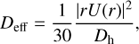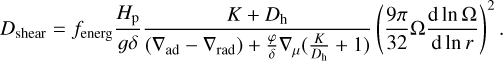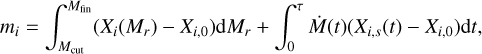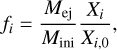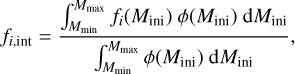EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 618 (October 2018) A&A, 618 (2018) A133 Full HTML
Free Access
Issue
A&A
Volume 618, October 2018
Article Number A133
Number of page(s) 15
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/201833283
Published online 23 October 2018

© ESO 2018

1. Introduction

The standard view of the s-process in massive stars is that it occurs in He- and C-burning regions and contributes to the production of elements up to about A = 90, hence giving only s-elements up to the first peak, at N = 50, where N is the number of neutrons (e.g. Peters 1968; Couch et al. 1974; Lamb et al. 1977; Langer et al. 1989; Raiteri et al. 1991a,b, 1993; Käppeler et al. 2011, and references therein). In standard models of massive stars, both the neutron source (mainly 22Ne) and the seed (mainly 56Fe) decrease with initial metallicity, while the main neutron poison (16O) remains similar whatever the metallicity, leading to a threshold of about Z/Z⊙ = 10−2 below which the s-process becomes negligible (Prantzos et al. 1990).

Meynet et al. (2006) and Hirschi (2007) suggested that this picture would be modified in rotating stars because of the rotational mixing operating between the H-shell and He-core during the core helium burning phase. The abundant 12C and 16O isotopes in the convective He-burning core are mixed within the H-shell, boosting the CNO cycle and forming primary 14N (e.g. Meynet & Maeder 2002b; Ekström et al. 2008). The 14N is mixed back into the convective He-burning core and allows the synthesis of extra 22Ne, via the reaction chain 14N(α, γ)18F(e+ νe)18O(α, γ)22Ne. The growth of the convective He-burning core also helps to reach layers that had been previously enriched in 14N. Neutrons are finally released by the 22Ne(α, n)25Mg reaction. The production of 22Ne in rotating stars is extensively discussed in Frischknecht et al. (2016; Sect. 3.1, their Figs. 2–5; see also Fig. 1 of Choplin et al. 2016, for a schematic view of this mixing process). By investigating the effect of rotation in a 25 M⊙ model, Pignatari et al. (2008) have shown that rotational mixing would allow the production of s-elements up to A ≂ 140. Since then, a few studies (e.g. Frischknecht et al. 2012, 2016, F12 and F16 hereafter) have started to build a picture of the s-process in massive rotating stars by computing models of different masses (15 < M < 40 M⊙) and metallicities (10−7 < Z < Z⊙) while following the complete s-process during evolution. So far, the most complete s-process study from rotating massive star models was carried out in F16. They computed 29 non-rotating and rotating models of 15, 20, 25, and 40 M⊙, with metallicities of Z = 0.014, 10−3, 10−5, and 10−7 and with a nuclear network of 613 or 737 isotopes, depending on the burning phase.

thumbnail Fig. 1.

Comparison between different sources of the important reaction rates for the s-process in massive stars as a function of the temperature. “ja01”: Jaeger et al. (2001), “nacr”: Angulo et al. (1999), “li12”: Longland et al. (2012), “cf88”: Caughlan & Fowler (1988), “il10”: Iliadis et al. (2010), “rath”: Rauscher & Thielemann (2000), “ths8”: Cyburt et al. (2010), “bg11”: Best et al. (2011), “bg13”: Best et al. (2013). We note that the Best et al. (2011) rate is an experimental lower limit. The shaded bands indicate the approximate ranges of temperature of interest for the s-process in massive stars: the first area named “He–c” is associated to the s-process during the core helium burning phase and the second area (“C–sh”) during carbon shell burning.

Several observational signatures tend to support the view of an enhanced s-process in massive rotating stars. The first one is that of globular cluster NGC 6522, located in the Galactic bulge and possibly being about 12.5 Gyr old (Kerber et al. 2018). It contains eight stars whose pattern is enriched in s-elements (Barbuy et al. 2009) and consistent with the yields of massive rotating models (Chiappini et al. 2011).

The second signature regards the iron-poor low-mass stars enriched in s-elements in the halo of the Milky Way. Using an inhomogeneous Galactic chemical evolution model, Cescutti et al. (2013) have shown that the observed scatter in the [Sr/Ba] ratio of normal (i.e. not enriched in carbon, see next discussion) halo stars with [Fe/H] < −2.5 can be reproduced if yields from fast-rotating massive stars are included.

The third one regards some of the [Fe/H] ≲ −4 stars enriched in s-elements. At such a low metallicity, asymptotic giant branch (AGB) stars might not have contributed yet to the chemical enrichment. HE 1327-2326 (Aoki et al. 2006; Frebel et al. 2006, 2008) has [Fe/H] = −5.7, [Sr/Fe] = 1.08, [Ba/Fe] < 1.39 and is enriched in light elements (C, N, O, Na, Mg, Al) relative to Fe. As discussed in the Sect. 7.2 of Maeder et al. (2015), this is consistent with the ejecta of a fast-rotating, low-metallicity massive star, where a strong mixing between H- and He-burning zones occurred, triggering the synthesis of a variety of elements, including Sr and Ba.

A fourth signature concerns the CEMP-s stars, which are Carbon-Enhanced Metal-Poor stars enriched in s-elements (Beers & Christlieb 2005). CEMP-s stars are mostly found at [Fe/H] > −3 (e.g. Yong et al. 2013; Norris et al. 2013). Some significantly s-rich stars also exist at [Fe/H] < −3, like HE 1029-0546 or SDSSJ1036+1212 with [Fe/H] around −3.3 (Behara et al. 2010; Aoki et al. 2013; Hansen et al. 2015). The peculiar chemical pattern of such stars is generally considered as acquired from an AGB star companion during a mass-transfer (or wind-mass-transfer) episode (Stancliffe & Glebbeek 2008; Lau et al. 2009; Bisterzo et al. 2010, 2012; Lugaro et al. 2012; Abate et al. 2013, 2015a,b; Hollek et al. 2015). A consequence of such a scenario is that CEMP-s stars should mostly be in binary systems, which seems to be the case for most CEMP-s since they show radial velocity variations (Lucatello et al. 2005; Starkenburg et al. 2014; Hansen et al. 2016). Nevertheless, some CEMP-s stars are very likely single stars (four out of 22 in the sample of Hansen et al. 2016), challenging the AGB scenario. The yields of a fast-rotating 25 M⊙ model can reproduce the pattern of three out of the four apparently single CEMP-s stars (Choplin et al. 2017b). Furthermore, we cannot exclude the possibility that some CEMP-s stars in binary systems show the nucleosynthetic signature of massive rotating stars since massive rotating stars could have enriched the cloud in which the binary system formed. On the other hand, single CEMP-s stars may be explained by the AGB scenario anyway since (1) single CEMP-s stars might have lost their companion, or (2) they might be in a binary system with very long period, explaining the non-detection of radial velocity variation.

Extensive and homogeneous grids of massive stellar models including rotation and full s-process network are needed to further investigate the role of such stars in the chemical enrichment of the universe. In this work, we study the impact of rotation on the s-element production at a metallicity Z = 10−3 in mass fraction and in the range 10−150 M⊙. We focus on one metallicity but extend significantly the range of mass compared to the study of F16. It allows us to draw a more complete picture of the s-process in massive stars at the considered metallicity. We investigate also the impact of a faster initial rotation and a lower 17O(α, γ)21Ne reaction rate. Section 2 describes the physical ingredients used throughout this work. Results are presented in Sect. 3. In Sect. 4 we investigate the effect of the mass cut and describe the table of yields. Section 5 presents the conclusions and additional discussions.

2. Physical ingredients

2.1. Input parameters

We used the Geneva stellar evolution code (Eggenberger et al. 2008). The models were computed at Z = 10−3 ([Fe/H] = −1.8) with initial masses of 10, 15, 20, 25, 40, 60, 85, 120, and 150 M⊙. The initial rotation rate on the zero-age main-sequence (ZAMS), υini/υcrit1 is 0, 0.4 or 0.7. Only the 25 M⊙ was computed with υini/υcrit = 0.7. As in Ekström et al. (2012) and Georgy et al. (2013), we use υini/υcrit = 0.4 for the grid. It corresponds well to the peak of the velocity distribution of the sample of 220 young main-sequence B-type stars of Huang et al. (2010, their Fig. 6). At lower metallicities, stars are more compact and the mass loss by line-driven winds is weaker so that the removal of angular momentum during evolution is smaller. Consequently, for a given υini/υcrit ratio, lower metallicity stars have higher surface rotational values during the main-sequence (MS) phase (Maeder & Meynet 2001).

At the metallicity considered here, F16 computed (with the same stellar evolution code) non-rotating 15, 20, and 25 M⊙ and 15, 20, 25, and 40 M⊙ models with υini/υcrit = 0.4. These models were computed again in the present work with the latest version of the code and with updated nuclear reaction rates (see below, the present section). A comparison of the yields is done in Sect. 3.2. Our models are generally stopped at the end of the neon photo-disintegration phase. Only the 10 M⊙ models are stopped at the end of C-burning and the rotating 120 M⊙ is stopped at the end of He-burning. Computing the advanced stages is important since the s-process occurs in the C-burning shell (also in the He-burning shell to a smaller extent, see The et al. 2007). However, the contribution from He-core burning dominates both in non-rotating and rotating models, and the C-shell contribution decreases quickly with initial metallicity (F16, especially their Fig. 13). Table 1 shows the initial properties of the models computed in this work as well as the final nuclear phase computed, the total lifetimes, and the final masses.

Table 1.

Main characteristics of the models.

The nuclear network is fully coupled to the evolution and used throughout all of it. It comprises 737 isotopes, from hydrogen to polonium (Z = 84). The size of the network is similar to the network used in The et al. (2000), F12, and F16, and allows us to follow the complete s-process. At the end of evolution, before computing stellar yields, unstable isotopes are decayed to stable ones. The initial composition of metals (elements heavier than helium2) is α-enhanced (we refer to Sect. 2.1 of F16 where more details are given).

Opacity tables are computed with the OPAL tool3. At low temperature, the opacities from Ferguson et al. (2005) are used to complement the OPAL tables. Radiative mass-loss rates are from Vink et al. (2001) when log Teff ≥ 3.9 and if Mini > 15 M⊙. Otherwise, they are from de Jager et al. (1988). For rotating models, the radiative mass-loss rates are corrected with the factor described in Maeder & Meynet (2000). Following Ekström et al. (2012), the mass-loss rate is increased by a factor of three when the luminosity of any layer in the stellar envelope becomes higher than five times the Eddington luminosity.

The Schwarzschild criterion is used for convection. During the H- and He-burning phases, overshoot is considered: the size of the convective core is extended by dover = αHP, where HP is the pressure scale height and α = 0.1. α was calibrated so as to reproduce the observed MS width of stars with 1.35 < M < 9 M⊙ (Ekström et al. 2012). Rotation is included according to the shellular theory of rotation (Zahn 1992). The angular momentum is transported according to an advection-diffusion equation (Chaboyer & Zahn 1992), which is fully solved during the main sequence. Only the diffusive part of the equation is solved after the main sequence. For chemicals species, the combination of meridional circulation and horizontal turbulence can be described as a pure diffusive process (Chaboyer & Zahn 1992). The associated diffusion coefficient is

Deff=130|rU(r)|2Dh,$${D_{{\rm{eff}}}} = {1 \over {30}}{{{\rm{|}}rU(r){|^2}} \over {{D_{\rm{h}}}}},$$(1)

with U(r) the amplitude of the radial component of the meridional velocity (Maeder & Zahn 1998) and Dh the horizontal shear diffusion coefficient from Zahn (1992). The equation for the transport of chemical elements is therefore purely diffusive with a total diffusion coefficient Dtot = D + Deff, where D is the sum of the various instabilities (convection, shear). After the main sequence, the advective effects are not considered so that Deff = 0. The secular shear diffusion coefficient is from Talon & Zahn (1997). It is expressed as

Dshear=fenergHpgδK+Dh(∇ad−∇rad)+φδ∇μ(KDh+1)(9π32ΩdlnΩdlnr)2.$${D_{{\rm{shear}}}} = {f_{{\rm{energ}}}}{{{H_{\rm{p}}}} \over {g\delta }}{{K + {D_{\rm{h}}}} \over {({\nabla _{{\rm{ad}}}} - {\nabla _{{\rm{rad}}}}) + {\varphi \over \delta }{\nabla _\mu }({K \over {{D_{\rm{h}}}}} + 1)}}{\left( {{{9\pi } \over {32}}\Omega {{{\rm{d}}\ln \Omega } \over {{\rm{d}}\ln r}}} \right)^2}.$$(2)

The efficiency of the shear is calibrated with the fenerg parameter. We set fenerg = 4, which is the value needed for a 15 M⊙ model at solar metallicity and with υini = 300 km s−1 to obtain an enhancement of the surface N abundance by a factor of three at core H depletion (a similar calibration is done in e.g. Heger et al. 2000; Chieffi & Limongi 2013). Such a surface enrichment agrees qualitatively with observations of 10−20 M⊙ rotating stars (e.g. Gies & Lambert 1992; Villamariz & Herrero 2005; Hunter et al. 2009).

Except for some nuclear rates, we used the same inputs as those used in F16 so that the interested reader can refer to this work for further details. Table 2 lists the rates important for the s-process that were updated in the present work. In the stellar evolution code, the rates in their analytical form (Rauscher & Thielemann 2000) are used. The new rates of 17O(α, γ) and 17O(α, n) from Best et al. (2013), used in stellar evolution models for the first time, are only tabulated. As a consequence, we derived the analytical form of these rates4. We checked that the difference between the fit and the tabulated rate was less than 5%. The rates of 17O(α, γ), 17O(α, n), 22Ne(α, γ), and 22Ne(α, n) are still uncertain in the range of temperature of interest for the s-process in massive stars (e.g Best et al. 2011; Nishimura et al. 2014). Figure 1 compares the different available rates in the literature for these four reactions. In the range of temperature of interest for us (mainly 0.2−0.3 GK, corresponding to the temperature of the helium burning core), the most uncertain rate is 17O(α, γ). It varies by about 3 dex from the rate of Caughlan & Fowler (1988) to the rate of Best et al. (2011; see the bottom right panel of Fig. 1). This motivated us to test the impact of a lower 17O(α, γ) rate in some models. We tried a rate divided by ten (dotted line in Fig. 1) for the fast-rotating 25 M⊙ and non-rotating 120 M⊙ models.

Table 2.

Updated reactions important for the s-process.

2.2. Yields and production factors

The yields provided contain a contribution from the wind and a contribution from the supernova. The yields from the supernova depend on the mass cut5 Mcut. Explosive nucleosynthesis, which is not considered here, will mostly affect the iron-group elements in the innermost layers of the star (Woosley & Weaver 1995; Thielemann et al. 1996; Limongi & Chieffi 2003; Nomoto et al. 2006; Heger & Woosley 2010) and is not expected to strongly modify the yields of s-elements (Rauscher et al. 2002; Turetal. 2009). Our results hence provide good predictions for the yields of light nuclei and s-process nuclei. The yield of an isotope i is calculated according to the relation

mi=∫McutMfin(Xi(Mr)−Xi,0)dMr+∫0τM˙(t)(Xi,s(t)−Xi,0)dt,$${m_i} = \int_{{M_{{\rm{cut}}}}}^{{M_{{\rm{fin}}}}} {({X_i}(} {M_r}) - {X_{i,0}}){\rm{d}}{M_r} + \int_0^\tau {\dot M} (t)({X_{i,s}}(t) - {X_{i,0}}){\rm{d}}t,$$(3)

where Mfin and τ are the mass at the end of the evolution and the total lifetime of the model, respectively (both given in Table 1), Xi(Mr) is the mass fraction of isotope i at coordinate Mr, at the end of the calculation, Xi,0 is the initial mass fraction, and Xi,s(t) and Ṁ(t) are the surface mass fraction and the mass-loss rate at time t respectively. As a first step, Mcut is estimated using the relation of Maeder (1992), which links the mass of the CO-core to the mass of the remnant. Such remnant masses are defined as Mrem and are given in the last column of Table 3 for our models6. The impact of different assumptions on the mass cut, and hence on the remnant mass, are discussed in Sect. 4.1.

Table 3.

Initial and final masses, mass lost through winds and size of the cores of the models computed in the present work.

In addition to the yields, we use in this work the production factors. For an isotope i, the production factor is defined as

fi=MejMiniXiXi,0,$${f_i} = {{{M_{{\rm{ej}}}}} \over {{M_{{\rm{ini}}}}}}{{{X_i}} \over {{X_{i,0}}}},$$(4)

with Mej the total mass ejected by the star, Mini the initial mass, and Xi the mass fraction of isotope i in the ejecta. It expresses the ratio of what is given back by the star divided by what was present initially in the whole star.

3. Massive stars with rotation and s-process

3.1. Non-rotating models

The central temperature at the beginning of the helium-burning stage (when the central helium mass fraction Yc = 0.95) is 182, 210, and 220 MK for the 25, 85, and 150 M⊙ models, respectively. Above 220 MK, the 22Ne(α, n)25Mg and 22Ne(α, γ)26Ne reactions start to be active and provide the main source of neutrons. Below 220 MK, the neutrons are provided by other (α, n) reactions from elements between C and Ne (especially 13C(α, n)16O). The top panels of Fig. 2 show the neutron profile (black dashed lines) in the 25 and 150 M⊙ models at the beginning of the core helium burning phase. The central neutron peak is bigger for the 150 M⊙ because of the higher central temperature that activates more efficiently the (α, n) reactions between N and Ne. At this early stage of core He-burning, the s-process is not activated significantly (see the flat 88Sr and 138Ba profiles in the top panels of Fig. 2) and leads only to slight overabundances of light s-elements like 63Cu (dashed magenta line).

thumbnail Fig. 2.

Abundance profile of the non-rotating 25 M⊙ (left panels) and 150 M⊙ (right panels) models at the beginning (top panels) and at the end (bottom panels) of central helium burning phase. Grey areas show the convective zones. The neutron profile is scaled up by a factor of 1018.

At the end of core helium burning (bottom panels), the temperature is T > 220 MK in the core so that the main neutron source in the He-burning core is 22Ne for both models. Also, in both models and during all the core He-burning phase, the second neutron peak (at higher mass coordinates) is mainly due to 13C(α, n). The s-process is not efficient in this region (see the 63Cu, 88Sr, and 138Ba profiles) because of the high 14N abundance, acting as a strong neutron poison.

In more massive models, the temperature required for the efficient activation of the 22Ne(α, n) reaction (220 MK) is reached earlier during the core helium burning phase: while the 150 M⊙ model reaches a central temperature Tc = 220 MK at the very start of core He-burning, the 25 M⊙ model reaches this temperature only close to the end of He-burning, when Yc ∼ 0.2. The duration of the stage where the central temperature is Tc > 220 MK is 0.16, 0.22, and 0.25 Myr for the 25, 85, and 150 M⊙ models, respectively. The amount of burnt 22Ne during core Heburning therefore increases with initial mass (dashed line in the left panel of Fig. 3). As the initial mass increases, it converges toward a plateau whose value is almost equal to the sum of the initial CNO mass fraction X(CNO)ini (horizontal blue line in the left panel of Fig. 3). Indeed, during the main sequence, the CNO cycle mainly transforms 12C and 16O into 14N. Consequently, at the end of the main sequence, X(CNO)ini ≂ X(14N) in the core. When the core helium burning phase starts, 14N is transformed into 22Ne by successive α captures. Hence, at core He depletion, the maximum amount of burnt 22Ne is about X(CNO)ini.

thumbnail Fig. 3.

Mass fraction of burnt (left panel) and remaining (right panel) 22Ne at the end of core helium burning as a function of initial mass. The blue line on the left panel shows the sum of the initial mass fraction of CNO isotopes.

Since more 22Ne is burnt in more massive stars, less is left at core He depletion (e.g. Fig. 4 and the dashed line in the right panel of Fig. 3). For stars with Mini > 40 M⊙, almost all the available 22Ne burns during the core helium burning phase so that the contribution of the C-shell burning in producing s-element is in general negligible. Additional contributions from 13C(α, n)7 or 12C(12C, n)23Mg are in principle possible during carbon burning (see Bennett et al. 2012; Pignatari et al. 2013, for more details) but these contributions generally remain much smaller than the 22Ne contribution during He-burning for very massive stars.

thumbnail Fig. 4.

Kippenhahn diagrams of the non-rotating 25 M⊙ (left panel) and 85 M⊙ (right panel) models. The colour map shows the mass fraction of 22Ne (the initial 22Ne mass fraction is log(X(22Ne))ini = −5.6). The duration of the core helium burning phase is indicated at the top of the panels.

A higher temperature also favours the production of s-elements because the ratio of the rate of 17O(α, n)20Ne over the rate of 17O(α, γ)21Ne increases with increasing temperature. It means that for higher temperatures, the poisoning effect of 16O is reduced since neutrons are more efficiently recycled8 by 17O. The mean central temperatures of the 25 and 150 M⊙ models during He-burning are 207 and 233 MK, respectively. At 233 MK, the ratio (α, n)/ (α, γ) is roughly twice that at 207 MK.

Finally, s-elements are also overproduced in more massive stars because these stars have larger He-burning cores. The mass of the He-burning core corresponds roughly to the mass of the CO-core at the end of the evolution, which increases with initial mass (Col. 6 in Table 3) and also represents a larger fraction of the final stellar mass.

The effects discussed above lead to an increasing production of s-elements with initial stellar mass (Fig. 5), as has been found before (Langer et al. 1989; Prantzos et al. 1990; Käppeler 1999; The et al. 2007). In our models, the production factors of the s-elements for the 150 M⊙ model exceed the factors of the 25 M⊙ model by about two orders of magnitude at maximum (e.g. for Sr, see Fig. 5). Whatever the mass, the production factors of elements with Z ≳ 50 stay very small. Considering a lower 17O(α, γ)21Ne rate mostly affects the range 30 ≲ Z ≲ 50 (see red dashed line on Fig. 5). Even if the production factors of heavy s-elements like Pb do not vary much (a factor of ∼2) in the considered mass range, the Pb yield in M⊙ (Eq. (3)) is about 3 dex higher in the 150 M⊙ compared to the 10 M⊙, because much more mass (hence Pb) is ejected in the case of the 150 M⊙.

thumbnail Fig. 5.

Production factors (Eq. (4)) of non-rotating models. The mass cut is set according to the relation of Maeder (1992).

3.2. Rotating models

The boost in the production of s-elements due to rotation is the highest between 20 and 60 M⊙. Figure 6 shows indeed that the production factors first increase from 10 to 40 M⊙ and decrease for M > 40 M⊙. As shown in Fig. 6, the 60, 85, 120, and 150 M⊙ models with rotation have similar patterns. Figure 7 shows that our models agree well with the 15, 20, 25, and 40 M⊙ of F16 (green pattern). It means that overall, the new rates used in the present work (cf. Table 2) do not affect much the yields compared to the yields published in F16. Figure 7 also shows that rotation only significantly affects the yields if Mini < 60 M⊙.For 10 < Mini < 40 M⊙, the 88Sr, 138Ba, and 208Pb yields are boosted by ∼2−3, ∼1, and ∼1 dex, respectively (see Fig. 7). There are two main reasons for that:

  • First, close to the convective helium burning core, the Dshear coefficient (Eq. (2)) is generally smaller in more massive models (Fig. 8, red line between the two convective zones) and hence transports less efficiently the He-burning products to the H-shell. It ultimately leads to a smaller amount of extra 22Ne, hence less neutrons. The smaller Dshear is explained by the fact that (1) more massive stars have higher K/Dh ratios just above the convective core (dashed line in Fig. 8, this point was already discussed in F16, Sect. 3.1), and (2) Ω and its gradient are smaller in this same region (magenta line). Also, for the 25 M⊙ (left panel of Fig. 8), the Dshear drops just below the convective H-shell. This is because the convective H-shell migrates upward and leaves behind an almost flat Ω profile (at Mr ∼ 10 M⊙), which strongly reduces the Dshear (see also F16, Sect. 3.1). However, the bottom of the H-envelope extends down to about 9 M⊙ so that the He products reach the H-rich region anyway and extra 14N can be synthesized.

  • The second reason is that the most massive stars have a more active H-burning shell. The shell remains convective during the whole He-burning stage and contributes well to the total stellar luminosity. This limits the growth of the He-core of the most massive stars. The growth of the convective He-burning core contributes to form extra 22Ne by engulfing 14N. Since the He-core of the most massive stars does not grow as much as the core of less massive stars, less primary 14N is engulfed in the He-core, leading to a smaller production of s-elements. A word of caution is here required: the previous statement may be affected by the current uncertainties in convective boundaries and the mixing across these boundaries. For example, using Ledoux criterion instead of Schwarzschild criterion may limit the extent and growth of both the convective H-burning shell and He-burning core. These uncertainties can be tackled with multi-dimensional hydrodynamic simulations and asteroseismology (e.g. Arnett et al. 2015; Arnett & Moravveji 2017; Cristini et al. 2017).

thumbnail Fig. 6.

Same as Fig. 5 but for rotating models.

thumbnail Fig. 7.

Stellar yields in M⊙ (Eq. (3)) as a function of the initial mass Mini for the non-rotating (dashed lines) and rotating (solid lines) models. The mass cut is set using the relation of Maeder (1992). Isotopes 88Sr, 138Ba, and 208Pb are shown. Green patterns between 15 and 40 M⊙ are the yields of the F16 models. The small and big red arrows at Mini = 25 M⊙ indicate the yields of 138Ba for the fast-rotating 25 M⊙ model and the fast-rotating 25 M⊙ models with a lower 17O(α, γ) rate respectively. The same arrows are plotted for 88Sr and 208Pb. Arrows at Mini = 120 M⊙ represent the 120 M⊙ model with a lower 17O(α, γ) rate. We note that some arrows are not visible because there are too small.

thumbnail Fig. 8.

Internal Ω profile, Dshear coefficient, and other diffusion coefficients in Eq. (2) for the rotating 25 (left panel) and 150 M⊙ models (right panel) during the core He-burning phase (Yc = 0.66). Grey areas represent the convective zones and the dashed lines show the K/Dh ratio.

For these reasons, more extra 22Ne is available and burnt in Mini < 60 M⊙ models, as shown by the bump between 20 and 60 M⊙ in Fig. 3 (solid line, both panels). The bottom panels of Fig. 9 show the abundance profiles at the end of the core Heburning phase for the rotating 25 M⊙ (left) and 150 M⊙ (right) models. We see indeed that less primary 14N is synthesized in the 150 M⊙ model (compare the 14N bumps at Mr ∼ 9 and 80 M⊙ for the 25 and 150 M⊙ models, respectively).

thumbnail Fig. 9.

Abundance profile of the rotating 25 M⊙ (left panels) and 150 M⊙ (right panels) models at the beginning (top panels) and at the end (bottom panels) of central helium burning phase. Grey areas show the convective zones. The neutron profile is scaled up by a factor of 1018.

Another important product of rotation is 19F, which is synthesized after the core He-burning phase, in the He-burning shell. Figure 10 shows the convective He-burning shell (between ∼8 and ∼10.5 M⊙) of the rotating 25 M⊙ model. The abundance of 19F is about 10−4 in the He-shell (it is only about 10−7 in the non-rotating 25 M⊙ model). Fluorine comes from the 14N(α, γ)18F(β+)18O(p, α)15N(α, γ)19F chain (Goriely et al. 1989). The protons mainly come from the 14N(n, p)14C reaction. The neutrons needed for the previous reactions are released by (α, n) reactions, especially 13C(α, n) and 22Ne(α, n). Figure 10 shows the abundances of the species involved in the synthesis of 19F. The additional 13C, 14N, and 22Ne synthesized in rotating models largely contributes to boost the sequence described above and consequently the 19F production.

thumbnail Fig. 10.

Abundance profile of the rotating 25 M⊙ during the shell Heburning phase. Grey areas show the convective zones (the convective He-burning shell is in-between ∼8 and ∼10.5 M⊙). The neutron profile is scaled up by a factor of 1018.

In general, rotating models lose more mass during their evolution. It occurs mainly for three reasons:

  • rotation increases the mass losses by line-driven winds,

  • rotation changes the distribution of the chemical species in the stellar interior. It can modify the tracks in the HR diagram and therefore the mass loss experienced by the star,

  • rotation can also induce mechanical mass losses when the stellar surface reaches the critical velocity.

The surfaces of the 25, 40, and 60 M⊙ models reach critical velocity at the end of the main sequence so that mechanical mass loss occurs. The mass lost due to that effect remains modest (less than 0.1 M⊙). For the models of this work, the most important effect comes from the second reason mentioned above. After the main sequence, rotating models have higher luminosities than non-rotating models (Fig. 11). This is due to internal mixing, which tends to produce larger helium burning cores. The higher luminosity (1) increases directly the mass-loss rate, and (2) makes the model more likely to enter the supra-Eddington regime. In this regime, additional mass loss occurs (cf. Sect. 2.1). The rotating 25 M⊙ model becomes supra-Eddington close to the end of the core helium burning stage, while its non-rotating counterpart never enters this regime. In the end, the rotating 25 M⊙ model loses eight more solar masses compared to the non-rotating model (Table 1, last column). Quickly after core He ignition, the rotating 60 M⊙ model reaches log Teff ∼ 3.8 and experiences a supra-Eddington stage that removes ∼8 M⊙. The stellar surface in then enriched in helium and makes the star go back to the blue (Fig. 11). The non-rotating 60 M⊙ enters the supra-Eddington regime only at the very end of core He-burning. Its surface is not very enriched in helium so that it stays red.

thumbnail Fig. 11.

Tracks of the models in the Hertzsprung–Russell diagram. Dashed and solid lines show non-rotating and rotating models respectively. Circles and squares denote the endpoint of the evolution for the non-rotating and rotating models, respectively.

3.3. Integrated production factors

The integrated production factor fi,int for an isotope i is

fi,int=∫MminMmaxfi(Mini) ϕ(Mini) dMini∫MminMmaxϕ(Mini) dMini,$${f_{i,{\rm{int}}}} = {{\int_{{M_{{\rm{min}}}}}^{{M_{{\rm{max}}}}} {{f_i}} ({M_{{\rm{ini}}}})\;\phi ({M_{{\rm{ini}}}})\;{\rm{d}}{M_{{\rm{ini}}}}} \over {\int_{{M_{{\rm{min}}}}}^{{M_{{\rm{max}}}}} \phi ({M_{{\rm{ini}}}})\;{\rm{d}}{M_{{\rm{ini}}}}}},$$(5)

where Mmin = 10 M⊙, Mmax = 150 M⊙, and φ(Mini) is the initial mass function. Here we take the initial mass function of Chabrier (2003) defined as 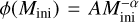ϕ(Mini)=AMini−α$\phi ({M_{{\rm{ini}}}}) = AM_{{\rm{ini}}}^{ - \alpha }$ with A = 7.1 10−5 and α = 2.3. The fi,int factors were computed for the non-rotating and rotating (40% of critical velocity) models (black and red lines in Fig. 12).

thumbnail Fig. 12.

Integrated production factors fi,int (Eq. 5) for the population of non-rotating and rotating models. The mass function of Chabrier (2003) is used. The green line shows the ratio between the two curves. The mass cut is set using the relation of Maeder (1992). The grey area highlights the elements that are likely affected by explosive nucleosynthesis.

Because of the low weight associated with very massive stars (cf. Eq. (5)), the contribution of such stars to the integrated pattern is small. The final pattern resembles that of an ∼20 M⊙ model. Strong differences between the rotating and nonrotating pattern occur between 30 < Z < 50, especially around Z = 38 (strontium). Also of interest is the fluorine, which is overproduced by more than 2 dex by the rotating population (cf. Sect. 3.2).

3.4. Faster rotation

Increasing the initial rotation rate from 40% to 70% of the critical velocity for the 25 M⊙ model allows the production of s-elements up to Z ∼ 60 (dashed purple line in Fig. 6). Compared to the 25 M⊙ model with slower rotation, Sr and Ba are overproduced by ∼0.2 and 1 dex respectively. This is shown by the small blue and red arrows in Fig. 7. Fast rotation boosts more the second than the first s-process peak with respect to the 40% case. This is because faster rotation gives more 22Ne, hence more neutrons, and a higher source (neutrons) over seed (heavy elements) ratio shifts the production of s-elements towards higher masses (Gallino et al. 1998).

3.5. Lower 17O(α, γ) rate

When the 17O(α, γ) rate is reduced in the fast-rotating 25 M⊙ model, the source over seed ratio is also increased since more neutrons are recycled. This allows the production of even more massive elements, up to Pb (dotted line in Fig. 6). The largest difference between the two fast-rotating models with different reaction rates occurs for Z > 55. In particular, Ba and Hg are overproduced by more than 1 dex. Reducing the rate of 17O(α, γ) in the non-rotating 120 M⊙ model boosts the production of light s-elements by ∼0.5 dex but does not allow the significant production of elements heavier than Z ∼ 50. A better knowledge of the 17O(α, γ) rate is crucial to better constrain the production of the s-elements, especially from the second peak, which are greatly affected when changing this nuclear rate.

4. Effect of the mass cut and table of yields

4.1. Effect of the mass cut

In the previous section, we discussed the yields assuming a specific mass cut (following Maeder 1992). However, how massive stars explode is still poorly constrained, and even less if rotation is included. It is generally difficult to state definitively which part of the star is expelled and contributes to the chemical enrichment of the interstellar medium (ISM). In what follows, we discuss the effect of varying the mass cut. In the table of yields provided with this work, the mass cut is let as a free parameter.

Figures 13 and 14 show the dependence of the yields on the mass cut for the 25 and 150 M⊙ models. They show how elements are produced (positive yield, red colour) or destroyed (negative yield, blue colour) when varying the mass cut between the final mass Mfin and the remnant mass Mrem of the model. The gaps at Z = 43 and 61 in every panel correspond to the elements Tc and Pm, which have no stable isotope and are consequently neither produced nor destroyed in the final yields. Considering the fast-rotating 25 M⊙ model with lower17 O(α, γ) (Fig. 13, bottom right panel), we see that a mass cut below ∼10.5 M⊙ is needed to expel s-elements with 27 < Z < 60 and a mass cut below ∼7.5 M⊙ (corresponding to the bottom of the He-burning shell) to expel s-elements with Z > 60. Interestingly, elements with 60 < Z < 70 (among them Eu) are exclusively produced in the inner regions of the two fast-rotating 25 M⊙ models (bottom panels of Fig. 13). Also, out of these two models, only the one with a lower 17O(α, γ) is able to produce elements with 75 < Z < 80.

thumbnail Fig. 13.

Yields of elements (characterized here by the atomic number Z) for different values of the mass cut. The colour map shows the yields for the non-rotating 25 M⊙ (top left panel), rotating 25 M⊙ (top right), fast-rotating 25 M⊙ (bottom left panel), and fast-rotating 25 M⊙ with lower 17O(α, γ)(bottom right panel). The ticks labelled Mrem show the location of the remnant mass using the relation of Maeder (1992; last column of Table 3). “CO” and “He” denote the location of the top of the CO and He core, respectively (fifth and sixth columns of Table 3).

thumbnail Fig. 14.

Same as Fig. 13 but for the non-rotating 150 M⊙ (left panel) and rotating 150 M⊙ (right panel).

Models including rotation generally lose more mass during their evolution (cf. Sect. 3.2) and have larger helium cores so that s-elements are located closer to the stellar surface at the end of the evolution. A large mass cut (i.e. close to the surface) will then already eject some s-elements in the case of the rotating models. Without rotation, s-elements are located deeper inside the star so that a smaller mass cut (i.e. deeper inside the star) is required to eject these elements. As an example, Mcut = 70 M⊙ will eject some s-elements for the rotating 150 M⊙ model while it will not for the non-rotating 150 M⊙ model (Fig. 14). Ejecting deeper layers likely requires a more powerful explosion. Consequently, rotation in massive stars not only boosts the production of s-elements but might also make it easier to expel these elements. This could be viewed as an indirect effect of the rotation providing more s-elements to the ISM.

4.2. Table of yields

Yields is available online9. In this table, the mass cut Mcut is varied between the final mass of the considered stellar model and the remnant mass Mrem from Maeder (1992). One hundred values of Mcut are considered for each model, equally spaced between Mrem and Mfin. The entire table therefore contains 21 stellar models times 100 Mcut, which means 2100 different ejecta compositions. For each model, the first value of Mcut is equal to the final mass of the model Mfin (given in Table 3). It corresponds to the case where only the mass lost through stellar wind is taken into account (also given in Table 3). In all the other cases, the yield of an isotope is the sum of the yields in the wind plus the yields in the material ejected by a supernova of the indicated mass cut. The last value of Mcut corresponds to the case where all the material above Mcut = Mrem is ejected (also the stellar wind is taken into account). Yields below 10−15 M⊙ in absolute value are set to zero.

5. Summary and discussions

We computed a grid of 21 models with and without rotation, at Z = 10−3 and with initial masses between 10 and 150 M⊙. Rotating models were computed with an initial rotation of 40% of the critical velocity. One model was computed with 70% of the critical velocity and two models with the rate of 17O(α, γ) divided by 10. With this paper, we provide a table of yields including the effect of varying the mass cut.

The main result of this work is that rotation has the strongest impact on s-element production for 20 < Mini < 60 M⊙. The first s-process peak is the most affected by rotation. In the 25 M⊙ rotating model, the yield of 88Sr is increased by ∼3 dex (Fig. 7). Although to a smaller extent, the second and third peaks are also affected: 138Ba and 208Pb are overproduced by ∼1 dex. Faster rotation boosts even more the s-element production in the range 40 < Z < 60. Taking a reasonably lower 17O(α, γ) reaction rate in the fast-rotating model overproduces the s-elements with Z > 55 (among them Pb) by about 1 dex compared to the standard fast-rotating model.

5.1. Initial rotation of the models

The boost of s-process element production in massive stars is obtained here through rotational mixing. The importance of the boost depends, amongst other parameters, on the initial angular momentum content of the star, here determined by the choice of the surface rotation velocity on the ZAMS where the star is supposed to rotate as a solid body. The present results have been obtained for only one initial rotation for each initial mass and of course, to obtain a broader view of the impact of rotation, families of models with different initial rotation rates should be computed for each initial mass. Here, to limit the computational time (which is significant when following the changes in the abundances of such a large number of isotopes), we focused on a particular choice (40% of the critical velocity at the ZAMS). We adopted this value for the following reasons: first, at solar metallicity, this choice is consistent with the peak of the velocity distribution of young main-sequence B-type stars (cf. Sect. 2.1). Second, we wanted to use the same initial rotations as those used in F12 and F16 in order to check what some changes brought to the code since these computations may have affected the results. Since there are no observational constraints concerning the velocity distributions at the metallicity considered here, it is difficult to know whether such a choice is representative or not. At the moment, in the absence of such a confirmation, we can see the present computations as an exploration of how the boost of the s-process due to rotation varies as a function of the initial masses over a large range of initial masses. The reader has to keep in mind that the absolute values of the yields depend here on the choice of the initial rotation.

5.2. Model uncertainties

One has also to keep in mind that the yields of stellar models are affected by several sources of uncertainty. By changing the rate of 17O(α, γ), we provided an example of how current nuclear rate uncertainties can affect the yields. The three other key reactions for s-process in massive stars (shown in Fig. 1), which are still not completely constrained, add another source of uncertainty in the yields. Uncertainties on neutron-capture and β-decay rates also affect the s-process yields by a factor of two at maximum, in general (Nishimura et al. 2017, 2018).

Also, even if we know that stars rotate, important uncertainties remain on the effects of rotation in the stellar interiors, and hence on the s-process yields of rotating stars. The production of s-elements is highly sensitive to the amount of 22Ne available, which in turn depends on stellar evolution inputs such as the way rotational mixing (also convection) is treated in the code. Different recipes exist in the literature for the horizontal diffusion (Zahn 1992; Maeder 2003; Mathis et al. 2004) and the shear diffusion coefficients (Talon & Zahn 1997; Maeder 1997; Maeder et al. 2013) that govern the transport of chemical elements (see Meynet et al. 2013, for a review). Different combinations of these coefficients will lead to a higher or lower production of extra 22Ne, hence a possibly different production of s-elements. Such uncertainties might be at the origin of the differences between this work and the recent work of Prantzos et al. (2018). They used a chemical evolution model to discuss the abundance evolution of elements up to uranium in the Milky Way. They included yields of rotating massive stars from Chieffi & Limongi. Elements from Ba to Pb are generally overproduced compared to our models. Since these stellar models are not published yet, we do not know the detailed physics ingredients and cannot do extensive comparisons.

5.3. Fluorine and s-elements

From discussions in Sect. 3.3 and Fig. 12, we note that the production of s-elements in massive rotating stars should be correlated with the production of several light elements, particularly fluorine. This correlation might be found in the next generation of low-mass halo field stars. Importantly, AGB stars are also believed to contribute to the production of both fluorine and s-elements (e.g. Jorissen et al. 1992; Lugaro et al. 2004, 2008; Abia et al. 2010; Karakas 2010; Bisterzo et al. 2010; Gallino et al. 2010), leaving open the possibility for AGB and massive stars to be responsible for such abundance patterns. In addition to AGB and massive rotators, the ν-process in core-collapse supernovae is also generally expected to contribute to fluorine production (Woosley 1977; Woosley et al. 1990; Kobayashi et al. 2011; Izutani et al. 2012). Recent studies suggest, however, that both the ν-process in supernovae (Jönsson et al. 2017) and AGB stars (Abia et al. 2015) might be insufficient to explain the observed evolution of fluorine in the solar neighbourhood. This potentially makes rotating massive stars interesting complementary fluorine sources that might improve the agreement between Galactic chemical evolution models and observations (Meynet & Arnould 2000; Palacios et al. 2005).

Around the metallicity considered in this work ([Fe/H] ∼ −2), the few iron-poor halo field stars whose fluorine abundance was determined are generally F-rich (Otsuka et al. 2008; Lucatello et al. 2011; Li et al. 2013; Schuler et al. 2007). One star (HD 5223) with [Fe/H] ∼ −2 has both fluorine and heavy element abundances available. It is enriched in F, Sr, Ba, and Pb (Goswami et al. 2006; Lucatello et al. 2011) and shows radial velocity variations (McClure & Woodsworth 1990). The enhancement in Pb may not be reproduced by the massive stellar models of the present work. A mass transfer episode from an AGB star’s companion may be the main process for explaining the abundances of HD 5223. Further determinations of fluorine and s-elements abundances in metal-poor stars should help to test stellar model predictions.

5.4. Rotation from solar to very low metallicity

As a final note, we would like to emphasize here that the impact of rotation on the evolution of stars (in particular on the stellar yields) allows us to unify in the same theoretical framework the properties of stars observed, for instance, in the solar neighbourhood to the properties of stars and their impact on nucleosynthesis at very low metallicities (see e.g. Maeder et al. 2015; Chiappini 2013).

Let us first recall that rotational mixing was first included in stellar models to account for surface enrichments observed at the surface of main-sequence B-type stars in the solar neighbourhood (see e.g. Maeder & Meynet 2012, and references therein). In general, rotating models need to be calibrated in order to constrain the efficiency of rotation-induced mixing (cf. Sect. 2.1). In the present work, the value of fenerg (Eq. (2)) is chosen in order for solar metallicity models with initial masses around 15 M⊙ to fit the averaged observed chemical enrichments of Galactic B-type stars rotating with an average surface velocity. Although the calibration can be done using different observations (Brott et al. 2011, for instance, used a sample of B-type stars in the Large Magellanic Cloud), at very low metallicities there are no observations allowing us to check whether a different value of fenerg is be needed. At the moment the most reasonable choice is to keep this quantity constant. Once the calibration is done, the physics describing the transport processes of both chemical elements and angular momentum due to rotation is not changed. As a consequence, the results of the stellar models for other initial masses and metallicities can be seen as stellar model predictions. Interestingly, when this physics is used for low metallicity rotating stars of both intermediate and high masses, the rotational mixing produces, without any artificial tuning, primary nitrogen production (Meynet & Maeder 2002a). Rotating massive star models have been invoked to explain the N/O plateau shown by metal-poor halo stars, the C/O upturn (Chiappini et al. 2006), and have provided predictions concerning the 12C/13C ratio (Chiappini et al. 2008).

Rotation is also interesting to explain the CEMP stars with [Fe/H] < −3 that are not highly enriched in s- and/or r-elements (Meynet et al. 2006, 2010; Hirschi 2007; Joggerst et al. 2010; Takahashi et al. 2014; Maeder et al. 2015; Maeder & Meynet 2015; Choplin et al. 2016, 2017a). It was reported by Placco et al. (2014) that 43% of stars with [Fe/H] < −3 are CEMP (with [C/Fe] > 0.7 and excluding the stars showing clear overabundances of neutron-capture elements). A major difference between CEMP stars and normal metal-poor halo stars is likely due to the degree of mixing of the cloud of interstellar material from which these two types of stars formed. CEMP stars likely formed from pockets of the ISM that have been enriched by the ejecta of a few objects, maybe only one, while normal halo stars are likely formed from a much better mixed reservoir in which the ejecta of many more sources have accumulated. In both cases (normal halo stars and at least some CEMP stars), rotational mixing provides a very interesting mechanism for explaining the surface abundances of many of these objects, while still being able to account for observed features of massive stars at solar metallicity. Of course alternative explanations exist (e.g. Umeda & Nomoto 2003; Limongi et al. 2003; Iwamoto et al. 2005; Tominaga et al. 2014; Clarkson et al. 2018) and in the future some specific signatures will hopefully allow us to decide which of these models or combination of models are the most probable. A comparison between the different models for explaining the most iron-poor stars is beyond the scope of this work, which focuses on higher metallicities. We plan to compute similar models as done in the present paper but with a lower metallicity ([Fe/H] ∼ −4).

1

The initial equatorial velocity is υini and υcrit is the initial equatorial velocity at which the gravitational acceleration is balanced by the centrifugal force. It is defined as 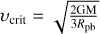υcrit=2GM3Rpb${\upsilon _{{\rm{crit}}}} = \sqrt {{{{\rm{2GM}}} \over {3{R_{{\rm{pb}}}}}}} $, where Rpb is the polar radius at the break-up velocity (see Maeder & Meynet 2000).

2

The initial helium mass fraction Y is calculated according to the relation Y = Yp + ΔY/ΔZ × Z, where Z is the metallicity, Yp the primordial helium abundance, and ΔY/ΔZ = (Y⊙ − Yp)/Z⊙ the average slope of the helium-to-metal enrichment law. We set Yp = 0.248, according to Cyburt et al. (2003). We use Z⊙ = 0.014 and Y⊙ = 0.266 as in Ekström et al. (2012), derived from Asplund et al. (2005). The initial mass fraction of hydrogen is deduced from 1 − Y − Z = 0.752.

4

More details can be found at http://nucastro.org/forum/viewtopic.php?id=22

5

At the time of the supernova, the mass cut delimits the part of the star that is expelled from the part that is locked into the remnant. The mass cut is equal to the mass of the remnant.

6

In Maeder (1992), the relation between the mass of the CO core and the mass of the remnant is applied for Mini ≤ 120 M⊙. For our 150 M⊙model, we have extrapolated the relation linearly.

7

Starting from 12C(p, γ), with the protons coming from 12C(12C , p)23Na.

8

The isotope 16O is an abundant poison that absorbs neutrons in the He-core and limits the production of s-elements. With the chain 16O(n, γ)17O(α, γ)21Ne, the neutron captured by 16O is definitely lost. With the chain 16O(n, γ)17O(α, n)20Ne, the neutron is captured by 16O and then recycled.

Acknowledgments

This work was supported by the SNF project number 200020-172505. The authors acknowledge support from the “ChETEC” COST Action (CA16117), supported by COST (European Cooperation in Science and Technology). RH acknowledges the European Research Council under the European Union’s Seventh Framework Programme (FP/2007-2013)/ERC Grant Agreement no. 306901. RH acknowledges support from the World Premier International Research Center Initiative (WPI Initiative), MEXT, Japan. CC acknowledges support from DFG Grant CH1188/2-1.

References

  1. Abate, C., Pols, O. R., Izzard, R. G., Mohamed, S. S., & de Mink, S. E. 2013, A&A, 552, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Abate, C., Pols, O. R., Izzard, R. G., & Karakas, A. I. 2015a, A&A, 581, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Abate, C., Pols, O. R., Karakas, A. I., & Izzard, R. G. 2015b, A&A, 576, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Abia, C., Cunha, K., Cristallo, S., et al. 2010, ApJ, 715, L94 [NASA ADS] [CrossRef] [Google Scholar]
  5. Abia, C., Cunha, K., Cristallo, S., & de Laverny, P. 2015, A&A, 581, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Angulo, C., Arnould, M., Rayet, M., et al. 1999, Nucl. Phys. A, 656, 3 [NASA ADS] [CrossRef] [Google Scholar]
  7. Aoki, W., Frebel, A., Christlieb, N., et al. 2006, ApJ, 639, 897 [NASA ADS] [CrossRef] [Google Scholar]
  8. Aoki, W., Beers, T. C., Lee, Y. S., et al. 2013, AJ, 145, 13 [NASA ADS] [CrossRef] [Google Scholar]
  9. Arnett, W. D., & Moravveji, E. 2017, ApJ, 836, L19 [NASA ADS] [CrossRef] [Google Scholar]
  10. Arnett, W. D., Meakin, C., Viallet, M., et al. 2015, ApJ, 809, 30 [NASA ADS] [CrossRef] [Google Scholar]
  11. Asplund, M., Grevesse, N., & Sauval, A. J. 2005, in Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis, eds. T. G. Barnes, & F. N. Bash, ASP Conf. Ser., 336, 25 [NASA ADS] [Google Scholar]
  12. Barbuy, B., Zoccali, M., Ortolani, S., et al. 2009, A&A, 507, 405 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Beers, T. C., & Christlieb, N. 2005, ARA&A, 43, 531 [NASA ADS] [CrossRef] [Google Scholar]
  14. Behara, N. T., Bonifacio, P., Ludwig, H.-G., et al. 2010, A&A, 513, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Bennett, M. E., Hirschi, R., Pignatari, M., et al. 2012, MNRAS, 420, 3047 [NASA ADS] [CrossRef] [Google Scholar]
  16. Best, A., Görres, J., Couder, M., et al. 2011, Phys. Rev. C, 83, 052802 [NASA ADS] [CrossRef] [Google Scholar]
  17. Best, A., Beard, M., Görres, J., et al. 2013, Phys. Rev. C, 87, 045805 [NASA ADS] [CrossRef] [Google Scholar]
  18. Bisterzo, S., Gallino, R., Straniero, O., Cristallo, S., & Käppeler, F. 2010, MNRAS, 404, 1529 [NASA ADS] [Google Scholar]
  19. Bisterzo, S., Gallino, R., Straniero, O., Cristallo, S., & Käppeler, F. 2012, MNRAS, 422, 849 [NASA ADS] [CrossRef] [Google Scholar]
  20. Brott, I., de Mink, S. E., Cantiello, M., et al. 2011, A&A, 530, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Caughlan, G. R., & Fowler, W. A. 1988, At. Data Nucl. Data Tables, 40, 283 [Google Scholar]
  22. Cescutti, G., Chiappini, C., Hirschi, R., Meynet, G., & Frischknecht, U. 2013, A&A, 553, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Chaboyer, B., & Zahn, J.-P. 1992, A&A, 253, 173 [Google Scholar]
  24. Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] [Google Scholar]
  25. Chiappini, C. 2013, Astron. Nachr., 334, 595 [NASA ADS] [CrossRef] [Google Scholar]
  26. Chiappini, C., Hirschi, R., Meynet, G., et al. 2006, A&A, 449, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Chiappini, C., Ekström, S., Meynet, G., et al. 2008, A&A, 479, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Chiappini, C., Frischknecht, U., Meynet, G., et al. 2011, Nature, 472, 454 [NASA ADS] [CrossRef] [Google Scholar]
  29. Chieffi, A., & Limongi, M. 2013, ApJ, 764, 21 [NASA ADS] [CrossRef] [Google Scholar]
  30. Choplin, A., Maeder, A., Meynet, G., & Chiappini, C. 2016, A&A, 593, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Choplin, A., Ekström, S., Meynet, G., et al. 2017a, A&A, 605, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Choplin, A., Hirschi, R., Meynet, G., & Ekström, S. 2017b, A&A, 607, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Clarkson, O., Herwig, F., & Pignatari, M. 2018, MNRAS, 474, L37 [NASA ADS] [CrossRef] [Google Scholar]
  34. Couch, R. G., Schmiedekamp, A. B., & Arnett, W. D. 1974, ApJ, 190, 95 [NASA ADS] [CrossRef] [Google Scholar]
  35. Cristini, A., Meakin, C., Hirschi, R., et al. 2017, MNRAS, 471, 279 [NASA ADS] [CrossRef] [Google Scholar]
  36. Cyburt, R. H., Fields, B. D., & Olive, K. A. 2003, Phys. Lett. B, 567, 227 [NASA ADS] [CrossRef] [Google Scholar]
  37. Cyburt, R. H., Amthor, A. M., Ferguson, R., et al. 2010, ApJS, 189, 240 [NASA ADS] [CrossRef] [Google Scholar]
  38. de Jager, C., Nieuwenhuijzen, H., & van der Hucht, K. A. 1988, A&AS, 72, 259 [NASA ADS] [Google Scholar]
  39. Eggenberger, P., Meynet, G., Maeder, A., et al. 2008, Ap&SS, 316, 43 [NASA ADS] [CrossRef] [Google Scholar]
  40. Ekström, S., Meynet, G., Chiappini, C., Hirschi, R., & Maeder, A. 2008, A&A, 489, 685 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Ekström, S., Georgy, C., Eggenberger, P., et al. 2012, A&A, 537, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Ferguson, J. W., Alexander, D. R., Allard, F., et al. 2005, ApJ, 623, 585 [NASA ADS] [CrossRef] [Google Scholar]
  43. Frebel, A., Christlieb, N., Norris, J. E., Aoki, W., & Asplund, M. 2006, ApJ, 638, L17 [NASA ADS] [CrossRef] [Google Scholar]
  44. Frebel, A., Collet, R., Eriksson, K., Christlieb, N., & Aoki, W. 2008, ApJ, 684, 588 [NASA ADS] [CrossRef] [Google Scholar]
  45. Frischknecht, U., Hirschi, R., & Thielemann, F.-K. 2012, A&A, 538, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Frischknecht, U., Hirschi, R., Pignatari, M., et al. 2016, MNRAS, 456, 1803 [NASA ADS] [CrossRef] [Google Scholar]
  47. Gallino, R., Arlandini, C., Busso, M., et al. 1998, ApJ, 497, 388 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  48. Gallino, R., Bisterzo, S., Cristallo, S., & Straniero, O. 2010, Mem. Soc. Astron. It., 81, 998 [NASA ADS] [Google Scholar]
  49. Georgy, C., Ekström, S., Eggenberger, P., et al. 2013, A&A, 558, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Gies, D. R., & Lambert, D. L. 1992, ApJ, 387, 673 [NASA ADS] [CrossRef] [Google Scholar]
  51. Goriely, S., Jorissen, A., & Arnould, M. 1989, in Proc. 5th Workshop on Nuclear Astrophys, eds. W. Hillebrandt, & E. Müller, Max Planck Inst. für Astrophys. Rep., 60 [Google Scholar]
  52. Goswami, A., Aoki, W., Beers, T. C., et al. 2006, MNRAS, 372, 343 [NASA ADS] [CrossRef] [Google Scholar]
  53. Guo, B., Li, Z. H., Lugaro, M., et al. 2012, ApJ, 756, 193 [NASA ADS] [CrossRef] [Google Scholar]
  54. Hansen, T., Hansen, C. J., Christlieb, N., et al. 2015, ApJ, 807, 173 [NASA ADS] [CrossRef] [Google Scholar]
  55. Hansen, T. T., Andersen, J., Nordström, B., et al. 2016, A&A, 588, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Heger, A., & Woosley, S. E. 2010, ApJ, 724, 341 [NASA ADS] [CrossRef] [Google Scholar]
  57. Heger, A., Langer, N., & Woosley, S. E. 2000, ApJ, 528, 368 [NASA ADS] [CrossRef] [Google Scholar]
  58. Hirschi, R. 2007, A&A, 461, 571 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  59. Hollek, J. K., Frebel, A., Placco, V. M., et al. 2015, ApJ, 814, 121 [NASA ADS] [CrossRef] [Google Scholar]
  60. Huang, W., Gies, D. R., & McSwain, M. V. 2010, ApJ, 722, 605 [NASA ADS] [CrossRef] [Google Scholar]
  61. Hunter, I., Brott, I., Langer, N., et al. 2009, A&A, 496, 841 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Iliadis, C., Longland, R., Champagne, A. E., Coc, A., & Fitzgerald, R. 2010, Nucl. Phys. A, 841, 31 [NASA ADS] [CrossRef] [Google Scholar]
  63. Iwamoto, N., Umeda, H., Tominaga, N., Nomoto, K., & Maeda, K. 2005, Science, 309, 451 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  64. Izutani, N., Umeda, H., & Yoshida, A. J. 2012, in Death of Massive Stars: Supernovae and Gamma-Ray Bursts, eds. P. Roming, N. Kawai, & E. Pian, IAU Symp., 279, 339 [NASA ADS] [Google Scholar]
  65. Jaeger, M., Kunz, R., Mayer, A., et al. 2001, Phys. Rev. Lett., 87, 202501 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  66. Joggerst, C. C., Almgren, A., Bell, J., et al. 2010, ApJ, 709, 11 [NASA ADS] [CrossRef] [Google Scholar]
  67. Jönsson, H., Ryde, N., Spitoni, E., et al. 2017, ApJ, 835, 50 [NASA ADS] [CrossRef] [Google Scholar]
  68. Jorissen, A., Smith, V. V., & Lambert, D. L. 1992, A&A, 261, 164 [NASA ADS] [Google Scholar]
  69. Käppeler, F. 1999, Prog. Part. Nucl. Phys., 43, 419 [NASA ADS] [CrossRef] [Google Scholar]
  70. Käppeler, F., Gallino, R., Bisterzo, S., & Aoki, W. 2011, Rev. Mod. Phys., 83, 157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  71. Karakas, A. I. 2010, MNRAS, 403, 1413 [NASA ADS] [CrossRef] [Google Scholar]
  72. Kerber, L. O., Nardiello, D., Ortolani, S., et al. 2018, ApJ, 853, 15 [NASA ADS] [CrossRef] [Google Scholar]
  73. Kobayashi, C., Izutani, N., Karakas, A. I., et al. 2011, ApJ, 739, L57 [NASA ADS] [CrossRef] [Google Scholar]
  74. Kunz, R., Fey, M., Jaeger, M., et al. 2002, ApJ, 567, 643 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  75. Lamb, S. A., Howard, W. M., Truran, J. W., & Iben, I., Jr. 1977, ApJ, 217, 213 [NASA ADS] [CrossRef] [Google Scholar]
  76. Langer, N., Arcoragi, J.-P., & Arnould, M. 1989, A&A, 210, 187 [NASA ADS] [Google Scholar]
  77. Lau, H. H. B., Stancliffe, R. J., & Tout, C. A. 2009, MNRAS, 396, 1046 [NASA ADS] [CrossRef] [Google Scholar]
  78. Li, H. N., Ludwig, H.-G., Caffau, E., Christlieb, N., & Zhao, G. 2013, ApJ, 765, 51 [NASA ADS] [CrossRef] [Google Scholar]
  79. Limongi, M., & Chieffi, A. 2003, ApJ, 592, 404 [NASA ADS] [CrossRef] [Google Scholar]
  80. Limongi, M., Chieffi, A., & Bonifacio, P. 2003, ApJ, 594, L123 [CrossRef] [Google Scholar]
  81. Longland, R., Iliadis, C., & Karakas, A. I. 2012, Phys. Rev. C, 85, 065809 [NASA ADS] [CrossRef] [Google Scholar]
  82. Lucatello, S., Tsangarides, S., Beers, T. C., et al. 2005, ApJ, 625, 825 [NASA ADS] [CrossRef] [Google Scholar]
  83. Lucatello, S., Masseron, T., Johnson, J. A., Pignatari, M., & Herwig, F. 2011, ApJ, 729, 40 [NASA ADS] [CrossRef] [Google Scholar]
  84. Lugaro, M., Ugalde, C., Karakas, A. I., et al. 2004, ApJ, 615, 934 [NASA ADS] [CrossRef] [Google Scholar]
  85. Lugaro, M., de Mink, S. E., Izzard, R. G., et al. 2008, A&A, 484, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  86. Lugaro, M., Karakas, A. I., Stancliffe, R. J., & Rijs, C. 2012, ApJ, 747, 2 [NASA ADS] [CrossRef] [Google Scholar]
  87. Maeder, A. 1992, A&A, 264, 105 [NASA ADS] [Google Scholar]
  88. Maeder, A. 1997, A&A, 321, 134 [NASA ADS] [Google Scholar]
  89. Maeder, A. 2003, A&A, 399, 263 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  90. Maeder, A., & Meynet, G. 2000, A&A, 361, 159 [NASA ADS] [Google Scholar]
  91. Maeder, A., & Meynet, G. 2001, A&A, 373, 555 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  92. Maeder, A., & Meynet, G. 2012, Rev. Mod. Phys., 84, 25 [NASA ADS] [CrossRef] [Google Scholar]
  93. Maeder, A., & Meynet, G. 2015, A&A, 580, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  94. Maeder, A., & Zahn, J.-P. 1998, A&A, 334, 1000 [NASA ADS] [Google Scholar]
  95. Maeder, A., Meynet, G., Lagarde, N., & Charbonnel, C. 2013, A&A, 553, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  96. Maeder, A., Meynet, G., & Chiappini, C. 2015, A&A, 576, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  97. Mathis, S., Palacios, A., & Zahn, J.-P. 2004, A&A, 425, 243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  98. McClure, R. D., & Woodsworth, A. W. 1990, ApJ, 352, 709 [NASA ADS] [CrossRef] [Google Scholar]
  99. Meynet, G., & Arnould, M. 2000, A&A, 355, 176 [NASA ADS] [Google Scholar]
  100. Meynet, G., & Maeder, A. 2002a, A&A, 390, 561 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  101. Meynet, G., & Maeder, A. 2002b, A&A, 381, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  102. Meynet, G., Ekström, S., & Maeder, A. 2006, A&A, 447, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  103. Meynet, G., Hirschi, R., Ekstrom, S., et al. 2010, A&A, 521, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  104. Meynet, G., Ekstrom, S., Maeder, A., et al. 2013, in Lect. Notes Phys., eds. M. Goupil, K. Belkacem, C. Neiner, F. Lignières, & J. J. Green (Berlin: Springer Verlag), 865, 3 [NASA ADS] [CrossRef] [Google Scholar]
  105. Nishimura, N., Hirschi, R., Pignatari, M., et al. 2014, Am. Inst. Phys. Conf. Ser., 1594, 146 [NASA ADS] [Google Scholar]
  106. Nishimura, N., Hirschi, R., Rauscher, T., Murphy, A. S. J., & Cescutti, G. 2017, MNRAS, 469, 1752 [NASA ADS] [CrossRef] [Google Scholar]
  107. Nishimura, N., Hirschi, R., & Rauscher, T. 2018, J. Phys. Conf. Ser., 940, 012051 [CrossRef] [Google Scholar]
  108. Nomoto, K., Tominaga, N., Umeda, H., Kobayashi, C., & Maeda, K. 2006, Nucl. Phys. A, 777, 424 [NASA ADS] [CrossRef] [Google Scholar]
  109. Norris, J. E., Yong, D., Bessell, M. S., et al. 2013, ApJ, 762, 28 [NASA ADS] [CrossRef] [Google Scholar]
  110. Otsuka, M., Izumiura, H., Tajitsu, A., & Hyung, S. 2008, ApJ, 682, L105 [NASA ADS] [CrossRef] [Google Scholar]
  111. Palacios, A., Arnould, M., & Meynet, G. 2005, A&A, 443, 243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  112. Peters, J. G. 1968, ApJ, 154, 225 [NASA ADS] [CrossRef] [Google Scholar]
  113. Pignatari, M., Gallino, R., Meynet, G., et al. 2008, ApJ, 687, L95 [NASA ADS] [CrossRef] [Google Scholar]
  114. Pignatari, M., Wiescher, M., Timmes, F. X., et al. 2013, ApJ, 767, L22 [NASA ADS] [CrossRef] [Google Scholar]
  115. Placco, V. M., Frebel, A., Beers, T. C., & Stancliffe, R. J. 2014, ApJ, 797, 21 [NASA ADS] [CrossRef] [Google Scholar]
  116. Prantzos, N., Hashimoto, M., & Nomoto, K. 1990, A&A, 234, 211 [NASA ADS] [Google Scholar]
  117. Prantzos, N., Abia, C., Limongi, M., Chieffi, A., & Cristallo, S. 2018, MNRAS, 476, 3432 [NASA ADS] [CrossRef] [Google Scholar]
  118. Raiteri, C. M., Busso, M., Gallino, R., Picchio, G., & Pulone, L. 1991a, ApJ, 367, 228 [NASA ADS] [CrossRef] [Google Scholar]
  119. Raiteri, C. M., Busso, M., Picchio, G., & Gallino, R. 1991b, ApJ, 371, 665 [NASA ADS] [CrossRef] [Google Scholar]
  120. Raiteri, C. M., Gallino, R., Busso, M., Neuberger, D., & Kaeppeler, F. 1993, ApJ, 419, 207 [NASA ADS] [CrossRef] [Google Scholar]
  121. Rauscher, T., Heger, A., Hoffman, R. D., & Woosley, S. E. 2002, ApJ, 576, 323 [NASA ADS] [CrossRef] [Google Scholar]
  122. Rauscher, T., & Thielemann, F.-K. 2000, At. Data Nucl. Data Tables, 75, 1 [NASA ADS] [CrossRef] [Google Scholar]
  123. Schuler, S. C., Cunha, K., Smith, V. V., et al. 2007, ApJ, 667, L81 [NASA ADS] [CrossRef] [Google Scholar]
  124. Stancliffe, R. J., & Glebbeek, E. 2008, MNRAS, 389, 1828 [Google Scholar]
  125. Starkenburg, E., Shetrone, M. D., McConnachie, A. W., & Venn, K. A. 2014, MNRAS, 441, 1217 [NASA ADS] [CrossRef] [Google Scholar]
  126. Takahashi, K., Umeda, H., & Yoshida, T. 2014, ApJ, 794, 40 [NASA ADS] [CrossRef] [Google Scholar]
  127. Talon, S., & Zahn, J.-P. 1997, A&A, 317, 749 [Google Scholar]
  128. The, L.-S., El Eid, M. F., & Meyer, B. S. 2000, ApJ, 533, 998 [NASA ADS] [CrossRef] [Google Scholar]
  129. The, L.-S., El Eid, M. F., & Meyer, B. S. 2007, ApJ, 655, 1058 [NASA ADS] [CrossRef] [Google Scholar]
  130. Thielemann, F.-K., Nomoto, K., & Hashimoto, M.-A. 1996, ApJ, 460, 408 [NASA ADS] [CrossRef] [Google Scholar]
  131. Tominaga, N., Iwamoto, N., & Nomoto, K. 2014, ApJ, 785, 98 [NASA ADS] [CrossRef] [Google Scholar]
  132. Tur, C., Heger, A., & Austin, S. M. 2009, ApJ, 702, 1068 [NASA ADS] [CrossRef] [Google Scholar]
  133. Umeda, H., & Nomoto, K. 2003, Nature, 422, 871 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  134. Villamariz, M. R., & Herrero, A. 2005, A&A, 442, 263 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  135. Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2001, A&A, 369, 574 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  136. Woosley, S. E. 1977, Nature, 269, 42 [NASA ADS] [CrossRef] [Google Scholar]
  137. Woosley, S. E., Hartmann, D. H., Hoffman, R. D., & Haxton, W. C. 1990, ApJ, 356, 272 [NASA ADS] [CrossRef] [Google Scholar]
  138. Woosley, S. E., & Weaver, T. A. 1995, ApJS, 101, 181 [NASA ADS] [CrossRef] [Google Scholar]
  139. Xu, Y., Takahashi, K., Goriely, S., et al. 2013, Nucl. Phys. A, 918, 61 [NASA ADS] [CrossRef] [Google Scholar]
  140. Yong, D., Norris, J. E., Bessell, M. S., et al. 2013, ApJ, 762, 26 [NASA ADS] [CrossRef] [Google Scholar]
  141. Zahn, J.-P. 1992, A&A, 265, 115 [NASA ADS] [Google Scholar]

All Tables

Table 1.

Main characteristics of the models.

In the text
Table 2.

Updated reactions important for the s-process.

In the text
Table 3.

Initial and final masses, mass lost through winds and size of the cores of the models computed in the present work.

In the text

All Figures

thumbnail Fig. 1.

Comparison between different sources of the important reaction rates for the s-process in massive stars as a function of the temperature. “ja01”: Jaeger et al. (2001), “nacr”: Angulo et al. (1999), “li12”: Longland et al. (2012), “cf88”: Caughlan & Fowler (1988), “il10”: Iliadis et al. (2010), “rath”: Rauscher & Thielemann (2000), “ths8”: Cyburt et al. (2010), “bg11”: Best et al. (2011), “bg13”: Best et al. (2013). We note that the Best et al. (2011) rate is an experimental lower limit. The shaded bands indicate the approximate ranges of temperature of interest for the s-process in massive stars: the first area named “He–c” is associated to the s-process during the core helium burning phase and the second area (“C–sh”) during carbon shell burning.
In the text
thumbnail Fig. 2.

Abundance profile of the non-rotating 25 M⊙ (left panels) and 150 M⊙ (right panels) models at the beginning (top panels) and at the end (bottom panels) of central helium burning phase. Grey areas show the convective zones. The neutron profile is scaled up by a factor of 1018.
In the text
thumbnail Fig. 3.

Mass fraction of burnt (left panel) and remaining (right panel) 22Ne at the end of core helium burning as a function of initial mass. The blue line on the left panel shows the sum of the initial mass fraction of CNO isotopes.
In the text
thumbnail Fig. 4.

Kippenhahn diagrams of the non-rotating 25 M⊙ (left panel) and 85 M⊙ (right panel) models. The colour map shows the mass fraction of 22Ne (the initial 22Ne mass fraction is log(X(22Ne))ini = −5.6). The duration of the core helium burning phase is indicated at the top of the panels.
In the text
thumbnail Fig. 5.

Production factors (Eq. (4)) of non-rotating models. The mass cut is set according to the relation of Maeder (1992).
In the text
thumbnail Fig. 6.

Same as Fig. 5 but for rotating models.
In the text
thumbnail Fig. 7.

Stellar yields in M⊙ (Eq. (3)) as a function of the initial mass Mini for the non-rotating (dashed lines) and rotating (solid lines) models. The mass cut is set using the relation of Maeder (1992). Isotopes 88Sr, 138Ba, and 208Pb are shown. Green patterns between 15 and 40 M⊙ are the yields of the F16 models. The small and big red arrows at Mini = 25 M⊙ indicate the yields of 138Ba for the fast-rotating 25 M⊙ model and the fast-rotating 25 M⊙ models with a lower 17O(α, γ) rate respectively. The same arrows are plotted for 88Sr and 208Pb. Arrows at Mini = 120 M⊙ represent the 120 M⊙ model with a lower 17O(α, γ) rate. We note that some arrows are not visible because there are too small.
In the text
thumbnail Fig. 8.

Internal Ω profile, Dshear coefficient, and other diffusion coefficients in Eq. (2) for the rotating 25 (left panel) and 150 M⊙ models (right panel) during the core He-burning phase (Yc = 0.66). Grey areas represent the convective zones and the dashed lines show the K/Dh ratio.
In the text
thumbnail Fig. 9.

Abundance profile of the rotating 25 M⊙ (left panels) and 150 M⊙ (right panels) models at the beginning (top panels) and at the end (bottom panels) of central helium burning phase. Grey areas show the convective zones. The neutron profile is scaled up by a factor of 1018.
In the text
thumbnail Fig. 10.

Abundance profile of the rotating 25 M⊙ during the shell Heburning phase. Grey areas show the convective zones (the convective He-burning shell is in-between ∼8 and ∼10.5 M⊙). The neutron profile is scaled up by a factor of 1018.
In the text
thumbnail Fig. 11.

Tracks of the models in the Hertzsprung–Russell diagram. Dashed and solid lines show non-rotating and rotating models respectively. Circles and squares denote the endpoint of the evolution for the non-rotating and rotating models, respectively.
In the text
thumbnail Fig. 12.

Integrated production factors fi,int (Eq. 5) for the population of non-rotating and rotating models. The mass function of Chabrier (2003) is used. The green line shows the ratio between the two curves. The mass cut is set using the relation of Maeder (1992). The grey area highlights the elements that are likely affected by explosive nucleosynthesis.
In the text
thumbnail Fig. 13.

Yields of elements (characterized here by the atomic number Z) for different values of the mass cut. The colour map shows the yields for the non-rotating 25 M⊙ (top left panel), rotating 25 M⊙ (top right), fast-rotating 25 M⊙ (bottom left panel), and fast-rotating 25 M⊙ with lower 17O(α, γ)(bottom right panel). The ticks labelled Mrem show the location of the remnant mass using the relation of Maeder (1992; last column of Table 3). “CO” and “He” denote the location of the top of the CO and He core, respectively (fifth and sixth columns of Table 3).
In the text
thumbnail Fig. 14.

Same as Fig. 13 but for the non-rotating 150 M⊙ (left panel) and rotating 150 M⊙ (right panel).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.