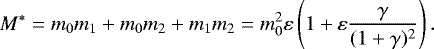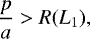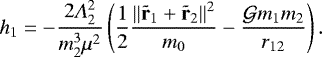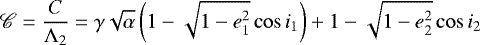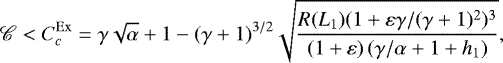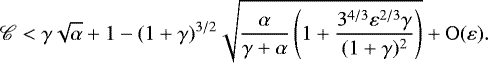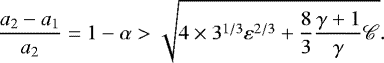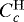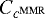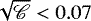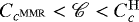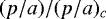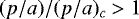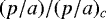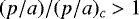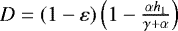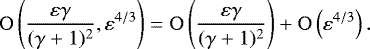| Issue |
A&A
Volume 617, September 2018
|
|
|---|---|---|
| Article Number | A93 | |
| Number of page(s) | 10 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201833088 | |
| Published online | 21 September 2018 | |
Hill stability in the AMD framework
IMCCE, CNRS-UMR8028, Observatoire de Paris, PSL University, Sorbonne Université,
77 Avenue Denfert-Rochereau,
75014
Paris,
France
e-mail: antoine.petit@obspm.fr
Received:
23
March
2018
Accepted:
19
June
2018
In a two-planet system, a topological boundary that is created by Sundman (1912, Acta Math., 36, 105) inequality can forbid close encounters between the two planets for an infinite time. A system is said to be Hill stable if it verifies this topological condition. Hill stability is widely used in the study of extrasolar planet dynamics. However, the coplanar and circular orbit approximation is often used. In this paper, we explain how the Hill stability can be understood in the framework of angular momentum deficit (AMD). In the secular approximation, AMD allows us to discriminate between a priori stable systems and systems for which a more in-depth dynamical analysis is required. We show that the general Hill stability criterion can be expressed as a function of only semimajor axes, masses, and total AMD of the system. The proposed criterion is only expanded in the planets-to-star mass ratio ε and not in the semimajor axis ratio, eccentricities, nor the mutual inclination. Moreover, the expansion in ε remains excellent up to values of about 10−3 even for two planets with very different mass values. We performed numerical simulations in order to highlight the sharp change of behavior between Hill stable and Hill unstable systems. We show that Hill stable systems tend to be very regular, whereas Hill unstable systems often lead to rapid planet collisions. We also note that Hill stability does not provide protection from the ejection of the outer planet.
Key words: planets and satellites: general / planets and satellites: dynamical evolution and stability / celestial mechanics
© ESO 2018
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
The chaotic nature of planetary dynamics has made the development of stability criteria necessary because the complete study of individual systems for the lifetime of the central star would require too much computational power. Moreover, in the context of exoplanet dynamics, the orbital parameters are often not known with great precision, making it impossible to conduct a precise dynamical study. For multiplanetary systems, the best solutions yet are empirical stability criteria based on minimum spacing between planets obtained from numerical simulations (Chambers et al. 1996; Pu & Wu 2015). For tightly packed systems, Tamayo et al. (2016) have suggested a solution based on short integrations and a machine-learning algorithm.
Another approach consists in the study of the angular momentum deficit (AMD; see Laskar 1997, 2000). The AMD is a weighted sum of the eccentricities and mutual inclinations of planets and can be interpreted as a dynamical temperature of the planetary system. The AMD is conserved at all orders of averaging over the mean motions. In Laskar & Petit (2017), it was shown that if the AMD is small enough, collisions are impossible. We can define a sufficient stability condition from the secular conservation of the AMD, i.e., the AMD-stability. Systems that are AMD-stable are long-lived, whereas a more in-depth dynamical study is necessary for AMD-unstable systems.
The initial AMD-stability definition is based on the secular approximation. In Petit et al. (2017), the criterion was slightly modified to exclude systems experiencing short-term chaos due to first-order mean motion resonances (MMR) overlap. The MMR overlap is the main source of chaos and instability in planetary dynamics. Based on Chirikov (1979) resonance overlap criterion, Wisdom (1980) has derived an analytical stability criterion for the two-planet systems that has since been widely used. Wisdom’s criterion is obtained for circular and coplanar planets. It was improved to take into account moderate eccentricities (Mustill & Wyatt 2012; Deck et al. 2013). We have shown in Petit et al. (2017) that this MMR overlap criterion can be expressed solely as a function of the AMD, semimajor axes, and masses for almost coplanar and low eccentricity systems.
The MMR overlap criterion gives a clear limit between regular and chaotic orbits for small eccentricities. However, this criterion is based on first-order expansions in the planets-to-star mass ratio, the spacing between planets, eccentricities, and inclinations. As a result, for wider orbit separations, the secular collision criterion from Laskar & Petit (2017) remains a better limit (Petit et al. 2017). Moreover, the MMR overlap criterion only takes into account the interaction between a couple of planets, making it really accurate only for two-planet systems.
In the case of two-planet systems, the topology of the phase space gives a far simpler criterion of stability, that is the Hill stability. Based on a work by Sundman (1912) on the moment of inertia in the three-body problem, Marchal & Saari (1975) noted the existence of forbidden zones in the configuration space. In Marchal & Bozis (1982), they extended the notion of Hill stability to the general three-body problem and showed that some systems can forbid close encounters between the outer body and any of the inner bodies. In particular, the Hill stability ensures that collisions between the outer body and the close binary (in a two-planet system, between the outer planet and the inner planet or the star) are impossible for infinite time.
The results of Marchal & Saari (1975) and Marchal & Bozis (1982) have many applications outside of the Hill stability. It is possible to cite a sufficient condition for the ejection of a body from the system (Marchal et al. 1984a,b) or the determination of the limit of a triple close approach for bounded orbits (Laskar & Marchal 1984).
Marchal & Bozis (1982) presented the planetary problem (one body with a much larger mass) as a particular case, but the result was mainly popularized by Gladman (1993) who introduced a minimal spacing for initially circular and coplanar systems. Gladman also proposed some criteria for eccentric orbits in some particular configurations of masses. The result by Gladman was refined to cover other situations as, for example, the case of inclined orbits (Veras & Armitage 2004). Georgakarakos (2008) provided a review of stability criteria for hierarchical three-body problems.
The Hill stability is consistent with numerical integrations, where a sharp transition between Hill stable and Hill unstable systems is often observed (Gladman 1993; Barnes & Greenberg 2006; Deck et al. 2013). Moreover, Deck et al. (2013) analyzed the differences between the MMR overlap and Hill stability criteria. They remarked that there exists an area where orbits are chaotic because of the overlap of MMR but long-lived owing to Hill stability.
In this paper, we show that Marchal & Bozis (1982) Hill stability criterion fits extremely well in the AMD-stability framework. In Sect. 2, we derive a criterion for Hill stability solely expressed as a function of the total AMD, semimajor axes, and masses. Our criterion does not need any expansion in the spacing, eccentricities, or inclinations of the orbits and admits all previous Hill criteria as particular approximations. In order to do so, we follow the reasoning proposed by Marchal & Bozis (1982).
We then compare the Hill stability criterion with the AMD-stability criteria proposed in Laskar & Petit (2017) and Petit et al. (2017). In the last section, we carry numerical integrations of two-planet systems over a large part of the phase space. We show that the only parameters of importance are the initial AMD and semimajor axis ratio.
2 Hill stability in the three-body problem
2.1 Generalized Hill curves
Let us use the formalism proposed in Marchal & Saari (1975) and Marchal & Bozis (1982) for the definition of the Hill regions for the general three-body problem. We mainly consider the planetary case and therefore slightly adapt their notations to this particular problem. Let us consider two planets of masses m1, m2 orbiting a star of mass m0. Let 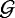 be the constant of gravitation,
be the constant of gravitation, 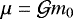 ,
,
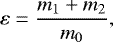 (1)
(1)
the planet mass to star mass ratio and
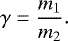 (2)
(2)
As in Laskar & Petit (2017), we use the heliocentric canonical coordinates 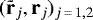 . In those coordinates, the Hamiltonian is
. In those coordinates, the Hamiltonian is
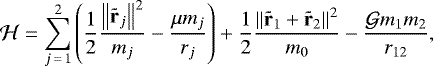 (3)
(3)
where r12 = ∥r1 −r2∥. We denote G the total angular momentum of the system:
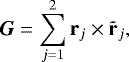 (4)
(4)
and G its norm. From now, we assume G to be aligned along the z-axis. We also define
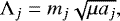 (5)
(5)
where aj is the semimajor axis of the jth planet. We also note ej, the eccentricity, and ij, the inclination of the orbital plane with the horizontal plane. The AMD, C (Laskar 1997, 2000) is expressed
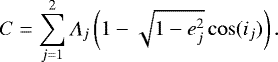 (6)
(6)
Following Marchal & Bozis (1982), we define a generalized semimajor axis:
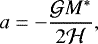 (7)
(7)
and a generalized semilatus rectum:
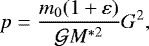 (8)
(8)
The values a and p are the two length units that can be built from the first integrals 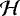 and G.
and G.
We finally define two variable lengths. First, ρ the mean quadratic distance
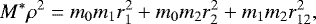 (10)
(10)
that is proportional to the moment of inertia I computed in the center of mass frame (Marchal & Bozis 1982):
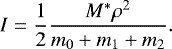 (11)
(11)
We also define ν, the mean harmonic distance:
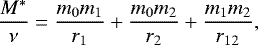 (12)
(12)
which is proportional to the potential energy:
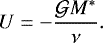 (13)
(13)
For a system with given  and G, some configurations of the planets are forbidden. Indeed, the value of the ratio ρ∕ν is constrained by the inequality (Marchal & Saari 1975):
and G, some configurations of the planets are forbidden. Indeed, the value of the ratio ρ∕ν is constrained by the inequality (Marchal & Saari 1975):
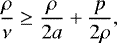 (14)
(14)
derived from Sundman’s inequality (Sundman 1912). Moreover, if the system has a negative energy, the right-hand side of Eq. (14) has a minimum value obtained for 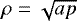 . We therefore have the inequality (Marchal & Bozis 1982):
. We therefore have the inequality (Marchal & Bozis 1982):
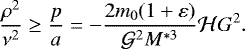 (15)
(15)
If p∕a is high enough, the inequality (15) makes some regions of the phase space inaccessible. In this case, we can ensure that certain initial conditions forbid collisions between the two planets for all times.
Let us study the values of the function 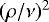 . Since this ratio only depends on the ratios of mutual distances, we can always place ourselves in the planegenerated by the three bodies. We can also choose to place the first planet on the x-axis and normalize the lengths by r1. Let us call this plane
. Since this ratio only depends on the ratios of mutual distances, we can always place ourselves in the planegenerated by the three bodies. We can also choose to place the first planet on the x-axis and normalize the lengths by r1. Let us call this plane 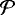 and note (x, y) the coordinates of the second planet. In the plane
and note (x, y) the coordinates of the second planet. In the plane 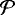 (see Fig. 1), the star S is at the origin, the first planet P1 is situated at the point (1, 0). For the planar restricted three-body problem, this reduction is equivalent to study the dynamics in the corotating frame. We note
(see Fig. 1), the star S is at the origin, the first planet P1 is situated at the point (1, 0). For the planar restricted three-body problem, this reduction is equivalent to study the dynamics in the corotating frame. We note
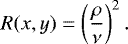 (16)
(16)
The shape of the function R in 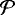 only depends on the mass distribution, for example, the two ratios ε and γ. In Fig. 1, we can see level curves of the function R plotted in
only depends on the mass distribution, for example, the two ratios ε and γ. In Fig. 1, we can see level curves of the function R plotted in 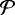 for ε = 10−3 and γ = 1. The value R is minimal and equal to 1 at the two Lagrange points L4 and L5 and goes to + ∞ for ∥r2∥→ 0, ∥r2 −r1∥→ 0 or ∥r2 ∥ → +∞. The function has three saddle nodes at the Lagrange points L1, L2, and L3. We give the method to compute the position of the Lagrange points in Appendix A. Let us denote x1, x2, and x3 their abscissa, respectively. At the lowest order in ε, we have
for ε = 10−3 and γ = 1. The value R is minimal and equal to 1 at the two Lagrange points L4 and L5 and goes to + ∞ for ∥r2∥→ 0, ∥r2 −r1∥→ 0 or ∥r2 ∥ → +∞. The function has three saddle nodes at the Lagrange points L1, L2, and L3. We give the method to compute the position of the Lagrange points in Appendix A. Let us denote x1, x2, and x3 their abscissa, respectively. At the lowest order in ε, we have
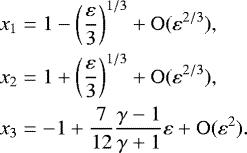 (17)
(17)
At the lowest order in ε, the value of R at the Lagrange points are as follows:
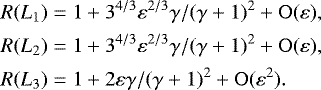 (18)
(18)
The values R(L1) and R(L2) have the same first-order term but differ in the expansion of higher order. Indeed, if m0 ≥ m1 ≥ m2, we have R(L1) ≥ R(L2) (Marchal & Bozis 1982). From now on, let us assume R(L1) ≥ R(L2) (if not, we can just substitute R(L2) to R(L1) in further equations).
For p∕a ≥ R(L1), the accessible domain is split into three parts: the Hill sphere of the star S, which is around the origin; the first planet Hill sphere1  (in green in Fig. 1); and the outer region. In this case, if the second planet is not initially inside
(in green in Fig. 1); and the outer region. In this case, if the second planet is not initially inside  , it will never be able to enter this region. However, if P2 is in the outer region, the Hill stability cannot constrain the possibility of ejection. Similarly, if P2 is closer to the star (in the inner region), a collision with the star is still possible.
, it will never be able to enter this region. However, if P2 is in the outer region, the Hill stability cannot constrain the possibility of ejection. Similarly, if P2 is closer to the star (in the inner region), a collision with the star is still possible.
The study of the function R and the inequality (15) gives a noncollision criterion for an infinite time. Marchal and Bozis called it the Hill stability.
Proposition 1 (Marchal & Bozis 1982).
Let us consider a negative energy three-body problem with a body S of mass m0 and two others P1 and P2 of mass m1 and m2 such that m0 ≥ m1 ≥ m2. We place ourselves in the  plane defined by S, P1, and P2 (Fig. 1). If P2 is not initially inside the Hill sphere
plane defined by S, P1, and P2 (Fig. 1). If P2 is not initially inside the Hill sphere  of P1, the system is Hill stable if
of P1, the system is Hill stable if
where a is defined in (7), p in (8), and R in (16).
From this inequality, Gladman (1993) obtained criteria for initially circular orbits and for two particular cases of eccentric orbits: the case of equal masses and small eccentricities and the case of equal masses and large, but equal eccentricities.
While Gladman’s Hill stability criterion for initially circular orbits is useful, the eccentric criteria are too particular to be used in the context of a generic system. It is, however, possible to obtain a very general Hill stability criterion using the AMD to take into account the eccentricities and inclinations of the orbits.
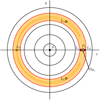 |
Fig. 1 Some levels of the function R defined in (16) for ε = 10−3 and γ = 1 in the |
2.2 AMD condition for Hill stability
The total energy of the system can be written
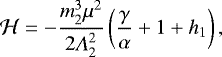 (20)
(20)
From now on, we assume that initially α ≤ 1 (if not we can just renumber the two planets). Similarly, the angular momentum can be rewritten:
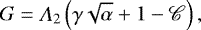 (22)
(22)
is the relative AMD (Laskar & Petit 2017). Combining Eqs. (15), (20), and (22), we obtain
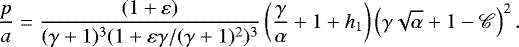 (24)
(24)
The Hill stability criterion (19) can be rewritten without any approximation as a condition on 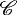 and we have the following formulation of the Hill stability.
and we have the following formulation of the Hill stability.
Proposition 2 (Hill stability).
With the hypotheses of the proposition 1, assuming the elliptical elements can be defined (i.e., both Keplerian energies are negative), a system is Hill stable if
where 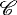 is the relative AMD (23) and h1 is the normalized perturbation part (21).
is the relative AMD (23) and h1 is the normalized perturbation part (21).
The inequality (25) is equivalent to Proposition 1, but we isolated the contribution from the AMD on the left-hand side. Up to the perturbation term h1, the right-hand side of Eq. (25) only depends on the masses and the semimajor axis ratio α. If we only keep the terms of leading order in ε in the square root of the right-hand side of Eq. (25), we obtain an expression that depends only on α, ε, and γ.
Proposition 3 (Hill stability, planetary case).
For small enough ε, a two-planet system is Hill stable if the relative AMD 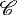 verifies the inequality:
verifies the inequality:
As explained in Appendix B, h1 is of smaller order in ε and can be neglected if the criterion is verified. We want to stress that the expression (26) is obtained with only an expansion in ε and only depends on α, 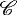 , and the masses of the bodies. The term of order ε2∕3 in Eq. (26) also depends on
, and the masses of the bodies. The term of order ε2∕3 in Eq. (26) also depends on 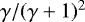 , but we show in Appendix B that (26) is still valid for γ ≪ 1 or γ ≫ 1.
, but we show in Appendix B that (26) is still valid for γ ≪ 1 or γ ≫ 1.
2.3 Close planets approximation
Assuming 1 − α ≪ 1, and a smallAMD value, further approximations can be made. At leading order in 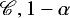 , and ε, the inequality (26) becomes
, and ε, the inequality (26) becomes
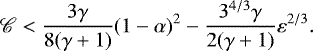 (27)
(27)
We can isolate 1 − α in this expression to obtain an approximate minimum spacing for Hill stable systems.
Proposition 4 (Hill stability, close planets case).
For a close planets system, the minimum spacing criterion for Hill stability is
Gladman’s eccentric criteria can be recovered from Eq. (28) if the AMD is developed under the assumptions (same planet masses, small or large, and equal eccentricities) made in Gladman (1993). However, Eq. (28) is more general as it takes into account mutual inclinations or uneven mass distribution.
In the case of circular orbits, we also get the well-known formula (Gladman 1993):
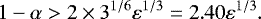 (29)
(29)
2.4 Comparison of the Hill criteria
We can compare the right-hand side of Eqs. (25)–(27), and Gladman’s circular approximation (29) to test how relevant are the approximations made here. In Fig. 2, we plot the exact expression 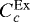 (Eq. (25); in green), the expansion in ε (Eq. (26); in orange), the approximation for close planets (Eq. (27); in red), and the minimum spacing for circular orbits (Eq. (29); in blue). We see that the expansion in ε (Eq. (26)) cannot be distinguished from the exact curve (Eq. (25)). In order to better quantify this, we plot in Fig. 3 the maximum difference between the two curves as a function of ε for various values of the mass ratio γ.
(Eq. (25); in green), the expansion in ε (Eq. (26); in orange), the approximation for close planets (Eq. (27); in red), and the minimum spacing for circular orbits (Eq. (29); in blue). We see that the expansion in ε (Eq. (26)) cannot be distinguished from the exact curve (Eq. (25)). In order to better quantify this, we plot in Fig. 3 the maximum difference between the two curves as a function of ε for various values of the mass ratio γ.
We seein Fig. 3 that for the range of ε used in planetary dynamics (typically from 10−6–10−2), the expression (26) developed in ε is accurate even for very uneven planet mass distribution. From now, we use Eq. (26) to define the Hill stability.
 |
Fig. 2 Comparison of the right-hand sides of the inequalities – Eq. (25) (orange), Eq. (26) (green), and Eq. (27) (red) – as a function of α for γ = 1 and ε = 10−5 (upper three curves) or ε = 10−3 (lower three curves). The black curve is the critical AMD for the collision condition (Laskar & Petit 2017). The green and orange curves are on top of each other (see Fig. 3). The critical AMD from MMR overlap |
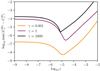 |
Fig. 3 Maximum difference between |
3 Comparison with the AMD-stability
In Laskar &Petit (2017), the AMD-stability of a system is defined by comparing its AMD to a critical value Cc above which the stability of the system cannot be guaranteed. The AMD-stability is a sufficient condition for long-lived stability of a system. The result from Laskar & Petit (2017) was obtained by finding the minimal AMD needed for a system to allow for collisions in the secular approximation, i.e., assuming the semimajor axes are fixed. We completed, in Petit et al. (2017), the AMD-stability definition by excluding the configurations such that the overlap of first-order MMR occurs. The modified critical AMD is hereafter noted 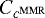 .
.
We can use Eq. (26) to define a critical AMD 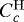 for the Hill stability:
for the Hill stability:
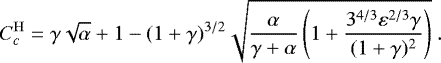 (30)
(30)
A system isHill stable if its initial relative AMD is smaller than the initial critical AMD 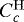 .
.
We see that for two planets, the Hill stability definition fits extremely well in the AMD-stability framework. We can also compare 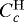 to the previously proposed critical AMD. The collision critical AMD Cc is plotted in Fig. 2 with two values of
to the previously proposed critical AMD. The collision critical AMD Cc is plotted in Fig. 2 with two values of 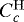 for ε = 10−5 (resp. 10−3). We can see that the Hill stability criterion is stricter (
for ε = 10−5 (resp. 10−3). We can see that the Hill stability criterion is stricter (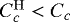 ) than the collision condition for secular dynamics. It can be easily understood since the Hill stability forbids the planets to approach each other.
) than the collision condition for secular dynamics. It can be easily understood since the Hill stability forbids the planets to approach each other.
Indeed, let us consider a Hill stable system, i.e., such that 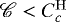 . As a result, the two planets cannot approach each other by less than their mutual Hill radius for any variation of semimajor axes and thus also in the secular system. In particular, a configuration such that the two orbits intersect is impossible. Therefore, the system is AMD-stable and
. As a result, the two planets cannot approach each other by less than their mutual Hill radius for any variation of semimajor axes and thus also in the secular system. In particular, a configuration such that the two orbits intersect is impossible. Therefore, the system is AMD-stable and 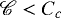 . Since we are not making any additional hypothesis regarding
. Since we are not making any additional hypothesis regarding 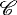 , we have
, we have 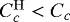 . The strict inequality comes from the positive minimal distance between the two planets.
. The strict inequality comes from the positive minimal distance between the two planets.
As a comparison, we also plot in Fig. 2 the MMR critical AMD 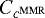 . For small relative AMD,
. For small relative AMD, 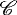 ,
, 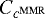 , and
, and 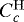 are almost identical.
are almost identical.
4 Numerical simulations
The Hill criterion proposed by Marchal & Bozis (1982) has already been tested numerically in particular cases (Gladman 1993; Veras & Armitage 2004; Barnes & Greenberg 2006). In their comparison between the Hill and the overlap of MMR criteria, Deck et al. (2013) noted a sharp transition in the proportion of chaotic orbits at the Hill limit (p∕a) = (p∕a)|c. It also appears that for small ε and α close to 1, the overlap of MMR criterion provides a better limit for the chaotic region.
We want to test whether the Hill criterion gives a good limit to the chaotic region for wider separations. Moreover, we want our initial conditions to sample homogeneously the phase space. Indeed, the Hill stability criterion studied in this paper only depends on few quantities, the relative AMD 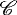 , and the ratio of semimajor axis and not the angles or the actual distribution of the AMD between the degrees of freedom of eccentricities or inclinations. Choosing an homogeneous sampling of the initial conditions also avoids giving too much importance to regions protected by MMR owing to particular combinations of angles while another choice of angles would have given an unstable orbit.
, and the ratio of semimajor axis and not the angles or the actual distribution of the AMD between the degrees of freedom of eccentricities or inclinations. Choosing an homogeneous sampling of the initial conditions also avoids giving too much importance to regions protected by MMR owing to particular combinations of angles while another choice of angles would have given an unstable orbit.
4.1 Numerical setup
We ran numerical simulations using the symplectic scheme ABAH1064 from Farrés et al. (2013). We chose our initial conditions such that
the outerplanet semimajor axis a2 is fixed at 1 au;
the AMD and inner planet semimajor axis a1 are chosen such that, we have a regular grid in the plane
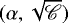 . Such a scaling in
. Such a scaling in 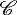 is chosen to have an approximately uniform distribution in terms of eccentricities and inclination;
is chosen to have an approximately uniform distribution in terms of eccentricities and inclination;the AMD is on average equipartitioned between the eccentricity and inclination degrees of freedom;
the inclinations are chosen such that the angular momentum is on the z-axis;
the angles are chosen randomly;
the star mass is taken as 1 M⊙ and the planets masses do not vary for each grid of initial conditions.
We then integrate each initial condition for 500 kyr using a time-step of 10−3 yr. The numerical integration is stopped if the planets approach each other by less than a quarter of their mutual Hill radius, if a planet reaches 10−2 or 20 AU or if the relative variation of energy is higher than 10−8.
In order to measure the stability of a system, we use frequency map analysis (Laskar 1990, 1993). Our criterion is based on the relative variation of the main frequencies in the quasiperiodic best fit. More precisely, let 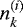 (respectively
(respectively 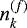 ) be the frequency obtained by frequency analysis for the planet k for the first (resp. last) 100 kyr of integration. We consider an orbit to be chaotic if
) be the frequency obtained by frequency analysis for the planet k for the first (resp. last) 100 kyr of integration. We consider an orbit to be chaotic if
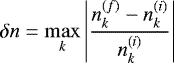 (31)
(31)
is greater than 10−4. The chosen threshold is such that the variation of semimajor axis changes by about 1% in a few Gyr if we assume a constant diffusion process as it would happen for a random walk. Indeed, δn measures the variation of frequency over 500 kyr. If the diffusion rate remains constant, a variation on the order of 1% on average needs a time 10 000 times larger, i.e., 5 Gyr.
If the integration time is shorter due to a collision or ejection, we set δn to 1. Since we randomly draw most of the initial parameters, we bin the results into a two-dimensional grid in 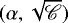 and average the frequency variation in each bin.
and average the frequency variation in each bin.
4.2 Results
We first integrate 1 00 000 initial conditions on a uniform grid with α taking values from 0.5 to 1 and 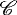 from 0 to 0.1. The masses of the two planets are equal to 0.5 × 10−5 M⊙, such that ε = 10−5 and γ = 1. In this simulation, 78.4% of the orbits survive up to 500 kyr, 21.1% end up in a collision between the two planets, and 0.5% ofthe integrations are stopped because of the nonconservation of energy due to an unresolved close encounter.
from 0 to 0.1. The masses of the two planets are equal to 0.5 × 10−5 M⊙, such that ε = 10−5 and γ = 1. In this simulation, 78.4% of the orbits survive up to 500 kyr, 21.1% end up in a collision between the two planets, and 0.5% ofthe integrations are stopped because of the nonconservation of energy due to an unresolved close encounter.
The results of the frequency analysis are shown in Fig. 4. We see that the chaotic region is well constrained by the Hill curve 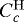 . Indeed, very few orbits with
. Indeed, very few orbits with 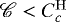 appear to be chaotic. The region where Hill stable orbits (
appear to be chaotic. The region where Hill stable orbits (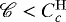 ) are chaotic seems restricted to the region, where
) are chaotic seems restricted to the region, where 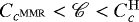 around α ≃ 0.94 and low
around α ≃ 0.94 and low 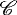 , i.e., for orbits experiencing MMR overlap (a zoomed view of Fig. 4 is given in Fig. 5). The behavior of planets initially in this region was already discussed in (Deck et al. 2013). Orbits that are Hill unstable (
, i.e., for orbits experiencing MMR overlap (a zoomed view of Fig. 4 is given in Fig. 5). The behavior of planets initially in this region was already discussed in (Deck et al. 2013). Orbits that are Hill unstable (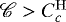 ) appear to be largely chaotic up to some resonant islands situated at α ≃1 (co-orbital resonance) and near the 3:2 and 4:3 resonances (α ≃ 0.76 and 0.82). We also see that for larger separations (α ≲ 0.6), orbits are less chaotic. However, it is probable that for longer integration times, these orbits would end up unstable.
) appear to be largely chaotic up to some resonant islands situated at α ≃1 (co-orbital resonance) and near the 3:2 and 4:3 resonances (α ≃ 0.76 and 0.82). We also see that for larger separations (α ≲ 0.6), orbits are less chaotic. However, it is probable that for longer integration times, these orbits would end up unstable.
In order to highlight how the Hill criterion separates the chaotic orbits from the stable orbits, we can plot the fraction of regular orbits as a function of 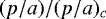 as suggested in Barnes & Greenberg (2006). We see in Fig. 6 that there is a sharp limit at
as suggested in Barnes & Greenberg (2006). We see in Fig. 6 that there is a sharp limit at 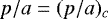 . All Hill stable integrations go to 500 kyr and very few are chaotic. For Hill unstable orbits (
. All Hill stable integrations go to 500 kyr and very few are chaotic. For Hill unstable orbits (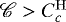 ), we see a slight increase of regular and surviving orbits with p∕a but the decrease is not as significant as the change at the Hill limit. On average 64.9% of the Hill unstable orbits survive and 52.3% are regular.
), we see a slight increase of regular and surviving orbits with p∕a but the decrease is not as significant as the change at the Hill limit. On average 64.9% of the Hill unstable orbits survive and 52.3% are regular.
We plot in Fig. 7 the average time of the integrations as a function of initial α and 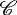 . The initial conditions are binned in a 160 × 75 grid. We see in this figure that the average lifetime of a system is almost always smaller than 500 kyr in the Hill unstable region. We also remark that the average lifetime is less than 50 kyr for a system with α ≳0.9 and not too large
. The initial conditions are binned in a 160 × 75 grid. We see in this figure that the average lifetime of a system is almost always smaller than 500 kyr in the Hill unstable region. We also remark that the average lifetime is less than 50 kyr for a system with α ≳0.9 and not too large 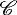 but increases for wider separations or greater AMD. Indeed, for higher
but increases for wider separations or greater AMD. Indeed, for higher 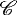 , the planets are on average initially further away from crossing orbits because the initial choice of eccentricities and inclinations is random.
, the planets are on average initially further away from crossing orbits because the initial choice of eccentricities and inclinations is random.
 |
Fig. 4 Frequency variation δn (31) for 1 00 000 initial conditions binned in a 160 × 75 grid with ε = 10−5 and γ = 1. The black curve is the Hill critical AMD |
 |
Fig. 5 Zoomed view of Fig. 4 for 0.9 < α < 1 and |
 |
Fig. 6 Proportion of orbits that survived for 500 kyr (green curve) and nonchaotic orbits (δn < 10−4; red curve) asa function of |
 |
Fig. 7 Average lifetime of the system as a function of α and |
4.3 Influence of the masses
To highlight the role of the mass of the planets, we ran another simulation with the same method but with ε = 10−3 and γ = 1. We integrate 40 000 initial conditions and carry out a similar analysis. After 500 kyr, 54.6% of the systems leads to a collision between the two planets, 2% to an ejection, and 0.5% is stopped due to nonconservation of energy. If we consider only the Hill unstable systems (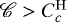 ), only 24.0% have survived and 15.7% are regular. As expected, larger masses lead to much more unstable systems.
), only 24.0% have survived and 15.7% are regular. As expected, larger masses lead to much more unstable systems.
The results of the frequency analysis are plotted in Fig. 8. We observe that the 3:2 MMR is still very stable in comparison to the surrounding regions. The 2:1 MMR appears to create an area of moderate chaos in the Hill stable region but is not as marked in the Hill unstable part. The co-orbital resonance also appears more unstable.
We see in Fig. 9 that some of the Hill stable systems do not survive for 500 kyr. These systems have led to an ejection of the outer planet. As a result, the Hill stability line appears to be more porous in comparison to the case ε = 10−5.
We also see that a larger percentage of Hill stable orbits appear to be chaotic. This can be quantified, thanks to Fig. 10. We see that the proportion of regular orbits drops before it reaches the Hill stability limit. However, the more important change of behavior is still at the Hill stability limit.
 |
Fig. 8 Frequency variation δn (31) for 40 000 initial conditions binned in a 100 × 50 grid with ε = 10−3 and γ = 1. The three curves are similar to Fig. 4. |
 |
Fig. 9 Average lifetime of the system as a function of α and |
 |
Fig. 10 Proportion of orbits that survived for 500 kyr (green curve) and nonchaotic orbits (δn < 10−4; red curve) asa function of |
5 Conclusions
In a two-planet system, Hill stability is a topological limit that forbids close encounters between the outer planet and the inner planet or the star. If verified, the system remains stable if the outer planet does not escape or if the inner planet does not collide with the star. Moreover, since a minimal distance between planets is imposed, the planet perturbation remains moderate and the system is most likely regular.
We have generalized Gladman’s Hill stability criterion and have shown that it is natural to express the Hill criterion in the AMD framework. Indeed, we obtained a simple expression for this criterion (Proposition 3) with only an expansion in ε (Eq. (1)). Moreover, it is easy to recover all former published criteria as particular cases of this expression. Because of its formulation as a function of the AMD, the expression (26) is valid in the general spatial case for any value of eccentricities and inclinations. Moreover, our Hill criterion is accurate even for very different planet masses. We also highlight that the AMD and the semimajor axis ratio α are the main parameters to consider in a stability study.
We show that the Hill stability allows us to give an accurate stability limit up to large orbital separations. The sharp change of behavior at the Hill stability limit has already been studied in Barnes & Greenberg (2006) or in Deck et al. (2013). Nevertheless, our numerical integrations confirm it for a much larger range of α and AMD with randomized initial conditions for the parameters not taken into account.
Our simulations for large planet masses also show that the expansion in ε is valid even for larger planets and that the Hill stability accurately segregates between regular and short-lived initial conditions. However, it appears that for large mass values, ejections cannot be neglected and a model should be developed to understand this further behavior.
As shown in several works on tightly packed systems (Chambers et al. 1996; Pu & Wu 2015), Gladman’s Hill criterion is no longer adapted in these cases. Such a sharp limit between almost eternal and short-lived systems no longer exists. Instead, it appears that there exists a scaling between the initial orbital separation and the time of instability, wider separated orbits becoming unstable after a longer time. In the cited works, the empirical stability criteria give stability spacing as a function of the mutual radius
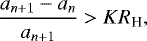 (32)
(32)
where 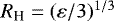 is the Hill radius. In the context of multiplanetary systems, an analytical work on long-term stability is still necessary. This will be the subject of future work.
is the Hill radius. In the context of multiplanetary systems, an analytical work on long-term stability is still necessary. This will be the subject of future work.
Acknowledgements
This work was granted access to the HPC resources of MesoPSL financed by the Region Ile de France and the project Equip@Meso (reference ANR-10-EQPX-29-01) of the programme Investissements d’Avenir supervised by the Agence Nationale pour la Recherche. We acknowledge the support of the PNP and the CS of the Observatoire de Paris.
Appendix A Computation of R at the Lagrange points
The function 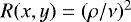 defined in Eq. (16) admits three saddle points situated on the x-axis, which are the Lagrange points L1, L2, and L3. If xj is the abscissa of the point Lj, we have 0 < x1 < 1, x2 > 1, and x3 < 0. The xj quantities only depends on the mass ratio ε and on
defined in Eq. (16) admits three saddle points situated on the x-axis, which are the Lagrange points L1, L2, and L3. If xj is the abscissa of the point Lj, we have 0 < x1 < 1, x2 > 1, and x3 < 0. The xj quantities only depends on the mass ratio ε and on
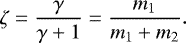 (A.1)
(A.1)
They are the roots of the three different polynomial equations:
![\begin{align*} &(1+\zeta\varepsilon)x_1^5-(2+3\zeta\varepsilon)x_1^4\nonumber\\ &\quad+(1+2\varepsilon+\zeta\varepsilon)x_1^3-(1+3\varepsilon(1-\zeta))x_1^2\nonumber\\ &\quad+(2+3\varepsilon(1-\zeta))x_1-(1+\varepsilon(1-\zeta))=0,\\[10pt] &(1+\zeta\varepsilon)x_2^5-(2+3\zeta\varepsilon)x_2^4\nonumber\\ &\quad+(1+3\zeta\varepsilon)x_2^3-(1+3\varepsilon-\zeta\varepsilon))x_2^2\nonumber\\ &\quad+(2+3\varepsilon(1-\zeta))x_2-(1+\varepsilon(1-\zeta))=0,\\[10pt] &(1+\zeta\varepsilon)x_3^5-(2+3\zeta\varepsilon)x_3^4\nonumber\\ &\quad+(1+3\zeta\varepsilon)x_3^3+(1+3\varepsilon(1-\zeta))x_3^2\nonumber\\ &\quad+(2+3\varepsilon(1-\zeta))x_3+(1+\varepsilon(1-\zeta))=0, \end{align*}](/articles/aa/full_html/2018/09/aa33088-18/aa33088-18-eq92.png)
At up to terms of order ε4∕3, we have
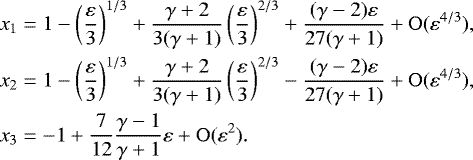 (A.5)
(A.5)
We can then evaluate R (Eq. (16)) at those points and we have at order, ε4∕3:
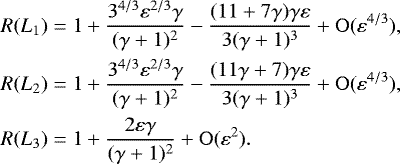 (A.6)
(A.6)
Appendix B Expansion of 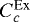 and h1
and h1
In Sect. 2, the Hill stability criterion (26) is obtained by the expansion at the leading order in ε of
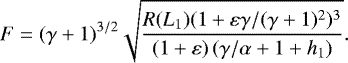 (B.1)
(B.1)
In F, the main term depending on ε comes from the expansion of
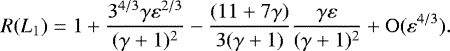 (B.2)
(B.2)
However, wealso need to make sure that h1 remains small in comparison to this term. Thus, the expansion of F requires an estimate of h1 with respect to ε and γ. As explained in Sect. 2, h1 is the renormalized perturbation part of the Hamiltonian (3):
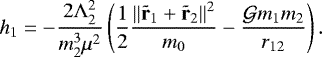 (B.3)
(B.3)
If we note 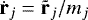 and simplify the expression (B.3), we obtain
and simplify the expression (B.3), we obtain 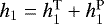 , where
, where
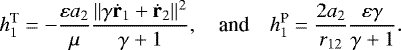 (B.4)
(B.4)
As one cansee in Fig. 2, the value of ε is only relevant for small values of the critical AMD  , i.e., for close planets. Using the expansion in 1 − α (27), we can estimatethat we need to compute h1 for systems such that
, i.e., for close planets. Using the expansion in 1 − α (27), we can estimatethat we need to compute h1 for systems such that 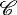 is of order ε2∕3. This corresponds to systems with eccentricities of order ε1∕3. We can therefore use the circular approximation in our estimation of h1. In particular, we have rj = aj(1 + O(ε1∕3)).
is of order ε2∕3. This corresponds to systems with eccentricities of order ε1∕3. We can therefore use the circular approximation in our estimation of h1. In particular, we have rj = aj(1 + O(ε1∕3)).
We first consider the term coming from the gravitational interaction between the two planets, 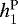 . If the system is Hill stable, the distance r12 is greater than the radius ofthe Hill sphere
. If the system is Hill stable, the distance r12 is greater than the radius ofthe Hill sphere 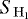 :
:
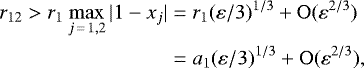 (B.5)
(B.5)
where xj is defined in (A.5). For all times, we therefore have
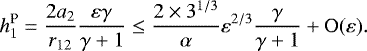 (B.6)
(B.6)
The gravitational potential term 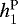 is at most of the same order as the leading term in ε of R(L1). However, we can always choose to estimate the energy and actions values when the two planets are far from each other. In this case, a2 ∕r12 = O(1) and
is at most of the same order as the leading term in ε of R(L1). However, we can always choose to estimate the energy and actions values when the two planets are far from each other. In this case, a2 ∕r12 = O(1) and 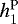 is linear in ε. From now on, we assume that we have
is linear in ε. From now on, we assume that we have
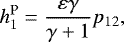 (B.7)
(B.7)
with p12 = O(1).
Moreover, F is a decreasing function of h1, so 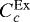 is an increasing function of h1. Since
is an increasing function of h1. Since 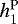 is positive, neglecting it is equivalent to have a more conservative criterion.
is positive, neglecting it is equivalent to have a more conservative criterion.
Let us now consider the kinetic term 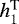 . We develop (B.4) for almost circular orbits. In this limit, we have
. We develop (B.4) for almost circular orbits. In this limit, we have 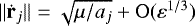 . We have
. We have
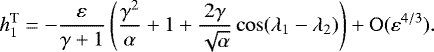 (B.8)
(B.8)
Therefore, 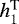 is always linear in ε. Combining the estimations (B.7) and (B.8), we see that h1 = O(ε).
is always linear in ε. Combining the estimations (B.7) and (B.8), we see that h1 = O(ε).
We can now use the expansions of h1, (B.8) and (B.7), to obtain the expansion of F in function of ε and γ. Because of the term 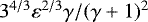 from R(L1), we do not keep terms of order
from R(L1), we do not keep terms of order 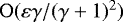 . We keep all other terms depending on ε up to the order O(ε4∕3). We obtain
. We keep all other terms depending on ε up to the order O(ε4∕3). We obtain
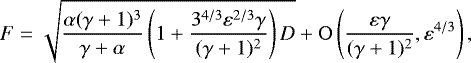 (B.9)
(B.9)
Let us develop D on the same order than F. We have
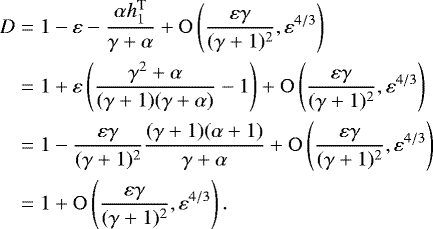 (B.10)
(B.10)
We see that D has no contribution to F at the considered orders. Therefore, we can write
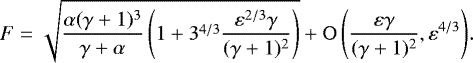 (B.11)
(B.11)
As an immediate consequence of (B.11), the expression proposed in Eq. (26) remains valid in the case of a very uneven mass distribution between the two planets (e.g., for O (ε1∕3) < γ < O(ε−1∕3)).
References
- Barnes, R., & Greenberg, R. 2006, ApJL, 647, L163 [NASA ADS] [CrossRef] [Google Scholar]
- Chambers, J., Wetherill, G., & Boss, A. 1996, Icarus, 119, 261 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Chirikov, B. V. 1979, Phys. Rep., 52, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Deck, K. M., Payne, M., & Holman, M. J. 2013, ApJ, 774, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Farrés, A., Laskar, J., Blanes, S., et al. 2013, Celest. Mech. Dyn. Astron., 116, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Georgakarakos, N. 2008, Celest. Mech. Dyn. Astron., 100, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Gladman, B. 1993, Icarus, 106, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Laskar, J. 1990, Icarus, 88, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Laskar, J. 1993, Physica D Nonlinear Phenom., 67, 257 [Google Scholar]
- Laskar, J. 1997, A&A, 317, L75 [NASA ADS] [Google Scholar]
- Laskar, J. 2000, Phys. Rev. Lett., 84, 3240 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Laskar, J., & Marchal, C. 1984, Celest. Mech. Dyn. Astron., 32, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Laskar, J., & Petit, A. C. 2017, A&A, 605, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marchal, C., & Bozis, G. 1982, Celest. Mech. Dyn. Astron., 26, 311 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Marchal, C., & Saari, D. G. 1975, Celest. Mech. Dyn. Astron., 12, 115 [CrossRef] [Google Scholar]
- Marchal, C., Yoshida, J., & Yi-Sui, S. 1984a, Celest. Mech. Dyn. Astron., 33, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Marchal, C., Yoshida, J., & Yi-Sui, S. 1984b, Celest. Mech. Dyn. Astron., 34, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Mustill, A. J., & Wyatt, M. C. 2012, MNRAS, 419, 3074 [NASA ADS] [CrossRef] [Google Scholar]
- Petit, A. C., Laskar, J., & Boué, G. 2017, A&A, 607, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pu, B., & Wu, Y. 2015, ApJ, 807, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Sundman, K. F. 1912, Acta Math., 36, 105 [CrossRef] [Google Scholar]
- Tamayo, D., Silburt, A., Valencia, D., et al. 2016, ApJ, 832, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Veras, D., & Armitage, P. J. 2004, Icarus, 172, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Wisdom, J. 1980, AJ, 85, 1122 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Some levels of the function R defined in (16) for ε = 10−3 and γ = 1 in the |
| In the text | |
 |
Fig. 2 Comparison of the right-hand sides of the inequalities – Eq. (25) (orange), Eq. (26) (green), and Eq. (27) (red) – as a function of α for γ = 1 and ε = 10−5 (upper three curves) or ε = 10−3 (lower three curves). The black curve is the critical AMD for the collision condition (Laskar & Petit 2017). The green and orange curves are on top of each other (see Fig. 3). The critical AMD from MMR overlap |
| In the text | |
 |
Fig. 3 Maximum difference between |
| In the text | |
 |
Fig. 4 Frequency variation δn (31) for 1 00 000 initial conditions binned in a 160 × 75 grid with ε = 10−5 and γ = 1. The black curve is the Hill critical AMD |
| In the text | |
 |
Fig. 5 Zoomed view of Fig. 4 for 0.9 < α < 1 and |
| In the text | |
 |
Fig. 6 Proportion of orbits that survived for 500 kyr (green curve) and nonchaotic orbits (δn < 10−4; red curve) asa function of |
| In the text | |
 |
Fig. 7 Average lifetime of the system as a function of α and |
| In the text | |
 |
Fig. 8 Frequency variation δn (31) for 40 000 initial conditions binned in a 100 × 50 grid with ε = 10−3 and γ = 1. The three curves are similar to Fig. 4. |
| In the text | |
 |
Fig. 9 Average lifetime of the system as a function of α and |
| In the text | |
 |
Fig. 10 Proportion of orbits that survived for 500 kyr (green curve) and nonchaotic orbits (δn < 10−4; red curve) asa function of |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.