| Issue |
A&A
Volume 616, August 2018
|
|
|---|---|---|
| Article Number | A140 | |
| Number of page(s) | 21 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201731858 | |
| Published online | 11 September 2018 | |
3D radiative transfer: Continuum and line scattering in non-spherical winds from OB stars
1
LMU München, Universitätssternwarte, Scheinerstr. 1, 81679 München, Germany
e-mail: levin@usm.lmu.de, levin@usm.uni-muenchen.de
2
Institut für Astronomie und Astrophysik, Universität Tübingen, Auf der Morgenstelle 10, 72076 Tübingen, Germany
3
Instituut voor Sterrenkunde, KU Leuven, Celestijnenlaan 200D, 3001 Leuven, Belgium
Received:
30
August
2017
Accepted:
29
April
2018
Context. State of the art quantitative spectroscopy utilizes synthetic spectra to extract information from observations. For hot, massive stars, these synthetic spectra are calculated by means of 1D, spherically symmetric, NLTE atmosphere and spectrum-synthesis codes. Certain stellar atmospheres, however, show strong deviations from spherical symmetry, and need to be treated in 3D.
Aims. We present and test a newly developed 3D radiative transfer code, tailored to the solution of the radiation field in rapidly expanding stellar atmospheres. We apply our code to the continuum transfer in wind-ablation models, and to the UV resonance line formation in magnetic winds.
Methods. We have used a 3D finite-volume method for the solution of the time-independent equation of radiative transfer, to study continuum- and line-scattering problems, currently approximated by a two-level-atom. Convergence has been accelerated by coupling the formal solver to a non-local approximate Λ-iteration scheme. Particular emphasis has been put on careful tests, by comparing with alternative solutions for 1D, spherically symmetric model atmospheres. These tests allowed us to understand certain shortcomings of the methods, and to estimate limiting cases that can actually be calculated.
Results. The typical errors of the converged source functions, when compared to 1D solutions, are of the order of 10–20%, and rapidly increase for optically thick (τ ≳ 10) continua, mostly due to the order of accuracy of our solution scheme. In circumstellar discs, the radiation temperatures in the (optically thin) transition region from wind to disc are quite similar to corresponding values in the wind. For MHD simulations of dynamical magnetospheres, the line profiles, calculated with our new 3D code, agree well with previous solutions using a 3D-SEI method. When compared with profiles resulting from the so-called analytic dynamical magnetosphere (ADM) model, however, significant differences become apparent.
Conclusions. Due to similar radiation temperatures in the wind and the transition region to the disc, the same line-strength distribution can be applied within radiation hydrodynamic calculations for optically thick circumstellar discs in “accreting high-mass stars”. To properly describe the UV line formation in dynamical magnetospheres, the ADM model needs to be further developed, at least in a large part of the outer wind.
Key words: radiative transfer / methods: numerical / circumstellar matter / stars: magnetic field / stars: winds, outflows
© ESO 2018
1. Introduction
Hot, massive stars are key tools to interpret the Universe. For example, they both enrich the interstellar medium with highly processed material due to their strong stellar winds, as well as end their lives as supernovae, enriching the surroundings with metals even further. Additionally, the latter produce strong shocks within the interstellar medium, thus triggering star formation.
Massive stars are thought to be the progenitors of massive black holes (MBH ≳ 25 M⊙) when their final fate is a direct collapse into a black hole instead of a supernova explosion. The collapse into a black hole, however, is only possible when the progenitor stars exhibit a weak wind, or, more generally, do not lose too much mass during their lifetime. Belczynski et al. (2016) proposed a low-metallicity environment to explain the massive black hole merger GW150914 (M1 ≈ 36 M⊙, M2 ≈ 29 M⊙, Abbott et al. 2016) observed at the Laser Interferometric Gravitational-Wave Observatory (LIGO), whereas Petit et al. (2017) showed that magnetic surface fields could also lower the mass loss to form such progenitor stars.
The physical properties of massive stars are generally derived by means of quantitative spectroscopy, that is by modelling their atmospheres numerically and comparing the calculated synthetic spectra with observations. When using one-dimensional (1D), spherically symmetric codes (e.g. CMFGEN Hillier & Miller 1998, PHOENIX1 Hauschildt 1992, POWR Gräfener et al. 2002, WM-BASIC Pauldrach et al. 2001, FASTWIND Puls et al. 2005; Rivero González et al. 2012, as a non-exhaustive list for massive star atmospheric models), this has meanwhile become a routine job and is widely applied. Within the last decade, however, it became more and more evident, from both the theoretical and observational side, that many stars differ from spherical symmetry, rendering the results from 1D codes questionable for such objects. The deviations can be of different origin and shape:
(i) Magnetic winds: Wade et al. (2012) showed within the Magnetism in Massive Stars (MiMeS) survey, that about 7% of all (Galactic) OB-stars have detectable magnetic fields. Magneto-hydrodynamic (MHD) calculations from ud-Doula & Owocki (2002) and ud-Doula et al. (2008) revealed, that large scale magnetic fields, possibly of fossil origin (Alecian et al. 2013), have a direct impact on the stellar wind by channeling the wind outflow along magnetic-field lines, often producing disc-like structures around the magnetic equator. Depending on the competition between wind energy and magnetic-field energy (characterized by the so called Alfvén-radius, RA), and the rotational velocities (characterized by the Kepler-radius, RK), a dynamical (RA < RK) or centrifugal (RA > RK) magnetosphere may form (see also Petit et al. 2013). In the former case, confined material in the equatorial disc falls back onto the stellar surface, whereas in the latter case, material is supported by centrifugal forces, forming a quite stable and strongly confined disc structure. Townsend & Owocki (2005) were able to explain the observed Balmer-line variability in σ Ori E, a magnetic Bp star, by applying the oblique-rotator model. Recently, Owocki et al. (2016) developed a simplified model, the “analytic dynamical magnetosphere” (ADM), in order to provide a framework for the analysis of magnetic winds, and were able to reproduce the observed Hα-line variations of HD 191612. However, a test of the ADM model for UV resonance lines is still missing, and will be addressed in this paper.
(ii) Accretion and decretion discs: Both pre-main-sequence and a significant fraction of massive main-sequence stars are observed to have circumstellar discs, from which material is either accreted onto the star, or decreted by different mechanisms, respectively. For classical Be stars, Kee et al. (2016) proposed that the destruction of the circumstellar disc by wind-ablation, that is by radiative forces along the disc surface, is the major mechanism, which possibly plays also a significant role for stars that already have ignited hydrogen burning, however are still accreting material through a disc. These objects will be named “accreting high-mass stars” within this paper. Although Kee (2015) applied reasonable approximations in order to derive the incident intensity at the disc’s surface layers, the local ionization stages are not treated explicitly. Since the line-force depends on the line-strength distribution function (e.g. Castor et al. 1975; Puls et al. 2000), which crucially depends on the local ionization stages of the ions and therefore also on the mean intensity, a consistent treatment of the (pseudo) continuum radiative transfer (RT) is needed.
(iii) Fast rotation: Stellar rotation is a natural consequence of the classical star-formation scenario, that means of the collapse of an initially rotating molecular cloud. Within the VLT-FLAMES Tarantula survey (VFTS), Ramírez-Agudelo et al. (2013) derived the distribution of projected rotational velocities of (LMC) O-type stars, and found that it peaks at relatively low values (v sin i ≈ 50–100 km s−1), and has an extended tail towards higher ones, thought to be due to binary interaction. For example, the very rapidly rotating O-star, VFTS102, rotates at a nearly critical rotation rate (Dufton et al. 2011). Nearly critically rotating stars are highly distorted, with a ratio of equatorial to polar radius approaching a value of three half. Additionally, the emergent flux at the stellar surface becomes latitude-dependent due to gravity darkening (see von Zeipel 1924 for uniform rotation, and Maeder 1999; Maeder & Meynet 2000 for shellular rotation).
(iv) Binary interaction: By a detailed investigation of binarity within the VFTS, Sana et al. (2013) found that about 50% of the observed O-star population in the Tarantula nebula have binary companions, that will interact with the primary star during its lifetime via Roche-lobe-overflow, or even merging. Roughly 30%–40% of these stars have periods less than six days (see also Sana & Evans 2011), which influences already the main-sequence evolution. Due to the mass transfer, the donor star will be stripped and spins down, whereas the companion will spin up due to the transport of angular momentum (e.g. de Mink et al. 2013). In case of two massive stars being part of the binary system, their winds will collide and lead to strong shocks and X-ray emission (e.g. Prilutskii & Usov 1976; Cherepashchuk 1976; Stevens et al. 1992; Pittard 2009), in addition to phase-locked variations of recombination lines (see Sana et al. 2001).
Since all these effects break the symmetry of many observed objects, a 3D treatment of the RT has to be applied to derive the (possibly dynamical) spectral energy distributions. This, however, is computationally expensive due to the dependence of the radiation field on frequency and direction, in addition to the three spatial dimensions. Nevertheless, solution schemes have been developed already from the early 70s on, starting with the long-characteristics (LC) method (see Jones & Skumanich 1973 and Jones 1973), over the short-characteristics (SC) method (see Kunasz & Auer 1988), to finite-volume methods (FVM, see Adam 1990). Within the LC method, the equation of radiative transfer (EQRT) is solved for a given direction along a ray intersecting a considered grid point. Thus, for a 3D grid with N3 grid points, and assuming on average N/2 grid points along the ray, N4/2 operations have to be performed to obtain the intensities at all grid points for a single direction. Each operation consists of interpolating the physical properties from the 3D grid onto the ray, and solving the formal integral along all points on the ray. The SC method solves the EQRT only across each grid cell, with incident intensities on the cell surfaces obtained by interpolation from the already known grid points. The number of operations is thus reduced by a factor of N/2. For both methods, the accuracy of the applied interpolation scheme is crucial for the final performance of the obtained solution.
Instead of considering discrete rays, as in the above methods, the FVM solves the EQRT for a single direction, by considering the complete set of rays with the given direction entering the volume of a grid cell, and assuming that the physical properties at the corresponding grid point are representative averages for the complete cell. Though this still gives N3 operations for the solution for a single direction, all interpolations are avoided. Thus, when compared to the LC or SC method, the amount of work needed for each operation is reduced considerably. Interestingly, the development of methods underwent an evolution from computationally most expensive methods (LC) to cheaper methods (SC and FVM).
The above mentioned tools are called formal solvers, since they calculate the radiation field for given source- and sink-terms. However, the most important problem arises in scattering dominated atmospheres, where the sources (and sinks) depend on the radiation field, and vice versa. Such atmospheres need to be calculated by applying, for instance, the so-called Λ-iteration and associated acceleration techniques (e.g. Cannon 1973).
Meanwhile, various 2D and 3D codes exist, with widely differing assumptions on the underlying geometry and designated applications. In this respect, one important point is the assumption of local thermodynamic equilibrium (LTE), which cannot be applied in expanding atmospheres, when the radiation field dominates the level populations. For the latter problem, the coupling between the non-LTE (NLTE) rate equations and radiation field is mostly performed using the aforementioned acceleration techniques (e.g. the accelerated Λ-iteration, ALI). We briefly mention specific codes designated to the multi-D RT in stellar atmospheres (for other applications, there are many more such codes; e.g. for multi-D codes related to the ionization balance in the interstellar medium, see Weber et al. 2013 and references therein):
WIND3D (Lobel & Blomme 2008) is a 3D FVM code, which has been developed to calculate the line transport in scattering dominated environments using Cartesian coordinates, and with level populations approximated by a two-level-atom (TLA). It adopts the classical Λ-iteration scheme, which has poor convergence properties for optically thick, scattering-dominated lines. WIND3D is thus restricted to the treatment of weak lines. For those, however, Lobel & Blomme (2008) were able to model the time variations of discrete absorption components (DACs), as observed for the Si IV 1400 Å doublet of the B0.5Ib supergiant HD 64760. Together with the hydrodynamic code ZEUS3D, they were able to reproduce these DACs, supporting the suggestion of Mullan (1984), that they arise from co-rotating interaction regions (see also Cranmer & Owocki 1996).
ASTAROTH (Georgiev et al. 2006; Zsargó et al. 2006) is a 2D SC code, which is capable of solving the RT in parallel with the NLTE rate equations for axisymmetric problems with non-monotonic velocity fields. It uses spherical coordinates and includes a (local) ALI scheme. Many tests have been performed by a comparison to 1D spherically symmetric models from CM-FGEN, giving errors of a few percent only. Zsargó et al. (2008) applied the code to investigate the H and He ionization stages in the envelopes of B[e] supergiants, and modelled, among others, the Hα line.
IRIS (Ibgui et al. 2013a) is a 3D SC code, which, to our knowledge, has been only applied for studying laboratory-generated radiative shocks (Ibgui et al. 2013b) thus far. Ibgui et al. (2013a) performed test cases (searchlight beam test and 1D plane-parallel models), which show an astonishing accuracy for the solution of intensity, mean intensity, radiative flux, and radiation pressure tensor, on non-uniform Cartesian coordinates and including velocity field gradients. By now, the code assumes LTE. However, the inclusion of scattering terms is planned for the future.
MULTI3D (Leenaarts & Carlsson 2009) is a 3D SC code developed to accurately solve the NLTE rate equations in cool FGK-type stars. Amarsi et al. (2016) used this code to predict, among other lines, the O I 777 nm line for a grid of 3D hydrodynamical models, by setting up a 23-level model atom. This code, however, has been developed (and optimized) for the application to cool stars (with subsonic velocity fields, at most), and cannot be used in our context.
PHOENIX/3D (Hauschildt & Baron 2006 and other papers in this series) is a 3D LC solver, which is capable of solving the RT together with the multi-level NLTE rate equations. They use spherical, cylindrical or Cartesian coordinates, and implemented a non-local ALI scheme. With the extension from Seelmann et al. (2010), arbitrary velocity fields can be included as well. To our knowledge, PHOENIX/3D has not been applied, thus far, to real, multi-dimensional, problems.
In this paper, we develop a 3D solution scheme to calculate continuum and line source functions in expanding atmospheres. As a first step, we implement a FVM to determine the formal solution, since this method has already been applied in the context of 3D structures (e.g. Adam 1990; Stenholm et al. 1991; Lobel & Blomme 2008), and is supposed to have the lowest computational cost, when compared to the SC and LC methods. To calculate optically thick continua and strong lines, an ALI technique is required, and developed for the first time within the 3D FVM framework by means of a non-local approximate Λ-operator (ALO, see Sect. 3). In Sect. 4, we present, also for the first time, an error analysis of the 3D FVM for the case of 1D spherical atmospheres, both for optically thin and optically thick environments. This error analysis allows us to understand certain shortcomings of the methods, and to estimate limiting cases that can actually be calculated. As first applications for our 3D solver, we study specific aspects related to the circumstellar discs of ac-creting high-mass stars (Sect. 5), and to the UV line formation in magnetic winds (Sect. 6).
2. Basic assumptions
The problems considered within this paper assume an (almost) stationary atmospheric structure, meaning that the densities, velocities and boundary conditions are assumed to be constant in time, or are at least changing much slower than the radiation field. Thus, we use the time-independent EQRT (e.g. Mihalas 1978):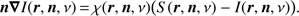 (1)
(1)
In the following, we skip the explicit notation for the spatial (r) and directional (n) dependencies, and write the frequency dependence as subscript, or, when appropriate, skip also this notation. The source function, S ν, and the opacity, χν, consist of the sum of continuum and line processes. By splitting the continuum emissivity and opacity into true2 and scattering processes, the corresponding source function can be parameterized by a single parameter, ϵc, the ratio of true absorption to total opacity, which is called the thermalization parameter: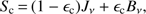 (2)
(2)
where Jν is the mean intensity, and Bν the Planck function. As a first approach, we treat the line transfer similarly by considering a TLA only. This is well suited to describe resonance lines, but for future applications the complete rate equations need to be taken into account, of course. The line source function in the TLA approach reads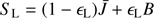 (3)
(3)
![$ {{\epsilon }_{L}}=\frac{{{\epsilon }'}}{1+{\epsilon }'},{\epsilon }'=\frac{{{C}_{\text{ul}}}}{{{\text{A}}_{\text{ul}}}}\left[ \exp \left( -\frac{h\nu }{{{k}_{\text{B}}}T} \right) \right], $](/articles/aa/full_html/2018/08/aa31858-17/aa31858-17-eq4.gif) (4)
(4)
with Cul and Aul being the collisional rate (from the upper to the lower level) and the Einstein-coeffcient for spontaneous emission, respectively. J̄ = 1/4π ∫ IνΦx dx dΩ is the profile-weighted and frequency-integrated, angle-averaged intensity, the so-called scattering integral. The profile function, Φx, has been approximated by a Doppler profile. Further, we did not calculate the profile in frequency space, but rather in the variable xCMF, describing the comoving frame (CMF) frequency shift from line centre, in units of a fiducial Doppler width, 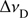 :
: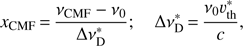 (5)
(5)
where ν0 and 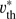 are the line-centre transition frequency, and the fiducial thermal velocity, respectively. The fiducial width is required to enable a depth-independent frequency grid. xCMF is related to the corresponding observer’s frame quantity via xCMF = xOBS − n · V, with
are the line-centre transition frequency, and the fiducial thermal velocity, respectively. The fiducial width is required to enable a depth-independent frequency grid. xCMF is related to the corresponding observer’s frame quantity via xCMF = xOBS − n · V, with 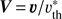 the local velocity vector in units of
the local velocity vector in units of 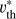 . In most cases, we do not label x explicitly to distinguish between comoving and observer’s frame (nor from the spatial x-coordinate), since the meaning should be clear wherever it occurs.
. In most cases, we do not label x explicitly to distinguish between comoving and observer’s frame (nor from the spatial x-coordinate), since the meaning should be clear wherever it occurs.
The profile function (in frequency-space) is
![$ {{\Phi }_{\nu }}=\frac{1}{\sqrt{\pi }\Delta {{\nu }_{\text{D}}}}\exp \left[ -{{\left( \frac{{{\nu }_{\text{CMF}}}-{{\nu }_{\text{0}}}}{\Delta {{\nu }_{\text{D}}}} \right)}^{2}} \right]=\frac{1}{\sqrt{\pi }\Delta {{\nu }_{\text{D}}}}\exp \left[ -{{\left( \frac{{{x}_{\text{CMF}}}}{\delta } \right)}^{2}} \right], $](/articles/aa/full_html/2018/08/aa31858-17/aa31858-17-eq10.gif) (6)
(6)
is the ratio between the local thermal velocity (including micro-turbulence, see Sect. 3.1) and the fiducial velocity, T is the local temperature, and mA is the mass of the considered ion. With the profile function, normalized in x-space,![$ {{\Phi }_{x}}=\frac{1}{\sqrt{\pi }\delta }\exp \left[ -{{\left( \frac{{{x}_{\text{CMF}}}}{\delta } \right)}^{2}} \right]=\frac{1}{\sqrt{\pi }\delta }\exp \left[ -{{\left( \frac{{{x}_{\text{OBS}}}-n\cdot V}{\delta } \right)}^{2}} \right], $](/articles/aa/full_html/2018/08/aa31858-17/aa31858-17-eq12.gif) (8)
(8)
the line opacity, which needs to be described in frequency-space (because the RT and Planck function are formulated w.r.t. frequency), is given by
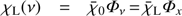 (9)
(9)
![$ {{\bar{\chi }}_{\text{0}}}=\frac{\pi {{\text{e}}^{2}}}{{{m}_{\text{e}}}c}(gf)\left[ \frac{{{n}_{l}}}{{{g}_{l}}}-\frac{{{n}_{u}}}{{{g}_{u}}} \right]\approx \frac{\pi {{\text{e}}^{2}}}{{{m}_{\text{e}}}c}\cdot f\cdot {{n}_{l}}, $](/articles/aa/full_html/2018/08/aa31858-17/aa31858-17-eq14.gif) (10)
(10)
with (g f ) the g f -value of the considered transition, and nl, nu, gl, gu the occupation numbers and statistical weights of the lower and upper level, respectively. Since nl ≫ nu for resonance lines, we have neglected stimulated emission on the right-hand side. χ̄0 is the frequency integrated opacity3, and is related to χ̄L by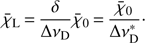 (11)
(11)
We finally parameterize the continuum and line opacities in terms of the Thomson-opacity, χTh = neσe, (12)
(12)
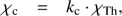 (13)
(13)
where we use kL as a depth-independent parameter, since the ratio nl/ne remains almost constant in the atmosphere for resonance lines (almost frozen-in ionization).
The radiation field depends on the source functions via the EQRT, and the source functions depend on the radiation field via Eqs. (2) and (3). Although this coupled problem could be solved directly, at least in principle, we note already here that this would require the inversion of a very large matrix, which is computationally prohibitive in 3D calculations (see Sect. 3.2). Thus, we apply a Λ-iteration, for which a formal solution (FS) of the EQRT is obtained, given the continuum and line source functions. These are subsequently updated according to Eqs. (2) and (3), given the formal solution of the previous iterate. For large optical depths and low ϵc (ϵL), however, the strong non-local coupling between the source functions and the radiation field results in the well known convergence-problem of the classical Λ-iteration. This problem is based on the fact that, due to scattering processes, photons can travel over many mean-free-paths before being destroyed or escaping from the atmosphere. On the other hand, information is propagated in each iteration step only over roughly one mean-free-path. Therefore, a large number of iteration steps would be required, until a consistent solution was obtained (if at all). Thus, acceleration techniques are urgently needed, and developed in this work in terms of an ALI scheme using operator-splitting techniques (Cannon 1973).
3. Numerical methods
The ALI scheme can be split into two parts, namely the calculation of the FS, and the construction of a new iterate, by means of an approximate Λ-operator. There are various solution schemes to obtain the FS, differing in required computing power, and using different assumptions on the geometry and physical properties of the considered problems, as outlined in the introduction. Among those, the FVM (Adam 1990) is expected to be the fastest and most simple one, and is used here as a first step to tackle 3D radiative transfer problems.
Since we aim at modelling non-monotonic velocity fields, for which a comoving-frame formulation, if at all, is very complicated to implement, we solve the EQRT in the observer’s frame. We also use a Cartesian coordinate system, which has the advantage of constant angular directions w.r.t. the spatial grid. Anyhow, a description of the atmospheric structure in spherical coordinates loses its advantages for the problems considered in this (and future) work.
In the first part of this section, we describe the FVM, and the angular and frequency integration methods. Main focus is put on the development of the ALI scheme tailored to the FVM (Sect. 3.2).
3.1. Finite-volume method
The main ideas of the FVM originate from heat transfer (Patankar 1980), and have been already applied to radiative transfer problems in accretion discs by Adam (1990), as well as to the formation of discrete absorption components in hot star winds (Lobel & Blomme 2008). Although the derivation of the discretized EQRT can be found, for instance, in Adam (1990), we outline the basic ideas in more detail in Appendix A. The final solution scheme reads: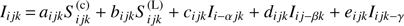 (14)
(14)

with α, β, γ set to ±1 for direction-vector components nx, ny, nz ≷ 0. All quantities except χc, χ̄L, and the source terms, depend on the considered direction n as well as on frequency. Equation (14) represents a pure upwind scheme, with projected ∆τ-steps4 calculated from a central-differencing approach (following Patankar 1980, see also Appendix A). Due to the upwind scheme, and because the coeffcients ai jk … ei jk ∈ [0, 1], the solution method is unconditionally stable (Adam 1990).
Contrasted to our central-differencing approach, Adam (1990) and Lobel & Blomme (2008) used backward differences for the calculation of the ∆τ-steps. We have tested both methods, and found superior results when using central differences.
Instead of using an equidistant grid, a grid-construction procedure is applied in order to resolve the important regions of the atmosphere. In the case of nearly spherical winds, this basically consists of setting up a 3D spherical grid in the first octant, with uniformly distributed latitude- and azimuth-angles, and with radial coordinates such that ∆τc and ∆vr are (nearly) equidistant. ∆τc and ∆vr are the step-sizes in continuum optical-depth and radial velocity, respectively. The final (Cartesian) x (y, z)-coordinates are chosen such that they correspond to the distribution of the xs (ys, zs)-coordinates from the spherical grid. If not indicated explicitly, we use Nx = Ny = Nz = 133 grid points for the continuum, and Nx = Ny = Nz = 93 grid points for the line formation, distributed over the complete range, [−Rmax, Rmax]. We allow for a higher grid resolution within the continuum calculations, since only one frequency point needs to be considered, and we thus have lower computation times anyhow. As a comparison, Lobel & Blomme (2008) used only Nx = Ny = Nz = 71 grid points for their (optically thin) models. A typical grid in the x–z-plane is shown in the top panel of Fig. 3. The applied grid resolution is required to properly resolve the resonance zones (where the CMF line opacity and corresponding profile function is non-negligible), and to obtain reasonable optical-depth steps within our (first-order5) method. We emphasize that a large number of grid points would be required to properly describe the radiation field in the optically thick limit, since a first-order scheme is generally unable to reproduce the (second-order) diffusion equation. This problem, however, arises only at large optical depths (e.g. when considering the winds of Wolf–Rayet stars), and is only of minor importance for the winds of OB stars, where the total continuum optical depth is of the order unity. To consider only the regions where we actually know the structure of the atmosphere, we calculate the RT within a predefined “calculation volume”, defined by the constraint r(xi, yj, zk) ∈ [R∗, 1.1Rmax].
Angular integration. The mean intensity at each grid point is obtained from the solutions of the EQRT for many directions, where the distribution of these directions over the unit sphere depends on the used quadrature formula. The resulting intensities are numerically integrated via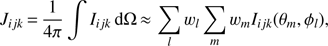 (15)
(15)
with θm, φl being the co-latitude (measured from the z-axis) and the azimuth (measured from the x-axis), respectively, and wm, wl the corresponding integration weights. The projection factor sin(θm), and the normalization have been included into wm, wl. Several different techniques and directional distributions have been tested, including the standard trapezoidal rule with equidistant θ, φ-grids, as well as using the approach of Lobel & Blomme (2008), who basically use an ansatz dΩ = const, and obtain different φ-grids on each θ-level. To obtain a fair angular resolution of the unit sphere, that means without preferring certain directions, we split the integration into a sum over all oc-tants, with the same nodes and weights within each octant. The mean relative errors6 of the mean intensity for a zero-opacity model, using Nx = Ny = Nz = 133 grid points and different angular grids, are summarized in Table 1. The corresponding theoretical solution has been calculated from J(theo) = WIc, with ![$ W=1/2\left[ 1-\sqrt{1-{{({{R}_{*}}/r)}^{2}}} \right] $](/articles/aa/full_html/2018/08/aa31858-17/aa31858-17-eq21.gif) the dilution factor, and Ic the intensity emitted from the stellar core.
the dilution factor, and Ic the intensity emitted from the stellar core.
Mean relative errors of the mean intensity for a zero-opacity model, using either Gauss–Legendre quadrature, or the trapezoidal rule with integration nodes from Lobel & Blomme (2008).
The best results have been obtained using a Gauss–Legendre quadrature, for which the integration nodes are fixed, and cannot be chosen arbitrarily. Using this quadrature, already Nθ·Nϕ = 512 grid points would be suffcient for an accurate integration, at least in principle. We note, however, that the solution in the outer part of the atmosphere oscillates around the theoretical value, because the star is not resolved by the angular grid in these regions. This effect becomes even worse for the trapezoidal rule. The corresponding errors, however, contribute only weakly to the mean error, because most grid points are located near to the star. Additionally, the dependence of the profile function on the local projected velocity (see Eq. (8)) requires a much finer angular resolution in the line case. Thus, to safely avoid artefacts from the angular integration scheme, we use Nθ · Nϕ = 2048 throughout this paper. This is a factor of three lower than the number of angular integration points used by Lobel & Blomme (2008), (Nθ·Nϕ)Wind3D = 6400. We finally note that the calculation of integration nodes for the Gauss–Legendre quadrature requires the inversion of a large matrix, which directly shows the advantage of a Cartesian grid, for which the angular nodes and weights are the same at all grid points, and can be calculated prior to the complete solution scheme. Using a spherical grid, Gaussian quadrature would be computationally very time-consuming, because the involved angles w.r.t. the coordinate system depend on position in the atmosphere.
Frequency integration. The integration over frequency is only performed when solving for J̄ in the line case. Due to its simplicity, we apply the trapezoidal rule with equidistant steps,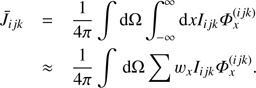 (16)
(16)
The integration is performed over the complete frequency range, ![$ {x_{{\rm{OBS}}}} = \left[ {{{ - {\upsilon _\infty } - 3{\upsilon_{{\rm{th}}}}({R_{{\rm{max}}}})} \over {\upsilon_{{\rm{th}}}^ * }},{{{\upsilon_{{\rm{\infty}}}} + 3{\upsilon_{{\rm{th}}}}({R_{{\rm{max}}}})} \over {\upsilon_{{\rm{th}}}^ * }}} \right] $](/articles/aa/full_html/2018/08/aa31858-17/aa31858-17-eq23.gif) , with maximum velocity, υ∞, corresponding thermal velocity, υth(Rmax), and a rapidly vanishing Doppler profile for |xCMF/δ| > 37. To resolve the profile function everywhere in the atmosphere, we require ∆xCMF/δ ≲ 1/3 at each position, which is achieved by defining
, with maximum velocity, υ∞, corresponding thermal velocity, υth(Rmax), and a rapidly vanishing Doppler profile for |xCMF/δ| > 37. To resolve the profile function everywhere in the atmosphere, we require ∆xCMF/δ ≲ 1/3 at each position, which is achieved by defining 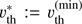 , and choosing the number of frequency points, NF, such that
, and choosing the number of frequency points, NF, such that 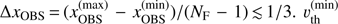 is the minimum thermal velocity (including micro-turbulence) of the atmosphere. However, since the comoving frame frequency depends on the projected velocity, the corresponding integration nodes may not be centred around the profile maximum anymore. This issue is only of minor importance and has been checked by a comparison to model calculations that use ∆xOBS ≲ 1/6. In atmospheres with very low micro-turbulent velocities, a number of NF ≈ 1200 frequency points would be required, for typical values of
is the minimum thermal velocity (including micro-turbulence) of the atmosphere. However, since the comoving frame frequency depends on the projected velocity, the corresponding integration nodes may not be centred around the profile maximum anymore. This issue is only of minor importance and has been checked by a comparison to model calculations that use ∆xOBS ≲ 1/6. In atmospheres with very low micro-turbulent velocities, a number of NF ≈ 1200 frequency points would be required, for typical values of 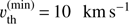 (if no micro-turbulent velocities were present), and typical wind terminal speeds, υ∞ = 2000 km s−1. When using a rather high micro-turbulent velocity, υturb = 100 km s−1, NF is reduced considerably, by a factor of ten. Fortunately, such high values are not un-typical in the winds of hot stars (see next paragraph). Again, when compared to Lobel & Blomme (2008), who used NF = 100 frequency points for a thermal velocity of υth = 30 km s−1, we have a much finer resolved frequency grid, with ≈15 frequency points distributed over the complete line profile, whereas they resolved the profile function with only three frequency points.
(if no micro-turbulent velocities were present), and typical wind terminal speeds, υ∞ = 2000 km s−1. When using a rather high micro-turbulent velocity, υturb = 100 km s−1, NF is reduced considerably, by a factor of ten. Fortunately, such high values are not un-typical in the winds of hot stars (see next paragraph). Again, when compared to Lobel & Blomme (2008), who used NF = 100 frequency points for a thermal velocity of υth = 30 km s−1, we have a much finer resolved frequency grid, with ≈15 frequency points distributed over the complete line profile, whereas they resolved the profile function with only three frequency points.
Microturbulence. To correctly treat the radiative transport in the line, we need to resolve the resonance zones, and demand that ∆(n · v/υth) ≈ 1/3. Again, for low micro-turbulent velocities, we would require a resolution of at least 1200 grid points per spatial dimension (for a spherical wind accounting for both hemispheres). On the other hand, including a large micro-turbulent velocity (υturb = 100 km s−1), as applied here, results in a much lower required resolution, both in space and frequency. Due to the linear (cubic) scaling of computation time with the number of frequency (spatial) grid points, this results in a reduction of computation time by a factor of 104, when compared to models without large micro-turbulent velocities. Putting it the other way round, and already mentioning here that typical model-calculations take about 50 min of wallclock time per iteration (and using 16 processors, see next paragraph), a large micro-turbulent velocity is needed thus far to keep the computation time on a reasonable scale.
Hamann (1981) showed that such micro-turbulent velocities can indeed be used to correctly model the black absorption troughs observed in the P Cygni profiles of hot star winds. From a theoretical point of view, a large velocity dispersion mimicks the effects of multiply non-monotonic velocity fields, as originating from the line-driven instability (see, e.g. Lucy 1983; Puls et al. 1993).
Parallelization and timing. In the line case, a number of Nθ × Nϕ × NF formal solutions of the EQRT are required to calculate the scattering integrals. In order to obtain accurate angular and frequency integrals, the minimum number of integration nodes is basically fixed, and the computation time can only be reduced further by parallelization. In our case, the most simple and straightforward procedure is a parallelization in frequency, which was done here using OPENMP. The computation time of a typical model with Nx = Ny = Nz = 93, Nθ · Nϕ = 2048, NF = 139 spatial, angular and frequency grid points, respectively, is about 50 min of wallclock time per iteration on a 16 CPU INTEL XEON X5650 (2.67 GHZ) machine. As a reference, WIND3D (Lobel & Blomme 2008) requires about 30 min per iteration for their grid parameters (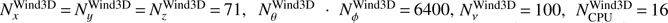 ). To obtain a more meaningful comparison, we scale the computation time by the number of applied angular and frequency grid points, and perform a test calculation, which uses the same spatial grid as Lobel & Blomme (2008). Although our CPUs are more modern and faster, our code performs only slightly better than WIND3D, with computation times
). To obtain a more meaningful comparison, we scale the computation time by the number of applied angular and frequency grid points, and perform a test calculation, which uses the same spatial grid as Lobel & Blomme (2008). Although our CPUs are more modern and faster, our code performs only slightly better than WIND3D, with computation times 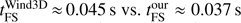 , per iteration, per angular and frequency point, and per CPU. We note, however, that our algorithm requires at least a factor of two more operations per formal solution, since we additionally compute the (non-local) approximate Λ-operator in parallel (see next section).
, per iteration, per angular and frequency point, and per CPU. We note, however, that our algorithm requires at least a factor of two more operations per formal solution, since we additionally compute the (non-local) approximate Λ-operator in parallel (see next section).
3.2. Λ-iteration
By now, we are able to construct a formal solution for a given source function. In this section, we discuss the iteration procedure. The following discussion considers the line case alone, with a frequency-independent background continuum (i.e. constant continuum opacity and source function), assumed to be known (either in form of an optically thin continuum, or from previous calculations in the absence of the line). For convenience, we summarize the basic ideas and corresponding acceleration techniques via the ALI from first principles.
Matrix equation. To show that the Λ formalism can also be applied to our 3D formulation, we derive a matrix equation for the scattering integral, and show that this equation is consistent with an affne representation of the Λ operator. Since, however, the fi-nal ALO will be calculated differently, a detailed description of the involved matrices is skipped in the following.
All 3D quantities are expressed as vectors of length Nx × Ny × Nz, by introducing a unique ordering of the (i, j, k)-triple: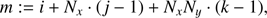 (17)
(17)
where i, j, k ∈ [1, Nx, y, z], and m ∈ [1, NxNyNz]. Replacing the (i, j, k)-indices in Eq. (14) with this unique index, m, and after collecting all intensity terms on the left-hand side, we obtain: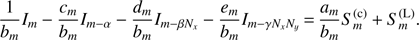 (18)
(18)
This equation is written in matrix form,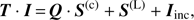 (19)
(19)
where Iinc refers to the boundary condition. Since we use a TLA with given opacity (i.e. the opacity does not change during the iteration), and consider time-independent boundary conditions, we combine the constant vectors from Eq. (19), Ĩinc := Q · S(c) + Iinc. Inverting the matrix T and integrating over all angles and frequencies gives:![$ \begin{array}{*{35}{l}} 4\pi \boldsymbol{\bar{J}} & =\int{{{\Phi }_{x}}\cdot I\text{d}\Omega \,\text{d}x} \\ {} & =\int{{{\boldsymbol{\Phi} }_{x}}\cdot {{T}^{-1}}\cdot {{S}^{(\text{L})}}\text{d}\Omega \,\text{d}x}+\int{{{\boldsymbol{\Phi} }_{x}}\cdot {{T}^{-1}}\cdot {{{\tilde{I}}}_{inc}}\text{d}\Omega \,\text{d}x} \\ {} & =\int{{{\boldsymbol{\Phi} }_{x}}\cdot {{T}^{-1}}\cdot \text{d}\Omega \,\text{d}x\cdot {{S}^{(\text{L})}}+4\pi {{\boldsymbol{\Phi} }_{B}}} \\ {} & =:4\pi \left[ \Lambda \cdot {{S}^{(\text{L})}}+{{\boldsymbol{\Phi} }_{B}} \right]. \\ \end{array} $](/articles/aa/full_html/2018/08/aa31858-17/aa31858-17-eq32.gif) (20)
(20)
The diagonal matrix Φx and the vector ΦB describe the local profile function, and the contribution of the boundary conditions and the background continuum to the scattering integral, respectively. As shown below, an explicit calculation of these quantities is not required to obtain the finally used ALO. We note that also for the continuum case, which is calculated close (w.r.t. frequency) to the line, Eq. (20) is applicable, with a different Λ-matrix and boundary contribution though. A comparison of Eq. (20) with the common Λ-operator formalism (i.e. formally writing J̄= Λ[S L]) directly shows that the Λ-operator is an affne operator, that means a linear operator given by the Λ-matrix plus a constant displacement vector ΦB (see also Puls 1991), also for our 3D method.
From Eqs. (3) and (20), we could formulate an explicit solution of the radiation field already now. This, however, would require the calculation, storage and inversion of the complete Λ-matrix, which is computationally prohibitive:
Firstly, the Λ-matrix is a full matrix with NxNyNz × NxNyNz elements, which would require, for typical grid sizes of N := Nx = Ny = Nz = 93, N6 ≈ 6.5 × 1011 numbers, equivalent to 5.2 TB data to be stored in memory, when double-precision numbers are used. Secondly, the Λ-matrix elements can be obtained, at least in principle, by inversion (see also Puls 1991),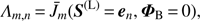 (21)
(21)
with en being the n-th unit vector. Thus, Nx × Ny × Nz formal solutions would be needed to calculate the complete Λ-matrix, which again is computationally prohibitive on reasonably well-resolved grids.
An iterative solution is therefore the only possibility to solve problems of this kind. Due to the well known convergence problems of the classical Λ-iteration, we directly focus on the ALI. For completeness, let us mention here a similar approach, the “non-linear multi-grid method” (see Fabiani Bendicho et al. 1997 and references therein), which has even better convergence properties, and, in contrast to the ALI method, does not depend on the spatial resolution of the grid. For simplicity, however, we only implement an ALI scheme. The ALI is an operator-splitting technique, which splits the original Λ-operator into the combination
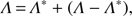 (22)
(22)with an appropriately chosen ALO, Λ∗ (see Cannon 1973). Appropriately chosen means that Λ∗ should be easily calculated (preferentially in parallel with the formal solution), and easily inverted. Moreover, the ALO should reflect the basic physical properties of the original Λ-matrix, in order to significantly boost the convergence.
ALI. Using Eq. (22), where now the first term acts on the current iterate of the source function, and the second one on the previous iterate, we obtain in combination with Eq. (3)
![${S^{(n)}}\, = \zeta \,\cdot\,{J^{(n)}} + {\rm{ }}\Psi \approx \zeta \,\cdot\,{\Lambda ^ * }[{S^{(n)}}]\, + \,\zeta \,\cdot\,(\Lambda - {\Lambda ^ * })[{S^{(n - 1)}}]\, + \,\Psi, $](/articles/aa/full_html/2018/08/aa31858-17/aa31858-17-eq35.gif) (23)
where the approximate relation becomes an exact one for the converged solution. Here we have used the notation and definitions of the diagonal matrix, ζ := 1 − ϵ L, and the thermal contribution vector, Ψ := ϵ L · Bν(T), from Puls & Herrero (1988).
(23)
where the approximate relation becomes an exact one for the converged solution. Here we have used the notation and definitions of the diagonal matrix, ζ := 1 − ϵ L, and the thermal contribution vector, Ψ := ϵ L · Bν(T), from Puls & Herrero (1988).
Again, all quantities are ordered according to Eq. (17). After some algebra, we obtain![$\matrix{ {} \hfill & {(1\, - \,\zeta \cdot{\rm{ }}{\Lambda ^ * }){S^{(n)}}{\mkern 1mu} \approx {\mkern 1mu} {\rm{ }}\zeta \cdot(\Lambda - {\Lambda ^ * })[{S^{(n - 1)}}] + \zeta \,\,\cdot\,\,{\Phi _{\rm{B}}}\, + \,\Psi } \hfill \cr {} \hfill & { = \zeta \,\,\cdot\,\,{(^{(n - 1)}}\, - \,{\Lambda ^ * }\,\,\cdot\,\,{S^{(n - 1)}})\, + \,\,\Psi. } \hfill \cr } $](/articles/aa/full_html/2018/08/aa31858-17/aa31858-17-eq36.gif) (24)
(24)
Since also the ALO is an affne operator (analogous to the original Λ-operator), the displacement vector ΦB only cancels if it remains constant over subsequent iteration steps, that is, when the background and the boundary conditions remain constant over the iteration. (In realistic, multi-level NLTE calculations, this means in practice that the ALI cycle shows a fast convergence only when the continuum is close to convergence).
Given a previous iterate of the source function, S(n−1), and
the corresponding formal solution, Eq. (24) is used to calculate the next iterate, S(n). The detailed choice of the ALO is the crucial point, and finally determines the convergence behaviour. We could, for instance, choose Λ∗ = Λ, which would result in the direct solution via inversion, and is computationally not feasible, as discussed above. On the other hand, choosing Λ∗ = 0 would result in the classical Λ-iteration, with the known convergence problems. Olson et al. (1986) showed that an ALO containing only the diagonal of the exact Λ-matrix is very effcient, because the matrix (1 − ζ · Λ∗) becomes diagonal, and Eq. (24) could be solved by a simple scalar division. Furthermore, the diagonal, that means the local part, already contributes most to the radiative transfer (at least in the critical optically thick case), and thus, is quite a good approximation for the original Λ-operator. Such an ALO corresponds to the well known Jacobi-iteration (see also Trujillo Bueno & Fabiani Bendicho 1995 for a thoughtful discussion, also about a Gauss–Seidel method with successive over-relaxation in the context of the ALI).
In 3D calculations, however, a diagonal ALO will not converge fast enough (see Sect. 4.1). To achieve faster convergence rates, a multi-band ALO is favourable, as already shown by Olson & Kunasz (1987) for 1D cases, and extended to a 3D, long-characteristics solver by Hauschildt & Baron (2006). For such ALOs, the matrix (1 − ζ · Λ∗) is sparse, whereas its inverse is a full matrix, and cannot be stored due to the N6 scaling of required memory. Therefore, we have already formulated Eq. (24) as a fix-point iteration, A · S(n) = b, which can be solved for the new iterate by applying Jacobi or Gauss–Seidel methods. We found that a Jacobi-iteration, coupled with the storage of the iteration-matrix in coordinate-format (COO)8, is particularly fast and easy, because its computationally most expensive term is a matrix-vector multiplication, which reduces to NNZ operations only, where NNZ is the number of non-zero elements (e.g. Tessem 2013).
Constructing the ALO. To construct a multi-band ALO as aimed at above, we need to to calculate the corresponding elements of the exact Λ-matrix. This could be done, in principle, by using Eq. (20), which would require the inversion of T. Due to the upwind scheme, however, we can simply use Eq. (21), in combination with Eqs. (14) and (16). Since the (m, n)-th element of the Λ-matrix describes the impact of a non-vanishing source term at point n ↔ (i′ j′ k′) onto a point m ↔ (i jk), the local contribution is given by n = m, whereas the coupling with directly neighbouring points is found from:
n(i − 1, j, k) = m − 1 for nx > 0
n(i, j − 1, k) = m − Nx for ny > 0
n(i, j, k − 1) = m − NxNy for nz > 0
n(i + 1, j, k) = m + 1 for nx < 0
n(i, j + 1, k) = m + Nx for ny < 0
n(i, j, k + 1) = m + NxNy for nz < 0.
One big advantage of our method is that the exact elements of local and neighbouring terms can be easily calculated from Eq. (14),
We call this ALO “direct neighbour” (DN)-ALO, to discriminate from the “nearest neighbour” ALO from Hauschildt & Baron (2006), who use all 26 surrounding grid points and the local term, whereas we are using the local term and the contribution from the six direct neighbours only9. Although it would be possible to include also the other neighbouring terms in our calculations, we note that the calculation of the ALO elements in parallel to the formal solution requires already 50% of the calculation-time in our case, which would increase rapidly when including even more terms for the ALO. On the other hand, the inversion of the ALO, that means the calculation of the new iterate via Jacobi-iterations, requires only about 0.5% of the calculation time needed for the complete FS. We emphasize that the ALO actually needs to be calculated only once, because the opacity of the (simplified) TLA remains constant over subsequent iteration cycles. When considering multi-level atoms (as planned in the future), the situation changes, and the opacity depends on the occupation numbers, and thus, also on the radiation field. We therefore implemented the calculation of the ALO in parallel to the formal solution at each iteration step already at the current stage of our code.
To accelerate the iteration scheme further, we implemented the extrapolation technique from Ng (1974, see also Olson et al. 1986). In order to use independent extrapolations, the Ng-acceleration is applied in every fifth iteration step. We finally note that the convergence behaviour depends on the grid resolution, which determines the optical-depth steps, ∆τx, y, z, and affects the coeffcients ci jk, di jk, ei jk. The finer the grid, the poorer the convergence behaviour (Kunasz & Olson 1988).
Input parameters for the spherically symmetric models used for our test calculations.
To summarize, we have implemented a 3D FVM in Cartesian coordinates, to determine the FS for a given source function, and to calculate, in parallel, a DN-ALO applied within an ALI scheme.
4. Spherically symmetric models
Before applying our method to first non-spherical test problems, we have checked its reliability by investigating the convergence properties, and by comparing our 3D solution for a spherical wind with an accurate 1D solution. The 1D solution for the line case has been found by a ray-by-ray solution scheme in p–z-geometry, which has been formulated in the comoving frame and accelerated by an appropriate ALO (Puls 1991). The 1D solution for the continuum transport has been found by applying the Rybicki-algorithm (e.g. Mihalas 1978).
Three major error sources of our 3D code will be discussed in the following: Firstly, errors occurring due to false convergence (Sect. 4.1), secondly, errors originating from the incorporation of the boundary conditions and from numerical diffusion (Sect. 4.2), and finally, errors occurring for optically thick media, due to the order of accuracy of our method (Sect. 4.3).
The spherically symmetric models to be compared with have been calculated from a prescribed β-velocity law, the equation of continuity, and a temperature structure from the 1D code (which plays almost no role in our test cases).
For opacities and source functions, see Sect. 2, and the required electron density, ne, has been derived from a completely ionized H and He plasma, with NHe/NH = 0.1. For all following model calculations, we used a fixed set of prototypical input parameters, summarized in Table 2. These parameters roughly correspond to the wind from ζ Pup, when assuming an unclumped wind. Within the line transfer, we considered a generic UV resonance transition, with different line-strengths following Eq. (12). To calculate the thermal width, we used mA = 12 mp, mp being the proton mass. The total width of the line profile, however, is mainly controlled by the (large) turbulent velocities. Different optical depths,
(for the model considered in Table 2), and scattering properties of the model atmosphere were simulated by varying the scaling factors, kc, kL, and the thermalization parameters, ϵc, ϵL, in the continuum and line case, respectively.
 |
Fig. 1. Convergence behaviour of the continuum transfer with ϵc = 10−6 (left), and of the line transfer with ϵL = 10−6 (right), for different acceleration techniques applied to the RT, and for a spherical model atmosphere. The optical depth scale varies according to kc = 10, kL = 10 (top) and kc = 100, kL = 105 (bottom). See text. |
4.1. Convergence behaviour
To test the convergence behaviour of our ALI implementation with corresponding ALO, we only considered scattering dominated atmospheres by setting ϵc and ϵL to 10−6. We discuss the continuum transfer in the absence of a line, and the line transfer assuming an optically thin continuum. In both cases, we applied the classical Λ-iteration, and compare to ALI schemes using a diagonal or DN-ALO, with Ng-extrapolation switched on or off.
Pure continuum. The left panel of Fig. 1 shows the maximum relative corrections of the mean intensity after each iteration step, for an intermediate grid resolution of Nx = Ny = Nz = 93 spatial points and NθNϕ = 968 angular points. Two different continua are shown, referring to an optically thick (kc = 100), and marginally optically thick (kc = 10) case. Obviously, the classical Λ-iteration converges only very slowly (if at all) in the high optical-depth regime, requiring 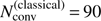 iterations until the convergence criterion of maximum relative corrections being less than 10−3 is fulfilled. We emphasize that a (steep) gradient of the “convergence curve” is required to achieve actual convergence, rather than this (arbitrarily chosen) number.
iterations until the convergence criterion of maximum relative corrections being less than 10−3 is fulfilled. We emphasize that a (steep) gradient of the “convergence curve” is required to achieve actual convergence, rather than this (arbitrarily chosen) number.
For the optically thick problem, even the diagonal and also the DN-ALO have severe convergence problems, with 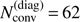 and
and 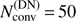 , respectively. To ensure fast convergence, the Ng-acceleration is urgently needed, since it boosts the relative corrections significantly, reducing the number of required iterations for the optically thick problem to
, respectively. To ensure fast convergence, the Ng-acceleration is urgently needed, since it boosts the relative corrections significantly, reducing the number of required iterations for the optically thick problem to 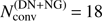 (lower left panel of Fig. 1).
(lower left panel of Fig. 1).
Line case. With the same set-up as above, we display the maximum relative corrections of the scattering integral after each iteration step in the right panel of Fig. 1. We applied two different line-strength parameters, kL = 10, 105, which correspond to a weak and strong line, respectively. Since the line transport is restricted to the finite widths of the resonance zones, and is therefore intrinsically much more local than the continuum, the convergence behaviour is accelerated significantly already by the diagonal and DN-ALO. For the strong line, the required number of iterations until convergence is reduced from 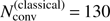 to
to 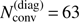 ,
, 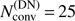 and
and 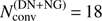 , for the diagonal and DN-ALO, excluding or including the Ng-acceleration, respectively (lower right panel of Fig. 1).
, for the diagonal and DN-ALO, excluding or including the Ng-acceleration, respectively (lower right panel of Fig. 1).
4.2. Boundary conditions and zero-opacity models
Two important points still to be explained refer to the incorporation of boundary conditions and to numerical diffusion. The latter can be best understood by considering continuum models with an opacity set to zero.
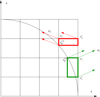 |
Fig. 2. Boundary conditions for two different points, r1, r2, and different directions, n1, n2. Green: a ray originating from the stellar photosphere. To calculate the intensity at r1 in direction n1, the intensities at the neighbouring grid points, |
Boundary conditions. At the outer boundary, the intensities coming from outside are set to zero, whereas those coming from inside are calculated within the RT scheme, and need not to be specified. Close to the star, the situation is more complicated: The inner grid points are generally located close to the boundary, but not directly on it, due to the difference of Cartesian and spherical grids. The intensities at those grid points are calculated by the standard FVM-RT (Eq. (14)), but using different grid cells, defined by the intersection(s) of the original grid cell with the (spherical) photosphere (see Fig. 2). The intensity for certain directions needs to be specified at those so-called phantom points. Figure 2 displays phantom points corresponding to two distinct grid points, r1, r2, and different ray directions, n1, n2. Radiation originating from the stellar surface (direction n1 in Fig. 2) is set to Bν(Teff)10 at the corresponding phantom point, 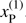 . For some grid points and ray directions, however (e.g. direction n2 in Fig. 2), even intensities incident onto the photosphere need to be specified at the corresponding phantom point.
. For some grid points and ray directions, however (e.g. direction n2 in Fig. 2), even intensities incident onto the photosphere need to be specified at the corresponding phantom point.
Within the core-halo approximation used here, inwards directed intensities should, in principle, be set to zero at the lower boundary, that is Iphantom-point = 0. If, on the other hand, the lower boundary is located at significant optical depths (as for the majority of the cases considered here), a specification within a simplified diffusion approximation, Iphantom-point ≈ Bν(Teff), is more appropriate. Although the diffusion approximation is no longer justified when concentrating on purely scattering atmospheres, backscattering of photons in such environments mimicks a similar effect, at least if the optical depths are not too low.
Mean and maximum relative errors of our 3D solution scheme, when compared to an “accurate” 1D solution.
We have tested this issue by considering an optically thin model as the most extreme test-bed, using both alternative descriptions for those critical directions. The mean relative errors for both alternatives are of the same order, and do not significantly differ from those arising under more physical conditions discussed later (with larger optical depths at the lower boundary, see Sect. 4.3 and Table 3). Thus, we apply Bν(Teff) as the inner boundary condition for those critical rays as well, also because this procedure is less time-consuming, since it avoids conditional clauses in the innermost loop of the code.
Zero-opacity models. Numerical diffusion is a major error source within the FVM (it also occurs in the SC method, though to a lesser extent, see Kunasz & Auer 1988 and Ibgui et al. 2013a for an analysis of this effect in the context of multi-D SC methods). Quite generally, rays propagating parallel to the grid axes are nearly undisturbed by this effect, whereas those propagating at different angles are effectively widened, due to the diffusion of intensity into neighbouring cells. This diffusion results from the finite size of the grid cells, and the competition between the ∆x/∆y, ∆x/∆z and ∆y/∆z terms in the discretized EQRT (Eq. (14)), for any given direction, and can only be minimized by increasing the grid resolution.
To obtain a qualitative measure of numerical diffusion errors, we performed a searchlight beam test with ray direction n= (1, 0, 1), by setting the opacity to zero. For consistency, the critical boundary conditions have been set to zero.
The top panel of Fig. 3 shows the contours of the specific intensity in the x–z-plane, and the middle panel displays the intensity through an aperture perpendicular to the ray direction. In our projection, the aperture appears as a straight line in the x–z-plane, specified by its distance from the origin and the impact parameter. Finally, the bottom panel of Fig. 3 shows the intensity along the considered direction, at the centre of the beam.
Evidently, numerical diffusion plays a crucial role. We expect corresponding errors to be most severe when photons propagate over large distances, for instance, for optically thin continua, or, in the line case, before they hit the resonance zones. Since the resonance zones are mostly quite narrow, while the path-length of freely propagating line photons is usually quite large (at least if the continuum is comparatively weak, as in most realistic conditions), numerical diffusion errors are of major significance for the line transfer.
To address the impact of numerical diffusion on the final solution, we consider the mean intensity for zero-opacity models. Figure 4 shows the mean intensity (scaled by its theoretical value obtained from the dilution factor) for such models on spherical surfaces at two distinct radii, r = 1.1R∗ and r = 3R∗. We find a clear pattern of the shape of the mean intensities: Close to the star, the mean intensities are reasonably accurate on the axes, in contrast to the regions away from the axes, where they become overestimated. Far from the star, the situation reverses, with reasonable results away from the axes, and an overestimate on the axes. This behaviour is explained in the following.
 |
Fig. 3. Top: specific intensities for direction n= (1, 0, 1) in the x–z-plane, for a zero-opacity model. Overplotted is the spatial grid with a typical size of Nx = Ny = Nz = 133 grid points. The thick lines indicate the theoretical boundary of the beam. Middle: projected intensity profile through the area indicated by a straight line in the top panel, covering all rays with direction n and impact parameter p = ±2R∗, and theoretical intensity profile denoted by dotted lines. The central distance from the origin is 3R∗. Bottom: specific intensity along n, compared to the theoretical value indicated by the dotted line. |
 |
Fig. 4. Contours of the mean intensity for a zero-opacity model, normalized by its theoretical value, on spherical surfaces, r = 1.1R∗ (left) and r = 3R∗ (right). The line of sight is along the vector n= (1, 1, 1). Nx = Ny = Nz = 133 grid points have been used. |
For a given grid point on or close to a coordinate axis, and far from the stellar surface, core-rays, that means those originating from the stellar surface, remain nearly undisturbed by numerical diffusion. Without diffusion, only such core-rays would contribute to the mean intensity. Due to numerical diffusion, however, also non-core rays contribute, that means those which form a certain angle w.r.t. the considered grid axis, since they have been fed with intensity by corresponding core-rays propagating in the same direction (widening of the effective aperture, see above). Consequently, the mean intensity becomes overestimated.
For grid points far from the star, and away from the major axes, core-rays and non-core rays are both affected by numerical diffusion, resulting in an under- and over-estimation of the intensity, respectively. Consequently, there is a significant cancellation of both effects, and the mean intensity remains close to its expected value.
At points located on the grid axes close to the star, numerical diffusion plays only a minor role, mostly because the contributing non-core rays are propagating almost perpendicular to the considered axis, which means parallel to one of the other axes, with negligible diffusion errors.
Away from the axes, and close to the star, contributing non-core rays are significantly inclined w.r.t. the coordinate axes, and thus strongly fed by diffusion effects. Thus, the mean intensities become overestimated.
Due to the different effects for different ray directions and for different regions in the atmosphere, any symmetry will be broken. This error cannot be avoided, and is minimized only for higher grid resolutions. As the important part of the radiative transfer is mainly located near to the star (where the densities are largest), and the numerical diffusion errors are not too large in this regime (up to a radius of r ≲ 3–4R∗), the 3D solution scheme should deliver at least qualitatively correct results.
4.3. Variation of optical depth
We finally compare the results from our 3D solutions for a spherically symmetric wind with corresponding ones from 1D solutions using spherical coordinates, as a function of optical depth. Within the continuum transport, the optical depth has been varied by increasing the linear scaling factor, kc = (100, 101, 102), which defines a radial optical-depth scale, τr = (0.17, 1.7, 17.0), at the lowermost point. The solutions for the mean intensities, together with the 1D solution, are shown in Fig. 5, top panel. The line transitions have been calculated for the same model, assuming an optically thin continuum in order to extract the error from the line transport alone. The adopted line-strength parameters, kL = (100, 103, 105), describe a weak, intermediate and strong line, respectively. The corresponding solutions are shown in the bottom panel of Fig. 5. To ensure convergence, we have used the DN-ALO together with the Ng-acceleration (see Sect. 4.1) for all test calculations. Thus, the differences between the 1D and 3D solution originate from the formal solution scheme alone, and not from a false convergence. The mean and maximum relative errors are summarized in Table 3.
 |
Fig. 5. Top: mean intensities (scaled by the emitted intensity from the stellar core, Ic) for the continuum transport, with ϵc = 10−6, and kc = (100, 101, 102) corresponding to τr = (0.17, 1.7, 17.0), from left to right. Bottom: line source functions (scaled by Ic) assuming an optically thin continuum, and with ϵL = 10−6, and kL = (100, 103, 105) from left to right. The red line corresponds to the accurate 1D solution, the blue line is the solution along the x-axis, and the dots (mainly located in between the red and the blue line) correspond to the solution of (arbitrarily) selected grid points (only a subset of all grid points is shown to compress the images). |
 |
Fig. 6. Emergent line profiles for spherically symmetric models with different line-strengths, kL = (100, 103, 105), from left to right. The red line corresponds to the accurate 1D solution, and the black line is the solution corresponding to our 3D calculations. |
The mean errors are increasing together with the optical thickness, because the FVM becomes a first-order scheme for increasing optical-depth steps11. The errors in the line case do not exceed roughly 25%, and are generally lower than those for the continuum, because the RT is much more local (see above)12,
and thus, the error is not being propagated through the complete grid. On the other hand, numerical diffusion plays a larger role (see Sect. 4.2), resulting in minimum errors of ≳10% even for very weak lines.
For optically thick continua (with τr ≳ 20), the continuum transfer breaks down, giving mean errors larger than 100%. Figure 5 shows that the errors for the continuum and line transport are mostly due to an overestimation of the mean intensities and scattering integrals, respectively. With respect to the local distribution of the errors, we find a similar behaviour as for the zero-opacity models (on vs. away from the axes for different radii). The maximum errors are mostly found at the same locations as in Fig. 4.
Finally, we conclude that the overall error is a combination of errors introduced by numerical diffusion, and the first-order scheme for optically thick environments. The line transport is generally more reliable than the continuum transport, which should be treated with higher spatial resolution.
4.4. Emergent flux profile
To calculate the line profiles, we implemented a postprocessing LC method. Within this method, the converged source function is used to derive the formal solution along characteristics in a cylindrical coordinate system, with the z-axis aligned with the line of sight. The emergent intensity is finally integrated over the projected stellar disc, which gives the flux (see, e.g. Lamers et al. 1987; Busche & Hillier 2005; Sundqvist et al. 2012, for more details). To obtain the source functions at each position of a given characteristics, a 3D tri-linear interpolation is performed in log-space. Though this could be applied to the velocity components and opacities as well, we calculate those properties from analytic expressions whenever possible. This way, we avoid errors introduced by the interpolation scheme, which have been found to be of the order of only few percent for a β-velocity law, but have rather strong influence for the ADM models, where the interpolation of shear-velocities is not a simple task.
The emergent profiles for the same models as above are shown in Fig. 6, with differences between the 1D and 3D models originating from the line source function alone. Generally, when compared to the 1D solution, the line profiles from our 3D code overestimate the emission part due to the larger source functions. The absorption edge is slightly red-shifted from its theoretical value at xobs ≈ 1+vth/v∞, because the calculation volume extends only up to 13.2R∗ (where v(13.2R∗) = 0.92 v∞). This issue, however, could be improved by enlarging the size of the calculation volume.
Overall, despite the slightly enhanced emission peak, we find that the line profile can be reproduced by our FVM, in combination with an accurate postprocessing routine, for a wide range of line-strength parameters. Thus, our method allows for a qualitative interpretation of line profiles even for the most extreme test cases, that is for strong scattering lines.
5. Wind-ablation
Using 3D radiation-hydrodynamic simulations, Kee (2015) and Kee et al. (2016) modelled the ablation of circumstellar discs around massive stars, due to radiative line driving. They showed that a significant line-force arises due to the coupling of non-radially streaming photons to the non-radial velocity field of circumstellar discs (see also Kee et al. 2016, their Fig. 1). The line-force has been calculated within a Sobolev-approach, by means of line-strength distribution functions. Contrasted to the original formulation by Castor et al. (1975), they followed the parameterization by Gayley (1995). The full 3D line acceleration can then be written as13
Stellar and wind parameters for the wind-ablation model.
where n and v describe the direction of the considered ray and the velocity-vector, respectively. ρ is the density, Q̄, Q0, and α describe the line-strength distribution, and were taken from the calibration of Puls et al. (2000, their Table 2), for the considered Teff.
For optically thin continua (e.g. in classical Be stars), the incident intensity I(n) can be directly replaced by the intensity originating from the stellar core, Ic, and Eq. (35) can be solved by quadrature, for a given density and velocity structure. For accreting high-mass stars (see Sect. 1), that means for massive objects in their late formation phases, however, the circumstellar discs are optically thick, and at least two major problems arise:
Firstly, due to absorption and scattering processes, the incident intensity at a considered point needs to be calculated by a global solution of the radiation field, which is very time consuming in hydrodynamic simulations. Kee (2015) developed an effcient method to delimit the contribution by either calculating the absorption part alone (giving a lower limit of the incident intensity), or assuming the disc to be optically thin (giving an upper limit). A comparison between the irradiation obtained from their method to the irradiation obtained from our 3D code (including scattering of photons) will be presented in a forthcoming paper, and shall not be discussed here.
In this paper, we only consider the second problem of optically thick environments: Since the disc partly blocks the irradiation from the star, the radiation field might become considerably reduced. However, it is this (ionizing) radiation field, which mainly determines the ionization stages of the considered plasma, and consequently might influence the line-strength distribution function. To address this issue, we proceed as follows: First, the radiation field for a specific hydrodynamic structure (see below) is computed by our 3D code, and the resulting mean intensity is translated to a corresponding radiation temperature (using Jν =: W · Bν(Trad) with dilution factor W; the derived radiation temperature would correspond to Teff if the star had an optically thin, spherically symmetric atmosphere). Corresponding line-strength parameters could again be obtained from Puls et al. (2000). In regions where the local radiation temperature is similar to the effective one, one can safely assume that the parameters of the line-strength distribution remain at their original input values, and indeed can be used to calculate the line force throughout all following hydro-timesteps. If, on the other hand, Trad differed significantly from Teff, this would imply that these parameters would need to be consistently adapted within the hydrodynamical evolution.
For our analysis, we used a wind+Keplerian-disc model similar to the initial conditions for the accreting O7-star system as considered by Kee et al. (2016). This model describes such objects as already defined in the introduction as accreting high-mass stars (see Hosokawa et al. 2010; Kuiper et al. 2016). The wind and stellar parameters are given in Table 4, following Kee et al. (2016). A radial optical depth of the disc, τdisc = 1400, has been adopted. We approximated the continuum by pure Thomson-scattering, ϵc = 0, to ensure frequency independence. This is a fair assumption for the 500–2000 Å range, where the majority of line-driving happens (e.g. Puls et al. 2000). Of course, we would expect thermalization in the disc’s deeper layers. Due to the dominating ρ−α-dependence of the line force (Eq. (35)) and the large densities inside the disc, however, most of the wind-ablation occurs at the surface layers, and we do not need to care about the details in the inner parts. This fact is even more important, since it allows us to apply our 3D FVM method, although being aware of the large errors of the continuum transfer for optically thick media. To ensure that the transition region from the wind to the disc is not subject to (larger) numerical uncertainties, we have performed a test calculation with doubled grid resolution  . Although we found, as expected, differences in the inner part of the disc, our results for the outer part and the wind region are (almost) identical. We can, therefore, safely assume that the obtained solutions, at least in the aforementioned regions, are only mildly affected by numerical artefacts.
. Although we found, as expected, differences in the inner part of the disc, our results for the outer part and the wind region are (almost) identical. We can, therefore, safely assume that the obtained solutions, at least in the aforementioned regions, are only mildly affected by numerical artefacts.
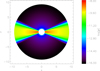 |
Fig. 7. Density structure for the wind-ablation model with τdisc = 1400, in the x–z-plane. |
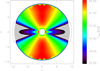 |
Fig. 8. As Fig. 7, but for the radiation temperature. Additionally, the density contours corresponding to a decrease in line force by f = 10 (solid) and f = 100 (dashed) are displayed. Both contours indicate the transition region from wind to disc (see text). The grey colour corresponds to radiation temperatures less than the colour-coded minimum value. |
The density structure and radiation temperature (the latter computed by our code) are shown in Figs. 7 and 8, respectively. The radiation temperature in the wind (here: along the z-axis) exceeds the effective temperature by a factor of roughly 1.25. In order to ensure that this is not a numerical effect, we have checked this issue by calculating the same wind model, however applying an optically thin disc with τdisc = 1.4 × 10−3. For such a model, Trad and Teff turned out to be fairly identical. We thus conclude that the enhancement of radiation temperature in our original model is due to additional irradiation of the wind from the disc, by scattering off photons from the disc. Most likely, this effect will induce latitudinal line-force components (also to be addressed in a forthcoming paper).
Wind-ablation dominates in the transition region between wind and disc. We define this region by calculating the decrease in line-force by a certain factor, f, due to density effects alone, that means assuming the same ionization stages and the same velocity structure. Such a reduction of line-force or line-acceleration is easily cast into an enhancement of density via Eq. (35),
where the radius-dependent quantities from the wind can be measured along the z-axis. In this picture, f should be chosen such that the corresponding decrease in line-force represents the border from the wind region to the region where the line-force is negligible (i.e. inside the disc). As a first guess, we adopted f = 10, and display the corresponding density contour in Fig. 8. Since a factor f = 10 seems to be somewhat artificial, we additionally display the density contour corresponding to f = 100.
From our simulations, we then find that both contours are located within a range of Trad between roughly 31 and 33 kK, which is of the same order as the effective temperature, Teff = 36 kK. We thus conclude that the ionization stages at the disc surface are not changing too much, when compared to the ionization stages in the wind, and that the line-strength param-eterization of the wind can also be used to calculate the line-force at the surface of such optically thick circumstellar discs. Due to significant scattering of photons off the disc, a multi-D description of the radiative transfer might need to be incorporated into the hydrodynamic simulations, to account for all force-components.
6. Dynamical magnetospheres: HD 191612
As a first application to line transitions, we modelled UV resonance lines in dynamical magnetospheres, that means atmospheres which form in slowly rotating magnetic OB-stars (in contrast to the so-called centrifugal magnetospheres, which form in fast rotating magnetic OB-stars). As a prototypical case, we considered the Of?p star HD 191612, which has a negligible equatorial rotation speed of vrot ≈ 1.4 km s−1 (Howarth et al. 2007; Sundqvist et al. 2012). Marcolino et al. (2013) already calculated corresponding resonance lines for this star, by extending the 3D formal solver developed by Sundqvist et al. (2012) to a “3D Sobolev with exact integration” method (SEI, Lamers et al. 1987), and applying this method to a set of 100 two-dimensional MHD-simulation snapshots, equidistantly distributed over the azimuth-angle to enable a 3D description of the atmosphere. At least for the Hα line (where the source function is taken from prototypical 1D NLTE-calculations), such a patching-technique produces quite similar results as full 3D MHD simulations (see ud-Doula et al. 2013). In Sect. 6.1, we use the same simulations as a benchmark for our 3D code, and compare the obtained line profiles to those from Marcolino et al. (2013). In Sect. 6.2, we calculate analogous line profiles for the ADM model developed by Owocki et al. (2016), to investigate in how far their simplified description of the magnetosphere can be used as a reasonable substitute for elaborate MHD simulations. We already note here, that such a simplified approach would be favourable to MHD simulations, because it provides (within the applied approximations) an average, steady state solution for the magnetospheric structure, and avoids time-consuming hydrodynamic simulations.
6.1. MHD models
To understand the behaviour of the line profiles presented below, we first explain the basic characteristics of (non-rotating) magnetic winds. For a more detailed discussion, we refer the reader to the seminal work by ud-Doula & Owocki (2002) and ud-Doula et al. (2008). These authors introduced a magnetic dipole field as an initial condition, and evolved the (initially spherical) stellar wind according to the MHD equations. Within ideal MHD14, the material follows the (closed) magnetic-field lines in regions where the magnetic energy exceeds the kinetic energy of the wind (close to the star), whereas, in the opposite case, the field lines follow the (almost radial) mass flow (far from the star). The border of both regions can be roughly described by the Alfvén-Radius, 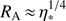 , with wind-confinement parameter
, with wind-confinement parameter 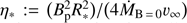 and Bp the polar magnetic-field strength evaluated at the stellar radius (see ud-Doula & Owocki 2002).
and Bp the polar magnetic-field strength evaluated at the stellar radius (see ud-Doula & Owocki 2002).
Within closed-field regions, material originating from opposite footpoints shocks (and accumulates) in the equatorial plane. Due to the 1/ρα-dependence of the line-force (see Eq. (35)), the net-force becomes dominated by gravity, and produces an inflow along the magnetic field lines in a “snake-like” pattern.
In the open-field regions, the presence of the magnetic field, together with a frozen-in mass flow, results in a density decrease when compared with spherically symmetric models, due to the faster-than-radial expansion of the flow-tube area (see Fig. 7 in ud-Doula & Owocki 2002). Consequently, the line-force becomes increased, resulting in higher terminal velocities than in 1D non-magnetic models. A single snapshot and an azimuthal average of the applied MHD simulations are shown in Fig. 9.
Based on such MHD simulations, Sundqvist et al. (2012) calculated corresponding Hα-line profiles, while Marcolino et al. (2013) investigated the UV resonance line formation. To remain consistent with the calculations by Marcolino et al. (2013), we apply ϵL = 0, and use their description of the line-strength parameter, κ0, originally introduced by Hamann (1980). κ0 is related to the line-strength parameter from Eq. (12) by
with IHe = 2 and YHe = NHe/NH = 0.1, the number of free electrons per helium atom, and helium abundance by number, respectively.
Although we use a micro-turbulent velocity of vturb = 100 km s−1 for the determination of the source function, we calculate the final line profile (somewhat inconsistently) for vturb = 50km s−1, as done by Marcolino et al. (2013). The line profiles obtained from our 3D code and the SEI line profiles from Marcolino et al. (2013) are displayed in Fig. 10, for two different line-strength parameters, κ0 = 0.1 and 1.0, respectively.
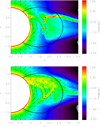 |
Fig. 9. Upper panel: density structure for an example snapshot from the MHD simulations for HD 191612, as performed by Sundqvist et al. (2012). Lower panel: azimuthal average of the MHD simulations. In both figures, the density has been normalized by a typical down-flow density, |
The agreement between the two methods is excellent. The minor differences in the emission part are related to two effects: Firstly, the methods for determining the source functions (SEI implying very narrow resonance lines vs. FVM accounting for much broader ones, due to vturb = 100 km s−1) are quite different, and a certain deviation must be present. Secondly, the (general) overestimation of the scattering integrals and thus source functions due to the FVM might play a role as well. Also the absorption parts of the line profiles observed equator-on (lower panel of Fig. 10) are not perfectly matched. This (small) effect is most likely simply due to different formulations of the numerical solvers.
A comparison of these line profiles with those from corresponding spherically symmetric models has already been performed by Marcolino et al. (2013), and we summarize only the most important characteristics: (1) The absorption trough for pole-on and equator-on observers extends beyond the 1D terminal velocity, as expected from the MHD atmospheric structure. We note that such a large extension has not been observed for HD 191612. (2) The emission for equator-on observers is reduced (compared to the 1D case), due to the lower densities in the emission plane (e.g. the polar plane for line-centre frequencies with xOBS = 0). (3) The particular form of the line profiles is determined by the different mapping of projected velocities for different observer directions.
 |
Fig. 10. UV resonance-line profiles for the MHD models, as obtained from our 3D-code (black) and from the SEI method by Marcolino et al. (2013; red). Two different line-strength parameters, κ0 = 0.1 and 1.0, have been used. For convenience, the line profiles for κ0 = 0.1 have been shifted vertically by 1.5. The upper and lower panels show the synthetic line profiles for pole-on and equator-on observers, respectively. The abscissa has been scaled to v∞ = 2700 km s−1, the “observed” 1D value applied by Marcolino et al. (2013). |
Given the overall agreement of the two different methods, we conclude that the SEI and our 3D FVM solutions are consistent. Additionally, we are highly confident that the line formation is described correctly (at least qualitatively), since both methods are completely independent. Under this assumption we are able to study the UV line formation within the ADM model.
6.2. ADM models
Owocki et al. (2016) developed an analytic description of dynamical magnetospheres, in order to set a framework similar to the β-velocity-field prescription for spherically symmetric winds. This ADM formalism provides a time-independent, steady-state solution for dynamical magnetospheres, which is comparable to the average of several MHD-simulation snapshots, and has been corroborated by a comparison of synthetic Hα lines with observations. The formation of resonance lines within the ADM framework, however, has not been analysed yet, and is the focus of this section. For that purpose, we aim at modelling the MHD atmospheric structure from above with the ADM method, and compare the resulting line profiles.
Within the ADM method, Owocki et al. (2016) divide the atmosphere into two major zones. The border between both regions is given by the condition rm = RA, where the apex-radius, rm, is defined as the distance between the origin and the intersection of magnetic equator and closed dipole magnetic-field line attached to a considered point (see left panel of Fig. B.1 for clarification). In the following, we call these two regions the “closed-field region” (rm < RA) and the “outer wind” (rm > RA).
The closed-field region consists of three different components:
wind-upflow component: The magnetic loops are fed with material ejected from the stellar surface. The matter flow follows the dipole magnetic-field lines, with absolute velocities calculated from a β-velocity law, using β = 1.
post-shock component: The collision of outflows following the B-field lines from opposite foot points leads to a shock at the magnetic equator, resulting in a hot and dense post-shock region. The extent of this region is controlled by a (dimensionless) cooling parameter, χ∞, where 1/χ∞ describes the effciency of radiative cooling by X-ray emission (see ud-Doula et al. 2014 for details). In test calculations, however, this component turned out to have only very small influence on the UV line formation. Thus, and to keep the model as simple as possible, we neglect the post-shock component in this work.
cooled-downflow component: As the post-shock gas cools, its density increases, and the line-force decreases. Thus, the cooled and compressed gas is pulled back onto the stellar surface by gravity, resulting in a downflow starting at the magnetic equator. The gas is accelerated from zero velocity along the B-field lines to the escape speed at the stellar surface.
For their Hα analysis, Owocki et al. (2016) only considered the cooled downflow, because of the mostly larger densities of this component. Since the infall occurs in episodic infall events, the closed-field region is actually highly structured, and the authors found rather large clumping factors ⟨ρ2⟩/⟨ρ⟩ (of the order of several tens). Under the assumption of clumps that are optically thin then, this clumping factor can be used to translate the actual (structured) density-distribution to the mean opacities and emissivities of recombination lines (ρ2-processes, see e.g. Puls et al. 2008). For the UV resonance line formation (linear in ρ), micro-clumping has no direct impact on the mean opacities. Therefore, and because of the different densities and velocities within the upflow and downflow components, an explicit description of the structured medium is required when considering UV resonance lines. As it is not a priori clear how to treat the combination of the above mentioned components, we consider four different approaches, and model the closed-field region by:
-
(i)
Applying only the cooled-downflow component.
-
(ii)
Introducing a statistical treatment, where the probabilities of using either the wind-upflow or the cooled downflow-component when calculating the radiative transfer are here defined as
This approach preferentially chooses the component with higher density and lower velocity15, in other words that component with the larger timescale for the matter flow.
-
(iii)
Introducing flux-tubes that alternating consist of the down-flow and upflow component.
-
(iv)
Applying only the wind-upflow component.
The models are ordered such that the contribution of the wind-upflow component is increasing from model (i) to (iv).
As a zeroth-order approximation, Owocki et al. (2016) model the outer wind (at rm > RA) by the wind-upflow component, that means by a flow following closed magnetic-field lines even in that region. This is a fair assumption for modelling the polar regions, since it accounts for the faster than radial decline of the density (see also Owocki & ud-Doula 2004). Moreover, the magnetic field lines are nearly radial in these regions, thus resulting in a nearly radial outflow similar to the MHD simulations. On the other hand, the velocity vectors near the equatorial regions are modelled with a large latitudinal component, whereas they are radially directed within the (more realistic) MHD simulations. Thus, a match of the ADM and MHD mag-netospheric structure in the equatorial region cannot be achieved within the standard formulation. With respect to UV line formation, this is the major drawback of the ADM formalism, and will influence the line formation (see below).
To set the base density, Owocki et al. (2016) introduced the mass-loss rate of the star if it had no magnetic field, ṀB= 0, which determines the loop-feeding rate. With the input parameters from Table 5, the dynamical magnetosphere can be modelled according to the recipe from Owocki et al. (2016)16. We used the values of ṀB= 0 and 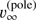 in Table 5, right panel, to adapt the ADM model to the MHD simulations. For our model parameters, the Alfvén-Radius, RA = 2.7R∗, has been calculated from the mass-loss rate, terminal velocity and magnetic-field strength. We stress that the adopted mass-loss rate is not necessarily the “true” one, nor the mass-loss rate the star would have if no magnetic field was present. For the applied ADM models, the resulting density stratification, magnetic-field lines and velocity vectors in the xz-plane are shown in the left panel of Fig. B.1. Here and in the following, the equatorial plane coincides with the plane of the magnetic equator, since we assume the magnetic axis to be aligned with the z-axis.
in Table 5, right panel, to adapt the ADM model to the MHD simulations. For our model parameters, the Alfvén-Radius, RA = 2.7R∗, has been calculated from the mass-loss rate, terminal velocity and magnetic-field strength. We stress that the adopted mass-loss rate is not necessarily the “true” one, nor the mass-loss rate the star would have if no magnetic field was present. For the applied ADM models, the resulting density stratification, magnetic-field lines and velocity vectors in the xz-plane are shown in the left panel of Fig. B.1. Here and in the following, the equatorial plane coincides with the plane of the magnetic equator, since we assume the magnetic axis to be aligned with the z-axis.
Compared to the MHD structure (see Fig. 9), the ADM densities in the closed-field region are best represented by model (ii) and (iii), that is by a combination of downflow and upflow component. In the outer wind near the equator, the densities are underestimated due to the aforementioned different description of the velocity field (see Fig. B.1, left panel).
 |
Fig. 11. UV resonance-line profiles obtained from our 3D code, for the MHD simulation (black, as Fig. 10), and the different ADM models, (i)–(iv) (see text). The line-strength parameter has been set to κ0 = 1. The upper and lower panels show the synthetic profiles for pole-on and equator-on view, respectively. As in Fig. 10, the abscissa has been scaled to v∞ = 2700 km s−1, the “observed” 1D value applied by Marcolino et al. (2013). |
Once again we apply ϵL = 0, and compare the corresponding line profiles with line-strength parameter, κ0 = 1, for equator-on and pole-on observers, with the line profiles obtained from the MHD simulations (see Fig. 11). For clarification, Fig. B.1 additionally displays all line profiles with their emission and absorption parts. The differences between the profile-sets can be explained as follows.
For pole-on observers. With increasing contribution from the upflow component, the emission peak becomes broader, because the emitting volume at intermediate to high velocities increases. Simultaneously, the cooled downflow component with only low absolute velocities decreases, resulting in a lower emission peak near the line centre. An exception is model (i), for which the emission peak at low frequency shifts is lowest, because the emission of the upflow component near the star (with high densities and low velocities) is missing. When compared to the line profiles from the MHD simulations, the best result is obtained for model (ii), that is for the statistical description of upflow and downflow component in the closed-field region. Even for this model, however, we only get a relatively poor match with the MHD profiles. Since our ADM models cover a large range of combinations of upflow and downflow component (including the most extreme cases of a pure upflow and a pure downflow), this finding suggests that the outer wind region is inadequately modelled. Indeed, the major differences of the line profiles can be explained (at least qualitatively) by the different description of the outer wind: (1) In the ADM models, the emission peaks close to line centre (i.e. at xOBS ≈ 0, with corresponding resonance zones at projected velocities n · u ≈ 0) are underestimated compared to the MHD model, since within all ADM models also the mass flow in the outer wind is adopted to follow closed magnetic field lines. This assumption becomes problematic in equatorial regions, since here the ADM wind flows almost perpendicular to the plane, whereas it is almost radial in the MHD case. Consequently, when viewed pole on, only large projected velocities are present in the corresponding area of the equatorial plane, where the latter creates a large part of low-velocity emission in the MHD model. This part is now missing in the ADM models, and the emitting area is almost limited to the downflow component (with generally low projected velocities). Thus, the profile becomes shallower than in the MHD case. (2) Within the blue absorption trough, the absorption column in front of the star is slightly decreased, because the velocity vectors are once again following the magnetic field lines, and do not perfectly match the MHD simulations. The differences of the line profiles can thus be explained by the different description of the outer wind region alone.
For equator-on observers. The emission peak of the ADM models becomes stronger and shifted to the blue side with increasing contribution of the upflow component. Additionally, the absorption part on the blue side increases, while it decreases on the red side. This behaviour is readily explained: as the upflow contribution in front of the star (with projected velocities directed towards the observer, thus affecting the blue side of the profile) grows, the downwind contribution (with projected velocities directed away from the observer, and affecting the red side of the profile) is diminished. Consequently, the absorption in front of the star increases on the blue side, and decreases on the red one. Again, when compared to the MHD model, none of the obtained profiles provides a good agreement. While model (iv) reproduces the absorption part on the blue side relatively well, the red-sided absorption part is highly underestimated. On the other hand, a better model for the red-sided absorption (e.g. model iii) underestimates the absorption part on the blue side. In fact, it is not possible to simultaneously model the blue and red absorption by only tuning the composition of the closed-field region, suggesting that (at least) the outer wind needs to be treated differently. For instance, assuming a radial outflow in the equatorial plane of the outer wind region would increase the blue-sided absorption (and emission), while preserving the rather good behaviour of model (iii) on the red side.
Taking all this evidence together, we conclude that the (present) ADM model needs to be improved for the modelling of UV resonance lines, at least in the outer wind. Such a reformulation then needs to include a consistent description of the actual velocity and density stratification, accounting for the delicate interplay between B-field and wind.
7. Summary and conclusions
In this paper, we introduced a newly developed 3D FVM code, which solves the equation of radiative transfer for continuum-and line-scattering problems (the latter approximated by a two-level-atom in the present version). An observer’s-frame formulation allows us to consider arbitrary velocity fields (and density structures).
Within the ALI scheme, the code iterates the source functions to convergence, using a non-local approximateΛ-operator, and ex-trapolating subsequent iterates by the Ng-formalism. For the most challenging problems of optically thick, scattering dominated atmospheres, we obtained a satisfying convergence behaviour, with relative corrections between subsequent iterates of less than 10−3 within 20 iteration steps. Due to this convergence behaviour, we were able to analyse the performance of the 3D FVM for such optically thick, scattering dominated atmospheres.
A comparison of spherically symmetric problems calculated with our 3D code and an accurate 1D solver shows that the FVM requires a relatively high spatial resolution. Continuum errors are of the order of ≲20% for marginally optically thick atmospheres, that is for typical O-star conditions, however increase rapidly for larger optical depths, due to the first-order scheme. These errors can only be reduced by applying either a higher grid resolution, or when using more accurate solution schemes (e.g. the SC method with appropriate interpolations). To analyse rapidly expanding stellar winds with large continuum optical depths, the development of a 3D SC method is planned for the future in our group.
The line transfer, on the other hand, performs much better, with relative errors less than 25% even for strong lines. The resulting profiles as obtained from a postprocessing LC method are reasonably accurate.
Due to significant numerical diffusion, intrinsic to the FVM, we found a minimum error (for optically thin continua and weak lines) of roughly 10%. Additionally, any symmetry of a considered problem is broken, due to the distinct behaviour of numerical diffusion for different ray directions and in different regions of the atmosphere. Numerical diffusion errors, however, could be minimized by increasing the grid resolution in the outer parts of the atmosphere. Accounting for the sound reproduction of line profiles for spherically symmetric models, we conclude that our code is ready to be used also for arbitrary 3D atmospheric structures, at least if the continuum displays an only moderate optical depth.
As a first application to continuum-scattering problems, we estimated the radiation temperatures of wind-ablation models, focusing on the transition region between a line-driven wind and the optically thick circumstellar disc (as present during the late phases of massive star formation in accreting high mass stars). We found a reduction of radiation temperatures by only few percent, which indicates that the ionization stages in this region are (almost) the same as in the wind. Thus, a line-distribution formalism with the same set of line-strength parameters as used in the wind can be applied to obtain the line acceleration that finally ablates the disc. Because of the numerical inaccuracies of the FVM, our findings must be taken with caution, and possibly rechecked with more elaborate methods or a much higher grid resolution. To analyse the complete evolution of optically thick circumstellar discs, the impact of continuum scattering on latitudinal forces still needs to be investigated, and is left to future studies.
As a benchmark for our code regarding the line transfer in non-spherical models, we considered the same MHD simulations of dynamical magnetospheres as used by Marcolino et al. (2013), and compared the resulting UV resonance-line profiles to those obtained from their 3D-SEI analysis. The profiles as viewed both polar-on and equator-on are in excellent agreement, indicating that our 3D FVM performs well also for such atmospheric models. We additionally applied the analytic dynamical magnetosphere framework (ADM, Owocki et al. 2016), and modelled the corresponding atmospheric structure by adopting four different descriptions of the closed-field regions. A comparison between the obtained line profiles and those for the MHD simulations from above showed significant differences. These were explained by the (somewhat insuffcient) description of the outer wind region within the (present) ADM formulation, primarily in the equatorial plane. An improvement of the underlying assumptions is planned for future work.
The projected ∆τ-steps represent the optical depth of the cell for a given direction, and are easily obtained from Eq. (14) and the definition of the coeffcients cijk … eijk, e.g. cijk =: 1/(1 + ∆τx).
We emphasize that for the line transfer, the ratio of the photon destruction probability, ϵL, to the photon escape probability is less than unity for all our models, indicating that the line-transfer is, in principal, non-local. However, for the considered spherically symmetric problems, no multiple resonances arise, and the line is formed within a single, well-localized resonance region.
Strictly speaking, Eq. (35) holds only when the strongest line is optically thick. See Kee (2015), Chap. 2, for a complete derivation and discussion.
Acknowledgments
We thank our anonymous referee for valuable comments and suggestions. Many thanks to V. Petit and S. Owocki for fruitful discussions about the ADM. LH gratefully acknowledges support from the German Research Foundation, DFG, under grant PU 117/9-1. NDK acknowledges support from the German DFG under grant KU 2849/3-1, which funds the Emmy Noether research group on “Accretion Flows and Feedback in Realistic Models of Massive Star Formation”. JOS acknowledges funding from the Euro-pean Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement no. 656725.
References
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2016, Phys. Rev. Lett., 116, 061102 [Google Scholar]
- Adam, J. 1990, A&A, 240, 541 [NASA ADS] [Google Scholar]
- Alecian, E., Wade, G. A., Catala, C., et al. 2013, MNRAS, 429, 1001 [NASA ADS] [CrossRef] [Google Scholar]
- Amarsi, A. M., Asplund, M., Collet, R., & Leenaarts, J. 2016, MNRAS, 455, 3735 [NASA ADS] [CrossRef] [Google Scholar]
- Belczynski, K., Holz, D. E., Bulik, T., & O’Shaughnessy, R. 2016, Nature, 534, 512 [NASA ADS] [CrossRef] [Google Scholar]
- Busche, J. R., & Hillier, D. J. 2005, AJ, 129, 454 [NASA ADS] [CrossRef] [Google Scholar]
- Cannon, C. J. 1973, ApJ, 185, 621 [NASA ADS] [CrossRef] [Google Scholar]
- Castor, J. I., Abbott, D. C., & Klein, R. I. 1975, ApJ, 195, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Cherepashchuk, A. M. 1976, Sov. Astron. Lett., 2, 138 [NASA ADS] [Google Scholar]
- Cranmer, S. R., & Owocki, S. P. 1996, ApJ, 462, 469 [NASA ADS] [CrossRef] [Google Scholar]
- de Mink, S. E., Langer, N., Izzard, R. G., Sana, H., & de Koter, A. 2013, ApJ, 764, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Dufton, P. L., Dunstall, P. R., Evans, C. J., et al. 2011, ApJ, 743, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Fabiani Bendicho, P., Trujillo Bueno, J., & Auer, L. 1997, A&A, 324, 161 [Google Scholar]
- Gayley, K. G. 1995, ApJ, 454, 410 [NASA ADS] [CrossRef] [Google Scholar]
- Georgiev, L. N., Hillier, D. J., & Zsargó, J. 2006, A&A, 458, 597 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gräfener, G., Koesterke, L., & Hamann, W.-R. 2002, A&A, 387, 244 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hamann, W.-R. 1980, A&A, 84, 342 [NASA ADS] [Google Scholar]
- Hamann, W.-R. 1981, A&A, 93, 353 [NASA ADS] [Google Scholar]
- Hauschildt, P. H. 1992, J. Quant. Spectr. Rad. Transf., 47, 433 [Google Scholar]
- Hauschildt, P. H., & Baron, E. 2006, A&A, 451, 273 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hillier, D. J., & Miller, D. L. 1998, ApJ, 496, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Hosokawa, T., Yorke, H. W., & Omukai, K. 2010, ApJ, 721, 478 [NASA ADS] [CrossRef] [Google Scholar]
- Howarth, I. D., Walborn, N. R., Lennon, D. J., et al. 2007, MNRAS, 381, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Ibgui, L., Hubeny, I., Lanz, T., & Stehlé, C. 2013a, A&A, 549, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ibgui, L., Hubeny, I., Lanz, T., et al. 2013b, ASP Conf. Ser., 474, 66 [NASA ADS] [Google Scholar]
- Jones, H. P. 1973, ApJ, 185, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, H. P., & Skumanich, A. 1973, ApJ, 185, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Kee, N. D. 2015, PhD Thesis, University of Delaware, USA [Google Scholar]
- Kee, N. D., Owocki, S., & Sundqvist, J. O. 2016, MNRAS, 458, 2323 [NASA ADS] [CrossRef] [Google Scholar]
- Kuiper, R., Turner, N. J., & Yorke, H. W. 2016, ApJ, 832, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Kunasz, P., & Auer, L. H. 1988, J. Quant. Spectr. Rad. Transf., 39, 67 [Google Scholar]
- Kunasz, P. B., & Olson, G. L. 1988, J. Quant. Spectr. Rad. Transf., 39, 1 [Google Scholar]
- Lamers, H. J. G. L. M., Cerruti-Sola, M., & Perinotto, M. 1987, ApJ, 314, 726 [NASA ADS] [CrossRef] [Google Scholar]
- Leenaarts, J., & Carlsson, M. 2009, ASP Conf. Ser., 415, 87 [Google Scholar]
- Lobel, A., & Blomme, R. 2008, ApJ, 678, 408 [NASA ADS] [CrossRef] [Google Scholar]
- Lucy, L. B. 1983, ApJ, 274, 372 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A. 1999, A&A, 347, 185 [NASA ADS] [Google Scholar]
- Maeder, A., & Meynet, G. 2000, A&A, 361, 159 [NASA ADS] [Google Scholar]
- Marcolino, W. L. F., Bouret, J.-C., Sundqvist, J. O., et al. 2013, MNRAS, 431, 2253 [NASA ADS] [CrossRef] [Google Scholar]
- Mihalas, D. 1978, Stellar Atmospheres, 2nd edition (San Francisco: W. H. Freeman and Co) [Google Scholar]
- Mullan, D. J. 1984, ApJ, 283, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Ng, K.-C. 1974, J. Chem. Phys., 61, 2680 [NASA ADS] [CrossRef] [Google Scholar]
- Olson, G. L., & Kunasz, P. B. 1987, J. Quant. Spectr. Rad. Transf., 38, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Olson, G. L., Auer, L. H., & Buchler, J. R. 1986, J. Quant. Spectr. Rad. Transf., 35, 431 [Google Scholar]
- Owocki, S. P., & ud-Doula, A. 2004, ApJ, 600, 1004 [NASA ADS] [CrossRef] [Google Scholar]
- Owocki, S. P., ud-Doula, A., Sundqvist, J. O., et al. 2016, MNRAS, 462, 3830 [NASA ADS] [CrossRef] [Google Scholar]
- Patankar, S. V. 1980, Numerical Heat Transfer and Fluid Flow (Hemisphere Publishing Corporation), Series on Computational Methods in Mechanics and Thermal Science [CrossRef] [Google Scholar]
- Pauldrach, A. W. A., Hoffmann, T. L., & Lennon, M. 2001, A&A, 375, 161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petit, V., Owocki, S. P., Wade, G. A., et al. 2013, MNRAS, 429, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Petit, V., Keszthelyi, Z., MacInnis, R., et al. 2017, MNRAS, 466, 1052 [NASA ADS] [CrossRef] [Google Scholar]
- Pittard, J. M. 2009, MNRAS, 396, 1743 [NASA ADS] [CrossRef] [Google Scholar]
- Prilutskii, O. F., & Usov, V. V. 1976, Sov. Astron., 20, 2 [NASA ADS] [Google Scholar]
- Puls, J. 1991, A&A, 248, 581 [NASA ADS] [Google Scholar]
- Puls, J., & Herrero, A. 1988, A&A, 204, 219 [NASA ADS] [Google Scholar]
- Puls, J., Owocki, S. P., & Fullerton, A. W. 1993, A&A, 279, 457 [NASA ADS] [Google Scholar]
- Puls, J., Springmann, U., & Lennon, M. 2000, A&AS, 141, 23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Puls, J., Urbaneja, M. A., Venero, R., et al. 2005, A&A, 435, 669 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Puls, J., Vink, J. S., & Najarro, F. 2008, A&ARv, 16, 209 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramírez-Agudelo, O. H., Simón-Díaz, S., Sana, H., et al. 2013, A&A, 560, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rivero González, J. G., Puls, J., Najarro, F., & Brott, I. 2012, A&A, 537, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sana, H., & Evans, C. J. 2011, IAU Symp., 272, 474 [NASA ADS] [CrossRef] [Google Scholar]
- Sana, H., Rauw, G., & Gosset, E. 2001, A&A, 370, 121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sana, H., de Koter, A., de Mink, S. E., et al. 2013, A&A, 550, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seelmann, A. M., Hauschildt, P. H., & Baron, E. 2010, A&A, 522, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stenholm, L. G., Stoerzer, H., & Wehrse, R. 1991, J. Quant. Spectr. Rad. Transf., 45, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Stevens, I. R., Blondin, J. M., & Pollock, A. M. T. 1992, ApJ, 386, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Sundqvist, J. O., ud-Doula, A., Owocki, S. P., et al. 2012, MNRAS, 423, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Tessem, T. 2013, Master’s Thesis, University of Bergen, Norway [Google Scholar]
- Townsend, R. H. D., & Owocki, S. P. 2005, MNRAS, 357, 251 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Trujillo Bueno, J., & Fabiani Bendicho, P. 1995, ApJ, 455, 646 [NASA ADS] [CrossRef] [Google Scholar]
- ud-Doula, A., & Owocki, S. P. 2002, ApJ, 576, 413 [NASA ADS] [CrossRef] [Google Scholar]
- ud-Doula, A., Owocki, S. P., & Townsend, R. H. D. 2008, MNRAS, 385, 97 [NASA ADS] [CrossRef] [Google Scholar]
- ud-Doula, A., Sundqvist, J. O., Owocki, S. P., Petit, V., & Townsend, R. H. D. 2013, MNRAS, 428, 2723 [NASA ADS] [CrossRef] [Google Scholar]
- ud-Doula, A., Owocki, S., Townsend, R., Petit, V., & Cohen, D. 2014, MNRAS, 441, 3600 [NASA ADS] [CrossRef] [Google Scholar]
- von Zeipel, H. 1924, MNRAS, 84, 665 [NASA ADS] [CrossRef] [Google Scholar]
- Wade, G. A., Howarth, I. D., Townsend, R. H. D., et al. 2011, MNRAS, 416, 3160 [NASA ADS] [CrossRef] [Google Scholar]
- Wade, G. A., et al. (MiMeS Collaboration) 2012, ASP Conf. Ser., 464, 405 [NASA ADS] [Google Scholar]
- Weber, J. A., Pauldrach, A. W. A., Knogl, J. S., & Hoffmann, T. L. 2013, A&A, 555, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zsargó, J., Hillier, D. J., & Georgiev, L. N. 2006, A&A, 447, 1093 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zsargó, J., Hillier, D. J., & Georgiev, L. N. 2008, A&A, 478, 543 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: The discretized EQRT within the FVM
Following the ideas of Patankar (1980) and Adam (1990), we here describe the discretization scheme of the time-independent equation of radiative transfer, Eq. (1). At each grid point, Eq. (1) is integrated over a finite control volume (see Fig. A.1). Applying Gauss’s theorem, we obtain:
Here and in the following, we omit the notation for the explicit frequency dependence. The left-hand side of Eq. (A.1) describes the intensity propagating into and out of the control-volume surfaces, and the right-hand side corresponds to the grid-cell contribution from sources and sinks. Assuming that the variables at the grid points are appropriate mean values within the corresponding control volume, the right-hand side is easily integrated, and gives for grid point (i, j, k),
Since we are using Cartesian coordinates, the integral on the left-hand side can be readily calculated:
Again, assuming that the intensities at the midpoints of the control-volume surfaces are representative averages of the corresponding surfaces, we obtain:
Since the control-volume coordinates are positioned at the midpoints of the grid coordinates, we substitute:
Finally, we use the upwind approximation to replace the (unknown) intensities at the control-volume surfaces:
 |
Fig. A.1. Geometry used within the control-volume approach: The dis-cretized 3D spatial grid is shown in blue. The dashed lines indicate the control volume, corresponding to a grid-point (i, j, k). The control-volume surfaces are located at the centre between the grid-point coordinates. |
Combining Eqs. (A.1), (A.2), (A.4), (A.5)–(A.7), and the definitions of α, β, γ, the discretized EQRT finally reads:
where we already have separated the continuum and line contribution of the opacity and source function. Collecting terms, and solving for Iijk leads to:
Appendix B: UV line profiles for different ADM models
 |
Fig. B.1. Left panel: as Fig. 9, but for the corresponding ADM model structures. To clarify the definition of the apex radius, rm, we have displayed a specific value, rm = 2R∗, as a red arrow, where this value corresponds to all points located on the red magnetic-field line. In the closed-field region (inside rm = RA, displayed by a thick line), the models contain, from top to bottom: (i) the cooled-downflow component alone. (ii) A statistical approach for the downflow and upflow component. (iii) Alternating flux tubes with cooled-downflow and wind-upflow component. (iv) The wind-upflow component alone. Middle panel: as Fig. 11, for pole-on observers, and for the different ADM models (i)–(iv). The dashed and dotted lines display the emission part and the absorption part of the line profiles, respectively. Right panel: as middle panel, but for equator-on observers. |
All Tables
Mean relative errors of the mean intensity for a zero-opacity model, using either Gauss–Legendre quadrature, or the trapezoidal rule with integration nodes from Lobel & Blomme (2008).
Input parameters for the spherically symmetric models used for our test calculations.
Mean and maximum relative errors of our 3D solution scheme, when compared to an “accurate” 1D solution.
All Figures
 |
Fig. 1. Convergence behaviour of the continuum transfer with ϵc = 10−6 (left), and of the line transfer with ϵL = 10−6 (right), for different acceleration techniques applied to the RT, and for a spherical model atmosphere. The optical depth scale varies according to kc = 10, kL = 10 (top) and kc = 100, kL = 105 (bottom). See text. |
| In the text | |
 |
Fig. 2. Boundary conditions for two different points, r1, r2, and different directions, n1, n2. Green: a ray originating from the stellar photosphere. To calculate the intensity at r1 in direction n1, the intensities at the neighbouring grid points, |
| In the text | |
 |
Fig. 3. Top: specific intensities for direction n= (1, 0, 1) in the x–z-plane, for a zero-opacity model. Overplotted is the spatial grid with a typical size of Nx = Ny = Nz = 133 grid points. The thick lines indicate the theoretical boundary of the beam. Middle: projected intensity profile through the area indicated by a straight line in the top panel, covering all rays with direction n and impact parameter p = ±2R∗, and theoretical intensity profile denoted by dotted lines. The central distance from the origin is 3R∗. Bottom: specific intensity along n, compared to the theoretical value indicated by the dotted line. |
| In the text | |
 |
Fig. 4. Contours of the mean intensity for a zero-opacity model, normalized by its theoretical value, on spherical surfaces, r = 1.1R∗ (left) and r = 3R∗ (right). The line of sight is along the vector n= (1, 1, 1). Nx = Ny = Nz = 133 grid points have been used. |
| In the text | |
 |
Fig. 5. Top: mean intensities (scaled by the emitted intensity from the stellar core, Ic) for the continuum transport, with ϵc = 10−6, and kc = (100, 101, 102) corresponding to τr = (0.17, 1.7, 17.0), from left to right. Bottom: line source functions (scaled by Ic) assuming an optically thin continuum, and with ϵL = 10−6, and kL = (100, 103, 105) from left to right. The red line corresponds to the accurate 1D solution, the blue line is the solution along the x-axis, and the dots (mainly located in between the red and the blue line) correspond to the solution of (arbitrarily) selected grid points (only a subset of all grid points is shown to compress the images). |
| In the text | |
 |
Fig. 6. Emergent line profiles for spherically symmetric models with different line-strengths, kL = (100, 103, 105), from left to right. The red line corresponds to the accurate 1D solution, and the black line is the solution corresponding to our 3D calculations. |
| In the text | |
 |
Fig. 7. Density structure for the wind-ablation model with τdisc = 1400, in the x–z-plane. |
| In the text | |
 |
Fig. 8. As Fig. 7, but for the radiation temperature. Additionally, the density contours corresponding to a decrease in line force by f = 10 (solid) and f = 100 (dashed) are displayed. Both contours indicate the transition region from wind to disc (see text). The grey colour corresponds to radiation temperatures less than the colour-coded minimum value. |
| In the text | |
 |
Fig. 9. Upper panel: density structure for an example snapshot from the MHD simulations for HD 191612, as performed by Sundqvist et al. (2012). Lower panel: azimuthal average of the MHD simulations. In both figures, the density has been normalized by a typical down-flow density, |
| In the text | |
 |
Fig. 10. UV resonance-line profiles for the MHD models, as obtained from our 3D-code (black) and from the SEI method by Marcolino et al. (2013; red). Two different line-strength parameters, κ0 = 0.1 and 1.0, have been used. For convenience, the line profiles for κ0 = 0.1 have been shifted vertically by 1.5. The upper and lower panels show the synthetic line profiles for pole-on and equator-on observers, respectively. The abscissa has been scaled to v∞ = 2700 km s−1, the “observed” 1D value applied by Marcolino et al. (2013). |
| In the text | |
 |
Fig. 11. UV resonance-line profiles obtained from our 3D code, for the MHD simulation (black, as Fig. 10), and the different ADM models, (i)–(iv) (see text). The line-strength parameter has been set to κ0 = 1. The upper and lower panels show the synthetic profiles for pole-on and equator-on view, respectively. As in Fig. 10, the abscissa has been scaled to v∞ = 2700 km s−1, the “observed” 1D value applied by Marcolino et al. (2013). |
| In the text | |
 |
Fig. A.1. Geometry used within the control-volume approach: The dis-cretized 3D spatial grid is shown in blue. The dashed lines indicate the control volume, corresponding to a grid-point (i, j, k). The control-volume surfaces are located at the centre between the grid-point coordinates. |
| In the text | |
 |
Fig. B.1. Left panel: as Fig. 9, but for the corresponding ADM model structures. To clarify the definition of the apex radius, rm, we have displayed a specific value, rm = 2R∗, as a red arrow, where this value corresponds to all points located on the red magnetic-field line. In the closed-field region (inside rm = RA, displayed by a thick line), the models contain, from top to bottom: (i) the cooled-downflow component alone. (ii) A statistical approach for the downflow and upflow component. (iii) Alternating flux tubes with cooled-downflow and wind-upflow component. (iv) The wind-upflow component alone. Middle panel: as Fig. 11, for pole-on observers, and for the different ADM models (i)–(iv). The dashed and dotted lines display the emission part and the absorption part of the line profiles, respectively. Right panel: as middle panel, but for equator-on observers. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



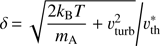
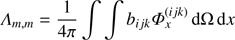
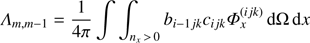
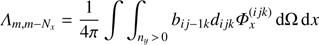
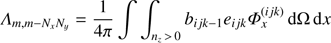
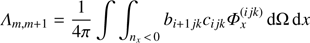
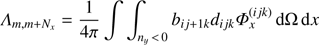
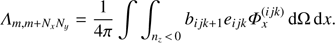
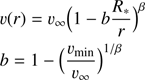
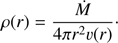
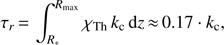
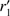
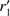
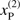
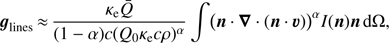
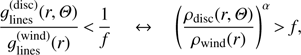
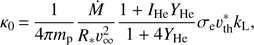
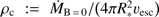
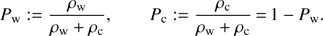
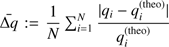
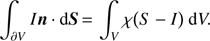
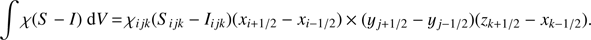
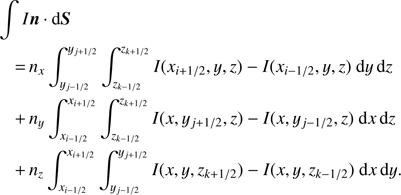
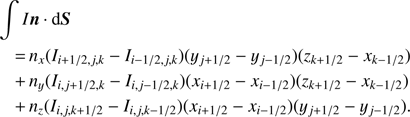
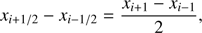
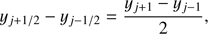
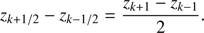
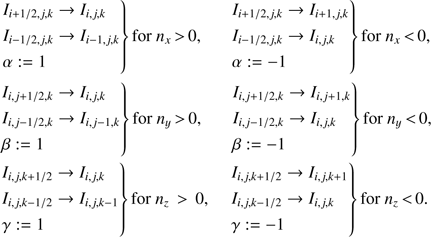
![$ \begin{array}{*{20}{l}} {{n_x}({I_{ijk}} - {I_{i - \alpha jk}})\frac{{{y_{j + \beta }} - {y_{j - \beta }}}}{2}\frac{{{z_{k + \gamma }} - {z_{k - \gamma }}}}{2}}\\ { + {\rm{ }}{n_y}({I_{ijk}} - {I_{ij - \beta k}})\frac{{{x_{i + \alpha }} - {x_{i - \alpha }}}}{2}\frac{{{z_{k + \gamma }} - {z_{k - \gamma }}}}{2}}\\ { + {\rm{ }}{n_z}({I_{ijk}} - {I_{ijk - \gamma }})\frac{{{x_{i + \alpha }} - {x_{i - \alpha }}}}{2}\frac{{{y_{j + \beta }} - {y_{j - \beta }}}}{2}}\\ { = [{\rm{ }}\chi _{ijk}^{({\rm{c}})}S_{ijk}^{({\rm{c}})} + {\rm{ }}\bar \chi _{ijk}^{({\rm{L}})}\Phi _x^{ijk}S_{ijk}^{({\rm{L}})} - (\chi _{ijk}^{({\rm{c}})} + {\rm{ }}\bar \chi _{ijk}^{({\rm{L}})}\Phi _x^{ijk}){I_{ijk}}]{\rm{ }} \times \frac{{{x_{i + \alpha }} - {x_{i - \alpha }}}}{2}\frac{{{y_{j + \beta }} - {y_{j - \beta }}}}{2}\frac{{{z_{k + \gamma }} - {z_{k - \gamma }}}}{2},} \end{array} $](/articles/aa/full_html/2018/08/aa31858-17/aa31858-17-eq80.gif)
