| Issue |
A&A
Volume 614, June 2018
|
|
|---|---|---|
| Article Number | A136 | |
| Number of page(s) | 13 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201731463 | |
| Published online | 03 July 2018 | |
Pulsational instabilities driven by the ∈ mechanism in hot pre-horizontal branch stars
I. The hot-flasher scenario
1
Instituto de Astrofísica de La Plata, CONICET–UNLP, Paseo del Bosque s/n, 1900 La Plata, Argentina
2
Grupo de Evolución Estelar y Pulsaciones, Facultad de Ciencias Astronómicas y Geofísicas, Universidad Nacional de La Plata, Paseo del Bosque s/n, 1900 La Plata, Argentina
e-mail: tbattich@fcaglp.unlp.edu.ar
Received:
28
June
2017
Accepted:
19
January
2018
Context. The ∈ mechanism is a self-excitation mechanism of stellar pulsations that acts in regions inside the star where nuclear burning takes place. It has been shown that the ∈ mechanism can excite pulsations in models of hot pre-horizontal branch stars before they settle into the stable helium core-burning phase. Moreover, it has been shown that this mechanism could explain the shortest periods of LS IV-14°116, a mild He-sdBV star.
Aims. We aim to study the ∈ mechanism in stellar models appropriate for hot pre-horizontal branch stars to predict their pulsational properties and the instability domain in the log g − log Teff plane.
Methods. We performed detailed computations of non-adiabatic non-radial pulsations on stellar models during the helium subflashes just before the helium-core burning phase. Computations were carried out for different values of initial helium composition, metallicity, and envelope mass at the moment of helium flash.
Results. We find an instability domain of long-period gravity modes due to the ∈ mechanism in the log g − log Teff plane at roughly 22 000 K ≲ Teff ≲ 50 000 K and 4.67 ≲ log g ≲ 6.15. Consequently, we find instabilities due to the ∈ mechanism on pre-extreme horizontal branch stellar models (Teff ≳ 22 000 K), but not on pre-blue horizontal branch stellar models (Teff ≲ 21 000 K). The periods of excited modes range between ~200 and ~2000 s. Comparison with the three known pulsating He-rich subdwarfs shows that ∈ mechanism can excite gravity modes in stars with similar surface properties (He abundances, log g, log Teff), but in our models it is only able to excite modes in the range of the shortest observed periods.
Conclusions. We predict a new instability strip for hot-subdwarf stars of which LS IV-14°116 could be the first inhabitant. Based on simple estimates we expect 1 to 10 stars in the current samples of hot-subdwarf stars to be pulsating by the ∈ mechanism. Our results could constitute a theoretical basis for future searches of pulsators in the Galactic field.
Key words: stars: horizontal-branch / stars: oscillations / stars: low-mass / stars: interiors / – asteroseismology
© ESO 2018
1. Introduction
Low-mass stars during the core helium (He)-burning phase of stellar evolution are located in a well defined region of the Hertzsprung-Russell (HR) diagram called the horizontal branch (HB). The HB derives its name from its locus in the theoretical HR diagram, which spans a much thinner range in luminosity than in effective temperature. Some globular clusters present a population of HB stars that are hotter than the RR Lyrae instability strip. This hot part of the HB is called the blue horizontal branch (BHB) and is located approximately in the effective temperature (Teff) range of 7000 K ≲ Teff ≲ 21 000 K. Some clusters also show an extension of the HB, at even higher temperatures (Teff ≳ 22 000 K), called the extreme horizontal branch (EHB). These EHB stars correspond to the hot-subdwarf stars of spectral type B (sdB), which can also be found in the Galactic disk (Heber 2016). The Teff of stars in the BHB or the EHB depend mainly on the mass of their hydrogen (H)-rich envelopes. Extreme horizontal branch stars (or sdBs) are core He-burning stars with H envelopes that are too thin to sustain H burning (Heber 2016). In low-mass stars the beginning of the He-core burning phase occurs in the form of a violent He-core flash. This happens because in these stars He ignition occurs under degenerate conditions of the stellar plasma. After the main He-core flash, subsequent subflashes take place, although with less nuclear energy release than in main He flash (see Kippenhahn et al. 2012). Finally, He burning becomes stable and the stars settle into the zero age horizontal branch (ZAHB). In this paper we call pre-EHB (pre-BHB) stars to stars undergoing the He subflashes before the ZAHB and with temperatures corresponding to the EHB (BHB).
The atmospheres of sdB stars are mostly H pure as a result of the action of gravitational settling, which carries the elements heavier than H to the interior of the star. However, there are some sdBs with He-enriched atmospheres (He-sdB). The short duration (~1.5–2 Myr) of the pre-EHB phase along with the action of stellar winds would prevent the formation of a H-pure envelope in this evolutionary stage. It has been argued that He-sdBs could be stars during the He-core subflashes just before the beginning of the quiescent He-core burning phase (Naslim et al. 2010). Hot-subdwarf stars of spectral type O (sdO) have an evolutionary status that is less clear. In contrast to the sdB stars, their atmospheres show a wide range of He abundances and their temperatures are higher (37 000 K ≲ Teff ≲ 70 000 K). The sdO population is believed to be a mixture of post-EHB stars, post-asymptotic giant branch stars, the progeny of double He-core white dwarf (He-WD) mergers, and post red-giant branch (RGB) stars that had undergone a late He-core flash (Heber 2009, 2016). In particular, the He-rich sdO stars (He-sdO) are thought to be formed by double He-WD mergers (Zhang & Jeffery 2012) and late helium-core flashes (Miller Bertolami et al. 2008). If the last scenario holds, a fraction of the He-sdOs could also be stars undergoing He subflashes.
Among sdB stars, some of these exhibit periodic photometric variations likely due to global pulsations. There are two main classes of known pulsating stars among sdB stars: slow pulsators (sdBVs or V1093 Her stars; Green et al. 2003) with long periods (~2500–8000 s) associated with gravity (g) modes, and rapid pulsators (sdBVr or V361 Hya stars; Charpinet et al. 1996; Kilkenny et al. 1997) with short periods (~80–400 s) associated with radial and non-radial pressure (p) modes (Kilkenny et al. 2010). In both cases the pulsational instabilities are explained by means of the κ mechanism acting on the partial ionization zone of the iron group (Charpinet et al. 1997a; Fontaine et al. 2003). Apart from the pulsating sdB stars, there also exist some sdO stars that exhibit variability (Woudt et al. 2006; Rodríguez-López et al. 2010a; Randall et al. 2016). Pulsating sdO stars, the most of which belong to the globular cluster ω Cen, are rapid pulsators with periods of ~60–130 s, and are also understood by means of the κ mechanism (Fontaine et al. 2008; Rodríguez-López et al. 2010b; Randall et al. 2016). However, there are a few hot-subdwarf stars, LS IV-14°116, KIC 1718290, and UVO 0825+15, whose pulsations cannot be explained by means of the κ mechanism. All these stars have in common the peculiarity that they are mild He-enhanced hot-subdwarf stars. LS IV-14°116 is a He-sdB star whose pulsations have periods in the range of sdBVs stars but its log g and log Teff values correspond to that of sdBVr stars (Ahmad & Jeffery 2005; Green et al. 2011). KIC 1718290 is a cool sdB star or a hot BHB star (Teff ~ 22100 K, Østensen et al. 2012). The effective temperature of this cool sdB star is close to the sdBVs stars and its pulsation modes are compatible with long-period g modes, but this star has periods that are too long compared with those of the sd-BVs stars (up to 11 h; Østensen et al. 2012). Finally, Jeffery et al. (2017) recently reported variability in the light curve of UVO 0825+15, a He-sdO star, which is compatible with non-radial pulsations associated with long-period g modes. UVO 0825+15 is located outside the instability region of sdBVs stars and its periods are also of the order of a few hours (~12 h).
Miller Bertolami et al. (2011) suggested that the pulsations of LS IV-14°116 could be due to ∈ mechanism acting during the He subflashes before the star settles into the quiescent He-burning phase. The ∈ mechanism is a self-excitation mechanism of stellar pulsations that acts on the regions inside the star where nuclear burning takes place. Because of the strong dependence of nuclear burning on the temperature, even tiny perturbations of the temperature inflicted by oscillations translate into huge increases in the amount of nuclear energy released, which in turn increases the local temperature. The process is fed back, resulting in a global instability that grows with time. Generally, the ∈ mechanism is not a very efficient mechanism of excitation since the pulsation amplitudes tend to be small in the high-temperature layers where nuclear energy is generated. The ∈ mechanism was studied in a variety of scenarios, including white dwarf (WD) stars (Charpinet et al. 1997b; Córsico & Althaus 2014, 2016; Camisassa et al. 2016b), pre-WD stars (Kawaler et al. 1986; Saio 1996; Gautschy 1997; Córsico et al. 2009; Maeda & Shibahashi 2014), post He-WD mergers (Miller Bertolami et al. 2013), postmain sequence B stars (Moravveji et al. 2012), and main sequence low-mass stars (Palla & Baraffe 2005; Rodríguez-López et al. 2012; Sonoi & Shibahashi 2012) among others. All these studies predict instabilities due to the ∈ mechanism. Indeed, this mechanism was proposed as the responsible of the pulsations of a few stars, as the supergiant B star Rigel (Moravveji et al. 2012), the PNNV star VV 47 (González Pérez et al. 2006; Córsico et al. 2009) and, as mentioned, the He-sdB star LS IV-14°116 (Miller Bertolami et al. 2011), although none of these suggestions are conclusive. Therefore, if the pulsations of LS IV-14°116, or another He-enhanced hot-subdwarf star, are confirmed to be triggered by ∈ mechanism, it would represent the first evidence that ∈ mechanism can indeed excite pulsations in stars.
Moreover, observational proof of the existence of the He flash and subflashes is lacking, as pointed out by Bildsten et al. (2012). Particularly, there is no hint of any star passing through the He flash or subflashes. Mocák et al. (2009) performed 3D and long-term (36 h) 2D simulations of the evolution of the core He flash. They found that the convective zone that develops as a result of the He burning grows rapidly, and argued that if this zone continues to grow at the same rate for ~ a month, the convection would eventually lift the electron degeneracy and the He flash would not be followed by subsequent subflashes. In this context, an observational hint of the existence of the subflashes would be very interesting. If any star is identified as pulsating by ∈ mechanism in a pre-EHB phase, it would represent a first proof of the existence of He subflashes.
Therefore, faced with the possibility that the ∈ mechanism is responsible for the pulsations in LS IV-14°116, along with the recent discovery of new long-period pulsating He-enriched hot-subdwarf stars, it is of interest to have a detailed study of the pulsations triggered by the ∈ mechanism on pre-BHB and pre-EHB model stars. Such a study is lacking, since Miller Bertolami et al. (2011) studied just a single evolutionary sequence. In this work we largely extend the study of Miller Bertolami et al. (2011) by performing a comprehensive stability analysis on stellar models appropriate for stars on the pre-BHB and pre-EHB that undergo the He subflashes. We extend the previous work of Miller Bertolami et al. (2011) by computing models of different hot flashers flavours and different initial compositions, and performing non-adiabatic pulsation studies for the whole range of temperatures of the hot horizontal branch. This allows us to determine the domain of instability due to the ∈ mechanism. In addition we provide a detailed theoretical study of the excitation and damping of the oscillations and provide the expected growth rates of the modes as well as the expected rates of period changes. This allows us to make better comparisons with the available and future observations. Moreover, our results could constitute a theoretical basis to guide future searches of pulsating stars of this kind.
The paper is organized as follows. In Sect. 2 we present the input physics and numerical tools of the simulations. In Sect. 3 we discuss the evolutionary sequences in the hot-flasher scenario, their predicted surface abundances, and compare these with previous works. In Sect. 4 we present in detail the results of the stability analysis. In Sect. 5 we compare the results with the available observations and give a brief discussion. Finally, in Sect. 6 we summarize our conclusions.
2. Input physics and numerical tools
All the stellar evolutionary calculations in this work were performed with the LPCODE stellar evolutionary code. The LPCODE is a well tested code (Salaris et al. 2013; Miller Bertolami 2016) that has been used for a variety of studies regarding low-mass stars and WDs (see e.g. García-Berro et al. 2010; Wachlin et al. 2011; Camisassa et al. 2016a). In particular, LPCODE was used in the computation of He flashes, including the born again episode (Miller Bertolami et al. 2006) and the hot-flasher scenario (Miller Bertolami et al. 2008). Recently this code has been used to develop a new grid of post-asymptotic giant branch models (Miller Bertolami 2016) and study the evolution of WDs originated from He-enhanced, low-metallicity progenitors (Althaus et al. 2017). The LPCODE is well described in Althaus et al. (2003, 2005) and the improvements of the last version are detailed in Miller Bertolami (2016). Next, we mention the relevant input physics for this work.
The nuclear network of LPCODE accounts for 16 elements along with 34 nuclear reactions for the p–p chains, CNO bicycle, He burning, and carbon ignition. The reaction rates are the same as in Althaus et al. (2005) with the exception of the reactions 12C + p →13 N + →13 C + νe+ + e, 13C(ρ, γ) 14N and 14N(ρ, γ)15O. The first two are taken from Angulo et al. (1999), and the last is taken from Imbriani et al. (2005). Radiative opacities are those of OPAL (Iglesias & Rogers 1996), complemented at low temperature with the molecular opacities of Ferguson et al. (2005) and Weiss & Ferguson (2009). The conductive opacities are included according to Cassisi et al. (2007). The neutrino emission due to plasmon-emission process is calculated according to Haft et al. (1994). Convection is solved within the standard mixing length theory (MLT). The free parameter of the MLT was chosen to be αMLT = 1.822, which corresponds to solar calibration for the LPCODE (Miller Bertolami 2016). The mixing and burning processes are computed simultaneously in the context of diffusive convective mixing (Althaus et al. 2005). No extra-mixing processes were included in the simulations.
All the stellar pulsation calculations were performed with the linear, non-radial, non-adiabatic stellar pulsation code LP-PUL, which is coupled to the LPCODE. The LP-PUL was widely used in studies of pulsation properties of low-mass stars (see e.g. Córsico et al. 2006; Romero et al. 2012; Córsico et al. 2016; Sánchez Arias et al. 2017). In particular it was used to study the ∈-mechanism effects on WD and pre-WD stars (Córsico et al. 2009; Córsico & Althaus 2014; Camisassa et al. 2016b). The LP-PUL is fully described in Córsico et al. (2006) and references therein and this includes the ∈-mechanism mode driving as described in Córsico et al. (2009). The non-adiabatic computations in this work rely on the frozen-in convection approximation, in which the perturbation of the convective flux is neglected. In addition, it was assumed that dS/dt = 0 in the non-perturbed background model adopted in the non-adiabatic computations. For a discussion of the validity of these assumptions in the study of the ∈ mechanism on the subflashes stage, see the work of Miller Bertolami et al. (2011).
3. Evolutionary sequences
In the canonical stellar evolution picture, the He-core flash takes place when stellar models reach the tip of the RGB. However, under certain conditions, most of the H-rich envelope mass can be removed before the development of the He-core flash. These conditions could be enhanced winds due to stellar rotation (Sweigart 1997; Tailo et al. 2015), mass transfer due to stable Roche lobe overflow or common envelope systems (Han et al. 2003; Paczynski 1976), or the ingestion of a substellar companion (Schaffenroth et al. 2014). In addition, in He-enriched populations even standard winds can lead to the (almost) complete removal of the H-rich envelope before the RGB-tip in very low-mass stars (Villanova et al. 2012; Althaus et al. 2017). When this happens models depart from the RGB contracting towards higher effective temperatures at constant luminosity. Castellani & Castellani (1993) demonstrated that a He flash can still develop when the model is entering the WD cooling stage. This scenario leads to He-core burning models with a wide range of envelope masses, thus populating the hot end of the horizontal branch (Faulkner 1972, and references therein). D’Cruz et al. (1996) introduced the term “hot flashers” for this scenario.
We constructed pre-EHB and pre-BHB models within the hot-flashers scenario, i.e., removing different amounts of the H-rich envelope by an artificially enhanced mass loss at the RGB tip. We calculated the evolution of initially 1 M⊙ models from the ZAMS to the RGB. At the tip of the RGB we switched on artificially enhanced mass loss, removing different amounts of envelope mass. For the purpose of this work, the particular value of the mass at the ZAMS and the treatment of mass loss at RGB are not relevant, since it is the total mass at He ignition that determines the behaviour of the hot flashers. Moreover, the actual mass loss rate cannot be determined without a clear understanding of the exact process responsible for the formation of hot horizontal branch stars.
Models were computed for three different initial compositions. The adopted initial compositions are shown in Table 1. Two sets were computed with canonical initial He abundances according to the relation Y = 2 Z + 0.245. Based on the evidence of He-enhanced populations in globular clusters (e.g. Marino et al. 2017), we decided to calculate evolutionary sequences with Y = 0.4 to characterize the impact of He-enriched feature on ∈-mechanism driven pulsations on the hot subflashes stage. Next we describe the qualitative behaviour of hot flashers and compare our sequences with other works.
Initial abundances by mass fraction of the stellar sequences computed in this work.
3.1. Qualitative behaviour of hot flashers
Lanz et al. (2004) classified the hot flashers into three cases, the early hot flasher, the late hot flasher with shallow mixing, and the late hot flasher with deep mixing (Fig. 1). In the early hot flasher (EHF), the He flash occurs when the model star is moving from the tip of the RGB towards the top of the WD cooling curve. In this case, as in canonical He-core flashes, the convective zone that develops as a consequence of the He-core flash (He-core flash driven convective zone; HeFCZ) does not reach the H-rich envelope. This is a consequence of the existence of an entropy barrier at the H-burning shell (Iben 1976). Consequently, the surface abundances are not altered during the He flash but the models end up settling down at hotter effective temperatures than canonical HB models owing to their thinner H-rich envelopes. In late hot flashers, the He flash takes place when the model stars are entering the WD cooling curve. As the model stars descend the WD cooling curve, the energy liberation by H-shell burning decreases, and therefore the entropy barrier also decreases. At some point the H-burning shell becomes too weak to prevent the contact between the H-rich envelope and the He-flash driven convective zone. The penetration, or not, of the He-flash driven convective zone into the H-rich envelope divides the late hot flashers into deep-mixing and shallow-mixing events. Regardless the kind of late hot flasher, after the He flash, the stellar envelope expands due to the energy liberated by it, and the surface became cooler. As a consequence, an outer convective zone develops in the envelope which moves progressively inwards. In the shallow mixing (SM) case the He-core flash driven convective zone eventually splits giving rise to a convective zone that persists in the outer region of the core by several thousands years. This convective zone eventually merges with the outer convective zone of the envelope, and some material of the core is taken to the surface. In this case there is no H burning, but the H surface abundance decreases. Miller Bertolami et al. (2008) found that in some cases the convective region that develops after the He flash can penetrate slightly into the H-rich material, and some H is burned. This case is labelled as SM*. In a late hot flasher with deep mixing (DM), the flash occurs where the model star is well down the WD cooling curve and the entropy barrier is small. The convective region reaches the H-rich layer shortly after the maximum of He flash, and the H is mixed within the hot HeFCZ (Sweigart 1997) leading to a violent burning of H as first calculated by Cassisi et al. (2003). This H-burning leads to a further outward growth of the convective zone, and more H is burned. Therefore, the burning is unstable and a H-flash develops, where almost all H is burned. The superficial abundances change drastically, and the envelope becomes highly He enriched. The absence of H leads to even higher effective temperatures on the resulting ZAHB models.
 |
Fig. 1. HR diagram for evolutionary sequences with Z = 0.02. The evolutionary sequences correspond to two cases of early hot flashers (EHF, dotted and full red lines) and two cases of late hot flashers: one with shallow mixing (SM; full yellow line) and the other with deep mixing (DM; full light blue line). |
With the EHF scenario we are able to populate the pre-BHB and the pre-EHB up to Teff ≃ 37 000 K. Late hot flashers are able to produce models of even higher temperatures, up to Teff ≃ 50 000 K (depending on metallicity).
3.2. Description of the sequences
In Fig. 2 we show the typical evolution of the He-burning luminosity (LHe) on He flash and subflashes for each choice of initial chemical compositions. As in canonical He flashes (Kippenhahn et al. 2012), LHe reaches values as high as LHe ~ 1.3 × 1010 L⊙ (LHe ~ 3.6 × 109 L⊙) for Z = 0.001 (Z = 0.02) and standard He abundances. The energy released due to the He flash in the case of Y = 0.4 is a factor ~4 lower than in the cases with canonical initial He composition (LHe ~ 8.1 × 108 L⊙). Also, the number of subflashes is lower for higher values of Z and Y. These trends are related to lower degree of degeneracy and lower core masses for higher values of Z and Y. In all cases, the timescale of the subflashes stage is about ~2 Myr.
 |
Fig. 2. Luminosity due to nuclear energy liberation at the He flash and subflashes vs. the time after the maximum energy liberation. |
Figure 3 shows the mass of the stellar models at the moment of He ignition for each choice of initial chemical abundances. The He-core mass at He ignition is lower for higher metallicities and higher He abundances. Stars with He-enhanced abundances during the main sequence have a larger mean molecular weight. These stars are hotter and brighter for a given mass than stars with canonical He contents. In particular, the higher core temperatures during the RGB phase mean that the temperature needed for He ignition is reached at lower He-core mass than in the case of normal He abundances (Salaris & Cassisi 2005). Because of the well-known core-luminosity relation (Kippenhahn et al. 2012), hot-flasher models corresponding to sequences with higher initial He abundances are less luminous, and lie at higher gravities on the Kiel diagram than their canonical counterparts.
 |
Fig. 3. Upper panel: mass of the stellar models at He ignition for the different initial chemical compositions computed in this work. Lower panel: same as upper panel but for the works of Xiong et al. (2017) (X+2016) and Miller Bertolami et al. (2008) (MB+2008) for Z = 0.02; and Castellani et al. (2006) (Castellani+2006) and Cassisi et al. (2003) (Cassisi+2003) for Z = 0.0015. |
The qualitative behaviour of our sequences is the same as in previous works (D’Cruz et al. 1996; Brown et al. 2001; Cassisi et al. 2003; Castellani et al. 2006; Miller Bertolami et al. 2008). In the lower panel of Fig. 3 we show the masses at He flash obtained by Cassisi et al. (2003) and Castellani et al. (2006) for Z = 0.0015, and by Miller Bertolami et al. (2008) and Xiong et al. (2017) for Z = 0.02. The masses of our stellar models at He ignition for Z = 0.001 are lower than those of Cassisi et al. (2003) and Castellani et al. (2006) in spite of their values corresponding to a higher metallicity. This is due to the adoption in our work of the updated conductive opacities of Cassisi et al. (2007). The masses of the hot-flasher sequences computed in this work for Z = 0.02 are similar of those obtained by Miller Bertolami et al. (2008) and Xiong et al. (2017) for the same metallicity, in particular, the Xiong et al. (2017) values are slightly lower and the Miller Bertolami et al. (2008) values slightly higher than in the present work. Xiong et al. (2017) computed the formation of sdB stars within the common-envelope ejection channel. These authors mimic the envelope ejection just by enhancing the mass loss at the RGB tip. Since the behaviour of the hot-flasher sequences depends only on the remaining envelope mass, and not on the detailed treatment of mass loss, their evolutionary sequences also belong to the hot-flasher scenario, and are comparable with other hot-flasher scenario sequences.
Figure 4 depicts the surface abundances of various models at the ZAHB for various metallicities in terms of the total mass of the model at He ignition. The mass ranges for the different flavours of hot flashers are shown in different colours. As in previous works, we find that the mass range for the different flavours of hot flashers is dependent on the initial metallicity of the sequences. In fact, for Z = 0.001 we did not find a SM case, leaving the range for SM at Z = 0.001 to be below δM⋆SM < 10−6 M⊙. Instead, for Z = 0.001, we found a DM case where the maximum of energy liberation is much lower (L/L⊙ ~ 108) than in standard DM events (L/L⊙ ~ 1010). In this case the mixing is still deep into the HeFCZ and the surface abundances change as in a DM case. This case is an intermediate case between a normal DM case and a SM* case where the depth of the outer convective mixing is much shallower. We label this case as DM*. For Z = 0.02 we found all flavours of hot flasher including a DM* case.
 |
Fig. 4. Surface abundances by mass fraction at the onset of stable He burning in terms of the mass at He ignition (full lines). The typical abundances of the He core after the primary He flash has ended, but before the He subflashes (dashed lines), are shown for comparison. Upper panel: corresponds to initial chemical compositions of Z = 0.02 and Y = 0.285. Lower panel: corresponds to initial chemical compositions of Z = 0.001 and Y = 0.247. |
Now we discuss briefly the obtained surface abundances after the He flash. In EHF cases the abundances are left unchanged and are the same as in the case where the He flash occurs at the RGB tip. On the other hand, late hot flashers lead to the dredging up of material from the stellar interior to the photosphere. Depending on the deepness of the mixing, different surface abundances arise. When shallow mixing (SM) occurs, the surface abundances of 12C and 16O decrease and the abundances of He and 14N increase respect to the EHF and canonical cases. This is because in SM events the envelope is mixed with the H-free region rich in He and 14N that lies immediately below the H-rich envelope. This region displays the typical abundances left behind by the stable CNO burning during the RGB (see Fig. 5). Also, as H is diluted into the H-free material coming from the interior, the surface H abundance decreases. This is shown in Fig. 4. The exact values depend on metallicity and the depth of the outer convective zone. In deep mixing (DM) episodes, the H-rich envelope is mixed into the hot HeFCZ where large amounts of 12C have already been created by the 3α reaction during the primary He-core flash (see Fig. 5) and a violent H flash develops. As H is burned in a 12C rich environment, 13C is created. Once enough 13C has been created, H is burned with 13C increasing the final 14N superficial abundance. In addition, during He flash the 14N, which comes from previous CNO burning on the RGB, is burned with particles to produce 18O. In turn, 18O is burned producing 22Ne. Once the H-rich material is mixed and burned in the hot interior, the violent H flash splits the HeFCZ into two (due to the huge energy release). The outer convective zone, driven by H-flash burning is too cold for He burning to take place and 18O and 22Ne in the outer convective zone are left unchanged after that. As 18O and 22Ne keep increasing during the He flash, the exact final abundances of 18O and 22Ne in DM episodes depend on how many years after the peak of the He flash the mixing takes place. As 12C also keeps increasing during the He flash, meanwhile 14N keeps decreasing, the same holds for the abundances of these elements; the difference is that their exact values are also affected by H burning. All in all the 12C and 22Ne superficial abundances are higher for cases where the H flash takes more time to develop, meanwhile the 14N superficial abundance is lower for those cases. These are the DM cases closer to the SM region in Fig. 4.
 |
Fig. 5. Typical chemical stratification below the H-rich envelope (at mr ≳ 0.468 M⊙) during the main He-core flash for a model with initial chemical compositions of Z = 0.02 and Y = 0.285. The chemical inversions at about mr = 0.468 are a consequence of the H-shell burning. |
The same holds for Z = 0.001 and for the sequences with Y = 0.4. Some quantitative differences are due to the different initial compositions. The resulting surface abundances at the onset of stable core He burning for the case of late hot flashers are listed in Table 2.
Surface abundances of the late hot-flasher scenario at the ZAHB.
The typical differences between our derived surface abundances and those derived for Miller Bertolami et al. (2008) represent less than the 20% of our surface abundances values for both the DM and SM cases. The exceptions are the abundances of C, H, and O in the DM case. The larger difference is for the abundance of O, as the abundances derived by Miller Bertolami et al. (2008) are around twice the values that we obtain. As Xiong et al. (2017) have not provided a classification of the flavour of the sequences in their tables (DM or SM), we compared those that are clearly deep mixing cases with our DM cases. The differences for He, C, N, and O (the only surface abundances provided in Xiong et al. 2017) are always below 20% except for the abundance of O, as their values are also about twice the values of our derived O abundances. In all cases the differences are smaller than a factor of 2. Therefore, the final surface abundances computed in this work for the different late hotflasher scenarios are in good qualitative agreement with those of Xiong et al. (2017) (for Z = 0.02) and Miller Bertolami et al. (2008) (for Z = 0.02 and Z = 0.001).
4. Stability analysis
We performed a stability analysis over a total of 20 stellar evolutionary sequences for different values of initial chemical abundances and masses of the H-rich envelope. We computed non-adiabatic non-radial pulsations in stellar models going through He subflashes. For each evolutionary sequence we performed a stability analysis over 300 to 800 stellar structure models (the exact value depending on initial chemical abundances), covering the whole subflashes stage. For each of these models we explored ℓ = 1 modes within a period range of 50–7000 s. For one of the evolutionary sequences we also performed calculations of ℓ = 2 and ℓ = 3 modes to determine the trend of the periods and excitation with the value of ℓ.
We found a new theoretical instability domain in the log Teff − log g plane (also known as Kiel diagram). The domain of instability corresponds to low- or intermediate-order g modes excited by ∈ mechanism, which agrees with what was found for one evolutionary sequence by Miller Bertolami et al. (2011). The period range of excited modes is from 200s to 2000s. We found that pulsations are only excited in the hottest models with Teff ≳ 20 000 K (see Fig. 6). As a consequence pre-EHB models show ∈-mechanism driven pulsations during the He subflashes, while pre-BHB models do not. Also, oscillations are excited in models with surface gravities higher than log g ≃ 4.8. Within the hot-flasher scenario the He sub-flashes occupy a region in the Kiel diagram of about 1 dex above the ZAHB, and never attain temperatures higher than 50 000 K (see Figs. 1 and 6). The instability domain in the Kiel diagram predicted by our sequences is therefore the intersection of the locus of the evolutionary sequences during the He subflashes and the temperature and gravity boundaries mentioned before (Teff ≳ 20 000 K and log g ≳ 4.8), see Fig. 6. The location of the ZAHB depends on both the initial metal (Z) and helium (Y) content of the models. In particular, in the He-enriched models the ZAHB is located at higher gravities owing to the smaller He cores and the consequent lower luminosities. While the high temperature and gravity boundaries of the instability domain are the direct consequence of the locus of the hot-flasher models in the Kiel diagram, the lower temperature and gravity boundaries requires a detailed analysis of the excitation and damping mechanisms.
 |
Fig. 6. Phase of the He subflashes of the evolutionary sequences in the log Teff − log g diagram (grey and pink lines). Coloured points correspond to models with excited modes and the colour coding shows the minimum e-folding time for each model. Evolutionary sequences in pink lines have their pulsational quantities listed in Table 3. Also shown for comparison is the location of the known He-rich hot-subdwarf pulsators LS IV-14°116 (Randall et al. 2015), UVO 0825+15 (Jeffery et al. 2017), and KIC 1718290 (Østensen et al. 2012). The upper panel also shows the models discussed in Sect. 4.1. |
4.1. Driving and damping of pulsations
All g modes have relatively high amplitudes in the layers where the He subflashes take place, and consequently undergo some degree of excitation through the ∈ mechanism. Yet, whether or not a mode is actually excited is determined by the competition between the driving mechanism and the damping of oscillations, mostly through radiative damping. To understand the excitation and damping mechanisms it becomes useful to look at the mechanical structure of the pre-HB models through a propagation diagram. In Fig. 7 we show the propagation diagrams of two different models during the peak of energy release in a He subflash. The logarithm of the squared Brunt–Väisälä (Lamb) frequency is plotted with full violet (red) lines. There are two peaks of the Brunt–Väisälä frequency near to log(1 − mr/M⋆) = −2. The outermost peak corresponds to the He–H transition, and the innermost peak corresponds to the most external position reached by the outer edge of the convective zone during the main He flash, which reduces the abundance of He in 0.04% and increases the abundance of 12C. The majority of the nodes of the radial eigenfunctions are clustered in the core, in particular in the regions of high values of the Brunt–Väisälä frequency. At about log(1 − mr/M⋆) = −0.2, the Brunt–Väisälä frequency drops to zero in the convective zone (the zone without any nodes). The pulsation driving region is located at the base of this convective zone. The model on the upper panel of Fig. 7 corresponds to a high-gravity, high-temperature model (log g = 5.12, log Teff/K = 4.53, and M⋆ = 0.4868 M⋆, hereafter model HG) that displays unstable modes with periods in the range ~880–1130 s, while the lower panel of Fig. 7 corresponds to a lowgravity, low-temperature model (log g = 4.25, log Teff/K = 4.35, and M⋆ = 0.4908 M⊙, hereafter model LG, see also Fig. 6) without unstable modes. The Brunt–Väisälä frequency (N) of model LG reaches lower values in the outer layers. N can be written as1 (Brassard et al. 1991)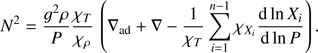 (1)
(1)
 |
Fig. 7. Logarithm of the squared Lamb and Brunt–Väisälä frequencies (violet and red lines) in terms of the outer mass fraction coordinate. The black points indicate the nodes of the radial eigenfunctions. The upper panel corresponds to a model with log g = 5.12, log Teff/K = 4.53, M⋆ = 0.4868 M⋆ (model HG) with excited modes. The lower panel corresponds to a model with log g = 4.25, log Teff/K = 4.35, M⋆ = 0.4908 M⊙ (model LG) and no excited modes. The region of periods in the range ~880–1130 s is shown with a green strip. This corresponds to the region of excited modes for model HG. At about log(1 − mr/M⋆) = −0.2 the Brunt–Väisälä frequency drops to zero in the convective zone. The pulsation driving region is located at the base of this convective zone. |
Therefore, N is lower for lower values of the local gravity g. As a consequence, all the modes of model LG that have periods shorter than 3000 s (log !2 > −5.3) oscillate as mixed modes – i.e., they behave as g modes in the core and as p modes in the envelope; see e.g. Hekker & Christensen-Dalsgaard (2017). Modes with periods in the range ~880–1130 s are locally excited by the ∈ mechanism in both models. The running work integral2 of three modes with periods in this range is shown for both models in the lower panel of Fig. 8. At − log(1 − mr/M⋆) ~ 0.2 the work function becomes W > 0 due to the excitation by the ∈ mechanism. For model LG, the modes in the period range of ~880–1130 s are mixed modes that oscillate as p modes in the outer layers (lower panel of Fig. 7), where they have large amplitudes (upper panel of Fig. 8, red lines). As a consequence, these modes are strongly stabilized by radiative damping in the outer layers, and turn out to be globally stable modes. On the other hand, for model HG (upper panel of Fig. 7) the excited modes have frequencies at or below the local minimum of N2 (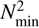 ; at around − log(1 − mr/M⋆) ~ 4.5). As a consequence, those modes oscillate as pure g modes in the stellar core. On the contrary, modes with frequencies higher than
; at around − log(1 − mr/M⋆) ~ 4.5). As a consequence, those modes oscillate as pure g modes in the stellar core. On the contrary, modes with frequencies higher than 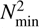 oscillate as mixed modes. Because of their relative large amplitudes in the envelope, modes with frequencies above
oscillate as mixed modes. Because of their relative large amplitudes in the envelope, modes with frequencies above 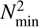 are also strongly stabilized by radiative damping in the outer layers. This explains the high-frequency limit for the driving of pulsations. The lowfrequency limit of the excited modes is a consequence of the radiative damping of pure g modes in the core. This can be understood as follows. The local radiative damping rate rad(r) depends on the local wavenumber of the modes. For modes with higher local wavenumbers, γrad(r) is higher. Locally, the temperature perturbations can be approximated as δT/T∝ / e−ik, r, and within the diffusion approximation, γrad(r) for g modes can be written as (Shiode et al. 2013; Kumar & Quataert 1998)
are also strongly stabilized by radiative damping in the outer layers. This explains the high-frequency limit for the driving of pulsations. The lowfrequency limit of the excited modes is a consequence of the radiative damping of pure g modes in the core. This can be understood as follows. The local radiative damping rate rad(r) depends on the local wavenumber of the modes. For modes with higher local wavenumbers, γrad(r) is higher. Locally, the temperature perturbations can be approximated as δT/T∝ / e−ik, r, and within the diffusion approximation, γrad(r) for g modes can be written as (Shiode et al. 2013; Kumar & Quataert 1998)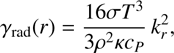 (2)
(2)
 |
Fig. 8. Upper panel: Lagrangian perturbation of the temperature for three modes of each of the models of Fig. 7. These modes have periods between 880–1130s and are excited by ∈ mechanism in the inner region (− log(1 − mr/M⋆) ~ 0.2). Blue (red) lines correspond to the modes of the model HG (LG). Lower panel: Running work integral for the same models is shown. The quantities W and δT/T are normalized to have the radius perturbation at the surface δr/R = 1. In the lower panel the running work integral is normalized arbitrarily for each model to be able to plot them in the same panel. |
where the temperature T, density ρ, opacity κ, and specific heat cP are functions of the radial coordinate r, and kr is the local wavenumber. The dispersion relation for gravity modes with frequency ω << N, L leads to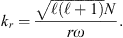 (3)
(3)
Lower frequencies have larger local wavenumber and are more strongly radiatively damped. For frequencies lower than a particular value, the damping in the radiative core becomes more important than the excitation by ∈ mechanism and the modes become stable.
Once the excitation and damping mechanisms are understood, the origin of the low-gravity and low-temperature limits of the pulsation domain in the Kiel diagram (Fig. 6) becomes clear. In models that undergo the He subflashes at low surface gravities (like model LG) all modes with frequencies higher than Nmin are mixed modes strongly damped by radiative diffusion in the outer regions. Also, because of the low value of Nmin, pure g modes have frequencies that are too low and are strongly damped in the core. Consequently, no mode is actually excited in these models. The low-temperature limit of the pulsation domain is a consequence of the previous effect and the lower energy release of the later subflashes: as we move to lower effective temperatures, the first (and more intense) subflashes take place at too low gravities where modes are strongly radiatively damped in the outer layers of the star, and once the model has attained gravities closer to the ZAHB, the He subflashes do not release enough energy to excite pulsations.
4.2. Properties of excited modes
We have obtained excited modes (ℓ = 1) with periods in the range ~200–2000 s and radial orders in the range ~1–25. In all cases, the range of excited periods becomes shorter with subsequent subflashes. This is exemplified in Fig. 9, which shows the periods as a function of time for a sequence with Z = 0.02, Y = 0.285 and M⋆ = 0.457 M⊙. The trend of the periods is a natural consequence of the continuous shrinking of the model as it approaches the ZAHB, which shifts the global pulsational properties to shorter periods. The short-period limit (high-frequency limit) is given by the local minimum of the Brunt–Väisälä frequency (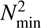 ) discussed in the previous section. The value
) discussed in the previous section. The value 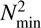 slightly increases in later subflashes, as shown in Fig. 10, which depicts the Brunt–Väisälä frequency for each subflash of the same evolutionary sequence of Fig. 9. As a consequence, the short-period limit slightly decreases in the last subflashes (see Fig. 9). This trend is more notorious for the long-period limit. This limit is due to the radiative damping of g modes at the stellar core. For periods longer than a particular value, the radiative damping becomes more important than the excitation. For our models during the first subflash, for ℓ = 1, this happens for periods longer than about ≃2000 s. As subflashes take place, the nuclear energy release is lower and the ∈ mechanism is less efficient. Therefore, the damping becomes more important than the excitation for shorter periods than in the first subflashes.
slightly increases in later subflashes, as shown in Fig. 10, which depicts the Brunt–Väisälä frequency for each subflash of the same evolutionary sequence of Fig. 9. As a consequence, the short-period limit slightly decreases in the last subflashes (see Fig. 9). This trend is more notorious for the long-period limit. This limit is due to the radiative damping of g modes at the stellar core. For periods longer than a particular value, the radiative damping becomes more important than the excitation. For our models during the first subflash, for ℓ = 1, this happens for periods longer than about ≃2000 s. As subflashes take place, the nuclear energy release is lower and the ∈ mechanism is less efficient. Therefore, the damping becomes more important than the excitation for shorter periods than in the first subflashes.
 |
Fig. 9. Upper panel: period vs. time of a sequence with Z = 0.02, Y = 0.285 and M⋆ = 0.457 M⊙. Excited periods are coloured with the e-folding time in colour coding. This sequence is indicated as a pink DM in middle panel of Fig. 6, and its pulsation properties are tabulated in Table 3. Lower panel: zoom on first subflash. |
 |
Fig. 10. Brunt–Väisälä frequency (N) of models at the top of each subflash, for the same evolutionary sequence of Fig. 9. The red solid line corresponds to the first subflash, and upwards, to successive subflashes. |
The range of excited periods is also sensitive to the harmonic degree ℓ. Meanwhile the short-period limit does not change with ℓ as it depends only on the value of N, the long-period limit of excited modes is lower for higher values of the harmonic degree ℓ. This is illustrated in Fig. 11, where we show the unstable periods for each computed value of ℓ. This is a consequence of the dependence of the radiative damping on ℓ (see Eqs. (2) and (3)). As rad increases with ℓ, the period at which radiative damping overwhelms the excitation is shorter for higher values of the harmonic degree ℓ.
 |
Fig. 11. Period vs. number of model of sequences with Z = 0.02, Y = 0.4 and M⋆ = 0.445M⊙, corresponding to ℓ = 1 (green points), ℓ = 2 (grey points), and ℓ = 3 (red points). This sequence is indicated as the "Shallow mixing" case in Table 3. |
Another feature of the excitation by ∈ mechanism is the sharp transition between excited and non-excited modes at the short-period limit. The sudden transition from a pure g-mode behaviour to a mixed mode one at 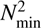 explains this sharp transition. On the contrary, the transition between excited and non-excited modes at the long-period limit occurs smoothly as the radiative damping increases with the increasing radial order.
explains this sharp transition. On the contrary, the transition between excited and non-excited modes at the long-period limit occurs smoothly as the radiative damping increases with the increasing radial order.
Table 3 shows some quantitative pulsational properties of selected sequences in Fig. 6 at each subflash before the sequences settle on the ZAHB. Column 2 shows the maximum He-burning luminosity in each subflash. Column 3 shows an estimate of the time span ∆tex in which the modes are effectively being excited. Before and after this time interval the excitation due to ∈ mechanism is marginal. The value ∆tex is assessed as the time interval in which modes are excited with e-folding times shorter than the duration of the subflash3. The e-folding time (τ) is a measure of the time required by a given unstable mode to grow to observable amplitudes. Modes with τ < Δ tex are excited by the ∈ mechanism long enough to grow to observable amplitudes. This allow us to estimate characteristic quantities for those modes that can actually reach observable amplitudes during the subflash. Therefore, all the other quantities in Table 3 were computed taking into account only unstable modes with e-folding times shorter than Δtex. As shown in Col. 4 of Table 3 our computations predict that for all stellar models within the instability strip and for all the initial chemical compositions, there are several modes with values of τ lower than the time interval Δtex. The values τmin and <τ> indicate the minimum and mean e-folding times of all the significantly excited modes during each subflash. We note, in particular, that the shortest e-folding times (τmin) are typically one order of magnitude lower than (Δtex). As it is apparent from Table 3 (and also Figs. 6 and 9), the e-folding times are shorter during the earlier subflashes, when the intensity of He burning is higher and the ∈ mechanism is consequently more effective. The exception to this rule are those evolutionary sequences in which the first subflashes occur at lower surface gravities than the limit of the instability strip.
Another interesting property predicted by our computations is the rate of period change Ṗ of the unstable modes. Because of the large structural changes driven by the sudden energy injection in the He subflashes, the periods of normal g modes are strongly affected with typical values of Ṗ in the range of 〈 Ṗ〉 ~ 10−5 − 10−7 s/s (see Table 3). This corresponds to a period drift typically between 1 and 300 seconds per year that could be easily measured. These values are even higher than the typical 〈 Ṗ〉 derived by Silva Aguirre et al. (2008) for radial modes of RR Lyrae at the subflashes phase, 〈 Ṗ〉 ~ 10−8 s/s. This is not surprising since, contrary to the RR Lyrae case, the modes excited in our compact models are pure g modes. These kinds of modes live in the core and are evanescent in the convective region that develops as a consequence of the He flash. Therefore, pure g modes are very sensitive to changes in the structure of the stellar core.
5. Discussion
We now compare our predictions with the pulsational properties of the small number of known pulsating He-rich subdwarfs with mild He enhancements, namely LS IV-14°116 with observed periods P ≃ 1950–5080 s (Teff = 35150 ± 111, log g = 5.88 ± 0.02, log n(He)/n(H) = −0.62 ± 0.01; Randall et al. 2015; Ahmad & Jeffery 2005; Green et al. 2011), KIC 1718290 with P ≃ 1–12 h (Teff = 22 100, log g = 4.72, log n(He)/n(H) = −0.45; Østensen et al. 2012) and UVO 0825+156 with P ≃ 10.8–13.3 h (Teff = 38900 ± 270, log g = 5.97 ± 0.11, log n(He)/n(H) = −0.57 ± 0.01; Jeffery et al. 2017); see Fig. 6. Interestingly, as shown in Fig. 6, all these stars fall within the range of surface gravities and temperatures predicted by our computations of the ∈ mechanism acting on hot-flasher sequences. The fact that the ∈ mechanism qualitatively predicts the excitation of g modes in stellar models with similar values of Teff, log g, and log n(He)/n(H) is very encouraging. Quantitatively, however, the range of excited periods in our sequences (P ~ 200–2000 s) can only account for the shortest observed periods in these stars. This could be pointing to shortcomings in the stellar evolution models in this very fast and badly tested stage of the evolution. If He subflashes were more intense than predicted by our sequences, the range of excited periods would reach longer periods. This is particularly interesting in the case of LS IV-14°116, which shows periods below 2 h and whose Teff, log g, and log n(He)/n(H) values are well reproduced by our He-enhanced sequences, as shown in the bottom panel, Fig. 6. On the other hand, because of the very strong radiative damping of higher order g modes, the longest periods of the order of 10 h shown by KIC 1718290 and UVO 0825+156 can hardly be explained by the ∈ mechanism.
Another interesting question concerns the number of pre-HB stars expected to pulsate due to the ∈ mechanism. From Table 3 we see that, within the hot-flasher scenario, the total amount of time spent by the sequences in the stages of pulsation instability is between ~35 000 yr and ~65 000 yr. Therefore, comparing this time with the timescale typical of the whole pre-HB (~2 Myr, see Fig. 2) we can estimate that ~2–3 % of all pre-EHB stars should be pulsating owing to the ∈ mechanism. The question now turns to how many stars in the current sdB samples (Fontaine et al. 2014; Geier et al. 2017) are in the pre-EHB phase. Because of the short duration of this phase (~2 Myr) in comparison with the core He-burning phase (~100 Myr) pre-EHB stars should be 50 times less common than quiescent He-burning EHB stars in a volume-limited sample. However, pre-EHB stars can be up to one order of magnitude more luminous than EHB stars and can consequently be detected in much larger volumes (up to 30 times larger) for magnitude-limited samples. Consequently, the number of pre-EHB stars in a sample of field subdwarfs could be much higher than just a small percentage of the total. Under the optimistic assumption that most He-rich subdwarfs are indeed hot flashers on the pre-HB, we should expect ~1 out of the ~50 field He-rich subdwarfs in the sample of Fontaine et al. (2014) and ~10 out of the ~500 He-rich subdwarfs in the sample of Geier et al. (2017) to be pulsating by the ∈ mechanism. But even if we make the conservative assumption that only a fraction of ~0.00054 of the whole sdB sample is undergoing ∈-mechanism driven pulsations, we still find that at least ~3 stars should be pulsating by the ∈ mechanism in the sample of 5613 sdB stars presented by Geier et al. (2017).
Pulsating subdwarfs have been observed in globular clusters such as ω Cen (Randall et al. 2016) and NGC 2808 (Brown et al. 2013) and one might wonder about the possibility to detect ∈-mechanism driven pulsations in those clusters. The most favourable case is ω Cen, which is the most massive globular cluster and, in addition, has 30% of its horizontal branch stars in the blue hook (Tailo et al. 2015). A simple estimate of the expected number of pre-horizontal branch pulsating stars can be carried out by means of Renzini?(tm)s evolutionary flux method (Greggio & Renzini 2011). Within this approximation, the number of stars (Nj) in a given stellar population (with total brightness Lt) for an evolutionary phase of duration tj is,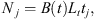 (4)
(4)
where B(t) is the specific evolutionary flux, that is very close to 2 × 10−11 stars 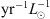 (Greggio & Renzini 2011). In the case of ω Cen (log L/L⊙ = 6.2; Harris 2010; Worthey 1994), taking ~50 000 yr for the total duration of the excitation of ∈-driven pulsations and that only 30% of ω Cen horizontal branch stars are in the blue hook, we get Nj ≃ 0.4. Consequently, about only one star in the whole cluster is expected to be in this stage. The situation is worse in other clusters; the total number of EHB stars in globular clusters is well below 1000. Therefore, based on these simple considerations it seems unlikely to find stars pulsating by ∈ mechanism in the EHB of globular clusters.
(Greggio & Renzini 2011). In the case of ω Cen (log L/L⊙ = 6.2; Harris 2010; Worthey 1994), taking ~50 000 yr for the total duration of the excitation of ∈-driven pulsations and that only 30% of ω Cen horizontal branch stars are in the blue hook, we get Nj ≃ 0.4. Consequently, about only one star in the whole cluster is expected to be in this stage. The situation is worse in other clusters; the total number of EHB stars in globular clusters is well below 1000. Therefore, based on these simple considerations it seems unlikely to find stars pulsating by ∈ mechanism in the EHB of globular clusters.
6. Summary and conclusions
We performed non-adiabatic computations of stellar pulsations in pre-hot horizontal branch stellar models within the hot-flasher scenario. Our computations predict a new instability strip for hot-subdwarf stars centred in the log Teff − log g diagram at slightly lower gravities than the canonical hot-subdwarf pulsators. The locus of the instability domain is roughly 22 000 K ≲ Teff ≲ 50 000 K and 4.67 ≲ log g ≲ 6.15. The range of excited periods is P ~ 200–2000 s corresponding to low- and intermediate-order g modes. Consequently, our computations show the excitation of long-period g modes driven by the ∈ mechanism associated with pre-EHB stellar models, but not with pre-BHB stellar models.
We found that a considerable number of excited modes are very likely to grow to observable amplitudes during the subflashes. Also, the rates of period change predicted are very high (1–300 s yr−1). These features show that ∈-mechanism driven pulsations in hot-subdwarf stars can be detected and identified.
The location of known He-rich hot subdwarf pulsators (Fig. 6) is well reproduced by our theoretical predictions, although the observed periods in these stars are systematically longer than the predicted periods. In the cases of the longest observed periods in KIC 1718290 and UVO 0825+156 the pulsations cannot be explained by ∈ mechanism owing to the strong radiative damping of high-order g modes in the stellar core. For LS IV-14°116, our computations are able to explain the shortest observed period along with its location in the log Teff − log g diagram and its He-enriched composition. For this star it was proposed that a magnetic field could be involved in its variability (Naslim et al. 2011; Green et al. 2011). But Randall et al. (2015) searched for a magnetic field in LS IV-14°116 and found no evidence of it. Therefore, we conclude that the ∈ mechanism remains the best available explanation for the pulsations in this star. Although, as only the shortest period can be explained it is necessary to continue exploring alternative scenarios.
Miller Bertolami et al. (2013) showed that the ∈ mechanism can excite pulsations during the off-centred He-shell flashes that take place after a double He-white dwarf merger. The merger of two He-WDs is also a very favourable scenario for the formation of He-sdO stars (Zhang & Jeffery 2012). Therefore, in future works we intend to study the properties of ∈-mechanism excited pulsations in detailed double He-WD post-merger models.
Finally, we conclude that our work could constitute a theoretical basis for future searches of pulsators in the Galactic field. In particular, based on simple numerical estimates we expect 1 to 10 stars in the current samples of hot-subdwarf stars to be pulsating by the ∈ mechanism.
Acknowledgments
The authors thank the anonymous referee for her/his suggestions that improved the original version of the article. This project has been partially supported by ANPCyT through grant PICT-2014-2708, MinCyT-DAAD bilateral cooperation through grant DA/16/07 and by a Return Fellowship from the Alexander von Humboldt Foundation. This research has made use of NASA’s Astrophysics Data System Bibliographic Services.
The running work integral at a radius coordinate r represents the work done by the sphere of radius r on the layer at radius r. The value of this function at the surface, W(R), depends of the stability nature of modes. If W(R) > 0 the mode is unstable. If W(R) < 0 the mode is stable, see Unno et al. (1989).
References
- Ahmad, A., & Jeffery, C. S. 2005, A&A, 437, L51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Althaus, L. G., Serenelli, A. M., Córsico, A. H., & Montgomery, M. H. 2003, A&A, 404, 593 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Althaus, L. G., Serenelli, A. M., Panei, J. A., et al. 2005, A&A, 435, 631 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Althaus, L. G., De Gerónimo, F., Córsico, A., Torres, S., & García-Berro, E. 2017, A&A, 597, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Angulo, C., Arnould, M., Rayet, M., et al. 1999, Nucl. Phys. A, 656, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Bildsten, L., Paxton, B., Moore, K., & Macias, P. J. 2012, ApJ, 744, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Brassard, P., Fontaine, G., Wesemael, F., Kawaler, S. D., & Tassoul, M. 1991, ApJ, 367, 601 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, T. M., Sweigart, A. V., Lanz, T., Landsman, W. B., & Hubeny, I. 2001, ApJ, 562, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, T. M., Landsman, W. B., Randall, S. K., Sweigart, A. V., & Lanz, T. 2013, ApJ, 777, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Camisassa, M. E., Althaus, L. G., Córsico, A. H., et al. 2016a, ApJ, 823, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Camisassa, M. E., Córsico, A. H., Althaus, L. G., & Shibahashi, H. 2016b, A&A, 595, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cassisi, S., Schlattl, H., Salaris, M., & Weiss, A. 2003, ApJ, 582, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Cassisi, S., Potekhin, A. Y., Pietrinferni, A., Catelan, M., & Salaris, M. 2007, ApJ, 661, 1094 [NASA ADS] [CrossRef] [Google Scholar]
- Castellani, M., & Castellani, V. 1993, ApJ, 407, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Castellani, M., Castellani, V., & Prada Moroni, P. G. 2006, A&A, 457, 569 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Charpinet, S., Fontaine, G., Brassard, P., & Dorman, B. 1996, ApJ, 471, L103 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Charpinet, S., Fontaine, G., Brassard, P., et al. 1997a, ApJ, 483, L123 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Charpinet, S., Fontaine, G., Brassard, P., & Dorman, B. 1997b, ApJ, 489, L149 [NASA ADS] [CrossRef] [Google Scholar]
- Córsico, A. H., & Althaus, L. G. 2014, ApJ, 793, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Córsico, A. H., & Althaus, L. G. 2016, A&A, 585, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Córsico, A. H., Althaus, L. G., & Miller Bertolami, M. M. 2006, A&A, 458, 259 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Córsico, A. H., Althaus, L. G., Miller Bertolami, M. M., González Pérez, J. M., & Kepler, S. O. 2009, ApJ, 701, 1008 [NASA ADS] [CrossRef] [Google Scholar]
- Córsico, A. H., Althaus, L. G., Serenelli, A. M., et al. 2016, A&A, 588, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D’Cruz, N. L., Dorman, B., Rood, R. T., & O’Connell, R. W. 1996, ApJ, 466, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Faulkner, J. 1972, ApJ, 173, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Ferguson, J. W., Alexander, D. R., Allard, F., et al. 2005, ApJ, 623, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Fontaine, G., Brassard, P., Charpinet, S., et al. 2003, ApJ, 597, 518 [Google Scholar]
- Fontaine, G., Brassard, P., Green, E. M., et al. 2008, A&A, 486, L39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fontaine, G., Green, E., Brassard, P., Latour, M., & Chayer, P. 2014, in 6th Meeting on Hot Subdwarf Stars and Related Objects, eds. V. van Grootel, E. Green, G. Fontaine, & S. Charpinet, ASP Conf. Ser., 481, 83 [NASA ADS] [Google Scholar]
- García-Berro, E., Torres, S., Althaus, L. G., et al. 2010, Nature, 465, 194 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gautschy, A. 1997, A&A, 320, 811 [Google Scholar]
- Geier, S., Østensen, R. H., Nemeth, P., et al. 2017, A&A, 600, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- González Pérez, J. M., Solheim, J.-E., & Kamben, R. 2006, A&A, 454, 527 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Green, E. M., Fontaine, G., Reed, M. D., et al. 2003, ApJ, 583, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Green, E. M., Guvenen, B., O’Malley, C. J., et al. 2011, ApJ, 734, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Greggio, L., & Renzini, A. 2011, Stellar Populations. A User Guide from Low to High Redshift (Weinheim: Wiley-VCH) [Google Scholar]
- Haft, M., Raffelt, G., & Weiss, A. 1994, ApJ, 425, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Han, Z., Podsiadlowski, P., Maxted, P. F. L., & Marsh, T. R. 2003, MNRAS, 341, 669 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, W. E. 2010, ArXiv e-prints [arXiv:1012.3224] [Google Scholar]
- Heber, U. 2009, ARA&A, 47, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Heber, U. 2016, PASP, 128, 082001 [NASA ADS] [CrossRef] [Google Scholar]
- Hekker, S., & Christensen-Dalsgaard, J. 2017, A&ARv, 25, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iben, Jr., I. 1976, ApJ, 208, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Imbriani, G., Costantini, H., Formicola, A., et al. 2005, Eur. Phys. J. A, 25, 455 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jeffery, C. S., Baran, A. S., Behara, N. T., et al. 2017, MNRAS, 465, 3101 [NASA ADS] [CrossRef] [Google Scholar]
- Kawaler, S. D., Winget, D. E., Hansen, C. J., & Iben, Jr., I. 1986, ApJ, 306, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Kilkenny, D., Koen, C., O’Donoghue, D., & Stobie, R. S. 1997, MNRAS, 285, 640 [Google Scholar]
- Kilkenny, D., Fontaine, G., Green, E. M., & Schuh, S. 2010, Information Bulletin on Variable Stars, (Budapest: Konkoly Observatory), 5927 [Google Scholar]
- Kippenhahn, R., Weigert, A., & Weiss, A. 2012, Stellar Structure and Evolution (Heidelberg: Springer) [Google Scholar]
- Kumar, P., & Quataert, E. J. 1998, ApJ, 493, 412 [NASA ADS] [CrossRef] [Google Scholar]
- Lanz, T., Brown, T. M., Sweigart, A. V., Hubeny, I., & Landsman, W. B. 2004, ApJ, 602, 342 [NASA ADS] [CrossRef] [Google Scholar]
- Maeda, K., & Shibahashi, H. 2014, PASJ, 66, 76 [Google Scholar]
- Marino, A. F., Milone, A. P., Yong, D., et al. 2017, ApJ, 843, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Miller Bertolami, M. M. 2016, A&A, 588, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miller Bertolami, M. M., Althaus, L. G., Serenelli, A. M., & Panei, J. A. 2006, A&A, 449, 313 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miller Bertolami, M. M., Althaus, L. G., Unglaub, K., & Weiss, A. 2008, A&A, 491, 253 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miller Bertolami, M. M., Córsico, A. H., & Althaus, L. G. 2011, ApJ, 741, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Miller Bertolami, M. M., Córsico, A. H., Zhang, X., Althaus, L. G., & Jeffery, C. S. 2013, EPJ Web Conf., 43, 04004 [Google Scholar]
- Mocák, M., Müller, E., Weiss, A., & Kifonidis, K. 2009, A&A, 501, 659 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moravveji, E., Moya, A., & Guinan, E. F. 2012, ApJ, 749, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Naslim, N., Jeffery, C. S., Ahmad, A., Behara, N. T., & Şahín, T. 2010, MNRAS, 409, 582 [NASA ADS] [CrossRef] [Google Scholar]
- Naslim, N., Jeffery, C. S., Behara, N. T., & Hibbert, A. 2011, MNRAS, 412, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Østensen, R. H., Degroote, P., Telting, J. H., et al. 2012, ApJ, 753, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Paczynski, B. 1976, in Structure and Evolution of Close Binary Systems, eds. P. Eggleton, S. Mitton, & J. Whelan, IAU Symp., 73, 75 [Google Scholar]
- Palla, F., & Baraffe, I. 2005, A&A, 432, L57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Randall, S. K., Bagnulo, S., Ziegerer, E., Geier, S., & Fontaine, G. 2015, A&A, 576, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Randall, S. K., Calamida, A., Fontaine, G., et al. 2016, A&A, 589, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rodríguez-López, C., Lynas-Gray, A. E., Kilkenny, D., et al. 2010a, MNRAS, 401, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Rodríguez-López, C., Moya, A., Garrido, R., et al. 2010b, MNRAS, 402, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Rodríguez-López, C., MacDonald, J., & Moya, A. 2012, MNRAS, 419, L44 [NASA ADS] [CrossRef] [Google Scholar]
- Romero, A. D., Córsico, A. H., Althaus, L. G., et al. 2012, MNRAS, 420, 1462 [Google Scholar]
- Saio, H. 1996, in Hydrogen Deficient Stars, eds. C. S. Jeffery, & U. Heber, ASP Conf. Ser., 96, 361 [Google Scholar]
- Salaris, M., & Cassisi, S. 2005, Evolution of Stars and Stellar Populations, (Weinheim: Wiley-VCH), 400 [Google Scholar]
- Salaris, M., Althaus, L. G., & García-Berro, E. 2013, A&A, 555, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sánchez Arias, J. P., Córsico, A. H., & Althaus, L. G. 2017, A&A, 597, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schaffenroth, V., Classen, L., Nagel, K., et al. 2014, A&A, 570, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shiode, J. H., Quataert, E., Cantiello, M., & Bildsten, L. 2013, MNRAS, 430, 1736 [NASA ADS] [CrossRef] [Google Scholar]
- Silva Aguirre, V., Catelan, M., Weiss, A., & Valcarce, A. A. R. 2008, A&A, 489, 1201 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sonoi, T., & Shibahashi, H. 2012, MNRAS, 422, 2642 [NASA ADS] [CrossRef] [Google Scholar]
- Sweigart, A. V. 1997, in The Third Conference on Faint Blue Stars, eds. A. G. D. Philip, J. Liebert, R. Saffer, & D. S. Hayes, 3 [Google Scholar]
- Tailo, M., D’Antona, F., Vesperini, E., et al. 2015, Nature, 523, 318 [NASA ADS] [CrossRef] [Google Scholar]
- Unno, W., Osaki, Y., Ando, H., Saio, H., & Shibahashi, H. 1989, Nonradial Oscillations of Stars (Tokyo: University of Tokyo Press) [Google Scholar]
- Villanova, S., Geisler, D., Piotto, G., & Gratton, R. G. 2012, ApJ, 748, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Wachlin, F. C., Miller Bertolami, M. M., & Althaus, L. G. 2011, A&A, 533, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weiss, A., & Ferguson, J. W. 2009, A&A, 508, 1343 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Worthey, G. 1994, ApJS, 95, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Woudt, P. A., Kilkenny, D., Zietsman, E., et al. 2006, MNRAS, 371, 1497 [NASA ADS] [CrossRef] [Google Scholar]
- Xiong, H., Chen, X., Podsiadlowski, P., Li, Y., & Han, Z. 2017, A&A, 599, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, X., & Jeffery, C. S. 2012, MNRAS, 419, 452 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Initial abundances by mass fraction of the stellar sequences computed in this work.
All Figures
 |
Fig. 1. HR diagram for evolutionary sequences with Z = 0.02. The evolutionary sequences correspond to two cases of early hot flashers (EHF, dotted and full red lines) and two cases of late hot flashers: one with shallow mixing (SM; full yellow line) and the other with deep mixing (DM; full light blue line). |
| In the text | |
 |
Fig. 2. Luminosity due to nuclear energy liberation at the He flash and subflashes vs. the time after the maximum energy liberation. |
| In the text | |
 |
Fig. 3. Upper panel: mass of the stellar models at He ignition for the different initial chemical compositions computed in this work. Lower panel: same as upper panel but for the works of Xiong et al. (2017) (X+2016) and Miller Bertolami et al. (2008) (MB+2008) for Z = 0.02; and Castellani et al. (2006) (Castellani+2006) and Cassisi et al. (2003) (Cassisi+2003) for Z = 0.0015. |
| In the text | |
 |
Fig. 4. Surface abundances by mass fraction at the onset of stable He burning in terms of the mass at He ignition (full lines). The typical abundances of the He core after the primary He flash has ended, but before the He subflashes (dashed lines), are shown for comparison. Upper panel: corresponds to initial chemical compositions of Z = 0.02 and Y = 0.285. Lower panel: corresponds to initial chemical compositions of Z = 0.001 and Y = 0.247. |
| In the text | |
 |
Fig. 5. Typical chemical stratification below the H-rich envelope (at mr ≳ 0.468 M⊙) during the main He-core flash for a model with initial chemical compositions of Z = 0.02 and Y = 0.285. The chemical inversions at about mr = 0.468 are a consequence of the H-shell burning. |
| In the text | |
 |
Fig. 6. Phase of the He subflashes of the evolutionary sequences in the log Teff − log g diagram (grey and pink lines). Coloured points correspond to models with excited modes and the colour coding shows the minimum e-folding time for each model. Evolutionary sequences in pink lines have their pulsational quantities listed in Table 3. Also shown for comparison is the location of the known He-rich hot-subdwarf pulsators LS IV-14°116 (Randall et al. 2015), UVO 0825+15 (Jeffery et al. 2017), and KIC 1718290 (Østensen et al. 2012). The upper panel also shows the models discussed in Sect. 4.1. |
| In the text | |
 |
Fig. 7. Logarithm of the squared Lamb and Brunt–Väisälä frequencies (violet and red lines) in terms of the outer mass fraction coordinate. The black points indicate the nodes of the radial eigenfunctions. The upper panel corresponds to a model with log g = 5.12, log Teff/K = 4.53, M⋆ = 0.4868 M⋆ (model HG) with excited modes. The lower panel corresponds to a model with log g = 4.25, log Teff/K = 4.35, M⋆ = 0.4908 M⊙ (model LG) and no excited modes. The region of periods in the range ~880–1130 s is shown with a green strip. This corresponds to the region of excited modes for model HG. At about log(1 − mr/M⋆) = −0.2 the Brunt–Väisälä frequency drops to zero in the convective zone. The pulsation driving region is located at the base of this convective zone. |
| In the text | |
 |
Fig. 8. Upper panel: Lagrangian perturbation of the temperature for three modes of each of the models of Fig. 7. These modes have periods between 880–1130s and are excited by ∈ mechanism in the inner region (− log(1 − mr/M⋆) ~ 0.2). Blue (red) lines correspond to the modes of the model HG (LG). Lower panel: Running work integral for the same models is shown. The quantities W and δT/T are normalized to have the radius perturbation at the surface δr/R = 1. In the lower panel the running work integral is normalized arbitrarily for each model to be able to plot them in the same panel. |
| In the text | |
 |
Fig. 9. Upper panel: period vs. time of a sequence with Z = 0.02, Y = 0.285 and M⋆ = 0.457 M⊙. Excited periods are coloured with the e-folding time in colour coding. This sequence is indicated as a pink DM in middle panel of Fig. 6, and its pulsation properties are tabulated in Table 3. Lower panel: zoom on first subflash. |
| In the text | |
 |
Fig. 10. Brunt–Väisälä frequency (N) of models at the top of each subflash, for the same evolutionary sequence of Fig. 9. The red solid line corresponds to the first subflash, and upwards, to successive subflashes. |
| In the text | |
 |
Fig. 11. Period vs. number of model of sequences with Z = 0.02, Y = 0.4 and M⋆ = 0.445M⊙, corresponding to ℓ = 1 (green points), ℓ = 2 (grey points), and ℓ = 3 (red points). This sequence is indicated as the "Shallow mixing" case in Table 3. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


