| Issue |
A&A
Volume 612, April 2018
H.E.S.S. phase-I observations of the plane of the Milky Way
|
|
|---|---|---|
| Article Number | A5 | |
| Number of page(s) | 10 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201527843 | |
| Published online | 09 April 2018 | |
The supernova remnant W49B as seen with H.E.S.S. and Fermi-LAT★
1
Centre for Space Research, North-West University,
2520 Potchefstroom,
South Africa
2
Universität Hamburg, Institut für Experimentalphysik, Luruper Chaussee 149,
22761
Hamburg, Germany
3
Max-Planck-Institut für Kernphysik,
PO Box 103980,
69029
Heidelberg, Germany
4
Dublin Institute for Advanced Studies, 31 Fitzwilliam Place,
Dublin 2, Ireland
5
National Academy of Sciences of the Republic of Armenia, Marshall Baghramian Avenue,
24, 0019 Yerevan, Republic of Armenia
6
Yerevan Physics Institute, 2 Alikhanian Brothers St.,
375036 Yerevan, Armenia
7
Institut für Physik, Humboldt-Universität zu Berlin, Newtonstr. 15,
12489 Berlin, Germany
8
University of Namibia, Department of Physics, Private Bag 13301,
Windhoek, Namibia
9
GRAPPA, Anton Pannekoek Institute for Astronomy, University of Amsterdam, Science Park 904,
1098 XH Amsterdam, The Netherlands
10
Department of Physics and Electrical Engineering, Linnaeus University,
351 95 Växjö, Sweden
11
Institut für Theoretische Physik, Lehrstuhl IV: Weltraum und Astrophysik, Ruhr-Universität Bochum,
44780 Bochum, Germany
12
GRAPPA, Anton Pannekoek Institute for Astronomy and Institute of High-Energy Physics, University of Amsterdam, Science Park 904,
1098 XH Amsterdam, The Netherlands
13
Institut für Astro- und Teilchenphysik, Leopold-Franzens-Universität Innsbruck,
6020 Innsbruck, Austria
14
School of Physical Sciences, University of Adelaide,
5005 Adelaide, Australia
15
LUTH, Observatoire de Paris, PSL Research University, CNRS, Université Paris Diderot, 5 Place Jules Janssen,
92190 Meudon, France
16
Sorbonne Universités, UPMC Université Paris 06, Université Paris Diderot, Sorbonne Paris Cité, CNRS, Laboratoire de Physique Nucléaire et de Hautes Energies (LPNHE), 4 place Jussieu,
75252 Paris Cedex 5, France
17
Laboratoire Univers et Particules de Montpellier, Université Montpellier, CNRS/IN2P3, CC 72, Place Eugène Bataillon,
34095 Montpellier Cedex 5, France
18
DSM/Irfu, CEA Saclay,
91191 Gif-Sur-Yvette Cedex, France
19
Astronomical Observatory, The University of Warsaw, Al. Ujazdowskie 4,
00-478 Warsaw, Poland
20
Aix Marseille Université, CNRS/IN2P3, CPPM UMR 7346,
13288 Marseille, France
21
Instytut Fizyki Ja̧drowej PAN, ul. Radzikowskiego 152,
31-342 Kraków, Poland
22
Funded by EU FP7 Marie Curie, grant agreement No. PIEF-GA-2012-332350
23
School of Physics, University of the Witwatersrand, 1 Jan Smuts Avenue, Braamfontein,
2050 Johannesburg, South Africa
24
Laboratoire d’Annecy-le-Vieux de Physique des Particules, Université Savoie Mont-Blanc, CNRS/IN2P3,
74941 Annecy-le-Vieux, France
25
Landessternwarte, Universität Heidelberg, Königstuhl,
69117 Heidelberg, Germany
26
Université Bordeaux, CNRS/IN2P3, Centre d’Études Nucléaires de Bordeaux Gradignan,
33175 Gradignan, France
27
Oskar Klein Centre, Department of Physics, Stockholm University, Albanova University Center,
10691 Stockholm, Sweden
28
Wallenberg Academy Fellow
29
Institut für Astronomie und Astrophysik, Universität Tübingen,
Sand 1, 72076 Tübingen, Germany
30
Laboratoire Leprince-Ringuet, Ecole Polytechnique, CNRS/IN2P3,
91128 Palaiseau, France
31
APC, AstroParticule et Cosmologie, Université Paris Diderot, CNRS/IN2P3, CEA/Irfu, Observatoire de Paris, Sorbonne Paris Cité, 10 rue Alice Domon et Léonie Duquet,
75205 Paris Cedex 13, France
32
Univ. Grenoble Alpes, IPAG CNRS, IPAG,
38000 Grenoble, France
33
Department of Physics and Astronomy, The University of Leicester, University Road,
Leicester, LE1 7RH, UK
34
Nicolaus Copernicus Astronomical Center, ul. Bartycka 18,
00-716 Warsaw, Poland
35
Institut für Physik und Astronomie, Universität Potsdam, Karl-Liebknecht-Strasse 24/25,
14476 Potsdam, Germany
36
Friedrich-Alexander-Universität Erlangen-Nürnberg, Erlangen Centre for Astroparticle Physics, Erwin-Rommel-Str. 1,
91058 Erlangen, Germany
37
DESY,
15738 Zeuthen, Germany
38
Obserwatorium Astronomiczne, Uniwersytet Jagielloński, ul. Orla 171,
30-244 Kraków, Poland
39
Centre for Astronomy, Faculty of Physics, Astronomy and Informatics, Nicolaus Copernicus University, Grudziadzka 5,
87-100 Torun, Poland
40
Department of Physics, University of the Free State, PO Box 339,
9300 Bloemfontein, South Africa
41
Heisenberg Fellow (DFG), ITA Universität Heidelberg,
69029 Heidelberg, Germany
42
GRAPPA, Institute of High-Energy Physics, University of Amsterdam, Science Park 904,
1098 XH Amsterdam, The Netherlands
43
W. W. Hansen Experimental Physics Laboratory, Kavli Institute for Particle Astrophysics and Cosmology, Department of Physics and SLAC National Accelerator Laboratory, Stanford University,
Stanford, CA 94305, USA
44
Department of Physics, Rikkyo University, 3-34-1 Nishi-Ikebukuro, Toshima-ku,
171-8501 Tokyo, Japan
45
Department of Physical Sciences, Hiroshima University, Higashi-Hiroshima,
739-8526 Hiroshima, Japan
46
Now at Santa Cruz Institute for Particle Physics and Department of Physics, University of California at Santa Cruz,
Santa Cruz, CA 95064, USA
★★ Corresponding author: H.E.S.S. Collaboration,
e-mail: contact.hess@hess-experiment.eu
Received:
26
November
2015
Accepted:
24
August
2016
The supernova remnant (SNR) W49B originated from a core-collapse supernova that occurred between one and four thousand years ago, and subsequently evolved into a mixed-morphology remnant, which is interacting with molecular clouds (MC). Gamma-ray observations of SNR-MC associations are a powerful tool to constrain the origin of Galactic cosmic rays, as they can probe the acceleration of hadrons through their interaction with the surrounding medium and subsequent emission of non-thermal photons. We report the detection of a γ-ray source coincident with W49B at very high energies (VHE; E > 100 GeV) with the H.E.S.S. Cherenkov telescopes together with a study of the source with five years of Fermi-LAT high-energy γ-ray (0.06–300 GeV) data. The smoothly connected, combined source spectrum, measured from 60 MeV to multi-TeV energies, shows two significant spectral breaks at 304 ± 20 MeV and 8.4−2.5+2.2 GeV; the latter is constrained by the joint fit from the two instruments. The detected spectral features are similar to those observed in several other SNR-MC associations and are found to be indicative of γ-ray emission produced through neutral-pion decay.
Key words: gamma rays: general / ISM: supernova remnants / ISM: clouds
The H.E.S.S. gamma-ray excess map (see Fig. 1, in FITS format) of the W49 region is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/612/A5
© ESO 2018
1 Introduction
The strong shocks associated with supernova remnants (SNRs) are very good candidates for accelerating hadronic Galactic cosmic rays to at least 1015 eV through the diffusive shock acceleration mechanism (e.g. Drury 1983). The detection of very high energy (VHE) γ-rays above 20 TeV in objects such as RX J1713.7-3946 (Aharonian et al. 2006b) or RCW 86 (Aharonian et al. 2009) shows that these objects can accelerate particles up to at least 100 TeV. However, whether the bulk of accelerated particles that radiate in the high-energy (HE; 0.1 < E < 100 GeV) and very high-energy (E > 100 GeV) γ-ray range is of leptonic or hadronic nature is still under debate (Blasi 2013).
A growing number of SNRs interacting with molecular clouds (SNR-MC) are being revealed in the GeV and TeV γ-ray domain. This includes W44 (Abdo et al. 2010b), W28 (Aharonian et al. 2008b; Abdo et al. 2010a), CTB 37A (Aharonian et al. 2008a; Castro & Slane 2010), and IC 443 (Albert et al. 2007; Acciari et al. 2009; Abdo et al. 2010c). Even though isolated SNRs are obviously cleaner laboratories to study cosmic-ray acceleration processes, SNR-MC associations are good candidates to test the presence of hadronic acceleration in SNRs; this is in part because the HE and VHE γ-ray emissions from the decay of π0 mesons are expected to be strongly enhanced. The neutral pions, which are produced when high-energy protons (or nuclei) collide with interstellar material, each decay into two γ-rays with equal energies in the rest frame of the pion. This translates into a steep rise below ~200 MeV in the γ-ray spectral energy distribution (often referred to as the pion-decay bump). This characteristic spectral feature has been recently detected at high energies for three interacting SNRs: IC 443, W44 (Ackermann et al. 2013), and W51C (Jogler & Funk 2016). However, whether this feature is the signature of the acceleration of freshly injected protons may be questioned, as re-acceleration of diffuse cosmic rays for a limited time period is also possible (Uchiyama et al. 2010; Cardillo et al. 2016).
In this context, the W49 region, discovered in the 22 cm survey of Westerhout (1958), represents one of the most interesting regions in the Galaxy to study cosmic-ray acceleration. This region contains two remarkable objects: a young SNR (W49B) and a star-forming region (W49A). The SNR W49B (G43.3−0.2) is another example of a SNR-MC association. It is a mixed-morphology (Rho & Petre 1998) SNR with a bright shell of diameter ~ 4′ that is resolved at radio wavelengths and centrally filled with thermal X-rays (Hwang et al. 2000). With a flux density of 38 Jy at 1 GHz, this source is one of the brightest SNRs of the Galaxy at radio wavelengths. Extensive infrared and X-ray studies revealed that the progenitor of W49B was a supermassive star that created a wind-blown bubble in a dense molecular cloud in which the explosion occurred (Keohane et al. 2007). It has recently been shown that the progenitor of W49B experienced a jet-driven, core-collapse explosion (Lopez et al. 2013; González-Casanova et al. 2014). Observations of mid-infrared lines from shocked molecular hydrogen show that W49B is interacting with molecular clouds. Near-infrared Fe ii observations revealed filamentary structures, which is evidence of radiative shocks (Keohane et al. 2007). This interaction is also suggested by H i line observations (Brogan & Troland 2001). The age of the remnant is estimated to be between 1000 and 4000 years (Moffett & Reynolds 1994; Hwang et al. 2000; Zhou et al. 2011) and the distance of this object is still not very well constrained. From H i absorption analyses, Radhakrishnan et al. (1972) derived a distance, which Moffett & Reynolds (1994) later recalculated to be ~ 8 kpc using an updated Galactic rotation model. Brogan & Troland (2001), using more recent VLA data, have shown that an association of W49B with the nearby star-forming region W49A is also possible, extending the range of possible distances (8 ≤ D ≤ 12 kpc) for this source. More recently, Zhu et al. (2014) obtained a distance of ~10 kpc.
As mentioned above, the other notable component of the W49 region is W49A (Mezger et al. 1967). This is one of the brightest giant radio H ii regions in the Galaxy. This star-forming region is located in the densest ~15 pc of a 106 M⊙ giant molecular cloud of ~100 pc in size. It contains numerous compact and ultra-compact (UC) H ii regions and its emission is equivalent to the presence of about 100 O7 stars (Brogan & Troland 2001). The presence of a very massive star with an initial mass of 100− 180 M⊙ has been reported by Wu et al. (2014). W49A is associated with a molecular outflow and strong H2 O masers (Walker et al. 1982; Scoville et al. 1986), the proper motion of which was used by Zhang et al. (2013) to determine a distance of 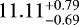 kpc. Star-forming regions are considered potential VHE γ-ray emitters since they generally host massive stars that could accelerate particles to VHEs through interactive or collective wind effects. As an example, the TeV γ-ray source coincidentwith Westerlund 1 (Abramowski et al. 2012), detected with the High Energy Stereoscopic System (H.E.S.S.), may be the site of such processes.
kpc. Star-forming regions are considered potential VHE γ-ray emitters since they generally host massive stars that could accelerate particles to VHEs through interactive or collective wind effects. As an example, the TeV γ-ray source coincidentwith Westerlund 1 (Abramowski et al. 2012), detected with the High Energy Stereoscopic System (H.E.S.S.), may be the site of such processes.
In the HE domain, a bright source coincident with W49B is detected with the Fermi Large Area Telescope (LAT) (3FGL J1910.9+0906 in the Fermi-LAT 3FGL catalogue; Acero et al. 2015). This bright source was one of the 205 most significant sources after the first three months of observation1 and is one of the 360 sources detected above 50 GeV in 80 months of data (Ackermann et al. 2016). This source is the subject of a detailed analysis presented in Abdo et al. (2010d). In that paper, the detection of HE γ-ray emission was reported towards W49B at a significance of 38σ with 17 months of data. The authors disfavoured a possible pulsar origin for the emission observed towards W49B in the GeV range. Furthermore, from X-ray measurements, the presence of a neutron star as the result of the collapse of the progenitor star appears unlikely (Lopez et al. 2013).
In the present paper, the detection of a source coincident with the SNR W49B in the VHE γ-ray domain with H.E.S.S. is reported. The analysis of the Fermi-LAT data is applied in this work to five years of data using an updated calibration and updated source and background models. The spectral and morphological results in the GeV and TeV regime are discussed in the context of a SNR interacting with a molecular cloud.
2 Data analysis
2.1 H.E.S.S. observations and analysis
2.1.1 H.E.S.S. data set and analysis methods
H.E.S.S. is an array of five imaging Cherenkov telescopes located in the Khomas Highland in Namibia (23°16′ 18″ S, 16°30′ 01″ E) at an altitude of 1800 m above sea level (Hinton 2004). The fifth telescope was added in July 2012 but observations with the upgraded system are not used in this work. With the initial four-telescope array, γ-rays are detected above an energy threshold of ~100 GeV with an angular resolution better than 0.1° and an energy resolution below 15%.
A standard data quality selection procedure was used to remove observations affected by bad weather or instrumental problems (Aharonian et al. 2006a). Extrapolating the Fermi-LAT γ-ray spectrum to higher energies, W49B is expected to have a steep spectrum in the TeV range; this is also a common feature for GeV-detected SNRs interacting with molecular clouds. Therefore, observations with an energy threshold above 600 GeV , which can be determined a priori from the observation conditions, were not used in this study. This resulted in a data set comprising 75 h (live time) of observations towards the W49 region taken from 2004 to 2013 with a mean pointing offset of 1.1° and a mean zenith angle of 37°. The data set comprises dedicated observations as well as observations of other nearby sources or dedicated to the survey of the Galactic plane (H.E.S.S. Collaboration 2018).
The data were analysed using the Model Analysis (de Naurois & Rolland 2009), in which shower images of all triggered telescopes are compared to a precalculated model by means of a log likelihood optimisation. This advanced reconstruction technique improves the sensitivity with respect to more conventional techniques. The standard cuts of the Model Analysis were adopted. This set of cuts includes a minimum charge in the shower images of 60 photoelectrons resulting, for this data set, in an energy threshold of 290 GeV. This set of cuts was used for signal extraction and for the spectral and morphological analyses. The results presented in this paper have been cross-checked with the analysis methods described in Ohm et al. (2009) and Parsons & Hinton (2014) and yield compatible results.
2.1.2 H.E.S.S. analysis results
The signal was extracted from a circular region with a radius of 0.1° around the position of W49B, taken inside the radio shell, at the position of the maximum of the emission in X-rays determined by Hwang et al. (2000), that is 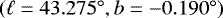 . From the correlated excess map, which is computed using the ring background subtraction method (Berge et al. 2007) and shown in Fig. 1, a significant excess of VHE γ-rays is detected at the position of W49B, with a peak significance of 12.9σ (Eq. (17) of Li & Ma 1983). With the primary analysis, VHE γ-ray emission is observed towards W49A, but this observation could not be confirmed (above 5σ) with the cross-check analysis. Therefore, only the VHE emission coincident with W49B is discussed in the following.
. From the correlated excess map, which is computed using the ring background subtraction method (Berge et al. 2007) and shown in Fig. 1, a significant excess of VHE γ-rays is detected at the position of W49B, with a peak significance of 12.9σ (Eq. (17) of Li & Ma 1983). With the primary analysis, VHE γ-ray emission is observed towards W49A, but this observation could not be confirmed (above 5σ) with the cross-check analysis. Therefore, only the VHE emission coincident with W49B is discussed in the following.
In order to derive the source position at VHE and therefore the best-suited spectral extraction region, the excess map of VHE γ-rays towards the W49 region was fitted with a two-source model. This is undertaken to model the region in the best possible way, given the possible excess towards W49A, which is ~0.2° away from W49B (a model with only one source for the fit leads to compatible results). The model is convolvedwith the H.E.S.S. point spread function before being fit to the measured excess counts. The VHE γ-ray emission towards W49B is found to be point-likewith a best-fit position of 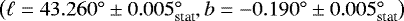 with a systematic error of ± 0.006° on each axis. As can be seen in Fig. 2, the obtained position is compatible with the centre of the SNR observed in radio and X-rays (e.g. Pye et al. 1984). This position corresponds to α2000 =19h11m7.3s, δ2000 = 09°05′37.0″ and the detectedsource is therefore given the identifier HESS J1911+090.
with a systematic error of ± 0.006° on each axis. As can be seen in Fig. 2, the obtained position is compatible with the centre of the SNR observed in radio and X-rays (e.g. Pye et al. 1984). This position corresponds to α2000 =19h11m7.3s, δ2000 = 09°05′37.0″ and the detectedsource is therefore given the identifier HESS J1911+090.
The reflected background subtraction method (Berge et al. 2007) was used at the best-fit position to derive the spectrum of the VHE emission coincident with W49B. From a region of radius 0.1° around this position, thetotal number of counts is 1141, while 16 017 events are used to estimate the background with an average normalisation factor α = 0.047. This corresponds to an excess of 392.3 events detected with a significance of 13.0σ. The differential energy spectrum is derived above 290 GeV using a forward-folding method described in Piron et al. (2001). The data are described well (χ2 ∕ndf = 60.6∕61) by a power-law model 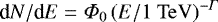 with a flux normalisation
with a flux normalisation 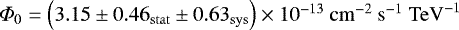 and a spectral index of Γ = 3.14 ± 0.24stat ± 0.10sys (see Fig. 3). The integrated flux above 1 TeV is
and a spectral index of Γ = 3.14 ± 0.24stat ± 0.10sys (see Fig. 3). The integrated flux above 1 TeV is 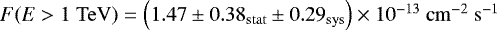 , corresponding to 0.65% of the Crab nebula flux above the same energy (Aharonian et al. 2006a). Two other spectral shapes were tested (log parabolic power law and power law with exponential cut-off) but they do not fit the data significantly better.
, corresponding to 0.65% of the Crab nebula flux above the same energy (Aharonian et al. 2006a). Two other spectral shapes were tested (log parabolic power law and power law with exponential cut-off) but they do not fit the data significantly better.
 |
Fig. 1 γ-ray excess map of the W49 region obtained with H.E.S.S. The map is smoothed with a Gaussian of width 0.06°, corresponding to the 68% radius containment of the H.E.S.S. point spread function (PSF; shown in the inset). The black triangle denotes the position of the supernova remnant W49B (Green 2014). The white triangle denotes the position of W49A (Lockman 1989). |
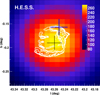 |
Fig. 2 Zoomed-in version of Fig. 1. The crosses show the best-fit positions of the source with H.E.S.S. (black) and Fermi-LAT (blue). The size of the crosses represents the size of the 95% confidence level (CL) contours on the best-fit positions, including systematic uncertainties. The white contours show the radio intensity obtained at a wavelength of 20 cm with MAGPIS (Helfand et al. 2006). |
2.2 Fermi-LAT analysis
2.2.1 Fermi-LAT observations and data reduction
The LAT detects γ-ray photons by conversion into electron-positron pairs in the energy range between 20 MeV to higher than 300 GeV, as described by Atwood et al. (2009). It contains a high-resolution converter/tracker (for direction measurement of the incident γ rays), a CsI(Tl) crystal calorimeter (for energy measurement), and an anti-coincidence detector to identify the background of charged particles. The following analysis was performed using five years of Fermi-LAT data collected primarily in survey mode (2008 August 04−2013 August 04). This new data set consists of Pass 7 LAT data that have been reprocessed using updated calibration constants for the detector systems (Bregeon et al. 2013). The primary differences with respect to the Pass7_V6 instrument response functions (IRFs) are the correction of a slight (1% per year) expected degradation in the calorimeter light yield and significant improvement of the position from the calorimeter reconstruction, which in turn significantly improves the LAT point spread function above 5 GeV. Only γ-rays in the Source class events were selected, excluding those coming from a zenith angle larger than 100° with respect to the detector axis so as to reduce γ-ray contamination from protons interacting with the atmosphere of the Earth. The 15th version of the reprocessed Pass 7 IRFs for this class of events (P7REP_SOURCE_V15; Bregeon et al. 2013) were adopted.
Two different tools were used to perform the spatial and spectral analysis: gtlike and pointlike. The tool gtlike is a binned maximum likelihood method (Mattox et al. 1996) implemented in the Science Tools distributed by the Fermi Science Support Center (FSSC)2. The tool pointlike is an alternate binned likelihood technique, optimised for characterising the extension of a source, a functionality that is not implemented in gtlike. The pointlike tool was extensively tested against gtlike (Lande et al. 2012). These tools fit a source model to the data along with models for isotropic γ-ray emission that also accounts for the residual charged particles and a diffuse γ-ray emission model. The obtained log likelihood is then compared between different source model assumptions to find an optimal description of the region. For quantitative evaluation between models, the test-statistic value (TS) was defined as 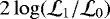 , where
, where 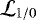 corresponds to the likelihood value for the source/no-source hypothesis (Mattox et al. 1996). The TS value is a measure of the detection significance or description improvement.
corresponds to the likelihood value for the source/no-source hypothesis (Mattox et al. 1996). The TS value is a measure of the detection significance or description improvement.
For this work, the Galactic diffuse emission model gll_iem_v05_rev1.fits and isotropic diffuse model iso_source_v05.txt provided by the Fermi-LAT collaboration were used3. A 20° × 20° region of interest binned in 0.1° bins and centred on the position of W49B was defined. Sources within 25° of W49B were extracted from the Fermi-LAT 3FGL catalogue (Acero et al. 2015) and included in the likelihood fit. The spectral parameters of sources closer than 5° to W49B or with a TS larger than 400 were left free and shown with diamonds in Fig. 4, while the parameters of all other sources were fixed at the values from the 3FGL catalogue.
Two main systematic errors have been taken into account: imperfect modelling of the Galactic diffuse emission and uncertainties in the effective area calibration. The first was estimated by comparing the results obtained using the standard Galactic diffuse model with the results based on eight alternative interstellar emission models (IEMs) as performed in de Palma et al. (2013). The alternative IEMs do not necessarily bracket the standard IEM, but provide a good insight into deviations from fit results obtained by the standard IEM expected from variations in the IEM. Comparing results between analyses performedusing the standard and alternative IEMs is currently the best method to estimate systematic uncertainties related to the IEM modelling. The second major systematic uncertainty was estimated using modified IRFs whose effective areas bracket the nominal areas. These bracketing IRFs are defined by envelopes above and below the nominal energy dependence of the effective area by linearly connecting differences of (10%, 5%, 5%, and 15%) at log10 (E∕MeV) of (2, 2.5, 4, and 6), respectively4.
 |
Fig. 4 Fermi-LAT count map of the 20° × 20° around W49B between 60 MeV and 300 GeV, smoothed with a Gaussian of width 0.3°. Spectral parameters of sources indicated by a diamond are left free in the analysis while sources indicated with crosses are frozen in the likelihood fit. Events were spatially binned in pixels of side-length 0.1°. The dominant source seen at a Galactic longitude of 34.6° in this counts map is W44. |
2.2.2 Fermi-LAT analysis results
The spatial analysis was performed using all events above 1 GeV, thus providing a good compromise between statistics and angular resolution. The source position, determined by pointlike is 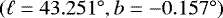 with a statistical uncertainty of 0.015° (95% CL), which is compatible with the radio shell of W49B (see Fig. 2). At this position, the TS value above 1 GeV is 1504. No significant extension was found with pointlike.
with a statistical uncertainty of 0.015° (95% CL), which is compatible with the radio shell of W49B (see Fig. 2). At this position, the TS value above 1 GeV is 1504. No significant extension was found with pointlike.
The spectral analysis was then performed with gtlike including all events between 0.06 and 300 GeV. Here the best-fit point-sourceposition for W49B obtained by pointlike was used in the log likelihood fit. Figure 3 shows the spectral energy distribution obtained for W49B through the maximum likelihood estimation. To derive the flux points, the 0.06−300 GeV range was divided into 20 logarithmically spaced energy bins and a maximum likelihood spectral analysis was performed in each interval, assuming a power-law shape with a fixed spectral index of Γ = 2 for W49B. The normalisations of the diffuse Galactic and isotropic emission were left free in each energy bin as well as those of sources located within 5° from W49B. A 95% CL upper limit is computed when the statistical significance is lower than 2σ. At the highest energies, bins containing no significant signal were combined to compute a meaningful upper limit. The errors on the spectral points represent the statistical and systematic uncertainties added in quadrature.
The spectrum below 300 MeV is steeply rising, clearly exhibiting a break at around 300 MeV. To quantify the significance of this spectral break, a log likelihood fit of W49B between 60 MeV and 4 GeV was performed (below the high-energy break previously found in the one-year spectra, Abdo et al. 2010d) using both a single power law of the form 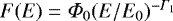 and a smoothly broken power law of the form
and a smoothly broken power law of the form 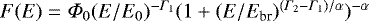 , where Φ0 is the differential flux at E0 = 200 MeV and α = 0.1, as was carried out previously for the cases of IC 443 and W44 (Ackermann et al. 2013). The improvement in log likelihood when comparing the broken power law to a single power law corresponds to a formal statistical significance of 8σ for the low-energy break (TS of 84 for 2 additional degrees of freedom), as reported in Table 1. Another fit in the same energy band using a log parabola was also performed, showing that the log parabola improves the likelihood by only 5σ (TS of 28 for 1 additional degree of freedom). Therefore the best spectral shape for this energy band is the broken power law.
, where Φ0 is the differential flux at E0 = 200 MeV and α = 0.1, as was carried out previously for the cases of IC 443 and W44 (Ackermann et al. 2013). The improvement in log likelihood when comparing the broken power law to a single power law corresponds to a formal statistical significance of 8σ for the low-energy break (TS of 84 for 2 additional degrees of freedom), as reported in Table 1. Another fit in the same energy band using a log parabola was also performed, showing that the log parabola improves the likelihood by only 5σ (TS of 28 for 1 additional degree of freedom). Therefore the best spectral shape for this energy band is the broken power law.
 |
Fig. 3 Fermi-LAT and H.E.S.S. spectrum of W49B. The red line shows the best fit of a smoothly broken power law derived between 60 MeV and 4 GeV and the blue data points indicate the fluxes measured in each energy bin with the Fermi-LAT. The statistical errors are shown in blue, while the red lines take both the statistical and systematic errors into account as discussed in Sect. 2.2.2. The grey band shows the 68% confidence level (CL) uncertainty of the best-fit power-law model with H.E.S.S. The open black circles indicate the spectral points computed from the forward-folding fit with their statistical errors shown in black. For both instruments, a 95% CL upper limit is computed when the statistical significance is lower than 2σ. The dotted green line shows the best smoothly broken power-law model obtained from the joint fit of the Fermi-LAT and H.E.S.S. data between 500 MeV and 10 TeV, as described in Sect. 2.3. |
Spectral parameters in the energy ranges of 60 MeV–4 GeV and 500 MeV–300 GeV for power-law (PL) and smoothly broken power-law (SBPL) models, using Fermi-LAT data and 290 GeV–10 TeV with H.E.S.S.
2.3 H.E.S.S. and Fermi-LAT combined results
The best-fit position obtained with the Fermi-LAT is coincident with the radio shell, while the fitted position in the TeV range is more compatible with its centre (see Fig. 2). However, the size of the shell detected at radio wavelengths is comparable to the size of the H.E.S.S. point spread function, preventing discrimination between the emission originating from the centre of the remnant or from its shell. Furthermore, the spectra derived in the GeV and TeV energy ranges are in good agreement (see Fig. 3). The positions and spectra are also compatible with those reported in the recently published second Fermi-LAT catalogue of sources above 50 GeV (Ackermann et al. 2016). It is therefore reasonable to assume that the detected γ-ray photons are emitted in the same physical region of the W49B remnant.
Taking advantage of the smooth connection between the HE and VHE spectra, the presence of another break at high energy was evaluated through a likelihood ratio test statistic applied to both the H.E.S.S. and Fermi-LAT data. For this test, a single power law and a smoothly broken power law between 500 MeV and 10 TeV, which is above the low energy break found above, were used, and the statistical and systematic uncertainties were taken into account. The minimum of the likelihood ratio is reached at 8.4 GeV with a 6.5σ improvement of the smoothly broken power-law model with respect to the power-law model. The 68% confidence interval is [5.9; 10.6] GeV and the spectral indices below and above the break are 2.17 ± 0.06 and 2.80 ± 0.04, respectively. This result was checked by fitting the Fermi-LAT fluxes of W49B between 500 MeV and 300 GeV with both a single power law and a smoothly broken power law. A 3.3σ (TS of 14 for 2 additional degrees of freedom) improvement is obtained for an energy break at 9.4 ± 2.9stat ± 3.8sys GeV. This energy,as well as the spectral indices above and below the break (listed in Table 1), are compatible with the values obtained from the Fermi-LAT and H.E.S.S. joint fit.
3 Discussion of the results
3.1 General considerations
A spectral break is detected at 304 ± 20 MeV with the Fermi-LAT, with properties (break energy, spectral indices) similar to those detected in the SNRs IC 443 and W44 (Ackermann et al. 2013) and interpreted as the signature of γ-ray emission produced through neutral-pion decay. In addition, the H.E.S.S. and Fermi-LAT joint spectral fit allowed for the estimation of a second spectral break at 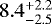 GeV, which is compatible with the break energy position found using the Fermi-LAT data alone (9.4 ± 2.9 GeV). Such a spectral break has been found in several other interacting SNRs, for instance in W51C (Abdo et al. 2009b), W28 (Abdo et al. 2010a), and G349.7+0.2 (H.E.S.S. Collaboration 2015). The energy at which this break occurs is found to be in the range 1− 20 GeV, except for G349.7+0.2 where it is found at a higher energy (~ 50 GeV). Interestingly, while W49B is estimated to be 1−4 thousand years old, it exhibits spectral features similar to the other detected SNR/MC systems that are believed to be ~ 10 times older. Likewise, G349.7+0.2 which has roughly the same age as W49B, shows an energy break that is ~ 5 times higher. This emphasises the importance of the environment in the evolution of the γ-ray luminosity of these objects.
GeV, which is compatible with the break energy position found using the Fermi-LAT data alone (9.4 ± 2.9 GeV). Such a spectral break has been found in several other interacting SNRs, for instance in W51C (Abdo et al. 2009b), W28 (Abdo et al. 2010a), and G349.7+0.2 (H.E.S.S. Collaboration 2015). The energy at which this break occurs is found to be in the range 1− 20 GeV, except for G349.7+0.2 where it is found at a higher energy (~ 50 GeV). Interestingly, while W49B is estimated to be 1−4 thousand years old, it exhibits spectral features similar to the other detected SNR/MC systems that are believed to be ~ 10 times older. Likewise, G349.7+0.2 which has roughly the same age as W49B, shows an energy break that is ~ 5 times higher. This emphasises the importance of the environment in the evolution of the γ-ray luminosity of these objects.
The origin of the break in the 1−20 GeV range has been the subject of several theoretical works. It could be explained either by the diffusion of particles escaping the shock (e.g. Ohira et al. 2011; Li & Chen 2012), acceleration and wave evanescence effects (e.g. Inoue et al. 2010; Malkov et al. 2012), or time-limited re-acceleration of CRs already present in the surroundings (e.g. Uchiyama et al. 2010; Cardillo et al. 2016). Other phenomena might be at play in such objects, such as a so-called neutral return flux that can modify the dynamics of the shock when propagating into a partially neutral medium (Blasi et al. 2012). The maximum energy that accelerated particles can achieve could be limited by the ion-neutral damping (Ptuskin & Zirakashvili 2005) and their spectrum could be steepened due to the feedback of amplified magnetic fields (Ptuskin et al. 2010; Caprioli 2012). Future precision modelling may be able to take the whole history and environment of W49B into account to predict the spectra of accelerated particles in this source and resultant radiation from radio to TeV energies. In this work, a simple one-zone model that assumes an empirical distribution of accelerated particles is used specifically to constrain the energetics and the dominant processes in the source.
3.2 Molecular gas density estimates
In order to use appropriate values for the modelling, the mass and density of the molecular gas inside a spherical volume of radius 0.025°, which is consistent with that of the radio SNR radius, were estimated using the Galactic Ring Survey 13CO data (Jackson et al. 2006). For the three velocity ranges (1−15, 38−47, and 57−67 km s−1 at their kinematic distances of 11, 9.3, and 5 kpc, respectively) examined by Zhu et al. (2014) (see also Chen et al. 2014), and using the 13CO “X-factor” of 4.92 × 1020 (K km/s)−1 from Simon et al. (2001), masses of 5 × 103 to 17 × 103 M⊙ with densities of 400 to 4000 cm−3 were obtained. Allowing for a larger radius to the outer edge of the radio SNR features (0.05°) reduces the molecular gas densities by a factor ~2 to 3.
Chen et al. (2014) and Zhu et al. (2014) have argued that the CO bubble in the 38−47 km s−1 range was blown out by the W49B progenitor star, suggesting a distance of about 10 kpc for the SNR. Additionally for this, and the 57−67 km s−1 ranges, the H2 column densities (about 5 × 1022 cm−2) inferred in this work are consistent with that derived from the X-ray spectral studies of Keohane et al. (2007).
3.3 High-energy particles in W49B
The observed γ-ray emission is most likely to originate from SNR W49B, as discussed in Abdo et al. (2010d). In this section, the properties of the relativistic particles that radiate at γ-ray energies are investigated. Given the smooth connection of the observed Fermi-LAT and H.E.S.S. spectra (see Fig. 3), it is assumed that the γ-ray photons are emitted in the same region. In addition, the observed radio emission (e.g. Moffett & Reynolds 1994) is assumed to come from the same shell region where a constant hydrogen density nH and magnetic field strength B are considered. Given the evidence that W49B interacts with the surrounding molecular clouds (e.g. Keohane et al. 2007; Zhu et al. 2014), we consider a scenario where the γ-ray emission comes from the shocked molecular clouds in the SNR shell. The emitting region may originate from swept-up stellar wind and/or interstellar gas as discussed in Abdo et al. (2010d). However, adopting such a scenario would not significantly change the spectra calculated in this section.
The γ-ray emission is reproduced using the (relatively) simple model described in Abdo et al. (2009b). Empirical injection distributions of protons and electrons are assumed as follows:
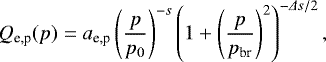 (1)
(1)
where p0 = 1 GeV c−1, pbr is the break momentum, s is the spectral index below pbr, and Δs is the difference between the spectral indices values below and above pbr. The kinetic equation for the momentum distribution of high-energy particles in the shell can be written as
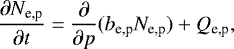 (2)
(2)
where be,p = −dp∕dt is the momentum loss rate; only the synchrotron, inverse-Compton, bremsstrahlung, and neutral pion decay radiative losses were considered; and Qe,p(p), which is assumed to be time independent, is the particle injection rate. To obtain the radiation spectrum from the remnant, Ne,p (p, T0) is numerically calculated for T0 = 2000 yr.
The γ-ray emission mechanisms include the π0-decay γ-rays due to high-energy protons, bremsstrahlung, and inverse-Compton scattering processes by high-energy electrons. The radio emission is calculated by considering the synchrotron radiation from the population of high-energy electrons. To reproduce the multi-wavelength spectra, two cases of the relativistic electrons to protons number ratio (Kep ≡ ae∕ap) were considered, Kep = 0.01 and Kep = 1. The value of 0.01 is similar to what is locally observed for cosmic rays at GeV energies (e.g. Beischer et al. 2009) whereas Kep = 1 corresponds to an upper limit of the ratio that is most likely too high for realistic applications due to the faster cooling of the electrons compared to the protons. In the calculation, the same indices and break momenta for both the electrons and the protons were chosen. Given that the radio synchrotron index α = 0.48 (Moffett & Reynolds 1994) corresponds to s ~ 2, three values for s were considered: 1.8, 2.0, and 2.2. The observed γ-ray spectra are calculated by adjusting spectral parameters of the relativistic particles: the normalisation, the break momentum pbr , and Δs. The magnetic field B is then determined to explain the observed radio data. Only thermal X-rays, which are not useful in constraining the non-thermal electron population energy distribution, are observed from the SNR (Hwang et al. 2000). In the energy range 1–10 keV, our model synchrotron X-ray predictions would be at least one order of magnitude below the measured thermal X-ray values; thus no constraining limits exist in this part of the spectrum. Two conservative cases of 100 cm−3 and 1000 cm−3 for the ambient medium density nH were considered (see Sec. 3.2). The seed photons for inverse-Compton scattering processes include infrared (kTIR = 3 × 10−3 eV, UIR = 0.7 eV cm−3), optical (kTopt= 0.3 eV, Uopt = 0.8 eV cm−3), and the CMB. These values were taken to match the axisymmetric estimates of the GALPROP code at the assumed distance of W49B (Porter et al. 2008, and references therein). For a more precise modelling, dedicated analysis of the infrared and optical emission around the source should be performed. The derived parameters and spectra are shown in Tables 2 and 3, and Figs. 5 and 6.
In the case of Kep = 0.01 (the hadronic scenario), the obtained γ-ray spectrum is dominated by the π0-decay emission due to the relativistic protons as shown in Fig. 5. The observed spectra can be formally explained in all the cases except for the case (a4) where the reproduced synchrotron spectrum seems a little harder than the observed radio data. The rather high values derived for the magnetic field of models (a4–6) are needed to explain the radio data. This is because Kep is fixed to 0.01; allowing for higher values of Kep would implyhigher total kinetic energies for the electrons and lower magnetic field values would be needed to explain the radio data.
The reproduced spectral shape is independent of the value of nH , as long as the range is set to reasonable values (nH ~ 100–1000 cm−3).
In the case of Kep = 1 (the leptonic scenario), the obtained γ-rays are dominated by the bremsstrahlung emission due to the relativistic electrons as shown in Fig. 6. The figure shows that s ≲ 1.8 is required to explain the LAT data below ~300 MeV. The synchrotron radiation loss modifies the reproduced spectra at the ≳ TeV range; its break momentum of the electrons are 16 TeV c−1 and 0.6 TeV c−1 for B of 20 μG (corresponding to the cases (b1–3)) and 100 μG (corresponding to the cases (b4–6)), respectively. On the other hand, the spectral shape does not significantly change in the energy bandbelow the break.
As discussed in Sect. 2.2, the LAT data show a clear spectral break at 304 ± 20 MeV. Given the systematic errors of the data, both the hadronic and leptonic scenarios can explain this spectral shape. In the leptonic scenario, however, a limit to the spectral index of s ≲ 1.8 must be set to reproduce such a sharp break. On the other hand, the hadronic scenario can naturally explain the break by the π0 -decay bump irrespective of the spectral index. The obtained B-field values in Tables 2 and 3 are significantly larger than typical interstellar values. To some extent, these values correspond to those expected in a MC (Crutcher et al. 2010). They are also consistent with predictions of magnetic field amplification from cosmic-ray-excited turbulence (Bell 2004; Zirakashvili et al. 2008). The values adopted in this modelling are set to reasonable values and different assumptions for the parameters (age, distance, nH , and Kep ) would change the quantitative results of the modelling slightly (derived magnetic field or energy values), but would not change these conclusions.
 |
Fig. 5 SEDs of W49B with model curves for the hadronic-dominant scenario. The upper and lower panels show (a1–3) and (a4–6), respectively (see Table 2). The red diamonds, red circles, and magenta squares represent observed data in the radio (Moffett & Reynolds 1994), LAT, and H.E.S.S. bands, respectively. The radio emission is explained by the synchrotron radiation from the relativistic electrons. The γ-ray emission canbe decomposed into π0-decay (dotted line), bremsstrahlung (dashed line), and IC scattering (dot-dashed line). The solid line represents the total flux of the components. The cases (a1)/(a4), (a2)/(a5), and (a3)/(a6) are represented by cyan, blue, and green lines, respectively,in the upper/lower panel. The decomposed emissions are shown for the cases (a2) and (a5) in the upper and lower panels, respectively. |
Parameters for the hadronic scenario.
 |
Fig. 6 Same as Fig. 5 but for the leptonic-dominant scenario. The upper and lower panels show reproduced spectra of (b1–3) and (b4–6), respectively (see Table 3). The cases (b1)/(b4), (b2)/(b5), and (b3)/(b6) are represented by cyan, blue, and green lines, respectively, in the upper/lower panel. The decomposed emission is shown for the cases (b2) and (b5) in the upper and lower panels, respectively. |
Parameters for the leptonic scenario.
4 Conclusions
A source of very high-energy γ rays is detected towards the supernova remnant W49B with H.E.S.S. and a joint study is conducted together with the analysis of five years of Fermi-LAT data towards the source. The point spread functions of these instruments are comparable to the physical size of the SNR and do not allow for detailed morphology studies. However, the significantly increased data set compared to previous publications allowed for the derivation of the γ-ray spectrum of the source between 60 MeV and a few TeV. Two spectral breaks could be identified in the γ-ray spectrum: one at 304 MeV and the other at 8.4 GeV. The latter, constrained from a joint fit of the Fermi-LAT and H.E.S.S. data, is similar to the spectral breaks observed in other supernova remnants interacting with molecular clouds and further supports the evidence of interaction observed in other wavelengths for this object. The broadband spectrum of W49B could be explained either by leptonic or hadronic models. However, the sharp break detected with the Fermi-LAT data at 304 MeV seems to favour a hadronic origin of the γ-ray emission since the leptonic models would require an even harder spectrum for the electron population than those tested in this work, which would fail to explain the radio observations.
In the near future, W49B and the nearby star-forming region W49A will be of particular interest to study at VHE with improved analysis methods and with the next generation of instruments such as the Cherenkov Telescope Array. Observations or analyses of the W49 region with improved angular resolution and higher sensitivity would help to constrain the morphology and the origin of the emission towards W49B and possibly confirm the hint of emission towards W49A. Furthermore, if one assumes that the distances to W49A and W49B are comparable, then the observed difference between the γ-ray luminosities of the two sources would become especially interesting. This would imply that, in the absence of recognizable supernova remnants, as in W49A, the other possible energetic particle sources, such as shocks expected from interacting or collective stellar winds, do not appear very effective for HE and VHE γ-ray emission in this case. Therefore, a truly reliable distance determination for these sources (see Sect. 1) would be of great astrophysical importance.
Acknowledgements
The support of the Namibian authorities and of the University of Namibia in facilitating the construction and operation of H.E.S.S. is gratefully acknowledged, as is the support by the German Ministry for Education and Research (BMBF), the Max Planck Society, the German Research Foundation (DFG), the French Ministry for Research, the CNRS-IN2P3 and the Astroparticle Interdisciplinary Programme of the CNRS, the UK Science and Technology Facilities Council (STFC), the IPNP of the Charles University, the Czech Science Foundation, the Polish Ministry of Science and Higher Education, the South African Department of Science and Technology and National Research Foundation, the University of Namibia, the Innsbruck University, the Austrian Science Fund (FWF), and the Austrian Federal Ministry for Science, Research and Economy, and by the University of Adelaide and the Australian Research Council. We appreciate the excellent work of the technical support staff in Berlin, Durham, Hamburg, Heidelberg, Palaiseau, Paris, Saclay, and in Namibia in the construction and operation of the equipment. This work benefited from services provided by the H.E.S.S. Virtual Organisation, supported by the national resource providers of the EGI Federation. The Fermi LAT Collaboration acknowledges generous ongoing support from a number of agencies and institutes that have supported both the development and the operation of the LAT as well as scientific data analysis. These include the National Aeronautics and Space Administration and the Department of Energy in the United States, the Commissariat à l’Énergie Atomique and the Centre National de la Recherche Scientifique/Institut National de Physique Nucléaire et de Physique des Particules in France, the Agenzia Spaziale Italiana and the Istituto Nazionale di Fisica Nucleare in Italy, the Ministry of Education, Culture, Sports, Science and Technology (MEXT), High Energy Accelerator Research Organization (KEK), and Japan Aerospace Exploration Agency (JAXA) in Japan, and the K. A. Wallenberg Foundation, the Swedish Research Council, and the Swedish National Space Board in Sweden. Additional support for science analysis during the operations phase is gratefully acknowledged from the Istituto Nazionale di Astrofisica in Italy and the Centre National d’Études Spatiales in France. This publication makes use of molecular line data from the Boston University-FCRAO Galactic Ring Survey (GRS). The GRS is a joint project of Boston University and Five College Radio Astronomy Observatory, funded by the National Science Foundation under grants AST-9800334, AST-0098562, AST-0100793, AST-0228993 & AST-0507657.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009a, ApJS, 183, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009b, ApJ, 706, L1 [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010a, ApJ, 718, 348 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010b, Science, 327, 1103 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010c, ApJ, 712, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010d, ApJ, 722, 1303 [NASA ADS] [CrossRef] [Google Scholar]
- Abramowski, A., Acero, F., Aharonian, F., et al. 2012, A&A, 537, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Acciari, V. A., Aliu, E., Arlen, T., et al. 2009, ApJ, 698, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Acero, F., Ackermann, M., Ajello, M., et al. 2015, ApJS, 218, 23 [Google Scholar]
- Ackermann, M., Ajello, M., Allafort, A., et al. 2013, Science, 339, 807 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ackermann, M., Ajello, M., Atwood, W. B., et al. 2016, ApJS, 222, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2006a, A&A, 457, 899 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2006b, A&A, 449, 223 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Barres de Almeida, U., et al. 2008a, A&A, 490, 685 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2008b, A&A, 481, 401 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., de Almeida, U. B., et al. 2009, ApJ, 692, 1500 [NASA ADS] [CrossRef] [Google Scholar]
- Albert, J., Aliu, E., Anderhub, H., et al. 2007, ApJ, 664, L87 [NASA ADS] [CrossRef] [Google Scholar]
- Atwood, W. B., Abdo, A. A., Ackermann, M., et al. 2009, ApJ, 697, 1071 [NASA ADS] [CrossRef] [Google Scholar]
- Beischer, B., van Doetinchem, P., Gast, H., et al. 2009, New J. Phys., 11, 105021 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, A. R. 2004, MNRAS, 353, 550 [Google Scholar]
- Berge, D., Funk, S., & Hinton, J. 2007, A&A, 466, 1219 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blasi, P. 2013, A&ARv, 21, 70 [Google Scholar]
- Blasi, P., Morlino, G., Bandiera, R., Amato, E., & Caprioli, D. 2012, ApJ, 755, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Bregeon, J., Charles, E., & M. Wood (for the Fermi-LAT Collaboration) 2013, 2012 Fermi Symp. Proc. eConf. C121028 [arXiv:1304.5456] [Google Scholar]
- Brogan, C. L., & Troland, T. H. 2001, ApJ, 550, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Caprioli, D. 2012, J. Cosmol. Astropart. Phys., 7, 038 [NASA ADS] [CrossRef] [Google Scholar]
- Cardillo, M., Amato, E., & Blasi, P. 2016, A&A, 595, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castro, D., & Slane, P. 2010, ApJ, 717, 372 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, Y., Jiang, B., Zhou, P., et al. 2014, in IAU Symp. 296, eds. A. Ray, & R. A. McCray, 170 [Google Scholar]
- Crutcher, R. M., Wandelt, B., Heiles, C., Falgarone, E., & Troland, T. H. 2010, ApJ, 725, 466 [NASA ADS] [CrossRef] [Google Scholar]
- de Naurois M., & Rolland, L. 2009, Astropart. Phys., 32, 231 [NASA ADS] [CrossRef] [Google Scholar]
- de Palma, F., Brandt, T. J., Johannesson, G., Tibaldo, L., (for the Fermi-LAT Collaboration) 2013, 2012 Fermi Symp. Proc. eConf. C121028 [arXiv:1304.1395] [Google Scholar]
- Drury, L. O. 1983, Rep. Prog. Phys., 46, 973 [NASA ADS] [CrossRef] [Google Scholar]
- González-Casanova, D. F., De Colle, F., Ramirez-Ruiz, E., & Lopez, L. A. 2014, ApJ, 781, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Green, D. A. 2014, Bull. Astron. Soc. India, 42, 47 [NASA ADS] [Google Scholar]
- Helfand, D. J., Becker, R. H., White, R. L., Fallon, A., & Tuttle, S. 2006, AJ, 131, 2525 [NASA ADS] [CrossRef] [Google Scholar]
- H.E.S.S. Collaboration (Abramowski, A., Aharonian, F., et al.) 2015, A&A, 574, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- H.E.S.S. Collaboration (Abdalla, H., Abramowski, A., et al.) 2018, A&A, 612, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hinton, J. A. 2004, New Astron., 48, 331 [Google Scholar]
- Hwang, U., Petre, R., & Hughes, J. P. 2000, ApJ, 532, 970 [NASA ADS] [CrossRef] [Google Scholar]
- Inoue, T., Yamazaki, R., & Inutsuka, S.-I. 2010, ApJ, 723, L108 [NASA ADS] [CrossRef] [Google Scholar]
- Jackson, J. M., Rathborne, J. M., Shah, R. Y., et al. 2006, ApJS, 163, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Jogler, T., & Funk, S. 2016, ApJ, 816, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Keohane, J. W., Reach, W. T., Rho, J., & Jarrett, T. H. 2007, ApJ, 654, 938 [NASA ADS] [CrossRef] [Google Scholar]
- Lande, J., Ackermann, M., Allafort, A., et al. 2012, ApJ, 756, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Li, H., & Chen, Y. 2012, MNRAS, 421, 935 [NASA ADS] [CrossRef] [Google Scholar]
- Li, T.-P., & Ma, Y.-Q. 1983, ApJ, 272, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Lockman, F. J. 1989, ApJS, 71, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Lopez, L. A., Ramirez-Ruiz, E., Castro, D., & Pearson, S. 2013, ApJ, 764, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Malkov, M. A., Diamond, P. H., & Sagdeev, R. Z. 2012, Phys. Plasmas, 19, 082901 [NASA ADS] [CrossRef] [Google Scholar]
- Mattox, J. R., Bertsch, D. L., Chiang, J., et al. 1996, ApJ, 461, 396 [NASA ADS] [CrossRef] [Google Scholar]
- Mezger, P. G., Schraml, J., & Terzian, Y. 1967, ApJ, 150, 807 [NASA ADS] [CrossRef] [Google Scholar]
- Moffett, D. A., & Reynolds, S. P. 1994, ApJ, 437, 705 [NASA ADS] [CrossRef] [Google Scholar]
- Ohira, Y., Murase, K., & Yamazaki, R. 2011, MNRAS, 410, 1577 [NASA ADS] [Google Scholar]
- Ohm, S., van Eldik, C., & Egberts, K. 2009, Astropart. Phys., 31, 383 [NASA ADS] [CrossRef] [Google Scholar]
- Parsons, R. D., & Hinton, J. A. 2014, Astropart. Phys., 56, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Piron, F., Djannati-Atai, A., Punch, M., et al. 2001, A&A, 374, 895 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Porter, T. A., Moskalenko, I. V., Strong, A. W., Orlando, E., & Bouchet, L. 2008, ApJ, 682, 400 [NASA ADS] [CrossRef] [Google Scholar]
- Ptuskin, V. S., & Zirakashvili, V. N. 2005, A&A, 429, 755 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Ptuskin, V., Zirakashvili, V., & Seo, E.-S. 2010, ApJ, 718, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Pye, J. P., Becker, R. H., Seward, F. D., & Thomas, N. 1984, MNRAS, 207, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Radhakrishnan, V., Goss, W. M., Murray, J. D., & Brooks, J. W. 1972, ApJS, 24, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Rho, J., & Petre, R. 1998, ApJ, 503, L167 [NASA ADS] [CrossRef] [Google Scholar]
- Scoville, N. Z., Sargent, A. I., Sanders, D. B., et al. 1986, ApJ, 303, 416 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, R., Jackson, J. M., Clemens, D. P., Bania, T. M., & Heyer, M. H. 2001, ApJ, 551, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Uchiyama, Y., Blandford, R. D., Funk, S., Tajima, H., & Tanaka, T. 2010, ApJ, 723, L122 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, R. C., Matsakis, D. N., & Garcia-Barreto, J. A. 1982, ApJ, 255, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Westerhout, G. 1958, Bull. Astron. Inst. Netherlands, 14, 215 [NASA ADS] [Google Scholar]
- Wu, S.-W., Bik, A., Henning, T., et al. 2014, A&A, 568, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, B., Reid, M. J., Menten, K. M., et al. 2013, ApJ, 775, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, X., Miceli, M., Bocchino, F., Orlando, S., & Chen, Y. 2011, MNRAS, 415, 244 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, H., Tian, W. W., & Zuo, P. 2014, ApJ, 793, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Zirakashvili, V. N., Ptuskin, V. S., & Völk, H. J. 2008, ApJ, 678, 255 [NASA ADS] [CrossRef] [Google Scholar]
It was designated as 0FGL J1911.0+0905 in this so-called Bright Sources List (Abdo et al. 2009a).
More information about the performance of the LAT can be found at the FSSC (http://fermi.gsfc.nasa.gov/ssc).
These models are available at: http://fermi.gsfc.nasa.gov/ssc/data/access/lat/BackgroundModels.html
All Tables
Spectral parameters in the energy ranges of 60 MeV–4 GeV and 500 MeV–300 GeV for power-law (PL) and smoothly broken power-law (SBPL) models, using Fermi-LAT data and 290 GeV–10 TeV with H.E.S.S.
All Figures
 |
Fig. 1 γ-ray excess map of the W49 region obtained with H.E.S.S. The map is smoothed with a Gaussian of width 0.06°, corresponding to the 68% radius containment of the H.E.S.S. point spread function (PSF; shown in the inset). The black triangle denotes the position of the supernova remnant W49B (Green 2014). The white triangle denotes the position of W49A (Lockman 1989). |
| In the text | |
 |
Fig. 2 Zoomed-in version of Fig. 1. The crosses show the best-fit positions of the source with H.E.S.S. (black) and Fermi-LAT (blue). The size of the crosses represents the size of the 95% confidence level (CL) contours on the best-fit positions, including systematic uncertainties. The white contours show the radio intensity obtained at a wavelength of 20 cm with MAGPIS (Helfand et al. 2006). |
| In the text | |
 |
Fig. 4 Fermi-LAT count map of the 20° × 20° around W49B between 60 MeV and 300 GeV, smoothed with a Gaussian of width 0.3°. Spectral parameters of sources indicated by a diamond are left free in the analysis while sources indicated with crosses are frozen in the likelihood fit. Events were spatially binned in pixels of side-length 0.1°. The dominant source seen at a Galactic longitude of 34.6° in this counts map is W44. |
| In the text | |
 |
Fig. 3 Fermi-LAT and H.E.S.S. spectrum of W49B. The red line shows the best fit of a smoothly broken power law derived between 60 MeV and 4 GeV and the blue data points indicate the fluxes measured in each energy bin with the Fermi-LAT. The statistical errors are shown in blue, while the red lines take both the statistical and systematic errors into account as discussed in Sect. 2.2.2. The grey band shows the 68% confidence level (CL) uncertainty of the best-fit power-law model with H.E.S.S. The open black circles indicate the spectral points computed from the forward-folding fit with their statistical errors shown in black. For both instruments, a 95% CL upper limit is computed when the statistical significance is lower than 2σ. The dotted green line shows the best smoothly broken power-law model obtained from the joint fit of the Fermi-LAT and H.E.S.S. data between 500 MeV and 10 TeV, as described in Sect. 2.3. |
| In the text | |
 |
Fig. 5 SEDs of W49B with model curves for the hadronic-dominant scenario. The upper and lower panels show (a1–3) and (a4–6), respectively (see Table 2). The red diamonds, red circles, and magenta squares represent observed data in the radio (Moffett & Reynolds 1994), LAT, and H.E.S.S. bands, respectively. The radio emission is explained by the synchrotron radiation from the relativistic electrons. The γ-ray emission canbe decomposed into π0-decay (dotted line), bremsstrahlung (dashed line), and IC scattering (dot-dashed line). The solid line represents the total flux of the components. The cases (a1)/(a4), (a2)/(a5), and (a3)/(a6) are represented by cyan, blue, and green lines, respectively,in the upper/lower panel. The decomposed emissions are shown for the cases (a2) and (a5) in the upper and lower panels, respectively. |
| In the text | |
 |
Fig. 6 Same as Fig. 5 but for the leptonic-dominant scenario. The upper and lower panels show reproduced spectra of (b1–3) and (b4–6), respectively (see Table 3). The cases (b1)/(b4), (b2)/(b5), and (b3)/(b6) are represented by cyan, blue, and green lines, respectively, in the upper/lower panel. The decomposed emission is shown for the cases (b2) and (b5) in the upper and lower panels, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


