| Issue |
A&A
Volume 610, February 2018
|
|
|---|---|---|
| Article Number | A52 | |
| Number of page(s) | 14 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201731227 | |
| Published online | 27 February 2018 | |
The influence of convective blueshift on radial velocities of F, G, and K stars
1
Institut für Astrophysik (IAG), Georg-August-Universität Göttingen,
Friedrich-Hund-Platz 1,
37077
Göttingen, Germany
e-mail: fbauer@astro.physik.uni-goettingen.de
2
Max Planck Institut für Sonnensystem Forschung,
37077
Göttingen, Germany
Received:
23
May
2017
Accepted:
30
October
2017
Context. Apparent radial velocity (RV) signals induced by stellar surface features such as spots and plages can result in a false planet detection or hide the presence of an orbiting planet. Our ability to detect rocky exoplanets is currently limited by our understanding of such stellar signals.
Aims. We model RV variations caused by active regions on the stellar surface of typical exoplanet-hosting stars of spectral type F, G, and K. We aim to understand how the stellar magnetic field strength, convective blueshift, and spot temperatures can influence RV signals caused by active regions.
Methods. We use magneto-hydrodynamic (MHD) simulations for stars with spectral types F3V, a G2V, and a K5V. We quantify the impact of the magnetic field strength inside active regions on the RV measurement using the magnetic and non-magnetic FeI lines at 6165 Å and 6173 Å. We also quantify the impact of spot temperature and convective blueshift on the measured RV values.
Results. Increasing the magnetic field strength increases the efficiency to suppress convection in active regions which results in an asymmetry between red- and blueshifted parts of the RV curves. A stronger suppression of convection also leads to an observed increase in RV amplitude for stronger magnetic fields. The MHD simulations predict convective motions to be faster in hotter stars. The suppression of faster convection leads to a stronger RV amplitude increase in hotter stars when the magnetic field is increased. While suppression of convection increases the asymmetry in RV curves,c a decreasing spot temperature counteracts this effect. When using observed temperatures for dark spots in our simulations we find that convective blueshift effects are negligible.
Key words: techniques: radial velocities / stars: activity / starspots
© ESO 2018
1 Introduction
For about two decades the radial velocity (RV) method has been successfully used to detect extrasolar planets. Since the first planet detection by Mayor & Queloz (1995), the RV technique has undergone major improvements (Latham et al. 1998; Fischer et al. 2016). Current instruments like HARPS (Mayor et al. 2003) can reach a precision of a few m/s in the optical. Several instruments like CARMENES (Quirrenbach et al. 2011), SPIROU (Artigau et al. 2011), IRD (Kotani et al. 2014), and HPF (Mahadevan et al. 2010) aim to extend this precision to the near-infrared. Furthermore, ESPRESSO (D’Odorico et al. 2007) aims to achieve an unprecedented precision of 20 cm/s at optical wavelengths. With this next generation of RV machines, instrumental noise will no longer be the limiting factor in detecting exoplanets similar to Earth. However, astrophysical noise sources such as stellar activity will become a concern and hinder planet detections (Fischer et al. 2016).
Current exoplanet surveys focus on solar-like stars of spectral type F, G, K, and M to detect rocky planets in the habitable zone of their host stars. Unfortunately these stars exhibit a variety of intrinsic signals as well which are often referred to as stellar noise or jitter in the exoplanet community. Asteroseismic oscillations and granulation cause signals on the timescales of minutes to days (Butler et al. 2004; Dumusque et al. 2011; Meunier et al. 2015), and magnetic activity, manifested as spots, produces signals associated with the rotation period of the stars (Radick et al. 1983; Benedict et al. 1993) in the range of hours to months. Because of the similar timescales, the signals of small spots are often hard to disentangle from planetary companions in RV searches. This has lead to several examples in the literature where proposed planets have been identified later as stellar activity or are still under debate today (e.g., Udry et al. 2007; Vogt et al. 2010; Robertson et al. 2014, 2015; Anglada-Escudé et al. 2014, 2016).
Hence, new tools are needed to understand and possibly correct for activity signals of the host star to be able to detect small exoplanets reliably in the future. In this context, many attempts have been made to model the activity modulation of RV curves from stellar spots. All of them have in common that the RVs are estimated from the disk integrated spectrum which is constructed from a grid of quiet and spotted regions. The spectra of quiet and active regions differ from each other because of temperature and magnetic field, and therefore the choice of the model spectra influences the resulting RVs. As an overview we summarize here the approaches that have been used by other authors in their studies of activity-related RV simulations.
Saar & Donahue (1997) started to simulate the spot induced RV jitter by measuring the apparent line shift of atmospheric models of a single FeI line around 6000 Å. They used a solar-like star with an effective temperature of Teff = 5750 K and set the spot temperature to 0 K. In this way the spot is totally dark and no spot spectrum has to be considered. Hatzes (2002) used a similar technique to derive RV amplitudes due to spots. In his case the spot was 1200 K cooler than the quiet stellar photosphere which corresponds to the mean between temperatures measured in the umbra and penumbra of the Sun (Berdyugina 2005). As in Hatzes (2002), spots are not completely dark; they also contribute to the disk-integrated stellar spectra. Although the RV amplitudes should be sensitive to spot temperatures, the results in Hatzes (2002) and Saar & Donahue (1997) are seemingly consistent. As a next step, Desort et al. (2007) used the full spectral range of HARPS to simulate RV amplitudes of dark spots for an F, G, and K star using Kurucz (1993) models. Desort et al. (2007) showed that using different single spectral lines can lead to different spot RV amplitudes. Thus the consistency in the spot RV amplitudes despite the spot temperature difference between Hatzes (2002) and Saar & Donahue (1997) could be the result of different lines used in both works. In order to use broader spectral regions while saving computational time when computing spot RVs, Boisse et al. (2012) suggested to directly use a Gaussian cross correlation function (CCF) instead of a full spectrum in each grid point. However, all of the above mentioned works have been done taking into account only the contrast of active regions. Lagrange et al. (2010), Meunier et al. (2010), Lanza et al. (2010), Jeffers et al. (2014), Dumusque et al. (2014), and Borgniet et al. (2015) realized the importance of the convective blueshift for activity-induced RVs: as magnetic fields hinder convection inside active regions, spectra of spots are expected to appear redshifted compared to the surrounding disk. This apparent redshift of the active region changes the RV signature of spots and gives rise to stronger RV amplitudes of bright plages compared to simulations only taking into account the flux effect.
Nevertheless, measuring the convective blueshift proves to be difficult even for the Sun. Absolute values of the convective blueshift of the Sun differ significantly throughout the literature (e.g., 200 m/s in Meunier et al. 2010; or 500 m/s in Lanza et al. 2010). This large range of convective blueshift values found in the literature can at least partly be attributed to the fact that the measured convective blueshift depends on the depth of the lines used to derive it (Gray 2009; Meunier et al. 2017). As the convective blueshift is even difficult to measure in the Sun, only recently hasthere been first attempts to measure convective blueshifts in other stars (e.g., Meunier et al. 2017). The best guess of the convective blueshift in stars we have today therefore comes from simulations (e.g., Beeck et al. 2013b). Convection patterns might be different in other stars and extrapolation of activity models based on solar parameters might lead to under- or overestimation of activity effects. With the help of simulated line profiles we can explore which differences arise in the RV curves of spots and plages in stars other than the Sun. Hence in this workwe investigate the effects of convective blueshift on the RV curves of spots and plages not only in the Sun butalso in other stars. Instead of relying on measured spectra, we chose to use magneto-hydrodynamic (MHD) simulations (Beeck et al. 2013a,b) where convective blueshift can be simulated for the Sun and other stars.
While so far only the projection effect of the convective blueshift has been taken into account, Herrero et al. (2016) also included a more complex variation of the convective blueshift with μ (where μ = cos θ with θ being the angle between the line of sight and the normal to the stellar surface, which is what we call the limb angle) by using simulation results from Ludwig et al. (2009). By using the line profiles of Beeck et al. (2013b,a) we automatically include variations of convective blueshift in a consistent way.
The magnetic fields that hinder convection in active regions and lead to the importance of including convective effects in the simulations of activity RV jitter also alter the line profiles in spots and plages (e.g., by Zeeman broadening; Reiners et al. 2013; Reiners 2014). Strong magnetic fields present in active regions can be taken into account by using observed spectra of the quiet photosphere and a sunspot as done by Dumusque et al. (2014). While this approach might hold for G-type stars, expanding the simulations to fit stars of spectral types F, K, or M might not work well. The line profile simulations of Beeck et al. (2013a,b) enable us to include the line profile altering effects of the magnetic field into our activity simulation. In this work we also investigate the influence that the line profiles in active regions have on the resulting RV curves.
In this work we investigate activity RV curves from spots and plages on stars other than the Sun. In Sect. 2 we describe the fundamental effects causing active regions to produce apparent RV jitter in stars. In Sect. 3 we present our model including the properties of the simulated stars. In Sect. 4 we show how magnetic fields, convective blueshift, line profiles and spot temperatures influence the RV signals of spots and plages. The bisector span has become an important parameter in exoplanet studies during the last years. However, it is beyond the scope of this work to investigate bisectors in detail, which will therefore be done in a separate article.
2 Effect of active regions on stellar RVs
When active regions appear on the stellar disk they can cause apparent variations in RV measurements of the star. The parameters of the active region play an important role in determining which signatures are observed. In this section we summarize the most important effects influencing the RV curves of active regions.
2.1 Temperature
On the Sun we can observe active regions as dark spots or bright faculae and plages. Spots are regions in which a strong magnetic field hindersthe plasma moving perpendicular to the field lines. This suppresses the supply of new, hot material into the active region and causes a cool down in the vicinity of a strong magnetic field. On the Sun a dark spot is about 500–1700 K cooler than the rest of the stellar surface (Lagrange et al. 2010; Berdyugina 2005).
If a dark spot rotates into view it disturbs the flux balance between the approaching part of the disk that rotates towards the observer and the receding part of the disk that rotates away from the observer. As a result more light from the receding part of the stellar disk reaches the observer when the spot first comes into view resulting in line profile distortions (e.g., Reiners et al. 2010)and an apparent redshift of the disk integrated spectral lines. When the spot proceeds with stellar rotation across the disk it blocks light from areas with different projected rotational velocities. The result is a variation of the RV during one rotation period of the star. This effect is commonly referred to as the flux effect which produces symmetric, sinusoidal RV curves (while the spot is visible and if the size of the spot is constant throughout its lifetime). The upper panel of Fig. 11 indicates a schematic path of a dark active region on the equator of the stellar disk and the middle panel shows the characteristic RV variations caused by the dark spot on an active star.
Compared to dark spots, bright faculae and plages behave differently. As explained in Foukal (2008) faculae are conglomerates of narrow flux tubes with diameters in the order of 100 km. These flux tubes are much thinner than spots and the strong magnetic field inside sustains it against the outside gas pressure. The walls of the flux tube are hot and radiation is entering the tube horizontally. If the tube is thin enough the horizontal flux reaches the center and the interior of the tube is heated which results in an increase of vertical flux turning the tube bright (Ortiz et al. 2002). Plages show a significant limb brightening effect. While the disk dims towards the limb (at small μ), the hot walls of the plages seen by the observer increase the plages contrast. Meunier et al. (2010) published an empirical law for the temperature of plages on the Sun as a function of μ:
![\begin{equation*} \delta T_p = 250.9 - 407.7\mu + 190.9\mu^2~[\mathrm{K}].\end{equation*}](/articles/aa/full_html/2018/02/aa31227-17/aa31227-17-eq1.png) (1)
(1)
Because of the smaller temperature difference between quiet stellar photosphere and active region, plages have a much lower contrast than dark spots and consequently the flux effect expected from faculae and plages leads to lower RV amplitudes. In the lower panel of Fig. 11 the RV curve due to the flux effect of an equatorial plage with the same size as the dark spot can be seen. Because the plage is bright its RV curve shows a reversed behavior as compared to the dark spot. Nevertheless, RV amplitudes caused by the flux effect of plages are much lower than for dark spots in the scenario shown here. Although in our similar size scenario plages produce lower RV signals than spots, plages occupy larger surface areas on the Sun than spots do. Therefore the total RV amplitudes from plages are similar to those of spots (Meunier et al. 2010).
The very different RV amplitudes of spots and plages caused by the flux effect show the importance of active region contrast. While the dark spot is 550 K cooler than the rest of the disk, the bright plage is only 250 K hotter than the quiet photosphere at maximum. The contrast of active regions can be estimated by dividing the Planck curves from spot and plage by the Planck curve of the quiet photosphere (this is a simple estimate without the line variations studied later in Sect. 4.3). At a visible wavelength of 6200 Å this results in a spot contrast of 0.68 and a plage contrast of 1.18 for the Sun. Hence, larger temperature differences, ΔT, between active region and quiet photosphere lead to a larger contrast and thereby to larger flux effect in the RV signal. However, spot temperatures are not necessarily the same in all stars which gives rise to the assumption that RV curves of spotted stars can be very different depending on the active region contrast. Therefore, we investigate the behavior of spot RV curves with changing spot contrast in Sect. 4.4 in more detail.
 |
Fig. 1 Upper panel: schematic view of the G2 star with a dark spot rotating across the projected stellar disk. The color code indicates the intensity across the disk. Middle panel: RV curve produced by the flux effect of a dark spot. Lower panel: RV curve produced by the flux effect of a bright plage. The stellar effective temperature in this models is Teff = 5780 K. The spot is 550 K cooler than the quiet stellar photosphere and the plage temperature is derived from Eq. (1). |
2.2 Convection
Convection is present in the outer layers of late-type stars of spectral types F, G, K, and M. Uprising material in the outer convective layers of these stars is hotter, brighter, and covers a larger surface area than the down-flowing material. Hence, lines formed in the unperturbed quiet photosphere are blueshifted due to the rising convection cells. The strong magnetic fields that create dark spots and bright plages suppress the supply of new material into the active regions. As a consequence, convection inside dark spots and faculae is reduced. Lines formed in active regions are thus less blueshifted and the entire active region appears redshifted as compared to the surrounding quiet photosphere. For the Sun, the inhibition of the convective blueshift within active regions is estimated to be in the range between 200 and 500 m/s (Meunier et al. 2010; Lanza et al. 2010; Dumusque et al. 2014). This large range of values found in the literature is not only the result of the technical challenges faced when measuring the absolute convective blueshift; in fact, the convective blueshift also depends on the lines and wavelength range used to measure it (Gray 2009; Meunier et al. 2017). For a quantitative description of the effect of reduced convection on RVs of active stars we choose here to use 300 m/s as a value for the apparent active region redshift. This value corresponds to the mean of the estimated range for the Sun.
The effect of reduced convective motions changes what we observe in RV curves of spotted stars. In addition to the flux balance being perturbed by spots or plages, the velocity field also becomes disturbed by magnetic fields. The RV curves of spots and plages incorporating different mechanisms are shown in the middle and lower panels of Fig. 21. The different lines in Fig. 2 represent different cases. The broken gray line is our reference and represents the RV curve we get only from the flux effect of the spot and the plage.
In addition to the RV curve caused by the flux effect we also plot the RV curve caused only by the suppression of the convective blueshift as blue dashed line. The temperature of the spot and the plage are the same as the quiet photosphere (contrast of 1) but the spectra inside the active regions are redshifted by 300 m/s. Hence the blue dashed line involves no flux effect. In this case the RV shift caused by the active region is entirely produced by the spectral lines being redshifted relative to the quiet photosphere. This constant apparent redshift of 300 m/s causes the active region to produce an RV curve only showing a redshift.
When both the flux effect and the suppression of convection are combined, the result is the black solid line. Compared to the RV curves of the spot and the plage involving only the flux effect, the RVs including the convective blueshift become biased towards positive Doppler velocities. However, there is a significant difference between what happens to the spot and the plage RV curves when the suppression of convection is considered. A dark spot emits less light than the rest of the disk and the contrast is high. Thus the redshift of this region is less important for the RV curve and the differences between RV curves with pure flux effect and flux effect in combination with convection effects in Fig. 2 are rather small. For a bright plage, however, the contrast is low and therefore the RV curve changes considerably from the case where only the flux effect is considered to the case where the suppression of convection is included. In the case of the plage, the RV curve is almost entirely governed by the reduction of convection while for the dark spot the flux effect plays the major role. The brightness is the key parameter here. RVs of stars with bright active regions are more sensitive to the reduction ofconvective motions than stars with dark spots because dark regions contribute less to the integrated disk spectrum.
Parameters that influence the strength of convection effects in spots and plages are the speed of the convective motions andthe magnetic field strength. The faster the convective motions are in the quiet photosphere, the greater the impact on RV curves if convection is suppressed, because the apparent redshift of the active region becomes larger. The magnetic field strength plays a role because the ability to prevent convection grows with increasing magnetic field strength. A weak magnetic field might not suppress convection efficiently; therefore only the flux effect is observed. Strong magnetic fields can stop convection, and then apparent redshifts of active regions become important.
 |
Fig. 2 Upperpanel: spot RV curve produced by the flux effect only (gray dashed line), the RV curve produced by the active region by only suppressing the convective blueshift (blue dashed line) and the spot RV curve produced by taking into account the flux effect and the suppression of convection (black solid line). Lower panel: RV curves for the bright plage plotted in the same way as for the dark spot in the upper panel. |
3 Methods
Observations of stars other than the Sun only give us access to their disk-integrated spectra. Active regions have different spectra than the quiet photosphere. Hence the presence of active regions on the stellar surface alters the integrated disk spectrum and leads to observable effects, for example, in radial velocity. In order to model the effects of activity on RVs we must reconstruct the unresolved surface of the star and mimic observations by integrating contributions of single surface elements. In this section we explain step by step how we built our model.
Stellar parameters of stars simulated in this work.
3.1 Model grid
We start by defining a grid of surface elements for the star. We define the number of grid points at the equator and adjust the number of grid points for each latitude so that all surface elements roughly cover the same surface area. This has the advantage that an active region of given size is sampled with the same number of grid points anywhere on the sphere. Typically we use 500 grid points on the equator so that the star is sampled with about 80 000 grid points in total.
When observing stars, we only see a projection of the stellar disk. Therefore the second step is to project the three-dimensional (3D) sphere onto a two-dimensional (2D) disk. With our grid definition the projected area of grid points at the limb is smaller then in the center. Towards the edges changes in projected velocities and intensity are large and smaller grid points avoids covering large velocity or intensity ranges with only one grid point.
The last step is to fill the plain grid with information. Each grid cell holds information about its effective temperature, intensity (limb darkening), and projected rotational velocity. In this work we present results for three stars of spectral types F3, G2, andK5. In what follows we describe their properties, which are summarized in Table 1:
-
We estimated the effective temperatures of the F3 and the K5 star from their spectral types by fitting a 4th order polynomial to the spectral type – temperature data of Gray et al. (2006). For the G2 star we adopted the solar value. We use 6900 K, 5780 K, and 4300 K for the F3, G2, and K5 star, respectively throughout this paper.
-
The center to limb brightness variation for the F, G, and K stars was computed by Beeck et al. (2013b). We fit their data with a cubic limb darkening law of the form:
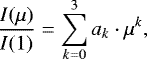 (2)
(2)
where 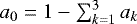 . The derived coefficients for all stars are listed in Table 1.
. The derived coefficients for all stars are listed in Table 1.
-
In this work we only consider slow rotators because current exoplanet surveys focus mainly on these stars as the RV content of the stellar spectra are higher when line profiles are narrow (Bouchy et al. 2001). The rotational velocity of our stars was chosen to resemble the Sun and was set to 2 km s−1 at the equator. However, stars are not rigid bodies and we use the relation between effective temperature and differential rotation derived by Küker & Rüdiger (2011) to include the differential rotation into our model. The differential rotation parameter δΩ for all stars are also given in Table 1 and range between
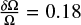 and 0.45.
and 0.45.
3.2 Line profiles
After the stellar parameters are inserted to the grid the next ingredient for our model is the spectral contribution of each cell. There are different approaches to choosing which spectrum to use in the grid points. Some authors used atmospheric models of single lines (e.g., Saar & Donahue 1997; Hatzes 2002), full model spectra in the wavelength ranges of different spectrographs (e.g., Desort et al. 2007; Herrero et al. 2016), or directly the CCF (e.g., Boisse et al. 2012).
In our implementation we can choose between two spectral contributions. The first one is a Voigt profile with solar parameters which is similar to the CCF approach of Boisse et al. (2012). The second one uses single line profiles of full MHD simulations of Beeck et al. (2013b, 2015b). From now on we refer to this line profile as the MHD line profile. We give here a short summary of the line synthesis but for more detailed information we refer the reader to the paper series covering the simulations used in this work (Beeck et al. 2013a,b, 2015a,b).
In this work we consider the FeI lines at 6165 Å and 6173 Å. Both are relatively isolated (no blends) and their effective Landé factors are geff, 6165 Å = 0.69, geff, 6173 Å = 2.5. Hence, the FeI line at 6165 Å is rather insensitive to magnetic fields while the FeI lines at 6173 Å can be considered magnetically sensitive. Differences in the RVs derived from both lines can give us an idea as to whether or not Zeeman splitting is important in our simulations. The FeI lines were synthesized in simulations of the stellar surface convection with parameters matching those of F3, G2, and K5 stars. The 3D stellar convection process was simulated with average magnetic field strengths of 0 G (no magnetic field), 20 G, 100 G, and 500 G. However, local magnetic field strength can exceed several kG in the surface simulations. Although no spots or faculae form in these simulations, areas of local strong magnetic fields exhibit significant changes in temperatures and convection patterns. Because theMHD simulations incorporate a realistic treatment of surface convection and magnetic fields, the resulting line profiles include the suppression of the convective blueshift by magnetic fields. Therefore the MHD line profiles capture one main mechanism believed to influence RV curves of active stars that is not yet observationally accessible.
The MHD line profiles capture intensity and convection effects not only globally but also locally because they are available for different μ, from 0.1 to 1. Therefore any spatial changes in convective blueshift, line shape, or line depth due to changes of the optical surface as a function of μ are simulated inour models. All three quantities influence the RV signals from active regions, as is discussed in Sect. 4.3.
To involve the spatial information from the MHD line profiles in our grid defined in Sect. 3.1 we have to interpolate the line profiles between the discrete μ values and also extrapolate the line profiles to μ values below 0.1. Although the portion of the disk with μ values below 0.1 is negligible and is expected to have no influence on our derived RV curves we still fill these grid points with extrapolated MHD line profiles to avoid numerical discontinuities at the disk edges. The extrapolation is done by fitting a low-order polynomial to the line intensities as a function of μ. We do this for individual wavelengths so that our model can be written as Ŝ (μ, λj) = poly(S(μ, λj), where Ŝ is the polynomial fit and the index j denotes the individual wavelength points of the line profile. This polynomial model is then used to extrapolate the line profile to μ = 0. When we have gained line profiles ranging from μ = 0 to μ = 1 we interpolate between the discrete μ sampling steps of 0.1 using 2D B-splines (de Boor 2001; Dierckx 1995).
3.3 Disk integrated line profiles and radial velocities
To derive the disk integrated spectra we need to sum the contribution of all grid points (quiet or active) visible to the observer. In the following section we explain the three steps we take to derive the disk integrated stellar spectrum.
3.3.1 Step 1: immaculate star
To compute the disk integrated spectrum is computationally expensive. However, we can save computation time if we compute the disk integrated spectrum of quiet disk elements only once and not for every active region configuration again. Therefore we start by computing the surface integrated disk spectrum of the immaculate star first (no spots or plages on the surface). This spectrum is what we call the quiet spectrum Squiet. For the quiet spectrum we use line profiles computed without magnetic field. All grid points on the visible disk are assigned the corresponding interpolated line profile, S(μ, λ, B = 0). The line profiles, S(μ, λ, B = 0), are then Doppler shifted by the projected rotational velocity of the grid points including differential rotation. Interpolation of the Doppler shifted line profiles to a fixed wavelength grid is necessary to enable summation. We use spline interpolation here and denote the interpolated profile with 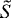 . Then the contribution of all grid points is weighted by the Planck function, P(Teff, λ), and the cubic limb darkening law fitted to the data of Beeck et al. (2013b). Finally the spectra of all grid points are summed to get the disk integrated quiet spectrum Squiet:
. Then the contribution of all grid points is weighted by the Planck function, P(Teff, λ), and the cubic limb darkening law fitted to the data of Beeck et al. (2013b). Finally the spectra of all grid points are summed to get the disk integrated quiet spectrum Squiet:
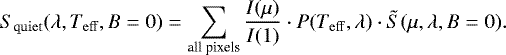 (3)
(3)
3.3.2 Step 2: spectra of active regions
After having computed the immaculate star spectrum we compute the spectrum integrated over active regions only. The spectrum resulting from integrating all active regions is denoted Sact here. Spots or plages have lower or higher temperatures than the quiet stellar disk. Consequently the Planck weight for these grid points are different. Along with the temperature change there is also a strong magnetic field present in active regions. We use the MHD line profiles of B = 0 G, B = 20 G, B = 100 G, and B = 500 G and calculate the integrated spectrum for grid points defined to be active by the user (active pixels) for each B value. The integrated active region spectrum is then:
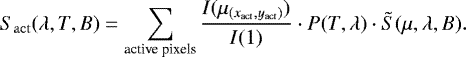 (4)
(4)
We note that we also compute the integrated active region spectrum using the B = 0 G line profile and calculate Sact twice using once the temperature for active region T = Tact and once with the temperature of the quiet photosphere T = Teff. We call the latter case the quiet photosphere spectrum of active elements. This is necessary to compute the full disk integrated spectrum of a star with spots or plages on the surface in the next step.
3.3.3 Step 3: full disk integrated spectrum
To derive the full disk integrated spectrum of a spotted star we add the integrated active region spectrum (from step 2) to the immaculate star (from step 1). Thus we need to subtract the quiet photosphere spectrum of active elements to effectively replace the quiet disk elements with active disk elements. The full disk integrated spectrum including active regions is then simply:
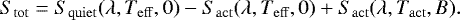 (5)
(5)
To computethe RVs from active regions we first convolve the template spectrum Squiet with the resolution of the spectrograph we want to simulate (in our case HARPS; R = 115 000). For the template we measure the line centroid and define this as reference wavelength. Then we measure the line centroid of the spectra including active regions Stot and compute the RV shift relative to the reference.
4 Results
In this section we will describe how different stellar parameters and line profiles affect RV curves of spotted stars. We investigate spectral types from F3 to K5. Unless explicitly stated we follow Lagrange et al. (2010) and adopt their temperature difference for dark spots of ΔT = 550 K relative to the quiet photosphere for all stars. For plages we use the temperature law of Meunier et al. (2010) given in Eq. (1).
We remind the reader here that neither the spot temperature difference of 550 K nor the plage temperature law in Eq. (1) might be representative for active regions on stars other than the Sun. For the dark spots observational efforts have been made to measure their temperatures in other stars. We investigate the influence of spot temperature on RVs of other stars in Sect. 4.4. However, for plages, no observational constraints exist. Therefore we use the temperature relation for the Sun (Eq. (1)) throughout this paper.
In this section we keep the spot and plage sizes constant at 1% of the visible stellar disk which corresponds to a radius of about 6 degrees. The upper panel of Fig. 1 shows a schematic picture of our simulation set up with the dark spot moving across the stellar disk of the G2 star. The color code indicates the intensity of the surface elements. The dark spot starts at the anticenter coming into view after 90 degrees of rotation and leaving the stellar disk at 270 degrees.
4.1 Influence of the magnetic field strength on RV curves
4.1.1 RV curves derived from MHD line profiles
In order to derive meaningful results from the MHD line profiles we start by testing the influence of the mean magnetic field on the RV curves. We simulate the dark spot and a bright plage for our three F, G, K stars with their parameters given in Table 1. We use the MHD line profiles of both FeI lines and derive the RVs induced by the active regions. We compute four simulations per star with different field strength inside the active region: B = 0 G, B = 20 G, B = 100 G, and B = 500 G. The results for both FeI lines are shown in Fig. 3 for the spot and in Fig. 4 for the plage. In both cases the results of the FeI line at 6165 Å do not substantially differ from the ones derived from the FeI line at 6173 Å (see solid gray and red dotted lines on the right panel of Figs. 3 and 4). Although the two FeI lines differ in their effective Landé factors (geff, 6165 Å = 0.69, geff, 6173 Å = 2.5) the fact that the results are very similar leads us to the conclusion that Zeeman broadening plays no important role in both lines at the magnetic field strengths considered here. This result is consistent with Reiners et al. (2013) where the RV amplitude caused by a purely magnetic spot (considering only the Zeeman effect and no temperature contrast) is predicted to be below 1 m/s in the optical for a magnetic field strength of 600 G.
In Figs. 3 and 4 we can see the evolution of the RV curves with increasing mean magnetic field inside the active region for the spot and plage respectively. In the case of B = 0 G we only see the flux effect for all stars causing symmetric, sinusoidal RV variations when the active region is visible (and a flat RV curve when the active region rotates behind the star). When the magnetic field inside the active region increases we start to see growing asymmetries in the RV curves of both spot and plage. Up to an average magnetic field strength of 100 G these asymmetries are small and we mainly observe the flux effect in the RV curves. The only exception is the F3 star where a magnetic field strength of 100 G already has impact on the RV curves. When we increase the average magnetic field strength further to 500 G the RV curves of the F and G stars show a significant change. However, for the K5 star there is little change in the active region RV curves even at B = 500 G. Do determine why different stellar types show different sensitivities to the magnetic field inside the active region we look into the convection of each star in more detail.
 |
Fig. 3 Influence of magnetic field strength on spot RVs. Line profiles with different field strengths were used inside the spot. Spot RVs calculated with B = 0 G (black solid line), with B = 20 G (green long dashed line), with B = 100 G (blue short dashed line), and with B = 500 G (red dotted line). The results for the FeI line at 6165 Å are shown in the left panel, and the results of the FeI line at 6173 Å can be seen in the right panel. The gray solid line in the right panel indicates the results of the FeI line at 6165 Å for comparison. |
 |
Fig. 4 Influence of magnetic field strength on plage RVs. Line profiles with differentfield strengths were used for the plage. Plage RVs calculated with B = 0 G (black solid line), with B = 20 G (green long dashed line), with B = 100 G (blue short dashed line) and with B = 500 G (red dotted line). The results for the FeI line at 6165 Å are shown in the left panel, and the results of the FeI line at 6173 Å can be seen in the right panel. The gray solid line in the right panel indicates the results of the FeI line at 6165 Å for comparison. |
4.1.2 Convection at different magnetic field strengths
We attribute the RV amplitude and symmetry changes seen with increasing magnetic field strength in Figs. 3 and 4 to the suppression of convection inside the active region (as explained in Sect. 2.2). To test this idea we measure the suppression of the convective blueshift as a function of the magnetic field strength. We use the local MHD line profiles at μ = 1 here. First we determine the line centers of the two FeI lines at B = 0 G, B = 20 G, B = 100 G, and B = 500 G by fitting a Gaussian to the ten data points around the minimum of the line profile. The effective velocity difference between active region and quiet photosphere is then calculated from the difference of the line centers with magnetic field (B = 20 G, B = 100 G, and B = 500 G) relative to the line center determined for the B = 0 G line: ((λB − λB=0)∕λB=0) ⋅ c. This method will be denoted as the Gaussian method from now on.
A second way to measure the apparent active region velocity is to use the line centroids instead of a Gaussian fit. This method will be denoted as centroid method from now on.
The resulting apparent active region velocity are plotted in the left panel of Fig. 5. As the results differ slightly between the FeI line at 6165 Å and the FeI line at 6173 Å we shaded the area between the two measurements. Open symbols in Fig. 5 indicate the measurements of the Gaussian method and filled symbols show the results obtained by the centroid method. A summary of the mean velocity shifts plotted in Fig. 5 can also be found in Table 2 for each B step.
Before exploring the details of Fig. 5, we remind the reader here that the active region velocity measured depends on the depth of the line used and the lines wavelength (Gray 2009; Meunier et al. 2017). The flux at the bottom of the FeI lines (at μ = 1), F, are F6165 = 0.9 and F6173 = 0.83 for the F3 star, F6165 = 0.6 and F6173 = 0.34 for the G2 star and F6165 = 0.47 and F6173 = 0.17 in the K5 star. Therefore, the lines we used here to compute the apparent active region velocity are not representative for all spectral lines. Nevertheless, the two lines used here give us a first impression how the active region velocities (derived from a consistent line list) change over spectral type and allow us to study the impact of this change on activity-induced RVs.
For the K5 and G2 stars the results obtained from the Gaussian method and the centroid method are similar (see Table 2). For the K5 star there is only a small change in the apparent active region velocity when changing the magnetic field from B = 20 G to B = 500 G. Moreover, the apparent active region velocities are low. Therefore, the absence of a change of the RV curves with increasing B shown in Figs. 3 and 4 can be explained by the small values of the apparent active region velocities.
For the G2 star the apparent active region velocities are also low and relatively stable for B = 20 G and B = 100 G. However, at B = 500 G the suppression of convection becomes significant. Therefore, also in the G2 star the observed change in the RV curves of spot and plage coincide with the apparent active region velocities which increases for stronger magnetic fields.
For the F3 star the apparent active region velocities obtained with the Gaussian method differ significantly from the results of the centroid method (see left panel of Fig. 5 and Table 2). The reason for the large differences in apparent active region velocities among the two methods lies in the MHDline profiles themselves. In the right panel of Fig. 5 we plot the FeI line profile at 6165 Å for all simulated magnetic field strengths and indicate the line centers obtained by the Gaussian method with crosses and with the centroid method as x. The line centers obtained for B = 0 G and B = 20 G are similar when measured with both methods. However, with increasing magnetic field strength the centroid method returns highly redshifted values because the spectral line becomes significantly asymmetric. We argue that the apparent active region velocity should be measured by the Gaussian method (as also used in Beeck et al. 2013b) because it measures the line core and thereby avoids a bias of the line centers towards redder wavelengths as a result of line asymmetries. Hence, the change in the RV curves of the F3 star in Fig. 3 (spot) and Fig. 4 (plage) only partially coincide with the inhibition of convection. The picture for the F3 star is more complex and line asymmetries as a function of magnetic field strength also play an important role here.
Becauseof the results obtained for the F3 star we decide to use the Gaussian method and its results of the apparent active region velocity in what follows in this work. Line asymmetries and their effect on RV curves of active regions are discussed later in more detail in Sect. 4.3.
 |
Fig. 5 Left panel: variation of the active region velocity with the magnetic field strength B for different stellar types and measurement methods. Right panel: MHD line profile of the FeI line at 6165 Å for different magnetic field strength (solid lines) and line center measurements with the Gaussian method (crosses) and the centroid method (x). The color code for the line profiles and the center measurements are the same: black for B = 0 G, green for B = 20 G, blue for B =100 G, and red for B = 500 G. |
Measured active region velocities as a function of magnetic field strength B.
4.1.3 RV amplitudes across different stellar types
It is interesting to note that the growth in asymmetry and RV amplitude with increasing magnetic field is seen more in hot stars than in cool ones. In the K star simulation the spot RV amplitude increases only from 6.8 m/s to 7.4 m/s (factor of 1.09) between the B = 0 G and B = 500 G run. For the G star the spot RV amplitude increases from 4 m/s to 6.6 m/s (factor of 1.65) if the magnetic field is increased from 0 G to 500 G and on the F star the RV amplitude grows from 2.8 m/s in the 0 G run to 11.2 m/s in the 500 G run (factor of 4).
For the plage simulation we observe a similar behavior. Changing the magnetic field inside the plage from 0 G to 500 G changes the RV amplitude in the K star simulation from 0.9 m/s to 2 m/s (factor of 2.2) in the G star simulation from 0.6 m/s to 5 m/s (factor of 8.3) and in the F star simulation from 0.5 m/s to 15.5 m/s (factor of 31).
We have to be careful when comparing the growth of the RV amplitude in Figs. 3and 4 between the F, G, and K stars. Because the same spot temperature contrast (ΔT = 550 K) and the same plage temperature contrast law (Eq. (1)) are used for all stars, the intensity contrasts of the active regions depend on the stellar type. Thus, one possibility for the increase in amplitude towards hotter stars could be the changing active region intensity contrast.
The dark spot has a contrast of 0.74 on the F star, a contrast of 0.65 on the G star and a contrast of 0.45 on the K star. As explained in Sect. 2.2, the suppression of convection is greater in RV curves of brighter active regions. Because the dark spot is relatively brighter on the F star compared to the G or K star, the suppression of convection is seen more in the spot RV curves of the hotter stars. However, for plages the effect should be exactly reversed because the plage is relatively brighter on the K star (contrast 1.35) than on the G star (contrast 1.19) or F star (contrast 1.13). According to the contrast we expect the plage signal to have the largest amplitude growth in the K star. Nevertheless, we observe the opposite and the plage RV amplitudes are also larger for hotter stars.
The decreasing sensitivity of the RV curves to magnetic fields in cooler stars is therefore not primarily caused by changing contrast. The spectral type dependence of the RV amplitude growth from B = 0 G to B = 500 G is better explained by the convection speeds. As shown in Sect. 4.1.2 the measured active region velocity increases towards earlier-type stars (76 m/s for the K5 star, 300 m/s for the G2 star, and 781 m/s for the F3 star). Suppressing fast convective motions leads to a strong impact on the RV curves. Thus the increase in asymmetry and RV amplitude towards the B = 500 G simulation is well explained by the different convective speeds of the stars and their suppression caused by the magnetic field.
A further consequence of the decreasing convective motion speeds towards late-type stars is that plages contribute less to the RV variation of an active star with decreasing effective temperature. As plages have low contrasts their signal comes mainly from the inhibition of convection within them. If convection is slow in the quiet photosphere plage signals become weaker. Nevertheless, we remind the reader that we simulate spots and plages covering only 1% of the visible stellar surface. On the Sun, plages cover larger areas than spots; therefore one has to be careful here when comparing absolute RV amplitudes of spots and plages. Plages can still produce large RV variations in cool stars because they are typically larger than simulated here.
4.2 Comparison to the literature
After finding that only simulations using the 500 G line profiles lead to a noticeable effect in the RV curves through the suppression of the convective blueshift we go ahead and attempt to validate our results by comparing them with published studies. The simulation of the G2 star is the perfect test ground for inter comparison as most other works in this field have been done with sun-like stars. Especially interesting is the comparison between our results and the ones obtained by Dumusque et al. (2014). Their simulations are based on observed spectra of the solar quiet photosphere and a solar spot while our results are completely based on MHD simulations. Although Reiners et al. (2016b) pointed out that the absolute wavelength scale of the data used in Dumusque et al. (2014) has some problems, a close match of the results can thus give us confidence to extend our method used to simulate activity RV curves to stars other than the Sun.
The setup of the simulations in this section is the same as before using an equatorial active region with a size of 1% of the visible stellar disk and the stellar parameters of Table 1. For the active region we now only use the MHD line profiles with a mean magnetic field of 500 G because only then the suppression of the convective blueshift is significant. We use our active region setup and simulate the same configuration with the SOAP 2.0 code of Dumusque et al. (2014). We show our RV curves and the ones obtained with SOAP 2.0 for the dark spot and the bright plage in Fig. 6.
For the dark spot our RV curve agrees well with the prediction of SOAP 2.0. We see in Fig. 6 that the maximum deviation of the two curves occurs around a rotation angle of 240 degrees and is found to be 1.14 m/s or 17% of the amplitude. If we compare our plage RV results of the G2 star to SOAP 2.0 we find the maximum difference between thetwo curves again around a rotation angle of 240 degrees. This time the maximum difference is 1.57 m/s or 31% of the amplitude.
Both dark spot and plage RV curves agree well with the findings of SOAP 2.0. Nevertheless, we take a closer look at how the RV curves are derived in both cases and give a possible explanation for the differences. Equivalent width, FWHM, line bisectors, and convective blueshift of the MHD line profiles are known to be functions of μ (Beeck et al. 2013b, 2015b). Changes in these parameters have impact on the RV signals computed from the line profiles. SOAP 2.0 uses observed high-resolution, spatially resolved spectra of a quiet part and a sunspot on the solar surface close to the disk center to simulate RV curves for spots and plages. As there are no observations available for different μ, the model of SOAP 2.0 uses constant line profiles and therefore a constant convective blueshift (corresponding to the convective blueshift close to the Suns disk center) to derive RV signals from spots and plages. Hence, the differences between our models and SOAP 2.0 are likely related to the fact that SOAP 2.0 uses constant line profiles while we use limb-angle dependent MHD line profiles.
However, we note here that the MHD line profiles might not fully cover all changes in line shape and line depth with changing μ. This was recently pointed out by Reiners et al. (2016a) who compared the MHD line profiles to observations made during a solar eclipse. Observations of line profile changes with μ will be useful for future work in this area of research.
Despite the differences between our results and SOAP 2.0 the general results of both spot and plage on the G2 star agree well. The amplitudes match for both spot and plage, and the shape of the RV curves also agrees. In the following sections we move on and explore the role of convective blueshift, line profiles, and spot contrast for activity RV curves of hotter and cooler main sequence stars.
 |
Fig. 6 Comparison between the RV curves derived by our code using the MHD line profiles (black solid lines) and SOAP 2.0 (red dotted lines) for a dark spot (upper panel) and a bright plage (lower panel). |
4.3 Influence of limb-angle-dependent convective blueshift and line profiles on RV curves
In this section we try to understand the role of changes in the convective blueshift and line profiles from center to limb in RV curves in more detail. For this purpose we try to recover the RV curves derived from the MHD line profiles with a simulation based on Voigt profiles with solar parameters. Also in this section we explain how we can use this method to test whether or not convective blueshift variations and line profile changes across the disk effect the resulting RV curves.
4.3.1 The apparent active region velocity across the disk
As a first step we derive the apparent active region velocity across the disk for all spectral types. We use the local MHD line profiles for 0 G and 500 G available for 10 μ values between 0.1 and 1 and measure the line centers with the Gaussian method as described in Sect. 4.1.2. The measurement is taken for both FeI lines at 6165 Å and 6173 Å. The resulting velocity difference between active region and quiet photosphere is plotted in Fig. 7 for different μ on the stellar disk.
It is important to note that our result is different in amplitude and span from the estimate of the convective blueshift in Beeck et al. (2013b). They measure the line core shift of the B = 0 lines relative to the laboratory wavelength of the FeI lines. This results in an estimate of the absolute velocities of the convective motions. For our purpose however, it is important to measure the suppression of the convection by the magnetic field because this is what is seen in the RV curves of spots and plages.
From Fig. 7 we can study the evolution of the convective blueshift from center to limb. As already shown in Beeck et al. (2013b) the convective blueshift can turn into a redshift towards the limb of stars. Active region can therefore appear blueshifted when observed at low μ values. Previous works studying the RV variation caused by active regions have often taken into account only the projection effect of the convective blueshift with μ, shown as black line in Fig. 7 for the G2 star. Hence, the effect that active regions can also become blueshifted at the limb was not taken into account.
The area on the disk where active regions appear red or blueshifted changes with spectral type. As shown by the red-blue circles in the lower-left corner of Fig. 7 the active regions on the K5 star appear redshifted almost on the entire disk. Only on the outermost 2% of the projected disk do active regions appear blueshifted. In the G2 star active regions appear blueshifted in the outer 33% of the disk and for the F3 star we measure this value to be 18%. Also the apparent convective motions across the stellar disk are changing with spectral type. The span is considerably high for the F3 and G2 stars, about 1800 m/s and 600 m/s, respectively,from center to limb. However, for the K5 star there is almost no variation.
 |
Fig. 7 Variation of the active region velocity field between B = 0 and B = 500 G as a functionof μ for the F3 star (blue squares), G2 star (green circles), and the K5 star (red triangles). The results of the FeI line at 6165 Å is shown with open symbols and the result of the FeI line at 6173 Å is indicatedas filled symbols. For comparison the constant active region velocity field taking into account only the projection effect with μ (as done in previous works) is plotted as black line. Red-blue circles in the bottom left indicate where on the stellar disk active regions appear redshifted or blueshifted relative to the quiet photosphere. |
4.3.2 Using Voigt profiles with different convective blueshift parameters
With the measurement of the active region velocity field in hand, we try to recover the RV curves derived from the MHD line profiles witha model parametrized as simply as possible. We want to test if we can reproduce the RV curve from MHD line profiles by using a constant Voigt profile throughout the disk and different models for the effective velocity field of the active region. We calculate three sets of RV curves for each star. The first one uses a constant effective redshift for the active region of 781 m/s for the F3 star, 300 m/s for the G2 star, and 76 m/s for the K5 star corresponding to the redshift seen at μ = 1. This approach is close to the one used by Dumusque et al. (2014) with observed Sun spectra. In our second setup we take the projection effect of the convective blueshift into account (see black line in Fig. 7 for the G2 example). The third simulation uses a variable effective active region velocity field. To simulate the variable velocity field we place the Voigt profiles at the measured line center positions of the MHD profiles. For the quiet photosphere we place the Voigt profiles at the center wavelength of the B = 0 G line profiles while for active regions we place the Voigt profiles at the center wavelength of the B = 500 G MHD line profiles. In this way we reproduce exactely the active region velocity fields shown in Fig. 7 and any remaining difference between the spot and plage RV curves derived from MHD and Voigt profiles can only originate from the line shape. The four models for the spot are compared in Fig. 8 and the models for the plage can be seen in Fig. 9. The black solid lines are the MHD (B = 500 G) simulations, the green dashed lines represent the models with constant active region velocities, the blue dashed lines represent the model taking into account the projection effect of the active region velocities and the red dashed lines use the variable active region velocity field from Fig. 7.
 |
Fig. 8 Spot RVs calculated for different stellar types with different line profiles. Calculations done with the 500 G MDH line profiles (black solid lines), Voigt profiles and a constant convective blueshift (green long dashed lines), and Voigt profiles including a varying convective blueshift (blue short dashed lines). |
4.3.3 Changes induced by convective blueshift models
In order to single out the influence of the convective blueshift alone on the RV curves of active regions we analyze the Voigt profile simulations. The only difference between the Voigt profile simulations shown in Figs. 8 and 9 is the active region velocity field across the disk. When the spot or plage is at disk center, at μ =1, which corresponds to a rotation angle of 180 degrees, all three simulations return the same result because the active region velocities are the same. However, when the active region moves towards the limb the difference in apparent active region velocity field impacts the RV curves.
For the spot as well as the plage we observe that the maximum differences among the Voigt profile simulations occur for all spectral types at rotation angles between 110 and 120 degrees and between240 and 250 degrees (60 to 70 degrees from the disk center at 0.34 < μ < 0.5). Although the difference in the apparent active region velocity among the simulations increases towards the limb (see Fig. 7 for the G2 example), the projected active region size decreases towards the limb. Therefore the maximum RV difference between the Voigt profile simulations is found at a distance to the disk center at which the active region velocities differ significantly while the active region itself does not appear too small to produce a significant RV signal. The maximum differences between the three Voigt profile simulations are summarized inTable 3.
In Table 3 we see that differences in the treatment of the convective blueshift can result in differences of the simulated RV curves in the order of a few m/s. From our results we conclude that for future RV models it is not only important to have accurate constraints for the absolute value of the convective blueshift but it is also necessary to take the variation of the convective blueshift from center to limb into account.
 |
Fig. 9 Plage RVs calculated for different stellar types with different line profiles. Calculations done with the 500 G MDH line profiles (black solid lines), Voigt profiles and a constant convective blueshift (green long dashed lines) and Voigt profiles including a varying convective blueshift (blue short dashed lines). |
Differences between Voigt profile models using different convective blueshift models.
4.3.4 Changes induced by line shape
Figures 8 and 9 show that the model using a variable active region velocity field (red broken line, cb (μ) model) can follow the spot RV curves from the MHD line profiles best. This is not surprising because the cb (μ) model follows the change in convective blueshift of the MHD line profiles from center to limb exactly. Nevertheless, we also observe large differences between the MHD and cb(μ) models. Forthe F3 star, the maximum difference between the MHD and the cb (μ) model is 3.1 m/s for the spot and 5.5 m/s for the plage. For the G2 star we find this difference to be 1.5 m/s for the spot and 2.3 m/s for the plage while the differences for the K5 star are 1 m/s for the spot as well as the plage. Spot RVs are generally less sensitive to line profile changes than plage RVs are. This is because spots are cooler than the surrounding photosphere and consequently darker. Hence the line profile inside the spot has less weight than the surrounding photosphere and the flux effect is dominant. For plages the situation is exactly the opposite and the RV curves become very sensitive to line profiles changes.
The differences between the RV curves derived from MHD and Voigt profiles suggest that the line profiles play an important role for the derived RV curves. Because the Voigt profile is a symmetric function, the remaining differences in the RV curves of spot and plage come from line shape and line depth (line bisectors, FWHM and equivalent width) changes with μ in the MHD line profiles. The line profiles of both the quiet photosphere and the active region vary from center to limb as can be seen in Fig. 10 for the G2 star (Beeck et al. 2013b, 2015b). As reference we plot the Voigt profile used to derive the models in Figs. 8 and 9 as black (at μ = 1) and gray (at μ = 0) broken lines. To visualize the differences between the line profiles we plot the residuals of the MHD minus the Voigt profile in the bottom of Fig. 10.
It is interesting to note that the maximum difference between the MHD and the cb (μ) model in the F3 star occurs at disk center (rotation angle 180 degrees) for both spot and plage models (see Figs. 8 and 9). This is not the case for the G2 and K5 star where the differences are largest at rotation angles between 30 and 50 degrees away from the disk center. The fact that the maximum occurs at different rotation angles in the F3 star compared to the G2 and K5 star is related to the relative line profile changes of the MHD lines in different stars between the B = 0 G (quiet photosphere) and B = 500 G (active region) lines.
In Fig. 11 we plot the difference between the B = 500 G and B = 0 G line profiles normalized by the line depth ofthe B = 0 G line. We show two rows of plots: one at μ = 1 and one at μ = 0.7 (where the maximum differences between Voigt and MHD simulations occur). As a reference we also depict the results obtained for the Voigt profiles of our cb(μ) model in the rightmost panels. The vertical black dashed lines mark the line center of the B = 0 G lines as measuredby the Gaussian method. We note that the results shown in Fig. 11 are for a temperature contrast of ΔT = 0.
Figure 11 can be interpreted as the perturbation introduced to the local line profiles by the magnetic field. The rightmost panels show the ideal cases in which the line profiles themselves do not change with B. The perturbation observed in the Voigt profile case originates from the two lines being shifted with respect to each other because of the suppression of convection. The MHD line profiles show different perturbation patterns that are asymmetric and not necessarily centered at line center. These asymmetric perturbation patterns are caused by the change in line depth and shape (asymmetries) when the magnetic field is turned on. Even in the disk center perturbations can be asymmetric resulting in the large differences between the cb(μ) and MHD models seen in the F3 star (see Figs. 8 and 9). For this reason we cannot reproduce the RV curves of spots and plages using symmetric Voigt profiles.
 |
Fig. 10 Variation of the FeI line at 6165 Å with μ for B = 0 G left, and B = 500 G right panel. MHD line profiles at different μ values are color coded from blue (μ = 1) to red (μ = 0). For comparison, Voigt profiles with solar parameters are overplotted as black (μ = 1) and gray (μ = 0) broken lines. |
 |
Fig. 11 Difference between the B = 500 G and B = 0 G line profiles normalized by the line depth of the B = 0 G line. Panel from left to right show the result for the F3, G2, K5 MHD lines, respectively. The rightmost panel depicts results from the cb(μ) simulation using Voigt profiles with solar parameters. Upper panels: results at μ = 1. Lower panel:results at μ = 0.7. |
4.4 Influence of spot temperatures in F, G, and K stars
Until now we have assumed that spots have the same temperature difference relative to the quiet photosphere in all stars. The spot temperatureis a crucial parameter in our models as it directly influences the RV amplitude and the asymmetry of the RV curve. As explained in Sect. 2.1 a lower spot temperature leads to a larger spot contrast. For high spot contrasts the flux effect is dominant. For low spot contrasts however the suppression of convective motions in active regions becomes important and can be seen as asymmetries in the RV curves. The temperature difference between quiet photosphere and a spot of ΔT = 550 K seen in the Sun might not necessarily represent the situation in F and K stars. Therefore, we investigate the influence of spot temperatures on the RV curves of F to K stars in this section. We aim to use realistic spot temperatures for individual spectral types and investigate what influence convective blueshift has on spot RVs if the spot temperature on other stars is taken into account.
4.4.1 Spot temperatures
There have been many efforts to measure the spot temperatures in other stars with a variety of methods. Berdyugina (2005) presented a summary of such measurements in their Table 5. We plot the measurements summarized in Berdyugina (2005) in Fig. 12 and fit a linear relation to the data excluding EK Dra as done in Berdyugina (2005). The relation found between effective temperature and temperature difference to the quiet photosphere of dark spots will be used in our simulations to produce more realistic spot RV curves for other stars.
The relation we find between effective temperature and temperature difference of the spot is ΔT = 0.64 ⋅ Teff − 1842.64. The spot temperature measurements cover a range of stellar effective temperatures from Teff= 3300 K up to Teff= 6000 K which corresponds to spectral types of mid M to late F type stars. The F3 star is not covered by this temperature range. We extrapolate the spot temperature difference with our linear relation and find a temperature difference of ΔTF3 = 2553 K (contrast of 0.13). For the G2 star we find ΔTG2 = 1840 K (contrast of 0.15) and following our relation for the K5 star we find spot temperature differences ΔTK5 = 897 K (contrast of 0.24).
 |
Fig. 12 Measured spot temperatures in red giants (red filled squares) and main sequence dwarfs (blue filled circles). Measurements of the Suns umbra and penumbra are shown as yellow open circles and EK Dra is shown as blue open circle. All values are taken from Berdyugina (2005). Our fit to the data is indicated as gray line and our simulated stars are indicated as green star symbols. |
4.4.2 The symmetry parameter
To rate the change in the RV curves as a function of spot temperature we introduce here the symmetry parameter. We measure the maximum and minimum of the RV curve and name the two points A and B, respectively. Our measure for the symmetry s is then simply the strength of the minimum B relative to the maximum A:
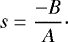 (6)
(6)
The closer the symmetry parameter s is to 1, the stronger the flux effect. The closer s approaches 0, the more influence the convective blueshift has. In the upper panel of Fig. 13 we show the RV curves for an equatorial spot of 1% size with different temperatures for the F3 star. The blue dashed line represents the reference case of ΔT = 550 K. To show the RV curve evolution with decreasing spot temperature we also indicate the RVs for ΔT = 1100 K as green dashed line (arbitrary chosen intermediate case) and the RVs with the temperature of the spot derived from the model in Fig. 12, ΔTF3 = 2553 K, as black solid line. The points A, B are indicated as dots for each curve.
From the upper panel of Fig. 13 we can see that there is an increase in symmetry for the spot RV curve with decreasing spot temperature (or increasing spot contrast). In the lower panel of Fig. 13 we plot the symmetry parameter as a function of the spot contrast. Higher values on the x-axis correspond to larger spot contrasts (or darker spots). The lines seen in the lower panel of Fig. 13 are calculated from both FeI lines of the MHD simulations and the area between the two results is shaded. For all three stars simulated in this work we see an increase in symmetry of the RV curves for cooler spots with higher contrasts. However, the symmetry in the spot RV curves is different in F, G, and K stars for the same spot contrast. As explained in Sect. 4.1 this is likely related to the different convective speeds for different spectral types. If the spot temperatures from our fit to Fig. 12 are used for the RV simulations, the symmetry parameter is above 90% for all stars (see gray crosses in Fig. 13). In these cases the spot contrast is large and the convective blueshift plays only a minor role because the flux effect is dominant.
However, it is not clear whether or not the values of ΔT used are typical for the F, G, and K stars. For the G2 star the temperature difference of ΔTG2 = 1840 K corresponds to the Umbra in the Sun. The average temperature difference of spots is lower if the Penumbra is also considered. It is debatable whether observations of spot temperatures on other stars are sensitive mainly to the darker parts of the spots (Berdyugina 2005). If so, we underestimate the influence of the reduction of convection on the RV curves of spots in other stars.
When RV curves of active stars are modeled there is a degeneracy between active region temperature and size (decreasing the spot temperature and increasing the spot size both increase the RV amplitudes). The symmetry parameter could help to break this degeneracy because it quantifies the interplay between convection and spot temperature which gives the RV curves a characteristic shape. In practice, however, active stars have more than one spot on the surface and the convective blueshift is hard to constrain which will make it difficult to disentangle spot temperatures and sizes.
 |
Fig. 13 Top panel: influence of spot temperature on spot RVs of the F3 star. Calculations done with ΔT = 550 K (blue short dashed line), ΔT = 1100 K (green long dashed), and ΔT = 2553 K chosen according to the spectral type (black solid line). Lower panel: fractional symmetry parameter as a function of spot contrast for spectral types F3 (blue), G2 (green) and K5 (red). The gray crosses mark the contrasts of the spot temperatures derived from Fig. 12 for the F3, G2, and K5 stars, and the cyan “x” symbols mark the contrasts associated to a spot temperature contrast of 550K used in the earlier sections. |
5 Summary and conclusion
This work presents simulations of activity-induced RV variations of cold, dark spots and hot, bright plages on stars of spectral type F3, G2, and K5. In all of our simulations, spots and plagues have the same size, covering 1% of the visible stellar disk and are placed at the equator. Although plages are observed to cover a larger surface area on the Sun, this setup enables us to investigate a variety of parameters and effects and allows us to compare our results obtained with different model setups.
We investigate the influence of convective blueshift, line shape, and spot temperature on activity-related RV variations on stars other than the Sun. Other approaches in this field use synthetic model spectra without magnetic fields or observed spectra of the Sun to simulate RV curves. In contrast to previous studies we use MHD line profiles of two FeI lines at 6165 Å and 6173 Å. These line profiles are available at ten different μ and four different mean magnetic field strengths from B = 0 G to B = 500 G. In addition these line profiles are available for different stellar types which enables us to investigate the differences in the activity RV curves on different stars.
Magnetic fields are important when RV curves of spots and plages are investigated. If the magnetic field is strong enough it hinders the supply of new material into the active region and suppresses convection. The result is an apparent redshift of the active region relative to the surrounding quiet disk which results in a bias of the RV curves towards positive Doppler velocities. We have calculated four spot and plage models with magnetic fields of B = 0 G, B = 20 G, B = 100 G, and B = 500 G inside the active regions. All models using low magnetic fields of up to 100 G show no significant signs of reduced convective motions in the active region and the flux effect dominates the RV curves. However, our simulations using a mean magnetic field of 500 G inside the active region produce significantly asymmetric RV curves because convection is suppressed.
For F and G stars the suppression of the convective blueshift is significant and easily seen in RV curves of both spots and plages. The amplitudes of plage RV signals, especially, increase with increasing magnetic field strength in F and G stars. Increasing the magnetic field from 0 G to 500 G in the plage increases the RV amplitude from 0.5 m/s to 15.5 m/s in the F star and from 0.6 m/s to 5 m/s in the G star. For K stars, however, the magnetic field does not influence the shape of the RV curves significantly. As the convective blueshift of spectral lines is very weak, the suppression of convection has only a weak influence on the RV curves in the K5 star. This leads to a symmetric spot RV signal and a negligible plage signal.
Convective blueshift is not constant across the disk and we investigate the influence a variable convective blueshift has on the RV curves of spots and plages. We find that using symmetric Voigt profiles in combination with a constant convective blueshift does not well reproduce the results from the MHD line profiles. Differences are as large as 3.5 m/s for the spot on the F star and 5.5 m/s for the plage. Including a variable convective blueshift for the Voigt profile simulation improves the match with the RV curves derived from the MHD line profiles. However, especially for the plage simulations of the F and G stars, the maximum differences remain large. As a general trend we find that differences between the Voigt and MHD simulations are larger for hotter stars.
As we placed the Voigt profiles at the wavelength measured for the MHD line centers, there is a possibility that the remaining differences between the simulations originate from line profile differences. Voigt profiles are symmetric while MHD profiles have a red tail due to fast downstreams which create line asymmetries. As the projected velocity fields change across the disk, the MHD line profiles change with limb angle and we suspect these line profile changes to be the reason for the differences seen in simulations computed with Voigt and MHD line profiles. However, the differences between simulations with MHD and Voigt profiles are larger for the plages than for the dark spots. We conclude that this is a result of the active region brightness. For brighter active regions, line profile changes result in larger changes of the RV signal because the line profiles of bright active regions contribute more to the disk integrated spectrum of the star than to the line profiles of dark active regions.
We alsotested the influence of spot temperatures on the RV curves. The literature suggests that spots in early-type stars are cooler as compared to the quiet photosphere than in late-type stars. We simulate RV curves with the MHD line profiles and vary the spot temperature (and contrast). We define the symmetry parameter that allows us to measure the influence of the convective blueshift on spot RVs as a function of spot contrast. If spot temperatures according to observational values are used in our simulations we find that the flux effect is dominating the spot RV curve in all stars. Thus we can conclude that for high spot contrasts convective blueshift effects are negligible in RV signals, while for bright plages the situation is reversed and convection effects dominate the RV signatures.
Acknowledgements
We thank the anonymous referee, Efşan Sökmen, and Denis Shulyak for their careful reading and helpful comments on the article. Florian Franziskus Bauer acknowledges support from the Deutsche Forschungsgemeinschaft under DFG GrK 1351. Part of this work was supported by the ERC Starting Grant 279347, Wavelength Standards.
References
- Anglada-Escudé, G., Arriagada, P., Tuomi, M., et al. 2014, MNRAS, 443, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Anglada-Escudé, G., Tuomi, M., Arriagada, P., et al. 2016, ApJ, 830, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Artigau, É., Donati, J.-F., & Delfosse, X. 2011, in 16th Cambridge Workshop on Cool Stars, Stellar Systems, and the Sun, eds. C. Johns-Krull, M. K. Browning, & A. A. West, ASP Conf. Ser., 448, 771 [NASA ADS] [Google Scholar]
- Beeck, B., Cameron, R. H., Reiners, A., & Schüssler, M. 2013a, A&A, 558, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beeck, B., Cameron, R. H., Reiners, A., & Schüssler, M. 2013b, A&A, 558, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beeck, B., Schüssler, M., Cameron, R. H., & Reiners, A. 2015a, A&A, 581, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beeck, B., Schüssler, M., Cameron, R. H., & Reiners, A. 2015b, A&A, 581, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benedict, G. F., Nelan, E., McArthur, B., et al. 1993, PASP, 105, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Berdyugina, S. V. 2005, Living Rev. Solar Phys., 2 [Google Scholar]
- Boisse, I., Bonfils, X., & Santos, N. C. 2012, A&A, 545, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borgniet, S., Meunier, N., & Lagrange, A.-M. 2015, A&A, 581, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouchy, F., Pepe, F., & Queloz, D. 2001, A&A, 374, 733 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Butler, R. P., Bedding, T. R., Kjeldsen, H., et al. 2004, ApJ, 600, L75 [Google Scholar]
- de Boor C. 2001, A Practical Guide to Splines, Applied Mathematical Sciences (New York: Springer) [Google Scholar]
- Desort, M., Lagrange, A.-M., Galland, F., Udry, S., & Mayor, M. 2007, A&A, 473, 983 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dierckx, P. 1995, Curve and Surface Fitting with Splines, Monographs on numerical analysis (Clarendon Press) [Google Scholar]
- D’Odorico, V., & CODEX/ESPRESSO Team 2007, Mem. Soc. Astron. It., 78, 712 [NASA ADS] [Google Scholar]
- Dumusque, X., Udry, S., Lovis, C., Santos, N. C., & Monteiro, M. J. P. F. G. 2011, A&A, 525, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dumusque, X., Boisse, I., & Santos, N. C. 2014, ApJ, 796, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Fischer, D. A., Anglada-Escude, G., Arriagada, P., et al. 2016, PASP, 128, 066001 [NASA ADS] [CrossRef] [Google Scholar]
- Foukal, P. 2008, Solar Astrophysics (Wiley) [Google Scholar]
- Gray, D. F. 2009, ApJ, 697, 1032 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, R. O., Corbally, C. J., Garrison, R. F., et al. 2006, AJ, 132, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Hatzes, A. P. 2002, Astron. Nachr., 323, 392 [NASA ADS] [CrossRef] [Google Scholar]
- Herrero, E., Ribas, I., Jordi, C., et al. 2016, A&A, 586, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jeffers, S. V., Barnes, J. R., Jones, H. R. A., et al. 2014, MNRAS, 438, 2717 [NASA ADS] [CrossRef] [Google Scholar]
- Kotani, T., Tamura, M., Suto, H., et al. 2014, in Ground-based and Airborne Instrumentation for Astronomy V, Proc. SPIE, 9147, 914714 [Google Scholar]
- Küker, M., & Rüdiger, G. 2011, Astron. Nachr., 332, 933 [NASA ADS] [CrossRef] [Google Scholar]
- Kurucz, R. 1993, ATLAS9 Stellar Atmosphere Programs and 2 km s−1 grid. Kurucz CD-ROM No. 13. (Cambridge, Mass.: Smithsonian Astrophysical Observatory), 13 [Google Scholar]
- Lagrange, A.-M., Desort, M., & Meunier, N. 2010, A&A, 512, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lanza, A. F., Bonomo, A. S., Moutou, C., et al. 2010, A&A, 520, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Latham, D. W., Stefanik, R. P., Mazeh, T., Torres, G., & Carney, B. W. 1998, in Brown Dwarfs and Extrasolar Planets, eds. R. Rebolo, E. L. Martin, & M. R. Zapatero Osorio, ASP Conf. Ser., 134, 178 [NASA ADS] [Google Scholar]
- Ludwig, H.-G., Caffau, E., Steffen, M., et al. 2009, Mem. Soc. Astron. It., 80, 711 [NASA ADS] [Google Scholar]
- Mahadevan, S., Ramsey, L., Wright, J., et al. 2010, in Ground-based and Airborne Instrumentation for Astronomy III, Proc. SPIE, 7735, 77356 [CrossRef] [Google Scholar]
- Mayor, M., & Queloz, D. 1995, Nature, 378, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
- Meunier, N., Desort, M., & Lagrange, A.-M. 2010, A&A, 512, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meunier, N., Lagrange, A.-M., Borgniet, S., & Rieutord, M. 2015, A&A, 583, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meunier, N., Lagrange, A.-M., Mbemba Kabuiku, L., et al. 2017, A&A, 597, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ortiz, A., Solanki, S. K., Domingo, V., Fligge, M., & Sanahuja, B. 2002, A&A,388, 1036 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Quirrenbach, A., Amado, P. J., Caballero, J. A., et al. 2011, in IAU Symp. 276, eds. A. Sozzetti, M. G. Lattanzi, & A. P. Boss, 545 [NASA ADS] [Google Scholar]
- Radick, R. R., Mihalas, D., Lockwood, G. W., et al. 1983, PASP, 95, 621 [NASA ADS] [CrossRef] [Google Scholar]
- Reiners, A. 2014, in Magnetic Fields throughout Stellar Evolution, eds. P. Petit, M. Jardine, & H. C. Spruit, IAU Symp., 302, 156 [NASA ADS] [Google Scholar]
- Reiners, A., Bean, J. L., Huber, K. F., et al. 2010, ApJ, 710, 432 [NASA ADS] [CrossRef] [Google Scholar]
- Reiners, A., Shulyak, D., Anglada-Escudé, G., et al. 2013, A&A, 552, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reiners, A., Lemke, U., Bauer, F., Beeck, B., & Huke, P. 2016a, A&A, 595, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reiners, A., Mrotzek, N., Lemke, U., Hinrichs, J., & Reinsch, K. 2016b, A&A, 587, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Robertson, P., Mahadevan, S., Endl, M., & Roy, A. 2014, Science, 345, 440 [NASA ADS] [CrossRef] [Google Scholar]
- Robertson, P., Roy, A., & Mahadevan, S. 2015, ApJ, 805, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Saar, S. H., & Donahue, R. A. 1997, ApJ, 485, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Udry, S., Bonfils, X., Delfosse, X., et al. 2007, A&A, 469, L43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vogt, S. S., Butler, R. P., Rivera, E. J., et al. 2010, ApJ, 723, 954 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
The RV curves in Figs. 1 and 2 are derived with our method explained in Sect. 3. The spot parameters are similar to what is observed on the Sun. The spot covers 1% of the visible disk and is 550 K cooler than the surrounding photosphere. The plage has the same size as the spot but its temperature is derived from Eq. (1). The star rotates with a projected velocity of v ⋅ sin(i) = 2 km s−1. The line profile used is a Voigt profile and the value for the convective blueshift in Fig. 2 is constant at 300 m/s.
All Tables
Differences between Voigt profile models using different convective blueshift models.
All Figures
 |
Fig. 1 Upper panel: schematic view of the G2 star with a dark spot rotating across the projected stellar disk. The color code indicates the intensity across the disk. Middle panel: RV curve produced by the flux effect of a dark spot. Lower panel: RV curve produced by the flux effect of a bright plage. The stellar effective temperature in this models is Teff = 5780 K. The spot is 550 K cooler than the quiet stellar photosphere and the plage temperature is derived from Eq. (1). |
| In the text | |
 |
Fig. 2 Upperpanel: spot RV curve produced by the flux effect only (gray dashed line), the RV curve produced by the active region by only suppressing the convective blueshift (blue dashed line) and the spot RV curve produced by taking into account the flux effect and the suppression of convection (black solid line). Lower panel: RV curves for the bright plage plotted in the same way as for the dark spot in the upper panel. |
| In the text | |
 |
Fig. 3 Influence of magnetic field strength on spot RVs. Line profiles with different field strengths were used inside the spot. Spot RVs calculated with B = 0 G (black solid line), with B = 20 G (green long dashed line), with B = 100 G (blue short dashed line), and with B = 500 G (red dotted line). The results for the FeI line at 6165 Å are shown in the left panel, and the results of the FeI line at 6173 Å can be seen in the right panel. The gray solid line in the right panel indicates the results of the FeI line at 6165 Å for comparison. |
| In the text | |
 |
Fig. 4 Influence of magnetic field strength on plage RVs. Line profiles with differentfield strengths were used for the plage. Plage RVs calculated with B = 0 G (black solid line), with B = 20 G (green long dashed line), with B = 100 G (blue short dashed line) and with B = 500 G (red dotted line). The results for the FeI line at 6165 Å are shown in the left panel, and the results of the FeI line at 6173 Å can be seen in the right panel. The gray solid line in the right panel indicates the results of the FeI line at 6165 Å for comparison. |
| In the text | |
 |
Fig. 5 Left panel: variation of the active region velocity with the magnetic field strength B for different stellar types and measurement methods. Right panel: MHD line profile of the FeI line at 6165 Å for different magnetic field strength (solid lines) and line center measurements with the Gaussian method (crosses) and the centroid method (x). The color code for the line profiles and the center measurements are the same: black for B = 0 G, green for B = 20 G, blue for B =100 G, and red for B = 500 G. |
| In the text | |
 |
Fig. 6 Comparison between the RV curves derived by our code using the MHD line profiles (black solid lines) and SOAP 2.0 (red dotted lines) for a dark spot (upper panel) and a bright plage (lower panel). |
| In the text | |
 |
Fig. 7 Variation of the active region velocity field between B = 0 and B = 500 G as a functionof μ for the F3 star (blue squares), G2 star (green circles), and the K5 star (red triangles). The results of the FeI line at 6165 Å is shown with open symbols and the result of the FeI line at 6173 Å is indicatedas filled symbols. For comparison the constant active region velocity field taking into account only the projection effect with μ (as done in previous works) is plotted as black line. Red-blue circles in the bottom left indicate where on the stellar disk active regions appear redshifted or blueshifted relative to the quiet photosphere. |
| In the text | |
 |
Fig. 8 Spot RVs calculated for different stellar types with different line profiles. Calculations done with the 500 G MDH line profiles (black solid lines), Voigt profiles and a constant convective blueshift (green long dashed lines), and Voigt profiles including a varying convective blueshift (blue short dashed lines). |
| In the text | |
 |
Fig. 9 Plage RVs calculated for different stellar types with different line profiles. Calculations done with the 500 G MDH line profiles (black solid lines), Voigt profiles and a constant convective blueshift (green long dashed lines) and Voigt profiles including a varying convective blueshift (blue short dashed lines). |
| In the text | |
 |
Fig. 10 Variation of the FeI line at 6165 Å with μ for B = 0 G left, and B = 500 G right panel. MHD line profiles at different μ values are color coded from blue (μ = 1) to red (μ = 0). For comparison, Voigt profiles with solar parameters are overplotted as black (μ = 1) and gray (μ = 0) broken lines. |
| In the text | |
 |
Fig. 11 Difference between the B = 500 G and B = 0 G line profiles normalized by the line depth of the B = 0 G line. Panel from left to right show the result for the F3, G2, K5 MHD lines, respectively. The rightmost panel depicts results from the cb(μ) simulation using Voigt profiles with solar parameters. Upper panels: results at μ = 1. Lower panel:results at μ = 0.7. |
| In the text | |
 |
Fig. 12 Measured spot temperatures in red giants (red filled squares) and main sequence dwarfs (blue filled circles). Measurements of the Suns umbra and penumbra are shown as yellow open circles and EK Dra is shown as blue open circle. All values are taken from Berdyugina (2005). Our fit to the data is indicated as gray line and our simulated stars are indicated as green star symbols. |
| In the text | |
 |
Fig. 13 Top panel: influence of spot temperature on spot RVs of the F3 star. Calculations done with ΔT = 550 K (blue short dashed line), ΔT = 1100 K (green long dashed), and ΔT = 2553 K chosen according to the spectral type (black solid line). Lower panel: fractional symmetry parameter as a function of spot contrast for spectral types F3 (blue), G2 (green) and K5 (red). The gray crosses mark the contrasts of the spot temperatures derived from Fig. 12 for the F3, G2, and K5 stars, and the cyan “x” symbols mark the contrasts associated to a spot temperature contrast of 550K used in the earlier sections. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


