EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 609 (January 2018) A&A, 609 (2018) A110 Full HTML
Open Access
Issue
A&A
Volume 609, January 2018
Article Number A110
Number of page(s) 20
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/201629108
Published online 25 January 2018

© ESO, 2018

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

1. Introduction

A pulsar wind nebula (PWN) is formed when the wind of a pulsar interacts with the ambient medium, either the supernova ejecta or the interstellar medium (e.g., Rees & Gunn 1974; Kennel & Coroniti 1984; Chevalier 2004; Gaensler & Slane 2006; Bucciantini 2008). It is generally believed that a PWN is mainly composed of a relativistic nonthermal lepton (electron/positron) plasma and magnetic field and can emit nonthermal photons from radio to γ-rays via synchrotron radiation and the inverse Compton (IC) process. Observations have shown that some PWNe, such as the Crab nebula, Kes 75, MSH 15-52, can emit nonthermal emission from radio to very high-energy (VHE) γ-ray bands (e.g., Bühler & Blandford 2014; Reynolds et al. 2017). Currently, about 37 TeV PWNe are firmly identified1. More recently, the observations and relevant physical analysis of 19 TeV PWNe have been presented in Abdalla et al. (2017), where 14 TeV PWNe are firmly identified as PWNe by HESS observations. These observations provide an essential reason for studying PWNe.

Various models have been proposed to explain the nonthermal properties of PWNe and a brief review of current models and differences can be found in Torres et al. (2014). Here we focus on the one-dimensional (1D) model of the dynamical and radiative evolution of a PWN in a nonradiative SNR. Here we focus on the 1D model of the dynamical and radiative evolution of a PWN in a nonradiative supernova remnant (SNR) presented in Gelfand et al. (2009). In the frame of the model, the radiative properties during different phases of the PWN evolution are investigated with a single power-law injection spectrum for the electrons/positrons (Gelfand et al. 2009), with the relativistic Maxwellian and a high-energy power-law tail injection spectrum for the electrons/positrons (Fang & Zhang 2010a), and with two possible forms of injected electron spectra: a broken power law and the sum of a power law at low energy, and a relativistic Maxwellian plus a high-energy power-law tail (Zhu et al. 2015). It has been shown that the broken power-law form for the electron injection is required when the model applies to the Crab nebula (Zhu et al. 2015). Recently, a model for describing PWN radiative properties during the dynamical evolutions of the PWN and the SNR is presented in Martin et al. (2016), the radius of the PWN during the free expansion phase and compression in this model is calculated through solving the equations given by Chevalier (2005), where the prescription is similar to that in Gelfand et al. (2009). The model is applied to a TeV PWN CTA 1 (Martin et al. 2016). We note that there is a kind of model in which a broken power-law injection spectrum for the electrons/positrons is assumed but the dynamics beyond reverberation is not included (e.g., Zhang et al. 2008; Bucciantini et al. 2011; Tanaka & Takahara 2011).

To investigate nonthermal radiative properties of each PWN and statistical features of PWNe, observed multiwaveband data for each PWN are required. However, not all PWNe are observed at different bands, due to observation limits, so 18 PWNe from known PWNe are selected here according to the following criteria: (1) the period and period derivative of central pulsar in each PWN are known, and (2) nonthermal emission at radio, X-ray, and TeV bands are detected. In this selection, N 158A is not detected at TeV band, G310.6-1.6 is detected with an upper limit at TeV band, G292.0+1.8 is detected with upper limits at GeV band. These three PWNe are included in the sample because of their energetic pulsars. These PWNe are divided into three groups based on the ages of PWNe that are adopted in our calculations (see Sect. 3). The nonthermal radiative property for each PWN is studied in the leptonic model with a broken power-law injection for the electrons/positrons, and the correlation features of all 18 PWNe are presented.

The structure of this article is as follows. In Sect. 2 we briefly review the model. In Sect. 3 we apply the model to 18 PWNe, and calculate the spectral energy distibution (SED) of each PWN. In Sect. 4 we study correlation properties of the PWNe, and we give our conclusions and discussions in Sect. 5.

2. Model description

For completeness, we briefly review the model for dynamical and radiative evolution of a PWN inside a SNR given in Zhu et al. (2015), which is closely based on that developed by Gelfand et al. (2009; see also Fang & Zhang 2010a). In this model, the large-scale evolution of a composite SNR depends on the mechanical energy Esn of the explosion, the density nH of the ambient medium, the mass Mej of the supernova ejecta, and the spin-down power L(t) of the pulsar. For a given pulsar with a period P, a period derivative Ṗ, a braking index n, and an initial spin-down power L0, the spin-down power L(t) at time t is given by (Gaensler & Slane 2006) 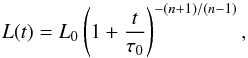L(t)=L0(1+tτ0)−(n+1)/(n−1),\begin{equation} {L}(t)={L}_0\left(1+\frac{t}{\tau_0}\right)^{-(n+1)/(n-1)} ,\label{Lum} \end{equation}(1)where τ0 = (2τc)/(n−1)−Tage is the initial spin-down timescale of the pulsar, τc = P/ 2Ṗ is the characteristic age of the pulsar, and Tage is the age of the PWN. Since L(t) can be estimated by L(t) = 4π2IṖ/P3, where I is the pulsar moment of inertia (here I = 1045 g cm2 is used), the evolution of the spin-down power can be determined (i.e., L0 and τ0 can be estimated) if Tage is known. Therefore, the main parameters of a given pulsar are P, Ṗ, and n. At present, the vaules of the braking index n for some pulsars have been measured, and we use the measured values if available, otherwise we assume n = 3. We call these parameters the pulsar and ejecta parameters.

The evolution of isotropic electron distribution N(E,t) in the PWN is calculated by using ∂N(E,t)∂t=∂∂E[ĖN(E,t)]+N(E,t)τ(E,t)+Q(E,t),\begin{equation} \frac{\partial N(E,t)}{\partial t}= \frac{\partial }{\partial E} \left [\dot{E} N(E,t) \right] + \frac{N(E,t)}{\tau(E,t)} + Q(E,t), \label{NE} \end{equation}(2)where Ė is the energy-loss rate of the particles with an energy E which includes the contributions of synchrotron radiation, inverse Compton scattering, and adiabatic losses and τ(E,t) is the escape time (for the details of their processes, see Zhang et al. 2008). The last term on the right-hand side in Eq. 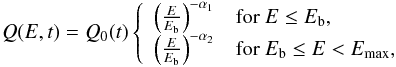(2), Q(E,t), is a source term, i.e., the injected electron number per unit energy per unit time, and is assumed to be a broken power-law form Q(E,t)=Q0(t){(EEb)−α1forE≤Eb,(EEb)−α2forEb≤E<Emax,\begin{equation} Q(E,t) = Q_0(t)\left\{\begin{array}{ll} \left(\frac{E}{E_{\rm b}}\right)^{-\alpha_1}& {\rm for}~E\le E_{\rm b},\\ \left(\frac{E}{E_{\rm b}}\right)^{-\alpha_2}& {\rm for}~E_{\rm b}\le E < E_{\rm max}, \end{array} \right. \label{Inj1} \end{equation}(3)where Q0(t) is a time-dependent parameter, Eb is the break energy, α1< 2 and α2> 2 are respectively the spectral indexes of the injection rate at E ≤ Eb and E>Eb, and Emax is the maximum energy of the electrons.

Here the spin-down power of the pulsar is assumed to be distributed between electrons (Ėe(t) = ηeL(t)) and magnetic fields (ĖB = ηBL(t)) [ηe + ηB = 1] (Gelfand et al. 2009), then Q0(t) can be estimated from 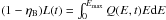(1−ηB)L(t)=∫0EmaxQ(E,t)EdE\hbox{$(1-\eta_{\rm B})L(t) = \int_{0}^{E_{\rm max}} Q(E, t) E {\rm d}E$}, which gives Q0(t)={(1−ηB)L(t)Eb2(2−α1)(2−α2)α1−α2α2>2(1−ηB)L(t)Eb2[12−α1+log(EmaxEb)]α2=2.\begin{equation} Q_0(t) = \left\{\begin{array}{ll} \dfrac{(1-\eta_{\rm B})L(t)}{{E_{\rm b}}^2}\frac{(2-\alpha_1)(2-\alpha_2)}{\alpha_1-\alpha_2} & \alpha_2> 2\\[6mm] \dfrac{(1-\eta_{\rm B})L(t)}{{E_b}^2}\left[\dfrac{1}{2-\alpha_1} + \log\left({\frac{E_{\rm max}}{E_{\rm b}}}\right)\right] & \alpha_2 =2. \end{array} \right . 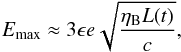\label{Q0I} \end{equation}(4)On the other hand, the maximum energy of the electrons can be estimated by the condition that the Larmor radius of the electrons inside the PWN is smaller than the termination shock radius of the PWNe by the containment factor ϵ< 1, which is given by Emax≈3ϵeηBL(t)c,\begin{equation} \label{} E_{\rm max} \approx 3\epsilon e\sqrt{\frac{\eta_{\rm B}L(t)}{c}}, \end{equation}(5)where e is the electron charge (e.g., Zhu et al. 2015). We note that Emax can also be estimated by the balance between the synchrotron loses and acceleration, which gives Emaxsyn≈[3(mec2)2/4e]π/eBpwn\hbox{$E^{\rm syn}_{\rm max}\approx [3(m_{\rm e}c^2)^2/4e]\sqrt{\pi/e B_{\rm pwn}}$}. 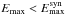For the parameters of PWNe used here (see Tables 1–3), Emax<Emaxsyn\hbox{$E_{\rm max}< E^{\rm syn}_{\rm max}$} is always satisfied. Hence, the injection parameters involving electron injection are Eb, α1, α2, ηB, and ϵ.

In such a model, the dynamical and radiative properties for a given PWN can be self-consistently studied Gelfand et al. (2009; see also Fang & Zhang 2010a; and Zhu et al. 2015). On the one hand, the time evolutions of the SNR radius Rsnr(t), reverse shock radius Rrs(t), PWN radius Rpwn(t), the position of the neutron star Rpsr(t), the termination shock radius Rts(t), and the magnetic field Bpwn(t) of the PWN can be calculated. On the other hand, the time evolutions of electron spectrum and the spectral energy distribution (SED) of nonthermal photons can be obtained. It should be pointed out that different electron injection forms and electron energy losses will lead to the change in dynamical features of the PWN. In this paper, the broken power-law injection of the electrons (see Eq. (3)) and escape term of the electrons (see the second term on the left-hand side of Eq. (2)) are considered, so the dynamical features for a given PWN will be different from those given in Gelfand et al. (2009), who assumed a single power-law injection without electron escape (e.g., Crab nebulae, see Zhu et al. 2015). We note that both Rpwn(t) and Bpwn(t) play important roles in the evolution of the energy losses and the SED for a given PWN. Therefore, in our calculations the allowed ranges of Rpwn(t) are limited by the values given in Abdalla et al. (2017; see their Tables 1 and 3).

In our calculations, nonthermal photons are produced through synchrotron radiation and inverse Compton (IC) scattering of relativistic electrons (e.g., Zhu et al. 2015). For the synchrotron radiation, the emissivity given in Zhang et al. (2008) is used, which includes the effect of electron pitch angle. The magnetic field Bpwn of a PWN evolves with time and can be estimated by Eq. (A.6) in Appendix A. We note that Torres et al. (2014) did not consider the effect of electron pitch angle (see also Tanaka & Takahara 2010; Martin et al. 2012), which will result in parameter differences between our model and the model in Torres et al. (2014) for a given PWN.

Table 1

Parameters for young PWNe.

For IC scattering, soft photon fields consist of four components: the cosmic microwave background (CMB) in our calculations, the galactic far-infrared (FIR) background, the near-infrared (NIR) and optical photon field due to the stars, and synchrotron radiation. The energy density and temperature of the CMB photons are UCMB = 0.25 eV cm-3 and TCMB = 2.7 K, and the energy densities and temperatures of FIR (UFIR and TFIR) and NIR (UNIR and TNIR) can be different for PWNe. We refer to these parameters as soft photon parameters. The emissivity of IC scattering used here is given by Zhang et al. (2008).

To fit the observed spectral energy distribution (SED) for each PWN, pulsar and ejecta parameters and soft photon parameters are fixed, and injection parameters are considered as fitting parameters (see Tables 1–3). The Levenberg-Marquardt (LM) method of the χ2 minimization fitting procedure is used to find the best-fitting values of injection parameters and their uncertainties. However, because of the lack of data (from radio to optical) for most PWNe, the best-fitting values and their uncertainties of α1 and Eb cannot be easily obtained. Therefore, at first, visual fitting is used to determine the values of α1 and Eb, and then the LM method is used to obtain the values of α2, ηB, and ϵ. With this procedure, we fit 14 PWNe, except for N 158A, G310.6-1.6, G292.0+1.8, and HESS J1303-631. Since the observed data at GeV–TeV and from radio to X-ray band are upper limits for these four PWNe, the LM method can only determine the values of α2 and ηB for N 158A, G310.6-1.6, and G292.0+1.8, and α2 for HESS J1303-631; other injection parameters are estimated via visual fitting. These values are shown in Tables 1–3.

In addition to the above parameters, six derived parameters (Emax,Bpwn,Rpwn,Rrs,Rsnr, and Rts) are also given (see Tables 1–3). We note that Emax and Bpwn, which relate to ϵ and ηB, are calculated. Because the slight difference in the injection spectrum has little effect on the dynamical properties of PWNe, the uncertainties of Rpwn,Rrs,Rsnr, and Rts are not calculated here.

thumbnail Fig. 1

Comparisons of predicted SEDs and observed data for young PWNe (from upper left panel for N 158A to bottom right panel for 3C 58). In each panel, the black line represents synchrotron SED; the magenta, blue, green, and cyan lines represent the SEDs of inverse Compton scatterings with the synchrotron photons, IR, CMB, and starlight, respectively; and the total SED is shown by the red line. See text for the descriptions of the observed data; the relevant parameters are listed in Table 1.

3. Applications to individual PWNe

The model described in Sect. 2 is now applied to explain the observed SEDs of nonthermal photons for 18 PWNe. The detailed descriptions of observed and derived properties of each PWN are summarized in Appendix B. The PWN sample is divided into three groups based on possible ages Tage of PWNe. The first group consists of the PWNe with Tage ≤ 2400 yr (we call them young PWNe), the second group with 2400 < Tage < 5000 yr (called evolved PWNe), and the third group with Tage ≥ 5000 yr (called mature/old PWNe). Although the division of the three groups is arbitrary, it is convenient for us to study the properties of PWNe that lie in different age ranges.

Some of the 18 PWNe have been already investigated (e.g., Fang & Zhang 2010a; Tanaka & Takahara 2011; Torres et al. 2014; Martin et al. 2014; Zhu et al. 2015; Martin et al. 2016). Two important quantities that influence the electron energy loss and photon SED of a PWN are Rpwn(t) and Bpwn(t). In Torres et al. (2014), Rpwn(t) ∝ t6/5 is calculated during the SNR’s free expansion phase (van der Swaluw et al. 2001, 2003) and Bpwn(t) is estimated with a method similar to that used in Gelfand et al. (2009). In Tanaka & Takahara (2011), Bpwn(t) is calculated by using the magnetic field energy conservation, i.e., 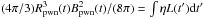(4π/3)Rpwn3(t)Bpwn2(t)/(8π)=∫ηL(t′)dt′\hbox{$(4\pi/3)R^3_{\rm pwn}(t)B^2_{\rm pwn}(t)/(8\pi)=\int\eta L(t'){\rm d}t'$}, and Rpwn is estimated by reproducing photon SED.

Table 2

Parameters for evolved PWNe.

thumbnail Fig. 2

Comparisons of predicted SEDs and observed data for evolved PWNe (from upper left panel for HEES J1813-178 to bottom right panel for N 157B). In each panel, the black line represents the synchrotron SED; magenta, blue, green, and cyan lines represent the SEDs of inverse Compton scatterings with the synchrotron photons, IR, CMB, and starlight, respectively; and the total SED is shown by the red line. See text for the descriptions of the observed data; the relevant parameters are listed in Table 2.

3.1. Group 1: young PWNe

Table 3

Parameters for mature/old PWNe.

thumbnail Fig. 3

Comparisons of predicted SEDs and observed data for mature/old PWNe (from upper left panel for HEES J1356-645 to bottom right panel for HESS J1303-631). In each panel, the black line represents the synchrotron SED; magenta, blue, green, and cyan lines represent the SEDs of inverse Compton scatterings with the synchrotron photons, IR, CMB, and starlight, respectively; and the total SED is shown by the red line. See text for the descriptions of the observed data; the relevant parameters are listed in Table 3.

There are six young PWNe in this group, N 158A, G21.5-0.9, Crab nebula, Kes 75, G310.6-1.6, and 3C 58, whose ages range from 700 yr to 2400 yr. The parameters of pulsar and ejecta, electron injections, and soft photon fields for these young PWNe are listed in Table 1, and the details for each PWN is given in Appendix B. Using the parameters in Table 1, the SEDs of these young PWNe are calculated. The comparisons of the calculated and observed SEDs are shown in Fig. 1 and derived parameters are listed in Table 1. The multiband SEDs of these young PWNe have been studied (e.g., Tanaka & Takahara 2011; Torres et al. 2014; Martin et al. 2014). These PWNe are in the SNR’s free expansion phases and the dynamical evolution in the free expansion phase used here is similar that used in Torres et al. (2014).

The fluxes, FX ≡ F1−10 keV and Fγ ≡ F1−10 TeV, in X-ray (1–10 keV) and γ-ray (1–10 TeV) bands for each PWN are calculated.

At an age of 760 yr N 158A was not detected in GeV and TeV γ-ray bands, so the sensitivity curves of the Cherenkov Telescope Array (CTA) is used as an upper limit to restrict soft photon parameters (see Table 1). Our results are shown in Table 1 and Fig. 1, and give that Rpwn = 0.68 pc and Bpwn = 45.22 μG, which is roughly consistent with the values given in Martin et al. (2014, Rpwn = 0.7 pc and Bpwn = 32 μG). The observed SED can be reproduced and predicted as FX/Fγ ~ 118.

Our results for G21.5-0.9 are shown in Table 1 and Fig. 1. Here the age is assumed to be Tage = 900 yr, which is close to Tage = 870 yr in Torres et al. (2014). Our results give Rpwn = 0.86 pc and Bpwn ≈ 84 μG, which are consistent with those in Torres et al. (2014; Rpwn = 0.9 pc and Bpwn = 71 μG) and those in Tanaka & Takahara (2011; Rpwn = 1.0 pc and Bpwn = 64, and 47 μG). We note that Rpwn is less than that given in Abdalla et al. (2017; <4 pc). The predicted FX/Fγ ~ 130.

For Crab nebulae, the results are the same as those given in Zhu et al. (2015). As mentioned above, the main differences between our results and those in Tanaka & Takahara (2011) and Torres et al. (2014) come from the use of different synchrotron emissivity. Our results give Rpwn ≈ 1.95 pc (<3 pc in Abdalla et al. 2017) and Bpwn ≈ 116 μG. The predicted FX/Fγ ~ 460.

For Kes 75, its age is assumed to be 1000 yr, which is slightly older than the ages given in Tanaka & Takahara (2011) and Torres et al. (2014), and its SED is calculated with the same values of pulsar and ejecta parameters and soft photon parameters as those in Torres et al. (2014) and can reproduce the observed SED well with FX/Fγ ~ 13 (see Fig. 1). However, our injection parameters are different from those given in Torres et al. (2014) because the formula of synchrotron emissivity used here (see Eq. (12) of Zhang et al. 2008) is different from that used in Torres et al. (2014, see Eqs. (27) and (28) of Martin et al. 2012), resulting in different values of Rpwn = 0.99 pc and Bpwn ≈ 14 μG of Table 1 in comparison with those (Rpwn = 0.9 pc and Bpwn = 19 μG) in Torres et al. (2014) and those (Rpwn = 0.29 pc and Bpwn = 20 μG) in Tanaka & Takahara (2011).

The HESS observation gives the upper limit of the flux at TeV band for G310.6-1.6, which can roughly restrict model parameters. With Tage = 1500 yr, which is less than the age of <1900 yr found in Renaud et al. (2010), Rpwn = 1.32 pc and Bpwn ≈ 13 μG are obtained here. We note that Tanaka & Takahara (2013) gave Rpwn = 1.3 pc and Bpwn = 17 μG with Tage = 600 yr, and Martin et al. (2014) obtained Rpwn = 1.3 pc and Bpwn = 8.2 μG with Tage = 1100 yr. The predicted FX/Fγ ~ 11.

3C 58 has an age of ~ 2400 yr (Chevalier 2005; Tanaka & Takahara 2013; Torres et al. 2013). With Tage = 2400 yr, Rpwn = 3.05 pc and Bpwn ≈ 24 μG are obtained, which can compare with the values in Tanaka & Takahara (2013, Rpwn = 2.0 pc and Bpwn = 17 μG) and those in Torres et al. (2013, Rpwn = 3.7 pc and Bpwn = 35 μG). We note that the distance of the PWN is assumed to be 2 kpc here, which is the same as that in Tanaka & Takahara (2013), but is different from that in Torres et al. (2013; 3.2 kpc). The predicted FX/Fγ ~ 20.

3.2. Group 2: evolved PWNe

The group of evolved PWNe consists of HESS J1813-178, G54.1+0.3, G292.0+1.8, G0.9+0.1, MSH 15-52, and N 157B whose ages range from 2500 yr to 4600 yr. Since the SN explosion energy Esn are unknown for these PWNe, here we assume Esn = 1.0 × 1051 erg. The related parameters for the evolved PWNe are listed in Table 2 and the comparisons of the modeled and observed SEDs are shown in Fig. 2.

HESS J1813-178 is observed to have a distance d ≈ 4.7 kpc (Brogan et al. 2005; Halpern et al. 2012) and Rpwn = 4.0 ± 0.3 pc (Abdalla et al. 2017). With Tage = 2500 yr, Rpwn ≈ 3.7 pc and Bpwn = 8.11 μG are obtained here. The predicted FX/Fγ ~ 6. We note that Fang & Zhang (2010b) investigated the PWN in detail, and obtained Rpwn = 1.7 pc and Bpwn = 5 μG with Tage = 1200 yr.

The age of G54.1+0.3 is uncertain, which ranges from 1500 to 6000 yr (Camilo et al. 2002a), or from 2100 to 3600 yr (Gelfand et al. 2015). Because the characteristic age is ~ 2872 yr, Tage = 2600 yr is assumed, and our results give Rpwn ~ 2.4 pc, Bpwn ≈ 9.5 μG, and FX/Fγ ~ 3. With different ages, Tanaka & Takahara (2011) gave Rpwn = 1.8 pc and Bpwn = 10 μG (6.7 μG) for Tage = 1700 yr (2300 yr) and Torres et al. (2014) obtained Rpwn = 1.4 pc and Bpwn = 14 μG for Tage = 1700 yr.

Although the age of G292.0+1.8 is uncertain, Rpwn ≈ 3.0 pc is given in Bhalerao et al. (2015). With Tage = 2700 yr (Tanaka & Takahara 2013), which is larger than 1600 yr given in Murdin & Clark (1979) and 2500 yr in Martin et al. (2014), our results show that Rpwn = 3.12 pc and Bpwn ≈ 24 μG, which are consistent with Rpwn = 3.5 pc and Bpwn = 16 μG obtained by Tanaka & Takahara (2013) and Rpwn = 3.5 pc and Bpwn = 21 μG by Martin et al. (2014). The predicted FX/Fγ ~ 14.

The age (from 2000 yr to 3000 yr, see Camilo et al. 2009) and distance (from 8.0 kpc to 16 kpc, see Dubner et al. 2008) of G0.9+0.1 are both uncertain. Here Tage = 3000 yr and d = 13.3 kpc are assumed; the results show that Rpwn = 3.51 pc, Bpwn ≈ 20 μG, and FX/Fγ ~ 4. Tanaka & Takahara (2011) obtained Rpwn = 2.3 pc (3.8 pc) and Bpwn = 15 μG (12 μG) for d = 8.0 kpc (13 kpc) and Tage = 2000 yr (4500 yr). Torres et al. (2014) obtained Rpwn = 2.5 pc (3.8 pc) and Bpwn = 14 μG (15 μG) for d = 8.5 kpc (13 kpc) and Tage = 2000 yr (3000 yr).

For MSH 15-52, its radius is Rpwn = 11.1 ± 2.0 pc (Abdalla et al. 2017). Our results give Rpwn = 11.21 pc, Bpwn ≈ 19 μG, and FX/Fγ ~ 10 with Tage = 4000 yr. We note that younger age in previous studies is used; for example, Tage ~ 1600 yr, Rpwn = 3.0 pc, and Bpwn = 21 μG were obtained by Torres et al. (2014), and Rpwn = 3.6 pc and Bpwn = 19.0 μG by Fang & Zhang (2010a).

N 157B has an estimated distance of 48 kpc (Macri et al. 2006), and its radius is about 10.6 pc (Lazendic et al. 2000), or 3.5 pc (Chen et al. 2006), or <94 pc (Abdalla et al. 2017). Here, Tage = 4600 yr is used, and the results show that Rpwn = 10.02 pc, Bpwn ≈ 26 μG, and FX/Fγ ~ 5. With Tage = 4600 yr, Martin et al. (2014) obtained Rpwn = 10.6 pc and Bpwn = 13 μG.

3.3. Group 3: mature/old PWNe

The third group of mature/old PWNe consists of HESS J1356-645, CTA 1, HESS J1418-609, HESS J1420-607, HESS J1119-614, and HESS J1303-631 whose ages range from 6500 yr to 13 000 yr. The related parameters for these mature/old PWNe are listed in Table 3 and the comparisons of modeled and observed SEDs are shown in Fig. 3.

HESS J1356-645 is a TeV PWN with a distance of 2.5 kpc (Cordes & Lazio 2002; Chang et al. 2012) and a radius of Rpwn = 10.1 ± 0.9 pc (Abdalla et al. 2017). With Tage = 6500 yr, the values of Rpwn = 10.34 pc, Bpwn ≈ 4 μG, and FX/Fγ ~ 0.9 are obtained. With Tage = 6000 (8000) yr, Torres et al. (2014) obtained Rpwn = 9.5 (9.9) pc and Bpwn ≈ 3.1 (3.5) μG.

CTA 1 has a radius of Rpwn = 6.6 ± 0.5 pc (Abdalla et al. 2017). With Tage = 7500 yr, the values of Rpwn = 6.24 pc, Bpwn ≈ 5.66 μG, and FX/Fγ ~ 4 are obtained here. There have been several studies of CTA 1 (e.g., Zhang et al. 2009; Torres et al. 2014; Martin et al. 2016). Torres et al. (2014) found Rpwn = 8 pc and Bpwn ≈ 4.1 μG with Tage = 7500 yr. Martin et al. (2016) studied both radiative and dynamical properties of CTA 1; they obtained that Tage = 9200 (11 400) yr, Rpwn = 6.7 (6.7) pc, and Bpwn ≈ 4.3 (1.8) μG in the free expansion (compression) phase of CTA 1.

For HESS J1418-609, its radius is Rpwn = 9.4 ± 0.9 pc (Abdalla et al. 2017). In the current paper Rpwn = 9.4 pc, Bpwn ≈ 4.4 μG, and FX/Fγ ~ 1 are obtained with Tage = 8000 yr.

The radius of HESS J1420-607 is Rpwn = 7.9 ± 0.6 pc (Abdalla et al. 2017). Here the values of Rpwn = 7.73 pc, Bpwn ≈ 3.7 μG, and FX/Fγ ~ 0.8 are obtained with Tage = 8500 yr.

HESS J1119-614 has a radius of Rpwn = 14 ± 2 pc (Abdalla et al. 2017). The values reported here are Rpwn = 14.67 pc, Bpwn ≈ 1.3 μG, and FX/Fγ ~ 0.01 with Tage = 9000 yr here. Torres et al. (2014) gave Rpwn = 13 pc and Bpwn ≈ 4 μG with Tage = 4200 yr.

HESS J1303-631 has a radius of Rpwn = 20.6 ± 1.7 pc (Abdalla et al. 2017). In the current paper Rpwn = 20.44 pc, Bpwn ≈ 1.6 μG and FX/Fγ ~ 0.02 are obtained with Tage = 13 000 yr.

Table 4

Pair multiplicities and wind Lorentz factors in the sample.

Table 5

Parameters of the central pulsars in the sample.

Table 6

Calculated luminosity at different wave bands and synchrotron cooling break energies in the sample.

3.4. Estimate of pair multiplicity and wind Lorentz factor

Pair multiplicity, κmulti, and the Lorentz factor, γw, are calculated for a PWN based on our model. The pair multiplicity can be expressed as 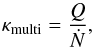κmulti=QṄ,\begin{equation} \kappa_{\rm multi} = \frac {Q}{\dot {N}}, \end{equation}(6)where Q is the injection rate by integrating Eq. (2), 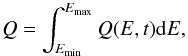Q=∫EminEmaxQ(E,t)dE,\begin{equation} Q = \int_{E_{\rm min}}^{E_{\rm max}} Q(E, t) {\rm d}E, \end{equation}(7)and Ṅ is the injection rate with electrodynamic minimum suggested by Goldreich & Julian (1969), i.e., 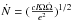Ṅ=(cIΩΩ̇e2)1/2\hbox{$\dot {N} =({\frac {cI \Omega \dot {\Omega}}{e^2}})^{1/2} $}. The values are shown in Table 5. The pair multiplicity ranges from ~ 105 to ~ 108. The Lorentz factor of the pulsar wind can be estimated by 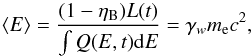⟨E⟩=(1−ηB)L(t)∫Q(E,t)dE=γwmec2,\begin{equation} \left<E\right> = \frac {(1-\eta_{\rm B})L(t)} {\int Q(E, t) {\rm d}E} = \gamma_w m_{\rm e} c^2, \end{equation}(8)where ⟨E⟩ is the average energy for the SED of each PWN. The values of γw are listed in Table 4. Clearly, Eb is larger than ⟨E⟩ by up to several orders of magnitude.

3.5. Brief summary of calculated results

Here, the main results in the above calculations are briefly summarized.

The observed SEDs of 18 PWNe can be reproduced well in the frame of the model. For the electron injection, five free parameters (α1,α2,Eb,ηB,ϵ) are used. Our results give α1 ≈ 1.0–1.8, α2 ≈ 2.0–3.1, Eb ≈ 104–107 MeV, ηB ≈ 0.1%–11% for the PWNe except for MSH 15-52 (ηB ≈ 45%) and CTA 1 (ηB ≈ 49%), and ϵ ≈ 0.1–0.70. The results for spectral indices are consistent with previous studies (e.g., Bucciantini et al. 2011; Tanaka & Takahara 2011; Torres et al. 2014). According to Sironi & Spitkovsky (2011, 2012, 2013), these low-energy electrons are accelerated by relativistic magnetic reconnection in a PWN; its spectral slope in the range at 1.0–2.0. Therefore, the low-energy electron component possibly originates from relativistic magnetic reconnection. The high-energy electron component with spectral slope from 2.0–3.0 are consistent with that produced by the Fermi-type process (e.g., Achterberg et al. 2001); thus, high-energy electrons are from the Fermi-type process in the termination shock. The PWN magnetization is weak, which means that most PWNe are particle-dominated. This conclusion is consistent with result of Torres et al. (2014). The values of ϵ are in the range 0.1–0.45, except for HESS J1119-614, and of the break energy Eb are in the range 104–107 MeV.

The fluxes, FX ≡ F1−10 keV and Fγ ≡ F1−10 TeV, in X-ray (1–10 keV) and γ-ray (1–10 TeV) bands for each PWN are obtained from our calculations. Our results show that FX/Fγ> 10 for young PWNe, 1 <FX/Fγ ≤ 10 for evolved PWNe except for G292.0+1.8 (FX/Fγ ~ 20.6), and FX/Fγ ≤ 1 for mature/old PWNe except for CTA 1 (FX/Fγ ~ 5). The results indicate that FX/Fγ decreases with increasing PWN age.

4. Correlation analysis of the PWNe

In this section, the correlations of various physical quantities in our model are studied. To this end, the best linear fit y = p1x + p0 to the data with the minimum χ2 technique is used. For each fit, the values of p1 and p0 are given, and the Pearson’s correlation coefficient r and the probability of the null hypothesis Pnull are calculated. Here, it is assumed that the correlation between two physical quantities is noneffective if Pnull ≥ 0.05. In correlation analysis, the sample of 14 PWNe is used in which α2, ηB, and ϵ are obtained through the LM method. All results have been recalculated and various luminosities with uncertainties are listed in Table 6. The uncertainties of the various physical quantities are included. We note that although four PWNe (N 158A, G310.6-1.6, G292.0+1.8, and HESS J1303-631) are not included in the best linear fits, the values of relevant physical quantities of these four PWNe are listed in Tables 4–6 and shown in Figs. 4–10. Here, the 2σ confidence band for each panel shown in Figs. 4−10 are from the dispersion of the fit to the points.

thumbnail Fig. 4

Correlations between Emax (upper panels) and Bpwn (bottom panels) and pulsar parameters BLC, Φ, and L(t). The solid lines represent the best linear fits (from top left to bottom right): log Emax = (0.42 ± 0.10)log BLC + (6.59 ± 0.54), log Emax = (0.88 ± 0.19)log Φ−(5.31 ± 2.97), log Emax = (0.44 ± 0.09)log L(t)−(7.65 ± 3.46), log Bpwn = (0.59 ± 0.08)log BLC−(1.72 ± 0.47), log Bpwn = (1.11 ± 0.12)log Φ−(16.47 ± 2.04), and log Bpwn = (0.56 ± 0.06)log L(t)−(19.44 ± 2.42); the correlation coefficient r = 0.71, 0.76, 0.76, 0.88, 0.91, and 0.91; and the probability of the null hypothesis Pnull = 8.95 × 10-4,2.26 × 10-4,2.24 × 10-4,1.14 × 10-6,1.23 × 10-7, and 1.71 × 10-7. The dashed lines are the 2σ confidence bands for the sample.

thumbnail Fig. 5

Correlations between L(t) and Lr, LX, and Lbol. The solid lines represent the best linear fits (from left to right): log Lr = (1.21 ± 0.17)log L(t)−(13.20 ± 6.38), log LX = (1.54 ± 0.12)log L(t)−(22.50 ± 4.68), and log Lbol = (1.24 ± 0.12)log L(t)−(10.15 ± 4.57); the correlation coefficients r = 0.88, 0.95, and 0.93; and the probability of the null hypothesis Pnull = 1.87 × 10-6,1.03 × 10-9, and 1.52 × 10-8. The dashed lines are the 2σ confidence bands for the sample.

4.1. Correlations between pulsar parameters with injection spectrum parameters and with derived parameters

For a given central pulsar with a period P (s) and a period derivative Ṗ (s s-1) in a PWN, it is commonly assumed that the magnetic field around it can be approximated as a dipole, so the surface magnetic field Bs is given by 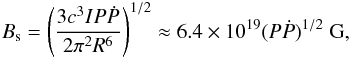Bs=(3c3IPṖ2π2R6)1/2≈6.4×1019(PṖ)1/2G,\begin{eqnarray} B_{\rm s} = \left(\frac{3c^3IP\dot{P}}{2\pi^2R^6}\right)^{1/2} \approx 6.4 \times 10^{19}(P\dot{P})^{1/2}\;{\rm G}, \end{eqnarray}(9)where c is the light speed, I = 1045 g cm2 is the inertia moment, and R = 106 cm is the surface radius of the pulsar. At the light cylinder with a radius RLC = (cP)/(2π) ≈ 4.77 × 109P cm, the magnetic field is described as 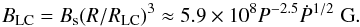BLC=Bs(R/RLC)3≈5.9×108P-2.5Ṗ1/2G.\begin{equation} B_{\rm LC} = B_{\rm s}(R/R_{\rm LC})^3 \approx {5.9} \times 10^8 P^{-2.5}\dot{P}^{1/2} \;{\rm G}. \end{equation}(10)For such a pulsar, the potential difference at the polar cap, Φ, can be expressed as 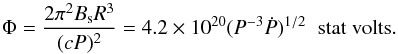Φ=2π2BsR3(cP)2=4.2×1020(P-3Ṗ)1/2statvolts.\begin{equation} \Phi =\frac{ 2\pi^2B_{\rm s}R^3}{(cP)^2} = {4.2} \times 10^{20}(P^{-3}\dot P)^{1/2}\;\;{\rm stat~volts}. \end{equation}(11)We note that the spin-down power L(t) at time t (see Eq. (3)) can be also expressed in terms of P and Ṗ as 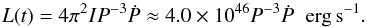L(t)=4π2IP-3Ṗ≈4.0×1046P-3Ṗerg s-1.\begin{equation} L(t) = 4\pi^2I P^{-3}\dot{P} \approx 4.0 \times 10^{46} P^{-3}\dot{P}\;\;{\rm erg\, {\rm s}^{-1}}. \end{equation}(12)For each pulsar, the L(t) and τc are shown in Tables 1–3, and Bs, BLC, and Φ are listed in Table 5.

The correlation analysis indicate that (1) there are no correlations between Eb, ηB, α1, α2, ϵ and the pulsar parameters such as Bs, BBL, Φ, L(t), and τc; (2) two derived parameters Emax and Bpwn have positive correlations with BBL, Φ, and L(t); and (3) there are no correlations between Bs and Emax and Bpwn. The correlations between Emax and BBL, Φ, and L(t) are shown in the upper panel of Fig. 4, and the correlations between Bpwn and BBL, Φ, and L(t) in the bottom panel. Since Emax ~ L(t)1/2, L(t) ~ (PṖ)1/2, BLC ~ P5/2Ṗ1/2, and Φ ~ (P-3Ṗ)1/2, these correlations are only consistent with the logical conclusions.

thumbnail Fig. 6

Correlations between L(t) and Lr/Lγ and LX/Lγ. The solid lines represent the best linear fits (from left to right): log Lr/Lγ = (1.28 ± 0.28)log L(t)−(50.38 ± 10.53) and log LX/Lγ = (1.41 ± 0.22)log L(t)−(50.21 ± 8.33); the correlation coefficients r = 0.76, and 0.85; and the probability of the null hypothesis Pnull = 2.81 × 10-4 and 7.81 × 10-6. The dashed lines are the 2σ confidence bands for the sample.

thumbnail Fig. 7

Correlation between Ls, Es and L(t), Ls, and Es. The solid lines are the best linear fits, which are log Ls = (1.64 ± 0.09)log L(t)−(26.39 ± 3.55), log Es = −(0.78 ± 0.11)log L(t) + (24.46 ± 3.99), and log Ls = −(1.15 ± 0.11)log Es + (30.47 ± 0.64); the correlation coefficients r = 0.98, 0.88, and 0.93; and the probability of the null hypothesis Pnull = 5.59 × 10-12,1.70 × 10-6, and 2.27 × 10-8 (from left to right). The dashed lines are the 2σ confidence bands for the sample.

4.2. Correlations between luminosities at various bands and L(t)

The possible correlations between the luminosities at radio (1.4 GHz), Lr; X-ray (1–10 keV), LX; VHE γ-ray (1–10 TeV), Lγ; bolometric luminosity at all wave bands, Lbol (which can be obtained from our model results, the corresponding values and errors are listed in Table 5); and the pulsar’s spin-down power, L(t), were analyzed. The results show that there are significant positive correlations between Lr and L(t), between LX and L(t), and between Lbol and L(t) (see Fig. 5), and the best linear fits yield Lr ~ L(t)1.21 ± 0.17, LX ~ L(t)1.54 ± 0.12, and Lbol ~ L(t)1.24 ± 0.12, respectively. The correlation between LX and L(t) is in agreement with the recent conclusions of Mattana et al. (2009), Kargaltsev & Pavlov (2010), and Kargaltsev et al. (2013). As expected, there is no correlation between Lγ and L(t), which is consistent with Mattana et al. (2009), Kargaltsev & Pavlov (2010), and Kargaltsev et al. (2013). This phenomenon may be due to the differences in the IR background and uncertain distance.

Since Lr/Lγ and LX/Lγ are distance-independent, the correlations between Lr/Lγ and L(t) and between LX/Lγ and L(t) are analyzed. Our results are shown in Fig. 6 where the best linear fits give LR/Lγ ~ L(t)1.28 ± 0.28, and LX/Lγ ~ L(t)1.41 ± 0.22. In fact, the correlation between LX/Lγ and L(t) is found in Mattana et al. (2009).

thumbnail Fig. 8

Correlations between L(t) and Sr, SX, and Sγ. The solid lines represent the best linear fits (from left to right): log Sr = (1.78 ± 0.20)log L(t)−(36.89 ± 7.60), log SX = (1.89 ± 0.32)log L(t)−(37.79 ± 12.42), and log Sγ = (0.71 ± 0.17)log L(t) + (5.89 ± 6.59); the correlation coefficients r = 0.91, 0.82, and 0.71; and the probability of the null hypothesis Pnull = 1.24 × 10-7,2.57 × 10-5, and 9.05 × 10-4, respectively. The dashed lines are the 2σ confidence bands for the sample.

thumbnail Fig. 9

Correlations between Rpwn and LX, LX/Lγ, and Ls. The solid lines are the best linear fits, which are log LX = −(1.36 ± 0.68)log Rpwn + (37.03 ± 0.38), log LX/Lγ = −(2.54 ± 0.52)log Rpwn + (2.69 ± 0.31), and log Ls = −(1.90 ± 0.75)log RPWNe + (37.48 ± 0.24); the correlation coefficients r = 0.45, 0.77, and 0.54; and the probability of the null hypothesis Pnull = 6.40 × 10-2,1.73 × 10-4, and 2.18 × 10-2 (from left to right). The dashed lines are the 2σ confidence bands for the sample.

4.3. Correlations between synchrotron luminosity and L(t)

Because synchrotron radiation dominates over the radiation from radio to X-ray bands, it is important to study the correlations of synchrotron cooling break energy (Es) and synchrotron radiation luminosity (Ls) with L(t). Following Tanaka & Takahara (2011), the inverse Compton cooling is assumed to be ineffective in most of the evolutionary phases, and the synchrotron cooling break frequency νs is given by 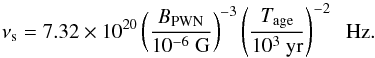νs=7.32×1020(BPWN10-6G)-3(Tage103yr)-2Hz.\begin{equation} \nu_{\rm s} = 7.32 \times 10^{20} \left(\frac{B_{\rm PWN}}{10^{-6}~{\rm G}}\right)^{-3}\left({\frac {T_{\rm age}}{10^3~\rm yr}}\right)^{-2} \;\;{\rm Hz}. \end{equation}(13)Using Eq. (13) and based on our model calculation, Es = hνs and Ls are calculated for each PWN in our sample. The results show that there is a strong positive correlation between Ls and L(t), the best linear fit yields Ls ~ L(t)1.64 ± 0.09, and that there are strong negative correlation between Es and L(t), where Es ~ L(t)− 0.78 ± 0.11, and Es and Ls, where 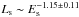Ls~Es−1.15±0.11\hbox{$L_{\rm s} \sim E_{\rm s}^{-1.15 \pm 0.11}$}. The best linear fit results are shown in Fig. 7.

4.4. Correlations between surface brightness S and L(t)

The surface brightness is defined as (e.g., Abdalla et al. 2017) 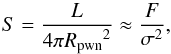S=L4πRpwn2≈Fσ2,\begin{equation} S = {\frac {L}{4\pi {R_{\rm pwn}}^2}} \approx {\frac {F}{{\sigma}^2}}, \end{equation}(14)where L is the luminosity at a given band, RPWN is the radius of the PWN, F is the energy flux at a given band, and σ is its angular extent as seen from the Earth. Using our model and Eq. (14), the surface brightness, SR, SX, and Sγ, at radio (1.4 GHz), X-ray (1–10 keV), and γ-ray (1–10 TeV) bands are calculated. The results are shown in Fig. 8 and show that there are correlations between L(t) and SR, SX, and Sγ. The best linear fits give Sr ~ L(t)1.78 ± 0.20, SX ~ L(t)1.89 ± 0.32, and Sγ ~ L(t)0.71 ± 0.17. We note that Sγ ~ L(t)0.81 has been given in Abdalla et al. (2017).

thumbnail Fig. 10

Correlations between Tage and LX, LX/Lγ, and Ls. The solid lines are the best linear fits, which are log LX = −(2.44 ± 0.59)log Tage + (44.23 ± 1.89), log LX/Lγ = −(3.37 ± 0.29)log Tage + (12.47 ± 0.94), and log Ls = −(2.83 ± 0.53)log Tage + (45.37 ± 1.59); the correlation coefficients r = 0.72, 0.95, and 0.80; and the probability of the null hypothesis Pnull = 7.81 × 10-4,3.15 × 10-9, and 7.22 × 10-5. The dashed lines are the 2σ confidence bands for the sample.

4.5. Correlations between luminosity and Rpwn and Tage

The correlations between the luminosities at various bands and Rpwn are analyzed here. In our model, the PWN radius for each PWN can be calculated (see Tables 1–3). The results show that there are no correlations between Rpwn and Lr, Lγ, and Lbol, but there are correlations between Rpwn and LX, Ls, and LX/Lγ. 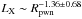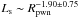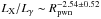The best linear fits give that LX~Rpwn−1.36±0.68\hbox{$L_{\rm X} \sim R_{\rm pwn}^{-1.36 \pm 0.68}$}, Ls~Rpwn−1.90±0.75\hbox{$ L_{\rm s} \sim R_{\rm pwn}^{-1.90 \pm 0.75}$}, and LX/Lγ~Rpwn−2.54±0.52\hbox{$ L_{\rm X}/L_\gamma \sim R_{\rm pwn}^{-2.54\pm 0.52}$}, respectively. We note that the correlation between LX and Rpwn is marginal here. The results are shown in Fig. 9.

The same procedure is performed for the correlations between Tage and the luminosities at various bands, and almost the same correlations are found. We found that there are correlations between Tage and LX, Ls, and LX/Lγ. 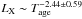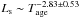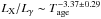These correlations mean that LX~Tage−2.44±0.59\hbox{$L_{\rm X} \sim T_{\rm age}^{-2.44 \pm 0.59}$}, Ls~Tage−2.83±0.53\hbox{$L_{\rm s} \sim T_{\rm age}^{-2.83 \pm 0.53}$}, and LX/Lγ~Tage−3.37±0.29\hbox{$ L_{\rm X}/L_\gamma \sim T_{\rm age}^{-3.37\pm 0.29}$}. The best linear fit results are shown in Fig. 10.

5. Discussions and conclusions

In this paper, the leptonic model with a broken power-law injection for the electrons/positrons is applied to the sample of 18 PWNe. The sample is divided into three groups: young, evolved, and mature/old PWNe. Observed SEDs of all 18 PWNe can be reproduced well in this model (see Figs. 1–3). The model parameters obtained in our calculations are listed in the Tables 1−3, and the relevant discussion are described in Sect. 3.

Using a time-dependent modeling of PWNe given by Martin et al. (2012), Torres et al. (2014) modeled the SEDs of nine PWNe and studied their statistical properties. These nine PWNe are included in our sample. As mentioned in Sect. 1, the model given in Torres et al. (2014) does not include the dynamical evolution of a PWN, but our model does. Therefore, some model parameters obtained in these two models are different. Meanwhile, our sample is larger than some previous works. So it is worth comparing our correlation results with the results of Torres et al. (2014) and some previous works.

For the relation between the derived parameters and pulsar’s parameter, our results indicate that the maximum electron energy has positive correlations with the magnetic field at the light cylinder, the potential difference at the polar cap, and the pulsar’s spin-down power and that the magnetic field in the PWN is positively correlated with the magnetic field at the light cylinder, the potential difference at the polar cap, and the pulsar’s spin-down power (see Fig. 4). Other parameters that describe pulsar properties and electron injection have no correlations. These results are consistent with those of Torres et al. (2014).

The results presented in this paper indicate that the spin-down power L(t) is correlated with Lr, LX, and Lbol (see Fig. 5). The results of L(t) versus Lr and L(t) versus LX are consistent with those in Torres et al. (2014). Meanwhile, our results show that the L(t) correlates with the ratio Lr/Lγ and the ratio LX/Lγ (see Fig. 6). These correlations are consistent with those given in previous papers (e.g., Mattana et al. 2009; Kargaltsev & Pavlov 2010; Torres et al. 2014).

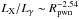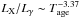In this paper, the correlations between L(t) and surface brightness at different bands are presented here (see Fig. 8). Moreover, the correlations between Rpwn (Tage) and LX, LX/Lγ, and Ls are analyzed (see Figs. 9 and 10). For example, the results show that LX/Lγ~Rpwn-2.54\hbox{$L_{\rm X}/L_\gamma \sim R_{\rm pwn}^{-2.54}$} and LX/Lγ~Tage-3.37\hbox{$L_{\rm X}/L_\gamma \sim T_{\rm age}^{-3.37}$}, which means that old PWNe have smaller values of LX/Lγ than do young PWNe. In fact, our results show that the LX/Lγ ≥ 10 for young PWNe, 1 <LX/Lγ ≲ 10 for evolved PWNe, and LX/Lγ ≤ 1 for mature/old PWNe. This result may provide a new tool for classifying the evolution state of PWNe. It should be pointed out that the results presented in this paper require confirmation from further observations.

Acknowledgments

We would like to thank the anonymous referee for the very constructive comments. This work is partially supported by the National Natural Science Foundation of China (NSFC 11433004, 11173020, 11563009), the Doctoral Fund of the Ministry of Education of China (RFDP 20115301110005), and the Research Innovation Fund for Graduate Students of Yunnan University.

References

  1. Abdalla, H., Abramowski, A., Aharonian, F., et al. 2017, A&A, in press, DOI: 10.1051/0004-6361/201629377 [Google Scholar]
  2. Abdo, A. A., Ackermann, M., Atwood, W. B., et al. 2008, Science, 322, 1218 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  3. Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010, ApJ, 714, 927 [NASA ADS] [CrossRef] [Google Scholar]
  4. Abdo, A. A., Wood, K. S., DeCesar, M. E., et al. 2012, ApJ, 744, 146 [NASA ADS] [CrossRef] [Google Scholar]
  5. Abdo, A. A., Ajello, M., Allafort, A., et al. 2013, ApJS, 208, 17 [NASA ADS] [CrossRef] [Google Scholar]
  6. Abramowski, A., Acero, F., Aharonian, F., et al. 2011, A&A, 533, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Abramowski, A., Acero, F., Aharonian, F., et al. 2012a, A&A, 545, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Abramowski, A., Acero, F., Aharonian, F., et al. 2012b, A&A, 548, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Abramowski, A., Aharonian, F., Ait Benkhali, F., et al. 2015, Science, 347, 406 [NASA ADS] [CrossRef] [Google Scholar]
  10. Acciari, V. A., Aliu, E., Arlen, T., et al. 2010, ApJ, 719, L69 [NASA ADS] [CrossRef] [Google Scholar]
  11. Acero, F., Ackermann, M., Ajello, M., et al. 2013, ApJ, 773, 77 [CrossRef] [Google Scholar]
  12. Achterberg, A., Gallant, Y. A., Kirk, J. G., & Guthmann, A. W. 2001, MNRAS, 328, 393 [NASA ADS] [CrossRef] [Google Scholar]
  13. Aharonian, F., Akhperjanian, A. G., Aye, K.-M., et al. 2005a, A&A, 435, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Aharonian, F., Akhperjanian, A. G., Aye, K.-M., et al. 2005b, A&A, 432, L25 [Google Scholar]
  15. Aharonian, F., Akhperjanian, A. G., Aye, K.-M., et al. 2005c, A&A, 439, 1013 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2006a, A&A, 456, 245 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2006b, ApJ, 636, 777 [NASA ADS] [CrossRef] [Google Scholar]
  18. Ackermann, M., Ajello, M., Baldini, L., et al. 2011, ApJ, 726, 35 [NASA ADS] [CrossRef] [Google Scholar]
  19. Ackermann, M., Ajello, M., Allafort, A., et al. 2013, ApJS, 209, 34 [NASA ADS] [CrossRef] [Google Scholar]
  20. Aleksić, J., Ansoldi, S., Antonelli, L. A., et al. 2014, A&A, 567, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Aliu, E., Archambault, S., Arlen, T., et al. 2013, ApJ, 764, 38 [NASA ADS] [CrossRef] [Google Scholar]
  22. Archibald, R. F., Kaspi, V. M., Beardmore, A. P., Gehrels, N., & Kennea, J. A. 2015, ApJ, 810, 67 [NASA ADS] [CrossRef] [Google Scholar]
  23. Becker, R. H., & Kundu, M. R. 1976, ApJ, 204, 427 [NASA ADS] [CrossRef] [Google Scholar]
  24. Bhalerao, J., Park, S., Dewey, D., et al. 2015, ApJ, 800, 65 [NASA ADS] [CrossRef] [Google Scholar]
  25. Bietenholz, M. F., & Bartel, N. 2008, MNRAS, 386, 1411 [NASA ADS] [CrossRef] [Google Scholar]
  26. Bock, D. C.-J., & Gaensler, B. M. 2005, ApJ, 626, 343 [NASA ADS] [CrossRef] [Google Scholar]
  27. Bocchino, F., Bandiera, R., & Gelfand, J. 2010, A&A, 520, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Brogan, C. L., Gaensler, B. M., Gelfand, J. D., et al. 2005, ApJ, 629, L105 [NASA ADS] [CrossRef] [Google Scholar]
  29. Bucciantini, N. 2008, in 40 Years of Pulsars Millisecond Pulsars, Magnetars and More, eds. C. Bassa, Z. Wang, A. Cumming, & V. M. Kaspi, AIP Conf. Ser., 983, 186 [Google Scholar]
  30. Bucciantini, N., Arons, J., & Amato, E. 2011, MNRAS, 410, 381 [Google Scholar]
  31. Bühler, R., & Blandford, R. 2014, Rept. Progr. Phys., 77, 066901 [CrossRef] [Google Scholar]
  32. Camilo, F., Kaspi, V. M., Lyne, A. G., et al. 2000, ApJ, 541, 367 [NASA ADS] [CrossRef] [Google Scholar]
  33. Camilo, F., Manchester, R. N., Gaensler, B. M., Lorimer, D. R., & Sarkissian, J. 2002a, ApJ, 567, L71 [NASA ADS] [CrossRef] [Google Scholar]
  34. Camilo, F., Stairs, I. H., Lorimer, D. R., et al. 2002b, ApJ, 571, L41 [NASA ADS] [CrossRef] [Google Scholar]
  35. Camilo, F., Manchester, R. N., Lyne, A. G., et al. 2004, ApJ, 611, L25 [NASA ADS] [CrossRef] [Google Scholar]
  36. Camilo, F., Ransom, S. M., Gaensler, B. M., et al. 2006, ApJ, 637, 456 [NASA ADS] [CrossRef] [Google Scholar]
  37. Camilo, F., Ransom, S. M., Gaensler, B. M., & Lorimer, D. R. 2009, ApJ, 700, L34 [NASA ADS] [CrossRef] [Google Scholar]
  38. Campana, R., Mineo, T., De Rosa, A., et al. 2008, MNRAS, 389, 691 [NASA ADS] [CrossRef] [Google Scholar]
  39. Caswell, J. L., Milne, D. K., & Wellington, K. J. 1981, MNRAS, 195, 89 [NASA ADS] [Google Scholar]
  40. Caswell, J. L., McClure-Griffiths, N. M., & Cheung, M. C. M. 2004, MNRAS, 352, 1405 [NASA ADS] [CrossRef] [Google Scholar]
  41. Chang, C., Pavlov, G. G., Kargaltsev, O., & Shibanov, Yu. A. 2012, ApJ, 744, 81 [NASA ADS] [CrossRef] [Google Scholar]
  42. Chevalier, R. A. 2004, Adv. Space Res., 33, 456 [NASA ADS] [CrossRef] [Google Scholar]
  43. Chevalier, R. A. 2005, ApJ, 619, 839 [NASA ADS] [CrossRef] [Google Scholar]
  44. Chen, Y., Wang, Q. D., Gotthelf, E. V., et al. 2006, ApJ, 651, 237 [NASA ADS] [CrossRef] [Google Scholar]
  45. Condon, J. J., Griffith, M. R., & Wright, A. E. 1993, AJ, 106, 1095 [NASA ADS] [CrossRef] [Google Scholar]
  46. Cordes, J. M., & Lazio, T. J. W. 2002, ArXiv e-prints [arXiv:astro-ph/0207156] [Google Scholar]
  47. Crawford, F., Gaensler, B. M., Kaspi, V. M., et al. 2001, ApJ, 554, 152 [NASA ADS] [CrossRef] [Google Scholar]
  48. D’Amico, N., Kaspi, V. M., Manchester, R. N., et al. 2001, ApJ, 552, L45 [NASA ADS] [CrossRef] [Google Scholar]
  49. De Rosa, A., Ubertini, P., Campana, R., et al. 2009, MNRAS, 393, 527 [NASA ADS] [CrossRef] [Google Scholar]
  50. Djannati-Atai, A., deJager, O. C., Terrier, R., Gallant, Y. A., & Hoppe, S. 2008, Proc. 30th International Cosmic Ray Conference, eds. R. Caballero et al., 2, 823 [Google Scholar]
  51. Dubner, G., Giacani, E., & Decourchelle, A. 2008, A&A, 487, 1033 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Duncan, A. R., Stewart, R. T., Haynes, R. F., & Jones, K. L. 1995, MNRAS, 277, 36 [NASA ADS] [Google Scholar]
  53. Fang, J., & Zhang, L. 2010a, A&A, 515, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Fang, J., & Zhang, L. 2010b, ApJ, 718, 467 [NASA ADS] [CrossRef] [Google Scholar]
  55. Ferdman, R. D., Archibald, R. F., & Kaspi, V. M. 2015, ApJ, 812, 95 [NASA ADS] [CrossRef] [Google Scholar]
  56. Forot, M., Hermsen, W., Renaud, M., et al. 2006, ApJ, 651, L45 [NASA ADS] [CrossRef] [Google Scholar]
  57. Funk, S., Hinton, J. A., Moriguchi, Y., et al. 2007, A&A, 470, 249 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  58. Gaensler, B. M., & Slane, P. O. 2006, ARA&A, 44, 17 [NASA ADS] [CrossRef] [Google Scholar]
  59. Gaensler, B. M., & Wallace, B. J. 2003, ApJ, 594, 326 [NASA ADS] [CrossRef] [Google Scholar]
  60. Gaensler, B. M., Brazier, K. T. S., Manchester, R. N., Johnston, S., & Green, A. J. 1999, MNRAS, 305, 724 [NASA ADS] [CrossRef] [Google Scholar]
  61. Gaensler, B. M., Arons, J., Kaspi, V. M., et al. 2002, ApJ, 569, 878 [CrossRef] [Google Scholar]
  62. Gaensler, B. M., Arons, J., Kaspi, V. M., et al. 2008, ApJ, 569, 878 [Google Scholar]
  63. Gallant, Y. A., & Tuffs, R. J. 1998, Mem. Soc. Astron. It., 69, 963 [NASA ADS] [Google Scholar]
  64. Gallant, Y. A., & Tuffs, R. J. 1999, ESASP, 427, 313 [NASA ADS] [Google Scholar]
  65. Gelfand, J. D., Slane, P. O., & Zhang, W. 2009, ApJ, 703, 2051 [NASA ADS] [CrossRef] [Google Scholar]
  66. Gelfand, J. D., Slane, P. O., & Temim, T. 2014, Astron. Nachr., 335, 318 [NASA ADS] [CrossRef] [Google Scholar]
  67. Gelfand, J. D., Slane, P. O., & Temim, T. 2015, ApJ, 807, 30 [NASA ADS] [CrossRef] [Google Scholar]
  68. Gonzalez, M., & Safi-Harb, S. 2003, ApJ, 591, L143 [NASA ADS] [CrossRef] [Google Scholar]
  69. Gotthelf, E. V., & Halpern, J. P. 2009, ApJ, 700, L158 [NASA ADS] [CrossRef] [Google Scholar]
  70. Gotthelf, E. V., Vasisht, G., Boylan-Kolchin, M., & Torii, K. 2000, ApJ, 542, L37 [NASA ADS] [CrossRef] [Google Scholar]
  71. Green, D. A. 1985, MNRAS, 216, 691 [NASA ADS] [CrossRef] [Google Scholar]
  72. Green, D. A. 1986, MNRAS, 218, 533 [NASA ADS] [CrossRef] [Google Scholar]
  73. Green, D. A. 1994, ApJS, 90, 817 [NASA ADS] [CrossRef] [Google Scholar]
  74. Griffith, M. R., & Wright, A. E. 1993, AJ, 105, 1666 [NASA ADS] [CrossRef] [Google Scholar]
  75. Gupta, Y., Mitra, D., Green, D. A., & Acharyya, A. 2005, CSci, 89, 853 [Google Scholar]
  76. Goldreich, P., & Julian, W. 1969, ApJ, 157, 869 [NASA ADS] [CrossRef] [Google Scholar]
  77. Gvaramadze, V. V. 2001, A&A, 374, 259 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  78. Halpern, J. P., Gotthelf, E. V., Camilo, F., Helfand, D. J., & Ransom, S. M. 2004, ApJ, 612, 398 [NASA ADS] [CrossRef] [Google Scholar]
  79. Halpern, J. P., Gotthelf, E. V., & Camilo, F. 2012, ApJ, 753, L14 [NASA ADS] [CrossRef] [Google Scholar]
  80. Harris, D. E., & Roberts, J. A. 1960, PASP, 72, 347 [Google Scholar]
  81. Helfand, D. J., Collins, B. F., & Gotthelf, E. V. 2003, ApJ, 582, 783 [NASA ADS] [CrossRef] [Google Scholar]
  82. Hughes, J. P., Slane, P. O., Burrows, D. N., et al. 2001, ApJ, 559, L153 [NASA ADS] [CrossRef] [Google Scholar]
  83. Indebetouw, R., de Messières, G. E., Madden, S., et al. 2009, ApJ, 694, 84 [NASA ADS] [CrossRef] [Google Scholar]
  84. Kaaret, P., Marshall, H. L., Aldcroft, T. L., et al. 2001, ApJ, 546, 1159 [NASA ADS] [CrossRef] [Google Scholar]
  85. Kargaltsev, O., & Pavlov, G. G. 2010, in X-Ray Astronomy 2009; Present Status, Multi-wavelength Approach and Future Perspectives, eds. A. Comastri, M. Cappi, & L. Angelini (Melville, NY: AIP), AIP Conf. Proc. 1248, 25 [Google Scholar]
  86. Kargaltsev, O., Rangelov, B., & Pavlov, G. G. 2013, in The Universe Evolution. Astrophysical and Nuclear Aspects, eds. Strakovsky & Blokhintsev (Nova Science Publishers, Inc) [Google Scholar]
  87. Kennel, C. F., & Coroniti, F. V. 1984, ApJ, 283, 694 [NASA ADS] [CrossRef] [Google Scholar]
  88. Khélifi, B., Masterson, C., Pita, S., & Oña-Wilhelmi, E. 2008, in New Companions for the Lonely Crab? VHE Emission from Young Pulsar Wind Nebulae Revealed by HESS Universidad Nacional Autónoma de México, Mexico City, eds. R. Caballero, J. Carlos D’Olivo, G. Medina-Tanco, et al., Proc. 30th Int. Cosm. Ray Conf., 2, 803 [Google Scholar]
  89. Kirshner, R. P., Morse, J. A., Winkler, P. F., & Blair, W. P. 1989, ApJ, 342, 260 [NASA ADS] [CrossRef] [Google Scholar]
  90. Kishishita, T., Bamba, A., Uchiyama, Y., Tanaka, Y., & Takahashi, T. 2012, ApJ, 750, 162 [NASA ADS] [CrossRef] [Google Scholar]
  91. Kothes, R. 2010, in The Dynamic Interstellar Medium: A Celebration of the Canadian Galactic Plane Survey, eds. R. Kothes, T. L. Landecker, & A. G. Willis (San Francisco: ASP), ASP Conf. Ser., 438, 347 [Google Scholar]
  92. Kothes, R. 2013, A&A, 560, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  93. Kumar, H. S., Safi-Harb, S., & Gonzalez, M. E. 2012, ApJ, 754, 96 [NASA ADS] [CrossRef] [Google Scholar]
  94. Lang, C. C., Wang, Q. D., Lu, F., & Clubb, K. I. 2010, ApJ, 709, 1125 [NASA ADS] [CrossRef] [Google Scholar]
  95. Lazendic, J. S., Dickel, J. R., Haynes, R. F., Jones, P. A., & White, G. L. 2000, ApJ, 540, 808 [NASA ADS] [CrossRef] [Google Scholar]
  96. Leahy, D. A., & Tian, W. W. 2008, ApJ, 480, L25 [Google Scholar]
  97. Leahy, D., Tian, W., & Wang, Q. D. 2008, ApJ, 136, 1477 [NASA ADS] [CrossRef] [Google Scholar]
  98. Livingstone, M. A., Kaspi, V. M., Gavril, F. P., & Manchester, R. N. 2005a, ApJ, 619, 1046 [NASA ADS] [CrossRef] [Google Scholar]
  99. Livingstone, M. A., Kaspi, V. M., & Gavriil, F. P. 2005b, ApJ, 633, 1095 [NASA ADS] [CrossRef] [Google Scholar]
  100. Livingstone, M. A., Kaspi, V. M., Gotthelf, E. V., & Kuiper, L. 2006, ApJ, 647, 1286 [NASA ADS] [CrossRef] [Google Scholar]
  101. Livingstone, M. A., Ransom, S. M., Camilo, F., et al. 2009, ApJ, 706, 1163 [NASA ADS] [CrossRef] [Google Scholar]
  102. Lorimer, D. R., Faulkner, A. J., Lyne, A. G., et al. 2006, MNRAS, 372, 777 [NASA ADS] [CrossRef] [Google Scholar]
  103. Lu, F. J., Aschenbach, B., & Song, L. M. 2001, A&A, 370, 570 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  104. Lu, F. J., Wang, Q. D., Aschenbach, B., Durouchoux, P., & Song, L. M. 2002, ApJ, 568, L49 [NASA ADS] [CrossRef] [Google Scholar]
  105. Lu, F., Wang, Q. D., Gotthelf, E. V., et al. 2007, ApJ, 663, 315 [NASA ADS] [CrossRef] [Google Scholar]
  106. Manchester, R. N., Staveley-Smith, L., & Kesteven, M. J. 1993, ApJ, 411, 756 [NASA ADS] [CrossRef] [Google Scholar]
  107. Manchester, R. N., Hobbs, G. B., Teoh, A., & Hobbs, M. 2005a, ViZier On-line Data Catalog: VII/245 [Google Scholar]
  108. Manchester, R. N., Hobbs, G. B., Teoh, A., & Hobbs, M. 2005b, AJ, 129, 1993 [NASA ADS] [CrossRef] [Google Scholar]
  109. Macri, L. M., Stanek, K. Z., Bersier, D., Greenhill, L. J., & Reid, M. J. 2006, ApJ, 652, 1133 [NASA ADS] [CrossRef] [Google Scholar]
  110. Mattana, F., Falanga, M., Götz, D., et al. 2009, ApJ, 694, 12 [NASA ADS] [CrossRef] [Google Scholar]
  111. Martin, J., Torres, D. F., & Rea, N. 2012, MNRAS, 427, 415 [NASA ADS] [CrossRef] [Google Scholar]
  112. Martin, J., Torres, D. F., Cillis, A., & de Ona Wilhelmi, E. 2014, MNRAS, 443, 138 [NASA ADS] [CrossRef] [Google Scholar]
  113. Martin, J., Torres, D. F., & Pedaletti, G. 2016, MNRAS, 459, 3868 [NASA ADS] [CrossRef] [Google Scholar]
  114. Marshall, F. E., Gotthelf, E. V., Zhang, W., Middleditch, J., & Wang, Q. D. 1998, ApJ, 499, L179 [NASA ADS] [CrossRef] [Google Scholar]
  115. Matheson, H., & Safi-Harb, S. 2005, Adv. Space Res., 35, 1099 [NASA ADS] [CrossRef] [Google Scholar]
  116. Mereghetti, S., Bandiera, R., Bocchino, F., & Israel, G. L. 2002, ApJ, 574, 873 [NASA ADS] [CrossRef] [Google Scholar]
  117. Mills, B. Y., Slee, O. B., & Hill, E. R. 1961, Austr. J. Phys., 14, 497 [NASA ADS] [CrossRef] [Google Scholar]
  118. Mignani, R. P., De Luca, A., Hummel, W., et al. 2012, A&A, 544, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  119. Mineo, T., Cusumano, G., Maccarone, M. C., et al. 2001, A&A, 380, 695 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  120. Morsi, H. W., & Reich, W. 1987, A&AS, 69, 533 [NASA ADS] [Google Scholar]
  121. Murphy, T., Mauch, T., Green, A., et al. 2007, MNRAS, 382, 382 [NASA ADS] [CrossRef] [Google Scholar]
  122. Murdin, P., & Clark, D. H. 1979, MNRAS, 189, 501 [NASA ADS] [CrossRef] [Google Scholar]
  123. Murray, S. S., Slane, P. O., Seward, F. D., Ransom, S. M., & Gaensler, B. M. 2002, ApJ, 568, 226 [NASA ADS] [CrossRef] [Google Scholar]
  124. Nynka, M., Hailey, C. J., Reynolds, S. P., et al. 2014, ApJ, 789, 72 [NASA ADS] [CrossRef] [Google Scholar]
  125. Ng, C.-Y., Roberts, M. S. E., & Romani, R. W. 2005, ApJ, 627, 904 [NASA ADS] [CrossRef] [Google Scholar]
  126. Pineault, S., Landecker, T. L., Madore, B., & Gaumont-Guay, S. 1993, AJ, 105, 1060 [NASA ADS] [CrossRef] [Google Scholar]
  127. Porquet, D., Decourchelle, A., & Warwick, R. S. 2003, A&A, 401, 197 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  128. Porter, T. A., Moskalenko, I. V., & Strong, A. W., 2006, ApJ, 648, L29 [NASA ADS] [CrossRef] [Google Scholar]
  129. Rees, M. J., & Gunn, J. E. 1974, MNRAS, 167, 1 [NASA ADS] [CrossRef] [Google Scholar]
  130. Reich, W., Fuerst, E., Altenhoff, W. J., Reich, P., & Junkes, N. 1985, A&A, 151, L10 [NASA ADS] [Google Scholar]
  131. Renaud, M., Marandon, V., Gotthelf, E. V., et al. 2010, ApJ, 716, 670 [Google Scholar]
  132. Reynolds, S. P. 1985, ApJ, 291, 152 [NASA ADS] [CrossRef] [Google Scholar]
  133. Reynolds, S. P., Pavlov, G. G., Kargaltsev, O., et al. 2017, Space Sci. Rev., 207, 175 [NASA ADS] [CrossRef] [Google Scholar]
  134. Roberts, D. A., Goss, W. M., Kalberla, P. M. W., Herbstmeier, U., & Schwarz, U. J. 1993, A&A, 274, 427 [NASA ADS] [Google Scholar]
  135. Roberts, M. S. E., Romani, R. W., Johnston, S., & Green, A. J. 1999, ApJ, 515, 712 [NASA ADS] [CrossRef] [Google Scholar]
  136. Roberts, M. S. E., Romani, R. W., & Kawai, N. 2001, ApJS, 133, 451 [NASA ADS] [CrossRef] [Google Scholar]
  137. Salter, C. J., Reynolds, S. P., Hogg, D. E., Payne, J. M., & Rhodes, P. J. 1989, ApJ, 338, 171 [NASA ADS] [CrossRef] [Google Scholar]
  138. Safi-Harb, S., & Kumar, H. S. 2008, ApJ, 684, 532 [NASA ADS] [CrossRef] [Google Scholar]
  139. Safi-Harb, S., & Kumar, H. S. 2012, Neutron Stars and Pulsars: Challenge and Opportunities after 80 yr, Proc. IAU Symp., 291 [Google Scholar]
  140. Seward, F. D., Harnden, F. R., Jr., Murdin, P., & Clark, D. H. 1983, ApJ, 267, 698 [NASA ADS] [CrossRef] [Google Scholar]
  141. Seward, F. D., Harnden, F. R., & Helfand, D. J. 1984, ApJ, 287, L19 [NASA ADS] [CrossRef] [Google Scholar]
  142. Sironi, L., & Spitkovsky, A. 2011, ApJ, 741, 39 [NASA ADS] [CrossRef] [Google Scholar]
  143. Sironi, L., & Spitkovsky, A. 2012, Comput. Sci. Discovery, 5, 014014 [NASA ADS] [CrossRef] [Google Scholar]
  144. Sironi, L., & Spitkovsky, A. 2014, ApJ, 783, L21 [NASA ADS] [CrossRef] [Google Scholar]
  145. Slane, P. O., Seward, F. D., Bandiera, R., Torii, K., & Tsunemi, H. 1997, ApJ, 485, 221 [NASA ADS] [CrossRef] [Google Scholar]
  146. Slane, P., Zimmerman, E. R., Hughes, J. P., et al. 2004, ApJ, 601, 1045 [NASA ADS] [CrossRef] [Google Scholar]
  147. Slane, P., Helfand, D. J., Reynolds, S. P., et al. 2008, ApJ, 676, L33 [NASA ADS] [CrossRef] [Google Scholar]
  148. Spyrou, N. K., & Stergioulas, N. 2002, A&A, 395, 151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  149. Tanaka, S. J., & Takahara, F. 2010, ApJ, 715, 1248. [NASA ADS] [CrossRef] [Google Scholar]
  150. Tanaka, S. J., & Takahara, F. 2011, ApJ, 741, 40 [NASA ADS] [CrossRef] [Google Scholar]
  151. Tanaka, S. J., & Takahara, F. 2013, MNRAS, 429, 2945 [NASA ADS] [CrossRef] [Google Scholar]
  152. Taylor, J. H., & Cordes, J. M. 1993, ApJ, 411, 674 [NASA ADS] [CrossRef] [Google Scholar]
  153. Temim, T., Slane, P., Reynolds, S. P., Raymond, J. C., & Borkowski, K. J. 2010, ApJ, 710, 309 [NASA ADS] [CrossRef] [Google Scholar]
  154. Temim, T., Dwek, E., Arendt, R. G., et al. 2017, ApJ, 836, 129 [NASA ADS] [CrossRef] [Google Scholar]
  155. Tian, W. W., & Leathy, D. A. 2008, MNRAS, 391, 54 [Google Scholar]
  156. Torres, D. F., Cillis, A. N., & Martín, J. 2013, ApJ, 763, L4 [NASA ADS] [CrossRef] [Google Scholar]
  157. Torres, D. F., Cillis, A., Martín, J., & de Oña Wilhelmi, E. 2014, J. High Energy Astrophys., 1, 31 [NASA ADS] [CrossRef] [Google Scholar]
  158. Torii, K., Slane, P. O., Kinugasa, K., Hashimotodani, K., & Tsunemi, H. 2000, PASJ, 52, 875 [NASA ADS] [CrossRef] [Google Scholar]
  159. Tsujimoto, M., Guainazzi, M., Plucinsky, P. P., et al. 2011, A&A, 525, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  160. Ubertini, P., Bassani, L., Malizia, A., et al. 2005, ApJ, 629, L109 [NASA ADS] [CrossRef] [Google Scholar]
  161. Van Etten, A., & Romani, R. W. 2010, ApJ, 711, 1168 [NASA ADS] [CrossRef] [Google Scholar]
  162. Velusamy, T., & Becker, R. H. 1988, AJ, 95, 1162 [NASA ADS] [CrossRef] [Google Scholar]
  163. Velusamy, T., Goss, W. M., & Arnal, E. M. 1986, J. Astrophys. Astron., 7, 105 [NASA ADS] [CrossRef] [Google Scholar]
  164. Wang, Q. D., & Gotthelf, E. V. 1998, A&A, 494, 623 [Google Scholar]
  165. Wang, Z. R., Liu, J. Y., Gorenstein, P., & Zombeck, M. V. 1986, Proc. Nineteenth IAU General Assembly, 7, Delhi, India, Highlights of Astronomy (Dordrecht: Reidel), 583 [Google Scholar]
  166. Weiler, K. W., & Panagia, N. 1978, A&A, 70, 419 [NASA ADS] [Google Scholar]
  167. Weltevrede, P., Johnston, S., & Espinoza, C. M. 2011, MNRAS, 411, 1917 [NASA ADS] [CrossRef] [Google Scholar]
  168. Williams, B. J., Borkowski, K. J., Reynolds, S. P., et al. 2008, ApJ, 687, 1054 [NASA ADS] [CrossRef] [Google Scholar]
  169. Wilson, A. S., & Weiler, K. W. 1976, A&A, 53, 89 [NASA ADS] [Google Scholar]
  170. Winkler, P. F., Twelker, K., Reith, C. N., & Long, K. S. 2009, ApJ, 692, 1489 [NASA ADS] [CrossRef] [Google Scholar]
  171. Zhang, L., Chen, S. B., & Fang, J. 2008, ApJ, 676, 1216 [Google Scholar]
  172. Zhang, L., Jiang, Z. J., & Lin, G. F. 2009, ApJ, 699, 507 [NASA ADS] [CrossRef] [Google Scholar]
  173. Zhu, B. T., Fang, J., & Zhang, L. 2015, MNRAS, 451, 3145 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Calculations of Rpwn(t) and Bpwn(t)

In this appendix, the calculations of Rpwn and Bpwn are briefly described in the frame of the model for dynamical and radiative evolution of a PWN inside an SNR presented in Gelfand et al. (2009).

Appendix A.1: Calculation of Rpwn(t)

To compute the radius of the PWN during the evolution process of the PWNe, the following initial conditions are required (Gelfand et al. 2009). The first is the equation of motion of the PWN for the pressure of the SNR ejecta Psnr(Rpwn) ≡ 0, Msw,pwndvpwndt=4πRpwn2[Ppwn−ρej(Rpwn)×(υpwn−υej(Rpwn))2],\appendix \setcounter{section}{1} \begin{equation} \label{A1} M_{\rm sw,pwn} \frac{{\rm d}v_{\rm pwn}}{{\rm d}t} = 4\pi R_{\rm pwn}^2 [P_{\rm pwn} - \rho_{\rm ej}(R_{\rm pwn}) \times (\upsilon_{\rm pwn}-\upsilon_{\rm ej}(R_{\rm pwn}))^2 ], \end{equation}(A.1)where υpwn = dRpwn/ dt, Msw,pwn, Ppwn, and Rpwn are the velocity, mass, pressure, and radius of the PWN shell; ρej and vej are the density and velocity of SNR ejecta and dEpwndt=Ė−Ppwn4πRpwn2υpwn.\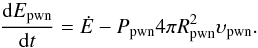appendix \setcounter{section}{1} \begin{equation} \label{A2} \frac{{\rm d}E_{\rm pwn}}{{\rm d}t} = \dot{E} - P_{\rm pwn} 4\pi R_{\rm pwn}^2 \upsilon_{\rm pwn}. \end{equation}(A.2)In the above treatment, the adiabatic losses dominate and the PWN is expanding with a constant velocity.

The second is expression of Rpwn is 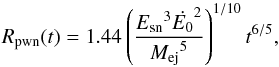Rpwn(t)=1.44(Esn3E0˙2Mej5)1/10t6/5,\appendix \setcounter{section}{1} \begin{equation} \label{A3} R_{\rm pwn}(t) = 1.44\left(\frac{{E_{\rm sn}}^3{\dot{E_{\rm 0}}}^2}{{M_{\rm ej}}^5}\right)^{1/10}t^{6/5} , \end{equation}(A.3)where Esn is the explosion energy of the supernova, Ė0 ≈ Ė, and Mej is the mass of the SNR ejecta.

The PWN expands outwards due to the energy provided by the central pulsar and sweeps out the material of the SNR ejecta, so a thin shell is formed around the PWN. Because there is a pressure Ppwn inside the PWN and a pressure Psnr(Rpwn) outside the PWN, the net force suffered by the PWN is FΔP = 4πRpwn2 [Ppwn−Psnr(Rpwn)], and the change rate of the momentum is ddt(Msw,pwnυpwn)=FΔP=4πRpwn2[Ppwn−Psnr(Rpwn)].\appendix \setcounter{section}{1} \begin{equation} \label{A4} \frac {{\rm d}}{{\rm d}t}(M_{\rm sw,pwn}\upsilon_{\rm pwn}) = F_{\rm \Delta P}=4\pi {R^2_{\rm pwn}} [P_{\rm pwn}-P_{\rm snr}(R_{\rm pwn})]. \end{equation}(A.4)In Eq. (A.4), the pressure of the PWN Ppwn is calculated as follows. 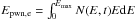Assuming the PWN is mainly composed of a relativistic nonthermal lepton (electron/positron) plasma and magnetic field Epwn = Epwn,e + Epwn,B (the spin-down power is described as L(t) = Ė = ηBĖ + ηeĖ), where Epwn,e is the total energy contained in the leptons and is given by Epwn,e=∫0EmaxN(E,t)EdE\hbox{$E_{\rm pwn,e}=\int_{0}^{E_{\rm max}}N(E, t) E {\rm d}E$}, and Epwn,B is the energy stored in the magnetic field of the PWN and reads 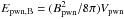Epwn,B=(Bpwn2/8π)Vpwn\hbox{$E_{\rm pwn,B}=(B^2_{\rm pwn}/8\pi)V_{\rm pwn}$}. 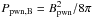The corresponding pressures contributed by the leptons and stored in the magnetic field of the PWN are Ppwn,e=[(γpwn−1)Epwn,e]/Vpwn=Epwn,e/(4πRpwn3)\hbox{$P_{\rm pwn,e}=[(\gamma_{\rm pwn}-1)E_{\rm pwn,e}]/V_{\rm pwn}=E_{\rm pwn,e}/(4\pi R^3_{\rm pwn})$} and Ppwn,B=Bpwn2/8π\hbox{$P_{\rm pwn,B}=B^2_{\rm pwn}/8\pi$}, where γpwn = 4/3 and 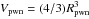Vpwn=(4/3)Rpwn3\hbox{$V_{\rm pwn}=(4/3)R^3_{\rm pwn}$} is the volume of the PWN. Therefore, Ppwn = Ppwn,e + Ppwn,B. Psnr(Rpwn) is the pressure of the shocked material at r = Rpwn and its calculation (see Appendix A in Gelfand et al. 2009).

If the density, velocity, pressure of the ejecta, and the inner pressure of the PWN at some time t are given, then the radius and velocity of the PWN shell are calculated using above expressions. The calculation process here is the same as that in Gelfand et al. (2009, see their Sect. 2.2, in details).

Appendix A.2: Calculation of Bpwn(t)

From the relation of Bpwn and L(t) is given by 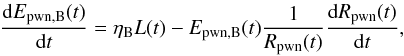dEpwn,B(t)dt=ηBL(t)−Epwn,B(t)1Rpwn(t)dRpwn(t)dt,\appendix \setcounter{section}{1} \begin{eqnarray*} \frac{{\rm d}E_{\rm pwn, B}(t)}{{\rm d}t}=\eta_{\rm B}L(t)- E_{\rm pwn, B}(t)\frac{1}{R_{\rm pwn}(t)}\frac{{\rm d}R_{\rm pwn}(t)}{{\rm d}t}, \end{eqnarray*}the following equation can be derived: d[Epwn,B(t)Rpwn(t)]dt=ηBRpwn(t)L(t).\appendix \setcounter{section}{1} \begin{equation} \label{A5} \frac{{\rm d}[E_{\rm pwn, B}(t)R_{\rm pwn}(t)]}{{\rm d}t}=\eta_{\rm B}R_{\rm pwn}(t)L(t). \end{equation}(A.5)Integrating Eq. 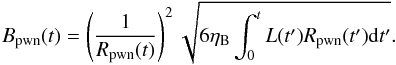(A.5) from t = 0 to t and noting that Epwn,B(t) = 0 at t = 0, the magnetic field Bpwn(t) is given by Bpwn(t)=(1Rpwn(t))26ηB∫0tL(t′)Rpwn(t′)dt′.\appendix \setcounter{section}{1} \begin{equation} B_{\rm pwn}(t) = \left(\frac{1}{R_{\rm pwn}(t)}\right)^2 \sqrt{6\eta_{\rm B}\int_{0}^{t}L(t')R_{\rm pwn}(t'){\rm d}t'}. \end{equation}(A.6)

Appendix B: Basic properties of PWNe in the sample

Appendix B.1: Group 1: young PWNe

N 158A. It is also known as G279.7-31.5, and is powered by an energetic pulsar PSR B0540-69 with a rotation period of 50.5 ms, a period derivative of 4.79 × 10-13 s s-1 (Seward et al. 1984; Livingstone et al. 2005b; Ferdman et al. 2015), and a braking index n for the PSR B0540-69 is 2.08 (Kaaret et al. 2001), very recent measurement shows n = 2.129 ± 0.012 (Ferdman et al. 2015), which is used here. Therefore, the pulsar has a characteristic age of ~ 1672 yr, and a spin-down luminosity L(t) = 1.47 × 1038 erg s-1. The system lies at a distance of 49 kpc (Seward et al. 1984; Taylor & Cordes 1993). Meanwhile, according to Manchester et al. (1993), the physical size of the N 158A is 0.7 pc. Observationally, N 158A has been detected in radio (Manchester et al. 1993), IR and optical (Mignani et al. 2012), and X-ray bands (Kaaret et al. 2001; Campana et al. 2008), but it was not detected in GeV and TeV γ-ray bands. The age of the system is ~760 yr by measurements of the expansion velocity of the SNR shell in the optical spectral band (Reynolds 1985; Kirshner et al. 1989; Chevalier 2005), and the mass of 20–25 M⊙ for the progenitor star is inferred by Williams et al. (2008). The parameters used in our calculation are Esn = 2.0 × 1051 erg, Mej = 23.0 M⊙, and nH = 0.01 cm-3. In Martin et al. (2014), UIR = 5.0 eV cm-3 and UOPT = 0.2 eV cm-3 were used to compute the energy density needed for the PWN to be detected by CTA. Here, UIR = 1.0 eV cm-3 and UOPT = 1.0 eV cm-3 are used in our calculation.

PWN G21.5-0.9 or HESS J1833-105. It is powered by an energetic PSR J1833-1034. The pulsar has a 61.8 ms rotation period, a period derivative of 2.02 × 10-13 s s-1 (Gupta et al. 2005; Camilo et al. 2006), and n = 3.0 is assumed. Thus, the pulsar has a characteristic age τc = 4850 yr and spin-down power L(t) = 3.4 × 1037 erg s-1. According to Camilo et al. (2006), the distance of the system is 4.7 ± 0.4 kpc; the same value was obtained by Tian & Leathy (2008). Here the distance of 4.1 kpc (Abdalla et al. 2017) is used. Observationally, PWN G21.5-0.9 is detected in radio (Salter et al. 1989; Morsi & Reich 1987; Wilson & Weiler 1976; Becker & Kundu 1976), IR (Gallant & Tuffs 1998, 1999), X-ray (De Rosa et al. 2009; Tsujimoto et al. 2011; Nynka et al. 2014), and TeV γ-ray bands by HESS (Djannati-Atai et al. 2008). Although Wang et al. (1986) suggested that the age of PWN G21.5-0.9 is about 2000 yr because it might be the historical supernova of 48 BC, Bietenholz & Bartel (2008) estimated Tage ~ 900 yr through the observation of the expansion rate of the PWN. Following Bietenholz & Bartel (2008) or Tanaka & Takahara (2011), Tage = 900 yr is assumed here. The parameters used in our calculation are nH = 0.1 cm-3, which is constrained to be between 0.1 and 0.4 cm-3 by Matheson & Safi-Harb (2005), and Mej = 8.0 M⊙. The values UIR = 1.4 eV cm-3 and UOPT = 5.0 eV cm-3 given in the GALPROP code of Porter et al. (2006) are used.

Crab nebula. It is a famous PWN that has been widely studied. The details of the observed and derived properties for the Crab nebula can be found in many papers (e.g., Torres et al. 2014; Zhu et al. 2015).

Kes 75. It is also known as HESS J1846-029 or G29.7-0.3, which is a typical composite supernova remnant. The central pulsar is PSR 1846-0258 (Gotthelf et al. 2000), and it has a rotational period P = 324 ms, a period derivative Ṗ = 7.08 × 10-12 s s-1, and a braking index n = 2.65 ± 0.01 (Livingstone et al. 2006). Very recently, the braking index n = 2.19 ± 0.03 was measured by Archibald et al. (2015); this value is applied in our paper. Thus, the pulsar has a characteristic age τc = 730 yr and its spin-down power L(t) = 8.21 × 1036 erg s-1. Leahy & Tian (2008) estimated a distance for the system between 5.1 to 7.5 kpc; the distance of 5.8 kpc (Abdalla et al. 2017) is adopted in our model. Observationally, Kes 75 has been detected in radio band (Salter et al. 1989; Bock & Gaensler 2005), X-ray band (Helfand et al. 2003), and TeV γ-ray band by HESS (Djannati-Atai et al. 2008). The ambient medium density of 1 cm-3 is estimated by Safi-Harb & Kumar (2012). Recently, the ambient medium density is constrained to be between 0.005 and 0.1 cm-3 by Gelfand et al. (2014); here, 0.1 cm-3 is used. The PSR 1846-0258 is very young; the actual age was constrained to be between 980 and 1770 yr by Mereghetti et al. (2002). Here, the age of 1000 yr and Mej = 10.0 M⊙ are used. The values UIR = 1.2 eV cm-3 and UOPT = 2.0 eV cm-3 are taken from Tanaka & Takahara (2011).

G310.6-1.6. It is powered by an energetic pulsar PSR J1400-6325, which has a rotation period of 31.18 ms, a period derivative 3.89 × 10-14 s s-1 (Renaud et al. 2010), and n = 3.0 is assumed. Thus, these parameters derive the characteristic age τc = 12 700 yr and spin-down power L(t) = 5.1 × 1037 erg s-1. The system lies at a distance of 7 kpc (Renaud et al. 2010; Tanaka & Takahara 2013). Observationally, G310.6-1.6 has been measured in radio band (Murphy et al. 2007; Griffith & Wright 1993; Condon et al. 1993; Duncan et al. 1995), X-ray band (Renaud et al. 2010), and TeV γ-ray band by HESS (e.g., Khélifi et al. 2008). The parameters used here are Mej = 13.0 M⊙, and nH = 0.01 cm-3. The values UIR = 0.3 eV cm-3 and UOPT = 0.3 eV cm-3 are taken from Tanaka & Takahara (2013).

3C 58. It is also known as SNR G130.7+3.1 or SN 1181, which is a composite SNR (Weiler & Panagia 1978). Its central pulsar is PSR J0205+6449, which is detected in radio, X-ray, and γ-ray bands. The pulsar has a rotation period 65.7 ms, a period derivative of 1.93 × 10-13 s s-1 (Murray et al. 2002; Camilo et al. 2002b; Livingstone et al. 2009), and n = 3.0 is assumed. These parameters derive a characteristic age of ~ 5397 yr and a spin-down luminosity L(t) = 2.68 × 1037 erg s-1. According to Roberts et al. (1993), 3C 58 is located at a distance of 3.2 kpc (Roberts et al. 1993) or 2 kpc (Kothes et al. 2010; Kothes 2013). Here, the distance of 2 kpc is adopted. Observationally, 3C 58 has been detected in radio (Green 1986; Morsi & Reich 1987; Salter et al. 1989), IR (Green 1994; Slane et al. 2008), X-ray (Torii et al. 2000), and GeV by Fermi-LAT (Abdo et al. 2013; Ackermann et al. 2013) and TeV bands by MAGIC (Aleksić et al. 2014). Chevalier (2005) estimated that the age of the system is ~ 2400 ± 500 yr by the PWN evolution and energetics, so 2400 yr is used in our paper. The parameters used in our calculation are Mej = 8.0 M⊙, and nH = 0.01 cm-3. The values UIR = 0.3 eV cm-3 and UOPT = 0.3 eV cm-3 are taken from Tanaka & Takahara (2013).

Appendix B.2: Group 2: evolved PWNe

HESS J1813-178 or G12.8-0.0. It is powered by an energetic pulsar PSR J1813-1749, which is the third most energetic pulsar in the Galaxy (Halpern et al. 2012). The pulsar has a rotation period of 44.7 ms (Gotthelf & Halpern 2009), a period derivative of 1.265 × 10-13 s s-1 (Halpern et al. 2012), and n = 3.0 is assumed. These parameters lead to a characteristic age of ~ 5600 yr and a spin-down luminosity L(t) = 5.6 × 1037 erg s-1. According to Brogan et al. (2005) and Halpern et al. (2012), the distance of the PWN is 4.7 kpc, and the corresponding radius of 4.0 ± 0.3 pc (Funk et al. 2007; Abdalla et al. 2017). Observationally, Brogan et al. (2005) presented the discovery of nonthermal radio emission of the radio shell (SNR G12.8-0.0) that is spatially coincident with HESS J1813-178, so we assume that the radio emission comes from HESS J1813-178, which was observed in X-ray band (Funk et al. 2007; Ubertini et al. 2005), GeV band by Fermi-LAT (Acero et al. 2013), and TeV γ-ray band by HESS (Aharonian et al. 2006b). In our model, we assume an age of 2500 yr. The parameters used in our calculation are the density of ambient medium of 1.0 cm-3 (Brogan et al. 2005), and Mej = 8.0 M⊙. For the soft seed photons, UIR = 1.0 eV cm-3 and UOPT = 1.5 eV cm-3 are used in Fang & Zhang (2010b). Here, UIR = 0.1 eV cm-3 and UOPT = 0.5 eV cm-3 are used to reproduce observed γ-ray SED.

G54.1+0.3. It is also known as VER J1930+188, which was first discovered by Reich et al. (1985). The PWN is powered by an energetic pulsar PSR J1930+1852, which was observed in radio (Camilo et al. 2002a) and X-ray bands (Lu et al. 2007). The pulsar has a period of 136 ms, a period time derivative 7.51 × 10-13 s s-1 (Camilo et al. 2002a), and n = 3.0 is assumed. These parameters lead to a characteristic age of ~ 2872 yr, and the spin-down power L(t) = 1.16 × 1037 erg s-1. PWN G54.1+0.3 has a distance of 6.2-0.6+1.0\hbox{$6.2^{+1.0}_{-0.6}$} kpc (Leahy et al. 2008). Here, the distance of 7.0 kpc (Abdalla et al. 2017) is used. Observationally, the PWN has been observed in radio band (Green 1985; Velusamy et al. 1986; Velusamy & Becker 1988; Lang et al. 2010), X-ray band (Lu et al. 2001, 2002; Bocchino et al. 2010), and TeV band by HESS (Acciari et al. 2010). The age of G54.1+0.3 is estimated to be between 1500 and 6000 yr (Camilo et al. 2002a). Recently, the age is constrained to be between 2100 and 3600 yr (Chevalier 2005; Bocchino et al. 2010; Gelfand et al. 2015). Here Tage = 2600 yr is used. The ejected mass Mej = 20 M⊙, which is constrained between 16 and 27 M⊙ (Temim et al. 2010, 2017) and nH = 1.0cm-3 are used here. The values UIR = 0.8 eV cm-3 and UOPT = 1.1 eV cm-3 are taken from the GALPROP code of Porter et al. (2006).

G292.0+1.8. It is also known as MSH 11-54 or HI 122-59. The system is powered by an energetic pulsar PSR J1124-5916 with a rotation period of 135.31 ms and a period derivative of 7.47 × 10-13 s s-1 (Camilo et al. 2002a); n = 3.0 is assumed. Thus, the pulsar has a characteristic age of ~ 2872 yr and a spin-down luminosity L(t) = 1.19 × 1037 erg s-1. The system lies at a distance of 6.0 kpc (Winkler et al. 2009). The radius of the PWN is about 3 pc (Bhalerao et al. 2015). Observationally, G292.0+1.8 has been observed in radio band (Gaensler & Wallace 2003), X-ray band (Hughes et al. 2001), and GeV band with an upper limit (Ackermann et al. 2011). The age of the system is uncertain, and ranges from ≤1600 yr (Murdin & Clark 1979) to ~3000 yr (Winkler et al. 2009); here Tage = 2700 yr is used, which is consistent with Tanaka & Takahara (2013). The values of nH = 0.5 cm-3 and Mej = 18.0 M⊙ are adopted. For the soft seed photons, UIR = 0.3 eV cm-3, UOPT = 0.3 eV and UIR = 0.42 eV cm-3, UOPT = 0.7 eV are applied in Tanaka & Takahara (2013) and Martin et al. (2014), respectively. Here, UIR = 1.0 eV cm-3 and UOPT = 0.7 eV cm-3 are used.

G0.9+0.1 or HESS J1747-281. It is powered by an energetic pulsar PSR J1747-2809 with a rotation period of 52.2 ms and a period derivative of 1.56 × 10-13 s s-1 (Camilo et al. 2009), and n = 3.0 is assumed. This pulsar has a characteristic age τc = 5305 yr and the spin-down power L(t) = 4.32 × 1037 erg s-1. The distance of the system is likely in the range from 8.0 kpc to 16 kpc, due to the uncertainty of the electron density model toward the distant inner Galactic regions (Dubner et al. 2008). Here, the distance of 13.3 kpc (Abdalla et al. 2017) is used. The PWN was detected in radio (Dubner et al. 2008), X-ray (Porquet et al. 2003), and TeV γ-ray bands by HESS (Aharonian et al. 2005b). Camilo et al. (2009) estimated the age of the system in the range between 2000 yr and 3000 yr. Here the age of the PWN is assumed to be 3000 yr; the density of the ambient medium of 0.01 cm-3 and Mej = 14.0 M⊙ are used in our calculation. The values UIR = 3.8 eV cm-3 and UOPT = 25.0 eV cm-3 given in Torres et al. (2014) are used.

MSH 15-52. A typical composite supernova remnant, which is also known as HESS J1514-591 or SNR G320.4-1.2 (Caswell et al. 1981). The system was first discovered as an extended nonthermal radio source by Mills et al. (1961). The PWN is powered by an energetic pulsar PSR B1509-58 (Gaensler et al. 2008), and it has a 150 ms rotation period, a period derivative of 1.5 × 10-12 s s-1, and a braking index n = 2.839 ± 0.003 (Livingstone et al. 2005a). Therefore, the pulsar has a characteristic age τc ~ 1585 yr and spin-down power L(t) = 1.75 × 1037 erg s-1. This system is located at a distance of 5.2 ± 1.4 kpc based on the HI absorption measurement (Gaensler et al. 1999). It is consistent with the vale of 4.2 ± 0.6 kpc derived from the dispersion measure Cordes & Lazio (2002). Here, the distance of 4.4 kpc (Abdalla et al. 2017) is used. Observationally, MSH 15-52 has been detected in radio band (Gaensler et al. 1999, 2008), X-ray band (Mineo et al. 2001; Forot et al. 2006), GeV band by Fermi-LAT (Abdo et al. 2010), and TeV γ-ray band by HESS (Aharonian et al. 2005a). Although the spin-down age is ~1600 yr, the true age of the system could be much older than the spin-down age (Seward et al. 1983; Gvaramadze 2001). To reconcile the age of the system, the braking index has to be <2.0. Here Tage = 4000 yr and n = 1.4 are assumed. The density of ambient medium nH = 0.01cm-3 and the ejected mass Mej = 6.0 M⊙ are adopted; UIR = 1.2 eV cm-3 and UOPT = 2.2 eV cm-3 are taken from the GALPROP code of Porter et al. (2006).

N 157B. It was the first extragalactic PWN to be detected in TeV γ-rays with HESS (Abramowski et al. 2012a, 2015). Its central pulsar is PSR J0537-6910 (Marshall et al. 1998). The pulsar has a rotation period of 16.12 ms and a period derivative of 5.13 × 10-14 s s-1 (Spyrou & Stergioulas 2002; Manchester et al. 2005b); n = 3.0 is assumed. Thus, the pulsar has a characteristic age of ~ 4982 yr, and a spin-down luminosity L(t) = 4.82 × 1038 erg s-1. The system has an estimated distance of 48 kpc (Macri et al. 2006), and the radius of the PWN is 10.6 pc (Lazendic et al. 2000). However, this radius is not very well defined, and it could include parts of the remnant. Following Abdalla et al. (2017), the distance of 53.7 kpc is used here. Observationally, this PWN has been detected in radio band (Lazendic et al. 2000), X-ray band (Chen et al. 2006), and TeV γ-ray band by HESS (Abramowski et al. 2012a, 2015). For the whole system, the Sedov age of ~5000 yr was estimated by Wang & Gotthelf (1998). Here, Tage = 4600 yr, which is consistent with Martin et al. (2014), and nH = 0.03 cm-3 and Mej = 20.0 M⊙, which is consistent with Chen et al. (2006), are used. For far-IR photons, according to the OB association LH99 and the nearby star-forming region 30 Doradus, using observations from Spitzer (Indebetouw et al. 2009), the infrared photon fields are modeled as blackbody radiation with a temperature of 80 K and an energy density of 8.9 eV cm-3 for LH99, and a temperature of 88 K and an energy density of 2.7 eV cm-3 for 30 Doradus. These are only upper limits to the infrared fields since the distances of N157B to these objects are unknown. Here, UIR = 5.0 eV cm-3 and UOPT = 4.0 eV cm-3 are used.

Appendix B.3: Group 3: mature/old PWNe

HESS J1356-645 or G309.9-2.51. It is powered by an energetic pulsar PSR J1357-6429 with a 166 ms rotation period, a 3.6 × 10-13 s s-1 period derivative (Camilo et al. 2004; Lorimer et al. 2006), and n = 3.0 is assumed. So the characteristic age of this pulsar is ~ 7310 yr and the spin-down luminosity is L(t) = 3.1 × 1036 erg s-1. Its distance is estimated to be 2.5 kpc (Cordes & Lazio 2002; Chang et al. 2012) and its radius is 10.1 ± 0.9 pc (Abdalla et al. 2017). Observationally, the PWN has been observed at radio band (Duncan et al. 1995; Griffith & Wright 1993; Murphy et al. 2007), X-ray band (Abramowski et al. 2011), GeV γ-ray band by Fermi-LAT (Acero et al. 2013), and TeV γ-ray band by HESS (Abramowski et al. 2011). Because the age of the system is not clear, Tage = 6500 yr is used here, which is similar to Torres et al. (2014). The values Mej = 7.0 M⊙ and nH = 0.05 cm-3 are assumed; UIR = 0.4 eV cm-3 and UOPT = 0.5 eV cm-3 are the same as those in Torres et al. (2014).

CTA 1. It is also known as VER J0006+727 or G 119.5 + 10.2, which was first discovered by Harris & Roberts (1960). The PWN is powered by PSR J0007+7303 with a rotation period of 316.86 ms, a period derivative of 3.614 × 10-13 s s-1 (Abdo et al. 2008), and n = 3.0 is assumed. Thus, the pulsar has a characteristic age of ~ 13 900 yr and a spin-down luminosity L(t) = 4.48 × 1035 erg s-1. CTA 1 has a distance of 1.4 ± 0.3 kpc (Pineault et al. 1993). The radius of the CTA 1 is estimated to be Rpwn ~ 7.2 pc because of the large synchrotron nebula observed by Slane et al. (1997, 2004), Halpern et al. (2004). Here, Rpwn = 6.6 ± 0.5 (Abdalla et al. 2017) is used. Observationally, CTA 1 has been detected in radio band (Aliu et al. 2013), X-ray band (Slane et al. 1997, 2004), GeV γ-ray band by Fermi-LAT (Abdo et al. 2012), and TeV γ-ray band by VERITAS (Aliu et al. 2013). The parameters used here are Tage = 7500 yr (which is between the values of 5000 yr and 15 000 yr found by Pineault et al. 1993; Slane et al. 2004), Mej = 8.0 M⊙, and nH = 0.1 cm-3. The values UIR = 0.3 eV cm-3 and UOPT = 0.6 eV cm-3 are taken from the GALPROP code of Porter et al. (2006).

HESS J1418-609. It is also known as Rabbit or G313.3+0.1. The PWN is powered by PSR J1418-6058 (Acero et al. 2013). The pulsar has a rotation period of 110.6 ms, a period derivative of 1.69 × 10-13 s s-1 (Abdo et al. 2013), and n = 3.0 is assumed. This pulsar has a characteristic age of ~ 10 380 yr and a spin-down luminosity L(t) = 4.93 × 1036 erg s-1. The distance of the system is 5.0 kpc (Ng et al. 2005; Aharonian et al. 2006a), which is used here. The radius of the system was estimated as 6.5 ± 0.3 pc (Kishishita et al. 2012) or 9.4 ± 0.9 (Abdalla et al. 2017). HESS J1418-609 has been detected in radio band (Roberts et al. 1999), X-ray band (Roberts et al. 2001; Ng et al. 2005; Kishishita et al. 2012), GeV γ-ray band by Fermi-LAT (Acero et al. 2013), and TeV γ-ray band by HESS (Aharonian et al. 2006a). So far, the age of HESS J1418-609 has not been clearly determined. The parameters used in our calculation are Tage = 8000 yr, Mej = 10.0 M⊙, and nH = 0.2 cm-3; UIR = 0.4 eV cm-3 and UOPT = 1.0 eV cm-3 are used to reproduce observed γ-ray SED here.

HESS J1420-607. It is also known as K3 PWN. The central pulsar is PSR J1420-6048 with a rotation period of 68 ms, a period derivative of 8.3 × 10-14 s s-1 (D’Amico et al. 2001; Roberts et al. 2001; Ng et al. 2005; Kishishita et al. 2012), and n = 3.0 is assumed. Therefore, the characteristic age of ~ 13 000 yr and the spin-down luminosity L(t) = 1.0 × 1037 erg s-1 are derived. The distance of the system is estimated as d = 5.6 kpc (Cordes & Lazio 2002), and the PWN radius is 7.9 ± 0.6 pc (Abdalla et al. 2017), which is consistent with Kishishita et al. (2012). HESS J1420-607 has been detected in radio band (Van Etten & Romani 2010), X-ray band (Van Etten & Romani 2010; Kishishita et al. 2012), GeV γ-ray band by Fermi-LAT Acero et al. (2013), and TeV γ-ray band by HESS Aharonian et al. (2006a). The age of the system is not clear. The parameters used here are Tage = 8500 yr, nH = 0.5 cm-3, and Mej = 15.0 M⊙; UIR = 0.3 eV cm-3 and UOPT = 0.3 eV cm-3 are used to reproduce observed γ-ray SED here.

HESS J1119-614 or G292.2-0.5. The PWN associates with the pulsar J1119-6127 (Caswell et al. 2004), which was discovered by Camilo et al. (2000). The pulsar has a rotational period of 408 ms, a period derivative of 4 × 10-12 s s-1, and the braking index n = 2.684 ± 0.002 (Weltevrede et al. 2011), which derives the characteristic age τc = 1617 yr and spin-down power L(t) = 2.32 × 1036 erg s-1. It lies at a distance of 8.4 ± 0.4 kpc (Caswell et al. 2004). The radius of the system is 14 ± 2 pc (Abdalla et al. 2017). Observationally, this PWN is detected in X-ray band (Gonzalez & Safi-Harb 2003; Safi-Harb & Kumar 2008) and the X-ray unabsorbed flux between 0.5 and 7 keV is 2.5 × 10-14 erg cm-2 s-1 and spectral index 1.4±0.90.8\hbox{$1.4\pm^{0.8}_{0.9}$}. It is detected in GeV band by Fermi-LAT (Acero et al. 2013), and TeV band by HESS (e.g., Abdalla et al. 2017). Here the whole SNR G292.2-0.5 flux measurement at 1.4 GHz flux density of 5.6 ± 0.3 Jy and 2.5 flux density of 1.6 ± 0.1 Jy (Crawford et al. 2001) are taken as a safe upper limit for the PWN radio emission. The age of HESS J1119-614 lies between 4200 yr (free expansion phase) and 7100 yr (Sedov phase; Kumar et al. 2012). We note that Tage = 4200 yr and n = 1.7 are used in Torres et al. (2014). These ages are older than the characteristic age ~1617 yr. Here Tage = 9000 yr and n = 1.2 are assumed. The parameters used in our calculation are Mej = 35.0 M⊙ and nH = 0.06 cm-3; UIR = 0.3 eV cm-3 and UOPT = 0.7 eV cm-3 are taken from the GALPROP code of Porter et al. (2006).

HESS J1303-631. It was first discovered in the VHE band by Aharonian et al. (2005c) and is associated with the pulsar J1301-6305 (Abramowski et al. 2012b). The pulsar has a 184 ms rotation period, a 2.65 × 10-13 s s-1 period derivative, and n = 3.0 is assumed. So a characteristic age of ~11 000 yr and a spin-down luminosity L(t) = 1.7 × 1036 erg s-1 are derived (Manchester et al. 2005a; Abramowski et al. 2012b). The pulsar’s distance was estimated to be 15.8 kpc by Taylor & Cordes (1993) and 6.6 kpc by Cordes & Lazio (2002). The distance of 6.6 kpc is used here. The radius of the system was estimated as 20 pc by (Abramowski et al. 2012b) and 20.6 ± 1.7 (Abdalla et al. 2017). Observationally, HESS J1303-631 has been detected in radio band (Condon et al. 1993), X-ray band (Abramowski et al. 2012b), GeV γ-ray band by Fermi-LAT (Acero et al. 2013), and TeV γ-ray band by HESS (Abramowski et al. 2012b); the X-ray unabsorbed flux between 2 and 10 KeV is 1.6 × 10-13 and the spectral index is unknown. Here, the value is assumed as a safe upper limit. The multiband spectrum of HESS J1303-631 was first studied by a simple stationary leptonic model (Abramowski et al. 2012b). The age of the system is not clear; here Tage = 13 000 yr and n = 2.5 are assumed. In our calculations, Mej = 9.0 M⊙ and nH = 0.02 cm-3; UIR = 6.0 eV cm-3 and UOPT = 2.0 eV cm-3 are used to reproduce observed γ-ray SED.

All Tables

Table 1

Parameters for young PWNe.

In the text
Table 2

Parameters for evolved PWNe.

In the text
Table 3

Parameters for mature/old PWNe.

In the text
Table 4

Pair multiplicities and wind Lorentz factors in the sample.

In the text
Table 5

Parameters of the central pulsars in the sample.

In the text
Table 6

Calculated luminosity at different wave bands and synchrotron cooling break energies in the sample.

In the text

All Figures

thumbnail Fig. 1

Comparisons of predicted SEDs and observed data for young PWNe (from upper left panel for N 158A to bottom right panel for 3C 58). In each panel, the black line represents synchrotron SED; the magenta, blue, green, and cyan lines represent the SEDs of inverse Compton scatterings with the synchrotron photons, IR, CMB, and starlight, respectively; and the total SED is shown by the red line. See text for the descriptions of the observed data; the relevant parameters are listed in Table 1.
In the text
thumbnail Fig. 2

Comparisons of predicted SEDs and observed data for evolved PWNe (from upper left panel for HEES J1813-178 to bottom right panel for N 157B). In each panel, the black line represents the synchrotron SED; magenta, blue, green, and cyan lines represent the SEDs of inverse Compton scatterings with the synchrotron photons, IR, CMB, and starlight, respectively; and the total SED is shown by the red line. See text for the descriptions of the observed data; the relevant parameters are listed in Table 2.
In the text
thumbnail Fig. 3

Comparisons of predicted SEDs and observed data for mature/old PWNe (from upper left panel for HEES J1356-645 to bottom right panel for HESS J1303-631). In each panel, the black line represents the synchrotron SED; magenta, blue, green, and cyan lines represent the SEDs of inverse Compton scatterings with the synchrotron photons, IR, CMB, and starlight, respectively; and the total SED is shown by the red line. See text for the descriptions of the observed data; the relevant parameters are listed in Table 3.
In the text
thumbnail Fig. 4

Correlations between Emax (upper panels) and Bpwn (bottom panels) and pulsar parameters BLC, Φ, and L(t). The solid lines represent the best linear fits (from top left to bottom right): log Emax = (0.42 ± 0.10)log BLC + (6.59 ± 0.54), log Emax = (0.88 ± 0.19)log Φ−(5.31 ± 2.97), log Emax = (0.44 ± 0.09)log L(t)−(7.65 ± 3.46), log Bpwn = (0.59 ± 0.08)log BLC−(1.72 ± 0.47), log Bpwn = (1.11 ± 0.12)log Φ−(16.47 ± 2.04), and log Bpwn = (0.56 ± 0.06)log L(t)−(19.44 ± 2.42); the correlation coefficient r = 0.71, 0.76, 0.76, 0.88, 0.91, and 0.91; and the probability of the null hypothesis Pnull = 8.95 × 10-4,2.26 × 10-4,2.24 × 10-4,1.14 × 10-6,1.23 × 10-7, and 1.71 × 10-7. The dashed lines are the 2σ confidence bands for the sample.
In the text
thumbnail Fig. 5

Correlations between L(t) and Lr, LX, and Lbol. The solid lines represent the best linear fits (from left to right): log Lr = (1.21 ± 0.17)log L(t)−(13.20 ± 6.38), log LX = (1.54 ± 0.12)log L(t)−(22.50 ± 4.68), and log Lbol = (1.24 ± 0.12)log L(t)−(10.15 ± 4.57); the correlation coefficients r = 0.88, 0.95, and 0.93; and the probability of the null hypothesis Pnull = 1.87 × 10-6,1.03 × 10-9, and 1.52 × 10-8. The dashed lines are the 2σ confidence bands for the sample.

In the text
thumbnail Fig. 6

Correlations between L(t) and Lr/Lγ and LX/Lγ. The solid lines represent the best linear fits (from left to right): log Lr/Lγ = (1.28 ± 0.28)log L(t)−(50.38 ± 10.53) and log LX/Lγ = (1.41 ± 0.22)log L(t)−(50.21 ± 8.33); the correlation coefficients r = 0.76, and 0.85; and the probability of the null hypothesis Pnull = 2.81 × 10-4 and 7.81 × 10-6. The dashed lines are the 2σ confidence bands for the sample.

In the text
thumbnail Fig. 7

Correlation between Ls, Es and L(t), Ls, and Es. The solid lines are the best linear fits, which are log Ls = (1.64 ± 0.09)log L(t)−(26.39 ± 3.55), log Es = −(0.78 ± 0.11)log L(t) + (24.46 ± 3.99), and log Ls = −(1.15 ± 0.11)log Es + (30.47 ± 0.64); the correlation coefficients r = 0.98, 0.88, and 0.93; and the probability of the null hypothesis Pnull = 5.59 × 10-12,1.70 × 10-6, and 2.27 × 10-8 (from left to right). The dashed lines are the 2σ confidence bands for the sample.

In the text
thumbnail Fig. 8

Correlations between L(t) and Sr, SX, and Sγ. The solid lines represent the best linear fits (from left to right): log Sr = (1.78 ± 0.20)log L(t)−(36.89 ± 7.60), log SX = (1.89 ± 0.32)log L(t)−(37.79 ± 12.42), and log Sγ = (0.71 ± 0.17)log L(t) + (5.89 ± 6.59); the correlation coefficients r = 0.91, 0.82, and 0.71; and the probability of the null hypothesis Pnull = 1.24 × 10-7,2.57 × 10-5, and 9.05 × 10-4, respectively. The dashed lines are the 2σ confidence bands for the sample.
In the text
thumbnail Fig. 9

Correlations between Rpwn and LX, LX/Lγ, and Ls. The solid lines are the best linear fits, which are log LX = −(1.36 ± 0.68)log Rpwn + (37.03 ± 0.38), log LX/Lγ = −(2.54 ± 0.52)log Rpwn + (2.69 ± 0.31), and log Ls = −(1.90 ± 0.75)log RPWNe + (37.48 ± 0.24); the correlation coefficients r = 0.45, 0.77, and 0.54; and the probability of the null hypothesis Pnull = 6.40 × 10-2,1.73 × 10-4, and 2.18 × 10-2 (from left to right). The dashed lines are the 2σ confidence bands for the sample.
In the text
thumbnail Fig. 10

Correlations between Tage and LX, LX/Lγ, and Ls. The solid lines are the best linear fits, which are log LX = −(2.44 ± 0.59)log Tage + (44.23 ± 1.89), log LX/Lγ = −(3.37 ± 0.29)log Tage + (12.47 ± 0.94), and log Ls = −(2.83 ± 0.53)log Tage + (45.37 ± 1.59); the correlation coefficients r = 0.72, 0.95, and 0.80; and the probability of the null hypothesis Pnull = 7.81 × 10-4,3.15 × 10-9, and 7.22 × 10-5. The dashed lines are the 2σ confidence bands for the sample.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.