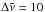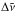| Issue |
A&A
Volume 605, September 2017
|
|
|---|---|---|
| Article Number | A95 | |
| Number of page(s) | 9 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201731026 | |
| Published online | 18 September 2017 | |
A hybrid line list for CH4 and hot methane continuum⋆
1 Department of Physics and Astronomy, University College London, London WC1E 6BT, UK
e-mail: s.yurchenko@ucl.ac.uk
2 Astrophysics Group, University of Exeter, Exeter, EX4 4QL, UK
3 Department of Applied Physics and Applied Mathematics, Columbia University, New York, NY 10025, USA
4 NASA Goddard Institute for Space Studies, New York, NY 10025, USA
Received: 23 April 2017
Accepted: 14 June 2017
Aims. Molecular line lists (catalogues of transition frequencies and line strengths) are important for modelling absorption and emission processes in atmospheres of different astronomical objects, such as cool stars and exoplanets. In order to be applicable for high temperatures, line lists for molecules like methane must contain billions of transitions, which makes their direct (line-by-line usage) application in radiative transfer calculations impracticable. Here we suggest a new, hybrid line list format to mitigate this problem, based on the idea of temperature-dependent absorption continuum.
Methods. The line list is partitioned into a large set of relatively weak lines and a small set of important, stronger lines. The weaker lines are then used either to construct a temperature-dependent (but pressure-independent) set of intensity cross sections or are blended into a greatly reduced set of “super-lines”. The strong lines are kept in the form of temperature-independent Einstein A coefficients.
Results. A line list for methane (CH4) is constructed as a combination of 17 million strong absorption lines relative to the reference absorption spectra and a background methane continuum in two temperature-dependent forms of cross sections and super-lines. This approach significantly eases the use of large high temperature line lists as the computationally expensive calculation of pressure-dependent profiles (e.g. Voigt) only need to be performed for a relatively small number of lines. Both the line list and cross sections were generated using a new 34 billion methane line list (known as 34to10), which extends the 10to10 line list to higher temperatures (up to 2000 K). The new hybrid scheme can be applied to any large line lists containing billions of transitions. We recommend using super-lines generated on a high resolution grid based on a resolving power of R = 1 000 000 to model the molecular continuum as a more flexible alternative to the temperature-dependent cross sections.
Key words: molecular data / opacity / infrared: stars / infrared: planetary systems / line: profiles / methods: numerical
The line list is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/605/A95
© ESO, 2017
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
Methane is one of the key absorbers in the atmospheres of exoplanets and cool stars. Due to a large number of relatively strong lines (up to several billion) at high temperatures, the calculation of cross sections becomes extremely computationally expensive. The contribution of each line to the total absorption must be taken into account by summing their individual cross sections, usually computed using Voigt profiles, on a grid of wavelengths. To make radiative transfer calculations using these line lists more tractable the line lists are usually converted into pre-computed tables of temperature- and pressure-dependent cross sections, or k-coefficients, for specific atmospheric conditions (temperature, pressure, broadeners; Amundsen et al. 2014; Malik et al. 2017). Subsequent radiative transfer calculations interpolate in these tables. However, the calculation of these cross sections and k-coefficients still requires the contributions of all lines to be summed, if only once for each atmospheric condition. Both pre-tabulated cross sections and k-coefficients are less flexible than a line-by-line approach, but are computationally more efficient.
As part of the ExoMol project (Tennyson & Yurchenko 2012) we produced an extensive line list for methane (12CH4), called 10to10 (Tennyson & Yurchenko 2012), containing almost 10 billion transitions. The line list was constructed to describe the opacity of methane for temperatures up to 1500 K. The 10to10 line list has been shown to be important for modelling the atmospheres of brown dwarfs and exoplanets (Yurchenko et al. 2014; Canty et al. 2015), and has been used as an input in a number of models such as TauREX (Waldmann et al. 2015b,a), NEMESIS (Irwin et al. 2008), VSTAR (Bailey & Kedziora-Chudczer 2012; Yurchenko et al. 2014), ATMO (Tremblin et al. 2015, 2016; Drummond et al. 2016), and the UK Met Office global circulation model (GCM) when applied to hot Jupiters (Amundsen et al. 2016). The ExoMol database contains line lists for about 40 other molecular species and has recently been upgraded (Tennyson et al. 2016). The line lists for polyatomic molecules usually contain more than 10 billion lines; examples include phosphine (PH3; Sousa-Silva et al. 2015), hydrogen peroxide (H2O2; Al-Refaie et al. 2015a), formaldehyde (H2CO; Al-Refaie et al. 2015b), and SO3 (Underwood et al. 2016); see also our review of molecular line lists (Tennyson & Yurchenko 2017).
A promising alternative to the line-by-line approach was recently proposed by Hargreaves et al. (2015), where an accurate experimental line list of the strongest CH4 transitions was complemented by a set of experimental quasi-continuum cross sections, measured for a set of different temperatures. Rey et al. (2016) recently proposed an alternative, super-line (SL), approach to speed up the line-by-line calculations. The idea is to build intensity histograms from transition intensities binned for a given temperature into wavenumber grid points. Each wavenumber bin is then treated as a super-line for computing cross sections for different line profiles, which brings the computational cost of a line-by-line approach almost down to that using pre-tabulated cross sections. The serious disadvantage, however, is that only very simplistic line profiles, i.e. ones which do not depend on quantum numbers, can be used. Indeed, each super-line loses memory of its upper and lower states; only the wavenumber is preserved. This is not a problem for the Doppler profile as it does not depend on quantum numbers. However, pressure-dependent profiles such as Voigt profiles often show strong dependence on the rotational J and other quantum numbers, which cannot be modelled using the SL approach.
In the present work we combine these two approaches and provide a synthetic hybrid line list for methane using the following compilation of data: (i) a line list of strong Nstr lines given explicitly using the ExoMol format (Hill et al. 2013; Tennyson et al. 2016) and (ii) all other Nweak weak lines converted into a temperature-dependent but pressure-independent background continuum. Thus the aim of this work is to select the most important lines (both the strongest and most sensitive to the variation of line profiles with pressure and broadener) for the direct line-by-line treatment, while the rest are processed either as cross sections or as super-lines (Rey et al. 2016). The hybrid approach is able to retain the key features of line lists and to significantly ease the computation of total cross sections and k-coefficient tables (including both weak and strong lines). We investigate two approaches to represent the temperature-dependent continuum: using pressure-independent cross sections described by the Doppler profile and using the profile-free histograms (super-lines).
As demonstrated by Rey et al. (2014) and Nikitin et al. (2017), in order to extend the temperature coverage of the 10to10 CH4 line list, the lower state energy threshold should be increased with respect to that used by Yurchenko & Tennyson (2014). Our 10to10 line list was based on the lower state energy threshold 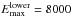 cm-1, which was estimated to be sufficient for temperatures up to 1500 K. In this work we extend the 10to10 line list by increasing
cm-1, which was estimated to be sufficient for temperatures up to 1500 K. In this work we extend the 10to10 line list by increasing 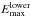 to 10 000 cm-1, which should extend the temperature coverage to about 2000 K. To be consistent with the extension of the lower state energy threshold, the rotational coverage had to be increased from the value of Jmax = 46 used by Yurchenko & Tennyson (2014) to about Jmax = 50. The cost of this improvement, however, is a dramatic increase in the number of lines, from 9.8 billion to 34 billion. The resulting “34to10” line list is used in this work to build a continuum absorption model for methane as described above.
to 10 000 cm-1, which should extend the temperature coverage to about 2000 K. To be consistent with the extension of the lower state energy threshold, the rotational coverage had to be increased from the value of Jmax = 46 used by Yurchenko & Tennyson (2014) to about Jmax = 50. The cost of this improvement, however, is a dramatic increase in the number of lines, from 9.8 billion to 34 billion. The resulting “34to10” line list is used in this work to build a continuum absorption model for methane as described above.
The partitioning of the 34 billion line list into a set of Nstr strong lines and Nweak weak lines is presented in Sect. 2, where we also define and test the strong/weak partitioning. In Sect. 3 our continuum model is tested by comparing it to the traditional approach of explicitly summing up the cross section contributions from all lines, at different temperatures and pressures. Section 4 presents our final results.
2. Strong/weak line list partitioning
In the following, the new line list for methane, which we have named 34to10, is used in all our examples. The line list is an extension of the 10to10 line list, produced using the same computational approach (Yurchenko & Tennyson 2014) by extending the lower state energy range from 8000 cm-1 to 10 000 cm-1. Calculations were performed with nuclear motion code TROVE (Yurchenko et al. 2007). As before, here calculations used a spectroscopically determined potential energy surface (Yurchenko & Tennyson 2014) and ab initio dipole moment surfaces (Yurchenko et al. 2013). The new line list contains 8 194 057 energies below 18 000 cm-1 and 34 170 582 862 transitions covering rotational excitations up to Jmax = 50. The calculation of the additional 28 billion transitions took approximately 5 million CPU hours on the Cambridge High Performance Computing Cluster Darwin. The wavenumber coverage, however, is kept the same as in the 10to10 line list, which means that the region from 10 000 to 12 000 cm-1 is less complete for the target temperature of 2000 K. All other computational components (potential energy and dipole moment surfaces, basis sets, etc.) are the same as in Yurchenko & Tennyson (2014).
In order to mitigate the difficulty of using such an extremely large line list, we propose dividing it into two subsets, responsible for strong and weak absorptions. The first question is how to define and separate “strong” and “weak” transitions. The large dynamic variation of the methane intensities means that a single intensity threshold would be not optimal. The following factors were taken into consideration when defining the intensity partitioning thresholds:
-
(i)
In regions of very strong bands many lines with moderateintensities are barely visible, while weak lines which lie betweenthe main bands can be relatively important.
-
(ii)
The definition of “strong” and “weak” must be temperature-dependent as “hot” bands, which are weak at low temperatures owing to the Boltzmann factor, become stronger with increasing population of excited lower states at higher temperatures.
-
(iii)
At the same time, the intensities of the fundamentals and overtones decrease with temperature owing to the decrease in their relative populations (e.g. due to a larger partition function).
-
(iv)
Finally, even relatively weak lines at longer wavelengths are very sensitive to pressure variations, due to their lower density.
To aid in the strong/weak partitioning, we introduced a reference CH4 opacity 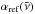 based on two temperatures, T1 = 300 K and T2 = 2000 K, and two pressures, P1 = 0 bar and P2 = 50 bar, on a wavenumber grid of
based on two temperatures, T1 = 300 K and T2 = 2000 K, and two pressures, P1 = 0 bar and P2 = 50 bar, on a wavenumber grid of 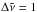 cm-1 (
cm-1 ( cm-1) by choosing the maximum cross section value among these four at each wavenumber grid point k:
cm-1) by choosing the maximum cross section value among these four at each wavenumber grid point k: 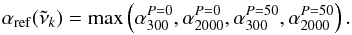 (1)The reference average intensities (cm/molecule) can then be defined as
(1)The reference average intensities (cm/molecule) can then be defined as 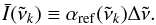 (2)Figure 1 shows the reference cross section curve used here for the 34to10 line list.
(2)Figure 1 shows the reference cross section curve used here for the 34to10 line list.
 |
Fig. 1 Reference cross sections obtained using the Doppler profile at T = 300 K and T = 2000 K on the uniform |
We then define the strong/weak partitioning using two criteria, one dynamic and one static. According to the static criterion, all lines stronger than the threshold Ithr are automatically taken into the strong section (e.g. Ithr = 10-25 cm/molecule). The dynamic criterion characterizes the line 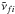 from the wavenumber bin k (
from the wavenumber bin k (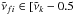 cm-1,
cm-1, 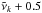 cm-1]) as strong if all four reference absorption intensities are stronger than the reference (average)
cm-1]) as strong if all four reference absorption intensities are stronger than the reference (average) 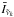 intensity by some scaling factor Cscale (e.g. stronger than
intensity by some scaling factor Cscale (e.g. stronger than 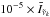 ). The scaling factor Cscale is made wavenumber-dependent using the following exponential form, also shown in Fig. 2:
). The scaling factor Cscale is made wavenumber-dependent using the following exponential form, also shown in Fig. 2: ![\begin{equation} \label{e:scale} C_{\rm scale} ({\tilde\nu}) = 10^{-5} \times \left[1{-}0.9\, {\rm e}^{-0.0005{\tilde\nu}}\right]. \end{equation}](/articles/aa/full_html/2017/09/aa31026-17/aa31026-17-eq43.png) (3)This scaling is necessary to take into account the importance of the varying density of lines at different spectroscopic regions for the accurate description of the line profiles: the smaller number of lines at the longer wavelengths means the cross sections are more sensitive to the shape of the profiles and to the sampling of the grid points. At the shorter wavelengths the spectrum is smoothed out by the large number of overlapping lines, which is therefore less sensitive to these factors. With this expression we thus assume a quasi-exponential increase in the density of lines vs. wavenumber, or, colloquially, a quasi-exponential decrease in their importance.
(3)This scaling is necessary to take into account the importance of the varying density of lines at different spectroscopic regions for the accurate description of the line profiles: the smaller number of lines at the longer wavelengths means the cross sections are more sensitive to the shape of the profiles and to the sampling of the grid points. At the shorter wavelengths the spectrum is smoothed out by the large number of overlapping lines, which is therefore less sensitive to these factors. With this expression we thus assume a quasi-exponential increase in the density of lines vs. wavenumber, or, colloquially, a quasi-exponential decrease in their importance.
Figures 3 and 4 illustrate how these partitioning criteria affect the absorption cross sections and the size of the strong and weak lines partitions, respectively, using the constant scale factor Cscale for simplicity. For example, the combination (Cscale = 10-2, Ithresh × [cm/molecules] -1 = 10-23) with Cscale constant leads to 262 470 lines. Using the scale factor Cscale = 10-5 increases the number of strong lines by one order of magnitude. For example, for the partitioning (10-5, 10-21) we obtain 125 million strong lines. The dynamic partitioning defined by Eq. (3) in combination with Ithresh = 10-23 cm/molecules is also shown in Fig. 4 as a large triangle. This partitioning is our preferred choice used in the following discussions and to construct the hybrid line list presented in this work. It results in 17 million selected lines (16 776 857) as part of the strong section, out of the original 34 × 1010. This is a huge reduction and should ease line-by-line calculations significantly. The remaining lines are converted into temperature-dependent histograms (super-lines) and/or cross sections to form our methane quasi-continuum, which is described below. By comparison, the HITRAN 2012 (Rothman et al. 2013) databases contains 336 830 12CH4 transitions.
 |
Fig. 3 Intensity partitioning for Ithr = 10-25 cm/molecule and Cscale = 10-5. The dashed line indicates the Ithr threshold; the blue (T = 300 K) and red (T = 2000 K) areas are the regions of the strong lines; the grey area at the bottom indicates all transitions which were excluded from the line list to form the weak lines of the continuum. Here all cross sections were obtained using the Doppler profile on a grid of 10 cm-1. |
 |
Fig. 4 Number of strong lines for different partitionings. |
3. Absorption continuum cross sections
3.1. Quasi-continuum from the Doppler line profile
The main difficulty associated with modelling cross sections (i.e. dressing lines with appropriate absorption profiles) is the pressure effect, which requires line shapes to be described using Lorentzian profiles (high pressure), Voigt profiles (moderate to high pressure), or even more sophisticated profiles (Tennyson et al. 2014). The Doppler profile (zero pressure), however, is much simpler; it is fast to compute, with a simple parametrization of the line width (mass- and frequency-dependent only), and no dependence on the transition quantum numbers, mixing ratios of broadeners, etc. (Amundsen et al. 2014).
We assume that the weak lines quasi-continuum forms a nearly featureless background that is not very sensitive to the variation of pressure (at least for moderate pressures). This means the exact shape of the lines that form this quasi-continuum is relatively unimportant and can be modelled using a pressure-independent, temperature-dependent profile. Basically, our assumption is that any realistic line profile would be applicable as long as it preserves the area as the frequency integrated cross section of each line. In order to illustrate this approach, we show in Fig. 5 the quasi-continuum cross section from the weak lines. The cross section was computed at 2000 K using the ExoCross code (Yurchenko et al. 2017) as described by Hill et al. (2013) for our selected partitioning using a Doppler line profile.
 |
Fig. 5 Upper panel: methane continuum at 2000 K, P = 10 bar (blue) and the total absorption (red). Lower panel: relative differences of the P = 0 and P = 10 bar continuum cross sections for the three wavenumber grids of |
In order to benchmark the zero pressure Doppler-based model of the continuum absorption we also computed the corresponding cross sections using the Voigt line profile at P = 10 bar, T = 2000 K. We use the simple ExoMol pressure-broadening diet of Barton et al. (2017) to describe the Voigt broadening of CH4 lines by 100% H2. The J dependence of the pressure-broadened half-width, γ, is similar to that used by Amundsen et al. (2014), and the temperature-dependence exponent, n, is assumed to be a constant. The broadening model is provided as part of the supplementary material to this paper. A grid spacing of 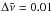 cm-1 was chosen. Figure 5 (bottom panel) also shows the relative difference between the Doppler-based continuum (P = 0) and the realistic P = 10 bar continuum (Voigt) on three grids of 0.01, 0.1, and 1 cm-1 at T = 2000 K. The grid of 0.01 cm-1 shows the fluctuations of the error within 2–8%. Here the relative difference of cross sections is defined as
cm-1 was chosen. Figure 5 (bottom panel) also shows the relative difference between the Doppler-based continuum (P = 0) and the realistic P = 10 bar continuum (Voigt) on three grids of 0.01, 0.1, and 1 cm-1 at T = 2000 K. The grid of 0.01 cm-1 shows the fluctuations of the error within 2–8%. Here the relative difference of cross sections is defined as 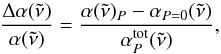 (4)where αP = 0, αP, and
(4)where αP = 0, αP, and 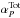 are the P = 0 (Doppler) continuum, P ≠ 0 continuum (Voigt), and the P ≠ 0 total cross section, respectively. The largest error is for the long wavelength region, characterized by the weakest intensities and least densities of lines. In this region the Doppler-broadened lines become increasingly narrow, which makes the cross section very sensitive to the grid sampling used. The best agreement is in the spectral regions with large cross sections and at short wavelengths, where the density is highest. Using coarser grids of 0.1 or 1 cm-1 drops the fluctuations to within 4 and 1.5%, respectively. The total integrated difference should be zero by definition since the area of the Voigt profile is conserved (subject to the numerical error). However, we note that unless the background lines are optically thin the resulting integrated flux will not be conserved.
are the P = 0 (Doppler) continuum, P ≠ 0 continuum (Voigt), and the P ≠ 0 total cross section, respectively. The largest error is for the long wavelength region, characterized by the weakest intensities and least densities of lines. In this region the Doppler-broadened lines become increasingly narrow, which makes the cross section very sensitive to the grid sampling used. The best agreement is in the spectral regions with large cross sections and at short wavelengths, where the density is highest. Using coarser grids of 0.1 or 1 cm-1 drops the fluctuations to within 4 and 1.5%, respectively. The total integrated difference should be zero by definition since the area of the Voigt profile is conserved (subject to the numerical error). However, we note that unless the background lines are optically thin the resulting integrated flux will not be conserved.
A more detailed example of the P = 0 and P = 10 bar cross sections for the region 6000–7000 cm-1 is shown in Fig. 6 for 300 K (left) and 2000 K (right). Even on the very small scale (see a zoom-in in the middle panels of this figure) the P = 0 and P = 10 bar continuum cross sections are almost identical: the difference between the two continuum curves (P = 0 and P = 10 bar) is barely seen. The bottom panels of Fig. 6 show absolute relative differences 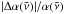 between these two cross sections. For our partitioning a 1–2% accuracy (measured as the relative difference between these two profiles) is achieved for this region. In fact, the difference is not systematic; therefore, the integrated effect should be even smaller. For example, integration of the relative difference
between these two cross sections. For our partitioning a 1–2% accuracy (measured as the relative difference between these two profiles) is achieved for this region. In fact, the difference is not systematic; therefore, the integrated effect should be even smaller. For example, integration of the relative difference 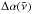 for T = 2000 K in the region 6700–6800 cm-1 gives an error of only 0.004% using the grid spacing of
for T = 2000 K in the region 6700–6800 cm-1 gives an error of only 0.004% using the grid spacing of 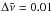 cm-1. The fluctuations for T = 300 K between the high pressure and zero pressure cases are slightly higher, but still within approximately 1–2%. The integrated relative difference in this case is about 0.06% (6700–6750 cm-1, see Fig. 6).
cm-1. The fluctuations for T = 300 K between the high pressure and zero pressure cases are slightly higher, but still within approximately 1–2%. The integrated relative difference in this case is about 0.06% (6700–6750 cm-1, see Fig. 6).
 |
Fig. 6 Comparison of the P = 0 and P = 10 bar cross sections for 300 K (left) and 2000 K (right): black (total P = 0), blue (continuum P = 0), and red (continuum P = 10). The middle panels are a zoom-in of the continuum, also for P = 0 and P = 10 bar, which are almost indistinguishable in the upper panels. The lower panels show the relative difference between the P = 0 and P = 10 bar continuum cross sections as defined in Eq. (4). The integrated area of the relative difference is 0.06% over the region 6700–6750 cm-1. A wavenumber grid of |
The corresponding line shapes are very different at these temperatures and pressures. The total P = 0 and P = 10 bar cross sections have very different profiles (see Fig. 7). However the difference between continuum curves is negligible (see also Fig. 6).
 |
Fig. 7 Comparison of the P = 0 and P = 10 bar line profiles used to generate cross sections at 2000 K in the region of 1.615 μm. The a0 model with the J-independent line broadening was used. The wavenumber grid |
3.2. Super-line approach
In this section we consider temperature-dependent lists of super-lines (Rey et al. 2016), which present a more flexible alternative to the Doppler-broadened continuum in terms of the line-profile modelling. The super-lines are constructed as temperature-dependent intensity histograms as follows (see also detailed instructions in Rey et al. 2016). The wavenumber range ![\hbox{$[\tilde\nu_{\rm A},\tilde\nu_{\rm B}]$}](/articles/aa/full_html/2017/09/aa31026-17/aa31026-17-eq71.png) is divided into N frequency bins, each centred around a grid point
is divided into N frequency bins, each centred around a grid point 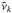 . Here we assume a general case of non-equidistant grids with variable widths
. Here we assume a general case of non-equidistant grids with variable widths 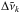 . For each
. For each 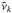 the total absorption intensity Ik(T) is computed as a sum of absorption line intensities Iif
the total absorption intensity Ik(T) is computed as a sum of absorption line intensities Iif![\begin{equation} \label{eq:int} I_{if} = \frac{1}{8\pi c \tilde{\nu}^2} \frac{g_{\rm ns}(2J' + 1)}{Q(T)} A_{if} \exp\left( \frac{-c_2 \tilde{E}''}{T} \right) \left[1-\exp\left({\frac{c_2\tilde{\nu}}{T}}\right)\right], \end{equation}](/articles/aa/full_html/2017/09/aa31026-17/aa31026-17-eq77.png) (5)from all i → f transitions falling into the wavenumber bin
(5)from all i → f transitions falling into the wavenumber bin ![\hbox{$[\tilde\nu_k-\Delta \tilde{\nu}_k/2 \ldots \tilde\nu_k+\Delta \tilde{\nu}_k/2 ] $}](/articles/aa/full_html/2017/09/aa31026-17/aa31026-17-eq79.png) at the given temperature T. Here Aif is the Einstein A coefficient (s-1), c is the speed of light (cm s-1), Q(T) is the partition function,
at the given temperature T. Here Aif is the Einstein A coefficient (s-1), c is the speed of light (cm s-1), Q(T) is the partition function, 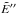 is the lower state term value (cm-1), c2 is the second radiation constant (K cm), gns is the nuclear statistical weight, J′ is the rotational angular momentum quantum number of the upper state, and Iif is the line intensity or absorption coefficient (cm2/molecule cm-1). Each grid point
is the lower state term value (cm-1), c2 is the second radiation constant (K cm), gns is the nuclear statistical weight, J′ is the rotational angular momentum quantum number of the upper state, and Iif is the line intensity or absorption coefficient (cm2/molecule cm-1). Each grid point 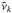 is then treated as a line position of an artificial transition (super-line) with an effective absorption intensity Ik(T). The super-line lists are then formed as catalogues of these artificial transitions
is then treated as a line position of an artificial transition (super-line) with an effective absorption intensity Ik(T). The super-line lists are then formed as catalogues of these artificial transitions 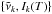 with pre-computed intensities Ik. This can be compared to the temperature-independent ExoMol-type
with pre-computed intensities Ik. This can be compared to the temperature-independent ExoMol-type 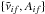 or temperature-dependent HITRAN-type
or temperature-dependent HITRAN-type 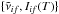 line lists.
line lists.
As in the case of the conventional line lists, the super-lines can be used in line-by-line modelling of absorption cross sections, which significantly reduces the computational costs. Indeed, each super-line can be dressed with the corresponding line profile to generate actual cross sections for the corresponding T and any given pressure broadening, provided that these line profiles depend only on the line positions and temperature, and not on the quantum numbers, for example. In fact, the main disadvantage of the histograms is that they lose any information on the upper and lower states, including the quantum numbers. This information is important when dealing with the pressure-dependent line profiles, which often show strong variation with quantum numbers, particularly J. It is still possible to assume, however, that the continuum is nearly featureless and thus not very sensitive to dependence of the line profiles on the quantum numbers of the upper or lower states.
In order to illustrate the applicability of this approximation, in Fig. 8 we show the error of the methane continuum at T = 2000 K and P = 10 bar as the difference between two cross sections: (i) obtained using the J-dependent Voigt-profile model by Barton et al. (2017) and (ii) obtained using constant Voigt parameters, relative to the total methane cross sections at these values of T and P. The error is within 0.05% for most of the frequency range and not larger than 0.1%. Another artefact of the histogram method (apart from the limited profile description) is the error of the line position within a bin. Therefore, the smaller the bin, the better the accuracy of the super-line list.
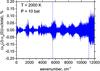 |
Fig. 8 Relative error from using J-independent line broadening to describe methane continuum at high temperature (T = 2000 K) and pressure (P = 10 bar) as the difference between two cross sections (J-dependent a0 model vs. J-independent model) relative to the total cross sections. The wavenumber grid of |
An important advantage of histograms is that they are very robust and efficient for computing cross sections thanks to a relatively small number of super-lines defined by the density of the wavenumber grid, which is therefore much smaller (at least for methane) than the number of the original lines. For example, with the 0.01 cm-1 grid spacing, the size of a histogram at a given T is only 1 200 000 grid points (super-lines) for our line list coverage (<12 000 cm-1), which is much smaller than the original 34 billion lines. Even for the more sophisticated four-grid model suggested by Tennyson et al. (2016; 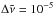 cm-1 for 10–100 cm-1, 10-4 cm-1 for 100–1000 cm-1, 0.001 cm-1 for 1000–10 000 cm-1, and 0.01 cm-1 for >10 000 cm-1) we obtain only 28 200 000 super-lines, which also should not be a problem for line-by-line practical applications. Since the long wavelength region is always more demanding in terms of the accuracy, such dynamic grids are more accurate. In the following we propose another dynamic grid based on a constant resolving power, R.
cm-1 for 10–100 cm-1, 10-4 cm-1 for 100–1000 cm-1, 0.001 cm-1 for 1000–10 000 cm-1, and 0.01 cm-1 for >10 000 cm-1) we obtain only 28 200 000 super-lines, which also should not be a problem for line-by-line practical applications. Since the long wavelength region is always more demanding in terms of the accuracy, such dynamic grids are more accurate. In the following we propose another dynamic grid based on a constant resolving power, R.
In order to benchmark the super-line approach we have computed three sets of histograms for T = 2000 K representing the continuum of methane (i.e. from the weak lines only) using the following grid models: histogram I with a constant grid spacing of 0.01 cm-1 (1 200 000 points); histogram II with four subgrids proposed by Tennyson et al. (2016; 28 million points); and histogram III with a constant resolving power R of 1 000 000 (7 090 081 points). The constant R-grid can be defined to have variable grid spacings as given by 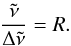 Thus, the vavenumber grid point
Thus, the vavenumber grid point 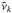 (k = 0...N(R)) is given by
(k = 0...N(R)) is given by 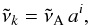 (6)where a = (R + 1) /R and
(6)where a = (R + 1) /R and 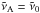 is the left-most wavenumber grid point (cm-1). The total number of bins, N(R) is given by
is the left-most wavenumber grid point (cm-1). The total number of bins, N(R) is given by 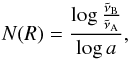 (7)where
(7)where 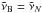 is the right-most grid point and N(R) + 1 is the total number of the grid points.
is the right-most grid point and N(R) + 1 is the total number of the grid points.
Histograms I, II, and III were used to generate the continuum cross sections of CH4 at P = 10 bar. Here we assumed the Voigt profile with constant parameters (γ0 = 0.051 cm-1, n = 0.44, T0 = 298 K, and P0 = 1 bar) and used the grid with 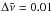 cm-1. These cross sections were then compared to the corresponding continuum cross sections (T = 2000 K, P = 10 bar) computed line-by-line directly from the 34to10 line list. All histogram models show very similar, almost identical deviations, well below 0.1% for most of the range. Figure 9 illustrates the relative errors obtained for the R = 1 000 000 histogram model.
cm-1. These cross sections were then compared to the corresponding continuum cross sections (T = 2000 K, P = 10 bar) computed line-by-line directly from the 34to10 line list. All histogram models show very similar, almost identical deviations, well below 0.1% for most of the range. Figure 9 illustrates the relative errors obtained for the R = 1 000 000 histogram model.
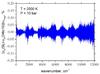 |
Fig. 9 Relative errors using the histogram model R = 1 000 000 to describe the methane continuum at T = 2000 K and P = 10 bar as the difference with the 34to10 cross sections (Voigt model) relative to the total 34to10 cross sections. The wavenumber grid of |
Now we turn to the case of the pure Doppler broadening (P = 0 bar, T = 2000 K, grid spacing 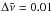 cm-1), where the lines are sharper and narrower, such that the line width may become comparable or even smaller than the grid spacing. Figure 10 illustrates the errors for the same three histogram models. The uniform histogram I of 0.01 cm-1 (1 200 000 points) exhibits the largest errors in the low frequency region, while the two adaptive grids show errors within about 4–5%. Clearly,
cm-1), where the lines are sharper and narrower, such that the line width may become comparable or even smaller than the grid spacing. Figure 10 illustrates the errors for the same three histogram models. The uniform histogram I of 0.01 cm-1 (1 200 000 points) exhibits the largest errors in the low frequency region, while the two adaptive grids show errors within about 4–5%. Clearly, 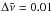 cm-1 is too coarse for the super-line approach to describe the low frequency range in the the zero pressure case; therefore, we recommend using grids with more points (lines) in the region below 1000 cm-1. For the denser histograms II and III the error drops to <0.2–0.5%. Histogram III (resolving power R = 1 000 000) shows a more even error distribution.
cm-1 is too coarse for the super-line approach to describe the low frequency range in the the zero pressure case; therefore, we recommend using grids with more points (lines) in the region below 1000 cm-1. For the denser histograms II and III the error drops to <0.2–0.5%. Histogram III (resolving power R = 1 000 000) shows a more even error distribution.
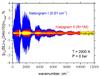 |
Fig. 10 Relative error from the histogram model for three different grids to describe the methane continuum at T = 2000 K and P = 0 bar as the difference with the 34to10 cross sections (pure Doppler model) relative to the total 34to10 cross sections at P = 0 bar. The wavenumber grid of |
A similar comparison for T = 300 K showed even better agreement, with errors about an order of magnitude smaller than those found for T = 2000 K. Using a coarser grid to simulate cross sections (e.g. 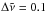 cm-1) also drops the errors by an order of magnitude.
cm-1) also drops the errors by an order of magnitude.
For super-lines it is obviously important that the underlying grid spacing is not too large compared to the line width. This is illustrated in Fig. 11, which shows the P = 0, T = 2000 K continuum cross sections modelled using the R = 100 000 histogram with the Doppler profile. It is clear that the Doppler line width is smaller than the separation between the super-lines, which leads to strong oscillations. In fact, the same histogram performs well in the case of much broader lines when modelling P = 10 bar, Fig. 8.
 |
Fig. 11 Inappropriate use of the super-line approach when the grid is too coarse. The super-lines use a resolution of R = 100 000, which is not sufficient, due to the narrow Doppler profiles at zero pressure, T = 2000 K. The cross section was computed on a |
In order to estimate the impact of the errors in the continuum models on actual atmospheric radiative transfer and retrieval calculations, we have calculated the transmission 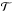 and the relative error in the transmission
and the relative error in the transmission 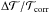 from the continuum models, where
from the continuum models, where ![\begin{equation} \mathcal T = \exp \left[ -\alpha(\tilde \nu) u \right], \qquad \frac{\Delta \mathcal T}{\mathcal T_\text{corr}} = \frac{\mathcal T - \mathcal T_\text{corr}}{\mathcal T_\text{corr}}, \end{equation}](/articles/aa/full_html/2017/09/aa31026-17/aa31026-17-eq118.png) (8)and
(8)and 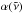 is the total cross section, u is the column amount, and
is the total cross section, u is the column amount, and  is the correct transmission calculated from the direct line-by-line evaluation of the 34to10 line list using the a0 Voigt model (Barton et al. 2017). We show the transmissions and errors in Fig. 12 obtained using both continuum models with column amounts ranging from 1019 to 1024molecule/cm2 at T = 2000 K, and P = 0 and P = 10 bar. The histogram model performs extremely well for the high pressure case (lower panel) with the errors within 1 % and significantly better than the Doppler grid model (upper panel). The errors in the histogram model at zero pressure are higher, due to the very narrow lines at small wavenumbers (middle panel), but should be acceptable for most of the applications (within 5 %). If higher accuracy is required, the histogram resolution should be increased.
is the correct transmission calculated from the direct line-by-line evaluation of the 34to10 line list using the a0 Voigt model (Barton et al. 2017). We show the transmissions and errors in Fig. 12 obtained using both continuum models with column amounts ranging from 1019 to 1024molecule/cm2 at T = 2000 K, and P = 0 and P = 10 bar. The histogram model performs extremely well for the high pressure case (lower panel) with the errors within 1 % and significantly better than the Doppler grid model (upper panel). The errors in the histogram model at zero pressure are higher, due to the very narrow lines at small wavenumbers (middle panel), but should be acceptable for most of the applications (within 5 %). If higher accuracy is required, the histogram resolution should be increased.
 |
Fig. 12 Transmissions computed using the Doppler model (upper panel) and histogram continuum models (R = 1 000 000, middle and lower panels) with relative errors for the column amounts 1019, 1020, 1021, 1022, 1023, and 1024 molecule/cm2 at T = 2000 K, P = 0 and P = 10 bar. The upper part of each panel shows the total transmission obtained from both the strong and weak lines at this temperature, while the lower part shows the relative error compared to the direct line-by-line evaluation from the 34to10 line list using the a0 Voigt model (Barton et al. 2017). The error in regions with very low transmissions (<10-4) are removed as the medium is optically thick. |
4. Hybrid line list and temperature-dependent continuum cross sections
Our partitioning of the total 34 170 582 862 lines in our new 34to10 line list leads to 16 776 857 strong and 34 153 806 005 weak lines. The latter were used to (i) generate temperature-dependent continuum cross sections (Doppler-broadened) and (ii) temperature-dependent histograms of super-lines for the following set of temperatures: 296 K, 400 K, 500 K, 600 K, 700 K, 800 K, 900 K, 1000 K, 1100 K, 1200 K, 1300 K, 1400 K, 1500 K, 1600 K, 1700 K, 1800 K, 1900 K, and 2000 K. A wavenumber grid with constant R = 1 000 000 consisting of 7 090 081 points (super-lines) was adopted for the total range of 0–12 000 cm-1. The remaining 16 776 857 strong lines together with the. states file containing 8 194 057 energies form a line list in the standard ExoMol format (Tennyson et al. 2016). The super-lines are stored in the two-column format with the frequency wavenumbers (cm-1) and absorption coefficients (cm/molecule), which is the same as the format used for the ExoMol cross sections (Tennyson et al. 2016). Thus, the histogram format does not require any information on the upper/lower states, temperature, partition function, or statistical weights; only the line profile specifications are needed. The line broadening can only depend on the wavenumber. The hybrid line list is given as supplementary material to this paper via the CDS database and can also be found on the ExoMol website1. We also include the Voigt model used in the simulations of cross sections.
5. Conclusion
We have extended our previous 10to10 methane line list to higher temperatures, the result of which is a new line list containing 34 billion transitions. Line lists of this size are impractical to work with as the calculation of cross sections becomes extremely computationally expensive. We have therefore explored the idea of partitioning this line list into a relatively small subset of strong lines which are retained; these lines will be fully treated in any cross section calculation, and augmented by a temperature-dependent quasi-continuum which represents the contribution of the remaining lines. A key assumption is that this quasi-continuum is essentially featureless and not very sensitive to the variation of the pressure broadened line shape. The strong lines are selected such that they retain the flexibility required to describe the variation of the shape of the methane absorption with pressure.
Two P-independent models were tested to represent the continuum built from the weak lines, Doppler-broadened cross sections, and super-lines. For the Doppler-broadened scheme, the assumption is that the methane continuum does not strongly depend on pressure and can be modelled using the pressure-independent line profiles. The error of this approach on dense grids (0.01 cm-1) ranges from within 8% for long wavelengths down to within 3% above 1 μm. The coarser grid of 0.1 cm-1 gives errors within 2%.
The super-lines approach is more flexible as it allows the continuum to depend on pressure. The variation with pressure, however, should not depend on the upper or lower states, only on the line position. For this model we also introduced the dynamic grid representation with a constant resolution, with the grid spacing changing as a function of the wavenumber to keep 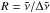 the same. Each grid in this histogram model point containing the total absorption within the
the same. Each grid in this histogram model point containing the total absorption within the 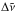 bin is then used as a super-line. We find that the super-lines built as histograms on an adaptive grid of a high resolution are more accurate for absorption modelling, and therefore was put forward as the ExoMol standard. The typical errors even for dense grids are within 1%. With our selected partitioning we retain 17 million strong lines for our strong line lists and computed a set of histograms containing 7 090 081 points (super-lines) for a set of 18 temperatures using a dynamic wavenumber grid with a resolution of R = 1 000 000. The strong lines are given as the ExoMol line list while the continuum histograms are presented using the ExoMol format developed for cross sections (Tennyson et al. 2016). We recommend using this hybrid line list based on the super-line approach for line-by-line atmospheric modelling of methane absorption. For low pressures and long wavelengths, the resolution might need to be increased to higher than 1 000 000, due to the very narrow Doppler-broadened lines and their low density in this region.
bin is then used as a super-line. We find that the super-lines built as histograms on an adaptive grid of a high resolution are more accurate for absorption modelling, and therefore was put forward as the ExoMol standard. The typical errors even for dense grids are within 1%. With our selected partitioning we retain 17 million strong lines for our strong line lists and computed a set of histograms containing 7 090 081 points (super-lines) for a set of 18 temperatures using a dynamic wavenumber grid with a resolution of R = 1 000 000. The strong lines are given as the ExoMol line list while the continuum histograms are presented using the ExoMol format developed for cross sections (Tennyson et al. 2016). We recommend using this hybrid line list based on the super-line approach for line-by-line atmospheric modelling of methane absorption. For low pressures and long wavelengths, the resolution might need to be increased to higher than 1 000 000, due to the very narrow Doppler-broadened lines and their low density in this region.
The integrated errors of cross sections over an extended frequency range (significantly larger than than linewidth) are found to be vanishingly small if the line profiles used preserve the area (subject to numerical accuracy). That is, for optically thin atmospheres both continuum models will guarantee that exact answer for the integrated opacities. We have also shown that even in the case of realistic, not optically thin media, the super-line approach leads to very small error transmission.
The data can be accessed via the CDS database or from the ExoMol database2.
Acknowledgments
This work was supported by the UK Science and Technology Research Council (STFC) No. ST/M001334/1, ERC Advanced Investigator Projects 267219 and 247060-PEPS, and the COST action MOLIM No. CM1405. D.S.A. acknowledges support from the NASA Astrobiology Program through the Nexus for Exoplanet System Science. This work made extensive use of the DiRAC@Darwin and DiRAC@COSMOS HPC clusters. DiRAC is the UK HPC facility for particle physics, astrophysics, and cosmology which is supported by STFC and BIS. Some calculations for this paper were performed on the University of Exeter Supercomputer, a DiRAC Facility jointly funded by STFC, the Large Facilities Capital Fund of BIS, and the University of Exeter.
References
- Al-Refaie, A. F., Ovsyannikov, R. I., Polyansky, O. L., Yurchenko, S. N., & Tennyson, J. 2015a, J. Mol. Spectr., 318, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Al-Refaie, A. F., Yurchenko, S. N., Yachmenev, A., & Tennyson, J. 2015b, MNRAS, 448, 1704 [NASA ADS] [CrossRef] [Google Scholar]
- Amundsen, D. S., Baraffe, I., Tremblin, P., et al. 2014, A&A, 564, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Amundsen, D. S., Mayne, N. J., Baraffe, I., et al. 2016, A&A, 595, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bailey, J., & Kedziora-Chudczer, L. 2012, MNRAS, 419, 1913 [NASA ADS] [CrossRef] [Google Scholar]
- Barton, E. J., Hill, C., Czurylo, M., et al. 2017, J. Quant. Spectr. Rad. Transf. 187, 453 [NASA ADS] [CrossRef] [Google Scholar]
- Canty, J. I., Lucas, P. W., Yurchenko, S. N., et al. 2015, MNRAS, 450, 454 [NASA ADS] [CrossRef] [Google Scholar]
- Drummond, B., Tremblin, P., Baraffe, I., et al. 2016, A&A, 594, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hargreaves, R. J., Bernath, P. F., Bailey, J., & Dulick, M. 2015, ApJ, 813, 12 [Google Scholar]
- Hill, C., Yurchenko, S. N., & Tennyson, J. 2013, Icarus, 226, 1673 [NASA ADS] [CrossRef] [Google Scholar]
- Irwin, P. G. J., Teanby, N. A., de Kok, R., et al. 2008, J. Quant. Spectr. Rad. Transf., 109, 1136 [NASA ADS] [CrossRef] [Google Scholar]
- Malik, M., Grosheintz, L., Mendonça, J. M., et al. 2017, ApJ, 153, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Nikitin, A. V., Rey, M., & Tyuterev, V. G. 2017, J. Quant. Spectr. Rad. Transf., 200, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Rey, M., Nikitin, A. V., & Tyuterev, V. G. 2014, ApJ, 789, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Rey, M., Nikitin, A. V., Babikov, Y. L., & Tyuterev, V. G. 2016, J. Mol. Spectr., 327, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Rothman, L. S., Gordon, I. E., Babikov, Y., et al. 2013, J. Quant. Spectr. Rad. Transf., 130, 4 [Google Scholar]
- Sousa-Silva, C., Al-Refaie, A. F., Tennyson, J., & Yurchenko, S. N. 2015, MNRAS, 446, 2337 [Google Scholar]
- Tennyson, J., & Yurchenko, S. N. 2012, MNRAS, 425, 21 [Google Scholar]
- Tennyson, J., & Yurchenko, S. N. 2017, Mol. Astrophys., 8, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tennyson, J., Bernath, P. F., Campargue, A., et al. 2014, Pure Appl. Chem., 86, 1931 [Google Scholar]
- Tennyson, J., Yurchenko, S. N., Al-Refaie, A. F., et al. 2016, J. Mol. Spectr., 327, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Tremblin, P., Amundsen, D. S., Mourier, P., et al. 2015, ApJ, 804, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Tremblin, P., Amundsen, D. S., Chabrier, G., et al. 2016, ApJ, 817, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Underwood, D. S., Tennyson, J., Yurchenko, S. N., Clausen, S., & Fateev, A. 2016, MNRAS, 462, 4300 [NASA ADS] [CrossRef] [Google Scholar]
- Waldmann, I. P., Rocchetto, M., Tinetti, G., et al. 2015a, ApJ, 813, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Waldmann, I. P., Tinetti, G., Barton, E. J., Yurchenko, S. N., & Tennyson, J. 2015b, ApJ, 802, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Yurchenko, S. N., & Tennyson, J. 2014, MNRAS, 440, 1649 [NASA ADS] [CrossRef] [Google Scholar]
- Yurchenko, S. N., Thiel, W., & Jensen, P. 2007, J. Mol. Spectr., 245, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Yurchenko, S. N., Tennyson, J., Barber, R. J., & Thiel, W. 2013, J. Mol. Spectr., 291, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Yurchenko, S. N., Tennyson, J., Bailey, J., Hollis, M. D. J., & Tinetti, G. 2014, Proc. Nat. Acad. Sci., 111, 9379 [NASA ADS] [CrossRef] [Google Scholar]
- Yurchenko, S. N., Al-Refaie, A. F., & Tennyson, J. 2017, Comput. Phys. Commun., submitted [Google Scholar]
All Figures
 |
Fig. 1 Reference cross sections obtained using the Doppler profile at T = 300 K and T = 2000 K on the uniform |
| In the text | |
 |
Fig. 2 Dynamic scaling factor used in Eq. (3). |
| In the text | |
 |
Fig. 3 Intensity partitioning for Ithr = 10-25 cm/molecule and Cscale = 10-5. The dashed line indicates the Ithr threshold; the blue (T = 300 K) and red (T = 2000 K) areas are the regions of the strong lines; the grey area at the bottom indicates all transitions which were excluded from the line list to form the weak lines of the continuum. Here all cross sections were obtained using the Doppler profile on a grid of 10 cm-1. |
| In the text | |
 |
Fig. 4 Number of strong lines for different partitionings. |
| In the text | |
 |
Fig. 5 Upper panel: methane continuum at 2000 K, P = 10 bar (blue) and the total absorption (red). Lower panel: relative differences of the P = 0 and P = 10 bar continuum cross sections for the three wavenumber grids of |
| In the text | |
 |
Fig. 6 Comparison of the P = 0 and P = 10 bar cross sections for 300 K (left) and 2000 K (right): black (total P = 0), blue (continuum P = 0), and red (continuum P = 10). The middle panels are a zoom-in of the continuum, also for P = 0 and P = 10 bar, which are almost indistinguishable in the upper panels. The lower panels show the relative difference between the P = 0 and P = 10 bar continuum cross sections as defined in Eq. (4). The integrated area of the relative difference is 0.06% over the region 6700–6750 cm-1. A wavenumber grid of |
| In the text | |
 |
Fig. 7 Comparison of the P = 0 and P = 10 bar line profiles used to generate cross sections at 2000 K in the region of 1.615 μm. The a0 model with the J-independent line broadening was used. The wavenumber grid |
| In the text | |
 |
Fig. 8 Relative error from using J-independent line broadening to describe methane continuum at high temperature (T = 2000 K) and pressure (P = 10 bar) as the difference between two cross sections (J-dependent a0 model vs. J-independent model) relative to the total cross sections. The wavenumber grid of |
| In the text | |
 |
Fig. 9 Relative errors using the histogram model R = 1 000 000 to describe the methane continuum at T = 2000 K and P = 10 bar as the difference with the 34to10 cross sections (Voigt model) relative to the total 34to10 cross sections. The wavenumber grid of |
| In the text | |
 |
Fig. 10 Relative error from the histogram model for three different grids to describe the methane continuum at T = 2000 K and P = 0 bar as the difference with the 34to10 cross sections (pure Doppler model) relative to the total 34to10 cross sections at P = 0 bar. The wavenumber grid of |
| In the text | |
 |
Fig. 11 Inappropriate use of the super-line approach when the grid is too coarse. The super-lines use a resolution of R = 100 000, which is not sufficient, due to the narrow Doppler profiles at zero pressure, T = 2000 K. The cross section was computed on a |
| In the text | |
 |
Fig. 12 Transmissions computed using the Doppler model (upper panel) and histogram continuum models (R = 1 000 000, middle and lower panels) with relative errors for the column amounts 1019, 1020, 1021, 1022, 1023, and 1024 molecule/cm2 at T = 2000 K, P = 0 and P = 10 bar. The upper part of each panel shows the total transmission obtained from both the strong and weak lines at this temperature, while the lower part shows the relative error compared to the direct line-by-line evaluation from the 34to10 line list using the a0 Voigt model (Barton et al. 2017). The error in regions with very low transmissions (<10-4) are removed as the medium is optically thick. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.