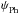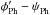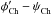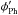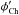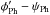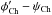| Issue |
A&A
Volume 604, August 2017
|
|
|---|---|---|
| Article Number | A98 | |
| Number of page(s) | 12 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201730875 | |
| Published online | 17 August 2017 | |
Three-dimensional magnetic structure of a sunspot: Comparison of the photosphere and upper chromosphere
1 Max-Planck-Institut für Sonnensystemforschung, Justus-von-Liebig-Weg 3, 37077 Göttingen, Germany
2 Institute for Solar Physics, Department of Astronomy, Stockholm University, AlbaNova University Centre, 106 91 Stockholm, Sweden
e-mail: jayant.joshi@astro.su.se
3 School of Space Research, Kyung Hee University, Yongin, 446-701 Gyeonggi Do, Republic of Korea
Received: 27 March 2017
Accepted: 21 May 2017
Aims. We investigate the magnetic field of a sunspot in the upper chromosphere and compare it to the photospheric properties of the field.
Methods. We observed the main leading sunspot of the active region NOAA 11124 during two days with the Tenerife Infrared Polarimeter-2 (TIP-2) mounted at the German Vacuum Tower Telescope (VTT). Through inversion of Stokes spectra of the He i triplet at 10 830 Å, we obtained the magnetic field vector of the upper chromosphere. For comparison with the photosphere, we applied height-dependent inversions of the Si i 10 827.1 Å and Ca i 10 833.4 Å lines.
Results. We found that the umbral magnetic field strength in the upper chromosphere is lower by a factor of 1.30–1.65 compared to the photosphere. The magnetic field strength of the umbra decreases from the photosphere toward the upper chromosphere by an average rate of 0.5–0.9 G km-1. The difference in the magnetic field strength between both atmospheric layers steadily decreases from the sunspot center to the outer boundary of the sunspot; the field, in particular its horizontal component, is stronger in the chromopshere outside the spot and this is suggestive of a magnetic canopy. The sunspot displays a twist that on average is similar in the two layers. However, the differential twist between the photosphere and chromosphere increases rapidly toward the outer penumbral boundary. The magnetic field vector is more horizontal with respect to the solar surface by roughly 5–20° in the photosphere compared to the upper chromosphere. Above a lightbridge, the chromospheric magnetic field is equally strong as that in the umbra, whereas the field of the lightbridge is weaker than its surroundings in the photosphere by roughly 1 kG. This suggests a cusp-like magnetic field structure above the lightbridge.
Key words: Sun: chromosphere / Sun: infrared / Sun: magnetic fields / sunspots / techniques: spectroscopic / techniques: polarimetric
© ESO, 2017
1. Introduction
The photospheric structure of the magnetic field of sunspots has been studied very extensively in the last few decades through Zeeman diagnostics from various magnetically sensitive spectral lines (Solanki 2003; Borrero & Ichimoto 2011). The study of the three-dimensional structure of sunspots up to the chromosphere is much more challenging observationally and therefore less explored.
Line parameters of the He i triplet at 10 830 Å.
The He i triplet at 10 830 Å provides a promising avenue to study the upper chromospheric magnetic field (see overview by Lagg et al. 2007, 2015). The special formation process of this triplet (Penn & Kuhn 1995; Rüedi et al. 1995) makes it a simpler tool to diagnose the magnetic field, compared to most other chromospheric spectral lines. Many studies of the magnetic field vector in the upper chromospheric layer use the He i triplet (e.g., Rüedi et al. 1996; Solanki et al. 2003; Lagg et al. 2004; Trujillo Bueno et al. 2005; Solanki et al. 2006; Xu et al. 2010; Merenda et al. 2011; Xu et al. 2012; Schad et al. 2015; Joshi et al. 2016). The He i triplet is produced by transitions between the 1s2s 3S1 and the 1s2p 3P0,1,2 energy levels. Extreme ultraviolet (EUV) radiation from the corona ionizes neutral helium atoms in the upper chromosphere, which then populate the lower level of the transition by recombination (Avrett et al. 1994; Andretta & Jones 1997; Centeno et al. 2008). The fine scale structures observed in the He i triplet images are caused by ionizing radiation from the transition region (Leenaarts et al. 2016).
Trujillo Bueno et al. (2002) have shown that the He i triplet observed in polarized light is influenced by both the Zeeman effect and Hanle effect. At solar disk center, the Hanle effect acts in forward scattering and can produce linearly polarized light in the He i triplet only in the presence of a magnetic field inclined with respect to the solar radius vector. In the presence of strong magnetic fields, as in sunspots, linear polarization is dominated by the transverse Zeeman effect.
Rüedi et al. (1995), Orozco Suarez et al. (2005), and Schad et al. (2015) studied the upper chromospheric magnetic field of a sunspot using the He i triplet and compared it with its photospheric counterpart. The vertical gradient of the magnetic field strength in the umbra found by Rüedi et al. (1995) is around 0.35–0.60 G km-1 with positive values that denote increasing field strength with increasing depth. This value is similar to that found by Abdussamatov (1971) who compared magnetograms derived from the Hα line with those derived from the Fe i 6302.5 Å line. Values of the vertical magnetic field gradient found by Henze et al. (1982) and Hagyard et al. (1983) fall in the same range. They derived this value from the C iv 1548 Å emission line in the transition region and the photospheric Fe i 5250 Å absorption line. In penumbrae, Rüedi et al. (1995) reported a value of the vertical gradient of the magnetic field of around 0.1–0.3 G km-1. They also find a canopy-like structure in the longitudinal magnetic field at the upper chromosphere around the sunspot (see also Schad et al. 2015). Recently, Joshi et al. (2016) observed a spine and inter-spine structure in the magnetic field inclination of the penumbra using high spatial resolution observations in the He i triplet obtained with the GREGOR Infrared Spectrograph (GRIS; Collados et al. 2012) at the 1.5-m GREGOR telescope (Schmidt et al. 2012).
Here we present inversions of the full Stokes vectors of the He i triplet at 10 830 Å, the Si i 10 827.1 Å, and the Ca i 10 833.4 Å lines. The latter two give us maps of the magnetic vector in two different height layers of the photosphere. These maps are analyzed to discuss the differences between the photospheric and upper chromospheric magnetic field structure of the sunspot.
2. VTT/TIP-2 observations
We used the same data set as presented by Joshi et al. (2017, hereafter Paper I). The full Stokes vector of the photospheric Si i 10 827.1 Å and Ca i 10 833.4 Å lines and the upper chromospheric He i triplet at 10 830 Å was recorded in a sunspot and its close surroundings using the Tenerife Infrared Polarimeter-2 (TIP-2; Collados et al. 2007) mounted on the German Vacuum Tower Telescope (VTT). The sunspot was recorded on 14 November 2010 (12°N, 10°W, μ = 0.96) and 16 November 2010 (14°N, 32°W, μ = 0.84). Atomic parameters of the He i triplet are provided in Table 1. Hereafter we refer to the blue component of the triplet as He ia and the red components of the triplet as He ib and He ic. Since the latter two lines are blended, we refer to them together as He ibc.
Maps of the continuum intensity at 10 832.6 Å, the depression of the Si i line core, 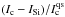 , and of the line core of the He ibc,
, and of the line core of the He ibc, 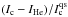 , observed on 14 November 2010 are shown in Fig. 1. Here Ic and
, observed on 14 November 2010 are shown in Fig. 1. Here Ic and 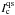 represent the continuum intensity of the individual Stokes profile and the averaged continuum intensity in the quiet Sun, respectively. The intensities of the Si i line core and the He ibc line core are represented by ISi and IHe, respectively. An arc filament can be seen in the He ibc line core depression map at position x = 18′′ − 26′′, y = 5′′ − 38′′. Figure 2 shows maps of the continuum intensity at 10 832.6 Å and the depression of the Si i and He ibc line core observed on 16 November 2010. The sunspot was observed in a growing phase on 14 November 2010; the increase of its projected area from 450 Mm2 on 14 November 2010 to 1054 Mm2 on 16 November 2010 corresponded to an increase of 234%. If we correct for foreshortening then it grew by 281% in two days.
represent the continuum intensity of the individual Stokes profile and the averaged continuum intensity in the quiet Sun, respectively. The intensities of the Si i line core and the He ibc line core are represented by ISi and IHe, respectively. An arc filament can be seen in the He ibc line core depression map at position x = 18′′ − 26′′, y = 5′′ − 38′′. Figure 2 shows maps of the continuum intensity at 10 832.6 Å and the depression of the Si i and He ibc line core observed on 16 November 2010. The sunspot was observed in a growing phase on 14 November 2010; the increase of its projected area from 450 Mm2 on 14 November 2010 to 1054 Mm2 on 16 November 2010 corresponded to an increase of 234%. If we correct for foreshortening then it grew by 281% in two days.
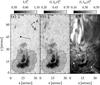 |
Fig. 1 Panel a: observed field-of-view (FOV) on 14 November 2010 in the continuum. Panels b and c: depression of the line core of the Si i 10 827 Å line and He ibc, respectively. The inner and outer contours in all panels indicate the umbra-penumbra boundary and the outer boundary of the sunspot, respectively. The arrow in panel a indicates the direction to the solar disk center. Three white arrows in panel c mark positions of downflow intrusions in the penumbra in the upper chromosphere (see Fig. 4d). |
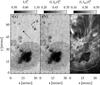 |
Fig. 2 Same as Fig. 1, but showing the observed FOV on 16 November 2010. The red plus in panel b indicates the position for which observed and the best fit Stokes profiles are shown in Fig. 3. |
3. Inversions
The He i absorption is thought to arise in a thin slab located at the upper boundary of the chromosphere. The reason for this is the special formation process of the triplet requiring coronal UV illumination. The chromosphere is highly opaque to this radiation, which therefore affects only its uppermost layer, justifying the assumption that the atmospheric parameters do not vary within the thin slab where the He i triplet forms. Hence, we inverted all three components of the He i triplet with the HeLIx+ inversion code assuming a Milne-Eddington type atmosphere. For details about HeLIx+, see Lagg et al. (2004, 2009). The HeLIx+ code includes a consideration of the incomplete Paschen-Back effect regimes (cf. Socas-Navarro et al. 2005; Sasso et al. 2006).
The blue component of the He i triplet is blended by the red wing of the Si i line. This blending is taken into account in a self-consistent manner by inverting the He i triplet and Si i line simultaneously. Our model atmosphere used for this purpose consists of eight free parameters to fit the observed Stokes profiles of the He i triplet: the magnetic field strength, B, the inclination of the magnetic field vector, γ, the azimuth angle of the magnetic field vector, φ, the LOS velocity, vlos, the Doppler width, ΔλD, the damping constant, a, the gradient of the source function, S1, and the opacity ratio between line center and continuum, η0. To fit the Si i line, the model atmosphere consists of the same free parameters as the He i triplet along with two additional free parameters, the global stray-light factor, α and the line-of-sight velocity for the global stray-light components. The approach for global stray light is similar to that used in Paper I, where the global stray light is assumed to originate from the broad wings of the point-spread function and therefore resembles the shape of the average quiet Sun Stokes I profile.
To take into account the blends from the Si i line into the He i triplet in the inversions, we took a multi-step approach. We first inverted the Stokes profiles from the Si i line. Then, in a second run, we fitted the Stokes profiles of the He i triplet and we fixed the free parameters for the Si i line to the values retrieved from the first run. Finally, we fitted both the Si i line and He i triplet simultaneously, but we allowed the parameters to vary only within ± 5% of the values fitted in the previous runs. The H20 telluric line at 10 832 Å, which can blend the He i triplet when it is strongly redshifted, is fitted with a Voigt function. Observed Stokes profiles at one penumbral pixel along with the best fits are depicted in Fig. 3. The purpose of including the Si i line in the inversions of the He i triplet is only to account for blending of the He i triplet.
 |
Fig. 3 Best fit HeLIx+ inversions of typical Stokes profiles in the penumbra. Their spatial location is marked by a red plus sign in Fig. 2a. Black dots represent observed data points and solid blue curves represent the best fits. |
For the analysis presented in this paper we use the magnetic field vector in the photosphere inferred from the SPINOR (Frutiger et al. 1999, 2000) inversions of the Si i and Ca i lines. The combination of the strong Si i line and weak Ca i line puts more constraints especially on the height information of the free parameters in the inversion process compared to an inversion of a single line only. Our model atmosphere consists of three nodes, log τ630 = 0.0, − 0.7, and − 2.3 for the line-of-sight (LOS) velocity, vlos, and the temperature, T, where τ630 corresponds to the optical depth at 630 nm. The magnetic field strength is assumed to vary linearly with respect to log τ. The other atmospheric parameters, such as inclination of the magnetic field relative to LOS, γ; its azimuth direction, φ; and the micro-turbulent velocity, vmic, were assumed to be constant with height. Only the height-dependent atmosphere inferred from the SPINOR inversions can take into account the strong asymmetries due to gradients in the Doppler velocities and the magnetic field in the Stokes profiles of the Si i line. More detailed information on the inversions are mentioned in Paper I.
4. Analysis and results
Maps of the magnetic field vector and the LOS velocity retrieved from the observations recorded on 14 November 2010 are shown in Fig. 4. In each panel the maps on the left correspond to the parameters obtained in the photosphere through the SPINOR inversions of the Si i and Ca i lines. In the SPINOR inversions we obtained B and its linear gradient with respect to log τ, but for comparison of the photospheric magnetic field properties with the upper chromosphere we use values of B obtained by averaging between log τ = 0.0 and log τ = − 2.3. The atmospheric parameters obtained from the upper chromosphere through the HeLIx+ inversions of the He i triplet are shown in the right panels. Figure 5 shows the same plots for the data observed on 16 November 2010.
 |
Fig. 4 Maps of a) Magnetic field strength B, b) inclination angle, γ′, of the magnetic field vector with respect to the solar surface normal, c) azimuth direction, φ′, of the magnetic field vector and d) line-of-sight velocity obtained from the observations recorded on 14 November 2010. Left and right maps in all panels represent atmospheric parameters obtained in the photosphere and upper chromosphere, respectively. An arrow in the left map of panel d indicates the disk center direction and three arrows in the right map point three downflow intrusions in the penumbra. |
Overall, within the visible boundary of the sunspot the magnetic field strength in the upper chromosphere is weaker than in the photosphere. This is particularly striking in the umbra, as can be seen in the maps of B from both days. The lightbridge observed on 14 November 2010 shows weaker B compared to the umbra in its photospheric layer and in the upper chromosphere no signature of the lightbridge is present in the B map. The values of B in the upper chromosphere at the location of the lightbridge are comparable to the umbral magnetic field strength, although the He i line depth in the lightbridge is considerably bigger than in the surrounding umbra (see Fig. 1).
The 180° ambiguity in the azimuth direction was resolved by applying the “acute angle” method (Sakurai et al. 1985; Cuperman et al. 1992). The magnetic field vectors presented here are projected to disk center coordinates using the transformation matrix by Wilkinson et al. (1989). The inclination angle with respect to solar surface normal and the ambiguity resolved azimuth angle are denoted by γ′ and φ′, respectively.
 |
Fig. 6 Cross sections through the observed sunspots: panels b and f, c and g and d and h depict profiles of B, γ′ and φ′, respectively, along an artificial slit represented by the red lines in panels a and e. Panels a–d refer to observations recorded on 14 November 2010 and panels e–h correspond to 16 November 2010. The black and blue curves in panels b–d and f–h correspond to the photosphere and upper chromosphere, respectively, while the dotted curves represent the continuum intensity. |
The inclination of the magnetic field vector in the upper chromosphere looks qualitatively similar to that in the photosphere. In the photosphere, outside the boundary, but close to the sunspot, we see a few small patches where γ′ has values less than 90°, i.e., at those locations the magnetic field has polarity that is opposite to that of the umbra. These opposite polarity patches are not visible in the upper chromosphere, suggesting that they do not reach the height of the formation of the He i triplet, as it is covered by the canopy of the sunspot. Maps of γ′ from both days show more fine structure in the photosphere as compared to the upper chromosphere. In the sunspot the magnetic field azimuth in the upper chromosphere is generally similar to that in the photosphere. One exception is the lightbridge, which shows an indication of the field from the umbra expanding over it in the photosphere on both sides, but no signature at all in the upper chromosphere. Outside the sunspot, maps of the magnetic field vectors in the upper chromosphere are much noisier than in the photosphere. This has its source in the much weaker Stokes Q and U in the He i triplet compared to the Si i line.
The LOS velocity maps are shown in Figs. 4d and 5d. In the photosphere these refer to log τ = 0.0. We use this layer since it displays stronger signature of the Evershed flow than the other nodes higher in the atmosphere. The magnitude of velocities is considerably stronger on 16 November 2010, when the sunspot was closer to the limb (μ = 0.84). The LOS velocities derived in the upper chromosphere show radial inflows on 16 November 2010, which is consistent with the inverse Evershed effect. On 14 November 2010 the situation is less clear cut with no clear sign of the inverse Evershed effect in the He i triplet. Three intrusions of denser (brighter in Fig. 1c) downflowing gas are identified in the chromosphere (see small arrows in Figs. 1c and 4d). These may be associated with sunspot plumes (Fludra et al. 1997; Maltby et al. 1998, 1999; Brynildsen et al. 1998, 1999, 2001; Fludra 2001; Brosius & White 2004; Brosius 2005). The maps of vlos derived from the He i triplet show wave-like structures in the sunspot umbra and in the inner penumbra. This wave structure is elongated in the direction of the y-axes (i.e., in the direction of the slit of the spectrograph). This pattern is produced by running penumbral waves and umbral flashes (Zirin & Stein 1972; Christopoulou et al. 2000; Georgakilas et al. 2000; Christopoulou et al. 2001; Bogdan & Judge 2006; Centeno et al. 2006; Tziotziou et al. 2006, 2007; Bloomfield et al. 2007; Felipe et al. 2010; de la Cruz Rodríguez et al. 2013).
We expect a small offset between the parameter maps obtained in the photosphere and upper chromosphere because of the viewing geometry; the sunspot was observed away from disk center on both days. If we assume a height difference of 1000 km (see Centeno et al. 2006) between the two observed layers of the atmosphere, which is a conservative estimate, then the chromospheric parameter maps are offset by ~275 km and ~575 km toward the limb on 14 and 16 November 2010, respectively. The analysis described in the following sections was carried out after correcting for these offsets.
For a more detailed and quantitative insight into the magnetic field properties of the sunspot and the connection between its photospheric layer and upper chromospheric layer, B, γ′, and φ′ are plotted along an artificial 3.0′′ wide slit laid across the sunspot (see Fig. 6). The parameters B, γ′, and φ′ are averaged perpendicularly to the slit direction. On 14 November 2010 the profile of B along the slit in the photosphere shows a dip at the location of the lightbridge with a minimum value of B ~ 1.2 kG, which is ~1.0 kG weaker than in the surrounding umbra. In the upper chromosphere, at the location of the lightbridge B is ~1.4 kG. This value is comparable with and maybe even slightly higher than the value in the surrounding umbra and higher than in the photopshere. A similar B in a lightbridge and umbra in chromospheres was already noticed by Rüedi et al. (1995). The difference between the photospheric and upper chromospheric magnetic field strength becomes rather small in the penumbra. Just outside of the visible boundary of the sunspot, the values of B are higher by up to ~300 G in the upper chromosphere as compared to the photosphere. Rüedi et al. (1995) interpreted this behavior as evidence of a magnetic canopy.
Profiles of γ′ along the slit on 14 November 2010 indicate that inside the sunspot, except in the inner part of the umbra, the magnetic field is in general more horizontal in the photosphere compared to the upper chromosphere. This is particularly pronounced in the penumbra and more so on the 14 November 2010. At the center of the lightbridge the magnetic field in the photosphere becomes more horizontal in agreement with results in the literature (see, e.g., Lagg et al. 2014, and references therein). In the chromosphere the field in the center of the lightbridge is as vertical as everywhere else along the cut and more vertical than in the umbra directly at the edge of the lightbridge. In summary, the field in the light bridge is more vertical in the upper chromosphere than in the photosphere. The umbra close to the lightbridge shows the opposite trend. On 16 November 2010, the photospheric and the upper chromospheric profile of γ′ are quantitatively more similar.
On 14 November 2010 profiles of φ′ in the photosphere along the slit show a sudden change of ~180° (compared to that in the nearby umbra) at the both edges of the lightbridge, which suggests that the magnetic field lines are fanning out at the location of the lightbridge. The sunspot has negative polarity and so magnetic field line points inward. Variation in φ′ in the upper chromosphere is rather steady.
The small difference in the magnetic field strength and inclination between the lightbridge and its immediate surroundings may be due to a difference in the formation height of the He i 10 830 Å over the lightbridge compared to the umbra. The sudden difference in the gradient of B between umbra, on the one hand, and the penumbra and lightbridge, on the other, also suggest a difference in formation height.
 |
Fig. 7 Division of the sunspot into umbral, penumbral, and lightbridge areas. Red and blue contours in both panels encircle umbral and penumbral areas, which are used to compare the magnetic field vector retrieved in the photosphere and upper chromosphere. The area within the black contour in the left panel represents the lightbridge. The left and right panels correspond to the observations recorded on 14 and 16 November 2010, respectively. |
 |
Fig. 8 Two-dimensional histograms of the magnetic field components obtained in the upper chromosphere vs. those obtained in the photosphere from the observations recorded on 14 November 2010. Panels a–c show plots of B from the umbral, penumbral , and lightbridge pixels, respectively (see Fig. 7). The γ′ values of data points from the same spatial positions are shown in panels d–f, respectively. |
 |
Fig. 9 Same as Fig. 8 but for the observations recorded on 16 November 2010 and restricted to umbral and penumbral pixels. |
To emphasize the differences between the umbra, penumbra, and lightbridge, we show two-dimensional histograms of the magnetic field components in the upper chromosphere versus those of the photosphere in Figs. 8 and 9 for 14 and 16 November 2010, respectively. The areas considered here for the different regions of the sunspot are indicated in Fig. 7 with red, blue and black contours. The blue contours exclude the strongly distorted parts of the penumbra. Also, the boundary region between the umbra and penumbra is excluded to make sure that the pixels under consideration are either from the umbra or penumbra and to the avoid the transition between them in the analysis as such pixels are likely to be more affected by stray light.
All the pixels in the umbrae indicate that the B in the upper chromosphere is lower by a factor of 1.30–1.65 than that in the photosphere on both days of the observations. In the penumbra the magnetic field strength in the upper chromosphere is, in general, a factor 1.00–1.55 lower than that in the photosphere, while a few pixels even indicate higher values in the upper chromosphere. The lower the penumbral field strength, B, the smaller the difference between the photosphere and upper chromosphere.
 |
Fig. 10 Averaged radial distribution of the magnetic field properties in the observed sunspot: panel a: continuum intensity map with overplotted contours used to calculate azimuthal averages for 14 November 2010. The area above the red line was not included to calculate the azimuthal averages. Panel b: relative continuum intensity (normalized to the quiet Sun) of the sunspot as a function of the normalized radial distance, r/Rspot. Panels c–f: radial dependence of B, γ′, the vertical component of the magnetic field, Bz, and the transverse component of the magnetic field, Bt, respectively. The black and blue curves correspond to the magnetic field vector derived in the photosphere and upper chromosphere, respectively. The dotted vertical lines in panels b–f indicate the umbra-penumbra boundary and the outer boundary of the sunspot. |
The two-dimensional histograms of γ′ from the observations on both days indicate that the upper chromospheric magnetic field is more vertical compared to the photospheric magnetic field by roughly 5–20°. The signal-to-noise ratio is lower in the He i triplet, especially for Q and U. Since low signal-to-noise ratios lead inversion codes to return to more horizontal B (Borrero & Kobel 2012; Jafarzadeh 2013; Jafarzadeh et al. 2014), this result is not an artifact of the noise. The values of B and γ′ in the lightbridge observed on 14 November 2010 are comparable both in the photosphere and in the upper chromosphere.
We take azimuthal averages along smoothed iso-intensity contours to derive the average radial dependence of the components of the magnetic field vector. Figures 10a and 11a show these contour lines. Areas above the red line are excluded in the computation of azimuthal averages because of their complex photospheric structure. The remainder of the panels depicts the azimuthal averages of Ic and various magnetic parameters and corresponding standard deviations as a function of normalized radial distance, r/Rspot, from the sunspot center for 14 and 16 November 2010.
On 14 November 2010, B has an average value of ~2.3 kG in the darkest part of the umbra in the photosphere, decreasing to ~1.8 kG at the umbra-penumbra boundary. In the upper chromosphere B amounts to ~1.3 kG at the sunspot center and it remains almost constant to the umbra-penumbra boundary. On 16 November 2010 the center of the sunspot has a value of B around ~2.5 kG and of ~1.9 kG at the umbra-penumbra boundary in the photosphere. In the upper chromosphere B is nearly constant at a value ~1.4 kG from the sunspot center to the umbra-penumbra boundary. The difference in the values of B between the photosphere and upper chromosphere decreases from the umbra-penumbra boundary toward the outer boundary of the sunspot; the same field strength of ~400 G at both layers is reached close to the outer sunspot boundary. This is valid for both days. Outside the boundary of the sunspot, B is larger in the upper chromosphere than in the photosphere on both days.
Azimuthally averaged radial profiles of γ′ from both days suggest that the magnetic field in the upper chromosphere is more vertical than the magnetic field in the photosphere both in the umbra and the penumbra (see Figs. 10 and 11). The magnetic field in the upper chromosphere is on average 10–20° less inclined compared to the photosphere on 14 November 2010. On 16 November 2010 it is only 5–10° less inclined in the upper chromosphere.
 |
Fig. 11 Same as Fig. 10, but for the observations recorded on 16 November 2010. Here the area to the upper left of the red lines is not included in making the radial averages. |
The vertical component of the magnetic field, Bz, shows a negligible difference between the upper chromosphere and the photosphere for r ≥ 0.60 Rspot on both days. The maximum of the transverse component of the magnetic field, Bt, in the photosphere is found at the r ≃ 0.40 − 0.45 Rspot while in the upper chromosphere it is at r ≃ 0.50 − 0.60 Rspot. This move of the maximum horizontal field to further out in the spot is consistent with the fact that the horizontal field is considerably larger in the upper chromosphere than in the photosphere outside the outer boundary of the spot. This is particularly evident on 16 November 2010. The chromospheric field is also more horizontal there. These properties are consistent with the presence of a magnetic canopy whose lower boundary may lie between the two layers considered here.
We estimated the vertical gradient of the magnetic field, ΔB/ Δd (here d denotes the geometrical depth, i.e., d increases into the Sun), between the photosphere and upper chromosphere by assuming that the He i triplet forms approximately 1000 km above the formation height of the Si i line in the sunspot. This difference is inferred from the study of Centeno et al. (2006) who retrieved this height difference between the photosphere and formation height of the He i triplet in the sunspot umbra by analyzing phase spectra of LOS velocities inferred from the Si i and He i triplet. We are aware that the formation height of the He i triplet could be significantly different for the umbra and penumbra. Joshi et al. (2016) estimated the difference in the formation height of these lines to be 1250 km in sunspot penumbrae by looking at the shift in the apparent neutral lines in the Stokes V images of the respective spectral lines. The method takes into account the difference in the inclination of magnetic field at a certain radial position in the penumbra. According to Fig. 10 the field in the chromosphere is somewhat more vertical, although Fig. 11 shows that this difference can be quite small for a relatively regular spot. This implies that the 1250 km found by Joshi et al. (2016) is an upper limit for the height difference. In the following we therefore mainly employ the 1000 km given by Centeno et al. (2006).
 |
Fig. 12 Vertical gradient of B, ΔB/ Δd, between the photosphere and upper chromosphere as a function of r/Rspot. Solid curves represent ΔB/ Δd estimated with the average value of B in the photosphere. Dashed and dot-dashed curves show ΔB/ Δd from log τ = 0.0 and log τ = − 2.3, respectively. Panels a and b correspond to 14 and 16 November 2010, respectively. |
We learned from Paper I that due to the highly corrugated iso-τ surfaces of sunspot penumbrae we can see a decreasing magnetic field strength within the photosphere with optical depth in the azimuthal averages. So, it is important to know how this configuration affects the estimation of ΔB/ Δd between the photosphere and upper chromosphere. This is why we also estimate ΔB/ Δd between log τ = 0.0 and the upper chromosphere and between log τ = − 2.3 and the upper chromosphere. First we computed the difference of geometrical depth, ddiff between log τ = 0.0 and log τ = − 2.3 for each pixel, assuming hydrostatic equilibrium. Then the geometrical depth difference, Δd, between log τ = 0.0 and the upper chromosphere and between log τ = –2.3 and the upper chromosphere is estimated to be 1000 + (ddiff/ 2) km and 1000 − (ddiff/ 2) km, respectively.
 |
Fig. 13 Maps of the twist and differential twist angles of magnetic field of the sunspot. Panels a and d: twist of the photospheric field defined as the difference between the azimuth angle of the photospheric field |
The radial dependence of ΔB/ Δd between the photosphere and upper chromosphere is shown in Fig. 12 for both days. Solid curves represent ΔB/ Δd between the average photosphere and upper chromosphere. The value ΔB/ Δd from log τ = 0.0 and log τ = − 2.3 to the upper chromosphere is represented by dot-dashed dashed curves, respectively. In the center of the umbra ΔB/ Δd is similar for both log τ layers, irrespective of the photospheric layer used in estimating the gradient. B increases with depth in the darkest part of the umbra, i.e., on average by 0.9 G km-1 between the upper chromosphere and photosphere. From the center of the sunspot toward its outer boundary, the values of ΔB/ Δd decrease, i.e., B increases with geometrical depth with a slower rate in the penumbra compared to umbra. The way ΔB/ Δd drops with r/Rspot depends significantly on the layer at which the photospheric field is taken. The higher this is the closer to linear ΔB/ Δd becomes with respect to r/Rspot. As mentioned earlier, the difference in the formation height between the He i triplet and the Si i 10 827.1 Å line can be significantly different from the umbra to that in the penumbra; similarly, it may also change from one sunspot to another sunspot. If we consider the difference in the formation heights to be 1250 km, following Joshi et al. (2016), then the resulting vertical gradient of the magnetic field on average would be ~0.7 G km-1 in the darkest part of the umbra. We consider this to be a lower limit to the gradient.
Statistics of the twist and differential twist.
To learn how strongly the magnetic field of the sunspot is twisted, we calculated the difference between the azimuth angle of the magnetic field in the photosphere and that of a potential field, 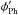 – ψPh, where
– ψPh, where 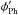 and ψPh denotes the azimuth angle in the photosphere and the azimuth angle of the potential field is derived from the vertical component of photospheric magnetic field, respectively. The potential field is calculated with the Fourier method (Alissandrakis 1981; Gary 1989). We also calculated the twist of the upper chromospheric magnetic vector,
and ψPh denotes the azimuth angle in the photosphere and the azimuth angle of the potential field is derived from the vertical component of photospheric magnetic field, respectively. The potential field is calculated with the Fourier method (Alissandrakis 1981; Gary 1989). We also calculated the twist of the upper chromospheric magnetic vector,  – ψCh, where
– ψCh, where  denotes the azimuth angle in the upper chromosphere and ψCh represents the azimuth angle of the potential field calculated from the vertical component of the chromospheric magnetic field. Finally, we determined the differential twist between the photosphere and upper chromopshere, i.e., the difference of the azimuth angle between the upper chromosphere and photosphere,
denotes the azimuth angle in the upper chromosphere and ψCh represents the azimuth angle of the potential field calculated from the vertical component of the chromospheric magnetic field. Finally, we determined the differential twist between the photosphere and upper chromopshere, i.e., the difference of the azimuth angle between the upper chromosphere and photosphere,  –
–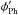 . All twist maps are shown in Fig. 13 for both days of observations. Positive values denote counterclockwise twist. The sunspot obviously exhibits twist in both directions, but clockwise twist (green and blue in Fig. 13) are more common in both atmospheric layers on both days. Figures 13a, b, d, and e suggest a field of the sunspot diverging slightly away from the negative y-axes on 14 November 2010 and away from roughly the direction of the disk center on 16 November 2010. The maps of
. All twist maps are shown in Fig. 13 for both days of observations. Positive values denote counterclockwise twist. The sunspot obviously exhibits twist in both directions, but clockwise twist (green and blue in Fig. 13) are more common in both atmospheric layers on both days. Figures 13a, b, d, and e suggest a field of the sunspot diverging slightly away from the negative y-axes on 14 November 2010 and away from roughly the direction of the disk center on 16 November 2010. The maps of  –
–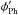 show differential twists in both directions in some areas, but
show differential twists in both directions in some areas, but  –
–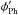 is small in most parts of the penumbra. Maps of
is small in most parts of the penumbra. Maps of  –
–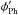 also show that the differential twist is higher in the outer penumbra compared to inner penumbra.
also show that the differential twist is higher in the outer penumbra compared to inner penumbra.
 |
Fig. 14 Histograms of the twist and differential twist of the magnetic field of the sunspot, with the differential twist denoting the difference between the azimuthal direction of the field in the photosphere, |
Figure 13 suggests that both senses of the twist are present in the observations of both days. To better quantify this fact we divide the spots in two halves (identified as part-A and part-B) with the divisions line selected to maximize the difference in the twist (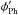 – ψPh, solid black lines in Fig. 13). Figure 14 shows histograms of the twists for the same panels as in Fig. 13, individually for both halves of the sunspot. On average part-A has clockwise twist and part-B has counterclockwise twist at both atmospheric heights on both days. On 14 November 2010, the average twist of the photospheric and upper chromospheric azimuth angle was − 6°, and − 7°, respectively (see Table 2). The average twist is − 13° in the photosphere and − 12° in the upper chromosphere on 16 November 2010. Histograms of twist maps indicate that the distribution of the upper chromospheric twist is wider than that of the photosphere, although a part of the excess may be due to the higher noise in the chromospheric values. On average, the differential twist between the photosphere and the chromosphere is very small with values between − 1° and 3°.
– ψPh, solid black lines in Fig. 13). Figure 14 shows histograms of the twists for the same panels as in Fig. 13, individually for both halves of the sunspot. On average part-A has clockwise twist and part-B has counterclockwise twist at both atmospheric heights on both days. On 14 November 2010, the average twist of the photospheric and upper chromospheric azimuth angle was − 6°, and − 7°, respectively (see Table 2). The average twist is − 13° in the photosphere and − 12° in the upper chromosphere on 16 November 2010. Histograms of twist maps indicate that the distribution of the upper chromospheric twist is wider than that of the photosphere, although a part of the excess may be due to the higher noise in the chromospheric values. On average, the differential twist between the photosphere and the chromosphere is very small with values between − 1° and 3°.
 |
Fig. 15 Radial dependence of |
The radial dependence of the differential twist,  –
– 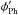 for both days is presented in Fig. 15. Azimuthal averages are only calculated for areas shown below the red lines in Figs. 10a and 11a for 14 and 16 November 2010, respectively. On 14 November 2010 the differential twist increases from 0° to ~21° between the umbra-penumbra boundary and the outer boundary of the sunspot. On 16 November 2010 the differential twist also increases outward through most of the penumbra, but then abruptly drops to near zero close to Rspot. The average differential twist is on average ~4° out to r = Rspot. Hence, although the average differential twist is always very small, this may be masked by the fact that the inner penumbra displays a very small differential twist.
for both days is presented in Fig. 15. Azimuthal averages are only calculated for areas shown below the red lines in Figs. 10a and 11a for 14 and 16 November 2010, respectively. On 14 November 2010 the differential twist increases from 0° to ~21° between the umbra-penumbra boundary and the outer boundary of the sunspot. On 16 November 2010 the differential twist also increases outward through most of the penumbra, but then abruptly drops to near zero close to Rspot. The average differential twist is on average ~4° out to r = Rspot. Hence, although the average differential twist is always very small, this may be masked by the fact that the inner penumbra displays a very small differential twist.
5. Discussion and conclusions
5.1. Magnetic field strength and its vertical gradient
We have measured and compared the magnetic field vector of a sunspot in its photospheric and upper chromospheric layers. In the umbra we found the maximum value of B to be around 2.5/2.8 kG in the photosphere and 1.6/1.8 kG in the upper chromosphere from observations recorded on 14 and 16 November 2010. On average the upper chromospheric umbral magnetic field strength is reduced by a factor 1.30–1.65 compared to the photosphere. These differences between the upper chromospheric and the photospheric magnetic field strength are comparable with the results of Rüedi et al. (1995) and Schad et al. (2015), who used the same spectral lines analyzed in this paper. A striking feature of the upper chromospheric magnetic field is that it is almost constant from the center of the sunspot to the umbra-penumbra boundary; i.e., it decreases by less than a factor of 1.1. In the photosphere it decreases from the center of the sunspot to the umbra-penumbra boundary by a factor of 1.2–1.4, which is consistent with values found earlier (Solanki et al. 1992; Balthasar & Schmidt 1993; Skumanich et al. 1994; Keppens & Martinez Pillet 1996; Westendorp Plaza et al. 2001; Mathew et al. 2003; Borrero & Ichimoto 2011; Tiwari et al. 2015)1.
The ratio of the magnetic field strength between the photosphere and chromosphere drops from a factor of 1.4 in the umbra and the umbra-penumbra boundary steadily over the whole penumbra to reach a value of 1.0 at the outer boundary of the sunspot. We see a magnetic canopy structure outside the visible boundary of the sunspot, in the sense that the upper chromospheric field is higher by up to ~300 G compared to the field in the photosphere. This magnetic canopy results from an expansion of the magnetic field of the sunspot with height beyond its visible boundary as seen in continuum images. Results of the height-dependent inversions of the Si i and Ca i lines, as discussed in Paper I, show that the base of the canopy lies in the photosphere. Sunspot magnetic canopies have been observed by Jones & Giovanelli (1982) by comparing magnetograms obtained in the photosphere using the Fe i 8688 Å line with those obtained from the chromospheric Ca ii 8542 Å line. Sunspot magnetic canopies in the photosphere have been regularly detected using different spectral lines as a diagnostic (Solanki et al. 1992; Lites et al. 1993; Adams et al. 1993; Solanki et al. 1994; Skumanich et al. 1994; Keppens & Martinez Pillet 1996; Rüedi et al. 1998; Solanki et al. 1999; Tiwari et al. 2015).
We find that in the umbra, the magnetic field strength decreases from the photosphere toward the upper chromosphere at a rate of 0.5–0.9 G km-1. These values are higher than the values of 0.4–0.6 G km-1 found by Rüedi et al. (1995). The reason for this discrepancy lies mainly in the assumption about the formation height of the He i triplet. Whereas Rüedi et al. (1995) assumed that in sunspots the He i triplet forms 1500–2000 km above the photosphere, we considered a height difference of 1000 km following Centeno et al. (2008). Schad et al. (2015) report a vertical gradient of the magnetic field strength around 0.5 G km-1 in the umbra. They also used the Si i 10 827.1 Å and He i 10 830 Å triplet in their study and assumed a 1000 km difference in formation height of these lines.
In the penumbra the magnetic field strength decreases more slowly with vertical gradients between 0 and 0.7 G km-1. In the outer penumbra and outside the visible boundary of the sunspot the gradient has negative values, indicating the presence of a magnetic canopy. Here the vertical gradient in the penumbra may be underestimated because of the underestimation of the magnetic field strength in the photosphere due to unresolved opposite polarities (see Zakharov et al. 2008; Scharmer et al. 2013; Ruiz Cobo & Asensio Ramos 2013; Franz & Schlichenmaier 2013; Tiwari et al. 2013; van Noort et al. 2013; Joshi 2014; Joshi et al. 2017).
If we consider the difference in formation heights to be 1250 km, as estimated by Joshi et al. (2016), then the vertical gradient of the magnetic field in the umbra and penumbra would be 0.4–0.7 G km-1 and 0.0–0.6 G km-1, respectively.
The lightbridge exhibits ~1 kG lower magnetic field strength compared to the surrounding umbra at photospheric layers present on 14 November 2010. This is a well-known property of lightbridges (Rimmele 1997; Berger & Berdyugina 2003; Jurčák et al. 2006; Rimmele 2008; Sobotka et al. 2013; Lagg et al. 2014). Signatures of the lightbridge are visible in the He i 10 830 Å spectrum, for example, the higher values of the line depression in the lightbridge compared to those in the surrounding umbra (see Fig. 1c). However, the magnetic field in the upper chromosphere does not seem to be influenced by the lightbridge; at this height, the magnetic field above the lightbridge is not distinguishable from the field in the surrounding umbra. This result is consistent with the findings of Rüedi et al. (1995), but is in contrast to that of Schad et al. (2015), who obtained a lower value of the magnetic field strength in the chromosphere at the location of a lightbridge. Our results show that lightbridge is stronger by ~200 G compared to the photosphere. This and other results of our work indicate a cusp-like shape of the magnetic field lines above the lightbridge forming a canopy directly above the photosphere, which is completely covered by the umbral field at the chromospheric heights (see also, Jurčák et al. 2006; Lagg et al. 2014; Felipe et al. 2016). In the deep photosphere, magneto-convection can lower the field in a lightbridge considerably. In the upper atmosphere the strong field from the surrounding umbra expands to fill the volume above the lightbridge.
5.2. Inclination
We found that the magnetic field in the penumbra is less inclined in the upper chromosphere compared to the photosphere by 10–20°/5–10° on 14 and 16 November 2010. Our results are in agreement with Joshi et al. (2016), who found the upper chromospheric magnetic field in the penumbra to be more vertical by ~12° compared to that in the photosphere. More vertical magnetic fields in penumbrae at higher photospheric layers compared to the deep photosphere have already been reported by Westendorp Plaza et al. (2001), Sánchez Cuberes et al. (2005), Borrero & Ichimoto (2011). Tiwari et al. (2015) have also found that in azimuthal averages, the magnetic field becomes more vertical with height in the photosphere everywhere in the sunspot. They obtained the height-dependent magnetic field vector using spatially coupled inversions (van Noort 2012; van Noort et al. 2013) from observations recorded by the Spectropolarimeter of the Solar Optical Telescope (SOT/SP; Tsuneta et al. 2008). Joshi et al. (2016) also observed a more vertical magnetic field in the higher layers of the photosphere than in its lower layers in a sunspot penumbra using high spatial resolution data obtained with the 1.5-m GREGOR telescope (Schmidt et al. 2012) using the GRIS spectropolarimeter (Collados et al. 2012).
A monolithic flux tube expanding with height should have a more vertical field in the higher layers at a given spatial pixel; this is consistent with our observation. In addition to this, the more inclined magnetic field in the lower photospheric layer may be further explained by the penumbral fine structure. Borrero et al. (2008), Tiwari et al. (2013), and Paper I have shown that the more vertical field of spines expands and covers the relatively horizontal magnetic field lines (intra-spines or filaments) in general accordance with the geometry proposed by Solanki & Montavon (1993). In the upper chromosphere, Joshi et al. (2016) therefore see that the peak-to-peak variation in the magnetic field inclination due to spine and inter-spine structure is reduced to 10° − 15° compared to 20° − 25° in the photosphere, again in qualitative agreement with this picture. In the azimuthal averages, the field appears to be more horizontal in the deeper photosphere, resulting from the smearing of horizontal and vertical field lines. This effect could also play a role in the umbra due to the presence of umbral dots and lightbridges harboring a more horizontal magnetic field than the surrounding umbra in the deeper layers of the photosphere (see, e.g., Riethmüller et al. 2013; Lagg et al. 2014).
5.3. Twist of the magnetic field of the sunspot
At different places, the sunspot exhibits different senses of twist of the magnetic field vector in the azimuthal direction with respect to a potential field for both the photosphere and chromosphere. However, the clockwise twist dominates and the average twist angle is found to be ≈6° on 14 November 2010 in the photosphere and the upper chromosphere. On 16 November 2010 the twist increases to ≈12° in both the photosphere and upper chromosphere. A clockwise twist corresponds to negative magnetic helicity (Tiwari et al. 2009). The observed sunspot therefore follows the helicity hemispheric rule (Hale 1925, 1927; Richardson 1941; Hagino & Sakurai 2004; Nandy 2006; Bernasconi et al. 2005; Pevtsov et al. 2008). Sunspots with both senses of twist at the same time have been observed earlier (Tiwari et al. 2009; Socas-Navarro 2005; Tiwari et al. 2015). We found that the sunspot has on average a negligible twist in azimuth angle between the chromospheric and photospheric magnetic field when considering the whole sunspot. However, locally the twist maps show significant values of both signs in the sunspot. The radial dependence of the twist between the chromosphere and photospheric magnetic field indicates an increase from the inner penumbra to the outer penumbra. Similar twist gradients have been reported by Tiwari et al. (2015) in the photospheric layers of a sunspot. Peter (1996) demonstrated that the decreasing radial magnetic field leads to increasing twist under influence of the Coriolis force on the radial flows (the inverse Evershed flow) in chromospheric penumbrae and superpenumbrae.
The present study has revealed a number of basic properties of the magnetic field in the upper chromosphere of a sunspot. The differences between the results on the two days at which the sunspot was studied suggest that it would be worthwhile to observe and analyze a number of sunspots at the two layers to determine the commonality of their behavior and to learn of the full range that the properties of the upper chromospheric magnetic field in sunspots can cover. Recently, the work of Joshi et al. (2016) has given intriguing signs of small-scale structure (spine and interspine) in the upper chromosphere, i.e., in a layer in which magnetoconvection, the driver of similar structure seen in the photosphere, cannot be the cause of the structure. The higher spatial resolution now afforded by the GRIS instrument (Collados et al. 2012) on the GREGOR telescope makes it attractive to redo a similar analysis as presented in the current paper, but applied to data with a higher spatial resolution.
Acknowledgments
The German Vacuum Tower Telescope is operated by the Kiepenheuer-Institut für Sonnenphysik at the Spanish Observatorio del Teide of the Instituto de Astrofísica de Canarias (IAC). This work was partly supported by the BK21 plus program through the National Research Foundation (NRF) funded by the Ministry of Education of Korea.
References
- Abdussamatov, H. I. 1971, Sol. Phys., 16, 384 [NASA ADS] [CrossRef] [Google Scholar]
- Adams, M., Solanki, S. K., Hagyard, M., & Moore, R. L. 1993, Sol. Phys., 148, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Alissandrakis, C. E. 1981, A&A, 100, 197 [NASA ADS] [Google Scholar]
- Andretta, V., & Jones, H. P. 1997, ApJ, 489, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Avrett, E. H., Fontenla, J. M., & Loeser, R. 1994, in Infrared Solar Physics, eds. D. M. Rabin, J. T. Jefferies, & C. Lindsey, IAU Symp., 154, 35 [Google Scholar]
- Balthasar, H., & Schmidt, W. 1993, A&A, 279, 243 [NASA ADS] [Google Scholar]
- Berger, T. E., & Berdyugina, S. V. 2003, ApJ, 589, L117 [NASA ADS] [CrossRef] [Google Scholar]
- Bernasconi, P. N., Rust, D. M., & Hakim, D. 2005, Sol. Phys., 228, 97 [Google Scholar]
- Bloomfield, D. S., Lagg, A., & Solanki, S. K. 2007, ApJ, 671, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Bogdan, T. J., & Judge, P. G. 2006, Roy. Soc. London Philos. Trans. Ser. A, 364, 313 [Google Scholar]
- Borrero, J. M., & Ichimoto, K. 2011, Liv. Rev. Sol. Phys., 8, 4 [Google Scholar]
- Borrero, J. M., & Kobel, P. 2012, A&A, 547, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borrero, J. M., Lites, B. W., & Solanki, S. K. 2008, A&A, 481, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brosius, J. W. 2005, ApJ, 622, 1216 [NASA ADS] [CrossRef] [Google Scholar]
- Brosius, J. W., & White, S. M. 2004, ApJ, 601, 546 [NASA ADS] [CrossRef] [Google Scholar]
- Brynildsen, N., Maltby, P., Brekke, P., et al. 1998, ApJ, 502, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Brynildsen, N., Maltby, P., Brekke, P., Haugan, S. V. H., & Kjeldseth-Moe, O. 1999, Sol. Phys., 186, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Brynildsen, N., Maltby, P., Fredvik, T., Kjeldseth-Moe, O., & Wilhelm, K. 2001, Sol. Phys., 198, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Centeno, R., Collados, M., & Trujillo Bueno, J. 2006, ApJ, 640, 1153 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Centeno, R., Trujillo Bueno, J., Uitenbroek, H., & Collados, M. 2008, ApJ, 677, 742 [NASA ADS] [CrossRef] [Google Scholar]
- Christopoulou, E. B., Georgakilas, A. A., & Koutchmy, S. 2000, A&A, 354, 305 [NASA ADS] [Google Scholar]
- Christopoulou, E. B., Georgakilas, A. A., & Koutchmy, S. 2001, A&A, 375, 617 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Collados, M., Lagg, A., Díaz Garcí A, J. J., et al. 2007, in The Physics of Chromospheric Plasmas, eds. P. Heinzel, I. Dorotovič, & R. J. Rutten, ASP Conf. Ser., 368, 611 [Google Scholar]
- Collados, M., López, R., Páez, E., et al. 2012, Astron. Nachr., 333, 872 [NASA ADS] [CrossRef] [Google Scholar]
- Cuperman, S., Li, J., & Semel, M. 1992, A&A, 265, 296 [NASA ADS] [Google Scholar]
- de la Cruz Rodríguez, J., Rouppe van der Voort, L., Socas-Navarro, H., & van Noort, M. 2013, A&A, 556, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Felipe, T., Khomenko, E., Collados, M., & Beck, C. 2010, ApJ, 722, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Felipe, T., Collados, M., Khomenko, E., et al. 2016, A&A, 596, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fludra, A. 2001, A&A, 368, 639 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fludra, A., Brekke, P., Harrison, R. A., et al. 1997, Sol. Phys., 175, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Franz, M., & Schlichenmaier, R. 2013, A&A, 550, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frutiger, C., Solanki, S. K., Fligge, M., & Bruls, J. H. M. J. 1999, in Polarization, eds. K. N. Nagendra, & J. O. Stenflo, Astrophys. Space Sci. Lib., 243, 281 [Google Scholar]
- Frutiger, C., Solanki, S. K., Fligge, M., & Bruls, J. H. M. J. 2000, A&A, 358, 1109 [NASA ADS] [Google Scholar]
- Gary, G. A. 1989, ApJS, 69, 323 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Georgakilas, A. A., Christopoulou, E. B., & Koutchmy, S. 2000, A&A, 363, 306 [NASA ADS] [Google Scholar]
- Hagino, M., & Sakurai, T. 2004, PASJ, 56, 831 [NASA ADS] [CrossRef] [Google Scholar]
- Hagyard, M. J., Teuber, D., West, E. A., et al. 1983, Sol. Phys., 84, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Hale, G. E. 1925, PASP, 37, 268 [NASA ADS] [CrossRef] [Google Scholar]
- Hale, G. E. 1927, Nature, 119, 708 [NASA ADS] [CrossRef] [Google Scholar]
- Henze, J. W., Tandberg-Hanssen, E., Hagyard, M. J., et al. 1982, Sol. Phys., 81, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Jafarzadeh, S. 2013, Ph.D. Thesis, Göttingen University [Google Scholar]
- Jafarzadeh, S., Solanki, S. K., Lagg, A., et al. 2014, A&A, 569, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, H. P., & Giovanelli, R. G. 1982, Sol. Phys., 79, 247 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Joshi, J. 2014, Ph.D. Thesis, Braunschweig University [Google Scholar]
- Joshi, J., Lagg, A., Solanki, S. K., et al. 2016, A&A, 596, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Joshi, J., Lagg, A., Hirzberger, J., Solanki, S. K., & Tiwari, S. K. 2017, A&A, 599, A35 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jurčák, J., Martínez Pillet, V., & Sobotka, M. 2006, A&A, 453, 1079 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Keppens, R., & Martinez Pillet, V. 1996, A&A, 316, 229 [NASA ADS] [Google Scholar]
- Lagg, A., Woch, J., Krupp, N., & Solanki, S. K. 2004, A&A, 414, 1109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lagg, A., Woch, J., Solanki, S. K., & Krupp, N. 2007, A&A, 462, 1147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lagg, A., Ishikawa, R., Merenda, L., et al. 2009, in The Second Hinode Science Meeting: Beyond Discovery-Toward Understanding, eds. B. Lites, M. Cheung, T. Magara, J. Mariska, & K. Reeves, ASP Conf. Ser., 415, 327 [Google Scholar]
- Lagg, A., Solanki, S. K., van Noort, M., & Danilovic, S. 2014, A&A, 568, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lagg, A., Lites, B., Harvey, J., Gosain, S., & Centeno, R. 2015, Space Sci. Rev., 1 [Google Scholar]
- Leenaarts, J., Golding, T., Carlsson, M., Libbrecht, T., & Joshi, J. 2016, A&A, 594, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lites, B. W., Elmore, D. F., Seagraves, P., & Skumanich, A. P. 1993, ApJ, 418, 928 [NASA ADS] [CrossRef] [Google Scholar]
- Maltby, P., Brynildsen, N., Brekke, P., et al. 1998, ApJ, 496, L117 [NASA ADS] [CrossRef] [Google Scholar]
- Maltby, P., Brynildsen, N., Fredvik, T., Kjeldseth-Moe, O., & Wilhelm, K. 1999, Sol. Phys., 190, 437 [NASA ADS] [CrossRef] [Google Scholar]
- Mathew, S. K., Lagg, A., Solanki, S. K., et al. 2003, A&A, 410, 695 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Merenda, L., Lagg, A., & Solanki, S. K. 2011, A&A, 532, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nandy, D. 2006, J. Geophys. Res. (Space Phys.), 111, 12 [CrossRef] [Google Scholar]
- Orozco Suarez, D., Lagg, A., & Solanki, S. K. 2005, in Chromospheric and Coronal Magnetic Fields, eds. D. E. Innes, A. Lagg, & S. A. Solanki, ESA SP, 596 [Google Scholar]
- Penn, M. J., & Kuhn, J. R. 1995, ApJ, 441, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Peter, H. 1996, MNRAS, 278, 821 [NASA ADS] [Google Scholar]
- Pevtsov, A. A., Canfield, R. C., Sakurai, T., & Hagino, M. 2008, ApJ, 677, 719 [NASA ADS] [CrossRef] [Google Scholar]
- Richardson, R. S. 1941, ApJ, 93, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Riethmüller, T. L., Solanki, S. K., van Noort, M., & Tiwari, S. K. 2013, A&A, 554, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rimmele, T. R. 1997, ApJ, 490, 458 [NASA ADS] [CrossRef] [Google Scholar]
- Rimmele, T. 2008, ApJ, 672, 684 [NASA ADS] [CrossRef] [Google Scholar]
- Rüedi, I., Solanki, S. K., & Livingston, W. C. 1995, A&A, 293, 252 [NASA ADS] [Google Scholar]
- Rüedi, I., Keller, C. U., & Solanki, S. K. 1996, Sol. Phys., 164, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Rüedi, I., Solanki, S. K., Keller, C. U., & Frutiger, C. 1998, A&A, 338, 1089 [NASA ADS] [Google Scholar]
- Ruiz Cobo, B., & Asensio Ramos, A. 2013, A&A, 549, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sakurai, T., Makita, M., & Shibasaki, K. 1985, in Theo. Prob. High Resolution Solar Physics, ed. H. U. Schmidt, 313 [Google Scholar]
- Sánchez Cuberes, M., Puschmann, K. G., & Wiehr, E. 2005, A&A, 440, 345 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sasso, C., Lagg, A., & Solanki, S. K. 2006, A&A, 456, 367 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schad, T. A., Penn, M. J., Lin, H., & Tritschler, A. 2015, Sol. Phys., 290, 1607 [NASA ADS] [CrossRef] [Google Scholar]
- Scharmer, G. B., de la Cruz Rodríguez, J., Sütterlin, P., & Henriques, V. M. J. 2013, A&A, 553, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schmidt, W., von der Lühe, O., Volkmer, R., et al. 2012, Astron. Nachr., 333, 796 [NASA ADS] [CrossRef] [Google Scholar]
- Skumanich, A., Lites, B. W., & Martínez Pillet, V. 1994, in Solar Surface Magnetism, eds. R. J. Rutten, & C. J. Schrijver, 99 [Google Scholar]
- Sobotka, M., Švanda, M., Jurčák, J., et al. 2013, A&A, 560, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Socas-Navarro, H. 2005, ApJ, 631, L167 [NASA ADS] [CrossRef] [Google Scholar]
- Socas-Navarro, H., Trujillo Bueno, J., & Landi Degl’Innocenti, E. 2005, ApJS, 160, 312 [NASA ADS] [CrossRef] [Google Scholar]
- Solanki, S. K. 2003, A&ARv, 11, 153 [Google Scholar]
- Solanki, S. K., & Montavon, C. A. P. 1993, A&A, 275, 283 [NASA ADS] [Google Scholar]
- Solanki, S. K., Rüedi, I., & Livingston, W. 1992, A&A, 263, 339 [NASA ADS] [Google Scholar]
- Solanki, S. K., Montavon, C. A. P., & Livingston, W. 1994, A&A, 283, 221 [NASA ADS] [Google Scholar]
- Solanki, S. K., Finsterle, W., Rüedi, I., & Livingston, W. 1999, A&A, 347, L27 [NASA ADS] [Google Scholar]
- Solanki, S. K., Lagg, A., Woch, J., Krupp, N., & Collados, M. 2003, Nature, 425, 692 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Solanki, S. K., Lagg, A., Aznar Cuadrado, R., et al. 2006, in ASP Conf. Ser., 358, eds. R. Casini, & B. W. Lites, 431 [Google Scholar]
- Tiwari, S. K., Venkatakrishnan, P., & Sankarasubramanian, K. 2009, ApJ, 702, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Tiwari, S. K., van Noort, M., Lagg, A., & Solanki, S. K. 2013, A&A, 557, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tiwari, S. K., van Noort, M., Solanki, S. K., & Lagg, A. 2015, A&A, 583, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Trujillo Bueno, J., Landi Degl’Innocenti, E., Collados, M., Merenda, L., & Manso Sainz, R. 2002, Nature, 415, 403 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Trujillo Bueno, J., Merenda, L., Centeno, R., Collados, M., & Landi Degl’Innocenti, E. 2005, ApJ, 619, L191 [NASA ADS] [CrossRef] [Google Scholar]
- Tsuneta, S., Ichimoto, K., Katsukawa, Y., et al. 2008, Sol. Phys., 249, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Tziotziou, K., Tsiropoula, G., Mein, N., & Mein, P. 2006, A&A, 456, 689 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tziotziou, K., Tsiropoula, G., Mein, N., & Mein, P. 2007, A&A, 463, 1153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Noort, M. 2012, A&A, 548, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Noort, M., Lagg, A., Tiwari, S. K., & Solanki, S. K. 2013, A&A, 557, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Westendorp Plaza, C., del Toro Iniesta, J. C., Ruiz Cobo, B., et al. 2001, ApJ, 547, 1130 [NASA ADS] [CrossRef] [Google Scholar]
- Wilkinson, L. K., Emslie, G. A., & Gary, G. A. 1989, Sol. Phys., 119, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, Z., Lagg, A., & Solanki, S. K. 2010, A&A, 520, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Xu, Z., Lagg, A., Solanki, S., & Liu, Y. 2012, ApJ, 749, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Zakharov, V., Hirzberger, J., Riethmüller, T. L., Solanki, S. K., & Kobel, P. 2008, A&A, 488, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zirin, H., & Stein, A. 1972, ApJ, 178, L85 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Panel a: observed field-of-view (FOV) on 14 November 2010 in the continuum. Panels b and c: depression of the line core of the Si i 10 827 Å line and He ibc, respectively. The inner and outer contours in all panels indicate the umbra-penumbra boundary and the outer boundary of the sunspot, respectively. The arrow in panel a indicates the direction to the solar disk center. Three white arrows in panel c mark positions of downflow intrusions in the penumbra in the upper chromosphere (see Fig. 4d). |
| In the text | |
 |
Fig. 2 Same as Fig. 1, but showing the observed FOV on 16 November 2010. The red plus in panel b indicates the position for which observed and the best fit Stokes profiles are shown in Fig. 3. |
| In the text | |
 |
Fig. 3 Best fit HeLIx+ inversions of typical Stokes profiles in the penumbra. Their spatial location is marked by a red plus sign in Fig. 2a. Black dots represent observed data points and solid blue curves represent the best fits. |
| In the text | |
 |
Fig. 4 Maps of a) Magnetic field strength B, b) inclination angle, γ′, of the magnetic field vector with respect to the solar surface normal, c) azimuth direction, φ′, of the magnetic field vector and d) line-of-sight velocity obtained from the observations recorded on 14 November 2010. Left and right maps in all panels represent atmospheric parameters obtained in the photosphere and upper chromosphere, respectively. An arrow in the left map of panel d indicates the disk center direction and three arrows in the right map point three downflow intrusions in the penumbra. |
| In the text | |
 |
Fig. 5 Same as Fig. 4, but for the observations recorded on 16 November 2010. |
| In the text | |
 |
Fig. 6 Cross sections through the observed sunspots: panels b and f, c and g and d and h depict profiles of B, γ′ and φ′, respectively, along an artificial slit represented by the red lines in panels a and e. Panels a–d refer to observations recorded on 14 November 2010 and panels e–h correspond to 16 November 2010. The black and blue curves in panels b–d and f–h correspond to the photosphere and upper chromosphere, respectively, while the dotted curves represent the continuum intensity. |
| In the text | |
 |
Fig. 7 Division of the sunspot into umbral, penumbral, and lightbridge areas. Red and blue contours in both panels encircle umbral and penumbral areas, which are used to compare the magnetic field vector retrieved in the photosphere and upper chromosphere. The area within the black contour in the left panel represents the lightbridge. The left and right panels correspond to the observations recorded on 14 and 16 November 2010, respectively. |
| In the text | |
 |
Fig. 8 Two-dimensional histograms of the magnetic field components obtained in the upper chromosphere vs. those obtained in the photosphere from the observations recorded on 14 November 2010. Panels a–c show plots of B from the umbral, penumbral , and lightbridge pixels, respectively (see Fig. 7). The γ′ values of data points from the same spatial positions are shown in panels d–f, respectively. |
| In the text | |
 |
Fig. 9 Same as Fig. 8 but for the observations recorded on 16 November 2010 and restricted to umbral and penumbral pixels. |
| In the text | |
 |
Fig. 10 Averaged radial distribution of the magnetic field properties in the observed sunspot: panel a: continuum intensity map with overplotted contours used to calculate azimuthal averages for 14 November 2010. The area above the red line was not included to calculate the azimuthal averages. Panel b: relative continuum intensity (normalized to the quiet Sun) of the sunspot as a function of the normalized radial distance, r/Rspot. Panels c–f: radial dependence of B, γ′, the vertical component of the magnetic field, Bz, and the transverse component of the magnetic field, Bt, respectively. The black and blue curves correspond to the magnetic field vector derived in the photosphere and upper chromosphere, respectively. The dotted vertical lines in panels b–f indicate the umbra-penumbra boundary and the outer boundary of the sunspot. |
| In the text | |
 |
Fig. 11 Same as Fig. 10, but for the observations recorded on 16 November 2010. Here the area to the upper left of the red lines is not included in making the radial averages. |
| In the text | |
 |
Fig. 12 Vertical gradient of B, ΔB/ Δd, between the photosphere and upper chromosphere as a function of r/Rspot. Solid curves represent ΔB/ Δd estimated with the average value of B in the photosphere. Dashed and dot-dashed curves show ΔB/ Δd from log τ = 0.0 and log τ = − 2.3, respectively. Panels a and b correspond to 14 and 16 November 2010, respectively. |
| In the text | |
 |
Fig. 13 Maps of the twist and differential twist angles of magnetic field of the sunspot. Panels a and d: twist of the photospheric field defined as the difference between the azimuth angle of the photospheric field |
| In the text | |
 |
Fig. 14 Histograms of the twist and differential twist of the magnetic field of the sunspot, with the differential twist denoting the difference between the azimuthal direction of the field in the photosphere, |
| In the text | |
 |
Fig. 15 Radial dependence of |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.