| Issue |
A&A
Volume 603, July 2017
|
|
|---|---|---|
| Article Number | A106 | |
| Number of page(s) | 63 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201630337 | |
| Published online | 18 July 2017 | |
Near-infrared time-series photometry in the field of Cygnus OB2 association
I. Rotational scenario for candidate members⋆
1 Departamento de Física, ICEx, UFMG,, Av. Antônio Carlos, 6627, 30270-901 Belo Horizonte, MG, Brazil
e-mail: roquette@fisica.ufmg.br
2 Univ. Grenoble Alpes, CNRS, IPAG, 38000 Grenoble, France
3 INAF–Osservatorio Astronomico di Palermo, Piazza del Parlamento 1, 90134 Palermo, Italy
Received: 22 December 2016
Accepted: 7 April 2017
Context. In recent decades, the picture of early pre-main sequence stellar rotational evolution has been constrained by studies targeting different regions at a variety of ages with respect to young star formation. Observational studies suggest a dependence of rotation with mass, and for some mass ranges a connection between rotation and the presence of a circumstellar disk. The role of environmental conditions on the rotational regulation, however, has still not been fully explored.
Aims. We investigate the rotational properties of candidate members of the young massive association Cygnus OB2. By evaluating their rotational properties, we address questions regarding the effect of environment properties on PMS rotational evolution.
Methods. We studied JHK-band variability in 5083 candidate members (24% of them are disk-bearing stars). We selected variable stars with the Stetson variability index and performed the period search with the Lomb-Scargle periodogram for periods between 0.83–45 days. Period detections were verified using false alarm probability levels, Saunders statistics, the string and rope length method, and visual verification of folded light curves.
Results. We identified 1224 periodic variable stars (24% of the candidate member sample, 8% of the disk-bearing sample, and 28% of the non-disk-bearing sample). Monte Carlo simulations were performed in order to evaluate completeness and contamination of the periodic sample, out of which 894 measured periods were considered reliable. Our study was considered reasonably complete for periods between 2 and 30 days.
Conclusions. The general scenario for the rotational evolution of young stars seen in other regions is confirmed by Cygnus OB2 period distributions with disc-bearing stars rotating on average more slowly than non-disk-bearing stars. A mass-rotation dependence was also verified, but as in NGC 6530, very low mass stars (M ≤ 0.4 M⊙) are rotating on average slower than higher mass stars (0.4M⊙<M ≤ 1.4 M⊙). We observed an excess of slow rotators among the lower mass population. The disk and mass-rotation connection was also analyzed by taking into account the incident UV radiation arising from O stars in the association. Results compatible with the disk-locking scenario were verified for stars with low UV incidence, but no statistical significant relation between rotation and disk presence was verified for stars with high UV incidence suggesting that massive stars can have an important role in regulating the rotation of nearby low mass stars.
Key words: infrared: stars / stars: variables: T Tauri, Herbig Ae/Be / stars: formation / stars: low-mass / stars: pre-main sequence / stars: rotation
The full Table 1 is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/603/A106
© ESO, 2017
1. Introduction
The angular momentum (AM) evolution during the early stages of the stellar life is one of the most fundamental questions currently under debate (e.g., Bodenheimer 1995). If AM conservation was solely responsible for early rotational evolution during star contraction toward the zero age main sequence (ZAMS) phase pre-main sequence (PMS) stars should reach their first few Myr with spin rates close to critical values (when the centrifugal forces balance gravity). On the contrary, observations mapping rotational velocities of low mass PMS stars, (hereafter T Tauri stars; TTS; Joy 1945) found that their typical rotational velocities are only a fraction of their critical velocities (e.g., Vogel & Kuhi 1981; Bouvier et al. 1986). This suggests that there must exist some ongoing physical mechanisms on such stars that counteract the spin-up expected from stellar contraction.
The AM of a forming star is determined by both internal and external physical processes. Internal processes determine how AM is transported in the stellar interior. The most popular scenario assumes that a radiative core and a convective envelope rotate as solid bodies but with different angular velocities (e.g., Gallet & Bouvier 2013). External processes are responsible for the AM loss from the stellar surface, and models for such processes include the magnetic star-disk interaction (e.g., Ghosh & Lamb 1979; Matt & Pudritz 2005), accretion-powered stellar winds (e.g., Matt et al. 2012), and mass ejections (e.g., Conical Winds: Zanni & Ferreira 2013; Romanova et al. 2009). To constrain the physical models, recent studies have looked for correlations between stellar rotation rates and parameters such as stellar mass, circumstellar disk indicators, X-ray emission, and mass accretion rates.
A controversial issue still under debate is the “disk-locking” process (e.g., Ghosh & Lamb 1979; Koenigl 1991), which is based on the observational evidence that accreting stars are on average slower rotators than non-accreting stars. According to the disk-locking scenario, PMS stars that still magnetically interact with their disks would be prevented from spinning-up via star-disk interaction even though they are contracting toward the ZAMS. Consequently, these stars would maintain almost constant rotational velocity during their first few Myr. The disk-locking model can be validated by observing a correlation between existent or absent mass accretion diagnosis and the rotational status of the star as a slow or fast rotator. Studies supporting the disk-locking scenario found that during the first few Myr of their evolution, PMS stars of solar mass (0.4 M⊙ ≤ M ≤ 1.4 M⊙) present a bimodal period distribution, in which disk-bearing stars have typical periods between 3–10 days, while non-disk-bearing stars have periods between 1–7 days (e.g., Rebull et al. 2004; Irwin et al. 2008; Rodríguez-Ledesma et al. 2009; Littlefair et al. 2010; Affer et al. 2013; Venuti et al. 2017). Recently, Vasconcelos & Bouvier (2015) have used semi-empirical Monte Carlo simulations to investigate the effect of the disk-locking hypothesis on the period distributions of groups of coeval stars. They have adopted a model in which accreting stars have constant rotational periods (disk-locking) and non-disk-bearing stars conserve AM. They have applied to the model values of mass accretion rates and disk lifetimes from the literature. They have succeeded in reproducing the scenario observed in young clusters of several ages when they started their simulations with a bimodal period distribution at the age of 1 Myr in which disk-bearing stars rotate with periods of 8 ± 6 days and non-disk-bearing stars rotate with periods of 3 ± 2 days. Nevertheless, disk-locking seems to be less efficient for very low mass stars (Lamm et al. 2005; Bouvier et al. 2014), and Cody & Hillenbrand (2010) found no correlation between disk presence and rotational periods for stars with masses below 0.5 M⊙.
Interpreting period distributions in the light of disk-locking models may be a delicate process. Often, conclusions regarding the statistical significance of the differences between the rotational period distributions for classical TTS (CTTS) and weak-lined TTS (WTTS), which are commonly seen as supportive of disk-locking scenario, are controversial. The results reported in some studies are often not verified by other studies, even for the same group of stars. This is because external factors can easily introduce ambiguities in the period distribution interpretation. Among the typical observational biases are the one day aliasing phenomenon introduced by the rotation of the Earth in ground-based observations (to be discussed in Sect. 3.1); sample incompleteness; periodic samples with small statistics numbers; and physical aspects, such as the fact that the rotational scenario is mass dependent and, therefore, uncertainties in mass estimation can easily contaminate the results. Another recurrent physical contamination factor is the disk diagnosis used to identify disk-bearing stars. Several studies (including the present one) used IR excess as indicative of disk presence; despite being a good diagnosis for a dusty local environment that is interpreted as a disk, this diagnosis does not tell whether there is indeed an active accretion process in the disk and thus whether the star is still magnetically interacting with the disk.
Even with all those caveats, the best way to date to study AM evolution is still to measure rotational periods of groups of coeval stars in open cluster or associations and then to assemble period distributions for clusters of different ages in an evolutionary sequence. In this direction, thousands of rotational periods of stars in young clusters and associations have been measured in recent decades (for a review see Bouvier et al. 2014). However, the assumption that each group represents a piece of the same time line assumes that global environmental conditions do not play a significant role in the overall rotational evolution. Notwithstanding, some discrepant observational results for regions of similar ages show that environmental conditions may have an important effect in the evolution of AM during the first Myr. Some examples are the case of CepOB3b region (of 4–5 Myr in age, according to Littlefair et al. 2010), where the authors reported significantly different rotational period distributions at very low mass (M ≤ 0.4 M⊙) than Irwin et al. (2008) reported for the similar aged NGC 2362; and the case of IC 348 and NGC 2264 (age 1–3 Myr, according to Littlefair et al. 2005), where stars of the former cluster were reported to be rotating more slowly than those of the latter cluster.
It is, therefore, mandatory to build statistically significant samples of stars with measured rotational periods in young regions with similar ages but different environments to improve our understanding of the role of the environmental conditions in regulating the AM during PMS. In this context, massive young associations such as Cygnus OB2 (CygOB2) are valuable targets for investigating the effects of environment on the AM evolution.
CygOB2 is the closest young massive association to the Sun. Kiminki et al. (2015) recently reviewed its distance by studying four double-lined eclipsing binaries within the association, analyzed using both photometry and spectroscopy. They found an average distance of 1.33 ± 0.06 kpc to the association.
CygOB2 massive population has been investigated by photometric and spectroscopic studies in both optical and infrared bands (e.g., Reddish et al. 1966; Torres-Dodgen et al. 1991; Knödlseder 2000; Comerón et al. 2002; Hanson 2003; Drew et al. 2008; Rauw et al. 2015; Wright et al. 2015, 2016; Kiminki et al. 2015), and it is known for harboring some of the brightest stars in the Galaxy. Some examples of its rich population are the peculiar B supergiant CygOB2#12 (Massey & Thompson 1991), two O3If stars (#7 and 22-A from Walborn et al. 2002), and some Wolf-Rayet stars (e.g., WR 142a from Pasquali et al. 2002). There are 169 confirmed OB stars (Wright et al. 2015) among the association members.
Wright et al. (2016), as part of the DANCe (Dynamical Analysis of Nearby Clusters, Bouy et al. 2013) project, used high-precision proper motions of stars in the association to investigate its kinematic and dynamic. These authors suggested that CygOB2 formed pretty much as it is today: a highly substructured, globally unbound association. Beyond its massive population, CygOB2 is also a valuable target for studying the environmental influence on the formation and early evolution of low mass stars (M ≤ 1.4 M⊙), and, in particular, to probe low mass star evolution in the vicinity of massive stars.
In the last decade, CygOB2 low mass population has been the target of several studies (e.g., Vink et al. 2008; Wright & Drake 2009; Guarcello et al. 2012, 2013; Wright et al. 2014; Guarcello et al. 2015, 2016) and while some massive stars are as young as 2 Myr in age (e.g., Hanson 2003), the low mass population age ranges mainly between ~3 Myr and ~5 Myr (Wright et al. 2010). Guarcello et al. (2013) used wide and deep photometry from r band to 24 μm to unveil its disk-bearing population, finding 1843 disk-bearing candidates. As result of the Chandra Cygnus OB2 Legacy Survey, Wright et al. (2014) identified 7924 X-ray sources in the direction of the association. Guarcello et al. (2015) found that 5703 of the X-ray sources had optical and/or infrared counterparts. Using the optical and infrared photometry merged by Guarcello et al. (2015), Kashyap (2017) classified 5022 sources as candidate members. Guarcello et al. (2016) recently used the disk-bearing and non-disk-bearing candidate members to investigate the dissipation timescale of protoplanetary disks of low mass stars in the vicinity of massive stars. These authors analyzed the spatial variation of the disk fraction across the association and its correlation with the local ultraviolet radiation and stellar density. They found evidence that disks are more rapidly dissipated in regions with higher stellar density and more intense UV radiation within the association. They also found that disk dissipation due to close encounters is negligible in the association and that disk dissipation is dominated by photoevaporation.
We used the results of a near-infrared (NIR) photometric variability survey in the direction of the association to address some questions regarding the low mass population of the association. We will present the first results of the survey in two papers. In this first paper we focus on a sample of periodic stars that were listed as candidate members in the literature. As most of periodic variability can be explained by the rotational modulation by spots at the stellar surface, we analyze the periodic sample in the context of angular momentum (AM) evolution for young stars. The general characteristics of the NIR variable sample, and the description of their variable behavior inside the color-magnitude and color–color diagrams will be presented in the second paper (Roquette et al., in prep.).
The present paper is organized as follows: in Sect. 2 we outline the observations carried out for the present survey, data processing, and light-curve production, as well as data taken from the literature used to complement the study. In Sect. 3 we describe the methods applied for time-series analysis and periodicity search. In Sect. 4 we present the results regarding the periodic stars, and in Sect. 5 we present conclusions and discuss the results inside the general young stellar AM scenario.
2. Analyzed data
2.1. Observations
Our observational dataset was obtained with the 3.8 m United Kingdom Infra-Red Telescope (UKIRT), at Manua Kea, Hawaii, equipped with the Wide Field Camera (WFCAM; Casali et al. 2007); the programs were U/07A/H16 and U/07B/H60. Our complete dataset is composed of up to 115 nights observed using the J, H, and K filters (Hewett et al. 2006). The observations were carried during 2007 in two seasons (Fig. 1): the first season comprises 43 observed nights between April 1 and May 21; the second season comprises 73 observed nights between August 4 and November 3. The two observational seasons span a total of 217 days. The exposures were short, 2 s in each filter.
 |
Fig. 1 Scheme showing the nights when observations were taken in the given filters. |
The WFCAM is composed of four 2048 × 2048 Rockwell Hawaii-II detectors (Casali et al. 2007, hereafter CCDs W, X, Y, and Z). The detectors are spaced with a separation of 94% of the width of each detector, such that four exposures (exposures A–D) are required to image a contiguous area of 0.87 squared degrees. The layout of WFCAM is schematically shown in Fig. 2. The observed area was centered on α2000 = 20h33m, δ2000 = + 41°12′, which comprises approximately the center of CygOB2 association.
 |
Fig. 2 Schematic representation of WFCAM layout. A sequence of 4 exposures (ABCD) with the 4 CCDs (WXYZ) produces a mosaic of 16 observed regions covering a total area of 0.87 squared degrees in the sky. For each region composing the mosaic, we also show the number of observations in the J, H, and K filters after data processing and cleaning. |
The data were pipeline-reduced and calibrated at the Cambridge Astronomy Survey Unit (CASU; Irwin et al. 2004; Hodgkin et al. 2009) and a source catalog was provided. The source catalog is composed of a set of fluxes measured with different aperture radii per source. As we need a single number for the flux in all images (in order to link the objects building consistent light curves), we followed the CASU documentation and adopted flux number 3, which is a soft-edge aperture of 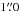 radius. Data calibration was made by the CASU pipeline using 2MASS sources with extinction-corrected color 0.0 ≤ J − K ≤ 1.0 and signal-to-noise ratio S/N ≥ 10 in each filter (Hodgkin et al. 2009).
radius. Data calibration was made by the CASU pipeline using 2MASS sources with extinction-corrected color 0.0 ≤ J − K ≤ 1.0 and signal-to-noise ratio S/N ≥ 10 in each filter (Hodgkin et al. 2009).
The images and catalogs were retrieved from the CASU server in January 2008. Owing to the layout of the WFCAM 4 detectors (Fig. 2), one night of observation in J, H, and K filters is composed of 4 × 4 × 3 = 48 frames/source catalogs. In order to build a light-curve catalog from the 5640 tables, we created an IDL procedure to read, manipulate, and link sources from the tables provided by CASU. We excluded all sources with the classification flag in the CASU catalogs indicating noise, borderline stellar, or saturated objects.
Candidate member catalog:
our main goal is to determine the variability characteristics of young stellar objects (YSO) that belong to the CygOB2 association. We searched the literature for candidate members and used their coordinates to build an input catalog for cross-matching and merging all CASU tables together in a single multi-band light-curve catalog.
The candidate member catalogs used to compose the input catalog were
-
the list of disk-bearing stars from Guarcelloet al. (2013,,which contains 1843 stars;
-
the X-ray sources from Chandra Cygnus OB2 Legacy Survey with optical/infrared counterparts from Guarcello et al. (2015, 2016, hereafter GDW15), considered members by Kashyap (in prep.), which contains 4864 sources
Each object from this input catalog was examined for companions in CASU tables inside a radius of 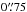 . Every time two objects were found inside this search radius, both objects were excluded to avoid contaminations into the light curves, and this selection rule accounts for most objects we could not recover inside our field of view (FOV). The catalog was built processing region by region (AW, AX, and so on; cf. Fig. 2). At the end, the 16 light-curve catalogs were merged and objects in the overlapping region between the CCDs were merged into a single identifier.
. Every time two objects were found inside this search radius, both objects were excluded to avoid contaminations into the light curves, and this selection rule accounts for most objects we could not recover inside our field of view (FOV). The catalog was built processing region by region (AW, AX, and so on; cf. Fig. 2). At the end, the 16 light-curve catalogs were merged and objects in the overlapping region between the CCDs were merged into a single identifier.
There were 100 OB stars on GDW15 and all those stars were saturated in our images. GDW15 and GDW13 have 403 low mass stars in common, and we recovered 354 of them (87.84%). We recovered 1272 (69.02%) disk-bearing stars from GDW13 and 4165 (85.63%) X-ray sources from GDW15. Our final candidate member light-curve catalog is composed of 5083 stars. The spatial distribution of those stars is shown in Fig. 3.
 |
Fig. 3 Spatial distribution of candidate members. Stars from GDW15 are shown as black squares, and stars from GDW13 are shown as gray points. Membership candidates with valid light curve in the present study are shown as blue dots. OB stars from Wright et al. (2015) are shown as red circles. |
Control sample:
we built a control sample including all stars in the three central regions (AW, BZ, and CY in Fig. 2) regardless of confirmed membership. Non-variable stars selected from the control sample (as described in Sect. 3.2) were used to estimate limit values of the statistical indexes used for evaluating periodic stars, such as the false alarm probability for peaks in the Lomb/Scargle periodogram, as described in Sect. 3.1. For each region, we chose the best night in K band in terms of seeing and generated an initial catalog with the coordinates of all the stars observed on that night. The typical number of detected sources in the central fields was around 25 000 for nights with good seeing. For each subsequent night and/or filter exposure for that region, we used a searching radius of 0.75 arcsec for each object already in the catalog. After a complete inspection, the objects in each exposure not matched with the light-curve catalog were added as new objects. A human operator was necessary in the procedure to judge parameters and make decisions on how to proceed in case of ambiguities due to 1) objects in the central fields being too crowded and causing more than one object to be found inside the 0.75 arcsec radius search; 2) seeing variations from night to night, causing variations in how many resolved objects were detected from one night to the other; 3) some objects presented proper motion with varying coordinates; and 4) spurious objects inside the source catalog, caused by defects in the data reduction, which were not flagged by CASU processing.
Using this method, we catalogued 42 777 objects with more than 10 valid observations in at least one filter. Objects catalogued in the control sample are shown in gray in Fig. 4, while objects in the candidate member catalog are shown as red dots.
 |
Fig. 4 Spatial distribution of the stars with an analyzed light curve. Control sample objects are shown as gray circles and candidate member stars are shown as red dots. |
Corrected errors:
after completing the multi-band light-curve catalogs, we applied the empirically derived correction presented by Hodgkin et al. (2009) to the pipeline-estimated photometric errors, 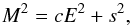 (1)where M is the correct measured total error, E is the pipeline-estimated photometric error, and c (=1.082) and s (=0.021) were empirically determined by Hodgkin et al. (2009). With this updated error, we confirmed the 2% level of night to night variations estimated by Hodgkin et al. (2009) for UKIRT/WFCAM data pipeline reduced by the CASU, as can be verified in Fig. 5.
(1)where M is the correct measured total error, E is the pipeline-estimated photometric error, and c (=1.082) and s (=0.021) were empirically determined by Hodgkin et al. (2009). With this updated error, we confirmed the 2% level of night to night variations estimated by Hodgkin et al. (2009) for UKIRT/WFCAM data pipeline reduced by the CASU, as can be verified in Fig. 5.
 |
Fig. 5 Errors vs. magnitude distributions for all data points in both control sample catalog (left) and candidate member catalog (right), for J, H, and K filters. The limit of 0.1 mag for the error, adopted in the present study, is shown as a red dashed line. |
For each light curve, to remove individual points with errors that were unusually higher than the mean error of the light curve, we did a two-iteration 2σ clipping in the error distribution around the mean error. After cleaning the complete candidate member sample, we analyzed the outlier points and identified and removed the nights suffering from systematic errors (those for which more than 40% of the valid points in a certain filter). Eight observed nights were removed from the light curves given this criterion. Figure 5 shows the error distribution for each filter after removing these points and nights. To guarantee high quality photometry, we only used data points with error smaller than 0.1 mag.
2.2. Data from literature
GDW13 composed an Optical-Infrared (OIR) catalog using wide and deep photometry, from r band to 24 μm, extracted from the literature. Their OIR catalog is composed of 328 540 sources in the field of CygOB2. The surveys used by the authors to build their catalog were
-
GTC/OSIRIS catalog
(hereafter GDW12; Guarcelloet al. 2012). This catalog covers ther, i, and z bands with 65 349 sources. For sources with good photometry, as defined by GDW12, the catalog reaches r = 25m; for objects at the distance of 1400 pc, using a 3.5 Myr isochrone (Wright et al. 2010) with the average extinction
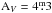 (from GDW12); this limit corresponds to a 0.16 M⊙ star (Guarcello et al. 2013).
(from GDW12); this limit corresponds to a 0.16 M⊙ star (Guarcello et al. 2013). -
WFC/IPHAS catalog
. This catalog comprises the r′ , i′ , and Hα filters and contains 24 072 sources. First release (Drew et al. 2005) for GDW13 and second release (Barentsen et al. 2014) for GDW15. The limit for good photometry is around
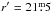 (Guarcello et al. 2013).
(Guarcello et al. 2013). -
SDSS DR8 catalog
(Aihara et al. 2011). This catalog is in the u, g, r, i, and z bands with 27 531 sources. The limit for good photometry is at r = 22m (~0.4 M⊙) but with a higher limit of saturation than GTC/OSIRIS catalog, allowing the study of stars up to r = 16m (~2.5 M⊙Guarcello et al. 2013).
-
UKIDSS/GPS catalog. This catalog covers
the J, H, and K bands with 273 473 sources. The original UKIDSS (Lucas et al. 2008) photometry extraction was redone by Guarcello et al. (2013), and reaches J = 21mJ = 21m corresponding to a mass limit of ~0.1 M⊙ at the distance of Cygnus OB2.
-
2MASS/PSC
(Cutri et al. 2003). The catalog comprises the J, H, and Ks filters and contains 43 485 sources. According to Guarcello et al. (2013), it was used because it has a higher limit of saturation than UKIDSS.
-
Spitzer Legacy Survey of the Cygnus X region
(Beerer et al. 2010). This catalog covers the IRAC 3.6, 4.5, 5.8, 8.0 μm, and MIPS 24 μm (149 381 sources) bands with sources detected down to 0.5 M⊙ (Guarcello et al. 2013).
To select the disk-bearing stars, GDW13 applied several disk-diagnosis techniques to their OIR-catalog, finding 1843 candidates. They also inferred the evolutionary status of the disk-bearing objects by studying their infrared spectral index, 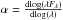 , using Wilking et al. (2001) classification scheme: 8.4% of the disk-bearing stars were class I, 13.1% were flat-spectrum sources, 72.9% were class II sources, 2.3% were pre-transition disks, and 3.3% were transitional disks.
, using Wilking et al. (2001) classification scheme: 8.4% of the disk-bearing stars were class I, 13.1% were flat-spectrum sources, 72.9% were class II sources, 2.3% were pre-transition disks, and 3.3% were transitional disks.
As part of the Chandra Cygnus OB2 Legacy Survey (Wright et al. 2014), a region of 1 square degree was covered using 36 Chandra/ACIS-I overlapping fields, and the authors detected and verified 7924 X-ray point sources in the observed region. GDW15 cross matched those X-ray sources with GDW13 OIR catalog and found 5703 X-ray sources with OIR counterparts. From the list of X-ray OIR sources, Kashyap (2017) selected 4864 candidate members.
2.3. Completeness of the analyzed data
The completeness of the analyzed data was estimated based on the drop in the number of detected objects in the magnitude distribution histograms for the J, H, and K filters, which are shown in Fig. 6, for the control and member candidate samples.
For the control sample (left plots), the limit magnitude detected in each band was Jmax ~ 20.2 mag, Hmax ~ 19.4 mag, and Kmax ~ 19.0 mag. The samples are complete up to magnitudes Jcomplete ~ 19.2 mag, Hcomplete ~ 17.9 mag, and Kcomplete ~ 16.9 mag.
For the candidate member sample (right plots), the limit magnitude detected in each band was Jmax ~ 18.8 mag, Hmax ~ 18.2 mag, and Kmax ~ 17.4 mag. The samples are complete up to magnitudes Jcomplete ~ 16.1 mag, Hcomplete ~ 14.9 mag, and Kcomplete ~ 14.3 mag.
 |
Fig. 6 Magnitude distributions for the control sample (left) and candidate member sample (right) for J, H, and K filters. |
From Fig. 6 one can see that the control sample goes deeper than the candidate member sample. This happens because of the lower completeness limits in the studies used to compose the candidate member sample. Also, there can be an incompleteness toward the brighter stars in both samples. But this incompleteness is not thought to interfere with the present work because, at the distance of CygOB2, the brightest stars in our sample would correspond to stars with intermediate mass and those are out of the mass range of interest in the present work.
3. Time-series analysis
Initial variable selection was carried out via the Stetson variability index (Stetson 1996), which is defined as 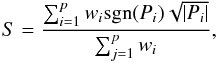 (2)where i is a pair of observations, which has a weight wi; and p is the total number of pairs of observations. The value Pi is defined as the product of the normalized residuals of two observations j and k that constitute the ith pair, Pi = δj(i)δk(i), and as
(2)where i is a pair of observations, which has a weight wi; and p is the total number of pairs of observations. The value Pi is defined as the product of the normalized residuals of two observations j and k that constitute the ith pair, Pi = δj(i)δk(i), and as 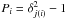 when there is only one valid observation (j = k). If one night has valid observations in all J, H, and K filters, then there are three pairs of observations for that night. Following Carpenter et al. (2001), if the star has valid J, H, and K, then each pair of observation has weight
when there is only one valid observation (j = k). If one night has valid observations in all J, H, and K filters, then there are three pairs of observations for that night. Following Carpenter et al. (2001), if the star has valid J, H, and K, then each pair of observation has weight 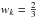 (total weight of 2 for the whole set), when there was a missing point, i.e., nonexistent observation in one or two filters, then a weight wk = 1 was assigned. The normalized residuals are defined as
(total weight of 2 for the whole set), when there was a missing point, i.e., nonexistent observation in one or two filters, then a weight wk = 1 was assigned. The normalized residuals are defined as 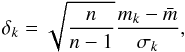 (3)for a given filter, where n is the number of measurements used for determining the mean magnitude,
(3)for a given filter, where n is the number of measurements used for determining the mean magnitude, 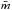 , and σk is the photometric uncertainty for the measurement k.
, and σk is the photometric uncertainty for the measurement k.
Designed this way, the Stetson index sets uncorrelated non-variable stars with values of S ~ 0, and significant variables with S ≥ 1. Different authors adopt different Stetson index limits for accounting for low-amplitude variable stars. For example, Carpenter et al. (2001) adopts S ≥ 0.55, and Plavchan et al. (2008) found periodic variables down to S ~ 0.2. For the purposes of the present work we adopted a selection limit of S ≥ 0.25 for variable stars. The distribution of Stetson variability index as a function of magnitude H is shown in Fig. 7.
 |
Fig. 7 Distribution of 3-band Stetson variability index vs. mean H magnitude. Top: 36 365 objects from control sample with 3 band light curve. Higher density of points is shown as darker gray. Bottom: 5083 stars from the candidate member catalog. In both panels, the 3-band light curve is plotted as light gray dots, and darker gray shows regions with high density of points. The dashed red lines show the selection value S = 0.25. In the right plot, periodic stars are plotted in black. |
From the candidate member sample, 4079 (80%) stars met the Stetson variability criterion. We did a visual inspection of these candidate variable stars and organized them in morphological classes1: eclipse-like variables (110 objects, 2.2% of the total candidate member sample), candidate periodic variables (1679, 33.0%), and non-periodic variable stars (1288, 25.3%). 1002 stars (20%) met the Stetson variability index criteria, but were not considered variables after light curve visual inspection. In the present study, since we target measurements of rotational periods, we only focus on the second group. Stars from the candidate periodic sample with confirmed period (Sect. 3.1) are shown in black in the right panel of Fig. 7.
3.1. Period search
The main technique used for identifying and determining periods was the Lomb-Scargle normalized periodogram (hereafter LSP; Lomb 1976; Scargle 1982), which is a widely used modified version of the classical periodogram based on fast Fourier transforms that can be applied to unevenly spaced datasets. The LSP algorithm used here was implemented according to Press et al. (1992) and Horne & Baliunas (1986), and it was normalized by the total variance of the data. This normalization guarantees that the power of the peak of a certain frequency in the periodogram, (z), is related to the false alarm probability (FAP) for that frequency as 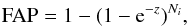 (4)where Ni is the number of independent frequencies used to compose the periodogram.
(4)where Ni is the number of independent frequencies used to compose the periodogram.
To apply the LSP algorithm to the sample, an oversampling factor of 260 and a scale factor of 5 for the Nyquist frequency were used; this sets the lower limit in the period search as ~0.83 day and is discussed in more detail in Appendix. A.1. For evenly spaced data, the higher limit in the frequency search would be given by 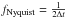 , where Δt is the time between consecutive data points. For unevenly spaced data, the Nyquist frequency, calculated with Δt being the mean time between two consecutive measurements, gives only a rough estimation for the higher limit in the frequency search (Scholz & Eislöffel 2004). Since we are dealing with unevenly spaced data, we extended our search over higher frequencies than the limit imposed by the Nyquist frequency (which is around 2 days for our dataset), and potential contamination because this choice is discussed in Sect. 3.2. Our dataset is composed of two observational seasons of ~45 days and ~75 days, respectively. For the lower limit in the frequency search, we adopted the resolution of the smaller season, i.e.,
, where Δt is the time between consecutive data points. For unevenly spaced data, the Nyquist frequency, calculated with Δt being the mean time between two consecutive measurements, gives only a rough estimation for the higher limit in the frequency search (Scholz & Eislöffel 2004). Since we are dealing with unevenly spaced data, we extended our search over higher frequencies than the limit imposed by the Nyquist frequency (which is around 2 days for our dataset), and potential contamination because this choice is discussed in Sect. 3.2. Our dataset is composed of two observational seasons of ~45 days and ~75 days, respectively. For the lower limit in the frequency search, we adopted the resolution of the smaller season, i.e., 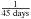 . Hence, periods were searched in the interval 0.83–45 days.
. Hence, periods were searched in the interval 0.83–45 days.
The search for periods via LSP consists in studying the highest peaks inside the periodogram and determining their significance. Judging a certain frequency’s power peak significance can be a tricky task and it is up to now one of the main limitations in studies regarding periodic stars. First, there is the one day aliasing phenomenon that can be written as 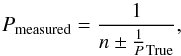 (5)with n integer, and it is caused by the limitations in observation imposed by the rotation of the Earth (cf. Tanner 1948). Second, we are here dealing with young stars and they typically show irregular variability that may be mixed with the periodic signal. The combination of irregular variability with discrete and uneven sampling may cause the occurrence of spurious periodogram power peaks, which despite being high peaks, are not truly associated with a periodic signal.
(5)with n integer, and it is caused by the limitations in observation imposed by the rotation of the Earth (cf. Tanner 1948). Second, we are here dealing with young stars and they typically show irregular variability that may be mixed with the periodic signal. The combination of irregular variability with discrete and uneven sampling may cause the occurrence of spurious periodogram power peaks, which despite being high peaks, are not truly associated with a periodic signal.
Horne & Baliunas (1986) reduced the problem of estimating the FAP (FAPh when referring to their concept of FAP) to the problem of finding the number of independent frequencies adequate to be applied in Eq. (4). They used Monte Carlo simulations to generate a large number of datasets with pseudo-Gaussian noise, and different time samplings. From the simulated data, they estimated Ni for a set of unevenly and non-clumped data, as Ni = − 6.3 + 1.2N + 0.00098N2, where N is the number of valid data points. Even though it is largely used in the literature, this method for estimating FAPh may not be adequate. As pointed out by Littlefair et al. (2010), FAPh calculations via Monte Carlo simulations with Gaussian noise are not reliable since they can only account for variability due to photometric errors, while often there is also some intrinsic variability characteristic of YSOs. Littlefair et al. (2010) propose, as an alternative, to use the light curves themselves as a mean of estimating the height of spurious peaks from their intrinsic variability. When using the light curves themselves, we are accounting for spurious peaks introduced into the periodogram by all factors affecting the dataset, from imperfect photometry to intrinsic variability (Littlefair et al. 2010).
False alarm probability from a control sample:
when studying the sample of member candidates of CygOB2, we expect to be dealing with a sample of young stars, and possibly with a high fraction of periodic stars. On the contrary, when studying the sample of all objects in CygOB2 FOV, we expect a sample rich in field stars, and a lower fraction of periodic stars. This gives us an alternative method for estimating the FAP, that consists in studying known constant stars in our field of view and estimating the recurrence and typical height of spurious periodogram peaks for them.
We estimated the FAP by using data from the control sample. LSPs were calculated for all the objects in the sample, and the power of the highest periodogram peak for each object was recorded. A sample of objects with frequency of the highest peak in the range20.3 <f< 0.5 day-1, and Stetson Variability Index smaller than S = 0.15 was selected, building this way a constant star sample, composed of 3999, 3077 and 3064 objects in J, H and K filters respectively. The false alarm probability, FAPc, was estimated from the cumulative distribution of the highest periodogram power peak in each filter as the power peak bin that contains the desired percentage of constant stars data. This way, the 0.01% FAPc level for J, H, and K filters were found at the power value 11.11, 10.52 and 10.47 respectively.
In spite of being a more accurate FAP estimator than analytical estimates or Monte Carlos simulations as derived by Horne & Baliunas (1986), FAPc gives only a reference value. Using it alone as a cut for selecting periodic stars may minimize spurious detections, but will not be enough for rejecting all of them. As discussed by Littlefair et al. (2010), very irregular variables and stars with poor rotational phase coverage are two common sources of contaminants in such analysis. Looking for a sample with the least contamination possible, we relied on the comparison of the periodograms in each of the three observed bands, and in two complementary statistical analysis, independent on the LSP.
 |
Fig. 8 Periodogram power peak vs. frequency from the selected peak distributions for the H band. All candidate members are shown as gray dots. (Top-left) Stars discarded owing to frequencies around 1 day-1 are shown in blue. (Top-right) Stars discarded owing to S-statistics limit are shown in red. (Bottom-left) Stars discarded owing to RL-statistics limit are shown in yellow. (Bottom-right) Stars selected as periodic stars are shown as black empty circles. The PFAc limit for the H band is shown as a black dashed line. |
Automatized period search:
the first test for periodicity was to evaluate the existence of significant peaks in each of the J, H, and K periodograms. In some cases, the same frequency was responsible for the highest peak in all three periodograms and thus that frequency was recorded as a possible valid periodic signal. Because of some missing points, differences in photometric errors and amplitudes, the same periodic signal sometimes produced different values of power peaks for each band. In particular, some missing points may favor the detection of an alias instead of the true period. Therefore, when the highest peak frequency was not the same for each of the three periodograms, we chose the one with the highest power. We then checked in the other two bands periodograms if the same frequency was responsible for one of the three highest peaks. If this was the case, that frequency and its power peak in each filter were recorded. If the same frequency was not found within the three highest peaks in the periodogram of each filter, or if the power of the that highest peak was smaller than the FAPc of 0.01%, the light curve was rejected as periodic. Periodogram power peak versus frequency from the selected peaks are shown in Fig. 8 for the H band. All candidate members with valid periodograms are shown as gray dots.
Next, we used the string/rope length method (Clarke 2002; Lafler & Kinman 1965), which is a non-parametric period search method based on Lafler-Kinman statistics (Lafler & Kinman 1965). For each trial period, the original data is folded in phase and reordered for ascending phases, and the string-length statistics (hereafter SL-statistics) was calculated as the summation of the squares of the differences between the consecutive phases reordered measurement values, normalized by the variance of the data. Given the normalization proposed by Clarke (2002), values of SL-statistics fluctuate around the unity with periodic stars presenting minimum values. The SL-statistics can be extended to the case of multi-band data, which Clarke (2002) calls the rope-length statistics (RL-statistics). In the multi-band case, the SL-statistics of each band is summed and divided by the total number of bands. The SL- and RL-statistics values can be calculated for a set of trial periods, and used to compose a periodogram. In the present study we do not used SL- or RL-statistics for searching for periods, as the two indexes were only evaluated for the periods selected via LSP, and they were used to check each period reliability. We chose the limit value for RL-statistics using Monte Carlo simulations with 78 000 synthetic periodic light curves built as described in Sect. 3.2. For each synthetic light curve, RL-statistics was calculated for the true period and for the two aliases formed around 1 day. From the comparison between the RL-statistics versus amplitude distributions for true period and aliases, we adopted an RL-statistics of 0.8 as a limit between true periods and probable aliases.
The Saunders statistics (S-statistics; Saunders et al. 2006) is a technique that may be used for investigating the aliasing effect of sampling. It is a normalized phase coverage metric and it is defined as the sum of the squares of the distances between two consecutive points in the folded in phase light curve, ordered for ascending phases, and normalized by the value of the sum for an ideal spacing of equally spaced observations across the phase space. A uniform phase coverage gives a S-statistics of order unity. Growing irregular phase coverage makes S-statistics increase. The S-statistics is especially good for removing the spurious periods arising from the one day-1 natural frequency introduced by the rotation of the Earth (e.g., Littlefair et al. 2010). Monte Carlo simulations were also performed to obtain a limit value for S-statistics. For each synthetic light curve in the simulated sample, LSP analysis was applied and the highest peak in the periodogram was recorded. We selected light curves for which the difference between the LSP period and the input period was smaller than 10% the input period; this resulted in a subsample of 64 102 synthetic light curves for which S-statistics was calculated. A cumulative distribution was built for this subsample and from the bin from which 99% of the data is contained, we defined the limit value of S-statistics equal to 5 for selecting stars with true period.
The effect of the chosen RL-statistics and S-statistics limit selection are shown in the frequency versus highest periodogram power peak distribution in Fig. 8. Even though the filter for S-statistics significantly reduces the ~1 day excess in the power peak versus frequency distribution (cf. Fig. 8), it is not enough to account completely for such aliasing effect. This conclusion was achieved after visually inspecting some light curves and folded light curves, for stars with detected period very close to 1 day that were not filtered out by S-statistics limits: in their majority, those stars were long-term non-periodic variables, and not truly periodic stars. To deal with the remaining contamination, a filter for frequencies in the range 0.92–1.08 day-1 was added. We chose this range of about 1 day based on simulations discussed in Appendix A.1.
The final selection was composed of 1291 stars: 25 eclipse-like, 1256 from the candidate periodic variables list, 2 non-periodic variables (stars selected as periodic stars, but with no visible periodic signal in the light curve), and 8 non-variable stars (stars not considered as variable according to the visual selection). Each period was measured as the mean value of the inverse of the frequencies obtained via LSP, 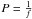 for each filter. From that, it follows that the rms error for each band period is δP = δf × P2. Simulations, as described in Sect. 3.2, were used to estimate the resolution δf for each filter. For each synthetic periodic light curve, we calculated the LSP and estimated the full width at half maximum (FWHM) of the highest periodogram power peak frequency. We estimated δf = ⟨ FWHM ⟩ from the FWHM versus period distributions for each filter, and by propagating the error it follows that the error in the periods are around δP = 0.002P2, which gives a 4.8 h error for a 10-day period.
for each filter. From that, it follows that the rms error for each band period is δP = δf × P2. Simulations, as described in Sect. 3.2, were used to estimate the resolution δf for each filter. For each synthetic periodic light curve, we calculated the LSP and estimated the full width at half maximum (FWHM) of the highest periodogram power peak frequency. We estimated δf = ⟨ FWHM ⟩ from the FWHM versus period distributions for each filter, and by propagating the error it follows that the error in the periods are around δP = 0.002P2, which gives a 4.8 h error for a 10-day period.
3.2. Period detection completeness and reliability
We ran Monte Carlo simulations on synthetic light curves to estimate the efficiency and limitations of the techniques employed in the period search method. We used a modified version of this type of simulation commonly presented in the literature (e.g., Littlefair et al. 2010; Moraux et al. 2013), since we used candidate members to build synthetic light curves instead of non-members in the field. To build synthetic light curves, “constant” stars were selected from the candidate members catalog as follows. First, we selected stars with a Stetson variability index smaller than 0.15 and more than 60 valid observations in each filter. From those, we selected stars classified as non-variable stars during the visual light curve inspection (stars with very small and uncorrelated variability). Finally, for each filter, we analyzed the peak to peak (ptp) amplitude versus magnitude distribution; using a bin of size one for magnitudes between 10 and 18, we randomly selected stars in the minimum outlier of the distribution. Whenever possible, two stars were selected per magnitude bin. A total of 39 stars were selected this way, and as they were considered the most constant stars in the candidate member sample, their light curves reflect the fingerprints of the dataset, including the window of observations and the kind of photometric and instrumental errors contained on the light curves. Each light curve in this constant stars sample was then used as a template for building synthetic light curves. For each light curve, the time sampling, magnitude, and error values were kept, and a periodic signal with random waveform, period (Pin), amplitude, and phase was added to it. We generated 2000 synthetic light curves per constant star, totaling 78 000 synthetic light curves. We generated random periods, amplitudes, and phases with uniform distributions.
From the visual inspection phase in the light-curve analysis, it was noticed that even though periodic behavior was often observed, they were usually not perfect sinusoidal signals. This may have direct consequences on the period analysis performed, as certain wave forms may favor the detection of aliases or harmonics in the LSP, instead of the true frequency. In fact, when inserting periodic eclipse-like wave forms in our synthetic light curves, we notice a favoring of the detection of harmonics instead of the true period. As we already distinguished between eclipse-like and candidate periodic light curves, eclipse-like wave forms are not included in the completeness analysis. For simulation purposes, we used single period sine-wave, sawtooth wave, triangle wave, and cycloidal wave as wave forms. The wave form was randomly chosen at the beginning of the creation of each synthetic light curve.
 |
Fig. 9 Ptp amplitude distributions for each band. Black: membership candidate catalog. Gray: periodic stars (Sect. 3.1). Black dashed lines show the median value for the member candidate sample: 0.094, 0.075, and 0.074 mag for J, H, and K band, respectively. Gray lines show the same for the periodic sample: 0.102, 0.087, and 0.080 mag. |
Two series of simulations were performed. The first considers periods as large as the maximum period searched (45 days; cf. Sect. 3.1), and as short as 0.2 days, which is about the minimum rotational periods verified in other young regions (e.g., Irwin et al. 2008; Littlefair et al. 2010; Moraux et al. 2013). It also considers a large range of amplitudes from 0.015–1.5 magnitudes. The second series considers amplitudes in the range 0.015–0.2 mag and periods in the range 0.2–20.0 days, which considers a more realistic amplitude and period upper limit given that Figs. 9 and 13 show that most of the stars have amplitudes smaller than 0.2 mag and periods smaller than 20 days. Random ptp amplitudes were generated for the J filter, and H and K magnitudes were set according to the ratio between the median value for each band periodic star ptp amplitude distribution (gray dashed lines; in Fig. 9); i.e., 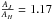 and
and 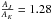 .
.
 |
Fig. 10 Period detection completeness and contamination levels for a mix of periodic synthetic light curves, with periods between 0.2 and 45 days and amplitudes between 0.015 and 1.5 mag. Upper left panel shows Pin × Pout diagram with every synthetic light curve shown as a gray dot, recovered sample periods shown in green, and selected sample periods shown in blue. Harmonic paths are shown as blue dotted line, and 1 day aliasing (cf. Eq. (5)) paths are shown as dashed black lines. Bottom plots: completeness distributions per magnitude (left), amplitude (medium), and period (right) bins. Top: given the selected sample, contamination levels are shown per amplitude (middle) and period (right) bins. Fraction of true recovers are shown as empty bars, and fraction of contamination are shown as filled gray bars. |
We applied the same analysis and filtering to the synthetic light curves as for the candidate member catalog. Both input and output periods were recorded. From the results, we defined two samples as follows: synthetic light curves flagged as periodic were considered as in the “selected”-sample and synthetic light curves were considered as in the “recovered” sample if the input and output periods were the same, i.e., if the deviation between them was smaller than 10% the input period ((| Pin − Pout | ) ≤ 0.1Pin)). The results for the J band in the two samples are shown in the Pin × Pout distribution in Figs. 10 and 11.
For the completeness analysis, a period in a synthetic light curve was considered successfully recovered if it was present in both the selected and recovered samples. The completeness, i.e., successfully recovered periods divided by the number of input periods, for the first series of simulations is presented in Fig. 10 (middle, top, and bottom plots). In these plots, one can see that the completeness decreases slightly for increasing magnitude (plot at the bottom left), going from ~69% for magnitudes about 12 to 47% for magnitudes larger than 18. The completeness of the sample is quite uniform and is ~67% for amplitudes between 0.18 and 1.5 mag with a significant drop between 0.015 and 0.18 mag, reaching only 37%. The completeness is also quite uniform and is ~ 87% for periods between 1.2 and 24 days (bottom plot); but it drops to ~12% for periods smaller than ~1 day and to ~12% for periods larger than 36 days, which can be explained by strong aliasing factors in the very large and very small period extremes.
 |
Fig. 11 Same as Fig. 10, but for a mix of periodic synthetic light curves with periods between 0.2 and 20 days and amplitudes between 0.015 and 0.2 mag. |
Figure 10 also shows the contamination analysis for the selected sample. In the top middle and right panels, 100% means the complete selected sample, empty bars show the percentage of light curves in this sample with successfully recovered periods per period or amplitude bins, and filled bars show the percentage of light curves in the selected sample, but that do not have (| Pin − Pout | ) ≤ 0.1Pin and, therefore, are contaminants to the sample. We point out the samples used to build each histogram in Figs. 10 and 11; while the completeness analysis takes into account the total number of periods available to be measured (i.e., every gray dot inside the Pin × Pout), the contamination analysis accounts only for periods that were measured by the process described in the previous section (i.e., blue and gray points inside the Pin × Pout). From the amplitude versus contamination fraction histogram one can see that the contamination level is quite small for a given amplitude, going from a maximum of about 16% for the smallest amplitude bin and reaching only 5% for the highest amplitude bin. The period versus contamination fraction histogram shows that the contamination level is insignificant (~1%) for periods longer than 6 days, and that it increases significantly up to 70% for measured periods shorter than ~1 day.
Even though the simulations presented in Fig. 10 comprise the whole amplitude and period ranges measured for our periodic sample, these simulations assume uniform distributions for the ranges considered, which is unrealistic if we consider the real distributions of periods and amplitudes. Only ~1% of the periodic sample had measured periods longer than 20 days, and Fig. 9 shows that the measured amplitudes are mostly low amplitudes up to 0.2 mag, which corresponds to the first bin of amplitude in Fig. 10. Therefore, we ran a second series of simulations to consider, in more detail, a sample that is dominated by periods shorter than 20 days and low amplitudes.
The second series of simulations are presented in Fig. 11. The completeness versus amplitude panel shows that the completeness of the sample increases from merely 4% for amplitudes smaller than 0.035, which is very close to the 2% error level of the data, to ~78% for amplitudes larger than 0.18 mag in J filter. The completeness for given period is quite homogeneous and is about 57% for periods larger than 2 days and as small as about 12% for periods smaller than 2 days. The completeness for given J magnitude bin is quite flat and is about 67% until magnitude 15, but it decreases toward larger magnitudes up to ~14% for magnitudes larger than 18. The completeness increase with amplitude and completeness decrease with magnitude can be explained by the error distributions in Fig. 5, since higher amplitudes result in higher S/N, while stars with larger magnitudes have larger errors and therefore smaller S/N.
There is a small contamination level as a function of amplitude, which decreases from ~16% to ~5% with increasing amplitude. From the upper left plot in Fig. 11, one can see in the Pout>Pin region that there exists some contamination arising from short Pin values aliased toward larger periods. The effect of this contamination can also be seen in the region filled in gray inside the contamination fraction as a function of period plot (upper right): the contamination is very high for period bins up to ~2 days, reaching ~44% for periods between 1.0 and 2.0 days and ~86% for periods smaller than 1 day. But this contamination decreases to very low values for periods between 2 and 7 days, and it is almost insignificant for periods larger than that. Additional sources of contamination are discussed in Appendix A.
3.3. Comparison with periods in the literature and binary stars contamination
Henderson et al. (2011) observed CygOB2 in two seasons of 19 and 18 nights with a few observations per night. They presented 121 stars variable in the R and I bands, 95 of which had measured periods. Within a distance of 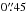 we found 79 of their variable stars that were also present in our catalog: 7 of them were classified by the present study as non-variable stars; 9 were eclipse-like variables; 17 were classified as non-periodic variable stars; and 46 were periodic candidates. Figure 12 shows a comparison between the periods measures by Henderson et al. (2011), and those measured in the present study. Both studies measured periods of 32 stars in common and the same period for 14 of them. Since we are only interested in periodic behavior that may be reflecting the rotation of the star, all the variables presented by Henderson et al. (2011) as eclipsing binary candidates (10 stars) were excluded from our periodic stars list. Taking out the eclipsing binary candidates from the plot in Fig. 12, all remaining stars without equal periods measured in both studies fall on the aliasing paths, and the 8 objects in this situation were also ruled out from our periodic list.
we found 79 of their variable stars that were also present in our catalog: 7 of them were classified by the present study as non-variable stars; 9 were eclipse-like variables; 17 were classified as non-periodic variable stars; and 46 were periodic candidates. Figure 12 shows a comparison between the periods measures by Henderson et al. (2011), and those measured in the present study. Both studies measured periods of 32 stars in common and the same period for 14 of them. Since we are only interested in periodic behavior that may be reflecting the rotation of the star, all the variables presented by Henderson et al. (2011) as eclipsing binary candidates (10 stars) were excluded from our periodic stars list. Taking out the eclipsing binary candidates from the plot in Fig. 12, all remaining stars without equal periods measured in both studies fall on the aliasing paths, and the 8 objects in this situation were also ruled out from our periodic list.
 |
Fig. 12 Comparison between periods measured in the present work and in Henderson et al. (2011). Gray circles show the periodic stars in common between the two works. Stars with the same period measured in both works fall over the red dashed line. Red circles show the eclipsing binaries candidates from Henderson et al. (2011). Continuous black lines show 1 day aliasing paths and dashed black lines show the path for harmonics. |
3.4. Visual light-curve crosscheck
Finally, we visually crosschecked the folded light curves for periodic stars selected in Sect. 3.1, and verified if a periodic signal was indeed present in them. We considered the stars that were selected as periodic but did not show a visible periodic signal in the folded light curve to be contaminants. We found 23 (1.8% of the periodic sample) contaminant stars this way. We also visually checked the light curves for the stars selected as periodic, but classified during the visual inspection as non-variable and verified that 4 (0.3%) of them did not show a periodic signal in the folded light curve, as they were considered extra contaminations to the periodic sample.
4. Results
4.1. General period distributions
After excluding eclipse-like variables, and possible visually selected contaminants (see Sect. 3.4), we compiled a final list of 1211 candidate members of CygOB2 with periodic variability and periods between 0.86 and 32.49 days. The period distribution for the 1196 stars with P< 20 days is shown in Fig. 13. Since only 15 stars (~1% of periodic sample) have periods longer than 20 days, we kept those stars outside the distributions shown in the rest of the paper. Error bars were estimated taking into account the completeness and contamination analysis for periods up to 20 days (Fig. 11); upper error bars account for the incompleteness of the sample for each magnitude bin (Fig. 11) and lower error bars account for the contamination level per magnitude. Even though they were not used in the present results analysis, periods shorter than 2 days are shown in red in the distribution in Fig. 13, and also in the following figures in this section. While not accounting for the shortest periods, the mean, standard deviation and median values for the general period distribution are P(μ,σ,ν) = 6.67, 4.18, and 5.92 days.
 |
Fig. 13 Period distributions for the 1196 periodic stars with P< 20 days found in the present study in both linear (top) and logarithm (bottom) scale. The median value for P ≥ 2 days stars is shown as a dotted line. There were 879 stars with P ≥ 2 days and P< 20 days. The red bins show the fast rotators with P< 2 days excluded from the analysis. |
 |
Fig. 14 Top: period vs. ptp H amplitude for periodic stars. Bottom: median H magnitude vs. ptp amplitude H for periodic stars. Stars with P< 2 days are shown as red dots; stars with P ≥ 2 days are shown as gray dots; and disk-bearing periodic stars are shown as blue dots. |
The photometric ptp amplitudes for the H band are shown as a function of periods in the top panel of Fig. 14. The amplitude of 90% of the periodic stars is widely distributed between 0.03 and 0.18 mag; 9% of them exhibit amplitudes between 0.18 and 0.51 mag and 1% exhibit amplitudes as high as 1 mag.
The bottom panel in Fig. 14 shows the photometric ptp amplitudes for the H band as a function of magnitude. The increase of the lower amplitude envelope with magnitude is due to an observational bias related to the dependence of the minimum photometric errors on the magnitude (cf. Fig. 5), which makes it increasingly difficult to detect low amplitude variables among fainter stars. On the other hand, the upper envelope of the distribution also shows an increase with amplitude, which can be explained by a larger and/or more uneven spot coverage for fainter (less massive) stars. There are 61 periodic star outliers in the median H magnitude versus amplitude distribution, showing higher amplitude than most of the stars with the same brightness. While 46% of the disk-bearing stars follow the main distribution, 74% of all the outliers are disk-bearing stars. This is consistent with the idea that most of periodicity observed in the light curves for disk-bearing stars arises mainly from two physical mechanisms: the rotational modulation by hot spots, which are expected to show higher variability amplitudes than cold spots (e.g., Carpenter et al. 2001; Scholz et al. 2009), and by circumstellar obscuration, which may be the responsible for the higher amplitudes observed (e.g., AA Tauri stars; Bouvier et al. 2003).
Rotational periods for CygOB2 periodic candidate members.
The 894 periodic stars with P> 2 days are listed in Table 1, which includes their identification within our variability survey catalog; their identification in the catalogs presented by GDW13 and GDW15; their coordinates in the present study; their Stetson variability index (Sect. 3); period (Sect. 3.1); mass and AV (Sect. 4.3.1); median J, H, and K magnitudes, their propagated errors, and their ptp amplitude for each band (Sect. 3); their IR-class according to GDW13 (Sects. 2 and 4.2); and a flag indicating the presence of disk, assuming the value 1 for disk-bearing stars, and 0 for non disk-bearing stars.
4.2. Period distribution for disk-bearing versus non-disk-bearing stars
To further investigate the nature of the period distribution presented in Fig. 13, we compared the period distributions of disk-bearing and non-disk-bearing stars. Since we do not have reliable mass accretion rate measurements for Cygnus OB2 low mass stars3, we rely on X-ray emission and IR disk diagnosis to distinguish between CTTs and WTTs samples and investigate the star/disk connection effect in the period distributions. The disk-bearing stars in the sample are the disk-bearing stars listed by GDW13. The non-disk-bearing stars in the sample are the X-ray emitter sources from Wright et al. (2014), which were classified as members by Kashyap (2017) without IR-excess.
 |
Fig. 15 Period distributions for periodic disk-bearing stars with P ≤ 20 days (top) and periodic non-disk-bearing stars with P ≤ 20 days (bottom) for both linear and logarithm distributions. The median value for P ≥ 2 days stars is shown as dotted line. There were 80 disk-bearing stars and 799 non-disk-bearing stars with P ≥ 2 days and P< 20 days. The red bins show the fast rotators with P< 2 days excluded from the analysis. |
There were 91 disk-bearing periodic stars, 82 with P ≥ 2 days, and 1120 non-disk-bearing periodic stars, 812 with P ≥ 2 days4. The period distributions for disk-bearing and non-disk-bearing stars are shown in Fig. 15. A visual inspection of the distributions suggests that the two samples exhibit different rotational properties, even without taking into account the bins with P< 2 days. The disk-bearing stars distribution is quite flat for periods in the range 4–11 days, decreasing for periods smaller than 4 days. The non-disk-bearing stars distribution is flat for periods between 4 and 7 days, but it decreases for periods larger than that and a larger number of stars have periods smaller than 4 days.
The mean, standard deviation, and median values are P(μ,σ,ν) = 7.87, 4.36, and 7.34 days for disk-bearing stars, and P(μ,σ,ν) = 6.55, 4.14, and 5.80 days for non-disk-bearing stars. A visual inspection in the distributions of Fig. 15, and a quick look at the statistical values suggest that although both distributions show a large dispersion, disk-bearing stars are on average rotating slower than non-disk-bearing stars. A Kolmogorov-Smirnov (KS) test5 considering only periods higher than 2 days statistically supports this idea, with a probability of only 0.4% that the two distributions came from the same parent distribution.
4.3. Period distributions for given masses
4.3.1. Mass estimation
Knowledge of individual extinctions would be necessary to estimate masses for the candidate members, which in turn would require knowledge of spectral types for the stars. Since there is no available information about the spectral type for the low mass members coming from spectroscopic studies in the literature, individual extinction for candidate members could not be formally determined. An alternative to that is to look for optical counterparts in other surveys and use optical colors to estimate the reddening of each object. Since colors are not affected by the distance, a distance independent individual AV can be estimated for each star using color–color diagrams (CCD). This can be carried out with a chosen extinction law to estimate the displacement of a star in the CCD from an appropriate isochrone with zero extinction, which is plotted in the same diagram.
As described in Sect. 2.2, riz photometry is available from GDW12, who give riz indices for 1086 stars of our periodic sample with errors smaller than 0.2 mag in each filter: 991 from GTC/OSIRIS observations and 95 from SDSS DR8. Thus, we used the i − z versus r − i color–color diagram to estimate individual extinctions. Instead of using a 3.5 Myr Siess et al. (2000) isochrone to estimate AV, as in GDW12, we used an empirical dwarf sequence from Covey et al. (2007). We adopted relative extinction for riz bands from Schlegel et al. (1998)6, where the authors used a RV = 3.1 extinction law from Cardelli et al. (1989) to evaluate relative extinctions. Since both Covey et al. (2007) dwarf sequence, and the riz data used from GDW12 (cf. Sect. 5.1 of their paper) are in SDSS photometric system, no transformation was required; this justifies the differences in our method of estimating individual extinctions and that used by GDW12. The CCD for riz colors is shown on the bottom plot of Fig. 16.
 |
Fig. 16 Top: individual AV distribution for periodic stars. The red line shows the median value, 4.1m. Bottom: riz CCD for periodic stars. Covey et al. (2007) empirical dwarf sequence is shown as dotted lines. A black arrow shows a reddening vector from Schlegel et al. (1998) for AV = 2m. |
 |
Fig. 17 Top: histogram with mass distribution for periodic stars. Bottom: r − i vs. r-DM CMD for periodic stars. Mass tracks from Bell et al. (2014) for Pisa models (Tognelli et al. 2012) with semi-empirical corrections are shown as dotted lines. A black arrow shows a reddening vector from Schlegel et al. (1998) for AV = 2m. Black Xs show stars excluded from the mass estimation because they were too far away from the minimum mass track. |
We were able to estimate AV for 1058 periodic stars, 971 using GTC/OSIRIS data, and 86 using SDSS DR8 data. The distribution of individual extinctions obtained is shown in the top of Fig. 16. The median AV obtained for the periodic sample was 4.1m, which is in good accordance with the 4.33m value obtained by GDW12 for stars in CygOB2 center.
We then used our estimations of individual extinction values and the r − i versus r CMD to estimate masses. We adopted a distance modulus DM = 10.62 (d = 1.33 kpc Kiminki et al. 2015). For each periodic star with estimated AV, we dereddened it for the individual AV and applied the distance modulus. Masses were then estimated given the position of the dereddened, and distance-corrected star inside the CMD in relation to a grid of PMS semi-empirical isochrones from Bell et al. (2014), with PISA models (Tognelli et al. 2011, 2012) for solar metallicity (Z⊙ = 0.013) and ages in the range 0.1–30 Myr. The grid of semi-empirical isochrones was built with the CMDfit software7 and the bolometric corrections applied were calculated by the software authors by folding spectra with opacities from BT-Settl (Allard et al. 2011) through the desired filter response and applying empirical corrections from Bell et al. (2014). In our case, we chose the filter responses for SDSS filters (Doi et al. 2010) with an AB zero point. The isochrones used in the grid comprise masses in the range 0.1–8 M⊙. We estimate masses for 1054 periodic stars. The bottom plot in Fig. 17 shows a r − i versus r CMD for dereddened periodic stars and mass tracks from 0.1 to 1.4 M⊙. The middle plot in Fig. 17 shows a histogram with the distribution of estimated masses for periodic stars. The CMD in Fig. 17 also shows a lack of stars with masses larger than ~0.9 M⊙, which is mainly because most of the stars with masses larger than that are very close to the saturation limit in our WFCAM/UKIRT observations.
A caveat on using optical colors for estimating masses is that stars with disks may be affected by accretion, scattering, or obscuration of the central star by the inner disk. Only 65 stars in our sample are periodic, have disks, and had masses estimated as described in this section. We verified that only 3 of those stars had an evolutionary status from GDW13, which is compatible with some ongoing phenomena that could affect their optical colors; of these 3 stars, 1 star has Hα emission, 1 star has colors that are compatible with scattering, and 1 star has a disk in high inclination. Since they correspond to a very small fraction of our sample, we consider that these effects do not influence our mass estimation.
4.3.2. Period distributions in different mass ranges
Mass estimations for PMS stars can be extremely model dependent, but for all models, lower effective temperatures correspond to lower mass stars, and thus the sense of variation of rotation with mass is model independent (Herbst et al. 2001). To test a possible mass-rotation connection in our data, we split the periodic sample into two mass bins: M ≤ 0.4 M⊙ (90 stars with P ≥ 2.0 days) and M> 0.4 M⊙ (687 stars with P ≥ 2.0 days). Histograms showing the period distribution for each of the three mass bins are shown in Fig. 19. From the distributions, it is evident that the period distribution for medium and slower rotators present a mass dependence. The period mean, standard deviation, and medium values are P(μ,σ,ν) = 7.0, 2.9 and 6.9 days for the M ≤ 0.4 M⊙ sample, and P(μ,σ,ν) = 6.5, 4.2 and 5.7 days for the M> 0.4 M⊙ sample.
Figure 18 shows the mass versus rotational period distribution for Cygnus OB2. The blue dashed line indicates the limits between the mass bins adopted and are meant to allow a simple comparison between Figs. 18 and 19. Keeping in mind that our data sampling does not allow us to access the complete fast rotators population, a lack of periods in the 2–5 day range can be verified for the M ≤ 0.4 M⊙ mass bin. Both linear and log scaled rotational period distributions are strongly peaked for the lower mass interval, but the peak, around 6.1 days, is more evident in log-scaled distribution. The overall distribution gets broader for the M> 0.4 M⊙ mass bin, which is reflected as an increase in the distribution’s σ. The peaked distribution verified for lower masses is less evident here, and an increase in the number of faster and intermediate rotators makes the period distribution flatter.
A KS test gives a probability of ~0.02% that the distributions for M ≤ 0.4 M⊙ and M> 0.4 M⊙ samples came from the same parent population. The results therefore indicate that for the periodic sample analyzed here, the lower mass stars are rotating on average more slowly than higher mass stars.
Since masses derived from CMD are highly model dependent, we verified that our results hold for masses estimated from different models. We repeated the process for estimating masses described in Sect. 4.3.1 using 3 other models: Baraffe et al. (1998), Baraffe et al. (2015) with Bell et al. (2014) empirical corrections, and Siess et al. (2000). The first two models result in masses very similar to our adopted masses. For Siess et al. (2000) model, masses larger than 0.4 M⊙, PISA models yield masses ~1.2 times larger. For masses bigger than 0.4 M⊙ PISA and Siess et al. (2000) can be different up to a factor of 2.
We adopted the mass limit of 0.4 M⊙ because the convective boundary, i.e., the mass under which all the stars are fully convective even in the MS, is around ~0.3 M⊙ for the model used. On the other hand, all low mass PMS stars are initially fully convective. Gregory et al. (2012) estimated the age at which a PMS star first develops a radiative core for the Pisa models, and according to their estimates a 0.5 M⊙ star develops its radiative core around ~9.3 Myr, and a 0.4 M⊙ star around ~15 Myr. As we discuss in Sect. 5.1, CygOB2 low mass stars age estimates are between 2.5–6.75 Myr (Wright et al. 2010), but these estimates were based on Siess et al. (2000) models, which, when applied to PMS stars, may result in underestimated ages down to a 1.5–2.0 factor. Accounting for this, we split the sample at 0.4 M⊙ as a way to guarantee that the lower mass sample is not contaminated by stars that are no longer fully convective.
We also investigated the effect of other choices of mass limit and concluded that the results hold for different values. Using 0.5 M⊙ gives results that are qualitatively similar to 0.4 M⊙ (lower mass stars rotate slower) and a KS test yields statistically different samples. When splitting the periodic stars in several mass ranges, the overall result is kept the same. Stars with M< 0.4M⊙ rotate slower than stars in the mass range 0.4–0.6 M⊙ and a KS test results in a 0.05% chance that they came from the same parent distribution. The 0.4–0.6 M⊙ and 0.6–0.8 M⊙ samples have very similar rotational properties and cannot be distinguished according to a KS test. When comparing the 0.4–0.5 M⊙ sample with the 0.5–0.8 M⊙ sample, the former is slower than the latter, but according to the KS test it is not possible to say whether they are different; this supports our choice of 0.4 M⊙ as mass limit for the comparison.
 |
Fig. 18 Mass vs. period distribution for periodic candidate members of CygOB2. Stars with reliable periods (P ≥ 2 days) are shown as black circles, and stars with dubious periods (P< 2 days) are shown as red circles. Dashed red lines delimit for periods equal to 2 and 10 days. The blue dashed line indicates the limit between the mass bins analyzed in the present section. |
5. Discussion
Given the CygOB2 rich population and the fraction of candidate members with periodic variability, Cygnus OB2 is a valuable target for testing the theory of stellar angular momentum evolution during the PMS.
In this section we discuss our results in the context of early rotational evolution for low mass stars. It is of utmost importance to keep in mind the limitations of our sample. Since the faster rotators (P< 2 days) in the sample are strongly contaminated, our discussion is based on a few fast, intermediate, and slow rotators. As in Herbst et al. (2002), we based our definition of rotational regimes on values of rotational angular velocity. Given that rotational angular velocity relates to the measured periods as 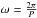 , we called stars with
, we called stars with 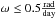 (P> 12.56 days) very slow rotators, stars with 0.5
(P> 12.56 days) very slow rotators, stars with 0.5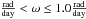 (P> 6.28 days) slow rotators, and stars with
(P> 6.28 days) slow rotators, and stars with 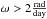 (P< 3.14 days) fast rotators. Median rotators are stars rotating with rotational angular velocity in the range 1
(P< 3.14 days) fast rotators. Median rotators are stars rotating with rotational angular velocity in the range 1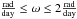 .
.
In Sect. 4.2 we considered the stars listed by GDW13 as disk-bearing stars to be CTTS, and the stars selected as candidate members because they had X-ray emission from Kashyap (2017) and not listed as disk-bearing stars to be WTTS. A caveat arises from this selection procedure, since it does not guarantee that the disk-bearing stars are still interacting with their disks nor does it account for disk-bearing stars with inclinations that do not produce IR excess. Nonetheless, using this criterion the disk fraction in the full candidate member sample is 24%8 and about 10% among candidate periodic stars. Given that the sample of stars with reliable period measured (with P ≥ 2 days) contains only 82 stars with disks, the disk fraction in this sample is only 7.5%. When looking at the light-curve morphological classification for the non-disk-bearing sample: 39.1% of the stars were classified as periodic candidates, 1.1% as eclipse-like, 14.5% as non-periodic variable stars, and 45.3% as non-variable stars. For the disk-bearing stars: 13.8% were periodic candidates, 5.7% were eclipse-like, 59.7% were non-periodic variables, and 10.8% where non-variables. This indicates that the data sampling used here is more efficient in detecting periodicity among non-disk-bearing stars, or equivalently, that the sample is biased toward WTTS.
The origin of the bias toward WTTS can be explained by taking the different physical mechanisms responsible for variability in CTTS and WTTS into account. Within WTTS we expect to detect mainly stars with variability caused by cold spots, which are expected to produce a low amplitude JHK variability (typically smaller than one tenth of magnitude), even for large spot coverages (e.g., Carpenter et al. 2001). For the CTTS the variability scenario may be more complicated. Besides the variability caused by the presence of cold spots, the most common sources of variability in CTTS are obscuration by circumstellar material, accretion driven variability, such as the presence of hot spots and variable mass accretion rates, and instabilities in the accretion disk (e.g., Carpenter et al. 2001; Cody et al. 2014; Stauffer et al. 2014; Rice et al. 2015; McGinnis et al. 2015; Sousa et al. 2016; Roquette, in prep.). While a single physical process may sometimes dominate the light curve of the star, often several concurrent variability sources exist. Adding up common limitation in the datasets, such as limited time and wavelength coverage, multiple physical processes that compose a complex light curve may not be distinguishable. Thus, rotational periods in CTTS are often masked by other variability sources in the light curve.
 |
Fig. 19 Histograms showing period distributions for given mass bins in linear (left) and logarithm scale (right). The top panels represent M ≤ 0.4MM⊙ and the bottom panels M> 0.4 M⊙. The median value for P ≥ 2 days stars is shown as a dotted line. There were 89 stars with M ≤ 0.4MM⊙ and P ≥ 2 days and P< 20 days, and 676 stars with M> 0.4 M⊙ in the same period interval. The red bins show the fast rotators with P< 2 days excluded from the analysis. |
This bias toward WTTS has been reported by other studies in the literature (e.g., Cohen et al. 2004; Herbst & Mundt 2005) and it is assumed to be present in all the studies comparing the rotation of CTTS and WTTS. In the present study, a direct consequence of this bias is that the size of the CTTS sample is much smaller than the size of the WTTS sample. Consequently the results regarding disk-bearing stars are less statistically significant. For this reason, we did not separate CTTS and WTTS by mass ranges in our comparison. Therefore, we could not verify the statistics correlation of rotational periods with disk diagnosis for restricted mass ranges to test the evidence that disk locking acts differently in different mass ranges.
Another bias arising from the use of disk diagnosis based on IR excess is that a correlation of rotation with disk presence diagnosed via IR excess can be a secondary effect due to the dependence of IR excess on mass suggested by some authors (Littlefair et al. 2005). Hillenbrand et al. (1998) showed that the IR excess produced by the disk is a function of the disk properties, but also of the mass and radius of the star. The contrast between the disk and photosphere of the star is larger for higher mass stars, so with lower contrast it is more difficult to detect disks of lower mass stars. In regions where lower mass stars rotate faster than higher mass stars (e.g., NGC 2362; Irwin et al. 2008), lower mass stars with undetected disks can mimic a correlation between fast rotators and non-disk-bearing stars. This effect can be minimized using longer IR wavelengths to identify stars with IR excess, and Cieza & Baliber (2007) showed that since the photosphere/disk contrast is higher in the mid-IR, disks can be detected even for lower mass stars with Spitzer/IRAC colors. We discarded the possibility that our sample was affected by such bias. The analysis of rotation as a function of mass bin presented in Sect. 4.3.2 showed that, contrary to several other young regions studied, lower mass stars in CygOB2 rotate on average slower than higher mass stars. Given that even if disks around some lower mass stars were undetectable within the limits of the Spitzer data used by GDW13 for evaluating disk-bearing stars, the contamination by those stars would introduce slow rotators to the non-disk-bearing sample. This would produce contamination in the sense of occluding the correlation between IR excess and slow rotators. Hence we rule out the possibility that a correlation between IR excess and slow rotators in our sample could be mimicked by a secondary effect.
Focusing on the whole list of members with periodic variability in CygOB2 (see Sect. 4.2), and even though our dataset is only complete for rotators with P ≥ 2 days, our results corroborate the general idea that the star-disk interaction has some influence in the rotational regulation of young stars. Disc-bearing stars in our sample are rotating on average slower than non-disk-bearing stars.
Cieza & Baliber (2007) present an alternative way of looking for observational evidence of the disk-locking phenomenon by studying the disk fraction as a function of period. A plot of disk fraction per period bin is shown in Fig. 20 (top). The black circle shows the central period for each bin, and the bars show the length of each bin. The bins were built considering fast rotators, intermediate rotators, slow rotators, and very slow rotators defined as in the beginning of the present section. Even though the disk fraction for periodic stars is low (~9%), the top plot of Fig. 20 shows that the disk fraction is actually quite dependent on the rotational period, having a maximum value of ~13% for stars with rotational periods between 8.4 days, and 12.6 days.
 |
Fig. 20 Disk fraction as a function of period. In both plots, circles show the center of each period bin, while horizontal bars indicate the size of the bin. The bins show fast, intermediate, slow, and very slow rotators. Observational data from the present study are shown as black. Top: the number of stars in each bin is shown for each point. Bottom: disk fractions resulting from M2 simulations from Vasconcelos & Bouvier (2015) for 5.1 Myr and 10.1 Myr are shown together with the fraction observed in CygOB2. |
Vasconcelos & Bouvier (2015) investigated the disk fraction variations as a function of period for simulated populations under disk-locking effect of between 1.0 Myr and 12.1 Myr in age. Figure 7 of their paper shows, for a model starting with different period distributions for disk-bearing and non-disk-bearing stars, that the disk fraction increases with increasing rotational periods at all ages. Their M2 model has, at age 5.1 Myr, a disk fraction varying from 15% to 77% for periods from 2 days to 18 days, and from 5% to 72% at 10.1 Myr. Their results for 5.1 Myr, and 10.1 Myr are shown in the bottom plot in Fig. 20, together with the results for our sample. In both plots in Fig. 20 vertical bars follow standard errors of a Poisson counting, as the error bars used by Vasconcelos & Bouvier (2015). Results from Guarcello et al. (2016, hereafter GDW16) investigation on the disk survival in CygOB2 suggest that the environmental feedback on disk evolution for CygOB2 members may be responsible for a decrease of about 20% of the disk fraction. The red vertical error bars in the bottom plot in Fig. 20 shows a tentative correction for this effect and adds up 20% of the disk fraction of each point. Remembering that the disk-bearing periodic sample is biased owing to the variability mechanisms acting on disk-bearing stars, as described early in the present section, our dataset seems to corroborate the disk-locking results for periods up to 12.6 days, even though the increase of the disk fraction with period occurs in a less accentuated way when compared with Vasconcelos & Bouvier (2015) results. For periods longer than that, i.e., for the slowest rotator bins in the plots of Fig. 20, the disk fraction decreases, which may indicate that our dataset suffers from contamination from field stars.
A possible explanation for the lower disk fraction compared to the models could be a strong premature disk loss due to the high energy radiation coming from the OB stars in the association, and Fig. 20 (top panel) would show signatures of a primordial disk-locking with a reduced disk fraction due to fast disk dissipation in the association. In this case, the disk lifetime distribution in CygOB2 would be very different from those used by Vasconcelos & Bouvier (2015), since they assume in their simulations that most stars are born with disks and suffer from a smooth decrease in disk fraction with time. Consequently, a comparison with their results would not be possible. Other possible explanations would be that the CygOB2 low mass population is a few Myr older than previously thought, or that the environmental conditions in CygOB2 make the disk fraction decrease with time more steeply than considered in Vasconcelos & Bouvier (2015). It seems reasonable that a combination of the two effects could explain the differences between CygOB2 data and the simulated data for the fast, slow, and intermediate rotators points in the bottom panel of Fig. 20.
Since Fig. 20 suggests that the very slow rotator sample suffers from strong contamination, we re-examine the results in Sect. 4.2 by removing stars with P> 12.56 days from the analysis. By doing so, we found that P(μ,σ,ν) = 7.0, 2.7, and 7.1 days for disk-bearing stars, and P(μ,σ,ν) = 5.7, 2.6, and 5.5 days for non-disk-bearing stars. A KS test gives an 0.0001% chance that the two distributions came from the same parent distribution, showing that the results from Sect. 4.2 hold even when excluding the very slow rotators from the analysis.
5.1. CygOB2 inside the picture of PMS rotational evolution
Figure 21 presents distributions of mass versus rotational period for several young regions. These regions were selected from the list presented by Bouvier et al. (2014) in their review on the evolution of the AM in young low mass stars. The clusters and associations chosen are up to 15 Myr in age and their rotational period samples are numerous enough to be considered statistically significant. The selected regions are NGC 6530 (Henderson & Stassun 2012), with 244 measured periods in the mass range 0.2–2.0 M⊙; Orion Nebulae Cluster (ONC; Irwin & Bouvier 2009; Rodríguez-Ledesma et al. 2009), with 528 measured periods in the mass range 0.015–1.4 M⊙; NGC 2264 (Lamm et al. 2005; Affer et al. 2013; Venuti et al. 2017), with about 581 measured periods in the mass range 0.22–3.0 M⊙; CepOB3b (Littlefair et al. 2010) in the mass range 0.1–1.3 M⊙, with 460 measured periods; NGC 2362 (Irwin et al. 2008), with 271 measured periods in the mass range 0.1–1.2 M⊙; and hPer (Moraux et al. 2013), with 586 measured periods in the mass range 0.4–1.4 M⊙.
The panels in Fig. 21 are presented in order of age. For each cluster, we adopted the most recent age estimation available in the literature: NGC 6530 has ~2 Myr (Bell et al. 2013), ONC has 2.8–5.2 Myr (Naylor 2009), NGC 2264 has 2.4–6 Myr (Naylor 2009), CepOB3b has ~6 Myr (Bell et al. 2013), NGC 2362 has 9.5–12.6 Myr (Bell et al. 2013), and hPer has 13 Myr (Mayne & Naylor 2008). Those age estimates partially explain the different rotational scenarios observed in CepOB3b and NGC 2362 by Littlefair et al. (2010), since the reviewed ages put the two regions in different evolutionary stages.
One can see a large spread in period for all ages from the mass versus period plots in Fig. 21. The youngest region is NGC 6530 and it presents rotational periods that are widely scattered between 0.5 days and 19 days. The oldest one is hPer, and its distributions, also widely scattered, present a lower envelope at periods around 0.3 days, and maximum rotational periods around 15 days. While in NGC 6530 only 32% of the sample is composed of fast rotators, for hPer the fast rotators percentage is ~56%. The ONC, NGC 2264, CepOB3b, and NGC 2362 seem to present some transitional properties from the rotational state of NGC 6530 to the rotational state of hPer. For some clusters, such as ONC, CepOB3b, and NGC 2362, the spin up of the lower envelope of the distribution seems to be more efficient for lower mass stars.
 |
Fig. 21 Rotational periods as a function of mass for several young regions with ages between 1–15 Myr. Dashed red lines delimit the periods between 2 and 10 days. Stars used for comparison with the present study are shown in dark gray. |
In order to make the comparison between the samples presented in Fig. 21 and the CygOB2 sample (Fig. 22), we filtered each sample for stars with masses larger than 1.4 M⊙ and smaller than 0.1 M⊙, and periods smaller than 2 days. Stars filtered by this selection rule are shown as light gray circles in the mass versus period plots in Fig. 21. Figure 22 shows the same plot as in Fig. 18, but in the same scale as the plots in Fig. 21. After filtering each sample, their sizes are as follows: 187 stars in the NGC 6530 sample; 351 in ONC; 288 in NGC 2264; 342 in CepOB3b; 198 in NGC 2362; and 309 in hPer. This compares to 894 stars in CygOB2.
Wright et al. (2010) derived ages between 2.75 and 6.75 Myr for the CygOB2 low mass population, with a median value of 3.5 Myr for the center field and 5 Myr for the northwestern field. For deriving stellar properties, they used Siess et al. (2000) models converted to 2MASS photometric system using Kenyon & Hartmann (1995). Given that the methods used by Mayne & Naylor (2008), Naylor (2009), and Bell et al. (2013) to evaluate stellar parameters result in ages 1.5–2.0 greater than ages estimated by previous methods, we stress that comparisons with other clusters in the literature using CygOB2 age as a parameter must be carried out with caution. That being said, using the age range as the unique criterion would place CygOB2 somewhere between ONC and NGC 2362.
 |
Fig. 22 Mass vs. period distribution for periodic candidate members of CygOB2. Stars with reliable periods (P ≥ 2 days) are shown as black circles, and stars with dubious periods (P< 2 days) are shown as red circles. Red dashed lines delimit the periods between 2 and 10 days, while blue dashed lines delimit the mass bin analyzed in the present section. |
One feature that markedly varies from cluster to cluster in the plots of Figs. 21 and 22 is the slope of the upper envelope of the distribution for lower mass stars. Irwin et al. (2008) suggest that this varying slope for masses between 0.1–0.5 M⊙ was a result of cluster evolution with age. Following this suggestion, Henderson & Stassun (2012) used such slope as an age proxy and suggest that NGC 6530 would be in an earlier evolutionary stage compared to ONC. They argued that this younger age would justify the remarkable differences between the mass versus period distributions for NGC 6530 and other clusters. In particular, they found that lower mass stars in NGC 6530 are rotating much more slowly than the higher mass stars, unlike observations of most other young clusters where lower mass stars rotate faster than higher mass stars. The authors argued that, given a younger age, the explanation for the opposite sense in the period-mass relationship would be that the lowest mass stars in the cluster are currently spinning up and that in a future step of evolution they would end up rotating faster than the higher mass stars.
We found in Sect. 4.3.2 that lower mass stars in CygOB2 also rotate more slowly than higher mass stars. Given the much older age of CygOB2, compared to NGC 6530, we argued that the different age of these clusters could not explain the observational results of lower mass stars rotating on average slower than higher mass stars. An alternative explanation to this inverse period-mass relation for lower mass stars would be the role of environmental conditions on regulating the stellar AM.
5.2. Are the mass versus period relations sensitive to the environment?
A mass-rotation connection was first reported for stars in ONC (2.5–5.2 Myr), where Herbst et al. (2001) found that while stars in the cluster with spectral types between M2 and K presented a bimodal distribution with one peak around fast rotators (~2 days) and another around slow rotators (~8 days), stars with spectral type later than M2 presented a unimodal distribution with a single peak around fast rotators (~2 days). Given the observed differences in the period distribution, and given that the stars with later spectral type were on average faster rotators than the earlier, the authors called attention to a possible mass-rotation connection. Studies for other regions such as NGC 2264 (Lamm et al. 2005) and IC 348 (Littlefair et al. 2005) favored this connection.
A role of the environment in determining the mass-rotation relation has been suggested by Littlefair et al. (2010). They found that even though lower mass stars rotate faster than higher mass stars in CepOB3b, this difference is less pronounced than in other clusters, since CepOB3b has an excess of slow rotating low mass stars compared to other regions.
As is the case in NGC 6530 (Henderson & Stassun 2012), lower mass stars in CygOB2 rotate on average more slowly than higher mass stars (Sect. 4.3.2) with a median rotational period of 6.9 days for lower mass stars and 5.7 days for higher mass stars. Since our data is incomplete for fast rotators, we do not have enough information to discuss the existence of bimodality in the period distributions, but apart from that, the shape of period distributions for different mass ranges presented in Fig. 19 shows clear sign of a mass dependence. While period distribution for higher mass stars (M ≥ 0.4M⊙) is quite flat for periods between 2–9 days, with a long tail toward slower rotators, it is peaked around slow rotators for the lower mass stars (M ≤ 0.4 M⊙) in the sample showing a lack of fast rotators.
Before putting these results in context, we examine the possibility that a bias due to underestimated extinction could affect the results. An underestimated extinction would cause highly extincted higher mass stars to be considered low mass stars. Since differences in the period distributions for lower and higher mass stars have been repeatedly reported in the literature, including studies for regions with relatively low and homogeneous extinction, higher mass stars mistaken by lower mass stars would bring contamination to the lower mass period sample. One such example of such as region is the case of NGC 2264 (AV ~ 0.4;Dahm 2008), where this contamination effect is probably minimal. In regions where higher mass stars are slower rotators than lower mass stars, this bias would introduce slow rotators to the lower mass period distributions, which was initially composed of faster rotators, biasing the distribution toward slower rotators and masking the differences between the two mass-regime distributions. In the case of higher mass stars rotating on average faster than lower mass stars, this bias would introduce fast rotators to the lower mass stars distribution and the distribution would be biased toward such faster rotators. In both cases, we would expect the period distribution for lower mass stars to be somehow flattened due to the contamination. When comparing CygOB2 mass versus period distributions (Fig. 22) with the other regions (Fig. 21), one can see that CygOB2 presents a clear lack of fast and intermediate rotators within its lower mass stars, and therefore we ruled out the possibility that the result may be mimicked by a contamination due to higher mass stars with underestimated extinction. A third possibility that remains is that the extinction for the stars in our sample is underestimated as a whole and in this case our observations would not reach lower mass at all, and the whole lower mass bin would actually be composed of higher mass stars with underestimated masses. Since we saw in Sect. 4.3.2 that a KS test between the samples with M ≤ 0.4 M⊙, and M ≥ 0.4 M⊙ returned a probability of only ~0.02% that the two samples came from the same parent population, we also excluded the hypothesis that the smaller mass sample could be a subsample of higher mass stars with underestimated extinction.
A final caveat on interpreting our results arises from the fact that our sample is incomplete for fast rotators with periods under 2 days. To check whether the statistical difference between the rotational scenario of different mass regimes holds after removing the faster rotators from the sample, we present in Table 2 the mean, standard deviation, and median values (μ,σ,ν) for the period distributions of the young regions presented in Fig. 21 for both full and P ≥ 2 day samples. We divided each cluster sample into two mass ranges using M = 0.4 M⊙ as a cut. For each cluster, the mass regime that rotates slower on average is stressed in bold. Since hPer sample includes only a few stars with masses M ≤ 0.4 M⊙, we present the results from this cluster in Table 2, but we did not use this sample for the present investigation. From Table 2, one can see that filtering the samples for P ≥ 2 days does not qualitatively change the rotation-mass connection. Nevertheless, for NGC 2264, KS tests between the samples of higher and lower mass stars without faster rotators than P = 2 days, changes significantly. The last column of Table 2 shows a KS test between the lower mass stars from each cluster and the low mass stars in CygOB2 and shows that the lower mass end of CygOB2 mass versus period distribution is dissimilar to all the other clusters considered.
The observational results for CygOB2 could be explained if the lower mass stars in the sample were remaining locked to their disks for a longer time than the higher mass stars in the sample (solar type). One possible reason why the lower mass stars could keep their disks for a longer time is if primordial mass segregation occurs, i.e., very low mass stars are more widely distributed than solar-type stars. They would thus lie further away from the ionizing radiation of central OB stars than the more concentrated solar-type stars. They would be in lower stellar density regions as well, thus avoiding disk-disruptive encounters. However, Wright et al. (2014, and 2016) found no signal of mass segregation in the association, and additionally GDW16 showed that close encounters in CygOB2 are not important in regulating disk dissipation, so this explanation may not apply.
The present study shows that, similar to NGC 6530, CygOB2 presents qualitatively a mass-rotation connection in the opposite sense from other clusters with lower mass stars rotating on average slower than higher mass stars. We consider that the statistical differences between the distributions from the two regions are due to different rotational ages, since NGC 6530 is about 2 Myr old and CygOB2 stars range in age from 2.5 to 6.75 Myr. Also, because of this age difference between the two regions, we refute the explanation given by Henderson & Stassun (2012) based on youth to explain lower mass stars being slower rotators than higher mass stars in the region, since for CygOB2 this explanation would not apply. Instead, we raise the hypothesis that the environmental influence on regulating the rotation may be a better explanation.
Since both CepOB3b, and CygOB2 are OB associations with similar ages, it would be reasonable to expect they would have similar rotational properties. Even though they both present an excess of slow rotators within their lower mass members, their period distributions are statistically different, and their rotational-mass connection is qualitatively inverse. Those differences could be explained by a smaller concentration of O stars: CygOB2 is a notoriously massive OB association with more than 160 confirmed OB stars (Wright et al. 2015) within its members, 73 of which are O stars, while CepOB3b is a small association with a massive population composed o only 3 O stars and 33 B stars (Blaauw et al. 1959; Blaauw 1964) stars spread over ~10 pc (Blaauw 1964). On the other hand, NGC 6530 is a core cluster of the Sgr OB1 association and is located in the eastern part of the very bright Lagoon Nebula (Sung et al. 2000). NGC 6530 is also 3–4 times richer in OB stars than ONC (Damiani et al. 2004), whose population is similar in age.
5.3. Does CygOB2 massive population regulate low mass star rotation?
OB stars can influence their environment owing to their strong UV field. Far ultraviolet (FUV) photons (6 eV <hν< 13.6 eV) can dissociate H2 molecules, and extreme ultraviolet (EUV) photons (hν> 13.6 eV) are capable of ionizing hydrogen atoms. Because of that, regions with intense local UV fields can be hostile to the evolution of circumstellar disks and to the processes of star formation (e.g., Johnstone et al. 1998; Adams et al. 2004; Guarcello et al. 2010, 2016). In particular, GDW16 recently found evidence that disks are more rapidly dissipated in regions of CygOB2 with intense local UV.
To test the effect of CygOB2 massive stars on the rotational properties of nearby YSO we investigated how the rotational period distributions vary as a function of local UV fields. To estimate local UV fluxes, we used the technique adopted in GDW16 and Guarcello et al. (2007). We propagated the FUV and EUV fluxes emitted by each O star to the position of each periodic stars using 2D projected distances. The effect of using 2D projected distances instead of real distances is discussed on Sect. 3.1 of GDW16, and it was shown by the authors to have very little impact on the analysis.
The UV flux emitted by each of the 73 O stars and 3 Wolf-Rayet (WR) stars in CygOB2 was estimated by GDW16 (Table 1 in their study). Their estimates of FUV flux are presented in terms of Habing flux9G0 = 1.6 × 10-3 erg/cm2/s and their EUV fluxes10 are in photons/s/cm2. A map of incident FUV and EUV fluxes for CygOB2 candidate member stars was presented by the authors in their Fig. 3. Using their estimates for the O stars UV flux, we calculated the incident UV flux at the position of each periodic star. As in GDW16, B stars are omitted because their census is still incomplete and their contribution to the whole UV field in the association is negligible compared to the O and WR stars.
Using the FUV and EUV local fluxes, we define as regions with low UV incidence star positions, where log (FFUV) ≤ 3.7 G0 or log (FEUV) ≤ 11.42 photons/s/cm2, and regions with high UV incidence star positions, where log (FFUV) > 3.7 G0 or log (FEUV) > 11.42 photons/s/cm211.
For each UV flux sample and for samples of disk-bearing and non-disk-bearing stars, mean, standard deviation, and median for each period distribution.
Disk fraction as a function of rotational period plots for stars in regions with high and low UV incidence are shown in Fig. 23. From the plots, one can see that the maximum disk fraction goes from 21% for slow rotators stars in low FUV incidence regions to 7.3% for slow rotators in high FUV incidence regions; this fraction goes from 20.3% for slow rotators in low EUV incidence regions to 7.1% for slow rotators in high EUV incidence regions. Figure 23 suggests that high incident UV yields faster disk dissipation, even though it does not qualitatively change the trend of increasing disk fraction for longer periods.
While GDW16 results suggest that regions with high UV incident fields can rapidly erode disks, our results suggest that this can directly influence disk-rotation connection. Table 3 shows the (μ,σ,ν) values for each period sample for disk-bearing and non-disk-bearing stars in each UV incidence sample. The number of stars in each sample and a KS test between samples of disk-bearing and non-disk-bearing stars are also included in the table. From the table one can see that while the disk-bearing and non-disk-bearing stars samples are different for regions with low UV incidence (a KS test gives 0.1% probability that they came from the same parent distribution for FUV samples, and 0.01% probability for the EUV sample), in regions with high UV incidence a disk-rotation connection cannot be verified and results from KS test does not discard the possibility that disk-bearing and non-disk-bearing period distributions came from the same parent distribution in such samples.
For each UV flux sample and for each mass range considered, mean, standard deviation, and median for each period distribution.
 |
Fig. 23 Same as Fig. 20 but for periodic stars with low UV incident radiation (top) and stars with high UV incident radiation (bottom). |
Next, as in Sect. 4.3.2, we built period distributions for different mass ranges for low and high UV incident radiation. The shape of the distribution does not seem to be significantly affected by the amount of UV incident radiation. Both low and high local UV incidence samples show a mass-rotation connection with lower mass stars rotating on average slower than higher mass stars. Table 4 shows the (μ,σ,ν) values for each distribution. The number of stars in each sample and a KS test between the two mass range for each subsample is also shown. We performed KS tests between each pair of samples for the same mass range and regions with low and high UV incidence, but for all pairs of samples the KS test yielded that we cannot exclude the possibility that the two samples came from the same parent distribution. From Table 4, one can see that KS tests between period distributions for different mass ranges in samples with high incident UV flux give smaller probabilities that the two samples came from the same parent distribution as regions with low incident UV. This difference, even if less strong than that one found for the case of disk-rotation connection, may be a hint that UV incident fluxes can also influence the mass-rotation connection.
The magnitude distributions for the samples of high and low UV incidence were analyzed as in Sect. 2.3, and the completeness limits found for the two samples were qualitatively the same. The magnitude range in which the two samples can be considered complete is the same as for the full candidate member sample (Fig. 6), hence we do not consider that completeness issues in the UV-selected samples may be impacting the results. Nevertheless, variability surveys sensitive to fainter stars may improve the size and completeness of the samples toward the fainter stars and help confirm the results presented here.
Further investigations are needed to improve these results, especially to complete the present analysis for faster rotators. But so far, our results suggest that local incident UV radiation may have a role in regulating the AM of YSO. In this sense, evaluating the UV radiation arising from massive stars may help to explain differences in the rotational properties of low mass stars in young cluster similarly aged presented in the literature.
6. Conclusions
In this study we presented the first analysis of rotation properties for low mass stars in the young OB association Cygnus OB2. We presented results for stars in the mass range 0.1–1.4 M⊙. We identified and studied a sample of 1679 stars with signs of periodic variability in their NIR light curves out of a sample of 5083 candidate members. After time-series analysis, we confirmed the periodicity in 1291 stars (25% of total candidate member sample), but after completeness analysis, only 894 of those were considered to be reliable period measurements. Since the periodic sample is strongly aliased for periods shorter than about 2 days, most of our analysis was limited to the intermediate (3.14 ≤ P ≤ 6.28 days) and slow (P> 6.28 days) rotators, with detected fast rotators only in the range 2–3.14 days. The main findings of this work are
-
1.
We found periods widely distributed between0.83 days, and 32.49 days, but dueto completeness and contamination issues, we only analyzedperiods longer than 2 days. The amplitudes ofvariability for periodic stars were in the range0.03–1.2 mag and the masses were in the range0.1–1.4 M⊙.
-
2.
We found disk-bearing and non-disk-bearing stars are statistically distinct in their rotational properties. Even though there is a significant overlap between their period distributions, disk-bearing stars rotate on average more slowly (median period: 7.34 days) than non-disk-bearing stars (median period 5.80 days). Also, period detection is more common among non-disk-bearing stars, than among disk-bearing stars.
-
3.
We found that the disk fraction increases as a function of period, except for the very slow rotator bin (P> 12.56 days), which has smaller statistics number and seems to suffer from contamination from field stars. The disk fraction varies from ~4% for fast rotators (P = 2–3.14 days) to ~13% for slow rotators (P = 6.28–12.56 days). This corroborates the results expected for the disk-locking hypothesis, but when compared with semi-empirical simulations from Vasconcelos & Bouvier (2015) testing disk locking hypothesis, the variation of disk-fraction as a function of period is shallower than predicted by the simulations.
-
4.
We verified a period-mass connection, i.e., statistically distinct properties were found for different mass ranges. A median period of 5.7 days was found for the mass range M> 0.4 M⊙, and 6.9 days for M ≤ 0.4 M⊙. However this mass-rotation connection is different from other regions. As is the case of NGC 6530, lower mass stars in CygOB2 rotate more slowly than higher mass stars.
We also investigated the possibility of a correlation between the incident UV flux arising from O stars in CygOB2 and the rotational properties of low mass stars described in the previous items.
-
5.
We verified that while the distinction in the rotational propertiesof disk-bearing and non- disk-bearing stars is stronger in regionswith low UV incidence, in regions with high UV incidence it is notpossible to distinguish between the two samples.
-
6.
We found that the increase of the disk fraction with period is stronger for a sample of stars with low local UV incidence and weaker for a sample of stars with high local UV incidence. A maximum disk fraction of 21%, and 7.3% for slow rotators was found for low and high local UV incidence, respectively.
-
7.
We determined that both low and high local UV incidence samples show a mass-rotation connection with lower mass stars rotating in average slower than higher mass stars. For stars with low local UV incidence, a KS test indicates that this difference is barely significant, but for stars with high local UV incidence, a KS test shows stronger evidence that the two mass ranges have different rotational period distributions.
Our results suggest a link between environmental conditions and the rotational evolution of PMS stars. However, it is urgent to complement the sample presented in this study for fast rotators and lower masses to achieve a better understanding of the rotational scenario in the association and to confirm such suggestions.
Details on the morphological classification will be present on Roquette (in prep.), but for the purposes of the present study it is worth mentioning that eclipse-like variables are stars whose light-curve points are in a maximum value of bright most of the time, but present several dimmings in bright; they may also be periodic. Candidate periodic stars present light curve oscillating between maximum and minimum values. Other variables encompass all stars with a visibly variable light curves but that did not fit in the previous categories, such as stars with long-term variability (e.g., stars that are slowly dimming with time), and also stars with a mixed light curve (e.g., long-term variability mixed with a short-term variability in their light curves). Stars that met the Stetson index criteria, but presented low amplitude stochastic variability in their light curves were not considered in the study.
We chose this interval based on the frequency versus periodogram power peak plots in Fig. 8. This frequency interval is outside the bulk produced by the one day alias and also outside the bulk of longer periods (lower frequencies).
These numbers are slightly different from the numbers presented in Fig. 15. This is because the plot in the refereed figure presents only stars with P ≤ 20 days, and there are 3 disk-bearing and 13 non-disk-bearing stars with periods larger than that.
Transformed from u′g′r′i′z′ (USNO 40 in) to ugriz (SDSS 2.5 m) according to http://classic.sdss.org/dr7/algorithms/jeg_photometric_eq_dr1.html
CMDfit software, author: Tim Naylor: http://www.astro.ex.ac.uk/people/timn/tau-squared/software.html
As reference, the disk fraction of similarly aged CepOB3b is 33% (Allen et al. 2012).
For reference, the average UV flux in the spectra range 912–2000 Å in the solar neighborhood is 1.7 G0 (Habing 1968).
Acknowledgments
This study was part of JR Ph.D. thesis, which was granted by CNPq (Conselho Nacional de Desenvolvimento Científico e Tecnológico) and CAPES (Coordenação de Aperfeiçoamento de Pessoal de Nível Superior). S.H.P.A. acknowledges financial support from CNPq, CAPES, and FAPEMIG. We thank Bo Reipurth for kindly providing us with the WFCAM/UKIRT dataset used in the present study. J.B. acknowledges the support of ANR grant 2011 Blanc SIMI5-6 020 01 Toupies: Towards understanding the spin evolution of stars (http://ipag.osug.fr/Anr_Toupies/).
We also thank Laura Venuti, Francisco Maia, Alana Souza, and Jaqueline Vasconcelos for useful comments over the development of the work.
This study has made use of NASA’s Astrophysics Data System Bibliographic Services. This research made extensive use of TOPCAT software (Taylor 2005).
References
- Adams, F. C., Hollenbach, D., Laughlin, G., & Gorti, U. 2004, ApJ, 611, 360 [NASA ADS] [CrossRef] [Google Scholar]
- Affer, L., Micela, G., Favata, F., Flaccomio, E., & Bouvier, J. 2013, MNRAS, 430, 1433 [NASA ADS] [CrossRef] [Google Scholar]
- Aihara, H., Allen de Prieto, C., An, D., et al. 2011, ApJS, 193, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Allard, F., Homeier, D., & Freytag, B. 2011, in 16th Cambridge Workshop on Cool Stars, Stellar Systems, and the Sun, eds. C. Johns-Krull, M. K. Browning, & A. A. West, ASP Conf. Ser., 448, 91 [Google Scholar]
- Allen, T. S., Gutermuth, R. A., Kryukova, E., et al. 2012, ApJ, 750, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Baraffe, I., Chabrier, G., Allard, F., & Hauschildt, P. H. 1998, A&A, 337, 403 [NASA ADS] [Google Scholar]
- Baraffe, I., Homeier, D., Allard, F., & Chabrier, G. 2015, A&A, 577, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barentsen, G., Farnhill, H. J., Drew, J. E., et al. 2014, MNRAS, 444, 3230 [NASA ADS] [CrossRef] [Google Scholar]
- Beerer, I. M., Koenig, X. P., Hora, J. L., et al. 2010, ApJ, 720, 679 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, C. P. M., Naylor, T., Mayne, N. J., Jeffries, R. D., & Littlefair, S. P. 2013, MNRAS, 434, 806 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, C. P. M., Rees, J. M., Naylor, T., et al. 2014, MNRAS, 445, 3496 [NASA ADS] [CrossRef] [Google Scholar]
- Blaauw, A. 1964, ARA&A, 2, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Blaauw, A., Hiltner, W. A., & Johnson, H. L. 1959, ApJ, 130, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Bodenheimer, P. 1995, ARA&A, 33, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Bouvier, J., Bertout, C., Benz, W., & Mayor, M. 1986, A&A, 165, 110 [NASA ADS] [Google Scholar]
- Bouvier, J., Grankin, K. N., Alencar, S. H. P., et al. 2003, A&A, 409, 169 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouvier, J., Matt, S. P., Mohanty, S., et al. 2014, Protostars and Planets VI, 433 [Google Scholar]
- Bouy, H., Bertin, E., Moraux, E., et al. 2013, A&A, 554, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Carpenter, J. M., Hillenbrand, L. A., & Skrutskie, M. F. 2001, AJ, 121, 3160 [NASA ADS] [CrossRef] [Google Scholar]
- Casali, M., Adamson, A., Alves de Oliveira, C., et al. 2007, A&A, 467, 777 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cieza, L., & Baliber, N. 2007, ApJ, 671, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Clarke, D. 2002, A&A, 386, 763 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cody, A. M., & Hillenbrand, L. A. 2010, ApJS, 191, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Cody, A. M., Stauffer, J., Baglin, A., et al. 2014, AJ, 147, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, R. E., Herbst, W., & Williams, E. C. 2004, AJ, 127, 1602 [NASA ADS] [CrossRef] [Google Scholar]
- Comerón, F., Pasquali, A., Rodighiero, G., et al. 2002, A&A, 389, 874 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Covey, K. R., Ivezić, Ž., Schlegel, D., et al. 2007, AJ, 134, 2398 [NASA ADS] [CrossRef] [Google Scholar]
- Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, 2MASS All Sky Catalog of point sources [Google Scholar]
- Dahm, S. E. 2008, The Young Cluster and Star Forming Region NGC 2264, ed. B. Reipurth, 966 [Google Scholar]
- Damiani, F., Flaccomio, E., Micela, G., et al. 2004, ApJ, 608, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Doi, M., Tanaka, M., Fukugita, M., et al. 2010, AJ, 139, 1628 [NASA ADS] [CrossRef] [Google Scholar]
- Drew, J. E., Greimel, R., Irwin, M. J., et al. 2005, MNRAS, 362, 753 [NASA ADS] [CrossRef] [Google Scholar]
- Drew, J. E., Greimel, R., Irwin, M. J., & Sale, S. E. 2008, MNRAS, 386, 1761 [NASA ADS] [CrossRef] [Google Scholar]
- Gallet, F., & Bouvier, J. 2013, A&A, 556, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ghosh, P., & Lamb, F. K. 1979, ApJ, 234, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Gregory, S. G., Donati, J.-F., Morin, J., et al. 2012, ApJ, 755, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Guarcello, M. G., Prisinzano, L., Micela, G., et al. 2007, A&A, 462, 245 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guarcello, M. G., Micela, G., Peres, G., Prisinzano, L., & Sciortino, S. 2010, A&A, 521, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guarcello, M. G., Wright, N. J., Drake, J. J., et al. 2012, ApJS, 202, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Guarcello, M. G., Drake, J. J., Wright, N. J., et al. 2013, ApJ, 773, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Guarcello, M. G., Drake, J. J., Wright, N. J., et al. 2015, ApJ, submitted [arXiv:1501.03761] [Google Scholar]
- Guarcello, M. G., Drake, J. J., Wright, N. J., et al. 2016, ApJS, submitted [arXiv:1605.01773] [Google Scholar]
- Habing, H. J. 1968, Bull. Astron. Inst. Netherlands, 19, 421 [Google Scholar]
- Hanson, M. M. 2003, ApJ, 597, 957 [NASA ADS] [CrossRef] [Google Scholar]
- Henderson, C. B., & Stassun, K. G. 2012, ApJ, 747, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Henderson, C. B., Stanek, K. Z., Pejcha, O., & Prieto, J. L. 2011, ApJS, 194, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Herbst, W., & Mundt, R. 2005, ApJ, 633, 967 [NASA ADS] [CrossRef] [Google Scholar]
- Herbst, W., Bailer-Jones, C. A. L., & Mundt, R. 2001, ApJ, 554, L197 [NASA ADS] [CrossRef] [Google Scholar]
- Herbst, W., Bailer-Jones, C. A. L., Mundt, R., Meisenheimer, K., & Wackermann, R. 2002, A&A, 396, 513 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hewett, P. C., Warren, S. J., Leggett, S. K. T. d., & Hodgkin, S. T. 2006, MNRAS, 367, 454 [NASA ADS] [CrossRef] [Google Scholar]
- Hillenbrand, L. A., Strom, S. E., Calvet, N., et al. 1998, AJ, 116, 1816 [NASA ADS] [CrossRef] [Google Scholar]
- Hodgkin, S. T., Irwin, M. J., Hewett, P. C., & Warren, S. J. 2009, MNRAS, 394, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Horne, J. H., & Baliunas, S. L. 1986, ApJ, 302, 757 [NASA ADS] [CrossRef] [Google Scholar]
- Irwin, J., & Bouvier, J. 2009, in IAU Symp. 258, eds. E. E. Mamajek, D. R. Soderblom, & R. F. G. Wyse, 363 [Google Scholar]
- Irwin, J., Hodgkin, S., Aigrain, S., et al. 2008, MNRAS, 384, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Johnstone, D., Hollenbach, D., & Bally, J. 1998, ApJ, 499, 758 [NASA ADS] [CrossRef] [Google Scholar]
- Joy, A. H. 1945, ApJ, 102, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Kashyap, V. L. 2017, ArXiv e-prints [arXiv:1702.03678] [Google Scholar]
- Kenyon, S. J., & Hartmann, L. 1995, ApJS, 101, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Kiminki, D. C., Kobulnicky, H. A., Vargas Álvarez, C. A., Alexander, M. J., & Lundquist, M. J. 2015, ApJ, 811, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Knödlseder, J. 2000, A&A, 360, 539 [NASA ADS] [Google Scholar]
- Koenigl, A. 1991, ApJ, 370, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Lafler, J., & Kinman, T. D. 1965, ApJS, 11, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Lamm, M. H., Mundt, R., Bailer-Jones, C. A. L., & Herbst, W. 2005, A&A, 430, 1005 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Littlefair, S. P., Naylor, T., Burningham, B., & Jeffries, R. D. 2005, MNRAS, 358, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Littlefair, S. P., Naylor, T., Mayne, N. J., Saunders, E. S., & Jeffries, R. D. 2010, MNRAS, 403, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Lomb, N. R. 1976, Ap&SS, 39, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Lucas, P. W., Hoare, M. G., Longmore, A., et al. 2008, MNRAS, 391, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Massey, P., & Thompson, A. B. 1991, AJ, 101, 1408 [NASA ADS] [CrossRef] [Google Scholar]
- Matt, S., & Pudritz, R. E. 2005, ApJ, 632, L135 [NASA ADS] [CrossRef] [Google Scholar]
- Matt, S. P., Pinzón, G., Greene, T. P., & Pudritz, R. E. 2012, ApJ, 745, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Mayne, N. J., & Naylor, T. 2008, MNRAS, 386, 261 [NASA ADS] [CrossRef] [Google Scholar]
- McGinnis, P. T., Alencar, S. H. P., Guimarães, M. M., et al. 2015, A&A, 577, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moraux, E., Artemenko, S., Bouvier, J., et al. 2013, A&A, 560, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Naylor, T. 2009, MNRAS, 399, 432 [NASA ADS] [CrossRef] [Google Scholar]
- Pasquali, A., Comerón, F., Gredel, R., Torra, J., & Figueras, F. 2002, A&A, 396, 533 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Plavchan, P., Jura, M., Kirkpatrick, J. D., Cutri, R. M., & Gallagher, S. C. 2008, ApJS, 175, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Flannery, B. P., Teukolsky, S. A., & Veterling, W. T. 1992, Numerical Recipes in C: the art of scientific computing, 2nd edn. (Cambridge: Cambridge University Press) [Google Scholar]
- Rauw, G., Nazé, Y., Wright, N. J., et al. 2015, ApJS, 221, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Rebull, L. M., Wolff, S. C., & Strom, S. E. 2004, AJ, 127, 1029 [NASA ADS] [CrossRef] [Google Scholar]
- Reddish, V., Lawrence, L. C., & Pratt, N. M. 1966, Publications of the Royal Observatory of Edinburgh, 5, 111 [NASA ADS] [Google Scholar]
- Rice, T. S., Reipurth, B., Wolk, S. J., Vaz, L. P., & Cross, N. J. G. 2015, AJ, 150, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Rodríguez-Ledesma, M. V., Mundt, R., & Eislöffel, J. 2009, A&A, 502, 883 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Romanova, M. M., Ustyugova, G. V., Koldoba, A. V., & Lovelace, R. V. E. 2009, MNRAS, 399, 1802 [NASA ADS] [CrossRef] [Google Scholar]
- Saunders, E. S., Naylor, T., & Allan, A. 2006, Astron. Nachr., 327, 783 [NASA ADS] [CrossRef] [Google Scholar]
- Scargle, J. D. 1982, ApJ, 263, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Scholz, A., & Eislöffel, J. 2004, A&A, 419, 249 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scholz, A., Xu, X., Jayawardhana, R., et al. 2009, MNRAS, 398, 873 [NASA ADS] [CrossRef] [Google Scholar]
- Siess, L., Dufour, E., & Forestini, M. 2000, A&A, 358, 593 [NASA ADS] [Google Scholar]
- Sousa, A. P., Alencar, S. H. P., Bouvier, J., et al. 2016, A&A, 586, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stauffer, J., Cody, A. M., Baglin, A., et al. 2014, AJ, 147, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Stetson, P. B. 1996, PASP, 108, 851 [NASA ADS] [CrossRef] [Google Scholar]
- Sung, H., Chun, M.-Y., & Bessell, M. S. 2000, AJ, 120, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Tanner, R. W. 1948, JRASC, 42, 177 [NASA ADS] [Google Scholar]
- Taylor, M. B. 2005, in Astronomical Data Analysis Software and Systems XIV, eds. P. Shopbell, M. Britton, & R. Ebert, ASP Conf. Ser., 347, 29 [Google Scholar]
- Tognelli, E., Prada Moroni, P. G., & Degl’Innocenti, S. 2011, A&A, 533, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tognelli, E., Degl’Innocenti, S., & Pra da Moroni, P. G. 2012, Mem. Soc. Astron. It. Suppl., 22, 225 [Google Scholar]
- Torres-Dodgen, A., Carroll, M., & Tapia, M. 1991, MNRAS, 249, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Vasconcelos, M. J., & Bouvier, J. 2015, A&A, 578, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Venuti, L., Bouvier, J., Cody, A. M., et al. 2017, A&A, 599, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vink, J. S., Drew, J. E., Steeghs, D., et al. 2008, MNRAS, 387, 308 [NASA ADS] [CrossRef] [Google Scholar]
- Vogel, S. N., & Kuhi, L. V. 1981, ApJ, 245, 960 [NASA ADS] [CrossRef] [Google Scholar]
- Walborn, N. R., Howarth, I. D., Lennon, D. J., et al. 2002, AJ, 123, 2754 [NASA ADS] [CrossRef] [Google Scholar]
- Wilking, B. A., Bontemps, S., Schuler, R. E., Greene, T. P., & André, P. 2001, ApJ, 551, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, N. J., & Drake, J. J. 2009, ApJS, 184, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, N. J., Drake, J. J., Drew, J. E., & Vink, J. S. 2010, ApJ, 713, 871 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, N. J., Drake, J. J., Guarcello, M. G., et al. 2014, ApJS, submitted [arXiv:1408.6579] [Google Scholar]
- Wright, N. J., Drew, J. E., & Mohr-Smith, M. 2015, MNRAS, 449, 741 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, N. J., Bouy, H., Drew, J. E., et al. 2016, MNRAS, 460, 2593 [NASA ADS] [CrossRef] [Google Scholar]
- Zanni, C., & Ferreira, J. 2013, A&A, 550, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Other possible sources of contamination to the periodic sample
Appendix A.1: Contamination by periods outside the observations resolution
Given the evidence of high contamination in the shorter periods bin (Figs. 10 and 11), we performed some extra simulations focusing on periods outside the period range considered.
Longer Periods:
first, we focused on the possible contamination due to periods longer than 20 days. We repeated the simulation described in Sect. 3.2, but this time considering periods (Pin) between 20 and 100 days with amplitudes between 0.015 and 0.5 mag. For those specific simulations, we kept the filtering for FAP, RL-, and S-statistics, but we did not perform any further cleaning for periods of about 1 day. The recovery success on this range is only ~12% in a sample of 78 000 synthetic periodic light curves for the amplitude range considered. For the 680 (9%) synthetic light curves in contaminant sample (i.e., synthetic light curves selected as periodic, but with Pout ≠ Pin), we analyzed the distribution of measured periods (Pout) and verified that ~98% of the contaminant sample had Pout around 1 ± 0.2 days. This justifies the filtering for periods in the range 0.92–1.08 days applied in Sect. 3.1.
Shorter Periods:
second, we focus on the contamination due to periods shorter than our data sampling is capable of resolving. For the set of simulations presented in Fig. 11, we analyzed the input characteristics of the synthetic light curves.
Figure A.1 shows the input period (Pin) distribution for the synthetic light curves with Pout< 2 days, which is composed of the two shortest period bins in Fig. 11. The y-axis shows the fraction of contaminants with Pout< 2 days. From this plot, we can estimate that ~15% of the contamination arises from aliased periods smaller than 1 day and ~49% of the contamination arises from unresolved periods between 1 and 2 days. Despite the fact that these short period aliases account for ~64% of the contamination, there is a lower level contamination arising from all period bins larger than 2 days up to ~15 days, which adds up to ~36% of contamination. Since it is not possible to untangle the two contaminant sources, we conclude that the periodic sample with P< 2.0 days suffers from strong contamination and it should not be used in further analysis.
 |
Fig. A.1 Period distribution histogram for the input periods for synthetic light curves measured Pout< 2.0 days (2 shorter period bins in Fig. 11) after the automatized period search procedure. |
Appendix A.2: Contamination due to non-periodic variability
We performed additional Monte Carlo simulation for non-periodic wave forms and applied the automatized period search for the non-periodic sample. For each synthetic light curve, a random amplitude was generated and two possible wave forms were randomly assigned. The first wave form assumes that the light curve is a straight line with slope defined as the ratio between the randomly selected amplitude and the total number of observations. The second wave form was composed of random numbers generated between 0.015 and the amplitude value.
A total of 78 000 synthetic light curves were generated this way with amplitudes between 0.015 and 1.5 mag. While ~49% of the sample presented periodogram power peaks in the three bands with a power higher enough to be automatically selected as periodic, they were however not wrongly selected as periodic, since most of them are distributed for at about 1 day and were ruled out of the periodic selection. The few objects with periods outside this range were ruled out by the RL-statistics or S-statistics filters. Finally, after applying the automatized period search procedure to this sample, we concluded that the procedure is robust enough to avoid any contamination due to these non-periodic wave forms in our periodic sample.
Appendix B: 894 folded light curves
 |
Fig. B.1 Phased light curves of periodic CygOB2 candidate members for H filter. |
 |
Fig. B.1 continued. |
 |
Fig. B.1 continued. |
 |
Fig. B.1 continued. |
 |
Fig. B.1 continued. |
 |
Fig. B.1 continued. |
 |
Fig. B.1 continued. |
 |
Fig. B.1 continued. |
 |
Fig. B.1 continued. |
 |
Fig. B.1 continued. |
 |
Fig. B.1 continued. |
 |
Fig. B.1 continued. |
 |
Fig. B.1 continued. |
 |
Fig. B.1 continued. |
 |
Fig. B.1 continued. |
 |
Fig. B.1 continued. |
 |
Fig. B.1 continued. |
 |
Fig. B.1 continued. |
 |
Fig. B.1 continued. |
 |
Fig. B.1 continued. |
 |
Fig. B.1 continued. |
 |
Fig. B.1 continued. |
 |
Fig. B.1 continued. |
 |
Fig. B.1 continued. |
 |
Fig. B.1 continued. |
 |
Fig. B.1 continued. |
 |
Fig. B.1 continued. |
 |
Fig. B.1 continued. |
 |
Fig. B.1 continued. |
 |
Fig. B.1 continued. |
 |
Fig. B.1 continued. |
 |
Fig. B.1 continued. |
 |
Fig. B.1 continued. |
 |
Fig. B.1 continued. |
 |
Fig. B.1 continued. |
 |
Fig. B.1 continued. |
 |
Fig. B.1 continued. |
 |
Fig. B.1 continued. |
All Tables
For each UV flux sample and for samples of disk-bearing and non-disk-bearing stars, mean, standard deviation, and median for each period distribution.
For each UV flux sample and for each mass range considered, mean, standard deviation, and median for each period distribution.
All Figures
 |
Fig. 1 Scheme showing the nights when observations were taken in the given filters. |
| In the text | |
 |
Fig. 2 Schematic representation of WFCAM layout. A sequence of 4 exposures (ABCD) with the 4 CCDs (WXYZ) produces a mosaic of 16 observed regions covering a total area of 0.87 squared degrees in the sky. For each region composing the mosaic, we also show the number of observations in the J, H, and K filters after data processing and cleaning. |
| In the text | |
 |
Fig. 3 Spatial distribution of candidate members. Stars from GDW15 are shown as black squares, and stars from GDW13 are shown as gray points. Membership candidates with valid light curve in the present study are shown as blue dots. OB stars from Wright et al. (2015) are shown as red circles. |
| In the text | |
 |
Fig. 4 Spatial distribution of the stars with an analyzed light curve. Control sample objects are shown as gray circles and candidate member stars are shown as red dots. |
| In the text | |
 |
Fig. 5 Errors vs. magnitude distributions for all data points in both control sample catalog (left) and candidate member catalog (right), for J, H, and K filters. The limit of 0.1 mag for the error, adopted in the present study, is shown as a red dashed line. |
| In the text | |
 |
Fig. 6 Magnitude distributions for the control sample (left) and candidate member sample (right) for J, H, and K filters. |
| In the text | |
 |
Fig. 7 Distribution of 3-band Stetson variability index vs. mean H magnitude. Top: 36 365 objects from control sample with 3 band light curve. Higher density of points is shown as darker gray. Bottom: 5083 stars from the candidate member catalog. In both panels, the 3-band light curve is plotted as light gray dots, and darker gray shows regions with high density of points. The dashed red lines show the selection value S = 0.25. In the right plot, periodic stars are plotted in black. |
| In the text | |
 |
Fig. 8 Periodogram power peak vs. frequency from the selected peak distributions for the H band. All candidate members are shown as gray dots. (Top-left) Stars discarded owing to frequencies around 1 day-1 are shown in blue. (Top-right) Stars discarded owing to S-statistics limit are shown in red. (Bottom-left) Stars discarded owing to RL-statistics limit are shown in yellow. (Bottom-right) Stars selected as periodic stars are shown as black empty circles. The PFAc limit for the H band is shown as a black dashed line. |
| In the text | |
 |
Fig. 9 Ptp amplitude distributions for each band. Black: membership candidate catalog. Gray: periodic stars (Sect. 3.1). Black dashed lines show the median value for the member candidate sample: 0.094, 0.075, and 0.074 mag for J, H, and K band, respectively. Gray lines show the same for the periodic sample: 0.102, 0.087, and 0.080 mag. |
| In the text | |
 |
Fig. 10 Period detection completeness and contamination levels for a mix of periodic synthetic light curves, with periods between 0.2 and 45 days and amplitudes between 0.015 and 1.5 mag. Upper left panel shows Pin × Pout diagram with every synthetic light curve shown as a gray dot, recovered sample periods shown in green, and selected sample periods shown in blue. Harmonic paths are shown as blue dotted line, and 1 day aliasing (cf. Eq. (5)) paths are shown as dashed black lines. Bottom plots: completeness distributions per magnitude (left), amplitude (medium), and period (right) bins. Top: given the selected sample, contamination levels are shown per amplitude (middle) and period (right) bins. Fraction of true recovers are shown as empty bars, and fraction of contamination are shown as filled gray bars. |
| In the text | |
 |
Fig. 11 Same as Fig. 10, but for a mix of periodic synthetic light curves with periods between 0.2 and 20 days and amplitudes between 0.015 and 0.2 mag. |
| In the text | |
 |
Fig. 12 Comparison between periods measured in the present work and in Henderson et al. (2011). Gray circles show the periodic stars in common between the two works. Stars with the same period measured in both works fall over the red dashed line. Red circles show the eclipsing binaries candidates from Henderson et al. (2011). Continuous black lines show 1 day aliasing paths and dashed black lines show the path for harmonics. |
| In the text | |
 |
Fig. 13 Period distributions for the 1196 periodic stars with P< 20 days found in the present study in both linear (top) and logarithm (bottom) scale. The median value for P ≥ 2 days stars is shown as a dotted line. There were 879 stars with P ≥ 2 days and P< 20 days. The red bins show the fast rotators with P< 2 days excluded from the analysis. |
| In the text | |
 |
Fig. 14 Top: period vs. ptp H amplitude for periodic stars. Bottom: median H magnitude vs. ptp amplitude H for periodic stars. Stars with P< 2 days are shown as red dots; stars with P ≥ 2 days are shown as gray dots; and disk-bearing periodic stars are shown as blue dots. |
| In the text | |
 |
Fig. 15 Period distributions for periodic disk-bearing stars with P ≤ 20 days (top) and periodic non-disk-bearing stars with P ≤ 20 days (bottom) for both linear and logarithm distributions. The median value for P ≥ 2 days stars is shown as dotted line. There were 80 disk-bearing stars and 799 non-disk-bearing stars with P ≥ 2 days and P< 20 days. The red bins show the fast rotators with P< 2 days excluded from the analysis. |
| In the text | |
 |
Fig. 16 Top: individual AV distribution for periodic stars. The red line shows the median value, 4.1m. Bottom: riz CCD for periodic stars. Covey et al. (2007) empirical dwarf sequence is shown as dotted lines. A black arrow shows a reddening vector from Schlegel et al. (1998) for AV = 2m. |
| In the text | |
 |
Fig. 17 Top: histogram with mass distribution for periodic stars. Bottom: r − i vs. r-DM CMD for periodic stars. Mass tracks from Bell et al. (2014) for Pisa models (Tognelli et al. 2012) with semi-empirical corrections are shown as dotted lines. A black arrow shows a reddening vector from Schlegel et al. (1998) for AV = 2m. Black Xs show stars excluded from the mass estimation because they were too far away from the minimum mass track. |
| In the text | |
 |
Fig. 18 Mass vs. period distribution for periodic candidate members of CygOB2. Stars with reliable periods (P ≥ 2 days) are shown as black circles, and stars with dubious periods (P< 2 days) are shown as red circles. Dashed red lines delimit for periods equal to 2 and 10 days. The blue dashed line indicates the limit between the mass bins analyzed in the present section. |
| In the text | |
 |
Fig. 19 Histograms showing period distributions for given mass bins in linear (left) and logarithm scale (right). The top panels represent M ≤ 0.4MM⊙ and the bottom panels M> 0.4 M⊙. The median value for P ≥ 2 days stars is shown as a dotted line. There were 89 stars with M ≤ 0.4MM⊙ and P ≥ 2 days and P< 20 days, and 676 stars with M> 0.4 M⊙ in the same period interval. The red bins show the fast rotators with P< 2 days excluded from the analysis. |
| In the text | |
 |
Fig. 20 Disk fraction as a function of period. In both plots, circles show the center of each period bin, while horizontal bars indicate the size of the bin. The bins show fast, intermediate, slow, and very slow rotators. Observational data from the present study are shown as black. Top: the number of stars in each bin is shown for each point. Bottom: disk fractions resulting from M2 simulations from Vasconcelos & Bouvier (2015) for 5.1 Myr and 10.1 Myr are shown together with the fraction observed in CygOB2. |
| In the text | |
 |
Fig. 21 Rotational periods as a function of mass for several young regions with ages between 1–15 Myr. Dashed red lines delimit the periods between 2 and 10 days. Stars used for comparison with the present study are shown in dark gray. |
| In the text | |
 |
Fig. 22 Mass vs. period distribution for periodic candidate members of CygOB2. Stars with reliable periods (P ≥ 2 days) are shown as black circles, and stars with dubious periods (P< 2 days) are shown as red circles. Red dashed lines delimit the periods between 2 and 10 days, while blue dashed lines delimit the mass bin analyzed in the present section. |
| In the text | |
 |
Fig. 23 Same as Fig. 20 but for periodic stars with low UV incident radiation (top) and stars with high UV incident radiation (bottom). |
| In the text | |
 |
Fig. A.1 Period distribution histogram for the input periods for synthetic light curves measured Pout< 2.0 days (2 shorter period bins in Fig. 11) after the automatized period search procedure. |
| In the text | |
 |
Fig. B.1 Phased light curves of periodic CygOB2 candidate members for H filter. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


