| Issue |
A&A
Volume 603, July 2017
|
|
|---|---|---|
| Article Number | A3 | |
| Number of page(s) | 19 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201630133 | |
| Published online | 30 June 2017 | |
The VLT/NaCo large program to probe the occurrence of exoplanets and brown dwarfs at wide orbits
IV. Gravitational instability rarely forms wide, giant planets⋆
1 Aix Marseille Univ, CNRS, LAM, Laboratoire d’Astrophysique de Marseille, 13013 Marseille, France
e-mail: arthur.vigan@lam.fr
2 SUPA, Institute for Astronomy, The University of Edinburgh, Royal Observatory, Blackford Hill, Edinburgh, EH9 3HJ, UK
3 INAF - Osservatorio Astronomico di Padova, Vicolo dell’Osservatorio 5, 35122, Padova, Italy
4 Max-Planck Institute for Astronomy, Königstuhl 17, 69117 Heidelberg, Germany
5 SUPA, School of Physics and Astronomy, University of St Andrews, North Haugh, St. Andrews KY16 9SS, UK
6 St. Andrews Centre for Exoplanet Science, UK
7 Université Grenoble Alpes, IPAG, 38000 Grenoble, France
8 CNRS, IPAG, 38000 Grenoble, France
9 NASA Exoplanet Science Institute, California Institute of Technology, 770 S. Wilson Ave., Pasadena, CA, USA
10 Department of Physics and Astronomy, College of Charleston, Charleston, SC 29424 , USA
11 INAF Osservatorio Astronomico di Capodimonte via Moiarello 16, 80131 Napoli, Italy
12 Department of Astronomy, Stockholm University, AlbaNova University Center, 106 91 Stockholm, Sweden
13 Institute for Astronomy, ETH Zurich, Wolfgang-Pauli-Strasse 27, 8093 Zurich, Switzerland
14 Núcleo de Astronomía, Facultad de Ingeniería, Universidad Diego Portales, Av. Ejercito 441, Santiago, Chile
15 Millennium Nucleus “Protoplanetary Disk”, Departamento de Astronomía, Universidad de Chile, Casilla 36- D Santiago, Chile
16 LESIA, Observatoire de Paris, CNRS, Université Paris Diderot, Université Pierre et Marie Curie, 5 place Jules Janssen, 92190 Meudon, France
17 European Southern Observatory, 3107 Alonso de Cordova, Vitacura, Santiago, Chile
18 European Southern Observatory, Karl-Schwarzschild-Str. 2, 85748 Garching, Germany
19 INAF – Catania Astrophysical Observatory, via S. Sofia 78, 95123 Catania, Italy
20 Observatoire de Haute-Provence, CNRS, Université d’Aix-Marseille, 04870 Saint-Michel-l’ Observatoire, France
21 Physikalisches Institut, University of Bern, Sidlerstrasse 5, 3012 Bern, Switzerland
22 CNRS, CFHT, 65-1238 Mamalahoa Hwy, Kamuela HI, USA
23 Observatoire Astronomique de l’Université de Genève, Chemin des Maillettes 51, 1290 Sauverny, Switzerland
Received: 25 November 2016
Accepted: 6 March 2017
Understanding the formation and evolution of giant planets (≥1 MJup) at wide orbital separation (≥5 AU) is one of the goals of direct imaging. Over the past 15 yr, many surveys have placed strong constraints on the occurrence rate of wide-orbit giants, mostly based on non-detections, but very few have tried to make a direct link with planet formation theories. In the present work, we combine the results of our previously published VLT/NaCo large program with the results of 12 past imaging surveys to constitute a statistical sample of 199 FGK stars within 100 pc, including three stars with sub-stellar companions. Using Monte Carlo simulations and assuming linear flat distributions for the mass and semi-major axis of planets, we estimate the sub-stellar companion frequency to be within 0.75–5.70% at the 68% confidence level (CL) within 20–300 AU and 0.5–75 MJup, which is compatible with previously published results. We also compare our results with the predictions of state-of-the-art population synthesis models based on the gravitational instability (GI) formation scenario with and without scattering. We estimate that in both the scattered and non-scattered populations, we would be able to detect more than 30% of companions in the 1–75 MJup range (95% CL). With the threesub-stellar detections in our sample, we estimate the fraction of stars that host a planetary system formed by GI to be within 1.0–8.6% (95% CL). We also conclude that even though GI is not common, it predicts a mass distribution of wide-orbit massive companions that is much closer to what is observed than what the core accretion scenario predicts. Finally, we associate the present paper with the release of the Direct Imaging Virtual Archive (DIVA), a public database that aims at gathering the results of past, present, and future direct imaging surveys.
Key words: techniques: high angular resolution / methods: statistical / infrared: planetary systems / planetary systems / planets and satellites: formation
© ESO, 2017
1. Introduction
Among the various exoplanet detection methods, direct imaging is the best suited to look for sub-stellar companions orbiting at large orbital separation (>10 AU) around nearby stars (<100 pc). Over the past 15 yr, multiple surveys targeting a variety of stars with different spectral type, distance, age, or metallicity have been successful at placing tight constraints on the frequency of giant planets and brown dwarfs in the 50–1000 AU range (see Bowler 2016, for a recent review). Despite the development of optimized observing strategies and data analysis methods, only a limited number of sub-stellar companions have been detected, leading to the conclusion that the frequency of these objects is very low (typically ≲5%; Galicher et al. 2016). At closer orbital separations, in the 5–50 AU range, the question remains largely unanswered, although initial results (Macintosh et al. 2015; Wagner et al. 2016) from on-going large-scale direct imaging surveys with the new generation of high-contrast imagers and spectrographs (Beuzit et al. 2008; Macintosh et al. 2014; Guyon et al. 2010) suggest that the frequency of young giant planets is within a few percent.
The few known directly imaged giant planets as well as the overall paucity of this type of object at large separations raise the question of planetary formation. The two competing mainstream scenarios are core accretion (CA) and gravitational instability1 (GI). In the CA model, giant planets are formed in a multi-stage process entailing the buildup of a 10–15 M⊕ core followed by rapid accretion of gas from the protoplanetary disk (Pollack et al. 1996; Alibert et al. 2004). This model has been very powerful in explaining a lot of the properties of the exoplanet population detected within 5 AU, but it faces major difficulties in explaining the formation of giant planets farther out than ~20 AU because of the timescales involved (Alibert et al. 2005; Kennedy & Kenyon 2008). Pebble accretion has been proposed as a potential solution to this issue (Lambrechts & Johansen 2012; Levison et al. 2015), but the most recent simulations show that this mechanism does not really form giant planets (several MJup) at large orbital distances (Bitsch et al. 2015, their Figs. 4 and 5).
In the GI model, the planets are the result of gravitational fragmentation and collapse of clumps in the disk (Boss 1998; Vorobyov 2013). This model could more readily explain the existence of gas giants very far from their star, but the conditions that can lead to disk fragmentation are still not fully understood (Meru & Bate 2011; Paardekooper 2012; Rice et al. 2012, 2014; Young & Clarke 2016). In any case, disk-planet interactions (Kley & Nelson 2012) or planet-planet scattering (Veras et al. 2009; Dawson & Murray-Clay 2013) will likely impact on the original semi-major axis distribution of planets, resulting in exoplanets covering a wide range of possible masses, sizes, locations, and compositions.
Observational constraints are crucial in validating or invalidating planetary formation models, and in investigating the migration processes at play during the early evolution of planetary systems. In this regard, planet population synthesis is an interesting approach to statistically compare observations with theory and detect potential shortcomings in the modeling (see the review by Benz et al. 2014). One of the important early successes of planet population synthesis has been to be able to provide a consistent picture of the mass versus semi-major axis diagram for planets up to a few AUs (Ida & Lin 2004; Mordasini et al. 2009).
For directly imaged planets, population synthesis has so far mainly been used for comparison with individual objects, like the giant planet around β Pictoris (Bonnefoy et al. 2013), or as an illustration of the potential for future exoplanet imagers (Rameau et al. 2013). One of the reasons is that population synthesis developments have been primarily based on the CA model, which forms very few massive planets at large separations, therefore making any comparison with results from past direct imaging surveys pointless. Although planet-planet scattering can send planets much farther out in the systems and allow their direct detection, population synthesis models based on CA only recently started to incorporate several planet embryos per disk and their subsequent dynamical evolution (Alibert et al. 2013; Ida et al. 2013). Predictions are currently too premature for comparison with past direct imaging surveys, but will be a key aspect for the forthcoming analysis of the large surveys on-going with VLT/SPHERE (Spectro-Polarimetric High contrast Exoplanet REsearch; Beuzit et al. 2008) and Gemini/GPI (Gemini Planet Imager; Macintosh et al. 2014).
Comparison between direct imaging observations and predictions of the GI theory has only been explored statistically in two surveys (Janson et al. 2011, 2012; Rameau et al. 2013). They used physical considerations to define the domains in the (mass, semi-major axis) parameter space where formation by GI would be allowed, and used the non-detection in their surveys to set upper limits on the giant planet frequency. These studies, however, do not consider the subsequent evolution of a population that may form via GI. Planet population synthesis based on the GI theory has taken much longer than CA to mature, and only lately has a consistent model including multi-object systems been formulated (Forgan & Rice 2013; Forgan et al. 2015). This model predicts the formation of a wide range of sub-stellar objects, a large portion of which could be detected by direct imaging with conventional or extreme adaptive optics systems.
In the present paper, we put the Forgan & Rice (2013) population synthesis model to the test by comparing its outcome to direct imaging results obtained around 200 young, solar-type (FGK) stars. In Sect. 2 we describe our full statistical sample based on 13 previously published direct imaging surveys spanning more than ten years. In Sect. 3, we discuss the detection limits and we present the Direct Imaging Virtual Archive (DIVA), a public database associated with this paper. In Sect. 5 we detail the population synthesis and evolutionary models considered in our analysis and then in Sect. 6 we present our statistical analysis based on outputs of population synthesis. Finally, we discuss our results and present our conclusions in Sect. 7.
2. Sample description
Surveys considered for the construction of the NACO-LP archive sample.
The current work was started in the context of the VLT/NaCo large program to probe the occurrence of exoplanets and brown dwarfs at wide orbits (ESO program 184.C-0157, P.I. J.-L. Beuzit), hereafter NaCo-LP. The general philosophy of the NaCo-LP sample selection has previously been described in Desidera et al. (2015) and Chauvin et al. (2015), but we summarize here the details that led to the definition of the final sample used in our work.
The target selection was originally based on a large compilation of ~1000 young nearby stars that were selected in preparation of the VLT/SPHERE SpHere INfrared survey for Exoplanets (SHINE; Chauvin et al., in prep.) survey. The age determination was based on various youth indicators including lithium content, Ca ii H and K line chromospheric emission, Hα emission, X-ray activity, rotation rate, and kinematics. From this initial compilation, we selected solar-type stars (FGK; 0.4 mag ≤ B−V ≤ 1.2 mag) within a distance horizon of 100 pc and with an age ≤200 Myr, in order to be sensitive to planetary-mass objects in the 50–1000 AU range. An additional cutoff at R ≤ 9.5 was applied, corresponding to the limit for full-performance of the visible wavefront sensor of VLT/SPHERE expected at that time (Fusco et al. 2006). Known spectroscopic and visual binaries (≤6′′) were also removed to have a sample as free as possible from dynamical perturbations to planets in wide orbits (see Sect. 5), as well as to avoid any decrease in performance of the adaptive optics system related to the presence of a stellar companion. Although spectroscopic binaries do not pose technical difficulties for wavefront sensing, they were discarded to focus the study on single stars and stars in extremely wide binary systems. The frequency of circumbinary giant planets has recently been the subject of a dedicated study (Bonavita et al. 2016).
The list was then cross-correlated to the targets observed in previous high-contrast imaging surveys with sensitivities similar to the expected NaCo-LP sensitivity (Masciadri et al. 2005; Lowrance et al. 2005; Kasper et al. 2007; Biller et al. 2007; Lafrenière et al. 2007; Chauvin et al. 2010), resulting in a selection of 110 targets observable from the VLT and that were never previously observed at high-contrast. From this final selection, 85 were observed with VLT/NaCo from 2009 to 2013, while the other 24 could not be observed due to weather or technical losses. The results of the observations and a first statistical analysis of the NaCo-LP observed sample are presented in Chauvin et al. (2015) and Reggiani et al. (2016).
For the final analysis that we present in this work, the observed sample was combined with the results from direct imaging surveys published prior to the start of the NaCo-LP, as well as surveys subsequently published (Heinze et al. 2010; Vigan et al. 2012; Rameau et al. 2013; Biller et al. 2013; Brandt et al. 2014). We also added the results of an unpublished HST/NICMOS survey2 by Song and collaborators and for which we performed a dedicated analysis. The candidates’ identification and follow-up of this program was performed with VLT/NaCo (Chauvin et al. 2010; Song, Farihi priv. com.). Only surveys targeting solar-type stars were included, and we did not include surveys targeting only stars with debris disks (Apai et al. 2008; Wahhaj et al. 2013b) to avoid any significant astrophysical bias. However this selection criterion does not mean that we do not have debris disk targets in our sample. We simply included only surveys that did not use the presence of a known debris disk as their primary selection criterion. The color, R-mag, and distance criteria were also applied to the archival data, but we did not apply the age criterion so as to increase the number of targets in the sample. Table 1 presents a summary of these surveys including the telescope and instrument, the band of the observations, the number of targets in their respective sample (Nsurvey), and the number that we use in the current work (NNaCo−LP). From here on, we refer to the combination of the observed and archive samples as the full NaCo-LP sample, which comprises a total of 199 stars, some of which were observed in several surveys.
Ages and other stellar parameters for the literature surveys were rederived in an homogeneous way following the procedures described in Desidera et al. (2015) for the NaCo sample. However, the ages of some young moving groups were updated, following the recent results by Bell et al. (2015) and correspondingly the ages of stars based on indirect methods (e.g., lithium) taking as reference moving groups members were also updated. Further details on the adopted ages for individual groups are described in Bonavita et al. (2016). The ages of the targets from Desidera et al. (2015) were also revised following the above procedure. The properties of the sample are summarized in Fig. 1, and all the values are detailed in Appendix A.
 |
Fig. 1 Histograms summarising the properties of all the targets considered in the final sample: spectral type, age, distance, and metallicity (from left to right). The complete sample includes 199 individuals targets. All the properties are detailed in Appendix A. |
From Fig. 1 we notice that the metallicity of the sample is quite narrowly distributed around solar value. This is the result of the fact that young stars in solar vicinity have typically metallicity close to the solar values (see, e.g., Santos et al. 2008; D’Orazi et al. 2009; Biazzo et al. 2012). Furthermore, the few stars with metallicity significantly above or below solar are typically among the oldest in the sample, and therefore carry limited information in the statistical analysis. This metallicity distribution and in particular the lack of super-metal-rich young stars should be taken into account in the interpretation of the statistical results of imaging surveys and in the comparison with the samples observed with other techniques like radial velocity, characterized by a broader metallicity distribution.
3. Detection limits
 |
Fig. 2 Summary plot of all the mass detection limits considered in this work (blue dashed lines). The big dot points correspond to the detections of sub-stellar companions that have been considered in the analysis (see Sect. 4). With an estimated mass of 0.1095 ± 0.0022M⊙, HD 130948 BC lies outside the considered mass range, and it is therefore not shown. |
Detection limits for the various surveys were collected from their respective authors. The challenges of defining a reliable detection limit in high-contrast imaging have already been underlined by several authors in the case of angular differential imaging (Marois et al. 2008; Mawet et al. 2014) or its combination with spectral differential imaging (Rameau et al. 2015; Vigan et al. 2015). To simplify the combination of many different detection limits from various surveys in our work, we adopt the commonly used 5σ threshold for all detection limits. Although this may not be completely accurate, there is no simple alternative when considering many surveys, unless one has the capability of reprocessing all the corresponding data in a consistent manner. The only exception to this 5σ threshold is the Biller et al. (2013) survey, where the detection limit is given by a 95% completeness curve, which represents the delta magnitude limit above which 95% of all objects in the field should be detected at a given separation. Wahhaj et al. (2013a), who defined this metric, showed that in most cases it agrees well (at the ~10%–30% level) with the nominal 5σ contrast curves.
While collecting all these detection limits, we realized that there is currently no public database that gathers all the results of past direct imaging surveys. In particular, the position and status of all companion candidates in the field is not always reported or easily accessible in machine-readable format. The availability of such data is of prime importance for the large imaging surveys being performed with VLT/SPHERE and Gemini/GPI, but also for the surveys that will be performed in the future. To remedy this lack, we associate the current paper with the release of DIVA3, a public database designed to contain results from published direct imaging surveys: images, detection limits, signal-to-noise ratio maps, position, and status (when available) of detected companion candidates. To simplify and standardize these heterogeneous data, all the relevant information is packaged into HCI-FITS files, a standard for high-contrast imaging data recently proposed by Choquet et al. (2014b) in the context of the ALICE4 (Archival Legacy Investigations of Circumstellar Environments) project (Choquet et al. 2014a; Soummer et al. 2014).
All the 5σ detection limits and detection maps calibrated in contrast were then converted into companion mass using the AMES-COND2003 evolutionary models (Baraffe et al. 2003) specifically calculated in the filters of the observations (Fig. 2). The post-formation luminosity of giant planets is likely to be the result of the way the material is accreted onto the protoplanetary core, resulting in a broad range of possible luminosities for a similar mass (Fortney et al. 2008; Spiegel & Burrows 2012; Mordasini 2013). However, comparisons of the luminosity of some giant planets with sets of evolutionary tracks or formation models (e.g., Janson et al. 2011; Bonnefoy et al. 2013) tend to show that they do not appear to be compatible with very low initial entropy models (“cold-start”) but instead with intermediate or high initial entropy models (“warm-start” or “hot-start”). For the mass conversion we therefore use the AMES-COND2003 models which correspond to the highest possible initial entropy, but keeping in mind that it is the most favorable scenario. Future studies will need to address the initial entropy problem in large direct imaging surveys more specifically.
4. Sub-stellar companion detections
During the course of the NaCo-LP, we detected twelve previously unknown binaries (Chauvin et al. 2015) and one white dwarf (Zurlo et al. 2013), but no new sub-stellar companions. However, our full statistical sample includes four known companions discovered by other surveys and that must be considered in the analysis. We summarize below the main properties of these companions:
-
GSC 08047-00232 B(TYC 8047-0232 B) is a25 ± 10MJup BD with a derived spectral type of M9.5±1 (Chauvin et al. 2005a) at a projected separation of ~280 AU. It is a probable member of the Tucana-Horologium association, with an age of 10–50 Myr. While the age indicators of GSC 08047-00232 are consistent with other K-type members of Tuc-Hor, its available kinematics are not a strong match to the bulk of the association. For the purpose of this paper we keep this star as a member of Tucana-Horologium;
-
AB Pic b (HIP 30034 b) is a 10–14 MJup object at a projected separation of 275 AU (Chauvin et al. 2005b; Bonnefoy et al. 2010). The object AB Pic b could alternatively be a member of the similarly aged, but less well defined, Carina association (Malo et al. 2013). This has no impact because the ages of Tuc-Hor and Carina are the same within uncertainties;
-
PZ Tel B (HIP 92680 B) is a
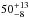 MJup BD companion (Biller et al. 2010; Maire et al. 2016) orbiting on a very eccentric orbit (e> 0.66) at 49–77 AU. It is a member of the β Pictoris moving group.
MJup BD companion (Biller et al. 2010; Maire et al. 2016) orbiting on a very eccentric orbit (e> 0.66) at 49–77 AU. It is a member of the β Pictoris moving group. -
HD 130948 BC (HIP 72567 BC) is a BD binary discovered by Potter et al. (2002), with a total mass estimated at 0.1095 ± 0.0022M⊙ (Dupuy & Liu 2011) and orbiting at a projected separation of ~50 AU from the Sun-like star HD 130948 A. As this is a hierarchical triple system, it is considered in our sample as a binary with masses MA and MBC. As the secondary has a mass outside the mass ranges of interest of this study, we will not consider this as a detection in our analysis.
5. Planet population synthesis models
 |
Fig. 3 Mass (MJup) versus physical separation (AU) for all the companions in the synthetic planet populations generated as described in Sect. 5. Left panel: non-scattered population (Forgan & Rice 2013). Right panel: same population including scattering (Forgan et al. 2015). Different colors are used for single (green), double (blue), triple (orange), and quadruple (purple) systems. The size of the symbols increases from single to quadruple systems to make the plots easier to read. |
The standard planet formation scenario is typically referred to as the core accretion model (Safronov 1972). This involves the growth of micron-sized dust grains to form kilometre-sized planetesimals that then collide and grow to form planetary-mass bodies (Wetherill 1990; Kokubo & Ida 1998). If these become sufficiently massive prior to the dispersal of the disk gas, they may accrete a gaseous envelope (Mizuno 1980) to become a gas giant planet (Pollack et al. 1996). If not, they remain as rocky and icy planets with masses similar to that of the Earth (Chambers & Wetherill 1998).
The detection of giant planets on wide orbits, however, provides a challenge to the standard core accretion scenario, as the growth time for cores at these radii should far exceed the gas disk lifetime (Levison & Stewart 2001). The accretion of centimeter-sized pebbles has been proposed as a possible way of rapidly forming gas giant cores (Lambrechts & Johansen 2012), but this model is relatively young so further exploration of this mechanism is still necessary. An alternative scenario involves direct gravitational collapse in massive, self-gravitating protostellar disks (Kuiper 1951; Boss 1998). The basic idea is that if a protostellar disk is both massive and cold, it becomes susceptible to the growth of gravitational instability (Toomre 1964). If these disks can cool rapidly (Gammie 2001; Rice et al. 2003), or maintain sufficiently high accretion rates while remaining quasi-isothermal (Kratter & Murray-Clay 2011), then this can lead to fragmentation to form bound objects that may then collapse to form planetary-mass bodies, brown dwarfs, or low-mass stars (Stamatellos & Whitworth 2009a).
Furthermore, it has been suggested (Nayakshin 2010a) that within these fragments, dust grains may grow and sediment to form cores, and that the fragments may rapidly migrate into the inner disk. If the contraction of the fragment is slow enough, and the migration and sedimentation fast enough, then the fragment may be stripped of gas by tidal interactions with the host star and this process could in principle form both close-in, and wide orbit, planets (Nayakshin 2017).
It is therefore possible to generate a synthetic population of planets – or brown dwarfs – that form via disk fragmentation, undergo grain sedimentation, and evolve via migration in the protostellar disks and, potentially, via tidal interactions with the host star. We briefly describe the main parameters of the models below, but the reader is encouraged to read Forgan & Rice (2013) and Forgan et al. (2015) for a complete description. The models combine:
-
1.
semi-analytic self-gravitating disk models withphotoevaporation (Rice &Armitage 2009; Owenet al. 2011);
-
2.
analytic fragmentation criteria which measure the local Jeans mass inside a spiral perturbation (Forgan & Rice 2011);
-
3.
a system of fragment evolution equations which follow the evolution of the fragment’s dust and gas components (Nayakshin 2010a,b, 2011);
-
4.
equations that describe the orbital evolution of the protoplanet via disk migration (Kley & Nelson 2012; Baruteau & Masset 2013); and
-
5.
equations describing the tidal disruption of the planetary embryo if it exceeds its Hill radius (Faber et al. 2005).
Once fragmentation has occurred, the embryos continue to collapse in a manner analogous to protostellar collapse, while their internal dust population grows and begins to sediment towards the pressure maximum at the center. This sedimentation is suppressed partially by gas turbulence and high-velocity collisional destruction, and eventually by evaporation as the gas temperature continues to increase. The embryo migrates radially inward according to the local disk properties, and can be tidally disrupted as it overflows its own Roche lobe. Indeed, almost half of all embryos are destroyed during this process.
 |
Fig. 4 Histogram (top) and cumulative histogram (bottom) of the population before and after scattering as a function of semi-major axis, normalized with respect to the total number of planets in the population. Only objects below 75 MJup are considered. Approximately 50% of the planets are ejected from the systems during the scattering, resulting in a much smaller total number of planets in the scattered population. The vertical dashed lines at 10 and 400 AU mark the semi-major axis range where the average detection probability of our observations is ~50% or more for massive companions. |
In this work, we assume a disk with maximum radius of 100 AU, with a surface density profile Σ ∝ r-1, and with solar metallicity. The stellar mass and disk mass are varied for each iteration of the model, as is the X-ray luminosity of the star, which affects the timescale for disk photoevaporation and hence sets a time limit on the fragments’ evolution. The resulting population generated is described in detail in Sect. 3.1 of Forgan & Rice (2013).
The population synthesis model yields (mainly) relatively massive gas giants and brown dwarfs, with the majority of these objects residing at semi-major axes above 30 AU. As this model does not consider the dynamical evolution of these bodies after the protostellar disk has dispersed, the systems for which more than two embryos have formed are evolved for 106 yr using n-body simulations to ascertain the effect of object-object scattering on the planetary orbital parameters (Forgan et al. 2015). Although each system is evolved for a time that is smaller than the observed ages of objects which we would like to compare to disk fragment models, this relatively low simulation time was used partly to reduce computational expense and partly because systems that produce scattering events express this instability within a few tens of thousands of years (Chambers et al. 1996; Chatterjee et al. 2008). As such, the results should reasonably reflect the likely outcome of fragment-fragment interactions. Having said this, we must note that secular evolution of these systems may occur over timescales greater than 106 yr (e.g., Veras et al. 2009). As a result, we may underestimate the number of bodies ejected from their host star systems, and we may also underestimate the final semimajor axis of the bodies that do remain bound.
This procedure therefore gives two data sets to consider: the first is the output of the population synthesis model (hereafter non-scattered population; Forgan & Rice 2013), and the second is the dynamically evolved, post-disk dispersal population (hereafter scattered population; Forgan et al. 2015).
Figure 3 shows the output of the population synthesis models for both the scattered (left panel) and non-scattered (right panel) population. We can see that for both before and after scattering, the majority of the population resides at semi-major axes >20 AU, with masses of the order of one Jupiter mass (MJup) and larger. This is despite the model’s ability to tidally downsize the bodies into the Neptune and Earth mass regime, which some authors predict (Nayakshin 2010a), but we find such events are statistically rare enough not to occur, despite synthesising a total of one million disk fragments. Crucially, whatever subsequent modification occurs to the bodies after fragmentation, the process preferentially generates large populations of bodies with masses above 1 MJup and semi-major axes above 20 AU, well within the sweet spot of direct imaging observation sensitivity reported in the present work.
Figures 4 and 5 show the evolution of the two populations in terms of semi-major axis distribution and repartition of the number of planets in the systems. For the semi-major axis, the scattering creates a tail of planets that go much beyond 100 AU, but the population remains largely dominated by a large peak in the 10–100 AU range. However, the cumulative histogram shows that ~50% of the planets are ejected from the systems during the scattering. This process affects mainly systems with three or more planets (Fig. 5), which are sometimes transformed into systems with one or two planets, but which more generally end up with not planets at all.
We should note of course that the population synthesis models of Forgan & Rice (2013) are the first steps towards a complete description of disk fragmentation and the tidal downsizing process. The post-processing of the model’s output by Forgan et al. (2015) highlights the importance of fragment-fragment interactions in setting the distribution of orbital parameters (especially eccentricity). However, these interactions only occur after the disk dissipates – interactions between fragments while still embedded in the disk are neglected. Simulations of fragmenting disks demonstrate that these early fragment interactions can determine whether a fragment survives tidal downsizing to become a detectable sub-stellar object (Stamatellos & Whitworth 2009a,b; Hall et al. 2017).
The model does not permit accretion of further gas from the disk by the fragment, and therefore the masses derived by the model are lower limits. Mass accretion can encourage the opening of gaps in the disk and reduce the migration speed, which allows more massive objects to remain at larger semi-major axis. That being said, Baruteau et al. (2011) and Zhu et al. (2012) show that migration rates in self-gravitating disks are rapid compared to theoretical calculations based on low-mass disks, and Malik et al. (2015) show that this can frustrate gap opening even for high fragment masses. If fragments do survive the tidal downsizing process, these results suggest such objects are likely to be more massive, and hence easier to detect than the Forgan & Rice (2013) model currently predicts.
 |
Fig. 5 Fraction of systems in the scattered and non-scattered populations as a function of the number of planets in the system. The total number of systems and planets before and after scattering is displayed in the top-right corner of the plot. The bins are normalized to the total number of systems in each of the two populations independently. The ~2% of systems with zero planets before scattering correspond only to cases where all the companions in the systems have masses above 75 MJup, while for the scattered case it also includes systems where all the companions were ejected as a result of the scattering process. |
The accretion of solid material (e.g., Helled et al. 2006) is also not modeled, which in turn affects the microphysics of dust settling in the fragment (Nayakshin 2016). As this is responsible for the formation of solid cores in the GI formalism, this affects the survival rates of disk fragments. The physics of fragment evolution is at its heart the study of dust-gas interactions in a collapsing environment, a process that is challenging to describe semi-analytically. The interested reader should consult Nayakshin (2017) for a review of the multiple physical processes at play.
Finally, it is still somewhat unclear as to how stellar companions might influence the evolution of self-gravitating protostellar disks, which is one of the reasons why visual binaries with separations below 6′′ have been removed from the sample. Much of the early work in this area investigated the role of stellar encounters, which indicate how the impulse induced by a companion can promote or inhibit fragmentation. Boffin et al. (1998) suggested that encounters might promote disk fragmentation, while more recent work has suggested that they will typically inhibit fragmentation (Lodato et al. 2007; Forgan & Rice 2009). This latter work, however, considered disks that were initially sufficiently compact that fragmentation in isolation was unlikely. If disks can be sufficiently extended that they become irradiation dominated, then encounters may well trigger fragmentation in the outer regions of these disks (Thies et al. 2010). It is, however, still unclear as to whether or not such extended disks actually exist at such early times (Maury et al. 2010).
More recent studies now consider the secular evolution of self-gravitating protostellar disks by companions on closed orbits. For example, Fu et al. (2017) demonstrated for isothermal disks that if the companion’s orbit is sufficiently tilted compared to the disk plane, Kozai-Lidov oscillations can induce fragmentation even when the disk has a Toomre parameter Q> 2. Further work is required to fully ascertain the role of binary companions in disk fragmentation, with particular attention needing to be paid to disk thermodynamics and sweeping the relatively large parameter space of both binary and disk configurations.
6. Statistical analysis
6.1. Giant planet and brown dwarf frequency estimation
The statistical analysis of the survey results has been done using the MESS code (Multi-purpose Exoplanet Simulation System, see Bonavita et al. 2012) and its QMESS evolution (Bonavita et al. 2013). The code allows a high level of flexibility in terms of possible assumptions on the synthetic planet population to be used for the determination of the detection probability. For consistency with previous work (see, e.g., Lafrenière et al. 2007; Vigan et al. 2012; Rameau et al. 2013) and to allow a straightforward comparison of the results, we started our analysis by generating a population of planets using a given set of assumptions on the planet parameter distributions, and comparing the detectability of this population of planets with our detection limits to obtain a mean probability of detection map. We assumed flat distributions in linear space for the mass and semi-major axis respectively, in the 1–75 MJup range by steps of 1 MJup and in the 1–1000 AU range by steps of 1 AU. Following Hogg et al. (2010), we adopt a Gaussian eccentricity distribution with μ = 0 and σ = 0.3. The implications of choosing this distribution over a flat eccentricity distribution are discussed in Bonavita et al. (2013). The mean sensitivity map that we obtain, plotted in Fig. 6 for the optimal stellar ages of the sample, illustrates the high sensitivity of the full NaCo-LP sample of brown dwarfs and massive planets down to ~10 MJup in the 50–300 AU range.
Following Lafrenière et al. (2007) and Vigan et al. (2012), we can estimate the fraction of stars that host at least one brown dwarf or giant planet, Fps, using the detection probability maps of individual targets and the confirmed detections in our sample (see Sect. 4). Since we have no a priori information on Fps, we assume a flat prior. The probability density function (PDF) of Fps in different semi-major axis and mass intervals is plotted in Fig. 7, and the results are summarized for the best stellar ages in Table 2 (results for the extreme ages are provided in Appendix B). As mentioned in Sect. 4, HD 130948 BC is considered in our sample as a binary and is therefore not used in this analysis. The frequency values are in agreement with the results presented by Galicher et al. (2016) for a sample of a similar size to ours. They support a frequency between 1–2% and 3–4% for planetary-mass and brown dwarfs around FGK stars within 100 pc.
To remain as unbiased as possible when deriving the PDF of Fps, this analysis assumes flat distributions in mass and semi-major axis (i.e., linear-flat priors). A more realistic approach would be to consider log-uniform priors, which would favor less massive, closer-in planets compared to distant giant planets. The main qualitative effect on our results would be to increase the number of planets that we cannot detect, and would therefore broaden significantly the PDFs showed in Fig. 7. Instead of relying on these modified priors, which are more realistic but still disconnected from the physics of planetary formation, we propose to use population synthesis models to constrain the planetary system frequency.
6.2. Analysis based on population synthesis models
 |
Fig. 6 Mean detection probability map for the complete sample of 199 stars as a function of mass and semi-major axis. In this plot we adopt the best estimate for the stellar ages. The four detections of the sample are over-plotted. The probability map assumes flat distributions of planets in mass and semi-major axis. |
Fraction of stars that host a planetary system, assuming linear flat mass and semi-major axis distributions.
 |
Fig. 7 Probability distribution of the frequency of stars with at least one giant planet in the mass and semi-major axes ranges indicated in the top-right of the plot. The results are summarized in Table 2. The plain lines represent the probability density function obtained when considering the best age estimate for all the stars in the sample, and the colored envelopes represent the variations when considering the minimum and maximum ages. |
 |
Fig. 8 Comparison of the non-scattered (left) and scattered (right) GI populations (Forgan & Rice 2013; Forgan et al. 2015) with the mean detection probabilities of the observations (best age estimate). A significant fraction of the GI population could potentially be detected, even in the non-scattered case. The colors and symbols for the populations and the known companions are the same as in Figs. 3 and 6. |
 |
Fig. 9 Histogram of the mass and separation of companions detectable at various confidence levels, for the scattered (right panels) and non-scattered (left panels) population. Similarly to Fig. 7, the plain lines represent the values for the best age estimate of the stars, and the colored envelopes show the variations observed when considering the minimum and maximum ages. The fraction of detected companions is smaller for the maximum ages and larger for the minimum ages. For the histograms in mass, semi-major axes from 1 to 500 AU are considered, and for the histograms in semi-major axis, masses from 1 to 75 MJup are considered. A confidence level of 95% means that for a given bin, the height of the bin represents the fraction of companions in that bin that have been detected in 95% (or more) of the simulated surveys. The small drop at 330 AU in the scattered population is numerical. |
 |
Fig. 10 Probability distribution of the frequency of stars hosting at least one planetary system, based on the non-scattered (left) and scattered (right) populations described in Sect. 5. Similarly to Figs. 7 and 9, the plain lines represent the probability density function obtained when considering the best age estimate, and the shaded areas show the variations obtained when considering the full age range. The results are summarized in Table 3. |
One of the goals of our work is to test the predictions of the Forgan & Rice (2013) population synthesis model based on the GI formation mechanism and described in Sect. 5. The output of the GI models provides mass, physical separation, and eccentricity for all the planets in the population. We use this information to compare the non-scattered and scattered populations with the detection limits of the survey presented in Fig. 2. Qualitatively, it appears that if a large population of planets formed by GI exists, it should be detectable from these observations.
To try to quantify this statement, we use the MESS code to assess the detectability of this GI population for our survey. The masses, semi-major axes, and eccentricities are taken directly from the generated population, and the code takes care of randomly generating all the missing orbital parameters needed to project the planetary orbit and evaluate the projected separation at the time of the observation. The detectability of the full population is then tested against the detection limits described in Sect. 3, individually for all the stars in the sample.
This process allows us to estimate the probability of detection of each companion in the population5. Figure 9 summarizes the result of the analysis: for each panel the fraction of companions with average detection probability greater than 68%, 90%, and 95% are shown as a function of the companion mass (top) or separation (bottom) for both the scattered and non-scattered populations. The fraction of companions detected in each bin is of course highly correlated to the planets distribution in the original populations (Fig. 4). The apparent inconsistency between Figs. 8 and 9 is caused by the fact that Fig. 8 compares the populations to the mean probability, which is pessimistic in the case of stars with poor detection limits (see Fig. 2), whereas Fig. 9 is based on a per-star analysis which is then combined together to produce the figure.
The plots as a function of semi-major axis in Fig. 9 show that more than 30% of companions with masses in the 1–75 MJup range and separations in the 70–200 AU range would be detected in 95% of the simulated surveys, for both the scattered and non-scattered scenarios. This number even goes above 50% when considering 68% of the simulated surveys. In the plots as a function of mass, there is a significant loss of sensitivity towards small masses (<10 MJup) because the population contains a large fraction of 1–20 MJup planets to which we are not very sensitive. Nevertheless, the population also contains a significant fraction of 20–50 MJup objects to which we are highly sensitive, both in the scattered and non-scattered scenarios. In other words, this analysis shows that under the hypothesis of the model, a population of GI-formed planets would have a great chance of being detected by our survey, even if scattering is negligible.
The MESS code provided us with a probability of detecting each companion belonging to the GI populations around each star in our sample, taking into account the observed detection limits and the projection effects (see above). Such results can be used to constrain the value of the frequency companions compatible with our survey results, in a similar fashion to what is described in Sect. 6.1. Most companions in the populations are part of multiple systems (both in the non-scattered and scattered case, see Fig. 5). We therefore decided that a more meaningful way to interpret our results would be to consider the probability of detecting a system with one or more companions, instead of considering each companion singularly. We therefore considered a synthetic system detected if at least one of its components had a detection probability greater than zero. In cases where more than one component satisfied such a requirement, then the highest value of the detection probability among the components was adopted as the detection probability of that system. Instead of limiting our analysis to a specific mass and semi-major axis range, we considered all the systems in the populations with companions up to 75 MJup. Once the detection probability of each synthetic system was obtained for all the stars in the sample, the average over all the systems was adopted as the detection probability for each star. This allowed us to estimate the fraction of stars hosting at least one system consisting of one or more companions formed via GI, compatible with our observations. The results are shown in Fig. 10 and summarized in Table 3 for both the non-scattered and scattered case.
All but one companion (AB Pic b) detected in our survey have estimated masses considerably higher than 14 MJup, therefore they are more properly characterized as brown dwarfs than planets. Thus, we have calculated limits on Fps both for planets and higher mass companions as well as for the planets only case (in this case, defining “planet” as anything with mass ≤14 MJup). When considering all companions (three detections), we estimate 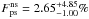 at the 95% confidence level for the non-scattered population and
at the 95% confidence level for the non-scattered population and 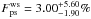 for the scattered case. For companions with masses ≤14MJup (one detection), these estimations drop to
for the scattered case. For companions with masses ≤14MJup (one detection), these estimations drop to 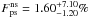 and
and  respectively.
respectively.
It is interesting to note that the best estimates of Fps are very similar in the scattered and non-scattered case. This is likely the result of the shape of the semi-major axis distribution of the population: in Fig. 4 we see that although the scattering sends many objects at very large orbital separations, the overall shape of the distribution remains dominated by a large peak in the 10–100 AU range where our observations are the most sensitive. The effect of the tail of the population that is scattered in the 100–400 AU range is almost negligible and has little influence on the Fps estimation. The main consequence is that if we assume that all the detected companions are the result of a GI-like formation scenario, then our observations cannot distinguish between the scattered and non-scattered scenarios: both scenarios appear equally likely when compared to the observations.
7. Discussion and conclusions
The dearth of detections of massive bodies at large radii challenges the gravitational instability theory of planet formation. This theory proposes that giant planets and brown dwarfs may be formed via disk fragmentation, which is predicted to occur at semi-major axes of at least 30–50 AU and larger.
In a previous attempt at constraining the GI formation mechanism using the Gemini Deep Planet Survey sample (Lafrenière et al. 2007), Janson et al. (2012) used a toy model (Klahr et al., unpublished) to define the range of mass and semi-major axis where formation by GI would in principle be allowed around FGKM-type stars. In their approach, they consider that two criteria need to be satisfied simultaneously to form a planet by GI: the Toomre parameter (Toomre 1964) needs to be small enough for an instability to occur, which translates into a minimum mass of the resulting planet, and the cooling timescale of the disk needs to be short enough for fragmentation to occur (Gammie 2001), which translates into a minimum semi-major axis of the resulting planet. The upper limit of Fps< 10% with 98% confidence derived by Janson et al. (2012) is in very good agreement with our findings for the non-scattered population, based on a much more realistic model. We also note that Rameau et al. (2013) reached similar conclusions as Janson et al. (2012) regarding the rarity of planets formed by GI around A-stars using the same toy model approach.
Our study goes one step further and considers for the first time a more complete formation model based on GI that includes the scattering of the planets. The semi-major axis distribution of GI objects can be significantly modified by orbital migration (Baruteau et al. 2011; Zhu et al. 2012), dynamical interactions with neighboring GI objects, and nearby stellar systems (Forgan et al. 2015). The masses of these bodies can also be reduced by Roche lobe overflow as they migrate inwards, drawing them into the parameter space more associated with core accretion (Nayakshin 2010a). That being said, it is equally true that statistical studies of these processes produce populations with properties that do overlap with core accretion, but they necessarily produce a large fraction of objects which remain at large semi-major axis and with masses greater than a few Jupiter masses.
The fact that this high mass component, easily detectable, is not present in most of the observations presented here places strong constraints on how frequently disk fragmentation occurs. With only three detections in the brown-dwarf and planetary-mass regime, our analysis suggests that if GI is the predominant formation scenario for these objects then it is rare (<5%). This result holds whether or not scattering is considered. We note that even though our observations are not sensitive to the very widest separations over which outward-scattered planets reside in the GI population, the Spitzer/IRAC direct imaging survey by Durkan et al. (2016) has placed a frequency upper limit of 9% for planets in the 0.5–13 MJup and 100–1000 AU ranges, which is compatible with our results closer in.
 |
Fig. 11 Density plots representing scattered populations based on GI (Forgan & Rice 2013; Forgan et al. 2015) and CA (Ida et al. 2013) compared to the detections in our sample and to the mean detection probabilities of the observations (contour lines are at 5%, 25%, 50%, 90%, and 95%). Density colors go from dark blue (low occurrence) to cyan (high occurrence) for the CA population, and from red (low occurrence) to yellow (high occurrence) for the GI population. The histograms on top and on the right represent the relative frequency in each bin of semi-major axis and planetary mass respectively. The histograms take into account the whole population, including the planets that are outside of the visibility window of the main plot. The semi-major axis and mass of the known companions are represented with dashed lines in the histograms. |
Our conclusion that GI is rare is also consistent with an analysis by Rice et al. (2015), who considered the scattering and then tidal evolution of a population of planetary-mass bodies initially on wide orbits. Their analysis suggested that if GI were common, there should be a large population of “hot”, or proto-“hot”, Jupiters that formed via GI on wide orbits, were scattered onto eccentric orbits by more distant stellar companions, and were then tidally circularized by interactions with their host star. That the population of known “hot”, and proto-“hot”, Jupiters is inconsistent with this origin suggests that the formation of planetary-mass bodies by GI is rare.
Even though GI cannot be common, it is predicting a mass distribution of wide-orbit sub-stellar companions that is much closer to what is observed than what CA scenarios predict. To illustrate this, we compare in Fig. 11 two populations that include scattering: one based on the GI scenario, produced by the model of Forgan et al. (2015), and the other based on the CA scenario, produced by the model of Ida et al. (2013). While the bulk of the CA population is dominated by sub-Jupiter mass planets within ~10 AU, there is an overlap with the GI population in the 1–10 MJup range within 10 AU. However, the mass histogram clearly shows that GI dominates when considering masses above 5 MJup and separations above 20 AU, similar to those of the imaged companions. CA cannot form massive brown dwarfs such as PZ Tel B, and even if extreme cases of scattered CA could form objects similar to TYC 8047-0232 B and AB Pic B, observing two cases of very large separation (>200 AU) massive companions while not observing the more common and easily detectable population that is predicted in the 50–200 AU range appears extremely improbable. Using a simple Monte Carlo simulation based on the mass and semi-major axis distributions of the two populations, and on the average detection probability map of the survey (Fig. 6), we estimate that it is ~600 000 times more likely to obtain three detections from the GI population than from the CA population. It seems therefore extremely unlikely for CA to be the preferential mechanism that explains the formation of the three imaged companions in the full NaCo-LP sample. This is of course even more the case when scattering is not included, since in that case the CA model produces no planets at separations wider than 20–30 AU.
We cannot completely rule out the formation of some of the observed companions by gravo-turbulent fragmentation (Hopkins 2013), that is, following a binary star-like formation scenario. Reggiani et al. (2016) have showed that the NaCo-LP observations are compatible with a sub-stellar companion mass function constituted by a superposition of the stellar mass-ratio distribution and a planet mass function extrapolated from radial velocity detections. In that framework, our conclusions would still be valid because their model shows that to be compatible with the observations, they need to apply a cutoff of the RV extrapolation well below 100 AU, that is, typically in the range where CA still manages to produce a large fraction of planets. This value of the cutoff is actually supported by many previous direct imaging surveys (e.g., Lafrenière et al. 2007; Kasper et al. 2007; Chauvin et al. 2010).
Our analysis of the planet frequency in Sect. 6.1 assumes a linear flat distribution for the planet’s mass and semi-major axis to derive the young giant planet frequency at large orbital separation. It can be argued that this approach, which does not rely on unknown or improperly modeled physics, is less prone to bias the estimation of the planet frequency. However, it puts an equal statistical weight on planets at all masses and separations, which is in contradiction with all models of planet formation, either based on CA (Mordasini et al. 2009; Ida & Lin 2004; Ida et al. 2013) or GI (Forgan & Rice 2013; Forgan et al. 2015; Nayakshin 2017), which all agree that the formation of very massive companions at large orbital separation occurs much less frequently than less massive, closer-in planets. Although based on models, this information is important to take into account prior to the analysis. Despite the limitations highlighted at the end of Sect. 5, the models of Forgan & Rice (2013) constitute state-of-the-art models of formation by GI. It is important to be cautious in deriving quantitative estimations based on these models, but the fact that our frequency estimations in Sect. 6.1 are compatible with the ones derived from the population synthesis models is a good sanity check.
It is also an essential first step for on-going large scale surveys with new-generation high-contrast imagers. These surveys, which are sensitive to lower masses at smaller orbital separations, are exploring the regime where CA and GI could have similar chances to form giant planets. In that context, statistical analysis work based on the outcomes of these surveys will need to make a stronger link between the observations and planet formation theories. This means focusing not only on deriving the occurrence rate of giant companions, but more importantly on deriving the properties of their underlying mass, separation, and eccentricity distributions. We have tried to initiate a first step in this direction using population synthesis models, and we hope that more work will soon follow.
HST, cycle 13, PI Inseok Song, GO10176: “Coronagraphic Survey for Giant Planets Around Nearby Young Stars”.
Acknowledgments
The authors warmly thank B. Biller, T. Brandt, G. Chauvin, A. Heinze, M. Kasper, D. Lafrenière, P. Lowrance, E. Masciadri, T. Meshkat, J. Rameau, I. Song and A. Vigan for providing the detection limits and candidates information for their surveys. We are also extremely grateful to S. Ida for providing planetary populations. Finally, AV is extremely grateful to Élodie Choquet, Rémi Soummer, Laurent Pueyo and Brendan Hagan for fruitful discussions on the definition of a standard file format for high-contrast imaging surveys. J.L.B., M.B., G.C., P.D., J.H., A.M.L., C.M., A.V. and A.Z. acknowledge support in France from the French National Research Agency (ANR) through project grants ANR10-BLANC0504-01 (GUEPARD) and ANR-14-CE33-0018 (GIPSE). DHF gratefully acknowledges support from the ECOGAL project, grant agreement 291227, funded by the European Research Council under ERC-2011-ADG. M.B., S.D., E.C., R.G., D.M. and S.M. acknowledge support from PRIN-INAF “Planetary systems at young ages and the interactions with their active host stars” and from the “Progetti Premiali” funding scheme of the Italian Ministry of Education, University, and Research. BB gratefully acknowledges support from STFC grant ST/M001229/1. J.C. was supported by the U.S. National Science Foundation under award no. 1009203. C.M. acknowledges the support from the Swiss National Science Foundation under grant BSSGI0_155816 “Planets In Time”. The research leading to these results has received funding from the European Union Seventh Framework Programme (FP7/2007-2013) under grant Agreement No. 313014 (ETAEARTH).
References
- Alibert, Y., Mordasini, C., & Benz, W. 2004, A&A, 417, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alibert, Y., Mordasini, C., Benz, W., & Winisdoerffer, C. 2005, A&A, 434, 343 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alibert, Y., Carron, F., Fortier, A., et al. 2013, A&A, 558, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Apai, D., Janson, M., Moro-Martín, A., et al. 2008, ApJ, 672, 1196 [NASA ADS] [CrossRef] [Google Scholar]
- Baraffe, I., Chabrier, G., Barman, T. S., Allard, F., & Hauschildt, P. H. 2003, A&A, 402, 701 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baruteau, C., & Masset, F. 2013, in Lect. Notes Phys., 861, eds. J. Souchay, S. Mathis, & T. Tokieda (Berlin: Springer Verlag), 201 [Google Scholar]
- Baruteau, C., Meru, F., & Paardekooper, S.-J. 2011, MNRAS, 416, 1971 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, C. P. M., Mamajek, E. E., & Naylor, T. 2015, MNRAS, 454, 593 [NASA ADS] [CrossRef] [Google Scholar]
- Benz, W., Ida, S., Alibert, Y., Lin, D., & Mordasini, C. 2014, in Protostars and Planets VI (University of Arizona Press), 691 [Google Scholar]
- Beuzit, J.-L., Feldt, M., Dohlen, K., et al. 2008, in Ground-based and Airborne Instrumentation for Astronomy II, Proc. SPIE, 7014, 701418 [CrossRef] [Google Scholar]
- Biazzo, K., D’Orazi, V., Desidera, S., et al. 2012, MNRAS, 427, 2905 [NASA ADS] [CrossRef] [Google Scholar]
- Biller, B. A., Close, L. M., Masciadri, E., et al. 2007, ApJS, 173, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Biller, B. A., Liu, M. C., Wahhaj, Z., et al. 2010, ApJ, 720, L82 [NASA ADS] [CrossRef] [Google Scholar]
- Biller, B. A., Liu, M. C., Wahhaj, Z., et al. 2013, ApJ, 777, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Bitsch, B., Lambrechts, M., & Johansen, A. 2015, A&A, 582, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boffin, H. M. J., Watkins, S. J., Bhattal, A. S., Francis, N., & Whitworth, A. P. 1998, MNRAS, 300, 1189 [NASA ADS] [CrossRef] [Google Scholar]
- Bonavita, M., Chauvin, G., Desidera, S., et al. 2012, A&A, 537, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonavita, M., de Mooij, E. J. W., & Jayawardhana, R. 2013, PASP, 125, 849 [NASA ADS] [CrossRef] [Google Scholar]
- Bonavita, M., Desidera, S., Thalmann, C., et al. 2016, A&A, 593, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonnefoy, M., Chauvin, G., Rojo, P., et al. 2010, A&A, 512, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonnefoy, M., Boccaletti, A., Lagrange, A.-M., et al. 2013, A&A, 555, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boss, A. P. 1998, ApJ, 503, 923 [NASA ADS] [CrossRef] [Google Scholar]
- Bowler, B. P. 2016, PASP, 128, 102001 [NASA ADS] [CrossRef] [Google Scholar]
- Brandt, T. D., Kuzuhara, M., McElwain, M. W., et al. 2014, ApJ, 786, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Chambers, J. E., & Wetherill, G. W. 1998, Icarus, 136, 304 [NASA ADS] [CrossRef] [Google Scholar]
- Chambers, J. E., Wetherill, G. W., & Boss, A. P. 1996, Icarus, 119, 261 [Google Scholar]
- Chatterjee, S., Ford, E. B., Matsumura, S., & Rasio, F. A. 2008, ApJ, 686, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Chauvin, G., Lagrange, A.-M., Lacombe, F., et al. 2005a, A&A, 430, 1027 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chauvin, G., Lagrange, A.-M., Zuckerman, B., et al. 2005b, A&A, 438, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chauvin, G., Lagrange, A.-M., Bonavita, M., et al. 2010, A&A, 509, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chauvin, G., Vigan, A., Bonnefoy, M., et al. 2015, A&A, 573, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Choquet, É., Pueyo, L., Hagan, J. B., et al. 2014a, in Space Telescopes and Instrumentation 2014: Optical, Infrared, and Millimeter Wave, Proc. SPIE, 9143, 914357 [CrossRef] [Google Scholar]
- Choquet, É., Vigan, A., Soummer, R., et al. 2014b, in Ground-based and Airborne Instrumentation for Astronomy V, Proc. SPIE, 9147, 914751 [CrossRef] [Google Scholar]
- Dawson, R. I., & Murray-Clay, R. A. 2013, ApJ, 767, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Desidera, S., Covino, E., Messina, S., et al. 2015, A&A, 573, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D’Orazi, V., Randich, S., Flaccomio, E., et al. 2009, A&A, 501, 973 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dupuy, T. J., & Liu, M. C. 2011, ApJ, 733, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Durkan, S., Janson, M., & Carson, J. C. 2016, ApJ, 824, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Faber, J. A., Rasio, F. A., & Willems, B. 2005, Icarus, 175, 248 [NASA ADS] [CrossRef] [Google Scholar]
- Forgan, D., & Rice, K. 2009, MNRAS, 400, 2022 [NASA ADS] [CrossRef] [Google Scholar]
- Forgan, D., & Rice, K. 2011, MNRAS, 417, 1928 [NASA ADS] [CrossRef] [Google Scholar]
- Forgan, D., & Rice, K. 2013, MNRAS, 432, 3168 [NASA ADS] [CrossRef] [Google Scholar]
- Forgan, D., Parker, R. J., & Rice, K. 2015, MNRAS, 447, 836 [NASA ADS] [CrossRef] [Google Scholar]
- Fortney, J. J., Marley, M. S., Saumon, D., & Lodders, K. 2008, ApJ, 683, 1104 [NASA ADS] [CrossRef] [Google Scholar]
- Fu, W., Lubow, S. H., & Martin, R. G. 2017, ApJ, 835, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Fusco, T., Rousset, G., Sauvage, J.-F., et al. 2006, Optics Express, 14, 7515 [Google Scholar]
- Galicher, R., Marois, C., Macintosh, B., et al. 2016, A&A, 594, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gammie, C. F. 2001, ApJ, 553, 174 [Google Scholar]
- Guyon, O., Martinache, F., Garrel, V., et al. 2010, in Adaptive Optics Systems II, Proc. SPIE, 7736, 773624 [CrossRef] [Google Scholar]
- Hall, C., Forgan, D., & Rice, K. 2017, MNRAS, submitted [Google Scholar]
- Heinze, A. N., Hinz, P. M., Sivanandam, S., et al. 2010, ApJ, 714, 1551 [NASA ADS] [CrossRef] [Google Scholar]
- Helled, R., Podolak, M., & Kovetz, A. 2006, Icarus, 185, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Hogg, D. W., Myers, A. D., & Bovy, J. 2010, ApJ, 725, 2166 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F. 2013, MNRAS, 430, 1653 [NASA ADS] [CrossRef] [Google Scholar]
- Ida, S., & Lin, D. N. C. 2004, ApJ, 604, 388 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ida, S., Lin, D. N. C., & Nagasawa, M. 2013, ApJ, 775, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Janson, M., Bonavita, M., Klahr, H., et al. 2011, ApJ, 736, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Janson, M., Bonavita, M., Klahr, H., & Lafrenière, D. 2012, ApJ, 745, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Kasper, M., Apai, D., Janson, M., & Brandner, W. 2007, A&A, 472, 321 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kennedy, G. M., & Kenyon, S. J. 2008, ApJ, 673, 502 [NASA ADS] [CrossRef] [Google Scholar]
- Kley, W., & Nelson, R. P. 2012, ARA&A, 50, 211 [Google Scholar]
- Kokubo, E., & Ida, S. 1998, Icarus, 131, 171 [Google Scholar]
- Kratter, K. M., & Murray-Clay, R. A. 2011, ApJ, 740, 1 [Google Scholar]
- Kuiper, G. P. 1951, in 50th Anniversary of the Yerkes Observatory and Half a Century of Progress in Astrophysics, ed. J. A. Hynek (New York: McGraw-Hill), 357 [Google Scholar]
- Lafrenière, D., Doyon, R., Marois, C., et al. 2007, ApJ, 670, 1367 [NASA ADS] [CrossRef] [Google Scholar]
- Lambrechts, M., & Johansen, A. 2012, A&A, 544, A32 [CrossRef] [EDP Sciences] [Google Scholar]
- Levison, H. F., & Stewart, G. R. 2001, Icarus, 153, 224 [NASA ADS] [CrossRef] [Google Scholar]
- Levison, H. F., Kretke, K. A., & Duncan, M. J. 2015, Nature, 524, 322 [CrossRef] [Google Scholar]
- Lodato, G., Meru, F., Clarke, C. J., & Rice, W. K. M. 2007, MNRAS, 374, 590 [NASA ADS] [CrossRef] [Google Scholar]
- Lowrance, P. J., Becklin, E. E., Schneider, G., et al. 2005, AJ, 130, 1845 [NASA ADS] [CrossRef] [Google Scholar]
- Macintosh, B., Graham, J. R., Ingraham, P., et al. 2014, Proc. Nat. Acad. Sci., 111, 12661 [Google Scholar]
- Macintosh, B., Graham, J. R., Barman, T., et al. 2015, Science, 350, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Maire, A.-L., Bonnefoy, M., Ginski, C., et al. 2016, A&A, 587, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Malik, M., Meru, F., Mayer, L., & Meyer, M. 2015, ApJ, 802, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Malo, L., Doyon, R., Lafrenière, D., et al. 2013, ApJ, 762, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Marois, C., Lafrenière, D., Macintosh, B., & Doyon, R. 2008, ApJ, 673, 647 [NASA ADS] [CrossRef] [Google Scholar]
- Masciadri, E., Mundt, R., Henning, T., Alvarez, C., & Barrado y Navascués, D. 2005, ApJ, 625, 1004 [NASA ADS] [CrossRef] [Google Scholar]
- Maury, A. J., André, P., Hennebelle, P., et al. 2010, A&A, 512, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mawet, D., Milli, J., Wahhaj, Z., et al. 2014, ApJ, 792, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Meru, F., & Bate, M. R. 2011, MNRAS, 411, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Mizuno, H. 1980, Prog. Theor. Phys., 64, 544 [Google Scholar]
- Mordasini, C. 2013, A&A, 558, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mordasini, C., Alibert, Y., Benz, W., & Naef, D. 2009, A&A, 501, 1161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nayakshin, S. 2010a, MNRAS, 408, L36 [NASA ADS] [CrossRef] [Google Scholar]
- Nayakshin, S. 2010b, MNRAS, 408, 2381 [NASA ADS] [CrossRef] [Google Scholar]
- Nayakshin, S. 2011, MNRAS, 413, 1462 [NASA ADS] [CrossRef] [Google Scholar]
- Nayakshin, S. 2016, MNRAS, 461, 3194 [NASA ADS] [CrossRef] [Google Scholar]
- Nayakshin, S. 2017, PASA, 34, e002 [NASA ADS] [CrossRef] [Google Scholar]
- Owen, J. E., Ercolano, B., & Clarke, C. J. 2011, MNRAS, 412, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Paardekooper, S.-J. 2012, MNRAS, 421, 3286 [NASA ADS] [CrossRef] [Google Scholar]
- Pollack, J. B., Hubickyj, O., Bodenheimer, P., et al. 1996, Icarus, 124, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Potter, D., Martín, E. L., Cushing, M. C., et al. 2002, ApJ, 567, L133 [Google Scholar]
- Rameau, J., Chauvin, G., Lagrange, A.-M., et al. 2013, A&A, 553, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rameau, J., Chauvin, G., Lagrange, A.-M., et al. 2015, A&A, 581, A80 [NASA ADS] [EDP Sciences] [Google Scholar]
- Reggiani, M., Meyer, M. R., Chauvin, G., et al. 2016, A&A, 586, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rice, K., Lopez, E., Forgan, D., & Biller, B. 2015, MNRAS, 454, 1940 [NASA ADS] [CrossRef] [Google Scholar]
- Rice, W. K. M., & Armitage, P. J. 2009, MNRAS, 396, 2228 [NASA ADS] [CrossRef] [Google Scholar]
- Rice, W. K. M., Armitage, P. J., Bate, M. R., & Bonnell, I. A. 2003, MNRAS, 339, 1025 [Google Scholar]
- Rice, W. K. M., Forgan, D. H., & Armitage, P. J. 2012, MNRAS, 420, 1640 [NASA ADS] [CrossRef] [Google Scholar]
- Rice, W. K. M., Paardekooper, S.-J., Forgan, D. H., & Armitage, P. J. 2014, MNRAS, 438, 1593 [NASA ADS] [CrossRef] [Google Scholar]
- Safronov, V. S. 1972, Evolution of the protoplanetary cloud and formation of the earth and planets, Translated from Russian. Jerusalem (Israel): Israel Program for Scientific Translations (Keter Publishing House) [Google Scholar]
- Santos, N. C., Melo, C., James, D. J., et al. 2008, A&A, 480, 889 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Soummer, R., Perrin, M. D., Pueyo, L., et al. 2014, ApJ, 786, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Spiegel, D. S., & Burrows, A. 2012, ApJ, 745, 174 [Google Scholar]
- Stamatellos, D., & Whitworth, A. P. 2009a, MNRAS, 392, 413 [Google Scholar]
- Stamatellos, D., & Whitworth, A. P. 2009b, MNRAS, 400, 1563 [NASA ADS] [CrossRef] [Google Scholar]
- Thies, I., Kroupa, P., Goodwin, S. P., Stamatellos, D., & Whitworth, A. P. 2010, ApJ, 717, 577 [NASA ADS] [CrossRef] [Google Scholar]
- Toomre, A. 1964, ApJ, 139, 1217 [Google Scholar]
- Veras, D., Crepp, J. R., & Ford, E. B. 2009, ApJ, 696, 1600 [Google Scholar]
- Vigan, A., Patience, J., Marois, C., et al. 2012, A&A, 544, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vigan, A., Gry, C., Salter, G., et al. 2015, MNRAS, 454, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Vorobyov, E. I. 2013, A&A, 552, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wagner, K., Apai, D., Kasper, M., et al. 2016, Science, 353, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Wahhaj, Z., Liu, M. C., Biller, B. A., et al. 2013a, ApJ, 779, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Wahhaj, Z., Liu, M. C., Nielsen, E. L., et al. 2013b, ApJ, 773, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Wetherill, G. W. 1990, Annual Rev. Earth Planet. Sci., 18, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Young, M. D., & Clarke, C. J. 2016, MNRAS, 455, 1438 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, Z., Hartmann, L., Nelson, R. P., & Gammie, C. F. 2012, ApJ, 746, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Zurlo, A., Vigan, A., Hagelberg, J., et al. 2013, A&A, 554, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Full sample
The names and properties of the targets considered in the full NaCo-LP sample are detailed in Table A.1. Different properties of the sample are plotted in Fig. 1.
Full NaCo-LP sample (observed + archive).
Appendix B: Impact of stellar ages on the frequency estimation
The values of the probability density function of f in Tables 2 and 3 are provided for the best age estimates of the stars. In Tables B.1 and B.2 we also provide the values for the minimum and maximum stellar ages. The assumptions are the same as detailed in Sect. 6.1 and Sect. 6.2 respectively.
Fraction of stars that host a planetary system, assuming linear flat mass and semi-major axis distributions.
All Tables
Fraction of stars that host a planetary system, assuming linear flat mass and semi-major axis distributions.
Fraction of stars that host a planetary system, assuming linear flat mass and semi-major axis distributions.
All Figures
 |
Fig. 1 Histograms summarising the properties of all the targets considered in the final sample: spectral type, age, distance, and metallicity (from left to right). The complete sample includes 199 individuals targets. All the properties are detailed in Appendix A. |
| In the text | |
 |
Fig. 2 Summary plot of all the mass detection limits considered in this work (blue dashed lines). The big dot points correspond to the detections of sub-stellar companions that have been considered in the analysis (see Sect. 4). With an estimated mass of 0.1095 ± 0.0022M⊙, HD 130948 BC lies outside the considered mass range, and it is therefore not shown. |
| In the text | |
 |
Fig. 3 Mass (MJup) versus physical separation (AU) for all the companions in the synthetic planet populations generated as described in Sect. 5. Left panel: non-scattered population (Forgan & Rice 2013). Right panel: same population including scattering (Forgan et al. 2015). Different colors are used for single (green), double (blue), triple (orange), and quadruple (purple) systems. The size of the symbols increases from single to quadruple systems to make the plots easier to read. |
| In the text | |
 |
Fig. 4 Histogram (top) and cumulative histogram (bottom) of the population before and after scattering as a function of semi-major axis, normalized with respect to the total number of planets in the population. Only objects below 75 MJup are considered. Approximately 50% of the planets are ejected from the systems during the scattering, resulting in a much smaller total number of planets in the scattered population. The vertical dashed lines at 10 and 400 AU mark the semi-major axis range where the average detection probability of our observations is ~50% or more for massive companions. |
| In the text | |
 |
Fig. 5 Fraction of systems in the scattered and non-scattered populations as a function of the number of planets in the system. The total number of systems and planets before and after scattering is displayed in the top-right corner of the plot. The bins are normalized to the total number of systems in each of the two populations independently. The ~2% of systems with zero planets before scattering correspond only to cases where all the companions in the systems have masses above 75 MJup, while for the scattered case it also includes systems where all the companions were ejected as a result of the scattering process. |
| In the text | |
 |
Fig. 6 Mean detection probability map for the complete sample of 199 stars as a function of mass and semi-major axis. In this plot we adopt the best estimate for the stellar ages. The four detections of the sample are over-plotted. The probability map assumes flat distributions of planets in mass and semi-major axis. |
| In the text | |
 |
Fig. 7 Probability distribution of the frequency of stars with at least one giant planet in the mass and semi-major axes ranges indicated in the top-right of the plot. The results are summarized in Table 2. The plain lines represent the probability density function obtained when considering the best age estimate for all the stars in the sample, and the colored envelopes represent the variations when considering the minimum and maximum ages. |
| In the text | |
 |
Fig. 8 Comparison of the non-scattered (left) and scattered (right) GI populations (Forgan & Rice 2013; Forgan et al. 2015) with the mean detection probabilities of the observations (best age estimate). A significant fraction of the GI population could potentially be detected, even in the non-scattered case. The colors and symbols for the populations and the known companions are the same as in Figs. 3 and 6. |
| In the text | |
 |
Fig. 9 Histogram of the mass and separation of companions detectable at various confidence levels, for the scattered (right panels) and non-scattered (left panels) population. Similarly to Fig. 7, the plain lines represent the values for the best age estimate of the stars, and the colored envelopes show the variations observed when considering the minimum and maximum ages. The fraction of detected companions is smaller for the maximum ages and larger for the minimum ages. For the histograms in mass, semi-major axes from 1 to 500 AU are considered, and for the histograms in semi-major axis, masses from 1 to 75 MJup are considered. A confidence level of 95% means that for a given bin, the height of the bin represents the fraction of companions in that bin that have been detected in 95% (or more) of the simulated surveys. The small drop at 330 AU in the scattered population is numerical. |
| In the text | |
 |
Fig. 10 Probability distribution of the frequency of stars hosting at least one planetary system, based on the non-scattered (left) and scattered (right) populations described in Sect. 5. Similarly to Figs. 7 and 9, the plain lines represent the probability density function obtained when considering the best age estimate, and the shaded areas show the variations obtained when considering the full age range. The results are summarized in Table 3. |
| In the text | |
 |
Fig. 11 Density plots representing scattered populations based on GI (Forgan & Rice 2013; Forgan et al. 2015) and CA (Ida et al. 2013) compared to the detections in our sample and to the mean detection probabilities of the observations (contour lines are at 5%, 25%, 50%, 90%, and 95%). Density colors go from dark blue (low occurrence) to cyan (high occurrence) for the CA population, and from red (low occurrence) to yellow (high occurrence) for the GI population. The histograms on top and on the right represent the relative frequency in each bin of semi-major axis and planetary mass respectively. The histograms take into account the whole population, including the planets that are outside of the visibility window of the main plot. The semi-major axis and mass of the known companions are represented with dashed lines in the histograms. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


