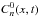| Issue |
A&A
Volume 599, March 2017
|
|
|---|---|---|
| Article Number | A111 | |
| Number of page(s) | 9 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201629846 | |
| Published online | 08 March 2017 | |
The amplitude of the cross-covariance function of solar oscillations as a diagnostic tool for wave attenuation and geometrical spreading
1 Max-Planck-Institut für Sonnensystemforschung, Justus-von-Liebig-Weg 3, 37077 Göttingen, Germany
e-mail: nagashima@mps.mpg.de
2 Institut für Numerische und Angewandte Mathematik, Georg-August-Universität Göttingen, Lotzestraße 16-18, 37083 Göttingen, Germany
3 Institut für Astrophysik, Georg-August-Universität Göttingen, Friedrich-Hund-Platz 1, 37077 Göttingen, Germany
Received: 5 October 2016
Accepted: 22 December 2016
Context. In time-distance helioseismology, wave travel times are measured from the two-point cross-covariance function of solar oscillations and are used to image the solar convection zone in three dimensions. There is, however, also information in the amplitude of the cross-covariance function, for example, about seismic wave attenuation.
Aims. We develop a convenient procedure to measure the amplitude of the cross-covariance function of solar oscillations.
Methods. In this procedure, the amplitude of the cross-covariance function is linearly related to the cross-covariance function and can be measured even for high levels of noise.
Results. As an example application, we measure the amplitude perturbations of the seismic waves that propagate through the sunspot in active region NOAA 9787. We can recover the amplitude variations due to the scattering and attenuation of the waves by the sunspot and associated finite-wavelength effects.
Conclusions. The proposed definition of cross-covariance amplitude is robust to noise, can be used to relate measured amplitudes to 3D perturbations in the solar interior under the Born approximation, and provides independent information from the travel times.
Key words: Sun: helioseismology / Sun: oscillations / sunspots / methods: data analysis
© ESO, 2017
1. Introduction
Solar oscillations are excited stochastically by turbulent convection and can be used to probe solar interior dynamics and structure (e.g., Christensen-Dalsgaard 2003; Gizon & Birch 2005; Gizon et al. 2010). The starting point in time-distance helioseismology is the temporal cross-covariance function of the observed oscillation signal, 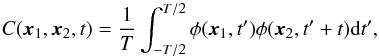 (1)where the φ(xi,t′) are the oscillation signals (e.g., Doppler velocity observations) at time t′ and positions xi (i = 1,2) on the solar surface, t is the time lag, and T is the duration of the observation (Duvall et al. 1993, 1997). Throughout this paper, for the sake of simplicity, we treat the observable φ as a continuous function of time.
(1)where the φ(xi,t′) are the oscillation signals (e.g., Doppler velocity observations) at time t′ and positions xi (i = 1,2) on the solar surface, t is the time lag, and T is the duration of the observation (Duvall et al. 1993, 1997). Throughout this paper, for the sake of simplicity, we treat the observable φ as a continuous function of time.
From the cross-covariance, one then generally measures wave travel times (e.g., Duvall et al. 1997; Gizon & Birch 2002, 2004; Langfellner et al. 2015) in order to constrain physical properties in the solar interior. The cross-covariance function, however, contains additional information other than the travel times (e.g., Tong et al. 2003a). It is possible to use all the information in the cross-covariance by performing a full waveform inversion; this approach is widely used in geophysics (see e.g., the review of Virieux & Operto 2009) and has been attempted in helioseismology by, for example, Hanasoge & Tromp (2014), but only in rather simple cases. Here, instead of full waveform inversion, we extract a second parameter from the cross-covariance in addition to the travel time, i.e., the amplitude.
In the field of helioseismology, only a few studies have reported measurements of the amplitude of the cross-covariance function. Jensen et al. (2006) used Michelson Doppler Imager (MDI; Scherrer et al. 1995) observations to show that the amplitude of the cross-covariance is reduced for waves propagating away from an active region. In this study, amplitudes were measured by fitting the measured cross-covariance function with a Gabor wavelet (Kosovichev & Duvall 1997). Similar reduction of the cross-covariance amplitude is shown for an example plage region in Nagashima et al. (2009) but without a quantitative calculation of amplitudes. Burtseva et al. (2007) measured the amplitude of the cross-covariance function (Gabor-wavelet fitting) and used the exponential decrease of the amplitude with the number of skips to estimate the solar p-mode lifetime.
Cameron et al. (2008) compared forward-modeled and observed f-mode cross-covariances for an almost circular sunspot in active region NOAA 9787. For a parametric magnetohydrostatic sunspot model with an axisymmetric magnetic field, these investigators found good agreement in both the amplitude and phase of the forward modeled and observed cross-covariances when the magnetic field peak at the photospheric level is 3kG (see also Gizon et al. 2010). We use observations of this region in the current study (see Sect. 6).
Liang et al. (2013) measured the amplitude reduction of waves propagating through the same sunspot and used 2D ray theory calculations to show that the amplitude reduction is, in part, due to the defocusing of waves caused by the enhanced wave speed in the sunspot.
Two definitions for the amplitude of the cross-covariance are used in helioseismology: first, the amplitude parameter obtained from fitting a Gabor wavelet to the cross-covariance (e.g., Kosovichev & Duvall 1997; Jensen et al. 2006; Burtseva et al. 2007) and, second, the maximum of the analytic signal associated with the cross-covariance between the observed cross-covariance and a reference cross-covariance (Liang et al. 2013, see our Sect. 5.1 for details). These definitions link the amplitude to the cross-covariance via complex transformations. It is thus complicated to compute the sensitivity of the amplitude measurement to small changes in a model of the solar interior. These sensitivity calculations (kernel calculations) are necessary for inversions that would use measured amplitudes to infer subsurface physical conditions.
In order to interpret amplitude measurements, a relationship between measured amplitudes and physical parameters, such as attenuation or wave velocities, is needed. As the first step, after reviewing what we could learn from the amplitude in Sect. 2, we propose a new definition of the amplitude of the cross-covariance function: the formulation procedure is described in Sect. 3 and the definition is given in Sect. 4. In this definition, changes in the amplitude are linearly related to changes in the cross-covariance. This linearity greatly simplifies the calculation of sensitivity kernels and, thus, opens the possibility of using amplitudes as inputs for inversions. It also has advantages in terms of the noise behavior as described in Sect. 5. To show that our proposed definition is reasonable, in Sect. 6 we compare the amplitude measurements of Liang et al. (2013) with the amplitudes obtained from our definition. Conclusions and outlooks of this study are given in Sect. 7.
2. What could we learn from the amplitude?
We expect the amplitude of the cross-covariance function to be useful for investigating wave properties in the Sun. For example, the amplitude is a more natural physical quantity for measuring attenuation than travel times (e.g., Woodard 1997; Tong et al. 2003b).
In Earth seismology, the amplitude of the seismogram signals (i.e., seismic waves from a single source) as well as the amplitude of the cross-covariance of seismogram signals (i.e., due to ambient seismic noise field) are used to infer physical properties in the interior of the Earth.
Amplitudes have been used to characterize the seismic signals caused by earthquakes (e.g. Nolet et al. 2005; Dalton & Ekström 2006). Dahlen & Baig (2002) showed body-wave speed Fréchet kernels for travel times and amplitudes of seismogram signals and a 1D reference Earth model. The kernels for travel times have a “banana-doughnut” shape: travel times are insensitive to changes in the wave speed along the ray path but are sensitive to changes in the surroundings. In contrast, the amplitudes are most sensitive to the wave speed along the ray path. Nolet et al. (2005) computed kernels for a volcano (Mount Vesuvius) model as well: travel times and amplitudes provide independent information about subsurface structure.
The amplitude of the cross-covariance of seismogram signals (ambient seismic noise field), as in time-distance helioseismology, has also been used in Earth seismology. The ambient noise field is produced by, for example, ocean swells (Yang & Ritzwoller 2008) or the interaction of storms with the ocean (Gerstoft & Bromirski 2016). Prieto et al. (2011) showed, using several observation examples, that the amplitude of the cross-covariance is useful for detecting attenuation and temperature perturbations in the interior. Liu & Ben-Zion (2013) modeled the effect of attenuation on amplitudes and the travel times (phases in their terminology) of the cross-covariance function.
The amplitude of earthquake seismogram signals has been used to create attenuation maps of Earth interior (Romanowicz 1995; Dalton et al. 2008). Amplitude measurements have also been used for highly nonlinear problems to infer the attenuation (more precisely, the quality factor Q) inside the volcanoes Mount St. Helens and Mount Vesuvius from the seismogram data (De Siena et al. 2014).
As another example, the amplitude of the cross-covariance of ambient seismic noise is discussed in Yang & Ritzwoller (2008). They used the signal-to-noise ratio of the cross-covariance to detect ambient noise sources.
In one ambient seismic noise analysis, Meier et al. (2010) reported the detection of seasonal wave velocity variations in the Los Angeles basin using the travel-time shift measured from the cross-covariance function of the ambient seismic noise. Later Zhan et al. (2013) and Daskalakis et al. (2016) suggested that the observed effect is caused by seasonal variations in the frequency content of the wave sources and does not actually imply velocity variations. This is another example in which using amplitude information might help to improve the understanding of a physical system.
3. Measuring the amplitude of a noise-free cross-covariance function
Gizon & Birch (2002) define the travel time t = τ as the time lag that minimizes the cost function ![\begin{eqnarray} X(t) = \int^{+\infty}_{-\infty} w(t^\prime) \left[\overline{C}(t^\prime) - \Cref(t^\prime-t) \right]^2 \mathrm{d}t^\prime , \label{eq:GB1para_chisq} \end{eqnarray}](/articles/aa/full_html/2017/03/aa29846-16/aa29846-16-eq13.png) (2)where w is a window function,
(2)where w is a window function, 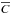 is a noise-free cross-covariance, and Cref is a reference cross-covariance. The noise-free cross-covariance
is a noise-free cross-covariance, and Cref is a reference cross-covariance. The noise-free cross-covariance 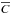 can be understood as the expectation value of C (see Sect. 4). In Eq. (2) and hereafter, we drop x1 and x2 from C(x1,x2,t) and write C(t) to simplify the notation. It is reasonable to use the noise-free cross-covariance when the observation duration, T, is long enough. The window function w is chosen to select the target wavepacket. As an example, one choice could be w(t) = 1 at the time lags t, where the target wave packet has significant amplitude and a smooth transition to zero outside this range of time lags (for an example, see Fig. 1).
can be understood as the expectation value of C (see Sect. 4). In Eq. (2) and hereafter, we drop x1 and x2 from C(x1,x2,t) and write C(t) to simplify the notation. It is reasonable to use the noise-free cross-covariance when the observation duration, T, is long enough. The window function w is chosen to select the target wavepacket. As an example, one choice could be w(t) = 1 at the time lags t, where the target wave packet has significant amplitude and a smooth transition to zero outside this range of time lags (for an example, see Fig. 1).
Here, we extend this one-parameter fit to a two-parameter fit for an amplitude, a = A, and a travel time, t = τ, which minimize the cost function ![\begin{eqnarray} X(a,t) = \int^{+\infty}_{-\infty} w(t^\prime) \left[\overline{C}(t^\prime) - a \Cref(t^\prime-t) \right]^2 \mathrm{d}t^\prime . \label{eq:2para_chisq} \end{eqnarray}](/articles/aa/full_html/2017/03/aa29846-16/aa29846-16-eq24.png) (3)Figure 1 shows example cross-covariances
(3)Figure 1 shows example cross-covariances 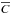 and Cref and the associated cost function X(a,t). In this figure,
and Cref and the associated cost function X(a,t). In this figure, 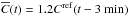 and the minimum of X, X(A,τ) = 0, is reached for τ = 3 min and A = 1.2 as expected.
and the minimum of X, X(A,τ) = 0, is reached for τ = 3 min and A = 1.2 as expected.
 |
Fig. 1 Left: illustrative sketch of a perturbed and reference cross-covariances ( |
As described in the Introduction (Sect. 1), we aim to have a definition in which changes in the amplitude are linearly related to changes in the cross-covariance. Thus, we linearize Eq. (3) using 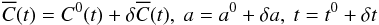 (4)and assume the perturbations (with δ) are small. This is justified when the reference cross-covariance is close enough to the observed cross-covariance, that is to say, the perturbation to the solar model is small. For the sake of simplicity, we consider the case where
(4)and assume the perturbations (with δ) are small. This is justified when the reference cross-covariance is close enough to the observed cross-covariance, that is to say, the perturbation to the solar model is small. For the sake of simplicity, we consider the case where 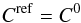 (5)and is even in time. In this case, the zeroth-order terms of Eq. (3) give a0 = A0 = 1 and t0 = τ0 = 0. Appendix A shows the details of the calculation. The cross-covariance C0 is obtained either from a model or from a spatial average of the observed cross-covariance function.
(5)and is even in time. In this case, the zeroth-order terms of Eq. (3) give a0 = A0 = 1 and t0 = τ0 = 0. Appendix A shows the details of the calculation. The cross-covariance C0 is obtained either from a model or from a spatial average of the observed cross-covariance function.
If we choose a window function w(t) to select a particular wave packet (for example, a smooth box like in Fig. 1), the minimum of Eq. (3), at first order, occurs at a = A0 + δA = 1 + δA and t = τ0 + δτ = 0 + δτ, where 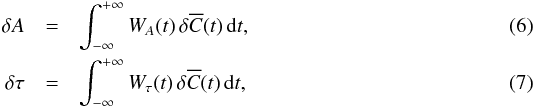 with the weight functions
with the weight functions ![\begin{equation} W_{A}(t) = \frac{w(t) \C0(t) }{\int^{+\infty}_{-\infty} w(t^\prime ) [\C0 (t^\prime )]^2 \mathrm{d}t^\prime} \label{eq:F2para_a_weight_new} \end{equation}](/articles/aa/full_html/2017/03/aa29846-16/aa29846-16-eq50.png) (8)and
(8)and ![\begin{equation} W_{\tau} (t) = - \frac{w(t) \bigdot{C}{}^0(t) }{\int^{+\infty}_{-\infty} w(t^\prime) [\bigdot{C}{}^0(t^\prime)]^2 \mathrm{d}t^\prime} \label{eq:F2para_t_weight_new} , \end{equation}](/articles/aa/full_html/2017/03/aa29846-16/aa29846-16-eq51.png) (9)where
(9)where 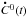 denotes the time derivative of C0(t).
denotes the time derivative of C0(t).
Thus, if the window function selects a wave packet properly, the measurements for travel time and amplitude are decoupled. In particular, Appendix A shows that the two measurements (δA and δτ) are decoupled when the integral I2 (defined by Eq. (A.8)) in Eq. (A.6) is negligible. In this case, the weight functions WA and Wτ are identical to what we would obtain from two independent single-parameter fits. In particular, Wτ is identical to the definition obtained in Gizon & Birch (2002) by minimizing Eq. (2).
 |
Fig. 2 Illustrative sketch of a reference cross-covariance C0 and the corresponding weight functions for the amplitude, WA, and for the travel time, Wτ, as well as the window function, w. The scaling is arbitrary as the different quantities have different units. |
Figure 2 illustrates the weight functions for amplitude and travel-time given by Eqs. (8) and (9). Multiplying these weight functions by the change in the cross-covariance 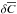 and integrating over time lag give the travel-time and amplitude perturbations δτ and δA. The weight function WA is proportional to C0, while Wτ is proportional to the derivative of C0. Thus WA is in phase with C0 while Wτ is shifted by a quarter of a period.
and integrating over time lag give the travel-time and amplitude perturbations δτ and δA. The weight function WA is proportional to C0, while Wτ is proportional to the derivative of C0. Thus WA is in phase with C0 while Wτ is shifted by a quarter of a period.
4. Definition of the amplitude
So far, we minimized the cost function by supposing that the cross-covariance function is noise free. This is the limit of the infinite length of observation duration and is not the case in observations with finite duration. If the data are too noisy then the minimization of Eq. (3) would not make sense. In this case, similarly to Gizon & Birch (2004), we can introduce a smoothed cross-covariance function Cϵ, 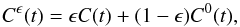 (10)where C(t) is the observed cross-covariance function with noise and ϵ is a small positive number, and perform the minimization of Eq. (3) with Cϵ instead of
(10)where C(t) is the observed cross-covariance function with noise and ϵ is a small positive number, and perform the minimization of Eq. (3) with Cϵ instead of 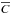 . In Appendix B we show that in the limit of ϵ → 0+, this procedure leads to the same expressions for the amplitude and travel time as given by Eqs. (6)–(9).
. In Appendix B we show that in the limit of ϵ → 0+, this procedure leads to the same expressions for the amplitude and travel time as given by Eqs. (6)–(9).
Another way to see that the amplitude defined by Eq. (6) is applicable to a noisy cross-covariance is to use the linearity of the definition. We decompose the cross-covariance function with noise into the expectation value, 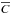 , and the noise, n(t),
, and the noise, n(t), 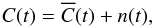 (11)where the expectation value of the noise is zero:
(11)where the expectation value of the noise is zero: 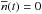 . Then, the expectation value of the amplitude is given by
. Then, the expectation value of the amplitude is given by 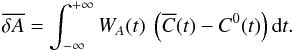 (12)Thus, the average value of the amplitude measured from the cross-covariance function with noise is the amplitude defined by the noise-free cross-covariance function.
(12)Thus, the average value of the amplitude measured from the cross-covariance function with noise is the amplitude defined by the noise-free cross-covariance function.
Therefore, the expectation value of the amplitude of the observation cross-covariance function can be measured based on Eqs. (6) and (8) as follows: first, the cross-covariance C0 is obtained either from a model or from a spatial average of the observed cross-covariance function. Second, the weight function WA is obtained via Eq. (8) using the window function for the targeted wave packet w. The amplitude is then defined with the weight function as 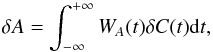 (13)where δC(t) = C(t)−C0(t). Hereafter in this paper we use Eq. (13) as the definition of the amplitude. We note that this is different from Eq. (6) in that δC contains noise.
(13)where δC(t) = C(t)−C0(t). Hereafter in this paper we use Eq. (13) as the definition of the amplitude. We note that this is different from Eq. (6) in that δC contains noise.
This definition is analogous to the amplitude definition in the Earth seismology analysis given by Eq. (26) in Nolet et al. (2005).
 |
Fig. 3 p1-mode cross-covariance functions (thin solid lines) and the weight functions (thick solid lines) calculated from a solar noise model datacube (Langfellner et al. 2015) and the window functions (dashed lines) w(t) to select the p1-mode wave packet. Panel a): the cross-covariance function averaged over the field of view as the reference cross-covariance function, C0, and the weight function for amplitude WA. Panel b): similar to a) but with the weight function for travel time Wτ. Panel c): one example cross-covariance function (at the central point of the field of view) and C0. The measured amplitude and travel time for this example cross-covariance are written in the panel. The cross-covariance functions in these plots are normalized by the maximum of the absolute value of C0. The cross-covariance functions and Wτ are dimensionless; the weight functions are calculated using the normalized cross-covariance and choosing seconds as the unit of time. In the figure, WA is multiplied by 102 for visibility and the units are s-1. |
5. Comparison with the definition of Liang et al. (2013)
5.1. Definition from Liang et al. (2013)
Another way to measure the amplitude was proposed by Liang et al. (2013) in the context of sunspot seismology. The amplitude was obtained from the function ![\begin{equation} F(t) = \frac{\int^{+\infty}_{-\infty} w(t^\prime) C(t^\prime) C^{0}(t^\prime-t)\mathrm{d}t^\prime}{\int^{+\infty}_{-\infty} w(t^\prime) [C^{0}(t^\prime)]^2 \mathrm{d}t^\prime } , \label{eq:Liang_F} \end{equation}](/articles/aa/full_html/2017/03/aa29846-16/aa29846-16-eq77.png) (14)where C0 here is an average of the quiet-Sun cross-covariance function. They computed the analytic signal of F, s [F] = F + iℋ [F], where ℋ [F] denotes the Hilbert transform of F. Finally, the amplitude AL13 was given by the maximum of the envelope of the analytic signal
(14)where C0 here is an average of the quiet-Sun cross-covariance function. They computed the analytic signal of F, s [F] = F + iℋ [F], where ℋ [F] denotes the Hilbert transform of F. Finally, the amplitude AL13 was given by the maximum of the envelope of the analytic signal | . \label{eq:aL13_adef} \end{equation}](/articles/aa/full_html/2017/03/aa29846-16/aa29846-16-eq83.png) (15)It is natural to ask whether there are any relations between this definition and our linear definition. As we are measuring a perturbation to the amplitude, we define a perturbed amplitude for Liang et al. (2013) as
(15)It is natural to ask whether there are any relations between this definition and our linear definition. As we are measuring a perturbation to the amplitude, we define a perturbed amplitude for Liang et al. (2013) as 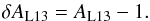 (16)In Appendix C, we show that
(16)In Appendix C, we show that 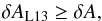 (17)and that we have equality if the maximum of F is obtained at t = 0 and the cross-covariances are symmetric with respect to time. Thus, if the time lag between the quiet-Sun cross-covariance and the measured cross-covariance is small, both definitions are equivalent; otherwise our linear definition always gives a smaller amplitude than the definition from Liang et al. (2013).
(17)and that we have equality if the maximum of F is obtained at t = 0 and the cross-covariances are symmetric with respect to time. Thus, if the time lag between the quiet-Sun cross-covariance and the measured cross-covariance is small, both definitions are equivalent; otherwise our linear definition always gives a smaller amplitude than the definition from Liang et al. (2013).
5.2. Noise properties
Using the quiet-Sun noise data from Langfellner et al. (2015) based on the solar noise model (realization noise) from Gizon & Birch (2004), we calculate the amplitudes in a quiet-Sun noise field. For this calculation, we use only the realization noise field with the p1-ridge filter, and center-to-annulus cross-covariance functions for a 10-Mm-radius annulus. Figure 3 shows the reference cross-covariance function (i.e., averaged cross-covariance over the field of view), window function, weight functions, and one example cross-covariance function with its amplitude and travel-time perturbations calculated using our definition.
Figure 4 compares δA and δAL13. In this plot the two amplitude measurements show a good correlation; Pearson’s correlation coefficient is 0.996 in this case. Thus, both definitions seem to behave similarly with noise. However, an advantage of the linear definition is that the noise can be estimated easily. Because of linearity, we can use the noise covariance matrix from Gizon & Birch (2004) and Fournier et al. (2014) by replacing the weight function for travel-time Wτ by the weight function for amplitude WA. In particular, the measurement of the amplitude is unbiased and its standard deviation decreases as 1/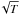 as the observation time T increases. Also, Fig. 4 shows that δAL13 is greater than δA, which is consistent with Eq. (17).
as the observation time T increases. Also, Fig. 4 shows that δAL13 is greater than δA, which is consistent with Eq. (17).
An important question is the independence of the travel-time and amplitude measurements. As a first step, we look at the correlation between the noise for travel time and amplitude for the case of realization noise. Figure 5 shows the scatter plot between δτ and δA. As expected the mean value is zero for both δτ and δA, confirming that the linear definitions are unbiased. Moreover, the distribution of the points indicates that the amplitude and travel-time noise measurements are largely uncorrelated; the Pearson correlation coefficient between δτ and δA is 0.02.
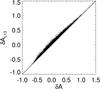 |
Fig. 4 Scatter plot between the linear definition of the amplitude δA and δAL13 for the case of a (quiet-Sun) realization noise calculation. These two amplitude measurements show a good correlation; the Pearson correlation coefficient is 0.996. This plot also shows δAL13 ≥ δA, which is expected from Eq. (17). |
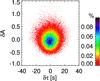 |
Fig. 5 Scatter plot of the amplitudes δA and travel times δτ for the case of the (quiet-Sun) realization noise calculation. The color indicates the percentage of points in each grid cell of size 0.4 s for δτ and 0.01 for δA. The total number of the data points is 51 465. |
6. Example: Cross-covariance amplitude around a sunspot
In this section, we use our new definition to compute the amplitude perturbations from the cross-covariance function around a sunspot measured by Liang et al. (2013) and show that the results are consistent with their measurements.
6.1. Observations used by Liang et al. (2013)
We use the cross-covariance functions calculated by Liang et al. (2013). These cross-covariance functions were calculated from a nine-day Dopplergram dataset around active region NOAA 9787 obtained by MDI (Scherrer et al. 1995). Here we use the same coordinate system as Liang et al. (2013); the sunspot center is the origin of the local coordinates, (x,y) = (0,0). Since they calculated cross-covariance functions in a transverse cylindrical equidistant projection centered at the sunspot center (i.e., the origin), the wave front, if in the quiet Sun, would be parallel to the y-axis (great circle on the Sun) in these x–y coordinates.
 |
Fig. 6 Observed amplitude perturbations around the sunspot NOAA 9787 with respect to the quiet Sun using SOHO/MDI observation. From left to right the results for f, p1, p2, p3, and p4 modes are shown. The black circle shows the outer boundary of the penumbra. The upper panels show the linear amplitude, δA, while the lower panels are replots of Fig. 2 of Liang et al. (2013); for better comparison, here we show δAL13 = AL13−1 instead of AL13 as in Fig. 2 of Liang et al. (2013). The central points of the squares in p1 and p3 panels are the positions of the cross-covariance functions shown in Fig. 7. The measurement results in the near field are not shown in the plots; the near field is defined as x−x0< 3λ, where λ is the typical wavelength for each mode, and x0 = −43.73 Mm is the leftmost point of these plots over which ⟨ φn ⟩ in Eq. (18) is averaged (see Table 1 in Liang et al. 2013 for details). |
As for the cross-covariance function definition, Liang et al. (2013) replaced Eq. (1) by 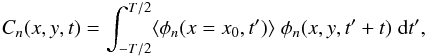 (18)where (x,y) is the spatial position on the surface, t is the time lag, φn is the filtered Doppler velocity, ⟨ φn ⟩ is the average of φn over y along the line x = x0 ≡ −43.73 Mm, and with T = 1 day. The Doppler velocity signals, φn, are obtained by applying ridge filters to select the modes with radial order n = 0−4. The cross-covariance function is then averaged over nine days and over rotations around the sunspot center (i.e., the origin) as well. The details of the ridge filters and other parameters are found in Liang et al. (2013).
(18)where (x,y) is the spatial position on the surface, t is the time lag, φn is the filtered Doppler velocity, ⟨ φn ⟩ is the average of φn over y along the line x = x0 ≡ −43.73 Mm, and with T = 1 day. The Doppler velocity signals, φn, are obtained by applying ridge filters to select the modes with radial order n = 0−4. The cross-covariance function is then averaged over nine days and over rotations around the sunspot center (i.e., the origin) as well. The details of the ridge filters and other parameters are found in Liang et al. (2013).
In their calculation they defined the quiet-Sun cross-covariance 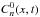 for each mode with radial order n at each x as the average of Cn(x,y,t) over the line segments, where 100 Mm < | y | < 200 Mm and also
for each mode with radial order n at each x as the average of Cn(x,y,t) over the line segments, where 100 Mm < | y | < 200 Mm and also 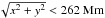 (to avoid the effect of the apodization). We use this
(to avoid the effect of the apodization). We use this 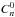 as the reference cross-covariance for our linear travel-time and amplitude calculations as well.
as the reference cross-covariance for our linear travel-time and amplitude calculations as well.
6.2. Comparison of amplitudes measured using the two methods
Figure 6 shows two amplitude measurements (δA and δAL13) around the sunspot. In both amplitude maps, the amplitude behind the sunspot shows a deficit along the x-axis and small enhancements off-axis on each side. These are mainly explained by geometrical spreading. As shown by Liang et al. (2013), using 2D ray tracing, the refraction of the waves resulting from the increased sound speed in the sunspot is responsible for most of the observed amplitude variations, namely the amplitude reduction along the y = 0 axis (defocusing) and the amplitude enhancement away from the axis (wavefront folding). See Fig. 3.7-5 of Stein & Wysession (2003) and Chap. 15.4 of Dahlen & Tromp (1998) as well as Nolet & Dahlen (2000) for geophysical analogs. In addition, part of the amplitude perturbations might be due to wave absorption in the sunspot as a result of the mode conversion of incoming p modes into downward propagating magneto-acoustic wave in the strong magnetic field (e.g., Spruit & Bogdan 1992; Cally & Bogdan 1997; Cameron et al. 2008).
 |
Fig. 7 Example cross-covariance functions used in Liang et al. (2013). Panels a) and b) are p1 cross-covariances at (x,y) = (50 Mm,30 Mm) and p3 cross-covariances at (x,y) = (160 Mm,55 Mm), respectively (see the squares drawn in Fig. 6). In each panel |
In Fig. 6 the linear (δA) and nonlinear (δAL13) amplitude measurements show reasonable agreement, even in the rather faint details away from the x-axis. Figure 7 shows a few examples of local changes in the cross-covariance function. The change in the amplitude is negative in Fig. 7a (δA = −0.45 and δAL13 = −0.28), where the amplitude of the perturbed cross-covariance is smaller than the quiet-Sun cross-covariance, and positive (δA = 0.19 and δAL13 = 0.25) in Fig. 7b. We note that δA is not the ratio between the maximum of the amplitudes of C and C0, but is the value that gives the best fit in the least-squares sense between C and C0 in the whole window function.
To better compare both measurements, Fig. 8 shows the scatter plot between δA and δAL13. The correlation is very good, in particular when the absolute value of the travel-time perturbation in the result of Liang et al. (2013), | δτL13 |, is less than 20 s (red points in Fig. 8). In this case, the Pearson correlation coefficient between δA and δAL13 is above 0.95 not only for p1 (shown in Fig. 8) but also for all other modes. As expected from Eq. (17), the values of δAL13 are always greater than the linear measurement, δA. Moreover, there is no saturation of the linear measurement and the linear and nonlinear values are consistent even for strong amplitude variations, although the measurements where the perturbation is larger show larger deviation from the line with a slope of one.
 |
Fig. 8 Scatter plot of amplitudes for the p1 cross-covariance functions. The data points in the field of the view of the p1 panels of Fig. 6 are used for this plot; the Pearson correlation coefficient is 0.91. The red points are the points in the area where | δτL13 | < 20 s. The Pearson correlation coefficient for these red data points is 0.98. |
7. Conclusions
We have developed a convenient linear procedure to measure the amplitude of the cross-covariance function of solar oscillations. We have shown that this new definition qualitatively reproduces the amplitude measurements computed by the more complex and nonlinear definition of Liang et al. (2013) even for strong perturbations in a sunspot.
The main advantage of our definition of the amplitude given by Eq. (13) is the linear relation between cross-covariance and amplitude. It allows easy generalization of the procedure developed in Gizon & Birch (2002) for computing travel-time sensitivity kernels under the Born approximation to compute kernels for amplitudes as well. The linear definition presented here also enables straightforward calculation of the amplitude noise covariance matrix by following the approach Gizon & Birch (2004) and Fournier et al. (2014). Thus, all the tools are in place for linear forward modeling and inversions using amplitude measurements in addition to, or instead of, travel times.
The conclusions from Earth seismology show that amplitudes contain information that is not in the travel times alone. In particular, the kernel calculation by Nolet et al. (2005) shows that the sensitivity kernels for amplitude and travel time have different spatial sensitivity.
For problems where linear theory is insufficient, numerical simulations of wave propagation are an important tool for interpreting helioseismic measurements (e.g., Cameron et al. 2008). Typically, these simulations have been used to predict the travel times that would be expected for a particular model of physical conditions in the solar interior (e.g., a sunspot) and then these modeled travel times are compared with travel times determined from observations. Comparison of forward-modeled amplitudes with observed amplitudes, in general, provides additional constraints on models. Schunker et al. (2013) used wave propagation simulations to compute the sensitivity of travel times to small changes in a model sunspot; the extension of this work to amplitudes will help quantify the diagnostic power of amplitudes in the context of sunspot seismology.
Another case in which amplitudes may be an important diagnostic is in characterizing small-scale turbulence. Scattering from small-scale (granulation scale) turbulence is, in some regimes, thought to be an important contributor to wave attenuation (Duvall et al. 1998) and thus should play a role in determining amplitudes.
Acknowledgments
We thank Zhi-Chao Liang and Thomas Duvall for useful discussions. The German Data Center for SDO, funded by the German Aerospace Center (DLR), provided the IT infrastructure for this work. K.N. and L.G. acknowledge support from EU FP7 Collaborative Project “Exploitation of Space Data for Innovative Helio- and Asteroseismology” (SpaceInn). SOHO is a project of international cooperation between ESA and NASA.
References
- Burtseva, O., Kholikov, S., Serebryanskiy, A., & Chou, D.-Y. 2007, Sol. Phys., 241, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Cally, P. S., & Bogdan, T. J. 1997, ApJ, 486, L67 [NASA ADS] [CrossRef] [Google Scholar]
- Cameron, R., Gizon, L., & Duvall, Jr., T. L. 2008, Sol. Phys., 251, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Christensen-Dalsgaard, J. 2003, Lecture Notes on Stellar Oscillations. Fifth Edition, http://astro.phys.au.dk/~jcd/oscilnotes/ [Google Scholar]
- Dahlen, F. A., & Baig, A. M. 2002, Geophys. J. Int., 150, 440 [NASA ADS] [CrossRef] [Google Scholar]
- Dahlen, F. A., & Tromp, J. 1998, Theoretical Global Seismology (Princeton University Press) [Google Scholar]
- Dalton, C. A., & Ekström, G. 2006, J. Geophys. Res., 111, B05317 [NASA ADS] [CrossRef] [Google Scholar]
- Dalton, C. A., Ekström, G., & Dziewoński, A. M. 2008, J. Geophys. Res, 113, B09303 [NASA ADS] [CrossRef] [Google Scholar]
- Daskalakis, E., Evangelidis, C. P., Garnier, J., et al. 2016, Geophys. J. Int., 205, 1926 [NASA ADS] [CrossRef] [Google Scholar]
- De Siena, L., Thomas, C., & Aster, R. 2014, J. Volcanology and Geothermal Res., 277, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Duvall, Jr., T. L., Jefferies, S. M., Harvey, J. W., & Pomerantz, M. A. 1993, Nature, 362, 430 [NASA ADS] [CrossRef] [Google Scholar]
- Duvall, Jr., T. L., Kosovichev, A. G., & Murawski, K. 1998, ApJ, 505, L55 [NASA ADS] [CrossRef] [Google Scholar]
- Duvall, Jr., T. L., Kosovichev, A. G., Scherrer, P. H., et al. 1997, Sol. Phys., 170, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Fournier, D., Gizon, L., Hohage, T., & Birch, A. C. 2014, A&A, 567, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gerstoft, P., & Bromirski, P. D. 2016, Science, 353, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Gizon, L., & Birch, A. C. 2002, ApJ, 571, 966 [NASA ADS] [CrossRef] [Google Scholar]
- Gizon, L., & Birch, A. C. 2004, ApJ, 614, 472 [NASA ADS] [CrossRef] [Google Scholar]
- Gizon, L., & Birch, A. C. 2005, Liv. Rev. Sol. Phys., 2, 6 [Google Scholar]
- Gizon, L., Birch, A. C., & Spruit, H. C. 2010, ARA&A, 48, 289 [Google Scholar]
- Hanasoge, S. M., & Tromp, J. 2014, ApJ, 784, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Jensen, J. M., Pijpers, F. P., & Thompson, M. J. 2006, ApJ, 648, L75 [NASA ADS] [CrossRef] [Google Scholar]
- Kosovichev, A. G., & Duvall, Jr., T. L. 1997, in SCORe’96: Solar Convection and Oscillations and their Relationship, eds. F. P. Pijpers, J. Christensen-Dalsgaard, & C. S. Rosenthal (Dordrecht: Kluwer), Astrophys. Space Sci. Lib., 225, 241 [Google Scholar]
- Langfellner, J., Gizon, L., & Birch, A. C. 2015, A&A, 581, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liang, Z.-C., Gizon, L., Schunker, H., & Philippe, T. 2013, A&A, 558, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liu, X., & Ben-Zion, Y. 2013, Geophys. J. Int., 194, 1966 [NASA ADS] [CrossRef] [Google Scholar]
- Meier, U., Shapiro, N. M., & Brenguier, F. 2010, Geophys. J. Int., 181, 985 [NASA ADS] [Google Scholar]
- Nagashima, K., Sekii, T., Kosovichev, A. G., Zhao, J., & Tarbell, T. D. 2009, in The Second Hinode Science Meeting: Beyond Discovery-Toward Understanding, eds. B. Lites, M. Cheung, T. Magara, J. Mariska, & K. Reeves, ASP Conf. Ser., 415, 417 [Google Scholar]
- Nolet, G., & Dahlen, F. A. 2000, J. Geophys. Res., 105(B8), 19043 [NASA ADS] [CrossRef] [Google Scholar]
- Nolet, G., Dahlen, F. A., & Montelli, R. 2005, in Seismic Earth: Array Analysis of Broadband Seismograms (Washington, D. C.: American Geophysical Union), 37 [Google Scholar]
- Prieto, G. A., Denolle, M., Lawrence, J. F., & Beroza, G. C. 2011, Comptes Rendus Géoscience, 343, 600 [NASA ADS] [CrossRef] [Google Scholar]
- Romanowicz, B. 1995, J. Geophys. Res., 100(B7), 12375 [NASA ADS] [CrossRef] [Google Scholar]
- Scherrer, P. H., Bogart, R. S., Bush, R. I., et al. 1995, Sol. Phys., 162, 129 [Google Scholar]
- Schunker, H., Gizon, L., Cameron, R. H., & Birch, A. C. 2013, A&A, 558, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spruit, H. C., & Bogdan, T. J. 1992, ApJ, 391, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Stein, S., & Wysession, M. 2003, An Introduction to Seismology, Earthquakes, and Earth Structure (Blackwell Publishing) [Google Scholar]
- Tong, C. H., Thompson, M. J., Warner, M. R., & Pain, C. C. 2003a, ApJ, 593, 1242 [NASA ADS] [CrossRef] [Google Scholar]
- Tong, C. H., Thompson, M. J., Warner, M. R., & Pain, C. C. 2003b, ApJ, 596, L263 [NASA ADS] [CrossRef] [Google Scholar]
- Virieux, J., & Operto, S. 2009, Geophysics, 74, WCC1 [Google Scholar]
- Woodard, M. F. 1997, ApJ, 485, 890 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, Y., & Ritzwoller, M. H. 2008, Geochemistry, Geophysics, Geosystems, 9, Q02008 [Google Scholar]
- Zhan, Z., Tsai, V. C., & Clayton, R. W. 2013, Geophys. J. Int., 194, 1574 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Derivation of the amplitude of the noise-free cross-covariance function
Here we briefly summarize the derivation of the two-parameter fitting formula and discuss when the two measurements (the amplitude and the travel time) are decoupled.
We look for a = A and t = τ that minimize X(a,t) (Eq. (3)), 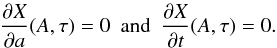 (A.1)We write
(A.1)We write 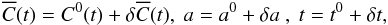 (A.2)where the superscript 0 is for the reference medium and δ for the perturbation. The zeroth-order cost function is given by
(A.2)where the superscript 0 is for the reference medium and δ for the perturbation. The zeroth-order cost function is given by ![\appendix \setcounter{section}{1} \begin{equation} X^0(a^0, t^0) = \int^{+\infty}_{-\infty} w(t^\prime) \left[\C0(t^\prime) - a^0 \C0 (t^\prime - t^0) \right]^2 \mathrm{d}t^\prime \end{equation}](/articles/aa/full_html/2017/03/aa29846-16/aa29846-16-eq135.png) (A.3)and is minimal for
(A.3)and is minimal for 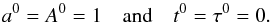 (A.4)Then, δA and δτ are obtained by solving
(A.4)Then, δA and δτ are obtained by solving 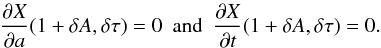 (A.5)To first order, we obtain
(A.5)To first order, we obtain 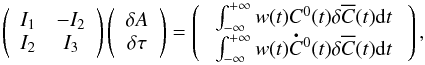 (A.6)where
(A.6)where ![\appendix \setcounter{section}{1} \begin{eqnarray} I_1 &=& \int^{+\infty}_{-\infty} w(t) \left[\C0(t)\right]^2 \mathrm{d}t , \\ I_2 &=& \int^{+\infty}_{-\infty} w(t) \C0(t) \bigdot{C}{}^0 (t) \mathrm{d}t , \label{eq:2para_I2} \\ I_3 &=& -\int^{+\infty}_{-\infty} w(t) \left[\bigdot{C}{}^0 (t)\right]^2 \mathrm{d}t . \end{eqnarray}](/articles/aa/full_html/2017/03/aa29846-16/aa29846-16-eq139.png) We show that the term I2 can be dropped if the window function is chosen such that it isolates a wave packet. We can write
We show that the term I2 can be dropped if the window function is chosen such that it isolates a wave packet. We can write ![\appendix \setcounter{section}{1} \begin{eqnarray} I_2 &=& \int^{+\infty}_{-\infty} w(t) \C0 (t) \bigdot{C}{}^0 (t)\mathrm{d}t = \frac{1}{2}\int^{+\infty}_{-\infty} w(t) \frac{\mathrm{d}}{ \mathrm{d}t}\left[\C0(t)\right]^2 \mathrm{d}t \ \nonumber \\ &=&\frac{1}{2} \left[w(t)\left[\C0(t) \right]^2 \right] ^{+\infty}_{-\infty} -\frac{1}{2} \int^{+\infty}_{-\infty} \bigdot{w}(t)\left[{\C0} (t)\right]^2 \mathrm{d}t . \end{eqnarray}](/articles/aa/full_html/2017/03/aa29846-16/aa29846-16-eq140.png) (A.10)The first term is zero, since C0(t) tends to zero at infinity. The second term is small if w(t) is constant or varies slowly over the duration of the wave packet, for example, by using a smooth rectangular function as shown in Fig. 1.
(A.10)The first term is zero, since C0(t) tends to zero at infinity. The second term is small if w(t) is constant or varies slowly over the duration of the wave packet, for example, by using a smooth rectangular function as shown in Fig. 1.
Therefore, we define δA and δτ as 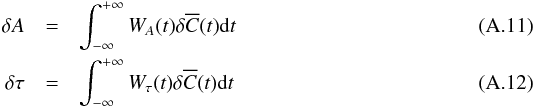 with the weight functions given by Eqs. (8) and (9).
with the weight functions given by Eqs. (8) and (9).
The weight functions WA and Wτ are identical to what we would obtain from two independent single-parameter fits. In other words, the weight function Wτ is identical to the weight function obtained by minimizing X(t) defined by Eq. (2). This is exactly the same as in Gizon & Birch (2002). In the same manner, the weight function WA is identical to the weight function obtained by minimizing ![\hbox{$X(a)=\int^{+\infty}_{-\infty} w(t) \left[\overline{C}(t) - a \C0 (t) \right]^2 \mathrm{d}t $}](/articles/aa/full_html/2017/03/aa29846-16/aa29846-16-eq144.png) .
.
Appendix B: Derivation of the amplitude in the noisy case
Here we extend the method used in Gizon & Birch (2004) in the case of noisy data. This is important since the observations of finite duration can be so noisy that the minimization problem defined by Eq. (3) does not make sense. We show that this leads to our linearized formulae (Eq. (A.6)).
In this case we introduce a smoothed cross-covariance function, Cϵ, defined by 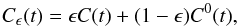 (B.1)where ϵ is a small positive number. In the limit ϵ → 0+ (no noise), Cϵ → C0.
(B.1)where ϵ is a small positive number. In the limit ϵ → 0+ (no noise), Cϵ → C0.
We are looking for aϵ = Aϵ and tϵ = τϵ, which minimize the cost function ![\appendix \setcounter{section}{2} \begin{equation} X_{\epsilon}(a_\epsilon, t_\epsilon) = \int^{+\infty}_{-\infty} w(t) \left[C_{\epsilon} (t) - a_\epsilon \C0 (t - t_\epsilon) \right]^2 \, \mathrm{d}t . \end{equation}](/articles/aa/full_html/2017/03/aa29846-16/aa29846-16-eq150.png) (B.2)We write
(B.2)We write 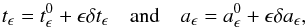 (B.3)where
(B.3)where 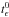 and
and 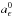 represent the zeroth-order terms in ϵ, while δtϵ and δtϵ are of order 1. At zeroth order, the cost function is given by
represent the zeroth-order terms in ϵ, while δtϵ and δtϵ are of order 1. At zeroth order, the cost function is given by ![\appendix \setcounter{section}{2} \begin{equation} X_{\epsilon}^0(a_\epsilon^0, t_\epsilon^0) = \int^{+\infty}_{-\infty} w(t) \left[\C0(t) - a_\epsilon^0 \C0 (t - t_\epsilon^0) \right]^2 \, \mathrm{d}t \end{equation}](/articles/aa/full_html/2017/03/aa29846-16/aa29846-16-eq155.png) (B.4)and is thus minimal for
(B.4)and is thus minimal for 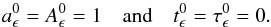 (B.5)In order to find δAϵ and δτϵ, we minimize the cost function Xϵ
(B.5)In order to find δAϵ and δτϵ, we minimize the cost function Xϵ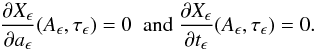 (B.6)Keeping only the first-order terms in ϵ, we obtain
(B.6)Keeping only the first-order terms in ϵ, we obtain 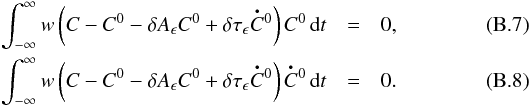 At the limit ϵ → 0+, it leads to the noise-free formulation given by Eq. (A.6) and thus δτϵ → δτ and δAϵ → δA. So the formulation given by Eq. (A.6) makes sense even in the case of noisy observations.
At the limit ϵ → 0+, it leads to the noise-free formulation given by Eq. (A.6) and thus δτϵ → δτ and δAϵ → δA. So the formulation given by Eq. (A.6) makes sense even in the case of noisy observations.
Appendix C: Comparison of amplitudes A and AL13
In this appendix, we compare our linear definition with that proposed by Liang et al. (2013), where the amplitude was obtained as the maximum of the analytic signal s [F] of the function F defined by Eq. (14), namely | = \max_t |F(t) + \textrm{i} \mathcal{H}[F](t)|, \end{equation}](/articles/aa/full_html/2017/03/aa29846-16/aa29846-16-eq166.png) (C.1)where ℋ [F] denotes the Hilbert transform of F. As the maximum of | s [F] (t) | over all t is larger than the value at t = 0, | s [F] (0) |, we have
(C.1)where ℋ [F] denotes the Hilbert transform of F. As the maximum of | s [F] (t) | over all t is larger than the value at t = 0, | s [F] (0) |, we have | \geq F(0). \label{eq:majoration} \end{equation}](/articles/aa/full_html/2017/03/aa29846-16/aa29846-16-eq171.png) (C.2)Adding and subtracting C0 in the definition of the function F, we obtain
(C.2)Adding and subtracting C0 in the definition of the function F, we obtain ![\appendix \setcounter{section}{3} \begin{eqnarray} F(0) &=& \frac{\int^{+\infty}_{-\infty} w(t^\prime) \left(C(t^\prime) + \C0(t^\prime) - \C0(t^\prime) \right) C^0(t^\prime) \mathrm{d}t^\prime }{\int^{+\infty}_{-\infty} w(t^\prime) [C^0(t^\prime)]^2 \mathrm{d}t^\prime} \nonumber \\ &=& 1 + \int^{+\infty}_{-\infty} W_A(t^\prime) \delta C(t^\prime) \mathrm{d}t^\prime \nonumber \\ &=& 1 + \delta A. \label{eq:F0} \end{eqnarray}](/articles/aa/full_html/2017/03/aa29846-16/aa29846-16-eq172.png) (C.3)
(C.3)
Then, combining Eqs. (C.2) and (C.3), we obtain 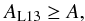 (C.4)and thus Eq. (17).
(C.4)and thus Eq. (17).
Moreover if the maximum of F is obtained at t = 0, then AL13 = | F(0) + iℋ [F] (0) |. If additionally, C and C0 are symmetric then F is symmetric and ℋ [F] is antisymmetric, which implies that ℋ [F] (0) = 0. In this case, AL13 = F(0) = A, and our linear definition coincides with that from Liang et al. (2013).
All Figures
 |
Fig. 1 Left: illustrative sketch of a perturbed and reference cross-covariances ( |
| In the text | |
 |
Fig. 2 Illustrative sketch of a reference cross-covariance C0 and the corresponding weight functions for the amplitude, WA, and for the travel time, Wτ, as well as the window function, w. The scaling is arbitrary as the different quantities have different units. |
| In the text | |
 |
Fig. 3 p1-mode cross-covariance functions (thin solid lines) and the weight functions (thick solid lines) calculated from a solar noise model datacube (Langfellner et al. 2015) and the window functions (dashed lines) w(t) to select the p1-mode wave packet. Panel a): the cross-covariance function averaged over the field of view as the reference cross-covariance function, C0, and the weight function for amplitude WA. Panel b): similar to a) but with the weight function for travel time Wτ. Panel c): one example cross-covariance function (at the central point of the field of view) and C0. The measured amplitude and travel time for this example cross-covariance are written in the panel. The cross-covariance functions in these plots are normalized by the maximum of the absolute value of C0. The cross-covariance functions and Wτ are dimensionless; the weight functions are calculated using the normalized cross-covariance and choosing seconds as the unit of time. In the figure, WA is multiplied by 102 for visibility and the units are s-1. |
| In the text | |
 |
Fig. 4 Scatter plot between the linear definition of the amplitude δA and δAL13 for the case of a (quiet-Sun) realization noise calculation. These two amplitude measurements show a good correlation; the Pearson correlation coefficient is 0.996. This plot also shows δAL13 ≥ δA, which is expected from Eq. (17). |
| In the text | |
 |
Fig. 5 Scatter plot of the amplitudes δA and travel times δτ for the case of the (quiet-Sun) realization noise calculation. The color indicates the percentage of points in each grid cell of size 0.4 s for δτ and 0.01 for δA. The total number of the data points is 51 465. |
| In the text | |
 |
Fig. 6 Observed amplitude perturbations around the sunspot NOAA 9787 with respect to the quiet Sun using SOHO/MDI observation. From left to right the results for f, p1, p2, p3, and p4 modes are shown. The black circle shows the outer boundary of the penumbra. The upper panels show the linear amplitude, δA, while the lower panels are replots of Fig. 2 of Liang et al. (2013); for better comparison, here we show δAL13 = AL13−1 instead of AL13 as in Fig. 2 of Liang et al. (2013). The central points of the squares in p1 and p3 panels are the positions of the cross-covariance functions shown in Fig. 7. The measurement results in the near field are not shown in the plots; the near field is defined as x−x0< 3λ, where λ is the typical wavelength for each mode, and x0 = −43.73 Mm is the leftmost point of these plots over which ⟨ φn ⟩ in Eq. (18) is averaged (see Table 1 in Liang et al. 2013 for details). |
| In the text | |
 |
Fig. 7 Example cross-covariance functions used in Liang et al. (2013). Panels a) and b) are p1 cross-covariances at (x,y) = (50 Mm,30 Mm) and p3 cross-covariances at (x,y) = (160 Mm,55 Mm), respectively (see the squares drawn in Fig. 6). In each panel |
| In the text | |
 |
Fig. 8 Scatter plot of amplitudes for the p1 cross-covariance functions. The data points in the field of the view of the p1 panels of Fig. 6 are used for this plot; the Pearson correlation coefficient is 0.91. The red points are the points in the area where | δτL13 | < 20 s. The Pearson correlation coefficient for these red data points is 0.98. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.