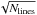| Issue |
A&A
Volume 599, March 2017
|
|
|---|---|---|
| Article Number | A97 | |
| Number of page(s) | 15 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201629650 | |
| Published online | 06 March 2017 | |
Insights into the chemical composition of the metal-poor Milky Way halo globular cluster NGC 6426⋆,⋆⋆
1 Landessternwarte, Zentrum für Astronomie der Universität Heidelberg, Königstuhl 12, 69117 Heidelberg, Germany
2 Astronomisches Rechen-Institut, Zentrum für Astronomie der Universität Heidelberg, Mönchhofstr. 12-14, 69120 Heidelberg, Germany
e-mail: mhanke@ari.uni-heidelberg.de
3 Department of Physics, Lancaster University, Bailrigg, Lancaster LA1 4YB, UK
4 Dark Cosmology Centre, The Niels Bohr Institute, Juliane Maries Vej 30, 2100 Copenhagen, Denmark
5 Carnegie Observatories, 813 Santa Barbara St., Pasadena, CA 91101, USA
Received: 5 September 2016
Accepted: 6 December 2016
We present our detailed spectroscopic analysis of the chemical composition of four red giant stars in the halo globular cluster NGC 6426. We obtained high-resolution spectra using the Magellan2/MIKE spectrograph, from which we derived equivalent widths and subsequently computed abundances of 24 species of 22 chemical elements. For the purpose of measuring equivalent widths, we developed a new semi-automated tool, called EWCODE. We report a mean Fe content of [Fe/H] =−2.34 ± 0.05 dex (stat.) in accordance with previous studies. At a mean α-abundance of [(Mg, Si, Ca)/3 Fe] = 0.39 ± 0.03 dex, NGC 6426 falls on the trend drawn by the Milky Way halo and other globular clusters at comparably low metallicities. The distribution of the lighter α-elements as well as the enhanced ratio [Zn/Fe] = 0.39 dex could originate from hypernova enrichment of the pre-cluster medium. We find tentative evidence for a spread in the elements Mg, Si, and Zn, indicating an enrichment scenario, where ejecta of evolved massive stars of a slightly older population have polluted a newly born younger one. The heavy element abundances in this cluster fit well into the picture of metal-poor globular clusters, which in that respect appear to be remarkably homogeneous. The pattern of the neutron-capture elements heavier than Zn points toward an enrichment history governed by the r-process with little, if any, sign of s-process contributions. This finding is supported by the striking similarity of our program stars to the metal-poor field star HD 108317.
Key words: stars: abundances / Galaxy: abundances / Galaxy: evolution / Galaxy: halo / globular clusters: individual: NGC 6426
This paper includes data gathered with the 6.5-m Magellan Telescopes located at Las Campanas Observatory, Chile.
Equivalent widths and full Table 2 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/599/A97
© ESO, 2017
1. Introduction
Amongst the oldest stellar systems known to exist in the Milky Way (MW) are metal-poor globular clusters (GCs). These accumulations of stars do not seem to have undergone substantial star formation for extended periods. Given the limited quality of the available data, for a long time color-magnitude diagrams (CMDs) of GCs appeared to be narrow and could be readily described by a single isochrone. These observations have justified the establishment of the long-lasting paradigm that considers CGs as prime examples of simple stellar populations (SSPs), that is, the results of very short bursts of star formation in their natal clouds. However, improved photometric precision indicates the presence of sub-populations in the cluster CMDs that are inconsistent with the SSP assumption, for a number of luminous GCs in a variety of bandpasses. Thus, early detections of chemical abundance variations (e.g., Cohen 1978) could be more easily explained in a scenario involving several populations. Moreover, in recent years evidence has grown supporting the statement that GCs are generally composed of two or three chemically distinct populations. These subpopulations are separated by a few tens to hundreds of Myr in age and show vastly varying abundances of light elements such as C, N, O, Na, Mg, and Al (see, e.g., Carretta et al. 2009b; Gratton et al. 2012, and references therein). Theoretical considerations (see, e.g., D’Ercole et al. 2008, 2011) imply that GCs could have lost the majority of the initial stellar content of the first population, which consequently should have ended up in the Galactic halo. In fact, numerous studies found metal-poor GCs to be consistent with the abundance trends of the MW halo at equally low metal content (e.g., Pritzl et al. 2005; Koch et al. 2009; Koch & McWilliam 2014; Villanova et al. 2016). We address this scenario by adding NGC 6426 to the short list of metal-poor clusters with available information on detailed chemical abundances. There are only two GCs in the Harris catalog (Harris 1996, 2010 edition) more metal poor than NGC 6426. At 12.9 ± 1.0 Gyr, the cluster is the oldest in the age compilation by Salaris & Weiss (2002). At a galactocentric distance of Rgc = 14.4 kpc and a galactic latitude of 16.23° it is located in the transition region between inner and outer halo. Previous studies found consistent [Fe/H]1 values: −2.20 ± 0.17 dex (Zinn & West 1984), −2.33 ± 0.15 (Hatzidimitriou et al. 1999), and −2.39 ± 0.04 dex (Dias et al. 2015). The latter value originates from the very first spectroscopic analysis of NGC 6426 at low resolution, which also stated [Mg/Fe] = 0.38 ± 0.06 dex. To date, there has been no study further addressing the detailed metal content of this cluster.
In this work, we have derived chemical abundances of 22 elements from high resolution spectroscopy of four giant stars attributed to NGC 6426. For the first time, we detected elements heavier than Fe in NGC 6426 and identify potential sites of nucleosynthesis that contributed to their enrichment. Furthermore, we relate NGC 6426’s chemical composition to the framework of other GCs and the MW halo.
This paper starts by introducing the sample and basic steps of data gathering and subsequent reduction (Sect. 2). Next, we introduce the analysis methods applied, including a brief introduction to the newly developed semi-automated equivalent width code, EWCODE (Sect. 3). There too, we describe the methods applied in order to derive the basic stellar photospheric parameters entering our model atmospheres. In Sect. 4, the results of this study are presented. Finally, Sect. 5 recapitulates all essential findings and the conclusions we draw from them.
2. Observations and data reduction
Our four NGC 6426 target stars were selected from what we identified as the tip of the red giant branch (RGB) in a 2MASS (Skrutskie et al. 2006) Ks vs. J−Ks CMD covering the region of two half-light radii (~0.92′) around the cluster’s center at α = 17:44:54.65, δ = + 03:10:12.5 (J2000, Harris 1996). The selection is indicated in Fig. 1. We decided against the usage of the recent Hubble Space Telescope (HST) photometry by Dotter et al. (2011), because the bright stars in question were labeled with bad fit quality flags and are thus likely to have saturated in the imaging process. As a consequence, only three of our targets have available HST V and I magnitudes.
 |
Fig. 1 Dereddened (J−Ks)0 vs. 2MASS Ks,0 (Schlafly & Finkbeiner 2011) color-magnitude diagram (CMD) of NGC 6426. Black dots correspond to stars within two half light radii and open red circles highlight the sample analyzed in this study. |
2.1. Data acquisition and reduction
The spectra were gathered over three nights in August 2014 and August 2015 using the Magellan Inamori Kyocera Echelle (MIKE) spectrograph (Bernstein et al. 2003), which is mounted at the Clay/Magellan2 Telescope at Las Campanas Observatory in Chile. We chose a slit width of 0.5″ together with an on-chip 2 × 1 binning. Using this configuration and both the blue and red arms of the instrument, we ended up with full wavelength coverage in the range 3340 Å ≤ λ ≤ 9410 Å. From the full widths at half maximum (FWHM) of the calibration lamp emission lines we derived a median spectral resolving power R = λ/FWHM ~ 45 000, and ~40 000 for the blue and the red arms respectively. The average seeing ranged from 0.6″ for the star 5659 up to 0.9″ for 2314. The basic observational settings are provided in Table 1.
The data were processed with the pipeline reduction package of Kelson (2003), which takes into account flat field division, order tracing from quartz lamp flats, and wavelength calibrations using built-in Th-Ar lamp spectra, that were obtained immediately following each science exposure.
Observing information.
2.2. Radial velocities
Radial velocities (RVs) of our targets were derived by cross correlating a portion of the spectra around Hα against a synthetic template spectrum with stellar parameters similar to the ones for our red giant targets (Sect. 3.3). All four targets have very similar heliocentric velocities, with a mean of vhelio = −212.2 ± 0.5 km s-1 and a 1σ-dispersion of 1.0 ± 0.4 km s-1, this low value being in line with the cluster’s moderately low mass and luminosity (MV = −6.67; Harris 1996). While the Harris catalog lists a considerably higher velocity of −162 km s-1, the more recent work of Dias et al. (2015) led to a systemic velocity of −242 ± 11 km s-1 based on five measurements at low resolution (R ~ 2000).
3. Stellar atmospheric parameters and abundance analysis
Most of our analysis relied on the technique of measuring equivalent widths (EWs), the computation of synthetic line profiles and their EWs for the respective transition under the assumption of local thermodynamic equilibrium (LTE), and the comparison of both in order to derive elemental abundances for a given set of stellar parameters. For this purpose we employed the June 2014 release of the LTE radiation transfer code MOOG (Sneden 1973). For the elements Na and K we provide non-LTE (NLTE) corrections using the respective LTE abundances as a baseline. Throughout this work we have made use of the α-enhanced ATLAS9 model atmospheres and AODFNEW opacity distribution functions as described in Castelli & Kurucz (2004). Because of reasons explained in Sect. 3.3 we derived the stellar parameters from differential Fe abundances with respect to the benchmark giant star HD 122563. A MIKE spectrum for this star was kindly provided by I. U. Roederer (priv. comm.).
3.1. Atomic data
Our line list comprises the line data compiled in Koch et al. (2016) for a set of stars with similar parameters and metallicities as well as minor additions from the VALD2 database. Lines that seemed to be affected by heavy blending (where the FWHM appeared exceptionally large or were we detected asymmetries in the profile), were rejected as well as those where telluric contamination was present. We accounted for hyperfine splitting of the transitions of the elements Sc (Kurucz & Bell 1995), V (Kurucz & Bell 1995), Mn (Den Hartog et al. 2011), Co (Kurucz & Bell 1995), Sr (Bergemann et al. 2012a; Hansen et al. 2013), Ba (McWilliam 1998), La (Lawler et al. 2001a) and Eu (Lawler et al. 2001b) and assumed a solar scaled isotope distribution for each chemical species (Lodders 2003).
3.2. Equivalent width measurements: EWCODE
In order to have a fast and reproducible method of measuring EWs without losing the ability to visually inspect every line, we developed a semi-automated Python 3 script we call EWCODE. This code works on RV-corrected, one-dimensional input spectra and fits Gaussian profiles at wavelengths predefined by an input line list. The fitting procedure does not rely on a global continuum or normalization, but on a more local approach of masking the region of the expected feature position. The local continuum is subsequently approximated by fitting a straight line to the flux levels of the neighboring wavelength ranges. Typical widths of these ranges, which decisively determine the stability of the continuum, are two profile FWHMs each. This value can be manually adapted. After the continuum placement, a Gaussian profile with the amplitude a, the position, and the FWHM as free parameters is fitted via a Levenberg-Marquardt least square algorithm. The whole procedure is iterated with the width of the fitted profile as input mask parameter for the next continuum placement step. The code also provides an estimate for the total EW error, which is computed via 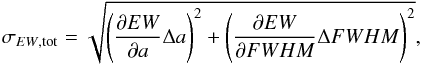 (1)following standard Gaussian error propagation. Covariances between Δa and ΔFWHM are not taken into account here, which renders σEW,tot a conservative upper estimate. One main advantage of this treatment is that it is applicable down to S/N values as low as approximately five, provided that the continuum windows are free of absorption lines (see, e.g., Fulbright et al. 2006). Our metal-poor spectra satisfy this condition over a wide spectral range, that is, there are many isolated transitions without substantial blending above wavelengths of 4000 Å which were reliably fitted by EWCODE.
(1)following standard Gaussian error propagation. Covariances between Δa and ΔFWHM are not taken into account here, which renders σEW,tot a conservative upper estimate. One main advantage of this treatment is that it is applicable down to S/N values as low as approximately five, provided that the continuum windows are free of absorption lines (see, e.g., Fulbright et al. 2006). Our metal-poor spectra satisfy this condition over a wide spectral range, that is, there are many isolated transitions without substantial blending above wavelengths of 4000 Å which were reliably fitted by EWCODE.
We tested the code extensively and found it to be very robust. In particular, we synthesized a fictitious Fe i line (λ = 5000 Å, χex = 3 eV, log gf = −1) 104 times for a fixed representative atmosphere (Teff = 4200, log g = 1, [Fe/H] =−2 dex, vmic = 2 km s-1) and an EW interval of [1 mÅ, 200 mÅ]. The pixel size was chosen to be δλ = 0.02 Å, representative for the typical values of our MIKE setup. We mimicked instrumental broadening by convolving the spectra with a Gaussian function of FWHM = 0.15 Å and added noise drawn from Poissonian distributions to implement different S/N characteristics. These profiles were then measured with EWCODE.
 |
Fig. 2 Residuals of measured and true equivalent widths ΔEW for S/N of 30 pixel-1 (top panel) and 10 pixel -1 (lower panel). Measurements which were already rejected within EWCODE are shown as red dots. Thick black points indicate the means of the respective EW bins. Red, gray and black error bars illustrate the theoretical and true rms scatters within the trust region (see text) and the error provided by EWCODE, respectively. The corresponding abundance for this particular synthesized transition (see text) for a given EWtrue is indicated by the top axis. |
Figure 2 illustrates the residuals of measured and input EWs versus the input EWs and the resulting logarithmic abundance log ϵ for S/N = 30 pixel-1 and S/N = 10 pixel-1.
Line list.
Binned mean deviations are shown in the figure, which indicate that there are two turnoffs from the zero-relation present at the lower (below 15/40 mÅ for S/N = 30/10) and the upper EW ranges (above 150 mÅ), respectively. The former was already rejected within the code, since we only claimed “detection” of a feature, if the computed EW is larger than 2.5 times its corresponding individual error σEW,tot (rejected points are highlighted in the figure). The latter trend sets in, once the assumption of absorption profiles with Gaussian shape looses justification. This case occurs once the core of the line saturates and an increasing amount of absorption moves in the damping wings. Such profiles cannot be correctly fit by EWCODE, because a substantial amount of line depth is not included in the Gaussian fit and therefore the derived EW drops with respect to the true one. A more accurate treatment of these profiles should involve the fitting of Voigt profiles, which can account for Lorentzian wings. We will implement this option in a future version of EWCODE. Here, we have limited our analysis to profiles which can be readily described by our Gaussian approximation.
Photometric and spectroscopic properties
We distinguish three properties to evaluate the quality of our EWCODE results. First, we introduce the theoretical root mean square (rms) deviation  (2)as derived by Cayrel (1988) and slightly modified by Battaglia et al. (2008). This relation establishes the lower limit of the measurement uncertainty due to sampling for very high S/N spectra. In fact, EWCODE nearly reaches this limit, judging from the standard deviation σstd of points within the trusted region below 150 mÅ. For completeness we included the mean of the individual errors
(2)as derived by Cayrel (1988) and slightly modified by Battaglia et al. (2008). This relation establishes the lower limit of the measurement uncertainty due to sampling for very high S/N spectra. In fact, EWCODE nearly reaches this limit, judging from the standard deviation σstd of points within the trusted region below 150 mÅ. For completeness we included the mean of the individual errors 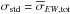 provided by the code. At an S/N of 30/10 pixel-1 we reached precisions of σstd = 3.0/8.7 mÅ and
provided by the code. At an S/N of 30/10 pixel-1 we reached precisions of σstd = 3.0/8.7 mÅ and 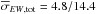 mÅ, compared to σCayrel,rms = 2.5/7.5 mÅ.
mÅ, compared to σCayrel,rms = 2.5/7.5 mÅ.
Since many features were to be found in more than one spectral order of the spectrograph, we selected those EWs that have been measured in the orders with the highest flux levels. Our EW results are presented in Table 2.
3.3. Atmospheric parameters
For each stellar model atmosphere the input quantities effective temperature Teff, metallicity [Fe/H] and microturbulence vmic were derived spectroscopically from line-by-line abundances of the neutral (log ϵ(Fe i)) and singly ionized (log ϵ(Fe ii)) iron species with respect to the abundances estimated for the same lines in the reference star (the choice of lines is further discussed in Sect. 3.3.3). Through this treatment we strongly reduced the influences of uncertain oscillator strengths on the atmosphere parameters. Here we adopted Teff = 4587 K, log g = 1.61 dex and [Fe/H] =−2.64 dex for HD 122563 as listed by Heiter et al. (2015). For the microturbulence we derived vmic = 2.16 km s-1 from our spectrum. These parameters agree reasonably well with the expected ones of our stars (ΔTeff ~ + 40–+ 270 K, Δlog g ~ + 0.5–+ 0.9 dex, Δ [Fe/H] ~ −0.2–−0.3 dex, Δvmic ~ 0–+ 0.35 km s-1), which makes HD 122563 a reliable benchmark. We note, however, that this star is strongly enhanced in all r-process elements so that an analysis of the heavy elements in our targets, differentially to HD 122563, would complicate our interpretations. This will be addressed further in Sect. 4.2.
The metallicity for HD 122563 stated by Heiter et al. (2015) is based on Jofré et al. (2014), who derived [Fe/H] from Fe i lines which have been corrected for NLTE effects. Hence, as Jofré et al. (2014) already pointed out, in order to compare their Fe abundances for HD 122563 to ours, one has to subtract their mean NLTE correction of Δlog ϵ(Fe i)NLTE = + 0.10 dex from the reference to get the mean LTE abundance of neutral lines. Likewise, the ionization imbalance of −0.19 dex provided in their work has to be subtracted from the reference to end up with [Fe ii/H]. In addition, since we relied on the solar reference values of Asplund et al. (2009) (log ϵ(Fe)⊙ = 7.50 dex), one has to bear in mind the discrepancy of 0.05 dex to the Grevesse et al. (2007) value (log ϵ(Fe)⊙ = 7.45 dex) which was used by Jofré et al. (2014). From our line list and EWs for HD 122563, we computed mean absolute abundances of log ϵ(Fe i) = 4.66 ± 0.11 dex (1σ scatter) and log ϵ(Fe ii) = 4.97 ± 0.10 dex, respectively. These are consistent with the reference value after applying the aforementioned adjustments, that is, log ϵ(Fe i)ref = 4.71 dex and log ϵ(Fe ii)ref = 5.00 dex.
In order to achieve accurate results for the model parameters of our stars, we tuned the atmospheric parameters to simultaneously attain balance between differential Fe i abundances at low and high excitation potentials (χex) and a zero-trend of abundance with reduced EW (log EW/λ). We accounted for spectral noise by the propagation of EW errors throughout the process of fitting the respective trends. Therefore we approximated the local curve of growth (COG) for a given EW and a fixed set of transition parameters by calling MOOG twice, with EW + σEW,tot and EW−σEW,tot. The individual assumed symmetric abundance error was then considered as the average. This value was incorporated as individual line weight for all fit procedures explained below. The methods of establishing the equilibria are not completely independent (see, e.g., McWilliam et al. 1995). Thus, for each set of model parameters we computed the full gradients of the log ϵ-χex- and log ϵ-log EW/λ slopes with respect to Teff and vmic. These were used to iteratively alter the stellar parameters until simultaneous convergence toward zero-slopes was reached. Our final photometric and spectroscopic solutions are listed in Table 3.
3.3.1. Effective temperature
The criterion that most affects the choice of Teff is the abundance trend of neutral lines with low excitation potential χex. To emphasize the importance of a differential treatment, we note the implications indicated by Fig. 3, where we present the log ϵ(Fe i)-χex relations of HD 122563 as fitted by a least-squares method to the absolute abundances derived from our line list and EW-measurements. We realized two temperatures while keeping the other parameters fixed at their reference values. The data points at higher abundances were computed using the reference of Teff,true = 4587 K. The fitted linear trend of −0.07 dex eV-1 points to a severe excitation imbalance, which could be resolved by lowering Teff by 200 K. This, however, would represent an unfeasibly low temperature with respect to the value of Heiter et al. (2015), which should be very accurate considering its origin from bolometric flux calibrations. In addition, this lower temperature would lead to a higher theoretical occupation number of Fe i low excitation states and thus strengthen their lines. This, in turn, leads to a lower derived abundance for a fixed EW. The effect on the weighted average of Fe i abundances for HD 122563 turns out to be as large as Δ(log ϵ(Fe i)) = −0.3 dex. Mashonkina et al. (2011) also encountered a negative excitation trend for this star. They were able to considerably flatten their slope from −0.054 dex eV-1 to −0.030 dex eV-1 by introducing NLTE effects in their line calculations but still could not completely get rid of the imbalance. We note here that there are possible additional sources for excitation imbalances. These comprise, for example, systematic errors in the oscillator strengths log gf, 3D- and hydrodynamical effects as well as systematic errors in the model atmospheres. Because of the similarity of our stars to HD 122563, we expected them to be subject to the same slope offset at the “true” Teff if we used absolute abundances. This could lead to an underestimated Teff by 200 K and consequently a lower log ϵ(Fe i). Thus we determined our stellar parameters from a strict line-by-line differential analysis relative to the respective Fe i and Fe ii abundances established by HD 122563, when employing the Heiter et al. (2015) value of Teff,true = 4587 K.
 |
Fig. 3 Absolute iron abundance trends with excitation potential χex of Fe i lines in HD 122563 for the reference effective temperature (Teff,true = 4587 K, gray points) and the one that satisfies excitation equilibrium best (Teff = 4387 K, red points). Error bars are the results of propagating σEW,tot through the abundance analysis. The weighted means for each realization are represented by the black dashed lines. |
In doing so we removed another issue, that becomes evident in Fig. 3. Apparently, the abundance scatter is not well reproduced by the individual errors due to σEW,tot, only. Since this is already an upper estimate, the substantially larger scatter was believed to originate from the systematic uncertainty of the line properties, especially of log gf. Following the differential approach, in our program stars we could in fact reduce the scatter, which is now significantly better described by σEW,tot only. This can be seen in the top panel of Fig. 4, where we show the findings for the star 5659. For this star the scatter in log ϵ(Fe i) decreased from 0.15 dex for absolute abundances to 0.08 dex in the differential case.
 |
Fig. 4 Exemplary final solutions for Teff,spec and vmic from balanced differential Fe i abundances with excitation potential (top) and line strength (bottom) for the star 5659. Errors are again computed from the EW uncertainties. The red shaded areas emphasize the slope errors corresponding to ±33 K and ±0.14 km s-1. |
We clipped those points from the fit that deviated by more than 2.5 times their corresponding uncertainty. These might just represent features with additional blending which was not recognized by EWCODE or profile fits with underestimated EW uncertainties. Under the above assumption we computed a 1σ slope error (indicated in Fig. 4 corresponding to ± 0.013 dex eV-1), which was used in the code to estimate the respective temperature uncertainties of our sample between 33 K and 42 K. At this point, we note that these are differential uncertainties with respect to the HD 122563 reference, which according to Heiter et al. (2015) has an uncertainty of 60 K.
For completeness, we included the photometric Teff using the relations of Casagrande et al. (2010) based on our dereddened (J−Ks)0 colors. We note that they are on average 120 K hotter than their spectroscopic counterparts. However, we emphasize the large uncertainties introduced by the photometry errors. In principle, it would be desirable to compute the more robust temperatures from V−Ks colors, but – as mentioned previously – we don’t have reliable V magnitudes for our stars at hand. Using V−Ks colors nevertheless – incorporating the Dotter et al. (2011)V magnitudes – would increase the listed Teff by ~300 K on average. Moreover, the extinction maps by Schlafly & Finkbeiner (2011) are badly resolved for our purposes, that is, if any differential reddening (see, e.g., Hendricks et al. 2012) was present, the Teff,phot of our stars would be grossly misjudged. For NGC 6426, Dotter et al. (2011) reported “signs of differential reddening”. Therefore, we claim our spectroscopic, reddening-independent results to be more reliable.
3.3.2. Surface gravity and metallicity
The surface gravity entering our models was calculated during each iteration step from the relation  (3)where we used log g⊙ = 4.44, Teff, ⊙ = 5777 K, Mbol, ⊙ = 4.74 and a stellar mass of M = 0.8 M⊙ for our red giants (see, e.g., Koch & McWilliam 2008). We computed the absolute magnitude MK using an adopted distance of 20.6 kpc (Harris 1996). In addition, we employed the relation provided in Eq. (4) of Buzzoni et al. (2010) for the bolometric Ks-band correction BCK. The presented uncertainties of 0.09 dex originate from a Monte-Carlo error propagation of our Teff and Ks errors and a mass range of ±0.15 M⊙ (see Roederer et al. 2016). Lind et al. (2012) showed for metal-poor giant stars that the spectroscopic method of deducing log g (with absolute abundances) is heavily biased by NLTE effects on Fe i lines. In particular, their NLTE calculations indicate that due to a stronger net UV-radiation field compared to the LTE case the ionization equilibrium gets shifted toward the ionized state, leading to a weakening of neutral Fe lines. Thus, in LTE, one underestimates log ϵ(Fe i). This is confirmed by the derivation of NLTE abundances for several of our HD 122563 Fe i lines from our measured EWs using the grid of Bergemann et al. (2012b) and Lind et al. (2012)3. We found typical corrections of the order of Δlog ϵ(Fe i)NLTE ≈ + 0.14 dex for low-excitation lines around χex ≈ 0 eV and Δlog ϵ(Fe i)NLTE ≈ + 0.26 dex at χex ≈ 4 eV. Because Fe ii is already the dominant species, overionization only marginally affects its abundance (typical corrections for HD 122563 range from −0.002 dex to −0.010 dex). A decrease in the model log g, however, tends to lower log ϵ(Fe ii) and has a vanishingly small impact on log ϵ(Fe i). Consequently, by forcing both abundances into equilibrium, one would underestimate the surface gravity and the metallicity, respectively. We report on a mean ionization imbalance of log ϵ(Fe ii)−log ϵ(Fe i) ~ 0.3 dex in terms of absolute abundances in the four program stars. Our usage of a differential measurement levels out the mentioned discrepancies to some degree, because we found log ϵ(Fe ii)−log ϵ(Fe i) = 0.31 dex for HD 122563 and its literature stellar parameters. Hence, our photometric gravities appear to establish ionization balance in the differential case. Nevertheless, we would like to stress that our stars span a range of effective temperatures and gravities below the values of HD 122563 and expose higher [Fe/H]. Owing to the fact that Lind et al. (2012) also pointed out that the magnitude of NLTE corrections depends strongly on the particular choice of stellar parameters and Fe lines, we cannot claim to be fully unaffected by them. Accordingly, the metallicities [Fe/H] in this work are based on the weighted mean of the Fe ii abundances, which we consider more reliable (see also Kraft & Ivans 2003). Again, we applied the clipping of outliers that deviated by more than 2.5σlog ϵ,EW. This mean value was computed during each iteration and set the metallicity of the successive step (for a more detailed discussion on Fe abundances see Sect. 4.2.1).
(3)where we used log g⊙ = 4.44, Teff, ⊙ = 5777 K, Mbol, ⊙ = 4.74 and a stellar mass of M = 0.8 M⊙ for our red giants (see, e.g., Koch & McWilliam 2008). We computed the absolute magnitude MK using an adopted distance of 20.6 kpc (Harris 1996). In addition, we employed the relation provided in Eq. (4) of Buzzoni et al. (2010) for the bolometric Ks-band correction BCK. The presented uncertainties of 0.09 dex originate from a Monte-Carlo error propagation of our Teff and Ks errors and a mass range of ±0.15 M⊙ (see Roederer et al. 2016). Lind et al. (2012) showed for metal-poor giant stars that the spectroscopic method of deducing log g (with absolute abundances) is heavily biased by NLTE effects on Fe i lines. In particular, their NLTE calculations indicate that due to a stronger net UV-radiation field compared to the LTE case the ionization equilibrium gets shifted toward the ionized state, leading to a weakening of neutral Fe lines. Thus, in LTE, one underestimates log ϵ(Fe i). This is confirmed by the derivation of NLTE abundances for several of our HD 122563 Fe i lines from our measured EWs using the grid of Bergemann et al. (2012b) and Lind et al. (2012)3. We found typical corrections of the order of Δlog ϵ(Fe i)NLTE ≈ + 0.14 dex for low-excitation lines around χex ≈ 0 eV and Δlog ϵ(Fe i)NLTE ≈ + 0.26 dex at χex ≈ 4 eV. Because Fe ii is already the dominant species, overionization only marginally affects its abundance (typical corrections for HD 122563 range from −0.002 dex to −0.010 dex). A decrease in the model log g, however, tends to lower log ϵ(Fe ii) and has a vanishingly small impact on log ϵ(Fe i). Consequently, by forcing both abundances into equilibrium, one would underestimate the surface gravity and the metallicity, respectively. We report on a mean ionization imbalance of log ϵ(Fe ii)−log ϵ(Fe i) ~ 0.3 dex in terms of absolute abundances in the four program stars. Our usage of a differential measurement levels out the mentioned discrepancies to some degree, because we found log ϵ(Fe ii)−log ϵ(Fe i) = 0.31 dex for HD 122563 and its literature stellar parameters. Hence, our photometric gravities appear to establish ionization balance in the differential case. Nevertheless, we would like to stress that our stars span a range of effective temperatures and gravities below the values of HD 122563 and expose higher [Fe/H]. Owing to the fact that Lind et al. (2012) also pointed out that the magnitude of NLTE corrections depends strongly on the particular choice of stellar parameters and Fe lines, we cannot claim to be fully unaffected by them. Accordingly, the metallicities [Fe/H] in this work are based on the weighted mean of the Fe ii abundances, which we consider more reliable (see also Kraft & Ivans 2003). Again, we applied the clipping of outliers that deviated by more than 2.5σlog ϵ,EW. This mean value was computed during each iteration and set the metallicity of the successive step (for a more detailed discussion on Fe abundances see Sect. 4.2.1).
3.3.3. Microturbulence
Since our microturbulence parameter vmic was tuned toward erasing the slope of the log ϵ(Fe i) vs. line strength (reduced EW, log EW/λ) relation, we again had to ensure that this slope was free of intrinsic influences causing the “true” microturbulent velocity to produce non-zero slopes. First, we followed the common procedure of limiting the analysis to weak and intermediately strong lines, that is, excluding the strongest, possibly saturated lines, that originate from the flat part of the COG. The reasoning behind this is that these features emerge from the highest, most dilute atmospheric layers of a star, where our LTE treatment and model atmospheres as well as the assumption of Gaussian line profiles are likely to fail. As a consequence we established an upper limit for the iron line strength of log EW/λ = −4.7. Since the uncertainties of log ϵ(Fe i) and log EW/λ are not independent, but coupled through the COG, a systematic bias for the slope and therefore the microturbulence can be expected. In order to decouple these quantities, Magain (1984) suggested using theoretical line strengths when fitting the slope. Unfortunately, this treatment does not account for an additional effect that becomes apparent in Fig. 2. When working with low S/N spectra one encounters a selection bias at the lower end of the EW distribution due to the noise-induced detection threshold. This threshold runs diagonally in the ΔEW-EWtrue plane. Hence, low-EW lines are more likely to be over- than underestimated in their magnitude with respect to their true values. Once propagated through the abundance analysis, one will end up with systematically higher log ϵ(Fe i) in the regime of low line strength and therefore measure a negative slope for the correct vmic. The vast majority of our iron lines resides in Echelle orders with S/N well above 30, so we decided to apply a reasonable lower EW cut of 20 mÅ. In his Monte-Carlo analysis with various S/N characteristics, Mucciarelli (2011) found that a proper treatment of the errors within the classical approach of finding vmic is superior to the Magain method. Following the suggestions made in that work, we used an orthogonal distance regression algorithm to fit the desired slopes. This enabled us to treat both abscissa and ordinate uncertainties. As an example we present the fit outcome for star 5659 in the lower panel of Fig. 4. Again, we used the slope error to constrain a respective vmic uncertainty.
4. Abundance results
In Table A.1 we present the weighted mean abundance ratios using our final model atmosphere solutions. While using differential abundances of Fe transitions to constrain the stellar parameters, we relied on absolute abundances – log gf values – for our final elemental abundance results. We emphasize the fact that – depending on χex – this treatment potentially introduces systematic errors to the abundances (see Sect. 3.3.1), which ultimately leads to increased values for the scatter around the weighted mean in Table A.1. All ratios of neutral and ionized species in the following sections were computed relative to their counterparts Fe i and Fe ii. Our results for the mean chemical abundances of NGC 6426 together with the rms scatter of the stars are shown in Table 4.
Mean abundances for NGC 6426
4.1. Abundance errors
In order to quantify the errors of our abundance analysis with respect to the uncertainties of the stellar parameters, we followed the procedure described in Koch & McWilliam (2014). In particular, we repeated the analysis for all the stars with the stellar parameters being lowered and elevated by the uncertainties given in Table 3, while keeping the others fixed. To account for uncertainties of the opacity distribution function with respect to the α-content, we also ran a computation with ODFNEW opacity distributions resembling solar [α/Fe] ratios.
In Table A.2 we demonstrate the impact of stellar parameters on the abundances and how their uncertainties propagate into the corresponding abundance uncertainties. This is shown for the stars 14853 and 2314 which have the largest separation in parameter space and should therefore be representative for the whole sample. The total uncertainty due to the model atmospheres used, σatm, was computed by quadratically summing all the mean absolute deviations. For this calculation we divided the ODFNEW contribution by four in order to mimic 0.1 dex of α-content uncertainty. We emphasize that we did not account for correlations of the parameters such as the Teff-log g dependency (see McWilliam et al. 1995, for further discussion). Hence, the given uncertainties are to be seen as upper estimates. We find variations of Teff to have the largest impact, which is especially pronounced for low excitation transitions of neutral species. Except in a few cases, the σatm reside well below 0.1 dex.
Our final statistical uncertainty σstat for the abundance of a species was computed from the 1σ rms line-to-line scatter. Consequently, this uncertainty accounts for spectral noise as well as errors of the atomic data. Once again, we clipped those lines that deviate more than 2.5σstat from the weighted mean of all lines belonging to that species. For those cases, where only one line was detectable, we provide the error based on the EW uncertainty, which has been propagated through the analysis. Finally, the total error budget σtot reported in Table A.1 represents the quadratic sum of σstat and σatm.
4.2. Notes on individual elements
In the following sections, we will comment on individual results of our abundance measurements. Figure 5 shows a compilation of the mean cluster abundance ratios of all elements analyzed here.
 |
Fig. 5 Mean abundance results of all elements analyzed in this study. All ratios of neutral and ionized species are scaled to their Fe counterpart. The only exceptions made are Fe i and Fe ii, which are given with respect to the cluster mean and Fe i abundances, respectively. The black error bars indicate the rms scatter around the mean, while the light blue error bars represent the mean σtot including stellar parameter uncertainties. |
4.2.1. Fe
Our final mean [Fe/H] for NGC 6426 is −2.34 dex with a scatter of 0.05 dex as derived from Fe ii lines. When looking at the ratios of abundances of neutral to ionized iron species, [Fe i/Fe ii], we found a spurious anti-correlation with [Fe ii/H], indicated in Fig. 6.
 |
Fig. 6 Ionization imbalance between Fe i and Fe ii. Color coding of the stars was chosen to represent the membership of the potential sub-populations MP (blue) and MR (red). The indicated errors were computed by dividing the line-to-line abundance scatter by |
There, we highlight two groups of two stars each by color. One group appears to be deficient in [Fe ii/H] by 0.08 dex and exposes an ionization imbalance [Fe i/Fe ii] elevated by ~+0.08 dex compared to the other group, which tends to higher Fe ii abundances and lower ionization imbalances. These imbalance deviations cannot be assigned to NLTE-effects, because either group contains both a mildly warmer, higher surface gravity star (14853/5659) and a cooler, lower surface gravity star (736/2314). Thus departures from LTE could be held responsible for an intra-group scatter of [Fe i/Fe ii] but not for the presented inter-group deviation. We can only speculate about the origin of this imbalance. If it is real, a possible explanation could be a significantly deviating He composition in both groups, which ultimately affects the model surface gravity and therefore the Fe ii abundance (see Strömgren et al. 1982; Lind et al. 2011b, for a detailed discussion). On the other hand, we encountered rather large uncertainties in the photometry and extinction maps, which could have a systematic effect on the surface gravities and as a consequence on the Fe ii abundances, so that the small separation could also be linked to these. Owing to these doubts, at this point we can neither accept nor reject the hypothesis that we have actually observed two distinct populations in NGC 6426. We will discuss these and further tentative evidence from other elements in Sect. 4.3.
4.2.2. Alpha elements Mg, Si, Ca, Ti
In terms of light α-elements, we found [Mg/Fe] = 0.44 ± 0.05 dex, confirming previous results from low-resolution spectroscopy (0.38 ± 0.06 dex, Dias et al. 2015), and – for the first time – [Si/Fe] = 0.49 ± 0.07 dex. These two species will be discussed in more detail in Sect. 4.3. For the heavy α-elements Ca and Ti in NGC 6426 we report mean abundances and rms scatters of 0.25 ± 0.03 dex and 0.20 ± 0.04 dex for [Ca/Fe] and [Ti/Fe], respectively. Hence, the cluster falls in line with metal-poor halo stars at the same metallicity (see Fig. 7), which show elevated levels of pure α- and Ti abundances (see Pritzl et al. 2005; Koch & McWilliam 2014). There is no intrinsic separation in these two elements and the scatter is fully consistent with the uncertainties. Our analysis reveals a mean [Mg/Ca] that is enhanced by 0.19 dex. Yield models for massive core-collapse supernovae (SNe) – with progenitor masses of 15 M⊙ and above – predict enhancements of [Mg/Ca] (see, e.g., Koch 2009, and references therein). Consequently, a possible explanation for our finding is the imprint of nucleosynthesis by such SN events (see Sect. 4.2.5 and Fig. 9 for further constraints and discussion).
 |
Fig. 7 Mean results and scatter for [X/Fe] for all species detected with 11 ≤ Z ≤ 27. NGC 6426 (this study) is represented by red stars. For the case of K, the red bar indicates the region where [K/Fe] is to be expected after an NLTE correction. The gray points resemble the compilation of abundances of stars in the MW halo by Roederer et al. (2014) in the range −3 dex ≤ [Fe/H] ≤−1.5 dex. We also include (in blue) the mean abundances of the similarly metal-poor GCs NGC 5897 (crosses, Koch & McWilliam 2014), NGC 4833 (diamonds, Roederer & Thompson 2015), NGC 5824 (squares, Roederer et al. 2016), M15 (filled circles, RGB targets of Sobeck et al. 2011), NGC 5634 and NGC 5053 (up and down triangles, Sbordone et al. 2015). |
4.2.3. Light elements Na, O, Al, K
Unfortunately, due to limited spectrum quality and the metal-poor nature of our sample we were not able to derive O and Al abundances using either EW measurements or with spectrum synthesis. For Na we were only able to measure one line for the star 5659. An NLTE-corrected abundance for this line has been computed from Lind et al. (2011a)3. The NaD lines were too strongly saturated and affected by interstellar absoption for all targets. The existence or non-existence of the popular Na-O and Mg-Al anti-correlations (Carretta et al. 2009b; Gratton et al. 2012) could be used to put further constraints on the multiple population hypothesis.
Our LTE analysis of the K i resonance line at 7698.97 Å shows [K/Fe] ~ 0.53 dex. However this has to be treated with caution, since for this particular line strong NLTE-corrections can be expected as stated by Takeda et al. (2009). From their work, we expect corrections between −0.2 and −0.3 dex in the regime of our derived stellar parameters. Consequently NGC 6426’s K abundances fall on the trend of the GC M15 in Takeda et al. (2009) and the MW halo at comparable metallicities (see again Fig. 7).
4.2.4. Iron peak elements Sc, V, Cr, Mn, Co, Ni
Concerning the iron peak, given its metallicity we can report on a regular behavior of NGC 6426. Our study reveals little scatter among the sample stars for the iron peak element abundances. The rms scatter values range from 0.01 dex for [Sc/Fe] to 0.05 dex for [Mn/Fe], which is well within the respective individual uncertainties. Again, we found the cluster mean abundances for Sc, V, Cr, Mn, Co and Ni to coincide well with other GCs and the halo at comparable [Fe/H] (see Figs. 7 and 8).
4.2.5. Neutron-capture elements Zn, Sr, Y, Zr, Ba, La, Nd, Sm, Eu
The mean [Zn/Fe] ratio for NGC 6426 appears to be enhanced by 0.39 dex and falls on the observed trend of increasing [Zn/Fe] with decreasing [Fe/H] of galactic halo field stars first reported by Johnson (1999). Possible production sites of Zn are the complete Si-burning layers of massive stars (Umeda & Nomoto 2002). In these layers, Si is completely destroyed. Umeda & Nomoto (2005) concluded that observed supersolar [Zn/Fe] in metal-poor halo stars imply an enrichment by very energetic massive supernovae (the so-called hypernovae, HN). In their models of such events, the fraction of complete Si-burning layer (high Zn production rate) to incomplete Si-burning layer (low Zn production rate) is elevated, such that the abundance observations are matched.
 |
Fig. 9 Model yields from Nomoto et al. (2013) for Z = 0.001, different SN explosion energies, and progenitor masses compared to this study’s individual stellar abundances for the elements Na to Zn. |
Figure 9 shows a comparison of predicted yields for normal supernovae and HNe models with assumed explosion energies ten times larger than in normal core-collapse SNe. The respective yields for progenitor masses of 20 M⊙,25 M⊙,30 M⊙ and 40 M⊙ were taken from Nomoto et al. (2013) and are presented along with our findings for the elements from Na to Zn. Apparently, normal SN fail to reproduce the overall trend from Fe to Zn, especially the Ni-Zn relation. In terms of minimum χ2, the best global fit is achieved by the 40 M⊙ HN model, whereas a 25 M⊙ HN seems to resemble the Fe to Zn pattern best because of the predicted close to solar [Ni/Fe]. Hence it is feasible that the pristine gas, from which NGC 6426 evolved, has experienced HN enrichment.
As shown in previous studies comparing observations to a number of different yield predictions (e.g., Hansen et al. 2011) finding a perfect match to SN or HN yields can be very challenging even for the less polluted extremely metal-poor stars. A number of factors cloud such comparisons, such as the number of free parameters in the model predictions (mass, energy, number of electrons per nucleon, Tpeak, jets, fallback and the contribution from neutrino-driven winds). Also uncertainties in stellar abundances (systematics, abundance assumptions such as LTE and 1D) combined with various unknowns in ISM mixing add to the uncertainty in the yield comparison. Unless a perfect match to a given model is found, one model cannot be singled out as the only donor, but mixing of various contributions is likely to have taken place and changed the original composition of the yielded abundance ratios. At this metallicity (~−2.3 dex) we are most likely not seeing the clean trace of one event and the somewhat poor match to the predictions confirms this. We therefore do not believe that strong constraints on the SN/HN origin can be obtained, however, quantitative predictions as to the mass (based on the high level of lighter alpha-elements and the enhancement of [Mg/Ca]) and the energy being high (high Ni and Zn abundances) can be made. The number of events can, to date, not be derived with confidence, owing to degeneracies like the number of free model parameters and the uncertainties in the elemental abundances.
We were not able to reliably measure EWs of isolated lines of Sr, because of strong blending in the blue wavelength regime. Thus, we applied spectrum synthesis for the resonance feature of Sr ii at 4215 Å and adjusted the input abundance to achieve the best fit (see Hansen et al. 2013, for a detailed discussion). Typical errors introduced this way are of order ~0.2 dex.
Elements heavier than Zn (Z> 30, the elements mainly attributed to neutron-capture processes) do not appear to show any means of separation in sub-populations when considering uncertainties. A possible exception is La which exposes the largest star-to-star scatter among all elements measured here (0.2 dex). On the other hand, being based on only one highly uncertain EW, La abundances have a typical uncertainty of ~0.25 dex. We note that the abundances of heavy elements from La to Eu are consistent with an r-dominated enrichment history with little to no contribution of the main slow neutron-capture process (s-process) attributed to low-mass AGB stars. This finding is supported by a low [Ba/Eu] of −0.46 dex, setting the upper limit of the formation timescale of NGC 6426 to a few hundred Myr.
The distribution of the light neutron-capture elements Sr, Y and Zr cannot be assigned to either of the r- and s-process patterns, because of the deep depression of Y between enhanced Sr and Zr. The same sequence has previously been reported for other GCs, for example, for M15 by Sobeck et al. (2011) and partly for NGC 5897 (low Y) by Koch & McWilliam (2014). Both groups assign these findings to the contribution of a yet unknown lighter element primary process (LEPP, McWilliam 1998; Travaglio et al. 2004), which ought to be active in metal-poor environments. Low Y abundances have also been reported by Hansen et al. (2012) for a large sample of halo stars.
4.3. Indications for multiple populations
During our analysis we found several weak indications for a separation in two subpopulations within the sample of four NGC 6426 stars. None of the following individual arguments is significant on a 3σ-level – but taken together, they draw a consistent, yet still uncertain picture.
The first clue is the already discussed ionization imbalance among the Fe ionization states (Sect. 4.2.1). Two-tailed t-tests of the separations in the two dimensions [Fe ii/H] and [Fe i/Fe ii] revealed statistical significances of 89.2% and 99.6%, respectively. Hence, at this point, the null hypothesis of actually having observed only one population cannot be rejected in neither of these abundance ratios. Nevertheless, for labeling purposes, we will from now on refer to the (mildly) more metal-poor (MP, stars 14853 and 736) and (mildly) more metal-rich population (MR, stars 5659 and 2314), when elaborating on their distinct nature.
The abundance results for Mg are consistent within the given uncertainties, though we note that both stars, which we previously attributed to the MP population expose the more enhanced [Mg/Fe] compared to the MR population. There is evidence of a more pronounced separation when looking at the [Si/Fe] ratios. The MP stars expose an enhancement of 0.41 and 0.43 dex, while the MR stars seem to be even more enhanced by additional 0.15 dex (absolute 0.59 and 0.54 dex). There is a weak indication for a Mg-Si anti-correlation with a correlation coefficient of −0.89. In order to get a handle on the significance of this anti-correlation and to account for our large uncertainties, we randomly generated 105 sets of four points in the [Mg/Fe]-[Si/Fe] plane where each point was drawn from a normal distribution resembling the means and uncertainties of the underlying cluster star. For each of the sets we computed the Pearson correlation coefficient rPearson. The result is presented in Fig. 10.
 |
Fig. 10 Top: abundance results for Si and Mg. Color coding is the same as in Fig. 6. The contours show the smoothed distribution, which was used in order to evaluate the significance of the correlation. Bottom: discrete probability distribution of the correlation coefficients for the 105 realizations. |
The lower panel shows a histogram from which we conclude that 79.5% of all realizations actually are anti-correlations. Thus we excluded the cases correlation (r> 0) and no correlation at all (r = 0) with a confidence level of 79.5%. This is far from enabling us to claim significance, but it is the same stars that already separated in [Fe i/Fe ii].
Mg is depleted in the H-burning phases of hot and massive stars, where the Mg-Al cycle is active. There, Mg gets destroyed at the expense of producing Al through a series of proton captures and successive β-decays (see, e.g., Karakas & Lattanzio 2003). Since the circle is not entirely closed, Si can be produced by further proton captures on Al seed nuclei. Therefore a depletion in Mg as a result of this process should come with an enhancement of Si. Carretta et al. (2009a) proposed this “leakage” in the Mg-Al chain to be responsible for their observations of Mg-Si anti-correlations in metal-poor and/or massive clusters. Consequently, assuming its existence, the observed anti-correlation in NGC 6426 points toward the two population scenario, where the ejecta of evolved, massive stars are depleted in Mg and enhanced in Si, which affects the composition of the ISM and eventually the newly formed stars.
The rms scatter in [Zn/Fe] of our four stars is lower than the individual uncertainties. Nevertheless, the left panel of Fig. 11 once again indicates a systematic separation of ~0.2 dex between MP and MR stars. Moreover, we report on a weak, non-significant correlation of [Zn/Fe] with [Si/Fe] (rPearson = 0.75, confidence level 73.4%, see Fig. 11).
If the intra-cluster correlation of [Zn/Fe] with [Si/Fe] is real, it further supports the argument that the enhancement of [Si/Fe] between MP and MR stars originates from pollution by hot and massive MP stars. In those stars with masses above 15 M⊙, the weak component of the s-process is active. This process is believed to be a production site of elements between Fe and Sr such as Zn (Käppeler et al. 1989; Frischknecht et al. 2012). Consequently both, elevated [Zn/Fe] and higher [Si/Fe] levels of MR stars point toward an additional contribution from massive star nucleosynthesis – weak s-process and hot H-burning cycles – to the element budget of these stars. Taking the aforementioned scenarios for granted, the MP population should resemble the unpolluted HN yield patterns presented in Fig. 9 more closely than the MR population. In fact, the fit quality of the 40 M⊙ HN model for the global pattern and the 25 M⊙ HN case for the Fe to Zn trend improves slightly, once we only consider the MP population. Nevertheless, we emphasize once again that the uncertainties involved remain high and the conclusions drawn here are highly speculative.
4.4. Similarity to HD 108317
In terms of abundances of Zn and the neutron-capture elements, we note a remarkable overlap of our target stars with the analysis of HD 108317 by Roederer et al. (2012). Their study of this close-by halo red giant (Teff = 5100 K, log g = 2.67 dex, vmic = 1.50 km s-1) revealed an Fe abundance of [Fe ii/H] =−2.37 ± 0.14 (stat.) dex, which falls right on top of our findings for NGC 6426. Its heavy element pattern in conjunction with the one of NGC 6426 is shown in Fig. 12. Neither of them have been scaled to fit the other, meaning both patterns are the original results. The Nd uncertainty does not change the results, since the combined uncertainties from both studies remain high. It is tempting to say that this striking congruence points to the conclusion that whatever processes contributed to the chemical enrichment of heavy elements in HD 108317, have also been active in NGC 6426. Roederer et al. (2012) claim these to be mainly the r-process with a possible minority component of the s-process. In light of published abundance measurements of HD 108317 other than the aforementioned, however, the s-process might have had a more pronounced contribution. Hansen et al. (2012) and Burris et al. (2000), for example, consistently report on [Ba/Eu] = 0.00 dex and [Ba/Eu] =−0.13 dex, respectively, compared to [Ba/Eu] =−0.61 dex from Roederer et al. (2012). These results indicate a mixed r-/s- origin of this star which is supported by Simmerer et al. (2004) who – based on their [La/Eu] ratio – excluded pure r-process enrichment.
 |
Fig. 12 Top panel: mean abundance pattern for NGC 6426. The color coding is the same as in Fig. 5. The red line and red shaded region state the abundances and uncertainties of HD 108317 as derived by Roederer et al. (2012). Both patterns are unscaled, i.e., represent their original values. Bottom panel: residual pattern for the cluster stars after subtracting HD 108317. |
5. Summary
We have carried out the first spectroscopic high-resolution study of four stars of the GC NGC 6426 using the MIKE spectrograph. In doing so, we have spectroscopically derived the stellar parameters of the targets and computed chemical abundances of 22 elements, including α-, iron peak- and several neutron-capture elements. We derived a metallicity of [Fe/H] =−2.34 ± 0.05 dex, which is in good agreement with the spectroscopic results of Dias et al. (2015, −2.39 ± 0.04 from low-resolution Ca triplet spectroscopy and the photometric ones by Hatzidimitriou et al. (1999, −2.33 ± 0.15.
The pattern of elemental abundances of the cluster fits well into the picture drawn by the MW halo and other GCs at comparable metallicities. In particular, we found a mean α enhancement of [(Mg, Si, Ca)/3 Fe] = 0.39 ± 0.03 dex and heavy element distributions that both fall in line with the abundance trends of the MW halo. There are weak indications for correlations and anti-correlations among the elements Mg, Si and Zn. Assuming these trends are real, we suggest that they point toward a pollution by heavy star nucleosynthesis of an older population toward a slightly younger one. We report on an overall enhancement of [Zn/Fe] by 0.39 dex, possibly indicating an early enrichment of the pre-cluster medium by hypernova events. Our results for the heavier neutron-capture elements La, Nd, Sm and Eu point toward an enrichment history governed by the r-process. However, the light neutron-capture elements Sr, Y and Zr neither fit the typical r- or s-process patterns nor a combination of both, because of the depletion of [Y/Fe] and the enhancement of [Sr/Fe] and [Zr/Fe]. We follow the argumentation of previous authors and attribute the results to an additional, yet unknown, source of these elements, called LEPP.
In terms of heavy elements, we encountered an extraordinary similarity of the MW field star HD 108317 and our program stars. Despite the disagreement in literature about the amount of s-process contributions to the enrichment of HD 108317, we suggest that this star was born in an environment similar to NGC 6426’s natal cloud.
In this paper, we have employed the common abundance notation log ϵ(X) = log (n(X) /n(H)) + 12 for the element X. The bracket notation [A/B] relates the stellar abundances to the respective solar ratios for the elements A and B taken from Asplund et al. (2009).
Data obtained from the INSPECT database, version 1.0 (www.inspect-stars.net).
Acknowledgments
A.K. acknowledges the Deutsche Forschungsgemeinschaft for funding from Emmy-Noether grant Ko 4161/1. C.J.H. was supported by a research grant (VKR023371) from VILLUM FONDEN. We are grateful to the referee for helpful and constructive inputs. The authors thank Ian Roederer for providing the MIKE spectrum of HD 122563. This research made use of atomic data from the INSPECT database, version 1.0 (www.inspect-stars.net), the NASA’s Astrophysics Data System and the SIMBAD database, operated at CDS, Strasbourg, France. Moreover, we applied results from the NASA/ IPAC Infrared Science Archive, which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. Atomic data were partly retrieved from the VALD database, operated at Uppsala University, the Institute of Astronomy RAS in Moscow, and the University of Vienna.
References
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Battaglia, G., Irwin, M., Tolstoy, E., et al. 2008, MNRAS, 383, 183 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Bergemann, M., Hansen, C. J., Bautista, M., & Ruchti, G. 2012a, A&A, 546, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bergemann, M., Lind, K., Collet, R., Magic, Z., & Asplund, M. 2012b, MNRAS, 427, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Bernstein, R., Shectman, S. A., Gunnels, S. M., Mochnacki, S., & Athey, A. E. 2003, in Instrument Design and Performance for Optical/Infrared Ground-based Telescopes, eds. M. Iye, & A. F. M. Moorwood, Proc. SPIE, 4841, 1694 [Google Scholar]
- Burris, D. L., Pilachowski, C. A., Armandroff, T. E., et al. 2000, ApJ, 544, 302 [NASA ADS] [CrossRef] [Google Scholar]
- Buzzoni, A., Patelli, L., Bellazzini, M., Pecci, F. F., & Oliva, E. 2010, MNRAS, 403, 1592 [NASA ADS] [CrossRef] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R., & Lucatello, S. 2009a, A&A, 505, 139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2009b, A&A, 505, 117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casagrande, L., Ramírez, I., Meléndez, J., Bessell, M., & Asplund, M. 2010, A&A, 512, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castelli, F., & Kurucz, R. L. 2004, ArXiv Astrophysics e-prints [arXiv:astro-ph/0405087] [Google Scholar]
- Cayrel, R. 1988, in The Impact of Very High S/N Spectroscopy on Stellar Physics, eds. G. Cayrel de Strobel, & M. Spite, IAU Symp., 132, 345 [Google Scholar]
- Cohen, J. G. 1978, ApJ, 223, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Den Hartog, E. A., Lawler, J. E., Sobeck, J. S., Sneden, C., & Cowan, J. J. 2011, ApJS, 194, 35 [NASA ADS] [CrossRef] [Google Scholar]
- D’Ercole, A., Vesperini, E., D’Antona, F., McMillan, S. L. W., & Recchi, S. 2008, MNRAS, 391, 825 [NASA ADS] [CrossRef] [Google Scholar]
- D’Ercole, A., D’Antona, F., & Vesperini, E. 2011, MNRAS, 415, 1304 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Dias, B., Barbuy, B., Saviane, I., et al. 2015, A&A, 573, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dotter, A., Sarajedini, A., & Anderson, J. 2011, ApJ, 738, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Frischknecht, U., Hirschi, R., & Thielemann, F.-K. 2012, A&A, 538, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fulbright, J. P., McWilliam, A., & Rich, R. M. 2006, ApJ, 636, 821 [NASA ADS] [CrossRef] [Google Scholar]
- Gratton, R. G., Carretta, E., & Bragaglia, A. 2012, A&ARv, 20, 50 [CrossRef] [Google Scholar]
- Grevesse, N., Asplund, M., & Sauval, A. J. 2007, Space Sci. Rev., 130, 105 [Google Scholar]
- Hansen, C. J., Nordström, B., Bonifacio, P., et al. 2011, A&A, 527, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hansen, C. J., Primas, F., Hartman, H., et al. 2012, A&A, 545, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hansen, C. J., Bergemann, M., Cescutti, G., et al. 2013, A&A, 551, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harris, W. E. 1996, AJ, 112, 1487 [NASA ADS] [CrossRef] [Google Scholar]
- Hatzidimitriou, D., Papadakis, I., Croke, B. F. W., et al. 1999, AJ, 117, 3059 [NASA ADS] [CrossRef] [Google Scholar]
- Heiter, U., Jofré, P., Gustafsson, B., et al. 2015, A&A, 582, A49 [NASA ADS] [CrossRef] [EDP Sciences] [PubMed] [Google Scholar]
- Hendricks, B., Stetson, P. B., VandenBerg, D. A., & Dall’Ora, M. 2012, AJ, 144, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Jofré, P., Heiter, U., Soubiran, C., et al. 2014, A&A, 564, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johnson, J. A. 1999, Ph.D. thesis, University of California, Santa Cruz, USA [Google Scholar]
- Käppeler, F., Beer, H., & Wisshak, K. 1989, Rep. Prog. Phys., 52, 945 [Google Scholar]
- Karakas, A. I., & Lattanzio, J. C. 2003, PASA, 20, 279 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Kelson, D. D. 2003, PASP, 115, 688 [NASA ADS] [CrossRef] [Google Scholar]
- Koch, A. 2009, Astron. Nachr., 330, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Koch, A., & McWilliam, A. 2008, AJ, 135, 1551 [NASA ADS] [CrossRef] [Google Scholar]
- Koch, A., & McWilliam, A. 2014, A&A, 565, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Koch, A., Côté, P., & McWilliam, A. 2009, A&A, 506, 729 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Koch, A., McWilliam, A., Preston, G. W., & Thompson, I. B. 2016, A&A, 587, A124 [Google Scholar]
- Kraft, R. P., & Ivans, I. I. 2003, PASP, 115, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Kurucz, R. L., & Bell, B. 1995, Atomic line list (Cambridge, MA: Smithsonian Astrophysical Observatory) [Google Scholar]
- Lawler, J. E., Bonvallet, G., & Sneden, C. 2001a, ApJ, 556, 452 [NASA ADS] [CrossRef] [Google Scholar]
- Lawler, J. E., Wickliffe, M. E., den Hartog, E. A., & Sneden, C. 2001b, ApJ, 563, 1075 [CrossRef] [Google Scholar]
- Lind, K., Asplund, M., Barklem, P. S., & Belyaev, A. K. 2011a, A&A, 528, A103 [Google Scholar]
- Lind, K., Charbonnel, C., Decressin, T., et al. 2011b, A&A, 527, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lind, K., Bergemann, M., & Asplund, M. 2012, MNRAS, 427, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Lodders, K. 2003, ApJ, 591, 1220 [NASA ADS] [CrossRef] [Google Scholar]
- Magain, P. 1984, A&A, 134, 189 [NASA ADS] [Google Scholar]
- Mashonkina, L., Gehren, T., Shi, J.-R., Korn, A. J., & Grupp, F. 2011, A&A, 528, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McWilliam, A. 1998, AJ, 115, 1640 [NASA ADS] [CrossRef] [Google Scholar]
- McWilliam, A., Preston, G. W., Sneden, C., & Searle, L. 1995, AJ, 109, 2757 [NASA ADS] [CrossRef] [Google Scholar]
- Mucciarelli, A. 2011, A&A, 528, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nomoto, K., Kobayashi, C., & Tominaga, N. 2013, ARA&A, 51, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Pritzl, B. J., Venn, K. A., & Irwin, M. 2005, AJ, 130, 2140 [NASA ADS] [CrossRef] [Google Scholar]
- Roederer, I. U., & Thompson, I. B. 2015, MNRAS, 449, 3889 [NASA ADS] [CrossRef] [Google Scholar]
- Roederer, I. U., Lawler, J. E., Sobeck, J. S., et al. 2012, ApJS, 203, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Roederer, I. U., Preston, G. W., Thompson, I. B., et al. 2014, AJ, 147, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Roederer, I. U., Mateo, M., Bailey, J. I., et al. 2016, MNRAS, 455, 2417 [NASA ADS] [CrossRef] [Google Scholar]
- Salaris, M., & Weiss, A. 2002, A&A, 388, 492 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sbordone, L., Monaco, L., Moni Bidin, C., et al. 2015, A&A, 579, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Simmerer, J., Sneden, C., Cowan, J. J., et al. 2004, ApJ, 617, 1091 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Sneden, C. 1973, Ph.D. Thesis, Univ. of Texas at Austin, USA [Google Scholar]
- Sobeck, J. S., Kraft, R. P., Sneden, C., et al. 2011, AJ, 141, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Strömgren, B., Gustafsson, B., & Olsen, E. H. 1982, PASP, 94, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Takeda, Y., Kaneko, H., Matsumoto, N., et al. 2009, PASJ, 61, 563 [NASA ADS] [Google Scholar]
- Travaglio, C., Gallino, R., Arnone, E., et al. 2004, ApJ, 601, 864 [NASA ADS] [CrossRef] [Google Scholar]
- Umeda, H., & Nomoto, K. 2002, ApJ, 565, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Umeda, H., & Nomoto, K. 2005, ApJ, 619, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Villanova, S., Monaco, L., Moni Bidin, C., & Assmann, P. 2016, MNRAS, 460, 2351 [NASA ADS] [CrossRef] [Google Scholar]
- Zinn, R., & West, M. J. 1984, ApJS, 55, 45 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Additional tables
Final abundance results for individual stars.
Abundance deviations from uncertainties in the stellar parameters for the stars 14853 and 2314.
All Tables
Abundance deviations from uncertainties in the stellar parameters for the stars 14853 and 2314.
All Figures
 |
Fig. 1 Dereddened (J−Ks)0 vs. 2MASS Ks,0 (Schlafly & Finkbeiner 2011) color-magnitude diagram (CMD) of NGC 6426. Black dots correspond to stars within two half light radii and open red circles highlight the sample analyzed in this study. |
| In the text | |
 |
Fig. 2 Residuals of measured and true equivalent widths ΔEW for S/N of 30 pixel-1 (top panel) and 10 pixel -1 (lower panel). Measurements which were already rejected within EWCODE are shown as red dots. Thick black points indicate the means of the respective EW bins. Red, gray and black error bars illustrate the theoretical and true rms scatters within the trust region (see text) and the error provided by EWCODE, respectively. The corresponding abundance for this particular synthesized transition (see text) for a given EWtrue is indicated by the top axis. |
| In the text | |
 |
Fig. 3 Absolute iron abundance trends with excitation potential χex of Fe i lines in HD 122563 for the reference effective temperature (Teff,true = 4587 K, gray points) and the one that satisfies excitation equilibrium best (Teff = 4387 K, red points). Error bars are the results of propagating σEW,tot through the abundance analysis. The weighted means for each realization are represented by the black dashed lines. |
| In the text | |
 |
Fig. 4 Exemplary final solutions for Teff,spec and vmic from balanced differential Fe i abundances with excitation potential (top) and line strength (bottom) for the star 5659. Errors are again computed from the EW uncertainties. The red shaded areas emphasize the slope errors corresponding to ±33 K and ±0.14 km s-1. |
| In the text | |
 |
Fig. 5 Mean abundance results of all elements analyzed in this study. All ratios of neutral and ionized species are scaled to their Fe counterpart. The only exceptions made are Fe i and Fe ii, which are given with respect to the cluster mean and Fe i abundances, respectively. The black error bars indicate the rms scatter around the mean, while the light blue error bars represent the mean σtot including stellar parameter uncertainties. |
| In the text | |
 |
Fig. 6 Ionization imbalance between Fe i and Fe ii. Color coding of the stars was chosen to represent the membership of the potential sub-populations MP (blue) and MR (red). The indicated errors were computed by dividing the line-to-line abundance scatter by |
| In the text | |
 |
Fig. 7 Mean results and scatter for [X/Fe] for all species detected with 11 ≤ Z ≤ 27. NGC 6426 (this study) is represented by red stars. For the case of K, the red bar indicates the region where [K/Fe] is to be expected after an NLTE correction. The gray points resemble the compilation of abundances of stars in the MW halo by Roederer et al. (2014) in the range −3 dex ≤ [Fe/H] ≤−1.5 dex. We also include (in blue) the mean abundances of the similarly metal-poor GCs NGC 5897 (crosses, Koch & McWilliam 2014), NGC 4833 (diamonds, Roederer & Thompson 2015), NGC 5824 (squares, Roederer et al. 2016), M15 (filled circles, RGB targets of Sobeck et al. 2011), NGC 5634 and NGC 5053 (up and down triangles, Sbordone et al. 2015). |
| In the text | |
 |
Fig. 8 Same as in Fig. 7 for 28 ≤ Z ≤ 63. |
| In the text | |
 |
Fig. 9 Model yields from Nomoto et al. (2013) for Z = 0.001, different SN explosion energies, and progenitor masses compared to this study’s individual stellar abundances for the elements Na to Zn. |
| In the text | |
 |
Fig. 10 Top: abundance results for Si and Mg. Color coding is the same as in Fig. 6. The contours show the smoothed distribution, which was used in order to evaluate the significance of the correlation. Bottom: discrete probability distribution of the correlation coefficients for the 105 realizations. |
| In the text | |
 |
Fig. 11 Same as in Fig. 10 but for Zn and Si. |
| In the text | |
 |
Fig. 12 Top panel: mean abundance pattern for NGC 6426. The color coding is the same as in Fig. 5. The red line and red shaded region state the abundances and uncertainties of HD 108317 as derived by Roederer et al. (2012). Both patterns are unscaled, i.e., represent their original values. Bottom panel: residual pattern for the cluster stars after subtracting HD 108317. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.