EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 599 (March 2017) A&A, 599 (2017) A113 Full HTML
Free Access
Issue
A&A
Volume 599, March 2017
Article Number A113
Number of page(s) 10
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/201629556
Published online 08 March 2017

© ESO, 2017

1. Introduction

Protoplanetary disks have been extensively studied in the past decades with infrared (IR) surveys (Haisch et al. 2001; Hernández et al. 2007; Evans et al. 2009). Furthermore, several attempts have been carried out to study the structure and bulk content of disks independently in gas and dust (see, e.g., Thi et al. 2001; Panić et al. 2008, 2009; Andrews et al. 2012; Boneberg et al. 2016; Andrews 2015, as a review). However, these studies have been limited to small, not statistically significant samples of mostly Herbig disks, often with partially unresolved and limited-sensitivity observations. The Atacama Large Millimeter/sub-millimeter Array (ALMA) now has the sensitivity and resolving power needed to image large numbers of disks in continuum and molecular lines in a modest amount of time. The first near-complete survey of protoplanetary disks in both dust and gas with ALMA in a single star-forming region has been carried out in Lupus (Ansdell et al. 2016). For the first time, about 80 disks in the same region have been observed at a resolution of 0.3′′ (22–30 au radius for a distance of 150–200 pc). At the same time, the unprecedented sensitivity of ALMA allowed detection of a fraction of these disks in the faint CO isotopologue lines with just one minute observations per source. Moreover, stellar properties and mass accretion rates have been estimated from VLT/X-shooter spectra for the same sample, allowing us to build a complete picture for the Lupus sources (Alcalá et al. 2014, 2017; Manara et al. 2016). More recently, other star-forming regions have been surveyed with similar aims by ALMA, such as Chameleon I (Pascucci et al. 2016) and the more evolved Upper Scorpius region (Barenfeld et al. 2016). An era has started in which gas and dust can be observed independently in protoplanetary disks.

Together with the physical structure of the gas, the total gas mass is one of the crucial properties needed to describe the disk evolution. Starting from the process of grain-growth, planetesimal formation sensitively depends on the physical structure of the gaseous disk (see, e.g., Armitage 2011, for a review). For this reason, it is crucial to directly observe the bulk of the gas in protoplanetary disks. CO lines are commonly used to estimate the total disk gas mass. In particular, less abundant CO isotopologues, which become optically thick deeper in the disk than 12CO, can trace the bulk gas mass present in the molecular layer (van Zadelhoff et al. 2001; Dartois et al. 2003).

The main caveat when employing CO isotopologues as mass tracers is related to the conversion of the observed CO mass into total gas mass. There are various arguments why CO/H2 is lower than the canonical value of 10-4 (Aikawa et al. 1997) when averaged over the entire disk, as indicated by early observations (Dutrey et al. 1997). Processes such as CO photodissociation in the upper layers and freeze-out in the disk midplane have been identified as the main cause (van Zadelhoff et al. 2001; Aikawa et al. 2002), and these processes are well understood from a molecular physics point of view. They are included in all recent physical-chemical disk models (Hollenbach et al. 2005; Gorti & Hollenbach 2009; Nomura et al. 2009; Woitke et al. 2009; Bruderer et al. 2012; Bruderer 2013). When less abundant CO isotopologues are involved, the well-understood process of isotope-selective photodissociation, which destroys relatively more C18O, needs to be taken into account (Visser et al. 2009; Miotello et al. 2014, 2016).

Williams & Best (2014) have shown that by combining multiple CO isotopologues, such as 13CO and C18O, and accounting in a parametrized way for photodissociation and freeze-out, it is possible to estimate disk gas masses, regardless of the disk properties. Traditionally, then a constant interstellar medium (ISM)-like overall volatile carbon abundance is used to calculate the total H2 mass (XC = [C]/[H] = 1.35 × 10-4). This assumption may be incorrect, however, as high levels of carbon depletion have been inferred for at least one disk. This is the case of TW Hya, the closest and probably best-studied disk, for which the fundamental rotational transition of hydrogen deuteride (HD) has been observed by the Herschel Space Observatory (Bergin et al. 2013). Comparing these data with SMA C18O data, Favre et al. (2013) found that a carbon depletion of two orders of magnitude was needed in order to recover the HD-based disk mass determination from C18O. This result has been confirmed by physical-chemical modeling of the source, which was able to reproduce, among other lines, spatially resolved ALMA data and atomic carbon lines (Kama et al. 2016; Schwarz et al. 2016). This result is interpreted as chemical evolution, that is, carbon has been turned from CO into more complex species either in the gas or in the ice (Aikawa et al. 1996; Bergin et al. 2014; Drozdovskaya et al. 2015; Eistrup et al. 2016), or alternatively, as a grain growth effect, carbon has been locked up in large icy bodies that no longer participate in the gas-phase chemistry (Du et al. 2015; Kama et al. 2016), resulting in less bright CO lines. This hints at the possible existence of a class of disks where CO is not the main carbon reservoir.

In this paper we apply the detailed modeling technique developed by Miotello et al. (2016) to the ALMA 13CO and C18O Lupus observations. Our modeling procedure allows us to also employ the 13CO-only detections to provide a disk gas mass determinations for a total of 34 disks, which extends and refines the initial analysis presented in Ansdell et al. (2016) for only 10 disks, for which both 13CO and C18O lines are available. Our derived gas masses are generally very low, often lower than the mass of Jupiter, consistent with Ansdell et al. (2016). This translates into very low global gas-to-dust ratios that often approach unity (Sect. 5). Low CO-based gas masses and gas-to-dust ratios may indicate rapid disk evolution, which is usually taken to be a loss of gas. An alternative is that the CO abundance may be low, as discussed above. Since current data cannot distinguish between these scenarios, we have simulated both of them, but model results do not allow us to rule out one of the two. Future ALMA observations of more complex tracers are needed to calibrate CO-based masses. Alternatively, Manara et al. (2016) and Rosotti et al. (2017) have proposed a method that allows tracing the gaseous disk component independently of chemistry by exploiting the availability of dust disk mass and mass accretion rate measurement. The implications of these data are discussed in Sect. 5.3.

2. ALMA observations

Lupus is one of the youngest (3 ± 2 Myr; Alcalá et al. 2014) and closest complexes and is composed of four main star-forming regions (Lupus I-IV, see Comerón 2008, for a review). Lupus III is located at a distance of ~ 200 pc to the Sun, while Lupus I, II, and IV are at ~ 150 pc.

The sample employed for this paper was observed in the Cycle 2 Lupus ALMA Disk Survey, it is composed of 88 objects with 0.1 < M⋆/M⊙ < 2.84 and is presented in detail by Ansdell et al. (2016). The observations were obtained on 2015 June 14 and 15. The disks were observed in continuum (890 μm) and CO isotopologue line emission (13CO and C18O 3–2 transitions). More details on the observational settings and data reduction are presented in Ansdell et al. (2016). Of the 88 targets, 34 were detected in 13CO, while only 10 were detected in C18O at more than a 3σ level.

3. Model

The observed CO isotopologue fluxes were compared with the model results presented in Miotello et al. (2016). These models are computed with the physical-chemical code DALI, which has been tested extensively with benchmark test problems (Bruderer et al. 2012; Bruderer 2013) and against observations (Bruderer et al. 2012, 2014; Fedele et al. 2013). The dust temperature, Tdust, and local continuum radiation field from UV to mm wavelengths are calculated by a 2D Monte Carlo method, given an input disk density structure and a stellar spectrum. Then the chemical composition is obtained with a time-dependent chemical network simulation (1 Myr). Finally, the gas temperature, Tgas, is obtained from an iterative balance between heating and cooling processes until a self-consistent solution is found, and the non-LTE excitation of the molecules is computed. The final outputs are spectral image cubes created with a raytracer. As in Miotello et al. (2014) and in Miotello et al. (2016), a complete treatment of CO isotope-selective processes is included.

The grid by Miotello et al. (2016) is composed of around 800 disk models that have been run for a range of realistic disk and stellar parameters. Disk masses varied between 10-5M⊙ and 10-1M⊙ , and stellar luminosities were set to 1 L⊙ (plus excess UV for mass accretion rates of 10-8M⊙ yr-1) for T Tauri disks and 10 L⊙ for Herbig disks (see Table 1 in Miotello et al. 2016). Coupling of the UV excess to an accretion rate is merely a convenient prescription to obtain a value for the UV luminosity, which controls the thermal and chemical structure of the gas, including the number of CO dissociating photons (Kama et al. 2016). It should not be taken here as a measure for disk evolution timescales. A consistent description of the accretion process and disk evolution is beyond the scope of our models. Line luminosities for different CO istopologues and transitions have been ray traced. The majority of Lupus sources detected in both CO isotopologues have stellar luminosity L⋆ between 0.1 L⊙ and 1 L⊙ (Alcala et al. 2017). As a check, a smaller grid of T Tauri disk models with L⋆ = 0.1 L⊙ and excess UV for mass accretion rates of 10-8M⊙ yr-1, which generates about 0.2 L⊙ of UV accretion luminosity, was run to reproduce the extreme cases. However, we found that CO isotopologue line luminosities are reduced only up to 25%. As this is well within the uncertainties on the CO-based gas mass derivations by Miotello et al. (2016), the original grid of T Tauri disk models with L⋆ = 1 L⊙ was used for the analysis.

4. Results

4.1. Dust masses revisited

Continuum observations at sub-mm wavelengths are traditionally employed to trace large (mm-sized) grains that are present in the cold midplane of disks. Since the bulk of the dust mass is expected to be retained in large grains, their thermal emission is generally used to derive disk dust masses, following 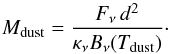Mdust=Fν d2κνBν(Tdust)·\begin{equation} M_{\rm dust}=\frac{F_{\nu} \, d^2}{\kappa_{\nu}B_{\nu}(T_{\rm dust})}\cdot \label{eq_Mdust} \end{equation}(1)The sub-mm flux Fν is directly related to the dust mass Mdust under the assumption that the emission is optically thin and in the Rayleigh-Jeans regime (Beckwith et al. 1990). Equation (1) has been employed by Ansdell et al. (2016) to derive dust masses for the Lupus disks, assuming a dust opacity κν = 3.4 cm2 g-1 at 340 GHz and a characteristic dust temperature Tdust = 20 K. This first-order analysis does not account for the effects of disk inclination and temperature variation on the spatially integrated dust emission. However, the inclination angle i has been derived for many of the Lupus disks from continuum data by Ansdell et al. (2016) and Tazzari et al. (in prep.).

In this work we exploit the results obtained by Miotello et al. (2016) with DALI continuum radiative transfer to estimate Lupus disks dust masses, accounting for the disk inclination and temperature structure. The assumed dust opacity, κν = 4.3 cm2 g-1 at 340 GHz, is the standard value in DALI (Weingartner & Draine 2001; Bruderer 2013) and is slightly higher than that used by Ansdell et al. (2016). Our models assume that the dust surface density distribution follows a radial power-law with an exponential taper and a Gaussian distribution in the vertical direction. Two dust populations are considered: large (mm-sized) grains are settled toward the midplane, and small (sub-μm to μm-sized) grains are coupled to the gas and present in the disk atmosphere (see Miotello et al. 2016, for more detail). Finally, grain-growth and migration are not included in the models, except in an ad hoc fashion by including small and large grains.

The continuum and line emission obtained with the disk models presented in Miotello et al. (2016) were both ray-traced assuming disk inclinations of 10° and 80°. Submillimeter fluxes are not expected to vary significantly for intermediate inclinations, that is, up to 70° (Beckwith et al. 1990). On the other hand, line intensities and dust emission are extremely modified in the rarer case of edge-on disks, that is, with an inclination close to 90°. Lupus disks with i< 70° or with unknown inclination are compared with models where i = 10°, elsewhere we employ models with i = 80°.

The medians of the simulated continuum luminosities at 890 μm can be calculated for different dust masses (Fig. 1). They can be fitted by simple functions of the disk dust mass and be employed to estimate Lupus disk masses. In particular, the continuum luminosity at 890 μm L0.9 mm can be expressed by L0.9mm={ Mdust<Mtr Mdust>Mtr.\begin{equation} L_{\rm 0.9~mm}= \begin{cases} a+b\cdot M_{\rm dust}^c & \quad M_{\rm dust} < M_{\rm tr}\\[1.5mm] d + e\cdot M_{\rm dust}^f & \quad M_{\rm dust} > M_{\rm tr}.\\ \end{cases} \label{Lcont_Mdust} \end{equation}(2)The coefficients a,b,c,d,e,f, and Mtr are reported in Table 1 for disk inclinations of both 10° and 80°. For dust masses below the transition mass Mtr the dependence is linear, while for higher masses it is sublinear. This reflects the fact that the dust emission becomes optically thick for high enough dust masses, even at 890 μm. This occurs at lower masses for edge-on disks, as the high inclination enhances the dust column density.

thumbnail Fig. 1

Medians of the simulated T Tauri continuum luminosities at 890 μm for different mass bins, presented by the green dots for disk inclinations of 10° and 80° in panels a) and b), respectively. The solid lines show the fit function of the 890 μm continuum luminosity as a function of the disk mass (see Eq. (2)). The dotted black lines present the transition mass between the two dependencies of the luminosity on the mass expressed in Eq. (2). The colored bands show the maximum and minimum simulated continuum luminosities for the different mass bins.

Table 1

Polynomial coefficients a,b,c,d,e,f, and Mtr, in Eq. (2).

The Lupus disk dust masses derived in this work are generally a factor of a few lower than the estimates given by Ansdell et al. (2016; see Fig. 2). In particular, between 5 × 10-7M⊙ and 3 × 10-5M⊙, dust masses derived by Ansdell et al. (2016) are a factor of 2.2 higher than those estimated by this analysis (1.7 if we correct for the dust opacity difference at 340 GHz). For disks with dust masses higher than Mtr = 3 × 10-5M⊙, the derivations obtained with the two methods become similar because the emission becomes marginally optically thick. This effect is only considered by our models and leads to higher mass determinations. Finally, a bimodality can be seen in Fig. 2, with six points being displaced from the main trend. These represent the highly inclined disks (i> 70°) with dust masses higher than Mtr = 5 × 10-6M⊙. For the most massive of these sources, the dust masses derived in this work are generally a factor of a few higher than the estimates given by Ansdell et al. (2016). The dust masses derived for the highly inclined disks are Mdust = 9.6 × 10-4, 5.2 × 10-4, 4.4 × 10-4, 8.0 × 10-5, 1.7 × 10-5, 1.6 × 10-5, 7.0 × 10-6, 3.4 × 10-6,and 2.2 × 10-6M⊙ for J16083070-3828268, MY Lup, J16070854-3914075, Sz 133, J16090141-3925119, Sz 84, Sz 74, J16102955-3922144, and J16070384-3911113, respectively.

thumbnail Fig. 2

Disk dust masses derived in this work compared with the dust masses obtained by Ansdell et al. (2016). Full symbols show the current model results. Empty circles present mass estimates corrected for the dust opacity difference at 340 GHz between the two studies.

thumbnail Fig. 3

C18O (3–2) vs. 13CO (3–2) line luminosities. The color–coded dots show the line luminosities simulated by the T Tauri models in the Miotello et al. (2016) grid. The Lupus observations are overplotted. The disks detected in both isotopologues are shown with green stars, while the C18O non detections are presented with empty circles.

4.2. Gas masses

Measuring disk gas masses is essential for understanding disk evolution up to the formation of planetary systems. The aim of this analysis is to employ the CO isotopologue lines observed in Lupus for deriving gas masses for a statistically significant number of disks. The 13CO and C18O model results shown by Miotello et al. (2016) can be presented in the same way as done by Williams & Best (2014) and be compared with Lupus observations (Fig. 3). As explained by Miotello et al. (2016), the two sets of model results differ throughout the whole disk mass range because of a temperature effect. Williams & Best (2014) find a wider range of CO luminosities because they parameterize a wider range of temperatures than Miotello et al. (2016) find in their models. Miotello and collaborators compute the disk temperature structure through full radiative transfer. Furthermore, the divergence is maximized in the lower mass regime where the implementation of isotope-selective processes reduces C18O line intensities compared with the results by Williams & Best (2014). The same disk mass model results cover a limited region of the line luminosity-luminosity space. Lupus disks that are detected in both isotopologues are presented in Fig. 3 with green stars, while C18O non-detections are shown with white circles as upper limits on the y direction. This plot can only be used to derive disk masses when C18O is also detected. For Lupus, this is the case for only 10 sources. Four of them are not reproduced by any of our models, presenting either lower 13CO and regular C18O luminosities, or regular 13CO and higher C18O luminosities (see Fig. 3). This shows that the current model grid may not apply to all disks, but a source-by-source detailed modeling may be needed. Knowledge about disk properties such as the radial extent and vertical structure would help to predict the line fluxes with higher confidence.

thumbnail Fig. 4

Medians of the 13CO (3–2) and C18O (3–2) simulated T Tauri line luminosities for different mass bins, presented with red and blue dots in panels a) and b), respectively (i = 10°). The red and blue lines show the fit function of the line luminosity as a function of disk mass. The dotted black lines present the transition mass between the linear and the logarithmic dependence of the line luminosity on the mass (see Eq. (3)). The colored bands show the maximum and minimum simulated line luminosities for the different mass bins.

thumbnail Fig. 5

Zoom of Fig. 4 top: medians of the 13CO (3–2) simulated line luminosities for different mass bins, presented with red dots in the region where the luminosity dependence on mass is linear (see Eq. (3)). The red line shows the fit function of the line luminosity as a function of disk mass. The 13CO-only detections are shown with gray dashed lines. The pink band shows the maximum and minimum simulated line luminosities.

For disks that have been detected in 13CO, but not in C18O (henceforth, 13CO-only detections), 13CO alone can only be employed as a mass tracer when its emission is optically thin. Similarly to Miotello et al. (2016), the median of the 13CO and C18O J = 3−2 simulated line luminosities, rather than J = 2–1, are expressed by fit functions of the disk mass: 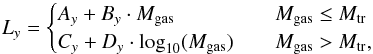Ly={ Mgas≤Mtr Mgas>Mtr,\begin{equation} L_{y} = \begin{cases} A_y+B_y\cdot M_{\rm gas} & \quad M_{\rm gas} \leq M_{\rm tr}\\ C_y + D_y\cdot \text{log}_{10}(M_{\rm gas}) & \quad M_{\rm gas} > M_{\rm tr},\\ \end{cases} \label{L_13} \end{equation}(3)where y = 13 or 18, for 13CO and C18O, respectively. For low-mass disks, the line luminosity has a linear dependence on the disk mass, while for more massive disks the trend is logarithmic because of the optical depth. The transition point Mtr is different for the two isotopologues because 13CO becomes optically thick at lower column densities than C18O. The polynomial coefficients Ay, By, Cy, and Dy, as well as the transition masses Mtr, are reported in Table 2 for disk models with inclination angle i = 10° and i = 80°. The fit functions are shown in Fig. 4 with red and blue lines for 13CO and C18O, respectively.

Interestingly, all the 13CO-only detections fall in the region of panel (a) where the dependence is linear, that is, for Mdisk<Mtr (Fig. 6). Accordingly, we can use the fit function presented in Eq. (3) to calculate the gas masses of these sources, as 13CO is optically thin for the observed range of luminosities, which is confirmed by the absence of C18O emission. The uncertainties on the gas mass determinations are defined by the shadowed region in Fig. 5 (which is a zoom of Fig. 4), which covers the range of line luminosities simulated by the grid of models for different mass bins. Similarly, we can employ this line luminosity-mass relation to derive mass upper limits for disks that are undetected in both CO isotopologues. The disk mass determinations together with the calculated upper limits are presented in Table 3 and are shown in the middle panel of Fig. 6. Total gas masses are generally low, often lower than 1 MJup. The implications of this result are discussed in Sect. 5.

Table 2

Polynomial coefficients Ay, By, Cy, and Dy, in Eq. (3).

thumbnail Fig. 6

Disk dust masses (upper panel), gas masses (middle panel), and gas-to-dust ratios (lower panels) for all the sources detected in the continuum. Gas non-detections are shown with gray triangles, while all detections are presented as filled circles. Objects that are classified as transitional disks (TD) are shown in orange, and edge-on disks are circled in blue. Red rectangles show the subsample of disks discussed in Sect. 5.2.1.

Table 3

Disk mass determination for all the detected sources in Lupus.

5. Discussion

5.1. Gas-to-dust ratio

Dust masses were calculated for all Lupus disks detected in the continuum as described in Sect. 4.1. For the 34 sources for which at least one of the two CO istopologues was detected, disk gas masses were derived as explained in Sect. 4.2. When we divide the gas masses by the newly determined dust masses, it is possible to obtain global gas-to-dust mass ratios. Figure 6 shows that these are often much lower than the expected ISM value of 100 and occasionally reach unity or lower.

Only full-disk models were employed for the mass determinations, but three disks in the Lupus sample show resolved dust cavities and three other sources show possible cavities with diameter ≲0.4′′ (Ansdell et al. 2016). Moreover, six other disks are classified as transition disk candidates, but do not show cavities in the ALMA images (Merín et al. 2010; Romero et al. 2012; van der Marel et al. 2016; Bustamante et al. 2015). All these sources, presented with orange symbols in Fig. 6, are not properly described by our grid of full-disk models. However, these moderate-resolution Lupus data primarily trace the outer disks, which should be well represented by a full-disk model even for transitional disks. Therefore the calculated gas-to-dust ratios provide a first-order description of the disk properties in Lupus, including the transitional disks.

An alternative way to present the results is shown in Fig. 7. The global gas-to-dust ratios obtained for the sources detected in both gas and dust are shown in a histogram. Most of the disks, 23 out of 34, present gas-to-dust ratios lower than 10, with 13 of these sources showing ratios between 3 and 10.

Traditionally, disk masses are thought to be dominated by the gaseous component with ISM-like gas-to-dust ratios of 100 assumed to convert Mdust into total disk mass. Many disks in Lupus instead have lower measured gas-to-dust ratios, as shown in the bottom panel of Fig. 6. A similar result was found by Ansdell et al. (2016) with only 10 gas mass determinations, and this has been confirmed with a larger sample of 34 gas mass measurements. A possible interpretation is that Lupus disks are evolved and that the gas has been physically dissipated, while the large dust grains are still retained in the midplane. The finding of disks that are depleted in gas by a few Myr would place strong constraints on disk evolution and planet formation theories (Thommes et al. 2008; Lissauer et al. 2009; Levison et al. 2015), as discussed by Ansdell et al. (2016).

5.2. Carbon depletion vs low gas masses

An alternative interpretation of low CO-based gas masses and gas-to-dust ratios is that the CO abundance is low, for example, because of sequestering of carbon from CO to more complex molecules or because it is locked up into larger bodies (Aikawa et al. 1996; Bergin et al. 2014; Du et al. 2015; Eistrup et al. 2016; Kama et al. 2016; Yu et al. 2016). However, current data cannot distinguish between these scenarios.

Clues on tracers to probe these two cases come from the well-studied TW Hya disk. In this unique case, HD far-infrared emission has been employed to independently determine an accurate gas mass (Bergin et al. 2013) and thereby calibrate the weak C18O detection. These observations have been interpreted to imply a much lower abundance of CO, caused by carbon depletion of two orders of magnitude (Favre et al. 2013; Schwarz et al. 2016). This finding has been confirmed by an independent analysis, where other lines such as [CI], [CII], [OI], C2H, and the CO ladder have been fit self-consistently (Kama et al. 2016). Unfortunately, no current facility is able to detect the fundamental HD transition in the Lupus disks. However, detection of more complex carbon-bearing species can help to distinguish between the two cases of gas-poor versus carbon-poor disks.

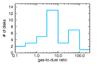thumbnail Fig. 7

Histogram showing the number of disks presenting different levels of gas-to-dust ratio. Only sources detected in both continuum and line emission are considered.

There is some debate about the mechanism(s) responsible for carbon depletion in protoplanetary disks. A possible explanation comes from gas-phase reactions initiated by X-ray and cosmic-ray ionization of He in the disk. The resulting He+ atoms can react with gaseous CO and gradually extract the carbon, which can then be processed into more complex molecules that can freeze onto cold dust grains at higher temperatures than CO (Aikawa et al. 1997; Bruderer et al. 2012; Favre et al. 2013; Bergin et al. 2014; Kama et al. 2016; Yu et al. 2016). Moreover, oxygen will also be removed from the gas by freeze-out of H2O, CO2 , and CO, even more than carbon (Hogerheijde et al. 2011; Öberg et al. 2011; Walsh et al. 2015). Accordingly, a way to test the level of carbon depletion in disks is to compare observations of CO isotopologues with species such as C2H and c-C3H2, whose gas-phase abundances are sensitive to the gaseous carbon abundance and [C]/[O] ratio. Indeed, C2H is observed to have very strong emission in the TW Hya disk (Kastner et al. 2015) and is particularly strong when both elements are depleted, but gaseous [C]/[O] > 1 (Kama et al. 2016). If the difference in the global gas-to-dust ratios found in Lupus disks is due to different levels of carbon depletion, then this should be reflected in C2H and c-C3H2 fluxes, and this may be tested by future ALMA observations. Alternatively, ice chemistry may be the fundamental process that turns CO into more complex organics, such CH3OH, or into CO2 and CH4 ice (see, e.g., Fig. 3c in Eistrup et al. 2016). Finally, volatile elements, such as oxygen and carbon, may be locked up in large icy bodies in the midplane (Bergin et al. 2010; Ros & Johansen 2013; Guidi et al. 2016). These large pebbles cannot diffuse upward and participate in the gas-phase chemistry (see Du et al. 2015; Kama et al. 2016). Such a process is most likely the cause of the underabundance of gas-phase water in disk atmospheres.

thumbnail Fig. 8

13CO (J = 3−2) luminosity as a function of dust mass. Light blue circles present the simulated line luminosities with different levels of carbon depletion: no depletion (δC = 1, black contoured circles), depletion by a factor of 10 (δC = 0.1, filled light blue circles), and depletion by two orders of magnitude (δC = 0.01, light blue empty circles). Purple circles present the simulated line luminosities obtained without carbon depletion, fixing the gas mass Mgas = 10-4M⊙ and increasing the dust mass to Mdust = 10-5,10-4M⊙, accordingly with gas-to-dust ratios Δgd = 10, 1. A subsample of six Lupus sources is shown with gray stars. Models run with Rc = 30 au and with Rc = 60 au are shown in the left and right panels, respectively.

5.2.1. Test models

From the modeling side, it is possible to simulate the two different scenarios (low gas-to-dust ratio or high carbon depletion) and to compare the predictions with the observations. As done by Miotello et al. (2016), the loss of gas is simulated by fixing the gas mass and increasing the dust mass, that is, by obtaining lower gas-to-dust ratios. The carbon depletion scenario is obtained by reducing the initial ISM-like carbon abundance by different levels. We define carbon depletion as δC = 1 if the carbon over hydrogen ratio is set to the ISM-level, [C]/[H] = 1.35 × 10-4. We then assume higher values of carbon depletion δC = 0.1, 0.01 if the abundance ratio is [C]/[H] = 1.35 × 10-5, 1.35 × 10-6, respectively.

Two interesting groups of sources can be identified in Fig. 6 for which the gas mass is Mgas = 10-4M⊙, while the dust mass is either Mdust = 10-4M⊙ (Sz71, Sz114, Sz129) or Mdust = 10-5M⊙ (J16085324-3914401, Sz90). These five disks present similar 13CO emission, but different continuum fluxes. This may be interpreted as the first group of sources presenting a lower gas-to-dust ratio, or a higher level of carbon depletion. Four additional models were run with Rc = 30, 60 au, fixing the gas mass Mgas = 10-4M⊙ and increasing the dust mass from Mdust = 10-6M⊙ to Mdust = 10-5,10-4M⊙, that is, with gas-to-dust ratios of 10 and 1 (see purple circles in Fig. 8). Moreover, another eight models were run with Rc = 30, 60 au, Mdust = 10-5,10-4M⊙, gas-to-dust ratios of 100, but with initial carbon abundances reduced by a factor δC = 0.1, 0.01 (see Fig. 8). Remarkably, for a fixed gas mass and δC, the CO line intensities do not depend strongly on dust masses.

From comparing the results from the two sets of models presented in Fig. 8 with the observations, it is not possible to rule out one of the two scenarios, which indicates that we need to calibrate CO-based masses with other tracers. The first group of sources (Sz71, Sz114, and Sz129), bright in the continuum, but faint in CO emission, are well described either by models with gas-to-dust ratios equal to unity or with a carbon depletion of around two orders of magnitudes. The fluxes of the second set of disks (J16085324-3914401 and Sz90) are instead reproduced with less precision by models with a gas-to-dust ratio equal to 10, or with carbon depletion of about a factor of 10. Carbon depletion and gas dissipation processes may both playing a role, but it is not possible to estimate the relative importance.

5.3. Correlation between disk gas mass and stellar mass

Ansdell et al. (2016) found a positive correlation between Mgas and M⋆ (computed by Alcalá et al. 2014, 2017), but were unable to produce a meaningful fit given the low number of disks detected in the two CO isotopologues and the large uncertainties on the gas mass determinations. This changes when the sample is enlarged from 10 to 34 sources. Using the Bayesian linear regression method (Kelly 2007), which accounts for the upper limits, we find a correlation with r = 0.74 and a two-sided p-value of 3 × 10-2 for the null hypothesis that the slope of this correlation is zero. This is shown in Fig. 9, where the red line gives the Bayesian linear regression fit, which considers errors on both axes and is applied to detected and undetected targets. The slope of the correlation is 0.63 and the intercept is –3.92.

Ansdell et al. (2016) found a clear correlation between Mdust and M⋆. Furthermore, Manara et al. (2016) found a linear relation between the mass accretion rate onto the central star and the disk mass inferred from the dust by combining ALMA and VLT/X-shooter data (Alcalá et al. 2014, 2017). A relation between Ṁacc and Mdisk has been theoretically predicted for viscously evolving disks (Hartmann et al. 1998), and it was found observationally in Lupus for the first time using dust masses to measure the bulk disk mass, which is equivalent to assume a constant gas-to-dust ratio (Manara et al. 2016). For a gas-to-dust ratio of 100, the ratio of Mdisk/Ṁacc is comparable with the age of the region, as expected for viscous disks and under the effect of other disk evolution processes (Jones et al. 2012; Rosotti et al. 2017). On the other hand, no correlation was found with disk masses derived from CO isotopologue lines by Ansdell et al. (2016). Even expanding the sample of gas masses to 34 sources, no correlation is found in this work. Furthermore, the ratio of Mdisk/Ṁacc when using Mdisk derived from CO isotopologues is much lower than the age of the region. This is expected only in cases where external disturbances, such as external photoevaporation, play a major role in the evolution of disks (Rosotti et al. 2017). As this is probably not be the case in the Lupus region, this method suggests that CO-based disk masses are generally underestimated.

When we assume that all Lupus disks have evolved mainly through viscous processes over the past few Myr, the observed correlation between the current mass accretion rate and dust mass found by Manara et al. (2016) implies a constant gas-to-dust ratio, which is close to 100 based on the observed Mdisk/Macc ratio. This in turn points to a scenario in which carbon-depletion mechanisms are in play and affect CO line emission. Moreover, the non-correlation found between mass accretion rate and CO-based gas masses implies that carbon is non-homogeneously depleted throughout the Lupus sample. This opens an interesting question on the stellar and disk properties that maximize the sequestering of carbon from gas-phase CO. As discusses in Sect. 5.2, if an anticorrelation of complementary gas tracers, such as C2H, with CO lines were observed, then this would help in solving the controversy.

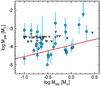thumbnail Fig. 9

Disk gas mass as a function of stellar mass for Lupus disks. Gas non-detections are shown as upper limits with gray triangles. For the gas detections the error bars are reported. The red line gives the Bayesian linear regression fit (Kelly 2007).

6. Summary and conclusion

We have employed the grid of physical-chemical models presented in Miotello et al. (2016) to analyze continuum and CO isotopologue ALMA observations of Lupus disks (Ansdell et al. 2016). By also employing the 13CO-only detections in the optically thin regime, we calculated disk gas masses for a total of 34 sources, expanding the sample of 10 disks for which Ansdell et al. (2016) were able to derive gas masses. As previously found, overall, the gas masses are very low, often lower than MJup. Accordingly, global gas-to-dust ratios are much lower than the expected ISM-value of 100; they lie predominantly between 1 and 10. Low CO-based gas masses and gas-to-dust ratios may indicate rapid loss of gas, or alternatively, carbon depletion. The latter may occur through sequestering of carbon from CO that is either locked into large icy bodies in the midplane, or converted into more complex molecules by either gas-phase chemistry or ice chemistry (Aikawa et al. 1996; Bergin et al. 2014; Du et al. 2015; Eistrup et al. 2016; Kama et al. 2016; Yu et al. 2016). However, current ALMA data alone cannot distinguish between these scenarios. We have simulated both of them, but model results did not allow us to rule out one of the two hypotheses, which means that we need to calibrate CO-based masses with other tracers. Alternatively, exploitation of disk mass and mass accretion rate measurements simultaneously available in protoplanetary disks can give insight into the nature of low CO-based masses (Manara et al. 2016) and point to non-homogeneous carbon depletion throughout the Lupus sample.

Acknowledgments

This paper makes use of the following ALMA data: ADS/JAO.ALMA#2013.1.00220.S. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada), NSC and SIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/ NRAO, and NAOJ. Astrochemistry in Leiden is supported by the Netherlands Research School for Astronomy (NOVA), by a Royal Netherlands Academy of Arts and Sciences (KNAW) professor prize, and by the European Union A-ERC grant 291141 CHEMPLAN. This work was partly supported by the Italian Ministero dell’Istruzione, Universita e Ricerca through the grant Progetti Premiali 2012-iALMA (CUP C52I13000140001). C.F.M. gratefully acknowledges an ESA Research Fellowship. J.P.W. is supported by funding from the NSF and NASA through grants AST- 1208911 and NNX15AC92G.

References

  1. Aikawa, Y., Miyama, S. M., Nakano, T., & Umebayashi, T. 1996, ApJ, 467, 684 [NASA ADS] [CrossRef] [Google Scholar]
  2. Aikawa, Y., Umebayashi, T., Nakano, T., & Miyama, S. M. 1997, ApJ, 486, L51 [NASA ADS] [CrossRef] [Google Scholar]
  3. Aikawa, Y., van Zadelhoff, G. J., van Dishoeck, E. F., & Herbst, E. 2002, A&A, 386, 622 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Alcalá, J. M., Natta, A., Manara, C. F., et al. 2014, A&A, 561, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Alcalá, J. M., Manara, C. F., Natta, A., et al. 2017, A&A, in press, DOI: 10.1051/0004-6361/201629929 [Google Scholar]
  6. ALMA Partnership, Brogan, C. L., Pérez, L. M., et al. 2015, ApJ, 808, L3 [NASA ADS] [CrossRef] [Google Scholar]
  7. Andrews, S. M. 2015, PASP, 127, 961 [NASA ADS] [CrossRef] [Google Scholar]
  8. Andrews, S. M., Wilner, D. J., Hughes, A. M., et al. 2012, ApJ, 744, 162 [NASA ADS] [CrossRef] [Google Scholar]
  9. Ansdell, M., Williams, J. P., van der Marel, N., et al. 2016, ApJ, 828, 46 [Google Scholar]
  10. Armitage, P. J. 2011, ARA&A, 49, 195 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Barenfeld, S. A., Carpenter, J. M., Ricci, L., & Isella, A. 2016, ApJ, 827, 142 [NASA ADS] [CrossRef] [Google Scholar]
  12. Beckwith, S. V. W., Sargent, A. I., Chini, R. S., & Guesten, R. 1990, AJ, 99, 924 [NASA ADS] [CrossRef] [Google Scholar]
  13. Bergin, E. A., Hogerheijde, M. R., Brinch, C., et al. 2010, A&A, 521, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Bergin, E. A., Cleeves, L. I., Gorti, U., et al. 2013, Nature, 493, 644 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  15. Bergin, E. A., Cleeves, L. I., Crockett, N., & Blake, G. A. 2014, Faraday Discussions, 168, 61 [NASA ADS] [CrossRef] [Google Scholar]
  16. Blake, G. A., van Dishoeck, E. F., & Sargent, A. I. 1992, ApJ, 391, L99 [NASA ADS] [CrossRef] [Google Scholar]
  17. Boneberg, D. M., Panić, O., Haworth, T. J., Clarke, C. J., & Min, M. 2016, MNRAS, 461, 385 [NASA ADS] [CrossRef] [Google Scholar]
  18. Bruderer, S. 2013, A&A, 559, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Bruderer, S., van Dishoeck, E. F., Doty, S. D., & Herczeg, G. J. 2012, A&A, 541, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Bruderer, S., van der Marel, N., van Dishoeck, E. F., & van Kempen, T. A. 2014, A&A, 562, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Bustamante, I., Merín, B., Ribas, Á., et al. 2015, A&A, 578, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Comerón, F. 2008, Handbook of Star Forming Regions, Volume II, 5, 295 [Google Scholar]
  23. Dartois, E., Dutrey, A., & Guilloteau, S. 2003, A&A, 399, 773 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Drozdovskaya, M. N., Walsh, C., Visser, R., Harsono, D., & van Dishoeck, E. F. 2015, MNRAS, 451, 3836 [NASA ADS] [CrossRef] [Google Scholar]
  25. Du, F., Bergin, E. A., & Hogerheijde, M. R. 2015, ApJ, 807, L32 [NASA ADS] [CrossRef] [Google Scholar]
  26. Dunham, M. M., Allen, L. E., Evans, N. J., II, et al. 2015, ApJS, 220, 11 [NASA ADS] [CrossRef] [Google Scholar]
  27. Dutrey, A., Guilloteau, S., & Guelin, M. 1997, A&A, 317, L55 [NASA ADS] [Google Scholar]
  28. Eistrup, C., Walsh, C., & van Dishoeck, E. F. 2016, A&A, 595, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Evans, N. J., II, Dunham, M. M., Jørgensen, J. K., et al. 2009, ApJS, 181, 321 [NASA ADS] [CrossRef] [Google Scholar]
  30. Favre, C., Cleeves, L. I., Bergin, E. A., Qi, C., & Blake, G. A. 2013, ApJ, 776, L38 [NASA ADS] [CrossRef] [Google Scholar]
  31. Fedele, D., Bruderer, S., van Dishoeck, E. F., et al. 2013, ApJ, 776, L3 [NASA ADS] [CrossRef] [Google Scholar]
  32. Gorti, U., & Hollenbach, D. 2009, ApJ, 690, 1539 [Google Scholar]
  33. Guidi, G., Tazzari, M., Testi, L., et al. 2016, A&A, 588, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Haisch, K. E., Jr., Greene, T. P., Barsony, M., & Ressler, M. 2001, BAAS, 33, 04.10 [Google Scholar]
  35. Hartmann, L., Calvet, N., Gullbring, E., & D’Alessio, P. 1998, ApJ, 495, 385 [NASA ADS] [CrossRef] [Google Scholar]
  36. Hernández, J., Calvet, N., Briceño, C., et al. 2007, ApJ, 671, 1784 [NASA ADS] [CrossRef] [Google Scholar]
  37. Hogerheijde, M. R., Bergin, E. A., Brinch, C., et al. 2011, Science, 334, 338 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  38. Hollenbach, D., Gorti, U., Meyer, M., et al. 2005, ApJ, 631, 1180 [NASA ADS] [CrossRef] [Google Scholar]
  39. Jones, M. G., Pringle, J. E., & Alexander, R. D. 2012, MNRAS, 419, 925 [NASA ADS] [CrossRef] [Google Scholar]
  40. Kama, M., Bruderer, S., van Dishoeck, E. F., et al. 2016, A&A, 592, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Kastner, J. H., Qi, C., Gorti, U., et al. 2015, ApJ, 806, 75 [NASA ADS] [CrossRef] [Google Scholar]
  42. Kelly, B. C. 2007, ApJ, 665, 1489 [NASA ADS] [CrossRef] [Google Scholar]
  43. Levison, H. F., Kretke, K. A., & Duncan, M. J. 2015, Nature, 524, 322 [CrossRef] [Google Scholar]
  44. Lissauer, J. J., Hubickyj, O., D’Angelo, G., & Bodenheimer, P. 2009, Icarus, 199, 338 [NASA ADS] [CrossRef] [Google Scholar]
  45. Manara, C. F., Rosotti, G., Testi, L., et al. 2016, A&A, 591, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Merín, B., Brown, J. M., Oliveira, I., et al. 2010, ApJ, 718, 1200 [NASA ADS] [CrossRef] [Google Scholar]
  47. Miotello, A., Bruderer, S., & van Dishoeck, E. F. 2014, A&A, 572, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Miotello, A., van Dishoeck, E. F., Kama, M., & Bruderer, S. 2016, A&A, 594, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Nomura, H., Aikawa, Y., Nakagawa, Y., & Millar, T. J. 2009, A&A, 495, 183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Öberg, K. I., Murray-Clay, R., & Bergin, E. A. 2011, ApJ, 743, L16 [NASA ADS] [CrossRef] [Google Scholar]
  51. Panić, O., Hogerheijde, M. R., Wilner, D., & Qi, C. 2008, A&A, 491, 219 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Panić, O., Hogerheijde, M. R., Wilner, D., & Qi, C. 2009, A&A, 501, 269 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Pascucci, I., Testi, L., Herczeg, G. J., et al. 2016, ApJ, 831, 125 [NASA ADS] [CrossRef] [Google Scholar]
  54. Ricci, L., Testi, L., Natta, A., et al. 2010, A&A, 512, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Romero, G. A., Schreiber, M. R., Cieza, L. A., et al. 2012, ApJ, 749, 79 [NASA ADS] [CrossRef] [Google Scholar]
  56. Ros, K., & Johansen, A. 2013, A&A, 552, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Rosotti, G., Clarke, C., Manara C. F., & Facchini, S. 2017, MNRAS, submitted [Google Scholar]
  58. Schwarz, K. R., Bergin, E. A., Cleeves, L. I., et al. 2016, ApJ, 823, 91 [NASA ADS] [CrossRef] [Google Scholar]
  59. Thi, W. F., van Dishoeck, E. F., Blake, G. A., et al. 2001, ApJ, 561, 1074 [NASA ADS] [CrossRef] [Google Scholar]
  60. Thommes, E. W., Matsumura, S., & Rasio, F. A. 2008, Science, 321, 814 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  61. van der Marel, N., Verhaar, B. W., van Terwisga, S., et al. 2016, A&A, 592, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. van Zadelhoff, G.-J., van Dishoeck, E. F., Thi, W.-F., & Blake, G. A. 2001, A&A, 377, 566 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  63. Visser, R., van Dishoeck, E. F., & Black, J. H. 2009, A&A, 503, 323 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  64. Walsh, C., Nomura, H., & van Dishoeck, E. 2015, A&A, 582, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  65. Weingartner, J. C., & Draine, B. T. 2001, ApJ, 548, 296 [NASA ADS] [CrossRef] [Google Scholar]
  66. Williams, J. P., & Best, W. M. J. 2014, ApJ, 788, 59 [NASA ADS] [CrossRef] [Google Scholar]
  67. Woitke, P., Kamp, I., & Thi, W.-F. 2009, A&A, 501, 383 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  68. Yu, M., Willacy, K., Dodson-Robinson, S. E., Turner, N. J., & Evans, N. J., II 2016, ApJ, 822, 53 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Polynomial coefficients a,b,c,d,e,f, and Mtr, in Eq. (2).

In the text
Table 2

Polynomial coefficients Ay, By, Cy, and Dy, in Eq. (3).

In the text
Table 3

Disk mass determination for all the detected sources in Lupus.

In the text

All Figures

thumbnail Fig. 1

Medians of the simulated T Tauri continuum luminosities at 890 μm for different mass bins, presented by the green dots for disk inclinations of 10° and 80° in panels a) and b), respectively. The solid lines show the fit function of the 890 μm continuum luminosity as a function of the disk mass (see Eq. (2)). The dotted black lines present the transition mass between the two dependencies of the luminosity on the mass expressed in Eq. (2). The colored bands show the maximum and minimum simulated continuum luminosities for the different mass bins.
In the text
thumbnail Fig. 2

Disk dust masses derived in this work compared with the dust masses obtained by Ansdell et al. (2016). Full symbols show the current model results. Empty circles present mass estimates corrected for the dust opacity difference at 340 GHz between the two studies.
In the text
thumbnail Fig. 3

C18O (3–2) vs. 13CO (3–2) line luminosities. The color–coded dots show the line luminosities simulated by the T Tauri models in the Miotello et al. (2016) grid. The Lupus observations are overplotted. The disks detected in both isotopologues are shown with green stars, while the C18O non detections are presented with empty circles.
In the text
thumbnail Fig. 4

Medians of the 13CO (3–2) and C18O (3–2) simulated T Tauri line luminosities for different mass bins, presented with red and blue dots in panels a) and b), respectively (i = 10°). The red and blue lines show the fit function of the line luminosity as a function of disk mass. The dotted black lines present the transition mass between the linear and the logarithmic dependence of the line luminosity on the mass (see Eq. (3)). The colored bands show the maximum and minimum simulated line luminosities for the different mass bins.
In the text
thumbnail Fig. 5

Zoom of Fig. 4 top: medians of the 13CO (3–2) simulated line luminosities for different mass bins, presented with red dots in the region where the luminosity dependence on mass is linear (see Eq. (3)). The red line shows the fit function of the line luminosity as a function of disk mass. The 13CO-only detections are shown with gray dashed lines. The pink band shows the maximum and minimum simulated line luminosities.
In the text
thumbnail Fig. 6

Disk dust masses (upper panel), gas masses (middle panel), and gas-to-dust ratios (lower panels) for all the sources detected in the continuum. Gas non-detections are shown with gray triangles, while all detections are presented as filled circles. Objects that are classified as transitional disks (TD) are shown in orange, and edge-on disks are circled in blue. Red rectangles show the subsample of disks discussed in Sect. 5.2.1.
In the text
thumbnail Fig. 7

Histogram showing the number of disks presenting different levels of gas-to-dust ratio. Only sources detected in both continuum and line emission are considered.
In the text
thumbnail Fig. 8

13CO (J = 3−2) luminosity as a function of dust mass. Light blue circles present the simulated line luminosities with different levels of carbon depletion: no depletion (δC = 1, black contoured circles), depletion by a factor of 10 (δC = 0.1, filled light blue circles), and depletion by two orders of magnitude (δC = 0.01, light blue empty circles). Purple circles present the simulated line luminosities obtained without carbon depletion, fixing the gas mass Mgas = 10-4M⊙ and increasing the dust mass to Mdust = 10-5,10-4M⊙, accordingly with gas-to-dust ratios Δgd = 10, 1. A subsample of six Lupus sources is shown with gray stars. Models run with Rc = 30 au and with Rc = 60 au are shown in the left and right panels, respectively.
In the text
thumbnail Fig. 9

Disk gas mass as a function of stellar mass for Lupus disks. Gas non-detections are shown as upper limits with gray triangles. For the gas detections the error bars are reported. The red line gives the Bayesian linear regression fit (Kelly 2007).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.