| Issue |
A&A
Volume 598, February 2017
|
|
|---|---|---|
| Article Number | A4 | |
| Number of page(s) | 20 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201629468 | |
| Published online | 24 January 2017 | |
Modeling the early evolution of massive OB stars with an experimental wind routine
The first bi-stability jump and the angular momentum loss problem
1 LMU Munich, Universitätssternwarte, Scheinerstr. 1, 81679 München, Germany
e-mail: zsolt.keszthelyi@rmc.ca
2 Royal Military College of Canada, PO Box 17000 Station Forces, Kingston, K7K 7B4 Ontario, Canada
3 Queen’s University, Stirling Hall, Kingston, K7L 3N6 Ontario, Canada
Received: 3 August 2016
Accepted: 13 October 2016
Context. Stellar evolution models of massive stars are very sensitive to the adopted mass-loss scheme. The magnitude and evolution of mass-loss rates significantly affect the main sequence evolution, and the properties of post-main sequence objects, including their rotational velocities.
Aims. Driven by potential discrepancies between theoretically predicted and observationally derived mass-loss rates in the OB star range, we aim in particular to investigate the response to mass-loss rates that are lower than currently adopted, in parallel with the mass-loss behavior at the “first” bi-stability jump.
Methods. We performed 1D hydrodynamical model calculations of single 20−60 M⊙ Galactic (Z = 0.014) stars where the effects of stellar winds are already significant in the main sequence phase. We have developed an experimental wind routine to examine the behavior and response of the models under the influence of different mass-loss rates. This observationally guided, simple and flexible wind routine is not a new mass-loss description but a useful tool based on the wind-momentum luminosity relation and other scaling relations, and provides a meaningful base for various tests and comparisons.
Results. The main result of this study indicates a dichotomy between solutions of currently debated problems regarding mass-loss rates of hot massive stars. In a fully diffusive approach, and for commonly adopted initial rotational velocities, lower mass-loss rates than theoretically predicted require to invoke an additional source of angular momentum loss (either due to bi-stability braking, or yet unidentified) to brake down surface rotational velocities. On the other hand, a large jump in the mass-loss rates due to the bi-stability mechanism (a factor of 5–7 predicted by Vink et al. (2000, A&A, 362, 295), but a factor of 10–20 in modern models of massive stars) is challenged by observational results, and might be avoided if the early mass-loss rates agreed with the theoretically predicted values.
Conclusions. We conclude that simultaneously adopting lower mass-loss rates and a significantly smaller jump in the mass-loss rates over the bi-stability region (both compared to presently used prescriptions) would require an additional mechanism for angular momentum loss to be present in massive stars. Otherwise, the observed rotational velocities of a large population of B supergiants, that are thought to be the evolutionary descendants of O stars, would remain unexplained.
Key words: stars: massive / stars: mass-loss / stars: evolution
© ESO, 2017
1. Introduction
During their complete evolution, massive stars lose a significant fraction of their initial mass in the form of stellar winds. This mass loss has a significant impact on the evolution of massive stars (e.g., Maeder 2009), influencing their properties in two important ways. First, evidently the actual stellar mass (as a function of time) is affected by mass loss. The winds of hot OB stars and of their descendants are sufficiently powerful to remove a significant amount of mass that their evolutionary paths depend sensitively on the strength of the wind at the various evolutionary phases. As a consequence, mass loss (together with rotation, binarity and metallicity effects) is a key determinant of the final end-states of massive star evolution. Second, it has recently been noted (Vink et al. 2010) that mass loss is also influential for massive star evolution due to the removal of angular momentum from surface layers (see also Langer 1998) by the stellar wind. In particular, the surface rotational velocities and their evolution are determined by the joint effects of internal transport mechanisms and surface angular momentum loss due to mass loss. Our main goal in this study is to investigate the evolutionary implications of currently-debated uncertainties regarding the magnitude of mass-loss rates of hot massive stars.
In recent years, it has become clear that the original assumptions of the radiation-driven wind theory (pioneered by Lucy & Solomon 1970; and Castor et al. 1975, hereafter CAK) need to be reconsidered. The discovery of small-scale inhomogeneities in stellar winds has had a significant impact on the derived mass-loss rates (e.g., Hillier 1991; Feldmeier et al. 2003; Puls et al. 2006; Oskinova et al. 2007; Sundqvist et al. 2011; Šurlan et al. 2013, and summarized by Puls et al. 2008; Sundqvist 2013; Puls et al. 2015). Mass-loss rates of hot OB stars derived both from current X-ray (Cohen et al. 2013; Leutenegger et al. 2013; Hervé et al. 2013; Rauw et al. 2015), UV (Sundqvist et al. 2011; Bouret et al. 2012; Šurlan et al. 2013), and IR (Najarro et al. 2011) diagnostics do not agree with the widely-used theoretical rates derived by Vink et al. (2000) and Vink et al. (2001). The apparent discrepancy is of a factor of between two and three, where rates derived from observations are lower, when taking the “Vink-rates” at face value (see above references), and typically a factor of two when accounting for up-to-date abundances in the mass-loss recipe (Petrov et al. 2016). Such changes in the overall mass-loss rates might have severe consequences for the evolution of massive stars (e.g., Meynet et al. 1994).
Simulating the wind of the famous Luminous Blue Variable, P Cygni (B1 Ia+), Pauldrach & Puls (1990) noted a bi-stable behavior. In their self-consistent calculations, keeping Teff = 19.3 kK and varying log (L/L⊙) = 5.74,5.86,5.97, they showed that for a small increase in the Eddington Γ, a large impact is seen on the dynamics of the stellar wind. Instead of a gradual increase, Ṁ showed a strong discontinuity versus Γ, and the behavior resulted in a jump in Ṁ accompanied by a corresponding jump (in the opposite direction) in the terminal velocity. The triggering mechanism of this bi-stability was attributed to the behavior of the hydrogen Lyman continuum, namely that it becomes optically thick at a critical wind density or effective temperature. The high opacity blocks the flux bluewards of the Lyman edge, and the metals that have ground state photoionisation edges in this frequency range shift to a lower ionisation state. The recombination of metals enhances the radiative line acceleration (since lower ions typically exhibit more lines), and thus leads to an increase in Ṁ.
Even if the Lyman continuum were to remain optically thin, a shift in the ionisation equilibrium could still occur, mainly due to reaching a critical Teff. Regarding this more general situation, Vink et al. (1999) identified the dominant role of iron recombination in the wind. As a massive star evolves and reaches lower effective temperatures, Fe iv recombines to Fe iii, giving rise to an increased mass-loss rate corresponding to the “first” bi-stability jump in the mass-loss rate and terminal velocity of the wind.
Calculations by Vink et al. (1999) confirm the presence of bi-stable behavior (both with respect to the above theoretical findings and observational results demonstrating the presence of a jump in the terminal velocities of B star winds, Lamers et al. 1995), however their prediction of the jump temperature falls into the range 27.5–22.5 kK. This is higher than the Pauldrach & Puls (1990) result, 19.3 kK, and the values derived by Lamers et al. (1995) and others (see below), which indicate a jump temperature of 20.5 kK.
Parameter setup in the evolutionary grids and models discussed in this work.
As also noted by Vink et al. (1999), a second bi-stability jump should be expected at around 12 kK, because of the recombination of Fe iii. The presence of such a jump has been theoretically confirmed by Petrov et al. (2016), although typically at lower effective temperatures, around 9 kK. Interestingly, the model calculations by Petrov et al. (2016) predict the first bi-stability to occur at around 20 kK, in agreement with observations.
Irrespective of the actual position of the jump, the calculations by Vink et al. (2000) indicate an increase of mass-loss rates by a factor of between five and seven over the first jump, if the ratio v∞/vesc decreases by a factor of two. On the other hand, quantitative spectroscopy of a sample of Galactic OB supergiants by Markova & Puls (2008) provided an (observational) upper limit for any such increase, namely that the mass-loss rates should at maximum increase by the same factor as the terminal velocities decrease, meaning by a factor of between two and three. However, those results are most consistent with mass-loss rates that remain constant or even decrease in parallel with v∞. These and similar findings from other investigations (e.g., Crowther et al. 2006) have incited vigorous debate about the behavior of Ṁ around the expected positions of the bi-stability jumps (see also Vink et al. 2010), noting as well that Lamers et al. (1995) found a steep decrease of v∞/vesc over a quite narrow temperature range, while Crowther et al. (2006) identified a much more gradual change (see also Markova & Puls 2008).
Vink et al. (2010) argued that a large increase in the mass-loss rate due to the first bi-stability jump would lead to an efficient mechanism to brake surface rotational velocities, the so-called bi-stability braking (BSB). As already outlined, however, the description of the jump itself is hampered by at least two uncertainties. Firstly, the observed jump temperature (Teff,jump1 ≈ 20 kK, Lamers et al. 1995; Prinja & Massa 1998; Crowther et al. 2006; Markova & Puls 2008, based on the behavior of v∞ and/or v∞/vesc) is much lower than originally considered. Petrov et al. (2016) have also confirmed that improved model calculations yield results quite similar to observed values. Secondly, the change of the observed mass-loss rate, that is, the size of the jump at the first bi-stability location (a factor of 0.4–2 when following the analysis of Markova & Puls 2008) does not agree with the Vink et al. (1999) and Vink et al. (2000) values (a factor of between five and seven). Even more troublesome is that massive star evolutionary models that adopt the Vink recipe result in an increase of mass-loss rates by a factor of 10–20 at the first theoretical bi-stability jump location (≈25 kK) (Brott et al. 2011; Ekström et al. 2012; Groh et al. 2014).
Since stellar evolution models of massive stars commonly adopt the Vink recipe, both issues (regarding the overall rates and their behavior at the bi-stability) might have a fundamental impact on massive star evolution that has until now not been investigated. Although we will focus on hot stars, we remind the reader that due to the adopted position of the second jump, the mass-loss rates of blue supergiants might also be significantly overpredicted.
Close to the zero age main sequence (ZAMS) of O-type stars, rotational velocities are relatively high (200−400 km s-1, e.g., Howarth et al. 1997), while there is overwhelming evidence for a large population of slowly rotating B supergiants below 20 kK (Howarth et al. 1997; Hunter et al. 2008; Fraser et al. 2010; Huang et al. 2010). Since these B supergiants are thought to be the evolutionary descendants of rapidly rotating O-type stars, a significant angular momentum loss should occur during their evolution.
In this paper, we investigate the impact on massive star evolution models caused firstly by decreasing the overall mass-loss rates, and secondly, avoiding a large increase in Ṁ at the first bi-stability. In this sense, the angular momentum content of massive stars is considered to account for observational constraints. In particular, we investigate the model and parameter dependence inherent to this problem (already noted by Vink et al. 2010), namely we evaluate whether there is an actual need for a significant increase in Ṁ around ≈20 kK.
We will compare the mass-loss rates and surface rotational velocities resulting from two widely used grids of massive star evolutionary models that were calculated with different computational codes: the grids presented by Ekström et al. (2012) and by Brott et al. (2011). A variety of comparisons between these two model grids and the underlying codes are available in the literature (Martins & Palacios 2013; Paxton et al. 2013; Chieffi & Limongi 2013; Jones et al. 2015). However, these works primarily focus on aspects different from those considered in the present work, which concentrates on the impact of mass loss. Thus, to independently test the influence of mass-loss rates on massive stars, we calculate our models by means of the 1D-hydrodynamical code MESA (Paxton et al. 2011, 2013, 2015), after implementing an observationally guided, simple and flexible wind routine based on the wind-momentum luminosity relation (WLR, Kudritzki et al. 1995; Puls et al. 1996). This experimental routine – which includes the possibility of bi-stability jumps – is a powerful tool in the sense that it can be adjusted to either reproduce observed wind parameters or to modify these parameters in a simple way. We underscore that this routine is by no means a new wind model, and will not be suitable (at least in its present form) for actual production runs.
This paper is structured as follows. Section 2 introduces the stellar evolution models/codes considered in the following, while in Sect. 3 we present our first test with the MESA code. In Sect. 4 we describe our experimental wind tool used within our own calculations. In Sect. 5 we present the outcome of various model calculations, and discuss the role of the bi-stability jump. In Sect. 6 we show that reduced mass-loss rates (compared to the Vink rates) and the avoidance of a large jump in Ṁ at the bi-stability location cannot be present simultaneously. In Sect. 7 we summarize our findings and address relevant issues that require forthcoming observational tests.
2. Stellar evolution model
To perform our calculations, we adopt a widely used, rapidly developing 1D hydrodynamical stellar evolution code, Modules for Experiments in Stellar Astrophysics (MESA, Paxton et al. 2011, 2013, 2015) version r67941. MESA has a wide range of applicability, and our purpose was to explore the physics and the evolution of single massive stars through experiments with the mass-loss rates.
In our comparisons we refer to two often-cited grids of evolutionary models of massive stars, those of Ekström et al. (2012) using the Geneva code (GENEC, Eggenberger et al. 2008), and those of Brott et al. (2011) using the Bonn evolution code (STERN, Langer et al. 1988; Petrovic et al. 2005). Although these grids span extensive ranges in mass and rotational velocity, in our investigation we focus on 20–60 M⊙ models, either with no rotation or with an equatorial surface rotational velocity vrot = 300 km s-1.
MESA is similar to, and to some extent modeled upon, the Bonn code (Paxton et al. 2013). The bi-stability braking mechanism suggested by Vink et al. (2010) was based on models similar to those published by Brott et al. (2011). For this reason, we adopt a similar parameter setup (see Table 1). In the following we will comment on important details and on the major differences from the Ekström et al. (2012) models.
2.1. Abundances
Our models have been calculated for a metallicity of Z = 0.014, using the Asplund et al. (2005) mixture of elements, and adopting the Lodders (2003) isotopic ratios. This choice has been made so that our comparisons to other models (see below) would not suffer from large differences (as would be the case with the default Z = 0.020 in MESA, or very different mixtures). For simplicity, we refer to this particular choice as “Galactic metallicity” considering that it provides a good description of massive stars in the solar neighborhood.
Brott et al. (2011) used Z = 0.0088 for the chemical evolution of their Galactic metallicity models, when individual compositions are required (e.g., for surface element enrichment). The detailed metallicity mixture is described by Brott et al. (2011), supplemented with the Asplund et al. (2005) values for some other elements. The resulting metallicity is lower than found in other studies, as a consequence of tailoring the adopted individual elemental abundances. Isotopic ratios were taken from Lodders (2003). When the opacity tables (from Iglesias & Rogers 1996) are required, the Grevesse et al. (1996) mixture of elements was adopted and tailored for Z = 0.014. (For different metallicities this is scaled by the iron abundance.) Ekström et al. (2012) used the Asplund et al. (2005) mixture of elements, except for a different Ne abundance, taken from Cunha et al. (2006). This particular mixture was then scaled to Z = 0.014. Again, isotopic ratios are from Lodders (2003). The opacities were then generated for this particular mixture of elements.
2.2. Convective core overshooting
In our MESA models, the convective core boundary is determined by the Ledoux criterion2, 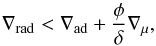 (1)where the nablas are the radiative, adiabatic and chemical gradients, that is,
(1)where the nablas are the radiative, adiabatic and chemical gradients, that is, 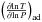 ,
, 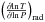 , and
, and 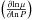 . φ, and δ are derivatives from the equation of state, denoting
. φ, and δ are derivatives from the equation of state, denoting 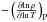 , and
, and 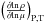 , respectively (Kippenhahn et al. 2012). We have adopted a step-overshooting parameter of αov = 0.335 consistent with the Brott et al. (2011) models. Overshooting is a sensitive parameter which can significantly modify the outcome of model calculations since it directly affects the MS lifetime, as it is well known from evolutionary models (Langer 1986; Schaller et al. 1992; Brott et al. 2011; Ekström et al. 2012; Chieffi & Limongi 2013; Castro et al. 2014). This issue might deserve an extended discussion; here we provide only some brief comments.
, respectively (Kippenhahn et al. 2012). We have adopted a step-overshooting parameter of αov = 0.335 consistent with the Brott et al. (2011) models. Overshooting is a sensitive parameter which can significantly modify the outcome of model calculations since it directly affects the MS lifetime, as it is well known from evolutionary models (Langer 1986; Schaller et al. 1992; Brott et al. 2011; Ekström et al. 2012; Chieffi & Limongi 2013; Castro et al. 2014). This issue might deserve an extended discussion; here we provide only some brief comments.
Currently two methods are adopted to treat convective overshooting in stellar evolution models: the step method, and the exponential or diffusive method. Both model grids from Brott et al. (2011) and Ekström et al. (2012) use a step overshooting which refers to an extension of the convective core lov by a fraction αov of the local pressure scale height HP, 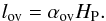 (2)Other studies (mostly of individual stars, e.g., Moravveji et al. 2015) use the exponential method based on Herwig (2000), which accounts for the change in diffusive mixing using an additional diffusion coefficient,
(2)Other studies (mostly of individual stars, e.g., Moravveji et al. 2015) use the exponential method based on Herwig (2000), which accounts for the change in diffusive mixing using an additional diffusion coefficient, 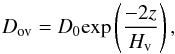 (3)where D0 is the diffusion coefficient at the core boundary, z is the vertical distance from the core boundary, and Hv is the local velocity scale height, defined as the exponential overshooting parameter times the local pressure scale height:
(3)where D0 is the diffusion coefficient at the core boundary, z is the vertical distance from the core boundary, and Hv is the local velocity scale height, defined as the exponential overshooting parameter times the local pressure scale height: 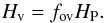 (4)Although our MESA models contain an exponential overshoot parameter, this is effectively not used, and we rely on the step overshoot method alone, since we aim to perform a consistent comparison.
(4)Although our MESA models contain an exponential overshoot parameter, this is effectively not used, and we rely on the step overshoot method alone, since we aim to perform a consistent comparison.
In this context, we note that it has become possible to use asteroseismological measurements to constrain the overshoot parameter for hot, massive stars (e.g., Aerts 2015). This has been done, for example for θ Ophiuchi by Briquet et al. (2007), resulting in a step overshoot parameter, αov = 0.44 ± 0.07 (at Teff ≈ 22 kK and log g ≈ 3.95).
Recently, Moravveji et al. (2015) claimed that, based on asteroseismological measurements, the exponential method (plus diffusive mixing in the radiative zone) better reproduces observations than the step overshoot method. For a B-type dwarf star, they derived an exponential overshoot parameter, fov = 0.016−0.017.
Petermann et al. (2015) argued that in stars with strong, observable magnetic fields, these fields might be sufficiently strong in the deep interior to suppress core overshooting. Briquet et al. (2012) showed that the observed magnetic star, V2052 Ophiuchi, is reproduced with models adopting a small overshoot parameter. Dynamos operating in the convective core have been proposed to suppress core overshooting in intermediate-mass stars (Stello et al. 2016). It is reasonable to speculate that this is also the case for high-mass stars.
It should be also pointed out that even though stellar models with a calibrated value of overshooting (Moravveji et al. 2015; McEvoy et al. 2015; Castro et al. 2014) can reproduce observed stellar properties, in 1D models the implementation of the physical problem (small-scale convective motions) is challenging (Arnett et al. 2009). We also note that Köhler et al. (2015) argue that in very massive stars (>60 M⊙) the value of overshooting is of less significance since the size of the convective core is large enough that possible extensions are not relevant.
At a specific mass (16 M⊙), the effective temperature where the models reach the terminal age main sequence (TAMS) coincides with the effective temperature at which the rotational velocities are observed to drop significantly (Vink et al. 2010). Indeed, this was the criterion for calibrating the overshoot parameter as applied by (Brott et al. 2011, based on Hunter et al. 2008). This calibration was obtained for stars in the Large Magellanic Cloud (LMC), and also adopted for Galactic conditions without modifications. Ekström et al. (2012) determined the overshooting parameter based on the observed width of the main sequence using models with lower initial masses, in the range from 1.35 to 9 M⊙. If the overshoot parameter was smaller than the value αov = 0.335 which is used in our models (e.g., αov = 0.1 as adopted by Ekström et al. 2012, or the corresponding value using exponential overshooting), and thus the models reached the end of the main sequence at higher Teff, then our quantitative results would need to be reconsidered. However, our qualitative picture does not depend on this issue.
2.3. Rotation, mixing, and magnetic fields
In MESA (and STERN), the effects of rotation are considered in a fully diffusive approach. The inclusion of rotation in stellar evolution models is critical for mixing chemical elements and angular momentum transport. It has been argued that the implementation of meridional (Eddington-Sweet) circulation requires an advective treatment (Maeder 2009). Most importantly, the choice of advective or diffusive approach for the Eddington-Sweet circulation leads to a qualitatively different behavior of the evolution of the surface rotational velocities. Moreover, there is also a difference in calculating the meridional circulation velocity. In MESA and STERN, Eq. (35) from Heger et al. (2000) is used, while in the Geneva code, Eq. (4.38) from Maeder & Zahn (1998) is adopted. This can also affect the way chemical elements and angular momentum are transported in the stellar interiors.
Ekström et al. (2012) did not include any effects of magnetic fields, while Brott et al. (2011) considered angular momentum transport due to a Spruit-Tayler (ST) dynamo (Tayler 1973; Spruit 2002). Although simulations by Braithwaite (2006) were reported to produce a closed dynamo loop using the Tayler instability, Zahn et al. (2007) were unable to obtain a closed loop. As a consequence, the existence of the Spruit-Tayler dynamo is heavily debated (Rüdiger et al. 2012; Neiner et al. 2015). Even more problematic is that if magnetic fields were present throughout the radiative zone, a possible interaction with large scale meridional currents might occur and the combined effects would need to be considered (Maeder 2009). On the other hand, such effects might justify the use of a fully diffusive treatment (Song et al. 2016).
The Ekström et al. (2012) grid was computed for an initial ratio of vrot(init) /vcrit = 0.4 where the critical velocity for an Eddington Γ < 0.639 is 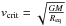 . The choice of the assumed initial ratio is based on the peak of the observed rotational velocity distribution of B-type stars from Huang et al. (2010). Georgy et al. (2013) have shown that this choice reproduces well the observed surface nitrogen enrichment.
. The choice of the assumed initial ratio is based on the peak of the observed rotational velocity distribution of B-type stars from Huang et al. (2010). Georgy et al. (2013) have shown that this choice reproduces well the observed surface nitrogen enrichment.
On the other hand, the Brott et al. (2011) grid was calculated for a wide range of rotational velocities. To reproduce the observed nitrogen enrichment from Hunter et al. (2008), the mixing efficiency parameters from Heger et al. (2000) were adopted, and calibrated to fc = 0.0228 and fμ = 0.1, respectively. While fc accounts for the contribution of the rotationally-induced instabilities to the total diffusion coefficient, fμ relates to the inhibiting effect of chemical gradients on the efficiency of rotational mixing processes. Since MESA follows the Bonn code implementations, after several tests (see also Chieffi & Limongi 2013) we also adopted these values for the sake of consistency, keeping in mind that these parameters introduce a considerable uncertainty, though most likely will not modify our final conclusions. We also note that the calibration of mixing efficiencies should depend on initial mass, initial rotational velocity and metallicity (de Mink et al. 2009; Ekström et al. 2012; Georgy et al. 2013). Thus far, it has not been justified why, for example, the Brott et al. (2011) mixing efficiencies calibrated for a LMC composition have been also used for their Galactic and SMC model grids. Furthermore, it must be noted that the calibration of the rotational mixing efficiency is not independent of the size of the convective core, hence of the adopted overshoot parameter. Finally, any adjustment of mixing efficiencies will have an impact on the angular momentum transport.
2.4. Mass-loss rates
We have specifically investigated models that adopt the Vink et al. prescription, and we have also adopted our experimental wind routine (see Sect. 4). Besides the actual treatment of the mass-loss rates (which will be discussed in detail later in the paper), two major factors deserve special attention.
2.4.1. Metallicity dependence
The Brott et al. (2011) models include a scaling of Ṁ with respect to the surface iron abundance. Instead of an overall metallicity dependence (e.g., as present in the Vink recipe and adopted by Ekström et al. 2012 and in the MESA models), they use a scaling: 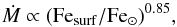 (5)where (for reasons of consistency) Brott et al. adopted a value of 7.50 (in units of log (Fe/H) + 12 when using number densities) for the solar iron abundance, following Grevesse et al. (1996). Although metallicity effects are of major interest in a more general context, we have restricted our investigations to a Galactic environment. Investigation of other environments require additional studies, due to the large impact of metallicity on the mass-loss rates.
(5)where (for reasons of consistency) Brott et al. adopted a value of 7.50 (in units of log (Fe/H) + 12 when using number densities) for the solar iron abundance, following Grevesse et al. (1996). Although metallicity effects are of major interest in a more general context, we have restricted our investigations to a Galactic environment. Investigation of other environments require additional studies, due to the large impact of metallicity on the mass-loss rates.
2.4.2. Dependence on rotation
In most cases, stellar rotation has a minor influence on the winds of massive O-type stars, since for typical rotation rates (far from the critical value) the centrifugal forces are low, and the distortion of the stellar shape is insignificant. In extreme cases, two limits become decisive. The so-called Ω-limit is reached at critical rotation (at which point the gravitational and centrifugal forces are equal), while the Eddington limit is reached when Γ = 1, that is, when the luminosity is equal to the Eddington luminosity (L = LEdd). Maeder & Meynet (2000) combine these limits as the ΩΓ-limit which is reached when the total acceleration (at the surface) becomes zero, that is, ggrav + gcent + grad = 0. Before proceeding any further, we must address a basic problem which illustrates another difference between the Geneva and the Bonn models.
The definition of the critical velocity by the Bonn group (e.g., Langer 1998) and in the MESA models is 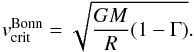 (6)On the other hand, Maeder & Meynet (2000) pointed out that Eq. (6) is only valid if the surface radiative flux has a uniform value (and the surface is not distorted). This is in contradiction with von Zeipel’s theorem for rotating stars (for a generalization of the von Zeipel theorem for shellular rotation, see Maeder 1999, and for an alternative approach see Espinosa Lara & Rieutord 2011). If Γ is well below a specific critical value, explicitly calculated as Γ < 0.639 by Maeder & Meynet (2000), the critical velocity can be calculated independent of the Eddington Γ,
(6)On the other hand, Maeder & Meynet (2000) pointed out that Eq. (6) is only valid if the surface radiative flux has a uniform value (and the surface is not distorted). This is in contradiction with von Zeipel’s theorem for rotating stars (for a generalization of the von Zeipel theorem for shellular rotation, see Maeder 1999, and for an alternative approach see Espinosa Lara & Rieutord 2011). If Γ is well below a specific critical value, explicitly calculated as Γ < 0.639 by Maeder & Meynet (2000), the critical velocity can be calculated independent of the Eddington Γ, 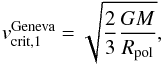 (7)where at critical rotation
(7)where at critical rotation 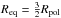 . For Γ > 0.639, a modified critical velocity needs to be defined, which includes the Γ-dependence.
. For Γ > 0.639, a modified critical velocity needs to be defined, which includes the Γ-dependence.
Now, let us introduce the corresponding scaling factors which are applied in the evolutionary codes to correct Ṁ for rotational effects. Langer (1998) (and STERN) use the factor 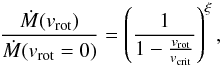 (8)with ξ = 0.43 (following a fit to the results of Friend & Abbott 1986 performed by Bjorkman & Cassinelli 1993) and
(8)with ξ = 0.43 (following a fit to the results of Friend & Abbott 1986 performed by Bjorkman & Cassinelli 1993) and 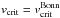 . This formulation gives a reasonable agreement with the alternative calculations of Pauldrach et al. (1986) when the actual velocity is far from the critical one, and the enhancement of the mass-loss rate due to rotation is on the order of 30%. Equation (8) has also been adopted in MESA where ξ is an adjustable free parameter, and the right-hand side of this equation is referred to as the rotational Ṁ boost (Paxton et al. 2013). We note that both Friend & Abbott (1986) and Pauldrach et al. (1986) considered a sort of maximum rotational effect, by accounting only for particles in the equatorial plane. A physically motivated alternative to Eq. (8), using the same assumptions, would result in a rotational Ṁ boost of (1−(vrot/vcrit)2)1−1 /α′, where α′< 1 is related to the force multiplier parameters of the modified CAK theory (see Eq. (13); cf. Puls et al. 2008, and references therein). The major point, however, is that gravity darkening is not considered in this simplified approach.
. This formulation gives a reasonable agreement with the alternative calculations of Pauldrach et al. (1986) when the actual velocity is far from the critical one, and the enhancement of the mass-loss rate due to rotation is on the order of 30%. Equation (8) has also been adopted in MESA where ξ is an adjustable free parameter, and the right-hand side of this equation is referred to as the rotational Ṁ boost (Paxton et al. 2013). We note that both Friend & Abbott (1986) and Pauldrach et al. (1986) considered a sort of maximum rotational effect, by accounting only for particles in the equatorial plane. A physically motivated alternative to Eq. (8), using the same assumptions, would result in a rotational Ṁ boost of (1−(vrot/vcrit)2)1−1 /α′, where α′< 1 is related to the force multiplier parameters of the modified CAK theory (see Eq. (13); cf. Puls et al. 2008, and references therein). The major point, however, is that gravity darkening is not considered in this simplified approach.
Maeder & Meynet (2000) include the effects of gravity darkening and derive the enhancement factor due to rotation as ![\begin{equation} \label{eq:rotf_g} \frac{\dot{M}(\Omega)}{\dot{M} (\Omega = 0)} = \frac{(1- \Gamma_{\rm e})^{\frac{1}{\alpha}-1}} {\left[ 1 - \frac{\Omega^2}{2 \pi G \rho_m} - \Gamma_{\rm e} \right]^{\frac{1}{\alpha} - 1}}, \end{equation}](/articles/aa/full_html/2017/02/aa29468-16/aa29468-16-eq84.png) (9)where α< 1 is the corresponding force multiplier parameter (to be replaced by α′ if ionization effects are accounted for), Γe is the Eddington factor for electron scattering opacity in a a non-rotating star, Ω is the angular velocity, ρm is the average density of the star, and the term in the denominator can be approximated by
(9)where α< 1 is the corresponding force multiplier parameter (to be replaced by α′ if ionization effects are accounted for), Γe is the Eddington factor for electron scattering opacity in a a non-rotating star, Ω is the angular velocity, ρm is the average density of the star, and the term in the denominator can be approximated by 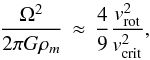 (10)with
(10)with 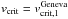 . The latter relations are used in GENEC. Finally, we note that in contrast to all of the relations above which result in an increase of mass-loss close to the Ω or ΩΓ limit, Müller & Vink (2014) suggested alternative rotating wind models that imply a potential decrease of the total mass-loss rate, at least for specific models.
. The latter relations are used in GENEC. Finally, we note that in contrast to all of the relations above which result in an increase of mass-loss close to the Ω or ΩΓ limit, Müller & Vink (2014) suggested alternative rotating wind models that imply a potential decrease of the total mass-loss rate, at least for specific models.
3. First tests with MESA
3.1. Non-rotating models – comparisons with MESA
A variety of model grids for massive stars are available in the literature and online (and numerous comparisons between them, for example, Martins & Palacios 2013; Paxton et al. 2013; Chieffi & Limongi 2013; Jones et al. 2015). To convince ourselves of the capabilities of MESA, as a first step we compared or reproduced the main sequence of non-rotating Galactic (Z = 0.014) model grids published by Ekström et al. 2012 (using GENEC) and Brott et al. 2011 (using STERN). We recall that Brott et al. (2011) also use Z = 0.014 for the opacity calculations in their Galactic models. Although non-rotating models are somewhat unphysical, it is useful to compare such models calculated by different codes, since this provides valuable information independent of the different treatment of rotation in the various codes. Particularly, clues about the sensitivity of the model calculations to the input parameters can be obtained, by testing their influences on the HRD tracks. Note that we did not attempt to compare the post-MS phases nor the Teff range in which line-driven winds are no longer applicable.
The overall reproduction of the main sequence as calculated in both grids is excellent, although small qualitative and quantitative differences exist (see Figs. 1 and 2). One of these issues refers to the starting point of the ZAMS which occurs at higher effective temperatures in the Geneva tracks. Moreover, a sensitive point of comparison is the evolution during and right after core hydrogen exhaustion (the terminal age main sequence, TAMS). There are indeed small differences around the “hooks” where the stars first turn back on the HRD towards increasing Teff, and then turn again redward. The reason for this behavior (in a simplified picture) is that at this point the star undergoes significant internal structural changes. The core, which at this point consists almost entirely of helium, starts to contract on a thermal timescale. This contraction is due to exceeding the Schönberg-Chandrasekhar limit, which states that the pressure in the core cannot sustain the weight of the envelope above a given core mass to total mass ratio (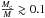 ). The core contraction leads to an overall contraction, and an increase of the core temperature, which maintains the star in hydrostatic equilibrium. This also results in heating the envelope which will then initiate hydrogen shell burning in the envelope, which leads to increasing radius and decreasing surface temperature. Therefore, the hook in the HRD corresponds to a contracting phase with increasing Teff, and the following redward evolution is due to shell H-burning. This process, however, is sensitive to the prescription of convective mixing: using either instantaneous (GENEC) or diffusive mixing (STERN, MESA) might partly be responsible for small differences when comparing the tracks.
). The core contraction leads to an overall contraction, and an increase of the core temperature, which maintains the star in hydrostatic equilibrium. This also results in heating the envelope which will then initiate hydrogen shell burning in the envelope, which leads to increasing radius and decreasing surface temperature. Therefore, the hook in the HRD corresponds to a contracting phase with increasing Teff, and the following redward evolution is due to shell H-burning. This process, however, is sensitive to the prescription of convective mixing: using either instantaneous (GENEC) or diffusive mixing (STERN, MESA) might partly be responsible for small differences when comparing the tracks.
To reproduce these models as closely as possible, we used an identical parameter setup as described in the studies of Ekström et al. (2012) and Brott et al. (2011), from which one of the most important is the (step-) overshooting, set to αov = 0.1 in the former, and αov = 0.335 in the latter case. Furthermore, for this comparison we applied the mass-loss prescription of Vink et al. (2001), as was also done in the other two studies. It should be noted, however, that the implementation of the Vink prescription is not exactly the same in the three codes.
 |
Fig. 1 Comparison between non-rotating Galactic Z Geneva evolutionary tracks on the MS published by Ekström et al. (2012, black dashed), and our MESA models calculated with a similar setup (colored lines). Initial masses in solar units are indicated next to the tracks. A step overshoot parameter, αov = 0.1, was used. |
 |
Fig. 2 Comparison between non-rotating Galactic Z Bonn evolutionary tracks on the MS published by Brott et al. (2011, black dashed), and our MESA models calculated with a similar setup (colored lines). A step overshoot parameter, αov = 0.335, was used. Stars above 40 M⊙ are still on the main sequence at rather low effective temperatures. The lack of hooks at higher masses is due to envelope inflation (N. Langer, priv. comm.), treated similarly in STERN and MESA. |
To conclude, we have demonstrated that the general behavior of the MS evolution of massive stars, as reported previously using the Geneva and Bonn codes, can be reproduced using MESA. However, the following points must be taken into account. Firstly, this reproduction does not mean that the models agree for all of their detailed physical parameters. As an example, the MS lifetimes of the models are different. Secondly, the free parameters are not independent, and hence it is possible to obtain similar results with a different parameter setup. For example, simultaneously increasing the overshooting and reducing the convective mixing efficiency can produce (almost) the same evolutionary track. This situation becomes further complicated in rotating models. Thirdly, since the codes are not identical, but have certain differences in their implementations, their results will always have at least small discrepancies. For instance, the difference of the model properties at the initial timestep(s) reflect the parameters of the starting model which is loaded. The differences at the TAMS might be attributed to more delicate issues, since it is quite challenging to simulate the very rapid and very large internal changes that these models undergo immediately after core hydrogen exhaustion. The most influential free parameter in this respect is overshooting.
3.2. Rotating models – comparison between MESA and the Brott et al. models.
Rotation plays a crucial role in the evolution of stars: it is responsible for the mixing of elements and the transport of angular momentum (e.g., Langer 1998; Maeder 2009). Moreover, fast rotation modifies the strength and the topology of hot star winds (see Sect. 2.4.2). The inclusion of rotation in 1D stellar evolution codes is a non-trivial task. In a spherically symmetric, non-rotating case the models are well described by concentric, spherically-symmetric equipotential layers. However, if rotation is present, and shellular rotation (Zahn 1992) is assumed, the (pseudo-)equipotentials are deformed due to the centrifugal force, and the distance to the center of two given surface elements on the same (pseudo-)equipotential is no longer described by a unique radius. Therefore a one-dimensional treatment of rotation must work with suitable averages along pseudo-equipotential surfaces. The inclusion of rotation and its effects requires a special treatment in evolutionary codes which shows remarkable differences between the two schools, that is, the Bonn (e.g., Langer 1998; Heger et al. 2000, 2005; Petrovic et al. 2005; Yoon & Langer 2005; Brott et al. 2011) and Geneva (e.g., Maeder & Meynet 2000, 2003; Hirschi et al. 2004; Eggenberger et al. 2008; Ekström et al. 2012) groups. An attempt to present a unified description of stellar rotation in 1D evolution codes was provided by Potter et al. (2012) using the ROSE code.
Surface rotational velocities in the Brott et al. (2011) grid and our experimental model grid for four representative initial masses.
Since the MESA implementation of rotation follows (but is by no means identical to) the Bonn code, a comparison of MESA with this code can be conveniently performed by tuning the free parameters as described by Brott et al. (2011) (fc = 0.0228 and fμ = 0.1). Thus we consider rotationally induced instabilities as diffusive processes (see Heger et al. 2000; Paxton et al. 2013), including the dynamical and secular shear, the Goldreich-Schubert-Fricke instability, and the Eddington-Sweet circulation for chemical mixing. For consistency, we also turn off the Solberg-Hoiland instability for any transport mechanism (I. Brott & N. Langer, priv. comm.). In analogy to the work by Brott et al. (2011), transport of chemical elements due to the Spruit-Tayler dynamo is ignored. However, angular momentum transport due to the Spruit-Tayler dynamo is included.
After relaxation of the initial models, the rotational velocities provide an excellent match to the Brott et al. (2011) values. In Table 2, we show the initial surface rotational velocities, noting that besides relaxation effects, the surface vrot remains close to its initial value. We conclude that this behavior is mainly due to the effects caused by meridional circulation and the Spruit-Tayler dynamo. As already pointed out, the real challenge is that magnetic fields and meridional circulation may interact (Maeder 2009). Such potential interaction, however, is not yet understood and needs to be explored in detail. Thus the inclusion or exclusion of magnetic fields, and the advective-diffusive vs. purely diffusive treatment of angular momentum transport lead to major differences between the models from different authors (Brott et al. 2011; Ekström et al. 2012; Chieffi & Limongi 2013; Paxton et al. 2013).
In Fig. 3, we compare our experimental MESA models with the rotating Galactic models of Brott et al. (2011), and we can confidently rule out a possible degenerate solution resulting from interacting input parameters, since the most important quantities related to rotation (vrot on the MS, diffusion coefficients for mixing and transport processes) agree extremely well. For further details, we refer to the comparisons provided by Paxton et al. (2013).
 |
Fig. 3 Comparison between rotating Galactic Z Bonn evolutionary tracks on the MS published by Brott et al. 2011 (black dashed) and our MESA models calculated with a similar setup (colored lines). The average initial surface rotational velocity of the grid models is ≈270 km s-1 (exact values indicated in Table 2). A step overshoot parameter, αov = 0.335, was used. |
Finally, we note that due to the similarities between STERN and MESA and because of the good reproduction of the results of Brott et al. (2011) as obtained here, we will adopt similar parameters for most of our standard evolutionary models in the following (see Table 1).
4. An experimental wind routine for hot stars
Mass loss has a major impact on the evolution of hot, massive stars (e.g., Meynet et al. 1994), but consequences of uncertainties related to wind strength and the behavior of (at least) the first bi-stability jump (see Sect. 1) have not been tested in stellar evolution model calculations thus far. To this end, we aimed to develop a simple and flexible tool to reproduce different mass-loss scenarios. To avoid confusion regarding the different wind schemes in evolutionary codes, we stress that our new routine can only be applied for hot (≈50−15 kK)3 and massive (≈8−60 M⊙) main-sequence and post-MS stars. In its current state, it is in an experimental phase, and not applicable for production runs.
In brief, we implemented a wind routine based on the semi-empirical WLR, which in turn can be understood from theoretical scaling relations of mass-loss rate and terminal velocity (Kudritzki et al. 1995; Puls et al. 1996). Multiplying the wind momentum rate with the square-root of the stellar radius, the WLR can be written as 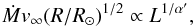 (11)if α′ (see below) is close to 2/3. Conveniently, this equation is expressed in logarithmic form:
(11)if α′ (see below) is close to 2/3. Conveniently, this equation is expressed in logarithmic form: 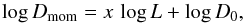 (12)where x = 1 /α′, and the offset D0 depends on metallicity and spectral type. In these relations,
(12)where x = 1 /α′, and the offset D0 depends on metallicity and spectral type. In these relations, 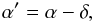 (13)depends on the force multiplier parameters α and δ (Abbott 1982; Pauldrach et al. 1986), related to the radiative line acceleration
(13)depends on the force multiplier parameters α and δ (Abbott 1982; Pauldrach et al. 1986), related to the radiative line acceleration 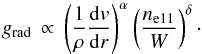 (14)Here, ne11 is the electron density (in units of 1011 cm-3), and W the dilution factor. α refers to the exponent of the line-strength distribution function, and also provides the ratio between the line force from optically thick lines and the total one. δ quantifies changes in the ionization balance. Since, for typical OB star wind conditions, α = 0.6−0.7 and δ = 0.02−0.1 (Puls et al. 2000; Kudritzki & Puls 2000), the above requirement of α′ ≈ 2/3 is usually fulfilled.
(14)Here, ne11 is the electron density (in units of 1011 cm-3), and W the dilution factor. α refers to the exponent of the line-strength distribution function, and also provides the ratio between the line force from optically thick lines and the total one. δ quantifies changes in the ionization balance. Since, for typical OB star wind conditions, α = 0.6−0.7 and δ = 0.02−0.1 (Puls et al. 2000; Kudritzki & Puls 2000), the above requirement of α′ ≈ 2/3 is usually fulfilled.
This is, however, not true for the whole spectral range. For example, for A supergiants, α′ ≈ 0.4 (Puls et al. 2000), and according to Lamers et al. (1995) the force multiplier parameters and thus α′ become discontinuous around Teff = 21 kK. Nevertheless, for simplicity we assume a global α′ = 1 /x to be representative for the complete Teff range under consideration. For future studies, we advise accounting for a proper temperature dependence, i.e., α′(Teff) and log D0(Teff). In most cases we have adopted a fixed value of x = 1.84 from Mokiem et al. (2007b), which is consistent with theoretical values in the OB star range (see above).
The wind momentum rate is a very useful quantity, particularly when comparing observations with theoretical predictions. This is why many studies (e.g., Puls et al. 1996; Kudritzki & Puls 2000; Repolust et al. 2004; Mokiem et al. 2005; Martins et al. 2005; Mokiem et al. 2007a) have tried to constrain the WLR observationally. In the following, we will concentrate on Galactic conditions. We recall that the observed WLR in most cases constrains very well luminosity class I stars, whereas for other classes this relation may be ambiguous (e.g., the “weak wind problem”, see Puls et al. 2008, and references therein, and also Huenemoerder et al. 2012). Note that to first order, at least the theoretical WLR does not depend on the luminosity class (see also Vink et al. 2000).
Different studies have derived different parameters for the WLR. For comparison, some of these are listed in Table 3. Note that α′ and log D0 correlate strongly with one another (since they are derived from a linear fit). This becomes obvious when, for example, comparing corresponding values with and without clumping correction from the same study.
WLR parameters for Galactic early-type stars.
In most cases, these observational results confirm the validity of the WLR concept, although there is significant scatter in the corresponding coefficients. Moreover, most of these values overestimate the actual wind momentum rates, since they were derived for “smooth” winds, without correcting for wind inhomogeneities (e.g., clumping).
In the following, we outline some details of our experimental wind routine. The terminal velocity scales with the escape velocity, 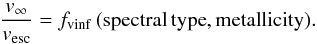 (15)For typical O-star conditions, fvinf = 2.65 (Kudritzki & Puls 2000). We note that in our description fvinf is an adjustable input parameter that can be calibrated based on observations (Groenewegen et al. 1989; Lamers et al. 1995; Prinja & Massa 1998; Prinja et al. 1990; Crowther et al. 2006; Markova & Puls 2008). The effective escape velocity (accounting for Thomson scattering) is
(15)For typical O-star conditions, fvinf = 2.65 (Kudritzki & Puls 2000). We note that in our description fvinf is an adjustable input parameter that can be calibrated based on observations (Groenewegen et al. 1989; Lamers et al. 1995; Prinja & Massa 1998; Prinja et al. 1990; Crowther et al. 2006; Markova & Puls 2008). The effective escape velocity (accounting for Thomson scattering) is 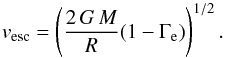 (16)In our formulation (which is consistent with the basic CAK approach), the Eddington factor needs to be calculated for pure electron scattering,
(16)In our formulation (which is consistent with the basic CAK approach), the Eddington factor needs to be calculated for pure electron scattering, 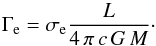 (17)Furthermore, we assume hydrogen to be fully ionized. The number of free electrons per helium nucleus (IHe) is approximated as a simple function of Teff. As a reasonable assumption, we adopt for OB stars with Teff> 20 kK IHe = 2, while for Teff< 20 kK we adopt IHe = 1 (Kudritzki et al. 1989). The electron scattering opacity per unit mass (in units of cm2 g-1) is then provided by
(17)Furthermore, we assume hydrogen to be fully ionized. The number of free electrons per helium nucleus (IHe) is approximated as a simple function of Teff. As a reasonable assumption, we adopt for OB stars with Teff> 20 kK IHe = 2, while for Teff< 20 kK we adopt IHe = 1 (Kudritzki et al. 1989). The electron scattering opacity per unit mass (in units of cm2 g-1) is then provided by 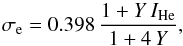 (18)where Y is the surface helium number fraction, Y = NHe/NH.
(18)where Y is the surface helium number fraction, Y = NHe/NH.
Using the WLR, the mass-loss rates are then derived according to 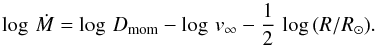 (19)The parameters required to estimate both Dmom and v∞ are obtained from the evolutionary calculations. In addition, two further input parameters need to be provided, namely, α′ and log D0 (cf. Table 3). The specification of these parameters provides a simple way to calibrate the mass-loss rates to observed WLRs, and to account for new observational or theoretical results.
(19)The parameters required to estimate both Dmom and v∞ are obtained from the evolutionary calculations. In addition, two further input parameters need to be provided, namely, α′ and log D0 (cf. Table 3). The specification of these parameters provides a simple way to calibrate the mass-loss rates to observed WLRs, and to account for new observational or theoretical results.
Furthermore, it is convenient to apply a global scaling factor, denoted here as fscal, for the calculated mass-loss rate, so that 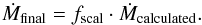 (20)It is evident that similar results could be obtained with other parameter settings, for example, by changing α′ (cf. Fig. 7) and/or log D0. However, while in the following we mostly consider fscal and α′ as fixed, the specification of log D0 provides a simple way to account for arbitrary changes in the mass-loss rates at the bi-stability jump.
(20)It is evident that similar results could be obtained with other parameter settings, for example, by changing α′ (cf. Fig. 7) and/or log D0. However, while in the following we mostly consider fscal and α′ as fixed, the specification of log D0 provides a simple way to account for arbitrary changes in the mass-loss rates at the bi-stability jump.
The implementation of the bi-stability jumps depends on the position of the jump (Teff,jump), the method used to calculate the mass loss around the jump (interpolation), and the size of the jump. We emphasize that the observed behavior of the ratio of v∞/vesc over the jump is gradual (Prinja & Massa 1998; Crowther et al. 2006) which implies that the change in Ṁ should be gradual as well (Markova & Puls 2008).
4.1. The position of the jump
Based on the discrepancy between theoretical predictions from Vink et al. (1999) and observational results, it is useful to control the position of the jump in terms of a jump temperature Teff,jump. Theoretically, the jump temperature is predicted to depend on the wind density, and Vink et al. (2000) calculate it via Γe, while Vink et al. (2001) calculate it via Z. Since observations suggest that there may be a well-defined Teff where the bi-stability jump occurs (for a given metallicity), we specify Teff,jump1 and Teff,jump2 as input parameters for the first and the second bi-stability jump temperatures, respectively. This provides the flexibility to adjust these parameters to observed or new theoretical values. Indeed, the very recent study by Petrov et al. (2016) indicates that the (theoretical) jump temperature needs to be shifted toward lower effective temperatures (≈20 kK in case of the first bi-stability, in agreement with observations) than predicted previously by Vink et al. (1999) and Vink et al. (2000) (≈25 kK). This change will need to be adopted in future stellar evolution models.
The bi-stability region itself is defined by its central jump temperature (Teff,jump) and the half width of interpolation (ΔT). For simplicity, we have adopted the same interpolation technique as present in the MESA Vink scheme. In particular, a larger interpolation region will yield results similar to a gradual change, while a small value of ΔT implies a steep increase in Ṁ. Considering observational constraints, we set Teff,jump1 = 20 500 K, and use ΔT = 3500 K, unless otherwise stated.
4.2. The size of the jump
There are several parameters that control the size of the jump. It is reasonable to consider that the (input) parameter fvinf decreases over the jump, based on the observed ratio of terminal velocity and escape velocity (Lamers et al. 1995; Prinja & Massa 1998; Crowther et al. 2006). The adjustment of this parameter directly influences the mass-loss rates. For example, if v∞/vesc steeply decreases by a factor of two from the hot to the cool side of the jump (following the studies by Lamers et al. 1995; Vink et al. 2000), then, without further adjustment, Ṁ would steeply increase by a factor of two as long as the WLR is continuous. Since the change in v∞/vesc is fairly well constrained by observations, and we intend to test the effects of different behaviors of Ṁ alone, we use the following parametrization for simplicity.
We consider the offset value of the WLR at the hot side of the jump, log D0(hot), as fixed, and define a corresponding 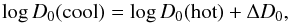 (21)at the cool side of the jump, with ΔD0 an adjustable parameter, allowing us to control the size of the jump in a simple and flexible way.
(21)at the cool side of the jump, with ΔD0 an adjustable parameter, allowing us to control the size of the jump in a simple and flexible way.
5. Results
5.1. The Vink mass-loss rates in evolutionary codes
In Fig. 4 we compare the implementation of the Vink mass-loss recipe for the case of two non-rotating Galactic 40 M⊙ models as computed by Ekström et al. (2012) and Brott et al. (2011). This plot shows one of the main foci of the present study: The implementation of the first bi-stability jump predicts an increase in the mass-loss rates by a factor of 15.4 in the Ekström et al. (2012) model (at 25 kK) and by a factor of 10.7 in the Brott et al. (2011) model (at 27–22 kK). The Ekström et al. (2012) model results in a steep increase of Ṁ across the first and the second bi-stability jumps. The Brott et al. (2011) model, on the other hand, uses a linear interpolation over the first bi-stability jump region, noting that the expressions from Vink et al. (2001) do not account for the intermediate range between 22.5 and 27.5 kK. The latter method may provide a closer match to observational constraints (J. Vink, priv. comm.), while the former is not compatible with the behavior of mass-loss rates and terminal velocities derived from observations (see Sect. 4).
 |
Fig. 4 Mass-loss histories for non-rotating Galactic 40 M⊙ models from Ekström et al. (2012) and Brott et al. (2011), adopting the Vink mass-loss prescription. See text. |
The second bi-stability jump is not implemented in the Bonn models. Instead, a switch is performed to the Nieuwenhuijzen & de Jager (1990) mass-loss rates whenever Teff<Teff,jump1 ≈ 25 kK, and when the Vink rates would yield lower Ṁ values than the corresponding Nieuwenhuijzen & de Jager (1990) values (typically around 16 kK). Brott et al. (2011) argue that this strategy accounts for the increased mass-loss rates at the second bi-stability jump. The Ekström et al. (2012) models, including the second bi-stability jump, apply the Vink et al. (2001) recipe until 12.5 kK, that is, to the minimum temperature considered, and then switch to the de Jager et al. (1988) prescription (cf. Fig. 4). This yields mass-loss rates on the order of 10-4M⊙ yr-1 close to Teff = 17 kK, in stark contrast with observations from typical B supergiants (Crowther et al. 2006; Markova & Puls 2008). The values derived from observations are typically two orders of magnitude lower than from these models.
By estimating theoretical mass-loss rates based on a work-integral method4, Petrov et al. (2016) found that both the first and the second bi-stability jump should be located at lower effective temperatures than predicted by Vink et al. (2000). Namely, the first jump (Fe iv recombining to Fe iii) should lie around 20 kK, and the second jump (Fe iii recombining to Fe ii) around 9 kK. Note that these values are much lower than the corresponding jump temperatures in the evolutionary models displayed in Fig. 4.
The reason why a comparison of mass-loss rates from higher mass models calculated by different numerical codes (using different assumptions and parameters) is challenging is a consequence of the different evolution in the HRD, which is more distinct for higher masses. The main differences arise from overshooting, and in rotating models from the treatment of angular momentum transport and chemical mixing. Since the mass-loss rates have a strong dependence on luminosity, it is evident that models with different luminosities will lead to different mass-loss histories, namely more luminous models will lose more mass. This effect can be clearly seen in Fig. 5 if one compares the evolutionary tracks of the two models that include rotation, and considers that the increase in luminosity of the 40 M⊙Ekström et al. (2012) track corresponds to an increase in the mass loss-rate (beginning at around 39 kK).
 |
Fig. 5 As Fig. 4, but for rotating models. Both evolution models have vrot(initial) ≈ 315 km s-1. The Geneva model becomes more luminous from ≈39 kK on, which results in higher mass-loss rates. |
To conclude, with some dependence on the details of individual codes, rotating models will show different mass-loss rates throughout their evolution, even when adopting the same wind prescription. Referring to the Vink rates, the size of the first bi-stability jump is barely affected by the different mass-loss implementations though.
MESA uses a mixture of the Bonn and Geneva approaches to implement the Vink mass-loss rates. The first bi-stability jump is implemented in a similar way to the Geneva code. A small difference concerns the temperature region close to the jump. While the Geneva code uses either Eqs. (14) or (15) from Vink et al. (2001) to determine the mass-loss rate directly at the hot and at the cool side, respectively, the MESA implementation interpolates between the two equations, with a very small half width of ΔT = 100 K.
The second jump is discarded in the MESA implementation. However, an alternative is incorporated in the code, allowing to switch to other schemes at effective temperatures below the range of applicability of the Vink rates (<12.5 kK). However, while the Bonn group adopts such a switch whenever the Vink rates would result in Ṁ lower than the Nieuwenhuijzen & de Jager (1990) rates, MESA conservatively switches at 12.5 kK to any other mass-loss prescription specified by the user. (We note that in the newest MESA release, r8118, this has been changed, and the switch between the wind schemes can be set to occur at a user-defined effective temperature.) This implies, considering the properties of the Vink recipe, that the MESA implementation results in a decreasing Ṁ from ≈16 kK to 12.5 kK, in contrast to the Bonn models that have an increasing mass loss in this range.
5.2. The size of the first bi-stability jump in stellar evolution models
The Vink formula predicts a large jump in the mass-loss rates from the hot to the cool side of the jump, and this has often been quoted as an average factor of 5 (Vink et al. 2000). However, apart from a few studies (e.g., Groh et al. 2014), no further check of this statement has been performed, namely whether evolutionary model calculations actually result in such an average value. To this end, the size of the jump as present in the Galactic Ekström et al. (2012) and Brott et al. (2011) evolutionary grids is compared in Table 4. For this comparison we have concentrated on non-rotating models, but the results for rotating models are similar.
In a conservative approach, we considered the local minima on the hot side, and the local maxima on the cool side, but using mean values on both sides would result in similar ratios. The jump temperatures are simply read off from the corresponding timestep, if the jump region is not wider than 0.9 kK. This applies to almost all cases from Ekström et al. (2012), except for the 20 and 25 M⊙ models at the second bi-stability jump, and we suspect that the wider jump in these cases is a result of a fast change in radius. The Bonn models apply a linear interpolation for the transient Teff regime, and thus the corresponding jump temperature is provided as a range.
The outcome of our comparison is somewhat surprising. The average increase in Ṁ over the first bi-stability jump corresponds to a factor of 16.5 and 12.3 for the non-rotating Galactic Ekström et al. (2012) and Brott et al. (2011) models, respectively. Almost all of the entries denote an increase larger than a factor of 10. The 20 M⊙ models display the largest jumps (a factor beyond 15), while the size of the jump decreases for higher initial masses. For comparison, in the study by Vink et al. (1999) a 20 M⊙ non-rotating Galactic model shows an increase in Ṁ of only a factor of 6.5 (see their Fig. 3). The source of this discrepancy is still unclear, but it is likely that the actual stellar parameters at the position of the jump are different from those adopted by Vink et al. (1999). Nevertheless, these values result in high Ṁ on the cool side of the jump, in stark contrast with mass-loss rates derived from current diagnostics (see previous sections). Therefore it seems that stellar evolution models might significantly overestimate the mass-loss rates after the bi-stability jump(s).
One further difficulty relates to overshooting. The Geneva models with smaller step overshooting always reach the TAMS before the first bi-stability jump, while the Bonn models reach the TAMS at lower effective temperatures, because of the larger overshoot parameter (see, e.g., their published HRDs). However, thus far it is unclear what happens when the end of the main sequence and the first bi-stability jump occur simultaneously. We need to understand whether there might be a physical interaction between the significant internal changes and the mass loss driven by the wind. Stellar parameters do change rapidly upon reaching the TAMS, and the mass-loss rates will change accordingly. If the TAMS coincides with the jump temperature a more complex behavior may occur. This might also become important if one additionally accounts for the accompanying angular momentum-loss (bi-stability braking, see Sect. 5.8).
Comparison of the increase of mass-loss rates over the bi-stability jump(s) in the non-rotating Galactic Ekström et al. (2012) and Brott et al. (2011) evolutionary grids.
5.3. Pre-bi-stability behavior (PBB)
In our first step, we aimed at calibrating our experimental wind routine to recover the Vink rates, with particular emphasis on the first bi-stability jump. Our description (see end of Sect. 4) allows for an approximate reproduction of the jumps (as a function of Minit) as computed by the Vink wind scheme (Fig. 6). For the complete mass range considered, 20–60 M⊙, good agreement (at least when concentrating on the average behavior) was obtained when using fvinf = v∞/vesc = 2.6 on the hot side of the first jump, fvinf = 1.3 on the cool side, and simultaneously increasing the WLR offset at the cool side by ΔD0 = 0.35 (see Eq. (21)). This choice of parameters corresponds to an average increase in Ṁ by a factor of ≈4.5. Additional parameters for this test are as follows. We adopted x = 1.83 (following the theoretical value provided by Vink et al. 2000), corresponding to α′ ≈ 0.55. The jump temperature was fixed at Teff,jump1 = 25 kK, and the second bi-stability jump had been ignored. All models were calculated for Galactic metallicity and without rotation.
 |
Fig. 6 Comparison between MESA models applying either the Vink recipe or our experimental wind scheme, in terms of mass-loss rates versus effective temperature. Initial masses (in solar units) indicated next to the tracks. See text. |
At the hot side of the jump and towards higher temperatures, however, an important qualitative difference in the behavior of the mass-loss rates needs to be discussed. While the mass-loss rates from our experimental routine monotonically increase from higher Teff until the jump, the Vink rates display a curvature, with a local maximum well before the jump temperature (see Fig. 6). This difference relates to the fact that the Vink recipe has a strong dependence on Teff, being the potentially largest factor influencing Ṁ on the hot side of the jump, log Ṁ ∝ 10.92 · { log (Teff/ 40 000) } 2. Thus, the Vink prescription is calibrated at 40 kK, which roughly corresponds to the ZAMS temperature of a 30 M⊙ Galactic star. This scaling keeps the temperature dependence small around temperatures close to 40 kK, while close to the bi-stability jump this dependence dominates and decreases Ṁ compared to higher values of Teff. Furthermore, since Ṁ decreases before the bi-stability jump, the size of the jump is effectively larger than if such a decrease was not present.
On the other hand, our wind tool includes only an indirect dependence on Teff, via L and R. As long as there is no explicit dependence via defining log D0 = log D0(Teff) (and we refrained from including such a dependence in the present study), Ṁ mainly depends on luminosity5, and because of the monotonic increase of this quantity for our 40 M⊙ model (see Fig. 1), the mass-loss rate also increases towards the jump.
Thus, the most important qualitative difference between the Vink rates and our experimental wind scheme is their “pre-bi-stability behavior” (PBB). We define the PBB as the behavior of the mass-loss rates at effective temperatures higher than the first bi-stability jump temperature, and the starting point of the PBB is where the mass-loss rates derived from the Vink formula start to decrease with decreasing Teff (and thus where the Vink and the experimental wind begin to depart qualitatively). This is, of course, initial-mass dependent: for larger masses, the PBB will start earlier, at higher Teff (see Fig. 6).
Although one can easily identify the source of this difference, originating from the specific temperature scaling of the Vink prescription, a corresponding decrease in the mass-loss rate with decreasing Teff cannot be identified from the semi-empirical WLR as used here (i.e., with constant D0), due to the dominating effect of increasing luminosity (see above).
Even though the luminosity increases, Vink et al. (2000) argue that there is a physical explanation why the line acceleration should become less effective at lower Teff (when considering the range between 50 and 30 kK): due to the shift of the flux maximum towards longer wavelengths, the number of effective lines decreases. With respect to our approach, this would mean that D0 should decrease as well. Unfortunately, there is no strict observational evidence to support either scenario (Crowther et al. 2006; Markova & Puls 2008; Fraser et al. 2010). This means that it is not established whether the mass-loss rates increase or decrease with Teff in the PBB region. In order to discriminate between the two cases, a meaningful analysis of mass-loss rates (and not only wind-momenta) should be performed in this quite narrow Teff range, for a significant sample of massive stars.
In any case, a comparison between WLRs derived from observations and model calculations is a non-trivial task. While from observations a sample of stars with different (initial and actual) masses can be analyzed at a certain point in their evolution, evolutionary models provide the complete path of a stellar model for a given initial mass. In particular, any WLR derived from a grid of evolutionary models with different masses will diminish the actual PBB seen when concentrating on individual tracks. Such an effect can be already noted in the wind momentum vs. luminosity diagram presented by Vink et al. (2000, their Fig. 9, upper panel), where individual patterns (e.g., the Ṁ(Teff) behavior) are smeared out, and an almost strictly linear relation over the complete range between 50 and 27.5 kK “survives”, consistent with our approach of adopting a constant D0.
When interpreting theoretical or observed WLRs, potential degeneracies (same luminosity, but other parameters different) need to be taken into account as well. For instance, HD 210809 and HD 15629 are two O stars with similar luminosities (Repolust et al. 2004), and the derived Ṁ is higher for HD 210809, which is the cooler object. This would be consistent with model calculations if the cooler star was less massive and more evolved. For instance, our 30 and 40 M⊙ models with the experimental wind scheme may be appropriate for such a case. These two models reach the same luminosity at Teff = 27.5 kK and Teff = 44 kK, respectively. At these positions, the Ṁ of the cooler object is slightly larger indeed, when predicted following our approach (see Fig. 6).
Increase of mass-loss rates over the first bi-stability jump in non-rotating Galactic models using the Vink and the experimental wind scheme.
The PBB has a large impact on the size of the jump in mass-loss rate, when considering the immediate region in Teff enclosing the jump temperature. To provide a numerical comparison between the Vink and the experimental wind scenario, Table 5 displays the increase of Ṁ from the hot to the cool side of the jump. For the considered masses between 20 to 60 M⊙, the average increase of Ṁ is a factor of 13.5 using the Vink recipe, while it is 4.4 for the experimental wind (consistent with the adopted change in v∞/vesc by a factor of two, and ΔD0 = 0.35 dex; note that for this test the experimental wind rates have been calibrated to match the Vink rates at early phases and at the cool side of the bi-stability jump). In other words, the increase of Ṁ during the PBB results in a much smaller jump at the bi-stability than predicted by the Vink recipe when considering individual tracks.
We add here that within our prescription of the experimental wind, the choice of a sufficiently large ΔT (increasing the width of the jump) would lead to similar effects as produced by the Brott et al. (2011) interpolation of mass-loss rates between 27.5 and 22.5 kK (see above). In particular, such a procedure would also diminish the pre-bi-stability decrease in Ṁ in the Vink recipe, leading to a somewhat smaller effective jump (cf. Figs. 4 and 5). It might be useful to consider such a choice of ΔT for future studies.
 |
Fig. 7 Mass-loss histories for non-rotating Galactic 30 M⊙ MESA models, adopting different values for the WLR-parameter related to its slope, α′ = 0.61 to 0.69 (indicated next to the tracks). A model with the same initial parameters but using the Vink recipe (without the second jump) is shown for reference. |
5.4. The experimental wind scheme: impact of α′
There are four global parameters (α′, log D0, fvinf, and fscal) in our setup that can influence the calculated mass-loss rates, and in Fig. 7 we show an important test case for a 30 M⊙, Galactic Z, non-rotating model, when α′ is varied (we recall that this parameter has a physical meaning, and is most commonly adopted in the range between 0.50 and 0.70), and the other parameters remain unchanged. Following the clumping-corrected values from Mokiem et al. (2005) and Mokiem et al. (2007b), α′ has been specified to lie in the range between 0.61 and 0.69 (corresponding to x = 1.63−1.45), while log D0 has been fixed at a value corresponding to smooth winds, log D0 = 18.40. Obviously, the choice of α′ has a significant impact on the produced mass-loss rates: even for the rather small range of α′ considered, Ṁ varies by a factor of ≳10. Similar results would have been obtained if α′ was fixed, and log D0 was varied. This degeneracy of Ṁ with respect to α′ and D0 is an important issue; for example, when adopting values which are both corrected for wind-inhomogeneities, the mass-loss rates might become significantly reduced compared to the displayed situation (see Sect. 1 and below).
To obtain an impression of the overall mass-loss history, we follow the evolution until the coolest regime of line-driven winds. In these models, the first bi-stability jump temperature has been set to Teff,jump1 = 20.5 kK, according to observational constraints, and we adopted ΔD0(1) = 0.35, following our calibration from the previous section. Interestingly, a variation of α′ affects also the position of the TAMS, because of different mass-loss rates: when lowering α′ and thus increasing Ṁ, the TAMS is shifted to lower effective temperatures.
Moreover, we also considered the second jump, at a temperature Teff,jump2 = 12 kK. For example, when assuming a continuous WLR for late B and early A-type supergiants (i.e., ΔD0(2) = 0), and a decrease in v∞/vesc from 1.3 to 0.7 (e.g., Markova & Puls 2008), this second jump would produce only a minor increase of the mass-loss rates.
5.5. The experimental wind scheme: jump properties
To test the response to different Ṁ prescriptions at the first bi-stability jump, we again considered non-rotating Galactic models. Figure 8 shows a corresponding 40 M⊙ MESA model, where alternative bi-stability scenarios have been simulated, by varying the offset of the WLR over the jump, quantified by ΔD0. Here, we used again a “high” Teff,jump1 = 25 kK, and we simulated increasing, continuous, and moderately decreasing mass-loss rates, by adopting ΔD0 = 0.35,−0.20, and −0.50, respectively. The latter two scenarios are in agreement with the results from Markova & Puls (2008), while a significant jump corresponds to the Vink et al. (1999) predictions. We note that for a continuous Ṁ over the bi-stability region, the offset of the WLR must be decreased to compensate for the decrease in v∞/vesc, 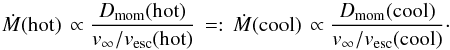 (22)
(22)
 |
Fig. 8 Mass-loss histories for non-rotating Galactic 40 M⊙ MESA models, with different bi-stability jump properties. Red: increase in Ṁ (ΔD0 = 0.35); blue: (almost) continuous Ṁ (ΔD0 = −0.20); green: moderate decrease in Ṁ (ΔD0 = −0.50). A model with the same initial parameters but using the Vink recipe (without the second jump) is shown for reference. |
5.6. Reducing the mass-loss rates in rotating models
After the simple parameter tests presented above, we turn our attention to rotating Galactic models. In the following model calculations, we set the initial rotational velocities to vrot(initial) = 300 kms-1, and we varied only the overall scaling factor (fscal = 1.0,0.6,0.3), while keeping α′ = 0.543 and log D0 = 18.40, respectively. For the mass range (20–60 M⊙) and metallicity (Z = 0.014) considered in this work, this setup recovers the Vink rates when fscal = 1.
Figure 9 shows the result of this test, which aims at simulating the effects from globally reduced mass-loss rates (compared to presently used values), a scenario which is quite likely in view of the current debate (cf. Sect. 1).
It is immediately clear that the inclusion of rotation has a very large impact on the resulting mass-loss rates and vice versa. This effect, however, is rather complex. Close to the ZAMS, the mass-loss rates indeed correspond to their reduced values, and in non-rotating models these differences would remain preserved throughout the evolution, as shown, for example, in our α′ parameter study (Fig. 7). In the rotating models, on the other hand, the initially different mass-loss rates converge to almost identical values between 28–23 kK, before diverging again at lower temperatures. Since we have used quite a large value of ΔT = 3500 K when interpolating over the bi-stability region, the corresponding change in Ṁ is rather gradual (again, we adopted ΔD0(1) = 0.35 to recover the Vink mass-loss rate at the cool side of the jump).
 |
Fig. 9 Mass-loss histories for rotating Galactic 40 M⊙ MESA models, with vrot(initial) = 300 km s-1, and different mass-loss rates corresponding to scaling factors fscal = 1.0 (red), fscal = 0.6 (blue), and fscal = 0.3 (green). The corresponding HRD is provided as an inset. See text for further details. |
To investigate the reason for this interesting behavior, most prominent in the model with fscal = 0.3, we turned off the Spruit-Tayler dynamo which otherwise helps to preserve the surface angular momentum due to a coupled core-envelope configuration. Figure 10 displays the outcome of this test, namely that the internal effects related to rotation can, indeed, have an influence on the (reduced) mass-loss rates.
 |
Fig. 10 As Fig. 9, for two models with fscal = 0.3. The only difference between the models is the inclusion of magnetic-field effects from an internal Spruit-Tayler dynamo on the angular momentum transport (green line; this model is identical to the fscal = 0.3 model from Fig. 9), and the exclusion of such effects (black line). Additionally, we show the corresponding rotational Ṁ boost factors (dashed lines and right ordinate). |
The large difference between the mass-loss rates from the coupled and uncoupled models originates, in fact, from their rotational properties. When the Spruit-Tayler (ST) dynamo is used for angular momentum transport (as in Brott et al. 2011), the model behaves as a solid body rotator (this process also induces an efficient chemical mixing, because of an efficient Eddington-Sweet circulation), therefore it must maintain a flat internal angular velocity profile (see Paxton et al. 2013, their Fig. 29). When this mechanism is not considered, the core angular velocity is higher than in the envelope.
The reason that the originally reduced mass-loss rates become higher than anticipated (the model with fscal = 0.3 reaches mass-loss rates as high as the model with fscal = 1, see Fig. 9), is the “rotational Ṁ boost” (Paxton et al. 2013) implemented in MESA (see Eq. (8)), which approximately accounts for an increased mass-loss due to centrifugal acceleration. We remind the reader that the Brott et al. (2011) models account for a similar mechanism. Additionally, we note that due to these differences the two models do not evolve at identical luminosities, though the corresponding differences are very small (≤0.02 dex until 15 kK).
The boost itself results from a significant difference in the development of the surface rotational velocities of the ST coupled (magnetic) and uncoupled (non-magnetic) models. From Fig. 11, we see that the quasi solid body rotator (i.e., the ST coupled model, green line) approaches its critical velocity around 30 kK. While the rotational velocity remains almost constant, the critical velocity decreases, mostly because of an increasing radius (and, in the problematic formulation of Eq. (6), also because of the increase in luminosity). The reason for the almost constant surface rotational velocity in the ST coupled model is that the surface angular momentum lost due to the wind can be efficiently replaced by angular momentum extracted from the core, thus keeping the surface rotation high. In other words, when strong coupling is present, the whole star must be braked, not only the surface.
When the rotational velocity approaches the critical velocity, the approximate expression for the rotational boost of Ṁ becomes inadequate, but we refrained from manipulating the formulation adopted in MESA – this would require a separate investigation of its own.
Nevertheless, since the basic effects should be qualitatively correct, we conclude that in these test cases an original reduction (referring to slow rotation) of the mass loss, and hence angular momentum loss, is able to significantly influence stellar evolution. In this regard, the treatment of internal angular momentum transport (strongly affected by the presence or absence of internal magnetic fields) plays a major role. Therefore, the revision of mass-loss rates (from the perspective of angular momentum loss) cannot be studied separately, since when changing the angular momentum transport, significant feedback effects will influence the angular momentum loss.
As a side note, we remark that the model with fscal = 0.3 and internal magnetic field displays only a marginal bi-stability jump in Ṁ. In this case, the rotational boost is more efficient at the hot than at the cool side, since at the cool side the rotational velocity departs from the critical one, presumably due to the significant mass loss and angular momentum loss just before and across the jump. Thus, the change in mass loss over the jump is weaker than if both sides would be similarly affected. Further studies on this issue might be required, since it might partly explain a jump lower than predicted, assuming that indeed the mass-loss rates (when discarding rotational effects) were weaker than presently adopted.
5.7. The evolution of surface rotational velocities
If the mass-loss rates are reduced, the angular momentum loss decreases under typical conditions, which has a severe effect on the rotational properties at all stages of stellar evolution. This is one of the issues that can be constrained via observations of vsini, particularly for main sequence and blue supergiant stars. Later and pre-supernova phases are affected even more, since the actual mass and angular momentum content determines the final fate of the star.
To investigate the evolution of vrot in various scenarios, we compare, in a step-by-step approach, our MESA models utilizing the experimental wind scheme with the Ekström et al. (2012) and Brott et al. (2011) tracks (Fig. 12, red and green lines, respectively).
First, we display a 40 M⊙ (Z = 0.014) model (MB1, blue line) that has similar characteristics as the corresponding one from Brott et al. (2011). In particular, we adopted (i) αov = 0.335; (ii) Spruit-Tayler dynamo generated magnetic fields when accounting for the angular momentum transport; (iii) meridional circulation in a diffusive approach; and (iv) mixing efficiencies fc = 0.0228 and fμ = 0.1. The (experimental) mass-loss rates have been calibrated in such a way that they roughly agree, in earlier phases and at the cool side of the first bi-stability jump, with the Vink rates, though the PBB and consequently the change of Ṁ over the jump are different.
A departure between the rotational velocities as predicted by our MESA and the Brott et al. (2011) model is already seen at early phases (around 40 kK). We speculate that these early differences are a consequence of differences in the implementation accounting for the effects of a dynamo generated field in the radiative zones (Heger et al. 2005; Petrovic et al. 2005). We note, for example, that without magnetic fields the rotational velocity decreases even more drastically in early phases, as obvious from the corresponding Ekström et al. (2012) model. The differences in the slope from 35 kK on might be associated with the different PBB, that is, the differences in Ṁ(Teff), of the Vink rates and our experimental wind scheme (see Fig. 6). Since the Bonn models have a shorter MS lifetime (compared to analogous MESA models), they evolve faster, and lose less mass (thus less angular momentum). This issue may explain why their vrot values are consequently higher on the MS compared to our MESA models. Further differences relate to a cooler bi-stability jump temperature in the experimental wind scheme (see next section).
It is well known that internal magnetic fields are predicted to have a major impact on the evolution of surface rotational velocities (see, e.g., Fig. 3 from Maeder & Meynet 2005; and also Maeder 2009). Based on our previous finding that internal magnetic fields can also affect mass-loss rates, via angular momentum transport, we calculated a second model without internal magnetic fields (MB2, black line). Evidently, this model displays considerably lower vrot during its complete MS evolution, compared to the magnetic one. At early stages, this model has a similar vrot history as the corresponding model from Ekström et al. (2012).
Subsequently, we decreased the overall mass-loss rates in the latter non-magnetic model to 30% of its original value (MB3, black dashed line). Very interestingly, this modification results in a similar evolution of vrot as in the original Bonn model. (This similarity could, of course, be also achieved by a somewhat weaker reduction of the mass-loss rates in the magnetic model).
 |
Fig. 12 Surface rotational velocities vs. effective temperature, for rotating Galactic models at 40 M⊙. Models shown are published by (Brott et al. 2011, B11, green line), (Ekström et al. 2012, E12, red line), and three MESA models (MB1, blue line; MB2, black line; MB3, black dashed line). See text. |
The large effect of the reduced mass-loss rates on the surface rotational velocities is remarkable. Though Maeder & Meynet (2005) pointed out that the loss of angular momentum at the surface has a limited impact on the internal rotational properties, here we have shown that the surface angular momentum loss has a large impact on the observable rotational velocities, though it also depends on the effects of internal transport mechanisms (coupled vs. uncoupled configuration). Thus, the evolution of the surface rotational velocities can only be studied if both the surface angular momentum loss and the internal angular momentum transport are considered in a realistic manner. Conversely, a study of the surface rotational velocities can provide severe constraints on these issues.
One may now ask to what extent these findings depend on initial mass. To this end, we calculated a small grid of models with similar assumptions as above, for the range of 20–60 M⊙. In the following section, we quantify the strong impact of Ṁ on vrot as a function of initial mass, and discuss the outcome of our simulations in the context of bi-stability braking proposed by Vink et al. (2010).
5.8. The need for bi-stability braking
For Galactic O-type stars, the measured (projected) rotational velocities display a large scatter, reaching up to vrotsini ≈ 400 km s-1 (e.g., Howarth et al. 1997), though the average initial rotational velocities of massive O stars are currently debated. For example, Simón-Díaz & Herrero (2014) find that essentially all O supergiants of their northern Galactic sample and 71% of all O dwarfs therein have vrotsini< 200 km s-1. In the Howarth et al. (1997) sample, a significant drop in the rotational velocities of B supergiants is observed at around 22 kK. To date, there is overwhelming observational evidence supporting an average surface rotational velocity on the order of vrotsini ≈ 50 km s-1 for late blue supergiants (Huang et al. 2010; Hunter et al. 2009; Fraser et al. 2010). If the blue supergiants are the direct descendants of O-type stars, then the steep drop in the rotational velocities implies that a braking mechanism must be present. To this end, Vink et al. (2010) proposed that a large jump in the mass-loss rates at the first bi-stability (the bi-stability braking, BSB) could efficiently remove surface angular momentum, and hence reduce the surface rotation of the star. However, we stress again that at least a large jump in Ṁ is debated, and that the jump temperature which is used in current evolutionary models most likely needs to be shifted to cooler temperatures.
Moreover, Vink et al. (2010) emphasized that the possibility of BSB depends on the adopted evolutionary models. However, it has not been investigated in detail which models would require a BSB to reach low vrot in the B supergiant regime, and which would not.
The 32–60 M⊙ tracks of Ekström et al. (2012) can be easily inspected (Fig. 13). These models do not need a BSB; they already brake the surface rotational velocities at high temperatures, because of discarding internal magnetic fields and applying Vink mass-loss rates, which in most cases are larger than those used in the Bonn models, due to a higher luminosity (see Sect. 5.1). The 20 and 25 M⊙ tracks (the latter not shown here) are somewhat misleading: because of the comparatively small overshoot parameter, these tracks reach the end of the main sequence just before the bi-stability jump. Here, we interpret the hooks in the vrot-tracks as a result from the corresponding hooks in the HRD, meaning those related to changes in the internal structure of the star, and not as a result of bi-stability braking. This assumption can be justified if one recalls that the adopted jump temperature is at 24 and 25 kK for the 20 and 25 M⊙ model, respectively. These values clearly do not coincide with the drop in vrot that occurs at higher temperatures, therefore the braking in this case is attributed to reaching the TAMS. We conclude that none of the Ekström et al. (2012) models would require a BSB to account for slowly rotating B supergiants. One might now argue that these models, with weak overshooting, would yield lifetimes in the B supergiant regime that are too short to be compatible with the observed large population of such objects, at least when relying on the hypothesis that they were the immediate descendants of O stars. However, even when increasing the overshoot parameter to account for this possibility, the large angular momentum loss in early phases would not be affected, and still no BSB would be required.
The Brott et al. (2011) models maintain a higher surface angular momentum before the first jump, mainly due to the coupled core-envelope configuration achieved by the effects of a Spruit-Tayler dynamo mechanism in the radiative zone (as discussed before in Sect. 5.6). For most of these models, it can be safely stated that bi-stability braking is required to reduce the rotational velocities and to match the observed values. Only the 20 M⊙ case is problematic. Even with an increase of a factor of 15 in the mass-loss rates, the bi-stability jump seems to be insufficient to brake this model’s large surface rotational velocity. To investigate the impact of important assumptions regarding internal momentum transport and mass loss (which obviously cannot be tested when relying on published models alone), we calculated a small grid of MESA models with different setup, labeled as MB1 to MB4, respectively. The general setup of models MB1 to MB3 has already been described in the previous section, and these models are augmented here by an additional magnetic model MB4 with fscal = 0.3. These models are summarized in Table 6 for easy comparison.
 |
Fig. 13 Various Galactic metallicity models to investigate the potential role of bi-stability braking, with initial masses between 20 to 60 M⊙, and initial rotational velocities ≈300 km s-1. For reference, the Geneva models (red, E12) and the Bonn models (green B11) are indicated. (Note that there is no 30 M⊙ but a 32 M⊙ model available from the Ekström et al. (2012) grid.) For the set-up of MESA models MB1 to MB4, see Table 6 and Sect. 5.7. |
Evaluating the results displayed in Fig. 13, the role of the BSB can be determined. As a conclusion on its necessity, the following (crude) criterion was checked for each model: is there a steep drop in the surface rotational velocity required to obtain models in the region Teff < 20 kK and vrot < 100 km s-1? In other words, would the models evolve to Teff < 20 kK with vrot > 100 km s-1 without the benefit of an increase in Ṁ related to the bi-stability of the winds? If the answer to both questions is yes, then the BSB may be required - keeping in mind that the BSB is not the only mechanism capable of reducing angular momentum. By inspecting Fig. 13 (see also the last column of Table 6), we find the following situation: whereas in models MB1 and MB2 a BSB is only required for stars with M < 30 M⊙, models with a decreased mass-loss rate (MB3 and MB4, respectively) would always require a BSB – except for the 60 M⊙ MB3 model – to enable slowly-rotating B supergiants.
Various models to check the requirement for BSB.
However, there is also the problem that in almost all 20 M⊙ models (except for the one presented by Ekström et al. 2012), and in models MB3/MB4 with 30 M⊙, the bi-stability braking alone is still not sufficient to push the rotational velocities below 100 km s-1 for Teff< 20 kK. This is a serious challenge, as we note that the increase in Ṁ as adopted here may already overestimate the actual situation.
6. Discussion
As shown by our model calculations, the evolution of the surface rotational velocities of massive stars are not only determined by the effects of internal angular momentum transport, but are strongly and qualitatively influenced by the magnitude and evolution of mass-loss rates. Although the existence and origin of internal magnetic fields, and their role in determining the internal angular momentum transport are debated, such magnetic fields – when included in evolutionary models – often dominate this transport mechanism (Maeder & Meynet 2005; Heger et al. 2005). Moreover, the actual treatment of the Eddington-Sweet circulation (i.e., a diffusive or advective approach) must also be considered when relying on specific evolutionary models, since in a diffusive approach this is the largest term contributing to chemical mixing (see also Song et al. 2016).
Regardless of the differences in the treatment of meridional circulation, mixing efficiencies, or the consideration of internal magnetic fields, a reduction of the mass-loss rates (i.e. fscal = 0.3) compared to the currently used theoretical prescriptions (fscal = 1) would result in less angular momentum loss, which in turn would keep the surface rotation in massive stars closer to their initial velocities throughout the main sequence evolution. According to our simulations, only for M ≳ 60 M⊙ it is still possible to brake stellar rotational velocities significantly, when internal magnetic fields are not included (see Fig. 13). This is a very drastic and observable effect, especially as the mass-loss rates were changed by a factor of only between two and three when accounting for the different overall rates.
In our models with a fully diffusive scheme, the current disagreement between mass-loss rates predicted by the standard Vink recipe and those derived from observations leads to a dichotomy of potential scenarios:
-
(i)
If the mass-loss rates derived from observations are considered(a factor of between two and three less than the Vink rates), thenthere is a need for bi-stability braking, requiring a large jump inṀ which has not been observed thus far. Otherwise, model calculations would predict a large sample of late B supergiants with high surface rotational velocities.
-
(ii)
If, on the other hand, the Vink rates (for Teff >Teff,jump1) are correct, there may be no need for a large jump in Ṁ at the bi-stability (depending on the particular evolutionary model), in agreement with observational evidence.
In this context, we must also consider (at least) two observational constraints. Namely, is the average surface rotational velocity adopted at the ZAMS (300 km s-1) too high? Or, is it possible that there are late B supergiants with vrot > 100 km s-1 that are not observed, for example, due to their short lifetime in that region?
Indeed, it is not clear that all O stars are fast rotators at or close to the ZAMS. As already pointed out, the majority of northern Galactic O stars analyzed by Simón-Díaz & Herrero (2014) has vrotsini < 200 km s-1. If these values were common, then for a considerable number of stars, mass-loss rates lower (by a factor of between two and three) than those currently adopted would mean that BSB is not required. In this case, no significant angular momentum loss would be required to brake rotation and thus to enable the production of slowly rotating B supergiants.
Whether a larger number of late B supergiants with vrot > 100 km s-1 exists but has not been detected might also be an observational issue. Adopting a large overshoot parameter for consistency reasons in our model calculations from Brott et al. (2011) ensures that our late B supergiants are still core hydrogen burning, although the typical main sequence lifetime of the models below 20 kK is short. For example, in case of our 40 M⊙ models (Fig. 13) only the last 3% of their main sequence lifetime is spent in that regime.
There is no clear consensus whether the observed B supergiants are core-hydrogen burning main sequence or core-helium burning post-main sequence objects (e.g., Vink et al. 2010; Meynet et al. 2015). Indeed, it might be possible that B supergiants are not a homogeneous sample, which would make the evaluation of a requirement for BSB even more challenging. Nevertheless, if B supergiants are the direct descendants of O stars, a physical mechanism for angular momentum loss must be established, whether or not the BSB exists.
7. Conclusions and future work
In this study we have investigated the impact of mass loss on the early stages of massive star evolution. We aimed to understand whether the discrepancy between mass-loss rates from theoretical predictions and from recent diagnostics could be clarified in terms of evolutionary constraints. To this extent, we developed a simple wind routine which has been implemented into MESA, and we simulated stellar evolution using various mass-loss rates, particularly rates that are either compatible with those predicted by Vink et al. (2000) or with state-of-the-art observational diagnostics.
Our experimental wind description is based on the semi-empirical WLR, and has been implemented within an easily adjustable, flexible and fast routine. For the sake of simplicity, we considered the corresponding parameters, slope x = 1 /α′ (see Eq. (13)), and offset log D0, as constant for Teff > Teff,jump1. For more sophisticated models a Teff-dependence might need to be considered (e.g., Lamers et al. 1995; Puls et al. 2000). Furthermore, due to the line-driving mechanism, both parameters depend on metallicity, though in this work we only considered Galactic models, thus avoiding such an explicit dependence. We emphasize that this observationally guided routine relies on existing scaling relations, and that it is not a new mass-loss description, in contrast to the much more complex approaches by, for example, Gräfener & Hamann (2005), Bouret et al. (2012), or Petrov et al. (2016).
From our model calculations, in which we adopted a fully diffusive scheme, we draw the following conclusions that are mostly independent of assumptions about internal magnetic fields and their coupling with angular momentum transport: for a mass range between 20 to 60 M⊙, and canonical initial rotational speeds, vrot(init) ≈ 300 km s-1, it is not possible to simultaneously account for (i) lower overall mass-loss rates (here: by a factor of between two and three); and (ii) a smaller increase of Ṁ over the bi-stability region, compared to the predictions by Vink et al. (2000, 2001). Otherwise, the models would retain too high surface rotational velocities in the late B supergiant regime. An obvious alternative would become feasible if either the rotational velocities at/close to the ZAMS were significantly lower than adopted here, or if a yet unidentified, efficient braking mechanism would operate during the early stages of massive star evolution.
As an interesting secondary result, we also found that initially weaker winds can become significantly amplified in their subsequent evolution by the rotational boost, for models which account for a coupled core-envelope configuration due to magnetic fields (quasi solid body rotators). This effect would lead to a lower effective Ṁ jump across the bi-stability region, and might help to understand corresponding observational findings.
During our investigation, we identified the following problems that must be studied to enable further progress:
-
What are the real mass-loss rates before the onset of thebi-stability, for temperatures lower than roughly35 kK? Do they increase (experimental wind) ordecrease (Vink rates) with time? This pre-bi-stability behavior(PBB) plays a crucial role in determining the actual value of thebi-stability jump regarding Ṁ.
-
Is there a gradual change in mass-loss rates at ≈18−23 kK, corresponding to the observed gradual behavior of vesc/v∞?
-
What are the average ZAMS surface rotational velocities of O-type stars, and are there any rapidly-rotating (single) B supergiants below 20 kK?
-
Approximately 10% of massive stars have detected surface magnetic fields (e.g., Wade et al. 2014), and thus could experience magnetic braking accounting for slow rotation (see Meynet et al. 2011). Is it possible that weaker, as-yet undetected surface magnetic fields in massive stars result in an efficient removal of surface angular momentum? The challenge of detecting magnetic fields in the often complex and variable spectra of O stars makes this question worthy of further investigation.
-
Stellar evolution codes do not agree on the implementation of the first and second bi-stability jump adopting the Vink rates, and the size of the jump in Ṁ is much larger than the originally considered value by Vink et al. (2000). This is in contradiction with observations (and also with recent wind calculations by Petrov et al. 2016), and evolutionary models might significantly overestimate the mass-loss rates at the cool side of the bi-stability.
-
The necessarily simplified treatment of the complex interactions and evolution of magnetic fields in 1D hydrodynamical calculations implies that results will be approximate. While the characteristics of internal fields and their effects are still debated, it is clear that such fields, if present, could have extremely important consequences for stellar evolution. Moreover, the existence of strong surface magnetic fields is now known for a handful of O stars (e.g., Wade & MiMeS Collaboration 2015). The direct effects of these surface magnetic fields – on both mass loss and rotation – also urgently need to be implemented in stellar evolution calculations (e.g., Petit et al., in prep.).
Although, in our opinion, the predicted evolution vs. diagnostics of vrot is an ideal tool to study open issues in evolutionary calculations, particularly regarding mass loss, there are also other constraints that need to be considered. Most important in this respect are diagnostics of the abundances of nuclear-processed material mixed into the stellar surface layers, where the mixing efficiency strongly depends on the angular velocity profile between the core and the envelope. Since diagnostics of surface CNO abundances have made considerable progress in recent years (e.g., Hunter et al. 2008; Przybilla et al. 2010; Rivero González et al. 2012; Bouret et al. 2012; Martins et al. 2015a,b), the inclusion of such results into studies similar to the present work will certainly lead to further understanding of the evolution of massive stars during the main sequence and beyond.
MESA is free, open source software, available for download from: http://mesa.sourceforge.net
Using radiative accelerations as calculated by the NLTE atmosphere code CMFGEN (Hillier & Miller 1998).
When combining the second and third term on the rhs of Eq. (19) and assuming v∞ ∝ vesc, any explicit radius dependence vanishes
Acknowledgments
We appreciate fruitful discussions with Jorick Vink, Ines Brott, Norbert Langer, Raphael Hirschi, and Jose Groh, and we acknowledge the MESA developers for making their code publicly available. We thank the referee of this paper, Cyril Georgy, for his valuable comments and suggestions. G.A.W. acknowledges Discovery Grant support from the Natural Science and Engineering Research Council (NSERC) of Canada.
References
- Abbott, D. C. 1982, ApJ, 259, 282 [NASA ADS] [CrossRef] [Google Scholar]
- Aerts, C. 2015, New windows on massive stars: asteroseismology, interferometry, and spectropolarimetry, Proc. International Astronomical Union, IAU Symp., 307, 154 [Google Scholar]
- Angulo, C., Arnould, M., Rayet, M., et al. 1999, Nucl. Phys. A, 656, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Arnett, D., Meakin, C., & Young, P. A. 2009, ApJ, 690, 1715 [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., & Sauval, A. J. 2005, Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis, eds. T. G. Barnes III, & F. N. Bash, ASP Conf. Ser., 336, 25 [Google Scholar]
- Bjorkman, J. E., & Cassinelli, J. P. 1993, ApJ, 409, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Bouret, J.-C., Hillier, D. J., Lanz, T., & Fullerton, A. W. 2012, A&A, 544, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Braithwaite, J. 2006, A&A, 449, 451 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Briquet, M., Morel, T., Thoul, A., et al. 2007, MNRAS, 381, 1482 [NASA ADS] [CrossRef] [Google Scholar]
- Briquet, M., Neiner, C., Aerts, C., et al. 2012, MNRAS, 427, 483 [NASA ADS] [CrossRef] [Google Scholar]
- Brott, I., de Mink, S. E., Cantiello, M., et al. 2011, A&A, 530, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castor, J. I., Abbott, D. C., & Klein, R. I. 1975, A&A, 195, 154 [Google Scholar]
- Castro, N., Fossati, L., Langer, N., et al. 2014, A&A, 570, A13 [Google Scholar]
- Chieffi, A., & Limongi, M. 2013, ApJ, 764, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, D., Sundqvist, J., & Leutenegger, M. 2013, Massive Stars: From alpha to Omega, held 10–14 June 2013 in Rhodes, Greece, 36 [Google Scholar]
- Crowther, P. A., Lennon, D. J., & Walborn, N. R. 2006, A&A, 446, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cunha, K., Hubeny, I., & Lanz, T. 2006, ApJ, 647, 143 [Google Scholar]
- Cyburt, R. H., Amthor, A. M., Ferguson, R., et al. 2010, ApJSS, 189, 240 [NASA ADS] [CrossRef] [Google Scholar]
- de Jager, C., Nieuwenhuijzen, H., & van der Hucht, K. A. 1988, A&AS, 72, 259 [NASA ADS] [Google Scholar]
- de Mink, S. E., Cantiello, M., Langer, N., et al. 2009, A&A, 497, 243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eggenberger, P., Meynet, G., Maeder, A., et al. 2008, Astrophys. Space Sci., 316, 43 [Google Scholar]
- Ekström, S., Georgy, C., Eggenberger, P., et al. 2012, A&A, 537, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Espinosa Lara, F., & Rieutord, M. 2011, A&A, 533, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feldmeier, A., Oskinova, L., & Hamann, W.-R. 2003, A&A, 403, 217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fraser, M., Dufton, P. L., Hunter, I., & Ryans, R. S. I. 2010, MNRAS, 404, 1306 [NASA ADS] [Google Scholar]
- Friend, D. B., & Abbott, D. C. 1986, ApJ, 311, 701 [NASA ADS] [CrossRef] [Google Scholar]
- Georgy, C., Ekström, S., Granada, A., et al. 2013, A&A, 553, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gräfener, G., & Hamann, W.-R. 2005, A&A, 432, 633 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grevesse, N., Noels, A., & Sauval, A. J. 1996, Astrophysics Conference in College Park; Maryland; 9–11 October 1995; San Francisco, Proc. Sixth annual October Astrophysics Conference, eds. S. S. Holt, & G. Sonneborn, ASP Conf. Ser., 99, 117 [Google Scholar]
- Groenewegen, M. A. T., Lamers, H. J. G. L. M., & Pauldrach, A. W. A. 1989, A&A, 221, 78 [NASA ADS] [Google Scholar]
- Groh, J. H., Meynet, G., Ekström, S., & Georgy, C. 2014, A&A, 564, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heger, A., Langer, N., & Woosley, S. E. 2000, ApJ, 528, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Heger, A., Woosley, S. E., & Spruit, H. C. 2005, ApJ, 626, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Hervé, A., Rauw, G., & Naze, Y. 2013, A&A, 551, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Herwig, F. 2000, A&A, 360, 952 [NASA ADS] [Google Scholar]
- Hillier, D. J. 1991, A&A, 247, 455 [NASA ADS] [Google Scholar]
- Hillier, D. J., & Miller, D. L. 1998, ApJ, 496, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Hirschi, R., Meynet, G., & Maeder, A. 2004, A&A, 425, 649 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Howarth, I., Siebert, K., Hussain, G., & Prinja, R. 1997, MNRAS, 284, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, W., Gies, D., & McSwain, M. V. 2010, ApJ, 722, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Huenemoerder, D. P., Oskinova, L. M., Ignace, R., et al. 2012, ApJ, 756, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, I., Brott, I., Lennon, D. J., et al. 2008, ApJ, 676, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, I., Brott, I., Langer, N., et al. 2009, A&A, 496, 841 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iglesias, C. A., & Rogers, F. J. 1993, ApJ, 412, 752 [NASA ADS] [CrossRef] [Google Scholar]
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, S., Hirschi, R., Pignatari, M., et al. 2015, MNRAS, 447, 3115 [NASA ADS] [CrossRef] [Google Scholar]
- Kippenhahn, R., Weigert, A., & Weiss, A. 2012, Stellar Structure and Evolution 2nd edn. (Berlin Heidelberg: Springer-Verlag) [Google Scholar]
- Köhler, K., Langer, N., de Koter, A., et al. 2015, A&A, 573, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kudritzki, R. P., & Puls, J. 2000, ARA&A, 38, 613 [NASA ADS] [CrossRef] [Google Scholar]
- Kudritzki, R. P., Pauldrach, A. W. A., Puls, J., & Abbott, D. C. 1989, A&A, 219, 205 [NASA ADS] [Google Scholar]
- Kudritzki, R. P., Lennon, D. J., & Puls, J. 1995, in ESO Astrophysics Symposia, Science with the VLT, eds. J. R. Walsh, & I. J. Danziger (Heidelberg: Springer), 46 [Google Scholar]
- Langer, N. 1986, A&A, 164, 45 [NASA ADS] [Google Scholar]
- Langer, N. 1998, A&A, 329, 551 [NASA ADS] [Google Scholar]
- Langer, N., Kiriakidis, M., El Eid, M. F., Fricke, K. J., & Weiss, A. 1988, A&A, 192, 177 [NASA ADS] [Google Scholar]
- Lamers, H. J. G. L. M., Snow, T. P., & Lindholm, D. M. 1995, ApJ, 455, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Leutenegger, M. A., Cohen, D. H., Sundqvist, J. O., & Owocki, S. P. 2013, ApJ, 770, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Lodders, K. 2003, ApJ, 591, 1220 [NASA ADS] [CrossRef] [Google Scholar]
- Lucy, L. B., & Solomon, P. M. 1970, ApJ, 159, 879 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A. 1999, A&A, 347, 185 [NASA ADS] [Google Scholar]
- Maeder, A. 2009, Physics, Formation and Evolution of Rotating Stars (Berlin Heidelberg: Springer-Verlag) [Google Scholar]
- Maeder, A., & Meynet, G. 2000, A&A, 361, 159 [NASA ADS] [Google Scholar]
- Maeder, A., & Meynet, G. 2003, A&A, 411, 543 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maeder, A., & Meynet, G. 2005, A&A, 440, 1041 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maeder, A., & Zahn, J.-P. 1998, A&A, 334, 1000 [NASA ADS] [Google Scholar]
- Markova, N., & Puls, J. 2008, A&A, 478, 823 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Markova, N., Puls, J., Repolust, T., & Markov, H. 2004, A&A, 413, 693 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martins, F., & Palacios, A. 2013, A&A, 560, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martins, F., Schaerer, D., & Hillier, D. J. 2005, A&A, 436, 1049 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martins, F., Hervé, A., Bouret, J.-C., et al. 2015a, A&A, 575, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martins, F., Simón-Díaz, S., Palacios, A., et al. 2015b, A&A, 578, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McEvoy, C. M., Dufton, P. L., Evans, C. J., et al. 2015, A&A, 575, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meynet, G., Maeder, A., Schaller, G., Schaerer, D., & Charbonnel, C. 1994, A&AS, 103, 97 [Google Scholar]
- Meynet, G., Eggenberger, P., & Maeder, A. 2011, A&A, 525, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meynet, G., Kudritzki, R. P., & Georgy, C. 2015, A&A, 581, A15 [Google Scholar]
- Mokiem, M. R., de Koter, A., Puls, J., et al. 2005, A&A, 441, 711 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mokiem, M. R., de Koter, A., Evans, C. J., et al. 2007a, A&A, 465, 1003 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mokiem, M. R., de Koter, A., Vink, J. S., et al. 2007b, A&A, 473, 603 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moravveji, E., Aerts, C., Papics, P. I., Triana, S. A., & Vandoren, B. 2015, A&A, 580, A14 [Google Scholar]
- Müller, P. E., & Vink, J. S. 2014, A&A, 564, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Najarro, F., Hanson, M. M., & Puls, J. 2011, A&A, 535, A25 [Google Scholar]
- Neiner, C., Mathis, S., Alecian, E., et al. 2015, Proc. IAU, 305, 61 [Google Scholar]
- Nieuwenhuijzen, H., & de Jager, C. 1990, A&A, 231, 134 [NASA ADS] [Google Scholar]
- Oskinova, L. M., Hamann, W.-R., & Feldmeier, A. 2007, A&A, 476, 1331 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pauldrach, A. W. A., & Puls, J. 1990, A&A, 237, 409 [NASA ADS] [Google Scholar]
- Pauldrach, A. W. A., Puls, J., & Kudritzki, R. P. 1986, A&A, 164, 86 [NASA ADS] [Google Scholar]
- Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
- Paxton, B., Cantiello, M., Arras, P., et al. 2013, ApJS, 208, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Paxton, B., Marchant, P., Schwab, J., et al. 2015, ApJS, 2, 4 [Google Scholar]
- Petermann, I., Langer, N., Castro, N., & Fossati, L. 2015, A&A, 584, A7 [Google Scholar]
- Petrov, B., Vink, J., & Gräfener, G. 2016, MNRAS, 458, 1999 [NASA ADS] [CrossRef] [Google Scholar]
- Petrovic, J., Langer, N., Yoon, S.-C., & Heger, A. 2005, A&A, 435, 247 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Potter, A. T., Tout, C. A., & Edridge, J. J. 2012, MNRAS, 419, 748 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Prinja, R. K., & Massa, D. L. 1998, in Boulder-Munich II: Properties of Hot, Luminous Stars, ed. Ian Howarth, ASP Conf. Ser., 131, 218 [Google Scholar]
- Prinja, R. K., Barlow, M. J., & Howarth, I. D. 1990, ApJ, 361, 607 [NASA ADS] [CrossRef] [Google Scholar]
- Przybilla, N., Firnstein, M., Nieva, M. F., Meynet, G., & Maeder, A. 2010, A&A, 517, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Puls, J., Kudritzki, R.-P., Herrero, A., et al. 1996, A&A, 305, 171 [NASA ADS] [Google Scholar]
- Puls, J., Springmann, U., & Lennon, M. 2000, A&A, 141, 23 [Google Scholar]
- Puls, J., Markova, N., Scuderi, S., et al. 2006, A&A, 454, 625 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Puls, J., Vink, J. S., & Najarro, F. 2008, ARA&A, 16, 209 [Google Scholar]
- Puls, J., Sundqvist, J. O., & Markova, N. 2015, in New windows on massive stars: asteroseismology, interferometry, and spectropolarimetry, Proc. IAU Symp., 307, 25 [Google Scholar]
- Rauw, G., Hervé, A., Nazé, Y., et al. 2015, A&A, 580, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Repolust, T., Puls, J., & Herrero, A. 2004, A&A, 414, 349 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rivero González, J. G., Puls, J., Najarro, F., & Brott, I. 2012, A&A, 537, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rüdiger, G., Kitchatinov, L. L., & Elstner, D. 2012, MNRAS, 425, 2267 [NASA ADS] [CrossRef] [Google Scholar]
- Schaller, G., Schaerer, D., Meynet, G., & Maeder, A. 1992, A&AS, 96, 269 [Google Scholar]
- Simón-Díaz, S., & Herrero, A. 2014, A&AS, 562, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Song, H. F., Meynet, G., Maeder, A., Ekstrom, S., & Eggenberger, P. 2016, A&A, 585, A21 [Google Scholar]
- Spruit, H. C. 2002, A&A, 381, 923 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stello, D., Cantiello, M., Fuller, J., et al. 2016, Nature, 529, 364 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Sundqvist, J. O. 2013, Massive Stars: From alpha to Omega, held 10–14 June 2013 in Rhodes, Greece, 47 [Google Scholar]
- Sundqvist, J. O., Puls, J., Feldmeier, A., & Owocki, S. P. 2011, A&A, 528, 16 [Google Scholar]
- Tayler, R. J. 1973, MNRAS, 161, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Šurlan, B., Hamann, W.-R., Aret, A., et al. 2013, A&A, 559, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 1999, A&A, 350, 181 [NASA ADS] [Google Scholar]
- Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2000, A&A, 362, 295 [NASA ADS] [Google Scholar]
- Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2001, A&A, 369, 574 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vink, J. S., Brott, I., Gräfener, G., et al. 2010, A&A, 512, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wade, G. A., Grunhut, J., Alecian, E., et al. 2014, in Magnetic Fields throughout Stellar Evolution, Proc. IAU Symp., 302, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Wade, G. A., & MiMeS Collaboration. 2015, in Physics and Evolution of Magnetic and Related Stars, eds. Y. Y. Balega, I. I. Romanyuk, & D. O. Kudryavtsev, ASP Conf. Ser., 494, 30 [Google Scholar]
- Yoon, S.-C., & Langer, N. 2005, A&A, 443, 643 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zahn, J.-P. 1992, A&A, 265, 115 [NASA ADS] [Google Scholar]
- Zahn, J.-P., Brun, A. S., & Mathis, S. 2007, A&A, 474, 145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Surface rotational velocities in the Brott et al. (2011) grid and our experimental model grid for four representative initial masses.
Comparison of the increase of mass-loss rates over the bi-stability jump(s) in the non-rotating Galactic Ekström et al. (2012) and Brott et al. (2011) evolutionary grids.
Increase of mass-loss rates over the first bi-stability jump in non-rotating Galactic models using the Vink and the experimental wind scheme.
All Figures
 |
Fig. 1 Comparison between non-rotating Galactic Z Geneva evolutionary tracks on the MS published by Ekström et al. (2012, black dashed), and our MESA models calculated with a similar setup (colored lines). Initial masses in solar units are indicated next to the tracks. A step overshoot parameter, αov = 0.1, was used. |
| In the text | |
 |
Fig. 2 Comparison between non-rotating Galactic Z Bonn evolutionary tracks on the MS published by Brott et al. (2011, black dashed), and our MESA models calculated with a similar setup (colored lines). A step overshoot parameter, αov = 0.335, was used. Stars above 40 M⊙ are still on the main sequence at rather low effective temperatures. The lack of hooks at higher masses is due to envelope inflation (N. Langer, priv. comm.), treated similarly in STERN and MESA. |
| In the text | |
 |
Fig. 3 Comparison between rotating Galactic Z Bonn evolutionary tracks on the MS published by Brott et al. 2011 (black dashed) and our MESA models calculated with a similar setup (colored lines). The average initial surface rotational velocity of the grid models is ≈270 km s-1 (exact values indicated in Table 2). A step overshoot parameter, αov = 0.335, was used. |
| In the text | |
 |
Fig. 4 Mass-loss histories for non-rotating Galactic 40 M⊙ models from Ekström et al. (2012) and Brott et al. (2011), adopting the Vink mass-loss prescription. See text. |
| In the text | |
 |
Fig. 5 As Fig. 4, but for rotating models. Both evolution models have vrot(initial) ≈ 315 km s-1. The Geneva model becomes more luminous from ≈39 kK on, which results in higher mass-loss rates. |
| In the text | |
 |
Fig. 6 Comparison between MESA models applying either the Vink recipe or our experimental wind scheme, in terms of mass-loss rates versus effective temperature. Initial masses (in solar units) indicated next to the tracks. See text. |
| In the text | |
 |
Fig. 7 Mass-loss histories for non-rotating Galactic 30 M⊙ MESA models, adopting different values for the WLR-parameter related to its slope, α′ = 0.61 to 0.69 (indicated next to the tracks). A model with the same initial parameters but using the Vink recipe (without the second jump) is shown for reference. |
| In the text | |
 |
Fig. 8 Mass-loss histories for non-rotating Galactic 40 M⊙ MESA models, with different bi-stability jump properties. Red: increase in Ṁ (ΔD0 = 0.35); blue: (almost) continuous Ṁ (ΔD0 = −0.20); green: moderate decrease in Ṁ (ΔD0 = −0.50). A model with the same initial parameters but using the Vink recipe (without the second jump) is shown for reference. |
| In the text | |
 |
Fig. 9 Mass-loss histories for rotating Galactic 40 M⊙ MESA models, with vrot(initial) = 300 km s-1, and different mass-loss rates corresponding to scaling factors fscal = 1.0 (red), fscal = 0.6 (blue), and fscal = 0.3 (green). The corresponding HRD is provided as an inset. See text for further details. |
| In the text | |
 |
Fig. 10 As Fig. 9, for two models with fscal = 0.3. The only difference between the models is the inclusion of magnetic-field effects from an internal Spruit-Tayler dynamo on the angular momentum transport (green line; this model is identical to the fscal = 0.3 model from Fig. 9), and the exclusion of such effects (black line). Additionally, we show the corresponding rotational Ṁ boost factors (dashed lines and right ordinate). |
| In the text | |
 |
Fig. 11 Rotational and critical velocities for the two models from Fig. 10. |
| In the text | |
 |
Fig. 12 Surface rotational velocities vs. effective temperature, for rotating Galactic models at 40 M⊙. Models shown are published by (Brott et al. 2011, B11, green line), (Ekström et al. 2012, E12, red line), and three MESA models (MB1, blue line; MB2, black line; MB3, black dashed line). See text. |
| In the text | |
 |
Fig. 13 Various Galactic metallicity models to investigate the potential role of bi-stability braking, with initial masses between 20 to 60 M⊙, and initial rotational velocities ≈300 km s-1. For reference, the Geneva models (red, E12) and the Bonn models (green B11) are indicated. (Note that there is no 30 M⊙ but a 32 M⊙ model available from the Ekström et al. (2012) grid.) For the set-up of MESA models MB1 to MB4, see Table 6 and Sect. 5.7. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


