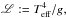| Issue |
A&A
Volume 597, January 2017
|
|
|---|---|---|
| Article Number | A71 | |
| Number of page(s) | 16 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201629612 | |
| Published online | 03 January 2017 | |
Metallicity dependence of envelope inflation in massive stars
1 Argelander-Insitut für Astronomie, Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
e-mail: dsanyal@astro.uni-bonn.de
2 Department of Physics and Astronomy, Seoul National University, 151-747 Seoul, Korea
3 Astronomical Institute of the Czech Academy of Sciences, 251 65 Ondřejov, Czech Republic
Received: 30 August 2016
Accepted: 18 November 2016
Context. Recently it has been found that models of massive stars reach the Eddington limit in their interior, which leads to dilute extended envelopes.
Aims. We perform a comparative study of the envelope properties of massive stars at different metallicities, with the aim to establish the impact of the stellar metallicity on the effect of envelope inflation.
Methods. We analysed published grids of core-hydrogen burning massive star models computed with metallicities appropriate for massive stars in the Milky Way, the Large Magellanic Cloud, and the Small Magellanic Cloud, the very metal poor dwarf galaxy I Zwicky 18, and for metal-free chemical composition.
Results. Stellar models of all the investigated metallicities reach and exceed the Eddington limit in their interior, aided by the opacity peaks of iron, helium, and hydrogen, and consequently develop inflated envelopes. Envelope inflation leads to a redward bending of the zero-age main sequence and a broadening of the main-sequence band in the upper part of the Hertzsprung-Russell diagram. We derive the limiting L/M-values as a function of the stellar surface temperature above which inflation occurs, and find them to be higher for lower metallicity. While Galactic models show inflation above ~29 M⊙, the corresponding mass limit for Population III stars is ~150 M⊙. While the masses of the inflated envelopes are generally low, we find that they can reach 1−100 M⊙ in models with effective temperatures below ~8000 K, with higher masses reached by models of lower metallicity.
Conclusions. Envelope inflation is expected to occur in sufficiently massive stars at all metallicities, and is expected to lead to rapidly growing pulsations, high macroturbulent velocities, and might well be related to the unexplained variability observed in luminous blue variables such as S Doradus and η Carina.
Key words: stars: evolution / stars: massive / stars: interiors / stars: mass-loss
© ESO 2017
1. Introduction
Massive stars, although rare, are cosmic engines in the Universe. They drive the dynamical and chemical evolution of galaxies with their strong stellar winds, high luminosities, and spectacular explosions. The earliest massive stars, that is, the metal-free Population III stars, may have played a major role in the reionisation of the Universe (Bromm et al. 2009). Furthermore, massive stars in low-metallicity environments are primary candidates for progenitors of long-duration gamma-ray bursts (Yoon & Langer 2005; Woosley & Heger 2006), pair instability supernovae (Heger & Woosley 2002; Langer et al. 2007), and superluminous supernovae (Quimby et al. 2013; Inserra & Smartt 2014). Accurate models of massive stars across a wide range of metallicities are therefore needed to facilitate comparisons with the available observational data (Maeder & Meynet 2012; Langer 2012).
Recently, evidence has accumulated that stars more massive than the often quoted upper mass limit of ~150 M⊙ (Figer 2005) exist in the local Universe. For example, Crowther et al. (2010) estimated present-day masses of up to 260 M⊙ for several stars in the Tarantula nebula of the Large Magellanic Cloud (LMC). Furthermore, in the recently concluded VLT-FLAMES Tarantula Survey of massive stars in the LMC (Evans et al. 2011), Bestenlehner et al. (2014) identified three stars with initial mass estimates above 150 M⊙. Models of very massive stars with up-to-date physics have therefore become increasingly relevant.
Initial chemical compositions (in mass fraction), the metallicities, and the range of initial masses of the stellar evolutionary sequences.
The mass-luminosity (M−L) relation for main-sequence stars, L ∝ Mα, has α > 1. However, for constant opacity, α → 1 for M → ∞ (Kippenhahn & Weigert 1990). Therefore one might wonder whether the Eddington limit, which is proportional to L/M, is ever reached by stars.
The classical Eddington limit, which is proportional to the electron-scattering opacity and the stellar L/M ratio, is not reached for stars below ~105M⊙ for solar composition (Kato 1985, 1986). Sanyal et al. (2015) showed that even when the Rosseland mean opacity is considered, stars below ~500 M⊙ do not reach the Eddington limit at their surface. When the Eddington limit is defined in the stellar interior (Langer 1997), however, Sanyal et al. (2015) showed that main-sequence models with LMC composition reach and exceed the Eddington limit at masses M ≳ 40 M⊙. Such stellar models, instead of developing a strong outflow, re-adjust their structure such that a dilute and extended envelope is produced, a process that is called envelope inflation. This effect was earlier pointed out by Ishii et al. (1999) for zero-age main-sequence models and by Petrovic et al. (2006) and Gräfener et al. (2012) for helium star models. As a result of such an envelope structure, the surface temperatures of these models are much lower than they would have been without this effect, which has consequences for the further evolution of the stars (Köhler et al. 2015). The distribution of OB stars in our Galaxy shows many stars with masses >30 M⊙ in the effective temperature range 10 000−30 000 K, and it has been suggested that these stars are affected by envelope inflation (Castro et al. 2014).
The metallicity (Z) of a star affects many of its physical properties such as the wind mass-loss rate, opacity, and the equation of state. The OPAL opacity tables from Iglesias et al. (1992) introduced an opacity peak at a temperature of T ~ 2 × 105K caused by bound-bound and bound-free transitions of iron-group elements. This so-called Fe-bump opacity drastically changed the envelope structure of stellar models (Stothers & Chin 1993), and even new pulsational instability strips were discovered in the Hertzsprung-Russell diagram (Pamyatnykh 1999). Since the Eddington factor depends on opacity, the Fe-bump, which is a function of Z, plays a major role in determining the extent of envelope inflation in a massive-star model.
In this paper, we extend the study by Sanyal et al. (2015) over a wide range of metallicities from Galactic to metal-free, and investigate the properties of the stellar models in the context of the Eddington limit and envelope inflation. Section 2.1 presents an overview of the grids of models used in this study, while in Sects. 3 and 4 we explain our concept of the Eddington limit and envelope inflation. We discuss how the Eddington limit and envelope inflation change with metallicity in Sect. 5 and conclude in Sect. 6.
2. Method
2.1. Stellar models
The stellar models used in the present study were computed with a one-dimensional hydrodynamic Lagrangian code (BEC) that includes the most recent input physics, including rotation (for details, see Heger et al. 2000; Yoon et al. 2006; Brott et al. 2011; Köhler et al. 2015, and references therein). Grids of models computed with five metallicities were used that are appropriate for the Milky Way (MW), LMC, Small Magellanic Cloud (SMC), I Zwicky 18 (I Zw18 ), and for Population III (Pop III) stars. The MW, the LMC, and the SMC models are published in Brott et al. (2011) and Köhler et al. (2015), whereas the I Zw18 and the Pop III models are from Szécsi et al. (2015) and Yoon et al. (2012), respectively. The initial chemical compositions and the initial mass ranges in each of these grids are summarised in Table 1. In this paper, we consider only core-hydrogen burning models that are either non-rotating or slowly rotating, that is, with vrot ≤ 100 km s-1, vrot being the equatorial rotational velocity at the photosphere.
The standard non-adiabatic mixing length theory (MLT, Böhm-Vitense 1958; Kippenhahn & Weigert 1990) was used to model the energy transport in the convective zones in the stellar interior with a mixing length parameter of α = l/Hp = 1.5 (Langer 1991), where l is the mixing length and Hp is the pressure scale height. A discussion of the properties of convection in the inflated envelopes of our LMC models can be found in Sanyal et al. (2015). The parameters for core-convective overshooting (α = 0.335) and rotationally induced chemical mixing (fc = 0.0228, fμ = 0.1) were adopted from Brott et al. (2011). Transport of angular momentum by Spruit-Tayler dynamo (Spruit 2002) was treated following Petrovic et al. (2005). Radiative opacities from the OPAL tables (Iglesias & Rogers 1996) were used for temperatures above 8000 K. For temperatures below 8000 K the opacity tables from Alexander & Ferguson (1994) were used.
2.2. Mass loss
Models for the MW, LMC, SMC, and I Zw18
For stellar models with effective temperatures higher than 22 000 K, the mass-loss prescription from Vink et al. (2001) was employed to account for the winds of O- and B-type stars. The mass-loss rate prescription from Nieuwenhuijzen & de Jager (1990) was used at effective temperatures lower than 22 000 K when the Nieuwenhuijzen & de Jager (1990) mass-loss rate exceeded that of Vink et al. (2001). In the Wolf-Rayet (WR) evolutionary phases, that is, when the surface helium mass fraction (Ys) is greater than 70%, the empirical mass-loss rates from Hamann et al. (1995) were used, scaled down by a factor of 10 (Yoon et al. 2006). For 0.4 ≤ Ys ≤ 0.7, a linear interpolation between the Vink et al. (2000, 2001) mass-loss rate and the Hamann et al. (1995) mass-loss rate reduced by a factor of 10 was used.
Pop III models
For metal-free hot stars, a very low mass-loss rate of 10-14M⊙ yr-1 is predicted near the classical Eddington limit (Marigo et al. 2003; Krtička & Kubát 2006; Yoon et al. 2012). Therefore, in the Pop III grid, stellar wind mass-loss rates were applied only when there was any surface enrichment of CNO elements by rotational mixing. Hence the non-rotating models practically did not suffer from any mass loss over their lifetime. For rotating stars, the mass-loss prescriptions from Kudritzki et al. (1989) and Nieuwenhuijzen & de Jager (1990) were used for Teff> 104K and Teff< 104K respectively, with a metallicity scaling of Z0.69.
Rotationally enhanced mass loss
The effect of rotationally enhanced mass loss (Friend & Abbott 1986; Langer 1997) is treated in our models as 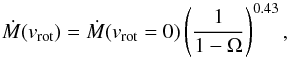 (1)where
(1)where 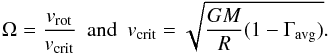 (2)HerevΓavg is the Eddington factor averaged over the region with an optical depth of between 2/3 and 100. The enhancement of the mass-loss rate is limited by the thermal timescale mass-loss rate of the star to avoid the singularity in Eq. (1)as v approaches vcrit (Yoon et al. 2012). We note that for the models analysed in this paper the enhancement to the mass-loss rate is negligible.
(2)HerevΓavg is the Eddington factor averaged over the region with an optical depth of between 2/3 and 100. The enhancement of the mass-loss rate is limited by the thermal timescale mass-loss rate of the star to avoid the singularity in Eq. (1)as v approaches vcrit (Yoon et al. 2012). We note that for the models analysed in this paper the enhancement to the mass-loss rate is negligible.
2.3. Additional models
In the evolutionary sequences computed by Brott et al. (2011) and Köhler et al. (2015), the data regarding the structure of a stellar model are stored for every 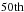 computed model, that is, at non-regular time intervals since the time steps are not uniform during the evolution. For the I Zw18 sequences, every
computed model, that is, at non-regular time intervals since the time steps are not uniform during the evolution. For the I Zw18 sequences, every 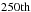 model is stored. To obtain a higher model density in certain parts of the Hertzsprung-Russell (HR) diagram for the present study, several evolutionary tracks (without rotation) were re-computed with the same input parameters, as summarised in Table 2.
model is stored. To obtain a higher model density in certain parts of the Hertzsprung-Russell (HR) diagram for the present study, several evolutionary tracks (without rotation) were re-computed with the same input parameters, as summarised in Table 2.
Initial masses (in units of M⊙) of the non-rotating evolutionary sequences that were re-computed.
3. Eddington limit
Conventionally, a star is considered to be at the Eddington limit when its luminosity L equals its Eddington luminosity (LEdd), which is defined as the condition when the radiative acceleration (grad) balances the gravitational acceleration (g) at the stellar surface. The radiative acceleration is proportional to the stellar luminosity and the opacity κ. When electron scattering is considered as the only source of opacity, that is, κ = κe, the classical Eddington factor is defined as 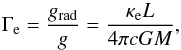 (3)where the physical constants have their usual meaning. With this definition, stellar models reach the Eddington limit only at masses M ≳ 105M⊙ (Kato 1986).
(3)where the physical constants have their usual meaning. With this definition, stellar models reach the Eddington limit only at masses M ≳ 105M⊙ (Kato 1986).
When the Rosseland mean opacities are used, the LMC models from Köhler et al. (2015) do not reach the Eddington limit at their surface, even at 500 M⊙ (Sanyal et al. 2015). However, we can also define an Eddington factor locally (Langer 1997), such that 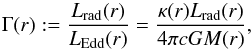 (4)where M(r) is the Lagrangian mass coordinate, κ(r) is the Rosseland mean opacity, and L(r) is the local luminosity. Since the convective luminosity does not contribute to the radiative acceleration, it is not considered in Eq. (4). With this definition, core-hydrogen burning LMC models with masses as low as ~40 M⊙ reach the Eddington limit in their interior (Sanyal et al. 2015). However, instead of a super-Eddington outflow, a hydrostatic structure with an extended envelope is obtained (cf. Sect. 4), often associated with a density inversion (cf. Fig. 9 in Sanyal et al. 2015). It has been argued in the literature (Langer 1997; Sanyal et al. 2015) that the concept of the Eddington limit as a stability criterion does not apply in the stellar interior. If not explicitly stated otherwise, we use the definition in Eq. (4) for the Eddington factor in the rest of the paper.
(4)where M(r) is the Lagrangian mass coordinate, κ(r) is the Rosseland mean opacity, and L(r) is the local luminosity. Since the convective luminosity does not contribute to the radiative acceleration, it is not considered in Eq. (4). With this definition, core-hydrogen burning LMC models with masses as low as ~40 M⊙ reach the Eddington limit in their interior (Sanyal et al. 2015). However, instead of a super-Eddington outflow, a hydrostatic structure with an extended envelope is obtained (cf. Sect. 4), often associated with a density inversion (cf. Fig. 9 in Sanyal et al. 2015). It has been argued in the literature (Langer 1997; Sanyal et al. 2015) that the concept of the Eddington limit as a stability criterion does not apply in the stellar interior. If not explicitly stated otherwise, we use the definition in Eq. (4) for the Eddington factor in the rest of the paper.
Since the Rosseland mean opacity κ depends on the chemical composition and hence the metallicity, the Eddington factor is also expected to be a function of metallicity. Sanyal et al. (2015) showed that in the LMC models from Köhler et al. (2015), the opacity peaks caused by the partial ionisation of iron group elements, helium and hydrogen, shape the profile of the Eddington factor inside a massive star model. In this paper we investigate how the metallicity influences the Eddington factor in the stellar interior.
4. Envelope inflation
As mentioned above, stellar models reaching the Eddington limit in their interior have extended and dilute envelopes (Ishii et al. 1999; Gräfener et al. 2012; Köhler et al. 2015; Sanyal et al. 2015). When the Eddington limit is reached in the interior, either Lrad or the opacity κ needs to be reduced. Since energy transport by convection may be inefficient because of low densities, however, Lrad cannot be significantly reduced in this case, and hence the opacity needs to decrease by a further drop in density. As a result, an inflated envelope develops such that Γ ≈ 1 is maintained across the inflated region. An example of the density structure of such an inflated stellar model is shown in Fig. 1, where the region with a steeply declining density profile is referred to as the non-inflated core and the region with a relatively flat density profile is referred to as the inflated envelope. While the core radius (rcore) of this model is 25.2 R⊙, the extent of the inflated envelope is about 1.7 times that of rcore. The profile of the Eddington factor shows that in the core it is Γ < 1, but in the envelope Γ ≈ 1. At the surface of the star, Γ drops to 0.82.
 |
Fig. 1 Density profile of a 79 M⊙ solar metallicity core-hydrogen burning model showing the inflated envelope. The model had an initial mass of 100 M⊙. The radial co-ordinate has been scaled with the core radius rcore. The blue line (right Y-axis) shows the run of the Eddington factor Γ (Eq. (4)) in the interior of the model. The Eddington factor almost reaches unity in the inflated region. |
To our knowledge, an analytical criterion for inflation is not available in the literature (however, see Sects. 3.4 and 3.5 in Owocki 2015) for models at various evolutionary stages, that is, from hot WR stars (Petrovic et al. 2006) to cool core-hydrogen burning red supergiants (Gräfener et al. 2012; Sanyal et al. 2015; Szécsi et al. 2015). We note that envelope inflation is different from the formation of extended envelopes in classical red supergiants, as those are post-main-sequence stars with a shell-burning source that is responsible for the envelope expansion, through the so-called mirror principle (Kippenhahn & Weigert 1990). In this study we follow Sanyal et al. (2015) to determine whether a stellar model is inflated. Since inflation is related to high values of the Eddington factor, which in turn implies dominance of radiation pressure over gas pressure, the inflated region must have a low enough value of β, where β is the ratio of the gas pressure (Pgas) to the total pressure (P). For all the model grids except for the Pop III grid, we therefore adopt a threshold value of β = 0.15 to identify the base of the inflated envelope rcore in a stellar model, in accordance with Sanyal et al. (2015). For the Minit = 1000 M⊙ sequences in the Pop III grid, we use a lower threshold β = 0.1 because the mass averaged value of β (and the β-value in the centre) drops below 0.15 for some models in these sequences, as expected for models with extremely high luminosities. For all other model sequences of lower masses in the Pop III grid, we use β = 0.15. We motivate our choice of using a threshold value of β to identify the occurrence of an inflated envelope below.
The equation of hydrostatic equilibrium inside a star is given as 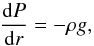 (5)where ρ is the density at r. When we write P = Pgas + Prad, where the radiation pressure is
(5)where ρ is the density at r. When we write P = Pgas + Prad, where the radiation pressure is 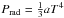 , this is
, this is 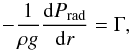 (6)and
(6)and 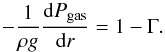 (7)Therefore, Γ → 1 leads to a vanishing gas pressure gradient, and Γ > 1 in the hydrostatic stellar interior merely implies a positive gas pressure gradient (Joss et al. 1973; Paxton et al. 2013). Using Eq. (5)in Eq. (7), we obtain
(7)Therefore, Γ → 1 leads to a vanishing gas pressure gradient, and Γ > 1 in the hydrostatic stellar interior merely implies a positive gas pressure gradient (Joss et al. 1973; Paxton et al. 2013). Using Eq. (5)in Eq. (7), we obtain  Locally, for β either constant or slowly varying, which is generally true in inflated envelopes (Sanyal et al. 2015, cf. Fig. 1), it is
Locally, for β either constant or slowly varying, which is generally true in inflated envelopes (Sanyal et al. 2015, cf. Fig. 1), it is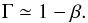 (11)Therefore Γ ≲ 1 implies a low value of β. Since we adopted β = 0.15 as the inflation criterion, we expect to find inflated models with Γ > 0.85, and this is indeed the case (Sanyal et al. 2015). Equation (11) was earlier arrived at by Gräfener et al. (2012), and the validity of the assumption of a constant β in the inflated envelope was shown in studies by Gräfener et al. (2012) and Sanyal et al. (2015).
(11)Therefore Γ ≲ 1 implies a low value of β. Since we adopted β = 0.15 as the inflation criterion, we expect to find inflated models with Γ > 0.85, and this is indeed the case (Sanyal et al. 2015). Equation (11) was earlier arrived at by Gräfener et al. (2012), and the validity of the assumption of a constant β in the inflated envelope was shown in studies by Gräfener et al. (2012) and Sanyal et al. (2015).
To show that Eq. (11)is consistent with the occurrence of a flat density profile, Eq. (7)can also be written as 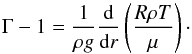 (12)Rearranging Eq. (12)and dividing by ρT on both sides (assuming a constant μ), we obtain
(12)Rearranging Eq. (12)and dividing by ρT on both sides (assuming a constant μ), we obtain 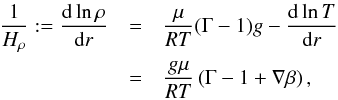 where Hρ is the density scale height and ∇ is the temperature gradient defined as
where Hρ is the density scale height and ∇ is the temperature gradient defined as 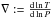 . Substituting β = 1−Γ in the above expression, we obtain
. Substituting β = 1−Γ in the above expression, we obtain 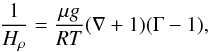 (13)which implies that Hρ → ∞ as Γ → 1. Therefore, when Γ(r) is close to unity, the density scale height becomes very large and leads to an extended, flat density profile, which we identify as a signature of inflation. We furthermore note that a vanishing density gradient, that is,
(13)which implies that Hρ → ∞ as Γ → 1. Therefore, when Γ(r) is close to unity, the density scale height becomes very large and leads to an extended, flat density profile, which we identify as a signature of inflation. We furthermore note that a vanishing density gradient, that is, 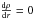 , is equivalent to the condition
, is equivalent to the condition 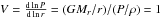 .
.
Quantitatively, we define inflation in a stellar model as Δr/rcore: = (R⋆−rcore) /rcore, where R⋆ is the stellar radius and rcore is the radial co-ordinate where the β value drops below 0.15 for the first time in the stellar interior. Since there is some arbitrariness in our inflation criterion, only those models for which our criterion predicts Δr/rcore> 0.05 are considered to be inflated.
Langer (1997) showed that if the Eddington factor is defined in the stellar interior as 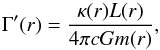 (14)that is, taking the total luminosity into account, then the Schwarzschild criterion for convective instability can be written in the following form:
(14)that is, taking the total luminosity into account, then the Schwarzschild criterion for convective instability can be written in the following form: 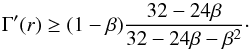 (15)For β ≪ 1, the above inequality reduces to
(15)For β ≪ 1, the above inequality reduces to 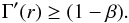 (16)Since
(16)Since 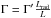 from Eqs. (4)and (15), the above inequality can be written as
from Eqs. (4)and (15), the above inequality can be written as 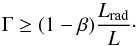 (17)Since Lrad ≤ L everywhere inside the star, from Eqs. (11)and (16)we conclude that the inflated envelope will always be convectively unstable. Furthermore, the densities in the sub-surface convection zones of massive stars are low, and convection is strongly non-adiabatic. As a consequence, particularly in the hot models (Teff ≳ 15 000 K), the luminosity carried by convection is much lower than that carried by radiation, and hence Lrad/L ≈ 1, or Γ ≈ Γ′.
(17)Since Lrad ≤ L everywhere inside the star, from Eqs. (11)and (16)we conclude that the inflated envelope will always be convectively unstable. Furthermore, the densities in the sub-surface convection zones of massive stars are low, and convection is strongly non-adiabatic. As a consequence, particularly in the hot models (Teff ≳ 15 000 K), the luminosity carried by convection is much lower than that carried by radiation, and hence Lrad/L ≈ 1, or Γ ≈ Γ′.
5. Results
5.1. Hertzsprung-Russell diagram
 |
Fig. 2 Zero-age main-sequence (solid lines) and the terminal-age main-sequence lines (dotted lines) above log (L/L⊙) > 4 of the analysed stellar models at different metallicities. The masses of some representative models (black squares) are indicated along the ZAMS. The position of the TAMS (in the model grid) where they bend towards cooler effective temperatures are marked with coloured dots, and the corresponding initial masses of these models are labelled alongside. |
The HR diagram in Fig. 2 shows the zero-age main-sequence (ZAMS) and the terminal-age main-sequence (TAMS) of the analysed non-rotating models. The ZAMS is defined by the condition that 3% of hydrogen (by mass) has been burnt, whereas the TAMS is defined by the location at which the models reach the maximum radius over their main-sequence lifetime, that is, until the central helium mass fraction is <0.98.
The ZAMSs of the different metallicities are located roughly parallel to one another up to log (L/L⊙) ~ 6 in the HR diagram , such that the Pop III ZAMS has the highest Teff (and smallest radius) and the MW ZAMS has the lowest Teff (and largest radius) for corresponding model masses.
The LMC ZAMS reaches a maximum Teff of ~57 000 K and then starts to bend towards lower values around log (L/L⊙) ~ 6.6, which corresponds to a mass of ~200 M⊙. Above this critical mass the surface temperature of the ZAMS models decreases for increasing mass. The lower the metallicity, the higher the luminosity and the effective temperature at which the bend is expected to be located (Ishii et al. 1999). This feature is not seen for all the metallicities in Fig. 2 because the initial mass ranges of the evolutionary sequences do not extend to high enough values (see Table 1). Nevertheless, an increase in the slope of the ZAMSs in the upper HR diagram is observed.
The latest OPAL opacities were used to investigate the bending of the ZAMS by Ishii et al. (1999). The authors computed models with metallicities ranging from Z = 0.1 to Z = 0.004 and found that the ZAMS curves redwards at sufficiently high masses for all the metallicities. The solar metallicity ZAMS in their study had a bend at M ~ 100 M⊙, which is consistent with our results.
The redwards curving of the ZAMS is a consequence of envelope inflation of massive luminous stars, as discussed in Sect. 4. When the layers in the stellar interior reach the Eddington limit either because of an opacity bump or because of a high L/M ratio, the high radiation pressure pushes the layers outwards such that density and hence opacity decreases, and the Eddington factor obtains a value ≲1.
If convection is efficient, then the star does not need to re-adjust its structure, but in the luminous stars discussed here, the low densities in their outer layers imply that convective energy transport within the framework of the standard MLT is not efficient enough to bring down the Eddington factor below one, even though the fraction of the total luminosity carried by convection can exceed 90% in the coolest models (cf. Sanyal et al. 2015). Therefore the envelope expands, giving rise to a core-halo density structure (Fig. 1).
The redward bend is also present in the TAMS lines of all metallicities. The higher the metallicity, the lower the luminosity at which the bend occurs, similar to the trend expected for the ZAMS lines. The TAMS, however, curves redwards at a lower luminosity than the ZAMS. For example, the TAMS for the LMC bends at log (L/L⊙) ≈ 5.3, whereas the ZAMS bends at log (L/L⊙) ≈ 6.6. From the mass-luminosity relation for homologous stars, we know that L ∝ μβ for a fixed mass, where the exponent β lies in the range ~1.3...2 for masses between 100−500 M⊙ on the ZAMS (cf. Fig. 17 in Köhler et al. 2015) such that higher masses have lower values of β. Therefore, at the TAMS a model has a higher L/M value than at ZAMS because of a higher mean molecular weight.
The stellar parameters at the points (marked with filled dots in Fig. 2) where the TAMS lines bend towards cooler effective temperatures are noted in Table 3. This feature indicates the onset of envelope inflation because below this bend we do not find any TAMS model to be inflated, but above the bend, we find inflated models. With a decrease in metallicity, the opacity in the stellar envelope decreases (cf. Sect. 5.4) and hence Γ ≈ 1 can be achieved only with a higher L/M value. Therefore the low-Z TAMS models show envelope inflation at higher luminosities. The TAMS extends to temperatures below ~5000 K, leading to core-hydrogen burning red supergiant models. We note that the lowest luminosity at which we identify an inflated model on the TAMS is higher than the luminosity at which the bend is located. This might be related to our ad hoc criterion for inflation.
The TAMS lines for the MW, LMC, and I Zw18 models bend bluewards above log (L/L⊙) of 5.7, 6.0, and 6.8, respectively (Brott et al. 2011; Köhler et al. 2015). This has not been included in Fig. 2 for the sake of clarity. The blueward bend occurs because the mass-loss rates in this part of the HR diagram are high enough to strip the hydrogen-rich outer layers of the models and produce helium-rich WR models (Brott et al. 2011; Köhler et al. 2015). Once the helium-rich layers are exposed, the mass-loss rates increase even further, such that the models evolve towards higher surface temperatures, towards the helium ZAMS.
 |
Fig. 3 Spectroscopic Hertzsprung-Russell diagrams showing the non-rotating and slowly rotating core-hydrogen burning models in the five grids corresponding to the different metallicities (see labels). The left Y-axis shows the quantity log (L/ L⊙) with |
5.2. Spectroscopic HR diagram
In the spectroscopic HR (sHR) diagram introduced by Langer & Kudritzki (2014), instead of the luminosity, the quantity 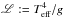 is plotted as a function of the effective temperature. The quantity L is proportional to Γe, such that
is plotted as a function of the effective temperature. The quantity L is proportional to Γe, such that 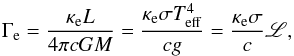 (18)where the constants have their usual meaning. Hence for solar hydrogen abundance,
(18)where the constants have their usual meaning. Hence for solar hydrogen abundance,  (19)Figure 3 shows the maximum Eddington factor Γmax in the interior of the analysed models for the five grids. Since the iron bump opacity increases non-linearly (cf. Sect. 5.4) with increasing iron abundance, that is, with increasing metallicity (Fig. 7), layers in the stellar interior reach the Eddington limit at a lower L, that is, at a lower L/M. This is demonstrated in the different panels of Fig. 3. Whereas we find models with Γmax> 0.9 for masses as low as ~30 M⊙ in the MW grid, the same is achieved at M ~ 100 M⊙ in the Pop III grid. Furthermore, an evolutionary model with a higher initial mass encounters a higher Γmax earlier in its evolution because of its higher L/M ratio. For example, the 50 M⊙ MW sequence starts to develop super-Eddington layers in the midst of its main-sequence life, whereas the 80 M⊙ sequence already has Γmax> 1 on its ZAMS.
(19)Figure 3 shows the maximum Eddington factor Γmax in the interior of the analysed models for the five grids. Since the iron bump opacity increases non-linearly (cf. Sect. 5.4) with increasing iron abundance, that is, with increasing metallicity (Fig. 7), layers in the stellar interior reach the Eddington limit at a lower L, that is, at a lower L/M. This is demonstrated in the different panels of Fig. 3. Whereas we find models with Γmax> 0.9 for masses as low as ~30 M⊙ in the MW grid, the same is achieved at M ~ 100 M⊙ in the Pop III grid. Furthermore, an evolutionary model with a higher initial mass encounters a higher Γmax earlier in its evolution because of its higher L/M ratio. For example, the 50 M⊙ MW sequence starts to develop super-Eddington layers in the midst of its main-sequence life, whereas the 80 M⊙ sequence already has Γmax> 1 on its ZAMS.
In the MW and the LMC grids, there are models with Γmax> 1 in the Teff range 35−55 kK. These models have the Fe opacity peak close to their surface where convective energy transport is inefficient, such that Γmax reaches values above one (Sanyal et al. 2015). In the temperature range 20−30 kK but at log (L/ L⊙) > 4.4, we also find models with Γmax> 1. These models are hydrogen deficient, either because of strong wind mass-loss or because of rotationally induced mechanical mass loss in the past. The super-Eddington layers in these models are caused by the helium opacity bump located close to their surface, coupled with inefficient convection. The models with SMC metallicity or lower do not evolve to have helium-rich envelopes during their main-sequence evolution, at least not in the mass and rotational velocity range considered here. For the SMC and the I Zw18 metallicity, the Fe-opacity peak, although present, is much weaker than the peak in the MW and the LMC. In other words, to reach the same value of Γmax, the models with lower metallicity need to have a higher L/M ratio.
In the 60 M⊙ MW sequence for example, Γmax exceeds unity very close to the ZAMS, but at Teff< 32 kK Γmax falls below one. This drop in Γmax is explained by relatively efficient convection in the envelope as the Fe-bump moves deeper into the star where densities are relatively higher. The evolution of Γmax versus Teff for the 60 M⊙ sequence is shown in Fig. 4. The increase of Γmax at Teff< 14 000 K is explained by strong mass loss that increases the L/M ratio and the surface helium abundance. However, we note that Γe increases throughout its main-sequence evolution. A similar trend exists in other evolutionary sequences in Fig. 3.
None of the Pop III models in the investigated parameter range have Γmax> 1 at Teff> 10 000 K. Since the Fe-bump is completely absent, Γ = 1 is never reached. Neither are these models helium-enriched at their surface because of negligible wind mass-loss that would have increased their L/M ratio.
The log Γe values shown on the right Y-axis in Fig. 3 gives little information about the Γmax in the stellar interior. For example, the 80 M⊙ MW ZAMS model has super-Eddington layers in its envelope, but its Γe value is only 0.27. This shows that Γe is not a good proxy for the true Γ while investigating the structure and the stability of massive star envelopes.
At the stellar surface the classical Eddington factor cannot exceed unity if hydrostatic equilibrium is to be maintained. Therefore Γe = 1 is an impenetrable upper limit (Eddington 1926; Langer & Kudritzki 2014). However, in the LMC grid there are apparently many models with Γe> 1 (Fig. 3), but their surface helium mass fraction exceeds Ys = 0.8 (Köhler et al. 2015). The true Γe = 1 for these models is therefore located at a higher L such that they all lie below it. For example, if X = 0, then the Γe = 1 line in Fig. 3 shifts upwards by 0.24 dex.
Across all the metallicities, there are models with Γmax> 1 at Teff< 9000 K. This is because of the opacity peak caused by hydrogen recombination, and hence is not influenced by the metal content in the star. The Γmax values of these models can be as high as 6 for the MW models to ≳8 for the Pop III models, meaning that in the outer envelope (around the hydrogen recombination temperature) of such a model the luminosity transported by radiation can be a few times the Eddington luminosity (Sanyal et al. 2015). The opacities in the hydrogen recobination zone can be ~10 times that of the Fe-opacity peak. Hydrostatic equilibrium in these super-Eddington layers is maintained by building up a positive gas pressure gradient and a positive density gradient (Joss et al. 1973; Sanyal et al. 2015).
It might be expected that these peculiar structures, coupled with the fact that they are located beyond the observed Humphreys-Davidson (H-D) limit (Humphreys & Davidson 1979) are prone to various instabilities and possibly undergo violent mass-loss episodes such that it prevents them from staying long enough on the cool side of the H-D limit. However, in our hydrodynamic 1D models we find no sign of a super-Eddington outflow.
 |
Fig. 4 Evolution of Γmax with Teff for the 60 M⊙ZMWsequence. The colour depicts the surface helium mass fraction. |
5.3. Dependence of envelope inflation on metallicity
The extent of envelope inflation in the analysed models is summarised in the sHR diagrams in Fig. 5. Comparing this with Fig. 3, we note that barring a few, none of the models with Γmax < 0.9 are inflated, whereas models with Γmax > 1 all have inflated envelopes. Therefore, as mentioned in Sect. 4, the occurrence of inflated envelopes is related to models approaching the Eddington limit (as defined by Eq. (4)) in their interior. In general, the hotter models are less inflated than the cooler models for a given L, in agreement with the results obtained by Sanyal et al. (2015). This is expected because the effective temperature is strongly affected by inflation. The strongest inflation is found in models with Teff ≲ 8000 K, for all Z. The most extreme cases are found in the I Zw18 and the Pop III models, where Δr/rcorecan increase to a few hundred.
The Eddington limit is either approached with high opacities or with a high L/M ratio. Models with lower metal abundances, that is, with a weaker Fe-opacity bump, need to attain a higher L/M ratio, or a higher Γe, to reach the Eddington limit and inflate their envelopes. Therefore inflation starts at higher L as Z decreases. However, we reiterate that reaching the Eddington limit is a sufficient but not a necessary condition for envelope inflation to occur (cf. Eqs. (11)and (13)) because the gas pressure gradient might also contribute to inflating the envelope.
Figure 6 marks the regions in the sHR diagram that separate the non-inflated models from the inflated ones, considering the same sample as in Fig. 5. For each model grid the Teff range of the models was divided into 20 equi-spaced bins, and in each bin the un-inflated model with the highest L was selected. These data points were then joined, and the resulting line was smoothed using Bézier splines. These lines do not extend to Teff values below ~10 000 K (see Fig. 5) because we did not find any core-hydrogen burning model that is not inflated in this temperature range and hence the boundaries cannot be drawn.
The lines for ZMWand ZLMCshow a pronounced dip around Teff ~ 35 kK. This is because of the influence of the Fe-bump coupled with inefficient convection, as previously mentioned. At lower temperatures, convection becomes more efficient, and therefore these lines move upwards to higher L. For lower metallicities this dip is not clearly identified because the Fe-bump is either weak or absent.
In the MW and LMC grids, the models start to develop inflated envelopes even on the ZAMS at masses above ~80 M⊙ and ~125 M⊙, respectively. At lower metallicities this is also expected to occur, although at higher masses and hence at higher L, which is beyond the parameter space explored here.
 |
Fig. 5 Spectroscopic HR diagram showing the metallicity dependence of inflation for the analysed models in our grid. The left Y-axis shows the quantity log (L/ L⊙), whereas the right Y-axis shows the corresponding values of log (Γe). The Γe values are computed assuming a solar hydrogen abundance (completely ionised). Models marked with open black dots are not inflated, whereas the coloured dots represent models with inflated envelopes. The colour of the dots indicates the strength of inflation, log (Δr/rcore ). The black line is the ZAMS, and the masses of some representative models (in units of M⊙) are indicated along it. |
 |
Fig. 6 Spectroscopic HR diagram showing the boundaries (dotted lines) between non-inflated and inflated models for different metallicities such that below a given line, we do not find any inflated model for that metallicity. The solid lines represent the ZAMS. The masses at ZAMS for some of the models have been indicated. The right Y-axis represents the logarithm of the classical Eddington factor considering X = 0.73, similar to Figs. 3 and 5. The horizontal line marks the location Γe = 1 and the hatched region above it is the forbidden zone where no hydrostatic model can lie. |
5.4. Role of opacity in determining the envelope structure
5.4.1. OPAL opacities
The Rosseland mean opacity κ is a function of density, temperature, and chemical composition such that for a given ρ and T, κ increases with an increase in metallicity. This is demonstrated in Fig. 7, where the three opacity peaks caused by partial ionisation of iron, helium, and hydrogen at their characteristic temperatures are visible. We note that the opacity does not vary linearly with metallicity around the Fe bump temperature. The slope 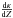 is higher for lower values of Z. In this section we investigate how the strength of these opacity peaks determines the density structure of the inflated envelope.
is higher for lower values of Z. In this section we investigate how the strength of these opacity peaks determines the density structure of the inflated envelope.
In Fig. 8 we show the OPAL opacities around the Fe-bump for the MW and LMC metallicities. As mentioned before, in the inflated envelope the condition Γ ≈ 1 holds true. Let the corresponding opacity be κEdd such that Γ = κEddLrad/ 4πcGm ≈ 1. Consider two models with the same L/M but with metallicities ZMWand ZLMCsuch that κEdd = 0.6 (dot-dashed line), and assume that the convective efficiency is negligible. At the peak of the Fe-bump marked by the vertical black line, the MW model has to decrease its density by two orders of magnitude, from 10-8 g cm-3 to ≈10-10 g cm-3, whereas the LMC model only has to decrease to ~10-9 g cm-3 to satisfy the constraint Γ = 1. Therefore, the higher metallicity model will adjust its envelope structure such that it has a lower envelope density. In practice, however, convection may mediate this effect (Sanyal et al. 2015).
5.4.2. Opacity in the inflated envelope
As mentioned before, the opacity bumps caused by the partial ionisation zones at characteristic temperatures play a major role in determining the structure of an inflated envelope. As prototypical examples, we have selected three sequences with Z = ZLMC and with initial masses of 60 M⊙,70 M⊙, and 100 M⊙. The base of the inflated envelope in these models is located around the characteristic Fe-bump temperature TFe ≈ 170 000 K. The maximum opacity within the Fe-bump (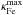 ), that is, between 5 < log (T/K) < 5.5, for the three sequences are shown in the top panel of Fig. 9 for that part of the evolution where the models are not helium enriched at the surface, that is, for Ys < 0.3. At any given value of Δr/rcore, the higher mass model has a lower
), that is, between 5 < log (T/K) < 5.5, for the three sequences are shown in the top panel of Fig. 9 for that part of the evolution where the models are not helium enriched at the surface, that is, for Ys < 0.3. At any given value of Δr/rcore, the higher mass model has a lower 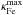 because it has a higher luminosity, and hence needs to decrease its opacity further to maintain κ ≈ κEdd.
because it has a higher luminosity, and hence needs to decrease its opacity further to maintain κ ≈ κEdd.
The 60 M⊙ sequence, for example, develops a larger inflated envelope as it evolves, while increasing its L. The opacity within the Fe-bump and 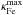 therefore decrease in the initial phase because convection is relatively inefficient. As the model evolves to cooler effective temperatures, the Fe-bump occurs deeper inside the star where densities are higher, and convection becomes efficient. Hence,
therefore decrease in the initial phase because convection is relatively inefficient. As the model evolves to cooler effective temperatures, the Fe-bump occurs deeper inside the star where densities are higher, and convection becomes efficient. Hence, 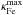 increases at Teff ≲ 25 000 K. In the case of the 70 M⊙ sequence, however, there is a drop in
increases at Teff ≲ 25 000 K. In the case of the 70 M⊙ sequence, however, there is a drop in 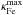 at Teff < 5000 K. In this phase of the evolution, a high mass-loss rate (~10-5M⊙ yr-1) causes a sharp increase in L. As a result, Lrad increases in the Fe-bump region. The convective efficiency does not increase enough (for details, see Appendix A), however, such that it can prevent κFe from decreasing.
at Teff < 5000 K. In this phase of the evolution, a high mass-loss rate (~10-5M⊙ yr-1) causes a sharp increase in L. As a result, Lrad increases in the Fe-bump region. The convective efficiency does not increase enough (for details, see Appendix A), however, such that it can prevent κFe from decreasing.
Models with a higher metallicity have a stronger Fe-bump, the effect of which is seen in the bottom panel of Fig. 9. While 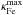 for the 80 M⊙ZMW model with the highest Teff is ~1.2 cm2 g-1, the same quantity for the 196 M⊙ZI Zw18 model is ~0.5 cm2 g-1. The slope of
for the 80 M⊙ZMW model with the highest Teff is ~1.2 cm2 g-1, the same quantity for the 196 M⊙ZI Zw18 model is ~0.5 cm2 g-1. The slope of 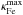 versus Δr/rcore is steeper for the ZMWevolutionary sequences than for the other sequences at lower metallicities because of the nature of the OPAL opacities that we explained in Sect. 5.4.1.
versus Δr/rcore is steeper for the ZMWevolutionary sequences than for the other sequences at lower metallicities because of the nature of the OPAL opacities that we explained in Sect. 5.4.1.
5.5. Mass contained in the inflated envelopes
 |
Fig. 7 Interpolated opacities from the OPAL tables for Teff> 8000 K and from Alexander & Ferguson (1994) for Teff > 8000 K. The density is fixed at ρ = 10-10 g cm-3, and opacities for the five metallicities used in this study are shown. The opacity peaks caused by iron, helium, and hydrogen ionisation are marked. |
 |
Fig. 8 OPAL opacities for two metallicities ZMWand ZLMC, and three different values of log (ρ [g cm-3]) each, i.e., −8, −9 and −10, as indicated in the plot. The dot-dashed line at κ = 0.6 is the assumed location of κEdd. |
 |
Fig. 9 Top: maximum opacity within the Fe-bump region for three different evolutionary sequences with initial masses of 60,70, and 100 M⊙ from the LMC grid as a function of Δr/rcore. The effective temperature of the model is colour coded. Only the part of the evolution where Ys< 0.3 has been plotted. Bottom: same as in the top panel, but for four metallicities. |
 |
Fig. 10 Envelope mass versus effective temperature for the 80 M⊙ sequences from the MW, LMC, and SMC grids. Only models in the Teff range 20−50 kK and with Ys< 0.3 are shown. |
In this section we investigate the inflated envelope masses of our models. In Fig. 10 we compare the 80 M⊙ sequences in the MW, LMC, and SMC model grids and show that for a given Teff, the higher metallicity model has a lower envelope mass. At relatively high effective temperatures (Teff > 45 000 K), that is, when the sequences start developing inflated envelopes for the first time during their evolution, the envelope masses for all three sequences are similar, but at as they evolve to lower Teff, the distinction becomes clear. For example, at Teff = 30 000 K the 80 M⊙ MW model has a distinctly lower envelope mass than the corresponding LMC and SMC models, the difference in their core radii being negligible. The LMC and the SMC models, however, have comparable envelope masses over the whole Teff range. This trend is likely related to the relative strength of the iron opacity peaks for these metallicities (cf. Fig. 7).
 |
Fig. 11 Top: inflated envelope masses for three sequences from the LMC grid as a function of Δr/rcore, such that Ys < 0.3. Bottom: same as in the top panel, but for four metallicities. |
For evolutionary sequences of a given metallicity, for instance, ZLMC, the sequences with higher Ls have lower envelope masses (Menv), as shown in the top panel of Fig. 11. For small inflation, that is, for Δr/rcore<0.1, the envelope mass in the three LMC sequences is comparable, but as Δr/rcore increases, the sequences separate out such that for a given Δr/rcore, the 100 M⊙ sequence with the highest L has the lowest envelope mass and comparing with Fig. 9, the lowest 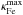 . We note that for the 70 M⊙ sequence for example, the envelope mass varies by more than five orders of magnitude over its main-sequence lifetime. The drop in Menv near the end of the 70 M⊙ sequence is caused by its blueward evolution in the HR diagram, which in turn is caused by strong mass-loss (cf. Sect. 5.3).
. We note that for the 70 M⊙ sequence for example, the envelope mass varies by more than five orders of magnitude over its main-sequence lifetime. The drop in Menv near the end of the 70 M⊙ sequence is caused by its blueward evolution in the HR diagram, which in turn is caused by strong mass-loss (cf. Sect. 5.3).
 |
Fig. 12 Mass contained in the envelope of inflated models as a function of their effective temperatures for the five metallicities considered in this study. Only models with Ys < 0.3 are shown. The black dotted line has been drawn to guide the eye (see text). The bottom panel only shows models with Menv > 10-2M⊙ and Teff < 30 000 K. The colour bar on the right represents the fraction of the stellar mass contained in the inflated envelope. |
In the bottom panel of Fig. 11, several representative sequences from the MW, LMC, SMC, and I Zw18 grids are shown that depict how Menv changes with inflation. The higher metallicity models have a lower envelope mass for a fixed Δr/rcore. For example, at Δr/rcore = 1, the 60 M⊙ LMC sequence has Menv = 3 × 10-3M⊙, while the 60 M⊙ SMC sequence has Menv = 6 × 10-3M⊙. At high inflation (Δr/rcore > 10), some of the lines touch each other, which may be related to the different L/M ratios of the models induced by mass loss.
We investigate the envelope masses of all the inflated models in Fig. 12. The envelope mass spans several orders of magnitude from ~10-5M⊙ to ~100 M⊙. In general, we find that Menvincreases with a decrease in Teff for a given metallicity. This increase in Menvis distinctly steeper at Teff ≲ 8000 K (bottom panel of Fig. 12) compared to that at Teff > 10 000 K. Below 10 000 K, the low-Z models have very massive envelopes (bottom panel of Fig. 12). The models that contain the hydrogen opacity bump show strong density inversions (Sanyal et al. 2015), and because of the sharp rise in density the envelope mass increases.
At Teff > 10 000 K, there is a spread in Menv over a few orders of magnitude, but the spread is much narrower at the lowest effective temperatures. This is because the sequences that evolve to effective temperatures below ~8000 K do so for a narrow mass range. At higher initial masses strong mass loss prevents them from evolving to low surface temperatures, and at lower initial masses, inflation is not strong enough.
Gräfener et al. (2012) found from analytical estimates that the inflated envelope mass scales as Menv ~ R4/M. For constant M and L, this translates into 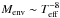 . The shape of this curve (Fig. 12) is well reproduced by our model grids at higher Teff, although at Teff < 8000 K the dependence is steeper than the analytical estimate. We note that the envelope mass estimates of the Minit = 1000 M⊙ and the Minit = 500 M⊙ models in the Pop III grid (some of these are the black dots located above the dotted line in Fig. 12) are particularly uncertain because they are sensitive to the choice of the threshold value of β that marks the location of rcore. Although these models have inflated envelopes, the absence of an opacity peak complicates the process of identifying rcore. A more detailed investigation of the envelope structures of massive Pop III models is beyond the scope of the present paper and will be pursued in a forthcoming study.
. The shape of this curve (Fig. 12) is well reproduced by our model grids at higher Teff, although at Teff < 8000 K the dependence is steeper than the analytical estimate. We note that the envelope mass estimates of the Minit = 1000 M⊙ and the Minit = 500 M⊙ models in the Pop III grid (some of these are the black dots located above the dotted line in Fig. 12) are particularly uncertain because they are sensitive to the choice of the threshold value of β that marks the location of rcore. Although these models have inflated envelopes, the absence of an opacity peak complicates the process of identifying rcore. A more detailed investigation of the envelope structures of massive Pop III models is beyond the scope of the present paper and will be pursued in a forthcoming study.
The envelope mass is determined by both the extent of inflation (Δr/rcore) and the metallicity. As the metallicity increases, the models with the most massive inflated envelopes (the cool supergiants) are found at lower masses. This is a consequence of the applied mass-loss rates. The wind mass-loss prescriptions used in stellar evolution calculations are functions of luminosity, temperature, mass, radius, and chemical composition of the model. With an increase in luminosity or mass, the wind mass-loss rates increase and the most massive stars in our MW and LMC grids become helium-rich WR stars (Köhler et al. 2015) and do not become cool enough to contain massive envelopes (≳1 M⊙), as explained in the previous paragraph. At lower Z, this occurs at higher masses. At Z = 0, models never become helium-rich at the surface unless they are very fast rotators (Yoon et al. 2012).
6. Discussion and conclusions
We have performed a study of the envelope structures of core-hydrogen burning massive star models computed with the following metallicities: ZMW, ZLMC, ZSMC, ZI Zw18 , and ZPopIII. We investigated the Eddington factors in their interior and the connection of this factor to envelope inflation as a function of metallicity.
As expected, we found that the Eddington limit is metallicity dependent such that models with a higher Z reach Γ = 1 in their interior at a lower mass. While a 30 M⊙ MW model reaches Γ ≈ 1 in its interior, it requires a 150 M⊙ Pop III model to obtain similar Eddington factors on the hot side of the HR diagram, that is, at Teff > 10 000 K. For models with Teff below the hydrogen recombination temperature, metallicity has little effect, and super-Eddington layers can be found down to ~5 M⊙ models, although in the post-main-sequence phase (Langer et al. 2015; Grassitelli et al. 2015a). Proximity to the Eddington limit leads to envelope inflation in our models. We find inflated models at all the metallicities investigated, albeit at different L/M-ratios (Fig. 6). At a higher Z, envelope inflation starts at lower masses because of higher opacities that help approach Γ ≈ 1. We reiterate that envelope inflation might already start to develop before reaching the Eddington limit because of the contribution from the gas pressure gradient (cf. Sect. 4). Envelope inflation is responsible for the redward bending of the ZAMS and the TAMS in the upper HR diagram (Fig. 2), which is also supported by observations, which show that the upper part of the Galactic HR diagram is well populated by stars up to Teff ~ 10 000 K (Castro et al. 2014). The extent of inflation might be used to infer the value of αMLT for massive stars by comparing the main-sequence width of the models with the observational TAMS (Castro et al. 2014; Bestenlehner et al. 2014).
We find that the mass contained in the inflated envelopes can range from ~10-6M⊙ in the hot luminous models to ~100 M⊙ in the cool supergiant type models across the range of metallicities we investigated. While the observational signatures of these envelopes needs to be explored further, the envelopes with high masses (Menv > 1 M⊙) seem to be promising candidates for explaining the violent LBV eruptions, for example, the 1860 outburst η Car, and other η Car analogues (Khan et al. 2015) or supernova imposters. These models are near the Eddington limit and have several solar masses in the loosely bound envelope. The details of the instability that are responsible for the outburst still need to be investigated. On the other hand, if the inflated envelopes are lost episodically from the models with low envelope masses, it will cause them to shrink to the non-inflated core radius, but will not be able to change the bolometric luminosity appreciably. These models have been put forward to explain the S-Doradus-type variations by Gräfener et al. (2012) and Sanyal et al. (2015).
Moriya et al. (2015) proposed that an observational consequence of a supernova progenitor with an inflated envelope is that it extends the rise time of the supernova shock-breakout signal. This naturally explains the long (~50 s) shock-breakout X-ray signal detected from the Type Ic SN 2008D (Soderberg et al. 2008) that is believed to have had a compact WR progenitor.
Luminous helium stars also show pronounced core-halo structures, and such models have been investigated in the past (Ishii et al. 1999; Petrovic et al. 2006; Gräfener et al. 2012; Tramper et al. 2015; Grassitelli et al. 2016a). The apparent mismatch in radii between model atmosphere calculations and stellar interior models of massive Galactic WR stars has been claimed to have been reconciled by envelope inflation (Gräfener et al. 2012).
The inflated models are potentially unstable against the so-called strange-mode instability (Gautschy & Glatzel 1990; Glatzel & Kiriakidis 1993) because of low heat capacities in their dilute envelopes (Glatzel 1994). Glatzel & Kiriakidis (1993) reported that their solar metallicity models with log (L/ L⊙) ≳ 4 are unstable to strange-mode oscillations. This result coincides with the boundary between the inflated and non-inflated models in our ZMWgrid. Furthermore, these oscillations might drive mass loss from the star (Grott et al. 2005), although Moriya & Langer (2015) and Grassitelli et al. (2016a) find that mass-loss dampens the pulsations. The pulsational properties of our models will be explored in detail in a forthcoming study.
A critical ingredient in the physics of envelope inflation is convection, that is, how convective energy transport is treated in these regions. In the literature, stellar models computed with increased convective efficiency show little or no envelope inflation (Ekström et al. 2012; Yusof et al. 2013). A discussion of the convective efficiencies in our ZLMCmodels can be found in Sect. 6 of Sanyal et al. (2015). Jiang et al. (2015) performed 3D radiation hydrodynamics simulations of massive star envelopes and concluded that for a 80 M⊙ ZAMS model, standard MLT overestimates the convective flux in the inflated region around the Fe-bump. In that case, inflation in our 1D models has been underestimated. Jiang et al. (2015) also found turbulent velocities that exceed the isothermal sound speed, driving shocks in the envelope and creating an inhomogeneous clumpy medium, which, however, does not lead to a break-down of the inflation.
Grassitelli et al. (2016b) recently investigated the role of turbulent pressure (Pturb) in stellar models computed with MW, LMC, and SMC metallicities, and found that its effect on stellar structure is negligible regardless of the metallicity (Grassitelli et al. 2015b). However, the ratio of Pturb to Ptotal in the stellar envelopes of the hot stellar models decreases for lower metallicities at a given temperature and luminosity. This trend is consistent with our results for inflation (Figs. 5 and 6). At higher metallicities the density in the inflated envelope is lower, which implies inefficient convection and therefore a large and negative entropy gradient. Hence the convective velocities and the Mach number is also higher, which leads to higher turbulent pressure.
Furthermore, Grassitelli et al. (2015b) found a correlation between macroturbulent velocities in Galactic OB stars and the fraction of turbulent pressure in the stellar envelope models. Since the turbulent pressure contribution in the inflated envelope becomes stronger in the upper HR diagram, high macroturbulent velocities (≳50 km s-1, Simón-Díaz 2015; Grassitelli et al. 2015b; Simón-Díaz et al. 2017) might well be a signature of envelope inflation in hot massive stars. The conditions in the inflated envelope might be inferred through asteroseismic studies (Aerts et al. 2014), especially if the connection between inefficient convection and high-order non-radial pulsations is confirmed (Aerts et al. 2009; Grassitelli et al. 2015a,b).
It might be interesting to study the fate of the inflated envelopes in close binaries, since ~70% of all massive stars are believed to interact during their lifetimes (Sana et al. 2012). The loosely bound envelopes might help to stabilise mass-transfer in close massive binary systems, especially in metal-rich systems where this is expected to occur at lower masses. In close binaries, the hydrogen envelope is typically lost from the mass donor that bares its helium core and increases the L/M ratio. Helium stars with solar metallicity start to develop inflated envelopes from ~10 M⊙ (see Fig. 19 in Köhler et al. 2015). Massive Type Ib/c progenitors in binary systems are thus expected to have inflated envelopes (Yoon et al. 2010).
Acknowledgments
D. Szécsi was supported by GAČR grant 14-02385S. S.C.Y. acknowledges support from the Korea Astronomy and Space Science Institute under the R&D program (Project No. 3348- 20160002) supervised by the Ministry of Science, ICT and Future Planning.
References
- Aerts, C., Puls, J., Godart, M., & Dupret, M.-A. 2009, A&A, 508, 409 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aerts, C., Simón-Díaz, S., Groot, P. J., & Degroote, P. 2014, A&A, 569, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alexander, D. R., & Ferguson, J. W. 1994, ApJ, 437, 879 [NASA ADS] [CrossRef] [Google Scholar]
- Bestenlehner, J. M., Gräfener, G., Vink, J. S., et al. 2014, A&A, 570, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Böhm-Vitense, E. 1958, Z. Astrophys., 46, 108 [Google Scholar]
- Bromm, V., Yoshida, N., Hernquist, L., & McKee, C. F. 2009, Nature, 459, 49 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Brott, I., de Mink, S. E., Cantiello, M., et al. 2011, A&A, 530, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castro, N., Fossati, L., Langer, N., et al. 2014, A&A, 570, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crowther, P. A., Schnurr, O., Hirschi, R., et al. 2010, MNRAS, 408, 731 [NASA ADS] [CrossRef] [Google Scholar]
- Eddington, A. S. 1926, The Internal Constitution of the Stars (New York: Cambridge University Press) [Google Scholar]
- Ekström, S., Georgy, C., Eggenberger, P., et al. 2012, A&A, 537, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Evans, C. J., Taylor, W. D., Hénault-Brunet, V., et al. 2011, A&A, 530, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Figer, D. F. 2005, Nature, 434, 192 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Friend, D. B., & Abbott, D. C. 1986, ApJ, 311, 701 [NASA ADS] [CrossRef] [Google Scholar]
- Gautschy, A., & Glatzel, W. 1990, MNRAS, 245, 597 [NASA ADS] [Google Scholar]
- Glatzel, W. 1994, MNRAS, 271, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Glatzel, W., & Kiriakidis, M. 1993, MNRAS, 263, 375 [NASA ADS] [Google Scholar]
- Gräfener, G., Owocki, S. P., & Vink, J. S. 2012, A&A, 538, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grassitelli, L., Fossati, L., Langer, N., et al. 2015a, A&A, 584, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grassitelli, L., Fossati, L., Simón-Diáz, S., et al. 2015b, ApJ, 808, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Grassitelli, L., Chené, A.-N., Sanyal, D., et al. 2016a, A&A, 590, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grassitelli, L., Fossati, L., Langer, N., et al. 2016b, A&A, accepted [Google Scholar]
- Grott, M., Chernigovski, S., & Glatzel, W. 2005, MNRAS, 360, 1532 [NASA ADS] [CrossRef] [Google Scholar]
- Hamann, W.-R., Koesterke, L., & Wessolowski, U. 1995, A&A, 299, 151 [NASA ADS] [Google Scholar]
- Heger, A., & Woosley, S. E. 2002, ApJ, 567, 532 [NASA ADS] [CrossRef] [Google Scholar]
- Heger, A., Langer, N., & Woosley, S. E. 2000, ApJ, 528, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Humphreys, R. M., & Davidson, K. 1979, ApJ, 232, 409 [NASA ADS] [CrossRef] [Google Scholar]
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Iglesias, C. A., Rogers, F. J., & Wilson, B. G. 1992, ApJ, 397, 717 [NASA ADS] [CrossRef] [Google Scholar]
- Inserra, C., & Smartt, S. J. 2014, ApJ, 796, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Ishii, M., Ueno, M., & Kato, M. 1999, PASJ, 51, 417 [NASA ADS] [Google Scholar]
- Jiang, Y.-F., Cantiello, M., Bildsten, L., Quataert, E., & Blaes, O. 2015, ApJ, 813, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Joss, P. C., Salpeter, E. E., & Ostriker, J. P. 1973, ApJ, 181, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Kato, M. 1985, PASJ, 37, 311 [NASA ADS] [Google Scholar]
- Kato, M. 1986, Ap&SS, 119, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Khan, R., Adams, S. M., Stanek, K. Z., Kochanek, C. S., & Sonneborn, G. 2015, ApJ, 815, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Kippenhahn, R., & Weigert, A. 1990, Stellar Structure and Evolution (Berlin: Springer) [Google Scholar]
- Köhler, K., Langer, N., de Koter, A., et al. 2015, A&A, 573, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krtička, J., & Kubát, J. 2006, A&A, 446, 1039 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kudritzki, R. P., Pauldrach, A., Puls, J., & Abbott, D. C. 1989, A&A, 219, 205 [NASA ADS] [Google Scholar]
- Langer, N. 1991, A&A, 252, 669 [NASA ADS] [Google Scholar]
- Langer, N. 1997, in Luminous Blue Variables: Massive Stars in Transition, eds. A. Nota, & H. Lamers, ASP Conf. Ser., 120, 83 [Google Scholar]
- Langer, N. 2012, ARA&A, 50, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, N., & Kudritzki, R. P. 2014, A&A, 564, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Langer, N., Norman, C. A., de Koter, A., et al. 2007, A&A, 475, L19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Langer, N., Sanyal, D., Grassitelli, L., & Szésci, D. 2015, in Wolf-Rayet Stars: Proceedings of an International Workshop held in Potsdam, Germany, 1–5 June 2015, eds. W.-R. Hamann, A. Sander, & H. Todt, 241 [Google Scholar]
- Maeder, A., & Meynet, G. 2012, Rev. Mod. Phys., 84, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Marigo, P., Chiosi, C., & Kudritzki, R.-P. 2003, A&A, 399, 617 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moriya, T. J., & Langer, N. 2015, A&A, 573, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moriya, T. J., Sanyal, D., & Langer, N. 2015, A&A, 575, L10 [Google Scholar]
- Nieuwenhuijzen, H., & de Jager, C. 1990, A&A, 231, 134 [NASA ADS] [Google Scholar]
- Owocki, S. P. 2015, in Very Massive Stars in the Local Universe, ed. J. S. Vink, Astrophys. Space Sci. Libr., 412, 113 [Google Scholar]
- Pamyatnykh, A. A. 1999, Acta Astron., 49, 119 [Google Scholar]
- Paxton, B., Cantiello, M., Arras, P., et al. 2013, ApJS, 208, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Petrovic, J., Langer, N., Yoon, S.-C., & Heger, A. 2005, A&A, 435, 247 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petrovic, J., Pols, O., & Langer, N. 2006, A&A, 450, 219 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Quimby, R. M., Yuan, F., Akerlof, C., & Wheeler, J. C. 2013, MNRAS, 431, 912 [NASA ADS] [CrossRef] [Google Scholar]
- Sana, H., de Mink, S. E., de Koter, A., et al. 2012, Science, 337, 444 [Google Scholar]
- Sanyal, D., Grassitelli, L., Langer, N., & Bestenlehner, J. M. 2015, A&A, 580, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simón-Díaz, S. 2015, in New Windows on Massive Stars, eds. G. Meynet, C. Georgy, J. Groh, & P. Stee, IAU Symp., 307, 194 [Google Scholar]
- Simón-Díaz, S., Godart, M., Castro, N., et al. 2017, A&A, 597, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Soderberg, A. M., Berger, E., Page, K. L., et al. 2008, Nature, 453, 469 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Spruit, H. C. 2002, A&A, 381, 923 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stothers, R. B., & Chin, C.-W. 1993, ApJ, 408, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Szécsi, D., Langer, N., Yoon, S.-C., et al. 2015, A&A, 581, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tramper, F., Straal, S. M., Sanyal, D., et al. 2015, A&A, 581, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2000, A&A, 362, 295 [NASA ADS] [Google Scholar]
- Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2001, A&A, 369, 574 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woosley, S. E., & Heger, A. 2006, ApJ, 637, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Yoon, S.-C., & Langer, N. 2005, A&A, 435, 967 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yoon, S., Langer, N., & Norman, C. 2006, A&A, 460, 199 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yoon, S.-C., Woosley, S. E., & Langer, N. 2010, ApJ, 725, 940 [NASA ADS] [CrossRef] [Google Scholar]
- Yoon, S.-C., Dierks, A., & Langer, N. 2012, A&A, 542, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yusof, N., Hirschi, R., Meynet, G., et al. 2013, MNRAS, 433, 1114 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Evolution of a 70 M⊙ inflated LMC model
We present the evolution of a typical inflated model, the 70 M⊙ LMC sequence, with respect to its inflated envelope and the properties around the iron opacity bump. Only that part of the evolution has been studied where the surface helium mass fraction (Ys) is lower than 0.3.
 |
Fig. A.1 Maximum opacity in the temperature range 5 < log (T/K) < 5.5 as a function of Δr/rcorefor that part of the evolution where Ys < 0.3. The colour bar indicates the effective temperature of the models. |
 |
Fig. A.2 Variation in density at the position of |
 |
Fig. A.3 Lrad/M-ratio at the position of |
The maximum value of the opacity around the Fe-bump (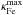 ; Fig. A.1) and the density at the location of
; Fig. A.1) and the density at the location of 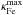 (Fig. A.2) decrease initially as Δr/rcoreincreases, because of an increase in Lrad/M (Fig. A.3). The product of the quantities
(Fig. A.2) decrease initially as Δr/rcoreincreases, because of an increase in Lrad/M (Fig. A.3). The product of the quantities 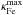 and Lrad/M, which is proportional to Γ, also initially increases up to Δr/rcore≈ 0.1 (Fig. A.4). Thereafter it starts decreasing with a decrease in Lrad/M. The Lrad/M decreases in this phase of the evolution because of a rise in convective efficiency at this location, shown in Fig. A.5. This is because as Teff of the model
and Lrad/M, which is proportional to Γ, also initially increases up to Δr/rcore≈ 0.1 (Fig. A.4). Thereafter it starts decreasing with a decrease in Lrad/M. The Lrad/M decreases in this phase of the evolution because of a rise in convective efficiency at this location, shown in Fig. A.5. This is because as Teff of the model
continues to decrease, the Fe-bump occurs deeper inside the star where density is higher and hence convection is relatively efficient. When convection is capable of transporting the energy, the radiative luminosity Lrad decreases, and hence the Eddington factor at this location (ΓFe) decreases. The inflated envelope continues to increase even though ΓFe decreases to values as low as 0.91.
At Δr/rcore≳ 20, Lrad/M and ΓFe increase again, while 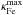 decreases. Since the star experiences high mass-loss rates at such low effective temperatures, its L/M ratio increases sharply in this phase (Fig. A.6), but the convective efficiency does not increase as much. Hence to let the relatively high radiative flux pass through, the model reduces its opacity, which increases the value of Γ at that location. We note that at Teff below ~8000 K the location of Γmax is in the hydrogen recombination zone and not within the Fe-bump.
decreases. Since the star experiences high mass-loss rates at such low effective temperatures, its L/M ratio increases sharply in this phase (Fig. A.6), but the convective efficiency does not increase as much. Hence to let the relatively high radiative flux pass through, the model reduces its opacity, which increases the value of Γ at that location. We note that at Teff below ~8000 K the location of Γmax is in the hydrogen recombination zone and not within the Fe-bump.
 |
Fig. A.4 Value of the Eddington factor at the position of |
 |
Fig. A.5 Ratio of convective flux to the total flux at the position of |
 |
Fig. A.6 Evolution of the quantity log (L/ L⊙) as a function of Δr/rcorefor that part of the evolution where Ys < 0.3. The colour bar indicates the effective temperature of the models. |
All Tables
Initial chemical compositions (in mass fraction), the metallicities, and the range of initial masses of the stellar evolutionary sequences.
Initial masses (in units of M⊙) of the non-rotating evolutionary sequences that were re-computed.
All Figures
 |
Fig. 1 Density profile of a 79 M⊙ solar metallicity core-hydrogen burning model showing the inflated envelope. The model had an initial mass of 100 M⊙. The radial co-ordinate has been scaled with the core radius rcore. The blue line (right Y-axis) shows the run of the Eddington factor Γ (Eq. (4)) in the interior of the model. The Eddington factor almost reaches unity in the inflated region. |
| In the text | |
 |
Fig. 2 Zero-age main-sequence (solid lines) and the terminal-age main-sequence lines (dotted lines) above log (L/L⊙) > 4 of the analysed stellar models at different metallicities. The masses of some representative models (black squares) are indicated along the ZAMS. The position of the TAMS (in the model grid) where they bend towards cooler effective temperatures are marked with coloured dots, and the corresponding initial masses of these models are labelled alongside. |
| In the text | |
 |
Fig. 3 Spectroscopic Hertzsprung-Russell diagrams showing the non-rotating and slowly rotating core-hydrogen burning models in the five grids corresponding to the different metallicities (see labels). The left Y-axis shows the quantity log (L/ L⊙) with |
| In the text | |
 |
Fig. 4 Evolution of Γmax with Teff for the 60 M⊙ZMWsequence. The colour depicts the surface helium mass fraction. |
| In the text | |
 |
Fig. 5 Spectroscopic HR diagram showing the metallicity dependence of inflation for the analysed models in our grid. The left Y-axis shows the quantity log (L/ L⊙), whereas the right Y-axis shows the corresponding values of log (Γe). The Γe values are computed assuming a solar hydrogen abundance (completely ionised). Models marked with open black dots are not inflated, whereas the coloured dots represent models with inflated envelopes. The colour of the dots indicates the strength of inflation, log (Δr/rcore ). The black line is the ZAMS, and the masses of some representative models (in units of M⊙) are indicated along it. |
| In the text | |
 |
Fig. 6 Spectroscopic HR diagram showing the boundaries (dotted lines) between non-inflated and inflated models for different metallicities such that below a given line, we do not find any inflated model for that metallicity. The solid lines represent the ZAMS. The masses at ZAMS for some of the models have been indicated. The right Y-axis represents the logarithm of the classical Eddington factor considering X = 0.73, similar to Figs. 3 and 5. The horizontal line marks the location Γe = 1 and the hatched region above it is the forbidden zone where no hydrostatic model can lie. |
| In the text | |
 |
Fig. 7 Interpolated opacities from the OPAL tables for Teff> 8000 K and from Alexander & Ferguson (1994) for Teff > 8000 K. The density is fixed at ρ = 10-10 g cm-3, and opacities for the five metallicities used in this study are shown. The opacity peaks caused by iron, helium, and hydrogen ionisation are marked. |
| In the text | |
 |
Fig. 8 OPAL opacities for two metallicities ZMWand ZLMC, and three different values of log (ρ [g cm-3]) each, i.e., −8, −9 and −10, as indicated in the plot. The dot-dashed line at κ = 0.6 is the assumed location of κEdd. |
| In the text | |
 |
Fig. 9 Top: maximum opacity within the Fe-bump region for three different evolutionary sequences with initial masses of 60,70, and 100 M⊙ from the LMC grid as a function of Δr/rcore. The effective temperature of the model is colour coded. Only the part of the evolution where Ys< 0.3 has been plotted. Bottom: same as in the top panel, but for four metallicities. |
| In the text | |
 |
Fig. 10 Envelope mass versus effective temperature for the 80 M⊙ sequences from the MW, LMC, and SMC grids. Only models in the Teff range 20−50 kK and with Ys< 0.3 are shown. |
| In the text | |
 |
Fig. 11 Top: inflated envelope masses for three sequences from the LMC grid as a function of Δr/rcore, such that Ys < 0.3. Bottom: same as in the top panel, but for four metallicities. |
| In the text | |
 |
Fig. 12 Mass contained in the envelope of inflated models as a function of their effective temperatures for the five metallicities considered in this study. Only models with Ys < 0.3 are shown. The black dotted line has been drawn to guide the eye (see text). The bottom panel only shows models with Menv > 10-2M⊙ and Teff < 30 000 K. The colour bar on the right represents the fraction of the stellar mass contained in the inflated envelope. |
| In the text | |
 |
Fig. A.1 Maximum opacity in the temperature range 5 < log (T/K) < 5.5 as a function of Δr/rcorefor that part of the evolution where Ys < 0.3. The colour bar indicates the effective temperature of the models. |
| In the text | |
 |
Fig. A.2 Variation in density at the position of |
| In the text | |
 |
Fig. A.3 Lrad/M-ratio at the position of |
| In the text | |
 |
Fig. A.4 Value of the Eddington factor at the position of |
| In the text | |
 |
Fig. A.5 Ratio of convective flux to the total flux at the position of |
| In the text | |
 |
Fig. A.6 Evolution of the quantity log (L/ L⊙) as a function of Δr/rcorefor that part of the evolution where Ys < 0.3. The colour bar indicates the effective temperature of the models. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.