| Issue |
A&A
Volume 597, January 2017
|
|
|---|---|---|
| Article Number | A120 | |
| Number of page(s) | 12 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201629408 | |
| Published online | 12 January 2017 | |
Anisotropy in the all-sky distribution of galaxy morphological types
1 Argelander Institut für Astronomie der Universität Bonn Auf dem Hügel 71 53121 Bonn Germany
e-mail: behnam@astro.uni-bonn.de
2 Helmholtz-Institut fuer Strahlen und Kernphysik, Nussallee 14-16, 53115 Bonn, Germany
3 Charles University in Prague, Faculty of Mathematics and Physics, Astronomical Institute, V Holešovičkách 2, 180 00 Praha 8, Czech Republic
Received: 26 July 2016
Accepted: 19 September 2016
We present the first study of the isotropy of the all-sky distribution of morphological types of galaxies in the Local Universe out to around 200 Mpc using more than 60 000 galaxies from the HyperLeda database. We use a hemispherical comparison method where the sky is divided into two opposite hemispheres and the abundance distribution of the morphological types, T, are compared using the Kolmogorov-Smirnov (KS) test. By pointing the axis of symmetry of the hemisphere pairs to different directions in the sky, the KS statistic as a function of sky coordinates is obtained. For three samples of galaxies within around 100, 150, and 200 Mpc, we find a significant hemispherical asymmetry with a vanishingly small chance of occurring in an isotropic distribution. Astonishingly, regardless of this extreme significance, the observed hemispherical asymmetry for the three distance ranges is aligned with the celestial equator at the 97.1−99.8% confidence level and with the ecliptic at 94.6−97.6%, estimated using a Monte Carlo analysis. Shifting T values randomly within their uncertainties has a negligible effect on this result. When a magnitude limit of B ≤ 15 mag is applied to these samples, the galaxies within 100 Mpc show no significant anisotropy after randomization of T. However, the direction of the asymmetry in the samples within 150 and 200 Mpc and the same magnitude limit is found to be within an angular separation of 32 degrees from (l,b) = (123.7,24.6) with a 97.2% and 99.9% confidence level, respectively. This direction is only 2.6 degrees away from the celestial north pole. Unless the Local Universe has a significant anisotropic distribution of galaxy morphologies aligned with the orientation or the orbit of the Earth (which would be a challenge for the Cosmological Principle), our results show that there seems to be a systematic bias in the classification of galaxy morphological types between the data from the northern and the southern equatorial sky. Further studies are absolutely needed to find the exact source of this anisotropy.
Key words: galaxies: structure / galaxies: statistics / galaxies: abundances / cosmology: observations / methods: data analysis
© ESO, 2017
1. Introduction
Galaxies appear in various shapes and are observed to have a range of different properties; one of the main ways of studying their evolution is to classify them based on these observed features. The most widely known classification of galaxies, which is famously known as “Hubble’s tuning fork”1, categorizes the (mostly nearby) galaxies into a range of morphological types based on bulge/disk domination. This classification was later revised by de Vaucouleurs (1959) who added a numerical value to each Hubble type and also to the intermediate stages.
The morphology of galaxies is closely linked to their physical properties and those of their environments (Sandage 1975; Kormendy 1982; van den Bergh 1998; Abraham 1998; Calvi et al. 2012), and is one of the important tools for studying galaxy formation and evolution. Bulge formation scenarios depend on galaxy formation models (Hopkins et al. 2010; Kroupa 2015; López-Corredoira & Kroupa 2016; Combes 2016); distinct galaxy types are observed to have very different stellar populations and star formation rates (Grebel 2011) and different spectral properties (Sánchez Almeida et al. 2011), and their inner structure, such as bar and bulge types, is connected with their observed kinematics (Molaeinezhad et al. 2016). For a study on the evolution of the Hubble sequence see Delgado-Serrano et al. (2010) and for a recent review on galaxy morphology see Buta (2013).
Though the majority of the bright nearby galaxies fit into the Hubble’s tuning fork classification, the high redshift galaxies detected by deep surveys and the low surface brightness dwarf galaxies, whose number is increasing thanks to various surveys inside and outside the Local Group (e.g., Bechtol et al.2015; Javanmardi et al.2016, respectively), are hard to classify using the standard morphological classification system (Naim et al. 1997; Abraham & van den Bergh 2001).
One of the most widely used classification schemes is that of de Vaucouleurs compiled in the Third Reference Catalogue of Bright Galaxies (RC3; de Vaucouleurs et al. 1991) from which many other catalogs extract the morphological types of different galaxies. As pointed out by Makarov et al. (2014), visual inspection has been the main method of classification in RC3.
The need for an automated morphology classification has been known for decades (Naim 1995) and has been used in recent years (see, e.g., the recent studies by Huertas-Company et al.2015; and Kuminski & Shamir2016, and references therein). Nair & Abraham (2010) and Baillard et al. (2011) used the data from the Sloan Digital Sky Survey (SDSS) and attempted to improve the visual classification of galaxy morphologies with the aim of paving the way for automated galaxy classification by providing training sets and calibration samples (for other catalogs of galaxy morphologies see Fukugita et al. 2007; Shibuya et al. 2015; Herrera-Endoqui et al. 2015; Krywult et al. 2017; Poudel et al. 2016; Psychogyios et al.2016). In general, the goal is to achieve a catalog of the morphological types of the observed galaxies as complete and systematic-free as possible and to have a well-defined classification method applicable to future large galaxy surveys. A catalog of this kind is obviously crucial for studies of galaxy formation and evolution.
In this work, and for the first time, we search for possible deviations from isotropy in the all-sky distribution of the morphological types of galaxies within ≈200 Mpc using the HyperLeda database. Based on the Cosmological Principle (generally understood to be confirmed by most of the observations so far), on sufficiently large scales the properties of the Universe, including the distribution of galaxy types, should be statistically isotropic. Therefore, deviations from isotropy can be a hint of systematic issues with the morphological classification of galaxies or with the homogenization of catalogs.
On the other hand, it is vital to re-inspect the assumption of isotropy with various observations (Maartens 2011) and this is one of the motivations of our study. If a significant deviation from cosmic isotropy is detected and confirmed by various data sets, cosmology will face a major paradigm change. During the last decade, probing isotropy in all-sky extragalactic data has become a vibrant research topic and continues to deliver interesting results. Tegmark et al. (2003), Eriksen et al. (2004), and Hansen et al. (2004) reported some large-scale anisotropies (hemispherical asymmetry and quadrupole-octopole alignment) in the cosmic microwave background (CMB) radiation data from the WMAP satellite. These CMB anomalies have recently been confirmed by the Planck Collaboration XXIII (2014) suggesting that they are not artifacts caused by the detectors or data-reduction procedures (see also Akrami et al. 2014; Rassat et al. 2014; Copi et al. 2015; Mukherjee et al. 2016). Javanmardi et al. (2015) found an anisotropy in the magnitude-redshift relation of high redshift Type Ia Supernovae (SNe Ia) that is significantly aligned with the direction of the CMB dipole and very close to the CMB quadrupole-octopole alignment (for similar studies see Carvalho & Marques 2016; Bengaly 2016; Migkas & Plionis 2016; Lin et al. 2016, and references therein). Also, an inconsistency between the amplitude of the observed dipole in the distribution of radio galaxies and the value expected from the CMB dipole has been reported in Singal (2011), Rubart & Schwarz (2013), and Tiwari & Nusser (2016). For a recent review on various isotropy studies see Zhao & Santos (2016).
The isotropy of the spatial distribution of galaxies has been probed by various authors (Gibelyou & Huterer 2012; Yoon et al. 2014; Appleby & Shafieloo 2014; Alonso et al. 2015; Bengaly et al. 2017). These studies have found some mild anisotropies with different directions, but none of them has reported a significant deviation.
In our analysis, we consider three distance ranges separately: galaxies with radial velocity less than 7000, 10 000, and 14 000 km s-1 (equivalent to around 100, 150, and 200 Mpc from us, respectively2). Based on the standard model of cosmology, at such distance scales and especially beyond ≈150 Mpc (Marinoni et al. 2012) the distribution of galaxies should be statistically isotropic. For each distance range, we separate the galaxies by dividing the sky into two opposite hemispheres and compare their morphological type distribution using the Kolmogorov-Smirnov test. By pointing the axis of symmetry of our hemispheric cut towards different directions on the sky and repeating the test, we find the pair of hemispheres with the greatest difference in the distribution of morphological types and quantify the significance of the difference.
This paper is organized as follows. In Sect. 2 we describe our sample from the HyperLeda database. Our method of analysis is explained in Sect. 3. We present the results in Sect. 4, discuss them critically in Sect. 5, and finally we summarize and conclude in Sect. 6.
2. Data
HyperLeda (Paturel et al. 2003a,b; Makarov et al. 2014) is a large database of more than three million objects, around 1.5 million of which are confirmed galaxies that uniformly cover the entire sky except for the region around the Galactic plane. This database contains different observed properties like magnitude, surface brightness, color, redshift, and morphological type of galaxies. These measurements have been homogenized to standard systems and are updated when new measurements become available (Makarov et al. 2014).
The morphological types, T, in HyperLeda are homogenized values based on compilation of morphology measurements from the literature. These types are in the de Vaucouleurs scale (de Vaucouleurs et al. 1991) ranging from T = −5 for elliptical galaxies to T = 10 for irregular galaxies. Most of these measurements are obtained by visual inspection of optical images. After the homogenization (which also takes into account the quality of each measurement), the best possible value and its uncertainty for each galaxy is determined. They are not limited to integer values and have an accuracy up to the first decimal digit in the HyperLeda database (e.g., T = 2.2 ± 0.7 for the galaxy NGC 3368). The information on the instruments used for these measurements are not kept in the database, but can be found in the individual works3.
For the purpose of this study, we limit our sample to all the confirmed galaxies that have a radial velocity in the CMB reference frame, VCMB, lower than 14 000 km s-1. This velocity corresponds to a distance of about 200 Mpc. This gives us around 200 000 galaxies from the HyperLeda database. For each galaxy, we obtain its equatorial and Galactic coordinates, its morphological type (if available), its corresponding uncertainty (σT), corrected apparent total B magnitude, and absolute B-band magnitude (MB) from the database.
More than 65 000 of these galaxies (≈33% of the sample) have a measured morphological type assigned to them in the database4. In order to increase the robustness of our analysis, we exclude the ≈3000 galaxies (around 5% of the galaxies with T) for which an absolute B-band magnitude is not available5. This condition gives us the final sample of more than 62 000 galaxies that we used for our statistical analysis, hereafter referred to as “the whole sample”. The faintest object in the sample has B = 23.5 mag, but only around 2500 galaxies in the sample have B ≥ 17.0 mag6. The number distribution of the T values of the whole sample is shown in Fig. 1 and its sky distribution in the Galactic coordinate system is shown in Fig. 2 with the color code being VCMB in units of km s-1. We see that galaxies are distributed uniformly across the sky (except for the region around the Galactic plane) and we see no trace of any particular survey.
 |
Fig. 1 Number distribution of the T values for the galaxies in the HyperLeda database with VCMB< 14 000 km s-1 and a measured MB. In all the bins only the left edge is included in the counting (e.g., for the the first bin −5 ≤ T< 4) except for the last bin, which also includes the right edge (i.e., 9 ≤ T ≤ 10). This is the same for the rest of the histogram plots in this paper. |
 |
Fig. 2 Sky distribution of all the galaxies in the HyperLeda database with VCMB < 14 000 km s-1 that have T and MB, in the Galactic coordinate system. The color code is radial velocity, VCMB, in km s-1 and the celestial equator is shown by a black solid curve. The sample uniformly covers all the sky (except for the regions in and around the disk of our Galaxy). |
3. Method
3.1. Hemispherical comparison
We consider a particular hemisphere of the sky whose pole is pointing at a direction 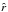 with longitude and latitude (l,b) in the Galactic coordinate system. We then separate the galaxies into two groups: those inside that hemisphere and the ones that are in the opposite hemisphere whose pole is pointing towards
with longitude and latitude (l,b) in the Galactic coordinate system. We then separate the galaxies into two groups: those inside that hemisphere and the ones that are in the opposite hemisphere whose pole is pointing towards 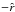 with coordinates (l + 180°,−b). We then compare the morphological distribution of these two sets of galaxies. The aim is to vary
with coordinates (l + 180°,−b). We then compare the morphological distribution of these two sets of galaxies. The aim is to vary 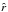 to point towards different directions on the sky and repeat the hemispheric division and distribution comparison in order to find the pair of hemispheres with the greatest difference in the distribution of T and to calculate the significance of the difference. We start from the northern Galactic hemisphere, so
to point towards different directions on the sky and repeat the hemispheric division and distribution comparison in order to find the pair of hemispheres with the greatest difference in the distribution of T and to calculate the significance of the difference. We start from the northern Galactic hemisphere, so 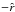 will be in the southern hemisphere. We pixelize the sky using a HEALPix7 grid (Górski et al. 2005) with 768 pixels (or directions). This gives us 384 pairs of opposite hemispheres for our analysis.
will be in the southern hemisphere. We pixelize the sky using a HEALPix7 grid (Górski et al. 2005) with 768 pixels (or directions). This gives us 384 pairs of opposite hemispheres for our analysis.
3.2. Kolmogorov-Smirnov test
A simple but powerful statistical method for quantifying the level of consistency of the distribution of two data sets is the Kolmogorov-Smirnov (KS) test. This non-parametric method is used to test whether two data sets come from the same parent distribution. After separating the galaxies into two groups using the hemispheric cut (see Sect. 3.1), we obtain the cumulative distribution functions, 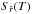 and
and 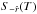 , of the morphological types in the hemispheres pointing at
, of the morphological types in the hemispheres pointing at 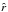 and
and 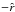 , respectively. These distribution functions are normalized so that their highest value is equal to unity. The KS statistic as a measure of the difference between these two distributions is simply the maximum value of the absolute difference between
, respectively. These distribution functions are normalized so that their highest value is equal to unity. The KS statistic as a measure of the difference between these two distributions is simply the maximum value of the absolute difference between 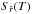 and
and 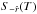 (Press et al. 1986):
(Press et al. 1986): 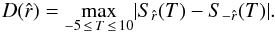 (1)We find
(1)We find 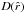 for the 384 hemisphere pairs to determine the direction with the highest D.
for the 384 hemisphere pairs to determine the direction with the highest D.
 |
Fig. 3 Left: sky maps of D from the KS test in the Galactic coordinate system from top to bottom for VCMB < 7000, 10 000, and 14 000 km s-1. The value in each pixel is obtained from the KS comparison of the pair of hemispheres with axis of symmetry along the center of that pixel. The opposite direction of each pixel has exactly the same value. On each map, the direction |
4. Results
4.1. Hemispherical comparison and the directions with the greatest difference
Sky maps of 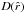 for the three radial velocity ranges are shown in the left panel of Fig. 3. The value in each pixel is obtained by applying the KS test on the hemisphere whose pole is pointing towards the center of that pixel and its opposite hemisphere. Obviously, the D for each direction
for the three radial velocity ranges are shown in the left panel of Fig. 3. The value in each pixel is obtained by applying the KS test on the hemisphere whose pole is pointing towards the center of that pixel and its opposite hemisphere. Obviously, the D for each direction 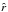 and its opposite direction
and its opposite direction 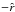 is exactly the same since it is a measure of the difference between them. On each map, the direction with the greatest difference,
is exactly the same since it is a measure of the difference between them. On each map, the direction with the greatest difference,  , and its opposite direction,
, and its opposite direction, 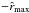 , are marked by a star and a circle, respectively. It can be seen that the general trend and the
, are marked by a star and a circle, respectively. It can be seen that the general trend and the  in all three maps are very close to each other.
in all three maps are very close to each other.
In Table 1, we list the coordinates of the  and the corresponding KS results, Dmax, for the three VCMB ranges. The number of total galaxies in the HyperLeda database within each radial velocity range, Ntot, and the number of galaxies that have both T and MB and were used in our analysis, Na, are also listed in this table. We see that Dmax decreases when the distance increases from VCMB< 7000 to 10 000 km s-1, but increases again when going to VCMB< 14 000 km s-1, while
and the corresponding KS results, Dmax, for the three VCMB ranges. The number of total galaxies in the HyperLeda database within each radial velocity range, Ntot, and the number of galaxies that have both T and MB and were used in our analysis, Na, are also listed in this table. We see that Dmax decreases when the distance increases from VCMB< 7000 to 10 000 km s-1, but increases again when going to VCMB< 14 000 km s-1, while  remains unchanged in this step.
remains unchanged in this step.
In this table, we also list the number of galaxies in the pair of hemispheres corresponding to Dmax, namely 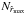 and
and 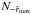 . We see that their difference is small for all three distance ranges, but to check whether these directions are related or are close to the directions with the greatest difference in the number of galaxies, we can look at the variation in the number of galaxies in each sample across the sky. In the right panel of Fig. 3, the number of galaxies in the hemispheres whose poles are pointing towards each pixel is plotted. We also show
. We see that their difference is small for all three distance ranges, but to check whether these directions are related or are close to the directions with the greatest difference in the number of galaxies, we can look at the variation in the number of galaxies in each sample across the sky. In the right panel of Fig. 3, the number of galaxies in the hemispheres whose poles are pointing towards each pixel is plotted. We also show  and
and 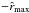 as in the left panel. Although these are only the galaxies that have a T value, the change in the number is smooth; the maximum, M, is consistently close to the direction that the Local Group moves towards (with respect to the CMB rest frame; see, e.g., Gibelyou & Huterer 2012), and the minimum, m, is in the opposite direction. Hence, the directions corresponding to Dmax are very different from those with the greatest difference in the number of galaxies.
as in the left panel. Although these are only the galaxies that have a T value, the change in the number is smooth; the maximum, M, is consistently close to the direction that the Local Group moves towards (with respect to the CMB rest frame; see, e.g., Gibelyou & Huterer 2012), and the minimum, m, is in the opposite direction. Hence, the directions corresponding to Dmax are very different from those with the greatest difference in the number of galaxies.
In the first two columns of Fig. 4 we show the distribution of T in the hemispheres towards  and
and 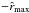 for the three VCMB ranges. Their cumulative distributions are shown in the third column of this figure. We can see two prominent differences between the morphological distribution of galaxies in these opposite hemispheres. First, the number of galaxies with 9 ≤ T ≤ 10 (i.e., Sm and Im types) in the direction of
for the three VCMB ranges. Their cumulative distributions are shown in the third column of this figure. We can see two prominent differences between the morphological distribution of galaxies in these opposite hemispheres. First, the number of galaxies with 9 ≤ T ≤ 10 (i.e., Sm and Im types) in the direction of  is around twice as high as the number of these types in the direction
is around twice as high as the number of these types in the direction 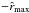 in all three VCMB ranges. Second, the number of galaxies with −1 ≤ T < 0 (i.e., S0+ types) in the direction of
in all three VCMB ranges. Second, the number of galaxies with −1 ≤ T < 0 (i.e., S0+ types) in the direction of 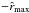 is more than twice the number of these galaxies in the direction of
is more than twice the number of these galaxies in the direction of  , again for all three VCMB ranges. In the latter case, a clear jump in the cumulative distribution functions is visible. Another increase in this function is at T = 5 (i.e., Sc galaxies) and their number is higher towards
, again for all three VCMB ranges. In the latter case, a clear jump in the cumulative distribution functions is visible. Another increase in this function is at T = 5 (i.e., Sc galaxies) and their number is higher towards 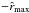 in all the three VCMB ranges.
in all the three VCMB ranges.
Finally, we emphasize that the results are almost the same in all three of the distance ranges.
Our three radial velocity ranges and their corresponding estimated distances, the total number of galaxies from the HyperLeda database Ntot for each range and the number of galaxies Na used in our analysis (i.e., having T and MB).
4.2. Significance of the observed asymmetry
Given the assumption that the distribution of galaxies is statistically isotropic in the distance ranges under consideration and therefore that the distribution of morphologies is statistically similar in different directions, we calculate the significance of the observed anisotropy using the KS distribution and different Monte Carlo (MC) analyses.
4.2.1. KS distribution
The null hypotheses here is that the morphological types in the opposite hemispheres towards  and
and 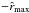 come from the same parent distribution. The probability that this hypothesis is true is equal to the probability of obtaining a difference greater than (or equal to) the observed difference: p(Dmax) = ProbKS(D ≥ Dmax). This can be calculated using the standard two-sided Kolmogorov-Smirnov distribution, which is a function of the number of data points (see Press et al. 1986, for the details). The third column of Table 2, contains the probabilities, p(Dmax), obtained for each Dmax (which are listed again in this table for ease of comparison). These values are dramatically low and basically consistent with zero. To better understand these values, we can compare them to those for the directions with the smallest difference, Dmin, which are also listed in Table 2 as p(Dmin). In other words, p(Dmin) corresponds to the pair of opposite hemispheres with the most similar distributions of T. We see that p(Dmin) is many orders of magnitude higher than p(Dmax) for all the three distance ranges.
come from the same parent distribution. The probability that this hypothesis is true is equal to the probability of obtaining a difference greater than (or equal to) the observed difference: p(Dmax) = ProbKS(D ≥ Dmax). This can be calculated using the standard two-sided Kolmogorov-Smirnov distribution, which is a function of the number of data points (see Press et al. 1986, for the details). The third column of Table 2, contains the probabilities, p(Dmax), obtained for each Dmax (which are listed again in this table for ease of comparison). These values are dramatically low and basically consistent with zero. To better understand these values, we can compare them to those for the directions with the smallest difference, Dmin, which are also listed in Table 2 as p(Dmin). In other words, p(Dmin) corresponds to the pair of opposite hemispheres with the most similar distributions of T. We see that p(Dmin) is many orders of magnitude higher than p(Dmax) for all the three distance ranges.
4.2.2. Monte Carlo: isotropic realizations
In an effort to investigate the significance calculated from the KS distribution even further, we can use MC analyses. In the first method, we create mock galaxy samples with an isotropic distribution of morphologies by shuffling the position of the galaxies in the analysis while keeping the sky distribution fixed to the original one. Although shuffling can (in some cases) place a late-type galaxy at the center of a galaxy cluster (where an elliptical is usually located), it is still a good way to have an estimate of the distribution of D in the case of a fully random sky distribution. We create 1000 random realizations with an isotropic distribution and repeat the hemispherical comparison method and find the pair of hemispheres with the highest D for each of the realizations. For all three distance ranges, the number of realizations having a Dmax equal to or higher than the observed values is zero. Actually, the highest Dmax values obtained in 1000 realizations are 0.029, 0.027, and 0.019 for VCMB < 7000, 10 000, and 14 000 km s-1, respectively, which are much lower than the observed values of Dmax.
4.2.3. Monte Carlo: random sampling
In the second MC approach, we randomly draw 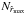 galaxies from each of the distance ranges (regardless of their coordinates) and compare their T distribution with the rest of the galaxies (whose number amounts to
galaxies from each of the distance ranges (regardless of their coordinates) and compare their T distribution with the rest of the galaxies (whose number amounts to 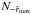 ) with the KS test. We repeat this 100 000 times and again in none of the random samples do we find a D as high as or higher than the observed Dmax values. In this case, the highest D values obtained in 100 000 realizations are 0.028, 0.022, and 0.020 for VCMB < 7000, 10 000, and 14 000 km s-1, respectively, which are similar to those obtained by the shuffling method.
) with the KS test. We repeat this 100 000 times and again in none of the random samples do we find a D as high as or higher than the observed Dmax values. In this case, the highest D values obtained in 100 000 realizations are 0.028, 0.022, and 0.020 for VCMB < 7000, 10 000, and 14 000 km s-1, respectively, which are similar to those obtained by the shuffling method.
These MC results (and the ones from Sect. 4.2.2) were expected from the calculated probabilities from the KS distribution and together they show that it is extremely improbable that the observed values of Dmax can occur out of an isotropic distribution of galaxy morphologies.
 |
Fig. 4 Distribution of morphologies in the hemisphere pairs with the greatest difference, i.e., towards |
Probability p(Dmax) (from the KS distribution) that the observed difference, Dmax, occurs if the morphologies in the pair of hemispheres are from the same parent distribution.
 |
Fig. 5 The probability distribution of Dmax for 1000 realizations in which Ti of each galaxy is replaced by Ti + ΔT where ΔT is randomly drawn from a Gaussian distribution with zero mean and standard deviation σTi. From left to right for VCMB< 7000, 10 000 and 14 000 km s-1, respectively. See Sect. 4.4. |
4.3. Alignment with the celestial equator and the ecliptic
The observed significant anisotropy has a peculiar feature that requires further analysis. The direction  for all three distance ranges is very close to the celestial north pole (CNP) and is also relatively close to the ecliptic north pole (ENP); in other words, the plane separating the hemispheres corresponding to Dmax is aligned with the celestial equator and the ecliptic. The angular separations between
for all three distance ranges is very close to the celestial north pole (CNP) and is also relatively close to the ecliptic north pole (ENP); in other words, the plane separating the hemispheres corresponding to Dmax is aligned with the celestial equator and the ecliptic. The angular separations between  and the CNP, αCNP, and the ENP, αENP, are listed in Table 3. Such an alignment is totally unexpected even if the result from the KS test would not have been significant. Since
and the CNP, αCNP, and the ENP, αENP, are listed in Table 3. Such an alignment is totally unexpected even if the result from the KS test would not have been significant. Since  is close to both the CNP and the ENP, we quantify the significance of the alignment to both of them.
is close to both the CNP and the ENP, we quantify the significance of the alignment to both of them.
Angular separation between  and the celestial, αCNP, and the ecliptic, αENP, north poles.
and the celestial, αCNP, and the ecliptic, αENP, north poles.
4.3.1. Significance of the alignment from Monte Carlo analysis
Using the 1000 isotropic realizations from the MC analysis in Sect. 4.2.2, we find the fractions, fCNP and fENP, of isotropic samples in which the direction with the highest D has the same or better alignment with the CNP and the ENP. These values are also listed in Table 3. To obtain these fractions we do not consider the significance of the anisotropy (i.e., the value of Dmax) and we only take the direction into account. The fraction of random samples with better alignment and higher Dmax would be zero as is obvious from the results in Sect. 4.2. Interestingly, fCNP shows that even when the significance of the KS test is not taken into account, the hemispherical asymmetry is aligned with the celestial equator at the 97.1%, 99.7%, and 99.8% confidence levels for VCMB < 7000, 10 000, and 14 000 km s-1, respectively. The alignment of the observed hemispherical asymmetry with the ecliptic is at the 94.6−97.6% confidence levels, depending on the distance range under consideration. Actually, the alignment with the ENP is slightly more significant than with the CNP for the sample with VCMB < 7000 km s-1. It may be worth noting that one of the CMB anomalies, i.e., the hemispherical asymmetry in the power spectrum, is also aligned with the ecliptic plane (Planck Collaboration XXIII 2014).
4.4. Effect of shuffling T within σT on the significance and the direction of the anisotropy
The uncertainty of the morphological types, σT, for the whole sample ranges between 0.1 and 6.6 with an average 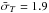 . The majority of galaxies have σT ≈ 2.0. When a σT is available for a galaxy in the HyperLeda database, it means that several astronomers have classified that galaxy. All the galaxies in our sample have a σT assigned to their T values. By performing another MC analysis, we check the extent to which random uncertainties reduce the significance of the observed asymmetry and change its direction. To achieve this, we replace the morphological type Ti of each galaxy by Ti + ΔT where ΔT is randomly drawn from a Gaussian distribution with zero mean and standard deviation σTi. We then perform the hemispherical comparison on the new T values. This process of randomization of T and search for asymmetry is repeated 1000 times for the three distance ranges. Figure 5 shows the distribution of Dmax obtained from this MC analysis.
. The majority of galaxies have σT ≈ 2.0. When a σT is available for a galaxy in the HyperLeda database, it means that several astronomers have classified that galaxy. All the galaxies in our sample have a σT assigned to their T values. By performing another MC analysis, we check the extent to which random uncertainties reduce the significance of the observed asymmetry and change its direction. To achieve this, we replace the morphological type Ti of each galaxy by Ti + ΔT where ΔT is randomly drawn from a Gaussian distribution with zero mean and standard deviation σTi. We then perform the hemispherical comparison on the new T values. This process of randomization of T and search for asymmetry is repeated 1000 times for the three distance ranges. Figure 5 shows the distribution of Dmax obtained from this MC analysis.
In 99.9% of these realizations, p(Dmax) is lower than 1.5 × 10-58, 4.2 × 10-58, and 3.2 × 10-96 for VCMB < 7000, 10 000, and 14 000 km s-1, respectively. For the VCMB < 7000 km s-1 range, the direction  remains exactly the same in 73.4% of the realizations, while in the rest
remains exactly the same in 73.4% of the realizations, while in the rest  is within
is within 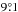 of the observed direction. For the sample with VCMB< 10 000 km s-1, 83.3% of the cases yield the same
of the observed direction. For the sample with VCMB< 10 000 km s-1, 83.3% of the cases yield the same  and the rest have an
and the rest have an  within
within 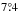 of the observed direction. Finally, for the distance range VCMB< 14 000 km s-1, in all 1000 realizations the direction
of the observed direction. Finally, for the distance range VCMB< 14 000 km s-1, in all 1000 realizations the direction  remains exactly the same as the observed direction. Therefore, shuffling T within σT has little to no effect on the direction of the asymmetry found in these distance limited samples.
remains exactly the same as the observed direction. Therefore, shuffling T within σT has little to no effect on the direction of the asymmetry found in these distance limited samples.
In Fig. 6, we show the distribution of galaxy morphologies for the three radial velocity ranges in our study in the equatorial coordinate system8. The black dotted line is the plane of the ecliptic, and the red solid line is the plane separating the pair of hemispheres corresponding to Dmax for each case. As can be seen, the observed hemispherical asymmetry is very close to both the ecliptic plane and the celestial equator for VCMB < 7000 km s-1, but is closer to the celestial equator for VCMB < 10 000 and 14 000 km s-1. In the case of VCMB < 14 000 km s-1, the number of galaxies in the analysis increases by more than 30% with respect to this number for VCMB < 10 000 km s-1; however, the direction of  does not change. We can clearly see a region to the south of the celestial equator occupied mostly with early-type galaxies and the northern sky is more populated by late-type galaxies.
does not change. We can clearly see a region to the south of the celestial equator occupied mostly with early-type galaxies and the northern sky is more populated by late-type galaxies.
5. Discussion
At the moment, our results cannot be compared with other studies because this is the first time that the isotropy of galaxy morphological types has been investigated. The previous statistical studies of the morphological types (e.g., Nair & Abraham 2010; de Lapparent et al. 2011) were limited to only a fraction of the sky. The studies on the isotropy of the number distribution of galaxies by Gibelyou & Huterer (2012) and Alonso et al. (2015) and on the isotropy of the luminosity function of galaxies by Appleby & Shafieloo (2014) did not report a significant deviation from isotropy, but their reported directions are relatively close to the direction of the CMB dipole. The studies by Yoon et al. (2014) and Bengaly et al. (2017) of the isotropy of the galaxy number counts both found (with low significance) similar dipole directions of (l,b) = (310,−15) and (l,b) = (323,−5) that are different from the above-mentioned studies, but are not far from the 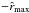 directions in our study.
directions in our study.
5.1. Sample selection effects
Since the anisotropy we found in the distribution of morphological types is very significant and unexpectedly aligned with the CNP and ENP, it is necessary to examine the results more closely. In this section we discuss the cases regarding our sample that could affect the results.
5.1.1. Including the galaxies without MB
As we mentioned in Sect. 2, the galaxies that do not have an available MB in the HyperLeda database were excluded from our analysis. Although they constitute only about 5% of the galaxies with T, we checked their effect on the results. We repeated the hemispherical comparison analysis for the whole sample of galaxies with VCMB < 14 000 km s-1, this time including the ≈3000 galaxies without MB. The direction with the greatest difference remains exactly the same and Dmax = 0.124. Hence, including these galaxies does not affect the final results.
5.1.2. Excluding galaxies with large error on T
Here we applied a strict cut and excluded all the galaxies with σT ≥ 3.0 from the whole sample with VCMB< 14 000 km s-1, which left us with 50 195 galaxies for the analysis. The hemispherical comparison again results in exactly the same direction and a slightly smaller difference, Dmax = 0.121. Therefore, excluding the galaxies with large error on T does not have a significant effect on the results either.
5.1.3. Distance tomography
The subsamples we considered are not independent of each other, i.e., the whole sample with all the galaxies within VCMB < 14 000 km s-1 includes the other two samples with VCMB< 7000 and 10 000 km s-1. Here we repeat the hemispherical comparison analysis for the two independent subsamples of galaxies with 7000 <VCMB/ (km s-1) < 10 000, and 10 000 <VCMB/ (km s-1) < 14 000. For the first sample, Dmax = 0.132 and p(Dmax) = 4.6 × 10-63, and for the second sample, Dmax = 0.203 and p(Dmax) = 9.0 × 10-139. For both of them, the direction  is (l,b) = (118.1,30.0), i.e., exactly the same as those of the samples with VCMB< 10 000 and 14 000 km s-1 (see Table 1). The KS test shows that the distance range 10 000 <VCMB/ (km s-1) < 14 000 has the greatest asymmetry in the distribution of T. The overall results remain unchanged.
is (l,b) = (118.1,30.0), i.e., exactly the same as those of the samples with VCMB< 10 000 and 14 000 km s-1 (see Table 1). The KS test shows that the distance range 10 000 <VCMB/ (km s-1) < 14 000 has the greatest asymmetry in the distribution of T. The overall results remain unchanged.
5.1.4. Applying a magnitude limit to the sample
The factor that is more likely to affect the results is that a large number of galaxies within 14 000 km s-1 in the HyperLeda database do not have a T value. Had we known the morphological types of these galaxies, the result could be different. Unfortunately, this information is not available at the moment.
However, we can test the effect of completeness by limiting the analysis to all the galaxies brighter than a certain magnitude. We put a conservative magnitude limit and confine our hemispherical comparison analysis to the galaxies with B ≤ 15 mag. The galaxy sample from HyperLeda with VCMB< 14 000 km s-1 and B ≤ 15 mag is around 99% complete, i.e., around 99% of galaxies in the database with these two conditions have a T value. This is the same for the samples with VCMB< 7000 and 10 000 km s-1 and the same magnitude limit. The results of the hemispherical comparison for the three distance ranges are shown in Table 4. We see that the Dmax values are lower than the values for the samples without the magnitude limit. Although the level of anisotropy decreases and the values of p(Dmax) are orders of magnitude higher than those for the samples without the B ≤ 15 mag limit, they are still quite low and the KS result is still very significant (compare the values of p(Dmax) to those of p(Dmin) which are also listed in Table 4). The direction of  did not change for the range VCMB< 7000 km s-1; however, for VCMB< 10 000 and 14 000 km s-1, the
did not change for the range VCMB< 7000 km s-1; however, for VCMB< 10 000 and 14 000 km s-1, the  is farther away from the ENP, but interestingly is even more aligned with the CNP having only a
is farther away from the ENP, but interestingly is even more aligned with the CNP having only a 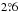 angular separation.
angular separation.
We apply the MC method explained and used in Sect. 4.4 to check the effect of shuffling T within σT on the anisotropy observed in these samples. For VCMB< 10 000 and 14 000 km s-1, 97.2% and 99.9% of the realizations have their  within 32
within 32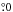 of the observed direction9, and all the realizations have their p(Dmax) lower than 2.2 × 10-5 and 6.8 × 10-7, respectively. However, in the case of the sample with VCMB< 7000 km s-1, only 17.0% of the realizations have their
of the observed direction9, and all the realizations have their p(Dmax) lower than 2.2 × 10-5 and 6.8 × 10-7, respectively. However, in the case of the sample with VCMB< 7000 km s-1, only 17.0% of the realizations have their  within 32
within 32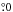 of the observed direction, the rest have their
of the observed direction, the rest have their  towards various directions and ranging to more than 80
towards various directions and ranging to more than 80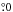 away from the observed
away from the observed  . Although shuffling T within σT washes out the asymmetry in the sample with VCMB< 7000 km s-1 and B ≤ 15 mag, the anisotropy in the samples with VCMB< 10 000 and 14 000 km s-1 and B ≤ 15 (especially the latter) remain significantly close to the observed direction of
. Although shuffling T within σT washes out the asymmetry in the sample with VCMB< 7000 km s-1 and B ≤ 15 mag, the anisotropy in the samples with VCMB< 10 000 and 14 000 km s-1 and B ≤ 15 (especially the latter) remain significantly close to the observed direction of  .
.
Figure 7 shows the number distribution of different T values in the hemisphere pairs corresponding to Dmax for the magnitude limited samples. We also show the difference in the number of each T bin between the two hemispheres. The greatest difference is for the galaxies with −5 ≤ T ≤ −4, −3 ≤ T ≤ −2, 3 ≤ T ≤ 4, and 5 ≤ T ≤ 6, in the order of relative difference. Based on these number differences we see that if ≈30% of galaxies with 3 ≤ T ≤ 4 in the north and ≈34% of galaxies with 5 ≤ T ≤ 6 in the south had their morphological types in the range 4 ≤ T ≤ 5, and at the same time ≈35% of galaxies with −5 ≤ T ≤ −4 in the north and ≈40% of galaxies with −3 ≤ T ≤ −2 in the south had their morphological types in the range −4 ≤ T ≤ −3, then the anisotropy would be partially alleviated. However, even in this case, the number of galaxies with 4 ≤ T ≤ 5 would be ≈17% more in the south and the number of galaxies with −4 ≤ T ≤ −3 would be ≈25% more in the north. Actually, it is not straightforward to tell what sort of shift in the T values will remove the asymmetry. Figure 8 shows the distribution of the morphological types of the magnitude limited samples in the equatorial coordinate system. By comparing this with Fig. 6 we can see that the obvious sharp contrast between the north and the south in the case of the VCMB< 10 000 and 14 000 km s-1 samples is no longer visible, but the hemispherical asymmetry (shown by the red solid curve) is more aligned with the celestial equator. Applying the B ≤ 15.0 mag limit reduces the level of anisotropy, but does not remove it.
 |
Fig. 6 Equatorial coordinate system distribution of all the galaxies in the HyperLeda database with measured T and MB, from top to bottom corresponding to VCMB< 7000, 10 000, and 14 000 km s-1. The color code is T, the empty parts are the region around the disk of the Milky Way, the plane of the ecliptic is shown with a dotted line, and the pair of hemispheres with the greatest difference in the distribution of morphologies are divided by a red solid line. |
However, given that the sky coverage of the distance limited sample is fairly uniform and covers a wide range of apparent magnitude as well as a full range of distances, and that the two hemispheres with the greatest difference have a similar number of galaxies, the question is raised as to why the distance limited sample, though incomplete, should be biased by a certain type of galaxy in one hemisphere and by a different type in the opposite one.
Results for the samples with B ≤ 15 mag.
 |
Fig. 7 Distribution of morphologies in the hemispheres towards |
6. Summary and conclusion
We presented the first probe of isotropy of the distribution of morphological types of galaxies in the Local Universe. Using the de Vaucouleurs morphological types of more than 60 000 galaxies with radial velocity VCMB < 14 000 km s-1 (corresponding to a distance within ≈200 Mpc) from the HyperLeda database, we searched for any directional difference in the distribution of morphological types. We used a hemispherical comparison method and by dividing the sky into two opposite hemisphere pairs, compared the frequency of morphological types, T, using a Kolmogorov-Smirnov test. The KS test was applied to hemisphere pairs with the axis of symmetry pointing at the centers of the pixels of a HEALPix grid. This gave us all-sky maps of the KS statistics, D. We performed this analysis for three radial velocity ranges, i.e., for galaxies with VCMB < 7000, 10 000, and 14 000 km s-1 (corresponding to distances of about 100, 150, and 200 Mpc).
 |
Fig. 8 Equatorial coordinate system distribution of all the galaxies in the HyperLeda database with B ≤ 15.0 mag and measured T and MB, from top to bottom corresponding to VCMB< 7000, 10 000, and 14 000 km s-1. The color code is T, the empty parts are the region around the disk of the Milky Way, the plane of the ecliptic is shown with a dotted line, and the pair of hemispheres with the greatest difference in the distribution of morphologies are divided by a red solid line. Though the sharp contrast seen in Fig. 6 is no longer visible, the hemispherical asymmetry obtained from the KS test is even more aligned with the celestial equator for galaxies with VCMB< 10 000 and 14 000 km s-1. |
The directions  corresponding to the hemisphere pairs with the greatest difference, Dmax, were found to be similar for the three distance ranges. These directions are very far from the directions with the greatest difference in the number of galaxies. Under the assumption that the galaxy morphologies should be statistically isotropic in the distance ranges under consideration, the probability of obtaining the observed difference or greater from the KS distribution, p(Dmax), was found to be ≤10-133. In addition, using a Monte Carlo analysis and by creating 1000 isotropic realizations, the number of realizations with equal or higher Dmax was found to be zero and the highest values of Dmax obtained from the 1000 realizations were found to be an order of magnitude lower than the observed values.
corresponding to the hemisphere pairs with the greatest difference, Dmax, were found to be similar for the three distance ranges. These directions are very far from the directions with the greatest difference in the number of galaxies. Under the assumption that the galaxy morphologies should be statistically isotropic in the distance ranges under consideration, the probability of obtaining the observed difference or greater from the KS distribution, p(Dmax), was found to be ≤10-133. In addition, using a Monte Carlo analysis and by creating 1000 isotropic realizations, the number of realizations with equal or higher Dmax was found to be zero and the highest values of Dmax obtained from the 1000 realizations were found to be an order of magnitude lower than the observed values.
Interestingly, the hemispherical asymmetry that we found in the distribution of the morphological types of galaxies is aligned with both the ecliptic and the celestial equator planes. The direction  for the sample with VCMB < 7000 km s-1 is only
for the sample with VCMB < 7000 km s-1 is only 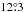 and
and 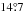 away from the celestial and the ecliptic north poles, respectively. Using our Monte Carlo analysis with 1000 isotropic realizations, we quantified the significance of the alignment with the ecliptic to be at the 97.6% confidence level, and that of the alignment with the celestial equator to be at the 97.1% (both not taking into account the extreme significance obtained from the KS test). It may be interesting to note that the hemispherical asymmetry in the CMB power spectrum discovered in the WMAP data and confirmed by the Planck satellite is also aligned with the plane of the ecliptic (Planck Collaboration XXIII 2014).
away from the celestial and the ecliptic north poles, respectively. Using our Monte Carlo analysis with 1000 isotropic realizations, we quantified the significance of the alignment with the ecliptic to be at the 97.6% confidence level, and that of the alignment with the celestial equator to be at the 97.1% (both not taking into account the extreme significance obtained from the KS test). It may be interesting to note that the hemispherical asymmetry in the CMB power spectrum discovered in the WMAP data and confirmed by the Planck satellite is also aligned with the plane of the ecliptic (Planck Collaboration XXIII 2014).
For the other two samples with VCMB< 10 000 and 14 000 km s-1, the observed anisotropy is aligned with the celestial equator at the 99.7% confidence level, with an angular separation of only 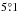 . In general, when looking at the sky distribution of morphological types of the whole sample (VCMB< 14 000 km s-1), the northern sky is more populated by late-type galaxies whereas early-type galaxies are the dominant type in the southern sky. In particular, the greatest difference in the abundance of morphological types is observed to be related to the galaxies with 9 ≤ T ≤ 10 (i.e., Sm and Im types) whose number is two times higher towards the northern sky, and the galaxies with −1 ≤ T< 0 (i.e., S0+ types) whose number is more than twice as high in the southern sky. Excluding galaxies with large uncertainty on T (i.e., σT ≥ 3.0) does not affect the direction of the asymmetry. Also, repeating the analysis on the independent subsamples of galaxies with 7000 <VCMB (km s-1)<10 000 and 10 000 <VCMB (km s-1)<14 000 yields similar directions for the greatest difference in the distribution of T.
. In general, when looking at the sky distribution of morphological types of the whole sample (VCMB< 14 000 km s-1), the northern sky is more populated by late-type galaxies whereas early-type galaxies are the dominant type in the southern sky. In particular, the greatest difference in the abundance of morphological types is observed to be related to the galaxies with 9 ≤ T ≤ 10 (i.e., Sm and Im types) whose number is two times higher towards the northern sky, and the galaxies with −1 ≤ T< 0 (i.e., S0+ types) whose number is more than twice as high in the southern sky. Excluding galaxies with large uncertainty on T (i.e., σT ≥ 3.0) does not affect the direction of the asymmetry. Also, repeating the analysis on the independent subsamples of galaxies with 7000 <VCMB (km s-1)<10 000 and 10 000 <VCMB (km s-1)<14 000 yields similar directions for the greatest difference in the distribution of T.
To increase the completeness of our sample, we applied a conservative magnitude limit and included only the galaxies with B ≤ 15.0 mag in our analysis. This resulted in a decrease in the values of Dmax, though still with a small probability of consistency with the null hypothesis of isotropy of p(Dmax) ≤ 10-21 for all three distance ranges. For the sample with VCMB < 7000 km s-1, the direction of  remained unchanged with respect to the sample without the magnitude limit; however, for the samples with VCMB< 10 000 and 14 000 km s-1 and B ≤ 15.0 mag the direction of
remained unchanged with respect to the sample without the magnitude limit; however, for the samples with VCMB< 10 000 and 14 000 km s-1 and B ≤ 15.0 mag the direction of  was found to be closer to the celestial north pole with only
was found to be closer to the celestial north pole with only 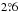 angular separation, i.e., the hemispherical asymmetry is even more aligned to the celestial equator than in the samples with the same distance ranges but without the magnitude limit.
angular separation, i.e., the hemispherical asymmetry is even more aligned to the celestial equator than in the samples with the same distance ranges but without the magnitude limit.
Using an additional 1000 Monte Carlo realizations in each of which the T values are shifted randomly within their uncertainties, we quantified the effect of random errors on the anisotropy in the distance limited samples to be negligible. However, for the VCMB< 7000 km s-1 and B ≤ 15.0 mag sample, shuffling T within σT can change the direction of anisotropy towards various directions in each realization, meaning that the anisotropy in this sample is not significant. On the other hand, in 97.2% and 99.9% of the realizations for VCMB< 10 000 and 14 000 km s-1 and B ≤ 15.0 mag, the direction  is within
is within 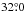 of the observed direction showing that the anisotropy in these samples (especially in the latter one) is robust against the effect of random errors. For these two samples, the number of galaxies with −5 ≤ T< −4 and with 3 ≤ T< 4 is respectively around 50% and 40% higher and the number of galaxies with −3 ≤ T< −2 and 5 ≤ T< 6 is respectively around 40% and 34% lower in the northern sky. A simple shift (e.g., +1 or −1) in the T values of one hemisphere does not decrease the value of Dmax (it actually increases it in most cases). Various combinations of shifts in T around −5 ≤ T< −2 and around 3 ≤ T< 6 can only partially alleviate the tension in the number of morphological types between north and south.
of the observed direction showing that the anisotropy in these samples (especially in the latter one) is robust against the effect of random errors. For these two samples, the number of galaxies with −5 ≤ T< −4 and with 3 ≤ T< 4 is respectively around 50% and 40% higher and the number of galaxies with −3 ≤ T< −2 and 5 ≤ T< 6 is respectively around 40% and 34% lower in the northern sky. A simple shift (e.g., +1 or −1) in the T values of one hemisphere does not decrease the value of Dmax (it actually increases it in most cases). Various combinations of shifts in T around −5 ≤ T< −2 and around 3 ≤ T< 6 can only partially alleviate the tension in the number of morphological types between north and south.
If this significant deviation from isotropy is real and not due to issues with the catalog and the classifications, it could mean that the galaxies in these two opposite directions have different evolution and/or formation histories which would be a major challenge for the Cosmological Principle. However, the fact that the asymmetry has an equatorial north-south alignment indicates that most probably its source is a systematic bias in the classification of morphological types between the data of the northern and the southern sky possibly because different telescopes (with different systematics) were used to observe these galaxies.
The morphological types cataloged in RC3 and the HyperLeda database have been used for many studies, and some other catalogs and online databases extract the morphological information from them. Our results indicate that some of the studies based on this morphological information may need to be reconsidered. In addition, we should not forget that these classifications have mostly been done visually and it is necessary to put even more effort into making well-defined quantitative and automated approaches for morphological classifications. Further investigations are indispensable in order to uncover the exact reason for the anisotropy we found in this study.
Based on a classification originally published in Reynolds (1920) and later by Hubble (1926), and on the tuning fork of Jeans (1928). Its famous form was later presented in Hubble (1936). See Block & Freeman (2015) for a historical note.
We consider the effect of including them in our analysis in Sect. 5.1.1.
We also apply magnitude limits to our sample in Sect. 5.1.4.
Hierarchical Equal Area isoLatitude Pixelation, http://healpix.sourceforge.net/
Acknowledgments
We thank the referee for the critical and constructive comments. We are very grateful to Dmitry Makarov for his kind and helpful correspondence and very useful information on the HyperLeda database. We thank Christian Henkel and David Martinez-Delgado for useful discussions; Jan Pflamm-Altenburg, Cristiano Porciani, Fateme Kamali, and Hosein Haghi for their constructive comments; Jens Erler for his kind help with HEALPix; and Michael Marks and Patrick Simon for useful discussions on statistics. We acknowledge the usage of the HyperLeda database (http://leda.univ-lyon1.fr), HEALPix package, and the matplotlib plotting library.
References
- Abraham, R. G. 1998, ArXiv Astrophysics e-prints [astro-ph/9809131] [Google Scholar]
- Abraham, R. G., & van den Bergh, S. 2001, Science, 293, 1273 [NASA ADS] [CrossRef] [Google Scholar]
- Akrami, Y., Fantaye, Y., Shafieloo, A., et al. 2014, ApJ, 784, L42 [NASA ADS] [CrossRef] [Google Scholar]
- Alonso, D., Salvador, A. I., Sánchez, F. J., et al. 2015, MNRAS, 449, 670 [NASA ADS] [CrossRef] [Google Scholar]
- Appleby, S., & Shafieloo, A. 2014, J. Cosmol. Astropart. Phys., 10, 070 [Google Scholar]
- Baillard, A., Bertin, E., de Lapparent, V., et al. 2011, A&A, 532, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bechtol, K., Drlica-Wagner, A., Balbinot, E., et al. 2015, ApJ, 807, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Bengaly, Jr., C. A. P. 2016, J. Cosmology Astropart. Phys., 4, 036 [NASA ADS] [Google Scholar]
- Bengaly, Jr., C. A. P., Bernui, A., Alcaniz, J. S., Xavier, H. S., & Novaes, C. P. 2017, MNRAS, 464, 768 [NASA ADS] [CrossRef] [Google Scholar]
- Block, L. D., & Freeman, C. K. 2015, A Walk with Dr Allan Sandage–Changing the History of Galaxy Morphology, Forever, eds. K. Freeman, B. Elmegreen, D. Block, & M. Woolway (Cham: Springer International Publishing), 1 [Google Scholar]
- Buta, R. J. 2013, Galaxy Morphology, eds. J. Falcón-Barroso, & J. H. Knapen, 155 [Google Scholar]
- Calvi, R., Poggianti, B. M., Fasano, G., & Vulcani, B. 2012, MNRAS, 419, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Carvalho, C. S., & Marques, K. 2016, A&A, 592, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Combes, F. 2016, Galactic Bulges, 418, 413 [NASA ADS] [CrossRef] [Google Scholar]
- Copi, C. J., Huterer, D., Schwarz, D. J., & Starkman, G. D. 2015, MNRAS, 449, 3458 [NASA ADS] [CrossRef] [Google Scholar]
- de Lapparent, V., Baillard, A., & Bertin, E. 2011, A&A, 532, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Vaucouleurs, G. 1959, Handbuch der Physik, 53, 275 [Google Scholar]
- de Vaucouleurs, G., de Vaucouleurs, A., Corwin, Jr., H. G., et al. 1991, Third Reference Catalogue of Bright Galaxies, Vol. I: Explanations and references, Vol. II: Data for galaxies between 0h and 12h, Vol. III: Data for galaxies between 12h and 24h [Google Scholar]
- Delgado-Serrano, R., Hammer, F., Yang, Y. B., et al. 2010, A&A, 509, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eriksen, H. K., Hansen, F. K., Banday, A. J., Górski, K. M., & Lilje, P. B. 2004, ApJ, 605, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Fukugita, M., Nakamura, O., Okamura, S., et al. 2007, AJ, 134, 579 [NASA ADS] [CrossRef] [Google Scholar]
- Gibelyou, C., & Huterer, D. 2012, MNRAS, 427, 1994 [NASA ADS] [CrossRef] [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Grebel, E. K. 2011, in Computational Star Formation, eds. J. Alves, B. G. Elmegreen, J. M. Girart, & V. Trimble, IAU Symp., 270, 335 [Google Scholar]
- Hansen, F. K., Banday, A. J., & Górski, K. M. 2004, MNRAS, 354, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Herrera-Endoqui, M., Díaz-García, S., Laurikainen, E., & Salo, H. 2015, A&A, 582, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hopkins, P. F., Bundy, K., Croton, D., et al. 2010, ApJ, 715, 202 [NASA ADS] [CrossRef] [Google Scholar]
- Hubble, E. P. 1926, ApJ, 64, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Hubble, E. P. 1936, Realm of the Nebulae (New Haven: Yale University Press) [Google Scholar]
- Huertas-Company, M., Gravet, R., Cabrera-Vives, G., et al. 2015, ApJS, 221, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Javanmardi, B., Porciani, C., Kroupa, P., & Pflamm-Altenburg, J. 2015, ApJ, 810, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Javanmardi, B., Martinez-Delgado, D., Kroupa, P., et al. 2016, A&A, 588, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jeans, J. H. 1928, Astronomy and Cosmogony (Cambridge University Press) [Google Scholar]
- Kormendy, J. 1982, Morphology and dynamics of galaxies, Proc. of the Twelfth Advanced Course, Saas-Fee, Switzerland, March 29−April 3, Sauverny, Switzerland, Observatoire de Genève, 1983, 12, 113 [Google Scholar]
- Kroupa, P. 2015, Can. J. Phys., 93, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Krywult, J., Tasca, L. A. M., Pollo, A., et al. 2017, A&A, in press, DOI: 10.1051/0004-6361/201628953 [Google Scholar]
- Kuminski, E., & Shamir, L. 2016, ApJS, 223, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, H.-N., Li, X., & Chang, Z. 2016, MNRAS, 460, 617 [NASA ADS] [CrossRef] [Google Scholar]
- López-Corredoira, M., & Kroupa, P. 2016, ApJ, 817, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Maartens, R. 2011, Philosoph. Trans. Roy. Soc. Lond. Ser. A, 369, 5115 [NASA ADS] [CrossRef] [Google Scholar]
- Makarov, D., Prugniel, P., Terekhova, N., Courtois, H., & Vauglin, I. 2014, A&A, 570, A13 [Google Scholar]
- Marinoni, C., Bel, J., & Buzzi, A. 2012, J. Cosmol. Astropart. Phys., 10, 036 [Google Scholar]
- Migkas, K., & Plionis, M. 2016, Rev. Mex. Astron. Astrofis., 52, 133 [Google Scholar]
- Molaeinezhad, A., Falcón-Barroso, J., Martínez-Valpuesta, I., et al. 2016, MNRAS, 456, 692 [NASA ADS] [CrossRef] [Google Scholar]
- Mukherjee, S., Aluri, P. K., Das, S., Shaikh, S., & Souradeep, T. 2016, J. Cosmol. Astropart. Phys., 6, 042 [NASA ADS] [CrossRef] [Google Scholar]
- Naim, A. 1995, Astrophys. Lett. Commun., 31, 87 [NASA ADS] [Google Scholar]
- Naim, A., Ratnatunga, K. U., & Griffiths, R. E. 1997, ApJ, 476, 510 [NASA ADS] [CrossRef] [Google Scholar]
- Nair, P. B., & Abraham, R. G. 2010, ApJS, 186, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Paturel, G., Petit, C., Prugniel, P., et al. 2003a, A&A, 412, 45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paturel, G., Theureau, G., Bottinelli, L., et al. 2003b, A&A, 412, 57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXIII. 2014, A&A, 571, A23 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Poudel, A., Heinämäki, P., Nurmi, P., et al. 2016, A&A, 590, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Press, W. H., Flannery, B. P., & Teukolsky, S. A. 1986, Numerical recipes, The art of scientific computing [Google Scholar]
- Psychogyios, A., Charmandaris, V., Diaz-Santos, T., et al. 2016, A&A, 591, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rassat, A., Starck, J.-L., Paykari, P., Sureau, F., & Bobin, J. 2014, J. Cosmol. Astropart. Phys.„ 8, 006 [Google Scholar]
- Reynolds, J. H. 1920, MNRAS, 80, 746 [NASA ADS] [CrossRef] [Google Scholar]
- Rubart, M., & Schwarz, D. J. 2013, A&A, 555, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sánchez Almeida, J., Aguerri, J. A. L., Muñoz-Tuñón, C., & Huertas-Company, M. 2011, ApJ, 735, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Sandage, A. 1975, Classification and Stellar Content of Galaxies Obtained from Direct Photography, eds. A. Sandage, M. Sandage, & J. Kristian (The University of Chicago Press), 1 [Google Scholar]
- Shibuya, T., Ouchi, M., & Harikane, Y. 2015, ApJS, 219, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Singal, A. K. 2011, ApJ, 742, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Tegmark, M., de Oliveira-Costa, A., & Hamilton, A. J. 2003, Phys. Rev. D, 68, 123523 [NASA ADS] [CrossRef] [Google Scholar]
- Tiwari, P., & Nusser, A. 2016, J. Cosmol. Astropart. Phys., 3, 062 [Google Scholar]
- van den Bergh, S. 1998, Galaxy Morphology and Classification [Google Scholar]
- Yoon, M., Huterer, D., Gibelyou, C., Kovács, A., & Szapudi, I. 2014, MNRAS, 445, L60 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, W., & Santos, L. 2016, ArXiv e-prints [arXiv:1604.05484] [Google Scholar]
All Tables
Our three radial velocity ranges and their corresponding estimated distances, the total number of galaxies from the HyperLeda database Ntot for each range and the number of galaxies Na used in our analysis (i.e., having T and MB).
Probability p(Dmax) (from the KS distribution) that the observed difference, Dmax, occurs if the morphologies in the pair of hemispheres are from the same parent distribution.
Angular separation between  and the celestial, αCNP, and the ecliptic, αENP, north poles.
and the celestial, αCNP, and the ecliptic, αENP, north poles.
All Figures
 |
Fig. 1 Number distribution of the T values for the galaxies in the HyperLeda database with VCMB< 14 000 km s-1 and a measured MB. In all the bins only the left edge is included in the counting (e.g., for the the first bin −5 ≤ T< 4) except for the last bin, which also includes the right edge (i.e., 9 ≤ T ≤ 10). This is the same for the rest of the histogram plots in this paper. |
| In the text | |
 |
Fig. 2 Sky distribution of all the galaxies in the HyperLeda database with VCMB < 14 000 km s-1 that have T and MB, in the Galactic coordinate system. The color code is radial velocity, VCMB, in km s-1 and the celestial equator is shown by a black solid curve. The sample uniformly covers all the sky (except for the regions in and around the disk of our Galaxy). |
| In the text | |
 |
Fig. 3 Left: sky maps of D from the KS test in the Galactic coordinate system from top to bottom for VCMB < 7000, 10 000, and 14 000 km s-1. The value in each pixel is obtained from the KS comparison of the pair of hemispheres with axis of symmetry along the center of that pixel. The opposite direction of each pixel has exactly the same value. On each map, the direction |
| In the text | |
 |
Fig. 4 Distribution of morphologies in the hemisphere pairs with the greatest difference, i.e., towards |
| In the text | |
 |
Fig. 5 The probability distribution of Dmax for 1000 realizations in which Ti of each galaxy is replaced by Ti + ΔT where ΔT is randomly drawn from a Gaussian distribution with zero mean and standard deviation σTi. From left to right for VCMB< 7000, 10 000 and 14 000 km s-1, respectively. See Sect. 4.4. |
| In the text | |
 |
Fig. 6 Equatorial coordinate system distribution of all the galaxies in the HyperLeda database with measured T and MB, from top to bottom corresponding to VCMB< 7000, 10 000, and 14 000 km s-1. The color code is T, the empty parts are the region around the disk of the Milky Way, the plane of the ecliptic is shown with a dotted line, and the pair of hemispheres with the greatest difference in the distribution of morphologies are divided by a red solid line. |
| In the text | |
 |
Fig. 7 Distribution of morphologies in the hemispheres towards |
| In the text | |
 |
Fig. 8 Equatorial coordinate system distribution of all the galaxies in the HyperLeda database with B ≤ 15.0 mag and measured T and MB, from top to bottom corresponding to VCMB< 7000, 10 000, and 14 000 km s-1. The color code is T, the empty parts are the region around the disk of the Milky Way, the plane of the ecliptic is shown with a dotted line, and the pair of hemispheres with the greatest difference in the distribution of morphologies are divided by a red solid line. Though the sharp contrast seen in Fig. 6 is no longer visible, the hemispherical asymmetry obtained from the KS test is even more aligned with the celestial equator for galaxies with VCMB< 10 000 and 14 000 km s-1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


