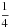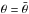| Issue |
A&A
Volume 597, January 2017
|
|
|---|---|---|
| Article Number | A75 | |
| Number of page(s) | 10 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201628998 | |
| Published online | 03 January 2017 | |
Constraining the geometry of PSR J0855−4644: A nearby pulsar wind nebula with double torus/jet morphology
1 Laboratoire AIM, IRFU/Service d’Astrophysique – CEA/DRF – CNRS – Université Paris Diderot, Bât. 709, CEA-Saclay, 91191 Gif-sur-Yvette Cedex, France
e-mail: cmaitra@mpg.mpe.de
2 Centre for Space Research, North-West University, Potchefstroom Campus, Private Bag X6001, 2520 Potchefstroom, South Africa
Received: 25 May 2016
Accepted: 17 October 2016
Aims. PSR J0855−4644 is a fast-spinning, energetic pulsar discovered at radio wavelengths near the south-eastern rim of the supernova remnant RX J0852.0−4622. A follow-up XMM-Newton observation revealed the X-ray counterpart of the pulsar and a slightly asymmetric pulsar wind nebula, which suggests possible jet structures. Lying at a distance d ≤ 900 pc, PSR J0855−4644 is a pulsar with one of the highest Ė/d2 from which no GeV γ-ray pulsations have been detected. With a dedicated Chandra observation we aim to further resolve the possible jet structures of the nebula and study the pulsar geometry to understand the lack of γ-ray pulsations.
Methods. We performed detailed spatial modelling to constrain the geometry of the pulsar wind nebula and in particular the pulsar line of sight (observer angle) ζPSR, which is defined as the angle between the direction of the observer and the pulsar spin axis. We also performed geometric radio and γ-ray light-curve modelling using a hollow-cone radio beam model together with two-pole caustic and outer gap models to further constrain ζPSR and the magnetic obliquity α defined as the angle between the magnetic and spin axes of the pulsar.
Results. The Chandra observation reveals that the compact XMM source, thought to be the X-ray pulsar, can be further resolved into a point source surrounded by an elongated axisymmetric nebula with a longitudinal extent of 10′′. The pulsar flux represents only ~1% of the XMM compact source, and its spectrum is well described by a blackbody of temperature kT = 0.2 keV, while the surrounding nebula has a much harder spectrum (Γ = 1.1 for a power-law model). Assuming the origin of the extended emission is a double torus yields ζPSR = 32.5° ± 4.3°. The detection of thermal X-rays from the pulsar may point to a low value of | ζ−α | if this emission originates from a heated polar cap. Independent constraints from geometric light-curve modelling yield α ≲ 55° and ζ ≲ 55°, and 10° ≲ | ζ−α | ≲ 30°. A χ2 fit to the radio light curve yields a best fit at (α,ζPSR) = (22°,8°), with an alternative fit at (α,ζPSR) = (9°,25°) within 3σ. The lack of non-thermal X-ray emission from the pulsar further supports low values for α and ζ under the assumption that X-rays and γ-rays are generated in the same region of the pulsar magnetosphere. Such a geometry would explain, in the standard caustic pulsar model picture, the radio-loud and γ-ray-quiet behaviour of this high Ė/d2 pulsar.
Key words: acceleration of particles / pulsars: individual: PSR J0855-4644 / X-rays: general / methods: miscellaneous
© ESO, 2017
1. Introduction
Pulsar wind nebulae (PWNe) are powered by young energetic pulsars and are excellent sites for studying the energetics of and particle spectrum injected by young rotation-powered pulsars. The unprecedented spatial resolution of Chandra has unravelled highly structured compact PWNe around many of these sources, including equatorial and polar outflows Gaensler & Slane 2000; 2006; 2008). An accurate knowledge of the PWN morphology is crucial to constrain the geometry of the pulsar, especially the pulsar line of sight ζPSR, which is defined as the angle between the direction of the observer and the pulsar spin axis, and the magnetic obliquity α defined as the angle between the magnetic axis and the spin axis of the pulsar. These constraints can in turn provide useful insights for models of high-energy emission from pulsar magnetospheres, such as the polar cap (PC) model (Daugherty & Harding 1996), the outer gap (OG) model (Cheng et al. 1986; Romani & Yadigaroglu 1995; Romani 1996), and the slot gap or two-pole caustic (TPC) model (Arons 1983; Dyks & Rudak 2003).
PSR J0855−4644 was discovered by the Parkes multibeam radio survey lying on the south-eastern rim of the RX J0852.0−4622 supernova remnant (SNR; Kramer et al. 2003). The measured spin characteristics, such as the spin period P = 65 ms and its first derivative Ṗ = 7.3 × 10-15 s s-1, gives a spin-down luminosity Ė = 1.1 × 1036 erg/s (assuming a moment of inertia I = 1045 g cm2 for standard neutron star parameters), and characteristic age τc ≡ P/ (2Ṗ) = 140 kyr. A dedicated XMM-Newton observation revealed that the X-ray counterpart of the pulsar is surrounded by extended non-thermal emission; this is the associated PWN (Acero et al. 2013). The emission was 150′′ in extent, including two large-scale structures with an angular separation of ~180°, resembling possible jets. In addition, comparison of column densities provided an upper limit to the distance of the pulsar PSR J0855−4644 of d ≤ 900 pc. With this revised distance, PSR J0855−4644 is the second most energetic pulsar, after the Vela pulsar, within a distance of 1 kpc from Earth, and could therefore contribute to the local cosmic-ray e−/e+ spectrum (Acero et al. 2013). This furthermore makes this pulsar the highest Ė/d2 system not detected at γ-ray energies with the Fermi-LAT instrument (Abdo et al. 2013). As mentioned earlier, determination of the pulsar and/or PWN geometry holds the key to understand this paradox.
We present results of a 38 ks on-axis Chandra observation to study the small-scale morphology of the nebula surrounding PSR J0855-4644 and its geometry. With the arcsecond spatial resolution of Chandra we have resolved the compact XMM-Newton source that was assumed to be the X-ray counterpart of the pulsar into a ~10′′ extended emission with jets and a possible double torus. We performed a morphological and spectral analysis, and constrained the observer angle of the system. From geometric light curve modelling, we were also able to independently constrain the (α, ζPSR) space by comparing our predictions to the radio pulse profile of the pulsar (and taking the non-detection of pulsed γ rays into account).
The observations and analysis are described in Sect. 2. Section 3 presents the spatial analysis including the imaging and morphological fitting of the source. Section 4 presents the detailed spectral analysis of the pulsar, the surrounding nebula, and its decomposed regions. Section 5 details our geometric light-curve modelling and comparison with observations. Section 6 presents the discussion, and Sect. 7 the summary and future work.
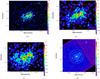 |
Fig. 1 Panel a) Chandra ACIS-S (0.5–8 keV) full-resolution image of the PWN around PSR J0855−4644. The image size is 29′′× 27′′. The box shows the extraction region for the count profile in Fig. 2. The white dashed line inside shows the symmetry axis along which the nebula is extended. Panel b) ACIS-S (0.5–2 keV) sub-pixel image (image size is 18′′× 15′′) produced at |
2. Observations and analysis
The Advanced CCD Imaging Spectrometer (ACIS) onboard Chandra offers simultaneous high-resolution images and moderate-resolution spectra. ACIS consists of ten planar CCDs, four front-illuminated CCDs (ACIS-I) are arranged in a 2 × 2 array, and six back-illuminated CCDs (ACIS-S) in a 1 × 6 array. The Chandra observation (ObsID 13780) was carried out with the ACIS-S as the primary instrument and was performed in full-frame timed-exposure (TE) mode, which uses the standard 3.2 s frame time and the FAINT telementry format. The observation was performed on 3 September 2012 with PSR J0855−4644 positioned at the aimpoint of the S3 CCD with an exposure of 38.02 ks. Data reduction was performed using CIAO 4.7, CALDB 4.6.7, and the standard prescribed analysis procedure1. The event file was reprocessed with chandra_repro, which incorporates the subpixel repositioning algorithm EDSER as a default to obtain a better angular resolution for sources near the centre of the field of view. The effective exposure of the observation after filtering was 37.98 ks. We also checked for the possible presence of pileup in the data. Many times, multiple photons impinge on a single pixel during readout, leading to it being read out as one single photon with a large pulse height, and causing photon pileup. Using the tool pileup_map, the estimated fraction of pileup in the centremost pixel was <5% and so the effect was not important for our observation. Images were created using the task dmcopy. Spatial analysis was performed using the Sherpa analysis package 4.42. The task specextract was used to extract source and background spectra and response files from regions of interest. The selection of regions used for spectral extraction is described in Sect. 4. Spectra were fitted using XSPEC v12.8.23.
Figure 1a shows a full-resolution Chandra image in the energy range 0.5–8 keV centred on PSR J0855−4644. The point source seen with XMM that was previously thought to be the pulsar X-ray counterpart is composed of an extended structure elongated in the south-east/north-west direction along a symmetry axis (see Fig. 1a). This component of the PWN is more compact (~10′′) than the much larger diffuse nebula seen with XMM, which measures 150′′ (Acero et al. 2013). Signatures of the diffuse nebula can be seen in the Chandra image in the high-energy 2–8 keV band (free of emission from the Vela Senior SNR) after smoothing it at the scale of the compact PWN, that is, 10′′ (see Fig. 1d). The fine structures of the compact PWN can be seen more clearly from its subpixel images of the same region after dividing them into soft (0.5–2 keV) and hard (2–8 keV) energy bands (see Figs. 1b and c). The elongated PWN structure is composed of two lobes lying on the symmetry axis, more or less equidistant from the pulsar in the middle. The pulsar spectrum is soft and almost disappears in the 2–8 keV energy band. The nebular structure, on the other hand, is much harder and extends more to the east in the form of a tail-like elongation. The structure is reminiscent of axisymmetric features commonly seen in young PWN systems like the equatorial outflows (tori), and collimated polar outflows (jets) (Gaensler & Slane 2006; Kargaltsev & Pavlov 2008). The two lobes symmetric about the pulsar can be explained by three possible scenarios: (a) a double-torus; (b) a double-torus and jets; and (c) a jets-only morphology. In the first scenario the lobes could be the two rings of a double-torus structure as it would appear in sky projection, spaced more or less equidistant from the pulsar centred on the torus axis (which is coincident with the symmetry axis, hence the spin axis). The brightened central parts of the lobes are caused by the doppler boosting of the torus. In the second scenario, the morphology of the PWN around PSR J0855−4644 is that of a double torus-jet structure, with both the equatorial torus and polar jet features contributing to the lobes. This is similar to the PWNe systems seen in Vela and PSR J2021+3651 (Helfand et al. 2001; Hessels et al. 2004). In the third case, the lobes could be the jets along the pulsar spin axis (the symmetry axis in Fig. 1a). In all three cases, however, the eastern part of the nebula shows an additional protrusion in the form of an outer jet. While it is hard to distinguish between these scenarios and separate the dominance of either the jets or torus in the present observation, the presence of torus and/or jets are strong indicators of ζPSR and can constrain the geometry of the system, as shown in Sect. 3.
To accurately determine the position of the point source (pulsar), we created a subpixel image of the same (at one-fifth of the ACIS pixel resolution) and applied the source detection algorithm celldetect in the soft energy band of 0.5–2 keV where the pulsar is visible. The coordinates of the point source are RA(J2000)= 08h55m36.138s Dec =−46°44′13.57′′ considering an error of 0.6′′ at 90 % confidence level in absolute Chandra astrometry. This is consistent with the radio position of the pulsar.
The net count rate from the point source after subtracting the nebular component is 0.0005 counts/s, and from the entire nebula it is 0.02 counts/s. The details of background subtraction are discussed in the spectral analysis in Sect. 4.
3. X-ray spatial analysis
We performed a detailed spatial analysis of the compact PWN surrounding PSR J0855−4644. To probe the structures of the nebula, especially the axisymmetric features, we created a count profile in the box region shown in Fig. 1a. We also performed morphological fitting of the PWN using the torus-fitting model of Ng & Romani (2004, 2008), and determined its geometrical parameters such as the torus radii, the position angle, and ζTORUS. Figure 2 shows the 0.5–8 keV count profile decomposed into two energy bands. The profile was created in the box region of length 10′′ shown in Fig. 1a, along the symmetry axis, averaged over a region (4.5′′ in width) perpendicular to it. The box was centred on the X-ray counterpart of the pulsar, and we overlaid the point-spread function (PSF) in the figure. The PSF of the observation was simulated using the Chandra ray tracer chaRT4, which simulates the High-Resolution Mirror Assembly based on the energy spectrum of the source and the observation exposure. The output of chaRT was modelled with the software MARX5 taking the instrumental effects and the EDSER subpixel algorithm into account to be consistent with the observational data. The best-fit spectrum of the point source (see Sect. 4) was used. The profile clearly shows all the structures of the nebula, including the two lobes, which are symmetric about the pulsar. The western lobe has higher counts than the eastern lobe, although it is consistent within errors. The region west of the pulsar declines more steeply with radius, almost immediately after the lobed feature. The eastern part, on the other hand, has two additional bumps, the farthest one corresponding to a tail-like protrusion seen in the images, which might be the outer jet. The decomposed count profile highlights the dominance of some features of the PWN in certain energy ranges. As seen from the images and also from spectral analysis (described below in Sect. 4), the X-ray counterpart of the pulsar is clearly seen in the energy band of 0.5–2 keV, while it is less dominant above 2 keV. The east lobe of the nebula shows an indication of being harder; it is more dominant in the energy range of 2–8 keV. The eastern outer jet has equal dominance in the soft and hard energy bands.
 |
Fig. 2 Top panel: counts profile of the source extracted from the box region in Fig. 1a (0.5–8 keV) compared with the 2D PSF (0.5–8 keV, red dashed line). The bottom panel portrays the same profile in the two energy bands 0.5–2 keV and 2–8 keV. |
Section 2 discusses three possible scenarios for the morphology of the PWN around PSR J0855−4644. In two of the three scenarios where the lobes either correspond entirely to the arcs of the torus, or to one of the torus components along with the jets, it is possible to provide quantitative measurements of the PWN geometry by modelling the lobes as a double torus as in the pulsar wind torus by fitting scheme of Ng & Romani (2008). In the third case, identifying the lobes entirely as jets instead does not alter the geometry of the system as the torus axis is coincident with the spin axis of the pulsar along which jets are formed (Ng & Romani 2008). The parameters of the torus model are the torus axis position angle (PA) Ψ (N-E)6
Spatial fitting was performed on the full-resolution image in a region of size 47′′× 45′′ centred on the pulsar to constrain the background better. The PSF described in the previous section was loaded as a table model in Sherpa to model the pulsar emission. The remaining excess consisted of the background and the emission from the nebula. The background was modelled with a constant. The lobes of the nebula were modelled with the relativistic torus model of Ng & Romani (2008) as a double torus seperated by a distance d. The background and the double-torus model was then convolved with the PSF. The δ, if left free, has a tendency to grow and absorb the unmodelled larger-scale PWN components. As this parameter does not provide any physical information on the shock or the geometry of the system, it was frozen to 0.5′′ provided by an initial visual estimate.
Figure 3 shows the best-fit model along with the data used for fitting and the residuals. The best-fit parameters were determined using the C-statistics (Cash 1979)7. The best-fit parameters are listed in Table 1. The 1σ confidence intervals are quoted here. The statistical errors were estimated by performing Monte Carlo Poisson realizations of the best-fit model as recommended in Ng & Romani (2008). To characterize the uncertainty on the estimates associated with the unmodelled components in the fit, especially the eastern tail region, we blanked out the region in the fit and noted the change in parameters. Considering that the two errors add in quadrature, we find that the pulsar line of sight ζPSR is inclined at 32.5° ± 4.3° with an upper limit of ζPSR< 37°.
Final morphological best fit with a double-torus model.
4. X-ray spectral analysis
We have performed a detailed spectral analysis of the X-ray counterpart of PSR J0855−4644 and the surrounding compact PWN. To determine changes in the spectral parameters in different parts of the nebula, we also extracted spectra from different regions by dividing the PWN into an inner and outer annular part, and examined the spectra of the east and west lobes separately. The analysis was performed in the energy range of 0.5–8 keV. The C-statistics was used for spectral fitting, and errors were estimated at a 90% confidence interval. The regions used for spectral extraction are shown in Fig. 4. For the pulsar, a circular region of radius 0.7′′ was extracted, centred on the best-fit coordinates of the source. In the case of the compact PWN, the outer radius was optimized from the spatial fitting, with the region corresponding to the pulsar excised. For all the regions, the background spectrum was extracted from an annular region with inner and outer radii of 75′′ and 100′′ (extent of the diffuse nebula seen with XMM: see Fig. 1d). This ensured that the background was free from the fainter diffuse nebular emission that was seen with the XMM-Newton observations. In the case of the pulsar, the astrophysical background due to the nebula was considered in addition to the annular background spectrum, and it was modelled with the best-fit spectrum of the entire PWN, scaled with the ratio of the two extraction regions. We also checked for an additional astrophysical background contribution from the pulsar in the nebular region and found it to be a negligible fraction of the total background.
 |
Fig. 3 First panel: data in the energy range of 0.5–8 keV. Second panel: corresponding best-fit geometric model with a double torus (Ng & Romani 2008). The arcs of the torus are marked as black dashed lines to illustrate the geometry. The third panel displays the residuals after the best-fit has been subtracted.The colour bar is in square root, and units are counts for all the images. |
 |
Fig. 4 Chandra image (0.5–8 keV) of the PWN around PSR J0855−4644 along with the regions used for spectral extraction shown in white. The value of the Γ (or kT) obtained from spectral fitting is also indicated in each panel. |
We used an absorbed power law as the spectral model for the compact PWN and all the decomposed regions marked in Fig. 4. To account for the photoelectric absorption by the interstellar gas along the line of sight, a free absorption (XSPEC model tbabs) component was used. This component was determined from the fit of the entire nebula and frozen henceforth for all other regions as it is not expected to vary locally. The value obtained with Chandra is 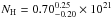 cm-2, which is consistent with that obtained using XMM-Newton, derived from a 15′′ radius region (NH = 0.64
cm-2, which is consistent with that obtained using XMM-Newton, derived from a 15′′ radius region (NH = 0.64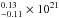 cm-2). The spectrum of the PWN is hard with a power-law index Γ of 1.12 ± 0.25. The unabsorbed bolometric luminosity Leff (0.5–8 keV) is 3.3 × 1031 erg s-1 assuming a distance of d ~ 900 pc. Comparing the spectra of the inner and outer nebula, we did not detect any steepening of the power-law spectral index Γ that could have been indicative of synchrotron cooling. In the case of the east and west lobe, while there is an indication from the counts profile (Fig. 2) that the eastern lobe has a harder spectrum than the western region (higher counts in 2–8 keV band in the east lobe compared to 0.5–2 keV), we do not find a significant difference in the spectral indices, given the current level of statistics. The pulsar spectrum is faint and soft with the statistics deteriorating drastically beyond 5 keV. The spectrum was fitted with an absorbed blackbody as well as a neutron star hydrogen atmosphere model (nsa; Gänsicke et al. 2002; Zavlin 2009). Both models provide acceptable fits to the data with comparable C-stat values. The fit with the nsa model shows an effective temperature Teff of 2.2 × 106 K and an unabsorbed bolometric luminosity Leff (0.5–8 keV) of 1.4 × 1030 erg s-1 assuming a distance of d = 900 pc. The blackbody fit of the thermal component gives a similar temperature TBB of 2.0 × 106 K and Leff of 1.3 × 1030 erg s-1. Both indicate an effective radius Reff of ~1.5 km, suggesting that the emission originates from hot spots on the poles of the neutron star and is not emission from the entire surface. No additional power-law component (related to potential non-thermal emission) was required for the fit. The pulsar and the compact PWN spectrum along with its best-fit model and residuals are shown in Fig. 5a and b, and the best-fit parameters for all the regions along with the C-statistics values are given in Table 2.
cm-2). The spectrum of the PWN is hard with a power-law index Γ of 1.12 ± 0.25. The unabsorbed bolometric luminosity Leff (0.5–8 keV) is 3.3 × 1031 erg s-1 assuming a distance of d ~ 900 pc. Comparing the spectra of the inner and outer nebula, we did not detect any steepening of the power-law spectral index Γ that could have been indicative of synchrotron cooling. In the case of the east and west lobe, while there is an indication from the counts profile (Fig. 2) that the eastern lobe has a harder spectrum than the western region (higher counts in 2–8 keV band in the east lobe compared to 0.5–2 keV), we do not find a significant difference in the spectral indices, given the current level of statistics. The pulsar spectrum is faint and soft with the statistics deteriorating drastically beyond 5 keV. The spectrum was fitted with an absorbed blackbody as well as a neutron star hydrogen atmosphere model (nsa; Gänsicke et al. 2002; Zavlin 2009). Both models provide acceptable fits to the data with comparable C-stat values. The fit with the nsa model shows an effective temperature Teff of 2.2 × 106 K and an unabsorbed bolometric luminosity Leff (0.5–8 keV) of 1.4 × 1030 erg s-1 assuming a distance of d = 900 pc. The blackbody fit of the thermal component gives a similar temperature TBB of 2.0 × 106 K and Leff of 1.3 × 1030 erg s-1. Both indicate an effective radius Reff of ~1.5 km, suggesting that the emission originates from hot spots on the poles of the neutron star and is not emission from the entire surface. No additional power-law component (related to potential non-thermal emission) was required for the fit. The pulsar and the compact PWN spectrum along with its best-fit model and residuals are shown in Fig. 5a and b, and the best-fit parameters for all the regions along with the C-statistics values are given in Table 2.
 |
Fig. 5 ACIS-S spectra for the X-ray counterpart of the pulsar (panel a)) and the entire PWN (panel b)). The solid lines correspond to the respective best-fit spectral models (absorbed blackbody and absorbed power law, respectively). In the panel a), the pulsar blackbody component (red) and the nebular contribution in the same region (green) are shown. The unbinned spectrum fitted using C-statistics has been rebinned in the plot for visual clarity. |
Parameters of the best-fit spectral model to the putative pulsar and nebula with background, without diffuse emission.
5. Constraints from geometric light-curve modelling
The fact that PSR J0855−4644 is radio-loud but γ-quiet (despite its high pseudo-luminosity Ė/d2) may be used to derive constraints on the pulsar geometry. The radio-peak multiplicity and width may also aid in obtaining geometric constraints. We can compare the predictions of geometric light-curve models with the observed radio profile to constrain both α and ζPSR. We used the TPC model (Dyks & Rudak 2003) and a geometric version of the OG model (Cheng et al. 1986; Romani 1996), in conjuction with a semi-empirical hollow-cone radio model (Gonthier et al. 2004; Harding et al. 2007). The latter model is based on work by Rankin (1993), Arzoumanian et al. (2002), with the radio emission altitude expression as in Kijak & Gil (2003). For more details, see Venter et al. (2009).
We generated an atlas of γ-ray and radio light curves on an (α, ζPSR) grid with a 5° resolution. In the next two sections, we attempt to provide conservative limits on α and ζPSR based on the qualitative features of the observed radio profile (peak multiplicity, duty cycle) and the non-detection of γ-ray pulsations. Additionally, we perform a χ2 fit using the observed radio profile to further constrain α and ζPSR in a subsequent section.
5.1. Radio visibility and peak multiplicity
For the radio models, we used a period of P = 65 ms. This important parameter sets the radio beam width (assuming emission from a single altitude for simplicity), which scales as P− 1/2 (as does the polar cap opening angle θPC, with which it is closely associated). The beam width, in conjunction with the observer angle ζPSR, determines the radio visibility of the pulsar. Conversely, the γ-ray emission originates from a range of altitudes and undergoes beaming effects, so that the caustic γ-ray beam shape in this case is relatively independent of the period (unless the observer line of sight crosses the non-emitting polar cap on the stellar surface when α ≈ ζPSR, which will cause a dip in the γ-ray light curves). We set the radio frequency to ν = 1400 MHz (same as for the observed profile). The observer orientation with respect to the radio beam provides three regimes in terms of predicting the radio pulse shape. For an impact angle β ≡ ζPSR−α ~ 0°, a double-peaked structure will be seen. For higher values of | β |, a single peak will be visible, since the observer skims the edge of the hollow cone. For even higher values of | β |, the cone will be completely missed, and the pulsar will be radio quiet. Additionally, for small α, the duty cycle is large, and for large α and small enough | β |, we start to see radio beams from both magnetic poles (leading to two profiles with a difference of about 0.5 in normalized phase). Therefore, the fact that the observed radio peak of PSR J0855−4644 is single provides a lower limit | β | ≳ 10°−15° (the lower value is for low values of α). On the other hand, radio visibility provides an upper limit on | β |: from the radio model we can derive the constraint | β | ≲ 30°. This result is somewhat dependent on the assumed emission profile of the cone. Currently, we use an offset-Gaussian flux profile that peaks at a co-latitude 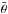 . Since we assume emission from a single height, this maximum relative flux is independent of α and ζPSR. The Gaussian profile has tails reaching beyond the last open B-field lines (which are tangent to the light cylinder at a cylindrical radius r = cP/ 2π, where the corotation speed equals the speed of light), into the corotating region. If we wish to restrict the emission by not allowing any radio flux from this region (i.e. terminating the tails at
. Since we assume emission from a single height, this maximum relative flux is independent of α and ζPSR. The Gaussian profile has tails reaching beyond the last open B-field lines (which are tangent to the light cylinder at a cylindrical radius r = cP/ 2π, where the corotation speed equals the speed of light), into the corotating region. If we wish to restrict the emission by not allowing any radio flux from this region (i.e. terminating the tails at 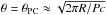 ), this would lead to smaller radio beams (by a few degrees) and therefore to tighter constraints on | β |. However, given the inherent uncertainties in the beam geometry, it might not be wise to pursue such stricter constraints on | β | that depend on the detailed beam structure. We can therefore summarize our constraint from this section as 10° ≲ | β | ≲ 30°. This constraint is also borne out by the χ2 fit to the data performed below.
), this would lead to smaller radio beams (by a few degrees) and therefore to tighter constraints on | β |. However, given the inherent uncertainties in the beam geometry, it might not be wise to pursue such stricter constraints on | β | that depend on the detailed beam structure. We can therefore summarize our constraint from this section as 10° ≲ | β | ≲ 30°. This constraint is also borne out by the χ2 fit to the data performed below.
5.2. γ-ray invisibility (non-detection)
The pulsar geometry is much better constrained when radio and γ-ray data (or a non-detection in the latter case) are used simultaneously (Pierbattista et al. 2015). In our case, the lack of γ-ray visibility leads to further constraints on α and ζPSR within the context of the TPC and OG models. In Fig. 6 we plot γ-ray (black) and radio (magenta) light curves on an (α,ζPSR) grid with a resolution of 10°. We have normalized the γ-ray intensity so that the maximum (typically at α = ζPSR = 90°) is unity and the flux of the other combinations of α and ζPSR relative to this maximum is clear8. The geometric models cannot predict absolute9γ-ray fluxes, neither can they give an indication of the γ-ray flux relative to the radio flux at a particular viewing geometry, therefore we cannot use a sensitivity-limit argument to constrain α and ζPSR. Instead, we can only use visibility (and radio pulse shape) arguments to constrain these angles.
We note that we have followed Venter et al. (2009) and assumed a gap width of 0.05θPC for both the TPC and OG models. It is true that the gap width sensitively depends on the pulsar period and magnetic field in physical pulsar models. For example, Muslimov & Harding (2003) derived expressions for the slot gap width as a function of P and B, and the width scales linearly with P. When using geometrical models, however, the common approach is to assume a reasonable value for this width that results in good light-curve fits. Our choice of 5% is also supported by the results of Johnson et al. (2014), who fitted the light curves of 40 γ-ray millisecond pulsars, finding that their best-fit gap width never exceeded 10%, but is usually smaller. Further justification comes from Fig. 2 of Muslimov & Harding (2003). While it is true that the gap width influences the shape of the resulting γ-ray light curves, the actual γ-ray pulse shape is of less importance in our case for the following reasons: (i) observational data imply that the gaps must be narrow to reproduce the observed shapes; and (ii) we only use the geometrical gap models to decide for which parameter ranges (α and ζPSR) the γ-ray pulse should be visible. Therefore, the width of the pulse is less important than the relative intensity at different (α,ζPSR), and different gap width choices should not alter our main conclusions. We have assumed the vacuum retarded dipole (Deutsch 1955; Cheng et al. 2000; Dyks et al. 2004) for the magnetice field structure, which has been standard in recent years, allowing other authors to compare their results to ours.
For the TPC model the γ-ray light curves are visible at almost all angles (except α = ζPSR ~ 10°). The low-level γ-ray emission reflects the emission outside of the main caustic beam. However, the relative flux increases dramatically when the observer samples the bright caustic (e.g. compare (α,ζPSR) = (10°,60°) and (α,ζPSR) = (10°,70°)). Given the γ-quiet and single visible radio pulse constraints, this would imply both α and ζPSR ≲ 50°, assuming that the low level of γ-ray flux (and broad γ-ray peaks) were not detectable. The case of the OG model is perhaps slightly clearer. Since no γ-ray emission is generated below the null charge surface where the Goldreich-Julian charge density is zero (Goldreich & Julian 1969), γ rays are only visible for ζPSR ≳ 50° and for large α. For example, at (α,ζPSR) ~ (50°,50°) we starts to sample the main caustic beam. (For larger ζPSR, we sample the caustic twice during one rotation, leading to double peaks.) Since the radio model is the same for the TPC and OG cases, we derive the same constraints on α and ζPSR for both γ-ray models. At a finer resolution, we find that the constraint may be written as α ≲ 55° and ζPSR ≲ 55°. It would be difficult to pick a best model between the OG and TPC in this case, since this would depend on whether the low-level TPC emission is deemed detectable. This is difficult to decide given the lack of absolute flux predictions.
 |
Fig. 6 Plot of predicted TPC (panel a)) and OG (panel b)) γ-ray (black) and radio (magenta) light curves on a (α,ζPSR) grid. The γ-ray intensity has been normalized globally so that the maximum (typically at α = ζPSR = 90°) is unity and the flux of the other combinations of α and ζPSR relative to this maximum is clear. The x-axis denotes normalized from –0.5 to 0.5. A phase offset of 0.5 has been artificially imposed to centre the radio pulses for visual clarity. The coordinate pair in each panel refers to the value of α and ζPSR in each case. |
5.3. Radio profile fit
In this section, we constrain α and ζPSR by fitting the observed radio profile from Kramer et al. (2003) using our radio model and a χ2 minimization procedure. We are only interested in reproducing the pulse shape, therefore we normalize the flux maximum to unity. We estimate the error on the data by calculating the standard deviation of the flux for the phase range φ< 0.4 (this range was chosen as the “off-peak region”), yielding σdata ~ 0.06. The number of degrees of freedom is Ndof = 255. We used χ2 = ∑ i [(Ymodel−Ydata) /σdata] 2 for i = 1,...,Nbins. The radio model was run for α ∈ [0°,90°] and ζPSR ∈ [0°,90°] at a 1° resolution, for P = 65 ms and ν = 1400 MHz, and initially for 720 phase bins. To perform a χ2 fit, we rebinned (smoothed) the model to have the same number of bins as that of the data (Nbins = 256) using a Gaussian Kernel Density Estimator (KDE) with step size h = 1 /Nbins (Rosenblatt 1956; Parzen 1962). We furthermore minimized χ2(α,ζPSR) for each fixed value of α and ζPSR over a phase-shift parameter dφ ∈ [0,0.99] with a resolution of 0.01. This is to allow alignment of the model and observed light curves, circumventing any issues that may stem from the uncertain definition of φ = 0 (cf. Johnson et al. 2014). The background level was set to zero, and the model curve was treated as being cyclical.
Figure 7 shows the log 10 [χ2(α,ζPSR)] map. Dark red indicates where the radio is invisible (| β | ≳ 30° as mentioned above). Moving inward from higher to lower | β | values, the edge of the cone is clipped and the pulse is too narrow (cyan, | β | ~ 25°); at | β | ~ 10°−15° a wider single peak is obtained that reasonably fits the data (blue), and at even smaller | β | ≲ 10°, a double peak is obtained (green). At small α and | β | (e.g. α ~ 15° and β ~ 5°), the predicted single peak is very wide (yellow), and at α ≳ 0° and | β | ~ 5°, the edge of the cone is clipped for most of the rotation, so that the light curve is nearly flat, or very broad, with a very large duty cycle (light red). The best fit is found at (α,ζPSR) = (22°,8°) for dφ = 0.73, giving χ2/Nd.o.f. = 285/255. The sigma contours (yellow lines) are calculated using ![\hbox{$\log_{10}[\chi^2_{\rm min}+\sigma_i]$}](/articles/aa/full_html/2017/01/aa28998-16/aa28998-16-eq152.png) , with σ1 = 2.3, σ2 = 6.18, and σ3 = 11.83 (Lampton et al. 1976). They are quite small (and barely visible on the χ2 contour plot), and the 1σ contours imply strong constraints on the best-fit values of α and ζPSR. However, we note that there is an alternative fit at (α,ζPSR) = (9°,25°) for dφ = 0.74, giving χ2/Nd.o.f. = 294/255, which lies within 3σ of the best fit. Other fits within 3σ are (α,ζPSR) = (23°,10°) and (α,ζPSR) = (24°,9°). These best-fit values satisfy the constraints derived in the two preceding sections. Figure 8 shows the best-fit radio light curve overplotted on the data.
, with σ1 = 2.3, σ2 = 6.18, and σ3 = 11.83 (Lampton et al. 1976). They are quite small (and barely visible on the χ2 contour plot), and the 1σ contours imply strong constraints on the best-fit values of α and ζPSR. However, we note that there is an alternative fit at (α,ζPSR) = (9°,25°) for dφ = 0.74, giving χ2/Nd.o.f. = 294/255, which lies within 3σ of the best fit. Other fits within 3σ are (α,ζPSR) = (23°,10°) and (α,ζPSR) = (24°,9°). These best-fit values satisfy the constraints derived in the two preceding sections. Figure 8 shows the best-fit radio light curve overplotted on the data.
 |
Fig. 7 log 10χ2/Nd.o.f.(α,ζPSR) map with the best fit indicated by a yellow cross. The 1σ, 2σ, and 3σ contours are very small and are indicated by yellow lines. |
6. Discussion
Thanks to a dedicated Chandra observation, the compact PWN around the fast-spinning energetic pulsar PSR J0855−4644 has been resolved. The two lobes, located axisymmetric about a fainter pulsar counterpart, can receive contributions from either the torus or the jet structures or from both of them, with the dominance of one component over the other indistinguishable by the present observation. Using the double torus model of Ng & Romani (2008) to spatially fit the lobes, we capture the characteristic features of the PWN. Most importantly, it provides a reliable estimate of ζPSR that agrees with constraints derived from geometric modelling of the radio pulse profile and non-detection of γ-ray pulsations from the pulsar.
6.1. X-ray pulsar
The X-ray counterpart of PSR J0855−4644 is faint and soft with a blackbody temperature of 0.2 ± 0.05 keV and Leff of 1.3 × 1030 erg s-1. The blackbody is emitted from a region with Reff ~ 1.5 km, which indicates a polar cap nature of this emission, rather than emission from the surface of the neutron star. Assuming co-located non-thermal X-ray and γ-ray emission regions, detection of thermal emission from the polar cap and the lack of non-thermal X-rays indicate that we are viewing the source close to the pole of the neutron star, that is, with small | β |. Given the absence of detection of non-thermal emission from the pulsar, we cannot determine the parameters of the system such as the X-ray efficiency of the pulsar (ηpsr ≡ Lpsr/Ė) or the ratio of the efficiency of the PWN to its pulsar (ηpwn/ηpsr). Given the spin period and its first derivative (P and Ṗ) as determined from radio observations (Kramer et al. 2003), the equatorial surface magnetic field can be estimated to be 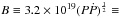 0.7 × 1012 G (assuming a dipole magnetic field). This is in the range expected for a neutron star powering a PWN.
0.7 × 1012 G (assuming a dipole magnetic field). This is in the range expected for a neutron star powering a PWN.
6.2. Morphology and properties of the compact PWN
The spectrum of the compact nebula is hard, compatible with a power law of Γ = 1.12 ± 0.25. This is compatible with that observed in other PWNe (Kargaltsev & Pavlov 2008) and is also compatible with predictions of particle wind models assuming relativistic Fermi acceleration (Achterberg et al. 2001).
 |
Fig. 8 Best-fit radio light curves overplotted on the data. |
At a distance of d = 900 pc, the compact PWN radius ~10′′ corresponds to a physical size of 0.06 pc. This is similar to the inner PWN of Vela (~0.1 pc; Pavlov et al. 2001). The fainter and diffuse PWN extends much farther, as indicated by the XMM observation (Acero et al. 2013), which corresponds to a physical size of ~0.6 pc. An Leff (0.5–8 keV) of 3.3 × 1031 erg s-1 indicates a nebular efficiency (ηpwn ≡ Lpsr/Ė) of ~10-5, which is similar to what is observed for Vela and some Vela-like pulsars and their PWNe (which have their Ė in the same range). This is, however, only a lower limit as the contribution from the diffuse nebula has not been taken into account in this case.
Morphological modelling of the inner PWN with a double-torus model provides a reasonable fit, resulting in an observer angle ζPSR< 37°. The eastern outer tail-like feature that is not accounted for in the spatial model could represent the outer jet of the nebula. In that case the system would be dominated by one of the jet components, which also supports a low value of ζPSR.
6.3. Pulsar geometry and its implications
Constraints obtained from spatial modelling indicate ζPSR ≲ 37° (although with some uncertainty, since we cannot rule out a higher value of ζPSR based on spatial modelling alone). Constraints from geometric10 light-curve modelling indicate α ≲ 55° and ζ ≲ 55°, and 10° ≲ | β | ≲ 30° (because of a single visible radio peak and the width of the radio pulse). A χ2 fit to the radio light curve yields a best fit at (α,ζPSR) = (22°,8°), with a few alternative fits within 3σ, including one at (α,ζPSR) = (9°,25°). Assuming (nearly) co-located regions of non-thermal X-ray and γ-ray emission, this is also consistent with the lack of (pulsed) non-thermal X-rays from the pulsar. To further break the degeneracy of α-ζPSR parameter space and improve constraints on the individual values of α and ζPSR, we might pursue radio polarization modelling, as well as X-ray light curve modelling, should radio polarization data become available and X-ray pulsations be detected11. The obtained range of (α, ζPSR) implies that we are viewing the system relatively close to the spin axis of the pulsar. Limits on β further imply that we are also viewing the system relatively close to the magnetic poles of the pulsar.
Interestingly, Rookyard et al. (2017) recently found that radio profile widths of a sample of 35 young, energetic radio pulsars that are not detected in γ-rays are typically broader than those of another sample of 35 pulsars that are detected in both radio and γ rays, and that the boundary between these two populations increases with Ė. The most plausible scenario to qualitatively explain this is the geometry: we need a small α (to have wide radio pulses) and a small | β | (to cross the radio beam and thus detect the radio pulsar), implying a small ζ (which also, crucially, ensures missing the γ-ray emission concentrated at the equator, making the pulsar invisible in γ rays). This exactly corresponds to the independent arguments we used above to constrain the geometry of PSR J0855-4644. Guillemot & Tauris (2014) have furthermore argued for small ζPSR in the case of nearby, energetic millisecond pulsars that are undetected in γ rays, suggesting that the geometric arguments made above hold for the entire pulsar population.
7. Summary and future work
We have carried out a detailed spatial and spectral study of the compact PWN and X-ray counterpart of the fast-spinning and energetic pulsar PSR J0855−4644. The pulsar is faint and soft in the X-rays (accounts for ~1% of the total emission) surrounded by a brighter hard and compact PWN of about 0.06 pc in extent. The PWN is elongated along a symmetry axis composed of two lobes that are more or less equidistant from the pulsar in the middle. The morphology is compatible with a double-torus morphology, although other models (double-torus and jets or jets alone) cannot be ruled out in the present observation. Spatial modelling of the two lobes of the PWN with a double-torus model captures the overall structure of the nebula and provides an estimate of the observer angle of the pulsar ζPSR< 37°. Spectral analysis confirms the hard nature of the PWN spectrum (Γ = 1.12 ± 0.25) with no changes in spectral parameters detected between the outer and inner PWN, or the east and west lobe in the present observation. The pulsar spectrum is compatible with that of a blackbody of TBB = 2.0 × 106 K and effective radius Reff ~ 1.5 km, suggesting that the emission originates from the hot spots on the poles of the neutron star.
We find a consistent scenario emerging from constraints on the geometry of the system, derived independently from the X-ray morphological modelling of the nebula and from the radio and γ-ray light-curve modelling. These constraints are compatible with values of α ≲ 55° and ζPSR ≲ 55°, and 10° ≲ | β | ≲ 30°, (additionally, we find a best-fit radio profile at (α,ζPSR) = (22°,8°)), which implies that we are viewing the pulsar relatively close to one of its magnetic poles, and relatively close to the spin axis of the pulsar. In this scenario, we do not expect to see the γ-ray pulsations that are assumed to originate from the outer magnetosphere (e.g. Grenier & Harding 2015) from caustics mostly located near the equatorial regions at large ζPSR. This proposed scenario (which we do not claim to be the only plausible one) would explain why, despite the high Ė/d2 value for this system, no γ-ray pulsations have been detected so far with the Fermi-LAT telescope. For co-located regions of non-thermal X-ray and γ-ray emission, this is also consistent with the lack of non-thermal X-rays from the pulsar.
PSR J0855−4644 is the most energetic pulsar after Vela in the nearby environment (distance <1 kpc) and therefore has a great appeal for studying the morphology in detail and enhancing our understanding of the PWNe. A future Chandra observation will be used to further test for changes in position and brightness of the lobes with respect to the pulsar symmetry axis to determine which of the two components (torus vs. jet) dominates. Radio polarization data to look for sweeps of the position angle will also be useful to place further constraints on β. Finally, X-ray pulsations and the light-curve shape may lead to independent constraints on the pulsar geometry and mass-to-radius ratio (e.g. Bogdanov 2013).
Position angle 0° corresponds to North and 90° to East, observer angle ζTORUS between the torus axis and the observer line of sight, radius R, and a finite thickness or “blur” δ of the cross section of the torus, and the post-shock flow velocity βshock. For the double torus, an additional parameter d denotes the separation between the two torii. It is symmetrically offset along the torus axis with the pulsar positioned in the middle. The torus axis is coincident with the pulsar spin axis, ζTORUS = ζPSR and so ζTORUS is referred to as ζPSR in the rest of the paper.
The Cash statistics is a likelihood function defined using Poisson statistics. The probability Px,y of observing dx,y counts out of the expected cx,y counts in pixel (x,y) is 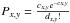 . It may be used regardless of the number of counts in each pixel and passes to χ2 statistics at cx,y ≥ 20. The best-fit parameters are determined by the negative logarithm of the likelihood function summed over all image pixels.
. It may be used regardless of the number of counts in each pixel and passes to χ2 statistics at cx,y ≥ 20. The best-fit parameters are determined by the negative logarithm of the likelihood function summed over all image pixels.
We note that while the geometric models assume constant emissivity in the co-rotating frame, it is very likely that there will be an azimuthal dependence of this quantity in more detailed models, given such a dependence of the electric field. This should terminate some of the low-level (off-peak) TPC radiation at small α and ζPSR. More physical models that self-consistently modulate the emissivity through an electric field and associated particle transport and radiation calculations are beyond the scope of the current geometric models.
Acknowledgments
We gratefully acknowledge fruitful discussions with Alice Harding. This work is based on the research supported wholly and in part by the National Research Foundation of South Africa (Grant No. 87613, 90822, 92860, 93278, and 99072). The grantholder acknowledges that opinions, findings and conclusions or recommendations expressed in any publication generated by the NRF supported research is that of the author(s), and that the NRF accepts no liability whatsoever in this regard.
References
- Abdo, A. A., Ajello, M., Allafort, A., et al. 2013, ApJS, 208, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Acero, F., Gallant, Y., Ballet, J., Renaud, M., & Terrier, R. 2013, A&A, 551, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Achterberg, A., Gallant, Y. A., Kirk, J. G., & Guthmann, A. W. 2001, MNRAS, 328, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Arons, J. 1983, ApJ, 266, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Arzoumanian, Z., Chernoff, D. F., & Cordes, J. M. 2002, ApJ, 568, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Bogdanov, S. 2013, ApJ, 762, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Cash, W. 1979, ApJ, 228, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Cheng, K. S., Ho, C., & Ruderman, M. 1986, ApJ, 300, 500 [NASA ADS] [CrossRef] [Google Scholar]
- Cheng, K. S., Ruderman, M., & Zhang, L. 2000, ApJ, 537, 964 [NASA ADS] [CrossRef] [Google Scholar]
- Daugherty, J. K., & Harding, A. K. 1996, ApJ, 458, 278 [NASA ADS] [CrossRef] [Google Scholar]
- Deutsch, A. J. 1955, Annales d’Astrophysique, 18, 1 [Google Scholar]
- Dyks, J., & Rudak, B. 2003, ApJ, 598, 1201 [NASA ADS] [CrossRef] [Google Scholar]
- Dyks, J., Harding, A. K., & Rudak, B. 2004, ApJ, 606, 1125 [NASA ADS] [CrossRef] [Google Scholar]
- Gaensler, B. M., & Slane, P. O. 2006, ARA&A, 44, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Gänsicke, B. T., Braje, T. M., & Romani, R. W. 2002, VizieR Online Data Catalog: III/38 [Google Scholar]
- Goldreich, P., & Julian, W. H. 1969, ApJ, 157, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Gonthier, P. L., Van Guilder, R., & Harding, A. K. 2004, ApJ, 604, 775 [NASA ADS] [CrossRef] [Google Scholar]
- Grenier, I. A., & Harding, A. K. 2015, C. R. Acad. Sci. Phys. Paris, 16, 641 [Google Scholar]
- Guillemot, L., & Tauris, T. M. 2014, MNRAS, 439, 2033 [NASA ADS] [CrossRef] [Google Scholar]
- Harding, A. K., Grenier, I. A., & Gonthier, P. L. 2007, Ap&SS, 309, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Helfand, D. J., Gotthelf, E. V., & Halpern, J. P. 2001, ApJ, 556, 380 [NASA ADS] [CrossRef] [Google Scholar]
- Hessels, J. W. T., Roberts, M. S. E., Ransom, S. M., et al. 2004, ApJ, 612, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, T. J., Venter, C., Harding, A. K., et al. 2014, ApJS, 213, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Kargaltsev, O., & Pavlov, G. G. 2008, in 40 Years of Pulsars: Millisecond Pulsars, Magnetars and More, eds. C. Bassa, Z. Wang, A. Cumming, & V. M. Kaspi, AIP Conf. Ser., 983, 171 [Google Scholar]
- Kijak, J., & Gil, J. 2003, A&A, 397, 969 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kramer, M., Bell, J. F., Manchester, R. N., et al. 2003, MNRAS, 342, 1299 [NASA ADS] [CrossRef] [Google Scholar]
- Lampton, M., Margon, B., & Bowyer, S. 1976, ApJ, 208, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Muslimov, A. G., & Harding, A. K. 2003, ApJ, 588, 430 [NASA ADS] [CrossRef] [Google Scholar]
- Ng, C.-Y., & Romani, R. W. 2004, ApJ, 601, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Ng, C.-Y., & Romani, R. W. 2008, ApJ, 673, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Parzen, E. 1962, Ann. Math. Statist., 33, 1065 [CrossRef] [Google Scholar]
- Pavlov, G. G., Kargaltsev, O. Y., Sanwal, D., & Garmire, G. P. 2001, ApJ, 554, L189 [NASA ADS] [CrossRef] [Google Scholar]
- Pierbattista, M., Harding, A. K., Grenier, I. A., et al. 2015, A&A, 575, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rankin, J. M. 1993, ApJ, 405, 285 [NASA ADS] [CrossRef] [Google Scholar]
- Romani, R. W. 1996, ApJ, 470, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Romani, R. W., & Yadigaroglu, I.-A. 1995, ApJ, 438, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Rookyard, S. C., Weltevrede, P., Johnston, S., & Kerr, M. 2017, MNRAS, 464, 2018 [NASA ADS] [CrossRef] [Google Scholar]
- Rosenblatt, M. 1956, Ann. Math. Statist., 27, 832 [CrossRef] [MathSciNet] [Google Scholar]
- Venter, C., Harding, A. K., & Guillemot, L. 2009, ApJ, 707, 800 [NASA ADS] [CrossRef] [Google Scholar]
- Weisskopf, M. C., Hester, J. J., Tennant, A. F., et al. 2000, ApJ, 536, L81 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Zavlin, V. E. 2009, in Astrophys. Space Sci. Lib. 357, ed. W. Becker, 181 [Google Scholar]
All Tables
Parameters of the best-fit spectral model to the putative pulsar and nebula with background, without diffuse emission.
All Figures
 |
Fig. 1 Panel a) Chandra ACIS-S (0.5–8 keV) full-resolution image of the PWN around PSR J0855−4644. The image size is 29′′× 27′′. The box shows the extraction region for the count profile in Fig. 2. The white dashed line inside shows the symmetry axis along which the nebula is extended. Panel b) ACIS-S (0.5–2 keV) sub-pixel image (image size is 18′′× 15′′) produced at |
| In the text | |
 |
Fig. 2 Top panel: counts profile of the source extracted from the box region in Fig. 1a (0.5–8 keV) compared with the 2D PSF (0.5–8 keV, red dashed line). The bottom panel portrays the same profile in the two energy bands 0.5–2 keV and 2–8 keV. |
| In the text | |
 |
Fig. 3 First panel: data in the energy range of 0.5–8 keV. Second panel: corresponding best-fit geometric model with a double torus (Ng & Romani 2008). The arcs of the torus are marked as black dashed lines to illustrate the geometry. The third panel displays the residuals after the best-fit has been subtracted.The colour bar is in square root, and units are counts for all the images. |
| In the text | |
 |
Fig. 4 Chandra image (0.5–8 keV) of the PWN around PSR J0855−4644 along with the regions used for spectral extraction shown in white. The value of the Γ (or kT) obtained from spectral fitting is also indicated in each panel. |
| In the text | |
 |
Fig. 5 ACIS-S spectra for the X-ray counterpart of the pulsar (panel a)) and the entire PWN (panel b)). The solid lines correspond to the respective best-fit spectral models (absorbed blackbody and absorbed power law, respectively). In the panel a), the pulsar blackbody component (red) and the nebular contribution in the same region (green) are shown. The unbinned spectrum fitted using C-statistics has been rebinned in the plot for visual clarity. |
| In the text | |
 |
Fig. 6 Plot of predicted TPC (panel a)) and OG (panel b)) γ-ray (black) and radio (magenta) light curves on a (α,ζPSR) grid. The γ-ray intensity has been normalized globally so that the maximum (typically at α = ζPSR = 90°) is unity and the flux of the other combinations of α and ζPSR relative to this maximum is clear. The x-axis denotes normalized from –0.5 to 0.5. A phase offset of 0.5 has been artificially imposed to centre the radio pulses for visual clarity. The coordinate pair in each panel refers to the value of α and ζPSR in each case. |
| In the text | |
 |
Fig. 7 log 10χ2/Nd.o.f.(α,ζPSR) map with the best fit indicated by a yellow cross. The 1σ, 2σ, and 3σ contours are very small and are indicated by yellow lines. |
| In the text | |
 |
Fig. 8 Best-fit radio light curves overplotted on the data. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.