| Issue |
A&A
Volume 594, October 2016
|
|
|---|---|---|
| Article Number | A38 | |
| Number of page(s) | 12 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201628299 | |
| Published online | 07 October 2016 | |
Direct illumination calibration of telescopes at the quantum precision limit
LPNHE, CNRS-IN2P3 and Universités Paris 6 and 7, 4 place Jussieu, 75252 Paris Cedex 05, France
e-mail: barrelet@lpnhe.in2p3.fr
Received: 12 February 2016
Accepted: 3 July 2016
The electronic response of a telescope under direct illumination by a point-like light source is based on photon counting. With the data obtained using the SNDICE light source and the Megacam camera on the CFHT telescope, we show that the ultimate precision is only limited by the photon statistical fluctuation, which is below 1 ppm. A key feature of the analysis is the incorporation of diffuse light that interfers with specularly reflected light in the transmission model to explain the observed diffraction patterns. The effect of diffuse light, usually hidden conveniently in the Strehl ratio for an object at infinity, is characterized with a precision of 10 ppm. In particular, the spatial frequency representation provides some strong physical constraints and a practical monitoring of the roughness of various optical surfaces.
Key words: instrumentation: detectors / techniques: photometric / methods: statistical / telescopes / methods: numerical / methods: miscellaneous
© ESO, 2016
1. Introduction
The calibrated light sources developed for our SNDICE project (Barrelet & Juramy 2006) are based on a direct illumination concept (Barrelet & Juramy 2008) using the new generation of light emitting diodes (LEDs) to reach a high stability of about 10-4. This opens the possibility of measuring the sensitivity of good space-based CCD cameras such as those of the CoRoT and Kepler telescopes with a good precision. We have tested the calibration of a telescope and a large-field camera by using the images of the SNDICE light source taken by the CFHT telescope equipped with the Megacam camera (Boulade et al. 2003). We placed the limiting precision of the direct illumination calibration of the CFHT telescope at the quantum bound (≈10-6), which only depends on the potential improvement of the CCD readout electronics described in Sect. 3. Our proof-of-concept goals are distinct from those of the more practical study by Regnault et al. (2015) who used SNDICE to yield an improved photometric calibration of the SNLS experiment of about 10-3.
A novel feature of the present paper is the comprehensive model of the telescope transmission, including its optical defects. This model, defined in Sect. 2.1, combines diffuse and specular light in a common photon wave packet (WP) model. It extends the conventional models called here “specular models”, where the optical surfaces are mathematically defined and the properties of optical media are represented by continuous reflection and refraction functions, while the primary light propagation is symbolized by ray optics. Our WP model, which parametrizes the whole interference pattern, is validated quantitatively with an exquisite precision.
In Sect. 2.2, the spatial frequency spectrum of the interference signal is shown to separate the effect of light propagation in free space from that of electronic and optical defects. The former is used as a validation of the model and then taken as a prior. The latter is used as an ultra precise control of the optical quality and of the CCD electronic response. Following this spectrum allowed us to monitor during one or two hours runs the stability of the interference signal at the quantum precision limit. The only deviation found is due to the microscopic motion of the LED source. It is then integrated in the spectral analysis and corrected for. Independently of this analysis of the mirror surface, we provide efficient algorithms for detecting, localizing, and parametrizing the defects of the Megacam camera in Sect. 2.5. This is a first step, since there are about 105 such defects to monitor individually during the life of the camera. Their effect on astronomical images is obviously diverse and cannot be represented by a simple pixel-to-pixel correction.
The last part of our analysis describes the successive steps of a complete telescope photometry based purely on photon counting. This analysis implicitly uses the spectral properties of the interference pattern found in Sect. 2.2 and the mitigation of the electronic problems found in Sect. 3. First Sect. 4.1 defines the four operators (pixel combinations) that permit a clean photon counting analysis and introduces their pure Gaussian properties that allow precisely applying the law of large numbers up to the 1013 photons contained in a Megacam image. Second, Sects. 4.2 and 4.3 establish the second-order corrections to the pure Gaussian model needed for multinomial statistics and for LED motion checks, respectively. Last, Sects. 4.4 and 4.5 apply these methods to flux and noise estimation respectively. Combining these two methods, we show that the fluctuation of pixel counts is rigorously proportional to the square root of the flux.
More generally, these methods offer a perspective to replace the paradigms of the classical optics and the photometric standards by paradigms relying on fundamental physics. The technical breakthrough behind these progresses, beyond the new optical sources and the detectors already mentioned, is clearly the data processing power which is essential for the analyses presented in this paper.
2. Using coherent light for calibration
Measuring the overall response of a telescope by placing a point illumination source (i.e. a partially coherent source) at the focal distance is attractive because it is expected to yield smooth images, and each pixel of the camera would define a single light ray. Previous attempts1 have met the obstacle also seen by SNDICE (Fig. 1), which is a plethora of diffraction patterns that is due to the imperfections in the mirror surface. We can consider these artifacts as a nuisance caused by the partial coherence, but they alter an image exactly as they would for a target object at infinity, as suggested by Fig. 2, based on the classical Fraunhofer diffraction theory (Born & Wolf 1999, chapter VIII, Fig. 8.6). Therefore they need to be taken into account by astronomical calibration. The first goal of this section is to demonstrate the exact correspondance of the light diffracted by the same area of the mirror, either from a point source at infinity or at a focal distance. Diffracted light is expressed by the Fresnel diffraction integral as a convolution product of an aperture function representing the defects of the mirror and the impulse response of the free space propagation from the mirror to the focal plane. This property is used in Sect. 2.2 to extract by Fourier analysis pure diffracted light from non-diffracted light. In Sect. 2.3 we measure the effect of the translation of the point source on the diffracted light. By joining these two developments, we can compare extended source and point source images. We can also measure the stability of the SNDICE source with high precision.
 |
Fig. 1 Left: wave packet signal (WP) measured in a 1024 × 1024 pixel2 area. The gray scale covers ⟨WP⟩± 1.5σ. Right: the 1% of pixels in this area with a sharp WP gradient due to defects of the camera optics (∥ ∇(WP) ∥ ≥ 16σ). Four camera defects a–d of different types are circled in the two figures for discussion in Sect. 2.5. |
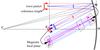 |
Fig. 2 Ray optics and wave packet: in red we plot a star source at infinity imaged at focus F and its diffuse reflection falling in the Strehl ratio area around F; in blue we show a LED source S at focal distance and diffuse reflection interfering with specular reflection (reflected beam MF displaced for clarity into M’F’). |
2.1. SNDICE geometrical setup and the generation of a CCD image
In our setup drawn in Fig. 2, the SNDICE LED source in S is a 0.1 mm2 chip situated at a focal distance f = 13.5 m (19 m in reality) from the mirror. The SNDICE axis SM is aligned with the telescope axis FO. It pierces the mirror in M within its 1.8 m radius. The SNDICE beam one degree aperture just covers focal plane (no stray light). The Megacam camera is centered on the focus F of the parabolic mirror. A pixel covers a 13.5 × 13.5 μm2 area, that is, a 1.0 μrad2 solid angle. The center of curvature C of the mirror is used for geometrical ray tracing. The optics is completed by an image corrector, made of four lenses and one out of five filters. Filters are not used in this study. The optical band-pass provided by a LED spectrum is Δλ/λ≈ 5%, a third of the band-pass of a typical astronomical filter.
The base concept is to consider the photon transmission through the telescope as a quantum process as well as the photon emission (LED) and the photon absorption (CCD). Telescope calibration establishes the balance sheet between a photon-counting calibrated light source and a photon-counting light detector. The LED emits a thin spherical wave packet (WP). Planar after reflection on the mirror around M, the wave packet collapses when absorbed by the focal plane in F. The WP probability of counting a photon in a given CCD pixel { v } is 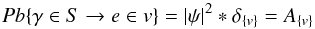 (1)where |ψ(x,y)|2 is the modulus square of the wave function amplitude and δ(x,y){v} the electron collection efficiency. The total number of photons falling on the channel k is
(1)where |ψ(x,y)|2 is the modulus square of the wave function amplitude and δ(x,y){v} the electron collection efficiency. The total number of photons falling on the channel k is 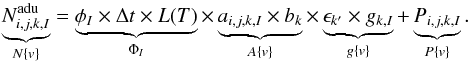 (2)Assuming an uniform photon emission rate φI, the expected photon total count ΦI during the exposure I is proportional to the exposure duration ΔtI, with a temperature correction L(TI). The photoelectron count in one pixel follows a Poisson law with an expected value ΦI×A{ v }. The counting rates in all individual pixels or any subset inside the complete 3.4 × 108 pixel set { v } follows a multinomial law.
(2)Assuming an uniform photon emission rate φI, the expected photon total count ΦI during the exposure I is proportional to the exposure duration ΔtI, with a temperature correction L(TI). The photoelectron count in one pixel follows a Poisson law with an expected value ΦI×A{ v }. The counting rates in all individual pixels or any subset inside the complete 3.4 × 108 pixel set { v } follows a multinomial law.
The last part of the Eq. (2) represents the digitization of the pixel counts, represented ideally by two constants: a gain factor g{ v } that transforms a number of photons into a number of ADUs (analog to digital unit) and the pedestal P{ v }. These electronic constants are two Gaussian variables whose fluctuations have to be added to the multinomial fluctuations of the photon counts to constitute the global statistical factor studied in Sect. 4.5. Both electronic constants are studied specially in the electronic section Sect. 3, but we state here that they have defects that introduce strong variations (1.5 ×10-3 RMS) from one image I to the next, depending on the electronic channel k. For this reason, these constants are indexed with I and k instead of being considered as long-term constants. We take into account that the gain fluctuation equally affects all the pixels read by one channel k and that the quantum efficiency ϵk is the same for the two channels inside one CCD. For this purpose, Eq. (2) introduces the fraction bk of the total number of photons falling on the channel k and the respective quantum efficiency 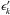 . The image matrix ai,j,k,I depends on I because the interference pattern slides (LED jitter), which we extensively study in Sect. 4.3 and which is normalized by ∑ i,jai,j,k,I = 1.
. The image matrix ai,j,k,I depends on I because the interference pattern slides (LED jitter), which we extensively study in Sect. 4.3 and which is normalized by ∑ i,jai,j,k,I = 1.
2.2. Wave packet signal and its Fresnel spectrum
Within the quantum mechanical framework, each individual photon wave function carries the complete interference pattern, and the image builds up by independently piling up a large number of photoelectrons (1012/s) in all pixels. Accordingly, the optical modulation of an image is perfectly represented in Eqs. (1) and (2) by a probability density, constant at a 10-6 precision level for hours. Before proving it in Sect. 4.5, we show here that the wave packet signal conforms to the laws of optics. Our LED light propagates in free space excepted for the reflection on the mirror surface, which can be represented by a Fresnel integral. (We neglect the diffraction on the optical surfaces of the image corrector optics, which is treated separately in Sect. 2.5.) We subdivided the mirror into sections covered by some 1024 × 1024 pixel sub-matrices. The WP signal in each section (e.g., in Fig. 1 left) was then Fourier transformed. The Fresnel integral being a convolution of the Fresnel free space propagation function and a mirror defect distribution, its transform is the product of two terms: the well-known Fresnel diffraction figure, and the transform of the mirror defect distribution. We call the distribution of the modulus the Fresnel spectrum. The quadratic average of all spectra is shown in Fig. 3(left).
 |
Fig. 3 Effect of the Fourier transform on a 1024 × 1024 vignette of the Sndice image. Left: applied to the original field; right: applied to the 3 PDE transformed fields – ∇x, ∇y, Δ2/ ΔxΔy –. The 288 vignettes covering the focal plane are quadratically averaged. The frames are set by |νx| and |νy| = νnyq. The horizontal and vertical lines passing through the center are due to electronic noise. Dashed circles mark radial cuts ν1 and ν2 in Fig. 4. The three points β, γ, and δ mark the three real FFT components averaging same name filters (α is at the center). |
The spectrum is contained in a square defined by spatial frequencies |νx| and |νy| ≤νnyq. The Nyquist frequency νnyq is 37 mm-1, that is, the inverse of twice the pixel width 1/(2 × 13.5 μm). The spectrum, being the digital Fourier transform (DFT) of a real function, is centrally symmetric. The rotational invariance around the center (νx = νy = 0) is predicted by Fresnel symmetry.
We explain the two lines on the x and y axes crossing at the center by residual electronic problems2 such as pixel-to-pixel (e.g., dead column) or line-to-line (e.g., microphonic noise), respectively. The bright spot at the center is due to specular reflection, which is in this way separated from diffraction.
The rotational invariance of the DFT field reduces the amount of empirical data representing the surface state of the mirror by a huge factor. Instead of a two-dimensional spatial frequency plot such as Fig. 3, we can make two one-dimensional spectral curves: one radial frequency distribution (Fig. 4), and one angular distribution (Fig. 5).
Each sample of the field in the spatial frequency plane { νx,νy } is taken as a sample at the radial frequency νρ and the angle θ:  (3)
(3)
 |
Fig. 4 Radial spectra of the sum and the difference of two images (image v is close to u; w distant). All are normalized to the 0.7% rms photon noise. The [ν1,ν2] cut yields the angular plots in Fig. 5. The Nyquist frequency is νnyq. |
 |
Fig. 5 Spectral angular distribution of u+v, normalized by the photon noise and then by subtracting 1. The angular average S/N≈ 6 equals the radial average inside the [ν1, ν2] cut. The electronic noise peaks at θ = 0 and θ = ± π/ 2. |
The samples can either be integrated in angular and radial bins, or averaged3. We remark that the radial sampling along a diagonal is defined by a spacing divided by 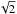 and that the square pixel sampling filter projected on a diagonal is a triangle with a 13.5 ×
and that the square pixel sampling filter projected on a diagonal is a triangle with a 13.5 ×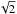 micron base. The highest radial sampling frequency νmax is
micron base. The highest radial sampling frequency νmax is 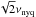 (νmax = 52.4 mm-1). The radial spectrum corresponding to the field in Fig. 3 is found in Fig. 4. Two images are added to this spectrum. This allows comparing in the same figure the radial spectrum of the sum of two images (in black) with their difference (blue and red). For a sum there is no effect depending on the choice of the images. In contrast, for a difference there is an effect that is related to the vicinity of the images in time. There is a greater difference between the images u and w taken after waiting for one hour (blue) than between u and v taken within a one-minute delay (red). This effect is explained in Sect. 4.3 by a progressive drift of the LED position with respect to the optical axis of the telescope.
(νmax = 52.4 mm-1). The radial spectrum corresponding to the field in Fig. 3 is found in Fig. 4. Two images are added to this spectrum. This allows comparing in the same figure the radial spectrum of the sum of two images (in black) with their difference (blue and red). For a sum there is no effect depending on the choice of the images. In contrast, for a difference there is an effect that is related to the vicinity of the images in time. There is a greater difference between the images u and w taken after waiting for one hour (blue) than between u and v taken within a one-minute delay (red). This effect is explained in Sect. 4.3 by a progressive drift of the LED position with respect to the optical axis of the telescope.
The angular distribution of the sum spectrum, seen in Fig. 5, is computed within the ring ν1<νρ<ν2. The two-dimensional Fourier transform of a real function being centrally symmetric, we need to plot only one half of the unit circle (− π/ 2 <θ<π/ 2). As predicted by our model, the distribution is flat, except for the electronic noise, which yields accumulations and peaks at θ = 0 and θ ± π/ 2 (where line or column frequencies are null).
A Fresnel spectrum is a stable and reproductible characteristic of the status of a section of mirror (2 cm2 (one CCD vignette), 0.1 m2 (one SNDICE image), or 8 m2 (the whole mirror)). A complete mirror scan lasts about two hours. Systematic studies such as aging or color dependence have not been made so far.
2.3. Effect of a transverse LED motion on the Fresnel spectrum
Figure 2 shows that moving the source S moves its projection M, the center of the illuminated section of the mirror, but keeps it projected on the center of the focal plane. We call Tx and Ty the two translation operators representing a shift of the mirror points reflected on a given pixel by one pixel leftward or upward. Partial derivatives of the WP signal are approximated by the finite differences of the translation operators Tx and Ty and the identity operator U, 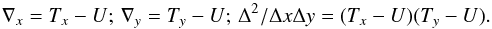 (4)When we apply these operators, commonly named gradient and hessian partial derivative equation (PDE) filters, to a CCD image, we obtain three rather uniform new images. The Fresnel spectra of these images are seen on the right of the main spectrum in Fig. 3. Simple mathematics predict the shape of these images. For instance, the DFT of the translation Ty yields the product of the complex DFT by a phase shift factor exp(iπνy/νnyq). Subtracting unity and taking the modulus gives the observed result: the two-dimensional spectrum of ∇y is the whole spectrum multiplied by a sin(πνy/ 2νnyq) factor. The ∇x formula is obtained by exchanging x and y and Δ2/ ΔxΔy by multiplying the two angular factors.
(4)When we apply these operators, commonly named gradient and hessian partial derivative equation (PDE) filters, to a CCD image, we obtain three rather uniform new images. The Fresnel spectra of these images are seen on the right of the main spectrum in Fig. 3. Simple mathematics predict the shape of these images. For instance, the DFT of the translation Ty yields the product of the complex DFT by a phase shift factor exp(iπνy/νnyq). Subtracting unity and taking the modulus gives the observed result: the two-dimensional spectrum of ∇y is the whole spectrum multiplied by a sin(πνy/ 2νnyq) factor. The ∇x formula is obtained by exchanging x and y and Δ2/ ΔxΔy by multiplying the two angular factors.
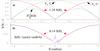 |
Fig. 6 a) Spectral angular distribution of u+w after applying PDE operators, divided by the unity distribution U of Fig. 5. b) Spectral angular distribution of u–w, divided by U (inside the radial cut [ν1, ν2]). The uncorrelated random spectra, null after subtraction of unity, are plotted in yellow. Fitted curves are shown in red. |
The angular spectra resulting from the application of PDE filters to the sum of the images are found in Fig. 6a. They are explained by the factor introduced in DFT by differentiation. For ∇y, the factor is |sin(πνy/ 2νnyq)|. Inside the ring ν1<νρ<ν2 the average value of νρ is νnyq/2 and νy = νρ × sin θ, therefore the angular factor is: 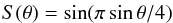 The ∇y spectrum in Fig. 6a and the spectrum of the image u–w in Fig. 6b are both proportional to S(θ). A fit yields the respective factors 1.34 and 0.14. For the other pair of images u and v taken at one-minute intervals, the angular spectrum is almost null. This proves that a LED drift in the y direction is the cause of the small difference between exposures u and w. When we apply a proportional rule of thumb, the u–w shift distance is a tenth of that of a one CCD line shift computed in ∇y (13.7 μ). Hence we estimate a 1.4 μ LED shift in one hour!
The ∇y spectrum in Fig. 6a and the spectrum of the image u–w in Fig. 6b are both proportional to S(θ). A fit yields the respective factors 1.34 and 0.14. For the other pair of images u and v taken at one-minute intervals, the angular spectrum is almost null. This proves that a LED drift in the y direction is the cause of the small difference between exposures u and w. When we apply a proportional rule of thumb, the u–w shift distance is a tenth of that of a one CCD line shift computed in ∇y (13.7 μ). Hence we estimate a 1.4 μ LED shift in one hour!
2.4. Orthogonal basis of differential operators: α,β,γ, and δ
Similarly we introduce four orthogonal operators α,β,γ, and δ which have a crucial role in our image analysis method: 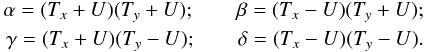 (5)We modified these operators to project the original CCD images { ai,j } into lower resolution images (scale 1/2 × 1/2) by restricting indices to even values. More explicitly, we developed Eq. (5) using the pixels ai,j defined in Eq. (2):
(5)We modified these operators to project the original CCD images { ai,j } into lower resolution images (scale 1/2 × 1/2) by restricting indices to even values. More explicitly, we developed Eq. (5) using the pixels ai,j defined in Eq. (2): 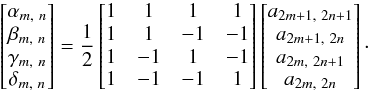 (6)The operator α = { αm,n } sums pixels with adjacent even and odd indices. Its spectrum in Fig. 4 follows the original spectrum (U), but stops at half the frequency range.
(6)The operator α = { αm,n } sums pixels with adjacent even and odd indices. Its spectrum in Fig. 4 follows the original spectrum (U), but stops at half the frequency range.
β and γ are similar to the gradient ∇ = { ∇x,∇y }, and δ to the Hessian Δ2/ ΔxΔy. Taking the four α,β,γ, and δ images together, we have an efficient lossless encoding of the original image, represented by the orthogonal matrix of Eq. (6).
 |
Fig. 7 Radial spectra of the sum and difference of two images after the application of four filters (α,β,γ,δ). |
In Fig. 7 we show the radial spectra of α,β,γ, and δ for image sums and differences. The spectra of the image differences are almost drowned in the noise, except for those of β and γ for distant images u and w. The radial spectra of the β,γ, and δ operators are cut severely at low frequencies, but higher frequencies are unchanged. The four radial spectra converge at 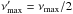 .
.
The uncorrelated photon noise spectrum was obtained by simulation, using a Gaussian variable generator4 with an rms equal to 98 adu for each pixel, which corresponds to about 4 × 104 photon/pixel. It was processed in the same way as for a real image. The resulting radial and angular spectra are flat for the α,β,γ, and δ operators but not for the PDEs. We tested with the highest precision defined by the photon statistics of whole images the hypothesis that the δ operator applied to a difference of images yields a pure photon noise spectrum. For this we fit a flat δ radial spectrum on the u–v and u–w images. The histograms of the residuals are shown in Fig. 8. The reference level of 1 corresponds to the approximate level of the noise (98 adu). The dispersion of the radial samples is 0.17 adu (rms) on a mean signal of 17 000 adu, that is, ≈10-5. The number of photons contributing to one sample is the whole content of two images: 56 × 1012 divided by 4 (the number of estimators) and then by 1500 (the number of samples), that is, ≈1010. This verifies that the dispersion of the radial samples (10-5) is consistent with photon statistical error (1010)−1/2.
 |
Fig. 8 Residuals of δ(u–v)/noise and δ(u–w)/noise linear fits of radial frequency spectra (noise = 98 adu). The precision for each sample is ≈10-5, and for the whole image the average is ≈0.3 × 10-6. |
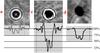 |
Fig. 9 Camera defects a, c, and d circled in Fig. 1. Top: the flux map around the defects. Bottom: the profile of the adc content drawn along a line passing through the center of the defects. |
2.5. Detection of camera defects
The photon propagation from the camera lens to the focal plane is shorter than from the mirror by a factor larger than 15. Therefore its Fresnel spectrum is much sharper. We developed a test on this premise (Barrelet 2010a), using the gradient vector length:
-
1% of the pixels are tagged by the ||∇|| ≥ 16σ cut (see Fig. 1), (46 000 per channel). All are connected to an isolated defect (or to dead columns).
-
There are around 1000 defects per CCD channel, that is, about 105 for the whole camera.
-
Many types of defects are found. Some with a few tagged pixels and some with hundreds of tagged pixels. For instance, the defects a, c and d, circled in Fig. 1, are examined in Fig. 9: a) is circular with no absorption; c) is strongly absorbing with a complex shape; d) is slightly absorbing with no interference rings. In addition, b) is a single absorbing pixel surrounded by 8 pixels at half level, that is, a dead pixel.
-
The defect distribution is sufficiently sparse to separate individual defects and to build a comprehensive catalog.
-
For each tagged pixel, we measure a significant ∇ vector. Therefore a given defect is characterized by a vector field.
 |
Fig. 10 a) Gradient field pattern around a defect A is characterized by a regression analysis of angle Θ (cotgΘ = ∇.Ox) versus pixel x in each CCD line y. The regression equation is x = a + (b−y)cotgΘ. b) Four horizontal slices of six lines each are drawn corresponding to groups of lines in a). The field lines converge on the point A x = a, y = b. |
Figure 10 shows how the analysis of the vector field transforms the cloud of pixels produced by tagging into field lines and a center of curvature A. It defines piecewise the phase contours by joining some concentric arcs of circle. This method was adapted for contours that are more circular at the periphery of a cluster than in the central region where the center of gravity A of the defect is. A regression analysis fits a common center of curvature A(a, b) for parallel phase contours defined by the property of field lines: (x−a)sinΘ + (y−b)cosΘ = 0.
3. High-precision CCD electronics
The aim of this paper is to track the precision limit of photometry as it is applied in astronomy. The basic concept is to count photons along the three quantum steps: LED emission, telescope transmission and CCD absorption. The second step is the only one that uses optics. It has been treated above in Sect. 2. The remaining analysis in Sect. 4 is pure statistics. However, the precision of the third step, photon counting by Megacam, is currently limited by the instability of the electronics. We observe hourly fluctuations of the gain in a 0.8% interval and of the pedestal around 0.1 mV (15 adu). The resulting problems are mitigated for astronomers by the empirical subtraction of local sky background and by the comparison to local reference stars, but maybe not as well as needed. In Sect. 3.1 we expose the mitigating techniques developed especially for Sndice images that reach a 1−30 ppm fluctuation range. Then in Sect. 3.2 we describe why we are confident that better CCD readout electronics might yield all the precision needed without resorting to mitigation.
3.1. Mitigation of Megacam electronics problems
Megacam electronics problems (cf. Barrelet 2013) are expressed by a variation of the pedestal and gain constants in Eq. (2) depending on the image number and by fluctuations during image readout. The pedestal fluctuations, which yield horizontal and vertical lines in Fig. 3, are controlled using the ∇x and ∇y filters, which suppress these lines selectively. The gain fluctuations are controlled using the stability of the Sndice light source. This could yield a vicious circle because we need gain corrections to yield CCD data and vice versa. To break the loop, we introduce the concept of a flux × efficiency × gain (FEG) scale. It is based on the fact that the fraction of the total number of photons impinging a half CCD, noted bk in Eq. (2), is constant within its ≈3 × 10-6 statistical fluctuation. The observed fluctuation of the CCD count is due to a common multiplicative factor ψk,I of the flux, the gain, or the efficiency in the Eq. (2). We slightly transform this equation by replacing the global flux ΦI by the FEG average ψI: 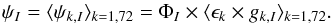 (7)The average of the gains of the 72 channels is an order of magnitude more stable than the gain of one channel (≈0.02% rms versus ≈0.2% rms). This fluctuation is on the same order of magnitude as the effect of the LED thermal fluctuations (0.1 °C) on the flux ΦI. Both contribute equally to the FEG fluctuations. Using only ADC counts, we cannot distinguish between them. We determine ψI at ≈3 × 10-5 precision, an order of magnitude better than each of its components ψk,I. The relative gain parameter of each channel is the real one divided by the 72-channel gain average. In practice, we fix a reference image and fix the gains for the other images relative to this reference. With this FEG scale, we mimic what would be done with an ideal electronics: we would check that the gains in each image are compatible with those of the reference image at a 3 × 10-5 level. Then their average could be tested at the next order of precision, that is, 3 × 10-6, which is the limiting precision of the photon statistics in one channel (i.e., one half CCD). This precision is reached after mitigation in the remaining study, except in Sect. 4.5, where the FEG mitigating method is replaced by the use of the real gain of each channel determined by the photon noise in the actual frame.
(7)The average of the gains of the 72 channels is an order of magnitude more stable than the gain of one channel (≈0.02% rms versus ≈0.2% rms). This fluctuation is on the same order of magnitude as the effect of the LED thermal fluctuations (0.1 °C) on the flux ΦI. Both contribute equally to the FEG fluctuations. Using only ADC counts, we cannot distinguish between them. We determine ψI at ≈3 × 10-5 precision, an order of magnitude better than each of its components ψk,I. The relative gain parameter of each channel is the real one divided by the 72-channel gain average. In practice, we fix a reference image and fix the gains for the other images relative to this reference. With this FEG scale, we mimic what would be done with an ideal electronics: we would check that the gains in each image are compatible with those of the reference image at a 3 × 10-5 level. Then their average could be tested at the next order of precision, that is, 3 × 10-6, which is the limiting precision of the photon statistics in one channel (i.e., one half CCD). This precision is reached after mitigation in the remaining study, except in Sect. 4.5, where the FEG mitigating method is replaced by the use of the real gain of each channel determined by the photon noise in the actual frame.
3.2. Making high-precision CCD electronics
We claim that making an ideal CCD readout electronics is feasible rather easily with modern technology. We base this claim on our experience with a large electronic system in the H1 experiment (Appuhn et al. 1999) calibrated at a 30 ppm level for 15 yr and on a R&D on Megacam electronics (Barrelet et al. 2004; Juramy 2006) reaching a 0.2 e equivalent noise charge. High-precision electronics would open a wide range of applications to the methods developed in this paper. One example is the preventive maintenance of a telescope using a measurement much more sensitive than the usual scientific requirements (i.e., detecting problems before they hurt). Another example is the creation of photometric standards and the photometric calibration of any instrument (not only telescope) at the ppm level. This paper also prooves that for the low light fluxes of astronomy, cooled CCDs are the best photometric calibrators5.
4. Coherent illumination calibration at the quantum precision limit
We have regrouped in Sect. 4.1 the mathematical methods used when comparing CCD images. Readers interested in bare results could skip it. However, this paragraph is needed to understand why the precision of our regression analyses is so good. These methods are used in Sects. 4.2 and 4.4 to measure the single parameter that defines a particular image inside a sequence: the total number of photons emitted by the LED during the exposure. In Sect. 4.3 we show how the stability of the led position during a sequence has to be controled. Finally, in Sect. 4.5 we check for two image sequences (8.5 and 24 billions of pixels, respectively) that the content of each pixel in each image is entirely defined by quantum mechanics and photon statistics.
4.1. Mathematical properties of the statistical distributions of the four-vector α,β,γ,δ
Our measurement model is Eq. (2). Groups of four pixels are replaced by the four filters6, according to Eq. (6). The uncorrelated noise, which is the quadratic average of the noises coming from the four individual pixels, is the same for each filter. In contrast the correlated electronic noise and the led-jitter noise are different. As shown in Sect. 2, the δ filter suppresses the pedestal, the correlated gain fluctuations, and the led jitter at a 10-6 level. The β and γ filters suppress correlated noises down to a few 10-4 level. The α filter keep most correlated noises that are at a few 10-3 level and the led jitter noise. (We recall that according to the Parseval theorem, signal and noise power are globally conserved in the Fourier transform and in the orthogonal change from the pixel basis to the filter basis in Eq. (6).)
The next step is to consider the 1.18 million four-vectors inside a given half-CCD k of a given image I as the successive occurrence of four random variables αk,I, βk,I, γk,I, and δk,I, themselves the components of a random four-vector Ξk,I. Equation (2) yields that the expected value of Ξk,I is the result of applying the filters to the WP signal seen by one given half-CCD. The sequence of 1.18 million four-vectors almost perfectly simulates those taken by a multivariate Gaussian variable whose distribution is represented by Eq. (8): ![\begin{eqnarray} \begin{split} &\langle\Xi_{k,I}\rangle = [\Psi_{k,I}\quad 0\quad 0\quad 0]\quad\quad\; \Xi_{k,I}' = \Xi_{k,I} - \langle\Xi_{k,I}\rangle \quad \\ \label{eq:9} &\langle\Xi_{k,I}' \times \Tilde{\Xi}_{k,I}' \rangle =\Psi^2_{k, I} \begin{bmatrix} \sigma^2_{\alpha_{k}} & 0 & 0 & 0 \\ 0 & \sigma^2_{\beta_{k}} & 0 & 0 \\ 0 & 0 & \sigma^2_{\gamma_{k}} & 0 \\ 0 & 0 & 0 & \sigma^2_{\delta_{k}} \\ \end{bmatrix} \quad \sigma^2_{\beta_{k}} = \sigma^2_{\gamma_{k}}. \end{split} \end{eqnarray}](/articles/aa/full_html/2016/10/aa28299-16/aa28299-16-eq127.png) (8)The relations in Eq. (8) have all been verified. First, the mean of α has been defined in Eq. (7). The three other means are null within a fraction of an adu. This property is explained theoretically using the Fourier analysis of the WP signal as reported in Sect. 2. Second, the covariance matrices are diagonal due to the algebraic properties of the WP phase contours and because of the rotation invariance. The values of σα, σβ, σγ, and σδ are directly related to the Fresnel spectra seen in Fig. 7 (σα≈ 3.5%, σβ = σγ≈ 0.9%, and σδ≈ 0.4%). They do not depend on the flux of image I and not much on the channel number k. Therefore we sometimes dropped the indices k and I in their expression. Moreover, ⟨ β|γ ⟩ = 0 and σβ = σγ because of rotation invariance. After associating a 4 × 4 diagonal Gaussian with each CCD channel, we added to it the diagonal Gaussian noise in Eq. (9).
(8)The relations in Eq. (8) have all been verified. First, the mean of α has been defined in Eq. (7). The three other means are null within a fraction of an adu. This property is explained theoretically using the Fourier analysis of the WP signal as reported in Sect. 2. Second, the covariance matrices are diagonal due to the algebraic properties of the WP phase contours and because of the rotation invariance. The values of σα, σβ, σγ, and σδ are directly related to the Fresnel spectra seen in Fig. 7 (σα≈ 3.5%, σβ = σγ≈ 0.9%, and σδ≈ 0.4%). They do not depend on the flux of image I and not much on the channel number k. Therefore we sometimes dropped the indices k and I in their expression. Moreover, ⟨ β|γ ⟩ = 0 and σβ = σγ because of rotation invariance. After associating a 4 × 4 diagonal Gaussian with each CCD channel, we added to it the diagonal Gaussian noise in Eq. (9). 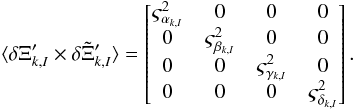 (9)The 72 four-vector variables
(9)The 72 four-vector variables 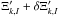 are also centered Gaussians. Their means are null and their variances, measured independently for each image, are the raw Ψσ flux estimators. They are plotted in Fig. 15b for the level ramp and in Fig. 17 for the flux ramp (after dividing the expression by
are also centered Gaussians. Their means are null and their variances, measured independently for each image, are the raw Ψσ flux estimators. They are plotted in Fig. 15b for the level ramp and in Fig. 17 for the flux ramp (after dividing the expression by  and averaging all channels). To extract the pure WP signal from the noise, we compared different images two by two. Extending Eq. (8) to all pairs of images I1 and I2 leads to Eq. (10).
and averaging all channels). To extract the pure WP signal from the noise, we compared different images two by two. Extending Eq. (8) to all pairs of images I1 and I2 leads to Eq. (10). 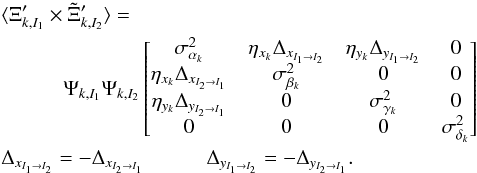 (10)The compact matrix form of Eqs. (8)–(10) hides a great complexity. For example, the total number of variables Nt = 4 × 72 ×NI is 20 160 for the sequence of NI = 70 images in the flux ramp. This yields 20 160 diagonal terms and 2 812 320 pairs of non-diagonal terms of interest. This is the number of terms that we analyse in Sect. 4.2. When we restrict the distribution of these enormous Gaussian variables to some components x and y, it yields a bivariate Gaussian law with a two × two covariance matrix Cxy. The Cxy matrix is written conventionally with the two marginal variances
(10)The compact matrix form of Eqs. (8)–(10) hides a great complexity. For example, the total number of variables Nt = 4 × 72 ×NI is 20 160 for the sequence of NI = 70 images in the flux ramp. This yields 20 160 diagonal terms and 2 812 320 pairs of non-diagonal terms of interest. This is the number of terms that we analyse in Sect. 4.2. When we restrict the distribution of these enormous Gaussian variables to some components x and y, it yields a bivariate Gaussian law with a two × two covariance matrix Cxy. The Cxy matrix is written conventionally with the two marginal variances 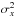 and
and 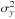 on the diagonal and a non-diagonal term ρσxσy (ρ being the correlation coefficient). The additivity of covariance matrices allows us to add the noise in Eq. (9) to the WP signal of Eq. (10). This yields the following equation:
on the diagonal and a non-diagonal term ρσxσy (ρ being the correlation coefficient). The additivity of covariance matrices allows us to add the noise in Eq. (9) to the WP signal of Eq. (10). This yields the following equation: 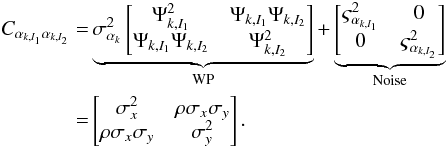 (11)In Sect. 4.2 we assume for the bivariate Gaussian distribution of two αk,I variables a common representation of the regression analysis: x is the marginal variable, y the conditional variable, and the three parameters are σx, σy/x, and the slope ay/x. Classical formulas7 that relate the two parametrizations of the regression analysis are used in Sect. 4.2 to evaluate the difference between the slope ay/x of the regression line and the gain ratio of WP signal Ψy/ Ψx (x = αk,I1; y = αk,I2). This difference D = 2(σy/x/σα)2≈ 1% is small for the α variables at the reference flux, supporting the choice of a regression estimator for the gain ratio in this case. But D is large for the other three variables β, γ, and δ, imposing another type of noise estimator, the variance of Δδ (in which δ by may be replaced by β or γ):
(11)In Sect. 4.2 we assume for the bivariate Gaussian distribution of two αk,I variables a common representation of the regression analysis: x is the marginal variable, y the conditional variable, and the three parameters are σx, σy/x, and the slope ay/x. Classical formulas7 that relate the two parametrizations of the regression analysis are used in Sect. 4.2 to evaluate the difference between the slope ay/x of the regression line and the gain ratio of WP signal Ψy/ Ψx (x = αk,I1; y = αk,I2). This difference D = 2(σy/x/σα)2≈ 1% is small for the α variables at the reference flux, supporting the choice of a regression estimator for the gain ratio in this case. But D is large for the other three variables β, γ, and δ, imposing another type of noise estimator, the variance of Δδ (in which δ by may be replaced by β or γ): 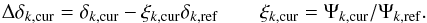 (12)This linear combination of the current and the reference images eliminates the WP signal on a pixel-by-pixel basis and yields a pure noise variable. Its mean is null and its variance, using Eq. (11) is:
(12)This linear combination of the current and the reference images eliminates the WP signal on a pixel-by-pixel basis and yields a pure noise variable. Its mean is null and its variance, using Eq. (11) is: 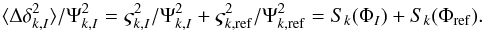 (13)The identification of the square of ςδ/α with the so-called statistical factor S(Φ) is a key of the analysis of uncorrelated noise in Sect. 4.5.
(13)The identification of the square of ςδ/α with the so-called statistical factor S(Φ) is a key of the analysis of uncorrelated noise in Sect. 4.5.
In summary, the four-vector Gaussian model yields four mean estimators and a variance matrix (four variances and six covariances) for one image. Three means and four covariances are null. We are left with the mean of α and four variances used in the following as five redundant flux estimators, plus two covariances used as led motion estimators. For a sequence of images we extract four sequences of noise estimators based on the variance of the flux-weighted difference of two images (one for each filter).
 |
Fig. 11 Left: histogram of α in the reference image subdivided in slices 40-adu wide. Right: histogram of the projection of each reference slice in any current image is a Gaussian. Only one slice for every five is represented. Top (inset): the means of the current slices are fit as a linear function of the means of the reference slices. The distribution of the residuals is shown in Fig. 12. |
4.2. High-precision flux ratio estimates
The algorithm estimating the flux ratio of the two images I1 (reference) and I2 (current) was introduced by Guyonnet (2012). Its principle, which is illustrated in Fig. 11, considers that the photon distribution is multinomial (not Gaussian). The ratio of the FEG variables αk,I in a given four-pixel matches the ratio of exposure duration, which is about 5/6 in this example. We reconstructed the joint probability distribution as a product of the marginal distribution of the reference variable αk,ref (left) and the conditional probability of the current variable αk,cur (right). The joint distribution has three properties:
-
The marginal distribution is Gaussian: A Gaussian fit8 yields ⟨ αk,ref ⟩ = Ψk,ref and σ(αk,ref) = Ψk,refσα.
-
b)
The regression curve is a straight line (see inset of Fig. 11):
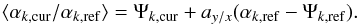 (14)In each bin of the αk,ref histogram, we fit a Gaussian on the αk,cur distribution and hence give a value of the conditional mean ⟨ αk,cur/αk,ref ⟩ and of the conditional standard deviation σ(αk,cur/αk,ref). The quality of the fit of Eq. (14) is excellent, as shown in Fig. 12a, where individual errors bars are the Gaussian width divided by the root of event number, or more conservatively, in Fig. 12b by the width (0.4 adu rms) of the distribution of residuals. It determines Ψk,cur with a 0.06 adu (rms) point precision (4 × 10-6). Particular care is taken for such high-precision point measurements involving a small fraction of an adu. They are valid only as representing an average of the digital sampling of a continuous analog variable over a wide ADC range. In this example, where αk,cur is sampled within a 14 000 ± 750 adu interval, the precision of the fit of the slope ay/x is −1.7 × 10-4.
(14)In each bin of the αk,ref histogram, we fit a Gaussian on the αk,cur distribution and hence give a value of the conditional mean ⟨ αk,cur/αk,ref ⟩ and of the conditional standard deviation σ(αk,cur/αk,ref). The quality of the fit of Eq. (14) is excellent, as shown in Fig. 12a, where individual errors bars are the Gaussian width divided by the root of event number, or more conservatively, in Fig. 12b by the width (0.4 adu rms) of the distribution of residuals. It determines Ψk,cur with a 0.06 adu (rms) point precision (4 × 10-6). Particular care is taken for such high-precision point measurements involving a small fraction of an adu. They are valid only as representing an average of the digital sampling of a continuous analog variable over a wide ADC range. In this example, where αk,cur is sampled within a 14 000 ± 750 adu interval, the precision of the fit of the slope ay/x is −1.7 × 10-4. -
c)
The conditional standard deviation σ(αk,cur/αk,ref) varies as a square root of the flux (because of the multinomial law of photon counts). We fit a polynomial on the data, as shown in Fig. 13a. Its first-order linear approximation is:
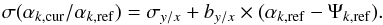 (15)The central value ςk,cur = σy/x will take the place of the constant value defined for a Gaussian. The point precision in this example is excellent (0.02 adu ≈Ψk,ref× 10-6). The precision on by/x is 0.023 adu/adu. This process of extrapolation at the central reference flux Ψ = Ψk,ref of the flux-dependent quantities f(Ψ), used in Eqs. (14) and (15), is applied systematically to all other variables.
(15)The central value ςk,cur = σy/x will take the place of the constant value defined for a Gaussian. The point precision in this example is excellent (0.02 adu ≈Ψk,ref× 10-6). The precision on by/x is 0.023 adu/adu. This process of extrapolation at the central reference flux Ψ = Ψk,ref of the flux-dependent quantities f(Ψ), used in Eqs. (14) and (15), is applied systematically to all other variables.
 |
Fig. 12 Residuals of the linear fit of Fig. 11: a) as a function of αk,reference; b) as a histogram (0.4 adu rms). In red: points included in the fit (α ∈ [ ⟨ α ⟩ ± 1.5σ]). |
 |
Fig. 13 a) Fit of the width of the joint distribution as a function of αk,reference in the { ⟨ α ⟩ ± 1.5σ } interval. b) Histogram of the residuals of the previous fit, fitted by a Gaussian (0.14 adu rms). |
4.3. Determining the LED jitter using the α′/β and α′/γ correlation
Two correlation terms, ⟨ β|α ⟩ or ⟨ γ|α ⟩, appear in the covariance matrix of Eq. (10), while they are null in the autocovariance matrix of Eq. (8). An intuitive explanation of this puzzle is found in Barrelet (2013). The point of interest here is that the non-diagonal matrix elements noted Ψk,I1 × Ψk,I2 × ηyk × Δy1 → 2 are a very sensitive probe of the LED jitter projected on y axis (idem for x). LED jitter is the only source of noise found in the optical signal in addition to the photon noise. The ⟨ γ|α ⟩ terms for each CCD channel k (0 ≤k≤ 71) in the sequence of NI = 25 images at constant flux level yields a NI × NI matrix. In Fig. 14, we only keep the last row (I1 = 24, I2 = 0 to 24) of the matrix, but we repeat the operation for the 72 channels. The raw data (in blue) are the slopes aγ/α of the regression fit in Eq. (14). They are ordered by time (that is, by image number I) and by electronic channel number k. Here α24 is the marginal variable and γ0,...,γ24 are the conditional variables. The reason for taking the reference image from among the last eleven images in Fig. 14 is obvious: it belongs to a group of images (I = 14,...,24) in which led jitter is minimal.
The result of a complementary method is shown in Fig. 14. It is a principal component analysis that fits the 1800 raw data using 72 ϵkηk and 25 ΔyI parameters (aγ/α = ϵkηk × ΔyI; ⟨ ϵkηk ⟩ = 1). The index ϵk = ±1 is introduced to take the up/down orientation of the CCD readout within the focal plane into account. It explains the characteristic data pattern: negative for the first 36 and positive for the last 36 channels, or vice versa. The fit values of the vertical displacement ΔyI are drawn in green and the residuals of the fit in black. The calibration of the Δy scale was made using Fig. 6, where the displacement of the LED between image w (I = 2 and Δy = 0.016) and image u (I = 17 and Δy = 0.0005) is estimated at 1.4 μ. This yields a 1% per micron calibration ratio of the aγ/α slope change per LED displacement. The distribution of residuals in the inset of Fig. 14 displays a 0.05% Gaussian width, that is, a sensitivity for the LED position given by one channel equal to 0.05 μ rms. The average sensitivity for all 72 channels is 0.006 μ, that is, a mean angular position of the LED defined at 0.4 nrad.
 |
Fig. 14 Signal of γ vs. α correlation as a function of channel k and image I (noted ηkΔyI, with ΔyI fixed to 0 for I = 24) (blue). Residual of the fit of this signal with one ηk parameter per channel and one ΔyI per image (black). Images I = 2, 17, 18 were called w, u, v in the spectral studies of Sect. 2. Δy is calibrated by comparison with Δyw → u. The inset shows a Gaussian fit of the residuals (1 point/channel/image) with a 5 × 10-4 rms, yielding Δyk = 0.05 μ or ⟨ Δyk ⟩ = 0.006 μ. The green line indicate the effect of a 1 μ LED drift. |
We conclude this study by observing that we are fortunate to have a rather good mechanical stability of the telescope illumination system, because there was no provision for this effect during the construction of Sndice. We did not yet perform a study of the mechanical stability, but we note that the flux ramp run during two hours was affected by no δy displacement and only one significant δx displacement. This is used in the next paragraph to obtain a full flux ramp unaffected by led jitter.
4.4. Determining the fluxes for a sequence of images
The integrated flux ΦI emitted by an LED is a product of LED current, exposure time, and temperature terms (cf. Eq. (2)). It is measured by the LED electronics. In Fig. 15 we represent the trend due to the linear temperature variation of 1 °C and 2 °C per hour (due to the warming of the CFHT dome after dawn). Under these conditions, the test-bench calibration of Sndice tells us that the precision is limited to a few 10-4 and could be improved to a few 10-5 by monitoring the LED current and the temperature (Barrelet 2010b, Sect. 4)9. In the constant level run the exposure time was kept constant by means of an electronic LED shutter defined at a 0.3 μs time resolution. In the flux ramp the exposure time was varied using the megacam shutter (1 ms resolution).
Alternatively, we measured the mean flux absorbed in the CCDs. The linear fit of Eq. (14) yields for each channel k a constant term Ψk,cur/ Ψk,ref and a slope term ay/x, with a statistical precision of 4 × 10-6 and 1.7 × 10-5/(0.1 ×Ψk,ref), respectively. LED jitter has no effect on the constant term of the fit. The large error bars seen in Fig. 15.b) show the spread of the gain fluctuations in the 72 channel data. The mitigation method described in Sect. 3.1 reduces the gain fluctuations (δgk,cur / ref≈ 1.5 × 10-3 rms) and yields an average FEG flux ratio (black points), 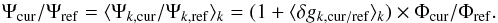 (16)The deviation from the linear trend is 1.8 × 10-4 rms. It is compatible with the averaging of 72 channels (δg/
(16)The deviation from the linear trend is 1.8 × 10-4 rms. It is compatible with the averaging of 72 channels (δg/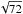 = 1.5 × 10-3/
= 1.5 × 10-3/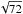 ). Thermal fluctuations of LED, around 0.1 °C per minute, have comparable effects.
). Thermal fluctuations of LED, around 0.1 °C per minute, have comparable effects.
 |
Fig. 15 Effect of LED temperature on light flux (warming of CFHT dome at dawn): a) variable exposure (1s < Δt < 8s); b) constant exposure (Δt = 8s): two independent estimators ⟨ αk ⟩≈ 16 000 adu (black points) and ⟨ Ψσδ ⟩≈ 100 adu (red points) agree within 0.8 × 10-4 rms. Deviation from linearity is 1.8 × 10-4 rms. The precision on ⟨ Ψσδ ⟩ is ≈0.008 adu, i.e., 0.6 × 10-6. Error bars cover gain spread before averaging. The two other estimators ⟨ Ψσβ ⟩ and ⟨ Ψσγ ⟩ (green and blue) are more sensitive to LED jitter. |
 |
Fig. 16 Setting up the relative fluxes within a sequence of 70 images: 1) three sequences, covered by horizontal lines, are built around three reference images (black, blue, and brown arrows). Gain × fluxes ratios are determined as in Fig. 11 (Icur = 9, Iref = 11). 2) The reference image of sequence 2 is measured relative to reference 1 and reference 3 relative to reference 2. By transitivity all fluxes are related. 3) The two overlap regions 1 over 2 and 2 over 3 yield a set of double determinations. The relative fluxes of all 70 images agree within 3 × 10-5 rms. They give the relations flux vs. exposure time (shaded area: 28 images at a common LED current) and flux vs. LED current (constant exposure time). The only significant LED jitter occurs between images 55 and 56. |
For the variable exposure run, the 70 images in Fig. 16 yield a point representing Ψcur/ Ψref the ratio of its averaged FEG flux over that of a reference image. Integrated fluxes are varied by two different means: exposure time using shutter speed (magenta shade) or LED current (plain). As a precaution, because the long periods at low flux destroy the continuity of high-precision data, we took three reference images marked by vertical arrows (one for each peak of flux). To reconnect the results based on different references, we measured the relation between each pair of reference images and checked the transitivity of the flux ratio measurements. The relative flux precision that we obtained at highest flux is ≈3 × 10-5 rms. The mechanical shutter yields the error bars (δ(Δt) = 1 ms) seen in Fig. 15a). Clearly, the electronic shutter is prefered. The ⟨ α ⟩ flux ratio estimator Ψcur/ Ψref measured so far reaches a precision of around 10-4 after mitigation of the electronics errors. It is essentially a measurement of the flux of specular light.
Four other measurements, Ψk,I(σα,σβ,σγ,σδ), the square root of the covariances in Eq. (8), yields four completely independent estimates of the flux based on the diffused light (≈10% of specular light). The application of these covariance estimators provides a positive test of the WP model with the spectacular precision shown in Fig. 15b. The Ψk,Iσδ estimate yields the red points superimposed on the black ones. There is a 0.8 × 10-4 rms agreement between the two types of estimators. The agreement is better than the 1.8 × 10-4 precision resulting from averaging the gains in Eq. (16). This is explained by considering that both types of estimators are based on the same FEG scale and not on the real flux scale. The 0.8 × 10-4 precision on σδ corresponds to a 0.008 adu precision on the pixel counts. This result, relative to the average pixel content of 16 000 adu, entails a remarkable precision on the WP hessian signal width Ψσδ of 0.5 × 10-6 rms, almost at the statistical precision limit of the 1013 photons. The two other quantities shown in the figure – Ψσβ,Ψσγ – yield similar results, but the analysis is complicated by the introduction of the LED jitter noise, which adds up quadratically to the WP signal dispersion. The limiting precision for the WP estimators is set by the photon noise. The filtering of the low spatial frequencies suppresses the effect of electronic bugs.
4.5. α, β, γ, and δ noise estimators
The raw variance of a filter content in Eq. (11) is the sum of the WP variance Ψk,Iσδ and the noise variance ςδ. Figure 17 reproduces the variances of three filters in a relative form (divided by the FEG flux ⟨ α ⟩). This figure is one half of the consistency check of our model. It shows on a very broad dynamical range that the interference pattern is proportional to the flux (because it is defined by the probability density of the wave packet). The second half of the demonstration is contained in the analysis of the noise variance as a function of flux (Fig. 20), because it demonstrates that in most of the range the noise is dominated by the photon statistics.
Without too many technical details, we report that we applied the slicing method and the fits shown in Figs. 12 and 13 to the distributions (δk,cur, 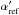 ) and (Δδk,cur,
) and (Δδk,cur, 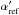 ). The variances of δk,cur and Δδk,cur (Eq. (12)) yield the estimates for the raw WP signal and for the pure noise, respectively. Both are shown in Fig. 17 for three filters.
). The variances of δk,cur and Δδk,cur (Eq. (12)) yield the estimates for the raw WP signal and for the pure noise, respectively. Both are shown in Fig. 17 for three filters.
 |
Fig. 17 Pure noise ςδ is extracted by subtracting the raw reference image (with its relative weight) from all other raw images. Then pure WP signals Ψσβ, Ψσγ, and Ψσδ are extracted from raw images by subtracting noise ςδ. Check: σβ,σγ, and σδ are constant and σβ = σγ (superimposed). |
We used the constant level run as a benchmark for the high-precision noise estimators. A good summary of the study is seen in Fig. 18. It represents two versions of the same four (α, β, γ, and δ) noise variance estimators. For the upper one (Fig. 18a), mitigation yields only one average adu count per image per filter proportional to the average adu count of the reference image. A global LED jitter noise correction was applied using the parameter Δy from Fig. 14 (open circles before and full circles after correction). In the lower one (Fig. 18b), there are 72 data per image (one relative noise per channel). Relative noise is not affected by gain fluctuations (cancelled between the numerator and the denominator). Data are represented in the plot by their mean and rms. The precision is sufficient to fit the flux dependence of the noise (proportional to 1/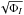 ). The comparison of the four filters after LED jitter correction gives the size of the correlated fluctuations among four neighboring pixels. Fully correlated fluctuations such as pedestal or gain fluctuations are seen by the ςα variable. Their effect is in a 0.5−3 adu range. The line-to-line (or column-to-column) fluctuations sensed by ςβ (or ςγ) yield a 0.25 adu effect. The fourth variable ςδ serves as a pure sample of uncorrelated noise to be used for a fine study of the photon noise on the whole flux range covered by the 70 images flux ramp.
). The comparison of the four filters after LED jitter correction gives the size of the correlated fluctuations among four neighboring pixels. Fully correlated fluctuations such as pedestal or gain fluctuations are seen by the ςα variable. Their effect is in a 0.5−3 adu range. The line-to-line (or column-to-column) fluctuations sensed by ςβ (or ςγ) yield a 0.25 adu effect. The fourth variable ςδ serves as a pure sample of uncorrelated noise to be used for a fine study of the photon noise on the whole flux range covered by the 70 images flux ramp.
 |
Fig. 18 a) Fluctuations ςα,...,δ (rms) of α,...,δ between the last image I = 25 and any other one I = 1, 24 in temporal order (72 channels average). Open circles represent raw data and full circles data corrected for LED jitter. Variable α senses all noise sources; β (γ) suppresses the line (column) correlated electronic noise and the LED jitter along x (y) axes; δ suppresses all correlated noises and LED jitter. b) Relative fluctuations 2 ×⟨ ςβ(,γ,δ)/α ⟩ are compared to the prediction. The continuous line representing the prediction ∝1/ |
The three uncorrelated random processes affecting the WP signal have a different flux dependence: the pedestal noise is constant, the gain noise is proportional to the flux, and the photon noise to the square root of the flux. The variances were added to constitute what is classically called the statistical factor (Eq. (17)). We could take into account the LED jitter variance in the statistical factor, but we do not need it because the flux ramp is divided into two sequences with no internal LED jitter, 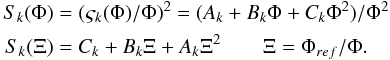 (17)The link between the variance of the noise variable Δδk,I in Eq. (12) and the statistical factor has been given in Eq. (13), which sums the statistical factors of the current image and the reference image. This eliminates not only the WP signal, but also the fluctuation of gains of both current and reference images, which are the root of our electronic problems. The change of variable from the flux Φ to its inverse Ξ = Φref/ Φ in Eq. (17) transforms S(Φ) into a second-degree polynomial in Ξ. The photo-electron noise is in the BkΞ term and the pedestal noise in AkΞ2.
(17)The link between the variance of the noise variable Δδk,I in Eq. (12) and the statistical factor has been given in Eq. (13), which sums the statistical factors of the current image and the reference image. This eliminates not only the WP signal, but also the fluctuation of gains of both current and reference images, which are the root of our electronic problems. The change of variable from the flux Φ to its inverse Ξ = Φref/ Φ in Eq. (17) transforms S(Φ) into a second-degree polynomial in Ξ. The photo-electron noise is in the BkΞ term and the pedestal noise in AkΞ2.
Figure 20b shows one of the 72 curves representing the S(Ξk,I) vs. Ξk,I data and their fit by a second-degree polynomial on a flux range of two orders of magnitude. The second-degree term is visible only when extending the flux range down, from hundreds to tens of photo-electrons per pixel. For each point of a Sk(Ξ) curve a gain fluctuation does not alter the ordinate Sk(ΞI) but shift the abscissa ΞI. The shift of ΞI from Ψref/ΨI to Φref/ΦI is common to all the 72 channels of an image. Figure 19a displays the residuals of the 72 linear fits of Sk(ΨI) vs. ΨI, which contain the common mode effect of the ΦI−ΨI shift in addition to the random noise. This effect is statistically significant, therefore we corrected for it. The correction reduces the dispersion of residuals seen in Fig. 20a by a factor two for all channels. This amounts to replacing the FEG flux ΨI by an FE flux ΦI (or to correct the fluctuation of the average gain assuming that the average efficiency is constant). Figure 19a represents a continuous drift of the average gain with time independently of the flux. The overall distribution of final residuals, shown in Fig. 20a, is an unbiased Gaussian with a 2.7 × 10-8 rms. For channel 72, whose S(Ξ) vs. Ξ fit is given in Fig. 20b, this entails a 0.30% Gaussian width of ΔSk/Sk. Using the S = (ςδ/α)2 relation, Δςδ/α = 0.5 × (ΔS/S) ×ςδ/α = 4.5 × 10-6 rms (at reference flux Ξ = 1)10. This is the number expected from a pure photo-electron statistical noise, which proves that there is no other unknown or uncorrected systematic fluctuation in the CCD measurement.
 |
Fig. 19 a) Bias ⟨ δSk(ΞI) ⟩ k (in blue) drift continuously with time. It equally affects all 72 residuals of the fit S(Ψ) vs. Ψ. When corrected, the width of the residual distribution is reduced to its photon statistics value (Fig. 20a). This correction is equivalent to a modification of the flux scale ΨI→ΦI. b) The flux ramp sequence ΨI (red), taken from Fig. 16, is correlated to the dispersion of biases (error bars in Fig. 19-a). For ΨI < 2000 adu (black boxes) the dispersion of the pedestals dominates the dispersion of the photon number. |
 |
Fig. 20 a) Residuals of Sk(ΞI) vs. ΞI fits (k = 1, 72, I = 1, 70). In black we plot data and Gaussian fit for ΨI > 2000 adu with a width =2.7 × 10-8 rms; in blue we show the complete data. b) Extrapolation at infinite flux for any channel k yields a negligible value of Ck = Sk(0). |
In addition to photon noise, our random noise model in Eq. (17) contains the two auxiliary terms Ck and Ak. In Eq. (13), our noise estimator, Sk(Φref) is a constant added to Ck. In practice, we fit a second-degree polynomial P2(Ξ) to the data and evaluate it at Ξ = 1. This yielded P2(1) = 2 ×Sk(Φref). The constant Sk(Φref) = P2(1)/2 was subtracted from the data. Then we repeated the fit on these reduced data. The new constant term is the real Ck seen in Fig. 20b. For all channels Ck is null within a good approximation: there is no need to envisage a noise component other than photon statistics in the wide range above 2000 adu. The coefficient Ak includes the Johnson noise of the amplifier and fluctuations of the pedestal, reaching a few adus. We see in Fig. 19b that, first in the 2000−20 000 adu range (above the yellow line) the Ak term is too small compared to the signal to be sensed and a linear fit is perfect, then in the 200−2000 adu range (inside rectangles) Ak is needed and the dispersion of the residuals (error bars) increases as a result of the pedestal fluctuations, and finally in the range below 200 adu (not sampled in the ramp), pedestals should be processed differently.
In the present section we emphasized the importance of an accurate Φ scale for the photon noise ramp. Previously in Sect. 4.4, we developped an accurate Ψ scale needed for the WP signal ramp. This does not set the two scales on the same footing. The Φ scale is already at its theoretical precision limit of 1.8 × 10-4 because of the photon statistics, while the Ψ scale precision is limited by the poor stability of electronics, also at 1.8 × 10-4. Ψ scale could be improved by two orders of magnitude by using high precision electronics, to reach its photon statistical limit, and both scale could be reconciled at a common value better than 10-5.
5. Conclusions and perspectives
We have shown in this paper that there is no other limit for a photometry based on the Megacam camera than the statistical fluctuations of the photon count in any CCD area, set in our case to below 1 ppm per exposure for the whole image. The proof, using the properties of some difference operators applied to the photon field, is indirect because of the defects of the electronics. The single photo-electron response is calibrated by statistics and the integrated flux is measured for each exposure using the total response of the whole detector or a part of it. We might call this type of photometry self-consistent or self-calibrated.
If the LED flux or the CCD flux are deduced from electronic readings alone, the precision is limited by the stability and the calibration of electronics. After optimizing the electronics this precision limit should be around 20−30 ppm. In practice, with either Sndice or Megacam electronics, the current precision is degraded to 100−200 ppm. We showed how electronics might be optimized to suppress these practical limitations. We call this type of photometry electrically calibrated. The precision of an optimized electric calibration could be maintained for years. It surpasses the best photometric results obtained using stable stellar sources. Electric calibration allows comparing different exposures of a varying light source or monitoring the evolution of a detector with a constant LED source, while self-calibrated fluxes are used to compare even more precisely two sources with a common detector or two detectors with a common source (e.g., for calibration transfer). Based on these examples, we can build a large set of direct illumination calibration applications. A third type of calibration, the absolute calibration, is done in SNDICE by a common practice method using a NIST calibrated photodiode in a test bench. In this case, we would speak of accuracy instead of precision. We did not discuss accuracy because the absolute calibration procedure mentioned above is not sufficiently reliable. First, because it does not consider either the angular dependence and the map of the detector quantum efficiencies or the emission pattern of the light sources. Second, because in the light of our study of cooled large area photodiodes for other Sndice publications, we cannot take the accuracy of the photovoltaic quantum efficiency used by NIST for granted as the reference photodiode yield.
At this point, we could have concluded the review of the instrumental results obtained from our Sndice-on-Megacam data by observing that we had reached a level of precision better by two order of magnitude than best astronomical photometry and that we measure the effect of diffuse reflection on the mirror that is not seen by other means with the same precision.
However, it was more fruitful to take a new point of view: to consider the interference patterns that we called the WP signal like a signal to be studied instead of a noise to hide (as calibration systems using incoherent extended illumination do). The WP signal represents 10% of the flux seen in Megacam. It is stable and we measure it at an overall 10-5 precision level. Classical signal processing methods have been applied to the WP signal. They produced simple and useful results. In frequency space, the WP spectrum separates the specular and diffuse components of light. It measures the effect of the photon propagator in free space and yields optical surface quality estimators. It also maps the defects of optical surfaces individually. As compared with holographic or phase-contrast systems with similar abilities, we have had a large-scale high-performance system for free already built in the camera.
In direct space, we have used and developed pixel difference operators (PDE) with extremely useful results. In particular, the extraction of photon statistical noise is performed by four independent operators that first define the angular position of an LED in the telescope frame at a 0.4 nrad rms precision and then yield four noise estimators at better than 1 ppm.
The perspective of entering a new territory of high-precision photometry should be seriously considered. The first steps might easily be to build dedicated photometric systems and improve commercial components such as LEDs for our purposes.
Take a white-noise CCD image (photon flat field): its |DFT| field is flat. The integrated radial spectrum, proportional to the surface in a given ring, rises linearly with radius and then decreases when the rings are no longer contained in the square. The averaged radial and angular spectra are flat, as seen in Figs. 4 and 5.
Adjusted in the residual plot in Fig. 8.
Introduced as differential operators in Sect. 2.4, they act as filters on a Fresnel spectrum.
Formulas and their application to our problem are found in Barrelet (2013), Appendix C.
The truncated Gaussian fit is good within ± 2σα; 4 out of 72 channels have non-Gaussian tails due to stains on the mirror (see Barrelet 2013, Fig. 12).
Acknowledgments
This work incorporates a number of important contributions to the subject that must be quoted and for which I express all my gratitude. First of all is the Megacam camera including its E2V CCDs, which represents an epochal realization. I am grateful to Pierre Borgeaud, who introduced us to the Megacam electronics and helped starting the electronic developments described in Claire Juramy’s thesis. In this thesis we also found the first proposition of a direct illumination calibration of a telescope with LEDs that we developed together in a later article. Reynald Pain together with the CFHT scientific and technical team transformed this concept into the SNDICE project. Kyan Schahmaneche has led the realization of Sndice with its associated calibration bench in record time and its installation in Hawaii. Kyan and Augustin Guyonnet did the calibration of Sndice on the bench. Augustin’s thesis started the study of the high-precision methods presented here. Sndice calibration tools were developed and advanced in an article by Nicolas Regnault. He applied these tools with Marc Betoule to the calibration of the SNLS experiment. Last but not least, we benefited from illuminating discussions with Pierre Astier.
References
- Appuhn, R. D., Arndt, C., Barrelet, E., et al. 1999, Nucl. Instr. and Meth. A, 426, 518 [NASA ADS] [CrossRef] [Google Scholar]
- Barrelet, E. 2010a, Digital Image Processing for SNDICE, LPNHE Report 2010-06 [Google Scholar]
- Barrelet, E. 2010b, Optoelectronic tests for SNDICE, LPNHE Report 2010-03 [Google Scholar]
- Barrelet, E. 2013, Testing Megacam with SNDICE, LPNHE Report 2010-04 [Google Scholar]
- Barrelet, E., & Juramy, C. 2006, Direct Illumination Led Calibration for Ia Supernovae Photometry, LPNHE Report 2006-02 [Google Scholar]
- Barrelet, E., & Juramy, C. 2008, Nucl. Instr. and Meth. A, 585, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Barrelet, E., Juramy, C., Lebbolo, H., & Sefri, R. 2004, Dual Gain Clamp and Sample ASIC, LPNHE Report 2004-11 [Google Scholar]
- Born, M., & Wolf, E. 1999, Principles of Optics (Cambridge: Cambridge University Press) [Google Scholar]
- Boulade, O., Charlot, X., Abbon, P., et al. 2003, in SPIE Conf. Ser. 4841, eds. M. Iye, & A. F. M. Moorwood, 72 [Google Scholar]
- Guyonnet, A. 2012, Thesis, Université Paris 7, Denis Diderot, France [Google Scholar]
- Juramy, C. 2006, Thesis, Université Pierre et Marie Curie, Paris, 6, France [Google Scholar]
- Regnault, N., Guyonnet, A., Schahmanèche, K., et al. 2015, A&A, 581, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1 Left: wave packet signal (WP) measured in a 1024 × 1024 pixel2 area. The gray scale covers ⟨WP⟩± 1.5σ. Right: the 1% of pixels in this area with a sharp WP gradient due to defects of the camera optics (∥ ∇(WP) ∥ ≥ 16σ). Four camera defects a–d of different types are circled in the two figures for discussion in Sect. 2.5. |
| In the text | |
 |
Fig. 2 Ray optics and wave packet: in red we plot a star source at infinity imaged at focus F and its diffuse reflection falling in the Strehl ratio area around F; in blue we show a LED source S at focal distance and diffuse reflection interfering with specular reflection (reflected beam MF displaced for clarity into M’F’). |
| In the text | |
 |
Fig. 3 Effect of the Fourier transform on a 1024 × 1024 vignette of the Sndice image. Left: applied to the original field; right: applied to the 3 PDE transformed fields – ∇x, ∇y, Δ2/ ΔxΔy –. The 288 vignettes covering the focal plane are quadratically averaged. The frames are set by |νx| and |νy| = νnyq. The horizontal and vertical lines passing through the center are due to electronic noise. Dashed circles mark radial cuts ν1 and ν2 in Fig. 4. The three points β, γ, and δ mark the three real FFT components averaging same name filters (α is at the center). |
| In the text | |
 |
Fig. 4 Radial spectra of the sum and the difference of two images (image v is close to u; w distant). All are normalized to the 0.7% rms photon noise. The [ν1,ν2] cut yields the angular plots in Fig. 5. The Nyquist frequency is νnyq. |
| In the text | |
 |
Fig. 5 Spectral angular distribution of u+v, normalized by the photon noise and then by subtracting 1. The angular average S/N≈ 6 equals the radial average inside the [ν1, ν2] cut. The electronic noise peaks at θ = 0 and θ = ± π/ 2. |
| In the text | |
 |
Fig. 6 a) Spectral angular distribution of u+w after applying PDE operators, divided by the unity distribution U of Fig. 5. b) Spectral angular distribution of u–w, divided by U (inside the radial cut [ν1, ν2]). The uncorrelated random spectra, null after subtraction of unity, are plotted in yellow. Fitted curves are shown in red. |
| In the text | |
 |
Fig. 7 Radial spectra of the sum and difference of two images after the application of four filters (α,β,γ,δ). |
| In the text | |
 |
Fig. 8 Residuals of δ(u–v)/noise and δ(u–w)/noise linear fits of radial frequency spectra (noise = 98 adu). The precision for each sample is ≈10-5, and for the whole image the average is ≈0.3 × 10-6. |
| In the text | |
 |
Fig. 9 Camera defects a, c, and d circled in Fig. 1. Top: the flux map around the defects. Bottom: the profile of the adc content drawn along a line passing through the center of the defects. |
| In the text | |
 |
Fig. 10 a) Gradient field pattern around a defect A is characterized by a regression analysis of angle Θ (cotgΘ = ∇.Ox) versus pixel x in each CCD line y. The regression equation is x = a + (b−y)cotgΘ. b) Four horizontal slices of six lines each are drawn corresponding to groups of lines in a). The field lines converge on the point A x = a, y = b. |
| In the text | |
 |
Fig. 11 Left: histogram of α in the reference image subdivided in slices 40-adu wide. Right: histogram of the projection of each reference slice in any current image is a Gaussian. Only one slice for every five is represented. Top (inset): the means of the current slices are fit as a linear function of the means of the reference slices. The distribution of the residuals is shown in Fig. 12. |
| In the text | |
 |
Fig. 12 Residuals of the linear fit of Fig. 11: a) as a function of αk,reference; b) as a histogram (0.4 adu rms). In red: points included in the fit (α ∈ [ ⟨ α ⟩ ± 1.5σ]). |
| In the text | |
 |
Fig. 13 a) Fit of the width of the joint distribution as a function of αk,reference in the { ⟨ α ⟩ ± 1.5σ } interval. b) Histogram of the residuals of the previous fit, fitted by a Gaussian (0.14 adu rms). |
| In the text | |
 |
Fig. 14 Signal of γ vs. α correlation as a function of channel k and image I (noted ηkΔyI, with ΔyI fixed to 0 for I = 24) (blue). Residual of the fit of this signal with one ηk parameter per channel and one ΔyI per image (black). Images I = 2, 17, 18 were called w, u, v in the spectral studies of Sect. 2. Δy is calibrated by comparison with Δyw → u. The inset shows a Gaussian fit of the residuals (1 point/channel/image) with a 5 × 10-4 rms, yielding Δyk = 0.05 μ or ⟨ Δyk ⟩ = 0.006 μ. The green line indicate the effect of a 1 μ LED drift. |
| In the text | |
 |
Fig. 15 Effect of LED temperature on light flux (warming of CFHT dome at dawn): a) variable exposure (1s < Δt < 8s); b) constant exposure (Δt = 8s): two independent estimators ⟨ αk ⟩≈ 16 000 adu (black points) and ⟨ Ψσδ ⟩≈ 100 adu (red points) agree within 0.8 × 10-4 rms. Deviation from linearity is 1.8 × 10-4 rms. The precision on ⟨ Ψσδ ⟩ is ≈0.008 adu, i.e., 0.6 × 10-6. Error bars cover gain spread before averaging. The two other estimators ⟨ Ψσβ ⟩ and ⟨ Ψσγ ⟩ (green and blue) are more sensitive to LED jitter. |
| In the text | |
 |
Fig. 16 Setting up the relative fluxes within a sequence of 70 images: 1) three sequences, covered by horizontal lines, are built around three reference images (black, blue, and brown arrows). Gain × fluxes ratios are determined as in Fig. 11 (Icur = 9, Iref = 11). 2) The reference image of sequence 2 is measured relative to reference 1 and reference 3 relative to reference 2. By transitivity all fluxes are related. 3) The two overlap regions 1 over 2 and 2 over 3 yield a set of double determinations. The relative fluxes of all 70 images agree within 3 × 10-5 rms. They give the relations flux vs. exposure time (shaded area: 28 images at a common LED current) and flux vs. LED current (constant exposure time). The only significant LED jitter occurs between images 55 and 56. |
| In the text | |
 |
Fig. 17 Pure noise ςδ is extracted by subtracting the raw reference image (with its relative weight) from all other raw images. Then pure WP signals Ψσβ, Ψσγ, and Ψσδ are extracted from raw images by subtracting noise ςδ. Check: σβ,σγ, and σδ are constant and σβ = σγ (superimposed). |
| In the text | |
 |
Fig. 18 a) Fluctuations ςα,...,δ (rms) of α,...,δ between the last image I = 25 and any other one I = 1, 24 in temporal order (72 channels average). Open circles represent raw data and full circles data corrected for LED jitter. Variable α senses all noise sources; β (γ) suppresses the line (column) correlated electronic noise and the LED jitter along x (y) axes; δ suppresses all correlated noises and LED jitter. b) Relative fluctuations 2 ×⟨ ςβ(,γ,δ)/α ⟩ are compared to the prediction. The continuous line representing the prediction ∝1/ |
| In the text | |
 |
Fig. 19 a) Bias ⟨ δSk(ΞI) ⟩ k (in blue) drift continuously with time. It equally affects all 72 residuals of the fit S(Ψ) vs. Ψ. When corrected, the width of the residual distribution is reduced to its photon statistics value (Fig. 20a). This correction is equivalent to a modification of the flux scale ΨI→ΦI. b) The flux ramp sequence ΨI (red), taken from Fig. 16, is correlated to the dispersion of biases (error bars in Fig. 19-a). For ΨI < 2000 adu (black boxes) the dispersion of the pedestals dominates the dispersion of the photon number. |
| In the text | |
 |
Fig. 20 a) Residuals of Sk(ΞI) vs. ΞI fits (k = 1, 72, I = 1, 70). In black we plot data and Gaussian fit for ΨI > 2000 adu with a width =2.7 × 10-8 rms; in blue we show the complete data. b) Extrapolation at infinite flux for any channel k yields a negligible value of Ck = Sk(0). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.