| Issue |
A&A
Volume 593, September 2016
|
|
|---|---|---|
| Article Number | A53 | |
| Number of page(s) | 10 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201628784 | |
| Published online | 21 September 2016 | |
Spatially resolved observation of the fundamental and second harmonic standing kink modes using SDO/AIA⋆
Centre for Fusion, Space and Astrophysics, Department of Physics, University of Warwick, CV4 7AL, UK
e-mail: D.J.Pascoe@warwick.ac.uk
Received: 25 April 2016
Accepted: 23 June 2016
Aims. We consider a coronal loop kink oscillation observed by the Atmospheric Imaging Assembly (AIA) of the Solar Dynamics Observatory (SDO) which demonstrates two strong spectral components. The period of the lower frequency component being approximately twice that of the shorter frequency component suggests the presence of harmonics.
Methods. We examine the presence of two longitudinal harmonics by investigating the spatial dependence of the loop oscillation. The time-dependent displacement of the loop is measured at 15 locations along the loop axis. For each position the displacement is fitted as the sum of two damped sinusoids, having periods P1 and P2, and a damping time τ. The shorter period component exhibits anti-phase oscillations in the loop legs.
Results. We interpret the observation in terms of the first (global or fundamental) and second longitudinal harmonics of the standing kink mode. The strong excitation of the second harmonic appears connected to the preceding coronal mass ejection (CME) which displaced one of the loop legs. The oscillation parameters found are P1 = 5.00±0.62 min, P2 = 2.20±0.23 min, P1/ 2P2 = 1.15±0.22, and τ/P = 3.35 ± 1.45.
Key words: magnetohydrodynamics (MHD) / Sun: atmosphere / Sun: corona / Sun: magnetic fields / Sun: oscillations / waves
A movie associated to Fig. 5 is available in electronic form at http://www.aanda.org
© ESO, 2016
1. Introduction
Kink oscillations of coronal loops have been intensively studied since their detection with the Transition Region And Coronal Explorer (TRACE; Handy et al. 1999) in 1999 (Aschwanden et al. 1999; Nakariakov et al. 1999). Much of this study is motivated by the potential for using these oscillations to probe the physical plasma parameters with coronal seismology (e.g. Stepanov et al. 2012; Liu & Ofman 2014). Kink oscillations are typically detected as strongly damped transverse displacements of coronal loops following eruptive or flare events detected using EUV imaging instruments. The quality and detail of these observations have improved (e.g. Aschwanden & Schrijver 2011; White & Verwichte 2012) following the launch of the Solar Dynamics Observatory (SDO) Atmospheric Imaging Assembly (AIA; Lemen et al. 2012). More recently, AIA data has been exploited for systematic statistical studies of decaying kink oscillations, which include a catalogue and study of their excitation mechanism (Zimovets & Nakariakov 2015). Goddard et al. (2016) studied the distributions of the oscillation parameters, such as the derived kink speed, as well as the damping of the oscillations. In contrast to this strongly damped regime, low amplitude decay-less kink oscillations have also been detected (Nisticò et al. 2013; Anfinogentov et al. 2013) and confirmed to be a common phenomenon in the corona (Anfinogentov et al. 2015).
The simultaneous detection of different wave modes – or different harmonics of the same wave mode – in the same coronal loop can provide additional seismological information about the plasma structure. For standing modes in coronal loops with a length L, the footpoints are nodes for the oscillation and the longitudinal wavenumber k is required to be an integer multiple of π/L i.e. kn = nπ/L. The global or fundamental standing mode has n = 1, and the second harmonic is n = 2. The period of oscillation for the harmonic of order n is denoted as Pn. Fast MHD waves in a waveguide are highly dispersive. This can be expressed in terms of the periods of longitudinal harmonics not being integer multiples of the fundamental mode; P1/ 2P2 is generally less than unity for fast MHD waves. Verwichte et al. (2004) analysed oscillations in an arcade of coronal loops. For two of the nine paths analysed, two periods of oscillation were detected and interpreted as the first and second harmonic kink modes. Andries et al. (2005) used the period ratios reported by Verwichte et al. (2004) to estimate the density scale height and in taking the large observational errors into account considered the possibility of a negative scale height for one of the two loops, i.e. the density for that loop being greater at the apex than the footpoints. Similar calculations were also performed by McEwan et al. (2006), and McEwan et al. (2008) derived an analytical expression for the dependence of the period ratio on the density scale height. Macnamara & Roberts (2011) produced analytical expressions for the period ratio P1/ 2P2 of sausage and kink modes in a magnetic slab with an Epstein profile for the transverse density structure. Ruderman (2003) studied the period of oscillation and resonant damping of coronal loops with elliptic cross-sections. Morton & Erdélyi (2009) demonstrated that an elliptic curvature of the loop axis has a small effect on the period ratio, while Orza & Ballai (2013) showed that asymmetry in coronal loops also has a small effect on the ratio. Chen et al. (2014) studied the effect of steady siphon flows and found that it significantly reduces the P1/nPn ratio.
De Moortel & Brady (2007) reported the observation of flare-induced higher harmonic kink oscillations using TRACE. Spatial information is provided by four slits across the loop and demonstrates the antiphase motions of the loop either side of the apex. The authors noted the absence of the fundamental mode, although there was an initial displacement of the loop apex associated with the physical displacement immediately after the flare. Wang et al. (2008) considered the observational signatures of first and second kink harmonics with horizontal and vertical polarisations and demonstrated that in some cases it can be difficult to distinguish between the different modes. Van Doorsselaere et al. (2007) also used the first and second kink harmonics to determine the density scale height. The accuracy of their measurements was significantly increased by considering the oscillation signals at many locations in the loop leg, although the length of the loop segment considered was too small to demonstrate the full spatial structure of the different harmonics. Srivastava et al. (2013) observed kink harmonics in a cool loop system and also reported a period ratio P1/ 2P2 greater than unity, which they interpreted as being due to loop expansion rather than the longitudinal density profile, and used the analytical result of Verth & Erdélyi (2008) to calculate an expansion factor of Γ = 1.27. Zaqarashvili et al. (2013) used radio observations to perform seismology for the outer solar corona, i.e. sufficiently high that EUV intensities are too weak to measure. They interpret quasi-periodic variations in terms of the first and second harmonics of the vertical kink oscillation of transequatorial coronal loops. Kupriyanova et al. (2013) detected three periodicities, ≥ 30, 20, and 10 s in a short loop seen in microwave emission with the Nobeyama Radioheliogaph (NoRH), and concluded that the observed spatial structure of the oscillations is consistent with the fundamental, second, and third harmonics of kink mode standing waves. The apparent integer ratios of the oscillation periods could be attributed to the negligible stratification in a short and hot flaring loop. Kolotkov et al. (2015) also used NoRH observations of quasi-periodic pulsations and discovered three periodicities in flare microwave emission of 15, 45, and 100 s. The shortest period is interpreted as a fundamental standing sausage mode, and the other two as first and second kink harmonics with a period radio P1/ 2P2 ≈ 1.1. As with Zaqarashvili et al. (2013), the interpretation of a second harmonic kink mode is not based on direct observation of the spatial dependence of the mode. Rather, it is based on the relationship to other periodicities and comparison with those expected for known wave modes when realistic loop and plasma properties are assumed. Zhang et al. (2015) reported an observation of a coronal funnel with SDO/AIA which demonstrates fast and slow waves propagating along the same field-aligned path, consistent with numerical simulations of Pascoe et al. (2013b; 2014) and Nisticò et al. (2014). Measurement of the propagation speeds allowed the plasma-β to be estimated as approximately 0.01. Guo et al. (2015) analysed the anti-node positions of the first two harmonics, which were found to shift towards a weak field region. Despite all these studies and observations, a clear and unambiguous detection of multiple kink oscillation harmonics along most of the length of a loop has not been reported until now.
The curved geometry of coronal loops can potentially introduce effects in addition to those present in models of straight slabs or cylinders (e.g. review by van Doorsselaere et al. 2009). Curved loops require a non-uniform equilibrium magnetic field and so can produce a varying Alfvén speed outside the loop structure (also depending on the density profile). This can allow the tunnelling of wave energy from the inside to the outside of the loop and so can introduce an additional damping mechanism for oscillations in the form of lateral wave leakage (e.g. Smith et al. 1997; Brady et al. 2006; Díaz et al. 2006; Verwichte et al. 2006). However, Terradas et al. (2006) found that this lateral leakage was typically weaker than the effect of resonant absorption or mode coupling which applies to kink waves in loops where there is a finite transition layer between the high density core and the background.
Based on numerical (Pascoe et al. 2012) and analytical investigations (Hood et al. 2013) of mode coupling, Pascoe et al. (2013a) described how the damping of kink oscillations by mode coupling can exhibit two different regimes. A Gaussian damping profile applies for early times, and an exponential damping profile at later times. The time of the switch between damping profiles depends on the loop density contrast ratio, such that the Gaussian damping profile is dominant for low contrast loops, and the exponential profile is dominant for high contrast loops (see also reviews by Pascoe 2014; De Moortel et al. 2016). Pascoe et al. (2016b) have examined the damping profile of standing kink oscillations observed by SDO/AIA and found examples of both Gaussian and exponential damping behaviour. Pascoe et al. (2013a) have proposed that a unique seismological inversion for the transverse density profile would be possible in cases of oscillations for which both regimes were observed. This method has recently been applied to three coronal loops by Pascoe et al. (2016a).
Kink modes may be excited by any mechanism which perturbs the axis of a coronal loop. The mechanism initially proposed (e.g. Nakariakov et al. 1999) is based on a solar flare exciting a fast MHD wave which propagates outwards and interacts with nearby loops. There have been several numerical investigations for the interaction of fast waves with active regions (e.g. Terradas & Ofman 2004a) and coronal loops (Terradas et al. 2008; McLaughlin & Ofman 2008; De Moortel & Pascoe 2009; Pascoe & De Moortel 2014). Pascoe et al. (2009a) have demonstrated that the second harmonic is efficiently excited by waves which perturb loops with an attack angle of approximately 45 degrees, i.e. which perturb one of the legs before the other. The statistical study by Zimovets & Nakariakov (2015) suggests the majority of kink oscillations are associated with plasma ejections.
The aim of this paper is to examine the case of a coronal loop oscillation containing different periods of oscillation and present evidence from the periods of oscillation, spatial dependence, and phase information to support our interpretation in terms of the fundamental and second longitudinal harmonic standing kink modes. In Sect. 2 we describe our observation with SDO/AIA. In Sect. 3 we determine the oscillation parameters by fitting the oscillation at several points along the loop with a signal based on two damped sinusoids. The discussion and conclusions are presented in Sect. 4.
2. Observations by SDO/AIA
 |
Fig. 1 SDO/AIA 171 Å images of the loop before and during the oscillation. The dashed red line (left panel) shows the elliptical fit to the loop axis. Slits (solid blue lines) are taken perpendicular to this axis. The middle panel shows the loop after the lower leg (red arrow) has been displaced by the CME. The right panel shows the apparent plasma outflow (purple arrow) associated with the CME which obscures the view of the lower leg for most of the oscillation. |
Pascoe et al. (2016b) studied the damping profile of kink oscillations compiled by Goddard et al. (2016) to demonstrate the existence of the Gaussian damping regime predicted by numerical (Pascoe et al. 2012, 2013a) and analytical (Hood et al. 2013) modelling of mode coupling. One of the requirements for that investigation was for the oscillating loop to have a period of oscillation that remains stable over several cycles so that the damping profile could be accurately examined. The event we examine in this paper was initially chosen for the study by Pascoe et al. (2016b) on the basis of the high quality of the data. However, it had to be excluded because there were two strong periodicities evident in the time series and so the oscillation could not be easily modelled as a decaying global (fundamental) standing kink mode. On the other hand, the shorter period of oscillation (about one-half of the longer period) suggested the presence of the second harmonic. This is further implied by the EUV images of the event which give the strong impression of the two sides of the loop oscillating in anti-phase, consistent with the second harmonic standing mode (see online movie and Fig. 5).
The event occurred on 9 February 2011 at 01:30:02 UT, which Goddard et al. (2016) refer to as Event 4 Loop 1 and report a period 2.29 ± 0.03 mins (which corresponds to the higher frequency component in our analysis). Figure 1 shows SDO/AIA images at several times during the event. A flare is accompanied by a coronal mass ejection (CME), which strikes the lower leg of the loop as it propagates away from the Sun. This perturbation causes the loop to oscillate about its initial position for several cycles. During the oscillation, there is a slowly varying intensity which may be associated with flows. Plasma appears to flow upwards (and later downwards) along the magnetic field lines of the flaring active regions. These flows (or other perturbations) obscure the lower leg of the oscillating loop, and so we are only able to track the loop for part of its length (approximately 2L/ 3) during the oscillation. The loop segment is fitted with an ellipse. Time-distance (TD) maps were created with SDO/AIA EUV 171 Å data (spatial resolution of 0.6 arcsec per pixel and temporal cadence of 12 s) by taking linear slits perpendicular to the oscillating loop. Each slit has a width of 5 pixels over which the intensity is averaged to increase the signal-to-noise ratio. A series of 100 slits are calculated along the fitted loop segment. Each of these were inspected and those with sufficient quality were chosen for further analysis. This produced 15 time series at different positions along the loop which we will use to determine the spatial dependence of the two periodicities evident in our initial study. The positions of the slits used (numbers 17, 25, 30, 33, 37, 41, 55, 60, 65, 70, 75, 80, 85, 95, and 98) are shown in the left panel of Fig. 1.
 |
Fig. 2 Time-distance map for slit 70. The symbols (with error bars) represent the fitted locations of the loop axis. The vertical dotted lines denote the interval used for fitting in Fig. 3. |
 |
Fig. 3 Analysis of kink oscillation signals for slits 17 (top), 37 (middle), and 70 (bottom). The left panels show the position of the loop axis varying in time. The blue curves correspond to the two-component fits given by Eq. (2). The dashed lines show the polynomial background trends and the vertical dotted lines denote the time interval over which the oscillation is analysed. The middle panels show the periodogram analysis of the detrended signals. The symbols correspond to the observational data and the blue curve to the two-component fit. The red and green curves give the spectral profile of the two components separately; the fitted frequencies are indicated by the vertical lines of the same colour. The vertical dashed and dotted lines show the frequencies of the two components averaged over 15 analysed slits. The right panels show the detrended signals with the fitted oscillation (blue curves) and the two individual comopnents (red and green curves). |
Figure 2 shows an example TD map using slit 70. From such TD maps, the loop centre (symbols with error bars) is located by fitting the intensity with a Gaussian profile. The time series for the location of the loop centre as a function of time is then taken as the kink mode signal. The spectral and spatial properties of this signal are investigated in the following section.
3. Fitting standing kink mode harmonics
Figure 3 shows the kink oscillation signals calculated from the TD maps for slits 17 (top panels), 37 (middle panels), and 70 (bottom panels). These slits correspond to the lower leg, apex, and upper leg of the oscillating loop, respectively, and the fits for all the slits we use are shown in Figs. A.1−A.3. The left panels show the position of the loop axis as a function of time. The dashed lines show the background trend, which is assumed to be a polynomial. For example White & Verwichte (2012) use a third-order polynomial for the background, while Aschwanden et al. (2002) contains examples of polynomial trends with order 1−6. The solid blue curves represent the fitted oscillation with two spectral components, described below. The middle panels show the periodogram analysis of the detrended signals. The peaks at these fitted frequencies have a finite width, as expected for time series which only contain a few cycles of oscillation. The vertical dashed and dotted lines correspond to the frequencies of the two components averaged over all 15 slits we analysed. These frequencies are consistent with those determined by the periodogram analysis; in most cases they align with the peak in spectral amplitude, or near to it in cases where the peak is broad.
The damping time of kink oscillations is observed to scale linearly with the oscillation period (e.g. Ofman & Aschwanden 2002; Goddard et al. 2016). For damping of kink oscillations by mode coupling, the damping time τ is proportional to the period of oscillation P (in both the Gaussian and exponential damping regimes). We can therefore consider the signal quality τ/P to be determined by loop properties, specifically the transverse density profile. Since we are considering the case of two longitudinal harmonics of the same coronal loop, the two harmonics are expected to have the same signal quality, i.e. 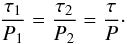 (1)This condition is used to constrain our two-component sinusoidal fits to the data, which have the form
(1)This condition is used to constrain our two-component sinusoidal fits to the data, which have the form 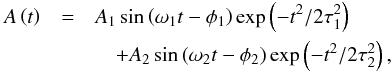 (2)where A1, A2, ω1 = 2π/P1, ω2 = 2π/P2, φ1, φ2, and τ1 are determined by a Levenberg-Marquardt least-squares fit with data points weighted according to their errors. Equation (1) defines τ2 so this is not fitted separately. The right panels of Fig. 3 show the detrended oscillations with the two fitted harmonics plotted individually; the red and green lines correspond to the components with period P1 and P2, respectively. In Eq. (2) we use a Gaussian damping profile as we found this gives better quality fits than an exponential damping profile for this event (see also Pascoe et al. 2016b,a).
(2)where A1, A2, ω1 = 2π/P1, ω2 = 2π/P2, φ1, φ2, and τ1 are determined by a Levenberg-Marquardt least-squares fit with data points weighted according to their errors. Equation (1) defines τ2 so this is not fitted separately. The right panels of Fig. 3 show the detrended oscillations with the two fitted harmonics plotted individually; the red and green lines correspond to the components with period P1 and P2, respectively. In Eq. (2) we use a Gaussian damping profile as we found this gives better quality fits than an exponential damping profile for this event (see also Pascoe et al. 2016b,a).
 |
Fig. 4 Dependence of the amplitudes of the two fitted components on loop position. The dashed lines show the dependence expected for fundamental (top) and second harmonic (bottom) standing modes. |
 |
Fig. 5 Demonstration of the anti-phase motion of the loop legs due to the second harmonic standing kink mode. The top panel shows the slit (solid blue line) used to create the TD map shown in the bottom panel. The slit is taken near the location of the anti-nodes of the second harmonic. The vertical dashed lines denote the times of the extrema in the TD map. See also the associated movie. |
 |
Fig. 6 Dependence of the periods (top) of the two fitted components and their ratio (middle) on loop position. The bottom panel shows the signal quality. Horizontal lines denote mean values. |
Figure 4 shows the spatial dependence of A1 (top panel) and A2 (bottom panel) determined by fitting the oscillations for each slit with Eq. (2). The amplitudes are plotted as a function of the position s along the loop, normalised to the loop length L. The corresponding slit numbers are indicated by the upper axis. As discussed in Sect. 2, the slits do not cover the entire loop because part of the lower leg is obscured. For the purpose of this mapping from slit number to loop position, slit 100 is taken to be at s = L and slit 37 to be at s = L/ 2. Determining the position of the loop apex more accurately was not possible as the footpoints and apex could not be reliably identified in the available STEREO data. The dashed lines indicate the expected dependence for the fundamental and second harmonic standing modes (ignoring possible distortions or shifts caused by longitudinal structuring or line-of-sight effects). There is significant scatter in the data points, shown by the shaded regions, which is indicative of the variable quality of the fitting for different slits. Nonetheless, the expected spatial dependence is evident in the two plots in terms of the number of nodes and anti-nodes and their positions.
Figure 5 demonstrates the anti-phase motion of the loop legs due to the second harmonic standing kink mode. The top panel shows the slit (solid blue line) used to create the TD map shown in the bottom panel. The slit is taken near the location of the anti-nodes of the second harmonic, but again constrained by the presence of flows obscuring part of the lower leg (see Fig. 1). The vertical dashed lines denote the times of the extrema in the TD map. It can be seen that the lower leg which is perturbed by the CME begins oscillating slightly earlier than the upper leg. However, the subsequent extrema occur at the same time and are in anti-phase, indicating that a second longitudinal harmonic standing mode has been established.
The top panel of Fig. 6 shows the variation of the periods P1 (triangles) and P2 (squares) with slit position. The dashed and dotted horizontal lines denote the mean values for each period (and correspond to the same lines in the middle panels of Fig. 3). For our interpretation in terms of harmonic (kink) modes, we expect the periods to be constant, i.e. independent of position. The variations in periods therefore reflect the errors in observational data and fitting procedures. The variations in P1 are greater than for P2 since fewer cycles are observed in a fixed interval, and possibly also because the longer period component is more sensitive to the trend describing the evolution of the loop. Similarly, the dependence of the period ratio P1/ 2P2 and signal quality τ/P are shown in the middle and bottom panels, respectively. The average values for these parameters are P1 = 5.00±0.62 min, P2 = 2.20 ± 0.23 min, P1/ 2P2 = 1.15 ± 0.22, and τ/P = 3.35 ± 1.45.
Using slits perpendicular to the loop axis (see Fig. 1) is a common method used to detect loop displacements. However, when used across the entire loop or a large segment this method has the effect that mode polarisation is not accurately accounted for when the motions are not aligned with the direction of the slits. Consequently, we did not obtain consistent phase values for the information from our fitting of the two components using Eq. (2), although the anti-phase motion of loop legs due to the second harmonic is evident in the movie (available online) and also shown in Fig. 5. In addition, the motion may be further complicated by the presence of multiple polarisations of the same mode. For example, if the CME generates a horizontally polarised (parallel to the solar surface) second harmonic standing mode by strongly displacing one loop leg, then we would also expect a fundamental standing mode with the same polarisation. There might simultaneously be a vertically polarised fundamental standing mode generated associated with large-scale changes to the environment after the eruption. The combination of these line-of-sight and polarisation effects likely contributes to the spread in amplitudes provided by our fitting (Fig. 4), and to the shape departing from a sinusoid, e.g. the larger amplitude near the apex for the fundamental standing mode. On the other hand, the method appears sufficiently robust to provide spatial information in terms of the number and locations of nodes and anti-nodes. Wang et al. (2008) discuss the issue of mode identification for a single harmonic with the possible presence of both horizontal and vertical polarisations. For the observation we report, the identification is simplified in that we have two strong periods of oscillation present and so can interpret the fundamental and second harmonic components using their relative periods of oscillation in addition to the spatial information.
 |
Fig. 7 Analysis of kink oscillation signal for slit 70 as in Fig. 3 but without the assumption of Eq. (1), i.e. the damping times τ1 and τ2 are fitted independently. The signal qualities of the two components τ1/P1 ≃ τ2/P2 are consistent with damping due to mode coupling. |
4. Discussion and conclusions
In this paper we have examined the case of a coronal loop oscillation containing different periods of oscillation. The interpretation in terms of the first and second harmonic is based on the ratio of the periods of oscillation, the spatial dependence of the amplitudes for each mode, and the anti-phase oscillation of the loop legs in the case of the second harmonic.
The method of directly fitting the signal with Eq. (2) uses the physical interpretation to more accurately constrain the oscillation parameters, namely that we have two harmonics, and that we expect the two components to have the same signal quality when damped by mode coupling. This assumption of mode coupling being the damping mechanism is considered further in Fig. 7 which performs a two component fit as in Fig. 3 but without the assumption of Eq. (1), i.e. τ1 and τ2 are fitted independently. This particular slit is chosen as being located near the anti-node for the second harmonic, and so with a large amplitude of both harmonics for accurate fitting. The signal qualities are consistent with our interpretation of the damping mechanism being mode coupling, i.e. τ1/P1 ≃ τ2/P2.
The observations of the fundamental and second harmonic kink mode by Van Doorsselaere et al. (2007) gave a period ratio of P1/ 2P2 ≈ 0.9, which was used to estimate a density scale height of 109 Mm (compared with the estimated hydrostatical value of 50 Mm). In Fig. 6, this value is within the range of our measured values, but our average over all positions is close to or slightly greater than unity.
The departure of the period ratio P1/ 2P2 from unity may be indicative of dispersion. The kink mode is typically weakly dispersive in the long wavelength limit; however, additional effects such as longitudinal structuring of the density or magnetic field can also produce a departure. Our mean value of 1.15 ± 0.22 is consistent with weak dispersion, but is not sufficiently accurate to support or exclude additional effects. Being greater than unity implies a negative scale height as also considered by Andries et al. (2005) for the coronal loop arcade observed by Verwichte et al. (2004). A negative scale height may arise from inhomogeneous heating. Increases in plasma density at the loop apex can also arise from the ponderomotive force (e.g. Terradas & Ofman 2004b), although this effect is suppressed by finite values of plasma β (e.g. Pascoe et al. 2009a). Lomineishvili et al. (2014) also discuss a kink mode period ratio greater than unity for prominence threads, which are denser at the apex than the footpoints.
Transverse velocity perturbations discovered to be ubiquitous in the corona (Tomczyk et al. 2007) have been interpreted as propagating kink waves (e.g. van Doorsselaere et al. 2008). They are strongly damped in loop structures (Tomczyk & McIntosh 2009) which is also accounted for by mode coupling (e.g. Pascoe et al. 2010; Terradas et al. 2010). The propagating kink waves are observed to have a broadband power spectrum. When damped by mode coupling, each spectral component has the same signal quality τ/P (or, equivalently, the ratio of damping length to wavelength Ld/λ) and so components with larger periods propagate further along waveguides. This frequency filtering effect was considered by Verth et al. (2010b) for the exponential damping regime and (Pascoe et al. 2015) for the Gaussian and/or exponential damping regimes. In the case of standing modes, the possible frequencies are quantised but the switch between Gaussian and exponential damping regimes is proportional to the period. Extension of the seismology using the general damping profile performed by Pascoe et al. (2016a) to multiple longitudinal harmonics would require this effect to be taken into account.
More accurate spatial resolution of harmonics would also allow further information about structuring to be determined. Spatial seismology connects the shifts in the positions of kink mode nodes and anti-nodes (in comparison to sinusoidal profiles) to effects such as stratification (Erdélyi & Verth 2007; Verth et al. 2007) or longitudinal inhomogeneities (Verth & Erdélyi 2008). These shifts have also been investigated for sausage modes in expanding loops (Pascoe et al. 2009b) and torsional Alfvén waves in stratified waveguides (Verth et al. 2010a).
Online material
Movie of Fig. 5 Access here
Acknowledgments
This work is supported by the Marie Curie PIRSES-GA-2011-295272 RadioSun project, the European Research Council under the SeismoSun Research Project No. 321141 (DJP, CRG, VMN) and the STFC consolidated grant ST/L000733/1 (VMN). The data is used courtesy of the SDO/AIA team.
References
- Andries, J., Arregui, I., & Goossens, M. 2005, ApJ, 624, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Anfinogentov, S., Nisticò, G., & Nakariakov, V. M. 2013, A&A, 560, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anfinogentov, S. A., Nakariakov, V. M., & Nisticò, G. 2015, A&A, 583, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aschwanden, M. J., & Schrijver, C. J. 2011, ApJ, 736, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J., Fletcher, L., Schrijver, C. J., & Alexander, D. 1999, ApJ, 520, 880 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J., de Pontieu, B., Schrijver, C. J., & Title, A. M. 2002, Sol. Phys., 206, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Brady, C. S., Verwichte, E., & Arber, T. D. 2006, A&A, 449, 389 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, S.-X., Li, B., Xia, L.-D., Chen, Y.-J., & Yu, H. 2014, Sol. Phys., 289, 1663 [NASA ADS] [CrossRef] [Google Scholar]
- De Moortel, I., & Brady, C. S. 2007, ApJ, 664, 1210 [NASA ADS] [CrossRef] [Google Scholar]
- De Moortel, I., & Pascoe, D. J. 2009, ApJ, 699, L72 [NASA ADS] [CrossRef] [Google Scholar]
- De Moortel, I., Pascoe, D. J., Wright, A. N., & Hood, A. W. 2016, Plasma Physics and Controlled Fusion, 58, 014001 [Google Scholar]
- Díaz, A. J., Zaqarashvili, T., & Roberts, B. 2006, A&A, 455, 709 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Erdélyi, R., & Verth, G. 2007, A&A, 462, 743 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goddard, C. R., Nisticò, G., Nakariakov, V. M., & Zimovets, I. V. 2016, A&A, 585, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guo, Y., Erdélyi, R., Srivastava, A. K., et al. 2015, ApJ, 799, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Handy, B. N., Acton, L. W., Kankelborg, C. C., et al. 1999, Sol. Phys., 187, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Hood, A. W., Ruderman, M., Pascoe, D. J., et al. 2013, A&A, 551, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kolotkov, D. Y., Nakariakov, V. M., Kupriyanova, E. G., Ratcliffe, H., & Shibasaki, K. 2015, A&A, 574, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kupriyanova, E. G., Melnikov, V. F., & Shibasaki, K. 2013, Sol. Phys., 284, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Lemen, J. R., Title, A. M., Akin, D. J., et al. 2012, Sol. Phys., 275, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, W., & Ofman, L. 2014, Sol. Phys., 289, 3233 [NASA ADS] [CrossRef] [Google Scholar]
- Lomineishvili, S. N., Zaqarashvili, T. V., Zhelyazkov, I., & Tevzadze, A. G. 2014, A&A, 565, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Macnamara, C. K., & Roberts, B. 2011, A&A, 526, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McEwan, M. P., Díaz, A. J., & Roberts, B. 2008, A&A, 481, 819 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McEwan, M. P., Donnelly, G. R., Díaz, A. J., & Roberts, B. 2006, A&A, 460, 893 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McLaughlin, J. A., & Ofman, L. 2008, ApJ, 682, 1338 [NASA ADS] [CrossRef] [Google Scholar]
- Morton, R. J., & Erdélyi, R. 2009, A&A, 502, 315 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nakariakov, V. M., Ofman, L., Deluca, E. E., Roberts, B., & Davila, J. M. 1999, Science, 285, 862 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Nisticò, G., Nakariakov, V. M., & Verwichte, E. 2013, A&A, 552, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nisticò, G., Pascoe, D. J., & Nakariakov, V. M. 2014, A&A, 569, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ofman, L., & Aschwanden, M. J. 2002, ApJ, 576, L153 [NASA ADS] [CrossRef] [Google Scholar]
- Orza, B., & Ballai, I. 2013, Astron. Nachr., 334, 948 [NASA ADS] [CrossRef] [Google Scholar]
- Pascoe, D. J. 2014, Res. Astron. Astrophys., 14, 805 [NASA ADS] [CrossRef] [Google Scholar]
- Pascoe, D. J., & De Moortel, I. 2014, ApJ, 784, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Pascoe, D. J., de Moortel, I., & McLaughlin, J. A. 2009a, A&A, 505, 319 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pascoe, D. J., Nakariakov, V. M., Arber, T. D., & Murawski, K. 2009b, A&A, 494, 1119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pascoe, D. J., Wright, A. N., & De Moortel, I. 2010, ApJ, 711, 990 [NASA ADS] [CrossRef] [Google Scholar]
- Pascoe, D. J., Hood, A. W., de Moortel, I., & Wright, A. N. 2012, A&A, 539, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pascoe, D. J., Hood, A. W., De Moortel, I., & Wright, A. N. 2013a, A&A, 551, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pascoe, D. J., Nakariakov, V. M., & Kupriyanova, E. G. 2013b, A&A, 560, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pascoe, D. J., Nakariakov, V. M., & Kupriyanova, E. G. 2014, A&A, 568, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pascoe, D. J., Wright, A. N., De Moortel, I., & Hood, A. W. 2015, A&A, 578, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pascoe, D. J., Goddard, C. R., Nisticò, G., Anfinogentov, S., & Nakariakov, V. M. 2016a, A&A, 589, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pascoe, D. J., Goddard, C. R., Nisticò, G., Anfinogentov, S., & Nakariakov, V. M. 2016b, A&A, 585, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ruderman, M. S. 2003, A&A, 409, 287 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smith, J. M., Roberts, B., & Oliver, R. 1997, A&A, 317, 752 [NASA ADS] [Google Scholar]
- Srivastava, A. K., Dwivedi, B. N., & Kumar, M. 2013, Ap&SS, 345, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Stepanov, A. V., Zaitsev, V. V., & Nakariakov, V. M. 2012, Stellar Coronal Seismology as a Diagnostic Tool for Flare Plasma (Wiley-VCH Verlag GmbH & Co) [Google Scholar]
- Terradas, J., & Ofman, L. 2004a, in SOHO 13 Waves, Oscillations and Small-Scale Transients Events in the Solar Atmosphere: Joint View from SOHO and TRACE, ed. H. Lacoste, ESA SP, 547, 469 [Google Scholar]
- Terradas, J., & Ofman, L. 2004b, ApJ, 610, 523 [NASA ADS] [CrossRef] [Google Scholar]
- Terradas, J., Oliver, R., & Ballester, J. L. 2006, ApJ, 650, L91 [NASA ADS] [CrossRef] [Google Scholar]
- Terradas, J., Arregui, I., Oliver, R., et al. 2008, ApJ, 679, 1611 [NASA ADS] [CrossRef] [Google Scholar]
- Terradas, J., Goossens, M., & Verth, G. 2010, A&A, 524, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tomczyk, S., & McIntosh, S. W. 2009, ApJ, 697, 1384 [NASA ADS] [CrossRef] [Google Scholar]
- Tomczyk, S., McIntosh, S. W., Keil, S. L., et al. 2007, Science, 317, 1192 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Van Doorsselaere, T., Nakariakov, V. M., & Verwichte, E. 2007, A&A, 473, 959 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Doorsselaere, T., Nakariakov, V. M., Verwichte, E., & Young, P. R. 2008, in Eur. Sol. Phys. Meet. 12, ed. H. Peter, 2.81 [Google Scholar]
- van Doorsselaere, T., Verwichte, E., & Terradas, J. 2009, Space Sci. Rev., 149, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Verth, G., & Erdélyi, R. 2008, A&A, 486, 1015 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verth, G., Van Doorsselaere, T., Erdélyi, R., & Goossens, M. 2007, A&A, 475, 341 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verth, G., Erdélyi, R., & Goossens, M. 2010a, ApJ, 714, 1637 [NASA ADS] [CrossRef] [Google Scholar]
- Verth, G., Terradas, J., & Goossens, M. 2010b, ApJ, 718, L102 [NASA ADS] [CrossRef] [Google Scholar]
- Verwichte, E., Nakariakov, V. M., Ofman, L., & Deluca, E. E. 2004, Sol. Phys., 223, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Verwichte, E., Foullon, C., & Nakariakov, V. M. 2006, A&A, 449, 769 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, T. J., Solanki, S. K., & Selwa, M. 2008, A&A, 489, 1307 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- White, R. S., & Verwichte, E. 2012, A&A, 537, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zaqarashvili, T. V., Melnik, V. N., Brazhenko, A. I., et al. 2013, A&A, 555, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, Y., Zhang, J., Wang, J., & Nakariakov, V. M. 2015, A&A, 581, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zimovets, I. V., & Nakariakov, V. M. 2015, A&A, 577, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Oscillation fitting for all slits used
In Figs A.1–A.3 we present the analysis of the kink oscillations for the 15 slits used in this paper.
All Figures
 |
Fig. 1 SDO/AIA 171 Å images of the loop before and during the oscillation. The dashed red line (left panel) shows the elliptical fit to the loop axis. Slits (solid blue lines) are taken perpendicular to this axis. The middle panel shows the loop after the lower leg (red arrow) has been displaced by the CME. The right panel shows the apparent plasma outflow (purple arrow) associated with the CME which obscures the view of the lower leg for most of the oscillation. |
| In the text | |
 |
Fig. 2 Time-distance map for slit 70. The symbols (with error bars) represent the fitted locations of the loop axis. The vertical dotted lines denote the interval used for fitting in Fig. 3. |
| In the text | |
 |
Fig. 3 Analysis of kink oscillation signals for slits 17 (top), 37 (middle), and 70 (bottom). The left panels show the position of the loop axis varying in time. The blue curves correspond to the two-component fits given by Eq. (2). The dashed lines show the polynomial background trends and the vertical dotted lines denote the time interval over which the oscillation is analysed. The middle panels show the periodogram analysis of the detrended signals. The symbols correspond to the observational data and the blue curve to the two-component fit. The red and green curves give the spectral profile of the two components separately; the fitted frequencies are indicated by the vertical lines of the same colour. The vertical dashed and dotted lines show the frequencies of the two components averaged over 15 analysed slits. The right panels show the detrended signals with the fitted oscillation (blue curves) and the two individual comopnents (red and green curves). |
| In the text | |
 |
Fig. 4 Dependence of the amplitudes of the two fitted components on loop position. The dashed lines show the dependence expected for fundamental (top) and second harmonic (bottom) standing modes. |
| In the text | |
 |
Fig. 5 Demonstration of the anti-phase motion of the loop legs due to the second harmonic standing kink mode. The top panel shows the slit (solid blue line) used to create the TD map shown in the bottom panel. The slit is taken near the location of the anti-nodes of the second harmonic. The vertical dashed lines denote the times of the extrema in the TD map. See also the associated movie. |
| In the text | |
 |
Fig. 6 Dependence of the periods (top) of the two fitted components and their ratio (middle) on loop position. The bottom panel shows the signal quality. Horizontal lines denote mean values. |
| In the text | |
 |
Fig. 7 Analysis of kink oscillation signal for slit 70 as in Fig. 3 but without the assumption of Eq. (1), i.e. the damping times τ1 and τ2 are fitted independently. The signal qualities of the two components τ1/P1 ≃ τ2/P2 are consistent with damping due to mode coupling. |
| In the text | |
 |
Fig. A.1 Same as Fig. 3, but for slits 17, 25, 30, 33, and 37. |
| In the text | |
 |
Fig. A.2 Same as Fig. 3, but for slits 41, 55, 60, 65, and 70. |
| In the text | |
 |
Fig. A.3 Same as Fig. 3, but for slits 75, 80, 85, 95, and 98. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


