| Issue |
A&A
Volume 593, September 2016
|
|
|---|---|---|
| Article Number | A102 | |
| Number of page(s) | 8 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201628591 | |
| Published online | 30 September 2016 | |
Microwave observations of a large-scale coronal wave with the Nobeyama radioheliograph
1 Leibniz-Institut für Astrophysik Potsdam (AIP), An der Sternwarte 16, 14482 Potsdam, Germany
e-mail: awarmuth@aip.de
2 Solar Physics Research Inc., Matsushin 2–24, Kasugai, 486-0931 Aichi, Japan
3 National Institute of Information and Communications Technology, 4-2-1 Nukui-kita, Koganei, 184-8795 Tokyo, Japan
Received: 24 March 2016
Accepted: 2 August 2016
Context. Large-scale globally propagating waves in the solar corona have been studied extensively, mainly using extreme ultraviolet (EUV) observations. In a few events, corresponding wave signatures have been detected in microwave radioheliograms provided by the Nobeyama radioheliograph (NoRH). Several aspects of these observations seem to contradict the conclusions drawn from EUV observations.
Aims. We investigate whether the microwave observations of global waves are consistent with previous findings.
Methods. We revisited the wave of 1997 Sep. 24, which is still the best-defined event in microwaves. We obtained radioheliograms at 17 and 34 GHz from NoRH and studied the morphology, kinematics, perturbation profile evolution, and emission mechanism of the propagating microwave signatures.
Results. We find that the NoRH wave signatures are morphologically consistent with both the associated coronal wave as observed by SOHO/EIT and the Moreton wave seen in Hα. The NoRH wave is clearly decelerating, which is typically found for large-amplitude coronal waves associated with Moreton waves, and its kinematical curve is consistent with the EIT wavefronts. The perturbation profile shows a pronounced decrease in amplitude. Based on the derivation of the spectral index of the excess microwave emission, we conclude that the NoRH wave is due to optically thick free-free bremsstrahlung from the chromosphere.
Conclusions. The wavefronts seen in microwave radioheliograms are chromospheric signatures of coronal waves, and their characteristics support the interpretation of coronal waves as large-amplitude fast-mode MHD waves or shocks.
Key words: Sun: corona / Sun: chromosphere / Sun: flares / Sun: coronal mass ejections (CMEs) / waves / shock waves
© ESO, 2016
1. Introduction
Signatures of large-scale, globally propagating wavelike disturbances in the solar atmosphere (for a recent review, see Warmuth 2015) were first observed in Hα filtergrams in the 1960s. Known as Moreton waves, these phenomena are observed as arc-shaped fronts in the chromosphere that propagate with typical speeds of 1000 km s-1. They are bright in the Hα line center and in the blue wing, while they appear dark in the red wing. This indicates that the Morton wave signatures are generated by a Doppler shift of the chromospheric plasma that is pushed downward. Together with the high speed of Moreton waves (which would imply Mach numbers larger than 10 in the chromosphere), this strongly suggests that the Hα signatures are not due to waves that are actually propagating in the chromosphere, but are caused by a coronal influence. Uchida (1968) proposed that Moreton waves are the chromospheric reaction to a dome-shaped coronal magnetohydrodynamic (MHD) wavefront that expands through the corona and sweeps over the chromosphere (“sweeping skirt hypothesis”; see also Uchida 1970; Uchida et al. 1973; Uchida 1974).
Potential coronal counterparts of Moreton waves were finally observed in 1997 (Moses et al. 1997; Thompson et al. 1998) with the Extreme ultraviolet Imaging Telescope (EIT; Delaboudinière et al. 1995) onboard the SOHO spacecraft, and have become known as EIT waves or coronal extreme UV (EUV) waves. However, EIT waves tend to be more diffuse than Moreton waves and have typical speeds of a few 100 km s-1 (e.g., Klassen et al. 2000), whereby they seem to be significantly slower than Moreton waves. These discrepancies have called the interpretation of EIT waves as the coronal counterpart of Moreton waves into doubt and have led to scenarios where EIT waves are interpreted not as waves, but as consequences of magnetic restructuring associated with a coronal mass ejection (CME, see, e.g., Delannée & Aulanier 1999; Delannée et al. 2008; Attrill et al. 2007). Accordingly, EIT waves were interpreted as being physically distinct from Moreton waves. In hybrid scenarios obtained from numerical simulations, Moreton waves were still attributed to MHD waves or shocks, while EIT wavefronts were interpreted as signatures of the changing magnetic configuration due to the CME expansion (Chen et al. 2002, 2005; Chen 2016).
As opposed to this hybrid interpretation, the notion of a single disturbance causing both Moreton and EIT wave signatures has been strongly supported by numerous kinematical studies, which have found that both chromospheric and coronal wavefronts lie on the same kinematical curve (cf. Warmuth et al. 2001, 2004a; Narukage et al. 2008; Muhr et al. 2010; Balasubramaniam et al. 2010; Warmuth 2010). The combined kinematical curves of these Moreton-EIT wave events always show deceleration, which explains the apparent speed discrepancy between Morteon and EIT waves. EUV observations with higher cadence have confirmed that initially fast coronal waves are decelerating (Warmuth & Mann 2011; Muhr et al. 2014)1.
The notion of a single disturbance generating the different signatures is additionally supported by observations of coronal wavefronts in soft X-rays (SXR; Khan & Aurass 2002; Narukage et al. 2002, 2004; Hudson et al. 2003; Warmuth et al. 2004a, 2005; Vršnak et al. 2006; Asai et al. 2008) and of chromospheric fronts seen in the helium I line at 10 830 Å (He I; Vršnak et al. 2002; Gilbert et al. 2004), and also by high-cadence EUV observations with SDO/AIA (Asai et al. 2012; Shen & Liu 2012). In addition to deceleration, both coronal and chromospheric wave signatures show a widening of the perturbation profile and a decrease in amplitude with increasing time and distance (Warmuth et al. 2001, 2004b; Veronig et al. 2010; Long et al. 2011; Muhr et al. 2011, 2014; Kienreich et al. 2011), which is expected for a nonlinear fast-mode MHD wave or shock (e.g., Mann 1995; Warmuth et al. 2004b; Lulić et al. 2013). The presence of shocks is also shown by the high association of coronal waves with metric type II radio bursts (cf. Klassen et al. 2000; Warmuth et al. 2004b).
The scenario of a single underlying disturbance generating coronal wavefronts, chromospheric wavefronts, and type II bursts is completely consistent with Uchida’s original model. Even Uchida’s prediction of a dome-shaped coronal front has now been confirmed (see Veronig et al. 2010), as has the prediction of the wavefront becoming progressively more inclined forward with respect to the solar surface (e.g., Hudson et al. 2003). The latter effect results from an increase in Alfvén speed with height in the quiet corona (cf. Mann et al. 1999; Warmuth & Mann 2005).
This wave/shock scenario does not preclude the possibility that additional disturbances are generated by non-wave processes associated with the CME expansion, as suggested by the various pseudo-wave and hybrid models introduced above. High-cadence EUV observations have found evidence for secondary wavefronts that are trailing behind the main perturbation segment (e.g., Patsourakos & Vourlidas 2009; Kienreich et al. 2009; Liu et al. 2010; Ma et al. 2011; Chen & Wu 2011; Dai et al. 2012; Liu & Ofman 2014). This is consistent with a hybrid scenario where a CME launches a fast-mode wave or shock (leading or main perturbation) that is followed by secondary brightenings that are generated by the magnetic restructuring associated with an expanding CME (e.g., Downs et al. 2012). Moreover, pseudo-wave scenarios can account for EUV perturbations that are propagating below the coronal sound speed or show erratic kinematics (cf. the class 3 events proposed by Warmuth & Mann 2011).
While coronal EUV and SXR emission as well as chromosopheric absorption lines have provided the bulk of observational data on large-scale coronal waves, a few events have been observed in radioheliograms. In addition to metric observations of a single event with the Nançay radioheliograph (Vršnak et al. 2005, 2006), several wave events have been recorded in microwaves by the Nobeyama radioheliograph (NoRH; Nakajima et al. 1994), which routinely provides radioheliograms at 17 and 34 GHz. Radio emission at these wavelengths arises from thermal bremsstrahlung and gyroresonance as well as nonthermal gyrosynchrotron radiation. In the quiet Sun, the main contribution is thermal bremsstrahlung from the chromosphere (with a brightness temperature of Tb ≈ 10 000 K).
The first indirect evidence for waves seen in microwave radioheliograms has been presented by Aurass et al. (2002), who observed a bright blob at 17 GHz moving with an EIT wave. In four Moreton wave events, Warmuth et al. (2004a) found corresponding NoRH waves at 17 GHz. They resembled the Moreton waves in terms of shape and angular extent, but were more diffuse. However, the NoRH waves appeared to be more diffuse, which was probably because an image synthesis algorithm was used that was optimized to deconvolve point sources such as flare emissions. The excess brightness temperatures were up to ΔTb ≈ 3500 K. In two limb events, no excess emission was observed above the limb, which would point to chromospheric optically thick bremsstrahlung as the emission mechanism.
White & Thompson (2005) have studied one of these waves (the disk event of 1997 Sep. 24) in more detail. Based on spectral characteristics (the ratio of 17 GHZ and 34 GHz wave signatures), they concluded that the emission generating the wavefronts is most likely due to coronal optically thin free-free bremsstrahlung. This interpretation creates a problem because the corresponding EIT wave emission (which is clearly due to optically thin coronal emission) could only be reproduced if the emitting plasma was not at the peak formation temperature of the Fe XII line (≈1.5 MK) or if the abundances were photospheric instead of coronal (see discussion in White & Thompson 2005). Moreover, the coronal interpretation of the microwave emission contrasts with the finding that the emission is not extended in height in limb events. In terms of kinematics, White & Thompson (2005) deduced a high constant speed that disagreed with the corresponding Moreton and EIT wavefronts, which showed clear deceleration (Warmuth et al. 2004a).
It is therefore unclear how the microwave signatures fit in the coherent picture of coronal waves that is emerging from observations in other spectral ranges and from simulations. We have therefore decided to revisit the event of 1997 Sep. 24 with the aim of better understanding and potentially resolving the discrepancies discussed above. In Sect. 2 the observations and the morphology of the wave are described, with an emphasis on microwave imaging. In Sect. 3 we discuss the kinematics and evolution of the wave and the physical nature of the microwave emission. Finally, the conclusions are given in Sect. 4.
 |
Fig. 1 Wave of 1997 Sep. 24 imaged with the Nobeyama radioheliograph at 02:49:30 UT. Shown are brightness temperature maps. The wave is seen as a bright semicircular front north of the flaring AR. Top left: 17 GHz radioheliogram synthesized with the Koshix algorithm. The sector over which the intensity profiles were measured is outlined in white. Top right: 17 GHz radioheliogram synthesized with the Hanaoka algorithm. Bottom left: 34 GHz radioheliogram (Koshix algorithm). Bottom right: 34 GHz radioheliogram (Hanaoka algorithm). |
2. Observations
The wave event of 1997 Sep. 24 originated from the active region NOAA 8088. It was associated with an M5.9 flare (IAU identification SOL1997-09-24T02:48) located at S31E19, and with a CME with an average speed of 532 km s-1 and a width of 76°. A northward-heading coronal wave was observed at 195 Å by SOHO/EIT, and a corresponding Moreton wave was recorded in three frames obtained in the red wing of Hα by an amateur astronomer (see Thompson et al. 2000). The event was also associated with a metric type II radio burst (see Warmuth et al. 2004b), which indicates the presence of a coronal shock wave.
Corresponding wave features were imaged in microwaves with the Nobeyama radioheliograph (NoRH) at 17 and 34 GHz. The full-disk radioheliograms were obtained at a cadence of 1 s. The radioheliograms were synthesized with two imaging algorithms: the Hanaoka algorithm, which is based on the standard CLEAN method, and the Koshix method (Koshiishi 2003), which uses the Steer-CLEAN algorithm (Steer et al. 1984). The Koshix algorithm has been implemented for 34 GHz data only recently (cf. Iwai et al. 2016). The brightness temperatures of the NoRH images are normalized by the quiet-Sun level, which corresponds to 10 000 K at 17 Ghz and 9000 K at 34 GHz, respectively (see, e.g., Iwai & Shibasaki 2013).
Figure 1 shows the wave at 02:49:30 UT as seen in brightness temperature maps at 17 GHz and 34 GHz. While the wave is very clearly seen in the 17 GHz Koshix image (top left panel in Fig. 1) as a bright arc-shaped front to the north of the flaring AR, it is much more diffuse in the corresponding Hanaoka image (top right). This is not surprising, since the Koshix algorithm is optimized for imaging extended sources, while the Hanaoka method is more suitable for compact sources like flares. In the two 34 GHz images the wavefront is barely perceptible as a result of the higher noise level at 34 GHz. To study the wave morphology and kinematics, we consequently focus on the 17 GHz Koshix radioheliograms.
The propagation and evolution of the NoRH wave is illustrated in Fig. 2 by a series of six 17 GHz radioheliograms obtained with the Koshix algorithm. Shown are difference images at a cadence of 1 min from which a pre-event frame (taken at 02:46 UT) has been subtracted. The wave first becomes visible around 02:48 UT as a rather irregular front of brightenings to the north of the flaring AR. It quickly develops into a well-defined semi-circular front (see, e.g., 02:50 UT). During its propagation to the north, the wavefront increases in thickness and decreases in brightness (i.e., it becomes more diffuse). Around 02:53:30 UT, the wave has become too diffuse to be identified visually.
Overall, the morphology of the NoRH wave and its evolution are very similar to what is typically found for Moreton waves. In Fig. 3 we now compare the NoRH wave (bottom panels) with the corresponding Hα (top left and right panels) and EIT fronts (top, middle panel). The Hα images were obtained on film in the red wing of the Hα line (see Thompson et al. 2000), hence they show a dark leading front that is followed by a brightening. This corresponds to the downward-upward motion of the chromosphere that reacts to coronal wave that sweeps over it. The shape of the Hα wavefront, a semicircular arc propagating northward, is very similar to what is seen at 17 GHz. However, a closer comparison of the Hα frames with co-temporal radioheliograms shows significant discrepancies. While the Hα wave is well developed at 02:47 UT, the NoRH wave has not yet appeared. At 02:50 UT, the Hα front (while being morphological similar) appears to lead the corresponding NoRH front significantly. A caveat here is that the times of the Hα images are only approximate (cf. Thompson et al. 2000), so that a timing error could explain the apparent discrepancies.
 |
Fig. 2 Temporal evolution of the wave as seen in a series of 17 GHz radioheliograms obtained with the Koshix algorithm. Shown are difference images from which a pre-event image (taken at 02:46 UT) has been subtracted. Note the propagation of the wavefront, the increase in width, and the decrease of amplitude. |
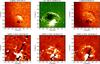 |
Fig. 3 Top row: Hα (left, right) and EIT (middle) images showing the wave event of 1997 Sep. 24. Shown are difference images from which a pre-event frame has been subtracted. The Hα frames were obtained in the red line wing, and the EIT image at 195 Å. The times of the Hα images are only approximate. Bottom row: 17 GHz difference images corresponding in time to the images in the top row. |
As shown in Fig. 3 (top middle), the EIT wave in this event was very sharp. Such waves are referred to as S-waves and are comparatively rare (cf. Biesecker & Thompson 2000). While the leading edge of the EIT wave corresponds rather well to the co-temporal NoRH wavefront, it seems to lead it by a few tens of Mm. In Sect. 3.2 we discuss the association of the NoRH wave features with the corresponding Hα and EUV signatures in more detail.
 |
Fig. 4 Space-time plots obtained from the sector shown in Fig. 2 using 17 GHz (top) and 34 GHz (bottom) NoRH difference images computed with the Koshix algorithm. The bright feature moving from small to large distances is a clear signature of the wave. |
 |
Fig. 5 Evolution of the NoRH wave derived from the 17 GHz stack plots shown in Fig. 4 (Koshix algorithm). Top: kinematics of the leading edge and the wave peak. Also shown are second-degree polynomial (red lines) and power-law fits (blue lines), and the corresponding mean acceleration a and the power-law index δ is indicated. For comparison, the leading edges of the Hα (red triangles) and EIT wavefronts (green diamond) are shown as well. Middle: evolution of the wavefront width (FWHM). Bottom: evolution of the perturbation amplitude, ΔTb. |
3. Discussion
3.1. Wave kinematics
To study the kinematics and evolution of the NoRH wave, we have derived intensity profiles along great circles on the solar surface that were then averaged over an angular sector that covers the area that the wave is expanding into and which emanates from the extrapolated radiant point of the wave (cf. Warmuth et al. 2001). The sector is shown in the first panel of Fig. 2. We used 17 GHz and 34 GHz NoRH difference images synthesized with the Koshix algorithm. We averaged over five images to increase the signal-to-noise ratio (cf. Iwai & Shibasaki 2013; Iwai et al. 2014), which results in a cadence of 5 s.
In Fig. 4 the resulting profiles are shown as a function of time in the form of space-time plots for 17 GHz and 34 GHz (upper and lower panel, respectively). The bright diagonal feature moving from small to large distances corresponds to the NoRH wavefront. While the wave is much better defined at 17 GHz, it can still be clearly identified in the 34 GHz profiles. In contrast, the wave is barely perceptible in the 34 GHz radioheliograms (see Fig. 1), which clearly demonstrates that the method of using averaged intensity profiles is ideally suited for studying the wave propagation and evolution. The RMS noise level is much lower at 17 GHz (≈40 K as compared to ≈150 K at 34 GHz), therefore we used the 17 GHz profiles to determine the wave kinematics and evolution. The wave signature was fit with a Gaussian in each profile, yielding (as a function of time) the distance dpeak of the wave peak from the radiant point, the FWHM width w of the wave, and its perturbation amplitude ΔTb (which is the maximum brightness temperature increase).
We first focus on the kinematics of the NoRH wave. The top panel of Fig. 5 show the distance of the wave peak dpeak (dots) from the radiant point as a function of time. We note that most studies of coronal waves consider the propagation of the leading edge instead. We therefore include in the plot a proxy for the leading edge, which we define as the location of the peak amplitude plus half the full width at half maximum (FHWM) width, that is, dlead = dpeak + 0.5w. We fit the wavefront distances with a second-degree polynomial and with a power-law of the form d = c(t−t0)δ, where d is the distance, c is a constant, t−t0 is the time relative to the initiation time of the wave, and δ is the power-law index (cf. Warmuth et al. 2004a).
We see already by eye that the NoRH wave does not propagate at a constant speed, but decelerates. The mean deceleration given by the polynomial fits is alead = −1388 m s-2 and apeak = −1121 m s-2 for the leading edge and the wave peak, respectively. The corresponding power-law indices are δlead = 0.57 and δpeak = 0.66. These values are typical for Moreton waves (cf. Warmuth et al. 2004a; Warmuth 2010; Zhang et al. 2011). While both functions provide a good fit of the distances, the power law gives a slightly better fit. This is consistent with previous kinematical studies of fast coronal waves (cf. Warmuth et al. 2004a; Warmuth & Mann 2011; Grechnev et al. 2011), and power laws are indeed predicted for the distance-time curves of freely propagating shock waves (Grechnev et al. 2008). The initial speed of the wave as given by the different fits is in the range of 900 km s-1, while the speed at the end of the traceable propagation is around 400 km s-1. For comparison, linear fits of the distances yield mean speeds of ≈600 km s-1.
We therefore conclude that the NoRH wave behaves in accordance with what is typically seen in Moreton waves in terms of kinematics, which contrasts with the constant speed of 835 km s-1 obtained by White & Thompson (2005). The reason might be that White & Thompson (2005) only considered the time interval 02:49–02:53:20 UT, while our selection of imaging algorithm, averaging, and analysis technique allowed us to track the wave over the significantly longer time range of 02:48–02:54:50 UT, which makes it much easier to clearly detect deceleration.
 |
Fig. 6 NoRH wave kinematics as compared to EIT wave. Top: power-law fit of the distances of the leading edge of the NoRH wavefront (blue line) and distances of the three EIT wavefronts (green diamonds). Bottom: corresponding NoRH and EIT wave speeds. |
3.2. Relationship with Moreton and EIT wave signatures
We can now check how the observed Hα and EIT wavefronts compare with the kinematical curve derived from the NoRH observations. In the top panel of Fig. 5 we have included the distances of the visually determined leading edges of the three detected Hα fronts (red triangles) and the single sharp EIT front (green diamond; note that this was followed by two diffuse EIT fronts later in the event). The Hα wavefronts seem to lie significantly (on the order of 100 Mm) ahead of the NoRH wave, and indeed the Moreton wave appears to be present well before the appearance of the NoRH signatures. This is an extremely improbable scenario. We conclude that the most likely explanation for the apparent discrepancy is a considerable error in Hα timing, which is quite likely considering that the Hα timing was reported as being only approximate. A systematic shift to later times is required to bring the Hα fronts in agreement with the NoRH wave, and the red arrows in Fig. 5 illustrate such a shift of 1 min. While this would bring the third Hα front right on the kinematical track of the NoRH wave, larger shifts of 90 s and 2 min would be required for the second and first Hα front, respectively.
Moving to coronal observations, no significant timing errors are expected for the EIT observations, and indeed the sharp EIT front agrees much more closely with the NoRH wave. Still, the EIT front leads the NoRH wave by some 20 Mm. This scenario is typically observed in Moreton waves, which often lag behind the associated coronal wavefront by up to 25 Mm (Warmuth 2010). This is attributed to the increase in propagation speed with height (Mann et al. 1999; Warmuth & Mann 2005), which causes coronal wavefronts to become inclined forward with respect to the solar surface (see, e.g., Hudson et al. 2003). Seen from the top, the observed wavefront is thus observed ahead of its actual position at the coronal base, where it impacts the chromosphere and generates the Moreton wave signatures. Thus, the EIT wave slightly leading the NoRH wave supports the scenario of a chromospheric origin of the enhanced microwave emission.
When the kinematical curve of the NoRH wave’s leading edge is extrapolated to later times using the power-law fit, it intersects the location of the second and third EIT wavefronts at 03:03 UT and 03:23 UT. This is shown in the top of Fig. 6. This strongly supports the notion that a single physical disturbance is generating the microwave and EUV wave signatures, in the same manner as has been conclusively shown for Moreton waves. The bottom panel of Fig. 6 shows the corresponding NoRH wave speeds derived from the power-law fit and the measured EIT wave speeds. We note that the extrapolated NoRH wave speeds at the times of the second and third EIT wavefront are 320 km s-1 and 230 km s-1. This is higher than the coronal sound speed (185 km s-1 for a temperature of 1.5 MK) and consistent with what is expected for the fast-mode speed in the quiet corona. This has been shown explicitly for this event by Warmuth & Mann (2005). The NoRH wave kinematics therefore support the scenario of a large-amplitude nonlinear fast-mode wave (a simple wave or a shock) that over the course of its propagation drops in amplitude and evolves finally to a small-amplitude linear MHD wave propagating at the ambient fast-mode speed.
3.3. Perturbation evolution
Moving from kinematics to the evolution of the perturbation profile of the wave, the middle panel in Fig. 5 shows the evolution of the perturbation width as given by the FWHM of the fitted Gaussians. While the disturbance initially widens from 30 to 80 Mm, it subsequently appears to oscillate between 40 and 80 Mm. For comparison, a pronounced broadening is typically seen in chromospheric Hα and in coronal EUV wavefronts (e.g., Warmuth et al. 2001, 2004a; Veronig et al. 2010; Long et al. 2011).
The bottom panel of Fig. 5 shows the evolution of the perturbation amplitude as given by the peak of the Gaussians fit to the brightness temperature difference profiles (i.e., the temperature excess ΔTb). Initially, the wave amplitude quickly rises to a maximum of ΔTb ≈ 2500 K around 02:48:20 UT, which is then followed by a rather steady and gradual decline. At the end of the time interval where the wave can be identified unambiguously (02:54:50 UT), ΔTb has dropped to ≈200 K. For comparison, the RMS noise level in the profiles is on the order of 40 K.
3.4. Emission mechanism
We now address the question of which mechanism is responsible for the excess microwave emission in the observed wavefronts. The brightness temperature excess is on the order of a few 100 to a few 1000 K, it comes from the quiet Sun, and the radiation is unpolarized. This is consistent with either optically thin thermal free-free emission from the corona, or with optically thick free-free emission from the chromosphere. The spectral index α of the emission can be used to distinguish between the two possibilities. We derived α from the ratio of the microwave flux density profiles at 17 and 34 GHz. We first converted the brightness temperature maps (using the Koshix images) to flux densities and then made the beam size the same between 17 and 34 GHz by deconvolving the 17 GHz beam with the 34 GHz images, and vice versa. The latter step is important since we wish to compare the same region with the same field of view at both frequencies. We then obtained the flux density profiles in a similar manner as the brightness temperature profiles discussed in Sect. 3.1, and finally derived α from the ratio of the wave amplitude at 34 and 17 GHz.
Assuming that the wavefronts are due to enhanced optically thin emission from the corona (caused by compression by the wave/shock), we expect to see a flat spectrum (α ≈ 0) when the chromospheric background is removed. The upper panel in Fig. 7 shows the measured spectral index α derived from the 17 and 34 GHz background-subtracted profiles as a function of time. We were only able to determine α up to 02:52:20 UT, after which the wave signature at 34 GHz became too close to the noise level. While the spectral index shows considerable scatter, it is very clear that α is larger than zero, and averaged over time, we find α = 1.5 ± 0.5. We therefore conclude that optically thin coronal emission is not the dominant emission mechanism in the wavefronts. The alternative is enhanced optically thick chromospheric emission, for which a spectrum increasing with α ≈ 2 is expected. For chromospheric emission, this value has to be reproduced using the total (i.e., not background-subtracted) emission. The spectral index derived from the total fluxes is shown in the lower panel in Fig. 7. Averaged over time, it amounts to α = 1.7 ± 0.1, which means that it is generally consistent with optically thick emission.
 |
Fig. 7 Spectral index α of the wave signature as derived from 17 GHz and 34 GHz radioheliograms as a function of time, derived for the background-subtracted excess emission (top) and the total emission (bottom). |
We therefore conclude that the excess microwave emission associated with the propagating wave is primarily due to optically thick thermal emission from the chromosphere. This is consistent with earlier observations of limb events where the excess emission did not extend beyond the solar limb (Warmuth et al. 2004a), and with the fact that the coronal EUV wavefront apparently leads the NoRH wave (see discussion in Sect. 3.2). While White & Thompson (2005) have concluded that the emission is optically thin, this result has mainly rested on the lack of a significant wave signature at 34 GHz in that study. Using the averaged brightness temperature profiles has enabled us to find and characterize this signature, resulting in a much more confident identification of the emission mechanism.
Finally, we have to address the question of how the enhanced optically thick emission is generated. We note that coronal waves are compressive, which is directly shown by the coronal emission increase over a wide spectral range in the EUV and SXR regime, and also by the chromospheric response (i.e., the downward-upward swing) to the impacting coronal wavefront. The passage of a coronal wave will thus also enhance pressure and density in the chromosphere, which will cause the chromosphere to become optically thick at a larger height as compared to the unperturbed state. Since temperature is increasing with height in the upper chromosphere, a higher brightness temperature will be observed. We note that adiabatic heating due to the compression may represent an additional minor contribution to the excess emission.
The positive identification of optically thick chromospheric emission represents a new and independent line of evidence for the compressive nature of coronal waves. At the same time, it resolves the apparent discrepancy between the observed emission increase at 17 GHz and in EUV that would arise if the microwave emission were optically thin (cf. White & Thompson 2005).
4. Conclusions
Over the past years, high-quality EUV observations have been instrumental in fostering a growing consensus on the physical nature of large-scale coronal waves. While there are still some debates on the generation mechanisms of EUV disturbances, the wave events that are associated with Moreton waves and/or metric type II bursts are generally interpreted as large-amplitude fast-mode MHD waves and/or shocks. In contrast, only a few observations of similar wave signatures in microwaves have been obtained with the Nobeyama radioheliograph. Several aspects of these observations have been interpreted controversially (see Warmuth et al. 2004a; White & Thompson 2005), and some findings seemed to contradict the results obtained in other wavelength ranges.
We have therefore revisited the best-defined event, the wave of 1997 Sep. 24, to resolve the open issues. A careful selection of image synthesis algorithms and analysis techniques has allowed us to extract more information from the microwave observations at 17 and 34 GHz than in previous studies and has enabled us to resolve the apparent discrepancies. The shape of the NoRH wavefront is morphologically similar to the associated coronal wave as imaged by EIT and the chromospheric Moreton wave signatures seen in Hα. The kinematics of the NoRH wave is consistent with what is typically found for large-amplitude coronal waves (the class 1 waves in the terminology of Warmuth & Mann 2011): an initially fast wave (900 km s-1 in the present case) that shows pronounced deceleration over the course of its propagation. The kinematical curve of the NoRH wave directly overlaps the first sharp EIT wavefront, and an extrapolation using a power-law fit of the NoRH wavefront kinematics shows that it is also consistent with the two diffuse EIT fronts observed later on. The corresponding Moreton wavefronts appear to precede the other signatures significantly, but this is most probably due to timing errors of the Hα data. Therefore, all observations are consistent with a single physical disturbance generating the different wave signatures. The decrease in amplitude of the 17 GHz perturbation profile is also typical for large-amplitude coronal waves. Finally, we have shown conclusively that the NoRH wave signatures are due to optically thick thermal free-free emission from the chromosphere.
We therefore conclude that the wavefronts seen in microwave radioheliograms are chromospheric signatures of coronal waves and that their characteristics support the interpretation of class 1 coronal waves (Warmuth & Mann 2011) as large-amplitude fast-mode MHD waves or shocks. We point out that imaging observations in microwaves provide several advantages that have yet to be exploited for the study of coronal waves. In particular, NoRH can image the wave signatures at cadences of up to one second, which is about one order of magnitude better than with any other chromospheric or coronal imager. Moreover, the fact that the microwave signatures are generated in the chromosphere implies that the height of detected features is known precisely, which is not the case of coronal emission, where line-of-sight integration through emitting structures often leads to ambiguities in height and consequently in kinematics. The NoRH observations thus allow the precise characterization of the kinematics of the wave propagation at the coronal base, and we are planning to use this technique on a larger event sample.
For potential counter-examples, see Nitta et al. (2013).
Acknowledgments
The work of A. W. was supported by DLR under grant No. 50 QL 0001. A. W. expresses his gratitude to the Nobeyama Solar Radio Observatory for the travel support and to its staff for their kind hospitality. NoRH had been operated by the Nobeyama Solar Radio Observatory/NAOJ. SOHO is a project of international cooperation between ESA and NASA. We thank the anonymous referee for constructive comments.
References
- Asai, A., Hara, H., Watanabe, T., et al. 2008, ApJ, 685, 622 [NASA ADS] [CrossRef] [Google Scholar]
- Asai, A., Ishii, T. T., Isobe, H., et al. 2012, ApJ, 745, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Attrill, G. D. R., Harra, L. K., van Driel-Gesztelyi, L., & Demoulin, P. 2007, ApJ, 656, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Aurass, H., Shibasaki, K., Reiner, M., & Karlický, M. 2002, ApJ, 567, 610 [Google Scholar]
- Balasubramaniam, K. S., Cliver, E. W., Pevtsov, A., et al. 2010, ApJ, 723, 587 [NASA ADS] [CrossRef] [Google Scholar]
- Biesecker, D. A., & Thompson, B. J. 2000, J. Atmos. Sol.-Terr. Phys., 62, 1449 [Google Scholar]
- Chen, P. F. 2016, Washington DC American Geophysical Union Geophysical Monograph Series, 216, 381 [NASA ADS] [Google Scholar]
- Chen, P. F., & Wu, Y. 2011, ApJ, 732, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, P. F., Wu, S. T., Shibata, K., & Fang, C. 2002, ApJ, 572, L99 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, P. F., Ding, M. D., & Fang, C. 2005, Space Sci. Rev., 121, 201 [Google Scholar]
- Dai, Y., Ding, M. D., Chen, P. F., & Zhang, J. 2012, ApJ, 759, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Delaboudinière, J.-P., Artzner, G. E., Brunaud, J., et al. 1995, Sol. Phys., 162, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Delannée, C., & Aulanier, G. 1999, Sol. Phys., 190, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Delannée, C., Török, T., Aulanier, G., & Hochedez, J.-F. 2008, Sol. Phys., 247, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Downs, C., Roussev, I. I., van der Holst, B., Lugaz, N., & Sokolov, I. V. 2012, ApJ, 750, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Gilbert, H. R., Holzer, T. E., Thompson, B. J., & Burkepile, J. T. 2004, ApJ, 607, 540 [NASA ADS] [CrossRef] [Google Scholar]
- Grechnev, V. V., Uralov, A. M., Slemzin, V. A., et al. 2008, Sol. Phys., 253, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Grechnev, V. V., Uralov, A. M., Chertok, I. M., et al. 2011, Sol. Phys., 273, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Hudson, H. S., Khan, J. I., Lemen, J. R., Nitta, N. V., & Uchida, Y. 2003, Sol. Phys., 212, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Iwai, K., & Shibasaki, K. 2013, PASJ, 65, S14 [NASA ADS] [CrossRef] [Google Scholar]
- Iwai, K., Shibasaki, K., Nozawa, S., et al. 2014, Earth, Planets, and Space, 66, 149 [Google Scholar]
- Iwai, K., Koshiishi, H., Shibasaki, K., et al. 2016, ApJ, 816, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Khan, J. I., & Aurass, H. 2002, A&A, 383, 1018 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kienreich, I. W., Temmer, M., & Veronig, A. M. 2009, ApJ, 703, L118 [Google Scholar]
- Kienreich, I. W., Veronig, A. M., Muhr, N., et al. 2011, ApJ, 727, L43 [Google Scholar]
- Klassen, A., Aurass, H., Mann, G., & Thompson, B. J. 2000, A&AS, 141, 357 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Koshiishi, H. 2003, A&A, 412, 893 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liu, W., & Ofman, L. 2014, Sol. Phys., 289, 3233 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, W., Nitta, N. V., Schrijver, C. J., Title, A. M., & Tarbell, T. D. 2010, ApJ, 723, L53 [Google Scholar]
- Long, D. M., Gallagher, P. T., McAteer, R. T. J., & Bloomfield, D. S. 2011, A&A, 531, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lulić, S., Vršnak, B., Žic, T., et al. 2013, Sol. Phys., 286, 509 [Google Scholar]
- Ma, S., Raymond, J. C., Golub, L., et al. 2011, ApJ, 738, 160 [CrossRef] [Google Scholar]
- Mann, G. 1995, J. Plasma Phys., 53, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Mann, G., Klassen, A., Estel, C., & Thompson, B. J. 1999, in ESA SP, 8th SOHO Workshop: Plasma Dynamics and Diagnostics in the Solar Transition Region and Corona, eds. J.-C. Vial, & B. Kaldeich-Schümann, 446, 477 [Google Scholar]
- Moses, D., Clette, F., Delaboudinière, J.-P., et al. 1997, Sol. Phys., 175, 571 [NASA ADS] [CrossRef] [Google Scholar]
- Muhr, N., Vršnak, B., Temmer, M., Veronig, A. M., & Magdalenić, J. 2010, ApJ, 708, 1639 [Google Scholar]
- Muhr, N., Veronig, A. M., Kienreich, I. W., Temmer, M., & Vršnak, B. 2011, ApJ, 739, 89 [Google Scholar]
- Muhr, N., Veronig, A. M., Kienreich, I. W., et al. 2014, Sol. Phys., 289, 4563 [NASA ADS] [CrossRef] [Google Scholar]
- Nakajima, H., Nishio, M., Enome, S., et al. 1994, IEEE Proc., 82, 705 [NASA ADS] [CrossRef] [Google Scholar]
- Narukage, N., Hudson, H. S., Morimoto, T., et al. 2002, ApJ, 572, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Narukage, N., Morimoto, T., Kadota, M., et al. 2004, PASJ, 56, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Narukage, N., Ishii, T. T., Nagata, S., et al. 2008, ApJ, 684, L45 [Google Scholar]
- Nitta, N. V., Schrijver, C. J., Title, A. M., & Liu, W. 2013, ApJ, 776, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Patsourakos, S., & Vourlidas, A. 2009, ApJ, 700, L182 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, Y., & Liu, Y. 2012, ApJ, 752, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Steer, D. G., Dewdney, P. E., & Ito, M. R. 1984, A&A, 137, 159 [NASA ADS] [Google Scholar]
- Thompson, B. J., Plunkett, S. P., Gurman, J. B., et al. 1998, Geophys. Res. Lett., 25, 2465 [Google Scholar]
- Thompson, B. J., Reynolds, B., Aurass, H., et al. 2000, Sol. Phys., 193, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Uchida, Y. 1968, Sol. Phys., 4, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Uchida, Y. 1970, PASJ, 22, 341 [NASA ADS] [Google Scholar]
- Uchida, Y. 1974, Sol. Phys., 39, 431 [NASA ADS] [CrossRef] [Google Scholar]
- Uchida, Y., Altschuler, M. D., & Newkirk, Jr., G. 1973, Sol. Phys., 28, 495 [Google Scholar]
- Veronig, A. M., Muhr, N., Kienreich, I. W., Temmer, M., & Vršnak, B. 2010, ApJ, 716, L57 [Google Scholar]
- Vršnak, B., Warmuth, A., Brajša, R., & Hanslmeier, A. 2002, A&A, 394, 299 [Google Scholar]
- Vršnak, B., Magdalenić, J., Temmer, M., et al. 2005, ApJ, 625, L67 [Google Scholar]
- Vršnak, B., Warmuth, A., Temmer, M., et al. 2006, A&A, 448, 739 [Google Scholar]
- Warmuth, A. 2010, Adv. Space Res., 45, 527 [NASA ADS] [CrossRef] [Google Scholar]
- Warmuth, A. 2015, Liv. Rev. Sol. Phys., 12, 3 [Google Scholar]
- Warmuth, A., & Mann, G. 2005, A&A, 435, 1123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Warmuth, A., & Mann, G. 2011, A&A, 532, A151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Warmuth, A., Vršnak, B., Aurass, H., & Hanslmeier, A. 2001, ApJ, 560, L105 [Google Scholar]
- Warmuth, A., Vršnak, B., Magdalenić, J., Hanslmeier, A., & Otruba, W. 2004a, A&A, 418, 1101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Warmuth, A., Vršnak, B., Magdalenić, J., Hanslmeier, A., & Otruba, W. 2004b, A&A, 418, 1117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Warmuth, A., Mann, G., & Aurass, H. 2005, ApJ, 626, L121 [NASA ADS] [CrossRef] [Google Scholar]
- White, S. M., & Thompson, B. J. 2005, ApJ, 620, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Y., Kitai, R., Narukage, N., et al. 2011, PASJ, 63, 685 [Google Scholar]
All Figures
 |
Fig. 1 Wave of 1997 Sep. 24 imaged with the Nobeyama radioheliograph at 02:49:30 UT. Shown are brightness temperature maps. The wave is seen as a bright semicircular front north of the flaring AR. Top left: 17 GHz radioheliogram synthesized with the Koshix algorithm. The sector over which the intensity profiles were measured is outlined in white. Top right: 17 GHz radioheliogram synthesized with the Hanaoka algorithm. Bottom left: 34 GHz radioheliogram (Koshix algorithm). Bottom right: 34 GHz radioheliogram (Hanaoka algorithm). |
| In the text | |
 |
Fig. 2 Temporal evolution of the wave as seen in a series of 17 GHz radioheliograms obtained with the Koshix algorithm. Shown are difference images from which a pre-event image (taken at 02:46 UT) has been subtracted. Note the propagation of the wavefront, the increase in width, and the decrease of amplitude. |
| In the text | |
 |
Fig. 3 Top row: Hα (left, right) and EIT (middle) images showing the wave event of 1997 Sep. 24. Shown are difference images from which a pre-event frame has been subtracted. The Hα frames were obtained in the red line wing, and the EIT image at 195 Å. The times of the Hα images are only approximate. Bottom row: 17 GHz difference images corresponding in time to the images in the top row. |
| In the text | |
 |
Fig. 4 Space-time plots obtained from the sector shown in Fig. 2 using 17 GHz (top) and 34 GHz (bottom) NoRH difference images computed with the Koshix algorithm. The bright feature moving from small to large distances is a clear signature of the wave. |
| In the text | |
 |
Fig. 5 Evolution of the NoRH wave derived from the 17 GHz stack plots shown in Fig. 4 (Koshix algorithm). Top: kinematics of the leading edge and the wave peak. Also shown are second-degree polynomial (red lines) and power-law fits (blue lines), and the corresponding mean acceleration a and the power-law index δ is indicated. For comparison, the leading edges of the Hα (red triangles) and EIT wavefronts (green diamond) are shown as well. Middle: evolution of the wavefront width (FWHM). Bottom: evolution of the perturbation amplitude, ΔTb. |
| In the text | |
 |
Fig. 6 NoRH wave kinematics as compared to EIT wave. Top: power-law fit of the distances of the leading edge of the NoRH wavefront (blue line) and distances of the three EIT wavefronts (green diamonds). Bottom: corresponding NoRH and EIT wave speeds. |
| In the text | |
 |
Fig. 7 Spectral index α of the wave signature as derived from 17 GHz and 34 GHz radioheliograms as a function of time, derived for the background-subtracted excess emission (top) and the total emission (bottom). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


