| Issue |
A&A
Volume 593, September 2016
|
|
|---|---|---|
| Article Number | A19 | |
| Number of page(s) | 10 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201526423 | |
| Published online | 30 August 2016 | |
Near-infrared spatially resolved spectroscopy of (136108) Haumea’s multiple system⋆
1 European Southern Observatory,
Alonso de Córdova 3107,
Vitacura, Santiago,
Chile
e-mail: florian.gourgeot@gmail.com
2 Observatório Nacional,
COAA, Rua General José Cristino
77, 20921-400
Rio de Janeiro,
Brazil
3 IMCCE, Observatoire de Paris, PSL
Research University, CNRS, Sorbonne Universités, UPMC Univ Paris 06, Univ. Lille,
France
4 Laboratoire Lagrange, Université de
Nice-Sophia Antipolis, CNRS, Observatoire de la Côte d’ Azur, France
5 Observatoire de Paris-Meudon / LESIA,
Meudon,
France
6 Université Denis Diderot,
Paris VII,
France
7 Max Planck Institute for Solar System
Research, Justus-von-Liebig-Weg
3, 37077
Göttingen,
Germany
Received:
28
April
2015
Accepted:
13
March
2016
Context. The transneptunian region of the solar system is populated by a wide variety of icy bodies showing great diversity in orbital behavior, size, surface color, and composition.
Aims. The dwarf planet (136108) Haumea is among the largest transneptunian objects (TNOs) and is a very fast rotator (~3.9 h). This dwarf planet displays a highly elongated shape and hosts two small moons that are covered with crystalline water ice, similar to their central body. A particular region of interest is the Dark Red Spot (DRS) identified on the surface of Haumea from multiband light-curve analysis (Lacerda et al. 2008). Haumea is also known to be the largest member of the sole TNO family known to date, and an outcome of a catastrophic collision that is likely responsible for the unique characteristics of Haumea.
Methods. We report here on the analysis of a new set of near-infrared Laser Guide Star assisted observations of Haumea obtained with the Integral Field Unit (IFU) Spectrograph for INtegral Field Observations in the Near Infrared (SINFONI) at the European Southern Observatory (ESO) Very Large Telescope (VLT) Observatory. Combined with previous data published by Dumas et al. (2011), and using light-curve measurements in the optical and far infrared to associate each spectrum with its corresponding rotational phase, we were able to carry out a rotationally resolved spectroscopic study of the surface of Haumea.
Results. We describe the physical characteristics of the crystalline water ice present on the surface of Haumea for both regions, in and out of the DRS, and analyze the differences obtained for each individual spectrum. The presence of crystalline water ice is confirmed over more than half of the surface of Haumea. Our measurements of the average spectral slope (1.45 ± 0.82% by 100 nm) confirm the redder characteristic of the spot region. Detailed analysis of the crystalline water-ice absorption bands do not show significant differences between the DRS and the remaining part of the surface. We also present the results of applying Hapke modeling to our data set. The best spectral fit is obtained with a mixture of crystalline water ice (grain sizes smaller than 60 μm) with a few percent of amorphous carbon. Improvements to the fit are obtained by adding ~10% of amorphous water ice. Additionally, we used the IFU-reconstructed images to measure the relative astrometric position of the largest satellite Hi‘iaka and determine its orbital elements. An orbital solution was computed with our genetic-based algorithm GENOID and our results are in full agreement with recent results.
Key words: Kuiper belt objects: individual: (136108) Haumea / planets and satellites: surfaces / techniques: imaging spectroscopy / techniques: high angular resolution
© ESO, 2016
1. Introduction
The object (136108) Haumea is one of the most remarkable transneptunian objects (TNO). Its visible light curve indicates a very short (~3.91 h) rotation period and an ellipsoidal shape (1000 × 800 × 500 km; Rabinowitz et al. 2006), while its gravity is determined to be sufficient for having relaxed into hydrostatic equilibrium, making Haumea a dwarf planet. Dynamically, it is considered a classical TNO, with an orbital period of 283 years, a perihelion at 35 AU, and an orbital inclination of 28° (Rabinowitz et al. 2006). Haumea is one of the bluest TNOs (Tegler et al. 2007) known to date. Its surface is covered by almost pure water ice (Trujillo et al. 2007; Merlin et al. 2007), though its high density (~2.6−3.3 g cm-3, Rabinowitz et al. 2006; Lacerda & Jewitt 2007; Carry et al. 2012) indicates a more rocky interior. It possesses two satellites (Brown et al. 2005, 2006), the largest of the two is also coated with crystalline water ice (Barkume et al. 2006; Dumas et al. 2011). Such dynamical and physical characteristics, added to the fact that Haumea is the largest body of a population of small water-ice TNOs, all sharing the same orbital parameters (Schaller & Brown 2008), point to the idea that Haumea is the remnant body of an ancient (>1 Gyr) catastrophic collision (Ragozzine & Brown 2007; Snodgrass et al. 2010; Carry et al. 2012).
High time-resolution observations, combined with multicolor photometry, provide evidence for a localized surface feature that is redder and darker than the surrounding material (Lacerda et al. 2008; Lacerda 2009). The presence of such a feature (perhaps of collisional origin) makes Haumea the second TNO (after Pluto) displaying strong surface heterogeneities. In this study, we combine two sets of observations taken four years apart to analyze the spectral behavior of the Dark Red Spot (DRS) and its surrounding areas and the ice properties of the surface material. Finally, we measure the astrometric positions of Hi‘iaka directly from our set of hyperspectral images, and determine the Keplerian elements of its orbit using Genoid, a genetic-based algorithm (Vachier et al. 2012).
2. Observations
Haumea was observed in H and K bands on 2007 March 15 and 2011 April 09 UT, using the Laser Guide-Star Facility (LGSF) and the Spectrograph for INtegral Field Observations in the Near Infrared (SINFONI) instrument installed at the 8-m “Yepun” telescope of the European Southern Observatory (ESO) Very Large Telescope (VLT). SINFONI is an integral-field spectrometer working in the 1.0–2.5 μm range. It is equipped with an adaptive optics (AO) system offering Natural Guide Star (NGS) and Laser Guide Star (LGS) channels. The use of this instrument for observing the large TNOs Haumea, Eris, and Orcus has been described in earlier papers (Merlin et al. 2007; Barucci et al. 2008; Dumas et al. 2007, 2011; Carry et al. 2012), and more information about SINFONI can be found in Eisenhauer et al. (2003) and Bonnet et al. (2004). The observations for both epochs were carried out using the AO system and its LGS facility. The laser produces an artificial visible-light star of R mag ~ 13.4 near the line of sight of Haumea (V-mag = 17.4), thus providing a gain of four magnitudes for characterizing the high orders of the wavefront (in comparison to non-laser observations). Haumea was used as the on-axis tip-tilt reference source, thus delivering optimal correction by the AO-LGS system.
The atmospheric conditions were extremely good during the 2007 observations with a seeing varying between 0.81′′ and 1.13′′. On March 15, between 6h34 UT and 7h24 UT, six exposures of 300 s each were obtained on Haumea (total integration time of 0.5 h), interspersed with three exposures of 300 s to record the sky background. The results of these data were already published (Dumas et al. 2011), but we decided to reduce them again using the same data processing and the latest data reduction tools for both epochs. On 2011 April 09, between 3h57 UT and 5h40 UT, six exposures of 600 s each were obtained on Haumea (total integration time of 1.15 h), interspaced by sky background measurements. However, as a result of relatively poor meteorological conditions (degraded sky transparency due to clouds and wind above 15 m/s after 6h00 UT), it was not possible to obtain the full mapping of Haumea during the 2011 observations (see Fig. 1). Still, combining the 2007 (sampling almost exactly the DRS longitudinal span) and the 2011 data allowed us to obtain a substantial longitudinal coverage of Haumea and explore any variations of its surface properties. The H + K spectral grating (resolving power of ~1500), covering both H and K bands simultaneously, as well as a plate scale of 100 mas/pixel (3′′ × 3′′ field of view), were used on each observation date.
 |
Fig. 1 Positions of all observed epochs (six for 2007 and seven for 2011, see Table 1 for notations) onto Haumea’s light curve. The location of the Dark Red Spot (Lacerda 2009) is represented by the red-shaded region. The combination of the data obtained on both dates returns the 230 degrees of rotational coverage of Haumea. The 2007 observations published in (Dumas et al. 2011) can be used to characterize the DRS region. The rotational phase (longitude) is also represented in degrees along the X-axis. The size of the diamond is proportional to the timespan between the start and end of each observation. with typical exposure times of 300 s in 2007 and 600 s in 2011. Haumea’s light curve is taken from Lellouch et al. (2010). The longitude uncertainties are not represented because they are too small (less than 0.13% and 0.07% over the period covering the 2007 and 2011 data). |
Observation logs for Haumea, with its associated central longitude at each epoch, and the solar analog calibrators.
 |
Fig. 2 A) Average spectra of Haumea obtained for each date (top) and for both regions: the DRS (including all the 2007 observations with H11_0 and H11_6) and no-DRS (all combined H11_x with x = [1..5]). See Table 1 and Fig. 1 for notations. The standard deviation at 1σ is also represented for each spectrum. Water-ice features are clearly visible at 1.5 μm, 1.65 μm (crystalline), and with the large band at 2.0 μm, but no significant differences were observed between each regions. All spectra were normalized at 2.20 μm (dashed line). B) Spectral ratios between the two data sets of 2007 and 2011: top: division of the two average spectra of Haumea and that of the two solar analogs. We note the bump observed in the 1.63−1.80 μm range (gray region), which is due to an artifact of the solar analog calibration star (see Dumas et al. 2011 for more explanation). Bottom: the ratio of the spectra 2007/2011 and DRS/no-DRS. The blue parts of the spectra correspond to the wavelengths range (1.51−1.63 μm in H and 2.03−2.30 μm in K) used to fit the polynomial regressions (red curves). The slopes are [0.81 ± 0.60]%/100 nm and [1.49 ± 0.60]%/100 nm for the 2007/2011 and DRS/no-DRS ratios, respectively, and they confirm the redder profile of the DRS region. |
Using the same settings (though in NGS), we also observed standard solar-analog stars that are close in time to observations of Haumea and at similar airmass. These stars were used to correct our spectra from the solar response and telluric absorption features (see Table 1).
3. Data reduction
The science and calibration data were reduced using the ESO pipeline version 2.3.2 (Modigliani et al. 2007). We first corrected all raw frames from the noise pattern of dark and bright horizontal lines introduced when reading the detector. We then used the ESO pipeline to produce all master calibration files needed by the data reduction process, such as the bad pixel masks, master darks, flat-field frames, and the wavelength and distortion calibration files, which are needed to associate a wavelength value with each pixel, respectively, and to reconstruct the final image cubes.
From each object (science or calibrator) frame, we subtracted the sky frame recorded closest in time. The quality of the sky subtraction was further improved by enabling the correction of sky residuals in the pipeline, i.e., by subtracting the residual median value of the sky from each image slice of the spectral-image cube. We extracted all individual spectra one by one and combined them after correction of any remaining bad pixels, which were replaced by the median of all frames at the corresponding wavelength. Airmass correction was applied by dividing the spectra of Haumea with their corresponding solar analogs. The final spectra were then normalized to unity at 2.20 μm. We determined the rotational phase of each of our spectra from the accurate knowledge of Haumea’s rotation period (3.915341 h ± 0.000005 h), based on the closest photometric observations acquired in December 2009 (Lellouch et al. 2010) and June 2007 (Lacerda 2009). The 2007 observations were acquired while the DRS region was facing the Earth (see Fig. 1). An arbitrary origin for the rotational phase of Haumea was chosen to correspond to the lowest of its two light-curve maxima. A detailed analysis of the combined 2007 and 2011 observations is shown in the next section.
4. Spectral analysis
4.1. Identification of the spectral features and comparison
Figure 2A shows the average spectra obtained in 2007 and 2011 in the 1.4–2.4 μm range. We also present the spectra corresponding to the different regions (DRS and no-DRS).
These four spectra look broadly similar with no major differences between the DRS and the no-DRS regions, and the main spectral features are that of water ice, with deep absorption bands at 1.5 μ and 2 μm. The shapes of these bands, and their relative depths between 1.50 and 1.57 μm, and around 1.65 μm, confirm that most of the H2O ice is in its crystalline state (amorphous ice lacks the 1.57 and 1.65 μm absorption bands, while the 1.5 and 2.0 μm band shapes remain; see Grundy & Schmitt 1998). This predominance of crystalline ice is not surprising, since it is the most thermodynamically stable phase of water ice and has been widely reported on the surface of other icy outer solar system objects (e.g., satellites of giant planets and TNOs).
It is important to note that the spectral difference observed in the 1.63−1.8 μm range is due to a feature of the solar analog (HD142093) used for our 2007 observations. It is clearly visible in Fig. 2A, between 1.63−1.80 μm (gray region in Fig. 2B), where we present the ratio between both dates for Haumea and the solar analog spectra. We decided not to remove this artifact in the spectra to conserve all the observed properties, but we excluded this wavelength region from our analysis of the spectral slope. We could not extract the spectra of the satellites because of their high proximity with Haumea.
4.2. Study of the spectral slope
As a result of the above analysis, we only considered the spectral ranges between 1.51−1.63 μm in H and 2.03−2.30 μm in K (represented in blue in Fig. 2B) to measure the overall spectral slope. We determined a slope of 0.81 (±0.60)%/100 nm for the ratio between the data acquired in 2007 and in 2011, and a slope of 1.49 (±0.60)%/100 nm for the ratio between the data taken inside and outside the DRS. These values confirm thereby a redder surface for the DRS region. This behavior was so far only known for the visible part of the spectrum; present measurements are the first detection of this redder slope in the near infrared. We refined the measurements by computing the ratio of each spectrum with the average spectrum of the no-DRS region (H11_x observations, with x = [2,3,4,5]). The spectral slopes are presented in Fig. 3 and were obtained from a simple linear fit of our data over the same wavelength range as Fig. 2.
The obtained slope coefficients are presented in Fig. 4, which shows the evolution of the spectral slope versus time. The dispersion of the data points is larger for the DRS region, which is also shown by their larger error bars. Still, the average slope obtained from all DRS measurements point to a redder surface in this region. Similarly, the points with the maximum slope values (3.25 and 3.26%/100 nm) are located at Haumea’s longitudes 30° and 81°, respectively, i.e., within the DRS region. Even though better data are needed to improve our measurements, we can confirm from this analysis that the DRS region is spectrally redder than the rest of the surface of Haumea.
 |
Fig. 3 Comparison of the spectra ratios obtained by dividing each spectrum by the average spectrum of the no-DRS region (H11_x with x = [2,3,4,5]). The slope is calculated considering the wavelength ranges 1.51−1.63 μm and 2.03−2.30 μm (red and blue parts for 2007 and 2011, respectively) and a simple linear regression. All spectra have been normalized at 2.20 μm (dashed line). The variation of the spectral slopes obtained for each spectra as a function of time is represented in Fig. 4. |
4.3. Analysis of the 2.0 μm band depth
The depth of an absorption feature is computed as ![\begin{equation} D_\lambda[\%] = 100 \times (1 - f_\lambda), \end{equation}](/articles/aa/full_html/2016/09/aa26423-15/aa26423-15-eq22.png) (1)where fλ is the normalized reflectance at the wavelength λ. This formula gives the percentile value of the absorption depth of a given band, which informs us about the relative quantity of the absorber and a possible indication of the path length traveled by the light. To compute this parameter we assume the ratio between the median values of the bottom band [2.00−2.05 μm] and the top band [2.20−2.25 μm], where all the spectra were normalized (at 2.225 μm). The results of the band depth are shown in Fig. 5. We see that the values of the absorption band depth are in the range 40% to 60% with no significant difference between DRS and no-DRS. However, the smallest water-ice absorption (41.5%) seems to coincide with the smallest longitude (10°, close to the lowest maximum of the light curve). As a result, the surface material present on the DRS region, even though dominated by crystalline water ice, could correspond to a less hydrated mixture than the remaining surface of Haumea.
(1)where fλ is the normalized reflectance at the wavelength λ. This formula gives the percentile value of the absorption depth of a given band, which informs us about the relative quantity of the absorber and a possible indication of the path length traveled by the light. To compute this parameter we assume the ratio between the median values of the bottom band [2.00−2.05 μm] and the top band [2.20−2.25 μm], where all the spectra were normalized (at 2.225 μm). The results of the band depth are shown in Fig. 5. We see that the values of the absorption band depth are in the range 40% to 60% with no significant difference between DRS and no-DRS. However, the smallest water-ice absorption (41.5%) seems to coincide with the smallest longitude (10°, close to the lowest maximum of the light curve). As a result, the surface material present on the DRS region, even though dominated by crystalline water ice, could correspond to a less hydrated mixture than the remaining surface of Haumea.
 |
Fig. 4 Representation of the spectral slopes (%/100 nm) from Fig. 3 as a function of time (in MJD-55 660 days). The rotational phase (longitude) is also represented on the top axis in degrees. The 2007 data have been shifted by an integer number of rotational period so that they can be overplotted on the 2011 data (see Table 1). The red circles and blue triangles correspond to the 2007 and 2011 data, respectively. A null slope corresponding to the no-DRS part (dashed line) and the black square represents the average of the slope values in the DRS equal to [1.46 ± 0.82]%/100 nm, highlighting the redder spectral slope for this region of the surface of Haumea. The error bars correspond to a standard deviation of 1σ. Haumea’s light curve (solid line) is also represented for clarity. |
4.4. Analysis of the area of H complex band
 |
Fig. 5 Variation of the depth of the 2.0 μm absorption band (in %) calculated as a function of time (MJD − 55 660 days). The 2007 data have been shifted by an integer number of rotational period so that they can be overplotted on the 2011 data (see Table 1). The red circles and blue triangles correspond to the 2007 and 2011 data, respectively. All spectra were normalized at 2.225 μm for this study. The error bars are 1σ uncertainty for both data. Haumea’s light curve (solid line) is also represented for clarity. Values corresponding to the absorption band depth are in the [40–60%] range with a smallest water-ice absorption at 10° close to the lowest minimum of the light curve with no significant difference between DRS and no-DRS. |
 |
Fig. 6 Variation of the integrated area of the [1.50−1.63] μm H2O ice complex band as a function of time (MJD − 55 660 days). The 2007 data have been shifted by an integer number of rotational period so that they can be overplotted on the 2011 data (see Table 1). The red circles and blue triangles correspond to the 2007 and 2011 data, respectively. The errors represented are 1σ for both data. Haumea’s light curve (solid line) is also represented for clarity. We see that the strongest H-band absorptions are localized in the DRS region. |
 |
Fig. 7 Spectra of Haumea (in gray) taken on 2007 (DRS, top figure) and 2011 (no-DRS, bottom figure; excluding data point H11_6, which is right on top of the DRS). The results of our spectral modeling is shown with red and blue lines. Crystalline water ice with grain sizes smaller than 60 μm as the major component, with only a few percent of amorphous carbon, are sufficient to fit our data nicely (Model 1, in blue dashed line). However, slight improvements to the fit can be obtained by adding ~10% of amorphous water ice (Model 2, in solid red line). See Table 2 for more details on the models. |
However, the most unambiguous characterization of the surface properties of the DRS might come from the spectral analysis of the H-band area. For this, we investigated the behavior of all Haumea spectra around the 1.50−1.63 μm absorption band (sadly, we could not study the crystalline water-ice band at 1.65 microns because of the artifact introduced by the solar analog used in our 2007 data). The integrated areas of the 1.5 μm water-ice absorption complex were computed by fitting the continuum level on either side of the absorption band (1.50 to 1.63 μm). Then we determined the value corresponding to “one minus the normalized spectrum” over the band interval, following a method proposed by Grundy et al. (2006). The results are shown in Fig. 6 where we see the variations of this integrated area with time (and rotational phase). The shallow 1.56 μm band, still included in our wavelength range of study, is also of interest to investigate possible differences between amorphous and crystalline ice, as was suggested in the laboratory (Mastrapa et al. 2008). Figure 6 shows that the strongest absorptions in the H-band region are located within the DRS with a band area almost twice larger (at longitude 10°) than for the region outside the DRS. Indeed, contrary to the 2.0 μm band behavior (see previously), the highest absorption seems to coincide with the smallest longitude (10°, close to the lowest maximum of the light curve). This result points to the fact that, although the DRS might represent the less hydrated region of the surface, it could still display a higher concentration of crystalline water ice than the rest of the surface. This result itself is confirmed by the analysis of our spectral modeling explained in the next section.
5. Compositional modeling
5.1. Methods
We use the spectral model developed by Hapke (1981, 1993) to investigate the chemical properties of the surface of Haumea. This approach allows us to model the reflectance spectrum and the albedo of a medium, from the physical properties of the different chemical compounds present on the surface. The albedo is approximated using Eq. (44) of Hapke (1981): 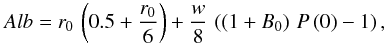 (2)where w is the single-scattering albedo and r0 the bi-hemispherical reflectance, which is purely single-scattering albedo dependent, i.e.,
(2)where w is the single-scattering albedo and r0 the bi-hemispherical reflectance, which is purely single-scattering albedo dependent, i.e., 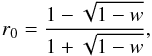 (3)where w depends on the optical constants and the size of the particles and is computed for a multicomponent surface that is assumed to be intimately or geographically mixed; see Poulet et al. (2002). The parameter B0 is the ratio of the near-surface contribution to the total particle scattering at zero phase angle and P is the phase function. The method follows the instruction provided by Merlin et al. (2010), assuming an albedo approximation model with a phase angle equal to 0, and B0 close to 0.67 for icy objects (Verbiscer & Helfenstein 1998). The surface roughness and interference were neglected in this work.
(3)where w depends on the optical constants and the size of the particles and is computed for a multicomponent surface that is assumed to be intimately or geographically mixed; see Poulet et al. (2002). The parameter B0 is the ratio of the near-surface contribution to the total particle scattering at zero phase angle and P is the phase function. The method follows the instruction provided by Merlin et al. (2010), assuming an albedo approximation model with a phase angle equal to 0, and B0 close to 0.67 for icy objects (Verbiscer & Helfenstein 1998). The surface roughness and interference were neglected in this work.
5.2. Results for intimate mixtures
The free parameters are the asymmetry parameters of the phase function (which is approximated by a single Henyey-Greenstein function), the particle sizes, and the abundances of the various compounds. In order to take the blue component in our model into account, we add two other parameters, a and b, to adjust the blue continuum of the spectrum with a second degree polynomial curve. We note x the wavelength, given by x = (λ[i] −1.75) μm, to normalize the spectra at 2.24 μm with an albedo of 0.67. In each case, the model is adjusted to the spectra using this continuum. The result is shown in Fig. 7. The normalization at 1.75 μm was correlated for each date (geometrical albedo: 0.75 and 0.702 for 2007 and 2011, respectively) taking into account the solar analog artifact described earlier and affecting the 2007 data. A previous model for the 2007 observations (Dumas et al. 2011) is also represented with a normalization at 0.60 at 1.75 μm.
We considered two sets of data: all 2007 observations in a first part (DRS) and all 2011 data (no-DRS, and excluding H11_6, which corresponds to the DRS region) in the second part. For each date, two models are used: one considering only crystalline water ice, and a second including some amorphous water ice. To constrain the free parameters, we use a best-fit model based on the Levenberg-Marquardt algorithm to minimize the reduced χ2. The minimization is applied outside the telluric absorption bands, which can affect the results. Best models are based on an intimate mixture of crystalline water ice (optical constants at 50 K from Grundy & Schmitt 1998), amorphous carbon (from Zubko et al. 1996), and amorphous water ice (at low temperature, from Mastrapa et al. 2008). For the 2007 data, the [1.63−1.80] μm range was considered but with a lower weight than the rest of the spectra to minimize the contamination of the solar analog artifact. All the results are shown in Table 2.
Crystalline water ice with grain sizes smaller than 60 μm as the major component, with a few percent of amorphous carbon, are sufficient to fit the data. Some improvements of the fit can be obtained by adding ~10% of amorphous water ice. Indeed, we see that, for the 2007 data, the presence of amorphous water ice (with large-size 0.1 mm grains) allows us to better fit the spectrum of the DRS region, as measured by the small difference of the reduced χ2. For the 2011 data, we obtain a nearly similar reduced χ2 between both models (with and without amorphous ice), although we get lower values than for 2007 owing to the analog artifact affecting our older data. If we focus on Model 2 for both epochs, we confirm our earlier result that a higher concentration of crystalline water ice is seen for the DRS region (87.0% for 2007 vs. 83.6% for 2011), considering all grain sizes. Finally, we note that the different amounts of amorphous carbon needed to fit the 2011 (more than 10%) and 2007 (less than 2%) also points to differences in composition between the DRS and no-DRS surfaces. It is also important to note that Hershel could not detect any “signature” associated with the DRS in its analysis of Haumea’s light curve (Lellouch et al. 2010), emphasizing the difficulty of quantifying any variation of surface properties at the spot’s location.
Model mixtures.
6. Orbit of Hi‘iaka and Namaka
6.1. Astrometric positions
 |
Fig. 8 Comparison of H+K band of SINFONI broadband images of Haumea obtained with the LGS-AO corrected mode for 2007 (left) and 2011 (right). North is up and east is left. The spatial and intensity scales are similar. The color represents the intensity given in ADU units. The improved contrast and spatial resolution of the AO image make the detection of the two faint satellites possible: Namaka (the faintest, just below Haumea) and Hi’iaka (the brightest, at the bottom of image) in 2007, only Hi’iaka (faint source northeast of Haumea) in 2011. |
Taking advantage of the imaging capabilities of SINFONI, we extracted the relative astrometric position of Haumea and its largest satellite Hi‘iaka from the hyperspectral cubes of 2172 × 64 × 64 pixels. We created a broadband image by stacking the cube along the wavelength, avoiding wavelength ranges affected by telluric absorption. The resulting image, shown in Fig. 8, contains all the slices in the wavelength intervals 1.524–1.764 μm and 2.077–2.332 μm.
We used Moffat 2D functions to determine the coordinates of the photocenters of the components, following the procedure described in Carry et al. (2011). The spatial accuracy of this measurement is about a quarter of a pixel. Owing to the rectangular shape of SINFONI pixels, it is twice as large in the north-south direction (100 mas) than along the east-west direction (50 mas). The relative positions of Hi‘iaka with respect to Haumea photocenter are listed in Table 3, and shown in Fig. 9. The brightness difference between Hi‘iaka and Haumea, which is normalized to the average brightness of Haumea, that is, removing the effect of Haumea’s high-amplitude light curve, is also reported as a magnitude difference (ΔMag) for each epoch. With the exception of the last epoch, the magnitude difference ranges from 2.6 to 3.1, with an average of 2.76 ± 0.18, in agreement with the value of 3.0 reported in Lacerda (2009). The estimation of the flux of the components is rather crude, and is reported here only for information. Namaka is not detected in 2011 image (see Fig. 8), although its detection is within SINFONI capabilities (see Fig. 8 and Dumas et al. 2011). It is likely that Namaka was angularly too close to Haumea at the time of the observations, as suggested by its predicted position at (0.̋008, −0.̋110), based on the orbit by Ragozzine & Brown (2009) and our own computations below, thus less than 2 pixels from the center of Haumea.
Relative positions of Hi’iaka on 2011 April 09. The uncertainty is 15 mas in right ascension, and 40 mas in declination.
 |
Fig. 9 Relative positions of Hi’iaka on 2011 April 09. Left: the seven positions on the plane of the sky listed in Table 3 are shown as open circles, with their uncertainty (15 × 40 mas). The bold diamond represents the average position. Right: evolution of the position with time (top: ΔRA and bottom: ΔDec). |
6.2. Orbital solutions
Ragozzine & Brown (2009) built a dynamic solution for Haumea’s system on the base of about 30 observations spanning a period of 1260 days from January 2005 to May 2008, acquired with the Hubble Space Telescope (HST). These authors used a dynamic three-body model in which the gravitational interaction between the satellites causes non-Keplerian perturbations on Namaka’s orbit on timescales much longer than a month. However, they found that the perturbation of Namaka on Hi‘iaka’s orbit was negligible, and that its orbit is described well by a Keplerian motion. Furthermore, they found no evidence for an effect of Haumea gravitational quadrupole (J2). Using the astrometric positions of Hi‘iaka and Namaka measured on SINFONI datacubes in 2007, Dumas et al. (2011) also studied the orbits of both satellites and discussed heating that could be generated by tidal effects.
We took advantage of another astrometric position, taken 431 days (about nine revolutions) after the latest position reported by Ragozzine & Brown (2009) to determine the orbital elements of Hi‘iaka. For that, we used the genetic-based algorithm Genoid (Vachier et al. 2012), which relies on a metaheuristic approach to find the best-fit set of orbital elements in a two-body problem. This approach can be used to search for Keplerian orbits, as well as to explore a more complex problem, including the gravitational field of the central body up to the fourth order. To define the set of orbital elements that best fit the data, Genoid minimizes a fitness function, fp, defined as a χ2 minimization function (Eq. (4)) ![\begin{equation} \label{eq:chi2} f_p = \chi^2 = \sum_{i=1}^{n} \left[ \left(\frac{x^{\rm o}_i - x^{\rm c}_i}{x^{\rm e}_i} \right)^2 + \left(\frac{y^{\rm o}_i - y^{\rm c}_i}{y^{\rm e}_i} \right)^2 \right] , \end{equation}](/articles/aa/full_html/2016/09/aa26423-15/aa26423-15-eq43.png) (4)where n is the number of observations, and xi and yi are the relative position between Hi‘iaka and Haumea along the right ascension and declination, respectively. The exponents o and c stand for observed and computed positions, and exponent e stands for measured error. For convenience, in the following text, we express the fitness function as the quadratic mean of the residuals. The main advantage of this fitness function is to provide a link between the quality of the fitted orbit and the uncertainties of the astrometric positions provided by the ephemeris. A definition and discussion about estimating uncertainties in astronomy can be found, for example, in Andrae (2010), Andrae et al. (2010), and references therein.
(4)where n is the number of observations, and xi and yi are the relative position between Hi‘iaka and Haumea along the right ascension and declination, respectively. The exponents o and c stand for observed and computed positions, and exponent e stands for measured error. For convenience, in the following text, we express the fitness function as the quadratic mean of the residuals. The main advantage of this fitness function is to provide a link between the quality of the fitted orbit and the uncertainties of the astrometric positions provided by the ephemeris. A definition and discussion about estimating uncertainties in astronomy can be found, for example, in Andrae (2010), Andrae et al. (2010), and references therein.
We used a total of 35 astrometric positions, spread over 2264 days or 46.2 orbital periods, to determine the orbit of Hi‘iaka. The orbit of Namaka is based on 30 observations spread over 1175 days or 64.1 orbital periods. We added to the set of HST observations, the positions measured on SINFONI spectral cubes in 2007 and 2011 (see above) and the set of observations obtained with NIRC2 on the W. K. Keck II telescope (pixel scale of 9.963 mas) between 2005 and 2008 reported by Brown et al. (2005), Brown et al. (2006), and Ragozzine & Brown (2009).
Albeit the intrinsic precision of Keck images is deemed cruder than that of HST, which benefits from highly stable PSF, and the absolute link between HST and Keck astrometry is unknown (pixel scale and field orientation), we favor orbital solutions based on a longer time baseline that are more sensitive to departures from a pure Keplerian motion. Because of these points, however, the goodness of fit is expected to be lower. The addition of Keck data here corresponds to an increase of 350 days of time coverage. Compared to the case using only HST data, as carried out by Ragozzine & Brown (2009), this represents 44% of the temporal baseline. This baseline is longer with the addition of the SINFONI measurements in 2011, the leverage provided by Keck data is of 20% (see Fig. 10).
 |
Fig. 10 Observed positions and model positions of Hi‘iaka and Namaka. Figure similar to Fig. 2 of Ragozzine & Brown (2009), with similar scale to ease comparison. From top to bottom, the curves represent the model on-the-sky position of Hi‘iaka in the x-direction (i.e., the negative offset in right ascension), Hi’iaka in the y-direction (i.e., the offset in declination), Namaka in the x-direction, and Namaka in the y-direction, all in arcseconds. Symbols represent astrometric observations. We note the much larger time coverage provided by the use of both Keck and VLT/SINFONI data set. |
Dynamical parameters of Hi‘iaka and Namaka reported in EQJ2000 and derived mass of Haumea.
6.3. Results
We run two separate orbital fits: one assuming the central object (Haumea) to be a point-like mass and the satellites to be massless test particles (i.e., Genoid-Kepler), and one considering the zonal harmonic coefficients J2 and J4 of the central object, its size, and the coordinates of its pole of sidereal rotation (i.e., Genoid-ANIS).
Our best-fit solution is obtained using a pure Keplerian motion with a fitness function fp = 11.3 mas for Hi‘iaka and fp = 17.3 mas for Namaka. This corresponds to reduced χ2 of 1.61 and 2.5, respectively. This level of accuracy is typical of the pixel size of the Keck NIRC2 camera of ≈10 mas, which is 5 and 10 times smaller than the pixel size of HST WFPC2 (≈50 mas) and ACS (≈100 mas) cameras, respectively. These reduced χ2 are to be compared with the reduced χ2 of 1.1 reported by Ragozzine & Brown (2009), based on a fit of both HST and Keck data.
Our calculations show clearly that there is no signature for non-Keplerian motion that would be caused by Haumea gravitational quadrupole, confirming Ragozzine & Brown (2009) results. Although the orbits determined here are restrained to the two-body assumption, compared with the three-body integration by Ragozzine & Brown (2009), they still allow us to predict the position of both satellites to a high accuracy over the period 2005−2020. Our Virtual Observatory web service Miriade1 (Berthier et al. 2009) allows anyone to compute the ephemeris of Hi‘iaka and Namaka for any arbitrary epoch and observer location, and can be used to plan future observations of the system.
 |
Fig. 11 Residuals (observed minus computed satellite – primary positions) normalized by the positional uncertainty σ for both Hi‘iaka and Namaka (filled and open symbols, respectively). The three circles represent the 1, 2, and 3σ contours. The color enlightens the different epochs of observation. The redder dot corresponds to the observation by SINFONI in 2011. |
Figure 11 shows the residual positions (between observed and computed) obtained normalized by the positional uncertainty. We list in Table 4 the orbital parameters of Hi‘iaka and Namaka obtained with Genoid-Kepler. They correspond to the same geometry as the orbits presented by Ragozzine & Brown (2009), albeit Namaka eccentricity is found to be lower (0.15 here vs. 0.25). We note the existence of a numerical solution with similar residuals (fp = 10.7 mas) in which the orbital motion of Hi‘iaka is reversed. We do not consider this solution here.
7. Conclusion
We presented a rotationally resolved spectroscopic study of the surface of the TNO Haumea derived from the 2007 and 2011 near-infrared (1.4–2.5 μm) observations obtained with the integral-field spectrograph SINFONI at the ESO VLT. Crystalline water ice is confirmed to be the major compound present over the entire surface of Haumea. We detected a steeper spectral slope in the near-infrared associated with the so-called DRS region over which the visible spectrum is redder, as reported by Lacerda (2009). We find that the reddening of the spectrum extends up to 2 microns.
A detailed analysis of the depth of the 2.0 μm absorption band shows that the weakest water-ice absorption is measured for 10° of rotation phase, i.e., near the center of the DRS region. Similarly, the analysis of the water absorption band around 1.6 μm reveals that the concentration of crystalline water ice is highest at the DRS location. Hapke modeling of our spectra also shows that amorphous carbon appears to be depleted in the DRS region in comparison to the rest of the surface. Although no major compositional differences have been found between the DRS region and the remaining surface, all the evidence hints at a slightly different composition for this region.
New astrometric positions of Hi‘iaka were reported and an orbital solution was computed with the genetic-based algorithm Genoid. The results are in agreement with the orbits originally presented by Ragozzine & Brown (2009) and ephemeris generation is proposed to the community.
Acknowledgments
We thank Darin Ragozzine for providing the expected positions of both satellites from his modeling at the time of our observations.
References
- Andrae, R. 2010, ArXiv e-prints [arXiv:1009.2755] [Google Scholar]
- Andrae, R., Schulze-Hartung, T., & Melchior, P. 2010, ArXiv e-prints [arXiv:1012.3754] [Google Scholar]
- Barkume, K. M., Brown, M. E., & Schaller, E. L. 2006, ApJ, 640, L87 [NASA ADS] [CrossRef] [Google Scholar]
- Barucci, M. A., Merlin, F., Guilbert, A., et al. 2008, A&A, 479, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berthier, J., Hestroffer, D., Carry, B., et al. 2009, in European Planetary Science Congress, 676 [Google Scholar]
- Bonnet, H., Abuter, R., Baker, A., et al. 2004, The Messenger, 117, 17 [NASA ADS] [Google Scholar]
- Brown, M. E., Bouchez, A. H., Rabinowitz, D., et al. 2005, ApJ, 632, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, M. E., van Dam, M. A., Bouchez, A. H., et al. 2006, ApJ, 639, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Carry, B., Hestroffer, D., DeMeo, F. E., et al. 2011, A&A, 534, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carry, B., Snodgrass, C., Lacerda, P., Hainaut, O., & Dumas, C. 2012, A&A, 544, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dumas, C., Merlin, F., Barucci, M. A., et al. 2007, A&A, 471, 331 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dumas, C., Carry, B., Hestroffer, D., & Merlin, F. 2011, A&A, 528, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eisenhauer, F., Abuter, R., Bickert, K., et al. 2003, in SPIE Conf. Ser. 4841, eds. M. Iye, & A. F. M. Moorwood, 1548 [Google Scholar]
- Grundy, W. M., & Schmitt, B. 1998, J. Geophys. Res., 103, 25809 [NASA ADS] [CrossRef] [Google Scholar]
- Grundy, W. M., Young, L. A., Spencer, J. R., et al. 2006, Icarus, 184, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Lacerda, P. 2009, AJ, 137, 3404 [NASA ADS] [CrossRef] [Google Scholar]
- Lacerda, P., & Jewitt, D. C. 2007, AJ, 133, 1393 [NASA ADS] [CrossRef] [Google Scholar]
- Lacerda, P., Jewitt, D., & Peixinho, N. 2008, AJ, 135, 1749 [NASA ADS] [CrossRef] [Google Scholar]
- Lellouch, E., Kiss, C., Santos-Sanz, P., et al. 2010, A&A, 518, L147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mastrapa, R. M., Bernstein, M. P., Sandford, S. A., et al. 2008, Icarus, 197, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Merlin, F., Guilbert, A., Dumas, C., et al. 2007, A&A, 466, 1185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Merlin, F., Barucci, M. A., de Bergh, C., et al. 2010, Icarus, 208, 945 [NASA ADS] [CrossRef] [Google Scholar]
- Modigliani, A., Hummel, W., Abuter, R., et al. 2007, ArXiv e-prints [arXiv:astro-ph/0701297] [Google Scholar]
- Poulet, F., Cuzzi, J. N., Cruikshank, D. P., Roush, T., & Dal le Ore, C. M. 2002, Icarus, 160, 313 [Google Scholar]
- Rabinowitz, D. L., Barkume, K., Brown, M. E., et al. 2006, ApJ, 639, 1238 [NASA ADS] [CrossRef] [Google Scholar]
- Ragozzine, D., & Brown, M. E. 2007, AJ, 134, 2160 [NASA ADS] [CrossRef] [Google Scholar]
- Ragozzine, D., & Brown, M. E. 2009, AJ, 137, 4766 [NASA ADS] [CrossRef] [Google Scholar]
- Schaller, E. L., & Brown, M. E. 2008, ApJ, 684, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Snodgrass, C., Carry, B., Dumas, C., & Hainaut, O. 2010, A&A, 511, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tegler, S. C., Grundy, W. M., Romanishin, W., et al. 2007, AJ, 133, 526 [NASA ADS] [CrossRef] [Google Scholar]
- Trujillo, C. A., Brown, M. E., Barkume, K. M., Schaller, E. L., & Rabinowitz, D. L. 2007, ApJ, 655, 1172 [NASA ADS] [CrossRef] [Google Scholar]
- Vachier, F., Berthier, J., & Marchis, F. 2012, A&A, 543, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verbiscer, A., & Helfenstein, P. 1998, in Solar System Ices, eds. B. Schmitt, C. de Bergh, & M. Festou, Astrophys. Space Sci. Lib., 227, 157 [Google Scholar]
- Zubko, V. G., Mennella, V., Colangeli, L., & Bussoletti, E. 1996, MNRAS, 282, 1321 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Observation logs for Haumea, with its associated central longitude at each epoch, and the solar analog calibrators.
Relative positions of Hi’iaka on 2011 April 09. The uncertainty is 15 mas in right ascension, and 40 mas in declination.
Dynamical parameters of Hi‘iaka and Namaka reported in EQJ2000 and derived mass of Haumea.
All Figures
 |
Fig. 1 Positions of all observed epochs (six for 2007 and seven for 2011, see Table 1 for notations) onto Haumea’s light curve. The location of the Dark Red Spot (Lacerda 2009) is represented by the red-shaded region. The combination of the data obtained on both dates returns the 230 degrees of rotational coverage of Haumea. The 2007 observations published in (Dumas et al. 2011) can be used to characterize the DRS region. The rotational phase (longitude) is also represented in degrees along the X-axis. The size of the diamond is proportional to the timespan between the start and end of each observation. with typical exposure times of 300 s in 2007 and 600 s in 2011. Haumea’s light curve is taken from Lellouch et al. (2010). The longitude uncertainties are not represented because they are too small (less than 0.13% and 0.07% over the period covering the 2007 and 2011 data). |
| In the text | |
 |
Fig. 2 A) Average spectra of Haumea obtained for each date (top) and for both regions: the DRS (including all the 2007 observations with H11_0 and H11_6) and no-DRS (all combined H11_x with x = [1..5]). See Table 1 and Fig. 1 for notations. The standard deviation at 1σ is also represented for each spectrum. Water-ice features are clearly visible at 1.5 μm, 1.65 μm (crystalline), and with the large band at 2.0 μm, but no significant differences were observed between each regions. All spectra were normalized at 2.20 μm (dashed line). B) Spectral ratios between the two data sets of 2007 and 2011: top: division of the two average spectra of Haumea and that of the two solar analogs. We note the bump observed in the 1.63−1.80 μm range (gray region), which is due to an artifact of the solar analog calibration star (see Dumas et al. 2011 for more explanation). Bottom: the ratio of the spectra 2007/2011 and DRS/no-DRS. The blue parts of the spectra correspond to the wavelengths range (1.51−1.63 μm in H and 2.03−2.30 μm in K) used to fit the polynomial regressions (red curves). The slopes are [0.81 ± 0.60]%/100 nm and [1.49 ± 0.60]%/100 nm for the 2007/2011 and DRS/no-DRS ratios, respectively, and they confirm the redder profile of the DRS region. |
| In the text | |
 |
Fig. 3 Comparison of the spectra ratios obtained by dividing each spectrum by the average spectrum of the no-DRS region (H11_x with x = [2,3,4,5]). The slope is calculated considering the wavelength ranges 1.51−1.63 μm and 2.03−2.30 μm (red and blue parts for 2007 and 2011, respectively) and a simple linear regression. All spectra have been normalized at 2.20 μm (dashed line). The variation of the spectral slopes obtained for each spectra as a function of time is represented in Fig. 4. |
| In the text | |
 |
Fig. 4 Representation of the spectral slopes (%/100 nm) from Fig. 3 as a function of time (in MJD-55 660 days). The rotational phase (longitude) is also represented on the top axis in degrees. The 2007 data have been shifted by an integer number of rotational period so that they can be overplotted on the 2011 data (see Table 1). The red circles and blue triangles correspond to the 2007 and 2011 data, respectively. A null slope corresponding to the no-DRS part (dashed line) and the black square represents the average of the slope values in the DRS equal to [1.46 ± 0.82]%/100 nm, highlighting the redder spectral slope for this region of the surface of Haumea. The error bars correspond to a standard deviation of 1σ. Haumea’s light curve (solid line) is also represented for clarity. |
| In the text | |
 |
Fig. 5 Variation of the depth of the 2.0 μm absorption band (in %) calculated as a function of time (MJD − 55 660 days). The 2007 data have been shifted by an integer number of rotational period so that they can be overplotted on the 2011 data (see Table 1). The red circles and blue triangles correspond to the 2007 and 2011 data, respectively. All spectra were normalized at 2.225 μm for this study. The error bars are 1σ uncertainty for both data. Haumea’s light curve (solid line) is also represented for clarity. Values corresponding to the absorption band depth are in the [40–60%] range with a smallest water-ice absorption at 10° close to the lowest minimum of the light curve with no significant difference between DRS and no-DRS. |
| In the text | |
 |
Fig. 6 Variation of the integrated area of the [1.50−1.63] μm H2O ice complex band as a function of time (MJD − 55 660 days). The 2007 data have been shifted by an integer number of rotational period so that they can be overplotted on the 2011 data (see Table 1). The red circles and blue triangles correspond to the 2007 and 2011 data, respectively. The errors represented are 1σ for both data. Haumea’s light curve (solid line) is also represented for clarity. We see that the strongest H-band absorptions are localized in the DRS region. |
| In the text | |
 |
Fig. 7 Spectra of Haumea (in gray) taken on 2007 (DRS, top figure) and 2011 (no-DRS, bottom figure; excluding data point H11_6, which is right on top of the DRS). The results of our spectral modeling is shown with red and blue lines. Crystalline water ice with grain sizes smaller than 60 μm as the major component, with only a few percent of amorphous carbon, are sufficient to fit our data nicely (Model 1, in blue dashed line). However, slight improvements to the fit can be obtained by adding ~10% of amorphous water ice (Model 2, in solid red line). See Table 2 for more details on the models. |
| In the text | |
 |
Fig. 8 Comparison of H+K band of SINFONI broadband images of Haumea obtained with the LGS-AO corrected mode for 2007 (left) and 2011 (right). North is up and east is left. The spatial and intensity scales are similar. The color represents the intensity given in ADU units. The improved contrast and spatial resolution of the AO image make the detection of the two faint satellites possible: Namaka (the faintest, just below Haumea) and Hi’iaka (the brightest, at the bottom of image) in 2007, only Hi’iaka (faint source northeast of Haumea) in 2011. |
| In the text | |
 |
Fig. 9 Relative positions of Hi’iaka on 2011 April 09. Left: the seven positions on the plane of the sky listed in Table 3 are shown as open circles, with their uncertainty (15 × 40 mas). The bold diamond represents the average position. Right: evolution of the position with time (top: ΔRA and bottom: ΔDec). |
| In the text | |
 |
Fig. 10 Observed positions and model positions of Hi‘iaka and Namaka. Figure similar to Fig. 2 of Ragozzine & Brown (2009), with similar scale to ease comparison. From top to bottom, the curves represent the model on-the-sky position of Hi‘iaka in the x-direction (i.e., the negative offset in right ascension), Hi’iaka in the y-direction (i.e., the offset in declination), Namaka in the x-direction, and Namaka in the y-direction, all in arcseconds. Symbols represent astrometric observations. We note the much larger time coverage provided by the use of both Keck and VLT/SINFONI data set. |
| In the text | |
 |
Fig. 11 Residuals (observed minus computed satellite – primary positions) normalized by the positional uncertainty σ for both Hi‘iaka and Namaka (filled and open symbols, respectively). The three circles represent the 1, 2, and 3σ contours. The color enlightens the different epochs of observation. The redder dot corresponds to the observation by SINFONI in 2011. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


