| Issue |
A&A
Volume 593, September 2016
|
|
|---|---|---|
| Article Number | A85 | |
| Number of page(s) | 19 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201423916 | |
| Published online | 27 September 2016 | |
Gravitational scattering of stars and clusters and the heating of the Galactic disk
1 Department of Physics and Astronomy, Uppsala University, Box 515, 751 20 Uppsala, Sweden
e-mail: Bengt.Gustafsson@physics.uu.se
2 Department of Astronomy and Theoretical Physics, Lund Observatory, Box 43, 221 00 Lund, Swedem
3 NORDITA, Roslagstullsbacken 23, 106 91 Stockholm, Sweden
4 PAS Space Research Center, Bartycka 18A, 00-716 Warsawa, Poland
Received: 31 March 2014
Accepted: 9 May 2016
Context. Could the velocity spread, increasing with time, in the Galactic disk be explained as a result of gravitational interactions of stars with giant molecular clouds (GMCs) and spiral arms? Do the old open clusters high above the Galactic plane provide clues to this question?
Aims. We explore the effects on stellar orbits of scattering by inhomogeneities in the Galactic potential due to GMCs, spiral arms and the Galactic bar, and whether high-altitude clusters could have formed in orbits closer to the Galactic plane and later been scattered.
Methods. Simulations of test-particle motions are performed in a realistic Galactic potential. The effects of the internal structure of GMCs are explored. The destruction of clusters in GMC collisions is treated in detail with N-body simulations of the clusters.
Results. The observed velocity dispersions of stars as a function of time are well reproduced. The GMC structure is found to be significant, but adequate models produce considerable scattering effects. The fraction of simulated massive old open clusters, scattered into orbits with |z| > 400 pc, is typically 0.5%, in agreement with the observed number of high-altitude clusters and consistent with the present formation rate of massive open clusters.
Conclusions. The heating of the thin Galactic disk is well explained by gravitational scattering by GMCs and spiral arms, if the local correlation between the GMC mass and the corresponding voids in the gas is not very strong. Our results suggest that the high-altitude metal-rich clusters were formed in orbits close to the Galactic plane and later scattered to higher orbits. It is possible, though not very probable, that the Sun formed in such a cluster before scattering occurred.
Key words: Galaxy: kinematics and dynamics / open clusters and associations: individual: M 67 / Sun: evolution / stars: formation
© ESO, 2016
1. Introduction
Several relatively metal-rich and massive open clusters are located high above the Galactic plane. From Vande Putte et al. (2010) we find that 8% of all 481 open clusters in their study have | z | > 400 pc. The number is decreased to about 4% if we limit ourselves to solar metallicities (cf. their Fig. 7). Among the 78 clusters with reliable spectroscopic metallicities compiled by Heiter et al. (2014), 7 have |z| > 400 pc and yet close to solar metallicity. In Fig. 1 we display the known open clusters with | z | > 400 pc. We find four such clusters with [Fe/H] > −0.1 and an age >1.0 Gyr, M 67, NGC 188, NGC 2420 and NGC 6791, all northern which could reflect incompleteness and selection effects in the data. Data for these clusters are listed in Table 1 as taken from the sources given.
The relatively old, metal-rich and yet populous open cluster M 67 is located at a height z above the Galactic plane of about 400–450 pc (Sarajedini et al. 2009; VandenBerg & Stetson 2004; Friel 1995) and +36 deg in Galactic longitude from the anti-centre direction. Its orbit currently has an eccentricity of about 0.13, and its distance from the centre of the Galaxy, now close to 9 kpc, is estimated to vary between 8 and 10 kpc or possibly 6 to 10 kpc, depending on the mass in spiral arms assumed at the orbit calculations (Pichardo et al. 2012). It has a metallicity very close to solar and an age of about 3.5–4.8 Gyr (see Önehag et al. 2011, for references).
The cluster NGC 188, although it is more distant and probably older than M 67, has a metallicity and mass similar to or even greater (Friel et al. 2010; Bonatto et al. 2005). Cluster NGC 2420 was earlier regarded to be a transition system between solar-metallicity open clusters and more metal-poor globular clusters. However, for this cluster more recent analyses with high-resolution spectroscopy suggest a metallicity ranging from [Fe/H] = −0.05 to –0.20 (see Carrera & Martínez-Vázquez 2013), i.e. rather close to solar ([Fe/H] ≡ 0.0). Age estimates vary between 1 and 3 Gyr see references in Table 1 and in Carrera & Martínez-Vázquez 2013). The highly interesting and relatively old cluster NGC 6791 (Brogaard et al. 2012) seems to be unique in showing different abundances for different stars, with an Na/O anti-correlation similar to that found in globular clusters, suggesting that several generations of stars have formed while the cluster was massive enough to retain the material expelled by AGB stars within the cluster. Carraro (2014) followed Jílková et al. (2012) in speculating that it formed in the Galactic bulge and then migrated to its present position, 7 kpc away from the Galactic centre. In addition to these four clusters, we have included one similarly metal-rich, old and populous cluster at a slightly lower altitude, NGC 7142.
Metal-rich and old Galactic clusters at high altitudes.
One fundamental reason for studying the nature of old metal-rich clusters at high latitudes is the problem of understanding the evolution of the Galactic disk and of galaxy disks in general. In their classic papers Spitzer & Schwarzschild (1951) and Spitzer & Schwarzschild (1953) suggested that the gradual increase of the scatter of stellar velocities with age in the solar neighbourhood is a result of gravitational scattering by “interstellar gas complexes”. Accordingly, the later-discovered giant molecular clouds (GMCs) became main candidates responsible for this so-called disk heating. Calculations by Lacey (1984) did, however, not reproduce the observed scatters in radial (σU), azimuthal (σV) and perpendicular (σW) directions relative to the disk; note however, that Villumsen (1983) obtained a better agreement with observations. Barbanis & Woltjer (1967), Carlberg & Sellwood (1985), Carlberg (1987) and Jenkins & Binney (1990) suggested that the acceleration in the plane was due to transient spiral structure, while the scattering against the GMCs partially redirected the velocities into the W direction. Later Ida et al. (1993) and Shiidsuka & Ida (1999) found that GMCs alone could, indeed give proper axis ratios for the velocity ellipsoid, see also Sellwood (2008) and Sellwood (2013). Yet, the effects of spiral structure, notably in the U and V velocities, and also the Galactic bar (see Saha et al. 2010; Grand et al. 2016; and Athanassoula 2013, and references therein) may indeed be significant. Other mechanisms that have been suggested to play a role are infall of satellite galaxies and other cosmic sub structures (Kazantzidis et al. 2009), including massive black holes (Hänninen & Flynn 2002, 2004) and dark-matter halos, as well as collective effects like buckling instabilites or bending waves in the disk (Sotnikova & Rodionov 2003; Saha et al. 2010; Griv et al. 1997). The observed and rather smooth increase of σU, σV and σW in unison with time may speak against more dramatic irregular mechanisms (cf. Sellwood 2013, see also Zasov et al. 2013). With van der Kruit & Freeman (2011) we conclude that there is still “much uncertainty about the heating of the thin disk. Some of this uncertainty is due to uncertainty in the observational relation between stellar ages and velocity dispersions, because stellar ages are so difficult to measure”. We limit the present study to the evolution of the Galactic disk from the formation of the Sun to the present, partly because the observations of heating for older thin-disk stars are limited and also influenced by the mixing-in of thick-disk stars, probably affected by additional heating mechanisms. Morevover, the conditions in the Galactic disk, for example as regards star formation and density of GMCs, are more uncertain the longer we look backwards in time, making simulations of the evolution more uncertain.
A reason for exploring the connection between the heating of the Galactic disk and the existence of high-altitude clusters is the possibility that the latter could illuminate the general heating mechanisms. The response of the young clusters close to the Galactic plane to the mechanisms, whatever they are, might not be similar to those of stars of similar ages. In particular, nearby interaction, for example with a GMC, may break up the cluster. Also, it is interesting in itself to explore whether the existence and frequency of the clusters at high latitudes could be at all consistent with reasonable heating mechanisms for the disk in general, or whether the clusters must be explained by other mechanisms, such as interaction between the disk gas and massive infalling objects like high velocity clouds or globular clusters, or shock interaction between spiral density waves and a thick magnetised Galactic disk, pushing up star-forming gas to high latitudes. For a review of such “unusual formation scenarios”, see Appendix A.2 and Vande Putte et al. (2010).
In the present paper, some focus will be on the cluster M 67, being the most well studied of the old metal-rich clusters, at high altitudes. One special reason for wondering about the origin of M 67 is its similarity in age and chemical composition with the Sun. In fact, Önehag et al. (2011) found one solar-twin star in the cluster to be more solar-like than almost any known twins in the solar neighbourhood and speculated that the Sun might even have had an origin in the cluster. The solar-identical abundances of the cluster were later verified by the analysis of 13 more stars in M 67 (Önehag et al. 2014). The possibility of a solar origin in the cluster was, however, refuted by Pichardo et al. (2012) who argued that the Sun being kicked out from the cluster to the rather different solar orbit would have damaged the outer parts of the solar system. Pichardo et al. (2012) carried out their simulations backwards in time by starting the cluster from the present locus of M 67. Although spiral arms and the Galactic bar were included in the Galactic potential, the more concentrated inhomogeneities in the mass distribution provided by the giant molecular clouds were not represented explicitly. The possibility that the cluster itself had an earlier, more solar-like orbit which evolved into its present high inclination orbit via scattering against one or several giant molecular clouds was not suggested.
Before the analysis of these possibilities of forming clusters in orbits close to the Galactic plane and subsequently scattering them to high altitudes, we will discuss the representativity of the clusters and field star at these heights in some detail in Sect. 2. In Sect. 3 orbit calculations for models of the Galaxy with the contributions to the potential from stars and gas, spiral arms, a central bar and GMCs and with detailed consideration of cluster destruction, are introduced and results of these simulations are presented. The significance of the detailed structure of the GMCs is explored in Sect. 4. The results will be further discussed in Sect. 5 where also conclusions are given. In Appendices A and B, the possible alternative formation of clusters by gas in high-altitude orbits is discussed, and some details of the numerical representation used for the gravity potentials are given.
2. The population of high-altitude clusters
2.1. Comparions with stellar distributions
One realistic explanation for the high-altitude clusters could be that they represent the tail of the z-velocity distribution of a considerable number of open clusters, most of which have now been dissolved into the older thin Galactic disk. The reason why they now stand out would then be a natural selection effect, since clusters spending their lives closer to the Galactic plane would dissolve more rapidly. This idea appears commonly in the literature, for example Friel (1995) states: “The old clusters not only spend their time in the outer disk away from the disruptive effects of giant molecular clouds, they spend their time at large distances from the Galactic plane, further enhancing their survivability.”
A question is then whether one could, adopting realistic destruction rates (cf. for example the empirical result of Wielen (1971) that about 2% of all open clusters in the Galactic disk survive beyond 1 Gyr), explain the present population of clusters at high altitudes with orbits from a “normal” velocity distribution of the thin disk population. In the present section this issue will be discussed from an empirical view point, on the basis of survey data concerning stars and stellar clusters at different heights above the plane and their metallicities.
In their UBV star counts towards the north Galactic pole Yoshii et al. (1987) found a scale height of the stellar disk of 250–325 pc. The z distribution of the high-altitude clusters in the WEBDA catalogue (Netopil et al. 2012) shows a steeper z gradient than the field stars in the old thin disk. For the 37 clusters significantly out of the Galactic plane in that catalogue, that is with | z | ranging from 0.2 to 1.0 kpc, we find that the ratio of the number density in the | z | interval 400−1000 pc relative to that in the interval 150−250 pc, is smaller by at least a factor of two compared with the corresponding ratio for field stars. Friel (1995) reviewed the knowledge about old open clusters in the Galaxy and quoted Janes & Phelps (1994) who found that the old cluster population is fit by a 375-pc scale-height exponential, an appreciably thicker distribution than that of the 55-pc scale-height young cluster population, but consistent with that found for other old disk populations. However, when studying Table 1 of 72 clusters in Janes & Phelps (1994), we find a clear tendency for the more distant ones to be at high altitudes, which seems to be because of the difficulty in identifying distant open clusters in the Galactic disk, due to extinction and crowding. If we confine the sample in Janes & Phelps (1994) to clusters within a Galactic cylinder with a radius of 3 kpc, we find a much steeper z gradient, more in agreement with that in the WEBDA catalogue (cf. also Fig. 14). Although one should not overinterpret the rather inhomogeneous latter compilation, it seems that the clusters with | z | > 0.2 kpc do show a significantly steeper gradient, that is a smaller scale-height than the general stellar field. Recently, Buckner & Froebrich (2014) have traced an increase of the scale height with age of the open cluster distribution from the Galactic plane, rising to 550 pc at 3.5 Gyr. They ascribe this tendency to scattering of the clusters from the plane in the past.
How does the metallicity z gradient for stars compare with that of open clusters in general? Yoshii et al. (1987) traced a stellar metallicity gradient, d[Fe/H]/dz, of –0.5 kpc-1. The average metallicity for stars of solar age in the solar neighbourhood is disputed but ranges between –0.2 and 0.0 which then, with the gradient quoted, implies an [Fe/H] at the height of 450 pc of –0.4 to –0.2. Cheng et al. (2012) determined metallicity gradients in the Galaxy as a function of z on basis of the Segue survey spectroscopic data. From their Fig. 7 we find a mean [Fe/H] of about −0.27 at z = 450 pc. From the metallicity distributions of the model of Galactic disk by Schönrich & Binney (2009), their Fig. 7, we estimate that about 90% of the stars at z = 450 pc are more metal-poor than the Sun, a number consistent with the statistics of Cheng et al. (2012). Also, the metallicity distributions of Schlesinger et al. (2012) from Segue suggest a similar tendency. Presumably, these field stars are also older than the Sun on average, although, according to Schönrich & Binney (2009), the thin disk still dominates the stellar populations at this height. Obviously, the stars at heights of 450 pc above the Galactic plane are on average less metal-rich than the metal-rich high-altitude clusters in Table 1. The open clusters in the plots of Cheng et al. (2012) also deviate in that they show systematically higher metallicities than indicated by the field-star relations. This departure is also found for the Cepheids. In fact, if we adopt the metallicities of open clusters listed in the WEBDA catalogue we find that the metallicity distributions for clusters in the height intervals 200 < | z | < 500 pc and 500 < |z| < 1000 pc depart significantly from the metallicity distributions at high altitudes for both G and K field stars by Schlesinger et al. (2012), such that the cluster distribution has a median [Fe/H] about 0.2 dex higher than the corresponding distributions for the field stars.
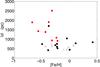 |
Fig. 1 Distribution of high-altitude (| z | > 400 pc) clusters with positive and negative Galactic latitudes (black and red/grey, respectively). Dots indicate clusters older than 1.0 Gyr while crosses correspond to lower ages. Data were taken from Heiter et al. (2014), Paunzen & Netopil (2006), Netopil et al. (2012). The four old clusters at highest metallicity are marked by the four black dots to the right (in order left to right: NGC 2420, M 67, NGC 188 and NGC 6791. |
In spite of possible selection effects in the data, it seems clear that the metallicity distribution for relatively old open clusters with 400 pc < | z | < 800 pc is skewed towards high values, as compared with the corresponding distribution for typical field-star metallicities. This effect may well be the result of systematic age differences due to the fact that older clusters (with smaller [Fe/H]) have been dissolved.
The possibilities that the clusters were formed by gas in high-inclination orbits from the outset seem small, on the basis of statistics of young early-type stars at high altitudes, see Appendix A.1, provided that the star-formation-rate in the disk was not orders of magnitude higher some Gyr ago than it is now. In Appendix A.2 we also make some comments on the possible “unusual” formation scenarios, as reviewed by Vande Putte et al. (2010). The high-altitude clusters could also possibly, after formation close to the Galactic plane, have been subsequently scattered to high orbits by infalling objects like globular clusters, high-velocity clouds, or even supermassive black holes or dark-matter sub-halos. Such alternatives are further discussed by Pfister & Gustafsson (in prep.), who find that these mechanisms do not seem to be probable explanations for the Galactic metal-rich high-altitude clusters, but nevertheless may possibly be important under certain other conditions.
2.2. Survival of massive clusters
Can we estimate the chance of a massive cluster formed in the Galactic disk surviving? Here we first attempt an empirical approach towards this problem, assuming that the formation of the M 67-like clusters occurred according to the same principles as other clusters in the disk. In next Section we shall explore this question with a more theoretical approach.
We may estimate the number of M 67-like clusters formed in the Galaxy, using the cluster initial mass function according to Lada & Lada (2003) of 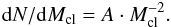 (1)
(1)
Assuming the total cluster-formation rate C to be independent of time, we find the constant C × A by integrating Eq. (1) using a formation rate representative for the solar neighbourhood (within 600 pc, the distance within which the surveyed volume is reasonably complete) of 400 M⊙ per Myr for bound clusters with masses Mcl in the interval 100 M⊙ to 3 × 104 M⊙ from Lamers & Gieles (2006). This gives C × A ≃ 70 M⊙/Myr which leads to the number of clusters formed in the mass interval 104 M⊙ to 3 × 104 M⊙ (representing M 67-like clusters in initial states according to Hurley et al. (2005)) of about 5 × 10-3 per Myr. For the period spanned by the clusters in Table 1 of 5 Gyr, and assuming that all started with masses of at least 1.0 × 104 M⊙, we find that about 1000 clusters of this magnitude should have formed in a Galactic cylinder with a radius of 4 kpc (to match the maximal distance in Table 1). We find four such clusters in the table. This suggests a fraction of survivals at high latitudes of the total number of clusters produced of about 0.4%. However, since the cluster formation rate, presumably following the star formation rate in general, may have been about a factor of two higher 4 Gyr ago (guided by the estimates of the history of the star formation rate in the disk of Just et al.2011; their model A and Fig. 1), this estimate could be decreased to about 0.2%.
We may alternatively follow a different approach in our estimate: the known young massive star clusters in the Galaxy with ages less than 20 Myr were listed by Portegies Zwart et al. (2010). These clusters, defined as having a mass greater than 104 M⊙, are 12, however, as noted by Portegies Zwart et al., they are almost all situated within the solar quadrant of the Galaxy which most probably reflects selection effects in the surveys. Thus, a reasonable assumption is that the true number of such clusters in the Galaxy as a whole is at least 40. Assuming the mean cluster formation rate some Gyr ago in the Galaxy to be about two times the present one (again following Just et al. 2011) we find that at least about 4000 such massive clusters should have formed per Gyr in the whole Galaxy. We may estimate from the data in Table 1 that about 12 old metal-rich clusters, still surviving at high altitudes, were produced per Gyr, This suggests a total fraction of high-altitude survivals of all massive clusters formed of 0.3%, which is also consistent with what we obtained from the cluster initial mass function of Lada & Lada (2003), Eq. (1) above. Allowing for the considerable uncertainties involved we thus estimate the observed fraction Fobs, of all massive open clusters that were formed in the Galactic disk about 4.5 Gyr ago and still survive at heights | z | > 400 pc, to be 0.2−0.5%.
3. Scattering in the Galactic disk
In this section we shall perform a detailed model study of the possibilities that the high-altitude clusters were formed in low-altitude orbits close to the Galactic plane, and were later scattered to the high altitudes by secular processes.
3.1. Encounters with giant molecular clouds and cluster destruction: preliminary considerations
The effects of encounters with GMCs in the Galactic disk will now be considered. The GMCs have typical masses of about 5 × 105 M⊙ (though the masses may extend up to ten times greater than that) and sizes of typically 40 pc and are located in particular at galacto-centric distances from 4 to 9 kpc. Their distribution perpendicular to the Galactic plane has a | z | scale height of 60 pc–120 pc with a value increasing with the distance from the Galactic centre, the latter value referring to the solar circle (data from Solomon et al. 1979, called SSS below, and Ferrière 2001), or even less for the heavier clouds (Stark & Lee 2005). The number of GMCs in the Galaxy was estimated by SSS to be 4000 which with the mean size given implies a filling factor of the clouds projected onto the Galactic plane of about 3% between 4 and 9 kpc from the centre (for further discussion of these estimates, see Sect. 3.2 below). The GMCs have typical 1D cloud-to-cloud velocity dispersions of about 8 km s-1 relative to the general Galactic rotation (Stark & Brand 1989), probably mainly generated by stellar winds and supernovae. Locally, however, the scatter may be smaller: Ramesh (1994) estimates it to of 3–6 km s-1. The observed structure of the individual clouds is more reminiscent of sheets or filaments than of spherical blobs (see, e.g. Allen & Shu 2000; and Butler et al. 2015).
The number of GMCs in the Galactic disk is high enough for a disk star of approximately solar age to come relatively close to a GMC several times during its life time. If a typical absolute velocity change of a cluster of v would result from each encounter with a GMC, the acquired velocity after n encounters might well be 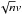 if the encounters are statistically independent. The question is then what the value of v might be. One way to estimate it is to apply the Rutherford impulse approximation. One may follow Binney & Tremaine (1987), their Eqs. (7.9a)–(7.10b), to show that the maximum possible addition to the velocity of the open cluster, with a mass significantly smaller that the mass M of the GMC, after the scattering in the z direction is
if the encounters are statistically independent. The question is then what the value of v might be. One way to estimate it is to apply the Rutherford impulse approximation. One may follow Binney & Tremaine (1987), their Eqs. (7.9a)–(7.10b), to show that the maximum possible addition to the velocity of the open cluster, with a mass significantly smaller that the mass M of the GMC, after the scattering in the z direction is 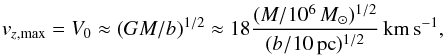 (2)where b is the impact parameter and V0 is the relative velocity at infinity. Thus, each encounter with a GMC may induce velocity changes of about 10 km s-1. However, relative velocities of about 18 km s-1 may not be unrealistic as such, due to the velocity spread of the GMCs and the clusters. Smaller impact parameters b than 10 pc will not lead to much greater effects since the radius of these relatively diffuse objects is typically 20 pc. Cloud masses significantly greater than 106 M⊙ will generate greater speeds, but the mass distribution observed for the GMCs suggests that such massive clouds are relatively rare (see SSS, and below). For vertical motion components of the GMCs, a disk half-width of 100 pc corresponds to cloud velocities of about 10 km s-1. In order for collisions with GMCs to be active in bringing a cluster into a high-elevation orbit (i.e. getting a cluster velocity perpendicular to the Galactic plane of about 30 km s-1) it is obvious either that the cluster or the cloud must depart from the typically low initial relative speeds of the Pop I objects, or that a number of encounters with GMCs must have occurred. These should then also happen to interfere constructively, systematically adding to the velocity of the cluster.
(2)where b is the impact parameter and V0 is the relative velocity at infinity. Thus, each encounter with a GMC may induce velocity changes of about 10 km s-1. However, relative velocities of about 18 km s-1 may not be unrealistic as such, due to the velocity spread of the GMCs and the clusters. Smaller impact parameters b than 10 pc will not lead to much greater effects since the radius of these relatively diffuse objects is typically 20 pc. Cloud masses significantly greater than 106 M⊙ will generate greater speeds, but the mass distribution observed for the GMCs suggests that such massive clouds are relatively rare (see SSS, and below). For vertical motion components of the GMCs, a disk half-width of 100 pc corresponds to cloud velocities of about 10 km s-1. In order for collisions with GMCs to be active in bringing a cluster into a high-elevation orbit (i.e. getting a cluster velocity perpendicular to the Galactic plane of about 30 km s-1) it is obvious either that the cluster or the cloud must depart from the typically low initial relative speeds of the Pop I objects, or that a number of encounters with GMCs must have occurred. These should then also happen to interfere constructively, systematically adding to the velocity of the cluster.
There may be several more complex acceleration mechanisms that hypothetically might affect the speed of the scattered star or cluster. One would be due to the transient character of the GMCs. If the cluster is falling in towards the centre of a cloud but star formation occurs in the cloud so that it is dissolved by supernovae explosions before the cluster has passed the cloud centre, the absolute momentum excess gained by the cluster during the infall phase may not be fully compensated for by retardation during the departure from the centre. It is easy to demonstrate, however, that this mechanism will not lead to greater contributions to the cluster speed than at most a few km s-1 as long as the dissolution of the cloud does not take place very abruptly. Another possibility is that the fragmented structure and internal dynamics of the GMC may contribute to the acceleration (or deceleration) of an incoming object. This possibility will be further commented on below. Still another mechanism would be that cluster stars are scattered or captured by the encounter with the GMC but that the core of the cluster picks up momentum and is thrown away at higher speed.
We must also consider the risk that the tidal forces at a nearby passage by a GMC may destroy the cluster. A simple measure of the critical distance bcrit for a tidal break-up may be obtained by adopting the impulse approximation and, following Spitzer & Härm (1958), estimating the inner kinetic energy change Δ(E) of the cluster with mass m due to an encounter with a GMC: 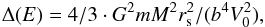 (3)where b is the impact parameter (at infinity), G Newton’s constant of gravity, V0 the relative velocity of the GMC and the cluster (at infinity), and rs is the root mean-square radius of the cluster. We assume that the cluster is in virial equilibrium such that the inner kinetic energy E of the cluster is half of the absolute gravitational one,
(3)where b is the impact parameter (at infinity), G Newton’s constant of gravity, V0 the relative velocity of the GMC and the cluster (at infinity), and rs is the root mean-square radius of the cluster. We assume that the cluster is in virial equilibrium such that the inner kinetic energy E of the cluster is half of the absolute gravitational one, 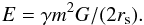 (4)The numerical coefficient γ depends on the distribution of stars in the cluster. Following Spitzer & Härm (1958) we set γ = 0.5 and obtain
(4)The numerical coefficient γ depends on the distribution of stars in the cluster. Following Spitzer & Härm (1958) we set γ = 0.5 and obtain 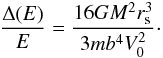 (5)We now assume that the cluster breaks up if Δ(E) /E> 1 and thus obtain for the critical impact parameter bcrit for which break-up is expected to occur
(5)We now assume that the cluster breaks up if Δ(E) /E> 1 and thus obtain for the critical impact parameter bcrit for which break-up is expected to occur 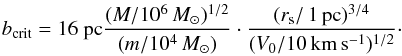 (6)More detailed numerical simulations of cluster destruction are presented in Sect. 5.2.
(6)More detailed numerical simulations of cluster destruction are presented in Sect. 5.2.
3.2. Scattering of M 67 to its high altitudes: a global synthetic approach. The detailed Galatic model
As discussed above, the spread of open clusters vertically relative to the Galactic plane may be the result of a process where many GMC collisions are involved. Also other phenomena may play important roles such as gravitational perturbations by spiral arms in the Galactic disk or the bar. In order to obtain realistic numbers on the probability of the scattering of stars and clusters to high latitudes in this “Galactic landscape” we have carried out numerical simulations of orbits of individual test particles moving in a model galaxy with stars, spiral arms, a central bar and GMCs included. Each of the test particles represents a star or a cluster. The destruction of the clusters by tidal interaction is considered schematically but is also studied in some detail (see Sects. 3.3 and 5.1, below).
The test particles move in an axially symmetric Galactic potential according to Potential I of Binney (2012), adjusted to be consistent with a circular speed of 220 km s-1 at R0 = 8 kpc and with some corrections for added masses described below. The mass distribution has components from thin and thick stellar disks, a gas disk, and a stellar and dark spheroid representing the Bulge and the Halo. (We have also made experiments with modifications of the z-gradient of the potential by ±10% to explore the effects of its uncertainties.) To this we have added two stellar spiral arms, following the recipe of Pichardo et al. (2003, 2012), with a pitch angle of 15.5 deg, a radial scale length exponential mass decrease along the arms of 3.9 kpc, a mass of 4 × 109 M⊙ and a constant pattern speed of 24 km s-1 kpc-1. Each arm is represented numerically by 100 oblate inhomogeneous spheroids with semi-major and minor axes of 1000 pc and 500 pc respectively, and with a mutual distance between the spheroid centres of 500 pc. The bar is represented by a prolate inhomogeneous spheroid following Pichardo et al. (2003) and Pichardo et al. (2012), with a total mass of 1.6 × 1010 M⊙, with density scale lengths in the Galactic disk of 1.7 kpc (along the major axis, which corresponds to an effective boundary of the bar at 3.13 kpc) and 0.54 kpc, respectively, with the axis perpendicularly to the plane also assumed to be 0.54 kpc, and with an angular speed of 55 km s-1, kpc-1. For the spheroids, representing the bulge as well as for those of the spiral arms, we adopted a linear density variation with radius, as used by Pichardo et al. For motivations and uncertainties in the parameters of these representations, see Pichardo et al. (2012). Both the set of spiral arms and the bar are assumed to be stationary rotating structures with constant angular speeds. It should be noted that the different elements in the model, including the overall Galactic potential, the spiral arms and the bar, are not dynamically consistent from the outset, nor are they allowed to relax to a dynamically consistent configuration. This kinematical, rather than dynamical, model has however the virtue that it may be supposed to describe a reasonably realistic semi-empirical potential. We consider it probable that its lack of consistency does not lead to extra scattering of the test particles. Sooner could such scatter be introduced if the model was made more dynamically consistent, before the various elements had relaxed. The numerical representation of the gravitational forces from these different components is described in Appendix B.
The GMCs were initiated from randomly chosen points in the spiral arms, within a distance of ±50 pc from the median line of the arm, and with a number density decreasing exponentially along the arm to match that of the stellar arm itself. As an alternative, the GMCs were generated randomly in the disk, also outside the arms, however, again with an exponential decrease of the formation probability with the distance from the galactic centre. It was found that the effects on the final statistical properties of the stellar/cluster orbits in the simulations of shifting between these two alternatives were astonishingly small – less than 2 km s-1 in the final velocity scatters for stars at a distance of about 8 kpc from the Galactic centre. Subsequently, only results for the first alternative, that is GMCs originating close to the spiral arms, are given. The GMCs were given initial velocities with Gaussian distributions and according to a characteristic velocity ellipsoid with axes of 7 km s-1, in agreement with observations of Stark (1984), see also Larson (1979) and Fukunaga (1984) but greater than those of Ramesh (1994); however, experiments with values lower than 7 km s-1 did not lead to very significant changes of our final results. We found that with this initial velocity distribution our ensemble of model clouds showed a z distribution with e-fold decrease relative to the plane at a z of ±75 pc which is close to the observed value of SSS. Again, however, the final result is relatively independent of our assumed starting-velocity distribution for GMCs. The maximum mass of cloud #i, Mi, was selected randomly with a distribution function (see Williams & McKee 1997; and Hopkins et al. 2012, HQM below) of 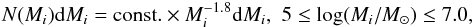 (7)while no clouds were generated with maximum mass outside this interval. In our standard models the GMCs were just added to the homogeneous disk with the total disk mass (and thus gas density) correspondingly globally reduced. In alternative models, mass conservation was considered more locally, see below. The evolution of the clouds was considered as follows: Each GMC was given an individual life time corresponding roughly to a few free-fall times of the cloud, that is 40 million years total, with a mass increasing to a value Mi over 20 million years, and then decreasing to zero over another 20 million years (see HQM), in fair agreement with the simulations of Krumholz et al. (2006) and Goldbaum et al. (2011), following a parabolic mass evolution:
(7)while no clouds were generated with maximum mass outside this interval. In our standard models the GMCs were just added to the homogeneous disk with the total disk mass (and thus gas density) correspondingly globally reduced. In alternative models, mass conservation was considered more locally, see below. The evolution of the clouds was considered as follows: Each GMC was given an individual life time corresponding roughly to a few free-fall times of the cloud, that is 40 million years total, with a mass increasing to a value Mi over 20 million years, and then decreasing to zero over another 20 million years (see HQM), in fair agreement with the simulations of Krumholz et al. (2006) and Goldbaum et al. (2011), following a parabolic mass evolution: ![\begin{eqnarray} M_t = \left\{-0.25 \cdot [(t-t_0)/10^7]^2 + (t-t_0)/10^7)\right\}\cdot M_i, \label{eq379} \end{eqnarray}](/articles/aa/full_html/2016/09/aa23916-14/aa23916-14-eq69.png) (8)where t0 is the time of the formation of the GMC and t the running time, both in years. The evolution effects made the distribution of average masses vary between the limits 2/3 × 105−2/3 × 107 M⊙ while the distribution for the clouds in general has the limits 0−107 M⊙. We note, however, that Fukui & Kawamura (2010) found a maximum GMC mass of 5 × 106 M⊙ in nearby galaxies. The mass distributions of Williams & McKee and HQM continue below our lower maximum-mass limit by one order of magnitude; these numerous lighter clouds were not included explicitly in the calculations of orbits, which in general are less strongly affected by these clouds, but included in the contribution from the gas disk to the general Galactic potential. The values of t0 for the individual clouds were taken at random through the time interval from 0 to 4.6 Gyr, adopting a probability distribution constant in time, that is we assume the number of GMCs in the Galaxy not to vary systematically with time. In the standard case, each GMC was represented by a Plummer sphere (Plummer 1911) with a typical radius Rc of about 20 pc (SSS), and Rc scaling with the square root of the cloud mass as suggested by HQM,
(8)where t0 is the time of the formation of the GMC and t the running time, both in years. The evolution effects made the distribution of average masses vary between the limits 2/3 × 105−2/3 × 107 M⊙ while the distribution for the clouds in general has the limits 0−107 M⊙. We note, however, that Fukui & Kawamura (2010) found a maximum GMC mass of 5 × 106 M⊙ in nearby galaxies. The mass distributions of Williams & McKee and HQM continue below our lower maximum-mass limit by one order of magnitude; these numerous lighter clouds were not included explicitly in the calculations of orbits, which in general are less strongly affected by these clouds, but included in the contribution from the gas disk to the general Galactic potential. The values of t0 for the individual clouds were taken at random through the time interval from 0 to 4.6 Gyr, adopting a probability distribution constant in time, that is we assume the number of GMCs in the Galaxy not to vary systematically with time. In the standard case, each GMC was represented by a Plummer sphere (Plummer 1911) with a typical radius Rc of about 20 pc (SSS), and Rc scaling with the square root of the cloud mass as suggested by HQM, 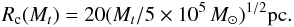 (9)
(9)
In some orbit simulations we also kept one tenth of the GMC mass concentrated into a homogeneous core with a radius of 1 pc to take the existence of condensed cores in the centres of the GMCs into reasonable consideration (see, e.g. Bergin et al. 1996). The modifications of the final results were, however, marginal. The effects of other modifications of the internal structure of the GMCs and their surroundings were found to be considerable. These will be discussed in Sect. 4.
The total number (4000) of GMCs in the present Galactic disk as estimated by SSS mainly includes clouds with masses ≥105 M⊙. Williams & McKee (1997) in their Table 4 favour a higher number of clouds, but most of these clouds have lower masses than the lower limit of our mass interval (and that of SSS), while if we limit the interval to our effective range of average masses from 6.7 × 104−6.7 × 106 M⊙ we find numbers of 2000–3000 from the distributions of Williams & McKee. We note, however, that a very considerable fraction of the clouds included in the study by Williams & McKee were still undetected, and only statistically and schematically corrected for. Willams & McKee have adopted the value of 1.0 × 109 M⊙ for the total Galactic molecular mass. 73% of this mass is then found in clouds with masses above 6.7 × 104 M⊙. The corresponding total GMC mass given by SSS is 2 × 109 M⊙, while Nakanishi & Sofue (2016) found an H2 mass of 8.5 × 108 M⊙. We here adopt the value of Williams & McKee for the total mass and then find, when reducing it to represent our mass interval, a total number of clouds of 2500 at present in the Galaxy. With a cloud life-time of 40 Myr and assuming the present density of GMCs to be representative for the last 4.6 Gyr in the Galaxy, our value for the total mass of the molecular gas corresponds to an ensemble of altogether about 300 000 GMCs, the action of which was included in our simulations. As an alternative, we also explored the results of increasing this number to 460 000, which then corresponds to the figures given by SSS.
In our rather complex Galaxy potential the molecular gas model clouds were moving, however the cloud-cloud interaction was not included in calculating the cloud orbits. As for the GMCs the test particles representing clusters or stars were initiated in the Galactic plane and their initial radial distances (between 4 and 9 kpc) from the Galactic centre and velocities were chosen randomly. Our main ambition has been to study the velocity distribution and the z-distribution for stars and clusters around the solar circle, while most stars form inside that due to the exponential density profile of the gas disk. Therefore, to get an optimal statistics we have biassed the distribution of test particles by giving an equal probability for their origins for every given value of their galactocentric distances R0, 4 kpc <R0< 10 kpc, and next, in the final calculation of distributions, means and standard deviations, given the particles different weights wp according to wps exp(−R0/ 4800) pc, following the exponential gas disk of Potential I of Binney (2012). It should be noted that the starting points for the particles were not correlated with the GMCs, except for the general concentration towards the Galactic disk. This statistical independence may underestimate the effects of GMCs on clusters and stars which are generally formed in dense gas clouds.
The particles were given random initial velocities according to a spherical velocity ellipsoid relative to the local circular rotation speed in the Galactic potential with a Gaussian spread of 7 km s-1 in the three velocity components U, V and W. The orbits of the test particles were followed for 4.6 × 109 yr. The number of test particles N∗ was in most runs typically chosen to be 500–1000 in order to secure enough of orbits for reliable statistics, for example on the resulting velocity distributions and the distribution of distances from the Galactic disk at the end of the integration. In some runs, N∗ was lowered to 200.
The orbits were obtained from the equations of motion (for a test particle of unit mass) in cylindrical coordinates:  Here, R is radial coordinate of the particle as measured from the Galactic centre in the Galactic plane, φ is the corresponding angular coordinate, measured relative to a fixed direction in space, Φ is the smooth axisymmetric gravitational potential, FR and F⊥ are the components of the sum of the forces, not represented by the potential Φ, that affect the motion of the particle. These components are directed away from the centre and perpendicularly to that direction, respectively, and are parallel to the Galactic plane. Fz is the corresponding force component in the z direction.
Here, R is radial coordinate of the particle as measured from the Galactic centre in the Galactic plane, φ is the corresponding angular coordinate, measured relative to a fixed direction in space, Φ is the smooth axisymmetric gravitational potential, FR and F⊥ are the components of the sum of the forces, not represented by the potential Φ, that affect the motion of the particle. These components are directed away from the centre and perpendicularly to that direction, respectively, and are parallel to the Galactic plane. Fz is the corresponding force component in the z direction.
Before proceeding to calculating the orbit numerically, we integrate the second of the equations above to obtain 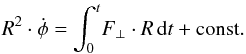 (13)The integration constant is determined by the initial conditions. Next, in order to guarantee a full angular-momentum versus torque balance,
(13)The integration constant is determined by the initial conditions. Next, in order to guarantee a full angular-momentum versus torque balance, 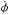 as obtained from Eq.(13) is substituted into Eq. (10), leading to the system
as obtained from Eq.(13) is substituted into Eq. (10), leading to the system
In practice, the system was solved for the variable r = R−R0 where R0 was chosen to be the initial R coordinate of the test particle and the variable ϕ = φ−R0·ω0 where ω0 is the angular speed of rotation at R0. During the integration, also velocities U, V and W were calculated. For this system, stable solutions were obtained for integration times extending to at least 5 × 109 yr by standard MATLAB routines such as ode23s based on a second-order Rosenbrock formula (Shampine & Reichelt 1997), as was demonstrated by comparison to detailed integration using the 15th order RADAU integrator by Everhart (1985). The particle was deleted from the cluster statistics if it ever came so close to a GMC, and with such small relative velocity that the condition Eq. (6) for disruption of the cluster was fulfilled. In adopting this criterion, however, we used Vn, the relative velocity when the particle was at its minimum distance from the GMC, instead of V0, the relative velocity at infinity. It is easy to prove that applying Eq. (6) in this way to calculate a critical distance bn and deleting all clusters within distances bn from the GMCs will lead to a systemactic overestimatation of the destruction rate of the clusters: all clusters with b<bcrit will (in the two-body case) come closer to the corresponding GMC than bn. The overestimate of the destruction rate will mainly be significant of low-velocity encounters.
For test particles that fulfilled this criterion of cluster destruction a flag was set but we continued the orbit calculation for totally 4.6 Gyr, in order to be able to apply the results also in comparsions with observations for individual field stars.
We performed test simulations with and without the effects of GMCs, spiral arms and the Galactic bar. As a standard, 500 test particles were followed for 4.6 Gyr in the model system in every run. The calculations were performed with the Tintin 2560 core cluster and the Milou 3338 core cluster at Uppsala Multidisciplinary Centre for Advanced Computational Science (Uppmax). In order to get satisfactory statistics for the calculation of the number of test particles ending up at high latitudes, we performed several of the runs repeatedly. The calculations were run in parallel in a simple manner such that the orbit for each test particle was run on its own core. Typical runs with N(GMC) = 300 000 took about 40 h on each core.
3.3. The cluster destruction in detail
We have tested the adequacy of Eq. (6), as a basis for estimating the risk of cluster destruction, by numerical N-body simulations, using the gravitational N-body code NBODY6, Aarseth (2003). In order to make the problem of modelling the encounters tractable, we consider only three initial cluster models. Inspired by the models for M 67 of Hurley et al. (2005) we started each of these models with an initial mass of 2.6 × 104 M⊙, made up of 36 000 stars distributed in mass according to a Kroupa et al. (1993) IMF. The stars were spatially distributed according to a Plummer (1911) distribution. The choice of initial half-mass radius is somewhat arbitrary. Hurley et al. (2005) choose an initial half-mass radius of rh,i ≃ 4 pc, which with the tidal field that they adopt ensures that the cluster is close to filling its tidal radius at formation time. However they point out that an adequate model of M 67 can be made using a smaller initial half-mass radius of, say, rh,i ≃ 1 pc, as in Hurley et al. (2001). In this case the cluster initially does not fill its tidal radius but evolves with a shorter dynamical timescale such that by a time of 4 Gyr both models have rather similar structures. We therefore considered models with initial half-mass radii of 1 pc, 2 pc and 4 pc. This covers the range of initial conditions indicated by Hurley et al. The significance of the choice of initial half-mass radius is discussed further at the end of this section.
The initial velocities were chosen so as to give a virial ratio of 0.5 in isolation. We chose to treat the stars in our simulations as point particles of constant mass and to ignore primordial binaries. The reason for this was two-fold. Firstly, the resulting simulations are computationally considerably more straightforward, both in terms of total runtime and reliability. Secondly, and more significantly, both the inclusion of primordial binaries and stellar evolution increase the variability of a cluster’s evolution; that is, they make the behaviour more stochastic. We were interested in isolating the dynamical effects of the encounters with GMCs, hence we chose to make our simulations as simple as possible.
We tested both the immediate effects of encounters with GMCs on stellar clusters and the subsequent evolution of the post-encounter clusters using a two-step process. In the first step, the encounter of a cluster with a GMC was modelled. The GMC was treated as a Plummer potential of total mass M, interacting with the cluster only through the gravitational force that it exerts on the stars; the force of the stars on the cloud was neglected. The cloud was set up at an initial spatial position of (x,y,z) = (−100 pc,−b,0) relative to the cluster, which was initially at rest at the origin. In addition, the cloud was given an initial velocity with respect to the cluster of (Vx,Vy,Vz) = (V0,0,0). The cluster was evolved in this varying potential until the cloud had travelled 200 pc from its starting position. A grid of values of GMC mass M, impact parameter b and relative velocity V0 were modelled, as summarised in Table 2. This part of the simulation was carried out with no external force; that is neglecting any effects of the Galactic tidal field.
Parameters of the cluster destruction simulations.
Once the cloud had reached a position of (100 pc,−b,0) the simulation was stopped. The cloud potential was removed and the simulation re-centred on the centre of momentum frame of the stars. A linearised solar circle Galactic tidal field was imposed following the method described in Aarseth (2003). and the simulations continued until the cluster had evaporated.
The outcome of the first step of one of the cluster destruction simulations can be seen in Fig. 2. It can be seen that the cluster has been accelerated in the -y direction. Two tidal tails of stripped stars are visible, as well as a small group of stars which have become entrained in the GMC and are visible as the small black halo towards the top right of the figure. The majority of stars in the tidal tails and the small halo have become unbound from the cluster, and hence are removed by the tidal field of the Galaxy when it is imposed. However the majority of the cluster has remained bound and can be identified as the solid black object located at approximately y = −100 pc. This model cluster survives the encounter with the loss of aproximately 8000 stars from its original 36 000.
 |
Fig. 2 Positions of stars projected onto the cloud-cluster orbit plane in one of our cluster-destruction simulations. Red/grey dots show the initial positions of stars in our model cluster. Black dots show the positions of stars at a time of 20 Myr, just before the GMC is removed from this simulation; i.e. at the end of step one of the two-step process described in Sect. 5.2. Positions are plotted in the frame in which the cluster centre of mass is initially at rest. Horizontal line shows the motion of the GMC in this frame from left to right, with the end points showing its position at the times when it is inserted and removed, and the encircling dashed line its half-mass radius. The star cluster in this example simulation had an initial half-mass radius rh,i = 2 pc and interacted with a cloud of mass M = 3 × 105 M⊙ and half-mass radius of 5 pc, moving at a relative velocity at infinity of V0 = 10 km s-1. The impact parameter was b = 10 pc. |
3.3.1. Results of N-body simulations of cluster/GMC encounters
In a small number of cases the cluster was completely disrupted by the encounter; that is, there was no discernible bound object remaining. In all cases such clusters were those predicted to be disrupted by the criterion of Eq. (6). All other cluster models were evolved, losing stars in the Galactic tidal field, until only a few tens of stars were left. We found that the evolution of the total number of stars Ni in cluster i as a function of time t was in each case fairly well-fitted by a function of the form 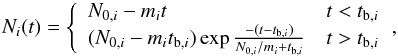 (17)where the initial number of stars, N0,i, the initial slope, mi, and the break time at which the function transitions from a straight line to an exponential decay, tb,i are parameters of the fit, which we obtained using a least-squares fitting procedure. Figure 3 shows an example fit.
(17)where the initial number of stars, N0,i, the initial slope, mi, and the break time at which the function transitions from a straight line to an exponential decay, tb,i are parameters of the fit, which we obtained using a least-squares fitting procedure. Figure 3 shows an example fit.
 |
Fig. 3 Evolution of the number of stars N with time t in one of our cluster destruction simulations. The example simulation had an initial half-mass radius rh,i = 2 pc and interacted with a cloud of mass M = 3 × 105 M⊙, moving at a relative velocity at infinity of v∞ = 10 km s-1. The impact parameter was b = 10 pc. The thin, black, solid line shows the evolution of N from the N-body simulation. The red, dashed, thick line shows the best-fit fitting function. |
The evolution of the half-mass radius with time is slightly more complex than that of the total number of stars since it initially increases owing to internal dynamical processes, then decreases once the cluster fills its tidal radius and starts to lose mass. After some experimentation we found that we could obtain an adequate fit from a broken quadratic function, although the fit is in general less accurate than that to the total number of stars, particularly in the later parts of the evolution. The fitting function that we adopted is 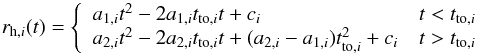 (18)where the fit parameters are the two curvatures, a1,i and a2,i, the initial value, ci, and the turnover time, tto,i. An example fit is shown in Fig. 4.
(18)where the fit parameters are the two curvatures, a1,i and a2,i, the initial value, ci, and the turnover time, tto,i. An example fit is shown in Fig. 4.
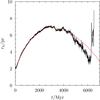 |
Fig. 4 Evolution of the cluster half-mass radius rh with time t in one of our cluster destruction simulations. As in Fig. 3, the example simulation had an initial half-mass radius rh,i = 2 pc and interacted with a cloud of mass M = 3 × 105 M⊙, moving at a relative velocity at infinity of v∞ = 10 km s-1. The impact parameter was b = 10 pc. The black solid line shows the evolution of rh from the N-body simulation. The red dashed line shows the best-fit fitting function. |
Having obtained fitting parameters for each of our clusters, we investigated their behaviour as a function of the analytically predicted fractional change in cluster-binding energy. Here we have here used a slightly different definition of the predicted fractional change in binding energy from that given in Eq. (5): 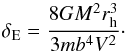 (19)We note that we here use the cluster half-mass radius rh, directly provided by our N-body simulations, rather than the root-mean-square radius rs. The fractional change in the binding energy is a quantity which relates to the degree of cluster dissolution but its exact absolute value is not of importance here. Therefore, the scaling difference between ΔE/E and δE is not significant. The reason for using δE rather than ΔE/E, as measured from the simulations, is that we wish to adapt our results to encounters which we have not made N-body models of. δE can be calculated for any encounter, whereas ΔE/E must be obtained from N-body simulations. Having plotted all the fitting parameters as functions of predicted δE, we found that there was a consistent trend. For each value of rh,i, up to a given value of δE, the values were constant, up to some scatter. This implies that weak encounters have very little effect on the evolution of the cluster. At larger values of δE we found that the fitting parameters varied, up to some much larger scatter, approximately linearly with log 10δE. Hence we fit, for each of our original fitting parameters, constant values breaking to a straight line as a function of log 10δE; see Fig. 5 for an example. This process allows us to, for any encounter, having calculated δE, generate fit parameters for the evolution of N and rh with time and hence easily simulate the evolution of the cluster.
(19)We note that we here use the cluster half-mass radius rh, directly provided by our N-body simulations, rather than the root-mean-square radius rs. The fractional change in the binding energy is a quantity which relates to the degree of cluster dissolution but its exact absolute value is not of importance here. Therefore, the scaling difference between ΔE/E and δE is not significant. The reason for using δE rather than ΔE/E, as measured from the simulations, is that we wish to adapt our results to encounters which we have not made N-body models of. δE can be calculated for any encounter, whereas ΔE/E must be obtained from N-body simulations. Having plotted all the fitting parameters as functions of predicted δE, we found that there was a consistent trend. For each value of rh,i, up to a given value of δE, the values were constant, up to some scatter. This implies that weak encounters have very little effect on the evolution of the cluster. At larger values of δE we found that the fitting parameters varied, up to some much larger scatter, approximately linearly with log 10δE. Hence we fit, for each of our original fitting parameters, constant values breaking to a straight line as a function of log 10δE; see Fig. 5 for an example. This process allows us to, for any encounter, having calculated δE, generate fit parameters for the evolution of N and rh with time and hence easily simulate the evolution of the cluster.
 |
Fig. 5 Behaviour of tb, break time in the fits of N with t, as a function of predicted δE. Model clusters with initial half-mass radii of 1, 2, and 4 pc are shown by black squares, red circles and blue triangles respectively. The solid black, dashed red and dotted blue lines show the fits adopted to the results for half-mass radii of 1, 2, and 4 pc respectively. |
3.3.2. Synthetic cluster encounters
In order to use our formalism to predict the effect of encounters on our clusters, we make two basic assumptions. The first is that we can treat multiple encounters by summing the fractional change in cluster binding energy δE. The second is that, following an encounter at time t, the properties of the cluster are the same as those of the same cluster with the same δE had the encounter occurred at time t. Having done this, we follow the history of each cluster in our global synthetic simulation. Starting at time zero, the cluster is taken to have δE = 0. When it first encounters a GMC we use the velocity and distance at closest approach to generate b and V0 for the encounter, and our fits to an unperturbed cluster evolution to obtain m and rh. We then use Eq. (19) to calculate the change in binding energy. Finally we step forwards to the next encounter and repeat the process, but this time using the fits for the newly increased value of δE = 0 to obtain the cluster properties at the time of encounter.
3.4. Resulting stellar orbits and velocity dispersions in the Galaxy simulations
We have generated a great number of sets of simulated orbits for test particles moving for 4.6 Gyr with different parameters in the recipes for the various potentials and the number and distribution of GMCs. Here, we concentrate on one homogenous set with varying the main contributors to the gravitational potential, the overall Galaxy, the spiral arms, the Galactic bar and the GMCs. Results of simulations with altogether 300 000 GMCs, are summarised in Table 3 and illustrated in Figs. 6 and 7. In the figures, some typical orbits are illustrated in the R−z plane, rotating in the Galaxy model with the momentary angular speed so that the test particle stays in the plane. Figure 7 shows an orbit that ended at high latitudes. As we can see, the effects of the inhomogeneities in the potential, in particular those caused by the GMCs, lead to considerable deviations from the standard box-shaped regular orbits shown in standard text books. The strengths and variations of the different forces that attract the test particles radially in the Galactic plane are illustrated in Fig. 8.
In Table 3 resulting dispersions after 4.6 Gyr are given in U, V and W velocities, that is in the R, φ and z-directions, respectively, as measured in the Galactic plane at the distance of 8 kpc from the Galactic centre. Here, all test particles around the solar circle after 4.6 Gyr are included, not only the surviving cluster-representing particles. However, in order to get good enough statistics, we had to widen the ring to include all particles within a range of 7 kpc <R< 9 kpc, then compensating for the R-dependent differential rotation. This, as well as the limited statistics, brought some errors into the dispersions. Based on a sequence of different simulations all including the effects of the bar, giant molecular clouds and spiral arms, here referred to as BGS simulations, and realistic variation of the model parameters, we estimate that the relative errors may amount to 10% in σU, 15% in σV, while σW is less affected. None of these errors affect our conclusions, but the values given in Table 3 should not be overinterpreted. In addition, local velocity dispersions are presented in the table for all the test particles, thus mainly biassed towards the inner parts of the Galaxy as a result of the exponential density distribution of the disk. Also given in the table are measures of migration in the radial direction of the test particles, as well as the fraction f400 of test particles that at 4.6 Gyr have | z | > 400 pc, and the probability of survival of those when representing clusters, S400, as following from Eq. (6).
 |
Fig. 6 An orbit of a test particle from a simulation with bar, GMCs and spiral arms (BGS) in the R−z plane, followed for 4.6 Gyr. |
 |
Fig. 7 An orbit of a test particle from a BGS simulation in the R−z plane, followed for 4.6 Gyr. This particle is one of the few that reached a height above the Galactic disk above 400 pc. |
 |
Fig. 8 Varying radial forces per mass unit from spiral arms (black curve, low frequency variation), GMCs (black curve, overlaid high frequency variations) and the Galactic bar (red/grey curve) as a function of time for 1/10 of the full simulation time range for a particular test particle. The mean distance of this particle from the Galactic centre is 6.8 kpc. Acceleration due to the overall-Galactic potential was about 2 × 10-11 pc yr-2. When calculating the comparatively little varying acceleration due to the bar, the mean acceleration from a point mass of corresponding mass in the centre of the Galaxy has been subtracted. |
As is seen in Table 3 the inclusion of forces from the GMCs and spiral arms contribute essentially to increasing σU in the inner Galaxy while spiral arms and the bar are less important for stars in the solar neighbourhood. For σV spiral arms and, less so, GMCs contribute importantly and, as it seems, nonlinearly. For the velocity dispersion perpendicular to the Galactic plane, the dominating factor is the scattering by the GMCs. It should be noted that the heating effects of the bar close to resonances may be of significance.
In Table 3, also the ratio σU/σW at the solar circle is given. We can see that the ratio stays safely below the critical value of 3.4 above which an infinite slab will be subject to bending instabilities, see Sellwood (1996) and references therein. In Fig. 9 we display the variation of the velocity dispersions as a function of time, compared with the observations of solar-type stars of different ages in the solar enviroment by Holmberg et al. (2009). A rather good agreement with observations is found, in particular for σU and σW. The calculated values for σV are somewhat high for ages less than 2 Gyr. It is interesting to note that the calculated values of the dispersions, for models with N(GMC) increased from 300 000 to 460 000, increase by typically 10% for the oldest stars and less than half of that for the younger ones. A model with a higher value of N(GMC) would have led to a better agreement with the observed slope of the σV-age relation, although the absolute values of σV would be too high.
We see from Table 3 that while the test particles in the model Galaxy as a mean have not moved substantially in the radial direction, the range of individual migration is fairly extensive, with a dispersion bf σδR of about 1 kpc for models with GMCs and/or spiral arms. The stars of solar age in the solar neighbourhood, however, are predicted to have formed further in, at a mean galactocentric distance ⟨ R0 ⟩ typically 300 to 600 pc closer to the Galactic centre, essentially reflecting the asymmetric effects of scattering, due to the exponential star density in the Galactic disk. This scattering is provided by both the spiral arms and the GMC scattering. The differences between the present Galactocentrick distance of the Sun and ⟨ R0 ⟩ are somewhat greater than that obtained in simulations by Yasutomi & Fujimoto (1991), but smaller than that (of 2 kpc) suggested by Wielen et al. (1996) for the Sun in an attempt to explain its comparatively high metal content, as well as by Sellwood & Binney (2002) as a result of transient spiral arms, see also Bland-Hawthorn et al. (2010) and Minchev et al. (2012).
A glance at Table 3 might give the impression that the effects of stationary (though rotating) spiral arms on the velocity dispersions and on the migration of stars are relatively small in general. This impression is misleading, however: the spiral arms contribute substantially to the velocity scatter in U and V in the inner Galaxy, albeit still little to the scatter in W. The differences between the spiral-arm effects at the solar circle and inside it may be ascribed to the general exponential profile of the spiral arms and the fact that the co-rotation radius (at 9.16 kpc with the data adopted) is not so distant from the solar circle.
 |
Fig. 9 Dispersions σU8 (red lines), σV8 (blue lines) and σW8 (black lines) in U, V and W velocity components, respectively, calculated for stars around R = 8 kpc in a BGS simulation (i.e. with bar, GMCs and spiral arms included), full lines, and when crossing the Galactic plane (for σW). Also plotted are the stellar observations of Holmberg et al. (2009) as dots (U: full, V: open) and asterisks (W), with a colour coding corresponding to that used for the models. |
Results after 4.6 Gyr of model simulations for different Galactic model.
In Fig. 10 the distribution of distances from the Galactic plane after 4.6 Gyr for the test particles of the BGS simulation is displayed. It is seen there and from Table 3 that there is a tail of high-latitude orbits resulting, but the fraction of orbits ending above 400 pc is low, ranging in the interval 0.5−2% for different runs, the exact value depending on the details of the Galaxy model such as the number of GMCs and the z dependence of the potential.
 |
Fig. 10 The | z | distribution of test particles after 4.6 Gyr, in a BGS simulation with 300 000 GMCs. Marked in red are the model star clusters that would survive for the full period, according to Eq. (6). |
4. The consequences of detailed GMC structures
An important circumstance to consider is to what extent the results of our simulations depend on the particular assumptions made concerning the structure of the GMCs. The referee of the present paper made the interesting comment that the formation of the GMCs may occur at the expense of gas in their surroundings, such that the scattering effects of the GMCs should be significantly reduced, as compared with our standard model where the GMCs are just added to the homogeneous disk with the total disk mass (and thus gas density) correspondingly globally reduced. The GMCs may have formed out of the neighbouring gas such that a hollow region might result around it. This hollow region, approximately a sphere, might produce a shielding effect, such that the net gravitational force from the GMC felt by the test particle/cluster at a distance greater than the radius of the hollow sphere (in practice beyond 50 to 200 pc, depending on the cloud mass and the height above the Galactic plane), would then be unimportant.
In testing these shielding effects, we complemented the standard GMCs in the BGS simulations by just adding an empty sphere, a void, centered around each of them, with a radius Rv determined by the mass of the GMC and the mean density of the surrounding disk. With such an approach one can easily prove that the ratio of the gravitational force from any individual GMC, relative to the standard case (when the GMC is just added to the general gas background and the gas density is correspondingly reduced), fi, is 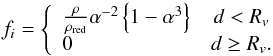 (20)Here, d is the distance from the cloud centre, α = d/Rv and ρ and ρred denote the density in the gas disk in the Galaxy and the density reduced to consider the corresponding formation of GMCs, respectively, so that the total mass of the Galactic gas disk is the same in both cases. In this approximation, the disk is considered a homogenous medium (except for the GMCs), infinite in all directions. In order to explore the effects of the finite extension of the disk gas in the z direction, we approximate it with an infinitely thin disk with constant surface density, though with a hole surrounding the GMC with a radius again corresponding to the mass of the cloud, and find the corresponding force fraction fiz to be supplementing Eq. (20) for the z-component of the force,
(20)Here, d is the distance from the cloud centre, α = d/Rv and ρ and ρred denote the density in the gas disk in the Galaxy and the density reduced to consider the corresponding formation of GMCs, respectively, so that the total mass of the Galactic gas disk is the same in both cases. In this approximation, the disk is considered a homogenous medium (except for the GMCs), infinite in all directions. In order to explore the effects of the finite extension of the disk gas in the z direction, we approximate it with an infinitely thin disk with constant surface density, though with a hole surrounding the GMC with a radius again corresponding to the mass of the cloud, and find the corresponding force fraction fiz to be supplementing Eq. (20) for the z-component of the force, 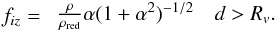 (21)While the spherical shielding of Eq. (20) should overestimate the effect of the shielding, the cylindrical shielding of Eq. (21) (within the approximation of the disk as a relatively homogenous body with a clear correlation between GMCs and hollow regions centred around them) should underestimate the effect. In Table 4 we present results of orbit simulations with the two different approaches, as compared with the standard BGS simulation. As is clearly seen, the effects of the spherical shielding on the fraction f400 of stars reaching high elevations above the Galactic plane, as well as on the velocity dispersions at the solar circle, are very considerable, while the consequences of “cylindrical shieldning” according to Eq. (21) are smaller.
(21)While the spherical shielding of Eq. (20) should overestimate the effect of the shielding, the cylindrical shielding of Eq. (21) (within the approximation of the disk as a relatively homogenous body with a clear correlation between GMCs and hollow regions centred around them) should underestimate the effect. In Table 4 we present results of orbit simulations with the two different approaches, as compared with the standard BGS simulation. As is clearly seen, the effects of the spherical shielding on the fraction f400 of stars reaching high elevations above the Galactic plane, as well as on the velocity dispersions at the solar circle, are very considerable, while the consequences of “cylindrical shieldning” according to Eq. (21) are smaller.
We performed another type of experiment in studying the effects of non-spherical structures of the GMCs: we divided each cloud into two spherical cores and displaced them horizontally and symmetrically within the still spherical void, with the void centre at their common centre of mass. Both cores were modelled with Plummer spheres. We chose the distances between the cores to be 30 pc and 100 pc, respectively (“dumbbell30” and “dumbbell100” in Table 4). This type of configuration was inspired by the fact that the observed GMCs often have an elongated and clumpy or even filamentary structure, see for example Blitz (1993). We set the angular momentum of each such pair of subclouds to zero, in view of the relatively low angular momenta found for GMCs by Imara & Blitz (2011). (An increase of their momenta to the specific momentum of their parent gas clouds due to differential galactic rotation was found to increase the scattering effects.) These systems act as quadrupoles outside the voids, with a gravitational potential decreasing with distance d in proportion to d-3. The resulting velocity scatters are shown in the table. It is seen that the scatters are smaller than for the displaced or reservoir cases (discussed below), and for the standard “naked” clouds (i.e. when the clouds are not enclosed in voids). When interpreting the results of these experiments one should note that all of the dumbbell bars were assumed to be initially directed towards the Galactic Centre. During the life times of the GMCs, the angle between the bars and the Galactic radius increased gradually, in the direction opposite to the rotation of the Galaxy, to a maximum of about 70 deg.
Results of changing the representation of GMCs from spherical clouds superposed onto an exponential gas disk model (the standard BGC case) to models with clouds surrounded by voids with a subtracted mass from the gas disk equal to the mass of the corresponding clouds.
The assumption of a spherical void in the gas disk, centred around each individual GMC is, however, not very realistic. A first argument against that configuration is that the density gradient in a stationary disk in itself implies an initial displacement of the GMC from the centre of the assumed spherical gas region from which it was formed, a region which is here supposed to define the borders of the void, by characteristically 1 pc. (Here we neglect dynamical effects except for a gravitational contraction of the cloud.) Displacements of this order of magnitude should grow exponentially, due to differential gravitational attraction from the disk, so that the GMC is moved in parallel to the disk plane a considerable distance towards the (assumed) spherical borders of the void within the lifetime of the GMC. In order to test the effects of such displacements, we have carried out simulations with the clouds randomly shifted to distances Δ from the void centres with 0 < Δ <Rv. The consequences of such cloud displacements are seen in Table 4. Basically, the scattering effects are due to the fact that empty voids as such are effective scatterers, in the sense that the net local effects of the remaining gas in the disk are unbalanced if the gas in the void is removed. In general, the scattering effects of inhomogeneities in the disk, whether due to clumps of dense gas or corresponding holes in the gas distrubution, may thus be rather similar. The effects of GMCs and local neigbouring or surrounding but off-centred voids may combine to significant scattering effects, producing wide scattering angles. Outside the voids, these systems act as dipoles, with a potential proportional to the dipole moment, mass×separation between the centre of the void and the GMC, and the inverse square of the distance from the system.
The degree to which local mass conservation prevails when GMCs form in the Galaxy certainly depends on the possible effects of non-circular and irregular mass motions in the Galactic field. We explored the effects of relaxing this condition locally by respresenting the Galactic gas disk between 4 kpc and 9 kpc from the Galactic centre as a whole by a number of 288 overlapping flat spheroids, with half axes in the Galactic plane of 500 pc each, and half axes perpendicular to the plane of 40 pc. The density distribution within the spheroids was assumed to vary linearly in all directions from their centres, and the total mass was equalled to that of the total gas disk – the corresponding potential was then subtracted from the general Galactic potential and replaced by the individual contributions from the spheroids. The spheroids were assumed to corotate in circular orbits around the Galactic centre with the local speed. Each GMC was then located within at least one such spheroid at any given time, and the gas forming the GMC was subtracted from the total mass of the spheroid, keeping the shape of its linear mass distribution. Similarly, when the GMC was dissolved its mass was given back to the spheroid where the GMC was located. If it was located in two spheroids simultaneously, its gas contribution was shared proportionally between them. The differential gas velocities needed for a model of this type to be dynamically realistic must be on the order of 6 km s-1 which is acceptable in view of the observed velocity scatter in the gas (see Sect. 3.2 above). The results of this experiment are shown in Table 4 in the row labelled “reservoir clouds”. It is seen that this arrangement causes a great velocity scatter. Obviously, the additional inhomogeneities introduced by representing the gas disk in this way (which is in itself not grossly unrealistic, cf. the observed maps in Nakanishi & Sofue 2016) adds to the scattering effects.
Summarising the results of the experiments with correlations between the GMCs and regions poor in gas (voids), supposed to represent the regions from which the GMC gas originated, we find that a high geometric correlation is needed in order to severely diminish the velocity scatter and spread perpendicularly to the Galactic plane from the results for the case with naked clouds. However, it is questionable whether this type of correlation, between GMCs and gas-poor regions surrounding them is present at all in real galaxy disks. The distribution of gas in galaxies has recently been explored in high spatial resolution, both observationally and theoretically. Thus, for 24−100 μm dust emission from the LMC, Block et al. (2010) found a structure with a power spectrum extending from k-1 ~ 7.6 pc–5000 pc with essentially two power laws, P ~ kν with ν values of 2 and 3, the latter applying for the interval k-1 ~ 7.6 pc–200 pc. This was well reproduced by hydrodynamic galaxy simulations by Bournaud et al. (2010). At a 50 pc resolution, the study by Druard et al. (2014) of CO gas in M33 does not seem to show any correlation between dense regions and surrounding voids. Altogether, these results suggest that high-density regions tend to be surrounded by regions with excess densities sooner than voids. We note that also studies of the distribution of young stars in neigbouring galaxies suggest similar correlations of dense regions with moderately dense regions, sooner than with relatively empty regions (Gieles et al. 2008; Bastian et al. 2009, 2011; Elmegreen et al. 2014).
We have studied the distribution of gas of our standard models, that is with no voids and a smooth exponential gas disk, projected onto the model plane, and found a typical slope of the logarithmic power spectrum of about 2.2 in the wavelength range extending from typical GMC radii to those of corresponding hypothetical hollow regions around them (k-1 ~ 10−100 pc). The corresponding slopes for models with the hollow spheres implemented around them is about 2.0. Corresponding differences occur in the two-point correlation functions, which is not unexpected, since they are directly related to the power spectra. From this, and the observed slope closer to three than two, we conclude that reduction of scattering effects by GMCs by surrounding voids is not expected to be important; more likely enhanced scattering effects may occur as a result of the piling up of gas around the GMCs.
We have found that the fragmented structure of the clouds may significantly affect the gravitational scattering by the GMCs. Also, the time evolution of their structure is important. This evolution, influenced by the gravitational interaction of the cluster with the fragments, each of a mass perhaps comparable to that of a young massive cluster, is supposed to accelerate/decelerate the cluster but may also lead to scattering into increased angles. We have studied this possibility in simulations by shooting point-mass particles onto schematic models of GMCs, consisting of between four and ten diffuse blobs in mutual gravitational interaction, each with masses of 105 M⊙ and with random velocities below the velocity of escape from the system. We then found the expected widening of the distribution of scattering angles and a change of the particle velocity distribution, when compared with scattering by a homogenous cloud of similar total radius and mass. Although most particles are braked by the dynamical friction from the cloud complex, as much as 10% of the particles were typically found to increase their speeds at infinity from 10 km s-1 to 20 km s-1 or more. Also, the break-up of clusters by cloud collisions may be severely dependent on the detailed cloud structure. More realistic studies of such effects, using detailed models of star-forming regions by Haugbølle, Nordlund & Padoan (cf. Padoan et al. 2014) are being pursued.
5. Discussion and conclusions
5.1. The heating of the Galactic disk and the destruction of clusters
Our simulations for test particles in a reasonably realistic Galactic potential suggest that at least for the last 5 Gyr, the observed heating of the thin Galactic stellar disk can be understood as the result of the effects of regular spiral arms, mainly accelerating the stars in the Galactic plane, and GMCs, linking the stellar orbits towards higher altitudes, a mechanism early on discussed by Carlberg (1987). In our simulations of the orbit evolution of star clusters, we have represented the clusters by simple test particles, however modelling the break up of the clusters by tidal forces due to the Galactic mean potential as well the GMCs. The effects of the latter are quite important.
The z distribution of the test particles that would have survived as clusters according to the first and standard recipe in the standard BGS simulation, is shown in red in Fig. 10. We find there and from Table 3 that only a relatively small fraction S400 of the M 67-like clusters should survive for 4.6 Gyr. We have studied the fraction of survivals as a function of the height zend above the Galactic plane in the end of the integration for a number of simulations and find the fraction to be typically a few percent for zend< 100 pc, rising to about 15% at about 200 pc, 35-50% at about 400 pc and next approaching even higher values. We stress that these estimates are based on small-number statistics and schematic; note for instance that clusters being close to the Plane but with high W velocities have a higher chance to survive individually. For N(GMC) increased to 460 000 the survival probability for the clusters that presently could be at heights above | z | = 400 pc is significantly reduced. This reduction is, however, roughly compensated for by a higher fraction of particles scattered to those heights, so that, in the end, a percentage f400 × S400 ~ 0.5% of all massive open clusters formed are predicted to end with | z | > 400 pc, rather independently of N(GMC) for the range 300 000 <N(GMC) < 460 000. Within the basic assumptions of the present Galaxy BGS model we find that the series of simulations suggest that this percentage has statistical standard errors of ±0.1%. As can be seen from the last column in Table 4, the systematic errors due to our limited understanding of the internal GMC structure could be considerably greater.
We have checked our rough standard procedure, according to Eq. (6), by applying the more detailed treament of Sect. 3.2. The survival of clusters at high latitudes turns out to be relatively independent of whether we use the criterion of Eq. (6) or the analysis based on N-body simulations described in Sect. 5.2. Figure 11 shows the internal energy absorbed by all eight particles that are scattered up to | z | > 350 pc at 4.6 Gyr in a model simulation 1000 test particles. In this particular calculation the clusters were all considered to have an initial half-mass radius of 1 pc. Four of these clusters undergo strong scatterings, which lead to vertical lines in the plot. This causes them to become rapidly disrupted thereafter, as can be seen by comparing the rate of loss of mass from the same clusters in Fig. 12. Four of the clusters do not suffer strong scatterings and hence survive until late times. One is destroyed by a series of moderate-intensity encounters, but the other three survive to an age of 4.6 Gyr. Similar results are obtained for larger initial half-mass radii.
 |
Fig. 11 History of the energy absorbed by clusters in our synthetic cluster encounter simulations, | δE |, as a function of time t. The clusters shown are the eight in total whose ultimate heights above the Plane | zend | > 350 pc. Each line shows a separate cluster, marked with a different point type and colour. Each point is an encounter between a cluster and a GMC. Large, filled, round points are those where | δE | > 1 for a single encounter. The dashed grey line indicates a cumulative | δE | value of ten, above which clusters are not found to survive. |
 |
Fig. 12 History of the stellar mass m in clusters in our synthetic cluster encounter simulations as a function of time t. The clusters shown are the eight in total whose ultimate heights above the Plane | zend | > 350 pc. Each line shows a separate cluster, indicated with a different point type and colour. Each point is an encounter between a cluster and a GMC. Colours and point types are the same as for the clusters in Fig. 11. |
The distribution of lifetimes in one of our BGS simulations with 1000 test particles/clusters, following the synthetic (N-body) cluster destruction model, are shown in Fig. 13. The median lifetime decreases with increasing initial half-mass radius, as the clusters are larger, more heated by encounters with GMCs. The median life time for rh,0 = 1 pc clusters is almost 2 Gyr which departs from the estimate given by Wielen (1971) that only 2% of the open clusters survive for more than 1 Gyr. The dominant reason for this is that our model clusters are at least one order of magnitude more massive than typical Galactic open clusters. Only a small number of clusters, however, survive until 4.6 Gyr (marked with a dashed line on the plot). For an initial half-mass radius of 1 pc the number of surviving clusters is close to that found using Eq. (6). In fact, all 36 clusters in the simulation that survived in the approximate treatment also survive in the N-body approach; the latter approach just adds one more cluster to this category. This agreement may seem astonishing, since the simulation was carried out with the standard choice of a cluster radius of 3 pc in Eq. (8) while the initial rh value in the N-body simulations is 1 pc. However, rh, representing the median radius, is supposed to be smaller than the radius used in the derivation of Eq. (6) and moreover, as is illustrated in Fig. 4, rh varies in the N-body simulations and is at all times greater than its initial value. The principal difference between the two formalisms is that the N-body treatment takes into account the variation of half-mass radius over the lifetime of the cluster.
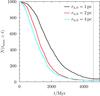 |
Fig. 13 Number of clusters N surviving for at least time t in a BGS simulation. The black, red and blue lines show initial cluster half-mass radii of 1, 2, and 4 pc. The grey dashed line represents 4.6 Gyr. |
There are shortcomings of the Rutherford (impulse) scattering approximation in treatments of the GMC-cluster interaction when a Galactic potential. Yet, this approximation is shown to give a good estimate of the critical impact parameter for the destruction of clusters, as we have demonstrated by N-body simulations of the cluster destruction process.
5.2. The origin of high-altitude old open clusters
We shall now address the question whether it is reasonable to assume that the massive high-altitude old open clusters like M 67 and NGC 188 could have originated in the Galactic plane and subsequently been brought to their high altitudes by scattering by GMCs, as well as interaction with spiral arms and the Galactic bar.
With the fraction for these clusters to be brought up to at least 400 pc, f400, of about 1.8% as a typical value from our standard BGS simulation, and a probability of survival for such clusters against tidal break-up, including GMC collisions, of S400 of typically 0.3, we find that the theoretical joint probability f400 × S400 for massive open clusters formed in the plane of the Galactic disk to be located after 4.5 Gyr at | z | > 400 pc, is about 0.5%. This is in fair agreement with the expected fraction of all formed massive Galactic clusters to be found at such high levels, as estimated to Fobs = 0.2−0.5% in Sect. 2. It should be noted here that the estimates in Sect. 2 were made after the model calculations of Sect. 5 had been completed; thus the empirical result did not at all affect the setup and constraints of the simulations. We have thus found consistency with the hypothesis that M 67 has its origin close to the Galactic plane in a normal disk orbit. As regards the significantly older NGC 188 its existence at an even higher altitude also seems consistent with the disk-origin hypothesis, and this may also be the case for the younger clusters NGC 2420 and NGC 7142.
Some verification of the present scenario for the formation of clusters, presently at relatively high altitudes, can also be found by comparing the distribution of the calculated heights z at 4.6 Gyr in Fig. 10, corrected with the probability of survival S. We find a relatively good agreement with the observed cluster distribution from the WEBDA data base as is seen in Fig. 14, as well as with the distribution of the open clusters of ages similar to that of the Hyades or older from the work by Janes & Phelps (1994), provided that we restrict the selection from their list of 72 clusters to those 42 that are within a Galactic cylinder with the Sun on its axis and a radius of 3 kpc. This restriction was applied in order to avoid the strong bias in their sample favouring high-altitude clusters at great distances, see the discussion in Sect. 2. The limited statistics makes it unclear whether the bumps in the Janes & Phelps distribution, when compared with our simulations, indicate that some extra heating phenomenon or even “unusual” formation mechanisms, like the ones discussed in Appendix A.2, are needed to explain any of these high-altitude clusters. This comparison should be extended to a sample of cluster models with a distribution in initial cluster mass and age.
In Fig. 14 we have also plotted the observed distribution of stars, as well as the calculated z (again after 4.6 Gyr) for our test particles, uncorrected with the S factor, which should then represent the distribution of stars of that age. It is seen that the observed stellar distribution is much broader – most probably due to the fact that many stars at high latitudes are significantly older than 4.6 Gyr, and this population also includes thick-disk stars.
Further simulation along the present lines, extending through the full life-time of the Galaxy, and more comparisons with more complete surveys of clusters of different ages, metallicities and at different locations, and not the least with coming Gaia data for both clusters and stars, would be valuable. Also, the dependence of the present results on the structure of the GMCs and their surroundings stresses the need for improved simulations with more detailed physical models of the insterstellar gas.
 |
Fig. 14 Predicted z-distribution of massive open clusters after 4.6 Gyr, as based on a BGS run with 1000 test particles subject to destruction due to GMC collisions (black dashed curve) and the corresponding distribution of stars (red dashed curve). The observed distribution from the WEBDA data base (Netopil et al. 2012) is indicated by black dots., and the distribution of old open clusters from Janes & Phelps (1994) within a Galactic cylinder with radius 3 kpc is marked with red circles. The bump around | z | ~ 850 pc in the latter data corresponds to altogether 2 individual clusters. The full red/grey curve denotes the observed stellar distribution, according to Yanny & Gardner (2013). We note that the scale of the N axis is ambigous, a relevant comparison is the ratio of the number of clusters around, say, z = 200, as compared with that at 500 pc. |
5.3. Did the Sun originate in M 67?
The possibility that the Sun was once formed in M 67 was discussed by Önehag et al. (2011) and Önehag et al. (2014), on the basis of their result that stars in M 67 have an abundance pattern more similar to that of the Sun than most solar twin candidates explored by Meléndez et al. (2009) and Ramírez et al. (2009). If the early M 67 really would have been the original environment of the Sun, the arguments by Pichardo et al. (2012) suggest that the Sun should have been formed in the cluster when it still had an orbit much closer to the Galactic plane and diffused out of the cluster. In some latter scattering process against one or several massive objects the cluster was then accelerated into its present high altitude orbit. In this paper we have demonstrated that this scenario is possible, in the respect that the cluster may well have formed in the plane and later been scattered up to its present locus by collisions with one or several giant molecular clouds, perhaps pre-accelerated in the plane by spiral arms.
There are, however, severe objections against this hypothesis. The first objection is based on the fact that the Sun, and the M 67 stars explored by Önehag et al. (2014), are not unique – several carefully studied field stars exist (see e.g. Meléndez et al. 2012; 2014) which have remarkably solar-like abundance profiles. Meléndez et al. (2009) note that a minor fraction (about 10–20%) of their solar twins from the solar neigbourhood resemble the Sun more than the majority of all twins (see also Nissen 2015). It thus seems possible that the number of stars with the solar abundance characteristics in the Galactic field is too great for all of them to come from one cluster. The detailed studies of the binary stars 16 Cyg (Tucci Maia et al. 2014) and XO-2 (Ramírez et al. 2015) should also be noted in this connection. In these stars, the components with discovered planets show a more solar-like abundance profile than their companions. The hypothesis brought forward by Meléndez et al. (2009) that the abundance pecularities of the Sun relate to its role as a planetary-system host, and not its more or less dense formation cluster, is supported by those findings.
The second objection arises from the expectation that the Sun left M 67 fairly early in the evolution of the solar system. There in one extra reason for such an early escape to be most probable, apart from the fact that it would give more time for the dynamical processes that we have discussed to bring M 67 into its current, highly inclined orbit. This reason relates to the existence of the Oort Cloud. In case the Sun was born in an M 67-like cluster, it has been shown by Nordlander et al. (in prep.) that any primordial Oort Cloud (i.e., one that was formed in connection with the scattering of planetesimals during the formation of the giant planets) would become disrupted in the course of some hundred Myr due to encounters with other cluster stars. This speaks in favour of a delayed Oort Cloud formation in connection with the late heavy bombardment (LHB, Brasser & Morbidelli 2013). Ongoing work on the same mechanism, when placed in the framework of M 67 or a similar dense solar birth environment (Rickman et al., in prep.), indicates a very efficient comet emplacement into the Cloud; however, any prolonged dwelling of the Sun within the cluster afterwards would cause a threat to the survival of the Cloud. Of course, if the Sun left M 67 before the LHB, the picture of Oort Cloud formation by Brasser & Morbidelli (2013) is also fairly attractive.
Nevertheless, an early exit implies that the Sun and its birth cluster have revolved many times in their Galactic orbits with somewhat different speeds. This raises our third objection against the hypothesis of an M 67 origin of the Sun: It would then be as probable that the Sun originated from any other of the M 67-like clusters that were suggested above to be around, and even much more probable that it would come from any of the other similar but more numerous clusters closer to the Galactic disk, a cluster which is since long dissolved. The only reason for believing that the Sun really has this specific origin would then be the similarity in the detailed chemical composition. It is important to study the chemical composition of other similar clusters to see if the specific solar composition profile is a characteristic signature of dense star-formation regions in general.
Acknowledgments
Johannes Andersen, Martin Asplund, Axel Brandenburg, Bruce Elmegreen, Gerry Gilmore, Ulrike Heiter, Oleg Kochukhov, Andreas Korn, Henny Lamers, Hal Levinson, Per Olof Lindblad, Jorges Meléndez, Poul Erik Nissen, Thomas Nordlander, Åke Nordlund, Hugo Pfister and Erik Zackrisson are thanked for valuable discussions and suggstions. The anonymous referee is thanked for several interesting points and valuable suggestions. Nordita is thanked by BG for hospitality. This work was supported by the Swedish Research Council, grant numbers 2008–4089, 2011–3991, 2012–2254, and 2012–5807. The simulations were performed on resources provided by the Swedish National Infrastructure for Computing (SNIC) at UPPMAX and LUNARC, using hardware funded in part by grants from the Royal Fysiographic Society of Lund. HR was supported by Grants 74/10:3 of the Swedish National Space Board and 2011/01/B/ST9/05442 of the Polish National Science Center
References
- Aarseth, S. J. 2003, Gravitational N-Body Simulations (Cambridge, UK: Cambridge University Press) [Google Scholar]
- Allen, A., & Shu, F. H. 2000, ApJ, 536, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Allen, C., & Kinman, T. 2004, in Rev. Mex. Astron. Astrofis. Conf. Ser. 21, eds. C. Allen, & C. Scarfe, 121 [Google Scholar]
- Athanassoula, E. 2013, in Bars and secular evolution in disk galaxies: Theoretical input, eds. J. Falcón-Barroso, & J. H. Knapen (Cambridge University Press), 305 [Google Scholar]
- Barbanis, B., & Woltjer, L. 1967, ApJ, 150, 461 [NASA ADS] [CrossRef] [Google Scholar]
- Bastian, N., Ercolano, B., & Gieles, M. 2009, Ap&SS, 324, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Bastian, N., Weisz, D. R., Skillman, E. D., et al. 2011, MNRAS, 412, 1539 [NASA ADS] [CrossRef] [Google Scholar]
- Bergin, E. A., Snell, R. L., & Goldsmith, P. F. 1996, ApJ, 460, 343 [NASA ADS] [CrossRef] [Google Scholar]
- Binney, J. 2012, MNRAS, 426, 1328 [NASA ADS] [CrossRef] [Google Scholar]
- Binney, J., & Tremaine, S. 1987, Galactic dynamics (Princeton, NJ: Princeton University Press) [Google Scholar]
- Bland-Hawthorn, J., Krumholz, M. R., & Freeman, K. 2010, ApJ, 713, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Blitz, L. 1993, in Protostars and Planets III, eds. E. H. Levy, & J. I. Lunine, 125 [Google Scholar]
- Block, D. L., Puerari, I., Elmegreen, B. G., & Bournaud, F. 2010, ApJ, 718, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Bonatto, C., Bica, E., & Santos, Jr., J. F. C. 2005, A&A, 433, 917 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bournaud, F., Elmegreen, B. G., Teyssier, R., Block, D. L., & Puerari, I. 2010, MNRAS, 409, 1088 [NASA ADS] [CrossRef] [Google Scholar]
- Brasser, R., & Morbidelli, A. 2013, Icarus, 225, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Brogaard, K., VandenBerg, D. A., Bruntt, H., et al. 2012, A&A, 543, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buckner, A. S. M., & Froebrich, D. 2014, MNRAS, 444, 290 [NASA ADS] [CrossRef] [Google Scholar]
- Butler, M. J., Tan, J. C., & Van Loo, S. 2015, ApJ, 805, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Carlberg, R. G. 1987, ApJ, 322, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Carlberg, R. G., & Sellwood, J. A. 1985, ApJ, 292, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Carraro, G. 2014, ASP Conf. Ser., 482, 245 [Google Scholar]
- Carrera, R., & Martínez-Vázquez, C. E. 2013, A&A, 560, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cheng, J. Y., Rockosi, C. M., Morrison, H. L., et al. 2012, ApJ, 746, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Comeron, F., & Torra, J. 1992, A&A, 261, 94 [Google Scholar]
- Conlon, E. S., Dufton, P. L., Keenan, F. P., McCausland, R. J. H., & Holmgren, D. 1992, ApJ, 400, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Druard, C., Braine, J., Schuster, K. F., et al. 2014, A&A, 567, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elmegreen, D. M., Elmegreen, B. G., Adamo, A., et al. 2014, ApJ, 787, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Everhart, E. 1985, in Dynamics of Comets: Their Origin and Evolution, Proc. IAU Colloq. 83, held in Rome, Italy, June 11–15, 1984, eds. A. Carusi, & G. B. Valsecchi (Dordrecht: Reidel, Astrophysics and Space Science Library), 115, 185 [Google Scholar]
- Ferrière, K. M. 2001, Rev. Mod. Phys., 73, 1031 [NASA ADS] [CrossRef] [Google Scholar]
- Friel, E. D. 1995, ARA&A, 33, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Friel, E. D., Jacobson, H. R., & Pilachowski, C. A. 2010, AJ, 139, 1942 [NASA ADS] [CrossRef] [Google Scholar]
- Fukui, Y., & Kawamura, A. 2010, ARA&A, 48, 547 [NASA ADS] [CrossRef] [Google Scholar]
- Fukunaga, M. 1984, PASJ, 36, 433 [NASA ADS] [Google Scholar]
- Gieles, M., Bastian, N., & Ercolano, B. 2008, MNRAS, 391, L93 [Google Scholar]
- Goldbaum, N. J., Krumholz, M. R., Matzner, C. D., & McKee, C. F. 2011, ApJ, 738, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Grand, R. J. J., Springel, V., Gómez, F. A., et al. 2016, MNRAS, 459, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Griv, E., Gedalin, M., & Yuan, C. 1997, A&A, 328, 531 [NASA ADS] [Google Scholar]
- Hänninen, J., & Flynn, C. 2002, MNRAS, 337, 731 [NASA ADS] [CrossRef] [Google Scholar]
- Hänninen, J., & Flynn, C. 2004, A&A, 421, 1001 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heiter, U., Soubiran, C., Netopil, M., & Paunzen, E. 2014, A&A, 561, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holmberg, J., Nordström, B., & Andersen, J. 2009, A&A, 501, 941 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hopkins, P. F., Quataert, E., & Murray, N. 2012, MNRAS, 421, 3488 [NASA ADS] [CrossRef] [Google Scholar]
- Hurley, J. R., Tout, C. A., Aarseth, S. J., & Pols, O. R. 2001, MNRAS, 323, 630 [NASA ADS] [CrossRef] [Google Scholar]
- Hurley, J. R., Pols, O. R., Aarseth, S. J., & Tout, C. A. 2005, MNRAS, 363, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Ida, S., Kokubo, E., & Makino, J. 1993, MNRAS, 263, 875 [NASA ADS] [CrossRef] [Google Scholar]
- Imara, N., & Blitz, L. 2011, ApJ, 732, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Janes, K. A., & Phelps, R. L. 1994, AJ, 108, 1773 [NASA ADS] [CrossRef] [Google Scholar]
- Jenkins, A., & Binney, J. 1990, MNRAS, 245, 305 [NASA ADS] [Google Scholar]
- Jílková, L., Carraro, G., Jungwiert, B., & Minchev, I. 2012, A&A, 541, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Just, A., Gao, S., & Vidrih, S. 2011, MNRAS, 411, 2586 [NASA ADS] [CrossRef] [Google Scholar]
- Kazantzidis, S., Zentner, A. R., Kravtsov, A. V., Bullock, J. S., & Debattista, V. P. 2009, ApJ, 700, 1896 [NASA ADS] [CrossRef] [Google Scholar]
- Knude, J. 1996, A&A, 306, 108 [NASA ADS] [Google Scholar]
- Knude, J. 1997, A&A, 327, 90 [NASA ADS] [Google Scholar]
- Kroupa, P. 2002, in Modes of Star Formation and the Origin of Field Populations, eds. E. K. Grebel, & W. Brandner, ASP Conf. Ser., 285, 86 [Google Scholar]
- Kroupa, P., Tout, C. A., & Gilmore, G. 1993, MNRAS, 262, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., Matzner, C. D., & McKee, C. F. 2006, ApJ, 653, 361 [NASA ADS] [CrossRef] [Google Scholar]
- Lacey, C. G. 1984, MNRAS, 208, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., & Lada, E. A. 2003, ARA&A, 41, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Lamers, H. J. G. L. M., & Gieles, M. 2006, A&A, 455, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Larson, R. B. 1979, MNRAS, 186, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Levy, V. V. 2000, Astron. Astrophys. Trans., 18, 621 [Google Scholar]
- Lindblad, P. O. 2000, A&A, 363, 154 [NASA ADS] [Google Scholar]
- Martos, M., Allen, C., Franco, J., & Kurtz, S. 1999, ApJ, 526, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Meléndez, J., Asplund, M., Gustafsson, B., & Yong, D. 2009, ApJ, 704, L66 [NASA ADS] [CrossRef] [Google Scholar]
- Meléndez, J., Bergemann, M., Cohen, J. G., et al. 2012, A&A, 543, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meléndez, J., Schirbel, L., Monroe, T. R., et al. 2014, A&A, 567, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Minchev, I., Famaey, B., Quillen, A. C., et al. 2012, A&A, 548, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nakanishi, H., & Sofue, Y. 2016, PASJ, 68, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Netopil, M., Paunzen, E., & Stütz, C. 2012, Star Clusters in the Era of Large Surveys, eds. A. Moitinho, & J. Alves (Springer Verlag: Astrophysics and Space Science Proceedings), 53 [Google Scholar]
- Nissen, P. E. 2015, A&A, 579, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oja, T. 1992, Balt. Astron., 1, 261 [NASA ADS] [Google Scholar]
- Önehag, A., Korn, A., Gustafsson, B., Stempels, E., & Vandenberg, D. A. 2011, A&A, 528, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Önehag, A., Gustafsson, B., & Korn, A. 2014, A&A, 562, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Padoan, P., Haugbølle, T., & Nordlund, Å. 2014, ApJ, 797, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Paunzen, E., & Netopil, M. 2006, MNRAS, 371, 1641 [NASA ADS] [CrossRef] [Google Scholar]
- Pichardo, B., Martos, M., Moreno, E., & Espresate, J. 2003, ApJ, 582, 230 [NASA ADS] [CrossRef] [Google Scholar]
- Pichardo, B., Moreno, E., Allen, C., et al. 2012, AJ, 143, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Plummer, H. C. 1911, MNRAS, 71, 460 [CrossRef] [Google Scholar]
- Portegies Zwart, S. F., McMillan, S. L. W., & Gieles, M. 2010, ARA&A, 48, 431 [NASA ADS] [CrossRef] [Google Scholar]
- Ramesh, B. 1994, J. Astrophys. Astron., 15, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Ramírez, I., Meléndez, J., & Asplund, M. 2009, A&A, 508, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramírez, I., Khanal, S., Aleo, P., et al. 2015, ApJ, 808, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Saffer, R. A., Keenan, F. P., Hambly, N. C., Dufton, P. L., & Liebert, J. 1997, ApJ, 491, 172 [NASA ADS] [CrossRef] [Google Scholar]
- Saha, K., Tseng, Y.-H., & Taam, R. E. 2010, ApJ, 721, 1878 [NASA ADS] [CrossRef] [Google Scholar]
- Sarajedini, A., Dotter, A., & Kirkpatrick, A. 2009, ApJ, 698, 1872 [NASA ADS] [CrossRef] [Google Scholar]
- Schlesinger, K. J., Johnson, J. A., Rockosi, C. M., et al. 2012, ApJ, 761, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Schönrich, R., & Binney, J. 2009, MNRAS, 399, 1145 [NASA ADS] [CrossRef] [Google Scholar]
- Sellwood, J. A. 1996, ApJ, 473, 733 [NASA ADS] [CrossRef] [Google Scholar]
- Sellwood, J. A. 2008, in Formation and Evolution of Galaxy Disks, eds. J. G. Funes, & E. M. Corsini, ASP Conf. Ser., 396, 341 [Google Scholar]
- Sellwood, J. A. 2013, ApJ, 769, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Sellwood, J. A., & Binney, J. J. 2002, MNRAS, 336, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Shampine, L. F., & Reichelt, M. W. 1997, SIAM J. Sci. Comput., 18, 1 [CrossRef] [Google Scholar]
- Shiidsuka, K., & Ida, S. 1999, MNRAS, 307, 737 [NASA ADS] [CrossRef] [Google Scholar]
- Solomon, P. M., Sanders, D. B., & Scoville, N. Z. 1979, in The Large-Scale Characteristics of the Galaxy, ed. W. B. Burton, IAU Symp., 84, 35 [Google Scholar]
- Sotnikova, N. Y., & Rodionov, S. A. 2003, Astron. Lett., 29, 321 [Google Scholar]
- Spitzer, Jr., L., & Härm, R. 1958, ApJ, 127, 544 [NASA ADS] [CrossRef] [Google Scholar]
- Spitzer, Jr., L., & Schwarzschild, M. 1951, ApJ, 114, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Spitzer, Jr., L., & Schwarzschild, M. 1953, ApJ, 118, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Stark, A. A. 1984, ApJ, 281, 624 [NASA ADS] [CrossRef] [Google Scholar]
- Stark, A. A., & Brand, J. 1989, ApJ, 339, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Stark, A. A., & Lee, Y. 2005, ApJ, 619, L159 [CrossRef] [Google Scholar]
- Tobin, W. 1991, in The Interstellar Disk-Halo Connection in Galaxies, ed. H. Bloemen, IAU Symp., 144, 109 [Google Scholar]
- Torres, G., Andersen, J., & Giménez, A. 2010, A&ARv, 18, 67 [Google Scholar]
- Tucci Maia, M., Meléndez, J., & Ramírez, I. 2014, ApJ, 790, L25 [NASA ADS] [CrossRef] [Google Scholar]
- van der Kruit, P. C., & Freeman, K. C. 2011, ARA&A, 49, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Van de Putte, D., & Cropper, M. 2009, MNRAS, 392, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Van de Putte, D., Garnier, T. P., Ferreras, I., Mignani, R. P., & Cropper, M. 2010, MNRAS, 407, 2109 [NASA ADS] [CrossRef] [Google Scholar]
- VandenBerg, D. A., & Stetson, P. B. 2004, PASP, 116, 997 [NASA ADS] [CrossRef] [Google Scholar]
- Villumsen, J. V. 1983, ApJ, 274, 632 [NASA ADS] [CrossRef] [Google Scholar]
- Wakker, B. P., Howk, J. C., Savage, B. D., et al. 1999, Nature, 402, 388 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Wallin, J. F., Higdon, J. L., & Staveley-Smith, L. 1996, ApJ, 459, 555 [Google Scholar]
- Wielen, R. 1971, A&A, 13, 309 [NASA ADS] [Google Scholar]
- Wielen, R., Fuchs, B., & Dettbarn, C. 1996, A&A, 314 [Google Scholar]
- Williams, J. P., & McKee, C. F. 1997, ApJ, 476, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Yanny, B., & Gardner, S. 2013, ApJ, 777, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Yasutomi, M., & Fujimoto, M. 1991, PASJ, 43, 9 [NASA ADS] [Google Scholar]
- Yoshii, Y., Ishida, K., & Stobie, R. S. 1987, AJ, 93, 323 [Google Scholar]
- Zasov, A., Saburova, A., & Katkov, I. 2013, Mem. Soc. Astron. Ital. Supp., 25, 70 [Google Scholar]
Appendix A: The possible formation of a M 67-like cluster at high latitudes
In this Appendix we explore whether the present location of the metal-rich high-altitude clusters directly discloses their mode of formation, and not a secular evolution of their orbits in the Galactic disk – this latter aspect is discussed in Sects. 3–5. First we investigate the possibility that such a cluster formed due to relatively normal star formation in an interstellar cloud belonging to the Galactic disk but in orbit with a considerable inclination to the Galactic plane, and next proceed to more “unusual” formation scenarios.
Appendix A.1: Formation from gas in high-inclination orbits
We can explore the possibility of star formation in high-inclination orbits by counting the number of known young stars at high altitudes, if we make the assumption of a non-drastically varying star-formation rate with time during the last 4–5 Gyr. Knude (1997), based on the survey by Oja (1992) of stars within 20 deg from the Northern Galactic pole and complete for V< 11.5 mag, explored the number density of stars of spectral type A2-A7 as a function of distance from the Galactic plane. From that we find a space density at z = 450 pc of 1.4 × 10-6 pc-3 for the A-type stars with ages ≤0.75 Gyr, while for the group of A-type stars with ages in the range 0.75 Gyr to 1.7 Gyr the corresponding density is 2.3 × 10-6 pc-3. Converting the spectral-type range to the mass interval 1.9−2.2 M⊙, following Torres et al. (2010), one finds from the IMF of Kroupa (2002) that this should correspond to a density of 2.6 × 10-5 stars pc-3 earlier than spectral type M or 19 × 10-5 pc-3, if also M dwarfs down to a mass of 0.08 M⊙ are included for the youngest age group. For stars in the older age range the corresponding number is 4.4 × 10-5 stars pc-3 or 31 × 10-5 pc-3, respectively. (It should be noted that here we have assumed all the stars of Knude (1997) to be main-sequence stars, i.e. we have neglected the contribution to his number-density estimates of blue horizontal-branch stars and other post-main-sequence stars, and of subdwarfs). Now, again guided by the estimates of the history of the star-formation rate in the disk of Just et al. (2011), we assume a two times larger star-formation rate 4.5 Gyr ago than presently at a height of 450 pc. We then find a maximum star-formation rate of ≤6 × 10-4 pc-3 Gyr-1. Thus, in order to provide the roughly 20 000 stars of a cluster like the initial M 67 cluster for every Gyr, one would then need to take all stars within a box of 0.5 kpc × 0.5 kpc × 100 pc that could possibly have been formed in an M 67-like orbit for 1 Gyr into consideration. Indeed, if our cluster is part of a mass distribution of clusters, so that, as discussed above, the total contribution of this (now dissolved) cluster distribution would amount to 500 000 stars, this population, now being represented by our single cluster, would then correspond to the total star production of a box on the order of 2.5 kpc × 2.5 kpc × 100 pc. This demonstrates that the assumption that the M 67-like clusters are just representative of the star formation in original high-inclination orbits, or even on high latitudes initially, seems not realistic if this star formation occurred at a rate proportional to the star formation rate in the Galactic disk today. In practice, a strong peak in star formation rate at high altitudes would have to be invoked, corresponding to an increase in this rate by about one order of magnitude. Thus, if the high-altitude clusters are just the result of normal star formation in the Galactic disk and not of such a considerable peak in the formation rate some Gyr ago, they should, as the other solar-type stars at high altitudes, have experienced a significant orbit evolution since the formation time, bringing them to greater heights above the Galactic plane, that is by disk heating.
Similar results are obtained if one considers the B-type stars at high altitudes. In his survey of stars within 20 degrees of the Northern Galactic pole and complete for V< 11.5 mag, Oja (1992) found 23 stars in the spectral-type interval B0-B8. Of these, most lie beyond 500 pc. From these we estimate, in a way similar to that for the A-type stars above, adopting an interstellar extinction AB of 0.077 mag., following Knude (1996), a corresponding total star formation rate of ≤10-4 pc-3 Gyr-1. Similar results were also obtained from the magnitude-limited spectroscopic survey of early-type hydrogen rich stars at high Galactic latitudes of Saffer et al. (1997).
We also note that Allen & Kinman (2004) have studied the samples of O and B stars found at high Galactic latitudes by Conlon et al. (1992) and others, and argue, on the basis of orbit calculations, that almost 90% of them may be run-away stars from the Galactic plane (see also Tobin 1991). This would then even more stress the need to invoke either a very high peak of star formation leading to stars at high Galactic latitudes about 4 Gyr ago, or alternatively to argue that the orbits of the high-altitude metal-rich clusters have indeed been considerably affected by disk heating.
These arguments show that if the high-altitude clusters were formed in orbits close to their present ones, they were the result of an unsusual event in the star-formation history of the Galaxy, at least if the present state of star-formation is assumed to be rather normal.
Appendix A.2: “Unusual” formation scenarios
Several “unusual” formation scenarios have been suggested for the metal-rich high-altitude clusters; see the summary by Vande Putte et al. (2010). Several of these may, however, be excluded in the case of the clusters in Table 1, primarily on the basis of their comparatively high metallicity. The following possibilities remain and should be further explored:
-
(1)
Martos et al. (1999) modelledthe gas response to the spiral arm density wave in a thickmagnetised Galactic disk and found that the spiral shock couldbring gas from the inter-arm region to high altitudes, followed bystar formation, albeit with a low efficiency.
-
(2)
Friel (1995) suggested that impact of high velocity clouds on to the Galactic disk could lead to star formation in the disk gas, a mechanism studied by Comeron & Torra (1992), who related an oblique collision of this kind to the formation of Gould’s belt. The cluster formed in the process could retain some kinetic memory of the event, leading to a high z and possibly eccentric Galactic orbits. This interpretation of Gould’s belt is, however, not generally accepted (for other alternatives, see, e.g., Lindblad 2000). It is not clear whether such high metallicities as that of M 67 could result in this case; Wakker et al. (1999) found that high velocity clouds have low metallicities of about 0.1 solar.
-
(3)
Globular clusters may impact the disk and cause disk-gas compression, either due to gravitational focussing (initially discussed by Wallin et al. (1996), who concluded that such passages, happening about once every 106 yr, may lead to a minor part of the star formation in the Galaxy) or shock wave formation, Levy (2000). Vande Putte & Cropper (2009) have tried to trace such effects caused by recent passages of globular clusters through the Galactic disk, with no very significant results. This would presumably produce clusters with metallicities representative of the disk, and perhaps high-inclination Galactic orbits with considerable eccentricities.
Appendix B: The numerical representation of the Galactic force field
The general Galactic force field has been pre-calculated from mass points in a spatial rectangular grid, representing the mass distribution adopted from Potential I of Binney (2012). The general mesh size was 50 pc, though with a decrease of the size in z (perpendicularly to the Galactic plane) to 10 pc for | z | < 120 pc and increase to 200 pc for | z] > 2000 pc. The forces in radial (R) direction, parallel to the plane, and in z were calculated along lines at equal distances between the mass points in the mesh in order to avoid spurious variation as a result of a force point close to a point in the mass grid. The force was tabulated for every 200 pc in R and every 50 pc in z, including one line in the Galactic plane. In these force tables, we interpolated using cublic splines. The resulting forces were carefully analysed as a function of distance and height above the plane, to avoid wiggles. We also tried, as an alternative, representation of the force components by polynomina in R and z (up to fourth degree), derived from the tables of Allen & Markos (1987), and found a quite satsifactory agreement with the results from the table representation. In particular, there were no tendencies for the resulting scatters in U, V and W to depart significantly from those obtained by interpolation in the force tables. We conclude that no additional velocity scatter was introduced as a result of the interpolations.
As a standard, the forces from the different spheroids used in representing the spiral arms and the central Galactic bar were pre-calculated as a function of r and angle β between the symmetry axis and direction to the point in question, and scaled with the squared distance from the centre and the cosine/sine of the angle, and next pretabulated as a function of distance and angle, for cubic spline interpolation in the orbit calculations. In the pre-calculation, a cubic grid representation of the mass distribution was used, with a mesh size of 2.5 pc. The mass at each mass point was then chosen to satisfy the density variation adopted for the spheroid. As an alternative, a Monte-Carlo approch was tried with N homogeneous spheres filling the spheroid, each sphere with a typical radius of RsN− 1/3, where Rs is the maximum size of the spheroid and the mass of each sphere was again chosen to satisfy the density variation adopted in the spheroid. Here, N was typically chosen to 108. In either case, the tables generated in r and β were typically 200 × 50 in size. In addition to the comparsion between the grid representation and the Monte-Carlo approach which showed satisfactory agreement, on the suggestion of the referee the method was checked in several ways. The appropriateness of the Monte-Carlo-representation was checked by some test cases relative to the formulae by Schmidt (1956), with high-order Gaussian quadatures to evaluate the integrals. An excellent agreement was then found. In an attempt to check the spline interpolation, and in particular the risks that wiggles in the interpolation could contribute to the scatter in resulting velocities, we approximated the tables from the pre-calculations by polynomina in β and r or 1 /r, for points inside and outside the spheroids, respectively. These polynomia were scrutinised to avoid wiggles. For points close to the spheroid surface, terms in both r and 1 /r were used, and special care was excercised in tying the approximations continuously together. Typically, 5 × 5 terms were necessary to approximate the tables with an accuracy on the order of 2%; an exception, however, was the force from the ellipsoids representing the spiral arms where both force approximations with both r and 1 /r terms were needed and the forces of the pre-tabulated tables were represented with maximum errors of 8%. When alternatively applying these polynomina instead of the standard interpolation in the tables, the resulting differences in calculated velocity scatters for the test particles were found to be less than 2 km s-1. Yet, the errors in calculating the forces from the spiral-arm spheroids seemed worrying, since the test particles/clusters in our simulations interact closely with them, and even may pass through them, with an abrupt change in the force derivates when the test particles enter from an assymptotic 1 /d2 to a d dependence, d here representing the distance from the centre of the spheroid.
In order to test this further we chose to apply our pre-calculation and interpolation techniques to spherical clouds, for which, alternatively, the forces could be calculated analytically, in our Galaxy model. We performed these experiments with only 200 test particles and a reduced number of model GMC:s (N(GMC) = 10 000) in order to save computer time; the reduction of N(GMC) is expected to exaggerate the effects of the numerical errors in the handling of the spiral spheroid forces since the test particles are not scattered so efficiently to high latitudes and thus spend more time close the Galactic plane, interacting with the spiral arms. The results are displayed in Table B.1. When replacing the spheroids in the spiral-arm representation with spheres with corresponding masses (again with a linear variation with radius of the linear density and with radii of 800 pc) we find differences in the resulting velocity scatters of the test particles of less than 5 km s-1. As seen in the table, the differences between the resulting velocity scatter when, in our spherical representation, changing from an analytical calculation of forces to the numerical interpolation are at the most 10% of the scatter as such, and not greater than what must be expected from the limited statistics. Obviously, the major change of velocity scatter in U and V velocities results from the spiral arms as such. From these different experiments we conclude that the numerical uncertainties in the calculation of forces and orbits are of little significance.
Test of the numerical errors when calculating forces from spiral-arms on test particles in our model simulations.
A probably much more severe source of error in our treatment than the numerical inaccuracies is the assumption that both the spiral arms and the Galactic bar are assumed to be stationary (although turning with constant angular velocities); more transient phenomena might induce different, and probably greater, momentum transfer to our test particles in the model.
All Tables
Results of changing the representation of GMCs from spherical clouds superposed onto an exponential gas disk model (the standard BGC case) to models with clouds surrounded by voids with a subtracted mass from the gas disk equal to the mass of the corresponding clouds.
Test of the numerical errors when calculating forces from spiral-arms on test particles in our model simulations.
All Figures
 |
Fig. 1 Distribution of high-altitude (| z | > 400 pc) clusters with positive and negative Galactic latitudes (black and red/grey, respectively). Dots indicate clusters older than 1.0 Gyr while crosses correspond to lower ages. Data were taken from Heiter et al. (2014), Paunzen & Netopil (2006), Netopil et al. (2012). The four old clusters at highest metallicity are marked by the four black dots to the right (in order left to right: NGC 2420, M 67, NGC 188 and NGC 6791. |
| In the text | |
 |
Fig. 2 Positions of stars projected onto the cloud-cluster orbit plane in one of our cluster-destruction simulations. Red/grey dots show the initial positions of stars in our model cluster. Black dots show the positions of stars at a time of 20 Myr, just before the GMC is removed from this simulation; i.e. at the end of step one of the two-step process described in Sect. 5.2. Positions are plotted in the frame in which the cluster centre of mass is initially at rest. Horizontal line shows the motion of the GMC in this frame from left to right, with the end points showing its position at the times when it is inserted and removed, and the encircling dashed line its half-mass radius. The star cluster in this example simulation had an initial half-mass radius rh,i = 2 pc and interacted with a cloud of mass M = 3 × 105 M⊙ and half-mass radius of 5 pc, moving at a relative velocity at infinity of V0 = 10 km s-1. The impact parameter was b = 10 pc. |
| In the text | |
 |
Fig. 3 Evolution of the number of stars N with time t in one of our cluster destruction simulations. The example simulation had an initial half-mass radius rh,i = 2 pc and interacted with a cloud of mass M = 3 × 105 M⊙, moving at a relative velocity at infinity of v∞ = 10 km s-1. The impact parameter was b = 10 pc. The thin, black, solid line shows the evolution of N from the N-body simulation. The red, dashed, thick line shows the best-fit fitting function. |
| In the text | |
 |
Fig. 4 Evolution of the cluster half-mass radius rh with time t in one of our cluster destruction simulations. As in Fig. 3, the example simulation had an initial half-mass radius rh,i = 2 pc and interacted with a cloud of mass M = 3 × 105 M⊙, moving at a relative velocity at infinity of v∞ = 10 km s-1. The impact parameter was b = 10 pc. The black solid line shows the evolution of rh from the N-body simulation. The red dashed line shows the best-fit fitting function. |
| In the text | |
 |
Fig. 5 Behaviour of tb, break time in the fits of N with t, as a function of predicted δE. Model clusters with initial half-mass radii of 1, 2, and 4 pc are shown by black squares, red circles and blue triangles respectively. The solid black, dashed red and dotted blue lines show the fits adopted to the results for half-mass radii of 1, 2, and 4 pc respectively. |
| In the text | |
 |
Fig. 6 An orbit of a test particle from a simulation with bar, GMCs and spiral arms (BGS) in the R−z plane, followed for 4.6 Gyr. |
| In the text | |
 |
Fig. 7 An orbit of a test particle from a BGS simulation in the R−z plane, followed for 4.6 Gyr. This particle is one of the few that reached a height above the Galactic disk above 400 pc. |
| In the text | |
 |
Fig. 8 Varying radial forces per mass unit from spiral arms (black curve, low frequency variation), GMCs (black curve, overlaid high frequency variations) and the Galactic bar (red/grey curve) as a function of time for 1/10 of the full simulation time range for a particular test particle. The mean distance of this particle from the Galactic centre is 6.8 kpc. Acceleration due to the overall-Galactic potential was about 2 × 10-11 pc yr-2. When calculating the comparatively little varying acceleration due to the bar, the mean acceleration from a point mass of corresponding mass in the centre of the Galaxy has been subtracted. |
| In the text | |
 |
Fig. 9 Dispersions σU8 (red lines), σV8 (blue lines) and σW8 (black lines) in U, V and W velocity components, respectively, calculated for stars around R = 8 kpc in a BGS simulation (i.e. with bar, GMCs and spiral arms included), full lines, and when crossing the Galactic plane (for σW). Also plotted are the stellar observations of Holmberg et al. (2009) as dots (U: full, V: open) and asterisks (W), with a colour coding corresponding to that used for the models. |
| In the text | |
 |
Fig. 10 The | z | distribution of test particles after 4.6 Gyr, in a BGS simulation with 300 000 GMCs. Marked in red are the model star clusters that would survive for the full period, according to Eq. (6). |
| In the text | |
 |
Fig. 11 History of the energy absorbed by clusters in our synthetic cluster encounter simulations, | δE |, as a function of time t. The clusters shown are the eight in total whose ultimate heights above the Plane | zend | > 350 pc. Each line shows a separate cluster, marked with a different point type and colour. Each point is an encounter between a cluster and a GMC. Large, filled, round points are those where | δE | > 1 for a single encounter. The dashed grey line indicates a cumulative | δE | value of ten, above which clusters are not found to survive. |
| In the text | |
 |
Fig. 12 History of the stellar mass m in clusters in our synthetic cluster encounter simulations as a function of time t. The clusters shown are the eight in total whose ultimate heights above the Plane | zend | > 350 pc. Each line shows a separate cluster, indicated with a different point type and colour. Each point is an encounter between a cluster and a GMC. Colours and point types are the same as for the clusters in Fig. 11. |
| In the text | |
 |
Fig. 13 Number of clusters N surviving for at least time t in a BGS simulation. The black, red and blue lines show initial cluster half-mass radii of 1, 2, and 4 pc. The grey dashed line represents 4.6 Gyr. |
| In the text | |
 |
Fig. 14 Predicted z-distribution of massive open clusters after 4.6 Gyr, as based on a BGS run with 1000 test particles subject to destruction due to GMC collisions (black dashed curve) and the corresponding distribution of stars (red dashed curve). The observed distribution from the WEBDA data base (Netopil et al. 2012) is indicated by black dots., and the distribution of old open clusters from Janes & Phelps (1994) within a Galactic cylinder with radius 3 kpc is marked with red circles. The bump around | z | ~ 850 pc in the latter data corresponds to altogether 2 individual clusters. The full red/grey curve denotes the observed stellar distribution, according to Yanny & Gardner (2013). We note that the scale of the N axis is ambigous, a relevant comparison is the ratio of the number of clusters around, say, z = 200, as compared with that at 500 pc. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.