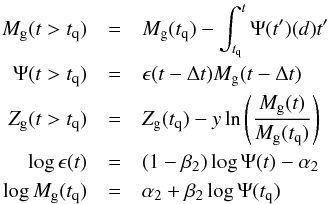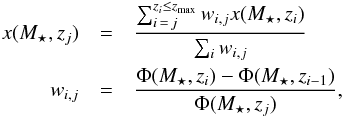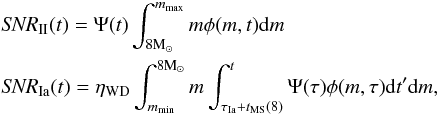| Issue |
A&A
Volume 592, August 2016
|
|
|---|---|---|
| Article Number | A96 | |
| Number of page(s) | 10 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201628834 | |
| Published online | 04 August 2016 | |
Evolution of galaxy habitability
School of Physics, Korea Institute for Advanced
Study, Hoegiro 85,
Dongdaemun-gu, Seoul
02455, Republic of
Korea
e-mail: rgobat@kias.re.kr
Received:
2
May
2016
Accepted:
20
May
2016
We combine a semi-analytic model of galaxy evolution with constraints on circumstellar habitable zones and the distribution of terrestrial planets in order to probe the suitability of galaxies of different mass and type to host habitable planets, and how it evolves with time. We find that the fraction of stars with terrestrial planets in their habitable zone (known as habitability) depends only weakly on galaxy mass, with a maximum around 4 × 1010M⊙. We estimate that 0.7% of all stars in Milky Way-type galaxies to host a terrestrial planet within their habitable zone, consistent with the value derived from Kepler observations. On the other hand, the habitability of passive galaxies is slightly but systematically higher, unless we assume an unrealistically high sensitivity of planets to supernovae. We find that the overall habitability of galaxies has not changed significantly in the last ~8 Gyr, with most of the habitable planets in local disk galaxies having formed ~1.5 Gyr before our own solar system. Finally, we expect that ~1.4 ×109 planets similar to present-day Earth have existed so far in our galaxy.
Key words: planets and satellites: terrestrial planets / galaxies: evolution / galaxies: star formation / galaxies: abundances / astrobiology
© ESO, 2016
1. Introduction
The idea of a plurality of worlds in which the universe is filled with a vast number of planets similar to our own has long been part of philosophical discourse and has acquired even more substance with the dawn of modern astronomy and the final shattering of the sphere of fixed stars. While Epicurus, Bruno, or Herschel might have had little doubt that all these worlds were inhabited, our explorations of the sky have made us finally realize how unforgiving the cosmos could be for life, and we are beginning to wonder what other environments in the universe, if any, might actually support it.
This question was partly answered in the last century with the concept of the circumstellar habitable zone (HZ; e.g., Huang 1959; Kasting et al. 1993), defined as the orbital belt around a star where the surface temperature of a planet would allow the existence of a biosphere. More recently, the idea of the HZ has by analogy been extended to that of the galactic habitable zone (GHZ; Gonzalez et al. 2001), i.e., the region within a galaxy where planets can form around stars and sustain a biosphere for a significant amount of time. Initially mostly speculative, the GHZ has become increasingly quantifiable thanks to the data accumulated by exoplanet surveys during the last decade (e.g., Wright & Gaudi 2013, and references therein), as well as an increasingly better understanding of galaxy-scale physics. Modeling of the GHZ then tends to focus either on our own Milky Way (MW; e.g., Lineweaver et al. 2004; Prantzos 2008; Gowanlock et al. 2011) or specific nearby galaxies (e.g., Spitoni et al. 2014; Forgan et al. 2015). The interest in our own surroundings is naturally high, and these studies benefit from the large amounts of data we have collected on them, allowing for fine-grained estimates. Generalizing then the GHZ to cosmic scales and epochs, we can discuss the capacity of the universe (or even universes; e.g., Adams et al. 2015) to sustain life up to the cosmic horizon, only limited by our understanding of galaxy evolution. This comes at the cost of simplification, however, either treating star-forming galaxies with (semi-)analytic recipes of galaxy evolution (Dayal et al. 2015; Zackrisson et al. 2016) or only considering the global star formation history (SFH) of the universe (Lineweaver 2001; Behroozi & Peeples 2015). This approach typically makes the simple assumption that the formation rate of habitable planets at any point in space and time is determined only by the local star formation rate (SFR) and metal content of the interstellar medium (ISM). Nevertheless, other factors can be expected to influence the number of habitable planets a galaxy can host, such as its stellar population, supernova rate (SNR), and structure. Moreover, early-type galaxies (ETGs), which are very common in the local universe, follow different scaling relations than star-forming disks and thus might have different habitability conditions.
Here we take a semi-analytical approach that considers both star-forming and passive galaxies in a consistent way, as well as the effects of stellar evolution. This paper is structured as follows: in Sect. 2 we describe the model and its underlying assumptions, in Sect. 3 we show the results under different initial parameters, while in Sect. 4 we summarize our conclusions1.
2. Method
In this section, we describe the different assumptions that underlie our estimates of galaxy habitability and its evolution with redshift. In particular, we rely on a treatment of galaxy evolution that includes the quenching of star formation. This is motivated by the predominance of passive galaxies in the local universe (e.g., Fukugita et al. 1998); while their structure and composition can not be directly equated with those of low star formation active systems, an analysis that considers both galaxy types requires that their evolution be approached in a consistent manner. Our objective here is not to recreate an accurate model of galaxy evolution and planetary formation, but to generate simple estimates that nevertheless self-consistently account for complexities (such as different stellar and galaxy types, that follow different evolutionary paths).
2.1. Galaxy evolution
We base our model of galaxy evolution on three main ingredients: a mass-dependent “universal” SFH, a single type of stellar initial mass function (IMF), and observed galaxy mass functions. We first assume that all galaxies start on the SFR – stellar mass relation (SFR − M⋆, or “main sequence” of star formation; e.g., Brinchmann et al. 2004; Daddi et al. 2007; Rodighiero et al. 2010), and describe the SFH of main sequence (MS) galaxies using the 2-SFM formalism (Béthermin et al. 2012; Sargent et al. 2014). The slope and evolution of the SFR − M⋆ relation imply a SFH peaking at redshift z = 1−2, with the SFR (here as a function of redshift) given by 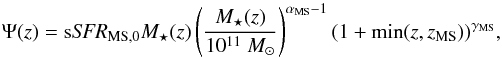 (1)where γMS = 3, zMS = 2.5, sSFRMS,0 = 10-10.2 yr-1 is the specific SFR (sSFR) of a 1011M⊙ galaxy at z = 0, and αMS = 1 is the slope of the SFR − M⋆ relation (Abramson et al. 2014; Schreiber et al. 2015). The stellar mass M⋆ of the galaxy is then given by the time-integrated SFR minus losses due to stellar death. It is thus dependent on the choice of IMF (see Sect. 2.1.2). This SFH also requires a “seed” mass as initial condition. Here we assume a single burst of star formation at zin = 10, with M⋆,in = 105−5 × 109M⊙. While the upper limit would yield an unrealistically high final galaxy mass at z = 0 of ~1013M⊙, such a large seed mass is necessary in this context to generate the highly star-forming progenitors of massive z ~ 2 passive galaxies (see Sect. 2.1.1). Examples of both a main sequence and quenched SFH are shown in Fig. 1. In addition, we assume that an evolving fraction rSB = 0.012 × (1 + min(z,1)) of star-forming galaxies are in starburst (SB) mode at any given time, with an average SFR enhancement of a factor 100.6 (Sargent et al. 2012; Béthermin et al. 2012). However, we here take the approximation that SBs do not contribute significantly to the M⋆ of the galaxy and only use the SB boost as a correction term to the SFR when estimating SNRs (Sect. 2.3.1). In this paper, all galaxies referred to as star-forming (SF) are either on the MS or are part of the SB fraction.
(1)where γMS = 3, zMS = 2.5, sSFRMS,0 = 10-10.2 yr-1 is the specific SFR (sSFR) of a 1011M⊙ galaxy at z = 0, and αMS = 1 is the slope of the SFR − M⋆ relation (Abramson et al. 2014; Schreiber et al. 2015). The stellar mass M⋆ of the galaxy is then given by the time-integrated SFR minus losses due to stellar death. It is thus dependent on the choice of IMF (see Sect. 2.1.2). This SFH also requires a “seed” mass as initial condition. Here we assume a single burst of star formation at zin = 10, with M⋆,in = 105−5 × 109M⊙. While the upper limit would yield an unrealistically high final galaxy mass at z = 0 of ~1013M⊙, such a large seed mass is necessary in this context to generate the highly star-forming progenitors of massive z ~ 2 passive galaxies (see Sect. 2.1.1). Examples of both a main sequence and quenched SFH are shown in Fig. 1. In addition, we assume that an evolving fraction rSB = 0.012 × (1 + min(z,1)) of star-forming galaxies are in starburst (SB) mode at any given time, with an average SFR enhancement of a factor 100.6 (Sargent et al. 2012; Béthermin et al. 2012). However, we here take the approximation that SBs do not contribute significantly to the M⋆ of the galaxy and only use the SB boost as a correction term to the SFR when estimating SNRs (Sect. 2.3.1). In this paper, all galaxies referred to as star-forming (SF) are either on the MS or are part of the SB fraction.
As long as a galaxy stays on the MS, we assume that its gas-phase metallicity Zg is given by the fundamental mass-metallicity relation (FMR; Mannucci et al. 2010). A stellar population forming at time t will then have a metallicity equal to Zg(t), with the average stellar metallicity of the galaxy Z⋆ being given by
where ℋ is the Heaviside function, φ(m,t) the IMF, and tMS(m) the stellar main sequence (sMS) life-time of a star of mass m (Sect. 2.1.2); mmin and mmax are, respectively, the lower and upper limit on star masses. Here we choose mmin = 0.1 M⊙ (see Sect. 2.2) and mmax = 100 M⊙. The parameter f⋆ is then the remaining stellar mass fraction at time t, after accounting for losses due to stellar death.
 |
Fig. 1 A) SFHs of a passive galaxy quenching at z = 0.4 (red) and a SF galaxy analogous to the MW (black), both having M⋆ = 5.2 × 1010M⊙. The gray dot shows the estimated SFR of the MW (Licquia & Newman 2015). B) Calculated SNII (green), SNIa (yellow), and total SN rate (black) for the M⋆ = 5.2 × 1010M⊙ SF galaxy. The estimated MW value is shown as a gray dot (Cappellaro et al. 1993; Meng & Yang 2010). |
2.1.1. Passive galaxies
In this model, passive galaxies follow the MS SFH until the start of quenching at tq, after which we follow a simple closed box formalism, with initial gas masses and SFR efficiencies based on the 2-SFM parameterization (Sargent et al. 2014). The evolution of the SFR Ψ, gas content Mg, and metallicity Z after tq are then given by the following equations, which we solve numerically in steps of Δt = 10 Myr:
where ϵ(t) and Mg(tq) are, respectively, the SF efficiency (SFE) at time t and molecular gas mass at the start of quenching. As a result, the SFR will then decrease more or less rapidly depending on galaxy mass. We then consider that a galaxy has become passive when its SFR is 1.5 dex below that of a same-mass galaxy on the MS. An example of a quenched SFH is shown in Fig. 1. In our case, the values for the slope β2 and intercept α2 of the Mg − SFR and SFE − SFR relations given in Sargent et al. (2014) would preclude the existence of passive galaxies with M⋆ below ~5 ×1010M⊙ at z ≥ 2, in contradiction with observations (e.g., Ilbert et al. 2013). This is not entirely surprising, since environmental effects play a more significant role in the quenching of low-mass galaxies than high-mass ones even at high redshift (Strazzullo et al. 2013; Gobat et al. 2013; Newman et al. 2014; Gobat et al. 2015) and can be expected to have different timescales than the simple case we are considering here. Letting both parameters vary, we find that values of α2 = 8.8 and β2 = 1 reproduce better – within the constraints of the model – the observed ages and metallicities of ETGs (Thomas et al. 2005; Gallazzi et al. 2006, 2014, see also Fig. 2). These values imply a SFE lower than that of main sequence galaxies by a factor ~3, consistent with the value reported at low redshift (Martig et al. 2013) and suggested by observation at z ~ 1.5 (Sargent et al. 2015). We also verify that Eq. (3) can reproduce reasonably well the observed stellar metallicity of passive galaxies at z< 1 (Gallazzi et al. 2006, 2014), as shown in Fig. 2. This can be achieved using a yield of y ~ 0.9, regardless of the IMF (Sect. 2.1.2).
While we assume that SF galaxies constitute a homogeneous population that always follows MS evolution, passive galaxies clearly form a composite population of objects that have quenched at different times and thus have different SFHs. To include this fundamental aspect of the ETG population, we use observed galaxy mass functions (GMFs) from Ilbert et al. (2013, at z = 0.2−2.5 and Baldry et al. (2012, at z ~ 0. The ETG population at z is then given by the combination of the ETGs present at z + Δz, and the systems that quenched between z + Δz and z, with their relative weights given by the value of the GMF,
where Φ is the GMF and x a derived observable (such as luminosity, total M⋆, or number of stars or planets as in Eq. (9)) for a passive galaxy of mass M⋆ quenched at zi. Here we choose zmax = 2, making the approximation that all z~2 ETGs quenched at this redshift. For ease of computation, we evaluate the GMFs in discrete bins of redshift with width Δz = 0.05.
We note that we do not consider galaxy mergers, except implicitly through the GMF and the SB fraction. The mass-weighted average SFH of two galaxies does not differ much from that of a galaxy of equivalent combined mass, and our assumed SFH can produce massive ETGs at high redshift without the need for mergers, with peak SFRs in their progenitors that are large (e.g., ~600 M⊙ yr-1 for ≳ 5×1011M⊙ ETG at z = 2), but compatible with observations (e.g., Fu et al. 2013; Tan et al. 2014; Schreiber et al. 2015). On the other hand, the metallicity of the final galaxy would be lower by up to 10−20% in the case of a merger, than that of a non-remnant galaxy. Furthermore, since higher mass galaxies are typically hosted in larger halos, with more surrounding substructure (i.e., satellites), galaxy mergers can be expected to play a more significant role in the case of large central galaxies (e.g., Feldmann et al. 2010; Carollo et al. 2013), and we can thus expect our estimates to match observables less well at large (>1011M⊙) masses.
 |
Fig. 2 A) Stellar metallicity of ETGs, as a function of M⋆, predicted by our model (orange to red) and observed at z ~ 0 and z ~ 0.7 (Gallazzi et al. 2006, 2014) (black line with gray scatter, and green lines with dashed uncertainty envelope). For comparison, the stellar metallicity of SF galaxies at z = 0 is shown in blue. B) M⋆ to bolometric light ratio (M/L) for z = 0 passive galaxies (solid line), with respect to the Salpeter case (dotted line). The red dots and green squares show, respectively, spectroscopic observations of low-redshift ETGs from Cappellari et al. (2013) and Spiniello et al. (2014). For consistency, we have converted M⋆ into velocity dispersions using Eq. (5) in Cappellari et al. (2013). |
2.1.2. Stellar initial mass function
For ease of comparison with the rest of the literature, most studies assume a single universal stellar IMF, typically either the canonical Salpeter (1955) IMF or a “bottom-light” function (Kroupa 2001; Chabrier 2003, these two IMFs have slightly different slopes and parameterization of the low-mass regime, but otherwise yield very similar M⋆ and SFRs). The choice of IMF typically only determines the scaling of derived quantities such as M⋆ or SFR, although it has a greater impact on the amount of metals produced and returned to the ISM. On the other hand, recent studies have shown evidence for a varying IMF in massive elliptical galaxies (e.g., van Dokkum & Conroy 2011, 2012; Cappellari et al. 2012, 2013; Spiniello et al. 2014), implying that the IMF of their SF progenitors are not universal either. Furthermore, the IMFs mentioned above have all been derived by measuring the distribution of stars in localized regions of the MW and might therefore not be directly applicable to extragalactic environments.
Here we adopt the integrated galactic IMF (IGIMF; Kroupa & Weidner 2003), i.e., a convolution of the IMF of individual star clusters with a distribution of star cluster masses. The IMF of individual clusters is assumed to correspond to the Kroupa (2001) function below m = 1.3 M⊙, with a slope at m> 1.3 M⊙ and maximum stellar mass mmax proportional to the embedded cluster mass (Pflamm-Altenburg et al. 2007; Weidner et al. 2011). The cluster mass function is, in turn, described by a power law with index β = 2 with a maximum cluster mass depending on the galaxy’s SFR (Weidner et al. 2013). Here we fix the minimum cluster mass at 50 M⊙. While clearly more complex, the IGIMF can reproduce some observables better than a fixed IMF (see Kroupa et al. 2013, and references therein). In particular, since more massive galaxies experience higher peak SFRs than lower mass ones, the variation of the IGIMF slope with SFR naturally translates into a variation with final M⋆ when integrated over the galaxy’s SFH. As an example, we show in Fig. 2 the ratio of M⋆ to bolometric luminosity (M/L) of passive galaxies compared to those derived from observations of ETGs in the nearby universe. While not a tight fit, the IGIMF reproduces reasonably well the observed offset in M/L compared to the Salpeter case for low-mass galaxies. It also yields an increase in M/L at higher M⋆ (although the latter is steeper than observed, possibly due to our neglect of galaxy mergers). This occurs because the IGIMF is by design very similar to the Kroupa IMF at low SFRs, if slightly top-light due to the cutoff M⋆, but becomes top-heavy at SFR>100M⊙ yr-1. Since Eqs. (1), (3), and the FMR and GMFs, assume a Chabrier IMF, we evaluate these expressions using the appropriate IMF and convert all quantities to the IGIMF afterwards. For comparison, in Sect. 3, we also give results with a Salpeter IMF. As noted in Sect. 2.1, here we evaluate the IMF between 0.1 and 100 M⊙.
2.2. Habitable planets
We assign a probability of hosting life-sustaining planets to the stars in each galaxy based on their age, metallicity and mass. What constitutes a habitable world, in the sense of a planetary body that can sustain life for some fraction of its lifetime, is somewhat conjectural as we are still limited by our incomplete understanding of the emergence and possible types of life. In principle, any environment allowing for liquid water and an energy source, whether internal or external, and stable over geological times could sustain life. These could include not only the usually considered icy moons of gas giants, but also more exotic environments such as free-floating planets (e.g., Stevenson 1999; Laughlin & Adams 2000; Abbot & Switzer 2011). Furthermore, biochemistries different from our own could exist, in which case the range of conditions favorable to the emergence of life might be much greater than what we can currently envision, and all the more unconstrained.
For the purpose of this work, we limit ourselves to environments similar to our own, i.e., terrestrial planets around stars on the sMS, with a combination of atmospheric pressure and temperature allowing them to sustain liquid water on their surface. We adopt the definition of circumstellar HZ given by Kopparapu et al. (2013), in this case the region bracketed by the “moist greenhouse” and “maximum greenhouse” limits (respectively, inner and outer). Kopparapu et al. (2013) define the HZ for effective temperatures between 2600 and 7200 K, corresponding to a mass interval of ~0.1−1.5 M⊙. We accordingly adopt a lower mass limit of 0.1 M⊙ and make the ad hoc assumption that only stars with ≤ 1.5M⊙ can host habitable planets. Furthermore, we only consider stars older than tmin = 1 Gyr as possible hosts for habitable planets, motivated by the presumably hostile surface conditions a planet would experience in its early eon, due to impacts from the large amount of debris left over from the protoplanetary disk and perturbed by planetary migration (e.g., Gomes et al. 2005). In addition, the HZ shifts during a star’s lifetime on the sMS as the latter brightens and its effective temperature changes. We take the effect of stellar aging into account by calculating the inner and outer HZ radii at each time step, using the fitting formulae of Hurley et al. (2000) to estimate accurate luminosities and effective temperatures.
The probability of a star hosting a terrestrial planet within its HZ is then given by the width of the HZ, the probability of planet formation, and the distribution of orbital periods. Despite recent advances, our knowledge of the distribution of low-mass or long-period exoplanets is still limited. In this paper, we mainly rely on the observed properties of short-period planets and use extrapolation when necessary. We assume that the distribution of the orbital periods P of terrestrial planets follows a simple power law of the form dN ∝ P(r,m)βPdP (r and m are, respectively, the radius of the orbit and mass of the host star) and set βP = −0.7 in accordance with observations (e.g., Cumming et al. 2008; Petigura et al. 2013; Burke et al. 2015). We also make the assumption that the fraction of stars with terrestrial planets, fT, depends principally on the host star’s metallicity rather than its mass. We consider two cases for this metallicity dependence: 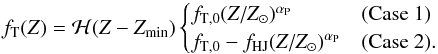 (5)
(5)
Case 1 is a straightforward power law, based on the historical assumption that planet formation requires an abundance of heavy elements, and represents the simplest form of metallicity dependence for fT. While Case 1 does not appear to fit very well the distribution of currently known terrestrial planets, it still describes accurately the observed correlation between the occurrence of giant planets and the host star metallicity (e.g., Fischer & Valenti 2005; Gonzalez 2014; Gaidos & Mann 2014). Because the value of the exponent is still somewhat uncertain, we choose a mid-range αP = 2 for simplicity. On the other hand, the presence of non-giant planets does not seem to be strongly correlated with stellar metallicity (e.g., Buchhave et al. 2012; Wang & Fischer 2015; Buchhave & Latham 2015; Schuler et al. 2015). Furthermore, the inward migration of a giant planet towards its host star would likely disrupt the formation of smaller planets or, if already present, their orbits. We can then simply assume that stars with short-period giants known as hot Jupiters cannot have terrestrial planets in their HZ (but see, e.g., Fogg & Nelson 2009; Becker et al. 2015). In Case 2 we therefore take a constant occurrence rate for terrestrial planets, but subtract from it the metallicity-dependent fraction of stars with hot Jupiters, fHJ(Z/Z⊙)αP, and therefore assume that fT is weakly anticorrelated with metallicity (see, e.g., Prantzos 2008; Zackrisson et al. 2016). We take fHJ = 0.012 for solar-type stars (Wright et al. 2012) and, in both cases, set fT,0 = 0.4 at Z = Z⊙ following Prantzos (2008) and in accordance with the occurrence rate of planets with a radius of <2 R⊕ and a period of P = 5−500 days derived by Petigura et al. (2013) from the Kepler sample. In both cases, we adopt a low-metallicity threshold of 0.1 Z⊙ under which the probability of forming terrestrial planets is zero (e.g., Fischer & Valenti 2005; Buchhave et al. 2012). The fraction of stars of a given mass, age, and metallicity with habitable planets can then be expressed as 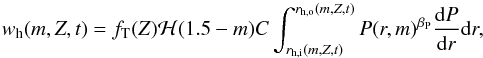 (6)
(6)
where C is a normalization constant so that 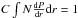 over the whole range of periods considered. Here we conservatively take a lower and upper limit of 3 days and 300 yr, respectively.
over the whole range of periods considered. Here we conservatively take a lower and upper limit of 3 days and 300 yr, respectively.
2.3. Supernovae and AGN
The habitable stellar fraction given in Eq. (6) can be considered an upper limit, as energetic phenomena such as supernovae (SN) and active galactic nuclei (AGN) can sterilize the surface of planets if they happen close enough.
2.3.1. Supernovae
The majority of supernova events falling into either the type Ia or type II category (e.g., Hakobyan et al. 2014; Cappellaro et al. 2015), we only consider these two classes (hereafter, SNIa and SNII). Both the SNII and SNIa rate depend on the IMF through the fraction of stars with, respectively, m ≥ 8M⊙ and m< 8M⊙. The SNII rate is directly proportional to the instant SFR, the lifetime of a m ≥ 8M⊙ star being shorter than the typical timescale normally considered for star formation in galaxies (~100 Myr). On the other hand, SNIa are significantly delayed by the longer time spent on the sMS by their progenitors and the additional time elapsed between the formation of the white dwarf (WD) and its detonation. The rates of the two SN types can thus be expressed as:
where ηWD = 0.01 is the WD conversion rate (Pritchet et al. 2008) and τ = t′ − tMS(m) − τIa, with tMS(m) and τIa = 500 Myr being, respectively, the main sequence lifetime of a progenitor of mass m and the average delay time between stellar death and the detonation of the WD (Raskin et al. 2009).
The impact of SN on galaxy habitability depends principally on two parameters: the distance rSN at which a SN can sterilize a planet and/or render it uninhabitable (hereafter the lethal radius) and the time required by a planet to recover from the effects of the SN, trec. There is circumstantial evidence that SN events might be implicated in some of the mass extinctions of species that have happened on Earth throughout its history (e.g., Ellis & Schramm 1993; Detre et al. 1998; Melott & Thomas 2009; Thomas et al. 2015), but the full range of SN effects on life-bearing worlds has, to our knowledge, not been extensively probed. The emphasis is usually put on hard radiation (e.g., gamma rays) owing to its disruptive effect on atmospheric ozone, which leads to an increase in biologically hazardous UV irradiance. For example, Gowanlock et al. (2011) and Forgan et al. (2015) use the ozone-depletion estimates of Gehrels et al. (2003) to set the lethal radius at 8 pc. However, the expected rate of SN within 8 pc (see Gehrels et al. 2003) suggests that the Earth might have experienced several during the last few Gyr while still ultimately retaining its capability to support life. Such an event would also only affect the unprotected areas of a planet: photosynthesis-independent benthic and lithoautotrophic organisms would be scarcely affected by hard radiation on the surface and the approximately tenfold decrease (in the case of Earth) in ocean water absorbance between UVB wavelengths and the first peak of chlorophyll absorbance (~300 nm and ~450 nm, respectively; see Shifrin 1988) suggests that even shallow marine ecosystems would be somewhat more resistant than surface ones. We can then surmise that, at 8 pc, trec is of the order of the recovery time of biodiversity after mass extinctions as inferred from the fossil record, i.e., small with respect to the timescales relevant to galaxies. In the { rSN = 8pc,trec ~ 0 } case, the effect of SN on habitability averaged over a whole galaxy is then likely negligible for all but the most active star-forming galaxies.
Instead, we focus here on thermal effects, i.e., how far a SN can occur from a planet and still push it out of the HZ of its host star. Since this distance depends on the position of a planet within the HZ and on the width of the HZ, we define the lethal radius as the distance at which 50% of planets normally within the HZ of their host star find themselves out of it for the duration of the event. We consider two different sources of heating: the initial bolometric radiation emitted by the SN over ~2 months and the blastwave arriving some time later. In the first case, we assume a radiative output of 1049 erg for SNII and 3 × 1049 erg for SNIa (Scalzo et al. 2014). In the second, we consider ~10 M⊙ of ejecta for SNII (e.g., Woosley et al. 2002) and 1.4 M⊙ for SNIa, adiabatically expanding with an initial kinetic energy of 1051 erg. We assume that the blastwave propagates in a surrounding ISM of pure hydrogen with an average density of 1 atom/cm3 (see, e.g., Draine 2011). We further posit that the ejected shell can only interact with a planet as long as its pressure is larger than that of the wind of the host star, for which we assume a constant density of 10 atoms/cm3 and a speed of 500 km s-1, and that the entire kinetic energy of the gas will be converted into heating the planet’s atmosphere. Because the bolometric radiation is mostly released in the days following the detonation, but the ejected material expands much more slowly, these two effects are considered independently. For our choice of dN/ dP, we find a lethal radius of rIa = 0.3 pc for SNIa and rII = 0.5 pc for SNII. We make the additional assumption that such an excursion from the HZ will sterilize a planet and permanently alter its surface conditions, rendering it inhospitable, and thus set the recovery time trec to a value greater than the Hubble time tH. On the other hand, feedback processes in the planet’s atmosphere might, depending on its composition, compensate for the increased energy input. However, ascertaining the actual impact of the SN would then require complex modeling that is beyond the scope of this paper.
We then estimate a fractional irradiated volume to use as a correction term to the time-varying habitable fraction. We approximate passive galaxies as spheres and SF galaxies as disks, both with constant stellar density and redshift-dependent radius set by the observed mass-size relation (van der Wel et al. 2014). We assume that the disks have a thickness of hd = 0.25 × re at high redshift, where re is the effective radius of the galaxy, and transition to a thin disk with hd = 0.15 × re (based on the structure of the MW disk; Bovy et al. 2012) after the peak of their SFH (Lehnert et al. 2014). The fractional irradiated volumes for passive (P) and SF galaxies are then 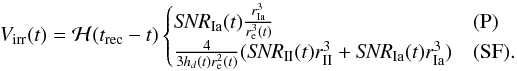 (8)
(8)
Since we do not include the growth of passive bulges in disk galaxies, we simply assume that the volume of ETGs is given by the disk case during their SF phase and the passive one after quenching, with a simple linear transition between both during quenching. We assume internal homogeneity for simplicity. This is however a clear limitation, especially in the case of SF galaxies, as we can expect SNII and SNIa to preferentially happen in comparatively dense star clusters (e.g. Shara & Hurley 2002; Maoz et al. 2010), which would increase SN lethality. In more extreme environments, such as massive star clusters or very compact galaxies, nearby main sequence stars might contribute enough to the ambient radiation field to adversely affect the HZ (Thompson 2013; Adams et al. 2015).
2.3.2. AGN
We estimate a lethal radius rAGN resulting from the activity of a galaxy’s central supermassive black hole (SMBH) in a similar manner. Although this activity is expected to be sporadic, we assume it to be frequent enough to define an exclusion region where planets cannot stay habitable over the long term. In this case, only thermal radiative effects are considered. We assume that the SMBH radiates at Eddington luminosity and use the local relation of Reines & Volonteri (2015) for ellipticals and bulges to derive the SMBH mass from a galaxy’s M⋆. The distance from the SMBH at which 50% of planets fall out of the HZ of their host star depends on the AGN luminosity, thus M⋆ through the relation log rAGN(kpc) = −6.1 + 0.7 × log M⋆(M⊙). We then add the spherical volume defined by this radius to the value of Virr given in Eq. (8).
2.4. Galaxy habitability
Combining all the elements described in the previous sections, we define the habitability hG of a galaxy at redshift z as the ratio of the number of main sequence stars of mass ≤ 1.5 M⊙, age ≤ tmin = 1 Gyr, and with planets in their HZ, to the total number of stars present in the galaxy at z. In a slightly shortened notation 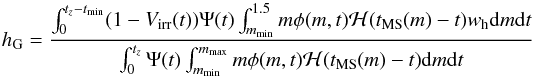 (9)
(9)
for SF galaxies. The habitability hG is here a function of the time tz after the onset of star formation and, through the SFH Ψ, the M⋆ of the galaxy at z. In the case of passive galaxies, both sides of the fraction are a combination of different age populations as described in Eq. (4).
3. Results
 |
Fig. 3 A) Galaxy habitability at z = 0 as a function of mass and IMF (IGIMF and Salpeter; solid and dashed lines, respectively), for SF (blue) and passive (red) galaxies and a metallicity-anticorrelated (Case 2) fT. To illustrate the effect of SN on the mass-dependency of hG, the dotted lines show the IGIMF case with the lethal radius of Gehrels et al. (2003)rII = rIa = 8 pc and trec>tH. B) Galaxy habitability at z = 0 of SF (blue) and passive (red) galaxies, using the IGIMF and for the two different cases of terrestrial planet incidence (Cases 1 and 2; dashed and solid lines, respectively). The filled gray circle shows the ratio of stars with terrestrial planet candidates in the habitable zone to the total number of stars with at least one planet candidate, taken from the NASA Exoplanet Archive using the same criteria (star mass, illuminance, planetary radius) as described in Sect. 2.2. The error bar assumes Poisson uncertainties. C) Galaxy habitability integrated over the range of galaxy masses, as a function of redshift and IMF (IGIMF and Salpeter; solid and dashed lines, respectively), for SF (blue) and passive (red) galaxies. As in A), this panel assumes a Case 2 fT. The dotted lines show the evolution of habitability in the IGIMF case if we use the larger (8 pc) SN lethal radius of Gehrels et al. (2003). D) As in C), evolution of galaxy habitability with redshift as a function of the metallicity dependence of fT. In both panels, the black lines show the evolution of habitability averaged over the whole galaxy population (SF and passives). |
Figure 3 shows the galaxy habitability hG, computed in the mass range 109<M< 3 × 1011M⊙, as a function of M⋆ at z = 0 and as a function of redshift. We consider several combinations of parameters: the IGIMF with Cases 1 and 2 metallicity dependence as defined in Eq. (5) (panels B and D), and Case 2 only with either an IGIMF or Salpeter IMF (panels A and C). For Case 2 at z = 0, between 0.65% and 0.8% of all stars host potentially habitable planets and hG is only weakly dependent on M⋆, with a maximum around 4 × 1010M⊙ (consistent with Zackrisson et al. 2016). The habitability of ETGs is ~0.03 dex higher than for disks of similar mass as a consequence of the 1 Gyr delay time before a planet becomes habitable. This reflects the typical fraction of stars formed in disks since that look-back time. The main factors determining the overall normalization and behavior of hG are, in order of importance:
-
Metallicity: lower mass galaxies also have lower metallicity andtherefore a higher fraction of stars below the threshold forterrestrial planets, while for higher mass galaxies the decrease inhG stems from fT being inversely proportional to metallicity. In contrast, the habitability for Case 1 increases monotonically with M⋆ and is comparable in behavior to the model of Dayal et al. (2015). The M⋆ − Z⋆ relation is well defined for both SF and passive galaxies, with an intrinsic scatter whose value is not precisely known, although it is believed to be small. Using a value of 0.1 dex close to the observed scatter would add a dispersion of 0.03 dex and 0.008 dex at the low- and high-mass end of Fig. 3, respectively, for Case 2, and a constant dispersion of 0.2 dex for Case 1.
-
IMF: while metallicity drives the mass dependence of hG, the IMF determines its average value because the number of habitable planets in a stellar population depends on its fraction of low-mass stars. For example, using a Salpeter IMF decreases the habitability by ~0.02 dex, owing to the lower fraction of ≲ 1M⊙ stars compared to the IGIMF, while the variation of hG with M⋆ is similar in both cases. The negative slope of the IMF in the range 0.1−100 M⊙ implies that most terrestrial planets will be hosted by subsolar mass stars, which have tighter HZs than solar mass stars. As a consequence, hG is rather sensitive to the slope of the distribution of orbital periods and an error of 0.1 in βP (Cumming et al. 2008) would offset hG by 0.2 dex, making this parameter as important as fT,0 in determining its normalization.
-
Supernovae: since our model assumes a small lethal radius, the effect of SN is very weak. It is slightly stronger at higher masses and for ETGs, which have SFHs that peak higher than disks of identical mass and at earlier times, when galaxies are denser. On the other hand, while we have ruled out large lethal radii in our model, the 8 pc value of Gehrels et al. (2003) might still be relevant if we were to consider a more restrictive criterion for planetary habitability (see Sect. 3.1). As shown in Fig. 3, the impact of SN would in this case lead to significant differences in the hG of passive and SF galaxies at high masses. Active galactic nuclei behave in a similar fashion, fractionally increasing the irradiated volume in high-mass galaxies. The larger irradiated volume and fraction of stars below the metallicity threshold make these two effects stronger at higher redshift as well.
We compare our estimates with observations from the Kepler mission using the NASA Exoplanet Archive2. If the Kepler sample is mostly unbiased and terrestrial planets have the same distribution of orbital inclinations as giant ones, the ratio of stars with planet candidates within the HZ to the total number of stars with planet candidates should represent an estimate of hG (if all stars host at least one planet) or an upper limit to it. We first select all stars observed by Kepler with at least one confirmed or candidate planet and Teff ≤ 7200 K, in accordance with Sect. 2.2. After taking multiplanetary systems into account, we find 3570 such objects in the database. This corresponds to 3924 stars, after correcting for the fraction of stars with <1.5M⊙ to the total and assuming a Kroupa (2001) IMF for simplicity. We repeat the procedure adding conditions for the planet’s radius (<2 R⊕) and insolation (between 0.22 and 1.13 times that of Earth) consistent with Sect. 2.2, and find 44 candidates. This corresponds to a ratio of ~1%, slightly higher but broadly consistent with our Case 2 estimate (assuming a mass of 5.2 × 1010M⊙ for the MW disk; Licquia & Newman 2015). This is not unexpected, since our model uses parameters derived from the Kepler sample. It would however tend to validate the use of Case 2 and our assumptions for galaxy evolution, as well as our chosen combination of fT,0 and βP. On the other hand, the Case 1 prediction lies significantly below the observed ratio, and can be reconciled only if fT,0 = 1, i.e., if all stars of solar metallicity or greater host a terrestrial planet, in conflict with observations.
In panels C and D of Fig. 3 we show the redshift dependence of hG, integrated over the mass range 109−3 × 1011M⊙. The evolution of the integrated galactic habitability is monotonic with time for both SF and passive galaxies, and in both cases can be broadly divided into an early linear rise followed by a plateau in which hG increases by no more than 0.1 dex, with the transition happening at z> 1.5 for passive galaxies and z< 0.5 for SF galaxies. We note that for Case 1 the integrated habitability is very sensitive to the number ratio of low-mass, low-metallicity (and hence low-hG) galaxies to high-mass, high-metallicity (and high-hG) ones. Therefore, the apparent decrease in habitability at z< 0.2 for SF galaxies shown in Fig. 3, panel D, is likely due to our use of different GMFs for z ~ 0 and z> 0.2 populations. On the other hand, extending our SFHs to future epochs, and assuming that the FMR holds, we find that the habitability of SF galaxies for Case 2 will asymptotically approach that of passive galaxies, increasing by just ~0.02 dex over the next 5 Gyr. For the total galaxy population, the shift occurs at z ~ 1, i.e., after the peak of SFR in galaxies (and thus of cosmic SFR; e.g., Madau & Dickinson 2014, and references therein). Since the stellar density does not appear to have changed significantly since this epoch as well, this implies that the total number of habitable planets in a given cosmological volume has remained roughly constant since z ~ 1, i.e., in the last 7−8 Gyr. In the local universe, most of the stellar mass is held in large passive galaxies that formed at z> 1. This suggests that most of the habitable planets in the present epoch should belong to stars older than our own. Indeed, as shown in Fig. 4, the median age of stars hosting habitable planets at z = 0 is ~9.5 Gyr, 5 Gyr older than our own Sun and close to the estimate of Behroozi & Peeples (2015). On the other hand, if we only consider SF galaxies the median age drops to ~6 Gyr, or ~1.5 Gyr older than the Sun, which formed after ~70% of stars in disks that host habitable planets at z = 0, in agreement with the earlier estimate of Lineweaver (2001). Unlike the work presented here, the studies referenced above did not consider stellar death. However, the shape of the IMF implies that most planets orbit long-lived subsolar mass stars, greatly mitigating its effect. On the other hand, the impact of stellar death would be more important when considering timescales longer than the Hubble time or non-standard IMFs. Finally, we note that we might be overestimating the number of presently habitable planets formed near the peak of SF in passive galaxies (z ~ 2, or ~10 Gyr ago) as a result of the simplistic assumptions on galaxy structure that our model uses, as stated in Sect. 2.3.1.
 |
Fig. 4 Distribution of the ages of habitable planets per unit volume at z = 0, for SF (blue) and passive (red) galaxies and with the total distribution shown as a black curve. The dotted lines show the respective median ages, while the dashed gray line marks the formation time of the solar system. |
3.1. On the plurality of Earths
In the previous sections we used a rather broad definition of planetary habitability, which likely includes environments that are at best marginal to life (e.g., planets that spend only a short amount of time in the HZ). However, we as a culture seem to be most fascinated by the possibility of existence of other worlds and intelligences similar to our own. The latter in particular has become a recurrent part of both our folklore and scientific discourse (e.g., Dyson 1960; Hewish et al. 1968; Bowyer et al. 1982; Wright et al. 2014). Complex surface ecosystems such as the ones present on Earth today, let alone intelligent species, require time to arise by random evolution and are more sensitive to outside catastrophes (e.g., SN) than life in general. If we simply assume that the emergence of complex and/or intelligent life on a habitable planet is not contingent upon the type and metallicity of its host star, the frequency of Earth-analog “garden worlds” and that of intelligent life (hereafter civilizations) should then be directly proportional to the number of habitable planets, with two modifications: first, we increase tmin, with the added condition that the planets stay within the (shifting) HZ for a period at least equal to tmin (e.g., the rise of our own species corresponds to tmin = 4.5 Gyr). This accounts for the delay between the appearance of life and that of complex organisms; for the latter to happen, conditions must remain favorable throughout. Second, in addition to the SN lethal radius described above, we include the 8 pc irradiation radius of Gehrels et al. (2003) with a recovery time of trec = 50 Myr to account for SN-induced mass extinctions.
On the other hand, the probabilities of the emergence of life, of Earth-like biospheres, and of intelligent species are so far unconstrained. Consequently, we can only estimate the frequency of civilizations with respect to some arbitrary reference point. Here we choose to normalize the number of planets estimated with the modified criterion to 1 at z = 0 for MW-type disks. We then find that, if the number of Earth-like biospheres or civilizations now present in the MW is 1, a typical 1011M⊙ galaxy has ~2−3, and 109−0.22 × (tmin/ Gyr) civilizations exist in the observable universe when accounting for look-back time. The occurrence rate of civilizations, as shown in Fig. 5, peaks 3 + 1.3 × tmin Gyr after the onset of star formation. This suggests that, if Earth is not unique in this galaxy and the timescale of our own evolution is typical, we exist ~4 Gyr after this maximum, with the median age of civilizations being ~3.5 Gyr. Conversely, assuming that tmin = 4.5 Gyr, 1.4 × 109 planets following the above criterion have formed in a MW-mass disk since the onset of star formation. For us to exist before most civilizations our galaxy will produce would then imply either that the incidence of civilizations per suitable planet is <7 × 10-10 or that, contrary to what the timescale of our evolution suggests, the typical delay time is >8 Gyr.
 |
Fig. 5 Occurrence rate of civilizations in a MW-type disk, normalized to 1 at z = 0, as a function of look-back time and for delay times of 2, 4.5, and 6 Gyr (dashed, solid, and dotted lines, respectively). The solid line corresponds to our own case. |
4. Conclusion
We have used an analytic model of galaxy evolution to estimate galaxy habitability, measured by the fraction of stars with habitable planets, as a function of galaxy type, M⋆, and redshift. Our model includes passive galaxies through a simple treatment of galaxy quenching and metal enrichment, as well as thermal effects of stellar evolution and supernovae on habitable zone planets. We summarize our findings as follows:
-
We consider two different types of metallicity dependence for thefrequency of terrestrial planets and find that, given theassumptions of the model, a weak negative metallicitydependence (Case 2) reproduces observationsbetter. In this case, between 0.65% and 0.8% of stars in>109M⊙ galaxies are expected to host planets in their HZ, close to the <1% inferred from Kepler observations. The habitability of galaxies at z = 0 varies then relatively little with galaxy mass, reaching a maximum at log M⋆ = 10.6.
-
We estimate that the radius where the thermal effects of SN on planets become significant is 0.3−0.5 pc. The impact of SN on galaxy habitability is therefore negligible, as the fractional irradiated volume is almost always very small except at high M⋆ and redshift, where SFRs are extreme and galaxies more compact. The effect of the central AGN is likewise limited.
-
The habitability of passive galaxies is slightly but systematically higher than that of star-forming galaxies and has remained mostly unchanged since z ~ 1.5. On the other hand, the habitability of SF galaxies has increased monotonically since z = 2 and has only recently started to plateau. Overall, the average habitability of galaxies has not varied much in the last 8 Gyr.
-
The median age of habitable planets is ~6 Gyr in SF galaxies, i.e., ~1.5 Gyr older than our own solar system, and ~10 Gyr in passive galaxies. Using a more restrictive criterion, the occurrence rate of habitable planets similar to present-day Earth (which we can assume is proportional to that of alien civilizations) peaked ~4 Gyr ago. For us to be unique in the history of the MW would imply that the probability for intelligent life to evolve on a suitable planet is lower than ~7× 10-10.
Acknowledgments
We thank E. Daddi for enlightening discussions, F. Adams, C. Park, O. Snaith, and H. S. Hwang for their helpful suggestions which helped improve this paper. This research has made use of the NASA Exoplanet Archive, which is operated by the California Institute of Technology, under contract with the National Aeronautics and Space Administration under the Exoplanet Exploration Program.
References
- Abbot, D. S., & Switzer, E. R. 2011, ApJ, 735, 27 [Google Scholar]
- Abramson, L. E., Kelson, D. D., Dressler, A., et al. 2014, ApJ, 785, 36 [Google Scholar]
- Adams, F. C., Coppess, K. R., & Bloch, A. M. 2015, J. Cosmology Astropart. Phys., 09, 030 [NASA ADS] [CrossRef] [Google Scholar]
- Baldry, I. K., Driver, S. P., Loveday, J., et al. 2012, MNRAS, 421, 621 [NASA ADS] [Google Scholar]
- Becker, J. C., Vanderburg, A., Adams, F. C., Rappaport, S. A., & Schwengeler, H. M. 2015, ApJ, 812, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Behroozi, P. S., & Peeples, M. 2015, MNRAS, 454, 1811 [NASA ADS] [CrossRef] [Google Scholar]
- Béthermin, M., Daddi, E., Magdis, G., et al. 2012, ApJ, 757, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Bovy, J., Rix, H.-W., Liu, C., et al. 2012, ApJ, 753, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Bowyer, S., Zeitlin, G., Tarter, J., Lampton, M., & Welch, W. 1982, BAAS, 14, 941 [NASA ADS] [Google Scholar]
- Brinchmann, J., Charlot, S., White, S. D. M., et al. 2004, MNRAS, 351, 1151 [NASA ADS] [CrossRef] [Google Scholar]
- Buchhave, L. A., & Latham, D. W. 2015, ApJ, 808, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Buchhave, L. A., Latham, D. W., Johansen, A., et al. 2012, Nature, 486, 375 [NASA ADS] [Google Scholar]
- Burke, C. J., Christiansen, J. L., Mullally, F., et al. 2015, ApJ, 809, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., McDermid, R. M., Alatalo, K., et al. 2012, Nature, 484, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., McDermid, R. M., Alatalo, K., et al. 2013, MNRAS, 432, 1862 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellaro, E., Turatto, M., Benetti, S., et al. 1993, A&A, 273, 383 [NASA ADS] [Google Scholar]
- Cappellaro, E., Botticella, M. T., Pignata, G., et al. 2015, A&A, 584, 62 [Google Scholar]
- Carollo, C. M., Bschorr, T. J., Renzini, A., et al. 2013, ApJ, 773, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Cumming, A., Butler, R. P., Marcy, G. W., et al. 2008, PASP, 120, 531 [CrossRef] [Google Scholar]
- Chabrier, G. 2003, ApJ, 586, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Daddi, E., Dickinson, M., Morrison, G., et al. 2007, ApJ, 670, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Dayal, P., Cockell, C., Rice, K., & Mazumdar, A., et al. 2015, ApJ, 810, 2 [Google Scholar]
- Detre, Cs. H., Tóth, I., Gucsik, A., et al. 1998, Lunar and Planetary Science, 29, 1030 [NASA ADS] [Google Scholar]
- Draine, B. T. 2011, Physics of the Interstellar and Intergalactic Medium (Princeton University Press) [Google Scholar]
- Dyson, F. J. 1960, Science, 131, 1667 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ellis, J., & Schramm, D. N. 1993, ArXiv e-prints [arXiv:hep-ph/9303206] [Google Scholar]
- Feldmann, R., Carollo, C. M., Mayer, L., et al. 2010, ApJ, 709, 218 [NASA ADS] [CrossRef] [Google Scholar]
- Fischer, D. A., & Valenti, J. 2005, ApJ, 622, 1102 [NASA ADS] [CrossRef] [Google Scholar]
- Fu, H., Cooray, A., Feruglio, C., et al. 2013, Nature, 498, 338 [NASA ADS] [CrossRef] [Google Scholar]
- Fukugita, M., Hogan, C. J., & Peebles, P. J. E. 1998, ApJ, 503, 518 [NASA ADS] [CrossRef] [Google Scholar]
- Fogg, M. J., & Nelson, R. P. 2009, A&A, 498, 575 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Forgan, D., Dayal, P., Cockell, C., & Libeskind, N. 2015, Int. J. Astrobiol., [arXiv:1511.01786] [Google Scholar]
- Gaidos, E., & Mann, A. W. 2014, ApJ, 791, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Gallazzi, A., Charlot, S., Brinchmann, J., & White, S. D. M. 2006, MNRAS, 370, 1106 [NASA ADS] [CrossRef] [Google Scholar]
- Gallazzi, A., Bell, E. F., Zibetti, S., Brinchmann, J., & Kelson, D. D. 2014, ApJ, 788, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrels, N., Laird, C. M., Jackman, C. H., et al. 2003, ApJ, 585, 1169 [NASA ADS] [CrossRef] [Google Scholar]
- Gobat, R., Strazzullo, V., Daddi, E., et al. 2013, ApJ, 776, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Gobat, R., Daddi, E., Béthermin, M., et al. 2015, A&A, 581, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gomes, R., Levison, H. F., Tsiganis, K., & Morbidelli, A. 2005, Nature, 435, 466 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gonzalez, G. 2014, MNRAS, 443, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Gonzalez, G., Brownlee, D., & Ward, P. 2001, Icarus, 152, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Gowanlock, M. G., Patton, D. R., & McConnell, S. M. 2011, Astrobiology, 11, 855 [NASA ADS] [CrossRef] [Google Scholar]
- Hakobyan, A. A., Nazaryan, T. A., Adibekyan, V. Zh., et al. 2014, MNRAS, 444, 2428 [NASA ADS] [CrossRef] [Google Scholar]
- Hewish, A., Bell, S. J., Pilkington, J. D. H., Scott, P. F., & Collins, R. A. 1968, Nature, 217, 709 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, S.-S. 1959, PASP, 71, 220 [NASA ADS] [CrossRef] [Google Scholar]
- Hurley, J. R., Pols, O. R., & Tout, C. A. 2000, MNRAS, 315, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., McCracken, H. J., Le Fèvre, O., et al. 2013, A&A, 556, 55 [Google Scholar]
- Kasting, J. F., Whitmire, D. P., & Reynolds, R. T. 1993, Icarus, 101, 108 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kopparapu, R. K., Ramirez, R., Kasting, J. F., et al. 2013, ApJ, 765, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P., & Weidner, C. 2003, ApJ, 598, 1076 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P., Weidner, C., Pflamm-Altenburg, J., et al. 2013, Planets, Stars and Stellar Systems Vol. 5, eds. T. D. Oswalt, & G. Gilmore, 115 [Google Scholar]
- Laughlin, G., & Adams, F. C. 2000, Icarus, 145, 614 [NASA ADS] [CrossRef] [Google Scholar]
- Lehnert, M. D., Di Matteo, P., Haywood, M., & Snaith, O. N. 2014, ApJ, 789, 30 [Google Scholar]
- Licquia, T. C., & Newman, J. A. 2015, ApJ, 806, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Lineweaver, C. H. 2001, Icarus, 151, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Lineweaver, C. H., Fenner, Y., & Gibson, B. K. 2004, Science, 303, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P., & Dickinson, M. 2014, ARA&A, 52, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Mannucci, F., Cresci, G., Maiolino, R., Marconi, A., & Gnerucci, A. 2010, MNRAS, 408, 2115 [NASA ADS] [CrossRef] [Google Scholar]
- Maoz, D., Keren, S., & Gal-Yam, A. 2010, ApJ, 722, 1879 [Google Scholar]
- Martig, M., Crocker, A. F., Bournaud, F., et al. 2013, MNRAS, 432, 1914 [NASA ADS] [CrossRef] [Google Scholar]
- Melott, A. L., & Thomas, B. C. 2009, Paleobiology, 35, 311 [CrossRef] [Google Scholar]
- Meng, X., & Yang, W. 2010, ApJ, 710, 1310 [NASA ADS] [CrossRef] [Google Scholar]
- Newman, A. B., Ellis, R. S., Andreon, S., et al. 2014, ApJ, 788, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Perryman, M., Hartman, J., Bakos, G. Á., & Lindegren, L. 2014, ApJ, 797, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Petigura, E. A., Marcy, G. W., & Howard, A. W. 2013, ApJ, 770, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Pflamm-Altenburg, J., Weidner, C., & Kroupa, P. 2007, ApJ, 671, 1550 [NASA ADS] [CrossRef] [Google Scholar]
- Prantzos, N. 2008, Space Sci. Rev., 135, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Pritchet, C. J., Howell, D. A., & Sullivan, M. 2008, ApJ, 683, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Raskin, C., Scannapieco, E., Rhoads, J., & Della Valle, M. 2009, ApJ, 707, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Rauer, H., Catala, C., Aerts, C., et al. 2014, Exp. Astron., 38, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Reines, A. E., & Volonteri, M. 2015, ApJ, 813, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Rodighiero, G., Cimatti, A., Gruppioni, C., et al. 2010, A&A, 518, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Sargent, M. T., Béthermin, M., Daddi, E., & Elbaz, D. 2012, ApJ, 747, 31 [Google Scholar]
- Sargent, M. T., Daddi, E., Béthermin, M., et al. 2014, ApJ, 793, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Sargent, M. T., Daddi, E., Bournaud, F., et al. 2015, ApJ, 806, 20 [Google Scholar]
- Scalzo, R., Aldering, G., Antilogus, P., et al. 2014, MNRAS, 440, 1498 [NASA ADS] [CrossRef] [Google Scholar]
- Schreiber, C., Pannella, M., Elbaz, D., et al. 2015, A&A, 575, 74 [Google Scholar]
- Schuler, S. C., Vaz, Z. A., Katime Santrich, O. J., et al. 2015, ApJ, 815, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Shara, M. M., & Hurley, J. R. 2002, ApJ, 571, 830 [NASA ADS] [CrossRef] [Google Scholar]
- Shifrin, K. S. 1988, Physical Optics of Ocean Water (AIP Press) [Google Scholar]
- Spiniello, C., Trager, S., Koopmans, L. V. E., & Conroy, C. 2014, MNRAS, 438, 1483 [NASA ADS] [CrossRef] [Google Scholar]
- Spitoni, E., Matteucci, F., & Sozzetti, A. 2014, MNRAS, 440, 2588 [NASA ADS] [CrossRef] [Google Scholar]
- Stevenson, D. J. 1999, Nature, 400, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Strazzullo, V., Gobat, R., Daddi, E., et al. 2013, ApJ, 772, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Tan, Q., Daddi, E., Magdis, G., et al. 2014, A&A, 569, 98 [Google Scholar]
- Thomas, D., Maraston, C., Bender, R., & Mendes de Oliveira, C. 2005, ApJ, 621, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, B. C., Neale, P. J., & Snyder, B. R. II 2015, Astrobiology, 15. 207 [Google Scholar]
- Thompson, T. A. 2013, MNRAS, 431, 63 [NASA ADS] [CrossRef] [Google Scholar]
- van Dokkum, P. G., & Conroy, C. 2011, ApJ, 735, 13 [NASA ADS] [CrossRef] [Google Scholar]
- van Dokkum, P. G., & Conroy, C. 2012, ApJ, 760, 70 [NASA ADS] [CrossRef] [Google Scholar]
- van der Wel, A., Franx, M., van Dokkum, P. G., et al. 2014, ApJ, 788, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, J., & Fischer, D. A. 2015, AJ, 149, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., Heger, A., & Weaver, T. A. 2002, Rev. Mod. Phys., 74, 1015 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, J. T., & Gaudi, B. S. 2013, Planets, Stars and Stellar Systems, Vol. 3: Solar and Stellar Planetary Systems, 489 [Google Scholar]
- Wright, J. T., Marcy, G. W., Howard, A. W., et al. 2012, ApJ, 753, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, J. T., Mullan, B., Sigurdsson, S., & Povich, M. S. 2014, ApJ, 792, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Weidner, C., Kroupa, P., & Pflamm-Altenburg, J. 2011, MNRAS, 412, 979 [NASA ADS] [Google Scholar]
- Weidner, C., Kroupa, P., & Pflamm-Altenburg, J. 2013, MNRAS, 436, 3309 [NASA ADS] [CrossRef] [Google Scholar]
- Zackrisson, E., Calissendorff, P., Gonzalez, J., et al. 2016, ArXiv e-prints [arXiv:1602.00690] [Google Scholar]
All Figures
 |
Fig. 1 A) SFHs of a passive galaxy quenching at z = 0.4 (red) and a SF galaxy analogous to the MW (black), both having M⋆ = 5.2 × 1010M⊙. The gray dot shows the estimated SFR of the MW (Licquia & Newman 2015). B) Calculated SNII (green), SNIa (yellow), and total SN rate (black) for the M⋆ = 5.2 × 1010M⊙ SF galaxy. The estimated MW value is shown as a gray dot (Cappellaro et al. 1993; Meng & Yang 2010). |
| In the text | |
 |
Fig. 2 A) Stellar metallicity of ETGs, as a function of M⋆, predicted by our model (orange to red) and observed at z ~ 0 and z ~ 0.7 (Gallazzi et al. 2006, 2014) (black line with gray scatter, and green lines with dashed uncertainty envelope). For comparison, the stellar metallicity of SF galaxies at z = 0 is shown in blue. B) M⋆ to bolometric light ratio (M/L) for z = 0 passive galaxies (solid line), with respect to the Salpeter case (dotted line). The red dots and green squares show, respectively, spectroscopic observations of low-redshift ETGs from Cappellari et al. (2013) and Spiniello et al. (2014). For consistency, we have converted M⋆ into velocity dispersions using Eq. (5) in Cappellari et al. (2013). |
| In the text | |
 |
Fig. 3 A) Galaxy habitability at z = 0 as a function of mass and IMF (IGIMF and Salpeter; solid and dashed lines, respectively), for SF (blue) and passive (red) galaxies and a metallicity-anticorrelated (Case 2) fT. To illustrate the effect of SN on the mass-dependency of hG, the dotted lines show the IGIMF case with the lethal radius of Gehrels et al. (2003)rII = rIa = 8 pc and trec>tH. B) Galaxy habitability at z = 0 of SF (blue) and passive (red) galaxies, using the IGIMF and for the two different cases of terrestrial planet incidence (Cases 1 and 2; dashed and solid lines, respectively). The filled gray circle shows the ratio of stars with terrestrial planet candidates in the habitable zone to the total number of stars with at least one planet candidate, taken from the NASA Exoplanet Archive using the same criteria (star mass, illuminance, planetary radius) as described in Sect. 2.2. The error bar assumes Poisson uncertainties. C) Galaxy habitability integrated over the range of galaxy masses, as a function of redshift and IMF (IGIMF and Salpeter; solid and dashed lines, respectively), for SF (blue) and passive (red) galaxies. As in A), this panel assumes a Case 2 fT. The dotted lines show the evolution of habitability in the IGIMF case if we use the larger (8 pc) SN lethal radius of Gehrels et al. (2003). D) As in C), evolution of galaxy habitability with redshift as a function of the metallicity dependence of fT. In both panels, the black lines show the evolution of habitability averaged over the whole galaxy population (SF and passives). |
| In the text | |
 |
Fig. 4 Distribution of the ages of habitable planets per unit volume at z = 0, for SF (blue) and passive (red) galaxies and with the total distribution shown as a black curve. The dotted lines show the respective median ages, while the dashed gray line marks the formation time of the solar system. |
| In the text | |
 |
Fig. 5 Occurrence rate of civilizations in a MW-type disk, normalized to 1 at z = 0, as a function of look-back time and for delay times of 2, 4.5, and 6 Gyr (dashed, solid, and dotted lines, respectively). The solid line corresponds to our own case. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\begin{eqnarray} Z_{\star}(t) &=& \frac{\int_0^t Z_{g}(t')\Psi(t')f_{\star}(t-t')\mathrm{d}t'}{\int_0^t \Psi(t')f_{\star}(t-t')\mathrm{d}t'}\nonumber\\[-1mm] f_{\star}(t) &=& \int_{m_{\text{min}}}^{m_{\text{max}}} m\phi(m,t)\mathcal{H}(t_{\text{MS}}(m)-t) \mathrm{d}m, \label{eq:Zstar} \end{eqnarray}](/articles/aa/full_html/2016/08/aa28834-16/aa28834-16-eq27.png)