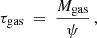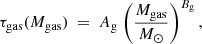| Issue |
A&A
Volume 689, September 2024
|
|
|---|---|---|
| Article Number | A221 | |
| Number of page(s) | 18 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202347928 | |
| Published online | 13 September 2024 | |
The effect of the environment-dependent stellar initial mass function on the photometric properties of star-forming galaxies
1
Helmholtz-Institut für Strahlen- und Kernphysik, Universität Bonn, Nussallee 14-16, 53115
Bonn, Germany
e-mail: mhaslbauer@astro.uni-bonn.de
2
School of Astronomy and Space Science, Nanjing University, Nanjing, 210093
PR China
e-mail: yan@nju.edu.cn
3
Key Laboratory of Modern Astronomy and Astrophysics (Nanjing University), Ministry of Education, Nanjing, 210093
PR China
4
European Southern Observatory, Karl-Schwarzschild-Straße 2, 85748
Garching bei München, Germany
e-mail: tereza.jerabkova@eso.org
5
Astronomical Institute, Faculty of Mathematics and Physics, Charles University, V Holešovičkách 2, 180 00
Praha 8, Czech Republic
6
Department of Physics, Institute for Advanced Studies in Basic Sciences (IASBS), PO Box 11365-9161
Zanjan, Iran
Received:
10
September
2023
Accepted:
30
April
2024
Context. Observational estimates of galaxy properties, including mass and star formation rates (SFRs), rely on the inherent galaxy-wide initial mass function (gwIMF), which systematically varies with the global SFR and metallicity, as proposed by the integrated-galactic IMF (IGIMF) theory and supported by empirical evidence.
Aims. We aim to evaluate the influence of the variable gwIMF on various galaxy properties, encompassing the Ks-, K3.6-, and V-band stellar mass-to-light ratio, SFR–luminosity relation, gas depletion timescale, and stellar mass buildup timescale of local star-forming galaxies.
Methods. We incorporate PARSEC and COLIBRI stellar isochrones into the GalIMF code, a galaxy chemical evolution (GCE) model featuring real-time updates of environment-dependent gwIMFs. This newly developed photometric GalIMF (photGalIMF) code allows the calculation of photometric properties for galaxies with diverse stellar populations. Subsequently, we analyze observed luminosities and metallicities of local star-forming galaxies to deduce their stellar masses assuming empirically-motivated SFHs of Local Cosmological Volume galaxies. We also compute SFR–Hα luminosity relations for varying stellar metallicities using a separate stellar population synthesis code based on PÉGASE.
Results. Comparing the IGIMF theory to the canonical universal IMF, our analysis reveals that estimates of the stellar masses and SFRs for local star-forming galaxies differ by factors of approximately 2 and 10, respectively. This disparity yields a well-defined galaxy main sequence extending to dwarf galaxies. The computed gas-depletion timescale increases with gas mass, implying lower star formation efficiencies in more massive galaxies, possibly due to stronger feedback regulation, aligning with theoretical expectations. Additionally, the characteristic stellar mass buildup timescale increases with stellar mass, indicating that massive disk galaxies initiate star formation earlier than their low-mass counterparts.
Conclusions. The photGalIMF code enables self-consistent computations of galactic photometry with GCE modelling adopting an environment-dependent gwIMF. Utilizing K-band and Hα luminosities of galaxies, the outcomes include galaxy mass, SFR, and fitting functions for the SFR correction factor.
Key words: galaxies: evolution / galaxies: formation / galaxies: fundamental parameters / galaxies: luminosity function / mass function / galaxies: photometry / galaxies: star formation
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Galaxies in the observed distant and local Universe constrain various galaxy evolution and cosmological models, which require precise measurements and a correct interpretation of the measured observables. The inferred physical properties of galaxies are not only sensitive to the underlying cosmological framework (Balakrishna Subramani et al. 2019; Haslbauer et al. 2022b) but also to the behaviour of baryonic physics (e.g. Schaye et al. 2015, Ludlow et al. 2017, Hopkins et al. 2018, Li et al. 2020, and Keller & Kruijssen 2022. Interestingly, the dependency on baryonic physics is much less pronounced when Milgromian gravitation is applied, Wittenburg et al. 2020; Eappen et al. 2022; Nagesh et al. 2023).
A fundamental parameter in galaxy evolution is the initial stellar mass function (IMF) which describes the mass distribution of newly formed stars (Hopkins 2018). The IMF together with the star formation history (SFH) determine the stellar population of systems, the masses in living stars and remnants, and affect the matter cycle and chemical enrichment. Deducing the SFRs of unresolved stellar systems requires measurements of SFR indicators which are available, for example, for the X-ray, ultra-violet, optical, infrared, and the radio regime (e.g. Kennicutt 1983; Donas & Deharveng 1984; Buat et al. 1989; David et al. 1992; Condon 1992; Kennicutt 1998; Yun et al. 2001; Kewley et al. 2002; Brinchmann et al. 2004; Moustakas et al. 2006; Rieke et al. 2009; Kennicutt & Evans 2012; Calzetti 2013; Brown et al. 2017; Mahajan et al. 2019, and references therein). Crucially, converting these tracers to a SFR depends on the shape of the IMF (Kroupa & Jerabkova 2021). A strong variation of the IMF can alter galaxy mass estimates by more than a factor of ten (Wang et al. 2024). Therefore, the properties and functional dependencies of the IMF are of great importance in interpreting the observations of stellar systems.
It has been commonly assumed in the past that the IMF is invariant (known as the canonical IMF, see Kroupa 2002 that highlights the uniformity of IMFs of nearby star clusters) meaning that the mass distribution of stars is independent of the star-forming environment. However, increasingly observations suggest that the IMF varies inside our Galaxy (Matteucci 1994; Vazdekis et al. 1997; Kroupa 2002; Marks et al. 2012; Dib 2014; Dib et al. 2017; Dib 2023; Li et al. 2023) and outside as assessed in systems ranging from dense star-formation regions (Dabringhausen et al. 2009, 2012; Schneider et al. 2018; Zhang et al. 2018) to dwarf galaxies (Meurer et al. 2009; Lee et al. 2009; Watts et al. 2018) and from very metal-poor satellite galaxies (Geha et al. 2013; Gennaro et al. 2018; Yan et al. 2020; Mucciarelli et al. 2021) to galaxies with about Solar metallicity (Gunawardhana et al. 2011; Parikh et al. 2018; Zhou et al. 2019; Martín-Navarro et al. 2019; Smith 2020; van Dokkum & Conroy 2021). The JWST observation of high-redshift galaxy spectra is also consistent with a top-heavy IMF (Cameron et al. 2023).
The integrated galactic IMF (IGIMF) theory, introduced by Kroupa & Weidner (2003), can largely account for the above variety of observations. It is a mathematical framework to calculate the galaxy-wide IMF (gwIMF) by adding up the stellar IMFs of all embedded clusters within a galaxy. Note that from here on we differentiate between the IMF which is the result of one star-formation event as an embedded star cluster in a molecular cloud and the gwIMF. Both have the same shape only if the former is a scale-invariant probability density distribution function (Kroupa & Jerabkova 2021). Qualitatively, the IGIMF theory relies on the empirical relations of star formation and has been constantly further constrained (Kroupa et al. 2013; Weidner et al. 2013a,b,c, 2014; Schulz et al. 2015; Yan et al. 2017, 2019b, 2020, 2023; Jeřábková et al. 2018; Fontanot et al. 2018, 2024; Dib & Basu 2018; Zonoozi et al. 2019).
According to the IGIMF theory, the gwIMF systematically varies with the properties of the star-forming environment such as the global SFR, ψ, and averaged gas-phase metallicity of a galaxy. For example, the gwIMF for galaxies with a higher SFR than the Milky Way (ψ ≳ few M⊙ yr−1) becomes top-heavy (Weidner et al. 2011; Gunawardhana et al. 2011; Zhang et al. 2018), meaning that the formation of more massive stars is favoured compared to the canonical IMF, and the gwIMF for low-SFR galaxies (ψ <1 M⊙ yr−1) becomes top-light (Lee et al. 2009; Yan et al. 2020; Mucciarelli et al. 2021), resulting in a steeper gwIMF slope for stars above 1 M⊙ relative to the canonical IMF of the Milky Way. The metallicity also correlates with the slope of the IMF for both massive (Marks et al. 2012) and low-mass stars (Yan et al. 2024, and references therein). For metal-poor and metal-rich stellar populations, their IMFs become bottom-light (relatively fewer low-mass stars) and bottom-heavy (steeper IMF slope for low-mass stars), respectively (see e.g. Fig. 2 of Jeřábková et al. 2018, and Sect. 2.1). The IMF is likely to be affected by more physical parameters, such as cosmic ray density (Papadopoulos 2010; Fontanot et al. 2018) and temperature (Sneppen et al. 2022), but these initial conditions are difficult to measure and can be affected by the SFR density. With only two environmental inputs, the galactic SFR and metallicity, the IGIMF model has successfully explained several observations over the last two decades. For example, the mass–metallicity relation (Köppen et al. 2007; Yan et al. 2019a, 2021), the [α/Fe] relation in early-type galaxies (Recchi et al. 2009; Yan et al. 2019a, 2021), the chemical evolution of ultra-faint dwarf galaxies (UFDs; Yan et al. 2020; Mucciarelli et al. 2021), the IMF of UFD galaxies (Dib 2022), the UV/Hα flux ratio of galaxies (Lee et al. 2009; Pflamm-Altenburg et al. 2009; Yan et al. 2017), the radial Hα cut-off in disk galaxies (Pflamm-Altenburg & Kroupa 2008; Rautio et al. 2024), and the mass correlation between spheroidal galaxies and their hosted supermassive black holes (Kroupa et al. 2020b).
We note that Dib (2022) argues for a possible random variation of the IMF from one star-forming region to another. This is an interesting possibility, but for the time being here we consider that the IMF is optimally sampled (Kroupa et al. 2013 and Yan et al. 2023, i.e. there are no random variations) from an underlying parent function which strictly only depends on the metallicity and density of the embedded-cluster forming gas cloud core, following Yan et al. (2017). This gives us complete analytical predictability and thus allows detailed controlled experiments ranging from the embedded cluster scale to the scale of whole galaxies. The possible random variations proposed by Dib (2022) will be studied in the future.
The implications of the systematic variation of the gwIMF given by the IGIMF theory are significant. For example, the number of ionizing photons depends on the shape of the gwIMF such that the relation between the SFR and Hα luminosity, LHα, of a galaxy becomes non-linear for a varying IMF (Pflamm-Altenburg et al. 2009; Jeřábková et al. 2018) violating therewith the Kennicutt law (Kennicutt 1998). Galaxies with LHα > 1041 ergs s−1 (LHα < 1041 ergs s−1) have SFRs lower (higher) than those given by the Kennicutt law. This affects the properties of star-forming galaxies such as the main sequence of star-forming galaxies, which is a tight correlation between the SFRs and stellar masses of galaxies (see e.g. Fig. 8 of Speagle et al. 2014). Applying an IGIMF-corrected SFR–Hα luminosity relation (see Fig. 7 of Jeřábková et al. 2018), the slope of the main sequence becomes flatter (Kroupa & Jerabkova 2021). Another consequence of the variable IMF is for the estimation of the gas depletion timescale, τgas = Mgas/ψ, and stellar-mass build-up timescale, τ⋆ = M⋆/ψ. Pflamm-Altenburg & Kroupa (2009) calculated these timescales for 200 nearby galaxies in the canonical IMF and IGIMF context. They demonstrated that in the IGIMF framework, the star formation efficiency (SFE),  , remains almost constant, while massive disk galaxies have much higher
, remains almost constant, while massive disk galaxies have much higher  than dwarf galaxies for a canonical IMF. Moreover, Pflamm-Altenburg & Kroupa (2009) find that τ⋆ increases with stellar mass in the IGIMF framework, implying that SFR may have been increasing slightly with time for dwarf galaxies but not for large disk galaxies. This is in agreement with observations (Fontanot et al. 2009) and in contrast to the expectations assuming the canonical IMF.
than dwarf galaxies for a canonical IMF. Moreover, Pflamm-Altenburg & Kroupa (2009) find that τ⋆ increases with stellar mass in the IGIMF framework, implying that SFR may have been increasing slightly with time for dwarf galaxies but not for large disk galaxies. This is in agreement with observations (Fontanot et al. 2009) and in contrast to the expectations assuming the canonical IMF.
The above studies mostly take into account the effect of the IMF variation on the estimation of the galactic SFR but not on the stellar mass. This simplification is reasonable because the SFR correction is much more significant than the stellar mass correction but still is not fully self-consistent if the latter is not also corrected. The effect of the IMF variation on the determination of the galaxy mass in stars and their remnants is more complicated than the SFR estimation because it involves the SFH and chemical enrichment history. A detailed galaxy evolution simulation incorporating an environment-dependent IMF, as developed in Yan et al. (2019b), is necessary (cf. Cueto et al. 2024).
This work expands the GalIMF galaxy chemical evolution code (Yan et al. 2019b) to include galaxy photometry, that is, the stellar isochrones provided by the PAdova and TRieste Stellar Evolution Code (PARSEC, Bressan et al. 2012) and COLIBRI code (Marigo et al. 2013). This expanded public code is available under the name “photometric GalIMF” (photGalIMF, Sect. 2.4). This code enables, for the first time, to study photometric properties of galaxies in self-consistent chemical evolution models with an environment-dependent gwIMF. Additionally, we integrate the methods developed in Jeřábková et al. (2018) to obtain the SFR–Hα-luminosity relation, as well as Pflamm-Altenburg & Kroupa (2009) to treat galactic gas depletion timescales. We then correct both the SFRs and the stellar masses of galaxies located in the Local Cosmological Volume (LV, Karachentsev et al. 2004, 2013).
The paper is organized as follows: Sect. 2 introduces our model and assumptions to calculate the stellar mass-to-light ratio (M⋆/L which includes the stellar remnants) in different photometric bands and the SFR–Hα-luminosity relation. Section 3 describes the observational constraints of our model and a sample of 603 star-forming galaxies in the LV (< 11Mpc). Section 4 presents the evolution of M⋆/L, the stellar-mass–SFR relation, the gas depletion timescale, and stellar-mass buildup times of local star-forming galaxies in the invariant canonical IMF and the IGIMF frameworks. The results are discussed in Sect. 5 which is followed by an outlook and a conclusion in Sect. 6. Throughout the analysis, we assume an age of the Universe of τh = 13.8 Gyr (Table 4 of Planck Collaboration XIII 2016).
2. Methods
As introduced in Sect. 1, the environment-dependent empirical IMF variation described by the IGIMF theory is both well-developed and rigorously tested. Here, we state the physical assumptions and mathematical framework of the IGIMF theory in Sect. 2.1, providing qualitative discussions on the functional dependence of the gwIMFs on the global SFR and the metallicity of different IGIMF formulations. A more comprehensive description and the observational constraints of the IGIMF theory can be found, for example, in Jeřábková et al. (2018) and Yan et al. (2021, 2024). Next, we summarize our chemical evolution model, which is necessary to obtain the evolution of stellar ages, masses, and metallicity in Sect. 2.2. The assumption on the SFH with a constant SFR is motivated in Sect. 2.3. We then present in Sect. 2.4 the new photGalIMF code, which tracks the stellar luminosity evolution of synthetic photometric bands. It is an extension to the chemical evolution code GalIMF (Yan et al. 2019b), which itself is built upon the IGIMF module (Yan et al. 2017). A schematic representation of the code structure is shown in Fig. 1. Finally, the SFR–Hα luminosity relations for different metallicities are provided in Sect. 2.5.
 |
Fig. 1. Flowchart of the photGalIMF code, original to the present work, which couples the galaxy chemical evolution code GalIMF (Yan et al. 2019b) with stellar evolution models to calculate photometric properties of galaxies. The GalIMF code calculates the stellar population of a galaxy for given galaxy evolution assumptions (Sect. 2.2) and a variable IMF that depends on the environment at each timestep. The metallicity, mass, and age distributions of stars are then combined with the photometric module to calculate the luminosity for selected photometric bands. See details in Sect. 2.4. |
2.1. The IGIMF theory
The stellar IMF, ξ⋆(m), describes the number of formed stars in an embedded star cluster, dN, in the mass interval m to m + dm. The IMF in embedded star clusters can be mathematically modelled as a three-part power law of the form
where ki are normalization constants (ensuring continuity of the function) and αi are the power-law indices or slopes. The canonical IMF (Kroupa 2001) has α1 = 1.3 ± 0.3, α2 = α3 = 2.3 ± 0.36 (Kroupa et al. 2013, their Eq. (4.55)). The uncertainties of the slope of the IMF can have different interpretations. It may originate from an environment-dependent IMF (Kroupa et al. 2013 their Sect. 9.5 and Yan et al. 2017, 2024) or a random IMF difference between different star clusters (Dib 2022). For this study, we consider only the average shape of the IMF and the dependence of this shape on the star-formation environment. The values of α1 and α2 have been verified by Reid et al. (2002) and Kirkpatrick et al. (2024) who suggest a possible flattening below 0.22 M⊙. The maximum mass of a star in a cluster, mmax, is given by the optimal sampling (Weidner & Kroupa 2006; Yan et al. 2023), which states that mmax depends on the cluster stellar mass Mecl.
Observations of the Milky Way show that about 70 − 90% of all stars are formed in embedded clusters in giant molecular clouds (Lada & Lada 2003), while the other 10 − 30% may be stars formed in short-lived clusters (Recchi et al. 2009; Dinnbier et al. 2022). The embedded cluster mass function (ECMF) is described by a single power law (Lada & Lada 2003; Lieberz & Kroupa 2017) of the form
where kecl is the normalization constant, 5 M⊙ is the minimum mass of an embedded cluster (e.g. Joncour et al. 2018) and Mecl, max is the maximum mass of an embedded star cluster forming in a galaxy with a SFR, ψ. The power-law index of the ECMF is about −2 (Lada & Lada 2003) with a possible variation in galaxies with different SFRs as suggested in Weidner et al. (2011, 2013c). We refer the readers to Yan et al. (2017) for more details. JWST observations will better constrain the ECMF and its possible variation.
Approximating that all stars of the galaxy are formed in embedded star clusters (Kroupa 1995), the IGIMF theory (Kroupa & Weidner 2003) gives the gwIMF, ξecl, by adding up the stellar IMFs in all embedded clusters of a galaxy, that is, combining the stellar IMF of each embedded star cluster (Eq. (1)) and the ECMF (Eq. (2)):
where Z is the metal mass fraction.
We note that the exact dependency of the shape of the IMF and ECMF on the environment is under debate (cf. Fontanot et al. 2018; Sneppen et al. 2022). For example, the original IGIMF version as proposed by Kroupa & Weidner (2003) and Weidner & Kroupa (2006) adopted the invariant IMF for low-mass stars (α1 = 1.3, α2 = 2.3) while Jeřábková et al. (2018) adopt variable IMF slopes with α1 and α2 coefficients that are functions of the stellar iron abundance in the logarithmic scale. Different from the previous works, Yan et al. (2020, 2021) assume that α1 and α2 depends on Z
where Δα = 63 is a constant constrained by observation (Yan et al. 2020, 2021). Z and Z⊙ = 0.0142 (Asplund et al. 2009) are the mean stellar metal-mass fraction of the system and the Sun, respectively. Although a strong IMF–metallicity correlation is reported (Geha et al. 2013; Martín-Navarro et al. 2015), the dependencies of the IMF on the stellar metallicity are different in different studies (Yan et al. 2024), probably due to systematic errors of the measurement methods or hidden parameters (Martín-Navarro et al. 2019). Equation (4) is only constrained by stellar populations with −3 < [Z] < 0.25. An extrapolation of this relation on other metallicities may not be correct.
The power-law index of the high-mass stars (1.00 ≤ m/M⊙ < mmax) is given by (Marks et al. 2012, 2014)
with
where Mecl is the initial stellar mass of the star cluster and [Z] ≡ log10(Z/Z⊙). The expression of x on Mecl was derived in Jeřábková et al. (2018, their Eq. (9)). Here we have the original IMF shape dependency on iron abundance modified to a dependency on metallicity (Yan et al. 2020) because carbon and oxygen are more abundant and more important metal coolants for the star formation process (Sharda & Krumholz 2022). A summary of IMF and ECMF variations in different IGIMF models is provided in Table 1.
Overview of different IGIMF formulations.
Throughout this work, we adopt either an invariant canonical IMF as the gwIMF (the “canonical gwIMF”) or the “IGIMF-2021” gwIMF that depends on galactic SFR and gas metallicity (Yan et al. 2021). The effect of the environment-dependent stellar gwIMF, IGIMF-2021, is qualitatively investigated in Fig. 2 by showing a grid of gwIMFs for different global SFRs in the range of ψ = [10−5,104] M⊙ yr−1 and metallicities in the range of [Z] = [ − 5, 0.2]. This grid is similar to the analysis of Fig. 2 by Jeřábková et al. (2018) but includes only the newer IGIMF-2021 formulation that results in bottom-heavier IMFs for metal-rich galaxies than IGIMF-2018, and therefore, a higher M⋆/L (discussed in Sect. 4.1 below). The most up-to-date version IGIMF-2024 (Yan et al. 2024) only has a minor modification on the IMF of low-mass stars, considering the sub-solar mean metallicity instead of a Solar metallicity for the field stars in the Solar neighbourhood.
 |
Fig. 2. Grid of simulated gwIMFs in dependence of the SFR (from left to right: |
Generally, the gwIMF constructed from the IGIMF-2021 (red lines in Fig. 2) systematically varies with the global SFR and metallicity but as it is constructed based on observational constraints, the gwIMF is consistent with the canonical IMF at Solar metallicity and ψ = 1 M⊙ yr−1 (dashed black line). The gwIMFs of the IGIMF-2021 formulation become bottom-heavy for [Z] > 0 and bottom-light for [Z] < 0 independent of the SFR, reproducing the observed correlation (Yan et al. 2024, and references therein). The gwIMF becomes top-heavy for ψ ≳ 10 M⊙ yr−1 and top-light for ψ ≲ 0.1 M⊙ yr−1, following the formulation of Marks et al. (2012). As illustrated more clearly in Fig. B1 of Yan et al. (2017) the top-heaviness of the gwIMFs for ψ > 1 M⊙ yr−1 slightly increases with decreasing metallicity.
2.2. Galaxy chemical evolution model
The GalIMF code is a Python 3 package that couples a gwIMF generator (galimf.py) with a chemical evolution model (galevo.py), introduced and described in full detail in Yan et al. (2017) and Yan et al. (2019b, 2021), respectively, and are publicly available on GitHub1. We provide here a summary of the most important assumptions and model parameters.
The chemical evolution calculation assumes a monolithic collapse for galaxy formation whereby primordial gas is transformed into living stars which subsequently evolve into white dwarfs, neutron stars, and black holes over cosmic time. In this study, the gas phase is modelled as a single-zone gas, which is continuously enriched by stellar evolution. The galactic gas outflow is turned off to reduce the number of free parameters and simplify the discussion since we assume a moderate and continuous SFH rather than starbursts (Sect. 2.3). Studies of star-forming galaxies including dwarfs show that outflows are local and do not affect the evolution significantly because observed star-bursting dwarfs have similar baryonic and neutral gas fractions to those of typical dwarfs (Lelli et al. 2014) and they also have similar properties of their ionized gas content (Marasco et al. 2023). Dwarf and massive star-forming galaxies at redshift z = 1 − 2 also have negligible large-scale outflows (Concas et al. 2022). A review of the relevance of feedback in star-forming dwarf galaxies can be found in Lelli (2022). Supernova feedback has an observable effect in star-forming galaxies, but it is largely local. It may also lead to outflows outside the disk plane, but the gas most likely falls back on the disk in the galactic fountain fashion, creating a small-scale gas circulation that can help metal mixing and gas recycling (Melioli et al. 2015). A strong stellar feedback stirs the gas inside the potential well and may generate too strong non-circular motions in the disk plane than observed (Lelli 2022). The survey by Valentino et al. (2021) demonstrates that feedback by AGN also has a minimal effect on the gas, dust fractions, and star formation efficiencies. At high redshifts, dwarfs likely experienced galactic outflow but the effect is a reduced metallicity and does not change our main conclusions.
Similar to Yan et al. (2021), the main input parameters of the galaxy evolution module are the SFH and the gas-convergence factor, gconv, which is the ratio between the total stellar mass ever formed and the initial mass of the gas reservoir that is involved in the instantaneous well-mixing assumption. The gconv value quantifies the SFE and correlates with the metal enrichment of the simulated galaxy. A higher value of gconv increases the metallicity while a lower value decreases the galactic metallicity. Therefore, the adopted gconv value is constrained by the observed metallicities of galaxies. For example, Yan et al. (2021, their figure 8) suggest that gconv = 0.25 for elliptical galaxies.
The timestep of the simulation is set to δt = 10 Myr, which corresponds, approximately, to the time span for large molecular clouds to collapse and form a population of embedded star clusters that can well represent the ECMF (Weidner et al. 2004; Yan et al. 2017). For each 10 Myr time step, the chemical evolution module updates the chemical abundances, the mass of stellar remnants, living stars, and gas mass by accounting for the contributions of stellar populations formed in all previous timesteps. Then the code calculates the instantaneous environment-dependent gwIMF as a function of ψ and Z according to Eq. (3) for the stars formed at this timestep.
2.3. SFHs of the local star-forming galaxies
Converting the observed luminosities of galaxies to stellar masses requires the mass-to-light ratio of the stellar population, M⋆/L, which mainly depends on the underlying stellar IMF, SFH, and chemical evolution. In the case of an invariant gwIMF, M⋆/L will depend on the shape of the SFH, but not on the absolute SFR values. On the other hand, with a SFR-dependent gwIMF, M⋆/L also depends on the absolute SFR (Zonoozi et al. 2019).
The real SFHs of observed galaxies are uncertain. Galaxies on the star-forming main sequence can have rising or declining SFRs. Assuming a rising SFR could result in an estimated present-day SFR that is 0.3 to 0.6 dex higher than the value when assuming a declining SFH (Sect. 3.1.4 of Speagle et al. 2014). On the other hand, Kroupa et al. (2020a) showed that most of the star-forming galaxies in the LV have near constant SFRs over a time-span of 12 Gyr. Therefore, it is reasonable to assume as a first approach SFH models with a constant SFR over time for star-forming galaxies. Assuming a fixed SFR is similar to the assumption that a fixed fraction of gas is converted to stars per time interval because the total gas mass in our closed-box model does not change more than 25%. In addition, we assume that all galaxies start forming their stars 0.2 Gyr after the Big Bang till the present time. Thus, throughout the analysis, the present-day properties of galaxies refer to an age of 13.6 Gyr.
A more comprehensive modelling of galaxies with different SFHs and ages is needed to extend the current study. Extreme SFH differences may lead to a M⋆/L variation by a factor of 2 (Fig. 5 in Bell & de Jong 2001) which is similar to the variation caused by a variable gwIMF for a constant SFH (Sect. 4.1). The discussion presented here is useful because adopting a constant NIR mass-to-light ratio without taking into account the variation of the IMF and SFH is common in practice (McGaugh & Schombert 2014). A systematic overestimation of stellar mass due to an unrealistic SFH would not affect our main conclusions.
2.4. photGalIMF: Evolution model of the stellar luminosity
The previous GalIMF code only considers the bolometric luminosity of zero-age main sequence stars (Sect. 4.4 of Yan et al. 2019b). To include the metallicity and age dependencies of stellar luminosities for pre-main sequence and giant stars, we develop the photGalIMF code2 which extends the GalIMF code by coupling it with the stellar isochrones of PARSEC (Bressan et al. 2012) and COLIBRI (Marigo et al. 2013). This correctly increases the luminosity estimation of a stellar population up to a factor of a few (Girardi et al. 2013). The concept of the photGalIMF code is illustrated in Fig. 1.
The PARSEC code models the evolutionary tracks from the pre-main sequence phase to the first thermal pulse or carbon ignition. The COLIBRI code adds the thermally-pulsing asymptotic giant branch (TP-AGB) evolution from the 1st thermal pulse to the total loss of envelope. In particular, the current version of the photGalIMF code implements the PARSEC (Bressan et al. 2012) version 1.2s, and the COLIBRI S_37 code (Pastorelli et al. 2020) for metallicities in the range of 0.008 ≤ Z ≤ 0.02, COLIBRI S_35 (Pastorelli et al. 2019) for 0.0005 ≤ Z ≤ 0.006, COLIBRI PR16 (Marigo et al. 2013) and the models by Rosenfield et al. (2016) for Z ≤ 0.0002 and Z ≥ 0.03 (see also the description on the CMD web interface version 3.73, hereafter CMD V3.7).
Considering the luminosities of galaxies in the Ks-band of the 2MASS sky survey (Jarrett et al. 2000, 2003) as an example, we downloaded from the CMD V3.7 the PARSEC-COLIBRI stellar isochrone tables for the photometric systems labeled “2Mass + Spitzer (IRAC + MPIS)” (Cohen et al. 2003; Groenewegen 2006), which list the Ks-band magnitudes with an effective wavelength of λeff = 21620.75 Å, a bandwidth of weff = 2714 Å, and an attenuation relative to the V-band of AKs/AV = 0.11675 as given by the CMD V3.7. We apply the default options of the CMD V3.7 which provide the bolometric correction “YBC+new Vega”, a dust composition of 60% Silicate and 40% AlOx for M stars and 85% AMC and 15% SiC for C stars (Groenewegen 2006), a total extinction of AV = 0.0 mag, and a long-period variability during the RGB and AGB phase as modelled by Trabucchi et al. (2021). In total, we incorporated the isochrones for ten different metallicities, Z = 0.0001, 0.0002, 0.0005, 0.001, 0.004, 0.008, 0.01, 0.02, 0.03, and 0.04.
The K-band magnitudes, MK, of the so-downloaded and incorporated isochrone tables are converted into luminosities via
where MK, ⊙ = 3.27 (Table 3 of Willmer 2018) is the absolute magnitude of the Sun in the VEGAMAG system.
We calculate the gwIMF for stars formed within a galaxy evolution timestep of δt = 10 Myr (Sect. 2.2) by assuming that individual stars are randomly forming at different times in this 10 Myr epoch. Therefore, the photGalIMF code calculates the time-averaged luminosity of stars formed with a given initial mass, m, metallicity, Z, and age, t, by
where δt = N ⋅ Δt, ti = t + i ⋅ Δt is the age of the isochrone, and N is the number of used isochrones between the time span t and t + δt in the photGalIMF code. The time resolution of the isochrones is set to Δt = 0.1 Myr for stars with ages of t < 1 Gyr and Δt = 1 Myr for t ≥ 1 Gyr.
The photGalIMF module assigns each formed star in the GalIMF module a time-averaged luminosity value  according to its m, Z, and t. To reduce the computational cost, we linearly interpolate the stellar-mass–time-averaged-luminosity relation (MLR) for stars with t < 108.5 yr, ensuring that the pre-main sequence is accurately described. For t ≥ 108.5 yr, the main sequence phase of the MLR is fitted with a 10-th order polynomial. The giant phase is again linearly interpolated to ensure that the TP-AGB is accurately traced. The sum of all
according to its m, Z, and t. To reduce the computational cost, we linearly interpolate the stellar-mass–time-averaged-luminosity relation (MLR) for stars with t < 108.5 yr, ensuring that the pre-main sequence is accurately described. For t ≥ 108.5 yr, the main sequence phase of the MLR is fitted with a 10-th order polynomial. The giant phase is again linearly interpolated to ensure that the TP-AGB is accurately traced. The sum of all  values is the total luminosity of the simulated galaxy.
values is the total luminosity of the simulated galaxy.
The Ks-band stellar (including remnants) mass-to-light ratio at a given time is then
where M⋆, living and Mrem are the mass of the living stars and stellar remnants (i.e. white dwarfs, neutron stars, black holes, calculated as in Yan et al. 2019b), respectively.
The photGalIMF code is freely available on GitHub2. As an example, Fig. A.1 shows the time evolution of M⋆/LK for stellar populations with fixed metallicities (Z = 0.0001, 0.004, 0.02, and 0.04) given by the photGalIMF code. The results are qualitatively in agreement with previous studies (e.g. Maraston 2005 and Busch et al. 2015) with minor differences likely due to different versions of adopted stellar evolution models.
The M⋆/L value depends on the photometric band. The current version of the photGalIMF code provides the galaxy luminosity evolution in the K-band of the 2Mass sky survey (Cohen et al. 2003), the IRAC [3.6]-band of the Spitzer survey (see e.g. Groenewegen 2006), and the V-band of the UBVRIJHK photometric system (Bessell 1990; Maíz Apellániz 2006). More bands, including the Gaia and JWST photometries and the hydrogen line emissions, can be added.
2.5. Calibration of the Hα luminosity as a SFR tracer
Equation (2) of Kennicutt (1998) empirically relates the SFR and the Hα nebular gas luminosity of a galaxy via
This relation assumes the solar abundance and the Salpeter IMF (Salpeter 1955) and is not valid for a different gwIMF or metallicity (Pflamm-Altenburg et al. 2007, 2009; Jeřábková et al. 2018).
To estimate the galactic Hα luminosity, we apply a separate stellar population synthesis code because the current version of the photGalIMF code does not include the calculation of nebular gas Hα luminosity. Following Sect. 4.3 of Jeřábková et al. (2018), we use the second version of the Programme d’Étude des GAlaxies par Synthèse Évolutive (PÉGASE) stellar population synthesis code (Fioc & Rocca-Volmerange 1999; Fioc et al. 2011) in combination with the PyPegase python wrapper4 to compute the SFR–Hα-luminosity relation for the here applied IGIMF-2021 formulation. The computation of this conversion uses the gwIMF as an input and calculates an average nebular gas Hα flux of a galaxy from the ionizing photons, assuming a constant SFR. Since the code only allows the implementation of a multi-power-law IMF, we adopted the same procedure developed in Jeřábková et al. (2018) where the gwIMF is approximated as a multi-part power law by fitting the power-law indices in the mass ranges of 0.08 to 0.5 [M⊙], 0.5 to 1 [M⊙], 1 to 0.8 ⋅ mmax [M⊙], and 0.8 ⋅ mmax to 150 [M⊙] (see their Sect. 4.3). The code calculates the average Hα flux value for a timescale over 100 Myr, as short-lived massive stars contribute most significantly to the ionizing flux.
The SFR–Hα-luminosity relations of the IGIMF-2021 formulation for different metallicities are presented in the left panel of Fig. 3. In general, galaxies with LHα ≳ 1041 ergs s−1 (LHα ≲ 1041 ergs s−1) have lower (higher) SFRs compared to the SFRs derived from Kennicutt (1998). This is consistent with Fig. 7 of Jeřábková et al. (2018).
 |
Fig. 3. SFR-Hα luminosity relations of the canonical invariant IMF and the IGIMF-2021 theory. Left panel: Star formation rate in dependence of the Hα luminosity assuming a canonical IMF (solid black line; Kennicutt 1998) and the IGIMF-2021 theory (coloured lines) for different metallicities [Z] shown on the right colorbar. The Hα fluxes are calculated with the PÉGASE code (see text). Right panel: Conversion factor of the SFRs, |
Following Kennicutt (1998), our provided relations based on the continuous-star-formation approximation only consider a systematic gwIMF variation and metallicity differences of the galaxies. Dust content, SFH, and other galaxy properties are assumed to be identical or irrelevant. Therefore, the SFR–Hα-luminosity relation can be different, for example, if massive galaxies have stronger dust attenuation (Nelson et al. 2016). Essentially, the photometry provided by the photGalIMF code assumes the effect of dust has been removed (see chapters in Zezas & Buat 2021).
To convert the observed Hα luminosities to SFRs within the IGIMF-2021 context, we provide, in the following, different fitting functions. The SFR–Hα-luminosity relations for different metallicities are fitted in the range of −6 < log10(LHα [1041 erg s−1]) < 4 with a fifth-order polynomial in log10-space of the form
where x ≡ log10(LHα [1041 erg s−1]).
The conversion factor between the SFRs based on the linear Kennicutt law (Kennicutt 1998) and the IGIMF theory (cf. Eq. (17) of Jeřábková et al. 2018) is defined as
and its LHα dependence is shown in the right panel of Fig. 3. This relation is also fitted in the range of −6 < log10(LHα [1041 erg s−1]) < 4 with a fifth-order polynomial
where y ≡ log10(LHα [1041 erg s−1]).
Finally, the relation between ψK98 (Kennicutt 1998) and ψIGIMF is fitted in the range of −6 < log10(ψK98 [M⊙ yr−1]) < 4 with a fifth-order polynomial in the log10-space of the form
where z ≡ log10(ψK98 [M⊙ yr−1]). For example, a galaxy traditionally thought to have ψK98 = 10−5 M⊙ yr−1 would have ψIGIMF = 10−3 M⊙ yr−1 for [Z] ≈ −0.5. That is, the SFR based on the nebular ionizing flux may be significantly underestimated for low-SFR galaxies because of a top-light gwIMF (e.g. Yan et al. 2017, their Fig. 6). Multi-tracer studies of the SFR of dwarf galaxies support the gwIMF predicted by the IGIMF theory (Lee et al. 2009), as already also emphasized by Pflamm-Altenburg et al. (2007, 2009) based on the IGIMF-2003 (Table 1).
The polynomial coefficients of the fitting functions given by the Eqs. (11), (13), and (14) are listed for different metallicities in Table B.1.
3. Observations
3.1. SFE constrained by the mass–metallicity relation
The gwIMF of a galaxy and the luminosity of stars depend on the metallicity. Therefore, the M⋆/L value of a galaxy depends on the metallicity distribution of the stars calculated by the galaxy chemical enrichment model and the galaxy models need to reproduce the observed mass–metallicity relation of the sample galaxies.
Assuming the closed-box GCE model and constant SFRs (reasons given in Sect. 2.3), between ψ = 10−5 M⊙ yr−1 and ψ = 103 M⊙ yr−1 in steps of 0.5 dex, over a time-span of 13.6 Gyr, we calculate for each SFH two different chemical enrichment models with gconv = 0.10 and gconv = 0.25 (as explained in Sect. 2.2). We find that the observed stellar mass–metallicity relation of star-forming galaxies (Gallazzi et al. 2005; Kirby et al. 2013) lies approximately in between these models as is shown in Fig. 4. Therefore, we consider that within the framework of our galaxy evolution model, most local star-forming galaxies should have a gconv value between 0.1 and 0.25. The uncertainties introduced by the unknown gconv value of galaxies are estimated by applying 0.1 and 0.25 as a lower and upper limit, respectively.
 |
Fig. 4. Present-day stellar (including remnants) mass–metallicity relation for galaxies with different constant SFRs over a time-span of 13.6 Gyr, adopting gconv = 0.10 (red line) and gconv = 0.25 (blue line), within the IGIMF-2021 context. The green stars refer to dwarf galaxies of the Milky Way and M31 galaxies (Table 4 of Kirby et al. 2013). The solid black line shows the median while the dashed lines show the 16th and 84th percentiles of the metallicity distribution of galaxies in the Sloan Digital Sky Survey Data Release 2 (Table 1 of Gallazzi et al. 2005). Note that the shown stellar masses of Kirby et al. (2013) and Gallazzi et al. (2005) are derived for the canonical gwIMF but the simulated mass–metallicity relations (red and blue lines) refers to a varying gwIMF within the IGIMF theory (see text). |
The galactic stellar masses estimated by Gallazzi et al. (2005) and Kirby et al. (2013) assume a canonical IMF while our calculations are based on the more realistic empirical environment-dependent gwIMF. However, the calculated masses differ by usually less than a factor of two (Sect. 4.2, cf. Yan et al. 2021), which is insignificant compared to the observed scatter in the mass–metallicity relation (Fig. 4) and, therefore, do not affect our conclusions. Note that the IGIMF-2021 model reproduces the observed mass-metallicity relation without invoking outflows. This was already noted by Köppen et al. (2007) and is consistent with the observational evidence of starforming and starbursting galaxies lacking large-scale gas outflows despite the presence of AGN activity (Valentino et al. 2021, Sect. 2.2).
3.2. Sample galaxies
The observational data are taken from the updated version (Karachentsev et al. 2013) of the Catalogue of Neighbouring Galaxies5 (Karachentsev et al. 2004), which lists galaxies in the LV defined by Galactocentric distances of D < 11 Mpc or radial velocities of V < 600 km s−1. In order to analyse the main sequence of star-forming galaxies (Sect. 4.3) and the characteristic stellar mass buildup timescales (Sect. 4.5), we extract the K-band luminosity, LK, and the SFR based on the integrated Hα luminosity assuming the Kennicutt law, ψK98 (Karachentsev & Kaisina 2013). Galaxies marked with ψK98 limit flags are excluded as only reliable SFR measurements should be included in the analysis. This gives a final sample of 603 galaxies. For calculating the gas depletion timescales (Sect. 4.4), we also select the measurements of the hydrogen mass, MHI, which reduces the sample to 544 galaxies. The total neutral gas mass of a galaxy is obtained via
where the prefactor 1.85 accounts for the helium mass and molecular gas mass (cf. Sect. 7 of Karachentsev & Kaisina 2013 and Sect. 2.3.4 of Fukugita & Peebles 2004).
4. Results
In this section, we calculate the M⋆/LK values and compare the stellar-mass–SFR relation, characteristic stellar mass buildup timescale, and gas depletion timescale of local star-forming galaxies assuming two different frameworks, the invariant canonical IMF and the IGIMF-2021 (Sect. 2.1) formulations.
4.1. Evolution of the mass-to-light ratio of the stellar population
As an example, Fig. 5 shows the time evolution of the gwIMF and the Ks-band mass-to-light ratio, M⋆/LK (Eq. (9)), assuming constant SFRs and gconv = 0.25, constructed assuming an invariant canonical IMF and the IGIMF. The gwIMF of the low-mass stars depends on the stellar metallicity according to the empirical IGIMF-2021 formulation. Compared to the invariant canonical gwIMF case, the IGIMF-2021 model leads to a significant increase of the M⋆/LK value for massive metal-rich galaxies and a lower M⋆/LK value for the low-SFR metal-poor galaxies.
 |
Fig. 5. Time evolution of the gwIMF (right panels) and the stellar mass-to-light ratio in the K-band (left panels) assuming a constant SFR of ψ = 103 M⊙ yr−1 (top panels), 1 M⊙ yr−1 (middle panels), and 10−3 M⊙ yr−1 (bottom panels) over a timescale of 14 Gyr in the invariant canonical gwIMF (dashed black lines in the left and right panels; Kroupa 2001) and IGIMF-2021 (solid black line in the left panels and coloured lines in the right panels) framework. The chemical evolution model adopts gconv = 0.25. The mass-to-light evolution curves adopting the invariant canonical IMF are not identical because they represent the evolution of galaxies with different metal enrichment histories. |
For the IGIMF-2021 formulation and assuming a constant SFR (Sect. 2.3), the M⋆/LK value slowly increases with time after about 2 × 108 yr, especially for bottom-heavier gwIMFs. We note that the significant increase of M⋆/LK for high-SFR galaxies (top panel in Fig. 5) near 10 Gyr is mainly driven by metal enrichment and the gwIMF dependency on metallicity. If a galaxy with a known metallicity has a shorter SFH duration than the 13.6 Gyr assumed above, the time variation of M⋆/LK could lead to an overestimation of the galaxy’s stellar mass, by a factor of ≲3.
4.2. M/L–L relation
The present-day M⋆/LK values of our grid galaxies with two different gconv parameters are calculated, given in Fig. 6. This corresponds to the M⋆/LK value of the final time step in Fig. 5. When assuming the invariant canonical gwIMF, the more massive galaxies have smaller gconv values because they have a higher metallicity (Fig. 4) that increases the K-band luminosity. In the IGIMF context, the gwIMF becomes bottom-heavy for metal-rich galaxies. Therefore, the present-day M⋆/LK also increases for the most massive galaxies as demonstrated in Fig. 6. This gwIMF-metallicity dependency is absent for models assuming gconv = 0.1 that result in metal-poor galaxies because the IMF of low-mass stars is no longer sensitive to metallicity when the metallicity is low enough. Our calculation, considering galaxies with a constant SFR over 13.6 Gyr and an empirical gwIMF variation, suggests that the stellar mass of a local star-forming galaxy is overestimated by a factor of ≲2 for dwarf galaxies, and the galactic stellar mass is underestimated by a factor of ≈2 for the most massive galaxies with a super-Solar metallicity ([Z] ≈ 0.2, see Fig. 4).
 |
Fig. 6. Stellar mass-to-light ratio, M⋆/LK (Eq. (9)), in the Ks-band in dependence of LK for galaxies with an age of 13.6 Gyr assuming gconv = 25% (red lines) and 10% (blue lines) in the canonical IMF (left panel) and IGIMF-2021 (right panel) context. The dashed black line shows the mean M⋆/LK of the two different chemical enrichment models (red and blue lines). |
4.3. Stellar-mass–SFR relation of star-forming galaxies
The stellar-mass–SFR relation of star-forming galaxies in the LV assuming the invariant canonical gwIMF and the IGIMF-2021 formulations is presented in Fig. 7. The observed Ks-band luminosities listed in the Catalogue of Neighbouring Galaxies (Sect. 3.2) are converted to stellar masses in the IGIMF context by applying the present-day M⋆/LK values shown in the right panel of Fig. 6. The M⋆/LK nominal-face-value for a given Ks-band luminosity is taken to be the mean value of the chemical enrichment models with gconv = 0.10 and gconv = 0.25 (Sect. 3.1). The upper and lower limit of M⋆/LK refer either to the gconv = 0.10 or gconv = 0.25 model depending on which yields the higher or lower M⋆/LK value. The IMF is affected by the metallicity more significantly in the metal-rich regime. As a consequence, the errorbar of M⋆ increases with higher LK. Here, the resulting uncertainty denotes the possible range of M⋆/LK for a constant SFR (Sect. 2.3), and if gconv is between 0.1 and 0.25. For any specific galaxy with an accurate metallicity measurement, its M⋆ can be estimated with a smaller uncertainty. Instead of applying the M⋆/LK values in the left panel of Fig. 6, we adopt a fixed M⋆/LK = 0.6 for the canonical IMF (McGaugh & Schombert 2014) in Sects. 4.3 and 4.5.
 |
Fig. 7. Star formation rate derived from the Hα luminosity in dependence of the stellar mass derived from the K-band luminosity (Karachentsev et al. 2013) assuming an invariant canonical gwIMF (left panels) and the IGIMF-2021 (right panels) for galaxies located in the LV. The errorbars of the IGIMF-corrected stellar mass values refer to the two different applied chemical enrichment models (Sect. 4.2) and the errorbars of the IGIMF-corrected SFR values refer to metallicities of [Z] = −2.20 (lower limit) and [Z] = 0.45 (upper limit; see Sect. 4.2). The SFR values have an uncertainty of about 30% due to distance uncertainties (see Fig. 1 of Kroupa et al. 2020a; Karachentsev et al. 2004, 2013). The solid green lines show the present-day main sequence of star-forming galaxies with 109.7 < M⋆/M⊙ < 1011.1 and a scatter of ±0.2 dex highlighted by the shaded area (i.e. Eq. (28) of Speagle et al. 2014, and Eq. (17)). The dashed green lines are extrapolations beyond the adopted fitted range of the stellar masses. The solid red lines show the linear best fit to the corresponding data (Eq. (18) for the right panel). Note the smaller scatter in the right panel. |
The SFRs are IGIMF corrected by using the fitting function defined by Eq. (14). The metallicities of the observed galaxies have not been estimated in the current version of the Catalogue of Neighbouring galaxies. Therefore, we apply for the nominal-face-value of the corrected SFRs Eq. (14) for a Solar metallicity (Table B.1). The corresponding errorbars are conservatively estimated by adopting the lower and upper limits [Z] = −2.20 and [Z] = 0.45, respectively.
In the canonical gwIMF context (left panel of Fig. 7), the resulting stellar-mass–SFR relation has a large scatter, especially for low-mass galaxies, such that the star-forming main sequence of low-mass galaxies is ill-defined. Star-forming galaxies with ψ ≳ 10−3 M⊙ yr−1 and M⋆ ≲ 1010 M⊙ are consistent with a constant SFR over a star-forming timescale of ≈12 Gyr (because M⋆ = ψ × 12 Gyr), while more massive galaxies typically follow the main sequence of galaxies (McGaugh et al. 2017; Schombert et al. 2019; Kroupa et al. 2020a; Haslbauer et al. 2023). For more massive galaxies, Speagle et al. (2014) quantified the main sequence for a given age, t, and found for star-forming galaxies with 109.7 < M⋆/M⊙ < 1011.1 a linear relation of the form (see their equation (28)),
For galaxies in the LV (t = τh), this relation reduces to
shown by the green dashed line in Fig. 7 (cf. Förster Schreiber & Wuyts 2020).
For gwIMFs given by the IGIMF-2021, galaxies with LK ≲ 109 LK, ⊙ (LK ≳ 109 LK, ⊙) have higher (lower) SFRs compared to a canonical gwIMF as discussed in Fig. 3. A tight stellar-mass–SFR relation similar to the main sequence of massive galaxies given in Speagle et al. (2014) is recovered, extending to low-mass galaxies. Approximating the resulting main sequence by a linear function over 104.4 < M⋆/M⊙ < 1011.1 yields,
as is shown by the red solid line in the right panel of Fig. 7 (see also Fig. 1.8 of Kroupa & Jerabkova (2021) demonstrating the IGIMF correction for the galaxy main sequence at different redshifts).
4.4. Gas depletion timescale
The present-day gas depletion timescale (cf. Sect. 5 of Pflamm-Altenburg & Kroupa 2009) is defined by
such that the inverse is a measure of the SFE of a galaxy. The gas depletion timescales in dependence of the total neutral gas mass for the invariant canonical gwIMF and IGIMF-2021 for galaxies in the LV are presented in Fig. 8. In the invariant canonical gwIMF context, the gas depletion timescale decreases with increasing gas mass, implying that low-mass galaxies have a lower SFE compared to more massive galaxies. The correlation is reversed assuming the gwIMF is given by the IGIMF-2021, in which low-mass galaxies have a higher SFE than massive galaxies. This is probably due to massive late-type galaxies having stronger feedback associated with a top-heavier gwIMF (Gunawardhana et al. 2011) and more AGB stars. For the low-mass galaxies, the metallicity-dependent feedback is weaker in a low-metallicity environment which allows a higher SFE (Dib et al. 2011; Dib 2011).
 |
Fig. 8. Gas depletion timescale, τgas, in dependence of the gas mass assuming the gwIMF in the invariant canonical IMF (left panel) and IGIMF-2021 (right panel) for galaxies located in the LV. The dashed red line shows the age of the Universe, τgas = τh = 13.8 Gyr, assuming the standard ΛCDM cosmology (Planck Collaboration XIII 2016). The error on the IGIMF-corrected τgas values (right panel) is estimated by adopting the SFR values for [Z] = −2.20 (upper limit) and [Z] = 0.45 (lower limit; Sect. 4.2). The solid red lines are fits of the data with Eq. (20). The green dotted line is the ‘minimum-1’ model of Pflamm-Altenburg & Kroupa (2009, their Fig. 7). Note the smaller scatter of the data in the right panel (see also Fig. 9). |
Following Pflamm-Altenburg & Kroupa (2009), the relation between the gas depletion timescale and total neutral gas is fitted with a function of the form
with Ag = 0.03 Gyr and Bg = 0.28 for the IGIMF-2021 case (solid red line in Fig. 8) broadly matching the ‘minimum-1’ model of Pflamm-Altenburg & Kroupa (2009, their Fig. 7) with Ag = 0.62 Gyr and Bg = 0.13 (green dotted line in Fig. 8) but significantly differs from their ‘standard’ IGIMF model with Ag = 2.52 Gyr and Bg = 0.01 (see their Eq. (7) and Fig. 6) implies only a weak correlation between τgas and Mgas.
Figure 9 shows the distribution of the gas depletion timescales fitted with a log-normal function of the form (following Eq. (8) of Pflamm-Altenburg & Kroupa 2009)
 |
Fig. 9. Distribution of the gas depletion timescale, τgas, assuming the gwIMF is given by the invariant canonical IMF (blue) and the IGIMF-2021 (green) in the log10-space. The τgas are calculated by adopting the IGIMF-corrected SFR values for a Solar metallicity. The histograms are fitted with a Gaussian (solid red curves) with expected values of μ = log10(τgas [Gyr]) = 1.12 (13.25 Gyr; canonical gwIMF) and μ = log10(τgas [Gyr]) = 0.67 (4.72 Gyr; IGIMF-2021) and variances of σ = 0.60 Gyr (canonical gwIMF) and σ = 0.41 Gyr (IGIMF-2021). |
where μ and σ are the mean and standard deviation, respectively, being μ = 1.12 (13.25 Gyr) and σ = 0.60 Gyr in the case of the invariant canonical gwIMF and μ = 0.67 (4.72 Gyr) and σ = 0.41 Gyr for the IGIMF-2021. The mean value but also the scatter of τgas become smaller in the IGIMF framework, in agreement with Fig. 8 of Pflamm-Altenburg & Kroupa (2009).
4.5. Characteristic stellar-mass buildup times
The characteristic stellar mass buildup timescale (Section 6 of Pflamm-Altenburg & Kroupa 2009) is defined as
In the invariant canonical gwIMF context, the characteristic stellar mass buildup timescale decreases with increasing stellar mass of the galaxies as shown in the left panel of Fig. 10. Galaxies with τ⋆ values much larger than the age of the Universe τh = 13.8 Gyr implies that they have a lower than average SFR at the present day, while on average, τ⋆ ≈ τh implies ψ ≈ M⋆/τh.
 |
Fig. 10. Characteristic stellar mass buildup timescale normalized by the age of the Universe of τh = 13.8 Gyr (Planck Collaboration XIII 2016) in dependence of the stellar mass in the invariant canonical IMF (left panel) and the IGIMF-2021 (right panel) context for galaxies located in the LV. The dashed red line refers to a characteristic stellar mass buildup timescale equal to τh = 13.8 Gyr. In the right panel, the uncertainty of the IGIMF effect is plotted while the measurement errors are not shown. The upper and lower limits of the IGIMF-corrected τ⋆ values (right panel) are estimated by adopting τup, ⋆ = Mupper, ⋆/ψ([Z] = −2.20) and τlow, ⋆ = Mlow, ⋆/ψ([Z] = 0.45), respectively. ψ([Z] = −2.20) and ψ([Z] = 0.45) refer to the IGIMF-corrected SFR values for [Z] = −2.20 and [Z] = 0.45 (Sect. 4.2). Mup, ⋆ and Mlow, ⋆ refer to the upper and lower IGIMF-corrected stellar masses by applying the maximum and minimum M⋆/LK values (Sect. 4.2). The solid red lines are fits of the data with Eq. (23). |
In contrast, the characteristic stellar mass buildup timescale increases with stellar mass in the IGIMF-2021 context. Fitting the relation between the stellar-mass buildup timescale normalized by τh and the stellar mass with
yields A⋆ = 3.86 × 10−4 and B⋆ = 0.37 for the IGIMF-2021 case (solid red line in Fig. 10). Most of the galaxies with M⋆ ≲ 1010 M⊙ have τ⋆ < τh but more massive galaxies have τ⋆ > τh.
Intriguingly, we see again that the scatter of the galaxies around this average relation is much tighter than the case when assuming the invariant canonical gwIMF, revealing a regulated formation history of galaxies located in the LV. This result is in agreement with the ‘minimum-1’ IGIMF formulation in Pflamm-Altenburg & Kroupa (2009) and is discussed further in Sect. 5.3.
5. Discussion
Following Sect. 4.1 of Jeřábková et al. (2018), we present in Sect. 2.1 a grid of gwIMFs in dependence of the averaged metallicity and global SFR constructed from the IGIMF-2021 formulation (Yan et al. 2021). The gwIMF systematically varies with metallicity and SFR in such a way that it becomes top-heavy for galaxies with ψ > few M⊙ yr−1, while being top-light when ψ < 1 M⊙ yr−1 compared to the invariant canonical gwIMF (Yan et al. 2017). The gwIMF becomes bottom-heavy and bottom-light for [Z] > 0 and [Z] < 0, respectively, independent of the SFR (Yan et al. 2024). The gwIMF is close to a canonical IMF when ψ = 1 M⊙ yr−1 and at solar metallicity (Sect. 2.1). The gwIMF variation for the most metal-rich galaxies will be discussed in Gjergo et al. (in prep.).
5.1. Stellar-mass–SFR relation of star-forming galaxies for a varying IMF
As the Kennicutt-law is invalid for a varying gwIMF, the stellar-mass–SFR relation and therefore also the main sequence of star-forming galaxies needs to be revised within the current parameterization of the IGIMF framework. We present the SFR–Hα luminosity relation in the IGIMF-2021 formulation for different metallicities using the PÉGASE stellar population synthesis code (Sect. 2.5) and provide fitting functions in order to transform observed Hα luminosities or Kennicutt SFRs to IGIMF SFRs (Appendix B).
For example, less luminous Hα galaxies with LHα = 5.5 × 1036 erg s−1 (e.g. the dwarf galaxy Leo P; Jeřábková et al. 2018) have SFRs about 15 (for [Z] = −2.20; Sect. 4.2) to 221 (for [Z] = 0.45) times higher than based on the Kennicutt law, while more Hα-luminous galaxies with LHα = 1044 erg s−1 have about 4.4 (for [Z] = 0.45) and 13 (for [Z] = −2.20) times lower SFRs. As a consequence, the IGIMF-corrected present-day main sequence of galaxies has a shallower slope (Fig. 7).
The IGIMF theory also has cosmological implications. Kroupa & Jerabkova (2021) study the redshift evolution of the main sequence by correcting the SFRs according to the IGIMF theory, finding a shallower slope and a weaker redshift dependence. Interestingly, several studies find inconsistencies between the observed and stellar mass density and SFR density over cosmic time (e.g. Grazian et al. 2015; Hopkins & Beacom 2006, 2008; Wilkins et al. 2008; Madau & Dickinson 2014; Leja et al. 2015; Tomczak et al. 2016; Yu & Wang 2016). A top-heavy or bottom-light gwIMF could alleviate this discrepancy (Yu & Wang 2016). However, such an analysis is beyond the scope of our article and depends on the physical interpretation of the Madau & Dickinson (2014) data of SFR density versus redshift z (Haslbauer et al. 2023). Given the near-constant SFRs for the galaxies observed in the LV, these data imply a significant matter over-density at z ≈ 1.8.
5.2. Gas depletion timescales
Pflamm-Altenburg & Kroupa (2009) applied a revised SFR–Hα luminosity relation based on 200 local galaxies for IGIMF versions which assume a canonical IMF per embedded star cluster and an ECMF with a single power-law index of β = 2.35 (their ‘standard’ IGIMF model) and a two-part power law with β = 1.00 for 5 < m/M⊙ < 50 and β = 2.00 for m/M⊙ > 50 (‘minimum-1’ IGIMF model). Their standard model shows a stronger IGIMF effect compared to the ‘minimum-1’ model by yielding higher SFRs (see their Fig. 1).
In the invariant canonical gwIMF case, the gas depletion timescale shows a decreasing trend with increasing gas mass implying that less massive galaxies have a lower SFE (Pflamm-Altenburg & Kroupa 2009). That is, galaxies with Mgas ≲ 109 M⊙ can have τgas up to 104 Gyr while more massive galaxies have τgas < 102 Gyr. In the IGIMF-2021 case, the situation differs as τgas slightly increases with gas mass such that low-mass galaxies have a higher SFE (i.e. shorter τgas values). Almost all galaxies have τgas ≲ 102 Gyr with a mean of a few Gyr (Fig. 9). The scatter of τgas is smaller assuming the IGIMF-2021 than for the invariant canonical gwIMF.
These findings are consistent with the ‘minimum-1’ IGIMF formalism of Pflamm-Altenburg & Kroupa (2009) while their standard IGIMF yields an almost constant gas depletion timescale between 2.5 and 3 Gyr over a stellar mass range of ≈106 to 1010 M⊙.
The result obtained here of a decreasing SFE with increasing gas (and thus galaxy) mass may suggest that dwarf late-type galaxies form more stars per unit gas mass per unit of time because their star-formation process occurs mostly in low-mass embedded clusters that do not have cloud-destroying ionizing stars.
5.3. Stellar-mass buildup timescales
In the invariant canonical gwIMF case, the characteristic stellar mass buildup timescale decreases with increasing stellar mass for galaxies located in the LV. The situation changes in the IGIMF-2021 context as the characteristic stellar mass buildup timescale increases with stellar mass. Thus, our findings, with a more self-consistent galaxy mass estimation in the IGIMF framework, qualitatively confirm the results of Pflamm-Altenburg & Kroupa (2009) for a larger sample size of local galaxies, suggesting that massive star-forming galaxies have a relatively constant or decreasing SFR, while dwarf galaxies have either started their star-formation activity recently or have an increasing SFR, as is indeed observed to be the case for the galaxies in the Local Group (Kroupa et al. 2020a; Ren et al. 2024). Compared to the results assuming an invariant canonical IMF, the dependency of the SFH on the stellar mass of a galaxy calculated using the IGIMF-2021 theory agrees better with simulation and population synthesis studies (e.g. Mitchell et al. 2014; Guglielmo et al. 2015; Lu et al. 2023).
For completeness we note that the characteristic stellar mass buildup timescale, calculated according to Eq. (22), can be different from the real stellar mass buildup time of a galaxy because (i) the present-day stellar mass, M⋆, is not the total stellar mass ever formed in a galaxy and (ii) the present-day SFR estimation based on the Hα luminosity is not the mean SFR of a galaxy. Not all galaxies have a relatively stable SFR. For example, Kroupa et al. (2020a) reported that most of the galaxies located in the LV have nearly constant SFRs over a star-formation timescale of 12 Gyr, while Speagle et al. (2014) showed that massive star-forming galaxies with M⋆ ≳ 1010 M⊙ strictly evolving along the main sequence of galaxies can be described by a delayed-tau SFH model with maximum SFRs when the galaxy was 3.5 − 4.5 Gyr old. Re-addressing the analysis for more complex SFHs would be required in upcoming studies.
5.4. Galaxy mergers
It is worth addressing the impact that galaxy mergers may have on the analysis of SFHs. In this context, however, their influence is generally deemed negligible for several reasons. First, we note that the vast majority of galaxies are thin disk galaxies (Binggeli et al. 1988; Delgado-Serrano et al. 2010; Haslbauer et al. 2022a), whose evolution is best characterized by in-situ star formation (e.g., Zonoozi et al. 2019). This is also evident in the Milky Way (e.g., Belokurov & Kravtsov 2024; Chen & Gnedin 2024). Therefore, our model is well suited to describe spiral galaxies. But even within a hierarchical mass assembly framework, our model remains applicable. In ΛCDM cosmological simulations (e.g. Lee & Yi 2013) and observations (Zhu et al. 2022), galaxies similar to or less massive than the Milky Way have a small fraction (≲20%) of merged stars, and our galaxy sample does not exceed this mass range. Ultimately, a comprehensive SFH analysis must include dynamical evolution and hence require the self-consistency of cosmological simulations, paired with stellar population synthesis studies. However, we advise caution in the excessive reliance on hierarchical mass assembly models, which lead to inconsistencies with observations. For example, Eappen et al. (2022) revealed that the stellar age distributions in hierarchically-formed elliptical galaxies span too wide an age range, in contrast with observations. Additionally, Haslbauer et al. (2022a) noted that ΛCDM-based simulations overproduce elliptical galaxies, contradicting the observation that the universe predominantly contains spirals.
Therefore, it would be valuable to implement the IGIMF theory in cosmological simulations. Attempts towards incorporating a varying IMF in Newtonian simulations have been made for example by Ploeckinger et al. (2014, 2015), who encoded the IGIMF theory in the FLASH code. This would allow us to revisit downsizing in self-consistent cosmological simulations of structure formation and to address if a top-heavy gwIMF could indeed explain the JWST observations of very luminous galaxy candidates at (photometric) redshifts z > 10 within the standard ΛCDM paradigm (Haslbauer et al. 2022b; Wang et al. 2024; Menon et al. 2024). Implementing the IGIMF theory in the Phantom of Ramses (PoR MOND patch developed by Lüghausen et al. 2015, and the corresponding user guide by Nagesh et al. 2021) will enable galaxy evolution in Milgromian dynamics (MOND, Milgrom 1983) where mergers are rare (Kroupa et al. 2023).
6. Conclusion
A systematically varying gwIMF has fundamental implications on the global properties of the galaxy as the stellar population is constructed from the IMF. In this contribution, we investigate the effect of the IGIMF theory, which is a mathematical framework to compute the gwIMF by integrating all IMFs of star-forming regions (embedded clusters) in a galaxy (Sect. 2.1), on the estimation of galaxy mass and SFR for a sample of local star-forming galaxies (Sect. 3.2).
To convert infrared luminosities to stellar masses, we developed the photGalIMF code to calculate the evolution of M⋆/L (including remnants) in the Ks-band (centred at ≈2.2 μm) in a galaxy chemical evolution model with an environment-dependent gwIMF according to the IGIMF theory (Sect. 2.4). The photGalIMF code provides at its current stage only the Ks-band, the IRAC [3.6]-band, and the V-band and will include further bands such as the Gaia and JWST photometries in the future.
The SFR–Hα-luminosity relation for different metallicities is calculated with the PÉGASE stellar population synthesis code. We provide new correcting functions for converting the measured Hα luminosity or SFRs derived from the Kennicutt-law to SFRs interpreted within the IGIMF-2021 context. The estimated SFR under these two assumptions can be different by a factor of 100 (Sect. 2.5). In the future, hydrogen line luminosities should be added to the photGalIMF code to allow a self-consistent calculation of the SFR–Hα luminosity relation in galaxy evolution simulations for different SFHs and chemical enrichment models.
Assessing the gwIMF in the framework of the IGIMF-2021 formulation, we find that
-
The M⋆/L ratio of a galaxy depends significantly on which description of the IMF (invariant canonical or the IGIMF) is applied (Sects. 4.1 and 4.2).
-
The SFR–stellar-mass relation of star-forming galaxies becomes flatter and has a smaller scatter compared to the results obtained with the canonical invariant IMF for dwarf galaxies, extending the main sequence to lower mass regimes (Sect. 4.3).
-
The gas depletion timescale of local star-forming galaxies increases with their total gas mass in the IGIMF context, suggesting a lower SFE (i.e. longer gas-consumption timescales) in massive galaxies (Sect. 4.4).
-
The characteristic stellar mass buildup timescale of local star-forming galaxies increases with their stellar masses, indicating that massive star-forming galaxies have on average a relatively constant or slightly decreasing SFR while dwarf galaxies either have an increasing SFR or that they started their star formation more recently (Sect. 4.5).
Interpreting photometric observations and subsequently testing cosmological and galaxy evolution models requires assumptions about the stellar IMF. The here-presented photGalIMF code enables a more accurate comparison of photometric observations with galaxy evolution and cosmological models.
https://github.com/coljac/pypegase (downloaded on 03.06.2022)
https://www.sao.ru/lv/lvgdb/introduction.php. Here, we use the latest update from 12.04.2023.
Acknowledgments
The authors thank Alice Concas, Federico Lelli, Xiaoting Fu, Yang Chen, Yunwei Deng and Zhi-Yu Zhang for helpful discussions. In particular, we thank Yang Chen for independently checking the implementation of the PARSEC model. M.H. acknowledges support from the ESO Early-Career Visitor Programme and the SPODYR group at Bonn University for a studentship. P.K. acknowledges support through the DAAD Bonn-Prague exchange programme. Z.Y acknowledges the support from the Jiangsu Funding Program for Excellent Postdoctoral Talent under grant number 2022ZB54, the National Natural Science Foundation of China under grant numbers 12203021, 12041305, and 12173016, and the Fundamental Research Funds for the Central Universities under grant number 0201/14380049. The authors thank an anonymous referee for very helpful comments. The data underlying this article are available in the article. The Python 3 code GalIMF1 version 1.1 developed by Yan et al. (2017, 2019b) with the package photGalIMF2 version 1.0 (Sect. 2.4) is publicly available on GitHub. The observational data are taken from the updated version of the Catalogue of Neighbouring Galaxies (Karachentsev et al. 2004, 2013) and have been IGIMF-corrected as described in Sect. 4.2.
References
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Balakrishna Subramani, V., Kroupa, P., Shenavar, H., & Muralidhara, V. 2019, MNRAS, 488, 3876 [Google Scholar]
- Bell, E. F., & de Jong, R. S. 2001, ApJ, 550, 212 [Google Scholar]
- Belokurov, V., & Kravtsov, A. 2024, MNRAS, 528, 3198 [CrossRef] [Google Scholar]
- Bessell, M. S. 1990, PASP, 102, 1181 [NASA ADS] [CrossRef] [Google Scholar]
- Binggeli, B., Sandage, A., & Tammann, G. A. 1988, ARA&A, 26, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Brinchmann, J., Charlot, S., White, S. D. M., et al. 2004, MNRAS, 351, 1151 [Google Scholar]
- Brown, M. J. I., Moustakas, J., Kennicutt, R. C., et al. 2017, ApJ, 847, 136 [Google Scholar]
- Buat, V., Deharveng, J. M., & Donas, J. 1989, A&A, 223, 42 [NASA ADS] [Google Scholar]
- Busch, G., Smajić, S., Scharwächter, J., et al. 2015, A&A, 575, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Calzetti, D. 2013, in Secular Evolution of Galaxies, eds. J. Falcón-Barroso, & J. H. Knapen, 419 [CrossRef] [Google Scholar]
- Cameron, A. J., Katz, H., Witten, C., et al. 2023, MNRAS, submitted [arXiv:2311.02051] [Google Scholar]
- Chen, Y., & Gnedin, O. Y. 2024, Open J. Astrophys., 7, 23 [NASA ADS] [Google Scholar]
- Cohen, M., Wheaton, W. A., & Megeath, S. T. 2003, AJ, 126, 1090 [Google Scholar]
- Concas, A., Maiolino, R., Curti, M., et al. 2022, MNRAS, 513, 2535 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J. 1992, ARA&A, 30, 575 [Google Scholar]
- Dabringhausen, J., Kroupa, P., & Baumgardt, H. 2009, MNRAS, 394, 1529 [Google Scholar]
- Dabringhausen, J., Kroupa, P., Pflamm-Altenburg, J., & Mieske, S. 2012, ApJ, 747, 72 [NASA ADS] [CrossRef] [Google Scholar]
- David, L. P., Jones, C., & Forman, W. 1992, ApJ, 388, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Delgado-Serrano, R., Hammer, F., Yang, Y. B., et al. 2010, A&A, 509, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dib, S. 2011, ApJ, 737, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Dib, S. 2014, MNRAS, 444, 1957 [NASA ADS] [CrossRef] [Google Scholar]
- Dib, S. 2022, A&A, 666, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dib, S. 2023, ApJ, 959, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Dib, S., & Basu, S. 2018, A&A, 614, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dib, S., Piau, L., Mohanty, S., & Braine, J. 2011, MNRAS, 415, 3439 [NASA ADS] [CrossRef] [Google Scholar]
- Dib, S., Schmeja, S., & Hony, S. 2017, MNRAS, 464, 1738 [NASA ADS] [CrossRef] [Google Scholar]
- Dinnbier, F., Kroupa, P., & Anderson, R. I. 2022, A&A, 660, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Donas, J., & Deharveng, J. M. 1984, A&A, 140, 325 [NASA ADS] [Google Scholar]
- Eappen, R., Kroupa, P., Wittenburg, N., Haslbauer, M., & Famaey, B. 2022, MNRAS, 516, 1081 [NASA ADS] [CrossRef] [Google Scholar]
- Fioc, M., & Rocca-Volmerange, B. 1999, ArXiv e-prints [arXiv: astro-ph/9912179] [Google Scholar]
- Fioc, M., Le Borgne, D., & Rocca-Volmerange, B. 2011, Astrophysics Source Code Library [record ascl:1108.007] [Google Scholar]
- Fontanot, F., De Lucia, G., Monaco, P., Somerville, R. S., & Santini, P. 2009, MNRAS, 397, 1776 [NASA ADS] [CrossRef] [Google Scholar]
- Fontanot, F., La Barbera, F., De Lucia, G., Pasquali, A., & Vazdekis, A. 2018, MNRAS, 479, 5678 [NASA ADS] [CrossRef] [Google Scholar]
- Fontanot, F., La Barbera, F., De Lucia, G., et al. 2024, A&A, 686, A302 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Förster Schreiber, N. M., & Wuyts, S. 2020, ARA&A, 58, 661 [Google Scholar]
- Fukugita, M., & Peebles, P. J. E. 2004, ApJ, 616, 643 [Google Scholar]
- Gallazzi, A., Charlot, S., Brinchmann, J., White, S. D. M., & Tremonti, C. A. 2005, MNRAS, 362, 41 [Google Scholar]
- Geha, M., Brown, T. M., Tumlinson, J., et al. 2013, ApJ, 771, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Gennaro, M., Tchernyshyov, K., Brown, T. M., et al. 2018, ApJ, 855, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Girardi, L., & Bertelli, G. 1998, MNRAS, 300, 533 [CrossRef] [Google Scholar]
- Girardi, L., Marigo, P., Bressan, A., & Rosenfield, P. 2013, ApJ, 777, 142 [Google Scholar]
- Grazian, A., Fontana, A., Santini, P., et al. 2015, A&A, 575, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Groenewegen, M. A. T. 2006, A&A, 448, 181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guglielmo, V., Poggianti, B. M., Moretti, A., et al. 2015, MNRAS, 450, 2749 [NASA ADS] [CrossRef] [Google Scholar]
- Gunawardhana, M. L. P., Hopkins, A. M., Sharp, R. G., et al. 2011, MNRAS, 415, 1647 [NASA ADS] [CrossRef] [Google Scholar]
- Haslbauer, M., Banik, I., Kroupa, P., Wittenburg, N., & Javanmardi, B. 2022a, ApJ, 925, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Haslbauer, M., Kroupa, P., Zonoozi, A. H., & Haghi, H. 2022b, ApJ, 939, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Haslbauer, M., Kroupa, P., & Jerabkova, T. 2023, MNRAS, 524, 3252 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, A. M. 2018, PASA, 35, e039 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, A. M., & Beacom, J. F. 2006, ApJ, 651, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, A. M., & Beacom, J. F. 2008, ApJ, 682, 1486 [CrossRef] [Google Scholar]
- Hopkins, P. F., Wetzel, A., Kereš, D., et al. 2018, MNRAS, 480, 800 [NASA ADS] [CrossRef] [Google Scholar]
- Jarrett, T. H., Chester, T., Cutri, R., et al. 2000, AJ, 119, 2498 [Google Scholar]
- Jarrett, T. H., Chester, T., Cutri, R., Schneider, S. E., & Huchra, J. P. 2003, AJ, 125, 525 [Google Scholar]
- Jeřábková, T., Hasani Zonoozi, A., Kroupa, P., et al. 2018, A&A, 620, A39 [Google Scholar]
- Joncour, I., Duchêne, G., Moraux, E., & Motte, F. 2018, A&A, 620, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Karachentsev, I. D., & Kaisina, E. I. 2013, AJ, 146, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Karachentsev, I. D., Karachentseva, V. E., Huchtmeier, W. K., & Makarov, D. I. 2004, AJ, 127, 2031 [Google Scholar]
- Karachentsev, I. D., Makarov, D. I., & Kaisina, E. I. 2013, AJ, 145, 101 [Google Scholar]
- Keller, B. W., & Kruijssen, J. M. D. 2022, MNRAS, 512, 199 [CrossRef] [Google Scholar]
- Kennicutt, R. C., Jr 1983, ApJ, 272, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., Jr 1998, ARA&A, 36, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., & Evans, N. J. 2012, ARA&A, 50, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L. J., Geller, M. J., Jansen, R. A., & Dopita, M. A. 2002, AJ, 124, 3135 [NASA ADS] [CrossRef] [Google Scholar]
- Kirby, E. N., Cohen, J. G., Guhathakurta, P., et al. 2013, ApJ, 779, 102 [Google Scholar]
- Kirkpatrick, J. D., Marocco, F., Gelino, C. R., et al. 2024, ApJS, 271, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Köppen, J., Weidner, C., & Kroupa, P. 2007, MNRAS, 375, 673 [CrossRef] [Google Scholar]
- Kroupa, P. 1995, MNRAS, 277, 1507 [NASA ADS] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2002, Science, 295, 82 [Google Scholar]
- Kroupa, P., & Jerabkova, T. 2021, arXiv e-prints [arXiv:2112.10788] [Google Scholar]
- Kroupa, P., & Weidner, C. 2003, ApJ, 598, 1076 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P., Weidner, C., Pflamm-Altenburg, J., et al. 2013, in Planets, Stars and Stellar Systems. Volume 5: Galactic Structure and Stellar Populations, eds. T. D. Oswalt, & G. Gilmore, 5, 115 [NASA ADS] [Google Scholar]
- Kroupa, P., Haslbauer, M., Banik, I., Nagesh, S. T., & Pflamm-Altenburg, J. 2020a, MNRAS, 497, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P., Subr, L., Jerabkova, T., & Wang, L. 2020b, MNRAS, 498, 5652 [Google Scholar]
- Kroupa, P., Gjergo, E., Asencio, E., et al. 2023, School and Workshops on Elementary Particle Physics and Gravity, 231 [Google Scholar]
- Lada, C. J., & Lada, E. A. 2003, ARA&A, 41, 57 [Google Scholar]
- Larsen, S. S. 2002, AJ, 124, 1393 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, J., & Yi, S. K. 2013, ApJ, 766, 38 [CrossRef] [Google Scholar]
- Lee, J. C., Gil de Paz, A., Tremonti, C., et al. 2009, ApJ, 706, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Leja, J., van Dokkum, P. G., Franx, M., & Whitaker, K. E. 2015, ApJ, 798, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Lelli, F. 2022, Nat. Astron., 6, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Lelli, F., Verheijen, M., & Fraternali, F. 2014, A&A, 566, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, H., Vogelsberger, M., Marinacci, F., Sales, L. V., & Torrey, P. 2020, MNRAS, 499, 5862 [NASA ADS] [CrossRef] [Google Scholar]
- Li, J., Liu, C., Zhang, Z.-Y., et al. 2023, Nature, 613, 460 [NASA ADS] [CrossRef] [Google Scholar]
- Lieberz, P., & Kroupa, P. 2017, MNRAS, 465, 3775 [NASA ADS] [CrossRef] [Google Scholar]
- Lu, S., Zhu, K., Cappellari, M., et al. 2023, MNRAS, 526, 1022 [NASA ADS] [CrossRef] [Google Scholar]
- Ludlow, A. D., Benítez-Llambay, A., Schaller, M., et al. 2017, Phys. Rev. Lett., 118, 161103 [NASA ADS] [CrossRef] [Google Scholar]
- Lüghausen, F., Famaey, B., & Kroupa, P. 2015, Can. J. Phys., 93, 232 [CrossRef] [Google Scholar]
- Madau, P., & Dickinson, M. 2014, ARA&A, 52, 415 [Google Scholar]
- Mahajan, S., Ashby, M. L. N., Willner, S. P., et al. 2019, MNRAS, 482, 560 [NASA ADS] [CrossRef] [Google Scholar]
- Maíz Apellániz, J. 2006, AJ, 131, 1184 [CrossRef] [Google Scholar]
- Marasco, A., Belfiore, F., Cresci, G., et al. 2023, A&A, 670, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maraston, C. 2005, MNRAS, 362, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Marigo, P., Bressan, A., Nanni, A., Girardi, L., & Pumo, M. L. 2013, MNRAS, 434, 488 [Google Scholar]
- Marks, M., Kroupa, P., Dabringhausen, J., & Pawlowski, M. S. 2012, MNRAS, 422, 2246 [NASA ADS] [CrossRef] [Google Scholar]
- Marks, M., Kroupa, P., Dabringhausen, J., & Pawlowski, M. S. 2014, MNRAS, 442, 3315 [CrossRef] [Google Scholar]
- Martín-Navarro, I., Vazdekis, A., La Barbera, F., et al. 2015, ApJ, 806, L31 [CrossRef] [Google Scholar]
- Martín-Navarro, I., Lyubenova, M., van de Ven, G., et al. 2019, A&A, 626, A124 [Google Scholar]
- Matteucci, F. 1994, A&A, 288, 57 [NASA ADS] [Google Scholar]
- McGaugh, S. S., & Schombert, J. M. 2014, AJ, 148, 77 [Google Scholar]
- McGaugh, S. S., Schombert, J. M., & Lelli, F. 2017, ApJ, 851, 22 [Google Scholar]
- Melioli, C., Brighenti, F., & D’Ercole, A. 2015, MNRAS, 446, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Menon, S. H., Lancaster, L., Burkhart, B., et al. 2024, ArXiv e-prints [arXiv:2405.00813] [Google Scholar]
- Meurer, G. R., Wong, O. I., Kim, J. H., et al. 2009, ApJ, 695, 765 [NASA ADS] [CrossRef] [Google Scholar]
- Milgrom, M. 1983, ApJ, 270, 365 [Google Scholar]
- Mitchell, P. D., Lacey, C. G., Cole, S., & Baugh, C. M. 2014, MNRAS, 444, 2637 [NASA ADS] [CrossRef] [Google Scholar]
- Moustakas, J., Kennicutt, R. C., Jr, & Tremonti, C. A. 2006, ApJ, 642, 775 [NASA ADS] [CrossRef] [Google Scholar]
- Mucciarelli, A., Massari, D., Minelli, A., et al. 2021, Nat. Astron., 5, 1247 [NASA ADS] [CrossRef] [Google Scholar]
- Nagesh, S. T., Banik, I., Thies, I., et al. 2021, Can. J. Phys., 99, 607 [NASA ADS] [CrossRef] [Google Scholar]
- Nagesh, S. T., Kroupa, P., Banik, I., et al. 2023, MNRAS, 519, 5128 [NASA ADS] [CrossRef] [Google Scholar]
- Nelson, E. J., van Dokkum, P. G., Momcheva, I. G., et al. 2016, ApJ, 817, L9 [CrossRef] [Google Scholar]
- Papadopoulos, P. P. 2010, ApJ, 720, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Parikh, T., Thomas, D., Maraston, C., et al. 2018, MNRAS, 477, 3954 [Google Scholar]
- Pastorelli, G., Marigo, P., Girardi, L., et al. 2019, MNRAS, 485, 5666 [Google Scholar]
- Pastorelli, G., Marigo, P., Girardi, L., et al. 2020, MNRAS, 498, 3283 [Google Scholar]
- Pflamm-Altenburg, J., & Kroupa, P. 2008, Nature, 455, 641 [Google Scholar]
- Pflamm-Altenburg, J., & Kroupa, P. 2009, ApJ, 706, 516 [NASA ADS] [CrossRef] [Google Scholar]
- Pflamm-Altenburg, J., Weidner, C., & Kroupa, P. 2007, ApJ, 671, 1550 [NASA ADS] [CrossRef] [Google Scholar]
- Pflamm-Altenburg, J., Weidner, C., & Kroupa, P. 2009, MNRAS, 395, 394 [CrossRef] [Google Scholar]
- Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ploeckinger, S., Hensler, G., Recchi, S., Mitchell, N., & Kroupa, P. 2014, MNRAS, 437, 3980 [NASA ADS] [CrossRef] [Google Scholar]
- Ploeckinger, S., Recchi, S., Hensler, G., & Kroupa, P. 2015, MNRAS, 447, 2512 [NASA ADS] [CrossRef] [Google Scholar]
- Cueto, E. R., Hutter, A., Dayal, P., et al. 2024, A&A, 686, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rautio, R. P. V., Watkins, A. E., Salo, H., et al. 2024, A&A, 681, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Recchi, S., Calura, F., & Kroupa, P. 2009, A&A, 499, 711 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reid, I. N., Gizis, J. E., & Hawley, S. L. 2002, AJ, 124, 2721 [NASA ADS] [CrossRef] [Google Scholar]
- Ren, Y., Jiang, B., Wang, Y., Yang, M., & Yan, Z. 2024, ApJ, 966, 25 [CrossRef] [Google Scholar]
- Rieke, G. H., Alonso-Herrero, A., Weiner, B. J., et al. 2009, ApJ, 692, 556 [NASA ADS] [CrossRef] [Google Scholar]
- Rosenfield, P., Marigo, P., Girardi, L., et al. 2016, ApJ, 822, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Schaye, J., Crain, R. A., Bower, R. G., et al. 2015, MNRAS, 446, 521 [Google Scholar]
- Schneider, F. R. N., Sana, H., Evans, C. J., et al. 2018, Science, 359, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Schombert, J., McGaugh, S., & Lelli, F. 2019, MNRAS, 483, 1496 [NASA ADS] [Google Scholar]
- Schulz, C., Pflamm-Altenburg, J., & Kroupa, P. 2015, A&A, 582, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sharda, P., & Krumholz, M. R. 2022, MNRAS, 509, 1959 [Google Scholar]
- Smith, R. J. 2020, ARA&A, 58, 577 [NASA ADS] [CrossRef] [Google Scholar]
- Sneppen, A., Steinhardt, C. L., Hensley, H., et al. 2022, ApJ, 931, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Speagle, J. S., Steinhardt, C. L., Capak, P. L., & Silverman, J. D. 2014, ApJS, 214, 15 [Google Scholar]
- Tomczak, A. R., Quadri, R. F., Tran, K.-V. H., et al. 2016, ApJ, 817, 118 [Google Scholar]
- Trabucchi, M., Wood, P. R., Mowlavi, N., et al. 2021, MNRAS, 500, 1575 [Google Scholar]
- Valentino, F., Daddi, E., Puglisi, A., et al. 2021, A&A, 654, A165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Dokkum, P., & Conroy, C. 2021, ApJ, 923, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Vazdekis, A., Peletier, R. F., Beckman, J. E., & Casuso, E. 1997, ApJS, 111, 203 [CrossRef] [Google Scholar]
- Wang, B., Leja, J., Atek, H., et al. 2024, ApJ, 963, 74 [CrossRef] [Google Scholar]
- Watts, A. B., Meurer, G. R., Lagos, C. D. P., et al. 2018, MNRAS, 477, 5554 [NASA ADS] [CrossRef] [Google Scholar]
- Weidner, C., & Kroupa, P. 2006, MNRAS, 365, 1333 [Google Scholar]
- Weidner, C., Kroupa, P., & Larsen, S. S. 2004, MNRAS, 350, 1503 [CrossRef] [Google Scholar]
- Weidner, C., Kroupa, P., & Pflamm-Altenburg, J. 2011, MNRAS, 412, 979 [NASA ADS] [Google Scholar]
- Weidner, C., Ferreras, I., Vazdekis, A., & La Barbera, F. 2013a, MNRAS, 435, 2274 [NASA ADS] [CrossRef] [Google Scholar]
- Weidner, C., Kroupa, P., & Pflamm-Altenburg, J. 2013b, MNRAS, 434, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Weidner, C., Kroupa, P., Pflamm-Altenburg, J., & Vazdekis, A. 2013c, MNRAS, 436, 3309 [NASA ADS] [CrossRef] [Google Scholar]
- Weidner, C., Kroupa, P., & Pflamm-Altenburg, J. 2014, MNRAS, 441, 3348 [CrossRef] [Google Scholar]
- Wilkins, S. M., Trentham, N., & Hopkins, A. M. 2008, MNRAS, 385, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Willmer, C. N. A. 2018, ApJS, 236, 47 [Google Scholar]
- Wittenburg, N., Kroupa, P., & Famaey, B. 2020, ApJ, 890, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Yan, Z., Jerabkova, T., & Kroupa, P. 2017, A&A, 607, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yan, Z., Jerabkova, T., & Kroupa, P. 2019a, A&A, 632, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yan, Z., Jerabkova, T., Kroupa, P., & Vazdekis, A. 2019b, A&A, 629, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yan, Z., Jerabkova, T., & Kroupa, P. 2020, A&A, 637, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yan, Z., Jeřábková, T., & Kroupa, P. 2021, A&A, 655, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yan, Z., Jerabkova, T., & Kroupa, P. 2023, A&A, 670, A151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yan, Z., Li, J., Kroupa, P., et al. 2024, ApJ, 969, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Yu, H., & Wang, F. Y. 2016, ApJ, 820, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Yun, M. S., Reddy, N. A., & Condon, J. J. 2001, ApJ, 554, 803 [Google Scholar]
- Zezas, A., & Buat, V. 2021, Star Formation Rates in Galaxies, 55 [CrossRef] [Google Scholar]
- Zhang, Z.-Y., Romano, D., Ivison, R. J., Papadopoulos, P. P., & Matteucci, F. 2018, Nature, 558, 260 [Google Scholar]
- Zhou, S., Mo, H. J., Li, C., et al. 2019, MNRAS, 485, 5256 [Google Scholar]
- Zhu, L., van de Ven, G., Leaman, R., et al. 2022, A&A, 664, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zonoozi, A. H., Mahani, H., & Kroupa, P. 2019, MNRAS, 483, 46 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: M/L evolution for stellar populations with fixed metallicities
As an example, Fig. A.1 shows the time evolution of M⋆/LK for single stellar populations (SSPs) and constant SFR models with different metallicities ([Z] = −2.17, -0.57, 0.13, 0.43) assuming the canonical IMF (Kroupa 2001). The sharp decrease at ≈2 × 109 yr is due to a pronounced peak in the production rate of AGB stars as explained in Girardi & Bertelli (1998) and Girardi et al. (2013). Our result is qualitatively in agreement with previous studies (e.g. Maraston 2005 their Fig. 23 and Busch et al. 2015 their Fig. 10). Other than the choices of wavelength, metallicity, and time resolution, the differences in the shape of the curve and the exact time of the pronounced luminosity peak are also due to updated stellar and TP-AGB evolution models of the PARSEC code.
 |
Fig. A.1. Time evolution of the Ks-band mass-to-light ratio, M⋆/LK, for stellar populations with a fixed canonical (Kroupa 2001) IMF and different metallicities denoted in the upper left corner of each panel. Red solid curves are SSPs formed at time zero. The sharp drop in the SSP models of M⋆/LK at t ≈ 2 × 109 yr is caused by a significant increase in the number of AGB stars. The blue dashed curves are stellar populations with the same fixed metallicity but a constant SFR over time, demonstrating a smooth curve of lower M⋆/LK value due to the luminosity contribution from young stars. The exact mass of the SSP or the SFR for the constant SFR model does not affect the IMF by definition, and therefore, does not affect the M⋆/LK evolution curve. |
Appendix B: Fitting parameters
Table B.1 lists the polynomial coefficients for different metallicities of the fitting functions presented in Section 2.5. We note that these fifth-order polynomial functions are only valid for the fitted range of parameters (see table caption) and should not be extrapolated.
Polynomial coefficients of the fitting functions presented in Section 2.5.
All Tables
All Figures
 |
Fig. 1. Flowchart of the photGalIMF code, original to the present work, which couples the galaxy chemical evolution code GalIMF (Yan et al. 2019b) with stellar evolution models to calculate photometric properties of galaxies. The GalIMF code calculates the stellar population of a galaxy for given galaxy evolution assumptions (Sect. 2.2) and a variable IMF that depends on the environment at each timestep. The metallicity, mass, and age distributions of stars are then combined with the photometric module to calculate the luminosity for selected photometric bands. See details in Sect. 2.4. |
| In the text | |
 |
Fig. 2. Grid of simulated gwIMFs in dependence of the SFR (from left to right: |
| In the text | |
 |
Fig. 3. SFR-Hα luminosity relations of the canonical invariant IMF and the IGIMF-2021 theory. Left panel: Star formation rate in dependence of the Hα luminosity assuming a canonical IMF (solid black line; Kennicutt 1998) and the IGIMF-2021 theory (coloured lines) for different metallicities [Z] shown on the right colorbar. The Hα fluxes are calculated with the PÉGASE code (see text). Right panel: Conversion factor of the SFRs, |
| In the text | |
 |
Fig. 4. Present-day stellar (including remnants) mass–metallicity relation for galaxies with different constant SFRs over a time-span of 13.6 Gyr, adopting gconv = 0.10 (red line) and gconv = 0.25 (blue line), within the IGIMF-2021 context. The green stars refer to dwarf galaxies of the Milky Way and M31 galaxies (Table 4 of Kirby et al. 2013). The solid black line shows the median while the dashed lines show the 16th and 84th percentiles of the metallicity distribution of galaxies in the Sloan Digital Sky Survey Data Release 2 (Table 1 of Gallazzi et al. 2005). Note that the shown stellar masses of Kirby et al. (2013) and Gallazzi et al. (2005) are derived for the canonical gwIMF but the simulated mass–metallicity relations (red and blue lines) refers to a varying gwIMF within the IGIMF theory (see text). |
| In the text | |
 |
Fig. 5. Time evolution of the gwIMF (right panels) and the stellar mass-to-light ratio in the K-band (left panels) assuming a constant SFR of ψ = 103 M⊙ yr−1 (top panels), 1 M⊙ yr−1 (middle panels), and 10−3 M⊙ yr−1 (bottom panels) over a timescale of 14 Gyr in the invariant canonical gwIMF (dashed black lines in the left and right panels; Kroupa 2001) and IGIMF-2021 (solid black line in the left panels and coloured lines in the right panels) framework. The chemical evolution model adopts gconv = 0.25. The mass-to-light evolution curves adopting the invariant canonical IMF are not identical because they represent the evolution of galaxies with different metal enrichment histories. |
| In the text | |
 |
Fig. 6. Stellar mass-to-light ratio, M⋆/LK (Eq. (9)), in the Ks-band in dependence of LK for galaxies with an age of 13.6 Gyr assuming gconv = 25% (red lines) and 10% (blue lines) in the canonical IMF (left panel) and IGIMF-2021 (right panel) context. The dashed black line shows the mean M⋆/LK of the two different chemical enrichment models (red and blue lines). |
| In the text | |
 |
Fig. 7. Star formation rate derived from the Hα luminosity in dependence of the stellar mass derived from the K-band luminosity (Karachentsev et al. 2013) assuming an invariant canonical gwIMF (left panels) and the IGIMF-2021 (right panels) for galaxies located in the LV. The errorbars of the IGIMF-corrected stellar mass values refer to the two different applied chemical enrichment models (Sect. 4.2) and the errorbars of the IGIMF-corrected SFR values refer to metallicities of [Z] = −2.20 (lower limit) and [Z] = 0.45 (upper limit; see Sect. 4.2). The SFR values have an uncertainty of about 30% due to distance uncertainties (see Fig. 1 of Kroupa et al. 2020a; Karachentsev et al. 2004, 2013). The solid green lines show the present-day main sequence of star-forming galaxies with 109.7 < M⋆/M⊙ < 1011.1 and a scatter of ±0.2 dex highlighted by the shaded area (i.e. Eq. (28) of Speagle et al. 2014, and Eq. (17)). The dashed green lines are extrapolations beyond the adopted fitted range of the stellar masses. The solid red lines show the linear best fit to the corresponding data (Eq. (18) for the right panel). Note the smaller scatter in the right panel. |
| In the text | |
 |
Fig. 8. Gas depletion timescale, τgas, in dependence of the gas mass assuming the gwIMF in the invariant canonical IMF (left panel) and IGIMF-2021 (right panel) for galaxies located in the LV. The dashed red line shows the age of the Universe, τgas = τh = 13.8 Gyr, assuming the standard ΛCDM cosmology (Planck Collaboration XIII 2016). The error on the IGIMF-corrected τgas values (right panel) is estimated by adopting the SFR values for [Z] = −2.20 (upper limit) and [Z] = 0.45 (lower limit; Sect. 4.2). The solid red lines are fits of the data with Eq. (20). The green dotted line is the ‘minimum-1’ model of Pflamm-Altenburg & Kroupa (2009, their Fig. 7). Note the smaller scatter of the data in the right panel (see also Fig. 9). |
| In the text | |
 |
Fig. 9. Distribution of the gas depletion timescale, τgas, assuming the gwIMF is given by the invariant canonical IMF (blue) and the IGIMF-2021 (green) in the log10-space. The τgas are calculated by adopting the IGIMF-corrected SFR values for a Solar metallicity. The histograms are fitted with a Gaussian (solid red curves) with expected values of μ = log10(τgas [Gyr]) = 1.12 (13.25 Gyr; canonical gwIMF) and μ = log10(τgas [Gyr]) = 0.67 (4.72 Gyr; IGIMF-2021) and variances of σ = 0.60 Gyr (canonical gwIMF) and σ = 0.41 Gyr (IGIMF-2021). |
| In the text | |
 |
Fig. 10. Characteristic stellar mass buildup timescale normalized by the age of the Universe of τh = 13.8 Gyr (Planck Collaboration XIII 2016) in dependence of the stellar mass in the invariant canonical IMF (left panel) and the IGIMF-2021 (right panel) context for galaxies located in the LV. The dashed red line refers to a characteristic stellar mass buildup timescale equal to τh = 13.8 Gyr. In the right panel, the uncertainty of the IGIMF effect is plotted while the measurement errors are not shown. The upper and lower limits of the IGIMF-corrected τ⋆ values (right panel) are estimated by adopting τup, ⋆ = Mupper, ⋆/ψ([Z] = −2.20) and τlow, ⋆ = Mlow, ⋆/ψ([Z] = 0.45), respectively. ψ([Z] = −2.20) and ψ([Z] = 0.45) refer to the IGIMF-corrected SFR values for [Z] = −2.20 and [Z] = 0.45 (Sect. 4.2). Mup, ⋆ and Mlow, ⋆ refer to the upper and lower IGIMF-corrected stellar masses by applying the maximum and minimum M⋆/LK values (Sect. 4.2). The solid red lines are fits of the data with Eq. (23). |
| In the text | |
 |
Fig. A.1. Time evolution of the Ks-band mass-to-light ratio, M⋆/LK, for stellar populations with a fixed canonical (Kroupa 2001) IMF and different metallicities denoted in the upper left corner of each panel. Red solid curves are SSPs formed at time zero. The sharp drop in the SSP models of M⋆/LK at t ≈ 2 × 109 yr is caused by a significant increase in the number of AGB stars. The blue dashed curves are stellar populations with the same fixed metallicity but a constant SFR over time, demonstrating a smooth curve of lower M⋆/LK value due to the luminosity contribution from young stars. The exact mass of the SSP or the SFR for the constant SFR model does not affect the IMF by definition, and therefore, does not affect the M⋆/LK evolution curve. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.






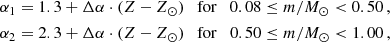

![$$ \begin{aligned} x~=~-0.14 {[Z]} + 0.6 \log _{10}\bigg (\frac{M_{\mathrm{ecl} }}{10^{6}M_{\odot }} \bigg )+2.82, \end{aligned} $$](/articles/aa/full_html/2024/09/aa47928-23/aa47928-23-eq8.gif)