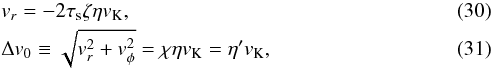| Issue |
A&A
Volume 591, July 2016
|
|
|---|---|---|
| Article Number | A72 | |
| Number of page(s) | 12 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201628099 | |
| Published online | 17 June 2016 | |
The radial dependence of pebble accretion rates: A source of diversity in planetary systems
I. Analytical formulation
1 Earth-Life Science Institute, Tokyo Institute of Technology, Meguro-ku, 152-8550 Tokyo, Japan
e-mail: ida@elsi.jp
2 Laboratoire J.-L. Lagrange, Université Côte d’Azur, Observatoire de la Côte d’Azur, CNRS, 06304 Nice, France
Received: 9 January 2016
Accepted: 5 April 2016
Context. The classical planetesimal accretion scenario for the formation of planets has recently evolved with the idea that pebbles, centimeter- to meter-sized icy grains migrating in protoplanetary disks, can control planetesimal and/or planetary growth.
Aims. We investigate how pebble accretion depends on disk properties and affects the formation of planetary systems.
Methods. We construct analytical models of pebble accretion onto planetary embryos that consistently account for the mass and orbital evolution of the pebble flow and reflect disk structure.
Results. We derive simple formulas for pebble accretion rates in the so-called settling regime for planetary embryos that are more than 100 km in size. For relatively smaller embryos or in outer disk regions, the accretion mode is three-dimensional (3D), meaning that the thickness of the pebble flow must be taken into account, and resulting in an accretion rate that is independent of the embryo mass. For larger embryos or in inner regions, the accretion is in a two-dimensional (2D) mode, i.e., the pebble disk may be considered infinitely thin. We show that the radial dependence of the pebble accretion rate is different (even the sign of the power-law exponent changes) for different disk conditions such as the disk heating source (viscous heating or stellar irradiation), drag law (Stokes or Epstein, and weak or strong coupling), and in the 2D or 3D accretion modes. We also discuss the effect of the sublimation and destruction of icy pebbles inside the snow line.
Conclusions. Pebble accretion easily produces a large diversity of planetary systems. In other words, to infer the results of planet formation through pebble accretion correctly, detailed prescriptions of disk evolution and pebble growth, sublimation, destruction and migration are required.
Key words: planets and satellites: formation / planets and satellites: dynamical evolution and stability / protoplanetary disks / planets and satellites: terrestrial planets / planet-disk interactions / methods: analytical
© ESO, 2016
1. Introduction
The conventional model of planet formation (e.g., Safronov 1972; Hayashi et al. 1985) assumed that the building blocks of planetary bodies are km-sized planetesimals. However, agglomerating dust grains in a protoplanetary disk to form these planetesimals leads to a serious problem, the so-called radial drift barrier (a.k.a. meter-size barrier). While small enough grains are strongly coupled to the disk gas, larger bodies migrate more rapidly through angular momentum loss by aerodynamical gas drag until they reach kilometric sizes. The migration of meter-sized bodies is as fast as ~ 10-2 au/yr (e.g., Weidenschilling 1980; Nakagawa et al. 1981).
For small dust grains, growth via pairwise collisions is faster than migration (if collisions result in coagulation rather than rebounding or fragmentation; see Sect. 3.4), so that they actually grow in situ. When they grow to O(10) cm-sized bodies called pebbles, migration dominates over growth and they actually start their migration. Although the migration of pebbles is slower than that of meter-sized bodies, it is still ≳10-4 au/yr and the migration timescale is shorter by a few orders than gas disk lifetimes that are observationally inferred. These bodies cannot bypass the radial drift barrier through more rapid growth, unless the fluffy structure of icy dust grains (Okuzumi et al. 2012) is considered or local disk structure such as long-lived turbulent anticlonic eddies (e.g., Barge & Sommeria 1995; Chavanis 2000; Johansen et al. 2004; Inaba & Barge 2006) or radial pressure bumps (e.g., Johansen et al. 2014,and references therein) exists.
However, a swarm of these fast migrating pebbles may cause a traffic jam resulting in a streaming instability and form large clumps that may become 100−1000 km-sized bodies (Youdin & Goodman 2005; Johansen et al. 2007, 2012, 2015). Some of these simulations (Johansen et al. 2012) suggest that only a few tens of percent of solid materials could be incorporated into these clumps. The clumps would subsequently grow by accreting the migrating pebbles (Lambrechts & Johansen 2012, 2014; Lambrechts et al. 2014), a process commonly called pebble accretion. This idea was applied among others, to the formation of Jovian cores (Levison et al. 2015), close-in super-Earths in exoplanetary systems (Chatterjee & Tan 2014, 2015; Moriarty & Fischer 2015), an explanation of the dichotomy of the solar system (Morbidelli et al. 2015), and to account for water delivery to the Earth (Morbidelli et al. 2016; Sato et al. 2016).
Planet formation through planetesimal accretion is a local process, that is, planetesimals are accreted in a local feeding zone, until planets acquire lunar to Martian mass for which type I migration becomes effective (e.g., Tanaka et al. 2002; Paardekooper et al. 2011). Because Kepler frequency and planetesimal spatial density are higher in inner regions, the planetesimal accretion timescale is shorter for smaller orbital radius with a relatively strong dependence (tacc ∝ r2−3).
On the other hand, in the case of pebble accretion, planets accrete pebbles migrating from outer regions with a small capture probability (Guillot et al. 2014), so that the accreting planets share the common pebble flux as building blocks. It is thus expected that the r-dependence of tacc should be very weak.
Fundamental formulas for pebble accretion rate have been studied in detail (Ormel & Klahr 2010; Ormel & Kobayashi 2012; Lambrechts & Johansen 2012, 2014; Guillot et al. 2014). Using these expressions, we investigate the radial dependence of pebble accretion rates onto planets, consistently taking pebble growth and migration and disk properties into account. In Sect. 2, we set up a simple empirical disk model based on detailed analytical calculations and radiative transfer simulations that includes both viscous heating and stellar irradiation. In Sect. 3, we model the collisional growth and radial migration of dust and pebbles. Based on the dust and pebble evolution model with the disk model, we derive simple analytical formulas of the pebble accretion rate onto planetary embryos. In Sect. 4, we provide expressions for the pebble accretion rate as a function of gas disk accretion rate (Ṁ∗) and orbital radius (r) and discuss the relations between the radial dependence and disk properties. Section 5 is a summary. Lastly, the symbols used in this work are listed in Table A.1.
2. Protoplanetary disk model
For simplification, we consider steady accretion disks with a constant α (the α-viscosity parameter) and parameterize the disk midplane temperature T and gas surface density Σg with power-law functions of the orbital distance r as 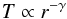 (1)and
(1)and 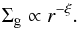 (2)Because the radial gradient is important in our arguments, the power indexes do not need to be the same values throughout the entire disk. The scaling laws that we provide below are the same as those derived by Chambers (2009). For numerical factors, we use the results from Garaud & Lin (2007) and Oka et al. (2011).
(2)Because the radial gradient is important in our arguments, the power indexes do not need to be the same values throughout the entire disk. The scaling laws that we provide below are the same as those derived by Chambers (2009). For numerical factors, we use the results from Garaud & Lin (2007) and Oka et al. (2011).
As we show here, the disk aspect ratio hg/r (where hg is the vertical gas disk scale height) is an important factor for pebble accretion. We set 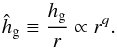 (3)We choose to define the scale height hg so that the vertical gas density is
(3)We choose to define the scale height hg so that the vertical gas density is 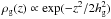 , or equivalently, hg = cs/ Ω, where cs is the sound velocity and Ω is Keplerian frequency (
, or equivalently, hg = cs/ Ω, where cs is the sound velocity and Ω is Keplerian frequency (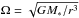 ; M∗ is the host star mass), both estimated at the midplane and for a given orbital distance1.
; M∗ is the host star mass), both estimated at the midplane and for a given orbital distance1.
Since  ,
, 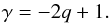 (4)From the assumption of steady disk accretion,
(4)From the assumption of steady disk accretion, 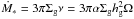 , is independent of r, so that
, is independent of r, so that 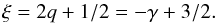 (5)The assumption of a steady accretion is generally good in the inner regions, i.e., when r ≪ rout where rout is the disk outer edge radius. In order to simplify the quantitative estimates, we introduce normalized parameters for the stellar mass M∗, stellar luminosity L∗, viscous alpha parameter α, disk accretion rate Ṁ∗, and pebble mass accretion flux through the disk ṀF as
(5)The assumption of a steady accretion is generally good in the inner regions, i.e., when r ≪ rout where rout is the disk outer edge radius. In order to simplify the quantitative estimates, we introduce normalized parameters for the stellar mass M∗, stellar luminosity L∗, viscous alpha parameter α, disk accretion rate Ṁ∗, and pebble mass accretion flux through the disk ṀF as 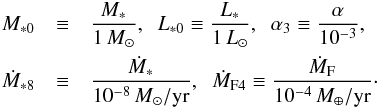 (6)The scaling factor Ṁ∗ = 10-8M⊙/ yr is typical of classical T Tauri stars, and ṀF4 = 10-4M⊕/ yr corresponds to a value that is often estimated from theoretical works (Sect. 3.4).
(6)The scaling factor Ṁ∗ = 10-8M⊙/ yr is typical of classical T Tauri stars, and ṀF4 = 10-4M⊕/ yr corresponds to a value that is often estimated from theoretical works (Sect. 3.4).
The disk temperature parameter γ (or equivalently q) is mostly determined by the heating source. As shown by, for example, Hueso & Guillot (2005) and Oka et al. (2011), viscous heating dominates in the inner disk regions while irradiation from the central star dominates the thermal structure of the outer regions of the disk. The disk midplane temperature can be approximated by T = max(Tvis,Tirr), where Tvis and Tirr are temperatures determined by viscous heating and stellar irradiation, respectively. The detailed results of Garaud & Lin (2007) and Oka et al. (2011) are empirically fitted by 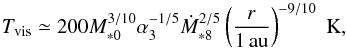 (7)and
(7)and 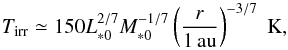 (8)where the power exponents are derived by analytical arguments. In the pre-main sequence stellar evolution phase, when protoplanetary disks are present,
(8)where the power exponents are derived by analytical arguments. In the pre-main sequence stellar evolution phase, when protoplanetary disks are present, 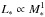 to
to 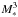 , implying that Tirr increases with M∗. Since it is observationally suggested that mean values of Ṁ∗ is proportional to
, implying that Tirr increases with M∗. Since it is observationally suggested that mean values of Ṁ∗ is proportional to 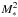 , Tvis would also increase with M∗.
, Tvis would also increase with M∗.
In order to derive Eq. (8), we implicitly assumed that the disk is vertically optically thin, but radially optically thick. When the disk is so depleted that the disk becomes optically thin even in the radial direction, 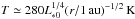 (e.g., Hayashi 1981). However, the radially thin condition is realized only for Ṁ∗ ≲ 10-10M⊙/ yr (e.g., Oka et al. 2011). This corresponds to a very low accretion rate and accordingly a very low disk gas surface density. We hence do not consider the optically thin limit in this paper. In the irradiated, radially thick limit, the midplane temperature of the disk is significantly lower than in the optically thin limit. When viscous heating becomes weak enough (Ṁ∗ ≲ 10-8M⊙/ yr), the snow line is inside 1 au (e.g., Oka et al. 2011)2.
(e.g., Hayashi 1981). However, the radially thin condition is realized only for Ṁ∗ ≲ 10-10M⊙/ yr (e.g., Oka et al. 2011). This corresponds to a very low accretion rate and accordingly a very low disk gas surface density. We hence do not consider the optically thin limit in this paper. In the irradiated, radially thick limit, the midplane temperature of the disk is significantly lower than in the optically thin limit. When viscous heating becomes weak enough (Ṁ∗ ≲ 10-8M⊙/ yr), the snow line is inside 1 au (e.g., Oka et al. 2011)2.
The corresponding disk scale heights in both temperature regimes are 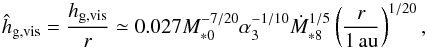 (9)and
(9)and 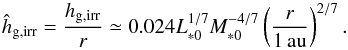 (10)The actual scale height is given by hg = max(hg,vis,hg,irr). The exponent is thus q = 1/20 in viscous regime and q = 2/7 in irradiation regime. In the optically thin limit, hg is given by hg/r ≃ 0.033(r/ 1 au)1/4(M∗/M⊙)−1/2(L∗/L⊙)1/8.
(10)The actual scale height is given by hg = max(hg,vis,hg,irr). The exponent is thus q = 1/20 in viscous regime and q = 2/7 in irradiation regime. In the optically thin limit, hg is given by hg/r ≃ 0.033(r/ 1 au)1/4(M∗/M⊙)−1/2(L∗/L⊙)1/8.
The assumption of a steady accretion disk enables us to calculate the gas surface density explicitly as ![\begin{equation} \begin{array}{ll} \sigg & {\displaystyle = \frac{\dot{M}_* }{3\pi \alpha \hg^2 \Omega} = \frac{\dot{M}_* T_K}{6\pi^2 \alpha \hhg^2 r^2}}\\[3mm] & {\displaystyle = \frac{10^{-5}}{6\pi^2} \dot{M}_{*8} M_{*0}^{-1/2} \left(\frac{r}{1\,\au}\right)^{1/2} \alpha_3^{-1} \hhg^{-2} \; \left[\msol/\au^2\right]} \\[3mm] & {\displaystyle = 1.5 \dot{M}_{*8} M_{*0}^{-1/2} \left(\frac{r}{1\,\au}\right)^{1/2} \alpha_3^{-1} \hhg^{-2} \; \left[{\rm g/cm}^2\right]}. \end{array} \end{equation}](/articles/aa/full_html/2016/07/aa28099-16/aa28099-16-eq54.png) (11)Substituting Eqs. (9) and (10) into the above equation, the surface density in the viscous and irradiation regimes, respectively, becomes
(11)Substituting Eqs. (9) and (10) into the above equation, the surface density in the viscous and irradiation regimes, respectively, becomes 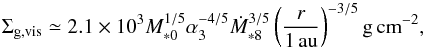 (12)and
(12)and 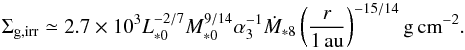 (13)At any point, the surface density can be calculated by Σg = min(Σg,vis,Σg,irr).
(13)At any point, the surface density can be calculated by Σg = min(Σg,vis,Σg,irr).
The boundary between the viscous and irradiation regimes given by Tvis = Tirr corresponds to an orbital distance, 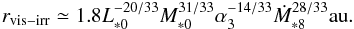 (14)Viscous heating dominates for r<rvis - irr and conversely, stellar irradiation dominates at larger orbital distances. For classical T Tauri stars, Ṁ∗ ~ 10-8M⊙/ yr, implying a value of rvis−irr ~ 2 au, i.e., in the middle of the expected planet formation region. As we show later, the properties of pebble accretion change significantly between the viscous and irradiation regimes.
(14)Viscous heating dominates for r<rvis - irr and conversely, stellar irradiation dominates at larger orbital distances. For classical T Tauri stars, Ṁ∗ ~ 10-8M⊙/ yr, implying a value of rvis−irr ~ 2 au, i.e., in the middle of the expected planet formation region. As we show later, the properties of pebble accretion change significantly between the viscous and irradiation regimes.
Because the water inside pebbles should vaporize inside the so-called snow line (defined by the region at which T ~ 170 K), the size of pebbles and properties of pebble accretion should change when r<rsnow. The location of the snow line can be obtained by rsnow ~ max(rsnow,vis,rsnow,irr), where ![\begin{eqnarray} &&r_{\rm snow,vis} \simeq 1.2 M_{*0}^{1/3} \alpha_3^{-2/9} \dot{M}_{*8}^{4/9}\au, \label{eq:r_snow_vis} \\[2mm] &&r_{\rm snow,irr} \simeq 0.75 L_{*0}^{2/3}M_{*0}^{-1/3}\au. \label{eq:r_snow_irr} \end{eqnarray}](/articles/aa/full_html/2016/07/aa28099-16/aa28099-16-eq66.png) Because Ṁ∗ decreases with time, the snow line migrates inward as long as it is in the viscous regime. When the snow line is in the irradiation region, shading effects may complicate its evolution (Bitsch et al. 2015a). For simplicity, we do not consider this possibility.
Because Ṁ∗ decreases with time, the snow line migrates inward as long as it is in the viscous regime. When the snow line is in the irradiation region, shading effects may complicate its evolution (Bitsch et al. 2015a). For simplicity, we do not consider this possibility.
In summary, in the viscously heated inner region, γ ≃ 9/10,ξ ≃ 3/5 and q ≃ 1/20, while in the irradiation outer region, γ ≃ 3/7,ξ ≃ 15/14 and q ≃ 2/7. The transition occurs at a few au. Pebble size can also change at a similar location because of ice sublimation. The size of pebbles is also bound to change in this region owing to ice sublimation. We see that the mode of accretion of pebbles and gas drag law also change in the same region, thus making planet formation through the accretion of pebbles particularly complex.
3. Pebble accretion rate
3.1. Stokes number
Another important parameter for pebble accretion is the Stokes number τs which expresses how the motion of pebbles are coupled to that of the circumstellar disk gas in sub-Keplerian rotation. It is defined by 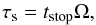 (17)where tstop is the stopping time due to gas drag. A general expression of the stopping time is provided by Guillot et al. (2014), but in our case, we can consider two limits that depend on the size of the pebbles considered:
(17)where tstop is the stopping time due to gas drag. A general expression of the stopping time is provided by Guillot et al. (2014), but in our case, we can consider two limits that depend on the size of the pebbles considered: ![\begin{equation} t_{\rm stop} = \left\{ \begin{array}{ll} {\displaystyle \frac{\rho_{\rm s} R}{c_{\rm s} \rho_{\rm g}} = \frac{\rho_{\rm s} R}{\hg \Omega \frac{\sigg}{\sqrt{2\pi} \hg}} = \frac{\sqrt{2\pi} \rho_{\rm s} R}{\Omega \sigg}} & [R \la \frac{9}{4} \lambda_{\rm mfp} {\rm : Epstein}], \\ {\displaystyle \frac{4\rho_{\rm s} R^2}{9c_{\rm s} \lambda_{\rm mfp} \rho_{\rm g}} } & [R \ga \frac{9}{4} \lambda_{\rm mfp} {\rm : Stokes}], \end{array} \right. \label{eq:t_stop} \end{equation}](/articles/aa/full_html/2016/07/aa28099-16/aa28099-16-eq74.png) (18)where λmfp is the mean free path, ρs and R are the bulk density and physical radius of a dust particle, respectively; we used the spatial gas density at the midplane of the disk,
(18)where λmfp is the mean free path, ρs and R are the bulk density and physical radius of a dust particle, respectively; we used the spatial gas density at the midplane of the disk, 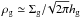 .
.
According to Eq. (18), the Stokes number is given by ![\begin{equation} \st = \left\{ \begin{array}{ll} {\displaystyle \frac{\sqrt{2\pi} \rho_{\rm s} R}{\sigg} } & [{\rm Epstein}] ,\\ {\displaystyle \frac{4 \rho_{\rm s} R^2}{9 \rho_{\rm g} \hg \lambda_{\rm mfp} } = \frac{4 \rho_{\rm s} \sigma R^2}{9 \mu m_{\rm H} \hg} } & [{\rm Stokes}]. \end{array} \right. \label{eq:tau_s} \end{equation}](/articles/aa/full_html/2016/07/aa28099-16/aa28099-16-eq79.png) (19)where σ (≃ 2 × 10-15cm2) is the collisional cross section for H2, mH (≃ 1.67 × 10-24g) is the mass of hydrogen, μ (≃ 2.34) is the mean molecular weight. In the viscous regime with Σg,vis (Eq. (12)) and hg,vis (Eq. (9)), the Stokes number is explicitly given by
(19)where σ (≃ 2 × 10-15cm2) is the collisional cross section for H2, mH (≃ 1.67 × 10-24g) is the mass of hydrogen, μ (≃ 2.34) is the mean molecular weight. In the viscous regime with Σg,vis (Eq. (12)) and hg,vis (Eq. (9)), the Stokes number is explicitly given by ![\begin{equation} \st = \left\{\!\!\! \begin{array}{l} \frac{\sqrt{2\pi} \rho_{\rm s} R}{\sigg}\! \sim\! 1.3 \times 10^{-3} M_{*0}^{-1/5} \alpha_3^{4/5} \dot{M}_{*8}^{-3/5} \rho_{s1} \left(\frac{r}{1\,\au}\right)^{3/5} \left(\frac{R}{1{\, \rm cm}}\right) \\ \hspace*{5cm} [{\rm Epstein}], \\ \frac{4 \rho_{\rm s} \sigma R^2}{9 \mu m_{\rm H} \hg} \!\sim\! 5.6 \times 10^{-4} M_{*0}^{7/20}\alpha_3^{1/10}\dot{M}_{*8}^{-1/5} \rho_{s1} \left(\frac{r}{1\,\au}\right)^{-21/20} \left(\frac{R}{1{\, \rm cm}}\right)^2 \\ \hspace*{5cm} [{\rm Stokes}], \end{array} \right. \label{eq:tau_s2} \end{equation}](/articles/aa/full_html/2016/07/aa28099-16/aa28099-16-eq89.png) (20)where ρs1 = ρs/ 1 g cm-3. In the irradiation regime with Σg,irr (Eq. (13)) and hg,irr (Eq. (13)),
(20)where ρs1 = ρs/ 1 g cm-3. In the irradiation regime with Σg,irr (Eq. (13)) and hg,irr (Eq. (13)), ![\begin{equation} \st = \left\{\!\!\! \begin{array}{l} \frac{\sqrt{2\pi} \rho_{\rm s} R}{\sigg} \! \sim\! 0.93 \times 10^{-3} L_{*0}^{2/7}M_{*0}^{-9/14} \alpha_3 \dot{M}_{*8}^{-1} \rho_{s1} \left(\frac{r}{1\,\au}\right)^{15/14} \left(\frac{R}{1{\rm cm}}\right) \\ \hspace*{5cm} [ {\rm Epstein}], \\ \frac{4 \rho_{\rm s} \sigma R^2}{9 \mu m_{\rm H} \hg}\! \sim\! 6.3 \times 10^{-4} L_{*0}^{-1/7}M_{*0}^{4/7} \rho_{s1} \left(\frac{r}{1\,\au}\right)^{-9/7} \left(\frac{R}{1{\rm cm}}\right)^2 \\ \hspace*{5cm} [{\rm Stokes}]. \end{array} \right. \label{eq:tau_s3} \end{equation}](/articles/aa/full_html/2016/07/aa28099-16/aa28099-16-eq93.png) (21)The mean free path is given by
(21)The mean free path is given by ![\begin{equation} \begin{array}{ll} \lambda_{\rm mfp} & {\displaystyle \simeq \frac{\mu m_{\rm H}}{\sigma \rho_{\rm g}} \simeq \frac{\sqrt{2\pi} \mu m_{\rm H} \hg}{\sigma \sigg} } \\ & \sim \left\{ \begin{array}{l} 1.0 M_{*0}^{-11/20} \alpha_3^{7/10} \dot{M}_{*8}^{-2/5} \left(\frac{r}{1\,\au}\right)^{33/20} {\rm cm} \\ \hspace*{3.5cm} [\mbox{viscous region}], \\ 0.65 L_{*0}^{3/7}M_{*0}^{-17/14} \alpha_3 \dot{M}_{*8}^{-1} \left(\frac{r}{1\,\au}\right)^{33/14}{\rm cm} \\ \hspace*{3.5cm} [\mbox{irradiation region}].\\ \end{array} \right. \end{array} \label{eq:l_g} \end{equation}](/articles/aa/full_html/2016/07/aa28099-16/aa28099-16-eq94.png) (22)Since the r-dependence of λmfp is relatively strong, a dust grain in the Epstein regime migrating inward must eventually enter the Stokes regime (also see Fig. 1 by Lambrechts & Johansen 2012).
(22)Since the r-dependence of λmfp is relatively strong, a dust grain in the Epstein regime migrating inward must eventually enter the Stokes regime (also see Fig. 1 by Lambrechts & Johansen 2012).
3.2. Basic relation for the pebble accretion rate
The mass accretion rate of pebbles onto a planetary embryo with mass M depends on whether the accretion may be considered as bidimensional (if the scale height of the pebble disk is small compared to the cross section of the collisions) or three-dimensional. In the first case, the accretion rate is 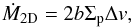 (23)where 2b is the linear cross section of the collision (b = R in the geometric limit), hp and Σp are the scale height and the surface density of a pebble subdisk, and Δv is the relative velocity between the embryo and the pebbles.
(23)where 2b is the linear cross section of the collision (b = R in the geometric limit), hp and Σp are the scale height and the surface density of a pebble subdisk, and Δv is the relative velocity between the embryo and the pebbles.
Otherwise, the situation becomes more complex. A limiting case is when the gravitational pull of the embryo is large enough that the pebble flux can be considered as isotropic. In that case, the accretion rate can be written as 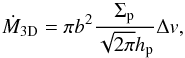 (24)where we used the fact that the pebble spatial density at the midplane is given by
(24)where we used the fact that the pebble spatial density at the midplane is given by 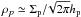 . The above equations can be combined into (see also Guillot et al. 2014)
. The above equations can be combined into (see also Guillot et al. 2014) 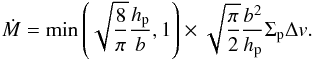 (25)The pebble scale height is related to the disk gas scale height as (Dubrulle et al. 1995; Youdin & Lithwick 2007; Okuzumi et al. 2012)
(25)The pebble scale height is related to the disk gas scale height as (Dubrulle et al. 1995; Youdin & Lithwick 2007; Okuzumi et al. 2012) 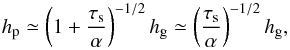 (26)where we assumed τs/α> 1, because for pebble accretion, we usually consider the parameter ranges of τs ≳ 0.1 and α ≲ 10-2. Because hg ∝ r, the accretion mode tends to be 2D in the inner disk regions (also see Sect. 4). In late phases, when planetary mass becomes so high that b ≳ hp, the accretion mode also changes from 3D to 2D (Sect. 3.5). The transitional planetary mass is O(10-1) M⊕, as shown in Eq. (66).
(26)where we assumed τs/α> 1, because for pebble accretion, we usually consider the parameter ranges of τs ≳ 0.1 and α ≲ 10-2. Because hg ∝ r, the accretion mode tends to be 2D in the inner disk regions (also see Sect. 4). In late phases, when planetary mass becomes so high that b ≳ hp, the accretion mode also changes from 3D to 2D (Sect. 3.5). The transitional planetary mass is O(10-1) M⊕, as shown in Eq. (66).
The radial and azimuthal components of pebble drift velocity are given by (e.g., Nakagawa et al. 1986; Guillot et al. 2014) ![\begin{eqnarray} \v_r &=& -\Lambda^2 \frac{2\st}{1+\Lambda^2 \st^2}\eta \vk + \frac{\Lambda}{1 + \Lambda^2 \st^2}u_\nu, \label{eq:vr} \\[-1.5mm] \v_\phi &=& -\Lambda \frac{1}{1+\Lambda^2 \st^2}\eta \vk + \frac{\Lambda^2 \st}{1 + \Lambda^2 \st^2} u_\nu, \label{eq:vphi} \end{eqnarray}](/articles/aa/full_html/2016/07/aa28099-16/aa28099-16-eq112.png) where η is the difference between gas and Keplerian velocities due to pressure gradient given by
where η is the difference between gas and Keplerian velocities due to pressure gradient given by 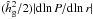 , Λ = ρg/ (ρg + ρp), and uν is the radial viscous diffusion velocity (
, Λ = ρg/ (ρg + ρp), and uν is the radial viscous diffusion velocity (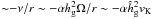 ). We hereafter assume Λ ≃ 1. Because
). We hereafter assume Λ ≃ 1. Because 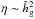 and we consider the cases with α ≲ 10-2 and τs ≳ 0.1, we neglect the 2nd terms proportional to uν We note that when pebbles migrate to the region inside the snow line and are broken apart into small silicate grains, the second terms in Eqs. (27)and (28)could become important. Since η regulates pebble migration speed, it is a very important quantity for pebble accretion. It is explicitly given by
and we consider the cases with α ≲ 10-2 and τs ≳ 0.1, we neglect the 2nd terms proportional to uν We note that when pebbles migrate to the region inside the snow line and are broken apart into small silicate grains, the second terms in Eqs. (27)and (28)could become important. Since η regulates pebble migration speed, it is a very important quantity for pebble accretion. It is explicitly given by ![\begin{equation} \eta = \frac{\hhg^2}{2} \left| \frac{{\rm d}\!\ln P}{{\rm d}\!\ln r} \right| \simeq \left\{ \begin{array}{l} 0.93 \times 10^{-3} M_{*0}^{-7/10} \alpha_3^{-1/5} \dot{M}_{*8}^{2/5} \left(\frac{r}{1\,\au}\right)^{2q} \\ \hspace*{2cm} [\mbox{viscous regime; } q = 1/20], \\ 0.80 \times 10^{-3} L_{*0}^{2/7}M_{*0}^{-8/7} \left(\frac{r}{1\,\au}\right)^{2q} \\ \hspace*{2cm} [\mbox{irradiation regime; } q = 2/7], \end{array} \right. \label{eq:eta} \vspace{-1.7mm} \end{equation}](/articles/aa/full_html/2016/07/aa28099-16/aa28099-16-eq120.png) (29)where we used dlnP/ dlnr = dln(ΣgT/hg)/dlnr ≃ −2.55 for the viscous region and ≃−2.78 for the irradiation region.
(29)where we used dlnP/ dlnr = dln(ΣgT/hg)/dlnr ≃ −2.55 for the viscous region and ≃−2.78 for the irradiation region.
Equations (27) and (28) are rewritten as
where 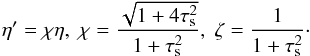 (32)For τs< 1, ζ,χ ≃ 1, while
(32)For τs< 1, ζ,χ ≃ 1, while 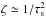 and χ ≃ 2 /τs for τs ≫ 1. As we show in what follows, the dependence on χ disappears in pebble accretion rates, while the ζ-factor remains. It is no problem to assume χ = 1 and η′ = η in the following.
and χ ≃ 2 /τs for τs ≫ 1. As we show in what follows, the dependence on χ disappears in pebble accretion rates, while the ζ-factor remains. It is no problem to assume χ = 1 and η′ = η in the following.
If a circular orbit is assumed for the embryo, the relative velocity between the embryo and a pebble is given by the sum of their relative velocities Δv0 and of a contribution due to the Keplerian shear (Ormel & Klahr 2010; Guillot et al. 2014) 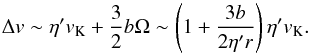 (33)Departures from this assumption occur if the eccentricities or inclinations of the embryos become larger than η ~ O(10-3) (Guillot et al. 2014). Density fluctuations from turbulence could excite eccentricities to
(33)Departures from this assumption occur if the eccentricities or inclinations of the embryos become larger than η ~ O(10-3) (Guillot et al. 2014). Density fluctuations from turbulence could excite eccentricities to 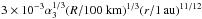 for R ≲ 1000 km (Guillot et al. 2014). The collision velocity could be dominated by the embryo eccentricity with R ~ 100–1000 km in the case of α ≳ 10-3. However, after R becomes larger than 1000 km, disk-planet interaction efficiently damps eccentricity and the second term of Eq. (33) becomes larger than the first term (a transition from Bondi (drift accretion) regime to Hill regime; see below). As a result, the effect of the embryo eccentricity becomes weak again. The self-stirring of the embryos could also become important. Since it depends on orbital separation, which has not been clarified in the case of their formation by streaming instability, this is difficult to estimate at this point. We leave analysis of this case for future work and assume here for simplicity that Δv is given by Eq. (33). In Eqs. (31) and (33), the relative velocity induced by turbulence,
for R ≲ 1000 km (Guillot et al. 2014). The collision velocity could be dominated by the embryo eccentricity with R ~ 100–1000 km in the case of α ≳ 10-3. However, after R becomes larger than 1000 km, disk-planet interaction efficiently damps eccentricity and the second term of Eq. (33) becomes larger than the first term (a transition from Bondi (drift accretion) regime to Hill regime; see below). As a result, the effect of the embryo eccentricity becomes weak again. The self-stirring of the embryos could also become important. Since it depends on orbital separation, which has not been clarified in the case of their formation by streaming instability, this is difficult to estimate at this point. We leave analysis of this case for future work and assume here for simplicity that Δv is given by Eq. (33). In Eqs. (31) and (33), the relative velocity induced by turbulence, 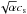 , is not included. It is negligible for pebble size bodies, as long as α ≲ 10-2 (e.g., Sato et al. 2016).
, is not included. It is negligible for pebble size bodies, as long as α ≲ 10-2 (e.g., Sato et al. 2016).
Moriarty & Fischer (2015) used Δv = vr, while vr is smaller than vθ for τs< 1 and the shear velocity is more important for high mass planets. Furthermore, although they discussed formation of close-in planets, they assumed irradiative scale height. In general, viscous heating is more important than the stellar irradiation in inner disk regions.
The set of Eqs. (25), (26), (29), (32)and (33)allows us to derive mass accretion rates for the different cases that we consider.
3.3. Cross section of pebble accretion
We now need to calculate the accretion cross section b. Here, we consider 1−100 cm-sized pebbles accreted by a planetary embryo with a size larger than 100 km. The gas drag effect is then combined with the gravitational pull of the embryo, which results in a significant increase of the collision cross section (settling regime; Ormel & Klahr 2010; Guillot et al. 2014). For τs< 1, the velocity change of a pebble with an impact parameter b by the gravitational force from the embryo is given approximately by (Lambrechts & Johansen 2012; Guillot et al. 2014) 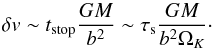 (34)If δv ≲ Δv/ 4, a collision occurs (Ormel & Klahr 2010). Then,
(34)If δv ≲ Δv/ 4, a collision occurs (Ormel & Klahr 2010). Then, 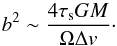 (35)When b ≲ (2/3)η′r and hence Δv ~ η′vK (Bondi regime), the equivalent radius cross section is
(35)When b ≲ (2/3)η′r and hence Δv ~ η′vK (Bondi regime), the equivalent radius cross section is ![\begin{equation} b \simeq \left(\frac{12 \st \RH^3}{\eta' r}\right)^{1/2} \simeq 2 \sqrt{\frac{t_{\rm stop}}{t_B}} R_B \; \; \; [{\rm Bondi \; regime}], \label{eq:b_Bondi} \end{equation}](/articles/aa/full_html/2016/07/aa28099-16/aa28099-16-eq151.png) (36)where RB = GM/ (η′vK)2 and tB = RB/η′vK [tstop/tB ≃ τsη′3(M∗/M)]. When b ≳ (2/3)η′r and hence Δv ~ (3/2)bΩ (Hill regime),
(36)where RB = GM/ (η′vK)2 and tB = RB/η′vK [tstop/tB ≃ τsη′3(M∗/M)]. When b ≳ (2/3)η′r and hence Δv ~ (3/2)bΩ (Hill regime), ![\begin{equation} b \simeq 2 \st^{1/3} \RH \simeq \left(\frac{\st}{0.1}\right)^{1/3} \RH \; \; \; [{\rm Hill\; regime}]. \label{eq:b_Hill} \end{equation}](/articles/aa/full_html/2016/07/aa28099-16/aa28099-16-eq157.png) (37)This expression assumes τs ≲ 0.1. As τs increases over this value, b asymptotes to ~ RH. However, while almost all trajectories with impact parameters <b result in collisions with the planetary embryo for τs ≲ 1, only a small fraction of the trajectories with impact parameters within ~ RH can actually collide for τs ≫ 1 (e.g., Ida & Nakazawa 1989; Ormel & Klahr 2010) because their motions are not dissipative. To take this effect into account, Ormel & Kobayashi (2012) proposed a reduction factor for b with τs ≫ 1 as
(37)This expression assumes τs ≲ 0.1. As τs increases over this value, b asymptotes to ~ RH. However, while almost all trajectories with impact parameters <b result in collisions with the planetary embryo for τs ≲ 1, only a small fraction of the trajectories with impact parameters within ~ RH can actually collide for τs ≫ 1 (e.g., Ida & Nakazawa 1989; Ormel & Klahr 2010) because their motions are not dissipative. To take this effect into account, Ormel & Kobayashi (2012) proposed a reduction factor for b with τs ≫ 1 as 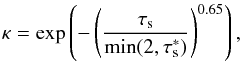 (38)where
(38)where 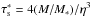 .
.
Taking the reduction factor into account, Eqs. (36) and (37) are combined into 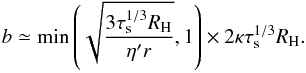 (39)The left-hand term in the bracket dominates for small M (Bondi regime). The transition from the Bondi regime to Hill regime (when the right-hand term in the bracket becomes comparable to the left-hand term) occurs at b ~ (2/3)η′r, which is equivalent to
(39)The left-hand term in the bracket dominates for small M (Bondi regime). The transition from the Bondi regime to Hill regime (when the right-hand term in the bracket becomes comparable to the left-hand term) occurs at b ~ (2/3)η′r, which is equivalent to 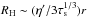 . The transition planetary mass is given by
. The transition planetary mass is given by 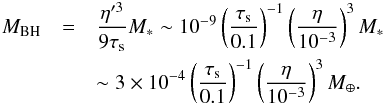 (40)In the last two equations, we assumed τs< 1.
(40)In the last two equations, we assumed τs< 1.
3.4. Pebble mass flux and surface density
To estimate the pebble mass flux, we first evaluate the size of migrating pebbles from the balance between growth and migration. The dust growth timescale is approximately given by (Takeuchi & Lin 2005; Brauer et al. 2008) 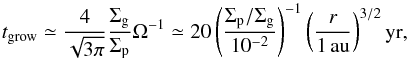 (41)where we assumed perfect sticking for simplicity. For high enough speed collisions, grains rebound or fragment rather than coagulate, which is called a bouncing or fragmentation barrier, and the threshold velocity may be 20−100 m/s for icy grains and about ten times smaller for silicate grains (Blum & Wurm 2000; Zsom et al. 2010, 2011; Wada et al. 2011, 2013; Weidling et al. 2012). We show in the following that the barrier does not affect the assumption of perfect sticking for icy grains. On the other hand, the barrier may prevent silicate grains from growing beyond millimeter sizes (Zsom et al. 2010, 2011; Wada et al. 2011; Weidling et al. 2012). We will also discuss this issue later.
(41)where we assumed perfect sticking for simplicity. For high enough speed collisions, grains rebound or fragment rather than coagulate, which is called a bouncing or fragmentation barrier, and the threshold velocity may be 20−100 m/s for icy grains and about ten times smaller for silicate grains (Blum & Wurm 2000; Zsom et al. 2010, 2011; Wada et al. 2011, 2013; Weidling et al. 2012). We show in the following that the barrier does not affect the assumption of perfect sticking for icy grains. On the other hand, the barrier may prevent silicate grains from growing beyond millimeter sizes (Zsom et al. 2010, 2011; Wada et al. 2011; Weidling et al. 2012). We will also discuss this issue later.
Although Eq. (41)differs slightly from more detailed calculations, for example, in the Stokes regime (Sato et al. 2016), it is useful for the purpose of the present paper. In the region of pebble formation from sub-micron dust grains, migration has not set in and we use a typical value Σp/ Σg ~ 10-2. In regions where pebbles are migrating, Σp/ Σg becomes much smaller than 10-2 (see below).
The timescale of radial migration of dust due to gas drag is given by 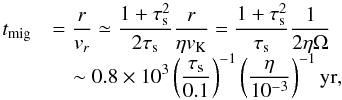 (42)where we assumed τs< 1, because we consider relatively outer regions for the formation site of pebbles.
(42)where we assumed τs< 1, because we consider relatively outer regions for the formation site of pebbles.
For small dust grains with τs ≪ 1, tmig is much longer than tgrow, so that they grow without significant migration. As pebbles grow, tmig decreases, while tgrow does not change. Since pebble growth occurs in an inside-out manner (Eq. (41)) and the largest bodies dominate the total pebble surface density (Sato et al. 2016), Σp/ Σg can be regarded as a constant behind the pebble formation front. Pebbles start their migration when tmig becomes shorter than tgrow. That is, migration starts when τs exceeds 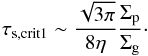 (43)The surface densities of migrating pebbles and disk gas are given by
(43)The surface densities of migrating pebbles and disk gas are given by 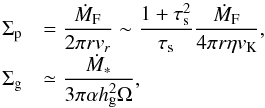 (44)where ṀF is the pebble mass flux through the disk. Since η = (1/2)(hg/r)2 | dlnP/ dlnr |,
(44)where ṀF is the pebble mass flux through the disk. Since η = (1/2)(hg/r)2 | dlnP/ dlnr |, 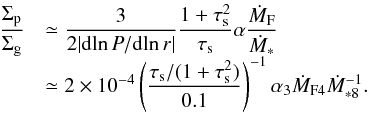 (45)If we use an expression of ṀF given by Eq. (54),
(45)If we use an expression of ṀF given by Eq. (54), 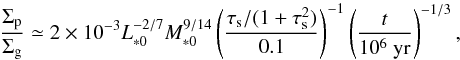 (46)which is consistent with the results by Sato et al. (2016) and Krijt et al. (2016).
(46)which is consistent with the results by Sato et al. (2016) and Krijt et al. (2016).
The parameter Σp is smaller than the solid surface density of the MMSN by two orders of magnitude for τs ~ 0.1 and ṀF ~ 10-4M⊕/ yr, which was also found by Lambrechts & Johansen (2014). This is because the pebble migration velocity vr is very large and we consider a steady-state solution in which ṀF is independent of r. If pebbles split into mm-sized silicate grains when they pass through the snow line as assumed by Morbidelli et al. (2015), we expect Σp to increase again inside the snow line.
Substituting Eq. (45) into Eq. (43) with τs ~ τs,crit1 and assuming τs< 1, we obtain 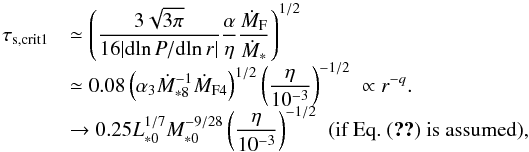 (47)In the Epstein regime, τs ∝ Rrξ (Eq. (19)), where Σg ∝ r− ξ. Both q and ξ are usually positive. As a pebble migrates inward, without growth, its τs would decrease. However, because τs,crit1 increases, growth must dominate over migration. Here we consider collisions between pebbles and used Eq. (45) for τs,crit1. This means that pebbles must migrate and grow so that τs ~ τs,crit1 (see Fig. 1 below). In the irradiation regime, the pebble size evolves with τs ~ τs,crit1 (Eq. (21)) as
(47)In the Epstein regime, τs ∝ Rrξ (Eq. (19)), where Σg ∝ r− ξ. Both q and ξ are usually positive. As a pebble migrates inward, without growth, its τs would decrease. However, because τs,crit1 increases, growth must dominate over migration. Here we consider collisions between pebbles and used Eq. (45) for τs,crit1. This means that pebbles must migrate and grow so that τs ~ τs,crit1 (see Fig. 1 below). In the irradiation regime, the pebble size evolves with τs ~ τs,crit1 (Eq. (21)) as 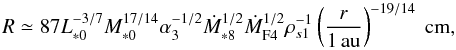 (48)where we used Eq. (29) in the irradiation region.
(48)where we used Eq. (29) in the irradiation region.
 |
Fig. 1 Evolution of a) size and b) Stokes number of pebbles migrating from gas drag for Ṁ∗ 8 = ṀF4 = α3 = 1. The dust grains are initially 0.001 cm in size and their growth and migration paths are calculated by directly integrating dR/ dt = R/tgrow and dr/ dt = −r/tmig with Eqs. (41) and (42) as bold lines. The dashed lines represent the analytical estimates of Eqs. (48) and (50) in panel a), and those in panel b) are τs,crit1 (Eqs. (47)) and Eq. (20) with Eq. (50). |
As pebbles further grow and migrate inward, λmfp becomes smaller until they eventually enter the Stokes regime when R ≳ (9/4)λmfp. Equations (22) and (48) show that the Epstein-Stokes transition in the irradiation region occurs at 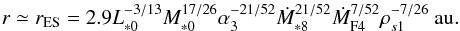 (49)Because τs ∝ R2 × r− 1−q in the Stokes regime, τs increases with inward migration and τs>τs,crit1 is always satisfied. In the Stokes regime, pebbles migrate without significant growth. Therefore, the pebble size in the Stokes regime is given by substituting Eq. (49) into Eq. (48) as
(49)Because τs ∝ R2 × r− 1−q in the Stokes regime, τs increases with inward migration and τs>τs,crit1 is always satisfied. In the Stokes regime, pebbles migrate without significant growth. Therefore, the pebble size in the Stokes regime is given by substituting Eq. (49) into Eq. (48) as 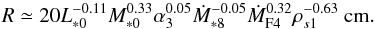 (50)The corresponding evolution of the Stokes number is obtained by substituting Eq. (50) into Eq. (20).
(50)The corresponding evolution of the Stokes number is obtained by substituting Eq. (50) into Eq. (20).
With a constant R, the Stokes parameter increases with inward migration as dlnτs/ dlnr ≃ −1−q in the Stokes regime. When τs exceeds unity, the migration quickly slows down (tmig ∝ τs for τs> 1). If τs would further exceed 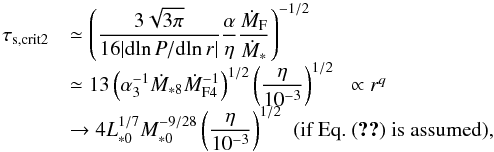 (51)before the pebbles pass the snow line, tmig would again become longer than tgrow and the pebbles would keep growing in situ. Furthermore, since τs ∝ R2, the condition τs>τs,crit2 would then always be satisfied, resulting in runaway coagulation (Okuzumi et al. 2012). Okuzumi et al. (2012), however, showed that τs does not reach τs,crit2 outside the snow line where the assumption of perfect accretion may be relevant, unless we consider the possibility that dust grains are highly porous. We do not consider this possibility in the present work.
(51)before the pebbles pass the snow line, tmig would again become longer than tgrow and the pebbles would keep growing in situ. Furthermore, since τs ∝ R2, the condition τs>τs,crit2 would then always be satisfied, resulting in runaway coagulation (Okuzumi et al. 2012). Okuzumi et al. (2012), however, showed that τs does not reach τs,crit2 outside the snow line where the assumption of perfect accretion may be relevant, unless we consider the possibility that dust grains are highly porous. We do not consider this possibility in the present work.
So far, we assumed perfect accretion. However, even for icy grains, the bouncing/fragmentation barrier exists as mentioned before. For collisions between dust grains, their collision velocity is likely to be dominated by that induced by turbulence as long as α ≳ 10-3, which is given by 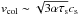 (Sato et al. 2016). For the threshold velocity vcol,crit, collisions result in coagulation when
(Sato et al. 2016). For the threshold velocity vcol,crit, collisions result in coagulation when 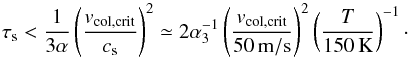 (52)If we use Tirr given by Eq. (8),
(52)If we use Tirr given by Eq. (8), 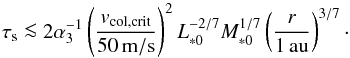 (53)Since collisions are efficient in Epstein regime, the result in Figure 1 shows that the bouncing/fragmentation barrier does not restrict the pebble growth as long as α ≲ 10-2.
(53)Since collisions are efficient in Epstein regime, the result in Figure 1 shows that the bouncing/fragmentation barrier does not restrict the pebble growth as long as α ≲ 10-2.
Figure 1a shows the growth and migration of pebbles obtained by directly integrating dR/ dt = R/tgrow and dr/ dt = −r/tmig with Eqs. (41) and (42). In panel b, the corresponding evolution of τs is plotted. The analytical estimates are represented by the dashed lines, which are given by Eq. (48) and τs,crit1 (Eq. (47)) in the Epstein regime and Eqs. (50) and (20) with Eq. (50) in the Stokes regime. They are consistent with the results by direct integration. These results are also consistent with the evolution of peak mass bodies obtained by more detailed dust growth/migration calculations taking the dust size distribution into account (e.g., Okuzumi et al. 2012; Sato et al. 2016).Lambrechts & Johansen (2014) derived a similar analytical result. However, they were focused on Epstein regime, so that the results differ in inner disk regions where Stokes regime is important.
From this plot, we find that runaway coagulation appears inside 0.1 au. Indeed, the threshold τs,crit2 crosses the point of r = 0.1 au and τs = 10 with a positive gradient q ≃ 1/20. However, the sublimation of icy components inside the snow line would prevent runaway coagulation from occurring.
The pebble mass flux is evaluated as follows. The pebble growth timescale (tgrow) is the timescale for a body to grow in size by a factor of e ~ 2.72. The timescale of growth from μm dust to cm pebbles (by a factor 104) is tp,grow ~ ln104 × tgrow ~ 10tgrow. From Eq. (41), tp,grow ~ 2 × 105(r/ 100 au)3/2 yr, where Σp is the small dust surface density as Σp/ Σg ~ 10-2.
We assume Σp/ Σg ~ 10-2 in the outer pebble-forming region and use the value of Σg that applies to the irradiation regime (Eq. (13)). The parameter tp,grow depends on Σp/ Σg but not on Σp. Once migration starts, pebbles quickly migrate and the dust surface density there is rapidly depleted. The timescale for pebbles to grow until migration dominates, tp,grow, is proportional to r3/2. Thereby, the region in which pebbles are forming is narrow and migrates outward. The pebble formation front rpf at t satisfies t ~ 2 × 105(rpf/ 100 au)3/2 yr, that is, rpf ~ 100(t/ 2 × 105 yr)2/3au. The pebble mass flux is estimated by calculating the dust mass swept by the pebble formation front per unit time (Lambrechts & Johansen 2014), 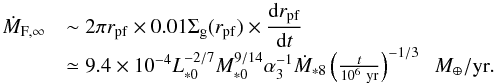 (54)The pebble mass flux ṀF is governed by the outward migration of pebble formation front, but not by the pebble migration speed.
(54)The pebble mass flux ṀF is governed by the outward migration of pebble formation front, but not by the pebble migration speed.
A disk with a surface density Σg,irr defined by Eq. (13) can be gravitationally unstable in its outer regions. The Toomre Q parameter is given by 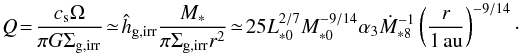 (55)If the turbulence due to the disk instability is so vigorous that even icy grains do not grow, the pebble formation front is given by
(55)If the turbulence due to the disk instability is so vigorous that even icy grains do not grow, the pebble formation front is given by 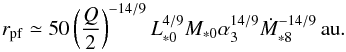 (56)According to our α disk evolution model, Ṁ∗ 8 decreases monotonously while rpf increases. If Ṁ∗ 8 ~ (t/ 106 yr)− 3/2, rpf ~ 50(t/ 106 yr)7/3au. In this case, ṀF is 2 times smaller than that given by Eq. (54).
(56)According to our α disk evolution model, Ṁ∗ 8 decreases monotonously while rpf increases. If Ṁ∗ 8 ~ (t/ 106 yr)− 3/2, rpf ~ 50(t/ 106 yr)7/3au. In this case, ṀF is 2 times smaller than that given by Eq. (54).
In the above derivation, it is assumed that the disk is extended to infinity. Sato et al. (2016) showed the existence of two phases for the flux of pebbles (their Fig. 6). First, the pebble mass flux ṀF is almost constant with time until rpf exceeds the disk size rout. After that, ṀF decays rapidly as a consequence of the depletion of solid materials in the outer regions. The transition time between the two regimes is 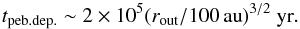 (57)If we assume an exponential taper to the surface density of the disk beyond rout, Σg ∝ r-1exp(−r/rout), the two phase evolution is described by addition of a decaying factor of exp(−rpf/rout) = exp(−(100 au /rout)(t/ 2 × 105 yr)2/3) to ṀF given by of Eq. (54). Because observations suggest that disks around T Tauri stars typically have rout ≲ 100 au (e.g., Andrews et al. 2009), the reduction cannot be neglected.
(57)If we assume an exponential taper to the surface density of the disk beyond rout, Σg ∝ r-1exp(−r/rout), the two phase evolution is described by addition of a decaying factor of exp(−rpf/rout) = exp(−(100 au /rout)(t/ 2 × 105 yr)2/3) to ṀF given by of Eq. (54). Because observations suggest that disks around T Tauri stars typically have rout ≲ 100 au (e.g., Andrews et al. 2009), the reduction cannot be neglected.
Furthermore, if the planetary embryos grow beyond Mars mass, a non-negligible fraction of ṀF may be filtered out by the accretion onto the embryos (see Sect. 3.5 hereafter). Thus, ṀF and Σp would be quickly depleted once such large embryos appear (see also Chambers 2016).
The time evolution of ṀF is very important for the final configuration of planetary systems formed through pebble accretion. However, a proper calculation of this quantity would be beyond the scope of the present work and we choose to treat ṀF as a constant parameter, adopting as a nominal value 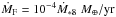 . This value, obtained from dust growth calculations (Lambrechts & Johansen 2012; Sato et al. 2016), is about an order of magnitude smaller than that obtained in Eq. (54). We note that there is considerable uncertainty on this value which also depends on the disk surface density profile.
. This value, obtained from dust growth calculations (Lambrechts & Johansen 2012; Sato et al. 2016), is about an order of magnitude smaller than that obtained in Eq. (54). We note that there is considerable uncertainty on this value which also depends on the disk surface density profile.
3.5. General form of the pebble accretion rate
We now seek to calculate the rate of pebble accretion by a protoplanet and whether its presence can affect the flow of pebbles. From Eqs. (33) and (44), 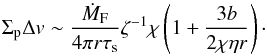 (58)Substituting this into Eq. (25), the pebble accretion rate is given by
(58)Substituting this into Eq. (25), the pebble accretion rate is given by 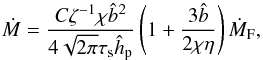 (59)with
(59)with 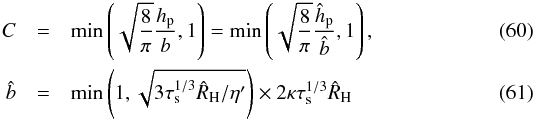 where the hat sign such as
where the hat sign such as 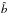 expresses lengths that have been divided by the orbital distance r. Here ṀF and τs are given as parameters, such as ṀF ~ 10-4M⊕ and τs ~ 0.1 (see Sect. 3.4). The formula for Ṁ given by Eq. (59) can exceed ṀF, in which case we limit it to that value.
expresses lengths that have been divided by the orbital distance r. Here ṀF and τs are given as parameters, such as ṀF ~ 10-4M⊕ and τs ~ 0.1 (see Sect. 3.4). The formula for Ṁ given by Eq. (59) can exceed ṀF, in which case we limit it to that value.
From Eq. (59), the accretion timescale is 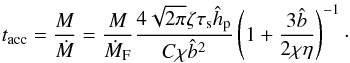 (62)In the 3D case (C ~ 1), the pebble accretion timescale (tacc,3D) has an identical simple form both in the Bondi and Hill regimes, as shown below. In the early Bondi phase (
(62)In the 3D case (C ~ 1), the pebble accretion timescale (tacc,3D) has an identical simple form both in the Bondi and Hill regimes, as shown below. In the early Bondi phase (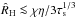 ),
), 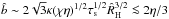 , and Eq. (62) reads as
, and Eq. (62) reads as 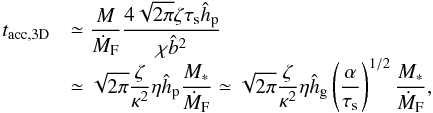 (63)where we used ĥp ~ [ 1 + (τs/α) ] − 1/2ĥg ~ (α/τs)1/2ĥg. In the late Hill phase in which
(63)where we used ĥp ~ [ 1 + (τs/α) ] − 1/2ĥg ~ (α/τs)1/2ĥg. In the late Hill phase in which 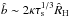 and
and 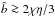 ,
, 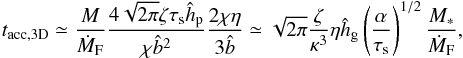 (64)which is identical to Eq. (63) except for the reduction factor for τs ≫ 1, although
(64)which is identical to Eq. (63) except for the reduction factor for τs ≫ 1, although 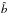 has a different form. Because the reduction does not actually occur in the Bondi regime, we can use Eq. (64) both in the Bondi and Hill regimes. For τs> 1, both ζ and κ3 decrease (Eqs. (32) and (38)). Since κ is a stronger function of τs, ζ/κ3 rapidly increases with τs so that pebble accretion slows down for τs ≫ 1. Using
has a different form. Because the reduction does not actually occur in the Bondi regime, we can use Eq. (64) both in the Bondi and Hill regimes. For τs> 1, both ζ and κ3 decrease (Eqs. (32) and (38)). Since κ is a stronger function of τs, ζ/κ3 rapidly increases with τs so that pebble accretion slows down for τs ≫ 1. Using 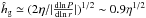 (Eq. (29)) and assuming τs< 1,
(Eq. (29)) and assuming τs< 1, 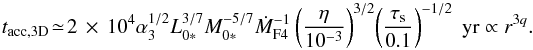 (65)The accretion mode is initially 3D. It becomes 2D when
(65)The accretion mode is initially 3D. It becomes 2D when 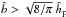 . In this case, since it is likely that a transition from the Bondi regime to the Hill regime (
. In this case, since it is likely that a transition from the Bondi regime to the Hill regime (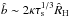 ) has already occurred, the transition to the 2D accretion mode occurs when
) has already occurred, the transition to the 2D accretion mode occurs when 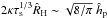 , that is, when
, that is, when 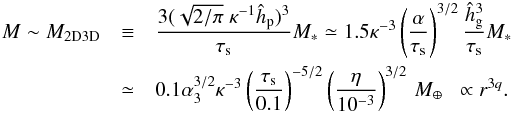 (66)The transition mass from the Bondi to the Hill regime, MBH given by Eq. (40), is actually much smaller than M2D3D. 2D accretion always takes place in the Hill regime.
(66)The transition mass from the Bondi to the Hill regime, MBH given by Eq. (40), is actually much smaller than M2D3D. 2D accretion always takes place in the Hill regime.
The accretion timescale in 2D is given by 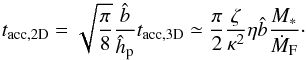 (67)Since the 2D mode occurs in the Hill regime,
(67)Since the 2D mode occurs in the Hill regime, 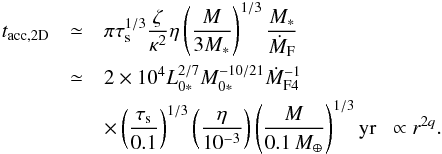 (68)In the last equation, we assumed τs< 1. This accretion timescale is consistent with that derived by Lambrechts & Johansen (2014, their Eq. (31)).
(68)In the last equation, we assumed τs< 1. This accretion timescale is consistent with that derived by Lambrechts & Johansen (2014, their Eq. (31)).
Following Guillot et al. (2014), we define the filtering efficiency by the ratio of the accretion rate onto the embryo (Ṁ) to that of the supplied pebble mass flux (ṀF). For τs< 1, the filtering efficiency in the 3D case (M ≲ 0.1 M⊕) is 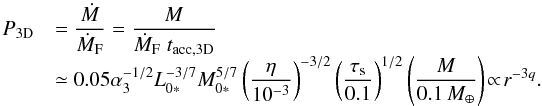 (69)The reduction of the pebble mass flux due to the accretion by a protoplanet is thus negligible until M becomes comparable to the mass of Mars. Because P3D ∝ M, the total reduction in pebble mass flux from the filtering depends only on the total mass of planetary embryos, as long as we consider the viscous (q ≃ 1/20), 3D-settling regime. The filtering probability in the 2D case (M ≳ 0.1 M⊕) is
(69)The reduction of the pebble mass flux due to the accretion by a protoplanet is thus negligible until M becomes comparable to the mass of Mars. Because P3D ∝ M, the total reduction in pebble mass flux from the filtering depends only on the total mass of planetary embryos, as long as we consider the viscous (q ≃ 1/20), 3D-settling regime. The filtering probability in the 2D case (M ≳ 0.1 M⊕) is 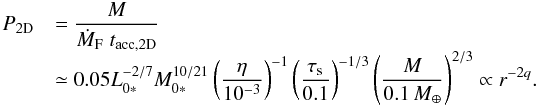 (70)These values of P3D and P2D coincide with those obtained by more detailed calculations by Guillot et al. (2014).
(70)These values of P3D and P2D coincide with those obtained by more detailed calculations by Guillot et al. (2014).
Substituting M3D2D given by Eqs. (66) into (69) or (70), we find that the 2D probability must be applied when 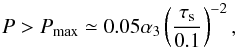 (71)which is independent of η. For P>Pmax, P increases proportionally to M2/3 rather than to M: the total filtering by all the embryos becomes less efficient as they grow.
(71)which is independent of η. For P>Pmax, P increases proportionally to M2/3 rather than to M: the total filtering by all the embryos becomes less efficient as they grow.
 |
Fig. 2 Pebble accretion timescale tacc of embryos with M = 0.1 M⊕ on the r-Ṁ∗ plane. Color bars represent log 10(tacc/ yr). Brighter parameter regions represent faster accretion. In panel a), the entire disk is assumed to be irradiation-heated, while it is viscously-heated in panel b). In panel c), the disk is the combination of irradiation-heated and viscously heated regimes. In panel d), the reduction factor for τs> 1 is taken into account in the disk in panel c). In panel e), the effect of ice sublimation is added to the disk in panel d). Details of individual sets are described in the main text. |
4. Radial dependence of the pebble accretion timescale
We consider the r-dependence of the pebble accretion timescale that controls the final configuration of planetary systems. We use τs< 1, ĥg ∝ rq (η ∝ r2q), τs ∝ rp, and Σg ∝ r− ξ. In the viscous region, q ≃ 1/20 and ξ = 3/5 and in the irradiation region q ≃ 2/7 and ξ = 15/14. The exponent p (τs ∝ rp) must be treated carefully. In the Epstein regime, pebbles grow by keeping τs ≃ τs,crit1. From Eq. (47), p ≃ −q. In the Stokes regime, pebbles migrate without significant growth, so that from Eq. (19), p ≃ −1−q.
From Eqs. (63) and (68), 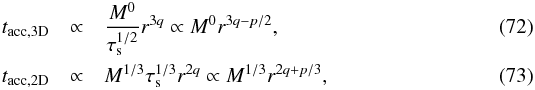 where we also explicitly included the dependences on the planet mass (M) and Stokes parameter (τs).
where we also explicitly included the dependences on the planet mass (M) and Stokes parameter (τs).
The 3D accretion timescale is independent of M, which means that planet growth is exponential. In the case of planetesimal accretion, the early runaway growth is superexponential: tacc ∝ M− 1/3, while the late oligarchic growth is subexponential: tacc ∝ M1/3 (e.g., Kokubo & Ida 1998, 2002). If conventional km-sized planetesimals are successfully formed, planetesimal accretion would dominate the early phases. Pebble accretion would dominate in the oligarchic growth stage. Pebble accretion then eventually enters the 2D mode and becomes comparable to planetesimal accretion. However the two forms differ in the sense that embryos can become isolated from planetesimals after depleting their feeding zones (e.g., Kokubo & Ida 1998, 2002), a process that would not occur in the case of pebbles at least until the planet mass becomes high enough to create a density gap in the disk that may halt the inward migration of pebbles and their supply to the embryos (e.g., Lambrechts & Johansen 2012). This mass (pebble isolation mass) is comparable to the inferred core masses of Jupiter and Saturn.
In the case of τs< 1, which is valid except in close-in regions, the exponent (tacc ∝ rδ) in the early 3D phase is: ![\begin{equation} \delta = 3q-p/2 \simeq \left\{ \begin{array}{ll} 7q/2 = 7/40 & [\mbox{viscous \& Epstein}], \\ 7q/2 = 1 & [\mbox{irradiative \& Epstein}], \\ 7q/2 + 1/2 = 27/40 & [\mbox{viscous \& Stokes}], \\ 7q/2 + 1/2 = 3/2 & [\mbox{irradiative \& Stokes}] . \end{array} \right. \end{equation}](/articles/aa/full_html/2016/07/aa28099-16/aa28099-16-eq290.png) (74)When embryos sufficiently grow or are located in sufficiently inner disk regions, M>M2D3D (Eq. (66)) is satisfied and pebble accretion enters a 2D mode. The exponent is
(74)When embryos sufficiently grow or are located in sufficiently inner disk regions, M>M2D3D (Eq. (66)) is satisfied and pebble accretion enters a 2D mode. The exponent is ![\begin{equation} \delta = 2q+p/3 \simeq \left\{ \begin{array}{ll} 5q/3 = 1/12 & [\mbox{viscous \& Epstein}], \\ 5q/3= 15/21 & [\mbox{irradiative \& Epstein}], \\ 5q/3 - 1/3 = -1/4 & [\mbox{viscous \& Stokes}],\\ 5q/3 - 1/3 = 1/21 & [\mbox{irradiative \& Stokes}]. \end{array} \right. \end{equation}](/articles/aa/full_html/2016/07/aa28099-16/aa28099-16-eq292.png) (75)When δ< 0, the outer planets grow more rapidly. Conversely, when δ> 0, the inner planets grow more rapidly (unless there is a significant reduction of the pebble flux from filtering by outer planets).
(75)When δ< 0, the outer planets grow more rapidly. Conversely, when δ> 0, the inner planets grow more rapidly (unless there is a significant reduction of the pebble flux from filtering by outer planets).
Pebble accretion hence has a weak dependence on r, but the fact that δ can be either positive or negative has strong implications for our understanding of planet formation. This is a very different situation than the classical planetesimal accretion scenario for which the timescale strongly depends on r (∝1/ΣpΩ ∝ rξ + 3/2), and planetary growth thus proceeds in an inside-out manner.
Figure 2 shows tacc calculated by the formulas in Sect. 3.5, as a function of r and Ṁ∗ for different disk conditions. We use α3 = 1 and ṀF4 = Ṁ∗ 8. The Stokes parameter τs is calculated from the prescriptions in section 3.4. The planetary embryo mass is set to be M = 0.1 M⊕. In the 3D regime, tacc is independent of M, while it increases in proportion to M1/3 in the 2D case. In general, the accretion is 2D in the inner disk regions and 3D in the outer regions (see Fig. 3). For larger M, the 2D region expands toward the outer disk.
Figure 2a assumes that the entire disk is in the irradiation regime and ζ,κ ≃ 1, which is an often used setting for pebble accretion calculations. The left half (≲1 au) is in a 2D-Stokes regime and the other half is in a 3D-Epstein regime (Fig. 3). At r ≲ 1 au, embryos would grow equally in all regions (| δ | ≪ 1), while they grow in a weak inside-out manner (δ ≃ 1) at r ≳ 1 au. In Fig. 2b, it is assumed that the entire disk is in the viscous regime and ζ,κ ≃ 1. Although the dependence is very weak, the growth mode is outside-in (δ< 0) at r ≲ 1 au. In Fig. 2c, we consider a more realistic model that includes a transition from an inner viscous regime to an outer irradiation regime as in Sect. 2. In this case, a fast-growing region is found at ~ 1 au. Figures 2a–c demonstrate how the disk conditions influence planetary growth by pebble accretion and ultimately, the configurations of final planetary systems.
Figure 2d corresponds to the case in which the correction factors ζ (Eq. (32)) and κ (Eq. (38)) are included along with the viscous and irradiation regimes. As shown in Sect. 3.4, since τs ∝ r− 1−q in the Stokes regime, τs increases with inward migration even without accounting for growth of the pebbles. As shown by Fig. 3, the inner disk regions are characterized by τs> 1 and a 2D-Stokes regime (see Fig. 3). As a result, tacc is proportional to ζ/κ. While κ-1 increases because of a decrease of the collision cross section, ζ decreases owing to an increase of pebble surface density caused by the reduction of vr, so that tacc increases or decreases corresponding to the change in ζ and κ-1, compared with Fig. 2c. In the limit of large τs, the κ-1-increase dominates over the ζ-decrease (see the upper left region of Fig. 2d), because κ is an exponential function. In order to study the formation of close-in Earths and super-Earths, a more detailed analysis of pebble accretion rates at τs ≳ 1 is necessary.
 |
Fig. 3 Boundaries of disk conditions and pebble accretion modes in the case of Fig. 2d. The Stokes-Epstein (brown dashed line) and 2D−3D (black dotted line) boundaries are common also in other panels in Fig. 2. The boundary of viscously heated and irradiation heated regimes (magenta solid line), snow line (blue dashed line), and τs = 1 line (green dashed line) depend on the disk mass accretion rate, dM∗/ dt. The left side is characterized by a viscous, 2D accretion, Stokes and high τs regime, while the right side is characterized by a irradiation, 3D, Epstein and lower τs regime. |
Lastly, Fig. 2e considers the full model which, following Morbidelli et al. (2015), assumes that the icy mantles of pebbles sublimate inside the snow line and release mm-sized silicate grains, resulting in a few orders of magnitude reduction of τs. Even if silicate components are present as larger clumps within the icy pebbles, collisional fragmentation would decrease their sizes below centimeters (Birnstiel et al. 2012; Banzatti et al. 2015). With the fact that the bouncing barrier would furthermore prevent their growth beyond millimeter sizes, we set the silicate pebble size to R = 1 mm. Because of the small τs, these small silicate pebbles (or dust grains) are stirred up and the accretion mode becomes 3D. As shown in Eq. (72), the pebble accretion timescale in the 3D mode increases as a result of the decrease of τs. The slowing down of the pebble accretion rate inside the snow line is evident.
As shown in Fig. 3, the snow line and transitions from viscous to irradiative, Stokes to Epstein and 2D to 3D occur at similar orbital distances. The location of τs ~ 1 is also similar. The radial dependence of the pebble accretion rate changes across these boundaries. Furthermore, since all planetary embryos share the same pebble flux, if the outer embryos efficiently filter the pebble flux, the inner embryos cannot grow even if the accretion cross section is larger. As demonstrated here, configurations of planetary systems formed by pebble accretion sensitively depend on the disk conditions3.
This means that the outcome of planet formation through pebble accretion is highly sensitive to the hypotheses made. It also means that pebble accretion could be responsible for the large diversity of planetary systems that we observe. Differences in disk outer radii, surface densities and radiative properties would naturally be generated through the collapse of molecular cloud cores of different densities and angular momentum (e.g., Hueso & Guillot 2005). Furthermore, as we discussed in Sect. 3.4, the timescale for the pebble formation front to reach the outer edge of the disk (see Eq. (57)) depends on disk size and is generally on order of 105 yr, which is much shorter than typical gas disk lifetimes (~a few million years). This implies that the initial total mass of solid materials, Ṁ∗, Σg and rout significantly affects the final configurations of planetary systems. The formation of planetary systems via pebble accretion should depend sensitively on initial disk parameters.
Detailed descriptions of the disk initial conditions, thermodynamic properties and evolution are required to correctly predict and interpret the distributions of exoplanetary systems by planet population synthesis simulations (e.g., Ida & Lin 2004, 2008; Mordasini et al. 2009; Ida et al. 2013; Alibert et al. 2013; Bitsch et al. 2015b). In a separate paper, we show the results of planet population synthesis simulations based on pebble accretion.
Another important issue is where and how planetary embryos are formed. Indeed, the formation of seed embryos is essential for efficient pebble accretion. Because the r-dependence of pebble accretion rate is weak, the initial locations of the embryos regulate the final planetary systems. Special sites at which the embryos would form preferentially (e.g., the inner edge of the dead zone, the snow line, locations of opacity jumps) could control the final configurations of planetary systems. The initial size of the embryos is also important: For example, for embryos smaller than 100 km in radius, pebble accretion is slower and less efficient than planetesimal accretion (see also Chambers 2016).
5. Summary
We have derived simple analytical formulas for pebble accretion timescales, assuming settling regime. The formulas are explicitly presented in Sect. 3.5. We next evaluated their radial dependence to discuss final configurations of planetary systems formed through pebble accretion (Sect. 4).
We found that the radial dependence of the pebble accretion rate is generally relatively weak but that it changes significantly (including sometimes changing sign) across the boundaries defined by different regimes, such as the transitions from the viscous-dominated to the irradiation-dominated disks, from the Epstein drag to the Stokes drag, from 2D to 3D accretion regimes, and whether Stokes number τs is smaller or larger than 1. All of these boundaries, as well as the snow line, occur at similar distances from the star, O(1) au. Inside the snow line, sublimation of icy mantle of grains may change Stokes number by orders of magnitude. Since the locations of the boundaries depend on the disk models, we expect intrinsic changes in the properties of the disk to lead to a large variety of final outcomes.
Self-consistent simulations of planet growth and disk evolution are much more important for pebble accretion scenario than for classical planetesimal accretion scenario. The variety of protoplanetary disks observed combined to the high sensitivity of pebble accretion on the properties of this disk indicates that the diversity of planetary systems formed should be larger than what can be obtained through classical planetesimal accretion. This diversity, as predicted by a planet population synthesis model including pebble accretion, will be discussed in a future paper.
In some works (e.g., Hayashi 1981; Hueso & Guillot 2005; Guillot et al. 2014), hg is defined by 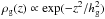 , or equivalently,
, or equivalently, 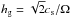 . In both cases, these expressions implicitly assume a disk that is vertically isothermal and in hydrostatic equilibrium (see Hueso & Guillot 2005).
. In both cases, these expressions implicitly assume a disk that is vertically isothermal and in hydrostatic equilibrium (see Hueso & Guillot 2005).
The reason terrestrial planets in our solar system are dry (almost ice-free) even though they would have formed in such low-temperature disks is discussed by Morbidelli et al. (2016) and Sato et al. (2016).
Acknowledgments
We thank Ramon Brasser and Soko Matsumura for careful proofreading. We also thank John Chambers for helpful comments as a reviewer. S.I. is thankful for the hospitality given during his visit to the Observatoire de la Côte d’Azur. This work was supported by Japan Society for the Promotion of Science (JSPS) KAKENHI Grant 15H02065, ANR grant ANR-13–13-BS05-0003-01 project MOJO (Modeling the Origin of JOvian planets), and European Research Council (ERC) Advanced Grant ACCRETE (contract number 290568).
References
- Alibert, Y., Carron, F., Fortier, A., et al. 2013, A&A, 558, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andrews, S. M., Wilner, D. J., Hughes, A. M., Qi, C., & Dullemond, C. P. 2009, ApJ, 700, 1502 [NASA ADS] [CrossRef] [Google Scholar]
- Banzatti, A., Pinilla, P., Ricci, L., et al. 2015, ApJ, 815, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Barge, P., & Sommeria, J. 1995, A&A, 295, L1 [NASA ADS] [Google Scholar]
- Birnstiel, T., Klahr, H., & Ercolano, B. 2012, A&A, 539, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., Johansen, A., Lambrechts, M., & Morbidelli, A. 2015a, A&A, 575, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., Lambrechts, M., & Johansen, A. 2015b, A&A, 582, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blum, J., & Wurm, G. 2000, Icarus, 143, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Brauer, F., Dullemond, C. P., & Henning, T. 2008, A&A, 480, 859 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chambers, J. 2016, ApJ, accepted [arXiv:1604.06362] [Google Scholar]
- Chambers, J. E. 2009, ApJ, 705, 1206 [NASA ADS] [CrossRef] [Google Scholar]
- Chatterjee, S., & Tan, J. C. 2014, ApJ, 780, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Chatterjee, S., & Tan, J. C. 2015, ApJ, 798, L32 [NASA ADS] [CrossRef] [Google Scholar]
- Chavanis, P. H. 2000, A&A, 356, 1089 [NASA ADS] [Google Scholar]
- Dubrulle, B., Morfill, G., & Sterzik, M. 1995, Icarus, 114, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Garaud, P., & Lin, D. N. C. 2007, ApJ, 654, 606 [Google Scholar]
- Guillot, T., Ida, S., & Ormel, C. W. 2014, A&A, 572, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hayashi, C. 1981, Suppl. Prog. Theoret. Phys., 70, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Hayashi, C., Nakazawa, K., & Nakagawa, Y. 1985, in Protostars and Planets II, eds. D. C. Black, & M. S. Matthews, 1100 [Google Scholar]
- Hueso, R., & Guillot, T. 2005, A&A, 442, 703 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ida, S., & Lin, D. N. C. 2004, ApJ, 604, 388 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ida, S., & Lin, D. N. C. 2008, ApJ, 673, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Ida, S., & Nakazawa, K. 1989, A&A, 224, 303 [NASA ADS] [Google Scholar]
- Ida, S., Lin, D. N. C., & Nagasawa, M. 2013, ApJ, 775, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Inaba, S., & Barge, P. 2006, ApJ, 649, 415 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johansen, A., Andersen, A. C., & Brandenburg, A. 2004, A&A, 417, 361 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johansen, A., Oishi, J. S., Mac Low, M.-M., et al. 2007, Nature, 448, 1022 [Google Scholar]
- Johansen, A., Youdin, A. N., & Lithwick, Y. 2012, A&A, 537, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johansen, A., Blum, J., Tanaka, H., et al. 2014, Protostars and Planets VI, 547 [Google Scholar]
- Johansen, A., Mac Low, M.-M., Lacerda, P., & Bizzarro, M. 2015, Sci. Adv., 1, 1500109 [NASA ADS] [CrossRef] [Google Scholar]
- Kokubo, E., & Ida, S. 1998, Icarus, 131, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Kokubo, E., & Ida, S. 2002, ApJ, 581, 666 [NASA ADS] [CrossRef] [Google Scholar]
- Krijt, S., Ormel, C. W., Dominik, C., & Tielens, A. G. G. M. 2016, A&A, 586, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lambrechts, M., & Johansen, A. 2012, A&A, 544, A32 [Google Scholar]
- Lambrechts, M., & Johansen, A. 2014, A&A, 572, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lambrechts, M., Johansen, A., & Morbidelli, A. 2014, A&A, 572, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Levison, H. F., Kretke, K. A., & Duncan, M. J. 2015, Nature, 524, 322 [CrossRef] [Google Scholar]
- Morbidelli, A., Lambrechts, M., Jacobson, S., & Bitsch, B. 2015, Icarus, 258, 418 [NASA ADS] [CrossRef] [Google Scholar]
- Morbidelli, A., Bitsch, B., Crida, A., et al. 2016, Icarus, 267, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Mordasini, C., Alibert, Y., & Benz, W. 2009, A&A, 501, 1139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moriarty, J., & Fischer, D. 2015, ApJ, 809, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Nakagawa, Y., Nakazawa, K., & Hayashi, C. 1981, Icarus, 45, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Nakagawa, Y., Sekiya, M., & Hayashi, C. 1986, Icarus, 67, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Oka, A., Nakamoto, T., & Ida, S. 2011, ApJ, 738, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Okuzumi, S., Tanaka, H., Kobayashi, H., & Wada, K. 2012, ApJ, 752, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Ormel, C. W., & Klahr, H. H. 2010, A&A, 520, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ormel, C. W., & Kobayashi, H. 2012, ApJ, 747, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Paardekooper, S.-J., Baruteau, C., & Kley, W. 2011, MNRAS, 410, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Safronov, V. S. 1972, Evolution of the protoplanetary cloud and formation of the earth and planets (Keter Publishing House) [Google Scholar]
- Sato, T., Okuzumi, S., & Ida, S. 2016, A&A, 589, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Takeuchi, T., & Lin, D. N. C. 2005, ApJ, 623, 482 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, H., Takeuchi, T., & Ward, W. R. 2002, ApJ, 565, 1257 [NASA ADS] [CrossRef] [Google Scholar]
- Wada, K., Tanaka, H., Suyama, T., Kimura, H., & Yamamoto, T. 2011, ApJ, 737, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Wada, K., Tanaka, H., Okuzumi, S., et al. 2013, A&A, 559, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weidenschilling, S. J. 1980, Icarus, 44, 172 [NASA ADS] [CrossRef] [Google Scholar]
- Weidling, R., Güttler, C., & Blum, J. 2012, Icarus, 218, 688 [NASA ADS] [CrossRef] [Google Scholar]
- Youdin, A. N., & Goodman, J. 2005, ApJ, 620, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Youdin, A. N., & Lithwick, Y. 2007, Icarus, 192, 588 [NASA ADS] [CrossRef] [Google Scholar]
- Zsom, A., Ormel, C. W., Güttler, C., Blum, J., & Dullemond, C. P. 2010, A&A, 513, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zsom, A., Sándor, Z., & Dullemond, C. P. 2011, A&A, 527, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Symbols used in this work
Definitions of symbols.
All Tables
All Figures
 |
Fig. 1 Evolution of a) size and b) Stokes number of pebbles migrating from gas drag for Ṁ∗ 8 = ṀF4 = α3 = 1. The dust grains are initially 0.001 cm in size and their growth and migration paths are calculated by directly integrating dR/ dt = R/tgrow and dr/ dt = −r/tmig with Eqs. (41) and (42) as bold lines. The dashed lines represent the analytical estimates of Eqs. (48) and (50) in panel a), and those in panel b) are τs,crit1 (Eqs. (47)) and Eq. (20) with Eq. (50). |
| In the text | |
 |
Fig. 2 Pebble accretion timescale tacc of embryos with M = 0.1 M⊕ on the r-Ṁ∗ plane. Color bars represent log 10(tacc/ yr). Brighter parameter regions represent faster accretion. In panel a), the entire disk is assumed to be irradiation-heated, while it is viscously-heated in panel b). In panel c), the disk is the combination of irradiation-heated and viscously heated regimes. In panel d), the reduction factor for τs> 1 is taken into account in the disk in panel c). In panel e), the effect of ice sublimation is added to the disk in panel d). Details of individual sets are described in the main text. |
| In the text | |
 |
Fig. 3 Boundaries of disk conditions and pebble accretion modes in the case of Fig. 2d. The Stokes-Epstein (brown dashed line) and 2D−3D (black dotted line) boundaries are common also in other panels in Fig. 2. The boundary of viscously heated and irradiation heated regimes (magenta solid line), snow line (blue dashed line), and τs = 1 line (green dashed line) depend on the disk mass accretion rate, dM∗/ dt. The left side is characterized by a viscous, 2D accretion, Stokes and high τs regime, while the right side is characterized by a irradiation, 3D, Epstein and lower τs regime. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.