| Issue |
A&A
Volume 590, June 2016
|
|
|---|---|---|
| Article Number | A77 | |
| Number of page(s) | 12 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201628325 | |
| Published online | 13 May 2016 | |
NuSTAR reveals the extreme properties of the super-Eddington accreting supermassive black hole in PG 1247+267
1 Dipartimento di Fisica e Astronomia, Università di Bologna, Viale Berti Pichat 6/2, 40127 Bologna, Italy
e-mail: giorgio.lanzuisi2@unibo.it
2 INAF−Osservatorio Astronomico di Bologna, via Ranzani 1, 40127 Bologna, Italy
3 INAF−Istituto di Astrofisica Spaziale e Fisica Cosmica, via Piero Gobetti 101, 40129 Bologna, Italy
4 Dipartimento di Matematica e Fisica, Università di Roma Tre, via della Vasca Navale 84, 00146 Roma, Italy
5 Dipartimento di Fisica, Università di Roma Tor Vergata, via della Ricerca Scientifica 1, 00133 Roma, Italy
6 Center for Relativistic Astrophysics, School of Physics, Georgia Institute of Technology, 837 State St., Atlanta, GA 30332, USA
7 Instituto de Astrofísica, Facultad de Física, Pontificia Universidad Católica de Chile, Casilla 306, Santiago 22, Chile
8 Millennium Institute of Astrophysics, Vicuna Mackenna 4860, 7820436 Macul, Santiago, Chile
9 Space Science Institute, 4750 Walnut Street, Suite 205, Boulder, CO 80301, USA
10 Space Science Laboratory, University of California, Berkeley, CA 94720, USA
11 Department of Astronomy and Astrophysics, 525 Davey Lab, The Pennsylvania State University, University Park, PA 16802, USA
12 Institute for Gravitation and the Cosmos, The Pennsylvania State University, University Park, PA 16802, USA
13 Department of Physics, 104 Davey Lab, The Pennsylvania State University, University Park, PA 16802, USA
14 DTU Space National Space Institute, Technical University of Denmark, Elektrovej 327, 2800 Lyngby, Denmark
15 Lawrence Livermore National Laboratory, Livermore, CA 94550, USA
16 Institute of Astronomy, Madingley Road, Cambridge CB3 0HA, UK
17 Department of Physics, Virginia Tech, Blacksburg, VA 24061, USA
18 Columbia Astrophysics Laboratory, Columbia University, New York, NY 10027, USA
19 Cahill Center for Astronomy and Astrophysics, California Institute of Technology, Pasadena, CA 91125, USA
20 School of Astronomy and Space Science, Nanjing University, Nanjing, 210093, PR China
21 Key laboratory of Modern Astronomy and Astrophysics (Nanjing University), Ministry of Education, 210093 Nanjing, PR China
22 INAF−Osservatorio Astronomico di Roma, via di Frascati, 33, 00040 Monteporzio Catone (Roma), Italy
23 ASDC–ASI, via del Politecnico, 00133 Roma, Italy
24 Korea Astronomy and Space Science Institute, 776 Daedeokdae-ro, Yuseong-gu, 305348 Daejeon, Korea
25 Jet Propulsion Laboratory, California Institute of Technology, Pasadena, CA 91109, USA
26 NASA Goddard Space Flight Center, Greenbelt, MD 20771, USA
Received: 17 February 2016
Accepted: 21 March 2016
PG1247+267 is one of the most luminous known quasars at z ~ 2 and is a strongly super-Eddington accreting supermassive black hole (SMBH) candidate. We obtained NuSTAR data of this intriguing source in December 2014 with the aim of studying its high-energy emission, leveraging the broad band covered by the new NuSTAR and the archival XMM-Newton data. Several measurements are in agreement with the super-Eddington scenario for PG1247+267: the soft power law (Γ = 2.3 ± 0.1); the weak ionized Fe emission line; and a hint of the presence of outflowing ionized gas surrounding the SMBH. The presence of an extreme reflection component is instead at odds with the high accretion rate proposed for this quasar. This can be explained with three different scenarios; all of them are in good agreement with the existing data, but imply very different conclusions: i) a variable primary power law observed in a low state, superimposed on a reflection component echoing a past, higher flux state; ii) a power law continuum obscured by an ionized, Compton thick, partial covering absorber; and iii) a relativistic disk reflector in a lamp-post geometry, with low coronal height and high BH spin. The first model is able to explain the high reflection component in terms of variability. The second does not require any reflection to reproduce the hard emission, while a rather low high-energy cutoff of ~100 keV is detected for the first time in such a high redshift source. The third model require a face-on geometry, which may affect the SMBH mass and Eddington ratio measurements. Deeper X-ray broad-band data are required in order to distinguish between these possibilities.
Key words: galaxies: active / galaxies: nuclei / quasars: individual: PG 1247+267 / accretion, accretion disks
© ESO, 2016
1. Introduction
The Eddington luminosity (expressed as LEdd = 4πGMmpc/σT) is an approximate upper bound to the total luminosity Lbol that can be radiated by a compact object of mass M, set by the equilibrium between the radiation pressure acting outward and the gravitational force acting inward, for a spherically symmetric geometry (Eddington 1916). The limit of Lbol/LEdd (hereafter λEdd) = 1 is thought to regulate the growth of supermassive black holes (SMBHs) over cosmic time and is observed to hold both at low (e.g., Schulze & Wisotzki 2010) and high redshift (e.g., Nobuta et al. 2012; Suh et al. 2015). However, super-Eddington accretion periods are thought to be possible (Zubovas & King 2013) and may even be required to explain the fast growth of the first SMBHs (see, e.g., Volonteri 2012, for a review); super-Eddington episodes could in fact be the transient phenomena in which SMBHs gain most of their mass (King 2003).
As implied by its rapid variability, the X-ray emission is produced in the inner regions surrounding the SMBH (few to tens of gravitational radii, rG; e.g., Chartas et al. 2009; Zoghbi et al. 2012; Reis & Miller 2013) and is the most direct probe for investigating accretion properties. There are several key observables in the X-ray spectra of active galactic nuclei (AGN) related to the accretion rate. First, a positive correlation between spectral slope (Γ) and flux (and hence λEdd) is thought to be a common feature of SMBH accretion and has been observed in individual, highly variable AGN at low redshift (e.g., Perola et al. 1986; Vaughan & Edelson 2001); in large samples of AGN, both locally and at high redshift (Shemmer et al. 2008; Risaliti et al. 2009; Brightman et al. 2013); and also derived theoretically for BHs in general (Laurent & Titarchuk 2011), with sources close to the Eddington limit showing softer spectra (Γ up to 2.5) compared to sources accreting at slower rates (Γ ~ 1.5). There is also evidence that this relation tends to flatten above λEdd= 1 (Shih et al. 2002; Ai et al. 2011). The relation between Γ and λEdd is based on the existence of a strong link between the accretion flow and the properties of both the disk and the corona: a high accretion rate drives the disk temperature up, producing more soft X-ray radiation and at the same time increases the Compton cooling of the corona, steepening the slope of the X-ray continuum (e.g., Shemmer et al. 2006).
Second, an anti-correlation has been observed between λEdd and the equivalent width (EW) of the narrow component of the Fe Kα emission line (EW ∝λEdd-0.19; Bianchi et al. 2007): at λEdd = 1 the line can be as weak as EW = 25 eV. This correlation is thought to be the fundamental cause underlying the observed X-ray Baldwin effect (Iwasawa & Taniguchi 1993), in which the EW anti-correlates with the X-ray luminosity. The nature of this correlation and the role of selection effects in this context, however, are still debated (see Shu et al. 2012).
The Γ-λEdd and EW-λEdd relations may be related; objects with higher values of λEdd have a steeper continuum, implying that the number of photons that can produce the fluorescent Fe Kα emission is smaller, leading to a smaller EW (Ricci et al. 2013). The intensity of the fluorescent emission line and the Compton hump are also related since for a given reflector geometry, ionization parameter, and Fe abundance the relative strength of the Fe Kα line and the reflected continuum is fixed (e.g., George & Fabian 1991); therefore, in highly accreting sources the last component should also be weaker. Furthermore, AGN with high λEdd, both at low and high redshift, tend to have stronger ionized Fe Kα emission at 6.9 keV, with respect to the neutral Fe Kα line at 6.4 keV (Nandra et al. 1996; Iwasawa et al. 2012). The same is observed in narrow-line Seyfert 1 galaxies (e.g., Comastri et al. 1998) that are also thought to have high λEdd. This is probably due to the fact that the inner disc is more strongly ionized when the central source is brighter (see, e.g., Keek & Ballantyne 2016).
Finally, gas outflows are naturally expected during super-Eddington accretion phases (Zubovas & King 2012) owing to the intense radiation pressure associated with these events. Such winds are one of the main candidates thought to produce the AGN “feedback” and to fine-tune the MBH−σ relation observed in the local Universe between quiescent SMBHs and their host bulges (see Kormendy & Ho 2013, for a review). These outflows are observed as blueshifted absorption features produced by ionized gas in optical/UV spectra of ~20% of optically selected quasars (e.g., Weymann et al. 1979; Gibson et al. 2009), and are also observed in 30−40% of X-ray spectra of local AGN (Tombesi et al. 2010) and in a few high redshift QSOs (Chartas et al. 2003; Saez et al. 2011; Lanzuisi et al. 2012; Vignali et al. 2015) in the form of highly ionized Fe absorption lines. These absorbers may be part of a single large-scale, stratified outflow observed at different locations from the black hole and spanning several orders of magnitude in ionization, column density, and velocity (Tombesi et al. 2013). Considering the few QSOs at low redshift that show strong signatures of massive winds and have reliable BH mass measurements, all appear to be accreting close to their Eddington limit: PG1211+143, PG0844+349, PDS 456, MCG-6-30-15 (Pounds et al. 2003a,b; Reeves et al. 2003).
The luminous QSO PG1247+267 (hereafter PG1247) at z = 2.048 is candidate to be an extreme example of super-Eddington accretion, and in this paper we present new NuSTAR observations obtained with the aim of characterizing its high-energy emission. The source properties are summarized in Sect. 2. The existing XMM-Newton data (Sect. 3) are combined with the hard X-ray data from NuSTAR (Sect. 4) to constrain the high-energy properties of this extreme QSO (Sect. 5). Results from the broad-band X-ray spectral fits are summarized and discussed in Sect. 6. Throughout the paper, a standard Λ −CDM cosmology with H0 = 70 km s-1 Mpc-1, ΩΛ = 0.7, and ΩM = 0.3 is used. Errors are quoted at the 90% confidence level for one parameter of interest.
2. Source properties
Having Lbol= 1.5 × 1048 erg s-1, an absolute magnitude of Mi ~ −30, and an observed magnitude of i = 15.37, PG1247 is the most luminous radio-quiet1 QSO at z ~ 2 ± 0.2 in the SDSS DR7 (Abazajian et al. 2009; Shen et al. 2011)2. PG1247 is also the second most luminous AGN with a reverberation mapping (RM) BH mass measurement available, obtained from a spectro-photometric monitoring campaign with the 1.82 m Copernicus Telescope at Asiago (Trevese et al. 2007), after the lensed quasar APM 08279+5255 at z ~ 4 (Saturni et al. 2016). The BH mass estimate from CIII] and CIV RM is MBH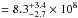 M⊙ (Trevese et al. 2014). The average Lbol obtained from the optical continuum (between 2500 Å and 5100 Å) measured in these observations is 1.1 × 1048 erg s-1. These values translate into a fiducial value of λEdd= 10.6, the highest reported in the literature to date for a QSO with a SMBH mass obtained via RM.
M⊙ (Trevese et al. 2014). The average Lbol obtained from the optical continuum (between 2500 Å and 5100 Å) measured in these observations is 1.1 × 1048 erg s-1. These values translate into a fiducial value of λEdd= 10.6, the highest reported in the literature to date for a QSO with a SMBH mass obtained via RM.
The source also has a single epoch (SE) BH mass estimate, reported in Shen et al. (2011), from MgII in the range Log(MBH/M⊙) = 9.7−9.9, depending on the calibration adopted, and Log(MBH/M⊙) ~ 9.8 from CIV. The authors take the latter as the MBH fiducial value for all the sources with z > 1.9 because of the SDSS observing band limits.
Although the statistical errors on these measurements are small (ΔMBH= 0.01−0.03) one must bear in mind that there are large systematic uncertainties (≳0.4 dex) associated with these estimates. In particular, SE estimates based on CIV are known to be affected by large uncertainties due to the presence of outflowing components contributing to the CIV line flux (see, e.g., the discussion in Shen et al. 2011). The strong blue wing in the CIV emission line and the presence of absorption systems observed in PG1247 SDSS spectrum support this possibility. In particular, a doublet absorption line at ~1508 Å with a rest-frame separation of 2.57 Å, FWHM ~ 200 km s-1 and EW doublet ratio of ~0.8 identify the 1548 and 1550 transitions of the CIV doublet line (see, e.g., Vestergaard 2003). The doublet is at ~–7700 km s-1 from the systemic and therefore can be associated with outflowing gas.
On the other hand, the RM measurements based on the same emission line are less affected by non-virial outflows if the root mean square spectrum (Peterson et al. 1998) is used instead of the average spectrum, because the outflow components are expected to vary on timescales longer than reverberation time lags (see the discussion in Trevese et al. 2014). In all cases, even taking into account the SE value, the source has an accretion rate in the range λEdd= 0.9−1.75, which is close to or above the Eddington limit. All these properties are summarized in Fig. 1 (top), where the Lbol and MBH values for PG1247 from Trevese et al. (2014) and from Shen et al. (2011) are shown in comparison with the 1.8 < z < 2.2 quasars from the SDSS DR7 catalog. PG1247 is a truly remarkable source that can be used as a laboratory for testing predictions of super-Eddington accretion theories.
A magnification factor of μ = 5−10 due to strong lensing could bring the Eddington ratio of PG1247 to ~1 (see discussion in Trevese et al. 2014). However, the quasar was observed several times between 1991 and 1998 with HST as a single point source, with no sign of multiple images, down to scales of ~0.1′′. Figure 1 (bottom) shows a 4″ × 4″ zoom around PG1247 from the combined HST-NICMOS observations of 1998 (F160W filter, total exposure time 1150s). The possibility of strong lensing is therefore excluded, as all known high-redshift lensed QSOs observed so far with HST have been resolved into multiple images at those scales3.
 |
Fig. 1 Top: Lbol and MBH for the 1.8 < z < 2.2 SDSS QSO sample (black points and gray contours). Values for PG1247 from SDSS (Shen et al. 2011) and from Trevese et al. (2014) are shown with empty and filled red diamonds, respectively. Dashed green lines mark different λEdd values. Bottom: 4″ × 4″ HST-NICMOS image of PG1247 (filter F160W). The 1′′ scale is shown. |
3. Existing X-ray data
 |
Fig. 2 Top: XMM-Newton pn (black) and MOS1+2 (red) spectra of PG1247. The model is a simple power law fitted to the 0.3−2 keV observed band to highlight the residuals above 2 keV due to the emission line complex and the strong reflection component. Bottom: contour plot (at 68, 90, and 99% c.l.) for the emission line energy (rest frame) and normalization. In both panels the dashed lines mark the expected neutral Fe, FeXXV, and FeXXVI Kα emission line energies. |
PG1247 was observed by XMM-Newton in 2003 for a total of 34 ks (20 ks after background-flare subtraction). No significant variability is detected within the XMM-Newton observation. Page et al. (2004) analyzed the data, and reported a strong reflection component (R ~ 2.8, modeled with PEXRAV, Magdziarz & Zdziarski 1995), a very soft power law (Γ = 2.23 ± 0.10), plus a broad and neutral Fe Kα line (σ = 0.52 ± 0.35 keV, EW = 421 ± 215 eV). As the authors pointed out, such a high reflection fraction is unphysical in the context of the PEXRAV model, which includes a primary power law and models reflection from cold material in a slab geometry, since R is defined to be Ω / 2π, i.e., the solid angle of the cold material visible from the Comptonizing source in units of 2π, and therefore R ~ 2.8 > 4π sr, the solid angle of the entire sphere.
We reanalyzed the data applying standard extraction procedures using the Scientific Analysis System (SAS) v13.5, and optimized extraction regions (40′′ for pn and 35′′ for MOS1 and 2) to obtain pn and MOS1+2 spectra4. The extracted spectra have ~4560 pn and ~2900 MOS1+2 counts in the 0.3−10 keV band (black and red data points in Fig. 2, top). We fitted the spectrum with a single power law plus Galactic absorption (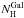 = 0.9 × 1020 cm-2, Kalberla et al. 2005) in the observed 0.3−2 keV band, corresponding to the rest frame 1−6 keV band at the source redshift. Indeed, extrapolating this model to the full 0.3−10 keV observed band, strong residuals can be seen around the expected position of the Fe Kα emission line, and at the reflection hump. We fitted the data with the same PEXRAV reflection model adopted in Page et al. (2004) to check for consistency. The best fit (χ2/d.o.f. = 278.5 / 300) is obtained with a very soft power law with Γ = 2.36 ± 0.08, again with an extremely high reflection component
= 0.9 × 1020 cm-2, Kalberla et al. 2005) in the observed 0.3−2 keV band, corresponding to the rest frame 1−6 keV band at the source redshift. Indeed, extrapolating this model to the full 0.3−10 keV observed band, strong residuals can be seen around the expected position of the Fe Kα emission line, and at the reflection hump. We fitted the data with the same PEXRAV reflection model adopted in Page et al. (2004) to check for consistency. The best fit (χ2/d.o.f. = 278.5 / 300) is obtained with a very soft power law with Γ = 2.36 ± 0.08, again with an extremely high reflection component 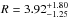 . The high-energy cutoff (Ecut) is fixed to 100 keV in the XMM-Newton data, given that the XMM-Newton spectra only reach ~30 keV (rest frame), and are therefore not able to constrain this parameter, given the available photon statistics. Also, the inclination angle (defined as the inclination angle between the line of sight and the vertical axis of the accretion disk) is fixed to the default value, cos(i) = 0.45 (see Sect. 5.1.1. for the effect of possible different geometries). The normalizations of pn and MOS1+2 are left free to vary independently, but they are in agreement within ~4%.
. The high-energy cutoff (Ecut) is fixed to 100 keV in the XMM-Newton data, given that the XMM-Newton spectra only reach ~30 keV (rest frame), and are therefore not able to constrain this parameter, given the available photon statistics. Also, the inclination angle (defined as the inclination angle between the line of sight and the vertical axis of the accretion disk) is fixed to the default value, cos(i) = 0.45 (see Sect. 5.1.1. for the effect of possible different geometries). The normalizations of pn and MOS1+2 are left free to vary independently, but they are in agreement within ~4%.
Residuals to the PEXRAV model in both the pn and MOS1+2 spectra around 6.4 keV rest frame suggest the presence of an emission line close to the rest-frame energies of the Fe Kα line. We added a narrow (σ = 10 eV fixed) emission line to the model at energy Eline = 6.4 keV, fixed. The improvement in the fit is small (Δχ2 = 1.9) and the addition of the emission line is justified only at a ~85% confidence level (c.l., F-test probability p = 0.15)5. Leaving the energy of the line as a free parameter, we obtain a further improvement of the fit of Δχ2 = 3.0. The addition of the new free parameter is justified at ~93% c.l. (p = 0.071 from an F-test). The best-fit line energy is 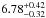 keV. Figure 2 (bottom) shows the confidence contours of the emission-line energy and normalization, obtained for a fixed σ = 10 eV. As can be seen in the contours, the observed feature could be the result of blending of Fe XXV and Fe XXVI, while the 6.4 keV energy is ruled out at 90% c.l. Leaving the line width σ as a free parameter, the best-fit values become
keV. Figure 2 (bottom) shows the confidence contours of the emission-line energy and normalization, obtained for a fixed σ = 10 eV. As can be seen in the contours, the observed feature could be the result of blending of Fe XXV and Fe XXVI, while the 6.4 keV energy is ruled out at 90% c.l. Leaving the line width σ as a free parameter, the best-fit values become 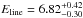 keV and σ ≤ 0.63 keV. The improvement in the fit is minimal (χ2/d.o.f. = 272.6 / 297) and the new free parameter is not justified (p = 0.30). As pointed out in Page et al. (2004), although there is evidence that the iron line may be broadened, no definite statement can be made. A narrow emission line with the same parameters derived above is included in all the following fits. The equivalent width of the line is
keV and σ ≤ 0.63 keV. The improvement in the fit is minimal (χ2/d.o.f. = 272.6 / 297) and the new free parameter is not justified (p = 0.30). As pointed out in Page et al. (2004), although there is evidence that the iron line may be broadened, no definite statement can be made. A narrow emission line with the same parameters derived above is included in all the following fits. The equivalent width of the line is 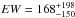 eV rest frame. Given the inferred luminosity of L2−10= 1046 erg s-1, the X-ray Baldwin effect predicts EW = 20−30 eV (Bianchi et al. 2007). Assuming that this value refers to a canonical, R = 1 reflection component with solar abundances, the observed emission line EW is broadly consistent with the strong reflection component (R = 3−4) found above.
eV rest frame. Given the inferred luminosity of L2−10= 1046 erg s-1, the X-ray Baldwin effect predicts EW = 20−30 eV (Bianchi et al. 2007). Assuming that this value refers to a canonical, R = 1 reflection component with solar abundances, the observed emission line EW is broadly consistent with the strong reflection component (R = 3−4) found above.
PG1247 was also observed by Swift-XRT 19 times between 2007 and 2014. We collected the spectra in all the observations with more than 1 ks exposure time (14 in total), and merged them using standard ftool procedures to obtain a single spectrum with statistics good enough to perform a basic spectral analysis. The final spectrum has ~560 net counts in the 0.3−10 keV band for a total exposure time of 43 ks. When fitted with the same reflection model described above, the XRT data give consistent results with the XMM-Newton spectra: a steep power law (Γ = 2.2 ± 0.4) and a strong reflection component (R ~ 2.5). Given the limited number of counts, and the fact that they have been collected over 7 years, we decided not to use the XRT spectrum for the following spectral analysis. However, we used this best-fit model to convert the observed count rate of each observation into full band (0.2−10 keV) fluxes, which will be relevant for the variability analysis of the source (see Sect. 35.2 and Fig. 7).
4. NuSTAR data
 |
Fig. 3 Top: 3−79 keV background-subtracted images of the NuSTAR observation of PG1247 (FPMA left and FPMB right). Contamination from the Coma cluster is visible in the upper left corner of FPMA. Bottom: 15−30 keV NuSTAR images, not background subtracted. In both panels the 1′ scale is shown, and the source and background extraction regions are shown with continuous and dashed lines, respectively. North is up and east is left. |
 |
Fig. 4 NuSTAR FPMA and FPMB data (blue and cyan points, respectively) fitted with a simple power law (top panel). The spectra have been further rebinned with respect to the S/N = 3 level to highlight the curvature of the spectrum in the residuals (central panel). The residuals with respect to the fit performed with the PEXRAV model are shown in the lower panel. |
PG1247 was observed by NuSTAR (Harrison et al. 2013) in December 2014 for a total of 94 ks. The raw data were processed using the NuSTAR Data Analysis Software package v. 1.4.1 (NuSTARDAS)6. Calibrated and cleaned event files were produced using the calibration files in the NuSTAR CALDB (version 20150312) and standard filtering criteria with the nupipeline task. The global light-curves extracted from the full FPMA and FPMB modules in the energy range 3−20 keV show a strong background flare – with a count-rate more than a factor of two higher than the stable level – due to solar activity, lasting ~2 h. We removed this high background period using the nustar_filter_lightcurve IDL script. The cleaned exposure time is 86 ks.
The NuSTAR observation of PG1247 is also affected by contamination (particularly in FPMA) by the Coma cluster, lying ~2.5° northeast of the quasar. Figure 3 (top), shows the 3−79 keV images of PG1247 obtained with the FPMA (left) and FPMB (right) detectors produced with the IDL code nuskybkg (Wik et al. 2014). This code takes into account all the background components usually observed in NuSTAR, i.e., the instrumental background, the focused cosmic X-ray background, and the aperture background. However, the code does not model and remove the contamination from the nearby cluster, which is evident in the upper left corner of the FPMA image. Therefore, we used annular regions to extract local background spectra instead of using the background files produced by nuskybkg. The background spectra were extracted from annular regions of inner radius 70′′ and outer radius 120′′. Circular extraction regions for the source, with different radii, were tested in order to find the radius that optimizes the S/N for each focal plane module. The final extraction radius is 40′′ for both FPMA and FPMB, which gives a S/N of ~14 and ~15, respectively. The nuproducts task was then used to extract the NuSTAR source and background spectra, plus the appropriate response and ancillary files. In the following the fits are performed leaving the relative normalizations between FPMA and FPMB as free parameters. The two normalizations agree within 15% and are consistent within 1σ.
 |
Fig. 5 Best-fit unfolded models for models 1, 2, 3, and 4, from top left to bottom right. The continuous curves represents the best fit to the XMM-Newton data (in red) and NuSTAR data (in blue). The dotted curves represent the primary power law, while the dashed curves represent the component reproducing the hump (either reflection or absorption). In the top right panel the magenta curve represents the constant reflection component underlying both XMM-Newton and NuSTAR data, modeled with PEXRAV. |
The spectra have been grouped using the tool Specgroup within SAS, to a minimum S/N = 3 per bin. The source is detected at this level between 3 and 30 keV in both instruments, with a total of 520 (590) net counts for FPMA (FPMB). Figure 3 (bottom) shows the 15−30 keV NuSTAR image of PG1247 without any background subtraction: the source is clearly detected even in this very hard band. Figure 4 shows the NuSTAR spectra (FPMA in cyan and FPMB in blue) fitted with a simple power law (Γ = 2.14 ± 0.13, χ2/d.o.f. = 65.46 / 73). The curved shape of the hard X-ray spectrum of PG1247 is visible in the residuals (central panel). Adopting a PEXRAV model, the fit is significantly improved (χ2/d.o.f. = 55.83 / 71). Residuals for this fit are shown in the lower panel of Fig. 4. However, owing to the limited photon statistics and to the complexity of the underlying model, the NuSTAR spectra alone do not provide interesting simultaneous constraints on the high-energy cutoff, the reflection fraction, and the photon index; the best-fit photon index is Γ = 1.9 ± 1.5, while the high-energy cutoff and reflection fraction are only loosely constrained (Ecut> 50 keV, R> 1.35).
The flux in the 2−10 keV band (extrapolated using the PEXRAV model) is F2−10= (4.2 ± 0.5) × 10-13 erg cm-2 s-1, while the 2−10 keV flux measured by XMM-Newton with the same model was F2−10= (2.3 ± 0.1) × 10-13 erg cm-2 s-1: the NuSTAR data show that the source has increased in flux between the XMM-Newton observation in 2003 and the NuSTAR observation in 2014 by a factor of ~1.8. Also, the intermediate Swift-XRT observations show an average flux level consistent with the NuSTAR measurement. The cross-calibration between NuSTAR and the other X-ray satellites is accurate within 10% (Madsen et al. 2015).
Because the correlation between Γ and flux (i.e., λEdd) saturates at high fluxes (e.g., Shih et al. 2002; Ai et al. 2011), we try to fit the NuSTAR spectra with Γ fixed at the XMM-Newton value to get more stringent constraints on the Ecut and R parameters, and test whether there is any difference, for example, in the R value derived from XMM-Newton due to the change in flux (i.e., accretion rate). The resulting best fit Ecut is Ecut> 60 keV, while the reflection fraction is 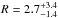 , and therefore consistent with the XMM-Newton results within the large errors.
, and therefore consistent with the XMM-Newton results within the large errors.
5. Joint spectral modeling
We modeled the XMM-Newton and NuSTAR spectra together with the aim of deriving a physically meaningful interpretation of the peculiar X-ray spectrum of PG1247, leveraging the broad band covered by the combined data and accounting for the higher flux measured during the NuSTAR observation. First, we adopted a cold reflection model and tested whether the addition of the new NuSTAR data allow for a less extreme value of R (Sect. 5.1). Then we tested whether the strong reflection seen in XMM-Newton can be explained in terms of variability of the continuum superimposed on a constant cold reflection component (Sect. 5.2). Third, we tested the possibility that the hump observed in the hard X-rays is produced by absorption of partial covering, dense material, rather than by reflection (Sect. 5.3). Finally we tested a model in which the reflection is produced in the inner regions of an ionized accretion disk, and is relativistically blurred (Sect. 5.4).
Fit parameters for the baseline models discussed in Sect. 5.
5.1. Variable cold reflection
 |
Fig. 6 Panel a) unfolded data and model for the best fit obtained with model 1. Panels b)−e) delta χ for model 1, 2, 3, and 4, respectively. In all panels XMM-Newton pn data are in black, MOS1+2 in red, NuSTAR module A in green, and B in blue. |
To account for the overall variability of the X-ray spectra between 2003 and 2014, we modeled the XMM-Newton+NuSTAR data with a cold reflection model (PEXRAV) as described in Sect. 3, but where the normalizations of the XMM-Newton and NuSTAR data are allowed to vary independently, while the rest of the free parameters, i.e., Γ, Ecut, and R, are forced to be the same for the two data sets (model 1); i.e., we are assuming that the spectral shape was the same in the two periods, and only the global normalization has changed. The inclination angle was first fixed to cos(i) = 0.45.
As a first step we fixed the value of the reflection parameter to R = 1 to check whether the addition of NuSTAR data allow for a less extreme reflection component with respect to the XMM-Newton data alone. The resulting fit gives χ2/d.o.f. = 347.8 / 369, with a soft photon index (Γ = 2.22 ± 0.05), while Ecut is not well constrained. We then left the reflection parameter R free to vary (model 1, Fig. 5, top left). The best-fit value for the reflection parameter is 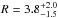 and the improvement in the fit is large (Δχ2 = 20.1). The F-test indicates that the addition of this extra free parameter provides a significant improvement to the fit (F-test probability p = 2.7 × 10-6). The best-fit photon index is again very soft (
and the improvement in the fit is large (Δχ2 = 20.1). The F-test indicates that the addition of this extra free parameter provides a significant improvement to the fit (F-test probability p = 2.7 × 10-6). The best-fit photon index is again very soft (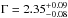 ), comparable to the one obtained from XMM-Newton alone. With this model the Ecut is constrained to a rather low value (Ecut
), comparable to the one obtained from XMM-Newton alone. With this model the Ecut is constrained to a rather low value (Ecut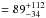 keV rest frame). The best-fit parameters are given in Table 1. The unfolded data and model for the best fit obtained in this way are shown in panel a of Fig. 6. Panel b shows the Δχ for the same model.
keV rest frame). The best-fit parameters are given in Table 1. The unfolded data and model for the best fit obtained in this way are shown in panel a of Fig. 6. Panel b shows the Δχ for the same model.
We note that a small inclination angle i between the line of sight and the accretion disk axis can increase the reflection component observed by at most a factor of ~2 with respect to the default geometry used in this section (cos(i) = 0.45). Therefore, even an extremely face-on geometry cannot entirely account for the R> 3 reflection observed in the data. We obtain 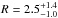 for cos(i) = 0.95, still significantly larger than R = 1, which is the reflection for a 2π sr solid angle. We therefore discard this model as unrealistic.
for cos(i) = 0.95, still significantly larger than R = 1, which is the reflection for a 2π sr solid angle. We therefore discard this model as unrealistic.
5.2. Constant cold reflection
To reproduce a case in which a variable primary power law is superimposed on a constant reflection component, we used a model that includes a power law with high-energy exponential cutoff and the normalization left free to vary between the XMM-Newton and NuSTAR observations, plus a PEXRAV component seen only in reflection (R = −1) and kept constant between the two observations (model 2, Fig. 5 top right). The photon index and Ecut are left as free parameters, but are forced to have the same value in the power-law and PEXRAV components. In this way, the extreme R parameter observed in the XMM-Newton spectra of 2003 could be explained in terms of a primary power law observed in a lower state with respect to the reflection hump, which is expected to be less variable and to exhibit significant time lags, being the result of reflection from distant material (i.e., the torus) with a range of different light paths. The goodness of the fit in this case is comparable with that of model 1 (χ2/d.o.f. = 327.7 / 367). The Δχ for this model are shown in panel c of Fig. 6. The resulting R parameters for the fit with a constant reflection component are R = 3.8 ± 1.4 for the XMM-Newton spectra and R = 1.7 ± 0.8 for the NuSTAR spectra. If this model is correct, the best-fit cutoff is Ecut~ 160 keV (rest frame), a factor of 2 higher than the value measured for model 1 and with larger errors: it is loosely constrained to be Ecut≲ 600 keV at 90% c.l. Given that the NuSTAR data only reach a 90 keV rest frame, some doubt can be cast on the reliability of this result.
The weak Fe line EW observed in the XMM-Newton data (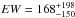 eV, see Sect. 3) is consistent, within the errors, with the expected Fe line EW computed taking into account the high reflection factor observed in that data set and the X-ray Baldwin effect (EW ~ 20−30 eV for the luminosity of PG1247, to be rescaled by a reflection parameter R = 3.8) without requiring any particularly low Fe abundance.
eV, see Sect. 3) is consistent, within the errors, with the expected Fe line EW computed taking into account the high reflection factor observed in that data set and the X-ray Baldwin effect (EW ~ 20−30 eV for the luminosity of PG1247, to be rescaled by a reflection parameter R = 3.8) without requiring any particularly low Fe abundance.
Figure 7 shows the 0.2−10 keV (rest-frame) light-curve of PG1247 as has been observed since 1993 by ROSAT, ASCA, XMM-Newton, and Swift. The light-curve is taken from Shemmer et al. (2014). We added four more Swift observations taken after November 2013, and as an empty square the flux obtained from the reanalysis of the ROSAT data performed in Boller et al. (2016), with a better background treatment. The NuSTAR data point (magenta) is added by extrapolating the hard X-rayflux to the 0.2−10 keV flux, using the spectral model described in this section. PG1247 is highly variable at X-raywavelengths despite its exceptional X-ray luminosity: the normalized excess variance (e.g., Nandra et al. 1997) is 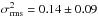 (Shemmer et al. 2014), higher than expected for its X-ray luminosity, i.e.,
(Shemmer et al. 2014), higher than expected for its X-ray luminosity, i.e., 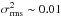 (Young et al. 2012; Lanzuisi et al. 2014). More importantly, the light-curve shows that the flux level of the XMM-Newton observation (red point) is the lowest measured in the last twenty years: the X-ray flux dropped from ~10 to 3.5 × 10-13 erg s-1 cm-2 between the ROSAT and the XMM-Newton measurements from 1993 to 2003 (~1200 days rest frame), while the flux measured by Swift between 2007 and 2013 spans the range 4−8 × 10-13 erg s-1 cm-2. In this scenario, we obtain a lower limit of the distance between the primary X-ray source and the reflector of ~1200 light-days, equivalent to ~1 pc, which is consistent with molecular torus size estimates obtained from the source luminosity (see Sect. 6).
(Young et al. 2012; Lanzuisi et al. 2014). More importantly, the light-curve shows that the flux level of the XMM-Newton observation (red point) is the lowest measured in the last twenty years: the X-ray flux dropped from ~10 to 3.5 × 10-13 erg s-1 cm-2 between the ROSAT and the XMM-Newton measurements from 1993 to 2003 (~1200 days rest frame), while the flux measured by Swift between 2007 and 2013 spans the range 4−8 × 10-13 erg s-1 cm-2. In this scenario, we obtain a lower limit of the distance between the primary X-ray source and the reflector of ~1200 light-days, equivalent to ~1 pc, which is consistent with molecular torus size estimates obtained from the source luminosity (see Sect. 6).
 |
Fig. 7 Rest-frame 0.2−10 keV light-curve of PG1247 since its first detection with ROSAT in 1993 (black filled square). The empty square shows the ROSAT data reanalyzed in Boller et al. (2016). The black triangle represents the ASCA measurement (1995). The red diamond represents the XMM-Newton measurement of 2003. The gray points represent the monitoring performed with Swift between 2007 and 2013 (Shemmer et al. 2014), and the magenta point shows the NuSTAR measurement in 2014. |
5.3. Ionized partial covering absorber
We then tested the possibility that an ionized, partial covering absorber could reproduce the shape observed in PG1247 without the need of any reflection component (or with a standard R = 1 cold reflection) by affecting mostly the X-ray data below 10 keV (rest frame). Model 3 (Fig. 5, bottom left) includes an ionized absorber with partial covering (ZXIPCF in Xspec7, Reeves et al. 2008), superimposed on a PEXRAV model with the reflection fraction parameter set to R = 0 (i.e., no reflection). Indeed, this model can accurately reproduce the continuum shape observed in PG1247: the best fit gives χ2/d.o.f. = 325.5 / 365.
To fit the XMM-Newton and NuSTAR data, a mildly ionized (log (ξ) ~ 2.4 erg cm s-1), almost Compton thick (NH~ 1.3 ± 0.3 × 1024 cm-2) absorber is required. The covering fraction (CF) of the absorber is CF ~ 0.6. Figure 8 (left) shows the confidence contours for the column density and the covering fraction. Adding a standard reflection component with R = 1 has the only effect of reducing the covering factor to CF ~ 0.4.
We note that the validity of Xstar is restricted to NH≤ 1 × 1024 cm-2 in order to avoid significant effects from Compton scattering (Kallman & Bautista 2001), even if the nominal NH range of ZXIPCF reaches NH= 5 × 1024 cm-2. However, even imposing an NH upper limit equal to NH= 1 × 1024 cm-2 in our fit, does not significantly change the results for the other parameters or the quality of the final best fit.
This model implies that the intrinsic luminosity of the source is a factor of ~2 higher than the value observed by XMM-Newton, going from L2−10= 8 × 1045 erg s-1 to L2−10= 1.5 × 1046 erg s-1. This, however, has a limited effect on the bolometric luminosity of the source, which is estimated to be Lbol= 1.5 × 1048 erg s-1 from the optical continuum, given that at these luminosities the X-ray contribution is expected to be a small fraction of the total luminosity: the bolometric correction kbol (defined as Lbol/L2−10) is ~100 already at Lbol= 1047 erg s-1 (Steffen et al. 2006; Lusso et al. 2012).
Interestingly, this model naturally produces absorption features at energies above the Fe Kα line and could also produce significant Fe Kα emission if the covering factor of the wind/outflow is large (i.e., P Cygni profile, see Nardini et al. 2015). A similar feature is indeed observed in the XMM-Newton spectrum of PG1247 (NuSTAR does not cover the energy of interest), albeit at low significance (~2σ) and at energies slightly higher (Eabs ~ 7.8 keV rest frame) than the value expected for FeXXV-FeXXVI Kα transitions (6.70−6.97 keV). Therefore, if produced by FeXXV-FeXXVI, the observed feature would imply an outflow velocity of vout ~ 0.15c, comparable to typical outflow velocities observed in local Seyferts (Tombesi et al. 2010). However, the quality of the spectrum and the low significance of the feature do not allow us to investigate in detail the properties of this potential outflow. Figure 8 (right) shows the ratio (in rest-frame energy) between the data and a simple power law in the region of the Fe Kα line. We note that the absorption feature is seen at energies Eabs ~ 2.4−2.6 keV observed frame, and therefore just above the prominent edge in the XMM-Newton mirror effective area at Eedge = 2.2−2.3 keV due to the Au M edge. This can produce some additional uncertainties in the instrumental calibration at these energies.
If this model is correct, we have detected for the first time the high energy cutoff of the primary continuum emission in a high redshift, non-lensed quasar (but see also Dadina et al. 2016, for the detection of a high-energy cutoff in a lensed QSO at z = 3.6). The low value measured may have important implications for the electron temperature of the corona (see discussion is Sect. 6.2).
 |
Fig. 8 Left: contour plot of the column density vs. covering fraction for model 3. Right: rest-frame residuals in the Fe Kα line region, after fitting with a simple power law. The gray dashed lines mark the expected neutral Fe, FeXXV, and FeXXVI Kα emission line energies. Symbols as in Fig. 6. |
 |
Fig. 9 Left: contour plot of the disk inclination angle vs. BH spin parameter for model 4. Right: contour plot of the corona height h vs. spin parameter for model 4. |
5.4. Relativistic reflection
Finally, to test the alternative possibility that the reflection continuum is produced in the inner regions of the accretion disk, i.e., by ionized material and under relativistic effects, we used the RELXILL model (Garcia et al. 2014), which is the convolution of the XILLVER reflection model (Garcia et al. 2010) for ionized accretion disk reflection, with the relativistic treatment of RELCONV (Dauser et al. 2010). In particular the RELXILL_LP configuration assumes a simple lamp post geometry, i.e., a point-like hard X-ray source (the corona) above the black hole that is irradiating the accretion disk (e.g., Matt et al. 1991; Dauser et al. 2013) and computes both the expected emissivity profile and the strength of the reflection self-consistently (model 4, Fig. 5 bottom right).
The free parameters, in addition to the primary power-law photon index, high-energy cutoff, and normalizations, are the height of the primary source (h), the BH spin (a), the inclination angle of the disk (i), and the ionization parameter (ξ), defined as the ionization parameter of the accretion disk. The inner radius of the accretion disk is fixed to the innermost stable circular orbit, which depends on the BH spin, while the outer radius is frozen to 400 rG.
Interestingly the high-energy cutoff seems to be unconstrained for this model. This is not entirely due to the limited spectral quality of PG1247 and the larger number of free parameters for this model, but also to the fact that – for a given primary power-law cutoff – the reflection component computed by RELXILL always has a sharper decline at high energies than the value computed by PEXRAV (see, e.g., Dauser et al. 2016). This means that the relativistic reflection model is able to reproduce the shape of the high-energy spectrum without the need of a cutoff. Therefore, we fixed it to Ecut= 100 keV, in order to be consistent with the measurements of the other parameters performed from the models discussed above. The goodness of this fit is comparable with the fits obtained for the previous three models (χ2/d.o.f. = 333.8 / 365). The photon index is very soft (Γ = 2.26 ± 0.04) also for this model.
The interesting aspect of this model is that the reflection fraction in this configuration is not a free parameter, but instead the reflection contribution is computed self-consistently as the result of the geometry, size, and ionization state of the emitting corona. The height of the corona, the BH spin, and the reflection fraction are indeed correlated in this model, in the sense that in order to produce a strong reflection fraction, both a low value of h (i.e., the corona is close to the BH and hence to the disk) and a high value of the BH spin (i.e., the disk has a small inner radius) are required (see Dauser et al. 2014). Figure 9 (left) shows the inclination angle vs. BH spin parameter confidence contours: to produce the strong reflection we see in the spectrum of PG1247, a nearly maximally rotating BH is required (a> 0.68), observed at a small inclination angle (cos(i) > 0.83). Figure 9 (right) shows the confidence contours between the coronal height h (in units of rG) and the spin parameter. The height of the emitting region is constrained to be h ≤ 3.5rG. Finally, the ionization parameter is constrained to be log (ξ) = 1.8 ± 0.5 erg cm s-1; i.e., the disk must be moderately ionized in order to produce the strong Compton hump, while a more ionized reflecting medium would produce a steeper reflection continuum. We note that a small height of the corona (h< 10rG) for a maximally rotating BH (a> 0.9), observed at small inclination angles (i< 30°), has also been estimated in a few local Seyferts through spectral-timing analysis and reverberation techniques (e.g., Cackett et al. 2014; see Uttley et al. 2014, for a review), while evidence is mounting that maximally rotating SMBHs may be common among AGN at low and high redshift (Walton et al. 2013; Reis et al. 2014; Reynolds et al. 2014), with the caveat that high spin means high accretion efficiency (Vasudevan et al. 2016) so the brightest objects (for which measuring the BH spin is feasible) in a population of objects with similar accretion properties will be those with high spin.
6. Discussion
Several aspects of the X-ray broad-band spectrum of PG1247 are in agreement with the possibility that this high-redshift QSO is accreting close to or above the Eddington limit, independent of the model adopted to reproduce the overall spectral shape:
-
The photon index is very soft: Γ ~ 2.3−2.4 for all models. These values are consistent with those expected for a nearly Eddington accreting SMBH, given the relation observed in individual, variable, local AGN (e.g., Perola et al. 1986; Vaughan & Edelson 2001; Vignali et al. 2008; Puccetti et al. 2014), and in samples of low- and high-redshift AGN (Shemmer et al. 2008; Risaliti et al. 2009; Brightman et al. 2013). The caveat is that the parameter space above the Eddington limit is currently unexplored. Unfortunately, owing to the limited data quality and the lack of simultaneity between the XMM-Newton and NuSTAR data, we cannot test whether PG1247 shows the softer when brighter behavior within the flux variation observed between the XMM-Newton and NuSTAR data.
-
The Fe emission line is most likely produced by ionized gas in the accretion disk (the rest-frame energy of 6.4 keV is ruled out at 90% c.l.), as observed in the stacked spectrum of large samples of AGN accreting close to the Eddington limit (Iwasawa et al. 2012). The EW of the line (
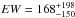 eV) is consistent, within the errors, with the value expected taking into account the high reflection factor derived from PEXRAV (possibly due to variability, see below) and the X-ray Baldwin effect (EW ~ 20−30 eV intrinsic, to be rescaled by a reflection parameter R = 3.8).
eV) is consistent, within the errors, with the value expected taking into account the high reflection factor derived from PEXRAV (possibly due to variability, see below) and the X-ray Baldwin effect (EW ~ 20−30 eV intrinsic, to be rescaled by a reflection parameter R = 3.8). -
The residuals above the expected energies of Fe Kα suggest the presence of an outflowing disk wind, as predicted by super-Eddington accretion models (e.g., Zubovas & King 2012), and observed in a handful of high-redshift QSOs accreting close to Eddington (Chartas et al. 2003; Lanzuisi et al. 2012; Vignali et al. 2015). The presence of ionized material surrounding the SMBH is indeed one of the characteristics of highly accreting BHs (see, e.g., Ballantyne et al. 2011).
6.1. Reflection and accretion
The intensity of the reflection component is usually thought to be anti-correlated with the flux state, and therefore λEdd, so that sources accreting closer to the Eddington limit show lower levels of reflection (see, e.g., Fabian et al. 2012; Keek & Ballantyne 2016). Therefore, the super-Eddington nature of PG1247 and the exceptional reflection component observed in its spectrum seem in tension. However, with the exception of model 1, which requires an unphysical value of the reflection fraction (R> 1), each of the other models discussed in Sect. 5 offers an explanation, even though the conclusions are strongly model-dependent.
In PG1247, the SMBH is on average accreting close to or above Eddington, while the XMM-Newton observation of 2003 can be considered a drop in the X-ray flux of a factor of ~2 with respect to the average, and a factor of ~3 with respect to the ROSAT measurements. The cold reflection scenario is therefore able to explain the exceptionally high reflection component in terms of variability (model 2): the source was a factor of ~3 fainter at the time of the XMM-Newton observation than during the ROSAT observation. In this scenario the super-Eddington accretion rate has nothing to do with the presence of a strong reflection component, which is only a light echo of the continuum level as it was 1200 days before the XMM-Newton observation. A reflection fraction R = 3−4 in the XMM-Newton data is therefore in agreement with this scenario, while the reflection fraction for the NuSTAR data in model 2 is consistent with R = 1 within the errors.
We note that the value R = 1 in the PEXRAV model is defined relative to the reflection produced by an infinite slab of cold material illuminated by the corona. If instead the reflector is the inner wall of the torus, we do not expect a reflection as high as R = 1 (the total solid angle seen by the reflector must be <2π sr). However, if we imagine a torus with a small half opening angle and large height (e.g., the one described in Ikeda et al. 2009), R could be close to ~1. Furthermore, if the reflection component is produced by cold material at the inner edge of the obscuring torus, the time delay between continuum and cold reflection variability would imply a radius of the torus inner edge of ~1 pc, roughly in agreement with the expected sublimation radius rin = 1−4 pc (Barvainis 1987; Kishimoto et al. 2007) given the UV luminosity of λLλ(1350 Å) ~ 4 × 1047 erg s-1 (Trevese et al. 2014) and with the torus half-light radius expected from the bolometric luminosity, i.e., 1−10 pc at 1048 erg s-1 (Burtscher et al. 2013).
The ionized absorber scenario (model 3) is able to explain the broad-band shape observed in PG1247 without the need of any reflection component. The spectral curvature is due to the effect of a mildly ionized (log ξ ~ 2.4 erg cm s-1) dense absorber (NH~ 1 × 1024 cm-2) with a covering factor of CF ~ 0.6 superimposed on a simple power law with a high-energy cutoff Ecut~ 100 keV. The addition of a standard cold reflection with R = 1 would reduce the required covering factor to CF ~ 0.4. In this case, the link between the shape of the X-ray spectrum of PG1247 and its extreme accretion properties would be in the presence of ionized, outflowing material close to the SMBH, a clear prediction of super-Eddington accretion theories that needs to be investigated with higher S/N spectra in the region of the Fe Kα emission line.
Finally, the relativistic reflection scenario (model 4) is able to explain the strong reflection component with an extreme geometry of the system, i.e., a rather small inclination angle (i< 30°), a small height of the corona (h< 3.5rG), and a maximally rotating BH (a ~ 0.97). The face-on geometry required to explain the strong reflection may actually affect the SMBH mass measurements, in particular requiring an increase in both the SE and RM mass estimates by a factor of up to 5 for very small angles (Pancoast et al. 2014). This would reduce the Eddington ratio of PG1247 by the same amount.
6.2. Ecut and the properties of the corona
 |
Fig. 10 Confidence contours (at 68, 90, and 99% c.l.) of Γ vs. Ecut (rest frame) parameters for model 1 (left), model 2 (center), and model 3 (right). |
The confidence contours for Γ and Ecut measured from the different models are shown in Fig. 10. The results on Ecut obtained from model 1 (left panel) are not considered here since, as discussed above, this model must be considered unrealistic. The best-fit Ecut measured with model 2 (central panel) is Ecut~ 160 keV, but it is only loosely constrained to be Ecut≲ 600 keV. For model 3 instead, we clearly constrain, for the first time at such high redshift, a rather low cutoff (right panel). Finally, for model 4 the Ecut is unconstrained and therefore fixed in the spectral fit.
The high-energy cutoff measured in model 3 is consistent with the average Ecut observed at low redshift (e.g., Malizia et al. 2014: ⟨Ecut⟩ = 128 keV, with standard deviation σ = 46 keV. This rather low value would imply a low plasma temperature of the Comptonizing region (kTe =Ecut/ 2 for τ ≲ 1 and large λEdd). Indeed, using Eq. (1) of Petrucci et al. (2001) and the derived Ecut and Γ values, we can derive the optical depth of the corona. Using the results from model 3, the optical depth is τ ~ 1.3, i.e., the corona is optically thick. We stress, however, that – as shown in Petrucci et al. (2001) – the kTe values derived from PEXRAV are in general underestimated, while the τ is overestimated with respect to a realistic, anisotropic Comptonization model, and therefore these results must be taken with caution.
We stress that the result obtained for model 3 is, to our best knowledge, the first detection of a high-energy cutoff at such high redshift. The rather low temperature derived from the high-energy cutoff and the high compactness of the corona (ℓ ≳ 10, with ℓ defined as ℓ = LσT/Rmec3, Guilbert et al. 1983) are in agreement with our current understanding of the heating and thermalization mechanisms operating in the corona where large powers are dissipated in the physically compact regions surrounding the SMBH (Fabian et al. 2015).
PG1247 is, therefore, a clear example of how NuSTAR is opening up the possibility of measuring the fundamental parameters of coronal emission (ℓ, τ, and kTe) beyond the local Universe, thanks to sensitive hard X-ray observations. However, a campaign of deep XMM-Newton observations, coupled with simultaneous hard X-ray data from NuSTAR, are required in order to understand which of the models discussed in Sect. 5 best represents the observed X-ray spectrum of PG1247, e.g., distinguishing between cold and relativistic reflection or clearly detecting absorption troughs associated with ionized obscuring gas.
The second considering SDSS 1521+5202 at z = 2.208 with Mi ~ −30.6, Luo et al. (2015).
See, e.g., the CASTLES database of HST gravitational lenses (https://www.cfa.harvard.edu/castles/) observed with comparable exposure times.
This model is based on the Xstar photo-ionization code (Kallman & Bautista 2001), where the ionization parameter is defined as ξ = L/ (n ∗ R2), L is the luminosity of the ionizing source, n the density of the ionized medium, and R the distance between the two.
Acknowledgments
We thank the anonymous referee for constructive comments that have helped us to improve the quality of the paper. G.L. thanks F. Gastaldello for useful insights on NuSTAR background issues, E. Dalessandro for advice about HST data, and O. Shemmer for help with the Swift data. G.L. acknowledges financial support from the CIG grant “eEASY” No. 321913 and from ASI-INAF 2014-045-R.0 and ASI/INAF I/037/12/0–011/13 grants. A.C.F. acknowledges support from ERC grant 340442. FEB acknowledges support from CONICYT-Chile (Basal-CATA PFB-06/2007, FONDECYT Regular 1141218, “EMBIGGEN” Anillo ACT1101), the Ministry of Economy, Development, and Tourism’s Millennium Science Initiative through grant IC120009, awarded to The Millennium Institute of Astrophysics, MAS. W.N.B. and B.L. acknowledges support from Caltech NuSTAR subcontract 44A-1092750. This work made use of data from the NuSTAR mission, a project led by the California Institute of Technology, managed by the Jet Propulsion Laboratory, and funded by NASA. This research also made use of the NuSTAR Data Analysis Software (NuSTARDAS) jointly developed by the ASI Science Data Center (ASDC, Italy) and the California Institute of Technology (USA).
References
- Abazajian, K. N., Adelman-McCarthy, J. K., Agüeros, M. A., et al. 2009, ApJS, 182, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Ai, Y. L., Yuan, W., Zhou, H. Y., Wang, T. G., & Zhang, S. H. 2011, ApJ, 727, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Ballantyne, D. R., McDuffie, J. R., & Rusin, J. S. 2011, ApJ, 734, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Barvainis, R. 1987, ApJ, 320, 537 [NASA ADS] [CrossRef] [Google Scholar]
- Bianchi, S., Guainazzi, M., Matt, G., & Fonseca Bonilla, N. 2007, A&A, 467, L19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boller, T., Freyberg, M. J., Trümper, J., et al. 2016, A&A, 588, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brightman, M., Silverman, J. D., Mainieri, V., et al. 2013, MNRAS, 433, 2485 [NASA ADS] [CrossRef] [Google Scholar]
- Burtscher, L., Meisenheimer, K., Tristram, K. R. W., et al. 2013, A&A, 558, A149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cackett, E. M., Zoghbi, A., Reynolds, C., et al. 2014, MNRAS, 438, 2980 [NASA ADS] [CrossRef] [Google Scholar]
- Chartas, G., Brandt, W. N., & Gallagher, S. C. 2003, ApJ, 595, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Chartas, G., Kochanek, C. S., Dai, X., Poindexter, S., & Garmire, G. 2009, ApJ, 693, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Comastri, A., Fiore, F., Guainazzi, M., et al. 1998, A&A, 333, 31 [NASA ADS] [Google Scholar]
- Dadina M., Vignali, C., Cappi, M., et al. 2016, A&A, submitted [Google Scholar]
- Dauser, T., Garcia, J., Wilms, J., et al. 2013, MNRAS, 430, 1694 [NASA ADS] [CrossRef] [Google Scholar]
- Dauser, T., García, J., Parker, M. L., Fabian, A. C., & Wilms, J. 2014, MNRAS, 444, L100 [NASA ADS] [CrossRef] [Google Scholar]
- Dauser, T., Garcia, J., Walton, D., et al. 2016, A&A, 590, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eddington, A. S. 1916, MNRAS, 77, 16 [NASA ADS] [Google Scholar]
- Fabian, A. C., Zoghbi, A., Wilkins, D., et al. 2012, MNRAS, 419, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C., Lohfink, A., Kara, E., et al. 2015, MNRAS, 451, 4375 [NASA ADS] [CrossRef] [Google Scholar]
- García, J., & Kallman, T. R. 2010, ApJ, 718, 695 [NASA ADS] [CrossRef] [Google Scholar]
- García, J., Dauser, T., Lohfink, A., et al. 2014, ApJ, 782, 76 [NASA ADS] [CrossRef] [Google Scholar]
- George, I. M., & Fabian, A. C. 1991, MNRAS, 249, 352 [NASA ADS] [CrossRef] [Google Scholar]
- Gibson, R. R., Jiang, L., Brandt, W. N., et al. 2009, ApJ, 692, 758 [NASA ADS] [CrossRef] [Google Scholar]
- Guilbert, P. W., Fabian, A. C., & Rees, M. J. 1983, MNRAS, 205, 593 [NASA ADS] [CrossRef] [Google Scholar]
- Harrison, F. A., Craig, W. W., Christensen, F. E., et al. 2013, ApJ, 770, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Iwasawa, K., & Taniguchi, Y. 1993, ApJ, 413, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Iwasawa, K., Mainieri, V., Brusa, M., et al. 2012, A&A, 537, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kallman, T., & Bautista, M. 2001, ApJS, 133, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Keek, L., & Ballantyne, D. R. 2016, MNRAS, 456, 2722 [NASA ADS] [CrossRef] [Google Scholar]
- King, A. 2003, ApJ, 596, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Kishimoto, M., Hönig, S. F., Beckert, T., & Weigelt, G. 2007, A&A, 476, 713 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kormendy, J., & Ho, L. C. 2013, ARA&A, 51, 511 [Google Scholar]
- Lanzuisi, G., Giustini, M., Cappi, M., et al. 2012, A&A, 544, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lanzuisi, G., Ponti, G., Salvato, M., et al. 2014, ApJ, 781, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Laurent, P., & Titarchuk, L. 2011, ApJ, 727, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Luo, B., Brandt, W. N., Hall, P. B., et al. 2015, ApJ, 805, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Lusso, E., Comastri, A., Simmons, B. D., et al. 2012, MNRAS, 425, 623 [NASA ADS] [CrossRef] [Google Scholar]
- Madsen, K. K., Harrison, F. A., Markwardt, C. B., et al. 2015, ApJS, 220, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Magdziarz, P., & Zdziarski, A. A. 1995, MNRAS, 273, 837 [NASA ADS] [CrossRef] [Google Scholar]
- Markowitz, A., Reeves, J. N., & Braito, V. 2006, ApJ, 646, 783 [NASA ADS] [CrossRef] [Google Scholar]
- Matt, G., Perola, G. C., & Piro, L. 1991, A&A, 247, 25 [NASA ADS] [Google Scholar]
- Nandra, K., George, I. M., Turner, T. J., & Fukazawa, Y. 1996, ApJ, 464, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Nandra, K., George, I. M., Mushotzky, R. F., Turner, T. J., & Yaqoob, T. 1997, ApJ, 476, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Nardini, E., Reeves, J. N., Gofford, J., et al. 2015, Science, 347, 860 [Google Scholar]
- Nobuta, K., Akiyama, M., Ueda, Y., et al. 2012, ApJ, 761, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Page, K. L., Reeves, J. N., O’Brien, P. T., Turner, M. J. L., & Worrall, D. M. 2004, MNRAS, 353, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Pancoast, A., Brewer, B. J., Treu, T., et al. 2014, MNRAS, 445, 3073 [NASA ADS] [CrossRef] [Google Scholar]
- Perola, G. C., Piro, L., Altamore, A., et al. 1986, ApJ, 306, 508 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, B. M., Wanders, I., Bertram, R., et al. 1998, ApJ, 501, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Petrucci, P. O., Haardt, F., Maraschi, L., et al. 2001, ApJ, 556, 716 [NASA ADS] [CrossRef] [Google Scholar]
- Pounds, K. A., Reeves, J. N., King, A. R., et al. 2003a, MNRAS, 345, 705 [NASA ADS] [CrossRef] [Google Scholar]
- Pounds, K. A., King, A. R., Page, K. L., & O’Brien, P. T. 2003b, MNRAS, 346, 1025 [NASA ADS] [CrossRef] [Google Scholar]
- Protassov, R., van Dyk, D. A., Connors, A., Kashyap, V. L., & Siemiginowska, A. 2002, ApJ, 571, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Puccetti, S., Comastri, A., Fiore, F., et al. 2014, ApJ, 793, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Reeves, J. N., O’Brien, P. T., & Ward, M. J. 2003, ApJ, 593, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Reeves, J., Done, C., Pounds, K., et al. 2008, MNRAS, 385, L108 [NASA ADS] [CrossRef] [Google Scholar]
- Reis, R. C., & Miller, J. M. 2013, ApJ, 769, L7 [Google Scholar]
- Reis, R. C., Reynolds, M. T., Miller, J. M., & Walton, D. J. 2014, Nature, 507, 207 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reynolds, M. T., Walton, D. J., Miller, J. M., & Reis, R. C. 2014, ApJ, 792, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Ricci, C., Paltani, S., Awaki, H., et al. 2013, A&A, 553, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Risaliti, G., Young, M., & Elvis, M. 2009, ApJ, 700, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Saez, C., & Chartas, G. 2011, ApJ, 737, 91 [Google Scholar]
- Saturni, F. G., Trevese, D., Vagnetti, F., Perna, M., & Dadina, M. 2016, A&A, 587, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schulze, A., & Wisotzki, L. 2010, A&A, 516, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shemmer, O., Brandt, W. N., Netzer, H., Maiolino, R., & Kaspi, S. 2006, ApJ, 646, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Shemmer, O., Brandt, W. N., Netzer, H., Maiolino, R., & Kaspi, S. 2008, ApJ, 682, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Shemmer, O., Brandt, W. N., Paolillo, M., et al. 2014, ApJ, 783, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, Y., Richards, G. T., Strauss, M. A., et al. 2011, ApJS, 194, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Shih, D. C., Iwasawa, K., & Fabian, A. C. 2002, MNRAS, 333, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Shu, X. W., Wang, J. X., Yaqoob, T., Jiang, P., & Zhou, Y. Y. 2012, ApJ, 744, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Steffen, A. T., Strateva, I., Brandt, W. N., et al. 2006, AJ, 131, 2826 [NASA ADS] [CrossRef] [Google Scholar]
- Suh, H., Hasinger, G., Steinhardt, C., Silverman, J. D., & Schramm, M. 2015, ApJ, 815, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Tombesi, F., Cappi, M., Reeves, J. N., et al. 2010, A&A, 521, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tombesi, F., Cappi, M., Reeves, J. N., et al. 2013, MNRAS, 430, 1102 [Google Scholar]
- Trevese, D., Paris, D., Stirpe, G. M., Vagnetti, F., & Zitelli, V. 2007, A&A, 470, 491 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Trevese, D., Perna, M., Vagnetti, F., Saturni, F. G., & Dadina, M. 2014, ApJ, 795, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Uttley, P., Cackett, E. M., Fabian, A. C., Kara, E., & Wilkins, D. R. 2014, A&ARv, 22, 72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vasudevan, R. V., Fabian, A. C., Reynolds, C. S., et al. 2016, MNRAS, 458, 2012 [NASA ADS] [CrossRef] [Google Scholar]
- Vaughan, S., & Edelson, R. 2001, ApJ, 548, 694 [NASA ADS] [CrossRef] [Google Scholar]
- Vestergaard, M. 2003, ApJ, 599, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Vignali, C., Piconcelli, E., Bianchi, S., & Miniutti, G. 2008, MNRAS, 388, 761 [NASA ADS] [CrossRef] [Google Scholar]
- Vignali, C., Iwasawa, K., Comastri, A., et al. 2015, A&A, 583, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Volonteri, M. 2012, Science, 337, 544 [NASA ADS] [CrossRef] [Google Scholar]
- Walton, D. J., Nardini, E., Fabian, A. C., Gallo, L. C., & Reis, R. C. 2013, MNRAS, 428, 2901 [NASA ADS] [CrossRef] [Google Scholar]
- Weymann, R. J., Williams, R. E., Peterson, B. M., & Turnshek, D. A. 1979, ApJ, 234, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Wik, D. R., Hornstrup, A., Molendi, S., et al. 2014, ApJ, 792, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Young, M., Brandt, W. N., Xue, Y. Q., et al. 2012, ApJ, 748, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Zoghbi, A., Fabian, A. C., Reynolds, C. S., & Cackett, E. M. 2012, MNRAS, 422, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Zubovas, K., & King, A. 2012, ApJ, 745, L34 [Google Scholar]
- Zubovas, K., & King, A. 2013, ApJ, 769, 51 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Top: Lbol and MBH for the 1.8 < z < 2.2 SDSS QSO sample (black points and gray contours). Values for PG1247 from SDSS (Shen et al. 2011) and from Trevese et al. (2014) are shown with empty and filled red diamonds, respectively. Dashed green lines mark different λEdd values. Bottom: 4″ × 4″ HST-NICMOS image of PG1247 (filter F160W). The 1′′ scale is shown. |
| In the text | |
 |
Fig. 2 Top: XMM-Newton pn (black) and MOS1+2 (red) spectra of PG1247. The model is a simple power law fitted to the 0.3−2 keV observed band to highlight the residuals above 2 keV due to the emission line complex and the strong reflection component. Bottom: contour plot (at 68, 90, and 99% c.l.) for the emission line energy (rest frame) and normalization. In both panels the dashed lines mark the expected neutral Fe, FeXXV, and FeXXVI Kα emission line energies. |
| In the text | |
 |
Fig. 3 Top: 3−79 keV background-subtracted images of the NuSTAR observation of PG1247 (FPMA left and FPMB right). Contamination from the Coma cluster is visible in the upper left corner of FPMA. Bottom: 15−30 keV NuSTAR images, not background subtracted. In both panels the 1′ scale is shown, and the source and background extraction regions are shown with continuous and dashed lines, respectively. North is up and east is left. |
| In the text | |
 |
Fig. 4 NuSTAR FPMA and FPMB data (blue and cyan points, respectively) fitted with a simple power law (top panel). The spectra have been further rebinned with respect to the S/N = 3 level to highlight the curvature of the spectrum in the residuals (central panel). The residuals with respect to the fit performed with the PEXRAV model are shown in the lower panel. |
| In the text | |
 |
Fig. 5 Best-fit unfolded models for models 1, 2, 3, and 4, from top left to bottom right. The continuous curves represents the best fit to the XMM-Newton data (in red) and NuSTAR data (in blue). The dotted curves represent the primary power law, while the dashed curves represent the component reproducing the hump (either reflection or absorption). In the top right panel the magenta curve represents the constant reflection component underlying both XMM-Newton and NuSTAR data, modeled with PEXRAV. |
| In the text | |
 |
Fig. 6 Panel a) unfolded data and model for the best fit obtained with model 1. Panels b)−e) delta χ for model 1, 2, 3, and 4, respectively. In all panels XMM-Newton pn data are in black, MOS1+2 in red, NuSTAR module A in green, and B in blue. |
| In the text | |
 |
Fig. 7 Rest-frame 0.2−10 keV light-curve of PG1247 since its first detection with ROSAT in 1993 (black filled square). The empty square shows the ROSAT data reanalyzed in Boller et al. (2016). The black triangle represents the ASCA measurement (1995). The red diamond represents the XMM-Newton measurement of 2003. The gray points represent the monitoring performed with Swift between 2007 and 2013 (Shemmer et al. 2014), and the magenta point shows the NuSTAR measurement in 2014. |
| In the text | |
 |
Fig. 8 Left: contour plot of the column density vs. covering fraction for model 3. Right: rest-frame residuals in the Fe Kα line region, after fitting with a simple power law. The gray dashed lines mark the expected neutral Fe, FeXXV, and FeXXVI Kα emission line energies. Symbols as in Fig. 6. |
| In the text | |
 |
Fig. 9 Left: contour plot of the disk inclination angle vs. BH spin parameter for model 4. Right: contour plot of the corona height h vs. spin parameter for model 4. |
| In the text | |
 |
Fig. 10 Confidence contours (at 68, 90, and 99% c.l.) of Γ vs. Ecut (rest frame) parameters for model 1 (left), model 2 (center), and model 3 (right). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


