EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 590 (June 2016) A&A, 590 (2016) A128 Full HTML
Free Access
Issue
A&A
Volume 590, June 2016
Article Number A128
Number of page(s) 26
Section Atomic, molecular, and nuclear data
DOI https://doi.org/10.1051/0004-6361/201628131
Published online 27 May 2016

© ESO, 2016

1. Introduction

Reliably determining the abundance of trans-iron elements in hot white dwarf (WD) stars, e.g., G191−B2B and RE 0503−289 (WD 0501+527 and WD 0501−289, respectively, McCook & Sion 1999a,b), recently became possible with the calculation of transition probabilities for highly ionized Zn (atomic number Z = 30), Ga (31), Ge (32), Mo (42), and Ba (56) (Rauch et al. 2014a, 2015, 2012, 2016, 2014b). These analyses were initiated by the discovery of lines of Ga, Ge, As (33), Se (34), Kr (36), Mo, Sn (50), Te (52), I (53), and Xe (54) in the Far Ultraviolet Spectroscopic Explorer (FUSE) spectrum of the hydrogen-deficient DO-type WD RE 0503−289 by Werner et al. (2012b). Owing to the lack of atomic data at that time, they could only measure the Kr and Xe abundances (−4.3 ± 0.5 and −4.2 ± 0.6 in logarithmic mass fractions, respectively). We calculated new Kr iv–vii transition probabilities to construct more detailed model atoms that are used in our non-local thermodynamic equilibrium (NLTE) model-atmosphere calculations to improve the Kr abundance determination.

In Sects. 2 and 3, we briefly describe the available observations, our model-atmosphere code, and the atomic data. Details of the transition-probability calculations and a comparison of the results with literature values are given in Sect. 4. Based on our state-of-the-art NLTE models, we start our spectral analysis with a verification of the previous determination of the effective temperature and surface gravity by Dreizler & Werner (1996, Teff = 70000 K, log  (g/ cm s-2) = 7.5 in Sect. 5. An improved Kr abundance analysis for RE 0503−289 is then presented in Sect. 6. The stellar mass and the distance of RE 0503−289 are revisited in Sect. 7. At the end (Sect. 8), we take a look at the velocity field of the observed interstellar line absorption and compare it with that of the nearby hydrogen-rich, DA-type WD RE 0457−281 (WD 0455−282, mV = 13.90, McCook & Sion 1999a,b; Gianninas et al. 2011). We summarize and conclude in Sect. 9.

2. Observations

We analyzed ultraviolet (UV) FUSE (described in detail by Werner et al. 2012b) and Hubble Space Telescope/Space Telescope Imaging Spectrograph (HST/STIS) observations (1144 Å <λ< 3073 Å) of RE 0503−289, that were performed on 2014-08-14. The latter spectrum was co-added from two observations with grating E140M (exposure times 2493 s and 3001 s, 1144 Å−1709 Å, resolving power R ≈ 45 800), and two observations with grating E230M (1338 s, 1690 Å−2366 Å and 1338 s, 2277 Å−3073 Å, R ≈ 30 000). These STIS observations are retrievable from the Barbara A. Mikulski Archive for Space Telescopes (MAST).

In addition to the UV observations, we used optical spectra that were obtained at the European Southern Observatory (ESO) and the Calar Alto (CA) observatory. In the framework of the Supernova Ia Progenitor Survey project (SPY, Napiwotzki et al. 2001, 2003), observations were performed on 2000-09-09 and 2001-04-08 with the Ultraviolet and Visual Echelle Spectrograph (UVES) attached to the Very Large Telescope (VLT) located at ESO. The co-added spectra cover the wavelength intervals [3290 Å, 4524 Å], [4604 Å, 5609 Å], and [5673 Å, 6641 Å] with a resolution of about 0.2 Å. Two spectra [4094 Å, 4994 Å] and [5680 Å, 6776 Å] were taken with the Cassegrain TWIN Spectrograph that was attached to the 3.5 m telescope at the CA observatory. Their resolution is about 3 Å (the same spectra were used by Dreizler & Werner 1996).

For RE 0457−281, we used FUSE spectra (ObsIds P1041101000, P1041102000, and P1041103000 from 2000-02-03, 2000-02-04, and 2000-02-07, respectively, with a total observation time of 47 465 s) that were obtained with the medium-resolution (MDRS) aperture. In addition, we used an IUE (International Ultraviolet Explorer) spectrum ([1153 Å, 1947 Å]) that was co-added from four observations that were obtained in high-resolution (R ≈ 10 000) mode with the large aperture (Data Ids SWP46302, SWP56213, SWP56262, and SWP56267 from 1992-11-19, 1995-11-18, 1995-12-02, and 1995-12-04, respectively, with a total exposure time of 168 360 s, Holberg et al. 1998). This is available via the MAST High-Level Science Products.

If not otherwise explicitly mentioned, all synthetic spectra shown in this paper, which are compared with an observation, are convolved with a Gaussian to model the respective resolving power. The observed spectra are shifted to rest wavelengths according to our measurement of the radial velocity vrad = 25.5 km s-1.

3. Model atmospheres and atomic data

We calculated plane-parallel, chemically homogeneous model-atmospheres in hydrostatic and radiative equilibrium with our Tübingen NLTE Model Atmosphere Package (TMAP1, Werner et al. 2003, 2012a). Model atoms were provided by the Tübingen Model Atom Database (TMAD2, Rauch & Deetjen 2003). TMAD was constructed as part of the Tübingen contribution to the German Astrophysical Virtual Observatory (GAVO3).

Our Kr model atom was designed with a statistical method (similar to Rauch et al. 2015) by calculating the so-called super levels and super lines with our Iron Opacity and Interface (IrOnIc4, Rauch & Deetjen 2003). Using our approach, we neglected spin system and parity of the individual levels in the calculation of the super levels. This is justified because, in the atmosphere of RE 0503−289, the deviation of the levels’ occupation numbers from LTE is small in the line-forming region of the atmosphere. The detailed fits of our theoretical line profiles to the observations (Sect. 6) do no give any hint of inconsistencies. To process our new Kr data, we transferred it into Kurucz’s format5, which is readable by IrOnIc. The statistics of our Kr model atom are summarized in Table 1.

Table 1

Statistics of Kr iv–vii atomic levels and line transitions from Tables A.9–A.12, respectively.

For the calculation of cross-sections, we followed Rauch & Deetjen (2003) for the transition types

  • collisional bound-bound: van Regemorter (1962) formula for known f-values and an approximate formula for unknown f-values,

  • radiative bound-bound: approximate formula by Cowley (1970, 1971) for the quadratic Stark effect, and

  • collisional and radiative bound-free: Seaton (1962) formula with hydrogen-like threshold cross-sections.

For Kr and all other species, level dissolution (pressure ionization) following Hummer & Mihalas (1988) and Hubeny et al. (1994) is accounted for. Stark broadening tables of Barnard et al. (1974) are used for He iλ 4471 Å and of Schoening & Butler (1989) for He ii lines.

4. Oscillator-strength calculations in krypton ions

New oscillator strengths were computed for transitions in Kr iv–vii ions in the present work. The method used was the same as the one considered in our previous studies that focused on Zn, Ga, Ge, Mo, and Ba ions (Rauch et al. 2014a, 2015, 2012, 2016, 2014b), namely the Relativistic Hartree-Fock (HFR) method (Cowan 1981) that was modified to take core-polarization effects into account (HFR+CPOL), as described by Quinet et al. (1999, 2002). In each Kr ion, the same core-polarization parameters were used, i.e., a dipole polarizability and a cut-off radius rc = 0.55 a0. The former value, taken from Johnson et al. (1983), corresponds to a Kr8+ closed-shell ionic core of the type 1s22s22p63s23p63d10, while the latter value was chosen as the mean value of ⟨r⟩ for the outermost core orbital (3d), as calculated by the HFR approach. Intravalence correlations were considered by explicitly including the following configurations in the physical models: Kr iv   4s24p3+ 4s24p25p + 4s24p26p + 4s24p24f + 4s24p25f + 4s24p26f + 4s4p34d + 4s4p35d + 4s4p36d + 4s4p35s + 4s4p36s + 4s24p4d2 + 4s24p4f2 + 4p5 + 4p44f (odd parity) and 4s4p4 + 4s24p24d + 4s24p25d + 4s24p26d + 4s24p25s + 4s24p26s + 4s4p34f+ 4s4p35f+ 4s4p36f+ 4s4p35p+ 4s4p36p+ 4p44d + 4p45s (even parity), Kr v   4s24p2 + 4s24p5p + 4s24p6p + 4s24p4f + 4s24p5f + 4s24p6f + 4s4p24d + 4s4p25d + 4s4p26d + 4s4p25s + 4s4p26s + 4s24d2 + 4s24f2 + 4p4 + 4p34f (even parity) and 4s4p3 + 4s24p4d + 4s24p5d + 4s24p6d + 4s24p5s + 4s24p6s + 4s4p24f + 4s4p25f + 4s4p26f + 4s4p25p + 4s4p26p + 4p34d + 4p35s (odd parity), Kr vi   4s24p + 4s25p + 4s26p + 4s24f + 4s25f + 4s26f + 4s4p4d + 4s4p5d + 4s4p6d + 4s4p5s + 4s4p6s + 4p3 + 4p24f + 4s4d4f + 4p4d2 + 4d24f + 4p4f2 (odd parity) and 4s4p2 + 4s24d + 4s25d + 4s26d + 4s25s + 4s26s + 4s4p5p + 4s4p6p + 4s4p4f + 4s4p5f + 4s4p6f + 4p24d + 4p25s + 4s4d5s + 4s4d2 + 4s4f2 (even parity), Kr vii   4s2 + 4p2 + 4d2 + 4f2 + 5s2 + 4s4d + 4s5d + 4s6d + 4s5s + 4s6s + 4p4f + 4p5f + 4d5s + 4p5p (even parity) and 4s4p + 4s5p + 4s6p + 4s4f + 4s5f + 4s6f + 4p5s + 4p4d + 4p5d + 4d4f (odd parity).

The HFR+CPOL method was then combined with a semi-empirical optimization of the radial parameters to minimize the discrepancies between calculated and experimental energy levels. More precisely, the energy levels reported by Saloman (2007) were used in Kr iv to adjust the radial parameters corresponding to the 4p3, 4p25p, 4s4p4, 4p24d, 4p25d, 4p25s, and 4p26s configurations. In Kr v, the experimental level values taken from Saloman (2007) and Rezende et al. (2010) were included in the adjustment of some parameters in the 4p2, 4p5p, 4s4p24d, 4p4, 4s4p3, 4p4d, 4p5d, 4p5s, and 4p6s configurations. In the case of Kr vi, the energy levels from Saloman (2007) and Farias et al. (2011) enabled us to optimize the radial parameters by describing the 4p, 5p, 4s4p4d, 4p3, 4s4p2, 4s24d, 4s25s, 4s4p4f, 4s4p5p, and 4p24d configurations. Finally, the energy levels measured by Raineri et al. (2014) were used to fit the parameters of the 4s2, 4p2, 4s4d, 4s5d, 4s6d, 4s5s, 4s6s, 4p4f, 4s4p, 4s5p, 4s6p, 4s4f, 4s5f, 4s6f, 4p5s, and 4p4d configurations in Kr vii.

The numerical values of the parameters adopted in the present calculations are reported in Tables A.1–A.4, while the computed energies for Kr iv–vii are compared with available experimental values in Tables A.5–A.8, respectively. Tables A.9–A.12 give the computed oscillator strengths (log gf) and transition probabilities (gA, in s-1) for Kr iv–vii, respectively, and the numerical values (in cm-1) of lower and upper energy levels, together with the corresponding wavelengths (in Å). The cancellation factor, CF, as defined by Cowan (1981) is also given in the last column of each table. For a specific transition, a very small value of this parameter (typically <0.05) indicates strong cancellation effects in the calculation of the line strength. In this case, the corresponding oscillator strength and transition probability could be affected by larger uncertainties and, as a consequence, should be considered with care.

Tables A.9–A.12 are provided in VO6-compliant format via the registered7 Tübingen Oscillator Strengths Service (TOSS8, Rauch et al. 2016) that has recently been developed by GAVO.

For Kr iv–vii, oscillator strengths were previously published by several authors. In the following, we compare our new data to theirs. Figure 1 illustrates this comparison.

thumbnail Fig. 1

Comparison of our weighted oscillator strengths for Kr iv–vii (from top to bottom) to those of Bredice et al. (2000), Raineri et al. (2012), Pagan et al. (1996), and Liang et al. (2013), respectively. Left panel: comparison of weighted oscillator strengths. Right panel: ratio of weighted oscillator strengths over wavelength. The wavelength ranges of our FUSE and HST/STIS spectra are marked. The larger, red symbols refer to the lines identified in RE 0503−289 (see Figs. 5 and 8).

Bredice et al. (2000) calculated weighted oscillator strengths for 471 spectral lines of Kr iv involving the 4s24p3, 4s4p4, 4s24p25p, and 4s24p2(5s + 6s + 4d + 5d) configurations within the wavelength interval [501.50 Å, 4703.85 Å]. Of these lines, 320 agree within 0.1 Å to lines reported in Table A.9. We selected them to compare their log gf values to ours in Fig.1. As seen from this figure, even if both sets of results agree for many lines, a large scatter is also observed for many other lines. This is obviously due to the very limited multiconfiguration Hartree-Fock model (including only two odd- and seven even-parity configurations) that was considered by Bredice et al. (2000).

Raineri et al. (2012) published transition probabilities for 313 lines of Kr v ([294.27 Å, 3614.10 Å]). They were calculated with Cowan’s package (Cowan 1981), i.e., the Hartree-Fock method with relativistic corrections using energy parameters from least-squares and dipole-reduced matrix from a core polarization calculation. A large set of 4s24p2, 4p5p, 4p4, 4s4p24d, 4p4f, 4s4p25s, 4s24d2, 4s4p4d5p, 4p34f, 4s4p4d4f, 4s24f2, and 4s4d3 even and 4s4p3, 4p4d, 4p5s, 4p5d, 4p6s, 4p5g, 4p6d, 4s4p25p, 4s4p24f, 4p34d, 4s4p26p, 4s4p4d2, 4p35s, 4s24d4f, 4s24f5s, 4p35d, 4s24f5d, 4s4d25p, and 4s4d24f odd configurations was considered.

Table 2

Photospheric abundances of RE 0503−289.

We selected 183 of these lines (by wavelength agreement within 0.1 Å to lines in Table A.10) and compared their log gf values to ours (Fig. 1). Although a good agreement between the two sets of data is observed for many lines, a large scatter is also obtained for a number of transitions, in particular for those corresponding to weak oscillator strengths, i.e., log gf< −2. This is mainly due to the rather large cancellation effects that appear in the calculations of these types of transition rates in both works. Moreover, it is worth noting that Raineri et al. (2012) modified only their electric dipole matrix elements to take core-polarization effects into account while, in our work, all the radial wave functions were also modified by a model potential, including one- and two-body core-polarization contributions, together with a core-penetration correction (see, e.g., Quinet et al. 2002). This could also explain some of the differences between the two sets of results.

Pagan et al. (1996) calculated 138 weighted Kr vi oscillator strengths ([331.65 Å, 2051.72 Å]) in a multiconfigurational HFR approach considering 4s24p, 4p3, 4s25p, 4s4p4d, 4s24f, 4s4p5s, 4s26p, 4s4d4f, 4p24f, 4p4d2, and 4d24f configurations for odd parity and 4s4p2, 4s24d, 4s25s, 4s25d, 4s4p4f, 4s4p5s, 4p24d, and 4s4d2 for even parity. Analogously to Kr v, we compared the log gf values of 115 selected Kr vi lines with our data (Fig.1). Although both sets of data are in good agreement, we note that our oscillator strengths are generally smaller than those obtained by Pagan et al. (1996). This is essentially due to the much more extended multiconfiguration expansions and the core-polarization effects that we include in our calculations.

Liang et al. (2013) presented oscillator strengths for 90 lines ([201.05 Å, 920.98 Å]) for Kr vii. For their calculations with the AUTOSTRUCTURE code (Badnell 2011), they only use nine configurations, i.e., 4s2, 4p2, 4s4d, 4s5s, 4s5d, and 4s4p, 4s4f, 4p4d, 4s5p for the even and odd parities, respectively. In particular, they omit some configurations, such as 4d2 and 4d4f which, according to our calculations, appeared to have non-negligible interactions with 4s2, 4p2 and 4s4p, 4s4f, 4p4d, respectively. The effect of this rather limited model is illustrated in Fig. 1, where our log gf values, obtained with an extended configuration interaction approach, are systematically smaller than those reported by Liang et al. (2013).

5. Effective temperature and surface gravity

Dreizler & Werner (1996) analyzed the optical TWIN spectra (Sect. 2) with NLTE model atmospheres that considered opacities of H, He, C, N, O, and Si. They derived Teff = 70000 ± 5000 K and log (g/ cm/s2) = 7.5 ± 0.3. In their spectral analysis based on H+He composed LTE model atmospheres, Vennes et al. (1998) determined Teff = 68600 ± 1800 K and log g = 7.20 ± 0.07. Dreizler (1999) improved the metal abundance analysis of C, N, O, and Ni based on HST/GHRS (Goddard High-Resolution Spectrograph) observations and used the previously determined Teff = 70000 K and log g = 7.5. The same did Werner et al. (2012b) for their Kr and Xe abundance analysis. In our latest models, much more species (Table 2) and, thus, a higher metal opacity is considered. Therefore, we start here with a new assessment of Teff and log g.

thumbnail Fig. 2

Section of the HST/STIS spectrum, compared with models with different log g of 7.0 (thin, green, dashed), 7.5 (thick, red), and 8.0 (thin, blue, dashed) and Teff = 70000 K. The synthetic spectra are normalized to match the flux of the observation at 2800 Å, respectively. All spectra are convolved with Gaussians (full width at half maximum of 1 Å) for clarity. Identified lines are indicated. “is” denotes interstellar origin.

The decrements of spectral series are very sensitive indicators for log g (e.g., Rauch et al. 1998; Ziegler et al. 2012). Figure 2 shows a comparison of theoretical line profiles of the He ii Fowler series (principal quantum numbers n − n′ with n = 3 and n′ ≥ 4) that are located in our HST/STIS spectrum. The central depressions of He ii 3− [ 5,...,13 ] are well matched at log g = 7.5, while the decrement is much too strong at log g = 8.0, and much too weak at log g = 7.0. We therefore verify log g = 7.5, which was the result of Dreizler & Werner (1996), and improved the error limit to ± 0.1 dex.

thumbnail Fig. 3

Sections of the HST/STIS spectrum compared with three log g = 7.5 models with different Teff of 66 000 K (thin, blue), 70 000 K (thick, red), and 74 000 K (thin, green). The synthetic spectra are normalized to match the observed flux at 1335 Å.

Figure 4 demonstrates that the line wings of the He ii n = 2 and n′ ≥ 3n = 4 and n′ ≥ 5 (Pickering) series are well in agreement with the observation at log g = 7.5. A different log g cannot be compensated for by adapted interstellar H i densities because this has a strong impact on the inner line wings (Sect. 6). The error range for these densities is below 20%. Our optical spectra corroborate the log g determination. Figure 4 shows the comparison of our models to the observations. He iiλ 6560 Å is too shallow in all our models and does not match the TWIN observation. The reason is still unknown. The UVES spectra show a slightly better fit of this line, which may be a hint for some data-reduction uncertainty in the TWIN and/or UVES spectra. To make a comparison with the FUSE observation, we selected those He ii n = 2−n′ lines that are not contaminated by interstellar H i line absorption. Their observed line profiles and the series’ decrement are well reproduced at log g = 7.5. The insufficient blaze correction of the HST/STIS spectrum only allows for an evaluation of the inner line wings of He iiλ 1640.42 Å (n = 2−3). He iiλ 1215.12 Å (n = 2−4) is shown in Fig. 13.

Dreizler & Werner (1996) used the O iv/O v ionization equilibrium as an indicator for Teff. They found a simultaneous match of theoretical line profiles of O ivλλ 1338.6,1343.0,1343.5 Å (2p22P–2p32Do) and O vλ 1371.3 Å (2p 1Po–2p21D) to a high-resolution IUE observation. In Fig. 3, we show the same lines compared to our much better HST/STIS observation. O vλ 1371.3 Å appears much more sensitive to Teff, compared to the O iv lines, and Teff = 70000 K is verified within an error range of ±2000 K.

We adopt Teff = 70000 ± 2000 K and log g = 7.5 ± 0.1. Many additional ionization equilibria, e.g., of He i–ii (Fig. 4), C iii–iv (Fig. 2), O iv–v (Dreizler & Werner 1996, and this paper, Fig. 3), Zn iv–v (Rauch et al. 2014a), Ga iv–v (Rauch et al. 2015), Ge iv–vi (Rauch et al. 2012), Kr v–vii (Werner et al. 2012b, and this paper), Mo v–vi (Rauch et al. 2016), Xe vi–vii (Werner et al. 2012b), and Ba vi–vii (Rauch et al. 2014b) are well matched at these values.

thumbnail Fig. 4

Three models (Teff = 70000 K) with log g = 7.0 (green, dashed), 7.5 (red), and 8.0 (blue, dashed) compared to FUSE (left panel), UVES (middle), and TWIN (right) observations. The dashed, horizontal lines indicate the location of the local continuum.

6. Line identification and abundance analysis

Table 3

Comparison of log gf values of Kr lines used in the abundance analysis (Figs. 5, 8).

We replaced our previously used Kr model atom and recalculated our latest model atmosphere (see Rauch et al. 2016). Figure 5 shows that, in general, the wavelengths of the old and the new data are in good agreement, while the line strengths calculated with the new data are much smaller. There are three reasons for this deviation. First, the Kr iv–vii model ions are much more complete, e.g., for Kr vi and Kr vii, Werner et al. (2012b) constructed model ions with 46 and 14 atomic levels that were combined with 140 and 2 line transitions with known oscillator strengths, respectively. These numbers were increased to 69 and 70 levels with 843 and 743 line transitions, respectively (Table 1). Second, the new oscillator strengths of the lines that were used in the Kr abundance analysis are smaller in general (Table 3). Third (with minor impact), the chemical composition of the model atmospheres is different and the C, N, and O abundances were fine-tuned, i.e., the background opacity was increased and, thus, the calculated atmospheric structure is different.

In their Kr abundance analysis, Werner et al. (2012b) use He+C+N+O+Kr+Xe models and adopt the C, N, and O abundances of Dreizler (1999). Our models also consider the opacities of Si, P, S, Ca, Sc, Ti, V, Cr, Mn, Fe, Co, Ni, Zn, Ga, Ge, As, Mo, Sn, and Ba. The C and O abundances were increased to better reproduce their observed lines. The abundances are compared in Table 2. Figure 6 shows the temperature structures of the respective models. Deviations are obvious in the outer atmosphere, but also in the line-forming region (−4 ≲ log  m ≲ + 0.5, m is the column mass, measured from the outer boundary of our model atmospheres).

thumbnail Fig. 5

Kr vi lines and one Kr vii line (bottom right) identified by Werner et al. (2012b) in the observed FUSE spectrum of RE 0503−289. Three synthetic spectra are overplotted. Thin, blue: the genuine spectrum of Werner et al. (2012b, Teff = 70000 K, classical Kr model atom with log Kr = −4.3. Thick red (Teff = 70000 K): our new Kr model atom with log Kr = −4.3. Dashed, red (Teff = 70000 K): our new Kr model atom with log Kr = −3.3. Kr lines are indicated with their wavelengths from Tables A.11 and A.12, and other lines by their ion’s name. “is” denotes interstellar origin.

thumbnail Fig. 6

Temperature structure of our model (thick, red) compared with the model of Werner et al. (2012b, thin, blue).

Due to the higher background opacity in our models, the calculated Kr lines are weaker compared with Werner et al. (2012b, log Kr = −4.3 ± 0.5. To match the observation, we have to increase the previously determined Kr mass fraction (log Kr = −4.3 ± 0.5, Werner et al. 2012b) by a factor of 10 to 5.1 × 10-4 (log Kr = −3.3 ± 0.3). Our given error is estimated, considering the error propagation that is due to the uncertainties of Teff, log g and the background opacity (Sect. 5).

Figure 7 shows that Kr v–vii are the dominant ions in the line-forming region. We newly identified Kr viλ 1052.067 Å (log gf = −0.55) in the FUSE observation and for the first time lines of Kr v, namely λλ 1384.611, 1387.961, 1392.594, 1393.603, 1515.611, 1566.073, 1583.456, 1589.269, 1591.875, 1764.478 Å (−0.59, −0.65, −0.67, −0.17, 0.40, 0.30, 0.25, 0.68, 0.49, −0.16, respectively) in the HST/STIS observation (Fig. 8). These lines are in agreement with the observation, while Kr vλλ 1583.456,1591.875,1764.478 Å are uncertain. Many more weak Kr v–vii lines are exhibited in the synthetic spectrum but they fade in the noise of the available observed UV and optical spectra. The Kr v–vii ionization equilibrium is well matched. Since ionization equilibria are sensitive indicators of the effective temperature, our value of Teff = 70000 K (Sect. 5) is corroborated.

thumbnail Fig. 7

Kr ionization fractions in our model for RE 0503−289.

With our new Kr oscillator strengths and also at the higher Kr abundance, a simultaneous fit of all 26 identified lines was achieved. For example, Kr vi λλ 944.046, 965.093, 1011.133, 1015.765, 1052.964 Å were much too weak before in our models but now reproduce the observation (Fig. 5).

thumbnail Fig. 8

Newly identified Kr v lines and a Kr vi (top, right) line in the FUSE and HST/STIS observations. The model is calculated with log Kr = −3.3.

In the optical wavelength range, Kr vλ 3579.739 Å (log gf = −1.15, air wavelength 3578.717 Å) is the strongest line in our model but very weak (central depression of about 1 % of the local continuum flux) and not detectable in the available observation.

Ba vii lines were newly identified in the observed FUSE spectrum during the search for Kr lines. These are one blend at Ba viiλλ 924.892,924.898 Å (log gf = −2.42 and −2.06, respectively, Fig. 12), and Ba viiλ 1143.317 Å (−2.54). Rauch et al. (2014b) previously discovered Ba viiλ 943.102 Å (−1.77) and Ba viiλ 993.411 Å (−1.57).

7. Mass, post-AGB age, and distance

We determined from a comparison of the evolutionary tracks of hydrogen-deficient post-AGB stars (Fig. 9). From these tracks, we calculated a post-AGB age of about 6.8 ± × 105 yr. For RE 0457−281, we measured 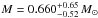and a post-AGB age of 1.14 ± 0.06 × 106 yr by comparing them with cooling sequences for old hydrogen-rich WDs (Fig. 10).

thumbnail Fig. 9

Location of RE 0503−289 in the log Teff–log g diagram (the ellipse indicates the error range) compared with evolutionary tracks for post-AGB stars that experienced a very late thermal pulse (Althaus et al. 2009). These are labeled with the respective stellar masses (in M⊙). Positions of hydrogen-deficient PG 1159-type stars and DO-type WDs are indicated by squares and circles, respectively.

thumbnail Fig. 10

Location of RE 0457−281 (Teff = 55875−60170 K, log g = 7.78−8.07, Marsh et al. 1997, the ellipse indicates the error range) in the log Teff–log g diagram compared with evolutionary tracks for DA-type WDs (Renedo et al. 2010) labeled with the respective stellar masses (in M⊙).

We used the flux calibration9 of Heber et al. (1984) to calculate the distance using mV0 = mV − RVEB − V, and the Eddington flux Hν = 1.018 ± 0.002 × 10-3 erg/cm2/ s/Hz at λeff = 5454 Å of our final model atmosphere. We used EB − V = 0.015 ± 0.002, RV = 3.1,  M⊙, and mV = 13.58 ± 0.01 (Faedi et al. 2011). We derive  pc. The height below the Galactic plane10 is 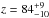 pc. This distance is smaller than the value of Vennes et al. (1998, 190 pc).

8. Interstellar line absorption

To measure the interstellar reddening in the line of sight (LOS), we first normalized our synthetic spectrum (Teff = 70000 K, log g = 7.5) to match the measured mH = 14.77 (Cutri et al. 2003). Then, interstellar reddening with EB − V = 0.015 ± 0.002 had to be applied to reproduce the observed FUV continuum flux, using the reddening law of Fitzpatrick (1999) with the standard Rv = 3.1. Our EB − V value is in good agreement with measurements of Schlegel et al. (1998, evaluating images from the Diffuse Infrared Background Experiment on board of the Cosmic Background Explorer satellite, COBE/DIRBE, and the Infrared Astronomy Satellite Sky Survey Atlas, IRAS/ISSA) and Schlafly & Finkbeiner (2011, based on Sloan Digital Sky Survey, SDSS, stellar spectra). They publish EB − V = 0.0160 and EB − V = 0.0138, respectively. The errors can be estimated from the mean values of EB − V within a 5° circle around RE 0503−289. These are and 0.0134 ± 0.0006, respectively. The dust distribution around RE 0503−289 and RE 0457−281 is illustrated by Fig. 11. While RE 0503−289 is apparently located in the middle of a voided area, RE 0457−281 lies at the rim of stronger emission, with a higher EB − V = 0.0201 (, Schlafly & Finkbeiner 2011).

thumbnail Fig. 11

Locations (J2000) of RE 0503−289, RE 0457−281, and WD 0458−303 (marked by green encircled red + signs) in a 10° × 10°100 μ dust map from http://irsa.ipac.caltech.edu/applications/DUST.

Table 4

Ionic column densities (in cm-2) and radial velocities (in km s-1) in interstellar clouds in the line of sight toward RE 0503−289.

The DAO-type WD 0458−303 (MCT 0458−3020, mB = 16.3, Teff = 91010 ± 3156 K, log g = 7.09 ± 0.10, M = 0.53 ± 0.02 M⊙, d = 928 pc, Demers et al. 1986; McCook & Sion 1999a,b; Gianninas et al. 2010, 2011) also lies close to RE 0503−289 (angular distance 1°53, Fig. 11) in an area with obviously less 100 μ emission and a lower EB − V = 0.0082 (, Schlafly & Finkbeiner 2011).

While RE 0503−289 and RE 0457−281 were newly identified in the ROSAT/WFC (Röntgensatellit/Wide Field Camera) extreme-ultraviolet (EUV) bright source catalogue (Pounds et al. 1993a; Pounds & et al. 1993b) and were later matched with their optical counterparts (Mason et al. 1995, 1996), the much hotter WD 0458−303 has no significant EUV flux. Therefore, an investigation, based on UV spectroscopy, of the ISM line absorption in the LOS toward this much more distant star is highly desirable. So far, only Galaxy Evolution Explorer (GALEX11) near and far UV imaging is available in MAST. Exploiting the GALEX GR6 and GR7 data releases, GalexView12 provides mFUV = 14.35 ± 0.01, mNUV = 15.08 ± 0.01 and EB − V = 0.0096 for WD 0458−303.

Figure 12 shows a section of the FUSE observation compared with our spectrum that was calculated with the new Kr model atom and log Kr = −3.3. Kr viiλ 918.444 Å and Kr viλλ 927.334,931.368 Å are prominent in the observed spectrum and are well reproduced, while Kr vλ 916.734 Å and Kr viλ 919.938 Å are weak in our model and fade in the noise of the observation.

thumbnail Fig. 12

Section of the FUSE observation (shifted to rest wavelengths) compared with our final synthetic spectrum (Teff = 70000 K, log g = 7.5). Prominent stellar and interstellar (is, blue) lines are indicated.

The program OWENS was used to model the line absorption by the interstellar medium (ISM). OWENS is able to consider individual ISM clouds with different radial and turbulent velocities, temperatures, column densities, and chemical compositions. Voigt profiles are fitted to the observation using a χ2 minimization. More details are given by, for example, Hébrard et al. (2002) or Hébrard & Moos (2003). To model the interstellar absorption of neutral hydrogen, we first considered two clouds with column densities of NH i = 1.2 × 1018 cm-2 and NH i = 9.3 × 1015 cm-2, and radial velocities of 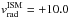and −39.3 km s-1, respectively. These column densities are smaller than the expected value of 9.2 ± 0.3 × 1018 cm-2 that was calculated from NH/EB − V = 6.12 ± 0.20 × 1021 cm-2 mag-1 (Gudennavar et al. 2012, with NH = NH i + 2N(H2)). In addition, we derive and 64.8 ± 4.2 km s-1 for the two clouds.

Vennes et al. (1994) analyzed Extreme Ultraviolet Explorer (EUVE) photometry data and measured column densities of log (NH i/ cm-2) = 17.75–18.00 and 17.80–17.90 in the LOS toward RE 0503−289 and the nearby (spatially separated by ) RE 0457−281. Since Hoare et al. (1993) and Vallerga et al. (1993) determined log (NH i/ cm-2) = 18.00–18.18 for β and ϵ CMa (located in about the same direction, at angular distances of 21° and 31°, respectively, but at larger distances of d = 206 pc and d = 188 pc, respectively), Vennes et al. (1994) suggested that the local cloud, agglomerated with a few parsecs from the Sun, is the main ISM structure along the LOS toward these stars. Vennes et al. (1998) used ORFEUS/BEFS13 observations and measured , which is within error limits in agreement with the mean velocity of our two clouds. Dupuis et al. (1995) investigated interstellar column densities based on EUVE spectra. For RE 0457−281, they found d = 90 pc and log (NH i/ cm-2) = 18.04–18.12. Vennes et al. (1996) measured . Pauli et al. (2006) investigated on the 3D kinematics of WDs from the SPY project and determined and a distance of d = 115.9 ± 14 pc.

The interstellar N iiλ 915.6 Å also exhibits a double feature (Fig. 12). We considered this line with column densities of NN ii = 7.5 × 1013 cm-2 at + 11.0 km s-1 and NN ii = 2.5 × 1013 cm-2 at −39.5 km s-1. The HST/STIS observation is used to verify our solution with two ISM clouds (Fig. 13). While Si iiiλ 1206.5 Å is not sufficiently well reproduced with NS iii = 1.8 × 1013 cm-2 at + 18.0 km s-1 and NS iii = 1.9 × 1012 cm-2 at −40.5 km s-1 (insert A), a multi-cloud solution for the ISM absorption could improve the agreement (main spectra). The assumed clouds’ column densities and radial velocities are summarized in Table 4.

thumbnail Fig. 13

Section of the STIS observation around L α, compared with our final synthetic spectrum (thick, red, Teff = 70000 K, log g = 7.5). The dashed, blue lines are the pure photospheric model-atmosphere spectra (Teff = 70000 K, log g = 7.0,7.5,8.0), i.e., no interstellar line absorption is applied. See text for the description of inserts A and B.

While the outer line wings of H i L α are dominated by stellar He ii absorption, the inner line wings are well matched at a total NH i = 1.5 × 1018 cm-2. To reproduce the blue side of the observed absorption core, a significant D i column density of ND i = 1.2 × 1014 cm-2 is necessary. This value is uncertain because this line is saturated and blended by stellar He ii and interstellar H i. Therefore, we consider D i with a single ISM cloud at 12.1 km s-1. The region around L α is well reproduced with either a two-cloud (insert “B”) or a multi-cloud solution for H i.

Figure 14 shows that a multi-cloud solution can explain the strong and weak ISM absorption lines in the observations of RE 0503−289 and RE 0457−281. To simulate the stellar flux of RE 0457−281, we used a synthetic spectrum (pure hydrogen, Teff = 58000 K, log g = 7.9) which was provided by the German Astrophysical Virtual Observatory (GAVO14) Theoretical Stellar Spectra Access service (TheoSSA15). The ISM line absorption was modeled with the same parameters that were used for RE 0503−289. We find a good agreement for RE 0457−281 and RE 0503−289, although they have different distances of 116 ± 14 pc and , respectively, which are in rough agreement within their error limits (Fig. 15). This issue will be clarified by the results of Gaia16 in the near future.

thumbnail Fig. 14

Sections of the FUSE, STIS, and IUE observations around interstellar lines compared with our synthetic spectra for RE 0503−289 (left) and RE 0457−281 (right). The pure stellar model spectra are shown with dashed, blue lines. The vertical lines indicate the assumed clouds’ velocities given in Table 4. The dashed, vertical lines in each panel show the radial velocities of the two stars.

This corroborates the suggestion of Vennes et al. (1994) that the major contribution to the ISM absorption stems from the so-called local fluff in which our Sun is located. Nearly all of the gas along the LOS toward RE 0503−289 and RE 0457−281, and at distances well beyond these, is very hot and highly ionized. The gas that we see occupies only a small fraction of the total distance to the stars.

The main interstellar gas component toward RE 0503−289 is located near vhelio = + 15 km s-1, as evident from the H i 21 cm emission spectrum in this direction from the Leiden-Argentina-Bonn (LAB) survey (Kalberla et al. 2005). Also the STIS spectrum of RE 0503−289 indicates strong interstellar absorption at vhelio ≈ + 15 km s-1 in the strong resonance lines of C iiλ 1334.5 Å, Si iiiλ 1206.5 Å, Si iiλ 1260.4 Å, and others. As well as this main absorption component, there is weaker interstellar/circumstellar absorption extending bluewards until −60 km s-1, including another distinct (weak) absorption component near vhelio = −40 km s-1 (Fig. 14). The strong C iiλ 1334.5 Å and Si iiiλ 1206.5 Å lines show additional weak absorption between −30 km s-1 and zero velocities, but without a clear component structure.

The H i Lyman series absorption can also be best fit with two neutral gas components at + 15 and −40 km s-1, with a total column density of NH i = 1.5 × 1018 cm-2.

In the metal ions, the satellite component at −40 km s-1 is relatively narrow with a b-value of just 2.5 km s-1. The simultaneous presence of weak C ii, Si ii, Si iii, and H i absorption (and possibly O vi; Fig. 14), together with the narrow line shape, indicates a relatively compact, low-column density gas structure with multiphase gas that causes the absorption at negative velocities.

To estimate the contribution of the circumstellar material to the ISM absorption in the LOS toward RE 0503−289 and RE 0457−281, we estimated the densities of planetary nebulae (PNe) that were ejected at the end of the AGB phases of both stars. We assumed expansion velocities of vexp = 20 km s-1. Because of the very long post-AGB times, these PNe have swept up all stellar material ejected in the slow (≈10 km s-1) AGB-wind phase before, and their so-called radii indicate the maximum distance from the star that ejected material would have reached.

Table 5 summarizes radii, volumes, masses, and densities of the expected PNe. The estimated column densities are orders of magnitude lower than those that are necessary to reproduce the observation, even if RE 0503−289 lies beyond the circumstellar material of RE 0457−281. However, the ejected PN material may have compressed accelerated ambient interstellar gas, so that the −40 km s-1 component toward RE 0503−289 may be a result of the interaction between circumstellar and interstellar material at the interface between both components.

Table 5

Parameters to estimate the circumstellar column densities around RE 0503−289 and RE 0457−281 owing to their AGB mass loss.

9. Results and conclusions

We reanalyzed the effective temperature and surface gravity and determined Teff = 70000 ± 2000 K and log g = 7.5 ± 0.1. This verifies the results of Dreizler & Werner (1996) within improved, rather small, error limits.

For precise NLTE spectral analyses, reliable transition probabilities are required, not only for lines that are identified in the observation, but also for the complete model atoms that are considered in the model-atmosphere calculations. Therefore, our new computation of a complete set of transition probabilities for Kr iv–vii was a prerequisite for an improved NLTE spectral analysis. The new data enabled us to construct a more realistic Kr model atom. We improved the previous determination of the Kr abundance in RE 0503−289 (Werner et al. 2012b), taking these oscillator strengths into consideration.

thumbnail Fig. 15

Constellation of Earth, RE 0457−281, and RE 0503−289. The circles indicate the estimated maximum distance reached by stellar material that was ejected from the stars on the AGB. The error bars show the distance uncertainties.

In addition to the already known 15 Kr vi-vii lines in the observed high-resolution UV spectrum of RE 0503−289 (Werner et al. 2012b), we identified one Kr vi line and, for the first time in this star, ten lines of Kr v. Our synthetic line profiles reproduce well the observation at a photospheric Kr abundance of 2.5 × 10-4−1.0 × 10-3 (log Kr = −3.3 ± 0.3). This is 2300–9200 times the solar abundance (Grevesse et al. 2015). This highly supersolar Kr abundance goes along with the high abundances of other trans-iron elements in RE 0503−289 (Fig. 16). The Kr v–vii ionization equilibrium is well reproduced (Figs. 5, 8).

thumbnail Fig. 16

Solar abundances (Asplund et al. 2009; Scott et al. 2015b,a; Grevesse et al. 2015, thick line; the dashed lines connect the elements with even and odd atomic numbers) compared with the determined photospheric abundances of RE 0503−289 (red squares, Dreizler & Werner 1996; Rauch et al. 2014a,b, 2015, 2012, 2016, and this work). The uncertainties of the WD abundances are about 0.2 dex, in general. For Fe, the arrow indicates the upper limit. Top panel: abundances given as logarithmic mass fractions. Bottom panel: abundance ratios to respective solar values, [X] denotes log (fraction/solar fraction) of species X. The dashed, green line indicates solar abundances.

Iron is the only element in Fig. 16 with an upper abundance limit (Fe/He < 10-6 by number, about a hundredth of the solar abundance, Scott et al. 2015a). Barstow et al. (2000) determined this value by a co-addition (in the velocity space) of the nine Fe v lines that were predicted to be strongest in the HST/GHRS spectrum. In Fig. 17, we compare theoretical line profiles of the most prominent Fe v lines in the FUSE and HST/STIS wavelength range to the observation. The upper limit for the Fe abundance of 0.01 times solar is verified. Therefore, the reason why the Ni/Fe abundance ratio is much higher compared to other post-AGB stars remains unexplained (see Barstow et al. 2000).

thumbnail Fig. 17

Sections of the FUSE (top panel) and HST/STIS (bottom) spectra compared with synthetic spectra (Teff = 70000 K, log g = 7.5) that were calculated with Fe abundances of 1.3 × 10-5 (dashed, green), 1.3 × 10-4 (full, red), and 1.3 × 10-3 (dashed, blue) (about 0.01, 0.1, 1 times solar, respectively). Fe v lines are indicated.

6

Virtual Observatory.

10

Galactic coordinates of RE 0503−289 for J2000: ,

13

Orbiting and Retrievable Far and Extreme Ultraviolet Spectrometer/Berkeley Extreme and Far-ultraviolet Spectrometer.

Acknowledgments

T.R. and D.H. are supported by the German Aerospace Center (DLR, grants 05 OR 1507 and 50 OR 1501, respectively). The GAVO project had been supported by the Federal Ministry of Education and Research (BMBF) at Tübingen (05 AC 6 VTB, 05 AC 11 VTB) and is funded at Heidelberg (05 AC 11 VH3). Financial support from the Belgian FRS-FNRS is also acknowledged. PQ is research director of this organization. Some of the data presented in this paper were obtained from the Mikulski Archive for Space Telescopes (MAST). STScI is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS5-26555. Support for MAST for non-HST data is provided by the NASA Office of Space Science via grant NNX09AF08G and by other grants and contracts. We thank Ralf Napiwotzki for putting the reduced ESO/VLT spectra at our disposal, Monica Raineri who sent us the electronic versions of the Kr iv (Bredice et al. 2000) and Kr v (Raineri et al. 2012) log gf data, and Liang Liang who provided the Kr vii data (Liang et al. 2013). This work used the profile-fitting procedure, OWENS, that was developed by M. Lemoine and the FUSE French Team. This research has made use of NASA’s Astrophysics Data System and the SIMBAD database, operated at CDS, Strasbourg, France. The TheoSSA service (http://dc.g-vo.org/theossa) used to retrieve theoretical spectra for this paper and the TOSS service (http://dc.g-vo.org/TOSS) that provides weighted oscillator strengths and transition probabilities were constructed as part of the activities of the German Astrophysical Virtual Observatory.

References

  1. Althaus, L. G., Panei, J. A., Miller Bertolami, M. M., et al. 2009, ApJ, 704, 1605 [NASA ADS] [CrossRef] [Google Scholar]
  2. Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
  3. Badnell, N. R. 2011, Comput. Phys. Comm., 182, 1528 [Google Scholar]
  4. Barnard, A. J., Cooper, J., & Smith, E. W. 1974, J. Quant. Spec. Radiat. Transf., 14, 1025 [NASA ADS] [CrossRef] [Google Scholar]
  5. Barstow, M. A., Dreizler, S., Holberg, J. B., et al. 2000, MNRAS, 314, 109 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bredice, F., Raineri, M., Almandos, J. R., Gallardo, M., & Trigueiros, A. G. 2000, J. Quant. Spec. Radiat. Transf., 65, 805 [NASA ADS] [CrossRef] [Google Scholar]
  7. Cowley, C. R. 1970, The theory of stellar spectra (New York: Gordon & Breach) [Google Scholar]
  8. Cowley, C. R. 1971, The Observatory, 91, 139 [NASA ADS] [Google Scholar]
  9. Cowan, R. D. 1981, The theory of atomic structure and spectra (Berkeley, CA: University of California Press) [Google Scholar]
  10. Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, VizieR Online Data Catalog: II/246 [Google Scholar]
  11. Demers, S., Beland, S., Kibblewhite, E. J., Irwin, M. J., & Nithakorn, D. S. 1986, AJ, 92, 878 [NASA ADS] [CrossRef] [Google Scholar]
  12. Dreizler, S. 1999, A&A, 352, 632 [NASA ADS] [Google Scholar]
  13. Dreizler, S., & Werner, K. 1996, A&A, 314, 217 [NASA ADS] [Google Scholar]
  14. Dupuis, J., Vennes, S., Bowyer, S., Pradhan, A. K., & Thejll, P. 1995, ApJ, 455, 574 [NASA ADS] [CrossRef] [Google Scholar]
  15. Faedi, F., West, R. G., Burleigh, M. R., Goad, M. R., & Hebb, L. 2011, MNRAS, 410, 899 [NASA ADS] [CrossRef] [Google Scholar]
  16. Farias, E. E., Raineri, M., Gallardo, M., et al. 2011, J. Quant. Spec. Radiat. Transf., 112, 2463 [NASA ADS] [CrossRef] [Google Scholar]
  17. Fitzpatrick, E. L. 1999, PASP, 111, 63 [NASA ADS] [CrossRef] [Google Scholar]
  18. Gianninas, A., Bergeron, P., Dupuis, J., & Ruiz, M. T. 2010, ApJ, 720, 581 [NASA ADS] [CrossRef] [Google Scholar]
  19. Gianninas, A., Bergeron, P., & Ruiz, M. T. 2011, ApJ, 743, 138 [NASA ADS] [CrossRef] [Google Scholar]
  20. Grevesse, N., Scott, P., Asplund, M., & Sauval, A. J. 2015, A&A, 573, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Gudennavar, S. B., Bubbly, S. G., Preethi, K., & Murthy, J. 2012, ApJS, 199, 8 [NASA ADS] [CrossRef] [Google Scholar]
  22. Heber, U., Hunger, K., Jonas, G., & Kudritzki, R. P. 1984, A&A, 130, 119 [NASA ADS] [Google Scholar]
  23. Hébrard, G., Friedman, S. D., Kruk, J. W., et al. 2002, Planet. Space Sci., 50, 1169 [NASA ADS] [CrossRef] [Google Scholar]
  24. Hébrard, G., & Moos, H. W. 2003, ApJ, 599, 297 [NASA ADS] [CrossRef] [Google Scholar]
  25. Hoare, M. G., Drew, J. E., & Denby, M. 1993, MNRAS, 262, L19 [NASA ADS] [CrossRef] [Google Scholar]
  26. Holberg, J. B., Barstow, M. A., & Sion, E. M. 1998, ApJS, 119, 207 [NASA ADS] [CrossRef] [Google Scholar]
  27. Hubeny, I., Hummer, D. G., & Lanz, T. 1994, A&A, 282, 151 [NASA ADS] [Google Scholar]
  28. Hummer, D. G., & Mihalas, D. 1988, ApJ, 331, 794 [NASA ADS] [CrossRef] [Google Scholar]
  29. Johnson, W. R., Kolb, D., & Huang, K.-N. 1983, Atomic Data and Nuclear Data Tables, 28, 333 [Google Scholar]
  30. Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Liang, L., Gao, W.-J., & Zhou, C. 2013, Can. J. Phys., 91, 554 [CrossRef] [Google Scholar]
  32. Marsh, M. C., Barstow, M. A., Buckley, D. A., et al. 1997, MNRAS, 286, 369 [NASA ADS] [CrossRef] [Google Scholar]
  33. Mason, K. O., Hassall, B. J. M., Bromage, G. E., et al. 1995, MNRAS, 274, 1194 [NASA ADS] [CrossRef] [Google Scholar]
  34. Mason, K. O., Hassall, B. J. M., Bromage, G. E., et al. 1996, VizieR Online Data Catalog: VII/27 [Google Scholar]
  35. McCook, G. P., & Sion, E. M. 1999a, ApJS, 121, 1 [NASA ADS] [CrossRef] [Google Scholar]
  36. McCook, G. P., & Sion, E. M. 1999b, VizieR Online Data Catalog: III/210 [Google Scholar]
  37. Napiwotzki, R., Christlieb, N., Drechsel, H., et al. 2001, Astron. Nachr., 322, 411 [NASA ADS] [CrossRef] [Google Scholar]
  38. Napiwotzki, R., Christlieb, N., Drechsel, H., et al. 2003, The Messenger, 112, 25 [NASA ADS] [Google Scholar]
  39. Pagan, C. J. B., Raineri, M., Bredice, F., et al. 1996, J. Quant. Spectr. Rad. Transf., 55, 163 [NASA ADS] [CrossRef] [Google Scholar]
  40. Pauli, E.-M., Napiwotzki, R., Heber, U., Altmann, M., & Odenkirchen, M. 2006, A&A, 447, 173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Pounds, K. A., Allan, D. J., Barber, C., et al. 1993a, MNRAS, 260, 77 [NASA ADS] [Google Scholar]
  42. Pounds, K. A., & et al. 1993b, VizieR Online Data Catalog: VII/26 [Google Scholar]
  43. Quinet, P., Palmeri, P., Biémont, E., et al. 1999, MNRAS, 307, 934 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Quinet, P., Palmeri, P., Biémont, E., et al. 2002, J. Alloys Comp., 344, 255 [CrossRef] [Google Scholar]
  45. Raineri, M., Gallardo, M., Pagan, C. J. B., Trigueiros, A. G., & Reyna Almandos, J. 2012, J. Quant. Spec. Radiat. Transf., 113, 1612 [NASA ADS] [CrossRef] [Google Scholar]
  46. Raineri, M., Farías, E. E., Souza, J. O., et al. 2014, J. Quant. Spec. Radiat. Transf., 148, 90 [NASA ADS] [CrossRef] [Google Scholar]
  47. Rauch, T., & Deetjen, J. L. 2003, in Stellar Atmosphere Modeling, eds. I. Hubeny, D. Mihalas, & K. Werner, ASP Conf. Ser., 288, 103 [Google Scholar]
  48. Rauch, T., Dreizler, S., & Wolff, B. 1998, A&A, 338, 651 [NASA ADS] [Google Scholar]
  49. Rauch, T., Werner, K., Biémont, É., Quinet, P., & Kruk, J. W. 2012, A&A, 546, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Rauch, T., Werner, K., Quinet, P., & Kruk, J. W. 2014a, A&A, 564, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Rauch, T., Werner, K., Quinet, P., & Kruk, J. W. 2014b, A&A, 566, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Rauch, T., Werner, K., Quinet, P., & Kruk, J. W. 2015, A&A, 577, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Rauch, T., Quinet, P., Hoyer, D., et al. 2016, A&A, 587, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Renedo, I., Althaus, L. G., Miller Bertolami, M. M., et al. 2010, ApJ, 717, 183 [NASA ADS] [CrossRef] [Google Scholar]
  55. Rezende, D. C. J., Borges, F. O., Cavalcanti, G. H., et al. 2010, J. Quant. Spec. Radiat. Transf., 111, 2000 [NASA ADS] [CrossRef] [Google Scholar]
  56. Saloman, E. B. 2007, J. Phys. Chem. Ref. Data, 36, 215 [NASA ADS] [CrossRef] [Google Scholar]
  57. Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [NASA ADS] [CrossRef] [Google Scholar]
  58. Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
  59. Schoening, T., & Butler, K. 1989, A&AS, 78, 51 [NASA ADS] [Google Scholar]
  60. Scott, P., Asplund, M., Grevesse, N., Bergemann, M., & Sauval, A. J. 2015a, A&A, 573, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  61. Scott, P., Grevesse, N., Asplund, M., et al. 2015b, A&A, 573, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Seaton, M. J. 1962, in Atomic and Molecular Processes, ed. D. R. Bates (New York: Academic Press), 375 [Google Scholar]
  63. Vallerga, J. V., Vedder, P. W., & Welsh, B. Y. 1993, ApJ, 414, L65 [NASA ADS] [CrossRef] [Google Scholar]
  64. van Regemorter, H. 1962, ApJ, 136, 906 [NASA ADS] [CrossRef] [Google Scholar]
  65. Vennes, S., Dupuis, J., Bowyer, S., et al. 1994, ApJ, 421, L35 [NASA ADS] [CrossRef] [Google Scholar]
  66. Vennes, S., Chayer, P., Hurwitz, M., & Bowyer, S. 1996, ApJ, 468, 898 [NASA ADS] [CrossRef] [Google Scholar]
  67. Vennes, S., Dupuis, J., Chayer, P., et al. 1998, ApJ, 500, L41 [NASA ADS] [CrossRef] [Google Scholar]
  68. Victor, G. A., & Taylor, W. R. 1983, Atomic Data and Nuclear Data Tables, 28, 107 [NASA ADS] [CrossRef] [Google Scholar]
  69. Werner, K., Deetjen, J. L., Dreizler, S., et al. 2003, in Stellar Atmosphere Modeling, eds. I. Hubeny, D. Mihalas, & K. Werner, ASP Conf. Ser., 288, 31 [Google Scholar]
  70. Werner, K., Dreizler, S., & Rauch, T. 2012a, Astrophysics Source Code Library [record ascl:1212.015] [Google Scholar]
  71. Werner, K., Rauch, T., Ringat, E., & Kruk, J. W. 2012b, ApJ, 753, L7 [NASA ADS] [CrossRef] [Google Scholar]
  72. Werner, K., Rauch, T., & Kruk, J. W. 2015, A&A, 582, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  73. Ziegler, M., Rauch, T., Werner, K., Köppen, J., & Kruk, J. W. 2012, A&A, 548, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

Appendix A: Additional tables

Table A.1

Radial parameters (in cm-1) adopted for the calculations in Kr iv.

Table A.2

Radial parameters (in cm-1) adopted for the calculations in Kr v.

Table A.3

Radial parameters (in cm-1) adopted for the calculations in Kr vi.

Table A.4

Radial parameters (in cm-1) adopted for the calculations in Kr vii.

Table A.5

Comparison between available experimental and calculated energy levels in Kr iv. Energies are given in cm-1.

Table A.6

Comparison between available experimental and calculated energy levels in Kr v. Energies are given in cm-1.

Table A.7

Comparison between available experimental and calculated energy levels in Kr vi. Energies are given in cm-1.

Table A.8

Comparison between available experimental and calculated energy levels in Kr vii. Energies are given in cm-1.

All Tables

Table 1

Statistics of Kr iv–vii atomic levels and line transitions from Tables A.9–A.12, respectively.

In the text
Table 2

Photospheric abundances of RE 0503−289.

In the text
Table 3

Comparison of log gf values of Kr lines used in the abundance analysis (Figs. 5, 8).

In the text
Table 4

Ionic column densities (in cm-2) and radial velocities (in km s-1) in interstellar clouds in the line of sight toward RE 0503−289.

In the text
Table 5

Parameters to estimate the circumstellar column densities around RE 0503−289 and RE 0457−281 owing to their AGB mass loss.

In the text
Table A.1

Radial parameters (in cm-1) adopted for the calculations in Kr iv.

In the text
Table A.2

Radial parameters (in cm-1) adopted for the calculations in Kr v.

In the text
Table A.3

Radial parameters (in cm-1) adopted for the calculations in Kr vi.

In the text
Table A.4

Radial parameters (in cm-1) adopted for the calculations in Kr vii.

In the text
Table A.5

Comparison between available experimental and calculated energy levels in Kr iv. Energies are given in cm-1.

In the text
Table A.6

Comparison between available experimental and calculated energy levels in Kr v. Energies are given in cm-1.

In the text
Table A.7

Comparison between available experimental and calculated energy levels in Kr vi. Energies are given in cm-1.

In the text
Table A.8

Comparison between available experimental and calculated energy levels in Kr vii. Energies are given in cm-1.

In the text

All Figures

thumbnail Fig. 1

Comparison of our weighted oscillator strengths for Kr iv–vii (from top to bottom) to those of Bredice et al. (2000), Raineri et al. (2012), Pagan et al. (1996), and Liang et al. (2013), respectively. Left panel: comparison of weighted oscillator strengths. Right panel: ratio of weighted oscillator strengths over wavelength. The wavelength ranges of our FUSE and HST/STIS spectra are marked. The larger, red symbols refer to the lines identified in RE 0503−289 (see Figs. 5 and 8).

In the text
thumbnail Fig. 2

Section of the HST/STIS spectrum, compared with models with different log g of 7.0 (thin, green, dashed), 7.5 (thick, red), and 8.0 (thin, blue, dashed) and Teff = 70000 K. The synthetic spectra are normalized to match the flux of the observation at 2800 Å, respectively. All spectra are convolved with Gaussians (full width at half maximum of 1 Å) for clarity. Identified lines are indicated. “is” denotes interstellar origin.

In the text
thumbnail Fig. 3

Sections of the HST/STIS spectrum compared with three log g = 7.5 models with different Teff of 66 000 K (thin, blue), 70 000 K (thick, red), and 74 000 K (thin, green). The synthetic spectra are normalized to match the observed flux at 1335 Å.

In the text
thumbnail Fig. 4

Three models (Teff = 70000 K) with log g = 7.0 (green, dashed), 7.5 (red), and 8.0 (blue, dashed) compared to FUSE (left panel), UVES (middle), and TWIN (right) observations. The dashed, horizontal lines indicate the location of the local continuum.

In the text
thumbnail Fig. 5

Kr vi lines and one Kr vii line (bottom right) identified by Werner et al. (2012b) in the observed FUSE spectrum of RE 0503−289. Three synthetic spectra are overplotted. Thin, blue: the genuine spectrum of Werner et al. (2012b, Teff = 70000 K, classical Kr model atom with log Kr = −4.3. Thick red (Teff = 70000 K): our new Kr model atom with log Kr = −4.3. Dashed, red (Teff = 70000 K): our new Kr model atom with log Kr = −3.3. Kr lines are indicated with their wavelengths from Tables A.11 and A.12, and other lines by their ion’s name. “is” denotes interstellar origin.

In the text
thumbnail Fig. 6

Temperature structure of our model (thick, red) compared with the model of Werner et al. (2012b, thin, blue).

In the text
thumbnail Fig. 7

Kr ionization fractions in our model for RE 0503−289.

In the text
thumbnail Fig. 8

Newly identified Kr v lines and a Kr vi (top, right) line in the FUSE and HST/STIS observations. The model is calculated with log Kr = −3.3.

In the text
thumbnail Fig. 9

Location of RE 0503−289 in the log Teff–log g diagram (the ellipse indicates the error range) compared with evolutionary tracks for post-AGB stars that experienced a very late thermal pulse (Althaus et al. 2009). These are labeled with the respective stellar masses (in M⊙). Positions of hydrogen-deficient PG 1159-type stars and DO-type WDs are indicated by squares and circles, respectively.

In the text
thumbnail Fig. 10

Location of RE 0457−281 (Teff = 55875−60170 K, log g = 7.78−8.07, Marsh et al. 1997, the ellipse indicates the error range) in the log Teff–log g diagram compared with evolutionary tracks for DA-type WDs (Renedo et al. 2010) labeled with the respective stellar masses (in M⊙).

In the text
thumbnail Fig. 11

Locations (J2000) of RE 0503−289, RE 0457−281, and WD 0458−303 (marked by green encircled red + signs) in a 10° × 10°100 μ dust map from http://irsa.ipac.caltech.edu/applications/DUST.

In the text
thumbnail Fig. 12

Section of the FUSE observation (shifted to rest wavelengths) compared with our final synthetic spectrum (Teff = 70000 K, log g = 7.5). Prominent stellar and interstellar (is, blue) lines are indicated.

In the text
thumbnail Fig. 13

Section of the STIS observation around L α, compared with our final synthetic spectrum (thick, red, Teff = 70000 K, log g = 7.5). The dashed, blue lines are the pure photospheric model-atmosphere spectra (Teff = 70000 K, log g = 7.0,7.5,8.0), i.e., no interstellar line absorption is applied. See text for the description of inserts A and B.

In the text
thumbnail Fig. 14

Sections of the FUSE, STIS, and IUE observations around interstellar lines compared with our synthetic spectra for RE 0503−289 (left) and RE 0457−281 (right). The pure stellar model spectra are shown with dashed, blue lines. The vertical lines indicate the assumed clouds’ velocities given in Table 4. The dashed, vertical lines in each panel show the radial velocities of the two stars.

In the text
thumbnail Fig. 15

Constellation of Earth, RE 0457−281, and RE 0503−289. The circles indicate the estimated maximum distance reached by stellar material that was ejected from the stars on the AGB. The error bars show the distance uncertainties.

In the text
thumbnail Fig. 16

Solar abundances (Asplund et al. 2009; Scott et al. 2015b,a; Grevesse et al. 2015, thick line; the dashed lines connect the elements with even and odd atomic numbers) compared with the determined photospheric abundances of RE 0503−289 (red squares, Dreizler & Werner 1996; Rauch et al. 2014a,b, 2015, 2012, 2016, and this work). The uncertainties of the WD abundances are about 0.2 dex, in general. For Fe, the arrow indicates the upper limit. Top panel: abundances given as logarithmic mass fractions. Bottom panel: abundance ratios to respective solar values, [X] denotes log (fraction/solar fraction) of species X. The dashed, green line indicates solar abundances.

In the text
thumbnail Fig. 17

Sections of the FUSE (top panel) and HST/STIS (bottom) spectra compared with synthetic spectra (Teff = 70000 K, log g = 7.5) that were calculated with Fe abundances of 1.3 × 10-5 (dashed, green), 1.3 × 10-4 (full, red), and 1.3 × 10-3 (dashed, blue) (about 0.01, 0.1, 1 times solar, respectively). Fe v lines are indicated.

In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.