| Issue |
A&A
Volume 588, April 2016
|
|
|---|---|---|
| Article Number | A112 | |
| Number of page(s) | 12 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201527516 | |
| Published online | 28 March 2016 | |
Dust properties across the CO snowline in the HD 163296 disk from ALMA and VLA observations
1 INAF–Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Firenze, Italy
e-mail: guidi@arcetri.astro.it
2 Dipartimento di Fisica e Astronomia, Università degli Studi di Firenze, 50121 Firenze, Italy
3 ESO, Karl Schwarzschild str. 2, 85748 Garching bei München, Germany
4 Excellence Cluster “Universe”, Boltzmannstr. 2, 85748 Garching bei Muenchen, Germany
5 Joint ALMA Observatory (JAO), Alonso de Cordova 3107 Vitacura – Santiago de Chile, Chile
6 National Radio Astronomy Observatory, Socorro, NM 87801, USA
7 Department of Physics and Astronomy, Rice University, 6100 Main Street, Houston, TX 77005, USA
8 School of Cosmic Physics, Dublin Institute for Advanced Studies, 31 Fitzwilliams Place, 2 Dublin, Ireland
9 Dipartimento di Fisica e Astronomia, Università di Padova, 35122 Padova, Italy
10 INAF–Osservatorio Astronomico di Padova, Vicolo dell Osservatorio 5, 35122 Padova, Italy
11 Max Planck Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany
12 Harvard-Smithsonian Center for Astrophysics, 60 Garden Street, Cambridge, MA 02138, USA
13 Department of Astronomy, California Institute of Technology, MC 249-17, Pasadena, CA 91125, USA
14 Department of Astronomy, University of Maryland, College Park, MD 20742, USA
15 Department of Astronomy, University of Michigan, 830 Dennison Building, 500 Church Street, Ann Arbor, MI 48109, USA
16 Institute for Theoretical Astrophysics, Heidelberg University, Albert-Ueberle-Strasse 2, 69120 Heidelberg, Germany
17 SUPA, School of Physics and Astronomy, University of St Andrews, North Haugh, St Andrews, KY16 9 SS Scotland, UK
18 Jet Propulsion Laboratory, California Institute of Technology Pasadena, CA 91109, USA
19 The Netherlands Institute for Radio Astronomy (ASTRON), 7991 Dwingeloo, The Netherlands
20 Korea Astronomy and Space Science Institute, 776 Daedeok-daero, Yuseong-gu, 34055 Daejeon, Republic of Korea
Received: 6 October 2015
Accepted: 27 January 2016
Context. To characterize the mechanisms of planet formation it is crucial to investigate the properties and evolution of protoplanetary disks around young stars, where the initial conditions for the growth of planets are set. The high spatial resolution of Atacama Large Millimeter/submillimeter Array (ALMA) and Karl G. Jansky Very Large Array (VLA) observations now allows the study of radial variations of dust properties in nearby resolved disks and the investigation of the early stages of grain growth in disk midplanes.
Aims. Our goal is to study grain growth in the well-studied disk of the young, intermediate-mass star HD 163296 where dust processing has already been observed and to look for evidence of growth by ice condensation across the CO snowline, which has already been identified in this disk with ALMA.
Methods. Under the hypothesis of optically thin emission, we compare images at different wavelengths from ALMA and VLA to measure the opacity spectral index across the disk and thus the maximum grain size. We also use a Bayesian tool based on a two-layer disk model to fit the observations and constrain the dust surface density.
Results. The measurements of the opacity spectral index indicate the presence of large grains and pebbles (≥1 cm) in the inner regions of the disk (inside ~50 AU) and smaller grains, consistent with ISM sizes, in the outer disk (beyond 150 AU). Re-analyzing ALMA Band 7 science verification data, we find (radially) unresolved excess continuum emission centered near the location of the CO snowline at ~90 AU.
Conclusions. Our analysis suggests a grain size distribution consistent with an enhanced production of large grains at the CO snowline and consequent transport to the inner regions. Our results combined with the excess in infrared scattered light suggests there is a structure at 90 AU involving the whole vertical extent of the disk. This could be evidence of small scale processing of dust at the CO snowline.
Key words: stars: pre-main sequence / protoplanetary disks / instrumentation: interferometers / submillimeter: stars
© ESO, 2016
1. Introduction
The mechanisms that cause small dust particles to grow into larger bodies and eventually form planets are still not fully understood, in spite of the large laboratory, theoretical, and observational efforts (see the review by Testi et al. 2014). These processes are thought to occur in circumstellar disks around young stars on rather short timescales: infrared surveys show that the number of low mass stars with disks drops dramatically for stars older than 10 Myr (Mamajek 2009; Hernández et al. 2007), suggesting that in order to form large solids before the disk disperses, the growth process has to take place within a few million years. Analysis of dust properties in protostellar envelopes and young circumstellar disks suggests that large grains (even up to few millimeter size) are formed during the disk formation stage in infalling envelopes (Kwon et al. 2009; Miotello et al. 2014); still, substantial growth of dust grains occurs in the cold midplane of protoplanetary disks, where most of the solid mass is confined and planetesimals and planets are thought to form. The recent ALMA results for the young protoplanetary disk surrounding HL Tau suggest that planet formation may indeed occur very early in the disk’s lifetime (ALMA Partnership et al. 2015; Dipierro et al. 2015; Tamayo et al. 2015).
The life of a growing dust grain in a protoplanetary disk is not an easy one. It was realized already four decades ago that aerodynamical friction may effectively prevent grain growth (Weidenschilling 1977). The process of rapid radial migration and fragmentation sets an upper limit to the grain sizes as a function of radius and a very rapid evolutionary timescale for dust particles in disks (Brauer et al. 2008; Birnstiel et al. 2012). These theoretical expectations are at odds with direct observations of dust properties in the outer disks from millimeter observations (Ricci et al. 2010; Birnstiel et al. 2010). This is a general result, although some authors have shown that disks with peculiar growth processes (e.g., Laibe 2014; Dra¸żkowska et al. 2014) or specific dust properties (Okuzumi et al. 2012) may retain large particles more efficiently. To overcome the general inconsistency between models and observations, the most commonly accepted scenarios involve local grain growth and trapping in small regions, with sizes close to or smaller than the local disk scale height (Klahr & Henning 1997; Pinilla et al. 2012; Testi et al. 2014; Johansen et al. 2014).
The regions in the disk midplane that correspond to the snowlines of major volatiles are particularly interesting. These may promote locally efficient grain growth through recondensation across the snowline or by changing the sticking properties of ice-coated grains and, in addition, the local release of volatiles from the ices may induce a local pressure bump that could trap large grains (e.g., Supulver & Lin 2000; Wada et al. 2009; Ros & Johansen 2013; Gundlach & Blum 2015).
The dense regions of disk midplanes can be investigated at submillimeter and millimeter wavelengths, where the dust emission is more optically thin and can now be spatially resolved with present-day facilities, such as the Atacama Large Millimeter/submillimeter Array (ALMA) and the Karl G. Jansky Very Large Array (VLA). These facilities allow us to obtain sensitive and high angular resolution observations of the dust continuum and gas emission lines from protoplanetary disks and therefore study the radial variations of the physical parameters of the disk. Recent results include the study of the dust properties as a function of radius in disks (e.g., Guilloteau et al. 2011; Banzatti et al. 2011; Pérez et al. 2012, 2015; Menu et al. 2014; Tazzari et al. 2016), and the clear identification of the CO snowline in nearby disks (Mathews et al. 2013; Qi et al. 2013, 2015), through its effects on DCO+ and N2H+ abundances. It is thus becoming possible to directly investigate the effect of the CO snowline on grain growth observationally. This snowline is thought to be one of the most important after that of water, because the CO abundance in protostellar ices is found to be about 30−40% of H2O (Öberg et al. 2011). In this work we focus on the Herbig Ae star HD 163296, a bright and isolated object at a distance of 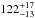 parsec (van den Ancker et al. 1998) with a relatively massive disk (~0.1 M⊙: Qi et al. 2011; Isella et al. 2007) and an excellent prototype for gas- and dust-rich protoplanetary disks. An estimated age of 5 Myr was obtained from the comparison between Hipparcos astrometric measurements and pre-main sequence evolutionary models by van den Ancker et al. (1998). The stellar parameters computed by Natta et al. (2004) are M∗ = 2.3 M⊙, L∗ = 36 L⊙, Teff = 9500 K. To study the dust properties in the protoplanetary disk around HD 163296, we re-analyse the ALMA science verification observations (de Gregorio-Monsalvo et al. 2013; Mathews et al. 2013; Rosenfeld et al. 2013) and for the first time discuss the continuum emission in Band 6, combined with new VLA observations from the Disks@EVLA collaboration. In Sect. 2 we describe the observational data, in Sect. 3 we report the main new results of our analysis, in Sect. 4 we present the result of our disk modeling, and in Sect. 5 we discuss the main implications for grain properties.
parsec (van den Ancker et al. 1998) with a relatively massive disk (~0.1 M⊙: Qi et al. 2011; Isella et al. 2007) and an excellent prototype for gas- and dust-rich protoplanetary disks. An estimated age of 5 Myr was obtained from the comparison between Hipparcos astrometric measurements and pre-main sequence evolutionary models by van den Ancker et al. (1998). The stellar parameters computed by Natta et al. (2004) are M∗ = 2.3 M⊙, L∗ = 36 L⊙, Teff = 9500 K. To study the dust properties in the protoplanetary disk around HD 163296, we re-analyse the ALMA science verification observations (de Gregorio-Monsalvo et al. 2013; Mathews et al. 2013; Rosenfeld et al. 2013) and for the first time discuss the continuum emission in Band 6, combined with new VLA observations from the Disks@EVLA collaboration. In Sect. 2 we describe the observational data, in Sect. 3 we report the main new results of our analysis, in Sect. 4 we present the result of our disk modeling, and in Sect. 5 we discuss the main implications for grain properties.
 |
Fig. 1 Continuum maps at different wavelengths, from the left: 850 μm, 1.3 mm, and 9 mm, the last obtained from the combination of VLA 8.0 mm and 9.8 mm bands. The contour levels correspond to −3 (dashed), 3, 6, 12, 24, 48, 100, 200, 400, 800, 1600σ. The bottom right of every panel shows the synthesized beam (see Table 1). |
2. Observations
2.1. ALMA observations
The ALMA observations of HD 163296 (also known as MWC 275) were part of the ALMA science verification Program 2011.0.000010.SV1. Band 6 observations were performed on 2012 June 9, June 23, and July 7 using a set of configurations comprising 20, 21 and 19 antennas, respectively. The total integration time was 3.14 h (1.4 h on the science source), the field of view was ~20 arcsec and the baselines ranged from 20 to 400 m, corresponding to spatial scales of 1600 AU to 80 AU at the distance of the object. The flux density calibrator for the three execution blocks were Juno, Neptune, and Mars, while the phase calibrator was J1733-130 and the bandpass calibrator J1924-292. The correlator was set with four spectral windows in dual polarization mode, two spectral windows in the upper side band and two in the lower side band. Two spectral windows, #0 (216.2−218 GHz) and #3 (233.1−234.9 GHz), were used to observe the line-free continuum with channel widths of 488 kHz; while at higher resolution (244 kHz) spectral window #1 (219.5−220.4 GHz) included the C18O(2−1) line at 219.560 GHz and the 13CO(2−1) line at 220.398 GHz, and spectral window #2 (230.5−231.5 GHz) covered the CO(2−1) line at 230.539 GHz. Imaging of the continuum emission of HD 163296 was performed excluding the above-mentioned lines (see Rosenfeld et al. 2013; Klaassen et al. 2013). Data was calibrated using version 4.1.0 of the Common Astronomy Software Application (CASA), self calibration was applied making use of the line-free channels, and using robust weighting during the CLEAN deconvolution, we were able to reach a resolution of 0.74′′ × 0.60′′ with a rms of 0.37 mJy/beam (see Table 1).
Band 7 observations were made on 2012 June 9, June 11, and June 22 with the same antenna configurations as for Band 6. Collectively, the five datasets covered an integration time of 3.9 h, with 2.3 h on the science target. The flux density calibrators were Juno and Neptune, while the bandpass and phase calibrators were the same as those used for Band 6. The two spectral windows in the lower side band were #2 (345.56−346.03 GHz) and #3 (346.52−347.47) with channel widths of 122 and 244 kHz, respectively. The ones in the upper side band were #1 (356.50−356.97 GHz) with 122 kHz channel width and #0 (360.11−360.23 GHz) at a high spectral resolution of 30.5 kHz; these included the emission lines: CO(3−2) at 345.796 GHz (#2), HCO+(4−3) at 356.734 GHz (#1), H13CO+(4−3) at 346.998 GHz (#3) and DCO+(5−4) at 360.160 GHz (#0). A detailed analysis of these spectral lines has been published by Mathews et al. (2013), de Gregorio-Monsalvo et al. (2013), and Rosenfeld et al. (2013). In this work we focus on the imaging of the continuum emission, obtained with the task CLEAN applying a robust weighting with Briggs parameter 0.5 and achieving a synthesized beam of 0.57′′ × 0.37′′ and a rms of 0.18 mJy/beam (see Table 1).
2.2. VLA observations
Observations of HD 163296 were made using the Karl G. Jansky Very Large Array (VLA) of the National Radio Astronomy Observatory2 as part of the Disks@EVLA project (AC982) in 2011 May and June in the BnA and A configurations. The Ka-band (λ ~ 1 cm) receivers were used with two 1 GHz basebands centered at 30.5 and 37.5 GHz, providing projected uv-spacings from 25 to 3800 kλ. The complex gain was tracked via frequent observations of J1755−2232, and the spectral shape of the complex bandpass was determined through observations of 3C 279. The absolute flux density scale was derived from observations of 3C 286 (e.g., Perley & Butler 2013), and its overall accuracy is estimated to be 10%. The data were calibrated, flagged, and imaged using a modified version of the VLA calibration pipeline3 with CASA. The astrometry reported here corresponds to what was derived from the A configuration data.
In addition, HD 163296 was observed with the C-band (λ ~ 6 cm) receivers in the DnC configuration in September 2010, in order to evaluate any potential contamination from ionized gas at shorter wavelengths. Two 1 GHz basebands were centered at 5.3 and 6.3 GHz. Complex gain variations were tracked through observations of J1820−2528, and the bandpass and absolute flux density scale was obtained through observations of 3C 286. The data were calibrated, flagged, and imaged using the CASA data reduction package. HD 163296 was detected with integrated flux density F5.2 cm = (410 ± 57) μJy.
3. Observational results
3.1. Continuum maps
In Fig. 1 we show the continuum intensity maps obtained from the line-free channels at three different wavelengths: ALMA Band 7, ALMA Band 6, and the combination of the two VLA frequency ranges at 30.5 and 37.5 GHz. The parameters of the images are listed in Table 1.
In agreement with previous work (de Gregorio-Monsalvo et al. 2013; Natta et al. 2004), we observe more compact emission at longer wavelengths, obtaining at 850 μm a projected radius of ~2.4′′ at a three-sigma level, corresponding to about 290 AU, while the outer radius of the emission is ~260 AU at 1.3 mm, and ~40 AU at 8−10 mm. We note that the low signal-to-noise of the VLA data at 8 and 10 mm can lead to underestimating the extent of the emission at these wavelengths, and it is critical to consider the visibility function for a proper analysis of the disk structure. We use 44° for the disk inclination and 133° for the disk position angle (from Qi et al. 2011) and plot the normalized real and imaginary part of the visibilities in Fig. 2.
These plots show that the real part of the visibilities declines more steeply at the shorter wavelengths (ALMA 850 μm and 1.3 mm) than at longer wavelengths (VLA 8 mm and 9.8 mm), demonstrating that the millimeter wavelength emission is intrinsically considerably more extended than the centimeter wavelength emission (a point source would be a constant 1.0 as a function of uv-distance in this plot). The integrated flux density above the 3σ level at 850 μm is F850 μm = 2.13 ± 0.02 Jy, similar to the value found by Isella et al. (2007) and de Gregorio-Monsalvo et al. (2013), while in Band 6 we find F1.3 mm = 0.59 ± 0.06 Jy. At the longer wavelengths, the flux density decreases by almost 3 orders of magnitude, with F8 mm = 2.0 ± 0.2 mJy and F10 mm = 1.6 ± 0.2 mJy. We include a calibration error of 10% in the measurements of the flux densities. We find a smoothly decreasing intensity profile at all wavelengths, consistent with the disk temperature and surface density decreasing with radius.
 |
Fig. 2 Real and imaginary parts of the measured visibilities as a function of uv-distance, deprojected assuming PA = 133°, i = 44° and bin-averaged every 40 kλ. Visibilities at each wavelength have been normalized by the average value at 40 kλ and error bars display the standard error of the mean, negligible for ALMA observations. |
 |
Fig. 3 Position of HD 163296 at the different observing epochs. The dashed line represents the proper motions from the Hipparcos measurement (J1991.25) to 2012, with respective proper motion error ellipses at 1, 2, and 3σ from the predicted positions. The black dot indicates our position estimate for the star at epoch 2012.5 based on the peak of the image in Band 7, while the red dot is the peak of the VLA image at 9 mm in 2011.5. The error bars are given by the astrometric accuracy of 0.1 arcsec for ALMA and 0.02 arcsec for VLA. The blue solid line represents the proper motions calculated from a least-squares regression between Hipparcos measurements and the observations. |
3.2. Proper motions
We checked whether the position of the star at the two different epochs of our observations was consistent with the proper motions reported in the literature: applying a Gaussian fit with to the images we find that the positions of the peaks fall within the 3σ error ellipse from the predicted position based on the Hipparcos astrometric mission measurements (J1991.25). For the ALMA observations (2012), we used Band 7 data because of its better signal-to-noise, with the peak position of the images obtained from the calibrated dataset before the self-calibration was applied. Figure 3 displays the estimated positions of the central star, and the astrometric error for interferometric observations is affected, among other things, by the phase calibration and depends on several factors (weather conditions, the separation between the target and the calibrator, etc.). We assume here that the absolute astrometry of the ALMA data is 0.1′′4, while for the VLA in A configuration, it is expected to be ~0.02′′5. The proper motions derived from a least-squares interpolation between our peaks at the two different epochs and the J1991.25 Hipparcos position are consistent with the latest reduction of the Hipparcos data (van Leeuwen 2007) within the errors and are listed in Table 2. The main difference we find is in the right ascension, where our best fit would imply a smaller proper motion. Nevertheless, the difference is still well within the uncertainties.
Coordinates and proper motions of HD 163296.
3.3. SED and free-free contribution
The integrated flux densities measured within a three-sigma level in our observations and the spectral energy distribution predicted by our model (see Sect. 4) are plotted in Fig. 4. Our model is consistent with the observed flux densities in the literature (Natta et al. 2004; Isella et al. 2007). At submillimeter and millimeter wavelengths, the continuum emission is due to the dust in the colder regions of the disk midplane, while at centimeter wavelengths the emission may also arise from free electrons in the stellar wind. Since this contribution is thought to come from a region in the inner part of the disk, we examined the longest baselines (≥1500 kλ) in the VLA 8.0 and 9.8 mm observations and we estimate an upper limit of 0.3 mJy for this wind emission, corresponding to the asymptotic value reached at the higher uv-distances by the real part of the visibilities. We fit a power law for the free-free emission by performing a least squares interpolation between our estimates at 8 and 10 mm and other VLA measurements at 3.6 cm (Natta et al. 2004) and 5.2 cm (see Sect. 2). The resulting power law is Fν ∝ ν− 0.19 ± 0.11, and is shown in Fig. 4 (where we plot νFν as a function of λ). According to this estimate, the free-free component at wavelengths shorter than 7 mm is negligible (see also Natta et al. 2004).
 |
Fig. 4 HD 163296 spectral energy distribution. Our measurements are represented in red filled squares, the white empty squares are taken from the literature (Isella et al. 2007; Natta et al. 2004), and the longer wavelength measurements used to evaluate the free free contribution are shown with full black circles (Natta et al. 2004) and a blue full circle (Disks@EVLA collaboration). Empty circles show the value of 0.3 mJy for the free free emission estimated in this paper. The dashed curve shows the best fit model from this paper (see Sect. 4), the dotted line is the estimated free-free emission, and the solid line the sum of the two. |
3.4. Excess emission at 850 μm
In Fig. 5 we show the intensity profile of the image at 850 μm: as the disk is inclined by 44° from the line of sight, the best angular resolution is reached using only the data along the projected disk major axis. We considered the pixels inside one beam across the major axis, each point corresponding to a pixel of 0.1 arcsec in the image (the points are therefore not all independent). The vertical spread is due to the shape and position angle of the synthesized beam, and to estimate the error when averaging on bins (Fig. 5, second panel) we weighted the points for the number of correlated pixels, i.e., 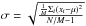 , where M is the number of correlated points and N the number of averaged pixels.
, where M is the number of correlated points and N the number of averaged pixels.
A simple analysis of the profiles reveals a bump in the emission between 80 and 150 AU: fitting a simple polynomial to outline a smooth profile does not produce an accurate fit (see Fig. 6). The degree of the polynomial was chosen as the lowest degree that would provide a reasonable fit to the intensity profile. To characterize the properties of this bump we fitted a combination of a 3rd degree polynomial plus a Gaussian curve to our flux density profile (see Fig. 6, right panel): subtracting the polynomial from the data leaves a Gaussian-shaped residual (see Fig. 5, second panel) centered at about (106 ± 4) AU, with a full width at half maximum (FWHM) of (71 ± 18) AU and a peak at (67±29)% of the smooth polynomial profile. An estimate of the maximum spatial extent of the feature can be derived from deconvolving our best fit Gaussian with the synthesized beam (~0.5′′ in Band 7), resulting in an upper limit of ~40 AU in FWHM. These values depend on the choice of the pixel size of the image and the tolerance we use for the points on the major axis, and thus are useful only for giving a rough estimate of the spatial scale of this unresolved emission excess. An independent analysis of this excess, obtained from modeling the visibilities directly, is shown in Sect. 4.
The feature cannot be clearly identified in Band 6 intensity profiles: we find an indication of a faint excess in the radial profiles along the disk projected major axis, but its detection depends on the small variation in the position angle and inclination parameters, making its characterization unreliable. This is consistent with the lower angular resolution of the Band 6 SV data: if we image the Band 7 dataset with a restoring beam equal to Band 6 resolution, the feature is diluted and cannot be reliably separated from the smooth disk emission (see Fig. 7).
Best fit parameters of the polynomial fits.
 |
Fig. 5 Top panel: flux density at 850 μm along the disk major axis from SE (left) to NW (right). The solid line represents the fit (polynomial profile + a Gaussian for the excess) performed excluding the inner 0.2 arcsec of the disk (gray shaded area). The vertical dashed line corresponds to the CO snowline at 90 ± 10 AU (from Qi et al. 2015). DCO+ emission in blue squares binned by 0.15 arcsec, the blue triangles show the upper limit of DCO+ emission in the inner 0.2 arcsec region of the disk, where we are limited by resolution. Bottom panel: residuals obtained by subtracting the polynomial fit from the data are shown with black dots binned by 0.15 arcsec. The blue solid line represents the Gaussian that best fits the excess (see Table 3), with the shaded area showing the 1σ fit uncertainty. The red triangles are the polarized light contrast in the Ks-band (from Garufi et al. 2014, the scale is on the right side vertical axis). |
 |
Fig. 6 Left: flux density across the disk major axis with a polynomial fit of degree 3 (dashed line in the upper panel). The second and third panels show the absolute residuals and the percentage residuals respectively. Right: the same intensity profile fitted with a 3rd-degree polynomial plus a Gaussian (see Table 3 for the best fit parameters). |
 |
Fig. 7 Left: radial profile at 1.3 mm across the disk major axis, with the dashed curve resulting from the polynomial fit of the data. Bottom panel: absolute residuals with respect to the polynomial interpolation. The excess emission found at 850 μm is not visible in Band 6. Right: radial profile of the image at 850 μm restored with the same beam as Band 6 (0.74′′ × 0.60′′, PA 77.3°). |
3.5. DCO+ emission
We extracted the DCO+(J = 5−4) emission lines at 360.160 GHz from the ALMA Band 7 observations in order to compare the dust continuum radial profile with a potential molecular tracer of the CO snowline (see Mathews et al. 2013). We used the CASA task “clean” with natural weighting to produce an integrated map of the DCO+ emission in the velocity range 0.8−10 km s-1, and the resulting synthesized beam is 0.62″ × 0.42″. We find a ring-like structure, similar to the one reported by Mathews et al. (2013), with a central radius of ~110 AU and a total extent of the DCO+ emission (detected at greater than 3σ) of 200 AU in radius. In Fig. 5 (top panel), we show the radial profile of the integrated DCO+ emission along the disk projected major axis: we note a symmetry between the southeast and the northwest directions, both displaying a double peak at a distance of ~60 AU and ~140 AU from the central star. We also point out that the minimum between the two peaks on both sides appears to fall at the position of the excess in the continuum emission at 850 μm (~110 AU). The signal-to-noise ratio of the DCO+ image is very low, so this result is very tentative and should be verified with higher sensitivity observations.
 |
Fig. 8 Temperature profile of the best fit model (see Sect. 4) in black dots and brightness temperature from the observations at 850 μm (red solid line) plotted in function of the distance, starting from 30 AU to have a reliable estimate considering the resolution of the observations. On the right axis, the optical depth from the comparison of the two temperatures, plotted as the dashed line. |
 |
Fig. 9 Left: flux density maps (top panel) at 850 μm and 9 mm with contour levels at −3 (dashed), 3, 6, 12, 24, 48, 100, 200, 400, 800, and 1600σ. Disk surface brightness profiles (middle panel) used to compute the spectral index, plotted on a logarithmic scale. The shaded region shows the dispersion of the individual data points in the images, while the error bars show the uncertainty on the mean for each bin. The flux density spectral index (bottom panel) was calculated between 850 μm and 9 mm as a function of radial distance. The profiles were averaged on ellipses of semi major axis r (shown in arcsec and AU in the top and bottom axes, respectively). The shaded region indicates the uncertainty of the measurement, resulting from the noise of the deconvolved images and the systematic calibration uncertainty; the low signal-to-noise ratio in the VLA map dominates the uncertainty on the spectral index determination beyond ~100 AU. Right: as above, but for the two ALMA datasets at 850 μm and 1.3 mm. |
3.6. Spectral index profiles
The dust opacity at millimeter and submillimeter wavelengths is usually approximated by a power law, κν ∝ νβ(e.g., Hildebrand 1983). The emission properties depend on the details of the composition, geometry, and size distribution of dust grains, most of which are very difficult to constrain. A general conclusion, however, is that in the conditions expected for dust in the densest regions of cores and disks, larger grain sizes correspond to lower values of the β index (e.g., Miyake & Nakagawa 1993; Stognienko et al. 1995; Natta & Testi 2004; Draine 2006). Even though directly connecting a value of β to the detailed properties of the dust population is not possible, measurements of β have been successfully used to infer the growth of dust in disks for many years (e.g., Beckwith & Sargent 1991; Wilner et al. 2000; Testi et al. 2001, 2003; Rodmann et al. 2006; Ricci et al. 2010; Kwon et al. 2015).
Previous measurements of the dust opacity power law between 0.87 and 7 mm (Isella et al. 2007) and between 1.3 and 7 mm (Natta et al. 2004) have already shown that grain growth occurs in the disk around HD 163296. With the high resolution of ALMA it is now possible to extend these studies and constrain the radial behavior of the opacity spectral index β(see, e.g., Pérez et al. 2012, 2015), not just its average value across the disk. We recall here that the emission from the disk midplane is generally optically thin, and at these wavelengths the Rayleigh-Jeans regime is a good approximation. To verify these assumptions, we compared the brightness temperature derived from our observations with the temperature profile of our best-fit model (see Sect. 4), in order to estimate the optical depth τ of the emission as τ ≃ −ln(1−Tb/Tmodel). We found τ increasing toward the central regions, as expected, with values <0.6 for the emission at 850 μm, and <0.5 for the emission at 1.3 mm outside a inner region of ~30 AU (see Fig. 8 for the 850 μm optical depth profile). At longer wavelengths, we estimate a lower optical depth with values of τ< 10-1 at both 8 and 10 mm. The assumption of optically thin continuum emission is therefore consistent with our data, and we expect a linear relation between flux density and dust opacity.
The flux density emitted from a ring dr at a given radius can be written as 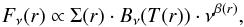 (1)where T(r) and Σ(r) are the midplane temperature and surface density at the distance r from the star, and Bν is the Planck function. In the Rayleigh-Jeans regime we therefore have Fν(r) ∝ Σ(r)·T(r)·ν2·νβ(r). Producing matched images (same beam, pixel size and centered on the peak of the emission) at different wavelengths and measuring the ratio of the flux densities as a function of distance from the star allows the spectral index, α (where Fν ∝ να), to be determined. Then, given the assumptions noted above, the power-law dependence of the dust opacity, β, can be derived as β = α−2 and does not depend on temperature or surface density. As discussed in Sect. 3.3, the observation at 8 and 10 mm includes gas emission from the stellar wind that needs to be subtracted to study the dust emissivity. The VLA maps used to compute the spectral index were produced by subtracting a point source at the center of the system with a flux density of 0.3 mJy from the calibrated visibilities (see Sect. 3.3).
(1)where T(r) and Σ(r) are the midplane temperature and surface density at the distance r from the star, and Bν is the Planck function. In the Rayleigh-Jeans regime we therefore have Fν(r) ∝ Σ(r)·T(r)·ν2·νβ(r). Producing matched images (same beam, pixel size and centered on the peak of the emission) at different wavelengths and measuring the ratio of the flux densities as a function of distance from the star allows the spectral index, α (where Fν ∝ να), to be determined. Then, given the assumptions noted above, the power-law dependence of the dust opacity, β, can be derived as β = α−2 and does not depend on temperature or surface density. As discussed in Sect. 3.3, the observation at 8 and 10 mm includes gas emission from the stellar wind that needs to be subtracted to study the dust emissivity. The VLA maps used to compute the spectral index were produced by subtracting a point source at the center of the system with a flux density of 0.3 mJy from the calibrated visibilities (see Sect. 3.3).
In the lefthand panel of Fig. 9 we show the intensity maps at 850 μm and 9 mm with a circular beam of 0.5′′, the corresponding averaged radial intensity profiles and the derived α profile. The intensity-averaged values (and consequently the spectral index) are plotted as long as they stay above the 1σ level. We see an increasing trend in the spectral index α from ~2.5 in the inner regions to ~3.5 at 150 AU. The profiles are displayed starting from and sampling every half resolution element of the images, corresponding to ~30 AU; the large error associated with this spectral index profile is dominated by the limited signal-to-noise ratio of the VLA images. With the same procedure we computed the spectral index between the ALMA Band 6 and 7 images, with a matching circular beam of 0.6′′, and obtained the profile shown in the righthand panel of Fig. 9. In this case the profile is sampled every 0.3′′ (~40 AU). In spite of the high signal-to-noise of the ALMA images, the large uncertainties are caused by the small wavelength leverage between the ALMA Band 6 and 7 observations. In propagating the uncertainty on α, we used a 10% calibration error for each flux, which in the case of α(850 μm−1.3 mm) represents a pessimistic estimate, because the two ALMA observations were carried out with the same phase calibrator and with Neptune as flux calibrator. Within the uncertainties the α profile seems to be consistent with the measurements between 850 μm and 9 mm. The spectral index remains below the value of 3 beyond 50 AU, corresponding to a β< 1 under the assumptions mentioned above, this indicates the presence of grains that have grown to at least 1 mm in size (using the dust opacity curves computed by Testi et al. 2014). We find no features in the α (and by implication, β) profiles across the CO snowline, as would be expected for localized grain growth, but it should be noted that the resolution of the spectral index maps is limited by the lower resolution of Band 6 observations (~0.6″), which would not be sufficient to detect small scale variations of the emission (see Sect. 3.4). We return to the estimate of β(r) in Sect. 5.
4. Modeling results
In Sect. 3.4 we have shown that the surface brightness radial profile for the continuum emission at 850 μm is compatible with having an excess peaked around 110 AU, with deconvolved FWHM ≤ 40 AU. To assess the robustness of this result, we performed a direct fit of the interferometric data (i.e., the visibilities) using the fitting scheme described by Tazzari et al. (2016) to which we refer for the analysis details. To estimate the disk thermal emission at 850 μm, we used a classical two layer disk model (Chiang & Goldreich 1997) with refinements by (Dullemond et al. 2001) and a reduced disk flaring that adequately describes the observed far-infrared flux (from Tilling et al. 2012). The resulting vertical scale height for the surface layer at R> 50 AU is h/R ~ 0.08. Moreover, we assumed a constant dust to gas mass ratio ζ = 0.01 and the following gas surface density profile: ![\begin{equation} \label{eq:sigma.parametrization} \Sigma_{\mathrm{g}}(R) = \Sigma_{0}\left(\frac{R}{R_{0}} \right)^{-\gamma} \exp{\left[-\left(\frac{R}{R_{\mathrm{c}}} \right)^{2-\gamma} \right]}, \end{equation}](/articles/aa/full_html/2016/04/aa27516-15/aa27516-15-eq94.png) (2)where R0 = 10 AU is a fixed scale length and Σ0, Rc, and γ are free parameters to be fitted. To compute the disk emission, the dust opacity is calculated using Mie theory (see Trotta et al. 2013, for details of the computation) assuming the same dust composition throughout the disk, given by the following fractional abundances adapted from Pollack et al. (1994): 5.4% astronomical silicates, 20.6% carbonaceaous material, 44% water ice, and 30% vacuum. Furthermore, we assume a power-law grain size distribution n(a) ∝ a− q for amin ≤ a ≤ amax, where a is the grain radius. To model the expectation that in the disk midplane there are larger grains than on the surface (Testi et al. 2014), we used different parametrization for the grain size distribution in these two regions: q = 3.5, amin = 10 nm, amax = 100 μm in the surface and q = 3, amin = 10 nm and amax = 0.8 ∗ (R/ 10 AU)-1.025 mm in the midplane, where this variable maximum grain size is chosen to reproduce the β(R) profiles found in Sect. 3.6. The modeling methodology is based on a Bayesian approach and employs an affine-invariant Markov chain Monte Carlo (MCMC) ensemble sampler (Foreman-Mackey et al. 2013) to explore the parameter space and find the best-fit models (Tazzari et al. 2016).
(2)where R0 = 10 AU is a fixed scale length and Σ0, Rc, and γ are free parameters to be fitted. To compute the disk emission, the dust opacity is calculated using Mie theory (see Trotta et al. 2013, for details of the computation) assuming the same dust composition throughout the disk, given by the following fractional abundances adapted from Pollack et al. (1994): 5.4% astronomical silicates, 20.6% carbonaceaous material, 44% water ice, and 30% vacuum. Furthermore, we assume a power-law grain size distribution n(a) ∝ a− q for amin ≤ a ≤ amax, where a is the grain radius. To model the expectation that in the disk midplane there are larger grains than on the surface (Testi et al. 2014), we used different parametrization for the grain size distribution in these two regions: q = 3.5, amin = 10 nm, amax = 100 μm in the surface and q = 3, amin = 10 nm and amax = 0.8 ∗ (R/ 10 AU)-1.025 mm in the midplane, where this variable maximum grain size is chosen to reproduce the β(R) profiles found in Sect. 3.6. The modeling methodology is based on a Bayesian approach and employs an affine-invariant Markov chain Monte Carlo (MCMC) ensemble sampler (Foreman-Mackey et al. 2013) to explore the parameter space and find the best-fit models (Tazzari et al. 2016).
In panel (a) of Fig. 10 we show the comparison between the observations at 850 μm and the best-fit model (obtained running a MCMC with 500 chains) that corresponds to the following median values: γ = 0.882 ± 0.002, Σ0 = (13.40 ± 0.03) g/cm2, Rc = (118.7 ± 0.2) AU. We note that the model with median values also gives the minimum χ2, with 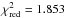 . The ring-shaped residuals are clearly visible in the righthand plot of panel (a), and this show that a simple two-layer disk model with a monotonically decreasing surface density (and thus surface brightness) is not sufficient to completely account for the observed flux density profile.
. The ring-shaped residuals are clearly visible in the righthand plot of panel (a), and this show that a simple two-layer disk model with a monotonically decreasing surface density (and thus surface brightness) is not sufficient to completely account for the observed flux density profile.
 |
Fig. 10 Continuum maps at 850 μm showing the results of the fits of the visibilities. The top left panel shows the observations, the two panels in the center the best-fit model, and the two panels on the right the residuals. The red solid curve represents the CO snowline at 90 AU. Panel a): we use a classical two-layer disk model that implements a monotonically decreasing surface brightness. Ring-shaped residuals are clearly visible. Panel b): we use the two layer disk model with an additional Gaussian peak. We fit the peak location (Rp = 96 AU) and width FWHMp = 58 AU. The residuals are substantially reduced. The parameters used for the CLEAN are the same as discussed in Sect. 2, and the contour levels are the same as those used in Figs. 1 and 9. |
To assess whether the residuals can be explained by adding a simple ring-like peak or whether they need a more complicated treatment, we performed another fit with a modified version of the two-layer model. This modified two-layer disk model implements an additional ring-like structure in the 850 μm emission, with a disk surface brightness I′(R) as follows: ![\begin{equation} I'(R) = I_{\mathrm{2L}}(R) + I_{\rm p} I_{\mathrm{2L}}(R_{\rm p})\exp\left[-\frac{(R-R_{\rm p})^2}{2\sigma_{\rm p}^2} \right], \end{equation}](/articles/aa/full_html/2016/04/aa27516-15/aa27516-15-eq119.png) (3)where I2L(R) is the brightness computed by the classical two layer model, Rp the peak center, σp the peak width, and Ip the peak intensity (in units of the brightness in the vicinity of the peak, namely I2L(Rp)). This new model therefore has six free parameters: three of them for the two-layer model (γ, Σ0,Rc) and another three to define the peak (Rp,σp,Ip). We performed the fit with the Tazzari et al. (2016) modeling tool discussed above, with the results shown in panel (b) of Fig. 10. The best-fit model (
(3)where I2L(R) is the brightness computed by the classical two layer model, Rp the peak center, σp the peak width, and Ip the peak intensity (in units of the brightness in the vicinity of the peak, namely I2L(Rp)). This new model therefore has six free parameters: three of them for the two-layer model (γ, Σ0,Rc) and another three to define the peak (Rp,σp,Ip). We performed the fit with the Tazzari et al. (2016) modeling tool discussed above, with the results shown in panel (b) of Fig. 10. The best-fit model (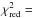 1.830) is described by γ = 1.32 ± 0.01, Σ0 = (24.6 ± 0.3) g/cm2, Rc = (111.3 ± 0.8) AU, which correspond to a radial profile that is slightly steeper than the simple power-law model but has a similar cut-off radius. For the Gaussian peak, we find that is described by Rp = (96 ± 1) AU, σp = (24.9 ± 0.5) AU and Ip = 128 ± 20%. This modified disk model is able to reproduce the observations with an extremely good agreement, as confirmed by the considerably smaller residuals (right plot of panel (b), Fig. 10). The midplane temperature is computed at every radius according to the two-layer approximation: in Fig. 8 (Sect. 3.6) we show the temperature profile of this best-fit model.
1.830) is described by γ = 1.32 ± 0.01, Σ0 = (24.6 ± 0.3) g/cm2, Rc = (111.3 ± 0.8) AU, which correspond to a radial profile that is slightly steeper than the simple power-law model but has a similar cut-off radius. For the Gaussian peak, we find that is described by Rp = (96 ± 1) AU, σp = (24.9 ± 0.5) AU and Ip = 128 ± 20%. This modified disk model is able to reproduce the observations with an extremely good agreement, as confirmed by the considerably smaller residuals (right plot of panel (b), Fig. 10). The midplane temperature is computed at every radius according to the two-layer approximation: in Fig. 8 (Sect. 3.6) we show the temperature profile of this best-fit model.
In conclusion, the peak inferred from the direct fit of the visibilities is evidence of a ring-like structure centered at 96 AU with a 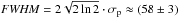 AU, compatible with the upper limit resulting from the simple polynomial+Gaussian fitting of the continuum surface brightness in Sect. 3.4.
AU, compatible with the upper limit resulting from the simple polynomial+Gaussian fitting of the continuum surface brightness in Sect. 3.4.
5. Discussion
In Sect. 3 we derived spatially resolved spectral index profiles for the dust emission from the HD 163296 protoplanetary disk and we identified and characterized an unresolved excess 850 μm emission centered at ~110 AU. The presence of this feature has also been confirmed through a detailed modeling of the visibilities in Sect. 4. In this section we analyze these results and their possible implications for the growth of grains in the HD 163296 disk.
5.1. β(r) profiles and grain growth
In Sect. 3.6 we derived the radial distribution of the spectral index as measured combining the ALMA 850 μm image with the ALMA 1.3 mm or the VLA 10 mm images. Under the assumptions of optically thin emission and Rayleigh-Jeans regime, the spectral index profiles can be directly converted into opacity power-law index profiles by subtracting a constant value of 2.0. Our modeling of the disk (Sect. 4) and the comparison of the measured brightness temperature with the expected temperature profile from our model (Sect. 3.6) confirm that the emission is optically thin throughout the disk, with the exception of the very inner region that is not resolved by the ALMA and VLA observations. On the other hand, the Rayleigh-Jeans approximation is not fully justified in the outer regions of the disk, especially for the ALMA Band 7 data. To estimate the value of the opacity power-law index as a function of radius we thus used (see Eq. (1)) ![\begin{equation} \label{eq:beta} \beta(r) = \left[\log \large \left(\frac{\nu_1}{\nu_2}\right ) \right]^{-1} \left[\log \left(\frac{F_{\nu_1}(r)}{F_{\nu_2}(r)}\right) - \log \left(\frac{B_{\nu_1}(T(r))}{B_{\nu_2}(T(r))}\right) \right] \end{equation}](/articles/aa/full_html/2016/04/aa27516-15/aa27516-15-eq135.png) (4)where T(r) are the temperature profiles derived from our models. In Fig. 11 we show the profiles of β(r) obtained from Eq. (4) using the intensity profiles shown in Fig. 9.
(4)where T(r) are the temperature profiles derived from our models. In Fig. 11 we show the profiles of β(r) obtained from Eq. (4) using the intensity profiles shown in Fig. 9.
Our analysis of the continuum emission at three different frequencies shows in the first place a decreasing spatial extent with increasing wavelength, confirming the presence of dust processing and radial transport in this disk, as already shown by the comparison between the size of the dust and gas disk by de Gregorio-Monsalvo et al. (2013) and confirm and extend the results of Natta et al. (2004, 2007), who showed the presence of large grains in the HD 163296 disk from integrated spectral indices and suggested a possible spectral index variation within the disk.
 |
Fig. 11 Dust opacity power-law index (β) profiles derived using Eq. (4). β(r) is computed between 850 μm and 9 mm in the top panel and between 850 μm and 1.3 mm in the bottom panel. The uncertainties are propagated from the surface brightness profiles presented in Fig. 9. The derived values of β(r) in the top panel are dominated by the low signal-to-noise in the VLA image from ~100 AU and are very uncertain beyond this radius. The CO snowline at 90 ± 10 AU from Qi et al. (2015) is pictured as the dashed vertical line. |
The β(r) profiles are qualitatively consistent with the results of similar analyses performed in other classical smooth disks (Guilloteau et al. 2011; Banzatti et al. 2011; Pérez et al. 2012, 2015; Trotta et al. 2013; Menu et al. 2014; Tazzari et al. 2016), with a significant variation of β throughout the disk (Δβ> 1), indicating a maximum grain size amax decreasing with the distance from the star. The ALMA and VLA data provide for the first time the combination of signal-to-noise ratio, angular resolution and image fidelity to successfully perform an analysis in the image plane. Unfortunately, the ALMA Band 6 science verification data do not have the angular resolution to probe the dust properties in a localized region across the CO snowline. Similarly, the VLA data do not have a high enough signal-to-noise ratio at 100 AU and beyond to derive strong constraints in the outer disk.
The conclusion that we can draw from the β(r) profiles is that there is convincing evidence of large grains inside the CO snowline, but at ~70 AU resolution the profile appears to be smooth with no features. The data are consistent with significant grain growth throughout the inner 150−200 AU of the disk. As discussed by many authors (see, e.g., Testi et al. 2014, and references therein), deriving a direct constraint on the level of grain growth from the β values is not trivial, because it requires assumptions on the dust structure and composition, which cannot be constrained outside the solar system. Nevertheless, a very broad range of reasonable assumptions on the grains properties imply that β values lower than 1 in the millimeter to centimeter regime can only be produced by grains and pebbles larger than a millimeter in size, and can be significantly larger under reasonable assumptions for grain porosity (Natta & Testi 2004). As an example, if we adopt an educated guess for the grain composition based on the constraints from our own Solar System (e.g., Pollack et al. 1994), combined with a fraction of vacuum of ~50%, we derive maximum grain sizes as large as ~1 cm at the CO snowline and even exceeding ~10 cm in the inner ~50 AU of the disk (see Fig. 4 of Testi et al. 2014).
5.2. The nature of the 850 μm excess
We found an excess emission at 850 μm located at about 105−115 AU from the star with a full width along the disk major axis of ≤40 AU. This excess appears to be located very close to the CO snowline at 90 AU as measured by Qi et al. (2015), who resolved the N2H+ emission in this disk with ALMA. The N2H+ molecule is thought to be a robust tracer of CO condensation fronts, because of the strong correlation between its abundance and gas phase CO depletion (see also Qi et al. 2013).
An analogous excess ring was found in the images of scattered light from HD 163296 taken with VLT/NACO (Garufi et al. 2014): polarized light images in Ks band displayed a “broken” ring feature with an excess along the major axis between ~0.5 and 1 arcsec, corresponding to 60 and 120 AU, respectively (shown in Fig. 5, middle panel). The upper limit on the extent of the excess we found corresponds to a total radial extent of ≲40 AU, while the dimension of the resolved ring found in infrared polarized light by Garufi et al. (2014) measured 0.45″ on the east side and 0.6″ on the west side, corresponding to 60 AU and 73 AU, respectively.
The interpretation of the ring in Ks-band polarized contrast given by Garufi et al. (2014) was the effect of self-shadowing of the disk created by a puffed-up inner region, with the outer disk emerging from the shadow at the location of the polarized emission. Garufi et al. (2014) could not exclude other effects that are possibly related to the CO snowline, but could not reach a conclusion as the polarized infrared light is tracing the τ ~ 1 (at 2 μm) surface of the disk atmosphere at much higher altitudes in the disk than the cold midplane where the CO snowline (and the bulk of the disk material) is located.
Our result provides an important contribution, since it shows that the excess is not purely a disk surface feature. The detection of the excess at the two different wavelengths, tracing two different vertical regions of the disk, suggests the presence of a structure that concerns the whole vertical extent of the disk. At millimeter wavelengths we are probing the disk midplane, and the emission is proportional to the surface density, the dust properties, and the temperature profile (see Sect. 3.6). In principle any localized change of one (or more) of these properties can explain the excess emission that we find in our images.
The lack of sensitivity or angular resolution in the VLA and ALMA Band 6 data do not allow us to probe the spectral index of the excess detected in Band 7. Future ALMA and/or VLA observations may allow us to probe the presence of large grains at the location of the excess emission. The possibility of large grains at the snowline may also be connected with a local increase in the surface density (or temperature), which could also explain the observed excess.
This is indeed expected from the simulations of grain growth across snowlines (e.g., Ros & Johansen 2013). We note that the effect of snowlines on grain growth is still poorly understood theoretically and much work is still needed. Recent simulations (Stammler, priv. comm.) show that, as grains maintain the (water) ice mantles across the CO snowline, this does not produce a discontinuity in the coagulation and fragmentation properties. The only effect would be a drop in the mass of solid particles inside the snowline because a fraction of the mantles is released in the gas. Such a variation in the surface density distribution across the snowline may produce an effect similar to the one we observe in the brightness profile and possibly also explain the effects on the disk surface observed in the near infrared.
Another mechanism that has been proposed to explain emission rings near snowlines in disks is sintering (Okuzumi et al. 2016): this process brings icy grains to bond at temperatures close to the sublimation temperature. As a consequence, these aggregates can easily fragment by collisions close to the snowline leading to the accumulation of smaller fragments, which are less affected by radial drift. Clearly more theoretical work is needed before a detailed comparison of our observations with models can be done.
An alternative explanation for this excess emission, which is not connected to the presence of the CO snowline, could be that particles are trapped by zonal flows (e.g., Dittrich et al. 2013) or by vortices (e.g., Klahr & Henning 1997). Such a mechanism has been invoked to explain the presence of annular dust confinement in some transitional disks (e.g., Pérez et al. 2014). Future higher angular resolution mm observations of the dust and gas will allow this possibility to be tested.
6. Summary
We have re-analyzed HD 163296 ALMA science verification data at 850 μm and 1.3 mm, and VLA data at 8 and 10 mm to study the radial behavior of dust properties in this disk. Our goal was to combine high resolution observations to derive the profile of the dust opacity spectral index, which is ultimately related to the size of grains throughout the disk, and look for evidence of grain growth across the CO snowline.
Our analysis shows, in the first place, more compact emission moving to longer wavelengths, confirming that dust processing and radial migration are taking place in this disk. A significant conclusion is that the dust opacity spectral index varies with radius and decreases toward the center to values ≤1, indicating the presence of large grains (≥1 mm) in the inner regions of the disk (inside 100 AU). Our β(r) profiles agree with those found in other resolved disks (e.g., Guilloteau et al. 2011; Pérez et al. 2012, 2015; Tazzari et al. 2016).
For this particular source, where a direct measurement of the location of the CO snowline is available, our analysis supports a scenario where the grains outside the snowline have not grown significantly, while the inner disk is populated by large grains. This general distribution would be consistent with an enhanced production of large grains at the CO snowline and subsequent transport to the inner regions. The alternative explanation of a smooth distribution of the grain sizes due to growth and transportation processes unrelated to the CO snowline is also consistent with the observed β(r) profile.
A second important finding is the evidence of an excess in the continuum emission at 850 μm near the location of the CO snowline and approximately at the same position of the excess in Ks-band polarized light as found by Garufi et al. (2014). Our finding confirms that the infrared excess emission is not only related to a disk surface layer effect, but also has more profound roots in the disk midplane, which is responsible for the 850 μm emission. The possible causes for this bump could be a local increase in the dust surface density due to dust trapping, for example caused by a local pressure maximum at the location of the snowline (Armitage 2013) or by turbulent eddies that can retain grains in their interior (Klahr & Henning 1997).
It is not clear whether the dust at this location has a different opacity spectral index β with respect to the bulk of the dust, since we lack the spatial resolution and/or sensitivity at 1.3 mm and ~10 mm to clearly detect the excess emission.
To conclusively probe whether this excess is a local change in the dust density and properties due to an effect of the CO snowline or another dust-trapping process, ALMA high resolution and sensitivity observations at mm wavelengths are needed, as well as higher sensitivity VLA measurements. As a future development, with ALMA longer baselines we might be able to resolve the iceline of the most important volatile, H2O, and investigate the role of snowlines in grain growth more extensively.
The ALMA science verification data can be found at: https://almascience.eso.org/alma-data/science-verification
Acknowledgments
This paper makes use of the following ALMA data: ADS/JAO.ALMA#2011.0.000010.SV. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada), NSC and ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ. We are grateful to Antonio Garufi for many discussions and for sharing his infrared polarization images. We thank Sebastian Stammler for insightful discussions on the effect of the CO snowline on dust and for showing us the results of his simulations in advance of publication. We thank the anonymous referee for the helpful comments. Part of this research was carried out at the Jet Propulsion Laboratory, California Institute of Technology, under a contract with the National Aeronautics and Space Administration. The fits have been carried out on the computing facilities of the Computational Center for Particle and Astrophysics (C2PAP) as part of the approved project “Dust evolution in protoplanetary disks”. M.T. and L.T. are grateful for the experienced support by F. Beaujean (C2PAP). This work was partly supported by the Italian Ministero dell’Istruzione, Università e Ricerca through the grant Progetti Premiali 2012 – iALMA (CUP C52I13000140001).
References
- ALMA Partnership, Brogan, C. L., Perez, L. M., et al. 2015, ApJ, 808, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Armitage, P. J. 2013, Astrophysics of Planet Formation (Cambridge University Press) [Google Scholar]
- Banzatti, A., Testi, L., Isella, A., et al. 2011, A&A, 525, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beckwith, S. V. W., & Sargent, A. I. 1991, ApJ, 381, 250 [NASA ADS] [CrossRef] [Google Scholar]
- Birnstiel, T., Ricci, L., Trotta, F., et al. 2010, A&A, 516, L14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Birnstiel, T., Klahr, H., & Ercolano, B. 2012, A&A, 539, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brauer, F., Dullemond, C. P., & Henning, T. 2008, A&A, 480, 859 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chiang, E. I., & Goldreich, P. 1997, ApJ, 490, 368 [NASA ADS] [CrossRef] [Google Scholar]
- de Gregorio-Monsalvo, I., Ménard, F., Dent, W., et al. 2013, A&A, 557, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dipierro, G., Price, D., Laibe, G., et al. 2015, MNRAS, 453, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Dittrich, K., Klahr, H., & Johansen, A. 2013, ApJ, 763, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2006, ApJ, 636, 1114 [NASA ADS] [CrossRef] [Google Scholar]
- Drążkowska, J., Windmark, F., & Dullemond, C. P. 2014, A&A, 567, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dullemond, C. P., Dominik, C., & Natta, A. 2001, ApJ, 560, 957 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [CrossRef] [Google Scholar]
- Garufi, A., Quanz, S. P., Schmid, H. M., et al. 2014, A&A, 568, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guilloteau, S., Dutrey, A., Piétu, V., & Boehler, Y. 2011, A&A, 529, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gundlach, B., & Blum, J. 2015, ApJ, 798, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Hernández, J., Hartmann, L., Megeath, T., et al. 2007, ApJ, 662, 1067 [NASA ADS] [CrossRef] [Google Scholar]
- Hildebrand, R. H. 1983, Quant. J. Roy. Astron. Soc., 24, 267 [Google Scholar]
- Isella, A., Testi, L., Natta, A., et al. 2007, A&A, 469, 213 [CrossRef] [EDP Sciences] [Google Scholar]
- Johansen, A., Blum, J., Tanaka, H., et al. 2014, Protostars and Planets VI, 547 [Google Scholar]
- Klaassen, P. D., Juhasz, A., Mathews, G. S., et al. 2013, A&A, 555, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klahr, H. H., & Henning, T. 1997, Icarus, 128, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Kwon, W., Looney, L. W., Mundy, L. G., Chiang, H.-F., & Kemball, A. J. 2009, ApJ, 696, 841 [NASA ADS] [CrossRef] [Google Scholar]
- Kwon, W., Looney, L. W., Mundy, L. G., & Welch, W. J. 2015, ApJ, 808, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Laibe, G. 2014, MNRAS, 437, 3037 [NASA ADS] [CrossRef] [Google Scholar]
- Mamajek, E. E. 2009, in AIP Conf. Ser. 1158, eds. T. Usuda, M. Tamura, & M. Ishii, 3 [Google Scholar]
- Mathews, G. S., Klaassen, P. D., Juhász, A., et al. 2013, A&A, 557, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Menu, J., van Boekel, R., Henning, T., et al. 2014, A&A, 564, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miotello, A., Testi, L., Lodato, G., et al. 2014, A&A, 567, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miyake, K., & Nakagawa, Y. 1993, Icarus, 106, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Natta, A., & Testi, L. 2004, in Star Formation in the Interstellar Medium: in Honor of David Hollenbach, eds. D. Johnstone, F. C. Adams, D. N. C. Lin, D. A. Neufeeld, & E. C. Ostriker, ASP Conf. Ser., 323, 279 [Google Scholar]
- Natta, A., Testi, L., Neri, R., Shepherd, D. S., & Wilner, D. J. 2004, A&A, 416, 179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Natta, A., Testi, L., Calvet, N., et al. 2007, Protostars and Planets V, 767 [Google Scholar]
- Öberg, K. I., Boogert, A. C. A., Pontoppidan, K. M., et al. 2011, ApJ, 740, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Okuzumi, S., Tanaka, H., Kobayashi, H., & Wada, K. 2012, ApJ, 752, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Okuzumi, S., Momose, M., Sirono, S.-I., Kobayashi, H., & Tanaka, H. 2016, ApJ, submitted [arXiv:1510.03556] [Google Scholar]
- Pérez, L. M., Carpenter, J. M., Chandler, C. J., et al. 2012, ApJ, 760, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez, L. M., Isella, A., Carpenter, J. M., & Chandler, C. J. 2014, ApJ, 783, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez, L. M., Chandler, C. J., Isella, A., et al. 2015, ApJ, 813, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Perley, R. A., & Butler, B. J. 2013, ApJS, 204, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Pinilla, P., Birnstiel, T., Ricci, L., et al. 2012, A&A, 538, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pollack, J. B., Hollenbach, D., Beckwith, S., et al. 1994, ApJ, 421, 615 [NASA ADS] [CrossRef] [Google Scholar]
- Qi, C., D’Alessio, P., Öberg, K. I., et al. 2011, ApJ, 740, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Qi, C., Öberg, K. I., Wilner, D. J., et al. 2013, Science, 341, 630 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Qi, C., Öberg, K. I., Andrews, S. M., et al. 2015, ApJ, 813, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Ricci, L., Testi, L., Natta, A., et al. 2010, A&A, 512, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rodmann, J., Henning, T., Chandler, C. J., Mundy, L. G., & Wilner, D. J. 2006, A&A, 446, 211 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ros, K., & Johansen, A. 2013, A&A, 552, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rosenfeld, K. A., Andrews, S. M., Hughes, A. M., Wilner, D. J., & Qi, C. 2013, ApJ, 774, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Stognienko, R., Henning, T., & Ossenkopf, V. 1995, A&A, 296, 797 [NASA ADS] [Google Scholar]
- Supulver, K. D., & Lin, D. N. C. 2000, Icarus, 146, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Tamayo, D., Triaud, A. H. M. J., Menou, K., & Rein, H. 2015, ApJ, 805, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Tazzari, M., Testi, L., Ercolano, B., et al. 2016, A&A, 588, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Testi, L., Natta, A., Shepherd, D. S., & Wilner, D. J. 2001, ApJ, 554, 1087 [Google Scholar]
- Testi, L., Natta, A., Shepherd, D. S., & Wilner, D. J. 2003, A&A, 403, 323 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Testi, L., Birnstiel, T., Ricci, L., et al. 2014, Protostars and Planets VI, 339 [Google Scholar]
- Tilling, I., Woitke, P., Meeus, G., et al. 2012, A&A, 538, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Trotta, F., Testi, L., Natta, A., Isella, A., & Ricci, L. 2013, A&A, 558, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van den Ancker, M. E., de Winter, D., & Tjin A Djie, H. R. E. 1998, A&A, 330, 145 [NASA ADS] [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wada, K., Tanaka, H., Suyama, T., Kimura, H., & Yamamoto, T. 2009, ApJ, 702, 1490 [NASA ADS] [CrossRef] [Google Scholar]
- Weidenschilling, S. J. 1977, MNRAS, 180, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Wilner, D. J., Ho, P. T. P., Kastner, J. H., & Rodríguez, L. F. 2000, ApJ, 534, L101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Continuum maps at different wavelengths, from the left: 850 μm, 1.3 mm, and 9 mm, the last obtained from the combination of VLA 8.0 mm and 9.8 mm bands. The contour levels correspond to −3 (dashed), 3, 6, 12, 24, 48, 100, 200, 400, 800, 1600σ. The bottom right of every panel shows the synthesized beam (see Table 1). |
| In the text | |
 |
Fig. 2 Real and imaginary parts of the measured visibilities as a function of uv-distance, deprojected assuming PA = 133°, i = 44° and bin-averaged every 40 kλ. Visibilities at each wavelength have been normalized by the average value at 40 kλ and error bars display the standard error of the mean, negligible for ALMA observations. |
| In the text | |
 |
Fig. 3 Position of HD 163296 at the different observing epochs. The dashed line represents the proper motions from the Hipparcos measurement (J1991.25) to 2012, with respective proper motion error ellipses at 1, 2, and 3σ from the predicted positions. The black dot indicates our position estimate for the star at epoch 2012.5 based on the peak of the image in Band 7, while the red dot is the peak of the VLA image at 9 mm in 2011.5. The error bars are given by the astrometric accuracy of 0.1 arcsec for ALMA and 0.02 arcsec for VLA. The blue solid line represents the proper motions calculated from a least-squares regression between Hipparcos measurements and the observations. |
| In the text | |
 |
Fig. 4 HD 163296 spectral energy distribution. Our measurements are represented in red filled squares, the white empty squares are taken from the literature (Isella et al. 2007; Natta et al. 2004), and the longer wavelength measurements used to evaluate the free free contribution are shown with full black circles (Natta et al. 2004) and a blue full circle (Disks@EVLA collaboration). Empty circles show the value of 0.3 mJy for the free free emission estimated in this paper. The dashed curve shows the best fit model from this paper (see Sect. 4), the dotted line is the estimated free-free emission, and the solid line the sum of the two. |
| In the text | |
 |
Fig. 5 Top panel: flux density at 850 μm along the disk major axis from SE (left) to NW (right). The solid line represents the fit (polynomial profile + a Gaussian for the excess) performed excluding the inner 0.2 arcsec of the disk (gray shaded area). The vertical dashed line corresponds to the CO snowline at 90 ± 10 AU (from Qi et al. 2015). DCO+ emission in blue squares binned by 0.15 arcsec, the blue triangles show the upper limit of DCO+ emission in the inner 0.2 arcsec region of the disk, where we are limited by resolution. Bottom panel: residuals obtained by subtracting the polynomial fit from the data are shown with black dots binned by 0.15 arcsec. The blue solid line represents the Gaussian that best fits the excess (see Table 3), with the shaded area showing the 1σ fit uncertainty. The red triangles are the polarized light contrast in the Ks-band (from Garufi et al. 2014, the scale is on the right side vertical axis). |
| In the text | |
 |
Fig. 6 Left: flux density across the disk major axis with a polynomial fit of degree 3 (dashed line in the upper panel). The second and third panels show the absolute residuals and the percentage residuals respectively. Right: the same intensity profile fitted with a 3rd-degree polynomial plus a Gaussian (see Table 3 for the best fit parameters). |
| In the text | |
 |
Fig. 7 Left: radial profile at 1.3 mm across the disk major axis, with the dashed curve resulting from the polynomial fit of the data. Bottom panel: absolute residuals with respect to the polynomial interpolation. The excess emission found at 850 μm is not visible in Band 6. Right: radial profile of the image at 850 μm restored with the same beam as Band 6 (0.74′′ × 0.60′′, PA 77.3°). |
| In the text | |
 |
Fig. 8 Temperature profile of the best fit model (see Sect. 4) in black dots and brightness temperature from the observations at 850 μm (red solid line) plotted in function of the distance, starting from 30 AU to have a reliable estimate considering the resolution of the observations. On the right axis, the optical depth from the comparison of the two temperatures, plotted as the dashed line. |
| In the text | |
 |
Fig. 9 Left: flux density maps (top panel) at 850 μm and 9 mm with contour levels at −3 (dashed), 3, 6, 12, 24, 48, 100, 200, 400, 800, and 1600σ. Disk surface brightness profiles (middle panel) used to compute the spectral index, plotted on a logarithmic scale. The shaded region shows the dispersion of the individual data points in the images, while the error bars show the uncertainty on the mean for each bin. The flux density spectral index (bottom panel) was calculated between 850 μm and 9 mm as a function of radial distance. The profiles were averaged on ellipses of semi major axis r (shown in arcsec and AU in the top and bottom axes, respectively). The shaded region indicates the uncertainty of the measurement, resulting from the noise of the deconvolved images and the systematic calibration uncertainty; the low signal-to-noise ratio in the VLA map dominates the uncertainty on the spectral index determination beyond ~100 AU. Right: as above, but for the two ALMA datasets at 850 μm and 1.3 mm. |
| In the text | |
 |
Fig. 10 Continuum maps at 850 μm showing the results of the fits of the visibilities. The top left panel shows the observations, the two panels in the center the best-fit model, and the two panels on the right the residuals. The red solid curve represents the CO snowline at 90 AU. Panel a): we use a classical two-layer disk model that implements a monotonically decreasing surface brightness. Ring-shaped residuals are clearly visible. Panel b): we use the two layer disk model with an additional Gaussian peak. We fit the peak location (Rp = 96 AU) and width FWHMp = 58 AU. The residuals are substantially reduced. The parameters used for the CLEAN are the same as discussed in Sect. 2, and the contour levels are the same as those used in Figs. 1 and 9. |
| In the text | |
 |
Fig. 11 Dust opacity power-law index (β) profiles derived using Eq. (4). β(r) is computed between 850 μm and 9 mm in the top panel and between 850 μm and 1.3 mm in the bottom panel. The uncertainties are propagated from the surface brightness profiles presented in Fig. 9. The derived values of β(r) in the top panel are dominated by the low signal-to-noise in the VLA image from ~100 AU and are very uncertain beyond this radius. The CO snowline at 90 ± 10 AU from Qi et al. (2015) is pictured as the dashed vertical line. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


