| Issue |
A&A
Volume 588, April 2016
|
|
|---|---|---|
| Article Number | A148 | |
| Number of page(s) | 14 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201526949 | |
| Published online | 01 April 2016 | |
MUSE crowded field 3D spectroscopy of over 12 000 stars in the globular cluster NGC 6397
I. The first comprehensive HRD of a globular cluster⋆,⋆⋆
1
Institut für Astrophysik, Georg-August-Universität Göttingen,
Friedrich-Hund-Platz 1,
37077
Göttingen,
Germany
e-mail:
husser@astro.physik.uni-goettingen.de
2
Leibniz-Institut für Astrophysik Potsdam (AIP),
An der Sternwarte 16,
14482
Potsdam,
Germany
3
Institut für Physik und Astronomie, Universität
Potsdam, 14476
Potsdam,
Germany
4
CRAL, Observatoire de Lyon, CNRS, Université Lyon 1,
9 avenue Ch. André,
69561
Saint-Genis-Laval Cedex,
France
5
Leiden Observatory, Leiden University,
PO Box 9513, 2300 RA
Leiden, The
Netherlands
6
GEPI, Observatoire de Paris, CNRS, Université
Paris-Diderot, Place Jules
Janssen, 92190
Meudon,
France
Received: 13 July 2015
Accepted: 13 February 2016
Aims. We demonstrate the high multiplex advantage of crowded field 3D spectroscopy with the new integral field spectrograph MUSE by means of a spectroscopic analysis of more than 12 000 individual stars in the globular cluster NGC 6397.
Methods. The stars are deblended with a point spread function fitting technique, using a photometric reference catalogue from HST as prior, including relative positions and brightnesses. This catalogue is also used for a first analysis of the extracted spectra, followed by an automatic in-depth analysis via a full-spectrum fitting method based on a large grid of PHOENIX spectra.
Results. We analysed the largest sample so far available for a single globular cluster of 18 932 spectra from 12 307 stars in NGC 6397. We derived a mean radial velocity of vrad = 17.84 ± 0.07 km s-1 and a mean metallicity of [Fe/H] = −2.120 ± 0.002, with the latter seemingly varying with temperature for stars on the red giant branch (RGB). We determine Teff and [Fe/H] from the spectra, and log g from HST photometry. This is the first very comprehensive Hertzsprung-Russell diagram (HRD) for a globular cluster based on the analysis of several thousands of stellar spectra, ranging from the main sequence to the tip of the RGB. Furthermore, two interesting objects were identified; one is a post-AGB star and the other is a possible millisecond-pulsar companion.
Key words: methods: data analysis / techniques: imaging spectroscopy / planets and satellites: fundamental parameters / stars: atmospheres / pulsars: general / globular clusters: individual: NGC 6397
Data products are available at http://muse-vlt.eu/science
© ESO, 2016
1. Introduction
In recent decades, globular cluster research has mainly been dominated by two complementary approaches. On the one hand, photometry at high spatial resolution, mainly using the Hubble Space Telescope (HST), aims to study the populations of clusters as a whole, down to the faintest stars (e.g. Sarajedini et al. 2007). On the other hand, spectroscopy at high spectral resolution attempts to infer cluster properties from detailed studies of individual stars, mainly giants (e.g. Carretta et al. 2009b). Both approaches were able to show that the stellar populations in the clusters are not as homogeneous as once thought. The photometrically detected splits in the main sequences of some massive clusters (see e.g. Piotto et al. 2007; Bellini et al. 2010) or the more common variations in the abundances of light elements found in high-resolution spectroscopic studies (for a review see Gratton et al. 2012) are famous examples in this respect.
These findings raised new questions. The variations in the light element abundances are often explained by a second generation of star formation from material polluted by the first stellar generation. However, the nature of the polluters is still under debate (see e.g. Ventura et al. 2001; Prantzos & Charbonnel 2006; de Mink et al. 2009). Alternatively, early disc accretion has been proposed by Bastian et al. (2013) to explain the variations without a second star formation period.
An observational approach that has not been followed as extensively as the two aforementioned methods is spectroscopy at low-to-medium resolution (with R ~ 3000). Obviously, this approach is unlikely to achieve the same accuracy in element abundances as high-resolution spectroscopy, but it has other advantages; the lower resolution usually comes with a longer wavelength range and shorter exposure times. The potential of applying full-spectrum fitting to medium-resolution spectra has been demonstrated, among others, by Koleva et al. (2009) and Kirby et al. (2008).
A common problem of spectroscopic studies is that only a limited number of stars in a globular cluster can be meaningfully observed. The catalogues of the ACS survey of Galactic globular clusters (Anderson et al. 2008) lists about 23 000 stars in just the central 1 arcmin2 of 47 Tuc (NGC 104), so blending is a common problem, usually limiting spectroscopy to brighter stars or outer regions of the clusters.
 |
Fig. 1 V-band image extracted from the mosaic of MUSE datacubes of NGC 6397. Overplotted are the single pointings, which have been observed multiple times at different position angles and with little offsets. Two of the planned pointings were not carried out, so the mosaic is incomplete. The colour coding indicates the number of stellar spectra that were extracted from each pointing, ranging from ~1700 in the central pointing to about 400 in the outer fields. The dashed blue line indicates the area covered by the ACS survey of Galactic globular clusters (Sarajedini et al. 2007). |
After the first attempts with long-slit spectroscopy, resulting in only handfuls of spectra of bright isolated giants (see e.g. Kinman 1959), multi-object spectroscopy (MOS) took over, increasing the number of observed objects steadily. For instance, Sommariva et al. (2009) managed to obtain 5973 individual high-resolution spectra of 2469 stars in M4 using the FLAMES+GIRAFE facility at the VLT. Still, this technique suffers from contamination from nearby, especially brighter, stars. Hence, MOS studies typically target giant stars in the outskirts of the clusters.
An important advantage of photometric studies has consisted in the ability to use the full spatial information within the field of view for deblending techniques, for example point spread function (PSF) fitting tools such as daophot (Stetson 1987). A usable approach for spectroscopy, for instance employed by Gebhardt et al. (1995), was scanning Fabry-Perot (FP) spectroscopy, giving full spatial information and thus allowing for efficient PSF deblending. The drawbacks are a small wavelength range and, especially, the risk of changing environmental properties such as seeing and sky brightness, which complicates the analysis.
 |
Fig. 2 Deblending of stellar spectra on MUSE data. The top left panel shows a white light image of the central MUSE datacube in NGC 6397. A zoom into the area indicated with a red square is shown in the top middle panel. In the top right panel, the same field of view is shown as seen with HST. All stars for which spectra were extracted are shown with crosses. Spectra extracted from the stars indicated with the red and green crosses are shown in the bottom panel and show clearly distinct features without any contamination from each other. The star indicated in red was determined to be a late-type G star, while the star in green is type A. The spectra are continuum subtracted and normalised and the areas dominated by telluric absorption are indicated in grey for clarity. |
Integral field spectrographs (IFS), which also preserve the full spatial information, provide a solution to this shortcoming, yet the limiting factor of these instruments has always been the small number of spatial pixels, which made the observation of large stellar samples very time consuming. However, the recently commissioned IFS MUSE (Bacon et al., in prep.; see also Bacon et al. 2010, 2014), mounted at UT4 (Yepun) of the ESO Very Large Telescope (VLT) changes this. This instrument provides an unprecedented combination of a large field of view (1′ × 1′) with a fine spatial sampling (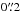 ). Dedicated simulations by Kamann et al. (2013) predict that up to 5000 stars can be simultaneously observed in a single MUSE pointing. This number would already exceed the largest spectroscopic samples obtained so far. In contrast to previous studies, MUSE observations are not limited to isolated stars alone, but promise to encompass the complete stellar population of a cluster in a single observation and, therefore, to bridge the gap to photometric studies.
). Dedicated simulations by Kamann et al. (2013) predict that up to 5000 stars can be simultaneously observed in a single MUSE pointing. This number would already exceed the largest spectroscopic samples obtained so far. In contrast to previous studies, MUSE observations are not limited to isolated stars alone, but promise to encompass the complete stellar population of a cluster in a single observation and, therefore, to bridge the gap to photometric studies.
In this paper, we discuss MUSE observations of the globular cluster NGC 6397 which is an extremely metal-poor, core-collapsed globular cluster with a moderate stellar mass. Because NGC 6397 is one of the closest clusters with a distance of only 2.4 kpc (Harris 1996), it has been subject of spectroscopic and photometric studies. This makes this globular cluster a perfect object for testing the capabilities of MUSE in the analysis of globular cluster populations.
The paper is structured as follows. In Sect. 2 the observations and basic data reduction are discussed, following by the source extraction in Sect. 3. In Sect. 4 we describe our full-spectrum fitting technique used for analysing the obtained spectra. The results are presented in Sect. 5, including a comprehensive Hertzsprung-Russell diagram (HRD), a peculiar trend in metallicity, and some interesting individual objects. The conclusions follow in Sect. 6. A more in-depth analysis of the kinematics and possible evidence for a black hole in the centre of NGC 6397 are discussed in Kamann et al. (2016, hereafter Paper II.
2. Observations and data reduction
We observed the globular cluster NGC 6397 during MUSE commissioning, lasting from July 26nd to August 3rd, 2014, to explore the capabilities of MUSE in crowded stellar fields. We created a 5 × 5 mosaic of the central part of the cluster, reaching out to a distance of ~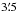 from the cluster centre. The various fields of the mosaic are shown in Fig. 1. The reason for the two missing fields in the outer rim is that the observations were embedded into the commissioning plan and, therefore, were interrupted occasionally to perform instrument tests.
from the cluster centre. The various fields of the mosaic are shown in Fig. 1. The reason for the two missing fields in the outer rim is that the observations were embedded into the commissioning plan and, therefore, were interrupted occasionally to perform instrument tests.
Each pointing was observed with a dither pattern and offsetting the derotator by 90 deg between exposures. This was performed to ensure that the light of each star is dispersed by multiple spectrographs, which improves the flat fielding and, hence, yields a homogeneous image quality across the field of view. The individual exposure times were always short, ≤60 s, to avoid saturation of the brightest cluster giants. In total, we obtained 127 exposures with a total integration time of 95 min. Including overheads, the observations took about 6 h.
The seeing during the observations was a bit variable, but never worse than ~1″. However, the observations of the central part of the cluster were carried out under excellent seeing conditions of ~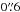 .
.
The data reduction was performed via the official MUSE pipeline (in versions 0.18.1, 0.92, and 1.0) written by Weilbacher et al. (in prep.; see also Weilbacher et al. 2012). It performs the basic reduction steps, that is bias subtraction, flat fielding, and wavelength calibration, on an IFU-per-IFU basis. In the next step, the data of each IFU was transformed into spatially calibrated coordinates before the data from all 24 IFUs were combined into a single pixtable, a FITS-file containing information about the flux and uncertainty, wavelength, and spatial position inside the field of view for each CCD pixel. To combine the pixtables from the individual exposures of each pointing into a single datacube, we had to account for the small offsets that occur during position angle changes, because the rotation centre is not perfectly aligned with the optical axis of the instrument; the so-called derotator wobble. We did so by creating a broadband image from each pixtable, measuring the coordinates of the brighter stars in the field of view, and feeding the measured average offsets to the pipeline when creating the final datacube for each pointing.
For visualisation purposes, we also created a datacube from the entire mosaic, but in a narrow wavelength range around 6000 Å. A collapsed image is shown in Fig. 1 and illustrates the remarkable image quality that is achieved by MUSE.
3. Extraction of stellar spectra
To obtain clean spectra in a crowded region such as a globular cluster, sophisticated analysis techniques are required. We developed a code to perform source deblending via PSF fitting on IFS data, described in detail in Kamann et al. (2013). This code relies on the existence of a photometric reference catalogue, including relative positions and brightnesses for the stars in the field of view. For NGC 6397, we used the catalogue prepared by Anderson et al. (2008) as part of the ACS survey of Galactic globular clusters (Sarajedini et al. 2007). Our MUSE mosaic extends beyond the ACS observations in this cluster (see Fig. 1), therefore we had to obtain positions and brightnesses of stars outside the area covered by the catalogue by other means. To this aim, we created broadband images from the datacubes of these fields and analysed them with daophot (Stetson 1987). Afterwards, we identified the stars that exist in the ACS catalogue, used those to calibrate the magnitudes measured with daophot, and added the missing stars to the catalogue. A possible shortcoming of this approach is that our deblending code works best with a reference catalogue obtained at higher spatial resolution, while the broadband images obviously have the same resolution as the IFS data. However, the areas in NGC 6397 without coverage by the ACS catalogue are not that densely crowded. Therefore we do not expect a significant impact on the results of the spectrum extraction.
Kamann et al. (2013) provide a detailed account of the method, and we give a brief summary of the methodology here. The extraction of the stellar spectra is performed in several steps. The analysis is started from an initial guess of the PSF in the MUSE data, which we model as an analytic Moffat profile with up to four free parameters: FWHM, kurtosis β, ellipticity e, and position angle θ, all of which can be wavelength dependent. For the initial guess, we tailor the FWHM to the seeing of the observation and set β to an average value of 2.5. The MUSE PSF did not show any signs of ellipticity, hence we set e = 0. In the next step, the PSF model is used to create a mock MUSE image from the reference catalogue. By cross-correlating this image against the MUSE cube, an initial guess for the coordinate transformation is obtained. For this purpose, we employ an affine transformation with up to six free parameters. Then, the sources for which meaningful spectra can be extracted are identified. To this aim, the signal-to-noise ratio (S/N) of each source is predicted based on its magnitude in the reference catalogue, the PSF, and the variances of the MUSE data. In addition, the density of brighter sources around the source in consideration is determined. Only sources that pass a S/N cut of 5, and for which the density calculation yields <0.4 brighter sources per resolution element, are used in the further analysis. This set of sources is then used in the actual extraction process, which works iteratively on every layer, i.e. every wavelength slice, of the datacube. In each layer, the analysis starts with a simultaneous fit to the fluxes of all sources, using the current estimate of the PSF and source coordinates. Afterwards, all sources except those identified as isolated enough to model the PSF are subtracted and the parameters of the PSF and coordinate transformation are refined. The new estimates are then used in another simultaneous flux fit. This process is iterated until convergence is reached on the source fluxes and the analysis of an adjacent layer is started. In this layer, the final estimates of the PSF and the coordinates are used as initial guesses.
After all layers have been processed in this way, a final PSF model is derived for the whole datacube. To this aim, the values of the PSF parameters obtained in the individual layers are fitted with polynomials. Polynomial fits are also performed to the source coordinates measured across the cube. We perform these polynomial fits to reduce the effect of small random jumps between layers and, thereby, to increase the S/N. Using polynomials for this task is justified because ambient characteristics such as atmospheric refraction or the seeing should result in a smooth change of the PSF and source coordinates with wavelength. Indeed, we found that the FWHM always shows a monotonic decrease with wavelength, which is very close to the theoretically expected behaviour. On the other hand, β does not vary strongly with wavelength.
In the last step, the final spectra are extracted by going through all layers of the cube once more and using the new estimates of the PSF and the source coordinates to extract the fluxes. This was carried out again by a simultaneous flux fit to all sources.
The results of the source extraction are summarised in Figs. 2 and 3. Figure 2 provides a good idea of the power of deblending techniques in integral field data. Our novel approach allows us to obtain clean spectra even in cases of heavily blended stars, such as the two stars indicated with coloured crosses in Fig. 2. Based on the magnitudes in the reference catalogue, one is a red giant (indicated by a red cross in Fig. 2) while the other is a horizontal branch (HB) star. The spectra we extracted and show in Fig. 2 confirm this classification nicely. Broad Paschen lines are visible in the red part of the spectrum of the HB star, while the red giant shows the characteristic calcium triplet lines in the same spectral window. Neither spectrum shows any contamination caused by the close neighbour. Also, we can reproduce the V − I colours of the reference catalogue to ~0.1 mag accuracy.
 |
Fig. 3 CMD of NGC 6397 generated from the input catalogue with colour-coded S/Ns of extracted spectra. The two stars denoted with circles are discussed in Sects. 5.6 and 5.7. Overplotted in black is an isochrone of 13.5 Gyrs in age and a metallicity of Z = 0.0014 (i.e. [Fe/H] ≈ –2.13). |
In Fig. 3 we show a colour−magnitude diagram (CMD) generated from the input catalogue where we colour coded the stars by the S/N of the extracted spectra. Our spectra cover a wide range of stellar types, ranging from red giants over HB stars and blue stragglers to main-sequence (MS) stars well below the turn-off (TO). The total exposure times per pointing were 4 min at most, but thanks to the high throughput of MUSE and our extraction method, which maximises the S/N of every extracted spectrum, we are still able to observe stars as faint as I ≈ 20 at a S/N of ~5.
In total, we were able to extract 18 932 spectra, 10 521 (~55.6%) of which have a S/N> 10, for 12 307 stars, i.e. some have been observed multiple times in overlapping pointings. The distribution of S/Ns is plotted in Fig. 4. Taking only those stars into account that we determined to be cluster members (see Sect. 5.2), we obtained spectra of 894 stars (13%) that are brighter than the turn-off (assumed to be at 15.7 mag in F814W) and of 6248 stars (87%) that are fainter, i.e. on the main sequence. To our knowledge, this is already the largest spectroscopic sample ever obtained for an individual cluster, which is an impressive demonstration of the unprecedented multiplexing capabilities of MUSE.
 |
Fig. 4 Distribution of S/Ns for the extracted spectra is plotted in red. Overplotted in blue is the cumulative distribution, showing that about 50% of the spectra have S/N> 10. |
3.1. Line spread function
In a low-to-medium resolution spectrograph such as MUSE, the knowledge of the line spread function (LSF) is important, since its shape has a stronger influence on the observed spectra than with high-resolution spectrographs. Each of the 24 IFUs of MUSE has slightly different characteristics and the LSF of each is highly wavelength dependent. The MUSE data reduction system tries to estimate those profiles, as shown in Fig. 5 for a single exposure, for each IFU at different wavelengths by fitting sky lines with Gauss-Hermite polynomials.
As one can see, the profiles change significantly both with wavelength and IFU. While the former variation can be dealt with easily using step-wise convolution, the latter poses a more serious problem, since the flux measured for a single star can be distributed over several IFUs. In that case, picking an appropriate LSF is not an obvious choice. For the present analysis we decided to use a mean LSF (see dashed line in Fig. 5), which overestimates the spectral resolution for some IFUs and underestimates it for others. Except for two IFUs, the deviation from this mean is never larger than 0.13 Å and is usually well below 0.05 Å.
The approach of using a mean LSF is further justified by the fact that we ran a dither pattern on each observed pointing by rotating 90 deg between exposures. This way the spectrum of a single star is a combined measurement of multiple spectrographs which, in turn, should have a LSF that is close to the mean LSF that we are using.
We pre-convolve all our model spectra with a kernel K that is slightly higher resolved than the LSF (with an offset σoff), i.e. 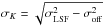 . This allows for some additional Gaussian line broadening during the fitting process (see Sect. 4.1), which should approximately compensate for the mean LSF that we are using and allow for some intrinsic line broadening.
. This allows for some additional Gaussian line broadening during the fitting process (see Sect. 4.1), which should approximately compensate for the mean LSF that we are using and allow for some intrinsic line broadening.
 |
Fig. 5 Full widths at half maximum (FWHM) of the line spread functions of all 24 IFUs of MUSE at different wavelengths as taken from a single exposure. |
To test this, we ran the analysis (as described in the next section) for the central pointing with two more grids of model spectra that have been convolved with different LSFs, namely those of IFUs #2 and #13, which correspond to the highest and lowest curve in Fig. 5, respectively. We could not find any systematic offsets and the scatter between the results was small, i.e. σ[ M / H ] = 0.06 dex for the metallicity and σTeff = 6 K for the effective temperature for S/N> 20, which we consider to be the lower limit for reliable results (see Table 2). As expected, the additional line broadening applied to the model spectra is smallest for those convolved with the LSF of IFU #2, i.e. the broadest one.
Although we already obtained reasonable results with this model for the LSF, we have to state that it still has room for improvement. For instance, the LSF of MUSE appears to be slightly asymmetric, which we do not take at all into account at the moment. Furthermore, we are currently ignoring the Hermite part of the LSF as given by the pipeline. As a result of this, currently we are not spectroscopically fitting the surface gravity, for which the fit highly depends on the line shapes and therefore on the LSF; instead, we use a value derived from comparison with an isochrone.
4. Analysis
Our analysis of the observed spectra is a multi-step process that is explained in detail in this section. The steps involved are:
-
1.
We compare the HST photometry with an isochrone with age, metallicity, and distance taken from the literature, with some minor manual adjustments for a better match, resulting in initial guesses for Teff and log g.
-
2.
We obtain a model spectrum with given Teff/log g/[M/H] and do a cross-correlation for each observed spectrum for deriving radial velocities.
-
3.
We run an optimisation with Teff, [M/H], vrad, line broadening, and telluric absorption as free parameters, fixing log g to the photometric value, i.e. assuming the stars belongs to the observed stellar cluster.
-
4.
We optimise again with [Fe/H] and [α/Fe] as free parameters, fixing the others to the previously obtained values.
This procedure yields a list of parameters for all the stars in the sample. For most of the further analyses of the results, a S/N cut of 20 is applied.
4.1. Full-spectrum fitting
The method we use for determining stellar parameters is similar to that described by Koleva et al. (2009) and was already discussed briefly in Husser et al. (2012). Instead of fitting only parts of an observed spectrum, for instance strong absorption features, we always use the whole available wavelength range and mask, if at all, only small regions with known template mismatches. During the fit, the observed spectrum O(x), given in pixel space, is never transformed in any way, i.e. convolved or rebinned. Instead, we try to find a best-fit model G as the weighted sum of model spectra Mk with coefficients ωk, each convolved with a corresponding kernel Bk, i.e. ![\begin{equation} G = \sum\limits_{k=1}^{K} \omega_k \left[ B_k \ast M_k \right]. \end{equation}](/articles/aa/full_html/2016/04/aa26949-15/aa26949-15-eq55.png) (1)We perform the convolution (denoted by ∗) in the logarithmic domain, which allows us to apply both line shifts (i.e. radial velocities) and broadenings in one single step. As the sum suggests, we can fit multiple models to a single observed spectrum, but for this work we always use K = 1, i.e. a single stellar component is fitted. This reduces the problem to finding a single model M1 with the convolution kernel B1 that matches the observation best. In case a spectrum is known to be a combination of multiple stars, K can be increased for determining the parameters of all stars.
(1)We perform the convolution (denoted by ∗) in the logarithmic domain, which allows us to apply both line shifts (i.e. radial velocities) and broadenings in one single step. As the sum suggests, we can fit multiple models to a single observed spectrum, but for this work we always use K = 1, i.e. a single stellar component is fitted. This reduces the problem to finding a single model M1 with the convolution kernel B1 that matches the observation best. In case a spectrum is known to be a combination of multiple stars, K can be increased for determining the parameters of all stars.
The best-matching model is then found by running a Levenberg-Marquardt optimisation. At each iteration a model spectrum is interpolated from a given spectral library (see next section). This is then convolved by a kernel that both broadens the lines by a given amount and shifts the spectrum to a given radial velocity. Finally, the model spectrum is rebinned to the same wavelength grid as the observed spectrum.
The model spectra that we use are usually not normalised and as mentioned before we never alter the observed spectrum in any way, so they still contain their continuum fluxes. Instead, we fit a Legendre polynomial, which, multiplied with the model, best matches the observation. We do this in every iteration and for every interpolated model spectrum, so we always find the best polynomial to match the two spectra. The order of the polynomial is chosen in a way that stellar features are not mistreated as continuum.
The free parameters in the fit are typically the effective temperature Teff and the metallicity [M/H]. Furthermore, we allow for a radial velocity vrad and an intrinsic line broadening using a Gaussian with the standard deviation σ. In general we can also fit the surface gravity log g, but because of our current problems with understanding the LSF (see Sect. 3.1) this has not been done for the analyses presented in this publication.
As stated before, we usually measure the metallicity as a scaled solar abundance [M/H]. Since most globular clusters have been found to be overabundant in alpha elements, this value changes when adding [α/Fe] as an additional free parameter to the fit. In that case, we denote the metallicity as [Fe/H] to be able to distinguish between both.
The convolution with a Gaussian kernel that we apply to the model spectra also allows us to account for effects like stellar rotation and macro-turbulence. The former is actually a non-Gaussian broadening, but at the spectral resolution of MUSE the difference is small. Furthermore, in globular clusters we expect only very old stars with relatively small masses (<1 M⊙), so we do not expect to observe large rotational velocities.
We tested the fitting procedure extensively against other publicly available medium-resolution stellar libraries, both synthetic and empirical. Among those were The Indo-US Library of Coudé Feed Stellar Spectra (also known as cflib, Valdes et al. 2004), ELODIE (Prugniel & Soubiran 2001), and SpectraLib (Munari et al. 2005). The results were all in good agreement and no systematic errors were found.
4.2. Model spectra and interpolation
Parameter space of the PHOENIX grid of model spectra used for fitting the observations.
For analysing the observed spectra, we use an extended version of the Göttingen Spectral Library (Husser et al. 2013). We increased the upper limit for the effective temperature Teff to 15 000 K and added some variations in alpha element abundances for the metallicities that were previously missing.
When creating the spectral library, we used values for the microturbulence vmicro empirically derived from 3D radiative hydrodynamic models models by Wende et al. (2009). They provide values for M stars only, but the extrapolation towards higher temperatures seemed plausible. This is a different approach than the commonly seen method of using a fixed value for microturbulence. Bergemann et al. (2015) suggested that there might be a vmicro-[Fe/H] degeneracy, which could affect our results; however, the same would be true with a fixed microturbulence.
Since with the Levenberg-Marquardt algorithm we use an optimisation routine that depends on gradients, interpolating linearly within the model grid is not an option because that would produce discontinuities in the first derivatives. Instead, we use a scheme based on cubic splines. The interpolation is performed under the assumption that each wavelength point is independent, so that we can interpolate them individually.
In a single dimension p of the grid, we derive second derivatives (along this dimension) by fitting a spline to the fluxes. Where p0 is the value of the parameter to interpolate and p1 and p2 are the two adjacent points in the grid, we can calculate the following coefficients (see Press et al. 2007):
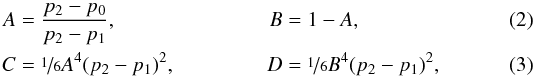 which in turn we can use to interpolate the flux f at p0 from the fluxes and second derivatives (along p) at p1 and p2, i.e.
which in turn we can use to interpolate the flux f at p0 from the fluxes and second derivatives (along p) at p1 and p2, i.e. 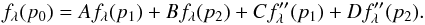 (4)Applying this interpolation scheme to higher dimensions can easily be accomplished by running it recursively, i.e. interpolating in one dimension after the other. By precomputing the second derivatives in one dimension (in our case Teff) we can significantly reduce the computation time for the interpolation.
(4)Applying this interpolation scheme to higher dimensions can easily be accomplished by running it recursively, i.e. interpolating in one dimension after the other. By precomputing the second derivatives in one dimension (in our case Teff) we can significantly reduce the computation time for the interpolation.
4.3. Initial guesses
The performance of optimisation algorithms such as Levenberg-Marquardt usually depends on good initial guesses. Therefore, we did comprehensive tests with varying starting parameters. We found that the results for the radial velocity are somewhat insensitive to its initial guess, provided that absorption lines in observation and model still overlap – which usually is the case for ±200 km s-1 around the real value. A similar result was observed for the effective temperature. Varying its initial guess across the full range of the used spectral library did not affect the results at all. For the metallicity we found that the real value could not be recovered reliably when starting with a low value like, for instance [M/H] = −4.0. This was to be expected, however, owing to the low number of absorption lines in those spectra. Thus, the initial guess for [M/H] is set to the mean cluster metallicity throughout this work.
Since we already used a catalogue including brightnesses in different passbands for the extraction of the spectra, we can use it again for a comparison with a matching isochrone with an age of 13.5 Gyr and Z = 0.0014 ([ Fe / H ] ≈ −2.13) from Bressan et al. (2012)1, as shown in Fig. 3. We fit a two-dimensional polynomial P(V,V − I) of third order to the effective temperatures from the isochrone as function of colour and magnitude. Evaluating this polynomial for each star in the catalogue yields initial guesses for the effective temperature. The same procedure is applied for the surface gravity. We estimate initial guesses for each star in the CMD by simply evaluating those two polynomials. The values obtained for Teff and log g are then used to create a template spectrum for a cross-correlation, which yields the initial radial velocity for the full-spectrum fit.
This method will most likely produce wrong log g values for field stars, since they are obtained by comparison with an isochrone with most probably wrong age, metallicity, and distance. As discussed above, we are currently fixing the surface gravity to this initial guess, and for these stars, we will see an impact on the results for Teff and [M/H]. As will be shown in Paper II, the measured metallicities of the field stars in the sample are distributed as expected by a Milky Way model and, therefore, we expect the effect on [M/H] to be small. As our membership determination depends on metallicities and radial velocities, which are not affected by these shortcomings, we can effectively remove such stars from further analysis.
 |
Fig. 6 Fraunhofer A band and the best-fitting model in the spectrum of a typical G subgiant in our sample. The positions of two K i absorption lines from the interstellar medium are indicated with blue arrows in the residuals. |
4.4. Telluric absorption
The concept of full-spectrum fitting can easily be extended to include telluric absorption as well (see also Husser & Ulbrich 2014). To accomplish this, we created model spectra for the Earth’s atmosphere with varying abundances for molecules that have absorption features in the wavelength range of MUSE (H2O, O2, and O3) with the FASCODE (Clough et al. 2005, 1992) based Line-By-Line Radiative Transfer Model (LBLRTM2). This model has been used before for removing telluric lines, among others, by Seifahrt et al. (2010). Unfortunately, LBLRTM always includes the absorption of water in the spectra, hence, we divided by the spectra for water to create the O2 spectra, for instance.
A simple polynomial interpolator is used for deriving the absorption spectra used in the fit. Since we handle all the molecules individually, a fifth order polynomial is fitted to each wavelength point for all the spectra for a given molecule. Evaluating this polynomial with the abundance of the corresponding molecule gives us the absorption spectra Tn, which are multiplied to obtain the final telluric spectrum; this spectrum is finally convolved with a kernel C to allow for a line shift and broadening as with the stellar model spectra.
The model spectrum used for fitting the observation now is just the stellar model multiplied with the telluric model ![\begin{equation} G = \sum\limits_{k=1}^{K} \omega_k \left[ B_k \ast M_k \right] \cdot C \ast \prod\limits_{n=1}^{N} T_n. \end{equation}](/articles/aa/full_html/2016/04/aa26949-15/aa26949-15-eq86.png) (5)By adding these terms, we increase the number of free parameters in the fit by N + 2, i.e. one for each of the N molecules plus line shift σtell and broadening vrad,tell. While N = 3 for MUSE, we have shown before in Husser & Ulbrich (2014) that this method works well for spectra with a wider wavelength range by using more molecules (CO2, N2O, and CH4). By using a simple polynomial for the interpolation, the increase in computation time as compared to a fit without tellurics is almost negligible.
(5)By adding these terms, we increase the number of free parameters in the fit by N + 2, i.e. one for each of the N molecules plus line shift σtell and broadening vrad,tell. While N = 3 for MUSE, we have shown before in Husser & Ulbrich (2014) that this method works well for spectra with a wider wavelength range by using more molecules (CO2, N2O, and CH4). By using a simple polynomial for the interpolation, the increase in computation time as compared to a fit without tellurics is almost negligible.
An example for the Fraunhofer A band found in a typical G subgiant from our sample is shown in Fig. 6. As one can see, the residuals are of the order of a few per cent of the flux, which is of the same order as the noise at a S/N of about 100. The positions of two K i absorption lines from the interstellar medium (ISM) are shown in the residuals with arrows. A detailed discussion on ISM and diffuse interstellar bands (DIBs) will be presented in another part of this series (Wendt et al., in prep.).
This method yields one telluric spectrum per extracted stellar spectrum, i.e. thousands of telluric spectra per pointing that can be averaged to obtain the most likely telluric spectrum. However, tests showed that fitting the extracted stellar spectra with this fixed telluric component neither improves the results nor reduces the computation time significantly.
5. Results
5.1. Uncertainties
For some of the stars in the sample, we have more than one spectrum from overlapping pointings or from multiple visits. These independent observations allow us to investigate the quality of the statistical uncertainties returned by the Levenberg-Marquardt optimisation. Having pairs X1 and X2 of results for the same star and their respective uncertainties σX1 and σX2, we can calculate the normalised error δX as 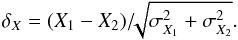 (6)Although in general δX is distributed in a Student-t distribution, for small uncertainties on the uncertainties it can be described using a normal distribution, which should have a standard deviation of 1 in the case of accurate uncertainties. Our results yielded 1.50 for Teff and 1.24 for [M/H], so the formal fitting errors underestimate the real statistical uncertainties by ~50% and ~24%, respectively.
(6)Although in general δX is distributed in a Student-t distribution, for small uncertainties on the uncertainties it can be described using a normal distribution, which should have a standard deviation of 1 in the case of accurate uncertainties. Our results yielded 1.50 for Teff and 1.24 for [M/H], so the formal fitting errors underestimate the real statistical uncertainties by ~50% and ~24%, respectively.
Average formal uncertainties from full-spectrum fit for Teff and [Fe/H] in given S/N intervals, scaled by the factor determined by the analysis of the statistical errors.
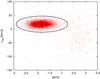 |
Fig. 7 Measured radial velocities vrad over metallicities [M/H]. A kappa-sigma clipping at 3σ (indicated by the overplotted ellipse) on this data is used for determining membership of stars to the cluster. |
A list of scaled uncertainties from the full-spectrum fit for several S/N intervals is given in Table 2. Hence, for a typical spectrum from a MUSE observation with a S/N of 20, we can expect to derive the effective temperature with an uncertainty of ~100 K and the metallicity is accurate to 0.16 dex.
 |
Fig. 8 HRD of NGC 6397 with luminosities plotted as a function of effective temperatures, colour coded by metallicity. The assumed reddening is E(B − V) = 0.18 with a distance modulus of 12.13 mag. The area on the giant branch indicated with a red rectangle is discussed in Sect. 5.4. |
 |
Fig. 9 Distributions of the effective temperature Teff, the surface gravity log g, the metallicity [M/H], and the radial velocity vrad as determined in the fits. |
These are of course only statistical errors. We excluded that there are strong systematic errors from our full-spectrum fits caused by the used spectral library by fitting some spectra against cflib (Valdes et al. 2004) and ELODIE (Prugniel & Soubiran 2004), which both yielded comparable results. As stated before, we also tested our spectral library directly against other libraries, which did not show any systematics either. However, some deviations are expected to be caused by non-local thermodynamic equilibrium (NLTE) effects, which are discussed in more detail in Sect. 5.5.
5.2. Radial velocities
We obtained all the following results for members of the globular cluster only. We defined membership using a simple 3σ clipping in vrad-[M/H] space as shown in Fig. 7. An implementation of the more elaborate method as described by Walker et al. (2009) is in progress. Since the results described in this publication do not depend critically on determination of membership, the application of that technique will be discussed in Paper II. With the current method, we determined 7142 (~56%) of the observed stars to be members of NGC 6397.
The distribution of all spectra with S/N> 20 is plotted in the right panel of Fig. 9. We measure a mean radial velocity of vrad = 17.84 ± 0.07 km s-1 (σ = 6.29 km s-1), which is a little smaller than the values given in previous studies, but still in good agreement
-
vrad = 18.26 ± 0.09 km s-1 by Milone et al. (2006),
-
vrad = 18.1 ± 0.3 km s-1 by Lind et al. (2008),
-
vrad = 22.75 ± 7.1 km s-1 by Carretta et al. (2009a),
-
vrad = 20.3 ± 0.3 km s-1 by Lovisi et al. (2012).
Another parameter coming from the full-spectrum fit is the radial velocity shift of the telluric spectrum. This can be used to investigate the quality of the velocity results, since it should be close to zero with only a small scatter. To achieve this, we had to subtract the barycentric correction, which is carried out automatically by the pipeline. From our results we obtain vtell = 0.4 km s-1 with a standard deviation of σtell = 2.0 km s-1s. These are consistent with the expected accuracy of the measurements. The little offset seen in the tellurics is most likely caused by a slight asymmetry of the MUSE LSF, which we have not yet modelled correctly.
A more in-depth analysis of the cluster dynamics, including a discussion of the corresponding uncertainties, will be presented in Paper II.
5.3. Effective temperatures and photometric surface gravities
We can easily determine absolute V magnitudes from our spectra with a reddening of E(B − V) = 0.18 and a distance modulus of 12.13 mag (see Reid & Gizis 1998). Applying the polynomial for the bolometric correction from Flower (1996) and the corrections in Torres (2010), those V magnitudes can be converted into luminosities. Together with the effective temperatures from the full-spectrum fit we can plot an HRD, which is shown in Fig. 8, colour coded with the metallicities derived from the fit. We plot the results for all member stars with spectra with S/N> 20, i.e. a total of 3870 stars (54% of the cluster members). To our knowledge, a HRD as detailed as this has never been presented before for a single globular cluster from spectroscopic data. All HB stars are missing in the HRD because we currently do not have matching templates for fitting their spectra.
A comparison of our photometrically obtained surface gravities for single stars with values from the literature is plotted in Fig. 10. Since most of the presented studies, some with a rather large sample, concentrated on outer fields of the cluster, we could only match a small number of stars to our data. The matching itself has been carried out by comparing RA/Dec coordinates and magnitudes.
All the studies that we have discussed determined Teff and log g photometrically, even though these studies used the FLAMES spectrograph at the VLT. Lovisi et al. (2012) used a method similar to the isochrone comparison that we used for our initial guesses, deriving values for Teff and log g from theoretical stellar models from the BaSTI database (Pietrinferni et al. 2006). Lovisi et al. (2012) compared those to another set of isochrones with different ages in order to use this procedure on blue straggler stars. The other three studies (Carretta et al. 2009a,b; Lind et al. 2009) utilised a calibration based on colour indices as described by Alonso et al. (1999), which only works for red giant stars.
Since we fix the surface gravities to the values obtained photometrically, we can compare those values directly to the literature (see Fig. 10), which yields an offset of δlog g = 0.01 with a scatter of 0.07. Ignoring the results from Lovisi et al. (2012) that mainly consists of blue stragglers, which we currently do not fit properly, this number decreases to δlog g = 0.00 ± 0.04.
 |
Fig. 10 Comparison of our results for log g for single stars that have been analysed before in other studies, all obtained photometrically. The values with the largest deviations by Lovisi et al. (2012) are mainly those of blue stragglers, which we currently cannot fit properly. |
A comparison of the photometric values for Teff from the same publications with our results yields a rather small δTeff = −68.34 ± 62.63 K. On the other hand, it is still unclear whether our photometric or spectroscopic results for Teff, which are compared in Fig. 11, are more accurate. Although the differences are usually small with δT< 200 K, we see some systematic discrepancies.
One possible explanation for these systematic discrepancies might be NLTE effects, which are discussed in Sect. 5.5, but these discrepancies seem more likely to be a simple mismatch of the isochrone. Since the comparison with an isochrone was only meant to obtain initial guesses, we picked the isochrone manually by eye. Tests showed that the error inflicted on the derived surface gravities is small (of the order of Δlog g ≲ 0.1 dex), but that the deviations in colour can be large, which directly affects the effective temperature. This is especially the case at the TO and on the red giant branch (RGB). Since the value for Teff is used as initial guess only, however, this discrepancy is acceptable.
 |
Fig. 11 Comparison of our photometric and spectroscopic results for Teff as a function of log g. The red error bars indicate the mean and standard deviation of the discrepancies in 0.5 dex wide bins. Overplotted in blue and green are predicted offsets due to neglected NLTE effects as shown in Lind et al. (2012). See text for details. |
5.4. Metallicities
As discussed before, we measure two different kinds of metallicities: if [α/Fe] is fixed to zero in the fit, we denote the metallicity [M/H], and [Fe/H] otherwise. The distribution for both is shown in Fig. 9. In the following, we mainly concentrate on [M/H], which we expect to be more accurate.
The mean values were fitted as [M/H] = −1.962 ± 0.002 (σ = 0.181) and [Fe/H] = −2.120 ± 0.002 (σ = 0.214). We employed a maximum likelihood technique, as described by Pryor & Meylan (1993) for determining the intrinsic dispersion, which is about 0.14 dex for both quantities. This also increases the mean values slightly by about 0.02 dex, since usually results for stars with lower metallicities have larger uncertainties.
As mentioned before, we found some discrepancies between the values for Teff obtained spectroscopically and from the comparison with an isochrone (see Fig. 11). Since shifting Teff also changes [M/H], we determined the metallicity for the central field again with both Teff and log g fixed to the values derived from the isochrone. As a result we found that the metallicity is shifted slightly with a maximum offset of [ M / H ] spec − [ M / H ] phot = −0.07 dex at the turnoff, where the difference in Teff is largest.
Most recent studies of NGC 6397 based their metallicity values on equivalent width measurements of Fe i and Fe ii lines, which correspond to our [Fe/H] values. For stars between the TO point and the tip of the RGB, Lind et al. (2009) found [Fe/H] = −2.10. A similar value of [Fe/H] = −2.12 ± 0.01 was found by Lovisi et al. (2012) for stars near the TO. All these results are in good agreement with our value for [Fe/H]. On the other hand, Carretta et al. (2009b) reported [Fe/H] = −1.993 ± 0.003 for stars along the RGB, which differs significantly from the other values.
A comparison of results for the metallicity of individual stars with values from the literature is plotted in Fig. 12. We present our results for [M/H], which show a deviation from the literature values of δ = 0.12 ± 0.10 dex. While the offset is in good agreement with the difference between our mean metallicity results, i.e. ⟨[ M / H ] ⟩ − ⟨ [ Fe / H ] ⟩ = 0.16 dex (indicated as a dashed cyan line), the small standard deviation confirms our goal of determining metallicities with an accuracy of 0.1 dex or better.
In the HRD (Fig. 8) we see a variation in metallicity, which gets more pronounced when plotting [M/H] over luminosity (see Fig. 13, for all spectra with S/N> 20). Starting on the main sequence with a metallicity of [ M / H ] ≈ −1.8 dex, this value decreases until it hits a minimum at the turnoff point with [ M / H ] ≈ −2.1 dex. Afterwards this value increases again and shows some minor oscillation within the uncertainties around [ M / H ] ≈ −1.9 dex. Altogether we see the largest variations on the MS and subgiant branch (SGB), while those on the RGB are significantly smaller.
 |
Fig. 12 Comparison of results for [M/H] with those from previous high-resolution studies. The dashed cyan line indicates the offset between our mean results for [Fe/H] and [M/H] of 0.16 dex. |
Figure 14 concentrates on the increase of metallicity on the RGB after this minimum (around 5750 K). We plot the metallicity as a function of effective temperature for all spectra with S/N> 50 and log g < 4.4, i.e. for all stars at the TO and on the RGB. Again, one can see a significant trend, which does not disappear with the photometric Teff described above.
A similar phenomenon has been reported by Korn et al. (2007) and Nordlander et al. (2012), who suggested that extremely metal-poor stars are heavily affected by atomic diffusion. In that scenario, heavy elements in stars on the main sequence sink deeper into the atmosphere and slowly disappear from the spectrum. When reaching the turn-off, convection kicks in and transports the heavy elements back up into the higher atmosphere, so we should observe an increase of metallicity for stars evolving on the RGB. Model calculations have been carried out by Korn et al. (2007), showing the expected trend. For iron abundance, those models (Olivier Richard, priv. comm., blue line in Fig. 14) predict a change of Δ [ Fe / H ] = 0.12 dex around 5750 K, which is a little shallower than what we see in our data (red line in the same figure), but still gives a better fit than a straight line.
 |
Fig. 13 Results for metallicity [M/H] plotted over luminosity L. The bins for the error bars contain at least 100 stars each (except for the last one). The HB stars are indicated with blue crosses and excluded from the binning. |
Bonifacio et al. (2009) also found discrepancies with the abundances for C, Sc, Ti, Cr, Mn, and Co, which are ~0.2 dex larger in TO stars than in giants. Since they see a physical explanation for the abundance shift in C only, they assume that this effect is not real and caused by shortcomings in their analysis.
Atomic diffusion would also explain the decrease in metallicity along the main sequence towards the turn-off as seen in the HRD (see Figs. 8 and 13). Unfortunately, we see a trend that is larger than predicted, so we believe this to be partly caused by the low S/N of the spectra on the main sequence.
When assuming that there is atomic diffusion happening in the atmospheres of the stars, giving a mean metallicity for the cluster is somewhat problematic; the majority of stars in our sample is near the TO, where the change in metallicity caused by diffusion is supposed to be strongest, which would result in a lower mean value. Therefore we measured the metallicity for stars near the tip of the RGB with log g < 3 and Teff < 5400 K, where the change in metallicity due to diffusion is negligible. The mean S/N of the spectra from those stars is ~150 and we get a mean metallicity of ⟨[ M / H ] ⟩RGB tip = −1.875 ± 0.003 dex. With the offset discussed before this yields ⟨[ Fe / H ] ⟩RGB tip = −2.04 dex, which is still in good agreement with literature values.
 |
Fig. 14 Metallicity trend with effective temperature for all spectra with log g < 4.4 (i.e. stars between the TO and the tip of the RGB) and S/N> 50. Overplotted with a solid red line are the mean values and standard deviations of the metallicity in 250 K wide bins. The same is plotted again with a dashed red line including a correction (Lind et al. 2012) for NLTE effects (with the same uncertainties). Overplotted in blue is an isochrone including atomic diffusion (Richard, priv. comm.). See text for details. |
5.5. Effects of NLTE
We are fully aware that analysing spectra of low-metallicity stars, such as those in our sample with LTE model spectra, has some shortcomings. An overview of this topic is given by Asplund (2005) and, more recently, by Bergemann & Nordlander (2014) for the FGK regime.
Possible errors that might occur when running an analysis with LTE model spectra were discussed in Lind et al. (2012), based on NLTE models presented in Bergemann et al. (2012). The authors determined the offsets in stellar parameters obtained from LTE and NLTE analyses. For Teff two different values are given, depending on the type of measurement, i.e. derived from either the ionisation balance of high-excitation Fe i and Fe ii lines (ΔTeff,ion) or from their excitation balance (ΔTeff,exc). Under the assumption that our Teff,spectroscopic is the real effective temperature, we calculated both corrections, which are shown with green and blue dashed lines in Fig. 11. While ΔTeff,exc can be ignored completely for our purposes (≲ 10 K), ΔTeff,ion is almost constant on the RGB and only shows some significant variations at the TO and on the MS. However, these corrections do not match the discrepancies between our photometric and spectroscopic results. So although errors due to the LTE analysis may be present, they cannot explain the observed deviations, making an isochrone mismatch (as discussed before) more likely.
It can be questioned whether these NLTE corrections apply to our results with their full amount. Instead of measuring Fe i and Fe ii lines only, we fit a model to the full observed spectrum. A closer look to the NLTE effects caused by other elements can be obtained when using corrections from Bergemann & Nordlander (2014). The most prominent lines in our spectra (besides those from hydrogen) are created by Mg, Ca, and Fe, so Table 3 lists the NLTE corrections for these elements for the three stars HD 84937 (TO), HD 140283 (SGB), and HD 122563 (RGB). As one can see, the variation of the corrections between TO and RGB is at most 0.05 dex, i.e. well within our targeted accuracies. Nevertheless, this correction would make the systematic offset between TO and RGB slightly larger.
NLTE effects might also be responsible for the metallicity trend discussed in Sect. 5.4. In Fig. 14 we also show the measured metallicities with applied NLTE corrections from Lind et al. (2012) with a dashed red line. As one can see, this results in a shift with almost constant offset of 0.06−0.08 dex with a maximum of ~0.1 dex in the coolest bin. The NLTE corrections for other elements provided by Bergemann & Nordlander (2014) also show only small variations between TO and RGB and would just shift the metallicity for all stars by ~0.15 dex (Mg) and ~0.20 dex (Ca), respectively.
Altogether the deviations caused by NLTE effects seem to be almost constant (within the uncertainties) for all stars within our sample. Therefore, it is unlikely that NLTE effects alone can explain the metallicity trend that we observe on the giant branch.
5.6. sdO star ROB 162
The massive multiplexing capabilities of MUSE offer the possibility of finding peculiar objects. One such object is ROB 162 (GSC 08729-01093), which can easily be identified in the CMD (see Fig. 3) because it is a little blueward of the HB. It was identified by Heber & Kudritzki (1986) as a post-AGB star with 0.5−0.55 M⊙ and these authors assume it is the central star of a planetary nebula. However, no nebula was found and we also cannot detect any emission features in the MUSE data, leaving the explanation that it is already dispersed or too faint. Using NLTE model atmospheres they found Teff = 52 000 K, log g = 4.5, and a solar helium abundance.
The observed spectrum of ROB 162 is plotted in Fig. 15. Overplotted is a TMAP3 spectrum with Teff = 52 000 K, log g = 4.5, and solar helium abundances by Dreizler et al. (1990) with updates described in Werner & Dreizler (1999).
 |
Fig. 15 Observed spectrum of sdO star ROB 162, in which the telluric lines have been removed. Overplotted in red in the inset is a synthetic spectra from Dreizler et al. (1990) with log g = 4.5, Teff = 52 000 K, and solar helium abundances. |
Since there are no spectra of post-AGB stars in our PHOENIX library, the general pipeline fit determined ROB 162 to be a very metal poor ([Fe/H] = −3.4) F type dwarf, which matches the hydrogen lines surprisingly well, of course without showing any He lines. The radial velocity resulting from this is vrad = 21 ± 2 km s-1. When fitting with the TMAP spectra we obtain 29 ± 1 km s-1 s. This difference is caused by the He ii absorption lines close to Hα and Hβ, which make their profiles slightly asymmetric. Therefore, the TMAP result should be the more trustworthy value, which can be compared to the radial velocity vrad = 28 ± 5 km s-1 found by Heber & Kudritzki (1986).
This result is only 2σ off the mean velocity of the cluster, so in combination with its position in the CMD near the HB and its proximity to the cluster centre (~2 arcmin, well within the 2.90 arcmin half-light radius), we conclude that ROB 162 really is a member of NGC 6397.
5.7. Possible pulsar companion
Another interesting object is Cl* NGC 6397 SAW V31, for which we have two observations 22 h apart. Our analysis identifies it as K subgiant with log g≈ 3.6 and Teff≈ 4200 K. It was fitted with a very low metallicity with [M/H] ≈−3.
Figure 16 shows the full-spectrum of one of the observations, where one can clearly identify the Hα emission line, which is also shown in the inset for both obtained spectra. In this emission line one can see a large radial velocity shift of Δvrad = 145.9 km s-1.
For this object, Kaluzny et al. (2006) observed a periodicity of ~1.3 days, possibly due to ellipsoidal variations. They also connected it to the hard X-ray source U18, which was discovered by Grindlay et al. (2001) and identified either as a BY Dra type variable or a millisecond pulsar. This connection, however, was challenged by Bogdanov et al. (2010), who claim the two objects are too far apart.
A radial velocity shift as large as the shift we have discovered can easily be caused by the motion of V31 within a binary system. If the companion is indeed a pulsar, we can furthermore speculate that our K subgiant may have a hot day and a cooler night side, which could explain both the reported variability and strong variation in the strength of the Hα line in our spectra. With the given period and velocity this yields a lower limit for the total mass of ~0.4 M⊙ in the system, which is consistent with our suggestion.
NLTE corrections for single elements as taken from Bergemann & Nordlander (2014).
6. Conclusions and outlook
We demonstrated how the use of an IFS such as MUSE dramatically increases the number of globular cluster stars available for spectroscopic analyses. Instead of a preselected list of just a few hundred spectra per observation campaign, we can obtain thousands of medium-resolution spectra of individual stars per exposure.
Although obtained with a spectral resolution lower than in most other studies, we showed that our spectra are still sufficient for investigating both the atmospheric parameters and kinematics of the stars. While the results for a single spectrum might be less accurate, the huge amount of data allows for new statistical approaches, resulting in uncertainties that are not larger than in high-resolution studies. On the other hand, the broad wavelength range of MUSE allows us to determine spectroscopically atmospheric parameters, such as Teff and [M/H]. In principle, this should also be possible for log g, for which we still suffer from our incomplete knowledge of the LSF that needs to be further investigated, resulting in the surface gravity that is currently determined photometrically. Overall, we can reproduce results from high-resolution spectroscopic studies very well.
 |
Fig. 16 One observation of the possible pulsar companion V31 as observed with MUSE. The best fit, identifying it as a K subgiant, is overplotted. The inset zooms into the region around Hα, showing the line in emission in both observed epochs and significantly shifted to each other. |
In this paper, we presented spectroscopic observations of 12 307 stars of which we determined 7142 to be members of the globular cluster NGC 6397, and most of them (87%) are below the TO. For 3870 of those stars, we obtained spectra with S/N> 20, from which we derived atmospheric parameters and constructed a HRD. To our knowledge, this is the most comprehensive HRD of a globular cluster obtained from spectroscopy so far.
The large number of stars in our sample allows us to investigate problems, which until now have only been explored using a few stars, for instance the variation of abundances with effective temperature in the atmospheres of RGB stars. There are indications that the trend that is visible in our data, a sample of almost 4000 spectra of more than 2000 stars at the TO and on the RGB, is real. Extending our methods for measuring the abundances of single elements (like Mg and Ca) and including NLTE effects will allow us to investigate this in more detail in many clusters.
We are aware of some shortcomings in our analysis and discussed the problems of using LTE model spectra and thus ignoring NLTE effects in detail. Fixing the surface gravity to a value obtained photometrically, which is an approach commonly found in the literature, is an inconsistency in our analysis; this effect should be small, however. The model spectra used for the analysis are another potential issue; each synthetic spectral library uses other parametrisations for, for example, the mixing length and macro- and microturbulence, uses other line data and opacities, and so on. Therefore, this is not a problem affecting our analyses alone. We are confident that our model spectra are suitable for the task at hand.
As for many other globular clusters, there have also been reports of multiple main sequences found in NGC 6397 (Milone et al. 2012; Nardiello et al. 2015). In this case, however, the effect is so small that we do not expect it to be measurable from MUSE spectra, especially with the rather low S/N values we obtained for spectra of main-sequence stars.
Since we are not observing only hand-picked targets as with classical spectroscopic techniques like long slit and MOS, we expect to get a lot of spectra from a variety of peculiar objects, such as the sdO and the possible pulsar companion described in this publication. While independent science cases will benefit from these findings, it will also help us to better understand the evolution of globular clusters.
The aspect of kinematics has not been addressed in this publication, although it is a topic of great interest with regard to claims of black holes in the centres of globular clusters over the last decade. A comprehensive discussion on the case of NGC 6397 will be presented in Paper II.
Altogether we have to emphasise that the observations presented in this publication were taken during the commissioning of MUSE, and we were constrained by the overall commissioning goals. However, with the start of regular MUSE observations, we began using GTO time for a large survey, targeting about 25 Galactic globular clusters over several epochs. Co-adding spectra from multiple visits will allow us to increase the S/N significantly, resulting in better results for single stars, making it, for instance, more feasible to contribute to the research on multiple populations in globular clusters.
Acknowledgments
S.K. and P.M.W. received funding through BMBF Verbundforschung (project MUSE-AO, grant 05A14BAC and 05A14MGA). Based on observations made with the NASA/ESA Hubble Space Telescope, and obtained from the Hubble Legacy Archive, which is a collaboration between the Space Telescope Science Institute (STScI/NASA), the Space Telescope European Coordinating Facility (ST-ECF/ESA), and the Canadian Astronomy Data Centre (CADC/NRC/CSA).
References
- Alonso, A., Arribas, S., & Martínez-Roger, C. 1999, A&AS, 140, 261 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anderson, J., Sarajedini, A., Bedin, L. R., et al. 2008, AJ, 135, 2055 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M. 2005, ARA&A, 43, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Bacon, R., Accardo, M., Adjali, L., et al. 2010, in SPIE Conf. Ser., 7735, 8 [Google Scholar]
- Bacon, R., Vernet, J., Borisova, E., et al. 2014, The Messenger, 157, 13 [NASA ADS] [Google Scholar]
- Bastian, N., Lamers, H. J. G. L. M., de Mink, S. E., et al. 2013, MNRAS, 436, 2398 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Bellini, A., Bedin, L. R., Piotto, G., et al. 2010, AJ, 140, 631 [NASA ADS] [CrossRef] [Google Scholar]
- Bergemann, M., & Nordlander, T. 2014, ArXiv e-prints [arXiv:1403.3088] [Google Scholar]
- Bergemann, M., Lind, K., Collet, R., Magic, Z., & Asplund, M. 2012, MNRAS, 427, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Bergemann, M., Kudritzki, R.-P., Gazak, Z., Davies, B., & Plez, B. 2015, ApJ, 804, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Bogdanov, S., van den Berg, M., Heinke, C. O., et al. 2010, ApJ, 709, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Bonifacio, P., Spite, M., Cayrel, R., et al. 2009, A&A, 501, 519 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R., & Lucatello, S. 2009a, A&A, 505, 139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2009b, A&A, 505, 117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clough, S. A., Iacono, M. J., & Moncet, J.-L. 1992, J. Geophys. Res., 97, 15761 [NASA ADS] [CrossRef] [Google Scholar]
- Clough, S. A., Shephard, M. W., Mlawer, E. J., et al. 2005, J. Quant. Spectr. Rad. Transf., 91, 233 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- de Mink, S. E., Pols, O. R., Langer, N., & Izzard, R. G. 2009, A&A, 507, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dreizler, S., Heber, U., Werner, K., Moehler, S., & de Boer, K. S. 1990, A&A, 235, 234 [NASA ADS] [Google Scholar]
- Flower, P. J. 1996, ApJ, 469, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Gebhardt, K., Pryor, C., Williams, T. B., & Hesser, J. E. 1995, AJ, 110, 1699 [NASA ADS] [CrossRef] [Google Scholar]
- Gratton, R. G., Carretta, E., & Bragaglia, A. 2012, A&ARv, 20, 50 [CrossRef] [Google Scholar]
- Grindlay, J. E., Heinke, C. O., Edmonds, P. D., Murray, S. S., & Cool, A. M. 2001, ApJ, 563, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, W. E. 1996, AJ, 112, 1487 [NASA ADS] [CrossRef] [Google Scholar]
- Heber, U., & Kudritzki, R. P. 1986, A&A, 169, 244 [NASA ADS] [Google Scholar]
- Husser, T.-O., & Ulbrich, K. 2014, in ASI Conf. Ser., 11, 53 [Google Scholar]
- Husser, T.-O., Kamann, S., Dreizler, S., & Hauschildt, P. H. 2012, in ASI Conf. Ser. 6, eds. P. Prugniel, & H. P. Singh, 71 [Google Scholar]
- Husser, T.-O., Wende-von Berg, S., Dreizler, S., et al. 2013, A&A, 553, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaluzny, J., Thompson, I. B., Krzeminski, W., & Schwarzenberg-Czerny, A. 2006, MNRAS, 365, 548 [NASA ADS] [CrossRef] [Google Scholar]
- Kamann, S., Wisotzki, L., & Roth, M. M. 2013, A&A, 549, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kamann, S., Husser, T.-O., Emsellem, E., et al. 2016, A&A, 588, A149 (Paper II) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kinman, T. D. 1959, MNRAS, 119, 157 [NASA ADS] [Google Scholar]
- Kirby, E. N., Guhathakurta, P., & Sneden, C. 2008, ApJ, 682, 1217 [NASA ADS] [CrossRef] [Google Scholar]
- Koleva, M., Prugniel, P., Bouchard, A., & Wu, Y. 2009, A&A, 501, 1269 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Korn, A. J., Grundahl, F., Richard, O., et al. 2007, ApJ, 671, 402 [NASA ADS] [CrossRef] [Google Scholar]
- Lind, K., Korn, A. J., Barklem, P. S., & Grundahl, F. 2008, A&A, 490, 777 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lind, K., Primas, F., Charbonnel, C., Grundahl, F., & Asplund, M. 2009, A&A, 503, 545 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Lind, K., Bergemann, M., & Asplund, M. 2012, MNRAS, 427, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Lovisi, L., Mucciarelli, A., Lanzoni, B., et al. 2012, ApJ, 754, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Milone, A. P., Villanova, S., Bedin, L. R., et al. 2006, A&A, 456, 517 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Milone, A. P., Marino, A. F., Piotto, G., et al. 2012, ApJ, 745, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Munari, U., Sordo, R., Castelli, F., & Zwitter, T. 2005, A&A, 442, 1127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nardiello, D., Milone, A. P., Piotto, G., et al. 2015, A&A, 573, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nordlander, T., Korn, A. J., Richard, O., & Lind, K. 2012, ApJ, 753, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Pietrinferni, A., Cassisi, S., Salaris, M., & Castelli, F. 2006, ApJ, 642, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Piotto, G., Bedin, L. R., Anderson, J., et al. 2007, ApJ, 661, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Prantzos, N., & Charbonnel, C. 2006, A&A, 458, 135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 2007, Numerical Recipes. The Art of Scientific Computing, 3rd edn. (New York: Cambridge University Press) [Google Scholar]
- Prugniel, P., & Soubiran, C. 2001, A&A, 369, 1048 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prugniel, P., & Soubiran, C. 2004, ArXiv e-prints [arXiv:astro-ph/0409214] [Google Scholar]
- Pryor, C., & Meylan, G. 1993, in Structure and Dynamics of Globular Clusters, eds. S. G. Djorgovski, & G. Meylan, ASP Conf. Ser., 50, 357 [Google Scholar]
- Reid, I. N., & Gizis, J. E. 1998, AJ, 116, 2929 [NASA ADS] [CrossRef] [Google Scholar]
- Sarajedini, A., Bedin, L. R., Chaboyer, B., et al. 2007, AJ, 133, 1658 [NASA ADS] [CrossRef] [Google Scholar]
- Seifahrt, A., Käufl, H. U., Zängl, G., et al. 2010, A&A, 524, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sommariva, V., Piotto, G., Rejkuba, M., et al. 2009, A&A, 493, 947 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stetson, P. B. 1987, PASP, 99, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, G. 2010, AJ, 140, 1158 [NASA ADS] [CrossRef] [Google Scholar]
- Valdes, F., Gupta, R., Rose, J. A., Singh, H. P., & Bell, D. J. 2004, ApJS, 152, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Ventura, P., D’Antona, F., Mazzitelli, I., & Gratton, R. 2001, ApJ, 550, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, M. G., Mateo, M., Olszewski, E. W., Sen, B., & Woodroofe, M. 2009, AJ, 137, 3109 [NASA ADS] [CrossRef] [Google Scholar]
- Weilbacher, P. M., Streicher, O., Urrutia, T., et al. 2012, in SPIE Conf. Ser., 8451 [Google Scholar]
- Wende, S., Reiners, A., & Ludwig, H.-G. 2009, A&A, 508, 1429 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Werner, K., & Dreizler, S. 1999, J. Comput. Appl. Math., 109, 65 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Parameter space of the PHOENIX grid of model spectra used for fitting the observations.
Average formal uncertainties from full-spectrum fit for Teff and [Fe/H] in given S/N intervals, scaled by the factor determined by the analysis of the statistical errors.
NLTE corrections for single elements as taken from Bergemann & Nordlander (2014).
All Figures
 |
Fig. 1 V-band image extracted from the mosaic of MUSE datacubes of NGC 6397. Overplotted are the single pointings, which have been observed multiple times at different position angles and with little offsets. Two of the planned pointings were not carried out, so the mosaic is incomplete. The colour coding indicates the number of stellar spectra that were extracted from each pointing, ranging from ~1700 in the central pointing to about 400 in the outer fields. The dashed blue line indicates the area covered by the ACS survey of Galactic globular clusters (Sarajedini et al. 2007). |
| In the text | |
 |
Fig. 2 Deblending of stellar spectra on MUSE data. The top left panel shows a white light image of the central MUSE datacube in NGC 6397. A zoom into the area indicated with a red square is shown in the top middle panel. In the top right panel, the same field of view is shown as seen with HST. All stars for which spectra were extracted are shown with crosses. Spectra extracted from the stars indicated with the red and green crosses are shown in the bottom panel and show clearly distinct features without any contamination from each other. The star indicated in red was determined to be a late-type G star, while the star in green is type A. The spectra are continuum subtracted and normalised and the areas dominated by telluric absorption are indicated in grey for clarity. |
| In the text | |
 |
Fig. 3 CMD of NGC 6397 generated from the input catalogue with colour-coded S/Ns of extracted spectra. The two stars denoted with circles are discussed in Sects. 5.6 and 5.7. Overplotted in black is an isochrone of 13.5 Gyrs in age and a metallicity of Z = 0.0014 (i.e. [Fe/H] ≈ –2.13). |
| In the text | |
 |
Fig. 4 Distribution of S/Ns for the extracted spectra is plotted in red. Overplotted in blue is the cumulative distribution, showing that about 50% of the spectra have S/N> 10. |
| In the text | |
 |
Fig. 5 Full widths at half maximum (FWHM) of the line spread functions of all 24 IFUs of MUSE at different wavelengths as taken from a single exposure. |
| In the text | |
 |
Fig. 6 Fraunhofer A band and the best-fitting model in the spectrum of a typical G subgiant in our sample. The positions of two K i absorption lines from the interstellar medium are indicated with blue arrows in the residuals. |
| In the text | |
 |
Fig. 7 Measured radial velocities vrad over metallicities [M/H]. A kappa-sigma clipping at 3σ (indicated by the overplotted ellipse) on this data is used for determining membership of stars to the cluster. |
| In the text | |
 |
Fig. 8 HRD of NGC 6397 with luminosities plotted as a function of effective temperatures, colour coded by metallicity. The assumed reddening is E(B − V) = 0.18 with a distance modulus of 12.13 mag. The area on the giant branch indicated with a red rectangle is discussed in Sect. 5.4. |
| In the text | |
 |
Fig. 9 Distributions of the effective temperature Teff, the surface gravity log g, the metallicity [M/H], and the radial velocity vrad as determined in the fits. |
| In the text | |
 |
Fig. 10 Comparison of our results for log g for single stars that have been analysed before in other studies, all obtained photometrically. The values with the largest deviations by Lovisi et al. (2012) are mainly those of blue stragglers, which we currently cannot fit properly. |
| In the text | |
 |
Fig. 11 Comparison of our photometric and spectroscopic results for Teff as a function of log g. The red error bars indicate the mean and standard deviation of the discrepancies in 0.5 dex wide bins. Overplotted in blue and green are predicted offsets due to neglected NLTE effects as shown in Lind et al. (2012). See text for details. |
| In the text | |
 |
Fig. 12 Comparison of results for [M/H] with those from previous high-resolution studies. The dashed cyan line indicates the offset between our mean results for [Fe/H] and [M/H] of 0.16 dex. |
| In the text | |
 |
Fig. 13 Results for metallicity [M/H] plotted over luminosity L. The bins for the error bars contain at least 100 stars each (except for the last one). The HB stars are indicated with blue crosses and excluded from the binning. |
| In the text | |
 |
Fig. 14 Metallicity trend with effective temperature for all spectra with log g < 4.4 (i.e. stars between the TO and the tip of the RGB) and S/N> 50. Overplotted with a solid red line are the mean values and standard deviations of the metallicity in 250 K wide bins. The same is plotted again with a dashed red line including a correction (Lind et al. 2012) for NLTE effects (with the same uncertainties). Overplotted in blue is an isochrone including atomic diffusion (Richard, priv. comm.). See text for details. |
| In the text | |
 |
Fig. 15 Observed spectrum of sdO star ROB 162, in which the telluric lines have been removed. Overplotted in red in the inset is a synthetic spectra from Dreizler et al. (1990) with log g = 4.5, Teff = 52 000 K, and solar helium abundances. |
| In the text | |
 |
Fig. 16 One observation of the possible pulsar companion V31 as observed with MUSE. The best fit, identifying it as a K subgiant, is overplotted. The inset zooms into the region around Hα, showing the line in emission in both observed epochs and significantly shifted to each other. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


