| Issue |
A&A
Volume 587, March 2016
|
|
|---|---|---|
| Article Number | A103 | |
| Number of page(s) | 11 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201527379 | |
| Published online | 25 February 2016 | |
Long-term radial-velocity variations of the Sun as a star: The HARPS view
1 INAF−Osservatorio Astrofisico di Catania, via S. Sofia, 78, 95123 Catania, Italy
e-mail: nuccio.lanza@oact.inaf.it
2 INAF−Osservatorio Astronomico di Trieste, via G. B. Tiepolo, 11, 34143 Trieste, Italy
e-mail: molaro@oats.inaf.it
3 Universidad Andres Bello, Departamento de Ciencias Fisicas, Republica 220, Santiago, Chile
e-mail: lorenzo.monaco@unab.cl
4 School of Physics and Astronomy, University of St. Andrews, St. Andrews KY16 9SS, UK
e-mail: rdh4@st-andrews.ac.uk
5 Harvard-Smithsonian Center for Astrophysics, 60 Garden Street, Cambridge, MA 02138, USA
e-mail: raphaelle.haywood@cfa.harvard.edu
Received: 16 September 2015
Accepted: 16 January 2016
Context. Stellar radial velocities play a fundamental role in the discovery of extrasolar planets and the measurement of their physical parameters as well as in the study of stellar physical properties.
Aims. We investigate the impact of the solar activity on the radial velocity of the Sun using the HARPS spectrograph to obtain measurements that can be directly compared with those acquired in the extrasolar planet search programmes.
Methods. We used the Moon, the Galilean satellites, and several asteroids as reflectors to measure the radial velocity of the Sun as a star and correlated this velocity with disc-integrated chromospheric and magnetic indexes of solar activity that are similar to stellar activity indexes. We discuss in detail the systematic effects that affect our measurements and the methods to account for them.
Results. We find that the radial velocity of the Sun as a star is positively correlated with the level of its chromospheric activity at ~95 percent significance level. The amplitude of the long-term variation measured in the 2006−2014 period is 4.98 ± 1.44 m/s, which is in good agreement with model predictions. The standard deviation of the residuals obtained by subtracting a linear best fit is 2.82 m/s and is due to the rotation of the reflecting bodies and the intrinsic variability of the Sun on timescales shorter than the activity cycle. A correlation with a lower significance is detected between the radial velocity and the mean absolute value of the line-of-sight photospheric magnetic field flux density.
Conclusions. Our results confirm similar correlations found in other late-type main-sequence stars and provide support to the predictions of radial velocity variations induced by stellar activity based on current models.
Key words: techniques: radial velocities / planets and satellites: detection / Sun: activity / Sun: magnetic fields / stars: activity
© ESO, 2016
1. Introduction
Extrasolar planets were first detected by measuring the radial velocity (hereafter RV) oscillations of the host stars induced by their orbital motion (cf. Mayor & Queloz 1995). This method allows us to measure the orbit eccentricity and true mass of a planet when it transits across the disc of the host star, thus, allowing us to measure the inclination of its orbital plane. The new frontier is the detection of Earth-mass planets and the measurement of their mass (cf. Dumusque et al. 2014; Haywood et al. 2014), which is made difficult by the apparent RV variations of the host star produced by its p-mode oscillations, surface convection, and magnetic activity. While the first two effects can be mitigated by averaging several observations on the same night (Dumusque et al. 2011) or on consecutive nights (Meunier et al. 2015), taking magnetic activity into account is much more complex and it can mimic a planetary signal on a variety of timescales (e.g., Santos et al. 2014). In particular, the detection of planets with orbital periods of several years or decades can be hampered by the RV modulations associated with stellar activity cycles (e.g., Santos et al. 2010; Lovis et al. 2011; Gomes da Silva et al. 2012; Carolo et al. 2014; Moutou et al. 2015).
A detailed understanding of this phenomenon and of the correlations between the RV and the magnetic activity indexes can be achieved by observations of the Sun as a star because we have simultaneous information on the disc position and parameters of the individual active regions. This allows us to test models that predict activity-induced RV perturbations from resolved images of the disc of the Sun such as those introduced by Lagrange et al. (2010) or Meunier et al. (2010a). They consider the effect of surface brightness inhomogeneities, either sunspots or faculae, which produce a distortion of the spectral line profiles that depend on their contrast, filling factor, position, and rotation velocity of the Sun. In addition to this effect, there is a quenching of convective motions by the magnetic fields that affects the line convective blueshifts. Which effect prevails depends on several factors, notably the filling factor of the active regions and the projected rotational velocity of the star. Moreover, while the effect of the brightness inhomogeneities can be either positive or negative, depending on the sign of their contrast and the location on the receding or approaching half of the solar disc, the magnetic quenching of convection always produces an apparent redshift (e.g., Lanza et al. 2010, 2011).
Meunier et al. (2010a) found that the main effect on the Sun-as-a-star RV measurements is produced by the quenching of the local convective flows in active regions. This leads to an apparent redshift in the synthetic RVs that appears to be positively correlated with activity indexes, such as the chromospheric Ca II H&K line core emission (Meunier & Lagrange 2013).
To confirm these model predictions, we need RV measurements of the Sun as a star that extend over a significant part of a solar activity cycle to sample the variations at different activity levels. Long-term sequences spanning more than 35 yr have been acquired to study the global oscillations of the Sun, but they are based on the measurement of the Doppler shift of a single or a few spectral lines. For example, Roca Cortés & Pallé (2014) found a clear anticorrelation between the RV variation as measured from the KI 769.9 nm line and the international sunspot number. These observations are not comparable to the stellar observations which are based on the simultaneous measurements of thousands of photospheric spectral lines to increase precision as, for example, in the case of the HARPS spectrograph (Mayor et al. 2003). Other investigations support this conclusion by confirming that the long-term RV variations of the Sun as a star depend on the specific spectral range considered (Jimenez et al. 1986; McMillan et al. 1993; Deming & Plymate 1994). Meunier et al. (2010b) extrapolated the RV variations as measured by the Michelson Doppler Imager on board of the Solar and Heliospheric Observatory (MDI/SoHO) in the Ni line at 676.8 nm to obtain the solar disc-integrated RV variations along cycle 23. They confirmed the dominant role of the suppression of convective line shifts in magnetized regions as predicted by Meunier et al. (2010a).
Instruments designed to integrate light over the solar disc and feed high-resolution spectrographs for star-like RV measurements are under construction or just beginning their commissioning phase (Glenday et al., in prep.; Dumusque et al. 2015; Strassmeier et al. 2015). Therefore, we adopt a different approach that exploits the optical solar spectrum as reflected by an asteroid, a Jupiter satellite, or a small area on the Moon (Zwitter et al. 2007; Molaro & Centurión 2011; Molaro & Monai 2012). This avoids the effects of the differential extinction across the disc of the Sun in the Earth atmosphere that can reach up to tens of m/s when integrating the flux over the solar disc (cf. McMillan et al. 1993).
2. Observations
We searched the ESO HARPS archive looking for RV observations of asteroids, the Galilean satellites, or the Moon, and found a good deal of measurements acquired between 2006 and 2014 (cf. Table 1)1. The Vesta time series acquired between 29 September and 7 December 2011 gives information on the impact of solar activity on the intra-night or daily variability of the RV of the Sun as a star and is investigated elsewhere (Haywood et al. 2016). Here we use only a few measurements of that dataset to complement our series because we are interested in variations over a longer timescale.
Individual HARPS spectra cover the range 378–691 nm with a gap between 530 and 533 nm. The instrument has a fixed configuration with a spectral resolution of λ/ Δλ ~ 120 000. The exposure time ranges from 30 to 3600 s according to the apparent magnitude of the target, thus giving a photon noise error from ~0.2 to ~1.0 m/s. The spectrograph is in vacuum and thermally isolated and is equipped with an image scrambler that provides a uniform pupil illumination, thus allowing very precise and stable RV measurements. The intra-night and long-term stability stays within 1.0 m/s for bright targets and it is checked by means of a reference Th–Ar lamp whose spectrum is occasionally sent on a second fiber for a simultaneous comparison with the target spectrum. The RV values are obtained through the HARPS Data Reduction System (DRS) by cross-correlating the source spectrum with a template obtained from the high-resolution Fourier Transform Spectrometer solar spectrum by Kurucz et al. (1984). The RV zero point of this spectrum is uncertain by ≈100 m/s, which explains the offset of about 100 m/s that we have in our measurements (see also Molaro & Monai 2012). An accurate estimate is not possible because the Sun is always active, thus we decided to leave it in our sequence because it is a constant that does not affect our investigation of the solar RV variations in any way.
HARPS radial velocity measurements of the Sun as a star.
The RV value given by the DRS is successively corrected for the Doppler shifts introduced by the orbital motion of the reflector with respect to the Sun and to the Earth (cf. Zwitter et al. 2007), calculated by means of the NASA JPL Horizon ephemerides2. The relativistic Doppler shift is not considered by Horizon, although light aberration is included, given its direct effect on the apparent positions of the bodies (Giorgini, priv. comm.). Therefore, we compute the relativistic Doppler shift as explained in Appendix A, where we provide details on the procedure applied to compute star-like RV for the Sun. Our RV time series is plotted in the top panel of Fig. 1, where we also plot the time series of the activity indexes as defined in Sect. 2.2. The red dots indicate measurements affected by the rotation or the non-uniform albedo of the reflecting body (see Sect. 4), while the measurement errors are derived in Sect. 4.2 in the case of the RV and in Sect. 2.3 for the activity indexes, respectively.
In Table 1 from left to right, we list the reflecting body, the epoch of each observation, its exposure time τ, the measured RV of the Sun referred to its barycentre(including the relativistic correction), the relativistic correction to the classic Doppler shift ΔVrel (cf. Appendix A), the time lag t′−t accounting for the different directions along which the Sun is seen from the reflecting body and the Earth (cf. Sect. 2.3), the chromospheric Ca II K index, and the mean total magnetic field ⟨ | B | ⟩ as defined in Sect. 2.2. The epoch of each observation in Table 1 is not the beginning of the exposure, but the time weighted according to the received stellar flux along the exposure as measured by the HARPS exposure meter.
Most of the measurements obtained with the Moon are average values over sequences extended for several hours (e.g. Molaro et al. 2013). In Fig. 2 we show an example of such lunar sequences. It was obtained on 5 July 2012 and its individual RV measurements show a rather flat behaviour with a mean of 98.3 m/s, considering the typical offset of about 100 m/s, and an rms of 0.83 m/s. The latter is mainly produced by the 5-min solar oscillations illustrating the sub m/s precision of HARPS observations. On 4 and 6 January 2014, Molaro et al. (2015) collected series of RV measurements by observing Ganymede and Europa, just before the beginning and after the end of the opposition surge effect that clearly affected the Europa data collected on 5 January. Therefore, we limit ourselves to only those parts of the dataset not affected by this effect. Ganymede data on 4 January 2014 were obtained by HARPS-N, the twin spectrograph mounted at Telescopio Nazionale Galileo in La Palma.
Regarding the asteroids, in most cases, the exposure times are of 600 s or longer, thus averaging out the 5-min p-mode oscillations that were clearly detected in the Moon sequences (cf. Figs. 2 and 4 in Molaro et al. 2013). The standard deviations of the RV measurements obtained in the course of the same night are within ~1.6−1.8 m/s, except for those acquired with Vesta and Ceres that are affected by the rotation of the asteroids (see Sect. 2.1). This is similar to the level of variability found on similar timescales in Sun-like stars (Dumusque et al. 2011).
 |
Fig. 1 Top panel: solar RV as derived by observing different reflecting bodies vs. the time in JD on the lower axis and in years on the top axis, respectively. The errors are derived in Sect. 4.2. The red dots indicate measurements that are affected by the rotation of the reflecting body or by other systematics and that are excluded from further analysis. Middle panel: chromospheric Ca II K index corresponding to our RV measurements vs. the time (see Sect. 2.2). The red dots indicate the excluded data points as in the top panel, while the errors are derived in Sect. 2.3. Lower panel: same as the middle panel, but for the total mean magnetic flux introduced in Sect. 2.2 and whose errors are derived in Sect. 2.3. |
 |
Fig. 2 Solar RV vs. the time for a sequence of 196 Moon measurements spanning about 4.5 h of total observation on 5 July 2012. The radial velocities are corrected by the radial motion components of the Moon relative to the observer and to the Sun as described in the text, but without rotational and relativistic corrections, which are added in Table 1. |
2.1. Effects of the reflector rotation
The RV variation produced by the rotation of the Moon has been corrected using an adequate observing strategy. Specifically, most of the Moon spectra were acquired close to the centre of the Moon’s disc, therefore, only the rotation velocity component in the direction of the Sun was relevant, while that in the direction of the Earth observer was negligible.
In the case of the asteroids or the Galilean satellites, we receive a disc-integrated spectrum that is affected by the rotation of the body and the non-uniform illumination by the Sun. In the case of a body of spherical shape with a uniform albedo, the Doppler shift induced by its rotation only averages to zero if the inclinations of its rotation axis to the direction of the Sun and to the observer on the Earth are the same. If this is not the case, there is a net Doppler shift because the opposite contributions coming from the receding and approaching parts of the illuminated disc do not balance each other exactly, as shown by Lanza & Molaro (2015). The amplitude of this effect can reach up to 2.6 m/s for Pallas, whose spin axis is inclined by ~16° to the plane of the ecliptic, but this amplitude is smaller than 0.06 m/s for Ceres or Vesta which have an inclination to the ecliptic greater than 60°, as well as for the Galilean satellites. In addition to the inclination of the spin axis to the plane of the ecliptic, the RV variation depends on the phase angle of the reflecting body and on the difference between its heliocentric ecliptic longitude and that of the Earth; therefore, it is modulated on timescales of weeks or months.
Another effect occurs when the surface of the reflecting body has a non-uniform albedo as indicated in the case of Ceres and Vesta by the rotational modulation of their optical flux and the resolved images of their surfaces. A dark spot of albedo produces a reduced continuum in the locally reflected spectrum of the Sun. The local spectra reflected by the different portions of the disc are Doppler shifted according to their projected rotational velocities and the lower continuum in the dark spot produces a bump in the spectral line profiles when we integrate the spectrum over the whole visible disc, akin to the case of a spotted star (cf. Fig. 1 in Vogt & Penrod 1983). Assuming a continuum flux reduced by a factor fc < 1 with respect to that without the spot, the maximum RV perturbation is of the order of 2(1−fc)Veq, where the factor 2 accounts for the worst case, i.e., when the rotational velocity components towards the Sun and the observer are equal to the equatorial rotation velocity of the asteroid Veq that reaches up to Veq ~ 90 m/s in the case of Vesta or Ceres (cf. Table 1 in Lanza & Molaro 2015). Given that 0.90 ≲ fc ≲ 0.98, RV perturbations of several m/s are possible as a consequence of albedo inhomogeneities on those fast-rotating asteroids with periods of Prot = 5.342 and 9.075 h, respectively.
A precise calculation of the effect is made difficult by our limited knowledge of the surface features of the different asteroids and by the variation of the angles between their spin axis and the directions to the Sun and the Earth along their orbit. Haywood et al. (2016) make an empirical investigation in the case of Vesta and find that a RV rotational modulation with a semi-amplitude of ~2.39 ± 0.55 m/s has been induced by this effect between 2011 September 29 and 2011 December 7. In the case of the data points of Vesta in Table 1, we find a maximum standard deviation of ~3.38 m/s in the course of the same night, which is compatible with their results and the very rough estimate given above. The amplitude is larger by a factor of ≈2 in the case of Ceres (Molaro et al. 2016), while a smaller amplitude by a factor of 3−10 is expected in the case of the other asteroids in our sample, owing to their smaller radii and longer rotation periods (cf. Lanza & Molaro 2015). For the Galilean satellites, the effect can only be larger than ~1 m/s for Io because it has the shortest rotation period.
2.2. Solar activity indexes
We use the normalized emission flux measured in a 0.1 nm bandpass centred in the core of the solar Ca II K line (central wavelength 393.3 nm) as a proxy for the solar chromospheric activity level (Keil & Worden 1984; Keil et al. 1998; Meunier & Lagrange 2013)3. The typical relative accuracy of this index is ~0.6 percent. Furthermore, we consider the magnetic field averaged over the disc of the Sun as another proxy for its activity to facilitate a comparison with the results of Deming & Plymate (1994), who used the mean absolute magnetic field over the solar disc as measured from Kitt Peak magnetograms. That time series terminated on 21 September 2003 and was then continued to date by the SOLIS Vector Spectromagnetograph (hereafter SOLIS VSM).
The mean field values are determined from daily measurements of the line-of-sight magnetic field flux density observed with 1 arcsecond pixels and averaged over the full disc. The solar line-of-sight magnetic field is measured with full-disc Fe I 630.15 nm (Landé factor of the line geff = 1.667) longitudinal photospheric magnetograms (Jones et al. 2002)4. The mean net magnetic flux is the sum of all the measurements divided by the number of pixels on the disc. The mean total magnetic flux is the average of the absolute value of the pixel measurements. Only pixels within 0.99 solar radii from disc centre and with absolute values greater than 0.2 G are included in the computation. The mean net magnetic flux during the time interval of our RV observations spanned between −0.89 and 1.0 G, while the range of the mean total flux was between 3.62 and 13.29 G. The mean standard deviations of the mean net and total fluxes are both ~0.017 G.
The variations of the chromospheric index and of the total magnetic flux vs. the time are plotted in Fig. 3. We see that the variations of the indexes are rather complex with the activity level of the Sun showing two relative maxima during cycle 24. Therefore, we cannot separate levels of low and high activity by simply considering the phase of the cycle as in the case of a single, well-defined maximum.
 |
Fig. 3 Top panel: Ca II K chromospheric index (black dots) vs. the time in JD on the lower axis and in years on the top axis. The continuous red line is obtained by smoothing the data with a time window of 60 days. The vertical dotted and dashed lines indicate the time intervals during which measurements of the RV of the Sun as a star were acquired by Haywood et al. (2016) and Dumusque et al. (2015), respectively. Lower panel: same as the upper panel, but for the total magnetic flux as measured by SOLIS VSM. |
2.3. Effect of the different lines of sight to the Sun
In general, the Sun is seen from different lines of sight from the Earth and the reflector, therefore we must account for the time lag introduced by this effect when dealing with solar activity proxies. For an RV observation made at the time t, we compute the angle α between the directions to the reflector and to the Earth as seen from the centre of the Sun. Assuming that the Ca II K emission comes from the faculae on the Sun and that they are rotating on average with the angular velocity ΩAR corresponding to a latitude of ~20°, we compute the effective time t′ = t−α/ ΩAR when the Sun is viewed by an Earth observer at the same rotation phase as viewed by an observer on the reflector at time t. Therefore, we compute the Ca II K index to be associated with the RV measurement at time t by linearly interpolating the chromospheric index time series at the time t′. The same method is used to compute the mean net and total magnetic fluxes corresponding to a given RV measurement.The difference t′−t ranges from −6.13 to 7.10 days with a mean value ⟨ | t′−t | ⟩ ≃ 3.42 days; this difference is much longer than the Sun-reflector-Earth light travel time that is always shorter than ~2 h. Therefore, we neglect light travel time when accounting for the different lines of sight.
The time lag t′−t introduces an additional error because of the intrinsic variations of the chromospheric and magnetic indexes over that timescale. To quantify it, we compute their average standard deviation considering time intervals between four and eight days for the period of high activity (Ca II K index greater than 0.092) and find values between 0.0020 and 0.0025 for the Ca II K index and 0.45 and 0.70 G for the total magnetic flux, respectively. These are significantly larger than the typical measurement errors and their mean values are used as statistical errors of the activity indexes in our analysis.
3. Methods
First we look for periodicities in our solar RV time series by computing its Lomb-Scargle periodogram (Horne & Baliunas 1986). Then we perform 10 000 random permutations of the RV values and measure the height of the highest peak in each of their periodograms. The frequency of occurrence of a peak equal to or higher than the maximum in the actual time series provides an a posteriori measurement of its false-alarm probability (hereafter FAP), i.e., the probability of its occurrence as a result of the time sampling and the uncorrelated noise present in the dataset. Another measure of the FAP can be obtained by adding to the individual RV measurements a normally distributed random variable with zero mean and standard deviation equal to the standard deviation of the measurements (cf. Sect. 4.2), and computing the corresponding periodogram. By repeating this procedure 10 000 times, we estimate the a posteriori probability of the occurrence of a peak of height equal to or greater than the highest peak of the original periodogram.
To investigate the correlations between the solar RV and the different activity indexes introduced in Sect. 2.2, we use Spearman and Pearson coefficients. The former measures the monotone correlation of one variable vs. the other, while the latter provides a measure of the linear correlation between them. Since the Spearman coefficient is based on the order ranks of the individual variables, it can sometimes have a low absolute value even if they are truly correlated. This happens if one of the variables has a larger scatter for some constant values of the other, which is indeed the case when we consider sequences of RV data acquired on the same night for which the chromospheric and magnetic indexes are constant because they are sampled once per day. In this case, the Pearson coefficient is more suitable to detect a correlation, although the estimate of its significance is much more complex than in the case of the Spearman coefficient for which a well-defined theoretical method is available (Press et al. 2002).
We use the IDL functions R_CORRELATE and CORRELATE to compute the correlation coefficients, respectively. The significance of the obtained values is estimated a posteriori by computing the coefficients for 10 000 random permutations of the RV values to evaluate the frequency of obtaining an absolute value equal to or greater than that measured for an uncorrelated dataset. Moreover, we test the significance by means of a Monte Carlo simulation of 10 000 datasets obtained by adding random deviates to the original variables. Their standard deviations are derived in Sect. 4.2 for the RV and in Sect. 2.3 for the Ca II K and the magnetic flux indexes, respectively.
4. Results
4.1. RV of the individual reflecting bodies
For a better characterization of the measurements obtained with the different bodies, we compute the mean ⟨ RV ⟩ and the standard deviation σRV for the objects with at least four measurements. In Table 2, we list the name of the object, the mean radial velocity, the standard deviation, and the number N of measurements.
Solar RV measurements obtained with individual reflecting bodies.
The mean of all the 88 measurements is 99.196 m/s, their standard deviation is 4.44 m/s, and their standard error is 0.47 m/s. Therefore, the mean value of Io is lower by 6.65 standard errors from the mean of all the measurements. This discrepancy is not associated with a specific range of orbital phases of the satellite. However, we find that Io’s measurements were obtained with an airmass ranging from 1.73 to 1.91 with five measurements out of seven taken at an airmass between 1.79 and 1.91. The high airmass and the variation of the albedo of Io from 0.10 to 0.75 between 380 and 690 nm (Nelson & Hapke 1978) may combine themselves to systematically modify the RV measurements because they reduce the weights of the echelle orders at shorter wavelengths in comparison to those at longer wavelengths, which corresponds to a change of the effective line mask used to cross-correlate the spectrum.
Ceres has the greatest standard deviation, likely as a consequence of its fast rotation (Veq = 92.3 m/s) in combination with its surface inhomogeneities (cf. Sect. 2.1), while Iris has the second largest standard deviation that is a consequence of one discrepant measurement taken on 2013 December 19 with an airmass of 1.7. After removing that measurement, the mean and standard deviation of the remaining four measurements of Iris are 99.03 and 3.25 m/s, respectively, in line with the other measurements.
In conclusion, we decided to discard the measurements obtained with Io and Ceres as well as the discrepant point of Iris and restrict our analysis to the remaining 73 data points. They have a mean RV of 100.26 m/s and a standard deviation of 3.056 m/s. The discarded datapoints are indicated with red dots in Fig. 1. We include in our analysis the measurements obtained with Vesta because they do not show any systematic effect that can affect our results, although its rotational modulation induces a significant scatter as measured by the standard deviation reported in Table 2 (cf. Sect. 2.1).
The smallest standard deviations are those of the measurements of the Moon, mostly mean values of sequences of several tens or hundreds of datapoints, and of Ganymede, the latter obtained over two nights. The rotation effects are small in the case of Ganymede and have been corrected in the case of the Moon, thus suggesting that the main source of the standard deviation at the level of 1.6−1.7 m/s is the intrinsic solar variability. This value is compatible with the 1.33 m/s rms measured by Dumusque et al. (2015) during one week between April and May 2014 that fell during a period of moderately high chromospheric activity (cf. Fig. 3). On a timescale of about two months, Haywood et al. (2016) find a mean standard deviation of ~3.9 m/s as a consequence of some large activity complexes that modulated the RV with the rotation of the Sun. These measurements encompassed the highest level of chromospheric activity during our time span (see Fig. 3). The simulations based on the models by Meunier et al. (2010a) and Borgniet et al. (2015) yield an rms of 1.53 m/s during a period of high activity and of 2.62 m/s over the entire cycle. These values are supported by the observations of Meunier et al. (2010b).
We conclude that the difference between the mean variance of our sequence of 73 points and those of the Moon and Ganymede is likely due in part to the intrinsic solar activity and in part to the effect of the body rotation through the phenomena introduced in Sect. 2.1. Given that our observations sample most of activity cycle 24, the difference in the standard deviation of 2.57 m/s appears to be comparable with the intrinsic solar rms expected on that timescale, according to the models and available observations.
4.2. Uncertainty of our RV measurements
Given the role of the intrinsic variability of the Sun in determining the standard deviation of our measurements, we expect that it depends on the level of activity of our star. In principle, we can compute the standard deviations of subsets of measurements belonging to intervals of low, intermediate, or high activity to empirically find that dependence. Nevertheless, the presence of a double maximum in cycle 24 and the sparseness of our measurements call for some caution in implementing this approach.
We subdivide the dataset according to the Ca II K index of each point. We consider the measurements with Ca II K below and above its median level, that is 0.09344, to obtain subsets with the same number of points; this allows us to obtain comparable levels of statistical fluctuation of the standard deviations, given the relatively low numbers of datapoints. The first subset consists of 37 datapoints with a mean value of 99.16 m/s and a standard deviation of 2.315 m/s, while the second consists of 36 points with a mean of 101.38 and a standard deviation of 3.338 m/s. The difference between the mean values is significant at 3.3 standard errors indicating that the solar apparent RV increases with its activity level.
We also consider the case of three intervals with 24, 24, and 25 datapoints in order of increasing mean value of the Ca II K index and find RV mean values of 98.87, 100.51, and 101.35 m/s with standard deviations of 2.460, 2.727, and 3.445 m/s, respectively. The difference between the mean value of the second subset and that of the first is significant at the level of 2.20 standard errors, while the difference between the third and the second is significant only at 0.94 standard errors.
Considering the case of four subsets with similar numbers of datapoints and increasing mean values of the Ca II K index, we find that the second subset consists of data taken during only one night and therefore it has a standard deviation that is significantly smaller than the other three subsets.
In conclusion, we adopt three subsets to estimate the standard deviations of our measurements as a function of the activity level and assign to each RV measurement the standard deviation of the subset to which it belongs. The effect of the body rotation is made random by the presence of different bodies in each subset, observed at widely different rotation phases, so we do not attempt any correction for it.
4.3. Periodogram analysis
The periodogram of our RV time series is plotted in the top panel of Fig. 4. It has the highest peak at 14.196 days with a FAP of 1.18 percent as estimated by 10 000 random shuffling of the RV data. However, if we estimate the FAP by adding random variates with zero mean and standard deviations equal to the estimated standard deviations of the RV measurements, it increases to 10.08 percent.
The periodogram of the chromospheric index Ca II K taken with the same cadence is similar to that of the RV variations (Fig. 4, middle panel). The peaks at the rotation period and its first harmonic are also present in the periodogram of the complete Ca II K time series where we see concentrations of power close to those periods. Another prominent peak at ~65 days is present in the chromospheric emission, which is probably related to large faculae in complexes of activity lasting for 1−2 solar rotations, but it is not particularly conspicuous in the RV periodogram. On a longer timescale, the sparseness of our time series strongly affects the periodogram, making it impossible to derive sound results. Nevertheless, we note the broad similarity between the distributions of the relative power of the RV and Ca II K index in the period range ≈1−3 yr.
Although the periodicity at half the solar rotation period has been reported by other authors (e.g., Jimenez et al. 1986), a more continuous sampling is certainly required to confirm its presence in the Sun-as-star RV time series.
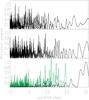 |
Fig. 4 Top panel: periodogram of our RV time series. Middle panel: periodogram of the Ca II K index interpolated on the same calendar as our RV time series. Lower panel: periodogram of the Ca II K time series with an almost even cadence of one measurement per day. To allow the identification of peaks at short periods, we overplot the periodogram with an amplitude amplified by a factor of five up to a period of about 300 days (green solid line). The dotted vertical lines in the three plots indicate the solar synodic rotation period and its first harmonic, respectively. |
 |
Fig. 5 Our solar RV measurements vs. the chromospheric Ca II K line index. The best-fit linear regression line is also plotted (red solid line). |
4.4. Correlations between RV and activity indexes
In Fig. 5, we plot our RV measurements vs. the chromospheric Ca II K line index. The Spearman correlation coefficient for our 73 points is 0.357 with a probability of obtaining an absolute value equal to or greater than this value of 0.19 percent in the case of an uncorrelated dataset, i.e., a significance of 99.8 percent. This result is found by computing the correlation coefficients for 10 000 shuffles of the RV time series. On the other hand, considering 10 000 datasets obtained from the observations by adding normally distributed random variates to the RV and the Ca II K index with their standard deviations, respectively, we find a significance of 95.4 percent.
The Pearson correlation coefficient is 0.385 with a significance of 97.2 percent, when it is estimated with 10 000 uncorrelated datasets, and of 97.6 percent, when it is estimated with 10 000 mock datasets obtained by adding random variates to the RV and chromospheric index with their standard deviations, respectively.
Since the Spearman coefficient is close to the Pearson coefficient, a linear model is not too different from the most general monotone correlation model as considered in the computation of the Spearman coefficient. Therefore, we computed a linear best fit to the RV−Ca II K correlation to estimate the amplitude of the RV variation over the time interval covered by our data and compare the RV variation to the variation expected on the basis of the model by Meunier & Lagrange (2013), who showed a linear best fit to their synthetic data in their Fig. 12. Considering the uncertainties on the RV values, we obtain an RV variation of 4.98 ± 1.44 m/s with the Ca II K index ranging between 0.0867 and 0.0990 in the 2006−2014 interval. This is in good agreement with a variation of ~6.0 ± 2.5 m/s as estimated from the work of Meunier & Lagrange.
The residuals of the linear best fit to our data range between −5.31 and 9.20 m/s (cf. Fig. 6)and a Smirnov-Kolmogorov test shows that they are compatible with a normal distribution with a probability of 0.67. We derive a standard deviation of 2.82 m/s, which can be associated with the effect of the rotation of the reflecting bodies and the variation of solar activity on timescales shorter than the 11-yr cycle (cf. Sects. 4.1 and 4.2).
In Fig. 7, we plot the RV measurements vs. the absolute value of the mean total magnetic flux measured by SOLIS VSM. This is the correlation with the highest Spearman and Pearson coefficients among those obtained with our two magnetic indexes (cf. Sect. 2.2). The Spearman coefficient is 0.131, giving an a posteriori significance of only 74.2 percent. On the other hand, the Pearson coefficient is 0.269 with a significance of 97.8 percent when we derive it from 10 000 random shuffles of the RV values. The significance decreases to 84.0 percent when we derive it from 10 000 mock datasets obtained by adding random deviates to the two variables. This is probably associated with the limited sensitivity of the Spearman coefficient because of the large spread in several RV measurements that have close values of the total mean magnetic flux (cf. Sect. 3). Therefore, we rely on the Pearson coefficient and conclude that a correlation is also present between the solar long-term RV variation and the mean total magnetic flux, although with a lower significance than in the case of the RV–Ca II K correlation. The minimum and maximum of the residuals of the linear best fit of the RV-⟨ | B | ⟩ correlation are −5.74 and 9.68 m/s. They follow a normal distribution with a probability of 0.93 according to the Kolmogorov-Smirnov test and have a standard deviation of 2.94 m/s.
 |
Fig. 6 Histogram of the distribution of the residuals of the linear best fit to the RV-Ca II K correlation (solid black line). The errorbars are equal to the square root of the number of residuals in each bin. The Gaussian best fit to the distribution is superposed (green solid line). |
 |
Fig. 7 Our solar RV measurements vs. the mean total magnetic flux as measured by SOLIS VSM. The best-fit regression line is also plotted (red solid line). |
5. Discussion and conclusions
We found a positive correlation between the solar RV variation and the level of chromospheric activity in our star as measured by the Ca II K line index. A similar correlation is found between the RV and the absolute value of the mean total photospheric magnetic field of our star, although with a lower significance. Therefore, the Sun behaves similarly to other low-activity late-type stars that show a positive correlation between the activity level and RV variations (e.g., Lovis et al. 2011; Gomes da Silva et al. 2012).
Our results support the theoretical prediction that the quenching of convective blueshifts associated with localized magnetic fields in active regions is the main source of long-term solar RV variations, while the flux perturbations associated with dark spots or bright faculae are of secondary importance (Meunier et al. 2010b; Meunier & Lagrange 2013; Dumusque et al. 2014). The former effect produces the strongest correlation between RV variation and facular areas because it depends on their disc-projected area, but is independent of their position on the solar disc. On the other hand, the flux effect has a different sign depending on the location of the active regions on the receding or approaching half of the solar disc. Therefore, a weaker RV-Ca II K correlation and a smaller amplitude of the variation are expected in that case (cf. Lagrange et al. 2010; Meunier et al. 2010a,b).
The measured amplitude of the long-term RV variation is in agreement with the models by Meunier & Lagrange (2013), suggesting that the predictions on the detectability of Earth-size planets based on their models can be regarded as realistic. Given that the amplitude of activity cycle 24 was smaller in comparison to those of the cycles observed in the 1980s and 1990s, we expect a larger RV variation than in the 2006–2014 period when the Sun is more active, as would be estimated from, for example, Fig. 12 of Meunier & Lagrange (2013).
The results of previous works such as those of McMillan et al. (1993) or Deming & Plymate (1994) cannot be directly compared with ours mainly because they used different and limited spectral ranges to measure the solar RV variations. However, the upper limit for the solar RV variation of ±4 m/s in the violet part of the optical spectrum found by McMillan et al. (1993) is compatible with our measured range. Contrary to Deming & Plymate (1994), we do not detect a highly significant correlation between the RV variation and the mean magnetic indexes; this is possibly because they base their measurements on infrared lines that sample a different level of the solar atmosphere where the convective blueshifts may have a different dependence on the magnetic field.
The correlation with the total magnetic flux density is remarkable during the two solar rotations observed by Haywood et al. (2016), who found a Pearson coefficient of 0.58 for 37 nightly-averaged observations, while it appears to be weaker on our longer timespan. This may be because those observations were taken close to the maximum of cycle 24 at the end of 2011 when the RV variation was dominated by a few relatively large active regions lasting up to two solar rotations. When we consider a longer time span, the intrinsic evolution of many smaller active regions and the size-dependent and non-linear relationship between the convective shift and the intensity of the magnetic field (cf. Fig. 6 in Meunier et al. 2010b) make the correlation with the mean magnetic flux noisier. On the other hand, the correlation with the chromospheric flux appears to be tighter. This is probably because the chromospheric emission is linearly related to the amplitude of the local convective motions that produce the heating of the chromosphere through magnetosonic waves, which is independent of any size effect that can affect the relationship with the magnetic field. Moreover, Haywood et al. (2016) could remove most of the variability induced by the rotation of Vesta, while our correlations are affected by the additional noise due to the rotation of our reflecting bodies.
Although a detailed analysis of the solar activity along cycle 24 is beyond the scope of the present work, we notice the difference between the amplitudes of the two relative maxima of the Ca II K and of the magnetic flux ⟨ | B | ⟩ at the end of 2011 and in 2014 in Fig. 1 (cf. middle and lower panels). The variation of the chromospheric index is more similar to the RV modulation (cf. Fig. 1, upper panel, black dots), which can explain why this modulation is better correlated with its variation than with the mean magnetic flux. Looking at the index time series in Fig. 3, we see the difference in the relative maxima of the mean magnetic flux that reaches a higher level in 2014. Conversely, the monthly sunspot number shows a more prominent and narrow peak in correspondence with the maximum at the end of 2011 (cf. Fig 1 in Kiess et al. 2014), thus suggesting a redistribution of magnetic flux from larger to smaller structures in the solar photosphere between the two maxima. Since the relationship between the chromospheric emission and the photospheric field depends on the size and type of structures (e.g. Loukitcheva et al. 2009, and references therein), this may account for the difference between the time series of the two activity indexes.
The residuals of the best fit to the RV variations in Fig. 5 range between −5.31 and 9.20 m/s and cannot only be attributed to the effect of the rotation of the asteroids or the Jupiter satellites. The latter may account for an amplitude up to 5−6 m/s, while the remaining variations are certainly intrinsic to the Sun. Variations with such an amplitude cannot be produced by the line profile distortions induced by surface brightness inhomogeneities, either sunspots or faculae, because their peak amplitude is ±2 m/s during the maximum of the activity cycle (cf. Lagrange et al. 2010). The reduction of convective blueshifts in the active regions can produce an amplitude that is larger by a factor of 3−4, which may account for the observed scattering on timescales shorter than ~100 days that we see in Fig. 1 (Meunier et al. 2010a). However, our time sampling is too sparse to reach definite conclusions on the cause of the short-term variations. The work by Haywood et al. (2016) addresses this point by means of a daily sampling extended for a couple of solar rotations and more information is expected to come in forthcoming studies (cf. Dumusque et al. 2015).
Available through: http://ssd.jpl.nasa.gov/horizons.cgi
Data are available from: http://nsosp.nso.edu/cak_mon
Data are available from: http://solis.nso.edu/vsm/vsm_mnfield.html
Acknowledgments
The authors are grateful to an anonymous referee for several valuable comments and suggestions that helped them to improve their work. They wish to thank Prof. Andrew Collier Cameron and Dr. Christophe Lovis for interesting discussions. AFL acknowledges support from the National Institute for Astrophysics (INAF) through the Progetti premiali funding scheme of the Italian Ministry of Education, University and Research. RDH was supported by STFC studentship grant ST/J500744/1 during the course of this work. R.D.H. gratefully acknowledges a grant from the John Templeton Foundation. The opinions expressed in this publication are those of the authors and do not necessarily reflect the views of the John Templeton Foundation. This work utilizes Ca II K solar data obtained at Sacramento Peak Observatory and SOLIS data obtained by the NSO Integrated Synoptic Program (NISP), managed by the National Solar Observatory, which is operated by the Association of Universities for Research in Astronomy (AURA), Inc. under a cooperative agreement with the National Science Foundation. The authors also gratefully acknowledge the availability of HARPS data obtained from the ESO Science Archive Facility and the use of JPL NASA Horizons Ephemerides.
References
- Borgniet, S., Meunier, N., & Lagrange, A.-M. 2015, A&A, 581, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carolo, E., Desidera, S., Gratton, R., et al. 2014, A&A, 567, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deming, D., & Plymate, C. 1994, ApJ, 426, 382 [Google Scholar]
- Dumusque, X., Udry, S., Lovis, C., Santos, N. C., & Monteiro, M. J. P. F. G. 2011, A&A, 525, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dumusque, X., Bonomo, A. S., Haywood, R. D., et al. 2014, ApJ, 789, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Dumusque, X., Glenday, A., Phillips, D. F., et al. 2015, ApJ, 814, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Gomes da Silva, J., Santos, N. C., Bonfils, X., et al. 2012, A&A, 541, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haywood, R. D., Collier Cameron, A., Queloz, D., et al. 2014, MNRAS, 443, 2517 [NASA ADS] [CrossRef] [Google Scholar]
- Haywood, R. D., Collier Cameron, A. C., Unruh, Y. C., et al. 2016, MNRAS, accepted [arXiv:1601.05651] [Google Scholar]
- Horne, J. H., & Baliunas, S. L. 1986, ApJ, 302, 757 [NASA ADS] [CrossRef] [Google Scholar]
- Jimenez, A., Palle, P. L., Regulo, C., Roca Cortes, T., & Isaak, G. R. 1986, Adv. Space Res., 6, 89 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Jones, H. P., Harvey, J. W., Henney, C. J., Hill, F., & Keller, C. U. 2002, SOLMAG Proc. Magnetic Coupling of the Solar Atmosphere Euroconference, 505, 15 [Google Scholar]
- Keil, S. L., & Worden, S. P. 1984, ApJ, 276, 766 [NASA ADS] [CrossRef] [Google Scholar]
- Keil, S. L., Henry, T. W., & Fleck, B. 1998, Synoptic Sol. Phys., 140, 301 [Google Scholar]
- Kiess, C., Rezaei, R., & Schmidt, W. 2014, A&A, 565, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kurucz, R. L., Furenlid, I., Brault, J., & Testerman, L. 1984, National Solar Observatory Atlas, Sunspot, New Mexico: National Solar Observatory [Google Scholar]
- Lagrange, A.-M., Desort, M., & Meunier, N. 2010, A&A, 512, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lanza, A. F., & Molaro, P. 2015, Exp. Astron., 39, 461 [NASA ADS] [CrossRef] [Google Scholar]
- Lanza, A. F., Bonomo, A. S., Moutou, C., et al. 2010, A&A, 520, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lanza, A. F., Boisse, I., Bouchy, F., Bonomo, A. S., & Moutou, C. 2011, A&A, 533, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lindegren, L., & Dravins, D. 2003, A&A, 401, 1185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Loukitcheva, M., Solanki, S. K., & White, S. M. 2009, A&A, 497, 273 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lovis, C., Dumusque, X., Santos, N. C., et al. 2011, unpublished [arXiv:1107.5325] [Google Scholar]
- Mayor, M., & Queloz, D. 1995, Nature, 378, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
- McMillan, R. S., Moore, T. L., Perry, M. L., & Smith, P. H. 1993, ApJ, 403, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Meunier, N., & Lagrange, A.-M. 2013, A&A, 551, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meunier, N., Desort, M., & Lagrange, A.-M. 2010a, A&A, 512, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meunier, N., Lagrange, A.-M., & Desort, M. 2010b, A&A, 519, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meunier, N., Lagrange, A.-M., Borgniet, S., & Rieutord, M. 2015, A&A, 583, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molaro, P., & Centurión, M. 2011, A&A, 525, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molaro, P., & Monai, S. 2012, A&A, 544, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molaro, P., Monaco, L., Barbieri, M., & Zaggia, S. 2013, MNRAS, 429, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Molaro, P., Barbieri, M., Monaco, L., Zaggia, S., & Lovis, C. 2015, MNRAS, 453, 1684 [NASA ADS] [CrossRef] [Google Scholar]
- Molaro, P., Lanza, A. F., Tosi, F., et al. 2016, MNRAS, accepted [arXiv:1602.03467] [Google Scholar]
- Moutou, C., Lo Curto, G., Mayor, M., et al. 2015, A&A, 576, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nelson, R. M., & Hapke, W. 1978, Icarus, 36, 304 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 2002, Numerical recipes in C++: the art of scientific computing by William H. Press. xxviii, 1002 p.: ill.; 26 cm. Includes bibliographical references and index [Google Scholar]
- Roca Cortés, T., & Pallé, P. L. 2014, MNRAS, 443, 1837 [NASA ADS] [CrossRef] [Google Scholar]
- Santos, N. C., Gomes da Silva, J., Lovis, C., & Melo, C. 2010, A&A, 511, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N. C., Mortier, A., Faria, J. P., et al. 2014, A&A, 566, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Strassmeier, K. G., Ilyin, I., Järvinen, A., et al. 2015, Astron. Nachr., 336, 324 [NASA ADS] [CrossRef] [Google Scholar]
- Vogt, S. S., & Penrod, G. D. 1983, PASP, 95, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Zwitter, T., Mignard, F., & Crifo, F. 2007, A&A, 462, 795 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Correction for the Doppler shifts
The HARPS DRS returns the radial velocity RVp relative to the solar system barycentre by taking the apparent position of the target into account. Therefore, we subtract the barycentric radial velocity correction, called BERV, which is recorded in the fits headers, to compute the RV relative to the observer on the Earth. This includes the Doppler shifts associated with the motions of the observer and the reflecting target. The Doppler shift z is measured by the relative line shift as follows: z ≡ (λobs−λ0) /λ0, where λobs is the observed wavelength and λ0 the rest-frame wavelength. The relativistic formula for the Doppler shift is 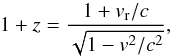 (A.1)where vr is the radial velocity of the source with respect to the observer, v its total velocity, and c the speed of light (e.g., Lindegren & Dravins 2003,Eq. (11)). In our case, Eq. (A.1) is applied first to the light received by the reflecting target from the Sun and then to the light received by the observer on Earth from the target. Indicating the wavelength received at the target with λa and the rest wavelength at the Sun with λ0, we obtain
(A.1)where vr is the radial velocity of the source with respect to the observer, v its total velocity, and c the speed of light (e.g., Lindegren & Dravins 2003,Eq. (11)). In our case, Eq. (A.1) is applied first to the light received by the reflecting target from the Sun and then to the light received by the observer on Earth from the target. Indicating the wavelength received at the target with λa and the rest wavelength at the Sun with λ0, we obtain 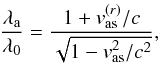 (A.2)\newpage\noindentwhere vas is the velocity of the target with respect to the Sun and
(A.2)\newpage\noindentwhere vas is the velocity of the target with respect to the Sun and 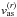 its radial component along the target-Sun direction, as given by VmagSn and rdot of NASA Horizon Ephemerides, respectively. The wavelength λobs measured by a geocentric observer, is written as
its radial component along the target-Sun direction, as given by VmagSn and rdot of NASA Horizon Ephemerides, respectively. The wavelength λobs measured by a geocentric observer, is written as 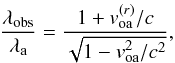 (A.3)where voa is the velocity of the target with respect to the barycentre of the Earth and
(A.3)where voa is the velocity of the target with respect to the barycentre of the Earth and 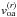 its radial component, as given by VmagOb and deldot of NASA Horizon Ephemerides, respectively.
its radial component, as given by VmagOb and deldot of NASA Horizon Ephemerides, respectively.
The total relativistic change in wavelength λobs/λ0 is computed by multiplying Eq. (A.3) by (A.2). Therefore, the RV relative to the barycentre of the Sun is obtained as RV = RVp−BERV −czrel, where zrel ≡ (λobs/λ0)−1. In other words, the special relativity correction to the classic Doppler shift is 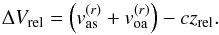 (A.4)For the sake of clarity, ΔVrel is reported in the right column of Table 1. The correction due to the rotation of the Earth is added classically because its relativistic expression differs from the classic expression by less than 1 cm/s in our case.
(A.4)For the sake of clarity, ΔVrel is reported in the right column of Table 1. The correction due to the rotation of the Earth is added classically because its relativistic expression differs from the classic expression by less than 1 cm/s in our case.
All Tables
All Figures
 |
Fig. 1 Top panel: solar RV as derived by observing different reflecting bodies vs. the time in JD on the lower axis and in years on the top axis, respectively. The errors are derived in Sect. 4.2. The red dots indicate measurements that are affected by the rotation of the reflecting body or by other systematics and that are excluded from further analysis. Middle panel: chromospheric Ca II K index corresponding to our RV measurements vs. the time (see Sect. 2.2). The red dots indicate the excluded data points as in the top panel, while the errors are derived in Sect. 2.3. Lower panel: same as the middle panel, but for the total mean magnetic flux introduced in Sect. 2.2 and whose errors are derived in Sect. 2.3. |
| In the text | |
 |
Fig. 2 Solar RV vs. the time for a sequence of 196 Moon measurements spanning about 4.5 h of total observation on 5 July 2012. The radial velocities are corrected by the radial motion components of the Moon relative to the observer and to the Sun as described in the text, but without rotational and relativistic corrections, which are added in Table 1. |
| In the text | |
 |
Fig. 3 Top panel: Ca II K chromospheric index (black dots) vs. the time in JD on the lower axis and in years on the top axis. The continuous red line is obtained by smoothing the data with a time window of 60 days. The vertical dotted and dashed lines indicate the time intervals during which measurements of the RV of the Sun as a star were acquired by Haywood et al. (2016) and Dumusque et al. (2015), respectively. Lower panel: same as the upper panel, but for the total magnetic flux as measured by SOLIS VSM. |
| In the text | |
 |
Fig. 4 Top panel: periodogram of our RV time series. Middle panel: periodogram of the Ca II K index interpolated on the same calendar as our RV time series. Lower panel: periodogram of the Ca II K time series with an almost even cadence of one measurement per day. To allow the identification of peaks at short periods, we overplot the periodogram with an amplitude amplified by a factor of five up to a period of about 300 days (green solid line). The dotted vertical lines in the three plots indicate the solar synodic rotation period and its first harmonic, respectively. |
| In the text | |
 |
Fig. 5 Our solar RV measurements vs. the chromospheric Ca II K line index. The best-fit linear regression line is also plotted (red solid line). |
| In the text | |
 |
Fig. 6 Histogram of the distribution of the residuals of the linear best fit to the RV-Ca II K correlation (solid black line). The errorbars are equal to the square root of the number of residuals in each bin. The Gaussian best fit to the distribution is superposed (green solid line). |
| In the text | |
 |
Fig. 7 Our solar RV measurements vs. the mean total magnetic flux as measured by SOLIS VSM. The best-fit regression line is also plotted (red solid line). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


