| Issue |
A&A
Volume 585, January 2016
|
|
|---|---|---|
| Article Number | A94 | |
| Number of page(s) | 11 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201526122 | |
| Published online | 23 December 2015 | |
Scaling of the photon index vs. mass accretion rate correlation and estimate of black hole mass in M101 ULX-1
1
Dipartimento di FisicaUniversità di Ferrara,
via Saragat 1,
44122
Ferrara,
Italy
e-mail:
titarchuk@fe.infn.it
2
National Research Nuclear University MEPhI (Moscow Engineering
Physics Institute), 115409
Moscow,
Russia
3
Goddard Space Flight Center, NASA, code 663,
Greenbelt, MD
20770,
USA
4
Moscow State University/Sternberg Astronomical Institute,
Universitetsky Prospect 13, 119992
Moscow,
Russia
e-mail:
seif@sai.msu.ru
Received: 18 March 2015
Accepted: 21 October 2015
We report the results of Swift and Chandra observations of an ultraluminous X-ray source, ULX-1 in M101. We show strong observational evidence that M101 ULX-1 undergoes spectral transitions from the low/hard state to the high/soft state during these observations. The spectra of M101 ULX-1 are well fitted by the so-called bulk motion Comptonization (BMC) model for all spectral states. We have established the photon index (Γ) saturation level, Γsat = 2.8 ± 0.1, in the Γ versus mass accretion rate (Ṁ) correlation. This Γ−Ṁ correlation allows us to evaluate black hole (BH) mass in M101 ULX-1 to be MBH ~ (3.2−4.3) × 104 M⊙, assuming the spread in distance to M101 (from 6.4 ± 0.5 Mpc to 7.4 ± 0.6 Mpc). For this BH mass estimate we apply the scaling method, using Galactic BHs XTE J1550-564, H 1743-322 and 4U 1630-472 as reference sources. The Γ vs. Ṁ correlation revealed in M101 ULX-1 is similar to that in a number of Galactic BHs and clearly exhibits the correlation along with the strong Γ saturation at ≈ 2.8. This is robust observational evidence for the presence of a BH in M101 ULX-1. We also find that the seed (disk) photon temperatures are low, on the order of 40−100 eV, which is consistent with high BH mass in M101 ULX-1. Thus, we suggest that the central object in M101 ULX-1 has intermediate BH mass on the order of 104 solar masses.
Key words: accretion, accretion disks / radiation mechanisms: general / black hole physics
© ESO, 2015
1. Introduction
The Pinwheel Galaxy (also known as Messier 101, M101) is a face-on spiral galaxy located 6 Mpc away in the constellation Ursa Major (Shappee & Stanek 2011). At this distance an Earth observer can only see very bright sources whose X-ray luminosity is greater than 1038 erg s-1 using current X-ray detectors. This galaxy has ten ultraluminous X-ray (ULX) sources (Pence et al. 2001). Among these are M101 ULX-1 and ULX N5457-X9,which are well seen in X-rays. M101 ULX-1 was discovered with ROSAT and identified as a ULX-1 by Pence et al. (2001). The bolometric luminosity is in the range of 1040−1041 erg s-1. Later, Chandra observations (see Mukai et al. 2003; Di Stefano & Kong 2003; Kong et al. 2004) found a very soft X-ray spectrum of this source with a blackbody temperature of about 100 eV. The source showed the low/hard and high/soft states in a quasi-recurrent manner during 160−190 day period as found by Chandra and XMM-Newton observations (Mukai et al. 2005).
Two scenarios for interpretation of ULX phenomena have been proposed. First, these sources could be stellar-mass black holes (BHs), which are significantly less than 100 solar masses (M⊙), radiating at Eddington or super-Eddington rates (Titarchuk et al. 1997; Mukai et al. 2005). Alternatively, they could be intermediate-mass black holes (IMBH; more than 100 M⊙) where the luminosity is essentially sub-Eddington. The exact origin of these objects still remains uncertain.
Given the faintness of the optical counterpart (typically V> 22 mag; see, e.g., Liu et al. 2004; Roberts et al. 2008), radial velocity studies of ULX-1 have mostly concentrated on strong emission lines in the optical spectrum. However, these attempts to provide a dynamical mass estimate of M101 ULX-1 fail because the emission lines are presumably associated with the accretion disk or a wind, instead of the donor star itself (cf. Liu et al. 2012; Roberts et al. 2011). Mukai et al. (2005) and Liu et al. (2013) estimated BH mass in the range of 20−40 M⊙, using the maximum of the bolometric luminosity for X-ray observations by Chandra and XMM-Newton during the high state. On the other hand, the estimates using the dynamical method based on the optical emission band provided a very broad BH mass range. For example, Liu et al. (2013) used optical HST observations of M101 ULX-1 to estimate dynamical BH mass in a wide range of MBH ~ 5−1000 M⊙.
The aformentioned BH mass evaluation, however, contradicts the relatively low seed (disk) photon temperature of the blackbody part of the spectrum, which is in the range of 40−70 eV. For example, Shakura & Sunyaev (1973) and Novikov & Thorne (1973) estimated an effective temperature of the accretion material of 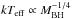 . Thus, it is desirable to have an independent BH identification for the compact object located in the center of M101 ULX-1 as an alternative to the dynamical method.
. Thus, it is desirable to have an independent BH identification for the compact object located in the center of M101 ULX-1 as an alternative to the dynamical method.
Swift observations of M101 ULX-1 used in our analysis.
Chandra observations of M101 ULX-1.
A new method of BH mass determination was developed by Shaposhnikov & Titarchuk (2009), hereafter ST09, using a correlation scaling between X-ray spectral and timing (or mass accretion rate) properties observed from many Galactic BH binaries during the spectral state transitions. It is possible to evaluate a BH mass applying this method when conventional dynamical methods cannot be used.Mukai et al. (2005), Kong et al. (2004), Kong & Di Stefano (2005) have analyzed the Chandraand XMM-Newton spectra. They fitted the low/hard state (LX ~ 2 × 1037 erg s-1) spectra with a power-law model, but they used a different model to fit the high/soft state spectra during the outbursts. Particularly, Kong et al. fitted the outburst spectra with the absorbed blackbody model of kTBB = 40−150 eV and NH = (1−4) × 1021 cm-2, and obtained outburst bolometric luminosities up to 3 × 1040 erg s-1. In contrast, Mukai et al. fitted the spectra with a model consisting of a blackbody plus a diskline component centered at 0.5 keV with NH fixed at 4 × 1020 cm-2, or with the absorbed blackbody with NH ranging from 0.4 to 3.7 × 1021 cm-2. Liu (2009) indicates a smaller absorption in the range (1−6) × 1020 cm-2 based on HST observations. Thus the absorbing column NH for M101 is in a wide range, depending on different X-ray and optical observations and also assuming various emission models of the source.
 |
Fig. 1 Color-intensity evolutionary diagram for M101 ULX-1 using Swift observations (2006–2012), where S and H are the source counts in the two bands: the soft [0.3−1.5 keV] and hard [1.5−10 keV] passbands. Spectral softness (hardness ratio) C and source soft brightness S increase to the right and, finally, the former saturates at high values of S. Larger values of C indicate a softer spectrum, and vice versa. Blue points are related to the decay part of the outburst (see the light curve in Fig. 4). |
As for the distance estimate for M101 ULX-1, Kelson et al. (1996) provide a value of 7.4 Mpc, while Freedman et al. (2001) argue that the distance is less and it is about 6.8 Mpc.Recently, Shappee & Stanek (2011) obtained a Cepheid distance to M101 using archival HST/ACS time series photometry of the inner fields of the galaxy based on a larger Cepheid sample. They improved the distance determination for M101 and obtained a distance value of dm101 = 6.4 ± 0.5 Mpc.
In this paper, we present an analysis of available Swift and Chandra observations of M101 ULX-1. In Sect. 2 we present the list of observations used in the data analysis, while in Sect. 3 we provide details of the X-ray spectral analysis. We discuss the evolution of the X-ray spectral properties during the high-low state transition and present the results of the scaling analysis to estimate BH mass of M101 ULX-1 in Sect. 4. We make our final conclusions in Sect. 5.
2. Observations and data reduction
As our first step, we analyzed the Swift data set for M101 ULX-1, which covered the longest observational interval (2006−2013). In this way, we studied the source behavior in X-rays (Sect. 2.1). Then we proceeded with a detailed spectral analysis using the Chandra (2000, 2004−2005) data (Sect. 2.2). A summary of the X-ray observations considered in this work is listed in Tables 1 and 2.
2.1. Swift data
We show the log of the Swift/XRT observations we used in Table 1. The Swift source count rates never exceed 0.02 count s-1, therefore, only photon-counting mode (PC) events (selected in grades 0−12) were considered. In this way, the Swift-XRT/PC data (ObsIDs, indicated in the first column of Table 1) were processed using the HEA-SOFT v6.14, the tool XRTPIPELINE v0.12.84 and the calibration files (CALDB version 4.1). The ancillary response files were created using XRTMKARF v0.6.0 and exposure maps generated by XRTEXPOMAP v0.2.7. We fitted the spectrum using the response file SWXPC0TO12S6_20010101v012.RMF. We also used the online XRT data product generator1 for an independent check on light curves and spectra (including background and ancillary response files, see Evans et al. 2007; 2009). We made the state identification in terms of the color ratio (see Sect. 3.2), using the Bayesian method developed by Park et al. (2006). Moreover, we applied the effective area option of the Park’s code, which includes the count-rate correction factors in their calculations. Our results, adapting this technique, indicate two color−intensity regimes in M101 ULX-1: i) with low color ratio at lower count-rate observations; and ii) high color ratio at higher count events (see Fig. 1). Furthermore the color−intensity diagram shows a smooth track. Therefore, we grouped the Swift spectra into four bands according to count rates (see Sect. 3.1) and fitted the combined spectra of each band using the XSPEC package (version 12.8.14).
 |
Fig. 2 Swift/XRT (0.3−10 keV) image of M101 field of view, where green circles are the locations of M101 ULX-1, and M101 galactic nucleus (NGC 5457), NGC 5461, and M101 H II regions. The image segment selected by dashed line box is also shown in Fig. 3 using Chandra data. |
2.2. Chandra data
M101 ULX-1 was also observed by Chandra in 2000, 2004−2005. The log of Chandra observations used is presented in Table 2. We extracted spectra from the ACIS-S detector via the standard pipeline CIAO v4.5 package and calibration database CALDB 2.27. All data were taken in very faint mode (VFAINT) except for the data taken in 2000, March 26 and October 29, which were used in faint mode (FAINT). We also identified intervals of high background level to exclude all high background events. The Chandra spectra were produced and modeled over the 0.3−7.0 keV energy range. The data during the low state are characterized by only a few photons (~10−30) for each observation. Therefore, we combined all the low state data to perform statistically significant spectral fits. Thus, we present the results for these low state data per observation using C-statistic. While the rest of the data are analyzed in terms of χ2-statistics.
3. Results
3.1. Images
We made a visual inspection of the obtained image (smoothed by a Gaussian with a full width at half maximum (FWHM) of 3′′2) to avoid possible contamination from nearby sources. Swift/XRT (0.3−10 keV) image of M101 field of view is presented in Fig. 2, where green circles indicate the locations of the M101 ULX-1, NGC 5457 (M101), NGC 5461, and M101 H II regions.
For deeper image analysis, we used the Chandra images with better data quality provided by ACIS-S onboard Chandra. We point out the Chandra region as shown by dashed line box in the Swift image in Fig. 2. The Chandra/ACIS-S (0.2−8 keV) image obtained during observations of M101 ULX-1 on March 26, 2000 (with exposure time of 99.5 ks, ObsID = 934) is shown in Fig. 3. Contour levels should demonstrate the minimal contamination by other point sources and diffuse emission within circle of 9 arcsec around M101 ULX-1. For each observation, we extracted the source spectrum from a 9′′ radius circular region centered on the source position of M101 ULX-1 ( ,
, 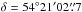 , J2000.0, see details in Kuntz et al. 2005), while an annulus region centered on the source with 10 and 18′′ radii was used to estimate the background contribution.
, J2000.0, see details in Kuntz et al. 2005), while an annulus region centered on the source with 10 and 18′′ radii was used to estimate the background contribution.
In addition, we extracted emission related to the other bright nuclear sources, NGC 5457 and NGC 5461, from circular regions with radius of 15′′ and retrace their time behavior. As a result we established that only M101 ULX-1 demonstrated significant variability during the analyzed observations.
 |
Fig. 3 Adaptively smoothed Chandra/ACIS-S (0.2−8 keV) image of the M101 field, in which localization is indicated with the selected dashed line box in Fig. 2. Contour levels demonstrate the minimal contamination by other point sources and diffuse emission within circle of 9′′ around M101 ULX-1. |
3.2. Color-intensity diagrams and light curves
Before detailed spectral fitting , we investigated a so-called color ratio to quantify and characterize the source spectrum. In particular, for our Swift data we consider R as a ratio of the counts S and H in the soft (0.3−1.5 keV) and hard (1.5−10 keV) bands, respectively. However, at low counts, the posterior distribution of the counts ratio, R, tends to be skewed because of the Poissonian nature of data. Therefore, we used the color, C = log 10(S/H), which is a log transformation of R and provides the skewed distribution more symmetric (see, e.g., Park et al. 2006). The ratio C is modified by taking background counts and instrumental effective areas into account. Figure 1 demonstrates the color-intensity diagram and thus one can see that different count-rate observations correspond to different color regimes. Larger values of C indicate a softer spectrum, and vice versa. We have applied a Bayesian approach to compute the ratio values C and their errors using BEHRs software (Park et al. 2006)2. Generally, this method is applicable when the source is faint or the background is relatively large (Evans et al. 2009; Burke et al. 2013; Jin et al. 2006). In our case, the most Swift observations are related to low count-rate regimes, which can confuse reliable color estimates. However, Bayesian analysis provides a simple way to overcome this problem. As a result, we found a clear low/hard-high/soft state evolution of X-ray emission from M101 ULX-1. Furthermore, Fig. 1 demonstrates that the color C monotonically increases with the soft flux S and achieves a noticeable stability at high/soft fluxes.The color−color diagram of M101 ULX-1 clearly demonstrates two groups of data points, related to the high/soft (HS) and low/hard (LH) states (see Fig. 1). More specifically, in outbursts, M101 ULX-1 evolves from the LH state to the HS state during the rise phase and then returned to the LH state during the decay phase. This evolution is similar to most outbursts of galactic X-ray binary transients (e.g., Homan et al. 2001; Shaposhnikov & Titarchuk 2006; Belloni et al. 2006; ST09; TS09; Shrader et al. 2010; Muñoz-Darias et al. 2014).
The source M101 ULX-1 is in the low/hard state (characterized by a low count rate) for most of the time except for relatively short outbursts (with a high count rate, see Fig. 4 for details). Because of the low count rate we combined all of the low/hard state data for Chandra and Swift data.
 |
Fig. 4 Swift/XRT light curve of M101 ULX-1 in the 0.3−10 keV band during 2006−2013. Red points denote the source signal and green points indicate the background level.Blue points indicate the decay part of the outburst for this light curve and correspond to blue points of color-intensity evolutionary diagram (see higher branch) shown in Fig. 1. |
 |
Fig. 5 Left: Swift/XRT spectra from band A (red) and band C (blue) fitted using the bmc model. Right: two representative Chandra spectra for different states of M101 ULX-1. Data taken for 2004 July 5 (red), correspond to the high/soft state spectrum and for 2004 January−May and November (blue), correspond to the low/hard state spectrum. Spectra are fitted by a phabs*bmc model with kTbb = 70 eV (red solid line), for the high state and with kTbb = 45 eV (blue solid line), for the low state. See also the best-fit parameters listed in Tables 3 and 4 for Swift and Chandra data, respectively. |
In Fig. 4 we present Swift/XRT light curve of M101 ULX-1 during 2006−2013 for the 0.3−10 keV band. Red points denote the source signal and green points indicate the background level. We detected an outburst of M101 ULX-1 at MJD = 55 800−56 100, while for the rest of the Swift observations this source remained in the low/hard state. Individual Swift/XRT observations of M101 ULX-1 in Photon Counting (PC) mode do not have enough counts to allow statistically meaningful spectral fits. To overcome this problem, we have examined the Swift/XRT light curve and grouped the observations into four bands: very high (A), high (B), medium (C), and low (D) count rates (see Fig. 4).We have also split Band C into two sub-bands. Blue points shown in Fig. 1 are associated with softer/higher track (see also related points in the light curve, Fig. 4). In fact, this softer track (blue points of Fig. 1) corresponds to the outburst decay part ( see Fig. 4). While Band Ch (red points) are related to the lower track of the color-intensity diagram.Finally, we combined the spectra in each related band and fitted them for all these observations using χ2 statistics. In addition, some of the brightest source spectra of A and B sets were regrouped with the task grppha and then analyzed in the 0.3−7 keV range using the Cash statistics.
3.3. Spectral analysis
We examine different spectral models in application to all available data for M101 ULX-1 to describe the source evolution between the low/hard and high/soft states. Specifically, we use the combined Swift spectra from different spectral states to test a number of spectral models: powerlaw, Bbody, bmc, and their possible combinations modified by an absorption model.We fitted all spectra using a tied neutral column, which provides the best-fit column NH of 3 × 1021 cm-2.
Best-fit parameters of the combined Swift spectra of M101 ULX-1 in the 0.3−7 keV energy range using the following four models†: phabs*power, phabs*bbody, phabs*(bbody+power), and phabs*bmc.
Best-fit parameters of the spectra using Chandra observations of M101 ULX-1 in the 0.3–7 keV energy range.
3.3.1. Choice of the spectral model
As our first step, we proceed with a model of an absorbed power law. This model (phabs*powerlaw) fits well the low/hard state data only (e.g., for D-spectra, 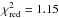 (18 d.o.f.), see the left column of Table 3). As one can see the power-law model is characterized by very large photon indices (much greater than 3, particularly for A and B event spectra, see notations of these events in Fig. 4) and furthermore, this model gives unacceptable fits (e.g., for all A, B, and C spectra of Swift data). On the other hand, for the high/soft state data, the thermal model (Bbody) provides better fits than the power-law model. However, the intermediate state spectra (B-, C-spectra for Swift data) cannot be fitted by any single-component model. In particular, a simple power-law model produces a soft excess. Significant positive residuals at low energies less than 1 keV suggest the presence of additional emission components. For this reason, we also use a sum of a blackbody and power-law component model (NH = 3 × 1021 cm-2, kTbb = 70−90 eV, and Γ = 1.4−2.2; see Table 3). The best fits of Swift spectra have been obtained by implementation of the so called Bulk Motion Comptonization model (BMC XSPEC model, Titarchuk et al. 1997), for which the photon index ranges in the interval of Γ ~ 1.4−2.8 for all observations (see Tables 3, 4 and Fig. 5). Furthermore, we achieve the best-fit results using the same model for all spectral (high/soft and low/hard) states.
(18 d.o.f.), see the left column of Table 3). As one can see the power-law model is characterized by very large photon indices (much greater than 3, particularly for A and B event spectra, see notations of these events in Fig. 4) and furthermore, this model gives unacceptable fits (e.g., for all A, B, and C spectra of Swift data). On the other hand, for the high/soft state data, the thermal model (Bbody) provides better fits than the power-law model. However, the intermediate state spectra (B-, C-spectra for Swift data) cannot be fitted by any single-component model. In particular, a simple power-law model produces a soft excess. Significant positive residuals at low energies less than 1 keV suggest the presence of additional emission components. For this reason, we also use a sum of a blackbody and power-law component model (NH = 3 × 1021 cm-2, kTbb = 70−90 eV, and Γ = 1.4−2.2; see Table 3). The best fits of Swift spectra have been obtained by implementation of the so called Bulk Motion Comptonization model (BMC XSPEC model, Titarchuk et al. 1997), for which the photon index ranges in the interval of Γ ~ 1.4−2.8 for all observations (see Tables 3, 4 and Fig. 5). Furthermore, we achieve the best-fit results using the same model for all spectral (high/soft and low/hard) states.
The BMC model is characterized by the seed photon temperature Ts, the energy index of the Comptonization spectrum is α (α = Γ−1), and the illumination parameter log (A) is related to the Comptonized (illumination) fraction f = A/ (1 + A). This model convolves a seed (disk) blackbody with an upscattering Green’s function.We also use a multiplicative phabs component to take an absorption by neutral material into account. The phabs model parameter is an equivalent hydrogen column NH. In Table 3 we demonstrate a good performance of the BMC model in application to the Swift data (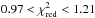 ).
).
 |
Fig. 6 Top to bottom: evolutions of the seed photon temperature kTs in eV, the BMC normalization and the spectral index α = Γ−1 during 2004−2005 outburst transitions observed with Chandra/ACIS-S. The outburst phases of the LS−HS transitions are indicated with blue vertical strips. |
3.3.2. Bulk motion Comptonization model and its application to M101 ULX-1
The bulk motion Comptonization (BMC) model has successfully fitted the M101 ULX-1 spectra for all spectral states. Specifically, Swift/XRT spectra for band A (red) and band C (blue) fitted using the BMC model are presented in Fig. 5 (left panel). The plot highlights the significant spectral variability between these sets of the observations (see Fig. 4 for our definition of Swift/XRT count-rate bands, and Table 3 for the best-fit parameters). In Table 3 (at the bottom), we present the results of spectral fitting Swift/XRT data of M101 ULX-1 using the phabs*bmc model. In particular, the low/hard state−high/soft state transition is related to the photon index Γ change from 1.4 to 2.5 when the relatively low seed photon temperature kTs changes from 40 eV to 90 eV. The bmc normalization varies by factor five, namely in the range of  erg s-1 kpc-2. However, the Comptonized (illumination) fraction is quite low (log A< −4 or f ~ 10-4) for all cases.
erg s-1 kpc-2. However, the Comptonized (illumination) fraction is quite low (log A< −4 or f ~ 10-4) for all cases.
As we have already pointed out above, Pence et al. (2001), Mukai et al. (2005), Kong et al. (2004), and Kong & Di Stefano (2005) analyzing the Chandra data investigated the spectral evolution of M101 ULX-1. We have also found a similar spectral behavior for the selected data set (see Table 2) with our model. In particular, we have revealed that M101 ULX-1 was in the high/soft state during three outbursts, including 2000 (March and October), 2004 (July), and 2004 December 30–2005 January 1. The other Chandra observations are related to the low/hard state when the source is seen at the detection limit. The low/hard state events of M101 ULX-1 covers long time intervals: during 2004 in January, March, May, November, and December. Usually in the low/hard state the X-ray luminosity of ULX-1 is about a factor 100 lower than that during the high/soft state, when the peak bolometric luminosity (for assumed isotropic emission) is about 1041 erg s-1.
In the right panel of Fig. 5 we demonstrate two representative Chandra spectra for different states of M101 ULX-1. Data taken for 2004 July 5 (red), which correspond to the high/soft state spectrum and for 2004 January–May and November (blue), which correspond to the low/hard state spectrum. These spectra have been fitted by a phabs*bmc model with the best-fit parameters kTs = 70 eV (red solid line for high state) and kTs = 45 eV (blue solid line for low/hard state). We list the best-fit spectral parameters in Table 4. The shapes of these spectra related to these two states, are different. In the low/hard state, the seed photons (with the lower kTs presumably related to lower mass accretion rate) are Comptonized more efficiently because the illumination fraction f [or log (A)] is higher. On the other hand, in the high state these parameters, i.e., kTs and log (A), show an opposite behavior, namely log (A) is lower for higher kTs. This means that a relatively small fraction of the seed photons, whose temperature is higher because of the higher mass accretion rate in the high state than that in the low state, is Comptonized.
We also evaluated the blackbody radius RBB derived using a relation 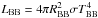 , where LBB is the luminosity of the blackbody and σ is Stefan’s constant. Assuming a distance D of 7.6 Mpc (as an upper estimate), the region associated with the blackbody has the radius RBB ≤ 3 × 106 km, which clearly indicates the IMBH presence in M101 ULX-1. In fact, RBB should be on order 10−30 km for a Galactic BH of mass around ten solar masses.
, where LBB is the luminosity of the blackbody and σ is Stefan’s constant. Assuming a distance D of 7.6 Mpc (as an upper estimate), the region associated with the blackbody has the radius RBB ≤ 3 × 106 km, which clearly indicates the IMBH presence in M101 ULX-1. In fact, RBB should be on order 10−30 km for a Galactic BH of mass around ten solar masses.
Our spectral model shows very good performance throughout all data sets. The reduced 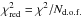 (where Nd.o.f. is the number of degree of freedom) is less or around 1.0 for the most of the observations. For a small fraction (less than 3%) of the spectra with high counting statistics
(where Nd.o.f. is the number of degree of freedom) is less or around 1.0 for the most of the observations. For a small fraction (less than 3%) of the spectra with high counting statistics 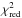 reaches 1.4. However, it never exceeds a rejection limit of 1.5.
reaches 1.4. However, it never exceeds a rejection limit of 1.5.
3.3.3. Evolution of X-ray spectral properties during spectral state transitions
We established common characteristics of the high/soft and low/hard state spectral transitions of M101 ULX-1 (as seen in Fig. 4) based on their spectral parameter evolution of X-ray emission in the energy range from 0.3 to 7 keV using Swift/XRT and Chandra/ACIS data. In Fig. 4 we show the light curves highlighting the X-ray variability of the source. In Fig. 6, from top to bottom we demonstrate an evolution of the seed photon temperature kTs, the BMC normalization, and the spectral index α = Γ−1 during 2004−2005 outburst transitions observed with Chandra/ACIS-S. The outburst phases of the low/hard state−high/soft state transitions are denoted by blue vertical strips.
During the rise phase and close to the peak of outburst, the softer emission [0.3−1 keV] dominates in the spectrum, which is associated with the seed photon temperatures kTs = 40−60 eV (see upper panel of Fig. 6). At the outburst we detected the maximum of the seed photon temperature kTs = 100 eV (see, e.g., MJD = 53 194 point) along with the maximum of the normalization Nbmc. Through the next days after outburst, mass accretion rate Ṁ drops by about a factor of ten (the BMC normalization parameter Nbmc ∝ Ṁ), kTs again drops to 60 eV when the source comes back its so-called standard low/hard state. In turn, a long standard low/hard state of M101 ULX-1 is associated with the low seed photon temperatures kTs = 40 eV (see, e.g., MJD = 53 000−53 150 interval in Ts-panel of Fig. 6) (see also Tables 3, 4).
From this plot we see that all spectral parameters correlate with each other during the LS−HS transitions. In particular, the correlations of the photon index Γ (= α + 1) versus BMC normalization NBMC are presented in Fig. 7, where blue triangles and red squares are related to Swift and Chandra data, respectively.In Fig. 7 we also show the photon index Γ (= α + 1) monotonically increases from 1.3 to 2.8 with NBMC (proportional to Ṁ) and saturates at Γsat = 2.8 ± 0.1 for high values of NBMC. One can see the strong saturation effect of the index Γ versus NBMC.
 |
Fig. 7 Correlations of the photon index Γ (= α + 1) vs. the BMC normalization NBMC (proportional to mass accretion rate) in units of |
4. Discussion
Before proceeding with the interpretation of the observations, let us briefly summarize these observations as follows: (1) the spectral data of M101 ULX-1 are well fitted by the BMC model for all analyzed the low/hard and high/soft state spectra (see Fig. 5 and Tables 3, 4). (2) The Green’s function index of the BMC component α (or the photon index Γ = α + 1) rises and saturates with an increase of the BMC normalization (proportional to Ṁ). The photon index saturation level of the BMC component is about 2.8 (see Fig. 7).
4.1. Saturation of the index is a signature of a BH
Using our analysis of the evolution of Γ in M101 ULX-1 we have firmly established that Γ saturates with the BMC-normalization NBMC, which is proportional to Ṁ. ST09 give strong arguments that this Γ saturation is a signature of converging flow into a BH.
Titarchuk et al. (1998) predicted that the transition layer (TL), the sub-Keplerian part of the accretion flow, should become more compact when Ṁ increases. For a BH case, Titarchuk & Zannias (2008), hereafter TZ98, obtain semianalytically and later Laurent & Titarchuk (1999; 2011, hereafter LT99 and LT11), find that Γ saturates for high mass accretion rates via Monte Carlo simulations. Analyzing a number of Galactic BHs (GBHs) ST09, Titarchuk & Seifina (2009, 2010), and Seifina et al. (2014, STS14) confirm the LT99-11 prediction that Γ increases and then it saturates with Ṁ. In Fig. 7 one can see that the values of Γ monotonically increase from 1.3 and then they finally saturate at a value of 2.8 for this particular source ULX-1 in M101.
We observed the luminosity increase along with the intrinsic softening of the spectrum lasting about three days. When the luminosity drops, we find the spectral hardening as a decrease of Γ in agreement with the theoretical expectations (see TZ98, LT99-11). This Γ vs. Ṁ correlation found using the M101 ULX-1 spectra are probably driven by the same physical process that causes the spectral evolutions seen in X-ray binaries due to the change of Ṁ. Moreover, we argue that the X-ray observations of M101 ULX-1 reveal the strong index saturation vs. Ṁ as a signature of the converging flow (or BH presence) in this source (see ST09). The index-NBMC normalization (or Ṁ) correlations found in a number of GBHs allow us to estimate a BH mass in M101 ULX-1 (see below Sect. 4.2).
Parameterizations for reference and target sources.
BH masses and distances.
4.2. Estimate of BH mass in M101 ULX-1
To scale BH mass MBH of the target source (M101 ULX-1), we select appropriate Galactic reference sources (XTE J1550-564, H 1742-322 (see ST09), and 4U 1630-47 (STS14)) whose masses and distances are known (see Table 6). We also select their BMC normalizations NBMC. We can compare the index vs. NBMC (proportional to Ṁ) correlations for these sources with that of the target source M101 ULX-1 (see Fig. 8). For all these sources, the index saturation level is at the almost same value of Γ. We used these three reference sources for an additional cross-check of the BH mass evaluation of M101 ULX-1.
 |
Fig. 8 Scaling of the photon index Γ versus the normalization NBMC for M101 ULX-1 (with red points – target source) and 4U 1630-472, XTE J1550-564, and H1743-322 (with pink, blue, and green indicating the reference sources), respectively. The bright blue vertical arrow schematically shows that the parameter A is the value of the index saturation level. The horizontal black arrow stresses the fact that the correlations of the target and reference sources are similar. The only difference is in terms of the BMC normalization because of the different values of the MBH/D2 ratio. |
All correlation patterns are self-similar, showing the same index saturation level, which allows us to perform a reliable scaling. The BH mass scaling technique is generally based on the parameterization of the Γ−NBMC correlation, which according to ST09 is fitted by a function ![\begin{equation} F(x)= A - (D\cdot B)\ln\left\{\exp\left[\left(1.0 - \left(x/(x_{\rm tr})^{\beta}\right)\right)/D\right] + 1\right\}, \end{equation}](/articles/aa/full_html/2016/01/aa26122-15/aa26122-15-eq138.png) (1)where x = NBMC.
(1)where x = NBMC.
By fitting this function to the correlation pattern, we find a set of parameters A, B, D, Ntr, and β that represent a best-fit form of the function F(x) for a particular correlation curve. For x ≫ xtr, the correlation function F(x) converges to a constant value A. Thus, A is the value of the index saturation level, β is the power-law index of the inclined part of the curve, xtr is a value at which index Γ starts growing, and β provides the slope of the correlation. Parameter D determines how smoothly the fitted function saturates to A. This function F(x) is widely used for a description of the correlation of Γ vs. NBMC (Sobolewska & Papadakis 2009, ST09; Seifina & Titarchuk 2010; Shrader et al. 2010, STS14; and Giacche et al. 2014).
The crucial assumption for this technique to be applied is that different reference sources show the same shape of the Γ−NBMC correlations and the only difference is in the ratio of a BH mass to the squared distance, namely in the coefficient MBH/d2. Figure 8 shows that a value of the parameter A (seebright blue vertical arrow) is almost the same for all scaling sources. In other words, the best-fit parameter A (within the limits of error bars) is almost the same for all these sources. In particular, AULX = 2.8 ± 0.1, A1550 = 2.84 ± 0.08, and A1743 = 2.97 ± 0.07 for M101 ULX-1, XTE J1550-564, and H 1743-322, respectively. Furthermore, the black horizontal arrow stresses that the correlations for a pair of sources (e.g., M101 ULX-1 red line and XTE J1550-564 blue line) are self-similar and the only difference is in the BMC normalization because of the different values of the MBH/D2 ratio.
Thus, to obtain the BH mass of M101 ULX-1, one should shift along NBMC-axis the related correlation of the reference source to the one of the target sources (see Fig. 8). This scaling technique provides a target BH mass value Mt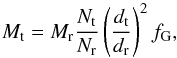 (2)where t denotes the target; r stands for the reference and the geometric factor; by definition, fG = (cosθ)r/ (cosθ)t; and the inclination angles θr, θt and dr, dt are distances to the reference and target sources, respectively (see details in ST09). The geometrical factor fG has to be considered when the accretion process is assumed to occur in disk-like geometry, while it is close to 1 in case of spherical accretion. Despite this uncertainty in the determination of fG, we adopt the above formula for fG in which θ ~ i if information on the system inclination angle i is available (see Table 6).
(2)where t denotes the target; r stands for the reference and the geometric factor; by definition, fG = (cosθ)r/ (cosθ)t; and the inclination angles θr, θt and dr, dt are distances to the reference and target sources, respectively (see details in ST09). The geometrical factor fG has to be considered when the accretion process is assumed to occur in disk-like geometry, while it is close to 1 in case of spherical accretion. Despite this uncertainty in the determination of fG, we adopt the above formula for fG in which θ ~ i if information on the system inclination angle i is available (see Table 6).
In Fig. 8 we plot the Γ−NBMC for M101 ULX-1 points extracted using Chandra and Swift spectra along with those for the three reference patterns (4U 1630-47 (pink), XTE J1550-564 blue, H 1743-322 green), which are similar to the correlation found for the target source. Scaling parameters for each of these pairs are presented in Table 6.
The target mass for M101 ULX-1 can be estimated using the relation 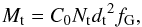 (3)where
(3)where 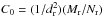 is the scaling coefficient for each scaling pair (target and reference sources), masses Mt and Mr are in solar units, and dr is the distance to a particular reference source measured in kpc.
is the scaling coefficient for each scaling pair (target and reference sources), masses Mt and Mr are in solar units, and dr is the distance to a particular reference source measured in kpc.
We take values of Mr, Mt, dr, dt, and cos(i) from Table 6 and then we obtain the lowest limit of the mass, using the best-fit value of Nt = (4.2 ± 0.2) × 10-4 taken at the begining of the index saturation (see Fig. 8) and measured in units of  erg s-1 kpc-2 (see Table 5 for values of the parameters of function f(Nt) Eq. (1)). We estimate C0 ~ 1.9, 1.72 1,83 for XTE J1550-564, H 1723-322, and 4U 1630-472, respectively using dr, Mr, Nr presented by ST09. Then, using formula (3), we obtain that MULX ≥ 3.4 × 104 M⊙ (MULX = Mt), assuming dULX ~ 6.4 Mpc (Shappee & Stanek 2011) and fG ~ 1 (inclinations for both objects are the same). To account for the spread in the distance to M101, we made the same estimates of MULX, assuming dULX = 7.4 ± 0.6 Mpc (Kelson et al. 2011), and derived higher values MULX≥ 4.3 × 104 M⊙. All these results are summarized in Table 6.
erg s-1 kpc-2 (see Table 5 for values of the parameters of function f(Nt) Eq. (1)). We estimate C0 ~ 1.9, 1.72 1,83 for XTE J1550-564, H 1723-322, and 4U 1630-472, respectively using dr, Mr, Nr presented by ST09. Then, using formula (3), we obtain that MULX ≥ 3.4 × 104 M⊙ (MULX = Mt), assuming dULX ~ 6.4 Mpc (Shappee & Stanek 2011) and fG ~ 1 (inclinations for both objects are the same). To account for the spread in the distance to M101, we made the same estimates of MULX, assuming dULX = 7.4 ± 0.6 Mpc (Kelson et al. 2011), and derived higher values MULX≥ 4.3 × 104 M⊙. All these results are summarized in Table 6.
It is evident that the inclination of M101 ULX-1 system may be different from the inclination for the reference sources (i ~ 60−70°), therefore, we take this BH mass estimate for M101 ULX-1 as a lowest BH mass value because MULX is reciprocal function of cos(iULX) (see Eq. (3) taking into account that fG = (cosθ)r/ (cosθ)t there).
The obtained BH mass estimate is in agreement with a high bolometrical luminosity for M101 ULX-1 and kTs value, which is in the range of 40−100 eV. In fact, a very soft spectrum is consistent with the relatively cold disk for ULXs, which have also been considered evidence for IMBHs (Miller et al. 2003; 2004; Wang et al. 2004).
In addition, Kong et al. (2004), based on the comparison between the observed temperature (kT ≤ 100 eV) and bolometric luminosity (Lbol ~ 1040−41 erg s-1) during the 2004 July outburst, obtained a similar estimate on BH mass of M101 ULX-1. In fact, they obtained that BH mass in M101 ULX-1, Mm101 is greater than 2800 M⊙. Furthermore, Kong & Di Stefano (2005) using the 90% lower limits of the disk blackbody fits derived from the 2004 December outburst, estimated Mm101 in the range of 1.3 × 103−3 × 104 M⊙.
Liu et al. (2013) report on optical observations of M101 ULX-1 by Gemini/GMOS and they find that the system contains a Wolf-Rayet star with an orbital period of 8.2 days. The optical spectrum of the source is characterized by a broad helium emission line, including the He II 4686 Ȧ line. Because of the absence of a broad hydrogen emission line the authors argue that the star must be a Wolf-Rayet (WR). They propose the scenario that the intensities of the helium emission lines can be reproduced by the atmospheric model (see Hiller & Miller 1998) and the mass is estimated to be 19 M⊙ based on the empirical mass-luminosity relation (Schaerer & Maeder 1992 and Crowther 2007). Liu et al. find the mass function is about 0.18 M⊙ for M101 ULX-1. Suggesting different values of inclination angle i, they propose that this BH mass is likely 20−30 M⊙. In Fig. 9 we present Liu’s BH estimate as a function of inclination angle i. The range of their BH mass estimates varies from 5 to 1000 solar masses, depending on inclination angle i. For smaller i a BH mass is higher (more than 1000 M⊙) and for i ≤ 90° it is about five solar masses.
Liu’s evaluation of the BH mass (20−30 M⊙) is too low in comparison with our BH mass estimate and also it is in contradiction with the lower values of the soft seed photon temperature kTs (see discussion above). In fact, for a BH of 20−30 M⊙ the seed temperature kTs is expected to be around 0.5 keV (see ST09). Liu et al. (2013) also point out that these low temperatures of the seed (disk) photons kTs ~ 70 eV combined with high luminosities (> 1039 erg s-1), which are observed in ULX-1 M101, complicate the interpretation of ULX-1 as a stellar-mass BH.
We derived the bolometric luminosity from the normalization of the BMC model between 7 × 1040 erg/s and 6 × 1041 erg/s (assuming isotropic radiation). This high luminosity is difficult to achieve in a X-ray binary unless the accretor has a mass greater than 1000 M⊙. While our luminosity estimate is higher than that for previous M101 ULX-1 outbursts observed by XMM-Newton in 2002–2005, it is closer to that derived by Kong et al. (2004) (who used a combined power law plus blackbody model). On average, Lx luminosity is lower than the bolometrical luminosity because the peak of the spectrum occurs at relatively low photon energies (E ~ 0.1 keV).
 |
Fig. 9 Estimates of BH mass MBH in M101 ULX-1. The blue line represents MBH versus the inclination angle i estimated using the dynamical method for HST data (taken from Liu et al. 2013), while the red line corresponds to our BH mass estimates based on X-ray data using the scaling technique (see Table 6). These two different methods give similar BH mass values with an assumption of small inclination angles. |
5. Conclusions
We have studied the low−high state transitions observed in M101 ULX-1 using Swift (2006–2013) and Chandra (2000, 2004–2005) observations. We argued that the source spectra can be fitted by the BMC model for all observations. Our study reveals that the index-normalization (or Ṁ) correlation observed in M101 ULX-1 is similar to those in GBHs. The photon index Γ is in the range Γ = 1.3−2.8. We also estimated the peak bolometric luminosity, which is about 6 × 1041 erg s-1.
We applied the scaling technique based on the observed correlations to estimate MBH in M101 ULX-1. This technique is commonly and successfully applied to estimate BH masses of Galactic black holes. In this work, for the first time the scaling technique is applied to estimate MBH in ULX. We obtain values ofMBH ~ (3.2−4.3) × 104 M⊙,which are in a good agreement with that estimated by peak bolometric luminosity estimates. The low limit of this BH mass estimate is in agreement with optical results (see Liu et al. 2013) assuming the face-on system configuration in ULX-1 (see Fig. 9).Combining these estimates with the inferred low temperatures of the seed disk photons Ts we can state that the compact object of ultraluminous source M101 ULX-1 is likely tobe an intermediate-mass black hole with at least MBH> 3.2 × 104 M⊙.
A Fortran and C-based program, which calculates the ratios via the methods described by Park et al. 2006 (see http://hea-www.harvard.edu/AstroStat/BEHR/).
Acknowledgments
This research was performed using data supplied by the UK Swift Science Data Centre at the University of Leicester. E.S. also thanks Phil Evans for useful scientific discussion. We appreciate editing the text of the paper by Mike Nowak and Tod Strohmayer. We also acknowledge the deep analysis of the paper by the referee.
References
- Belloni, T., Parolin, I., Del Santo, M., et al. 2006, MNRAS, 367, 1113 [NASA ADS] [CrossRef] [Google Scholar]
- Burke, M. J., Ralph, P., Kraft, R. P., et al. 2013, ApJ, 775, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Crowther, P. A. 2007, ARA&A, 45, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Di Stefano, R., & Kong, A. K. H. 2003, ApJ, 592, 884 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, P. A., Beardmore, A. P., Page, K. L., et al. 2007, A&A, 469, 379 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Evans, P. A., Beardmore, A. P., Page, K. L., et al. 2009, MNRAS, 397, 1177 [NASA ADS] [CrossRef] [Google Scholar]
- Freedman, W. L., Madore, B. F., Gibson, B. K., et al. 2001, ApJ, 553, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Giacche, S., Gili, R., & Titarchuk, L. 2014, A&A, 562, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hiller, D., & Miller, D. L 1998, ApJ, 496, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Homan, J., Wijnands, R., van der Klis, M., et al. 2001, ApJS, 132, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Jin, Y. K., Zhang, S. N., & Wu, J. F. 2006, ApJ, 653, 1566 [NASA ADS] [CrossRef] [Google Scholar]
- Kelson, D. D., Illingworth, G. D., Freedman, W. F., et al. 1996, ApJ, 463, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Kong, A. K. H., & Di Stefano, R. 2005, ApJ, 632, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Kong, A. K. H., Di Stefano, R., & Yuan, F. 2004, ApJ, 617, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Kuntz, K. D., Gruendl, R. A., Chu, Y.-H., et al. 2005, ApJ, 620, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Laurent, P., & Titarchuk, L. 1999, ApJ, 511, 289 (LT99) [NASA ADS] [CrossRef] [Google Scholar]
- Laurent, P., & Titarchuk, L. 2011, ApJ, 727, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, J. F. 2009, ApJ, 704, 1628 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, J. F., Bregman, J. N., Seitzer, P., Irwin, J. A. 2004, AAS Meeting 205, #104.03; BAAS, 36, 1515 [Google Scholar]
- Liu, J. F., Orosz, J., & Bregman, J. N. 2012, ApJ, 745, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, J. F., Bregman, J. N., Bai, Y., et al. 2013, Nature, 503, 500 [NASA ADS] [CrossRef] [Google Scholar]
- McClintock, J. E., Remillard, R. A., Rupen, M. P., et al. 2009, ApJ, 698, 1398 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, J. M., Fabbiano, G., Miller, M. C., & Fabian, A. C. 2003, ApJ, 585, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, J. M., Fabian, A. C., & Miller, M. C. 2004, ApJ, 614, L117 [NASA ADS] [CrossRef] [Google Scholar]
- Mukai, K., Pence, W. D., Snowden, S. L., & Kuntz, K. D. 2003, ApJ, 582, 184 [NASA ADS] [CrossRef] [Google Scholar]
- Mukai, K., Still, M., Corbet, R., Kuntz, K., & Barnard, R. 2005, ApJ, 634, 1085 [NASA ADS] [CrossRef] [Google Scholar]
- Muñoz-Darias, T., Fender, R. P., Motta, S. E., & Belloni, T. M. 2014, MNRAS, 443, 3270 [NASA ADS] [CrossRef] [Google Scholar]
- Novikov, I. D., & Thorne, K. S., 1973, in Black holes, 343 [Google Scholar]
- Orosz, J. A., Groot, P. J., van der Klis, M., et al. 2002, ApJ, 568, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Park, T., Kashyap, V. L., Siemiginowska, A., et al. 2006, ApJ, 652, 610 [NASA ADS] [CrossRef] [Google Scholar]
- Pence, W. D., Snowden, S. L., Mukai, K., & Kuntz, K. D. 2001, ApJ, 561, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Roberts, T. P., Levan, A. J., & Goad, M. R. 2008, MNRAS, 2008, 387, 73 [Google Scholar]
- Roberts, T. P., Gladstone, J. C., Goulding, A. D., et al. 2011, Astron. Nachr. 332, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Sańchez-Fernández, C., Castro-Tirado, A. J., Duerbeck, H. W., et al. 1999, A&A, 348, L9 [NASA ADS] [Google Scholar]
- Schaerer, D., & Maeder, A. 1992, A&A, 263, 129 [NASA ADS] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Seifina, E., & Titarchuk, L. 2010, ApJ, 722, 586 (ST10) [NASA ADS] [CrossRef] [Google Scholar]
- Seifina, E., & Titarchuk, L. & Shaposhnikov, N. 2014, ApJ, 789, 57 (STS14) [NASA ADS] [CrossRef] [Google Scholar]
- Shaposhnikov, N., & Titarchuk, L. 2006, ApJ, 643, 1098 (ST06) [NASA ADS] [CrossRef] [Google Scholar]
- Shaposhnikov, N., & Titarchuk, L. 2009, ApJ, 699, 453 (ST09) [NASA ADS] [CrossRef] [Google Scholar]
- Shappee, B., & Stanek, K. Z. 2011, ApJ, 733, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Shrader, Ch. R., Titarchuk, L., & Shaposhnikov, N. 2010, ApJ, 718, 488 [NASA ADS] [CrossRef] [Google Scholar]
- Sobczak, G. J., McClintock, J. E., Remillard, R. A., & Bailyn, C. D. 1999, ApJ, 520, 776 [NASA ADS] [CrossRef] [Google Scholar]
- Sobolewska, M. A., & Papadakis, I. E. 2009, MNRAS, 399, 1997 [Google Scholar]
- Titarchuk, L., & Seifina, E. 2009, ApJ, 706, 1463 [NASA ADS] [CrossRef] [Google Scholar]
- Titarchuk, L., & Zannias, T. 2008, ApJ, 499, 315 (TZ98) [Google Scholar]
- Titarchuk, L., Mastichiadis, A., Kylafis, N. D., et al. 1997, ApJ, 487, 834 [NASA ADS] [CrossRef] [Google Scholar]
- Titarchuk, L., Lapidus, I.I., & Muslimov, A. 1998, ApJ, 499, 315 (TLM98) [NASA ADS] [CrossRef] [Google Scholar]
- Wang, Q. D., Yao, Y., Fukui, W., Zhang, S. N., & Williams, R. 2004, ApJ, 609, 113 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Best-fit parameters of the combined Swift spectra of M101 ULX-1 in the 0.3−7 keV energy range using the following four models†: phabs*power, phabs*bbody, phabs*(bbody+power), and phabs*bmc.
Best-fit parameters of the spectra using Chandra observations of M101 ULX-1 in the 0.3–7 keV energy range.
All Figures
 |
Fig. 1 Color-intensity evolutionary diagram for M101 ULX-1 using Swift observations (2006–2012), where S and H are the source counts in the two bands: the soft [0.3−1.5 keV] and hard [1.5−10 keV] passbands. Spectral softness (hardness ratio) C and source soft brightness S increase to the right and, finally, the former saturates at high values of S. Larger values of C indicate a softer spectrum, and vice versa. Blue points are related to the decay part of the outburst (see the light curve in Fig. 4). |
| In the text | |
 |
Fig. 2 Swift/XRT (0.3−10 keV) image of M101 field of view, where green circles are the locations of M101 ULX-1, and M101 galactic nucleus (NGC 5457), NGC 5461, and M101 H II regions. The image segment selected by dashed line box is also shown in Fig. 3 using Chandra data. |
| In the text | |
 |
Fig. 3 Adaptively smoothed Chandra/ACIS-S (0.2−8 keV) image of the M101 field, in which localization is indicated with the selected dashed line box in Fig. 2. Contour levels demonstrate the minimal contamination by other point sources and diffuse emission within circle of 9′′ around M101 ULX-1. |
| In the text | |
 |
Fig. 4 Swift/XRT light curve of M101 ULX-1 in the 0.3−10 keV band during 2006−2013. Red points denote the source signal and green points indicate the background level.Blue points indicate the decay part of the outburst for this light curve and correspond to blue points of color-intensity evolutionary diagram (see higher branch) shown in Fig. 1. |
| In the text | |
 |
Fig. 5 Left: Swift/XRT spectra from band A (red) and band C (blue) fitted using the bmc model. Right: two representative Chandra spectra for different states of M101 ULX-1. Data taken for 2004 July 5 (red), correspond to the high/soft state spectrum and for 2004 January−May and November (blue), correspond to the low/hard state spectrum. Spectra are fitted by a phabs*bmc model with kTbb = 70 eV (red solid line), for the high state and with kTbb = 45 eV (blue solid line), for the low state. See also the best-fit parameters listed in Tables 3 and 4 for Swift and Chandra data, respectively. |
| In the text | |
 |
Fig. 6 Top to bottom: evolutions of the seed photon temperature kTs in eV, the BMC normalization and the spectral index α = Γ−1 during 2004−2005 outburst transitions observed with Chandra/ACIS-S. The outburst phases of the LS−HS transitions are indicated with blue vertical strips. |
| In the text | |
 |
Fig. 7 Correlations of the photon index Γ (= α + 1) vs. the BMC normalization NBMC (proportional to mass accretion rate) in units of |
| In the text | |
 |
Fig. 8 Scaling of the photon index Γ versus the normalization NBMC for M101 ULX-1 (with red points – target source) and 4U 1630-472, XTE J1550-564, and H1743-322 (with pink, blue, and green indicating the reference sources), respectively. The bright blue vertical arrow schematically shows that the parameter A is the value of the index saturation level. The horizontal black arrow stresses the fact that the correlations of the target and reference sources are similar. The only difference is in terms of the BMC normalization because of the different values of the MBH/D2 ratio. |
| In the text | |
 |
Fig. 9 Estimates of BH mass MBH in M101 ULX-1. The blue line represents MBH versus the inclination angle i estimated using the dynamical method for HST data (taken from Liu et al. 2013), while the red line corresponds to our BH mass estimates based on X-ray data using the scaling technique (see Table 6). These two different methods give similar BH mass values with an assumption of small inclination angles. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


