| Issue |
A&A
Volume 585, January 2016
|
|
|---|---|---|
| Article Number | A52 | |
| Number of page(s) | 14 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201525863 | |
| Published online | 16 December 2015 | |
Quiescent luminous red galaxies as cosmic chronometers: on the significance of mass and environmental dependence
1
College of Science, China Three Gorges University,
443002
Yichang,
PR China
2
Key Laboratory of Optical Astronomy, National Astronomical
Observatories, Chinese Academy of Science, 100012
Beijing, PR
China
e-mail:
luyj@nao.cas.cn
3
National Astronomical Observatories, Chinese Academy of
Science, 100012
Beijing, PR
China
4
Istituto Nazionale di Astrofisica (INAF), Osservatorio Astronomico
di Trieste, via Tiepolo 11, 34131
Trieste,
Italy
5
Center of High Energy Physics, Peking University,
100871
Beijing, PR
China
6
Department of Astronomy and Astrophysics, Peking
University, 100871
Beijing, PR
China
Received: 11 February 2015
Accepted: 23 September 2015
Context. Massive luminous red galaxies (LRGs) are believed to be evolving passively and can be used as cosmic chronometers to estimate the Hubble constant (the differential age method). However, different LRGs may be located in different environments. The environmental effects, if any, on the mean ages of LRGs, and the ages of the oldest LRGs at different redshift, may limit the use of the LRGs as cosmic chronometers.
Aims. We aim to investigate the environmental and mass dependence of the formation of “quiescent” LRGs, selected from the Sloan Digital Sky Survey (SDSS) data release 8, and to pave the way for using LRGs as cosmic chronometers.
Methods. Using the population synthesis software STARLIGHT, we derive the stellar populations in each LRG through the full spectrum fitting and obtain the mean age distribution and the mean star formation history (SFH) of those LRGs.
Results. We find that there is no apparent dependence of the mean age and the SFH of quiescent LRGs on their environment, while the ages of those quiescent LRGs depend weakly on their mass. We compare the SFHs of the SDSS LRGs with those obtained from a semi-analytical galaxy formation model and find that they are roughly consistent with each other if we consider the errors in the STARLIGHT-derived ages. We find that a small fraction of later star formation in LRGs leads to a systematical overestimation (~28%) of the Hubble constant by the differential age method, and the systematical errors in the STARLIGHT-derived ages may lead to an underestimation (~ 16%) of the Hubble constant. However, these errors can be corrected by a detailed study of the mean SFH of those LRGs and by calibrating the STARLIGHT-derived ages with those obtained independently by other methods.
Conclusions. The environmental effects do not play a significant role in the age estimates of quiescent LRGs; and the quiescent LRGs as a population can be used securely as cosmic chronometers, and the Hubble constant can be measured with high precision by using the differential age method.
Key words: Galaxy: evolution / Galaxy: formation / Galaxy: stellar content / galaxies: abundances
© ESO, 2015
1. Introduction
Luminous red galaxies (LRGs) are believed to evolve passively and host the oldest stellar population, and can thus be used as cosmic chronometers to measure the Hubble constants at different redshifts (the differential age method; Jimenez & Loeb 2002). For example, Jimenez et al. (2003) adopted the differential age method to measure the Hubble constant at redshift z ~ 0 by using the oldest LRGs at different redshifts among a large number of LRGs from the Sloan Digital Sky Survey (SDSS). The differential age method is also adopted to measure the Hubble constants at higher redshifts by using red galaxies from other surveys, and those measurements were used to constrain other cosmological parameters (e.g., Simon et al. 2005; Stern et al. 2010; Moresco et al. 2012, 2015). Liu et al. (2012) further developed the differential age method by using the mean ages of the SDSS LRGs, rather than the oldest LRGs, to constrain the Hubble constant at low redshift, for which a homogeneous sample of LRGs is required. However, different LRGs may be located in different environments, for example, some LRGs are the brightest central galaxies (BCGs) or satellite galaxies of clusters located in dense environments, and some LRGs are field galaxies located in less dense environments. Therefore, the environmental effects may affect the accuracy of the measurements of both the mean ages of LRGs and the ages of the oldest LRGs at different redshift (especially when they are not selected from a single uniform survey) and may thus limit the use of the LRGs as cosmic chronometers. Furthermore, the later star formation in the LRGs, if any, may also introduce systematic errors to the use of LRGs as cosmic chronometers (see a discussion in Liu et al. 2012). These effects must be addressed, not only for the validity of the use of LRGs as cosmic chronometers, but also to improve the accuracy of the estimates of the Hubble constant and other cosmological parameters via the differential age method.
The environmental effects on galaxy formation have been studied extensively in the past decade (e.g., Forbes et al. 1998; Blanton et al. 2005; Cooper et al. 2006; De Lucia et al. 2006; Poggianti et al. 2006; Lee et al. 2010; Thomas et al. 2010). The differences in the assembly histories of the dark matter halos of those galaxies in different environments appear to be the main driver of the environmental effects detailed below. Galaxies in high density environments may experience many more mergers, leading to multiple starburst episodes in their formation and evolution histories, compared to those in low density environments (e.g., Thomas et al. 2005); The BCGs in massive dark matter halos may have formed at early time and were then quenched because of internal quenching processes, such as the AGN feedback (De Lucia & Blaizot 2007); the hot gas in satellite galaxies may have been removed due to ram pressure stripping (an external process) when these galaxies fell into a group or cluster of galaxies, and thus the star formation in them was suppressed (Gómez et al. 2003; Balogh et al. 2004a; Pasquali et al. 2010; De Lucia et al. 2012); dynamical perturbations on those infalling galaxies may also have led to some instabilities and transformed disk galaxies to spheroidal galaxies (Naab et al. 2009). These differences in the formation histories of BCGs, satellite galaxies and field galaxies may be imprinted on their structure properties, as studied extensively over many decades (Matthews et al. 1964; Oemler 1973; Schombert 1988; Graham et al. 1996; Patel et al. 2006; Bernardi et al. 2007; Desroches et al. 2007; Lauer et al. 2007; von der Linden et al. 2007; De Lucia & Blaizot 2007; Liu et al. 2008).
In this paper, we adopt the spectral population synthesis technique to study the mass and environmental effects of the so-called quiescent SDSS LRGs and their star formation histories (SFHs), and check whether they can be securely used as cosmic chronometers to measure the Hubble constants at different redshifts. Several previous studies investigated the ages of early-type galaxies as a function of their environment and masses (Bernardi et al. 1998, 2006; Thomas et al. 2005, 2010. The present paper differs from previous studies in several aspects: (1) we adopt the largest LRG (or early type galaxy) sample (7882); (2) we use the full spectrum fitting method to extract galaxy properties; (3) we investigate the detailed SFHs for different type of early type galaxies, i.e., BCGs, member galaxies, and field galaxies. In Sect. 2, we describe the selection criteria for “quiescent” LRGs in different environments, e.g., the central and satellite galaxies in clusters of galaxies and dense environments, and field galaxies in less dense environments. In Sect. 3, we adopt the spectral population synthesis technique and the full spectrum fitting method to obtain the SFHs and age properties of these LRGs. In Sect. 4, we investigate the mass and environmental dependence of the formation of LRGs by comparing the obtained SFHs and age properties of LRGs with different mass and in different environments. In Sect. 5, we further investigate the underlying reasons for the little environmental effect in the formation of LRGs by comparing the SFHs and the age properties of the SDSS LRGs with mock LRGs from a semi-analytical galaxy formation model (Guo et al. 2011). We analyze the possible uncertainties in the estimates of the Hubble constant via the differential age method in Sect. 6. No significant environmental dependence of the age properties of quiescent LRGs suggests that these LRGs can be securely used as cosmic chronometers. Conclusions are given in Sect. 7.
2. Sample selection
A large number of (totaling 112, 191) LRGs were selected from the SDSS III data release 8 (DR8) based on color and magnitude criteria (see Eisenstein et al. 2001). By cross-matching the LRG sample with the cluster catalog given by Wen et al. (2012), we find that 28 336 LRGs are BCGs1. We also select those LRGs that are located within a projected separation of r200 from the BCGs and with a redshift difference of no more than 0.05 from the BCGs2. Here r200 is the radius within which the mean density of a cluster is 200 times that of the critical density of the universe (Wen et al. 2012, see Table 1), the redshift difference 0.05 is adopted to consider the uncertainties in the photometric redshift estimates; these LRGs are denoted as the “member galaxies” (MGs) of clusters. According to the above selection criteria, we obtain 11 703 MGs. The remaining LRGs (72 152), located in environments substantially less dense than those of the clusters, we denote as “field galaxies” (FGs). To obtain a passively evolving LRG sample, we use the following criteria (similar to those in Liu et al. 2012):
-
having the GALAXY_RED flag in Catalog Archive Server (CAS) database;
-
zWarning EQ 0, SNmedian> 10, 0.15 <z< 0.25, ph.fracDev_r> 0.8 and V_disp> 210,
Quiescent LRGs in different subgroups and their age properties.
The above LRG sample is further categorized into several different groups since the main purpose of this study is to investigate the mass and environment dependence of the formation of passively evolving LRGs.
-
Group I, BCGs are categorized into three subclasses according to the richness of their host clusters (RL). The richness boundaries for those subclasses of BCGs are 12 ≤ RL ≤ 22, 22 <RL ≤ 39 and RL> 39, respectively, where RL = 12 is the low limit for a galaxy system that is classified as a cluster in Wen et al. (2012). The richness of a cluster can be taken as a proxy of the cluster mass as log M200 = (−1.49 ± 0.05) + (1.17 ± 0.03)log RL(Wen et al. 2012), where M200, in unit of 1014M⊙, is the cluster mass enclosed in a region with an over-density of 200. According to this relation, the above richness boundaries correspond to the mass ranges of 0.6−1.2 × 1014M⊙, 1.2−2.4 × 1014M⊙, and > 2.4 × 1014M⊙, respectively.
-
Group II, LRGs with similar masses are categorized into BCGs, MGs, and FGs, which represent different environments. The mass of an LRG may be also indicated by its velocity dispersion (σv). Therefore, BCGs, MGs, and FGs are further categorized into four sub-groups according to their velocity dispersions. The boundaries for the velocity dispersion bins are 210−240 km s-1, 240 − 270 km s-1, 270−300 km s-1, and > 300 km s-1, respectively. According to the scaling relation between the stellar mass and the velocity dispersion of galaxies, e.g., log (M/M⊙) ≈ 0.63 + 4.52log σv (Thomas et al. 2005), the boundaries of the σv-bins correspond to the mass ranges of 1011.1 − 1011.4M⊙, 1011.4 − 1011.6M⊙, 1011.6 − 1011.8M⊙, and > 1011.8M⊙, respectively.
-
Group III, the satellite galaxies of BCGs (SCGs) are selected and categorized as a single group, of which the velocity dispersion range is different from that of the BCGs (see Table 1).
3. Spectral synthesis and spectrum fitting
 |
Fig. 1 Example for the full spectrum fitting of the spectrum of a BCG. The green, blue, and red lines in the top left panel represent the observed spectrum (Oλ), its error spectrum, and the model spectrum (Mλ), respectively. The residual spectrum (Eλ) is shown by the purple line in the bottom left panel. In the left panels, both Oλ and Mλ are scaled by normalizing the flux at wavelength 4020 Å to 1. The light-weighted and the mass-weighted fractions of stellar populations, i.e., xj and μj, are shown in the top and the bottom right panels, respectively. Several quantities (see Sect. 3) derived from the fitting are listed in the top right corner. |
In this section, we use the software STARLIGHT (see Cid Fernandes et al. 2005) to derive the stellar populations in each individual LRG in our sample through full spectrum fitting. Using STARLIGHT, the observed SDSS spectrum (Oλ) of each sample LRG can be fitted by a model spectrum (Mλ), a combination of a set of predefined base spectra, i.e., 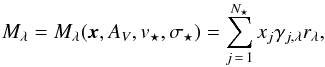 (1)where γj,λ ≡ bλ,j ⊗ G(v⋆,σ⋆), bλ,j ≡ Bλ,j/Bλ0,j is the normalized flux of the jth component, Bλ,j is the jth component of the base spectra, Bλ0,j is the flux of the jth component at wavelength λ0, G(v⋆,σ⋆) represents a Gaussian distribution centered at a velocity v⋆ and broadened by a line-of-sight velocity dispersion σ⋆, xj is the fraction of flux caused by component j at λ0, and rλ ≡ 10− 0.4(Aλ − AV) is the global extinction term represented by AV. The best-fit is obtained by using a simulated annealing plus Metropolis-Hastings scheme, which searches for the minimum of
(1)where γj,λ ≡ bλ,j ⊗ G(v⋆,σ⋆), bλ,j ≡ Bλ,j/Bλ0,j is the normalized flux of the jth component, Bλ,j is the jth component of the base spectra, Bλ0,j is the flux of the jth component at wavelength λ0, G(v⋆,σ⋆) represents a Gaussian distribution centered at a velocity v⋆ and broadened by a line-of-sight velocity dispersion σ⋆, xj is the fraction of flux caused by component j at λ0, and rλ ≡ 10− 0.4(Aλ − AV) is the global extinction term represented by AV. The best-fit is obtained by using a simulated annealing plus Metropolis-Hastings scheme, which searches for the minimum of ![\begin{equation} \chi^2 = \sum_{\lambda} \left[(O_\lambda - M_\lambda) w_\lambda\right]^2, \end{equation}](/articles/aa/full_html/2016/01/aa25863-15/aa25863-15-eq80.png) (2)where
(2)where 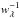 is the error in Oλ. The residual spectrum Eλ can also be obtained by subtracting the model spectrum from the observed one, i.e., Eλ = Oλ − Mλ.
is the error in Oλ. The residual spectrum Eλ can also be obtained by subtracting the model spectrum from the observed one, i.e., Eλ = Oλ − Mλ.
We first generate the base spectra by taking simple stellar populations (SSPs) from the Bruzal & Charlot (2003), hereafter referred to as BC03, evolutionary synthesis models (for more details, see Bruzual & Charlot 2003). We adopt the Padova 1994 evolutionary tracks (Bertelli et al. 1994) and the Salpeter initial mass function (Salpeter 1955). We adopt ten different SSP ages (i.e., 0.9, 1.4, 2.5, 5, 8, 9, 10, 11, 12, 13 Gyr) and four different metallicity values (0.2, 0.4, 1, and 2.5 Z⊙), and obtain a total of 40 SSPs to generate the base spectra. In addition, we model the extinction by using the dust extinction law given by Calzetti et al. (2000) and the global extinction term Av is a free parameter to be constrained by the fitting procedure. We use these 40 SSPs to fit the spectrum of each galaxy in our sample and extract the information on those SSPs in the formation and evolution of the galaxy.
Figure 1 shows an example of the fit to the spectrum of a typical BCG. The top left-hand panel of Fig. 1 shows both the observed SDSS spectrum Oλ (green) and the model spectrum Mλ (red); the bottom left-hand panel gives the residual spectrum Eλ (purple); the top right-hand panel shows the light-weighted stellar population fractions xj; and the bottom right-hand panel shows the mass-weighted stellar population fractions μj. As seen from Fig. 1, the spectrum of this BCG can be well fitted by a few SSPs with different ages, of which the dominant one in mass (and light) is an old population with age ~10 Gyr, and a young population with age ~1 Gyr contributes significantly to the total light at optical band (~20%), but is almost negligible to the total mass (less than a few percent).
The fraction of each stellar component, either in mass or in light, can be obtained through the full spectrum fitting for each galaxy. Therefore, the age properties and the mean SFHs for each subgroup of galaxies listed in Table 1 can be obtained. Following Cid Fernandes et al. (2005), we define the light-weighted mean age of a galaxy as 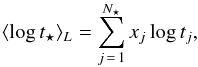 (3)and the mass-weighted mean age of a galaxy as
(3)and the mass-weighted mean age of a galaxy as 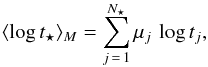 (4)respectively, where xj and μj are the fractions of flux and mass contributed by the jth component of the SSPs, respectively.
(4)respectively, where xj and μj are the fractions of flux and mass contributed by the jth component of the SSPs, respectively.
For the purposes of estimating the Hubble constant by using the differential age method, however, the mean age should be redefined later as 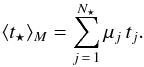 (5)In principle, the STARLIGHT code can deal with templates older than the age of the Universe properly, but the errors in the measurements (~0.1 dex, caused by the intrinsic degeneracies of stellar populations and measurement uncertainties) may cause the fitting ages of some galaxies to be larger than the age of Universe (13.7 Gyr), which will be discussed in Sect. 5 in detail.
(5)In principle, the STARLIGHT code can deal with templates older than the age of the Universe properly, but the errors in the measurements (~0.1 dex, caused by the intrinsic degeneracies of stellar populations and measurement uncertainties) may cause the fitting ages of some galaxies to be larger than the age of Universe (13.7 Gyr), which will be discussed in Sect. 5 in detail.
4. Results
Using the SSP information obtained above for each galaxy, we investigate statistically the formation and evolution histories of the LRGs in the different groups listed in Table 1.
4.1. Group I: BCGs with different RL
4.1.1. Age
Figure 2 shows the light-weighted (red histograms) and mass-weighted (blue histograms) mean age distributions of the BCGs in subgroups 1−3, respectively. The mean ages of these BCGs, which are hosted in clusters with different RL, are also listed in Table 1. According to Fig. 2 and Table 1, the mean mass- or light-weighted age of the BCGs, which are hosted in more massive clusters with larger RL, appear only slightly larger than that of those hosted in less massive clusters with smaller RL, and the differences among the mass-weighted (or light-weighted) age distributions are statistically insignificant, as indicated by the Kolmogorov-Smirnov (K-S) tests. It is apparent that the distributions of the light-weighted age are substantially offset from those of the mass-weighted age, mainly because stars with an age less than several Gyr contribute significantly to the total optical emission but contribute only a small fraction to the total stellar mass. However, the differences among the mass-weighted age distributions or among the light-weighted age distributions are all insignificant. For simplicity, hereafter we only show the relevant results for the mass-weighted age, if not otherwise stated.
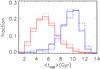 |
Fig. 2 Distributions of the mass-weighted (blue histograms) and the light-weighted ages (red histograms) of BCGs. Histograms shown by the solid dotted and long dashed lines represent the distributions of BCGs in galaxy clusters with richness RL in the range of 12−22, 22−39, and > 39, respectively. |
4.1.2. Star formation histories
The SSPs with different ages involved in the spectrum fitting of a galaxy roughly represent the SFH of the galaxy. For each (sub)group of galaxies, their mean SFH can be obtained by adding together the SSPs in each galaxy at each age, and as our results show, the difference in the SSP metallicities (mostly metal rich with 1 or 2.5 Z⊙) is negligible. Figure 3 shows the mean mass fractions and the corresponding standard deviations of the SSPs with each given age, which represent the mean SFH of each sub-group. As seen from Fig. 3, the mean SFHs of BCGs with different richness RL are similar; the old SSPs (with age ≳ 10 Gyr) are the dominant components to the mean SFHs of the BCGs in each subgroup; the evolutionary trend of the mean SFHs suggests that majority of the BCGs obtain most of their masses in a relatively short period at early time ≳ 10 Gyr; several young SSPs with age ≲ 1 Gyr do contribute to these BCGs, although they appear to be insignificant in the mass fraction (≲a few percent); and the later star formation appears to be extended and more or less at a constant rate over a period of more than several Gyr.
 |
Fig. 3 Mean mass fractions of SSPs in BCGs. Squares, triangles, and diamonds represent the subsamples with 12 <RL ≤ 22, 22 <RL ≤ 39, and RL> 39, respectively. The bars associated with each symbol represent the standard deviation of the mean mass fraction. For clarity, symbols representing an SSP with the same age but for BCGs in subsamples with RL from low to high are offset by δt = −0.1, 0, and 0.1, respectively. |
4.1.3. Young, intermediate and old SSPs
We divide the SSPs into three groups according to their ages, i.e., (1) the young SSP (YSP), including the SSPs with an age ≤ 1 Gyr; (2) the old SSP (OSP), including those SSPs with an age > 2.5 Gyr; and (3) the intermediate SSP (ISP), including those SSPs with an age in between the YSP and the OSP. Figure 4 shows the histograms for the distributions of mass fractions of YSP, ISP, and OSP in the BCGs with different richness, respectively. As shown in Fig. 4, the mass fractions of the YSP in most BCGs are small (≤ 0.5%), while the mass fractions of the OSP in most BCGs are large (≥ 90%). There are no apparent differences among the distributions of the mass fraction of the YSP, or the ISP, or the OSP, in the BCGs with different richness.
 |
Fig. 4 Distributions of the mass fraction of the YSP, ISP, and OSP in BCGs. Panels a)−c) show the distributions of the mass fraction of the YSP, ISP, and OSP, respectively. In each panel, histograms shown by the (green) solid, (red) dotted, and (blue) dashed lines represent the distributions of the sub-groups with 12 <RL ≤ 22, 22 <RL ≤ 39, and RL> 39, respectively. |
According to the analysis in this section, we conclude that the masses of the host clusters of BCGs have little effect on the SFHs and the age properties of those BCGs.
4.2. Group II: BCGs, member and field galaxies
To consider the mass and environmental effects on the formation of LRGs further, we explore the SFHs of the LRGs that are categorized as BCGs, MGs, and FGs (see Group II in Table 1). Galaxies in different σv bins are in different mass ranges as the mass of a galaxy is roughly proportional to the fourth power of σv (e.g., Faber & Jackson 1976), and the masses of those BCGs, MGs, and FGs are approximately the same in a given σv bin. However, the LRGs in the largest σv bin (σv> 300 km s-1) are roughly six or more times massive than those in the smallest σv bin (210 km s-1<σv< 240 km s-1).
 |
Fig. 5 Age distributions of BCGs (green solid line), MGs (red dotted line), and FGs (blue dashed line). The velocity dispersions of those BCGs, MGs, and FGs all span the range from 270 km s-1 to 300 km s-1. |
Figure 5 shows the age distributions of BCGs (green solid line), MGs (red dotted line), and FGs (blue dashed line), with σv in the range from 270 km s-1 to 300 km s-1, respectively. Apparently, there are no significant differences among the age distributions of these three subgroups, although BCGs and MGs appear to be slightly older than FGs. The mean mass-weighted ages of BCGs, MGs, and FGs are 9.34 ± 0.07, 9.51 ± 0.11, and 9.20 ± 0.06 Gyr, respectively. For each of the other σv bins, as shown in Appendix A , the differences among the age distributions of the BCGs, MGs, and FGs are also not significant, similar to those shown in Fig. 5 for the bin of 270 km s-1<σv< 300 km s-1. Part of reason that BCGs have a mean age similar to that of MGs might be that some BCGs are actually satellite galaxies rather than the central galaxies, which causes a mixing of the central galaxies with satellite galaxies in BCGs (Skibba et al. 2011).
Figure 6, as an example, shows the age distribution of BCGs in different σv bins. There is a weak tendency that the ages of the BCGs in a larger σv bin are slightly older than those of the BCGs in a smaller σv bin, though the difference is small. The mean age of the BCGs in the velocity dispersion bins of 210−240, 240−270, 270−300, and > 300 km s-1 are 9.09 ± 0.09, 9.28 ± 0.06, 9.34 ± 0.07, and 9.65 ± 0.1 Gyr, respectively (see Table 1). The apparent three-sigma difference of the means are due to the statistical errors that we adopt here are the errors for the means (i.e., 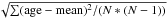 ) rather than the scatters (i.e.,
) rather than the scatters (i.e.,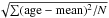 ) of the distributions. For MGs and FGs, we also find the tendency that their ages increase slightly with growing velocity dispersion, the same applying to BCGs (see also Table 1). We also perform the K-S test for the age distributions of BCGs within each of the four different velocity dispersion bins (subsamples 4, 5, 6, and 7), and find that the probability that any two of them draw from the same distribution is larger than 99%.
) of the distributions. For MGs and FGs, we also find the tendency that their ages increase slightly with growing velocity dispersion, the same applying to BCGs (see also Table 1). We also perform the K-S test for the age distributions of BCGs within each of the four different velocity dispersion bins (subsamples 4, 5, 6, and 7), and find that the probability that any two of them draw from the same distribution is larger than 99%.
 |
Fig. 6 Age distributions of BCGs in different velocity dispersion ranges. Histograms shown by the solid (magenta), dotted (green), dashed (red), and dash-dotted (blue) lines represent the age distribution for BCGs with velocity dispersions in the range of 210 km s-1<σv ≤ 240 km s-1, 240 km s-1<σv ≤ 270 km s-1, 270 km s-1<σv ≤ 300 km s-1, and σv ≥ 300 km s-1, respectively. |
 |
Fig. 7 Mean mass fraction of SSPs with different ages for the subsamples with different velocity dispersions. Squares, triangles, and diamonds represent the mean mass fraction of SSPs for BCGs, MGs, and FGs, respectively. The bar associated with each symbol represents the standard deviation of the mean mass fraction. For clarity, symbols representing an SSP with the same age but for different sub-samples are offset by δt = −0.1, 0, and 0.1, respectively. |
 |
Fig. 8 Distributions of the mass fraction of different SSPs for LRGs in different subsamples. As an example, only the distributions obtained for those galaxies with velocity dispersions σv> 300 km s-1 are shown here. Histograms shown by the solid (green), dotted (red), and dashed (blue) lines represent the distributions for BCGs, MGs, and FGs, respectively. |
4.2.1. Star formation histories
We also investigate and compare the SFHs of BCGs, MGs, and FGs in each σv bin, according to the SSPs obtained from the full spectrum fitting for each object. Figure 7 shows the mean mass fractions of SSPs formed per Gyr in the BCGs, MGs, and FGs for the four different σv bins, respectively, which represent the mean SFHs of those galaxies. As seen from Fig. 7, the mean SFHs of the BCGs, MGs, and FGs in each given σv bin are almost the same, and there is little difference between the SFHs of BCGs (or MGs, or FGs) in different σv bins, which suggests that the environmental dependence is weak and the mass dependence of the SFHs of quiescent LRGs is also not statistically significant. On average, most of the stars (≳ 90%) in BCGs, MGs, and FGs were formed about 8 Gyr ago; and less than 10% stars formed after 8 Gyr via a more or less constant rate; and the mean fraction of young SSP with an age < 1 Gyr is usually < 0.5% and can almost be neglected.
4.2.2. Young, intermediate and old SSPs
We compare the YSP, ISP, and OSP mass fractions for BCGs, MGs, and FGs, similar to the comparison done in Sect. 4.1.3, to illustrate the detailed distribution of SSPs in each subgroup of galaxies. Figure 8 shows the distributions of the mass fractions of YSP (left-hand panel), ISP (middle panel), and OSPs (right panel) among those BCGs (green line), MGs (red line) and FGs (blue line) with σv in the range from 270 km s-1 to 300 km s-1. (For other σv bins, the distributions of YSP, ISP, and OSP are shown in Appendix A. These are similar to those shown in Fig. 8 for the bin with σv in the range from 270 km s-1 to 300 km s-1.) We find that the mass fraction of YSP in majority of BCGs, MGs, or FGs is < 0.5% (as seen from the left-hand panel of Fig. 8), the mass fraction of ISP in majority of the BCGs/MGs/FGs is < 10%, and the mass fraction of OSP in majority of the BCGs, MGs, or FGs is > 90%.
4.3. Group III: BCGs and their associated MGs
In Sect. 4.2, we have explored the SFHs and the age properties of BCGs, MGs, and FGs, where the MGs are the member galaxies of the host clusters of the BCGs, and they are categorized into sub-groups with σv in the same range as that of the BCGs. Many MGs with small σv may exist in the host clusters of a BCG with large σv; and some MGs in a given σv bin may actually be the member galaxies of the host clusters of some BCGs grouped in a higher σv bin. We further investigate and compare the SFHs and age properties of these BCGs and their associated member galaxies (i.e., the SCGs in Table 1), without considering the differences of their velocity dispersion. The velocity dispersions of SCGs are systematically smaller than those of the BCGs. By comparison of both the SFHs and the age properties of the BCGs and the SCGs, as for those in Sect. 4.2, we find that the SFHs and age properties of SCGs are also similar to those of BCGs, and statistically there is no apparent difference between the SFHs/age properties of BCGs and those of SCGs.
4.4. Validity of the population synthesis results
The results obtained from the full spectrum fittings may depend on the initial settings of the base spectra. To close this section, we check the validity of the results obtained from the population synthesis above by exploring various different settings for the base spectra further. First, we alternatively adopt either fourteen different SSP ages (i.e., 0.9,1.4,2,3,4,5,6,7,8,9,10,11,12, and 13 Gyr) or eight different SSP ages (e.g., 0.9,1.4,2.5,3,5,8,10, and 13 Gyr) and four different metallicity values (0.2,0.4,1, and 2.5 Z⊙) to generate the base spectra. We redo the fits for all sample galaxies by using these base spectra. We find that there are no apparent differences in the resulting age distributions of SSPs in each velocity dispersion bin. These tests suggest that our results are not sensitive to the base spectra.
The results obtained from the population synthesis model may also depend on the adopted initial mass function (IMF). To check this, we alternatively adopt the Chabrier IMF and redo the fits for all sample galaxies. We find that the mean mass fractions of SSPs with different ages for BCGs, MGs, and FGs in each velocity dispersion bin are not much different from those that result from a Salpeter IMF, although the ages of the LRGs that are derived from using the Chabrier IMF are slightly older than those resulting from the Salpeter IMF. We also replace the BC03 model by the CB07 model to re-fit the LRG spectra and find that the results are almost the same.
The existence of multiple solutions is a well known problem in stellar population synthesis. It is necessary to assess the reliability of the model parameters that result from the full spectrum fittings, which may be quantified by Monte Carlo simulations. Cid Fernandes et al. (2005) have done such simulations and demonstrate that Starlight can produce reliable estimates of ⟨ log t⋆ ⟩ M and Av. They also investigate the age–metallicity degeneracy and find that this degeneracy may induce systematic biases in the estimates of ⟨ Z⋆ ⟩ and ⟨ log t⋆ ⟩ at the level of ≲ 0.1−0.2 dex. The statistical differences among the formation and evolution histories of different groups of LRGs in this paper are not affected by this level of precision, but the systematic biases in the age estimates will affect the constraints on the Hubble constant, as discussed in Sect. 6.
To close this section, we note that several previous studies have investigated the ages of early-type galaxies as a function of their environment and masses. Bernardi et al. (2006) studied the photometric and spectral properties of SDSS early-type galaxies as a function of their local environment and redshift, and they found that galaxies located in the densest regions are typically 1 Gyr older than those galaxies (with the same luminosities) in less dense regions. However, environment is quantified in two different ways in Bernardi et al. (2006), either by the distance to the nearest cluster of galaxies, or by the distance to the tenth nearest luminous neighbor, which are different to those in our paper; and their sample includes galaxies with strong OII emission, or with Hδ and Hγ Balmer absorption lines (however, these galaxies are excluded from our sample), which indicates significant star formation in the not very distant past. Thomas et al. (2005) analyze more than 100 early-type galaxies, including a roughly equal number of elliptical and lenticular (S0) galaxies, and they find that massive early-type galaxies in low-density environments appear to be two Gyr younger than their counterparts in high-density environments. In our study, most LRGs should be early-type galaxies but not S0. Thomas et al. (2010) study the effect of environment on the evolution of early-type galaxies by analyzing the stellar population properties of a large number of early-type massive galaxies selected from SDSS after a visual inspection of their morphologies, and they find that the influence of the effect of the environment increases with decreasing galaxy mass. Bernardi et al. (1998) found that the mass-weighted age differences between cluster and field elliptical galaxies could be significantly smaller than 1 Gyr and brighter field elliptical galaxies appear to be similar to their cluster counterparts. The latter two papers appear roughly consistent with our results because most LRGs studied in this paper are bright and massive early-type galaxies.
5. Comparison with the results from the semi-analytical model of galaxy formation
According to the analysis above, there are few differences between the age distributions and the mean SFHs of quiescent LRGs in different environments, which suggests that these LRGs, whether located in dense or less dense environments, can be securely used as cosmic chronometers. However, it appears that the little environmental dependence of the age properties of quiescent LRGs is in contradiction with basic expectations. For a deeper understanding of this problem, below we adopt the semi-analytical modeling of galaxy formation by Guo et al. (2011) to select mock LRGs, and compare the age properties and the SFHs of the mock LRGs with the observational ones obtained above.
We select LRGs from the mock galaxies that were generated by Guo et al. (2011) using the following criteria, i.e., M∗> 1011M⊙, Mbulge/M∗> 0.8 and | C⊥ | < 0.2 at z ~ 0, where | C⊥ | is defined as | C⊥ | = (r − i) − (g − r) / 4−0.18, Mbulge and M∗ are the mass of the bulge of a galaxy and the galaxy, respectively, g, r, and i represent the g-band, r-band and i-band magnitudes, respectively. These criteria were used to select LRGs in SDSS by Eisenstein et al. (2001).
Using a similar approach as for the SDSS LRGs, we also categorize the LRGs that have been selected from the mock galaxies into three groups, i.e., BCGs, MGs, and FGs, respectively. BCGs are the central galaxies in massive clusters that are hosted in dark matter halos with masses MH ≥ 6 × 1013M⊙ (corresponding to the low limit of richness RL = 12 for the clusters selected in Wen et al. 2012); MGs are massive satellite LRGs that are hosted in the same dark matter halos of BCGs; and FGs are the biggest galaxies in the dark matter halos with mass in the range of 1013M⊙<MH< 6 × 1013M⊙, where 1013M⊙ is set as the lower limit of the halo mass since (1) many studies indicate that the typical halo masses of LRGs are about a few times 1013h-1M⊙ or larger (Guo et al. 2014; Parejko et al. 2013; Hudson et al. 2015) and (2) Mandelbaum et al. (2006) found that the halos with mass ≳ 1013M⊙ host elliptical galaxies at their center while even the brightest central spirals are hosted by halos with masses < 1013M⊙. For each LRG, we trace its merger and assembly history back to high redshift.
The SFHs of galaxies are closely related to their assembly histories. In the semi-analytic models (SAM), most of the large elliptical galaxies, presumably massive LRGs or BCGs in the centers of the most massive halos, are formed through (many) major mergers of smaller progenitor galaxies, and most of the cold gas in each of them is consumed via a starburst triggered by the merger. These galaxies experienced little star formation after the last (wet) major mergers they experienced. Some satellite galaxies may transform to ellipticals due to the gravitational perturbation from their main halos. These satellite galaxies (MGs) may also have little gas to be cooled down to form new stars, after they fell into the main progenitor halos, because most of the hot gas in their progenitor halos may have been stripped off by their main halos. Less massive LRGs (or elliptical galaxies; FGs) may be hosted in less massive halos (e.g., with mass in the range of 1013M⊙<MH< 6 × 1013M⊙), they may experience less frequent major mergers in their assembly histories. Because the assembly histories of the above three populations of galaxies may be different, therefore the SFHs of these three populations may be different as well. Below we use the assembly histories extracted from the SAM model by Guo et al. (2011) for different populations of mock galaxies, i.e., BCGs, MGs, and FGs, to check the differences.
 |
Fig. 9 Distribution of the mass-weighted ages for sample galaxies in different types. The green, red, and blue lines represent the samples of BCGs, MGs, and FGs, respectively. The thin dotted lines represents the age distribution obtained for LRGs with velocity dispersion > 210 km s-1 by the full spectrum fitting in this paper, and the thick solid lines represent the age distributions obtained from a semi-analytic galaxy formation model (Guo et al. 2011). Some SDSS LRGs appear to have ages or lookback times of 15 Gyr, larger than the Hubble time, because of measurement errors in the STARLIGHT-derived ages. |
Figure 9 shows the mass-weighted age distributions of these mock BCGs, MGs, and FGs, respectively. Apparently, the age distribution of BCGs is limited to a small range, from 10 Gyr to 12 Gyr (or from redshift z ~ 2 to 4); the age distribution of MGs is more extended and skewed towards small values of ~8 Gyr, compared with that of BCGs; and the age distribution of FGs is even more extended and also skewed toward small values of ~8 Gyr. The mean age of the BCGs, MGs and FGs are 11.4 ± 0.006, 11.0 ± 0.007, and 10.6 ± 0.004 Gyr, respectively. The mean age of MGs is slightly younger than that of BCGs by 0.4 Gyr and older than that of FGs by 0.4 Gyr, and these differences are not significant considering the wide associated scatters. Figure 9 also shows the mass-weighted age distributions of the corresponding groups of the SDSS LRGs with σv ≥ 210 km s-1 (histograms in dotted lines). We note that the mock galaxies are selected at redshift z = 0, while the SDSS LRGs are selected in the redshift range from z = 0.15 to 0.25. To account for this difference, we assume no star formation in those galaxies at z ≲ 0.15−0.25 and re-calculate the stellar mass-weighted age by replacing Eq. (4) with 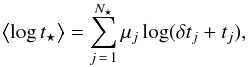 (6)where δtj is the lookback time of the galaxy j at zj. We adopt a flat ΛCDM cosmology with H0 = 73 km s-1 Mpc-1 and Ωm = 0.25 as used in Springel et al. (2005). The mean ages of the SDSS BCGs, MGs and FGs are 12.1 ± 0.04, 12.0 ± 0.06 and 11.8 ± 0.03 Gyr, respectively. It appears that the mean age of MGs is still slightly younger than that of BCGs, but older than that of FGs, respectively. The differences between the age distributions of those observed LRGs are less obvious than the ones seen for the mock LRGs. However, it is obvious that the age distributions obtained for the observed BCGs, MGs, and FGs are all broader than the corresponding distributions obtained from the SAM model, and the mean age of the observed ones are older than those obtained from the SAM model by ~1.0 Gyr, which might suggest that the mass-weighted ages of the observed LRGs, which were estimated using STARLIGHT, are systematically overestimated.
(6)where δtj is the lookback time of the galaxy j at zj. We adopt a flat ΛCDM cosmology with H0 = 73 km s-1 Mpc-1 and Ωm = 0.25 as used in Springel et al. (2005). The mean ages of the SDSS BCGs, MGs and FGs are 12.1 ± 0.04, 12.0 ± 0.06 and 11.8 ± 0.03 Gyr, respectively. It appears that the mean age of MGs is still slightly younger than that of BCGs, but older than that of FGs, respectively. The differences between the age distributions of those observed LRGs are less obvious than the ones seen for the mock LRGs. However, it is obvious that the age distributions obtained for the observed BCGs, MGs, and FGs are all broader than the corresponding distributions obtained from the SAM model, and the mean age of the observed ones are older than those obtained from the SAM model by ~1.0 Gyr, which might suggest that the mass-weighted ages of the observed LRGs, which were estimated using STARLIGHT, are systematically overestimated.
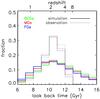 |
Fig. 10 Comparison between the mass-weighted ages obtained from simulation and those obtained from observations by considering the measurement errors. The green, red, and blue lines represent the samples of BCGs, MGs, and FGs, respectively. The thin dotted lines represent the age distributions obtained for different LRG samples by the full spectrum fitting in this paper, after adding a correction of −0.09 dex, and the thick solid lines represent the age distributions obtained from a semi-analytic galaxy formation model (Guo et al. 2011) by considering a scatter of 0.1 dex. |
We note that González & Cid Fernandes (2010) investigate the accuracy of the age estimates by using full spectrum fitting. They apply STARLIGHT to a sample of globular clusters, fitting the cluster-integrated light spectra with a suite of modern evolutionary synthesis models, such as the Galaxev/STELIB, as used in this study. By comparing the results obtained from the full spectrum fitting with those of other methods in the literature, they conclude that the ages estimated by the full spectrum fitting are older than those estimated by the S-color magnitude diagram (S-CMD) method (Girardi et al. 1995) by ~0.09 dex, and the accuracy of these age estimates is about ~0.1 dex. Galaxies are more complicated than globular cluster because of their SFHs and the errors of the STARLIGHT-derived ages for LRGs may be different from those for globular clusters. However, there is no such study on the possible biases or errors in the STARLIGHT-derived ages for galaxies or LRGs in the literature. Here we simply assume that the biases or errors in the STARLIGHT-derived ages for LRGs are the same as that for globular clusters, and we allocate an error following a normal distribution with standard deviation of 0.1 dex to the mass-weighted age of each mock LRG, and add a correction of −0.09 dex to the age obtained from the full spectrum fitting for each observed LRG. We reobtain the age distributions for both the mock and the observed BCGs, MGs, and FGs, as shown in Fig. 10. By these corrections, we find that the age distributions for the mock BCGs, MGs, and FGs appear to match well those obtained from the observations.
We further investigate the SFHs and the quench time of the mock BCGs, MGs, and FGs, to reveal the underlying physics for the small differences between the distributions of the ages and the SFHs of the observed BCGs, MGs, and FGs, as illustrated in Sect. 4. For a BCG or an FG, the time at which the star formation in it is quenched can be represented by the time of the last wet major merger it experienced; while for an MG the quench time is represented by the earlier occurrence of the last (wet) major merger time and the infall time. For the mock galaxies that result from the SAM model, we assume a merger as a wet major merger if the mass ratio of the two progenitor galaxies is in the range of 1 / 3 to 3 and the special star formation rates in the two galaxies are both > 0.01 Gyr-1. Figure 11 shows the distribution of the quench time for BCGs, MGs, and FGs, respectively. As seen from the figure, LRGs in dense environment, including BCGs and MGs, are quenched statistically earlier than those FGs in less dense environments; and FGs appear to be quenched slightly later than BCGs. Roughly half of BCGs and FGs experienced their last wet major mergers before 10.3 Gyr and 9.6 Gyr ago, respectively, and about half of MGs experienced their last wet major mergers or fell into main halos over 10 Gyr ago. However, the systematic differences between the distributions of the quench time of BCGs, MGs, and FGs are relatively small compared with the scatters of those found for the SDSS LRGs as listed in Table 1.
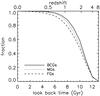 |
Fig. 11 Accumulated distribution of the quenching time of the simulated LRGs. The quenching time of a galaxy here is set as the lookback time of the universe at which the galaxy just experienced its last wet major merger or became a satellite. The solid, dotted, and dashed lines represent the distribution of BCGs, MGs, and FGs, respectively. |
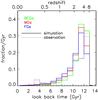 |
Fig. 12 Mean star formation histories of different types of LRGs. The SFH of a galaxy is represented by the mass ratio of stars formed per Gyr around any given lookback time t to the total stellar mass. The solid green, red, and blue histograms represent the mean value of the mass growth history for BCGs, MGs, and FGs obtained from a semi-analytical model (Guo et al. 2011), respectively; the dotted histograms are obtained from the full spectrum fitting for the SDSS BCGs, MGs, and FGs, respectively. |
The mean SFH of those galaxies in each subsample can be represented by the evolution of the mass fraction of the stars formed per Gyr around a given lookback time, as shown in Figs. 3 and 7. By recording the mass of formed stars in each mock galaxy at each snapshot, the SFH of each mock galaxy can be obtained, and consequently the mean SFH of any group of mock galaxies can also be obtained. Figure 12 shows the mean SFHs obtained from both the SAM model (solid lines) and the SDSS observations (dotted lines) for BCGs, MGs, and FGs, respectively. For the SFHs obtained from observations through STARLIGHT, a correction of −0.09 dex has been adopted for the age estimate of each SDSS LRG. As seen in Fig. 12, the SFHs of the SDSS LRGs show good consistenty with those of the mock LRGs, except that the SDSS LRGs have some recent star formation, on the order of less than a few percent per Gyr, at a lookback time ≲ 6 Gyr. The later star formation found in the SDSS LRGs may suggest that the feedback processes are not as efficient as those adopted in the SAM model by Guo et al. (2011) to suppress star formation. Because of this later star formation, the mean ages of the quiescent LRGs at a lower redshift, which were obtained from the full spectrum fitting, may be systematically younger than those at a higher redshift, even after correcting the difference in the lookback time. It is, therefore, necessary to correct this systematical error to get a more accurate estimation of the Hubble constant (and other cosmological parameters) by using the differential age method.
6. Uncertainties in estimating the Hubble constant by the differential age method
Estimates of the Hubble constant, obtained from the differential age method, may suffer some uncertainties caused by the later star formation in LRGs and the systematic errors in the age estimates of LRGs by using the stellar population synthesis technique.
We first estimate the systematical errors caused by the later star formation in LRGs. As shown in Fig. 7, the later star formation rate is on the percentage per Gyr level at t ≲ 6 Gyr. For illustration purposes, we assume that the mean later star formation rate is 2% per Gyr at t ≲ 6 Gyr. With this assumption, the mean SFHs of LRGs at any redshift bin from z = 0 to 0.4 (with a bin size of δz = 0.02) can be obtained because the mean SFHs at t> 6 Gyr of those galaxies are given by the mean SFHs obtained for the LRG samples given above. Consequently, the mean lifetime of those LRGs at redshift z can be estimated by 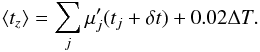 (7)Here
(7)Here 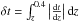 ,
, 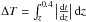 /Gyr,
/Gyr, 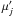 is the renormalized fraction of the j-th SSP, as shown in Fig. 7, and shifted to z = 0.4, the age of the j-th SSP is replaced by tj + δt,
is the renormalized fraction of the j-th SSP, as shown in Fig. 7, and shifted to z = 0.4, the age of the j-th SSP is replaced by tj + δt, 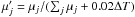 , and the summation ∑ jμj only covers those SSPs with tj + δt> 0. To generate mock observations, we set the Hubble constant as H0 = 73 km s-1 Mpc-1 and the fraction of matter to the critical density as Ωm = 0.25. According to the above procedures, we obtain the mean age of the mock LRGs that is located at each redshift bin from z = 0 to 0.4 with a redshift interval of δz = 0.02 , respectively, and consequently we obtain the age-redshift relation. We then directly fit the mock age-redshift relation using
, and the summation ∑ jμj only covers those SSPs with tj + δt> 0. To generate mock observations, we set the Hubble constant as H0 = 73 km s-1 Mpc-1 and the fraction of matter to the critical density as Ωm = 0.25. According to the above procedures, we obtain the mean age of the mock LRGs that is located at each redshift bin from z = 0 to 0.4 with a redshift interval of δz = 0.02 , respectively, and consequently we obtain the age-redshift relation. We then directly fit the mock age-redshift relation using 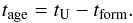 (8)Here tage is the mean age of the mock LRGs, tform is the mean formation time of those mock LRGs and assumed to be a constant for each sample, and tU is the cosmic age
(8)Here tage is the mean age of the mock LRGs, tform is the mean formation time of those mock LRGs and assumed to be a constant for each sample, and tU is the cosmic age 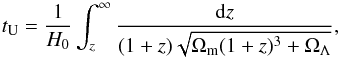 (9)where \begin{lxirformule}$\Omega_{\Lambda}$\end{lxirformule} is the fraction of the cosmological constant to the critical density at the present time (see details in Liu et al. 2012).
(9)where \begin{lxirformule}$\Omega_{\Lambda}$\end{lxirformule} is the fraction of the cosmological constant to the critical density at the present time (see details in Liu et al. 2012).
Adopting the standard χ2 statistics and assuming a flat universe, i.e., Ωm + ΩΛ = 1, we obtain the best fit value of the Hubble constant as 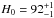 ,
, 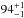 ,
, 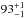 , and
, and 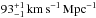 from the mock age-redshift relations obtained by using the mean SFHs, which were obtained for the sub-sample of SDSS LRGs in the velocity dispersion ranges of 210−240, 240−270, 270−300, and > 300 km s-1, respectively. Apparently, a later star formation, at a rate of two percent stellar mass per Gyr, can lead to an overestimation of the Hubble constant by ~28%, which is consistent with that argued in Liu et al. (2012, see discussions in Sect. 5.3 therein). We note that, if the later star formation rate is smaller, e.g., one percent in stellar mass per Gyr, the H0 value obtained from the mock age-redshift relation would be correspondingly overestimated by 16%.
from the mock age-redshift relations obtained by using the mean SFHs, which were obtained for the sub-sample of SDSS LRGs in the velocity dispersion ranges of 210−240, 240−270, 270−300, and > 300 km s-1, respectively. Apparently, a later star formation, at a rate of two percent stellar mass per Gyr, can lead to an overestimation of the Hubble constant by ~28%, which is consistent with that argued in Liu et al. (2012, see discussions in Sect. 5.3 therein). We note that, if the later star formation rate is smaller, e.g., one percent in stellar mass per Gyr, the H0 value obtained from the mock age-redshift relation would be correspondingly overestimated by 16%.
The mean age of quiescent LRGs may also not be accurate because of the possible systematic uncertainty in the populations synthesis tool. For example, the mean age of LRGs is probably overestimated by 0.09 dex in the logarithmic scale by using STARLIGHT, as discussed in Sect. 5). Therefore, it is important to investigate the systematic error on the estimation of the Hubble constant. Ignoring the later star formation in quiescent LRGs and assuming a systematic overestimation of 0.09 dex in the age measurements, we can also obtain the mock age-redshift relations by procedures similar to those above, except that Eq. (7) is replaced by 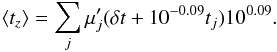 (10)We find the best-fit H0 = 63 ± 1, 62 ± 1, 62 ± 1, and 61 ± 1 km s-1 Mpc-1 by fitting the mock age-redshift relations obtained by using the mean SFHs for the SDSS LRGs in the σv ranges of 210−240, 240−270, 270−300, and > 300 km s-1, respectively. Apparently, the systematic errors in the age estimations from using STARLIGHT can lead to an underestimation of the Hubble constant of ~16%.
(10)We find the best-fit H0 = 63 ± 1, 62 ± 1, 62 ± 1, and 61 ± 1 km s-1 Mpc-1 by fitting the mock age-redshift relations obtained by using the mean SFHs for the SDSS LRGs in the σv ranges of 210−240, 240−270, 270−300, and > 300 km s-1, respectively. Apparently, the systematic errors in the age estimations from using STARLIGHT can lead to an underestimation of the Hubble constant of ~16%.
Considering both the systematic errors in the age estimates (0.09 dex) and the late star formation in LRGs (2 percent of stellar mass per Gyr), we can also obtain the mock age-redshift relation by using the SFHs obtained for each subsample. We find that the best-fit H0 = 74 ± 2, 73 ± 2, 74 ± 2, and 73 ± 2 km s-1 Mpc-1, respectively. In this case, the uncertainty in the estimation of the Hubble constant introduced by the later star formation is largely canceled by the uncertainty introduced by the systematic errors in the age estimates.
In summary, the later star formation in LRGs and the systematic errors in the LRG age estimates lead to substantial uncertainty in the estimation of the Hubble constant that is obtained from the differential age method. However, this error can be corrected provided that the mean SFH of the sample galaxies and the systematic error in the age estimation are identified by using a specific stellar population synthesis tool, such as STARLIGHT. We conclude that the Hubble constant can be measured with high accuracy through the age–redshift relation, taking the effect of both the later star formation and the systematic error in the age estimates into careful consideration.
7. Conclusions
Luminous red galaxies (LRGs) are believed to be passively evolving and host the oldest stellar population, and as such, can be used as cosmic chronometers to measure the Hubble parameters at different redshifts. Different LRGs may have different mass and locate in different environments. The mass and environmental effects on the LRG age properties, if significant, may limit the use of the LRGs as cosmic chronometers. In this paper, we have investigated the environmental and mass effects on the formation and evolution of quiescent SDSS LRGs through the stellar population synthesis technique and the full spectrum fitting method and have checked the importance of the environmental effects on the application of LRGs as cosmic chronometers. We find that (1) the ages of quiescent LRGs, whether they are BCGs of clusters, member galaxies of clusters (MGs), or field galaxies (FGs), correlate weakly with their velocity dispersions, i.e., the larger the velocity dispersion, the slightly older the ages; (2) the age distributions and the mean SFHs of quiescent LRGs with similar velocity dispersions in different environments do not show significant differences; (3) the SFHs of the SDSS LRGs are well consistent with those of the mock LRGs that result from a semi-analytical model of galaxy formation, except that the SDSS LRGs have some recent star formation (at a lookback time ≲ 6 Gyr of a few percent per Gyr; and (4) the systematic errors in the age estimates of LRGs and the later star formation in LRGs all lead to some errors in estimating the Hubble constant through the differential age method. We find that the late star formation in quiescent SDSS LRGs leads to a systematical overestimation of the Hubble constant; although the systematic errors in the STARLIGHT-derived ages of LRGs may lead to an underestimation of the Hubble constant. However, both effects may be corrected by a careful study of the mean SFH of those LRGs and by calibrating the STARLIGHT-derived ages with those obtained independently using other methods.
In summary, environmental effects do not play a significant role in the age estimates of quiescent LRGs; as a population, the quiescent LRGs can be securely used as cosmic chronometers and the Hubble constant can be measured with high precision by the differential age method, as performed by Jimenez et al. (2003), Simon et al. (2005), Stern et al. (2010), Moresco et al. (2012), and Liu et al. (2012).
Appendix A: Distribution of age and mass fraction
In the main text, Fig. 5 shows the age distributions of BCGs, MGs, and FGs with σv in the range from 270 km s-1 to 300 km s-1, and Fig. 8 shows the distribution of the mass
 |
Fig. A.1 Age distributions of BCGs (green solid line), MGs (red dotted line), and FGs (blue dashed line). |
fractions of YSP, ISP, and OSPs in the BCGs, MGs, and FGs with the same velocity dispersion bin. For completeness, we also show here the age distributions and the distributions of the mass fractions of BCGs, MGs, and FGs for other velocity dispersion bins in Figs. A.1 and A.2 , respectively.
 |
Fig. A.2 Distributions of the mass fractions of different SSPs of LRGs in different subsamples. Histograms shown by the solid (green), dotted (red), and dashed (blue) lines represent the distribution for BCGs, MGs, and FGs, respectively. |
Some BCGs may not locate at the centers of their host dark matter halos (Skibba et al. 2011).
According to Wen et al. (2012), the photo-z gap of z = 0.04(1+z) is adopted to select member galaxies. Since the redshifts of our sample galaxies is in the range of 0.15–0.25, a redshift gap of about 0.05 is applied to select the MGs. However, a redshift difference of 0.04 (1+z) is rather large and would introduce some interloper galaxies to the selected MG sample. To check the effect of this contamination, we adopt a more strict selection criterion for MGs, i.e., the spectroscopic redshift difference between an MG and its CG is smaller than 0.01, corresponding to a velocity difference of < 3000 km s-1, which is roughly on the same order of the velocity dispersion of massive galaxy cluster. By this criterion, we re-select a new MG sample, which is taken as the most conservative case. We analyze this new MG sample and find few differences in the results between those obtained from the conservative MG sample and the main MG sample.
Acknowledgments
We are grateful to the anonymous referee for constructive suggestion. Gaochao Liu thanks Zhonglue Wen for providing the BCG and LRG catalog and Xianmin Meng for helpful discussions on using STARLIGHT. This work is partly supported by NSFC grant support under Nos. 11303020, 11073024, 11203033, 11373031, 11390372, U1331113, U1231123, U1331202, the Strategic Priority Research Program “The Emergence of Cosmological Structures” of the Chinese Academy of Sciences, grant No. XDB09000000, and the CAS grant KJCX2-EW-W01. Funding for SDSS-III has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, and the USDepartment of Energy. The SDSS-III Web site is http://www.sdss3.org/. SDSS-III is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS-III Collaboration including the University of Arizona, the Brazilian Participation Group, Brookhaven National Laboratory, University of Cambridge, University of Florida, the French Participation Group, the German Participation Group, the Instituto de Astrofisica de Canarias, the Michigan State/Notre Dame/JINA Participation Group, Johns Hopkins University, Lawrence Berkeley National Laboratory, Max Planck Institute for Astrophysics, New Mexico State University, New York University, Ohio State University, Pennsylvania State University, University of Portsmouth, Princeton University, the Spanish Participation Group, University of Tokyo, University of Utah, Vanderbilt University, University of Virginia, University of Washington, and Yale University.
References
- Balogh, M. L., Baldry, I. K., Nichol, R., et al. 2004, ApJ, 615, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Bernardi, M., Renzini, A., da Costa, L. N., et al. 1998, ApJ, 508, L143 [Google Scholar]
- Bernardi, M., Nichol, R. C., Sheth, R. K., Miller, C. J., & Brinkmann, J. 2006, AJ, 131, 1288B [NASA ADS] [CrossRef] [Google Scholar]
- Bernardi, M., Hyde, J. B., Sheth, R. K., Miller, C. J., & Nichol, R. C. 2007, AJ, 133, 1741 [NASA ADS] [CrossRef] [Google Scholar]
- Bertelli, G., Bressan, A., Chiosi, C., Fagotto, F., & Nasi, E. 1994, A&AS, 106, 275 [NASA ADS] [Google Scholar]
- Blanton, M. R., Eisenstein, D., Hogg, D. W., et al. 2005, ApJ, 629, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000B [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Cid Fernandes, R., Mateus, A., Sodré, L., Stasińska, G., & Gomes, J. M. 2005, MNRAS, 358, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Cooper, M. C., Newman, J. A., Croton, D. J., et al. 2006, MNRAS, 370, 198 [NASA ADS] [CrossRef] [Google Scholar]
- Desroches, L., Quataert, E., Ma, C., & West, A. A. 2007, MNRAS, 377, 402 [NASA ADS] [CrossRef] [Google Scholar]
- De Lucia, G., & Blaizot, J. 2007, MNRAS, 375, 2 [NASA ADS] [CrossRef] [Google Scholar]
- De Lucia, G., Springel, V., White, Simon D. M., et al. 2006, MNRAS, 366, 499 [NASA ADS] [CrossRef] [Google Scholar]
- De Lucia, G., Weinmann, S., Poggianti, B. M., et al. 2012, MNRAS, 423, 1277 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenstein, D. J., Annis, J., Gunn, J. E., et al., 2001, AJ, 122, 2267 [NASA ADS] [CrossRef] [Google Scholar]
- Faber, S. M., & Jackson, R. E. 1976, ApJ, 204, 668 [NASA ADS] [CrossRef] [Google Scholar]
- Forbes, D. A., Ponman, T. J., & Brown, R. J. N. 1998, ApJ, 508, 43 [Google Scholar]
- Girardi, L., Chiosi, C., Bertelli, G., & Bressan, A. 1995, A&A, 298, 87 [NASA ADS] [Google Scholar]
- Gómez, P. L., Nichol, R. C., Miller, C. J., et al. 2003, ApJ, 584, 210 [NASA ADS] [CrossRef] [Google Scholar]
- González, Delgado, Rosa, M., & Cid Fernandes, R. 2010, MNRAS, 403, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Graham, A., Lauer, T. R., Colless, M., & Postman, M. 1996, ApJ, 465, 534 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, Q., White, S., Boylan-Kolchin, M., De Lucia, G., et al. 2011, MNRAS, 413, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, H., Zheng, Z., Zehavi, I., et al. 2014, MNRAS, 441, 2398 [NASA ADS] [CrossRef] [Google Scholar]
- Hudson, M. J., Gillis, B. R., Coupon, J., et al. 2015, MNRAS, 447, 298 [NASA ADS] [CrossRef] [Google Scholar]
- Jimenez, R., & Loeb, A. 2002, ApJ, 573, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Jimenez, R., Verde, L., Treu, T., & Stern, D. 2003, ApJ, 593, 622 [NASA ADS] [CrossRef] [Google Scholar]
- Lauer, T. R., Faber, S. M., Richstone, D., et al. 2007, ApJ, 662, 808 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, J. H., Lee, M. G., Park, C., et al. 2010, MNRAS, 403, 1930 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, F. S., Xia, X. Y., Mao, S., Wu, H., & Deng, Z. G. 2008, MNRAS, 385, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, G., Lu, Y., Chen, X., et al. 2012, ApJ, 758, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Mandelbaum, R., Seljak, U., Kauffmann, G., et al. 2006, MNRAS, 368, 715 [Google Scholar]
- Matthews, T. A., Morgan, W. W., & Schmidt, M. 1964, ApJ, 140, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Moresco, M. 2015, MNRAS, 450, 16 [Google Scholar]
- Moresco, M., Verde, L., Pozzetti, L., Jimenez, R., & Cimatti, A. 2012, JCAP, 7, 53 [Google Scholar]
- Naab, T., Johansson, P. H., & Ostriker, J. P. 2009, ApJ, 699, 178 [Google Scholar]
- Oemler, A. 1973, ApJ, 180, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Parejko, J. K., Sunayama, T., Padmanabhan, N., et al. 2013, MNRAS, 429, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Pasquali, A., Gallazzi, A., Fontanot, F., et al. 2010, MNRAS, 407, 937 [NASA ADS] [CrossRef] [Google Scholar]
- Patel, P., Maddox, S., Pearce, F. R., Aragón-Salamanca, A., & Conway, E. 2006, MNRAS, 370, 851 [NASA ADS] [Google Scholar]
- Poggianti, B. M., von der Linden, A., De Lucia, G., et al. 2006, ApJ, 642, 188 [NASA ADS] [CrossRef] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Schombert, J. M. 1988, ApJ, 328, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, J., Verde, L., & Jimenez, R. 2005, Phys. Rev. D, 71, 123001 [Google Scholar]
- Skibba, R. A., van den Bosch, F. C., Yang, X., et al. 2011, MNRAS, 410, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., White, S. D. M., Jenkins, A., et al. 2005, Nature, 435, 629 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Stern, D., Jimenez, R., Verde, L., Kamionkowski, M., & Stanford, S. A. 2010, JCAP, 2, 8 [Google Scholar]
- Thomas, D., Maraston, C., Bender, R., et al. 2005, ApJ, 621, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, D., Maraston, C., Schawinski, K., et al. 2010, MNRAS, 404, 1775 [NASA ADS] [Google Scholar]
- von der Linden, A., Best, P. N., Kauffmann, G., & White, S. D. M. 2007, MNRAS, 379, 867 [NASA ADS] [CrossRef] [Google Scholar]
- Wen, Z. L., Han, J. L., & Liu, F. S. 2012, ApJS, 199, 34 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Example for the full spectrum fitting of the spectrum of a BCG. The green, blue, and red lines in the top left panel represent the observed spectrum (Oλ), its error spectrum, and the model spectrum (Mλ), respectively. The residual spectrum (Eλ) is shown by the purple line in the bottom left panel. In the left panels, both Oλ and Mλ are scaled by normalizing the flux at wavelength 4020 Å to 1. The light-weighted and the mass-weighted fractions of stellar populations, i.e., xj and μj, are shown in the top and the bottom right panels, respectively. Several quantities (see Sect. 3) derived from the fitting are listed in the top right corner. |
| In the text | |
 |
Fig. 2 Distributions of the mass-weighted (blue histograms) and the light-weighted ages (red histograms) of BCGs. Histograms shown by the solid dotted and long dashed lines represent the distributions of BCGs in galaxy clusters with richness RL in the range of 12−22, 22−39, and > 39, respectively. |
| In the text | |
 |
Fig. 3 Mean mass fractions of SSPs in BCGs. Squares, triangles, and diamonds represent the subsamples with 12 <RL ≤ 22, 22 <RL ≤ 39, and RL> 39, respectively. The bars associated with each symbol represent the standard deviation of the mean mass fraction. For clarity, symbols representing an SSP with the same age but for BCGs in subsamples with RL from low to high are offset by δt = −0.1, 0, and 0.1, respectively. |
| In the text | |
 |
Fig. 4 Distributions of the mass fraction of the YSP, ISP, and OSP in BCGs. Panels a)−c) show the distributions of the mass fraction of the YSP, ISP, and OSP, respectively. In each panel, histograms shown by the (green) solid, (red) dotted, and (blue) dashed lines represent the distributions of the sub-groups with 12 <RL ≤ 22, 22 <RL ≤ 39, and RL> 39, respectively. |
| In the text | |
 |
Fig. 5 Age distributions of BCGs (green solid line), MGs (red dotted line), and FGs (blue dashed line). The velocity dispersions of those BCGs, MGs, and FGs all span the range from 270 km s-1 to 300 km s-1. |
| In the text | |
 |
Fig. 6 Age distributions of BCGs in different velocity dispersion ranges. Histograms shown by the solid (magenta), dotted (green), dashed (red), and dash-dotted (blue) lines represent the age distribution for BCGs with velocity dispersions in the range of 210 km s-1<σv ≤ 240 km s-1, 240 km s-1<σv ≤ 270 km s-1, 270 km s-1<σv ≤ 300 km s-1, and σv ≥ 300 km s-1, respectively. |
| In the text | |
 |
Fig. 7 Mean mass fraction of SSPs with different ages for the subsamples with different velocity dispersions. Squares, triangles, and diamonds represent the mean mass fraction of SSPs for BCGs, MGs, and FGs, respectively. The bar associated with each symbol represents the standard deviation of the mean mass fraction. For clarity, symbols representing an SSP with the same age but for different sub-samples are offset by δt = −0.1, 0, and 0.1, respectively. |
| In the text | |
 |
Fig. 8 Distributions of the mass fraction of different SSPs for LRGs in different subsamples. As an example, only the distributions obtained for those galaxies with velocity dispersions σv> 300 km s-1 are shown here. Histograms shown by the solid (green), dotted (red), and dashed (blue) lines represent the distributions for BCGs, MGs, and FGs, respectively. |
| In the text | |
 |
Fig. 9 Distribution of the mass-weighted ages for sample galaxies in different types. The green, red, and blue lines represent the samples of BCGs, MGs, and FGs, respectively. The thin dotted lines represents the age distribution obtained for LRGs with velocity dispersion > 210 km s-1 by the full spectrum fitting in this paper, and the thick solid lines represent the age distributions obtained from a semi-analytic galaxy formation model (Guo et al. 2011). Some SDSS LRGs appear to have ages or lookback times of 15 Gyr, larger than the Hubble time, because of measurement errors in the STARLIGHT-derived ages. |
| In the text | |
 |
Fig. 10 Comparison between the mass-weighted ages obtained from simulation and those obtained from observations by considering the measurement errors. The green, red, and blue lines represent the samples of BCGs, MGs, and FGs, respectively. The thin dotted lines represent the age distributions obtained for different LRG samples by the full spectrum fitting in this paper, after adding a correction of −0.09 dex, and the thick solid lines represent the age distributions obtained from a semi-analytic galaxy formation model (Guo et al. 2011) by considering a scatter of 0.1 dex. |
| In the text | |
 |
Fig. 11 Accumulated distribution of the quenching time of the simulated LRGs. The quenching time of a galaxy here is set as the lookback time of the universe at which the galaxy just experienced its last wet major merger or became a satellite. The solid, dotted, and dashed lines represent the distribution of BCGs, MGs, and FGs, respectively. |
| In the text | |
 |
Fig. 12 Mean star formation histories of different types of LRGs. The SFH of a galaxy is represented by the mass ratio of stars formed per Gyr around any given lookback time t to the total stellar mass. The solid green, red, and blue histograms represent the mean value of the mass growth history for BCGs, MGs, and FGs obtained from a semi-analytical model (Guo et al. 2011), respectively; the dotted histograms are obtained from the full spectrum fitting for the SDSS BCGs, MGs, and FGs, respectively. |
| In the text | |
 |
Fig. A.1 Age distributions of BCGs (green solid line), MGs (red dotted line), and FGs (blue dashed line). |
| In the text | |
 |
Fig. A.2 Distributions of the mass fractions of different SSPs of LRGs in different subsamples. Histograms shown by the solid (green), dotted (red), and dashed (blue) lines represent the distribution for BCGs, MGs, and FGs, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


