| Issue |
A&A
Volume 584, December 2015
|
|
|---|---|---|
| Article Number | A75 | |
| Number of page(s) | 19 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201526202 | |
| Published online | 24 November 2015 | |
A temperature inversion in WASP-33b?⋆,⋆⋆
Large Binocular Telescope occultation data confirm significant thermal flux at short wavelengths
1 Stellar Astrophysics Centre, Department of Physics and Astronomy, Aarhus University, Ny Munkegade 120, 8000 Aarhus C, Denmark
e-mail: cessen@phys.au.dk
2 Leibniz-Institut für Astrophysik Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany
3 N. Copernicus Astronomical Centre, Polish Academy of Sciences, Bartycka 18, 00-716 Warsaw, Poland
4 Institut für Astrophysik Göttingen, Friedrich-Hund-Platz 1, 33037 Göttingen, Germany
Received: 27 March 2015
Accepted: 10 July 2015
We observed a secondary eclipse of WASP-33 b quasi-simultaneously in the optical (~0.55 μm) and the near-infrared (~1.05 μm) using the 2×8.4 m Large Binocular Telescope. WASP-33 is a δ Scuti star pulsating with periods comparable to the eclipse duration, making the determination of the eclipse depth challenging. We use previously determined oscillation frequencies to model and remove the pulsation signal from the light curves, isolating the secondary eclipse. The determined eclipse depth is ΔF = 1.03 ± 0.34 parts per thousand, corresponding to a brightness temperature of TB = 3398 ± 302 K. Combining previously published data with our new measurement we find the equilibrium temperature of WASP-33 b to be TB = 3358 ± 165 K. We compare all existing eclipse data to a blackbody spectrum, to a carbon-rich non-inverted model and to a solar composition model with an inverted temperature structure. We find that current available data on WASP-33 b’s atmosphere can be best represented by a simple blackbody emission, without the need for more sophisticated atmospheric models with temperature inversions. Although our data cannot rule out models with or without a temperature inversion, they do confirm a high brightness temperature for the planet at short wavelengths. WASP-33 b is one of the hottest exoplanets known till date, and its equilibrium temperature is consistent with rapid reradiation of the absorbed stellar light and a low albedo.
Key words: asteroseismology / techniques: photometric / occultations / stars: oscillations / planets and satellites: atmospheres / methods: observational
The LBT is an international collaboration among institutions in the United States, Italy and Germany. LBT Corporation partners are: The University of Arizona on behalf of the Arizona university system; Instituto Nazionale di Astrofisica, Italy; LBT Beteiligungsgesellschaft, Germany, representing the Max-Planck Society, the Leibniz-Institute for Astrophysics Potsdam, and Heidelberg University; The Ohio State University, and The Research Corporation, on behalf of The University of Notre Dame, University of Minnesota and University of Virginia.
Appendix A is available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
Hot Jupiters offer us a great astrophysical laboratory for atmospheric science under extreme conditions as their atmospheres reach temperatures above 1000 K. Secondary eclipse measurements easily separate the stellar from the planetary lights and are therefore usually used to probe exoplanet atmospheres. Such measurements are most straight forward in the near infrared (NIR), where the planet-to-star contrast ratio is large (see e.g., Deming et al. 2007; Christiansen et al. 2010; Knutson et al. 2011). The first detection of secondary eclipses were made from the space using the infrared Spitzer Space Telescope (Charbonneau et al. 2005; Deming et al. 2005). Nonetheless, the planetary atmospheric composition and temperature structure has also been detected from the ground (see e.g., Snellen et al. 2008; Bean et al. 2010). Early studies suggest the existence of a temperature inversion layer caused by strong stellar absorption of certain molecules high up in the exoplanet atmospheres. For hot Jupiters, theoretical predictions place TiO and VO as favorite candidates (see e.g., Hubeny et al. 2003). However, this is still under debate (Spiegel et al. 2009). Fortney et al. (2008) proposed a differentiation of hot Jupiters into two populations divided by the amount of stellar irradiation. For these two families, the temperature profiles would be dominated by the state of TiO and VO. However, more recent observations have not been able to clearly show the existence of these two states (Knutson et al. 2010; Crossfield et al. 2012). A good example is WASP-12b, for which no inversion has been yet detected (Crossfield et al. 2012) despite being one of the most irradiated and hottest exoplanets known (Teq ~ 3000 K, Hebb et al. 2009; López-Morales et al. 2010). As observing techniques and data reduction strategies improve with time, past claimed detection of temperature inversions are being overruled. For example, HD 209458b was observed using Spitzer Space Telescope by Knutson et al. (2008). The four bandpass observations were represented by a thermal inversion in the exoplanet atmosphere (see e.g., Line et al. 2014). However, Diamond-Lowe et al. (2014) used state of the art techniques and models to perform a complete and self-consistent analysis of the data, finding no temperature inversion after all. To date, there doesn’t seem to be a clear determinant for which planets should present (or not) temperature inversions. Measuring the structure of one of the hottest exoplanet atmospheres could help to clarify the situation.
This work focuses on the transiting hot Jupiter WASP-33 b (Collier Cameron et al. 2010). With a wavelength-dependent brightness temperature of 3620 K, WASP-33 b is one of the hottest exoplanets known to date (Smith et al. 2011). WASP-33 (HD 15082) is a δ Scuti star, oscillating with amplitudes in the milli-magnitude regime and periods that are comparable to the transit duration (Herrero et al. 2011). WASP-33 b orbits the star each ~1.22 days in a retrograde orbit (Collier Cameron et al. 2010). Showing an unusually large radius, WASP-33 b belongs to the class of anomalously inflated exoplanets (Collier Cameron et al. 2010).
The first secondary eclipse was detected by Smith et al. (2011) at 0.91 μm. Deming et al. (2012) observed two events in the KS band (2.15 μm), and one secondary eclipse each at 3.6 μm and 4.5 μm using Warm Spitzer. The authors found the data to be consistent with two different atmospheric models, the first one with an inverted temperature structure and a solar composition, and the second one with a non-inverted temperature structure and a carbon-rich composition. Furthermore, de Mooij et al. (2013) re-observed WASP-33 b’s eclipses in the KS, finding consistency with Deming et al. (2012) and determined WASP-33 b’s effective temperature to be around 3300 K. Recently, Haynes et al. (2015) observed WASP-33 during two occultations using the Hubble Space Telescope between 1.13 and 1.63 μm. The authors represented their observations by a dayside atmosphere with a temperature inversion and an oxygen-rich composition with a slightly sub-solar abundance of H2O. Excluding this work, previous studies on WASP-33 b’s emission were observed in a broad wavelength range. At that time the authors didn’t count with a data-independent pulsation model nor with the characterization of the pulsation spectrum of the host star. In von Essen et al. (2014) we presented a two and a half years long follow-up campaign of WASP-33. We collected 457 h of in- and out- of transit data that were used to characterize the pulsation spectrum of WASP-33 with unprecedented precision, finding 8 statistically significant frequencies with periods comparable to the transit duration (~2.7 h). In this work, we observed WASP-33 during secondary eclipse at 1.05 μm using the Large Binocular Telescope. We make use of the identified pulsations to “clean” the photometry and determine the eclipse depth of WASP-33 b’s secondary eclipse. In this work, Sect. 2 presents the observations and the data reduction, Sect. 3 a detailed description of the model parameters and fitting procedures, Sect. 4 the secondary eclipse measurements in the context of the atmospheric structure of WASP-33, and Sect. 5 our final remarks.
2. Observations and data reduction
We observed WASP-33 on October 12/13, 2012, during a secondary eclipse with the 2 × 8.4 m Large Binocular Telescope1 (LBT) in binocular mode. In particular, we employed the NIR spectrograph LUCI (Seifert et al. 2010) simultaneously to the Large Binocular Cameras2 (LBC Giallongo et al. 2008). Unfortunately, due to technical problems the spectroscopic LUCI time-series lacks the pre-ingress part of the light curve. Therefore, our work focuses on the photometric data only.
The LBC consists of two wide-field cameras mounted on the prime focus swing arms of the LBT. Photometric data were acquired using the LBC Red camera, which is optimized for observations between 0.55 and 1 μm. The camera has four charge coupled devices (CCDs), each one of them with its own gain and read-out noise characteristics3. To minimize read-out time we used sub-frames of the CCDs with the brightest stars within the field of view centered on each chip. The size of the final sub-frames were approximately 1 × 3 arcmin, which reduced the read-out time from 30 to 15 s.
During the night the observing conditions were stable and the sky was clear. Seeing varied between 0.4 and 1.1 arcsec. The photometric data were acquired using the Johnson-Cousins V filter centered at 0.55 μm and a Y filter centered at 1.05 μm, the latter with a full-width at half-maximum of 0.2 μm. As WASP-33 is relatively bright (V ~ 8.3), we defocused the telescope to avoid saturation. The transmission function of the Y-band peaks around 95%, but the quantum efficiency of the CCD drops down to 10% in the filters wavelength range. This was also useful to avoid saturation. WASP-33 is located in a sparse stellar field. Therefore, the defocusing technique did not produce overlapping of the stellar point spread functions, except for the optical companion identified by Moya et al. (2011). A discussion on third-light contribution is addressed in Sect. 3.5. Exposure times were of 0.74 s for the V-band and 3.23 s for the Y-band. Every 3 images the filters were switched between the two bands. Since the readout time is shorter than the time that the filter wheel requires to go from one filter to the other (~20 s), the sampling between consecutive images is each ~18 s, while the sampling between consecutive groups of 3 images of the same filter is each ~2.3 min.
We used the IRAF’s package ccdproc for bias subtraction and the flat fielding, and the IRAF task apphot for aperture photometry. We measured fluxes of WASP-33 and three reference stars, namely BD+36 493, BD+36 487, and BD+36 488, using various aperture radii. We then fixed the aperture radius so that the scatter of the differential light curve is minimized. The chosen aperture radius was of 74 pixels, equivalently to 16 arcsec considering the plate scale of the LBC Red (0.2255′′/pixel). Next we divided WASP-33’s measured flux by the average of the three reference stars producing the final differential light curves (see Figs. 1 and 3). Since these are influenced by stellar pulsations, we estimated the scatter averaging the standard deviations calculated within 15 minutes bins, where the deformations caused by WASP-33’s intrinsic variability can be neglected. The derived uncertainties are ~0.8 parts-per-thousand (ppt) for the V-band and 0.6 ppt in the Y-band, four and three times the expected photometric precision assuming only photon noise (0.2 ppt), respectively. We believe that the difference between the achieved photometric precision and the theoretical photon-noise precision is caused by scintillation noise due to the short exposure times. To ensure that the photometry is based on proper references, the three reference stars were plotted against each other to check for constancy.
During the observations, the LUCI (spectroscopic) side of the LBT was the one guiding the telescope. The LBC side followed, however, its pointing stability was rather poor. After 3.5 h of observations WASP-33 and the reference stars drifted ~200 pixels in both x and y directions close to the edge of the read-out windows and flux was lost. These ~0.5 h of observations were omitted from our analysis. WASP-33 b eclipse lasts 2.7 h. Therefore, our observations account for ~25 min of off-eclipse data before eclipse begins and ends, respectively, and full eclipse coverage. As a final step the time stamps were converted from Julian Dates to Barycentric Julian Dates (BJDTDB) using the tools made available by Eastman et al. (2010).
3. Results
3.1. Analysis of the optical light curve
The data presented here comprise quasi-simultaneous observations during secondary eclipse of WASP-33 b around the V and Y bands. The predicted planet-star flux ratio in the V-band is 0.2 ppt, four times lower than the accuracy of our measurements. Therefore, we can neglect the planet imprint and use this band to measure the stellar pulsations, and most specifically to tune their current phases (see phase shifts in von Essen et al. 2014). Particularly, our model for the light contribution of the stellar pulsations consists of eight sinusoidal pulsation frequencies with corresponding amplitudes and phases. Hence, to reduce the number of 24 free parameters and the values they can take, we use prior knowledge about the pulsation spectrum of the star that was acquired during von Essen et al. (2014). As the frequency resolution is 1/ΔT (Kurtz 1983), 3.5 h of data are not sufficient to determine the pulsations frequencies. Therefore, during our fitting procedure we use the frequencies determined in von Essen et al. (2014) as starting values plus their derived errors as Gaussian priors. As pointed out in von Essen et al. (2014), we found clear evidences of pulsation phase variability with a maximum change of 2 × 10-3 c/d. In other words, as an example after one year time a phase-constant model would appear to have the correct shape with respect to the pulsation pattern of the star, but shifted several minutes in time. To account for this, the eight phases were considered as fitting parameters. The von Essen et al. (2014) photometric follow-up started in August, 2010, and ended in October, 2012, coinciding with these LBT data. We then used the phases determined in von Essen et al. (2014) during our last observing season as starting values, and we restricted them to the limiting cases derived in Sect. 3.5 of von Essen et al. (2014), rather than allowing them to take arbitrary values. The pulsation amplitudes in δ Scuti stars are expected to be wavelength-dependent (see e.g. Daszyńska-Daszkiewicz 2008). Our follow-up campaign and these data were acquired in the blue wavelength range. Therefore the amplitudes estimated in von Essen et al. (2014), listed in Table 1, are used in this work as fixed values. This approach would be incorrect if the pulsation amplitudes would be significantly variable (see e.g., Breger et al. 2005). Nonetheless, the short time span of LBT data, and the achieved photometric precision compared to the intrinsically low values of WASP-33’s amplitudes, make the detection of any amplitude variability impossible.
Comparison of derived pulsations between previous and current work.
For the fitting procedure we used the photometric errors that IRAF provides, but enlarged to meet the standard deviation of the data. Our model to the V-band light curve requires three additional free parameters to account for airmass and color-dependent extinction. Since the pulsations impede any visual inspection of how these effects impact on the photometry, the number of parameters was determined through 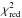 minimization. To derive the 16+3 parameters for our model we used a Markov chain Monte Carlo (MCMC) approach. Our MCMC calculations make extensive use of PyAstronomy4, a collection of Python routines providing a convenient interface for fitting and sampling algorithms implemented in the PyMC (Patil et al. 2010) and SciPy (Jones et al. 2001) packages. After 1 × 106 MCMC iterations and a burn-in of the initial 2 × 105 samples, we computed the mean and standard deviation (1σ) of the posterior distributions of the parameters and used them as best-fit values and uncertainties, respectively. Our results for the frequencies and phases are summarized in the sixth and seventh columns of Table 1. The small errors on the fitted frequencies are caused due to the priors imposed and due to the reduction of the fitting parameters compared to the ones in von Essen et al. (2014). In this work the eight amplitudes are considered as fixed parameters, making as consequence the statistical errors to appear smaller. To test if the MCMC chains were well-mixed and converged we followed two approaches. Firstly, we started the MCMC chains using different initial values. Secondly, we divided complete chains into sub-chains (normally dividing the 1 × 106 iterations into 4) confirming afterward that the best-fitting values obtained from the posterior distributions of each sub-chains were consistent to each other. Finally, we confirmed convergence by visually inspecting the traces and histograms of all the fitting parameters. Figure 1 shows the LBT optical data over-plotted to the best-fit model (top) along with the residual light curve (bottom).
minimization. To derive the 16+3 parameters for our model we used a Markov chain Monte Carlo (MCMC) approach. Our MCMC calculations make extensive use of PyAstronomy4, a collection of Python routines providing a convenient interface for fitting and sampling algorithms implemented in the PyMC (Patil et al. 2010) and SciPy (Jones et al. 2001) packages. After 1 × 106 MCMC iterations and a burn-in of the initial 2 × 105 samples, we computed the mean and standard deviation (1σ) of the posterior distributions of the parameters and used them as best-fit values and uncertainties, respectively. Our results for the frequencies and phases are summarized in the sixth and seventh columns of Table 1. The small errors on the fitted frequencies are caused due to the priors imposed and due to the reduction of the fitting parameters compared to the ones in von Essen et al. (2014). In this work the eight amplitudes are considered as fixed parameters, making as consequence the statistical errors to appear smaller. To test if the MCMC chains were well-mixed and converged we followed two approaches. Firstly, we started the MCMC chains using different initial values. Secondly, we divided complete chains into sub-chains (normally dividing the 1 × 106 iterations into 4) confirming afterward that the best-fitting values obtained from the posterior distributions of each sub-chains were consistent to each other. Finally, we confirmed convergence by visually inspecting the traces and histograms of all the fitting parameters. Figure 1 shows the LBT optical data over-plotted to the best-fit model (top) along with the residual light curve (bottom).
Our analysis over the V-band data was concluded trying to estimate an upper limit for the eclipse depth. For this end, we added to our model budget a secondary eclipse shape (see Sect. 3.2.2 for details on secondary eclipse modeling). After similar iterations and sample burn-in, we found the best-fit eclipse depth to be ΔF = 0.26 ± 0.48 ppt. 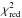 computations between the two models favor the case where the secondary eclipse is not considered. As previously assumed, the derived uncertainty is too large to compute a reasonable 3σ upper limit.
computations between the two models favor the case where the secondary eclipse is not considered. As previously assumed, the derived uncertainty is too large to compute a reasonable 3σ upper limit.
 |
Fig. 1 LBT V optical data during secondary eclipse of WASP-33 b as a function of the orbital phase and the hours relative to mid-eclipse. Top: normalized flux. The continuous black line shows the best-fitting model (24+3 parameters). The error bars were enlarged to meet the scatter of the data. Bottom: residual light curve. Vertical dashed lines indicate first to fourth contacts assuming a circular orbit (Deming et al. 2012). |
3.1.1. Residual light curve analysis
Pulsations not accounted for in our model would manifest themselves as correlated noise. To quantify to which extent the residual light curve is affected by it, we followed a similar approach as Gillon et al. (2006), Winn et al. (2008), and Carter & Winn (2009). We started dividing the residual light curve into M bins of equal duration. Since our data are not equally spaced, we calculated a mean value N of data points per bin. If the data are affected by correlated noise, the sample standard deviation of the binned data, σN, would differ by a factor βN from its theoretical expectation (see e.g., von Essen et al. 2013, for an extended mathematical description). For data sets free of correlated noise, βN = 1 is expected. βN’s smaller than 1 might occur due to statistical fluctuations and were neglected in our analysis. We estimated the amount of correlated noise, β, averaging βN’s that were calculated within bins of 0.5, 0.75, 1, 1.25 and 1.5 times the ingress time. Its derived value, β = 1.05, allows us to neglect the contribution of correlated noise in our future analysis. Finally, we searched for any residual pulsations computing a Lomb-Scargle periodogram (Lomb 1976; Scargle 1982; Zechmeister & Kürster 2009) from LBT-V’s residual data and found no significant peaks. Thus, our pulsation model satisfactory represents the intrinsic variability of WASP-33.
3.2. Analysis of the NIR light curve
3.2.1. Wavelength-dependency of fitting parameters for δ Scuti stars
The pulsations of δ Scuti stars are known to be wavelength-dependent (see e.g., Balona & Evers 1999; Daszyńska-Daszkiewicz et al. 2003). Thus, subtracting the V-model to the Y data would not properly account for WASP-33’s intrinsic variability. In von Essen et al. (2014) we tried to characterize the nature of the modes analyzing simultaneous multi-color photometry (see Sect. 3.6.3 of von Essen et al. (2014) for further details). However, we found no conclusive results. Consequently, an estimation of the V–to–Y change of the amplitudes and phases of the eight frequencies can only be obtained via theoretical modeling. To quantify these changes we used the Frequency Analysis and Mode Identification for AsteroSeismology code (FAMIAS), a collection of tools for the analysis of photometric and spectroscopic time series data (Zima 2008). To begin with, FAMIAS requires basic stellar parameters. Therefore, we adopted Teff = 7430 ± 100 K, log(g) = 4.3 ± 0.2, and [Fe/H] = 0.1 ± 0.2 (Collier Cameron et al. 2010). The non-adiabatic observables were calculated using the code MAD (Dupret 2001; Grigahcène et al. 2005), while as model atmospheres we used Kurucz (1997)’s grids. Furthermore, we assumed the degree, ℓ, and the azimuthal number, m, of the pulsation modes to be low (m,ℓ ≤ 2, see e.g. Aerts et al. 2010, geometric cancellation). From FAMIAS we computed the amplitude ratios and phase differences for each one of the eight frequencies relative to the V-band. Unfortunately, the wavelength coverage of FAMIAS goes up to 0.8 μm, i.e. not covering the Y wavelength range. Therefore, our estimates are an extrapolation of FAMIAS results, all of them summarized in Table 2. As an example, Fig. 2 shows FAMIAS results for ν1 = 20.1621 c/d, along with their respective extrapolations. Analyzing these theoretical expectations some relevant conclusions can be drawn. First, as it is expected for δ Scuti stars the amplitudes of the pulsations are larger where the star emits most of its flux (see e.g., Daszyńska-Daszkiewicz 2008). Therefore, for WASP-33 it is expected that the amplitudes will decrease for redder wavelengths. Second, the computed amplitude ratios for different ℓ degrees would make the proper identification of the modes impossible to achieve by means of these multi-color data. Indeed, for the eight frequencies that comprise our model the amplitudes are expected to scale down around 40−80% in the Y with respect to their V values. Considering the relative short duration of these observations, the photometric precision of the data, and the relation between this precision and the amplitude of the pulsations, for low ℓ-values it is impossible to determine their geometry (see Fig. 2). Finally, the phases in V and Y are expected to be similar. All these aspects will be considered in our NIR pulsation model.
 |
Fig. 2 Amplitude ratios (top) and phase differences bottom obtained with FAMIAS for the ν1 = 20.1621 c/d pulsation frequency, considering ℓ ≤ 2. Gray contours indicate the extrapolated area extended to the Y filter. Both V and Y filter transmission functions are plotted in gray continuous lines. |
Maximum theoretically-expected changes for amplitude ratios (AV/AYmin−AV/AYmax) and phase differences (φV,Y,min, φV,Y,max) between the V and Y-bands for the eight pulsation frequencies considering ℓ ≤ 2.
3.2.2. Planetary size versus secondary eclipse model
As secondary eclipse model we used a simple step function. Its shape was limited by the first to fourth contacts (Sackett 1999). The latter were estimated using the semi-major axis a/Rs, the orbital inclination i, the planet-to-star radius ratio RP/RS, the orbital period P, and the mid-eclipse time T0 that were computed in von Essen et al. (2014) accounting for the stellar pulsations. T0 was used to place the step function relative to mid-eclipse time, assuming a circular orbit (Deming et al. 2012). The chosen values are summarized in Table 3.
Orbital and physical parameters of WASP-33 b computed in von Essen et al. (2014).
 |
Fig. 3 Equivalently to Fig. 1, but around 1.05 μm. From top to bottom, WASP-33’s pulsations and secondary eclipse, the secondary eclipse once the pulsations have been removed, and the residual light curve once the secondary eclipse is removed. Black continuous lines show best-fit models for the pulsations and the secondary eclipse. Pink and green eclipse models correspond to Deming et al. (2012)’s predicted eclipse depths for inverted and non-inverted atmospheric structures integrated in the Y-band. |
Any potential change in the planetary radius as function of observing wavelength mainly manifests itself in a change of the eclipse shape. In addition, the times of contact might change by a small amount. We tested if our data is sensitive to this second order effect and if the use of one set of contact points for all wavelengths is justified. We simulated a secondary eclipse of a transiting planet 20% larger than the value measured in the optical (Table 3), adding to it the time stamps and noise properties of our data. We find that a change in the eclipse duration does not improve the fit to the simulated data compared to a fit where the radius obtained in the optical is used. Our data quality is such that we do not need to take this second order effect into account and we proceed using the times of contact as determined in the optical.
3.3. Fitting parameters and results
We now use our knowledge on the pulsations gained from the analysis of the optical light curve in the analysis of the NIR light curve. Our model consists of an eclipse light curve described by the parameters from Table 3. For all but the planet to star flux ratio ΔF, which we want to determine, we use the parameters and uncertainties given in the table as prior information. To describe the stellar pulsations we use the same model as in the optical plus the prior information on the eight frequencies, amplitudes and phases. All amplitudes are damped by a common factor ΔA relative to the optical. All parameters and their 1σ uncertainties are given in Table 1. In particular, we find an eclipse depth of ΔF = 1.03 ± 0.34 ppt in the Y-band.
The derived frequencies, phases, and the computed phase differences between both bands, are summarized in the last three columns of Table 1. Our results show that both φV−φY and ΔA = 0.73 ± 0.08 are consistent with their theoretical expectations. Figure 3 shows in the top panel the Y-band light curve, in the middle panel the pulsation model removed isolating the planetary eclipse and in the bottom panel the residuals model data. On top of our best-fit secondary eclipse model we show Deming et al. (2012)’s predicted eclipse depths integrated in the Y-band for the atmosphere of WASP-33 b when a carbon-rich non-inverted model (green) and a solar composition model with an inverted temperature structure (pink) are considered.
We calculated the Pearson, P, and Spearman, S, correlation coefficients between ΔA and ΔF. Both show a low positive correlation of ~0.4. No such correlation was found between the eclipse depth and the phases nor frequencies.
3.4. Robustness of our fitting approach
Measured eclipse depths and uncertainties can depend sensitively on the choice of model used to fit the light curve. To confirm that our final result is robust, we performed a number of additional fits. We compared the models using the Bayesian information criterion, BIC = χ + k ln N, which penalizes the number k of model parameters given N data points. The additional models for the stellar pulsations included the following fitting parameters:
- 1.
Frequencies fixed to the best-fit values found in von Essen et al. (2014), scaling factor for the amplitudes, eight phases with Gaussian priors, secondary eclipse and detrending function.
- 2.
Eight frequencies with Gaussian priors, eight amplitudes with uniform priors, eight phases with Gaussian priors, secondary eclipse and detrending function.
- 3.
Frequencies fixed to the best-fit values found in von Essen et al. (2014), eight amplitudes with uniform priors, eight phases with Gaussian priors, secondary eclipse and detrending function.
The resulting BIC values, along with the fitting parameters for each model and the derived best-fit eclipse depth for each model are summarized in Table 4. As the table reveals, the BIC favors our approach. All eclipse depths are consistent within 1σ errors.
Results for the four different pulsation models.
3.5. Potential third-light contributions
Moya et al. (2011) detected an optical companion to WASP-33 at an angular separation of ~2′′. This companion is included in our aperture and therefore reduces the measured eclipse depth relative to the undiluted case. Based on the color information obtained in the JC, HC, KC, and FII filters, Moya et al. (2011) estimated that the probable physical companion of WASP-33 has an effective temperature of Teff = 3050 ± 250 K. To compute the contribution of this third light we used the approach detailed in Tingley (2004). First, we represented the emission of the third body, F3, relative to WASP-33’s emission, FW33, with the ratio of two black body curves F3/FW33 of 3050 and 7430 K, respectively. Then, we converted the Δmag’s of the JC, HC, KC, and FII bands to fluxes and adjusted F3/FW33 to Moya et al. (2011)’s measurements with a diluting (scaling) factor, C, that accounts for the relative distances between the two stellar objects. Extrapolating this to the Y-band we found F3 to be 714 times dimmer than WASP-33. Given our data we can ignore such a contribution. Although strictly speaking stars are not blackbodies, the blackbody approximation was carried out in this case mainly due to two reasons. On one hand, WASP-33 is an A-type star and, therefore, is expected to have no strong absorption lines in the wavelength range of our interest. On the other hand, there is no knowledge about the metallicity nor the surface gravity of WASP-33’s companion, not allowing us to use appropriate stellar models without further speculation. Nonetheless, we caution the reader to carry out this approximation when a more complete knowledge of the spectral properties of the involved stars is known.
4. Thermal emission from WASP-33
4.1. Brightness and equilibrium temperatures
From the observed planet-star flux ratio at a given wavelength the exoplanet brightness temperature Tb at that wavelength can be derived. For this calculation we represent WASP-33’s emission by a spectrum from the PHOENIX library (Hauschildt & Baron 1999; Witte et al. 2009) with stellar parameters Teff = 7400 K, [Fe/H] = 0.1, and log g = 4.5, closely matching WASP-33’s values given by Collier Cameron et al. (2010). The planet contribution is represented by a black body and the measured eclipse depth represents the planet-to-star flux ratio FP/FS(Y), integrated within the Y-band (Charbonneau et al. 2005). We computed χ2 between our best-fit eclipse depth and FP/FS(Y), varying Tb between 2500 and 4500 K each 1 K. By means of χ2 minimization we found the brightness temperature of the exoplanet to be Tb(Y) = 3398 ± 302. Its error was determined from a Δχ2 contour equal to 1.
Observed eclipse depths (EDs) of WASP-33 b in ppt and the derived brightness temperatures (Tb).
 |
Fig. 4 Top: eclipse depth in ppt as a function of wavelength. The blue data point indicates our brightness temperature measurement, while the red circles show literature values. The gray area shows 1σ contour of WASP-33 b’s equilibrium temperature. Green continuous line corresponds to Deming et al. (2012)’s carbon-rich non-inverted model, while pink continuous line indicates a solar composition model with an inverted temperature structure. Squares mark the planetary fluxes integrated over the bandpasses. Bottom: the same data after multiplication by the PHOENIX stellar model revealing the SED for WASP-33 b. Overplotted are the expected SEDs for a zero-albedo instantly re-radiation (orange diamonds, f = 2/3) and instantly redistribution (cyan triangles, f = 1/4) day-sides. |
To date, six measurements of WASP-33 b’s eclipses along with their corresponding Tb’s have been obtained (Table 5). Assuming that the brightness temperatures can represent the equilibrium temperature Teq of WASP-33 b (see e.g., de Mooij et al. 2013, Sect. 4.1), we re-determined it following the approach explained in the previous paragraph but using all bibliographic data instead. We found the best-fit equilibrium temperature equal to Teq = 3358 ± 165 K (Fig. 4). Our determination of the equilibrium temperature is ~100 K higher than, but consistent with, the value determined by de Mooij et al. (2013), 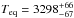 K. The corresponding
K. The corresponding 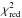 at 5 d.o.f. is 1.2. We calculated
at 5 d.o.f. is 1.2. We calculated 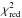 values between the observations and the two cases presented in Deming et al. (2012; see their Fig. 9 and our Fig. 4), i.e. a carbon-rich non-inverted model (green,
values between the observations and the two cases presented in Deming et al. (2012; see their Fig. 9 and our Fig. 4), i.e. a carbon-rich non-inverted model (green, 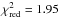 , 3 d.o.f.), and a solar composition model with an inverted temperature structure (pink,
, 3 d.o.f.), and a solar composition model with an inverted temperature structure (pink, 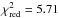 , 3 d.o.f.). We find that our simple blackbody curve seems to provide comparable results to the non-inverted scenario, and could also easily fit the inverted scenario if the emission from the TiO band centered at 0.9 μm is stronger than what current models predict. We notice that the measurement at 2 microns differs significantly with respect to the inverted (pink) model. This discrepancy has been solved by Haynes et al. (2015; see their Sect. 5.1 and their Fig. 5). We believe that these data can not be uniquely represented by a given model without the need of further speculation, and find our simple blackbody approach as sufficient. A more sophisticated analysis using different models with different inverted temperature structures is beyond our scope.
, 3 d.o.f.). We find that our simple blackbody curve seems to provide comparable results to the non-inverted scenario, and could also easily fit the inverted scenario if the emission from the TiO band centered at 0.9 μm is stronger than what current models predict. We notice that the measurement at 2 microns differs significantly with respect to the inverted (pink) model. This discrepancy has been solved by Haynes et al. (2015; see their Sect. 5.1 and their Fig. 5). We believe that these data can not be uniquely represented by a given model without the need of further speculation, and find our simple blackbody approach as sufficient. A more sophisticated analysis using different models with different inverted temperature structures is beyond our scope.
Special notice has to be given to the wavelength coverage of the data. The lower panel of Fig. 4 shows that all planet-to-star flux ratio measurements lie within the Rayleigh-Jeans region of the planets black body, making any temperature measurement prone to errors, since the raising part of the planetary emission curve is not being taken into account. A flux measurement at λ ~ 0.7−0.9 μm would significantly improve our knowledge on WASP-33 b’s temperature, because the shape of the planetary spectral energy distribution (SED) would be better constrained and the determination of the planetary temperature would not be determined only by the slope of the SED. However, secondary eclipse observations in the optical are extremely challenging, aggravated in this particular case by WASP-33’s intrinsic variability.
4.2. Albedo and re-distribution factor
Due to their proximity to the host star, the exoplanet atmospheres of short period exoplanets are strongly dominated by the stellar incident flux. An indicator for the fraction of light that gets reflected back into space immediately is the geometric albedo for which the majority of measurements yielded very low values (Heng & Demory 2013). How well the absorbed flux is redistributed from the dayside to the nightside is still a matter of debate (Perna et al. 2012; Heng & Showman 2015). López-Morales & Seager (2007) presented an analytic expression for the exoplanet equilibrium temperature as a function of the Bond albedo AB and the reradiation factor f, which describes how the stellar radiation absorbed by an exoplanet is redistributed in its atmosphere. Using their Eq. (1), we compute the equilibrium temperature of WASP-33 b for a zero-albedo and reradiation factors of 2/3 (instant reradiation) and 1/4 (instant redistribution) obtaining Teq = 3499 K and Teq = 3257 K. These are shown in the bottom panel of Fig. 4 as orange diamonds and cyan triangles respectively.
Instead of choosing two boundary conditions for AB and f, to constrain WASP-33 b’s values of bond albedo and redistribution efficiency we produced an equilibrium temperature map. Each point of the map was calculated in the same fashion as before, but defining a 300 × 300 grid in the AB−f space. The map is displayed in Fig. 5, where the cyan area defines WASP-33 b’s equilibrium temperature range. The shaded effect was produced considering the stellar (Teff, RS) and orbital (a/RS) parameters with their uncertainties.
Producing a statistical analysis of the bond albedo and redistribution efficiency over 24 transiting exoplanets with at least one published secondary eclipse, Cowan & Agol (2011) found that all the planets in the sample were consistent with low bond albedos (<10%), and planets hotter than 2400 K presented low redistribution efficiency (i.e., large f values). This is in good agreement with the cyan contours displayed in Fig. 5. Thus, WASP-33 b seems to have similar properties as atmospheres of other close-in gas giants orbiting cooler stars (AB< 0.38, 0.41 <f< 2/3).
 |
Fig. 5 Equilibrium temperature map as a function of albedo (AB) and re-distribution factor f. Cyan color shows the contours relative to WASP-33 b’s equilibrium temperature within 1σ error (top-left corner) for both planetary and stellar parameters. f values larger than 2/3 are unphysical. Therefore, the white-shaded area of the plot has not to be considered. |
A nonzero geometric albedo of the planet in the Y band would result in a contribution of reflected light to the eclipse depth. For example, the potential impact of a rather high geometric albedo of 0.5 would be ~350 ppt on the eclipse depth, which is on the order of our 1σ uncertainty. Such contribution of reflected light would not significantly affect our results of Sect. 4.1. However, any nonzero albedo would lower the estimated exoplanet equilibrium temperature.
4.3. Evidence for temperature inversion?
The observed diversity in the characteristics of hot Jupiter atmospheres has been a main subject of investigation. For instance, Knutson et al. (2010) suggested a direct relation between the activity of the host star and the presence of a temperature inversion. While active stars should host exoplanets without temperature inversions, the opposite should occur around quiet stars. To investigate WASP-33’s activity levels we analyzed calcium lines in high-resolution spectra acquired on December 28, 2012, using the High Resolution Echelle Spectrometer mounted at the Keck I telescope (program ID N116Hr, PI Howard). WASP-33 is X-ray dark and generally inactive, as seen in a lack of emission in the Ca II H and K lines (Fig. 6). Comparing the observations to Knutson et al. (2010)’s suggestions, WASP-33 b should present a temperature inversion. Also, planets with inversions are expected to have greater Spitzer/IRAC 4.5 μm than 3.6 μm flux, resulting from strong CO and CO2 absorption in the 4.5 μm bandpass (see e.g., Burrows et al. 2007; Madhusudhan & Seager 2010). This has been observed in WASP-33. However, both results seem to be in disagreement with the observed high re-radiation factor (Fortney et al. 2008). Although χ2 analysis would favor a non-inversion, the here presented disagreements caution ourselves to make any assumption about the atmospheric structure of WASP-33 b. A phase curve would help to constrain the albedo and the re-radiation factors. However, stellar pulsations might make the task more challenging.
 |
Fig. 6 WASP-33’s high resolution spectra around the Ca II H&K lines observed with Keck/HIRES. |
5. Conclusions
In this work we present simultaneous observations in the V and Y bands of WASP-33 during a secondary eclipse. We make use of the information about the stellar pulsations on the V light curve to “clean” the NIR data, minimizing the impact of stellar pulsations and correlated noise in the determination of the eclipse depth. The measured eclipse depth is ΔF = 1.03 ± 0.34 ppt, which corresponds to a brightness temperature of 3398 ± 302 K. We represent the SED of WASP-33 b by a black body curve and fit it to current data. We find an equilibrium temperature equal to 3358 ± 165 K, slightly hotter but still consistent with previous measurements. Comparing χ2 values between our approach and more sophisticated measurements we conclude that these observations can not provide a detailed description of the temperature structure of WASP-33 b’s atmosphere. In agreement with previous publications and hypothesis made by Cowan & Agol (2011), we find that WASP-33 b has a very low efficiency to circulate stellar radiation into the exoplanet night side.
Online material
Appendix A
Environmental and instrumental conditions during observations for the V-band.
Acknowledgments
C. von Essen acknowledges D. Deming, A. Mandell, K. Haynes, M. Breger and B.W. Tingley for fruitful discussions. We thank the LBTO support astronomers Olga Kuhn, Michelle Edwards, David Thompson and Barry Rothberg for their immense help in planning and executing the LBT observations. Funding for the Stellar Astrophysics Centre is provided by The Danish National Research Foundation (grant No. DNRF106). The research is supported by the ASTERISK project (ASTERoseismic Investigations with SONG and Kepler) funded by the European Research Council (Grant agreement No. 267864). A.M.S.S. acknowledges support from the Polish NCN through grant no. 2012/07/B/ST9/04422. This research has made use of the Keck Observatory Archive (KOA), which is operated by the W.M. Keck Observatory and the NASA Exoplanet Science Institute (NExScI), under contract with the National Aeronautics and Space Administration.
References
- Aerts, C., Christensen-Dalsgaard, J., & Kurtz, D. W. 2010, Asteroseismology (Springer) [Google Scholar]
- Balona, L. A., & Evers, E. A. 1999, Delta Scuti Star Newsletter, 13, 26 [NASA ADS] [Google Scholar]
- Bean, J. L., Miller-Ricci Kempton, E., & Homeier, D. 2010, Nature, 468, 669 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Breger, M., Lenz, P., Antoci, V., et al. 2005, A&A, 435, 955 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burrows, A., Hubeny, I., Budaj, J., Knutson, H. A., & Charbonneau, D. 2007, ApJ, 668, L171 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Carter, J. A., & Winn, J. N. 2009, ApJ, 704, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Charbonneau, D., Allen, L. E., Megeath, S. T., et al. 2005, ApJ, 626, 523 [NASA ADS] [CrossRef] [Google Scholar]
- Christiansen, J. L., Ballard, S., Charbonneau, D., et al. 2010, ApJ, 710, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Collier Cameron, A., Guenther, E., Smalley, B., et al. 2010, MNRAS, 407, 507 [NASA ADS] [CrossRef] [Google Scholar]
- Cowan, N. B., & Agol, E. 2011, ApJ, 729, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Crossfield, I. J. M., Barman, T., Hansen, B. M. S., Tanaka, I., & Kodama, T. 2012, ApJ, 760, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Daszyńska-Daszkiewicz, J. 2008, Commun. Asteroseismol., 152, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Daszyńska-Daszkiewicz, J., Dziembowski, W. A., & Pamyatnykh, A. A. 2003, A&A, 407, 999 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Mooij, E. J. W., Brogi, M., de Kok, R. J., et al. 2013, A&A, 550, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deming, D., Seager, S., Richardson, L. J., & Harrington, J. 2005, Nature, 434, 740 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Deming, D., Harrington, J., Laughlin, G., et al. 2007, ApJ, 667, L199 [NASA ADS] [CrossRef] [Google Scholar]
- Deming, D., Fraine, J. D., Sada, P. V., et al. 2012, ApJ, 754, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Diamond-Lowe, H., Stevenson, K. B., Bean, J. L., Line, M. R., & Fortney, J. J. 2014, ApJ, 796, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Dupret, M. A. 2001, A&A, 366, 166 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eastman, J., Siverd, R., & Gaudi, B. S. 2010, PASP, 122, 935 [NASA ADS] [CrossRef] [Google Scholar]
- Fortney, J. J., Lodders, K., Marley, M. S., & Freedman, R. S. 2008, ApJ, 678, 1419 [NASA ADS] [CrossRef] [Google Scholar]
- Giallongo, E., Ragazzoni, R., Grazian, A., et al. 2008, A&A, 482, 349 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gillon, M., Pont, F., Moutou, C., et al. 2006, A&A, 459, 249 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grigahcène, A., Dupret, M.-A., Gabriel, M., Garrido, R., & Scuflaire, R. 2005, A&A, 434, 1055 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hauschildt, P. H., & Baron, E. 1999, J. Comput. Appl. Math., 109, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Haynes, K., Mandell, A. M., Madhusudhan, N., Deming, D., & Knutson, H. 2015, ApJ, 806, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Hebb, L., Collier-Cameron, A., Loeillet, B., et al. 2009, ApJ, 693, 1920 [NASA ADS] [CrossRef] [Google Scholar]
- Heng, K., & Demory, B.-O. 2013, ApJ, 777, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Heng, K., & Showman, A. P. 2015, Ann. Rev. Earth Planet. Sci., 43, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Herrero, E., Morales, J. C., Ribas, I., & Naves, R. 2011, A&A, 526, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hubeny, I., Burrows, A., & Sudarsky, D. 2003, ApJ, 594, 1011 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, E., Oliphant, T., Peterson, P., et al. 2001, SciPy: Open source scientific tools for Python, http://www.scipy.org [Google Scholar]
- Knutson, H. A., Charbonneau, D., Allen, L. E., Burrows, A., & Megeath, S. T. 2008, ApJ, 673, 526 [NASA ADS] [CrossRef] [Google Scholar]
- Knutson, H. A., Howard, A. W., & Isaacson, H. 2010, ApJ, 720, 1569 [NASA ADS] [CrossRef] [Google Scholar]
- Knutson, H. A., Madhusudhan, N., Cowan, N. B., et al. 2011, ApJ, 735, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Kurtz, D. W. 1983, IBVS, 2285, 1 [NASA ADS] [Google Scholar]
- Kurucz, R. L. 1997, in IAU Symp. 189, eds. T. R. Bedding, A. J. Booth, & J. Davis, 217 [Google Scholar]
- Line, M. R., Knutson, H., Wolf, A. S., & Yung, Y. L. 2014, ApJ, 783, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Lomb, N. R. 1976, Ap&SS, 39, 447 [NASA ADS] [CrossRef] [Google Scholar]
- López-Morales, M., & Seager, S. 2007, ApJ, 667, L191 [NASA ADS] [CrossRef] [Google Scholar]
- López-Morales, M., Coughlin, J. L., Sing, D. K., et al. 2010, ApJ, 716, L36 [NASA ADS] [CrossRef] [Google Scholar]
- Madhusudhan, N., & Seager, S. 2010, ApJ, 725, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Moya, A., Bouy, H., Marchis, F., Vicente, B., & Barrado, D. 2011, A&A, 535, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Patil, A., Huard, D., & Fonnesbeck, C. J. 2010, Journal of Statistical Software, 35, 1 [Google Scholar]
- Perna, R., Heng, K., & Pont, F. 2012, ApJ, 751, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Sackett, P. D. 1999, in Planets Outside the Solar System: Theory and Observations, eds. J.-M. Mariotti, & D. Alloin, NATO ASIC Proc., 532, 189 [Google Scholar]
- Scargle, J. D. 1982, ApJ, 263, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Seifert, W., Ageorges, N., Lehmitz, M., et al. 2010, in SPIE Conf. Ser., 7735, 7 [Google Scholar]
- Smith, A. M. S., Anderson, D. R., Skillen, I., Collier Cameron, A., & Smalley, B. 2011, MNRAS, 416, 2096 [NASA ADS] [CrossRef] [Google Scholar]
- Snellen, I. A. G., Albrecht, S., de Mooij, E. J. W., & Le Poole, R. S. 2008, A&A, 487, 357 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spiegel, D. S., Silverio, K., & Burrows, A. 2009, ApJ, 699, 1487 [NASA ADS] [CrossRef] [Google Scholar]
- Tingley, B. 2004, A&A, 425, 1125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- von Essen, C., Schröter, S., Agol, E., & Schmitt, J. H. M. M. 2013, A&A, 555, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- von Essen, C., Czesla, S., Wolter, U., et al. 2014, A&A, 561, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Winn, J. N., Holman, M. J., Torres, G., et al. 2008, ApJ, 683, 1076 [NASA ADS] [CrossRef] [Google Scholar]
- Witte, S., Helling, C., & Hauschildt, P. H. 2009, A&A, 506, 1367 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zechmeister, M., & Kürster, M. 2009, A&A, 496, 577 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zima, W. 2008, Commun. Asteroseismol., 157, 387 [NASA ADS] [Google Scholar]
All Tables
Maximum theoretically-expected changes for amplitude ratios (AV/AYmin−AV/AYmax) and phase differences (φV,Y,min, φV,Y,max) between the V and Y-bands for the eight pulsation frequencies considering ℓ ≤ 2.
Orbital and physical parameters of WASP-33 b computed in von Essen et al. (2014).
Observed eclipse depths (EDs) of WASP-33 b in ppt and the derived brightness temperatures (Tb).
All Figures
 |
Fig. 1 LBT V optical data during secondary eclipse of WASP-33 b as a function of the orbital phase and the hours relative to mid-eclipse. Top: normalized flux. The continuous black line shows the best-fitting model (24+3 parameters). The error bars were enlarged to meet the scatter of the data. Bottom: residual light curve. Vertical dashed lines indicate first to fourth contacts assuming a circular orbit (Deming et al. 2012). |
| In the text | |
 |
Fig. 2 Amplitude ratios (top) and phase differences bottom obtained with FAMIAS for the ν1 = 20.1621 c/d pulsation frequency, considering ℓ ≤ 2. Gray contours indicate the extrapolated area extended to the Y filter. Both V and Y filter transmission functions are plotted in gray continuous lines. |
| In the text | |
 |
Fig. 3 Equivalently to Fig. 1, but around 1.05 μm. From top to bottom, WASP-33’s pulsations and secondary eclipse, the secondary eclipse once the pulsations have been removed, and the residual light curve once the secondary eclipse is removed. Black continuous lines show best-fit models for the pulsations and the secondary eclipse. Pink and green eclipse models correspond to Deming et al. (2012)’s predicted eclipse depths for inverted and non-inverted atmospheric structures integrated in the Y-band. |
| In the text | |
 |
Fig. 4 Top: eclipse depth in ppt as a function of wavelength. The blue data point indicates our brightness temperature measurement, while the red circles show literature values. The gray area shows 1σ contour of WASP-33 b’s equilibrium temperature. Green continuous line corresponds to Deming et al. (2012)’s carbon-rich non-inverted model, while pink continuous line indicates a solar composition model with an inverted temperature structure. Squares mark the planetary fluxes integrated over the bandpasses. Bottom: the same data after multiplication by the PHOENIX stellar model revealing the SED for WASP-33 b. Overplotted are the expected SEDs for a zero-albedo instantly re-radiation (orange diamonds, f = 2/3) and instantly redistribution (cyan triangles, f = 1/4) day-sides. |
| In the text | |
 |
Fig. 5 Equilibrium temperature map as a function of albedo (AB) and re-distribution factor f. Cyan color shows the contours relative to WASP-33 b’s equilibrium temperature within 1σ error (top-left corner) for both planetary and stellar parameters. f values larger than 2/3 are unphysical. Therefore, the white-shaded area of the plot has not to be considered. |
| In the text | |
 |
Fig. 6 WASP-33’s high resolution spectra around the Ca II H&K lines observed with Keck/HIRES. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


