| Issue |
A&A
Volume 581, September 2015
|
|
|---|---|---|
| Article Number | A80 | |
| Number of page(s) | 16 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201525879 | |
| Published online | 08 September 2015 | |
Detection limits with spectral differential imaging data⋆,⋆⋆
1 Univ. Grenoble-Alpes/CNRS, IPAG, 38000 Grenoble, France
2 Institut de Recherche sur les Exoplanètes (iREx), Université de Montréal, Département de physique, CP 6128 Succ. Centre-ville, Montréal, QC, H3C 3J7, Canada
e-mail: julien.rameau@astro.umontreal.ca
3 INAF, Osservatorio Astronomico di Padova, Vicolo dell’Osservatorio 5, 35122 Padova, Italy
4 LESIA, Observatoire de Paris, CNRS, Université Pierre et Marie Curie Paris 6 et Université Denis Diderot Paris 7, 5 place Jules Janssen, 92195 Meudon, France
Received: 12 February 2015
Accepted: 5 June 2015
Context. Direct imaging of exoplanets is polluted by speckle noise that severely limits the achievable contrast. Angular and spectral differential imaging have been proposed to make use of the temporal and chromatic properties of the speckles. Both modes, associated with extreme adaptive-optics and coronagraphy, are at the core of the new generation of planet imagers SPHERE and GPI.
Aims. We aim to illustrate and characterize the impact of the SDI and SDI+ADI (ASDI) data reduction on the detection of giant planets. We also propose an unbiased method to derive the detection limits from SDI/ASDI data.
Methods. Observations of AB Dor B and β Pictoris made with VLT/NaCo were used to simulate and quantify the effects of SDI and ASDI. The novel method is compared to the traditional injection of artificial point sources.
Results. The SDI reduction process creates a typical radial positive-negative pattern of any point-source. Its characteristics and its self-subtraction depend on the separation, but also on the spectral properties of the object. This work demonstrates that the self-subtraction cannot be reduced to a simple geometric effect. As a consequence, the detection performances of SDI observations cannot be expressed as a contrast in magnitude with the central star without the knowledge of the spectral properties of detectable companions. In addition, the residual noise cannot be converted into contrast and physical characteristics (mass, temperature) by standard calibration of flux losses. The proposed method takes the SDI bias into account to derive detection limits without the cost of massively injecting artificial sources into the data. Finally, the sensitivity of ASDI observations can be measured only with a control parameter on the algorithms that controls the minimum rotation that is necessary to build the reference image.
Key words: instrumentation: adaptive optics / techniques: high angular resolution / planets and satellites: detection / methods: data analysis
Based on observations collected at the European Organization for Astronomical Research in the Southern Hemisphere, Chile, ESO : 60.A-9026, 086.C-0164, 088.C-0358.
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
Direct imaging is the only technique that allows probing the outermost part (>5–10 astronomical units, au) of planetary systems. It is also a very efficient method for extracting spectra of exoplanets. However, the planets are angularly close to the central star and much fainter. The observations are therefore currently limited to self-luminous young giants around nearby stars.
Direct giant planet search has therefore been carried out on ground-based large telescopes fed by adaptive optics (AO) instruments to reach the necessary high-contrast and high-angular resolution. The contrast performances are limited by photon noise and speckle noise in the final image. Within the central arcsecond, AO systems are limited by two families of speckles, i) fast atmospheric speckles that can be averaged and then subtracted with long integration times (Angel 1994; Roddier & Roddier 1995; Racine et al. 1999); and ii) slowly evolving quasi-static speckles caused by telescope and instrument aberrations (Marois et al. 2003b; Masciadri et al. 2005). These quasi-static speckles evolve randomly over time and over the focal plane so that they produce a correlated speckle noise that prevents a longer integration time. The detection limit is therefore driven by the ability of calibrating and subtracting this speckle pattern.
Several observational strategies combined with advanced post-processing algorithms have been proposed and intensively used to estimate and remove the speckle pattern from the images. These techniques rely on the principle of differential imaging in which a reference frame is subtracted from the science image.
 |
Fig. 1 Spectra at a resolution of 60 around the CH4 band at 1.625 μm. Field dwarfs are from the SpeX Prism library. A peculiar red dwarf from Stephens et al. (2009) as well as young companions, free-floating planets, and Jupiter are plotted in color. They have been normalized to their highest values. The absorption bands of water and methane are labeled. The transmission of the SDI + filters (T1, T2, T3) is plotted in the bottom panel. |
Spectral differential imaging (SDI) was first proposed to attenuate the atmospheric speckles (Smith 1987; Racine et al. 1999). Two images are simultaneously recorded at different wavelengths; the theoretically identical speckle pattern can then be subtracted. To prevent the self-subtraction of any companion, the two channels are chosen to match a molecular absorption feature: one inside the absorption band, and one outside where the planet is bright. The signal of the companion will thus be partially preserved after the subtraction. SDI was first used on the Canada France Hawaii Telescope (CFHT) with the TRIDENT camera (Marois et al. 2000, 2003a), with NaCo on the Very Large Telescope (VLT/NaCo; Lenzen et al. 2003; Rousset et al. 2003) and with the Multiple Mirror Telescope (MMT) by Close et al. (2005) and Biller et al. (2007). Recently, Close et al. (2014) confirmed a close-in companion around HD 142527 with SDI with MagAO, based on a detection of the Hα emission, not a molecular absorption. However, SDI is limited by differential aberrations between the two channels, which create quasi-static speckles that cannot be removed. Angular differential imaging (ADI) was then developed to make use of the relative stability of the quasi-static speckle pattern with respect to the telescope and instrument configuration (Marois et al. 2006). The field of view (FoV) is rotating with the parallactic angle with an alt-az telescope, allowing temporally substracting the speckle pattern and recovering any off-axis companion by de-rotating the final residual images. ADI has been widely used during the past years in deep-imaging surveys of exoplanets (Lafrenière et al. 2007; Vigan et al. 2012; Rameau et al. 2013; Biller et al. 2013; Brandt et al. 2014; Chauvin et al. 2015). However, ADI is not efficient in calibrating and subtracting the fast atmospheric speckles. Therefore, ADI and SDI (ASDI) were combined to take advantage of both techniques. ASDI was intensively used in the NICI campaign (Biller et al. 2013; Nielsen et al. 2013; Wahhaj et al. 2013b,a) and is now a standard observing mode for the new planet imagers SPHERE (Beuzit et al. 2008) and GPI (Macintosh et al. 2008).
Estimating the sensitivity limits of direct-imaging observations is a key element to improve our knowledge of giant planets on wide orbits. Constraining the mass and position of a companion around a structured disk (e.g., Lagrange et al. 2012; Boccaletti et al. 2012, 2013) or in multiple planetary systems (e.g. Marois et al. 2010) helps to improve our understanding of planet-disk interaction and planetary system architecture. When a large number of stars are targeted, statistical analysis can be performed to constrain the population of giant planets on wide orbits, that is, occurrence, distribution of mass, and separation (Lafrenière et al. 2007; Kasper et al. 2007; Chauvin et al. 2010; Janson et al. 2011; Vigan et al. 2012; Rameau et al. 2013; Biller et al. 2013; Wahhaj et al. 2013b; Nielsen et al. 2013; Brandt et al. 2014). Therefore, it is mandatory to properly compute these detection limits and take into account any biases of reduction and analysis.
 |
Fig. 2 CH4 index (F1/F3) as a function of the spectral type (SpT). Values higher than 1 mean that CH4 is present in the atmosphere. The index is computed for field dwarfs from the SpeX Prism library (gray squares), references field dwarfs are plotted with larger squares, the peculiar red dwarfs from Stephens et al. (2009; open circles), young free-floating planetary-mass objects (triangles), and young companions (alternative symbols). The typical uncertainty on the index is 10%. |
SDI is expected to be efficient when the molecular features are deep enough. Spectra of several objects at different spectral types (SpTs)/temperatures can be used to investigate the regime for which SDI is interesting. H-band spectra of field MLT dwarfs from the SpeX Prism library are shown in Fig. 1 along with the peculiar red dwarfs (SD 1110+01) from Stephens et al. (2009), the young free-floating planetary-mass object CFBDSIR 2149 (Delorme et al. 2013), several low-mass companions to young stars (1RXS 1609 b Lafrenière et al. 2007; HN Peg b Luhman et al. 2007; HR 8799 b Marois et al. 2008; Barman et al. 2011), and Jupiter (Rayner et al. 2009)1. Spectra were rebinned and degraded to the same sampling and resolution, that is, R = 60, which corresponds to the lowest resolution spectrum. Methane seems to appear in the atmosphere of substellar objects around 1000 K, for early T-type objects with a rapid growth of the absorption band at 1.62 μm when the temperature decreases to 700 K and below. Intriguingly, HR 8799 b does not exhibit methane absorption, while the temperature corresponds to the expected transition. Discussing the reasons for this behavior is beyond the scope of this paper (e.g., Barman et al. 2011, 2015). However, the methane absorption band seems to be not only correlated with the temperature/SpT, but with other atmospheric parameters (reduced surface gravity, non-equilibrium chemistry, cloud, metallicity, see Barman et al. 2011; Zahnle & Marley 2014). Methane has nevertheless been detected in moderately young T-type companions to stars (Janson et al. 2013) and some moderately young T-type dwarfs (Luhman et al. 2007). For these reasons, the methane feature at 1.62 μm is most often used for SDI, but it can also be used with other bands, such as water or ammonia, at even lower temperatures.
The depth of the methane absorption with NaCo data can be measured with the SDI CH4 index in the H-band as defined in Biller et al. (2007),
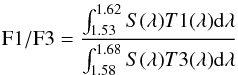 with S(λ) being the spectrum of the object, F1 and F3 referring to the flux measured in the filter centered at 1.575 μm and 1.625 μm, respectively, and T1 and T3 to the transmission in each filter. We note that the wavelength interval has the same length in both channels. With this definition, objects that show some absorption features in their spectra that are due to methane will have F1/F3 > 1. Objects in addition to those in Fig. 1 were considered for Fig. 2. Details are given in Appendix A.1. CH4 absorption starts to be significant around the type T2/T3 (Biller et al. 2007). Of the objects considered here, only CFBDSIR 2149 and the peculiar T5.5-dwarf SDSS 1110+01 exhibit strong CH4 absorption at 1.625 μm. Young L-type companions have lower CH4 indices than field L dwarfs (≃10%). Interestingly, the spectra of field M- and early-L type dwarfs have a plateau in this regime. HR 8799 b has the lowest value (≃0.77 ± 10%) of the objects. SDI therefore might be unsuitable for searching for planetary-mass companions earlier than T2/T3.
with S(λ) being the spectrum of the object, F1 and F3 referring to the flux measured in the filter centered at 1.575 μm and 1.625 μm, respectively, and T1 and T3 to the transmission in each filter. We note that the wavelength interval has the same length in both channels. With this definition, objects that show some absorption features in their spectra that are due to methane will have F1/F3 > 1. Objects in addition to those in Fig. 1 were considered for Fig. 2. Details are given in Appendix A.1. CH4 absorption starts to be significant around the type T2/T3 (Biller et al. 2007). Of the objects considered here, only CFBDSIR 2149 and the peculiar T5.5-dwarf SDSS 1110+01 exhibit strong CH4 absorption at 1.625 μm. Young L-type companions have lower CH4 indices than field L dwarfs (≃10%). Interestingly, the spectra of field M- and early-L type dwarfs have a plateau in this regime. HR 8799 b has the lowest value (≃0.77 ± 10%) of the objects. SDI therefore might be unsuitable for searching for planetary-mass companions earlier than T2/T3.
The efficiency of differential imaging relies on the ability to build a reference frame that contains speckles that are highly correlated with the science image. When part of the planetary signal is included in the reference frame, the subtraction will also reduce the flux of the object. For point-source objects observed with ADI, the self-subtraction can be calibrated as a function of the parallactic angle evolution and parameters used to reduce the data. For SDI, the correction is not straightforward.
The objective of the paper is twofold: first, to qualitatively and quantitatively estimate the effects and biases of the SDI reduction process, and second, to provide an SDI-unbiased method for deriving the detection limits computationally faster than is possible by injecting artificial sources. We do not attempt to compare the performances between ADI and ASDI observations, but refer to the companion paper (Maire et al. 2014) for this purpose.
After presenting the simulation procedures and the data in Sect. 2, we describe in Sect. 3 the pattern of an off-axis point source created by the SDI reduction and pinpoint the photometric and astrometric biases. We show that this SDI pattern and the biases depend on the flux ratio between the two images taken inside and outside the methane absorption feature. We provide a novel approach to derive the detection performances that take these effects into account. Their extensions by including additional effects of ADI are detailed in Sect. 4, for example, the reduction parameters that can be used to avoid to include additional biases. We finally discuss the use applicability of the method for data from integral field unit instruments.
2. Simulation procedure
2.1. Instrument consideration
VLT/NaCo SDI+ mode parameters.
Observations with VLT/NaCo were used to carry out this study. The observations made use of the SDI+ device (Lenzen et al. 2004; Close et al. 2005) mounted on the camera CONICA. The characteristics of this mode are presented in Table 1. The SDI+ was designed to benefit from the methane absorption feature at 1.62 μm into the spectrum of T-type companions. In this mode, four images are taken simultaneously on the same detector through a double Wollaston prism and three narrow-band filters in four quadrants. Two images (I1, I2) are taken outside the methane feature (at 1.575 and 1.600 μm)2, the other two (I3a, I3b) are taken inside (at 1.625 μm, left and right), but in two different quadrants. The λ1 and λ2 wavelengths were selected to be as close as possible to 1.625 μm to minimize the chromatic evolution of the point spread function (PSF; Strehl ~1–(2π/λ)2 following the Maréchal approximation) and the speckle pattern (local flux distribution; Marois et al. 2000). The second reason for this choice of λ was to optimize the sensitivity to T dwarfs (1.575 μm) and Y dwarfs (1.600 μm) because of the shape of the absorption feature. The SDI+ transmission curves are plotted in Fig. 1.
2.2. Datasets
VLT/NaCo SDI+ observating log of AB Dor and β Pictoris.
To first study the effect of the SDI mode and then that of using SDI and ADI (ASDI hereafter), we used two datasets: one of AB Dor B in SDI following the observing strategy of Biller et al. (2007), that is, four sets at two position angles to mimic ADI for the saturated and unsaturated observations. However, we focused on a single position angle to exploit the SDI alone. The second dataset was taken on β Pictoris in ASDI. Saturated images were recorded, along with one short set of unsaturated images to estimate the stellar PSF and serve as photometric calibrator. We chose to integrate during 5 s × 50 individual exposures into a data cube for the saturated observations. Sky observations were recorded after the sequence using the same set-ups and applying an offset of 1.7′′. The observing logs are summarized in Table 2. The detection limits for both modes are estimated from these two datasets in the following.
2.3. Reduction procedure
The two datasets were reduced with the IPAG-ADI pipeline (Lagrange et al. 2010; Chauvin et al. 2012). We developed an additional module to process the SDI-type data. Each quadrant was extracted from the raw data, cleaned (flat-field, bad pixel, sky) and aligned to a common central position, in parallel. The images I3a and I3b were demagnified to the spatial resolution of the images I1 or I2 by the ratio of the central wavelengths of the filters to be considered (1.625/1.600 or 1.625/1.575). The separation of the speckle and Airy pattern scale linearly with λ. This step is mandatory to align speckles in each filter at the same position. Then, the demagnified image (I′) was scaled in flux, computed as the ratio (α hereafter) of the total flux in both images in annuli of between 15 and 50 pixels (linear regime). This scaling removes the chromatic dependencies of the stellar flux, the atmospheric and instrument throughputs, and quantum efficiency. Finally, a simple difference was computed frame per frame to remove most of the speckle pattern, following 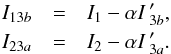 We focus on I13b as an example here.
We focus on I13b as an example here.
For SDI data alone, the subtracted images were then filtered out by unsharp-masking to remove low frequencies, and the images were median combined.
For ASDI data, SDI processing has to be done first because it benefits from the simultaneity of the speckle realization in the two channels. Because of differential aberrations between the two channels, the residual speckles were then suppressed by ADI processing, which benefits from the rotation of the FoV. To do this, the mono-λ and SDI-subtracted images were stored in data cubes together with their parallactic angles. The remaining stellar halo estimation and subtraction, de-rotation, and stacking were further processed in the standard way of the IPAG-ADI pipeline. We used several ADI algorithms that differ in the way the halo is estimated: cADI (Marois et al. 2006), rADI (Marois et al. 2006), LOCI (Lafrenière et al. 2007), and PCA (Amara & Quanz 2012; Soummer et al. 2012).
In all cases, we obtained six residual images, one per filter and two subtracted products.
Finally, we computed the noise as a function of the radius in each residual image from the standard deviation of all pixel values in a one-pixel wide annulus3.
While SDI+ provides images in three close narrow-band filters and thus allows the double difference method (Marois et al. 2000) to further improve the halo subtraction, we here only considered the simple difference for simplicity. Another reason is that the SDI mode is offered with only two spectral channels on NICI and SPHERE/IRDIS (Beuzit et al. 2008). However, the method presented here can be extended to multispectral data.
The unsaturated exposures were reduced in the same way, but were stacked without any SDI and/or ADI processing. We obtained four PSF templates for each quadrant. Zero points (ZP) were then computed using the peak value of each PSF and assuming the H-band magnitude of AB Dor (4.84 mag) and β Pictoris (3.51 mag, we address the error made on the broad-to-narrow band magnitude of the star in Sect. 3.4). These PSFs were used for all simulations here.
2.4. Standard derivation of detection performances
Two methods are commonly used in direct imaging to estimate the sensitivity limits in contrasts and masses.
The first method converts the noise (σ) in ADU into contrast after removing the SDI/ASDI photometric bias. In classical imaging, Eq. (1) is used, while in ADI, the photometric bias is removed as in Eq. (2), 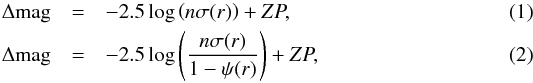 with n ∈R the detection threshold and ψ the flux loss due to the ADI reduction. The second method consists of injecting scaled versions of the PSFs (fake planets, FP hereafter) into the data cubes before the SDI/ASDI steps and reprocessing them as science data. Each FP is injected in order to explore the radius, position-angle, and flux space until it is recovered at a given threshold above the noise (usually 5σ). The contrast curves are then converted into mass detection limits using evolutionary models (e.g., Baraffe et al. 2003). However, the interpretation of contrast curves for SDI observations is not straightforward and depends on the spectral properties assumed for the detectable objects.
with n ∈R the detection threshold and ψ the flux loss due to the ADI reduction. The second method consists of injecting scaled versions of the PSFs (fake planets, FP hereafter) into the data cubes before the SDI/ASDI steps and reprocessing them as science data. Each FP is injected in order to explore the radius, position-angle, and flux space until it is recovered at a given threshold above the noise (usually 5σ). The contrast curves are then converted into mass detection limits using evolutionary models (e.g., Baraffe et al. 2003). However, the interpretation of contrast curves for SDI observations is not straightforward and depends on the spectral properties assumed for the detectable objects.
We here describe a method for converting the noise to mass without the injecting FPs and reprocessing the data from the beginning. We compared the detection performances derived by this technique to the method presented in Maire et al. (2014), who injected FP into the data by exploring a grid of masses (and therefore predicted flux in each filter) from evolutionary models. We considered a planet to be detected when its residual peak value lay above the 5σ threshold, the noise being measured in the FP-free images as described in the previous section.
As described in Maire et al. (2014), we made use of the atmospheric models from Allard et al. (2012) coupled to the evolutionary models of Baraffe et al. (2003) as a mass-luminosity relationship. We recall that these models have a cutoff at 500 K, that is, 1 MJup at 10 Myr, and 5 MJup at 200 Myr. The method described here can be used with other evolutionary or atmospheric models.
3. Influences of spectral differential imaging data reduction
3.1. Qualitative effect of self-subtraction
The spatial demagnification of I3b to align the speckle pattern causes a radial shift of all physical point sources, inward in our case, according to Δr = r(λ3−λ1) /λ3 (Thatte et al. 2007). Hence, first, the closer the spectral channels, the smaller the shift, and second, the farther the signal, the higher the shift (in absolute value). Thatte et al. (2007) defined the bifurcation point (rb) as the separation for which the shift is greater than the PSF full width at half-maximum (FWHM). The theoretical rb for the couple (I1, I3) is 29λ/D (1.3′′) for a diffraction-limited PSF with FWHM = 40 mas. We see that rb will increase for broader PSFs and closer spectral channels (for observations not in the diffraction-limited regime). In the present case, FWHM ≃ 63 mas and rb = 42λ/D = 1.9′′.
Subtracting 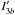 to I1 produces a characteristic radial negative-positive pattern; the gap between the two lobes increases with the separation. Therefore, an off-axis source will suffer from self-subtraction that will directly affect its resulting signal-to-noise ratio (S/N). In Fig. 3, we simulate the SDI effect on point sources as a function of the separation, but also of the flux-ratio F1/F3. We injected the PSFs in noise-free (void) images at ≃4, 9, 13, 18, 24, 33, and 42λ/D (0.2,0.4,0.6,0.8,1.1,1.5, and 1.9′′, i.e., at rb for the present PSFs) with a peak flux of 100 ADU in I1 at four considered position angles. In I3b, the PSFs were scaled to have F1/F3 = 1 at PA = 0 deg as an example, F1/F3 = 4.3 at 90 deg typical of an mid-T dwarf, F1/F3 = 1.1 at 180 deg typical of late-L dwarf, and F1/F3 = 0.87 at 270 deg as 2M 0122 b (see Fig. 2). It can be seen that the self-subtraction can be very significant, about 80–90%, at a separation as large as rb = 7λ/D (300 mas) and ≥40% below rb = 22λ/D (1′′) in the general case (see Fig. 6 in Maire et al. 2014 for a detailed measurement of the self-subtraction in the F1/F3 = 1 case for a range of measured FWHM). We also see that the residual signal suffers from some subtraction (20%) even at rb (see also Maire et al. 2014). Therefore, rb should not be considered as the separation beyond which SDI does not affect the signal anymore. The lobes of the SDI pattern still overlap at large separations. The self-subtraction typically becomes negligible (≤1%) beyond rb = 55λ/D (2.5′′). When there is very little to no flux counterpart in I3, that is, when F1/F3 higher than 1.5–2 for a T3 and later, SDI barely affects the signal and thus provides the best case for a detection. We recall that this behavior depends on the FWHM of the PSFs used, the self-subtraction being stronger for more spatially extended PSFs (see Maire et al. 2014). Moreover, when F1 ≠ F3, the way of subtraction (I1−I3 vs. I3−I1) becomes a major concern in optimizing the residual flux of the signal. When F1/F3 ≤ 1, that is, for methane-free hot companions, I3−I1 has to be preferred to enhance the power of SDI and the S/N (e.g., Close et al. 2005).
to I1 produces a characteristic radial negative-positive pattern; the gap between the two lobes increases with the separation. Therefore, an off-axis source will suffer from self-subtraction that will directly affect its resulting signal-to-noise ratio (S/N). In Fig. 3, we simulate the SDI effect on point sources as a function of the separation, but also of the flux-ratio F1/F3. We injected the PSFs in noise-free (void) images at ≃4, 9, 13, 18, 24, 33, and 42λ/D (0.2,0.4,0.6,0.8,1.1,1.5, and 1.9′′, i.e., at rb for the present PSFs) with a peak flux of 100 ADU in I1 at four considered position angles. In I3b, the PSFs were scaled to have F1/F3 = 1 at PA = 0 deg as an example, F1/F3 = 4.3 at 90 deg typical of an mid-T dwarf, F1/F3 = 1.1 at 180 deg typical of late-L dwarf, and F1/F3 = 0.87 at 270 deg as 2M 0122 b (see Fig. 2). It can be seen that the self-subtraction can be very significant, about 80–90%, at a separation as large as rb = 7λ/D (300 mas) and ≥40% below rb = 22λ/D (1′′) in the general case (see Fig. 6 in Maire et al. 2014 for a detailed measurement of the self-subtraction in the F1/F3 = 1 case for a range of measured FWHM). We also see that the residual signal suffers from some subtraction (20%) even at rb (see also Maire et al. 2014). Therefore, rb should not be considered as the separation beyond which SDI does not affect the signal anymore. The lobes of the SDI pattern still overlap at large separations. The self-subtraction typically becomes negligible (≤1%) beyond rb = 55λ/D (2.5′′). When there is very little to no flux counterpart in I3, that is, when F1/F3 higher than 1.5–2 for a T3 and later, SDI barely affects the signal and thus provides the best case for a detection. We recall that this behavior depends on the FWHM of the PSFs used, the self-subtraction being stronger for more spatially extended PSFs (see Maire et al. 2014). Moreover, when F1 ≠ F3, the way of subtraction (I1−I3 vs. I3−I1) becomes a major concern in optimizing the residual flux of the signal. When F1/F3 ≤ 1, that is, for methane-free hot companions, I3−I1 has to be preferred to enhance the power of SDI and the S/N (e.g., Close et al. 2005).
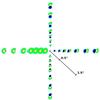 |
Fig. 3 Effects of SDI processing as a function of the separation and flux ratio (F1/F3) in noise-free images. Upward residuals have a flux ratio of 1 as an example; leftward residuals of 4.3, which is typical of a T7 dwarf; downward residuals have a ratio of 1.1, typical of a mid-L to early-T dwarf; rightward residuals have a ratio of 0.87, which is like that of 2M 0122 B. SDI residuals suffer from a strong self-subtraction (except for a highly methaned companion) and are thus difficult to characterize at small radii, i.e., in the region where the speckle pattern will be subtracted. The bifurcation point is at 1.9′′ with these PSFs. |
To summarize, SDI processing creates a typical positive-negative pattern of any point source. Its properties (separation between the two lobes, relative intensity) depend upon the star-to-planet separation and the flux ratio. Detecting a planet that does not exhibit strong methane absorption can therefore be difficult because of the high flux attenuation, even beyond the bifurcation radius.
3.2. Effect of the measurement on the self-subtraction
 |
Fig. 4 Left panel: flux measured on the peak of the residual and normalized to the injected F1 as a function of the flux ratio. The legend values indicate the separation in λ/D (equivalent to 87, 121, 173, 208, 259, 294, 346, 381, 433, 520, 690, and 866 mas). PSFs were reduced independently in noise-free images. Right panel: relative position between the peak in the residual pattern and the injected PSF. The 0.1 pixel in precision on the peak measurement leads to an unsmoothed curve. |
At first glance, the SDI self-subtraction might be thought to only depend on the geometry of the spatial rescaling and subtraction process. The differential flux would then be given by the following formulae expressed by Maire et al. (2014), with φ(r) the geometric flux loss: 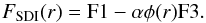 (3)φ would then be equal to 1 at r = 0 and 0 when r → ∞. For each radius, the planet PSF at a given wavelength is subtracted by a rescaled and shifted version of the PSF of the second wavelength. φ(r) would then be given by the ratio of the residual-to-original flux at the planet position.
(3)φ would then be equal to 1 at r = 0 and 0 when r → ∞. For each radius, the planet PSF at a given wavelength is subtracted by a rescaled and shifted version of the PSF of the second wavelength. φ(r) would then be given by the ratio of the residual-to-original flux at the planet position.
To test this hypothesis, we estimated φ(r) by measuring the differential flux FSDI by separately considering i) the interpolated flux at the planet position; ii) the maximum of the positive lobe of the SDI pattern in the image; or iii) the positive flux within an aperture centered on the positive lobe of the SDI pattern. The positivity constraint is commonly adopted in ADI processing and particularly when we have no a priori knowledge on the planet position. The same approach is used to derive F1 and F3. We therefore measured FSDI for different separations and F1/F3.
Each couple of PSFs (for a given separation) was reduced independently in noise-free images. In Fig. 4, we chose to display FSDI/F1 vs. F3/F1 so that Eq. (3), assuming α = 1, becomes linear. φ is therefore the slope that decreases with increasing radius. Based on this, a straight line as a function of F3/F1 is expected, starting from one.
As expected, FSDI/F1 so as φ on the pixel of injection decrease linearly with decreasing F1/F3 and increasing separation, respectively. For F1/F3 < 1, FSDI/F1 logically drops to negative values at short separations. This is illustrated for a position of injection of 6λ/D (300 mas) and a different F1/F3 ratio in Fig. 5. We also see that the maximum of the SDI pattern is shifted by a significant fraction of pixels after the SDI process. The right panel of Fig. 4 displays a detailed measurement of the shift of the peak. This shift can be as high as 0.6–0.8 λ/D (1.7–2 pixels) for non-methaned cases at the closest separations. But for F1/F3 ≳ 1, the peak can be shifted by half a resolution element (about one pixel). As mentioned earlier, the positivity constraint is commonly used when we have no a priori knowledge on the planet position. We then considered the cases where FSDI is either estimated on the true maximum or by aperture photometry (Rap = 0.75 FWHM4). The result for the aperture photometry is shown in the first panel of Fig. 4. It appears that FSDI/F1 differs from a linear function except for highly methaned cases (F1/F3 > 4, or late-T dwarfs). The simple geometric flux loss hypothesis does not hold anymore because FSDI now depends on F1/F3 in addition to the separation. This can be understood by the modification of the SDI pattern with F1/F3 at a given separation, particularly the positive lobe (as illustrated in Fig. 5).
 |
Fig. 5 Radial profiles of residual SDI patterns along the shift direction, separated by 6λ/D (300 mas) from the center of the image. PSF profiles are overplotted (dashed and dotted lines). The legend value indicates F1/F3 (and corresponds to F3/F1 = 0.5, 0.8, 0.9, 1.0, 1.2, and 1.5). All profiles have been centered on 0 for clarity. |
 |
Fig. 6 Top left panel: flux measured on the SDI residual maximum as a function of the mass and separation, assuming an age of 500 Myr, a distance of 15 pc, and H = 4.84 mag. Contours indicate FSDI in (ADU/s). White areas correspond to negative flux. Top right panel: mass map as a function of the separation and predicted FSDI. Regions where a degeneracy appears are specified with black contours, indicating the number of solutions. The first (and less massive) solution is plotted here. Cases without solution are plotted in white. Bottom left panel: the same, but considering the second solution in mass. Bottom right panel: the same, but considering the third solution in mass (see text). |
Consequently, the differential flux loss is not geometric when it is measured on the positive lobe of the SDI pattern. Therefore, the self-subtraction that is due to SDI strongly depends on the spectral properties of the companion and cannot be calibrated in an homogeneous way to unbias the photometry. Equation (3) thus becomes 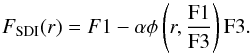 (4)
(4)
3.3. Estimation of spectral differential imaging detection limits
Biased limits for methaned companions.
Equation (4) implies that the noise (in ADU) measured in residual SDI images cannot be corrected for photometric bias by applying a simple multiplication factor. Because of that, the noise cannot be converted into magnitude to obtain a “contrast” curve without making strong assumptions of the spectral properties of any companion. Moreover, it cannot be used to assess the best observing strategy or reduction technique in terms of detections of planets. Comparing the noise between SDI and non-SDI reduction products only indicates the efficiency of this technique in reducing the speckle pattern. The “contrast curves” presented so far in all but one SDI publication made this direct translation. They thus assumed that this applies to strongly methaned companions (i.e., SpT of T8 or later). Very deep observations based on these contrast curves cannot be claimed without explicitly mentioning this strong hypothesis. It does also not mean that astrophysical objects with these contrasts can be detected, since they might have very different spectral properties. Macintosh et al. (2014) were the first to date to show multispectral contrast curves generated with different spectral properties. They considered the two extreme cases of a non-methaned companion and a strongly methaned companion. The effect is rather strong, that is, several ten orders of magnitude in flux, and increases at small separations, as expected. However, they did not consider the intrinsic brightness of such objets with these spectral features to show whether they are able to detect them or not. Translating these contrasts into masses is impossible for the same reasons. Therefore, the detection performances of SDI observations can be estimated with contrast curves as usual, but under strong hypotheses (Macintosh et al. 2014) or by directly incorporating the physics of the planets (predicted fluxes and mass; Maire et al. 2014; this work).
 |
Fig. 7 Left panel: residual radial noise in SDI and single-band images of AB Dor. Right panel: the same as the top right-hand panel of Fig. 6, but at 70 Myr. Five times the radial noise in the SDI residual image of AB Dor is overplotted in white and does not come across the degenerated region. |
New approach
We now provide a quantitative way to estimate the detection sensitivity of SDI-reduced images that overcomes the issue of estimating φ. This method directly translates the residual noise into mass without intensively injecting FPs into the full reduction process. The main idea is to limit the injection to explore a grid of separations and physical properties (mass and temperature) from models to create specific SDI patterns. The proposed approach is adapted for the determination of global detection limits of SDI surveys, but is not appropriate for a fine local analysis that would deserve a complete injection. We describe the different steps below.
The input parameters or data are, as for any injection,
-
1.
an evolutionary model with the magnitude in each filter for acorresponding mass at the age of the star;
-
2.
a zero point in each filter;
-
3.
a PSF in each filter;
-
4.
the spatial rescaling factor (the wavelength ratio) and flux normalization factor (α taken as the mean over the sequence) used in the SDI science reduction;
-
5.
a photometric measurement method to be kept throughout the process, maximum or aperture photometry.
The steps can be sorted as
-
1.
generating a (mass and flux) table for each filter;
-
2.
generating a template SDI-reduced PSF for the entire separation-mass parameter space;
-
3.
for each position in the grid, measuring the residual flux on the positive part of the signal; an FSDI(r,mass) map in ADU, called hereafter conversion map (Fig. 6, top left panel), is thus created;
-
4.
expressing the FSDI(r,mass) conversion map into a mass(r,FSDI) map in MJup;
-
5.
computing the radial profile of the noise in the residual science image;
-
6.
converting the noise into mass using the mass(r,FSDI) map to obtain the final sensitivity curve.
The conversion map is therefore only computed once for a given observing setup and estimation methods for the parameters of the SDI processing. On a standard laptop with a 2.6 Ghz dual-core processor, generating a map with 100 mass elements and 100 separation elements (in pixels, corresponding here to more than 1.5′′, beyond which SDI does not improve the performances for these data) takes five minutes, whereas the full fake-planet injection process requires several hours. The key point of this method is that the science data can be reduced independently to optimize the noise minimization without affecting the map.
Figure 6 displays a conversion map for a star at 15 pc, 500 Myr, and H = 4.84 mag built using the steps introduced above. FSDI is expressed as a function of the mass and separation in the top left panel. The mass limit does not go below 7 MJupas a result of the model5, and the separation has been limited beyond 2λ/D (80 mas) because the result is meaningless closer in. As expected, FSDI globally increases with increasing mass and separation. However, in this case, FSDI changes behavior in a region below 5λ/D (200 mas) and [20,70] MJup. As extensively discussed in Maire et al. (2014), different (F1,F3) can give the same FSDI. In other words, a given FSDI can be degenerated in mass. In the three remaining panels of Fig. 6, we plot the mass solution as a function of the radius and FSDI. While white areas correspond to a lack of solutions, regions where a degeneracy exists are highlighted by the contours, indicating the number of solutions, from 1 to 3 in this case. Other solutions are usually very massive and can be detected through single-band imaging. Combining SDI and classical imaging may help to break the degeneracy, as discussed in Maire et al. (2014).
Application to AB Dor
To test this approach, we reduced and analyzed the data of AB Dor. We measured the noise in I1, I3b, and I13b and translated it directly into masses. The left panel of Fig. 7 shows the residual radial noise in the three images. It is clear that SDI processing removes more noise than single-band imaging. We also built the conversion map from AB Dor’s parameters (15 pc, 70 Myr, H = 4.84 mag, right panel in Fig. 7, for the less-massive solution). We overplotted the noise measured in I13b to show the direct conversion of ADU into mass. The residuals do not cross the degenerated region. The conversion of the noise with the calibration results in the detection limits of these observations expressed in mass (“analytic”, solid lines, Fig. 8). The noise in I1 and I3b was converted into contrast with Eqs. (1) and then into mass. To assess whether this method works and is robust, we computed the detection limits with injected FPs at five different position angles until they reached the S/N threshold. We azimuthally averaged the S/N curve to obtain the radial sensitivity profile and took the standard deviation over the position angle to estimate an error (“FP”, dashed lines and shaded area, Fig. 8). The two methods agree very well, showing that the conversion map can be used to derive SDI detection limits while significantly reducing the CPU time. The SDI and 1.575 μm curves converge toward large separations and low masses because the SDI photometric bias is highly reduced to finally only obtain F1 (φ → 0, Eq. (3)). The sensitivity of I1 is better than the one of I3 at large radii because F1 is slightly greater than F3 for low-mass objects. To demonstrate that SDI processing plays a key role in the detection performance, we overplotted the limit curve by converting the SDI noise into mass assuming no flux in F3, that is, a T8 SpT for any companion with the associated mass. The error was found to be significant (several tens of magnitudes) at small radii. However, small separations are the regions of interest for using SDI, but these are the regions with the highest self-subtraction.
 |
Fig. 8 Detection limits on AB Dor at 1.575 μm (orange), 1.625 μm (red) in the top panel and in SDI (blue) in the bottom panel as a function of the separation. The solid lines (analytic) were estimated from a direct conversion of five times the noise into mass with the conversion map for SDI or with standard contrast conversion for single-band images. The limits were also estimated by injecting FP according to the predictions of the model, processed independently, until S/N = 5 was reached (“FP”, dashed lines), with a 1σ dispersion over five position angles (shaded area). The direct conversion from noise to contrast and mass without taking the SDI photometric bias into account, i.e., assuming a T8 SpT, is overplotted (“CH4”, triple-dotted dashed line). |
Possible degeneracy between differential flux and mass
To illustrate the degeneracy issue for the sensitivity derivation, we considered the same case as before, but we artificially reduced the noise measured in the SDI residual map by a factor of a hundred. The noise now reaches the degeneracy region in the conversion map (see Fig. 9, left panel). At large separation, the noise enters a region that reaches the limit of the model. We therefore set the corresponding mass to the lowest mass reached at the transition point. The corresponding sensitivity curve is shown in the right panel of Fig. 9. Out of the vertical dashed lines at 3 and 4λ/D (121 and 173 mas respectively), only one solution in mass exists for the noise; the observations are therefore sensitive to planets with higher masses than the limit (blue curve). In between, first three, then two solutions coexist for the same noise level; the SDI residual map can only reveal one of these three solutions for a corresponding separation and not other values. That is to say, in this region, the dots do not represent the minimum mass, but the exact solutions. As mentioned in Maire et al. (2014), the degeneracy can be overcome thanks to single-band observations that might exclude the more massive solutions.
Additional use: sensitivity forecast of planned observations
The conversion map can also be used to predict the mass sensitivity of planned observations. On the one hand, the conversion map at the age of the target can be generated following the previous procedure based on one and only one dataset (commissioning for instance, reference dataset hereafter). On the other hand, the expected noise profile of the observations can be generated with an exposure-time calculator based on the magnitude of the target and the observing setups (target coordinates, target SpT, exposure time, observing mode, etc.). The simulated noise profile can therefore be translated into masses thanks to the conversion map. However, one has to keep in mind the hypotheses behind this use of the conversion map. It assumes that the input parameters to build the conversion map (PSFs, α, zero points) from the reference dataset are close to those of the forecast observations. In summary, the predicted sensitivity of future observations can be estimated from the conversion map.
Summary of the estimation of SDI detection limits
We showed that computing detection limits for SDI-reduced data using standard single-band methods strongly biases the results for methaned companions. Expressing them in terms of contrast must be associated to the knowledge of the spectral properties of the companions. Therefore, they cannot be compared on average with other observing techniques. To derive proper detection limits, they need to be directly expressed in masses since the SDI self-subtraction cannot be calibrated. For this purpose, the injection of artificial sources cannot be avoided, but we here proposed a method that significantly limits the computing cost. We proposed to estimate the residual SDI flux for each mass and each separation independently of the science reduction. Assuming an evolutionary model, the PSFs in both filters, the mean flux normalization factor, and a photometry metric based on the positive signal, the conversion map FSDI(r, mass) can be produced in ADU/s. This map is used to translate the residual noise of the science data into sensitivity limits. We showed that this method works well compared to a massive injection of artificial sources into the data and that the standard contrast-to-mass technique differs from it. Finally, assuming that the flux normalization factor does not dramatically change from one observation to another, this map can be directly used to predict the sensitivity regime of SDI observations to be carried out.
3.4. Biases on the astrometry and photometry of a point source
 |
Fig. 9 Left panel: same as the bottom right panel of Fig. 8, but with the noise level artificially improved by a hundred to come across the degenerated region. Right panel: corresponding SDI sensitivity limit that gives the minimum detectable map. In between the vertical dashed lines, the noise-to-mass function is degenerated with three possible solutions, plotted with the circles. |
If point source is only detected in SDI residual maps and not in single-band images, it has to be characterized with caution. Because of the nature of the SDI pattern, its position cannot be measured by fitting a 2D function on the residual map. As we illustrated in Fig. 4, the peak shifts with respect to the true position as a function of both the separation and the flux ratio. Moreover, because of the steep profile of the SDI pattern along the direction of the magnification, the function to be fitted might be shifted even more. Therefore, the fitted position will be uncorrected. The astrometry and photometry of any point source therefore have to be estimated using the injection of artificial sources as described in several papers (Marois et al. 2006; Lagrange et al. 2010; Bonnefoy et al. 2011; Chauvin et al. 2012). However, since (F1,F3) can result in the same FSDI, the characterization has to be made by exploring the mass and its associated flux value in each spectral channel given by the evolutionary model. The flux and derived astrometry will therefore be model dependent.
 |
Fig. 10 Same as Fig. 1, but with typical spectra of class V stars from Ranade et al. (2004) at R ≃ 500. We also show prominent absorption features at play in the NaCo SDI+ filters such as the HI Brackett series for early-type stars and other elements for late-type stars. OBA spectra are taken from the library of Pickles (1998) at a resolution of 500 with a sampling of 5 Å, while FGKM spectra come from the IRTF/Spex library of Cushing et al. (2005), with an original resolution of 2000, but degraded to 500. A model spectrum of Vega is overplotted with a dashed line (Colina et al. 1996) and the 2MASS H-band relative spectral response curve from Cohen et al. (2003). |
As mentioned earlier, the fluxes of the primary star in the SDI filters are necessary to derive the photometry of the observations and convert predictions from models into observables (zero points). No value for any star is available in the literature for SDI magnitudes. It is usually assumed that stellar spectra have very little chromatic variation so that the SDI magnitude can be considered identical to the broad H-band magnitude. However, the precision of the photometry of any object also depends on the accuracy of the magnitude of the primary. These considerations have already been taken into account, but only for a specific case (e.g., Janson et al. 2013) or limited to late-M dwarfs (Biller et al. 2007).
In Fig. 10, we plot the H-band spectra of class V OBA stars from (Pickles 1998, R ≃ 500, sampling of 5 Å)6, FGKM stars from (Cushing et al. 2005, R ≃ 2000) and Vega (Colina et al. 1996), but interpolated over the same grid and degraded to the same resolution as the OBA spectra, and SDI+ transmission curves as for Fig. 1 and the 2MASS H-band relative spectral response (RSR) from Cohen et al. (2003). Atomic or molecular lines of interest are also displayed. While the H-band spectra of O stars are featureless, those of BA stars are dominated by the strong neutral hydrogen absorption lines of the Brackett series with a maximum depth for mid-A stars. The Brackett series still dominates the spectra of F stars, but to a lower level than for A stars. Lines of neutral metal species (e.g., Mg I, and Si I) are negligible for AF stars. They become dominant for G stars and significant for K and early-M stars with the Mg I at 1.58 μm. A bump due to the H− opacity minimum around 1.6 μm (and H2O absorption) significantly increases from K to late-M stars (Rayner et al. 2009). H-band M-type spectra are dominated by numerous but weak FeH absorption features. As a consequence of the lines and continuum shape, corrections to the broadband magnitude might be non-negligible.
We computed the offset between the H-band magnitude (2MASS RSR, TH, Cordelli et al. 1995) and the SDI narrowband magnitudes as a function of the SpT following Eq. (5), with an absolute flux-calibrated modeled-spectrum of Vega (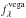 ),
), 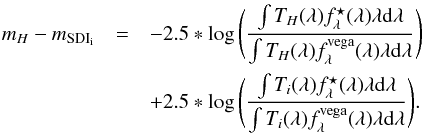 (5)Table 3 lists the results as a function of the SpT. First, Δm1.575 μm and Δm1.600 μm are on the order of 10-2−10-3, while Δm1.625 μm remains at the 10-3 level. For a given SpT, Δm1.575 μm is always higher in absolute value than the two others, as expected because of deep lines or red continuum. Variations are on the order of one magnitude within a SpT. Second, Δm1.575 μm and Δm1.600 μm decrease from O (positive) to M (negative) stars, while Δm1.625 μm remains nearly constant. The positive-negative transition occurs at the AF transition for Δm1.575 μm and for early-G stars for Δm1.600 μm. Input spectra of the GIRT library (Gupta et al. 2005) give similar results.
(5)Table 3 lists the results as a function of the SpT. First, Δm1.575 μm and Δm1.600 μm are on the order of 10-2−10-3, while Δm1.625 μm remains at the 10-3 level. For a given SpT, Δm1.575 μm is always higher in absolute value than the two others, as expected because of deep lines or red continuum. Variations are on the order of one magnitude within a SpT. Second, Δm1.575 μm and Δm1.600 μm decrease from O (positive) to M (negative) stars, while Δm1.625 μm remains nearly constant. The positive-negative transition occurs at the AF transition for Δm1.575 μm and for early-G stars for Δm1.600 μm. Input spectra of the GIRT library (Gupta et al. 2005) give similar results.
While these corrections are one to two orders of magnitude below the current photometric accuracy, they might become mandatory to prevent systematics for narrowband observations with the new generation of planet imagers.
H-band to SDI narrow-band magnitude corrections for dwarf stars using the Pickles and IRTF spectral libraries.
4. Influences of angular and spectral differential imaging
4.1. Structure of a point source reduced with angular and spectral differential imaging
The effect of any ADI algorithm is to subtract azimuthally offset copies of a point source, the effect of the subtraction depending on the algorithm and associated parameters, the field rotation, and the separation. The subtraction produces the typical negative sidelobes on both sides of the final processed point-source. These lobes might partially overlap the central point source and thus bias its photometry. They might also not be symmetrical when the observing sequence is not centered on the meridian time and/or little jitter is still present in the data. For ADI data, the self-subtraction can be calibrated by injecting artificial point sources with flat spectra into the data since the flux loss does not depend on an object’s spectrum. However, when applying SDI and ADI to reduce data, it becomes more complex. Because of the SDI two-lobe radial pattern, ADI creates additional sidelobes. The flux distributed into the sidelobes now also depends on the spectral properties of any point source.
We display in Fig. 11 the SDI map of Fig. 3 processed using the cADI algorithm to illustrate this effect. Other algorithms are discussed afterward. For F1 ≫ F3, the ASDI pattern is similar to the ADI one at short separation, but farther away, the negative counterpart of SDI becomes visible and positive sidelobes appear. For F1 ≳ F3, the positive sidelobes are as bright as the negative ones. Finally, for F1 ≪ F3 (west side), because of the strong negative SDI lobe, the positive sidelobes becomes brighter than the core of the PSF at very short separations.
By construction, cADI produces highly diluted azimuthal sidelobes. However, other ADI algorithms produce brighter (in absolute values) sidelobes because the best reference frames tend to be close in time to the target frame and thus have little relative field rotation. We show in Fig. 12 an ASDI pattern with F1/F3 = 1.1 at 9λ/D (400 mas) from the center, reduced in noise-free data cubes with rADI, LOCI (coefficients computed to minimize the noise in β Pic data and applied to the noise-free cube), and in science data cubes with PCA. It clearly shows that the positive sidelobes can be very bright, their positions being set by the separation criteria (1 FWHM here). We refer to the Appendix to for details on the effect of distance and flux ratio for different ADI algorithms.
The point source pattern after SDI and ADI processing therefore becomes very complicated, except for a highly methaned companion. In addition to the two lobes that are due to SDI, ADI induces four sidelobes, two of them being positive depending of the flux ratio of the initial point-source. The positions of these lobes are driven by the reduction parameters and the separation of the source. It is clear that these lobes might bias the photometry of the original point source, and we address this issue in the next section.
4.2. Coupling the self-subtraction calibration of spectral and angular differential imaging processing
 |
Fig. 12 ASDI reduced images using different ADI algorithms for a point source at 400 mas (23 px) in the original images with F1/F3 = 1.1. The LOCI coefficients derived to minimize the noise in the science data cube were applied on the noise-free image with the artificial source. For the PCA reduction, the artificial source was injected into the science data cube. All images have been normalized to their peak value. The scaling made use of the bytscl IDL function and is identical in the panels. |
 |
Fig. 13 Top panel: photometric bias due to cADI processing on SDI-reduced FPs as a function of F1/F3. The legend values indicate the separation in mas and correspond to about 4,8,13,17,21,26,30,34, and 38 λ/D. PSFs were reduced independently in noise-free images. Bottom panel: relative error of the bias measured on SDI-reduced FPs and non-SDI FPs as a function of separation for different measurement methods (color) for F1/F3 = 1.1. |
The key question we wish to address in this section is whether we can decouple the ADI self-subtraction from that of the SDI.
The ADI self-subtraction is usually estimated as the flux ratio of an artificial point source injected into the data to its flux measured in ADI-reduced images (either obtained on the peak value or by aperture photometry). For ASDI, if the aperture is too large, it will take part of the positive flux of the sidelobes into account and thus only bias the calibration of the ADI effect.
We tested whether the ADI flux-loss calibration is equivalent on SDI and non-SDI reduced point sources. We injected artificial point sources at different separations for different flux ratios, one by one, as for Fig. 4, and reduced them with and without SDI and different ADI algorithms. We measured the resulting flux on the maximum in an aperture of 1 FWHM in radius and by aperture photometry with diameter of 0.75,1,1.25, and 1.5 FWHM. In each case, we compared this residual flux to the one measured on I1 and I13b.
Figure 13 displays the results for the cADI algorithm for a first example. In the top panel, we consider the measurement on the maximum. We first note that the photometric bias is not constant with F1/F3, regardless of the separation for the considered range. It is only constant beyond F1/F3 = 1. It also decreases with the separation, as expected for cADI. Negative values mean that some flux was injected into the peak up to a higher level than F1. This behavior occurred during the cADI processing and came from the positive sidelobes, due to the SDI pattern, which contaminated it. The lower F1/F3, the higher the flux in the positive sidelobes, and therefore the lower the effect of ADI self-subtraction. In the bottom panel of Fig. 13, the relative difference of the ADI self-subtraction between the SDI and non-SDI pattern is shown as a function of the separation for different measurement methods, with F1/F3 = 1.1. Depending on the size of the aperture, the error can be as high as 15% for this flux ratio. The wider the aperture, the higher the error.
For rADI, Nδ is the parameter that directly controls the overlap of the sidelobes on the central lobe, regardless of the radius. It has to be large enough to avoid contamination. We tested parameters from 0.5 to 1.5 FWHM and measured the photometric bias with the same aperture photometry as for cADI. The bias remains below 10% as long as Nδ> 1.25 FWHM and the diameter of the aperture is smaller than 1 FWHM. This limitation has the cost of a high inner working angle, beyond 7λ/D (350 mas) in our case with the present rotation.
Therefore, the photometric biases of SDI and ADI in an ASDI reduction processing can be decoupled following some restrictions. To minimize the influence of the positive sidelobes resulting from the ADI after SDI processing, regardless of the separation, simple algorithms such as cADI and sADI have to be excluded. Moreover, the separation criterion has to be higher than 1.25 FWHM. Finally, the aperture photometry used to measure the ADI self-subtraction has to be smaller than 1 FWHM in diameter to exclude any contamination by the sidelobes.
4.3. Estimation of detection limits
 |
Fig. 14 Left panel: same as Fig. 7, but for β Pictoris with the SDI+rADI algorithm with Nδ = 1.25 FWHM. The rADI photometric bias has been computed on the residual peak value after ADI processing and without SDI reduction. Right panel: same as Fig. 8 for β Pictoris after ASDI processing. |
As for the SDI observations of AB Dor, we intend to demonstrate that our method also applies to ASDI data. With the β Pic dataset, we compared the detection limits after SDI and rADI reduction steps, computed by injecting artificial sources and by the technique introduced in this work. We tested this with Nδ = 1.25 FWHM. A conversion map was built according to the properties of β Pic with the two PSFs of interest. The self-subtraction due to rADI was calibrated on the peak value. The noise measured in the rADI residual map was corrected for the ADI flux loss and overplotted on the conversion map in Fig. 14. The conversion from ADU to mass was then made to obtain the sensitivity limits shown in Fig. 14 together with the curves from the FP injection. As for SDI, our method gives the same results as for the FP injection.
5. Discussion and concluding remarks
The effects of SDI and ASDI have been discussed in the context of the search for exoplanets and derivation of sensitivity limits to constrain their presence around young stars. The performance of this technique depends upon two parameters: the separation and the flux ratio of the companion between the two spectral channels. The ADI observing technique takes advantage of the rotation of the FoV with respect to the pupil to freeze the quasi-static speckle pattern over time, while an off-axis companion will rotate. At very short separations, the FoV rotation is usually not high enough to prevent a significant companion self-subtraction. The SDI technique can therefore be used before this to suppress the quasi-static speckle pattern taken simultaneously in two channels. SDI will be especially efficient at small separations for a highly methaned companion when little flux is present in the reference channel. However, differential aberrations might prevent a high-level speckle removal, and a following use of ADI might help to further subtract them.
This analysis clearly demonstrated that an ASDI-reduced point source can exhibit a peculiar six-lobe pattern that is not straightforward to predict. Moreover, in NaCo data, it is not guaranteed that ASDI is more efficient than ADI in detecting point sources. Indeed, differential aberrations between the two channels limit the speckle subtraction, and non-methaned objects suffer from high self-subtraction at short separations, which highly reduces their S/N (Maire et al. 2014). In contrast to ADI, the SDI self-subtraction is a physical quantity that can easily be incorrectly estimated. Because of simultaneous effects of the separation and flux ratio, it cannot be geometrically calibrated. The reason for this effect is the shift of the overall positive profile as well as the peak value. Therefore, the SDI geometric calibration for the self-subtraction cannot be applied as a correction factor to residual noise; this noise profile thus cannot be expressed in detection limits in terms of contrast and/or masses without significant bias. This observing strategy implies that these limits are model dependent.
SDI/ASDI detection performances must be computed by taking the specific and nonlinear SDI effects into account. As an alternative to the time-consuming injection of artificial point sources to explore a given evolutionary model until a detection threshold is reached, we here provided a method for calibrating the expected flux (positive) after SDI reduction and for translating the noise into masses. However, flux contamination by sidelobes needs to be prevented for the method to be valid, and to ensure this, the ADI reduction must be made using radial algorithms such as rADI or LOCI, with a separation criterion larger than 1.25 FWHM, which comes at the cost of reducing the inner working angle. 2D maps can be computed, while the injection of artificial sources is often limited to few PAs to save computing time. Finally, with NaCo data, these considerations can be limited to below one arcsecond since SDI and single-band observations reach the same sensitivity at this separation.
One of the focal instruments of SPHERE, IRDIS (Dohlen et al. 2008), will make use of a dual-band imaging mode (DBI) for SDI purposes using a variety of filter pairs from Y to K-band. The method we described here is straightforwardly applicable to derive its detection performances.
The conversion map computation can be generalized. The double difference proposed by Marois et al. (2000) to additionally suppress the speckle halo creates a negative-positive-negative SDI pattern that also depends on the flux ratio of the three spectral channels and the separation. The same method and reduction parameters can be used to estimate the detection performances using this reduction strategy. Moreover, with integral field units (IFU) being generalized to high-contrast ground-based AO fed-instruments (Beuzit et al. 2008; Macintosh et al. 2008), our method can be extended to multiwavelength techniques and the spectral deconvolution method (Sparks & Ford 2002; Thatte et al. 2007). Care must be taken at this point to compute the zero points if a 10-2 level in accuracy on the magnitude of any point source is expected to be reached.
The proposed method can be improved by using the sidelobes. Our choice was to focus on the central and positive part of the ASDI pattern, as is done for ADI. However, these sidelobes are additional parts of the signal that help the human eye to identify an astrophysical point source from a speckle. Therefore, the S/N might be higher and imply better sensitivity. Moreover, these lobes hold flux information of the point source to which they belong and might be brighter than the central part in some cases. They are implicitly used in characterizing point sources by standard techniques for ADI, but can help to improve the constraints on the presence of giant planets on wide orbits in the detection limits.
Finally, the solution to improving the sensitivity at very small angle might be to restore the use of RDI. With the higher stability of the new generation of planet imagers, RDI might help to remove the speckle pattern in this region with a higher efficiency than ADI or SDI. Moreover, this technique does not affect the signature of an off-axis companion, which is the limiting effect of the other differential techniques. Therefore, computing the detection limits with RDI in this technique is very straightforward and does not require any injection of an artificial point source. If the efficiency of RDI is proved with GPI/SPHERE with respect to ADI/ASDI at short separation, it might become a standard observation mode for probing the innermost part of planetary systems by direct imaging.
Online material
Appendix A: Properties of young substellar objects
We report in Table A.1 the properties of the young substellar objects used in Fig. 1.
Physical and atmospheric parameters of the young planetary-mass objects and companions used to investigate the depth of the 1.62 μm methane absorption band.
Appendix B: ASDI patterns using other ADI algorithms
We display in Fig. B.1 the ADI-reduced version of Fig. 3 with the sADI, rADI, PCA, and LOCI algorithms.
 |
Fig. B.1 Same as Fig. 11 with sADI (top left panel), rADI (top right panel), LOCI (bottom left panel), and PCA (bottom right panel) processing. The same parameters were used as in Fig. 12. The scaling made use of the bytscl IDL function and is identical in the panels. |
The notation follows Maire et al. (2014).
The noise calculation is beyond the scope of this paper. See Mawet et al. (2014) for details.
Acknowledgments
J.R. especially thanks Jérôme Bouvier for useful help with the photometric system. We also thank our referee for the comments that helped to improve the clarity and quality of this paper. This research has benefited from the SpeX Prism Spectral Libraries, maintained by Adam Burgasser at http://pono.ucsd.edu/~adam/browndwarfs/spexprism. This research has benefited from the Montreal Spectral Library, maintained by Jonathan Gagné at http://sites.google.com/site/mbderg/montreal-spectral-library. We acknowledge financial support from the French National Research Agency (ANR) through project grant ANR10-BLANC0504-01.
References
- Allard, F., Homeier, D., Freytag, B., & Sharp, C. M. 2012, in EAS Pub. Ser. 57, eds. C. Reylé, C. Charbonnel, & M. Schultheis, 3 [Google Scholar]
- Amara, A., & Quanz, S. P. 2012, MNRAS, 427, 948 [NASA ADS] [CrossRef] [Google Scholar]
- Angel, J. R. P. 1994, Nature, 368, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Baraffe, I., Chabrier, G., Barman, T. S., Allard, F., & Hauschildt, P. H. 2003, A&A, 402, 701 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barman, T. S., Macintosh, B., Konopacky, Q. M., & Marois, C. 2011, ApJ, 733, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Barman, T. S., Konopacky, Q. M., Macintosh, B., & Marois, C. 2015, ApJ, 804, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Beuzit, J.-L., Feldt, M., Dohlen, K., et al. 2008, in SPIE Conf. Ser., 7014 [Google Scholar]
- Biller, B. A., Close, L. M., Masciadri, E., et al. 2007, ApJS, 173, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Biller, B. A., Liu, M. C., Wahhaj, Z., et al. 2013, ApJ, 777, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Boccaletti, A., Augereau, J.-C., Lagrange, A.-M., et al. 2012, A&A, 544, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boccaletti, A., Pantin, E., Lagrange, A.-M., et al. 2013, A&A, 560, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonnefoy, M., Chauvin, G., Rojo, P., et al. 2010, A&A, 512, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonnefoy, M., Lagrange, A.-M., Boccaletti, A., et al. 2011, A&A, 528, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonnefoy, M., Chauvin, G., Lagrange, A.-M., et al. 2014, A&A, 562, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bowler, B. P., Liu, M. C., Shkolnik, E. L., & Dupuy, T. J. 2013, ApJ, 774, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Brandt, T. D., McElwain, M. W., Turner, E. L., et al. 2014, ApJ, 794, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Chauvin, G., Lagrange, A.-M., Dumas, C., et al. 2004, A&A, 425, L29 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Chauvin, G., Lagrange, A.-M., Zuckerman, B., et al. 2005, A&A, 438, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chauvin, G., Lagrange, A.-M., Bonavita, M., et al. 2010, A&A, 509, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chauvin, G., Lagrange, A.-M., Beust, H., et al. 2012, A&A, 542, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chauvin, G., Vigan, A., Bonnefoy, M., et al. 2015, A&A, 573, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Close, L. M., Lenzen, R., Guirado, J. C., et al. 2005, Nature, 433, 286 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Close, L. M., Follette, K. B., Males, J. R., et al. 2014, ApJ, 781, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, M., Wheaton, W. A., & Megeath, S. T. 2003, AJ, 126, 1090 [NASA ADS] [CrossRef] [Google Scholar]
- Colina, L., Bohlin, R. C., & Castelli, F. 1996, Instrument Science Report [Google Scholar]
- Cushing, M. C., Rayner, J. T., & Vacca, W. D. 2005, ApJ, 623, 1115 [NASA ADS] [CrossRef] [Google Scholar]
- Delorme, P., Gagné, J., Girard, J. H., et al. 2013, A&A, 553, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dohlen, K., Langlois, M., Saisse, M., et al. 2008, in SPIE Conf. Ser., 7014 [Google Scholar]
- Ducourant, C., Teixeira, R., Chauvin, G., et al. 2008, A&A, 477, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gupta, R., Ashok, N. M., Singh, H. P., & Ranade, A. C. 2005, Bull. Astron. Soc. India, 33, 175 [NASA ADS] [Google Scholar]
- Janson, M., Bonavita, M., Klahr, H., et al. 2011, ApJ, 736, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Janson, M., Brandt, T. D., Kuzuhara, M., et al. 2013, ApJ, 778, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Kasper, M., Apai, D., Janson, M., & Brandner, W. 2007, A&A, 472, 321 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kuzuhara, M., Tamura, M., Kudo, T., et al. 2013, ApJ, 774, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Lafrenière, D., Marois, C., Doyon, R., Nadeau, D., & Artigau, É. 2007, ApJ, 660, 770 [NASA ADS] [CrossRef] [Google Scholar]
- Lafrenière, D., Jayawardhana, R., & van Kerkwijk, M. H. 2010, ApJ, 719, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Lagrange, A.-M., Bonnefoy, M., Chauvin, G., et al. 2010, Science, 329, 57 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lagrange, A.-M., Milli, J., Boccaletti, A., et al. 2012, A&A, 546, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lenzen, R., Hartung, M., Brandner, W., et al. 2003, in SPIE, 4841, 944 [Google Scholar]
- Lenzen, R., Close, L., Brandner, W., Biller, B., & Hartung, M. 2004, in Ground-based Instrumentation for Astronomy, eds. A. F. M. Moorwood, & M. Iye, SPIE Conf. Ser., 5492, 970 [Google Scholar]
- Liu, M. C., Magnier, E. A., Deacon, N. R., et al. 2013, ApJ, 777, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Luhman, K. L., Patten, B. M., Marengo, M., et al. 2007, ApJ, 654, 570 [NASA ADS] [CrossRef] [Google Scholar]
- Macintosh, B., Graham, J. R., Ingraham, P., et al. 2014, Proc. National Academy of Sciences, 111, 12661 [Google Scholar]
- Macintosh, B. A., Graham, J. R., Palmer, D. W., et al. 2008, in SPIE Conf. Ser., 7015 [Google Scholar]
- Maire, A.-L., Boccaletti, A., Rameau, J., et al. 2015, A&A, 566, A126 [Google Scholar]
- Marois, C., Doyon, R., Racine, R., & Nadeau, D. 2000, in Optical and IR Telescope Instrumentation and Detectors, eds. M. Iye, & A. F. Moorwood, SPIE Conf. Ser., 4008, 788 [Google Scholar]
- Marois, C., Doyon, R., Nadeau, D., et al. 2003a, in High-Contrast Imaging for Exo-Planet Detection, ed. A. B. Schultz, SPIE, 4860, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Marois, C., Nadeau, D., Doyon, R., Racine, R., & Walker, G. A. H. 2003b, in Scientific Frontiers in Research on Extrasolar Planets, eds. D. Deming, & S. Seager,ASP Conf. Ser., 294, 103 [Google Scholar]
- Marois, C., Lafrenière, D., Doyon, R., Macintosh, B., & Nadeau, D. 2006, ApJ, 641, 556 [Google Scholar]
- Marois, C., Macintosh, B., Barman, T., et al. 2008, Science, 322, 1348 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Marois, C., Zuckerman, B., Konopacky, Q. M., Macintosh, B., & Barman, T. 2010, Nature, 468, 1080 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Masciadri, E., Mundt, R., Henning, T., Alvarez, C., & Barrado y Navascués, D. 2005, ApJ, 625, 1004 [NASA ADS] [CrossRef] [Google Scholar]
- Mawet, D., Milli, J., Wahhaj, Z., et al. 2014, ApJ, 792, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Naud, M.-E., Artigau, É., Malo, L., et al. 2014, ApJ, 787, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Nielsen, E. L., Liu, M. C., Wahhaj, Z., et al. 2013, ApJ, 776, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Patience, J., King, R. R., de Rosa, R. J., & Marois, C. 2010, A&A, 517, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pickles, A. J. 1998, PASP, 110, 863 [CrossRef] [Google Scholar]
- Racine, R., Walker, G. A. H., Nadeau, D., Doyon, R., & Marois, C. 1999, PASP, 111, 587 [NASA ADS] [CrossRef] [Google Scholar]
- Rameau, J., Chauvin, G., Lagrange, A.-M., et al. 2013, A&A, 553, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ranade, A., Gupta, R., Ashok, N. M., & Singh, H. P. 2004, Bull. Astron. Soc. India, 32, 311 [Google Scholar]
- Rayner, J. T., Cushing, M. C., & Vacca, W. D. 2009, ApJS, 185, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Roddier, C., & Roddier, F. 1995, Ap&SS, 223, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Rousset, G., Lacombe, F., Puget, P., et al. 2003, in SPIE, 4839, 140 [Google Scholar]
- Schneider, A. C., Cushing, M. C., Kirkpatrick, J. D., et al. 2014, AJ, 147, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, W. H. 1987, PASP, 99, 1344 [NASA ADS] [CrossRef] [Google Scholar]
- Soummer, R., Pueyo, L., & Larkin, J. 2012, ApJ, 755, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Sparks, W. B., & Ford, H. C. 2002, ApJ, 578, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Stephens, D. C., Leggett, S. K., Cushing, M. C., et al. 2009, ApJ, 702, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Thatte, N., Abuter, R., Tecza, M., et al. 2007, MNRAS, 378, 1229 [NASA ADS] [CrossRef] [Google Scholar]
- Vigan, A., Patience, J., Marois, C., et al. 2012, A&A, 544, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wahhaj, Z., Liu, M. C., Biller, B. A., et al. 2013a, ApJ, 779, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Wahhaj, Z., Liu, M. C., Nielsen, E. L., et al. 2013b, ApJ, 773, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Zahnle, K. J., & Marley, M. S. 2014, ApJ, 797, 41 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
H-band to SDI narrow-band magnitude corrections for dwarf stars using the Pickles and IRTF spectral libraries.
Physical and atmospheric parameters of the young planetary-mass objects and companions used to investigate the depth of the 1.62 μm methane absorption band.
All Figures
 |
Fig. 1 Spectra at a resolution of 60 around the CH4 band at 1.625 μm. Field dwarfs are from the SpeX Prism library. A peculiar red dwarf from Stephens et al. (2009) as well as young companions, free-floating planets, and Jupiter are plotted in color. They have been normalized to their highest values. The absorption bands of water and methane are labeled. The transmission of the SDI + filters (T1, T2, T3) is plotted in the bottom panel. |
| In the text | |
 |
Fig. 2 CH4 index (F1/F3) as a function of the spectral type (SpT). Values higher than 1 mean that CH4 is present in the atmosphere. The index is computed for field dwarfs from the SpeX Prism library (gray squares), references field dwarfs are plotted with larger squares, the peculiar red dwarfs from Stephens et al. (2009; open circles), young free-floating planetary-mass objects (triangles), and young companions (alternative symbols). The typical uncertainty on the index is 10%. |
| In the text | |
 |
Fig. 3 Effects of SDI processing as a function of the separation and flux ratio (F1/F3) in noise-free images. Upward residuals have a flux ratio of 1 as an example; leftward residuals of 4.3, which is typical of a T7 dwarf; downward residuals have a ratio of 1.1, typical of a mid-L to early-T dwarf; rightward residuals have a ratio of 0.87, which is like that of 2M 0122 B. SDI residuals suffer from a strong self-subtraction (except for a highly methaned companion) and are thus difficult to characterize at small radii, i.e., in the region where the speckle pattern will be subtracted. The bifurcation point is at 1.9′′ with these PSFs. |
| In the text | |
 |
Fig. 4 Left panel: flux measured on the peak of the residual and normalized to the injected F1 as a function of the flux ratio. The legend values indicate the separation in λ/D (equivalent to 87, 121, 173, 208, 259, 294, 346, 381, 433, 520, 690, and 866 mas). PSFs were reduced independently in noise-free images. Right panel: relative position between the peak in the residual pattern and the injected PSF. The 0.1 pixel in precision on the peak measurement leads to an unsmoothed curve. |
| In the text | |
 |
Fig. 5 Radial profiles of residual SDI patterns along the shift direction, separated by 6λ/D (300 mas) from the center of the image. PSF profiles are overplotted (dashed and dotted lines). The legend value indicates F1/F3 (and corresponds to F3/F1 = 0.5, 0.8, 0.9, 1.0, 1.2, and 1.5). All profiles have been centered on 0 for clarity. |
| In the text | |
 |
Fig. 6 Top left panel: flux measured on the SDI residual maximum as a function of the mass and separation, assuming an age of 500 Myr, a distance of 15 pc, and H = 4.84 mag. Contours indicate FSDI in (ADU/s). White areas correspond to negative flux. Top right panel: mass map as a function of the separation and predicted FSDI. Regions where a degeneracy appears are specified with black contours, indicating the number of solutions. The first (and less massive) solution is plotted here. Cases without solution are plotted in white. Bottom left panel: the same, but considering the second solution in mass. Bottom right panel: the same, but considering the third solution in mass (see text). |
| In the text | |
 |
Fig. 7 Left panel: residual radial noise in SDI and single-band images of AB Dor. Right panel: the same as the top right-hand panel of Fig. 6, but at 70 Myr. Five times the radial noise in the SDI residual image of AB Dor is overplotted in white and does not come across the degenerated region. |
| In the text | |
 |
Fig. 8 Detection limits on AB Dor at 1.575 μm (orange), 1.625 μm (red) in the top panel and in SDI (blue) in the bottom panel as a function of the separation. The solid lines (analytic) were estimated from a direct conversion of five times the noise into mass with the conversion map for SDI or with standard contrast conversion for single-band images. The limits were also estimated by injecting FP according to the predictions of the model, processed independently, until S/N = 5 was reached (“FP”, dashed lines), with a 1σ dispersion over five position angles (shaded area). The direct conversion from noise to contrast and mass without taking the SDI photometric bias into account, i.e., assuming a T8 SpT, is overplotted (“CH4”, triple-dotted dashed line). |
| In the text | |
 |
Fig. 9 Left panel: same as the bottom right panel of Fig. 8, but with the noise level artificially improved by a hundred to come across the degenerated region. Right panel: corresponding SDI sensitivity limit that gives the minimum detectable map. In between the vertical dashed lines, the noise-to-mass function is degenerated with three possible solutions, plotted with the circles. |
| In the text | |
 |
Fig. 10 Same as Fig. 1, but with typical spectra of class V stars from Ranade et al. (2004) at R ≃ 500. We also show prominent absorption features at play in the NaCo SDI+ filters such as the HI Brackett series for early-type stars and other elements for late-type stars. OBA spectra are taken from the library of Pickles (1998) at a resolution of 500 with a sampling of 5 Å, while FGKM spectra come from the IRTF/Spex library of Cushing et al. (2005), with an original resolution of 2000, but degraded to 500. A model spectrum of Vega is overplotted with a dashed line (Colina et al. 1996) and the 2MASS H-band relative spectral response curve from Cohen et al. (2003). |
| In the text | |
 |
Fig. 11 Same as Fig. 3 with cADI processing in addition to SDI. |
| In the text | |
 |
Fig. 12 ASDI reduced images using different ADI algorithms for a point source at 400 mas (23 px) in the original images with F1/F3 = 1.1. The LOCI coefficients derived to minimize the noise in the science data cube were applied on the noise-free image with the artificial source. For the PCA reduction, the artificial source was injected into the science data cube. All images have been normalized to their peak value. The scaling made use of the bytscl IDL function and is identical in the panels. |
| In the text | |
 |
Fig. 13 Top panel: photometric bias due to cADI processing on SDI-reduced FPs as a function of F1/F3. The legend values indicate the separation in mas and correspond to about 4,8,13,17,21,26,30,34, and 38 λ/D. PSFs were reduced independently in noise-free images. Bottom panel: relative error of the bias measured on SDI-reduced FPs and non-SDI FPs as a function of separation for different measurement methods (color) for F1/F3 = 1.1. |
| In the text | |
 |
Fig. 14 Left panel: same as Fig. 7, but for β Pictoris with the SDI+rADI algorithm with Nδ = 1.25 FWHM. The rADI photometric bias has been computed on the residual peak value after ADI processing and without SDI reduction. Right panel: same as Fig. 8 for β Pictoris after ASDI processing. |
| In the text | |
 |
Fig. B.1 Same as Fig. 11 with sADI (top left panel), rADI (top right panel), LOCI (bottom left panel), and PCA (bottom right panel) processing. The same parameters were used as in Fig. 12. The scaling made use of the bytscl IDL function and is identical in the panels. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


