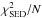| Issue |
A&A
Volume 581, September 2015
|
|
|---|---|---|
| Article Number | A97 | |
| Number of page(s) | 18 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201525664 | |
| Published online | 14 September 2015 | |
Collisional modelling of the AU Microscopii debris disc
1
Astrophysikalisches Institut und Universitätssternwarte,
Friedrich-Schiller-Universität Jena, Schillergäßchen 2–3, 07745
Jena, Germany
e-mail: christian.schueppler@uni-jena.de
2
European Southern Observatory, Alonso de Cordova 3107, Vitacura, Casilla 19001,
Santiago,
Chile
3
School of Physics, University of New South Wales,
NSW, 2052
Sydney,
Australia
4
Australian Centre for Astrobiology, University of New South Wales,
NSW, 2052
Sydney,
Australia
5
Institut für Theoretische Physik und Astrophysik,
Christian-Albrechts-Universität zu Kiel, Leibnizstraße 15, 24098
Kiel,
Germany
6
Institute of Astronomy, University of Cambridge,
Madingley Road, Cambridge
CB3 0HA,
UK
7
Université Grenoble Alpes, IPAG, 38000
Grenoble,
France
8
CNRS, IPAG, 38000
Grenoble,
France
9
University of Western Ontario, Department of Physics and
Astronomy, 1151 Richmond
Avenue, London,
ON
N6A 3K7,
Canada
Received: 14 January 2015
Accepted: 12 June 2015
AU Microscopii’s debris disc is one of the most famous and best-studied debris discs and one of only two resolved debris discs around M stars. We perform in-depth collisional modelling of the AU Mic disc including stellar radiative and corpuscular forces (stellar winds), aiming at a comprehensive understanding of the dust production and the dust and planetesimal dynamics in the system. Our models are compared to a suite of observational data for thermal and scattered light emission, ranging from the ALMA radial surface brightness profile at 1.3 mm to spatially resolved polarisation measurements in the visible. Most of the data are shown to be reproduced with dust production in a belt of planetesimals with an outer edge at around 40 au and subsequent inward transport of dust by stellar winds. A low dynamical excitation of the planetesimals with eccentricities up to 0.03 is preferred. The radial width of the planetesimal belt cannot be constrained tightly. Belts that are 5 au and 17 au wide, as well as a broad 44 au-wide belt, are consistent with observations. All models show surface density profiles that increase with distance from the star up to ≈40 au, as inferred from observations. The best model is achieved by assuming a stellar mass loss rate that exceeds the solar one by a factor of 50. The models reproduce the spectral energy distribution and the shape of the ALMA radial profile well, but deviate from the scattered light observations more strongly. The observations show a bluer disc colour and a lower degree of polarisation for projected distances <40 au than predicted by the models. These deviations may be reduced by taking irregularly shaped dust grains which have scattering properties different from the Mie spheres used in this work. From tests with a handful of selected dust materials, we favour mixtures of silicate, carbon, and ice of moderate porosity. We also address the origin of the unresolved central excess emission detected by ALMA and show that it cannot stem from an additional inner belt alone. Instead, it should derive, at least partly, from the chromosphere of the central star.
Key words: circumstellar matter / stars: individual: AU Mic (GJ 803, HD 197481) / submillimetre: planetary systems / scattering / polarisation / methods: numerical
© ESO, 2015
1. Introduction
Debris discs are remnants of the planet formation process, and they consist of (unobservable) planetesimals and collisionally replenished dust. They are ubiquitous around main-sequence stars with an incidence rate of about 20% for FGK stars with ages from hundreds of Myr to several Gyr (Eiroa et al. 2013). For 10−800 Myr-old A stars, Su et al. (2006) quote a higher detection rate of ≈30%, whereas Thureau et al. (2014) found a similar frequency to the one for FGK-type stars. The possible difference in the debris disc occurrence rate between the FGK and A stars appears to be largely due to the observed age ranges and the typical disc decay timescale for different spectral types (e.g., Decin et al. 2003; Wyatt et al. 2007; Kains et al. 2011).
The frequency of debris discs around M stars remains controversial (Lestrade et al. 2006, 2009, 2012; Gautier et al. 2007; Forbrich et al. 2008; Plavchan et al. 2009). Despite the high abundance of M dwarfs in the Galaxy (~80%, Lada 2006), only a few discs around them have been detected so far, for which there could be several reasons: (i) M dwarfs have low luminosities and are older on average than other stars so that their discs are faint and already mostly collisionally depleted. (ii) The blowout of dust around M stars may be favoured since they are likely to possess strong stellar winds (e.g., recently Johnstone et al. 2015a,b). (iii) Owing to their low stellar mass, it is easy to strip planetesimals from an M-dwarf disc during close encounters with massive objects. (iv) Debris disc surveys, including stars of various spectral types, reveal generic temperatures for warm and cold disc components of ~190 K and ~60 K, respectively (Morales et al. 2011; Ballering et al. 2013; Chen et al. 2014). If this also holds for M stars, the M-type discs would be close to the star, meaning a faster dynamic timescale of the disc and a quick depletion of the dust reservoir. Around a dozen non-resolved M-star discs have been found in recent years (Forbrich et al. 2008; Plavchan et al. 2009; Chen et al. 2014). Theissen & West (2014) find a much larger number of old M dwarfs that show mid-IR excesses, which can be interpreted as circumstellar dust emission. However, owing to the high fractional luminosities measured, the dust is more likely attributed to planetary impacts within the terrestrial zone than to asteroid belt-like debris discs. The discs around the M stars AU Microscopii and GJ 581 (Lestrade et al. 2012) are the only ones that have been spatially resolved thus far.
Since the discovery of the AU Mic disc (Kalas et al. 2004; Liu et al. 2004), it remains remarkable among the resolved debris systems in many respects. The disc is seen edge-on with an impressive radial extent of about 150 au and is resolved in the optical to near-IR (Krist et al. 2005; Metchev et al. 2005; Fitzgerald et al. 2007) where it appears blue relative to the star. The surface brightness profiles from the optical/near-IR images show shallow inner slopes at small projected distances but steepen substantially beyond 35 au. In addition, asymmetries on small and large scales with several local brightness maxima and minima have been detected at stellocentric distances beyond 20 au (Liu 2004; Krist et al. 2005; Fitzgerald et al. 2007). In the latest high spatial resolution Space Telescope Imaging Spectrograph (STIS) images, Schneider et al. (2014) have found a distinct brightness enhancement above the disc midplane on the south-eastern (SE) side at about 13 au from the star. Furthermore, a disc warp is discernible on the north-western (NW) side between 13 and 45 au, opposite to the SE brightness bump. There is also an NW-SE asymmetry, with the NW side brighter than the SE side inside 20 au. These disc inhomogeneities hint at the existence of planetary perturbers, causing radially localised structures such as rings, clumps, and gaps through planet-disc interactions (e.g., Ertel et al. 2012b; Nesvold & Kuchner 2015). However, no confirmation of planets in the AU Mic system has been found to date (Neuhäuser et al. 2003; Masciadri et al. 2005; Metchev et al. 2005; Hebb et al. 2007; Biller et al. 2013). Alternatively, clumpy disc structures may also be due to recent breakups of large planetesimals (e.g., Kral et al. 2015).
The disc has also been resolved at 1.3 mm with the Submillimetre Array (SMA), see Wilner et al. (2012), and with the Atacama Large Millimetre/submillimetre Array (ALMA), see MacGregor et al. (2013). From the ALMA observations two distinct emission components have been identified: a dust belt that extends up to 40 au and a central emission peak that remains unresolved. The dust belt shows an emission profile that rises with the distance from the star, indicating a steep surface density slope. The central emission peak is about six times brighter than the stellar photosphere. MacGregor et al. (2013) have surmised that this emission stems from an inner planetesimal belt, located ≲3 au from the star. Cranmer et al. (2013) propose that it comes solely or partly from an active stellar corona.
This great abundance of available observational data of the AU Mic disc provides valuable information from the smallest up to the largest dust particles, and further to planetesimals that produce the dust through collisional grinding. Constraints on the properties and spatial distribution of (sub)micron-sized particles can be inferred from the short-wavelength observations where the dust’s scattered light is detected. However, in the AU Mic edge-on system, this is impeded by the degeneracy between the scattering properties of grains and their supposed spatial distribution, and requires a good knowledge of the phase and polarisation function of small dust. The dynamics of small particles is strongly affected by radiative and corpuscular forces, resulting in radiative or stellar wind blowout and drag, depending on the grain and stellar properties. Observations at longer wavelengths show the thermal emission of larger grains and give insights into their spatial distribution. Especially, resolved images in the radio range reveal the locations of mm-sized, tracing the underlying parent bodies (planetesimals).
Much work has been done in the past to characterise and model the AU Mic system. Augereau & Beust (2006) performed a direct inversion of the visible and near-IR surface brightness profiles. From H-band observations, a disc surface number density was obtained that peaks around 35 au, close to the location of the break in the brightness profile, which hints at a planetesimal belt around that distance. Furthermore, by fitting the blue disc colour, they constrained the grain size distribution and found that grains smaller than 1 μm are mandatory to explain the observations. The study of Strubbe & Chiang (2006) included the dynamics of grains for the first time. There, a narrow birth ring of planetesimals at about 40 au was assumed. Micron-sized dust grains are produced through mutual collisions of the birth-ring objects. Grains with sizes <1 μm that are smaller than the radiative and corpuscular blowout limit are expelled from the system by direct radiation and stellar wind pressure. Slightly larger grains are either barely bound and launched into eccentric orbits, thereby forming a halo, or are transported into the inner regions of the system by Poynting-Robertson and stellar wind drag. The largest grains then follow the dynamics of their parents and remain in the birth ring. Strubbe & Chiang conclude that the disc is a collision-dominated system with an inner part devoid of submicron-sized grains (consistent with the polarisation measurements of Graham et al. 2007). Small grains mainly populate the outer part of the disc, causing the blue colour of the scattered light. Fitzgerald et al. (2007) attempted to simultaneously reproduce the scattered light profiles, the degree of polarisation, and the spectral energy distribution (SED) with a two-zone disc, using power-law descriptions for the radial and size distribution of the dust in each zone. They show that the first zone (35−40 au) of large particles, representative of a planetesimal ring, mainly accounts for the long-wavelength thermal emission, whereas the second zone (40−300 au), composed of small particles, reproduces the scattered light measurements well.
Recently, a dust halo has also been detected in far-IR resolved Herschel and James Clerk Maxwell (JCMT Telescope) images by Matthews et al. (in prep.). Their best fit supports the narrow birth-ring model of Strubbe & Chiang (2006), but is also consistent with an extended planetesimal ring from 8−40 au, according to the model explored in Wilner et al. (2012) and MacGregor et al. (2013).
In this study, we undertake collisional modelling to find a generic size and radial distribution of the dust in the AU Mic disc. We aim at a comprehensive understanding of the dust production and the dust and planetesimal dynamics in this system. For the first time, we combine constraints from scattered light and mm wavelength observations and search for a self-consistent collisional model that explains all these data. We assume an axisymmetric disc, and therefore do not account for the formation of substructures and asymmetries observed in the AU Mic disc. Section 2 gives an overview of the observational data and presents our re-reduction of the ALMA data, resulting in a star+disc flux density and a radial surface brightness profile at 1.3 mm. Section 3 explains our collisional model. Section 4 shows the modelling of the extended, ~40 au-wide emission zone, seen in the ALMA image, which we refer to as a resolved outer disc. Section 5 addresses a possible origin of the unresolved central emission. In Sect. 6, we compare our results from collisional modelling with a multidimensional power-law fitting approach. Conclusions are drawn in Sect. 7.
2. Data used
2.1. Stellar properties
AU Mic (GJ 803, HD 197481) is an M1 V dwarf at a distance of 9.9 pc (Perryman et al. 1997; van Leeuwen 2007). The star is a bright X-ray and UV emitter and shows strong flaring activity (e.g., Robinson et al. 2001). We used the photosphere model of Augereau & Beust (2006) with an effective temperature of 3700 K, a luminosity of 0.09 L⊙, and a surface gravity of log (g) = 4.5 (CGS). We assumed a stellar mass of 0.5 M⊙, motivated by the mean of the wide mass range given in the literature (0.3−0.6 M⊙, Plavchan et al. 2009; Houdebine & Doyle 1994). This assumption is roughly consistent with the photosphere model used that predicts ≈0.6 M⊙.
AU Mic belongs to the β Pic moving group (BPMG), and its age coincides with the BPMG age by assuming a coeval origin of all group members. Through the identification of the lithium depletion boundary, Binks & Jeffries (2014) and Malo et al. (2014) found BPMG ages of 21 ± 4 Myr and 26 ± 3 Myr, respectively. This agrees with traceback ages from Makarov (2007) and Mamajek & Bell (2014). The latter used revised Hipparcos astrometry data and also derived an isochronal age of 22 ± 3 Myr.
2.2. ALMA observations
ALMA observations of AU Mic in Band 6 (1.3 mm) have been carried out as part of the cycle 0 early science observations in the context of the projects 2011.0.00142.S (PI: D. Wilner) and 2011.0.00274.S (PI: S. Ertel). The data considered in the present work were taken on 16 June 2012 and are in agreement with the MacGregor et al. (2013) SB-4 observations. A total of 20 operational 12-m antennae were used, spanning baselines of 21−402 m with an effective angular resolution (FWHM of the reconstructed dirty beam) of 0.69″ × 0.79″ and an effective field of view of λ/D ≈ 22″ (with λ the observing wavelength and D the single-dish diameter). MacGregor et al. (2013) present a detailed description of the observations and data reduction. Our re-reduction of the data was carried out in the Common Astronomy Software Applications (CASA, McMullin et al. 2007). We followed the approach used by MacGregor et al. (2013) and came to consistent conclusions.
The edge-on disc has a radial extent of about 4′′ (≈40 au) and a position angle of 128.41 ± 0.13° (MacGregor et al. 2013). It is unresolved in its vertical direction. We refrain from presenting the ALMA image since it would not provide information beyond what is shown in Fig. 1 of MacGregor et al. (2013). To prepare the data for our modelling, we extracted a radial profile along the disc’s major axis. To this end, we largely adopted the approach used for Herschel data obtained in the context of the Open Time Key Programme DUst around NEarby Stars (DUNES, Löhne et al. 2012; Eiroa et al. 2013; Ertel et al. 2014). We first converted the flux units in the image from Jy/beam to Jy/pixel by multiplying them with a factor of 0.0185 derived by integrating the core of the reconstructed dirty beam. Then, we rebinned the image with an original pixel scale of 0.1′′/pixel to a ten times smaller pixel scale using a cubic spline interpolation and rotated it by an angle of 38.41° clockwise in order to align the disc major axis with the image x-axis. From this image, we measured the radial profile along the disc major axis by integrating over 11 × 11 subpixel-wide boxes centred on the disc midplane and spaced by 74 subpixels (0.74′′, about the FWHM of the reconstructed dirty beam, i.e. the resolution element of the image) left and right of the star, assumed to be located at the brightest subpixel. We averaged the SE and NW sides of the profile to fit an axisymmetric model to the data. Uncertainties were derived as a quadratic sum of the difference between the two sides of the profile and the background fluctuation measured in regions of the image where no flux is expected but where the sensitivity is comparable to the image centre. Since we were only interested in the dust distribution in the outer disc, we ignored the profile point at the image centre, which is affected by the inner, unresolved component. By extrapolating the disc profile from the outer points to the disc centre and assuming that the flux measured above the extrapolated value stems from the inner component (star and additional emission), we estimated a flux density of this component of 0.29 ± 0.05 mJy, which is consistent with 0.36 ± 0.07 mJy in MacGregor et al. (2013). We estimated the uncertainty of this measurement by adding in quadrature a typical uncertainty in the outer points (~15%) and an absolute photometric calibration uncertainty of 10% (MacGregor et al. 2013). The stellar contribution to this flux density is 0.04 mJy, obtained from the stellar photosphere spectrum (Augereau & Beust 2006) extrapolated to the ALMA wavelength using the Rayleigh-Jeans law. However, this might significantly underestimate the stellar flux and the whole central component might come from stellar emission (Cranmer et al. 2013).
Deviating from the complex fitting approach used by MacGregor et al. (2013) to derive the disc parameters (including the total flux density), we performed photometry of the disc by integrating the flux in the rotated image in a box of 101 × 21 native image pixels. The uncertainty was estimated from the scatter of the flux measured on eight positions above and below the disc, where no emission is expected. An additional calibration uncertainty of 10%, consistent with MacGregor et al. (2013), was added in quadrature. We found a total flux density of 8.75 ± 0.98 mJy, which is consistent with 7.46 ± 0.76 mJy from MacGregor et al. (2013), by summing both disc components and including calibration uncertainty. For the modelling, we subtracted the flux of the inner component estimated above, so that we are only left with the flux of the disc and the star as estimated using our photosphere spectrum.
The exact flux of the inner component has no significant impact on our profile or flux measurement, since we ignore the inner profile point affected by this component and because its contribution to the total flux density is only 0.2σ.
2.3. Auxiliary data
In addition to the ALMA data, we considered a variety of photometric data from earlier work for modelling. Furthermore, we included archival Herschel (Pilbratt et al. 2010) Photodetector Array Camera and Spectrometer (PACS, Poglitsch et al. 2010) and SPIRE (Spectral and Photometric Imaging Receiver, Griffin et al. 2010; Swinyard et al. 2010) data, obtained in the context of the debris disc guaranteed time observations programme (PI: G. Olofsson, see Matthews et al., in prep.). These data were treated following the Herschel/DUNES data reduction strategy (Eiroa et al. 2013). HIPE (Herschel Interactive Processing Environment, Ott 2010) version 11, and the calibration plan versions v56 and v11 for PACS and SPIRE, respectively, were used. PACS flux densities at 70 μm and 160 μm were measured with an aperture of 20′′ and annuli for the noise measurement of 30−40′′ and 40−60′′, respectively. The SPIRE flux density at 250 μm was measured with an aperture of 30′′, and the noise was estimated in a region of the image where no emission from the disc is expected. A nearby source is visible in all Herschel images, peaking at 250 μm. It is separated from the disc well at wavelengths up to 250 μm and easily removed by a point source subtraction. The two sources are not well separated at longer wavelengths. SPIRE flux densities at 350 μm and 500 μm were measured using SExtractor (Bertin & Arnouts 1996) and a point source approximation (PSF photometry), since the source is unresolved at these wavelengths. Aperture corrections were applied to the measured fluxes. Instrument calibration uncertainties of 7% for PACS and 6% for SPIRE were added in quadrature to the measured uncertainty. A more detailed reduction of the Herschel data will be given in Matthews et al. (in prep.). Minor differences to the data used here exist, but all within 2σ (B. Matthews, priv. comm.). The differences have no impact on the results presented in this work.
We did not consider the spatially resolved information from the Herschel images since the resolution is much lower than that of our ALMA image (e.g., FWHM = 5.8′′ for Herschel/PACS at 70 μm vs. FWHM = 0.74′′ for ALMA Band 6). However, we inspected the PACS data for signs of bright, warm central emission in the form of a significantly increasing extent of the disc from 70 μm to 160 μm (Ertel et al. 2014). Such behaviour is not visible suggesting that the inner component seen in the ALMA images indeed makes no or only a minor contribution to the fluxes at shorter wavelengths. Doering et al. (2005) report detecting the innermost disc regions up to ≈16 au in diameter via N-band imaging at Gemini South. However, only a low-level surface brightness extension along the direction of the edge-on disc was found that has not been taken into account in our study. Furthermore, we did not consider Spitzer/MIPS images because of the low angular resolution (e.g., the resolution of Spitzer at 24 μm is nearly as low as that of Herschel at 70 μm). Any confusion, such as from a background galaxy, would be difficult here to disentangle from the source.
Assuming the flux density to be proportional to λ−δ at long wavelengths, the mean spectral index beyond 250 μm amounts to δ = 1.7, close to the Rayleigh-Jeans (RJ) slope of a blackbody radiator (δRJ = 2). We fitted a blackbody curve to the far-IR excess in order to derive spectral slopes at all wavelengths. A temperature of 50 K fits the data very well, which is consistent with Rebull et al. (2008) and Plavchan et al. (2009). Interestingly, this is close to the generic temperature found for the outer cold components in many two-component disc systems (Morales et al. 2011; Ballering et al. 2013; Chen et al. 2014; Pawellek et al. 2014). The temperature that was found for the inner disc, 190 K, corresponds to a very small distance of 0.7 au for a putative warm component in the AU Mic system. This is well below the resolution limit and leaves room for further speculations about the presence of an inner unresolved disc component. We took the nearest tabulated values for the colour corrections listed in the literature for the instruments used and the spectral slopes of the source (star and disc) derived from this fit. The resulting colour-corrected flux densities and references for both the measurement and the colour correction are listed in Table 1.
Colour-corrected photometry of AU Mic.
2.4. Scattered light
The AU Mic disc is 60% brighter in B band than in I band relative to the star (Krist et al. 2005). A potential explanation is that there are many small grains that scatter more light at shorter wavelengths. Augereau & Beust (2006) constrained the grain size distribution by fitting the blue disc colour. They concluded that grains down to ~0.1 μm are needed to explain the observations when astronomical silicate or graphite grains are assumed. Graham et al. (2007) obtained polarisation maps in V band using the Hubble Space Telescope (HST) Advanced Camera for Surveys. They measured the degree of linear polarisation to be steeply rising from 5% to 40% within a distance of 80 au from the star. The light is polarised perpendicular to the disc plane that agrees with the expected scattering behaviour by small grains with size parameters x ≲ 1 (equivalent to typical grain sizes <1 μm). To model the V-band scattered light intensity and the degree of polarisation, Graham et al. (2007) assumed uniformly distributed dust between two distances from the star and adopted the empirical Henyey & Greenstein (1941) phase function in combination with a parameterized polarisation function. In their best-fit model, the particles exhibit strong forward scattering, and the innermost 40 au of the disc are devoid of grains. Later on, Shen et al. (2009) showed that the results from Graham et al. (2007) can be reproduced by a distribution of sphere cluster aggregates with size distribution index −3.5, volume-equivalent radii between 0.1 and 0.4 μm, and a porosity of 60%.
In this work, our models are compared with the optical and near-IR surface brightness profiles from Fitzgerald et al. (2007) and Schneider et al. (2014) and with the measured degree of polarisation from Graham et al. (2007). Since our modelling deals with axisymmetric discs, all observed profiles had been averaged over the SE and NW disc sides in order to remove the observed surface brightness anomalies.
2.5. Gas in the disc
Some studies searched for circumstellar gas in the AU Mic disc. From a non-detection of submillimetre CO emission, Liu et al. (2004) inferred an H2 mass of ≤1.3 M⊕. Roberge et al. (2005) reduced the H2 mass limit to 0.07 M⊕ due to a non-detection of far-UV H2 absorption. France et al. (2007) analysed fluorescent H2 emission and found a total gas mass between 4 × 10-4M⊕ and 6 × 10-6M⊕, but state that this detection might also come from a cloud that extends beyond the disc. From X-ray spectroscopy Schneider & Schmitt (2010) report a maximum H column density of ~1019cm-2, which is about five times higher than the interstellar value. However, since observational data point towards a very low gas content in the AU Mic disc, we neglect the influence of any gas in our investigations.
3. Collisional modelling
Collisional modelling with our code ACE (Analysis of Collisional Evolution) and its application to debris disc systems is described extensively in previous papers (Krivov et al. 2006, 2008; Müller et al. 2010; Reidemeister et al. 2011; Löhne et al. 2012; Krivov et al. 2013; Schüppler et al. 2014, among others). The code assumes a disc of planetesimals orbiting a central star, simulates their collisional grinding, and follows the collisional and dynamical evolution of the system under a variety of physical effects. ACE works with a three-dimensional logarithmic grid for objects’ mass, pericentric distance, and eccentricity. The simulations consider a number of parameters, including those that define the initial distribution of planetesimals, the strength of particle transport, and material properties such as the critical fragmentation energy. The following sections explain the parameters chosen in our modelling.
3.1. Stellar winds and mass loss rate
Stellar winds (SW) are expected to play a crucial role in discs around late-type stars such as AU Mic where they are typically stronger than for early-type stars (e.g., Plavchan et al. 2005, 2009; Strubbe & Chiang 2006; Reidemeister et al. 2011; Schüppler et al. 2014). The total stellar wind force that acts on the circumstellar dust can be decomposed to direct stellar wind pressure, which is directed radially outwards, and stellar wind drag, which works like a headwind on the particles and causes them to gradually lose orbital energy and angular momentum and, therefore, to spiral inwards (Burns et al. 1979). Depending on the stellar wind strengths and the size of the particles they are interacting with, the result could be either a grain transport towards the star or a blowout of smaller grains from the system.
Previous studies have proposed various stellar wind strengths for the AU Mic system, expressed in terms of multiples of the solar mass loss rate, Ṁ⊙ = 2 × 10-14 M⊙ yr-1. Strubbe & Chiang (2006) constrained the stellar mass loss rate to be Ṁ⋆< 10 Ṁ⊙, which was in good agreement with the observed SED and the V − H colour profile of the disc. This relatively weak wind strength means that the disc is dominated by destructive grain-grain collisions rather than transport processes. Plavchan et al. (2009) estimate Ṁ⋆< 50 Ṁ⊙ from considerations of Spitzer/IRS observations. Augereau & Beust (2006) took the active nature of AU Mic into account and found Ṁ⋆ ≈ 50 Ṁ⊙ during quiescent states and Ṁ⋆ ≈ 2500 Ṁ⊙ during flares. The star spends about 10% of the time in flare phases with typical flare durations of several minutes (Pagano et al. 2000). Averaging over quiescent and flare phases yields a mean stellar mass loss of Ṁ⋆ = 300 Ṁ⊙. This high wind strength means that the direct stellar wind pressure is greater than the radiation pressure, which causes an efficient transport of small dust into outer disc regions.
In our modelling, we considered moderate and strong wind strengths by assuming 50 Ṁ⊙ and 300 Ṁ⊙. Throughout this paper, we refer to both cases as SW50 and SW300. According to Augereau & Beust (2006), SW50 is a typical model where the flares are ignored, while SW300 is an attempt to account for the impact of the episodic stellar activity. In all simulations involving stellar winds, we used Eq. (7) of Gustafson (1994) for the total stellar wind force acting on a particle and assumed a wind speed vsw = 400 km s-1 (Strubbe & Chiang 2006).
3.2. Grain material
Graham et al. (2007) and Fitzgerald et al. (2007) found evidence of porous aggregates containing silicate, carbon, and ice. Guided by these results, we used porous grains composed of astronomical silicate (Draine 2003), ACH2 amorphous carbon (Zubko et al. 1996), and water ice (Li & Greenberg 1998). Since the ACH2 refractive data from Zubko et al. (1996) terminate at λ ≈ 1 mm and do not cover the full wavelength range for all available photometric measurements, we extrapolated the real and imaginary parts up to λ = 2 mm by the function c1 (λ/ 1 mm)c2. The extrapolation gives (c1,c2) = (16.2,0.27) and (c1,c2) = (5.6, −0.26) for real and imaginary parts, respectively.
We generated different porous silicate-carbon-ice mixtures and calculated the refractive indexes of the composites by applying the Bruggeman (1935) mixing rule. The materials considered in this study are given in Table 2. For brevity, we use the identifiers M1 to M5 when referring to the different compositions.
Materials used for modelling.
We assumed spherical dust grains. Each grain has a certain radius s which is denoted as its size. Optical properties of the grains were determined by means of Mie theory (Bohren & Huffman 1983). Figure 1 shows β = βrad + βsw = Frad/Fgrav + Fsw/Fgrav, the ratio of direct radiation and direct stellar wind pressure forces to stellar gravity (Burns et al. 1979) as a function of grain size. A detailed description of βsw includes a dependency on the distance from the star, r, owing to radial variations of the stellar wind velocity. However, this effect is weak for r> 15 au (Augereau & Beust 2006), and we considered βsw to be independent of r. Furthermore, we assumed the reflection of wind particles on the surface of the dust grains that means an efficiency of momentum coupling of CD = 2 (Gustafson 1994).
The orbits of the collisionally produced dust grains become more and more eccentric with increasing β. For β> 0.5, the grains get eccentricities >1 and are expelled from the system on hyperbolic orbits if they are released from bodies on circular orbits. As a measure of the blowout size, we define sblow = s (β = 0.5). However, when particles are released from eccentric orbits, the blowout occurs between β = (1 − e)/2 at the periastron and (1 + e)/2 at the apastron (Burns et al. 1979), where e is the typical eccentricity of the parent bodies that eject the dust. ACE computes the orbital elements of the fragments depending on the masses, semi-major axes, eccentricities, and β of the colliding bodies, so it automatically accounts for bound and unbound grains launched from non-circular orbits (Krivov et al. 2006). Therefore, the minimum size of bound grains in the debris disc system is slightly smaller than sblow. Nevertheless, we found this effect to be small, and sblow can be considered a representative value for the minimum grain size.
In the case of weak or no stellar winds, β is smaller than the blowout limit 0.5 for all grain sizes (see Fig. 1, Ṁ⋆ = 0). With increasing stellar wind strength, the dust particles experience a stronger radial wind pressure. Assuming a radiation pressure efficiency Qpr = 1 (Burns et al. 1979) yields Fsw/Frad ~ 0.5 for SW50 and Fsw/Frad ~ 3 for SW300. As a result, if the stellar winds are sufficiently strong, the β-ratio that would otherwise be smaller than 0.5 can exceed this critical value at the smallest dust sizes. This defines a blowout size, terminating the lower end of the size distribution (Table 2). Figure 1 shows β for M1 exemplarily. The other materials given in Table 2 follow a similar dependence of β on size.
 |
Fig. 1 β-ratio for different assumptions of AU Mic’s stellar mass loss rate Ṁ⋆. The material consists of 33% carbon, 33% silicate, and 33% vacuum (M1). The horizontal dashed line depicts β = 0.5. Particles with β> 0.5 are ejected from the system owing to radiation and stellar wind pressure. |
Description of ACE runs.
The mechanical strength of the materials was defined by a modified version of the Benz & Asphaug (1999) description of the critical
energy for fragmentation and dispersal,
![\begin{eqnarray} Q_\text{D}^\star=\left[Q_\text{D,s}\left(\frac{s}{1\,\text{m}}\right)^{b_\text{s}}+ Q_\text{D,g}\left(\frac{s}{1\,\text{km}}\right)^{b_\text{g}}\right] \left(\frac{v_\text{imp}}{3\,\text{km}~\text{s}^{-1}}\right)^{\kappa}, \end{eqnarray}](/articles/aa/full_html/2015/09/aa25664-15/aa25664-15-eq115.png) (1)where (QD,s,
bs) and (QD,g,
bg) are two pairs of constants,
characterising the strength and gravity regime, respectively, and vimp denotes the
impact speed. Here,
(1)where (QD,s,
bs) and (QD,g,
bg) are two pairs of constants,
characterising the strength and gravity regime, respectively, and vimp denotes the
impact speed. Here,  is the impact energy per unit target mass
necessary to disperse the target into fragments where the largest fragment contains at
most half of the original target mass. For objects smaller than 100 m,
is the impact energy per unit target mass
necessary to disperse the target into fragments where the largest fragment contains at
most half of the original target mass. For objects smaller than 100 m,
 is mainly determined by the material
strength, while the gravitational binding energy dominates for larger sizes. The material
strength also depends on the material composition, but this dependence is still
insufficiently constrained by laboratory work. Therefore, we used the same
is mainly determined by the material
strength, while the gravitational binding energy dominates for larger sizes. The material
strength also depends on the material composition, but this dependence is still
insufficiently constrained by laboratory work. Therefore, we used the same
 for all materials given in Table 2 and assumed QD,s =
QD,g = 5 × 106 erg
g-1,
bs =
−0.37, bg = 1.38, and κ = 0.5 (Löhne et al. 2012, and references therein).
for all materials given in Table 2 and assumed QD,s =
QD,g = 5 × 106 erg
g-1,
bs =
−0.37, bg = 1.38, and κ = 0.5 (Löhne et al. 2012, and references therein).
3.3. Setup
Table 3 lists all ACE simulations discussed in this paper. We distinguish between three disc types, named by the width and location of their planetesimal belt (PB): (i) a narrow outer PB; (ii) a radially extended PB; and (iii) a narrow inner PB. Configurations (i) and (ii) describe models for the outer resolved disc, whereas (iii) corresponds to a model for the central emission seen by ALMA.
In all simulations, we assumed the discs to be composed of planetesimals up to at least
10 m in radius with an initial size distribution ∝ s-3.5. The
planetesimals are large enough to ensure that their collisional lifetime is longer than
the time needed to reach a quasi-steady state material distribution at dust sizes (Löhne et al. 2008). Thus, the results of the
simulations are independent of the maximum size of the objects. Our code also accounts for
cratering and bouncing collisions where the bulk of one or both colliders stays intact but
fragments are released. For each collision, the distribution of fragments is assumed to
follow a power law with a mass distribution index −1.83 down to the smallest objects
represented in the grid. The planetesimal discs were assumed to be stirred to a maximum
eccentricity, emax. The bodies in the disc were assumed
to be uniformly distributed within a semi-opening angle imax =
emax/ 2 (energy equipartition). After
reaching a quasi-steady state, each simulation was evolved until the dust mass had reduced
sufficiently to reproduce the observed excess emission. In general, the simulation time,
tsim, does not coincide with the physical
age, tphys ≈
20−30 Myr, of the AU Mic system. For all models except the one with
planetesimals between 1 and 45 au, tsim was two to four times shorter than
tphys. These times are more than enough to
bring the model discs to collisional equilibrium. The initial conditions of our model
discs are, however, fiducial. Different combinations of total initial mass and initial
size distribution can lead to the same observed dust configuration, though after different
times. An estimate for the minimal initial disc mass that is needed to provide the
observed amount of dust after tphys can be obtained by assuming that
the collisional lifetimes, tcol, of the largest bodies equal the
system age, enabling them to sustain sufficient dust production over that time. The
required sizes for the largest bodies, 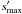 , typically exceed those in our simulation
runs. We extrapolated the size distributions and collisional lifetimes to derive
, typically exceed those in our simulation
runs. We extrapolated the size distributions and collisional lifetimes to derive
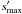 such that
such that
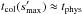 , and then, determined the minimum initial
disc masses Mmin for particle sizes up to
, and then, determined the minimum initial
disc masses Mmin for particle sizes up to
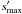 . The power-law distributions in the
m-to-km size range facilitate that extrapolation. The results are listed in Table 3. These masses reflect the minimum disc masses needed
to achieve simulation times that would approach tphys. Larger planetesimals and
potential exo-Plutos cannot be assessed this way because their direct contributions to the
collisional cascade are negligible.
. The power-law distributions in the
m-to-km size range facilitate that extrapolation. The results are listed in Table 3. These masses reflect the minimum disc masses needed
to achieve simulation times that would approach tphys. Larger planetesimals and
potential exo-Plutos cannot be assessed this way because their direct contributions to the
collisional cascade are negligible.
4. Resolved outer disc
We first seek to explain the available observational data on the resolved outer AU Mic disc, including the SED, the ALMA radial brightness profile, and scattered light measurements. In the following, we present several modelling attempts to illustrate the influence of different parameters on observables. We start with an investigation of the stellar wind strength to find an appropriate reference run (Sect. 4.1). In a subsequent analysis (Sects. 4.2−4.4), we vary other initial disc parameters of this reference run in order to more tightly constrain the parameters and reveal degeneracies among them.
 |
Fig. 2 Disc models of narrow planetesimal belts centred at 40 au with different assumptions
for the stellar wind (SW) strength (from left to right
Ṁ⋆ = 0,50,300
Ṁ⊙). a)−c): SEDs. Crosses show
photometric data and squares star-subtracted photometric data. The dashed lines depict
the stellar photosphere, the dash-dotted lines the disc emission, and the solid lines
the star+disc emission. The |
4.1. Stellar wind strength
In a first step, we sought a reasonable assumption for the stellar wind strength and carried out the runs SW0, SW50, and SW300. SW0 does not assume any stellar wind activity at all (Ṁ⋆ = 0). Here, the transport of particles is controlled by Poynting-Robertson drag alone. In SW50 and SW300, moderate and extreme stellar winds are considered, given by 50 times and 300 times the solar strength, respectively (see Sect. 3.1 for justification of these values).
For other disc parameters, we took reasonable values that have been preferred by previous studies. Inspired by the birth-ring scenario of Strubbe & Chiang (2006), we assumed a radially narrow planetesimal belt centred at a stellocentric distance rPB = 40 au, having the full width ΔrPB = 5 au. In all three runs, the maximum eccentricity of the planetesimals was set to emax = 0.03, motivated by Löhne et al. (2012) and Schüppler et al. (2014) who showed a preference for low dynamical excitations in debris discs around late-type stars. For the grain material, we chose a homogeneous mixture with volume filled in equal parts by astronomical silicate, amorphous carbon, and vacuum, denoted as M1 (Table 2). Other assumptions for the material composition, emax, and ΔrPB are probed in the Sects. 4.2−4.4.
4.1.1. Impact on thermal emission
Figure 2 shows SEDs and normal optical
thicknesses, τ⊥, for SW0, SW50, and SW300. The
vertical height of each SED was fitted by searching for the timestep in the ACE
simulations where the dust mass has an appropriate value to reproduce the observed level
of thermal emission. For the SEDs, we determined 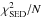 , which is the sum of the squares of the
deviations of our models from N individual photometric points, divided by
N. To
this end, we considered the N = 20 SED points for λ> 10μm (Table 1). We stress that the models are not fitted to the
data through variations in the initial disc parameters. The
, which is the sum of the squares of the
deviations of our models from N individual photometric points, divided by
N. To
this end, we considered the N = 20 SED points for λ> 10μm (Table 1). We stress that the models are not fitted to the
data through variations in the initial disc parameters. The
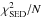 metric merely serves as a better
comparison of the SED models. All models show good fidelity with the photometry between
160−850 μm but markedly
underestimate or tend to underestimate the 1.3 mm data. At shorter wavelengths, SW50
provides a good match to the data, whereas SW0 significantly underestimates the mid-IR
points and SW300 the 70 μm point.
metric merely serves as a better
comparison of the SED models. All models show good fidelity with the photometry between
160−850 μm but markedly
underestimate or tend to underestimate the 1.3 mm data. At shorter wavelengths, SW50
provides a good match to the data, whereas SW0 significantly underestimates the mid-IR
points and SW300 the 70 μm point.
In the planetesimal zone of run SW0, the number of particles continuously increases with decreasing grain size apart from an underabundance around s = 0.4μm (Fig. 2d, r = 39 au). Although the smallest grains in the range of a few tens of microns are the most frequent, they barely affect the SED because their thermal emission is negligible in the IR. Thus, the effective minimum grain size is given by the maximum of the size distribution at around 10 μm. This large grain size is characteristic of discs with low dynamical excitation of the planetesimals (Thébault & Wu 2008; Löhne et al. 2012; Krivov et al. 2013; Schüppler et al. 2014). The size distributions in SW50 and SW300 show maxima near 0.07 μm and 0.5 μm, respectively (Figs. 2e, f). These values are close to the blowout sizes, sblow (Table 2). Most of the smaller grains move on unbound orbits and leave the system on short timescales. Towards larger grains, the size distributions in the parent belt are nearly flat until they become significantly steeper at sizes between 10 and 100 μm. This behaviour is caused by the strong transport due to stellar wind drag, which favours smaller particles and quickly removes them from the planetesimal ring (e.g., Vitense et al. 2010; Reidemeister et al. 2011; Wyatt et al. 2011; Krivov et al. 2013). As a result, the normal optical thickness is radially uniform for r<rPB in SW50 and SW300 (Figs. 2h, i).
Direct stellar radiation pressure, aided by stellar wind pressure in SW50 and SW300, pushes submicron-sized, barely bound grains to eccentric orbits resulting in extended dust halos. However, both because of low dynamical excitation (Thébault & Wu 2008) and fast transport (Strubbe & Chiang 2006), the halos are tenuous and exhibit radial profiles with outer slopes that are significantly steeper than the −1.5 predicted for “canonical” debris discs (Krivov et al. 2006; Strubbe & Chiang 2006).
For all three runs, the surface mass density of solids, Σ, is rising with distance up to rPB and shows a bow-like shape in a log-log Σ − r diagram. Averaged over r = 1−30 au, we measured Σ ∝ r2.0 for SW0 and Σ ∝ r2.7 for SW50 and SW300. The latter is close to r2.8, derived by MacGregor et al. (2013). The dust mass (objects with radii up to s = 1 mm) is about 2 × 10-3M⊕, consistent with previous estimates (Augereau & Beust 2006). The three models have a fractional luminosity of 4−5 × 10-4, which is not far from the 6 × 10-4 obtained by a modified blackbody fit (Liu et al. 2004).
 |
Fig. 3 ALMA radial surface brightness profile at 1.3 mm (dots) vs. models (lines). Synthetic profiles are multiplied by the factors given in the legend to compensate for imperfections in the modelling procedure (explained in the text). |
Figure 3 shows the surface brightness profile extracted from the ALMA 1.3 mm image. The profile increases with distance up to ≈30 au and drops steeply beyond. Since long-wavelength observations reveal the spatial distribution of large particles that have similar orbital elements as the planetesimals, this break indicates the outer edge of a dust-producing planetesimal zone. For modelling this profile, we assumed a disc inclination of 89.5° from face-on (Krist et al. 2005) and convolved the synthetic 1.3 mm images for SW0, SW50, and SW300 with the ALMA reconstructed dirty beam as produced by CASA after proper rotation. From these images, we extracted the radial profiles by integrating over a 0.1′′ central strip along the disc major axis. We allowed for vertical scaling of the gathered synthetic profiles. The scaling factors account for an imperfect reproduction of the total flux density at 1.3 mm, visible by comparing the models with the observed SED. Such imperfections stem, for example, from uncertainties in the absolute flux calibration or in the optical properties of the dust grains (Löhne et al. 2012). Furthermore, they derive from a definite inability of our models to reproduce the ALMA flux density along with the other photometric data. We surmise that the latter reason mainly causes the models to distinctly underestimate the ALMA flux density and necessitates high scaling factors (Fig. 2). In addition, the dust model used possibly underestimates the dust emissivity at mm wavelengths. Figure 3 clearly shows that the surface brightness peak moves to smaller projected distances with increasing stellar wind strength, reflecting the enhanced inward transport of particles.
 |
Fig. 4 Scattered light profiles of the AU Mic disc. a)−c): blue and red lines show synthetic midplane surface brightness profiles in V and H band relative to the stellar brightness for the disc models SW0, SW50, and SW300 (Sect. 4.1). Curves labelled with Mie in the legend were calculated with scattering phase functions obtained by means of Mie theory. The blue double-dotted line in panel b) depicts the V-band profile generated with the best-fit Henyey-Greenstein (HG) phase function model of Graham et al. (2007). Dots represent measurements with 1σ errors from Fitzgerald et al. (2007), abbreviated as F07, averaged over the SE and NW wings (circles for V band, squares for H band). The black dashed line shows the averaged V-band fit to both wings obtained by Schneider et al. (2014), abbreviated as S14. d)−f): observed and modelled colour profiles, V − H, obtained with the F07 data and the Mie profiles shown in panels a)−c). |
4.1.2. Impact on scattered light
We calculated the surface brightness of scattered light for our models along the
projected distance, b, in the disc midplane by
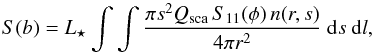 (2)where L⋆ is the luminosity of
the star, n(r,s)ds the
dust number density of grains with radii in [
s,s + ds ] at a distance
r, and
l = ±
(r2 −
b2)1/2 the line of sight.
Here, Qsca and S11(φ) are the
scattering efficiency and the scattering phase function of the grains, respectively. The
latter can be retrieved from the 4 ×
4 Mueller matrix Sij and is a function
of the scattering angle φ =
arcsin(b/r). We used Mie theory
to determine Qsca and S11(φ). The ACE
simulations provided the dust number density.
(2)where L⋆ is the luminosity of
the star, n(r,s)ds the
dust number density of grains with radii in [
s,s + ds ] at a distance
r, and
l = ±
(r2 −
b2)1/2 the line of sight.
Here, Qsca and S11(φ) are the
scattering efficiency and the scattering phase function of the grains, respectively. The
latter can be retrieved from the 4 ×
4 Mueller matrix Sij and is a function
of the scattering angle φ =
arcsin(b/r). We used Mie theory
to determine Qsca and S11(φ). The ACE
simulations provided the dust number density.
To compare with the observed V- and H-band surface brightness profiles presented in Fitzgerald et al. (2007), we integrated S(b) over the filter transmission curves of the HST Advanced Camera for Surveys F606W (central wavelength λc = 0.59μm, width Δλ = 0.23μm) and the Keck NIRC2 camera (λc = 1.63μm, Δλ = 0.30μm). The disc surface brightnesses were expressed relative to the star, for which we found 8.55 mag in V band and 4.84 mag in H band with our photosphere model. To account for the extended halo of small particles, the flux was integrated up to stellocentric distances of r = 150 au for each line of sight. We also compared with the radial profiles extracted from the high-resolution HST/STIS image by Schneider et al. (2014). In their Fig. 39, the surface brightness is given for both sides of the disc, along with their exponentional fits. We averaged both fits and converted the flux from mJy/arcsec2 to mag/arcsec2 using the zero-point magnitude flux of 3671 Jy and then subtracted a stellar V-band brightness of 8.837 mag according to Table 1 in Schneider et al. (2014). The resulting V-band profile was found to be in good agreement with the Fitzgerald et al. (2007) data.
Figure 4 depicts the modelled and observed V- and H-band profiles, as well as the disc colour, V − H. All models show significant deviations from the surface brightness data in both bands. Although roughly reproducing the observed slopes for b< 40 au, the synthetic profiles are steeper beyond, which is the halo zone, but get shallower with increasing stellar wind strength there. In terms of V − H, the SW0 and SW50 discs appear slightly blueish (V − H< 0), whereas the SW300 disc is red (V − H> 0), which completely disagrees with the observations. These effects are mainly due to the distribution of small grains in the disc. Increasing the stellar wind strength pushes more small particles into the halo zone (Fig. 2) and helps to enhance the scattered light flux beyond 40 au, thus approaching the observed level. However, the blowout size also increases, and the whole disc becomes more and more populated by larger particles that are stronger scatterers at longer wavelengths. The disc colour V − H therefore switches to red for winds that are too strong, clearly conflicting with the observational data.
Next, we considered the degree of linear polarisation, given by
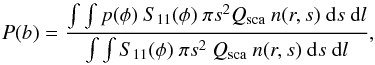 (3)where p(φ) is
the linear polarisation of a single particle. If P(b) is
positive (negative), the scattered light is partially polarised perpendicular (parallel)
to the scattering plane, i.e. the plane containing the star, the dust grains, and the
observer.
(3)where p(φ) is
the linear polarisation of a single particle. If P(b) is
positive (negative), the scattered light is partially polarised perpendicular (parallel)
to the scattering plane, i.e. the plane containing the star, the dust grains, and the
observer.
As shown in Fig. 5, the observed monotonous increase in the degree of polarisation up to 80 au is roughly reproduced by SW50 alone. In run SW300, the halo region is dominated by particles of ≈0.5 μm in size which are about one order of magnitude larger than in SW50. Their polarisation p(φ) strongly oscillates with the scattering angle. Accordingly, the polarisation integrated over a range of scattering angles along the line of sights tends to average to low values, and P(b) does not rise with distance. For SW0, P(b) increases up to the planetesimal belt as observed, but then decreases beyond.
 |
Fig. 5 Degree of polarisation as a function of projected distance. Squares and triangles are measurements for the SE and NW ansae, respectively (Graham et al. 2007). The double-dotted green line was obtained with the Henyey-Greenstein model of Graham et al. (2007), whereas the other lines are results from Mie theory. |
Although SW50 fits the measured degree of polarisation best, the data are markedly
overestimated by this model for b< 40 au. This is caused by particles dragged
from the parent belt to the inner zone. Graham et al.
(2007) and Fitzgerald et al. (2007)
conclude that the inner disc region has to be relatively free of scattering grains,
resulting in a low normal optical depth to scattering,
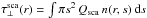 . In V band, SW50 gives
. In V band, SW50 gives
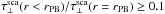 , which is at least two orders of
magnitude greater than the limit found by Graham et al.
(2007) and Fitzgerald et al. (2007).
However, owing to strong stellar winds, the inward transport of a significant amount of
dust is a natural outcome in the dynamical evolution of the outer planetesimal belt.
Even if planets exist at r<rPB, small
particles come through, because only slower, bigger particles can be efficiently
scattered by planets or get trapped in mean-motion resonances (e.g., Reidemeister et al. 2011; Shannon et al. 2015). It is important to note that the deviations in
the model from the data may be caused by the assumption of spherical dust grains. Real
particle shapes significantly deviate from spheres because the bodies underwent a rich
accretional and collisional history. While effective medium Mie spheres provide a good
approximation to the total scattering cross sections of irregular particles, they cannot
reproduce the scattering phase function and polarisation of such grains (Shen et al. 2008, 2009). As a result, Mie theory fails to reproduce the scattered light
observations as recently shown for HR 4796 A (Milli et
al. 2015; Perrin et al. 2015). In a
study of the HD 181327 disc, Stark et al. (2014)
also found an empirical scattering phase function, which is not fully reproducible with
Mie theory, indicating strongly forward scattering grains. Thus, if the AU Mic disc is
populated by similar particles, our models will fit the scattered light measurements
poorly by using Mie theory.
, which is at least two orders of
magnitude greater than the limit found by Graham et al.
(2007) and Fitzgerald et al. (2007).
However, owing to strong stellar winds, the inward transport of a significant amount of
dust is a natural outcome in the dynamical evolution of the outer planetesimal belt.
Even if planets exist at r<rPB, small
particles come through, because only slower, bigger particles can be efficiently
scattered by planets or get trapped in mean-motion resonances (e.g., Reidemeister et al. 2011; Shannon et al. 2015). It is important to note that the deviations in
the model from the data may be caused by the assumption of spherical dust grains. Real
particle shapes significantly deviate from spheres because the bodies underwent a rich
accretional and collisional history. While effective medium Mie spheres provide a good
approximation to the total scattering cross sections of irregular particles, they cannot
reproduce the scattering phase function and polarisation of such grains (Shen et al. 2008, 2009). As a result, Mie theory fails to reproduce the scattered light
observations as recently shown for HR 4796 A (Milli et
al. 2015; Perrin et al. 2015). In a
study of the HD 181327 disc, Stark et al. (2014)
also found an empirical scattering phase function, which is not fully reproducible with
Mie theory, indicating strongly forward scattering grains. Thus, if the AU Mic disc is
populated by similar particles, our models will fit the scattered light measurements
poorly by using Mie theory.
In an additional test, we aimed at illustrating the effect when deviating from the Mie sphere dust model. To this end, we adapted the Graham et al. (2007) best-fit Henyey-Greenstein (HG) model for S11(φ) and p(φ), and recomputed the V-band surface brightness profile and the degree of polarisation for SW50 (Figs. 4b and 5). We note that S11(φ) and p(φ) of the HG model are independent of grain size. Thus, all disc objects have the same scattering properties. The new synthetic V-band profile fits the absolute values of the surface brightness flux better for b< 40 au, whereas the degree of polarisation rises too steeply in that range. Reasons for this behaviour can be identified by comparing the S11(φ) and p(φ) predicted by Mie theory and the HG model (Fig. 6). The HG phase function is distinctly broader than for Mie spheres with s> 0.5μm. That is why bigger particles can scatter more light towards the observer that leads to the V-band flux enhancement for b< 40 au as shown in Fig. 4b. Beyond 40 au, only small particles are present and the HG profile resembles the one for the Mie spheres.
However, the HG model shows strong deviations from the observed degree of polarisation, which is attributable to the form of the polarisation curve as a function of scattering angle (Fig. 6). The maximum of the polarisation occurs at φmax = 90°, so that the main contribution to the polarised light comes from particles with distances from the star nearly equal to their projected distances (r ≈ b). The φmax of the Mie sphere polarisation functions strongly vary with s. This agrees with the trends found for irregularly shaped particles (Shen et al. 2009). With such shifts in φmax, the polarised light at a certain b mainly stems from particles at r>b. Furthermore, irregular grains smaller than 0.1 μm tend to be weaker polarisers than Mie spheres in the same size range. Both may help to generate a shallower increase in the degree of polarisation with projected distance. Thus, the consideration of irregular particles in the scattered light analysis seems to be an attractive possibility for mitigating the deviations between the observed and modelled degree of polarisation.
 |
Fig. 6 Normalised scattering phase function (top) and polarisation (bottom) vs. scattering angle in V band. Solid black lines have been inferred by Graham et al. (2007) via a Henyey-Greenstein model. The coloured lines are for Mie spheres with radii s, made of material M1. |
 |
Fig. 7 Influence of the dust composition on the SED (left) and the
degree of polarisation (right). The material names
M1−M4 are explained
in Table 2. For better comparison of the
SED models, |
In summary, all our models have a large amount of material in small grains within the parent belt in contrast to what was found in previous studies and none of our models provides good fits to the scattered light data. There are two ways to interpret this result: (1) our models may predict the actual dust distribution in the disc well, but Mie theory is not valid for simulating the scattering properties of the grains. Then, our analysis shows a preference for a scattered light model where the grains are weaker polarisers than Mie spheres with polarisation maxima at scattering angles different from 90°. (2) Mie theory is an appropriate technique for scattered light analysis, but there are shortcomings with respect to the dust density derived in the collisional modelling. The truth may also be a combination of (1) and (2). A consideration of point (1) goes along with the simulation of the emission from irregular particles, which is beyond the scope of this work. Thus in the following, we consider only point (2) in more detail. Since the scenario SW50 is found to be in best agreement with the data amongst the three stellar wind strengths tested, we consider SW50 a reference model, which is the starting point for further individual parameter variations influencing the dust distribution.
4.2. Material composition
The chemical composition of the AU Mic disc might be similar to discs around other BPMG stars because they have formed in the same molecular cloud from the same material and are coeval. However, the disc objects are heavily processed during the debris disc and preceding protoplanetary disc phases. Thus, their composition may depend on the mass and luminosity of the host star. Circumstellar dust compositions for some BMPG members have already been analysed previously. Smith et al. (2009) and Churcher et al. (2011) considered grains with a silicate core and a mantle of organic refractories for SED modelling in the η Tel and HD 191089 systems. They point out that particles with small silicate cores and a porosity of 20% (η Tel) and 60% (HD 191089) provide good fits to the observed excesses. A similar model that incorporates porous core-mantle silicate grains, additionally covered by ice in the outer region of the disc, also reproduces the β Pic observations (Pantin et al. 1997; Li & Greenberg 1998; Augereau et al. 2001). Lebreton et al. (2012) tested various chemical compositions for the debris around HD 181327. They find that the SED is mostly consistent with grains consisting of amorphous silicate and carbonaceous material with a dominant fraction of ice. In addition, the particles have to have a porosity of 65%.
The material composition affects the dust distribution and the SED by changing β and the dust temperature, Td (e.g., Kirchschlager & Wolf2013 for the influence of porosity on β and Td). We now depart from the mixture M1, which was used in our reference run SW50, to assess whether other materials can be viable for the AU Mic system. We repeated the simulation with the compositions M2, M3, and M4 explained in Table 2 and investigated modifications to observables (Fig. 7).
The material M2 represents compact particles composed of silicate and carbon. For these, we found a shift of the SED towards shorter wavelengths that deteriorates the fit in the submillimetre to radio range. In M3 and M4, we also included water ice. All constituents are present in equal volume fractions in M3, whereas the porosity and ice fraction are increased in M4. M3 is in fairly good agreement with the observed photometry, only tending to underestimate the near-IR excess. The icier and more porous M4 produces an SED whose peak position remains rather unchanged but increases and decreases more steeply. This narrower SED distinctly disagrees with the near-IR and submillimetre measurements.
No large differences in terms of the degree of polarisation are noticeable for M1, M2, and M3, whereas M4 markedly underestimates the data. The latter gives evidence that the material must not be too icy and porous. Modelling the degree of polarisation is possibly affected by limitations in the Mie theory (see Sect. 4.1.2) that do not allow us to find strong constraints for the upper limit of the ice and vacuum content.
We noticed little changes in the radial profile at 1.3 mm for all materials considered. This is caused by two characteristics of large grains, dominating the long-wavelength emission. First, large grains are weakly affected by stellar radiation and stellar winds, and their spatial distribution is equal for different materials. Second, the dust temperature approaches the blackbody temperature with increasing particle size at a given distance (e.g., Fig. 5 of Pawellek et al. 2014). Therefore, Td is nearly independent of the chemical composition for large grain sizes.
All in all, the SED and the degree of polarisation seem to be consistent with materials having a small fraction of ice and a moderate porosity.
 |
Fig. 8 SED models for different values of the maximum eccentricity, emax, of the planetesimals orbits. |
4.3. Dynamical planetesimal excitation
The maximum eccentricity of the planetesimals, emax, represents the disc’s dynamical excitation since this parameter affects the impact velocities of the objects, hence the number of small grains produced in collisions. In addition to the reference model with emax = 0.03, we considered emax = 0.01, a low value corresponding to the expected maximum level of pre-stirred discs (Matthews et al. 2014, and references therein), and emax = 0.1, a high value representing the dynamical excitation in the Edgeworth-Kuiper belt (e.g., Vitense et al. 2010). The resulting SEDs are shown in Fig. 8.
 |
Fig. 9 Influence of the planetesimal belt width, ΔrPB, on a) the SED, b) the 1.3 mm radial profile, c) the V- and H-band profiles, and d) the degree of polarisation. The filled patterns in panel b) depict the location and the radial width of the planetesimal belts (black-hatched 5 au, red-shaded 17 au). The profiles were vertically scaled by 1.7 (ΔrPB = 5 au) and 1.5 (ΔrPB = 17 au) to compensate for the modelling imperfections mentioned in Sect. 4.1.1. |
Increasing emax favours the production of small particles and shifts the SED maximum to shorter wavelengths. Thus, the model with emax = 0.1 agrees well with the excess data at λ< 70μm, but completely fails to reproduce the ones at longer wavelengths. In contrast, emax = 0.01 provides a good match to the photometry beyond 100 μm, but strongly deviates from the measurements at λ ≤ 70 μm. Improvements may be possible by additional variations in other parameters. For instance, shifting the planetesimal belt inwards (outwards) increases (decreases) the dust temperature and helps to find a better SED fit for emax = 0.01 (emax = 0.1). However, any significant rPB-shift would result in stronger deviations from the ALMA 1.3 mm profile, which constrains the location of a narrow planetesimal belt at around 40 au. Another possibility would be broadening the SED towards shorter wavelengths for emax = 0.01. This can be achieved by stronger stellar winds as depicted in Fig. 2. However, stronger winds also lead to an increase in the blowout size, and therefore, it is more difficult to reproduce the observed blue disc colour (Sect. 4.1.2). Furthermore, other dust materials may have a positive effect on the SEDs. None of the materials investigated in Sect. 4.2 strengthens the submillimetre flux density, as required to improve the SED for emax = 0.1. Only one composition – the non-porous M2 material – predicts a stronger mid-IR emission from which the low-emax model would benefit, but this material agrees less with the scattered light measurements. In summary, the reference run with emax = 0.03 matches the entire SED the best. Although values higher or lower than 0.03 seem to be unlikely, they cannot be ruled out completely if combined with other parameters, which was not explored here.
An observational constraint on the dynamical excitation can be put by the vertical thickness of the disc through the equilibrium condition i = e/ 2, where i and e are the orbital inclinations and eccentricities of the disc particles. Thus, measuring the disc’s opening angle at long wavelengths hints at the maximum eccentricity of the planetesimals. However, the AU Mic disc is vertically unresolved in the SMA and ALMA images (Wilner et al. 2012; MacGregor et al. 2013), which gives only upper limits of the disc extent in this direction. We compared synthetic vertical profiles of our emax = 0.1 model with the ones extracted from the ALMA image. The modelled profiles are marginally consistent with the ALMA data, which constrains the disc’s semi-opening angle to imax ≲ emax/ 2 = 0.05. Interestingly, Krist et al. (2005) and Metchev et al. (2005) derived imax = 0.04−0.07 from visible and near-IR images. Reading off the vertical scale height from the Schneider et al. (2014) high-resolution STIS image gives imax = 0.03. Thus, the observations yield a maximum eccentricity emax = 0.06−0.14 that is excluded by our modelling. Resolving this contradiction may be possible if the vertical disc thickness seen in short-wavelength images does not necessarily point towards the dynamical state of the planetesimals. Thébault (2009) propose a possibility that the AU Mic disc develops a vertical thickness close to the observed value in the visible and near-IR, although the disc is dynamically cold. In that model, the smallest grains have high in-plane velocities due to radiation and stellar wind pressure, and these velocities are partially converted into vertical ones in collisions with other particles. As a consequence, the disc becomes naturally thicker even without the gravitational perturbation of large, massive embedded bodies. In equilibrium, the disc has a large vertical dispersion of the smallest grains, whereas large particles remain close to the midplane. Thus, a low emax, as preferred in our collisional modelling, can be consistent with the observed vertical disc thicknesses at short wavelengths.
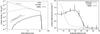 |
Fig. 10 Left: time evolution of the surface density in an extended planetesimal disc (ΔrPB ≈ 45 au). The wavy structures of the Σ-curves are numerical artefacts. For the sake of comparison, the straight line shows the Σ-slope derived by MacGregor et al. (2013). Right: time evolution of the 1.3 mm profile along with the ALMA data. The 0.01 Myr surface brightness profile was scaled by a factor of 0.05 for better visibility. |
4.4. Planetesimal belt width
4.4.1. 17 au-wide belt
As noted in Sect. 4.1.1, the outer edge of the planetesimal belt is well constrained by the ALMA profile. However, the edge-on orientation of the disc and the limited information on the innermost regions affected by the bright central source of unknown nature make the position of the inner edge of the disc, hence the disc extent, very uncertain. In another test, we increased the planetesimal belt width from ΔrPB = 5 au (reference model) to ΔrPB = 17 au by shifting the inner edge to 25.5 au while keeping the outer edge at 42.5 au. The initial surface density was assumed to be constant over the belt width. Figure 9 compares the 17 au-wide belt scenario with the reference model.
The broader planetesimal belt has nearly the same SED as in the reference run and does not increase the warm emission, although the dust production zone is more extended towards the star. The 1.3 mm profile of the 17 au-wide belt peaks closer to the star than for the reference model. Thus, it tends to underestimate the observed surface brightness farther out. This shortcoming does not hint at any implausibility of a broader planetesimal belt model since it can easily be compensated by shifting the outer edge from 42.5 au outwards. Although the broader belt scenario matches the V-band profile better than the reference run does, the degree of polarisation shows stronger deviations which may be attributed to the light scattering model (Sect. 4.1.2).
4.4.2. 44 au-wide belt
We now address the possibility that the AU Mic disc was populated by planetesimals over a wide range of distances. In such a disc, the innermost planetesimals have the shortest collisional lifetimes and are depleted within a few Myr, resulting in a surface density increasing outwards (Kennedy & Wyatt 2010). The inside-out erosion of objects means that an extended planetesimal disc may look like a narrow belt in long-wavelength observations, even if there are no planets within the disc that have swept up the inner region. In their study of the collisional evolution of a fiducial, 100 au-wide disc, Thébault & Augereau (2007) confirm that the surface brightness peaks at (sub)millimetre wavelengths close to the outer edge of the planetesimal distribution after several Myr. Thus, the extended-disc scenario is an auspicious alternative for explaining the rising ALMA profile up to projected distances of about 30 au in the AU Mic system. The significant fall beyond 30 au may mark the point beyond which planetesimals have not formed at all or where the disc was truncated.
To assess the feasibility of this scenario, we started an ACE simulation with a broad radial distribution of planetesimals from 1 to 45 au. Here we have already accounted for a slight shift in the outer edge from the reference value 42.5 au to 45 au, as suggested in Sect. 4.4.1. The run was initialised with a solid surface density given by the minimum mass solar nebula (MMSN) model, Σ ∝ r-1.5. We considered bodies up to 100 m in radius and assumed pre-stirred planetesimals with emax = 0.03 (Sect. 4.3).
Figure 10 depicts the evolution of the surface density and the 1.3 mm profile. The surface density quickly dropped close to the star owing to particle erosion, and the initially negative slope (−1.5) switched to a positive slope in a few ten thousand years. The particles’ collisional lifetimes were shorter than their orbital periods at the beginning of the simulation because of the high particle density at that phase. Thus, two consecutive collisions of one object are correlated, and the orbit averaging method, implemented in ACE, is a crude approximation for determining the phase space density. The results for the first one hundred thousand years of simulation time should therefore be treated with caution.
Owing to the progressive inside-out depletion of the planetesimals, the maximum of the 1.3 mm profile moved towards longer distances as time elapses. After 3 Myr, we noticed that the profile peak reached a maximum distance of about 30 au, which is in good agreement with the ALMA data. The absolute flux level of the observed dust emission was reproduced after 29 Myr. The final run fits the SED, the scattered light profiles, and the degree of polarisation with nearly the same fidelity as the 17 au-wide belt model (Sect. 4.4.1).
The collisional evolution of the disc was artificially shortened since the largest bodies in the disc had been 100 m in size. If the disc contains larger bodies, the inside-out planetesimal depletion is slower and the disc needs more time to reach the collisional equilibrium (Löhne et al. 2008). As a result, it takes longer than 3 Myr to reach the observed shape of the 1.3 mm profile. This way, scaling the model to the proper age of the system is possible. However, we refrained from further simulations, because of the numerical complexity of the extended planetesimal disc simulation1. The run presented here illustrates the feasibility of an extended planetesimal disc scenario sufficiently well.
5. Unresolved central emission
In Sect. 4, we did not care about the nature of the inner unresolved component and assumed its contribution to the flux densities at all wavelengths to be negligible. However, this may not be true if the unresolved central emission originates in an inner dust ring. The dust there would be much warmer than in the outer disc and would emit significantly at short wavelengths, while adding little flux in the mm range. We now consider the possibility of an additional inner planetesimal ring in the AU Mic system. If such a ring existed, we should also investigate its consequences for the modelling of the resolved outer disc, as discussed in Sect. 4.
A putative inner dust ring has to be six times brighter than the stellar photosphere at 1.3 mm (MacGregor et al. 2013, and Sect. 2.2 of this paper). Simultaneously, the ring has to emit weakly in the mid-IR in order not to contradict the measured excess there. Since an ALMA resolution of about 0.6′′ (≈6 au) was achieved, the ring should be located at distances ≲3 au to be compatible with remaining unresolved. We placed an inner planetesimal ring at rPB,in = 3 au, having a full width ΔrPB,in = 0.4 au, and assumed emax = 0.03 and 50 times the solar wind strength. We made sure that the ring emission did not exceed the excess shortwards of 24 μm and then investigated its emission at 1.3 mm. Figure 11 shows the results.
 |
Fig. 11 SEDs of the inner planetesimal rings centred at rPB,in = 3 au (width ΔrPB,in = 0.4 au) for the compositions M1, M3, and M5 (Table 2). Squares illustrate the photosphere-subtracted photometry. The black cross in the right lower corner shows the emission of the unresolved star-subtracted central component at 1.3 mm with 1σ uncertainty. The dashed line represents the M3 outer disc in Fig. 7 in combination with the M5 inner disc. |
First, we assumed two inner rings with M1 and M3 – materials we found suitable for the outer component (Sect. 4.2). Consistency with the short-wavelength excess was achieved with a maximum dust mass of ≈ 5 × 10-6M⊕. The rings are not bright enough to completely reproduce the central emission. Although M3 enhances the SED maximum, the long-wavelength slope is steeper and levels to nearly the same flux density at 1.3 mm as for M1. In another attempt, we considered highly porous grains (M5). This is motivated by the possibility that icy grains are produced beyond the ice line and then drift towards the star by drag forces. Accordingly, the particles get heated, and their sublimated ice fractions are replaced by vacuum inclusions, which increase the porosity. Assuming an ice sublimation temperature Tsubl = 100 K (e.g., Kobayashi et al. 2008) yields an iceline at rice = (L⋆/L⊙)0.5 (Tsubl/ 277 K)-2 au ≈ 2 au, which is close to rPB,in. The M5 material emits slightly more than M1 and M3 in the mm regime, but reproduces only about 60% of the observed central flux density. This constrains the maximum percentage of the central emission that can be explained by pure dust emission. Thus, the central emission must originate either totally or partially in another source. The star itself can contribute to the central emission, for instance, because of an active stellar corona (Cranmer et al. 2013). Furthermore, stars may emit more flux at long wavelengths than predicted by the purely photospheric models for their spectral class. ALMA observations of the G- and K-type stars α Cen A and B show a flux enhancement by 20−30% in Band 7 and almost doubling of the flux in Band 3 (Liseau et al. 2015). Provided such a trend continues to an M dwarf like AU Mic, we do expect a significant stellar contribution to the observed central emission.
To get the total SED, the inner ring should be combined with an appropriate model for the
outer disc. To avoid contradictions with the data, the outer disc has to emit less flux in
the mid-IR where the SED of the inner ring peaks. This is achieved by the M3 outer disc
(Sect. 4.2), and indeed, in combination with the M5
inner ring, the overall SED is reproduced well (Fig. 11). Furthermore, a combination of the icy material in the outer ring and iceless,
highly porous material in the inner ring is reasonable, as explained above. We adopted the
outer disc SED from the model described in Sect. 4.2
without any adjustments (e.g., vertical scaling) that one possibly expects owing to the
presence of the inner ring. Thus, even if the inner emission stems from dust, it seems to
barely affect the outer disc modelling. The 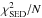 increases from 2.7 for the M3 outer disc to
3.3 for the combined M5 inner and M3 outer discs. The larger
increases from 2.7 for the M3 outer disc to
3.3 for the combined M5 inner and M3 outer discs. The larger
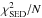 is mostly due to the deviation of the
inner+outer disc model from the Spitzer/MIPS 24 μm point. However, the
overestimated flux density at 24 μm may be counterbalanced by a modification of the
dust composition. As seen in Fig. 7, adding ice reduces
the flux in the mid-IR, while leaving it nearly unchanged at longer wavelengths. This
promises improvements if a material icier than M3 for the outer disc is used. We highlight
the small shift of the blowout size when going from iceless to icy grains (Table 2). Accordingly, the abundance of small grains will not
change significantly, still reproducing the scattered light data (Sect. 4.1.2).
is mostly due to the deviation of the
inner+outer disc model from the Spitzer/MIPS 24 μm point. However, the
overestimated flux density at 24 μm may be counterbalanced by a modification of the
dust composition. As seen in Fig. 7, adding ice reduces
the flux in the mid-IR, while leaving it nearly unchanged at longer wavelengths. This
promises improvements if a material icier than M3 for the outer disc is used. We highlight
the small shift of the blowout size when going from iceless to icy grains (Table 2). Accordingly, the abundance of small grains will not
change significantly, still reproducing the scattered light data (Sect. 4.1.2).
We stress that our two-component model does not account for the collisional interaction between inner and outer component which is mainly caused by two effects: (i) collisions of inner disc particles with inwards dragged grains from the outer disc and (ii) collisions between unbound particles produced in the inner ring with outer disc particles. By comparing the normal optical thicknesses of inner and outer components, including bound and unbound grains, we found τ⊥ ,out/τ⊥ ,in ~ 0.1 at 3 au and τ⊥ ,in/τ⊥ ,out ~ 0.001 at 40 au. Thus, collisional interaction between both is weak, justifying our modelling strategy.
Power-law fitting results.
6. Comparison with parametric modelling
Collisional modelling allows us to explore only a small number of parameter combinations. Although the models we found reproduce the data satisfactorily, they are not unique, and better solutions may exist. To find an independent confirmation of the collisional modelling results, we additionally analysed the data with a multi-dimensional fitting approach. In that approach, the dust number density was assumed to be a combination of two independent power laws, representing the size and radial distribution of the grains. This model does not consider the physical mechanisms of the dust production and evolution. However, it is well suited to exploring a wide parameter space to find the most likely solutions that we compared with the collisional modelling results.
In the power-law model, the surface density follows rα between the inner and outer cut-off radii, Rin and Rout, while the grain size distribution follows sγ between the lower and upper cut-off grain sizes, smin and smax. The influence of smax is negligible for reasonably steep grain size distributions with γ< −3. We fixed smax to 2 mm. The dust mass Md is an additional free parameter. The disc inclination was fixed to θ = 90°. For the dust composition, we assumed compact, spherical grains composed of pure astronomical silicate (Draine 2003). This makes a total of eight free parameters, Rin, Rout, α, smin, γ, Md, the dust composition (sampled by only one value, namely 100% astronomical silicate), and the vertical scaling of the ALMA profile. For the fitting of the SED and the ALMA profile, we used the SAnD code (Ertel et al. 2012a; Löhne et al. 2012), which was originally developed for fitting simultaneously SED data and spatially resolved Herschel data as part of the Herschel/DUNES modelling tool box. We did not include the scattered light data for this power-law fitting.
In a first approach, we fitted the model to the data neglecting the contribution of the central component. The best-fit model (Table 4) reveals features we already found, at least qualitatively, by collisional modelling: an outward-increasing surface density with an index close to 2.8, a well-constrained outer disc radius at about 40 au, a small lower grain size <1 μm consistent with a moderate level of stellar winds, and a relatively shallow slope of the grain size distribution, γ = −3.3, indicating that small particles are more affected by transport than collisions. Furthermore, the results are widely consistent with earlier studies of the disc (Augereau & Beust 2006; MacGregor et al. 2013).
In a second approach, we assumed that the inner component is an additional ring of dust. The ring was placed at 2 au from the star with an extent of 0.2 au and a constant surface density, which is just compatible with being mostly unresolved by the ALMA observations. The lower grain size, smin,in, and the exponent, γin, of the size distribution for this inner component were explored by hand. The model was scaled to the flux density of the central component seen in the ALMA data. We found that a very large lower grain size, smin,in = 5μm, as well as a very flat grain size distribution, γin = −3, is necessary in order to keep the dust cold enough (the grains large enough) not to produce too much excess at mid- to far-IR wavelengths. It is important to note that this model serves to estimate the potential contribution of the unknown inner component, which is probably not a debris disc, to the SED. However, the fitting result, even the large lower grain size, might be consistent with a normal debris disc. A large smin,in is naturally expected if the grains do not experience a radiation pressure blowout limit as is the case for AU Mic. Then, the dominant or critical grain size, sc, is the one where collisional and transport lifetimes are equal, which can be reached at much larger sizes. Including the effect of stellar wind drag in Eq. (6) of Kuchner & Stark (2010) and assuming an optical depth of 10-3 at 3 au in accordance with our M5 inner ring model yields a critical size sc ≈ 3μm, which is not far from smin,in = 5μm.
In a final step, we subtracted the contribution of the inner ring from the SED data and re-fitted the remaining flux by the two-power-law model used for our first approach (Table 4, last column). Comparing with the previous results illustrates the uncertainties of our first approach. The values are almost all within the 3σ-confidence interval of the first fit. This demonstrates that the inner component marginally influences the modelling of the resolved outer disc, as already found by collisional modelling.
7. Conclusions
We have performed in-depth collisional modelling of the AU Mic debris disc for the first time. A wealth of observational data was considered, including the densely sampled spectral energy distribution, the ALMA 1.3 mm thermal emission profile, the scattered light profiles in V and H bands, and the degree of scattered light polarisation as a function of projected distance in the disc midplane. Our study presents the first attempt to reproduce scattered light observations of a debris disc with collisional modelling.
Our models provide generic radial and size distributions of the particles in the whole disc. However, the disc also possesses several substructures and asymmetries, such as bumps and warps (Liu 2004; Schneider et al. 2014) that may be caused by the perturbing effects of so far undetected planets. As our modelling technique is limited to axisymmetric discs, the formation of such disc properties was not considered in this work.
Most of the data can be reproduced with a narrow belt of planetesimals centred at about 40 au with strong inward transport of dust by stellar winds, according to the birth-ring scenario of Strubbe & Chiang (2006). For modelling the ALMA 1.3 mm profile, a significant scaling factor ≲2 was necessary. This mainly hints at the inability of our simulated dust distributions to fully reproduce the observed ALMA flux density. Additionally, the synthetic dust material used may underestimate the dust emissivity at mm wavelengths. We find a clear preference for a belt with a low dynamical excitation where the planetesimals orbits have a maximum eccentricity of 0.03. Our modelling allows us to make inferences on the stellar mass loss rate Ṁ⋆, which is a measure of the stellar wind strength. We can exclude extreme values of hundreds of the solar mass loss rate, Ṁ⊙, because these would cause strong deviations from the observed V − H and the degree of linear polarisation. The best model was achieved with Ṁ⋆ = 50 Ṁ⊙ that corresponds to the estimated wind strength during quiescent phases (Augereau & Beust 2006).
Owing to strong dust transport from the planetesimal belt towards the star induced by the stellar wind drag, the inner disc region is filled with small scattering grains, unlike what was derived previously (Graham et al. 2007; Fitzgerald et al. 2007). Significant deviations between the modelled and observed V − H and the degree of linear polarisation are visible. The problem may be mitigated by irregularly shaped grains that have scattering properties different from the Mie spheres used in this study. We find a preference for particles that are weaker polarisers than Mie spheres and that have polarisation maxima at scattering angles different from 90°. This again demonstrates the necessity of incorporating more realistic light scattering physics in simulations of resolved debris discs.
Our models support the presence of ice-containing particles of moderate porosity. As found by a comparison with other works, porous particles seem to be ubiquitous in discs around stars of the β Pic moving group.
The radial width of the plantesimal belt cannot be constrained tightly. Belts with radial extents of 5 and 17 au are consistent with the observations. Furthermore, we have addressed an alternative scenario with a very broad planetesimal belt, extended over 1−45 au. The belt was assumed to be populated with particles up to 100 m in size and to have an MMSN-like surface density with initial radial index of −1.5. The inside-out evolution of this belt resulted in a rising surface density with distance from the star and a 1.3 mm profile as observed by ALMA. The scenario explains the formation of an outer ring-like planetesimal distribution and would be preferred if the presence of planets that cleared up the inner disc region are not confirmed in the future.
We have shown that the unresolved central emission at 1.3 mm, first reported by MacGregor et al. (2013), cannot stem from an inner dust ring alone. An inner ring located at ≲3 au, which is compatible with being unresolved in the ALMA image, emits 60% of the observed central emission at most. We found a fractional luminosity ratio between inner and outer components of ~0.4, which is a typical value for a two-temperature disc system (Kennedy & Wyatt 2014). As suggested in MacGregor et al. (2013), future ALMA observations at higher resolution should be able to test the inner ring hypothesis. If confirmed, this might argue against the very extended belt scenario, based on the assumption that the inner planetesimals have not survived the inside-out collisional erosion of the disc. However, this assumption remains controversial because some models would explain the presence of an inner dust ring even after the collisional depletion of an extended outer ring. For example, the innermost particles of the extended planetesimal belt could be less icy, since they have a higher mechanical strength, and thus would resist the collisional grinding more strongly. This increases the chance to detect left-over particles from the depleted, originally extended planetesimal disc. Furthermore, cometary activity may play a crucial role in creating hot dust in the inner disc zone. All in all, because the central emission cannot be explained by dust emission alone, it fully or at least partly derives from the stellar chromosphere.
Our work provides a good indication of the probable generic architecture of the system, characterised by the spatial and size distributions of planetesimals and their collisionally-produced dust. All the models presented here are not unique because a full exploration of the parameter space by collisional modelling is impossible. However, we verified the consistency of the collisional modelling results with a multi-dimensional power-law fitting approach for the radial and size distributions of the dust. This reduces the chance that our collisional models are “exotic” solutions.
Acknowledgments
We thank the reviewer for speedy and constructive comments that helped to improve the manuscript. This paper makes use of the following ALMA data: ADS/JAO.ALMA#2011.0.00274.S and ADS/JAO.ALMA#2011.0.00142. ALMA is a partnership of ESO (representing its member states), NSF (USA), and NINS (Japan), together with NRC (Canada) and NSC and ASIAA (Taiwan), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO, and NAOJ. We thank J. Rodmann for his support during the proposal writing process. T.L., A.V.K., and S.W. acknowledge the support by the Deutsche Forschungsgemeinschaft (DFG) through projects Lo 1715/1-1, Kr 2164/10-1, and Wo 857/7-1. S.E. acknowledges financial support from the DFG under contract Wo 857/7-1 and from ANR under contract ANR-2010 BLAN-0505-01 (EXOZODI). J.P.M. is supported by a UNSW Vice-Chancellor’s Fellowship. M.C.W. acknowledges the support of the European Union through ERC grant number 279973.
References
- Augereau, J.-C., & Beust, H. 2006, A&A, 455, 987 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Augereau, J. C., Nelson, R. P., Lagrange, A. M., Papaloizou, J. C. B., & Mouillet, D. 2001, A&A, 370, 447 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ballering, N. P., Rieke, G. H., Su, K. Y. L., & Montiel, E. 2013, ApJ, 775, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Beichman, C. A., Neugebauer, G., Habing, H. J., Clegg, P. E., & Chester, T. J., 1988, Infrared astronomical satellite (IRAS) catalogs and atlases, Vol. 1, Explanatory supplement [Google Scholar]
- Benz, W., & Asphaug, E. 1999, Icarus, 142, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Biller, B. A., Liu, M. C., Wahhaj, Z., et al. 2013, ApJ, 777, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Binks, A. S., & Jeffries, R. D. 2014, MNRAS, 438, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Bohren, C. F., & Huffman, D. R. 1983, Absorption and scattering of light by small particles (New York: Wiley) [Google Scholar]
- Bruggeman, D. A. G. 1935, Annalen der Physik, 416, 636 [NASA ADS] [CrossRef] [Google Scholar]
- Burns, J. A., Lamy, P. L., & Soter, S. 1979, Icarus, 40, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, C. H., Patten, B. M., Werner, M. W., et al. 2005, ApJ, 634, 1372 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, C. H., Mittal, T., Kuchner, M., et al. 2014, ApJS, 211, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Churcher, L., Wyatt, M., & Smith, R. 2011, MNRAS, 410, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Cranmer, S. R., Wilner, D. J., & MacGregor, M. A. 2013, ApJ, 772, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Cutri, R. M., et al. 2012, VizieR Online Data Catalog, II, 311 [Google Scholar]
- Decin, G., Dominik, C., Waters, L. B. F. M., & Waelkens, C. 2003, ApJ, 598, 636 [NASA ADS] [CrossRef] [Google Scholar]
- Doering, R. L., Meixner, M., Ardila, D., & Clampin, M. 2005, in Protostars and Planets V Posters, 8432 [Google Scholar]
- Draine, B. T. 2003, ApJ, 598, 1017 [NASA ADS] [CrossRef] [Google Scholar]
- Eiroa, C., Marshall, J. P., Mora, A., et al. 2013, A&A, 555, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ertel, S., Wolf, S., Marshall, J. P., et al. 2012a, A&A, 541, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ertel, S., Wolf, S., & Rodmann, J. 2012b, A&A, 544, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ertel, S., Marshall, J. P., Augereau, J.-C., et al. 2014, A&A, 561, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fitzgerald, M. P., Kalas, P. G., Duchêne, G., Pinte, C., & Graham, J. R. 2007, ApJ, 670, 536 [NASA ADS] [CrossRef] [Google Scholar]
- Forbrich, J., Lada, C. J., Muench, A. A., & Teixeira, P. S. 2008, ApJ, 687, 1107 [NASA ADS] [CrossRef] [Google Scholar]
- France, K., Roberge, A., Lupu, R. E., Redfield, S., & Feldman, P. D. 2007, ApJ, 668, 1174 [NASA ADS] [CrossRef] [Google Scholar]
- Gautier, III, T. N., Rieke, G. H., Stansberry, J., et al. 2007, ApJ, 667, 527 [NASA ADS] [CrossRef] [Google Scholar]
- Graham, J. R., Kalas, P. G., & Matthews, B. C. 2007, ApJ, 654, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Griffin, M. J., Abergel, A., Abreu, A., et al. 2010, A&A, 518, L3 [Google Scholar]
- Gustafson, B. A. S. 1994, Ann. Rev. Earth Planet. Sci., 22, 553 [Google Scholar]
- Hebb, L., Petro, L., Ford, H. C., et al. 2007, MNRAS, 379, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Henyey, L. G., & Greenstein, J. L. 1941, ApJ, 93, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Houdebine, E. R., & Doyle, J. G. 1994, A&A, 289, 185 [NASA ADS] [Google Scholar]
- Ishihara, D., Onaka, T., Kataza, H., et al. 2010, A&A, 514, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johnstone, C. P., Güdel, M., Brott, I., & Lüftinger, T. 2015a, A&A, 577, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johnstone, C. P., Güdel, M., Lüftinger, T., Toth, G., & Brott, I. 2015b, A&A, 577, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kains, N., Wyatt, M. C., & Greaves, J. S. 2011, MNRAS, 414, 2486 [NASA ADS] [CrossRef] [Google Scholar]
- Kalas, P., Liu, M. C., & Matthews, B. C. 2004, Science, 303, 1990 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kennedy, G. M., & Wyatt, M. C. 2010, MNRAS, 405, 1253 [NASA ADS] [Google Scholar]
- Kennedy, G. M., & Wyatt, M. C. 2014, MNRAS, 444, 3164 [NASA ADS] [CrossRef] [Google Scholar]
- Kirchschlager, F., & Wolf, S. 2013, A&A, 552, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kobayashi, H., Watanabe, S.-i., Kimura, H., & Yamamoto, T. 2008, Icarus, 195, 871 [NASA ADS] [CrossRef] [Google Scholar]
- Kral, Q., Thébault, P., Augereau, J.-C., Boccaletti, A., & Charnoz, S. 2015, A&A, 573, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krist, J. E., Ardila, D. R., Golimowski, D. A., et al. 2005, AJ, 129, 1008 [NASA ADS] [CrossRef] [Google Scholar]
- Krivov, A. V., Löhne, T., & Sremčević, M. 2006, A&A, 455, 509 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krivov, A. V., Müller, S., Löhne, T., & Mutschke, H. 2008, ApJ, 687, 608 [NASA ADS] [CrossRef] [Google Scholar]
- Krivov, A. V., Eiroa, C., Löhne, T., et al. 2013, ApJ, 772, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Kuchner, M. J., & Stark, C. C. 2010, AJ, 140, 1007 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J. 2006, ApJ, 640, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Lebreton, J., Augereau, J.-C., Thi, W.-F., et al. 2012, A&A, 539, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lestrade, J.-F., Wyatt, M. C., Bertoldi, F., Dent, W. R. F., & Menten, K. M. 2006, A&A, 460, 733 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lestrade, J.-F., Wyatt, M. C., Bertoldi, F., Menten, K. M., & Labaigt, G. 2009, A&A, 506, 1455 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lestrade, J.-F., Matthews, B. C., Sibthorpe, B., et al. 2012, A&A, 548, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, A., & Greenberg, J. M. 1998, A&A, 331, 291 [NASA ADS] [Google Scholar]
- Liseau, R., Vlemmings, W., Bayo, A., et al. 2015, A&A, 573, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liu, M. C. 2004, Science, 305, 1442 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, M. C., Matthews, B. C., Williams, J. P., & Kalas, P. G. 2004, ApJ, 608, 526 [NASA ADS] [CrossRef] [Google Scholar]
- Löhne, T., Krivov, A. V., & Rodmann, J. 2008, ApJ, 673, 1123 [NASA ADS] [CrossRef] [Google Scholar]
- Löhne, T., Augereau, J.-C., Ertel, S., et al. 2012, A&A, 537, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- MacGregor, M. A., Wilner, D. J., Rosenfeld, K. A., et al. 2013, ApJ, 762, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Makarov, V. V. 2007, ApJS, 169, 105 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Malo, L., Doyon, R., Feiden, G. A., et al. 2014, ApJ, 792, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Mamajek, E. E., & Bell, C. P. M. 2014, MNRAS, 445, 2169 [NASA ADS] [CrossRef] [Google Scholar]
- Masciadri, E., Mundt, R., Henning, T., Alvarez, C., & Barrado y Navascués, D. 2005, Mem. Soc. Astron. It., 76, 416 [NASA ADS] [Google Scholar]
- Matthews, B. C., Krivov, A. V., Wyatt, M. C., Bryden, G., & Eiroa, C. 2014, in Protostars and Planets VI, eds. H. Beuther, R. Klessen, C. Dullemond, & T. Henning (Univ. of Arizona Press), 521 [Google Scholar]
- McMullin, J. P., Waters, B., Schiebel, D., Young, W., & Golap, K. 2007, in Astronomical Data Analysis Software and Systems XVI, eds. R. A. Shaw, F. Hill, & D. J. Bell, ASP Conf. Ser., 376, 127 [Google Scholar]
- Metchev, S. A., Eisner, J. A., Hillenbrand, L. A., & Wolf, S. 2005, ApJ, 622, 451 [NASA ADS] [CrossRef] [Google Scholar]
- Milli, J., Mawet, D., Pinte, C., et al. 2015, A&A, 577, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morales, F. Y., Rieke, G. H., Werner, M. W., et al. 2011, ApJ, 730, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Moshir, M., Kopan, G., Conrow, T., et al. 1990, in BAAS, 22, 1325 [Google Scholar]
- Müller, S., Löhne, T., & Krivov, A. V. 2010, ApJ, 708, 1728 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvold, E. R., & Kuchner, M. J. 2015, ApJ, 798, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Neuhäuser, R., Guenther, E. W., Alves, J., et al. 2003, Astron. Nachr., 324, 535 [NASA ADS] [CrossRef] [Google Scholar]
- Ott, S. 2010, in Astronomical Data Analysis Software and Systems XIX, eds. Y. Mizumoto, K.-I. Morita, & M. Ohishi, ASP Conf. Ser., 434, 139 [Google Scholar]
- Pagano, I., Linsky, J. L., Carkner, L., et al. 2000, ApJ, 532, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Pantin, E., Lagage, P. O., & Artymowicz, P. 1997, A&A, 327, 1123 [NASA ADS] [Google Scholar]
- Pawellek, N., Krivov, A. V., Marshall, J. P., et al. 2014, ApJ, 792, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Perrin, M. D., Duchene, G., Millar-Blanchaer, M., et al. 2015, ApJ, 799, 182 [Google Scholar]
- Perryman, M. A. C., Lindegren, L., Kovalevsky, J., et al. 1997, A&A, 323, L49 [NASA ADS] [Google Scholar]
- Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
- Plavchan, P., Jura, M., & Lipscy, S. J. 2005, ApJ, 631, 1161 [NASA ADS] [CrossRef] [Google Scholar]
- Plavchan, P., Werner, M. W., Chen, C. H., et al. 2009, ApJ, 698, 1068 [NASA ADS] [CrossRef] [Google Scholar]
- Poglitsch, A., Waelkens, C., Geis, N., et al. 2010, A&A, 518, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rebull, L. M., Stapelfeldt, K. R., Werner, M. W., et al. 2008, ApJ, 681, 1484 [NASA ADS] [CrossRef] [Google Scholar]
- Reidemeister, M., Krivov, A. V., Stark, C. C., et al. 2011, A&A, 527, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roberge, A., Weinberger, A. J., Redfield, S., & Feldman, P. D. 2005, ApJ, 626, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Robinson, R. D., Linsky, J. L., Woodgate, B. E., & Timothy, J. G. 2001, ApJ, 554, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, P. C., & Schmitt, J. H. M. M. 2010, A&A, 516, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, G., Grady, C. A., Hines, D. C., et al. 2014, AJ, 148, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Schüppler, C., Löhne, T., Krivov, A. V., et al. 2014, A&A, 567, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shannon, A., Mustill, A. J., & Wyatt, M. 2015, MNRAS, 448, 684 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, Y., Draine, B. T., & Johnson, E. T. 2008, ApJ, 689, 260 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, Y., Draine, B. T., & Johnson, E. T. 2009, ApJ, 696, 2126 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R., Churcher, L. J., Wyatt, M. C., Moerchen, M. M., & Telesco, C. M. 2009, A&A, 493, 299 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stark, C. C., Schneider, G., Weinberger, A. J., et al. 2014, ApJ, 789, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Strubbe, L. E., & Chiang, E. I. 2006, ApJ, 648, 652 [NASA ADS] [CrossRef] [Google Scholar]
- Su, K. Y. L., Rieke, G. H., Stansberry, J. A., et al. 2006, ApJ, 653, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Swinyard, B. M., Ade, P., Baluteau, J.-P., et al. 2010, A&A, 518, L4 [Google Scholar]
- Thébault, P. 2009, A&A, 505, 1269 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thébault, P., & Augereau, J.-C. 2007, A&A, 472, 169 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thébault, P., & Wu, Y. 2008, A&A, 481, 713 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Theissen, C. A., & West, A. A. 2014, ApJ, 794, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Thureau, N. D., Greaves, J. S., Matthews, B. C., et al. 2014, MNRAS, 445, 2558 [NASA ADS] [CrossRef] [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vitense, C., Krivov, A. V., & Löhne, T. 2010, A&A, 520, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wilner, D. J., Andrews, S. M., MacGregor, M. A., & Hughes, A. M. 2012, ApJ, 749, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, E. L., Eisenhardt, P. R. M., Mainzer, A. K., et al. 2010, AJ, 140, 1868 [NASA ADS] [CrossRef] [Google Scholar]
- Wyatt, M. C., Smith, R., Su, K. Y. L., et al. 2007, ApJ, 663, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Wyatt, M. C., Clarke, C. J., & Booth, M. 2011, Celestial Mech. Dyn. Astron., 111, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Zubko, V. G., Mennella, V., Colangeli, L., & Bussoletti, E. 1996, MNRAS, 282, 1321 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 β-ratio for different assumptions of AU Mic’s stellar mass loss rate Ṁ⋆. The material consists of 33% carbon, 33% silicate, and 33% vacuum (M1). The horizontal dashed line depicts β = 0.5. Particles with β> 0.5 are ejected from the system owing to radiation and stellar wind pressure. |
| In the text | |
 |
Fig. 2 Disc models of narrow planetesimal belts centred at 40 au with different assumptions
for the stellar wind (SW) strength (from left to right
Ṁ⋆ = 0,50,300
Ṁ⊙). a)−c): SEDs. Crosses show
photometric data and squares star-subtracted photometric data. The dashed lines depict
the stellar photosphere, the dash-dotted lines the disc emission, and the solid lines
the star+disc emission. The |
| In the text | |
 |
Fig. 3 ALMA radial surface brightness profile at 1.3 mm (dots) vs. models (lines). Synthetic profiles are multiplied by the factors given in the legend to compensate for imperfections in the modelling procedure (explained in the text). |
| In the text | |
 |
Fig. 4 Scattered light profiles of the AU Mic disc. a)−c): blue and red lines show synthetic midplane surface brightness profiles in V and H band relative to the stellar brightness for the disc models SW0, SW50, and SW300 (Sect. 4.1). Curves labelled with Mie in the legend were calculated with scattering phase functions obtained by means of Mie theory. The blue double-dotted line in panel b) depicts the V-band profile generated with the best-fit Henyey-Greenstein (HG) phase function model of Graham et al. (2007). Dots represent measurements with 1σ errors from Fitzgerald et al. (2007), abbreviated as F07, averaged over the SE and NW wings (circles for V band, squares for H band). The black dashed line shows the averaged V-band fit to both wings obtained by Schneider et al. (2014), abbreviated as S14. d)−f): observed and modelled colour profiles, V − H, obtained with the F07 data and the Mie profiles shown in panels a)−c). |
| In the text | |
 |
Fig. 5 Degree of polarisation as a function of projected distance. Squares and triangles are measurements for the SE and NW ansae, respectively (Graham et al. 2007). The double-dotted green line was obtained with the Henyey-Greenstein model of Graham et al. (2007), whereas the other lines are results from Mie theory. |
| In the text | |
 |
Fig. 6 Normalised scattering phase function (top) and polarisation (bottom) vs. scattering angle in V band. Solid black lines have been inferred by Graham et al. (2007) via a Henyey-Greenstein model. The coloured lines are for Mie spheres with radii s, made of material M1. |
| In the text | |
 |
Fig. 7 Influence of the dust composition on the SED (left) and the
degree of polarisation (right). The material names
M1−M4 are explained
in Table 2. For better comparison of the
SED models, |
| In the text | |
 |
Fig. 8 SED models for different values of the maximum eccentricity, emax, of the planetesimals orbits. |
| In the text | |
 |
Fig. 9 Influence of the planetesimal belt width, ΔrPB, on a) the SED, b) the 1.3 mm radial profile, c) the V- and H-band profiles, and d) the degree of polarisation. The filled patterns in panel b) depict the location and the radial width of the planetesimal belts (black-hatched 5 au, red-shaded 17 au). The profiles were vertically scaled by 1.7 (ΔrPB = 5 au) and 1.5 (ΔrPB = 17 au) to compensate for the modelling imperfections mentioned in Sect. 4.1.1. |
| In the text | |
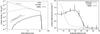 |
Fig. 10 Left: time evolution of the surface density in an extended planetesimal disc (ΔrPB ≈ 45 au). The wavy structures of the Σ-curves are numerical artefacts. For the sake of comparison, the straight line shows the Σ-slope derived by MacGregor et al. (2013). Right: time evolution of the 1.3 mm profile along with the ALMA data. The 0.01 Myr surface brightness profile was scaled by a factor of 0.05 for better visibility. |
| In the text | |
 |
Fig. 11 SEDs of the inner planetesimal rings centred at rPB,in = 3 au (width ΔrPB,in = 0.4 au) for the compositions M1, M3, and M5 (Table 2). Squares illustrate the photosphere-subtracted photometry. The black cross in the right lower corner shows the emission of the unresolved star-subtracted central component at 1.3 mm with 1σ uncertainty. The dashed line represents the M3 outer disc in Fig. 7 in combination with the M5 inner disc. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.