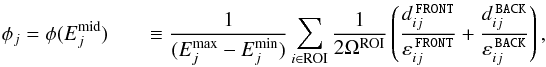| Issue |
A&A
Volume 581, September 2015
|
|
|---|---|---|
| Article Number | A126 | |
| Number of page(s) | 16 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201425172 | |
| Published online | 18 September 2015 | |
The denoised, deconvolved, and decomposed Fermi γ-ray sky⋆
An application of the D3PO algorithm
1
Max Planck Institut für Astrophysik,
Karl-Schwarzschild-Straße 1,
85748
Garching,
Germany
e-mail:
vvacca@mpa-garching.mpg.de
2
Ludwig-Maximilians-Universität München,
Geschwister-Scholl-Platz 1,
80539
München,
Germany
3
Canadian Institute for Theoretical Astrophysics,
60 St. George Street, Toronto,
ON
M5S 3H8,
Canada
Received: 17 October 2014
Accepted: 3 April 2015
We analyze the 6.5 year all-sky data from the Fermi Large Area Telescope that are restricted to γ-ray photons with energies between 0.6–307.2 GeV. Raw count maps show a superposition of diffuse and point-like emission structures and are subject to shot noise and instrumental artifacts. Using the D3PO inference algorithm, we modeled the observed photon counts as the sum of a diffuse and a point-like photon flux, convolved with the instrumental beam and subject to Poissonian shot noise. The D3PO algorithm performs a Bayesian inference without the use of spatial or spectral templates; that is, it removes the shot noise, deconvolves the instrumental response, and yields separate estimates for the two flux components. The non-parametric reconstruction uncovers the morphology of the diffuse photon flux up to several hundred GeV. We present an all-sky spectral index map for the diffuse component. We show that the diffuse γ-ray flux can be described phenomenologically by only two distinct components: a soft component, presumably dominated by hadronic processes, tracing the dense, cold interstellar medium, and a hard component, presumably dominated by leptonic interactions, following the hot and dilute medium and outflows such as the Fermi bubbles. A comparison of the soft component with the Galactic dust emission indicates that the dust-to-soft-gamma ratio in the interstellar medium decreases with latitude. The spectrally hard component exists in a thick Galactic disk and tends to flow out of the Galaxy at some locations. Furthermore, we find the angular power spectrum of the diffuse flux to roughly follow a power law with an index of 2.47 on large scales, independent of energy. Our first catalog of source candidates includes 3106 candidates of which we associate 1381 (1897) with known sources from the second (third) Fermi source catalog. We observe γ-ray emission in the direction of a few galaxy clusters hosting known radio halos.
Key words: methods: data analysis / methods: statistical / techniques: image processing / gamma rays: general / catalogs gamma rays: diffuse background
The results of this analysis (including full Table 3) are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/581/A126
© ESO, 2015
1. Introduction
Since August 2008, the Fermi Gamma-ray Space Telescope has observed the γ-ray sky with its main instrument, the Large Area Telescope (LAT, Atwood et al. 2009), which is sensitive to photons with energies ranging from around 20 MeV to above 300 GeV.
There is a diversity of astrophysical contributions to the total γ-ray flux. Most of the photons in the GeV-range are induced by cosmic rays (CRs), charged particles moving at (ultra-) relativistic speeds, through hadronic interactions of CR nuclei with the interstellar medium (ISM) or inverse Compton scattering (IC) of electrons with background light (Ackermann et al. 2012d; Dermer et al. 2013). In addition, there is emission from a spatially constant diffuse background, which is commonly denoted as “extragalactic” background (Dermer 2007, and references therein), and from sources that appear point-like.
The diffuse and point-like γ-ray fluxes appear superimposed to an observer. An observation through an instrument, like the Fermi LAT for example, additionally convolves the total flux with the instrument response functions (IRFs). The gathered data are, lastly, subject to noise, that is, Poissonian shot noise in the case of integer photon counts. To retrieve the physical photon flux from observations, we would need to reverse these processes. Unfortunately, neither a direct inversion of the convolution nor the separation of noise and signal components is feasible exactly, so that we have to resort to alternative approaches.
One possibility is forward modeling, whereby parametrized models of different emission components are fit to the data, for instance, by a maximum-likelihood procedure as suggested by Ackermann et al. (2008) for the analysis of Fermi LAT data. By inspection of residuals between the data and the best-fitting model(s), new features might be discovered. A famous example are the giant Fermi bubbles revealed by Su et al. (2010) using templates. Such templates are commonly constructed in accordance with surveys at lower energies or by modeling the relevant CR physics (Ackermann et al. 2008, 2012d, 2014b; Su et al. 2010; Su & Finkbeiner 2012, and references therein).
In this work, we investigate the backward reconstruction of flux contributions using Bayesian inference methods (Bayes 1763; Cox 1946; Shannon 1948; Wiener 1949). The idea is to obtain signal estimates (and uncertainties) from an algorithm based on a probabilistic model that denoises, deconvolves, and decomposes the input data. This probabilistic model includes prior constraints to remedy the complexity of the inverse problem. Assuming a sparsity-based regularization, for example, Schmitt et al. (2010, 2012) proposed an analysis strategy using waveforms, which they applied to simulated Fermi data. For the analysis of X-ray images, which pose the same challenges as γ-ray images, a Bayesian background-source separation technique was proposed by Guglielmetti et al. (2009).
We deploy the D3PO inference algorithm (Selig & Enßlin 2015) derived within the framework of information field theory (IFT, Enßlin et al. 2009; Enßlin 2013, 2014). It simultaneously provides non-parametric estimates for the diffuse and the point-like photon flux given a photon count map. This challenging inverse problem is thereby regularized by prior assumptions that provide a statistical description of the morphologically different components, that is, the priors define our naive understanding of “diffuse” and “point-like”. D3PO considers Poissonian shot noise, without Gaussian approximations, and takes the provided IRFs of the Fermi LAT fully into account. Furthermore, we can retrieve uncertainty information on the estimates.
Overview of the energy binning.
All this allows us to present a continuous reconstruction of the diffuse γ-ray sky up to around 300 GeV, as well as an estimate of the point-like contribution, from which we derive the first D3PO Fermi catalog of γ-ray source candidates. By analyzing the spectral behavior of the diffuse component, it is possible to investigate the underlying processes, especially with regard to the CRs responsible for the emission.
The remainder of this paper is structured as follows. Section 2 summarizes the analysis procedure, a more detailed description is given in Appendix A. We present and discuss our findings in Sect. 3, and conclude in Sect. 4.
 |
Fig. 1 γ-ray sky seen by the Fermi LAT in a Mollweide projection. Panel a) shows the (total) photon flux reconstructed from photon count data of 6.5 years mission elapsed time in the energy range from 0.6 to 307.2 GeV reconvolved with the LAT’s IRFs. Panel b) shows solely the reconvolved diffuse contribution. Panel c) shows the fractional residual map between data and reconstruction smoothed with a 0.5° Gaussian kernel. Panel d) shows the fractional difference map between the standard total, Galactic plus isotropic, diffuse model (short “std”) and the reconstructed diffuse contribution. |
2. Analysis summary
We analyzed the photon count data collected by the Fermi LAT within its 6.5 years of operation. All data selection criteria, the working principle of the applied D3PO inference algorithm (Selig & Enßlin 2015), and a description of the analysis procedure are detailed in Appendix A.
In summary, we make use of the reprocessed Pass 7 available within the Fermi science tools1 to retrieve the data, as well as the corresponding instrument response functions and exposure of the Fermi LAT (Atwood et al. 2009; Abdo et al. 2009; Ackermann et al. 2012a). We considered nine logarithmically spaced energy bands ranging from 0.6 to 307.2 GeV, cf. Table 1. For each band, we spatially binned all events classified as CLEAN in count maps, whereby we distinguished the front or back conversion of the photon within the LAT. Throughout this work, we discretize the sky using the Healpix scheme with nside = 128, which corresponds to an angular resolution of approximately 0.46°.
This data set was the input for the D3PO algorithm. To denoise, deconvolve, and decompose the data, we assumed the data d to be the result of a Poisson process with an expectation value given by the convolved sum of the diffuse and point-like flux, φ(s) and φ(u), that is, 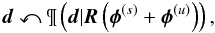 (1)where the operator R describes the full instrument response of the LAT. Under this model assumption, and with the aid of prior regularizations, D3PO computes estimates for the photon fluxes. The inference is performed iteratively until convergence and for each energy band separately. Further details regarding the inference can be found in Appendix A.
(1)where the operator R describes the full instrument response of the LAT. Under this model assumption, and with the aid of prior regularizations, D3PO computes estimates for the photon fluxes. The inference is performed iteratively until convergence and for each energy band separately. Further details regarding the inference can be found in Appendix A.
The results of this analysis – including, among others, the reconstructed fluxes, uncertainties, and the first D3PO Fermi (1DF) catalog of γ-ray source candidates – are publicly available2.
3. Results and discussion
3.1. γ-ray sky
The Fermi LAT has detected millions of γ-ray photons within the first 6.5 years of its mission. We can stack them in a binned all-sky count map disregarding the energy of the photons.
Figure 1 shows such all-sky maps for the total and the diffuse result of the reconstruction. D3PO denoises, deconvolves, and decomposes photon count maps and produces a reconstruction of the diffuse and point-like photon flux. A reconvolution of the reconstructed γ-ray flux with the instrument response functions demonstrates the quality of the performed denoising: the removal of Poissonian shot noise.
The fractional residual exhibits no significant structures, and the mean of its absolute value is below 5%3. As we compare the data with a denoised reproduction, the main difference is due to shot noise. We observe a weak ringing around the Galactic plane, which is a numerical artifact due to imperfections of spherical harmonic transformations applied during the inference. Previous comparisons with best-fitting templates created by the code GALPROP (Moskalenko & Strong 2000; Strong et al. 2000; Ackermann et al. 2008, 2012d, and references therein) often show significant residuals indicating features missed by the respective models; compare, for instance, Fig. 6 in Ackermann et al. (2012d). Since our inference machinery, in contrast, is free of an a priori assumption regarding the existence of any Galactic or extragalactic features, significant residuals are not to be expected.
When the point-like contribution is excluded from the reconvolved count map, the diffuse γ-ray sky becomes fully revealed, see Fig. 1b. The diffuse count map clearly displays Galactic features and substructures within the ISM. While the reconvolved photon count image appears somewhat smoothed, its deconvolved counterpart displays the Milky Way in more detail. In comparison to the standard total diffuse model4, we find obvious residuals. Figure 1d shows the difference between the standard total, Galactic plus isotropic, diffuse model and our reconstructed total diffuse emission, divided by the mean of the two images. Because of the different spectral ranges, the two images have been divided by their monopole before the computation. Diffuse structures on very small scales are not captured in the reconstruction because its effective resolution is limited due to the signal-to-noise ratio and IRFs. In the south and along the Galactic ridge, the standard total diffuse model is slightly higher than our reconstruction. The diffuse γ-ray fluxes in the individual energy bands are shown in Fig. 2. The coarseness of the images increases with energy because the number of detected photons, and thus the signal-to-noise ratio, drops drastically. The uncertainties of the reconstructions are illustrated in the lower panels of Fig. 2. Nevertheless, the Galactic disk and bulge are clearly visible at all energies.
 |
Fig. 2 Diffuse γ-ray flux and its relative reconstruction uncertainty on a logarithmic scale at different energies in a Mollweide projection. Panels a)−c) show the reconstructed diffuse photon flux at roughly 2 GeV, 10 GeV, and ~100 GeV. The photon flux is given in units of GeV-1 cm-2 s-1 sr-1. Note that the color scale varies. Panels d)–f) show the relative uncertainty on these reconstructions. Maps for all energy bands are available at the CDS. |
 |
Fig. 3 γ-ray sky in pseudocolor in a Mollweide projection. Panel a) shows the 6.5 year data. Panels b) and c) show the reconstructed (total) photon flux that in b) is reconvolved with the IRFs. Panel d) shows the reconstructed diffuse photon flux. Panels e) and f) reproduce the latter, but are overlaid with the feature contours found by Su et al. (2010) (white: giant Fermi bubbles, light magenta: Donut, light blue: North Arc, light gray: Radio Loop I) and contours of the 408 MHz radio map from Haslam et al. (1982). Panel g) highlights the contours defining the bulge-, cloud-, and bubble-like regions discussed in Sect. 3.3. |
3.1.1. Pseudocolor images
To obtain a better view on the spectral characteristics of the γ-ray sky, we combine the maps at different energies with a pseudocolor scheme. This scheme is designed to mimic the human perception of optical light in the γ-ray range. Intensity indicates the (logarithmic) brightness of the flux, red corresponds to low-energy γ-rays around 1 GeV, and blue to γ-rays up to 300 GeV. The resulting pseudocolor maps of the γ-ray sky are presented in Fig. 3. Thanks to a suitably tuned color response, spectrally different regions can easily be identified by eye. At a first glance, we can recognize the bright bulge of the Milky Way, the Fermi bubbles as two slightly green blue, somewhat round areas, and red to yellow cloud-like structures at low and intermediate latitudes, in particular around the Galactic anticenter.
The upper panels (a–d) illustrate the functionality of the D3PO inference algorithm, showing the raw data and the denoised, deconvolved, and decomposed reconstruction. The denoising applies most strongly to the high-energy bands, which appear slightly green-blue, where the signal-to-noise ratios are lowest. The deconvolution effect is most evident for point-like contributions in lower energy bands, which appear slightly red, because of the increasing width of the point spread function (PSF) for these bands. Finally, the decomposition reveals the purely diffuse γ-ray sky.
This view reveals many interesting features beyond the Galactic disk and bulge, which we discuss in the following.
3.1.2. Bubbles, features, and radio
The most striking features recovered by our reconstruction are the giant Fermi bubbles first found by Su et al. (2010). The bubbles extend up to | b | ≲ 50° in latitude and | l | ≲ 20° in longitude. They appear to emerge from the Galactic center, but their astrophysical origin is still under discussion (Su et al. 2010; Crocker & Aharonian 2011; Cheng et al. 2011; Dogiel et al. 2011; Su & Finkbeiner 2012; Yang et al. 2014; Ackermann et al. 2014b, and references therein). In agreement with previous studies, we find the bubbles to have relatively sharp edges and an overall homogeneous surface brightness; they appear slightly green-blue in Fig. 3. Yang et al. (2014) reported an energy-dependent morphology of the southern bubble, which is, in particular, more extended to the Galactic south and west at high energies. Our results confirm this extension, as can be seen in the reconstruction for the highest energy band in Fig. 2.
Figure 3e also shows the North Arc, Donut, and Cocoon (Su et al. 2010; Su & Finkbeiner 2012). However, we do not find evidence for the jet-like structure reported by Su & Finkbeiner (2012).
Moreover, there is a correlation with structures seen at radio frequencies. For example, a comparison with the synchrotron map from Haslam et al. (1982) taken at 408 MHz reveals γ-ray counterparts of Radio Loop I (Large et al. 1962) and smaller objects like the Large Magellanic Cloud at (l,b) ≈ (−80°,−30°), as well as the γ-ray glow around Centaurus A at (l,b) ≈ (−50°,20°), see Fig. 3f. However, the resolution of the all-sky reconstruction is too coarse to detail the morphology of such small sources. A reconstruction of a more focused field of view would be necessary to that end.
3.2. Energy spectra and spectral indices
To obtain a more quantitative view on the different contributions to the γ-ray flux, we now investigate photon flux energy spectra.
Figure 4 shows the measured5 and reconstructed energy spectra for the whole sky. Other regions of interest (ROIs), which typically in- or exclude the Galactic center or bulge, are investigated as well, see results in Table 2. The errors are dominated by systematics, that is, by the uncertainty in the absolute energy scale Δℰ / ℰ = ( + 2%,−5%) (Ackermann et al. 2012c) and in the normalization of the effective area, which is ± 10% up to 100 GeV and increases linearly with log (E) to ± 15% at 1 TeV (Bregeon et al. 2013)6. The statistical uncertainties determined from the inference tend to track the signal-to-noise ratio.
We split the total energy spectrum into a diffuse and a point-like contribution, whereby we additionally distinguished between isotropic7 and anisotropic diffuse components. Overall, the spectra from the reconstructed fluxes agree well with the data, except for the highest energy bin, where the point-like component seems to be strongly overestimated. There are two reasons for this. On the one hand, the signal-to-noise ratio is lowest, and on the other hand, the PSF is sharpest. Therefore, the distinction between point-like sources, noise peaks, and weak diffuse emission breaks down. For this reason, we excluded this highest energy band from further spectral analysis.
The diffuse γ-ray flux amounts to ~90% of the total flux with the majority being anisotropic contributions of Galactic origin. Both diffuse contributions, isotropic and anisotropic, are consistent with featureless power laws, φ ∝ E− γ. The results of the power-law fits are given in Table 2.
For the anisotropic component we find a spectral index γ(s) = 2.59 ± 0.05 that is slightly softer than the index of 2.44 ± 0.01 reported by Ackermann et al. (2012b), indicating a lack of flux at high energies, which can again be explained by the low signal-to-noise ratio in this regime. In low energy bands, the spectrum is dominated by the production and decay of π0-mesons induced by CR protons, while IC emission becomes increasingly strong at the highest energies (Ackermann et al. 2012b,d). The declining tail of the pion bump, peaking at 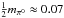 GeV c-2, is visible.
GeV c-2, is visible.
 |
Fig. 4 Energy spectra considering an all-sky ROI. Shown are the data (green squares) converted to flux units, and spectra from the reconstructed total (gray), anisotropic diffuse (dashed orange), isotropic diffuse (dotted magenta), and point-like photon flux (blue circles). Furthermore, power-law fits for the anisotropic (thick solid orange) and isotropic emission (thick dashed-dotted magenta) are shown. The errors include statistical and systematic uncertainties and are only shown for data and diffuse contributions for reasons of clarity. |
 |
Fig. 5 Spectral indices of featureless power-law fits, φaniso ∝ E− γ, at all positions in the sky using energy bands 1−8. |
The isotropic background is often referred to as extragalactic because it comprises unresolved extragalactic sources and might include possible signatures from large-scale structure formation or dark matter decay (Dermer 2007; Abdo et al. 2010b, and references therein). The isotropic diffuse background also follows a featureless power law with a spectral index 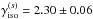 , if we ignore the last energy band. The excess of isotropic emission around ~3 GeV does not affect the uncertainties8. Abdo et al. (2010b) derived a spectral index of 2.41 ± 0.05 from one year Fermi LAT data in the energy range of 0.03−100 GeV. This indicates a slight spectral hardening of the isotropic background toward higher energies. In the same energy range, observations with the Energetic Gamma Ray Experiment Telescope (EGRET) yield a spectral index of 2.10 ± 0.03 that is considerably smaller (Sreekumar et al. 1998). This discrepancy, which might be an instrumental problem, is not yet clarified.
, if we ignore the last energy band. The excess of isotropic emission around ~3 GeV does not affect the uncertainties8. Abdo et al. (2010b) derived a spectral index of 2.41 ± 0.05 from one year Fermi LAT data in the energy range of 0.03−100 GeV. This indicates a slight spectral hardening of the isotropic background toward higher energies. In the same energy range, observations with the Energetic Gamma Ray Experiment Telescope (EGRET) yield a spectral index of 2.10 ± 0.03 that is considerably smaller (Sreekumar et al. 1998). This discrepancy, which might be an instrumental problem, is not yet clarified.
The recent analysis by Ackermann et al. (2015), who investigated an energy range of 0.1−820 GeV, reported the isotropic γ-ray background to be consistent with a power law with exponential cutoff at 280 GeV that has a spectral index of 2.32 ± 0.02. This is consistent with our findings.
Overview of the ROIs.
For smaller ROIs, we find fluctuations in the spectral index of the diffuse γ-ray flux. These fluctuations might give some indication about the CR spectrum, the composition of the local ISM, etc.
Since the D3PO algorithm provides a continuous estimate of the diffuse photon flux, we performed a spectral analysis in individual pixels. Although the energy spectra vary with location, for simplicity, we assumed a general power-law behavior everywhere, but with varying spectral index. Figure 5 shows the obtained spectral index map for the anisotropic γ-ray sky, centered on the average index of 2.6. The spatial smoothness of the spectral index map reflects that there are no discontinuities between neighboring pixels in the reconstructions.
From this spectral index map it is apparent that the Galactic disk is spectrally softer than the all-sky average. The same holds for the extensive structures that trace interstellar gas. These regions are dominated by hadronic interactions releasing γ-ray photons, for example, π0 production and decay (cf., e.g., Ackermann et al. 2012d).
In the region overlapping with the giant Fermi bubbles we find overall similar spectra that are harder than the all-sky average, however. This agrees with the results of Ackermann et al. (2014b), although they found a log-parabola to fit best. The strong hardening toward the high-latitude edge of the southern bubble arises because it is spatially more extented than at lower energies, cf. Yang et al. (2014). Additional local spots inside the bubble region are insignificant within the statistical and systematic uncertainties.
Although the morphology and spectra of the bubbles can be explained with hadronic and leptonic CR processes, IC scenarios also enable reproducing the microwave haze observed with WMAP and Planck (Planck Collaboration Int. IX 2013; Yang et al. 2013; Ackermann et al. 2014b). Furthermore, the low target densities at higher Galactic latitudes render the hadronic scenario unsatisfactory.
 |
Fig. 6 Cloud- and bubble-like component. Panel a) shows energy spectra from ROIs defined in Fig. 3g, cf. text. In addition to the spectra retrieved from the different regions, a linear combination of the cloud-, and bubble-like is fit to the bulge-like component, cf. legend. Panel b) shows the normalized latitude profiles of the cloud- and bubble-like component. |
 |
Fig. 7 γ-ray sky in pseudocolor in a Mollweide projection. Panel a) shows the cloud-like and panel b) the bubble-like diffuse component. |
 |
Fig. 8 Illustration of the brightness in a Mollweide projection. Panel a) shows the integrated brightness of the cloud-like component. Panel b) shows the monochromatic brightness of thermal dust emission at 353 GHz (Planck Collaboration XI 2014). Panel c) shows in white the area that was included in computing the latitude profile in Fig. 9. |
3.3. Diffuse emission components
The pseudocolor scheme introduced in Sect. 3.1.1 already allows us to visually inspect the continuous reconstruction of the diffuse γ-ray sky. By eye, we can make out the Galactic bulge, the Fermi bubbles, and also cloudy structures around the Galactic anticenter.
To confirm this impression of the visualization, we retrieved energy spectra from three characteristic regions: bulge-like (| l | < 40°, | b | < 1.5°), cloud-like (−150°<l< −120°, | b | < 3°), and bubble-like (for which we selected the southern bubble up to latitudes b< −27.5°). The contours of these regions are shown in Fig. 3g.
Figure 6a shows the energy spectra retrieved from the three regions. The cloud-like spectrum is rather soft (γ(s) ≈ 2.6) and features the tail of the pion bump. As expected, the cloud-like spectrum is dominated by emission from π0 decay, because the cloudy structures trace the gas content of the ISM that provides the target protons for π0 production. The bubble-like spectrum is significantly harder (γ(s) ≈ 2.4), indicating the dominance of hard processes like IC emission. The bulge-like region exhibits a spectrum that, besides having a higher absolute scale, can be described as a linear combination of the former two spectra, cf. Fig. 6a.
As the bulge-like spectrum is found to be a linear combination of cloud- and bubble-like, we tried to decompose the whole diffuse sky into those two components. For this purpose, we fit the spectrum in individual pixels by the cloud- and bubble-like component9. The fit coefficients then indicate the strength of the cloud- or bubble-like contribution at all locations. Multiplying the fit coefficients with the respective spectra, we obtained a pseudocolor visualization of the cloud- or bubble-like emission components as shown in Fig. 7.
In spite of the simplicity of this two-component model, the total diffuse emission and the sum of the two components agree well. The relative residuals are around 5−13%, except for the highest energy band, which was excluded from the fitting procedure, where the error is approximately 28%. Our findings demonstrate that the γ-ray sky in the energy range from 0.6 to 307.2 GeV can with high precision be described by cloud- and bubble-like emission components alone.
 |
Fig. 9 Latitude profile of the dust-to-cloud-like-gamma ratio. The thermal dust emission from Planck Collaboration XI (2014) and Finkbeiner et al. (1999) has been smoothed with a 0.7° Gaussian kernel to match the coarseness of the γ-ray map. |
 |
Fig. 10 Panel a) shows a magnification of the Chamaeleon complex from Fig. 7a. Panels b) and c) show magnifications of tentative outflows from Fig. 7b. The light gray line marks the Galactic plane (l = 0°). |
From the shape of the energy spectrum of the cloud-like component, we deduced that it is dominated by hadronic processes. We also compared its morphology with other ISM tracers. For this, we computed the brightness of the cloud-like component and show it in Fig. 8a. The resulting map agrees with the thermal dust emission seen by Planck (Planck Collaboration XI 2014) at 353 GHz shown in Fig. 8b. We emphasize the similar morphology of thermal dust microwave/IR emission and the cloud-like γ-ray component. In particular in the cloudy region in the Galactic East, the structures agree well, although we took the spectrum from a region in the West. As the thermal dust emission traces the densest part of the ISM, and hence the target gas for the CR protons, we are confident that the cloud-like component is indeed dominated by hadronic emission processes.
The Chamaeleon complex, around (l,b) ~ (−60°,−20°), hosting a number of star-forming clouds, is visible in the cloud-like component, cf. Fig. 10a. Recent work by the Planck Collaboration Int. XXVIII (2015) used γ, radio, and dust data to map the local gas content of the clouds.
 |
Fig. 11 Angular power spectra over angular quantum number ℓ. Panel a) shows the inferred spectra of the diffuse photon flux φ(s) in each energy band and a power-law fit thereof, cf. legend. Panel b) shows the direct realization spectra of the diffuse signal s = log (φ(s)/φ0) and the inferred, fitted, and averaged spectra, cf. legend. The colors (from red to violet to blue) indicate energy (from band 1 to 9) in both panels, and a white noise spectrum with arbitrary normalization is included for comparison. |
The cloud-like component is morphologically not exactly identical to the dust emission, however. For example, in the latitude profile shown in Fig. 9, the dust-to-gamma ratio decreases with increasing latitude. This profile was computed including only pixels outside the bubble region (| l | > 30°), where both the cloud- and bubble-like component contribute, and the estimated Planck dust emission is positive. The dust seems to be preferentially in the Galactic disk, differently from the thermal gas traced by γ-rays. The morphology of the bubble-like component is very different, cf. Fig. 7. Since the spectrum of the Fermi bubbles is spatially relatively constant, the shape of the northern bubble is well recovered based on the spectrum of the southern one. We also find an excess in the bubble-like emission in the bulge region (de Boer & Weber 2014) and in the star-forming region Cygnus-X around (l,b) ~ (80°,0°). Excess of emission following the bubble-like spectrum is also visible at intermediate latitudes where it exhibits mushroom-like shapes typical for hot outflows, for example, south of the Cygnus-X region ((l,b) ~ (90°,< −15°)), or along (l,b) ~ (130°,< −15°), cf. Fig. 10b and c. These are probable candidates for outflows from active star-forming regions of the Milky Way. Furthermore, the latitude profile shown in Fig. 6b indicates that the bubble-like disk is roughly twice as thick as the cloud-like component.
Since the bubble-like γ-ray emission is morphologically so distinct and different from the cloud-like component, we assume that the two components are dominated by different emission processes. The bubble-like spectrum is distinctly harder and less structured, therefore a leptonic emission process, in particular IC scattering, seems the more plausible origin for the bubble-like diffuse component.
The CR populations producing these two γ-ray emission components do not need to be very different. It might be that we observe two different phases of the ISM:
-
the cold and condensed phase carries most of the Galactic dust and has a sufficient nuclei target density to be predominately revealed through hadronic interactions with CR protons. Hence, the resulting γ-ray emission mostly traces the highly structured gas distribution.
-
the hot, diluted, and voluminous phase tends to flow out of the Galactic disk. The γ-ray emission from within is dominated by IC upscattering of the Galactic photon field by CR electrons. As the photon field is relatively homogeneous, the morphology of the bubble-like component is probably shaped by the spatial distribution of the CRs.
This simple two-component model of the diffuse γ-ray emission supports scenarios in which the Fermi bubbles are just outflows of the hot ISM (Yang et al. 2013; Cheng et al. 2011; Dogiel et al. 2011; Chernyshov 2011; Carretti et al. 2013).
 |
Fig. 12 Point sources in the γ-ray sky in pseudocolor and in a Mollweide projection. Markers show point sources from the second Fermi LAT source catalog (Nolan et al. 2012) for comparison; the gray scale indicates their average detection significance as listed in the catalog. Special markers show a selection of pulsars (squares), local SNRs (stars), and well-known galaxies (pentagons), as well as famous extragalactic objects (diamonds), cf. text. |
3.4. Angular power spectra
Under the assumption of statistical isotropy and homogeneity, the second moments of a diffuse signal field are defined by its angular power spectrum. Studying power spectra gives some indication of the strength of typical fluctuations on respective angular scales described by the angular quantum number ℓ. According to our chosen Healpix discretization, we examined spectra up to a maximum scale set by ℓmax = 2 nside = 256.
Figure 11 shows the angular power spectra of the diffuse photon flux φ(s) – the quantity we are interested in – and its logarithm, the diffuse signal field s. The power spectrum, which is a priori unknown, needs to be reconstructed from the data alongside the diffuse signal field (Wandelt et al. 2004; Jasche et al. 2010; Enßlin & Frommert 2011; Oppermann et al. 2012; Jasche & Wandelt 2013). This is done for each energy band separately. More details on the inference procedure can be found in Appendix A.
The inferred power spectra of s show a similar power-law behavior at all energies with some remarkable deviations. On large scales, 0 <ℓ ≲ 28, the spectra exhibit a strong distinction between even and odd ℓ-modes. The reason for this is the dominant contribution of the Galactic disk centered around b = 0° to the diffuse photon flux, which excites or suppresses even or odd ℓ-modes in the reconstruction. On smaller scales, on the other hand, the power spectra start to fall off because small-scale features cannot be resolved because of the finite exposure of the Fermi LAT. This effect has a clear energy dependence. Since events with higher energies are rarer, the decline of spectra from high-energy bands begins at lower ℓ. We note that the threshold set by the PSF is on very small scales; the 68% angular containment radius above 10 GeV is smaller than 0.2° corresponding to ℓ ≳ 900, for example.
We now consider the actual angular power spectrum Cℓ of the diffuse photon flux φ(s) ∝ exp(s). This can be computed by transforming10 the inferred (final) power spectra of s according to Greiner & Enßlin (2013). This transformation shifts power between different ℓ-modes, in particular toward smaller scales (larger ℓ). Again, we find a power-law behavior of the angular power spectrum, as can be seen in Fig. 11a. We fit a power-law with index 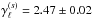 . There is an energy-dependent break point, however, beyond which the power drops. The break point should shift to higher ℓ with increasing observation time.
. There is an energy-dependent break point, however, beyond which the power drops. The break point should shift to higher ℓ with increasing observation time.
Extract from the 1DF catalog.
3.5. Point sources
Another result of our analysis of the 6.5 year Fermi data is a reconstruction of the point-like contribution to the photon flux, φ(u), which consists of Galactic and extragalactic point sources.
Figure 12 shows an all-sky map of all point source candidates in the pseudocolor scheme introduced in Sect. 3.1.1. Markers (and their opacity) in the map indicate the position (and detection significance) of point sources from the second Fermi LAT source catalog (Nolan et al. 2012)11. There is a diversity of sources, which is why we highlight a selection by special markers. The brightest γ-ray sources are pulsars (PSRs) like Vela (PSR J0835-4510), Geminga (PSR J0633+1746), and Crab (PSR J0534+2200), but there are also pulsars that have first been detected in γ-ray, such as LAT PSR J0007+7303 and LAT PSR J0357+3205. The Galactic disk, and especially the bulge, is clustered with point sources including, among others, supernova remnants (SNRs) such as W51C, W44, W30, and IC443. There are also many homogeneously distributed extragalactic sources, for example, the starburst galaxy Cigar (M 82) or our neighboring galaxy Andromeda (M 31). Furthermore, the core of Centaurus A (NGC 5128) and the Small and Large Magellanic Cloud are visible in γ-rays.
Deriving a catalog of source candidates from the point-like flux is difficult because a point source might, for example, appear in neighboring pixels at different energies due to different noise realizations and the aforementioned energy dependence of the signal-to-noise ratio and the PSF. To nominate a candidate, we checked whether the point-like contribution exceeded 2σ above the diffuse emission in at least two of the energy bands 1−8, which is a simple but conservative criterion taking the diffuse reconstruction uncertainty σ into account, cf. Fig. 2. We excluded the highest energy band from our search, since the point-like flux in this band seems to be contaminated, as discussed in Sect. 3.2. We refer to the compiled point source catalog as the first D3PO Fermi (1DF) catalog of γ-ray source candidates.
Qualitatively, the point-like flux found by D3PO agrees with the second Fermi LAT source catalog as shown in Fig. 12. A few sources appear slightly off-center or smeared out over two or more pixels. The reason for this is that these sources are positioned between grid points of the chosen Healpix grid. Image pixels in Fig. 12 do not represent Healpix pixels.
We found 3106 source candidates, see Table 3 for more details. For comparison, the one, two, and four year Fermi LAT source catalogs comprise 1451, 1873, and 3034 sources, respectively (Abdo et al. 2010a; Nolan et al. 2012; The Fermi-LAT Collaboration 2015). 1381 (1897) of our sources can be associated with known LAT sources from the second (third) catalog as the angular distance between 1DF candidate and catalog source is shorter than the angular resolution of our reconstruction. The reason why we do not confirm all objects in the second (third) Fermi LAT source catalog is the conservative criterion we applied. This still leaves 1253 (1209) new source candidates to be confirmed by future work.
We caution that a more detailed study is necessary to confirm or reject these candidates. The analysis of the individual sources, best constructed on more constrained ROIs and with higher angular resolution, is left for future work.
The present catalog includes extended objects such as SNRs. In the second Fermi LAT catalog 6 firm identifications, 4 associations, and 58 possible associations with SNRs are listed. We detected more than 55% of them. In particular, 5 out of their 6 firm identifications are listed as 1DF candidates. For SNRs with fluxes F ≳ 10-8 cm-2 s-1, our results agree well with those of the Fermi Collaboration. On the other hand, for faint sources we often recover lower fluxes, indicating that the missing flux might be attributed to the diffuse emission. For a few sources we estimate a higher flux than given in the Femi LAT catalog. For example, we measure 1.25 × 10-7 cm-2 s-1 for SNR W44 in comparison to 7.96 × 10-8 cm-2 s-1 in the Fermi LAT catalog. To overcome this discrepancy, a modeling that takes into account the presence of discrete extended sources would be required, which is left for future work.
 |
Fig. 13 Comparison of the second Fermi LAT source catalog (Nolan et al. 2012) and candidates from the reconstruction for which an association in the second Fermi LAT catalog has been found. Panel a) shows the histogram and scatter plot of the spectral indices γ(u) of candidates versus catalog sources. In the latter, a 1:1 line (black solid) is plotted for comparison, and the markers indicate the fit spectral shape, cf. legend. Panel b) shows the histogram and scatter plot of the logarithmic total fluxes log 10(F/F0), where F0 = 1 cm-2 s-1. The scatter plot contains a 1:1 line (black solid) for comparison. |
In the following, we compare the 1DF candidates for which we found a unique association within the second Fermi LAT source catalog (Nolan et al. 2012) by means of their spectral index and total flux. We note that the two studies are based on different data, exposure, calibration, and analysis algorithms12.
The spectral index of a source should not (or at least not strongly) be influenced by these differences. For each source, we attempted to fit three different spectral shapes: a plain power-law, 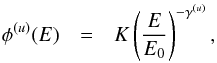 (2)a log-parabola,
(2)a log-parabola, 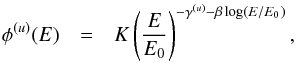 (3)and a power law with exponential cutoff,
(3)and a power law with exponential cutoff, 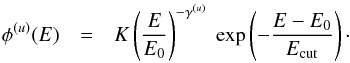 (4)Here E0 = 1 GeV serves as a reference energy, and the spectral index γ(u) is a fit parameter, as are K, β, and Ecut. The 1DF source catalog contains the best-fit parameters for all shapes if applicable.
(4)Here E0 = 1 GeV serves as a reference energy, and the spectral index γ(u) is a fit parameter, as are K, β, and Ecut. The 1DF source catalog contains the best-fit parameters for all shapes if applicable.
Figure 13a shows the comparison of the 1DF spectral indices and the indices listed in the second Fermi LAT source catalog (corrected to E0 where needed). The scatter of spectral indices is large, but comparable to the uncertainties. We find a rough agreement, although our distribution is broadened toward higher indices. Most of the outliers yielding a high (low) spectral index are modeled by a log-parabola (exponential cut-off) that has an additional degree of freedom compared to the plain power law. This implies that the versatility of point source spectra might not be covered by the considered spectral shapes.
Figure 13b shows a comparison of the total fluxes F(u), defined as 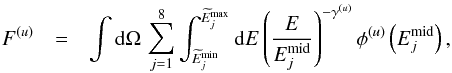 (5)with j labeling the energy bands and
(5)with j labeling the energy bands and ![\begin{eqnarray} {\widetilde E}_j^\mathrm{min} &=& \mathrm{min}\left\{1 \, \mathrm{GeV},\, E_j^\mathrm{min}\right\} \notag \\[1.5mm] {\widetilde E}_j^\mathrm{max} &=& \mathrm{max}\left\{E_j^\mathrm{max},\, 100 \, \mathrm{GeV}\right\}, \notag \end{eqnarray}](/articles/aa/full_html/2015/09/aa25172-14/aa25172-14-eq205.png) in a histogram and a scatter plot. The fluxes agree well overall. At the faint end, our fluxes tend to be lower than the fluxes reported in the second Fermi LAT source catalog (Nolan et al. 2012). Since our analysis benefits from a higher exposure and improved calibration, the fluxes from the Fermi Collaboration might rather be considered as upper limits in this comparison.
in a histogram and a scatter plot. The fluxes agree well overall. At the faint end, our fluxes tend to be lower than the fluxes reported in the second Fermi LAT source catalog (Nolan et al. 2012). Since our analysis benefits from a higher exposure and improved calibration, the fluxes from the Fermi Collaboration might rather be considered as upper limits in this comparison.
3.5.1. Galaxy clusters
Some galaxy clusters exhibit diffuse, extended radio emission, so-called radio halos, which proves the existence of relativistic electrons therein. If relativistic protons are present as well, γ-ray emission is to be expected due to hadronic interactions (Ackermann et al. 2010, 2014a, and references therein).
Feretti et al. (2012) provided a collection of clusters hosting radio halos. We investigated the presence of γ-ray emission in the direction of these clusters and in the direction of the clusters listed by Ackermann et al. (2010, 2014a), which would in our reconstruction appear point-like due to the pixelization of our reconstruction. Table 4 lists our upper limits on the total flux Fup and the level of the diffuse emission F(s) at the cluster locations. The upper limit flux is computed according to Fup = F(u) + 2σF(s), where σF(s) is the uncertainty of the total diffuse flux F(s)13. This is the highest possible flux hidden under the diffuse γ-ray emission.
We derived upper limit fluxes between 10-11 cm-2 s-1 and 10-8 cm-2 s-1 for the energy range 1−100 GeV. Ackermann et al. (2010, 2014a) provided upper limits for nearby clusters above 0.1 GeV. Some clusters are in both samples, for instance, A2256, A2319, Coma (A1656), Ophiuchus, Perseus (A0426), A1914, A2029, A2142, A2163, A2744, Bullet (1E 0657-56), and MACS J0717.5+3745. We computed comparable or slightly lower upper limit fluxes. For example, for the Coma (A1656) cluster Ackermann et al. (2014a) reported about 1.13 × 10-10 cm-2 s-1 above 1 GeV, which is comparable to the 1.1 × 10-10 cm-2 s-1 we obtained. However, we caution that our upper limits are not strict 95% confidence intervals, as they are not a direct outcome of our inference, but estimated as described above. A closer investigation is left for future work.
At the location of a few clusters in our sample we found a source in our point-source catalog. We marked these clusters in bold-face in Table 4 and reported the flux instead of an upper limit. Some of them are in projection to known γ-ray point-sources (active galaxies). These are, for example, Perseus (NGC 1275 and IC310), A2390, and Virgo. Others are already present either in the second or in the third Fermi LAT source catalog, while ten are new detections (clusters marked with the †). Noteworthy among the new detections are Hydra-A and seven clusters hosting large-scale diffuse synchrotron emission. These are A209, A2254, and RXC J1514.9-1523 (radio halo), A2029, A2626, and RX J1347.5-1145 (radio mini-halo), and A4038 (radio relic). An analysis at higher resolution is necessary to localize and better understand the origin of this emission.
Overview of total flux upper limits for clusters hosting a radio (mini-)halo from the collection by Feretti et al. (2012).
4. Conclusions and summary
We analyzed the Fermi LAT 6.5 year photon data in the energy range from 0.6 to 307.2 GeV. We applied the inference algorithm D3PO to effectively denoise, deconvolve, and decompose the data with Bayesian inference methods. In contrast to previous approaches by the Fermi Collaboration and others, our non-parametric reconstruction does not rely on emission templates.
We obtained estimates for the diffuse and point-like contributions to the γ-ray flux. Furthermore, D3PO also provided uncertainty information and the a priori unknown angular power spectrum of the diffuse contribution.
The inferred diffuse photon flux reveals the diversity of the γ-ray sky. We clearly reproduced the structure of the Galactic disk, bulge, and local interstellar gas, all of which are primarily illuminated by photons induced by hadronic interactions of CRs with the ISM. We confirmed the existence of the giant Fermi bubbles, as well as their homogeneous morphology, sharp edges, and hard spectra. Moreover, we were also able to resolve small diffuse structures such as the γ-ray glow around Centaurus A.
The continuous reconstruction of the diffuse flux allowed us to present the first spectral index map of the diffuse γ-ray sky, as well as a pseudocolor composite visualizing the spectrally different regions. Furthermore, the large-scale angular power spectrum of the diffuse emission seems to obey a power law with index 2.47 ± 0.02 across all energy bands.
Inspired by the pseudocolor visualization, we decomposed the diffuse γ-ray sky into a cloud-like and bubble-like emission component. The former, tracing the dense, cold ISM, is dominated by hadronic emission processes, while the latter, being morphologically and spectrally distinct, seems to be dominated by leptonic processes in hot, diluted parts of the ISM and outflows thereof. In particular, our findings indicate a preference for IC emission from the Fermi bubbles and support scenarios in which the Fermi bubbles are explained by hot outflows powered by strong activities in the Galactic center region (Yang et al. 2013; Cheng et al. 2011; Dogiel et al. 2011; Chernyshov 2011; Carretti et al. 2013). We reported additional, less extended outflows of a similar population of relativistic particles at other locations.
The reconstruction of the point-like photon flux qualitatively confirms most of the sources from the second and third Fermi LAT source catalog. Quantitatively, we derived the first D3PO Fermi catalog of γ-ray source candidates that comprises 3106 point sources. A more detailed analysis of this catalog is left for future research.
Finally, we observed γ-ray emission in the direction of a few galaxy clusters hosting known radio halos. An in-depth analysis is required to shed light on the origin of this emission.
at http://www.mpa-garching.mpg.de/ift/fermi/ and at the CDS.
The standard Galactic diffuse model is provided by http://fermi.gsfc.nasa.gov/ssc/data/analysis/software/aux/gll_iem_v05_rev1.fit.
This tentative excess might be a line-like signal from dark matter decay or annihilation (Conrad 2012), but this is highly speculative considering the available data.
For further details regarding the Fermi LAT source catalog see http://fermi.gsfc.nasa.gov/ssc/data/access/lat/2yr_catalog/
The main differences are the selection of SOURCE (CLEAN) events, the 2 (6.5) years of observation, and the use of the P7_V6 (P7REP_V15) IRFs in the second Fermi LAT source catalog (Nolan et al. 2012) (the candidate catalog presented here).
For further details regarding the Fermi LAT data products see http://fermi.gsfc.nasa.gov/ssc/data/.
Acknowledgments
We thank Martin Reinecke, Maksim Greiner, Sebastian Dorn, Dmitry Prokhorov, and Philipp Girichidis, Elena Orlando and the anonymous referee for the insightful discussions and productive comments. Moreover, we would like to thank Jean Ballet, Johann Cohen-Tanugi, Andrew W. Strong, Roland Crocker, and Stephan Zimmer for their very helpful annotations on the preprint version of this paper. We are grateful to the Fermi Collaboration for publicly providing their data and data analysis tools. This work has been carried out in the framework of the DFG Forschergruppe 1254 “Magnetisation of Interstellar and Intergalactic Media: The Prospects of Low-Frequency Radio Observations”. Furthermore, we thank the “MaxEnt and Bayesian Association of Australia, Inc.” for travel support in order to present preliminary results at MaxEnt 2013. Some of the results in this publication have been derived using Numpy/Scipy (Oliphant 2006), Matplotlib (Hunter 2007), Healpix (Górski et al. 2005), and especially the D3PO algorithm (Selig & Enßlin 2015) based on the Nifty package (Selig et al. 2013). This research has made use of NASA’s Astrophysics Data System. We acknowledge the use of the Legacy Archive for Microwave Background Data Analysis (LAMBDA), part of the High Energy Astrophysics Science Archive Center (HEASARC). HEASARC/LAMBDA is a service of the Astrophysics Science Division at the NASA Goddard Space Flight Center.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009, Astropart. Phys., 32, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010a, ApJS, 188, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010b, Phys. Rev. Lett., 104, 101101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ackermann, M., Jóhannesson, G., Digel, S., et al. 2008, in AIP Conf. Ser. 1085, eds. F. A. Aharonian, W. Hofmann, & F. Rieger, 763 [Google Scholar]
- Ackermann, M., Ajello, M., Allafort, A., et al. 2010, ApJ, 717, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Ackermann, M., Ajello, M., Albert, A., et al. 2012a, ApJS, 203, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Ackermann, M., Ajello, M., Albert, A., et al. 2012b, Phys. Rev. D, 86, 022002 [NASA ADS] [CrossRef] [Google Scholar]
- Ackermann, M., Ajello, M., Allafort, A., et al. 2012c, Astropart. Phys., 35, 346 [Google Scholar]
- Ackermann, M., Ajello, M., Atwood, W. B., et al. 2012d, ApJ, 750, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Ackermann, M., Ajello, M., Albert, A., et al. 2014a, ApJ, 787, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Ackermann, M., Albert, A., Atwood, W. B., & Fermi LAT Collaboration 2014b, ApJ, 793, 64 [Google Scholar]
- Ackermann, M., Ajello, M., Albert, A., & Fermi LAT Collaboration 2015, ApJ, 799, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Atwood, W. B., & Abdo, A. A., Ackermann, M., et al. 2009, ApJ, 697, 1071 [NASA ADS] [CrossRef] [Google Scholar]
- Bayes, T. 1763, Philosoph. Trans. Roy. Soc., 35, 370 [Google Scholar]
- Bregeon, J., Charles, E., & M. Wood, for the Fermi-LAT Collaboration 2013, ArXiv e-prints [arXiv:1304.5456] [Google Scholar]
- Carretti, E., Crocker, R. M., Staveley-Smith, L., et al. 2013, Nature, 493, 66 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Cheng, K.-S., Chernyshov, D. O., Dogiel, V. A., Ko, C.-M., & Ip, W.-H. 2011, ApJ, 731, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Chernyshov, D. 2011, International Cosmic Ray Conference, 7, 11 [NASA ADS] [Google Scholar]
- Conrad, J. 2012, in Conf. Ser., 1505, eds. F. A. Aharonian, W. Hofmann, & F. M. Rieger, 166 [Google Scholar]
- Cox, R. T. 1946, Am. J. Phys., 14, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Crocker, R. M., & Aharonian, F. 2011, Phys. Rev. Lett., 106, 101102 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- de Boer, W., & Weber, M. 2014, ApJ, 794, L17 [Google Scholar]
- Dermer, C. D. 2007, in The First GLAST Symposium, ed. S. Ritz, P. Michelson, & C. A. Meegan, AIP Conf. Ser., 921, 122 [Google Scholar]
- Dermer, C. D., Strong, A. W., Orlando, E., Tibaldo, L., for the Fermi Collaboration. 2013, ArXiv e-prints [arXiv:1307.0497] [Google Scholar]
- Dogiel, V. A., Chernyshov, D. O., Cheng, K., et al. 2011, ArXiv e-prints [arXiv:1109.6087] [Google Scholar]
- Enßlin, T. 2013, in AIP Conf. Ser., 1553, ed. U. von Toussaint, 184 [Google Scholar]
- Enßlin, T. 2014, in AIP Conf. Ser., 1636, 49 [Google Scholar]
- Enßlin, T. A., & Frommert, M. 2011, Phys. Rev. D, 83, 105014 [NASA ADS] [CrossRef] [Google Scholar]
- Enßlin, T. A., Frommert, M., & Kitaura, F. S. 2009, Phys. Rev. D, 80, 105005 [NASA ADS] [CrossRef] [Google Scholar]
- Feretti, L., Giovannini, G., Govoni, F., & Murgia, M. 2012, A&ARv, 20, 54 [Google Scholar]
- Finkbeiner, D. P., Davis, M., & Schlegel, D. J. 1999, ApJ, 524, 867 [NASA ADS] [CrossRef] [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Greiner, M., & Enßlin, T. A. 2013, ArXiv e-prints [arXiv:1312.1354] [Google Scholar]
- Guglielmetti, F., Fischer, R., & Dose, V. 2009, MNRAS, 396, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Haslam, C. G. T., Salter, C. J., Stoffel, H., & Wilson, W. E. 1982, A&AS, 47, 1 [NASA ADS] [Google Scholar]
- Hunter, J. D. 2007, Comp. Sci. Eng., 9, 90 [Google Scholar]
- Jasche, J., & Wandelt, B. D. 2013, ApJ, 779, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Jasche, J., Kitaura, F. S., Wandelt, B. D., & Enßlin, T. A. 2010, MNRAS, 406, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Johannesson, G., Orlando, E., for the Fermi-LAT collaboration. 2013, ArXiv e-prints [arXiv:1307.0197] [Google Scholar]
- Large, M. I., Quigley, M. J. S., & Haslam, C. G. T. 1962, MNRAS, 124, 405 [NASA ADS] [Google Scholar]
- Moskalenko, I. V., & Strong, A. W. 2000, ApJ, 528, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Nolan, P. L., Abdo, A. A., Ackermann, M., et al. 2012, ApJS, 199, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Oliphant, T. 2006, A Guide to NumPy (Trelgol Publishing) [Google Scholar]
- Oppermann, N., Selig, M., Bell, M. R., & Enßlin, T. A. 2013, Phys. Rev. E, 87, 032136 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration Int. IX. 2013, A&A, 554, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XI. 2014, 571, A11 [Google Scholar]
- Planck Collaboration Int. XXVIII. 2015, A&A, in press DOI: 10.1051/0004-6361/201424955 [Google Scholar]
- Portillo, S. K. N., & Finkbeiner, D. P. 2014, ApJ, 796, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Schmitt, J., Starck, J. L., Casandjian, J. M., Fadili, J., & Grenier, I. 2010, A&A, 517, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schmitt, J., Starck, J. L., Casandjian, J. M., Fadili, J., & Grenier, I. 2012, A&A, 546, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Selig, M., & Enßlin, T. A. 2015, A&A, 574, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Selig, M., Bell, M. R., Junklewitz, H., et al. 2013, A&A, 554, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shannon, C. E. 1948, Bell System Technical J., 27, 379 [Google Scholar]
- Sreekumar, P., Bertsch, D. L., Dingus, B. L., et al. 1998, ApJ, 494, 523 [NASA ADS] [CrossRef] [Google Scholar]
- Strong, A. W., Moskalenko, I. V., & Reimer, O. 2000, ApJ, 537, 763 [Google Scholar]
- Su, M., & Finkbeiner, D. P. 2012, ApJ, 753, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Su, M., Slatyer, T. R., & Finkbeiner, D. P. 2010, ApJ, 724, 1044 [NASA ADS] [CrossRef] [Google Scholar]
- The Fermi-LAT Collaboration. 2015, ApJS, 218, 23 [Google Scholar]
- Wandelt, B. D., Larson, D. L., & Lakshminarayanan, A. 2004, Phys. Rev. D, 70, 083511 [NASA ADS] [CrossRef] [Google Scholar]
- Wiener, N. 1949, Extrapolation, Interpolation and Smoothing of Stationary Time Series, with Engineering Applications (New York: Technology Press and Wiley) [Google Scholar]
- Yang, H.-Y. K., Ruszkowski, M., & Zweibel, E. 2013, MNRAS, 436, 2734 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, R.-z., Aharonian, F., & Crocker, R. 2014, A&A, 567, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Data analysis
Appendix A.1: Data selection
We analyzed the 6.5 years of observational data taken by the Fermi LAT, to be precise, data from mission weeks 9 to 346 (mission elapsed time 239,557,417 s to 443,556,512 s). The data were subject to multiple restrictions and cuts detailed in the following.
For our analysis we exclusively considered events classified as P7REP_CLEAN_V15 in the reprocessed Pass 7 data set. The CLEAN events, which are cleaned of CR interactions with the instrument, are recommended for studies of the diffuse γ-ray emission14. Events with rocking angles (between the LAT boresight and zenith) above 52° and zenith angles above 100° were excluded to suppress contaminations from CRs and the Earth’s limb (Atwood et al. 2009)15. In addition, we applied a (non-standard) cut with respect to the angular distance to the Sun that we required to exceed 20°. This way, almost all Solar γ-rays are rejected at the price of reducing the total number of events by less than 3%. A similar procedure regarding the moon is conceivable but was ignored because its contribution is negligible.
The individual events were labeled FRONT or BACK according to whether the photon had been converted in the front or back section of the LAT instrument. We retained this labeling, but combined these data vectors by a direct sum, 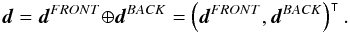 (A.1)The selected events were binned into nine (logarithmically equally spaced) energy bins ranging from 0.6 to 307.2 GeV, cf. Table 1. We also applied a spatial binning of the events into all-sky count maps using a Healpix discretization with nside = 128, which corresponds to 196,608 pixels with a size of roughly 64 μsr ≈ (0.46°)2 each.
(A.1)The selected events were binned into nine (logarithmically equally spaced) energy bins ranging from 0.6 to 307.2 GeV, cf. Table 1. We also applied a spatial binning of the events into all-sky count maps using a Healpix discretization with nside = 128, which corresponds to 196,608 pixels with a size of roughly 64 μsr ≈ (0.46°)2 each.
For a proper deconvolution, our analysis has to take the LAT PSF and exposure into account. The instrumental response functions of the Fermi LAT (Atwood et al. 2009; Abdo et al. 2009; Ackermann et al. 2012a), which are essential to do this, have been improved in the reprocessed Pass 7 release and are available within the Fermi science tools. According to our event selection, we made use of the P7REP_CLEAN_V15::FRONT and BACK IRFs. These can be assumed to be accurately calibrated, although further improvements, especially at low energies, are under discussion (Portillo & Finkbeiner 2014). Given the IRFs, the exposure 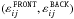 for each Healpix pixel i and each energy band j can be retrieved from the data archive. To compute ε, the Sun exposure was subtracted from the standard exposure due to the chosen rejection of potential solar events (Johannesson et al. 2013). The PSF of the Fermi LAT is a function of position and energy E. Its shape varies slightly with spatial translation and sharpens strongly with increasing energy. The forward application of the PSF is a linear operation that can be implemented in form of a convolution matrix evaluating the PSF at each pixel center and for each energy band. This matrix is fairly sparse because of the vanishing tails of the PSF, and is computed beforehand. The exposure and the PSF define the instrument response operator R,
for each Healpix pixel i and each energy band j can be retrieved from the data archive. To compute ε, the Sun exposure was subtracted from the standard exposure due to the chosen rejection of potential solar events (Johannesson et al. 2013). The PSF of the Fermi LAT is a function of position and energy E. Its shape varies slightly with spatial translation and sharpens strongly with increasing energy. The forward application of the PSF is a linear operation that can be implemented in form of a convolution matrix evaluating the PSF at each pixel center and for each energy band. This matrix is fairly sparse because of the vanishing tails of the PSF, and is computed beforehand. The exposure and the PSF define the instrument response operator R, 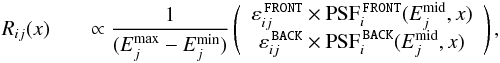 (A.2)up to a proportionality constant that can absorb numerical factors and physical units. This definition does not include a spectral convolution, meaning that no cross-talk between different energy bands is assumed.
(A.2)up to a proportionality constant that can absorb numerical factors and physical units. This definition does not include a spectral convolution, meaning that no cross-talk between different energy bands is assumed.
The primary target of our analysis is the physical photon flux φ = φ(x), which is a function of position x ∈ Ω. Here, the position space Ω is the observational sphere, and the position x might be given in spherical coordinates (ϕ,θ), or in Galactic longitude and latitude (l,b).
The response operator R describes the mapping of a photon flux φ to λ = Rφ by a convolution with the IRFs: 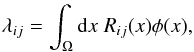 (A.3)where λ describes the noiseless (non-integer) number of photons one expects to observe through the IRFs given some photon flux in the sky. This expected number of counts λ relates to the observed (integer) photon counts d by a noise process, which is part of the statistical model detailed in the next section.
(A.3)where λ describes the noiseless (non-integer) number of photons one expects to observe through the IRFs given some photon flux in the sky. This expected number of counts λ relates to the observed (integer) photon counts d by a noise process, which is part of the statistical model detailed in the next section.
Appendix A.2: Inference algorithm
The foundation of the analysis presented in this work is the D3PO inference algorithm derived by Selig & Enßlin (2015) that targets the denoising, deconvolution, and decomposition of photon observations. Without going into technical details, we briefly review the underlying assumptions and characteristics of the D3PO algorithm in the following.
The observed photon count data d carries information about the astrophysical photon flux φ, as well as noise and instrumental imprints. To optimally reconstruct φ given d, we incorporated our knowledge about the actual measurement in a data model that consists of deterministic relations and probabilistic processes. Hence, D3PO is a probabilistic algorithm conducting Bayesian inference.
We can assume the photon counts to suffer from Poissonian shot noise, that is, the data entries dij are the outcomes of statistically independent Poisson processes given an expected number of counts λij each. Especially in low photon flux regions and at high energies, where the signal-to-noise ratios are lowest, using a Poissonian likelihood allows for an accurate noise treatment, whereas Gaussian noise approximations often fail.
The D3PO deconvolution task covers the correction of all effects that trace back to the instrumental response R. As discussed in Sect. A.1, this response establishes a relation between the astrophysical photon flux φ and the expected counts λ by taking the IRFs of the Fermi LAT fully into account. Since we assumed the IRFs to be thoroughly calibrated (to the best of our knowledge), this relation is deterministic.
The total photon flux φ consists of many different contributions that can be divided into two morphological classes, diffuse and point-like contributions. Diffuse emission, which is produced by the interaction of CRs with the ISM, unresolved point sources, and extragalactic background, is characterized by spatially smooth fluctuations. In contrast, point-like emission is fairly local originating primarily from resolved point sources. The D3PO algorithm reconstructs the total photon flux as the sum of a diffuse and point-like flux contribution, that is, 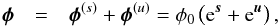 (A.4)where φ0 is a constant absorbing numerical factors and flux units, and the exponentiation is applied pixelwise to the diffuse and point-like signal fields, s and u. These signal fields describe the dimensionless logarithmic flux that ensures that the physical photon flux is positive in a natural way. Although the algorithm deals with the s and u fields for numerical reasons, we only regard the fluxes φ(s) and φ(u) in the following as they are physical.
(A.4)where φ0 is a constant absorbing numerical factors and flux units, and the exponentiation is applied pixelwise to the diffuse and point-like signal fields, s and u. These signal fields describe the dimensionless logarithmic flux that ensures that the physical photon flux is positive in a natural way. Although the algorithm deals with the s and u fields for numerical reasons, we only regard the fluxes φ(s) and φ(u) in the following as they are physical.
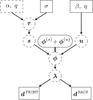 |
Fig. A.1 Graphical model of the model parameters α, q, σ, β, and η, the logarithmic angular power spectrum τ, the diffuse and point-like signal fields, s and u, the photon fluxes, φ, φ(s), and φ(u), and the expected and observed number of photons, λ and d. |
We can incorporate our naive understanding of “diffuse” and “point-like” by introducing prior assumptions. Embedding a priori knowledge on the solution, of course, biases the inference. However, priors also remedy the degeneracy of the inference problem as they suppress counterintuitive solutions.
The diffuse photon flux φ(s), being spatially smooth, is expected to exhibit a spatial correlation. Without enforcing concrete spatial features, such as a Galactic profile, we assumed φ(s) to obey multivariate log-normal statistics. Assuming, furthermore, statistical homogeneity and isotropy, the underlying covariance was determined by an a priori unknown angular power spectrum. To retain a flexible handle on this power spectrum, we further introduced hyperpriors (cf., e.g., Enßlin & Frommert 2011; Oppermann et al. 2012; Selig & Enßlin 2015). We assumed a (asymptotically) uniform prior for the logarithmic angular power and a spectral smoothness prior as suggested by Oppermann et al. (2012). This introduces the scalar model parameters α, q, and σ.
The point-like photon flux φ(u) exhibits strong features that appear to be fairly rare and local. We assumed φ(u) to follow statistically independent inverse-Gamma distributions described by the model parameters β and η.
For a detailed derivation and discussion of the probabilistic model that D3PO is based on, we refer to Selig & Enßlin (2015). An illustrative graphical model of the introduced hierarchy of Bayesian parameters is shown in Fig. A.1.
Appendix A.3: Analysis procedure
In theory, we could apply the D3PO algorithm to the whole data set at once. However, it is computationally more efficient to exploit the spectral separability of the response model by applying the algorithm to each energy band individually, cf. Eq. (A.2). To exploit spectral correlations, we propose to align the priors of the diffuse component after an initial inference run by defining a common angular power spectrum. This yields a three-step analysis procedure detailed in the following.
Initial inference:
the D3PO algorithm is applied to each energy band separately, which can be done in parallel.
We fixed the model parameters with fairly soft constraints by setting α = 1, q = 10-12, σ = 10, 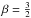 , and η = 10-2. The limit of (α,q) → (1,0) leads to a uniform prior for the logarithmic angular power spectrum τ of the diffuse photon flux (Enßlin & Frommert 2011), but choosing a non-zero q is numerically more stable. The spectral smoothness parameter σ is the a priori standard deviation of the second derivative of τ = τℓ with respect to the logarithm of the angular quantum number ℓ, that is, σ describes the tolerance of deviations from a power-law shape (Oppermann et al. 2012). The parameter tuple (β,η) determines the slope and scale of the inverse-Gamma prior of the point-like photon flux. While a slope of
, and η = 10-2. The limit of (α,q) → (1,0) leads to a uniform prior for the logarithmic angular power spectrum τ of the diffuse photon flux (Enßlin & Frommert 2011), but choosing a non-zero q is numerically more stable. The spectral smoothness parameter σ is the a priori standard deviation of the second derivative of τ = τℓ with respect to the logarithm of the angular quantum number ℓ, that is, σ describes the tolerance of deviations from a power-law shape (Oppermann et al. 2012). The parameter tuple (β,η) determines the slope and scale of the inverse-Gamma prior of the point-like photon flux. While a slope of 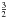 is generally applicable, the scale, for which we find 10-2 fitting, has to be adapted according to the chosen resolution (Selig & Enßlin 2015).
is generally applicable, the scale, for which we find 10-2 fitting, has to be adapted according to the chosen resolution (Selig & Enßlin 2015).
D3PO solves an inference problem that is non-linear and, in general, non-convex. To circumvent a dependence on its initialization, D3PO can generate suitable starting values by solving a coarse-grained inference problem first. For this purpose only, we provide a binary exposure masking the most prominent point sources.
Prior alignment:
the prior of the diffuse component describes our a priori expectation of how spatially smooth the emission is. If we find diffuse structures of a certain size at one energy band, we can expect to find similar structures at neighboring bands, especially since most diffuse emission processes exhibit power-law-like energy spectra. Thus, we expect significant spectral correlations, in particular for prominent features such as the Galactic bulge, for example. Since the incorporation of a spectral convolution in the response is computationally infeasible, we imposed an aligning of the diffuse priors to exploit spectral correlations, nonetheless.
The diffuse prior is defined by the logarithmic angular power spectrum τ. As discussed in Sect. 3.4, we found a rough power-law behavior of the power spectra with deviations due to the Galactic disk and finite exposure. Figure 11 shows the results of the initial inference, in particular including a power spectrum fit averaged across the energy bands. This average spectrum defines the aligned prior. The apparent excess of small-scale power for high-energy bands, comparing inferred and aligned power spectra, remedies potential perception thresholds occurring during the inference (Enßlin & Frommert 2011).
Afterwards, we also aligned the diffuse maps within the initially masked regions according to the aligned prior to avoid artifacts due to initialization16.
The alignment of the point-like priors, through β and η, has proven ineffective in tests and was therefore omitted.
Final inference:
the D3PO algorithm was again applied to each energy band separately. For this run, however, we ketp the (aligned) angular power spectrum fixed and provided the aligned diffuse maps as starting values. Hence, the initially used binary mask was not required any more. A fixed angular power spectrum renders the model parameters α, q, and σ obsolete.
All Tables
Overview of total flux upper limits for clusters hosting a radio (mini-)halo from the collection by Feretti et al. (2012).
All Figures
 |
Fig. 1 γ-ray sky seen by the Fermi LAT in a Mollweide projection. Panel a) shows the (total) photon flux reconstructed from photon count data of 6.5 years mission elapsed time in the energy range from 0.6 to 307.2 GeV reconvolved with the LAT’s IRFs. Panel b) shows solely the reconvolved diffuse contribution. Panel c) shows the fractional residual map between data and reconstruction smoothed with a 0.5° Gaussian kernel. Panel d) shows the fractional difference map between the standard total, Galactic plus isotropic, diffuse model (short “std”) and the reconstructed diffuse contribution. |
| In the text | |
 |
Fig. 2 Diffuse γ-ray flux and its relative reconstruction uncertainty on a logarithmic scale at different energies in a Mollweide projection. Panels a)−c) show the reconstructed diffuse photon flux at roughly 2 GeV, 10 GeV, and ~100 GeV. The photon flux is given in units of GeV-1 cm-2 s-1 sr-1. Note that the color scale varies. Panels d)–f) show the relative uncertainty on these reconstructions. Maps for all energy bands are available at the CDS. |
| In the text | |
 |
Fig. 3 γ-ray sky in pseudocolor in a Mollweide projection. Panel a) shows the 6.5 year data. Panels b) and c) show the reconstructed (total) photon flux that in b) is reconvolved with the IRFs. Panel d) shows the reconstructed diffuse photon flux. Panels e) and f) reproduce the latter, but are overlaid with the feature contours found by Su et al. (2010) (white: giant Fermi bubbles, light magenta: Donut, light blue: North Arc, light gray: Radio Loop I) and contours of the 408 MHz radio map from Haslam et al. (1982). Panel g) highlights the contours defining the bulge-, cloud-, and bubble-like regions discussed in Sect. 3.3. |
| In the text | |
 |
Fig. 4 Energy spectra considering an all-sky ROI. Shown are the data (green squares) converted to flux units, and spectra from the reconstructed total (gray), anisotropic diffuse (dashed orange), isotropic diffuse (dotted magenta), and point-like photon flux (blue circles). Furthermore, power-law fits for the anisotropic (thick solid orange) and isotropic emission (thick dashed-dotted magenta) are shown. The errors include statistical and systematic uncertainties and are only shown for data and diffuse contributions for reasons of clarity. |
| In the text | |
 |
Fig. 5 Spectral indices of featureless power-law fits, φaniso ∝ E− γ, at all positions in the sky using energy bands 1−8. |
| In the text | |
 |
Fig. 6 Cloud- and bubble-like component. Panel a) shows energy spectra from ROIs defined in Fig. 3g, cf. text. In addition to the spectra retrieved from the different regions, a linear combination of the cloud-, and bubble-like is fit to the bulge-like component, cf. legend. Panel b) shows the normalized latitude profiles of the cloud- and bubble-like component. |
| In the text | |
 |
Fig. 7 γ-ray sky in pseudocolor in a Mollweide projection. Panel a) shows the cloud-like and panel b) the bubble-like diffuse component. |
| In the text | |
 |
Fig. 8 Illustration of the brightness in a Mollweide projection. Panel a) shows the integrated brightness of the cloud-like component. Panel b) shows the monochromatic brightness of thermal dust emission at 353 GHz (Planck Collaboration XI 2014). Panel c) shows in white the area that was included in computing the latitude profile in Fig. 9. |
| In the text | |
 |
Fig. 9 Latitude profile of the dust-to-cloud-like-gamma ratio. The thermal dust emission from Planck Collaboration XI (2014) and Finkbeiner et al. (1999) has been smoothed with a 0.7° Gaussian kernel to match the coarseness of the γ-ray map. |
| In the text | |
 |
Fig. 10 Panel a) shows a magnification of the Chamaeleon complex from Fig. 7a. Panels b) and c) show magnifications of tentative outflows from Fig. 7b. The light gray line marks the Galactic plane (l = 0°). |
| In the text | |
 |
Fig. 11 Angular power spectra over angular quantum number ℓ. Panel a) shows the inferred spectra of the diffuse photon flux φ(s) in each energy band and a power-law fit thereof, cf. legend. Panel b) shows the direct realization spectra of the diffuse signal s = log (φ(s)/φ0) and the inferred, fitted, and averaged spectra, cf. legend. The colors (from red to violet to blue) indicate energy (from band 1 to 9) in both panels, and a white noise spectrum with arbitrary normalization is included for comparison. |
| In the text | |
 |
Fig. 12 Point sources in the γ-ray sky in pseudocolor and in a Mollweide projection. Markers show point sources from the second Fermi LAT source catalog (Nolan et al. 2012) for comparison; the gray scale indicates their average detection significance as listed in the catalog. Special markers show a selection of pulsars (squares), local SNRs (stars), and well-known galaxies (pentagons), as well as famous extragalactic objects (diamonds), cf. text. |
| In the text | |
 |
Fig. 13 Comparison of the second Fermi LAT source catalog (Nolan et al. 2012) and candidates from the reconstruction for which an association in the second Fermi LAT catalog has been found. Panel a) shows the histogram and scatter plot of the spectral indices γ(u) of candidates versus catalog sources. In the latter, a 1:1 line (black solid) is plotted for comparison, and the markers indicate the fit spectral shape, cf. legend. Panel b) shows the histogram and scatter plot of the logarithmic total fluxes log 10(F/F0), where F0 = 1 cm-2 s-1. The scatter plot contains a 1:1 line (black solid) for comparison. |
| In the text | |
 |
Fig. A.1 Graphical model of the model parameters α, q, σ, β, and η, the logarithmic angular power spectrum τ, the diffuse and point-like signal fields, s and u, the photon fluxes, φ, φ(s), and φ(u), and the expected and observed number of photons, λ and d. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.