| Issue |
A&A
Volume 581, September 2015
|
|
|---|---|---|
| Article Number | A101 | |
| Number of page(s) | 10 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201425164 | |
| Published online | 14 September 2015 | |
Constraining cosmology with shear peak statistics: tomographic analysis
1
UPMC Université Paris 06, UMR 7095, Institut d’Astrophysique de
Paris,
98bis Bd Arago,
75014
Paris,
France
e-mail:
martinet@iap.fr
2
APC, AstroParticule et Cosmologie, Université Paris Diderot,
CNRS/IN2P3, CEA/lrfu, Observatoire de Paris, Sorbonne Paris Cité, 10 rue Alice Domon et Léonie
Duquet, 75205
Paris Cedex 13,
France
3
Jet Propulsion Laboratory, California Institute of
Technology, 4800 Oak Grove
Drive, Pasadena,
California,
USA
4
Dipartimento di Fisica, Sezione di Astronomia, Università di
Trieste, via Tiepolo
11, 34143
Trieste,
Italy
5
INAF/Osservatorio Astronomico di Trieste, via Tiepolo
11, 34143
Trieste,
Italy
Received: 16 October 2014
Accepted: 8 April 2015
The abundance of peaks in weak gravitational lensing maps is a potentially powerful cosmological tool, complementary to measurements of the shear power spectrum. We study peaks detected directly in shear maps, rather than convergence maps, an approach that has the advantage of working directly with the observable quantity, the galaxy ellipticity catalog. Using large numbers of numerical simulations to accurately predict the abundance of peaks and their covariance, we quantify the cosmological constraints attainable by a large-area survey similar to that expected from the Euclid mission, focusing on the density parameter, Ωm, and on the power spectrum normalization, σ8, for illustration. We present a tomographic peak counting method that improves the conditional (marginal) constraints by a factor of 1.2 (2) over those from a two-dimensional (i.e., non-tomographic) peak-count analysis. We find that peak statistics provide constraints an order of magnitude less accurate than those from the cluster sample in the ideal situation of a perfectly known observable-mass relation; however, when the scaling relation is not known a priori, the shear-peak constraints are twice as strong and orthogonal to the cluster constraints, highlighting the value of using both clusters and shear-peak statistics.
Key words: gravitational lensing: weak / cosmological parameters
© ESO, 2015
1. Introduction
Weak gravitational lensing (WL) is a powerful probe of large-scale structure, dark matter, and dark energy (e.g., Bartelmann & Schneider 2001). In particular, cosmic shear surveys have demonstrated their ability to constrain cosmological parameters (e.g., Massey et al. 2007; Heymans et al. 2012), and the potential of large-area shear surveys covering thousands of square degrees to improve cosmological constraints to percent level accuracies is the prime motivation for ambitious programs like the on-going Dark Energy Survey (DES)1, and Stage IV experiments (Albrecht et al. 2006, 2009) like the Large Synoptic Survey Telescope2 (LSST, LSST Science Collaboration et al. 2009), the Wide Field Infrared Survey Telescope (WFIRST)3 (Spergel et al. 2013), and the Euclid4 (Laureijs et al. 2011) missions.
The shear correlation function (equivalently, power spectrum), a measure of the second moment of the mass distribution, is the standard tool for analyzing WL surveys. Other statistical measures of shear maps incorporating higher order moments are possible, and they become increasingly attractive in light of the significant gain in signal-to-noise expected from the planned large WL surveys.
In this paper, we consider the statistics of peaks in a shear map (or shear catalog) as a cosmological probe. We define shear peaks by filtering the map with an aperture designed to detect localized projected mass concentrations, such as galaxy clusters. Indeed, WL surveys can be used to detect galaxy clusters, and the cluster counts then used as a cosmological probe (Kruse & Schneider 1999; Marian & Bernstein 2006). Projection effects, however, severely limit the purity of cluster samples defined through WL, despite attempts at constructing optimal filters, because many peaks result from the alignment of small systems along the line of sight (White et al. 2002; Hamana et al. 2004; Hennawi & Spergel 2005).
An alternative is to abandon the correspondence between shear peaks and clusters and simply use the statistics of peaks to characterize the projected mass distribution (Reblinsky et al. 1999). This is the approach we adopt in the present work. These general shear peaks do not necessarily have any meaning as physical objects, being a combination of real clusters and chance alignments. Their abundance, however, like clusters, is sensitive to the underlying cosmology (Jain & Van Waerbeke 2000; Wang et al. 2009; Dietrich & Hartlap 2010; Kratochvil et al. 2010).
One disadvantage of this approach is that we do not posses a simple analytic form for the abundance of peaks as a function of cosmological parameters. This is in contrast to the situation with clusters, where practical expressions do exist for the mass function that greatly facilitate the theoretical prediction of cluster abundance and exploration of parameter space (Press & Schechter 1974; Jenkins et al. 2001; Tinker et al. 2008). We must instead resort to N-body simulations to predict WL peak abundance, and we require large suites of simulations to explore the parameter space.
Such studies have been undertaken by several authors in recent years (Dietrich & Hartlap 2010; Kratochvil et al. 2010; Yang et al. 2011; Hilbert et al. 2012; Marian et al. 2012, 2013). In this paper, we perform a Fisher analysis of the constraints from peak counts in the context of upcoming Stage IV dark energy surveys, comparing our results to constraints expected from cluster counts. We employ large suites of independent N-body simulations to mitigate what has been an important limitation of previous studies, and we work directly with shear measurements, rather than reconstructed convergence maps.
The SUNGLASS code (Kiessling et al. 2011) is a rapid simulation tool based on line-of-sight integration through N-body boxes to calculate the WL field. Its speed allows us to generate large numbers of simulated shear maps, and hence determine peak abundance as a function of cosmological parameters and its variance. In particular, we are able to accurately calculate the derivative of peak abundance with respect to the parameters needed for the Fisher matrix. It is important to note that while many previous works have employed N-body simulations for similar analyses, they have relied on statistically shifted maps generated from a limited number of simulations (e.g., Dietrich & Hartlap 2010; Kratochvil et al. 2010; Yang et al. 2011; Hilbert et al. 2012; Marian et al. 2012, 2013). By contrast, the maps in this work are truly independent, with each map generated from a separate N-body realization.
We work directly with ellipticity measurements, an unbiased estimator of the shear in the WL regime (e.g., Dietrich & Hartlap 2010; Maturi et al. 2011; Hamana et al. 2012; Hilbert et al. 2012), rather than convergence maps that have been used in several previous studies (e.g., Kratochvil et al. 2010; Yang et al. 2011; Marian et al. 2012, 2013). Convergence is not the direct observable, but must be reconstructed from shear measurements. Our approach avoids the complexity added by this inversion. In addition, the use of shear greatly simplifies the nature of map noise, which is non-trivial to estimate in the case of the reconstructed convergence.
Finally, we apply tomography to the peak statistics by dividing the lensed background galaxies into redshift bins. This offers a two-fold advantage; first it allows us to remove foreground galaxies (z ≤ 0.5) that tend to dilute the shear signal, although the mass distribution below this redshift still contributes to the statistics measured using only the higher redshift galaxies. Second, we can detect shear peaks in different redshift planes and examine the statistics both within and between planes. As with the shear correlation function, the additional radial information significantly increases precision on cosmological constraints. Building on the work of Hennawi & Spergel (2005) and Dietrich & Hartlap (2010), we quantify the constraining power of tomographic shear peak statistics for Stage IV dark energy missions, such as Euclid.
We begin by describing our WL simulations in Sect. 2. The peak detection procedure and its application to the simulations are detailed in Sect. 3. In Sect. 4 we examine peak statistics and their use as a cosmological probe. Section 5 extends the approach to tomography. We conclude with a final discussion and comment on future directions in Sect. 6. Throughout the paper, for concreteness, we consider the specific case of a survey similar to that of the Euclid mission with a fiducial flat ΛCDM cosmology specified by (ΩM, ΩΛ, Ωb, h, σ8, nS) = (0.272, 0.728, 0.0449, 0.71, 0.809, 1.000) (e.g., Hinshaw et al. 2013).
2. Weak lensing simulations
We employ the Fisher formalism to asses the cosmological constraints expected from peak counts in Stage IV dark energy experiments, taking as typical characteristics those of the Euclid (Laureijs et al. 2011) mission. Euclid will survey 15 000 deg2 in three infrared bands (Y, J, and H) and a single, wide optical filter (combined riz bands), the latter with a point spread function (PSF) of 0.1 arcsec. The survey reaches a mean source galaxy density usable for lensing of 30 gals. arcmin-2 with a median redshift of z = 0.8, following the redshift distribution 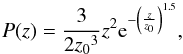 (1)with z0 = 0.7.
(1)with z0 = 0.7.
Calculation of the Fisher matrix requires the derivative of the mean peak counts with respect to cosmological parameters, evaluated at the fiducial model. We also need the covariance of the peak counts about their mean in this model. Since we do not posses an analytical expression for the WL peak abundance, we must use simulations to calculate the expected peak counts. We need enough simulations to accurately determine the mean peak counts for each parameter variation and to determine their covariance in the fiducial model. This is non-trivial as much of the signal comes from non-linear scales in the mass distribution, which can only be properly modeled by N-body simulations.
Simulation speed is therefore essential. In our study we use the SUNGLASS pipeline developed by Kiessling et al. (2011). We give a brief description of the SUNGLASS pipeline here but for a full prescription of how the SUNGLASS WL shear and convergence catalogs are generated, see Kiessling et al. (2011). For a given set of parameters, SUNGLASS first generates an N-body realization with the GADGET-2 code Springel (2005). These simulations are performed with 5123 paticles in a 512 h-1 Mpc box and the light cone is 100 square degrees and goes out to a redshift of z = 2.0. The convergence and shear of each mass point are calculated along the line of sight at multiple lensing source planes. This relies on the applicability of the Born approximation in the WL regime, i.e., that the mean path of the light bundle from a distant object remains adequately straight in the presence of lensing. The integration is much quicker than ray tracing through the simulation box, and allows the production of large suites of simulated WL observations. The shear and convergence is then interpolated on to the individual particles in the light cone, providing a highly sampled catalog of shear and convergence along the line of sight.
The speed of SUNGLASS enables us to produce many independent realizations, an improvement over previous studies that had to resort to shuffling the results from single realizations. The final WL catalogs are constructed by down-sampling the highly sampled SUNGLASS shear and convergence catalogs to 30 galaxies per square arc minute using the source galaxy redshift distribution of Eq. (1), and assuming that the galaxies trace the dark matter exactly. To model the shape noise arising from intrinsic galaxy ellipticity, we add a random ellipticity to each source galaxy in the simulated shear catalogs according to a Gaussian distribution with zero mean and standard deviation σϵ. In practice, we use a Box-Muller Gaussian random number generator, drawing two uniform numbers (x,y) over the interval (0,1) to obtain two Gaussian random numbers (ϵ1,ϵ2) that we add, respectively, to the shear components, γ1 and γ2: 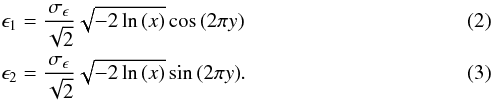 Null values in the first step are replaced by arbitrarily chosen values.
Null values in the first step are replaced by arbitrarily chosen values.
This procedure corresponds to drawing a tangential ellipticity from a Gaussian of zero mean and dispersion σϵ, which we take to be σϵ = 0.3 (e.g., Leauthaud et al. 2007). We note that the shear components, γ1 and γ2, are typically only a small percent of the noise, ϵ1 and ϵ2. Under the assumption that the noise is uncorrelated (i.e., in the absence of important intrinsic alignment effects), the mean ellipticity averaged over a number of source galaxies approaches the shear signal. We will discuss this fundamental hypothesis in Sect. 5.
3. Peak detection
3.1. Method
To identify peaks in a shear catalog, we employ aperture mass filtering (Schneider et al. 1998; Bartelmann & Schneider 2001) with an outer annulus to remove the integration constant, thereby resolving the finite space inversion problem. This technique does not return the true mass within the aperture, for example, when centered on a cluster; for that, one would have to know the true shape of the mass distribution as seen through the filter. By adopting a mass distribution, such as the NFW profile (Navarro et al. 1997), one can determine the true mass and also find clusters in WL surveys (e.g., Marian et al. 2012, 2013). Our goal, however, is not to measure the true mass of physical objects, but to compare the number of peaks expected in a WL survey for different cosmologies.
The aperture mass can be calculated either from the convergence field, κ, or the shear field, γ. In the former case, the aperture mass is calculated by integrating the convergence within the aperture centered at position θ0 (a two-dimensional vector in the plane of the sky), 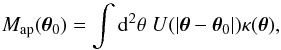 (4)where U is a filter chosen to best fit the lens mass density profile.
(4)where U is a filter chosen to best fit the lens mass density profile.
In a WL survey, the observable is actually the source galaxy ellipticity, ϵ. It is related to the reduced shear, g, by 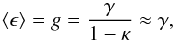 (5)which tends to the shear, γ, in the weak lensing regime where (κ,γ) ≪ (1,1). The indicated average is over random orientations of intrinsic galaxy ellipticity. A WL survey thus directly measures shear, γ, rather than the convergence. Working directly with the observable quantity, γ, we avoid the non-trivial step of integrating the shear to obtain the convergence field, which is a derived quantity.
(5)which tends to the shear, γ, in the weak lensing regime where (κ,γ) ≪ (1,1). The indicated average is over random orientations of intrinsic galaxy ellipticity. A WL survey thus directly measures shear, γ, rather than the convergence. Working directly with the observable quantity, γ, we avoid the non-trivial step of integrating the shear to obtain the convergence field, which is a derived quantity.
Shear and convergence are two mathematically distinct, although related, quantities, the first being a spinor of spin two and the second a scalar on the sphere. To adapt the expression for the aperture mass to the case of shear, we first define the scalar tangential shear, γt, for a galaxy image that accounts for both components of the shear (γ1 and γ2), ![\begin{equation} \gamma_{\rm t}(\vec{\theta},\vec{\theta}_0)=-\left[\gamma_1(\vec{\theta}) \cos 2\phi(\vec{\theta},\vec{\theta}_0) + \gamma_2(\vec{\theta}) \sin 2\phi(\vec{\theta},\vec{\theta}_0) \right], \end{equation}](/articles/aa/full_html/2015/09/aa25164-14/aa25164-14-eq41.png) (6)where φ is the angle giving the position of the galaxy image (θ) relative to an arbitrary fixed axis running through the center of the aperture, at position θ0, in the image plane; this fixed axis defines a local cartesian coordinate system in the plane of the sky with origin positioned on the filter center. The aperture mass equation can then be rewritten in terms of the tangential shear and the new filter function Q:
(6)where φ is the angle giving the position of the galaxy image (θ) relative to an arbitrary fixed axis running through the center of the aperture, at position θ0, in the image plane; this fixed axis defines a local cartesian coordinate system in the plane of the sky with origin positioned on the filter center. The aperture mass equation can then be rewritten in terms of the tangential shear and the new filter function Q:  The convergence has been used in several previous weak lensing peak studies (e.g., Kratochvil et al. 2010; Yang et al. 2011; Marian et al. 2012, 2013), although recent studies increasingly work directly with the shear (e.g., Dietrich & Hartlap 2010; Maturi et al. 2011; Hamana et al. 2012; Hilbert et al. 2012), which is also the approach adopted in this paper.
The convergence has been used in several previous weak lensing peak studies (e.g., Kratochvil et al. 2010; Yang et al. 2011; Marian et al. 2012, 2013), although recent studies increasingly work directly with the shear (e.g., Dietrich & Hartlap 2010; Maturi et al. 2011; Hamana et al. 2012; Hilbert et al. 2012), which is also the approach adopted in this paper.
We use the following weight functions, U for convergence and Q for shear, appropriate for a circular aperture (see Bartelmann & Schneider 2001): 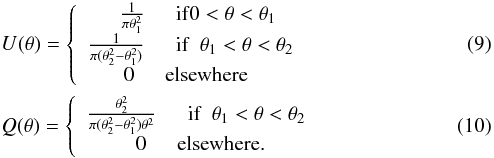 In practice, the integral over the aperture weight function becomes a sum weighted by the number density of galaxy images, n,
In practice, the integral over the aperture weight function becomes a sum weighted by the number density of galaxy images, n, 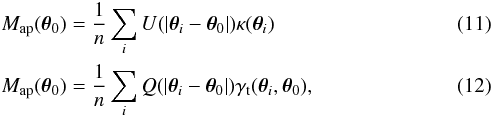 where γt(θi,θ0) and κ(θi) are the tangential shear and the convergence of the image at θi relative to the point θ0.
where γt(θi,θ0) and κ(θi) are the tangential shear and the convergence of the image at θi relative to the point θ0.
By expressing the equations in terms of discrete sums, we explicitly account for the sampling inherent in the observations, i.e., we only measure the shear where there is a source galaxy. Moreover, we use the actual number density of galaxies in the aperture, rather than a fixed, average value. The link from simulations to observations is trivial, as it is sufficient to replace the tangential shear, γt, in the last equation by the tangential component of the ellipticity, ϵt. This is the principal interest of using shear instead of convergence.
The aperture mass is convenient because in the case of the shear, it permits simple calculation of its variance due to the intrinsic ellipticity of the source galaxies, σϵ: 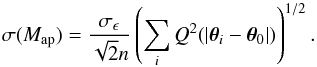 (13)This allows us to define a local noise level and peak detection threshold, which is another strong argument in favor of using shear peaks rather than convergence. We then define peak amplitude as
(13)This allows us to define a local noise level and peak detection threshold, which is another strong argument in favor of using shear peaks rather than convergence. We then define peak amplitude as 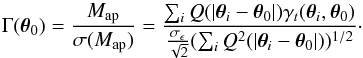 (14)The amplitude of a peak is independent of the normalization of the weight function, but does depend on the number of galaxies in the aperture through both the sums in numerator and denominator. Peak amplitude thus varies as the square root of the number of galaxies in the aperture. Intrinsic galaxy ellipticity also affects the signal-to-noise value, although it does not change the relative intensity of the peaks. As mentioned, we take σϵ = 0.3 (Leauthaud et al. 2007).
(14)The amplitude of a peak is independent of the normalization of the weight function, but does depend on the number of galaxies in the aperture through both the sums in numerator and denominator. Peak amplitude thus varies as the square root of the number of galaxies in the aperture. Intrinsic galaxy ellipticity also affects the signal-to-noise value, although it does not change the relative intensity of the peaks. As mentioned, we take σϵ = 0.3 (Leauthaud et al. 2007).
A critical point is the size and shape of the aperture. The chosen shape will preferentially select a specific form of structure, such as clusters or filaments, while the size will favor one cluster size over others. We must also adapt the aperture to include enough galaxies to optimize the signal-to-noise over the random shape noise (this point will be discussed in the section on tomography).
For simplicity, we adopt a radially symmetric aperture of fixed angular radius. The inner radius is set to θ1 = 3.5′, corresponding to the typical size of a cluster at redshift z = 0.3, where the contribution to shear peaks is the most important (Dietrich & Hartlap 2010), to exclude any contamination by cluster galaxies and the strong lensing regime, while the outer radius is set to θ2 = 10′, which is roughly the limit of the lensing effect at this redshift (see Hamana et al. 2012). In practice, we have found that the mass inside a given aperture strongly depends on the inner radius. In a future work, we plan to use a set of aperture sizes to extract information from different scales. One could also use an adaptive matched filter to preferentially select galaxy clusters (e.g., Marian et al. 2012). This is not our goal in this first study, and we leave the identification of an optimal filter to a future work. Finally, peaks are selected to be larger than all their neighbors in a radius equal to that of the aperture. Peaks situated at less than θ2 from the map edges are discarded as they are not computed in the proper aperture.
4. Peak statistics
We first present our statistical methodology and results from a non-tomographic analysis of the peak counts. Section 5 then extends the analysis to tomographic peak counts.
4.1. Method
We implemented two statistical measures: a χ2 test and the Fisher information matrix, both defined over bins of peak height. We chose our bins to include the same number of peaks based on the mean peak counts in our fiducial cosmology. This bin size is then maintained for the other cosmologies. Bin widths are given in Table 1, along with the number of peaks for one fiducial realization.
Bin widths and peak counts for one fiducial realization.
Let Ni,r be the number of peaks in bin i of realization r for a given cosmology, and R be the total number of realizations of this cosmology. Defining ⟨ N ⟩ i as the mean number of peaks in bin i, averaged over all R realizations, we calculate the covariance matrix of the binned peak counts as 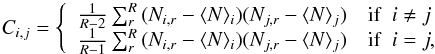 (15)using R = 150 independent realizations of the fiducial cosmology. Each of these realizations corresponds to a lightcone of 100 deg2, and we subsequently normalize the covariance matrix to an area of 15 000 deg2 (e.g., the useable extragalactic sky and Euclid target). Figure 1 shows the correlation matrix, i.e., the covariance matrix normalized to unity along the diagonal. We see that the correlation between bins is less than 20% except for the higher signal-to-noise bins where it can reach up to 40%. It seems reasonable that the stronger peaks would be more correlated between bins, with signal being dominated and seen by successive source planes, while the lower signal-to-noise peaks would be more affected by noise variations and projections between source planes. This agrees with the fact that high signal-to-noise peaks mostly correspond to galaxy clusters, while low signal-to-noise peaks are dominated by projections of large-scale structure and noise, as shown by Maturi et al. (2011).
(15)using R = 150 independent realizations of the fiducial cosmology. Each of these realizations corresponds to a lightcone of 100 deg2, and we subsequently normalize the covariance matrix to an area of 15 000 deg2 (e.g., the useable extragalactic sky and Euclid target). Figure 1 shows the correlation matrix, i.e., the covariance matrix normalized to unity along the diagonal. We see that the correlation between bins is less than 20% except for the higher signal-to-noise bins where it can reach up to 40%. It seems reasonable that the stronger peaks would be more correlated between bins, with signal being dominated and seen by successive source planes, while the lower signal-to-noise peaks would be more affected by noise variations and projections between source planes. This agrees with the fact that high signal-to-noise peaks mostly correspond to galaxy clusters, while low signal-to-noise peaks are dominated by projections of large-scale structure and noise, as shown by Maturi et al. (2011).
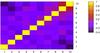 |
Fig. 1 Correlation matrix of the shear peak distribution for a 100 square-degree field, calculated by averaging over 150 realizations of the fiducial cosmology (see Eq. (15)). This is the covariance matrix normalized to unit diagonal. The x and y-axis values are the peak height bin numbers, defined in Table 1. |
This covariance matrix is then used to compute either the χ2 (Eq. (16)) or the Fisher matrix (Eq. (17)). The χ2 is expressed as 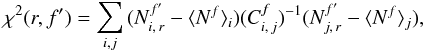 (16)where f represents the fiducial cosmology and f′ a reference cosmology. We note that f′ can be the same as f if we wish to compare one realization of a cosmology to all the other realizations of the same cosmology. This allows us, in particular, to test whether the χ2 variable is actually distributed according to a χ2-distribution. The Fisher matrix is given by
(16)where f represents the fiducial cosmology and f′ a reference cosmology. We note that f′ can be the same as f if we wish to compare one realization of a cosmology to all the other realizations of the same cosmology. This allows us, in particular, to test whether the χ2 variable is actually distributed according to a χ2-distribution. The Fisher matrix is given by 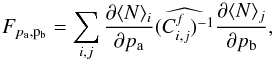 (17)where pa and pb are two cosmological parameters. We note that this expression is easily interpretable only in the case of Gaussian distributed bin counts, i.e., as the number of peaks becomes large. Cosmological parameter constraints are then obtained by inverting the Fisher matrix,
(17)where pa and pb are two cosmological parameters. We note that this expression is easily interpretable only in the case of Gaussian distributed bin counts, i.e., as the number of peaks becomes large. Cosmological parameter constraints are then obtained by inverting the Fisher matrix, 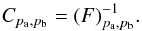 (18)Following Hartlap et al. (2007), we use the unbiased estimator,
(18)Following Hartlap et al. (2007), we use the unbiased estimator, 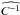 , for the inverse covariance matrix. Under the assumption of Gaussian errors and independent data vectors, it is related to the inverse of the estimated covariance matrix (Eq. (15)) through the number of realizations, R, and the number of degrees-of-freedom, D, as
, for the inverse covariance matrix. Under the assumption of Gaussian errors and independent data vectors, it is related to the inverse of the estimated covariance matrix (Eq. (15)) through the number of realizations, R, and the number of degrees-of-freedom, D, as
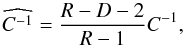 (19)where in our case D is the number of peak-height bins. This correction will thus be more important in our tomographic analysis where we build the covariance matrix through the assembled peak distributions of several redshift slices.
(19)where in our case D is the number of peak-height bins. This correction will thus be more important in our tomographic analysis where we build the covariance matrix through the assembled peak distributions of several redshift slices.
The derivative of the peak counts with respect to cosmological parameters averaged over all the realizations r is given by 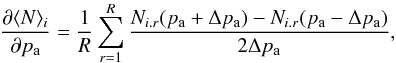 (20)where Δpa is the variation of the cosmological parameter pa. This calculation requires a sufficient number, R, of numerical simulations of each cosmology to accurately determine the derivatives. For a single parameter variation, we used 250 cosmological simulations (150 for the fiducial cosmology and 50 for a variation of + Δpa and 50 for a variation of −Δpa).
(20)where Δpa is the variation of the cosmological parameter pa. This calculation requires a sufficient number, R, of numerical simulations of each cosmology to accurately determine the derivatives. For a single parameter variation, we used 250 cosmological simulations (150 for the fiducial cosmology and 50 for a variation of + Δpa and 50 for a variation of −Δpa).
To determine if this is sufficient, we perform a convergence test on numbers of realizations by comparing the derivatives of the peak counts for increasing numbers of realizations of the modified cosmologies. In Fig. 2 we show the derivatives with respect to Ωm and σ8 when varying the number of realizations from 10 to 50 in increments of 10 realizations. We note that the derivatives do not significantly evolve beyond 30 realizations, justifying our choice of R = 50 for the modified cosmologies.
We use a larger number of realizations of the fiducial cosmology because the covariance matrix is computed for that model, while only the mean peak counts are required for the other cosmologies. Taylor & Joachimi (2014) calculated the accuracy of the covariance matrix given the number of realizations and of degrees of freedom of the data vectors. Following their Eq. (13), we estimate the precision of our covariance matrix to be better than ∼13% with our 150 realizations. The additive factor of 2ν-2, where ν is the desired accuracy, in the required number of realizations limits in practice the achievable accuracy on the covariance matrix; sub-percent accuracy, for instance, would demand at least 40 000 realizations. Our choice of 150 seems reasonable for the present test-study, but this issue calls for further attention and presents a crucial difficulty for many dark energy probes based on large-scale structure, such as cosmic shear.
 |
Fig. 2 Derivatives of the peak counts with respect to Ωm (top) and σ8 (bottom) as defined in Eq. (20) as a function of the number of realizations of the modified cosmologies. Results for R = (10,20,30,40,50) correspond, respectively, to the red, green, blue, purple and cyan curves. There is little change beyond R = 30. |
4.2. Results
As an illustration of peak count statistics, we study achievable constraints on two cosmological parameters: the total matter density, Ωm, and the present-day linear matter power spectrum normalization, σ8. In the standard ΛCDM model, these are well constrained by cosmic microwave background (CMB) observations (Hinshaw et al. 2013; Planck Collaboration XVI 2014). Methods measuring their values at low redshifts, such as peak counts or other gravitational lensing observations, are useful to search for extensions of this simple model. The power spectrum normalization, σ8, is a good example: differences between values obtained from the CMB and low redshift methods could indicate the need for a non-minimal neutrino mass (e.g., Planck Collaboration X 2014; Rozo et al. 2013; Battye & Moss 2014).
Each parameter was varied by 10% from its fiducial value given in Table 2 to define a reference cosmology. We generated 150 realizations of the fiducial cosmology and 50 realizations of each reference cosmology. When varying one parameter, the other remains at its fiducial value. However, when varying the matter density parameter, ΩM, the dark energy density parameter, ΩΛ, was also adjusted in order to maintain a flat Universe, ΩM + ΩΛ = 1.
4.2.1. Chi-squared distribution
We first examine the distribution of χ2 values (Eq. (16)) in the fiducial cosmology, using the covariance matrix calculated over the 150 realizations and dividing the peak heights into 10 bins of equal numbers of peaks, on average. The top panel of Fig. 3 shows that the distribution observed in the simulations is reasonably well represented by a true χ2 distribution with 10 degrees of freedom, although with a slight deviation manifest by the somewhat larger variance.
Cosmological parameter values for the fiducial and reference cosmologies.
When comparing a modified cosmology to the covariance matrix of the fiducial cosmology, we see that the χ2 distribution strongly diverges from a true χ2 law (lower panel of Fig. 3). This result illustrates the potential of this method to constrain cosmological parameters. The next step is to compute the constraints we would achieve with the Euclid survey using the Fisher formalism.
 |
Fig. 3 Normalized χ2 distribution based on the covariance matrix from the 150 realizations of the fiducial cosmology. We consider 10 bins in peak height with equal numbers of peaks in each bin (on average). Black histograms represent our data and red curve represents a theoretical χ2 distribution with 10 degrees of freedom. The top panel shows the distribution for 150 fiducial realizations. The bottom panel is the distribution for 50 realizations with Ωm increased by 10% from its fiducial value. |
4.2.2. Fisher information
Following Eq. (17) we compute the Fisher matrix and invert it to obtain constraints on the cosmological parameters. Two-dimensional constraints are plotted in Fig. 4 with 1σ and 2σ confidence contours. These constraints are summarized in Table 4.
 |
Fig. 4 Fisher joint conditional constraints on Ωm and σ8 with non-tomographic peak count statistics for a Euclid-like survey; the red and black contours delineate 1 and 2σ significance limits. |
Mean and one sigma variation of the number of peaks over the 150 realizations of the fiducial cosmology.
5. Tomography
We develop a tomographic approach to peak count statistics with the aim of exploiting the radial information by dividing the source galaxies into redshift bins and detecting peaks to each source plane separately. We then perform a joint statistical analysis of the multi-plane peak counts. For example, with two redshift bins we would have a peak distribution consisting of 20 bins in which the first 10 bins represent the distribution of peaks detected to the first source plane, and the remaining 10 the distribution to the second source plane. Our analysis employs the full covariance of these 20 bins. We note that this approach differs from that employed by Dietrich & Hartlap (2010) in that we do not attempt to localize individual peaks in redshift space; the two approaches, however, access the same information. An important issue with tomography is to ensure that we have enough galaxies in each aperture for the average ellipticity noise to be negligible compared to the average tangential shear.
5.1. How to slice the redshift dimension
Adopting a Gaussian random distribution of intrinsic galaxy ellipticities with zero mean and dispersion σϵ, the shape noise over an aperture is 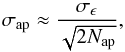 (21)where Nap is the average number of galaxies in the aperture. We denote y as the desired ratio between the average tangential shear, ⟨ γt ⟩ ap, and the aperture shape noise. An estimate of the number of source galaxies required per aperture is then
(21)where Nap is the average number of galaxies in the aperture. We denote y as the desired ratio between the average tangential shear, ⟨ γt ⟩ ap, and the aperture shape noise. An estimate of the number of source galaxies required per aperture is then 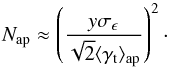 (22)We take a shape-noise dispersion of σϵ = 0.3 and an average shear value of 0.04 (e.g., Jain & Taylor 2003; Jain & Seljak 1997). These values with y = 7 yield a required number of about 1400 source galaxies per aperture.
(22)We take a shape-noise dispersion of σϵ = 0.3 and an average shear value of 0.04 (e.g., Jain & Taylor 2003; Jain & Seljak 1997). These values with y = 7 yield a required number of about 1400 source galaxies per aperture.
Working with fixed aperture size, the available number of galaxies per aperture depends on redshift. Using the distribution of redshifts in our simulations (Eq. (1)) normalized to the mean Euclid galaxy density of 30 galaxies per square arc-minute, we can estimate the number of galaxies per aperture for any slice of redshift. For the most distant redshift bin, the condition of having at least 1400 galaxies per aperture is satisfied for 1.43 <z ≤ 2. We adopt the same number of galaxies per redshift slice to avoid favoring any particular redshift bin. The condition on a minimal number of galaxies per aperture then directly translates into a condition on the maximum number of redshift bins. We also do not use the z ≤ 0.5 redshift range to avoid diluting the signal. These conditions allow us to perform a tomographic analysis with up to five redshift slices between redshift 0.5 and 2. We note that relaxing the constraint on the shear to ellipticity ratio would allow more redshift slices. We also note that this approach is limited by the uncertainty on the photometric redshift information, which is on the order of σ(z) = 0.05 × (1 + z).
For a first tomographic study, we use the following five redshift slices with equal numbers of galaxies: 0.5 <z ≤ 0.73, 0.73 <z ≤ 0.93, 0.93 <z ≤ 1.15, 1.15 <z ≤ 1.43, and 1.43 <z ≤ 2. The mean density in each slice is about five galaxies per square arc-minute. This corresponds to about 1400 galaxies per aperture and a shear to ellipticity ratio of about seven.
5.2. Results
We use the same simulations and shape noise realizations as in Sect. 4 when studying the two-dimensional peak counts. The size of the peak-amplitude bins is determined to include the same number of peaks in each bin of a given redshift slice, based on the mean peak counts in our fiducial cosmology. Figure 5 shows the full correlation matrix across all bins and source redshift planes, with the first 10 bins corresponding to the lowest redshift source plane and followed in sequence out to the highest redshift plane.
Table 3 gives the mean and one sigma variation of the number of peaks over the 150 realizations of the fiducial cosmology. The mean number of peaks are also shown in Fig. 6.
As seen from Table 3 and Fig. 6, peaks detected toward a low redshift source plane tend to also be detected when using higher redshift planes. This correlates the peak counts between source planes, as indicated by the non-zero off-diagonal elements of the correlation matrix, especially in the higher signal-to-noise bins. The bins are not fully correlated, however, because new peaks are detected beyond the lower redshift source planes as we move outward. This tomographic view of the peak distribution contains valuable cosmological information that increases the constraining power of the peak counts.
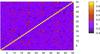 |
Fig. 5 Correlation matrix of the shear peak distribution for a 100 square-degree field with tomography, calculated by averaging over 150 realizations of the fiducial cosmology (see Eq. (15)). Each redshift slice is divided into ten bins of peak height. This is the covariance matrix normalized to unit diagonal. Correlations between bins are less than 20%, except at the highest signal-to-noise. |
 |
Fig. 6 Mean number of peaks over the 150 realizations of the fiducial cosmology. The red histogram corresponds to peaks detected in the 2D analysis while green, blue, pink, cyan, and yellow, respectively, correspond to peaks detected in the 0.5 <z ≤ 0.73, 0.73 <z ≤ 0.93, 0.93 <z ≤ 1.15, 1.15 <z ≤ 1.43, and 1.43 <z ≤ 2 redshift slices. |
This can be appreciated from the differences in the χ2 distributions shown in Fig. 7. The black histogram in the upper panel gives the distribution in the simulations, compared to a true χ2 distribution with 50 degrees-of-freedom traced by the solid red line. The lower panel gives the distribution of our χ2 variable for the same non-fiducial cosmology considered in the lower panel of Fig. 3. As before, the observed histogram strongly differs from the pure χ2 distribution. The fact that the histograms differ even more than in the two-dimensional case illustrates our increased ability to distinguish these cosmological models.
 |
Fig. 7 Normalized χ2 distributions with respect to the covariance matrix for 150 realizations of the fiducial cosmology with five source redshift planes. Each of the five source planes is associated with 10 signal-to-noise bins containing equal numbers of peaks. Black histograms trace the distribution observed in the simulations and the red curve represents a theoretical χ2 distribution with 50 degrees-of-freedom. The top panel gives the distribution for the 150 realizations of the fiducial model. The lower panel gives the distribution for the 50 realizations of the alternate cosmology with Ωm increased by 10% from its fiducial value. |
We quantify this gain with a Fisher analysis of the same cosmological parameters considered in the two-dimensional case. The increase in the number of effective degrees-of-freedom in the peak distribution drops the precision on our estimated covariance matrix to 15%, calculated according to Taylor & Joachimi (2014). Doubling the number of realizations to R = 300 would provide 10% precision, a small gain compared to the computational time required to generate twice as many realizations. We also verify that R = 50 realizations of the modified cosmologies is sufficient for calculation of the derivatives of the mean counts: as before, they are stable beyond 30 realizations. The constraints from our tomographic analysis are given in Fig. 8 and listed in Table 4, and they are compared to the two-dimensional case in Fig. 9.
Predicted cosmological parameter constraints for a Euclid-like survey.
6. Discussion
 |
Fig. 8 Predicted joint conditional constraints on Ωm and σ8 for a Euclid-like survey using tomographic peak count statistics. Solid red and dashed black contours correspond to 1σ and 2σ confidence regions, respectively. |
 |
Fig. 9 Fisher ellipses (at 1σ) for Ωm and σ8 for a Euclid-like survey. The blue dashed curve shows the joint conditional constraints without tomography, while the solid red contour gives those when using tomography with five redshift bins, demonstrating the important gain. |
A number of authors have investigated the potential of lensing peak counts as a cosmological probe, although few have considered large Stage IV projects such as Euclid (Yang et al. 2011; Maturi et al. 2011; Hilbert et al. 2012; Marian et al. 2012, 2013). Kratochvil et al. (2010), for example, examined the difference in the χ2 distributions from different cosmological models; however, it is difficult to make a direct comparison with our results since they varied a different set of cosmological parameters. In their pioneering study of tomographic peak counts, Dietrich & Hartlap (2010) considered a CFHTLS-like survey of about 180 deg2.
In this work we focus on a typical Stage IV survey characterized by the redshift distribution of a Euclid-like survey, using a suite of independent numerical simulations to examine possible cosmological constraints. Figure 9 and Table 4 quantify gains in constraining power by using tomography. We improve the marginal constraints on Ωm and σ8 by more than a factor of two over the two-dimensional (non-tomographic) analysis. As to be expected, the conditional constraints are improved by smaller factors: about 1.2 for Ωm and 1.3 for σ8.
Among previous studies of peak-statistics, only Dietrich & Hartlap (2010) and Yang et al. (2011) have applied tomography, the former maximizing the peak signal-to-noise given the redshift distribution of galaxies, and the latter placing source galaxies at either zs = 1 or zs = 2 and ray-tracing through simulations. Dietrich & Hartlap (2010) demonstrated the gain from tomographic peak counts for a survey of 180 deg2. In their LSST-like survey of 20 000 deg2, Yang et al. (2011) noted an improvement of the marginal constraints by factors of two to three when using tomography, in qualitative agreement with our results.
We also note that the impact of shape noise is effectively reduced with tomography, in particular for the peaks generated by structures at the higher redshifts. Binning the sources into redshift planes removes the shape noise contributed by foreground galaxies that do not carry any signal on the higher redshift peaks.
We compare our conditional constraints to those obtained by other authors. These vary over the range 0.0006 <δΩm< 0.0009, according to Hilbert et al. (2012) and Marian et al. (2012, 2013), and 0.0013 <δσ8< 0.0016, according to the same authors and Maturi et al. (2011). While these studies differ in a number of respects, the agreement on the conditional constraints among these authors and our results is very good. Indeed, we reach (δΩm,δσ8) = (0.0012,0.0018) without tomography, and (0.0010,0.0014) with tomography. The very small difference from the literature can be attributed to our use of a slightly lower survey area: 15 000 deg2 compared to 18 000 to 20 000 deg2 in these other studies.
Finally, we note that some authors have examined constraints on other cosmological parameters. In particular, it has been found that shear peaks have a good ability to constrain the dark energy equation-of-state w (e.g., Yang et al. 2011; Hilbert et al. 2012; Marian et al. 2012, 2013) and primordial non-Gaussianity fNL (e.g., Maturi et al. 2011; Hilbert et al. 2012).
We also compare our forecasted constraints with those from other cosmological probes, in particular from cluster abundance studies. While some lensing peaks do arise from individual clusters, peak statistics represent a more general description of the matter distribution because many originate from projections along the line of sight. Figure 10 compares our predicted constraints from tomographic peak statistics with those from current galaxy cluster constraints as summarized by Allen et al. (2011). The peak counts yield much tighter constraints than those from the current cluster analyses, which is not surprising because we are comparing present day cluster constraints to future lensing counts.
A more pertinent comparison is between constraints predicted from cluster photometric sample for the Euclid survey and the peak count constraints. This is shown in Fig. 11. The cluster constraints have been evaluated by Sartoris et al. (2015) for a Euclid cluster catalog considering the information provided by cluster number counts. We note that, unlike what has been done in Sartoris et al. (2015), constraints from clusters have been performed by varying only the σ8 and Ωm cosmological parameters and the 4 parameters that describe the bias, the scatter of the observable mass relation, and their redshift evolution. This has been done to compare in a more appropriate way the constraints obtained from the clusters and those from the shear peaks. The reduction in the number of free cosmological parameters explains why the cluster constraints shown in Fig. 11 are smaller than those shown in Sartoris et al. (2015). We see that the constraints from tomographic peak counts are weaker than cluster counts by an order of magnitude when supposing that the observable-mass relation is fully known a priori (blue dotted ellipse). However, the shear-peak constraints are almost twice as strong when not making any assumption on the scaling relation parameters and their evolution (green dash dotted ellipse). In addition, it is worth noting that the shear-peak contours are orthogonal to the clusters when the observable-mass relation is not known a priori. This essentially shows the value of using both clusters and shear-peak statistics. As it is difficult to predict how well we will be able to constrain the scaling relation, we show here two extreme cases for the cluster constraints, with the idea that the observational constraints should lie somewhere between the blue and green ellipses. In particular, the green contours are very conservative, as we could in principle already constrain the scaling relation at redshift z = 0, which would reduce the errors on the cosmological parameters.
We expect peak statistics to complement more standard two-point lensing statistics. In fact, the study by Dietrich & Hartlap (2010) suggests that peak statistics could yield tighter constraints than the classical 2-point correlation function, a result expected given that the peak statistics contain higher order correlations, and later confirmed by, e.g., Marian et al. (2012, 2013). Peak counts would also appear to be less affected by shape measurement systematics than the shear power spectrum in the sense that it is more difficult to reproduce the pattern necessary for peak identification than to affect the amplitude of two-point correlations. In similar vein, we expect that their respective sensitivities to photometric redshift uncertainties will not be the same. Overall, the two methods will not share the same systematics and therefore offer important complementarity.
 |
Fig. 10 Constraints from tomographic peak counts compared to current galaxy cluster constraints, with contours giving the 1 and 2σ confidence limits. The violet shading represents constraints from the maxBCG cluster catalog, blue those from WMAP-5, and the yellow their combination; they have been adapted from Allen et al. (2011). The green contours give the tomographic peak-count constraints for a Euclid-like survey covering 15 000 square degrees. |
 |
Fig. 11 Comparison of predicted constraints from Euclid clusters and peak counts for a Euclid-like survey (1σ confidence limits). The orange ellipse traces the tomographic peak-count results. The blue dotted ellipse reports the constraints obtained from cluster number counts with a 3σ selection function assuming a perfectly known observable-mass relation (see Sartoris et al. 2015). The green dash-dotted ellipse shows the same cluster constraints but leaving the 4 scaling relation parameters (bias, scatter, and their evolution) completely free to vary. We note the change of scale and shift of fiducial parameter values from Fig. 10. |
7. Conclusion
We have found that shear peak statistics offer a potentially powerful cosmological probe, in agreement with previous studies. As an advance along these lines, our results clearly illustrate the gain of using tomography in the framework of Stage IV dark energy surveys, i.e., separating the source galaxies into redshift planes and counting peaks to each plane. With tomography, we improve the conditional (respectively, marginal) constraints by a factor of 1.2 (resp. 2) on Ωm and σ8.
For a large-area survey, typified here as that from a Euclid-like mission, we estimate that the peak-count constraints are an order of magnitude less powerful than those predicated from galaxy cluster evolution when the observable-mass relation is fully known a priori, while they are twice as strong when not making any assumption on this relation. The peak counts, however, have the great advantage of not relying on such a scaling relation that may prove difficult to establish to high accuracy.
We have only explored the two parameters Ωm and σ8 in the present study, but plan to extend to other parameters, including the dark energy equation-of-state and primordial non-Gaussianity in future work. Further topics warranting exploration include the impact of various systematics, such as intrinsic alignments, photometric redshift errors, and shape measurement errors. These additional studies will quantify the extent to which peak counts are complementary to cosmic shear measurements.
The primary technical challenge in application of peak counts is the production of large suites of numerical simulations to calculate both the expected mean number of peaks and their covariance matrix over the cosmological parameter space. It is not, however, unique to the counts: all lensing studies face the same challenge because valuable signal, even in the two-point statistics of cosmic shear, originates in the non-linear regime. We therefore expect peak counts to accompany the more standard lensing measures in application to large lensing surveys.
Acknowledgments
We are grateful to the anonymous referee for his/her careful reading and helpful and constructive comments that improved the paper. N.M. thanks the École Normale Supérieure de Cachan and the Laboratoire AstroParticle et Cosmologie for financial support in the early stage of this work. B.S. acknowledges financial support from MIUR PRIN2010-2011 (J91J12000450001), from the PRIN-MIUR 201278X4FL grant, from a PRIN-INAF/2012 Grant, from the inDark INFN Grant and from the Consorzio per la Fisica di Trieste. A portion of the research described in this paper was carried out at the Jet Propulsion Laboratory, California Institute of Technology, under a contract with the National Aeronautics and Space Administration.
References
- Albrecht, A., Bernstein, G., Cahn, R., et al. 2006, ArXiv e-prints [arXiv:astro-ph/0609591] [Google Scholar]
- Albrecht, A., Amendola, L., Bernstein, G., et al. 2009, ArXiv e-prints [arXiv:0901.0721] [Google Scholar]
- Allen, S. W., Evrard, A. E., & Mantz, A. B. 2011, ARA&A, 49, 409 [NASA ADS] [CrossRef] [Google Scholar]
- Bartelmann, M., & Schneider, P. 2001, Phys. Rep., 340, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Battye, R. A., & Moss, A. 2014, Phys. Rev. Lett., 112, 051303 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Dietrich, J. P., & Hartlap, J. 2010, MNRAS, 402, 1049 [NASA ADS] [CrossRef] [Google Scholar]
- Hamana, T., Takada, M., & Yoshida, N. 2004, MNRAS, 350, 893 [NASA ADS] [CrossRef] [Google Scholar]
- Hamana, T., Oguri, M., Shirasaki, M., & Sato, M. 2012, MNRAS, 425, 2287 [NASA ADS] [CrossRef] [Google Scholar]
- Hartlap, J., Simon, P., & Schneider, P. 2007, A&A, 464, 399 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hennawi, J. F., & Spergel, D. N. 2005, ApJ, 624, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Heymans, C., Van Waerbeke, L., Miller, L., et al. 2012, MNRAS, 427, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Hilbert, S., Marian, L., Smith, R. E., & Desjacques, V. 2012, MNRAS, 426, 2870 [NASA ADS] [CrossRef] [Google Scholar]
- Hinshaw, G., Larson, D., Komatsu, E., et al. 2013, ApJS, 208, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Jain, B., & Seljak, U. 1997, ApJ, 484, 560 [NASA ADS] [CrossRef] [Google Scholar]
- Jain, B., & Taylor, A. 2003, Phys. Rev. Lett., 91, 141302 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Jain, B., & Van Waerbeke, L. 2000, ApJ, 530, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Jenkins, A., Frenk, C. S., White, S. D. M., et al. 2001, MNRAS, 321, 372 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Kiessling, A., Heavens, A. F., Taylor, A. N., & Joachimi, B. 2011, MNRAS, 414, 2235 [NASA ADS] [CrossRef] [Google Scholar]
- Kratochvil, J. M., Haiman, Z., & May, M. 2010, Phys. Rev. D, 81, 043519 [NASA ADS] [CrossRef] [Google Scholar]
- Kruse, G., & Schneider, P. 1999, MNRAS, 302, 821 [NASA ADS] [CrossRef] [Google Scholar]
- Laureijs, R., Amiaux, J., Arduini, S., et al. 2011, ArXiv e-prints [arXiv:1110.3193] [Google Scholar]
- Leauthaud, A., Massey, R., Kneib, J.-P., et al. 2007, ApJS, 172, 219 [NASA ADS] [CrossRef] [Google Scholar]
- LSST Science Collaboration, Abell, P. A., Allison, J., et al. 2009, ArXiv e-prints [arXiv:0912.0201] [Google Scholar]
- Marian, L., & Bernstein, G. M. 2006, Phys. Rev. D, 73, 123525 [NASA ADS] [CrossRef] [Google Scholar]
- Marian, L., Smith, R. E., Hilbert, S., & Schneider, P. 2012, MNRAS, 423, 1711 [NASA ADS] [CrossRef] [Google Scholar]
- Marian, L., Smith, R. E., Hilbert, S., & Schneider, P. 2013, MNRAS, 432, 1338 [NASA ADS] [CrossRef] [Google Scholar]
- Massey, R., Rhodes, J., Leauthaud, A., et al. 2007, ApJS, 172, 239 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Maturi, M., Fedeli, C., & Moscardini, L. 2011, MNRAS, 416, 2527 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration XVI. 2014, A&A, 571, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration X. 2014, A&A, 571, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Press, W. H., & Schechter, P. 1974, ApJ, 187, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Reblinsky, K., Kruse, G., Jain, B., & Schneider, P. 1999, A&A, 351, 815 [NASA ADS] [Google Scholar]
- Rozo, E., Rykoff, E. S., Bartlett, J. G., & Evrard, A. E. 2013, ArXiv e-prints [arXiv:1302.5086] [Google Scholar]
- Sartoris, B., Biviano, A., Fedeli, C., et al. 2015, MNRAS, submitted [arXiv:1505.02165] [Google Scholar]
- Schneider, P., van Waerbeke, L., Jain, B., & Kruse, G. 1998, MNRAS, 296, 873 [NASA ADS] [CrossRef] [Google Scholar]
- Spergel, D., Gehrels, N., Breckinridge, J., et al. 2013, ArXiv e-prints [arXiv:1305.5422] [Google Scholar]
- Springel, V. 2005, MNRAS, 364, 1105 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, A., & Joachimi, B. 2014, MNRAS, 442, 2728 [NASA ADS] [CrossRef] [Google Scholar]
- Tinker, J., Kravtsov, A. V., Klypin, A., et al. 2008, ApJ, 688, 709 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, S., Haiman, Z., & May, M. 2009, ApJ, 691, 547 [NASA ADS] [CrossRef] [Google Scholar]
- White, M., van Waerbeke, L., & Mackey, J. 2002, ApJ, 575, 640 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, X., Kratochvil, J. M., Wang, S., et al. 2011, Phys. Rev. D, 84, 043529 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Mean and one sigma variation of the number of peaks over the 150 realizations of the fiducial cosmology.
All Figures
 |
Fig. 1 Correlation matrix of the shear peak distribution for a 100 square-degree field, calculated by averaging over 150 realizations of the fiducial cosmology (see Eq. (15)). This is the covariance matrix normalized to unit diagonal. The x and y-axis values are the peak height bin numbers, defined in Table 1. |
| In the text | |
 |
Fig. 2 Derivatives of the peak counts with respect to Ωm (top) and σ8 (bottom) as defined in Eq. (20) as a function of the number of realizations of the modified cosmologies. Results for R = (10,20,30,40,50) correspond, respectively, to the red, green, blue, purple and cyan curves. There is little change beyond R = 30. |
| In the text | |
 |
Fig. 3 Normalized χ2 distribution based on the covariance matrix from the 150 realizations of the fiducial cosmology. We consider 10 bins in peak height with equal numbers of peaks in each bin (on average). Black histograms represent our data and red curve represents a theoretical χ2 distribution with 10 degrees of freedom. The top panel shows the distribution for 150 fiducial realizations. The bottom panel is the distribution for 50 realizations with Ωm increased by 10% from its fiducial value. |
| In the text | |
 |
Fig. 4 Fisher joint conditional constraints on Ωm and σ8 with non-tomographic peak count statistics for a Euclid-like survey; the red and black contours delineate 1 and 2σ significance limits. |
| In the text | |
 |
Fig. 5 Correlation matrix of the shear peak distribution for a 100 square-degree field with tomography, calculated by averaging over 150 realizations of the fiducial cosmology (see Eq. (15)). Each redshift slice is divided into ten bins of peak height. This is the covariance matrix normalized to unit diagonal. Correlations between bins are less than 20%, except at the highest signal-to-noise. |
| In the text | |
 |
Fig. 6 Mean number of peaks over the 150 realizations of the fiducial cosmology. The red histogram corresponds to peaks detected in the 2D analysis while green, blue, pink, cyan, and yellow, respectively, correspond to peaks detected in the 0.5 <z ≤ 0.73, 0.73 <z ≤ 0.93, 0.93 <z ≤ 1.15, 1.15 <z ≤ 1.43, and 1.43 <z ≤ 2 redshift slices. |
| In the text | |
 |
Fig. 7 Normalized χ2 distributions with respect to the covariance matrix for 150 realizations of the fiducial cosmology with five source redshift planes. Each of the five source planes is associated with 10 signal-to-noise bins containing equal numbers of peaks. Black histograms trace the distribution observed in the simulations and the red curve represents a theoretical χ2 distribution with 50 degrees-of-freedom. The top panel gives the distribution for the 150 realizations of the fiducial model. The lower panel gives the distribution for the 50 realizations of the alternate cosmology with Ωm increased by 10% from its fiducial value. |
| In the text | |
 |
Fig. 8 Predicted joint conditional constraints on Ωm and σ8 for a Euclid-like survey using tomographic peak count statistics. Solid red and dashed black contours correspond to 1σ and 2σ confidence regions, respectively. |
| In the text | |
 |
Fig. 9 Fisher ellipses (at 1σ) for Ωm and σ8 for a Euclid-like survey. The blue dashed curve shows the joint conditional constraints without tomography, while the solid red contour gives those when using tomography with five redshift bins, demonstrating the important gain. |
| In the text | |
 |
Fig. 10 Constraints from tomographic peak counts compared to current galaxy cluster constraints, with contours giving the 1 and 2σ confidence limits. The violet shading represents constraints from the maxBCG cluster catalog, blue those from WMAP-5, and the yellow their combination; they have been adapted from Allen et al. (2011). The green contours give the tomographic peak-count constraints for a Euclid-like survey covering 15 000 square degrees. |
| In the text | |
 |
Fig. 11 Comparison of predicted constraints from Euclid clusters and peak counts for a Euclid-like survey (1σ confidence limits). The orange ellipse traces the tomographic peak-count results. The blue dotted ellipse reports the constraints obtained from cluster number counts with a 3σ selection function assuming a perfectly known observable-mass relation (see Sartoris et al. 2015). The green dash-dotted ellipse shows the same cluster constraints but leaving the 4 scaling relation parameters (bias, scatter, and their evolution) completely free to vary. We note the change of scale and shift of fiducial parameter values from Fig. 10. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


