| Issue |
A&A
Volume 580, August 2015
|
|
|---|---|---|
| Article Number | A138 | |
| Number of page(s) | 17 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201424963 | |
| Published online | 19 August 2015 | |
The Good, the Bad, and the Ugly: Statistical quality assessment of SZ detections
1
Institut d’Astrophysique Spatiale, CNRS (UMR 8617) Université Paris-Sud
11, Bâtiment 121,
Orsay, France
e-mail: nabila.aghanim@ias.u-psud.fr
2
Instituto de Física de Cantabria (CSIC-Universidad de
Cantabria), Avda. de los Castros
s/n, 39005
Santander,
Spain
3
Laboratoire de Physique Subatomique et de Cosmologie, Université
Grenoble-Alpes, CNRS/IN2P3, Institut National Polytechnique de Grenoble,
53 rue des Martyrs,
38026
Grenoble Cedex,
France
4
CNRS, IRAP, 9
Av. colonel Roche, BP
44346, 31028
Toulouse Cedex 4,
France
5
Laboratoire AIM, IRFU/Service d’Astrophysique – CEA/DSM – CNRS –
Université Paris Diderot, Bât. 709,
CEA-Saclay, 91191
Gif-sur-Yvette Cedex,
France
Received:
11
September
2014
Accepted:
13
February
2015
We examine three approaches to the problem of source classification in catalogues. Our goal is to determine the confidence with which the elements in these catalogues can be distinguished in populations on the basis of their spectral energy distribution (SED). Our analysis is based on the projection of the measurements onto a comprehensive SED model of the main signals in the considered range of frequencies. We first consider likelihood analysis, which is halfway between supervised and unsupervised methods. Next, we investigate an unsupervised clustering technique. Finally, we consider a supervised classifier based on artificial neural networks. We illustrate the approach and results using catalogues from various surveys, such as X-rays (MCXC), optical (SDSS), and millimetric (Planck Sunyaev-Zeldovich (SZ)). We show that the results from the statistical classifications of the three methods are in very good agreement with each other, although the supervised neural network-based classification shows better performance allowing the best separation into populations of reliable and unreliable sources in catalogues. The latest method was applied to the SZ sources detected by the Planck satellite. It led to a classification assessing and thereby agreeing with the reliability assessment published in the Planck SZ catalogue. Our method could easily be applied to catalogues from future large surveys such as SRG/eROSITA and Euclid.
Key words: methods: statistical / galaxies: clusters: general
© ESO, 2015
1. Introduction
Astronomy and cosmology are witnessing a transition from specific point observations to larger and larger astronomical surveys covering large fractions of the sky, as large as the whole sky in some cases. In this context, there is a need for reliable classification tools to assess the quality and the confidence in detected sources. For example, in the context of galaxy cluster surveys several cosmological and astrophysical analyses need to be performed on samples with controlled selection effects. Moreover, follow-up observations are necessary to obtain crucial information such as redshifts. An a priori assessment of the quality of the detected sources is thus of great importance. For example, this is a crucial point for future surveys like SRG/eROSITA (see e.g. Merloni et al. 2012) or Euclid1 that expect to detect from 6 × 104 to 9 × 104 clusters of galaxies. In these experiments, a purity of 80 to 90% of the catalogues of clusters (defined as the fraction of detections associated with bona fide clusters) would translate into a few thousand false detections. These large numbers may pose serious issues for the cosmological interpretation of the number counts. They will also put a heavy load on the ground-based telescopes since the follow-up observations will need to mitigate the large number of false sources. In such a context, an assessment of the quality factor for the detections – or even better, a classification of the detected clusters in terms of their reliability – will be key information.
In the present article, we address the topic of multivariate tools for sample classification applying machine learning techniques that are commonly used in various scientific domains such as sociology, genetic classification, cosmology, and spectroscopy. Two distinct approaches can be used: Supervised and unsupervised learning. The difference relies on the utilization of hypotheses for supervised learning. Unsupervised learning can be used when no information on the potential classes are known a priori.
The traditional method for detecting structure within a population is some form of exploratory technique such as principal components analysis (PCA). Such methods do not use prior information on the classification of the candidate populations. Another unsupervised method commonly used is the clustering technique (see e.g. Hartigan 1975; Hartigan & Wong 1979). It consists of the search for the nearest neighbours in a canonic space and thus permits unknown populations to be automatically classified in relation to a reference population. This method has been in use since the 1980s in different domains ranging from apiculture (e.g. Tomassone & Fresnaye 1971; Cornuet et al. 1975) to planetary science (e.g. Forni et al. 2013). Clustering and in particular Voronoi tessellation is also used in astronomy to model and reproduce the cosmic web (e.g. Sheth & van de Weygaert 2004). Of the second type of classification methods, i.e. supervised methods, the most commonly used is the artificial neural networks (ANN; Du & Swamy 2014, and references therein). These networks are algorithms that mimic the learning abilities of brains; they have been successfully used in the analysis of datasets from many scientific domains (Reby et al. 1997; Bridges et al. 2011).
In our study, we illustrate the use and effects of the statistical classification techniques on the recently published catalogue of Sunyaev-Zeldovich (SZ) sources (Planck Collaboration XXIX 2014) which contains both confirmed galaxy clusters and candidate clusters detected through their SZ effect in the Planck frequency maps. Several astrophysical sources contribute to the measured signal and affect the SZ detection and lead to some false detections (see e.g. Planck Collaboration VIII 2011; Planck Collaboration XXIX 2014). Our aim is to assess whether an ensemble of sources detected through the SZ signal, including low-reliability sources, can be distinguishable on the basis of their spectral energy distribution (SED). First, we consider a likelihood analysis halfway between supervised and unsupervised methods. Next, we investigate a clustering technique. Finally, we consider ANN.
The article is organised as follows. We describe the data in Sect. 2; we then present both the SED model and the associated fitted parameters in Sects. 3 and 4. We describe the different classification methods used in the study in Sect. 5 and discuss the results in Sect. 6. We summarise our findings and conclusions in Sect. 7.
2. Data
For our study, we use catalogues and samples of sources including clusters of galaxies detected in the X-rays and in the optical and in SZ. We also use catalogues of radio and IR point sources as well as galactic cold sources. We use the Planck frequency maps. We finally construct a test set on 2000 random positions over the sky.
We use the Meta-Catalogue of X-ray detected Clusters of galaxies (MCXC, Piffaretti et al. 2011, and reference therein). It is a compilation constructed from the publicly available ROSAT All Sky Survey-based and serendipitous cluster catalogues, as well as the Einstein Medium Sensitivity Survey. It includes only clusters with available redshift information in the original catalogues which yields a dataset of 1789 clusters.
We also use a catalogue of clusters extracted from the Sloan Digital Sky Survey (SDSS, York et al. 2000) data, the WHL12 catalogue (132 684 objects, Wen et al. 2012). It provides an estimated richness. We apply a cut in richness, N200, of 50 to exclude low-mass systems and groups that have no significant SZ signal.
Finally, we use the Planck SZ source catalogue (PSZ1 hereafter, see Planck Collaboration XXIX 2014). It consists of 1227 sources detected through their SZ effect in the Planck frequency maps. As detailed in Planck Collaboration XXIX (2014), the PSZ1 catalogue contains 861 SZ sources associated with bona fide clusters. They are referred to as confirmed clusters. The remaining SZ sources are sorted into three categories, noted 1 to 3, from highest to lowest reliability according to an empirical assessment of their quality. The PSZ1 catalogue contains 54 class1 cluster candidates and 170 and 142 class2 and class3 candidates, respectively.
We also use catalogues of sources detected in the radio, at 30 GHz, and in the infrared (IR), at 353 GHz, both are extracted from the Planck Catalogue of Compact Sources (PCCS) (Planck Collaboration XXVIII 2014). We use a catalogue of cold Galactic sources (see Planck Collaboration XXIII 2011; Planck Collaboration XXII 2011) detected in the Planck channel maps following (Montier et al. 2010). We construct a catalogue of false SZ detections which consists of the major sources of contamination identified in Planck Collaboration VIII (2011) and Planck Collaboration XXIX (2014). Specifically, we take 200 sources outside the mask used for the Planck SZ detection, from the cold Galactic source catalogue, the IR sources at 353 GHz, and radio sources at 30 GHz. The obtained sample of false SZ detections is representative of unreliable SZ sources.
In order to compute the SED of the considered sources, we use the Planck channel maps from 70 to 857 GHz. Each map is set to a resolution of 13 arcmin, i.e. the lowest resolution associated with 70 GHz channel. This allows us to access to the emission in the radio domain (below 100 GHz) without decreasing the resolution too much.
3. SED fitting
In the context of multivariate classification, we need to resort to some dimensionality reduction approaches prior to any classification. There are standard dimensionality reduction techniques like PCA or independent component analysis (ICA) (Du & Swamy 2014) that do not include any pre-knowledge of the physical variables or processes. In the following, we choose to reduce the dimensionality by decomposing the signal in the form of a SED.
It is beyond the scope of our study to model the SED taking into account all the contributions to the signal. We focus instead on the astrophysical emissions that affect the most the SZ detection in multifrequency experiments. This was discussed in both Planck Collaboration VIII (2011) and Planck Collaboration XXIX (2014). From 70 to 857 GHz, several astrophysical sources contribute to the measured signal: Diffuse galactic free-free, synchrotron, and thermal dust emissions (The Planck Collaboration 2006; Planck Collaboration XXI 2011); anomalous microwave emission (AME, Planck Collaboration XX 2011); molecular Galactic emissions (mainly 12CO in the 100, 217, and 353 GHz bands; Planck Collaboration XIII 2013); emission from Galactic and extragalactic point sources (radio and infrared sources, Planck Collaboration Int. VII 2013; Planck Collaboration VII 2011); CIB (Planck Collaboration XVIII 2011); zodiacal light emission (Planck Collaboration XIV 2013); and thermal Sunyaev-Zeldovich effect (Sunyaev & Zeldovich 1972) in clusters of galaxies.
Therefore, we model the SED taking into account five components: the thermal SZ (tSZ) effect neglecting relativistic corrections; the cosmic microwave background (CMB) signal; and the CO emission. We also add an effective IR component representing the contamination by dust emission, cold Galactic sources, and CIB fluctuations; and an effective radio component accounting for diffuse radio and synchrotron emission and radio sources.
The flux in each channel, i.e. frequency, is then written as 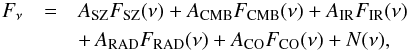 (1)where FSZ(ν), FCMB(ν), FIR(ν), FRAD(ν), and FCO(ν) are the spectra of SZ, CMB, IR, radio, and CO emissions shown in Fig. 1; ASZ, ACMB, AIR, ARAD, and ACO are the corresponding amplitudes; and N(ν) is the instrumental noise.
(1)where FSZ(ν), FCMB(ν), FIR(ν), FRAD(ν), and FCO(ν) are the spectra of SZ, CMB, IR, radio, and CO emissions shown in Fig. 1; ASZ, ACMB, AIR, ARAD, and ACO are the corresponding amplitudes; and N(ν) is the instrumental noise.
 |
Fig. 1 SED of the main astrophysical components. In orange is the tSZ effect, in red the infrared emission, in green the CMB, in dark blue the radio emission, and in light blue the CO molecular lines. |
For FIR(ν), we consider a modified black-body spectrum with temperature Td = 17 K and index βd = 1.6. This assumption is representative of the dust properties at high galactic latitudes. The contribution from CIB fluctuations affects the flux measurement, but is not a major contamination from the point of view of the detection, i.e. spurious sources. For FRAD(ν), we consider a power law emission, ναr, with index αr = −0.7 in intensity units representative of the average property of the radio emission. The SEDs of the different astrophysical components are given in Fig. 1.
We compute the flux at the position of each source of the catalogues described in Sect. 2 with aperture photometry. We set the aperture to 10 arcmin; the background level is estimated in an annulus between 20 to 50 arcmin. We have checked that varying the size of the aperture from 5 to 15 arcmin does not affect the results. Larger apertures obviously capture more contamination from the background.
Each derived spectrum, Fν, is fitted assuming the model in Eq. (1), where we fit for ASZ, ACMB, AIR, ARAD, and ACO through a linear fit of the form 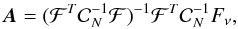 (2)with the mixing matrix ℱT, the instrumental noise covariance matrix
(2)with the mixing matrix ℱT, the instrumental noise covariance matrix 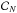 , and A a vector containing the fitted parameters. In this approach,
, and A a vector containing the fitted parameters. In this approach,  only accounts for the instrumental noise computed from the Planck half-ring maps, and we implicitly assume that the five components considered in the model reproduce the astrophysical signal in the data.
only accounts for the instrumental noise computed from the Planck half-ring maps, and we implicitly assume that the five components considered in the model reproduce the astrophysical signal in the data.
The efficiency of the dimensionality reduction is illustrated in Fig. 2 (right panel), where we show the SED fitted parameters correlation matrix, compared to the correlation matrix of measured fluxes from 30 to 857 GHz (left panel). We observe that we have a high degree of correlation between frequencies, especially at low frequency due to the CMB component (<217 GHz), and at higher frequency (>217 GHz) due to the thermal component. In contrast, in the SED parameter space, we observed that the correlation matrix is almost diagonal, except for a spatial correlation between thermal dust and CO emission.
 |
Fig. 2 Left panel: correlation matrix of the measured fluxes from 30 to 857 GHz estimated on 2000 random positions over the sky. Right panel: correlation matrix of fitted SED parameters from the same positions. |
4. Distribution of the fitted SED parameters
We start by fitting the amplitudes of the different components in the SED, namely ASZ, ACMB, AIR, ARAD, and ACO, at the positions of each source in the catalogue and samples described in Sect. 2. We examine the distribution of the fitted SED parameters and present, for each catalogue and sample, both the distributions and the correlation between fitted parameters. We also perform the same fitting at 2000 random positions in the sky.
 |
Fig. 3 Bottom line, from left to right: distribution of ASZ, ACMB, AIR, ARAD, and ACO at the position of MCXC galaxy clusters from Piffaretti et al. (2011). Top lines: 2D histograms showing the correlation between parameters. |
4.1. X-ray clusters from MCXC
In Fig. 3 we present the derived distribution for each amplitude fitted at the positions of MCXC galaxy clusters. Except for some negative values due to statistical noise, we observe an asymmetric distribution with positive values for ASZ, as is expected for galaxy clusters. We also note negative values for ASZ. These are associated with low signal-to-noise detections and are due to the combination of instrumental noise and the SED model-fitting. The distribution of ACMB is Gaussian, with a dispersion given by the amplitude of primordial CMB fluctuations; AIR presents a Cauchy distribution centred on zero; ARAD has a Gaussian distribution, except for a few outliers associated with contamination clusters from radio-loud active galactic nuclei (AGN) (e.g. Perseus, Virgo); and ACO presents a Gaussian distribution centred on zero.
We observe a positive correlation between ASZ and ARAD. Indeed, radio contamination mimics a tSZ effect at frequencies below 217 GHz, and thus an apparent increase on the tSZ flux can be compensated for by an increase of radio emission amplitude, leading to the observed degeneracy. Both radio and CO components induce an excess of emission at 100 GHz; as a result ARAD and ACO are anti-correlated. We notice that ACMB and AIR are not correlated with the other fitted parameters.
4.2. Optical clusters from SDSS
We now fit the amplitudes of the SED components at the position of optical clusters selected from the Wen et al. (hereafter WHL 2012) catalogue. In Fig. 4, we present the derived values for ASZ, ACMB, AIR, ARAD, and ACO. The distributions of amplitudes are similar to those of the MCXC clusters. They show the asymmetric distribution for ASZ and symmetric Gaussian or Cauchy distributions for the distributions of the other amplitudes.
 |
Fig. 4 Same as Fig. 3 for the SDSS galaxy clusters with richness above 50 from the WHL catalogue (Wen et al. 2012). |
 |
Fig. 5 same as Fig. 3 for the 861 confirmed SZ galaxy clusters from the PSZ1 catalogue (Planck Collaboration XXIX 2014). |
4.3. SZ clusters from PSZ1
The distributions of amplitudes of the fitted SED in the direction of 861 confirmed galaxy clusters from the PSZ1 catalogue share the same characteristics as the two other cluster catalogues detected in X-rays or the optical.
4.4. Radio, IR, and cold Galactic sources
We now examine the cases of sources emitting in the radio and in the IR that are not galaxy clusters. We focus on three sources that represent cases of spurious detections that affect the cluster extraction as described in Planck Collaboration VIII (2011) and in Planck Collaboration XXIX (2014). We fit for the SED in the direction of IR and radio sources from the PCCS catalogue, taken at 353 and 30 GHz, respectively, and we also consider GCS from Planck. All of the sources are taken outside a galactic mask leaving 85% of the sky.
The derived values are presented in Figs. 6–8. The distributions of fitted SED amplitudes are very different from the case of actual galaxy clusters. For the radio sources, we note that IR and CMB distributions are similar to those of the cluster catalogs and that the tSZ amplitude distribution is more symmetric than the case of galaxy clusters. For the IR sources detected at 353 GHz, the distribution of all amplitudes are “pathological”. The IR emission contaminates all the components including CMB and tSZ. For the cold Galactic sources, the distributions are much less compact. The ACMB distribution is mostly symmetric. The ASZ is symmetric and extends to very high values, unrealistic for clusters of galaxies. The distributions of AIR, ARAD, and ACO are mostly asymmetric and extend to large values similarly to the IR and radio-source cases.
4.5. Random positions
We perform the same SED fitting in random positions on the sky outside the mask. The distributions of the fitted amplitudes all show symmetric behaviour and do not extend to high values for any of the components considered here, as seen in Fig. 9.
4.6. PSZ1 sources
All the results presented above are either obtained for random positions on the sky or for catalogues and samples of actual clusters of galaxies or IR/radio or cold Galactic sources. The PSZ1 corresponds to a catalogue of sources detected through their tSZ effect. As such, it contains bona fide clusters of galaxies, 861 in total, but it also contains tSZ sources of different degrees of reliability including false detections.
We examine the distribution of the fitted SED amplitudes of all the PSZ1 sources. The derived values for ASZ, ACMB, AIR, ARAD, and ACO in the direction of PSZ1 sources are shown in Fig. 10. We note that the distribution of ASZ is similar to that of the clusters from MCXC and SDSS-based samples, i.e. asymmetric and extending to positive values. However, and contrary to the case of pure cluster samples of MCXC and SDSS, we observe a clear excess of IR and CO emissions. This is exhibited through the bimodal behaviour of the distribution extending to high AIR and ACO values. We also note a strong correlation of AIR and ACO that we can explain as the result of a combination of IR and CO contamination mimicking an offset SZ spectral distortion, see Fig. 3.
In Fig. 11, we show the distribution over the sky of the amplitudes ACMB, AIR, ARAD, and ACO. As expected, the distribution over the sky of CMB amplitudes does not show any particular trend or feature. It simply corresponds a Gaussian background. The distribution over the sky of the radio amplitudes is also featureless. We also note the absence of correlation on large scales, above a few tenths of degrees. As for the IR and the CO distributions, we clearly see that the contamination is, as expected, strongly correlated with the galactic emission in the galactic plane and the molecular clouds. For the AIR we also note some contamination at higher galactic latitudes.
 |
Fig. 11 From top to bottom: amplitude of ACMB, AIR, ARAD, and ACO as a function of the position on the sky for PSZ1 sources. |
5. Classification and SZ quality assessment
From the analysis of the SED fitted parameters ASZ, ACMB, AIR, ARAD, and ACO, we note that X-ray, optical, and SZ bona fide clusters show distributions of parameters consistent with no or low contamination. In contrast, the distribution of fitted SED parameters of the PSZ1 sources show some contamination both by IR and by CO emission. We thus construct quality assessments of tSZ detections based on the characteristics of SEDs. We use three different techniques to assess the quality of the tSZ detection and thus separate PSZ1 sources into two categories: reliable and unreliable.
As an intermediate step, we define a phenomenological quality assessment, hereafter called penalty factor QP, based on the data themselves, see Fig. 12. It does not rely on a model of the SED, but rather on the empirical assessments provided in the PSZ1 which define decreasing reliability classes 1, 2, and 3. Since the average spectrum of the class 3 sources of PSZ1 shows a clear excess of IR emission, we limit ourselves to a parametrization of the IR contamination. The penalty factor is defined as 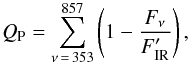 (3)with
(3)with 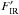 set to 2.8 × 10-4, 1.6 × 10-3, 2.4 × 10-2, and 1.9 K in CMB units from 353 to 857 GHz. As previously, Fν is estimated through aperture photometry in an aperture of 7 arcmin. The amplitude of the IR component corresponds to the average amplitude, at each frequency, of the class 3 sources in PSZ1 which represent the typical low-reliability sources as defined from empirical assessments. This estimator does not use error bars on the fluxes to derive the IR amplitude. The linear behaviour of QP penalizes cases that exceed the FIR.
set to 2.8 × 10-4, 1.6 × 10-3, 2.4 × 10-2, and 1.9 K in CMB units from 353 to 857 GHz. As previously, Fν is estimated through aperture photometry in an aperture of 7 arcmin. The amplitude of the IR component corresponds to the average amplitude, at each frequency, of the class 3 sources in PSZ1 which represent the typical low-reliability sources as defined from empirical assessments. This estimator does not use error bars on the fluxes to derive the IR amplitude. The linear behaviour of QP penalizes cases that exceed the FIR.
 |
Fig. 12 Piled-up distribution of the penalty factor for the PSZ1 catalog. Grey, blue, green, and red are for confirmed clusters, class 1, 2, and 3 sources respectively. |
5.1. Clustering-based quality assessment
The clustering algorithm is an unsupervised machine learning method often presented as assigning objects to the nearest cluster by distance. There are several choices for the distance: Euclidian, Manhattan, or generalized distance with the Mahalanobis metric. The number of clusters n is supplied as an input parameter.
We perform the classification of the sources, in n populations/clusters, using a standard k-means clustering (Hartigan 1975; Hartigan & Wong 1979) considering a Euclidian metric for the parameter space. In a first step, we define the distance, dcont, in the SED amplitude space from the zero contamination level as 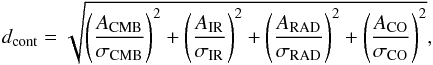 (4)where σCMB, σIR, σRAD, and σCO are the standard deviations of CMB, IR, radio, and CO amplitude distributions listed in Table 1.
(4)where σCMB, σIR, σRAD, and σCO are the standard deviations of CMB, IR, radio, and CO amplitude distributions listed in Table 1.
Best fitting parameters for ACMB, AIR, ARAD, and ACO distributions for random positions in the sky.
 |
Fig. 13 Piled-up distribution of the distance, dcont, in the clustering algorithm for PSZ1 sources. Grey is for confirmed clusters, blue is for class 1 sources, green for class 2 sources, and red is for class 3 sources. |
In Fig. 13, we present the piled-up distribution of the distance, dcont, for the PSZ1 sources. We observe that the confirmed clusters (grey), class 1 (blue), and class 2 (green) candidates present similar distributions, whereas class 3 objects (red) show larger values for dcont. This illustrates the presence of distinct populations of objects in the PSZ1 sample.
Then, we apply the k-means algorithm to the PSZ1 sources. One drawback of the k-means approach is that it requires each cluster of the population to be symmetric and to have the same extension with respect to the metric. This implies that we need a large number of populations. Moreover, an inappropriate choice of n may yield to poor results, which is why it is important to run diagnostic checks when performing k-means. We have tested the clustering techniques considering from n = 2 to 6 populations of sources. Below n = 3, the distribution of fitted amplitudes (ASZ, ACMB, AIR, ARAD, and ACO) showed residual contamination.
 |
Fig. 14 Same as Fig. 3 for the PSZ1 sources. In red we show the highest quality sources, in green and blue the sources are displayed with decreasing quality. |
We present the results for three populations in Fig. 14. We found that above three populations the results in terms of the distributions of fitted SED parameters were unchanged. We show the results of the clustering algorithm classification for the three populations (in red the highest quality sources; in yellow, cyan, and blue the sources with decreasing quality). We note that the population of good/reliable sources shows little sign of contamination and shares the same characteristics as the true clusters (see Figs. 3–5). In particular in the AIR/ACO plane, we observe a good separation between the three populations.
The clustering algorithm separates the low-quality and higher quality candidates and clusters of PSZ1 catalogue. However, the separation of populations is not optimal as the two populations of reliable and unreliable sources shows a large overlap.
5.2. Likelihood-based quality assessment
In this second approach halfway between supervised and unsupervised methods, we base the assessment of the SZ detection on the likelihood of the contamination. We thus define a quality factor, QL, as the product of SED parameter distributions estimated in random positions over the sky 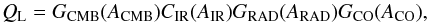 (5)with GCMB, CIR, GRAD, and GCO the distributions of the fitted SED parameters ACMB, AIR, ARAD, and ACO; G stands for Gaussian distribution, A exp(−(x − m)2/ 2σ2), and C for Cauchy distribution, A/ (1 + (x − m)2/σ2). In Table 1 we show the results of the adjustments for the random positions in the sky. We also conservatively set that high quality tSZ detections correspond to a 6σ limit, which translates into QL ~ 1.5 × 10-8.
(5)with GCMB, CIR, GRAD, and GCO the distributions of the fitted SED parameters ACMB, AIR, ARAD, and ACO; G stands for Gaussian distribution, A exp(−(x − m)2/ 2σ2), and C for Cauchy distribution, A/ (1 + (x − m)2/σ2). In Table 1 we show the results of the adjustments for the random positions in the sky. We also conservatively set that high quality tSZ detections correspond to a 6σ limit, which translates into QL ~ 1.5 × 10-8.
We first show in Fig. 15 the distribution of QL for the MCXC clusters. We note that the vast majority of these clusters fall above the quality factor of QL = 1.5 × 10-8. A small number of clusters from the MCXC have quality factors lower than the cut. They correspond to clusters exhibiting important contamination from AGN and radio sources. We also show in Fig. 16 the distribution of QL for the sample of false detections defined in Sect. 2. Only a handful of false detections lie above the quality factor cut.
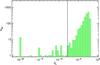 |
Fig. 15 Distribution of the quality factor QL for MCXC cluster of galaxies. The vertical solid line shows the threshold QL = 1.5 × 10-8. |
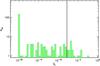 |
Fig. 16 Distribution of the quality factor QL for the sample of false detections. The vertical solid line shows the threshold QL = 1.5 × 10-8. |
In Fig. 17 we show the percentage of sources rejected by the quality factor cut QL = 1.5 × 10-8. We see that true confirmed clusters (red line) are not rejected. Applying the quality factor to the false sources (orange line) allows us to reject about 10% of the false detections. We see that the efficiency of the rejection differs if the contaminating sources are radio sources at 30 GHz (blue line), IR sources at 353 GHz (cyan line), or cold Galactic sources (green line).
 |
Fig. 17 Fraction of rejected sources as a function of the quality factor QL cut. In red and orange are the true/confirmed clusters from the PSZ1 catalogue and false detections, respectively. We also display in blue, cyan, and green the radio, IR, and cold Galactic sources. The vertical solid line shows the threshold QL = 1.5 × 10-8. |
 |
Fig. 18 Distribution of the quality factor for PSZ1 sources. In grey for confirmed clusters, in blue, green, and red for class 1, 2, and 3 sources, respectively. The vertical solid line shows the threshold QL = 1.5 × 10-8. |
We show in Fig. 18 the piled-up histograms of QL for the PSZ1 sources. We present classes 1, 2, and 3 together with the confirmed clusters in blue, green, red, and grey, respectively. We observe that the quality factor cut at QL = 1.5 × 10-8 clearly separates the confirmed clusters from the others. Moreover, the quality factor also separated the class 3 candidates of PSZ1 from the other PSZ1 sources, with most of the latter group being in the category of low-reliability sources. Some of the class 3 candidates, however, pass the cut and are in the category of highly reliable candidates. Confirmation of their status by follow-up observation will be an interesting test of the classification method.
We show the distributions of ASZ, ACMB, AIR, ARAD, and ACO in Figs. 19 and 20 for the PSZ1 sources with QL above the cut 1.5 × 10-8 and for the PSZ1 sources with QL< 1.5 × 10-8. We check that the high-quality sources (QL> 1.5 × 10-8) do not show significant contamination by IR, radio, or CO emissions, while we observe a clear contamination for the sources with QL< 1.5 × 10-8, especially in the IR-CO plane.
5.3. Neural network-based quality assessment
The third approach is based on ANN, the archetype of supervised machine learning methods. Artificial neural networks is a machine learning methodology based on parallelism and redundancy. The basic building block of an ANN is the neuron. Information is passed as inputs to the neuron, which processes them and produces an output which is a simple mathematical function of the inputs. The power of the ANN comes from assembling many neurons into a network. Well-designed networks are able to learn from a set of training data and to make predictions when presented with new, possibly incomplete, data.
We consider a standard three-layer back-propagation ANN to separate the tSZ detections into three populations of reliable quality (the Good), unreliable quality/false (the Bad), and noisy sources (the Ugly). A three-layer network consists of a layer of input neurons, a layer of hidden neurons, and a layer of output neurons. In such an arrangement each neuron is referred to as a node. The input layer consists of the five SED parameters and the output nodes represent the three classes of populations. The layout and number of nodes represent the architecture of the network.
Details on the ANN implementation can be found in Appendix A. We briefly present here the basics of this technique and illustrate the principle schematically in Fig. 21.
We define 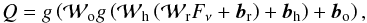 (6)where g(x) = 1 / (1 + exp(−x)) is the activation function,
(6)where g(x) = 1 / (1 + exp(−x)) is the activation function, 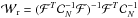 corresponds to a physically-based dimensional reduction,
corresponds to a physically-based dimensional reduction, 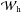 are the weights between input and hidden layers,
are the weights between input and hidden layers, 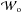 are the weights between hidden and output layers, bh are the biases between input and hidden layers, and bo are the biases between hidden and output layers.
are the weights between hidden and output layers, bh are the biases between input and hidden layers, and bo are the biases between hidden and output layers.
 |
Fig. 21 Neural network diagram. In our analysis, the input layer is composed of the five SED fitted parameters of each source at the seven frequencies. The hidden layer is composed of ten neurons. The output layer contains three values of Q for the categories, the Good, the Bad, and the Ugly, standing for reliable, unreliable, and noisy sources. |
To train the neural network, we use SED fitted parameters of the confirmed clusters of PSZ1 catalogue; they are representative of the Good high-quality source population. We use the fitted parameters of the sample of false detections defined in Sect. 2; they are representative of unreliable sources, the Bad. We also use the fitted parameters computed in random position over the sky; they are representative of noise-dominated population, the Ugly. We split each catalogue into two equal subsets, one training set and one checking set. Each of them contains of the order of 430, 300, and 100 Good (true clusters), Bad (false detections), and Ugly (noise at random positions) respectively. The second is used to estimate the efficiency of the ANN.
We defined the error on the classification as 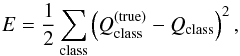 (7)where class stands for Good, Bad, or Ugly and
(7)where class stands for Good, Bad, or Ugly and 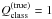 or 0 depending on whether the source belongs to the considered class. In order to avoid over-training, we stop the training at the iteration step that minimizes the error for the checking set.
or 0 depending on whether the source belongs to the considered class. In order to avoid over-training, we stop the training at the iteration step that minimizes the error for the checking set.
The ANN outputs a value of Qgood, Qbad, and Qugly (as given by Eq. (6)) for the source. We first show in Fig. 22 the distribution of ANN-based estimation of the Q values for the catalogue of false detections (checking-set subsample). We note that the distribution is dominated by high values of Qbad and low values of Qgood. We show by contrast in Fig. 23 the same distribution of Q values for actual clusters of galaxies from the MCXC catalogue. In this case, we note that most of the sources in this catalogue have low values of Qbad. The sources with lowest Qbad values are clusters exhibiting important contamination from AGNs. We also note a relatively large number of clusters with high values of Qugly. These clusters are associated with the low-mass clusters that have no significant SZ counterpart in the Planck data.
 |
Fig. 22 Distribution of neural-network-based estimation of Qgood, Qbad, and Qugly for the catalogue of false detections (checking-set subsample). The vertical solid line shows the threshold Qbad = 0.4. |
 |
Fig. 23 Distribution of ANN-based estimation of Qgood, Qbad, and Qugly for the MCXC catalogue. The vertical solid line shows the threshold Qbad = 0.6. |
 |
Fig. 24 Distribution of neural-network-based estimation of the quality factor for the PSZ1 catalog (used as training or checking sets). Grey, blue, green, and red are for confirmed clusters, class 1, 2, and 3 sources, respectively. The vertical solid line shows the threshold Qbad = 0.6. |
In Fig. 24, we present the piled-up histograms of Qgood, Qbad, and Qugly values for sources of the PSZ1 catalogue. We note that the ANN-based quality factor allows us to separate nicely the distribution of Qbad into two regimes of low and high values (associated mostly with class 3 PSZ1 sources), thus allowing us to identify clearly the Bad sources in the catalogue. The distribution of Qugly is flatter and shows that the category of Ugly noisy sources is evenly distributed, also among confirmed bona fide clusters. The distribution of Qgood is dominated by high values. The lowest end of the distribution is populated by class 3 sources from the PSZ1.
 |
Fig. 25 Distribution of PSZ1 sources as a function of Qgood, Qbad, and Qugly. Top panel: in grey for confirmed clusters, in blue for class 1 sources, in green for class 2 sources, and in red for class 3 sources. Bottom panel: density of sources as a function of Qgood, Qbad, and Qugly. |
In Fig. 25, we present the distribution of PSZ1 sources as a function of Qgood, Qbad, and Qugly. The abscissa, x, and ordinates, y, of each source is given by 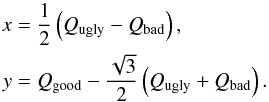 (8)We observe clearly three populations of sources associated with the Good, Bad, and Ugly categories. The PSZ1 sample is dominated by the Good sources; it also contains about 10% of Bad sources and a number of Ugly sources that have low signal-to-noise from the aperture photometry. We observe a clear separation between the Bad sources and the others. This representation illustrates the efficiency with which the neural network identifies and rejects Bad, most likely spurious, SZ sources.
(8)We observe clearly three populations of sources associated with the Good, Bad, and Ugly categories. The PSZ1 sample is dominated by the Good sources; it also contains about 10% of Bad sources and a number of Ugly sources that have low signal-to-noise from the aperture photometry. We observe a clear separation between the Bad sources and the others. This representation illustrates the efficiency with which the neural network identifies and rejects Bad, most likely spurious, SZ sources.
The same representation of Qgood, Qbad, and Qugly for other samples considered in this study can be found in Appendix B.
We now use the ANN results to find a quantitative way to identify the Bad sources from the catalogue. We thus define a quality factor of the SZ detection as, QN = 1 − Qbad. We show, in Fig. 26 and for the PSZ1 checking-set sample, the fraction of rejected sources as a function of the quality factor QN cut. In red and orange are the true clusters and false detections, respectively. In blue, cyan, and green are the radio, IR, and cold Galactic sources. We see that a cut at QN = 0.4 ensures that we remove 95% of the Bad sources without affecting the true cluster distribution. Such a cut allows us to reject 90% of the IR at 353 GHz and radio at 30 GHz sources and more that 95% of the cold Galactic sources. The cut in QN translates into a Qbad = 0.6 which marks the boundary of the Qbad distribution in Fig. 22.
 |
Fig. 26 For the PSZ1 checking-set sample: fraction of rejected sources as a function of the quality factor QN cut. In red and orange are the true clusters and false detections, respectively. We also display in blue, cyan, and green the radio, IR, and cold Galactic sources. The vertical solid line shows the threshold QN = 0.4. |
We show the distributions of ASZ, ACMB, AIR, ARAD, and ACO in Figs. 27 and 28 for the PSZ1 sources after applying the cut in QN and for the PSZ1 sources with QN< 0.4. We check that the good-quality sources (QN> 0.4) do not show significant contamination by IR, radio, or CO emissions, while for the sources with QN< 0.4 we observe a clear contamination, especially the IR-CO plane.
6. Discussion
We compare the efficiency with which the different quality factors distinguish between high-quality and low-quality SZ detections. We first illustrate this comparison by plotting in Fig. 29 the fraction of overlap between QN, QL, and QP as a function of the rejection percentage for the PSZ1 catalogue. We observe that the best agreement between QN and QL is obtained with an overlap of 91% for a rejection of 12%. For higher rejection percentage, we observe that the overlap decreases.
 |
Fig. 29 Overlap between QN and QL in red, QN and QP in green, and QL and QP in blue as a function of the rejection percentage for the PSZ1 catalogue. In black is shown the expected overlap between uncorrelated variables. |
We also examine the distribution of the PSZ1 sources as a function of the quality factors QN, QL, and the penalty QP, and we show the 2D scatter plots in the quality-factor planes in Fig. 30. On the one hand, we see that the cuts in QN and QL nicely separate the population of high- and low-quality SZ sources, with the ANN-based quality assessment seeming more efficient at identifying the Bad sources. Moreover, the two cuts preserve the confirmed clusters as only less that 2% of these fall in the category of low-quality sources. We have checked the status of the 22 confirmed clusters that are excluded by the combination of QN and QL cuts. We find that they are located mostly between −30°<b< 30°, and are contaminated by IR, radio point sources, or CO and thermal dust emission.
Finally, we check the effect of the classification in high- and low-quality sources through the average SED of the Bad and Good sources defined according to the cuts in QN, QL, and QP. For the last group we apply a cut at 7.4 that excludes a few tens of confirmed clusters. A smaller cut would increase the contamination at high frequencies, but would reduce the number of excluded clusters of galaxies. The SED are given in Figs. 31 and 32. We show in Fig. 31 that the SED is in perfect agreement with a dust-like SED. We also see the contamination from CO at 100 and 217 GHz. In contrast, we see in Fig. 32 that the average SED compatible with that of the SZ emission. Again, the quality assessment of Good sources from the ANN analysis shows a better performance (as traced by the low contamination level of the SED at the highest frequencies) than with the likelihood-based quality factor.
 |
Fig. 30 Piled-up distribution of the quality factors QN, QL, and QP for the PSZ1 sources (grey: confirmed clusters, blue: class1, green: class 2, red: class 3). The vertical solid line represents the cut separating the population of high- and low-quality detections. The 2D scatter plots show the cuts for the pair of quality factors under consideration. The vertical solid lines show the threshold QN = 0.4, QL = 1.5 × 10-8, and QP = 7.4. |
The classification from the ANN seems to give better results than the other methods. This is expected from supervised methods where the training is performed on pre-defined class memberships. We tested the ANN in a case where no pre-definition of the Bad class is given. Namely, we used the random positions as the Ugly class and we trained the network on a subsample constructed from the PSZ1 catalogue itself. The results applied on the checking set, i.e. the other subsample from PSZ1, are shown in Fig. 33. We note that without a training on the class of Bad candidates the ANN does not separate this type of source efficiently. The network separate the PSZ1 mostly into a population of Ugly, i.e. noisy, and Good. We also note that there is an ensemble of sources (middle of the lower panel, Fig. 33) for which the network is unable to set a class.
Although, the performance of the ANN is less efficient than when the classes are predefined, we nevertheless note that this method gives very satisfactory results.
Finally, we have investigated the ANN-based quality factors for SZ sources detected in Planck that were shown unambiguously to be false candidates by follow-up in X-rays based on Director’s Discretionary Time on the XMM-Newton observatory (Planck Collaboration IX 2011; Planck Collaboration Int. I 2012; Planck Collaboration Int. IV 2013). No significant extended X-ray emission was associated with eight SZ detections in Planck data: PLCK G321.410+19.941, PLCK G355.247-61.038, PLCK G93.139-19.040, PLCK G320.145-53.631, PLCK G10.161-11.706, PLCK G201.148-35.245, PLCK G34.92-19.263, and PLCK G120.218+11.093. We find that all SZ detections have very high Qugly factors (0.7 to 1) except the first (PLCK G321.410+19.941), which has a slightly smaller value of Qugly, but has Qugly = 0.4, i.e. is identified as a spurious detection. The quality factor Qgood for all but two detections is below 0.01. Only PLCK G201.148-35.245 and PLCK G34.92-19.263 have Qgood ~ 0.2 and 0.6, respectively, but they are both in the class of noisy Ugly sources.
The a posteriori quality assessment of the confirmed false SZ sources in Planck shows that these spurious detections were mostly related to noise fluctuations.
 |
Fig. 31 Average SED for Bad PSZ1 sources, i.e. with QN< 0.4, QL< 1.5 × 10-8 and QP< 7.4, respectively. In red is the best fit for an infrared SED and in blue the contribution from CO rotational lines. |
 |
Fig. 32 Average SED for good PSZ1 sources, i.e. with QN> 0.4, QL> 1.5 × 10-8, and QP> 7.4, respectively. In red is the expected SED for tSZ effect. |
 |
Fig. 33 Top panel: distribution of the PSZ1 sources as a function of Qgood, Qbad, and Qugly. In grey for confirmed clusters, in blue for class 1 sources, in green for class 2 sources, and in red for class 3 sources. Bottom panel: density of sources for the PSZ1 catalogue as a function of Qgood, Qbad, and Qugly. |
7. Summary and conclusions
We have addressed the question of classification of populations illustrating the approaches used on the catalogue of SZ sources detected by Planck. To this end, we build a SED model including all the major sources of signal in the range of frequencies considered for the dataset. This projection of the data onto a SED has allowed us to reduce the dimensionality of the problem and to resort to statistical classification techniques.
We explore three techniques (i) clustering, an unsupervised machine learning; (ii) artificial neural networks, a supervised machine learning; and (iii) likelihood, halfway between supervised and unsupervised. Each of the three methods outputs quantitative quality factors to the SZ sources. The classification techniques separate statistically the sources into populations of different quality and reliability.
We apply the techniques to cluster catalogues detected in the X-rays and in the optical and to catalogues of point sources. Each time the statistical classification was able to separate the cases of bona fide clusters and the cases of sources that are not clusters. We then applied our methods to the PSZ1 catalogue. All three classification results agree. They reproduce rather well the distribution of the PSZ1 sources in confirmed clusters and class 1, 2, and 3 candidates. For each technique, most of the class 3 objects are put in the least reliable population.
We show that although all methods agree, the supervised neural network-based classification performs better than the likelihood approach or the unsupervised clustering method. This is exhibited by the clean average SED of the sources in the Good population. The higher performance is expected since the supervised methods utilise more information. The performance is even better when we have an a priori definition of class membership. The classification then serves to determine whether or not the pre-defined populations are distinguishable. We show, however, that the ANN can detect differences between classes of populations even when the training is not performed on pre-defined populations.
Finally, we suggest on the basis of our results that a supervised learning approach should be the method of choice when classifying individuals into pre-defined populations. The classification methods applied in the present study to assess the quality factor of SZ detections and separate the populations focuses on photometric quantities only. It can easily be adapted and generalized to other quantities like morphological criteria, or to other contexts such as the detection of galaxy clusters, and more generally sources, in Euclid and in the X-rays in SRG/eROSITA where the classification is mainly an question of disentangling overlapping point sources and extended sources like clusters of galaxies. An adaptation is ongoing.
Acknowledgments
The authors thank A. Beelen, B. Bertincourt, O. Forni, and B. Roukema for useful remarks. We acknowledge the support of the French Agence Nationale de la Recherche under grant ANR-11-BD56-015. The development of Planck has been supported by: ESA; CNES and CNRS/INSU-IN2P3-INP (France); ASI, CNR, and INAF (Italy); NASA and DoE (USA); STFC and UKSA (UK); CSIC, MICINN and JA (Spain); Tekes, AoF and CSC (Finland); DLR and MPG (Germany); CSA (Canada); DTU Space (Denmark); SER/SSO (Switzerland); RCN (Norway); SFI (Ireland); FCT/MCTES (Portugal); and PRACE (EU).
References
- Bridges, M., Heron, E., O’Dushlaine, C., & Segurado, C. 2011, PLoS ONE, 6, e14802 [NASA ADS] [CrossRef] [Google Scholar]
- Cornuet, J.-M., Fresnaye, J., & Tassencourt, L. 1975, Apidologie, 6, 145 [CrossRef] [EDP Sciences] [Google Scholar]
- Du, K.-L., & Swamy, M. N. S. 2014, Neural Networks and Statistical Learning (London: Springer) [Google Scholar]
- Forni, O., Maurice, S., Gasnault, O., et al. 2013, Spectrochimica Acta Part B, 86, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Hartigan, J. 1975, Clustering Algorithms (John Wiley & Sons, Inc.) [Google Scholar]
- Hartigan, J., & Wong, M. A. 1979, J. Roy. Stat. Soc., 28, 100 [Google Scholar]
- Merloni, A., Predehl, P., Becker, W., et al. 2012, ArXiv e-prints [arXiv:1209.3114] [Google Scholar]
- Montier, L. A., Pelkonen, V., Juvela, M., Ristorcelli, I., & Marshall, D. J. 2010, A&A, 522, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Piffaretti, R., Arnaud, M., Pratt, G. W., Pointecouteau, E., & Melin, J.-B. 2011, A&A, 534, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration VII. 2011, A&A, 536, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration VIII. 2011, A&A, 536, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration IX. 2011, A&A, 536, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XVIII. 2011, A&A, 536, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XX. 2011, A&A, 536, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXI. 2011, A&A, 536, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXII. 2011, A&A, 536, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXIII. 2011, A&A, 536, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. I. 2012, A&A, 543, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. IV. 2013, A&A, 550, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. VII. 2013, A&A, 550, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XIII. 2014, A&A, 571, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XIV. 2014, A&A, 571, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXVIII. 2014, A&A, 571, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXIX. 2014, A&A, 571, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reby, D., Lek, S., Dimopoulos, I., et al. 1997, Behavioural Processes, 40, 35 [CrossRef] [Google Scholar]
- Sheth, R. K., & van de Weygaert, R. 2004, MNRAS, 350, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Sunyaev, R. A., & Zeldovich, Y. B. 1972, Comments Astrophys. Space Phys., 4, 173 [NASA ADS] [EDP Sciences] [Google Scholar]
- The Planck Collaboration 2006, ArXiv e-prints [arXiv:astro-ph/0604069] [Google Scholar]
- Tomassone & Fresnaye, J. 1971, Apidologie, 2, 49 [CrossRef] [EDP Sciences] [Google Scholar]
- Wen, Z. L., Han, J. L., & Liu, F. S. 2012, ApJS, 199, 34 [NASA ADS] [CrossRef] [Google Scholar]
- York, D. G., Adelman, J., Anderson, Jr., J. E., et al. 2000, AJ, 120, 1579 [Google Scholar]
Appendix A: Neural network
In this section we detail the concept of back propagation neural network that was used in the present analysis.
The concept of neural network consists in multiple layers of neurons. Each neuron is set to a value ranging from zero to one. The value of neurons, x(n), in the layer n is fully determined by the value of the neurons, x(n − 1), in layer n − 1 via a linear combination using weights, 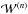 . This relation reads
. This relation reads 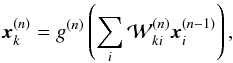 (A.1)where g(n)(x) is the activation function of the neuron. In the following, we do not mention the bias term as it can be considered an extra neuron added at each input layer for which the value is always set to one.
(A.1)where g(n)(x) is the activation function of the neuron. In the following, we do not mention the bias term as it can be considered an extra neuron added at each input layer for which the value is always set to one.
To be trained, this neural network needs a set of input neurons, x(0), for which the expected value of the neurons of the output layer, y, are known. Using the neural network, it is possible to estimate the values of y from the values of x(0). We can define the distance of the estimated value 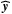 to the known solution y as
to the known solution y as 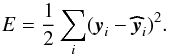 (A.2)Then, we aim at minimizing E by adjusting the weights,
(A.2)Then, we aim at minimizing E by adjusting the weights, 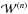 , of each layer.
, of each layer.
To do so we need to compute the derivative of E as a function of a given weight 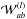 of the layer l ≠ m,
of the layer l ≠ m, 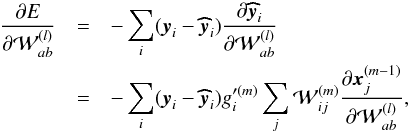 (A.3)where m is the total number of layers and
(A.3)where m is the total number of layers and 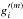 is the derivative of
is the derivative of 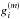 with respect to
with respect to 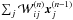 . Following the same approach, and considering m − 1 >l, it is possible to estimate
. Following the same approach, and considering m − 1 >l, it is possible to estimate 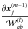 ,
, 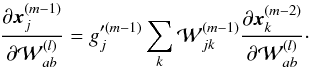 (A.4)We define the error,
(A.4)We define the error, 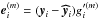 , and the back propagated error,
, and the back propagated error, 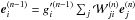 . Then we have
. Then we have 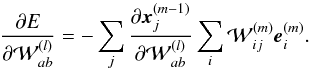 (A.5)Using Eq. (A.4), Eq. (A.5), and the relation between e(n − 1) and e(n) we obtain
(A.5)Using Eq. (A.4), Eq. (A.5), and the relation between e(n − 1) and e(n) we obtain 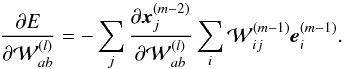 (A.6)Then, by iteration we can derive
(A.6)Then, by iteration we can derive 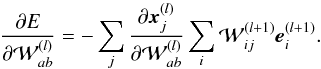 (A.7)We need to estimate
(A.7)We need to estimate 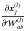 ,
, 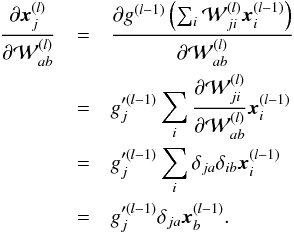 (A.8)Indeed, x(l − 1) does not depend on
(A.8)Indeed, x(l − 1) does not depend on 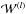 , as x(l − 1) is the input layer for weights
, as x(l − 1) is the input layer for weights 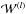 . Finally, we derive
. Finally, we derive 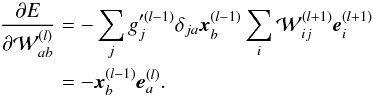 (A.9)As a consequence, the gradient of E with respect to
(A.9)As a consequence, the gradient of E with respect to 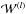 can be directly expressed from the input layer values x(l − 1) and the back propagated error e(l). Then the weights of the neural network can be adjusted iteratively through a gradient descent,
can be directly expressed from the input layer values x(l − 1) and the back propagated error e(l). Then the weights of the neural network can be adjusted iteratively through a gradient descent, 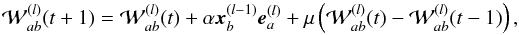 (A.10)where α is the learning rate and μ the momentum, both set to values ranging from 0 to 1.
(A.10)where α is the learning rate and μ the momentum, both set to values ranging from 0 to 1.
Low values for α prevent oscillations towards the minimum of E. High values for μ avoid local minima stabilization. However, extremely low values for both parameters can slow down the speed of training the network.
Appendix B: Neural network results for various samples of sources
 |
Fig. B.1 From left to right and top to bottom: density of sources as a function of Qgood, Qbad, and Qugly for MCXC, SDSS, random, bad, and PCCS at 30 and 353 GHz. |
In this section we present the distributions from various samples as a function of Qgood, Qbad, and Qugly. We test our neural network on the MCXC catalogue, the catalogue of clusters from Wen et al. (2012) based on SDSS data, a set of 2000 random positions over the sky, a set of bad detections, and PCCS sources at 30 and 353 GHz.
In Fig. B.1 we observe that galaxy clusters are flagged as Good quality sources or Ugly sources in the case of low signal-to-noise ratio for the tSZ emission. We observe that random positions over the sky are effectively classified as Ugly. We observe that the false detections are flagged as Bad quality sources. We note that PCCS sources are flagged as Bad quality sources or as Ugly for low signal-to-noise sources.
All these tests demonstrate that the neural network-based quality assessment is able to accurately separate classes of sources for which we have a significant signal-to-noise ratio.
All Tables
Best fitting parameters for ACMB, AIR, ARAD, and ACO distributions for random positions in the sky.
All Figures
 |
Fig. 1 SED of the main astrophysical components. In orange is the tSZ effect, in red the infrared emission, in green the CMB, in dark blue the radio emission, and in light blue the CO molecular lines. |
| In the text | |
 |
Fig. 2 Left panel: correlation matrix of the measured fluxes from 30 to 857 GHz estimated on 2000 random positions over the sky. Right panel: correlation matrix of fitted SED parameters from the same positions. |
| In the text | |
 |
Fig. 3 Bottom line, from left to right: distribution of ASZ, ACMB, AIR, ARAD, and ACO at the position of MCXC galaxy clusters from Piffaretti et al. (2011). Top lines: 2D histograms showing the correlation between parameters. |
| In the text | |
 |
Fig. 4 Same as Fig. 3 for the SDSS galaxy clusters with richness above 50 from the WHL catalogue (Wen et al. 2012). |
| In the text | |
 |
Fig. 5 same as Fig. 3 for the 861 confirmed SZ galaxy clusters from the PSZ1 catalogue (Planck Collaboration XXIX 2014). |
| In the text | |
 |
Fig. 6 Same as Fig. 3 for the sources detected in the 30 GHz channel of Planck. |
| In the text | |
 |
Fig. 7 Same as Fig. 3 for sources detected in the 353 GHz channel of Planck. |
| In the text | |
 |
Fig. 8 Same as Fig. 3 for cold Galactic sources from Planck. |
| In the text | |
 |
Fig. 9 Same as Fig. 3 at the 2000 random positions on the sky of our test sample. |
| In the text | |
 |
Fig. 10 Same as Fig. 3 for the PSZ1 sources. |
| In the text | |
 |
Fig. 11 From top to bottom: amplitude of ACMB, AIR, ARAD, and ACO as a function of the position on the sky for PSZ1 sources. |
| In the text | |
 |
Fig. 12 Piled-up distribution of the penalty factor for the PSZ1 catalog. Grey, blue, green, and red are for confirmed clusters, class 1, 2, and 3 sources respectively. |
| In the text | |
 |
Fig. 13 Piled-up distribution of the distance, dcont, in the clustering algorithm for PSZ1 sources. Grey is for confirmed clusters, blue is for class 1 sources, green for class 2 sources, and red is for class 3 sources. |
| In the text | |
 |
Fig. 14 Same as Fig. 3 for the PSZ1 sources. In red we show the highest quality sources, in green and blue the sources are displayed with decreasing quality. |
| In the text | |
 |
Fig. 15 Distribution of the quality factor QL for MCXC cluster of galaxies. The vertical solid line shows the threshold QL = 1.5 × 10-8. |
| In the text | |
 |
Fig. 16 Distribution of the quality factor QL for the sample of false detections. The vertical solid line shows the threshold QL = 1.5 × 10-8. |
| In the text | |
 |
Fig. 17 Fraction of rejected sources as a function of the quality factor QL cut. In red and orange are the true/confirmed clusters from the PSZ1 catalogue and false detections, respectively. We also display in blue, cyan, and green the radio, IR, and cold Galactic sources. The vertical solid line shows the threshold QL = 1.5 × 10-8. |
| In the text | |
 |
Fig. 18 Distribution of the quality factor for PSZ1 sources. In grey for confirmed clusters, in blue, green, and red for class 1, 2, and 3 sources, respectively. The vertical solid line shows the threshold QL = 1.5 × 10-8. |
| In the text | |
 |
Fig. 19 Same as Fig. 3 for the high-quality PSZ1 sources with QL> 1.5 × 10-8. |
| In the text | |
 |
Fig. 20 Same as Fig. 3 for the low-quality PSZ1 sources with QL< 1.5 × 10-8. |
| In the text | |
 |
Fig. 21 Neural network diagram. In our analysis, the input layer is composed of the five SED fitted parameters of each source at the seven frequencies. The hidden layer is composed of ten neurons. The output layer contains three values of Q for the categories, the Good, the Bad, and the Ugly, standing for reliable, unreliable, and noisy sources. |
| In the text | |
 |
Fig. 22 Distribution of neural-network-based estimation of Qgood, Qbad, and Qugly for the catalogue of false detections (checking-set subsample). The vertical solid line shows the threshold Qbad = 0.4. |
| In the text | |
 |
Fig. 23 Distribution of ANN-based estimation of Qgood, Qbad, and Qugly for the MCXC catalogue. The vertical solid line shows the threshold Qbad = 0.6. |
| In the text | |
 |
Fig. 24 Distribution of neural-network-based estimation of the quality factor for the PSZ1 catalog (used as training or checking sets). Grey, blue, green, and red are for confirmed clusters, class 1, 2, and 3 sources, respectively. The vertical solid line shows the threshold Qbad = 0.6. |
| In the text | |
 |
Fig. 25 Distribution of PSZ1 sources as a function of Qgood, Qbad, and Qugly. Top panel: in grey for confirmed clusters, in blue for class 1 sources, in green for class 2 sources, and in red for class 3 sources. Bottom panel: density of sources as a function of Qgood, Qbad, and Qugly. |
| In the text | |
 |
Fig. 26 For the PSZ1 checking-set sample: fraction of rejected sources as a function of the quality factor QN cut. In red and orange are the true clusters and false detections, respectively. We also display in blue, cyan, and green the radio, IR, and cold Galactic sources. The vertical solid line shows the threshold QN = 0.4. |
| In the text | |
 |
Fig. 27 Same as Fig. 3 for PSZ1 sources with the ANN-based quality factor QN> 0.4. |
| In the text | |
 |
Fig. 28 Same as Fig. 3 for PSZ1 sources with the ANN-based quality factor QN< 0.4. |
| In the text | |
 |
Fig. 29 Overlap between QN and QL in red, QN and QP in green, and QL and QP in blue as a function of the rejection percentage for the PSZ1 catalogue. In black is shown the expected overlap between uncorrelated variables. |
| In the text | |
 |
Fig. 30 Piled-up distribution of the quality factors QN, QL, and QP for the PSZ1 sources (grey: confirmed clusters, blue: class1, green: class 2, red: class 3). The vertical solid line represents the cut separating the population of high- and low-quality detections. The 2D scatter plots show the cuts for the pair of quality factors under consideration. The vertical solid lines show the threshold QN = 0.4, QL = 1.5 × 10-8, and QP = 7.4. |
| In the text | |
 |
Fig. 31 Average SED for Bad PSZ1 sources, i.e. with QN< 0.4, QL< 1.5 × 10-8 and QP< 7.4, respectively. In red is the best fit for an infrared SED and in blue the contribution from CO rotational lines. |
| In the text | |
 |
Fig. 32 Average SED for good PSZ1 sources, i.e. with QN> 0.4, QL> 1.5 × 10-8, and QP> 7.4, respectively. In red is the expected SED for tSZ effect. |
| In the text | |
 |
Fig. 33 Top panel: distribution of the PSZ1 sources as a function of Qgood, Qbad, and Qugly. In grey for confirmed clusters, in blue for class 1 sources, in green for class 2 sources, and in red for class 3 sources. Bottom panel: density of sources for the PSZ1 catalogue as a function of Qgood, Qbad, and Qugly. |
| In the text | |
 |
Fig. B.1 From left to right and top to bottom: density of sources as a function of Qgood, Qbad, and Qugly for MCXC, SDSS, random, bad, and PCCS at 30 and 353 GHz. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


