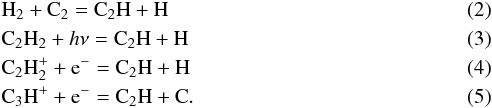| Issue |
A&A
Volume 578, June 2015
|
|
|---|---|---|
| Article Number | A124 | |
| Number of page(s) | 13 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201424220 | |
| Published online | 15 June 2015 | |
C2H observations toward the Orion Bar⋆
1
I. Physikalisches Institut, Universität zu Köln,
Zülpicher Str. 77, 50937
Köln,
Germany
e-mail:
zsofia.nagy.astro@gmail.com
2
Department of Physics and Astronomy, University of
Toledo, 2801 West Bancroft
Street, Toledo,
OH
43606,
USA
3
Kapteyn Astronomical Institute, University of
Groningen, PO box
800, 9700 AV
Groningen, The
Netherlands
4
SRON Netherlands Institute for Space Research,
Landleven 12, 9747 AD
Groningen, The
Netherlands
5
Université Joseph Fourier/CNRS, Institut de Planétologie et
d’Astrophysique de Grenoble (IPAG) UMR 5274, 38041
Grenoble,
France
6
University of Michigan, Ann Arbor, MI
48197,
USA
Received: 15 May 2014
Accepted: 20 April 2015
Context. The ethynyl radical (C2H) is one of the first radicals to be detected in the interstellar medium. Its higher rotational transitions have recently become available with the Herschel Space Observatory.
Aims. We aim to constrain the physical parameters of the C2H emitting gas toward the Orion Bar.
Methods. We analyze the C2H line intensities measured toward the Orion Bar CO+ Peak and Herschel/HIFI maps of C2H, CH, and HCO+ and a NANTEN map of [Ci]. We interpret the observed C2H emission using the combination of Herschel/HIFI and NANTEN data with radiative transfer and PDR models.
Results. Five rotational transitions of C2H (from N = 6−5 up to N = 10−9) have been detected in the HIFI frequency range toward the CO+ peak of the Orion Bar. Based on the five detected C2H transitions, a single component rotational diagram analysis gives a rotation temperature of ~64 K and a beam-averaged C2H column density of 4 × 1013 cm-2. The rotational diagram is also consistent with a two-component fit, resulting in rotation temperatures of 43 ± 0.2 K and 123 ± 21 K and in beam-averaged column densities of ~8.3 × 1013 cm-2 and ~2.3 × 1013 cm-2 for the three lower-N and for the three higher-N transitions, respectively. The measured five rotational transitions cannot be explained by any single parameter model. According to a non-LTE model, most of the C2H column density produces the lower−N C2H transitions and traces a warm (Tkin ~ 100−150 K) and dense (n(H2) ~ 105−106 cm-3) gas. A small fraction of the C2H column density is required to reproduce the intensity of the highest-N transitions (N = 9−8 and N = 10−9) originating in a high-density (n(H2) ~5 × 106 cm-3) hot (Tkin ~ 400 K) gas. The total beam-averaged C2H column density in the model is 1014 cm-2. A comparison of the spatial distribution of C2H to those of CH, HCO+, and [Ci] shows the best correlation with CH.
Conclusions. Both the non-LTE radiative transfer model and a simple PDR model representing the Orion Bar with a plane-parallel slab of gas and dust suggest that C2H cannot be described by a single pressure component, unlike the reactive ion CH+, which was previously analyzed toward the Orion Bar CO+ peak. The physical parameters traced by the higher rotational transitions (N = 6−5, ..., 10−9) of C2H may be consistent with the edges of dense clumps exposed to UV radiation near the ionization front of the Orion Bar.
Key words: stars: formation / ISM: molecules
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
The ethynyl radical (C2H) was one of the first radicals to be detected in the interstellar medium (Tucker et al. 1974). It has been observed toward several types of regions, including diffuse clouds (Lucas & Liszt 2000), massive star-forming regions (Beuther et al. 2008), photon-dominated regions (PDRs, e.g. Teyssier et al. 2004) and dark clouds (e.g., Pratap et al. 1997). C2H is an important molecule in the carbon-chemistry and is related to many C-bearing species. One example is the C3H+ ion, which has recently been detected toward the Horsehead PDR (Pety et al. 2012). C2H can also be an ingredient for the formation of carbon chain molecules, such as C5, via a reaction with C3. C2H can also be converted to CO either by a neutral-neutral reaction with O or by a reaction with carbon chain ions, such as HCO+. Its role in the carbon chemistry means that understanding the abundance of C2H is important to understanding the chemical network related to carbon. The recent access to the higher rotational transitions provided by the Herschel Space Observatory and the recently calculated inelastic collision rates (Spielfiedel et al. 2012) give an opportunity to probe the chemistry and excitation of C2H. Using the higher rotational transitions accessible by Herschel and the available collision rates we probe the excitation of C2H and the physical parameters that it traces toward the prototypical, high UV-illumination PDR, the Orion Bar. As photodissociation of larger carbon-chain molecules and polycyclic aromatic hydrocarbons (PAHs) is one of the possible formation routes of C2H, PDRs provide a good source to study C2H.
The Orion Bar is an ideal source for probing the excitation and chemistry of molecules in PDRs, thanks to its close distance of 414 pc (Menten et al. 2007) and its well-known structure and geometry. The Orion Bar is located between the Orion molecular cloud and an Hii region illuminated by the Trapezium cluster. The FUV radiation field of the Trapezium cluster at the location of the Orion Bar is equivalent to (1−4) × 104χ0 in Draine (1978) units. Its orientation changes from face-on to nearly edge-on where the molecular emissions peak. The observations presented in this paper also correspond to the nearly edge-on orientation part of the Orion Bar. The geometrical enhancement of the column densities toward the nearly edge-on part of the Orion Bar was derived by multiple studies and is in the range between 4 and 20. The tilt angle compared to a completely edge-on orientation was suggested to be 3° in the model of Hogerheijde et al. (1995) and Jansen et al. (1995). A tilt angle of 3° is equivalent to an enhancement factor of 20 for the measured column densities. Based on Oi 1.317 μm emission, Walmsley et al. (2000) find a model that requires a geometrical enhancement factor of 5 to convert the observed column densities into face-on values. Neufeld et al. (2006) find the geometrical enhancement factor to be 4 based on measured C+ column densities. Using a clumpy 3D PDR model, Andree-Labsch et al. (2014) successfully reproduced the Orion Bar stratification using a clumpy edge-on cavity wall, and they claim that a model of a convex filament fails to describe the structure of the Orion Bar. The average kinetic temperature was estimated to be 85 K (Hogerheijde et al. 1995). Closer to the ionization front, higher temperatures are also measured; for example, OH transitions observed with Herschel/PACS are consistent with 160−220 K gas (Goicoechea et al. 2011) and CH+ observations with temperatures around 500 K (Nagy et al. 2013). Part of the molecular line emission measured toward the Orion Bar corresponds to an “interclump medium” with densities between a few 104 and 2 × 105 cm-3 (Simon et al. 1997). It has been suggested that other molecular lines originate in clumps with densities in the range between 1.5 × 106 and 6 × 106 cm-3 (Lis & Schilke 2003).
Previous C2H observations toward the Orion Bar cover the lower-N rotational transitions. Cuadrado et al. (2015) analyze the N = 1−0, ..., 4−3 transitions. The N = 4−3 transition was observed by Hogerheijde et al. (1995), Jansen et al. (1995), and Van der Wiel et al. (2009)), and the N = 1−0 transition by Fuente et al. (1996). In this paper we analyze emission from five higher rotational transitions to constrain the physical parameters of the C2H emitting gas toward the Orion Bar.
2. Observations and data reduction
The observations presented in this paper are part of the HEXOS1 guaranteed-time key program (Bergin et al. 2010) for the HIFI instrument (De Graauw et al. 2010) of the Herschel Space Observatory (Pilbratt et al. 2010). The CO+ peak (αJ2000 = 05h35m20.6s, δJ2000 = −05°25′14′′) of the Orion Bar has been observed over the full HIFI range (480-1910 GHz) as a spectral scan. An overview of the full spectral line survey will be presented in a forthcoming paper (Nagy et al. 2015). The data were reduced using HIPE (Ott 2010) pipeline version 9.0 and 10.0 and are calibrated to 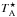 scale. The sideband deconvolution was done using the doDeconvolution task in HIPE. The double sideband (DSB) scans were first deconvolved with the strongest lines (
scale. The sideband deconvolution was done using the doDeconvolution task in HIPE. The double sideband (DSB) scans were first deconvolved with the strongest lines (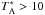 K) removed. This deconvolution results in a single sideband (SSB) spectrum with very little contribution from deconvolution ghosts, but without data at the frequencies of the strongest lines. Therefore, we performed another deconvolution of the data including the strongest lines. The data around the frequencies of the strong lines was then used with the first deconvolution result, providing a single sideband spectrum in the total observed frequency range.
K) removed. This deconvolution results in a single sideband (SSB) spectrum with very little contribution from deconvolution ghosts, but without data at the frequencies of the strongest lines. Therefore, we performed another deconvolution of the data including the strongest lines. The data around the frequencies of the strong lines was then used with the first deconvolution result, providing a single sideband spectrum in the total observed frequency range.
The continuum at the observed frequencies is negligible, because it is similar to the measured rms noise level. The C2H transitions detected in the HIFI survey are listed in Table 1 and include spectroscopic parameters from the Cologne Database for Molecular Spectroscopy (CDMS, Müller et al. 2005). The hyperfine structure is not resolved by HIFI, therefore the detected lines are blends of multiple hyperfine components. Table 1 lists the spectroscopic parameters for the strongest hyperfine components. The spectral resolutions at the frequencies of the observed transitions (from N = 6−5 to N = 10−9) are 0.29, 0.25, 0.21, 0.19, and 0.17 km s-1.
To compare the line intensities of the transitions detected with different beam sizes in the HIFI line survey, we converted all the observed line intensities to a common ~40.5′′ resolution. We derived conversion factors between the original beam sizes and ~40.5′′ based on the integrated intensity map of the C2H 4−3 transition from the James Clerk Maxwell Telescope (JCMT) Spectral Legacy Survey (Van der Wiel et al. 2009). The derived correction factors between the beam sizes of the C2H transitions and the 40.5′′ beam are 0.94, 0.88, 0.84, and 0.79 from beam sizes of 34.7′′, 30.4′′, 27.0′′, and 24.3′′ , respectively. Table 1 includes the parameters that are measured with the original beam sizes. For the non-local thermodynamic equilibrium (non-LTE) models in Sect. 5, we used the values that have been corrected for the changing beam size.
In addition to the HIFI spectral scans, a 115′′ × 65′′ area centered on αJ2000 = 05h35m20.81s, δJ2000 = −05°25′17.1′′ with a position angle of 145° was mapped in the N = 6−5 transition of C2H with HIFI, in on-the-fly (OTF) mapping mode with position-switch reference. The center of the maps is consistent with the CO+ peak (it is 4′′ off from the CO+ peak) where the spectral scans are pointed. The CO+ peak is close to the PDR surface and to the region where vibrationally excited H2 peaks (e.g., Walmsley et al. 2000 and Fig. 1. of Nagy et al. 2013). The fully sampled map was pipelined with HIPE 11.1 and exported to CLASS for further analysis, including baseline subtraction using linear baselines. As a comparison to the C2H emission, we used maps of the HCO+J = 6−5 transition (535 061.6 MHz) and of the CH 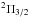 transitions around 536 GHz (N = 1−0, J = 3/2−1/2, F = 2−−1+ at 536.76115 MHz, N = 1−0, J = 3/2−1/2, F = 1−−1+ at 536782.0 MHz, N = 1−0, J = 3/2−1/2, F = 1−−0+ at 536.79568). These maps have the same parameters and were reduced with the same HIPE version and methods as the C2H N = 6−5 map. The spectral resolution of the observed HCO+ and CH transitions is 0.28 km s-1.
transitions around 536 GHz (N = 1−0, J = 3/2−1/2, F = 2−−1+ at 536.76115 MHz, N = 1−0, J = 3/2−1/2, F = 1−−1+ at 536782.0 MHz, N = 1−0, J = 3/2−1/2, F = 1−−0+ at 536.79568). These maps have the same parameters and were reduced with the same HIPE version and methods as the C2H N = 6−5 map. The spectral resolution of the observed HCO+ and CH transitions is 0.28 km s-1.
In addition to the HIFI maps, we used a [Ci] 3P1–3P0 (492.1607 GHz) map observed with the NANTEN2-4 m antenna, which is located at 4865 m altitude in Pampa la Bola in northern Chile. The observations were taken in October and November 2011 with a dual-channel 460/810 GHz SMART receiver. The receiver temperature was ~250 K at the band center. The velocity resolution (or channel spacing) is 0.68 km s-1 at 460 GHz. The observed spectra were calibrated using the atmospheric model atmospheric transmision at microwave (Pardo et al. 2001). The half power beam width (HPBW) is ~37′′. The data were calibrated to main beam temperature using main beam and forward efficiencies of 0.50 and 0.86, respectively.
3. The spatial distribution and velocity structure of C2H
Figure 1 shows the integrated intensity of the C2H N = 6−5J = 13/2−11/2 and J = 11/2−9/2 doublet. C2H emission has been detected toward the Bar and also perpendicular to the Bar, corresponding to the Orion Ridge. The C2H N = 6−5 emission is not as extended as other species, including CH and [Ci] (Fig. 4). The C2H integrated intensity does not peak at the CO+ peak (the center of the maps), but toward the northeastern part of the Bar covered by the C2H map around offsets (45′′, 25′′). The difference in the position where the C2H and CO+ line intensities peak is likely to be a result of different physical parameters toward the two positions. As mentioned in Sect. 7, C2H formation for the Orion Bar is expected to be dominated by a reaction of C2 with H2. CO+ is produced in a reaction between C+ and OH, where OH is produced from O and H2. Therefore, the CO+ and C2H peaks likely have different H2 volume densities. The region where C2H peaks overlaps with one of the OH+ intensity peaks (at a velocity of ~12 km s-1, Van der Tak et al. 2013), which lies about 10′′ southeast of the CO 10-9 intensity peak at a velocity of ~12 km s-1, which is observed toward the H13CN clumps 2 and 3 identified by Lis & Schilke (2003).
 |
Fig. 1 Integrated intensities of the C2H N = 6−5J = 13/2−11/2 (left) and J = 11/2−9/2 (right) doublet. The contour levels go from 0.2 to 2.8 K km s-1spaced by 0.4 K km s-1. |
Spectroscopic and Gaussian-fit parameters of the C2H lines observed toward the CO+ peak of the Orion Bar.
Apart from the N = 6−5 doublet, four more doublets (from N = 7−6 to N = 10−9) have been detected toward the CO+ peak of the Orion Bar, which the N = 6−5 map is centered on. Figure 2 shows the line profiles of the C2H doublets observed there. The observed two lines, which are blends of hyperfine transitions, are shifted with ~62 MHz in every case, which is equivalent to different velocity intervals due to the change in the frequency of the transitions. Table 1 lists the line intensities of these C2H transitions as obtained by Gaussian fitting. The observed doublet intensity ratios are 1.23, 1.16, 1.07, 1.26, and 0.66 for N = 6−5, ..., 10−9, respectively. In LTE, the doublet ratio is given by the ratio of the A coefficients so that we expect that the blueshifted component is about 2% brighter than the red one. The opposite ratio in N = 10−9 is probably due to the lower S/N, leading to an overestimate of the width and integrated intensity in the redshifted component. The peak velocities are in the range between 10.6−11.1 km s-1. The variation in the peak velocities falls slightly above the uncertainty from the frequency accuracy of the HIFI products and the fit accuracy so that it may indicate a small velocity variation within the C2H emitting gas, but it is very small compared to the line width, so that we can ignore it here, but still make certain that we analyze the same gas in all transitions. As shown in Fig. 3 on the velocity channel maps of C2H, the Orion Ridge is most prominent at velocities lower than 9 km s-1. Most C2H emission toward the Orion Bar is seen at velocities in the range between 9 and 11 km s-1. The velocity structure of C2H is similar to that seen in OH+ (Van der Tak et al. 2013): the blueshifted part of the emission peaks toward the Orion Ridge, emission around the expected source velocity (10 km s-1) has contributions both from the Orion Bar and the Orion Ridge, while emission corresponding to the redshifted velocities only comes from the Bar. However, the peak velocities at which the Orion Bar and Ridge are detected are slightly shifted for C2H compared to those for OH+. OH+ at velocities of 9−10 km s-1shows emission mainly toward the Orion Ridge. In the same velocity interval, C2H emission peaks toward the Orion Bar and shows little emission toward the Orion Ridge. This could be explained by low-density gas in the Orion Ridge at v< 9 km s-1 providing a lower C2H excitation compared to OH+ for that component.
 |
Fig. 2 Line profiles of the C2H doublets observed toward the CO+ peak of the Orion Bar from N = 6−5 (top) to N = 10−9 (bottom). The Gaussian fits shown in Table 1 are overlaid on the profiles. The black lines show the expected LSR velocity of 10 km s-1for both components. |
 |
Fig. 3 Velocity channel maps of the C2H N = 6−5J = 13/2−11/2 transition toward the Orion Bar. |
 |
Fig. 4 Integrated intensity maps of C2H N = 6−5, CH |
Figure 4 shows the spatial distribution of C2H N = 6−5 and lines of other species that are expected to trace regions relatively close to the PDR surface (equivalent to low visual extinctions): CH 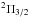 N = 1−0J = 3/2−1/2, HCO+J = 6−5, and [Ci] 3P
N = 1−0J = 3/2−1/2, HCO+J = 6−5, and [Ci] 3P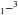 P0. Out of the four line emissions shown in Fig. 4, the lines of CH and [Ci] show the largest spatial extent over the area analyzed in this paper. All these lines peak at a similar position toward the Orion Bar. HCO+J = 6−5 emission toward the Orion Bar is less extended compared to the lines of the other molecules, especially [Ci] and CH. HCO+J = 6−5 is also the only line in Fig. 4 that peaks toward the Orion Ridge and not toward the Bar. The comparison of the spatial distribution of C2H to those of HCO+, CH, and [Ci] based on the line emissions shown in Fig. 4 is straightforward, due to the similar beam size of the observed transitions. In the following paragraphs while comparing the spatial distribution of C2H to those of CH, HCO+, and [Ci], we refer to the transitions shown in Fig. 4. The spatial distribution of the species may vary depending on the transitions used. The comparison of the spatial distributions can be converted to correlation plots (Fig. 5). C2H shows the strongest correlation with CH, compared to HCO+ and [Ci]. The corresponding correlation coefficients for CH, HCO+, and [Ci] are 0.93, 0.81, and 0.68, respectively.
P0. Out of the four line emissions shown in Fig. 4, the lines of CH and [Ci] show the largest spatial extent over the area analyzed in this paper. All these lines peak at a similar position toward the Orion Bar. HCO+J = 6−5 emission toward the Orion Bar is less extended compared to the lines of the other molecules, especially [Ci] and CH. HCO+J = 6−5 is also the only line in Fig. 4 that peaks toward the Orion Ridge and not toward the Bar. The comparison of the spatial distribution of C2H to those of HCO+, CH, and [Ci] based on the line emissions shown in Fig. 4 is straightforward, due to the similar beam size of the observed transitions. In the following paragraphs while comparing the spatial distribution of C2H to those of CH, HCO+, and [Ci], we refer to the transitions shown in Fig. 4. The spatial distribution of the species may vary depending on the transitions used. The comparison of the spatial distributions can be converted to correlation plots (Fig. 5). C2H shows the strongest correlation with CH, compared to HCO+ and [Ci]. The corresponding correlation coefficients for CH, HCO+, and [Ci] are 0.93, 0.81, and 0.68, respectively.
As seen in the velocity channel maps, the velocity range covered by the observed lines corresponds to at least two regions: the Orion Bar and the Orion Ridge. They represent two different PDRs with different conditions so that we expect a different behavior. Therefore, the spatial correlation may be different for the spatially different regions. Figure 6 shows spatial correlations between C2H, CH, HCO+, and [Ci] calculated in three velocity intervals: 7−8.5 km s-1, 8.5−10 km s-1, and 10−11.5 km s-1. The blueshifted velocity interval is dominated by emission from the Orion Ridge. The central velocity interval has contributions both from the Orion Bar and the Orion Ridge. The redshifted velocity interval is dominated by emission from the Orion Bar. The best correlation is found for the blueshifted (correlation coefficients of 0.69–0.92), and the worst for the intermediate velocity intervals (correlation coefficients of 0.38–0.68). The decrease in the correlation coefficient for the central velocity interval may be related to optical depth effects. Based on these results, CH and HCO+ may be good tracers of C2H for the Orion Ridge. Taking only the redshifted velocity interval into account, these species may probe a similar gas to C2H. Among the molecules studied here, the gas traced by [Ci] is the least related to the gas traced by C2H both for the Bar and the Ridge.
 |
Fig. 5 Integrated line intensity correlations between the C2H N = 6−5J = 13/2−11/2 line and HCO+, CH, and [Ci]. The corresponding correlation coefficients are shown in parentheses. |
 |
Fig. 6 Line intensity spatial correlations between the C2H N = 6−5J = 13/2−11/2 line and HCO+, CH, and [Ci]. The corresponding correlation coefficients are shown in parentheses. |
4. C2H column densities − single excitation temperature
One method of estimating the C2H column density is to interpret the intensities of the observed five doublets by a rotational diagram. The observed integrated intensities can be directly converted to upper state column densities by assuming that the transitions are optically thin, that the level populations can be characterized by a single excitation temperature, and that the line emission has a uniform beam filling. In the rotational diagram method, the measured integrated main-beam temperatures of lines (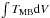 K km s-1) are converted to the column densities of the molecules in the upper level (Nu) using
K km s-1) are converted to the column densities of the molecules in the upper level (Nu) using 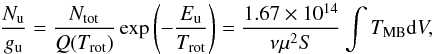 (1)with gu the statistical weight of level u, Ntot the total column density in cm-2, Q(Trot) the partition function for Trot, Eu the upper level energy in K, ν the frequency in GHz, μ the permanent dipole moment in Debye, and S the line strength value. A linear fit to ln(Nu/gu) − Eu gives Trot as the inverse of the slope, and Ntot, the column density as the intercept. The rotational temperature would be expected to be equal to the kinetic temperature if all levels were thermalized.
(1)with gu the statistical weight of level u, Ntot the total column density in cm-2, Q(Trot) the partition function for Trot, Eu the upper level energy in K, ν the frequency in GHz, μ the permanent dipole moment in Debye, and S the line strength value. A linear fit to ln(Nu/gu) − Eu gives Trot as the inverse of the slope, and Ntot, the column density as the intercept. The rotational temperature would be expected to be equal to the kinetic temperature if all levels were thermalized.
Figure 7 shows the resulting rotation diagram when adding the hyperfine components of each rotational transition, which corresponds to a rotation temperature of ~64 ± 11 K and a C2H column density of (4 ± 0.7) × 1013 cm-2. The ratios of the intensities of the hyperfine components are consistent with the optically thin assumption.
 |
Fig. 7 Rotational diagram of C2H, corresponding to a rotational temperature of 64 ± 11 K and a column density of (4 ± 0.02) × 1013 cm-2. |
The curved rotational diagram in Fig. 7 may be proof that multiple density and temperature components are present in the region covered by the HIFI beam. We therefore fitted the N = 6−5, ..., 8−7 and the N = 8−7, ..., 10−9 transitions separately as well. The rotation diagram of the lower-N transitions gives a rotation temperature of 43 ± 0.2 K and a column density of (8 ± 0.03) × 1013 cm-2. The rotation diagram fit for the higher-N transitions gives a rotation temperature of ~123 ± 21 K and a column density of (2 ± 0.4) × 1013 cm-2. For the two-component rotational diagram, the total beam-averaged C2H column density is 1014 cm-2. This is similar to the maximum value that Jansen et al. (1995) found along their observed cut toward the Orion Bar, and to the factors of 2−5 below the values that Van der Wiel et al. (2009) derived, both corresponding to beam sizes of ~15′′.
5. C2H column densities − non-LTE calculation
Since inelastic collision rates for C2H have recently become available, a non-LTE analysis is also possible. Non-LTE excitation is expected to be important because the transitions studied here have critical densities above the average ~105 cm-3 Orion Bar H2 volume density (Hogerheijde et al. 1995). For example, when assuming a gas temperature of 100 K, the N = 6−5, J = 13/2−11/2 transition for C2H-H2 collisions has a critical density of 6.8 × 107 cm-3, and the N = 8−7, J = 17/2−15/2 a critical density of 1.6 × 108 cm-3. While the LTE approach provides information on the C2H column density and excitation temperature, the non-LTE analysis also gives an estimate of the kinetic temperature and H2 volume density of the C2H emitting gas. This is, of course, only possible if the excitation deviates from LTE, but this is expected at least for the high-N transitions with very high critical densities. C2H-He collision rates were calculated by Spielfiedel et al. (2012), which we scaled to represent C2H-H2 collisions following Schöier et al. (2005) by a factor of 1.36, based on the ratio of the reduced mass of the C2H-He and C2H-H2 systems. These collision rates are available for energies up to 104.9 cm-1, covering three rotational transitions analyzed in this paper (N = 6−5, 7−6, and 8−7). The rates were calculated for a temperature range between 5 K and 100 K. We extrapolated these collision rates for temperatures up to 400 K and energies up to ~445 cm-1 (see Appendix B). Collisional rates for these higher levels and temperatures are clearly required and should be computed properly to avoid extrapolations. We also used collision rates with electrons, calculated in the Born approximation with infinite-order-sudden (IOS) recoupling, calculated for temperatures in the range between 10 K and 1000 K (see Appendix A). We ran several RADEX (Van der Tak et al. 2007) models with physical parameters that are expected for the Orion Bar, i.e., kinetic temperatures between 50 and 400 K and H2 volume densities between 5 × 104 cm-3 and 107 cm-3. We also used a background radiation field based on Arab et al. (2012), which is a modified blackbody distribution with a dust temperature of Td = 50 K and a dust emissivity index of β = 1.6. The used electron density has very little effect on the line intensities, which is a consequence of the small C2H dipole moment (Appendix A).
The observed line intensities are not consistent with C2H originating in a single gas component toward the Orion Bar CO+ peak. A two-component model is required to fit the observed C2H intensities. In this model the C2H column density is dominated by a gas component with a temperature of 100 K to 150 K, an H2 volume density of 5 × 105−106 cm-3, and a C2H column density of 8 × 1013 cm-2. To reproduce the integrated intensity of the highest-N (N = 9−8 and 10−9) doublets, a higher density (5 × 106 cm-3), hot (T ~ 400 K) gas component is required. This second component has a column density of 2 × 1013 cm-2. The sum of the line intensities predicted by this two-component model are overplotted on the observed line intensities in Fig. 8. This model is consistent with the N = 6−5, 7−6, and 10−9 doublets within the observational errors, and overpredict the 8−7 and 9−8 doublets by 40% and 30%, respectively. This model is also consistent with the assumption that the analyzed C2H transitions are optically thin: the opacity of every transition is less than 0.03 in each model. The doublet ratios are reproduced well (13% or better) by both two-component models for the N = 6−5,..., 9−8 transitions. The doublet ratio for the N = 10−9 transition is reproduced within a factor of two. The doublet ratios estimated with RADEX for the two-component model with n(H2) = 106 cm-3, Tkin = 100 K, n(H2) = 5 × 106 cm-3, and T = 400 K are 1.32, 1.27, 1.23, 1.22, and 1.22 for N = 6−5, ..., 10−9, respectively. The doublet ratios for the two component model with n(H2) = 5 × 105 cm-3, Tkin = 150 K, n(H2) = 5 × 106 cm-3 and T = 400 K are 1.28, 1.23, 1.20, 1.21, and 1.22.
The evidence of at least two different gas components observed toward the CO+ peak is consistent with the clumpy picture of PDRs. Different density and temperature components are expected to be covered by the HIFI beam. The existence of such high-density gas toward the Orion Bar CO+ peak is consistent with what was found for OH Goicoechea et al. (2011).
The non-LTE models suggest a total C2H column density of ~1014 cm-2, dominated by the lowest-N transitions. The models also suggest that there is a very high-density gas component that contributes only about 20% of the C2H column density, but is required to fit the highest-N transitions. The hot and dense gas that C2H traces toward the Orion Bar based on the transitions analyzed in this paper may be consistent with the UV-illuminated edges of dense clumps close to the ionization front of the PDR.
 |
Fig. 8 Non-LTE C2H line intensity predictions with RADEX vs. the observed line intensities (black symbols). Top panel: the models correspond to parameters of n(H2) = 106 cm-3, Tkin = 100 K, N(C2H) = 8 × 1013 cm-2 (green symbols), and to n(H2) = 5 × 106 cm-3, Tkin = 400 K, N(C2H) = 2 × 1013 cm-2 (blue symbols). The sum of the two components is given by the red symbols. Bottom panel: the models correspond to parameters of n(H2) = 105 cm-3, Tkin = 150 K, N(C2H) = 8 × 1013 cm-2 (green symbols), and to n(H2) = 5 × 106 cm-3, Tkin = 400 K, N(C2H) = 2 × 1013 cm-2 (blue symbols). The sum of the two components is given by the red symbols. |
6. Comparison to PDR models
In earlier works based on the Orion Bar HIFI line survey, we presented an isobaric PDR model, which explained the observed CH+ (Nagy et al. 2013) and OH+ (Van der Tak et al. 2013) emission toward the CO+ peak of the Orion Bar. This model was computed using the 1.4.4 version of the Meudon PDR code (Le Petit et al. 2006) and corresponds to a pressure of P = 108 cm-3 K and represents a plane-parallel slab of gas and dust illuminated from two sides by a radiation field of χ = 104 on the front and by χ/1000 on the back side. We implemented the collision rates used in Sect. 5 in order to compute integrated intensities for the observed transitions.
Figure 9 shows the calculated C2H integrated intensities corresponding to the model, overplotted on the observed integrated intensities. The model overpredicts the intensity of the N = 6−5, N = 7−6, and N = 9−8 doublets by about factors of 2, 1.5, and 20%. The model underpredicts the intensities of the N = 10−9 and N = 11−10 doublets by factors of 2.4 and 5.5. Even though the model predictions are close to most of the observed line intensities, it is clear that assuming a single pressure component is simplification, because the structure of PDRs is clumpy. The offset between the observed and modeled values may be explained by different gas components or clumps covered by the HIFI beam. The model predicts a face-on column density of 1.7 × 1014 cm-2. When assuming a geometrical enhancement factor of four (e.g., Neufeld et al. 2006), this is equivalent to an edge-on column density of 6.8 × 1014 cm-2. This value is about a factor of 7 above the values predicted by the two-component rotational diagram and RADEX models. Despite the higher column density than in the rotational diagram and RADEX models, this model underpredicts the intensity of the highest-N transitions. This confirms the result that the higher-N transitions contribute only a minor part of the total C2H column density. The difference between the observed and modeled C2H intensities suggests that most C2H originates in a different gas component than CH+, which was used to constrain the PDR model.
Figure 10 shows the abundances of C2H, CH, C+, HCO+, [Ci], and CH+ that correspond to the model, as a function of visual extinction up to a visual extinction of 10. Most C2H is located near the surface of the PDR in a relatively narrow region at visual extinctions of AV ~ 1−2. The gas temperature in this region predicted by the PDR model is in the range between ~570 K and 140 K, while the H2 volume densities are in the range of 105 cm-3 and 6 × 105 cm-3, as shown in Fig. 11. In the range of AV = 0.8...1.5 responsible for the main C2H emission, the PDR model predicts temperatures that cover both the components suggested by the RADEX models, 100−150 K and 400 K. The H2 volume densities suggested by the RADEX model for the lower-N transitions (105−106 cm-3) is close to those corresponding to the PDR model. There are, however, two discrepancies: the RADEX H2 volume density of 5 × 106 cm-3 for the hot component is above the density range predicted by the model for the C2H emitting gas. Moreover, the temperature-density structure calculated in the isobaric model would predict the highest temperature gas to trace the lowest H2 densities and the lowest temperature gas to trace the highest H2 densities. This behavior results in the overprediction of the intensities of lowest-N transitions and the underprediction of the intensities of the highest-N transitions. This suggests that a single isobaric model to describe the C2H emitting gas is an oversimplification. In contrast, the PDR is known to be out of balance, showing signs of photo-evaporation (Störzer & Hollenbach 1999). Figure 10 also shows that the CH+ abundance peaks at lower visual extinctions than for C2H and is consistent with gas at higher temperatures and lower H2 densities compared to C2H, which was also confirmed by non-LTE radiative transfer models (Nagy et al. 2013). This supports the assumption that most C2H originates in a different gas compared to what CH+ traces. The dominant C2H formation and destruction processes that the model suggests are shown in Sect. 7.
The PDR model quoted above is a simplification, but it confirms that C2H toward the Orion Bar originates in more than one pressure component. Based on the physical parameters suggested by the PDR model, the C2H emitting gas is also most likely to trace the edges of dense clumps exposed to UV irradiation close to the ionization front of the PDR. Moreover, C2H is predicted to be closely confined to the dense surface of the clump near AV ~ 1. This is consistent with our excitation analysis, which argues that this gas is directly heated by the UV photons.
 |
Fig. 9 C2H line intensity predictions from a PDR model with a pressure of P = 108 cm-3 K and a radiation field of χ = 104 (blue symbols) overplotted on the observations (black symbols). |
 |
Fig. 10 Abundances of C2H, CH, C+, HCO+, and [Ci] corresponding to a PDR model with a pressure of P = 108 cm-3 K, illuminated by a radiation field of χ = 104 on the front, and a radiation field of χ = 10 on the back side of the cloud. |
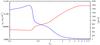 |
Fig. 11 Temperature (blue) and density (red) structure corresponding to the isobaric PDR model with a pressure of P = 108 cm-3 K, illuminated by a radiation field of χ = 104 on the front, and a radiation field of χ = 10 on the back side of the cloud. |
7. Formation and destruction processes
Even though we cannot constrain the formation and destruction of C2H with the observations presented in this paper, the PDR models explained above give an indication about the most important processes involved in the chemistry of C2H. For Orion Bar conditions represented by the isobaric model with P = 108 K cm-3 and χ = 104, the most important processes that contribute in the formation of C2H are
These processes contribute ~67.1%, ~27.2%, ~4.8%, and ~0.9% of the total C2H abundance, respectively. These values refer to a depth equivalent to AV ~ 1, which is part of the region, where C2H abundances peak. An alternative formation route of C2H can be expected in PDRs. Small hydrocarbons, such as C2H, can form via the photodissociation of small PAHs (NC ≤ 24) (Useli Bacchitta & Joblin 2007). This formation route is not included in the Meudon PDR code, however, based on a comparison of the spatial distribution of C2H to that of a Spitzer map at 8 μm Cuadrado et al. (2015) conclude that this formation route cannot dominate the formation of C2H for the Orion Bar. The most important destruction processes at the same AV ~ 1 are 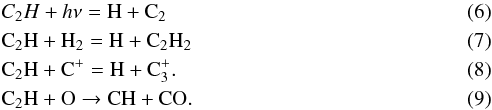 These processes are responsible for the destruction of ~68.1%, ~28.9%, ~1.5%, and 0.66% of C2H, respectively. C2H abundances therefore peak in a region, where the molecular fraction (f = 2N(H2)/(N(H) + 2N(H2))) or H2 density is high enough to produce C2H via reactions between H2 and C2, and the radiation field is low enough that the C2H production compensates for its destruction by FUV photons. With the used model parameters, the molecular fraction is 30%, the H2 volume density about 105 cm-3, and the gas temperature is around 570 K at AV ~ 1. At a depth equivalent to AV ~ 1.5, where significant C2H is still located, the temperature decreases to about 270 K, the molecular fraction increases to ~50%, and the H2 volume density is 3 × 105 cm-3. The reaction rates are summarized in Table 2.
These processes are responsible for the destruction of ~68.1%, ~28.9%, ~1.5%, and 0.66% of C2H, respectively. C2H abundances therefore peak in a region, where the molecular fraction (f = 2N(H2)/(N(H) + 2N(H2))) or H2 density is high enough to produce C2H via reactions between H2 and C2, and the radiation field is low enough that the C2H production compensates for its destruction by FUV photons. With the used model parameters, the molecular fraction is 30%, the H2 volume density about 105 cm-3, and the gas temperature is around 570 K at AV ~ 1. At a depth equivalent to AV ~ 1.5, where significant C2H is still located, the temperature decreases to about 270 K, the molecular fraction increases to ~50%, and the H2 volume density is 3 × 105 cm-3. The reaction rates are summarized in Table 2.
Rate coefficients for the formation and destruction reactions of C2H toward the Orion Bar.
8. Discussion
We presented C2H observations toward the Orion Bar that correspond to five rotational transitions, in order to probe the physical parameters of the C2H emitting gas. The observed line intensities are not consistent with a single gas component, but suggest that C2H originates in at least two different components. The total C2H column density of about 1014 cm-2 is dominated by gas corresponding to a kinetic temperature of 100 K to 150 K, which is consistent with the average value of 85 ± 30 K derived by Hogerheijde et al. (1995) and an H2 volume density of 105–106 cm-3. The intensities of the higher-N transitions suggest the existence of a higher density (5 × 106 cm-3) hot (T ~ 400 K) gas component. This high-pressure gas contributes only a small fraction of the C2H column density, but is required to explain the higher-N C2H transitions. The rotational diagram is also consistent with at least two different gas components. A high-density gas component toward the Orion Bar, interpreted as photoevaporating dense clumps, was previously found to be traced by OH (Goicoechea et al. 2011). The rotational Λ-doublets detected using Herschel/PACS are consistent with warm (160−220 K) gas at densities of nH = 106−107 cm-3. The high-N rotational transitions of C2H analyzed in this paper may trace similar areas of the dense filament surfaces.
Lower-N C2H doublets (N = 1−0, ..., 4−3) toward the Orion Bar were analyzed by Cuadrado et al. (2015). Based on a rotational diagram analysis and assuming a uniform beam filling factor, they derived C2H column densities of (4.2 ± 0.2) × 1014 cm-2 and (3.7 ± 0.6) × 1014 cm-2 toward the dissociation front and the molecular peak of the Orion Bar, about a factor of four above the total C2H column density derived from the high-N transitions presented in this paper. The rotational temperature they find for the N = 1−0, ..., 4−3 transitions is 26 ± 1 K, which is significantly below our cold-component temperature of 43 ± 0.2 K, determined from the N = 6−5, ..., 8−7 doublets. The combination of the higher column density and lower excitation temperature provides a similar flux around N = 5−4, which is consistent with our measurements, but leading to a continuation of our rotational diagram (Fig. 7) with a steeper slope towards lower energies. The low-N observations of Cuadrado et al. (2015) therefore also trace somewhat more extended colder gas than our measurements. Based on non-LTE radiative transfer models, Cuadrado et al. (2015) estimate an H2 volume density of ≳105 cm-3 and a kinetic temperature of ≳150 K. These parameters are close to those that our RADEX models suggest for the bulk of the C2H column density, corresponding mostly to the N = 6−5, ..., 8−7 doublets: n(H2) = 105−106 cm-3, Tkin ~ 100−150 K.
The C2H column density of 1014 cm-2 can be converted to a C2H abundance using C17O transitions observed as part of our HIFI line survey (Nagy et al., in prep.). The beam-averaged C17O column density based on the four observed transitions (from 5−4 to 8−7) based on a rotational diagram is 1.3 × 1015 cm-2. This C17O column density is equivalent to a CO column density of 2.3 × 1018 cm-2, when adopting abundance ratios of 16O/18O = 560 and 18O/17O = 3.2 (Wilson & Rood 1994). Assuming a CO abundance of 1.1 × 10-4 for the Orion Bar PDR (Johnstone et al. 2003), this CO column density is equivalent to an H2 column density of 2.1 × 1022 cm-2. This value is close to the N(H2) = 3 × 1022 cm-2 derived by Cuadrado et al. (2015) close to the CO+ peak position, based on the C18O 1−0, 2−1, and 3−2 transitions. This gives a C2H abundance of 5 × 10-9 with respect to H2. Van der Wiel et al. (2009) derived a C2H abundance of 2 × 10-9 for a beam size of 15′′. Fuente et al. (1996) derived a C2H abundance of 1.2 × 10-8 with respect to H2 toward the Orion Bar within a 26′′ beam size. When deriving the C2H abundance with respect to the total hydrogen column density NH = N(H) + 2N(H2),Cuadrado et al. (2015) measured C2H abundances of (0.7−2.7) × 10-8 with respect to H nuclei. Adding the N(H) = 3 × 1021 cm-2 from Van der Werf et al. (2013) to our H2 column, gives a C2H abundance of 2.2 × 10-9 with respect to H nuclei. The higher C2H abundance measured by Cuadrado et al. (2015) is due to tracing a cooler component as well as using lower-N transitions.
C2H has been detected toward other PDRs with various physical conditions, including Mon R2 (Rizzo et al. 2005; Ginard et al. 2012; Pilleri et al. 2013), the Horsehead PDR (Teyssier et al. 2004; Pety et al. 2005), and NGC 7023 (Fuente et al. 1993). Similar to what we found for the Orion Bar, multiple C2H transitions measured toward Mon R2 also suggest a two-component fit to describe C2H toward this region (Pilleri et al. 2013). However, only one of the two components found toward the Mon R2 region corresponds to a dense, highly UV-illuminated PDR, and the other to a low UV-illuminated lower density envelope. The PDR component toward Mon R2 originates in an H2 volume density of 3 × 106 cm-3, which is similar to what we found toward the Orion Bar for both components. Unlike the Orion Bar and Mon R2 PDRs, C2H toward the NGC 7023 region is likely to be related to a low-density envelope of NGC 7023, based on the comparison of the observations and chemical models (Fuente et al. 1993). C2H has also been detected toward the low UV-illumination (60 in Draine (1978) units) Horsehead PDR and was found to be spatially correlated with HCO (Gerin et al. 2009).
In addition to PDRs, C2H has also been detected in other types of regions. Watt et al. (1988) studied the C2H N = 4−3 transition in several molecular clouds. Based on the comparison of the observations and chemical models, they conclude that C2H emission arises from dense (104−105 cm-3) gas, but not from very dense gas with H2 densities of >106 cm-3. Padovani et al. (2009) studied the C2H N = 1−0 and N = 2−1 transitions toward two prestellar cores and found evidence of deviations from LTE-level populations. Deviations from LTE are also important in the case of the transitions studied here for the Orion Bar, since the excitation temperatures derived from the rotational diagrams are well below the kinetic temperatures derived using the non-LTE analysis. Beuther et al. (2008) studied C2H in regions that represent different evolutionary stages of high-mass star formation, including infrared dark clouds, high-mass protostellar objects, and ultracompact Hii regions. Based on chemical models, they suggest that C2H traces the initial conditions of massive star formation. In the outer cloud regions discussed in their models, the C2H abundance is high because of the interstellar UV radiation field, which dissociates CO, enlarging the abundance of carbon. These outer cloud regions discussed by Beuther et al. (2008) also represent a similar case to PDRs, including the Orion Bar. Toward the DR21(OH) high-mass star-forming region, Mookerjea et al. (2012) found that the observed C2H and c-C3H2 abundances are consistent with a chemical model with an H2 volume density of 5 × 106 cm-3, similar to what our RADEX models suggest toward the Orion Bar. Apart from star-forming regions, C2H has also been detected toward several cold dark clouds (Wootten et al. 1980). These models explain that the C2H/HC3N abundance ratio is consistent with gas-phase chemistry. C2H has been detected toward planetary nebulae including NGC 7027 (Zhang et al. 2008). Zhang et al. (2008) suggest that C2H is produced via the photodissociation of C2H2 toward this region. C2H has also been observed toward diffuse clouds (Lucas & Liszt 2000, Gerin et al. 2011). Both Lucas & Liszt (2000) and Gerin et al. (2011) suggest there is a correlation between C2H and c-C3H2 in diffuse clouds. Gerin et al. (2011) also suggest that C2H is a tracer of molecular hydrogen in diffuse and translucent gas.
Among the other environments mentioned above, C2H toward the Orion Bar is likely to trace a similar gas component to what was found toward Mon R2 and toward DR21(OH).
9. Conclusions
We have presented Herschel/HIFI observations of five high-N C2H rotational doublets (N = 6−5, ..., 10−9) toward the CO+ peak of the Orion Bar. These observations helped to constrain the excitation of C2H. A single-component rotational diagram of C2H suggests a rotation temperature of 64 K and a C2H column density of ~4 × 1013 cm-2. The rotational diagram is also consistent with two different gas components that correspond to rotation temperatures of 43 K and 123 K and to column densities of 8 × 1013 cm-2 and 2 × 1013 cm-2 for the three lower-N and for the three higher-N transitions, respectively.
A C2H N = 6−5 HIFI map shows C2H emission along the Orion Bar and perpendicular to it, corresponding to the Orion Ridge. Based on the comparison of the C2H integrated intensities to those of CH, HCO+, and [Ci], CH, and HCO+ are the best C2H tracers both toward the Orion Ridge and toward the Orion Bar among the molecules studied in this paper. The calculated correlation coefficients toward the Orion Ridge (in the velocity interval of 7−8.5 km s-1) are 0.92 and 0.89 for CH and HCO+, respectively. The correlation coefficients toward redshifted velocities compared to the expected LSR velocity of the Orion Bar (10−11.5 km s-1) are 0.88 and 0.89 for CH and HCO+, respectively. The correlation between C2H and [Ci] is lower toward both regions, suggesting that C2H and [Ci] do not entirely trace the same gas.
Based on non-LTE radiative transfer models, the detected C2H line intensities are consistent with C2H to originate at least in two different gas components. One of these gas components dominates the C2H total column density and the intensity of the lower-N transitions and can be related to warm (Tkin ~ 100−150 K) and dense (n(H2) ~ 105−106 cm-3) gas. The second component adds only a small fraction to the C2H column density, but is required to fit the intensity of the higher-N transitions. This component is related to hot (Tkin ~ 400 K) and dense (n(H2) ~5 × 106 cm-3) gas. A simple PDR model representing the Orion Bar with a plane-parallel slab of gas and dust confirms that C2H is likely to be related to more than a single pressure component, unlike CH+ toward the Orion Bar.
Based on the physical parameters derived for the high-N C2H transitions analyzed in this paper, the N = 6−5, ..., 10−9 C2H doublets may trace the edges of dense clumps exposed to UV radiation near the ionization front of the Orion Bar.
Online material
Appendix A: C2H–e− rate coefficients
The electronic ground-state symmetry of the radical C2H is 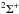 . Each rotational level N is therefore split by the spin-rotation coupling between N and the electronic spin S = 1/2 so that each rotational level N has two sublevels given by j = N ± 1/2. In addition, owing to the non-zero nuclear spin of the hydrogen atom (I = 1/2), each fine-structure level is further split into two hyperfine levels F = j ± 1/2. The rotational constant of C2H is 1.46 cm-1. The fine- and hyperfine-splittings are typically 0.01 and 0.001 cm-1, respectively. The dipole moment of C2H is 0.77 D (Woon 1995).
. Each rotational level N is therefore split by the spin-rotation coupling between N and the electronic spin S = 1/2 so that each rotational level N has two sublevels given by j = N ± 1/2. In addition, owing to the non-zero nuclear spin of the hydrogen atom (I = 1/2), each fine-structure level is further split into two hyperfine levels F = j ± 1/2. The rotational constant of C2H is 1.46 cm-1. The fine- and hyperfine-splittings are typically 0.01 and 0.001 cm-1, respectively. The dipole moment of C2H is 0.77 D (Woon 1995).
There is, to our knowledge, no previous estimate for the electron-impact hyperfine excitation rate coefficients of the C2H radical. Recent R-matrix calculations have considered electron scattering from C2H (Harrison & Tennyson 2011), but they concentrated on bound states of the anion and electronic excitation of the neutral. Here, electron-impact hyperfine rate coefficients for C2H were computed using a three-step procedure, similar to the one employed recently for the radicals OH+ (Van der Tak et al. 2013) and CN (Harrison et al. 2013): i) rotational excitation rate coefficients for the dipolar (ΔN = 1) transitions were first computed using the Born approximation; ii) fine-structure excitation rate coefficients were then obtained from the Born rotational rates using the (scaled) infinite-order sudden (IOS) approximation; and iii) hyperfine excitation rate coefficients were finally obtained again using the IOS approximation. In the case of polar molecules, the long-range electron dipole interaction is well known to control the rotational excitation, especially at low collision energies (Itikawa & Mason 2005). Although the C2H dipole is only moderate, the Born approximation is expected to be reasonably accurate for dipolar transitions. In practice, Born cross-sections were computed for collision energies ranging from 1 meV to 1 eV, and rate coefficients were deduced for temperatures from 10 K to 1000 K. The IOS approximation was employed to derive the fine-structure rate coefficients in terms of the rotational rates for excitation out of the lowest rotational level N = 0, following the general procedure of Faure & Lique (2012) (see Eqs. (1)−(3) of Harrison et al. 2013). The IOS approximation was also applied to derive the hyperfine rate coefficients (Eqs. (6)−(8) in Harrison et al. 2013).
The above three-step procedure was applied to the first 26 rotational levels of C2H, which is up to the level (N,j,F) = (25,24.5,24), which lies 945 cm-1 above the ground state (0, 0.5, 0), resulting in 246 collisional transitions. The largest rate coefficients are on the order of 5 × 10-7 cm3 s-1, i.e. typically four orders of magnitude more than the C2H-He rate coefficients, and they are expected to be accurate to within a factor of 2. The complete set of de-excitation rate coefficients is available online from the LAMDA (Schöier et al. 2005) and BASECOL (Dubernet et al. 2013) databases.
Appendix B: Extrapolation of collision rates
Spielfiedel et al. (2012) only provided collision rates for temperatures up to 100 K and for rotational levels with up to N = 8 corresponding to an upper level energy of about 150 K, as given in BASECOL. This is clearly insufficient for modeling our observations because we observed up to N = 10−9, the gas temperatures in the Orion Bar are around 150 K, and densities of more than 106 cm-3 allow for a collisional excitation of much higher levels that will eventually decay radiatively, feeding the rotational ladder from levels above N = 9. A solution of the rate equations for the Orion Bar conditions thus asks for the inclusion of levels with energies of a few times the kinetic temperature.
Thus we have to extrapolate the rate coefficients from Spielfiedel et al. (2012) in terms of both additional levels and higher temperatures. A very general, but numerically demanding approach to extrapolating collision rates was proposed by Neufeld (2010). It is applicable to any type of molecule, but needs some “training” through collision rates from similar species. For C2H we have, however, the advantage that it is basically a linear rotor, only superimposed by the hyperfine interaction. Since our measurements show no variation in the hyperfine ratio, and the collision rates from Spielfiedel et al. (2012) at temperatures above 20 K are dominated by the pure rotational transitions of the linear configuration with ΔN = ΔJ = ΔF (see Fig. B.1), it seems justified to concentrate on the rates for these transitions and to treat C2H as a simple linear rotor.
For such molecules, the IOS approximation is a handy approach to computing the collision rates for any series of ΔJ (see Appendix A) as long as the energy difference of the states is small compared to the kinetic energy of the collision partners. For higher levels, a correction is possible, as summarized by Schöier et al. (2005). We use here their Eq. (13) derived originally by de Jong et al. (1975), Bieging et al. (1998) to extrapolate the collision coefficients to higher levels based on the energy-level difference and the behavior of the collision rates for lower J levels in the series. Owing to the additional hyperfine split in C2H, we have to perform the fit individually for the different F − J combinations in a pure rotational series. This assumes that we have no further interaction of the states, as justified by the behavior of the collision rates at temperatures between 20 K and 100 K. The result is shown in Fig. B.1. This figure shows the collision-rate behavior within the dominant series for the levels computed by Spielfiedel et al. (2012) and the extrapolation of the rates up to N = 18. All other collision rates are much lower so that they are not important for the population of the upper levels.
 |
Fig. B.1 Rates for the de-excitation of C2H through collision with H2 at 100 K. Black crosses mark all collision rates from Spielfiedel et al. (2012) above 10-12 cm3s-1. The curves indicate the different transition series for pure rotational transitions of the molecule, i.e., ΔN = ΔJ = ΔF. Each series consists of four curves according to the fine and hyperfine structure split of the four N states with approximately the same energy: J = N ± /1/2 and F = J ± 1/2. The continuations of those curves into the colored symbols show the extrapolation of the rates to the higher level transitions using the formalism from Schöier et al. (2005) based on the IOS approximation. |
 |
Fig. B.2 Temperature dependence for the main collision rates of C2H with H2. The curves are sorted by ΔJ but cover all transitions of the corresponding series. Every connected dot in Fig. B.1 produces one temperature-dependence graph in this plot. To improve the readability, we have omitted the ΔN = ΔJ = ΔF = 3 series here. Up to 100 K, the lines show the rates computed by Spielfiedel et al. (2012), from 100 to 400 K, and we extrapolated as a power law with the same slope as measured between 90 and 100 K. |
Besides the extrapolation to higher level energies, we also need to extrapolate the rates from Spielfiedel et al. (2012) to higher temperatures. To obtain the rate at higher temperatures, we have to compute the integral over collision cross sections for energies of about ten times the kinetic temperature of the gas (Flower 2001). This makes the high-temperature computations demanding, in principle. However, since we only want to expand the temperature range by a small extent, from 100 K to 400 K, we can use the temperature behavior measured up to 100 K to estimate the rates above this temperature. The simplest approach would be an extrapolation with the square root of temperature, reflecting the velocity of the collision partners. When
inspecting the rate coefficients at temperatures up to 100 K, we see, however, that the majority of the rates show a temperature dependence that is very different from an exponent of 0.5 (see Fig. B.2). But the double-logarithmic plot shows straight lines for basically all rate coefficients at high temperatures, indicating that a power-law extrapolation with a free exponent is a good description of the temperature dependence. The curvature in the curves is very small.
We extrapolated from 100 K to 400 K using the power law determined either between 80 K and 100 K or between 90 K and 100 K. When comparing the two extrapolations, we found only 11 transitions with a deviation of about 10%. All other transitions showed better agreement of the rates, proving that the power-law description is quite accurate. One should take into account, however, that this approach should not be continued over wide dynamic ranges because we clearly expect the coupling to change when dealing with factors of ten or more.
To check the sensitivity of our overall results to the extrapolations, we also ran the RADEX fits performed in Sect. 5 with an alternative collision rate file created just by a constant continuation of the rates from 100 K toward higher temperatures and higher levels. For the same input parameters, the average excitation temperature then drops from 26.9 K to 24.6 K, eventually indicating an overall relatively minor sensitivity of our results to the details of the extrapolations.
We finally note that rate coefficients for the fine-structure excitation of C2H by para-H2(j = 0) have been published recently by Najar et al. (2014). The largest rate coefficients, which correspond to transitions with Δj = ΔN = 2, were found to differ from those of C2H-He by a factor of ~1.4, as assumed here. Larger differences were, however, observed for other transitions, especially those with Δj = ΔN = 1 (see Fig. 6 in Najar et al. 2014). Hyperfine-resolved rate coefficients for C2H-H2, for high levels and high temperatures, are therefore urgently required in order to avoid both collider-mass scaling and extrapolations.
Acknowledgments
We thank the referee and the editor Malcolm Walmsley for useful comments that helped to improve our manuscript. We thank Robert Simon for providing us with a [Ci] 1-0 NANTEN map. We also thank Franck Le Petit for discussions related to including the excitation of new species in the Meudon code. HIFI was designed and built by a consortium of institutes and university departments from across Europe, Canada, and the US under the leadership of SRON Netherlands Institute for Space Research, Groningen, The Netherlands, with major contributions from Germany, France, and the US. Consortium members are Canada: CSA, U.Waterloo; France: CESR, LAB, LERMA, IRAM; Germany: KOSMA,MPIfR,MPS; Ireland, NUIMaynooth; Italy: ASI, IFSI-INAF, Arcetri-INAF; Netherlands: SRON, TUD; Poland: CAMK, CBK; Spain: Observatorio Astronomico Nacional (IGN), Centro de Astrobiología (CSIC-INTA); Sweden: Chalmers University of Technology − MC2, RSS & GARD, Onsala Space Observatory, Swedish National Space Board, Stockholm University − Stockholm Observatory; Switzerland: ETH Zürich, FHNW; USA: Caltech, JPL, NHSC. HIPE is a joint development by the Herschel Science Ground Segment Consortium, consisting of ESA, the NASA Herschel Science Center, and the HIFI, PACS and SPIRE consortia.
References
- Andree-Labsch, S., Ossenkopf, V., & Röllig, M. 2014, A&A, submitted [arXiv:1405.5553] [Google Scholar]
- Arab, H., Abergel, A., Habart, E., et al. 2012, A&A, 541, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bergin, E. A., Phillips, T. G., Comito, C., et al. 2010, A&A, 521, L20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beuther, H., Semenov, D., Henning, T., & Linz, H. 2008, ApJ, 675, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Bieging, J. H., Knee, L. B. G., Latter, W. B., & Olofsson, H. 1998, A&A, 339, 811 [NASA ADS] [Google Scholar]
- Cuadrado, S., Goicoechea, J. R., Pilleri, P., et al. 2015, A&A, 575, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Jong, T., Dalgarno, A., & Chu, S.-I. 1975, ApJ, 199, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 1978, ApJS, 36, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Dubernet, M.-L., Alexander, M. H., Ba, Y. A., et al. 2013, A&A, 553, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Faure, A., & Lique, F. 2012, MNRAS, 425, 740 [Google Scholar]
- Florescu-Mitchell, A. I., & Mitchell, J. B. A. 2006, Phys. Rep., 430, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Flower, D. R. 2001, J. Phys. B, 34, 271 [Google Scholar]
- Fuente, A., Martín-Pintado, J., Cernicharo, J., & Bachiller, R. 1993, A&A, 276, 473 [NASA ADS] [Google Scholar]
- Fuente, A., Rodríguez-Franco, A., & Martín-Pintado, J. 1996, A&A, 312, 599 [NASA ADS] [Google Scholar]
- Gerin, M., Goicoechea1, J. R.,Pety, J., & Hily-Blant, P. 2009, A&A, 494, 977 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gerin, M., Kaźmierczak, M., Jastrzebska, M., et al. 2011, A&A, 525, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ginard, D., González-García, M., Fuente, A., et al. 2012, A&A, 543, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goicoechea, J. R., Joblin, C., Contursi, A., et al. 2011, A&A, 530, L16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harrison, S., & Tennyson, J. 2011, J. Phys. B: At. Mol. Opt. Phys., 44, 045206 [NASA ADS] [CrossRef] [Google Scholar]
- Harrison, S., Faure, A., & Tennyson, J. 2013, MNRAS, 435, 3541 [NASA ADS] [CrossRef] [Google Scholar]
- Hogerheijde, M. R., Jansen, D. J., & Van Dishoeck, E. F. 1995, A&A, 294, 792 [NASA ADS] [Google Scholar]
- Itikawa, Y., & Mason N., 2005, Phys. Rep. 414, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Jansen, D. J., Spaans, M., Hogerheijde, M. R., & van Dishoeck, E. F. 1995, A&A, 303, 541 [NASA ADS] [Google Scholar]
- Johnstone, D., Boonman, A. M. S., & van Dishoeck, E. F. 2003, A&A, 412, 157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kruse, T., & Roth, P. 1997, J. Phys. Chem. A., 101, 2138 [CrossRef] [Google Scholar]
- Le Petit, F., Nehmé, C., Le Bourlot, J., & Roueff, E. 2006, ApJS, 164, 506 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lis, D. C., & Schilke, P. 2003, ApJ, 597, 145 [Google Scholar]
- Lucas, R., & Liszt, H. S. 2000, 358, 1069 [Google Scholar]
- De Graauw, T., Helmich, F. P., Phillips, T. G., et al. 2010, A&A, 518, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Menten, K. M., Reid, M. J., Forbrich, J., & Brunthaler, A. 2007, A&A, 474, 515 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mookerjea, B., Hassel, G. E., Gerin, M., et al. 2012, A&A, 546, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, H. S. P., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Struct., 742, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Najar, F., Ben Abdallah, D., Spielfiedel, A., et al. 2014, Chem. Phys. Lett., 251 [Google Scholar]
- Nagy, Z., Van der Tak, F. F. S., Ossenkopf, V., et al. 2013, A&A, 550, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neufeld, D. A. 2010, ApJ, 708, 635 [NASA ADS] [CrossRef] [Google Scholar]
- Neufeld, D. A., Schilke, P., Menten, K. M., et al. 2006, A&A, 454, L37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ott, S. 2010, in Astronomical Data Analysis Software and Systems XIX, eds. Y. Mizumoto, K.-I. Morita, & M. Ohishi, ASP Conf. Ser., 434, 139 [Google Scholar]
- Padovani, M., Walmsley, C. M., Tafalla, M., Galli, D., & Müller, H. S. P. 2009, A&A, 505, 1199 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pardo, J., Cernicharo, J., & Serabyn, E. 2001, IEEE Transactions on Antennas and Propagation, 49, 1683 [NASA ADS] [CrossRef] [Google Scholar]
- Prasad, S. S., & Huntress, W. T. Tr. 1980, ApJS, 43, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Pety, J., Teyssier, D., Fossé, D., et al. 2005, A&A, 435, 885 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pety, J., Gratier, P., Guzmán, V., et al. 2012, A&A, 548, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
- Pilleri, P., Treviño-Morales, S., Fuente, A., et al. 2013, A&A, 554, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pitts, W. M. L., Pasternack, L., & McDonald, J. R. 1982, Chem. Phys. 68, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Pratap, P., Dickens, J. E., Snell, R. L., et al. 1997, ApJ, 486, 862 [Google Scholar]
- Rizzo, J. R., Fuente, A., & García-Burillo, S. 2005, ApJ, 634, 1133 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, R., Stutzki, J., Sternberg, A., & Winnewisser, G. 1997, A&A, 327, 9 [Google Scholar]
- Schöier, F. L., van der Tak, F. F. S., van Dishoeck, E. F., & Black, J. H. 2005, A&A, 432, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spielfiedel, A., Feautrier, N., Najar, F., et al. 2012, MNRAS, 421, 1891 [NASA ADS] [CrossRef] [Google Scholar]
- Störzer, H., & Hollenbach, D. 1999, ApJ, 515, 669 [CrossRef] [Google Scholar]
- Teyssier, D., Fossé, D., Gerin, M., et al. 2004, A&A, 417, 135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tucker, K. D., Kutner, M. L., & Thaddeus, P. 1974, ApJ, 193, L115 [NASA ADS] [CrossRef] [Google Scholar]
- Useli Bacchitta, F., & Joblin, C. 2007, in Molecules in Space and Laboratory, eds. P. J. L. Lemaire, & F. Combes (Publ. S. Diana), 89 [Google Scholar]
- Van der Tak, F. F. S., Black, J. H., Schöier, F. L., Jansen, D. J., & van Dishoeck, E. F. 2007, A&A, 468, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van der Tak, F. F. S., Nagy, Z., Ossenkopf, V., et al. 2013, A&A, 560, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van der Wiel, M. H. D., Van der Tak, F. F. S., Ossenkopf, V., et al. 2009, A&A, 498, 161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van der Werf, P. P., Goss, W. M., & O’Dell, C. R. 2013, ApJ, 762, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Van Dishoeck, E. F., Jonkheid, B., van Hermaet, et al. 2006, Faraday Discussions, 133, 231 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Van Hemert, M. C., & Van Dishoeck, E. F. 2008, Chem. Phys, 343, 292 [Google Scholar]
- Walmsley, C. M., Natta, A., Oliva, E., & Testi, L. 2000, A&A, 364, 301 [NASA ADS] [Google Scholar]
- Watt, G. D., White, G. J., Millar, T. J., & van Ardenne, A. 1988, A&A, 195, 257 [NASA ADS] [Google Scholar]
- Wilson, T. L., & Rood, R. 1994, ARA&A, 32, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Woon, D. E. 1995, Chem. Phys. Lett., 244, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Wootten, A., Bozyan, E. P., Garrett, D. B., Loren, R. B., Snell, R. L. 1980, ApJ, 239, 844 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Y., Kwok, S., & Dinh-V-Trung, 2008, ApJ, 678, 328 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Spectroscopic and Gaussian-fit parameters of the C2H lines observed toward the CO+ peak of the Orion Bar.
Rate coefficients for the formation and destruction reactions of C2H toward the Orion Bar.
All Figures
 |
Fig. 1 Integrated intensities of the C2H N = 6−5J = 13/2−11/2 (left) and J = 11/2−9/2 (right) doublet. The contour levels go from 0.2 to 2.8 K km s-1spaced by 0.4 K km s-1. |
| In the text | |
 |
Fig. 2 Line profiles of the C2H doublets observed toward the CO+ peak of the Orion Bar from N = 6−5 (top) to N = 10−9 (bottom). The Gaussian fits shown in Table 1 are overlaid on the profiles. The black lines show the expected LSR velocity of 10 km s-1for both components. |
| In the text | |
 |
Fig. 3 Velocity channel maps of the C2H N = 6−5J = 13/2−11/2 transition toward the Orion Bar. |
| In the text | |
 |
Fig. 4 Integrated intensity maps of C2H N = 6−5, CH |
| In the text | |
 |
Fig. 5 Integrated line intensity correlations between the C2H N = 6−5J = 13/2−11/2 line and HCO+, CH, and [Ci]. The corresponding correlation coefficients are shown in parentheses. |
| In the text | |
 |
Fig. 6 Line intensity spatial correlations between the C2H N = 6−5J = 13/2−11/2 line and HCO+, CH, and [Ci]. The corresponding correlation coefficients are shown in parentheses. |
| In the text | |
 |
Fig. 7 Rotational diagram of C2H, corresponding to a rotational temperature of 64 ± 11 K and a column density of (4 ± 0.02) × 1013 cm-2. |
| In the text | |
 |
Fig. 8 Non-LTE C2H line intensity predictions with RADEX vs. the observed line intensities (black symbols). Top panel: the models correspond to parameters of n(H2) = 106 cm-3, Tkin = 100 K, N(C2H) = 8 × 1013 cm-2 (green symbols), and to n(H2) = 5 × 106 cm-3, Tkin = 400 K, N(C2H) = 2 × 1013 cm-2 (blue symbols). The sum of the two components is given by the red symbols. Bottom panel: the models correspond to parameters of n(H2) = 105 cm-3, Tkin = 150 K, N(C2H) = 8 × 1013 cm-2 (green symbols), and to n(H2) = 5 × 106 cm-3, Tkin = 400 K, N(C2H) = 2 × 1013 cm-2 (blue symbols). The sum of the two components is given by the red symbols. |
| In the text | |
 |
Fig. 9 C2H line intensity predictions from a PDR model with a pressure of P = 108 cm-3 K and a radiation field of χ = 104 (blue symbols) overplotted on the observations (black symbols). |
| In the text | |
 |
Fig. 10 Abundances of C2H, CH, C+, HCO+, and [Ci] corresponding to a PDR model with a pressure of P = 108 cm-3 K, illuminated by a radiation field of χ = 104 on the front, and a radiation field of χ = 10 on the back side of the cloud. |
| In the text | |
 |
Fig. 11 Temperature (blue) and density (red) structure corresponding to the isobaric PDR model with a pressure of P = 108 cm-3 K, illuminated by a radiation field of χ = 104 on the front, and a radiation field of χ = 10 on the back side of the cloud. |
| In the text | |
 |
Fig. B.1 Rates for the de-excitation of C2H through collision with H2 at 100 K. Black crosses mark all collision rates from Spielfiedel et al. (2012) above 10-12 cm3s-1. The curves indicate the different transition series for pure rotational transitions of the molecule, i.e., ΔN = ΔJ = ΔF. Each series consists of four curves according to the fine and hyperfine structure split of the four N states with approximately the same energy: J = N ± /1/2 and F = J ± 1/2. The continuations of those curves into the colored symbols show the extrapolation of the rates to the higher level transitions using the formalism from Schöier et al. (2005) based on the IOS approximation. |
| In the text | |
 |
Fig. B.2 Temperature dependence for the main collision rates of C2H with H2. The curves are sorted by ΔJ but cover all transitions of the corresponding series. Every connected dot in Fig. B.1 produces one temperature-dependence graph in this plot. To improve the readability, we have omitted the ΔN = ΔJ = ΔF = 3 series here. Up to 100 K, the lines show the rates computed by Spielfiedel et al. (2012), from 100 to 400 K, and we extrapolated as a power law with the same slope as measured between 90 and 100 K. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.