| Issue |
A&A
Volume 576, April 2015
|
|
|---|---|---|
| Article Number | A13 | |
| Number of page(s) | 11 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201425256 | |
| Published online | 13 March 2015 | |
New view on exoplanet transits
Transit of Venus described using three-dimensional solar atmosphere STAGGER-grid simulations
1 Laboratoire Lagrange, UMR 7293, CNRS, Observatoire de la Côte d’Azur, Université de Nice Sophia-Antipolis, Nice, France
e-mail: andrea.chiavassa@oca.eu
2 Niels Bohr Institute, University of Copenhagen, Juliane Maries Vej 30, 2100 Copenhagen, Denmark
3 Centre for Star and Planet Formation, Natural History Museum of Denmark, University of Copenhagen, Øster Voldgade 5–7, 1350 Copenhagen, Denmark
4 Research School of Astronomy & Astrophysics, Australian National University, Cotter Road, Weston ACT 2611, Australia
Received: 31 October 2014
Accepted: 25 January 2015
Context. An important benchmark for current observational techniques and theoretical modeling of exoplanet atmospheres is the transit of Venus (ToV). Stellar activity and, in particular, convection-related surface structures, potentially cause fluctuations that can affect the transit light curves. Surface convection simulations can help interpreting the ToV as well as other transits outside our solar system.
Aims. We used the realistic three-dimensional (3D) radiative hydrodynamical (RHD) simulation of the Sun from the Stagger-grid and synthetic images computed with the radiative transfer code Optim3D to predict the transit of Venus (ToV) in 2004 that was observed by the satellite ACRIMSAT.
Methods. We computed intensity maps from the RHD simulation of the Sun and produced a synthetic stellar disk image as an observer would see, accounting for the center-to-limb variations. The contribution of the solar granulation was considered during the ToV. We computed the light curve and compared it to the ACRIMSAT observations as well as to light curves obtained with solar surface representations carried out using radial profiles with different limb-darkening laws. We also applied the same spherical tile imaging method as used for RHD simulation to the observations of center-to-limb solar granulation with Hinode.
Results. We explain ACRIMSAT observations of 2004 ToV and show that the granulation pattern causes fluctuations in the transit light curve. We compared different limb-darkening models to the RHD simulation and evaluated the contribution of the granulation to the ToV. We showed that the granulation pattern can partially explain the observed discrepancies between models and data. Moreover, we found that the overall agreement between real and RHD solar granulation is good, either in terms of depth or ingress/egress slopes of the transit curve. This confirms that the limb-darkening and granulation pattern simulated in 3D RHD of the Sun represent well what is imaged by Hinode. In the end, we found that the contribution of the Venusean aureole during ToV is ~10-6 times less intense than the solar photosphere, and thus, accurate measurements of this phenomena are extremely challenging.
Conclusions. The prospects for planet detection and characterization with transiting methods are excellent with access to large a amount of data for stars. Being able to consistently explain the data of 2004 ToV is a new step forward for 3D RHD simulations, which are becoming essential for detecting and characterizing exoplanets. They show that granulation has to be considered as an intrinsic uncertainty (as a result of stellar variability) on precise measurements of exoplanet transits of, most likely, planets with small diameters. In this context, it is mandatory to obtain a comprehensive knowledge of the host star, including a detailed study of the stellar surface convection.
Key words: planet-star interactions / Sun: granulation / techniques: photometric / stars: atmospheres / hydrodynamics / radiative transfer
© ESO, 2015
1. Introduction
The detection of exoplanets orbiting stars is now a routine with more that 1500 confirmed planets and about 3400 candidates (as in November 20141). The study of exoplanet atmospheres can generally be classified into two main categories: (i) measurement of time-varying signals, which include transits, secondary eclipses, and phase curves; and (ii) spatially resolved imaging and spectroscopy. These techniques allow exploring the property of exoplanet atmospheres and understanding the diversity of chemical compositions of exoplanets, their atmospheric processes, internal structures, and formation conditions (Madhusudhan et al. 2014).
A transit event occurs when one (or more) exoplanet moves across the face of the host star, hiding a small part of it, as seen by an observer at some particular vantage point. The exoplanet blocks some of the starlight during the transit and creates a periodic dip in the brightness of the star. The amount of light reduction is typically ~1%, 0.1%, and, 0.01% for Jupiter-, Neptune- and Earth-like planets, respectively (Borucki & Summers 1984). This depends on the size ratio of the star and planet and on the duration of the transit, which, in turn, depends on the distance of the planet from the host star and on the stellar mass. This method is mostly sensitive to large, short-period exoplanets that display the strongest atmospheric signatures, which makes them popular targets for time-varying characterization studies (Madhusudhan et al. 2014). During both the primary and secondary transits, the planet-stellar radius ratio can be deduced, and, for sufficiently bright stars, the exoplanet mass can also be determined from the host star’s radial velocity semi-amplitude (Mislis et al. 2012). If the mass and/or radius of the exoplanet is good enough, the atmospheric density can also be predicted, which can provide insight into the current understanding of exoplanet formation processes. Even more information can be retrieved by measuring the transit depth: the radiation from the host star passes through the atmopshere of the exoplanet and is absorbed to different degrees at different wavelengths. This wavelength-dependent depth of the transmission spectrum is directly linked to the absorption features imprinted on starlight transmitted through the exoplanet atmosphere (Seager & Sasselov 2000; Brown 2001).
However, the transit method has several drawbacks: (i) to be observed, the exoplanet must directly cross the line of sight from Earth (i.e., the star-planet system must be edge-on with respect to the observer), which is only the case for very few exoplanets. (ii) Another problem is the inter-transit duration, which can last from months to years and drastically reduces the number of detectable exoplanets. (iii) The alignment with a background eclipsing binary may cause blends that are difficult to separate from the transit data (Torres et al. 2011). (iv) A last potential complication are host-star surface inhomogeneities caused by stellar granulation (e.g., Chiavassa et al. 2014) or magnetic starspots (e.g., Strassmeier 2009).
A very important benchmark for current observational techniques and theoretical modeling of exoplanet atmospheres is the transit of Venus (ToV). Venus is in many ways an Earth analog and is the closest planet transit we can see in our solar system. ToV events are rare because they occur in pairs eight years apart, each pair separated by 121.5 or 105.5 years, alternating between descending node (June pairs: 1761/1769, 2004/2012, etc.), and ascending node (December pairs: 1631/1639, 1874/1882, 2117/ 2125, etc.). The 2004 and 2012 transits of Venus therefore represent a crucial leap on the human-life timescale because the modern imaging technologies allow for the first time a quantitative analysis of the atmospheric phenomena of the planet associated with its transit (Tanga et al. 2012). Spatial- and ground-based data have been collected and studied by different authors. Tanga et al. (2012) performed the first photometric analysis of the “aureole”2 using various ground-based systems and extracted fundamental parameters of the Venusian atmosphere. García Muñoz & Mills (2012) compared images of Venus during ingress and egress to 2004 data and provided guidelines to investigate the planet’s upper haze from vertically unresolved photometric measurements. Ehrenreich et al. (2012) provided a theoretical transmission spectrum of the atmosphere of Venus dominated by carbon dioxide absorption and droplets of sulfuric acid that compose an upper haze layer (features not expected for an Earth-like exoplanet) that were tested with spectroscopic observations of the 2012 transit.
In this work, we present the transit light-curve predictions obtained from 3D surface convection simulation of the Sun and compare them to the ToV of 2004. Furthermore, we compare 3D predictions to limb-darkening models of the Sun that are frequently used in the planetary community and to real observations of the granulation pattern on the Sun. The aim of this work is to determine whether the 3D surface convection approach to the transit technique yields reliable results for the benchmark case of the ToV, which is also important for interpreting other transits outside our solar system.
2. From solar hydrodynamical simulation to spherical tile imaging
The Sun is a natural reference for studying other stars, and solar models are essential for many studies in stellar and planetary astrophysics. Many of the observable phenomena occurring on the surface of the Sun are intimately linked to convection. Moreover, the atmospheric temperature stratification in the optically thin region in which the emerging flux form is also affected by the interaction between radiative and convective energy transport. To account for all these aspects, it is important to use realistic 3D radiative hydrodynamical (RHD) simulations of convection (Stein & Nordlund 1998; Freytag et al. 2012; Carlsson et al. 2004; Vögler et al. 2004). RHD simulations of the Sun are widely used and compared in detail with observations by the astrophysical community using different numerical codes (e.g., Nordlund et al. 2009; Asplund et al. 2009; Caffau et al. 2011; Pereira et al. 2013).
2.1. Stellar model atmospheres
We used the solar simulation from the Stagger-grid of realistic 3D RHD simulations of stellar convection for cool stars (Magic et al. 2013). This grid is computed using the Stagger-code (originally developed by Nordlund & Galsgaard 19953, and continuously improved over the years by its user community). In a Cartesian box located at the optical surface (i.e., τ ~ 1), the code solves the time-dependent equations for the conservation of mass, momentum, and energy coupled to a realistic treatment of the radiative transfer. The simulation domains are chosen to be large enough to cover at least ten pressure scale heights vertically and to allow for about ten granules to develop at the surface. Moreover, there are periodic boundary conditions horizontally and open boundaries vertically. At the bottom of the simulation, the inflows have a constant entropy and pressure. The simulations employ realistic input physics: (i) the equation of state is an updated version of the equation used by Mihalas et al. (1988); (ii) the radiative transfer is calculated for a large number over wavelength points merged into 12 opacity bins (Nordlund 1982; Skartlien 2000) with opacities including continuous absorption and scattering coefficients from Hayek et al. (2010) and line opacities as described from Gustafsson et al. (2008), which are in turn based on the VALD-2 database (Stempels et al. 2001) of atomic lines. The abundances employed in computing the solar simulation are those of the latest chemical composition reported by Asplund et al. (2009).
3D solar simulation from the Stagger-grid.
2.2. Three-dimensional radiative transfer
We computed the monochromatic emerging intensity using the 3D pure local thermal equilibrium radiative transfer code Optim3D (Chiavassa et al. 2009) and the snapshots of the RHD solar simulation (see Table 1). The radiative transfer equation was solved monochromatically using pretabulated extinction coefficients as a function of temperature, density, and wavelength based on the same extensive atomic and molecular continuum and line opacity data as the latest generation of MARCS models (Gustafsson et al. 2008). We assumed zero microturbulence and modeled the nonthermal Doppler broadening of spectral lines using only the self-consistent velocity fields present in the 3D simulations. We employed the same chemical composition as in the 3D RHD simulation (Asplund et al. 2009). The wavelength interval computed is 6684.0 ± 0.1Å. The detailed methods used in the code are explained in Chiavassa et al. (2009).
2.3. Spherical tile imaging
The computational domain of each simulation only represents a small portion of the stellar surface (see, e.g., the central panel of Fig. 1 in Chiavassa et al. 2012). To obtain an image of the whole solar disk that accounts for limb-darkened effects, we employed the same tiling method as explained in Chiavassa et al. (2010) that was also used in Chiavassa et al. (2012, 2014). Optim3D has been used to compute intensity maps from the solar simulation for different inclinations with respect to the vertical, μ ≡ cos(θ) = [1.0000, 0.9890, 0.9780, 0.9460, 0.9130, 0.8610, 0.8090, 0.7390, 0.6690, 0.5840, 0.5000, 0.4040, 0.3090, 0.2060, 0.1040], with θ being the angle with respect to the line of sight (vertical axis), and for 30 representative snapshots of the simulation adequately spaced apart so as to capture several convective turnovers.
We then used the synthetic images, chosen randomly among the snapshots in the time-series, to map them onto spherical surfaces to account for distortions especially at high latitudes and longitudes by cropping the square-shaped intensity maps when defining the spherical tiles. The computed value of the θ-angle used to generate each map depended on the position (longitude and latitude) of the tile on the sphere and was linearly interpolated among the inclination angles. The snapshots were chosen randomly to avoid assuming periodic boundary conditions. The resulting tiled spherical surface displays an artificial periodic granulation pattern (Fig. 1). The total number of tiles (Ntile) needed to cover half a circumference from side to side on the sphere is 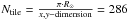 , where R⊙ (transformed into Mm) and the x,y-dimension are taken from Table 1. We generated 50 different synthetic solar-disk images. Since more tiles are necessary to cover the sphere than there are representative snapshots of the RHD simulation, some tiles may randomly appear several times on the solar disk at different inclinations. Therefore, the 50 synthetic images are not completely independent, but we assume that they are a good enough statistical representation to estimate the granulation changes with respect to time during the ToV. Figure 2 displays the fluctuation of the granulation structures for a particular cut in the synthetic disk images. The solar disk intensity fluctuates at the scale of the tile, and the highest intensity varies between [3.74–3.87] × 106 erg cm-2 s-1 Å-1.
, where R⊙ (transformed into Mm) and the x,y-dimension are taken from Table 1. We generated 50 different synthetic solar-disk images. Since more tiles are necessary to cover the sphere than there are representative snapshots of the RHD simulation, some tiles may randomly appear several times on the solar disk at different inclinations. Therefore, the 50 synthetic images are not completely independent, but we assume that they are a good enough statistical representation to estimate the granulation changes with respect to time during the ToV. Figure 2 displays the fluctuation of the granulation structures for a particular cut in the synthetic disk images. The solar disk intensity fluctuates at the scale of the tile, and the highest intensity varies between [3.74–3.87] × 106 erg cm-2 s-1 Å-1.
 |
Fig. 1 Synthetic solar-disk image computed at 6684.0 ± 0.1Å of the RHD simulation of Table 1. The intensity range is [0.0–3.79 × 106 erg cm-2 s-1 Å-1]. We generated 50 different synthetic solar-disk images to account for granulation changes with respect to time. |
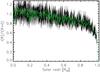 |
Fig. 2 Cut at x = 0,y> 0 for 50 different synthetic solar-disk images (one example reported in Fig. 1). The intensity profiles are normalized to the intensity at the disk center (R = 0.0). The green line is the RHD ⟨3D⟩ average profile. |
3. Modeling the transit of Venus in 2004
June 8, 2004 was a very important and rare date for monitoring the first of two close-in-time (2004 and 2012) transits of Venus visible from Earth before 2117. Schneider et al. (2006), hereafter SPW2006, took the opportunity and obtained space-based solar irradiance measurements with the ACRIMSAT spacecraft.
3.1. Observations with ACRIMSAT
The satellite mission ACRIMSAT4, launched in 1999 and founded by NASA through the Earth Science Programs Office at the Goddard Space Flight Center, measured a reduction of 0.0961% in solar intensity caused by the shadow of Venus during the transit in 2004 (SPW2006). These measurements were taken with the Active Cavity Radiometer Irradiance Monitor (ACRIM 3) instrument (Willson & Mordvinov 2003). ACRIM 3 was designed to provide accurate, highly precise, and traceable radiometry over decadal timescales to detect changes in the total energy received from the Sun by Earth. ACRIM 3 provides 32-second-exposure shutter measurements characterized by open (observations) and closed (calibration) measurements. The measurement precision is 0.01% (SPW2006).
ACRIMSAT cannot observe the Sun continuously because the line of sight is occulted by Earth during its orbit around the Sun. In SPW2006, these periodic interruptions were determined for time intervals spanning the ToV using a definitive a posteriori orbital ephemeris derived from a contemporaneous epochal satellite element set provided by the North American Aerospace Defense Command. SPW2006 reports (Fig. 2 in SPW2006) the apparent path of the center of Venus as seen from ACRIMSAT with respect to the heliocenter as the planet crossed the face of the Sun. ACRIMSAT observations are interrupted for ~30 min by Earth occultation during each of its ~100 min orbits. The duration of 2004 ToV is ~5.5 h.
We here used the trajectory coordinates of Venus extracted from SPW2006 to simulate the passage of the planet on the synthetic solar disk of Fig. 1.
3.2. Evaluation of the Venusian aureole with Hinode
Telescope images, with instruments of typically up to 15 to 20 cm, report that the cusp extension tends to transform the thin crescent of Venus into a ring of light since the mid-eighteenth century (for detailed historical reviews see Link 1969; Edson 1963). While these phenomena can be ascribed to light diffusion, during transits the contribution of refraction is clear (three to four orders of magnitude stronger). Traditionally, its discovery is attributed to Lomonosov (1711 and 1765; Marov 2005). As ToV are rare, the data concerning the aureole are sparse as well. However, thanks to the coordinated giant leap in the observation of the 2004 ToV, modern technologies allowed a quantitative analysis of the atmospheric phenomena associated with the ToV (Tanga et al. 2012). The authors performed the first photometric analysis and obtained spatially resolved data that provided measurements of the aureole flux as a function of the Venusian latitude along the limb.
The aureole is a distorted (strongly flattened) image of a portion of the solar photosphere. The surface brightness of the photosphere is the same in the aureole. For this reason, although the aureole is very thin (<40 km above the cloud deck), the overall contribution to the transit photometry clearly deserves a specific evaluation. To do this, we needed high spatial resolution images of Venus during a transit, and only the Hinode spacecraft could provide that. Unfortunately, the satellite was launched after 2004, thus we used observations carried out during the ToV of 2012, assuming that there were no changes in the Venusian atmosphere between 2004 and 2012.
Hinode (Kosugi et al. 2007) is a joint mission between the space agencies of Japan, the United States, Europe, and the United Kingdom that was launched in 2006, and since then, the spectropolarimeter SOT/SP (Lites et al. 2001; Tsuneta et al. 2008) allows the solar community to perform spectropolarimetry of the solar photosphere under extremely stable conditions. SOT/SP provides 0.32 arcsec angular resolution measurements of the vector magnetic fields on the Sun through precise spectropolarimetry of solar spectral lines with a spatial resolution of 0.32 arcsec and photometric accuracy of 10-3 (Ichimoto et al. 2008).
We obtained Hinode observations of the ToV on June 5, 2012 through the Hinode data on-line archive. We used SOT/SP Stokes I images (i.e., the total intensity measured) in the red filter (6684.0 ± 0.1Å). The data were reduced and calibrated for all the slit positions (i.e., corresponding to level 1 data). The solar diameter in that period was 31.7′ (~951.1′′ for the radius), the geometrical distance on the solar surface, seen under one arcsecond, was R⊙ SOHO/ 951.1 × 0.109 = 732.1 km (with R⊙ SOHO = 696 342 km measured by the SOHO spacecraft, Emilio et al. 2012). The spatial resolution of the image is 1024 × 1024 pixels (Fig. 3) and 1 pixel = 0.109′′, the size of each image is then 111.61 × 111.61″ or 81.71 × 81.71 Mm, with 1 pixel equal to 79.80 km.
 |
Fig. 3 Top panel: image (1024 × 1024 pixels) of Venus (dark circular subaperture) transiting the Sun (brighter areas) on June 5, 2012 as seen by the Hinode SOT/SP spectropolarimeter (total intensity Stoke parameter I) in the red filter centered at 6684.0 ± 0.1Å (red filter). The intensity range is 0.–2.7 × 103 DN pixel-1 s-1 (where DN is data number, Lites et al. 2013). The intensity plotted is the square root of the intensity to better display the “aureole”. Central panel: same figure as above with the contrast highly increased to fit the radius of the planet, yellow circle, with the procedure described in the text (Rfit = 274.91 pixels). The center of the Sun is located in southeast direction. Bottom panel: three-dimensional view of the images above. The contribution of the aureole is visible in the region just outside the solar disk. |
 |
Fig. 4 Representative radial intensity profiles within the ring region (Rfit ± 20 pixels) in the image of Fig. 3, which includes the aureole contribution. The blue dotted curve corresponds to the observations, the green solid line to the best fit (see text for details). The vertical red dashed line is the location of the Venusian radius. |
The contribution from the aureole was computed as follows:
-
1.
The dark circular subaperture corresponding to Venus inFig. 3 (central panel) was fitted using theNewton-based fit method (Pratt 1987). Weselected the points at which the Venusian radius is approximatelylocated (yellow numbered crosses in the figure). The fittingmethod returned the center of the planet and its radius (or impactparameter), a in the figure, with a Venusian radius Rfit = 274.91 pixels.
-
2.
When we knew the position of the center and radius, we extracted a ring of 40 pixels in the outer regions of Venus within the region Rfit ± 20 pixels.
-
3.
We extracted 215 radial intensity profiles within the ring region (a representative example is shown in Fig. 4).
-
4.
We fitted the aureole contribution using a Gaussian law (three free parameters) for the peak and a straight line equation (two free parameters) for the background. Then we integrated over the radius the intensity subtended by the Gaussian fitting curve for each of the 215 radial profiles. We obtained the radial contribution of the aureole.
-
5.
We repeated this procedure for 50 other images during the ingress and egress of the ToV with similar results.
Figure 4 shows the typical signal of the aureole in the ring region selected close to the Venusian radius. The peak is significant and much stronger than the background signal (always lower than ~20 DN pixel-1 s-1). The contribution of the aureole corresponding to the 215 radial intensity profiles is in the range Iaureole = [0.4 − 6.0] × 105 DN pixel-1 s-1 with an average value of ⟨ Iaureole ⟩ = 1.2 × 105 DN pixel-1 s-1 (Table 2).
To relate the aureole intensity to the full Sun, we used the 3D synthetic solar-disk image of Fig. 1. First, we defined IHinode as the total emerging intensity from Fig. 3 (top panel), Isynthglobal as the total emerging intensity from the synthetic Sun of Fig. 1, and Isynthcut as the intensity emerging from a cut in the synthetic disk of Fig. 1 corresponding to the same size and shape as the Hinode observation of Fig. 3. Then the relative intensity due to the aureole is 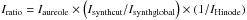 , knowing that
, knowing that  . Table 2 reports values of about 10-6, far too weak to be detected, also considering the precision level of ACRIMSAT (~10-5) and the height of the transit (10-4, Fig. 6). We therefore did not consider the aureole in our modeling.
. Table 2 reports values of about 10-6, far too weak to be detected, also considering the precision level of ACRIMSAT (~10-5) and the height of the transit (10-4, Fig. 6). We therefore did not consider the aureole in our modeling.
3.3. Modeling the transit with 3D RHD simulation of the Sun
The observations give transit parameters such as the geometrically derived transit depth and contact times, the ratio between the radii of Venus and the Sun, and the positions of Venus with respect to the heliocenter as functions of time given the spacecraft and planetary orbits. In the following, we explain how we modeled the ToV using RHD simulation of the Sun as a background. The steps were as follows:
-
1.
we used the synthetic solar image (Fig. 1) as thebackground-emitting source;
-
2.
Venus was modeled by a disk of radius RVenus = 0.0307 R⊙ ~ 8.5 pixels (Fig. 5) with total intensity 0.0961% of Isynthglobal (percentage flux decrement during the 2004 transit, SPW2006);
-
3.
the planetary disk crosses the solar disk following the apparent trajectory of Venus as seen from ACRIMSAT (see SPW2006 for more details and Fig. 5);
-
4.
the intensity of the system was collected for every transiting step.
The intensity map of Fig. 5 is a statistical representation of the Sun at a particular moment during the transit. The apparent trajectory of Venus on the Sun is characterized by (see SPW2006 for more details): (i) a periodic spatial and temporal modulation in the location of Venus as it traverses the solar disk caused by the projection on the Sun of the shifting of the line of sight induced by the spacecraft orbit; (ii) a vertical (north-south) amplitude variation resulting from the near-polar orbit of the spacecraft; (iii) an horizontal (east-west) component manifesting in nonlinear spacings in the planetary position along its projected path in equal time intervals because the orbit plane is not on the line-of-sight direction to the Sun.
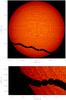 |
Fig. 5 Top panel: synthetic solar-disk image in the visible of the RHD simulation with the different positions of the ToV as seen from ACRIMSAT. The computed wavelength is the same as in Fig. 1. The unusual apparent trajectory of Venus is induced by the spacecraft orbit (see text). Bottom panel: enlargement of the top panel. |
The temporal fluctuations is taken into account using the 50 different synthetic solar-disk images computed. The resulting light curve from the ToV is reported in Fig. 6. The light curve has been averaged over 50 possible realizations of solar disk. The decrease of the Sun’s light is due to the planet occultation and depends on the ratio between the respective size of Venus and the Sun as well as on the brightness contrast. The magnitude of this intensity variation depends on the ratio of the size of Venus to the brightness contrast between the solar disk and the planet. As a result of the reflective spacecraft parallactic motion of Venus, the planet’s apparent path crosses regions of the Sun with surface brightnesses very close to the stellar limb. This affects the slope of the light curve, which is more shallow during egress than during ingress. This aspect is very constraining for transit modeling and crucial for validating the RHD simulation used.
 |
Fig. 6 Top panel: ToV 2004 light curve (black dashed line) for the 3D RHD simulation of the Sun (Fig. 5) compared to the photometric observations (red dots with error bars, Schneider et al. 2006) taken with ACRIM 3 mounted on ACRIMSAT. The observations have been normalized to 1, dividing the original data (Fig. 3 of Schneider et al. 2006) by 1365.88 W/m2. The light curve has been averaged (with the green shade denoting highest and lowest values) over 50 different synthetic solar-disk images to account for granulation changes with respect to time. Bottom panel: same as above, but for one particular realization among the 50 synthetic solar-disk images. |
The data obtained in 2004 for the ToV (see Sect. 3.1) were provided by Glenn H. Schneider (University of Arizona, priv. comm.). Unfortunately, data of the 2012 ToV were not helpful in our work because the error bars were too large. Venus occulted 0.0961% of the total area of the solar photosphere, and, ACRIM 3 provided calibrated observations with gaps resulting from the Earth occultations during the satellite orbit. Figure 6 shows that our RHD simulation and the data agree very well. The root-mean-square deviation (RMSD = 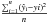 ; where ŷi are the predicted values, yi the observed values, and n the number of measurements) varies between [9.1–9.5] ×10-5 for all the 50 possible realizations of solar granulation and is equal to 9.1 × 10-5 for the average profile plotted in Fig. 6. At the bottom of the light curve (~8.4 h UT), there are some aperiodic variations. SPW2006 reported that this may result from intrinsic changes in the total solar irradiance over the same time interval or may arise as Venus occults isolated regions of the photosphere that differ in local surface brightness (e.g., sunspots or localized smaller spatial scale features). Indeed, it is possible that magnetic starspots contaminate the transit signal (e.g., Silva 2003; Lanza et al. 2009). In the end, accounting for the granulation fluctuations allows reducing the scatter on the observed points at about 7h, 9h, and 11h UT (Fig. 6, bottom panel).
; where ŷi are the predicted values, yi the observed values, and n the number of measurements) varies between [9.1–9.5] ×10-5 for all the 50 possible realizations of solar granulation and is equal to 9.1 × 10-5 for the average profile plotted in Fig. 6. At the bottom of the light curve (~8.4 h UT), there are some aperiodic variations. SPW2006 reported that this may result from intrinsic changes in the total solar irradiance over the same time interval or may arise as Venus occults isolated regions of the photosphere that differ in local surface brightness (e.g., sunspots or localized smaller spatial scale features). Indeed, it is possible that magnetic starspots contaminate the transit signal (e.g., Silva 2003; Lanza et al. 2009). In the end, accounting for the granulation fluctuations allows reducing the scatter on the observed points at about 7h, 9h, and 11h UT (Fig. 6, bottom panel).
Our approach is statistical and does not aim to fully explain the observed data but to show that our RHD simulation of the Sun is adapted (in terms of limb-darkening and emerging flux) to interpret these data and that the granulation fluctuations have a strong effect of the light curves during the transit. We evaluate the granulation contribution in Sect. 3.4.
3.4. 3D RHD granulation versus limb-darkening models
In the literature, the contribution of the star to the transit is typically approximated by a parametric representation of the radial limb-darkened surface profile. This approach neglects the surface inhomogenieties caused by the granulation pattern; the intensity brightness decrease is taken into account, depending on the limb-darkening law used. As a consequence, the slope of the light curve in ingress and egress may be affected differently. In SPW2006, the authors used this method and examined the causes that could affect their deficiency in light-curve fitting of the transit data. They argued that instrumental measurement errors and intrinsic solar variations compared to imperfections in the limb-darkening model itself may be the cause. In this context, RHD simulation of the Sun brings a new insight on the impact of the granulation thanks to the excellent match shown in Fig. 6. The numerical box of a RHD simulation is rotated with a determined μ-angle (see Sect. 2.3) before computing the emerging intensity. There is no pre-adopted limb-darkening function, and the final result is the direct output of the emerging intensity at a particular μ-angle.
Limb-darkening coefficients with the law 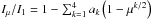 (Claret 2000) and a star with solar parameters or for the ⟨3D⟩ profile of the RHD simulation (Fig. 2, green line) or the intensity profile of Hinode data (Fig. 7, green line).
(Claret 2000) and a star with solar parameters or for the ⟨3D⟩ profile of the RHD simulation (Fig. 2, green line) or the intensity profile of Hinode data (Fig. 7, green line).
We tested different limb-darkening laws on the Sun. For this purpose, we built synthetic images representing the solar surface using radial profiles obtained with the limb-darkening law of Claret2000 (based on 1D model atmospheres of Kurucz1979): 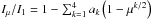 , expressed as the variation in intensity with μ-angle that is normalized to the disk center (Iμ/I1). The limb-darkening coefficients for a star with the stellar parameters of the Sun and for the visible range are listed in Table 3. Magic et al. (2015) used the same RHD simulation as listed in our Table 1 to extract their coefficients. Moreover, we used the law of Claret to fit the average RHD profile ⟨ 3D ⟩ of Fig. 2 (green curve) and report the coefficients in Table 3.
, expressed as the variation in intensity with μ-angle that is normalized to the disk center (Iμ/I1). The limb-darkening coefficients for a star with the stellar parameters of the Sun and for the visible range are listed in Table 3. Magic et al. (2015) used the same RHD simulation as listed in our Table 1 to extract their coefficients. Moreover, we used the law of Claret to fit the average RHD profile ⟨ 3D ⟩ of Fig. 2 (green curve) and report the coefficients in Table 3.
The normalized intensity profiles of the different laws are plotted in Fig. 7.
 |
Fig. 7 Cut at x = 0, y> 0 in different synthetic solar-disk images either built from Claret (2000; light blue curve), Magic et al. (2015; red curve), RHD ⟨3D⟩ profile (black curve, from Fig. 2) and Hinode data for the quiet Sun (green curve, used in Sect. 3.5). The intensity profiles are normalized to the intensity at the disk center (R = 0). |
 |
Fig. 8 Top panel: comparison of different ToV light curves. The black curve is the light curve combining the RHD simulation of the Sun (Figs. 5 and 6). The red and light blue curves represent the limb-darkening Magic et al. (2015) and Claret (2000), respectively. In the end, the purple curve represents the limb-darkening carried out using Claret’s law for the RHD ⟨ 3D ⟩ profile of Fig. 2 (green curve). In all the cases, a constant value is used for Venus intensity. Bottom panel: difference between the above curves with respect to the transit curve of the RHD simulation of Fig. 6. |
For the circular subaperture representing the disk of Venus we used a constant flux. Figure 8 (top) shows the three different limb-darkening models: Magic et al. (2015; RMSD = 9.0 × 10-5, red curve), Claret (2000; RMSD = 9.3 × 10-5, light blue curve), and the Claret law for the RHD ⟨3D⟩ profile (RMSD = 9.3 × 10-5, purple curve). Figure 8 (bottom) shows that the central depression of the ToV obtained with the limb-darkened disk of Claret (2000; light blue curve) is systematically smaller than the transit with the 3D RHD simulation (black curve), but it agrees better with the model of Magic et al. (2015; red curve) and with the RHD ⟨ 3D ⟩ limb-darkening. Since the magnitude of the intensity variation in the light curve depends on the brightness contrast between the solar disk and Venus, it is noticeable that the RHD synthetic disk image differs from limb-darkening models with particular emphasis at the stellar limb. The contribution of the granulation to the ToV can be retrieved by the absolute difference between the limb-darkening of the RHD ⟨3D⟩ profile and the full RHD ToV (purple curve in bottom panel of Fig. 8). We computed the RMS3D = 1.7 × 10-5 of this difference and found that it is ~5 smaller than the RMSDs of the different models. Even if the granulation contribution is not large enough to explain the whole observed discrepancies, it is the source of an intrinsic noise due to the stellar variability that may affect precise measurements of exoplanet transits of, most likely, planets with small diameters.
3.5. 3D RHD granulation versus observed solar granulation
The aim of this section is to create a solar-disk image using the same procedure as for the RHD simulation (Sect. 2.3) but with the granulation pattern observed on the Sun as input. For this purpose, we recovered the Hinode spectropolarimeter SOT/SP data product collected between December 19 and December 20 2007 from the High Altitude Observatory (HAO) website5. The data were reduced and calibrated for all the slit positions (i.e., corresponding to level 1 data). We used SOT/SP Stokes I images (i.e., the total intensity measured) integrated at the continuum wavelengths very close to the Fe I line pair at 6300 Å, but avoiding the spectral lines: the emerging intensity is then compatible, in term of wavelengths probed, to the intensity map of Fig. 1 and the Hinode red filter used in Fig. 3. The original images of 1024 pixel-spectrograph slit parallel to the north-south polar axis of the Sun was successively located at 20 latitudes, and scans of 370 steps of 0.16″ in the direction perpendicular to the slit were performed. At each position in the slit, the images were integrated for about 5 s and for a total time of about 30 min (i.e., 370 steps). This provided with 20 (1028 × 370 pixels) images allowing a complete recording of the center-to-limb variations of the solar disk. However, because the fields of view of the images are partly superimposed, we extracted from the Hinode images a set of 17 (370 × 370 pixels) images forming a continuous south-north stripe in the solar southern hemisphere. The solar diameter in that period was 32.5′ (~975.3′′ for the radius), the geometrical distance at the Sun surface, seen under one arcsecond was R⊙ SOHO/ 975.3 = 713.9 km. Each pixel is 0.16″, the size of each image (Fig. 9) is then 59.20 × 59.20″ or 42.18 × 42.18 Mm, with 1 pixel equal to 114 km.
 |
Fig. 9 Total solar intensity image (370 × 370 pixels) as seen by the Hinode SOT/SP spectropolarimeter at different Δμ and at continuum wavelengths close to 6300 Å. Top panel: center of the Sun, bottom panel: southern limb. The intensity range is, from the top, 18–27 × 103, 17–27 × 103, 14–21 × 103, and 18–25 × 103 DN pixel-1 s-1. |
 |
Fig. 10 Top panel: cut of 37 × 37 pixels from the top panel of Fig. 9. Central panel: intensity map of a small portion of the solar surface at μ = 1 from the RHD of Table 1. The intensity range is [2.0–4.3 × 106 erg cm-2 s-1 Å-1]. Bottom panel: ToV on the solar-disk image constructed with the tiling procedure of Sect. 2.3, but with real granulation observations (top panel and Fig. 9) of Hinode (see text for details). A constant value is used for the intensity of Venus. |
However, the images were too large compared to the synthetic maps (Fig. 10, central panel) we used for tiling the spherical surface of the Sun (Fig. 1) with the RHD simulation. We therefore divided each image by a factor 10 in the east-west axis and by a factor 10 in the north-south polar axis. We ultimately obtained several 37 × 37 images of ~4.2 Mm (Fig. 10, top panel) in 83 μ sub-steps.
In the end, we applied the tiling procedure of Sect. 2.3 and obtained the ToV for a granulation pattern based on Hinode observations (Fig. 10, bottom panel). The deviation from ACRIMSAT observations is RMSD = 8.7 × 10-5. Figure 11 displays the comparison between the light curve obtained from the RHD simulation (Fig. 6, black dashed line) and the one calculated from the ToV of Fig. 10 (bottom panel). The absolute difference between the ToV curves (Fig. 11, bottom panel) shows a typical value of ~5.0 × 10-5, which is close to what is reported in Fig. 8 (bottom). However, the agreement is better, in particular for the ingress/egress slopes of the transit. This confirms that the limb-darkening and the granulation pattern simulated in the 3D RHD solar simulation represent well what is imaged by Hinode. This comparison with Hinode data is important because allows another inspection of RHD simulation using data with lower noise than for the ToV data.
Following what we did in Sect. 3.4 for the RHD ⟨3D⟩ profile, we used the limb-darkening law of Claret to fit the intensity profile obtained from Hinode data (Fig. 7, green curve). The coefficients are reported in Table 3. The good agreement between the Hinode and RHD profiles is also visible in Fig. 7. To obtain the contribution from the granulation, we computed the limb-darkening ToV and subtracted it from the ToV of the Hinode image. The resulting granulation signature has an RMSHinode = 3.0 × 10-5, which is similar to the RMS3D = 1.7 × 10-5 as a result of the granulation signal in the RHD ToV. Both values are lower than or of about the same order as the smallest error bar of ACRIMSAT (2.7 × 10-5), however, and thus the granulation signal cannot be unveiled with these data. Nevertheless, we note that the small-scale variability produced by the RHD simulation might be slightly underestimated because of the snapshot we chose.
 |
Fig. 11 Top panel: ToV light curves for RHD simulation (Figs. 5 and 6) and Hinode SOT/SP spectropolarimeter data (Fig. 10, bottom panel). A constant value is used for the intensity of Venus. Bottom panel: difference between the Hinode ToV with respect to the RHD simulation. |
4. Conclusions and implications for transit studies of extrasolar planets
Modeling the transit light curve of Venus as seen from ACRIMSAT shows that a good representation of the background solar disk and of the planet itself is mandatory. For the Sun, we used the realistic, current, time-dependent, radiative-hydrodynamic stellar atmosphere of the Sun from the Stagger-grid. For Venus, we extracted and fitted radially averaged profiles from high spatial resolution images of Hinode.
We provided a synthetic solar-disk image using the spherical tile imaging method that was previously applied in Chiavassa et al. (2014, 2012, 2010). We applied a statistical approach to show that our RHD simulation of the Sun is adapted (in terms of limb-darkening and emerging flux) to interpret these data and that the granulation fluctuations have a strong effect of the light curves during the transit. Our procedure successfully explains ACRIMSAT observations of the 2004 ToV and showed that the granulation pattern causes fluctuations in the transit light curve. We compared different limb-darkening models to our RHD simulation and evaluated the contribution of the granulation to the ToV. We showed that the granulation pattern can partially explain the observed discrepancies between models and data. However, the amplitude of the signal is close to the typical differences between the different models used, and it is difficult to distinguish the signal of the granulation with the data used in this work. Moreover, we found that the contribution of the Venusian aureole during the ToV is ~10-6 times weaker than the contribution of the solar photosphere, and thus, accurate measurements of this phenomenon are extremely challenging.
Finally, we applied the same spherical tile imaging procedure to the observations of center-to-limb Sun granulation with Hinode and built a solar-disk image. We then compared the resulting transit curves and found that the overall agreement between real and RHD solar granulation is very good, either in terms of depth or ingress/egress slopes of the transit. This confirms that the limb-darkening and the granulation pattern simulated in 3D RHD images of the Sun represent well what is imaged by Hinode.
Three-dimensional RHD simulations are now established as realistic descriptions for the convective photospheres of various classes of stars. They have recently been employed (i) in predictions of differential spectroscopy during exoplanet transits to reconstruct spectra of small stellar surface portions that successively become hidden behind the planet (Dravins et al. 2014); (ii) and to assess the transit light-curve effects of the limb-darkening issued from 3D RHD simulations with respect to 1D models (Magic et al. 2015).
The ToV is an important benchmark for current theoretical modeling of exoplanet transits. Being able to explain consistently the data of 2004 transit is then a new step forward for 3D RHD simulations. This implies that our tiling procedure can be adapted to exoplanet transits. Moreover, our statistical approach in this work allowed us to show that the granulation has to be considered as an intrinsic uncertainty (as a result of the stellar variability) on precise measurements of exoplanet transits of, most likely, planets with small diameters. A possible solution to reduce this uncertainty is repeating the transit measurements several times instead of taking a single snapshot.
The prospects for planet detection and characterization with transiting methods are excellent with access to a large amount of data for different types of stars either with ground-based telescopes such as HATNet (Hungarian Automated Telescope Network, Bakos et al. 2004), NGTS (Next Generation Transit Survey, Wheatley et al. 2013), TRAPPIST (TRAnsiting Planets and PlanetesImals Small Telescope, Jehin et al. 2011), WASP (Wide Angle Search for Planets, Pollacco et al. 2006) or space-based missions like CHEOPS (CHaracterizing ExOPlanet Satellite, Broeg et al. 2013; Koch et al. 2010), COROT (Convection, Rotation and planetary Transits, Baglin et al. 2006b,a), Kepler (Borucki et al. 2010), TESS (Transit Exoplanet Survey Satellite, Ricker et al. 2010), PLATO (PLAnetary Transits and Oscillation of stars, Rauer et al. 2014).
In this context, 3D RHD simulations are essential for a detailed quantitative analysis of the transits. Indeed, interpreting and studying the effect of stellar granulation is not limited to the Sun (Nordlund et al. 2009), but RHD simulations cover a substantial portion of the Hertzsprung-Russell diagram (Magic et al. 2013; Trampedach et al. 2013; Ludwig et al. 2009), including the evolutionary phases from the main sequence over the turnoff up to the red giant branch for low-mass stars.
From http://exoplanets.org with Wright et al. (2011).
Acknowledgments
The authors thank G. Schneider, J. M. Pasachoff, R. C. Willson for providing 2004 ToV data and for the enlightening discussions. The authors acknowledge Alphonse C. Sterling (NASA/Marshall Space Flight Center) for the preparation and diffusion of the transit images. C.P. acknowledges funding from the European Union Seventh Framework Program (FP7) under grant agreement number 606798 (EuroVenus). R.C. is the recipient of an Australian Research Council Discovery Early Career Researcher Award (project number DE120102940).
References
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Baglin, A., Auvergne, M., Barge, P., et al. 2006a, in ESA SP 1306, eds. M. Fridlund, A. Baglin, J. Lochard, & L. Conroy, 33 [Google Scholar]
- Baglin, A., Auvergne, M., Boisnard, L., et al. 2006b, in COSPAR Meeting 36, 36th COSPAR Scientific Assembly, 3749 [Google Scholar]
- Bakos, G., Noyes, R. W., Kovács, G., et al. 2004, PASP, 116, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Borucki, W. J., & Summers, A. L. 1984, Icarus, 58, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Broeg, C., Fortier, A., Ehrenreich, D., et al. 2013, in EPJ Web Conf., 47, 3005 [Google Scholar]
- Brown, T. M. 2001, ApJ, 553, 1006 [NASA ADS] [CrossRef] [Google Scholar]
- Caffau, E., Ludwig, H.-G., Steffen, M., Freytag, B., & Bonifacio, P. 2011, Sol. Phys., 268, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Carlsson, M., Stein, R. F., Nordlund, Å., & Scharmer, G. B. 2004, ApJ, 610, L137 [NASA ADS] [CrossRef] [Google Scholar]
- Chiavassa, A., Plez, B., Josselin, E., & Freytag, B. 2009, A&A, 506, 1351 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Chiavassa, A., Collet, R., Casagrande, L., & Asplund, M. 2010, A&A, 524, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chiavassa, A., Bigot, L., Kervella, P., et al. 2012, A&A, 540, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chiavassa, A., Ligi, R., Magic, Z., et al. 2014, A&A, 567, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A. 2000, A&A, 363, 1081 [NASA ADS] [Google Scholar]
- Dravins, D., Ludwig, H.-G., Dahlén, E., & Pazira, H. 2014, in Proc. Lowell Observatory, eds. G. van Belle, & H. Harris, in press [arXiv:1408.1402] [Google Scholar]
- Edson, J. B. 1963, Adv. Astron. Astrophys., 2, 1 [CrossRef] [Google Scholar]
- Ehrenreich, D., Vidal-Madjar, A., Widemann, T., et al. 2012, A&A, 537, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Emilio, M., Kuhn, J. R., Bush, R. I., & Scholl, I. F. 2012, ApJ, 750, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Freytag, B., Steffen, M., Ludwig, H.-G., et al. 2012, J. Comp. Phys., 231, 919 [Google Scholar]
- García Muñoz, A., & Mills, F. P. 2012, A&A, 547, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hayek, W., Asplund, M., Carlsson, M., et al. 2010, A&A, 517, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ichimoto, K., Lites, B., Elmore, D., et al. 2008, Sol. Phys., 249, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Jehin, E., Gillon, M., Queloz, D., et al. 2011, The Messenger, 145, 2 [NASA ADS] [Google Scholar]
- Koch, D. G., Borucki, W. J., Basri, G., et al. 2010, ApJ, 713, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Kosugi, T., Matsuzaki, K., Sakao, T., et al. 2007, Sol. Phys., 243, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Kurucz, R. L. 1979, ApJS, 40, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Lanza, A. F., Pagano, I., Leto, G., et al. 2009, A&A, 493, 193 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Link, F. 1969, Eclipse phenomena in astronomy (Berlin: J. Springer) [Google Scholar]
- Lites, B. W., Elmore, D. F., & Streander, K. V. 2001, in Advanced Solar Polarimetry – Theory, Observation, and Instrumentation, ed. M. Sigwarth, ASP Conf. Ser., 236, 33 [Google Scholar]
- Lites, B. W., Akin, D. L., Card, G., et al. 2013, Sol. Phys., 283, 579 [NASA ADS] [CrossRef] [Google Scholar]
- Ludwig, H., Caffau, E., Steffen, M., et al. 2009, Mem. Soc. Astron. Italiana, 80, 711 [Google Scholar]
- Madhusudhan, N., Knutson, H., Fortney, J., & Barman, T. 2014, in Protostars and Planets VI, eds. H. Beuther, et al. (University of Arizona Press), 739 [Google Scholar]
- Magic, Z., Collet, R., Asplund, M., et al. 2013, A&A, 557, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magic, Z., Chiavassa, A., Collet, R., & Asplund, M. 2015, A&A, 573, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marov, M. Y. 2005, in Transits of Venus: New Views of the Solar System and Galaxy, ed. D. W. Kurtz, IAU Colloq. 196, 209 [Google Scholar]
- Mihalas, D., Dappen, W., & Hummer, D. G. 1988, ApJ, 331, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Mislis, D., Heller, R., Schmitt, J. H. M. M., & Hodgkin, S. 2012, A&A, 538, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nordlund, A. 1982, A&A, 107, 1 [NASA ADS] [Google Scholar]
- Nordlund, Å., Stein, R. F., & Asplund, M. 2009, Liv. Rev. Sol. Phys., 6, 2 [Google Scholar]
- Pereira, T. M. D., Asplund, M., Collet, R., et al. 2013, A&A, 554, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pollacco, D. L., Skillen, I., Collier Cameron, A., et al. 2006, PASP, 118, 1407 [NASA ADS] [CrossRef] [Google Scholar]
- Pratt, V. 1987, SIGGRAPH Comput. Graph., 21, 145 [Google Scholar]
- Rauer, H., Catala, C., Aerts, C., et al. 2014, Exper. Astron. (Dordrecht: Springer Science Business Media) [arXiv:1310.0696] [Google Scholar]
- Ricker, G. R., Latham, D. W., Vanderspek, R. K., et al. 2010, in AAS Meeting Abstracts. #215, BAAS, 42, 450.06 [NASA ADS] [Google Scholar]
- Schneider, G., Pasachoff, J. M., & Willson, R. C. 2006, ApJ, 641, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Seager, S., & Sasselov, D. D. 2000, ApJ, 537, 916 [NASA ADS] [CrossRef] [Google Scholar]
- Silva, A. V. R. 2003, ApJ, 585, L147 [NASA ADS] [CrossRef] [Google Scholar]
- Skartlien, R. 2000, ApJ, 536, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Stein, R. F., & Nordlund, A. 1998, ApJ, 499, 914 [Google Scholar]
- Stempels, H. C., Piskunov, N., & Barklem, P. S. 2001, in 11th Cambridge Workshop on Cool Stars, Stellar Systems and the Sun, eds. R. J. Garcia Lopez, R. Rebolo, & M. R. Zapaterio Osorio, ASP Conf. Ser., 223, 878 [Google Scholar]
- Strassmeier, K. G. 2009, A&ARv, 17, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Tanga, P., Widemann, T., Ambastha, A., et al. 2012, in AAS/Division for Planet. Sci. Meeting Abstracts., 44, 508.07 [Google Scholar]
- Torres, G., Fressin, F., Batalha, N. M., et al. 2011, ApJ, 727, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Trampedach, R., Asplund, M., Collet, R., Nordlund, Å., & Stein, R. F. 2013, ApJ, 769, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Tsuneta, S., Ichimoto, K., Katsukawa, Y., et al. 2008, Sol. Phys., 249, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Vögler, A., Bruls, J. H. M. J., & Schüssler, M. 2004, A&A, 421, 741 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wheatley, P. J., Pollacco, D. L., Queloz, D., et al. 2013, in EPJ Web Conf., 47, 13002 [Google Scholar]
- Willson, R. C., & Mordvinov, A. V. 2003, Geophys. Res. Lett., 30, 1199 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, J. T., Fakhouri, O., Marcy, G. W., et al. 2011, PASP, 123, 412 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Limb-darkening coefficients with the law 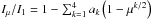 (Claret 2000) and a star with solar parameters or for the ⟨3D⟩ profile of the RHD simulation (Fig. 2, green line) or the intensity profile of Hinode data (Fig. 7, green line).
(Claret 2000) and a star with solar parameters or for the ⟨3D⟩ profile of the RHD simulation (Fig. 2, green line) or the intensity profile of Hinode data (Fig. 7, green line).
All Figures
 |
Fig. 1 Synthetic solar-disk image computed at 6684.0 ± 0.1Å of the RHD simulation of Table 1. The intensity range is [0.0–3.79 × 106 erg cm-2 s-1 Å-1]. We generated 50 different synthetic solar-disk images to account for granulation changes with respect to time. |
| In the text | |
 |
Fig. 2 Cut at x = 0,y> 0 for 50 different synthetic solar-disk images (one example reported in Fig. 1). The intensity profiles are normalized to the intensity at the disk center (R = 0.0). The green line is the RHD ⟨3D⟩ average profile. |
| In the text | |
 |
Fig. 3 Top panel: image (1024 × 1024 pixels) of Venus (dark circular subaperture) transiting the Sun (brighter areas) on June 5, 2012 as seen by the Hinode SOT/SP spectropolarimeter (total intensity Stoke parameter I) in the red filter centered at 6684.0 ± 0.1Å (red filter). The intensity range is 0.–2.7 × 103 DN pixel-1 s-1 (where DN is data number, Lites et al. 2013). The intensity plotted is the square root of the intensity to better display the “aureole”. Central panel: same figure as above with the contrast highly increased to fit the radius of the planet, yellow circle, with the procedure described in the text (Rfit = 274.91 pixels). The center of the Sun is located in southeast direction. Bottom panel: three-dimensional view of the images above. The contribution of the aureole is visible in the region just outside the solar disk. |
| In the text | |
 |
Fig. 4 Representative radial intensity profiles within the ring region (Rfit ± 20 pixels) in the image of Fig. 3, which includes the aureole contribution. The blue dotted curve corresponds to the observations, the green solid line to the best fit (see text for details). The vertical red dashed line is the location of the Venusian radius. |
| In the text | |
 |
Fig. 5 Top panel: synthetic solar-disk image in the visible of the RHD simulation with the different positions of the ToV as seen from ACRIMSAT. The computed wavelength is the same as in Fig. 1. The unusual apparent trajectory of Venus is induced by the spacecraft orbit (see text). Bottom panel: enlargement of the top panel. |
| In the text | |
 |
Fig. 6 Top panel: ToV 2004 light curve (black dashed line) for the 3D RHD simulation of the Sun (Fig. 5) compared to the photometric observations (red dots with error bars, Schneider et al. 2006) taken with ACRIM 3 mounted on ACRIMSAT. The observations have been normalized to 1, dividing the original data (Fig. 3 of Schneider et al. 2006) by 1365.88 W/m2. The light curve has been averaged (with the green shade denoting highest and lowest values) over 50 different synthetic solar-disk images to account for granulation changes with respect to time. Bottom panel: same as above, but for one particular realization among the 50 synthetic solar-disk images. |
| In the text | |
 |
Fig. 7 Cut at x = 0, y> 0 in different synthetic solar-disk images either built from Claret (2000; light blue curve), Magic et al. (2015; red curve), RHD ⟨3D⟩ profile (black curve, from Fig. 2) and Hinode data for the quiet Sun (green curve, used in Sect. 3.5). The intensity profiles are normalized to the intensity at the disk center (R = 0). |
| In the text | |
 |
Fig. 8 Top panel: comparison of different ToV light curves. The black curve is the light curve combining the RHD simulation of the Sun (Figs. 5 and 6). The red and light blue curves represent the limb-darkening Magic et al. (2015) and Claret (2000), respectively. In the end, the purple curve represents the limb-darkening carried out using Claret’s law for the RHD ⟨ 3D ⟩ profile of Fig. 2 (green curve). In all the cases, a constant value is used for Venus intensity. Bottom panel: difference between the above curves with respect to the transit curve of the RHD simulation of Fig. 6. |
| In the text | |
 |
Fig. 9 Total solar intensity image (370 × 370 pixels) as seen by the Hinode SOT/SP spectropolarimeter at different Δμ and at continuum wavelengths close to 6300 Å. Top panel: center of the Sun, bottom panel: southern limb. The intensity range is, from the top, 18–27 × 103, 17–27 × 103, 14–21 × 103, and 18–25 × 103 DN pixel-1 s-1. |
| In the text | |
 |
Fig. 10 Top panel: cut of 37 × 37 pixels from the top panel of Fig. 9. Central panel: intensity map of a small portion of the solar surface at μ = 1 from the RHD of Table 1. The intensity range is [2.0–4.3 × 106 erg cm-2 s-1 Å-1]. Bottom panel: ToV on the solar-disk image constructed with the tiling procedure of Sect. 2.3, but with real granulation observations (top panel and Fig. 9) of Hinode (see text for details). A constant value is used for the intensity of Venus. |
| In the text | |
 |
Fig. 11 Top panel: ToV light curves for RHD simulation (Figs. 5 and 6) and Hinode SOT/SP spectropolarimeter data (Fig. 10, bottom panel). A constant value is used for the intensity of Venus. Bottom panel: difference between the Hinode ToV with respect to the RHD simulation. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


