| Issue |
A&A
Volume 575, March 2015
|
|
|---|---|---|
| Article Number | A60 | |
| Number of page(s) | 19 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201424671 | |
| Published online | 24 February 2015 | |
Impact of mass-loss on the evolution and pre-supernova properties of red supergiants⋆
1 Geneva Observatory, University of Geneva, Maillettes 51, 1290 Sauverny, Switzerland
e-mail: georges.meynet@unige.ch
2 Astrophysics, Lennard-Jones Laboratories, EPSAM, Keele University, Staffordshire, ST5 5BG, UK
3 CASA, Department of Astrophysical and Planetary Sciences, University of Colorado 389-UCB, Boulder, CO 80309, USA
4 Lowell Observatory, 1400 W Mars Hill Road, Flagstaff, AZ 86001, USA
Received: 24 July 2014
Accepted: 30 October 2014
Context. The post-main-sequence evolution of massive stars is very sensitive to many parameters of the stellar models. Key parameters are the mixing processes, the metallicity, the mass-loss rate, and the effect of a close companion.
Aims. We study the change in the red supergiant (RSG) lifetimes, the tracks in the Hertzsprung-Russel diagram (HRD), the positions in this diagram of the pre-supernova progenitor and the structure of the stars at that time for various mass-loss rates during the RSG phase and for two different initial rotation velocities.
Methods. Stellar models were computed with the Geneva code for initial masses between 9 and 25 M⊙ at solar metallicity (Z = 0.014) with 10 times and 25 times the standard mass-loss rates during the RSG phase, with and without rotation.
Results. The surface abundances of RSGs are much more sensitive to rotation than to the mass-loss rates during that phase. A change of the RSG mass-loss rate has a strong impact on the RSG lifetimes and in turn on the luminosity function of RSGs. An observed RSG is associated with a model of higher initial mass when models with an enhanced RSG mass-loss rate are used to deduce that mass. At solar metallicity, models with an enhanced mass-loss rate produce significant changes in the populations of blue, yellow, and RSGs. When extended blue loops or blueward excursions are produced by enhanced mass-loss, the models predict that a majority of blue (yellow) supergiants are post-RSG objects. These post-RSG stars are predicted to show much lower surface rotational velocities than similar blue supergiants on their first crossing of the HR gap. Enhanced mass-loss rates during the RSG phase have little impact on the Wolf-Rayet populations. The position in the HRD of the end point of the evolution depends on the mass of the hydrogen envelope. More precisely, whenever at the pre-supernova stage the H-rich envelope contains more than about 5% of the initial mass, the star is a RSG, and whenever the H-rich envelope contains less than 1% of the total mass, the star is a blue supergiant. For intermediate situations, intermediate colors and effective temperatures are obtained. Yellow progenitors for core-collapse supernovae can be explained by models with an enhanced mass-loss rate, while the red progenitors are better fitted by models with the standard mass-loss rate.
Key words: supergiants / stars: Wolf-Rayet / stars: mass-loss / stars: rotation
Tracks of the enhanced mass loss rates models are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/575/A60
© ESO, 2015
1. Introduction
Red supergiants (RSG) represent a long-lasting stage during the core He-burning stage of all massive stars with masses between about 9 and 25 M⊙. Therefore, many post-main-sequence massive stars are expected to be in this evolutionary stage. These stars represent the end point of the evolution of about half of the massive stars. When such a star experiences core-collapse, it produces a type II-P or type II-L supernova (SN) event. Interactions of the supernova ejecta with the dense RSG wind may in some circumstances produce type II-n supernovae (see, e.g., Smith et al. 2011). These stars are the progenitors of neutron stars and possibly also of some black holes. Thanks to their high luminosities, they can be observed far away in the Universe and are used to probe the metallicity of distant galaxies (Davies et al. 2010), for instance. For all these reasons, it is important to understand RSGs.
While models can satisfactorily reproduce some observed properties of RSGs, such as their positions in the Hertzsprung-Russel diagrams (HRD; Levesque et al. 2005, 2006; Massey et al. 2009), these stars also pose some interesting questions. For instance, are all RSGs exploding in a type II core-collapse event? Or do some of them represent a transitory stage before the star evolves back to bluer regions of the HRD (Yoon & Cantiello 2010; Georgy et al. 2012; Georgy 2012; Groh et al. 2013a,b)? Can this later evolution explain the many blue supergiants observed in clusters of solar metallicity that have masses at the turn-off of about 9−15 M⊙ (Meylan & Maeder 1983; Eggenberger et al. 2002), the low-luminosity WC stars (Georgy et al. 2012), low-luminosity luminous blue variables (LBV) as SN progenitors (Groh et al. 2013a) and/or the yellow supergiants progenitors of core-collapse events (Georgy 2012), such as 2011dh (Van Dyk et al. 2013)?
 |
Fig. 1 Comparison between the mass-loss rates deduced from spectroscopy by different authors and the average values used in our models during the RSG phase. The data by van Loon et al. (2005) cover the region shaded in red. The data by Mauron & Josselin (2011) are distributed in the region shaded in blue. The two stars linked by a vertical line show the mass-loss rates for VY CMa; the lower value is taken from Table 1 of Mauron & Josselin (2011), the upper value from Matsuura et al. (2014). The heavy continuous, long-dashed and dotted lines are our averaged RSG mass-loss rates equal to 1, 10, and 25 times the standard mass-loss rate (see text). The upper thin long and short-dashed slanted lines mark the classical and multiple-scattering limits to the mass-loss rate (van Loon et al. 1999). The lower thin short-long-dashed line shows the Reimers law for an average temperature Teff = 3750 K (see Mauron & Josselin 2011). |
All these questions are somewhat intertwined and need to be addressed simultaneously. This is our aim here, which we intend to achieve by focusing on models with solar metallicity. A key point for answering these questions is a good knowledge of the mass-loss rates during the RSG phase. Unfortunately, this quantity is only poorly constrained observationally (see the discussion in the next section). The difficulty in deducing the mass-loss rates during the RSG phase comes from the complexity of the envelopes of these stars and thus from the difficulty of obtaining reliable spectroscopic diagnostics. Moreover, it is very likely that these stars do not lose mass uniformly as a function of time, but undergo strong and short outbursts. One spectacular example is VY CMa. This is a luminous M supergiant with a luminosity equal to 2–3 × 105L⊙ for the parallax distance of 1.14 ± 0.09 kpc (see Choi et al. 2008). The star has a dusty circumstellar envelope (Humphreys et al. 2007) that produces a reflection nebula at optical wavelengths. Smith et al. (2001) estimated the mass of the nebula surrounding VY CMa as 0.2−0.4 M⊙. Decin et al. (2006) deduced that VY CMa had undergone a phase of high mass-loss (about 3.2 × 10-4 M⊙ yr-1) some 1000 years ago (see Fig. 1).
If this outbursting mode of losing mass were common among RSGs, it would make modeling them quite difficult1. Even with reliable spectroscopic diagnostics of the current mass-loss rate, our vision might be biased toward mass-loss rate values representative of the long periods when the star is in a weak-wind regime. We may miss the much more rare and short mass-loss episodes during which most of the mass might be lost. Moreover, we have no firm theory at present for making predictions on the frequency and durations of such outbursts, although some authors have proposed that they may be triggered by pulsations (Yoon & Cantiello 2010). At the moment, the most promising way to make progress is therefore to compute models with various mass-loss rates during the RSG stage and to see whether some range of mass-losses seems to be preferred over others to predict some peculiar outcomes. This is the aim of the present work, where we build on initial efforts from Georgy (2012), who focused on the pre-SN phase.
In Sect. 2 we present the physical ingredients of our stellar models. Section 3 discusses the impact of different RSG mass-loss rates on the evolutionary tracks and lifetimes. The impacts on the properties of the RSG and of the post-RSG are investigated in Sects. 4 and 5. Implications for the populations of Wolf-Rayet, blue, yellow, and RSGs are discussed in Sect. 6. Conclusions and perspectives are presented in Sect. 7.
2. Stellar models
Except for the mass-loss rates in the non-standard cases (see below), the models were computed with exactly the same physical ingredients as the models computed by Ekström et al. (2012); we refer to this paper for a detailed account. We here recall that the models were computed with the Schwarzschild criteria for convection with a core overshooting. The core extension due to overshooting was taken to be equal to 10% of the pressure scale height estimated at the Schwarzschild core boundary. Nonadiabatic convection was considered in the outer convective zone with a mixing-length scale equal to 1.6 times the local pressure scale height. In rotating models, the shear turbulence coefficient was taken from Maeder (1997), while the horizontal turbulence and the effective diffusion coefficients were those from Zahn (1992).
The mass-loss prescription for the hot part of the evolutionary tracks was that of de Jager et al. (1988) for the initial masses 9 and 15 M⊙ and for Log (Teff/K) > 3.7. For Log (Teff/K) < 3.7, we used a fit on the data by Sylvester et al. (1998) and van Loon et al. (2005), as suggested by Crowther (2001). Above 15 M⊙, the prescription given by Vink et al. (2001) was used on the MS phase as long as Log (Teff/K) > 3.9, the recipe from de Jager et al. (1988) was used for outside the RSG phase. For Log (Teff/K) < 3.7, the prescription was the same as for stars with a lower initial mass. The effects of rotation on the mass-loss rates were accounted for as in Maeder & Meynet (2000). Note that these effects are quite negligible for the rotation rates considered in this work.
As explained in Ekström et al. (2012), for massive stars (>15 M⊙) in the RSG phase, some points in the most external layers of the stellar envelope might exceed the Eddington luminosity of the star: LEdd = 4πcGM/κ (with κ the opacity). This is due to the opacity peak produced by the variation of the ionization level of hydrogen beneath the surface of the star. We accounted for this phenomenon by increasing the mass-loss rate of the star (computed according to the prescription described above) by a factor of 3. When the supra-Eddington layers disappear, later during the evolution, we return to the usual mass-loss rate. Adopting this factor 3 for supra-Eddington luminosity layers and the mass-loss recipes indicated above produces the standard time-averaged mass-loss rates shown by the heavy continuous lines in Fig. 1. This agrees well with the average mass-loss rate determined for RSGs by various authors.
For the models with an enhanced mass-loss rate, we multiplied the mass-loss rates by a factor 10 or 25, as given by the prescriptions indicated above during the whole period when the star is a RSG. We considered the star to be a RSG when its effective temperature (Teff), as estimated by the Geneva code, is log (Teff/K) < 3.7. We chose this limit because for every stellar model considered here, it encompasses the evolutionary phase during which the tracks become vertical in the HRD. Although this is a slightly too high Teff for RSGs, using a lower limiting value such as log (Teff/K) < 3.6 would not have changed our results. This is because the part of the evolution comprised between log (Teff/K) = 3.6 and 3.7 is very short compared with the time spent with log (Teff/K) < 3.6. Note that when these enhanced mass-loss rates were used, we did not account for the effect of the supra-Eddington layers as described in Ekström et al. (2012). This means that the enhancement of the mass-loss rates with respect to those used in Ekström et al. (2012) are slightly lower than a factor 10 and 25. Figure 1 shows the enhancement factor with respect to the mass-loss rate used in Ekström et al. (2012).
The enhancement factors of 10 and 25 were chosen somewhat arbitrarily. The only guideline we considered was to avoid higher rates than the highest mass-loss rates estimated by van Loon et al. (2005, see the empty circles in Fig. 1). We could also have explored mass-loss rates lower than those indicated by the continuous line in Fig. 1. In that case, the differences with respect to the standard tracks presented here would be mainly an increase of the highest initial mass of stars that end their lifetimes as RSGs. The cases with enhanced mass-loss rates are the most interesting to study since they can propose a solution for the stars in the mass range between 9 and 25 M⊙ that end their lifetimes as yellow, blue, or even Wolf-Rayet stars; moreover, such models somewhat mimic the possible evolution in case of strong mass losses during the RSG phase that would be triggered by a mass transfer in a close binary system. Therefore we concentrate on these models here.
 |
Fig. 2 Evolutionary tracks for stellar models of 9 and 20 M⊙ for various prescriptions of the RSG mass-loss rates. Only partial tracks are shown. In the upper panel, the lowest line shows the first crossing from blue to red of the HR gap. The beginning of the portion of the track computed with an enhanced RSG mass-loss rate is indicated by a small empty circle. |
 |
Fig. 3 Upper panel: logarithm of RSG lifetimes as a function of the enhancement factor for the mass-loss rate during the RSG phase. Lower panel: fraction of the initial mass lost during the RSG phase, ΔM/M, as a function of the enhancement factor of the RSG mass-loss rate (see text). |
2.1. Comparisons with spectroscopically determined mass-loss rates
The question is whether these enhancement factors for the mass-loss rates are compatible with spectroscopically determined mass-loss rates. In Fig. 1, mass-loss rate determinations for RSG stars are shown as a function of their luminosity. The low (blue) shaded area covers the region where the sample of stars examined by Mauron & Josselin (2011, see their Tables 1 and 2) are located, while the upper (red) shaded area shows the region covered by the dust-enshrouded RSGs studied by van Loon et al. (2005). At a given luminosity, the scatter of the mass-loss rates is very high, as already noted by Jura & Kleinmann (1990) and Josselin et al. (2000). At a given luminosity, the mass-loss rates can show values that can differ by more than two orders of magnitude!
Is this very large scatter real or due to uncertainties in the techniques used to infer the mass-loss rates? We here assume that a significant part of that scatter is real. In Fig. 1, we compare the observationally deduced mass-loss rates with the time-averaged mass-loss rates we obtained for the RSG phase (see the heavy lines). The averaged mass-loss rates were obtained by simply extracting from the models the total mass lost and the duration of the RSG phase (see the numbers in Table 1). We also estimated for each initial mass model the time-averaged luminosity for the RSG phase. 1) The line showing the RSG mass-loss rate for the reference models (those of Ekström et al. 2012) lies approximately through the middle of the distribution of the points, indicating that this may be a good choice fro the mass-loss rate that represents the averaged evolution; 2) the models with mass-loss rates enhanced by a factor 10 and even 25 remain in a domain of mass-loss rates compatible with the mass-loss rates deduced from spectroscopy.
3. Evolutionary tracks and RSG lifetimes
The impact of the changes of the mass-loss rates during the RSG phase on the evolutionary tracks of the 9 and 20 M⊙ models are shown in Fig. 2. For the model with 9 M⊙ , the enhancement of the RSG mass-loss rate suppresses the blue loop, which in turn increases the time spent in the RSG phase, while for the 20 M⊙, the mass-loss rate enhancement has the opposite effect. Rotation does not change these trends qualitatively2.
Why does an increase in the mass-loss rate of the model with 9 M⊙ reduce or even suppress the blue loop while for the model with 20 M⊙ it favors a blueward evolution? The physics of the blueward evolution is not the same in the model with 9 and that with 20 M⊙ . For the model with 20 M⊙ the star is caused to evolve to the blue when the mass-loss increases because the star becomes more and more homogenous because the helium core still represents a large part of the total mass of the star (Giannone 1967). Typically, when the mass fraction of the He-core becomes greater than about 60−70% of the total actual mass (this limiting fraction depends on the initial mass of the model), the star evolves back to the blue part of the HRD.
For the model with 9 M⊙, the situation is different. The star is caused to evolve back to the blue because at some stage during the core-helium-burning phase, the core expands, which implies by mirror effect a contraction of the envelope. An expansion of the core occurs more easily in a model whose core is not too massive. Lauterborn et al. (1971) have shown that for such stars the red-to-blue motion in the HRD mainly depends on the gravitational potential of the He-core Φcore and how it compares with some critical potential Φcrit(M) that grows with the stellar mass. When the gravitational potential of the He-core is greater than this critical potential, the star remains in the RSG stage, while when the potential is lower, the core can expand and the envelope contracts, and the star reaches a blue location in the HRD. Therefore, we can write 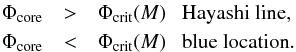 Masses equal to or higher than 15 M⊙ describe the first, masses of 9 M⊙ the second situation.
Masses equal to or higher than 15 M⊙ describe the first, masses of 9 M⊙ the second situation.
When the mass-loss rates increase, for the 9 M⊙ model, this decreases Φcrit(M). This favors the case where Φcore> Φcrit(M), and an evolution keeping the star in the red part of the HRD. For the more massive stars, an increase of the mass loss rates also disfavors the evolution back to the blue because of the mirror effect. But as explained above, these stars may nevertheless evolve back to the blue because the structure of the star becomes more and more homogeneous when mass loss is strong because of their massive convective cores, and thus these stars evolve in the direction of the helium-rich homogeneous sequence in the HRD, that is, in the blue part of the HRD.
Core He-burning lifetimes, RSG lifetimes, time-averaged mass-loss rates during the RSG phase, and different properties of the last computed models.
Various properties of the present stellar models are indicated in Table 1. Comparing the outputs of the stellar models obtained with different RSG mass-loss rates, one deduces the following points:
-
The core He-burning lifetimes are little affected by a change of theRSG mass-loss rates. This is because the stellar winds are neverstrong enough to modify the He-core masses significantly.
-
The RSG lifetimes are strongly affected by a change of the RSG mass-loss rates. This can be also seen in the upper panel of Fig. 3. When the RSG mass-loss rate increases, the RSG lifetime increases for the model with 9 M⊙ (by a factor 2 when the mass-loss rate is increased by a factor 10 with respect to the standard value) because the blue loop disappears. In contrast, the RSG lifetimes decrease for the model with 20 M⊙ computed with enhanced RSG mass-loss rates: by a factor 4 for the same change of the mass-loss rates as for the model with 9 M⊙. This is because the models with 20 M⊙ evolve back to the blue part of the HRD when they undergo strong mass-losses (see also Salasnich et al. 1999; Vanbeveren et al. 2007; Yoon & Cantiello 2010; Georgy 2012; Groh et al. 2013a,b). When the mass-loss rates are increased even more, the duration of the RSG phase for the model with 9 M⊙ does no longer change much, while for the model with 20 M⊙, it continues to decrease by about a factor 2.5.
-
The lower panel of Fig. 3 shows the fraction of the initial mass that is lost by stellar winds during the RSG phase for various mass-loss prescriptions. We first consider models with 15 M⊙. With the standard mass-loss rate, 10−20% (depending on rotation) is lost during the RSG phase. When the mass-loss rates are increased by an order of magnitude, the fraction increases by up to 55−60%. Increasing the mass-loss rates even more (from 10× to 25×) does not change this fraction further. This saturation of the mass lost arises because a star leaves the RSG region when the envelope mass is reduced to a certain value for a given core mass. As a consequence, an increase of the mass-loss rate reduces the time spent in the RSG phase, but not the total mass lost. The total mass lost during the RSG phase remains at about 40% for models with 20 M⊙ and is lower than 30% for models with 25 M⊙. This means that for stars with initial masses between 15 and 25 M⊙, a blueward evolution implies the loss of a relatively well-fixed amount of mass. The mass lost is not sufficient to produce a WC star, or in other words, a naked CO core (WC are Wolf-Rayet stars characterized by strong carbon and oxygen emission lines). Some mass can be lost after the RSG stage, but this amount is quite modest assuming only quiescent winds. Since the stars become LBVs when they return to the blue after losing significant amounts of mass as a RSG (Groh et al. 2013a), additional mass could be lost in LBV eruptions, but the total mass lost is unclear. This means that already at this stage, we can answer one of the question raised in the introduction: can such a blueward evolution (induced by an enhanced RSG mass-loss rate) explain the low-luminosity WC stars (Georgy et al. 2012)? The answer seems to be no, confirming the results from Georgy (2012). This conclusion remains valid even if the mass-loss were caused by a mass-transfer episode to a binary partner in a close multiple system during the RSG phase and not to an increase of the mass-loss rate, as computed here. It is interesting here to also mention the results by Chieffi & Limongi (2013), who obtained for the model with 20 M⊙ an evolution back to the blue after a RSG phase. The mass-loss rates used by these authors somewhat differ from the standard rate we used here. Their model with 20 M⊙ enters the WR phase, but never becomes a WC star, which somewhat supports our conclusion.
-
In general, including the effects of rotation does not change the results much. For a given initial mass, it shortens the RSG lifetimes, while it does not much affect the total mass lost during the RSG phase. This is because when rotation effects are included, the RSG is more luminous for a given initial mass, and in turn, the mass-losses are stronger. As explained above, this shortens the RSG lifetimes.
 |
Fig. 4 Evolutionary tracks of models with different initial velocities (nonrotating at the top, rotating at the bottom) with different RSG mass-loss rates (increasing from left to right). The (red) empty circles are the positions of the Galactic RSGs observed by Levesque et al. (2005). The blue pentagons are the positions of WC stars as observed by Sander et al. (2012). |
 |
Fig. 5 Left panel: number of RSGs as a function of luminosity in a region with constant star formation rate (see text). Numbers are normalized to the model with 9 M⊙. Dots indicate the values obtained for the models with 9, 15, 20, and 25 M⊙ from left to right. Right panel: radii of various stellar models during the RSG phase (Log Teff< 3.6) as a function of the luminosity. The shaded area indicates the region covered by the models with different initial masses, rotations, and mass-loss rates. The 25 times enhanced, rotating 15 M⊙ is the only model that evolves out of this region. The initial mass is indicated at the lowest luminosity predicted by the models for this mass. |
4. Properties of red supergiants
Figure 4 shows the location of the Galactic RSGs observed by Levesque et al. (2005) together with the evolutionary tracks computed with and without rotation and for different RSG mass-loss rates. A changing RSG mass-loss rate has no strong impact on the effective temperatures of RSGs, but it modifies the range of luminosities covered by a given initial mass when it is a RSG. The models with an enhanced RSG mass-loss rate encompass a smaller range of luminosities during the RSG phase than those with standard mass-loss rate (for instance, compare the RSG part of the tracks for models with 15 M⊙). This is caused by the much shorter lifetimes spent in the RSG phase for models with an enhanced mass-loss rate. Tracks computed with different RSG mass-loss rates to determine the range of initial masses of an observed RSG provide somewhat different values. To give a numerical example, if we observe a RSG with a luminosity equal to Log L/L⊙ = 5.0, the standard mass-loss rate can produce such a RSG starting, for instance, from a model with 15 M⊙, while models with 10 × and 25 × higher luminosity require a higher initial mass, around 18−19 M⊙.
The changes of RSG lifetimes shown in Fig. 3 may have an observable impact on the luminosity function of RSGs in regions of constant star formation rate3. To assess this in a quantitative way, a population-synthesis model is needed. This will be presented in a future work. At the moment, we may gain an idea of the strength of the effect using a more simple approach. In the left panel of Fig. 5, we plot the times spent in the RSG stage for our models with different initial masses weighted by the Salpeter initial mass function. We used the quantities for the model with 9 M⊙ as normalization. More precisely, the vertical axis of the left panel of Fig. 5 indicates 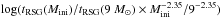 , where tRSG(Mini) is the RSG lifetime of a stellar model with an initial mass Mini. To each initial mass we attributed a time-averaged luminosity during the RSG phase, as can be deduced from the evolutionary tracks (these average luminosities are log L/L⊙ ≈ 3.9, 4.7, 5.0, and 5.3 for models with 9, 15, 20, and 25 M⊙). When the RSG mass-loss rate increases, the slope of this “luminosity function” becomes steeper. When the luminosity increases from Log L/L⊙ equal 4 to 5, the number of stars decreases by a factor 30 when standard mass-loss rates are used, while it decreases by a factor 500 when models with 25 × the standard mass-loss rate are used. The left panel of Fig. 5 shows that the impact of a change of mass-loss is much stronger than the impact caused by rotation (at least for the ranges of values explored here).
, where tRSG(Mini) is the RSG lifetime of a stellar model with an initial mass Mini. To each initial mass we attributed a time-averaged luminosity during the RSG phase, as can be deduced from the evolutionary tracks (these average luminosities are log L/L⊙ ≈ 3.9, 4.7, 5.0, and 5.3 for models with 9, 15, 20, and 25 M⊙). When the RSG mass-loss rate increases, the slope of this “luminosity function” becomes steeper. When the luminosity increases from Log L/L⊙ equal 4 to 5, the number of stars decreases by a factor 30 when standard mass-loss rates are used, while it decreases by a factor 500 when models with 25 × the standard mass-loss rate are used. The left panel of Fig. 5 shows that the impact of a change of mass-loss is much stronger than the impact caused by rotation (at least for the ranges of values explored here).
To use this feature to constrain the stellar models, a few conditions must be fulfilled: 1) it requires some completeness of the sample along the whole RSG sequence; 2) the RSGs, originating from masses equal to or larger than 9 M⊙ should be distinguished from luminous AGB stars; and 3) the star formation rate should have been constant in about the last 30 million years. If these conditions are fulfilled, using the RSG luminosity function to constrain the models has two interesting advantages: 1) it is based on a very simple observations (number ratios); and 2) this quantity will provide some constraint on the averaged mass-loss during the RSG phase, which is a more useful quantity than the instantaneous mass-loss rate, which might not be the one responsible for the loss of most of the material during that phase.
4.1. Effective temperatures and radii of RSG
The effective temperature or the radius of a RSG is not a very strong prediction of the stellar models since it depends on the choice of the mixing length used to compute the nonadiabatic convection in the envelope. The modeling of the convection may also be complicated by the fact that the velocity of the convective cells may approach or even supersede the sound speed, implying shocks (see, e.g., Maeder 2009). All models here assume a mixing length 1.6 times the pressure scale height (see Sect. 2, note that in these models we did not use a mixing-length proportional to the density scale height, as for instance in Maeder & Meynet 1987). The value 1.6 is calibrated on the Sun. This mixing length value incidentally also provides a good match of the observed positions of the red giant and supergiant branch (see Fig. 2 in Ekström et al. 2012, and Fig. 4).
The radii of our stellar models during the RSG phase are plotted as a function of the luminosity in the right panel of Fig. 5. The radii of the models span a wide range of values from 100 to 1570 R⊙. During the RSG phase, the variation of the radii for a given initial mass can be quite large for models with 9 and 15 M⊙ (by a factor 6 for models with 9 M⊙ and by a factor 2 for models with 15 M⊙). The range of radii covered by the more massive models is much smaller (5−20%). At a fixed luminosity, the range of possible radii for the RSG remains modest. Typically, the shaded area in the right panel of Fig. 5 has a width of 50−100 R⊙.
In the radius-luminosity plane, rotation pushes the tracks of a given mass at higher luminosities, but along the same general sequence as the one described by the nonrotating models. Enhancing the mass-loss rates during the RSG phase produces very small effects in general in this diagram. It shifts the tracks to slightly lower luminosities, but again along the same general trend as defined by the standard models. There is one exception, however, in the case of the rotating model with 15 M⊙ with 25 times the standard mass-loss rates. This model extends much below the general trend. This is because the luminosity during the RSG phase decreases strongly for this model as a result of the mass losses.
When comparisons are made with observed values (see the right panel of Fig. 5), we note a good agreement between models and observations for luminosities between 3.9 up to 5.1−5.2. For higher luminosities, the radii given by the models are too small by about 10−20% with respect to the observations. In this plot some interferometric determinations are also indicated; they are also larger than the predicted values. A possibility on the side of the theoretical models to improve the situation, namely to produce larger radii at higher luminosities, would be to decrease the mixing length in the upper luminosity range. It might also be that the values inferred from the observations are slightly too high. The radii of RSGs are not easy to measure, since these stars have a very extended and tenuous atmosphere. It is thus easy to understand that depending on wavelength, the radius may differ from the way the radius is determined in our stellar models. Moreover, if the wind is strong enough, it can be optically thick. In that case, the surface is no longer observable and a pseudo-photosphere at larger radius appears!
Some authors found that the observed radii of RSGs are smaller than those presented in the right panel of Fig. 5. The arguments come from two different approaches: 1) Davies et al. (2013) recently redetermined the effective temperatures of RSGs in the Magellanic Clouds, finding warmer temperatures than Levesque et al. (2006), and thus favoring radii of RSGs about 20−30% more compact. This affects all radii in the whole range of luminosities. The metallicity, however, is different than solar, therefore we can wonder whether applying their techniques on solar metallicity RSGs, these authors would obtain a similar systematic difference. We note that the effective temperatures of Galactic RSGs reported by Levesque et al. (2006) agree very well with results obtained quite independently by interferometric techniques (see Table 2 in van Belle et al. 2009). 2) Another indirect argument pointing toward smaller radii for RSGs is the one by Dessart et al. (2013), who argued, based on properties of the type II-P supernova light curve, that the progenitors should have a much more smaller radius than commonly assumed (note that this constraint applies to RSG that are the end point of the evolution of the considered star and not to RSGs in general). More precisely, Dessart et al. (2013) showed that light curves arising from the explosion of more compact RSG have less blue and shorter plateaus, which better agrees with the observation. Typically, these authors showed that their mdoel with 15 M⊙ with a radius of 500 R⊙ much better reproduces the light curves observed in different filters for the type II-P SN 1999em. The right panel of Fig. 5 shows that the model with 15 M⊙ ends with radii between 300 and 800 R⊙ depending on the RSG mass-loss rate used. To obtain a radius of 500 R⊙ at the end of the evolution, an enhancement factor of the mass-loss rate during the RSG phase between 10 and 25 should be used. Note, however, that this is not the only way to obtain a more compact radius. Another solution would be to change the way of computing the outer convective zone (Maeder & Meynet 1987; Dessart et al. 2013).
This discussion indicates that the radii (or effective temperatures) of RSGs are unclear. At the moment, we conclude that the mixing length considered in our models fit well in general. An enhanced RSG mass-loss rate can explain some more compact radii for RSGs at the pre-supernova stage, in the mass range of about 15 M⊙.
 |
Fig. 6 Upper left panel: surface N/C ratios during the RSG phase normalized to the initial ratio in logarithm and in mass fraction as a function of the luminosity for various models. The red full dots are for observed values; stars labeled 2, 3, and 6 are taken from Origlia et al. (2013), α Ori from Lambert et al. (1984), and IRS 7 from Carr et al. (2000). Upper right panel: same as upper left panel, but for the N/O surface abundance ratio. Lower left panel: tracks during the RSG phase in the N/C versus N/O plane (surface values). The models are the same as in the upper left figure. Lower right panel: surface 12C/13C ratios for the same models as in the upper left figure. The dots are observed values for 6, α Sco (Hinkle et al. 1976), 3, 2, alpha Ori, and VY CMa (Matsuura et al. 2014). |
4.2. Surface composition
Figure 6 shows how various abundance ratios evolve during the RSG phase for different initial masses, rotations, and RSG mass-loss rates. The nonrotating tracks enter into the RSG with N/C, N/O and 12C/13C ratios that are equal to the initial values (this means that the tracks begin at the ordinate 0 in the two upper panels, at the coordinate (0, 0) in the lower left panel, and at the ordinate around 90, well outside the range of values shown, in the lower right panel). Then the tracks go up (increases of nitrogen and decreases of carbon and oxygen), except for the lower right panel, where the tracks go down when time increases (12C/13C decreases).
We first focus on the nonrotating model with 20 M⊙ and standard mass-loss. The RSG tracks cover a very wide range of surface abundances, while the luminosity does not vary much. The change of the surface abundances comes from the deepening outer convective zone that dredges up some nuclearly processed material at the surface. For the N/C and N/O ratios, the changes are gradual and the different ratios are relatively well distributed along the time sequence. For the 12C/13C ratio, the decrease is quite rapid and most of the time, the model will show values below about 20. This is because the 12C/13C ratio is significantly decreased on a greater extent of the mass of the star than the N/C or the N/O ratio.
When the mass-loss rate is increased during the RSG phase, no significant differences appear for the model with 20 M⊙. However, because of the reduced RSG lifetime when the mass-loss rates are higher, the ranges of surface abundance values are slightly more restricted. The same occurs for the luminosity.
 |
Fig. 7 Left panel: evolutionary tracks in the HRD for the nonrotating models computed with the standard mass-loss rates, superposed the positions of progenitors of core-collapse supernovae. Empty stars indicate RSGs (see Table 2), filled pentagons those with a yellow supergiant as progenitors (see Table 6). A continuous segment links the positions of the same SN progenitors obtained by various authors. Progenitors of supernovae predicted by the nonrotating models computed with the various RSG mass-loss rates are found in the shaded area. Progenitors obtained with standard RSG mass-loss rates occupy the upper part as well as the right part of the shaded region, while the progenitors obtained from enhanced RSG mass-loss rate models are in the lower-left region of the shaded area. Lines of constant radius are indicated, the line intermediate between the 100 and 1000 R⊙ corresponds to a radius of 500 R⊙. Right panel: same as left panel with evolutionary tracks in the HRD for the rotating models computed with the standard mass-loss rates. Progenitors of supernovae predicted by the rotating models computed with the various RSG mass-loss rates are found in the shaded area. |
When for the model with 20 M⊙ rotational mixing is accounted for (continuous lines), two significant differences appear with respect to the nonrotating cases. First, at the entrance of the RSG phase, the N/C, N/O and 12C/13C ratios already reflect nuclearly processed material at the surface. Second, the ranges of surface abundance ratios covered during the RSG phase are much smaller. This is because the outer convective zone in the rotating model does not extend as far as in the nonrotating model because in rotating models, the helium cores are larger than in the nonrotating models. As a consequence, the H-burning shell, which acts as a barrier for the deepening of the convective envelope, is at a larger Lagrangian mass coordinate in the rotating models.
Similar qualitative behaviors as for the 20 M⊙ model are obtained for the 25 M⊙ models. For the model with 15 M⊙, we just note that when the RSG mass-loss rate increases, then a wider range of abundance ratios are obtained during the RSG phase for the N/C and N/O ratios. This is because for the model with 15 M⊙, the mass lost during the RSG strongly increases from the standard to the enhanced RSG mass-losses (see also Fig. 3). The model with 9 M⊙ appears in Fig. 6 just through the standard mass-loss rate models (the part of the track shown corresponds to the evolution back to the red after a blue loop). The models with an enhanced mass-loss rate are at too low luminosities to be visible in this plot.
The lower left plot shows the track in the N/C versus N/O plane. Regardless of the model considered, the tracks are very similar. As discussed by Przybilla et al. (2010) and Maeder et al. (2014), this results from the fact that the tracks in this plane reflect more the CNO cycle itself than the details of the stellar models.
Recently, surface abundances for three RSGs belonging to the cluster RSGC2 have been obtained using the near-infrared (NIR) spectrograph GIANO on the Telescopio Nazionale Galileo (TNG) by Origlia et al. (2013). The positions of these stars are indicated in Fig. 6. RSGC2 is a young massive cluster (40 000 M⊙) at a distance of about 3.5 kpc from the Galactic center (Davies et al. 2007). In this cluster, the [C/Fe] ratio is depleted by a factor between two and three, confirming the result by Davies et al. (2009). Origlia et al. (2013) also find that the 12C/13C ratio is low (between 9 and 11). Values for the N/C and N/O values are also indicated for Betelgeuse and IRS 7 (Lambert et al. 1984; Carr et al. 2000). The 12C/13C ratios are indicated for alpha Sco (Hinkle et al. 1976) and VY CMa (Matsuura et al. 2014).
With the exception of IRS 7, the ratios for N/C and N/O may be reproduced by the nonrotating models (regardless of the mass-loss rate during the RSG stage) or by models with an initial rotation lower than the one corresponding to υini/υcrit 0.4. IRS 7 belongs to the Galactic center and appears to be difficult to explain with the present models. It is also quite different from the predicted relations in the N/C versus N/O plane. The initial abundance ratios in the Galactic center may be different from solar ratios, which might explain part of these differences.
The observed 12C/13C ratios are all very low and appear to be slightly more compatible with models that include some mixing before entering the RSG stage. This is in line with the conclusions by Davies et al. (2009) and Origlia et al. (2013), and this conclusion is not changed when modifications of the RSG mass-loss rates are considered. The surface abundances are much more sensitive to rotation than to the mass-loss rates during the RSG phase. We can thus conclude that the constraints on the surface abundances of RSGs cannot be used to discard any of the models presented here, even those computed with the most extreme mass-loss rates during the RSG phase.
4.3. Surface and interior rotation of red supergiants
During the RSG phase, the surface velocities at the equator are in general lower than 1 km s-1. Surface velocities as low as 0.1 km s-1 or even a few 0.01 km s-1 can be reached. Models with enhanced mass-loss during the RSG phase present velocities that are not significantly different from the standard mass-loss rate.
The deprojected surface rotation velocity of Betelgeuse is about 15 km s-1 (Uitenbroek et al. 1998), which is significantly above the values obtained by our models, but still well below the typical critical velocity (between 40−60 km s-1). It is interesting to note that Betelgeuse is among the few RSGs that are runaway stars. Runaway stars move supersonically through the interstellar medium (Blaauw 1961). This high speed may be acquired through few-body dynamical encounters (Poveda et al. 1967) or binary-supernova explosions (Blaauw 1961; Stone 1991). The supersonic movement produces an arc-like bow shock that can be detected at many wavelengths from infrared to X-ray wavebands. As reported by Gvaramadze et al. (2014), most of the bow-shock producing stars are either on the main sequence or are blue supergiants, while there are no Wolf-Rayet stars and only three RSG: Betelgeuse (Noriega-Crespo et al. 1997), μ Cep (Cox et al. 2012), and IRC-10414 (Gvaramadze et al. 2014). Is the fast surface rotation observed for Betelgeuse related to the process that made it a runaway stars? We leave this question open.
The ratio between the angular velocity of the core and of the surface is very high, in the range of 105 − 109 for most models. Enhanced mass-loss rate models in general restrict these ratios to values below 107. We recall here that our models do not account for any transport mechanism in addition to those associated with shear turbulence and meridional currents. Asteroseismological analysis of red giants indicates that some additional transport mechanism is at work in stars with masses of about 1 M⊙ (Beck et al. 2012; Eggenberger et al. 2012; Marques et al. 2013). This additional mechanism produces stronger coupling between the core and envelope, reducing the ratio between the core and envelope rotation. It would be very interesting to obtain similar constraints for RSGs.
 |
Fig. 8 Left panel: evolutionary tracks in the HRD for the nonrotating models computed with the standard mass-loss rates with superposed observed positions of progenitors of core collapse supernovae. The observed data are the same as in Fig. 7. The error bars are not shown for clarity. Progenitors of supernovae predicted by the nonrotating models computed with the various RSG mass-loss rates are found in the shaded area. Right panel: same as the left panel for rotating stellar models. The shaded area shows the region where the progenitors of supernovae are found according to the rotating models with various RSG mass-loss rate prescriptions. |
4.4. Type II supernovae with a red supergiant progenitor
In Table 2, we list some properties of the RSGs identified as SN II-P progenitors according to the most recent determinations in the literature. We list only progenitors of type II-P supernovae for which the luminosity is available and exclude those for which only an upper limit is given. Note that when no effective temperature is given, an arbitrary value of 3.55 is attributed to the progenitor because according to the references quoted, the progenitor probably was a RSG. The metallicities given are very indicative.
Properties of RSGs identified as SN progenitors.
The positions in Fig. 7 of these nine progenitors allow the following comments:
-
Most of the progenitors have Log L/L⊙ between 4.2 and 4.8, which means that they are well within the luminosity range of stellar models according to which they end their lifetimes as RSGs when standard mass-loss rates are used. This holds for both rotating and nonrotating models. Models with a mass-loss rate increased by a factor of 10 can barely match the observed RSG at the pre-SN stage, meaning that we cannot rule out that models with modest mass-loss enhancements Ṁ (2–4) would be able to fit the observations. On the other hand, these progenitors cannot be fitted by models with a mass-loss rate enhanced by a factor of 25; they predict too low luminosities or too high effective temperatures in this luminosity range.
-
As discussed in Groh et al. (2013b), the initial mass of observed progenitors that are RSGs depends on rotation, with nonrotating models yielding a higher initial mass than rotating models. We refer to their Table 6 for determinations of the initial mass of SN II-P progenitors based on rotating and nonrotating models.
-
For SN 2004et, the nebular-phase spectral modeling made by Jerkstrand et al. (2012) constrains the progenitor mass to MZAMS = 15 M⊙, with a pre-SN oxygen mass of 0.8 M⊙. This oxygen mass is quite consistent with our nonrotating 15 M⊙ model with a standard mass-loss rate during the RSG phase, which predicts that an oxygen mass of 0.8 M⊙ would be ejected assuming a remnant mass of about 1 M⊙.
-
The case of 2012aw (the most luminous progenitor) might be explained by our nonrotating standard mass-loss rate model for a 20 M⊙ star or from a model with a slightly higher initial mass (although less massive than 25 M⊙). It appears more difficult to fit that progenitor from rotating models with standard mass-losses. Such a highly luminous RSG progenitor cannot be reproduced by models with an enhanced mass-loss rate, with or without rotation. More generally, the upper luminosity of stars ending their evolution as a RSG decreases when the initial rotation and/or the mass-loss rate during the RSG stage increases. This can be seen clearly in Fig. 8.
-
For models with 9 M⊙, an enhancement in the mass-loss rate at the RSG phase decreases the luminosity at the pre-SN stage. This may have interesting consequences for the nature of low-luminosity SN II-P progenitors and the lowest initial mass of stars that produce core-collapse SNe.
From these points, we conclude that the positions in the HRD of the present RSG supernova progenitors are best described by the standard mass-loss models (see Groh et al. 2013b), although modest mass-loss rate enhancements (2–4) cannot be discarded.
5. Evolution of post-RSG stars
In Fig. 4, the post RSG tracks clearly change when different RSG mass-loss rates are applied. For the model with 20 M⊙ , increasing the RSG mass-loss extends the post RSG track toward bluer positions. For the model with 15 M⊙, a qualitatively similar behavior is observed although less marked. For the model with 25 M⊙, on the other hand, we obtain that the evolution back to the blue, which was already present in the standard mass-loss rate model, is slightly shortened in its extension in effective temperatures and occurs at lower luminosities when models with an enhanced mass-loss rate are used. For all these cases (15 to 25 M⊙), the star would explode as an LBV or yellow hypergiant (Groh et al. 2013a,b). Finally, as already explained in Sect. 3, increasing the RSG mass-loss rate for the model with 9 M⊙ keeps the star in the red part of the HRD. When rotation is accounted for, these features remain very similar.
Duration of various post-MS stages in Myr.
Table 3 shows the time the stars spend according to our stellar models in the blue, yellow, and red regions of the HRD and as Wolf-Rayet stars. Following the recent results from Groh et al. (2014), we consider the models as producing WR stars when log (Teff/K) > 4.36 and the mass fraction of hydrogen at the surface is lower than 0.30. We consider the model as being in the blue region of the HRD when log (Teff/K) > 3.90 and when it is not a WR star. Our criteria for determining the blue region include blue supergiants, blue hypergiants, and LBVs. We distinguish the time spent in the blue before (tB1) and after the RSG phase (tB2). Yellow stars have 3.66 < log (Teff/K) < 3.90, which encompasses yellow supergiants and yellow hypergiants. We denote with tY1 and tY2 the duration of the yellow phase before and after the RSG phase. RSGs are stars with log (Teff/K) < 3.66 for the initial stellar masses shown in Table 3.
In general, the total time spent after the main-sequence phase (see tpMS in Table 3) is only little affected by a change of the RSG mass-loss rate. As mentioned before, the change of the RSG mass-loss rate has a deep impact on the duration of the post RSG phase (see tpRSG in Table 3). As an example, the model with 15 M⊙ with a standard mass-loss rate spends no time in post-RSG phases, while the model with an enhanced mass-loss rate spends a fraction of between 27 and 72% of the whole post MS period.
The fraction of the post-MS phase that is spent in the yellow and blue regions depends on the initial mass, rotation, and the RSG mass-loss rates. When the stellar model evolves back to the blue, then the duration of the post-RSG yellow or blue supergiant phase is in general longer than the duration of the corresponding phases before the RSG stage. Therefore, when a blueward evolution occurs, there is a greater chance that a given blue or yellow supergiant is a post-RSG object than a pre-RSG object.
The models with enhanced mass-loss never enter into the WR stage4! This might be surprising at first because one would have expected that stronger mass-losses during the RSG phase would favor the formation of WR stars. But as noted above, when the mass-loss rate is increased, the duration of the RSG phase is shortened while the total mass lost remains more or less constant. As a consequence, the star with an enhanced mass-loss rate will expose at the surface more or less the same interior layer, but at an earlier stage of its evolution. This explains why the surface composition will reflect a less advanced evolutionary phase. This means that increasing the mass-loss rate during the RSG phase would actually decrease the number of WR stars formed through the single star channel! A caveat applies for the occurrence of eruptions during the post-RSG phase, however, when the star becomes a yellow hypergiant or an LBV (Groh et al. 2013b), which could remove additional mass from the star and favor the formation of WRs. Therefore, it seems that the key for forming WR stars at low-luminosity from single stars is the post-RSG mass loss.
5.1. Effective temperatures and characteristics of SN progenitors
In Fig. 8, we show the regions in the HRDs (see the shaded areas) where the models computed with different RSG mass-loss rates predict the positions of the SNe progenitors5. When the RSG mass-loss rate is increased, as also discussed by Georgy (2012), the end point of the evolution is shifted to the blue for models with 15 and 20 M⊙.
 |
Fig. 9 Fraction of the initial mass of the star ejected by stellar winds during the whole stellar lifetime (red shaded area). The mass in the H-rich envelope, He-rich region, and CO core in the pre-supernova model as a function of the initial mass are indicated as black, white, and blue regions. Cases for various mass-loss rates during the RSG phase without and with rotation are shown. The symbols in the upper part of each panel indicate the range of effective temperatures of the model at the pre-supernova stage: log Teff lower than 3.65 is indicated by (red) stars, log Teff between 3.65 and 4.30 by (black) triangles, and log Teff greater than 4.3 by (blue) circles. |
 |
Fig. 10 Mass of hydrogen in solar masses at the pre-supernova stage for the various models of Table 1. Positions in this diagram of some supernovae are indicated by pentagons with error bars. For SN2008cn, the mass of hydrogen is not known, the range of effective temperatures is framed by the two dotted vertical segments. The three shaded regions from left to right correspond to stars ending their lifetime as blue, yellow, and RSGs. |
Figure 9 shows the structure of the pre-supernovae models for different initial masses, rotation, and prescriptions for the mass-loss rate during the RSG phase. In Table 4, the final radii, masses, masses of the hydrogen-rich envelope6, and the masses of the helium and carbon-oxygen cores of the remnants are indicated together with the integrated mass in the envelope of the quantities of hydrogen, helium, carbon, and oxygen. The angular momentum in the remnant, the angular velocity of the neutron star, and its period at birth are also provided for the rotating models. To compute these quantities we followed the same method as in Georgy et al. (2012). We can note the following effects of enhancing the mass-loss rate during the RSG phase:
-
Table 4 shows that models with enhanced mass-loss rates during the RSG phase in general posess smaller He and CO cores at the end of their evolution, which is of course expected. We note, however, that because of the interplay between mass loss and lifetime during the RSG stage, some models may present slightly larger He or even CO cores for higher RSG mass-loss rates (see for instance the case of the rotating model with 20 M⊙ with 1 and 10 × the standard mass-loss rate). On the whole, however, the effects on the cores remain modest.
-
In the most extreme case of mass loss during the RSG phase considered here, the final mass of the star contains 30−40% of the initial mass, regardless of the initial mass between models with 9 and 25 M⊙ (see the bottom panels of Fig. 9 and, in these panels, the bottom line framing the “WIND” region).
-
Does the change of the mass-loss rate during the RSG phase affect the angular momentum of the core? The angular momentum in the remnant decreases when the RSG mass-loss rate increases. However, the changes are very modest. Even considering the models with a mass-loss increased by a factor 25 would produce extremely rapidly rotating neutron stars. For instance, the longest period obtained here for a neutron star would be 3.6 ms. For comparison, the observed shortest periods for young pulsars are around 20 ms, thus five times longer than the periods obtained here. This means that some angular momentum is still lost, either during the previous phases (Heger et al. 2005) or at the time of the SN explosion (Blondin & Mezzacappa 2007) or during the early phases of the evolution of the newly born neutron star.
-
The RSG mass-loss increase has the strongest effect on the structure of the envelope in the range of initial masses between 9 and 15 M⊙. Very little changes for the model with 25 M⊙, while strong changes occur for the model with 9 or 15 M⊙. This is quite natural because the models with 25 M⊙ spend a very short time in the RSG phase so that changing the mass-loss rates during the short RSG phase will have only a marginal effect. This also justifies our stopping the investigation at this upper mass limit.
-
The H-rich envelope is significantly reduced by the high RSG mass-loss rates. On the other hand, as already noted above, the masses of the He-rich layer and of the CO core are generally only slightly changed.
-
The structure of stars that complete their life as RSGs (see red stars in the upper part of each panel of Fig. 9) shows that RSGs can exist for very different masses of the H-rich envelope (see also Groh et al. 2013b). The range for the masses of H-rich envelopes in RSG pre-supernova models can reach from more than 80% the initial mass to only a few percent of the total initial mass! Models with log Teff> 4.3 are probably WR stars (Groh et al. 2013b), and the mass of the H-rich envelope covers a much more restricted range from 0.004% to at most 1%. The pre-supernovae models with intermediate colors between the red and the blue (these are LBVs or YHGs at the pre-explosion phase; Groh et al. 2013b) posess a H-rich envelope covering the range between about 1 and 5%. Clearly, when the H-rich envelope contains more than about 5% of the initial mass, the star will end as a RSG, and when the whole H-rich envelope contains less than 1% of the total mass, the star appears as a WR star before the SN. For intermediate situations, intermediate colors and effective temperatures are obtained, and the star appears as an LBV or YHG at the pre-explosion stage.
-
Instead of considering the mass of the H-rich envelope, we can consider the integrated mass of hydrogen in the pre-supernova models. Figure 10 shows the mass of hydrogen in the star at the pre-SN stage as a function of the effective temperature. All stars with a mass of hydrogen above 0.4 M⊙ are RSGs, all stars with a mass of hydrogen lower than 0.1 M⊙ appear as WR stars. Stars with intermediate values appear as LBVs/YHGs with effective temperatures between those corresponding to RSGs and late-type WR stars.
Table 4Characteristics of the models at the end of the core He- or C-burning phase (models at the end of the C-burning phase are indicated by an asterisk).
Table 5Properties of the last computed models with effective temperatures between 3.6 and 4.3 ordered from top to bottom by increasing effective temperatures (in logarithm).
-
For stars with intermediate Teff (LBVs and YHGs), we need to determine the parameter that governs the effective temperature or the total radius of the model. In Table 5 we list various properties for the models belonging to the yellow region of Fig. 10. Models are ordered from top to bottom by increasing effective temperatures. In general, the effective temperature increases when the actual mass, the mass of the CO, or of the He core increases. In addition, the effective temperature generally increases when the mass of hydrogen in the envelope decreases or when the ratio of the mass of hydrogen to that of helium decreases.
We end this section by considering the surface rotational velocities of post RSG stars. There is a large difference between the model with 9 M⊙ and the more massive models considered here. The rotation velocity of the model with 9 M⊙ is higher along the blue loop than during the first crossing of the HR gap (standard mass-loss rate model). At an effective temperature of Log (Teff/K) = 3.8, the model with 9 M⊙ typically has a surface velocity of about 18 km s-1 during its first crossing. This velocity becomes about 106 km s-1 during the second crossing and nearly 43 km s-1 during the third crossing! In that case, the surface velocity increases rapidly from the RSG stage where the surface velocity is very low to the time when the star contracts to the blue. This is very different for the model with 15 M⊙ (model with ten times the standard mass-loss rate). At Log (Teff/K) = 3.8, the surface rotational velocity is between 9 and 10 km s-1 during the first crossing, and only 0.3 and 0. 1 km s-1 during the second and third crossing. This very different behavior results from the fact that in the model with 9 M⊙ , the blueward evolution results from the mirror effect (see Sect. 2), while for the 15 M⊙, as well as for more massive stars, the blueward evolution results from strong mass loss. The angular momentum is dredged up to the surface in the model with 9 M⊙ by the deep convective zone during the RSG phase. This model does not lose much mass (see Table 1), therefore this angular momentum remains in the star and produces an acceleration of the envelope when the star contracts to the blue (Heger & Langer 1998). For the model with 15 M⊙, the evolution to the blue part of the HRD is caused by strong mass-losses that also remove much angular momentum, which decreases the surface velocities to very low values during the post-RSG stages. Interestingly, the physical mechanism responsible for the blueward evolution therefore has a strong effect on the surface velocities in the yellow and blue supergiant domain.
5.2. Core-collapse supernovae with a post-red supergiant progenitor
Some supernovae are observed to have a yellow or a blue progenitor while being in the mass range of stars evolving into a RSG phase during their lifetime. Most likely, these stars reach that point because they have lost significant amounts of mass during the RSG phase. We present in Table 6 the list of known progenitors of type II supernovae for which the progenitors were not a RSG. Their positions in the HRD diagram are shown in Fig. 7.
Obviously, the nonrotating models with a normal RSG mass-loss rate cannot account for the existence of most if not all these stars. All the observed yellow progenitors can be explained in the frame of the nonrotating models computed with some enhancement of the RSG mass-loss rates. However, rotating models with standard mass-loss rates present blueward evolution above a luminosity of about 5.0, thus these models may be also invoked to explain some post-RSG progenitors with luminosities above this limit7. Thus there is some degeneracy between the effects of rotation and those induced by different RSG mass-loss rates. Can these two possibilities be distinguished by observing yellow supergiants? The surface velocities in these stages are very low, so are difficult to measure, and moreover, their values indicate very little about the initial rotation. The surface abundances do not appear to be very constraining either. Asteroseismology may be able to assist here. The possibility of probing the internal rotation, for instance, might be a way to distinguish between rotation or mass loss as the main cause for the existence of these yellow progenitors.
We now discuss each of the six supernovae identified as having a yellow supergiant as progenitor.
Properties of post-RSG identified as SN progenitor.
SN 1993J: this supernova originated very likely from a close binary system, consisting, a few thousand years before explosion, of a red (the primary) and a blue supergiant. Roche-lobe overflow from the RSG caused its blueward evolution (Podsiadlowski et al. 1993; Maund et al. 2004). This scenario is strongly supported by the detection of the hot component of this close binary system (Maund et al. 2004). Although our models here were computed for single stars, the enhanced mass-loss rate models can somewhat mimic the effect of a Roche-lobe overflow. The model with a rotating 15 M⊙ with a mass-loss increased by a factor 25 during the RSG stage would provide a reasonable fit to the progenitor of 1993J. The luminosity is 0.2 dex below the attributed luminosity, but still within the error bar. Interestingly, the light curve clearly matches models of an explosion of a He-core of mass 4−5 M⊙ with a low-mass H-envelope of about 0.2 M⊙ (Nomoto et al. 1993; Podsiadlowski et al. 1993; Woosley et al. 1994). Using the values of the effective temperature determined by Maund et al. (2004) and the mass of hydrogen in the envelope, we can place the position of this SN progenitor in Fig. 10. Our model with a rotating 15 M⊙ with 25 times the standard mass-loss ends its lifetime with 5.3 M⊙ and a low-mass H-envelope of 0.2 M⊙, the He-mass in the pre-supernova model is 1.9 M⊙, its CO core mass is 2.2 M⊙. This model would provide a good fit not only to the observed position in the HRD, but probably also for the evolution of the supernova light curve.
SN 2008cn: a progenitor candidate has been proposed by Elias-Rosa et al. (2009). Its yellow color (see the right panel of Fig. 7) would place it among the yellow supergiants. According to Elias-Rosa et al. (2009), the yellow progenitor might have arisen from the blend of two or more stars, such as a RSG and a brighter, blue supergiant. The light curve appeared as a type II-P plateau, which would favor the explosion of a RSG instead of a yellow one. Assuming that the progenitor was the yellow supergiant, we can deduce the following properties from comparisons with our models: a nonrotating model with 18 M⊙ with mass loss increased by more than ten times the standard mass-loss during the RSG phase could likely provide a good fit to the observed position of the progenitor. A rotating progenitor with masses between 15−17 M⊙ with an increased mass loss during the RSG phase (between 10 and 25 times the standard one) would probably provide a reasonable solution as well. This would mean that the actual mass of the progenitor would be between 5−8 M⊙, the mass of ejected hydrogen around 0.15−0.20 M⊙ and that of helium around 1.9 M⊙.
SN 2009hd: this object is heavily obscured by dust. By inserting artificial stars into the pre-SN HST images, Elias-Rosa et al. (2011) constrained the progenitor’s properties. The magnitude and color limits are compatible with a luminous RSG; they also allow for the possibility that the star could have been more yellow than red. The point placed in Figs. 7 represents the upper values for the luminosity and effective temperature. These limits are very similar to that attributed to SN 2008cn, and therefore the same estimates concerning the actual mass, the masses of H, and He ejected can be made (see Sect. 5.1).
SN 2009kr: properties of the progenitors have been obtained by two teams, Elias-Rosa et al. (2010) and Fraser et al. (2010). The properties obtained by the two teams agree relatively well. The only large difference is on the metallicity inferred for the region where the supernova occurred (see Table 6). This illustrates that metallicity estimates are at the moment difficult to make and not very reliable. Another difference is apparent in the SN type. Elias-Rosa et al. (2010) concluded from their own analysis that SN 2009kr is a type II-L supernova, while Fraser et al. (2010) reported that Tendulkar et al. (2009) indicated that SN 2009kr showed the features of a II-n SN. They also reported that Steele et al. (2009) claimed SN 2009kr to be a type II-P SN. In view of the inferred position in the HRD and the low mass of H that it implies, we tend to support the conclusion by Elias-Rosa et al. (2010) that this is a type II-L SN event. As for 2009kr, positions of the progenitor in the HRD support the view that the star is a post-RGS star that lost a great part of its envelope, as proposed by Georgy (2012).
SN 2011dh: this supernova attracted much attention, and the nature of its progenitor has been resolved only recently. It was uncertain for a long time whether the progenitor of this supernova was a compact or an extended star. Based on the properties of the early light curve and spectroscopy, some authors (Arcavi et al. 2011) suggested that the progenitor was a member of the compact IIb family (Chevalier & Soderberg 2010) and that the progenitor identified by Maund et al. (2011) was not the progenitor, but possibly a companion to the progenitor or a blended source, as its radius (~1013 cm) would be highly inconsistent with constraints from their post-explosion photometric and spectroscopic data. On the other hand, Bersten et al. (2012) used a set of hydrodynamical models to study the nature of the progenitor of SN 2011dh. Their modeling suggests that a large progenitor star with a radius about 200 R⊙ is needed to reproduce the early light curve. Their model would thus support the identification of the progenitor with the yellow supergiant detected at the location of the SN event in pre-explosion images. Their model indicates that mass of the ejecta were around 2 M⊙, the progenitor was composed of a helium core of 3−4 M⊙ and a thin hydrogen-rich envelope of about 0.1 M⊙. Van Dyk et al. (2013) have shown from HST observations of the regions of SN 2011dh about 641 days after the explosion that the yellow supergiant has disappeared, which implies that this star was the progenitor of the SN. Recently, a candidate for the companion of the progenitor of this supernova has been detected by Folatelli et al. (2014). From the models presented here we see that regardless of the cause of the mass loss, it probably was quite strong to cause the star to evolve at that position at the time of the supernova explosion. The progenitor position would be compatible with an initial mass around 15−18 M⊙ that experienced more than ten times the standard mass-loss during the RSG stage. Models with rotation would favor an initial mass of about 15 M⊙, while nonrotating models would favor a higher initial mass of about 18 M⊙. Interestingly, nonrotating and rotating models would again predict an actual mass at that position of between 4 and 6 M⊙, with a hydrogen mass in the envelope of about 0.2 M⊙, which is not far from the estimates made by Bersten et al. (2012) on the basis of the early light curve and spectra of the SN.
SN 2013df: Van Dyk et al. (2014) analyzed archived observations of the HST obtained 14 years before explosion and identified the progenitor to be a yellow supergiant. This supernova shows some similarities with SN 1993J, although with less 56Ni ejected and with a progenitor more extended in radius. It is clearly of type IIb.
For some of these SNe, the enhanced mass-loss models (both rotating and nonrotating) can provide a reasonable fit not only to the observed position in the HRD, but also to the masses of the progenitors and of the hydrogen and or helium, as can be deduced from the observed properties of the SN light curve. These post-RSG progenitors therefore provide some support to the enhanced mass-loss rate models, while, as we saw in the previous section, the RSG progenitors favor the standard mass-loss rate models more.
This implies that a star with a given mass and metallicity may evolve through different mass-loss regimes during the RSG phase. The different mass-loss regimes may be triggered by a close companion, rotation, the presence of a magnetic field, and other possibilities. Possible origins of the differences are not lacking, the question to answer is how to identify them and estimate their frequency.
 |
Fig. 11 Upper panels: expected number of Wolf-Rayet stars (dashed lines) and of RSGs in a coeval population (continuous lines) of 10 000 stars. Models with initial masses of between 9 and 25 M⊙ computed with different mass-loss rates during the RSG phases give the different continuous lines labeled by the enhancement factor considered for the mass-loss rate during the RSG phase. The populations of WR stars are very little affected by these changes of mass-loss recipes (see text). Lower panels: fraction between the number of RSG and the number of main-sequence stars two magnitudes below the turn-off. The black and empty squares correspond to observed ratios in stellar clusters with between 20 and 50 stars and with fewer than 20 stars. From left to right, the points correspond to the following clusters: NGC 1976, NGC 6231, NGC 884+4755, NGC 457, and NGC 581+2439 (see Meynet et al. 1993). |
6. Mass-loss rates and populations of evolved stars
When the mass-loss rate is increased during the RSG phase, we expect in general to observe fewer RSG stars since the RSG lifetimes are decreased. Moreover, the upper mass limit of stars spending some time in the RSG stage is lower. This can be seen in the upper panels of Fig. 11. For the standard mass-loss rates and no rotation (upper left panel), the number of RSGs varies between 1 and 28 in a cluster of 10 000 stars with ages between about 5 and 28 Myr. When a mass-loss rate one order of magnitude greater is used during the RSG phase, RSGs appear later than for standard mass-loss, the first RSGs appear around 8 Myr instead of 4 Myr8. The number expected is smaller than for the models computed with a standard mass-loss rate during the whole period between 8 and about 20 Myr. An increased factor of 25 yields a qualitatively similar behavior, but with a stronger decrease during the period between 8 and 20 Myr.
The two lower panels compare the predicted number ratios of RSG with MS stars (two magnitudes below the turn-off) with the observed numbers in a few open clusters having ages between 4 and 25 Myr. We recall that because of the small number of stars, stochastic effects can strongly blur the picture. The two youngest clusters do not show any RSG populations. This may be compatible with the rotating models. The other clusters present RSG/MS ratios between 8 and 14%. These values appear to be more compatible with the standard mass-loss rate models than with models with an increased mass-loss rate. Although this should be seen as a weak constraint at present, we consider that this situation would favor a time-averaged mass-loss rate compatible with the standard mass-losses used by the Ekström et al. (2012) models for the bulk of the RSG populations.
An enhanced RSG mass-loss rate increases the number ratio of blue to RSGs. Typically, for the nonrotating (rotating) 15 M⊙ model, the ratio B/R (=(tB1 + tB2) /tRSG) moves from a value equal to 0.20 (0.05) for the standard model to 0.3 (6.8) and 1.7 (6.9) for models with 10 and 25 × the RSG mass-loss rate. The ratio B/R observed in solar metallicity clusters with mass at the turn-off of about 9−15 M⊙ is about 2 (Meylan & Maeder 1983; Eggenberger et al. 2002). This means that if a fraction of the 15 M⊙ stars were to undergo stronger mass-losses during the RSG phase, then it would help in making the theoretical ratio compatible with the observed ratios. However, this question deserves more studies for the following reasons: 1) for the model with 9 M⊙, enhancing the mass-loss rate will decrease the (tB1 + tB2) /tRSG ratio by suppressing the blue loop; 2) we know that the enhanced mass-loss rates will most likely occur only for a fraction of stars, since some core-collapse progenitors are RSGs, which cannot be reproduced by RSG-enhanced mass-loss rate models and, as seen above, the number ratio of RSG to MS stars appears to be better fitted by the standard mass-loss rate models; and 3) finally, studies at other metallicities should be undertaken since the real challenge is not to reproduce the B/R at a given metallicity, but to reproduce the general trend, which is an increase of the ratio B/R with metallicity.
As we have shown, models with an enhanced RSG mass-loss rate (and no other changes such as enhanced post RSG mass-loss rates) do not produce WC stars. Our models indicate that simultaneous presence of RSG and WR stars of the WN type would only occur for a very limited age range, indicating that single-aged populations showing these two population are probably relatively rare. There are indeed not many cases of single-age populations showing both RSGs and Wolf-Rayet stars. We can cite Westerlund 1 (Clark et al. 2005, although it is so massive that not all the stars may be coeval) and clusters in the center of the Galaxy (Figer et al. 2004; Figer 2009). Interestingly, Shara et al. (2013) found from studying the massive star population in the ScI spiral galaxy M101 that the spatial distributions of the WR and RSG stars near a giant star-forming complex are strikingly different. WR stars dominate the complex core, while RSG dominate the complex halo. If this difference is linked to an age difference, it could be explained by the fact that these two populations originate from different initial mass ranges.
We mentioned above that models with enhanced mass-loss rates decrease the number of WR stars that form (see Table 3). However, the mass range considered here, of between 9 and 25 M⊙, contributes very little to the WR population that in our models mainly come from more massive stars. This is the reason why in Fig. 11 there is no difference in the WR populations between the different models.
7. Conclusions and perspectives
RSGs can be the end point of the evolution of massive stars or a transition phase before the star evolves into bluer parts of the HRD, exploding when it is a yellow, a blue, or even a WN-type Wolf-Rayet star. In this work, we explored how a change of the mass-loss rates during the RSG phase influences the properties of the RSG on the one hand and the evolution during the post-RSG phases and the nature of the core-collapse progenitors on the other. We conclude the following:
- 1.
For the RSG, the positions in the HRD, radii, surface abundances and rotation velocities are mostly insensitive to the RSG mass-loss rate used.
- 2.
Adopting different mass-loss rates during the RSG phase changes the initial mass attributed to a given RSG by evolutionary tracks. When enhanced mass-loss rates are used, higher initial masses are associated with a given RSG star in general.
- 3.
Since the mass to be lost for a given initial mass star to leave the RSG phase is more or less fixed, enhancing the RSG mass-loss rates beyond the point that causes a blueward evolution to appear does not change the total mass lost during the RSG phase, but the duration of the RSG phase. For a star with an initial mass of between 15 and 25 M⊙, the highest mass that can be lost during the RSG phase is between 40−60% of the initial mass.
- 4.
A consequence of the link between RSG lifetime and mass-loss rate is that a change of the RSG mass-loss rate has a strong effect on the luminosity function of RSGs.
- 5.
At solar metallicity, the enhanced mass-loss rate models do produce significant changes on the populations of blue, yellow, and RSGs. When extended blue loops are produced by enhanced mass loss, the models predict that a majority of blue (yellow) supergiants will be post-RSG objects9.
- 6.
Enhanced mass-loss rates during the RSG phase have little effect on the WR populations. We can safely say that even the enhanced mass-loss rate models cannot reproduce the low-luminosity WC stars. As indicated above, post-RSG mass-loss rates during the LBV pause might help. In a work in preparation, we investigate whether these stars can be produced in close binary systems, with mass transfer occurring before the RSG phase, but this does not appear to be a promising channel either for explaining these stars (Barblan et al., in prep.). Another possible solution would be that these stars come from massive stars with higher mass-loss rates (as in the models discussed by Maeder & Meynet 1994).
- 7.
We showed that the position in the HRD of the end point of the evolution depends on the mass of the hydrogen envelope, as was emphasized in Groh et al. (2013b) as well. More precisely, whenever the H-rich envelope contains more than 5% of the initial mass (the limit value may be between 5 and 10%), the star will end as a RSG, and whenever the whole H-rich envelope is lower than 1% of the total mass, the star is a blue supergiant. For intermediate situations, intermediate colors and effective temperatures are obtained.
- 8.
An enhanced mass-loss rate during the RSG has some effect on the angular momentum of the core, but at a level that is much too low to allow this effect to be invoked to explain the observed rotation rate of pulsars. This conclusion holds if no other couplings than those induced by shear and meridional currents exist. If there were a strong coupling (for instance, due to a strong magnetic coupling), this could be very different.
- 9.
To answer the question of which RSG mass-loss rates are favored by observations, we can bring the following elements of response: first, RSG mass-loss rates deduced from spectroscopy show a very large scatter and an outburst behavior for the mass-loss rates of RSGs. The mass lost by a star with a given initial mass and metallicity is probably different depending on some additional characteristics of the star (star may have a close companion, rotation10, etc.). Arguments based on the positions of the RSG progenitors of type II-P supernovae and on the RSG populations in clusters indicate that the standard mass-loss rates are most likely appropriate for describing the bulk of the RSG populations. On the other hand, the existence of yellow or blue progenitors with initial masses of between 15 and 25 M⊙ favors RSG-enhanced mass-loss rates. Interestingly, Humphreys et al. (2013) identified stars in the galaxies M 31 and M 33 that they called warm hypergiants, which present properties favoring a post-RSG phase. These stars thus probably formed through enhanced RSG (or possibly post-RSG) mass-loss rates. The properties of warm hypergiants are A- to F-type absorption spectra, winds with relatively slow outflows, extensive and dusty circumstellar ejecta, and relatively high mass-loss. The warm hypergiants show the small oscillations often referred to as α Cygni variability (van Genderen & Sterken 2002). This would be exactly in line with the conclusion by Saio et al. (2013), who explained the pulsational properties of the alpha Cygni variables, which are blue supergiants with masses of about 20−25 M⊙, by the fact that they are post-RSG stars (see also the discussion in Georgy et al. 2014). More work is needed to determine the main physical cause(s) for enhanced RSG mass-loss rates and their frequency of occurrence.
- 10.
The physical mechanism responsible for the blueward evolution has a strong effect on the surface velocities in the yellow and blue supergiant domain: when it is due to a mirror effect (core expansion+envelope contraction), high surface velocities are expected, while when the blueward evolution is due to strong mass-loss, very low surface velocities are expected.
Rotation produces marginal changes in the RSG lifetimes for the stellar model with 9 M⊙ (see Fig. 3), while it reduces the RSG lifetime by slightly more than 0.2 dex for the model with 20 M⊙ . This is mainly because the rotating models have higher luminosities and therefore suffer stronger mass-losses, which reduces the RSG lifetimes.
This of course is dependent on the way we define a WR star, but the feature that would remain is that regardless of the type of the star, the surface composition of models with an enhanced RSG mass-loss corresponds in general to less CNO-processed material than the surface composition of the standard models.
The models were computed until the end of the core C- or He-burning phase. The positions of the models at the end of the He-burning phase can still evolve during the core carbon-burning phase, but in absence of very strong mass-loss outbursts, the displacement in the HRD remains modest and we consider the positions of these models as a good proxy for the pre-supernova positions.
The mass of the hydrogen-rich envelope, ΔMH, is simply the difference between the final mass and Mα. Note that hydrogen can also be present outside ΔMH, in the outer layers of Mα. This is the reason why in some models the integrated mass of hydrogen, mH, can be higher than ΔMH. Here, Mα is defined as the Lagrangian mass coordinate where the mass fraction of helium becomes higher than 75% going from the surface to the center.
Note that we have computed only two sets of models with different rotational velocities (0 and 0.4υcrit). In reality, we have a distribution of initial rotations, and thus the domain of SN progenitors covered by the rotating models is larger than that shown in the right panel of Fig. 7.
One can wonder why changing the mass-loss rate only during the RSG phase can modify the time of appearance of the first supernovae after an instantaneous burst of star formation. The code computes the upper mass limit of stars becoming RSGs by computing through extrapolation the duration of the RSG phases, the upper initial mass model has a RSG lifetime equal to zero. This procedure implies that when stronger RSG mass-loss rates are used, since the RSG lifetimes are reduced, this limit is lowered and thus corresponds to older ages.
Acknowledgments
The authors thank Hideyuki Saio for his careful reading of the manuscript, as well as Luc Dessart and Ben Davies for interesting suggestions. G.M. acknowledges support from the Swiss National Science Foundation (project number 200020-146401) and thanks for the hospitality of the Lowell Observatory, where part of this work was done. C.G. acknowledges support from the European Research Council under the European Unions Seventh Framework Programme (FP/2007−2013)/ERC Grant Agreement No. 306901. P.M.’s involvement was supported by the National Science Foundation through AST-1008020.
References
- Arcavi, I., Gal-Yam, A., Yaron, O., et al. 2011, ApJ, 742, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Arnett, W. D., Bahcall, J. N., Kirshner, R. P., & Woosley, S. E. 1989, ARA&A, 27, 629 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, P. G., Montalban, J., Kallinger, T., et al. 2012, Nature, 481, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Bersten, M. C., Benvenuto, O. G., Nomoto, K., et al. 2012, ApJ, 757, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Blaauw, A. 1961, Bull. Astron. Inst. Netherlands, 15, 265 [NASA ADS] [Google Scholar]
- Blondin, J. M., & Mezzacappa, A. 2007, Nature, 445, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Carr, J. S., Sellgren, K., & Balachandran, S. C. 2000, ApJ, 530, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Chevalier, R. A., & Soderberg, A. M. 2010, ApJ, 711, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Chieffi, A., & Limongi, M. 2013, ApJ, 764, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Choi, Y. K., Hirota, T., Honma, M., et al. 2008, PASJ, 60, 1007 [NASA ADS] [Google Scholar]
- Clark, J. S., Negueruela, I., Crowther, P. A., & Goodwin, S. P. 2005, A&A, 434, 949 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cox, N. L. J., Kerschbaum, F., van Marle, A.-J., et al. 2012, A&A, 537, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crowther, P. A. 2001, in The Influence of Binaries on Stellar Population Studies, ed. D. Vanbeveren, Astrophys. Space Sci. Lib., 264, 215 [Google Scholar]
- Davies, B., Figer, D. F., Kudritzki, R.-P., et al. 2007, ApJ, 671, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, B., Origlia, L., Kudritzki, R.-P., et al. 2009, ApJ, 694, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, B., Kudritzki, R.-P., & Figer, D. F. 2010, MNRAS, 407, 1203 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, B., Kudritzki, R.-P., Plez, B., et al. 2013, ApJ, 767, 3 [NASA ADS] [CrossRef] [Google Scholar]
- de Jager, C., Nieuwenhuijzen, H., & van der Hucht, K. A. 1988, A&AS, 72, 259 [NASA ADS] [Google Scholar]
- Decin, L., Hony, S., de Koter, A., et al. 2006, A&A, 456, 549 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dessart, L., Hillier, D. J., Waldman, R., & Livne, E. 2013, MNRAS, 433, 1745 [NASA ADS] [CrossRef] [Google Scholar]
- Eggenberger, P., Meynet, G., & Maeder, A. 2002, A&A, 386, 576 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eggenberger, P., Montalbán, J., & Miglio, A. 2012, A&A, 544, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ekström, S., Georgy, C., Eggenberger, P., et al. 2012, A&A, 537, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elias-Rosa, N., Van Dyk, S. D., Li, W., et al. 2009, ApJ, 706, 1174 [NASA ADS] [CrossRef] [Google Scholar]
- Elias-Rosa, N., Van Dyk, S. D., Li, W., et al. 2010, ApJ, 714, L254 [NASA ADS] [CrossRef] [Google Scholar]
- Elias-Rosa, N., Van Dyk, S. D., Li, W., et al. 2011, ApJ, 742, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Figer, D. F. 2009, in Massive-star formation in the Galactic center, eds. M. Livio, & E. Villaver, 40 [Google Scholar]
- Figer, D. F., Rich, R. M., Kim, S. S., Morris, M., & Serabyn, E. 2004, ApJ, 601, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Folatelli, G., Bersten, M. C., Benvenuto, O. G., et al. 2014, ApJ, 793, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Fraser, M., Takáts, K., Pastorello, A., et al. 2010, ApJ, 714, L280 [NASA ADS] [CrossRef] [Google Scholar]
- Fraser, M., Ergon, M., Eldridge, J. J., et al. 2011, MNRAS, 417, 1417 [NASA ADS] [CrossRef] [Google Scholar]
- Fraser, M., Maund, J. R., Smartt, S. J., et al. 2012, ApJ, 759, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Fraser, M., Maund, J. R., Smartt, S. J., et al. 2014, MNRAS, 439, L56 [NASA ADS] [CrossRef] [Google Scholar]
- Georgy, C. 2012, A&A, 538, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Georgy, C., Ekström, S., Meynet, G., et al. 2012, A&A, 542, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Georgy, C., Ekström, S., Eggenberger, P., et al. 2013, A&A, 558, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Georgy, C., Saio, H., & Meynet, G. 2014, MNRAS, 439, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Giannone, P. 1967, Z. Astrophys., 65, 226 [NASA ADS] [Google Scholar]
- Groh, J. H., Meynet, G., & Ekström, S. 2013a, A&A, 550, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Groh, J. H., Meynet, G., Georgy, C., & Ekström, S. 2013b, A&A, 558, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Groh, J. H., Meynet, G., Ekström, S., & Georgy, C. 2014, A&A, 564, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gvaramadze, V. V., Menten, K. M., Kniazev, A. Y., et al. 2014, MNRAS, 437, 843 [NASA ADS] [CrossRef] [Google Scholar]
- Heger, A., & Langer, N. 1998, A&A, 334, 210 [NASA ADS] [Google Scholar]
- Heger, A., Woosley, S. E., & Spruit, H. C. 2005, ApJ, 626, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Hinkle, K. H., Lambert, D. L., & Snell, R. L. 1976, ApJ, 210, 684 [NASA ADS] [CrossRef] [Google Scholar]
- Humphreys, R. M., Helton, L. A., & Jones, T. J. 2007, AJ, 133, 2716 [NASA ADS] [CrossRef] [Google Scholar]
- Humphreys, R. M., Davidson, K., Grammer, S., et al. 2013, ApJ, 773, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Jerkstrand, A., Fransson, C., Maguire, K., et al. 2012, A&A, 546, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Josselin, E., Blommaert, J. A. D. L., Groenewegen, M. A. T., Omont, A., & Li, F. L. 2000, A&A, 357, 225 [NASA ADS] [Google Scholar]
- Jura, M., & Kleinmann, S. G. 1990, ApJS, 73, 769 [NASA ADS] [CrossRef] [Google Scholar]
- Lambert, D. L., Brown, J. A., Hinkle, K. H., & Johnson, H. R. 1984, ApJ, 284, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Lauterborn, D., Refsdal, S., & Weigert, A. 1971, A&A, 10, 97 [NASA ADS] [Google Scholar]
- Levesque, E. M., Massey, P., Olsen, K. A. G., et al. 2005, ApJ, 628, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Levesque, E. M., Massey, P., Olsen, K. A. G., et al. 2006, ApJ, 645, 1102 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A. 1997, A&A, 321, 134 [NASA ADS] [Google Scholar]
- Maeder, A. 2009, Physics, Formation and Evolution of Rotating Stars (Berlin: Springer) [Google Scholar]
- Maeder, A., & Meynet, G. 1987, A&A, 182, 243 [NASA ADS] [Google Scholar]
- Maeder, A., & Meynet, G. 1994, A&A, 287, 803 [Google Scholar]
- Maeder, A., & Meynet, G. 2000, A&A, 361, 159 [NASA ADS] [Google Scholar]
- Maeder, A., & Meynet, G. 2001, A&A, 373, 555 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maeder, A., Przybilla, N., Nieva, M.-F., et al. 2014, A&A, 565, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marques, J. P., Goupil, M. J., Lebreton, Y., et al. 2013, A&A, 549, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Massey, P., Silva, D. R., Levesque, E. M., et al. 2009, ApJ, 703, 420 [NASA ADS] [CrossRef] [Google Scholar]
- Matsuura, M., Yates, J. A., Barlow, M. J., et al. 2014, MNRAS, 437, 532 [NASA ADS] [CrossRef] [Google Scholar]
- Maund, J. R., Smartt, S. J., Kudritzki, R. P., Podsiadlowski, P., & Gilmore, G. F. 2004, Nature, 427, 129 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Maund, J. R., Fraser, M., Ergon, M., et al. 2011, ApJ, 739, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Maund, J. R., Mattila, S., Ramirez-Ruiz, E., & Eldridge, J. J. 2014, MNRAS, 438, 1577 [NASA ADS] [CrossRef] [Google Scholar]
- Mauron, N., & Josselin, E. 2011, A&A, 526, A156 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meylan, G., & Maeder, A. 1983, A&A, 124, 84 [NASA ADS] [Google Scholar]
- Meynet, G., Mermilliod, J.-C., & Maeder, A. 1993, A&AS, 98, 477 [NASA ADS] [Google Scholar]
- Meynet, G., Ekstrom, S., Maeder, A., et al. 2013, in Studying Stellar Rotation and Convection, eds. M. Goupil, K. Belkacem, C. Neiner, F. Lignières, & J. J. Green, Lect. Notes Phys. (Berlin Springer Verlag), 865, 3 [Google Scholar]
- Nomoto, K., Suzuki, T., Shigeyama, T., et al. 1993, Nature, 364, 507 [NASA ADS] [CrossRef] [Google Scholar]
- Noriega-Crespo, A., van Buren, D., Cao, Y., & Dgani, R. 1997, AJ, 114, 837 [NASA ADS] [CrossRef] [Google Scholar]
- Origlia, L., Oliva, E., Maiolino, R., et al. 2013, A&A, 560, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Podsiadlowski, P., Hsu, J. J. L., Joss, P. C., & Ross, R. R. 1993, Nature, 364, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Poveda, A., Ruiz, J., & Allen, C. 1967, Boletin de los Observatorios Tonantzintla y Tacubaya, 4, 86 [Google Scholar]
- Przybilla, N., Firnstein, M., Nieva, M. F., Meynet, G., & Maeder, A. 2010, A&A, 517, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Saio, H., Georgy, C., & Meynet, G. 2013, MNRAS, 433, 1246 [NASA ADS] [CrossRef] [Google Scholar]
- Salasnich, B., Bressan, A., & Chiosi, C. 1999, A&A, 342, 131 [NASA ADS] [Google Scholar]
- Sander, A., Hamann, W.-R., & Todt, H. 2012, A&A, 540, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shara, M. M., Bibby, J. L., Zurek, D., et al. 2013, AJ, 146, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Smartt, S. J. 2009, ARA&A, 47, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, N., Humphreys, R. M., Davidson, K., et al. 2001, AJ, 121, 1111 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, N., Li, W., Filippenko, A. V., & Chornock, R. 2011, MNRAS, 412, 1522 [NASA ADS] [CrossRef] [Google Scholar]
- Steele, T. N., Cobb, B., & Filippenko, A. V. 2009, Central Bureau Electronic Telegrams, 2011, 1 [NASA ADS] [Google Scholar]
- Stone, R. C. 1991, AJ, 102, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Sylvester, R. J., Skinner, C. J., & Barlow, M. J. 1998, MNRAS, 301, 1083 [NASA ADS] [CrossRef] [Google Scholar]
- Tendulkar, S. P., Kasliwal, M. M., Quimby, R., & Kulkarni, S. R. 2009, ATel, 2291, 1 [NASA ADS] [Google Scholar]
- Tomasella, L., Cappellaro, E., Fraser, M., et al. 2013, MNRAS, 434, 1636 [NASA ADS] [CrossRef] [Google Scholar]
- Uitenbroek, H., Dupree, A. K., & Gilliland, R. L. 1998, AJ, 116, 2501 [NASA ADS] [CrossRef] [Google Scholar]
- van Belle, G. T., Creech-Eakman, M. J., & Hart, A. 2009, MNRAS, 394, 1925 [NASA ADS] [CrossRef] [Google Scholar]
- Van Dyk, S. D., Li, W., Cenko, S. B., et al. 2011, ApJ, 741, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Van Dyk, S. D., Cenko, S. B., Poznanski, D., et al. 2012a, ApJ, 756, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Van Dyk, S. D., Davidge, T. J., Elias-Rosa, N., et al. 2012b, AJ, 143, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Van Dyk, S. D., Zheng, W., Clubb, K. I., et al. 2013, ApJ, 772, L32 [NASA ADS] [CrossRef] [Google Scholar]
- Van Dyk, S. D., Zheng, W., Fox, O. D., et al. 2014, AJ, 147, 37 [NASA ADS] [CrossRef] [Google Scholar]
- van Genderen, A. M., & Sterken, C. 2002, A&A, 386, 926 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Loon, J. T., Groenewegen, M. A. T., de Koter, A., et al. 1999, A&A, 351, 559 [NASA ADS] [Google Scholar]
- van Loon, J. T., Cioni, M.-R. L., Zijlstra, A. A., & Loup, C. 2005, A&A, 438, 273 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vanbeveren, D., Van Bever, J., & Belkus, H. 2007, ApJ, 662, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2001, A&A, 369, 574 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woosley, S. E., Eastman, R. G., Weaver, T. A., & Pinto, P. A. 1994, ApJ, 429, 300 [NASA ADS] [CrossRef] [Google Scholar]
- Yoon, S.-C., & Cantiello, M. 2010, ApJ, 717, L62 [NASA ADS] [CrossRef] [Google Scholar]
- Zahn, J.-P. 1992, A&A, 265, 115 [NASA ADS] [Google Scholar]
All Tables
Core He-burning lifetimes, RSG lifetimes, time-averaged mass-loss rates during the RSG phase, and different properties of the last computed models.
Characteristics of the models at the end of the core He- or C-burning phase (models at the end of the C-burning phase are indicated by an asterisk).
Properties of the last computed models with effective temperatures between 3.6 and 4.3 ordered from top to bottom by increasing effective temperatures (in logarithm).
All Figures
 |
Fig. 1 Comparison between the mass-loss rates deduced from spectroscopy by different authors and the average values used in our models during the RSG phase. The data by van Loon et al. (2005) cover the region shaded in red. The data by Mauron & Josselin (2011) are distributed in the region shaded in blue. The two stars linked by a vertical line show the mass-loss rates for VY CMa; the lower value is taken from Table 1 of Mauron & Josselin (2011), the upper value from Matsuura et al. (2014). The heavy continuous, long-dashed and dotted lines are our averaged RSG mass-loss rates equal to 1, 10, and 25 times the standard mass-loss rate (see text). The upper thin long and short-dashed slanted lines mark the classical and multiple-scattering limits to the mass-loss rate (van Loon et al. 1999). The lower thin short-long-dashed line shows the Reimers law for an average temperature Teff = 3750 K (see Mauron & Josselin 2011). |
| In the text | |
 |
Fig. 2 Evolutionary tracks for stellar models of 9 and 20 M⊙ for various prescriptions of the RSG mass-loss rates. Only partial tracks are shown. In the upper panel, the lowest line shows the first crossing from blue to red of the HR gap. The beginning of the portion of the track computed with an enhanced RSG mass-loss rate is indicated by a small empty circle. |
| In the text | |
 |
Fig. 3 Upper panel: logarithm of RSG lifetimes as a function of the enhancement factor for the mass-loss rate during the RSG phase. Lower panel: fraction of the initial mass lost during the RSG phase, ΔM/M, as a function of the enhancement factor of the RSG mass-loss rate (see text). |
| In the text | |
 |
Fig. 4 Evolutionary tracks of models with different initial velocities (nonrotating at the top, rotating at the bottom) with different RSG mass-loss rates (increasing from left to right). The (red) empty circles are the positions of the Galactic RSGs observed by Levesque et al. (2005). The blue pentagons are the positions of WC stars as observed by Sander et al. (2012). |
| In the text | |
 |
Fig. 5 Left panel: number of RSGs as a function of luminosity in a region with constant star formation rate (see text). Numbers are normalized to the model with 9 M⊙. Dots indicate the values obtained for the models with 9, 15, 20, and 25 M⊙ from left to right. Right panel: radii of various stellar models during the RSG phase (Log Teff< 3.6) as a function of the luminosity. The shaded area indicates the region covered by the models with different initial masses, rotations, and mass-loss rates. The 25 times enhanced, rotating 15 M⊙ is the only model that evolves out of this region. The initial mass is indicated at the lowest luminosity predicted by the models for this mass. |
| In the text | |
 |
Fig. 6 Upper left panel: surface N/C ratios during the RSG phase normalized to the initial ratio in logarithm and in mass fraction as a function of the luminosity for various models. The red full dots are for observed values; stars labeled 2, 3, and 6 are taken from Origlia et al. (2013), α Ori from Lambert et al. (1984), and IRS 7 from Carr et al. (2000). Upper right panel: same as upper left panel, but for the N/O surface abundance ratio. Lower left panel: tracks during the RSG phase in the N/C versus N/O plane (surface values). The models are the same as in the upper left figure. Lower right panel: surface 12C/13C ratios for the same models as in the upper left figure. The dots are observed values for 6, α Sco (Hinkle et al. 1976), 3, 2, alpha Ori, and VY CMa (Matsuura et al. 2014). |
| In the text | |
 |
Fig. 7 Left panel: evolutionary tracks in the HRD for the nonrotating models computed with the standard mass-loss rates, superposed the positions of progenitors of core-collapse supernovae. Empty stars indicate RSGs (see Table 2), filled pentagons those with a yellow supergiant as progenitors (see Table 6). A continuous segment links the positions of the same SN progenitors obtained by various authors. Progenitors of supernovae predicted by the nonrotating models computed with the various RSG mass-loss rates are found in the shaded area. Progenitors obtained with standard RSG mass-loss rates occupy the upper part as well as the right part of the shaded region, while the progenitors obtained from enhanced RSG mass-loss rate models are in the lower-left region of the shaded area. Lines of constant radius are indicated, the line intermediate between the 100 and 1000 R⊙ corresponds to a radius of 500 R⊙. Right panel: same as left panel with evolutionary tracks in the HRD for the rotating models computed with the standard mass-loss rates. Progenitors of supernovae predicted by the rotating models computed with the various RSG mass-loss rates are found in the shaded area. |
| In the text | |
 |
Fig. 8 Left panel: evolutionary tracks in the HRD for the nonrotating models computed with the standard mass-loss rates with superposed observed positions of progenitors of core collapse supernovae. The observed data are the same as in Fig. 7. The error bars are not shown for clarity. Progenitors of supernovae predicted by the nonrotating models computed with the various RSG mass-loss rates are found in the shaded area. Right panel: same as the left panel for rotating stellar models. The shaded area shows the region where the progenitors of supernovae are found according to the rotating models with various RSG mass-loss rate prescriptions. |
| In the text | |
 |
Fig. 9 Fraction of the initial mass of the star ejected by stellar winds during the whole stellar lifetime (red shaded area). The mass in the H-rich envelope, He-rich region, and CO core in the pre-supernova model as a function of the initial mass are indicated as black, white, and blue regions. Cases for various mass-loss rates during the RSG phase without and with rotation are shown. The symbols in the upper part of each panel indicate the range of effective temperatures of the model at the pre-supernova stage: log Teff lower than 3.65 is indicated by (red) stars, log Teff between 3.65 and 4.30 by (black) triangles, and log Teff greater than 4.3 by (blue) circles. |
| In the text | |
 |
Fig. 10 Mass of hydrogen in solar masses at the pre-supernova stage for the various models of Table 1. Positions in this diagram of some supernovae are indicated by pentagons with error bars. For SN2008cn, the mass of hydrogen is not known, the range of effective temperatures is framed by the two dotted vertical segments. The three shaded regions from left to right correspond to stars ending their lifetime as blue, yellow, and RSGs. |
| In the text | |
 |
Fig. 11 Upper panels: expected number of Wolf-Rayet stars (dashed lines) and of RSGs in a coeval population (continuous lines) of 10 000 stars. Models with initial masses of between 9 and 25 M⊙ computed with different mass-loss rates during the RSG phases give the different continuous lines labeled by the enhancement factor considered for the mass-loss rate during the RSG phase. The populations of WR stars are very little affected by these changes of mass-loss recipes (see text). Lower panels: fraction between the number of RSG and the number of main-sequence stars two magnitudes below the turn-off. The black and empty squares correspond to observed ratios in stellar clusters with between 20 and 50 stars and with fewer than 20 stars. From left to right, the points correspond to the following clusters: NGC 1976, NGC 6231, NGC 884+4755, NGC 457, and NGC 581+2439 (see Meynet et al. 1993). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


