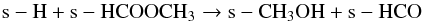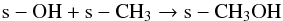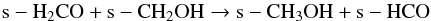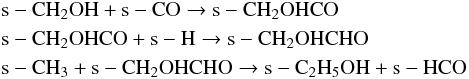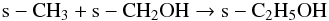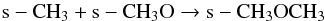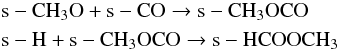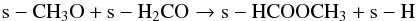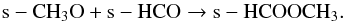| Issue |
A&A
Volume 575, March 2015
|
|
|---|---|---|
| Article Number | A68 | |
| Number of page(s) | 20 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201424499 | |
| Published online | 25 February 2015 | |
Evolution of complex organic molecules in hot molecular cores
Synthetic spectra at (sub-)mm wavebands⋆
1
I. Physikalisches Institut, Universität zu Köln,
Zülpicher Strasse 77,
50937
Köln, Germany
e-mail: rchoudhury@mpe.mpg.de
2
Max-Planck-Institut für extraterrestrische Physik,
Giessenbachstrasse 1,
85748
Garching,
Germany
3
LERMA, Observatoire de Paris, 61 Av. de l’Observatoire, 75014
Paris,
France
4
Department of Astronomy, University of Michigan,
Ann Arbor, MI
48109,
USA
Received: 30 June 2014
Accepted: 12 December 2014
Context. Hot molecular cores (HMCs) are intermediate stages of high-mass star formation and are also known for their rich chemical reservoirs and emission line spectra at (sub-)mm wavebands. Complex organic molecules (COMs) such as methanol (CH3OH), ethanol (C2H5OH), dimethyl ether (CH3OCH3), and methyl formate (HCOOCH3) produce most of these observed lines. The observed spectral feature of HMCs such as total number of emission lines and associated line intensities are also found to vary with evolutionary stages.
Aims. We aim to investigate the spectral evolution of these COMs to explore the initial evolutionary stages of high-mass star formation including HMCs.
Methods. We developed various 3D models for HMCs guided by the evolutionary scenarios proposed by recent empirical and modeling studies. We then investigated the spatio-temporal variation of temperature and molecular abundances in HMCs by consistently coupling gas-grain chemical evolution with radiative transfer calculations. We explored the effects of varying physical conditions on molecular abundances including density distribution and luminosity evolution of the central protostar(s) among other parameters. Finally, we simulated the synthetic spectra for these models at different evolutionary timescales to compare with observations.
Results. Temperature has a profound effect on the formation of COMs through the depletion and diffusion on grain surface to desorption and further gas-phase processing. The time-dependent temperature structure of the hot core models provides a realistic framework for investigating the spatial variation of ice mantle evaporation as a function of evolutionary timescales. We find that a slightly higher value (15 K) than the canonical dark cloud temperature (10 K) provides a more productive environment for COM formation on grain surface. With increasing protostellar luminosity, the water ice evaporation font (~100 K) expands and the spatial distribution of gas phase abundances of these COMs also spreads out. We calculated the temporal variation of the radial profiles of these COMs for different hot core models. These profiles resemble the so-called jump profiles with relative abundances higher than 10-9 within the evaporation font will furthermore be useful to model the observed spectra of hot cores. We present the simulated spectra of these COMs for different hot core models at various evolutionary timescales. A qualitative comparison of the simulated and observed spectra suggests that these self-consistent hot core models can reproduce the notable trends in hot core spectral variation within the typical hot core timescales of 105 year. These models predict that the spatial distribution of various emission line maps will also expand with evolutionary time; this feature can be used to constrain the relative desorption energies of the molecules that mainly form on the grain surface and return to the gas phase via thermal desorption. The detailed modeling of the thermal structure of hot cores with similar masses along with the characterization of the desorption energies of different molecules can be used to constrain the luminosity evolution of the central protostars. The model predictions can be compared with high resolution observation that can probe scales of a few thousand AU in high-mass star forming regions such as from Atacama Large Millimeter/submillimeter Array (ALMA). We used a spectral fitting method to analyze the simulated spectra and find that it significantly underestimates some of the physical parameters such as temperature. The coupling of chemical evolution with radiative transfer models will be particularly useful to decipher the physical structure of hot cores and also to constrain the initial evolutionary stages of high-mass star formation.
Key words: stars: formation / stars: massive / astrochemistry / ISM: molecules / ISM: lines and bands
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
Hot molecular cores (HMCs), also known as hot cores, are associated with the early evolutionary stages of high-mass star formation. Our current understanding of high-mass star formation is incomplete, but a plausible evolutionary scenario, emerging from the recent observational studies, is as follows: Infrared dark clouds (IRDCs) → HMCs → hyper/ultra-compact Hii regions → Hii region surrounding the ionizing high-mass stars (see Beuther et al. 2007). The intermediate phases between IRDCs and hypercompact Hii regions are known as hot cores; at this phase the central protostars heat up their surrounding gaseous and dusty materials to high temperatures (≥100 K) without ionizing it (due to lack of UV photons). Kurtz et al. (2000) characterized HMCs as a relatively compact phase of high-mass star formation (≤0.1 pc) with a typical density and temperature in the range of ≥107 cm-3 and ≥100 K. The evaporation of water and organic rich ice mantles leads to the detection of a wide variety of complex organic molecules (COMs) such as CH3OH, CH3OCH3, HCOOCH3, and C2H5OH in a number of HMCs (Herbst & van Dishoeck 2009).
The chemical richness and diversity of HMCs has received significant attention in recent times and has also triggered a number of studies that modeled the relevant chemical processes responsible for building up the molecular reservoir in HMCs (see Herbst & van Dishoeck 2009 for a detailed review of existing models). Among these, gas-grain models (which include both gas phase and grain surface chemical reactions) emerged as the most promising ones to explain the abundance of COMs in hot cores (Charnley et al. 1992). These studies suggested that the chemical richness of HMCs originates from the evaporation and subsequent gas phase processing of the molecules that became locked on icy mantles during the initial collapse phase of high-mass protostar formation. Recent hot core models (Garrod et al. 2008; Garrod 2013a) successfully reproduced the abundances of a number of COMs inferred from the observational studies of hot cores. One of the crucial parameters of these models is the gradual warm-up of hot cores to a temperature of 100 K and higher to facilitate the formation of COMs on grain surface and eventually their evaporation to the gas phase. Recent observations indicate that COMs are also present in cold dark clouds with a typical temperature of 10 K (Cernicharo et al. 2012; Bacmann et al. 2012). Vasyunin & Herbst (2013) suggested some alternative mechanisms that do not require high temperature (e.g., reactive desorption) for COM formation in these environments. However, these processes are probably less important in the hot core phase.
The salient observational feature of HMCs are numerous emission lines at (sub-)mm wavebands, mostly originating from the rotational transitions of COMs. Dedicated line surveys (e.g., Schilke et al. 1997, 2001; Zernickel et al. 2012; Crockett et al. 2014; Neill et al. 2014, see also Table 2 of Herbst & van Dishoeck 2009) are very useful to explore the inventory of COMs in hot cores. Most of these studies used local thermodynamic equilibrium (LTE) fitting of spectra, for example, rotational diagram analysis (Goldsmith & Langer 1999), XCLASS (Zernickel et al. 2012), or similar techniques for estimating the physical parameters and chemical abundances. However, these techniques, while useful to estimate the average physio-chemical scenario of the hot cores, are not suitable to explore the detailed structures (Herbst & van Dishoeck 2009). Investigations of the chemical evolution of selected molecules using a number of hot core sources are also carried out in selected studies (Bisschop et al. 2007; Beuther et al. 2009; Gerner et al. 2014). It has been found that the intensity as well as the spatial distribution of emission lines of various molecules also varies with evolutionary stages and from one hot core to another. These features can be attributed to the varying physio-chemical condition during the initial evolutionary stages of high-mass star formation. Although the results are promising, high angular resolution spectral line observations of the initial stages of high-mass star formation are still rare (Brouillet et al. 2013).
With the availability of the Atacama Large Millimeter/submillimeter Array (ALMA)1, it is now possible to explore the chemical segregation of high-mass star forming regions down to a spatial resolution of a few hundred AU in relatively short time. Observations of many sources at various evolutionary stages will also provide the opportunity to explore the chemical diversity. In short, these observed chemical probes can be used as powerful tools to decipher the internal structure and to constrain the evolutionary stages of hot cores. So far, only few astrochemical studies (e.g., Doty et al. 2002; Öberg et al. 2013; Gerner et al. 2014) incorporated a radial variation of density and temperature. However, a self-consistent approach to explore the temporal evolution of physical parameters associated with high-mass star formation is not considered in these models. Moreover, there are no dedicated studies that explore the trends of temporal variation in simulated spectra which arise due to the varying physical and chemical conditions of evolving hot cores. To bridge this gap, we investigated the effects of the spatio-temporal variation of physical conditions on the chemical evolution of hot cores in a self-consistent way. In this work, we investigate the chemical evolution of selected oxygen-bearing COMs such as, CH3OH, C2H5OH, HCOOCH3, and CH3OCH3 and simulate the spectral data cubes at (sub-)mm wavebands for various hot core models at different evolutionary stages.
We describe the model set-up, initial physical conditions and chemical modeling in Sect. 2. Spatio-temporal evolution of molecular abundances of selected COMs are summarized in Sect. 3. The simulated spectra and a qualitative comparison with the observed spectra are presented in Sect. 4. In Sect. 5, we summarize this study and discuss the possibilities of using these simulated spectra along with the observations to explore the evolution of hot cores, and finally we present our conclusion in Sect. 6.
2. Method
Most of the high-mass star forming regions are distant and heavily obscured. The physical structure, evolutionary sequence and timescales of high-mass star formation are thus only poorly understood. Molecular emission lines provide good diagnostics to understand the internal structure of these environments (Rolffs et al. 2011). In the case of low-mass star formation, several studies incorporated the results of hydrodynamic simulations into chemical models to investigate the role of evolving physical conditions on the chemical composition (Aikawa et al. 2008; Furuya et al. 2012). Similarly, the ideal way to model hot core chemistry would be to couple the chemical modeling with hydrodynamical simulations of high-mass star formation. However, models of high-mass protostellar evolution along with the surrounding gaseous and dusty materials are rare, with only a handful of available solutions (Kuiper & Yorke 2013). In order to investigate the coupling of physical conditions and molecular abundances, we set-up a simple physical model of hot cores guided by the current understanding of high-mass star formation and used this set-up to examine the spatio-temporal variation of chemical evolution of hot cores and finally generated synthetic spectra following the flowchart shown in Fig. 1. The flowchart is executed using a Python script (Schmiedeke et al., in prep.). We describe the physical parameters and chemical models in detail below.
2.1. Chemical model
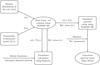 |
Fig. 1 Flowchart of the modeling framework. |
We developed a rate-equation-based 1D astrochemical code (Saptarsy) in Fortran90; it calculates the spatio-temporal evolution of various molecular species using gas phase reactions, gas-grain interactions, and surface chemistry (Choudhury et al., in prep.). The code has its origin in the Astrochem code of Bergin et al. (1995), and after several major modifications, it has become an improved and new astrochemical code that can be easily integrated with other external codes (e.g., RADMC-3D2). The ordinary differential equation solver from Netlib library dvodpk3 and MA284, the advance solver of sparse systems of linear equations from the HSL library, are used to compute the chemical evolution. Gas-grain interaction via accretion and desorption and surface reactions are implemented following the recipe of Hasegawa et al. (1992) and Hasegawa & Herbst (1993). The temporal evolution of grains such as grain coagulation and formation of the grain mantles etc. can affect the grain surface chemistry (Taquet et al. 2012; Garrod 2013b), but these processes are beyond the scope of this study and are, therefore, not considered in this work.
Saptarsy is suitable to explore the effects of spatio-temporal variation of physical parameters (e.g., temperature) on chemical evolution. It has been benchmarked against the models described in Semenov et al. (2010). The gas-grain chemical network5 from the Ohio State University Astrophysical Chemistry Group (~7840 reactions and ~840 species) is used in this study. The detailed description of the network and reaction rate calculations of the associated chemical reactions can be found in Garrod et al. (2008) and Semenov et al. (2010). We adopted standard grain parameters such as radius of 0.1 μm, density of 3 g cm-3 and a dust-to-gas mass ratio of 0.01. The initial abundance and desorption energy of the molecular species were adopted from Garrod et al. (2008) and Garrod (2013a). The ratio of diffusion-to-desorption energy is assumed to be 0.5. We used Saptarsy to obtain the spatio-temporal abundance evolution by solving the rate equations based on the overall molecular formation and destruction terms. Chemical evolutionary models are simulated up to a timescale of 1 × 105 year using discrete time-steps separated by few hundreds to thousands year. Conservative values of relative and absolute tolerances of 10-6 and 10-20, respectively, were used throughout the calculation. To avoid complexity, direct photo-dissociation and -ionization reactions are not considered in this work since hot core phases were not dominated by UV radiation. However, the effects of UV photons become prominent at the final phases of hot core evolution that is during the transformation to ultracompact Hii regions which require a detailed modeling of the radiation field inside hot cores; this is the focus of a separate study (Stéphan et al., in prep.).
2.2. Density distribution
Abbreviations used in the nomenclature of various models.
In a complex environment such as a hot core, the physical conditions (e.g., density, temperature) not only vary with time, but also with the distance from the central protostars. Recent (sub-)mm interferometric studies also indicated that internal rotational motion, outflows, etc. can be associated with HMCs (Beltrán et al. 2011; Furuya et al. 2011). Several studies investigated the density distribution of these objects using dust continuum emission (van der Tak et al. 2000; Beuther et al. 2002) and found a power-law density distribution on larger scales; recent studies using interferometric observations suggested a Plummer-type distribution at smaller scales (Rolffs et al. 2011). Plummer-type profiles can be represented as n(r) = nc(1 + c(r/rp)2)γ, where c is a constant and nc and rp represent the central density and Plummer radius (this parameter sets the size of the core at which nc drops to half of its value) and the exponent (γ) sets the density distribution at radii larger than the Plummer radius. We set up a spherical hot core model that contains a high-mass protostar at the center embedded in a dense core of gas and dust. We adopted a Plummer-type distribution for the hot core models with a peak density of 2 × 107 cm-3, c = 0.31951 and γ = −5/2 throughout this work. The density distribution profile does not change with time, but we have considered various types of density profiles by varying the Plummer radius (see Table 1). Assuming the standard dust-to-gas mass ratio, the mass of the model core with Plummer radius ~3000 AU is estimated to be around 45 M⊙, indicating that it barely has the potential to form a high-mass star (>10 M⊙).
2.3. Protostellar evolutionary models
The central protostar is the only source of heating in our model set-up and thus the temperature of hot cores depend on the luminosity of the protostar. We used the protostellar evolutionary models of Hosokawa & Omukai (2009; spherical accretion model with a constant accretion rate of 10-3 M⊙ yr-1, Rolffs et al. 2011) to investigate the spatio-temporal evolution of the temperature in our hot core models. The temperature evolution from IRDC phases (10–15 K) to the formation of protostars is not explicitly covered in this model. Garrod et al. (2008) explored the effect of warm-up timescales (the required time to reach the characteristic temperature of 100 K) and found that with a longer warm-up timescale the chemical complexity also increases. To imitate the luminosity evolution during the warm-up phase, we interpolated the luminosity over a fixed time interval (5 × 104 to 7.5 × 104 year) using different power-law indices of 2, 4, and 7.5 (see Fig. 3a). The starting point of the luminosity interpolation (5 × 104 year) was chosen in such a way that the temperature at the immediate vicinity of the protostars is around 15 K; the luminosity at the end point is adopted from the models of Hosokawa & Omukai so that the temperature reaches up to 100 K at the center. We then used these luminosity profiles to calculate the temperature. The power-law index 7.5 was chosen to reproduce a similar temperature evolution as used in Garrod et al. (2008). We restricted the highest value of the protostellar luminosity to 1 × 105L⊙ following the result of recent observational studies of hot cores (Beuther et al. 2009).
2.4. Nomenclature of the models
We developed various models by varying the physical parameters to explore the spatio-temporal variation of the chemical evolution. Instead of commonly used tags (e.g., model:a), we use different combinations of abbreviations to refer to a particular model. We summarize the physical parameters and associated abbreviations in Table 1. For example, a hot core model tagged as cr16-r3-l2 refers to a model where the Plummer radius is 3000 AU (r3), the power-law index of the protostellar luminosity evolution is 2 (l2), and the cosmic-ray ionization rate is 1.37 × 10-16s-1. Similarly, the cr-17 models refers to all the hot core models with a cosmic-ray ionization rate of 1.37 × 10-17s-1.
 |
Fig. 2 Evolution of molecular abundance on grains with respect to s-H2O in percent at 5 × 104 year for different cold core models: a) cc-cr17-t10; b) cc-cr16-t10; c) cc-cr17-t15; and d)cc-cr16-t15. |
2.5. Simulation of spectral data cubes
The radiative transfer code RADMC-3D was used to simulate the spectral data cubes of different COMs at various wavebands and evolutionary stages; the radius adopted for the hot core models was 0.1 pc (~20 600 AU). We started with a density distribution and a luminosity evolution profile of the central protostar and used RADMC-3D to calculate the spatio-temporal evolution of the temperature. In the next step, we extracted the 1D density and temperature distribution profiles from the 3D hot core models. These density-weighted profiles along with the initial abundance of selected molecules served as the input for Saptarsy, which calculates the spatio-temporal chemical evolution in hot cores. The 1D abundance distribution profiles of respective molecules were then used as input abundance profiles in RADMC-3D. Finally, simulated spectra spanning over a frequency range at desired evolutionary timescales were generated assuming LTE. As suggested by Herbst & van Dishoeck (2009), the ideal way to generate simulated spectra would be to use full non-LTE statistical equilibrium excitation of the molecules. However, collisional rate coefficients required for non-LTE modelings are available only for a few molecules. Moreover, the high densities and radiative coupling with far-infrared radiation fields make LTE a good approximation. Therefore, for this study we only considered LTE excitation to generate comparable simulated spectra for different COMs. To facilitate the comparison with observations, simulated spectra were convolved with different telescope beam sizes using MIRIAD6, also taking into account the distance to the source. The hot core models were placed at a fiducial distance of 2 kpc. Molecular data files of various COMs were retrieved from the Cologne Database for Molecular Spectroscopy (CDMS7; Müller et al. 2005, 2001), the JPL Catalog (Pickett et al. 1998), and the VAMDC database (Rixon et al. 2011).
3. Results
Molecular abundances on grains with respect to s-H2O in percent: observed and simulated values.
 |
Fig. 3 a) Luminosity evolution profiles for different power-law indices. b) Temperature evolution in the hot core model hmc-r3 at different radii: ~200 AU (blue), ~2000 AU (green) and ~10 000 AU (red). Temperature distribution obtained using different protostellar luminosity evolutions are shown with continuous (l2), dashed (l4), and dotted (l7) lines. c) Spatio-temporal evolution of the temperature in the hot core model hmc-r3. |
3.1. Molecular abundance on grains
The abundance of various species on grains that is the ice abundances, are important parameters that influence the chemical evolution of hot cores. At low temperature (10–15 K), molecules accrete onto grains and thus become locked on the grain surface; this is also known as freeze-out or depletion of molecules. We represent the grain surface species with s- meaning that s-H2O represents water on grain surface. A reduced abundance of some molecules at the center of the cores, that is in the high density regions, have been observed in a number of starless cores indicating the clear presence of molecular ice formation at this stage (Bergin & Tafalla 2007). The accretion rate of molecules onto grain surfaces depends on the sticking coefficient of molecules to the grain, the grain surface area, the velocity of the molecules in gas phase, and the number density of dust grains. Another critical factor that regulates the ice formation is the dust temperature at the early pre-stellar stages. Most of the hot core models so far considered the initial temperature as 10 K. However, recent large scale surveys of high-mass star forming regions indicate an average temperature of 15 K for starless cores (Wienen et al. 2012; Hoq et al. 2013). The slight increase of temperature from 10 to 15 K increases the mobility of molecules on grains (reactive radicals such as OH, CH3) and thus provides a more productive environment to form complex molecules.
We therefore explored models with temperatures of 10 K and 15 K during the prestellar
phase. Another factor that influences the abundance of molecules frozen to grain surfaces
is the interaction with cosmic rays that can dissociate and even evaporate ices. There is
a debate about the cosmic-ray rate in the literature based on the observations of
H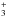 (Indriolo
& McCall 2012). Motivated by these studies, we also explored the effect of
cosmic-ray ionization rate with two distinct values of. 1.37 × 10-16s-1 and 1.37 × 10-17s-1 (Padovani et al. 2009). We ran four different models to calculate the
ice abundances, cc-cr17-t10, cc-cr16-t10,
cc-cr17-t15, and cc-cr16-t15. The timescale of the
starless phase is uncertain, but we have some guidance from large scale surveys of
high-mass star forming regions (Tackenberg et al.
2012); thus we adopted a timescale of 5 × 104 year for the pre-stellar phase. In Fig. 2 we present the grain surface abundance of selected
molecules at the pre-stellar stage with respect to s-H2O in percent. All these models
show a similar s-H2O relative abundance 2 × 10-4 with respect to the
total hydrogen number density (n(H+2H2)) at the center. We also tabulated the ice
abundance of these molecules from the literature in Table 2. Comparing the observed and our simulated values, it appears that cold
core models cc-cr17-t15 and cc-cr16-t15 produce
s-CH3OH
abundances close to the observed values among the other molecules. Since
s-CH3OH acts as
the parent molecule of other COMs, we have used these two models for the subsequent
calculations.
(Indriolo
& McCall 2012). Motivated by these studies, we also explored the effect of
cosmic-ray ionization rate with two distinct values of. 1.37 × 10-16s-1 and 1.37 × 10-17s-1 (Padovani et al. 2009). We ran four different models to calculate the
ice abundances, cc-cr17-t10, cc-cr16-t10,
cc-cr17-t15, and cc-cr16-t15. The timescale of the
starless phase is uncertain, but we have some guidance from large scale surveys of
high-mass star forming regions (Tackenberg et al.
2012); thus we adopted a timescale of 5 × 104 year for the pre-stellar phase. In Fig. 2 we present the grain surface abundance of selected
molecules at the pre-stellar stage with respect to s-H2O in percent. All these models
show a similar s-H2O relative abundance 2 × 10-4 with respect to the
total hydrogen number density (n(H+2H2)) at the center. We also tabulated the ice
abundance of these molecules from the literature in Table 2. Comparing the observed and our simulated values, it appears that cold
core models cc-cr17-t15 and cc-cr16-t15 produce
s-CH3OH
abundances close to the observed values among the other molecules. Since
s-CH3OH acts as
the parent molecule of other COMs, we have used these two models for the subsequent
calculations.
Abundance of COMs in Hot molecular cores: observed and simulated values.
3.2. Spatio-temporal variation of temperature
Temperature plays an important role in chemical evolution as the rate of most of the chemical reactions strongly depend on it. Previous studies (e.g., Viti & Williams 1999; Garrod & Herbst 2006) investigated the effect of temperature evolution assuming a power-law distribution in a constant density set-up. However no self-consistent treatment is used in these studies to calculate the spatial structure of temperature using any protostellar luminosity function. A significant improvement for temperature evolution is achieved by using a proper radiative transfer calculation that is tied to an evolving protostellar luminosity model. As required by the chemical evolutionary model Saptarsy, temperature evolution of the hot core models for different luminosity evolution are calculated at some discrete time-steps using RADMC-3D (Fig. 3). We estimated the heating and cooling timescales of dust grains explicitly to check whether dust temperature calculation at discrete time-steps would yield a realistic estimate of temperature evolution. To estimate the cooling timescales, we compared the absorption and emission processes of dust grains. A typical dust grain of radius 0.1 μm at 20 K would emit 1.14 × 10-12 erg s-1 assuming an efficiency factor of 10-4 (considering the opacities at (sub-)mm wavelengths). Similarly, considering our assumed density of grains (3 g cm-3), the thermal energy of the dust grain would be 2.5 × 10-6 erg. Therefore, the timescale for thermalization of dust grains would be about the fraction of a year (Dullemond, priv. comm.). As a result, any changes in temperature of the hot core model become nearly instantaneous compared to the changes in luminosity and thus ensure a nearly steady-state condition in the hot core models. Dust mass opacity coefficients were retrieved from Ossenkopf & Henning (1994). We also assumed that gas temperature is same as the dust temperature, which is a reasonable assumption considering the high density of hot cores. Doty et al. (2002) made a detailed calculation of the gas temperature for their hot core model and found that the values are similar to the ones obtained using the assumption of Tgas = Tdust. In Figs. 3b and c, the spatio-temporal evolution of temperature for hot core models hmc-r3 are shown. At the center of the hot cores, the temperature remains constant (15 K) up to 5 × 104 year (cold core phase), then it rises to the typical hot core temperature (100 K) during the next 2.5 × 104 year (warm-up phase), and after that, it reaches up to 500 K at the end of the evolutionary timescale that is 1 × 105 year (hot core phase). It is evident from the figures that the duration of these phases varies as a function of distance from the central star.
3.3. Spatio-temporal abundance variation
 |
Fig. 4 Spatio-temporal abundance variation of selected COMs on the grain (dot-dashed line) and in gas phases (continuous line) are shown for the hot core model cr16-r3-l2. Black dashed and continuous lines show the radial variation of the density and the temperature respectively. Time-stamps (in year) for different temporal snapshots are annotated in the upper right corner of the respective plots. Note the alternative labeling of the density and temperature axes on the right side of the respective plots. |
Simulated values of COMs at the center of various hot core models with the cosmic ray ionization rate of 1.37 × 10-16.
The most abundant molecule that dominates the spectra at (sub-)mm wavebands is CH3OH. Following CH3OH, the other oxygen-bearing COMs that contribute most of the lines in (sub-)mm wavebands (480–1907 GHz) are CH3OCH3, HCOOCH3, and C2H5OH (Zernickel et al. 2012). These COMs are also referred as first-generation molecules (Bisschop et al. 2007; Garrod et al. 2008; Herbst & van Dishoeck 2009); these molecules are mainly produced by reactions between primary ice species (also known as the zeroth-generation molecules). To investigate the favorable physical conditions for the formation of first-generation COMs during the warm-up phase, we ran further models using the initial physical conditions discussed in Sect. 3.1. We ran 24 hot core models in total up to 1 × 105 year with different physical parameters such as with four different static density distributions (r3, r3.5, r4, and r4.5) along with three different luminosity evolutions (l2, l4, and l7) and two different cosmic-ray ionization rates (cr-16 and cr-17) (see Table 1). The dust temperature is one of the most dominant factors that control the gas and grain surface abundances. Thanks to the spatio-temporal evolution of the temperature structure, our model set-up is particularly useful to investigate the transition from grain to gas phase abundance of various molecules as a function of evolutionary stages and distances from the central star. The spatio-temporal variations of grain and gas-phase abundance of selected COMs for various hot core models are shown in Figs. 4, A.1–A.4. At the initial stages, the ice abundance of COMs dominate over the gas phase abundances but with increased temperature ices evaporate from the grain surfaces and thus boost the gas phase abundances. With temporal evolution, the radius of the evaporation font (where the temperature is equal to the water ice evaporation temperature of 100 K) also increases (see Fig. B.1), and consequently, the spatial distribution of gas phase abundances also spreads out. However, at the outer region (>4.5 × 103 AU), where the temperature remains lower than 100 K, ice abundance of COMs dominate the gas phase abundances. One of the important features of this work is the derived temporal variation of the spatial distribution of COMs for solid and gaseous phases. These profiles will be particularly useful for modeling the observed high resolution emission line maps of these molecules. Gas phase abundance of selected COMs from the existing observational and modeling studies are collected in Table 3; a similar compilation of the observed value of these molecules for a number of hot cores can be found in Bisschop et al. (2007). The gas phase abundance of different COMs at the center of various hot core models are summarized in Tables 4 and 5. These abundances are comparable with the observed abundance of various COMs at least for the cr16 models. However, while comparing the observed and simulated values, one should also keep in mind that the quoted observed values are mostly conversions of the derived column densities with respect to H2 or CO column densities using a constant temperature, which introduces additional uncertainty. We discuss this aspect in detail in Sect. 4.2.
Simulated values of COMs at the center of various hot core models with the cosmic ray ionization rate of 1.37 × 10-17.
Garrod et al. (2008) suggested that cosmic-ray induced photodissociation of molecules (e.g. CH3OH) produce heavier radicals that effectively diffuse over grains at relatively higher temperature (>20 K) and produce other COMs such as C2H5OH. We found that a higher value of the cosmic-ray ionization rate of 1.37 × 10-16 supports the formation of more COMs over grains and eventually, also in the gas phase. At the initial stages of the evolution, the cr-16 models show nearly similar grain surface abundances for C2H5OH, CH3OCH3, and HCOOCH3 over larger radii; but for the cr-17 models, these abundances not only differ by orders of magnitude but also vary with radii. The relative abundance of these COMs with respect to CH3OH also differ significantly between the cr-17 and cr-16 models (see Figs. 4, A.1–A.4). During the warm-up phase, relative gas-phase abundances of COMs varies noticeably depending on the physical conditions. Moreover, even with a constant warm-up timescale, a slower rate of temperature increment provides favorable platforms to form more COMs (Tables 4 and 5); a similar behavior was also found by Garrod & Herbst (2006). In both models, the grain surface abundance of C2H5OH are higher than those of CH3OCH3 and HCOOCH3 at the center, but the final gas phase abundance of CH3OCH3 and HCOOCH3 are higher than that of C2H5OH, suggesting that CH3OCH3 and HCOOCH3 also have effective gas-phase formation routes in addition to the grain surface formation routes. The grain surface abundance of these COMs reach their highest values at the outer regions where the highest temperature reaches only ~50 K. Interestingly, a similar pattern for grain surface abundances of HCOOCH3< C2H5OH < CH3OCH3< CH3OH has been observed at the outer regions of both the cr-16 and cr-17 models. During the warm-up phase, the gas phase abundance of CH3OCH3 initially dominates other COMs; the final highest gas-phase CH3OCH3 abundance extends more than that of CH3OH in the cr-16 models, irrespective of density distribution and temperature evolution. In the cr-17 models the spatial distribution of CH3OCH3 shows two different peaks; the extent of the first peak is always narrower than the CH3OH distribution, but the extension and magnitude of the second peak depends on the density distribution (see Figs. A.3 and A.4).
3.4. Spatio-temporal variation of formation routes of COMs
As stated earlier, we used the OSU gas-grain chemical network (Garrod et al. 2008) and the associated chemical pathways are described
extensively in the corresponding paper (see also Herbst
& van Dishoeck 2009, for a general summary). For completeness, we briefly
summarize the important grain surface reactions and outline the variation of formation
routes of COMs depending on the physical conditions. At the initial stages, the ice
mantles primarily consist of s-H2O, s-CH4, s-H2CO, s-NH3, or s-CH3OH, etc., s-H2O, s-NH3, and s-CH4 are mainly formed by successive hydrogenation of O, N,
and C atoms (Tielens & Hagen 1982) and
s-H2CO and
s-CH3OH by
successive hydrogenation of CO (Charnley & Rodgers
2009). Cosmic-ray induced photodissociation of these molecules, specifically
s-H2CO and
s-CH3OH, produce
other important radicals (chemical species that actively react with other species) such as
s-OH, s-HCO, s-CH3,
s-CH3O. During
the warm-up phase (<100 K),
these radicals effectively diffuse over grains and produce highly abundant oxygen-bearing
COMs, for example, s-C2H5OH, s-HCOOCH3, and s-CH3OCH3; the following reactions act as the main formation
routes of these COMs depending on the physical conditions: 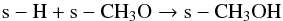 (1)
(1)
The mobility of the radicals strongly depend on the temperature, which shows a significant spatio-temporal variation and thus also affect the formation pathways of COMs. To facilitate the discussion, we divided the hot core models into three different subregions, central, middle, and outer regions. The typical temperatures of these zones at the end of the evolution are >100 K, 60–100 K, and <60 K. In Table 6, we summarize the important reactions at different regions that mainly produce the COMs described above.
Spatial variation of formation routes of selected COMs.
At the initial stages of evolution, that is at constant temperature (15 K), Reaction 1 acts as the primary pathway of s-CH3OH formation for all the models. For the cr-16 models, up to 30 K, Reaction 2 dominates and beyond that until the onset of evaporation (i.e., 100 K), Reaction 3 emerges as the main channel of s-CH3OH formation. Reaction 4 also occasionally becomes the main contributor of s-CH3OH formation in the middle region. However, in the outer region, Reaction 1 dominates up to 30 K, and beyond that, Reaction 3 produces most of the s-CH3OH. These trends do not vary significantly with different luminosity evolution models. However, for the cr-17 models, some differences are observed: although Reaction 1 initially dominates, Reaction 2 begins to contribute soon and remains the main contributory channel for temperatures up to 60–70 K. At higher temperatures Reaction 3 acts as the main formation route for s-CH3OH until it finally evaporates in the gas phase. But in the outer region Reaction 2 begins to strongly dominate at relatively higher temperatures (>15–40 K) also depending on the density. However, for temperatures around 60 K and above, the trend is similar to the cr-16 models that is Reaction 3 acts as the main formation pathway.
Formation of other COMs, for instance, s-C2H5OH, s-CH3OCH3, and s-HCOOCH3, also strongly depend on the temperature since the diffusion of relatively heavy radicals such as s-CH3, s-CH3O, and s-CH2OH is involved. For the cr-16 models the formation of s-C2H5OH is dominated by Reaction 5 around 20 K, and above that temperature until the desorption to the gas phase, Reaction 6 becomes the main contributing channel. For the cr-17 models, Reaction 5 dominates until the middle region up to 60 K and above that, Reaction 6 acts as the main formation route; but in the outer region both of these reactions contribute to the s-C2H5OH formation. The formation of s-CH3OCH3 is always dominated by Reaction 7. The formation of s-HCOOCH3 in the cr-16 models is controlled by Reaction 8 and 10 for temperatures lower than 60 K, and above that Reaction 9 acts as the main formation route. For the cr-17 models the behavior is similar, except that Reaction 10 does not contribute significantly to the formation of s-HCOOCH3. A more detailed discussion of the formation and destruction pathways of various molecular species including the COMs was reported in Garrod et al. (2008).
4. Analysis
4.1. Qualitative comparison of simulated and observed spectra
The most noticeable spectral features of high-mass star forming regions are the increase of the total number of spectral lines and their intensities with evolutionary stages (Beuther et al. 2009; Ceccarelli et al. 2010; Gerner et al. 2014). Spectral variations are also observed in different sources with similar evolutionary stages. Therefore, a characterization of the spectral evolution based on the inline physio-chemical models can be used as a unique tool to constrain the evolutionary sequence of the initial stages of high-mass star formation. Our simplistic model is unsuitable for any quantitative comparisons with the observed spectra, but it is expected that our model spectra at least reproduce the general trends of spectral variation provided that our input hot core models resemble the conditions of the observations. Comparing the simulated and observed spectra is thus also useful to determine the figure of merit of the input models. Motivated by this aim, we simulated the spectra for various hot core models at different evolutionary stages at various wavebands and present the simulated spectra in Figs. 5–8.
 |
Fig. 5 Simulated spectra of CH3OH for the hot core model cr16-r3-l2 at different evolutionary timescales. The adopted distance to the source and the telescope beam size are 2 kpc and 2.2′′. |
 |
Fig. 6 Simulated spectra of CH3OH for the hot core models cr16-r3-l2, cr16-r3.5-l2, cr16-r4-l2, and cr16-r4.5-l2 at 1.0 × 105 year. The adopted distance to the source and the telescope beam size are 2 kpc and 2.2′′. |
Simulated spectra of CH3OH for the hot core model cr16-r3-l2 at different evolutionary stages are shown in Fig. 5; the spectral range was chosen because it is often used in SMA/ALMA observations. In the literature the term line forest is often used when numerous complex molecules emit within a given frequency range and thereby create a forest of lines that perhaps hide emission from weaker molecules. In this paper we refer to the densely spaced ro-vibrational spectral lines of the COMs over a few GHz bandwidth as line forest. These lines arise from various transitions spanning over a range of energy states that trace different layers within the hot core. The spectra shown in Fig. 5 cover two different line forests of CH3OH with relatively lower (~60–300 K at ~338 GHz) to higher (~350–650 K at ~337 GHz) excitation energies. It can be easily seen from Fig. 5 that the number of spectral lines and their respective intensities vary with evolutionary timescales. Moreover, it is also evident from the spectra that temporal evolution of spectral features are not simply a scaled-up version of the previous time-steps but originated from the combined variation of spatial distribution of temperature and abundances with evolutionary stages (Fig. C.1). Simulated spectra of CH3OH around 337 GHz for various hot core models with different density distributions are shown in Fig. 6. To avoid the self absorption features in the simulated spectra the highest value of the CH3OH relative abundance was restricted to 1 × 10-6 (see Fig.13) compared with the values shown in Fig.4. This discrepancy also indicates that CH3OH is overproduced in our models compared with the other COMs. This trend is also seen in the recent chemical models for hot cores (Garrod 2013a). One possibility to explain this might be that there are some missing reactions in the chemical network that are useful to form other complex molecules using CH3OH. Since CH3OH is one of the parent molecules of other COMs, it would be interesting to compare the predicted relative abundance of other COMs with respect to CH3OH with the observations to improve our understanding of the chemical evolution in hot cores (Neill et al. 2014). However, this discrepancy also emphasizes the importance of simulated spectra over the chemical abundances that are generally quoted by the astrochemical models to provide a better constraint on physio-chemical model of hot cores.
 |
Fig. 7 Simulated spectra of selected COMs for the hot core model cr16-r3-l7 at 9 × 104 year (left) and 1 × 105 year (right) at different wavebands. The adopted distance to the source and the telescope beam size are 2 kpc and 2.2′′. |
 |
Fig. 8 Simulated spectra of selected COMs for the hot core model cr16-r3-l7 at 9 × 104 year (left) and 1 × 105 year (right) at Herschel-HIFI Band 1. The adopted distance to the source and the telescope beam size are 2 kpc and ~40′′. |
 |
Fig. 9 Integrated line intensity maps of the CH3OH (vt = 0) [7(0, 7)–6(0, 6)] transition at 338.1245 GHz for the hot core model cr16-r3-l2 at 7.0 × 104, 8.0 × 104, 9.0 × 104 and 1.0 × 105 year (left to right). The adopted distance to the source and the telescope beam size are 2 kpc and 2.2′′. |
 |
Fig. 10 Integrated line intensity maps of the CH3OH (vt = 1) [7(4, 4)–6(4, 3)] and [7(4, 3)–6(4, 2)] transitions at 337.68559 GHz for the hot core models cr16-r3-l2, cr16-r3.5-l2, cr16-r4-l2 and cr16-r4.5-l2 (left to right) at 1.0 × 105 year. The adopted distance to the source and the telescope beam size are 2 kpc and 2.2′′. |
Simulated spectra of different COMs such as CH3OH, C2H5OH, CH3OCH3, and HCOOCH3 of the hot core model cr16-r3-l7 for different frequency bands, evolutionary stages and angular resolution are shown in Figs. 7, 8. These spectra also follow the same trend: the specific line intensities become stronger and the spectra become more densely populated at later evolutionary stages. The frequency range shown in Fig. 8 is also covered by the Herschel-HIFI line surveys (Zernickel et al. 2012; Crockett et al. 2014). A qualitative comparison of the simulated and observed spectra reveals that the relative line intensities of CH3OCH3 and HCOOCH3 with respect to CH3OH are comparable with the observations (Fig. D.1).
Integrated line intensity maps of the CH3OH transition at 338.1245 GHz at different timescales are shown in Fig. 9. The corresponding radial profiles for the integrated intensity maps are shown in Fig. 11 (top panel). In both figures, the radial profiles of molecular emission expand with time. This is due to the radial expansion of the gas phase abundance of CH3OH with evolutionary time resulting from the increase in the stellar luminosity (Fig. 3a) and the successively higher mass that is heated to higher temperatures. However, as our models use a static density distribution and do not yet include dynamics, the spatial extension of temperature, abundance, emission maps, etc. should be considered as approximate values. In Fig. 10, integrated line intensity maps of CH3OH transition at 337.68559 GHz for various hot core models are shown. The corresponding radial profiles are shown in Fig. 11 (bottom panel). The variation in the emission maps can be attributed to the different density distributions of these models since the other input parameters are the same for all the models. These maps demonstrate the importance of the underlying physical structure on chemical evolution and spectra of HMCs. It also vouches for the potential of this study to achieve a better understanding of the hot cores and thus the high-mass star formation scenario.
One of the important parameters of astrochemical models is the desorption energy of the respective molecules8; it also controls the gas-phase abundance of COMs. Recent observational studies also started to compare the spatial distribution of COMs using high resolution emission line maps (Öberg et al. 2013). The relative gas phase abundance of CH3OCH3 is more extended than that of CH3OH in the hot core models, therefore, it will be interesting to verify whether this trend is also seen in observations. We show the integrated intensity maps of the CH3OH: 241.8877 GHz (Eu = 72.5 K) and CH3OCH3: 241.9465 GHz (Eu = 81.1 K) transitions for the model hot core cr16-r3-l7 at 1 × 105 year in Fig. 12. This figure demonstrates that the bond strength of the molecule to the grain can influence the size of the emissive region (i.e., a lower desorption energy places the molecule in the gas phase over a larger surface area). We can compare the observed emission maps from a range of parent molecular species, each with different desorption energies, but sampling transitions with comparable excitation conditions. Then these emission profiles can be used to constrain the relative desorption energies of the associated molecules. Moreover, with grounding to laboratory work for a particular molecule, we might be able to place this on an absolute scale.
It has been found that the abundances of various COMs in cr17 models are typically lower than that of cr16 models, and these values are unsuitable to reproduce the observed line strength of different COMs. Since our current approach is based on static density distribution, it is not possible to distinguish the effect of dynamics vs. cosmic-ray ionization rates on the initial ice formation and hence on the final gas phase abundance of COMs. More detailed studies are needed to constrain the cosmic-ray ionization rate at the sites of high-mass star formation.
4.2. myXCLASS fit to the simulated spectra
Many of the line-survey studies used XCLASS (Schilke et al. 1997, 2001; Zernickel et al. 2012; Crockett et al. 2014; Neill et al. 2014) or similar programs to estimate the physical parameters from the observed spectra and derived the relative abundances using H2 or CO column densities at constant temperature. We used the total hydrogen density to estimate the relative abundance of the respective molecules (see Tables 4 and 5). There is another notable difference between the XCLASS analysis and this work: the hot core models predict the temperature and abundance profiles for hot cores, whereas XCLASS and other methods can only derive beam-averaged values. Therefore, it would be interesting to compare these single-point physical parameters with the spatial distribution predicted by our hot core models. We carried out an analysis to re-estimate the physical parameters from the simulated spectra using the myXCLASS interface9 (Möller et al., in prep.) for CASA10; the interface also includes the model optimizer package MAGIX (Modeling and Analysis Generic Interface for eXternal numerical codes) (Möller et al. 2013). We fitted the simulated spectra of CH3OH, C2H5OH, CH3OCH3, and HCOOCH3 convolved with a telescope beam size of 2.2′′ at two different evolutionary stages over selected frequency ranges. The fitted spectra are overplotted on the simulated spectra in Fig. E.1. We list the physical parameters obtained from the myXCLASS analysis in Table 7; the relative abundances were derived using the hydrogen column density,1.05 × 1024 cm-2, as estimated for the hot core models hmc-r3. We also added white noise to our simulated spectra and fitted the noisy spectra with myXCLASS. We do not find any significant difference in the fitted parameters, indicating that the myXCLASS fitting values are robust against noise. We also plot the relative abundances as a function of temperature for different molecules at different evolutionary timescales and overplot the single-point physical parameters estimated by myXCLASS analysis in Fig. 13. The myXCLASS estimates are comparable with the physical parameters at the jump radius of these molecules (where the gaseous abundances sharply decrease; see also Fig. B.1); these regions have the largest area-filling factor in the beam, therefore, the results are expected. However, myXCLASS underestimates the temperature of the hot cores. Our analysis indicates that the typical temperatures of the hot cores are a few times higher than the canonical value of 100 K, which is also consistent with recent observations (Sridharan et al. 2014). These results also suggest that a comparison of the simulated spectra of the 3D hot core models with the high resolution observations (e.g., ALMA) will reveal a more realistic physio-chemical structure of the hot cores than the simple fitting methods.
5. Summary and discussion
 |
Fig. 11 Top: radial profiles of the CH3OH (vt = 0) [7(0, 7)–6(0, 6)] integrated intensity maps at 338.1245 GHz for the hot core model cr16-r3-l2 at various timescales. Bottom: radial profile of the CH3OH (vt = 1) [7(4, 4)–6(4, 3)] and [7(4, 3)–6(4, 2)] integrated intensity maps at 337.68559 GHz for various hot core models. The adopted distance to the source and the telescope beam size are 2 kpc and 2.2′′. |
 |
Fig. 12 Top: CH3OH 241.8877 GHz (Eu = 72.5 K), and bottom: CH3OCH3 241.9465 GHz (Eu = 81.1 K) integrated line intensity maps of the hot core model cr16-r3-l7 at 1 × 105 year. The adopted distance to the source and the telescope beam size are 2 kpc and 0.3′′. |
Molecular line observations are important probes to reveal the chemical reservoir of hot cores (Schilke et al. 1997, 2001). These observations are also useful to explore the physical conditions and chemical evolution of high-mass star forming regions (Beuther et al. 2009; Zernickel et al. 2012; Öberg et al. 2013). Recent studies also used single dish observations of a large number of sources at various evolutionary stages to investigate the chemical evolution of high-mass star forming regions (Hoq et al. 2013; Gerner et al. 2014). Selected studies also explored the radial distribution of density and temperature along with chemical evolutionary models to understand the underlying physical structure, abundance evolution, evolutionary stages, etc. (Doty et al. 2002; Öberg et al. 2013; Gerner et al. 2014). In general, these studies analyzed the observations by assuming a density distribution guided by empirical studies and an estimate of the thermal structure that would result from the density profile and a source with a particular luminosity. Doty et al. (2006) determined the temperature evolution including the luminosity evolution for high-mass protostars, but did not include any grain surface diffusion reactions, which are crucial for COM formation on grain surface.
 |
Fig. 13 Comparison of the input abundance distribution of the hot core model cr16-r3-l7 and the single-point physical parameters obtained by the myXCLASS analysis. |
In this work we have used different temporal evolution profiles of the luminosity for a forming high-mass star. The density distribution of the hot core models were setup using recent dust-continuum observations assuming a gas to dust mass ratio of 100. Within this framework, the thermal evolution was determined with the radiative transfer code RADMC3D based on the adopted protostellar luminosity evolution. This then resulted in a time-variable thermal profile that has a profound effect on the chemistry through sublimation and grain surface diffusion, subsequent gas phase processing, etc. We used the chemical evolutionary code Saptarsy along with a gas-grain chemical network to explore the spatio-temporal evolution of molecular abundances in hot cores. We then explored the evolution of abundance distribution of selected oxygen-bearing COMs such as CH3OH, C2H5OH, HCOOCH3, and CH3OCH3 in detail under varying physical conditions. We showed that the spatial distribution of gas phase abundances of the COMs expand with the increasing temperature of hot cores. These profiles provide a detailed variation in abundances against the physical structure of the hot cores. The average behavior of these profiles is similar to the so-called jump models (two different abundances are used for the upper and lower temperature regime relative to a characteristic temperature, typically 100 K) for species that primarily form on the grain surface and are transformed to the gas phase mainly via thermal desorption. In the evolutionary model the jump radius or the evaporation font (where the temperature is equal to the characteristic temperature of the jump abundance) also expands with time. We also showed the variation of the evaporation front associated with different temperatures for the hot core model hmc-r3-l7 (see Fig. B.1), which will be useful to set the jump abundances for any particular evolutionary stages. Moreover, the predicted abundance profiles can be used as templates to model the observed spectra of hot cores, but one should also keep in mind that these profiles vary significantly depending on the adopted physical structure and luminosity evolution.
Emission lines of COMs (often referred to as weeds) are one of the salient observational features of hot cores. These molecules are highly abundant (>10-7 with respect to hydrogen) and have rich ro-vibrational emission spectra. A significant improvement over previous studies was achieved by simulating the spectra for hot core models that can be directly compared with observations. The simulated spectra for different hot core models were generated by using RADMC-3D at different spectral wavebands to explore the spectral evolution in hot cores. The qualitative comparison of the observed and simulated spectra showed that the hot core models successfully reproduce the observed trends, that is the increase of the total number of emission lines and their associated intensities with evolutionary timescales. The adopted timescales for the chemical simulation of the cold core phase (~104 year) or the hot core lifetime (~105 year) are consistent with recent independent studies (Tackenberg et al. 2012; Gerner et al. 2014). These results indicate that the self-consistent models present a reasonable evolutionary scenario for hot cores. Based on these evolutionary models, we discuss some additional features that can be compared with observations.
Physical parameters of the hot core model cr16-r3-l7: myXCLASS analysis.
The hot core models predict that the emission line maps of various transitions of different COMs also expand with time. With increasing temperature, the material around the central protostars heats up, and consequently, the gas phase abundance of various COMs also spreads out, depending on the binding energies of the respective molecules. These processes collectively contribute to the expansion of the emitting regions of various transitions. We argue that for a given molecule the line forest (see Sect. 4.1) provides detailed information about the excitation conditions, which can be used to extract key information regarding the binding energies of the molecules to the grain surface, abundance profiles, etc. This will provide further constraint to the chemical models that sometimes suffer from lack of laboratory measurements of the binding energies. A satisfactory match between the observed and simulated spectra along with the emission line maps thus provides a well-constrained physio-chemical structure of the hot cores, which is a significant improvement over existing fitting methods that estimate the beam-averaged single-point physical parameters. High resolution observations (such as from ALMA) for a statistically significant samples of high-mass prestellar cores will be available soon. The temperature structure of these cores can be re-constructed by using radiative transfer modeling and can be further constrained by comparing the simulated emission line maps with the observations. The fitting process also place some constrain on the luminosity of the central stars, gas phase abundance profile and the desorption energy of the associated molecules. These models will be particularly useful for the molecules that primarily form on the grain surface and are transformed to gas phase mainly by thermal desorption. Moreover, modeling the high resolution observations of the high-mass protostellar cores with similar masses but at different evolutionary stages will be useful to estimate the protostellar luminosity function for high-mass protostars, which is an input parameter of these models. In summary, the full potential of these models can be explored by using the observations that can probe scales of few thousands AU. Currently, it is also possible to estimate the evolutionary stages using these models, but the estimated age should be considered with caution because a static density distribution is used. With a temporal variation of density distribution, it may be possible to diagnose the spectral features or abundance ratios that can be used as a proxy for the evolutionary stages, similar to the so-called chemical clocks.
Along with the variation in chemical abundances, the differences in formation and destruction pathways of various molecules as a function of physical conditions can be explored using our model. This is specifically helpful to verify the proposed chemical evolutionary scenarios. CH3OH acts as the parent molecule for the other COMs that are considered in this work. The spatio-temporal variation of the abundance ratio of these COMs with CH3OH can be used to verify the reaction pathways discussed in Sect. 3.4. The abundance and spectra of intermediate species such as CH3O and CH2OH will also be useful to constrain the formation scenario of COMs.
6. Conclusion
We investigated the formation and evolution of COMs in HMCs by constructing 3D physio-chemical models guided by recent empirical and modeling studies of high-mass star formation. We combined radiative transfer calculation with chemical evolution to explore the spatio-temporal evolution of the COMs in hot cores and also to generate the synthetic spectra at selective wavebands. The grain surface abundances of COMs are converted into gas phase, where the temperature is higher than the water ice evaporation temperature (100 K). The gas-phase abundance profile of various COMs will furthermore be useful for modeling the spectra of individual sources. We also find that jump abundance profiles are still a good approximation for the COMs that mainly form on the grain surface and return to the gas phase by thermal desorption (e.g., C2H5OH). We predicted the temporal variation of the jump radius that can be used as a template to set the jump abundances according to the evolutionary stages. We successfully reproduced the trends in spectral variation observed in hot cores within the typical lifetime of HMCs of 1 × 105 year. These results indicate that the adopted physical parameters and the chemical model (Garrod et al. 2008) are realistic estimates of the observed hot cores. We also discussed that a satisfactory match between the simulated and observed spectra obtained by iterating over the input parameter space will be useful to decipher the physio-chemical structure of the hot cores. This technique when applied to model the observation of a handful of hot cores can also constrain the luminosity evolution of the central protostars and the binding energies of the molecules to the grain surface. Our approach is more effective in extracting the physical parameters (such as temperature) using observations than the simple spectral fitting methods that estimate single-point values for the whole source. The modeling approach discussed in this paper will be particularly helpful to reconstruct the physical structures of hot cores and to constrain the timescales and chemical evolution during the initial stages of high-mass star formation.
Online material
Appendix A: Spatio-temporal variation of selected COMs in various hot core models
 |
Fig. A.1 Same as Fig. 4, but for hot core models cr16-r3-l7 (upper panel) and cr16-r3.5-l4 (lower panel). Note the alternative labeling of the density and temperature axes on the right side of the respective plots. |
 |
Fig. A.2 Same as Fig. 4, but for hot core models cr16-r4-l2 (upper panel) and cr16-r4.5-l4 (lower panel). Note the alternative labeling of the density and temperature axes on the right side of the respective plots. |
 |
Fig. A.3 Same as Fig. 4, but for hot core models cr17-r3-l2 (upper panel) and cr17-r3.5-l4 (lower panel). Note the alternative labeling of the density and temperature axes on the right side of the respective plots. |
 |
Fig. A.4 Same as Fig. 4, but for hot core models cr17-r4-l7 (upper panel) and cr17-r4.5-l4 (lower panel). Note the alternative labeling of the density and temperature axes on the right side of the respective plots. |
Appendix B: Temporal variation of the radii with temperature above 100 K, 150 K, and 200 K
 |
Fig. B.1 Temporal variation of the radii with temperature above 100 K, 150 K, and 200 K. Radii of the spatial distribution of various molecules as derived from the myXCLASS analysis (see Table 7) are overplotted with different colors. The arrow indicates that the radii of CH3OH and C2H5OH at 1 × 105 year are only lower limits. |
Appendix C: Comparison of simulated spectra for different evolutionary timescales
 |
Fig. C.1 Simulated spectra for the hot core model cr16-r3-l7 at 9 × 104 year, overplotted on the spectra at 1 × 105 year. The intensity of various spectral lines at two different epochs cannot be matched using a scaling factor. Spectral changes originate from the variation of temperature and abundances at different timescales. |
Appendix D: Comparison of simulated and Herschel-HIFI spectra
 |
Fig. D.1 Scaled-up version (multiplied by a factor of 2) of simulated spectra for the hot core model cr16-r3-l7 at 9 × 104 year, overplotted on the Herschel-HIFI spectra of NGC 6334I. |
Appendix E: myXCLASS fit to the simulated spectra
 |
Fig. E.1 Fitted spectra obtained from the myXCLASS analysis (solid black line), overplotted on the simulated spectra (colored dashed lines) of different COMs. |
A list of binding energies for various molecules can be found at http://www.astro.cornell.edu/~rgarrod/wp-content/uploads/2013/03/GH06_binding.txt
Acknowledgments
This work is carried out within the Collaborative Research Centre 956, sub-project Astrochemistry [C3], funded by the Deutsche Forschungsgemeinschaft (DFG). The authors would like to thank the referee and the editor, M. Walmsley, for a careful reading of the manuscript. R.C. would like to thank C. P. Dullemond, C. Endres, R. Garrod, N. Harada, G. Hassel, E. Herbst, A. Hindmarsh, Á. Sánchez-Monge, D. Semenov, S. Viti, and M. Walmsley for useful discussions. This research has made use of NASA’s Astrophysics Data System.
References
- Aikawa, Y., Wakelam, V., Garrod, R. T., & Herbst, E. 2008, ApJ, 674, 984 [NASA ADS] [CrossRef] [Google Scholar]
- Bacmann, A., Taquet, V., Faure, A., Kahane, C., & Ceccarelli, C. 2012, A&A, 541, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beltrán, M. T., Cesaroni, R., Zhang, Q., et al. 2011, A&A, 532, A91 [CrossRef] [EDP Sciences] [Google Scholar]
- Bergin, E. A., & Tafalla, M. 2007, ARA&A, 45, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Bergin, E. A., Langer, W. D., & Goldsmith, P. F. 1995, ApJ, 441, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Beuther, H., Schilke, P., Menten, K. M., et al. 2002, ApJ, 566, 945 [NASA ADS] [CrossRef] [Google Scholar]
- Beuther, H., Churchwell, E. B., McKee, C. F., & Tan, J. C. 2007, Protostars and Planets V, 165 [Google Scholar]
- Beuther, H., Zhang, Q., Bergin, E. A., & Sridharan, T. K. 2009, AJ, 137, 406 [NASA ADS] [CrossRef] [Google Scholar]
- Bisschop, S. E., Jørgensen, J. K., van Dishoeck, E. F., & de Wachter, E. B. M. 2007, A&A, 465, 913 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brouillet, N., Despois, D., Baudry, A., et al. 2013, A&A, 550, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cazaux, S., Tielens, A. G. G. M., Ceccarelli, C., et al. 2003, ApJ, 593, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Ceccarelli, C., Bacmann, A., Boogert, A., et al. 2010, A&A, 521, L22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cernicharo, J., Marcelino, N., Roueff, E., et al. 2012, ApJ, 759, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Charnley, S. B., & Rodgers, S. B. 2009, in Bioastronomy 2007: Molecules, Microbes and Extraterrestrial Life, eds. K. J. Meech, J. V. Keane, M. J. Mumma, J. L. Siefert, & D. J. Werthimer, ASP Conf. Ser., 420, 29 [Google Scholar]
- Charnley, S. B., Tielens, A. G. G. M., & Millar, T. J. 1992, ApJ, 399, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Crockett, N. R., Bergin, E. A., Neill, J. L., et al. 2014, ApJ, 787, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Doty, S. D., van Dishoeck, E. F., van der Tak, F. F. S., & Boonman, A. M. S. 2002, A&A, 389, 446 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Doty, S. D., van Dishoeck, E. F., & Tan, J. C. 2006, A&A, 454, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Furuya, R. S., Cesaroni, R., & Shinnaga, H. 2011, A&A, 525, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Furuya, K., Aikawa, Y., Tomida, K., et al. 2012, ApJ, 758, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Garrod, R. T. 2013a, ApJ, 765, 60 [Google Scholar]
- Garrod, R. T. 2013b, ApJ, 778, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Garrod, R. T., & Herbst, E. 2006, A&A, 457, 927 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garrod, R. T., Weaver, S. L. W., & Herbst, E. 2008, ApJ, 682, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Gerner, T., Beuther, H., Semenov, D., et al. 2014, A&A, 563, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gibb, E., Nummelin, A., Irvine, W. M., Whittet, D. C. B., & Bergman, P. 2000a, ApJ, 545, 309 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gibb, E. L., Whittet, D. C. B., Schutte, W. A., et al. 2000b, ApJ, 536, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Goldsmith, P. F., & Langer, W. D. 1999, ApJ, 517, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Hasegawa, T. I., & Herbst, E. 1993, MNRAS, 261, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Hasegawa, T. I., Herbst, E., & Leung, C. M. 1992, ApJS, 82, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Herbst, E., & van Dishoeck, E. F. 2009, ARA&A, 47, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Hoq, S., Jackson, J. M., Foster, J. B., et al. 2013, ApJ, 777, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Hosokawa, T., & Omukai, K. 2009, ApJ, 691, 823 [NASA ADS] [CrossRef] [Google Scholar]
- Indriolo, N., & McCall, B. J. 2012, ApJ, 745, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Kuiper, R., & Yorke, H. W. 2013, ApJ, 772, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Kurtz, S., Cesaroni, R., Churchwell, E., Hofner, P., & Walmsley, C. M. 2000, Protostars and Planets IV, 299 [Google Scholar]
- Möller, T., Bernst, I., Panoglou, D., et al. 2013, A&A, 549, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, H. S. P., Thorwirth, S., Roth, D. A., & Winnewisser, G. 2001, A&A, 370, L49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, H. S. P., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Struct., 742, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Neill, J. L., Bergin, E. A., Lis, D. C., et al. 2014, ApJ, 789, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Öberg, K. I., Boogert, A. C. A., Pontoppidan, K. M., et al. 2011, ApJ, 740, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Öberg, K. I., Boamah, M. D., Fayolle, E. C., et al. 2013, ApJ, 771, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Ossenkopf, V., & Henning, T. 1994, A&A, 291, 943 [NASA ADS] [Google Scholar]
- Padovani, M., Galli, D., & Glassgold, A. E. 2009, A&A, 501, 619 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pickett, H. M., Poynter, R. L., Cohen, E. A., et al. 1998, J. Quant. Spectr. Rad. Transf., 60, 883 [NASA ADS] [CrossRef] [Google Scholar]
- Rixon, G., Dubernet, M. L., Piskunov, N., et al. 2011, in AIP Conf. Ser. 1344, eds. A. Bernotas, R. Karazija, & Z. Rudzikas, 107 [Google Scholar]
- Rolffs, R., Schilke, P., Zhang, Q., & Zapata, L. 2011, A&A, 536, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schilke, P., Groesbeck, T. D., Blake, G. A., & Phillips, T. G. 1997, ApJS, 108, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Schilke, P., Benford, D. J., Hunter, T. R., Lis, D. C., & Phillips, T. G. 2001, ApJS, 132, 281 [NASA ADS] [CrossRef] [Google Scholar]
- Semenov, D., Hersant, F., Wakelam, V., et al. 2010, A&A, 522, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sridharan, T. K., Rao, R., Qiu, K., et al. 2014, ApJ, 783, L31 [Google Scholar]
- Tackenberg, J., Beuther, H., Henning, T., et al. 2012, A&A, 540, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Taquet, V., Ceccarelli, C., & Kahane, C. 2012, A&A, 538, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tielens, A. G. G. M., & Hagen, W. 1982, A&A, 114, 245 [NASA ADS] [Google Scholar]
- van der Tak, F. F. S., van Dishoeck, E. F., Evans, II, N. J., & Blake, G. A. 2000, ApJ, 537, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Vasyunin, A. I., & Herbst, E. 2013, ApJ, 769, 34 [Google Scholar]
- Viti, S., & Williams, D. A. 1999, MNRAS, 305, 755 [NASA ADS] [CrossRef] [Google Scholar]
- Wienen, M., Wyrowski, F., Schuller, F., et al. 2012, A&A, 544, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zernickel, A., Schilke, P., Schmiedeke, A., et al. 2012, A&A, 546, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Molecular abundances on grains with respect to s-H2O in percent: observed and simulated values.
Simulated values of COMs at the center of various hot core models with the cosmic ray ionization rate of 1.37 × 10-16.
Simulated values of COMs at the center of various hot core models with the cosmic ray ionization rate of 1.37 × 10-17.
All Figures
 |
Fig. 1 Flowchart of the modeling framework. |
| In the text | |
 |
Fig. 2 Evolution of molecular abundance on grains with respect to s-H2O in percent at 5 × 104 year for different cold core models: a) cc-cr17-t10; b) cc-cr16-t10; c) cc-cr17-t15; and d)cc-cr16-t15. |
| In the text | |
 |
Fig. 3 a) Luminosity evolution profiles for different power-law indices. b) Temperature evolution in the hot core model hmc-r3 at different radii: ~200 AU (blue), ~2000 AU (green) and ~10 000 AU (red). Temperature distribution obtained using different protostellar luminosity evolutions are shown with continuous (l2), dashed (l4), and dotted (l7) lines. c) Spatio-temporal evolution of the temperature in the hot core model hmc-r3. |
| In the text | |
 |
Fig. 4 Spatio-temporal abundance variation of selected COMs on the grain (dot-dashed line) and in gas phases (continuous line) are shown for the hot core model cr16-r3-l2. Black dashed and continuous lines show the radial variation of the density and the temperature respectively. Time-stamps (in year) for different temporal snapshots are annotated in the upper right corner of the respective plots. Note the alternative labeling of the density and temperature axes on the right side of the respective plots. |
| In the text | |
 |
Fig. 5 Simulated spectra of CH3OH for the hot core model cr16-r3-l2 at different evolutionary timescales. The adopted distance to the source and the telescope beam size are 2 kpc and 2.2′′. |
| In the text | |
 |
Fig. 6 Simulated spectra of CH3OH for the hot core models cr16-r3-l2, cr16-r3.5-l2, cr16-r4-l2, and cr16-r4.5-l2 at 1.0 × 105 year. The adopted distance to the source and the telescope beam size are 2 kpc and 2.2′′. |
| In the text | |
 |
Fig. 7 Simulated spectra of selected COMs for the hot core model cr16-r3-l7 at 9 × 104 year (left) and 1 × 105 year (right) at different wavebands. The adopted distance to the source and the telescope beam size are 2 kpc and 2.2′′. |
| In the text | |
 |
Fig. 8 Simulated spectra of selected COMs for the hot core model cr16-r3-l7 at 9 × 104 year (left) and 1 × 105 year (right) at Herschel-HIFI Band 1. The adopted distance to the source and the telescope beam size are 2 kpc and ~40′′. |
| In the text | |
 |
Fig. 9 Integrated line intensity maps of the CH3OH (vt = 0) [7(0, 7)–6(0, 6)] transition at 338.1245 GHz for the hot core model cr16-r3-l2 at 7.0 × 104, 8.0 × 104, 9.0 × 104 and 1.0 × 105 year (left to right). The adopted distance to the source and the telescope beam size are 2 kpc and 2.2′′. |
| In the text | |
 |
Fig. 10 Integrated line intensity maps of the CH3OH (vt = 1) [7(4, 4)–6(4, 3)] and [7(4, 3)–6(4, 2)] transitions at 337.68559 GHz for the hot core models cr16-r3-l2, cr16-r3.5-l2, cr16-r4-l2 and cr16-r4.5-l2 (left to right) at 1.0 × 105 year. The adopted distance to the source and the telescope beam size are 2 kpc and 2.2′′. |
| In the text | |
 |
Fig. 11 Top: radial profiles of the CH3OH (vt = 0) [7(0, 7)–6(0, 6)] integrated intensity maps at 338.1245 GHz for the hot core model cr16-r3-l2 at various timescales. Bottom: radial profile of the CH3OH (vt = 1) [7(4, 4)–6(4, 3)] and [7(4, 3)–6(4, 2)] integrated intensity maps at 337.68559 GHz for various hot core models. The adopted distance to the source and the telescope beam size are 2 kpc and 2.2′′. |
| In the text | |
 |
Fig. 12 Top: CH3OH 241.8877 GHz (Eu = 72.5 K), and bottom: CH3OCH3 241.9465 GHz (Eu = 81.1 K) integrated line intensity maps of the hot core model cr16-r3-l7 at 1 × 105 year. The adopted distance to the source and the telescope beam size are 2 kpc and 0.3′′. |
| In the text | |
 |
Fig. 13 Comparison of the input abundance distribution of the hot core model cr16-r3-l7 and the single-point physical parameters obtained by the myXCLASS analysis. |
| In the text | |
 |
Fig. A.1 Same as Fig. 4, but for hot core models cr16-r3-l7 (upper panel) and cr16-r3.5-l4 (lower panel). Note the alternative labeling of the density and temperature axes on the right side of the respective plots. |
| In the text | |
 |
Fig. A.2 Same as Fig. 4, but for hot core models cr16-r4-l2 (upper panel) and cr16-r4.5-l4 (lower panel). Note the alternative labeling of the density and temperature axes on the right side of the respective plots. |
| In the text | |
 |
Fig. A.3 Same as Fig. 4, but for hot core models cr17-r3-l2 (upper panel) and cr17-r3.5-l4 (lower panel). Note the alternative labeling of the density and temperature axes on the right side of the respective plots. |
| In the text | |
 |
Fig. A.4 Same as Fig. 4, but for hot core models cr17-r4-l7 (upper panel) and cr17-r4.5-l4 (lower panel). Note the alternative labeling of the density and temperature axes on the right side of the respective plots. |
| In the text | |
 |
Fig. B.1 Temporal variation of the radii with temperature above 100 K, 150 K, and 200 K. Radii of the spatial distribution of various molecules as derived from the myXCLASS analysis (see Table 7) are overplotted with different colors. The arrow indicates that the radii of CH3OH and C2H5OH at 1 × 105 year are only lower limits. |
| In the text | |
 |
Fig. C.1 Simulated spectra for the hot core model cr16-r3-l7 at 9 × 104 year, overplotted on the spectra at 1 × 105 year. The intensity of various spectral lines at two different epochs cannot be matched using a scaling factor. Spectral changes originate from the variation of temperature and abundances at different timescales. |
| In the text | |
 |
Fig. D.1 Scaled-up version (multiplied by a factor of 2) of simulated spectra for the hot core model cr16-r3-l7 at 9 × 104 year, overplotted on the Herschel-HIFI spectra of NGC 6334I. |
| In the text | |
 |
Fig. E.1 Fitted spectra obtained from the myXCLASS analysis (solid black line), overplotted on the simulated spectra (colored dashed lines) of different COMs. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.