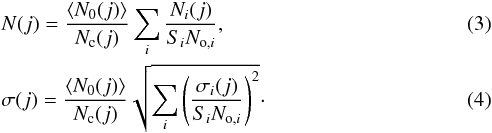| Issue |
A&A
Volume 575, March 2015
|
|
|---|---|---|
| Article Number | A116 | |
| Number of page(s) | 24 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201423796 | |
| Published online | 06 March 2015 | |
The evolution of the cluster optical galaxy luminosity function between z = 0.4 and 0.9 in the DAFT/FADA survey⋆
1 UPMC Université Paris 06, UMR 7095, Institut d’Astrophysique de Paris, 98bis Bd Arago, 75014 Paris, France
e-mail: martinet@iap.fr
2 Astrophysics and Cosmology Research Unit, University of KwaZulu-Natal, 4041 Durban, South Africa
3 LAM, OAMP, Université Aix-Marseille & CNRS, Pôle de l’Étoile, Site de Château Gombert, 38 rue Frédéric Joliot-Curie, 13388 Marseille 13 Cedex, France
4 INAF/Osservatorio Astronomico di Trieste, via Tiepolo 11, 34143 Trieste, Italy
5 Dept of Physics and Astronomy & centre for Interdisciplinary Exploration and Research in Astrophysics (CIERA), Northwestern University, Evanston, IL 60208-2900, USA
6 Department of Physics and Astronomy, Ohio University, 251B Clippinger Lab, Athens, OH 45701, USA
7 23 rue d’Yerres, 91230 Montgeron, France
8 Instituto de Astrofísica de Andalucía, CSIC, Glorieta de la Astronomía s/n, 18008 Granada, Spain
9 Gemini Observatory, Casilla 603, La Serena, Chile
10 Argelander-Institut für Astronomie, Universitët Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
Received: 12 March 2014
Accepted: 17 December 2014
Context. There is some disagreement about the abundance of faint galaxies in high-redshift clusters, with contradictory results in the literature arising from studies of the optical galaxy luminosity function (GLF) for small cluster samples.
Aims. We compute GLFs for one of the largest medium-to-high-redshift (0.4 ≤ z < 0.9) cluster samples to date in order to probe the abundance of faint galaxies in clusters. We also study how the GLF depends on cluster redshift, mass, and substructure and compare the GLFs of clusters with those of the field. We separately investigate the GLFs of blue and red-sequence (RS) galaxies to understand the evolution of different cluster populations.
Methods. We calculated the GLFs for 31 clusters taken from the DAFT/FADA survey in the B,V,R, and I rest-frame bands. We used photometric redshifts computed from BVRIZJ images to constrain galaxy cluster membership. We carried out a detailed estimate of the completeness of our data. We distinguished the red-sequence and blue galaxies using a V − I versus I colour−magnitude diagram. We studied the evolution of these two populations with redshift. We fitted Schechter functions to our stacked GLFs to determine average cluster characteristics.
Results. We find that the shapes of our GLFs are similar for the B,V,R, and I bands with a drop at the red GLF faint ends that is more pronounced at high redshift: αred ~ −0.5 at 0.40 ≤ z < 0.65 and αred > 0.1 at 0.65 ≤ z < 0.90. The blue GLFs have a steeper faint end (αblue ~ −1.6) than the red GLFs, which appears to be independent of redshift. For the full cluster sample, blue and red GLFs meet at MV = −20, MR = −20.5, and MI = −20.3. A study of how galaxy types evolve with redshift shows that late-type galaxies appear to become early types between z ~ 0.9 and today. Finally, the faint ends of the red GLFs of more massive clusters appear to be richer than less massive clusters, which is more typical of the lower redshift behaviour.
Conclusions. Our results indicate that these clusters form at redshifts higher than z = 0.9 from galaxy structures that already have an established red sequence. Late-type galaxies then appear to evolve into early types, enriching the red sequence between this redshift and today. This effect is consistent with the evolution of the faint-end slope of the red sequence and the galaxy type evolution that we find. Finally, faint galaxies accreted from the field environment at all redshifts might have replaced the blue late-type galaxies that converted into early types, explaining the lack of evolution in the faint-end slopes of the blue GLFs.
Key words: galaxies: clusters: general / galaxies: evolution / galaxies: formation / galaxies: luminosity function, mass function
Appendix is available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
It is widely accepted that cluster elliptical galaxies are a passively evolving population formed at high redshift (z> 1) in a short duration event (e.g. De Propris et al. 1999, 2007, 2013; De Lucia et al. 2004, 2007; Andreon 2006; Muzzin et al. 2008; Mancone et al. 2010, 2012). This scenario is strongly supported by the lack of evolution in the colour−magnitude relation for the bright galaxies in clusters from z = 1 to z = 0 (e.g. De Lucia et al. 2004). However, there is still a strong debate about whether cluster galaxies migrated from the field to clusters at lower redshift (z ~ 0.8; e.g. De Lucia et al. 2004, 2007; Poggianti et al. 2006) or if they joined clusters at higher redshift or still even originally formed in clusters. This debate arises from the different behaviours of the faint-end slope of galaxy luminosity functions (GLFs) observed at high z. At low z, cluster GLFs mainly have flat faint ends populated by low mass galaxies (e.g. Secker et al. 1997; Rudnick et al. 2009). We note that Popesso et al. (2006) find an upturn of the very faint population of the GLF for  in nearby clusters, but our data are not deep enough to investigate this population of dwarf galaxies at high redshift.
in nearby clusters, but our data are not deep enough to investigate this population of dwarf galaxies at high redshift.
The faint end of GLFs is found to either decrease with increasing redshift (e.g. Smail et al. 1998; De Lucia et al. 2004, 2007; Tanaka et al. 2005; Stott et al. 2007; Gilbank et al. 2008; Rudnick et al. 2009; Vulcani et al. 2011) or remain constant with redshift (e.g. De Propris et al. 2003, 2007, 2013; Andreon 2006). The first type of behaviour is the most commonly observed, but the cold dark matter scenario predicts a larger number of low mass galaxies (Andreon et al. 2006; Rudnick et al. 2009). Thus, additional processes are often invoked within clusters, such as ram pressure stripping (Gunn & Gott 1972) and harassment (e.g. Moore et al. 1996, 1998). These processes are found to weakly affect the results in the simulation of Lanzoni et al. (2005) and are likely to depend on mass (Muzzin et al. 2008). The study of the abundance of faint galaxies at high redshift is the main objective of this paper.
We also investigate whether GLFs are universal or depend on environment. This can help us determine whether the red cluster galaxy population originates in the field at higher redshift. Many studies find a universal GLF that does not depend on environment (Lugger 1986, 1989; Colless 1989; Gaidos 1997; Rauzy et al. 1998; Trentham 1998; Paolillo et al. 2001; Yagi et al. 2002; Andreon 2004), while others (Dressler 1978; Lopez-Cruz et al. 1997; Lumsden et al. 1997; Valotto et al. 1997; Driver et al. 1998a; Garilli et al. 1999; Goto et al. 2002; De Propris et al. 2003; Christlein & Zabludoff 2003; Popesso et al. 2006; Muzzin et al. 2008; Rudnick et al. 2009) observe differences between clusters and field GLFs. The most widely observed trend is a flattening of the GLF as the environment becomes less dense (see e.g. De Propris et al. 2003 for observations and Lanzoni et al. 2005 for simulations). This behaviour could be explained by either star formation being inhibited in dense environments (Tully et al. 2002; De Propris et al. 2003; Muzzin et al. 2008) or merging processes being more common in the field where the relative velocities of galaxies are lower (Menci et al. 2002). This last explanation does not apply to single objects falling onto groups of galaxies, which can trigger large amounts of star formation (e.g. Adami et al. 2009). In addition, we note that Ilbert et al. (2005) find a steepening of the faint end of the field GLF with increasing redshift such that they do not see the usual flattening of the field GLF at high redshift.
Additional support for the GLF dependence on the environment is the perturbation of the GLF caused by cluster merging (e.g. Durret et al. 2010). Finally, De Propris et al. (2003) and Boué et al. (2008) find different GLFs for cluster cores and outskirts. The first authors find an excess of bright galaxies in cluster cores and the second a steeper faint end in the outskirts.
The Dark energy American French Team (DAFT, in French FADA) survey is ideal for investigating the faint end of the GLF and field to cluster differences at relatively high redshift. The DAFT/FADA survey encompasses ~90 high-redshift (0.4 ≤ z ≤ 0.9) massive (M ≥ 2 × 1014M⊙) clusters of galaxies with Hubble Space Telescope (HST) imaging available, and multi-band optical and near infrared ground based imaging, using 4 m class telescopes, which is now almost complete. The main goals of the survey are to form a comprehensive database to study clusters and their evolution, and to test cosmological constraints geometrically by means of weak lensing tomography. In addition to the first DAFT/FADA paper establishing the reference basis for the photometric redshift (hereafter photo-z) determination (Guennou et al. 2010,hereafter G10), results concerning several topics have been obtained by the DAFT/FADA team1.
An outline of the paper is as follows; we first present the photo-z measurements and the improvements that we have made since G10. We then describe our method for computing GLFs. We present the optical GLFs for 31 clusters of the DAFT/FADA survey in the 0.4 ≤ z< 0.9 redshift range for the B,V,R, and I rest-frame bands. The cluster membership of galaxies is based on photo-zs computed with U or B,V,R,I,Z, and J or Ks band data and a field subtraction. We take special care to estimate the completeness of our data, and we show that the GLFs are strongly correlated to the 90% completeness limit. We investigate average cluster behaviours by stacking them and discuss the dependence of GLFs on cluster redshifts, masses, and substructures. We compare the GLF behaviour in the cluster core and outskirts. We also separate blue and red-sequence galaxies to investigate the evolution of different cluster galaxy populations. Finally, we compare our cluster GLFs to the field GLFs computed with COSMOS data (Ilbert et al. 2009) made in the same redshift intervals. We discuss our results in light of the literature. Throughout the paper, we use the standard cosmological model with ΩM = 0.3, ΩΛ = 0.7, and H0 = 70 km Mpc-1 s-1.
2. Photometric redshifts
2.1. Context
We measure our photo-zs as in G10, with the LePhare package (e.g. Arnouts et al. 1999; Ilbert et al. 2006a,b). We refer the reader to these papers for details but we provide here the salient points of the technique. The aim of the method is to compare observed magnitudes with predicted ones created by templates, in order to estimate the redshift and other parameters such as the photometric type. This type varies between 1 and 31 with the chosen templates (see below). Numbers 1–7 correspond to early-type galaxies, numbers 8–12 to early spiral galaxies, numbers 13–19 to late spiral galaxies, and numbers 20–31 to very blue galaxies. The last category corresponds to very blue templates which have been generated to compensate for the lack of very blue templates in Polletta et al. (2006, 2007).
In a similar way to G10, we select spectral energy distributions (hereafter SEDs) with emission lines from Polletta et al. (2006, 2007), with a Calzetti et al. extinction law (e.g. Calzetti & Heckman 1999) applied to different galaxy classes (see below).
The available spectroscopic redshift catalogues are another important ingredient (as in G10) of our calculations. As LePhare is able to estimate possible shifts in photometric zero points by comparing photometric and spectroscopic redshifts (used as training sets), this allows us to compensate for the various origins of our ground-based images. We collected spectroscopic catalogues for all clusters in the present paper.
2.1.1. Input magnitudes
The first difference from G10 is the photometric bands that we used. As already demonstrated, having near infrared bands is mandatory to obtain a robust estimate of photo-zs at z ≥ 1. In G10, we used space based IRAC data in the infrared. We did not do so in the present paper for the following reasons:
-
These data are unavailable for the entire sample presented here.
-
The angular resolution of IRAC is very poor compared to regular ground based data (typically 4 times worse) and this forced us in G10 to estimate correcting factors in order not to be biased. These factors were typically up to 1.5 mag for small objects.
-
Another problem is the small angular extent of our clusters, for which typical galaxy-galaxy separations are often smaller than the IRAC spatial resolution, leading to considerable confusion in the central parts of clusters.
-
The IRAC bands are very red (3.6 and 4.5 μm) compared to the reddest optical ground based images at our disposal (typically the z′ band at 0.9 μm), leading to a large wavelength gap, and making constraints on redshifts rather poor.
Here, we choose to use J and/or K band data instead of IRAC data. The typical seeings vary between 0.7 and 1.2 arcsec. Simulations similar to the ones we performed in G10 (see their Fig. 9) show that the shifts induced by the different spatial resolutions will be of the order of 0.1 to 0.2 mag, which can be easily compensated for by the capacity of LePhare to adapt the photometric zero points when spectroscopic redshift catalogues are available.
2.1.2. Image registration
Our data reduction procedure uses the Scamp and Swarp packages (Bertin et al. 2002; Bertin 2006) and is identical to that in G10. We produce calibrated median images with cosmic rays and other image defects removed.
The second difference from G10 resides in the image registration between different bands. In G10, we considered data acquired by only three different instruments (IRAC, ESO/FORS2, and CTIO/MOSAIC). It was therefore possible to align precisely all the images and to extract magnitude catalogues with SExtractor (Bertin & Arnouts 1996) in double-image mode.
In the present paper, we consider more than three times as many clusters (31 clusters, compared to 10 in G10) for which we collected near infrared data, in addition to optical band data. Owing to the relatively deep nature of our catalogues (with a typical 90% completeness limit of I ~ 24 for stellar objects), this represents a large survey, gathering about 350 h of observations in both hemispheres on 4 m class telescopes. Given also that we used all possible images available in public databases to minimize the amount of new data to be acquired, our project involves a wide range of very different ground-based data: we use data obtained with about 10 different telescopes and more than 12 different cameras (see Table 1). Although we reduced all the data from its raw form to ensure that the final imaging products are as homogeneous as possible, it is impossible to always have image astrometry more precise than 0.5 arcsec everywhere in the fields. Our final images are sometimes still plagued by high frequency astrometric differences of this order. As an example, we show in Fig. 1 the astrometric diagrams for CL J0152.7-1357, for which we collected B,V,R,i′,z′, and Ks data at SOAR (SOI), Subaru (Suprime), and ESO (HawkI). We see that for a non negligible number of objects, the astrometric shift is larger than 0.5 arcsec. However, the astrometry of sources in the data of CL J0152.7-1357 is among the poorest of all our collated data.
 |
Fig. 1 Astrometric shifts (α, δ) for CL J0152.7-1357 between the objects detected in the i′ band and the B,V,R,z′, and Ks bands. The figure at the lower right shows the histograms of the shifts between the i′ band and the other bands. |
2.1.3. Magnitude homogenization
As already mentioned, we have very different sources for our images, in contrast to G10. It is obviously uninteresting to compute GLFs in several bands that vary from one cluster to another. We therefore choose to take advantage of our spectroscopic catalogues and the ability of LePhare to compute magnitude zero-point shifts. This allows us to convert our various magnitudes homogeneously into a single system (the commonsystem in the following) that we choose to be VLT/FORS2 B,V,R,I,z′ (AB system), and VLT/HawkI J or Ks band (Vega system). These filter shifts are applied after the completion of the photo-z calculations.
Data used in our present study.
We therefore classify our images into several general classes. All U- and B-like magnitudes are translated into VLT/FORS2 B, all V- and g′-like magnitudes into VLT/FORS2 V, all R- and r′-like magnitudes into VLT/FORS2 R, all I- and i′-like magnitudes into VLT/FORS2 I, all z′-like magnitudes into VLT/FORS2 z′, all J-like magnitudes into VLT/HawkI J band, and all Ks-like magnitudes into VLT/HawkI Ks band. In the particular case of Abell 851, we also consider the CFHT/WIRCAM Y and H bands directly.
Since we cannot use SExtractor in double image mode here, we choose to apply it in single image mode, computing total magnitudes (MAG_AUTO) in each of the considered bands. We then cross-correlate the different catalogues to generate a final catalogue including all magnitudes for all objects, with an identification distance of 2 arcsec and a minimization of this distance when several objects are within the same radius. This is almost twice the maximum astrometric difference observed between the different bands. We checked that the results obtained with this correlation method do not differ considerably from those of a double image mode detection by comparing the results of both methods for clusters with imaging of good astrometry acquired with the same camera in the 5 optical bands. Both methods agree well except for very faint galaxies, which are detected in larger numbers in double image mode owing to the use of the deepest band (the i band) as the reference detection image for the double image mode. However, this only concerns objects far below the completeness limit of our images. In some cases, there is also a small difference at the bright end of the magnitude distribution because of foreground objects larger than our 2 arcsec criterion.
We also varied the MAG_AUTO minimum aperture radius from 3.5 to 1.5 pixels to verify that we were not missing light in faint objects, as explained in Rudnick et al. (2009). We did not find any significant variation in the magnitude distribution between these two radii.
 |
Fig. 2 Mean and uncertainty in the difference between the star and galaxy spectroscopic redshift-based shifts for the different magnitude bands considered over our 31 fields. |
2.2. Optimization and estimate of the LePhare performances
2.2.1. Zero-point shifts
We entered catalogues of galaxy spectroscopic redshifts into LePhare to correct for small zero-point variations and compute zero-point shifts when computing magnitudes in our commonsystem. We obviously need to estimate the typical errors induced by this process.
The zero-point shift computation in LePhare is a complex interplay between the selected templates, the considered redshifts, and the selection function of the spectroscopic catalogue, which is almost always impossible to compute precisely, owing to the wide range of origins of our spectroscopic redshifts. As a consequence, the only possible way to estimate the errors induced by the LePhare zero-point shift computation is to consider several catalogues of objects for which the redshifts are known.
We could have divided our galaxy spectroscopic catalogues into several subsamples and checked the robustness of the resulting magnitude zero-point shifts. However, this would only have been possible for a few clusters for which we have a sufficient number of spectroscopic redshifts. We therefore choose another approach, considering the only other object class for which the redshifts are known: the stars in our fields.
We select stars with both ground-based and space-based HST data. This is done by plotting all the detected objects in diagrams of central surface brightness versus total magnitude. Space-based data allow us to detect very faint stars albeit in rather limited sky areas, while ground-based data allow us to detect relatively bright stars across larger areas of the sky. By applying LePhare to these star catalogues and fixing the redshifts to 0, we can compute zero-point shifts for these star catalogues. The same is done for the catalogues of galaxies with a known spectroscopic redshift, giving us a second estimate of the zero-point shifts.
Both shifts have no reason to be identical, as we consider in one case only stellar templates (which are not adapted to our galaxy catalogues) and in the other case galaxy templates at various redshifts. However, we expect not to obtain dramatically different values, since galaxy templates are theoretically nothing but combinations of stellar templates.
 |
Fig. 3 Top: mean and uncertainty on the difference between the star and galaxy spectroscopic redshift-based shifts in the I band versus the number of spectroscopic redshifts available over our 31 fields. Bottom: histogram of the number of stars used for the calibration of each cluster. |
In Fig. 2, we show the mean value and the uncertainty in the difference between these two shifts for the various magnitude bands considered. As expected, the mean differences are always smaller than 0.2 mag. Similarly, typical uncertainties in the mean differences are of the order of 0.2 mag. The numbers of spectroscopic redshifts and stars used in the calibration are given in Fig. 3. On the one hand, this shows that we cannot exclude the hypothesis that the two shifts are the same, whatever the photometric band. On the other hand, this also means that given the uncertainties in the differences, it would be incorrect to use only star catalogues to estimate the zero-point shifts of our galaxy catalogues. A 0.2 mag shift is indeed large enough to induce significant errors in our photo-z estimates (see e.g. G10). Thus, star-based zero-point shifts were only used to roughly assess the spectroscopic redshift based shifts.
We also test how varying the number of spectroscopic redshifts affects our photo-z estimates. In Fig. 3, we plot the mean and uncertainty in the difference of the two shifts in the I band for different numbers of spectroscopic redshifts available in the considered catalogues. Except for the very sparse spectroscopic catalogues (≤10 redshifts) with uncertainties of about 0.3 mag, all shift differences are consistent with zero and all uncertainties are smaller than 0.2 mag. We therefore choose to consider only clusters for which we have at least 10 spectroscopic redshifts along the line of sight.
To conclude, our method of translating all our magnitudes to a commonsystem is robust, but cannot be efficiently applied without spectroscopic catalogues of at least 10 galaxies per cluster.
2.2.2. Extinction and photometric redshifts
One of the main results of G10 was that the precision of our photometric redshifts was sometimes degraded by a factor of two when considering cluster galaxies (see also Adami et al. 2011). This is probably due to a lack of galaxy templates typical of high density regions. Even the reddest galaxy templates are sometimes not red enough. Indeed, the mean type of cluster galaxies is 15 when taking all galaxies into account and 22 when taking only galaxies with photo-zs differing from spectroscopic redshifts by more than 1σ. These numbers highlight the lack of red templates (templates get bluer from type 1 to 31), and force LePhare to increase the galaxy redshifts.
In this framework, we note that in G10, we allowed LePhare to include extinction only in spiral galaxies. This was in good agreement with the galaxy properties generally observed, even though early-type galaxies are not always unobscured (e.g. Martini et al. 2013). Here, we allow LePhare to artificially introduce extinction in early-type galaxies, permitting galaxy templates to become redder. We are aware that this artificial extinction might not be physical but we choose to apply it nonetheless because it significantly improves the accuracy of our photo-zs.
 |
Fig. 4 Photometric versus spectroscopic redshifts when allowing extinction in all galaxies (left) or only in spiral galaxies (right) for the MS1054-03 field. The full lines show the lines of equality of the photometric and spectroscopic redshifts and the dotted lines show the scatter at ± 0.2. See text for details. |
To illustrate the effect of this approach, we show the example of MS 1054-03 at redshift z = 0.8231. The extinction in the I band is 0.3 ± 0.3 mag for early types and 0.4 ± 0.3 mag for late types. Figure 4 shows the photometric versus spectroscopic redshifts when allowing extinction only in spiral galaxies and in all galaxies. We achieve a higher photometric redshift accuracy when allowing extinction also in early-type galaxies. More quantitatively, the dispersion in the mean difference between the photometric and spectroscopic redshifts of cluster members is σ| zphot − zspec | = 0.20 when allowing extinction in early-type galaxies, while it is 0.30 when allowing extinction only in late-type galaxies. We therefore improve the quality of our photometric redshift estimates in the cluster by ~50% when allowing extinction in early-type galaxies. Outside the cluster, the effect is clearly less evident because the dispersion in the mean difference between photometric and spectroscopic redshifts is 0.22 when permitting extinction in early-type galaxies and 0.21 when allowing extinction only in late-type galaxies.
Permitting extinction in early-type galaxies therefore does not drastically change photometric redshifts outside the cluster but increases their accuracy by 50% within the cluster, enabling us to reach the same precision inside and outside the cluster. Furthermore, the number of catastrophic errors inside the cluster is reduced by more than 25% when extinction is allowed in early-type galaxies.
 |
Fig. 5 Top: mean individual photo-z uncertainties as a function of I magnitude in three redshift intervals, colour coded as: blue: z = [0.; 1.05], green: z = [1.05; 2.0], red: z = [2.0; 2.5]. Bottom: mean individual photo-z uncertainties as a function of photo-z for various I magnitude intervals, colour coded as: blue: I = [19.5; 22.5], red: F814W = [19.5; 24.5]. The vertical dotted line shows the z ≤ 1.5 limit we suggested to adopt in G10. In both plots, dotted lines correspond to G10 and continuous lines to the present work. The black curves correspond to the CFHTLS with I< 22.5 and z< 1.05 and should be compared with the blue curves (see text for details). |
2.2.3. Photometric redshift quality
We now discuss the quality of our photometric redshifts and compare our results with those of G10. The dotted lines in Fig. 5 come from G10 with slightly different redshift and magnitude intervals. At z ≤ 1.5 and I ≤ 22.5, our photometric redshifts have slightly smaller uncertainties than those of G10. The improvement is much more significant at I ≥ 22.5 and z ≥ 1.5.
We also compare our photo-zs to those of the CFHTLS (Coupon et al. 2009). To do so, we select cluster galaxies in the XXM-LSS survey (e.g. Adami et al. 2011) with spectroscopic redshifts and check their corresponding photo-zs in the CFHTLS. We then calculate the photo-z uncertainties for this sample (I< 22.5 and z< 1.05) using LePhare and plot them in Fig. 5. The precision of our photo-zs is comparable to that of the CFHTLS, and becomes higher for redshifts higher than z = 0.8 owing to the use of near infrared data.
 |
Fig. 6 Reduced σ of photo-zs versus I band absolute magnitude (top) and versus galaxy photometric type T (bottom). Left: field galaxies, and right: cluster galaxies inside a 1 Mpc radius. Error bars for the reduced σ are Poissonian and therefore directly proportional to the inverse square root of the number of galaxies within the considered bin. Error bars for each type are simply the second order momentum of the galaxy type distributions in the selected type bins ([1; 7], [8; 12], [13; 19], [20; 31]). Crosses correspond to the G10 values, and circles to the present values. Shifts in types and magnitudes arise from plotting average values for two different samples. Refer to Sect. 2.1 for details of the photometric types. |
Similarly, we reproduce Figs. 14 and 15 of G10 in Fig. 6, using data drawn only from spectroscopic catalogues. We find that our present photometric redshift computations lead to a modest improvement in the photometric redshift quality for field galaxies. However, cluster galaxy photometric redshifts are systematically improved for early-type galaxies, as expected, thanks to the extinction artificially allowed for such types.
As a conclusion, the present photometric redshift computations allow us to achieve a constant photometric redshift precision of σz ~ 0.06 for all galaxy environments (field or cluster), magnitudes, and galaxy types.
2.2.4. Improvement achieved by the use of more than one near infrared band
While the interest of having several near infrared bands is evident at z ≥ 1, the effect at z ≤ 1 (where all our clusters are) is not so clear. We test this with Abell 851. This cluster has a comprehensive range of data, with Y,J,H, and Ks near infrared bands available. Our spectroscopic redshift catalogue typically extends from z ~ 0.2 to z ~ 0.8, so is perfectly suited to testing the photometric redshift quality over the entire redshift range covered by our cluster sample. We therefore compute photometric redshifts for this cluster by considering, in addition to the optical bands, the z′ band, then the z′ and Y bands, the z′,Y, and J bands, the z′,Y,J, and H bands, and finally the z′,Y,J,H, and Ks bands.
The mean photometric redshift precision (with catastrophic errors removed) between z = 0.2 and 0.8 does not depend significantly on the number of near infrared bands included. However, the number of completely wrong photometric redshifts (i.e. for which the difference between the spectroscopic and photometric redshift is greater than 0.3) tends to increase when the number of bands decreases. In the case of Abell 851, this percentage is close to 25% when at least one band is used among Y,J,H, or Ks, in addition to B,V,R,I, and z′, while it suddenly jumps to 38% when only B,V,R,I, and z′ are used.
This shows that within the redshift range considered (typically z ≤ 1), the photo-z accuracy is not significantly improved by collecting data for more than one band among Y,J,H, or Ks. However, including data for at least one of these bands will notably diminish the number of catastrophic errors.
3. Galaxy luminosity functions
We now compute the B,V,R, and I rest-frame band GLFs for 31 clusters, using photo-zs to estimate the cluster membership of galaxies.
We consider that a galaxy belongs to the cluster when its photo-z is within a ±0.2 interval centred on the cluster redshift. Once a galaxy is identified as a potential cluster member, we set its photo-z to the cluster redshift and re-run LePhare to obtain better estimates of redshift dependent parameters (such as absolute magnitude, colour, k-correction, etc.). We then subtract galaxy field counts measured in the same redshift interval using COSMOS data (Ilbert et al. 2009) to exclude galaxies at ±0.2 from the cluster redshift that are not cluster members.
When single band catalogues are merged to estimate galaxy photo-zs, all objects that are not detected in every band are rejected from the catalogue. Galaxies missed in this approach are mainly very faint galaxies, and we need to correct for this incompleteness to have the same number of galaxies in each band than in the original single band catalogue. Schechter functions are fitted up to the limiting magnitude at which our galaxy catalogues are 90% complete. We measure the completeness independently within each image by inserting and re-detecting stars simulated with the image point spread function (PSF). We obtain the 90% completeness limit in absolute magnitude by applying the k-correction and distance modulus.
Further details of our analysis are described step by step in the rest of this section.
3.1. Completeness
For each image, we first measure the PSF by fitting the stars with a Gaussian light distribution using the PSFEx software (Bertin 2011). With this PSF, we can model a set of Gaussian stars of various magnitudes. For each bin of 0.5 apparent magnitude, we simulate a hundred stars, insert them into the image, and try to re-detect them with SExtractor. The 90% completeness limit corresponds to the faintest magnitude bin in which we still re-detect at least 90 stars. This star completeness limit can be transformed to an approximate galaxy completeness limit by subtracting 0.5 from the magnitude (e.g. Adami et al. 2006).
In some cases, it is impossible to measure the PSF accurately because there are too few stars in the field. We then take the magnitude of the bin just brighter than the peak of the selected band magnitude histogram to be the 90% completeness limit. We verified that in most cases both methods give the same completeness limit estimate for the clusters for which it was possible to measure the PSF in the I band. The I band completeness limits for both methods are equal for 40% of the clusters and always differ by less than 1 mag. The average galaxy 90% completeness limit of our sample in the I band is 23.2.
We then translate these apparent magnitude completeness limits to absolute magnitude completeness limits by applying the k-correction and distance modulus. LePhare uses galaxy SED model libraries to estimate the theoretical k-corrections, which depend on galaxy types and redshifts. For each type, we measure the mean and the dispersion of the k-correction over galaxy templates in a redshift range of ±0.1 around the cluster redshift. This redshift interval is narrower than the one chosen for cluster membership to avoid too much contamination from foreground and background galaxies. The redshift range for cluster membership is larger as we then subtract field counts. We then define our corrections to be the mean values plus 2σ to be representative of 95% of our galaxy population. To keep a 90% completeness limit for all types of galaxies, the final k-corrections are set to the maximal values over all types. This step is illustrated in Eq. (1), where CX and Cx are the completeness limit in absolute and apparent magnitude in the x band, DM(z) the distance modulus, kx(z) the k-correction in the x band at redshift z, and T the galaxy type: 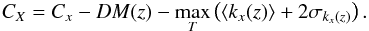 (1)
(1)
3.2. Computation of galaxy luminosity functions
We use the output catalogue of LePhare with photo-zs, positions, magnitudes, and absolute magnitudes for the B,V,R,I,Z, and J or Ks band data acquired by the original telescopes, and the magnitudes computed as if they had been observed with the VLT filters. We remove objects near saturated stars identified by eye in all our catalogues. Some stars are not assigned a null photo-z by LePhare. We then add an I band central surface brightness versus magnitude criterion to remove those stars. We correct for the dust extinction of the Milky Way using the cirrus maps of Schlegel et al. (1998). We assume that this correction is constant over each field and take the mean value of the extinction map area corresponding to the cluster position. This assumption is validated by the small area of our clusters compared to the resolution of the extinction maps. A cluster rarely occupies more than 4 × 4 pixel area of the cirrus map.
When combining all catalogues into a single one, we delete objects that are not detected in all 6 bands. We can estimate this loss of galaxies by comparing the number of galaxies in the merged catalogue to the single band catalogues. We first remove stars in single band catalogues using a surface brightness to magnitude diagram. This step mostly eliminates some very bright objects (bright and saturated stars) and faint spurious detections. We then measure the ratio of the numbers of galaxies from each of the single band catalogues to the combined catalogue in bins of 0.5 apparent magnitude. As we do not have the redshifts of the galaxies for which we wish to account for by applying this incompleteness correction, we apply these ratios as a weight coefficient to all galaxies belonging to the same apparent magnitude bin. Owing to the application of a k-correction, galaxies in the same apparent magnitude bin do not necessarily lie in the same absolute magnitude bin. Thus, applying this corrective factor directly to the magnitude bins instead of applying it to each galaxy would distort the absolute magnitude distribution. As we perform this correction on single band catalogues, we use the apparent magnitudes measured within the images. All subsequent steps are done using the magnitudes simulated by LePhare, which are as if they had been acquired with the VLT. This allows a more reliable comparison of clusters with each other.
We select galaxy cluster members as galaxies with photo-zs of ±0.2 around the cluster redshift. We verify in a V − I versus I colour−magnitude diagram that this subsample has a red sequence that agrees with that of simulated elliptical galaxies of Bruzual & Charlot (2003) at the cluster redshift. Once this pre-selection is done, we fix galaxy redshifts to the cluster redshift and re-run LePhare on this subsample without varying photo-zs. This allows LePhare to determine both the k-corrections and the absolute magnitudes of the cluster members more accurately because they are redshift dependent properties. The k-correction strongly depends on redshift at high redshift (Chilingarian et al. 2010). For example, mistaking a galaxy at z = 0.4 with a galaxy at z = 0.5 leads to a difference of 0.3 mag in the r band for an elliptical galaxy and 0.2 for a spiral galaxy, when adopting the galaxy colours g − r = 1.5 and 0.9 given in Fukugita et al. (1995) and using the on-line k-correction calculator of Chilingarian2.
We then perform a field galaxy background subtraction using COSMOS data (Ilbert et al. 2009), which are suitable for this subtraction because they include our redshift range and have accurate photo-zs. We first convert COSMOS magnitudes into our own set of filters by applying a correction factor that depends on galaxy type and redshift. Magnitudes in the COSMOS catalogue are already corrected for dust extinction. To avoid any k-correction effect, we do the background subtraction in apparent magnitude. Indeed, for our clusters, we compute the k-correction by setting all galaxies to the cluster redshift, while in COSMOS we have access to the k-correction of galaxies at their own photo-z. We apply the same photometric redshift cut applied to select our cluster members. We then count cluster and field galaxies in bins of 0.5 mag and apply a weight to all galaxies in each bin equal to the ratio of cluster to field galaxies in the bin. Field counts are first normalized to the cluster area assuming that the COSMOS field of view is 1.73 deg2 after eliminating the masked regions. This subtraction removes line of sight galaxies that are in our cluster redshift interval. Owing to the relatively small fields covered by our J band data, field counts cannot be estimated from our images, hence we use robust field counts taken from the literature. For the same reason, we are unable to investigate the properties of clusters at very large radii. We assume that our clusters lie in a region of radius 1 Mpc around their optical centre (position of the BCG or in some cases barycentre of bright galaxies). Once field counts are subtracted, we normalize GLFs by dividing by the 1 Mpc area converted to square degrees. We choose this normalization to compare our results to those of other authors who calculated GLFs normalized to 1 deg2.
We study the behaviour of clusters by fitting their B,V,R, and I band GLFs with a Schechter function (Eq. (2), Schechter 1976): ![\begin{equation} \label{eq:schech} N(M) = 0.4\log(10)\phi^*\left[10^{0.4(M^*-M)}\right]^{\alpha+1}\exp\left(-10^{0.4(M^*-M)}\right), \end{equation}](/articles/aa/full_html/2015/03/aa23796-14/aa23796-14-eq103.png) (2)where φ∗ is the characteristic number of galaxies per unit volume, M∗ the characteristic absolute magnitude, and α the faint-end slope of the GLF. We obtain these three parameters by applying a χ2 minimization algorithm. The error bars in these parameters are given by the covariance matrix (i.e. the second derivative matrix of the χ2 function with respect to its free parameters, evaluated at the best parameter values).
(2)where φ∗ is the characteristic number of galaxies per unit volume, M∗ the characteristic absolute magnitude, and α the faint-end slope of the GLF. We obtain these three parameters by applying a χ2 minimization algorithm. The error bars in these parameters are given by the covariance matrix (i.e. the second derivative matrix of the χ2 function with respect to its free parameters, evaluated at the best parameter values).
Since our clusters are rather distant, the numbers of points available to fit their GLFs do not justify the inclusion of a second function (either a second Schechter function, or a Gaussian) to fit our data, as sometimes found in the literature. Since we are particularly interested in the faint-end slope of the GLF, a single Schechter function is therefore appropriate.
3.3. Red-sequence and blue galaxy luminosity functions
To understand clearly the cluster properties, it is interesting to study their different galaxy populations. To do so, we need to distinguish the red sequence (RS) from the blue galaxies. The first roughly correspond to early-type galaxies and the second to late types.
To perform this separation, we use a V − I versus I colour−magnitude diagram plotting only galaxies selected as cluster members based on their photo-zs. As it has been observed that the RS slope does not evolve across our redshift range (e.g. De Lucia et al. 2007), we assume a fixed slope of −0.0436, as in Durret et al. (2011). For the ordinate of the RS, we first interpolate the elliptical galaxy colour value given in Fukugita et al. (1995) to each cluster redshift and select a wide RS with a width of 0.6 in magnitude. We then fit this preliminary RS with a free ordinate to get the final RS equation on which we set the smaller width of 0.3 used in De Lucia et al. (2007). We check that slightly modifying the value from Fukugita et al. (1995) does not significantly affect our RS selection: a shift of 0.2 to our first ordinate estimate results in only a few galaxies changing their population type.
Once we select our two galaxy populations, we compute GLFs for each population following the same method used for the whole sample. Field galaxies are separated using the red sequence calculated for each cluster.
The upper absolute magnitude limit for the Schechter fit is the magnitude corresponding to the 90% completeness and the lower limit is set to the magnitude of the cluster BCG, which is defined to be the brighest red sequence galaxy in the I band. Blue galaxies brighter than the BCG are removed as they are probably foreground galaxies incorrectly assumed to lie at the cluster redshift.
4. Results on galaxy luminosity functions
We present in this section our fitted Schechter functions to the GLFs of our clusters. We first analyse our fits to individual cluster GLFs and then study average behaviours by stacking the GLFs of several clusters. We consider the dependence of the Schechter parameters on redshift, mass, and cluster substructuring when our GLFs are stacked. For the stacked GLFs and their dependence on environment, we also derive GLFs for blue and red-sequence populations. To separate clusters in terms of redshifts, masses, and substructures, we limit our analysis to the RS galaxy population as there are too few blue galaxies for the considered number of clusters. This study will be conducted in a future paper when we have data for more clusters in hand.
 |
Fig. 7 Our GLFs in the B,V,R, and I rest-frame bands (from left to right) for CL0016+1609 (top) and LCDCS0504 (bottom). Red and blue points correspond to red-sequence and blue GLFs normalized to 1 deg2. The red vertical lines indicate the 90% completeness limit. The red and blue curves show the best Schechter fits to red-sequence and blue galaxies, and the faint-end slope parameter (α) is displayed in the corresponding colour. Only galaxies brighter than the 90% completeness limit are taken into account in the fits. In addition, we display GLFs only when more than 20 cluster galaxies are within the colour RS or blue bins and after subtracting the field. |
4.1. Individual cluster GLFs
We discuss individual cluster GLFs fitted with a Schechter function to the 90% magnitude completeness limits. These fits are done in the B,V,R, and I restframe bands and separately for red-sequence and blue galaxies. Two of our GLFs are shown in Fig. 7. All individual GLFs, and their Schechter fits when possible, are displayed for blue and RS populations in Appendix A (Fig. A.1 and Table A.1). As in Fig. 7, we only show galaxy counts when the selected cluster population has more than 20 members after removal of the background. We only display Schechter fits when they converge. In many cases, the fits indeed do not converge, probably because the completeness limit is too bright, even when the clusters have a relatively high number of galaxy counts. We display these clusters novertheless in Table A.1, as they are included in the stacked GLFs.
Figure 7 displays the GLFs for two clusters that span our redshift range: CL0016+1609 at z = 0.55 and LCDCS0504 at z = 0.79. CL0016+1609 represents our low-redshift clusters. We find rather flat RS GLFs but note the small decrease at the faint end characterized by an α parameter of about −0.5 in the V,R, and I restframe bands. In most of our low-redshift clusters, the observed cluster members lie primarily on the RS and too few blue galaxies are available to produce a blue GLF. LCDCS0504 represents our high-redshift clusters. Its RS GLFs sharply decline at their faint end. In contrast, its blue GLFs are rather flat except in the B band. For the high-redshift clusters, there are sometimes insufficient RS galaxies to obtain GLFs, as here in the B band. The large uncertainties in both counts and Schechter parameters highlight the need for stacking to draw any clear conclusion about the GLF behaviour.
For some clusters, the completeness limit is too bright to permit GLF fitting, especially for high-redshift clusters. This is true for CL_J0152.7-1357 and LCDCS 0853 for which deeper images would be required. Sometimes, the galaxy counts are too low to allow any fit of the GLF, placing in doubt the high masses assumed for these clusters. The masses we considered to select the DAFT/FADA clusters are drawn from X-ray surveys. The X-ray selection is often assumed to be superior to optical selection, because the X-ray flux is proportional to the gas density squared, while the rest-frame optical flux is roughly proportional to the galaxy density. However, compact X-ray sources may not have been subtracted reliably from many X-ray observations of our clusters (especially for ROSAT data), leading to overestimates of the cluster X-ray masses. This is true in particular for MACS J0647.7+7015, for which a bright source is very near the cluster in the XMM image. Clusters with a similarly small number of galaxy counts are F1557.19TC, MACS J0647.7+7015, MACS J0744.9+3927, SEXCLAS 12, GHO 1602+4312, and GHO 2155+0334. We eliminate them from our analysis.
As shown in Table A.1, the Schechter parameters derived for individual clusters can differ, even after removing the problematic clusters. The large error bars are due to the use of Poissonian errors and the large photo-z interval for cluster membership selection which causes more background galaxies to be subtracted. In the following parts we stack these clusters to study how the cluster properties depend on average on redshift, mass, substructures, and environment.
 |
Fig. 8 Our GLFs in the B,V,R and I rest-frame bands (from left to right) for clusters stacked together. Red and blue points respectively correspond to red-sequence and blue GLFs normalized to 1 deg2. The red and blue curves show the best Schechter fits to red-sequence and blue galaxies and the red and blue vertical lines indicate the corresponding 90% completeness limits. The slope of the fit α is given for each population. Refer to Table 2 for all Schechter fit parameters. |
Parameters of the best Schechter function fits for stacked cluster GLFs normalized to 1 deg2 for red-sequence and blue galaxies.
4.2. Stacked GLFs
We stack our clusters using the standard Colless method (Colless 1989) described in Popesso et al. (2006). The idea is to average cluster counts in each magnitude bin including all clusters that are 90% complete in this bin. Clusters first have to be normalized to the same area, chosen to be 1 deg2, and to a fixed richness. This richness is set to the number of galaxies detected to the completeness limit that encloses 90% of our sample. We do not choose our worst completeness limit because this would result in too few galaxies for the normalization. Also, we only include clusters that have more than 20 galaxies above the background for a given galaxy population (red or blue), to avoid a domination of the stack by the poorest clusters.
This method allows us to use the maximum amount of information for all our clusters. A more classical method would remove the information for the most complete bins as we would only be able to stack clusters reaching the same completeness limit. We could also stack different numbers of clusters for different completeness limits. This approach would allow to better control the evolution with completeness but it would generate many sets of figures partially containing the same information, thus affecting the legibility of the results.
For any method, the more complete our data, the farther we are from an average cluster. In a standard method, this problem affects only the stacks with the fewer clusters, while with the Colless method it affects the faintest bins of the GLF. We investigate this bias by stacking fixed numbers of clusters in each stack. We find that for the same completeness limit the stacked GLFs do not change much once we have four clusters in the stack. Thus, we require to have at least four clusters in each magnitude bin to take into account in the Colless stack, to avoid being dominated by individual cluster behaviours.
Error bars are calculated using the χ2 fit to our galaxy counts normalized to 1 deg2. Galaxy counts and their errors are summed following Eqs. (3) and (4) below, where N(j) and σ(j) are the stacked galaxy counts and galaxy count errors in magnitude bins j, the index i indicates single cluster values, Si is the area of cluster i, Nc(j) the number of clusters in bin j, and N0,i and ⟨ N0(j) ⟩ are the richness of the cluster i and the mean richness of clusters in bin j:
Individual variances are weighted by the square of the cluster area, as for the galaxy counts, and not simply the area. This is to retain the Poissonian distribution of the counts. We also fit Schechter functions to the stacked GLFs.
Stacked GLFs are shown in Fig. 8 for the RS and blue populations of the full cluster sample in the B,V,R, and I restframe bands. Results of their best Schechter fits are given in Table 2, along with the 90% completeness limit, the numbers of clusters in the stack, and the mean redshifts of the clusters in the stack.
We see a common behaviour for the V,R, and I bands. The RS GLF is close to that at low redshift but with a slight decline at the faint end. M∗ is almost the same for the three bands and α is slightly higher in the I band than in the other two bands. The blue GLFs are also very similar for these three bands, with steeper faint ends. In the I band, however, blue galaxy counts are smaller: as expected, blue galaxies are fainter in redder photometric bands. Blue and red GLFs cross at around V = −20, R = −20.5, and I = −20.3. These results represent clusters of mean redshift about z = 0.6. Results are quite different for the B band. The RS GLF also has a shallow decline at the faint end but the blue counts are higher than the red ones, implying that the blue galaxies are indeed brighter in the bluer bands.
There is also an excess of red-sequence galaxies at the bright end compared to the Schechter function, especially for the B and I bands. This kind of excess is often observed in clusters and some authors prefer to fit GLFs with a combination of a Schechter and a Gaussian (e.g. Biviano et al. 1995). However, this excess is puzzling for the B band, leading to very bright red-sequence galaxies for this optical band. This distribution of bright galaxies probably results from a complex interplay of intrinsic properties and applied k-correction. On examining the images, we indeed found that some BCGs appearing very bright in the I band are quite faint in the B band compared to other bright galaxies. The bright end of the red-sequence B band GLF is then dominated by the k-correction factor, which can be as high as 3 mag at these redshifts. It would be very useful to compare bright cluster galaxies in the B and I bands but this is beyond the scope of this paper. In the present study, we merely conclude that a Schechter function cannot simultaneously fit the bright and faint ends of the B band RS GLFs. In the rest of the paper, we concentrate mainly on the faint end of the GLFs, which is well constrained.
We wish to highlight several caveats of our method. The number of clusters with a sufficient number of blue galaxies to be stacked is two to three times lower than the number for RS galaxies. Thus, the blue GLFs are far more poorly constrained, as can be seen from their larger error bars for their best fit Schechter function parameters. In addition, as we used only clusters with a sufficient number of galaxies for each population, the RS GLF is biased toward red-galaxy rich clusters and the blue GLF toward blue-galaxy rich clusters. It would be more rigorous to consider the same clusters in both subsamples, but this would require deeper images. As a sanity check, we compared our GLFs with those obtained by considering only the few clusters presenting both large red and blue populations. Results are in good agreement, but error bars on the latest GLFs are much larger due to the very low number of clusters in the stack. When applying the Colless method for stacking, data for different clusters are stacked in different magnitude bins. As our survey spans a large redshift range (0.4 ≤ z< 0.9), each magnitude bin has a different mean redshift. Since the completeness limit is brighter for high-redshift clusters, the faint end of any stacked GLF will be dominated by lower redshift clusters. In the next subsection, we study GLFs in separate narrower redshift ranges to avoid this problem. We compare our stacked GLFs with field GLFs in Sect. 5.2.
 |
Fig. 9 Evolution of red-sequence GLFs with redshift in the B,V,R and I rest-frame bands (from left to right) for clusters stacked together. The first line of figures is for clusters with redshifts 0.40 ≤ z< 0.65 and the last line of figures is for clusters with redshifts 0.65 ≤ z< 0.90. Red crosses are red-sequence GLFs normalized to 1 deg2. The vertical red lines indicate the 90% completeness limit. Red curves are the best Schechter fits to red-sequence galaxies. The slope of the fit α is given with the number of clusters and the mean redshift of the stack. Refer to Table 3 for all Schechter fit parameters. |
Parameters of the best Schechter function fits for stacked cluster GLFs normalized to 1 deg2 for red sequence.
4.3. Evolution of GLFs with redshift
To investigate the evolution of the GLF with redshift, we apply the same analysis as previously, but separate our clusters between low (0.4 ≤ z< 0.65) and high (0.65 ≤ z< 0.9) redshifts. We obtain about 13 low and 4 high-redshift clusters, which each have more than 20 red-sequence galaxies depending on the photometric band. Unfortunatly, there are an unsufficient number of blue cluster galaxies to fit blue GLFs for these two redshift intervals. Our results for red-sequence galaxies are displayed in Fig. 9 and Table 3.
For the low-redshift sample, the faint end of the GLFs is similar to that of the stacked GLF for all clusters. This is evident from the similarity of the α parameters for both samples (Tables 2 and 3). This means that the faint end of our stacked GLF for all clusters is dominated by the low-redshift clusters. This is not surprising as there are fewer high redshift clusters than low-redshift ones. In addition, low-redshift clusters tend to have fainter completeness limits, hence are more likely to contribute to the faintest bins of the GLF than the high-redshift clusters.
The red GLFs of high-redshift clusters decline far more sharply at their faint end than the low-redshift clusters. The α parameter is significantly higher even with those large error bars. On the other hand, M∗ is slightly brighter than at low redshift and equal to that for the fit of all clusters taken together, meaning that the bright end is dominated by the high-redshift clusters. There may be more bright galaxies in high redshift clusters but this result can also be due to the k-correction which is higher for high-redshift clusters and tends to distort the bright end of the GLF such that the Schechter function is not appropriate any more. This can be clearly seen in the B band where there is a significantly larger number of red bright galaxies than predicted by the Schechter fit. The best-fit Schechter parameters for the B band are therefore unreliable for our high-redshift sample. We also note that there are very few clusters at high redshift, so that we need to target more high-redshift clusters to decrease the error bars in both the galaxy counts and Schechter parameters. In this particular case we took into account every magnitude bin with at least two clusters, a number that could be increased if we observed more clusters.
These dependences of the GLF properties on redshift are interpreted in terms of physical processes in our discussion.
We also note that overestimating the completeness limit in apparent magnitude would also lead to a sharp decline in the faint end of GLFs. This drop would also increase with redshift, because the completeness limit in absolute magnitude would be brighter at high redshift. Since we compute accurate 90% completeness limits for every image, we should not be affected by this effect.
 |
Fig. 10 Dependence of red-sequence GLFs on cluster X-ray luminosity in the B,V,R, and I rest-frame bands (from left to right) for clusters stacked together. The top line is for clusters with X-ray luminosities 8 × 1043<LX< 1045 erg s-1 and the bottom line is for clusters with X-ray luminosities LX> 1045 erg s-1. Red crosses are red-sequence GLFs normalized to 1 deg2. The vertical red lines indicate the 90% completeness limit. Red curves are the best Schechter fits to red-sequence galaxies. The slope of the fit α is given with the number of clusters and the mean redshift of the stack. |
4.4. Dependence of GLFs on cluster X-ray luminosity
We can similarly investigate the dependence of the GLF on a mass proxy. To achieve this, we separate clusters according to their X-ray luminosity, as measured in Guennou et al. (2014) who analysed the XMM-Newton data available for 42 DAFT/FADA clusters to derive their X-ray luminosities and temperatures, and search for substructures. We have about 5 clusters with a luminosity greater than 1045 erg s-1 and 4 with a lower luminosity depending on the considered optical band. These numbers are for RS galaxies; we do not have enough clusters with more than 20 blue galaxy members to compile blue GLFs in this case. We do not have accurate X-ray luminosities for the remaining clusters.
We find a steeper faint end for high-mass clusters than low-mass ones in every photometric band (Fig. 10). This could mean that the drop at the faint end of RS GLFs is essentially due to low mass clusters. In addition, the number of member galaxies is much larger for high X-ray luminosity clusters, which seems logical. However, we note that the number of clusters, especially for low-mass clusters, is small. In this particular case we recall that we consider every magnitude bin with at least two clusters. More data are needed to produce larger samples that cover a wide range of mass but similar in redshifts, and also to study the variations in the blue and red GLFs with mass. When our DAFT/FADA sample of about 90 clusters is complete, we should be able to draw conclusions about the GLF dependence on mass and redshift, provided that we have the same proportion of clusters with good completeness as in the present subsample. We also note that our clusters all have quite high X-ray luminosities. Our results therefore only concern clusters with X-ray luminosities LX> 8 × 1043 erg s-1.
 |
Fig. 11 Dependence of red-sequence GLFs on cluster substructures in the B,V,R, and I rest-frame bands (from left to right) for clusters stacked together. Only clusters with detected substructures are considered here (cf. Guennou et al. 2014). Red crosses are red-sequence GLFs normalized to 1 deg2. The vertical red lines indicate the 90% completeness limit. Red curves are the best Schechter fits to red-sequence galaxies. The slope of the fit α is given with the number of clusters and the mean redshift of the stack. |
4.5. Dependence of GLFs on substructures
We also search for differences between clusters with and without substructures. We consider clusters with substructures detected both with optical spectroscopy and X-ray data by Guennou et al. (2014). We have 3 clusters with substructures and 2 that are relaxed and sufficiently rich in red galaxies. For the remaining clusters, we have been unable to robustly confirm either the presence or absence of substructures and therefore discard these clusters in this subsection.
It is difficult to draw any conclusions about relaxed clusters as they are too few in number here and their completeness limit is too bright. Hence, we only study stacked clusters with substructures (Fig. 11). In this particular case we allow some bins to contain as few as two clusters to be able to draw the red-sequence GLFs. There is no clear difference in either the slope or M∗ of the Schechter function from those parameters for stacks containing all clusters, given the large error bars caused by the low number of clusters. In the I band, the very bright completeness limit does not allow us to study the faint part of the GLF.
For stacks of clusters with substructures, we also have higher counts for B band data than for other bands. This is consistent with a burst of star formation being produced as the clusters merge. These faint blue galaxies might also be the debris of any merging processes. However, we need data with a fainter completeness limit to investigate whether these debris dwarf galaxies exist.
Given the error bars in our Schechter parameters, our interpretations of the analysis of our substructured clusters are not statistically significant. We could reduce our error bars by either reducing the number of background galaxies, i.e. adding more clusters to the stacks, or computing more accurate photometric redshifts for field and cluster galaxies.
 |
Fig. 12 Galaxy luminosity functions in the B,V,R, and I rest-frame bands (from left to right) for stacked clusters in cores and outskirts. The first line of figures is for cluster cores (r ≤ 500 kpc) and the second line of figures for cluster outskirts (500 <r ≤ 1000 kpc). Red and blue points, respectively, correspond to red-sequence and blue GLFs normalized to 1 deg2. The red and blue curves show the best Schechter fits to red-sequence and blue galaxies and the red and blue vertical lines indicate the corresponding 90% completeness limits. The slope of the fit α is given for each population. |
4.6. Cluster cores and outskirts
In some cases, stellar formation can be triggered by in-fall in the outskirts of clusters (e.g. Biviano et al. 2011). To investigate whether this is true for clusters in general, we compute GLFs for the core (r ≤ 500 kpc) and outskirts (500 <r ≤ 1000 kpc) of clusters. We present the stacked GLFs for blue and red-sequence galaxies in different environments in Fig. 12. This figure is to be compared with Fig. 8 which displays cluster GLFs for the same cluster galaxies but in both the core and outskirt regions.
We only consider clusters which are richer than 20 galaxies once background galaxies have been subtracted, in the particular cluster area and for the selected colour population. For red-sequence GLFs, we see no difference between the faint ends for each cluster region. The α parameters are the same within the error bars for the cluster cores, outskirts, and both regions combined. However, the brighest galaxies tend to lie in cluster cores, so the excess seen at the bright end of GLFs diminishes in the cluster outskirts.
We find that there are more blue galaxies in the outskirts than in the cores, so blue GLFs in cluster cores can only be plotted for the B band for our data. In the B band, the blue core stacked GLF is much closer to the red-sequence GLF than when taking galaxies from all the regions together. In the outskirts, blue and red-sequence galaxies seem to equally contribute to the cluster population at any magnitude to our completeness limits for V,R, and I bands. However, the faint end of the GLF is steeper for blue galaxies, implying that at fainter magnitudes, blue galaxies are more numerous than red ones in cluster outskirts. In the B band, we detect far more bright blue galaxies than red-sequence galaxies, which indicates that the bright end of the blue B band GLF seen in Fig. 8 is dominated by the outskirts of clusters.
To conclude, we find an excess of blue galaxies in the outskirts compared to the core of clusters but in the cluster outskirts the GLFs of blue and red galaxies are very similar. This can be interpreted as an infall of blue galaxies on cluster outskirts from the field populations or by a burst of stellar formation.
 |
Fig. 13 Cluster and field GLFs in the B,V,R, and I rest-frame bands (from left to right). Red and blue points respectively correspond to red-sequence and blue stacked cluster GLFs normalized to 1 deg2. The red and blue plain curves show the best Schechter fits to red-sequence and blue galaxies and the red and blue vertical lines indicate the corresponding 90% completeness limits. The slope of the fit α is given for each population. Refer to Table 2 for cluster best Schechter fit parameters. The thin dotted and dashed curves correspond to the COSMOS field GLFs centered at redshifts z = 0.5 and z = 0.7 normalized to 1 deg2. The separation between red and blue field galaxies is done the same way than for clusters at the corresponding redshift (see text for details). |
5. Discussion
5.1. The faint end of the GLF
The GLF faint end depends on both colour and redshift. We have investigated this evolution by stacking cluster counts for blue and RS galaxies separated within colour-magnitude diagrams, and at either low redshift (0.40 ≤ z< 0.65) or high redshift (0.65 ≤ z< 0.90). We now interpret Fig. 8 and Table 2 in terms of colour evolution, and Fig. 9 and Table 3 in terms of redshift evolution.
Taking our full redshift cluster sample, we find steep blue GLFs with αblue ~ − 1.6 for all bands, owing to the large error bars caused by the small amount of clusters with a sufficient number of blue galaxies. This is more or less consistent with similar analyses for clusters at lower redshifts. For red-sequence galaxies, we see a small drop at the faint end with a slope αred ~ − 0.4 for B and I bands and αred ~ − 0.8 for V and R, while lower-redshift clusters usually present a flat faint end for the red-sequence population. In our redshift range, red galaxies dominate the blue population for magnitudes brighter than V = −20, R = −20.5, and I = −20.3. Above these magnitudes, blue faint counts become higher than red ones. In the B band, the blue galaxies dominate over red ones at all magnitudes, possibly because blue galaxies are brighter in the blue band. We note however that we draw this conclusion for only five clusters with sufficient blue galaxies in the B band.
If we now separate our clusters between high and low redshift, we find that the red-sequence faint-end drop is more important at high redshift. At low redshift, the slope is comparable to that for all clusters combined. This is because we perform our stacking using the Colless method, in which the faint end of the GLF is dominated by the low-redshift clusters in the stack. At higher redshifts, we find slopes of between αred ~ 0.1 and αred ~ 0.7. We have only a few clusters at high redshift, though the error bars in the slope are in the range 0.5 to 1. Data for more high-redshift clusters are needed to fully investigate this behaviour. We also have insufficient clusters with enough blue galaxies to produce blue GLFs at these redshifts.
When interpreting these results in terms of galaxy evolution, we can conclude that blue star forming galaxies are quenched in dense cluster environments to enrich the red-sequence population between high redshifts and today. However, that the properties of blue galaxies in clusters are similar at z ~ 0 and our redshift range (0.4 ≤ z< 0.9) implies that clusters continue to accrete galaxies from the field across a wide range of redshift.
This deficit of faint red galaxies at z ~ 0.7 has already been observed by many authors (e.g. Tanaka et al. 2005; De Lucia et al. 2007; Rudnick et al. 2009; Stott et al. 2007; Gilbank et al. 2008; Vulcani et al. 2011). In particular, our strong change in the RS faint-end slope is in good agreement with that found for EDisCs clusters (see Fig. 5 of Rudnick et al. 2009, and our Fig. 9). Kodama et al. (2004) also observed a compensation for the decrease in the faint red galaxy counts by those of bluer galaxies. Furthermore, this evolution agrees with the empirical model of Peng et al. (2010) which predicts a difference between the blue and red faint-end slopes of the order of unity owing to mass quenching being proportional to the star formation rate (SFR) of galaxies in our redshift range.
On the other hand, some authors find no evolution in the RS GLFs with redshift (e.g. Andreon 2006; De Propris et al. 2007, 2013). De Propris et al. (2013) wrote that surface brightness selection effects could account for claims of evolution at the faint end. Observations with various surface brightness limits are required to confirm this hypothesis.
We can only compare our results with GLFs that have been fitted by a single Schechter function. It is sometimes useful to fit GLFs with both a Gaussian and a Schechter function (Biviano et al. 1995) or with two Schechter functions (Popesso et al. 2006). The first case allows to better account for the excess of very bright galaxies observed in certain clusters, while the second fits well the upturn of very faint counts that can exist for dwarf galaxies at fainter magnitudes than the usual GLF flat faint end. In the present study, we chose to use a single Schechter fit, as our data are insufficiently complete to investigate the upturn of very faint galaxies found in Popesso et al. (2006). More sophisticated fitting with a higher number of degrees of freedom for the fit would require a larger number of data points and a fainter completeness limit. We cannot compare our results with those of the following authors because their approaches differ from ours:
-
Mancone et al. (2012) studied GLFs only in apparent magnitude. Thus, the k-correction is not taken into account and it is difficult to know exactly which population is studied and the precise completeness limit, particularly since they consider high-redshift clusters (1 <z< 1.5);
-
Muzzin et al. (2008) fixed the slope of the faint end α = −0.8 and fit the two other parameters (φ∗ and M∗).
5.2. Dependence on environment
Another important debate concerns the interaction between clusters and their environment. To properly address this problem, it is necessary to investigate it on three different scales. First, we compare cluster GLFs to field GLFs, then study the dependence of GLFs on various cluster properties before finally studying the variations inside clusters.
We first compare our cluster GLFs calculated in Sect. 4.2 with field GLFs derived from COSMOS data (Ilbert et al. 2009). We compute two field GLFs for redshifts of 0.5 and 0.7 with a width of ± 0.2 around these redshifts to be consistent with the way we made our cluster GLFs. We separate blue from red field galaxies by applying a colour-magnitude relation similar to the one used for our clusters. The ordinate of this red sequence is equal to the colour of elliptical galaxies at the central redshift taken from Fukugita et al. (1995) and the width of the RS is ± 0.3 in colour. This allows us to compare cluster and field GLFs computed in the same way with the same separation between red and blue galaxies. Results are shown in Fig. 13.
The GLFs of blue galaxies are similar for the field and clusters in the V,R, and I bands, while we find more blue galaxies in our clusters than the field for the B band but with a similar shape. The shape of the red-sequence GLFs are also almost identical. However, there are about ten times more red galaxies in clusters than the field. Another difference is the GLF of cluster RS galaxies has a sharper drop at the faint end at high redshift, while the field red GLFs remain unchanged across our redshift range. This apparent lack of evolution in early-type field galaxies was assessed in Zucca et al. (2006), who proposed that it highlights an efficient transformation of blue to red galaxies in higher density environments. Inside clusters, interactions between galaxies are more likely to happen, boosting this evolution, while in the field galaxy interactions are less frequent and the red population increases at a far lower rate.
We wrote above that the average cluster GLF of RS galaxies depends on mass. GLFs of more massive clusters ressemble more the GLFs of nearby clusters with a flat faint end. This implies that these high-redshift massive clusters are more evolved than their companions at the same redshift either because they formed earlier or in a denser environment.
We find no remarkable difference between the properties of general GLF and those of the GLF of only substructured clusters. However, we have only three clusters that can be studied in this way, leading to large error bars. We know that the merging of galaxy clusters can strongly affect the slope of the GLF, as illustrated by studies of cluster pairs or violently merging clusters (e.g. Durret et al. 2010, 2011, 2013). Hence we would expect that substructured clusters present a variation of their faint-end slope compared to others. More data at different stages of the merging process are needed before we can draw stronger conclusions.
Finally, we find differences in GLF behaviours between cluster cores and outskirts. We find more bright galaxies in the core compared to the outskirts, in agreement with CDM models that predict the most massive galaxies to lie at the cluster cores. We also find more blue galaxies in the outskirts than in the core. This larger number of blue galaxies in the outskirts could be explained by infalls from the field. However, the red GLF faint end remains the same in any part of the cluster. Some authors found steeper faint-end slopes in cluster outskirts (e.g. Adami et al. 2008; Boué et al. 2008). In particular, strong variations in α have been observed in the highly structured Coma cluster, which can be probed with high completeness and quality due to its proximity (Adami et al. 2007a,b).
5.3. Evolution of cluster galaxy types with redshift
With colour-selected populations, we analyse the variations of the galaxy types within clusters. We consider blue and red galaxies selected in a colour−magnitude diagram and for which field galaxies have been subtracted. We also remove galaxies that are outside disks of 1 Mpc radius centered on cluster optical centres. We compute the percentages of each type for every cluster and then average them over clusters by stacks of four clusters. Error bars correspond to the dispersion in values over all clusters within a stack. This allows us to study the evolution of cluster galaxy types with redshift from z = 0.4 to z = 0.9. We limit our sample to galaxies brighter than I = −21 and only consider clusters that are at least 90% complete at this magnitude.
Looking at Fig. 14, we note a clear decrease in the fraction of early-type galaxies from low to high redshift, while the fraction of late-type galaxies increases with redshift. This scenario agrees with galaxy-evolution scenarios where spiral galaxies evolve into ellipticals. Furthermore, it is consistent with the evolution of early-type and late-type GLF faint ends that we discussed in Sect. 5.1.
 |
Fig. 14 Evolution of cluster galaxy type percentages with redshift. Each point represents the mean value of a percentage over four clusters. Red dots are red (early type) galaxies and blue triangles correspond to blue (late type) galaxies. The blue dashed line corresponds to the blue fraction from Ellingson et al. (2001). |
Our early-type fraction decreases from fred = 0.81 ± 0.17 at z = 0.42 to fred = 0.50 ± 0.27 at z = 0.66. We compare these results to spectral classifications from Ellingson et al. (2001), and also to the morphology-density relation found by Smith et al. (2005) and Postman et al. (2005). In the first case, we overplot on Fig. 14 their best fit to the blue fraction of clusters between 0.18 <z< 0.55. The blue galaxies taken into account in this study are spectroscopic cluster members and are separated in a colour–magnitude diagram. They are also brighter than R = −20, such that it is very close to the low-redshift sample of galaxies we use. We find a very good agreement between our blue fraction and the one from Ellingson et al. (2001) at all redshifts. We do not attempt to separate our sample into high-density (cluster cores) and medium-density regions, so our results should compare with the Σ = 100 Mpc-2 and Σ = 1000 Mpc-2 curves in Fig. 3 of Smith et al. (2005) and Fig. 13 of Postman et al. (2005). We find an overall good agreement. At intermediate redshift (z = 0.4), our early-type fraction lies within the fractions of medium and high density of the cited authors (fE + S0 = 0.6 and fE + S0 = 0.85). At higher redshifts (z = 0.7), our values are also consistent with the interval 0.55 <fE + S0< 0.8 found by the previous authors, but only when taking our error bars into account. However, one must note that previous authors used a classification based on galaxy shapes while our work relies on the galaxy colours. The trend of a decreasing early-type fraction with increasing redshift is clearly seen whichever method is used. A comparison of both spectral and morphological methods for the same galaxy sample would help understanding the different biases of each method. Apart from possible biases, the morphological and spectral evolutions might also be different.
5.4. A scenario for the evolution of clusters
Peng et al. (2010) empirically showed that the red sequence is fed by two different types of quenching that happen at different redshifts. At high redshift (z> 2), environmental effects dominate and the red sequence grows through the quenching of blue star forming galaxies that fall into the dark matter halo of the forming group (“environment quenching”). At lower redshift (0 <z< 1), galaxies are quenched proportionally to their star forming rate and progressively enrich the red sequence (“mass quenching”).
Cosmological models of cluster mass assembly predict the most intense mass growth of clusters at redshifts earlier than z ~ 0.8 to 1 (e.g. Adami et al. (2013) from the Millennium simulation). In this redshift interval, clusters grow through accretion of major groups, and this already provides a pre-processed galaxy population formed by the cited “environment quenching”. This explains the fact that clusters at z> 1 already exhibit a red sequence (Gobat et al. 2011; Fassbender et al. 2011).
At lower redshifts (z< 0.8), group accretion only concerns more modest groups in terms of relative mass and Guennou et al. (2014) have shown in our survey that this accretion only involves less than 10% to 15% of the cluster mass. In the 0 <z< 0.8 redshift interval, the galaxies accreted by clusters are therefore not only coming from red populations preprocessed in groups but also from regular blue field galaxy populations. In the meantime, blue galaxies evolve into red ones following the “mass quenching” defined in Peng et al. (2010).
We can show that this evolutionary scenario for clusters is assessed by the main results of our paper as follows:
-
1)
Red-sequence cluster galaxies show a drop at their faint end which is more significant at higher redshift.
-
2)
Blue cluster GLFs are steeper than those of RS galaxies and are similar across our redshift range and at lower redshift.
-
3)
There is a large excess of red galaxies in clusters compared to the field while the blue galaxies behave more or less in the same way. The red GLFs of clusters continue to evolve across our redshift range, while for the field there is little evolution.
-
4)
There is a strong decrease of the early-type fraction in clusters with increasing redshift.
-
5)
There might be infalls of blue galaxies from the field to the cluster outskirts. This could explain why we find so few blue galaxies in cluster cores compared to the outskirts.
-
6)
When considering our more massive clusters, we find a red-sequence GLF that is consistent with those observed at z = 0 with a flat faint end.
6. Conclusion
We have computed GLFs in the B,V,R, and I rest-frame bands for 31 clusters of the DAFT/FADA survey using photo-zs, the largest medium-to-high redshift (0.4 ≤ z< 0.9) cluster sample to date.
To overcome the problem of lower photometric redshift precision in clusters mainly due to a lack of red enough spectral templates, we have artificially allowed the inclusion of extinction in early-type galaxies. This process does not affect drastically photometric redshifts outside clusters but increases their quality by ~50% inside clusters, allowing us to reach the same precision inside and outside the cluster.
Another result of this paper is that GLFs are strongly correlated to the completeness of the data. This should be kept in mind when comparing GLFs from different studies.
We have shown that GLFs have similar properties for the B,V,R, and I rest-frame bands with small differences for the B band blue GLFs. We found a sharp decline in the red faint end that increases with redshift: αred ~ − 0.5 at 0.40 ≤ z< 0.65 and αred> 0.1 at 0.65 ≤ z< 0.90. High mass clusters appear to have a flat faint end which may indicate that galaxy evolution is more rapid in denser environments or different formation epochs for clusters of different masses. Blue GLFs are steeper with αblue ~ − 1.6 and do not seem to evolve with redshift.
Our study of galaxy types with redshift shows an evolution of late-type galaxies to early types from high z until today that could account for the drop found at the red faint end.
We also found an excess of red galaxies in clusters compared to the field, while blue galaxies have more or less identical GLFs.
Our results imply that clusters have formed at high redshift (z> 0.9) and that blue cluster galaxies are efficiently quenched into red ones between z ~ 0.9 and today. During this time interval, galaxy clusters continue to accrete faint galaxies from the field environment.
Finally, we note an inversion of the red to blue population dominance at magnitudes V = −20, R = −20.5, and I = −20.3 at redshift 0.40 ≤ z< 0.90. We plan to compute stellar mass functions (SMFs) in a future paper, to see whether the blue and red populations have comparable behaviours in mass and luminosity. This would allow us to compare our results with simulations of galaxy cluster formation.
Online material
Appendix A: Individual cluster GLFs
 |
Fig. A.1 GLFs in the B,V,R and I rest-frame bands (from left to right) for individual clusters ordered by right ascension. Red and blue points correspond to red-sequence and blue GLFs normalized to 1 deg2. The red vertical lines indicate the 90% completeness limit. The red and blue curves show the best Schechter fits to red sequence and blue galaxies, and the faint-end slope parameter (α) is displayed in the corresponding colour. Only galaxies brighter than the 90% completeness limit are taken into account in the fits. Also, we only show GLFs richer than 20 galaxies after the colour separation and after subtracting the field. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
Parameters of the best Schechter function fit for every cluster normalized to 1 deg2.
The current status of the survey, with a list of refereed publications, can be found at http://cesam.lam.fr/DAFT/project.php
Acknowledgments
We thank Greg Rudnick for useful discussions. We also thank Eric Jullo, Marceau Limousin, Dennis Zaritsky for comments on earlier versions of this paper. We are grateful to the referee for interesting comments. F.D. acknowledges long-term financial support from CNES. I.M. acknowledges financial support from the Spanish grant AYA2010-15169 and from the Junta de Andalucia through TIC-114 and the Excellence Project P08-TIC-03531. Based on observations made with the FORS2 multi-object spectrograph mounted on the Antu VLT telescope at ESO-Paranal Observatory (programme 085.A-0016, 089A-0666, 191.A-0268; PI: C. Adami). Also based on observations made with the Italian Telescopio Nazionale Galileo (TNG) operated on the island of La Palma by the Fundación Galileo Galilei of the INAF (Istituto Nazionale di Astrofisica) at the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias. Based on observations obtained with MegaPrime/MegaCam, a joint project of CFHT and CEA/IRFU, at the Canada-France-Hawaii Telescope (CFHT) which is operated by the National Research Council (NRC) of Canada, the Institut National des Science de l’Univers of the Centre National de la Recherche Scientifique (CNRS) of France, and the University of Hawaii. This work is based in part on data products produced at Terapix available at the Canadian Astronomy Data Centre as part of the Canada-France-Hawaii Telescope Legacy Survey, a collaborative project of NRC and CNRS. Also based on observations obtained at the WIYN telescope (KNPO). The WIYN Observatory is a joint facility of the University of Wisconsin-Madison, Indiana University, Yale University, and the National Optical Astronomy Observatory. Kitt Peak National Observatory, National Optical Astronomy Observatory. It is operated by the Association of Universities for Research in Astronomy (AURA) under cooperative agreement with the National Science Foundation. Also based on observations obtained at the MDM observatory (2.4 m telescope). MDM consortium partners are Columbia University Department of Astronomy and Astrophysics, Dartmouth College Department of Physics and Astronomy, University of Michigan Astronomy Department, The Ohio State University Astronomy Department, and the Ohio University Dept. of Physics and Astronomy. Also based on observations obtained at the Southern Astrophysical Research (SOAR) telescope, which is a joint project of the Ministério da Ciência, Tecnologia, e Inovação (MCTI) da República Federativa do Brasil, the US National Optical Astronomy Observatory (NOAO), the University of North Carolina at Chapel Hill (UNC), and Michigan State University (MSU). Also based on observations obtained at the Cerro Tololo Inter-American Observatory, National Optical Astronomy Observatory, which are operated by the Association of Universities for Research in Astronomy, under contract with the National Science Foundation. Also based on observations made with the Gran Telescopio Canarias (GTC), installed at the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias, on the island of La Palma. Also based on archive data collected at the Subaru Telescope, which is operated by the National Astronomical Observatory of Japan. Finally, this research has made use of the VizieR catalogue access tool at the CDS, Strasbourg, France.
References
- Adami, C., Picat, J. P., Savine, C., et al. 2006, A&A, 451, 1159 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Adami, C., Durret, F., Mazure, A., et al. 2007a, A&A, 462, 411 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adami, C., Picat, J.-P., Durret, F., et al. 2007b, A&A, 472, 749 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adami, C., Ilbert, O., Pelló, R., et al. 2008, A&A, 491, 681 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adami, C., Le Brun, V., Biviano, A., et al. 2009, A&A, 507, 1225 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adami, C., Mazure, A., Pierre, M., et al. 2011, A&A, 526, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adami, C., Durret, F., Guennou, L., & Da Rocha, C. 2013, A&A, 551, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andreon, S. 2004, A&A, 416, 865 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andreon, S. 2006, MNRAS, 369, 969 [NASA ADS] [CrossRef] [Google Scholar]
- Andreon, S., Cuillandre, J.-C., Puddu, E., & Mellier, Y. 2006, MNRAS, 372, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Arnouts, S., Cristiani, S., Moscardini, L., et al. 1999, MNRAS, 310, 540 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E. 2006, ASP Conf. Ser., 351, 112 [Google Scholar]
- Bertin, E. 2011, ASP Conf. Ser., 442, 435 [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 317, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertin, E., Mellier, Y., Radovich, M., et al. 2002, ASP Conf. Ser., 281, 228 [Google Scholar]
- Biviano, A., Durret, F., Gerbal, D., et al. 1995, A&A, 297, 610 [NASA ADS] [Google Scholar]
- Biviano, A., Fadda, D., Durret, F., Edwards, L. O. V., & Marleau, F. 2011, A&A, 532, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boué, G., Adami, C., Durret, F., Mamon, G. A., & Cayatte, V. 2008, A&A, 479, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., & Heckman, T. M. 1999, ApJ, 519, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Chilingarian, I. V., Melchior, A.-L., & Zolotukhin, I. Y. 2010, MNRAS, 405, 1409 [NASA ADS] [CrossRef] [Google Scholar]
- Christlein, D., & Zabludoff, A. 2003, ApJ, 591, 764 [NASA ADS] [CrossRef] [Google Scholar]
- Colless, M. 1989, MNRAS, 237, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Coupon, J., Ilbert, O., Kilbinger, M., et al. 2009, A&A, 500, 981 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Lucia, G., Poggianti, B. M., Aragón-Salamanca, A., et al. 2004, ApJ, 610, L77 [NASA ADS] [CrossRef] [Google Scholar]
- De Lucia, G., Poggianti, B. M., Aragoń-Salamanca, A., et al. 2007, MNRAS, 374, 809 [NASA ADS] [CrossRef] [Google Scholar]
- De Propris, R., Stanford, S. A., Eisenhardt, P. R., Dickinson, M., & Elston, R. 1999, AJ, 118, 719 [NASA ADS] [CrossRef] [Google Scholar]
- De Propris, R., Colless, M., Driver, S. P., et al. 2003, MNRAS, 342, 725 [NASA ADS] [CrossRef] [Google Scholar]
- De Propris, R., Stanford, S. A., Eisenhardt, P. R., Holden, B. P., & Rosati, P. 2007, AJ, 133, 2209 [NASA ADS] [CrossRef] [Google Scholar]
- De Propris, R., Phillipps, S., & Bremer, M. N. 2013, MNRAS, 434, 3469 [NASA ADS] [CrossRef] [Google Scholar]
- Dressler, A. 1978, ApJ, 223, 765 [NASA ADS] [CrossRef] [Google Scholar]
- Driver, S. P., Fernandez-Soto, A., Couch, W. J., et al. 1998, ApJ, 496, L93 [NASA ADS] [CrossRef] [Google Scholar]
- Durret, F., Laganá, T. F., Adami, C., & Bertin, E. 2010, A&A, 517, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Durret, F., Laganá, T., & Haider, M. 2011, A&A, 529, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Durret, F., Perrot, C., Lima Neto, G. B., et al. 2013, A&A, 560, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ellingson, E., Lin, H., Yee, H. K. C., & Carlberg, R. G. 2001, ApJ, 547, 609 [NASA ADS] [CrossRef] [Google Scholar]
- Fassbender, R., Nastasi, A., Böhringer, H., et al. 2011, A&A, 527, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fukugita, M., Shimasaku, K., & Ichikawa, T. 1995, PASP, 107, 945 [NASA ADS] [CrossRef] [Google Scholar]
- Gaidos, E. J. 1997, AJ, 113, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Garilli, B., Maccagni, D., & Andreon, S. 1999, A&A, 342, 408 [NASA ADS] [Google Scholar]
- Gilbank, D. G., Yee, H. K. C., Ellingson, E., et al. 2008, ApJ, 673, 742 [NASA ADS] [CrossRef] [Google Scholar]
- Gobat, R., Daddi, E., Onodera, M., et al. 2011, A&A, 526, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gonzalez, A. H., Zaritsky, D., Dalcanton, J. J., & Nelson, A. 2001, ApJS, 137, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Goto, T., Okamura, S., McKay, T. A., et al. 2002, PASJ, 54, 515 [NASA ADS] [CrossRef] [Google Scholar]
- Guennou, L., Adami, C., Ulmer, M. P., et al. 2010, A&A, 523, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guennou, L., Adami, C., Durret, F., et al. 2014, A&A, 561, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gunn, J. E., & Gott, J. R., III 1972, ApJ, 176, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., Tresse, L., Zucca, E., et al. 2005, A&A, 439, 863 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ilbert, O., Arnouts, S., McCracken, H. J., et al. 2006a, A&A, 457, 841 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ilbert, O., Lauger, S., Tresse, L., et al. 2006b, A&A, 453, 809 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ilbert, O., Capak, P., Salvato, M., et al. 2008, ApJ, 690, 1236 [Google Scholar]
- Kodama, T., Yamada, T., Akiyama, M., et al. 2004, MNRAS, 350, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Lanzoni, B., Guiderdoni, B., Mamon, G. A., Devriendt, J., & Hatton, S. 2005, MNRAS, 361, 369 [NASA ADS] [CrossRef] [Google Scholar]
- Lopez-Cruz, O., Yee, H. K. C., Brown, J. P., Jones, C., & Forman, W. 1997, ApJ, 475, 97 [Google Scholar]
- Lugger, P. M. 1986, ApJ, 303, 535 [NASA ADS] [CrossRef] [Google Scholar]
- Lugger, P. M. 1989, ApJ, 343, 572 [NASA ADS] [CrossRef] [Google Scholar]
- Lumsden, S. L., Collins, C. A., Nichol, R. C., Eke, V. R., & Guzzo, L. 1997, MNRAS, 290, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Mancone, C. L., Gonzalez, A. H., Brodwin, M., et al. 2010, ApJ, 720, 284 [NASA ADS] [CrossRef] [Google Scholar]
- Mancone, C. L., Baker, T., Gonzalez, A. H., et al. 2012, ApJ, 761, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Martini, P., Dicken, D., & Storchi-Bergmann, T. 2013, ApJ, 766, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Menci, N., Cavaliere, A., Fontana, A., Giallongo, E., & Poli, F. 2002, ApJ, 575, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Moore, B., Katz, N., Lake, G., Dressler, A., & Oemler, A. 1996, Nature, 379, 613 [NASA ADS] [CrossRef] [Google Scholar]
- Moore, B., Lake, G., & Katz, N. 1998, ApJ, 495, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Muzzin, A., Wilson, G., Lacy, M., Yee, H. K. C., & Stanford, S. A. 2008, ApJ, 686, 966 [NASA ADS] [CrossRef] [Google Scholar]
- Paolillo, M., Andreon, S., Longo, G., et al. 2001, A&A, 367, 59 [Google Scholar]
- Peng, Y.-J., Lilly, S. J., Kovac, K., et al. 2010, ApJ, 721, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Poggianti, B. M., von der Linden, A., De Lucia, G., et al. 2006, ApJ, 642, 188 [NASA ADS] [CrossRef] [Google Scholar]
- Polletta, M., Wilkes, B. J., Siana, B., et al. 2006, ApJ, 642, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Polletta, M., Tajer, M., Maraschi, L., et al. 2007, ApJ, 663, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Popesso, P., Biviano, A., Böhringer, H., & Romaniello, M. 2006, A&A, 445, 29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Postman, M., Franx, M., Cross, N. J. G., et al. 2005, ApJ, 623, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Rauzy, S., Adami, C., & Mazure, A. 1998, A&A, 337, 31 [NASA ADS] [Google Scholar]
- Rudnick, G., Von der Linden, A., Pelló, R., et al. 2009, ApJ, 700, 1559 [NASA ADS] [CrossRef] [Google Scholar]
- Secker, J., Harris, W. E., & Plummer, J. D. 1997, PASP, 109, 1377 [NASA ADS] [CrossRef] [Google Scholar]
- Schechter, P. 1976, ApJ, 203, 297 [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Smail, I., Edge, A. C., Ellis, R. S., & Blandford, R. D. 1998, MNRAS, 293, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, G. P., Treu, T., Ellis, R. S., Moran, S. M., & Dressler, A. 2005, ApJ, 620, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Stott, J. P., Smail, I., Edge, A. C., et al. 2007, ApJ, 661, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, M., Kodama, T., Arimoto, N., et al. 2005, MNRAS, 362, 268 [NASA ADS] [CrossRef] [Google Scholar]
- Trentham, N. 1998, MNRAS, 294, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Tully, R. B., Somerville, R. S., Trentham, N., & Verheijen, M. A. W. 2002, ApJ, 569, 573 [NASA ADS] [CrossRef] [Google Scholar]
- Valotto, C. A., Nicotra, M. A., Muriel, H., & Lambas, D. G. 1997, ApJ, 479, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Vulcani, B., Poggianti, B., Aragón-Salamanca, A., et al. 2011, MNRAS, 412, 246 [NASA ADS] [CrossRef] [Google Scholar]
- Yagi, M., Kashikawa, N., Sekiguchi, M., et al. 2002, AJ, 123, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Zucca, E., Ilbert, O., Bardelli, S., et al. 2006, A&A, 455, 879 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Parameters of the best Schechter function fits for stacked cluster GLFs normalized to 1 deg2 for red-sequence and blue galaxies.
Parameters of the best Schechter function fits for stacked cluster GLFs normalized to 1 deg2 for red sequence.
Parameters of the best Schechter function fit for every cluster normalized to 1 deg2.
All Figures
 |
Fig. 1 Astrometric shifts (α, δ) for CL J0152.7-1357 between the objects detected in the i′ band and the B,V,R,z′, and Ks bands. The figure at the lower right shows the histograms of the shifts between the i′ band and the other bands. |
| In the text | |
 |
Fig. 2 Mean and uncertainty in the difference between the star and galaxy spectroscopic redshift-based shifts for the different magnitude bands considered over our 31 fields. |
| In the text | |
 |
Fig. 3 Top: mean and uncertainty on the difference between the star and galaxy spectroscopic redshift-based shifts in the I band versus the number of spectroscopic redshifts available over our 31 fields. Bottom: histogram of the number of stars used for the calibration of each cluster. |
| In the text | |
 |
Fig. 4 Photometric versus spectroscopic redshifts when allowing extinction in all galaxies (left) or only in spiral galaxies (right) for the MS1054-03 field. The full lines show the lines of equality of the photometric and spectroscopic redshifts and the dotted lines show the scatter at ± 0.2. See text for details. |
| In the text | |
 |
Fig. 5 Top: mean individual photo-z uncertainties as a function of I magnitude in three redshift intervals, colour coded as: blue: z = [0.; 1.05], green: z = [1.05; 2.0], red: z = [2.0; 2.5]. Bottom: mean individual photo-z uncertainties as a function of photo-z for various I magnitude intervals, colour coded as: blue: I = [19.5; 22.5], red: F814W = [19.5; 24.5]. The vertical dotted line shows the z ≤ 1.5 limit we suggested to adopt in G10. In both plots, dotted lines correspond to G10 and continuous lines to the present work. The black curves correspond to the CFHTLS with I< 22.5 and z< 1.05 and should be compared with the blue curves (see text for details). |
| In the text | |
 |
Fig. 6 Reduced σ of photo-zs versus I band absolute magnitude (top) and versus galaxy photometric type T (bottom). Left: field galaxies, and right: cluster galaxies inside a 1 Mpc radius. Error bars for the reduced σ are Poissonian and therefore directly proportional to the inverse square root of the number of galaxies within the considered bin. Error bars for each type are simply the second order momentum of the galaxy type distributions in the selected type bins ([1; 7], [8; 12], [13; 19], [20; 31]). Crosses correspond to the G10 values, and circles to the present values. Shifts in types and magnitudes arise from plotting average values for two different samples. Refer to Sect. 2.1 for details of the photometric types. |
| In the text | |
 |
Fig. 7 Our GLFs in the B,V,R, and I rest-frame bands (from left to right) for CL0016+1609 (top) and LCDCS0504 (bottom). Red and blue points correspond to red-sequence and blue GLFs normalized to 1 deg2. The red vertical lines indicate the 90% completeness limit. The red and blue curves show the best Schechter fits to red-sequence and blue galaxies, and the faint-end slope parameter (α) is displayed in the corresponding colour. Only galaxies brighter than the 90% completeness limit are taken into account in the fits. In addition, we display GLFs only when more than 20 cluster galaxies are within the colour RS or blue bins and after subtracting the field. |
| In the text | |
 |
Fig. 8 Our GLFs in the B,V,R and I rest-frame bands (from left to right) for clusters stacked together. Red and blue points respectively correspond to red-sequence and blue GLFs normalized to 1 deg2. The red and blue curves show the best Schechter fits to red-sequence and blue galaxies and the red and blue vertical lines indicate the corresponding 90% completeness limits. The slope of the fit α is given for each population. Refer to Table 2 for all Schechter fit parameters. |
| In the text | |
 |
Fig. 9 Evolution of red-sequence GLFs with redshift in the B,V,R and I rest-frame bands (from left to right) for clusters stacked together. The first line of figures is for clusters with redshifts 0.40 ≤ z< 0.65 and the last line of figures is for clusters with redshifts 0.65 ≤ z< 0.90. Red crosses are red-sequence GLFs normalized to 1 deg2. The vertical red lines indicate the 90% completeness limit. Red curves are the best Schechter fits to red-sequence galaxies. The slope of the fit α is given with the number of clusters and the mean redshift of the stack. Refer to Table 3 for all Schechter fit parameters. |
| In the text | |
 |
Fig. 10 Dependence of red-sequence GLFs on cluster X-ray luminosity in the B,V,R, and I rest-frame bands (from left to right) for clusters stacked together. The top line is for clusters with X-ray luminosities 8 × 1043<LX< 1045 erg s-1 and the bottom line is for clusters with X-ray luminosities LX> 1045 erg s-1. Red crosses are red-sequence GLFs normalized to 1 deg2. The vertical red lines indicate the 90% completeness limit. Red curves are the best Schechter fits to red-sequence galaxies. The slope of the fit α is given with the number of clusters and the mean redshift of the stack. |
| In the text | |
 |
Fig. 11 Dependence of red-sequence GLFs on cluster substructures in the B,V,R, and I rest-frame bands (from left to right) for clusters stacked together. Only clusters with detected substructures are considered here (cf. Guennou et al. 2014). Red crosses are red-sequence GLFs normalized to 1 deg2. The vertical red lines indicate the 90% completeness limit. Red curves are the best Schechter fits to red-sequence galaxies. The slope of the fit α is given with the number of clusters and the mean redshift of the stack. |
| In the text | |
 |
Fig. 12 Galaxy luminosity functions in the B,V,R, and I rest-frame bands (from left to right) for stacked clusters in cores and outskirts. The first line of figures is for cluster cores (r ≤ 500 kpc) and the second line of figures for cluster outskirts (500 <r ≤ 1000 kpc). Red and blue points, respectively, correspond to red-sequence and blue GLFs normalized to 1 deg2. The red and blue curves show the best Schechter fits to red-sequence and blue galaxies and the red and blue vertical lines indicate the corresponding 90% completeness limits. The slope of the fit α is given for each population. |
| In the text | |
 |
Fig. 13 Cluster and field GLFs in the B,V,R, and I rest-frame bands (from left to right). Red and blue points respectively correspond to red-sequence and blue stacked cluster GLFs normalized to 1 deg2. The red and blue plain curves show the best Schechter fits to red-sequence and blue galaxies and the red and blue vertical lines indicate the corresponding 90% completeness limits. The slope of the fit α is given for each population. Refer to Table 2 for cluster best Schechter fit parameters. The thin dotted and dashed curves correspond to the COSMOS field GLFs centered at redshifts z = 0.5 and z = 0.7 normalized to 1 deg2. The separation between red and blue field galaxies is done the same way than for clusters at the corresponding redshift (see text for details). |
| In the text | |
 |
Fig. 14 Evolution of cluster galaxy type percentages with redshift. Each point represents the mean value of a percentage over four clusters. Red dots are red (early type) galaxies and blue triangles correspond to blue (late type) galaxies. The blue dashed line corresponds to the blue fraction from Ellingson et al. (2001). |
| In the text | |
 |
Fig. A.1 GLFs in the B,V,R and I rest-frame bands (from left to right) for individual clusters ordered by right ascension. Red and blue points correspond to red-sequence and blue GLFs normalized to 1 deg2. The red vertical lines indicate the 90% completeness limit. The red and blue curves show the best Schechter fits to red sequence and blue galaxies, and the faint-end slope parameter (α) is displayed in the corresponding colour. Only galaxies brighter than the 90% completeness limit are taken into account in the fits. Also, we only show GLFs richer than 20 galaxies after the colour separation and after subtracting the field. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.