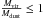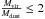| Issue |
A&A
Volume 575, March 2015
|
|
|---|---|---|
| Article Number | A27 | |
| Number of page(s) | 38 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201322955 | |
| Published online | 16 February 2015 | |
Star formation in Chamaeleon I and III: a molecular line study of the starless core population⋆
1
Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121
Bonn, Germany
e-mail: belloche@mpifr-bonn.mpg.de
2
Center for Radiophysics and Space Research, Cornell
University, Ithaca,
NY
14853-6801,
USA
3
School of Physics and Astronomy, Cardiff University,
Queen’s Buildings, The Parade,
Cardiff
CF24 3AA,
UK
Received: 31 October 2013
Accepted: 31 October 2014
Context. The Chamaeleon dark molecular clouds are excellent nearby targets for low-mass star formation studies. Even though they belong to the same cloud complex, Cha I and II are actively forming stars while Cha III shows no sign of ongoing star formation.
Aims. We aim to determine the driving factors that have led to the very different levels of star formation activity in Cha I and III and examine the dynamical state and possible evolution of the starless cores within them.
Methods. Observations were performed in various molecular transitions with the APEX and Mopra telescopes. We examine the kinematics of the starless cores in the clouds through a virial analysis, a search for contraction motions, and velocity gradients. The chemical differences in the two clouds are explored through their fractional molecular abundances, derived from a non-LTE analysis, and comparison to predictions of chemical models.
Results. Five cores are gravitationally bound in Cha I and one in Cha III. The so-called infall signature indicating contraction motions is seen toward 8–17 cores in Cha I and 2–5 cores in Cha III, which leads to a range of 13–28% of the cores in Cha I and 10–25% of the cores in Cha III that are contracting and may become prestellar. There is no significant difference in the turbulence level in the two clouds. Future dynamical interactions between the cores will not be dynamically significant in either Cha I or III, but the subregion Cha I North may experience collisions between cores within ~0.7 Myr. Turbulence dissipation in the cores of both clouds is seen in the high-density tracers N2H+ 1–0 and HC3N 10–9 which have lower non-thermal velocity dispersions compared to C17O 2–1, C18O 2–1, and C34S 2–1. Evidence of depletion in the Cha I core interiors is seen in the abundance distributions of the latter three molecules. The median fractional abundance of C18O is lower in Cha III than Cha I by a factor of ~2. The median abundances of most molecules (except methanol) in the Cha III cores lie at the lower end of the values found in the Cha I cores. A difference in chemistry is thus seen. Chemical models suitable for the Cha I and III cores are used to constrain the effectiveness of the HC3N to N2H+ abundance ratio as an evolutionary indicator. Both contraction and static chemical models indicate that this ratio is a good evolutionary indicator in the prestellar phase for both gravitationally bound and unbound cores. In the framework of these models, we find that the cores in Cha III and the southern part of Cha I are in a similar evolutionary stage and are less chemically evolved than the central region of Cha I.
Conclusions. The measured HC3N/N2H+ abundance ratio and the evidence for contraction motions seen towards the Cha III starless cores suggest that Cha III is younger than Cha I Centre and that some of its cores may form stars in the future if contraction does not cease. The cores in Cha I South may on the other hand be transient structures.
Key words: stars: formation / ISM: kinematics and dynamics
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
The Chamaeleon cloud complex is a prime target for studying the earliest phases of low-mass star formation. The molecular clouds Chamaeleon I and III contain a relatively large population of starless condensations at nearby distances. Only a few of these starless cores show signs of being gravitationally bound (Belloche et al. 2011a,b). One of our aims is to explore the dynamics and kinematics of these cores in more detail, and determine whether a significant fraction of the cores will become prestellar, or whether the majority are merely transient structures that will disperse as a result of turbulence. Throughout this paper, we use the definition that a starless core is a core without an embedded protostellar object. Prestellar cores are defined as the subset of starless cores that are gravitationally bound and will therefore likely form stars (André et al. 2000; di Francesco et al. 2007). Understanding which evolutionary path the condensations will undertake is important to assess the dynamical state and the likely future evolution of the clouds themselves.
Studying the initial phase of star formation can help establish the link between the stellar initial mass function (IMF) and the core mass function (CMF; e.g., André et al. 2007, 2009; Motte et al. 1998; Johnstone et al. 2000). Large and clustered core populations can also be used to shed light into the dominant dynamical processes taking place at the prestellar phase. On the one hand, in the competitive accretion scenario the dynamical interactions between the condensations play an important role in the subsequent core evolution and emergent IMF (e.g., Bate et al. 2003; Bonnell et al. 2004, 1998). On the other hand, the process of gravoturbulent cloud fragmentation suggests that stellar masses are determined at the prestellar phase and dynamical interactions with other cores and their surroundings are not significant (e.g., Padoan & Nordlund 2002; Myers 1998; Nakano 1998).
Chamaeleon I (Cha I) is a nearby, low-mass star forming cloud located at a distance of ~150 pc (Whittet et al. 1997; Knude & Høg 1998). The Chamaeleon cloud complex consists of Cha I, II, and III. Despite their close proximity to each other (all within ~16 pc in projection) they differ greatly in their level of star formation activity. Cha I has the highest level of star formation activity with more than 200 young stellar objects (YSOs) produced so far (Luhman 2008). A gas mass of ~950 M⊙ was derived from 12CO observations, as well as a diameter of 8 pc (Boulanger et al. 1998). It also has the highest dense gas fraction in the Chamaelon cloud complex (Mizuno et al. 1999). Belloche et al. (2011a) performed a deep, unbiased dust continuum survey of Cha I at 870 μm with the Large APEX Bolometer Camera (LABOCA; Siringo et al. 2009) at the Atacama Pathfinder Experiment telescope (APEX1). They identified 59 starless cores, 21 YSOs, 1 first hydrostatic core (FHSC) candidate, and a network of five filaments where most of the cores are located. They found that at most ~ 17% of the starless cores are prestellar based on a simple thermal analysis and concluded that the rate of star formation in Cha I is decreasing. Based on the YSO population, Luhman (2007) had similarly proposed that the star formation activity in Cha I is continuing but gradually declining. Haikala et al. (2005) identified 71 C18O 1–0 clumps in Cha I, but there is no one-to-one correspondence with the 870 μm continuum sources. The CMF of the starless cores in Cha I seems to be in good agreement with the shape of the IMF at the high-mass end (Belloche et al. 2011a), as was found for various other molecular clouds (Aquila, Taurus, Pipe nebula, Serpens & Perseus, Ophiuchus; André et al. 2010; Sadavoy et al. 2010; Alves et al. 2007; Enoch et al. 2008; Motte et al. 1998, respectively), but it ceases to be consistent at the low-mass end of the spectrum.
Chamaeleon III (Cha III) is also located at a distance of ~150 pc (Whittet et al. 1997; Knude & Høg 1998). Although it belongs to the same cloud complex as Cha I and has a 12CO mass of ~1400 M⊙ and a diameter of 10 pc (Boulanger et al. 1998), it contains a lower fraction of dense gas (Mizuno et al. 1999) and no YSO (e.g., Luhman 2008). Belloche et al. (2011b) identified 29 starless condensations in Cha III through an unbiased 870 μm dust continuum survey with LABOCA at APEX, performed with the same sensitivity as for Cha I. They found that only two sources out of the 29 starless cores are prestellar based on the Bonnor-Ebert critical mass criterion. A total of 38 clumps were previously detected in C18O 1–0 with the Swedish-ESO Submillimetre Telescope (SEST; Gahm et al. 2002). As in Cha I, no one-to-one correspondence is seen between the C18O 1–0 clumps and the detected 870 μm sources (Belloche et al. 2011b). Unlike for Cha I, no prominent filamentary structure is seen in the 870 μm dust continuum (Belloche et al. 2011b), but the core distribution within Cha III seems to trace out an underlying filamentary structure. The level of turbulence is of the same order in both Cha I and III based on C18O 1–0 (Mizuno et al. 1999) and CO 1–0 (Mizuno et al. 2001; Boulanger et al. 1998) data.
The striking difference in the number of YSOs in Cha I and III is bewildering given their proximity and the similar densities of their starless core population. A scenario that could explain why Cha III contains no YSOs, is that the cloud is at a younger evolutionary stage than Cha I and has not had enough time to produce protostars. To address this and other issues, we have undertaken a molecular line survey of the starless core population in Cha I and III, which aims to complement the results obtained from the dust continuum surveys of Belloche et al. (2011a,b). We start by presenting the observational details of our data in Sect. 2 and the basic results in Sect. 3. We then proceed to the analysis of the kinematics (velocity distribution, contraction motions, turbulence) of the cores in Sect. 4. Section 5 presents the analysis of the molecular abundances of the cores which are compared to predictions of chemical models. Finally, we discuss the implications of our results in Sect. 6 and give a summary of the conclusions in Sect. 7.
Molecular transitions observed with APEX for the cores in Cha I.
2. Observations
The observations were performed toward the starless condensations identified in the continuum surveys of Belloche et al. (2011a,b). The data was reduced with the CLASS software2.
2.1. Chamaeleon I data
The 60 cores detected in continuum emission were observed with the APEX telescope in 2010 May and July in the following molecular lines: C18O 2–1, 13CO 2–1, C17O 2–1, H2CO 31,2−21,1, HCN 3–2, HCO+ 3–2, and N2H+ 3–2 (project M-085.F-0022-2010). Table 1 lists the transitions observed for each core in our sample. The cores are numbered by decreasing 870 μm peak flux density (see Belloche et al. 2011a). All 60 cores were observed in C18O 2–1. 13CO 2–1 was observed in parallel to C18O 2–1. C17O 2–1 was observed toward the 33 cores with the strongest C18O 2–1 emission so that the transition pair can be used to determine line opacities. H2CO 31,2−21,1 was observed in parallel to C17O 2–1. Owing to observing time constraints only the brightest 30 cores were targeted in HCO+ 3−2 and HCN 3–2, which were observed in parallel. N2H+ 3−2 was observed only toward the cores Cha1-C1−C34 which had N2H+ 1–0 Mopra detections (see below).
Table 2 gives information about the frequencies,
resolutions, telescope receivers, forward/main beam efficiencies, system temperatures, and
root mean square (rms) noise values for all observed transitions. The coordinates of the
cores can be found in Table 2 of Belloche et al.
(2011a). The observations were conducted in position-switching mode with a
reference position for the CO isotopologues at αJ2000 = 11h24m33
 5, δJ2000 =−77°01′56.8′′, which was free
of emission in 13CO
2−1 with an rms of
~60 mK for the
spectral resolution given in Table 2. A second
reference position at
5, δJ2000 =−77°01′56.8′′, which was free
of emission in 13CO
2−1 with an rms of
~60 mK for the
spectral resolution given in Table 2. A second
reference position at 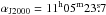 , δJ2000 =−77°11′02.2′′ was used for all
other transitions and was also free of emission at all frequencies with an rms of
~50 mK in
N2H+ 3−2 (spectral resolution listed in Table 2).
, δJ2000 =−77°11′02.2′′ was used for all
other transitions and was also free of emission at all frequencies with an rms of
~50 mK in
N2H+ 3−2 (spectral resolution listed in Table 2).
A subset of 57 cores from the continuum sample was observed with the Mopra telescope in
2010 June (project M506). The zoom mode of the high resolution spectrometer MOPS was used,
with the receiver tuned at 94 554 MHz with 12 zoom windows of 138 MHz selected within the
8 GHz bandwidth. The subset consists of cores Cha1-C1 to Cha1-C56 and core Cha1-C60. All
cores were observed in various molecular transitions from which the following were
detected: HNC 1−0,
HC3N
10−9, N2H+ 1−0, C4H 1010−99,
C34S 2–1,
CH3OH
21 −
11 E, CH3OH 20–10 A+, and CS 2–1. Information about the parameters of the
Mopra observations for each transition (frequency, angular resolution, main beam
efficiency, channel spacing, system temperature, rms) are given in Table 3. Position-switching observations were performed with
a reference position at 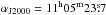 , δJ2000 = −
77°11′02.2′′ (free of emission with an rms of 40−53 mK for the transitions and spectral
resolutions given in Table 3). IRAM 04191+1522 and Oph A
SM1N were used as calibration sources. The pointing was checked every
~1 h. Tsitali et al. (2013) calculated a value of 0.34 for
the main beam efficiency of the telescope through a detailed calibration analysis.
, δJ2000 = −
77°11′02.2′′ (free of emission with an rms of 40−53 mK for the transitions and spectral
resolutions given in Table 3). IRAM 04191+1522 and Oph A
SM1N were used as calibration sources. The pointing was checked every
~1 h. Tsitali et al. (2013) calculated a value of 0.34 for
the main beam efficiency of the telescope through a detailed calibration analysis.
The northern part of Cha I was mapped in CO 3−2 with APEX in 2006 June with the on-the-fly mode (project
M-77.C-0016-2006). The mapped region has a size of 6.9′ × 5.4′, centred on the equatorial
offset position (60″,
60″) with respect to
Cha-MMS2 at 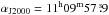 , δJ2000 = −
76°35′00.1″.
The rms of the cube at a region that is free of emission is ~ 0.6 K at a spectral resolution of 122
kHz. The reference position (
, δJ2000 = −
76°35′00.1″.
The rms of the cube at a region that is free of emission is ~ 0.6 K at a spectral resolution of 122
kHz. The reference position (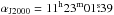 , δJ2000 = −
76°08′53.4″)
was also checked to be free of CO 3−2 emission with an rms of ~ 0.14 K at a spectral resolution of 122 kHz. The pointing was
checked every ~1 h on
07454-7112 and the focus was optimized on Saturn. Table 2 gives more information about the CO 3−2 observational setup.
, δJ2000 = −
76°08′53.4″)
was also checked to be free of CO 3−2 emission with an rms of ~ 0.14 K at a spectral resolution of 122 kHz. The pointing was
checked every ~1 h on
07454-7112 and the focus was optimized on Saturn. Table 2 gives more information about the CO 3−2 observational setup.
Parameters of Cha I and III observations with APEX.
Parameters of Cha I and III observations with Mopra.
2.2. Chamaeleon III data
Twenty starless cores in Cha III were observed with the Mopra telescope in 2012 May (project M627). The sample was chosen by selecting the cores with the highest peak flux density in 870 μm continuum emission (Belloche et al. 2011b). The receiver was tuned at two different frequencies, 94 554 MHz and 87 190 MHz. Single position observations were performed in various molecular transitions from which we detected the following: H13CO+ 1−0, HN13C 1−0, HNCO 40,4−30,3, HCN 1−0, HCO+ 1−0, HNC 1−0, HC3N 10−9, CH3OH 21−11 E, CH3OH 20–10 A+, N2H+ 1−0, CS 2−1. We list the observation parameters for all the detected transitions and some of the non-detected transitions in Table 3. The coordinates of the observed cores are given in Table 2 of Belloche et al. (2011b). The observations were performed in position-switching mode with the reference position at αJ2000 = 13h00m00s, δJ2000 = − 79°40′00′′. The reference position was free of emission at all frequencies with a maximum rms of 56 mK for the spectral resolution given in Table 3. IRAM 04191+1522 and Cha1-C1 were used as calibration sources.
We observed all 29 continuum sources in C18O 2−1 (and 13CO 2−1 in parallel) and two sources (Cha3-C1 and Cha3-C4) in C17O 2−1 with the APEX telescope in 2013 June (project M-091.F-0041-2013). Table 2 gives the respective observational parameters of the two transitions. The observations were done in position-switching mode with the same reference position at αJ2000 = 13h00m00s, δJ2000 = − 79°40′00′′ (free of emission in C18O 2−1 and 13CO 2−1 with an rms of ~ 100 mK). The pointing was checked every 1−1.5 h on 07454-7112.
2.3. Complementary C18O 1–0 data
We used the C18O 1−0 emission maps of Cha I and III observed with SEST from Haikala et al. (2005) and Gahm et al. (2002), respectively. Details about the observational setup can be found in these papers.
List of transitions to which Gaussian or hyperfine-structure fits were applied.
3. Results
We use a detection threshold of 3σ in peak temperature for all spectra used in the analysis. The cores’ systemic velocities and the linewidths of the detected transitions were extracted from single Gaussian or hyperfine-structure fits to the spectra. The fitting was performed in CLASS using the methods “GAUSS” or “HFS”, respectively. The transitions to which we applied fits are listed in Table 4. For the lines that do not have hyperfine structure we apply Gaussian fits as long as their shape is symmetric and not self-absorbed. The number of cores with two velocity components in their spectra is listed as N2vel. We define a core with two velocity components as a core with spectra having two emission peaks in both optically thick and optically thin transitions in order to exclude spectra that might be self-absorbed. The results of the “GAUSS” and “HFS” fits in CLASS are given in Tables A.1 and A.2 for Cha I and III, respectively. Transitions that are thought to be optically thick and in particular those that are self-absorbed toward most cores (HNC 1−0, 13CO 2−1, and CS 2−1) are not shown in Tables A.1 and A.2 and are not used to derive kinematical properties or column densities (Sect. 5).
In the following sections we also use a composite C18O and C17O sample when discussing non-thermal velocity dispersions in the clouds. The C18O 2−1 transition was observed and detected toward all sixty cores in Cha I so it is a very convenient starting point for a kinematic analysis. However, we calculated the opacity of the C18O 2−1 line for the sample of 32 cores that also have C17O 2−1 detections and found that only 50% of the cores are optically thin in the former line with an opacity τ ≤ 1 (see Sect. C.1). There is therefore a large fraction of cores that are somewhat optically thick in C18O 2−1. The 32 cores observed in C17O 2−1 were those with the strongest C18O 2−1 emission. Since C17O 2−1 is optically thin toward these cores, the C17O spectra are expected to be more reliable in deriving linewidths toward these 32 cores. The mean ratio of the C18O to C17O 2−1 linewidths for the sample of cores that are optically thick in C18O 2−1 is 1.19 ± 0.16. For the sample of cores optically thin in C18O 2−1, the mean ratio is 1.16 ± 0.29, slightly lower than for the optically thick sample, but the difference is not significant given the large dispersions. Even so, we create a composite sample that consists of the 32 cores observed in C17O and the remaining 28 cores observed only in C18O. Using this composite sample, we gain the advantage of having the full set of cores, while reducing possible biases introduced by the higher optical depth of C18O.
However, we do not use the composite sample for the centroid velocity analysis presented in Sect. 4.3 because we noticed a systematic difference between the systemic velocities derived from C18O and C17O 2−1. For the Cha I sample observed in both transitions, we find an average velocity difference V18−V17 of 0.17 ± 0.04 km s-1. This difference likely comes from either inaccurate spectroscopic predictions or an inaccurate frequency/velocity calibration of the observed spectra. We tested new spectroscopic predictions for C17O that take only laboratory measurements made in Bologna into account (H. S. P. Müller, priv. comm.), but this only reduces the discrepancy by 0.04 km s-1. Therefore, the problem is still unsolved.
 |
Fig. 1 Examples of spectra showing two emission peaks at different velocities that are not due to self-absorption, in Cha I (a) and in Cha III (b). a) Cha1-C7 and Cha1-C52 have two velocity components in C18O 2−1 (black) and in the optically thin C17O 2−1 and C34S 2−1 (red), respectively. Cha1-C15 (dashed) and Cha1-C12 (dotted) are located on either side of Cha1-C7 (see Fig. 2a). They both have only one emission peak that roughly coincides with either the lower velocity or the higher velocity peak of Cha1-C7. b) Cha3-C11 and Cha3-C21 have two velocity components in 13CO 2−1 (black) and in the optically thin C18O 2−1 (red), as well as in CS 2−1 for Cha3-C11. |
3.1. Multiple velocity components
Spectra with two emission peaks at different velocities are seen in the transitions C18O 2−1, C17O 2−1, and C34S 2−1 toward some dense structures in the northern and central parts of Cha I and in the central part of Cha III (see four examples in Fig. 1). Spectra with two velocity components that are not due to self-absorption might arise as projection effects if two physically unconnected regions coincide along the line of sight. Alternatively they could be an indication that different structures in the same region are interacting with one another. We used the C18O 1−0 maps of Haikala et al. (2005) and Gahm et al. (2002) alongside our data to better understand the physical origin of these features.
The spectrum of Cha1-C7, located in Cha I North, peaks at the velocities ~4.0 and ~4.8 km s-1 in C18O 2−1, C17O 2−1, and CS 2−1 (see Fig. 1a). The fact that we see the second velocity peak in the optically thin transition C17O 2−1 excludes the possibility that it is due to self-absorption. Cha1-C7 is located at the northern elongated structure as seen in the 870 μm dust continuum (Fig. 2a). Cores Cha1-C12 and Cha1-C15 lie on either side of Cha1-C7 but only have one component each, the former roughly corresponding to the higher velocity component of Cha1-C7 and the latter to the lower velocity one (Fig. 1a). We produced integrated intensity maps for the velocity ranges corresponding to each C18O 2−1 emission peak using the 1−0 map of Haikala et al. (2005). The intensity contours of both lower velocity and higher velocity emissions are overlaid on the 870 μm continuum in Fig. 2a. The lower velocity and higher velocity integrated intensity emissions peak at different locations on the continuum map. The lower velocity emission seems to follow the peak of the dust continuum emission. The higher velocity emission, however, peaks close to the position of Cha1-C12. Both velocity components overlap along the line of sight and Cha1-C7 lies in the overlap region which is the reason why its spectra show two velocity components.
 |
Fig. 2 C18O 1–0 blueshifted and redshifted emissions in a) Cha I North, b) Cha I Centre, and c) Cha III Centre overlaid on the 870 μm dust continuum maps of Cha I and III (Belloche et al. 2011a,b). The C18O 1−0 data are from Haikala et al. (2005) for Cha I and Gahm et al. (2002) for Cha III. The continuum contour levels (black) correspond to a, 2a, 4a, 8a, 16a, 32a, with a = 48 mJy/21″-beam (4σ) for a) and b), while a = 34.5 mJy/21″-beam (3σ) for c). The blueshifted (subscript b) and redshifted (subscript r) C18O 1−0 contours correspond to the levels a) 3σb (3σr), 4σb (4σr), 5σb (5σr) with σb = 0.17 K km s-1 and σr = 0.3 K km s-1, b) 3σb (3σr), 4.5σb (5σr) with σb = 0.33 K km s-1 and σr = 0.22 K km s-1, and c) 4σb (4σr), 6σb (6σr), 8σb with σb = 0.08 K km s-1 and σr = 0.09 K km s-1. The velocity ranges for the blueshifted and redshifted integrated intensity emissions are vb = 3.5 − 4.3 km s-1 and vr = 4.3−5.5 km s-1 for a), vb = 3.8 − 4.8 km s-1 and vr = 4.8−6.0 km s-1 for b), and vb = 0.5 − 1.5 km s-1 and vr = 1.5−2.5 km s-1 for c). The white dots show the location of the continuum cores in each region. The sources with spectra displayed in Fig. 1 are highlighted with a box around their name. |
A YSO, Cha-MMS2, is located very close to Cha1-C7 and drives a bipolar outflow (see, e.g., Bally et al. 2006; Reipurth et al. 1996; Mattila et al. 1989). We examined the possibility that the second, higher velocity component that we see in our spectra coincides with the redshifted outflow component. We use our CO 3−2 map of the Cha-MMS2 region (see Sect. 2.1) and find that the outflow does not contribute to the higher velocity emission in the velocity range 4.5 <v< 5.5 km s-1.
Two velocity components are seen toward three cores located in (or close to) the central elongated structrure of Cha I Centre: Cha1-C50, C52 (see Fig. 1a), and C54. Cha1-C52 and C54 are located at the northern edge of the filament as seen in the dust continuum (Fig. 2b) and C50 lies close to that part of the structure but is not embedded in it. The lower velocity component peaks close to ~4.5 km s-1 for all three cores and the higher velocity component peaks at ~5.2−5.5 km s-1. The integrated intensity contours of the lower and higher velocity C18O 1−0 emissions are shown in Fig. 2b overlaid on the dust continuum emission. The lower velocity emission closely follows the dust continuum emission, while the higher velocity component is less related to the continuum structure. Its emission seems to trace a direction perpendicular to the filamentary structure traced by the dust continuum and the lower velocity C18O 1−0 emission (see Sect. 6.5 for further discussion).
Two sources in Cha III have C18O 2−1 spectra with two emission peaks at different velocities, Cha3-C11 and Cha3-C21, which are located adjacent to each other (see Figs. 1b and 2c). The brightest peak of Cha3-C11 is at v ~ 2 km s-1 and the weakest peak is at v ~ 1.2 km s-1. The two emission peaks are also seen at the same velocities in the spectra of 13CO 2−1 and CS 2−1. The C18O 2−1 and 13CO 2−1 spectra of Cha3-C21 peak at ~2 km s-1 and ~ 0.9 km s-1, with the former being the strongest in emission in C18O 2−1 (the opposite is true for 13CO 2−1). Cha3-C11 and Cha3-C21 are located in the overlap region of two velocity components that are revealed in the C18O 1−0 map shown in Fig. 2c. The velocities of these two C18O 1−0 components match the velocities derived from our C18O 2−1, 13CO 2−1, and CS 2−1 spectra.
In the spectra that have two emission peaks in either Cha I or Cha III, we select the strongest emission peak as the main velocity component, and the weakest peak as the second velocity component. For the cores Cha1-C52 and Cha1-C54 we define the higher velocity peak as the second velocity component since we have an indication that it is not related to emission arising from the central elongated structure seen in the dust continuum. Finally, Fig. 2c suggests that the 870 μm dust continuum emission of Cha3-C11 and Cha3-C21 is closely related to the higher velocity component, which supports our decision to take the higher velocity component as the main component for these two cores.
 |
Fig. 3 Mass derived from dust emission versus virial mass of the Cha I (a),
c)) and Cha III (b), d)) cores computed for
the transitions HC3N 10−9, N2H+ 1−0, C34S 2−1, CH3OH 20−10 A+, CH3OH 21−11 E,
C18O
2−1, and
C17O
2−1. Panels a and b
show the total mass of the cores while panels c and d show the mass obtained for a
circular aperture of diameter 50′′. The solid line defines the region in which the cores are
virialized ( |
4. Analysis: kinematics
4.1. Turbulence
4.1.1. Virial analysis
If the external pressure is negligible, the virial mass of a spherically symmetric core
with a density distribution proportional to r-2 can be estimated through the
expression 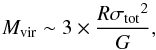 (1)where the radius R is given by the square
root of the product of the major and minor FWHM axes as measured in the dust maps (Belloche et al. 2011a,b),
(1)where the radius R is given by the square
root of the product of the major and minor FWHM axes as measured in the dust maps (Belloche et al. 2011a,b), 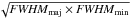 , and
, and
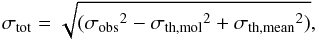 (2)with σobs the
measured velocity dispersion computed as
(2)with σobs the
measured velocity dispersion computed as
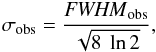 (3)where FWHMobs is the
observed spectral linewidth. The outer (radii ≥20 000 AU) gas kinetic temperature of the densest core in Cha I,
Cha1-C1 (Cha-MMS1) was constrained to 9 K
through radiative transfer modelling (Tsitali et al.
2013). Less dense cores may have a slightly higher kinetic temperature, and we
assume T =
10 K as an approximation. The mean thermal velocity dispersions are
computed as
(3)where FWHMobs is the
observed spectral linewidth. The outer (radii ≥20 000 AU) gas kinetic temperature of the densest core in Cha I,
Cha1-C1 (Cha-MMS1) was constrained to 9 K
through radiative transfer modelling (Tsitali et al.
2013). Less dense cores may have a slightly higher kinetic temperature, and we
assume T =
10 K as an approximation. The mean thermal velocity dispersions are
computed as  where kB is the
Boltzmann constant and T the kinetic temperature in K. The molecular
weight of the mean particle is μmH (μ = 2.37),
mmol =
μmolmH
is the molecular mass of the tracer, and mH the proton mass. Equation (1) therefore becomes
where kB is the
Boltzmann constant and T the kinetic temperature in K. The molecular
weight of the mean particle is μmH (μ = 2.37),
mmol =
μmolmH
is the molecular mass of the tracer, and mH the proton mass. Equation (1) therefore becomes
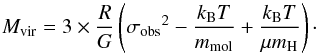 (6)A core is considered to be gravitationally
bound if its mass corresponds to at least half its virial mass and it is in
gravitational virial equilibrium if its mass and virial mass are equal (e.g., Bertoldi & McKee 1992). To calculate the
respective mass to virial mass ratios, we use the masses derived by Belloche et al. (2011a,b) through dust continuum observations at 870 μm. We calculate the mass
ratios both for the total dust mass derived from a Gaussian fit (Figs. 3a and b) and the dust mass derived for a circular
aperture of diameter 50′′
(Figs. 3c and d), which corresponds to typical mean
densities of ~0.5−1 ×
105 cm-3 (Belloche et al.
2011a,b). It is not straightforward to
decide which dust mass is the most appropriate to compare to the virial masses because
the lines trace material along the line of sight, the extent of which cannot be known
without a detailed radiative transfer modelling.
(6)A core is considered to be gravitationally
bound if its mass corresponds to at least half its virial mass and it is in
gravitational virial equilibrium if its mass and virial mass are equal (e.g., Bertoldi & McKee 1992). To calculate the
respective mass to virial mass ratios, we use the masses derived by Belloche et al. (2011a,b) through dust continuum observations at 870 μm. We calculate the mass
ratios both for the total dust mass derived from a Gaussian fit (Figs. 3a and b) and the dust mass derived for a circular
aperture of diameter 50′′
(Figs. 3c and d), which corresponds to typical mean
densities of ~0.5−1 ×
105 cm-3 (Belloche et al.
2011a,b). It is not straightforward to
decide which dust mass is the most appropriate to compare to the virial masses because
the lines trace material along the line of sight, the extent of which cannot be known
without a detailed radiative transfer modelling.
Table 4 and Fig. 3a show that at most five cores are gravitationally bound (Cha1-C1, C2, C3, C4, C5) and one is virialized in Cha I when taking the total dust mass into account. The virialized core is Cha1-C1 (also known as Cha-MMS1), which is a first hydrostatic core candidate (Belloche et al. 2006, 2011a; Tsitali et al. 2013). On the other hand, no single molecular line indicates that any core in Cha III is virialized and we find that only Cha3-C1 is gravitationally bound (see Tables 4 and A.2, and Fig. 3b). Repeating the calculations for the dust mass derived from a 50′′ aperture we find that only Cha1-C1 is gravitationally bound in Cha I and no core is gravitationally bound in Cha III (Figs. 3c and d). From now on, we will only use the total dust mass of the cores and consider the numbers of gravitationally bound and virialized cores as upper limits.
Comparison of systemic velocities, linewidths, and non-thermal velocity dispersions for selected pairs of transitions for Cha I and III.
“Infall” and opposite signatures.
Line shapes of optically thick tracersa for the cores that show the “infall” or opposite signature in Cha I and III.
4.1.2. Comparison between tracers
We compare the non-thermal velocity dispersions derived for a pair of transitions by using only the cores in which they are both detected. Table 5 lists the average systemic velocities, linewidths, non-thermal velocity dispersions, the ratio of the non-thermal velocity dispersions, and the mean ratio of the non-thermal to the mean thermal velocity dispersion for selected pairs of transitions in Cha I and III.
N2H+ 1–0 has systematically lower (by ~ 20–30%) non-thermal velocity dispersions when compared to either C17O 2−1, C34S 2−1, and the composite C18O/C17O sample in Cha I. HC3N 10–9 has a similar behaviour to N2H+ 1–0, with non-thermal dispersions lower than C17O 2–1, C34S 2–1, and the composite C18O/C17O by ~ 30–40%. The non-thermal dispersion ratio of the last two transitions is around unity. The two methanol species have similar non-thermal velocity dispersions. CH3OH 20–10 has higher non-thermal velocity dispersions than both N2H+ 1–0 and HC3N 10–9 by ~ 10% and ~ 20%, respectively. It has, however, a similar non-thermal dispersion to C17O 2–1. HC3N 10–9 similarly has a lower non-thermal dispersion in Cha III compared to C18O 2–1 by ~ 50% and CH3OH 20−10 A+ by ~40%. The methanol CH3OH 20–10 A+ and CH3OH 21–11 E transitions have similar non-thermal dispersions in both Cha I and III.
Overall, both high- and low-density tracers show subsonic to transonic turbulence in Cha I and III, with their non-thermal velocity dispersions being on average lower than or equal to the mean thermal velocity dispersion.
4.2. Contraction motions
The infall signature is an optical depth effect and is produced when the line excitation temperature increases toward the centre of a collapsing core (Evans 2003). Assuming spherical symmetry, the infall signature of a core consists of two elements. The first one is an asymmetric profile of an optically thick line that is skewed to the blue and sometimes features a self-absorption dip (due to absorption from the outer low-excitation material). In order to exclude the possibility that the observed spectral profile is due to two separate, overlapping velocity components, an optically thin, symmetric (and single-peaked) line is required to peak at a velocity in between the red and blue portions of the optically thick line (Leung & Brown 1977; Walker et al. 1986; Zhou 1992; Myers et al. 1995, 1996). Strictly speaking, the infall signature may in some cases trace early or large-scale contraction motions in layers that are not (yet) gravitationally collapsing. Therefore, we use the expression “infall” signature with quotation marks in the rest of the article to remind the reader that the signature may not trace proper infall motions but only contraction motions when gravity does not (yet) dominate the dynamical evolution of these layers.
The opposite signature, i.e., with the red peak emission of the self-absorbed transition stronger than the blue peak, has also been seen in other surveys of dense cores in the past (e.g., Gregersen et al. 1997; Mardones et al. 1997; Gregersen & Evans 2000, 2001). The red-skewed profiles are generally not very well understood. They may arise as a result of outflowing or expanding material (Evans 2003). In most of the aforementioned surveys, the blue profiles outnumbered the red profiles which was taken as an indication of “infall” motions.
Mardones et al. (1997) proposed a non-dimensional
parameter, δV, to quantify the observed asymmetry for both
blue-skewed and red-skewed profiles. This parameter is 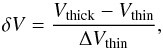 (7)where Vthick and
Vthin are the peak velocities of the
brightest optically thick peak and the optically thin peak, respectively, and
ΔVthin is the linewidth (FWHM) of the
optically thin transition. This parameter is given in Table 6 along with the peak temperature ratio of the blueshifted and
redshifted peaks of the optically thick line. This way we quantify both the peak asymmetry
in the optically thick spectrum and the amount by which the brightest peak of the
optically thick line is blueshifted or redshifted with respect to the peak of the
optically thin line. The peak velocities, linewidths, and respective uncertainties of the
optically thin transitions were derived by performing Gaussian fits in CLASS. The velocity
of the strongest optically thick peak (Vthick) was determined by applying
Gaussian fits to the spectrum after masking the channels of the weaker peak. We used the
rms of the spectrum as the uncertainty of Tblue and Tred, and the
velocity uncertainty from the Gaussian fit for Vthick. Negative values of
δV
correspond to blue-skewed profiles (“infall” signature) and positive values to red-skewed
profiles (opposite signature).
(7)where Vthick and
Vthin are the peak velocities of the
brightest optically thick peak and the optically thin peak, respectively, and
ΔVthin is the linewidth (FWHM) of the
optically thin transition. This parameter is given in Table 6 along with the peak temperature ratio of the blueshifted and
redshifted peaks of the optically thick line. This way we quantify both the peak asymmetry
in the optically thick spectrum and the amount by which the brightest peak of the
optically thick line is blueshifted or redshifted with respect to the peak of the
optically thin line. The peak velocities, linewidths, and respective uncertainties of the
optically thin transitions were derived by performing Gaussian fits in CLASS. The velocity
of the strongest optically thick peak (Vthick) was determined by applying
Gaussian fits to the spectrum after masking the channels of the weaker peak. We used the
rms of the spectrum as the uncertainty of Tblue and Tred, and the
velocity uncertainty from the Gaussian fit for Vthick. Negative values of
δV
correspond to blue-skewed profiles (“infall” signature) and positive values to red-skewed
profiles (opposite signature).
For Cha I, we look for the “infall” signature in pairs of optically thick/thin isotopologues in CS 2−1 and C34S 2−1. In the case of a non-detection in C34S 2−1 we use the detected optically thin transitions N2H+ 1−0, HC3N 10−9, CH3OH 20−10 A+, or C18O 2−1 for the cores in which it is optically thin (see Tables C.1 and C.2). If CS 2−1 is not self-absorbed, we search for the “infall” signature in the optically thick tracers HNC 1−0 and 13CO 2−1. CS 2−1 was detected toward all 20 cores in Cha III, but no spectrum shows a significant self-absorption in this transition. Only two cores have detections in C34S 2−1. We therefore use the HNC 1−0 and 13CO 2−1 as optically thick tracers for the “infall” signature in Cha III. 13CO 2−1 likely traces the outer core material (e.g., Onishi et al. 1999; Arce et al. 2011) and any “infall” signature found with this transition may only correspond to large-scale contraction motions. On the other hand, C18O and C17O 2−1 were found to correlate very well with the dust extinction between 6 and 15 mag in Cha I (Belloche et al. 2011a). These values correspond to H2 column densities of ~4−9 × 1021 cm-2, which are similar to the peak column densities of the cores in Cha I and III (see Belloche et al. 2011a,b). These two transitions are therefore expected to trace the bulk mass of the cores (excluding the innermost parts where depletion occurs) in Cha I and Cha III very well for extinctions in the aforementioned range. In general, the “infall” signatures discussed in this section may not signify gravitational collapse, but instead large-scale contraction motions of material accumulating onto the cores. This accumulation of material may turn some of the cores from unbound to gravitationally bound structures in the future. Table 7 lists the line shape characteristics of the optically thick spectra of all the cores that show an “infall” or opposite signature in Cha I and III. Figure E.1 shows the spectra of all transitions used to search for signatures of contraction motions in the sources listed in Table 7.
 |
Fig. 4 “Infall” signature toward cores in Cha I. The optically thick, self-absorbed transitions are shown with black thick lines and the optically thin transitions with red thin lines. The dashed red line shows the systemic velocity of each core derived from a Gaussian or hyperfine-structure fit to the optically thin line shown in red. The name of the cores is given on the right-hand side of each transition depicted. The factor by which each spectrum was multiplied is given next to the name of the transitions and it corresponds to 1 if not specified. |
 |
Fig. 7 Cores showing the “infall” signature in Cha I (corresponding to Fig. 4) are plotted as red filled circles, the cores showing the opposite signature as green triangles, and the cores showing both signatures as blue squares. The contours correspond to the 870 μm dust continuum emission obtained with LABOCA (Belloche et al. 2011a) with contour levels of a, 2a, 4a, 8a, 16a, 32a, and a = 48 mJy/21′′-beam (4σ). |
Starting with Cha I, a total of 18 cores have a negative δV parameter whose absolute value is greater than the 3σ uncertainty and thus appear to be contracting based on their “infall” signatures (Fig. 4). All of them have a peak temperature asymmetry Tblue/Tred deviating from unity by more than 1σ and 15 of them by more than 3σ, the three exception being Cha1-C9, Cha1-C18, and Cha1-C21 (Table 6). Cha1-C21, however, also shows the opposite signature in HNC 1–0 (see Fig. 5) and is therefore not a reliable candidate for contraction. The total number of cores showing the “infall” signature is therefore 17, or 28% of the Cha I cores. Their locations within the cloud are shown in Fig. 7. The optically thick, self-absorbed transitions CS 2–1, HNC 1–0, and 13CO 2–1, and the assumed optically thin transitions, C34S 2–1, HC3N 10–9, C18O 2–1, N2H+ 10,1–01,2 (isolated component), and CH3OH 20–10 A+, form this typical signature for the 18 cores in Cha I (Fig. 4). Table C.3 shows that C34S 2–1 is indeed optically thin for all the relevant cores (for which this transition is used) in Fig. 4, as well as the cores discussed later showing the opposite signature. We have no similar opacity estimates for HC3N 10–9 and CH3OH 20–10 A+, but these transitions have a Gaussian line shape for all cores in which they are detected. C18O 2–1 is optically thin toward approximately half of the cores that have C17O 2–1 detections (Table C.1). The core Cha1-C27 is optically thin in C18O 2–1. We do not have an estimate of the C18O 2–1 opacity for Cha1-C46 but the line looks symmetric and peaks in between the blue and red peaks of the 13CO 2–1 spectrum. We finally use the isolated, likely optically thin component of N2H+ 1–0 for only two cores, Cha1-C8 and Cha1-C11. It is interesting to note that 88% of the cores showing the “infall” signature (14 out of 17; the exceptions being Cha1-C1, C2, and C3) do not appear to be gravitationally bound based on the virial analysis (Sect. 4.1.1).
The opposite signature is seen in eight cores in Cha I (Fig. 5) and it corresponds to positive δV parameters (Table 6). As Cha1-C21 shows both an opposite and “infall” signature, it is not a reliable candidate either for contraction or expansion motions alone. We therefore take the remaining seven cores to be showing evidence of expansion (small- or large-scale depending on the tracer). Four of the seven cores showing the opposite signature have an asymmetric profile in 13CO 2−1. It is likely that this transition is sensitive to the ambient, low-density gas and might not be appropriate for tracing motions within the dense cores themselves. If we excluded the low-density tracer 13CO 2−1, the actual number of opposite signature spectra could be reduced to 3 and the number of “infall” signature spectra to 16.
The two signatures (“infall” and opposite) could be produced with the same probability by oscillations This interpretation was proposed for the starless core B68 where both blue-skewed and red-skewed spectra were seen in CS 2−1 (Lada et al. 2003) and HCO+ 3−2 across the core (Redman et al. 2006). This pattern was interpreted as an oscillation, or pulsation of the outer core layers about an equilibrium state due to external pressure perturbations (Lada et al. 2003; Redman et al. 2006; Keto & Field 2005). Aguti et al. (2007) also suggested pulsation as a possible physical state for the outer layers of the starless core FeSt 1-457.
If the “infall” and opposite signatures also trace oscillating motions, then given that we see the opposite signature in ~ 7 cores overall we could expect the sample of “infalling” cores to be contaminated by ~7 oscillating cores, which would reduce the number of infalling cores to ~ 10 in Cha I. The fact that we see both the “infall” and the opposite signature in Cha1-C21 may be an indication of such an oscillation. It is not straightforward to conclude if pulsations are occuring as most sources, apart from Cha1-C21, do not show both signatures simultaneously in different tracers and we do not have spatial information.
Five cores in Cha III show the classical “infall” signature (Fig. 6). The spectrum of Cha3-C1 in HNC 1–0 is not self-absorbed, but it is clearly skewed to the blue. CH3OH 20–10 A+ is redshifted with respect to the blue peak of HNC 1–0, thus making Cha3-C1 a probable collapsing core. The asymmetry is more pronounced for the cores Cha3-C9, Cha3-C10, Cha3-C13, and Cha3-C20 with optically thin lines peaking in between the blue and red peaks of the optically thick spectrum. Cha3-C1 is the only core that also appears to be gravitationally bound from our virial analysis (see Sect 4.1.1). All cores showing the “infall” signature in Cha III have a significant (negative) δV parameter at the 3σ level. The Tblue/Tred asymmetry is larger than ~ 1.2 in all cases. Three of the contracting cores, however, show the “infall” signature in 13CO 2–1. If this transition is not a good tracer of core motions, then only two cores are valid “infall” candidates.
Therefore, taking into account the observed line profiles, the parameter δV, and the ambiguity of the 13CO 2–1 profiles, the number of the “infall” candidates is 8–17 (with/without oscillations and without/with 13CO 2–1) cores in Cha I and ~ 2–5 (without/with 13CO 2–1) in Cha III. The opposite signature is seen toward 3–7 (without/with 13CO 2–1) cores in Cha I. Using these ranges, 13–28% of the core population in Cha I and 10−25% of the observed Cha III sample (or ~ 7–17% of the overall Cha III starless core population) are “infall” candidates.
Average velocity dispersions, crossing time, and collisional time for the Cha I and III cores detected in different tracers.
4.3. Centroid velocities
4.3.1. Core velocity distribution
We follow the analysis in André et al. (2007) to estimate if interactions between cores are likely to be dynamically important for the evolution of Cha I and III. This analysis assumes Maxwellian, isotropic velocities. We perform the analysis for the whole sample of cores in Cha I and Cha III, and also for the subsamples of cores in Cha I North, Centre, South, and Cha III North, Centre, and South, separately. We use the average velocity of all cores in each transition for our calculations (Table 8).
 |
Fig. 8 Systemic velocities of the cores in Cha I overplotted on the 870 μm continuum emission map obtained with LABOCA (Belloche et al. 2011a) for the transitions: a) C18O 2–1, b) C17O 2–1, c) CH3OH 20–10 A+, and d) N2H+ 1–0. The contour levels correspond to a, 2a, 4a, 8a, 16a, 32a, with a = 48 mJy/21′′-beam (4σ). The core velocities were derived from Gaussian or hyperfine-structure fits to the observed spectra. The filled circles are colour-coded and increase in size to emphasize increasing velocities. Cores with two velocity components are shown with the lower velocity overplotted onto the higher velocity component. The dashed arrow indicates the position angle of the velocity gradient fit. |
The global velocity dispersion of the cores in each tracer is given by
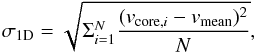 (8)where N is the number of cores
detected in the specific tracer, vcore,i the systemic
velocity of each individual core measured with this tracer, and vmean is the
average systemic velocity of all cores in this tracer. The 3D velocity dispersion is
(8)where N is the number of cores
detected in the specific tracer, vcore,i the systemic
velocity of each individual core measured with this tracer, and vmean is the
average systemic velocity of all cores in this tracer. The 3D velocity dispersion is
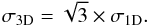 (9)We obtain the mean velocity relative to the
centre of mass of the system, vrel,COM, using the relation
(9)We obtain the mean velocity relative to the
centre of mass of the system, vrel,COM, using the relation
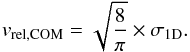 (10)Finally, the relative speed between cores
is computed as
(10)Finally, the relative speed between cores
is computed as 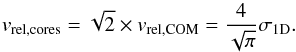 (11)The velocity dispersions are given in Table
8 for both Cha I and III as a whole, as well as
the subregions of Cha I and III.
(11)The velocity dispersions are given in Table
8 for both Cha I and III as a whole, as well as
the subregions of Cha I and III.
 |
Fig. 9 Same as Fig. 8 but for Cha III and the transitions a) C18O 2–1 and b) CH3OH 20–10 A+. The contour levels correspond to the 870 μm continuum emission obtained with LABOCA (Belloche et al. 2011b) at a, 2a, 4a, 6a, with a = 34.5 mJy/21′′-beam (3σ). |
Figure 8 shows the colour-coded (in terms of magnitude) systemic velocities of the cores in Cha I for the molecular tracers C18O 2–1, C17O 2–1, CH3OH 20–10 A+, and N2H+ 1–0 overlaid on the 870 μm continuum LABOCA map. Most of the cores are located in structures that appear to be filamentary in the dust continuum. We define four regions, Cha I North, Centre, South, and West, with the first three containing each at least one of the three distinct elongated structures in Cha I. The subregion Cha I West does not contain an elongated structure, but rather two small clumps with three cores altogether. Figure 9 overlays the systemic velocities that were derived for the Cha III cores in C18O 2–1 and CH3OH 20–10 A+ on the 870 μm map of the cloud. We also define the subregions Cha III North, Centre, and South, in which the cores appear more clustered.
We find a mean systemic velocity (vmean) of 4.72 ± 0.34 km s-1 for the C18O sample in Cha I. The uncertainty is the 1D velocity dispersion. Second velocity components are excluded in this calculation. We believe that the higher velocity peak, or second velocity component, is likely not associated with the material in the region we are studying and is either due to projection effects or due to material interacting with those regions (see Sect. 3.1). The mean velocities for Cha I North, Centre, and South yield 4.47 ± 0.29 km s-1, 4.48 ± 0.20 km s-1, and 4.83 ± 0.32 km s-1 for the C18O sample and for the number of cores given by Nfit in Table 8.
All 29 cores in Cha III were detected (>3σ) in C18O 2–1. We derive a mean velocity of 1.50 ± 0.23 km s-1, with the uncertainty being the 1D velocity dispersion. The mean systemic velocities in C18O 2–1 for the subregions of Cha III are 1.36 ± 0.09 km s-1 (Cha III North), 1.53 ± 0.31 km s-1 (Cha III Centre), and 1.59 ± 0.17 km s-1 (Cha III South) for the number of cores given by Nfit in Table 8.
4.3.2. Crossing and collisional times
To estimate the crossing and collisional times, tcross and
tcoll, for the Cha I and III clouds as a
whole and their subregions we assume cylindrical symmetry due to their elongated shape.
The only exception is Cha I South for which we assume spherical symmetry. For a number
of cores N, we take n to be the core number density in the respective
regions, given by 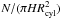 in the cylindrical case and
in the cylindrical case and
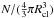 in the spherical case. We call
Dcl the largest projected distance
between two cores in the cloud or region. In the spherical case, Dcl
corresponds to the diameter of the sphere and the radius is Rcl =
Dcl/ 2. In the cylindrical case, the
height H of
the cylinder is assumed to be equal to Dcl. The diameter of the cylinder,
Dcyl, is estimated as the largest
distance between two cores in the direction perpendicular to the main axis of the
cylinder, and the radius is Rcyl = Dcyl/
2. Assuming isotropic, Maxwellian velocities we can estimate the
crossing and collisional times as (see Binney &
Tremaine 1987; André et al. 2007)
in the spherical case. We call
Dcl the largest projected distance
between two cores in the cloud or region. In the spherical case, Dcl
corresponds to the diameter of the sphere and the radius is Rcl =
Dcl/ 2. In the cylindrical case, the
height H of
the cylinder is assumed to be equal to Dcl. The diameter of the cylinder,
Dcyl, is estimated as the largest
distance between two cores in the direction perpendicular to the main axis of the
cylinder, and the radius is Rcyl = Dcyl/
2. Assuming isotropic, Maxwellian velocities we can estimate the
crossing and collisional times as (see Binney &
Tremaine 1987; André et al. 2007)
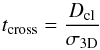 (12)for the long axis of the cylinder or for
the sphere in question, and
(12)for the long axis of the cylinder or for
the sphere in question, and 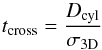 (13)for the short axis of the cylinder.
Finally,
(13)for the short axis of the cylinder.
Finally, 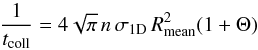 (14)where
(14)where
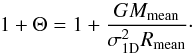 (15)The mean mass (Mmean), mean
core radius (Rmean), number of cores
(N) used
in each tracer and the resulting velocity dispersions and times are given in Table 8. The radii R of the cores are
calculated as
(15)The mean mass (Mmean), mean
core radius (Rmean), number of cores
(N) used
in each tracer and the resulting velocity dispersions and times are given in Table 8. The radii R of the cores are
calculated as 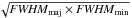 , as in André et al. (2007). We select the C18O 2–1 and CH3OH 20–10 A+ samples for Cha I as these
transitions were observed toward many cores. We use the same tracers for Cha III.
, as in André et al. (2007). We select the C18O 2–1 and CH3OH 20–10 A+ samples for Cha I as these
transitions were observed toward many cores. We use the same tracers for Cha III.
We compute maximum cloud crossing times, i.e., along the long axis in the cylindrical cases, tcross ~ 7 Myr for Cha I as a whole and ~ 2.5 Myr for each of its subregions. The time for core collisions is ~ 160 Myr for the whole Cha I cloud, but it is much lower in its subregions. We find collision times of ~ 0.7 Myr for Cha I North, ~ 1.3 Myr for Cha I Centre, and ~ 16 Myr for Cha I South. Interactions between cores in Cha I North and Cha I Centre could therefore occur at a higher rate than in Cha I South.
We perform the same calculations for the cores in Cha III and its subregions. The velocity dispersions and timescales for every transition are listed in Table 8. We find maximum cloud crossing times of ~13 Myr for the cloud as a whole, and ~ 4 Myr, ~ 2.3 Myr, and ~ 5.4 Myr for Cha III North, Centre, and South, respectively. The collisional time is ~ 40 Myr for the whole cloud. It decreases, however, by a large amount when focusing on the Cha III subregions, for which we find ~ 1 Myr (Cha III North), ~10 Myr (Cha III Centre), and ~12 Myr (Cha III South).
4.3.3. Velocity gradients
To search for velocity gradients in Cha I, we performed a 2D least-square fit on the
systemic velocities of the cores detected in each tracer. We perform the fitting with a
three-parameter function (Goodman et al. 1993),
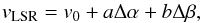 (16)where vLSR,
Δα, and
Δβ are
the systemic velocity of the cores, the offset of the cores in right ascension, and the
offset in declination (radians). The magnitude of the linear velocity gradient (which
assumes solid-body rotation) and its direction (east of north) are given by (Goodman et al. 1993)
(16)where vLSR,
Δα, and
Δβ are
the systemic velocity of the cores, the offset of the cores in right ascension, and the
offset in declination (radians). The magnitude of the linear velocity gradient (which
assumes solid-body rotation) and its direction (east of north) are given by (Goodman et al. 1993)  where d is the distance of the
cloud. The derived velocity gradients and their position angles are given in Table 9. They are shown in Fig. 8. We emphasize that the assumption of solid-body rotation only serves
as a rough approximation as the velocities across the cloud vary in a more complex
manner.
where d is the distance of the
cloud. The derived velocity gradients and their position angles are given in Table 9. They are shown in Fig. 8. We emphasize that the assumption of solid-body rotation only serves
as a rough approximation as the velocities across the cloud vary in a more complex
manner.
Velocity gradients in Cha I and III.
The higher velocities of the cores in the south-western part of Cha I (Fig. 8) are mostly responsible for the velocity gradient in Cha I. All tracers give consistent results, the higher value derived for N2H+ 1–0 being due to its non-detection in Cha I North. We tested the latter effect by computing the velocity gradients in C18O 2–1, C17O 2–1, CH3OH 20–10 A+ without taking the cores in Cha I North into account. We indeed found higher gradients (i.e., ~ 0.5–0.6 km s-1 pc-1) as in N2H+ 1–0. We find no significant velocity gradient in Cha III, but we list the CH3OH 20−10 A+ and C18O 2–1 upper limits in Table 9.
5. Analysis: Molecular abundances
5.1. Observational molecular abundances
We used the offline-version of the non-LTE radiative transfer code RADEX (van der Tak et al. 2007) to calculate the column densities of C18O, C17O, CH3OH, C34S, HC3N, and N2H+, applying the escape probability method for a uniform sphere. We assumed a kinetic temperature of 10 K for all observed transitions except for C18O and C17O 2–1 for which we used 12 K. The initial assumption of 10 K for C18O and C17O 2–1 gave rise to inconsistent (unrealistically high) column densities for a few cores. In addition, the dust temperature in the cold cores of the Chamaeleon clouds was found to be around 12 K (see Tóth et al. 2000). These two transitions may trace more diffuse material than the other higher-density tracers, which is likely to be at a higher kinetic temperature. RADEX calculates the column density and excitation temperature of a line, given the spectrum’s main-beam peak temperature, linewidth, and core density. The core densities for Cha I and III are taken from the 870 μm dust continuum surveys of Belloche et al. (2011a) and Belloche et al. (2011b), respectively. For each core, we interpolate between the peak density and the density computed from the flux contained in a 50″ aperture to derive the mean density in the beam (HPBW) corresponding to each transition (listed in Tables 2 and 3). Finally, the molecular datafiles are taken from the LAMDA database3.
We have no sign that HC3N 10–9, C34S 2–1, CH3OH 20−10 A+, CH3OH 21–11 E, and C17O 2–1 might be optically thick judging from the symmetric, Gaussian-like spectra (see Sects. C.1 and C.2 for estimates of C17O and C34S opacities). C18O 2–1 is slightly optically thick for some cores in Cha I (Sect. C.1). We do not expect the cores in Cha III to be optically thick in C18O 2–1 as the brightest core, Cha3-C1, is only at the limit of being optically thick. Cha3-C4 is optically thin in C18O 2–1 (see Sect. C.1).
Average and median molecular abundances in Cha I and III.
For HC3N 10–9, C17O 2–1, and N2H+ 1–0, which have a hyperfine structure, we apply hyperfine structure fits with CLASS to derive their linewidths. There are no molecular datafiles on LAMDA that consider the hyperfine structure of HC3N 10–9 and C17O 2–1. As approximately ~30% of the C17O 2–1 flux is missing from the central components, we apply a correction to the column density of 1 / 0.7, i.e., ~1.43. No correction is applied for HC3N 10–9. We use the strongest, single-frequency component N2H+ 12,3–01,2 along with its hyperfine structure datafile from LAMDA to derive its column density with RADEX. The four densest cores in Cha I, C1-C4, are optically thick in this transition. Therefore, for these four cores we use the weakest, optically thin component N2H+ 11,0–01,1 to derive their column densities.
The excitation temperatures we derive with RADEX show that C18O and C17O 2–1 are thermalized at Tk = 12 K. The two CH3OH species are also nearly thermalized with excitation temperatures around 8–9.5 K at a kinetic temperature of 10 K. C34S 2–1 and N2H+ 1–0 both have excitation temperatures of ~4–7 K in both clouds, while HC3N 10–9 has slightly higher excitation temperatures of ~6–8.5 K (excluding the two densest cores in Cha I).
We compute the abundances relative to H2 averaged along the line of sight using the H2 column densities of the cores derived from the dust emission by Belloche et al. (2011a,b). We use the interpolated column densities, using the same method as described above for the interpolated densities. We refer to the interpolated H2 column density as Ninter. The average and median abundances relative to H2 and the abundance dispersion derived from C18O 2–1, C17O 2–1, CH3OH 20–10 A+, CH3OH 21–11 E, C34S 2–1, HC3N 10–9, and N2H+ 1–0 are listed in Table 10 for both Cha I and III. Figure 10 plots the individual core abundances derived for each tracer against their interpolated H2 column densities.
Most of the Cha III molecular abundances lie at the lower end of the range of abundances in Cha I, apart from the core abundances of the two methanol species (Fig. 10). The fact that only a few cores in Cha III are detected in each molecule makes it difficult to conduct any reliable statistical comparisons between the two clouds, especially in C17O, HC3N, C34S, and N2H+. Nevertheless, it is apparent that C18O is on average more abundant in Cha I than in Cha III by a factor of ~ 1.6 (see Table 10). This difference in molecular abundances can also be seen in Fig. 10.
Benedettini et al. (2012) found that the ratio of HC3N/N2H+ varies between the (prestellar and protostellar) cores in the Lupus 1, 3, and 4 molecular clouds. They conclude that this ratio decreases as a dense core or a protostar evolves, both observationally in their core sample and in their chemical model predictions. The HC3N/N2H+ ratio for the cores in Cha I and III is shown in Fig. 11a. Figure 11b overplots the observed HC3N/N2H+ ratio in Cha I on the 870 μm continuum map. Two cores in Cha III have detections in both molecules (Cha3-C1, C15) and fourteen in Cha I. We calculate lower limits for one additional core in Cha III (Cha3-C13) and four cores in Cha I (Cha1-C17, C18, C26, C38) that have a HC3N detection and a N2H+ upper limit. The cores located in Cha I South and West have on average a higher HC3N/N2H+ ratio than the ones in Cha I Centre, while the cores in Cha III have values similar to Cha I South (Figs. 11a, b).
 |
Fig. 10 Molecular abundances relative to H2 against H2 column densities interpolated within an aperture of diameter equal to the HPBW of each transition. The abundances of the Cha I and III cores are shown as black squares and pink asterisks, respectively. Upper limits (3σ uncertainties) are shown as pink and black downward triangles for Cha III and Cha I, respectively. The N2H+ abundance of the four densest cores in panel g) was derived from the observed peak temperature of the weakest hyperfine component (11,0–01,1) while the strongest component (12,3–01,2) was used for all other cores (see Sect. 5.1). |
 |
Fig. 11 a) Observed HC3N/N2H+ abundance ratio as a function of H2 column density for the cores in Cha I Centre (black, filled squares), Cha I South (black, empty squares), Cha I West (black diamond), Cha I South lower limits (black, empty triangles), Cha III (pink asterisks), and Cha III lower limits (pink, empty triangle). b) Observed HC3N/N2H+ abundance ratios for Cha I (circles) and lower limits (triangles) overplotted on the 870 μm dust continuum emission obtained with LABOCA (Belloche et al. 2011a). The contour levels correspond to a, 2a, 4a, 8a, 16a, 32a, with a = 48 mJy/21′′-beam (4σ). |
5.2. Depletion
The distributions of the abundances of C18O, C17O, CH3OH, and C34S suggest that these molecules are affected by depletion in the core interiors in Cha I (Fig. 10). The abundances of these molecules appear to systematically decrease for cores of higher column density. C17O and C34S in particular show this abundance decrease with a narrower dispersion at each column density compared to C18O and CH3OH that have a larger spread of abundances. For instance, the abundances of C17O are of the order ~ 3–20 × 10-8 at a column density of ~5 × 1021 cm-2 and ~1–3 × 10-8 at a column density of ~15 × 1021 cm-2. There is also a hint of HC3N depletion at higher densities (Fig. 10f), but for this molecule the trend of abundance decrease as a function of increasing density is more uncertain than for C18O, C17O, CH3OH, and C34S. The sample of cores in Cha III is not large enough to draw a conclusion about depletion within the cores.
5.3. Comparison to predictions of chemical models
Both physically-static and core-contraction chemical models have been run for a selection of gas densities.
The static models adopt free-particle densities of 1 × 105, 3 × 105, and 1 × 106 cm-3 corresponding to total hydrogen number densities of nH = 1.7 × 105, 5.1 × 105, and 1.7 × 106 cm-3 (see Appendix D). The adopted densities are comparable to the interpolated (for 37″) averaged Mopra free-particle densities of the Cha I and III cores (Cha I; ninter ~ 7.4 × 104–1.7 × 106 cm-3, Cha III; ninter ~ 7.3 × 104–3.3 × 105 cm-3).
Visual extinctions are sufficient to render unimportant those processes that depend on the external UV radiation field. The chemical model (MAGICKAL) and reaction network are those presented by Garrod (2013), which employ a fully-coupled gas-phase and dust grain-surface chemistry. Because of the low dust temperatures assumed here (8 K), only surface chemistry is considered; chemistry within the bulk ices is switched off. All material except hydrogen begins in atomic/ionic form in the gas phase, as shown in Table 1 of Garrod (2013). A gas temperature of 9 K is assumed. We expect lower-density cores to have slightly higher temperatures (e.g., ~ 10–12 K). Somewhat higher temperatures do not significantly affect the model predictions (T = 12 K has been tested).
5.3.1. Static models
The evolution of the N2H+ and HC3N fractional abundances, and the HC3N/N2H+ abundance ratio for the static models are shown in Figs. 12a, c, and e. After an initial peak, the HC3N to N2H+ abundance ratio decreases from a value of ~ 103–104 down to ~ 10-3 (Fig. 12e). After it reaches a minimum value it increases once more by a factor of ~10 (highest density) to 100 (lowest density model) toward the end of the core evolution. The range of observed values of the HC3N/N2H+ abundance ratio (~ 0.2−11) is also shown in Fig. 12e. For the densities modelled in this section, the observed values match the model predictions in a phase during which the HC3N/N2H+ abundance ratio decreases with increasing time.
The static models therefore appear to support the hypothesis that a greater HC3N/N2H+ abundance ratio is associated with early-time chemistry. However, these models include no treatment of the time-dependent condensation of a core, nor account for the chemistry in regions outside of the central density peak. Furthermore, the initial chemical abundances correspond to diffuse, atomic conditions that are not appropriate for the higher densities observed in the cores. Since the early formation of HC3N appears to be dependent on the availability of atomic carbon, which is not fully locked up in CO at early times, the consideration of static models alone is not sufficient to support the interpretation of the observed trend.
5.3.2. Contraction models
To remedy these shortcomings, a comparison is made with chemical models of cloud cores investigated by Garrod et al. (2005) and later publications. These models trace the chemical evolution at 12 depth points arranged along a radius through a cloud core, as it condenses from diffuse to dense conditions over a period of 1 Myr, but without the re-expansion of the core that takes place after 1 Myr in the standard models of Garrod et al. (2005). Here, the physical conditions are kept steady after 1 Myr. The initial elemental abundances are the same for both the static and the core contraction models. Initial total hydrogen densities follow a Gaussian profile; values range from 300 to 1000 cm-3 between the outermost point and the central core position, with visual extinctions ranging from 0.65 to 1.7 mag. This profile is held steady for an arbitrary period of time until a chemical steady-state is achieved (no freeze-out onto dust grains is active during this time). This produces an initial chemical composition that is appropriate to the physical conditions.
 |
Fig. 12 Evolution of the N2H+a), b) and HC3N c), d) abundances, and the HC3N to N2H+ abundance ratio e), f) as a function of time for free-particle densities of 1 × 105 cm-3 (dotted), 3 × 105 cm-3 (solid), and 1 × 106 cm-3 (dashed line) and a kinetic temperature of 9 K. Each column shows predictions from one specific model (static, contraction). The predictions from the contraction models correspond to abundances derived from integrated (along all depth points) column densities (see Garrod et al. 2006a,b). The horizontal dot-dashed lines indicate the range of observed values for the N2H+ (top row), HC3N abundances (middle row), and the HC3N to N2H+ ratio (bottom row). The maximum H2 column densities for the contraction models are achieved at 1 Myr and they are ~4 × 1021 cm-2, ~ 1.3 × 1022 cm-2, and ~ 4 × 1022 cm-2, respectively. |
During the main period of physical evolution of the core, the density follows a Gaussian time-dependence. This process is described in detail by Garrod et al. (2005). Free-particle peak central densities of 1 × 105, 3 × 105, and 1 × 106 cm-3 with respective H2 peak edge-to-edge column densities of ~ 4 × 1021, ~ 1.3 × 1022, and ~ 4 × 1022 cm-2 are achieved after 1 Myr. The equivalent initial, edge-to-edge visual extinctions achieved are ~1, ~2, ~ 5 mag, while the final values are ~4, ~ 14, and ~ 43 mag (conversion factor of 9.4 × 1020 cm-2 mag-1; Bohlin et al. 1978). The densities and visual extinctions at each modelled depth point vary with time. As points achieve visual extinctions greater than 2.5 mag, the freeze-out of gas-phase material begins. No surface chemistry is explicitly modelled in this treatment; accreted atoms are assumed to be fully hydrogenated, and remain on the grain surfaces (until the visual extinction again falls below the threshold value of 2.5 mag).
These models allow column densities to be calculated along lines of sight passing through each depth point. Values calculated in this way take account of both the chemical abundances and gas densities specific to each point. Figures in Garrod et al. (2006a,b) show column densities calculated in this way, as a function of time during the physical evolution of the core. Species that are strongly dependent on carbon for their formation are found to peak prior to the attainment of maximum core density, while other species, such as N2H+, are found to trace the density more closely.
Figures 12b and d show the predicted peak column densities of N2H+ and HC3N for the contraction models, normalized to the total H2 column density to provide a comparison with the single-point fractional-abundance results. The range of the observed HC3N to N2H+ column density ratio is in agreement with predicted values (Fig. 12f), and shows the same trend in its time-dependent behaviour as is found in the case of the static models.
The observed H2 column densities for the Mopra beam of 37″ (for N2H+ 1–0) are found after interpolating between the peak H2 column density (for HPBW 21.2″, ~ 3200 AU) and the column density within an aperture of 50″. They are 3.3 × 1021−1.4 × 1022 cm-2 for the cores in Cha III and 3.6 × 1021−7.1 × 1022 cm-2 in Cha I (or 3.6 × 1021−1.4 × 1022 cm-2 excluding the three densest cores) (Belloche et al. 2011a,b). The HPBW of HC3N 10–9 is similar to N2H+ 1−0 (37.9″). The observed H2 column densities averaged over the Mopra beam are therefore comparable to the model values. The visual extinctions derived from 2MASS range from 5.1–19 mag for the Cha I cores with an average extinction of ~10 mag, and ~2–9 mag for the Cha III cores, with an average of ~ 5 mag (Belloche et al. 2011a,b). The cores in Cha III and the low AV cores in Cha I are therefore expected to be better described by the two lower-density, contraction models with final edge-to-edge extinctions of 4 and 14 mag, while the model with the final AV of ~ 43 mag is better suited for the Cha I cores with visual extinctions approaching 20 mag.
Linewidths and non-thermal velocity dispersions in Cha I and III.
The peak, predicted N2H+ and HC3N abundances for the contraction models shown in Figs. 12b and d are slightly lower (factor of ~1–5) than the equivalent observed abundances. The range of the observed HC3N to N2H+ abundance ratio is, on the other hand, in good agreement with the predicted values. The (downward) discrepancies in the individual abundances predicted for each molecule may result from the true density profiles of the cores being less sharp than the Gaussian density profile assumed in the contraction models. A more centrally-flattened density profile, with higher gas densities in the wings, would result in a somewhat larger region of molecule production. This could plausibly produce N2H+ and HC3N column densities that are a few times greater, while maintaining the same overall H2 column density, which would better match the observational fractional abundances. Nevertheless, given the agreement of the models and observations regarding the HC3N to N2H+ abundance ratio, this discrepancy is small enough that it is unlikely to affect the qualitative results.
While the hypothesized cause of the trend in the HC3N/N2H+ abundance ratio appears to agree with the models, i.e., that a lower ratio is indicative of a greater degree of physical evolution, it is unlikely that a more specific determination of core age may be made without a more specific model for individual cores in the cloud.
Finally, the models presented here for peak densities of ~ 1 × 105–1 × 106 cm-3 represent densities that match those of both prestellar (gravitationally bound) and currently unbound cores in Cha I and III. Our predictions in Fig. 12 therefore show that the HC3N/N2H+ abundance ratio cannot be used to differentiate between gravitationally bound and unbound cores. Instead, it only points to an early or late stage of chemical evolution.
5.4. Comparison to other clouds
Starting with the low-density tracers (in terms of critical density), the mean abundances of C18O and C17O in Cha I relative to H2 are ~4.2 × 10-7 and ~5.3 × 10-8, respectively. We derive lower abundances in Cha III by a factor of ~3 and ~2, respectively. Frerking et al. (1982) estimated a C18O abundance of 1.7×10-7 within cloud interiors in ρ Ophiuchus and Taurus. Miettinen et al. (2011) derived C17O abundances ranging from 4 × 10-8 to 1.6 × 10-7 toward seven clumps in massive infrared dark clouds (IRCDs). Friberg et al. (1988) observed methanol toward three dark clouds. They found CH3OH abundances of ~ 2 × 10-9 for TMC1 and L134N, and ~0.5−1 × 10-9 for the Class 0 object B335 and for a kinetic temperature of 10 K. The observed C18O, C17O, and CH3OH abundances toward the aforementioned clouds are all very similar to the mean (and median) abundances we derive for both Cha I and Cha III (see Table 10).
We now discuss the abundances of the high-density tracers. Vasyunina et al. (2011) report an average N2H+ abundance of 7.7 × 10-10 for a sample of low-mass IRDCs. The average N2H+ abundances we derive are lower by a factor of ~3 in Cha I and ~7 in Cha III. The low-mass IRDC abundance average for HC3N is ~ 1.5 × 10-9 (Vasyunina et al. 2011), which is higher than the mean abundance we find in Cha III by a factor of ~3. Molecular abundances of ~5.8−17 × 10-11 were found for C34S in the IC 5146 dark cloud (Bergin et al. 2001). Our reported C34S abundances in Cha I and III are similar to the high-end value. We therefore see a significant abundance difference between Cha (I and III) and other low-mass dark clouds only in N2H+ and in HC3N for Cha III, but the statistics are low in the last case. These molecules are both less abundant in Cha I and III than in other low-mass clouds.
6. Discussion
6.1. Turbulence in Cha I and III
In order to directly compare the linewidths and non-thermal velocity dispersions of the transitions detected in both clouds, we choose to only compare core samples of similar peak column densities. This way we compare cores of similar physical properties. For this reason we exclude the cores Cha1-C1, Cha1-C2, and Cha1-C3, whose observed peak column densities are higher by a factor of 1.5–6 than the maximum peak column densities in Cha III. We also omit the second velocity components (see definition in Sect. 3) for this comparison. We assume the same kinetic temperature of 10 K for both clouds, which is plausible since both clouds have similar dust temperatures (see Tóth et al. 2000) and mean densities (Belloche et al. 2011a,b).
A direct comparison of the non-thermal to thermal velocity dispersion ratios of the transitions C34S 2–1, CH3OH 20–10 A+, CH3OH 21–11 E, N2H+ 1–0, C18O 2–1, C17O 2–1, and HC3N 10–9 shows that they are similar in both clouds (see Table 11 and Fig. 13). This ratio is larger in C18O 2–1 in Cha I, but as the line is affected by optical depth effects (see Sect. C.1) the difference between the two clouds is most likely not significant. Hence, there is no significant difference in the turbulence level within Cha I and III that could account for the difference in their star formation activities.
6.1.1. Turbulence dissipation
C17O 2–1 and C18O 2–1 have critical densities of ~9 × 103 cm-3 at 10 K (see Table B.1). In addition, C17O and C18O are usually depleted in the interiors of cold starless cores. Therefore these transitions preferentially trace low-density material. Transitions with higher critical densities, such as N2H+ 1–0 and HC3N 10−9, are expected to trace core interiors. The dense, inner parts of the cores are expected to be regions of minimum turbulence in contrast to the less dense, outer parts of the cores, which are less shielded from the ambient turbulent motions (Goodman et al. 1998; Larson 1981). The low-density transitions likely trace these outer, and more turbulent core regions. The larger non-thermal dispersions that we find in C17O 2–1 and C18O 2–1 compared to HC3N and N2H+ in both clouds are consistent with the picture of turbulence dissipation in the core interiors in Cha I and III. CH3OH 20–10 A+ has a similar critical density to C17O, C18O, within a factor of ~3, as well as a similar abundance distribution (see Fig. 10). We also find that CH3OH 20–10 A+, C17O, and C18O have similar non-thermal velocity dispersions in both Cha I and III, therefore indicating that these transitions likely trace similar regions.
 |
Fig. 13 Mean ratio of non-thermal to thermal (of the mean particle) velocity dispersions against the critical density for the transitions listed in Table 11 for the Cha I (black squares) and III (pink asterisks) clouds. The errorbars show the dispersions from the mean. |
N2H+ 1–0 and HC3N 10–9 are both high-density tracers with critical
densities of ~2.4 ×
105 cm-3 and ~ 6.0 × 105 cm-3, respectively (Table B.1). Both transitions have non-thermal velocity
dispersions comparable to each other in both Cha I and III (Sect. 4.1.2). This is expected if they both trace regions of similar
density. The non-thermal velocity dispersions of these transitions are also found to be
systematically smaller than the non-thermal dispersions of C17O 2–1 and C18O 2–1 in both Cha I and III.
We obtain a N2H+ 1–0 to C34S 2–1 mean non-thermal velocity dispersion ratio of
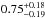 in Cha I. C34S 2–1 is excited at densities
similar to N2H+ 1–0 and these two transitions would therefore be
expected to have similar non-thermal velocity dispersions if they both have similar
abundance profiles. The higher C34S 2–1 non-thermal dispersions is a sign of
C34S depletion
in the core interiors, making this molecule sensitive to the outer, more turbulent core
regions. We also find evidence of C34S depletion in the distribution of core abundances in
Cha I as a function of their column density (Fig. 10e). The fact that C34S 2–1 and C17O 2–1 have a mean non-thermal dispersion ratio close
to unity is an additional hint that C34S 2–1 traces similar lower-density regions to
C17O 2–1 and
that N2H+ 1–0 and HC3N 10–9 trace the quiescent inner core regions.
in Cha I. C34S 2–1 is excited at densities
similar to N2H+ 1–0 and these two transitions would therefore be
expected to have similar non-thermal velocity dispersions if they both have similar
abundance profiles. The higher C34S 2–1 non-thermal dispersions is a sign of
C34S depletion
in the core interiors, making this molecule sensitive to the outer, more turbulent core
regions. We also find evidence of C34S depletion in the distribution of core abundances in
Cha I as a function of their column density (Fig. 10e). The fact that C34S 2–1 and C17O 2–1 have a mean non-thermal dispersion ratio close
to unity is an additional hint that C34S 2–1 traces similar lower-density regions to
C17O 2–1 and
that N2H+ 1–0 and HC3N 10–9 trace the quiescent inner core regions.
Overall, all tracers excluding C18O 2–1 have subsonic non-thermal dispersions, indicating that the core interiors in Cha I and III are indeed quiescent, as found in other clouds (Goodman et al. 1993).
6.2. Core interactions in Cha I and III
The free-fall time for spherically symmetric gravitational collapse is given by
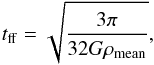 (19)where ρmean is the
mean mass density of the cores. We estimate the core densities as ρ = nmean ×
μmH, with
nmean taken from Belloche et al. (2011b) for Cha III, and computed using the total mass
and a radius of
(19)where ρmean is the
mean mass density of the cores. We estimate the core densities as ρ = nmean ×
μmH, with
nmean taken from Belloche et al. (2011b) for Cha III, and computed using the total mass
and a radius of 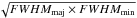 for the cores in Cha I (total mass and
radius from Belloche et al. 2011a). We use a mean
molecular weight of μ ~
2.37. We find average free-fall times of 0.18 Myr for
both Cha I and III.
for the cores in Cha I (total mass and
radius from Belloche et al. 2011a). We use a mean
molecular weight of μ ~
2.37. We find average free-fall times of 0.18 Myr for
both Cha I and III.
The expected lifetimes and evolution of dense cores largely depend on the theoretical model used to describe the gravitational collapse of the cloud (see Ward-Thompson et al. 2007 for a review on core lifetimes). Collapse models governed by ambipolar diffusion tend to predict core lifetimes longer than the free-fall time, which increases the more the initial core conditions depart from the magnetically supercritical state (Shu et al. 1987; Mouschovias 1991; Myers & Khersonsky 1995). The collapse proceeds faster when the core is initially nearly supercritical (e.g., Nakano 1998) and if turbulence is dynamically important (Ciolek & Basu 2001; Fatuzzo & Adams 2002; Vázquez-Semadeni et al. 2005). In models of initially magnetically subcritical, turbulent clouds the dense cores produced have lifetimes that range from ~1.5 to ~10 times the free-fall time (e.g., Nakamura & Li 2005). Models of magnetically supercritical, turbulent cloud collapse also predict core lifetimes of the order of a few times the free-fall time (Galván-Madrid et al. 2007; Vázquez-Semadeni et al. 2005) compared to the turbulence dominated star formation scenario that supports faster evolution timescales of the order of one free-fall time (Elmegreen 2000; Ward-Thompson et al. 2007; Kirk et al. 2005; Ballesteros-Paredes et al. 1999; Vazquez-Semadeni et al. 2000; Mac Low & Klessen 2004; Ballesteros-Paredes & Hartmann 2007). Galván-Madrid et al. (2007) find mean core lifetimes of the order of ~6tff in their numerical simulations of magnetically supercritical, turbulent, and isothermal clouds.
Observationally, there are various estimates of the core lifetimes, some of which are ~0.5 Myr (Evans et al. 2009), ~0.3−1.6 Myr (Lee & Myers 1999), ~0.4 Myr (Onishi et al. 1998, 2002), and ~0.3 Myr (Kirk et al. 2005). Ward-Thompson et al. (2007) conclude that most observational estimates yield core lifetimes of ~2–5 free-fall times for densities of ~104 − 105 cm-3.
If we assume core lifetimes of the order of 3–6 times the free-fall time as suggested by both the observational evidence (e.g., Ward-Thompson et al. 2007) and collapse models (e.g., Galván-Madrid et al. 2007), we obtain a dynamical lifetime of ~0.5–1 Myr for Cha I and III with dispersions of ~ 0.2−0.3 Myr. A comparison of these lifetime estimates to the collisional times we obtained in Table 8 for Cha I and III as a whole and their subregions shows that, with the exception of Cha I North (tcoll ~ 0.7 Myr), the collisional times are longer than the dynamical lifetimes, and in most cases even much longer. The cores in Cha I North might therefore be the only ones to experience dynamical interactions in the future, thus increasing the probability of competitive accretion in this region. We note, however, that the cores in Cha I Centre and Cha III North have collisional times only slightly longer than 1 Myr, so they may also experience dynamical interactions in the future.
The collision times we compute for the subregions of Cha I and III are of the same order as the ones found in André et al. (2007), while the deviations are large when we compare these values for the Cha I and III clouds as a whole. André et al. (2007) estimated a collision time of ~ 1–10 Myr between the 57 starless cores in Ophiuchus and a dynamical core lifetime of ~0.02 − 0.5 Myr (assuming 3 × tff and using the mean core density). They concluded that interactions between the condensations in Ophiuchus cannot happen within their lifetimes. Sadavoy et al. (2012) studied nine dense cores in Perseus B1-E and found that the cores have near-neighbour separations less than one Jeans length and interactions might occur on a timescale of ~1 Myr, which makes competitive accretion plausible for that region.
We conclude that, as is the case for Ophiuchus, dynamical interactions between cores are unlikely to be dynamically significant in either Cha I, Cha III, and the majority of their subregions. Competitive accretion may only affect the future dynamical state of the cores in Cha I North and, to a lesser extent, Cha I Centre and Cha III North.
6.3. Dynamical state of starless cores
Our virial equilibrium analysis suggests that up to five cores are gravitationally bound in Cha I (Cha1-C1, Cha1-C2, Cha1-C3, Cha1-C4, Cha1-C5) and only one is virialized (Cha1-C1, also known as Cha-MMS1). Cha1-C1 is virialized in most detected transitions (see Table 4). Therefore, ~ 8% of the whole sample at most, show evidence of already being gravitationally bound in Cha I.
Nevertheless, we found that 13%–28% of the total core population in Cha I are either already prestellar or likely to become gravitationally bound and therefore prestellar in the future based on the “infall” signature (see Sect. 4.2). For the number of cores not gravitationally bound, the “infall” signature is interpreted as contraction motions, which may turn the currently unbound cores into bound ones (prestellar). The upper limit corresponds to the full sample of cores showing the “infall” signature, while the lower limit reflects a more conservative number after excluding the number of “infall” signatures that may only trace large-scale contraction motions (as traced by 13CO 2–1) or pulsations. Anathpindika & Francesco (2013) also stress that inward motions are not a sufficient criterion for gravitational boundedness. Belloche et al. (2011a) found that ~17% of the starless cores are currently prestellar based on their Bonnor-Ebert analysis and Belloche et al. (2011b) estimated that up to ~50% might become unstable in the future based on theoretical predictions. We therefore find that the fraction of the cores that might become prestellar based on observational evidence and the “infall” signature (~ 13–28%) is in agreement with the ~ 50% upper limit of Belloche et al. (2011b).
The estimated fraction of prestellar cores in Aquila amounts to ~ 60% (André et al. 2010), while it is as high as ~ 70% in Ophiuchus (Motte et al. 1998). Curtis & Richer (2011) found that most of the dense cores in Perseus seem to be close to the critical virial ratio, thus implying that they are gravitationally bound, thus prestellar (see also Enoch et al. 2008). Belloche et al. (2011a) suggested that Cha I is experiencing the end of its star formation activity. Overall, the data show that Cha I is experiencing significantly lower star formation activity compared to other nearby clouds and our kinematical analysis so far suggests that only up to ~ 28% of the Cha I starless cores might become prestellar in the future. Morales Ortiz et al. (2012) also found that almost all the starless cores in the Vela-D molecular cloud are not virialized or gravitationally bound. Overall, they estimated that approximately 30% of the whole core population in Vela-D is gravitationally bound, which is comparable to the number of cores in Cha I that will likely become unstable in the future.
We find that no core is virialized in Cha III and only one, Cha3-C1, is gravitationally bound based on our virial analysis. We also find that 2–5 cores are likely to become prestellar based on the “infall” signature, which corresponds to 10–25% of the observed sample (see Sect. 4.2). Belloche et al. (2011b) concluded that two cores in Cha III are gravitationally unstable (Cha3-C1 and Cha3-C2) from their Bonnor-Ebert analysis.
The virial analysis of Cha I and Cha III confirms the result previously suggested that Cha I is in general more active than Cha III (Belloche et al. 2011b). When taking the “infall” signature into account we find that the cores suggested to be gravitationally bound in Cha III from the dust continuum survey are, indeed, infalling and that three additional cores are likely to become prestellar.
Smith et al. (2012) modelled the line emission of irregular cores embedded in filaments via radiative transfer and found that the number of collapsing cores are underestimated when only taking the “infall” signature into account. The line profiles are extremely variable depending on the viewing angle and other effects, such as one-sided accretion onto filaments. These may result in a line profile not showing the expected blue asymmetry even if the core is indeed collapsing. The fraction of contracting cores in Cha I and III might therefore be even larger than the observational evidence has shown so far.
6.4. Core evolutionary state
Observationally, we find a significant difference in the HC3N/N2H+ abundance ratio between Cha I Centre, and Cha I South and West (see Fig. 11b). The highest density cores belonging to Cha I Centre have on average lower HC3N/N2H+ abundance ratios than the lower density cores in Cha I South and West. In the framework of the static and collapse models presented in Sect. 5.3, the HC3N/N2H+ abundance ratio appears to be a good evolutionary tracer. Nevertheless, the use of abundance ratios as evolutionary clocks is strongly model dependent and requires knowledge of the initial conditions of the region being studied in order to be used as such.
The observed HC3N to N2H+ abundance ratios in Fig. 11 imply that the cores in the central part of Cha I (Cha I Centre) are more evolved than the cores in the southern part of the cloud (Cha I South). The densest and most evolved core in Cha I, Cha1-C1 (Cha-MMS1; first hydrostatic core candidate) is also located in Cha I centre and has an HC3N to N2H+ abundance ratio of ~ 0.3. It is interesting to note that all the cores in Cha I Centre show contraction motions manifested as the “infall” signature, while there are approximately equal numbers of cores showing the “infall” and opposite signatures in Cha I South (Fig. 7). Therefore, as there is no excess of “infall” signatures compared to the opposite signatures, the cores in Cha I South may only be transient structures or oscillating cores.
The HC3N to N2H+ abundance ratio for the Cha III cores is found to be similar to Cha I South, although with low statistics for Cha III. This points to the fact that Cha III, as well as Cha I South and West, are less chemically evolved than Cha I Centre. In addition, the evidence of contraction that we see for up to 25% of cores in Cha III through the “infall” signature and the fact that we see no opposite signatures for any cores indicate that some of the Cha III cores may become prestellar. Therefore, Cha III is likely to form stars in the future.
6.5. Overlapping velocity components
The Herschel image of Cha I shown in Winston et al. (2012) (PACS 160 μm, SPIRE 250 μm, and SPIRE 500 μm) reveals the dust structure of the cloud in great detail. The elongated filament in Cha I Centre (Fig. 2b) corresponds to the Ced 110 cluster on the Herschel image of Winston et al. (2012). It appears very bright and dense, while retaining the same elongated structure as in the 870 μm LABOCA map of Cha I (Belloche et al. 2011a). The direction as well as the location of the higher velocity emission in our maps seems to correspond to fainter, more dispersed and lower density material seen on the Herschel image that is threading the dense, elongated filament in the perpendicular direction. Alternatively, the higher velocity component could simply be a projection effect.
As the higher velocity component in Cha I North (Fig. 2a) is not related to the bipolar outflow of Cha-MMS2 (see Sect. 3.1) it might also be due to material in the cloud interacting with this elongated structure or a projection effect. The dust continuum Herschel map of Cha I North (Ced 112; Winston et al. 2012) shows that there is some fainter material close to the very northern part of the filament where the peak of the higher velocity emission is located and it seems to be oriented perpendicular to it. However, the material in Cha I North as seen on the Herschel map is not as dense and homogeneous in direction as it appears in Cha I Centre.
7. Summary and conclusions
We performed spectral line observations with the APEX and Mopra telescopes toward 60 cores in Cha I and 29 cores in Cha III. The aim of this study is to explore the kinematical state of the cores, their future dynamical evolution, and to determine what the main driver of the different star formation activities in the two clouds is. Our conclusions are the following:
-
1.
We find at most 5 prestellar cores (~8%) in Cha I and 1 in Cha III based on a virial analysis. Between 8 and 17 cores show contraction motions based on the “infall” signature in Cha I, bringing the total percentage of cores that might become, if not already, prestellar to 13–28%. Similarly, between 2 and 5 cores are contracting in Cha III, and thus 10–25% cores of the observed sample might become, if not already, prestellar in the future, which corresponds to 7–17% of the whole core population.
-
2.
Multiple velocity components are observed in Cha I toward a few cores in the northern and central parts of the cloud. The C18O 1–0 integrated emission of the higher velocity component in the central elongated structure in Cha I (Cha I Centre) is oriented perpendicular to the dust continuum emission. The higher velocity component might be caused by more disperse material interacting with the elongated structure along this direction, as suggested by the Herschel continuum data.
-
3.
We derive a C18O median abundance relative to H2 that is lower in Cha III than in Cha I by a factor of ~2. The distributions of the individual core abundances in Cha III in C18O, C17O, HC3N, and N2H+ lie at the lower end of the core abundances in Cha I, although with low statistics for Cha III.
-
4.
The C18O, C17O, CH3OH, and C34S abundances of the Cha I cores decrease with increasing density, therefore suggesting that these molecules are affected by depletion in the inner parts of the cores.
-
5.
The turbulence level is similar in both clouds in various transitions. There is therefore no indication of turbulence playing a role in the different star formation activities of Cha I and III.
-
6.
Turbulence dissipation in the core interiors is seen in both clouds with the non-thermal dispersions of the high-density tracers N2H+ 1–0 and HC3N 10–9 being smaller than the non-thermal dispersions of C18O 2–1 and C17O 2–1. C34S 2–1 has a higher non-thermal velocity dispersion compared to N2H+ 1–0 in Cha I, which is consistent with C34S being affected by depletion in the inner parts of the cores.
-
7.
A velocity distribution and collision time analysis adapted for cylindrical symmetry shows that the dynamical evolution of the cores in Cha I and III on a cloud scale is not likely to be affected by interactions between the cores and competitive accretion. Core interactions in Cha I North may, on the other hand, take place within ~0.7 Myr.
-
8.
Both contraction and static chemical models indicate that the HC3N to N2H+ abundance ratio is a good core evolutionary indicator, but it cannot distinguish between transient and gravitationally bound cores. In the framework of these models, the observed HC3N/N2H+ abundance ratios in Cha I and III suggest that the cores in Cha I South and Cha III are less chemically evolved than the cores in Cha I Centre. The Cha I South cores may just be oscillating or transient objects, whereas some of the Cha III cores may form stars in the future.
Online material
Appendix A: Detailed physical parameters of Cha I and III cores
Tables A.1 and A.2 provide a detailed list of the observationally derived physical parameters of the cores for each transition separately. The method for extracting these values is described in Sects. 3 and 4. For the spectra that have two velocity components, the derived properties based on both components are listed. The integrated intensities are listed only for the transitions that were used to derive column densities.
Line parameters and physical parameters of cores in Cha I.
Line parameters and physical parameters of cores in Cha III.
Appendix B: Critical densities
For the calculation of critical densities we use the Einstein A-coefficients, the collisional rate coefficients, and energies from the Leiden Atomic and Molecular Database (LAMDA4).
The critical density is the density at which the rate of spontaneous emission is equal
to the rate of collisional de-excitation,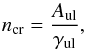 (B.1)where Aul is the
Einstein coefficient for spontaneous emission (s-1), Cul =
nH2γul
the collision coefficient (collision de-excitation rate, s-1), and γul the
collision rate (cm3 s-1). The critical densities we derive are listed in
Table B.1 for various molecular transitions.
(B.1)where Aul is the
Einstein coefficient for spontaneous emission (s-1), Cul =
nH2γul
the collision coefficient (collision de-excitation rate, s-1), and γul the
collision rate (cm3 s-1). The critical densities we derive are listed in
Table B.1 for various molecular transitions.
Critical densities.
Appendix C: Optical depths
Appendix C.1: C18O 2–1 opacity
C18O 2–1 was
observed toward all 60 cores in Cha I and C17O 2−1 toward 32. We estimate the optical depth of the
C18O 2–1
transition for this sample of 32 cores. We assume an isotopic ratio [18O]/[17O] of ~4.11, as was found for the nearby
(140 pc) low-mass star forming cloud ρ Ophiuchus (Wouterloot et al. 2005), to derive the opacity of C18O 2−1 with the relation
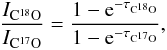 (C.1)where IC18O and IC17O are the integrated
intensities of the two transitions, τC18O and τC17O their opacities, and
τC17O =
τC18O/4.11. Table C.1 lists the opacity estimates for the sample of
32 cores in Cha I. Approximately half of them are somewhat optically thick
(4.2
>τC18O ≥ 1) in
C18O 2–1.
(C.1)where IC18O and IC17O are the integrated
intensities of the two transitions, τC18O and τC17O their opacities, and
τC17O =
τC18O/4.11. Table C.1 lists the opacity estimates for the sample of
32 cores in Cha I. Approximately half of them are somewhat optically thick
(4.2
>τC18O ≥ 1) in
C18O 2–1.
We can only calculate the C18O 2–1 opacities for the two cores in Cha III that were also observed in C17O 2–1, Cha3-C1 and Cha3-C4. Cha3-C1 is borderline optically thick/thin with an opacity of ~ 1, while Cha3-C4 is optically thin (Table C.2). They are both optically thin in C17O 2–1.
C18O 2–1 and C17O 2–1 opacities of the Cha I cores.
Appendix C.2: CS 2–1 opacity
We assume an isotopic ratio of [32S]/[34S] ~ 22 (Frerking et al. 1980) to calculate the opacity of the CS 2–1 line in Cha I. All 57 CS 2–1 spectra feature detections and 23 out of the 57 are detected in C34S 2–1. We follow the same method as above to estimate the CS 2–1 opacities toward the 23 cores that are detected in both transitions. The results are given in Table C.3.
For the remaining 34 spectra we calculate upper limits for the CS 2–1 opacity by using the ratio of the CS 2–1 integrated intensity to the value of 3 × rms of the C34S 2–1 spectra. The opacity upper limits are listed in Table C.4. All 23 cores that have detections in C34S 2–1 are optically thick in CS 2–1, with opacities ranging from ~2–10.
Two cores in Cha III are detected in C34S 2−1 and their CS 2−1 opacity is listed in Table C.5. Both have CS 2−1 opacities greater than one, while they are optically thin in C34S 2−1. CS 2−1 is detected toward all remaining cores, for which we calculate upper limits (Table C.6) in the same way as for the Cha I cores.
C18O 2–1 and C17O 2–1 opacities of the Cha III cores.
CS 2–1 and C34S 2–1 opacities of the Cha I cores.
CS 2–1 upper limit opacities of the Cha I cores.
CS 2–1 and C34S 2–1 opacities of the Cha III cores.
CS 2–1 upper limit opacities of the Cha III cores.
Appendix D: Density conversions
For the conversion of hydrogen densities to free-particle densities and vice versa we
use the mean molecular weight per free-particle, μ ~ 2.37 (see
Appendix A.1 in Kauffmann et al. 2008). The
cosmic mass ratio of hydrogen to the total mass of matter is ~ 0.71, while that of helium is
~0.27 (Cox 2000). The total hydrogen density,
nH, is equivalent to
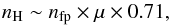 (D.1)which gives
(D.1)which gives
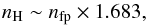 (D.2)with nfp the
free-particle density.
(D.2)with nfp the
free-particle density.
Appendix E: Spectra of Cha I and III cores
The spectra of the transitions used to search for signatures of contraction motions in the sources listed in Table 7 are displayed in Fig. E.1.
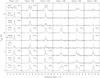 |
Fig. E.1 Spectra obtained with APEX and the Mopra telescope toward the Cha I and III sources listed in Table 7, displayed in main-beam temperature scale. Spectra that were rescaled to fit in the figure have their scaling factor indicated on the right. The vertical dashed line marks the systemic velocity as derived from a Gaussian fit to the CH3OH 20–10 A+ transition, except for sources Cha1-C6, Cha1-C24, Cha1-C27, Cha1-C35, and Cha3-C10 for which the C18O 2–1 transition was used. |
 |
Fig. E.1 continued. |
 |
Fig. E.1 continued. |
Acknowledgments
We thank the referee for the feedback that greatly improved the quality of this paper. We also thank the APEX and Mopra staff for their support during the observations, as well as Axel Weiß, Frédéric Schuller, Silvia Leurini, Arturo Gómez-Ruiz, Friedrich Wyrowski, and Keping Qiu for carrying out parts of the observations. In addition, we are very thankful to J. Harju for providing us with the Cha III C18O 1–0 data from their published work. A.E.T. was supported for this research through a stipend from the International Max Planck Research School (IMPRS) for Astronomy and Astrophysics at the Universities of Bonn and Cologne. R.T.G. acknowledges support from the NASA Astrophysics Theory Program through grant NNX11AC38G. The Mopra radio telescope is part of the Australia Telescope National Facility which is funded by the Commonwealth of Australia for operation as a National Facility managed by CSIRO. The University of New South Wales Digital Filter Bank used for the observations with the Mopra Telescope was provided with support from the Australian Research Council.
References
- Aguti, E. D., Lada, C. J., Bergin, E. A., Alves, J. F., & Birkinshaw, M. 2007, ApJ, 665, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Alves, J., Lombardi, M., & Lada, C. J. 2007, A&A, 462, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anathpindika, S., & Francesco, J. D. 2013, MNRAS, 430, 1854 [NASA ADS] [CrossRef] [Google Scholar]
- André, P., Ward-Thompson, D., & Barsony, M. 2000, Protostars and Planets IV (Tucson: University of Arizona Press), 59 [Google Scholar]
- André, P., Belloche, A., Motte, F., & Peretto, N. 2007, A&A, 472, 519 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- André, P., Basu, S., & Inutsuka, S. 2009, The formation and evolution of prestellar cores, ed. G. Chabrier (Cambridge University Press), 254 [Google Scholar]
- André, P., Men’shchikov, A., Bontemps, S., et al. 2010, A&A, 518, L102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arce, H. G., Borkin, M. A., Goodman, A. A., Pineda, J. E., & Beaumont, C. N. 2011, ApJ, 742, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Ballesteros-Paredes, J., & Hartmann, L. 2007, Rev. Mex. Astron. Astrofis., 43, 123 [NASA ADS] [Google Scholar]
- Ballesteros-Paredes, J., Vázquez-Semadeni, E., & Scalo, J. 1999, ApJ, 515, 286 [NASA ADS] [CrossRef] [Google Scholar]
- Bally, J., Walawender, J., Luhman, K. L., & Fazio, G. 2006, AJ, 132, 1923 [NASA ADS] [CrossRef] [Google Scholar]
- Bate, M. R., Bonnell, I. A., & Bromm, V. 2003, MNRAS, 339, 577 [NASA ADS] [CrossRef] [Google Scholar]
- Belloche, A., Parise, B., van der Tak, F. F. S., et al. 2006, A&A, 454, L51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belloche, A., Schuller, F., Parise, B., et al. 2011a, A&A, 527, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belloche, A., Parise, B., Schuller, F., et al. 2011b, A&A, 535, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benedettini, M., Pezzuto, S., Burton, M. G., et al. 2012, MNRAS, 419, 238 [Google Scholar]
- Bergin, E. A., Ciardi, D. R., Lada, C. J., Alves, J., & Lada, E. A. 2001, ApJ, 557, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Bertoldi, F., & McKee, C. F. 1992, ApJ, 395, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Binney, J., & Tremaine, S. 1987, Galactic dynamics (Princeton University Press) [Google Scholar]
- Bohlin, R. C., Savage, B. D., & Drake, J. F. 1978, ApJ, 224, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Bonnell, I. A., Bate, M. R., & Zinnecker, H. 1998, MNRAS, 298, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Bonnell, I. A., Vine, S. G., & Bate, M. R. 2004, MNRAS, 349, 735 [NASA ADS] [CrossRef] [Google Scholar]
- Boulanger, F., Bronfman, L., Dame, T. M., & Thaddeus, P. 1998, A&A, 332, 273 [NASA ADS] [Google Scholar]
- Ciolek, G. E., & Basu, S. 2001, ApJ, 547, 272 [NASA ADS] [CrossRef] [Google Scholar]
- Cox, A. N. 2000, Allen’s astrophysical quantities, 4th edn. (New York: AIP Press; Springer) [Google Scholar]
- Curtis, E. I., & Richer, J. S. 2011, MNRAS, 410, 75 [NASA ADS] [CrossRef] [Google Scholar]
- di Francesco, J., Evans, II, N. J., Caselli, P., et al. 2007, Protostars and Planets V (Tucson: University of Arizona Press), 17 [Google Scholar]
- Elmegreen, B. G. 2000, ApJ, 530, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Enoch, M. L., Evans,II, N. J., Sargent, A. I., et al. 2008, ApJ, 684, 1240 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, II, N. 2003, in SFChem 2002: Chemistry as a Diagnostic of Star Formation, eds. C. L. Curry, & M. Fich, 157 [Google Scholar]
- Evans,II, N. J., Dunham, M. M., Jørgensen, J. K., et al. 2009, ApJS, 181, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Fatuzzo, M., & Adams, F. C. 2002, ApJ, 570, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Frerking, M. A., Wilson, R. W., Linke, R. A., & Wannier, P. G. 1980, ApJ, 240, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Frerking, M. A., Langer, W. D., & Wilson, R. W. 1982, ApJ, 262, 590 [NASA ADS] [CrossRef] [Google Scholar]
- Friberg, P., Hjalmarson, A., Madden, S. C., & Irvine, W. M. 1988, A&A, 195, 281 [Google Scholar]
- Gahm, G. F., Lehtinen, K., Carlqvist, P., et al. 2002, A&A, 389, 577 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galván-Madrid, R., Vázquez-Semadeni, E., Kim, J., & Ballesteros-Paredes, J. 2007, ApJ, 670, 480 [NASA ADS] [CrossRef] [Google Scholar]
- Garrod, R. T. 2013, ApJ, 765, 60 [Google Scholar]
- Garrod, R. T., Williams, D. A., Hartquist, T. W., Rawlings, J. M. C., & Viti, S. 2005, MNRAS, 356, 654 [NASA ADS] [CrossRef] [Google Scholar]
- Garrod, R. T., Williams, D. A., & Rawlings, J. M. C. 2006a, ApJ, 638, 827 [NASA ADS] [CrossRef] [Google Scholar]
- Garrod, R. T., Williams, D. A., & Rawlings, J. M. C. 2006b, MNRAS, 373, 577 [NASA ADS] [CrossRef] [Google Scholar]
- Goodman, A. A., Benson, P. J., Fuller, G. A., & Myers, P. C. 1993, ApJ, 406, 528 [NASA ADS] [CrossRef] [Google Scholar]
- Goodman, A. A., Barranco, J. A., Wilner, D. J., & Heyer, M. H. 1998, ApJ, 504, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Gregersen, E. M., & Evans, II, N. J. 2000, ApJ, 538, 260 [NASA ADS] [CrossRef] [Google Scholar]
- Gregersen, E. M., & Evans, II, N. J. 2001, ApJ, 553, 1042 [NASA ADS] [CrossRef] [Google Scholar]
- Gregersen, E. M., Evans, II, N. J., Zhou, S., & Choi, M. 1997, ApJ, 484, 256 [NASA ADS] [CrossRef] [Google Scholar]
- Haikala, L. K., Harju, J., Mattila, K., & Toriseva, M. 2005, A&A, 431, 149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johnstone, D., Wilson, C. D., Moriarty-Schieven, G., et al. 2000, ApJ, 545, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, J., Bertoldi, F., Bourke, T. L., Evans, II, N. J., & Lee, C. W. 2008, A&A, 487, 993 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Keto, E., & Field, G. 2005, ApJ, 635, 1151 [NASA ADS] [CrossRef] [Google Scholar]
- Kirk, J. M., Ward-Thompson, D., & André, P. 2005, MNRAS, 360, 1506 [NASA ADS] [CrossRef] [Google Scholar]
- Knude, J., & Høg, E. 1998, A&A, 338, 897 [NASA ADS] [Google Scholar]
- Lada, C. J., Bergin, E. A., Alves, J. F., & Huard, T. L. 2003, ApJ, 586, 286 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. B. 1981, MNRAS, 194, 809 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, C. W., & Myers, P. C. 1999, ApJS, 123, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Leung, C. M., & Brown, R. L. 1977, ApJ, 214, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Luhman, K. L. 2007, ApJS, 173, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Luhman, K. L. 2008, Chamaeleon, Handbook of Star Forming Regions, Vol. II: The Southern Sky ASP Monograph Publications, ed. B. Reipurth, 169 [Google Scholar]
- MacLow, M.-M., & Klessen, R. S. 2004, Rev. Mod. Phys., 76, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Mardones, D., Myers, P. C., Tafalla, M., et al. 1997, ApJ, 489, 719 [NASA ADS] [CrossRef] [Google Scholar]
- Mattila, K., Liljeström, T., & Toriseva, M. 1989, in European Southern Observatory Conf. Workshop Proc. 33, ed. B. Reipurth, 153 [Google Scholar]
- Miettinen, O., Hennemann, M., & Linz, H. 2011, A&A, 534, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mizuno, A., Hayakawa, T., Tachihara, K., et al. 1999, PASJ, 51, 859 [NASA ADS] [CrossRef] [Google Scholar]
- Mizuno, A., Yamaguchi, R., Tachihara, K., et al. 2001, PASJ, 53, 1071 [NASA ADS] [CrossRef] [Google Scholar]
- Morales Ortiz, J. L., Olmi, L., Burton, M., et al. 2012, A&A, 543, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Motte, F., André, P., & Neri, R. 1998, A&A, 336, 150 [Google Scholar]
- Mouschovias, T. C. 1991, in The Physics of Star Formation and Early Stellar Evolution, eds. C. J. Lada, & N. D. Kylafis (Dordrecht: Kluwer), NATO ASIC Proc., 342, 449 [Google Scholar]
- Müller, H. S. P., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Struct., 742, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Myers, P. C. 1998, ApJ, 496, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Myers, P. C., & Khersonsky, V. K. 1995, ApJ, 442, 186 [NASA ADS] [CrossRef] [Google Scholar]
- Myers, P. C., Bachiller, R., Caselli, P., et al. 1995, ApJ, 449, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Myers, P. C., Mardones, D., Tafalla, M., Williams, J. P., & Wilner, D. J. 1996, ApJ, 465, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Nakamura, F., & Li, Z.-Y. 2005, ApJ, 631, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Nakano, T. 1998, ApJ, 494, 587 [NASA ADS] [CrossRef] [Google Scholar]
- Onishi, T., Mizuno, A., Kawamura, A., Ogawa, H., & Fukui, Y. 1998, ApJ, 502, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Onishi, T., Kawamura, A., Abe, R., et al. 1999, PASJ, 51, 871 [Google Scholar]
- Onishi, T., Mizuno, A., Kawamura, A., Tachihara, K., & Fukui, Y. 2002, ApJ, 575, 950 [NASA ADS] [CrossRef] [Google Scholar]
- Padoan, P., & Nordlund, Å. 2002, ApJ, 576, 870 [Google Scholar]
- Redman, M. P., Keto, E., & Rawlings, J. M. C. 2006, MNRAS, 370, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Reipurth, B., Nyman, L.-A., & Chini, R. 1996, A&A, 314, 258 [NASA ADS] [Google Scholar]
- Sadavoy, S. I., di Francesco, J., Bontemps, S., et al. 2010, ApJ, 710, 1247 [NASA ADS] [CrossRef] [Google Scholar]
- Sadavoy, S. I., di Francesco, J., André, P., et al. 2012, A&A, 540, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shu, F. H., Adams, F. C., & Lizano, S. 1987, ARA&A, 25, 23 [Google Scholar]
- Siringo, G., Kreysa, E., Kovács, A., et al. 2009, A&A, 497, 945 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smith, R. J., Shetty, R., Stutz, A. M., & Klessen, R. S. 2012, ApJ, 750, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Tóth, L. V., Hotzel, S., Krause, O., et al. 2000, A&A, 364, 769 [NASA ADS] [Google Scholar]
- Tsitali, A. E., Belloche, A., Commerçon, B., & Menten, K. M. 2013, A&A, 557, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van der Tak, F. F. S., Black, J. H., Schöier, F. L., Jansen, D. J., & van Dishoeck, E. F. 2007, A&A, 468, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vasyunina, T., Linz, H., Henning, T., et al. 2011, A&A, 527, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vazquez-Semadeni, E., Ostriker, E. C., Passot, T., Gammie, C. F., & Stone, J. M. 2000, Protostars and Planets IV (Tucson: University of Arizona Press), 3 [Google Scholar]
- Vázquez-Semadeni, E., Kim, J., Shadmehri, M., & Ballesteros-Paredes, J. 2005, ApJ, 618, 344 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, C. K., Lada, C. J., Young, E. T., Maloney, P. R., & Wilking, B. A. 1986, ApJ, 309, L47 [Google Scholar]
- Ward-Thompson, D., André, P., Crutcher, R., et al. 2007, Protostars and Planets V (Tucson: University of Arizona Press), 33 [Google Scholar]
- Whittet, D. C. B., Prusti, T., Franco, G. A. P., et al. 1997, A&A, 327, 1194 [NASA ADS] [Google Scholar]
- Winston, E., Cox, N. L. J., Prusti, T., et al. 2012, A&A, 545, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wouterloot, J. G. A., Brand, J., & Henkel, C. 2005, A&A, 430, 549 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhou, S. 1992, ApJ, 394, 204 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Comparison of systemic velocities, linewidths, and non-thermal velocity dispersions for selected pairs of transitions for Cha I and III.
Line shapes of optically thick tracersa for the cores that show the “infall” or opposite signature in Cha I and III.
Average velocity dispersions, crossing time, and collisional time for the Cha I and III cores detected in different tracers.
All Figures
 |
Fig. 1 Examples of spectra showing two emission peaks at different velocities that are not due to self-absorption, in Cha I (a) and in Cha III (b). a) Cha1-C7 and Cha1-C52 have two velocity components in C18O 2−1 (black) and in the optically thin C17O 2−1 and C34S 2−1 (red), respectively. Cha1-C15 (dashed) and Cha1-C12 (dotted) are located on either side of Cha1-C7 (see Fig. 2a). They both have only one emission peak that roughly coincides with either the lower velocity or the higher velocity peak of Cha1-C7. b) Cha3-C11 and Cha3-C21 have two velocity components in 13CO 2−1 (black) and in the optically thin C18O 2−1 (red), as well as in CS 2−1 for Cha3-C11. |
| In the text | |
 |
Fig. 2 C18O 1–0 blueshifted and redshifted emissions in a) Cha I North, b) Cha I Centre, and c) Cha III Centre overlaid on the 870 μm dust continuum maps of Cha I and III (Belloche et al. 2011a,b). The C18O 1−0 data are from Haikala et al. (2005) for Cha I and Gahm et al. (2002) for Cha III. The continuum contour levels (black) correspond to a, 2a, 4a, 8a, 16a, 32a, with a = 48 mJy/21″-beam (4σ) for a) and b), while a = 34.5 mJy/21″-beam (3σ) for c). The blueshifted (subscript b) and redshifted (subscript r) C18O 1−0 contours correspond to the levels a) 3σb (3σr), 4σb (4σr), 5σb (5σr) with σb = 0.17 K km s-1 and σr = 0.3 K km s-1, b) 3σb (3σr), 4.5σb (5σr) with σb = 0.33 K km s-1 and σr = 0.22 K km s-1, and c) 4σb (4σr), 6σb (6σr), 8σb with σb = 0.08 K km s-1 and σr = 0.09 K km s-1. The velocity ranges for the blueshifted and redshifted integrated intensity emissions are vb = 3.5 − 4.3 km s-1 and vr = 4.3−5.5 km s-1 for a), vb = 3.8 − 4.8 km s-1 and vr = 4.8−6.0 km s-1 for b), and vb = 0.5 − 1.5 km s-1 and vr = 1.5−2.5 km s-1 for c). The white dots show the location of the continuum cores in each region. The sources with spectra displayed in Fig. 1 are highlighted with a box around their name. |
| In the text | |
 |
Fig. 3 Mass derived from dust emission versus virial mass of the Cha I (a),
c)) and Cha III (b), d)) cores computed for
the transitions HC3N 10−9, N2H+ 1−0, C34S 2−1, CH3OH 20−10 A+, CH3OH 21−11 E,
C18O
2−1, and
C17O
2−1. Panels a and b
show the total mass of the cores while panels c and d show the mass obtained for a
circular aperture of diameter 50′′. The solid line defines the region in which the cores are
virialized ( |
| In the text | |
 |
Fig. 4 “Infall” signature toward cores in Cha I. The optically thick, self-absorbed transitions are shown with black thick lines and the optically thin transitions with red thin lines. The dashed red line shows the systemic velocity of each core derived from a Gaussian or hyperfine-structure fit to the optically thin line shown in red. The name of the cores is given on the right-hand side of each transition depicted. The factor by which each spectrum was multiplied is given next to the name of the transitions and it corresponds to 1 if not specified. |
| In the text | |
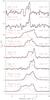 |
Fig. 5 Same as Fig. 4, for the cores in Cha I showing the opposite signature. |
| In the text | |
 |
Fig. 6 Same as Fig. 4, but for the cores in Cha III. |
| In the text | |
 |
Fig. 7 Cores showing the “infall” signature in Cha I (corresponding to Fig. 4) are plotted as red filled circles, the cores showing the opposite signature as green triangles, and the cores showing both signatures as blue squares. The contours correspond to the 870 μm dust continuum emission obtained with LABOCA (Belloche et al. 2011a) with contour levels of a, 2a, 4a, 8a, 16a, 32a, and a = 48 mJy/21′′-beam (4σ). |
| In the text | |
 |
Fig. 8 Systemic velocities of the cores in Cha I overplotted on the 870 μm continuum emission map obtained with LABOCA (Belloche et al. 2011a) for the transitions: a) C18O 2–1, b) C17O 2–1, c) CH3OH 20–10 A+, and d) N2H+ 1–0. The contour levels correspond to a, 2a, 4a, 8a, 16a, 32a, with a = 48 mJy/21′′-beam (4σ). The core velocities were derived from Gaussian or hyperfine-structure fits to the observed spectra. The filled circles are colour-coded and increase in size to emphasize increasing velocities. Cores with two velocity components are shown with the lower velocity overplotted onto the higher velocity component. The dashed arrow indicates the position angle of the velocity gradient fit. |
| In the text | |
 |
Fig. 9 Same as Fig. 8 but for Cha III and the transitions a) C18O 2–1 and b) CH3OH 20–10 A+. The contour levels correspond to the 870 μm continuum emission obtained with LABOCA (Belloche et al. 2011b) at a, 2a, 4a, 6a, with a = 34.5 mJy/21′′-beam (3σ). |
| In the text | |
 |
Fig. 10 Molecular abundances relative to H2 against H2 column densities interpolated within an aperture of diameter equal to the HPBW of each transition. The abundances of the Cha I and III cores are shown as black squares and pink asterisks, respectively. Upper limits (3σ uncertainties) are shown as pink and black downward triangles for Cha III and Cha I, respectively. The N2H+ abundance of the four densest cores in panel g) was derived from the observed peak temperature of the weakest hyperfine component (11,0–01,1) while the strongest component (12,3–01,2) was used for all other cores (see Sect. 5.1). |
| In the text | |
 |
Fig. 11 a) Observed HC3N/N2H+ abundance ratio as a function of H2 column density for the cores in Cha I Centre (black, filled squares), Cha I South (black, empty squares), Cha I West (black diamond), Cha I South lower limits (black, empty triangles), Cha III (pink asterisks), and Cha III lower limits (pink, empty triangle). b) Observed HC3N/N2H+ abundance ratios for Cha I (circles) and lower limits (triangles) overplotted on the 870 μm dust continuum emission obtained with LABOCA (Belloche et al. 2011a). The contour levels correspond to a, 2a, 4a, 8a, 16a, 32a, with a = 48 mJy/21′′-beam (4σ). |
| In the text | |
 |
Fig. 12 Evolution of the N2H+a), b) and HC3N c), d) abundances, and the HC3N to N2H+ abundance ratio e), f) as a function of time for free-particle densities of 1 × 105 cm-3 (dotted), 3 × 105 cm-3 (solid), and 1 × 106 cm-3 (dashed line) and a kinetic temperature of 9 K. Each column shows predictions from one specific model (static, contraction). The predictions from the contraction models correspond to abundances derived from integrated (along all depth points) column densities (see Garrod et al. 2006a,b). The horizontal dot-dashed lines indicate the range of observed values for the N2H+ (top row), HC3N abundances (middle row), and the HC3N to N2H+ ratio (bottom row). The maximum H2 column densities for the contraction models are achieved at 1 Myr and they are ~4 × 1021 cm-2, ~ 1.3 × 1022 cm-2, and ~ 4 × 1022 cm-2, respectively. |
| In the text | |
 |
Fig. 13 Mean ratio of non-thermal to thermal (of the mean particle) velocity dispersions against the critical density for the transitions listed in Table 11 for the Cha I (black squares) and III (pink asterisks) clouds. The errorbars show the dispersions from the mean. |
| In the text | |
 |
Fig. E.1 Spectra obtained with APEX and the Mopra telescope toward the Cha I and III sources listed in Table 7, displayed in main-beam temperature scale. Spectra that were rescaled to fit in the figure have their scaling factor indicated on the right. The vertical dashed line marks the systemic velocity as derived from a Gaussian fit to the CH3OH 20–10 A+ transition, except for sources Cha1-C6, Cha1-C24, Cha1-C27, Cha1-C35, and Cha3-C10 for which the C18O 2–1 transition was used. |
| In the text | |
 |
Fig. E.1 continued. |
| In the text | |
 |
Fig. E.1 continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.