| Issue |
A&A
Volume 573, January 2015
|
|
|---|---|---|
| Article Number | A138 | |
| Number of page(s) | 15 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201323019 | |
| Published online | 15 January 2015 | |
Detection of solar-like oscillations in the bright red giant stars γ Piscium and θ1 Tauri from a 190-day high-precision spectroscopic multi-site campaign⋆
1 Instituut voor Sterrenkunde, KU Leuven, 3001 Leuven, Belgium
e-mail: paul.beck@ster.kuleuven.be
2 Okayama Astrophysical Observatory, National Astron. Obs. of Japan, Kamogata, Asakuchi, 719-0232 Okayama, Japan
3 Department of Astrophysics, IMAPP, Radboud University Nijmegen, PO Box 9010, 6500 GL Nijmegen, The Netherlands
4 Observatoire de Genève, Université de Genève, Chemin des Maillettes 51, 1290 Sauverny, Switzerland
5 Université de Toulouse; UPS-OMP; IRAP; CNRS; IRAP ; 57 avenue d’Azereix, BP 826, 65008 Tarbes, France
6 Institut für Astronomie der Universität Wien, Türkenschanzstr. 17, 1180 Wien, Austria
7 Synergistic Exploitation of Atmospheric Data, Belgian Institute for Space Aeronomy, 1180 Brussels, Belgium
8 National Astronomical Observatory of Japan, 2-21-1 Osawa, Mitaka, 181-8588 Tokyo, Japan
9 Instituto de Astrofsica de Andalucía, Glorieta de la Astronomía s/n, 18009 Granada, Spain
10 School of Physics and Astronomy, University of Birmingham, UK
11 Department of Earth and Planetary Sciences, Tokyo Institute of Technology, 2-12-1 Ookayama, Meguro, 152-8551 Tokyo, Japan
12 Department of Physics & Astronomy, University of British Columbia, Vancouver, V6T 1Z1, Canada
13 Hiroshima Astrophysical Science Center, Hiroshima University, 1-3-1 Kagamiyama, 739-8526 Higashi-Hiroshima, Japan
14 OptCraft, 3-6-18 Higashi-Hashimoto, Midori-ku, 252-0144 Sagamihara, Japan
Received: 8 November 2013
Accepted: 16 July 2014
Context. Red giants are evolved stars that exhibit solar-like oscillations. Although a multitude of stars have been observed with space telescopes, only a handful of red giant stars were targets of spectroscopic asteroseismic observing projects.
Aims. We search for solar-like oscillations in the two bright red giant stars γ Psc and θ1 Tau from a time series of ground-based spectroscopy and determine the frequency of the excess of oscillation power νmax and the mean large frequency separation Δν for both stars. Seismic constraints on the stellar mass and radius will provide robust input for stellar modelling.
Methods. The radial velocities of γ Psc and θ1 Tau were monitored for 120 and 190 days, respectively. Nearly 9000 spectra were obtained. To reach accurate radial velocities, we used simultaneous thorium-argon and iodine-cell calibration of our optical spectra. In addition to the spectroscopy, we acquired interferometric observations of γ Psc for an independent estimate of the radius. We also analysed 22 days of observations of θ1 Tau with the MOST satellite.
Results. The frequency analysis of the radial velocity data of γ Psc revealed an excess of oscillation power around 32 μHz and a large frequency separation of 4.1 ± 0.1 μHz. θ1 Tau exhibits oscillation power around 90 μHz, with a large frequency separation of 6.9 ± 0.2 μHz. Scaling relations indicate that γ Psc is a star of about 1 M⊙ and 10 R⊙. The object θ1 Tau appears to be a massive star of about 2.7 M⊙ and 10 R⊙. The radial velocities of both stars were found to be modulated on timescales much longer than the oscillation periods.
Conclusions. The estimated radii from seismology are in agreement with interferometric observations and also with estimates based on photometric data. While the mass of θ1 Tau is in agreement with results from dynamical parallaxes, we find a lower mass for γ Psc than is found in the literature. The long periodic variability agrees with the expected timescales of rotational modulation.
Key words: asteroseismology / stars: rotation / techniques: interferometric / techniques: spectroscopic / stars: general
Based on observations made with the HERMES spectrograph mounted on the 1.2 m Mercator Telescope at the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofsica de Canarias; the CORALIE spectrograph mounted on the 1.2 m Swiss telescope at La Silla Observatory, the HIDES spectrograph, mounted on the 1.9 m telescope at Okayama Astrophysical Observatory, NAOJ, the MOST space telescope, and and observations made with ESO Telescopes at the La Silla Paranal Observatory under program ID 086.D-0101.
© ESO, 2015
1. Introduction
Solar-like oscillations are excited stochastically by motions in the convective envelope of stars. For low-mass stars, they are found in all evolutionary states, between the main sequence and horizontal branch of helium-core burning stars (e.g. Leighton et al. 1962; Frandsen et al. 2002; Carrier et al. 2003; Hekker et al. 2009; Chaplin et al. 2011; Huber et al. 2011; Kallinger et al. 2012; Mosser et al. 2013) and were even detected in the M5 super giant α Her (Moravveji et al. 2013). These very characteristic oscillations lead to a nearly regular spaced comb-like pattern in the power spectrum. It was shown by Deubner (1975) that this ridge structure is governed by the degree of oscillation modes and resembles the predictions made by Ando & Osaki (1975). Empirically, the frequency patterns of solar-like oscillations were described through scaling relations by Kjeldsen & Bedding (1995). Since then, these relations have been tested and revised from large sample studies based on high-precision space photometry of red giants in clusters and in eclipsing binaries besides single stars (e.g. Corsaro et al. 2012b; Frandsen et al. 2013; Kallinger et al. 2010). Indications of non-radial oscillation modes were found in the variations of the absorption lines of bright red giants (Hekker et al. 2006; Hekker & Aerts 2010), but were firmly established in a large set of red giants observed with the CoRoT satellite (De Ridder et al. 2009). The identification of dipole mixed modes extended the sensitivity of the seismic analyses towards the core of evolved stars also (Beck et al. 2011; Bedding et al. 2011; Mosser et al. 2011). The analysis of solar-like oscillations enabled us to unravel many open questions on stellar structure and evolution, such as constraining the internal rotational gradient (Elsworth et al. 1995; Beck et al. 2012; Deheuvels et al. 2012) or determining the evolutionary status in terms of nuclear burning of a given red giant star (Bedding et al. 2011; Mosser et al. 2011).
 |
Fig. 1 Example of radial velocity measurements of γ Psc in September 2010 (top panel) and θ1 Tau in November 2010 (bottom panel). The data sets of HERMES, HIDES, CORALIE, and SOPHIE are shown in red, blue, green, and cyan, respectively. The full data set is depicted in Fig. 2. The radial velocities of θ1 Tau have been detrended for the binary orbit, shown in Fig. 4. The grey line indicates the 16.57 d modulation of the radial velocities, found in θ1 Tau. |
Spectroscopic time series offer a different look at stars, as spectroscopy and photometry have different mode sensitivities because modes with an odd spherical degree l exhibit a better visibility in spectroscopy than in photometry (Aerts et al. 2010). Radial velocity data are less effected by granulation noise, providing a wider frequency range that can be investigated (Aerts et al. 2010). In addition, most targets of space observations are faint. As typical target stars for spectroscopy are bright, they are well studied and many complementary parameters are found in the literature. Furthermore, experience has shown that long-term stability is a major issue for space missions and it is very challenging to constrain weak signals on the order of several tens of days (e.g. Beck et al. 2014). With robust calibration techniques, we can also study variations on the order of more than 100 days and longer from stable spectrographs.
 |
Fig. 2 Radial velocity curve of γ Psc (top panel) and θ1 Tau (bottom panel). The radial velocities of θ1 Tau have been detrended for the binary orbit, shown in Fig. 4. The red, blue, green, and cyan data points have been acquired with the HERMES, HIDES, COARALIE, and SOPHIE spectrograph, respectively. |
 |
Fig. 3 Distribution of the radial velocity measurements of γ Psc (left panel) and θ1 Tau (right panel). The same colour code as in Fig. 1. The value of the airmass X at which the target was observed is also shown for HIDES and HERMES. Light grey shaded areas indicate 2.5 <X< 3 and dark grey X< 2.5. The solid blue and red lines indicate the nautical dawn for HIDES and HERMES, respectively. |
Although space-photometry is available for stars in all phases on the red giant branch, no spectroscopic time series have deliberately been obtained for stars in the red clump. Most campaigns concentrate on stars close to or on the main sequence, as the higher oscillation frequencies do not require extensive time series to resolve the variation. In this paper, we describe the definition, data acquisition, and analysis of an extensive observational campaign, focussed on the two red giants γ Psc and θ1 Tau, from high-precision spectroscopy. We also compare our results to interferometrically determined radii.
2. Project strategy and observations
Ground-based time series severely suffer from the contamination of alias frequencies. It has been shown in numerous photometric and spectroscopic campaigns however, that the coordinated, time-resolved observation of an object with telescopes at several, well distinguished geographic longitudes greatly improves the structure of the spectral window that originates from the gaps (e.g., Winget et al. 1990; Handler et al. 2004; Breger et al. 2006; Arentoft et al. 2008; Desmet et al. 2009; Kolenberg et al. 2009; Saesen et al. 2010, for various types of pulsators). To further improve the structure of the power spectrum, several recent works have modelled the effects of an incomplete duty cycle on solar-like oscillations for ground-based, multi-site observations and also for space observations with the Kepler space telescope (Arentoft et al. 2014; García et al. 2014, respectively). Our data consist of individual data sets however, originating from different telescopes and different calibration techniques with large gaps (Figs. 1 and 2). The structure of the data set is visualized in the graphical observing log in Fig. 3. We therefore decided not to apply such techniques, to avoid smearing or correlating systematic effects between data sets.
2.1. Target selection
We organised an extensive observational campaign, focussing on two red giant stars using spectrographs well distributed over geographical longitude and capable of meter-per-second precision. As such instruments are not numerous despite being located on both hemispheres, target stars had to be close to the celestial equator. To achieve high-precision radial velocity measurements with a high temporal resolution on the order of a few minutes, we limited our search to giants brighter than 4th magnitude in the visual.
Starting from the Hipparcos-catalogue, all stars, which did not fit the limitations in magnitude, colour index, or declination, were excluded. As a goal of this campaign is to study the effects of rotation on oscillation in red giants (Beck et al. 2010), stars with an unknown projected rotational velocity or with an averaged projected rotational velocity lower than 3 km s-1 were excluded from the target selection. For the remaining candidates, a photometric calibration following the grid of Flower (1996) has been carried out, obtaining the bolometric correction, effective temperature, and radius for each star. The Hipparcos-parallaxes from van Leeuwen (2007) have been used for the distance determination. To check if the frequency spectra would be suitable for this project, the asteroseismic parameters of solar-like oscillations of the remaining targets were computed following Kjeldsen & Bedding (1995).
Fundamental parameters and computed asteroseismic characteristics of the campaign targets.
Observatories participating in the campaign.
To use the observing time efficiently, we were searching for a target combination, that encompasses two targets, separated by approximately five hours in right ascension. After testing several target combinations, we finally selected the G9III star γ Psc (HD 219615) and the K0III star θ1 Tau (HD 28307) as targets for our campaign.
2.2. Characteristics of γ Psc and θ1 Tau
Both targets are evolved stars that are expected to exhibit solar-like oscillations. An overview of the fundamental parameters of these stars from the literature is given in Table 1. The object γ Psc is a single field star that was studied frequently in the past using photometric and spectroscopic measurements (e.g. Luck & Heiter 2007; Hekker & Meléndez 2007). The most important feature of γ Psc with respect to the present study is its sub-solar iron abundance (Table 1).
The star θ1 Tau is one of the four giants in the Hyades cluster and a well studied binary (e.g. Lunt 1919; Torres et al. 1997; Lebreton et al. 2001; Griffin 2012). The Hyades have a slightly higher metallicity than the Sun with Fe/H = +0.1 (Takeda et al. 2008). By comparing theoretical isochrones matching the measured helium and metal content of the cluster, Perryman et al. (1998) found a main-sequence turn-off point of ~2.3 M⊙ which corresponds to a cluster age of 625 ± 50 Myr. Therefore only the most massive stars are already in more advanced evolutionary stages after the main sequence. Very recently, Auriere et al. (2015) reported on the detection of a magnetic field in θ1 Tau whose unsigned longitudinal component peaked to 3 ± 0.5 G. From their measurements they find indications for a complex surface magnetic field structure.
Interferometric observations allow for a radius determination, independent of seismology. Interferometric observations of the Hyades’ giants were published by Boyajian et al. (2009), reporting a radius of 11.7 ± 0.2 R⊙ for θ1 Tau. For γ Psc no such observations are reported in the literature. We therefore obtained interferometric observations of this star with the Astronomical Multi-BEam combineR (AMBER) instrument at the Very Large Telescope Interferometer (VLTI, cf. Sect. 3).
2.3. Participating observatories
The main part of the campaign took place from August 2010 through January 2011 and utilised five different telescopes.We monitored γ Psc and θ1 Tau for ~120 d and ~190 d, respectively, during which in total 8844 spectra were taken with the High Efficiency and Resolution Mercator Echelle Spectrograph (HERMES), COARALIE, Spectrographe pour l’Observation des Phénomènes des Intérieurs stellaires et des Exoplanètes (SOPHIE), High Dispersion Echelle Spectrograph (HIDES), and Spettrografo ad Alta Risoluzione del Galileo (SARG) spectrographs.
Orbital parameters for θ1 Tau.
The majority of data were obtained with the HERMES spectrograph (Raskin et al. 2011) mounted at the 1.2 m Mercator telescope on La Palma, Canary Islands, the CORALIE spectrograph (e.g. Queloz et al. 2000) operated from Mercator’s twin 1.2 m Euler telescope on La Silla, Chile and the HIDES spectrograph (Izumiura 1999) at the Okayama 1.88 m telescope, Japan. We used the commissioning time of the fibre-fed high-efficiency observing mode of HIDES for the campaign (Kambe et al. 2013). Additional data were acquired with the SOPHIE spectrograph (Bouchy et al. 2009) at the 1.93 m telescope at the Observatoire de Haute-Provence (OHP) in the south of France. During the phase of best visibility for both targets, we obtained spectroscopic data with the SARG spectrograph (Gratton et al. 2001) mounted at the 3.58 m Telescopio Nazionale Galileo (TNG), on La Palma. Because of problems in the reduction of the SARG data, they could not be included in the present analysis. An overview of the applied calibration techniques, the observers, and the number of spectra taken with each instrument is provided in Table 2.
Additionally, for γ Psc we applied for and obtained two half nights with the AMBER instrument at the Very Large Telescope Interferometer, using the 1.8 m auxiliary telescopes (see Sect. 3).
In 2007 the Microvariability and Oscillations of STars (MOST) satellite (Walker et al. 2003) was used to search for photometric variability in the Hyades’ giants. The MOST team kindly provided us with the previously unpublished light curve of θ1 Tau, covering 22 days to compare the photometric and the radial velocity variations (See Sect. 6.2).
2.4. Radial velocity measurements and data set merging
In order to achieve m s-1 precision in our radial velocity measurements, we utilised the available simultaneous calibration techniques. The HERMES, CORALIE, and SOPHIE spectrographs use thorium-argon (ThAr) or thorium-argon-neon (ThArNe) reference lamps, from which light is simultaneously fed to the spectrograph through a reference fibre. On the CCD, the stellar and the reference spectrum are alternating in position. Radial Velocity information was derived from the spectra using the instrument pipelines. The HIDES instrument uses the absorption spectrum of an iodine (I2) cell, superimposed on the stellar spectrum in a wavelength range of 500 to 620 nm. Data from HIDES were reduced with IRAF (Image Reduction and Analysis Facility) and the radial velocity was estimated with the method described in Kambe et al. (2008) by a member of the HIDES team.
The mean radial velocity of each data set was subtracted from the observations of γ Psc to merge the results from all four different telescopes to obtain a consistent radial velocity curve. As θ1 Tau is a binary, we subtracted an orbital model (Table 3, Fig. 4), derived from the Griffin (2012) data set, equally distributed over 40 years (from 1969 through 2010). As we have no overlap of data, except for about 1 hour between HERMES and COARALIE and only a few radial velocity standards were observed, we manually corrected the offsets between the radial velocities from different spectrographs.
In addition to the Griffin data, we also monitored the radial velocity of θ1 Tau with HERMES between early 2010 up to late 2013. The radial velocity values from Griffin (2012) as well as from our monitoring, listed in Table 4, are compared in the phase diagram depicted in Fig. 4.
 |
Fig. 4 Orbital velocity phase diagram of θ1 Tau. Data by Griffin (2012) between the years 1969 and 2010 are shown as black dots. The duration of our multi-site asteroseismology campaign is marked with the blue bar. Red dots mark the values from the ongoing radial velocity monitoring with the HERMES spectrograph. The values are reported in Table 4. |
Radial velocities of θ1 Tau from HERMES observations in the high-resolution observing mode.
An inspection of the combined data subsets, as depicted in Fig. 1, shows that both stars exhibit radial velocity variations. The colours of the data points show the contribution of the different observatories. Although from single-site data the long periodic variations of γ Psc could be seen as long periodic trends, it becomes evident from the combination of multi-site data that it is a clear oscillation signal. Figure 1 also suggests that θ1 Tau oscillates at higher frequencies than γ Psc. The full radial velocity curves are shown in Fig. 2.
Figure 3 visualises the observational coverage of our campaign in an échelle diagram style. The vertical axis of both diagrams shows the distribution of observations during the project from August 2010 to January 2011. The horizontal axis shows the time of the day as a fraction of the Julian day. It therefore depicts the coverage of the multi-site campaign. For a more intuitive understanding of the diagram, the airmass of the object and the laps of the nautical twilight are given for the geographical location of the HIDES and HERMES spectrographs.
For improving the agreement between different data sets while merging, and for increasing the signal-to-noise ratio (S/N) in the amplitude spectrum, we normalised the uncertainties of the individual radial velocity measurements following the approach developed by Butler et al. (2004) and Bedding et al. (2007), which was described and adopted by Corsaro et al. (2012b). The analysis consists of two steps. First, the individual uncertainties in the radial velocity measurements are rescaled to be consistent with the amplitude of the noise level in the amplitude spectra, σamp, which is measured for each data set separately in a region far from the power excess. Second, a residual time series is derived by a complete pre-whitening of the oscillation signal, to end up with only noise remaining in the data sets.
The results of this approach in the case of HERMES data for γ Psc is depicted in Fig. 5. The upper panel shows the observed cumulative histogram of the ratio | ri/σi | of the residuals ri to the original uncertainty σi in each radial velocity measurement (black diamonds) with the theoretical distribution expected for Gaussian noise (red line). The uncertainty of the individual radial velocity measurement is then adjusted by the ratio f of the two distributions, which is shown in the lower panel. The ratio enhances the presence of a number of outliers, i.e. data points deviating from the expected distribution with | ri/σi | > 1.2, which are down-weighted when computing the amplitude spectrum.
 |
Fig. 5 Cumulative histograms for HERMES observations of γ Psc. Upper panel: the diamonds represent the ratio | ri/σi | between the residuals in the pre-whitened time series and the uncertainties of each radial velocity measurement. The solid red curve depicts the result expected for Gaussian noise. The diagram in the lower panel shows the ratio between the observed and theoretical distribution of the uncertainties. |
As a conclusion, we were able to reduce the noise level in the amplitude spectrum of the master data set from σamp = 0.09 m s-1 to 0.06 m s-1 for θ1 Tau, and from 0.12 m s-1 to 0.1 m s-1 for γ Psc. These values are the mean noise amplitude, derived for the frequency range 1000−1200 μHz of the power spectrum, which is supposedly free from leakage of oscillation power. The values of the mean noise amplitude in this range and how they were modified through the normalisation of weights is shown in Table 5. The frequency analyses of these data are presented in Sects. 5 and 6 and were performed on these adjusted residual radial velocity curves.
2.5. Instrument commissioning of HERMES
The campaign was also used for commissioning the fibre-fed high efficiency observing mode of the simultaneous ThArNe observing (low resolution with reference fibre, i.e. LRFWRF) of the HERMES spectrographs. In this observing mode, HERMES is simultaneously fed from the telescope and a ThArNe calibration unit through 60 μm fibres. The exposure times were chosen to achieve a S/N of 150 in the blue part of the stellar spectrum. To avoid saturation of the emission line spectrum and an eventual contamination of the stellar spectrum through blooming of strong lines on the CCD chip, a neutral density filter regulates the intensity of the reference source. The obtained spectra were reduced with the instrument specific pipeline, extracting a 1D spectrum for the stellar and reference fibre. From each spectrum, the radial velocities of the star were derived through the cross-correlation of the wavelength range between 478 and 653 nm with a line-list template of the spectrum of Arcturus (Raskin et al. 2011). The radial velocities are then corrected for the shift in radial velocity, determined from the cross correlation of the simultaneously exposed ThArNe spectrum with the reference ThArNe spectrum, obtained at the beginning of the night.
Accuracy per measurement of the radial velocity observations.
2.5.1. The sub giant δ Eri
To test the performance and the accuracy of the observing mode before the campaign, we have obtained observations of δ Eri, a well-known solar-like oscillator, exhibiting power between 500–900 μHz (Carrier et al. 2003). Our data set covers 14.4 h in two consecutive nights in late November 2009. In total, we obtained 235 spectra with an exposure time of 60 to 90 s. The resulting radial velocity time series and the corresponding power spectrum of δ Eri are shown in Figs. 6 and 7.
Observing log of the AMBER LR data.
From the comparison with earlier observations obtained by Carrier et al. (2003), we find that the region between 1500 and 4000 μHz is free from contamination through oscillations and resembles the average amplitude σnoise, which originates from instrumental noise and other noise sources. Following the Parseval theorem, we obtain 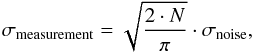 (1)the average noise amplitude of 0.24 m s-1 in this region translates into an accuracy of about 2.9 m s-1 per measurement, which is more than sufficient to explore solar-like oscillations in red giant stars. These observations were obtained in an early phase of the commissioning. As the instrument was improved since the observations of δ Eri, we did not find such noise in the data set of the campaign in 2010. Therefore, the noise in this frequency region is likely be coloured noise, originating from instrumental effects. These observations of δ Eri thus provided us with a proof-of-concept for the main observing campaign.
(1)the average noise amplitude of 0.24 m s-1 in this region translates into an accuracy of about 2.9 m s-1 per measurement, which is more than sufficient to explore solar-like oscillations in red giant stars. These observations were obtained in an early phase of the commissioning. As the instrument was improved since the observations of δ Eri, we did not find such noise in the data set of the campaign in 2010. Therefore, the noise in this frequency region is likely be coloured noise, originating from instrumental effects. These observations of δ Eri thus provided us with a proof-of-concept for the main observing campaign.
 |
Fig. 6 Radial velocity of δ Eri. Top panel shows the radial velocity values corrected for radial velocity drifts. The middle panel shows the uncorrected velocity values from the stellar spectrum while the bottom panel gives the radial velocity drift of the simultaneous ThArNe with respect to the wavelength reference, obtained in the beginning of the night. |
 |
Fig. 7 Power spectrum for the RV measurements of δ Eri. The red line illustrates the running average noise level in the spectrum. |
2.5.2. The red giants γ Psc and θ1 Tau
We performed the same analysis for γ Psc and θ1 Tau for the frequency range between 1000 and 1200 μHz on the campaign data, because we did not detect the signature of spectral leakage of oscillation power in this region. We calculated the noise amplitude for this region and estimated the accuracy per measurement from Eq. (1) for individual data sets. An overview is given in Table 5.
The numbers in Table 5 show that, although both stars were observed with the same instruments, the intrinsic scatter in the power spectra of γ Psc is consistently 1.8 times higher than for θ1 Tau. One possible explanation for this velocity jitter could be systematic effects as the accuracy of the measurements depend on how suited a star template for the cross correlation is for a given star. All pipelines used templates for K0 stars. Carney et al. (2003) concluded that neither orbital motion nor pulsation can explain such velocity jitter and suggest star spots or activity as another possible explanation.
3. Interferometric observations of γ Psc
The AMBER instrument (Petrov et al. 2007) on the Very Large Telescope Interferometer was used to observe γ Psc in its low spectral resolution (LR) observing mode (R = 30), covering the J, H and K atmospheric bands. Observations were procured during the nights of 4 and 5 October 2010, using two triplets of Auxiliary Telescopes (ATs) that included stations A0 and K1, the longest baseline (128 m) available at that time (see Table 6). The VLTI first-generation fringe tracker FINITO (Le Bouquin et al. 2008) was used to track the fringes.
3.1. Reduction
The data reduction was performed with the standard software amdlib (AMber. Dcs LIBrary) v3.0.5, provided by the Jean-Marie Mariotti Center (JMMC; Tatulli et al. 2007; Chelli et al. 2009). With amdlib, first a pixel-to-visibility-matrix (P2VM) is computed, which is then used to translate the detector frames into interferometric observables. In our case, a typical exposure consisted of 1000 frames, with integration times of 25 ms each. For each exposure, a frame selection and averaging is subsequently performed, typically using a S/N-based criterion. In the final raw data product additive biases should be removed, leaving only multiplicative terms to be divided away in the calibration stage. To this end, each sequence of five science (SCI) exposures is interleaved with similar sequences on well-chosen calibrators for which the visibility can be predicted with high precision. The estimated transfer function contains residual effects from the atmosphere as well as the interferometer’s response to a point source.
 |
Fig. 8 Left panel: calibrated squared visibilities of γ Psc. The colour denotes the baseline: K0-G1, A0-G1, and A0-K0 are shown in blue, green, and red, respectively. The dashed and dotted lines are the best-fit UD angular diameters in the H and K bands. Different symbols are used to represent the two calibrated exposures in the H (circles and diamonds) and K (squares and crosses) band. Right panel: closure phases as a function of the longest spatial frequency in the triplet. The same symbols are used as in the left panel, but the colour now denotes the exposure (blue being the first). |
During the first night only one sequence of exposures of the science target, as well as a sequence on a check star that has the same expected angular diameter could be obtained. Since no proper calibrator (CAL) could be observed, these data were not retained in our analysis. Two sequences of CAL-SCI-CAL were obtained in good observing conditions (seeing ~0.7″) during the second night. With a minimal S/N of ~2 at the longest baseline in the J band, where the VLTI throughput is low and the visibility is close to null, the intrinsic data quality is very good. This is also evidenced by the small spread between the subsequent exposures in each sequence. Despite the good S/N, the J band data were discarded for two reasons. First, the wavelength calibration is particularly unreliable in the J band. There is no way to do it reliably in the LR observing mode, so what the package amdlib does is to fit the position of the discontinuity between the H and K bands to its expected wavelength value. This works reasonably in the H and K bands, with an estimated systematic uncertainty of 2%, but leads to much larger uncertainties in the J band. Since the wavelength is used in the computation of the P2VM, and determines the spatial frequency of the observation, a wrong wavelength table can significantly bias the final result. Second, the spatial average of the phase of the incoming wave front (i.e. piston, cf. Vérinaud & Cassaing 2001) and its spread is large in the J band.
The critical step in the AMBER data reduction is the selection and averaging of frames within one exposure. Depending on the performance of FINITO, the contrast of a frame can be reduced by the residual effect of atmospheric jitter. At the time of our observations, no realtime FINITO data were recorded yet, so there is no objective way to do the frame selection. Instead, we resorted to the classical approach and selected frames based on piston (<10 μm) and S/N (best 15%) for the squared visibilities, while the 80% frames with the best S/N were retained for the closure phases as these are not sensitive to piston. The used criteria are a trade-off between competing effects: a too large piston will bias the visibilities, while a too strong selection criterion on piston will reduce the S/N too much and might bias the visibilities as well. In general, very few frames were removed based on piston, indicating that FINITO locked on the fringes properly, except in the H band on the longest baseline. For the latter, we note a systematic piston offset from zero, which appears in both science measurements despite their different detector integration times (DIT). Although the calibrator measurements are affected similarly, the brightness difference between the science target and the calibrator might result in a residual effect after the calibration. We tried different selection criteria, and we estimate a maximum bias on our derived angular diameter, because of our choice of selection criteria, of ~3% in K and ~6% in H.
The error on the final calibrated visibilities and closure phases is the quadratic sum of the intrinsic error on the science measurement, estimated from the spread between the consecutive exposures, with an error term for the transfer function. The latter is computed as the quadratic sum of the intrinsic error on the calibrator measurement, with the uncertainty on the calibrator’s theoretical visibility and the spread between the different calibrator measurements. The transfer function was very stable on the longest baseline, but less so on the shorter baselines; hence the large difference in the errors.
Special care was taken to estimate the wavelength-dependent uniform disc (UD) angular diameter of the calibrator. First, a bolometric diameter is determined from SED-fitting (using the grid-based procedures of Degroote et al. 2011). Then the formula from Hanbury Brown et al. (1974)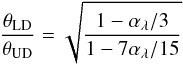 (2)was used to convert from bolometric to UD diameter. The parameter αλ is the band-dependent linear limb darkening coefficient for the appropriate stellar parameters, and is taken from the catalogue of Claret & Bloemen (2011). Since we use the ATLAS (Kurucz 1993) plane-parallel atmosphere models, the fitted bolometric diameter can be assumed equal to the limb-darkened diameter used in Eq. (2) (see e.g. Wittkowski et al. 2004, for a more detailed discussion about this assumption). The derived value (listed in Table 6) agrees perfectly with the diameter provided by the JMMC’s SearchCal tool (Bonneau et al. 2006).
(2)was used to convert from bolometric to UD diameter. The parameter αλ is the band-dependent linear limb darkening coefficient for the appropriate stellar parameters, and is taken from the catalogue of Claret & Bloemen (2011). Since we use the ATLAS (Kurucz 1993) plane-parallel atmosphere models, the fitted bolometric diameter can be assumed equal to the limb-darkened diameter used in Eq. (2) (see e.g. Wittkowski et al. 2004, for a more detailed discussion about this assumption). The derived value (listed in Table 6) agrees perfectly with the diameter provided by the JMMC’s SearchCal tool (Bonneau et al. 2006).
The final calibrated squared visibilities and closure phases are graphically depicted in Fig. 8. The visibility precision on the longest baseline is high, in contrast to the other baselines. The closure phases are very precise in the K band (~1–2°), and a bit less precise in H (~3–5°), but all are zero within 3σ.
 |
Fig. 9
|
3.2. Analysis
Fitting of simple geometric models to the interferometric data was performed with the LITpro (Lyons Interferometric Tool prototype) software tool (Tallon-Bosc et al. 2008) that is provided by the JMMC. LITpro does a simple but fast 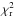 -minimisation, which also allows for easy examination of correlations between parameters through the computation of a correlation matrix and χ2-maps. Given the measured closure phases of zero degrees, we only fitted point-symmetric models to the squared visibilities. First, we try a uniform disc brightness profile. The H and K band were treated separately to account for the difference in the object’s limb darkening and the AMBER systematic errors. The best-fit uniform disc curves are shown in Fig. 8 and have diameters of
-minimisation, which also allows for easy examination of correlations between parameters through the computation of a correlation matrix and χ2-maps. Given the measured closure phases of zero degrees, we only fitted point-symmetric models to the squared visibilities. First, we try a uniform disc brightness profile. The H and K band were treated separately to account for the difference in the object’s limb darkening and the AMBER systematic errors. The best-fit uniform disc curves are shown in Fig. 8 and have diameters of 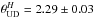 and
and 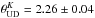 mas. Since LITpro assumes each data point to be independent, while the different AMBER wavelength channels are correlated, we corrected LITpro’s statistical errors here using
mas. Since LITpro assumes each data point to be independent, while the different AMBER wavelength channels are correlated, we corrected LITpro’s statistical errors here using 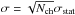 . The corresponding
. The corresponding 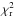 values (with its σ) are 1.3 ± 0.2 and 0.8 ± 0.2 for the H and K bands, respectively. Although the data do not require a more complex model, it is useful to fit a limb darkened model to check for internal consistency and because it is the limb darkened diameter that should be used for comparison with the seismic value. For simplicity we use a linear limb darkening law.
values (with its σ) are 1.3 ± 0.2 and 0.8 ± 0.2 for the H and K bands, respectively. Although the data do not require a more complex model, it is useful to fit a limb darkened model to check for internal consistency and because it is the limb darkened diameter that should be used for comparison with the seismic value. For simplicity we use a linear limb darkening law.
We note that the visibilities at shorter baselines are systematically above the model fit (Fig. 8). This is known to be the result of a calibration with poor transfer function stability, (which is mostly systematic across all wavelengths, i.e. it is to be expected that all visibilities fall on the same side of the model curve). Moreover, the diameter is constrained mostly by the measurements at the highest spatial frequencies, that have a higher resolving power, and in this particular case, also a more stable transfer function.
Figure 9 shows the 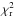 -map of the limb darkened K band angular diameter versus the linear limb darkening coefficient. Since our spatial frequencies only cover the first lobe of the visibility curve, the limb darkening cannot be constrained independently. However, for a given limb darkening coefficient we can determine the corresponding diameter. Taking the linear limb darkening coefficients from Claret & Bloemen (2011), using the parameters of γ Psc, which are αK ∈ [ 0.28,0.31 ] and αH ∈ [ 0.33,0.36 ], together with Eq. (2) and the measured UD diameters, we find limb darkened diameters of
-map of the limb darkened K band angular diameter versus the linear limb darkening coefficient. Since our spatial frequencies only cover the first lobe of the visibility curve, the limb darkening cannot be constrained independently. However, for a given limb darkening coefficient we can determine the corresponding diameter. Taking the linear limb darkening coefficients from Claret & Bloemen (2011), using the parameters of γ Psc, which are αK ∈ [ 0.28,0.31 ] and αH ∈ [ 0.33,0.36 ], together with Eq. (2) and the measured UD diameters, we find limb darkened diameters of 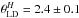 mas and
mas and 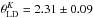 mas. The (conservative) errors are quadratic additions of all mentioned error terms. These limb darkened diameters agree well with the directly fitted values for the same value of αK and αH (see e.g. Fig. 9). A global fit to the full data set, and assuming the limb darkening coefficients αK = 0.295 and αH = 0.345, results in a final angular diameter of θLD = 2.34 ± 0.10 mas. With a Hipparcos parallax distance of 42.3 ± 0.3 pc, this angular diameter translates into a linear radius of 10.6 ± 0.5 R⊙.
mas. The (conservative) errors are quadratic additions of all mentioned error terms. These limb darkened diameters agree well with the directly fitted values for the same value of αK and αH (see e.g. Fig. 9). A global fit to the full data set, and assuming the limb darkening coefficients αK = 0.295 and αH = 0.345, results in a final angular diameter of θLD = 2.34 ± 0.10 mas. With a Hipparcos parallax distance of 42.3 ± 0.3 pc, this angular diameter translates into a linear radius of 10.6 ± 0.5 R⊙.
4. Long periodic variations
For both stars, the spectroscopic time series depicted in Fig. 2 reveal radial velocity variations on timescales longer than 100 d, that are present in the individual data sets from all sites. Such variations are too low in frequency to be connected to solar-like oscillations.
For the determination of these long periods, only data sets spanning over more than 100 days were used, i.e. HERMES, COARALIE, and HIDES. The data set from SOPHIE was excluded from this analysis, as it only covers about a week in time and suffers from strong night to night zero-point shifts. Also, the last observing run on θ1 Tau with HERMES in early January 2011 was excluded from the period determination because of zero-point shifts. We determined the periods by fitting a sine-wave to the variation in the data subset, using Period04 (Lenz & Breger 2005).
Long periodic variations found in the campaign stars.
For γ Psc we find a variation with a period of 113 d and a semi-amplitude of 22.8 ± 0.3 m s-1. The star θ1 Tau shows a dominant variation with a period of 165 d with 9.3 ± 0.2 m s-1 and a smaller variation on the order of 16.57 days (Table 7), which appears to be one-tenth of the main period. The close up on the radial velocity data of θ1 Tau in the bottom panel of Fig. 1 shows that all three data sets are modulated by this intermediate frequency.
Although we only cover a bit more than one cycle, we argue that these variations are real, as they occur in data sets from independent telescopes. Instrumental trends for a given star would not be consistently present with the same timescale and amplitude in both stars in independent data sets. In Fig. 2, all single-site data sets have been shifted by a constant offset in radial velocity. The variations in radial velocity follow a particular pattern throughout the full time span, independent of the used instrument. We therefore conclude that these trends are intrinsic to the stars.
Estimating the rotation period from the values of the stellar radius and the projected surface rotation velocity in Table 1 points toward a period of 113 and 138 days for γ Psc and θ1 Tau, respectively. This is a perfect match to the period of 113 ± 0.8 d we found in γ Psc and suggests that the inclination of the rotation axis of γ Psc is close to 90°. For θ1 Tau, the expected value deviates by ~30 days from the 165 ± 3 d variation found from our analysis. Torres et al. (1997) and Griffin (2012) have reported that the inclination of the eccentric binary orbit is probably close to 90 degrees. It is questionable if the orbital inclination is identical to the inclination of the rotation axis. For the eccentric system KIC 5006817, Beck et al. (2014) did not find a good match between the two axes. The orbital and rotation axis could be inclined by a few degrees. Yet, a lower inclination does not explain this difference.
In the literature, we find independent proof of the long periodic variability of θ1 Tau. The peak-to-peak amplitude we measure for θ1 Tau is compatible with the radial velocity scatter of ~20 m s-1, found by Sato et al. (2007) in the residuals of the binary model. The emission in the Ca ii H and K lines at 393.4 and 396.9 nm shows that θ1 Tau as well as γ Psc are chromospherically active. From about a decade of observations, Choi et al. (1995) found that the Ca ii H and K emission in θ1 Tau varies with a mean period of 140 ± 18 days, which is in agreement with our value of 165 ± 3 days. Given that our value is determined from only a bit more than one stellar revolution, we conclude that we measured the surface rotation of θ1 Tau but that our value could be affected by activity or the short temporal base line. The long periods found are typical rotation periods for red giants. Indeed, following a different approach, Beck et al. (2014) derived a similar period of 165 days for the surface rotation from forward modelling of the rotational splitting of dipole modes in the red giant component of KIC 5006817. Although this star has a radius of only 6 R⊙, this seismic result points to the same period regime of surface rotation. Ongoing studies of surface rotation of red giants from solar-like oscillations from Kepler photometry point to the same regime of rotation frequencies and show that there is a large spread of rotation periods that depends on the individual rotation history of the star (e.g. Garcia et al. 2014; McQuillan et al. 2014).
 |
Fig. 10 MOST photometry of θ1 Tau deconvolved from thermal trends. |
 |
Fig. 11 Comparison of the power spectra of γ Psc from the single instruments. The top panels show the original and the smoothed signal in the PDS for individual data sets. Two PDS are shown in the case of Hermes: the full data set was used for the red PDS and the set corrected for the radial velocity jump at 445 days (Fig. 2) was used for the black PDS. The estimate of νmax as the highest point of the smoothed PDS is marked as a dotted vertical line for each individual data set. The bottom panel shows the PDS of the combined data set, divided into two halves. The first and second half of the data set are shown as grey and black lines. The red line shows the power spectrum of the RV-subset with the best coverage (440 <t< 465 days in Fig. 2). |
We note that rotation does not explain the 5 m s-1 variation on 16.5 days found for θ1 Tau. The available MOST photometry suggests variations on the order of 11 days (Fig. 10) such that variability with this type of periodicity is confirmed in this independent data set.
 |
Fig. 12 Spectral windows of γ Psc (left panels) and θ1 Tau (right panels). The upper panels depict the spectral windows of the single-site data. The spectral window of the combined data set is shown in the lower left panel. |
 |
Fig. 13 Power density spectrum of γ Psc (left) and θ1 Tau (right). The original spectrum of the spectroscopic time series is shown in grey. The blue line shows the smoothed PDS. The red line depicts the multi-component fit to the original PDS. For γ Psc, no Gaussian profile was fitted for νmax. The vertical black line shows the adopted value of νmax for γ Psc and θ1 Tau of ~32 and 90 μHz. For both stars, Fig. 1 shows the clear variations on these timescales in the time series. |
5. Solar-like oscillations in γ Psc
The radial velocity curve of γ Psc, depicted in Figs. 1 and 2 (top panel) reveals the clear presence of long and multi-periodic radial velocity variations. Such patterns cannot originate from noise or instrumental trends as they are consistently present in independent single-site data sets. The key values to describe solar-like oscillations are the frequency of the maximum excess of oscillating power, νmax, and the large frequency separation, Δν, between consecutive pressure modes of the same spherical degree l.
From a data set contaminated with zero-point shifts we cannot determine a precise value for the frequency of maximum oscillation power. A typical approach would consist of shifting all individual nights to their nightly mean and then determine νmax from the combined master spectrum. From visual inspection of the radial-velocity variations (cf. Fig. 1) however, we estimated the frequency of the oscillations for γ Psc to be on the order of 2 to 3 per day. Therefore, shifting the nightly data sets by their zero point would act as a high-pass band filter that shifts power to higher values. From comparing the power spectra of zero-point shifted and unshifted data, we find that the frequency range up to ~30 μHz is severely affected, but also the distribution in the higher frequent part of the power density spectrum (PDS) is flattened. Such filter would change the shape of the power excess and mimic a higher νmax. To avoid unnecessary manipulations of the background signal, we only prewhitened the intrinsic long periodic variation of 110 days.
 |
Fig. 14 Frequency analysis of the combined data set for γ Psc (left) and θ1 Tau (right). The top panels show normalised comb response (NCR) of the six highest frequencies. The échelle diagrams (bottom panels) were calculated for the highest peak in the comb response function of γ Psc and θ1 Tau. Solid dots represent modes with an S/N ≥ 5. Open circles show the original position of modes that were shifted by 11.574 μHz. The crosses in the échelle diagram for γ Psc mark the position of multiples of the daily aliases. |
Before calculating the power spectrum for the full data set, the data sets for individual instruments were investigated. Nearly all single-site data already reveal a good approximation of the frequency of the oscillation power excess (Fig. 11, top panels). The HERMES data contain a source of instrumental noise that is dominated by long periodic noise and shows a maximum power at very low frequencies. This signal originates from small instabilities of the calibration lamp, which lead to night-to-night shifts. The main shift is visible in the red RV-curve in Fig. 2 between 440 and 460 days as a jump of ~25 m s-1. By correcting for this jump manually, the signal below ~1 d-1 drops (see Fig. 11, top left panel). For further understanding of the night-to-night shifts of the HERMES spectrograph, we have initialised a test program on HERMES during winter 2013/14.
From the smoothed power spectrum of theindividual single data sets (Fig. 11, top panels) and the power spectrum of the combined data set (Fig. 11, red line in the lower panel), we identify the highest signal as the maximum oscillation power at ~32 μHz. Variations on this timescale are found from detailed inspection of all independent nightly data sets. Such long-periodic oscillations are expected for red giants higher up on the RGB or red clump stars and are compatible with the position of γ Psc in the Hertzsprung-Russell diagram (HRD).
We subsequently combined all four single-site data sets of γ Psc. The spectral window of the single-site data sets and the full data set for γ Psc are presented in Fig. 12. The power excess of γ Psc is located exactly at the knee of the power law, describing the long periodic granulation noise (Fig. 13). Although we see the peak of the power excess (or aliases of it, shifted by 11.6 μHz) in the individual power spectra (Fig. 11), νmax is hardly visible in the power density spectrum of the combined data set. We argue that this is also a problem of the zero-point shift between data sets and nights. In addition, this region is contaminated by instrumental noise. It is therefore hard to reliably determine the value of νmax for γ Psc from a multi-component fit (Fig. 13).
In a wide frequency range around the identified maximum of oscillation power (15–50 μHz), all significant frequencies (i.e. S/N ≥ 5) were prewhitened, using the ISWF (iterative sine-wave fitting) method. The S/N compares the height of a mode to the mean noise in a selected frequency range. For γ Psc, it was determined to be between 50 and 70 μHz. Indeed, we find the highest peaks around ~32 μHz.
The large frequency separation was then computed from the generalised comb-response (CR) function (Bonanno et al. 2008; Corsaro et al. 2012a), based on the six frequencies with the highest power. The extracted frequencies are available in Table 8. With the CR function, we scanned a wide range of potential values of Δν, which includes a mass range that generously frames the mass estimates for the star in the literature. For γ Psc, the chosen range corresponds to ~0.5 to ~5 M⊙ (Fig. 14). The values of Δν, suggested by the highest peaks, were then tested with échelle diagrams.
The CR function, calculated from the extracted peaks, exhibits a clear peak at Δν = 4.1 ± 0.1 μHz (Fig. 14, left upper panel). The uncertainty originates from a Gaussian fit to the main peak and, given that we are dealing with ground-based and gapped data, can only be taken as a lower limit. In addition, we tested different step-sizes of the CR function (up to 0.02 μHz), but did not find a different result for the value and its uncertainty. This value remains stable up to the inclusion of the seventh highest out of the ten most significant frequencies. This is not surprising, because some of them are likely to be mixed modes, which do not follow the expected regular frequency pattern of pure p-modes. Using this value and the set of significant frequencies, we constructed an échelle diagram for this star, showing one ridge (Fig. 14). Most of the strongest modes are lined up on the left side of the diagram (i.e. ν modulo Δν ≤ 1, hereafter termed échelle phase). We note that the échelle phase is closely related through the modulo operation to the parameter ε from the asymptotic frequency relation (Aerts et al. 2010). One of the extracted frequencies is likely to be shifted by daily aliases. When we correct the strong mode at 29.7 μHz for the daily alias, it also falls in the ridge of strong modes. The original and the shifted position of a mode in the échelle diagram are marked by open circles. This structure could be the ridge of radial and quadrupole modes. We can compare our identification to the ε-values found in large samples of red giant stars, observed with the Kepler space telescope (e.g. Huber et al. 2010; Corsaro et al. 2012b). For these stars, we have a solid mode identification from uninterrupted data. Indeed, the study of Huber et al. (2010) shows that for a star with a Δν of ~4 μHz, one expects a value of ε ≃ 1 for radial modes suggesting that we correctly identified the radial modes. The remaining three extracted frequencies (at échelle phase of ~2) may originate from mixed dipole modes, which is in agreement with ε ≃ 1.5 for dipole modes. A comb-like pattern with a large separation of 4.1 μHz cannot be explained by daily aliasing as this value of Δν is not a multiple of the daily alias (11.574 μHz). For comparison, the position of the daily alias frequencies are depicted as crosses in the échelle diagrams.
Following the scaling relations described by Kjeldsen & Bedding (1995), using the revised reference values of Chaplin et al. (2011), we estimate γ Psc to be a star of M ≃ 0.9 M⊙ and R ≃ 10 R⊙. The stellar radius from the scaling relations is in good agreement with the independent radius of 10.6 ± 0.5 R⊙from interferometric observations (see Sect. 3). The mass obtained from both scaling relations are below the mass derived from spectroscopic calibrations by Luck & Heiter (2007) to be 1.87 M⊙. No uncertainty was given for this value. These values are likely affected by the lower constraining level of νmax, if compared to the case of θ1 Tau (see Sect. 6), however, from the échelle diagram (Fig. 14) the value of the large separation appears convincing. By using the value of the large separation found from our oscillation spectrum of γ Psc, and the independent radius from interferometry for the scaling relation for the stellar mass, 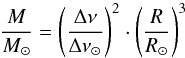 (3)we can derive the mass of the star without the use of \num. This approach leads to a mass of~\begin{lxirformule}$1.1\pm0.2~M$\end{lxirformule}⊙for γ Psc, which is in agreement with the mass found from the scaling relations. We therefore adopt 32 μHz and 4.1 μHz as good estimates of the νmax and Δν in γ Psc.
(3)we can derive the mass of the star without the use of \num. This approach leads to a mass of~\begin{lxirformule}$1.1\pm0.2~M$\end{lxirformule}⊙for γ Psc, which is in agreement with the mass found from the scaling relations. We therefore adopt 32 μHz and 4.1 μHz as good estimates of the νmax and Δν in γ Psc.
6. Solar-like oscillations in θ1 Tau
For θ1 Tau, we have two independent data sets that we can analyse for the signature of oscillations. Besides our spectroscopic campaign, covering 190-days, we also have photometric data from the MOST satellite.
6.1. Spectroscopic campaign
The data sets of θ1 Tau reveal a clear signature of the power excess at 90 ± 0.2 μHz. The value of νmax was obtained from the fit of a power law plus a Gaussian profile and a constant noise background to the power density spectrum (Fig. 13). This value is a formal error from the fit and we note that this is unrealistically small.
Frequencies extracted from the data sets of γ Psc and θ1 Tau.
To further improve the data, we corrected for zero-point shifts. As, visible from Fig. 2, SOPHIE data suffer from severe night to night jumps. Also, the last data from HERMES contain sudden jumps of up 50 m s-1 (at t> 560 d in Fig. 2). A visual inspection of the simultaneous ThArNe frames showed that these jumps originate from instabilities of the calibration lamp. Problematic frames were identified and deleted from the data set. The power excess of θ1 Tau is located at frequencies high enough to allow shifting the individual nights to their mean without manipulating the frequency region of νmax. Therefore, we subdivided the time string into individual nights and corrected them for the nightly mean. The frequency analysis was then performed at this time series of residuals. In total, we find seven frequencies with an S/N ≥ 5 in the frequency range around νmax. The extracted frequencies are listed in Table 8. From comparison with the MOST power spectrum, we find that the strong mode at 89.9 μHz falls on top of the ridge structure when shifting by +1 d-1. As we used the shifted data set for the prewhitening analysis, we could not use the background determined from the fit of the power laws but derived the mean noise from the frequency range between 140 and 170 μHz.
The comb response function of θ1 Tau (Fig. 14, top right) is complex as it exhibits three peaks in the range of 6 μHz < ΔνCR< 7 μHz. The CR function remains stable at this frequency range, independent of the number of significant oscillation peaks included and the resolution for which the CR function is calculated. From the échelle diagram we can exclude ΔνCR ≃ 6 μHz, as by plotting all significant frequencies in an échelle diagram, inclined ridges form and it is close to half of the daily aliasing. This indicates a wrong trial value for Δν. Peaks above ~8 μHz can be excluded, as they suggest a mass below ~1.5 M⊙and lead to a final radius (≲8 R⊙) which is ~30% smaller than the interferometric radius 11.7 ± 0.2 R⊙, determined by Boyajian et al. (2009). We therefore exclude these values from the possible solutions.
 |
Fig. 15 Comparison of the power spectra of the photometric and spectroscopic PDS of θ1 Tau. The top panel shows the power spectrum and the spectral window of the MOST data set as black line and red shaded region, respectively. The spectral window depicts the position of the orbital aliases and reveals that the range around νmax is nearly free of contaminations. The three main peaks in the region around 90 μHz in the MOST spectrum correspond to frequencies also detected with the ground-based campaign (red dashes). The bottom panel shows the unprewhitened power spectrum of the combined spectroscopic campaign data. The blue horizontal line indicates an average large frequency separation found for θ1 Tau. The lower and upper horizontal red line indicates the noise level and five times the noise level. |
The highest peak in the CR function indicates a large separation of 6.9 ± 0.2 μHz. Again we note, that the error is likely to be an underestimate. The échelle diagram of θ1 Tau shows eight frequencies with an S/N ≥ 5 folded with Δν = 6.9 μHz (Fig. 14, bottom right). From the scaling relations of Kjeldsen & Bedding (1995), we obtain from the mass of 2.7 ± 0.3 M⊙and a radius of 10.2 ± 0.6 R⊙for a given Δν = 6.9 ± 0.2 μHz. For this value, the mass of the red giant primary of the θ1 Tau-system is well in agreement with the mass estimate provided by the orbital parameters and the Hipparcos dynamical parallax. Torres et al. (1997) reported a mass of 2.9 ± 0.9 M⊙for the primary component, while using the parallax obtained from Hipparcos data Lebreton et al. (2001) derived a mass of 2.8 ± 0.5 M⊙ and 1.28 ± 0.1 M⊙ for the primary and secondary of θ1 Tau, respectively. All those values are substantially more massive than 2.3 M⊙of the turn-off point in the Hyades as must be the case (Perryman et al. 1998).
While this value of 6.9 μHz for the large frequency separation leads to a stellar radius that is slightly smaller than the interferometrically determined radius reported by Boyajian et al. (2009), there are indications that this interferometric radius is somewhat overestimated (by a few percent), to the extent that the disagreement is not significant. First, the diameters derived by Boyajian et al. (2009) for two other Hyades giants, δ1 Tau and ϵ Tau, are larger than other interferometric radii reported in the literature for these giants by 2–3σ, and it is thus also plausible that their diameter for θ1 Tau is too large. Since Boyajian et al. (2009) were limited to a single baseline, calibrator, and observing night, the calibration may have suffered undetected systematics. Second, this reasoning is further corroborated by the disagreement between the spectroscopic effective temperature from Hekker & Meléndez (2007) and the Teff derived by Boyajian et al. (2009), with the latter being 200 K lower than the former. This also suggests that the diameter derived by Boyajian et al. (2009) is slightly too large, as a Teff derived from a bolometric flux and a radius (the method used by Boyajian et al. 2009) scales inversely with assumed radius. For a more general discussion concerning possible biases in interferometric diameters, we refer to Casagrande et al. (2014). We therefore refrain from using this interferometric diameter as an argument against a seismic mass corresponding to 6.9 μHz frequency spacing, and suggest the need for a new interferometric diameter determination, based on multiple baselines and calibrators. Given the required time frame of such an observational campaign, it is outside the scope of the current paper.
6.2. Oscillation in MOST space photometry
Independent confirmation of the intrinsic variability and oscillations in θ1 Tau is provided by the MOST space photometry. Figure 15 compares the power spectra of the MOST data set and the spectroscopic campaign. The variability of θ1 Tau is on the detection limit of the satellite. The spectral window of the data set, depicted as red shaded surface, shows that the power spectrum of the photometric measurements does not follow the shape of the spectral window and that the contamination by aliasing in this region is minor. A typical power density diagram cannot be drawn, as the spectrum is dominated by the orbital aliasing. The main orbital alias frequencies are located well above this range at 164.35 μHz (14.2 d-1).
The strongest signal found in the photometric data is around 90 μHz and located in a region without contamination. We find that the three highest peaks from MOST photometry coincide with significant frequencies from the spectroscopic campaign data set. These frequencies are marked with red dashes in Fig. 15. This independently confirms our detection of oscillation power in this region from the spectroscopic campaign data.
7. Conclusions
In this paper, we report on the spectroscopic multi-site campaign performed in 2010, dedicated to the single field star γ Psc and on θ1 Tau, the primary component of an eccentric binary system in the Hyades open cluster. This campaign was supported by interferometric observations from the VLTI and space data from the MOST satellite.
We found clear evidence of long and multi-periodic variations in the radial velocity data set of γ Psc. No precise value of νmax could be deduced because of contamination by granulation noise and instrumental trends, however, we see clear indications that νmax is located around ~32 μHz. This value is typical for red clump stars and agrees with the position of γ Psc in the HRD. By analysing the frequency range around the adopted νmax, we find a large separation of 4.1 ± 0.1 μHz from the CR function. This value also leads to a convincing échelle diagram. The stellar radius from scaling relations shows good agreement with the radius from interferometry. We therefore estimate the mass of γ Psc to be ~1 M⊙.
The massive red giant star θ1 Tau exhibits a clear power excess at 90 μHz in the spectroscopic data sets. Oscillations in this range and the dominant peaks are independently confirmed from MOST space photometry. According to the CR function analysis, a large separation of either 6.9 μHz is preferred. Under the reasonable assumption that the interferometric radius of θ1 Tau (Boyajian et al. 2009) is overestimated, we find a rather good agreement between this value and the radius from the scaling relations. A new set of observations with the current instruments and the longest baselines on the CHARA array or similar instrumentation would allow a more reliable measurement of the radius of this star. The mass of θ1 Tau is 2.7 ± 0.3 M⊙.
The system θ1 Tau is of special interest because of its membership in the Hyades. Since 2010, the radial velocity of the binary system θ1 Tau has been monitored with HERMES. The binary is approaching its periastron passage early 2014. We hope to be able to perform a spectral disentangling analysis from these data.
In addition, we note that the value of the large separation for both stars comes from an attempt to measure the actual mean Δν of the stars because we only relied on the computation of the comb response function. Further investigations are needed to confirm these values. Unfortunately, the quality of the PDS does not allow us to discriminate between the evolutionary stages from mixed mode period spacings, however, the frequency of the maximum oscillation power excess is typical for red clump stars.
Besides the solar-like oscillations, we also detected long periodic modulations of the radial velocities, which occur on the order of 113 days and 165 days for γ Psc and θ1 Tau, respectively. These timescales are in good agreement with the estimates of the rotation period from the stellar radius and the measured vsini.
From this study we learned that the common approach to correct for zero-point variations by shifting the nightly data set of individual telescopes will suppress frequency information and shift νmax to higher frequencies for power excesses below ~40 μHz. We note that stars with Δν≃ 11.6 μHz, are also very challenging from the ground as their large separation Δν is identical to the 1-day aliasing in ground-based data. Very good spectral windows are needed to understand the oscillation spectra of such stars. Also, the interplay of solar-like oscillations and surface rotation requires a dense sampling and consistent data sets in order to disentangle the two effects. This can only be achieved with very dense telescope networks.
Finally, we note that in times of stunning asteroseismic results from space photometry, often the benefits of ground-based spectroscopy are forgotten. It is gradually becoming harder to successfully propose for sufficient telescope time for campaigns like the one described here. A promising future ground-based project is the Stellar Observations Network Group (SONG)1 which is a Danish led project to construct a global network of small 1 m telescopes around the globe (Grundahl et al. 2011). One of the main goals of the project is to obtain time series of radial velocity measurements with a high duty cycle, similar to our campaign. This will therefore allow us to investigate in detail the asteroseismic properties of the stars.
Acknowledgments
The research leading to these results has received funding from the European Research Council under the European Community’s Seventh Framework Programme (FP7/2007–2013)/ERC grant agreement No. 227224 (PROSPERITY). This research is (partially) funded by the Research Council of the KU Leuven under grant agreement GOA/2013/012. E.K. is supported by Grants-in-Aid for Scientific Research 20540240 from the Japan Society for the Promotion of Science (JSPS). K.Z. receives a Pegasus Marie Curie Fellowship of the Research Foundation Flanders (FWO).
M.Y., H.I., and B.S. are supported by Grants-in-Aid for Scientific Research 18340055 from JSPS. J.D.R. and E.C. acknowledge the support of the FWO-Flanders under project O6260 - G.0728.11. T.K. also acknowledges financial support from the Austrian Science Fund (FWF P23608). S.B. is supported by the Foundation for Fundamental Research on Matter (FOM), which is part of the Netherlands Organisation for Scientific Research (NWO). V.S.S. is an aspirant Ph.D. fellow at the Fonds voor Wetenschappelijk Onderzoek (FWO), Vlaanderen. E.M. is a beneficiary of a mobility grant from the Belgian Federal Science Policy Office co-funded by the Marie Curie Actions FP7-PEOPLE-COFUND-2008 n246540 MOBEL GRANT from the European Commission. The ground-based observations are based on spectroscopy made with the Mercator Telescope, operated on the island of La Palma by the Flemish Community, at the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofisica de Canarias. We are grateful to the Geneva Observatory’s technical staff for maintaining the 1.2 m Euler Swiss telescope and the COARALIE spectrograph. We are grateful to all staff members at OAO, National Astronomical Observatory of Japan (NAOJ) for their continuous and various support throughout our project with HIDES. We thank the technical team at Haute-Provence Observatory for their support with the SOPHIE instrument and the 1.93-m OHP telescope. We thank the referee for constructive comments and stimulating discussions.
References
- Aerts, C., Christensen-Dalsgaard, J., & Kurtz, D. W. 2010, Asteroseismology (Springer Science+Business Media B.V.) [Google Scholar]
- Ando, H., & Osaki, Y. 1975, PASJ, 27, 581 [NASA ADS] [Google Scholar]
- Arentoft, T., Kjeldsen, H., Bedding, T. R., et al. 2008, ApJ, 687, 1180 [NASA ADS] [CrossRef] [Google Scholar]
- Arentoft, T., Tingley, B., Christensen-Dalsgaard, J., et al. 2014, MNRAS, 437, 1318 [NASA ADS] [CrossRef] [Google Scholar]
- Auriere, M., Konstantinova-Antova, R., Charbonnel, C., et al. 2015, A&A, in press, DOI: 10.1051/0004-6361/201424579 [Google Scholar]
- Beck, P. G., Carrier, F., & Aerts, C. 2010, Astron. Nachr., 331, 32 [Google Scholar]
- Beck, P. G., Bedding, T. R., Mosser, B., et al. 2011, Science, 332, 205 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Beck, P. G., Montalban, J., Kallinger, T., et al. 2012, Nature, 481, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, P. G., Hambleton, K., Vos, J., et al. 2014, A&A, 564, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bedding, T. R., Kjeldsen, H., Arentoft, T., et al. 2007, ApJ, 663, 1315 [NASA ADS] [CrossRef] [Google Scholar]
- Bedding, T. R., Mosser, B., Huber, D., et al. 2011, Nature, 471, 608 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bonanno, A., Benatti, S., Claudi, R., et al. 2008, Mem. Soc. Astron. It., 79, 639 [NASA ADS] [Google Scholar]
- Bonneau, D., Clausse, J.-M., Delfosse, X., et al. 2006, A&A, 456, 789 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouchy, F., Hébrard, G., Udry, S., et al. 2009, A&A, 505, 853 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boyajian, T. S., McAlister, H. A., Cantrell, J. R., et al. 2009, ApJ, 691, 1243 [NASA ADS] [CrossRef] [Google Scholar]
- Breger, M., Beck, P., Lenz, P., et al. 2006, A&A, 455, 673 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Butler, R. P., Bedding, T. R., Kjeldsen, H., et al. 2004, ApJ, 600, L75 [Google Scholar]
- Carney, B. W., Latham, D. W., Stefanik, R. P., Laird, J. B., & Morse, J. A. 2003, AJ, 125, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Carrier, F., Bouchy, F., & Eggenberger, P. 2003, in Asteroseismology Across the HR Diagram, eds. M. J. Thompson, M. S. Cunha, & M. J. P. F. G. Monteiro (Dordrecht: Kluwer Academic Publishes), 311 [Google Scholar]
- Casagrande, L., Portinari, L., Glass, I. S., et al. 2014, MNRAS, 439, 2060 [Google Scholar]
- Chaplin, W. J., Kjeldsen, H., Christensen-Dalsgaard, J., et al. 2011, Science, 332, 213 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Chelli, A., Utrera, O. H., & Duvert, G. 2009, A&A, 502, 705 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Choi, H.-J., Soon, W., Donahue, R. A., Baliunas, S. L., & Henry, G. W. 1995, PASP, 107, 744 [NASA ADS] [CrossRef] [Google Scholar]
- Claret, A., & Bloemen, S. 2011, A&A, 529, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Corsaro, E., Grundahl, F., Leccia, S., et al. 2012a, A&A, 537, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Corsaro, E., Stello, D., Huber, D., et al. 2012b, ApJ, 757, 190 [NASA ADS] [CrossRef] [Google Scholar]
- De Ridder, J., Barban, C., Baudin, F., et al. 2009, Nature, 459, 398 [Google Scholar]
- Degroote, P., Acke, B., Samadi, R., et al. 2011, A&A, 536, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deheuvels, S., García, R. A., Chaplin, W. J., et al. 2012, ApJ, 756, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Desmet, M., Briquet, M., Thoul, A., et al. 2009, MNRAS, 396, 1460 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Deubner, F.-L. 1975, A&A, 44, 371 [NASA ADS] [Google Scholar]
- Elsworth, Y., Howe, R., Isaak, G. R., et al. 1995, Nature, 376, 669 [NASA ADS] [CrossRef] [Google Scholar]
- Flower, P. J. 1996, ApJ, 469, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Frandsen, S., Carrier, F., Aerts, C., et al. 2002, A&A, 394, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frandsen, S., Lehmann, H., Hekker, S., et al. 2013, A&A, 556, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garcia, R. A., Ceillier, T., Salabert, D., et al. 2014, A&A, 572, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García, R. A., Mathur, S., Pires, S., et al. 2014, A&A, 568, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gratton, R. G., Bonanno, G., Bruno, P., et al. 2001, Exp. Astron., 12, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Griffin, R. F. 2012, J. Astrophys. Astron., 33, 29 [Google Scholar]
- Grundahl, F., Christensen-Dalsgaard, J., Gråe Jørgensen, U., et al. 2011, J. Phys. Conf. Ser., 271, 012083 [NASA ADS] [CrossRef] [Google Scholar]
- Hanbury Brown, R., Davis, J., Lake, R. J. W., & Thompson, R. J. 1974, MNRAS, 167, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Handler, G., Shobbrook, R. R., Jerzykiewicz, M., et al. 2004, MNRAS, 347, 454 [NASA ADS] [CrossRef] [Google Scholar]
- Hekker, S., & Aerts, C. 2010, A&A, 515, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hekker, S., & Meléndez, J. 2007, A&A, 475, 1003 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hekker, S., Aerts, C., De Ridder, J., & Carrier, F. 2006, A&A, 458, 931 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hekker, S., Kallinger, T., Baudin, F., et al. 2009, A&A, 506, 465 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Huber, D., Bedding, T. R., Stello, D., et al. 2010, ApJ, 723, 1607 [NASA ADS] [CrossRef] [Google Scholar]
- Huber, D., Bedding, T. R., Stello, D., et al. 2011, ApJ, 743, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Izumiura, H. 1999, in Observational Astrophysics in Asia and its Future, ed. P. S. Chen, Chinese Academy of Sciences, 77 [Google Scholar]
- Kallinger, T., Mosser, B., Hekker, S., et al. 2010, A&A, 522, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kallinger, T., Hekker, S., Mosser, B., et al. 2012, A&A, 541, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kambe, E., Ando, H., Sato, B., et al. 2008, PASJ, 60, 45 [NASA ADS] [Google Scholar]
- Kambe, E., Yoshida, M., Izumiura, H., et al. 2013, PASJ, 65, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Kjeldsen, H., & Bedding, T. R. 1995, A&A, 293, 87 [NASA ADS] [Google Scholar]
- Kolenberg, K., Guggenberger, E., Medupe, T., et al. 2009, MNRAS, 396, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Kurucz, R. L. 1993, VizieR Online Data Catalog: VI/39 [Google Scholar]
- Le Bouquin, J.-B., Abuter, R., Bauvir, B., et al. 2008, in SPIE Conf. Ser., 7013 [Google Scholar]
- Lebreton, Y., Fernandes, J., & Lejeune, T. 2001, A&A, 374, 540 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leighton, R. B., Noyes, R. W., & Simon, G. W. 1962, ApJ, 135, 474 [NASA ADS] [CrossRef] [Google Scholar]
- Lenz, P., & Breger, M. 2005, Commun. Asteroseismol., 146, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Luck, R. E., & Heiter, U. 2007, AJ, 133, 2464 [NASA ADS] [CrossRef] [Google Scholar]
- Lunt, J. 1919, ApJ, 50, 161 [NASA ADS] [CrossRef] [Google Scholar]
- McQuillan, A., Mazeh, T., & Aigrain, S. 2014, ApJS, 211, 24 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Moravveji, E., Guinan, E. F., Khosroshahi, H., & Wasatonic, R. 2013, AJ, 146, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Mosser, B., Barban, C., Montalbán, J., et al. 2011, A&A, 532, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mosser, B., Dziembowski, W. A., Belkacem, K., et al. 2013, A&A, 559, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perryman, M. A. C., Brown, A. G. A., Lebreton, Y., et al. 1998, A&A, 331, 81 [NASA ADS] [Google Scholar]
- Petrov, R. G., Malbet, F., Weigelt, G., et al. 2007, A&A, 464, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Queloz, D., Mayor, M., Weber, L., et al. 2000, A&A, 354, 99 [NASA ADS] [Google Scholar]
- Raskin, G., van Winckel, H., Hensberge, H., et al. 2011, A&A, 526, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Saesen, S., Carrier, F., Pigulski, A., et al. 2010, A&A, 515, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sato, B., Izumiura, H., Toyota, E., et al. 2007, ApJ, 661, 527 [NASA ADS] [CrossRef] [Google Scholar]
- Takeda, Y., Sato, B., & Murata, D. 2008, PASJ, 60, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Tallon-Bosc, I., Tallon, M., Thiébaut, E., et al. 2008, in SPIE Conf. Ser., 7013 [Google Scholar]
- Tatulli, E., Millour, F., Chelli, A., et al. 2007, A&A, 464, 29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Torres, G., Stefanik, R. P., & Latham, D. W. 1997, ApJ, 485, 167 [NASA ADS] [CrossRef] [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vérinaud, C., & Cassaing, F. 2001, A&A, 365, 314 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walker, G., Matthews, J., Kuschnig, R., et al. 2003, PASP, 115, 1023 [NASA ADS] [CrossRef] [Google Scholar]
- Winget, D. E., Nather, R. E., Clemens, J. C., et al. 1990, ApJ, 357, 630 [NASA ADS] [CrossRef] [Google Scholar]
- Wittkowski, M., Aufdenberg, J. P., & Kervella, P. 2004, A&A, 413, 711 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Fundamental parameters and computed asteroseismic characteristics of the campaign targets.
Radial velocities of θ1 Tau from HERMES observations in the high-resolution observing mode.
All Figures
 |
Fig. 1 Example of radial velocity measurements of γ Psc in September 2010 (top panel) and θ1 Tau in November 2010 (bottom panel). The data sets of HERMES, HIDES, CORALIE, and SOPHIE are shown in red, blue, green, and cyan, respectively. The full data set is depicted in Fig. 2. The radial velocities of θ1 Tau have been detrended for the binary orbit, shown in Fig. 4. The grey line indicates the 16.57 d modulation of the radial velocities, found in θ1 Tau. |
| In the text | |
 |
Fig. 2 Radial velocity curve of γ Psc (top panel) and θ1 Tau (bottom panel). The radial velocities of θ1 Tau have been detrended for the binary orbit, shown in Fig. 4. The red, blue, green, and cyan data points have been acquired with the HERMES, HIDES, COARALIE, and SOPHIE spectrograph, respectively. |
| In the text | |
 |
Fig. 3 Distribution of the radial velocity measurements of γ Psc (left panel) and θ1 Tau (right panel). The same colour code as in Fig. 1. The value of the airmass X at which the target was observed is also shown for HIDES and HERMES. Light grey shaded areas indicate 2.5 <X< 3 and dark grey X< 2.5. The solid blue and red lines indicate the nautical dawn for HIDES and HERMES, respectively. |
| In the text | |
 |
Fig. 4 Orbital velocity phase diagram of θ1 Tau. Data by Griffin (2012) between the years 1969 and 2010 are shown as black dots. The duration of our multi-site asteroseismology campaign is marked with the blue bar. Red dots mark the values from the ongoing radial velocity monitoring with the HERMES spectrograph. The values are reported in Table 4. |
| In the text | |
 |
Fig. 5 Cumulative histograms for HERMES observations of γ Psc. Upper panel: the diamonds represent the ratio | ri/σi | between the residuals in the pre-whitened time series and the uncertainties of each radial velocity measurement. The solid red curve depicts the result expected for Gaussian noise. The diagram in the lower panel shows the ratio between the observed and theoretical distribution of the uncertainties. |
| In the text | |
 |
Fig. 6 Radial velocity of δ Eri. Top panel shows the radial velocity values corrected for radial velocity drifts. The middle panel shows the uncorrected velocity values from the stellar spectrum while the bottom panel gives the radial velocity drift of the simultaneous ThArNe with respect to the wavelength reference, obtained in the beginning of the night. |
| In the text | |
 |
Fig. 7 Power spectrum for the RV measurements of δ Eri. The red line illustrates the running average noise level in the spectrum. |
| In the text | |
 |
Fig. 8 Left panel: calibrated squared visibilities of γ Psc. The colour denotes the baseline: K0-G1, A0-G1, and A0-K0 are shown in blue, green, and red, respectively. The dashed and dotted lines are the best-fit UD angular diameters in the H and K bands. Different symbols are used to represent the two calibrated exposures in the H (circles and diamonds) and K (squares and crosses) band. Right panel: closure phases as a function of the longest spatial frequency in the triplet. The same symbols are used as in the left panel, but the colour now denotes the exposure (blue being the first). |
| In the text | |
 |
Fig. 9
|
| In the text | |
 |
Fig. 10 MOST photometry of θ1 Tau deconvolved from thermal trends. |
| In the text | |
 |
Fig. 11 Comparison of the power spectra of γ Psc from the single instruments. The top panels show the original and the smoothed signal in the PDS for individual data sets. Two PDS are shown in the case of Hermes: the full data set was used for the red PDS and the set corrected for the radial velocity jump at 445 days (Fig. 2) was used for the black PDS. The estimate of νmax as the highest point of the smoothed PDS is marked as a dotted vertical line for each individual data set. The bottom panel shows the PDS of the combined data set, divided into two halves. The first and second half of the data set are shown as grey and black lines. The red line shows the power spectrum of the RV-subset with the best coverage (440 <t< 465 days in Fig. 2). |
| In the text | |
 |
Fig. 12 Spectral windows of γ Psc (left panels) and θ1 Tau (right panels). The upper panels depict the spectral windows of the single-site data. The spectral window of the combined data set is shown in the lower left panel. |
| In the text | |
 |
Fig. 13 Power density spectrum of γ Psc (left) and θ1 Tau (right). The original spectrum of the spectroscopic time series is shown in grey. The blue line shows the smoothed PDS. The red line depicts the multi-component fit to the original PDS. For γ Psc, no Gaussian profile was fitted for νmax. The vertical black line shows the adopted value of νmax for γ Psc and θ1 Tau of ~32 and 90 μHz. For both stars, Fig. 1 shows the clear variations on these timescales in the time series. |
| In the text | |
 |
Fig. 14 Frequency analysis of the combined data set for γ Psc (left) and θ1 Tau (right). The top panels show normalised comb response (NCR) of the six highest frequencies. The échelle diagrams (bottom panels) were calculated for the highest peak in the comb response function of γ Psc and θ1 Tau. Solid dots represent modes with an S/N ≥ 5. Open circles show the original position of modes that were shifted by 11.574 μHz. The crosses in the échelle diagram for γ Psc mark the position of multiples of the daily aliases. |
| In the text | |
 |
Fig. 15 Comparison of the power spectra of the photometric and spectroscopic PDS of θ1 Tau. The top panel shows the power spectrum and the spectral window of the MOST data set as black line and red shaded region, respectively. The spectral window depicts the position of the orbital aliases and reveals that the range around νmax is nearly free of contaminations. The three main peaks in the region around 90 μHz in the MOST spectrum correspond to frequencies also detected with the ground-based campaign (red dashes). The bottom panel shows the unprewhitened power spectrum of the combined spectroscopic campaign data. The blue horizontal line indicates an average large frequency separation found for θ1 Tau. The lower and upper horizontal red line indicates the noise level and five times the noise level. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


