| Issue |
A&A
Volume 572, December 2014
|
|
|---|---|---|
| Article Number | A19 | |
| Number of page(s) | 17 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201424706 | |
| Published online | 20 November 2014 | |
SARCS strong-lensing galaxy groups
II. Mass-concentration relation and strong-lensing bias⋆
1
Instituto de Física y Astronomía, Universidad de Valparaíso,
Avda. Gran Bretaña 1111,
Valparaíso,
Chile
e-mail: foex.gael@gmail.com
2
Aix-Marseille Université, CNRS, LAM (Laboratoire d’Astrophysique
de Marseille) UMR 7326, 13388
Marseille,
France
3
Dark Cosmology Centre, Niels Bohr Institute, University of
Copenhagen, Juliane Maries Vej
30, 2100
Copenhagen,
Denmark
4
Centro de Investigaciones de Astronomía,
AP 264, Mérida 5101-A,
Venezuela
Received: 30 July 2014
Accepted: 20 September 2014
Aims. Various studies have shown a lensing bias in the mass-concentration relation of cluster-scale structures that is the result of an alignment of the major axis and the line of sight. In this paper, we aim to study this lensing bias through the mass-concentration relation of galaxy groups, thus extending observational constraints to dark matter haloes of mass ~1013−1014 M⊙.
Methods. Our work is based on the stacked weak-lensing analysis of a sample of 80 strong-lensing galaxy groups. By combining several lenses, we significantly increase the signal-to-noise ratio of the lensing signal, thus providing constraints on the mass profile that cannot be obtained for individual objects. The resulting shear profiles were fitted with various mass models, among them the Navarro-Frank-White (NFW) profile, which provides an estimate of the total mass and of the concentration of the composite galaxy groups.
Results. The main results of our analysis are the following: (i) the lensing signal does not allow us to firmly distinguish between a simple singular isothermal sphere mass distribution and the expected NFW mass profile; (ii) we obtain an average concentration c200 = 8.6-1.3+2.1 that is much higher than the value expected from numerical simulations for the corresponding average mass M200 = 0.73-0.10+0.11 × 1014 M⊙; (iii) the combination of our results with those at larger mass scales gives a mass-concentration relation c(M) of more than two decades in mass, whose slope disagrees with predictions from numerical simulations using unbiased populations of dark matter haloes; (iv) our combined c(M) relation matches results from simulations that only used haloes with a large strong-lensing cross-section, that is, elongated with a major axis close to the line of sight; (v) for the simplest case of prolate haloes, we estimate a lower limit on the minor-to-major axis ratio a/c = 0.5 for the average SARCS galaxy group with a toy model.
Conclusions. Our analysis based on galaxy groups confirmed the results obtained at larger mass scales: strong lenses apparently present concentrations that are too high, which arises because the triaxial haloes are preferentially oriented with the line of sight. Because more massive systems already have large lensing cross-sections, they do not require a strong elongation along the line of sight, contrary to less massive galaxy groups. Therefore it is natural to observe higher lensing (projected) concentrations for such systems, resulting in an overall mass-concentration relation steeper than that of nonlensing haloes.
Key words: gravitational lensing: strong / gravitational lensing: weak / galaxies: groups: general / dark matter
© ESO, 2014
1. Introduction
Among the challenges faced by modern cosmology, characterizing the mass distribution of groups and clusters of galaxies generates much interest, from both the observational and theoretical points of view. These objects, whose mass is thought to be dominated by the so-called dark matter, are theoretically forming in a hierarchical bottom-up fashion when considering only gravitational interactions (Kaiser 1986; White & Frenk 1991). Because the only scale of the process is the mass contained in the initial overdensity that leads to the formation of a virialized halo, groups and clusters are assumed to constitute a population of self-similar objects. This “universality” has been the subject of intensive work, for instance, through the theoretical scaling relations between the clusters’ total mass and their other observable physical quantities (see, e.g., Giodini et al. 2013 for a recent review). The analysis of these scaling laws is of prime importance for understanding the physics involved in the formation and evolution of structures, in particular with evidence of similarity breaks due to baryonic processes (e.g., Voit 2005).
Another way to test and constrain the model of structure formation consists of studying their internal mass distribution. For instance, the three-dimensional shape of the haloes, their average mass profile in the inner parts and at large scales, the influence of the central galaxy and its stellar mass, or the level of substructures resulting from the accretion history are some key aspects of the problem, reflecting the properties of dark matter coupled to the cosmological evolution of the Universe (see, e.g., the review by Bartelmann et al. 2013, and references therein). Some general predictions can be made from theoretical modeling with simplifying hypotheses, such as the profile of an isothermal mass distribution (Binney & Tremaine 1987), or the mass density contrast of a virialized halo in the case of spherical collapse in a matter-dominated Universe (Gunn & Gott 1972). However, owing to the complexity of the problem, one has to rely on numerical simulations to derive some statistical properties of the halo population. During the past two decades, tremendous efforts have been made in this direction, with the emergence of a rather well-defined model of dark matter halo formation within the framework of the Lambda cold dark matter (Λ-CDM) concordance cosmological model. Despite some intrinsic limitations of these simulations (e.g., spatial and mass resolution, treatment of baryonic physics, properties of the dark matter, etc.), they generated several expectations over the years about the mass distribution of group- and cluster-scale haloes. In particular, the dark matter N-body numerical simulations performed by Navarro et al. (1995, 1996, 1997) led to the prediction of a universal profile, able to recover the mass distribution of simulated haloes over three decades in mass. This Navarro-Frenk-White (NFW) profile is characterized by a rather flat central density and a steeper profile with a logarithmic slope of −3 at larger scales, the transition between the two asymptotical regimes occurring at a so-called scale radius. The properties of this profile and its ability to describe both real and simulated haloes have been intensively explored. Particular emphasis was placed on the so-called concentration parameter, the ratio between the virial radius and the scale radius. Intuitively, the Universe background density sets the characteristic density contrast of a halo at its formation epoch. In the case of the NFW model, this density contrast is related to the concentration parameter (see Sect. 4). Therefore, in a hierarchical scenario where more massive haloes form later, when the background density is lower, clusters are expected to be less concentrated than groups. This mass-concentration relation has mainly been studied in numerical simulations, with, indeed, a bottom-up formation of structures leading to haloes less concentrated at larger mass scales (e.g., Navarro et al. 1997; Bullock et al. 2001; Eke et al. 2001; Dolag et al. 2004; Neto et al. 2007; Duffy et al. 2008; Gao et al. 2008; Zhao et al. 2009). Interestingly, the recent work by Prada et al. (2012) resulted in a different relation, with a higher normalization and increasing concentrations for more massive galaxy clusters (an “upturn” in concentrations reported first by Klypin et al. 2011). On the one hand, Meneghetti & Rasia (2013) showed that the concentrations measured by Prada et al. (2012) are biased high compared with the conecntrations of Duffy et al. (2008) because of the haloes’ selection and binning (maximum circular velocity versus mass), along with a different methodology of estimating the concentrations (means of velocity ratio versus fitting of the spherically averaged mass profile). On the other hand, Ludlow et al. (2012) explained the upturn in concentrations by the dynamical state of the haloes. They found that the upturndisappears when selecting only relaxed clusters. Systems that are collapsing at the time they are identified in the simulations present a compact configuration: a large portion of the newly accreted mass is located at their pericenter, which results in higher concentrations. These apparent discrepancies highlight the importance of controlling the selection function and the estimator of the haloes’ parameters, two key aspects to be accounted for when comparing results from different analyses.
The mass-concentration relations derived in numerical simulations are very sensitive to the input cosmological parameters (e.g., Bullock et al. 2001; Neto et al. 2007; Macciò et al. 2008; Dutton & Macciò 2014; Ludlow et al. 2014), so they provide a powerful tool for testing the Λ-CDM cosmological model and the scenario of structure formation. Numerous observational studies, based on X-ray observations (e.g. Pointecouteau et al. 2005; Vikhlinin et al. 2006; Voigt & Fabian 2006; Zhang et al. 2006; Buote et al. 2007; Gastaldello et al. 2007; Schmidt & Allen 2007; Ettori et al. 2010, 2011) or galaxy kinematic data (e.g., Rines & Diaferio 2006; Wojtak & Łokas 2010), investigated the mass profile of galaxy clusters, successfully determining concentrations matching those from numerical simulations. On the other hand, most of the lensing-based analyses of galaxy clusters found haloes overconcentrated compared with Λ-CDM predictions (e.g., Broadhurst et al. 2005, 2008; Comerford & Natarajan 2007; Umetsu & Broadhurst 2008; Oguri et al. 2009, 2012; Umetsu et al. 2010, 2011b; Zitrin et al. 2010; Okabe et al. 2013). Only a few lensing studies found an agreement with the predicted mass-concentration relation (e.g., Halkola et al. 2006; Limousin et al. 2008; Okabe et al. 2010; Merten et al. 2014; Umetsu et al. 2014). This overconcentration problem raised questions about the Λ-CDM model and its scenario of structure formation, in which extremely high concentrations, or similarly large Einstein radii, are statistically very unlikely (e.g., Broadhurst & Barkana 2008; Zitrin et al. 2009, 2011; Meneghetti et al. 2011; see, however, Redlich et al. 2012). Several explanations can be invoked to overcome these discrepancies. First, dark matter haloes are not spherical, as seen from elliptical projected observational probes, and in numerical simulations where haloes have triaxial shapes with a preference for prolateness (see, e.g., the review by Limousin et al. 2013, and references therein). Because most of the observational studies assume spherical symmetry, the impact of projection effects for a highly elongated mass distribution aligned with the line of sight is easy to imagine: an enhancement of the projected mass density that leads to apparent overconcentrated haloes. On the other hand, when simulated haloes are treated in three dimensions, including or excluding the same hypothesis of spherical symmetry does not dramatically change the estimated masses and concentrations. These projections effects, which are inherent in any lensing reconstructions, have been widely studied and provided a solid way to reconcile observational results with theoretical predictions. For instance, Morandi et al. (2011b,a) performed a joint X-ray+lensing analysis to directly constrain the three-dimensional shape of the galaxy cluster A1689, for which several lensing-based studies derived very high concentrations (e.g., Halkola et al. 2006; Medezinski et al. 2007). In doing so, they obtained a highly elongated mass distribution with aconcentration compatible with the Λ-CDM predictions (see also Corless et al. 2009; Sereno & Umetsu 2011; Sereno & Zitrin 2012 for a different approach to treat projections effects, based on a Bayesian modeling with priors on the haloes’ elongation derived from numerical simulations).
Elongated haloes with a major axis close to the line of sight have an increased central surface mass density, therefore they are more likely to produce a strong-lensing signal. This consideration leads to a simple explanation for the systematically high concentrations derived for strong-lensing clusters: a coupling of projection effects with a selection bias in the orientation of haloes. The physical properties of strong lenses have been the subject of several studies based on numerical simulations that were targeting haloes with a large strong-lensing cross-section (e.g., Hennawi et al. 2007; Corless & King 2007; Oguri et al. 2009; Meneghetti et al. 2010b, 2014; Giocoli et al. 2014). These works highlighted that selecting objects with a large strong-lensing cross-section introduces an orientation bias in the population of haloes, resulting in higher concentrations derived form their surface mass density. They also revealed a bias in the intrinsic (3D) concentration of strong-lensing haloes, although the main enhancement of 2D concentrations comes from the projection of elongated mass distributions. By treating these simulated haloes as they would be from lensing observations, they derived specific mass-concentration relations characterized by steeper slopes and higher normalizations, leading to predicted concentrations that agree well with observational results of strong-lensing galaxy clusters.
This strong-lensing bias (projection effects of prolate haloes whose major axis is close to the line of sight) gives a natural explanation for overconcentrated haloes. However, the theoretical predictions derived from numerical simulations can also be adjusted in some way. In particular, including baryonic physics allows for a modification of the central mass distribution through radiative cooling and feedback processes, resulting in higher concentrations (e.g., Mead et al. 2010; Fedeli 2012). Finally, Waizmann et al. (2012, 2014), used the statistics of extreme values to show that very large Einstein radii are rare but not in conflict with Λ-CDM cosmology.
By comparing observational results with numerical predictions, a more accurate picture of the haloes’ mass distribution has emerged, in particular for the subpopulation of strong lenses and the “problem” of their high concentrations. However, most of the studies have been focused so far on cluster-scale objects. Therefore, we propose here to extend the analysis of the mass-concentration relation of strong lenses toward lower mass scales. Based on a sample of objects detected and selected by their strong lensing signal, our study focuses on haloes of masses ~1013−1014 M⊙, with concentrations derived from a stacked weak-lensing analysis. Our main goal is to perform the first analysis of the strong-lensing bias from galaxy groups to massive clusters, and to compare the resulting mass-concentration relation with those derived from numerical simulations that mimic lensing-based analyses on samples of lensing-selected haloes.
This paper is organized as follow: in Sect. 2, we briefly present the data used in this work. We define in Sect. 3 the SARCS composite lenses, and introduce the specifics of a stacked weak-lensing analysis. The fitting results of the average shear profiles are given in Sect. 4, along with a discussion of the several simplifying hypotheses and sources of uncertainty introduced in our method. Section 5 is dedicated to the analysis of the groups’ concentrations and the mass-concentration relation derived when combining our sample with massive strong-lensing galaxy clusters. Finally, we summarize our findings in Sect. 6. Throughout this paper, we use a standard Λ-CDM cosmology defined by ΩM = 0.3,ΩΛ = 0.7, and a Hubble constant H0 = 70 km s-1/ Mpc. Unless specified otherwise, masses are given in units of M⊙. Therefore, they should be re-scaled by our assumed h = (H0/ 100) = 0.7 before a comparison with results derived using a different Λ-CDM cosmology.
2. SARCS strong-lensing galaxy groups
2.1. Sample of group-scale strong lenses
To study the mass profile of strong-lensing galaxy groups, we used the Strong Lensing Legacy Survey sample (SL2S, Cabanac et al. 2007) and the recent compilation of its candidates with a group-scale gravitational arc (SARCS, More et al. 2012). The sample was constructed with a semi-automated searching of elongated and curved features on the full Canada-France-Hawaii Telescope Legacy Survey (CFHTLS). The arcfinder algorithm (Alard 2006; More et al. 2012) was used to scan the 150 deg2 of the CFHTLS optical images, leading to a number of ~1000 candidates per square degree. After a visual inspection and a selection based on the quality ranking attributed to each potential lens, a sample of 127 systems was obtained. A photometric redshift was assigned to each candidate using the catalog of Coupon et al. (2009), and different observing campaigns (Limousin et al. 2009; Thanjavur et al. 2010; Ruff et al. 2011; Muñoz et al. 2013) provided a spectroscopic redshift for several systems. More details about the CFHTLS data and the definition of the SARCS sample can be found in More et al. (2012).
2.2. Most secure galaxy group candidates
In Foëx et al. (2013, Paper I hereafter), we performed a weak-lensing and optical analysis of the SARCS sample of lens candidates, which provided two supplementary selection criteria to reduce the contamination of the sample by false detections and galaxy-scale lenses. With the fit of the systems’ shear profile, we estimated their velocity dispersion, σv, via the singular isothermal sphere (SIS) mass model. We obtained a positive weak-lensing detection with σv> 0 at the 1σ level for 89 objects. On the other hand, the study of the candidates’ luminosity map using the galaxies populating the red sequence led to a total of 96 objects with an evident light over-density associated with the strong-lensing system. The combination of these two criteria resulted in a sample of 80 objects, which is the basis of the present analysis. These most secure lens candidates span broad ranges in redshift (z ∈ [ 0.15−1.2 ]), mass (σv ∈ [ 300−1100 ] km s-1), and arc radius (RA ∈ [ 2−20 ] ′′). The average properties of this sample are given in the first row of Table 1, and we refer to Paper I for further details.
3. Methodology
3.1. Advantages of combining lenses
As mentioned above, we performed the weak-lensing analysis of each SARCS galaxy group
candidate in Paper I. However, the lensing signal-to-noise ratios (S/N) we measured were
not high enough to derive reliable constraints on the mass of individual systems. To
overcome this problem, we propose here to conduct a “stack” analysis, that is, combining
several objects to derive the properties of composite (average) galaxy groups. The main
limitation in obtaining well-constrained weak-lensing masses comes from the noise due to
the galaxies’ intrinsic ellipticity, whose dispersion is ~0.2−0.3. Recovering a shear signal with
intensities of ~0.1−0.01 is a difficult task and requires averaging the shape of a
large number N of lensed galaxies. Since this noise scales as
1/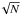 , one can artificially increase the source
density and derive a shear signal with higher confidence levels by combining several
lenses. For instance, Okabe et al. (2013) stacked
50 galaxy clusters and obtained a shear profile with a total S/N of ~30, compared with detection peaks of
~4 in the
two-dimensional mass map of individual objects (see also Okabe et al. 2010; Oguri et al. 2012;
Umetsu et al. 2011a, 2014).
, one can artificially increase the source
density and derive a shear signal with higher confidence levels by combining several
lenses. For instance, Okabe et al. (2013) stacked
50 galaxy clusters and obtained a shear profile with a total S/N of ~30, compared with detection peaks of
~4 in the
two-dimensional mass map of individual objects (see also Okabe et al. 2010; Oguri et al. 2012;
Umetsu et al. 2011a, 2014).
Stacking several lenses increases S/N, but it is not the only improvement it provides (e.g., Oguri & Takada 2011). In one-dimensional analyses, based on shear profiles, the assumption of circular symmetry can lead to biased estimates because of elliptically projected mass distributions (e.g., Corless & King 2008; Feroz & Hobson 2012). By combining several lenses, the projected ellipticity of the individual objects is averaged out, and a simple profile can provide a good description of the resulting average mass distribution. Furthermore, stacking several lenses reduces the impact of significant substructures in individual systems. In Paper I, we found 13 galaxy groups with complex light distributions, which presented two or more significant overdensities in their luminosity map. When combining these with regular systems, the substructures are naturally averaged, and their influence on the shear signal is diluted.
The final advantage of stacking/averaging several lenses is that weak-lensing deformations of source galaxies are produced by all the matter along the line of sight: large-scale structures (not correlated to the target lens) contribute to the shear signal, and can lead to biased mass estimates. As a result of the linearity of the shear, the contribution of these structures simply adds to the signal produced by the lens. Because these contributions can be positive or negative, they are averaged out when combining several lenses (assuming an isotropic Universe), and only produce an additional statistical noise to the measured signal (e.g., Hoekstra 2001, 2003).
3.2. Composite SARCS galaxy groups
While the advantages of a stacking analysis are evident, the lenses need to be carefully combined. A choice must be made between an increased S/N and a loss of information about the properties of the underlying population of lenses. As we have shown in Paper I, the SARCS sample mainly consists of group-scale lenses. However, it covers quite a very broad range in mass, up to galaxy clusters (arc radius up to 20′′, σv up to ~1000 km s-1). Therefore, we chose here to divide the sample into several stacks, which provides more data points to fit the mass-concentration relation (Sect. 5).
To select which objects can be stacked together while trying to reduce the scatter around the resulting composite lens, we used four selection criteria based on the individual properties of the groups. In Paper I, we derived for each object an estimate of the optical richness N and luminosity L, using the bright galaxies populating the red sequence and located within a projected radius of 1 Mpc from the strong-lensing system. Given the scaling relations between these two quantities and the total mass of a galaxy group, we expect these two observables to provide a fairly good way of stacking objects according to their mass. Despite the low S/N of the shear signal, we also have an estimate of the SIS velocity dispersion σv, which we expect to be the most robust way to combine objects of similar mass. Finally, we have the direct observable of the arc radius RA, values estimated in More et al. (2012). We have shown in Verdugo et al. (2014) that RA correlates with the groups’ total mass, even though a large intrinsic scatter was found. This quantity is tightly related to the central mass distribution, thus, we expect it to be a better tracer of the dark matter halo concentration.
After several tests, we decided to divide the sample of 80 objects into three stacks for each of the four selection criteria (richness, luminosity, velocity dispersion, and arc radius). In doing so, we obtained three uncorrelated points for the mass-concentration relation, while keeping a fairly high S/N of the stacked signal. We chose to put more objects in the low stacks (N1, L1, V1, and R1) because the lower mass lenses produce a more noisy shear signal. The limits of the middle and high stacks were chosen to have a similar number of objects, and to avoid a 1σ overlapping of the corresponding average selection criterion, that is, the richness ⟨N⟩ ± 1σ of the N stacks do not overlap, as for the ⟨L⟩ of the L stacks, ⟨σv⟩ of the V stacks, and ⟨RA⟩ of the R stacks. The general properties of the different stacks are given in Table 1 (using the individual properties derived in Paper I).
General properties of the different stacks.
3.3. Weak-lensing stacked analysis
Our weak-lensing pipeline is described in Paper I, and we review here some details of a stacked analysis.
Using the second derivative of the projected gravitational potential to express the shear
and convergence, one can show that for a lens with a circular-symmetric projected mass
distribution, the two weak-lensing deformations are simply related through (Miralda-Escude 1991)
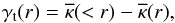 (1)where
(1)where 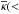 r) and
r) and 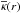 are the convergence averaged over the disk
and circle of radius r, respectively. Since the convergence
κ is equal
to the surface mass density Σ(r) normalized by a critical density
Σcrit, we can
rewrite the previous equation as
are the convergence averaged over the disk
and circle of radius r, respectively. Since the convergence
κ is equal
to the surface mass density Σ(r) normalized by a critical density
Σcrit, we can
rewrite the previous equation as 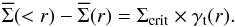 (2)The critical density reads
(2)The critical density reads
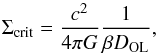 (3)where the factor β =
DLS/DOS
captures the geometrical configuration of the lensing optical bench. From Eq. (2), we see that the shear produced by a lens
equals its mass density contrast
(3)where the factor β =
DLS/DOS
captures the geometrical configuration of the lensing optical bench. From Eq. (2), we see that the shear produced by a lens
equals its mass density contrast 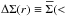
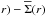 after a rescaling by the critical density.
In other words, one can combine (average, stack) the shear signal produced by lenses at
different redshifts to recover the mass of the corresponding composite lens.
after a rescaling by the critical density.
In other words, one can combine (average, stack) the shear signal produced by lenses at
different redshifts to recover the mass of the corresponding composite lens.
The density contrast of a circular-symmetric lens j can be locally estimated
by the tangential shear γt,ij it produces on
a galaxy source i located at the concentric radius rij:
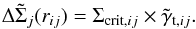 (4)To derive the shear, we employ the estimator
(4)To derive the shear, we employ the estimator
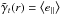 , that is, the average tangential
ellipticity component of the background galaxies located at a radius r ± δr.
Since we do not have an estimated redshift for each galaxy, we use the same critical
density Σcrit,j for all the source galaxies
i of a
given lens j.
This critical density is calculated with the average geometrical factor ⟨β(z)⟩,
whose values are given in Paper I for each SARCS lens.
, that is, the average tangential
ellipticity component of the background galaxies located at a radius r ± δr.
Since we do not have an estimated redshift for each galaxy, we use the same critical
density Σcrit,j for all the source galaxies
i of a
given lens j.
This critical density is calculated with the average geometrical factor ⟨β(z)⟩,
whose values are given in Paper I for each SARCS lens.
By combining the signal of several lenses, we increase the number of available sources
for the resulting composite object and reduce the noise due to the galaxies’ intrinsic
ellipticity. The corresponding average mass density contrast reads 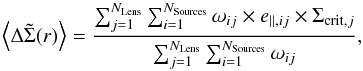 (5)where Nsources is the
number of source galaxies within the annulus of projected physical radius r ± δr
around the center of the jth lens.
(5)where Nsources is the
number of source galaxies within the annulus of projected physical radius r ± δr
around the center of the jth lens.
To reduce the impact of galaxies with a noisy estimate of their shape parameters, the
tangential component of the ellipticity is weighted according to the inverse variance of
its measurement: 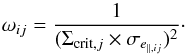 (6)Therefore, the statistical uncertainty
associated to our estimator
(6)Therefore, the statistical uncertainty
associated to our estimator 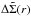 can be expressed as
can be expressed as 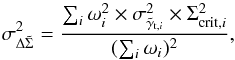 (7)where the sum runs over all the stacked
background galaxies in the radial bin r. The uncertainty on the tangential shear
(7)where the sum runs over all the stacked
background galaxies in the radial bin r. The uncertainty on the tangential shear
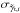 is given by the quadratic sum of the
errors on the shape measurement σe∥
,ij and the noise due to the galaxies’
intrinsic ellipticity, derived assuming a root mean square of 0.25 per component.
is given by the quadratic sum of the
errors on the shape measurement σe∥
,ij and the noise due to the galaxies’
intrinsic ellipticity, derived assuming a root mean square of 0.25 per component.
To quantify the detection level of the signal for a given stack, we define the total S/N
as follows: 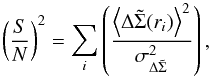 (8)where the sum runs over the bins in radius
used to fit the profile. Here we only consider the statistical uncertainty defined above
as source of noise, an approximation justified in Sect. 4.2. The total S/N of the profiles
are given Table 2; stacking the 80 SARCS galaxy
groups leads to S/N = 14.3 over the range
50−3000 kpc.
(8)where the sum runs over the bins in radius
used to fit the profile. Here we only consider the statistical uncertainty defined above
as source of noise, an approximation justified in Sect. 4.2. The total S/N of the profiles
are given Table 2; stacking the 80 SARCS galaxy
groups leads to S/N = 14.3 over the range
50−3000 kpc.
With Eq. (5), we have an estimator of the
mass density contrast for a stack of lenses. However, the signal that is actually measured
when averaging the shape of lensed galaxies is the reduced shear g = γ/ (1 −
κ). Therefore, one cannot simply fit the stacked
signal by the analytical expression ΔΣ(r) of a given mass model. Since we wish to take
full advantage of the stacking procedure to obtain constraints in the central regions of
the lenses where the weak-lensing approximation g ≈ γ no longer holds, we need to
evaluate what our estimator actually measures. It can be shown that, indeed, the estimator
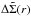 has a second-order contribution (Mandelbaum et al. 2006; Johnston et al. 2007):
has a second-order contribution (Mandelbaum et al. 2006; Johnston et al. 2007): 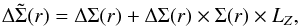 (9)with
(9)with  (10)Neglecting variations in the density of
source galaxies between the different radial bins (e.g., Johnston et al. 2007; Leauthaud et al.
2010), we estimate for each composite lens an average factor LZ over the range
0.1−2 Mpc from the lens
center. Following the methodology used in Paper I to derive the average geometrical factor
⟨β⟩, we
estimate the ratio
(10)Neglecting variations in the density of
source galaxies between the different radial bins (e.g., Johnston et al. 2007; Leauthaud et al.
2010), we estimate for each composite lens an average factor LZ over the range
0.1−2 Mpc from the lens
center. Following the methodology used in Paper I to derive the average geometrical factor
⟨β⟩, we
estimate the ratio 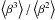 for each individual group. We then
calculate LZ for a given
composite lens as
for each individual group. We then
calculate LZ for a given
composite lens as 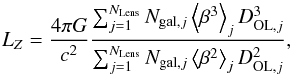 (11)with Ngal,j the number of
source galaxies within 0.1−2
Mpc from the center of the jth group. The value of LZ for each stack is
given in Table 2.
(11)with Ngal,j the number of
source galaxies within 0.1−2
Mpc from the center of the jth group. The value of LZ for each stack is
given in Table 2.
4. Mass profile of composite galaxy groups
4.1. Modeling the data
Most of the stacked weak-lensing analyses make use of the so-called halo model (e.g., Mandelbaum et al. 2005b, 2006; Johnston et al. 2007; Mandelbaum et al. 2008a, 2010; Leauthaud et al. 2010; Oguri & Takada 2011; Covone et al. 2014; Umetsu et al. 2014). With this approach, the mass density contrast is modeled as the sum of three components: the stellar mass contained in the central galaxy, the group- or cluster-scale main halo (the one-halo term), and a contribution from other groups and clusters surrounding the target (the two-halo term). While the first term only produces a significant contribution on very small scales (typically below 50 kpc), the two-halo term only has a dominant contribution well beyond the virial radius of the main halo (typically several Mpc, e.g., Oguri & Takada 2011). On intermediate scales, the signal is largely dominated by the contribution of the one-halo term. In the present work, we restrict our analysis to the one-halo term; thus, the expressions of ΔΣ(r) and Σ(r) (in Eq. (9)) do not include a stellar contribution or the large-scale two-halo term. We discuss the validity of this approximation in the next subsection.
To fit the observed density-contrast profiles of the SARCS galaxy groups, we employed
three mass models. First, we used the SIS, which is fully characterized by its velocity
dispersion σv, and has a
mass-density profile with a constant logarithmic slope of −2. While this model has proven to give a
good description for the mass distribution of individual galaxies, it is not expected to
accurately reproduce more massive dark matter haloes, which are expected to present a
steeper density profile at large scales. However, the SIS velocity dispersion
σv can be easily
compared with results from a dynamical analysis (e.g., Muñoz et al. 2013) or strong-lensing models providing an estimate of the
Einstein radius (e.g., Verdugo et al. 2014). The
shear produced by an SIS scales as 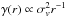 .
.
The second model we used is a mass distribution characterized by a power-law density profile with a constant but free slope (PLAW). We express its surface mass density as Σ(r) = Σ0rα, with Σ(1 Mpc) = Σ0. A slope α = −1 corresponds to the SIS model. The density contrast of the PLAW model reads ΔΣ(r) = (−α/ (2 + α))Σ0rα.
Finally, we used the NFW mass profile, derived from extensive dark matter numerical
simulations. This model is supposed to reproduce the mass distribution of dark matter
haloes over a wide range in mass, from galaxy to cluster scales (Navarro et al. 1995, 1996, 1997). Its density reads 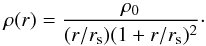 (12)The scale radius rs marks the
transition between the two asymptotic behaviors, ρ ∝
r-1 in the central part, and a steeper
profile ρ ∝
r-3 in the outskirts. Thus, the NFW model
provides more freedom to characterize the mass profile, in contrast to the two other
models whose slopes are constant at all radii. The normalization of the NFW profile
ρ0 is related to the 3D mass via
(12)The scale radius rs marks the
transition between the two asymptotic behaviors, ρ ∝
r-1 in the central part, and a steeper
profile ρ ∝
r-3 in the outskirts. Thus, the NFW model
provides more freedom to characterize the mass profile, in contrast to the two other
models whose slopes are constant at all radii. The normalization of the NFW profile
ρ0 is related to the 3D mass via
![\begin{equation} \label{eq:nfw} M(<\!r)=4\pi\rho_{0}^{3}r_{\rm s}^3\left[\ln(1+r/r_{\rm s})-(r/r_{\rm s})/(1+r/r_{\rm s})\right]. \end{equation}](/articles/aa/full_html/2014/12/aa24706-14/aa24706-14-eq171.png) (13)In the model of the gravitational collapse of
a spherical overdensity, one can show that a virialized object reaches a density contrast
Δvir ≈ 180 with
respect to the mean density
(13)In the model of the gravitational collapse of
a spherical overdensity, one can show that a virialized object reaches a density contrast
Δvir ≈ 180 with
respect to the mean density  of an Einstein-De Sitter Universe (Gunn & Gott 1972); Bryan & Norman (1998) derived an accurate approximation for Δvir(z) in a
ΛCDM Universe. This simple
prescription gives a natural parametrization of the NFW profile: the radius within which
the dark matter halo’s averaged density equals
of an Einstein-De Sitter Universe (Gunn & Gott 1972); Bryan & Norman (1998) derived an accurate approximation for Δvir(z) in a
ΛCDM Universe. This simple
prescription gives a natural parametrization of the NFW profile: the radius within which
the dark matter halo’s averaged density equals 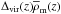 defines the virial mass,
defines the virial mass, 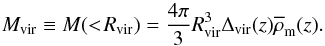 (14)This mass can be combined with Eq. (13) to simply express the normalization of the
NFW profile as
(14)This mass can be combined with Eq. (13) to simply express the normalization of the
NFW profile as 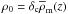 , where the characteristic overdensity
δc equals
, where the characteristic overdensity
δc equals 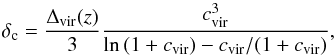 (15)with the concentration parameter
cvir =
Rvir/rs. It
is thus possible to express the NFW profile in terms of (Mvir,cvir)
rather than its normalization ρ0 and scale radius rs. Different
parametrizations can be found in the literature. For instance, instead of using the
Universe’s mean density
(15)with the concentration parameter
cvir =
Rvir/rs. It
is thus possible to express the NFW profile in terms of (Mvir,cvir)
rather than its normalization ρ0 and scale radius rs. Different
parametrizations can be found in the literature. For instance, instead of using the
Universe’s mean density 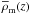 , one can use the critical density,
, one can use the critical density,
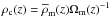 , which can be justified as follows: in a
ΛCDM Universe, an
overdensity will collapse if it behaves as a mini-closed Universe, that is, with an
average density higher than the critical density ρc. It is also
common to use a fixed density contrast for every redshift, often set to Δ = 200, a choice that can be motivated
because of the cosmology dependence of Δvir(z), and the assumption that galaxy
groups and clusters are not necessarily virialized at the time we observe them. Even
though these different parametrizations complicate the comparison between different
studies, it is easy to convert results from one definition to another by combining Eq.
(14), Eq. (15), and keeping constant the absolute normalization ρ0 (e.g., Hu & Kravtsov 2003). The NFW mass model has an
analytical expression for the shear (e.g., Bartelmann
1996), and in the remainder of the paper, we use the (M200,c200)
parametrization, with the density contrast expressed with respect to the critical density,
that is, ρ0 =
δcρc(z).
, which can be justified as follows: in a
ΛCDM Universe, an
overdensity will collapse if it behaves as a mini-closed Universe, that is, with an
average density higher than the critical density ρc. It is also
common to use a fixed density contrast for every redshift, often set to Δ = 200, a choice that can be motivated
because of the cosmology dependence of Δvir(z), and the assumption that galaxy
groups and clusters are not necessarily virialized at the time we observe them. Even
though these different parametrizations complicate the comparison between different
studies, it is easy to convert results from one definition to another by combining Eq.
(14), Eq. (15), and keeping constant the absolute normalization ρ0 (e.g., Hu & Kravtsov 2003). The NFW mass model has an
analytical expression for the shear (e.g., Bartelmann
1996), and in the remainder of the paper, we use the (M200,c200)
parametrization, with the density contrast expressed with respect to the critical density,
that is, ρ0 =
δcρc(z).
Even though the NFW model provides a fairly good description of the galaxy groups and clusters’ mass distribution, several improvements have been proposed, including triaxiality, core of constant density, or varying inner logarithmic slope (e.g., generalized NFW, Einasto profile). However, estimating the extra free parameters of such models requires observational data in the central part of the halo, a region not accessible with the present weak-lensing observations (see, e.g., Newman et al. 2009, 2013, for a combination of lensing and stellar kinematics to probe the mass profile down to ~kpc scales). Therefore, we limit our analysis to the classical NFW profile.
4.2. Error budget − validation of the method
Any weak-lensing study comes with several sources of both statistical and systematic error (e.g., Mandelbaum et al. 2005a). We review in the following the dominating errors and describe how we adapted our methodology accordingly.
Shear calibration In Foëx et al. (2012), we ran our lensing pipeline on the STEP1 simulations (Heymans et al. 2006) and derived a calibration bias of −0.1 ± 0.02. Therefore, before fitting the shear profiles, we corrected our measured signal by a boost factor of 10%. To further test whether our lensing measurements suffer from residual systematics, we computed shear profiles using the radial component of the galaxies’ ellipticity. Figure 3 shows that this signal, expected to be null, is indeed statistically consistent with 0 (within 3σ at most) over the range in radius used to fit the profiles.
Redshift distribution of the sources To translate the
geometrical weak-lensing signal into the mass of the deflector, one has to evaluate the
average geometrical factor ⟨β(zl,zs)⟩,
which depends on the redshift distribution of the lensed galaxies. Our approach, described
in Paper I (see also Limousin et al. 2009; Foëx et al. 2012), makes use of photometric redshifts
that were carefully calibrated with spectroscopic observations (Ienna & Pelló 2006). Because they were derived with the same CFHTLS
observations used for this work, it is straightforward to apply the selection criteria
(magnitude and color) to these catalogs, and derive the redshift distribution of the
lensing sources. We verified that differences in the value of ⟨β⟩ are typically of the
percent level when using the redshift distribution of the different CFHTLS fields. It is
much lower than the statistical noise due to the dispersion of the galaxies’ intrinsic
ellipticity, so this source of uncertainty can be neglected. In Paper I, we also
investigated the influence of uncertainties in the lens redshift zl, and we found
that an error of 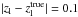 propagates to a 20%−30% error on the mass. The comparison
between spectroscopic and photometric redshifts has shown that the overall agreement is
better than this 0.1 uncertainty (Fig. 2 of Paper I); therefore, we can assume that the
optical benches of the stacks are well enough constrained to avoid generating significant
errors in the mass estimates.
propagates to a 20%−30% error on the mass. The comparison
between spectroscopic and photometric redshifts has shown that the overall agreement is
better than this 0.1 uncertainty (Fig. 2 of Paper I); therefore, we can assume that the
optical benches of the stacks are well enough constrained to avoid generating significant
errors in the mass estimates.
Center offset When using shear profiles, the position of the mass center has to be carefully chosen. Indeed, an incorrect center acts as a smoothing of the shear signal, which leads to biased-low mass and concentration estimates (e.g., Johnston et al. 2007; George et al. 2012; Covone et al. 2014). A dark matter halo is by definition dark and not visible, thus, locating its mass center can be a challenging task. The weak-lensing signal can be used itself to constrain the center position, but low spatial resolution, sparse constraints, and noisy data can lead to biased estimates, in particular with ground-based observations (e.g., Dietrich et al. 2012). Baryonic tracers are usually employed to locate the mass center, in particular with the position of the brightest central galaxy. However, this method suffers from two assumptions: that the brightest galaxy is correctly identified, and that it lies at the actual center of mass (see discussions in Johnston et al. 2007; and Mandelbaum et al. 2008a, for more details). George et al. (2012) compared different approaches for estimating the mass center, for instance, by using the centroid of the galaxy population rather than the brightest one, or including stellar mass and X-ray emission information: while the center of systems with a clear central galaxy is fairly well traced by its position (offsets smaller than 75 kpc), in most cases the best tracer is obtained by the position of the brightest/most massive galaxy close to the peak of the X-ray emission. However, this method requires X-ray observations, so we cannot use it here. On the other hand, for systems going through a major-merging event, the X-ray emission peak can be dislocated from the actual mass center, as observed in the so-called bullet clusters (Markevitch et al. 2004; Bradač et al. 2008; Merten et al. 2011; Dawson et al. 2012; Dahle et al. 2013). Recently, we found such a bullet-like object in the SARCS sample, the lowest mass system observed to date with a displacement between the X-ray emission peak and the mass center (Gastaldello et al. 2014). A parallel study based on numerical simulations showed that such low-mass systems are more frequent than bullet configurations in massive galaxy clusters (Fernández-Trincado et al. 2014). Thus we can expect that, although efficient in most cases, the actual mass center cannot be accurately traced by the X-ray emission for a non-negligible fraction of galaxy groups.
Since gravitational lensing does not rely on the baryonic content of a dark matter halo, the strong-lensing system can be expected to be an accurate tracer of the mass center, even in such dynamically perturbed galaxy groups (see Sect. 3.2 and Appendix of Paper I for further details). Therefore, we used the center of the SARCS gravitational arcs to define the center of the profiles, and we did not include a contribution to the signal by objects with a wrongly-identified mass center in our fitting procedure (see Johnston et al. 2007, for a method that accounts for center offsets in a stacked weak-lensing analysis). Furthermore, in the case of strong-lensing events produced by a subhalo of a more massive component, the weak-lensing signal of the larger-scale object will mainly contribute to the two-halo term of the stacked shear profiles. As shown below, we can neglect this term in our analysis, thus, our choice for the mass center provides a globally consistent approach.
Mass modeling The three mass models we used do not have any explicit contribution for the baryonic content of galaxy groups. A more complete description of their mass distribution should in fact account for the presence of the gas, and the stellar population within the galaxy members. For the former, it can be argued that its spatial distribution follows that of the dark matter (for relaxed objects at least), thus, its presence does not significantly modify the shape of the total mass density profile. For the stellar mass contribution, it can also be assumed that the distribution of satellite galaxies follows that of the dark matter (e.g., Leauthaud et al. 2011). Therefore, to first order, we can consider that the total mass distribution of our composite lenses is well represented by a single NFW component.
On the other hand, a massive central galaxy introduces a contribution to the lensing signal that needs to be accounted for because it can bias the results of the NFW fitting (e.g., Johnston et al. 2007; Leauthaud et al. 2010). The presence of baryons in the core of a dark matter halo can further modify its density profile by adiabatic contractions (e.g., Gnedin et al. 2004). However, we can expect that for the present data quality, our fitting method does not provide statistically significant differences in the best fit parameters when accounting or not for an additional central mass component (see also Okabe et al. 2013; Umetsu et al. 2014). Because we fit the shear profiles above 50 kpc, where the mass density of the central galaxy is negligible, we can model this component as a simple point mass rather than a more complex mass distribution, such as a Sersic profile. Figure 1 shows the relative contribution of such a point mass with ΔΣ(r) = M0/πr2 to the signal produced by an NFW halo characterized by the S0 best-fit parameters. Above 100 kpc, a point mass of M0 = 1012 M⊙ contributes less than 10% to the total signal. This value is lower than the typical uncertainty of our weak-lensing measurements over the range 50−300 kpc, which justifies excuding this component in the model. In Sect. 4.4, we investigate the contribution of a point mass when combining the stacked weak-lensing signal with strong-lensing constraints. Even though the central galaxy can bias the mass estimate of the dark matter halo itself, numerical (e.g., Laporte & White 2014) and observational (e.g., Newman et al. 2013) studies have shown that its presence leads to a the total mass profile that follows the NFW model. This considerationadditionally justifies the use of a simple single-component mass distribution.
The other main approximation in our mass modeling consists of neglecting the two-halo term. For instance, Umetsu et al. (2014) have shown that this component produces a signal that slowly decreases with increasing radius, which therefore does not significantly affect the shape of the weak-lensing profile. Moreover, since we limited the profiles to 3 Mpc, most of the constraints in the fit come from radii in the range 0.1−1 Mpc (up to ~Rv), a region where the two-halo term contributes less by ~1−2 orders of magnitude than the one-halo term (e.g., Fig. 8 of Johnston et al. 2007). Since we have a ~20% uncertainty on the measured signal in the same region, we can safely neglect this contribution in our mass modeling.
 |
Fig. 1 Relative contribution of a point mass component to the total measured signal, computed with Eq. (9), and using an NFW halo described by the best-fit parameters of the stack S0. The three curves show the contribution produced by a mass of 0.01, 0.1, and 1 × 1012 M⊙. The gray area represents the typical relative uncertainty of the measured signal in the region 50−300 kpc. |
Finally, it is worth mentioning that we only used spherical mass models, although dark matter haloes are known to be triaxial (see, e.g., the review of Limousin et al. 2013). We explore the effects of this approximation on the mass-concentration relation in Sect. 5.2 and provide a simple way to estimate the elongation along the line of sight of prolate haloes in Sect. 5.3.
Large-scale structures As briefly discussed in Sect. 3.1, the signal produced by uncorrelated large-scale structures can bias the lensing mass of a single lens, but their additional deformations are averaged out when stacking several objects. However, they introduce a statistical noise in the lensing signal. As shown in Oguri & Takada (2011) for stacked high-redshift galaxy clusters (Fig. 8), the dominant source of noise up to ~15 arcmin is produced by the intrinsic ellipticity of lensed galaxies. At the average redshift of our stacks z ~ 0.5, the limit in radius where we fit the profiles is 3 Mpc ~8 arcmin. Therefore, we can neglect this source of noise in our calculations, as done in similar studies of stacked weak-lensing analysis of galaxy groups (e.g., Leauthaud et al. 2010).
Stacking procedure The profiles are constructed with logarithmically-spaced annuli. We started to fit them at 50 kpc from the center, thus limiting the influence of mis-centering and reducing the contribution of the central baryonic mass component. The outer limit of the profiles was set to 2 Mpc for the low stacks, and 3 Mpc for the middle and high ones, resulting in eight and nine bins, respectively. We verified that slightly changing the inner and outer limits of the profiles does not give statistically different best-fit parameters.
To further test our stacking procedure, we performed several statistical simulations,
that is, simulating catalogs of lensed galaxies, analyzing them with our method, and
comparing the results with the expected values. The catalogs were generated with the code
Lenstool (Kneib et al. 1996; Jullo et al. 2007) as follows: based on our list of 80 groups with
measured richness N(r<1
Mpc), we assumed they were modeled with NFW density profiles, and their NFW parameters
were scaled with the following relations between the richness and the mass (Mandelbaum et al. 2008b): 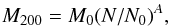 (16)with M0 = 1.56 ×
1014 M⊙, A = 1.15 and
N0 =
20, and between the mass and the concentration
(16)with M0 = 1.56 ×
1014 M⊙, A = 1.15 and
N0 =
20, and between the mass and the concentration 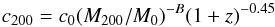 (17)with B = 0.13 and
c0 =
4.6.
(17)with B = 0.13 and
c0 =
4.6.
For each group, we simulated a catalog of about 3000 sources at redshift z = 1.171, with an intrinsic Gaussian shape noise eint = 0.25, and over an area of 15 × 15 arcmin2. The results we obtained by stacking the groups according to their richness are presented in Fig. 2, with masses and concentrations that are fully consistent with the average value of the simulated groups. Therefore, we can conclude that our methodology does not suffer any strong systematic bias.
 |
Fig. 2 Results of the stacked analysis on simulated catalogs of lensed galaxies that mimic our observations for the full sample of 80 strong lenses. Colored triangles show the best-fit mass and concentration for the three composite lenses corresponding to stacks in richness. The gray-shaded area covers the intrinsic dispersion of the simulated lenses (black stars) around their average mass and concentration. The overlap of these average values with the results of the stacked analysis indicate the absence of any strong systematic bias. |
4.3. Fitting results of the observed ΔΣ(r) profiles
To derive the set of parameters 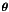 that describes best the data, we performed
a standard χ2 minimization:
that describes best the data, we performed
a standard χ2 minimization:
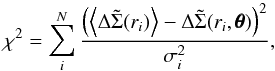 (18)where the sum runs over the N radial bins of
the profile. The model prediction
(18)where the sum runs over the N radial bins of
the profile. The model prediction 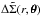 is derived from Eq. (9) using the corresponding analytical
expressions for ΔΣ(r) and Σ(r). The statistical uncertainties σi (Eq. (7)) are propagated on the best-fit parameters
with a Monte Carlo approach: we generated 10 000 new profiles, whose points were randomly
drawn from the normal distributions
is derived from Eq. (9) using the corresponding analytical
expressions for ΔΣ(r) and Σ(r). The statistical uncertainties σi (Eq. (7)) are propagated on the best-fit parameters
with a Monte Carlo approach: we generated 10 000 new profiles, whose points were randomly
drawn from the normal distributions 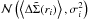 . The new profiles are fitted with the
previous equation, providing at the end an estimate of the probability distribution of the
model’s free parameters. The mode of the (marginalized) distribution gives the value of
the best-fit parameter, and the associated 1σ-confidence interval is given by the range
encompassing 68% of the drawings on each side. The fitting results for the SIS, PLAW, and
NFW mass models are given in Table 2. Figure 3 shows the results obtained for the stack S0, and Fig.
4 gathers the NFW masses and concentrations for the
all the stacks.
. The new profiles are fitted with the
previous equation, providing at the end an estimate of the probability distribution of the
model’s free parameters. The mode of the (marginalized) distribution gives the value of
the best-fit parameter, and the associated 1σ-confidence interval is given by the range
encompassing 68% of the drawings on each side. The fitting results for the SIS, PLAW, and
NFW mass models are given in Table 2. Figure 3 shows the results obtained for the stack S0, and Fig.
4 gathers the NFW masses and concentrations for the
all the stacks.
For every stack, the three mass models provide good fits, with reduced χ2 not exceeding
~2 (except for the
stack L1). For the stack S0, which has the largest difference in the fit quality between
the SIS and NFW models, we obtain a likelihood ratio
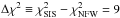 : the SIS model is only disfavored at the
3σ level.
Moreover, the slope of the PLAW model is fairly consistent with that of the SIS model
(i.e., α =
−1), results suggesting that group-scale objects are well described by an
SIS mass distribution in the range probed by our weak-lensing data. As shown by the study
of arc statistics (Oguri 2006; More et al. 2012), strong-lensing galaxy groups are,
indeed, expected to fall in between NFW massive galaxy clusters and SIS single galaxies.
Previous stacked analyses of galaxy clusters resulted in SIS fits rejected with a higher
significance: 11σ level in Okabe
et al. (2010; weak lensing, nine
clusters, Mvir =
9.7 ± 0.8 ×
1014h-1 M⊙),
8σ in Umetsu et al. (2011a; weak+strong lensing, four clusters, Mvir = 15.4 ± 1 ×
1014h-1 M⊙),
4σ in Umetsu et al. (2014; weak lensing + magnification, 20 clusters, M200 = 13.4 ± 1 ×
1014 M⊙). Okabe et al. (2010) found a better agreement between the SIS and NFW
fits when selecting objects with a lower mass, with an SIS fit disfavored at the
6σ level
(10 clusters, Mvir
= 4.8 ± 0.4 ×
1014h-1 M⊙),
a value closer to our findings. Therefore, we can explain the relatively good agreement
between the SIS and NFW fits that we obtain for the SARCS sample by the lower mass scales
it covers.
: the SIS model is only disfavored at the
3σ level.
Moreover, the slope of the PLAW model is fairly consistent with that of the SIS model
(i.e., α =
−1), results suggesting that group-scale objects are well described by an
SIS mass distribution in the range probed by our weak-lensing data. As shown by the study
of arc statistics (Oguri 2006; More et al. 2012), strong-lensing galaxy groups are,
indeed, expected to fall in between NFW massive galaxy clusters and SIS single galaxies.
Previous stacked analyses of galaxy clusters resulted in SIS fits rejected with a higher
significance: 11σ level in Okabe
et al. (2010; weak lensing, nine
clusters, Mvir =
9.7 ± 0.8 ×
1014h-1 M⊙),
8σ in Umetsu et al. (2011a; weak+strong lensing, four clusters, Mvir = 15.4 ± 1 ×
1014h-1 M⊙),
4σ in Umetsu et al. (2014; weak lensing + magnification, 20 clusters, M200 = 13.4 ± 1 ×
1014 M⊙). Okabe et al. (2010) found a better agreement between the SIS and NFW
fits when selecting objects with a lower mass, with an SIS fit disfavored at the
6σ level
(10 clusters, Mvir
= 4.8 ± 0.4 ×
1014h-1 M⊙),
a value closer to our findings. Therefore, we can explain the relatively good agreement
between the SIS and NFW fits that we obtain for the SARCS sample by the lower mass scales
it covers.
 |
Fig. 3 Average density contrast ΔΣ(r) for the stack S0 (Eq. (5)). The lower panel shows the profile obtained using the radial component of the lensed galaxies’ ellipticity, and should be equals to zero. The upper panel is the profile using the tangential component. Overplotted are the best-fit results (right side of Eq. (9)) for the three mass models, SIS (green-solid line), PLAW (dashed-blue line) and NFW (orange-shaded area, encompassing the combined 1σ uncertainty on M200 and c200). |
Even though we are not using an aperture scaling with mass or redshift to estimate the richnesses and luminosities, we observe the usual optical scaling relations: the mass parameters (σv, Σ0, and M200) increase for higher richnesses (N stacks) and luminosities (L stacks). As expected, the V stacks give the wider range in M200: although very noisy, the individual velocity dispersions derived in Paper I provide the best way to stack objects with a similar total mass. The sample covers one order of magnitude in mass, from M200 = 0.21 ± 0.07 × 1014 M⊙ for the stack V1 to M200 = 2.38 ± 0.5 × 1014 M⊙ for the stack V3. On the other hand, the arc radius appears to be a poor tracer of the total mass, with mass parameters roughly constant for the three R stacks. This result is expected because strong-lensing features are only related to the central part of the lens, whose projected mass density does not necessarily scale with the total mass of the dark matter halo (see Sect. 5.2, and Verdugo et al. 2014).
Results of the combined fit weak+strong lensing, with or without a central point mass.
4.4. Combining weak and strong lensing
To check the robustness of our results, in particular the determination of the NFW
concentrations, we combined our weak-lensing measurements with the strong-lensing models
obtained for eleven SARCS galaxy groups (see Limousin et
al. 2009; Verdugo et al. 2011, 2014). These strong-lensing constraints were stacked
as follows: using Lenstool, we constructed mass maps for each of the eleven objects (SA22,
SA39, SA50, SA63, SA66, SA72, SA80, SA83, SA112, SA123, and SA127) and we calculated the
mass inside their respective Einstein radius. Then we combined these masses to obtain a
mean mass of 7.89 ×
1012 M⊙. To be consistent with
the weak-lensing analysis we set up zl = 0.5 and zs = 1.5, and we
computed the corresponding Einstein radius for this mean mass,
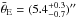 . The errors were estimated assuming that
the main source of uncertainty comes from the lack of a precise measurement on the source
redshift, i.e. zs =
1.5 ± 0.5 (this value is probably overestimated).
. The errors were estimated assuming that
the main source of uncertainty comes from the lack of a precise measurement on the source
redshift, i.e. zs =
1.5 ± 0.5 (this value is probably overestimated).
To perform the combined weak+strong lensing fit, we simply added in the χ2 a constraint
on this average Einstein radius 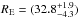 kpc, whose value is determined for the
analytical mass models by solving numerically g(RE) = 1. For the
weak-lensing constraints, we used the average profile for the stack S0, since the groups
with a strong-lensing model do not fall in one single of the bins defined in Table 1. Because the strong-lensing signal allows us to reach
a smaller radius, we checked the effect of including an extra central mass component (a
point mass as described in Sect. 4.2). The results of the combined fit are given in Table
3.
kpc, whose value is determined for the
analytical mass models by solving numerically g(RE) = 1. For the
weak-lensing constraints, we used the average profile for the stack S0, since the groups
with a strong-lensing model do not fall in one single of the bins defined in Table 1. Because the strong-lensing signal allows us to reach
a smaller radius, we checked the effect of including an extra central mass component (a
point mass as described in Sect. 4.2). The results of the combined fit are given in Table
3.
First of all, adding a point mass does not change the best-fit parameters with the weak lensing alone (third row compared with the first row). As shown in Sect. 4.2, we are not sensitive to the mass distribution within the inner regions of the groups, that is, for r< 50 kpc. The average shear profile only allows us to put an upper limit on the point mass, with values that are similar for the three mass models. Therefore, our approximation to exclude this mass component is valid.
For the weak+strong lensing fit and without a point mass (second row), we obtained a significant change in the results for the PLAW and NFW models. Because the SIS mass model does not have a freedom on the shape of its profile, the fit is dominated by the weak-lensing constraints. Adding a single strong-lensing constraint does not lead to a significant change in the SIS velocity dispersion (agreement within the errors). On the other hand, the PLAW and NFW models are more sensitive to the value of the Einstein radius, which results in a more concentrated mass distribution (larger c200 and steeper slope α). As expected, adding the strong lensing-signal does not change the total mass M200 significantly. Interestingly, the combined weak+strong lensing presents a high likelihood ratio when compared with the weak-lensing only fit, with Δχ2 = 8.5 for the NFW model, and Δχ2 = 13 for the PLAW model: a single mass component no longer provides a good description of the total mass profile when the strong-lensing constraints are taken into account (especially for the PLAW model with a reduced χ2/ d.o.f. ~ 3).
If we add the central mass component in the model (forth row of Table 3), the quality of the fits is improved. As expected, the SIS velocity dispersion remains the same. For the PLAW and NFW models, we obtained best-fit parameters that are fully compatible (within their 1σ error bars) with the values derived from the weak-lensing-only constraints: the two lensing regimes give consistent constraints on the total mass profile, providing the consideration of a supplementary mass component to the group-scale dark matter halo. While with the weak lensing alone we were unable to constrain the value of this central mass, we were able to estimate it with the combined fit. Depending on the model chosen to describe the group-scale halo, we obtained a mass M0 = (1.5−3.5) × 1012 M⊙. The constraints on the point mass are rather loose, and adding this component to the fit also increases the error bars on the other best-fit parameters. This result is expected because of the expected degeneracies between M0 and the models’ free parameters, that is, increasing the central mass will require a less concentrated/steep profile for the group-scale halo. To quantify them, we estimated the Pearson correlation factor over the Monte Carlo drawings used in our fitting procedure. We obtained r = 0.68 for α − M0 and r = −0.76 for c200 − M0. The mass M200 is mainly constrained by the weak lensing at large radii, and so has a very small correlation factor r = −0.02 with M0.
The interpretation of the point mass value is rather difficult because it most likely results from the combination of different contributions: the baryonic mass of the central galaxy, its dark matter halo, the intra-group gas, or possible adiabatic contractions modifying the central shape of the group-scale dark matter halo. Given the upper limit on this central component, we derive a ratio M200/M0> 17. Okabe et al. (2013) estimated a ratio M200/M0> 34 from the stacked weak-lensing analysis of 30 clusters with ⟨ M200 ⟩ ~ 6 × 1014 M⊙. With their upper limit on M0, Umetsu et al. (2014) found M200/M0> 30 from the stacked analysis of 20 clusters with ⟨ M200 ⟩ ~ 13 × 1014 M⊙. Our result on the SARCS galaxy groups is similar to those obtained for more massive galaxy clusters, which seems to indicate moderate variations of this ratio over the mass range of galaxy groups and clusters. Han et al. (2014) studied the stellar mass M⋆ associated with the central galaxy of group-scale haloes in detail: for a halo mass Mh ~ 1014 M⊙, the central stellar mass is expected to be ~5 × 1011 M⊙, which translates into a ratio Mh/M⋆ ~ 200 (see also Leauthaud et al. 2012, with expected ratios of 100−1000 for halo masses 1013−1015 M⊙). The ratio M200/M0 we derived is one order of magnitude lower, which suggests that the value of the central mass component added to the total mass NFW profile cannot be only due to the stars within the central galaxy. A possible explanation might be a different central slope of the total NFW mass distribution. With a shallower density profile, or equivalently, a core of almost constant density, the contribution of the dark matter halo would be larger in the inner part of the groups, thus requiring a less massive central point mass. The present lack of constraints to probe the central mass distribution of the composite SARCS lenses does not allow us to test this hypothesis by using, for instance, a generalized or cored NFW profile. Studying the inner slope of the galaxy groups’ mass profile is beyond the scope of this paper, and we refer to the work presented in Sand et al. (2002, 2004), where strong evidences of a shallower central dark matter profile are found for galaxy clusters.
5. Mass-concentration relation of strong lenses
5.1. Concentrations of the SARCS galaxy groups
 |
Fig. 4 Best-fit parameters of the NFW mass model for the stacks in richness N (red triangles), luminosity L (orange disks), SIS velocity dispersion σv (blue squares), and arc radius RA (purple stars). The large black rectangle shows the ⟨M200⟩ ± 1σ and ⟨c200⟩ ± 1σ obtained using the 80 groups (stack S0). The green-hatched area delimits the 1σ uncertainty around the mass-concentration relation derived with Lenstool, using a M200(σv) scaling. |
The results of the NFW model fitting are given Fig. 4, with similar concentrations for every stack. Using the 80 groups, we obtain a
concentration 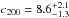 for a mass
for a mass
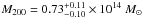 . Compared with the predictions from the
numerical simulations of Duffy et al. (2008), a
halo with the same redshift and mass as the stack S0 should present a concentration of
3.5, that is, we obtain an overconcentrated halo at the ~3σ level. Except for the
stacks in arc radius (see below), increasing the stacking criterion gives a larger mass
and a slightly lower concentration, hints of the expected c(M)
mass-concentration relation, which predicts less concentrated haloes of larger masses. We
further tested this c(M) relation with Lenstool, which
uses a different approach that does not involve a stacking analysis.
. Compared with the predictions from the
numerical simulations of Duffy et al. (2008), a
halo with the same redshift and mass as the stack S0 should present a concentration of
3.5, that is, we obtain an overconcentrated halo at the ~3σ level. Except for the
stacks in arc radius (see below), increasing the stacking criterion gives a larger mass
and a slightly lower concentration, hints of the expected c(M)
mass-concentration relation, which predicts less concentrated haloes of larger masses. We
further tested this c(M) relation with Lenstool, which
uses a different approach that does not involve a stacking analysis.
Lenstool ellipticity is defined as
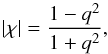 (19)where q =
b/a is the minor-to-major axis ratio.
The ellipticity is expressed in a coordinate system in which χ1 is positive
along the E-W axis, and χ2 is positive along the SE-NW diagonal.
The conversion from the im2shape ellipticity e = (a − b) / (a
+ b) is χ = 2e/ (1 +
e2).
(19)where q =
b/a is the minor-to-major axis ratio.
The ellipticity is expressed in a coordinate system in which χ1 is positive
along the E-W axis, and χ2 is positive along the SE-NW diagonal.
The conversion from the im2shape ellipticity e = (a − b) / (a
+ b) is χ = 2e/ (1 +
e2).
In contrast to the stacking analysis described above, Lenstool estimates a scaling
relation between an observable and the NFW mass M200 (e.g., Eq. (16)) in combination with the parameters of the
c(M) relation. The latter follows
the form of Eq. (17), with a scaling in
redshift fixed at (1 +
z)-0.45 (Duffy et al. 2008). Both relations are directly constrained from the measured
ellipticities of the background galaxies (for the full sample of 80 lenses), assuming that
the groups are modeled with 2D NFW potentials. For M weak-lensing sources in our catalog,
we define the likelihood as the product of M Gaussian likelihoods:
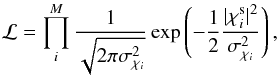 (20)where
(20)where  is the module of the predicted source
ellipticity obtained by multiplying the amplification matrix
is the module of the predicted source
ellipticity obtained by multiplying the amplification matrix
 with the second brightness moments of each image
with the second brightness moments of each image 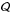 ,
through the equation
,
through the equation 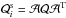 (Bartelmann
& Schneider 2001). In this formalism, the major and minor axes of a galaxy
correspond to the eigenvalues of its
(Bartelmann
& Schneider 2001). In this formalism, the major and minor axes of a galaxy
correspond to the eigenvalues of its 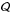 matrix. Although it is not really needed for this work, this matrix transformation is
valid in both the weak and the strong lensing regime. In this work, we assumed
matrix. Although it is not really needed for this work, this matrix transformation is
valid in both the weak and the strong lensing regime. In this work, we assumed
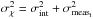 , that is, the variance is the quadratic
sum of the intrinsic ellipticity and the shape measurement errors for each galaxy.
, that is, the variance is the quadratic
sum of the intrinsic ellipticity and the shape measurement errors for each galaxy.
With Lenstool, we can directly derive a c(M) relation associated with a mass-observable scaling, and we tested this approach using either the optical richnesses or the SIS velocity dispersions; results are summarized in Table 4. In both cases, we observe an anticorrelation between M200 and c200. The c(M) relation derived with the scaling M200 − σv has a (logarithmic) slope B = 0.07 in fairly good agreement with predictions from numerical simulations, for example, B = 0.084 for the full sample of Duffy et al. (2008). However, its normalization is much higher, and we obtain a very good match with the results from the stacking analysis (green-hatched area in Fig. 4). The scaling mass-richness leads to a c(M) relation much steeper with B = 0.77, which is a result of a scaling shallower than expected, with A = 0.52 instead of ~1 (we have shown in Paper I that the high intrinsic dispersion of the groups leads to a reduced slope of the σv − N scaling). Interestingly, for the M200 − σv scaling, we obtain a lower limit on the slope A − 1σ = 3.11 in good agreement with its expected value A = 3 (e.g., Evrard et al. 2008; Saro et al. 2013): the velocity dispersions derived in Paper I provide a tracer of the groups’ mass that is less scattered than the optical observables. On the other hand, the scaling M200 − N also leads to a c(M) normalization that perfectly matches the average c200 derived from the stacked analysis: regardless of how the groups are combined or analyzed, the SARCS sample of strong lenses exhibits consistent concentrations that are higher than those measured in numerical simulations. A more precise analysis of the results derived with Lenstool via a combined fit of a scaling law and the c(M) relation will be presented in a forthcoming dedicated paper.
While an increase in richnesses, luminosities, and SIS velocity dispersions translates into larger masses and slightly lower concentrations, we observe a different behavior for the stacks in arc radius. The stacks R1 and R2 present no significant change in the mass parameters M200 and σv, but an increase in the concentration c200, as well as a slightly steeper slope for the PLAW model. The stack R3 corresponds to a more massive composite lens with an increased M200, but with a larger c200. This correlation between the arc radius and the concentration might seem surprising given the c(M) relation, and given that one would expect a correlation between the central projected mass (responsible for the size of the arc radius) and the total mass of a halo. Our results, which are consistent with the findings of Oguri et al. (2012), suggest that the strong-lensing efficiency is mainly driven by the concentration of the haloes and not by their total mass. The scaling M200 − RA appears to be weaker than the correlation c200 − RA, enough so to outbalance the c(M) relation. This correlation gives us a hint of the so-called strong-lensing bias: by combining lenses with a larger size of their gravitational arc (roughly equivalent to the Einstein radius), we introduce a selection bias resulting in a population with more concentrated projected mass distributions. Finally, we can explain the lower value of the R1 concentration by a larger contribution of the central galaxy relative to the group-scale halo. For small arc radii, the mass of the central galaxy contributes enough to the lensing efficiency, and the projected mass distribution of the dark matter halo does not need to be very concentrated. Therefore, the concentration of groups with small arc radius derived by weak lensing is less biased toward high values.
Lenstool constraints on the intermediate mass-observable scaling relation M200 = M0(X/X0)A, and the corresponding mass-concentration relation c200 = c0(M200/M0)− B(1 + z)-0.45.
5.2. Evidence of a strong-lensing bias
The NFW fit of the different stacks led to galaxy groups that were apparently overconcentrated compared with the expectations from numerical simulations for unbiased populations of dark matter haloes. Because the SARCS galaxy groups were selected for their strong-lensing signal, it is tempting to explain these high concentrations by a selection effect, which would mean that strong lenses are a somehow biased population of haloes. To further test this strong-lensing bias, we combined our stacked galaxy groups with more massive strong lenses to fit the corresponding c(M) relation. We used the 25 galaxy clusters binned in three stacks according to their virial mass from Oguri et al. (2012), and the stack of four massive galaxy clusters analyzed by Umetsu et al. (2011a). These two studies made use of a strong+weak lensing analysis to derive NFW masses and concentrations, which, after conversion in our definition, leads to a range of nearly two decades in mass. The stacked clusters from Umetsu et al. (2011a) have an average redshift z = 0.32, and the stacks from Oguri et al. (2012) have a redshift z = 0.46−0.48; these values are similar to our average redshift z = 0.55 for the full sample.
Assuming a log-normal distribution for the NFW concentration parameter (Jing 2000), we fitted a c(M)
relation expressed in logarithmic space:
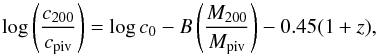 (21)where the pivots cpiv = 5 and
Mpiv =
1014 M⊙ were chosen to be
representative of the average mass and concentration of the combined samples, thus
reducing the correlation in the best-fit normalization c0 and slope
B. We
accounted for the slight differences in the average lens redshifts by rescaling them with
a redshift evolution (1 +
z)-0.45 (Duffy et al. 2008). To include in the fit error measurements on M200 and
c200, and to allow for an intrinsic
dispersion of the points around the best-fit relation, we used the BCES orthogonal
estimator (Akritas & Bershady 1996) in the same
way as described in Foëx et al. (2012).
(21)where the pivots cpiv = 5 and
Mpiv =
1014 M⊙ were chosen to be
representative of the average mass and concentration of the combined samples, thus
reducing the correlation in the best-fit normalization c0 and slope
B. We
accounted for the slight differences in the average lens redshifts by rescaling them with
a redshift evolution (1 +
z)-0.45 (Duffy et al. 2008). To include in the fit error measurements on M200 and
c200, and to allow for an intrinsic
dispersion of the points around the best-fit relation, we used the BCES orthogonal
estimator (Akritas & Bershady 1996) in the same
way as described in Foëx et al. (2012).
Because the V stacks (i.e., according to the SIS velocity dispersions) give the broader range in mass, we combined the corresponding masses and concentrations with those from Oguri et al. (2012) and Umetsu et al. (2011a). The results of the BCES fit are the following: a slope B = 0.30 ± 0.09, a normalization c0 = 1.63 ± 0.25, and an intrinsic dispersion σlog c200 = 0.11. Figure 5 presents this best fit: the different samples of stacked strong lenses are well constrained by a single c(M) relation over nearly two decades in mass. It has a slope much steeper than that obtained by Duffy et al. (2008), and a normalization such that concentrations are higher over the mass range 1013−1015 M⊙, by up to a factor ~3 at the low-mass end.
 |
Fig. 5 Combined fit of the mass-concentration relation, using the results from the stacks in velocity dispersion (open-blue squares, weak-lensing alone) and the values derived by Oguri et al. (2012; red triangles) and Umetsu et al. (2011a; open-green triangle) from the stacked analysis of strong-lensing galaxy clusters. The best-fit relation was obtained assuming a scaling in redshift of (1 + z)-0.45, and the black solid line show the results for z = 0.5 (the gray-shaded area delimits the statistical uncertainty from the best-fit parameters). Overplotted are the relations derived from numerical simulations by Duffy et al. (2008; black-dashed line, all haloes, z = 0.5) and Meneghetti et al. (2014; orange-solid line, strong-lensing selected haloes, z = 0.5). The magenta-dashed lines show the 1σ limit around the average relation derived by Oguri et al. (2012) from semi-analytical predictions (lensing bias using weights from the arc cross section+Einstein radii, z = 0.45). |
These results confirm the presence of a bias in the population of strong-lensing haloes. To explain why we obtain such discrepant concentrations compared with those from numerical simulations, we recall the differences in the way concentrations are estimated. From the simulation point of view, haloes are (usually) treated as spherical objects: the intrinsic shape is not accounted for, and the density contrasts are estimated by averaging within spheres, as for estimating masses and thus concentrations. In the case of our lensing analysis (and for the analyses of Oguri et al. 2012; and Umetsu et al. 2011a), we also assumed spherical symmetry. However, the shear signal only probes the projected mass distribution. In other words, depending on its orientation with respect to the line of sight, a triaxial halo can have very different projected mass distributions, therefore a different lensing signal. Intuitively, a prolate halo (cigar-shaped) with a major axis close to the line of sight will present an overconcentrated projected mass profile, leading to a higher lensing concentration compared with the value that would be obtained by analyzing it in three dimensions and assuming spherical symmetry. It is, therefore, tempting to attribute the high concentrations of strong lenses to an orientation bias of triaxial haloes, and not to intrinsically overconcentrated objects.
Several studies have explored this strong-lensing bias by extracting from numerical simulations only haloes with a large enough strong-lensing cross-section. The analysis of such peculiar populations of haloes have led to c(M) relations that exhibit a higher normalization and a steeper slope. In Fig. 5 we show, for instance, the recent work by Meneghetti et al. (2014), who simulated haloes that mimic the CLASH sample of strong-lensing galaxy clusters. By estimating the concentration of these haloes with their projected mass distribution, thus following what would be obtained from a lensing analysis, they derived a c(M) relation in very good agreement with our results (slope of −0.21). Oguri et al. (2012) estimated the apparent concentrations of strong-lensing galaxy clusters using a semi-analytic approach (magenta lines in Fig. 5), and they found a similar behavior: a strong-lensing bias resulting in larger concentrations. Their calculations fit the high-mass end of our c(M) relation very well, with a similar slope, that is, a stronger increase of the concentrations for the lower mass systems.
Because the strong-lensing efficiency is related to the projected mass distribution of a halo, an intrinsically very massive object will most likely produce a strong-lensing signal regardless of its shape and orientation. In the case of small galaxy groups, a large enough projected mass distribution can only be obtained for very elliptical haloes with a major axis close to the line of sight. Therefore, it is natural that a selection of haloes via strong lensing will result in a population more biased at lower mass scales. This mass-dependent selection bias translates into the observed c(M) relation for strong lenses, with slopes much steeper than those obtained considering unbiased populations of haloes. The study by Giocoli et al. (2014), who used simulated clusters, highlight this effect. They selected samples of haloes according to their Einstein radius and obtained steeper slopes for increasing θE (see their Table 2 and Fig. 14), from 0.21 for haloes with θE> 5′′ to 0.34 for haloes with θE> 20′′: the larger the Einstein radius, the larger the central projected mass, which can only be achieved for low-mass systems by a larger elongation, thus resulting in much higher apparent concentrations.
Although apparent too large concentrations can be explained by a combination of projection effects and an orientation bias, one cannot simply rule out the possibility that strong lenses are intrinsically a biased population of objects: intrinsically more concentrated (in three dimensions) and/or intrinsically more elongated haloes. Hennawi et al. (2007) have studied the properties of haloes with a large strong-lensing cross-section (see also Meneghetti et al. 2010a). They found that such haloes present a distribution of axis ratio that is very similar to that of normal haloes and that the largest source of bias in the strong-lensing selection is an orientation bias. Oguri & Blandford (2009) found, however, that in the case of a very large Einstein radius, an additional bias in the shape of the haloes is required, with larger elongations to increase the lensing efficiency. Hennawi et al. (2007) found apparent concentrations (derived from the projected mass distribution) that are 34% higher for the strong lenses, a result of the orientation bias+projection effects, mixed with intrinsically more concentrated haloes (in three dimensions). However, the latter effect was found to be responsible for an increase in the apparent concentrations of only 18%.
Finally, there is another possible bias in the population of strong lenses. The c(M) relation obtained by Prada et al. (2012) highlighted an alternative to explain high concentrations: a very rapid accretion of matter resulting in haloes with a more compact configuration. Moreover, mergers are known to increase the strong-lensing cross-section (Zitrin et al. 2012; Redlich et al. 2012). Therefore, a population of strong lenses is likely to be biased toward both elongated haloes along the line of sight and compact configurations due to recent mergers. However, at the group-scale, it is less likely that the haloes accreted large portions of their mass more recently than more massive galaxy clusters. With our observational results, it is impossible to distinguish the different possible sources of concentration enhancement, although we have shown in Paper I that a non-negligible fraction of the systems present a complex light morphology, a possible sign of merging events. In the next section, we provide a simple way to derive a lower limit on the minor-to-major axis ratio required to match the observed with the predicted concentrations. The value we derived for the SARCS sample is not unrealistic, thus we cannot conclude on the necessity of an additional bias to simple projection effects.
5.3. Toy model
To reconcile the observed concentration of the SARCS sample with the predicted value from
numerical simulations, we considered the effect of the halo triaxiality on the observed
lensing signal. The mass density of a triaxial NFW halo ρ(R) is
given by Eq. (12), with a radius
R expressed
as (Jing & Suto 2002)
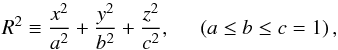 (22)where the coordinates x, y and z lie along the principal
axes of the halo. a, b and c are the semi-minor, semi-intermediate, and
semi-major axes, respectively, of the iso-density ellipsoid defined by R = 1. In the simplest case
of a halo whose semi-major axis is oriented along the line of sight, one can show (Oguri et al. 2003) that the convergence has the usual
NFW functional form κ(ζ), with the projected radius
(22)where the coordinates x, y and z lie along the principal
axes of the halo. a, b and c are the semi-minor, semi-intermediate, and
semi-major axes, respectively, of the iso-density ellipsoid defined by R = 1. In the simplest case
of a halo whose semi-major axis is oriented along the line of sight, one can show (Oguri et al. 2003) that the convergence has the usual
NFW functional form κ(ζ), with the projected radius
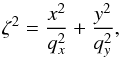 (23)whose expressions for qx and qy are given in Oguri et al. (2003). We can further simplify the
problem by considering a prolate halo, that is, a = b< 1, a valid
simplification when considering stacks of haloes whose projected ellipticity is averaged.
In doing so, we have qx =
qy =
a/c, leading to a density contrast
ΔΣ that is the same as that
of a spherical NFW halo (i.e., with spherical iso-densities) after a simple rescaling of
the concentric distance r →
ζ = r/a.
(23)whose expressions for qx and qy are given in Oguri et al. (2003). We can further simplify the
problem by considering a prolate halo, that is, a = b< 1, a valid
simplification when considering stacks of haloes whose projected ellipticity is averaged.
In doing so, we have qx =
qy =
a/c, leading to a density contrast
ΔΣ that is the same as that
of a spherical NFW halo (i.e., with spherical iso-densities) after a simple rescaling of
the concentric distance r →
ζ = r/a.
The NFW profile ΔΣ(r) is a function of the ratio r/rs, and its
normalization is proportional to (rsρ0).
Therefore, we can apply the rescaling 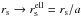 and
and
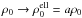 , so that the lensing signal produced by a
prolate NFW halo with
, so that the lensing signal produced by a
prolate NFW halo with 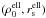 will be exactly the same as the signal of
a spherical halo with (ρ0,rs). To
mimic the results derived from simulations, we can numerically integrate the density
profile ρ(R) of this prolate NFW halo
will be exactly the same as the signal of
a spherical halo with (ρ0,rs). To
mimic the results derived from simulations, we can numerically integrate the density
profile ρ(R) of this prolate NFW halo
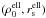 in spheres to find the spherical radius
R200,
s3D that defines the spherical mass
in spheres to find the spherical radius
R200,
s3D that defines the spherical mass
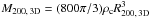 for a given critical density
ρc; the corresponding
spherical concentration is given by
for a given critical density
ρc; the corresponding
spherical concentration is given by 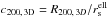 .
.
This toy model provides a simple way to convert the lensing masses and concentrations (i.e., derived from the shear signal using a spherical NFW halo) of a prolate halo into its “spherical” values as they would be derived in numerical simulations (i.e., measuring masses in spheres instead of in iso-density ellipsoids). Figure 6 presents the results of this toy model: as expected, the larger the elongation of the halo, the lower the concentration and mass have to be to produce the same lensing signal. For the stack S0, we see that a couple (M200, 3D,c200, 3D) in agreement with the prediction from Duffy et al. (2008) would have been obtained from the lensing analysis by using a prolate NFW halo with an axis ratio a/c ~ 0.5, a value similar to the median elongation of dark matter haloes in numerical simulations (e.g., Hennawi et al. 2007; Giocoli et al. 2014). Because we considered here the case of a prolate halo perfectly aligned with the line of sight, our estimated axis ratio can only be interpreted as a lower limit: introducing an angle would reduce the lensing efficiency, which would require a higher ratio a/c to produce the same shear profile (i.e., a mass distribution less stretched along the line of sight).
If we assume that the signal we measured for the stack S0 is, indeed, produced by a prolate halo in agreement with the relation of Duffy et al. (2008), we can use Fig. 6 to estimate the bias in our lensing measurements because of the hypothesis of spherical symmetry. With a ΔM200 ~ 0.15 × 1014 M⊙ and a Δc200 ~ 4.5 (shifts between the pink and black stars), we obtain a mass overestimated by ~25%, and a factor ~2 for the concentration. These values agree well with the results derived from the weak-lensing analysis of simulated catalogs, with typical biases in mass of ~30−40%, and up to a factor 2 for the concentration in the case of highly prolate lenses (e.g., Corless & King 2007, 2008; Feroz & Hobson 2012).
 |
Fig. 6 Values of the spherical mass and concentration of a prolate NFW halo producing the same signal as that of a spherical NFW halo characterized by the S0 best-fit parameters. The different stars show the required (M200, 3D,c200, 3D) as a function of the minor-to-major axis ratio a/c (starting from a/c = 1 in the top-right corner, and decreasing by 0.1). We consider here the case of a prolate halo (a = b<c) with a major axis aligned with the line of sight. The gray-shaded area and black curve indicate the relation of Duffy et al. 2008 (all haloes, z = 0.5). |
6. Conclusions
We presented the results derived from the stacked weak-lensing analysis of a sample
containing 80 strong-lensing galaxy groups. While in our first study (Paper I) the shear
signal for the individual lenses was too noisy to derive reliable information on their mass
distribution, we were here able to constrain the mass profiles of composite lenses. The
stacked profiles were fitted by three mass models, the singular isothermal sphere, a
power-law mass distribution, and the classical NFW model. When combining the 80 lenses, we
derived an average SIS velocity dispersion 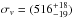 km s-1. The best PLAW model is
characterized by a normalization
km s-1. The best PLAW model is
characterized by a normalization 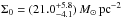 and a slope
and a slope
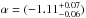 , a value close to that of an isothermal mass
distribution. For the NFW profile, we found
, a value close to that of an isothermal mass
distribution. For the NFW profile, we found 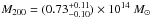 and
and 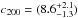 , a concentration in strong disagreement with
predictions from numerical simulations: it is higher at the 3σ level compared with the
prediction by Duffy et al. (2008). The best-fit PLAW
was not only found to be consistent with the SIS model, but with a likelihood ratio
, a concentration in strong disagreement with
predictions from numerical simulations: it is higher at the 3σ level compared with the
prediction by Duffy et al. (2008). The best-fit PLAW
was not only found to be consistent with the SIS model, but with a likelihood ratio
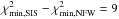 , we also concluded that for group-scale
haloes the isothermal mass distribution still provides a fairly good description of the
total mass, compared with galaxy clusters presenting higher rejection levels of the SIS
model.
, we also concluded that for group-scale
haloes the isothermal mass distribution still provides a fairly good description of the
total mass, compared with galaxy clusters presenting higher rejection levels of the SIS
model.
To check the reliability of our results derived from weak-lensing alone, in particular the NFW concentration parameter, we combined the stacked shear profiles with an average Einstein radius, derived from eleven strong-lensing models constructed in previous papers. When introducing a central mass component in the total mass distribution (modeled by a simple point mass), we obtained results that are fully consistent with those from the weak-lensing-only fitting. We derived an upper limit of the central mass M0 leading to a ratio M200/M0> 17, a value similar to those obtained for galaxy clusters. The comparison with the expected ratios between total mass and stellar mass within the central galaxy suggested the presence of another component or a modification of the classical NFW profile, for instance a core radius of constant density or a shallower inner slope of the density profile.
When stacking the groups according to their richness, luminosity, or SIS velocity dispersion, we obtained larger masses and lower concentrations when increasing the selection threshold, which indicates the expected mass-concentration relation. The opposite correlation was observed for the stacks in arc radius, with nearly no change in mass but a significant increase in c200 for larger RA. We explained this behavior by a selection bias that outbalances the mass-concentration relation, that is, higher strong-lensing efficiencies produced by more concentrated projected mass distributions rather than more massive haloes. The results of the stacked analysis were compared to those derived from a different approach, based on the code Lenstool. Instead of binning the lenses, Lenstool makes use of each galaxy group to constrain a scaling law to convert an observable into the NFW mass M200 together with the mass-concentration relation. Using either the richness or the individual σv, we derived a c(M) relation whose normalization is fully consistent with the concentrations obtained from the stacked analysis. The slope of the M200 − σv scaling derived by Lenstool was found to agree well with theoretical expectations, while the scaling M200 − N is shallower than expected and lead to a too steep c(M) relation.
We combined our results with those derived from stacked analyses of strong-lensing galaxy clusters, and constrained the specific c(M) relation of strong lenses over two decades in mass. We confirmed the existence of a strong-lensing bias: a c(M) relation with a steeper slope and that predicts higher concentrations than found for unbiased populations of haloes. This mass-dependent enhancement of the concentrations has also been observed in numerical simulations, extracting haloes with large strong-lensing cross-sections, and estimating concentrations from the projected mass distribution. Our c(M) relation, extended to group-scale haloes, perfectly matches these predictions derived for galaxy clusters. Finally, we presented a toy model to derive a lower limit on the elongation of a prolate NFW halo in the case of perfect alignment of the major axis and the line of sight. We have shown that our average (M200,c200) derived for a spherical NFW halo can be reconciled with the predictions of Duffy et al. (2008) assuming a prolate halo with a minor-to-major axis ratio a/c ~ 0.5. Because this elongation is a realistic value, as observed in numerical simulations, we concluded that simple projection effects are sufficient to explain the apparently overconcentrated mass distributions of strong lenses.
Acknowledgments
G.F. acknowledges support from FONDECYT through grant 3120160. V.M. acknowledges support from FONDECYT through grant 112074. T.V. acknowledges support from CONACYT through grant 165365 and 203489 through the program Estancias posdoctorales y sabáticas al extranjero para la consolidación de grupos de investigación. G.F, V.M., E.J., and M.L. acknowledge support from ECOS-CONICYT through grant C12U02. The authors thank M. Oguri for providing the results of the semi-analytic model used to derive the mass-concentration relation of strong lenses. Based on observations obtained with MegaPrime/MegaCam, a joint project of CFHT and CEA/DAPNIA, at the Canada-France-Hawaii Telescope (CFHT) which is operated by the National Research Council (NRC) of Canada, the Institut National des Science de l’Univers of the Centre National de la Recherche Scientifique (CNRS) of France, and the University of Hawaii. This work is based in part on data products produced at TERAPIX and the Canadian Astronomy Data Centre as part of the Canada-France-Hawaii Telescope Legacy Survey, a collaborative project of NRC and CNRS.
References
- Akritas, M. G., & Bershady, M. A. 1996, ApJ, 470, 706 [NASA ADS] [CrossRef] [Google Scholar]
- Alard, C. 2006 [arXiv:astro-ph/0606757] [Google Scholar]
- Bartelmann, M. 1996, A&A, 313, 697 [NASA ADS] [Google Scholar]
- Bartelmann, M., & Schneider, P. 2001, Phys. Rep., 340, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Bartelmann, M., Limousin, M., Meneghetti, M., & Schmidt, R. 2013, Space Sci. Rev., 177, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Binney, J., & Tremaine, S. 1987, Galactic dynamics (Princeton University Press) [Google Scholar]
- Bradač, M., Allen, S. W., Treu, T., et al. 2008, ApJ, 687, 959 [NASA ADS] [CrossRef] [Google Scholar]
- Broadhurst, T. J., & Barkana, R. 2008, MNRAS, 390, 1647 [NASA ADS] [Google Scholar]
- Broadhurst, T., Benítez, N., Coe, D., et al. 2005, ApJ, 621, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Broadhurst, T., Umetsu, K., Medezinski, E., Oguri, M., & Rephaeli, Y. 2008, ApJ, 685, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Bryan, G. L., & Norman, M. L. 1998, ApJ, 495, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Bullock, J. S., Kolatt, T. S., Sigad, Y., et al. 2001, MNRAS, 321, 559 [Google Scholar]
- Buote, D. A., Gastaldello, F., Humphrey, P. J., et al. 2007, ApJ, 664, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Cabanac, R. A., Alard, C., Dantel-Fort, M., et al. 2007, A&A, 461, 813 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Comerford, J. M., & Natarajan, P. 2007, MNRAS, 379, 190 [NASA ADS] [CrossRef] [Google Scholar]
- Corless, V. L., & King, L. J. 2007, MNRAS, 380, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Corless, V. L., & King, L. J. 2008, MNRAS, 390, 997 [NASA ADS] [CrossRef] [Google Scholar]
- Corless, V. L., King, L. J., & Clowe, D. 2009, MNRAS, 393, 1235 [NASA ADS] [CrossRef] [Google Scholar]
- Coupon, J., Ilbert, O., Kilbinger, M., et al. 2009, A&A, 500, 981 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Covone, G., Sereno, M., Kilbinger, M., & Cardone, V. F. 2014, ApJ, 784, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Dahle, H., Sarazin, C. L., Lopez, L. A., et al. 2013, ApJ, 772, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Dawson, W. A., Wittman, D., Jee, M. J., et al. 2012, ApJ, 747, L42 [NASA ADS] [CrossRef] [Google Scholar]
- Dietrich, J. P., Böhnert, A., Lombardi, M., Hilbert, S., & Hartlap, J. 2012, MNRAS, 419, 3547 [NASA ADS] [CrossRef] [Google Scholar]
- Dolag, K., Bartelmann, M., Perrotta, F., et al. 2004, A&A, 416, 853 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duffy, A. R., Schaye, J., Kay, S. T., & Dal la Vecchia, C. 2008, MNRAS, 390, L64 [NASA ADS] [CrossRef] [Google Scholar]
- Dutton, A. A., & Macciò, A. V. 2014, MNRAS, 441, 3359 [NASA ADS] [CrossRef] [Google Scholar]
- Eke, V. R., Navarro, J. F., & Steinmetz, M. 2001, ApJ, 554, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Ettori, S., Gastaldello, F., Leccardi, A., et al. 2010, A&A, 524, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ettori, S., Gastaldello, F., Leccardi, A., et al. 2011, A&A, 526, C1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Evrard, A. E., Bialek, J., Busha, M., et al. 2008, ApJ, 672, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Fedeli, C. 2012, MNRAS, 424, 1244 [NASA ADS] [CrossRef] [Google Scholar]
- Fernández-Trincado, J. G., Forero-Romero, J. E., Foex, G., Verdugo, T., & Motta, V. 2014, ApJ, 787, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Feroz, F., & Hobson, M. P. 2012, MNRAS, 420, 596 [NASA ADS] [CrossRef] [Google Scholar]
- Foëx, G., Soucail, G., Pointecouteau, E., et al. 2012, A&A, 546, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Foëx, G., Motta, V., Limousin, M., et al. 2013, A&A, 559, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gao, L., Navarro, J. F., Cole, S., et al. 2008, MNRAS, 387, 536 [NASA ADS] [CrossRef] [Google Scholar]
- Gastaldello, F., Buote, D. A., Humphrey, P. J., et al. 2007, ApJ, 669, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Gastaldello, F., Limousin, M., Foëx, G., et al. 2014, MNRAS, 442, L76 [NASA ADS] [CrossRef] [Google Scholar]
- George, M. R., Leauthaud, A., Bundy, K., et al. 2012, ApJ, 757, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Giocoli, C., Meneghetti, M., Metcalf, R. B., Ettori, S., & Moscardini, L. 2014, MNRAS, 440, 1899 [NASA ADS] [CrossRef] [Google Scholar]
- Giodini, S., Lovisari, L., Pointecouteau, E., et al. 2013, Space Sci. Rev., 177, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Gnedin, O. Y., Kravtsov, A. V., Klypin, A. A., & Nagai, D. 2004, ApJ, 616, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Gunn, J. E., & Gott, III, J. R. 1972, ApJ, 176, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Halkola, A., Seitz, S., & Pannella, M. 2006, MNRAS, 372, 1425 [NASA ADS] [CrossRef] [Google Scholar]
- Han, J., Eke, V. R., Frenk, C. S., et al. 2014, MNRAS, submitted [arXiv:1404.6828] [Google Scholar]
- Hennawi, J. F., Dalal, N., Bod, P., & Ostriker, J. P. 2007, ApJ, 654, 714 [NASA ADS] [CrossRef] [Google Scholar]
- Heymans, C., Van Waerbeke, L., Bacon, D., et al. 2006, MNRAS, 368, 1323 [NASA ADS] [CrossRef] [Google Scholar]
- Hoekstra, H. 2001, A&A, 370, 743 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hoekstra, H. 2003, MNRAS, 339, 1155 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, W., & Kravtsov, A. V. 2003, ApJ, 584, 702 [NASA ADS] [CrossRef] [Google Scholar]
- Ienna, F., & Pelló, R. 2006, in SF2A-2006: Semaine de l’Astrophysique Française, eds. D. Barret, F. Casoli, G. Lagache, A. Lecavelier, & L. Pagani, 347 [Google Scholar]
- Jing, Y. P. 2000, ApJ, 535, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Jing, Y. P., & Suto, Y. 2002, ApJ, 574, 538 [NASA ADS] [CrossRef] [Google Scholar]
- Johnston, D. E., Sheldon, E. S., Wechsler, R. H., et al. 2007 [arXiv:0709.1159] [Google Scholar]
- Jullo, E., Kneib, J., Limousin, M., et al. 2007, New J. Phys., 9, 447 [Google Scholar]
- Kaiser, N. 1986, MNRAS, 222, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Klypin, A. A., Trujillo-Gomez, S., & Primack, J. 2011, ApJ, 740, 102 [Google Scholar]
- Kneib, J., Ellis, R. S., Smail, I., Couch, W. J., & Sharples, R. M. 1996, ApJ, 471, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Laporte, C. F. P., & White, S. D. M. 2014, MNRAS, submitted [arXiv:1409.1924] [Google Scholar]
- Leauthaud, A., Finoguenov, A., Kneib, J., et al. 2010, ApJ, 709, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Leauthaud, A., Tinker, J., Behroozi, P. S., Busha, M. T., & Wechsler, R. H. 2011, ApJ, 738, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Leauthaud, A., Tinker, J., Bundy, K., et al. 2012, ApJ, 744, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Limousin, M., Richard, J., Kneib, J.-P., et al. 2008, A&A, 489, 23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Limousin, M., Cabanac, R., Gavazzi, R., et al. 2009, A&A, 502, 445 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Limousin, M., Morandi, A., Sereno, M., et al. 2013, Space Sci. Rev., 177, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Ludlow, A. D., Navarro, J. F., Li, M., et al. 2012, MNRAS, 427, 1322 [NASA ADS] [CrossRef] [Google Scholar]
- Ludlow, A. D., Navarro, J. F., Angulo, R. E., et al. 2014, MNRAS, 441, 378 [NASA ADS] [CrossRef] [Google Scholar]
- Macciò, A. V., Dutton, A. A., & van den Bosch, F. C. 2008, MNRAS, 391, 1940 [NASA ADS] [CrossRef] [Google Scholar]
- Mandelbaum, R., Hirata, C. M., Seljak, U., et al. 2005a, MNRAS, 361, 1287 [NASA ADS] [CrossRef] [Google Scholar]
- Mandelbaum, R., Tasitsiomi, A., Seljak, U., Kravtsov, A. V., & Wechsler, R. H. 2005b, MNRAS, 362, 1451 [NASA ADS] [CrossRef] [Google Scholar]
- Mandelbaum, R., Seljak, U., Cool, R. J., et al. 2006, MNRAS, 372, 758 [NASA ADS] [CrossRef] [Google Scholar]
- Mandelbaum, R., Seljak, U., & Hirata, C. M. 2008a, J. Cosmol. Astropart. Phys., 8, 6 [Google Scholar]
- Mandelbaum, R., Seljak, U., Hirata, C. M., et al. 2008b, MNRAS, 386, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Mandelbaum, R., Seljak, U., Baldauf, T., & Smith, R. E. 2010, MNRAS, 405, 2078 [NASA ADS] [Google Scholar]
- Markevitch, M., Gonzalez, A. H., Clowe, D., et al. 2004, ApJ, 606, 819 [NASA ADS] [CrossRef] [Google Scholar]
- Mead, J. M. G., King, L. J., Sijacki, D., et al. 2010, MNRAS, 406, 434 [NASA ADS] [CrossRef] [Google Scholar]
- Medezinski, E., Broadhurst, T., Umetsu, K., et al. 2007, ApJ, 663, 717 [NASA ADS] [CrossRef] [Google Scholar]
- Meneghetti, M., & Rasia, E. 2013 [arXiv:1303.6158] [Google Scholar]
- Meneghetti, M., Fedeli, C., Pace, F., Gottlöber, S., & Yepes, G. 2010a, A&A, 519, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meneghetti, M., Rasia, E., Merten, J., et al. 2010b, A&A, 514, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meneghetti, M., Fedeli, C., Zitrin, A., et al. 2011, A&A, 530, A17 [CrossRef] [EDP Sciences] [Google Scholar]
- Meneghetti, M., Rasia, E., Vega, J., et al. 2014, ApJ, submitted [arXiv:1404.1384] [Google Scholar]
- Merten, J., Coe, D., Dupke, R., et al. 2011, MNRAS, 417, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Merten, J., Meneghetti, M., Postman, M., et al. 2014, ApJ, submitted [arXiv:1404.1376] [Google Scholar]
- Miralda-Escude, J. 1991, ApJ, 370, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Morandi, A., Limousin, M., Rephaeli, Y., et al. 2011a, MNRAS, 416, 2567 [NASA ADS] [CrossRef] [Google Scholar]
- Morandi, A., Pedersen, K., & Limousin, M. 2011b, ApJ, 729, 37 [NASA ADS] [CrossRef] [Google Scholar]
- More, A., Cabanac, R., More, S., et al. 2012, ApJ, 749, 38 [Google Scholar]
- Muñoz, R. P., Motta, V., Verdugo, T., et al. 2013, A&A, 552, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1995, MNRAS, 275, 720 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1996, ApJ, 462, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Neto, A. F., Gao, L., Bett, P., et al. 2007, MNRAS, 381, 1450 [NASA ADS] [CrossRef] [Google Scholar]
- Newman, A. B., Treu, T., Ellis, R. S., et al. 2009, ApJ, 706, 1078 [NASA ADS] [CrossRef] [Google Scholar]
- Newman, A. B., Treu, T., Ellis, R. S., et al. 2013, ApJ, 765, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Oguri, M. 2006, MNRAS, 367, 1241 [NASA ADS] [CrossRef] [Google Scholar]
- Oguri, M., & Blandford, R. D. 2009, MNRAS, 392, 930 [NASA ADS] [CrossRef] [Google Scholar]
- Oguri, M., & Takada, M. 2011, Phys. Rev. D, 83, 023008 [NASA ADS] [CrossRef] [Google Scholar]
- Oguri, M., Lee, J., & Suto, Y. 2003, ApJ, 599, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Oguri, M., Hennawi, J. F., Gladders, M. D., et al. 2009, ApJ, 699, 1038 [NASA ADS] [CrossRef] [Google Scholar]
- Oguri, M., Bayliss, M. B., Dahle, H., et al. 2012, MNRAS, 420, 3213 [NASA ADS] [CrossRef] [Google Scholar]
- Okabe, N., Takada, M., Umetsu, K., Futamase, T., & Smith, G. P. 2010, PASJ, 62, 811 [NASA ADS] [Google Scholar]
- Okabe, N., Smith, G. P., Umetsu, K., Takada, M., & Futamase, T. 2013, ApJ, 769, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Pointecouteau, E., Arnaud, M., & Pratt, G. W. 2005, A&A, 435, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prada, F., Klypin, A. A., Cuesta, A. J., Betancort-Rijo, J. E., & Primack, J. 2012, MNRAS, 423, 3018 [NASA ADS] [CrossRef] [Google Scholar]
- Redlich, M., Bartelmann, M., Waizmann, J.-C., & Fedeli, C. 2012, A&A, 547, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rines, K., & Diaferio, A. 2006, AJ, 132, 1275 [NASA ADS] [CrossRef] [Google Scholar]
- Ruff, A. J., Gavazzi, R., Marshall, P. J., et al. 2011, ApJ, 727, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Sand, D. J., Treu, T., & Ellis, R. S. 2002, ApJ, 574, L129 [NASA ADS] [CrossRef] [Google Scholar]
- Sand, D. J., Treu, T., Smith, G. P., & Ellis, R. S. 2004, ApJ, 604, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Saro, A., Mohr, J. J., Bazin, G., & Dolag, K. 2013, ApJ, 772, 47 [CrossRef] [Google Scholar]
- Schmidt, R. W., & Allen, S. W. 2007, MNRAS, 379, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Sereno, M., & Umetsu, K. 2011, MNRAS, 416, 3187 [NASA ADS] [CrossRef] [Google Scholar]
- Sereno, M., & Zitrin, A. 2012, MNRAS, 419, 3280 [NASA ADS] [CrossRef] [Google Scholar]
- Thanjavur, K., Crampton, D., & Willis, J. 2010, ApJ, 714, 1355 [NASA ADS] [CrossRef] [Google Scholar]
- Umetsu, K., & Broadhurst, T. 2008, ApJ, 684, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Umetsu, K., Medezinski, E., Broadhurst, T., et al. 2010, ApJ, 714, 1470 [NASA ADS] [CrossRef] [Google Scholar]
- Umetsu, K., Broadhurst, T., Zitrin, A., et al. 2011a, ApJ, 738, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Umetsu, K., Broadhurst, T., Zitrin, A., Medezinski, E., & Hsu, L. 2011b, ApJ, 729, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Umetsu, K., Medezinski, E., Nonino, M., et al. 2014, ApJ, 795, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Verdugo, T., Motta, V., Muñoz, R. P., et al. 2011, A&A, 527, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verdugo, T., Motta, V., Foëx, G., et al. 2014, A&A, 571, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vikhlinin, A., Kravtsov, A., Forman, W., et al. 2006, ApJ, 640, 691 [NASA ADS] [CrossRef] [Google Scholar]
- Voigt, L. M., & Fabian, A. C. 2006, MNRAS, 368, 518 [NASA ADS] [CrossRef] [Google Scholar]
- Voit, G. M. 2005, Rev. Mod. Phys., 77, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Waizmann, J.-C., Redlich, M., & Bartelmann, M. 2012, A&A, 547, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Waizmann, J.-C., Redlich, M., Meneghetti, M., & Bartelmann, M. 2014, A&A, 565, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- White, S. D. M., & Frenk, C. S. 1991, ApJ, 379, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Wojtak, R., & Łokas, E. L. 2010, MNRAS, 408, 2442 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Y.-Y., Böhringer, H., Finoguenov, A., et al. 2006, A&A, 456, 55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhao, D. H., Jing, Y. P., Mo, H. J., & Börner, G. 2009, ApJ, 707, 354 [NASA ADS] [CrossRef] [Google Scholar]
- Zitrin, A., Broadhurst, T., Rephaeli, Y., & Sadeh, S. 2009, ApJ, 707, L102 [NASA ADS] [CrossRef] [Google Scholar]
- Zitrin, A., Broadhurst, T., Umetsu, K., et al. 2010, MNRAS, 408, 1916 [NASA ADS] [CrossRef] [Google Scholar]
- Zitrin, A., Broadhurst, T., Barkana, R., Rephaeli, Y., & Benítez, N. 2011, MNRAS, 410, 1939 [NASA ADS] [Google Scholar]
- Zitrin, A., Bartelmann, M., Umetsu, K., Oguri, M., & Broadhurst, T. 2012, MNRAS, 426, 2944 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Profiles of mass-density contrast
Figure A.1 presents the profile for each stack, along with the best-fit SIS, PLAW, and NFW mass models.
 |
Fig. A.1 Mass-density contrast for all the stacks in richness N (first row), luminosity L (second row), SIS velocity dispersion σv (third row), and arc radius RA (last row). See Fig. 3 for the legend. |
All Tables
Results of the combined fit weak+strong lensing, with or without a central point mass.
Lenstool constraints on the intermediate mass-observable scaling relation M200 = M0(X/X0)A, and the corresponding mass-concentration relation c200 = c0(M200/M0)− B(1 + z)-0.45.
All Figures
 |
Fig. 1 Relative contribution of a point mass component to the total measured signal, computed with Eq. (9), and using an NFW halo described by the best-fit parameters of the stack S0. The three curves show the contribution produced by a mass of 0.01, 0.1, and 1 × 1012 M⊙. The gray area represents the typical relative uncertainty of the measured signal in the region 50−300 kpc. |
| In the text | |
 |
Fig. 2 Results of the stacked analysis on simulated catalogs of lensed galaxies that mimic our observations for the full sample of 80 strong lenses. Colored triangles show the best-fit mass and concentration for the three composite lenses corresponding to stacks in richness. The gray-shaded area covers the intrinsic dispersion of the simulated lenses (black stars) around their average mass and concentration. The overlap of these average values with the results of the stacked analysis indicate the absence of any strong systematic bias. |
| In the text | |
 |
Fig. 3 Average density contrast ΔΣ(r) for the stack S0 (Eq. (5)). The lower panel shows the profile obtained using the radial component of the lensed galaxies’ ellipticity, and should be equals to zero. The upper panel is the profile using the tangential component. Overplotted are the best-fit results (right side of Eq. (9)) for the three mass models, SIS (green-solid line), PLAW (dashed-blue line) and NFW (orange-shaded area, encompassing the combined 1σ uncertainty on M200 and c200). |
| In the text | |
 |
Fig. 4 Best-fit parameters of the NFW mass model for the stacks in richness N (red triangles), luminosity L (orange disks), SIS velocity dispersion σv (blue squares), and arc radius RA (purple stars). The large black rectangle shows the ⟨M200⟩ ± 1σ and ⟨c200⟩ ± 1σ obtained using the 80 groups (stack S0). The green-hatched area delimits the 1σ uncertainty around the mass-concentration relation derived with Lenstool, using a M200(σv) scaling. |
| In the text | |
 |
Fig. 5 Combined fit of the mass-concentration relation, using the results from the stacks in velocity dispersion (open-blue squares, weak-lensing alone) and the values derived by Oguri et al. (2012; red triangles) and Umetsu et al. (2011a; open-green triangle) from the stacked analysis of strong-lensing galaxy clusters. The best-fit relation was obtained assuming a scaling in redshift of (1 + z)-0.45, and the black solid line show the results for z = 0.5 (the gray-shaded area delimits the statistical uncertainty from the best-fit parameters). Overplotted are the relations derived from numerical simulations by Duffy et al. (2008; black-dashed line, all haloes, z = 0.5) and Meneghetti et al. (2014; orange-solid line, strong-lensing selected haloes, z = 0.5). The magenta-dashed lines show the 1σ limit around the average relation derived by Oguri et al. (2012) from semi-analytical predictions (lensing bias using weights from the arc cross section+Einstein radii, z = 0.45). |
| In the text | |
 |
Fig. 6 Values of the spherical mass and concentration of a prolate NFW halo producing the same signal as that of a spherical NFW halo characterized by the S0 best-fit parameters. The different stars show the required (M200, 3D,c200, 3D) as a function of the minor-to-major axis ratio a/c (starting from a/c = 1 in the top-right corner, and decreasing by 0.1). We consider here the case of a prolate halo (a = b<c) with a major axis aligned with the line of sight. The gray-shaded area and black curve indicate the relation of Duffy et al. 2008 (all haloes, z = 0.5). |
| In the text | |
 |
Fig. A.1 Mass-density contrast for all the stacks in richness N (first row), luminosity L (second row), SIS velocity dispersion σv (third row), and arc radius RA (last row). See Fig. 3 for the legend. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


