| Issue |
A&A
Volume 569, September 2014
|
|
|---|---|---|
| Article Number | A5 | |
| Number of page(s) | 22 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201424136 | |
| Published online | 08 September 2014 | |
X-shooter spectroscopy of young stellar objects
V. Slow winds in T Tauri stars⋆,⋆⋆
1 INAF/Osservatorio Astrofisico of Arcetri, Largo E. Fermi, 5, 50125 Firenze, Italy
e-mail: natta@arcetri.astro.it
2 School of Cosmic Physics, Dublin Institute for Advanced Studies, 31 Fitzwilliams Place, 2 Dublin, Ireland
3 ESO/European Southern Observatory, Karl-Schwarzschild-Strasse 2, 85748 Garching bei München, Germany
4 INAF/Osservatorio Astronomico di Capodimonte, Salita Moiariello, 16 80131 Napoli, Italy
5 Department of Planetary Science, Lunar and Planetary Lab, University of Arizona, 1629, E. University Blvd, 85719, Tucson, AZ, USA
6 INAF/Osservatorio Astronomico di Palermo, Piazza del Parlamento 1, 90134 Palermo, Italy
7 ASI-Science Data Center, via del Politecnico snc, 00133 Rome, Italy
Received: 5 May 2014
Accepted: 13 June 2014
Disks around T Tauri stars are known to lose mass, as best shown by the profiles of the forbidden emission lines of low-ionization species. At least two separate kinematic components have been identified, one characterized by velocity shifts of tens to hundreds of km s-1 (HVC) and one with a much lower velocity of a few km s-1 (LVC). The HVC are convincingly associated to the emission of jets, but the origin of the LVC is still unknown. In this paper we analyze the forbidden line spectrum of a sample of 44 mostly low-mass young stars in Lupus and σ Ori observed with the X-shooter ESO spectrometer. We detect forbidden line emission of O i, O ii, S ii, N i, and N ii, and characterize the line profiles as LVC, blueshifted HVC, and redshifted HVC. We focus our study on the LVC. We show that there is a good correlation between line luminosity and both Lstar and the accretion luminosity (or the mass accretion rate) over a large interval of values (Lstar~ 10-2−1 L⊙; Lacc~ 10-5−10-1 L⊙; Ṁacc~ 10-11 − 10-7 M⊙/yr). The lines show the presence of a slow wind (Vpeak< 20 km s-1) that is dense (nH> 108 cm-3), warm (T ~ 5000−10 000 K), mostly neutral. We estimate the mass of the emitting gas and provide a value for the maximum volume it occupies. Both quantities increase steeply with the stellar mass, from ~ 10-12 M⊙ and ~0.01 AU3 for Mstar~ 0.1 M⊙, to ~ 3 × 10-10 M⊙ and ~1 AU3 for Mstar~ 1 M⊙, respectively. These results provide quite stringent constraints to wind models in low-mass young stars, that need to be explored further.
Key words: stars: low-mass / line: formation / ISM: jets and outflows / accretion, accretion disks
Based on observations collected at the European Souther Observatory at Paranal, under programs 084.C-0269(A), 085.C-0238(A), 086.C-0173(A), 087.C-0244(A) and 089.C-0143(A).
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2014
1. Introduction
Circumstellar disks of gas and dust surround young stars from their birth for a period of few million years; during this time planetary systems may form and evolve. The disk structure and its evolution affect the conditions for the formation of planets and their properties (Dutrey et al. 2014; Alexander et al. 2014). Disks are dynamical structures, with gas and dust accreting onto the central stars, but also being expelled from the systems. In particular, the way mass loss occurs and evolves with time has important consequences on the disk survival and on its properties.
Mass loss from magnetized accretion disks is expected, owing to the combined effect of rotation and magnetic fields; it is probably a very complex phenomenon, with different components: a so-called disk wind, due to the relic magnetic field that threads the disk at all distances from the star, an X-wind, which is launched in the region close to the star where the stellar magnetic field provides the pressure required to overcome the stellar gravity and, possibly, a stellar wind, where gas from the central star is expelled from the system (see, e.g., Ferreira 2013, and references therein). Under the action of the magnetic field, the gas is collimated and accelerated to terminal velocities of a few hundred km s-1, forming the bright jets observed in several young objects (e.g., Frank et al. 2014). As magnetocentrifugal winds extract angular momentum from the disk, they can control accretion (e.g., Turner et al. 2014).
Disks can also lose mass when their upper layers are heated to temperatures such that the gas’s thermal energy exceeds its binding energy and the gas escapes from the system (photoevaporation). This mechanism was firstly recognized to lead to dispersal of disks in the vicinity of a hot star (e.g., O’Dell & Wen 1994). More recently, it has been realized that the combined effect of the high energy photons (UV, far-UV (FUV), X) emitted by low-mass stars can heat the disk surface to sufficiently high temperatures to produce a centrifugally launched ouflow, driven by thermal pressure. Photoevaporation winds are possibly the cause of the quick disk dissipation, which ends their much longer phase of viscous evolution (see, e.g., Alexander et al. 2014, and references therein).
Observational evidence of mass loss from young stars (T Tauri stars; TTS) with disks (Class II) is provided by the intensity and profiles of forbidden lines of atomic and low-ionization species, which present at least two different components (Hartigan et al. 1995). One is emitted by gas moving at high velocity (HVC), which is clearly identified with the jets that have been imaged and carefully studied in several objects. The other component originates in a much slower moving gas (low velocity component, LVC). The LVC is detected in most Class II objects, and its origin is still unknown. It could be emitted at the base of a magnetically driven disk wind, as suggested by Hartigan et al. (1995) for the O i lines, but it can also be a tracer of a photoevaporative disk wind, as shown by, e.g., Pascucci & Sterzik (2009) for the LVC of the Ne ii mid-IR emission lines. Lately, Rigliaco et al. (2013) have shown that the LVC O i lines could also have multiple components, with one component tracing gas in Keplerian rotation and another component tracing a photoevaporative wind. Acke et al. (2005) find that in Herbig Ae/Be stars, the [O i] 630.03 nm emission could come from the disk surface layers. In this paper we focus on the properties of the LVC components of the winds from low-mass T Tauri stars.
As for other disk and stellar diagnostics, to find meaningful trends and to make full use of the diagnostic potential of the LVC forbidden line emission, it is necessary to simultaneously analize as many lines as possible and to have access to a large sample of objects that covers a wide range of stellar and accretion properties. The best sample available so far is still that of Hartigan et al. (1995), who observed 42 TTS in Taurus and detected forbidden line emission in about 30 of them. The number of stars with reliable measurements of the mass accretion properties is, however, smaller, in the range of 12–15 objects (Gullbring et al. 1998; Rigliaco et al. 2013), mostly of relatively high mass and accretion rate. In this paper, we analyze a sample of 44 low-mass stars in two star forming regions, Lupus and σ Ori, of ages 1–3 My. The two regions differ mostly due to the presence of a massive star (σ Ori) in the σ Ori region. The spectra have been obtained with VLT/X-shooter (Vernet et al. 2011), which gives medium-resolution spectra simultaneously over the spectral range from 310 to 2500 nm. They were collected as part of the Italian guaranteed time observation (GTO; Alcalá et al. 2011) and have already been used to derive the stellar parameters and the accretion properties of the stars (Rigliaco et al. 2012; Alcalá et al. 2014). This is, therefore, the largest sample of TTS with well-known accretion properties studied so far with the aim of characterizing the mass loss phenomenon and its origin.
In general, forbidden lines in the optical and near-IR are emitted by warm gas (temperature of a few thousand degrees), where collisions with electrons or neutral hydrogen excite the upper levels of the transitions, and we assume that this is the case throught this paper. However, an alternative, non-thermal mechanism has been proposed for the formation of the O i lines, namely that they have origin in a cooler disk region where OH is photodissociated by the stellar FUV photons (Acke et al. 2005; Gorti et al. 2011). We come back to this point at the end of the paper.
The paper is organized as follows. Sections 2 and 3 briefly summarize the observations, data reduction, and the sample properties, already discussed in Rigliaco et al. (2012) and Alcalá et al. (2014); Sect. 4 presents the forbidden line spectra; Sect. 5 the line profiles and the separation of the HVC and LVC. Section 6 is dedicated to the LVC. Discussion and summary follow in Sects. 7 and 8, respectively.
2. Observations
We use the spectra published in Alcalá et al. (2014) and Rigliaco et al. (2012). The instrument setup is described in those papers, including the spectral resolution in each wavelength range, the corresponding signal-to-noise ratio, the data reduction and calibration procedures, as well as the derivation of extinction, spectral type, and accretion luminosity. All the spectra used in this paper have been corrected for extinction. For most targets, the slit width was 1 arcsec, yielding a resolution of ~60 km s-1 in the UVB arm and ~35 km s-1 in the VIS arm.
In addition to the wavelength calibrations described in Alcalá et al. (2014) and Rigliaco et al. (2012), we have cross-checked and adjusted the wavelength scale of the UVB and VIS arms by aligning the [O i] 557.79 line, which is covered by both arms. This line is detected in all objects for which we have detections of other lines in the UVB arm, with the exception of SO587 and SO646. We detected and applied an offset to the UVB wavelength calibration only in 8 cases out of 31 objects, and in those cases the offset between the two scales was less than 24 km s-1. We assumed zero offset for SO587 and SO646. The emission line velocities reported in this paper are all relative to the photospheric rest velocity as measured by the Li i line at 670.78 nm.
All the measurements of the [O i] 557.79 line used for the scientific analysis in this paper come from the UVB arm. While the spectral resolution in this arm is lower than in the VIS, the signal-to-noise at the wavelength of the [O i] 557.79 line is better.
3. The sample
The sample studied in this paper comprises 36 low-mass Class II (i.e., with evidence of disk from the infrared) stars in Lupus (2 of these are brown dwarfs) and 8 in σ Ori. The spectra are publicly available in Vizier (J/A+A/561/A2 and J/A+A/548/A56). The Lupus sample contains about 50% of the total Class II population and is representative of the properties of the region, while the number of objects in σ Ori is small, and the targets were selected among low-mass Class II objects in different locations with respect to the bright star σ Ori. The objects are listed in Table A.1, which gives the stellar parameters and the accretion luminosity and mass accretion rates from Alcalá et al. (2014) for objects in Lupus and Rigliaco et al. (2012) for the σ Ori stars. As detailed in those papers, the X-shooter spectrum of each object is described as the sum of the photospheric emission, taken to be that of non-accreting diskless young objects (Class III; see Manara et al. 2013) and of a slab of hydrogen that represents the emission of the accretion shock. The spectral type, extinction, and slab luminosity (i.e., the accretion luminosity) are therefore self-consistently determined. In the following, we refer to stars in Table A.1 as the Lupus and σ Ori GTO (GTO for simplicity) sample.
The distribution of the stars in mass and accretion luminosity is shown in Fig. 1. About 70% of the objects have masses <0.3 M⊙. The accretion luminosity ranges from ~10-5 to ~1 L⊙ and the corresponding mass accretion rates between ~10-12 and ~10-7 M⊙/yr, with most of the objects having Ṁacc< 2 × 10-9 M⊙/yr. In the GTO sample, the accretion luminosity correlates with the stellar luminosity and the mass accretion rate with the mass of the star, with dispersions of about one order of magnitude, which is much less than in other samples, as discussed in Alcalá et al. (2014). The correlation between Lacc and Lstar for the GTO sample is significantly steeper than linear, with slope 1.53 ± 0.18, computed using ASURV (parametric EM algorithm; Feigelson & Nelson 1985; Fig. 2). We have not included Par-Lup3-4, for reasons discussed in Sect. 6.2. This relation extends also to the more massive TTS analyzed by Gullbring et al. (1998) and Ingleby et al. (2013) and to the low-mass (≲0.15 L⊙) objects studied by Herczeg & Hillenbrand (2008, 2014), which, however, have a large dispersion at low Lstar.
Given the tight correlation between Lacc and Ṁacc, in the following we use Lacc, which is derived directly from the observations, as a proxy for Ṁacc.
 |
Fig. 1 Accretion luminosity (top) and stellar mass (bottom) distribution. Red histogram for stars in Lupus, blue for stars in σ Ori. |
 |
Fig. 2 Lacc as function of Lstar for objects in Lupus (red dots) and σ Ori (filled blue squares). Open green squares plot the Taurus TTS of Gullbring et al. (1998); black diamonds the results of Herczeg & Hillenbrand (2008). The black line shows the best-fitting relation (GTO objects only) with slope 1.53; dashed lines are the locus Lacc/Lstar = 1, 0.1, 0.01 from top to bottom, respectively. |
Observed forbidden lines.
Kinematical components.
4. Results
We have searched the spectra of our targets for evidence of emission in the forbidden lines of O i, O ii, O iii, S ii, S iii, N i, N ii, C i, and Ca ii in the blue, visual, and near-IR wavelengths. The lines detected are [O i] 557.79; the O i doublet at 630.03, 636.37 nm; the O ii doublets at 372.88, 372.60 nm and 731.89, 732.97 nm; the S ii doublets at 407.63, 406.86 nm and 671.64, 673.08 nm; the N ii doublet at 654.80, 658.34 nm. The [N i] 519.79 nm is detected in many objects, but it is contaminated by Fe lines that cannot be reliably deconvolved at the resolution of our spectra, so that its intensity is very uncertain. In a few cases, we also detect the [N i] 346.649, 346.654 doublet, but in this spectral region the signal-to-noise ratio achieved is generally very low; there are no detections of the N i quadruplet around 1 micron. In Par-Lup3-4, which has the richest emission line spectrum, we also detect the [Ca ii] 729.15 nm and [C i] 982.40, 985.30 nm lines and the S ii quadruplet at ~1030 nm. In addition, there are some lines of Fe in different ionization states (Giannini et al. 2013).
Table 1 lists the spectroscopic parameters of the lines. For each line, it gives the ionization potential of the ion, the line wavelength in the vacuum and in air, the quantum number and multiplicity of the lower and upper states, the excitation temperature of the upper state of the transition, the value of the A21 coefficient, the critical density for collisions with electrons, and the number of stars in which the line is detected. The emissivity of the lines used in this paper has been kindly provided to us by Bruce Draine and computed using a five-level atomic model with collisional rates for electrons or atomic hydrogen (Draine 2011).
Some lines are detected in a large fraction of stars, for example the [O i] 630.03 nm (detected in 38 out of 44 stars) or the [S ii] 406.98 nm, which is detected in 26 stars; no forbidden line is detected in six stars (AKC2006-1, Lup713, Lup706, Sz115, SST-Lup3-1, SO397). Some lines of ions with high ionization potential, such as the [N ii] 658.34, are also seen in several stars.
There is a large variation in the number of forbidden lines detected in different stars. None of the low luminosity and low accretion luminosity objects show a rich forbidden line spectrum, with the exception of four objects (Par-Lup3-4, SO587, SO848, and SO1266), which are discussed in more detail in the following.
Of the stars with no forbidden line detections, four (AKC2006-1, Lup713, Lup706, SST-Lup3-1) are among the low luminosity, low Lacc objects, while two (Sz115 and SO397) are typical TTS, and the lack of lines is somewhat surprising. We note, however, that in all cases the upper limits to the line luminosities are not significantly lower than the detections.
5. Line profiles
Forbidden lines from TTS are known to show multiple components. Typically, one can identify a low velocity component, which is broad and roughly symmetric with a slightly blueshifted peak velocity, and high velocity components with peaks shifted to the blue and/or to the red (much less frequently) by tens of km s-1.
We have examined the lines [O i] 630.03, [O i] 557.79, [S ii] 406.86, [S ii] 673.08, [O ii] 372.60, [O ii] 731.89 and [N ii] 658.34 and classified them as high velocity blueshifted (HVC-blue), high velocity redshifted (HVC-red), and low velocity (LVC) components.
Because the spectral resolution of X-shooter is relatively low, we have adopted a conservative criterion to identify the presence of a HVC component in each line: i) when a line has a single component shifted by more than ± 40 km s-1, this is identified as a HVC; ii) when more than one component is present, the HVC is identified if it is well resolved from the LVC; iii) when a line shows a broad wing, this wing is identified as an HVC if another line has an HVC at the same velocity defined by one of the previous criteria. In Table 2 we report the components identified in each line for all stars in our sample. In this table “L” stands for LVC, “Hb” for HVC-blue, and “Hr” for HVC-red. LVC and HVC components are clearly detected in several objects. The star Sz83 (RU Lup) has very complex line profiles, not only for the forbidden lines but also for the permitted lines that directly trace the accreting matter (Alcalá et al. 2014) and is not discussed in this paper.
Our criteria in classifying the different components differ from those adopted by Hartigan et al. (1995). These authors define the LVC as the portion of the spectrum between −60 and +60 km s-1 and measured the HVC as the total flux (integrated over all the profile) minus the LVC flux. Note also that the spectral resolution they used is about 12 km s-1, which allowed them a better definition of the line wings.
We compute the intensity and the peak velocity of each component by fitting a Gaussian profile to the line. For each star Tables B.1–B.4 give the properties (flux, uncertainty, peak velocity and FWHM) of each component for the set of lines defined above. Upper limits (3σ) have been computed from the rms of the continuum, assuming a line FWHM width of 50 km s-1 (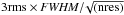 , where nrs is the number of resolution elements within 50 km s-1). The uncertainty on Vpeak is ~10 km s-1. Figure 3 shows the distribution of the peak velocity; almost all LVC have a blueshifted peak, with Vpeak smaller than ~ 20 km s-1. The Gaussian fit tends to overestimate Vpeak if there is a significant unresolved asymmetric wing. In general, our values of Vpeak are consistent, given the resolution of our spectra, with the typical value ~ 5 km s-1 of Hartigan et al. (1995). The large majority of the lines, both LVC and HVC, are broad and well resolved, with FWHM ranging from the resolution limit to ≳100 km s-1.
, where nrs is the number of resolution elements within 50 km s-1). The uncertainty on Vpeak is ~10 km s-1. Figure 3 shows the distribution of the peak velocity; almost all LVC have a blueshifted peak, with Vpeak smaller than ~ 20 km s-1. The Gaussian fit tends to overestimate Vpeak if there is a significant unresolved asymmetric wing. In general, our values of Vpeak are consistent, given the resolution of our spectra, with the typical value ~ 5 km s-1 of Hartigan et al. (1995). The large majority of the lines, both LVC and HVC, are broad and well resolved, with FWHM ranging from the resolution limit to ≳100 km s-1.
Examples of the observed line profiles are shown in Appendix C. Figure C.1 shows the observed profiles of the [O i] 630.03 line for all the GTO objects. Figures C.2–C.10 show line profiles for a selection of objects where several lines were detected, together with the results of the Gaussian fitting and deconvolution.
 |
Fig. 3 Distribution of the peak velocity shift with respect to the star (solid for LVC, hatched blue for HVC-blue, red for HVC-red) for different lines, as labeled. |
 |
Fig. 4 Ratio of the HVC to the LVC intensity in objects where both components are simultaneously detected. The bottom panel refers to the [O i] 630.03 lines; the top panel to the [S ii] 406.86| and [S ii] 673.08 lines, as labeled. Red and blue stand for Lupus and σ Ori, as before. |
5.1. Statistics
For each star, Table 2 characterizes the profile of the lines discussed in the following. LVC, HVC-blue and/or HVC-red may be present in all the lines we observe, but, as also shown by previous studies, the HVC-red is very rare. The exception is the [O i] 557.79 that does not show any HVCs clearly identifiable in our spectra, although in some cases there is a hint of emission in the line wings that could be resolved as a separate component in higher sensitivity and resolution spectra. This agrees with the results of other authors (i.e. Hartigan et al. 1995; Rigliaco et al. 2013).
When detected, the [O i] 630.03 always has a LVC, while a HVC is detected in 12 out of 37 cases. In general, HVCs are detected proportionally more often in high excitation/high ionization lines, such as [N ii] 658.34 and [O ii] 372.60, or in lines with low critical density, such as the [S ii] 673.08 doublet.
Of particular interest are stars where both LVC and HVC are detected, since in these cases, the potential confusion between the LVC emission and that of a jet projected on the plane of the sky does not exist. Our sample includes 12 stars with both LVC and HVCs in the [O i] 630.03 line. Of these, five show both components also in the [S ii] 406.86 line and two in the [S ii] 673.08 one. The intensity ratio between the two components is shown in Fig. 4 for the [O i] 630.03, [S ii] 406.86, and [S ii] 673.08 lines. The ratios range from very small to ~ 3.5; however, only a few objects have a very strong HVC (high value of the ratio), and in most cases the HVC has intensity lower than the LVC.
5.2. Contamination of the LVC sample by HVC in the plane of the sky
When only one component with low peak velocity is detected in any given object, it is possible that, rather than a bona-fide LVC, it is a HVC misclassified because of projection effects. This is certainly the case of Par-Lup3-4, which has a well resolved jet and an edge-on disk obscuring the central star so that both its stellar and its accretion luminosity are largely underestimated (Bacciotti et al. 2011; Alcalá et al. 2014). At the spatial resolution of our spectra (~1 arcsec, due to seeing), forbidden lines from Par-Lup3-4 have very low Vpeak, and we classify them as LVC. Unlike many other cases, however, the three lines, [S ii] 673.08, [O ii] 372.60, and [N ii] 658.34 are quite strong in this object, with ratios to the [O i] 630.03 line of 0.3, 0.1, and 0.05, respectively.
Two additional objects in Lupus also have rich LVC spectra, with all the lines clearly detected. They are Sz66 and Sz106. The high excitation lines are particularly strong, with ratios [O ii] 372.60/[O i] 630.03 and [N ii] 658.34/[O i] 630.03 of 0.02 and 0.05 for Sz66 and 0.25 and 0.3 for Sz106. For the latter object there is evidence in the literature for an edge-on geometry (Comerón et al. 2003; Alcalá et al. 2014). It is probable that, as in Par-Lup3-4, we are detecting the emission of a jet with axis close to the plane of the sky.
The presence of three “spurious” LVC objects in Lupus (about 10%) is consistent with the expectations for a randomly oriented sample. Assuming a velocity of 200 km s-1 for the HVC (e.g., Appenzeller & Bertout 2013), we expect that about 12% have projected velocities less than ~ 40 km s-1 and would therefore be classified as LVC in our analysis.
Given the small number of potentially spurious LVC, we include all the objects in the GTO sample in the following analysis (with the already noted exception of Sz83).
5.3. Doublets
All the lines in our sample are doublets, with the exception of the [O i] 557.79. In some cases (i.e., the [O i] 630.03 and the [N ii] 658.34 doublets), the ratio of the intensity of the two components only depends on atomic parameters; in others, it also depends on the physical conditions that determine the level population. If, for example, electronic collisions dominate, the intensity ratio depends on the electron density and, to a lower degree, on the temperature, as for the [S ii] 406.86 and [S ii] 673.08 case. The range, however, is not large. The [S ii] 673.08 ratio ranges from ~ 1.5 for density much lower than the critical density, to ~ 0.5 in the high density limits. In the case of the [S ii] 406.86 doublet, the [S ii] 407.63 is always weaker than the [S ii] 406.86, with a ratio of ~ 0.3 for ne ≪ ncr to ~ 0.2 in the high-density limit. Our observed ratios and upper limits are always consistent with the predictions. Unfortunately, the large errors, especially on the weaker components, prevent us from using these line ratios to constrain the density of the emitting regions.
6. The low velocity component
In the following, we focus our discussion on the region emitting the LVC and on its properties.
6.1. Line intensities
Figure 5 shows the luminosity of the LVC of the lines [O i] 630.03 and [O i] 557.79 as functions of Lstar (left panels) and Lacc (right panels). For the two O i lines, which are detected in a large fraction of objects, there is an excellent correlation of Lline with both Lstar and Lacc, with similar slopes for the two lines; using the ASURV, EM method (Feigelson & Nelson 1985), we find 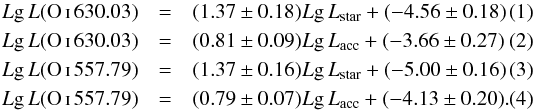 Upper limits to the line luminosity are taken into account. We have not included the object Par-Lup-3-4 in the correlations, because of its very uncertain values of Lstar and Lacc, and, in the case of the correlations with Lacc, the two objects in σ Ori that only have Lacc upper limits. If they are included, the correlations will be slightly flatter.
Upper limits to the line luminosity are taken into account. We have not included the object Par-Lup-3-4 in the correlations, because of its very uncertain values of Lstar and Lacc, and, in the case of the correlations with Lacc, the two objects in σ Ori that only have Lacc upper limits. If they are included, the correlations will be slightly flatter.
Figure 5 also plots the observed [O i] 630.03 and [O i] 557.79 luminosities for other stars in the literature. Values for DR Tau at different epochs (stellar, accretion and line luminosities) have been obtained from X-shooter spectra in the same manner as the objects analyzed in this paper (Banzatti et al. 2014). For the sample of TTS in Taurus firstly studied by Hartigan et al. (1995), we take extinction, Lstar and Lacc as remeasured by Gullbring et al. (1998). For the low-mass objects studied by Herczeg & Hillenbrand (2008), we use the new values of extinction, Lstar and Lacc given by Herczeg & Hillenbrand (2014), when available.
The correlations of Eqs. (1)–(4) also describe the higher luminosity TTS from the literature quite accurately. The slope of the Lline-Lacc correlation for the [O i] 630.03 line is similar within the uncertainties to that of Herczeg & Hillenbrand (2008). On the other hand, it is marginally steeper than the slope (0.52 ± 0.07) found by Rigliaco et al. (2013) using the [O i] 630.03 LVC luminosities of Hartigan et al. (1995) and new determinations of Lacc from the Hα luminosity. Inspection of Fig. 5 shows that in the TTS sample alone L([O i] 630.03) has a flat dependence on Lacc, and it is possible that the discrepancy comes from the different range of Lacc covered by the two samples. The possibility of a change in the slope at high Lacc is also suggested by the location of DR Tau; however, there are differences in the quality of the data and in the methods used to determine stellar and accretion properties for the various samples that prevent any conclusion at this stage.
 |
Fig. 5 Line luminosities for [O i] 630.03 and [O i] 557.79 are plotted as functions of the stellar luminosity (left panels) and of the accretion luminosity (right panels). Red filled dots are the Lupus objects, blue filled squares are objects in σ Ori, arrows show 3σ upper limits. The black crosses show the same quantities for the strongly accreting TTS DR Tau at different epochs (Banzatti et al. 2014). Black diamonds are values for Taurus very low-mass objects from Herczeg & Hillenbrand (2008, 2014, see text); green open squares denote Taurus TTS from Gullbring et al. (1998) and Hartigan et al. (1995), as described in the text. A few objects discussed in Sect. 6.2 are only labeled in some panels, to avoid confusion. Black lines show the relations derived in Eqs.(1)–(4) for the GTO sample. |
 |
Fig. 6 Line luminosities for the [S ii] 406.86 and [S ii] 673.08 lines are plotted as functions of the stellar luminosity (left panels) and of the accretion luminosity (right panels). Red dots are the Lupus objects, blue filled squares are objects in σ Ori, arrows show 3σ upper limits. Green open squares show the position of Taurus TTS from Gullbring et al. (1998) and Hartigan et al. (1995), as described in the text. |
As mentioned in Sect. 3, there is a rather tight correlation in the GTO objects between Lstar and Lacc. This makes it very difficult to identify which of the system properties controls the emission of the forbidden lines, the stellar or the accretion ones. It is interesting that the relation to Lacc is roughly linear, as for all the permitted lines that are tracers of the accretion process (Alcalá et al. 2014).
Figure 6 plots the luminosity of the [S ii] 406.86 and [S ii] 673.08 lines as a function of Lstar and Lacc respectively. As for the O i lines, there is a good correlation with both, with similar slopes, but with a larger number of upper limits, especially in the [S ii] 673.08 lines.
6.2. Individual objects
There are a few objects that deviate significantly from the general trends, and we have identified them in the figures. In addition to Par-Lup3-4, which we have already discussed, there are two stars in σ Ori with very strong forbidden lines. One is SO587, which has an upper limit to Lacc~ 10-4 L⊙, and a LVC spectrum with especially strong high excitation lines, i.e., [S ii] 673.08/[O i] 630.03 ~ 1.5, [N ii] 658.34/[O i] 630.03 ~ 1.7, and [N ii] 658.34/[O i] 630.03 ~ 3. Also the [S ii] 406.86 line is very strong for the observed Lacc (but not for the Lstar of the object). No [O i] 557.79 is detected. This object has been studied by Rigliaco et al. (2009), who interpreted it as a photoevaporative wind heated by the nearby O9.5 star σ Ori. The physical conditions in the outer wind should therefore be different from those in similar objects where no hot nearby star is present, explaining the strong emission in the high excitation lines.
Another object in σ Ori has a rich spectrum of forbidden lines, namely SO848. In this case both a LVC and a HVC-blue are detected and the LVC luminosities are as expected, given the Lstar and Lacc of the object. The only exception is the [S ii] 673.08 line, which is unusually strong. It is possible that the presence of the hot star σ Ori also affects the emission of SO848, which has a projected distance from σ Ori of 0.45 pc (to be compared with 0.35 for SO587). A deeper analysis of this aspect, however, requires line profiles of higher spectral resolution, which will allow a more accurate component separation and also the identification of spectral profiles typical of photoevaporated winds heated by an external source (see, e.g., Rigliaco et al. 2009).
SO1266 is a low luminosity object in σ Ori, with only an upper limit to Lacc from continuum excess measurement (Rigliaco et al. 2012). It has relatively strong emission lines of H and Ca ii, so that the mass accretion rate derived from the relation between line luminosity and Lacc would be about ten times higher than the continuum upper limit. Rigliaco et al. (2012) argue that chromospheric emission contributes about 80% of the line emission (see also Manara et al. 2013). We detected LVC of [O i] 630.03, [O i] 557.79, and [S ii] 673.08, which are stronger than in other objects with similarly low Lacc, but not when compared to other objects with similar Lstar. This is an interesting object that needs follow-up studies.
6.3. Physical conditions in the LVC emitting region
Line ratios provide very interesting information on the physical conditions of the emitting region. The top panel of Fig. 7 plots the values of the ratio of the two [O i] lines at 557.73 and 630.03 as functions of Lacc for the GTO sample and for the more luminous TTS from the literature described in the previous section. The ratio is impressively constant over the whole sample with values ranging from ~ 0.1 to ~ 1. There is no correlation with either the Lstar or the intensity of the [O i] 630.03 line. This is very similar to what has been found by Hartigan et al. (1995) for higher luminosity TTS, also shown in the figure.
The observed values can be compared in the bottom panel of Fig. 7 to the predictions of homogeneous and isothermal models where the excitation is due to electron collisions (bottom axis) or to collisions with neutral hydrogen (top axis). Different curves correspond to different temperatures, as labeled. The model predictions for the intensity of the [O i] 557.79 when collisional excitation by H dominates are uncertain, since the de-excitation cross section of the level 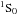 is not known. The calculations in Fig. 7 were performed assuming the same rate of the 1D2 level (see also the discussion in Gorti et al. 2011). The gray area shows the location of the observed ratios; one can see that, unless the temperature is significantly higher than 104, they are consistent with a rather dense gas, with ne ≫ ncr([O i] 630.03) ≳ 107 cm-3, or, alternatively, nH ≫ 1010 cm-3, if collisions with H dominate the level excitation. We have limited our models to T ≤ 104 K, but we note that at the high temperature T = 30 000 K, ne = 105 cm-3, the ratio [O i] 630.03/[O i] 557.79 is only ~ 0.1 barely consistent with the low end of the observed interval, and would decrease further for lower values of ne. Temperatures below ~ 5000 K cannot reproduce the observed ratios, regardless of the value of the density. In the following, we assume that the region emitting the [OI] lines have density ne ≥ 107 cm-3 (or nH ≥ 1010 cm-3) and temperature 5000 ≤ T ≤ 10 000 K.
is not known. The calculations in Fig. 7 were performed assuming the same rate of the 1D2 level (see also the discussion in Gorti et al. 2011). The gray area shows the location of the observed ratios; one can see that, unless the temperature is significantly higher than 104, they are consistent with a rather dense gas, with ne ≫ ncr([O i] 630.03) ≳ 107 cm-3, or, alternatively, nH ≫ 1010 cm-3, if collisions with H dominate the level excitation. We have limited our models to T ≤ 104 K, but we note that at the high temperature T = 30 000 K, ne = 105 cm-3, the ratio [O i] 630.03/[O i] 557.79 is only ~ 0.1 barely consistent with the low end of the observed interval, and would decrease further for lower values of ne. Temperatures below ~ 5000 K cannot reproduce the observed ratios, regardless of the value of the density. In the following, we assume that the region emitting the [OI] lines have density ne ≥ 107 cm-3 (or nH ≥ 1010 cm-3) and temperature 5000 ≤ T ≤ 10 000 K.
 |
Fig. 7 Top panel: ratio [O i] 557.79/[O i] 630.03 as function of Lacc for stars in Lupus (red dots) and σ Ori (filled blue squares). Arrows indicate 3σ upper limits. Objects where both a LVC and a HVC are detected are marked by large open circle. Black crosses show the values for the set of DR Tau spectra obtained at different epochs, and green open squares are stars in Taurus (see text). Bottom panel: model predictions for collisions with electron (solid curves) and with hydrogen atoms (dashed curves). Different curves refer to different temperatures in units of 104 K, as labeled. The ne scale is shown in the bottom axis, that for nH on the top axis. The gray area shows the location of the observed values, marked by the two dashed lines in the top panel. |
 |
Fig. 8 Same as Fig. 7 for the ratio [S ii] 406.86/[O i] 630.03. In the bottom panel, the dark-gray area shows the location of 65% of the observed values (dashed lines in the top panel). Three points lie in the upper light-gray area, the rest in the lower light-gray one (dotted lines in the top panel). |
The third most frequently observed line is [S ii] 406.86. The top panel of Fig. 8, plots the observed ratio of the intensity of the [S ii] 406.86 to [O i] 630.03 line as a function of Lacc. We marked the objects where there is unambiguous evidence that the two lines form in the LVC; i.e., both LVC and HVC are detected in the [O i] 630.03 line, as detailed in Sect. 5.1. The bottom panel of Fig. 8 plots the predictions for electronic collisions and atomic hydrogen collisions (same as Fig. 7). The [S ii] 406.86 line has a critical density for electronic collisions very similar to that of the [O i] 630.03 line and a difference in the energy of the upper level of ~ 10 000 K, so that their ratio is expected to vary little with the density and temperature of the emitting region. We have assumed that all oxygen is neutral, all sulfur is S ii and the Asplund (2005) solar elemental abundances (α(O) = 4.5 × 10-4, α(S) = 1.4 × 10-5). The ratio S/O is very similar if we take, instead, the protosolar abundances of Lodders (2003). The results in the case of collisions with neutral hydrogen are very uncertain, because no de-excitation rates for collisions with neutral hydrogen exist. The curves in the bottom panel of Fig. 8 have been computed in the orbiting collision approximation (see Eq. (2.34) of Draine 2011).
For the density and temperature values that account for the observed [O i] 630.03/[O i] 557.79 ratios, the models predict ratios [S ii] 406.86/[O i] 630.03 ~ 0.2 − 0.5. This interval is shown by the dashed horizontal lines in the top panel and the dark-shaded region in the bottom panel. About 65% of the measured values (and 5/6 of those with both components) lie in this interval, only three objects have ratios higher than 0.5, while five measurements plus five upper limits are lower than 0.2. In the objects within the dark gray region, the strength of the [S ii] 406.86 line is therefore as expected if the three lines [O i] 630.03, [O i] 557.79 and [S ii] 406.86 are emitted by the same region and are the result of thermal processes, namely collisional excitation. We note also that this emitting region cannot be much ionized. As the oxygen ionization is coupled to that of hydrogen by charge exchange, an ionization fraction ne/nH ~ 0.5, for example, would shift all model predicted ratios upward by 0.3 dex, i.e., above the observed range. Moreover, if O ii/O i~ 0.5, the [O ii] 731.89 line should have an intensity comparable to that of the [O i] 557.79, while it is detected in very few objects (Table 1). Neither of these is a strong quantitative argument, but, all together, it seems likely that the LVC emitting region is mostly neutral in these objects.
Very few objects have ratios [S ii] 406.86/[O i] 630.03 greater than ~0.5; in these cases, it is possible that a significant fraction of oxygen is ionized. The highest ratio is observed in Sz106, where we also detect the [O ii] 372.60 and [N ii] 658.34 lines at roughly zero velocity, and it is likely an object where the forbidden line emission is dominated by a jet aligned with the plane of the sky, where the ionization fraction (and therefore the ratio O ii/O ) could be of 20−30% (Bacciotti & Eislöffel 1999). We note, however, that the large values of the observed [S ii] 406.86/[O i] 630.03 ratio (~1.6) requires an ionization fraction ne/nH ≳ 0.5.
 |
Fig. 9 Same as Fig. 7 for the ratio of the LVC [S ii] 673.08/[S ii] 406.86. The shaded region in the bottom panel shows the locus of the four detections in the upper panel (excluding the special cases of Par-Lup3-4 and SO587, see text), between the two dashed lines in the top panel. |
Observed [S ii] 406.86/[O i] 630.03 below ~0.2 are difficult to explain if the line emission is thermal, even when the rather large errors of the observed points are taken into account. One would need to assume that a significant fraction of sulfur is either neutral or doubly ionized, which seems unlikely, or that the temperature is significantly lower than 5000 K, which is inconsistent with the constraints obtained from the [O i] 557.79/[O i] 630.03 ratio. In these objects, it is possible that a dominant part of the O i emission is due to non-thermal processes, namely photodissociation of OH, as advocated for TW Hya by Gorti et al. (2011); we go back to this point in Sect. 7.2.
A LVC [S ii] 673.08 is detected in few GTO objects. This line has a critical density much lower than either the [S ii] 406.86 or the [O i] 630.03 lines and is relatively stronger in lower density regions. The top panel of Fig. 9 plots the [S ii] 673.08/[S ii] 406.86 ratio as function of Lacc, and the bottom panel of Fig. 9 the predictions of the models. The ratios tend to be higher than expected for the physical conditions that account for the [O i] 630.03/[O i] 557.79 and [S ii] 673.08/[O i] 630.03 intensity ratios, suggesting that a region of lower electron density (but still higher than ~ 105 cm-3) is emitting most of the [S ii] 673.08 line. The two sources with the highest ratios [S ii] 673.08/[S ii] 406.86 are Par-Lup3-4 and SO587, which we have already discussed.
6.4. Mass, momentum and volume
The analysis of the O i and S ii lines in the previous section indicates that in 65% of the objects, we have evidence that the emission is coming from a warm (T ~ 5000 − 10 000 K), dense (ne ≳ 106 cm-3), mostly neutral gas. Since the density is larger than the critical density, the mass of gas in the emitting region can be derived from the luminosity of any forbidden line and is only a function of the temperature. If we consider the [O i] 630.03 line, which is detected in the largest number of stars, it is ![\begin{equation} M_{\rm gas} = \mu m_{\rm H} {{L({\rm [\ion{O}{i}]\,630.03})}\over{j({\rm [\ion{O}{i}]\,630.03}) \,\alpha(\ion{O}{i})}} \end{equation}](/articles/aa/full_html/2014/09/aa24136-14/aa24136-14-eq106.png) (5)where μmH = 2 × 10-24 is the mean molecular weight of neutral gas, L([O i] 630.03) the line luminosity, j( [O i] 630.03) the line emissivity and α(O i) the fractional abundance of neutral oxygen. For T ~ 5000 − 10 000 K, in the high density limit j( [O i] 630.03) ranges from 1.2 × 10-16 to 1.1 × 10-15 erg s-1 per O i atom. Assuming an average value ~ 6 × 10-16 and that most oxygen is O i, Mgas is
(5)where μmH = 2 × 10-24 is the mean molecular weight of neutral gas, L([O i] 630.03) the line luminosity, j( [O i] 630.03) the line emissivity and α(O i) the fractional abundance of neutral oxygen. For T ~ 5000 − 10 000 K, in the high density limit j( [O i] 630.03) ranges from 1.2 × 10-16 to 1.1 × 10-15 erg s-1 per O i atom. Assuming an average value ~ 6 × 10-16 and that most oxygen is O i, Mgas is ![\begin{equation} M_{\rm gas} \sim 1.4 \times 10^{-11}~ M_\odot \left({{L({\rm [\ion{O}{i}]\,630.03})}\over{10^{-6}\, L_\odot}}\right)\cdot \end{equation}](/articles/aa/full_html/2014/09/aa24136-14/aa24136-14-eq114.png) (6)In the GTO sample, Mgas increases from ~ 1.4 × 10-12 for the lowest luminosity objects (L([O i] 630.03)/ L⊙= 10-7) to ~ 1.4 × 10-9 M⊙ for the objects with the strongest [O i] 630.03. The corresponding momentum, assuming a velocity Vpeak ~ 10 km s-1, goes from ~ 1.4 × 10-11 to ~ 1.4 × 10-8 M⊙ km s-1.
(6)In the GTO sample, Mgas increases from ~ 1.4 × 10-12 for the lowest luminosity objects (L([O i] 630.03)/ L⊙= 10-7) to ~ 1.4 × 10-9 M⊙ for the objects with the strongest [O i] 630.03. The corresponding momentum, assuming a velocity Vpeak ~ 10 km s-1, goes from ~ 1.4 × 10-11 to ~ 1.4 × 10-8 M⊙ km s-1.
The volume occupied by the emitting gas can also be derived from the line luminosity if the gas density is known: ![\begin{equation} Vol_{\rm gas} = \left({{L({\rm [\ion{O}{i}]\,630.03})}\over{n_{\rm H}\, j({\rm[\ion{O}{i}]\,630.03})\, \alpha(\ion{O}{i})}}\right)\cdot \end{equation}](/articles/aa/full_html/2014/09/aa24136-14/aa24136-14-eq121.png) (7)If electron collisions dominate the level excitation, we can derive a very conservative upper limit of nH ~ 108 cm-3, assuming ne ~ 107 cm-3 and an ionization fraction ~0.1. The minimum nH will be at least hundred times higher if atomic hydrogen collisions dominate. Therefore, Volgas ranges from ≳1.4 × 1037 cm3 for objects with L([O i] 630.03) ~ 10-7 L⊙ to ≳1.4 × 1040 cm3 when L([O i] 630.03) ~ 10-4 L⊙. This would translate to a linear dimension of 0.16 AU to 1.6 AU, assuming spherical geometry.
(7)If electron collisions dominate the level excitation, we can derive a very conservative upper limit of nH ~ 108 cm-3, assuming ne ~ 107 cm-3 and an ionization fraction ~0.1. The minimum nH will be at least hundred times higher if atomic hydrogen collisions dominate. Therefore, Volgas ranges from ≳1.4 × 1037 cm3 for objects with L([O i] 630.03) ~ 10-7 L⊙ to ≳1.4 × 1040 cm3 when L([O i] 630.03) ~ 10-4 L⊙. This would translate to a linear dimension of 0.16 AU to 1.6 AU, assuming spherical geometry.
The values of the mass of the dense, warm gas and the maximum values it occupies are plotted in Fig. 10 as functions of the mass of the central object.
 |
Fig. 10 Properties of the dense, warm gas as a function of the stellar mass for the GTO sample. Red dots are objects in Lupus, blue filled squares in σ Ori; arrows are objects with upper limits of the [O i] 630.03 luminosity, from which we derive the properties of the emitting region. The top panel plots the mass of the gas in the region, the bottom panel the upper limit to the volume, computed for an electron density ne = 107 cm-3, ionization fraction 0.1 (nH = 108 cm-3). In both panels we have assumed a line emissivity that is the average between the values for T = 10 000 K (1.1 × 10-15 erg s-1 per O i) and T = 5000 K (1.2 × 10-16 erg s-1 per O i) once ne ≫ ncr. |
7. Discussion
The low, blueshifted velocity of the LVC line peaks is the main indication of their origin in a wind, ejected from the disk surface with low velocity (see Hartigan et al. 1995). The quality of our spectra does not allow us to constrain the peak velocity to an accuracy better than ~ 10 km s-1, but the blue shifts are clearly detected in all lines, and we therefore discuss their properties in the context of the wind models.
7.1. Mass loss rate
The mass loss rate is the fundamental global quantity that characterizes the mass loss process and its impact on the disk evolution. All the existing estimates of Ṁloss have been derived for the HVC (Hartigan et al. 1995; see Cabrit 2002, for a discussion) and do not necessarily apply to the outflowing gas traced by the LVC emission, which can trace a different mechanism of mass loss.
In spite of the number of spectroscopic data on the LVC, deriving a meaningful mass loss rate is difficult, since different assumptions on the geometry of the ouflowing matter lead to very different estimates. A crude estimate of Ṁloss can be obtained by dividing the mass of the emitting region (Eq. (6)) by a timescale τ = L/v where L and v are measured along the flow direction. We assume v ~ Vpeak and the maximum value of the volume occupied by the emitting matter derived in Sect. 6.4. Values of Ṁloss obtained assuming an outflow spherical geometry are in the range ~ 2 × 10-11 − 10-9 M⊙/yr, approximately between 1 and 0.1 Ṁacc. If the outflow is launched from a disk area A in the vertical direction and has a cylindrical geometry, then L = Vol /A. We have considered two possibilities. The first is that the outflow is emitted by a disk annulus at a distance from the star such that the Keplerian velocity Vkepler = Vpeak; assuming an annulus width ΔR/R = 0.1, we find that L is typically 10 to 30 times less than before and Ṁloss≫Ṁacc. The second possibility, suggested by models of photoevaporative winds, is that the emitting region is at a distance from the star of ~ 1.8 (Mstar/ M⊙) AU (Alexander et al. 2014). In this case L and Ṁloss are similar to those obtained for spherical geometry.
In fact, it is likely that L is much larger than our estimates. If the flow velocity is not orthogonal to the disk, but has a large tangential component as in a conical wind, then L can be much larger and is defined by a change in the physical conditions, density in particular, that are traced by the forbidden lines we observe. A detailed study of high spectral and spatial resolution line profiles is needed to obtain an estimate of the mass loss rate of the slow wind component.
7.2. Wind models
MHD disk winds have been associated to the LVC of the TTS forbidden lines (Kwan & Tademaru 1995), because at their base, when the disk material becomes unbound, they have high density and low velocities (see, e.g., Ferreira et al. 2006; Suzuki & Inutsuka 2009; Bai & Stone 2013; Zanni & Ferreira 2013; Lesur et al. 2013; Fromang et al. 2013; Bai 2014; Kurosawa & Romanova 2012). It is, however, very difficult to estimate whether any of these models can explain the observed properties of the LVC emitting region derived in this paper or, even more, to use the observations to discriminate between the various mechanisms that can trigger an MHD wind and constrain the model parameters. In very few cases have the results of the MHD models and simulations been coupled with calculations of the temperature (Safier 1993a,b; Shang et al. 1998, 2002; Cabrit et al. 1999, 2007; Garcia et al. 2001; Pesenti et al. 2004; Pyo et al. 2003, 2006; Panoglou et al. 2012), and they generally focused on jet-tracing lines for luminous, highly accreting TTS.
Photoevaporative winds are also characterized by a high density, low velocity region at their base, and in recent years, they have been associated to the LVC of the forbidden lines. Models that take into account the effect of the extreme UV (EUV), X-ray, and FUV radiation on the disk have been computed by various groups, using different simplifications and making different choices for the parameters (Font et al. 2004; Hollenbach & Gorti 2009; Ercolano et al. 2009; Owen et al. 2010; Ercolano & Owen 2010). The results from different models still show large discrepancies, as discussed most recently by Alexander et al. (2014). In addition, a few models predict luminosities of the optical forbidden lines, with the exception of the [O i] 630.03 line and are limited to a narrow range of stellar, disk, and radiation field properties.
The largest set of line luminosity calculations is from Ercolano & Owen (2010), who computed the forbidden line luminosity expected in a photoevaporative wind around a star of 0.7 M⊙ due to the combined effect of EUV and X-ray photons (no FUV photons were included). They find that the optical forbidden lines are produced in a warm neutral gas with temperatures of 3000–5000 K, where collisions with atomic hydrogen control the level populations. For the highest Lx ~ 2 × 1030 erg/s, the line luminosity is ~ 10-5 L⊙ for the [O i] 630.03, [S ii] 406.86, and [S ii] 673.08, roughly as observed. However, the predicted [O i] 557.79 is about two orders of magnitude lower than observed. Ercolano & Owen point out that in their models the excitation of the upper level of the [O i] 557.79 transition is highly underestimated, since the collision rates with neutral hydrogen are unknown and could therefore not be included in their excitation calculations. The calculations of the [O i] 630.03/[O i] 557.79 ratios in Sect. 6.2, albeit with a very crude approximation for the neutral hydrogen collisional de-excitation rates of the O i  level, suggest that one needs a gas density nH ≳ 1010 − 1011 cm-3 for T ~ 7000 − 5000 K, conditions that do not seem to occur in the models. These models reproduce the small blue shift of the line peaks quite well, but tend to underestimate the line width, which, for the [O i] 630.03 line, is always predicted to be smaller than ~ 20 km s-1. Photoevaporative wind models by Hollenbach & Gorti (2009), which also include EUV and X-ray, but make different assumptions and approximations, give somewhat lower luminosity for the [O i] 630.03 line. However, for a very soft X-ray spectrum, L([O i] 630.03) ~ 10-5 L⊙ for log LX = 30.3 (as in Ercolano & Owen 2010). Hollenbach & Gorti (2009) do not compute any other optical forbidden line.
level, suggest that one needs a gas density nH ≳ 1010 − 1011 cm-3 for T ~ 7000 − 5000 K, conditions that do not seem to occur in the models. These models reproduce the small blue shift of the line peaks quite well, but tend to underestimate the line width, which, for the [O i] 630.03 line, is always predicted to be smaller than ~ 20 km s-1. Photoevaporative wind models by Hollenbach & Gorti (2009), which also include EUV and X-ray, but make different assumptions and approximations, give somewhat lower luminosity for the [O i] 630.03 line. However, for a very soft X-ray spectrum, L([O i] 630.03) ~ 10-5 L⊙ for log LX = 30.3 (as in Ercolano & Owen 2010). Hollenbach & Gorti (2009) do not compute any other optical forbidden line.
The effect of the FUV photons (both of accretion and chromospheric origin) has been discussed by Gorti & Hollenbach (2009) for a range of stellar masses. They do not predict the line spectrum but only the disk-integrated mass loss rate. More recent models by Owen et al. (2012) compare the results for two stellar masses (0.1 and 0.7 M⊙) and include FUV photons as well; also in this case, no line luminosities are computed. In these models, as long as the ratio FUV/X is small, the disk-integrated mass-loss rate is roughly proportional to the X-ray luminosity and has a very weak dependence on the stellar mass (Gorti & Hollenbach 2009). Assuming that also in these more realistic models the line luminosity is roughly proportional to LX, as in Ercolano & Owen (2010), one would expect a relation between, say, L([O i] 630.03) and LX, which is not seen (Fig. 11; see also Rigliaco et al. 2013). It is possible that, in fact, the FUV flux controls the wind temperature and that the gas mass in the wind with density and temperature high enough to emit the optical forbidden lines is higher for more luminous, more accreting stars. We cannot estimate whether this is indeed the case from the published results of Owen et al. (2012), but we think that it is a possibility that should be explored further.
 |
Fig. 11 Luminosity of the [O i] 630.03 line plotted as a function of X-ray luminosity, when available, for the GTO sample. Red dots are the Lupus objects, blue filled squares are objects in σ Ori. The X-ray luminosities were collected from the ROSAT observations by Krautter et al. (1997) for Lupus and from the XMM-Newton observations by Franciosini et al. (2006) for σ Ori. |
The difficulty of wind models to reproduce the LVC spectrum and, in particular, the strength of the [O i] 557.79 line pushed some authors to consider a different mechanism for exciting the OI levels other than collisions with electrons and/or hydrogen atoms, namely photodissociation of OH in the disk surface layers (Störzer & Hollenbach 2000; Acke et al. 2005; Rigliaco et al. 2013). The most detailed study of the LVC spectrum in a TTS has been carried out for TW Hya (Mstar~ 0.7 M⊙, Lstar~ 0.53 L⊙, Ṁacc~ 10-9 M⊙/yr) by Gorti et al. (2011) and Pascucci et al. (2011). TW Hya has L([O i] 630.03) ~ 1.1 × 10-5 L⊙, a ratio [O i] 630.03/[O i] 557.79 ~ 7, [S ii] 406.86/[O i] 630.03 ~ 0.13, and [S ii] 673.08/[S ii] 406.86 ≲ 0.13, so not very different from the results we find in the GTO stars. Gorti et al. (2011) models that include X-ray and FUV photons fail to reproduce the [O i] 557.79 observed luminosity, which leads the authors to conclude that the strongest contribution to the two O i lines comes from photodissociation of OH, taking place on the disk surface and that O i lines do not trace a wind component. Only 20% of the [O i] 630.03 line is due to thermal processes in the dust-depleted inner disk, where the [S ii] 406.86 line is also emitted. The predicted global ratio [S ii] 406.86/[O i] 630.03 ~ 0.5, is roughly consistent with the observations. Among TTS, TW Hya has rather unusual line profiles, with narrow lines (FWHM ~ 10 km s-1) centered at zero velocity (Pascucci et al. 2011), which may support an origin on the disk surface, rather than in an unbound flow (but see Owen et al. 2010). Also, the presence of the dust-depleted inner ragion of radius ~4 AU seems crucial to the Gorti et al. (2011) model results.
The [S ii] 406.86 line provides the strongest discriminant between the two modes of line excitation, since it can only be produced by collisional excitation of S ii. As discussed in Sect. 6.3, in 65% of the GTO stars, the luminosity of the three lines [O i] 630.03, [O i] 557.79, and [S ii] 406.86 is consistent with the emission expected in a high-density, warm, and neutral gas, where the lines are all thermally excited: a significant non-thermal contribution to the O i lines will reduce the [S ii] 406.86/[O i] 630.03 well below the observed values. In these objects at least, a non-thermal origin of the O i lines could be ruled out. There is, however, a small but not negligible fraction of objects (10 in total) with ratios [S ii] 406.86/[O i] 630.03 lower than predicted by thermal excitation, where models like that of TW Hya may apply. On the other hand, they do not seem to be exceptional in any way: they are distributed over the whole range of Lstar, Lacc and LX, and the line profiles are similar to those of the other objects, broad with slightly blueshifted peaks. Also, there is no evidence of an inner dust-depleted region similar to that in TW Hya except in a couple of cases (Rigliaco et al. 2012; Alcalá et al., in prep.).
An obvious caveat is in order, namely that the GTO spectra have relatively low spectral resolution. Any detailed analysis and firm conclusion require higher quality data to validate our assumption that all the lines are emitted by the same kinematical component. In view of its importance, it is interesting that in the past [S ii] 406.86 has not been searched for as extensively as the [O i] 630.03 line, even if one expects that their intensity should be similar.
7.3. Bound or unbound gas?
The small velocity shift of the peak of the optical forbidden lines and their large width is difficult to understand in any wind model. Rigliaco et al. (2013) suggest that in two rather luminous TTS for which they have very high spectral resolution profiles of the [O i] 630.03 line, the LVC can be deconvolved into two different components, one narrower and slightly blueshifted and one much broader and symmetric. The broad component, which contributes to ~40% of the line intensity, traces not unbound gas, but rather the emission coming from the inner region of the disk (a few tenths of AU), where the gas is gravitationally bound and in Keplerian rotation around the star. The narrow component, on the other hand, could trace outflowing gas, ejected farther out in the disk at the low velocity traced by the peak velocity shift.
This may be a general occurrence in TTS disks: Acke & van den Ancker (2006) propose a disk surface origin for the [O i] 630.03 line in HAe stars and in two cases convincingly derive the Keplerian rotation and the disk orientation from high-resolution (Δv ~ 4 km s-1) spectra. We note that, if the Rigliaco et al. (2013) hypothesis is true for all objects, there should be an anticorrelation between the width of the broad, symmetric LVC component, which tends to zero if the disk is seen face-on, and the velocity of the HVC, which is maximum for face-on disk, since the jet is then expected to be oriented in the direction of the observer. A detailed study of high-resolution profiles of the optical forbidden lines detected in the LVC of the GTO spectra, including the two [O i] 630.03, [O i] 557.79 and the [S ii] 406.86 lines, will also be very valuable from this point of view.
8. Summary and conclusions
We have examined the forbidden line spectrum of a sample of 44 low-mass TTS in the star forming regions Lupus and σ Ori. The spectra were obtained with X-shooter as a part of the Italian GTO and were analyzed by Alcalá et al. (2014) and Rigliaco et al. (2012) to derive stellar and accretion properties. All the GTO objects have a disk, as inferred from their IR excess emission, and are all accretors, with the exception of two stars in σ Ori, where only upper limits to Lacc have been measured.
We detected forbidden lines of O i, O ii, S ii, N i, and N ii in a number of stars. The line profiles show the presence of two components, one peaked close to zero velocity (LVC) and one with a large peak velocity shift (>40 km s-1) to the blue and/or to the red (HVC). The HVC was identified with the emission of a high velocity jet, while the origin of the LVC is uncertain (Hartigan et al. 1995).
We focused our analysis on the LVC. The most commonly observed line is the [O i] 630.03, which is detected in 38 out of 44 objects, followed by the other neutral oxygen line [O i] 557.79 and the [S ii] 406.86. In very few objects do we have clear evidence of [S ii] 673.08 LVC emission. Higher excitation lines are detected with small peak velocity shifts in a few objects, and they probably trace a jet oriented along the plane of the sky. The spectral resolution of the GTO X-shooter spectra (~30−60 km s-1) does not allow us to perform a detailed study of the gas kinematics. However, we can measure the shift of the line peak, which is a few km s-1 to the blue for all the lines we have studied, and the line width, which is of ~30−100 km s-1, with very few cases of unresolved lines. For our low-mass sample, we confirm the properties of the LVC previously observed in solar-mass TTS; the small blue shift of the line peaks, in particular, seem to indicate their origin in outflowing, low velocity matter, which we call a slow wind. We do not find any correlation between line profiles and stellar properties.
The GTO spectra show that slow winds are ubiquitous in Class II stars, i.e., in stars with circumstellar disks, independently of their stellar and/or accretion properties, down to the lowest mass stars in our sample (approximately 0.1 M⊙, Ṁacc~ 10-11 − 10-12 M⊙/yr. The slow wind, whose properties we derived from the analysis of the LVC of forbidden lines of O i and S ii, is prevalently neutral, dense (nH ≳ 108 cm-3), and warm (T ~ 5000 − 10 000 K). These physical conditions do not seem to depend on the stellar and/or accretion properties. However, the mass of this gas varies by several orders of magnitude, from ~ 10-12 M⊙ for the lowest mass stars in our sample to ~ 10-9 M⊙ for solar-mass TTS. This may be accounted for by an increase in the density and/or the volume of the emitting matter.
We note that in about 65% of the objects, the ratio of the [S ii] 406.86 to the [O i] 630.03 and [O i] 557.79 lines agrees with the predictions for a collisionally excited gas with the physical properties given above. This seems to rule out (at least in these objects) a non-thermal origin of the O i lines, as proposed by Hollenbach & Gorti (2009). However, in about 30% of the cases, where we measured a relatively low [S ii] 406.86 intensity, this remains a viable hypothesis.
Line luminosities are strongly correlated with the stellar luminosity and with Lacc. In the latter case, the relation is not linear, but has a slope of ~0.81 ± 0.09. That the line luminosities correlate equally well with Lstar and Lacc is not surprising, since these two quantities are themselves tightly correlated (Lacc∝Lstar1.53 ± 0.18). As a consequence, we cannot establish which of these two properties drives the correlation with the line luminosity.
The comparison with the prediction of outflow models is difficult and so far the origin of the slow TTS winds remains elusive. In this context, the derivation of the mass and minimum volume of the low velocity, dense, and warm outflowing gas over a wide range of stellar masses, luminosities and mass accretion rates in Sect. 6.4 could provide crucial tests for wind models, even when calculations of the ionization and excitation conditions are not available.
On the observational side, we note that higher quality spectra with higher spectral resolution and better sensitivity are necessary to confirm the results of our analysis and to derive the detailed kinematics and the origin of the line broadening (see, e.g., Rigliaco et al. 2013). Variability studies of the line profiles could also provide very valuable information on the ejection mechanisms.
Online material
Appendix A: Stellar properties
The stellar and accretion parameters for the GTO sample are listed in Table A.1 (see Alcalá et al. 2014; Rigliaco et al. 2012).
Stellar properties.
Appendix B: Line properties
Tables B.1–B.4 list the properties of the LVC, HVC blueshifted, and HVC redshifted components of the lines [O i] 557.79, [O i] 630.03, [O ii] 372.60, [O ii] 731.89, [S ii] 406.86, [S ii] 673.08, and [N ii] 658.34. For each component the tables give the intensity, the uncertainty, the velocity shift of the line peak, and the FWHM of the observed component. When not detected, we give 3σ upper limit for only the LVC.
Fluxes, velocity peak, and full width at half maximun of [O i] lines.
Fluxes, velocity peak, and full width at half maximun of [O ii] lines.
Fluxes, velocity peak, and full width at half maximun of [S ii] lines.
Fluxes, velocity peak, and full width at half maximun of [N ii] lines.
Appendix C: Examples of line profiles in selected objects
In this Appendix we show examples of the line profiles discussed in this paper.
 |
Fig. C.1 Normalized, continuum subtracted line profile of the [O i] 630.03 line. The profiles are shifted vertically for an easier display. |
 |
Fig. C.2 Normalized, continuum subtracted line profiles (as labeled) for the object Sz66. In this and the following figures the dashed colored curves show the LVC (green), HVC blueshifted (blue) and HVC redshifted (red); the total is given by the dotted (black) line. In this object, only the LVC is detected. |
 |
Fig. C.5 Same as Fig. C.2 for Sz88A. The two panels for the lines [N ii] 658.34 and [S ii] 673.08 illustrate typical non-detections. |
Acknowledgments
We are indebted to Bruce Draine for computing the line emissivities used in this work and to Francesca Bacciotti, Barbara Ercolano, Ilaria Pascucci, and Malcolm Walmsley for useful discussions. We thank V. D’Odorico, P. Goldoni and A. Modigliani for their help with the X-shooter pipeline, and F. Getman and G. Capasso for the installation of the different pipeline versions at Capodimonte. Financial support from INAF, under PRIN2013 programe “Disks, jets and the dawn of planets” is also acknowledged.
References
- Acke, B., & van den Ancker, M. E. 2006, A&A, 449, 267 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Acke, B., van den Ancker, M. E., & Dullemond, C. P. 2005, A&A, 436, 209 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alcalá, J. M., Stelzer, B., Covino, E., et al. 2011, Astron. Nach., 332, 242 [Google Scholar]
- Alcalá, J. M., Natta, A., Manara, C., et al. 2014, A&A, 561, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alexander, R., Pascucci, I., Andrews, S., Armitage, P., & Cieza, L. 2014 in Protostars and Planets VI (Tucson: University of Arizona Press), in press [arXiv:1311.1819] [Google Scholar]
- Appenzeller, I., & Bertout, C. 2013, A&A, 558, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asplund, M. 2005, ARA&A, 43, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Bacciotti, F., & Eislöffel, J. 1999, A&A, 342, 717 [NASA ADS] [Google Scholar]
- Bacciotti, F., Whelan, E. T., Alcalá, J. M., et al. 2011, ApJ, 737, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Bai, X. 2014, ApJ, submitted [arXiv:1402.7102B] [Google Scholar]
- Bai, X., & Stone, J. 2013, ApJ, 769, 76B [NASA ADS] [CrossRef] [Google Scholar]
- Banzatti, A., Meyer, M. R., Manara, C. F., Pontoppidan, K. M., & Testi, L. 2014, ApJ, 780, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Cabrit, S. 2002, Star Formation and the Physics of Young Stars, eds. J. Bouvier, & J.-P. Zahn (Les Ulis: EDP Sciences), 147 [Google Scholar]
- Cabrit, S., Ferreira, J., & Raga, A. C. 1999, A&A, 343, 61 [Google Scholar]
- Cabrit, S., Codella, C., Gueth, F., et al. 2007, A&A, 468, 29 [Google Scholar]
- Comerón, F., Fernández, M., Baraffe, I., Neuhäuser, R., & Kaas, A. 2003, A&A, 406, 1001 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Draine, B. T. 2011, Physics of the Interstellar and Intergalactic Medium (Princeton University Press) [Google Scholar]
- Dutrey, A., Semenov, D., Chapillon, E., et al. 2014 in Protostars and Planets VI (Tucson: University of Arizona Press), in press [arXiv:1402.3503] [Google Scholar]
- Ercolano, B., & Owen, J. E. 2010, MNRAS, 406, 1553 [NASA ADS] [Google Scholar]
- Ercolano, B., Clarke, C. J., & Drake, J. J. 2009, ApJ, 699, 1639 [NASA ADS] [CrossRef] [Google Scholar]
- Feigelson, E. D., & Nelson, P. I. 1985, ApJ, 293, 192 [NASA ADS] [CrossRef] [Google Scholar]
- Ferreira, J. 2013, EAS Publ. Ser., 62, 16 [CrossRef] [EDP Sciences] [Google Scholar]
- Ferreira, J., Dougados, C., & Cabrit, S. 2006, A&A, 453, 785 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Font, A. S., McCarthy, I. G., Johnstone, D., & Ballantyne, D. R. 2004, ApJ, 607, 890 [NASA ADS] [CrossRef] [Google Scholar]
- Franciosini, E., Pallavicini, R., & Sanz-Forcada, J. 2006, A&A, 446, 501 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frank, A., Ray, T. P., Cabrit, S., et al. 2014 in Protostars and Planets VI (Tucson: University of Arizona Press), in press [arXiv:1402.3553] [Google Scholar]
- Fromang, S., Latter, H., Lesur, G., & Ogilvie, G. I. 2013, A&A, 552, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garcia, P. J. V., Cabrit, S., Ferreira, J., & Binette, L. 2001, A&A, 377, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giannini, T., Nisini, B., Antoniucci, A., et al. 2013, ApJ, 778, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Gorti, U., & Hollenbach, D. 2009, ApJ, 705, 1237 [NASA ADS] [CrossRef] [Google Scholar]
- Gorti, U., Hollenbach, D., Najita, J., & Pascucci, I. 2011, ApJ, 735, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Gullbring, E., Hartmann, L., Briceño, C., & Calvet, N. 1998, ApJ, 492, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Hartigan, P., Edwards, S., & Ghandour, L. 1995, ApJ, 452, 736 [NASA ADS] [CrossRef] [Google Scholar]
- Herczeg, G., & Hillenbrand, L. A. 2008, ApJ, 681, 594 [NASA ADS] [CrossRef] [Google Scholar]
- Herczeg, G., & Hillenbrand, L. A. 2014, ApJ, 786, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Hollenbach, D., & Gorti, U. 2009, ApJ, 703, 1203 [NASA ADS] [CrossRef] [Google Scholar]
- Ingleby, L., Calvet, N., Herczeg, G., et al. 2013, ApJ, 767, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Krautter, J., Wichmann, R., Schmitt, J. H. M. M., et al. 1997, A&AS, 123, 329 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kurosawa, R., & Romanova, M. M. 2012, MNRAS, 426, 290 [Google Scholar]
- Kwan, J., & Tademaru, E. 1995, ApJ, 454, 382 [NASA ADS] [CrossRef] [Google Scholar]
- Lesur, G., Ferreira, J., & Ogilvie, G. I. 2013, A&A, 550, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lodders, Katharina 2003, ApJ, 591, 1220 [NASA ADS] [CrossRef] [Google Scholar]
- Manara, C., Testi, L., Rigliaco, E., et al. 2013, A&A, 551, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- O’dell, C. R., & Wen, Z. 1994, ApJ, 436, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Owen, J. E., Ercolano, B., Clarke, C. J., & Alexander, R. D. 2010, MNRAS, 401, 1415 [NASA ADS] [CrossRef] [Google Scholar]
- Owen, J. E., Clarke, C. J., & Ercolano, B. 2012, MNRAS, 422, 1880 [NASA ADS] [CrossRef] [Google Scholar]
- Panoglou, D., Cabrit, S., Pineau Des Forets, G., et al. 2012, A&A, 538, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pascucci, I., & Sterzik, M. 2009, ApJ, 702, 724 [NASA ADS] [CrossRef] [Google Scholar]
- Pascucci, I., Sterzik, M., Alexander, R. D., et al. 2011, ApJ, 736, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Pesenti, N., Dougados, C., Cabrit, S., et al. 2004, A&A, 416, 9 [Google Scholar]
- Pyo, T., Kobayashi, N., Hayashi, M., et al. 2003, ApJ, 590, 340 [NASA ADS] [CrossRef] [Google Scholar]
- Pyo, T., Hayashi, M., Kobayashi, N., et al. 2006, ApJ, 649, 836 [NASA ADS] [CrossRef] [Google Scholar]
- Rigliaco, E., Natta, A., Randich, S., & Sacco, G. 2009, A&A, 495, 13 [Google Scholar]
- Rigliaco, E., Natta, A., Testi, L., et al. 2012, A&A, 548, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rigliaco, E., Pascucci, I., Gorti, U., Edwards, S., & Hollenbach, D. 2013, ApJ, 772, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Safier, P. N. 1993a, ApJ, 408, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Safier, P. N. 1993b, ApJ, 408, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Shang, H., Shu, F. H., & Glassgold, A. E. 1998, ApJ, 493, 91 [Google Scholar]
- Shang, H., Glassgold, A. E., Shu, F. H., & Lizano, S. 2002, ApJ, 564, 853 [NASA ADS] [CrossRef] [Google Scholar]
- Störzer, H., & Hollenbach, D. 2000, ApJ, 539, 751 [NASA ADS] [CrossRef] [Google Scholar]
- Suzuki, T. K., & Inutsuka, S. 2009, ApJ, 691, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, N. J., Fromang, S., Gammie, C., et al. 2014, in Protostars and Planets VI (Tucson: University of Arizona Press), in press [arXiv:1401.7306] [Google Scholar]
- Vernet, J., Dekker, H., D’Odorico, S., et al. 2011, A&A, 536, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zanni, C., & Ferreira, J. 2013, A&A, 550, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Accretion luminosity (top) and stellar mass (bottom) distribution. Red histogram for stars in Lupus, blue for stars in σ Ori. |
| In the text | |
 |
Fig. 2 Lacc as function of Lstar for objects in Lupus (red dots) and σ Ori (filled blue squares). Open green squares plot the Taurus TTS of Gullbring et al. (1998); black diamonds the results of Herczeg & Hillenbrand (2008). The black line shows the best-fitting relation (GTO objects only) with slope 1.53; dashed lines are the locus Lacc/Lstar = 1, 0.1, 0.01 from top to bottom, respectively. |
| In the text | |
 |
Fig. 3 Distribution of the peak velocity shift with respect to the star (solid for LVC, hatched blue for HVC-blue, red for HVC-red) for different lines, as labeled. |
| In the text | |
 |
Fig. 4 Ratio of the HVC to the LVC intensity in objects where both components are simultaneously detected. The bottom panel refers to the [O i] 630.03 lines; the top panel to the [S ii] 406.86| and [S ii] 673.08 lines, as labeled. Red and blue stand for Lupus and σ Ori, as before. |
| In the text | |
 |
Fig. 5 Line luminosities for [O i] 630.03 and [O i] 557.79 are plotted as functions of the stellar luminosity (left panels) and of the accretion luminosity (right panels). Red filled dots are the Lupus objects, blue filled squares are objects in σ Ori, arrows show 3σ upper limits. The black crosses show the same quantities for the strongly accreting TTS DR Tau at different epochs (Banzatti et al. 2014). Black diamonds are values for Taurus very low-mass objects from Herczeg & Hillenbrand (2008, 2014, see text); green open squares denote Taurus TTS from Gullbring et al. (1998) and Hartigan et al. (1995), as described in the text. A few objects discussed in Sect. 6.2 are only labeled in some panels, to avoid confusion. Black lines show the relations derived in Eqs.(1)–(4) for the GTO sample. |
| In the text | |
 |
Fig. 6 Line luminosities for the [S ii] 406.86 and [S ii] 673.08 lines are plotted as functions of the stellar luminosity (left panels) and of the accretion luminosity (right panels). Red dots are the Lupus objects, blue filled squares are objects in σ Ori, arrows show 3σ upper limits. Green open squares show the position of Taurus TTS from Gullbring et al. (1998) and Hartigan et al. (1995), as described in the text. |
| In the text | |
 |
Fig. 7 Top panel: ratio [O i] 557.79/[O i] 630.03 as function of Lacc for stars in Lupus (red dots) and σ Ori (filled blue squares). Arrows indicate 3σ upper limits. Objects where both a LVC and a HVC are detected are marked by large open circle. Black crosses show the values for the set of DR Tau spectra obtained at different epochs, and green open squares are stars in Taurus (see text). Bottom panel: model predictions for collisions with electron (solid curves) and with hydrogen atoms (dashed curves). Different curves refer to different temperatures in units of 104 K, as labeled. The ne scale is shown in the bottom axis, that for nH on the top axis. The gray area shows the location of the observed values, marked by the two dashed lines in the top panel. |
| In the text | |
 |
Fig. 8 Same as Fig. 7 for the ratio [S ii] 406.86/[O i] 630.03. In the bottom panel, the dark-gray area shows the location of 65% of the observed values (dashed lines in the top panel). Three points lie in the upper light-gray area, the rest in the lower light-gray one (dotted lines in the top panel). |
| In the text | |
 |
Fig. 9 Same as Fig. 7 for the ratio of the LVC [S ii] 673.08/[S ii] 406.86. The shaded region in the bottom panel shows the locus of the four detections in the upper panel (excluding the special cases of Par-Lup3-4 and SO587, see text), between the two dashed lines in the top panel. |
| In the text | |
 |
Fig. 10 Properties of the dense, warm gas as a function of the stellar mass for the GTO sample. Red dots are objects in Lupus, blue filled squares in σ Ori; arrows are objects with upper limits of the [O i] 630.03 luminosity, from which we derive the properties of the emitting region. The top panel plots the mass of the gas in the region, the bottom panel the upper limit to the volume, computed for an electron density ne = 107 cm-3, ionization fraction 0.1 (nH = 108 cm-3). In both panels we have assumed a line emissivity that is the average between the values for T = 10 000 K (1.1 × 10-15 erg s-1 per O i) and T = 5000 K (1.2 × 10-16 erg s-1 per O i) once ne ≫ ncr. |
| In the text | |
 |
Fig. 11 Luminosity of the [O i] 630.03 line plotted as a function of X-ray luminosity, when available, for the GTO sample. Red dots are the Lupus objects, blue filled squares are objects in σ Ori. The X-ray luminosities were collected from the ROSAT observations by Krautter et al. (1997) for Lupus and from the XMM-Newton observations by Franciosini et al. (2006) for σ Ori. |
| In the text | |
 |
Fig. C.1 Normalized, continuum subtracted line profile of the [O i] 630.03 line. The profiles are shifted vertically for an easier display. |
| In the text | |
 |
Fig. C.2 Normalized, continuum subtracted line profiles (as labeled) for the object Sz66. In this and the following figures the dashed colored curves show the LVC (green), HVC blueshifted (blue) and HVC redshifted (red); the total is given by the dotted (black) line. In this object, only the LVC is detected. |
| In the text | |
 |
Fig. C.3 Same as Fig. C.2 for Sz69. |
| In the text | |
 |
Fig. C.4 Same as Fig. C.2 for Sz73. |
| In the text | |
 |
Fig. C.5 Same as Fig. C.2 for Sz88A. The two panels for the lines [N ii] 658.34 and [S ii] 673.08 illustrate typical non-detections. |
| In the text | |
 |
Fig. C.6 Same as Fig. C.2 for Sz99. |
| In the text | |
 |
Fig. C.7 Same as Fig. C.2 for Sz100. |
| In the text | |
 |
Fig. C.8 Same as Fig. C.2 for Sz106. |
| In the text | |
 |
Fig. C.9 Same as Fig. C.2 for Sz113. Note that the [O i] 557.79 is a 3σ detection. |
| In the text | |
 |
Fig. C.10 Same as Fig. C.2 for SO848. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


