| Issue |
A&A
Volume 675, July 2023
|
|
|---|---|---|
| Article Number | A153 | |
| Number of page(s) | 22 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202346543 | |
| Published online | 14 July 2023 | |
PENELLOPE
IV. A comparison between optical forbidden lines and H2 UV lines in the Orion OB1b and σ-Ori associations★
1
ASI, Italian Space Agency,
Via del Politecnico snc,
00133
Rome, Italy
e-mail: manuele.gangi@asi.it
2
INAF – Osservatorio Astronomico di Roma,
Via Frascati 33,
00078
Monte Porzio Catone, Italy
3
European Southern Observatory,
Karl-Schwarzschild-Strasse 2,
85748
Garching bei München, Germany
4
Laboratory for Atmospheric and Space Physics, University of Colorado Boulder,
Boulder, CO
80303, USA
5
Kavli Institute for Astronomy and Astrophysics, Peking University,
Yiheyuan 5, Haidian Qu,
100871
Beijing, PR China
6
Department of Astronomy, Peking University,
Yiheyuan 5, Haidian Qu,
100871
Beijing, PR China
7
INAF – Osservatorio Astronomico di Capodimonte –
Salita Moiariello 16,
80131
Napoli, Italy
8
INAF – Osservatorio Astrofisico di Catania,
Via S. Sofia 78,
95123
Catania, Italy
9
Konkoly Observatory, Research Centre for Astronomy and Earth Sciences, Eötvös Loránd Research Network (ELKH),
KonkolyThege Miklós út 15–17,
1121
Budapest, Hungary
10
CSFK, MTA Centre of Excellence,
Konkoly-Thege Miklos út 15–17,
1121
Budapest, Hungary
11
SETI Institute,
339 Bernardo Ave, Suite 200,
Mountain View, CA
94043, USA
12
Hamburg Observatory,
Gojenbergsweg 11,
21029
Hamburg, Germany
13
Max Planck Institute for Astronomy,
Königstuhl 17,
69117
Heidelberg, Germany
14
ELTE Eötvös Loránd University, Institute of Physics,
Pázmány Péter sétány 1/A,
1117
Budapest, Hungary
15
INAF – Osservatorio Astronomico di Padova,
Vicolo dell'osservatorio 5,
35122
Padova, Italy
16
National Astronomical Research Institute of Thailand (NARIT),
Sirindhorn AstroPark, 260 Moo 4, T. Donkaew, A. Maerim,
Chiangmai
50180, Thailand
Received:
30
March
2023
Accepted:
28
May
2023
Context. Observing the spatial distribution and excitation processes of atomic and molecular gas in the inner regions (<20 au) of young (<10 Myr) protoplanetary disks helps us to understand the conditions for the formation and evolution of planetary systems.
Aims. In the framework of the PENELLOPE and ULLYSES projects, we aim to characterize the atomic and molecular component of protoplanetary disks in a sample of 11 classical T Tauri stars of the Orion OB1 and σ-Orionis associations.
Methods. We analyzed the flux-calibrated optical forbidden lines and the fluorescent ultraviolet H2 progressions using spectra acquired with ESPRESSO at VLT, UVES at VLT, and HST-COS. Line morphologies were characterized through Gaussian decomposition. We then focused on the properties of the narrow low-velocity (full width half maximum <40 km s−1 and |υp| < 30 km s−1) component (NLVC) of the [O I] 630 nm line and compared them with those of the UV-H2 lines.
Results. We found that the [O I]630 NLVC and the UV-H2 lines are strongly correlated in terms of peak velocities, full width at half maximum values, and luminosity. Assuming that the line width is dominated by Keplerian broadening, the [O I]630 NLVC originates from a disk region between 0.5 and 3.5 au, while that of UV-H2 originates in a region from 0.05 to 1 au. The luminosities of [O I]630 NLVC and UV-H2 correlate with an accretion luminosity with a similar slope, as well as with the luminosity of the C IV154.8, 155 nm doublet. We discuss such correlations in the framework of the currently suggested excitation processes for the [O I]630 NLVC.
Conclusions. Our results can be interpreted in a scenario in which the [O I]630 NLVC and UV-H2 have a common disk origin with a partially overlapped radial extension. We also suggest that the excitation of the [O I] NLVC is mainly induced by stellar far-ultraviolet continuum photons, than being of mostly thermal origin. This study demonstrates the potential of contemporaneous wide-band highresolution spectroscopy in linking different tracers of protoplanetary disks.
Key words: stars: pre-main sequence / stars: winds, outflows / techniques: spectroscopic
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Protoplanetary disks of young stellar objects (YSOs) are the birth site of planets. They undergo important processes that lead to mass accretion onto the star, ejection of outflows, and photoevap-orated disk winds (Hartmann et al. 2016; Ercolano & Pascucci 2017; Pascucci et al. 2022). Together, these processes affect the disk dissipation on timescales of a few million years (see review by Manara et al. 2022). In this framework, the composition and spatial distribution of atomic and molecular gas in the inner regions (i.e., with a spatial extension of a few astronomical units) of protoplanetary disks are some of the key ingredients for the formation and evolution of planetary systems.
The atomic protoplanetary disk components can be spec-troscopically traced by atomic or weakly ionized forbidden lines in the optical and infrared spectral range. These lines usually present a composite profile, with high-velocity components (HVCs; |υp| > 30 km s−1) attributed to extended colli-mated jets and low-velocity components (LVCs; |υp| < 30 km s−1) associated with compact (0.5–l0 au) protoplanetary disk winds (e.g., Hartigan et al. 1995). When observed at medium- or high-spectral resolution, the LVC often shows a contribution from a broad LVC (BLVC), having a full width at half maximum (FWHM) greater than 40 km s−1, and a narrow LVC (NLVC; FWHM <40 km s−1, e.g., Rigliaco et al. 2013; Simon et al. 2016; Banzatti et al. 2019; Giannini et al. 2019; Gangi et al. 2020). On the other hand, the molecular content in the inner disk region (<10 au) can be characterized through specific emission and absorption bands, such as those of H2, CO, H2O, and OH, observed from the UV to the IR spectral range (e.g., Najita et al. 2007; France et al. 2012; Banzatti et al. 2022).
One of the open questions concern the excitation mechanism of the oxygen LVC. Thermal excitation of atomic oxygen (i.e., collisional excitation with hydrogen atoms or electrons) was suggested as the major mechanism for the line emissions (e.g., Hartigan et al. 1995). Indeed, the [OI]5571/[OI]630 and [S II]406/[O I]630 line ratios are usually interpreted in terms of diagnostic models involving collisionally excited processes in order to set constraints on gas temperature and density (e.g., Natta et al. 2014; Giannini et al. 2015, 2019; Fang et al. 2018). This scenario is classically supported by the fact that the kinematic components of the [S II]406 line are found to be similar to those of the [O I]630 and the [S II]406 lines are collision-ally excited (e.g., Fang et al. 2018). However, the large spread observed in the [OI]557/[O I]630 and [S II]406/[O I]630 line ratios also suggest nonthermal contributions (e.g., Rigliaco et al. 2013; Nisini et al., in prep.).
A nonthermal contribution to the excitation of O may arise from the action of far-ultraviolet (FUV) photons (1400–1700 Å) through two distinct processes: (i) photodissociation of the OH molecule (Gorti et al. 2011; Rigliaco et al. 2013) and (ii) FUV pumping (Nemer et al. 2020). In the first process, OH molecules can be dissociated into the 1D and 1S fine-structure levels of the ground state of O by FUV photons reaching the disk surface. They eventually decay to the fundamental level along the [O I]630 and [O I]557 transitions. As pointed out by Rigliaco et al. (2013), this photodissociated layer may have both a bound component in Keplerian rotation and an unbound component at larger scales (≥10 au), making it kinematically indistinguishable from a photoevaporative wind. Regarding the second case, FUV pumping consists of excitation to higher O levels by absorption of FUV photons, with a subsequent cascade of radiative or col-lisional de-excitations toward the upper levels of the [O I] lines. Nemer et al. (2020) found that this process can appreciably contribute to the excitation of the [O I]557 and [O I]630 lines both in X-ray driven photoevaporative wind models (Owen et al. 2010) and in magnetothermal models (Wang et al. 2019), dominating the lines emission by as much as 90%. Along with stellar UV photons, an additional source of excitation may arise in the so-called external photoevaporative winds (e.g., Winter & Haworth 2022, and references therein) where the action of UV-dominated irradiation from close members of the star-forming region, such as OB stars, can contribute to the dissociation of OH. This would lead to an important increase of the [O I]630 line luminosity, as recently discussed in Ballabio et al. (2023).
From an observational point of view, the role of the aforementioned processes can be investigated by linking together the properties of the [O I] LVC and those of the dipole-allowed electronic transitions of the H2 molecules in the UV (hereafter, UV-H2). The UV-H2 are in fact photo-excited by Lyα photons (e.g., France et al. 2012), and therefore they can be used as an indirect probe of the role that an FUV continuum field may have in exciting the O species. This multiwavelength approach requires medium- or high-resolution spectroscopic investigation of large samples of YSOs as well as a wide and simultaneous spectral coverage from the UV to the NIR range. The simultaneity between different spectral bands is essential in order to avoid biases induced by variability.
In this framework, the Hubble Space Telescope (HST) Director's Discretionary Time ULLYSES program (Roman-Duval et al. 2020) is devoted to acquiring UV spectra for about 70 low-mass (~0.1–2M⊙) YSOs with ages from 1 to 10 Myr. This project is flanked by the public ESO VLT large program PENELLOPE (Manara et al. 2021), which obtains contemporaneous high-resolution optical and NIR spectra. With contemporaneous observations that minimize the spectral changes caused by variability, these complementary surveys offer a once-in-a-lifetime opportunity to make significant advances in the study of the physics of low-mass YSOs.
In this work, we add new observational constraints on the O excitation mechanism by comparing the properties of optical forbidden lines with those of the UV-H2 in a sample of 11 classical T Tauri stars (CTTs) observed in the framework of the ULLYSES and PENELLOPE collaborations. This is the first study on the PENELLOPE series devoted to the analysis of forbidden lines, and it is based on the sample of the Orion star-forming region (SFR) presented in Manara et al. (2021). The forbidden line properties of the other SFRs observed within the ULLYSES and PENELLOPE collaborations will be analyzed in forthcoming works. The paper is organized as follows. In Sect. 2, we present the sample and the data, while the analysis of the optical and UV spectra is reported in Sect. 3. Results are shown in Sect. 4, and the correlations between the properties of the different lines are reported in Sect. 5. A discussion and our conclusions are presented in Sects. 6 and 7, respectively.
2 Targets and data
Our sample consists of eight CTTs of the Orion OB1 and three CTTs of the σ-Orionis associations. Spectra from the FUV to the NIR were acquired from the framework of the PENELLOPE Large Program and the ULLYSES public survey. The list of the sources and their basic stellar and accretion parameters, characterized in Manara et al. (2021)2, are reported in Table 1. Masses are in the range between 0.25 and 1.09 M⊙, spectral types are between M0.5 and K7, and luminosities are between 0.13 and 3.61 L⊙.
For each target in this work, we used three high-resolution ESPRESSO (R = 140 000; λ 380–788 nm, Pepe et al. 2021) or UVES (R = 70 000, λ ~ 330–450, 480–680 nm, Dekker et al. 2000) spectra that were acquired with a one-day cadence and a contemporaneous flux-calibrated medium-resolution X-Shooter (R = 5400–18 400; λ ~ 300–2500 nm; Vernet et al. 2011) spectrum. We also included mediumresolution (R ~ 15 000) COS spectra acquired with HST and covering the FUV region (136 nm < λ < 177 nm).
Details on the observational strategy, standard data reduction, and analysis are reported in Manara et al. (2021) and Espaillat et al. (2022). In the following section, we describe the method used in this work.
List of sources with their stellar and accretion properties, and disk inclination when available.
Relevant parameters of the observed atomic lines.
3 Data analysis
3.1 Optical spectra
We focused on the five brightest optical forbidden transitions: the [O I] lines at 630 and 557 nm, the [S II] lines at 673 and 406 nm, and the [N II] lines at 658 nm. Their relevant atomic parameters retrieved from the NIST3 database are summarized in Table 2.
For each epoch, we retrieved the five UVES/ESPRESSO spectral segments (~100 Å larger) containing the emission profiles. The photospheric contribution was subtracted by the PENELLOPE collaboration, as described in Manara et al. (2021). We first corrected spectral segments for the radial velocity computed by Manara et al. (2021) through cross-correlation of appropriate template and target spectrum. The typical estimated wavelength accuracy of our calibration is about 0.5 km s−1. Each spectral profile was then normalized to the local continuum and flux calibrated on the basis on the local continuum extracted from the contemporaneous medium-resolution X-Shooter spectra. After checking that the multi-epoch profiles showed no appreciable line variability, we obtained the final profiles as the median of the available multi-epochs spectra. This allowed us to increase the signal-to-noise ratio to a sufficient level for the morphological analysis in the majority of cases.
Gaussian decomposition was performed employing an IDL procedure to fit multicomponent optical and infrared high-resolution profiles (Gangi et al. 2020, 2021). In short, this procedure is based on χ2 minimization and provides the width, peak velocity, and peak intensity values for each component. The total number of components was determined following the criteria adopted in Banzatti et al. (2019; i.e., the minimum number of Gaussians that yields a χ2 stable at 20% of its minimum value). To estimate the errors of the fit parameters, we simulated 104 data sets for each profile using random Gaussian distributions. In particular, the observed spectral points was set as the central value, and the standard deviation was the local S/N. Each simulated profile was then decomposed, and the errors were determined as the sigma of the fit parameter distributions. To limit the high level of degeneracy involved in this kind of analysis, we first applied the procedure to the highest S/N line profile for each star, namely [O I]630. We then used the obtained kinematic solutions as initial parameters for the decomposition of the other lines, since it is known that individual kinematic components share similar profiles among the different forbidden lines (e.g., Fang et al. 2018). Although this approach has significantly reduced the level of degeneracy, the high noise present in these profiles made it impossible to distinguish between BLVCs and NLVCs in most cases. We therefore note that a direct comparison with the respective low-velocity [O I]630 components must be taken with caution.
The FWHMs were deconvolved by instrumental width, σinstr, assuming a Gaussian profile with σinstr = 0.09 Å for UVES and σinstr = 0.04 Å for ESPRESSO. Finally, for each component, we derived the line flux and luminosity corrected for extinction, assuming the extinction coefficient (Av) values computed by Manara et al. (2021), and reported here in Table 1 for completeness, and the reddening law by Cardelli et al. (1989), with Rv = 3.1. In cases where a line was not detected, we estimated a 3-σ upper limit as 3× RMS ×Δλ, with RMS as the local flux noise and Δλ as the expected line width. The latter was estimated from the other detected lines, and the typical values ranged from 1 to 4 Å.
 |
Fig. 1 Example of H2 [1,4] (left) and H2 [1,7] (right) progression line profiles. The averaged profile is indicated in black. Flux units are 10−15 erg−1 cm−2 Å−1. |
3.2 Ultraviolet spectra
We restricted our analysis to the four brightest H2 emission lines in both of the progressions [υ′,J′] = [1,7] and [1,4], for a total of eight lines detected in all of the sources (Table 3). We corrected spectral profiles for the radial velocity, adopting the values reported by Manara et al. (2021). Peak velocities were found to be roughly consistent with stellar velocities, with differences well below the wavelength solution accuracy of COS (~15 km s−1). For each progression, we averaged the four spectral profiles, obtaining single lines to which we refer to as H2 [1,4] and H2 [1,7] (Fig. 1).
We performed a Gaussian fit of the profiles, taking into account the line broadening introduced by the COS line-spread-function (LSF). The LSF depends on both the telescope position and the wavelength range of the observation4, and it is approximately a Lorentzian profile. In addition to the instrumental broadening, broad LSF wings can substantially alter the line profile and mimic a BLVC. For this reason, it was particularly important to correct for this contribution. To do so, we followed the approach of France et al. (2012), in which a Gaussian component with infinite resolution is convolved with the appropriate LSF. We chose the COS LSF G160M/1611 corresponding to the telescope LifeTime position 4, and we averaged the LSFs at 1467, 1500, 1524, and 1556Å for the H2[1,7] line profile and those at 1431, 1446, 1489, and 1504Å for the H2[1,4] line profile. For each averaged profile, we then derived the peak intensity, FWHM, and peak velocity.
Finally, from a given progression, we computed the total line flux as
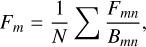 (1)
(1)
where Fmn is the integrated flux of the specific line from the rovibrational state m to the electronic state n, Bmn is the corresponding branching ratio, and N is the number of emission lines of the progression (France et al. 2012). Individual line fluxes (Fmn) were corrected for the extinction using the Av reported in Manara et al. (2021) and assuming the extinction law of Whittet et al. (2004) toward HD29647. The latter was shown to be better suited for use in the near-ultraviolet range than the law of Cardelli et al. (1989), in the case of Orion OB1 (Pittman et al. 2022). The total line fluxes were then converted into luminosity by adopting the distances reported in Table 1.
Relevant parameters of the observed molecular lines.
 |
Fig. 2 Example of Gaussian decomposition. The continuum-subtracted forbidden line profiles are shown with black lines. In blue, we have plotted the fit to the profile, while individual components are shown with red lines. Flux units are 10−15 erg−1 cm−2 Å−1. For each panel, the target name and line diagnostics are indicated. The complete sample is reported in Fig. A.1. |
 |
Fig. 3 Example of Gaussian fitting of continuum-subtracted H2 [1,4] and [1,7] averaged line profiles. Flux units are l0−15 erg−1 cm−2 Å−1. For each panel, the target name and line profile are indicated. The complete sample is reported in Figs. A.2 and A.3. |
4 Results
Figures 2 and 3 show examples of the observed atomic and H2 lines and their Gaussian analysis for the CVSO58 source, while the complete sample is reported in Figs. A.1, A.2 and A.3. Fitted parameters (i.e., peak velocity, FWHM, flux, and luminosity) are reported in Tables A.2 and A.1.
4.1 Detection statistics
The UV-H2 lines were detected in all the sources; their profiles can be always reproduced with a single Gaussian component, the current spectral resolution, and S/N. In contrast, the optical forbidden lines presented composite profiles where components at different velocities and FWHMs could be identified, which is in line with previous similar studies. A detailed view of the different detected components is reported in Table 4. In short, the two [O I] lines were detected in all the sources, with [O I]630 as the most structured one. The [O I] lines always show LVCs that peak at a velocity of zero, except in the case of four sources that showed slightly blueshifted values compatible with slow disk winds.
The [S II]637 and [S II]406 lines were detected in eight and nine sources out of eleven, respectively. Compared to the [O I] lines, the [S II] HVCs were detected more often, a behavior already observed in high excitation or ionization lines (e.g., Natta et al. 2014). Finally, the [N II]658 line was detected in four sources and only in the HVCs, as expected given the high ioniza-tion needed to have an appreciable N II abundance (e.g., Nisini et al., in prep.).
Detection of kinematical components drawn from Gaussian decomposition.
4.2 Line ratios
In this section, we investigate the line luminosity ratios under the assumption that the emission of the atomic components have a thermal origin. Figure 4 shows the diagnostic diagrams of line luminosity ratios based on the excitation model of Giannini et al. (2015, 2019). The model assumes an NLTE approximation for the line emission, with the population of levels determined by assuming equilibrium between collisional excitation and de-excitation with electrons and radiative decay. Different curves correspond to different temperatures, as labeled, while the range of ratios computed from the extinction-corrected LVCs luminosities are depicted in blue boxes.
In the top panel of Fig. 4, we observed that the [O I]557/[O I]630 ratios are consistent with density ne ≳ 106.5cm−3 and temperature 5000 ≤ T ≤ 10 000 K, in agreement with previous similar studies (e.g., Natta et al. 2014; Fang et al. 2018; Giannini et al. 2019). The [S II]406/[O I]630 ratio is expected to have a very little dependence on the density and temperature, since both the [S II]406 and [O I]630 lines have a similar critical density (bottom panel of Fig. 4). However, the observed [S II]406/[O I]630 ratios are consistent with the range of densities and temperatures indicated by the [O I]557/[O I]630 ratios, with the exception of three sources (i.e., CVSO90, CVSO104, and SO1153) whose [S II]406/[O I]630 ratios lie at around 0.1. This value would be compatible with a temperature of about 3000 K, which is not enough to sufficiently populate the S II atomic sublevels and give the observed line fluxes (e.g., Giannini et al. 2019).
4.3 Emitting sizes
Average emitting sizes can be deduced from the line width under the assumption that the width is dominated by the bulk motion of Keplerian rotation. As such, the average emitting size can be expressed as
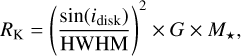 (2)
(2)
where idisk is the disk inclination angle and HWHM is the line half width at half maximum.
The assumption of a purely Keplerian broadening has been extensively applied for both the NLVC and BLVC of the [O I]630 line (Simon et al. 2016; Fang et al. 2018; McGinnis et al. 2018; Banzatti et al. 2019; Gangi et al. 2020), and it is usually assumed to be valid if the component originates in slow disk winds where the wind poloidal velocity is small and the broadening is still dominated by the Keplerian motion. However, as discussed in Weber et al. (2020), vertical velocity gradients might contribute to the line broadening, particularly at low inclinations (i.e., ≲20°). Regarding the UV-H2 lines, their widths can be reasonably considered to be dominated by Keplerian broadening, since significant thermal broadening would require temperatures higher than the dissociation temperature of H2 (Lepp & Shull 1983), so the broadening induced by the turbulence of the disk can be negligible (France et al. 2012).
In Fig. 5, we report the HWHM divided by the square root of the stellar mass as a function of sm(idisk) for the [O I]630 NLVC and BLVC and for the H2 [1,4] line. From the overplot-ted Keplerian models of constant radius, we inferred that the [O I]630 NLVC is emitted by regions with a size between ~0.5 and ~3.5 au, while the [O I]630 BLVC traces an innermost region between ~0.01 and ~0.2 au. In contrast, the UV-H2 emission appear to originate from an intermediate region partially superimposed on the previous two and that has a size between ~0.05 and ~1 au.
 |
Fig. 4 Diagnostic diagrams of line luminosity ratios due to thermal excitation as a function of density and temperature as computed by Giannini et al. (2019). Solar abundance was assumed for all involved species. Blue regions indicate the range of values measured in this work for the LVCs. |
 |
Fig. 5 Half width at half maximum divided by the square root of the stellar mass for the H2 (orange), [O I] NLVC (blue), and BLVC (red) as a function of the sine of the disk inclination. Keplerian models for gas emitted from disk radii of 0.01, 0.05, 0.2, 0.5, 1, 2, and 3.5 au are shown as solid black lines. |
5 Correlations
5.1 [O I]630 versus UV-H2 line properties
Figure 6 shows the correlations between vp, FWHM, and line luminosity of the [O I]630 NLVC, H2 [1,4], and [1,7] lines. The H2 [1,4] and [1,7] lines are well correlated in terms of both kinematics and luminosity. In particular, in six sources, the vp follows a one-to-one correlation, and in the other four, the H2 [1,4] line appears to be blueshifted but always within the velocity accuracy of COS (~15 km s−1). The FWHMs show a one-to-one relation, and the line luminosities correlate with a slope lower than one, that is, lines from the [1,4] progression are brighter than the corresponding lines of the [1,7] progression.
Regarding the [O I]630 NLVC, we found a similar behavior in the correlations with the H2 [1,7] and [1,4] lines. In particular, with the exception of SO518, the [O I] peak velocities are always consistent with zero. The SO518 source has a high disk inclination angle (idisk = 78°; see Table 1); thus, the LVC properties may be heavily contaminated by the HVC. For this reason, we have excluded this source in all of the correlations concerning the atomic forbidden lines. A high spread around the vp of both the H2 lines is present. Although this spread shows a predominance of blueshifted velocity, it is comparable to the velocity accuracy of COS. We also checked that the larger blueshifted peaks (up to −10 km s−1) were not associated with sources having a broad or an HVC in the [O I]630 emission, which could have contaminated the H2 line profile. The FWHMs are highly correlated, and for most cases, the FHWM of the [O I]630 is smaller than that of the H2 species. Finally, the line luminosities show a steep relation, as the luminosity of the H2 emission is 30–40 times higher than that of the [O I]630.
5.2 [O I]630 and UV-H2 line luminosity versus accretion luminosity
We can obtain insights on how the physical origin of the different line components are connected to the accretion mechanisms by looking at the correlation between Lline and Lacc. Indeed, the [O I]630 LVC and the HVC correlate with Lacc (e.g., Rigliaco et al. 2013; Natta et al. 2014; Simon et al. 2016; Nisini et al. 2018; Gangi et al. 2022). Moreover, Rigliaco et al. (2013) and Gangi et al. (2022) found a slightly different slope in the Lline − Lacc relation of these two components, which might suggest that they originate from distinct mechanisms, but both are nonetheless related to accretion processes.
Figure 7 (top panel) shows the Lline-Lacc correlation for the [O I]630 NLVC compared with the distribution found in Gangi et al. (2022) for a sample of CTTs of the Taurus-Auriga association. Both the Lline and the Lacc have been normalized to the stellar luminosity to exclude the correlation between Lline-L★ and Lacc-L★ (Mendigutía et al. 2015). We found that the NLVC luminosity correlates with Lacc, which is in good agreement with Gangi et al. (2022). A best linear regression fit in log scale yielded
![$\log {{{L_{\left[ {{\rm{OI}}} \right],{\rm{NLVC}}}}} \over {{L_ \star }}} = 0.44\left( { \pm 0.12} \right)\log {{{L_{{\rm{acc}}}}} \over {{L_ \star }}} - 4.21\left( { \pm 0.12} \right).$](/articles/aa/full_html/2023/07/aa46543-23/aa46543-23-eq9.png) (3)
(3)
In the bottom panel of Fig. 7, we report the Lline−Lacc distribution of the UV-H2 lines. To increase the statistics, we also included Lline values from France et al. (2012) and the corresponding Lacc from Gangi et al. (2022). We found a good correlation between the two quantities. More interestingly, the slope of the distribution is compatible, within errors, with that of [O I]630 NLVC. A best linear regression fit of the total sample yielded:
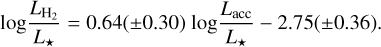 (4)
(4)
 |
Fig. 6 Correlations between kinematic and luminosity properties of the [O I]630 NLVC and UV H2 lines. From top to bottom: H2 [1,7] versus H2 [1,4], H2 [1,7] versus [O I], and H2 [1,4] versus [O I]. The black dashed lines represent the one-to-one correlations, while linear fits are shown as red dashed lines. The SO518 source (orange circled point) was excluded from the fit (see Sect. 5.1 for details). The Pearson coefficients are also reported. The vp errors on H2-UV lines reported in these plots are those resulting from the Gaussian decomposition procedure (Sect. 3). The estimated ~15 km s−1 uncertainty due to the wavelength calibration of COS should be added in quadrature. |
5.3 [O II]630 versus [S II]406 line properties
Figure 8 shows the correlations between vp and the FWHMs of the [O I]630 and [S II]406 lines obtained from the Gaussian decomposition of the profiles, as explained in Sect. 3. When it was possible to distinguish between NLVC from BLVC in the [O I]630 line but not in the [S II]406 line, we averaged the vp and FWHMs of the NLVC and BLVC using the peak intensities as weights. Overall, we found a good correlation between the two quantities, but we also note that a few sources (i.e., CVSO58, CVSO90, CVSO104, and CVSO107) whose [O I]630 LVC is centered at zero velocity showed slight blueshifts in their [S II]406 LVCs (see Table A.2). This might indicate different emitting regions for the two species.
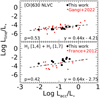 |
Fig. 7 Line luminosity as a function of accretion luminosity. Both quantities were normalized to the stellar luminosity. From top to bottom: [O I]630 NLVC and H2 [1,4] and [1,7] sum. Red dots indicate values found in Gangi et al. (2022) and France et al. (2012) for a sample of CTTs in the Taurus-Auriga association. Linear fits to the all data points are marked by dashed lines. The analytical solution and Pearson coefficients are also labeled. |
5.4 [O I]630, [S II]406, and UV-H2 versus ultraviolet emission
In this section, we look at a possible direct dependency of the line fluxes from the UV photons by means of the CIV-154.8, 155 nm doublet, which has been found to correlate with both the FUV continuum and the UV-H2 fluxes (France et al. 2012, 2014). Figure 9 correlates the luminosities of the UV-H2 with that of the C IV doublet. To increase the statistics, we also included values from the sample of CTTs reported in France et al. (2012). As expected, the UV-H2 luminosities are well correlated with those of the C IV, and they follow the same trend shown in France et al. (2012). In Fig. 10, we report the correlation between the line fluxes of the [O I]630 and [S II]406 lines with those of the C IV doublet. We found a good correlation for the [O I]630 line, while no evidence of a trend was present for the [S II]406 line.
6 Discussion
6.1 On the origin of the [O I]630 NLVC
As described in the introduction, the excitation mechanisms of the atomic oxygen component are still controversial. The similarities in the kinematical properties of [O I] and [S II], together with the consistency of the line ratios with simple thermal models, have supported a thermal origin for the oxygen component (see Natta et al. 2014; Fang et al. 2018), in contrast to suggestions of an origin from OH dissociation due to FUV photons (Rigliaco et al. 2013; Gorti et al. 2011) or from FUV pumping (Nemer et al. 2020).
In Sect. 5.3, we discussed a kinematic correlation between the different components of [O I]630 and [S II]406. However, for a few sources, the [S II] LVC peak velocity is more blueshifted than the [O I] LVC, suggesting different emitting regions for the two species. This evidence, along with the correlations between the [O I]630 NLVC and UV-H2 line transition properties (Sect. 5.1), can significantly alter the above scenario.
In particular, the positive correlation between the FWHMs of the [O I]630 NLVC and UV-H2 components presented in Sect. 5.1 may indicate that the two species are spatially connected. Under the assumption that the line broadening is dominated by Keplerian rotation, we estimated in Sect. 4.3 the average emitting sizes to be between ~0.5 and ~3.5 au for the [O I]630 NLVC and between ~0.05 and ~1 au for the UV-H2, a result in good agreement with previous studies of other CTTs samples (e.g., France et al. 2012; Fang et al. 2018; McGinnis et al. 2018; Gangi et al. 2020) and also consistent with the [O I] spatial size of TW Hya as recently measured by Fang et al. (2023). In Sect. 5.1, we also pointed out that the peak velocities of the [O I]630 NLVC are always centered at zero velocity. The same occurs for the UV-H2 lines, within the ~15 km s−1 wavelength resolution accuracy of COS (France et al. 2012). However, we stress that the decomposition of the [O I]630 LVC into a broad and narrow component, in contrast with a single Gaussian for the UV-H2 profile, may reflect the different spectral resolution and S/N in the optical and UV spectral regions. For example, previous studies with a higher S/N found that multicomponents or double-picked morphology for the UV-H2 profiles can be reproduced with simple disk emission models (e.g., Hoadley et al. 2015; Schneider et al. 2015). With this caveat in mind, these two pieces of evidence suggest that the atomic and molecular components originate from regions that might overlap and that both species mostly have a bound disk origin.
In Sect. 5.1, we also showed that the line luminosity of the [O I]630 NLVC and UV-H2 components are correlated, with the latter being 30–40 times higher than that of the [O I]. We additionally found line luminosities to be correlated with the accretion luminosities (Sect. 5.2). The Lline−Lacc dependence found in this study for the [O I]630 NLVC line is consistent with what has been measured in other samples of YSOs (Rigliaco et al. 2013; Natta et al. 2014; Simon et al. 2016; Nisini et al. 2018; Gangi et al. 2022). More interestingly, we found that the Lline−Lacc relation also persists for the UV-H2 species, and within the limit of the low statistics of this study, it shows the same dependence as that of [O I]630 NLVC. The UV-H2 Lline−Lacc correlation can be naturally explained by the fact that the H2 species are photoexcited by Lya photons, which in turn originate from the accretion processes (e.g., Hoadley et al. 2015; Arulanantham et al. 2023). These results suggest a non-negligible role of the FUV photons in exciting the [O I]630 NLVC for the sample analyzed in this work.
We investigated this conclusion further by looking at a possible link between line fluxes and the FUV continuum. In Sect. 5.4, we found that the [O I]630 NLVC fluxes are well correlated with those of the C IV-154.8, 155 nm doublet, a well-known tracer of UV continuum, while the [S II]406 NLVC did not show any particular trend. This different behavior supports the scenario in which the [O I]630 and [S II]406 NLVCs could have different dominant excitation mechanisms.
In conclusion, the above evidence point toward a framework where the [O I]630 NLVC and UV-H2 have a common disk origin with a partially overlapping region. An important contribution for the excitation of the [O I]630 NLVC component might be compatible with a nonthermal process due to the action of FUV photons.
6.2 Lyα and the FUV continuum penetration depths
We discuss in this section whether the above conclusion might be compatible with the capabilities of the exciting radiation to impact different disk layers. Figure 11 shows a schematic view of the disk vertical stratification and penetration depths of Lyα and the FUV continuum. The dust tends to settle in the inner layer where the temperature is low enough to freeze out molecules on the surface of dust grains. In contrast, the temperature in the upper layer is sufficiently warm to prevent freezing, and molecular species can form. We note, however, that while close to the disk surface, only the atomic species can survive. In this framework, the FUV continuum dominates in the atomic layer while the Lyα dominates in the molecular surface (Bethell & Bergin 2011). Such a behavior is particularly true in the inner disk regions (~1 au), which is where the bulk of UV-H2 and [O I]630 NLVC emission arise. Models have shown that, together with the fluorescence of H2, the Lya radiation is also responsible for the photodesorption of different molecular species, such as H2O and OH, trapped in the ice layer of dust (Fogel et al. 2011). The molecular layer can then be enriched with OH species, which in turn might be efficiently photodissociated by the action of FUV photons reaching the warm disk layer. In addition, the penetration efficiency of UV photons has been found to increase as dust settling increases (Dullemond & Dominik 2004), further facilitating OH photodissociation.
Therefore, the correlation between the UV-H2 and [O I]630 NLVC we found and the scenario in which the UV field could give a contribution to the oxygen atomic excitation appears to be consistent with the picture depicted here. However, we cannot discriminate between the OH photodissociation mechanism and the FUV pumping as a major UV contributor to the О excitation nor evaluate their relative contribution. Thermo-chemical models that simultaneously take into account the molecular and atomic species are necessary for that purpose. Similarly, and due to the low statistics of our data, we cannot point out any trend associated with a contribution from external UV fields. In particular, we note that the σ−Orionis sources of our sample might have an important external contribution due to their proximity to OB stars. However, complete samples in different star-forming regions are necessary to shed light on this latter point.
 |
Fig. 8 Peak velocities (left) and FWHMs (right) of individual [S II]4O6 and [O I]630 components. The different colors refer to different velocity components (see description in the panels). |
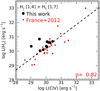 |
Fig. 9 Correlations between extinction-corrected line luminosities of H2 [1,4], [1,7], and С iv at 155 nm (black points) compared with those of a CTTs sample reported in France et al. (2012; red points). The linear fit to the total distribution is shown as a black dashed line. The Pearson coefficient is also reported. |
6.3 Comparison with near-infrared H2 emission
In a previous work (Gangi et al. 2020), we looked at the link between the [O I]630 NLVC and the ro-vibrational hydrogen 1–2 S(l) transition at 2.12 µm (hereafter NIR-H2) with a homogeneous and simultaneous dataset of 36 CTTs of the Taurus-Auriga star-forming region, in the framework of the GHOsT project (Alcalá et al. 2021). We found: (i) a strong kinematical link between the two species, both in terms of peak velocity and FWHM, and (ii) a weak correlation between the luminosities, with the NIR-H2 showing lower luminosity than that of the [O I]630 on average. The kinematic link was interpreted in the framework where the neutral atomic and near-infrared molecular components are part of the same disk wind, with the latter tracing a more external region with sizes between 2 and 20 au.
The weak correlation between the line luminosities was later examined by Rab et al. (2022), who interpreted the trend in terms of photoevaporative disk wind coupled with thermo-chemical models. These models included the UV pumping and the OH photodissociation for the calculation of the NLTE level populations of the О species and the pumping induced by dust grains for the NIR-H2. Their models are able to populate the distribution of the [O I]630 luminosity reasonably well, confirming the non-negligible role of UV photons. On the other hand, the NIR-H2 line luminosities were found to be underpredicted up to an order of magnitude. This might suggest that the dissociation mechanisms for this component could also depend on a detailed inclusion of the dynamical processes linked to the disk structure and wind radial extension.
Finally, in a subsequent work (Gangi et al. 2022), we found no significant correlation between the luminosity of the NIR-H2 line and Lacc. Again, this was explained in the framework where the NIR-H2 dissociation is strongly affected by several processes not necessarily connected with accretion.
 |
Fig. 10 Correlations between extinction-corrected line fluxes of [O I]63O NLVC, [S II]406 NLVC, and С IV at 155 nm. The flux units are 10−15 erg−1 cm2. The SO518 source was excluded (see Sect. 5.1 for details). Linear fit is shown as red dashed line. |
 |
Fig. 11 Schematic view of the vertical disk stratification and penetration depths of Lyα and FUV continuum photons. |
6.4 A schematic view of the O l and H2 protoplanetary disk components
If the scenario discussed in the previous subsection can be extended to the sample analyzed in this work, we can trace a global picture of the atomic [O I]630 NLVC, molecular UV-H2, and NIR-H2 emissions as schematized in Fig. 12. As already mentioned, we found evidence from line widths that all the three species are spatially connected, with the UV-H2 and the NIR-H2 regions partially overlapping with that of the [OI]63O LVC. The UV-H2 component traces the inner (≲1 au) molecular protoplanetary disk where stellar FUV photons are able to reach the warm disk and photoexcite the species. The NIR-H2 is the more extended component, with sizes up to ~20 au, but it is not present in the inner regions (≲ 1–2 au). In contrast, the atomic О component is emitted from a more internal region that reaches up to a few fractions of an astronomical unit.
The differences we found in the FWHMs between the [O I] BLVC and NLVC are consistent with the classical interpretation of the BLVC being a tracer of the innermost atomic protoplanetary disk region, in contrast to the corresponding NLVC (e.g., Ercolano & Pascucci 2017). In this framework, we stress that the spatial overlapping with the UV-H2 region supports the scenario in which the FUV photons provide a substantial contribution to the О line excitation.
Finally, we conclude that although the blueshifted [O I]630 LVC and NIR-H2 lines show that they can both be associated with slow winds, a contribution to the line emission from gas bound in the disk cannot be ruled out. Therefore, we highlight the importance of an accurate wavelength calibration and a precise correction for the stellar radial velocity (e.g., Campbell-White et al. 2023).
7 Summary and conclusion
In the framework of the PENELLOPE and ULLYSES projects, we presented a study of the atomic and molecular protoplanetary disk components in a sample of 11 CTTs of the Orion OBI and σ-Orionis associations. We analyzed contemporaneous high-resolution optical and ultraviolet spectra from ESPRESSO at VLT, UVES at VLT, and HST-COS, focusing on the five brightest optical forbidden lines and on the fluorescent ultraviolet H2 [1,4], [1,7] line progressions. We applied a Gaussian decomposition of the line profiles to separate different kinematic components. The optical forbidden lines were deconvolved into components at different velocities, in line with previous high-resolution studies of CTTs. In contrast, the H2 [1,4], [1,7] line progressions, which were detected in all sources, were fit as a single Gaussian. We then focused on the comparison between the [O I]630 NLVC (|υp| < 30 km s−1; FWHM < 40 km s−1) and the H2 line progressions, with the aim of investigating the О excitation mechanisms. The main results of our study are summarized below.
We found a strong kinematic link between the [O I]63O NLVC and the UV-H2. In particular, the FWHMs of the two components are tightly correlated, while the peak velocities are consistent with zero velocity.
Assuming that the line width is dominated by Keplerian broadening, we measured the average radius of the disk region where the emission originates. We found that the [O I]630 NLVC originates from radii between 0.5 au and 3.5 au, and the UV-H2 originates from radii between 0.05 au and 1 au.
We found a strong correlation between the line luminosities (Lline) of the [O I]630 NLVC and UV-H2, as well as between Lline and the accretion luminosities (Lacc)· In particular, the Lline−Lасс relations for the two species have a similar slope of the linear fit.
The UV-H2 Lline correlates with the luminosity of C IV-154.8, 155 doublet, in agreement with the results of France et al. (2012). In addition, we also found that such correlation is also valid for the [O I]630 NLVC, while no correlation was found for the [S II]406 LVC.
We interpreted these results in terms of a common disk origin for the [O I]630 NLVC and UV-H2 species, which partially overlap in space. We suggest a possible dominant role of the FUV photons in exciting the O I species, at variance with a thermal origin. Finally, we proposed a global picture of the distributions of atomic and molecular species in protoplanetary disks, including the near-infrared H2-2.12 µm emission properties from previous similar studies.
This work highlights the potential of contemporaneous wideband high-resolution spectroscopy to provide insights on the complex physical processes in the environments around YSOs. At the same time, we stress that a future observational strategy probing statistically significant samples in different star-forming regions, coupled with advanced thermo-chemical models, is essential to confirm the inferred gas distribution and the interaction between the exciting radiation and the inner disk structure. This can be achieved thanks to the effort of a large community, such as the one involved in the PENELLOPE and ULLYSE projects.
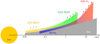 |
Fig. 12 Sketch (not in scale) showing a possible distribution of the atomic [O I] and molecular H2 components of a protoplanetary disk. The horizontal axis is in log scale. |
Acknowledgements
This work has been supported by the projects PRIN-INAF 2019 “Spectroscopically Tracing the Disk Dispersal Evolution (STRADE)”, PRIN-INAF 2019 “Planetary systems at young ages (PLATEA)” and by the Large Grant INAF 2022 YODA (YSOs Outflows, Disks and Accretion: toward a global framework for the evolution of planet forming systems). This work also benefited from discussions with the ODYSSEUS team (HST AR-16129), https://sites.bu.edu/odysseus/. Funded by the European Union under the European Union's Horizon Europe Research & Innovation Programme 101039452 (WANDA) and 716155 (SACCRED). Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Research Council. Neither the European Union nor the granting authority can be held responsible for them.
Appendix A Additional tables and images
 |
Fig. A.1 Continuum-subtracted optical forbidden line profiles (black). In blue is the fit to the profile obtained by adding single or multiple Gaussians (red lines). Flux units are 10−15 ergs−1cm−2 Å−1. For each panel, we indicate the target name and the line diagnostics. |
 |
Fig. A.2 Continuum-subtracted UV H2 [1,4] averaged profiles. In green is fit to the profile. Flux units are 10−15 ergs−1cm−2 Å−1. For each panel, we indicate the target name and the line diagnostics. |
 |
Fig.A.3 Continuum-subtracted UV H2 [1,7] averaged profiles. In green is the fit to the profile. Flux units are 10−15 ergs 1cm−2Å−1. For each panel we indicate the target name and the line diagnostics. |
Gaussian fit results for H2 [1,4] and H2 [1,7] lines.
Gaussian decomposition of optical forbidden lines.
References
- Agra-Amboage, V., Cabrit, S., Dougados, C., et al. 2014, A&A, 564, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alcalá, J. M., Gangi, M., Biazzo, K., et al. 2021, A&A, 652, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arulanantham, N., Gronke, M., Fiorellino, E., et al. 2023, ApJ, 944, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Ballabio, G., Haworth, T. J., & Henney, W. J. 2023, MNRAS, 518, 5563 [Google Scholar]
- Banzatti, A., Pascucci, I., Edwards, S., et al. 2019, ApJ, 870, 76 [Google Scholar]
- Banzatti, A., Abernathy, K. M., Brittain, S., et al. 2022, AJ, 163, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Bary, J. S., Weintraub, D. A., & Kastner, J. H. 2003, ApJ, 586, 1136 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, T. L., & Bary, J. S. 2019, ApJ, 884, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, T. L., McGregor, P. J., Takami, M., et al. 2008, ApJ, 676, 472 [NASA ADS] [CrossRef] [Google Scholar]
- Bethell, T. J., & Bergin, E. A. 2011, ApJ, 739, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Campbell-White, J., Manara, C. F., Sicilia-Aguilar, A., et al. 2023, A&A, 673, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [Google Scholar]
- Dekker, H., D’Odorico, S., Kaufer, A., et al. 2000, Proc. SPIE, 4008, 534 [Google Scholar]
- Dullemond, C. P., & Dominik, C. 2004, A&A, 421, 1075 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ercolano, B., & Pascucci, I. 2017, Roy. Soc. Open Sci., 4, 170114 [Google Scholar]
- Espaillat, C. C., Herczeg, G. J., Thanathibodee, T., et al. 2022, AJ, 163, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Fang, M., Pascucci, I., Edwards, S., et al. 2018, ApJ, 868, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Fang, M., Wang, L., Herczeg, G. J., et al. 2023, Nat. Astron., submitted [arXiv:2305.07929] [Google Scholar]
- Fogel, J. K. J., Bethell, T. J., Bergin, E. A., et al. 2011, ApJ, 726, 29 [NASA ADS] [CrossRef] [Google Scholar]
- France, K., Schindhelm, R., Herczeg, G. J., et al. 2012, ApJ, 756, 171 [NASA ADS] [CrossRef] [Google Scholar]
- France, K., Schindhelm, R., Bergin, E. A., et al. 2014, ApJ, 784, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Frasca, A., Boffin, H. M. J., Manara, C. F., et al. 2021, A&A, 656, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gangi, M., Nisini, B., Antoniucci, S., et al. 2020, A&A, 643, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gangi, M., Giarrusso, M., Munari, M., et al. 2021, MNRAS, 500, 926 [Google Scholar]
- Gangi, M., Antoniucci, S., Biazzo, K., et al. 2022, A&A, 667, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garcia Lopez, R., Caratti o Garatti, A., Weigelt, G., et al. 2013, A&A, 552, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giannini, T., Antoniucci, S., Nisini, B., et al. 2015, ApJ, 814, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Giannini, T., Nisini, B., Antoniucci, S., et al. 2019, A&A, 631, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gorti, U., Hollenbach, D., Najita, J., et al. 2011, ApJ, 735, 90 [CrossRef] [Google Scholar]
- Kounkel, M., Covey, K., Moe, M., et al. 2019, AJ, 157, 196 [NASA ADS] [CrossRef] [Google Scholar]
- Hartigan, P., Edwards, S., & Ghandour, L. 1995, ApJ, 452, 736 [Google Scholar]
- Hartmann, L., Herczeg, G., & Calvet, N. 2016, ARA&A, 54, 135 [Google Scholar]
- Hoadley, K., France, K., Alexander, R. D., et al. 2015, ApJ, 812, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Lepp, S., & Shull, J. M. 1983, ApJ, 270, 578 [NASA ADS] [CrossRef] [Google Scholar]
- Manara, C. F., Beccari, G., Da Rio, N., et al. 2013, A&A, 558, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Manara, C. F., Frasca, A., Venuti, L., et al. 2021, A&A, 650, A196 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Manara, C. F., Ansdell, M., Rosotti, G. P., et al. 2022, arXiv e-prints [arXiv:2203.09930] [Google Scholar]
- Maucó, K., Hernández, J., Calvet, N., et al. 2016, ApJ, 829, 38 [CrossRef] [Google Scholar]
- McGinnis, P., Dougados, C., Alencar, S. H. P., et al. 2018, A&A, 620, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mendigutía, I., Oudmaijer, R. D., Rigliaco, E., et al. 2015, MNRAS, 452, 2837 [Google Scholar]
- Najita, J. R., Carr, J. S., Glassgold, A. E., et al. 2007, Protostars and Planets V, 507 [Google Scholar]
- Natta, A., Testi, L., Alcalá, J. M., et al. 2014, A&A, 569, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nemer, A., Goodman, J., & Wang, L. 2020, ApJ, 904, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Nisini, B., Antoniucci, S., Alcalá, J. M., et al. 2018, A&A, 609, A87 [EDP Sciences] [Google Scholar]
- Owen, J. E., Ercolano, B., Clarke, C. J., et al. 2010, MNRAS, 401, 1415 [NASA ADS] [CrossRef] [Google Scholar]
- Pascucci, I., Cabrit, S., Edwards, S., et al. 2022, arXiv e-prints [arXiv:2203.10068] [Google Scholar]
- Pepe, F., Cristiani, S., Rebolo, R., et al. 2021, A&A, 645, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pittman, C. V., Espaillat, C. C., Robinson, C. E., et al. 2022, AJ, 164, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Rab, C., Weber, M., Grassi, T., et al. 2022, A&A, 668, A154 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rigliaco, E., Pascucci, I., Gorti, U., et al. 2013, ApJ, 772, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Roman-Duval, J., Proffitt, C. R., Taylor, J. M., et al. 2020, RNAAS, 4, 205 [NASA ADS] [Google Scholar]
- Schneider, P. C., France, K., Günther, H. M., et al. 2015, A&A, 584, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simon, M. N., Pascucci, I., Edwards, S., et al. 2016, ApJ, 831, 169 [Google Scholar]
- Vernet, J., Dekker, H., D’Odorico, S., et al. 2011, A&A, 536, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, L., Bai, X.-N., & Goodman, J. 2019, ApJ, 874, 90 [Google Scholar]
- Weber, M. L., Ercolano, B., Picogna, G., et al. 2020, MNRAS, 496, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Whittet, D. C. B., Shenoy, S. S., Clayton, G. C., et al. 2004, ApJ, 602, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Winter, A. J., & Haworth, T. J. 2022, Eur. Phys. J. Plus, 137, 1132 [NASA ADS] [CrossRef] [Google Scholar]
Accretion parameters were determined by Manara et al. (2021) through multicomponent accretion flows (Manara et al. 2013), and they were adopted here for homogeneity with previous works. However, another determination is also provided by Pittman et al. (2022).
This is due to the polishing errors on the HST primary and secondary mirrors: https://www.stsci.edu/hst/instrumentation/cos/performance/spectral-resolution
All Tables
List of sources with their stellar and accretion properties, and disk inclination when available.
All Figures
 |
Fig. 1 Example of H2 [1,4] (left) and H2 [1,7] (right) progression line profiles. The averaged profile is indicated in black. Flux units are 10−15 erg−1 cm−2 Å−1. |
| In the text | |
 |
Fig. 2 Example of Gaussian decomposition. The continuum-subtracted forbidden line profiles are shown with black lines. In blue, we have plotted the fit to the profile, while individual components are shown with red lines. Flux units are 10−15 erg−1 cm−2 Å−1. For each panel, the target name and line diagnostics are indicated. The complete sample is reported in Fig. A.1. |
| In the text | |
 |
Fig. 3 Example of Gaussian fitting of continuum-subtracted H2 [1,4] and [1,7] averaged line profiles. Flux units are l0−15 erg−1 cm−2 Å−1. For each panel, the target name and line profile are indicated. The complete sample is reported in Figs. A.2 and A.3. |
| In the text | |
 |
Fig. 4 Diagnostic diagrams of line luminosity ratios due to thermal excitation as a function of density and temperature as computed by Giannini et al. (2019). Solar abundance was assumed for all involved species. Blue regions indicate the range of values measured in this work for the LVCs. |
| In the text | |
 |
Fig. 5 Half width at half maximum divided by the square root of the stellar mass for the H2 (orange), [O I] NLVC (blue), and BLVC (red) as a function of the sine of the disk inclination. Keplerian models for gas emitted from disk radii of 0.01, 0.05, 0.2, 0.5, 1, 2, and 3.5 au are shown as solid black lines. |
| In the text | |
 |
Fig. 6 Correlations between kinematic and luminosity properties of the [O I]630 NLVC and UV H2 lines. From top to bottom: H2 [1,7] versus H2 [1,4], H2 [1,7] versus [O I], and H2 [1,4] versus [O I]. The black dashed lines represent the one-to-one correlations, while linear fits are shown as red dashed lines. The SO518 source (orange circled point) was excluded from the fit (see Sect. 5.1 for details). The Pearson coefficients are also reported. The vp errors on H2-UV lines reported in these plots are those resulting from the Gaussian decomposition procedure (Sect. 3). The estimated ~15 km s−1 uncertainty due to the wavelength calibration of COS should be added in quadrature. |
| In the text | |
 |
Fig. 7 Line luminosity as a function of accretion luminosity. Both quantities were normalized to the stellar luminosity. From top to bottom: [O I]630 NLVC and H2 [1,4] and [1,7] sum. Red dots indicate values found in Gangi et al. (2022) and France et al. (2012) for a sample of CTTs in the Taurus-Auriga association. Linear fits to the all data points are marked by dashed lines. The analytical solution and Pearson coefficients are also labeled. |
| In the text | |
 |
Fig. 8 Peak velocities (left) and FWHMs (right) of individual [S II]4O6 and [O I]630 components. The different colors refer to different velocity components (see description in the panels). |
| In the text | |
 |
Fig. 9 Correlations between extinction-corrected line luminosities of H2 [1,4], [1,7], and С iv at 155 nm (black points) compared with those of a CTTs sample reported in France et al. (2012; red points). The linear fit to the total distribution is shown as a black dashed line. The Pearson coefficient is also reported. |
| In the text | |
 |
Fig. 10 Correlations between extinction-corrected line fluxes of [O I]63O NLVC, [S II]406 NLVC, and С IV at 155 nm. The flux units are 10−15 erg−1 cm2. The SO518 source was excluded (see Sect. 5.1 for details). Linear fit is shown as red dashed line. |
| In the text | |
 |
Fig. 11 Schematic view of the vertical disk stratification and penetration depths of Lyα and FUV continuum photons. |
| In the text | |
 |
Fig. 12 Sketch (not in scale) showing a possible distribution of the atomic [O I] and molecular H2 components of a protoplanetary disk. The horizontal axis is in log scale. |
| In the text | |
 |
Fig. A.1 Continuum-subtracted optical forbidden line profiles (black). In blue is the fit to the profile obtained by adding single or multiple Gaussians (red lines). Flux units are 10−15 ergs−1cm−2 Å−1. For each panel, we indicate the target name and the line diagnostics. |
| In the text | |
 |
Fig. A.2 Continuum-subtracted UV H2 [1,4] averaged profiles. In green is fit to the profile. Flux units are 10−15 ergs−1cm−2 Å−1. For each panel, we indicate the target name and the line diagnostics. |
| In the text | |
 |
Fig.A.3 Continuum-subtracted UV H2 [1,7] averaged profiles. In green is the fit to the profile. Flux units are 10−15 ergs 1cm−2Å−1. For each panel we indicate the target name and the line diagnostics. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


