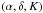| Issue |
A&A
Volume 569, September 2014
|
|
|---|---|---|
| Article Number | A69 | |
| Number of page(s) | 9 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201423666 | |
| Published online | 25 September 2014 | |
The Galactic bar and the large scale velocity gradients in the Galactic disk
1
Kapteyn Astronomical Institute,
Rijksuniversiteit Groningen, PO Box
800
9700 AV
Groningen
The Netherlands
e-mail:
monari@astro.rug.nl
2
ESA, European Space Research and Technology Center (ESTEC),
Keplerlaan 1, 2201
AZ
Noordwijk, The
Netherlands
3
Leibniz-Institut für Astrophysik Potsdam (AIP),
An der Sternwarte
16, 14482
Potsdam,
Germany
Received:
18
February
2014
Accepted:
28
July
2014
We investigate whether the cylindrical (galactocentric) radial velocity gradient of ~ −3 km s-1 kpc-1, directed radially from the Galactic center and recently observed in the stars of the solar neighborhood with the RAVE survey, can be explained by the resonant effects of the bar near the solar neighborhood. We compared the results of test particle simulations of the Milky Way with a potential that includes a rotating bar with observations from the RAVE survey. To this end we applied the RAVE selection function to the simulations and convolved these with the characteristic RAVE errors. We explored different “solar neighborhoods” in the simulations, as well as different bar models. We find that the bar induces a negative radial velocity gradient at every height from the Galactic plane, outside the outer Lindblad resonance and for angles from the long axis of the bar compatible with the current estimates. The selection function and errors do not wash away the gradient, but often make it steeper, especially near the Galactic plane, because this is where the RAVE survey is less radially extended. No gradient in the vertical velocity is present in our simulations, from which we may conclude that this cannot be induced by the bar.
Key words: Galaxy: kinematics and dynamics / solar neighborhood / Galaxy: structure / Galaxy: evolution
© ESO, 2014
1. Introduction
Many of the past efforts in modeling the mass distribution of the Milky Way have assumed that the Galaxy is axisymmetric and in a steady state. However, there is a wealth of evidence that these assumptions are not really valid. The two most important deviations from axisymmetry are the spiral arms and the bar. These features are not only apparent as non-axisymmetric density enhancements, but they also have long-range gravitational effects. In particular, the bar modifies the kinematics of the outer parts of the Galactic disks, far beyond its extension, through resonant interactions.
That the velocity distribution of stars very near to the Sun is not smooth (as one would expect in a steady state axisymmetric system), but instead rich in substructures, has been established observationally thanks to data from the Hipparcos satellite and other surveys (Dehnen 1998; Famaey et al. 2005; Antoja et al. 2008). Several authors have explained these substructures as being due to orbital resonant effects of the bar (Dehnen 2000; Fux 2001), of the spiral arms (Mayor 1970; De Simone et al. 2004; Antoja et al. 2011), or both (Antoja et al. 2009; Quillen et al. 2011).
Using data from the RAVE survey (Steinmetz et al. 2006), Antoja et al. (2012) discovered that some of the kinematic substructures detected in the vicinity of the Sun can be traced further, both on and above the plane of the Galaxy, up to ~0.7 kpc.
But RAVE also made it possible to discover large scale streaming motions. Siebert et al. (2011a, hereafter S11) used a sample of 213 713 stars to discover a gradient in the mean galactocentric radial velocity that decreases outward with Galactic radius. S11 show that this gradient was also present when using only the 29 623 red clump stars in their sample, whose distances are more accurate. Siebert et al. (2012) modeled the gradient as caused by a long-lived spiral pattern. Williams et al. (2013, hereafter W13) studied the 3D velocity distribution of red clump stars in RAVE in detail, confirmed the existence of the radial velocity gradient and also discovered a more complicated vertical velocity distribution than expected, attributing it to secular phenomena in the Galaxy. Faure et al. (2014) generalized to 3D the model for the spiral arms presented in Siebert et al. (2012), which now also depends on the distance from the Galactic plane. This model nicely predicts a behavior for the mean vertical velocity that is similar to what is observed in W13 (i.e., resembling “rarefaction-compression” waves), together with the radial velocity gradient.
On the other hand, Monari et al. (2013, hereafter M13), used 3D test particle simulations to show that the gravitational effects of the bar can significantly affect the kinematics of stars near the Sun, even at distances from the Galactic plane up to at least z ~ 1 kpc for the thin disk and z ~ 2 kpc for the thick disk. These results imply that some of the substructures found in Antoja et al. (2012) could also be caused by the bar.
In this paper we investigate an alternative explanation for the observed radial velocity gradient, beyond that caused by the spiral arms, by suggesting that it can be created by the bar. To do so, we compare the results of the test particle simulations in M13 with the RAVE data.
The paper is organized as follows. In Sect. 2 we summarize the salient characteristics of the simulations from M13, and in Sect. 3 we describe how we apply the RAVE selection function and error convolution to them, to mimic a RAVE catalog. In Sect. 4 we present the results. In Sect. 5 we explain how the bar can create a radial velocity gradient as observed. In Sect. 6 we discuss the similarities between our results and the ones in W13 and in Sect. 7 we conclude.
2. Simulations
We use the 3D test particle simulations of the thin and thick disk of the Milky Way described in M13. The rigid background gravitational potential in these simulations includes an axisymmetric part (composed of a dark halo and a thin and a thick disk) and a non-axisymmetric perturbation to represent the Galactic bar. The bar potential follows a Ferrers (1870) model and we varied its structural parameters (with values taken from the literature) but with a constant pattern speed Ωb = 50 km s-1 kpc-1. For the comparison with the RAVE data we focus on simulations with three bar potentials: the default bar, the long bar, and the less massive bar (corresponding to GB2, LB2, and GB1 in M13). We choose the snapshot of the simulations at t = 24Tbar, which corresponds to ~3 Gyr after the introduction of the bar in the simulations (see M13). In the default bar case, there are Nthin = 109 particles in the thin disk population and Nthick = 2 × 108 particles in the thick disk (to have a thick-to-thin density of particles normalization of ~10% at the Sun). For the remaining cases we only have low resolution simulations with Nthin = 5 × 107 and Nthick = 107 particles for the thin and the thick disk, respectively. The parameters of the simulations are summarized in Table 1.
In this paper, (R,φ,z) are the Galactocentric cylindrical coordinates,
where φ is the
angle from the long axis of the bar in the direction of rotation of the Galaxy. The
cylindrical velocities are 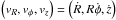 . Right
ascension, declination, and heliocentric distance are denoted as
. Right
ascension, declination, and heliocentric distance are denoted as
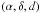 , and
the proper motions and line of sight velocity as (μα,μδ,vlos).
, and
the proper motions and line of sight velocity as (μα,μδ,vlos).
Parameters of the bar and location of the main resonances.
3. Selection function and errors
3.1. Red clump stars
Both S11 and W13 use red clump stars because they are promising standard candles, since
they are easy to identify in the HR diagram, and while being relatively unaffected by
extinction their K-band magnitude depends only weakly on metallicity
and age. In W13 the red clump is selected from the internal RAVE release from October
20111 (see the DR3 paper, Siebert et al. 2011b, for stellar parameter determination), as those
stars with 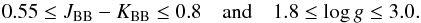 (1)The absolute magnitude
associated with the red clump stars is taken to be MK = −
1.65, following Alves (2000).
(1)The absolute magnitude
associated with the red clump stars is taken to be MK = −
1.65, following Alves (2000).
3.2. RAVE selection function
We applied the RAVE selection function in the space of observables
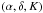 to the
simulations. We did this as follows:
to the
simulations. We did this as follows:
-
we chose the position of the Sun in the simulated Galaxy; the default position is (R,φ,z) = (8 kpc, −20°,0), in the range of current determinations (Bissantz & Gerhard 2002);
-
we transformed the spatial coordinates of the simulation into the observables
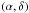 and
heliocentric distance d;
and
heliocentric distance d; -
we assigned K magnitudes to the particles in the simulation, assuming they are red clump stars with MK = − 1.65. Then the apparent magnitude is given by K = MK + 5(log 10d − 1);
-
we binned the red clump stars used in W13 in the (α,δ,K) space, with Nb bins of size 10° × 10° × 0.2 mag and α ∈ [ 0,360° ], δ ∈ [ − 90°,0 ], K ∈ [ 2,12 ];
-
we binned in the same space and in the same way the particles from the simulation that are inside a sphere of radius 3 kpc from the Sun;
-
for i = 1,...,Nb, if the i-th bin in the simulation contains
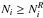 particles
(where
particles
(where 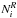 is the
number of stars in the same bin in RAVE) we randomly downsampled it to
is the
number of stars in the same bin in RAVE) we randomly downsampled it to
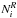 particles; if
particles; if 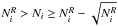 we kept the Ni particles
(because
we kept the Ni particles
(because 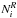 and
Ni differ less
than the corresponding Poisson noise error); however, not all the bins of the
simulations are populated enough: we excluded from the comparison those bins with
and
Ni differ less
than the corresponding Poisson noise error); however, not all the bins of the
simulations are populated enough: we excluded from the comparison those bins with
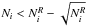 (this only happened for less than ~0.05% of the bins for the high resolution simulations, and also
in the low resolution case after the treatment explained in Sect. 4.3).
(this only happened for less than ~0.05% of the bins for the high resolution simulations, and also
in the low resolution case after the treatment explained in Sect. 4.3).
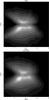 |
Fig. 1 (R,z) distribution of stars in the RAVE sample used in W13 (top) and in the simulation with default Sun’s position after the application of the RAVE selection function (bottom). The contours enclose 2,6,12,21,33,50,68,80,90,95 and 99% of the stars. |
3.3. Error convolution
For the comparison between data and simulations we proceeded to convolve the latter with the errors estimated for the RAVE survey.
We produced a simple error model, where the errors in proper motion and line of sight velocity are function of the K magnitude only. This was done by fitting second order polynomials to K vs. ep.m. and K vs. elos for the red clump stars in DR3. We also derived an error in distance ed propagating the error in K (eK ~ 0.04 mag) and the spread in absolute magnitudes of the red clump (eMK = 0.22 mag, Alves 2000). The resulting relative error in distance is ed/d ~ 0.1, that we assumed to be the same for all particles in our simulations.
The error convolution was done in the observable space (α,δ,d,μα,μδ,vlos), assuming Gaussian errors in each quantity.
4. Results
4.1. Default case
As a default case we place the Sun at (R,φ,z) = (8 kpc, − 20°,0) and we choose the default bar model. In this case R0/ROLR = 1.04, where R0 is R of the Sun and ROLR is the Galactocentric distance of the outer Lindblad resonance.
The top row of Fig. 2 shows the average velocities
as a function of R and z, for all the particles inside a sphere of radius
3 kpc from the Sun, with no
error convolution yet applied. From left to right we show contour plots of
 ,
,
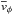 , and
, and
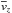 . As in W13, the
data are averaged inside bins of 100
pc size in (X′,Y′),
box smoothed on a scale of 200
pc. As it is apparent from these plots,
. As in W13, the
data are averaged inside bins of 100
pc size in (X′,Y′),
box smoothed on a scale of 200
pc. As it is apparent from these plots,
 decreases
increasing the R distance in the simulated Galaxy. Moreover,
decreases
increasing the R distance in the simulated Galaxy. Moreover,
 is rather
symmetric with z. The central panel shows that the rotational
velocity of the stars in the Galactic disk(s)
is rather
symmetric with z. The central panel shows that the rotational
velocity of the stars in the Galactic disk(s) 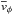 decreases with
distance from the plane. This is because the velocity dispersion increases with
z and
because the asymmetric drift increases with the velocity dispersion (Binney & Tremaine 2008). The rightmost panel shows instead how
decreases with
distance from the plane. This is because the velocity dispersion increases with
z and
because the asymmetric drift increases with the velocity dispersion (Binney & Tremaine 2008). The rightmost panel shows instead how
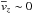 everywhere in the simulated sample, i.e., the distribution function of our simulations is
an even function of vz.
everywhere in the simulated sample, i.e., the distribution function of our simulations is
an even function of vz.
 |
Fig. 2 Average velocities for particles inside a sphere of radius 3 kpc, when the Sun is placed at (R,φ,z) = (8 kpc, −20°,0) and for the default bar model. Top row: contour plots in the (R,z) plane, with binsize 100 pc and box smoothing on a scale of 200 pc. Bottom row: as in the top row, but after the application of the RAVE selection function. The averages in the bottom panels correspond to those obtained using 100 random samples of the simulation. |
The bottom row of Fig. 2 shows the same quantities
as in the top panels, after the application of the RAVE selection function. The plotted
values were obtained averaging over the 100 random samples of the simulation, distributed in (α,δ,K) as in RAVE. We only
consider the bins including more than 50 particles. These contour plots show that the decreasing
 gradient is
preserved after the selection function has been applied to the simulation. In fact the
gradient is even enhanced: the yellow regions at R ~ 7 kpc are formed by
particles with
gradient is
preserved after the selection function has been applied to the simulation. In fact the
gradient is even enhanced: the yellow regions at R ~ 7 kpc are formed by
particles with 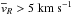 ,
and the blue/green regions at R ~ 8.5 kpc by particles with slightly negative
,
and the blue/green regions at R ~ 8.5 kpc by particles with slightly negative
 . From the second
and third panel we also see that the selection function does not induce any significant
difference in
. From the second
and third panel we also see that the selection function does not induce any significant
difference in 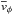 and
and
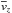 : unlike W13, in
the samples presented in this work we do not detect any significant
: unlike W13, in
the samples presented in this work we do not detect any significant
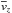 gradient with
respect to z
or R.
gradient with
respect to z
or R.
The reason why the selection function enhances the vR gradient is readily
understood from Fig. 3. Here X′ and
Y′ are the cartesian coordinates centered
at the Sun, the Galactic Center is placed at (X′,Y′) = (
−8 kpc,0), and the colors represent
 for particles
inside a sphere of radius 3
kpc from the Sun in bins of 100 pc size. The contours enclose 90% of particles with −1.5 kpc
<z<
0 (black) and 0
<z< 1.5
kpc (red), when the RAVE selection function is applied. These contours
therefore show that the selection function encloses mostly particles with negative
X′ and positive Y′ (with
φ< −
20°), where the gradient is steeper.
for particles
inside a sphere of radius 3
kpc from the Sun in bins of 100 pc size. The contours enclose 90% of particles with −1.5 kpc
<z<
0 (black) and 0
<z< 1.5
kpc (red), when the RAVE selection function is applied. These contours
therefore show that the selection function encloses mostly particles with negative
X′ and positive Y′ (with
φ< −
20°), where the gradient is steeper.
This analysis shows that vR is the velocity
component most influenced by the bar (and that no signature is readily apparent in
vz) and therefore we
focus in the rest of the paper on the R gradients of
 and on their
dependence on z.
and on their
dependence on z.
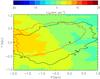 |
Fig. 3 Trends in |
In Figure 4 we look closer at the
 trends with
R, slicing
the particles at different z. The quantity
trends with
R, slicing
the particles at different z. The quantity
 is computed inside
R bins of
size 0.5 kpc. The black line
has been obtained using all the particles in the simulations inside a sphere of
3 kpc radius from the Sun,
the red line those that remain after applying the RAVE selection function only, and the
blue line the case where the error convolution is applied together with the selection
function. The shaded areas represent the standard errors of the mean inside each bin. For
the red and blue curves we show the maximum error amongst the 100 random samples2. We only show the bins with errors smaller than 5 km s-1 and including more than
50 particles. The black line
confirms what we saw in Fig. 2, namely that
is computed inside
R bins of
size 0.5 kpc. The black line
has been obtained using all the particles in the simulations inside a sphere of
3 kpc radius from the Sun,
the red line those that remain after applying the RAVE selection function only, and the
blue line the case where the error convolution is applied together with the selection
function. The shaded areas represent the standard errors of the mean inside each bin. For
the red and blue curves we show the maximum error amongst the 100 random samples2. We only show the bins with errors smaller than 5 km s-1 and including more than
50 particles. The black line
confirms what we saw in Fig. 2, namely that
 decreases with
R in each
of the 5 slices in
z.
decreases with
R in each
of the 5 slices in
z.
The numbers in the bottom right of each panel quantify the magnitude of the gradient:
m
represents the slope of the linear regression of the
 values inside the
plotted bins, and σm its uncertainty
(computed from the errors represented by the shaded areas). Although
values inside the
plotted bins, and σm its uncertainty
(computed from the errors represented by the shaded areas). Although
 slowly decreases
(m ~ −1 km s-1
kpc-1) with R in each z slice, the trend is not
simple. It is the composition of a flat/increasing gradient for R ≲ 7.5 kpc and a
decreasing one for R ≳ 7.5
kpc. This break happens almost in correspondence with the outer
Lindblad resonance (ROLR = 7.69 kpc). This composite
behavior makes m shallower than if only the data points with
R ≳ 7.5 kpc
were to be fitted.
slowly decreases
(m ~ −1 km s-1
kpc-1) with R in each z slice, the trend is not
simple. It is the composition of a flat/increasing gradient for R ≲ 7.5 kpc and a
decreasing one for R ≳ 7.5
kpc. This break happens almost in correspondence with the outer
Lindblad resonance (ROLR = 7.69 kpc). This composite
behavior makes m shallower than if only the data points with
R ≳ 7.5 kpc
were to be fitted.
The RAVE selection function (red line) in this default bar case makes the gradients
steeper, because the bins with R ≲ 7.5 kpc are excluded (or less populated) and
for this reason they do not reduce the slope. This is especially clear for the two slices
−0.5 kpc
<z<
0 and 0
<z< 0.5
kpc, where the retained bins are all very near to the Sun (because the
RAVE fields have | b |
> 25°, see Fig. 1). Since the Sun happens to be placed in the middle of
the region where  decreases and we
only have the nearest bins, the resulting gradient is very steep (m ~ −4 km s-1
kpc-1). This effect is mitigated further away from the
plane, because the R extent of the survey becomes larger.
decreases and we
only have the nearest bins, the resulting gradient is very steep (m ~ −4 km s-1
kpc-1). This effect is mitigated further away from the
plane, because the R extent of the survey becomes larger.
 |
Fig. 4 Average cylindrical radial velocity |
 |
Fig. 7 As in Fig. 4, but with the long bar. Note that in this case, the simulation has been mirrored with respect to the z = 0 plane, which implies that the black curves in the 2nd and 5th, and in the 3rd and 4th panels are identical. However, the RAVE selection function does depend on Galactic latitude, resulting in different blue and red curves in each panel. |
 |
Fig. 8 As in Fig. 4, but with less massive bar. As in the previous figure, the simulations have been mirrored with respect to the z = 0 plane. |
Finally, we note that the effect of error convolution is very small, with the blue curves within the red (error-free) uncertainty bands.
4.2. Other locations in the default bar
4.2.1. R = 8 kpc, φ = –40°
We consider now the effect of placing the Sun at a different position, namely (R,φ,z) = (8 kpc, −40°,0), thus at a larger angle from the long axis of the bar.
Figure 5 shows that, in this case, the vR gradient in the whole sphere is steeper than in the default case. In fact, the steepest gradient in the simulation is reached at φ = −45° (the gradient is a periodic function of φ, with period π; for a detailed analysis of the periodic response of a stellar disk to a bar see Mühlbauer & Dehnen 2003). We see that in the slices closest to the Galactic plane (| z | < 0.5 kpc) the effect of the selection function is similar to that of the default case: the Sun is placed in the region where the gradient is steepest and, since we remove the outermost bins, the mean velocity gradient is strongly enhanced. Again, at | z | > 0.5 kpc the slope is smaller, because of the larger R extent of the sample.
4.2.2. R = 9 kpc, φ = –20°
In Fig. 6 we present the analysis of the radial velocity gradient behavior in a volume further out in the Galaxy, namely at (R,φ,z) = (9 kpc, −20°,0). This case was chosen to illustrate the effect of the distance from the outer Lindblad resonance, here R0/ROLR = 1.17.
In this case the slope over the whole sphere is steeper than in the default case. This
happens because the volume is beyond the outer Lindblad resonance and is therefore less
affected by the particles with R ≲ 7.5 kpc (which were responsible for the
positive/flat gradient). However, the local gradient at R = 9 kpc is shallower
than the one at R = 8
kpc, i.e., 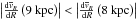 .
For this reason, when we apply the selection function, for | z | < 0.5
kpc the slope m becomes smaller in magnitude (than without
selection function and than the default case with selection function). On the contrary,
for the slice with −1 kpc
<z< −0.5
kpc it becomes steeper because in this case the steepest part of the
curve is included in the regression. Finally, in the outermost slice (−1.5 kpc
<z< −1
kpc) the low number of particles make the
.
For this reason, when we apply the selection function, for | z | < 0.5
kpc the slope m becomes smaller in magnitude (than without
selection function and than the default case with selection function). On the contrary,
for the slice with −1 kpc
<z< −0.5
kpc it becomes steeper because in this case the steepest part of the
curve is included in the regression. Finally, in the outermost slice (−1.5 kpc
<z< −1
kpc) the low number of particles make the
 profile noisy
and this washes out the
profile noisy
and this washes out the  gradient.
gradient.
4.3. Other bar models
The simulations in M13 include two other bar models: the long bar model with a different
geometry but with the same mass as the default bar, and a second one with same geometry
but half the mass, the low mass bar. However in these cases our simulations have lower
resolution than the default bar case (see Sect. 2).
In order to get the same number of objects as the RAVE red clump sample, we mirror the
particles above and below the z = 0 plane (so that we double the resolution).
However, we only do this for those 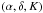 bins that
contain fewer particles than the observed number of red clump stars in RAVE. We are
allowed to do this because the potential is symmetric with the respect of the Galactic
plane and the same is true for our test particle simulations (at least when they reach a
steady state). After this operation, the discrepancy in total number of objects between
RAVE and the simulation is smaller than 1.5%. The regions slightly underpopulated are those with
0 ≲ α ≲
80°, 320° ≲ α ≲ 360° and
δ ≲ −
60°. In what follows we only consider the standard Sun’s
location, namely the case with the Sun at (R,φ,z) = (8 kpc, −
20°,0).
bins that
contain fewer particles than the observed number of red clump stars in RAVE. We are
allowed to do this because the potential is symmetric with the respect of the Galactic
plane and the same is true for our test particle simulations (at least when they reach a
steady state). After this operation, the discrepancy in total number of objects between
RAVE and the simulation is smaller than 1.5%. The regions slightly underpopulated are those with
0 ≲ α ≲
80°, 320° ≲ α ≲ 360° and
δ ≲ −
60°. In what follows we only consider the standard Sun’s
location, namely the case with the Sun at (R,φ,z) = (8 kpc, −
20°,0).
4.3.1. R = 8 kpc, φ = –20°, long bar
The long bar has a stronger effect than the default bar near the Sun, because its
gravitational force is larger in the solar neighborhood (see M13). This is evident
looking at the black line in Fig. 7, but also in
the red and blue curves which are obtained after applying the RAVE selection function
and error convolution. Moreover, for |
z | > 0.5 kpc,
 grows steeply
for R ≲ 7.5−8
kpc and decreases steeply for R ≳ 7.5−8 kpc. In the
central slices the effect of the selection function and error enhances the gradient, for
the same reasons as in the standard case. For | z | > 0.5 kpc the
selection function together with the errors preferentially pick out bins with smaller
R, where
grows steeply
for R ≲ 7.5−8
kpc and decreases steeply for R ≳ 7.5−8 kpc. In the
central slices the effect of the selection function and error enhances the gradient, for
the same reasons as in the standard case. For | z | > 0.5 kpc the
selection function together with the errors preferentially pick out bins with smaller
R, where
 increases, which
results in washing out the gradient.
increases, which
results in washing out the gradient.
4.3.2. R = 8 kpc, φ = –20°, less massive bar
As shown from the black lines in Fig. 8 and not surprisingly, the gradient induced by the less massive bar is shallower than the default bar because the bar is weaker. Formally the force of less massive bar is half that of the default bar. However the non-axisymmetric part of the force (i.e., excluding the monopole term associated to the bar) only differs by ~30% in the solar neighborhood (see M13).
Once the selection function and the error convolution have been applied, the resulting vR gradients are significantly shallower almost everywhere.
 |
Fig. 9 Velocity distribution in cylinders of radius 300 pc and height 600 pc, centered at φ = − 40°, z = 0 and different radii for the default bar case, inside the 3 kpc sphere centered at (R,φ,z) = (8 kpc, − 40°,0). The density distribution is obtained with an adaptive kernel estimator (see M13). |
5. Reasons for the velocity gradient
To explain the way the bar can induce a large scale radial velocity gradient in the Milky Way, as in the simulations discussed here, we show Fig. 9. In this figure we have plotted the velocity distribution in the vR and vφ components of the simulation with the default bar at φ =−40° and different R, inside small cylinders of radius 300 pc and height 600 pc, centered on the Galactic plane. The density field is estimated with an adaptive kernel estimator (see details in M13).
Let us consider an axisymmetric potential similar to the one of a disk galaxy. A star with
angular momentum Lz =
Rvφ is
associated with a circular orbit with radius Rg, the “guiding center”, such that
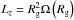 .
Therefore, when it passes from R, its tangential velocity is
.
Therefore, when it passes from R, its tangential velocity is
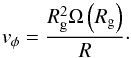 (2)Near the Sun, the bar
most strongly influences the stars with Rg = ROLR.
This is shown in Fig. 9, where the red dashed line
denotes vOLR, which is vφ of orbits that have
Rg =
ROLR, computed using the monopole component
of the Fourier decomposition of the potential in φ and where R is taken at the center of
the volumes. In fact, we note that around vOLR the velocity distribution is split in
two parts: the particles with vφ>vOLR
have
(2)Near the Sun, the bar
most strongly influences the stars with Rg = ROLR.
This is shown in Fig. 9, where the red dashed line
denotes vOLR, which is vφ of orbits that have
Rg =
ROLR, computed using the monopole component
of the Fourier decomposition of the potential in φ and where R is taken at the center of
the volumes. In fact, we note that around vOLR the velocity distribution is split in
two parts: the particles with vφ>vOLR
have 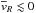 , the particles with
vφ<vOLR
have
, the particles with
vφ<vOLR
have 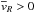 (Kalnajs 1991 introduced the idea that the outer Lindblad
resonance could account for bifurcation of the solar neighborhood velocity distribution). We
dub the former group “LSR mode” and the latter “OLR mode”, in the same fashion of Dehnen (2000), that linked the latter to the Hercules
stream. The division is particularly clear for the volume centered at R = 8 kpc.
(Kalnajs 1991 introduced the idea that the outer Lindblad
resonance could account for bifurcation of the solar neighborhood velocity distribution). We
dub the former group “LSR mode” and the latter “OLR mode”, in the same fashion of Dehnen (2000), that linked the latter to the Hercules
stream. The division is particularly clear for the volume centered at R = 8 kpc.
A first order treatment of nearly circular orbits in a weak bar potential (Binney & Tremaine 2008, Sect. 3.3.3) shows that the bar gravitational force stretches these orbits in two directions near the outer Lindblad resonance and in the frame of reference of the bar: the orbits with Rg<ROLR are stretched perpendicular to the long axis of the bar and the orbits with Rg>ROLR are aligned parallel to the long axis of the bar. The nearer Rg to ROLR, the stronger the effect. When they pass near the Sun, the orbits with Rg<ROLR (Rg>ROLR) have positive (negative) vR3. Orbits with Rg far enough from ROLR are not very affected by the bar, and on average have vR ~ 0. We see this reflected in Fig. 9: the OLR mode is formed by stars with Rg<ROLR, and the LSR mode by stars with Rg>ROLR.
When the volume is centered near ROLR (e.g., R = 7.5−8 kpc in Fig. 9), the orbits of the OLR mode with Rg<ROLR
dominate the velocity distribution of the particles, resulting in
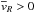 for the
whole volume. As we go further from the outer lindblad resonance less particles populate the
OLR mode. In particular, if we only consider volumes centered at R>ROLR,
this results in a negative
for the
whole volume. As we go further from the outer lindblad resonance less particles populate the
OLR mode. In particular, if we only consider volumes centered at R>ROLR,
this results in a negative  gradient (positive
for R<ROLR).
This is why we observe
gradient (positive
for R<ROLR).
This is why we observe  gradients and a
double behavior inside and outside the outer Lindblad resonance.
gradients and a
double behavior inside and outside the outer Lindblad resonance.
Note that, because of the symmetry of the problem, for volumes centered at positive
φ the
situation is reversed:  of the OLR mode is
negative and the gradient is positive.
of the OLR mode is
negative and the gradient is positive.
 |
Fig. 10 As in Fig. 4, but for the RAVE red clump stars used in W13. The shaded areas represent the measurement errors, the blue line the results obtained with the UCAC3 proper motions, the red line the results obtained with the SPM4 proper motions (see W13). |
 |
Fig. 11 Effect of a systematic errors in the distance determination on the
|
6. Discussion
In this section we compare our results in the case where the selection function and the error convolution are applied (red and blue lines in Figs. 4–8, that are similar) with the findings of W13 and in particular with the vR trends in their Fig. 8 (here reproduced in Fig. 10). Depending on the assumed Sun’s motion with the respect of the Local Standard of Rest, the curves may shift up or down in vR, but the overall trends remain unaffected (as shown in Fig. 9 in W13). Note that we have not included a correction for the solar motion in our analysis so far. Nonetheless, the vR values are comparable to those of W13.
However, only a qualitative comparison is warranted, as our simulation does not really reproduce in detail the properties of the Milky Way (e.g., the rotation curve is falling off near the Sun, the peak velocity is larger than observed, etc.). Furthermore, as we have noted, after the error convolution and RAVE selection function are applied, the underlying trends are sometimes modified, implying that care should be taken to avoid over interpretation of the results.
An important difference is that the radial velocity gradients found in RAVE (Fig. 10) are much steeper than in any of our models (Figs.
4−8), except perhaps for the slices
with z>
0. In magnitude, the model gradients resemble more the low limit of the
S11 estimate, i.e., 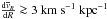 .
The trends are also different in the sense that most of the cases we have explored show a
flat/increasing part (e.g., at R< 7.5 kpc for the default
case) followed by a steeper decline at larger radii, a behavior that seems to be absent (or
is not as clear) in the data as shown in Fig. 10.
.
The trends are also different in the sense that most of the cases we have explored show a
flat/increasing part (e.g., at R< 7.5 kpc for the default
case) followed by a steeper decline at larger radii, a behavior that seems to be absent (or
is not as clear) in the data as shown in Fig. 10.
Although as stated above, in absolute terms the actual values of vR depend on the solar
motion, in Fig. 10 we note that the mean value of vR changes with distance
from the plane, when averaged over the whole radial distance range. This behavior is also
present, and in the same sense, in our default model, where for the three z slices at z> 0.5
kpc: in the central bins 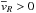 for
R< 8
kpc and vR ≳ 0 for
R> 8
kpc, and
for
R< 8
kpc and vR ≳ 0 for
R> 8
kpc, and 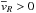 everywhere for z> 0.5 kpc.
everywhere for z> 0.5 kpc.
Systematic errors in the distances (and more specifically the assumed absolute magnitude for the red clump stars) could also affect our results. However, we find that when we use the other red clump magnitude normalizations considered in W13 (MK = 1.54 and MK = 1.64 + 0.0625 | z(kpc) |) our conclusions are not affected, because these only induce small distance changes (~5%). On the other hand, if the distances were more significantly overestimated, by for example 20%, the vR gradients would become steeper as shown by the red curves in the top panels of Fig. 11, while an underestimation by the same magnitude would lead to shallower gradients as shown by the black curves in the figure. Interestingly, in the case that the distances are overestimated a gradient in vz with radius is also induced as shown in the bottom panels of Fig. 11, which is positive below the plane, and negative above the plane, i.e. in the same sense as found by W13. Since in the literature (Alves 2000; Grocholski & Sarajedini 2002; Salaris & Girardi 2002; Groenewegen 2008) most other estimates of the red clump magnitude are fainter than what we have assumed, it may seem more likely that the distances in W13 have been systematically overestimated than underestimated4, however not as extremely as we have tested in these last examples.
It should be noted that the fact that the models explored in this work do not fit the
observed data, does not necessarily imply that the Galactic bar is not the cause for the
observed gradients. With our models we only have explored a very small portion of a large
parameter space and, for example, steeper gradients can be obtained by increasing the bar
strength near the Sun, or even with a circular speed curve falling more slowly with
R, at fixed
bar pattern speed5. Since some of the kinematic
substructure in the solar neighborhood can be explained by the bar, we expect that its
dynamical effect (for the current bar parameters estimates) should at least be partly
responsible for the observed negative  gradients.
gradients.
7. Conclusions
In this work we have proposed a new explanation for the recent discovery (S11, W13) of a negative R gradient of the (galactocentric) radial velocity. We found that the bar can create a negative gradient if the Sun is placed just outside the outer Lindblad resonance and at angles from the long axis of the bar similar to the current estimates from the literature. The velocity gradients become steeper when increasing the angle from the bar and also for the Long Bar model. On the other hand, in the less massive bar case they become shallower. Moreover, such gradients do not depend strongly on the height from the Galactic plane. This happens because the bar affects the kinematics of the Galaxy almost in the same way from z = 0 to z ~ 2 kpc, as explained in M13. Because of this, the bar provides a natural mechanism for the observed gradients at different heights.
We compared the 3D test particle simulations presented in M13 with the findings of RAVE, after applying the RAVE selection function and proper error convolution. The gradients exist in our simulations for all bar parameters and positions of the Sun explored (all outside the outer Lindblad resonance). These gradients are never completely washed out by the selection function and the errors, but rather they are enhanced in some cases. In fact, the gradients in the solar neighborhood spheres considered are in general shallower than those observed in the Milky Way, but the selection function can enhance them to the level of ~3 −4 km s-1 kpc-1 (as e.g., happens for all the studied simulation slices with | z | < 0.5 kpc and the Sun centered at R = 8 kpc).
However, none of the models that we explored in this work accurately describes the behavior
in RAVE of  at every
z: the
gradients are too shallow for z< 0. Some models resemble
RAVE for z> 0, especially our default
bar case at R = 8
kpc and φ ≤ −
20°. We conclude from this that the bar should at least contribute to the
negative gradient observed, for position angles with respect to the bar φ< 0
and for locations of the Sun near but outside the outer Lindblad resonance (R>ROLR).
at every
z: the
gradients are too shallow for z< 0. Some models resemble
RAVE for z> 0, especially our default
bar case at R = 8
kpc and φ ≤ −
20°. We conclude from this that the bar should at least contribute to the
negative gradient observed, for position angles with respect to the bar φ< 0
and for locations of the Sun near but outside the outer Lindblad resonance (R>ROLR).
Furthermore, our simulations do not show any kind of vertical velocity gradient as seen in the data for RAVE by W13. This result is consistent with the distribution function of the simulated disks being an even function of vz. On the other hand, the recent paper by Faure et al. (2014) shows that a 3D model for spiral arms is successful in reproducing radial and vertical velocity gradients similar to those observed in W13. In reality both effects of bar and spiral arms probably coexist and shape the velocity distribution of the solar neighborhood. However, while in the case of the bar the slope of the radial velocity gradient depends significantly on the angular location of the observer in the Galaxy, in the case of tightly wound spirals the angle is much less important (Figs. 6 and 7 in Faure et al. 2014). Future observations of the Galactic disk (e.g., obtained with the Gaia satellite) are expected to be sufficiently extended to distinguish whether the main cause of the radial velocity gradient is the bar or the spiral arms.
A natural future development of this work is to fit the kinematics of the extended solar neighborhood with the analytic predictions from the bar perturbation theory, in the same fashion as in Siebert et al. (2012) for the spiral arms, in order to retrieve the best fit values for the bar pattern speed, bar angle, and bar strength.
Here K is used to denote K-band magnitudes in the 2MASS system, while JBB and KBB denote the J and K-band magnitudes in the Bessell & Brett (1989) system.
This prediction of the first order treatment can be obtained from the time derivative of Eq. (3.148a) of Binney & Tremaine (2008), and is confirmed in our simulations.
In fact, Binney et al. (2014) recently estimated the absolute magnitude of the RAVE red clump stars to be ~0.1 mag fainter than in W13.
This can be shown in 2D with a simple potential with power-law velocity curve, applying Kuijken & Tremaine (1991) theory for the behavior of the mean velocities under the influence of a non-axisymmetric perturbation of multipole order m (see also Mühlbauer & Dehnen 2003).
Acknowledgments
We would like to thank T. Piffl and M. Williams for useful discussions. We also thank M. Williams for kindly providing the RAVE data used in Williams et al. (2013). The authors gratefully acknowledge support from the European Research Council under ERC Starting Grant GALACTICA-240271.
References
- Alves, D. R. 2000, ApJ, 539, 732 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Antoja, T., Figueras, F., Fernández, D., & Torra, J. 2008, A&A, 490, 135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Antoja, T., Valenzuela, O., Pichardo, B., et al. 2009, ApJ, 700, L78 [NASA ADS] [CrossRef] [Google Scholar]
- Antoja, T., Figueras, F., Romero-Gómez, M., et al. 2011, MNRAS, 418, 1423 [NASA ADS] [CrossRef] [Google Scholar]
- Antoja, T., Helmi, A., Bienayme, O., et al. 2012, MNRAS, 426, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Bessell, M. S., & Brett, J. M. 1989, in Infrared Extinction and Standardization, ed. E. F. Milone, Lect. Notes Phys. (Berlin: Springer Verlag), 341, 61 [Google Scholar]
- Binney, J., & Tremaine, S. 2008, Galactic Dynamics: 2nd edn. (Princeton University Press) [Google Scholar]
- Binney, J., Burnett, B., Kordopatis, G., et al. 2014, MNRAS, 437, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Bissantz, N., & Gerhard, O. 2002, MNRAS, 330, 591 [NASA ADS] [CrossRef] [Google Scholar]
- De Simone, R., Wu, X., & Tremaine, S. 2004, MNRAS, 350, 627 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Dehnen, W. 1998, AJ, 115, 2384 [NASA ADS] [CrossRef] [Google Scholar]
- Dehnen, W. 2000, AJ, 119, 800 [NASA ADS] [CrossRef] [Google Scholar]
- Famaey, B., Jorissen, A., Luri, X., et al. 2005, A&A, 430, 165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Faure, C., Siebert, A., & Famaey, B. 2014, MNRAS, 440, 2564 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrers, N. M. 1870, Roy. Soc. London Philos. Trans. Ser. I, 160, 1 [Google Scholar]
- Fux, R. 2001, A&A, 373, 511 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grocholski, A. J., & Sarajedini, A. 2002, AJ, 123, 1603 [NASA ADS] [CrossRef] [Google Scholar]
- Groenewegen, M. A. T. 2008, A&A, 488, 935 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kalnajs, A. J. 1991, in Dynamics of Disc Galaxies, ed. B. Sundelius, 323 [Google Scholar]
- Kuijken, K., & Tremaine, S. 1991, in Dynamics of Disc Galaxies, ed. B. Sundelius, 71 [Google Scholar]
- Mayor, M. 1970, A&A, 6, 60 [NASA ADS] [Google Scholar]
- Monari, G., Antoja, T., & Helmi, A. 2013 [arXiv:1306.2632] [Google Scholar]
- Mühlbauer, G., & Dehnen, W. 2003, A&A, 401, 975 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Quillen, A. C., Dougherty, J., Bagley, M. B., Minchev, I., & Comparetta, J. 2011, MNRAS, 417, 762 [NASA ADS] [CrossRef] [Google Scholar]
- Salaris, M., & Girardi, L. 2002, MNRAS, 337, 332 [NASA ADS] [CrossRef] [Google Scholar]
- Siebert, A., Famaey, B., Minchev, I., et al. 2011a, MNRAS, 412, 2026 [NASA ADS] [CrossRef] [Google Scholar]
- Siebert, A., Williams, M. E. K., Siviero, A., et al. 2011b, AJ, 141, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Siebert, A., Famaey, B., Binney, J., et al. 2012, MNRAS, 425, 2335 [NASA ADS] [CrossRef] [Google Scholar]
- Steinmetz, M., Zwitter, T., Siebert, A., et al. 2006, AJ, 132, 1645 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, M. E. K., Steinmetz, M., Binney, J., et al. 2013, MNRAS, 436, 101 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 (R,z) distribution of stars in the RAVE sample used in W13 (top) and in the simulation with default Sun’s position after the application of the RAVE selection function (bottom). The contours enclose 2,6,12,21,33,50,68,80,90,95 and 99% of the stars. |
| In the text | |
 |
Fig. 2 Average velocities for particles inside a sphere of radius 3 kpc, when the Sun is placed at (R,φ,z) = (8 kpc, −20°,0) and for the default bar model. Top row: contour plots in the (R,z) plane, with binsize 100 pc and box smoothing on a scale of 200 pc. Bottom row: as in the top row, but after the application of the RAVE selection function. The averages in the bottom panels correspond to those obtained using 100 random samples of the simulation. |
| In the text | |
 |
Fig. 3 Trends in |
| In the text | |
 |
Fig. 4 Average cylindrical radial velocity |
| In the text | |
 |
Fig. 5 As in Fig. 4, but with the Sun placed at (R,φ,z) = (8 kpc, −40°,0). |
| In the text | |
 |
Fig. 6 As in Fig. 4, but with the Sun placed at (R,φ,z) = (9 kpc, −20°,0). |
| In the text | |
 |
Fig. 7 As in Fig. 4, but with the long bar. Note that in this case, the simulation has been mirrored with respect to the z = 0 plane, which implies that the black curves in the 2nd and 5th, and in the 3rd and 4th panels are identical. However, the RAVE selection function does depend on Galactic latitude, resulting in different blue and red curves in each panel. |
| In the text | |
 |
Fig. 8 As in Fig. 4, but with less massive bar. As in the previous figure, the simulations have been mirrored with respect to the z = 0 plane. |
| In the text | |
 |
Fig. 9 Velocity distribution in cylinders of radius 300 pc and height 600 pc, centered at φ = − 40°, z = 0 and different radii for the default bar case, inside the 3 kpc sphere centered at (R,φ,z) = (8 kpc, − 40°,0). The density distribution is obtained with an adaptive kernel estimator (see M13). |
| In the text | |
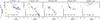 |
Fig. 10 As in Fig. 4, but for the RAVE red clump stars used in W13. The shaded areas represent the measurement errors, the blue line the results obtained with the UCAC3 proper motions, the red line the results obtained with the SPM4 proper motions (see W13). |
| In the text | |
 |
Fig. 11 Effect of a systematic errors in the distance determination on the
|
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.